(推荐)上海数学教材练习册高三全一册习题精选
上海中学高三数学综合练习三

7
3
1
bn
bn 1
an 1
4
4
an 2 an 1 1 bn, an 11 9 ( 1 ) n 1, bn 11 9 ( 1 ) n 1, 第9个观测点。 (0.68)
3
3
10 10 2
10 10 2
x2
22.(1)
4
y2 1
3
(2)(-4,0)
(3) x0 ( 2,0)
(0,2), 配对点 ( 4 ,0) x0
12.在一个给定的正 (2 n+1) 边形的顶点中随机地选取三个不同的顶点,任何一种选法的可能性是
相等的,则正多边形的中心位于所选三个点构成的三角形内部的概率为
.
二、选择题
13.已知 A x y
5x x2 4 , B x x 2 2ax a 2 0 , 若A B A ,那么实数 a 的取
值范围是 A. (-1,2)
a, y1, y2, … , yn, b 成等比数列,则点 A1,A2,…, An 与射线 L: y=x( x>0) 的关系为 ( ) A 各点均在射线 L 的上方; B 各点均在射线 L 的上面;
C 各点均在射线 L 的下方; D 不能确定
三、解答题
5
17. 已知函数 f ( x)
sin x 2
1 与 g( x)
.
0, ( x 0)
5.在 ABC 中,若 C 3 B, 则 c 的取值范围为 b
ax 3
6.已知函数 y
x2
对定义域内的任意
1
x 的值都有
1
f ( x)
4 ,则 a 的取值范围为
7 . 函 数 f ( x) a( x 2) 2 1 (a 0) 的 图 象 的 顶 点 A 在 直 线 mx ny 1 0 上 , 其 中
高等数学教材刷题推荐

高等数学教材刷题推荐一、导言随着高等数学课程的深入,掌握数学的基础知识和解题技巧变得尤为重要。
而解题训练是巩固和拓展数学知识的关键环节。
本文将向大家推荐几本高等数学教材中的刷题内容,帮助读者提高数学解题能力。
二、《高等数学(下册)》《高等数学(下册)》是大多数高校的高等数学教材之一,题量较大,题型较为全面。
在刷题过程中,可以将《高等数学(下册)》作为主要的参考教材。
这本教材覆盖了微分方程、无穷级数、多元函数等重要内容。
读者可以选择章节中的重点题目进行练习,重点关注典型的例题和习题,加深对相关知识点的理解。
三、《数学分析习题与解法》《数学分析习题与解法》是一本系统总结了高等数学分析部分典型题目的参考书。
书中按照章节分类,分别针对不同的数学分析题型进行了深入的解析。
该书不仅提供了题目的解答,还详细地讲解了解题的思路和方法。
通过反复刷题和思考,读者可以提高自己的解题思维和技巧。
四、《高等数学习题精选解析》《高等数学习题精选解析》是一本练习题和解析相结合的参考书。
书中精选了难度适中且常见的高等数学习题,并提供了详细的解题方法和步骤。
它可以作为配套的辅助教材,帮助读者针对性地进行刷题和巩固知识。
五、《高等数学研究性学习》《高等数学研究性学习》是一本提供了大量研究性学习问题和思考题的教辅材料。
这些问题和题目设计得更为复杂和有趣,旨在培养学生的创新思维和解决实际问题的能力。
通过挑战这些题目,读者可以提高自己的数学建模能力和问题解决能力。
六、小结刷题对于提高高等数学成绩和解题能力起到了至关重要的作用。
通过合理选择刷题教材,并结合教材的风格和特点进行刷题,可以提高解题效率和自信心。
本文推荐了几本适合刷题的高等数学教材,希望能够对读者的数学学习起到一定的辅助作用。
读者在刷题的同时,还要注重理论和实践的结合,通过反复训练和积累,逐渐提升自己的数学水平。
上海市上海中学高三数学综合练习(八) 新课标

上海市上海中学2010届高三综合练习(八)(数学)班级___________ 学号_______ 姓名_______________ 成绩________编辑:卢立臻 一、填空题 1.已知集合{}{}AB ax x B x x A ⊂====若,1,12,则a 的值为2.原命题是“已知a,b,c,d 是实数,若a=b,c=d,则a+c=b+d ”,则它的逆否命题是3.已知=+≤-=+-)1(,)1()1()1(12x f x x x f 则 . 4.抛物线1sin 22+-=αx x y 的顶点在椭圆122=+my x 上,这样的抛物线有且只有二条,则m 的取值范围是 . 5.已知函数)2(log )(x a x f a -=在(0,1)上是增函数,则a 的取值范围是 .6.已知与则,若不共线,且,0,=≠⋅的夹角7已知实数,log 21,log 21,log 2,,22121c b a c b a cba=⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛=满足这三个数从小到大排列为 .8.函数13342++-+-=x x x y 的值域为9.已知=+++++-+-+=)6()5()0()4()5(,221)(f f f f f x f x则 .10.有8本书,其中3本相同,其余各不相同,若有人来借书,每本书被借到的概率相同,则借得4本书中有相同书的概率为11.已知0322,022,,2=+-+=---∆c b a c b a a c b a ABC 满足中,三边长,则这个三角形最大角的大小为12.如果一个四面体的三个面是直角三角形,下列三角形:(1)直角三角形;(2)锐角三角形;(3)钝角三角形;(4)等腰三角形;(5)等腰直角三角形。
那么可能成为这个四面体的第四个面是 (填上你认为正确的序号) 二、选择题13.设A ,B 两点的坐标分别为(-1,0),(1,0)。
条件甲:A 、B 、C 三点构成以∠C为钝角的三角形;条件乙:点C 的坐标是方程)0(1222≠=+y y x 的解,则甲是乙的: ( )A .充分不必要条件B .必要不充分条件C. 充要条件D. 既不充分又不必要条件14.在直二面角B A B A l ,,,βαβα∈∈--中,都不在l 上,,x AB 所成角为与α222,c o s c o s s i n A B y A B l z x y z β++与所成角为与所成角为,则的值为 ( )A.2B. 2C.3D. 315.方程11122=---x y y x 所对应的曲线图形是:( )16.已知椭圆15922=+y x ,过右焦点F 做不垂直于x 轴的弦交椭圆于A 、B 两点,AB的垂直平分线交x 轴于N ,则=AB NF : ( )A .21B .31C .32D .41三、解答题17.已知函数b x xa x f ++=)sin 2cos 2()(2(0>a )(1)求)(x f 的单调增区间;(2)当0[∈x ,]π时,)(x f 值域为[3,4],求a ,b 的值。
高中数学沪教版 6.3 组合 课后练习、课时练习

一、单选题1. 在“3+1+2”模式的新高考方案中,“3”是指语文、数学、外语三科为必考科目,“1”指在物理和历史两门科目中必选一门,“2”指在化学、生物、政治、地理中任选两科,某学生根据自己实际情况确认了要选生物,那么此同学可能的选课方式共有()A.2种B.4种C.6种D.12种2. 算筹是一根根同样长短和粗细的小棍子,是中国古代用来记数、列式和进行各种数与式演算的一种工具,是中国古代的一项伟大、重要的发明.在算筹计数法中,以“纵式”和“横式”两种方式来表示数字,如表:1 2 3 4 5 6 7 8 9项目纵式横式用算筹计数法表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推,遇零则置空,如“”表示的三位数为732.如果把4根算筹以适当的方式全部放入表格“”中,那么可以表示不同的三位数的个数为()A.18 B.20 C.22 D.243. 如图所示为一电路图,从A到B共有条不同的线路可通电()A.1 B.2 C.3 D.44. 由数字1,2,3,4可以组成有重复数字的三位奇数的个数为()A.12 B.24 C.48 D.325. 重庆九宫格火锅,是重庆火锅独特的烹饪方式.九宫格下面是相通的,实现了“底同火不同,汤通油不通”它把火锅分为三个层次,不同的格子代表不同的温度和不同的牛油浓度,其锅具抽象成数学形状如图(同一类格子形状相同):“中间格“火力旺盛,不宜久煮,适合放一些质地嫩脆、顷刻即熟的食物;“十字格”火力稍弱,但火力均匀,适合煮食,长时间加热以锁住食材原香;“四角格”属文火,火力温和,适合焖菜,让食物软糯入味.现有6种不同食物(足够量),其中1种适合放入中间格,3种适合放入十字格,2种适合放入四角格.现将九宫格全部放入食物,且每格只放一种,若同时可以吃到这六种食物(不考虑位置),则有多少种不同放法()A.108 B.36 C.9 D.66. 在所有的两位数中,个位数字大于十位数字的两位数的个数是()A.18 B.36C.72 D.48二、多选题7. 现有不同的红球4个,黄球5个,绿球6个,则下列说法正确的是()A.从中选出2个球,正好一红一黄,有9种不同的选法B.若每种颜色选出1个球,有120种不同的选法C.若要选出不同颜色的2个球,有31种不同的选法D.若要不放回地依次选出2个球,有210种不同的选法8. 现有5幅不同的国画,2幅不同的油画,7幅不同的水彩画,下列说法正确的有()A.从中任选一幅画布置房间,有14种不同的选法B.从这些国画、油画、水彩画中各选一幅布置房间,有70种不同的选法C.从这些画中选出两幅不同种类的画布置房间,有59种不同的选法D.要从5幅不同的国画中选出2幅,分别挂在左、右两边墙上的指定位置,共有9种不同的挂法三、填空题9. 拟从5名班干部中选若干人在周一至周五期间值班(每天只需1人值班),要求同一名班干部不连续值班2天,则可能的安排方法有______种.(用数字作答)10. 某电商为某次活动设计了“和谐”“爱国”“敬业”三种红包,活动规定每人可以依次点击4次,每次都会获得三种红包中的一种,若集全三种即可获奖,但三种红包出现的顺序不同对应的奖次也不同.员工甲按规定依次点击了4次,直到第4次才获奖.则他获得奖次的不同情形种数为________.11. 若一个三位数的百位数字、十位数字、个位数字恰好构成等差数列,则称之为“等差三位数”,例如:147,642,777,420等.等差三位数的总个数为_________. 12. 在5张彩票中有2张有奖,甲、乙先后从中各任取一张,则乙中奖的概率为___________.四、解答题13. 乘积展开后共有多少项?14. 邮局发行10种新邮票,有一个集邮爱好者购买了15张邮票,他有多少种买法?15. 在图中的电路中,仅合上1只开关接通电路,有多少种不同的方法?16. 4名学生报名参加两项体育比赛,每名学生可参加的比赛数目不限,每项比赛参加的人数不限,共有多少种不同的报名结果?。
高等数学练习教材书籍推荐

高等数学练习教材书籍推荐高等数学是大多数理工科专业的重要课程之一,对于学生来说,选用一本好的练习教材可以有效提升自己的数学水平。
本文将为大家推荐几本优秀的高等数学练习教材,帮助学生更好地掌握这门学科。
一、《高等数学(下册)习题解析与考点评析》这本教材由清华大学出版社出版,是清华大学李永乐教授主编的高等数学习题解析与考点评析系列之一。
该书通过精选习题,对高等数学所涉及的重要知识点进行了详细解析,并结合考点分析,能够帮助学生快速理解和掌握高等数学的核心内容。
此外,书中还提供了大量的真实考试试题和模拟试题,供学生进行练习和考察。
该教材在难度、丰富程度和题型分布上都具有很高的水平,适合有一定数学基础的学生使用。
二、《高等数学(上册)习题精选与解析》这本教材由电子工业出版社出版,是北京大学数学学院编写的高等数学习题精选与解析系列之一。
该书通过对高等数学上册的经典习题进行精选,结合详细的解析,帮助学生理解和掌握数学的基本概念和方法。
书中的习题分布恰当,覆盖了课程中的各个知识点和技巧。
此外,书中还特别强调数学的应用能力培养,通过大量的实例和综合题目,帮助学生将数学应用于实际问题中。
该教材注重培养学生的解题思维和创新能力,适合学习高等数学的初学者使用。
三、《高等数学习题解析与教学指导》这本教材由浙江大学出版社出版,是浙江大学数学学院编写的高等数学教材系列之一。
该书通过对高等数学的习题解析,结合教学指导,帮助学生理解和掌握数学的基本原理和方法。
书中对每一个知识点都进行了详细的解释和示范,避免了学生对概念和方法的困惑。
此外,书中还提供了丰富的练习题和例题,供学生进行巩固和拓展。
教材注重培养学生的数学思维和创新能力,强调实际问题的应用,适合有一定数学基础的学生使用。
四、《高等数学习题与解析》这本教材由人民教育出版社出版,是清华大学陈建功教授编写的高等数学习题与解析系列之一。
该书通过对高等数学习题的分类和解析,帮助学生理清知识点之间的联系和应用方式。
高三数学练习册及答案

高三数学练习册及答案# 高三数学练习册及答案## 第一章:函数与方程### 1.1 函数的概念与性质- 练习题1:定义域与值域的确定- 练习题2:函数的单调性与奇偶性判断### 1.2 一次函数与二次函数- 练习题3:一次函数的图象与性质- 练习题4:二次函数的顶点式与性质### 1.3 高次函数与幂函数- 练习题5:高次函数的图象特征- 练习题6:幂函数的性质与应用### 1.4 指数函数与对数函数- 练习题7:指数函数的增长规律- 练习题8:对数函数的图象与性质### 1.5 三角函数- 练习题9:正弦函数与余弦函数的基本性质- 练习题10:正切函数与余切函数的图象与性质## 第二章:不等式与不等式组### 2.1 不等式的基本性质- 练习题11:不等式的基本性质与应用### 2.2 一元一次不等式的解法- 练习题12:线性不等式的解集确定### 2.3 一元二次不等式的解法- 练习题13:二次不等式的解集与判别式### 2.4 不等式组的解法- 练习题14:不等式组的解集确定与应用## 第三章:数列### 3.1 数列的概念与通项公式- 练习题15:数列的通项公式与性质### 3.2 等差数列与等比数列- 练习题16:等差数列的通项公式与求和公式- 练习题17:等比数列的通项公式与求和公式### 3.3 数列的极限与无穷等比数列- 练习题18:数列极限的概念与计算- 练习题19:无穷等比数列的求和问题## 第四章:解析几何### 4.1 直线与圆- 练习题20:直线方程的求解与应用- 练习题21:圆的方程与性质### 4.2 椭圆与双曲线- 练习题22:椭圆的标准方程与性质- 练习题23:双曲线的标准方程与性质### 4.3 抛物线- 练习题24:抛物线的方程与图象特征## 第五章:概率与统计### 5.1 概率的基本概念- 练习题25:概率的计算与应用### 5.2 条件概率与独立事件- 练习题26:条件概率的计算与理解### 5.3 统计初步- 练习题27:数据的收集与描述## 答案解析- 答案1-10:针对第一章的练习题,提供详细的解题步骤与答案。
2024年上海数学高考一轮复习必刷大题 专题1 解三角形大题综合含详解

专题01解三角形大题综合一、解答题1.(2023·上海长宁·上海市延安中学校考三模)已知()2sin cos c 2πos 6f x x x x ⎛⎫=++ ⎪⎝⎭.(1)求方程()0f x =的解集;(2)求函数()y f x =在[]0,π上的单调增区间.2.(2023·上海闵行·统考二模)在ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,已知sin sin 2A B =,4a =,6b =.(1)求cos B 的值;(2)求ABC 的面积.3.(2023·上海宝山·统考二模)已知函数()23sin cos 32f x x x x =-+.(1)求函数()y f x =的最小正周期和单调区间;(2)若关于x 的方程()0f x m -=在π0,2x ⎡⎤∈⎢⎥⎣⎦上有两个不同的实数解,求实数m 的取值范围.4.(2023·上海浦东新·华师大二附中校考模拟预测)在ABC 中,a b c 、、分别是角A B C 、、的对边.设()()2,,cos ,cos m a c b n B C =+= ,已知0m n ⋅=r r (1)求角B 的大小;(2)设()()2π2cos sin 2sin sin 2sin cos cos 3f x x x x B x x A C ⎛⎫=+-++ ⎪⎝⎭,当2,63ππx ⎡⎤∈⎢⎣⎦时,求函数()y f x =的最小值.5.(2023·上海闵行·上海市七宝中学校考三模)如图,P 是边长为2的正三角形ABC 所在平面上一点(点A 、B 、C 、P 逆时针排列),且满足CP CA =,记θ∠=CAP .(1)若π3θ=,求PB 的长;(2)用θ表示PAB 的面积S ,并求S 的取值范围.6.(2023·上海松江·校考模拟预测)已知向量())2sin ,cos2,3cos ,1m x x n x ωωω==,其中0ω>,若函数()f x m n=⋅的最小正周期为π.(1)求()f x 的单调增区间;(2)在ABC 中,若()2,f B BC B A =-==,求BA BC ⋅的值.7.(2023·上海奉贤·上海市奉贤中学校考三模)已知扇形OAB 的半径为1,π3AOB ∠=,P 是圆弧上一点(不与A ,B 重合),过P 作,PM OA PN OB ⊥⊥,M ,N为垂足.(1)若12PM =,求PN 的长;(2)设AOP x ∠=,PM ,PN 的线段之和为y ,求y 的取值范围.8.(2023·上海徐汇·上海市南洋模范中学校考三模)已知ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,()π4cos sin(6f x x x =-的最大值为()f A .(1)求角A ;(2)当a =2b =时,求ABC 的面积.9.(2023·上海·高三专题练习)在ABC 中,点D 在边AC 上,且2,AD CD BD AC ==.(1)若BD 平分ABC ∠,求sin sin ABDBDC∠∠的值;(2)若,,AB AC BC成递增的等比数列,AC =ABC 的面积.10.(2023·上海·高三专题练习)已知向量,2sin 22x x m ⎛⎫=- ⎪⎝⎭ ,cos ,cos 22x x n ⎛⎫= ⎝⎭ ,函数()y f x m n ==⋅ .(1)设ππ,22θ⎡⎤∈-⎢⎥⎣⎦,且()1f θ=,求θ的值;(2)在ABC 中,1AB =,()1f C =,且ABC的面积为2,求sin sin A B +的值.11.(2023春·上海杨浦·高三上海市杨浦高级中学校考开学考试)已知函数()()()sin 0,0,πf x A x A ωϕωϕ=+>><的部分图像如图所示.(1)求()f x 的解析式及对称中心;(2)先将()f x 的图像纵坐标缩短到原来的12,再向左平移π6个单位后得到()g x 的图像,求方程()12g x =在[]π,π-的解集.12.(2023春·上海·高三校联考阶段练习)已知函数()221cos sin 2f x x x =-+.(1)求()f x 的单调增区间;(2)设ABC 为锐角三角形,角A B C 、、所对的边分别是,,,5a b c a b ==,若()0f A =,求ABC 的面积.13.(2023·上海嘉定·统考二模)已知向量()sin ,1cos 2a x x =+ ,1cos ,2b x ⎛⎫= ⎪⎝⎭ ,()f x a b =⋅ .(1)求函数()y f x =的最大值及相应x 的值;(2)在ABC 中,角A 为锐角,且7π12A B +=,()1f A =,2BC =,求边AC 的长.14.(2023·上海黄浦·格致中学校考三模)在ABCcos cos C A =,6B π=,BC边中线AM (1)求A 的值;(2)求ABC 的面积.15.(2023·上海金山·统考二模)在ABC 中,角A 、B 、C 所对边的边长分别为a 、b 、c,已知a =45C =︒.(1)若sin A B =,求c ;(2)若15B A -=︒,求ABC 的面积.16.(2023春·上海·高三上海市实验学校校考阶段练习)已知函数25π()sin 2cos 16f x x x ⎛⎫=+-+ ⎪⎝⎭.(1)求函数()f x 的最小值和单调增区间;(2)设角A B 、、C 为ABC 的三个内角,若1cos 3B =,124C f ⎛⎫=- ⎪⎝⎭,求sin A .17.(2023·上海黄浦·统考二模)在ABC 中,53cos ,cos 135A B =-=.(1)求sin C 的值;(2)若4AB =,求ABC 的周长和面积.18.(2023·上海浦东新·统考三模)已知向量),cos a x x =,πsin ,cos 2b x x ⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭.设()f x a b =⋅ .(1)求函数()y f x =的最小正周期;(2)在ABC 中,角A 、B 、C 所对的边分别为a 、b 、c .若()1f A =,4b =,三角形ABC的面积为a 的长.19.(2023·上海奉贤·校考模拟预测)已知函数()ππsin 2cos sin 122f x x x x x ⎛⎫⎛⎫=+--+ ⎪ ⎪⎝⎭⎝⎭,(1)求函数()f x 的最值;(2)设ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若()2f A =,2b =,且2sin sin B C A +=,求ABC 的面积.20.(2023·上海·华师大二附中校考模拟预测)已知函数21()2cos 2f x x x =--,x R ∈.(1)求函数()y f x =在区间5,1212ππ⎡⎤-⎢⎥⎣⎦上的最大值和最小值;(2)设ABC 的内角A ,B ,C 的对边分别为a ,b ,c 且c =()0f C =,若sin 2sin B A =,求ABC S .21.(2023·上海普陀·曹杨二中校考三模)设函数()2cos 2f x x x ωω=+,其中02ω<<.(1)若()f x 的最小正周期为π,求()f x 的单调增区间;(2)若函数()f x 图像在π0,3⎛⎤⎥⎝⎦上存在对称轴,求ω的取值范围.22.(2023·上海徐汇·统考三模)如图,ABC 中,角A 、B 、C 的对边分别为a 、b 、c .(1)若33cos a c b C -=,求角B 的大小;(2)已知3b =、π3B =,若D 为ABC 外接圆劣弧AC 上一点,求ADC △周长的最大值.23.(2023·上海长宁·统考二模)(1)求简谐振动sin cos y x x =+的振幅、周期和初相位([0,2π))ϕϕ∈;(2)若函数11sincos 22y x x =+在区间(0,)m 上有唯一的极大值点,求实数m 的取值范围;(3)设0a >,()sin sin f x ax a x =-,若函数()y f x =在区间(0,π)上是严格增函数,求实数a 的取值范围.xπ0,3⎛⎫ ⎪⎝⎭π3π,π3⎛⎫ ⎪⎝⎭π5ππ,3⎛⎫ ⎪⎝⎭5π35π,3π3⎛⎫ ⎪⎝⎭y '+0-0+0-y极大值极小值极大值专题01解三角形大题综合一、解答题1.(2023·上海长宁·上海市延安中学校考三模)已知()2sin cos c 2πos 6f x x x x ⎛⎫=++ ⎪⎝⎭.(1)求方程()0f x =的解集;(2)求函数()y f x =在[]0,π上的单调增区间.【答案】(1)ππ,Z 26k x x k ⎧⎫=-∈⎨⎬⎩⎭(2)π0,12⎡⎤⎢⎥⎣⎦和7π,π12⎡⎤⎢⎥⎣⎦【分析】(1)化简得到()πsin 23f x x ⎛⎫=+ ⎪⎝⎭,取π2π,Z 3x k k +=∈,解得答案.(2)取πππ2π22π,Z 232k x k k -+≤+≤+∈,解不等式,取0k =和1k =得到单调增区间.【详解】(1)()312sin cos cos 2sin 2cos 2si 2622πn f x x x x x x x ⎛⎫=++=+- ⎪⎝⎭13sin 2222πsin 23x x x ⎛⎫=+ ⎪⎝⎭=,取()πsin 203f x x ⎛⎫=+= ⎪⎝⎭,则π2π,Z 3x k k +=∈,解得ππ,Z 26k x k =-∈.故方程()0f x =的解集为ππ,Z 26k x x k ⎧⎫=-∈⎨⎬⎩⎭.(2)取πππ2π22π,Z 232k x k k -+≤+≤+∈,解得5ππππ,Z 1212k x k k -+≤≤+∈,当0k =时,π0,12⎡⎤⎢⎣⎦满足条件;当1k =时,7π,π12⎡⎤⎢⎥⎣⎦满足条件;综上所述:单调增区间是π0,12⎡⎤⎢⎥⎣⎦和7π,π12⎡⎤⎢⎥⎣⎦2.(2023·上海闵行·统考二模)在ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,已知sin sin 2A B =,4a =,6b =.(1)求cos B 的值;(2)求ABC 的面积.【答案】(1)1cos 3B =(2)82【分析】(1)利用正弦定理结合二倍角公式可得解.(2)根据余弦定理可得c ,由cos B 可得sin B ,进而可得面积.【详解】(1)在ABC 中,由正弦定理sin sin a bA B=,又sin sin 22sin cos A B B B ==,所以2sin cos sin a b B B B=,即462sin cos sin B B B =,解得1cos 3B =;(2)由(1)得1cos 3B =,则sin 3B =,又由余弦定理222222461cos 2243a cbc B ac c +-+-===⨯,0c >,解得6c =,所以11sin 4622S ac B ==⨯⨯=3.(2023·上海宝山·统考二模)已知函数()2sin cos 2f x x x x =-+.(1)求函数()y f x =的最小正周期和单调区间;(2)若关于x 的方程()0f x m -=在π0,2x ⎡⎤∈⎢⎥⎣⎦上有两个不同的实数解,求实数m 的取值范围.【答案】(1)最小正周期πT =;单调递增区间为()π5ππ,πZ 1212k k k ⎡⎤-+∈⎢⎥⎣⎦;单调递减区间为()5π11π,πZ 2211k k k π⎡⎤++∈⎢⎥⎣⎦.(2)2⎫⎪⎪⎣⎭【分析】(1)利用降幂公式和辅助角公式化简函数解析式,用周期公式求周期,整体代入法求函数单调区间;(2)由区间内函数的单调性和函数值的变化范围求解实数m 的取值范围.【详解】(1)()21πsin cos cos sin 2cos 2sin 22223f x x x x x x x ⎛⎫=+=-=- ⎪⎝⎭,则函数()y f x =的最小正周期2ππ2T ==;令()πππ2π22πZ 232k x k k -≤-≤+∈,解得()π5πππZ 1122k x k k -≤≤+∈,可得函数()y f x =的单调递增区间为()π5ππ,πZ 1212k k k ⎡⎤-+∈⎢⎥⎣⎦·令()ππ3π2π22πZ 232k x k k +≤-≤+∈,解得()5π11ππZ 1122k x k k π+≤≤+∈,可得因数()y f x =的单调递减区间为()5π11π,πZ 2211k k k π⎡⎤++∈⎢⎥⎣⎦;(2)由(1)可知,π0,2x ⎡⎤∈⎢⎥⎣⎦时,()y f x =在5π0,12⎡⎤⎢⎥⎣⎦上单调递增,在5ππ,122⎡⎤⎢⎥⎣⎦上单调递减,当5π0,12x ⎡⎤∈⎢⎥⎣⎦,πππ2,332x ⎡⎤-∈-⎢⎣⎦,()f x 由增大到1,当5ππ212,x ⎡⎤∈⎢⎥⎣⎦,ππ2π2,323x ⎡⎤-∈⎢⎥⎣⎦,()f x 由1若关于x 的方程()0f x m -=在π0,2x ⎡⎤∈⎢⎥⎣⎦上有两个不同的实数解,则实数m 的取值范围为⎫⎪⎪⎣⎭4.(2023·上海浦东新·华师大二附中校考模拟预测)在ABC 中,a b c 、、分别是角A B C 、、的对边.设()()2,,cos ,cos m a c b n B C =+= ,已知0m n ⋅=r r(1)求角B 的大小;(2)设()()2π2cos sin 2sin sin 2sin cos cos 3f x x x x B x x A C ⎛⎫=+-++ ⎪⎝⎭,当2,63ππx ⎡⎤∈⎢⎣⎦时,求函数()y f x =的最小值.【答案】(1)2π3B =(2)最小值2-【分析】(1)利用向量的坐标运算和正弦定理即可求解;(2)先利用两角和的正弦公式及余弦的二倍角公式化简,再用辅助角公式化为()π2sin 23f x x ⎛⎫=+ ⎪⎝⎭,最后利用三角函数的性质求出最小值及其取得最小值时的x 值.【详解】(1)由题意可得:()2cos cos 0m n a c B b C ⋅=++=,由正弦定理得:()2sin sin cos sin cos 0A C B B C ++=,则()2sin cos sin cos sin cos 2sin cos sin 0A B C B B C A B B C ++=++=,可得2sin cos sin 0A B A +=,因为()0,πA ∈,则sin 0A ≠,可得2cos 10B +=,即1cos 2B =-,又因为()0,πB ∈,所以2π3B =.(2)由(1)可得2π3B =,则ππ3A CB +=-=,由题意可得:()2ππ2cos sin 2sin sin 2sin cos cos33f x x x x B x x ⎛⎫=+-+ ⎪⎝⎭212cos sin sin cos 2x x x x x x ⎛⎫=++ ⎪ ⎪⎝⎭222sin cos x x x x=πsin22sin 23x x x ⎛⎫==+ ⎪⎝⎭,因为2,63ππx ⎡⎤∈⎢⎥⎣⎦,则π2π5π2,333x ⎡⎤+∈⎢⎥⎣⎦,可得π22sin 23x ⎛⎫-≤+≤ ⎪⎝⎭,所以当π3π232x +=,即7π12x =时,()f x 有最小值2-.5.(2023·上海闵行·上海市七宝中学校考三模)如图,P 是边长为2的正三角形ABC 所在平面上一点(点A 、B 、C 、P 逆时针排列),且满足CP CA =,记θ∠=CAP .(1)若π3θ=,求PB 的长;(2)用θ表示PAB 的面积S ,并求S 的取值范围.【答案】(1)(2)(π2sin 20,23S θ⎛⎫=+++ ⎪⎝⎭【分析】(1)由余弦定理直接计算即可;(2)由正弦定理求出AP ,然后代入三角形面积公式,结合辅助角公式及三角函数值域求出面积范围.【详解】(1)由π3θ=,且ABC 是边长为2的正三角形,则2π3PAB ∠=,且2PA CP CA ===,所以在PAB 中,由余弦定理得22212cos 448122PB PA AB PA AB PAB ∠⎛⎫=+-⋅⋅=+-⨯-= ⎪⎝⎭,所以PB =;(2)由CP CA =,则CAP CPA θ∠=∠=,则π2PCA θ∠=-,在PAC △中,由正弦定理有()2sin π2sin sin AP BC θθθ==-,得()2sin π24cos sin AP θθθ-==,所以1ππsin 4cos sin 233S PA AB θθθ⎛⎫⎛⎫=⋅⋅+=⋅+ ⎪ ⎪⎝⎭⎝⎭2π2sin cos 2sin 22sin 23θθθθθθ⎛⎫=+=+=++ ⎪⎝⎭,又0πθ<<,且0π2πθ<-<,则π02θ<<,所以ππ4π2333θ<+<,所以πsin 23θ⎛⎤⎛⎫+∈ ⎥ ⎪ ⎝⎭⎝⎦,则(π2sin 20,23θ⎛⎫+++ ⎪⎝⎭,故S 的取值范围为(0,2⎤+⎦.6.(2023·上海松江·校考模拟预测)已知向量())2sin ,cos2,,1m x x n x ωωω==,其中0ω>,若函数()f x m n=⋅的最小正周期为π.(1)求()f x 的单调增区间;(2)在ABC 中,若()2,f B BC B A =-==,求BA BC ⋅的值.【答案】(1)πππ,π,36k k k ⎡⎤-+∈⎢⎥⎣⎦Z (2)32-【分析】(1)根据题意,由辅助角公式将函数()f x 化简,再由函数周期即可求得ω,再根据正弦型函数的单调区间即可得到结果;(2)根据题意,由(1)中函数()f x 的解析式可得2π3B =,再由正弦定理可得a c =,再结合平面向量数量积的定义代入计算,即可得到结果.【详解】(1)()πcos22sin 26f x m n x x x ωωω⎛⎫=⋅=+=+ ⎪⎝⎭ ()f x 的最小正周期为2ππ,π,12T ωω∴==∴=.故()π2sin 26f x x ⎛⎫=+ ⎪⎝⎭,令πππ2π22π262k x k -≤+≤+,解得,3πππ6πk x k k -≤≤+∈Z ,故函数()f x 的单调增区间为πππ,π,36k k k ⎡⎤-+∈⎢⎣⎦Z (2)设ABC 中角,,A B C 所对的边分别是,,a b c .()π2,2sin 226f B B ⎛⎫=-∴+=- ⎪⎝⎭ ,即πsin 216B ⎛⎫+=- ⎪⎝⎭,解得2π3B =.1sin ,,3,sin2BC a B A b b A ∴==∴=∴== ,πππ0,,,366A A C a c <<∴==∴== 13cos 322BA BC c a B ⎛⎫∴⋅=⋅⋅=⨯-=- ⎪⎝⎭.7.(2023·上海奉贤·上海市奉贤中学校考三模)已知扇形OAB 的半径为1,π3AOB ∠=,P 是圆弧上一点(不与A ,B 重合),过P 作,PM OA PN OB ⊥⊥,M ,N 为垂足.(1)若12PM =,求PN 的长;(2)设AOP x ∠=,PM ,PN 的线段之和为y ,求y 的取值范围.【答案】(1)12;(2)2.【分析】(1)在直角POM 与直角PON △中,利用锐角三角函数的定义求解作答.(2)由(1)中信息,把y 用x 的函数表示出,再借助正弦函数的性质求解作答.【详解】(1)在POM 中,PM OA ⊥,则1sin 2PM POM OP ∠==,显然π(0,3POM ∠∈,则π6POM ∠=,从而πππ366PON AOB POM ∠=∠-∠=-=,在PON △中,PN OB ⊥,所以π1sin 1sin 62PN OP PON =∠=⨯=.(2)依题意,ππ,(0,33PON AOB POM x x ∠=∠-∠=-∈πsin sin ,sin sin()3PM OP POM x PN OP PON x =∠==∠=-,因此π11πsin sin()sin sin sin sin()3223y x x x x x x x x =+-=+-=+=+,显然ππ2π(,)333x +∈,于是πsin()3x +∈,所以y 的取值范围是.8.(2023·上海徐汇·上海市南洋模范中学校考三模)已知ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,()π4cos sin(6f x x x =-的最大值为()f A .(1)求角A ;(2)当a =2b =时,求ABC 的面积.【答案】(1)π3;(2)2.【分析】(1)根据给定条件,利用三角恒等变换化简()f x ,再利用正弦函数性质求出角A 作答.(2)利用余弦定理求出c ,再利用三角形面积公式求解作答.【详解】(1)依题意,2ππ()4cos (sin cos cos sin )sin 2cos 66f x x x x x x x =-=-π2cos 212sin(216x x x =--=--,因为()0,πA ∈,则ππ11π2(,666A -∈-,又π()2sin(2)16f A A =--是()f x 的最大值,所以ππ262A -=,即π3A =.(2)在ABC 中,由余弦定理2222cos a b c bc A =+-,得222π222cos 3c c =+-⨯,即2230c c --=,解得3c =,所以ABC 的面积11πsin 23sin223ABC S bc A ==⨯⨯⨯ .9.(2023·上海·高三专题练习)在ABC 中,点D 在边AC 上,且2,AD CD BD AC ==.(1)若BD 平分ABC ∠,求sin sin ABDBDC∠∠的值;(2)若,,AB AC BC成递增的等比数列,AC =ABC 的面积.【答案】(1)11(2)4【分析】(1)运用余弦定理求出,CD BC 的关系,再运用正弦定理求解;(2)运用余弦定理求出AB ,BC 的值,再求出sin B ∠,用面积公式计算即可.【详解】(1)设CD m =,则2,3AD m BD AC m ===,因为BD 平分ABC ∠,所以2AB ADBC CD==,设BC n =,则2AB n =,在ABC 中,2222239cos 212AB AC BC n m A AB AC mn +-+==⋅,在ABD △中,2222245cos 28AB AD BD n m A AB AD mn+--==⋅,由22223945128n m n m nm mn+-=,得22112n m =,sin sinsin sin ABD CBD CD m BDC BDC BC n ∠∠====∠∠;(2)因为,,AB AC BC 成递增的等比数列,AC =26AB BC AC ⋅==,在ABD △中,2222263cos 28AB AD BD AB ADB AD BD -+-∠==⋅,在BCD △中,2222203cos 24BC BD CD BC BDC BD CD -+-∠==⋅,因为cos cos 0ADB BDC ∠+∠=,所以22262033084AB BC --+=,整理得22222AB BC +=,又6AB BC ⋅=,所以2236222BC BC+=,解得BC =3BC =,若BC =AB BC =>,不符合题意,若3BC =,则2AB =,符合题意,此时2227cos 212AB BC AC ABC AB BC +-∠==⋅,则sin ABC ABC ∠=△的面积1sin 2S AB BC ABC =⋅∠=10.(2023·上海·高三专题练习)已知向量,2sin 22x x m ⎛⎫=- ⎪⎝⎭ ,cos ,cos 22x x n ⎛⎫= ⎝⎭,函数()y f x m n ==⋅ .(1)设ππ,22θ⎡⎤∈-⎢⎥⎣⎦,且()1f θ=,求θ的值;(2)在ABC 中,1AB =,()1f C =,且ABC的面积为2,求sin sin A B +的值.【答案】(1)π2-或π6(2)1+【分析】(1)化简得到s π()2co 6f x x ⎛⎫=+ ⎪⎝⎭1cos 62πθ⎛⎫+= ⎪⎝⎭,得到2π(Z)63ππk k θ+=±∈,根据范围得到答案.(2)确定π6C =,根据面积公式得到=ab 227a b +=,得到2+=a b ,再根据正弦定理得到答案.【详解】(1)2π()cos2sin cos cos )sin 2cos 2226x x x f x x x x ⎛⎫=-+-=+ ⎪⎝⎭()π2cos 16f θθ⎛⎫=+= ⎪⎝⎭,得1cos 62πθ⎛⎫+= ⎪⎝⎭,故2π(Z)63ππk k θ+=±∈,ππ,22θ⎡⎤∈-⎢⎥⎣⎦,故π2θ=-或π6.(2)(0,π)C ∈,由(1)知π6C =,在ABC 中,设内角A 、B 的对边分别是,a b,则1s n πi 26S ab ==,故=ab 由余弦定理得2222π12cos66a b ab a b =+-=+-,故227a b +=.解得2a b =⎧⎪⎨=⎪⎩或2a b ⎧=⎪⎨=⎪⎩,于是2+=a b 由正弦定理得sin sin sin 112===A B C a b,故1sin sin ()12+=+=+A B a b 11.(2023春·上海杨浦·高三上海市杨浦高级中学校考开学考试)已知函数()()()sin 0,0,πf x A x A ωϕωϕ=+>><的部分图像如图所示.(1)求()f x 的解析式及对称中心;(2)先将()f x 的图像纵坐标缩短到原来的12,再向左平移π6个单位后得到()g x 的图像,求方程()12g x =在[]π,π-的解集.【答案】(1)()π2sin 23f x x ⎛⎫=- ⎪⎝⎭;对称中心为ππ,026k ⎛⎫+ ⎪⎝⎭,Z k ∈;(2)π5π11π7π,,,12121212⎧⎫⎨⎬⎩⎭--.【分析】(1)结合函数()()()sin 0,0,πf x A x A ωϕωϕ=+>><的部分图像特征可求()f x 的解析式及对称中心;(2)根据图象变换可得()g x 的解析式,从而方程可求.【详解】(1)根据函数()()()sin 0,0,πf x A x A ωϕωϕ=+>><的部分图像,可得32π5ππ2,4123A ω=⋅=+,∴2ω=.再根据五点法作图,5ππ2122ϕ⨯+=,∴π3ϕ=-,故()π2sin 23f x x ⎛⎫=- ⎪⎝⎭.令π2π,Z 3x k k -=∈,解得ππ,Z 62k x k =+∈,此时0y =.所以函数()f x 的对称中心为ππ,026k ⎛⎫+ ⎪⎝⎭,Z k ∈.(2)先将()f x 的图像纵坐标缩短到原来的12,可得πsin 23y x ⎛⎫=- ⎪⎝⎭的图像,再向左平移π6个单位,得到ππsin 2sin 632y x x ⎡⎤⎛⎫=+-= ⎪⎢⎥⎝⎭⎣⎦的图像,令1sin 22x =,[][]π,π,22π,2πx x ∈-∴∈- 所以π5π11π7π2,,,6666x =--,解得π5π11π7π,,,12121212x =--故方程()12g x =在[]π,π-的解集为π5π11π7π,,12121212⎧⎫⎨⎬⎩⎭--.12.(2023春·上海·高三校联考阶段练习)已知函数()221cos sin 2f x x x =-+.(1)求()f x 的单调增区间;(2)设ABC 为锐角三角形,角A B C 、、所对的边分别是,,,5a b c a b ==,若()0f A =,求ABC 的面积.【答案】(1)ππ,π,Z2k k k ⎡⎤-+∈⎢⎥⎣⎦(2)4【分析】(1)利用二倍角的余弦公式及三角函数的性质即可求解;(2)根据已知条件及余弦定理,利用余弦定理的推论及三角形的面积公式即可求解.【详解】(1)()2211cos sin cos 222f x x x x =-+=+由π2π22π,Z k x k k -+≤≤∈,得πππ,Z 2k x k k -+≤≤∈,所以()f x 的单调增区间为ππ,π,Z 2k k k ⎡⎤-+∈⎢⎥⎣⎦.(2)由(1)知,()1cos 22f x x =+,因为()0f A =,所以()1cos 202f A A =+=,即1cos 22A =-,因为π02A <<,所以02πA <<,所以2π23A =,即π3A =.由余弦定理可知,2222cos a b c bc A =+-,将5a b ==代入并整理得2560c c -+=,解得2c =或3c =.又因为ABC 为锐角三角形,所以222cos 0,02a c b B c ac+-=>>,即219250c +->,解得c 所以3c =.所以ABC的面积为11sin 5322ABC S bc A ==⨯⨯⨯△.13.(2023·上海嘉定·统考二模)已知向量()sin ,1cos 2a x x =+ ,1cos ,2b x ⎛⎫= ⎪⎝⎭ ,()f x a b =⋅ .(1)求函数()y f x =的最大值及相应x 的值;(2)在ABC 中,角A 为锐角,且7π12A B +=,()1f A =,2BC =,求边AC 的长.【答案】(1)ππ8x k =+,k ∈Z ;(2)AC =【分析】(1)利用向量数量积坐标运算、二倍角公式以及辅助角公式求得函数()y f x =的解析式,再由正弦函数的性质求解;(2)由(1)求出角A 的值,再利用正弦定理求出AC 边的长作答.【详解】(1)依题意,cos 2111π1()cos sin (sin 2cos 2))22242x f x x x x x x +=+=++=++当ππ22π42x k +=+,即ππ,Z 8x k k =+∈时,()y f x =取最大值12.(2)由(1)及()1f A =π12142A ⎛⎫++= ⎪⎝⎭,即πsin 24A ⎛⎫+= ⎪⎝⎭,因π02A <<,则ππ5π2444A <+<,因此,324ππ4A +=,则π4A =,而7π12A B +=,有π3B =,在ABC 中,由正弦定理sin sin BC AC A B =得,π2sinsin 3πsin sin 4BC B AC A ==所以边AC.14.(2023·上海黄浦·格致中学校考三模)在ABCcos cos C A =,6B π=,BC边中线AM (1)求A 的值;(2)求ABC 的面积.【答案】(1)π6【分析】(1)由正弦定理结合三角恒等变换得出A 的值;(2)由余弦定理得出2b =,最后由面积公式得出ABC 的面积.【详解】(1cos cos C A =cos cos CA=2sin cos cos sin cos sin()sin B A A C C A A C B+因为sin 0B ≠,所以cos 2A =,因为()0,πA ∈,所以π6A =.(2)因为6B π=,23C A B ππ=--=,可知ABC 为等腰三角形.在AMC 中,由余弦定理可得2222cos120AM AC MC AC MC =+-⋅︒即227(2cos12022b b b b =+-⨯⨯⨯︒,解得2b =.所以ABC的面积为2211sin 222S b C ==⨯=.15.(2023·上海金山·统考二模)在ABC 中,角A 、B 、C 所对边的边长分别为a 、b 、c,已知a =45C =︒.(1)若sin A B =,求c ;(2)若15B A -=︒,求ABC 的面积.【答案】(1)2c =(2)2+3【分析】(1)根据正弦定理求边长后再应用余弦定理求解即可.(2)先求出角,再求出边长,最后应用面积公式求解可得.【详解】(1)由sin A B =,应用正弦定理得a ==2b ∴=,2842242c ∴=+-⨯⨯,即得2c =.(2)因为15135B A B A -=︒⎧⎨+=︒⎩则7560B A =︒⎧⎨=︒⎩,c ==111sin =222ABC S ac B ==⨯⨯ 16.(2023春·上海·高三上海市实验学校校考阶段练习)已知函数25π()sin 2cos 16f x x x ⎛⎫=+-+ ⎪⎝⎭.(1)求函数()f x 的最小值和单调增区间;(2)设角A B 、、C 为ABC 的三个内角,若1cos 3B =,124C f ⎛⎫=- ⎪⎝⎭,求sin A .【答案】(1)()min 12f x =,单调递增区间()π3ππ,πZ 44k k k ⎡⎤++∈⎢⎥⎣⎦(2)6【分析】(1)由三角恒等变换得1()222f x x =-,结合正弦函数的性质求解即可;(2)由1cos 3B =,可得sin B =且β为锐角,60B >︒,由124C f ⎛⎫=- ⎪⎝⎭,可得60C =︒,再由()sin sin A B C =+求解即可.【详解】(1)解:由题意可得()2225ππππsin 2cos 1=sin 2++1cos =cos 2n 33si 62f x x x x x x x⎛⎫⎛⎫⎛⎫=+-++-++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ππ1cos 21cos 2cos sin 2sin 23322x x x x -=-+=-,所以当π2=2π+,Z 2x k k ∈,即ππ,Z 4x k k =+∈时,函数()f x 由π3π2π+22π+,Z 22k x k k ≤≤∈,解得π3ππ+π+,Z 44k x k k ≤≤∈,所以()f x 的单调递增区间()π3ππ,πZ 44k k k ⎡⎤++∈⎢⎥⎣⎦;综上所述:()min π1π42f x f k ⎛⎫=+= ⎪⎝⎭,单调递增区间()π3ππ,πZ 44k k k ⎡⎤++∈⎢⎥⎣⎦;(2)解:因为112224C f C ⎛⎫=-=- ⎪⎝⎭,sin C ∴=()0,πC ∈ ,60C ∴=︒或120︒,1cos sin 33662B B =⇒==>=Q ,且β为锐角,所以60B >︒,∴角C 只能为锐角60C =︒,()sin sin A B C ∴=+sin cos cos sin 6B C B C =+=.17.(2023·上海黄浦·统考二模)在ABC 中,53cos ,cos 135A B =-=.(1)求sin C 的值;(2)若4AB =,求ABC 的周长和面积.【答案】(1)1665;(2)周长32,面积24.【分析】(1)利用两角和的正弦公式即可求得sin C 的值;(2)先利用正弦定理求得ABC 的,a b 的长,进而求得ABC 的周长和面积.【详解】(1)在ABC 中,53cos ,cos 135A B =-=,又(),0,πA B ∈,则124sin ,sin 135A B ==,则1235416sin sin()sin cos cos sin 13513565C A B A B A B ⎛⎫=+=+=⨯+-⨯= ⎪⎝⎭.(2)4c AB ==,又124sin ,sin 135A B ==,16sin 65C =,则由正弦定理得124sin sin 135415,4131616sin sin 6565A Ba cbc C C =====⨯=,则ABC 的周长为1513432++=ABC 的面积为1116sin 1513242265ab C =⨯⨯⨯=.18.(2023·上海浦东新·统考三模)已知向量),cos a x x =,πsin ,cos 2b x x ⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭.设()f x a b =⋅ .(1)求函数()y f x =的最小正周期;(2)在ABC 中,角A 、B 、C 所对的边分别为a 、b 、c .若()1f A =,4b =,三角形ABC的面积为a 的长.【答案】(1)π(2)【分析】(1)利用数量积的坐标公式及二倍角公式、辅助角公式化简函数,利用最小正周期公式求解即可;(2)根据()1f A =求出角A ,结合条件及三角形面积公式求出c ,利用余弦定理即可求解a .【详解】(1)由题意,()f x a b =⋅=2πsin cos 2x x x ⎛⎫++ ⎪⎝⎭2cos cos x x x =+112cos 222x x =++π1sin 262x ⎛⎫=++ ⎪⎝⎭,因此函数()y f x =的最小正周期为2ππ2T ==;(2)由()1f A =得π1sin 262A ⎛⎫+= ⎪⎝⎭,因为()0,πA ∈,所以ππ7π2,666A ⎛⎫+∈ ⎪⎝⎭,解得π3A =,因为11sin 422ABC S bc A c ==⨯=V 2c =,由余弦定理解得2222212cos 42242122a b c bc A =+-=+-⨯⨯⨯=,所以a =.19.(2023·上海奉贤·校考模拟预测)已知函数()ππsin 2cos sin 122f x x x x x ⎛⎫⎛⎫=+--+ ⎪ ⎪⎝⎭⎝⎭,(1)求函数()f x 的最值;(2)设ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若()2f A =,2b =,且2sin sin B C A +=,求ABC 的面积.【答案】(1)最大值为2,最小值为2-(2)2或3【分析】(1)把()f x 化为“一角一函数”的形式:先用诱导公式把角化为x ,再用二倍角公式把二次项化为一次项,同时把角化为2x ,最后用辅助角公式把函数名化为正弦,即可求出函数的最值;(2)先求出角A ,由余弦定理得到关于,a c 的方程,再由正弦定理把已知的方程化简为含,a c 的方程,联立方程组即可解出,a c 的值,再代入三角形的面积公式即可.【详解】(1)因为()sin 2cos sin 122f x x x x x ππ⎛⎫⎛⎫=+--+ ⎪ ⎪⎝⎭⎝⎭2cos 2cos 12cos 2x x x x x=-+=-2sin 26x π⎛⎫=- ⎪⎝⎭,所以()f x 的最大值为2,最小值为2-.(2)结合(1)可知()2sin 226f A A π⎛⎫=-= ⎪⎝⎭,所以sin 216A π⎛⎫-= ⎪⎝⎭.因为()0,A π∈,所以112666A πππ⎛⎫-∈- ⎪⎝⎭,则2,623A A πππ-==.由余弦定理得2222241cos 242b c a c a A bc c +-+-===,化简得2224a c c =-+①.又2sin sin B C A +=,由正弦定理可得2b c +=,即4c +=②.结合①②得3a c ==或23a c ==.3c =时,1sin 22ABCS bc A ==;23c =时,1sin 23ABC S bc A ==△.综上,ABC 的面积为2或3.20.(2023·上海·华师大二附中校考模拟预测)已知函数21()2cos 2f x x x =--,x R ∈.(1)求函数()y f x =在区间5,1212ππ⎡⎤-⎢⎥⎣⎦上的最大值和最小值;(2)设ABC 的内角A ,B ,C 的对边分别为a ,b ,c 且c =()0f C =,若sin 2sin B A =,求ABC S .【答案】(1)max 0y =,min 22y +=-;(2)2.【分析】(1)利用辅助角公式将函数()f x 化简可得π()sin 216f x x ⎛⎫=-- ⎪⎝⎭,利用正弦函数的单调性得到()f x 在ππ,123⎡⎤-⎢⎥⎣⎦递增,在π5π,312⎡⎤⎢⎥⎣⎦递减,进而求出最值;(2)根据题意得到π3C =,然后利用正弦定理得到2b a =,再结合余弦定理和三角形面积公式即可求解.【详解】(1)()1cos 21π2sin 21226x f x x x +⎛⎫=-=-- ⎪⎝⎭,由ππ3π2π22π262k x k +≤-≤+,Z k ∈,得()f x 的单调递减区间为π5ππ,π36k k ⎡⎤++⎢⎥⎣⎦,Z k ∈,故()f x 在ππ,123⎡⎤-⎢⎥⎣⎦递增,在π5π,312⎡⎤⎢⎥⎣⎦递减,故max π03y f ⎛⎫== ⎪⎝⎭,min π5πmin ,1212y ff ⎧⎫⎛⎫⎛⎫=-=-⎨⎬ ⎪ ⎝⎭⎝⎭⎩⎭(2)π()sin 2106f C C ⎛⎫=--= ⎪⎝⎭,则πsin 2106C ⎛⎫--= ⎪⎝⎭,0πC <<,022πC <<,所以ππ11π2666C -<-<,所以ππ262C -=,π3C =,因为sin 2sin B A =,所以由正弦定理得2b a =,①由余弦定理得222π2cos3=+-c a b ab ,即2223c a b ab =+-=,②由①②解得:1a =,2b =.故1sin 2ABC S ab C ==△.21.(2023·上海普陀·曹杨二中校考三模)设函数()2cos 2f x x x ωω=+,其中02ω<<.(1)若()f x 的最小正周期为π,求()f x 的单调增区间;(2)若函数()f x 图像在π0,3⎛⎤⎥⎝⎦上存在对称轴,求ω的取值范围.【答案】(1)πππ,π36k k ⎡⎤-++⎢⎥⎣⎦,k ∈Z(2)122ω≤<【分析】(1)根据三角恒等变换化简函数表达式,然后根据最小正周期公式算出ω,然后利用正弦函数的单调性求解;(2)利用正弦函数sin y x =的对称轴公式求参数的范围.【详解】(1)由题意,()21π1sin2cos sin2(cos 21)sin 222262f x x x x x x ωωωωω⎛⎫=+++=++ ⎪⎝⎭,又02ω<<,于是2ππ2ω=,则1ω=,则()1sin 262πf x x ⎛⎫=++ ⎪⎝⎭,根据正弦函数的单调递增区间,令πππ22π,2π,622x k k k ⎡⎤+∈-+∈⎢⎥⎣⎦Z ,解得πππ,π36k k ⎡⎤-++⎢⎥⎣⎦,k ∈Z ,即为()f x 的单调递增区间.(2)当π0,3x ⎛⎤∈ ⎥⎝⎦,ππ2ππ2,6636x ωω⎛⎤+∈+ ⎥⎝⎦,注意到题干02ω<<,则2πππ3π,3662ω⎛⎫+∈ ⎪⎝⎭,根据正弦函数sin y x =的对称轴ππ,2x k k =+∈Z ,显然只有0k =时一条对称轴32π2ππ,6x =∈⎛⎫ ⎪⎝⎭,于是2πππ362ω+≥,解得12ω≥,结合02ω<<可得122ω≤<22.(2023·上海徐汇·统考三模)如图,ABC 中,角A 、B 、C 的对边分别为a 、b 、c .(1)若33cos a c b C -=,求角B 的大小;(2)已知3b =、π3B =,若D 为ABC 外接圆劣弧AC 上一点,求ADC △周长的最大值.【答案】(1)1arccos 3B =;(2)3+【分析】(1)根据给定条件,利用正弦定理边化角,再结合和角的正弦求解作答.(2)由(1)及给定条件,求出ADC ∠,再利用余弦定理结合均值不等式求解作答.【详解】(1)在ABC 中,由33cos a c b C -=及正弦定理,得3sin sin 3sin cos A C B C -=,即3sin()sin 3sin cos B C C B C +-=,则3(sin cos sin cos )sin 3sin cos B C C B C B C +-=,整理得sin (3cos 1)0C B -=,而sin 0C ≠,即1cos 3B =,又因为0B π<<,所以1arccos 3B =.(2)在ADC △中,2π,33ADC AC ∠==,由余弦定理得2222π2cos3AC AD DC AD DC =+-⋅,于是22()()994AD DC AD DC AD DC ++=+⋅≤+,解得AD DC +≤当且仅当AD DC ==所以当AD DC ==ADC △周长取得最大值3+23.(2023·上海长宁·统考二模)(1)求简谐振动sin cos y x x =+的振幅、周期和初相位([0,2π))ϕϕ∈;(2)若函数11sin cos 22y x x =+在区间(0,)m 上有唯一的极大值点,求实数m 的取值范围;(3)设0a >,()sin sin f x ax a x =-,若函数()y f x =在区间(0,π)上是严格增函数,求实数a 的取值范围.【答案】(12π2π1T ==,初相位π4ϕ=;(2)π5π,33⎛⎤ ⎥⎝⎦;(3)()0,1;【分析】(1)利用辅助角公式化简,即可得到振幅、周期和初相位;(2)求导,令0y '=,求出导函数的零点,利用三角函数的单调性判断导函数的正负,进而分析出()y f x =的单调,列表分析出有唯一的极大值点的情况,即可得到实数m 的取值范围;(3)求导,并对a 分类讨论,利用余弦函数的单调性分析导函数在区间(0,π)的正负,即可判断()y f x =是否为严格增函数,进而得到实数a 的取值范围.【详解】解:(1)πsin cos 4y x x x ⎛⎫=+=+ ⎪⎝⎭,2π2π1T ==,初相位π4ϕ=;(2)111111cos sin cos sin 222222y x x x '⎛⎫=-=- ⎪⎝⎭,令0y '=,得1cos 02x =,11sin 22x =,列表,x π0,3⎛⎫ ⎪⎝⎭π3π,π3⎛⎫ ⎪⎝⎭π5ππ,3⎛⎫ ⎪⎝⎭5π35π,3π3⎛⎫ ⎪⎝⎭y '+0-0+0-y 极大值 极小值 极大值函数11sin cos 22y x x =+在区间(0,)m 上有唯一的极大值点时,π5π33m <≤,即实数m 的取值范围为π5π,33⎛⎤ ⎥⎝⎦.(3)()cos cos f x a ax a x '=-,当01a <<时,因为0πx <<,所以0πax x <<<,进而cos cos ax x >,()(cos cos )0f x a ax x '=->此时,()y f x =在区间(0,π)上是严格增函数;当1a =时,()0f x =,()y f x =不是严格增函数;当1a >时,设π0,x a ⎛⎫∈ ⎪⎝⎭,则0πx ax <<<,进而cos cos x ax >,()0f x '<,此时,()y f x =在区间π0,a ⎛⎫ ⎪⎝⎭上是严格减函数;综上,若函数()y f x =在区间(0,π)上是严格增函数,则01a <<,即实数a 的取值范围()0,1.【点睛】思路点睛:分类讨论思想是高中数学一项重要的考查内容,分类讨论思想要求在不能用统一的方法解决问题的时候,将问题划分成不同的模块,通过分块来实现问题的求解,体现了对数学问题的分析处理能力和解决能力.。
高等数学训练教材推荐书目

高等数学训练教材推荐书目在高等数学学习中,选择一本合适的训练教材对于提高数学能力和解题能力非常重要。
本文将向大家推荐几本优秀的高等数学训练教材,帮助读者更好地掌握高等数学知识。
1.《高等数学(上、下册)》(同济大学数学系主编,高教社出版)这套教材是许多高校的教学用书,被广泛认可。
它全面系统地介绍了高等数学的各个分支,包括极限与连续、微分学、积分学等内容。
书中的习题设计合理,涵盖了各个难度层次,可以帮助读者提高解题能力。
此外,教材中还有详细的解答和习题选解,方便学生自我学习和巩固。
2.《高等数学辅导与习题精解》(全国高等教育自学考试办公室主编,北京理工大学出版社)这本书是为自学考试而编写的高等数学辅导教材,适合那些想自己学习高等数学的读者。
书中内容简洁明了,理论与应用结合紧密。
每章后都有大量的习题以及详细的解答,读者可以通过做题巩固所学知识,并了解解题思路和技巧。
3.《高等数学习题精选与解析》(清华大学数学系主编,北京大学出版社)这本教材是清华大学数学系的集体智慧之作,题目的设计和解析非常精细。
教材包含了大量有代表性的习题,不仅能够帮助读者巩固基础知识,还能提高解题能力和思维灵活性。
教材中提供的解析详尽,对于理解解题方法和技巧非常有帮助。
4.《高等数学习题解析与考点精研》(北京大学数学系主编,高等教育出版社)这本教材特别注重考点的讲解和解题思路的引导。
书中的习题精选了各类经典考题,并通过详细的解析,帮助读者理解考点和解题方法。
此外,该教材还提供了历年高等数学考试真题,并给出了详尽的解答和分析,方便读者进行针对性复习和训练。
5.《高等数学习题指导与训练》(浙江大学数学系主编,浙江大学出版社)这本教材强调对高等数学基本概念和方法的训练和巩固。
书中的习题按难易程度分层次设计,逐步引导读者提高解题能力。
每个章节后都附有大量的习题解答,供读者自我检验和巩固所学内容。
通过上述几本高等数学训练教材的推荐,相信读者可以找到适合自己的学习材料。
2022高三数学上册16.2《排列》同步练习沪教版

高考摆列问题的解决方案内容概要 : 本文把常有的摆列问题概括成三种典型问题,并在摆列的一般规定性下,对每一种种类的问题经过典型例题概括出相应的解决方案,并附以最近几年的高考原题及分析 , 使我们对摆列问题的认识更深入实质 , 对摆列问题的解决更有章法可寻.重点词 :“特别优先” ,“大元素”,“捆绑法” ,“插空法” ,“等机率法”, 笔者在教课中试试将摆列摆列问题的应用题是学生学习的难点,也是高考的必考内容问题概括为三种种类来解决:1.能排不可以排摆列问题摆列应用题 2.相邻不相邻摆列问题3.时机均等摆列问题下边就每一种题型联合例题总结其特色和解法,并附以最近几年的高考原题供读者参研.一.能排不可以排摆列问题即特别元素在特别地点上有特别要求的摆列问题解决此类问题的重点是特别元素或特别地点优先或使用间接法.例 1.(1) 7 位同学站成一排,此中甲站在中间的地点,共有多少种不一样的排法 27 位同学站成一排,甲、乙只好站在两头的排法共有多少种37 位同学站成一排,甲、乙不可以站在排头和排尾的排法共有多少种47 位同学站成一排,此中甲不可以在排头、乙不可以站排尾的排法共有多少种分析 :1 先考虑甲站在中间有 1 种方法,再在余下的 6 个地点排此外 6 位同学,共种方法;2 先考虑甲、乙站在两头的排法有种,再在余下的 5 个地点排此外 5 位同学的排法有种,共A22 A55种方法;3 先考虑在除两头外的 5 个地点选 2 个安排甲、乙有种,再在余下的 5 个地点排此外 5 位同学排法有种,共A52A55种方法;此题也可考虑特别地点优先, 即两头的排法有 , 中间 5个地点有种,共 A2A5种方法;254 分两类乙站在排头和乙不站在排头,乙站在排头的排法共有种,乙不站在排头的排法总数为:先在除甲、乙外的 5人中选 1人安排在排头的方法有种,中间5 个地点选 1 个安排乙的方法有,再在余下的 5 个地点排此外 5 位同学的排法有,故共有A66A51 A51A55种方法;此题也可考虑间接法,总排法为,不切合条件的甲在排头和乙站排尾的排法均为,但这两种状况均包含了甲在排头和乙站排尾的状况,故共有A772A66A55种.例 2 某天课表共六节课,要排政治、语文、数学、物理、化学、体育共六门课程,假如第一节不排体育,最后一节不排数学,共有多少种不一样的排课方法解法 1:对特别元素—数学和体育进行分类解决( 1)数学、体育均不排在第一节和第六节,有种,其余有种,共有A42 A44种;( 2)数学排在第一节、体育排在第六节有一种,其余有种,共有种;( 3)数学排在第一节、体育不在第六节有种,其余有种,共有A41 A44种;( 4)数学不排在第一节、体育排在第六节有种,其余有种,共有A41 A44种;因此切合条件的排法共有A422A41 1 A4421A44504 种解法 2:对特别地点—第一节和第六节进行分类解决( 1)第一节和第六节均不排数学、体育有种,其余有种,共有A42 A44种;( 2)第一节排数学、第六节排体育有一种,其余有种,共有种;( 3)第一节排数学、第六节不排体育有种,其余有种,共有A41A44种;( 4)第一节不排数学、第六节排体育有种,其余有种,共有A41A44种;因此切合条件的排法共有A422A41 1 A4421A44504 种.解法 3:此题也可采纳间接清除法解决不考虑任何限制条件共有种排法,不切合题目要求的排法有:(1)数学排在第六节有种;(2)体育排在第一节有种;考虑到这两种状况均包含了数学排在第六节和体育排在第一节的状况种因此切合条件的排法共有A662A55A44504 种附: 1、(2022 北京卷)五个工程队承建某项工程的五个不一样的子项目,每个工程队承建 1 项,此中甲工程队不可以承建 1 号子项目,则不一样的承建方案共有(A)种( B)种( C)种( D)种分析:此题在解答时将五个不一样的子项目理解为 5 个地点,五个工程队相当于 5 个不一样的元素,这时问题可归纳为能排不可以排摆列问题即特别元素在特别地点上有特别要求的摆列问题,先排甲工程队有,其余 4 个元素在 4 个地点上的排法为种,总方案为种.应选B.2、( 2022 全国卷Ⅱ)在由数字0,1, 2,3, 4, 5 所构成的没有重复数字的四位数中,不可以被5 整除的数共有个分析:此题在解答时只须考虑个位和千位这两个特别地点的限制,个位为1、 2、 3、 4 中的某一个有 4 种方法,千位在余下的 4 个非 0 数中选择也有 4 种方法,十位和百位方法数为种,故方法总数为 4 4A42192种.3、( 2022 福建卷)从 6 人中选出 4 人分别到巴黎、伦敦、悉尼、莫斯科四个城市旅行,要求每个城市有一人旅行,每人只旅行一个城市,且这 6 人中甲、乙两人不去巴黎旅行,则不一样的选择方案共有 ( )A .300 种B . 240 种C . 144 种D . 96 种分析:此题在解答时只须考虑巴黎这个特别地点的要求有 4 种方法,其余 3 个城市的排法看作标有这 3 个城市的 3 个签在 5 个地点( 5 个人)中的摆列有种,故方法总数为4 A 53 240种.应选( B ).上述问题归纳为能排不可以排摆列问题,从特别元素和特别地点下手解决, 抓住了问题的本质,使问题清楚了然,解决起来顺畅自然.二相邻不相邻摆列问题即某两或某些元素不可以相邻的摆列问题 相邻摆列问题一般采纳大元素法, 马上相邻的元素“捆绑”作为一个元素,再与其余元素进行摆列,解答时注意“开释”大元素,也叫“捆绑法” .不相邻摆列问题即某两或某些元素不可以相邻的摆列问题一般采纳“插空法” .例 3. 7 位同学站成一排,1 甲、乙和丙三同学一定相邻的排法共有多少种2 甲、乙和丙三名同学都不可以相邻的排法共有多少种( 3)甲、乙两同学间恰巧间隔2 人的排法共有多少种分析: 1 第一步、将甲、乙和丙三人“捆绑”成一个大元素与此外4 人的摆列为种,第二步、“开释”大元素,即甲、乙和丙在“捆绑”成的大元素内的排法有种, 因此共 A 5 A 3 72053种;2 第一步、先清除甲、乙和丙以外 4 人共种方法,第二步、甲、乙和丙三人排在4 人排好后产生的 5 个空挡中的任何 3 个都切合要求, 排法有种, 因此共有 A 44 A 531440种;( 3)先排甲、乙,有种排法,甲、乙两人中间插入的 2 人是从其余 5 人中选,有种排法,将已经排好的4人看作一个大元素作为“新人”参加下一轮4 人组的摆列,有种排法,因此总的排法共有A 22 A 52 A 44 960种.附: 1、( 2022 辽宁卷)用 1、 2、 3、4、 5、 6、 7、 8 构成没有重复数字的八位数,要求 1 和 2 相邻, 3 与 4 相邻, 5 与 6 相邻,而 7 与 8 不相邻,这样的八位数共有 个(用数字作答).分析:第一步、将 1 和 2“捆绑”成一个大元素, 3 和 4“捆绑”成一个大元素, 5 和 6“捆绑” 成一个大元素,第二步、摆列这三个大元素,第三步、在这三个大元素排好后产生的4 个空挡中的任何 2 个摆列7 和 8,第四步、“开释”每个大元素(即大元素内的每个小元素在“捆绑”成的大元素内部摆列) ,因此共有 A 33 A 42222576 个数.2、 (2022 重庆理)某校高三年级举行一次演讲赛共有 10 位同学参赛,此中一班有3 位,二班有 2 位,其余班有5 位,若采纳抽签的方式确立他们的演讲次序,则一班有3 位同学恰 好被排在一同(指演讲序号相连) ,而二班的 2 位同学没有被排在一同的概率为()A .1B .1C .1D .110 20 40 120分析:切合要求的基本领件(排法)共有:第一步、将一班的 3 位同学“捆绑”成一个大元素,第二步、这个大元素与其余班的 5 位同学共 6 个元素的全摆列,第三步、在这个大元素与其余班的 5 位同学共 6 个元素的全摆列排好后产生的7 个空挡中摆列二班的2 位同学,第四步、“开释”一班的3 位同学“捆绑”成的大元素,因此共有A 66 A 72 A 33 个;而基本领件总数为个,因此切合条件的概率为A 66A 72 A 33 1PA 1010.应选( B ).203、( 2022 京春理)某班新年联欢会原定的5 个节目已排成节目单,开演前又增添了两个新节目假如将这两个节目插入原节目单中,那么不一样插法的种数为().30C分析:分两类:增添的两个新节目不相邻和相邻,两个新节目不相邻采纳“插空法”,在 5个节目产生的 6 个空挡摆列共有A 6230 种,将两个新节目 “捆绑” 作为一个元素叉入 5 个节目产生的 6 个空挡中的一个地点, 再“开释”两个新节目 “捆绑”成的大元素, 共有 A 1A 2 1262种,再将两类方法数相加得42 种方法.应选( A ).三时机均等摆列问题即某两或某些元素按特定的方式或次序摆列的摆列问题解决时机均等摆列问题往常是先对全部元素进行全摆列 , 再借助等可能转变,即乘以切合要求的某两(或某些)元素按特定的方式或次序摆列的排法占它们(某两(或某些)元素)全摆列的比率,称为“等机率法” ;或将特定次序的摆列问题理解为组合问题加以解决例 4、 7 位同学站成一排.1 甲一定站在乙的左侧2 甲、乙和丙三个同学由左到右摆列分析:(1) 7 位同学站成一排总的排法共种, 包含甲、乙在内的 7 位同学排队只有甲站在乙的左侧和甲站在乙的右侧两类,它们的时机是均等的,故知足要求的排法为1A 77 ,此题也可将2特定次序的摆列问题理解为组合问题加以解决,即先在 7 个地点中选出 2 个地点安排甲、乙 ,因为甲在乙的左侧共有种,再将其余 5 人在余下的 5 个地点摆列有种, 得排法数为 C 72 A 55种;( 2)拜见( 1)的剖析得A 77(或C 73 A 44).A 33本文经过较为清楚的脉络把摆列问题分为三种种类,使我们对摆列问题有了比较系统的认识但因为摆列问题种类众多,总会有些问题不可以囊括此中,也必定存在很多不足 , 希望读者能和我一同研究完美.。
上海数学教材练习册高三全一册习题精选.doc
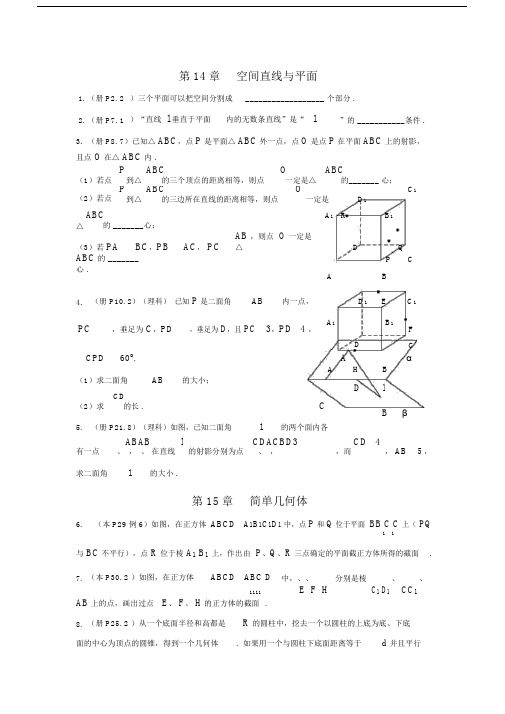
第14章 空间直线与平面1. (册 P2. 2 )三个平面可以把空间分割成 __________________ 个部分 .2. (册 P7. 1 )“直线 l 垂直于平面内的无数条直线”是“ l”的 ___________条件 .3. (册 P8. 7)已知△ ABC ,点 P 是平面△ ABC 外一点,点 O 是点 P 在平面 ABC 上的射影,且点 O 在△ ABC 内 .(1)若点 P到△ ABC OABC的三个顶点的距离相等,则点 一定是△的_______ 心;(2)若点 P到△ ABCO一定是D 1C 1的三边所在直线的距离相等,则点△ABCA 1 RB 1的 _______心;(3)若 PA BC ,PBAC , PCAB ,则点 O 一定是△DP QABC 的 _______心 .CAB4. (册 P10. 2)(理科) 已知 P 是二面角AB内一点,D 1EC 1 PC,垂足为 C ,PD,垂足为 D ,且 PC3,PD 4 , A 1B 1F60o .DCACPDAHBα(1)求二面角AB的大小;DlC(2)求 CD的长 .Bβ5. (册 P21. 8)(理科)如图,已知二面角l的两个面内各有一点 ABAB在直线 l 的射影分别为点 CDACBD3,而 CD 4, AB 5 ,、 , 、、 ,求二面角l的大小 .第 15章 简单几何体6.(本 P29 例 6)如图,在正方体 ABCD A 1B 1C 1D 1 中,点 P 和 Q 位于平面 BB C C 上( PQ1 1与 BC 不平行),点 R 位于棱 A 1 B 1 上,作出由 P 、Q 、R 三点确定的平面截正方体所得的截面 . 7. (本 P30. 2 )如图,在正方体ABCD ABC D 中,、、分别是棱C 1D 1 、 CC 1 、1111E F HAB 上的点,画出过点 E 、 F 、 H 的正方体的截面 .8. (册 P25. 2 )从一个底面半径和高都是 R 的圆柱中,挖去一个以圆柱的上底为底、下底面的中心为顶点的圆锥,得到一个几何体. 如果用一个与圆柱下底面距离等于d 并且平行于底面的平面去截这个几何体,求截面面积.9. (册 P29. 2)已知正六棱柱最长的一条对角线长为13 厘米,侧面积为180 平方厘米,求这个棱柱的体积.10. (册 P31. 1)维度为的纬度圈上有甲乙两地,它们的纬度圈上的弧长等于πRcos(R是地球的半径),求甲乙两地的球面距离.11.(册 P32. 2)现有以下三个命题:①底面是平行四边形的四棱柱是平行六面体;②底面是矩形的平行六面体是长方体;③直四棱柱是直平行六面体 . 其中真命题的序号是 _______.12. (册 P32. 3)如果一个三棱锥的底面是直角三角形,那么这个三棱锥的三个侧面()( A)都不是直角三角形(B)至多只能有一个是直角三角形( C)至多只能有两个是直角三角形(D)可能都是直角三角形13. (册 P35. 1)已知长方体ABCD A1B1C1D1的高为h P 1 1,底面积为,对角面BBDD的面积为Q,求它的侧面积.14. (册P36. 4 )设AB是球O的直径,AB 50, O1、 O2是AB上的两点,平面、分别通过点O1、 O2,且垂直于AB,截得圆O1、圆 O2,当圆O1、圆 O2的面积分别为49π、400π时,求O1、 O2两点的距离.第 16 章排列组合与二项式定理15.(本 P50 例 3)540 的不同正约数共有多少个?16.(本 P55 例 4)求证:P m n mP m n1P m n 1 .17.(本 P55 例 5)解方程:P42n 1140P3n .18. (本 P55. 2 )1! 2! 3! L 100! 的个位数为 __________.19. (本 P60 例 4)如果从 7 名运动员中选 4 名运动员组成接力队,参加 4 100 接力赛,那么甲乙两人都不跑中间两棒的安排方法有多少种?20. (本 P61 例 6)将a、b、c、d、e、f六个不同元素排成一列,其中a 不排在首位, b不排在末位,有几种排法?21.(本 P62. 3)A、B、C、D、E五人站成一排,如果B必须站在A的右边(A、B可以不相邻),那么共有多少种不同的排法?22. (本 P64 例 2)求证:C n m m 1 C n m 11 .n 123. (本 P65. 3 )解不等式:C n4 Cn6.24. (本 P67. 3 )求证: C m C m 2C m 1 C m 2.n 2 n n n25. (本 P67. 4 )解方程: C182x C18x 2 .26. (本 P71 例 3)求(1 a)12的二项展开式中倒数第 5 项 .1 n27. (本 P73 例 6)已知x 的二项展开式中,前三项系数成等差数列,求二项2 4 x展开式中的所有有理项.28.(本 P74. 3 )求5555被 8 除所得的余数 .29. (本 P75 例 11)利用二项式定理证明:2n n2 n 1 (n 5,n N*).30. (本 P76. 4 )求证:C n0 C n2 C n4 L C n n 2n 1(n是偶数).31.(册 P38. 2)要把 4 封信投入 3 个信箱,共有多少种不同的投法?(允许将信全部或部分投入某一个信箱)32. (册 P40. 8 )已知 P10m 10 9 L 5,求正整数 m的值.33. (册 P42. 3 )化简:12 3 L n 1 . ( n N* ,n 2 )2! 3! 4! n!34. (册 P42. 5 )求证: P11 2P 22 3P33 L nP n n P n n 11 1 .(n N* )35. (册 P43. 3)将 8 个相同的小球放入编号为1、2、3 的三个盒子内,要求每个盒子的球数不小于它的编号数,共有多少种不同的放法?36. (册 P48. 5 )在 (3 x 2 y)9 的展开式中,求二项式系数的和以及各项系数的和.37. (册 P49. 9 )求和: C1n 3C n2 9C n3 L 3n 1 C n n.的自然数,证明: 1 1 n38. (册 P49. 10 )已知n为大于 1 2 .n39. (册 P49. 11 )在x2 3x n的二项展开式中,有且只有第五项的二项式系数最大,求C0n 1C1n1C n2 L ( 1)n1n C n n.2 4 240. (册 P49. 1 )求和: C1000 C1002 C1004 L C10098 C100100 .41. (册 P50. 3 )在 (1 3 ) nx的二项展开式中,末三项的二项式系数之和等于631.(1)求二项展开式中二项式系数最大的项是第几项;(2)求二项展开式中系数最大的项.42. (册 P50. 4 )求 7777 15 除以 19 的余数 .43. (册 P50. 5 )用两种方法证明:26n 3 32 n 1能被11 整除 .44. (册 P50. 6 )已知 (x 1)n x n L ax3 bx2 cx 1 (n N* ),且a : b 3:1 ,求c 的值.45.(册 P50. 1 ( 4))用数字 0、 1、2、 3、 4、 5 可组成没有重复数字的六位数,其中数字2、 4 排在相邻数位上,满足条件的六位数共有___________个 .46. (册 P52. 1) 6 个人排成一列,其中甲乙两人之间至少有两个人的不同排法种数是___.第 17 章概率论初步47.(本 P90 例 7 改编为 2011 年高考试题)求随机抽取 10 个同学中至少有两个同学在同一个月份出生的概率 . (精确到)48. (册 P54. 4)某城镇共有 10000 辆自行车,牌照编号从00001 到 10000. 求在此城镇中偶然遇到的一辆自行车,其牌照号码中有数字8的概率 .49.(册 P56. 1 )将n间房分给n个人,每个人都以相等的可能性进入每一间房间,而且每间房间里的人数没有限制,求不出现空房的概率.50. (册 P56. 2 )把 10 本书随机地排在书架上,求其中指定的 3 本书排在一起的概率.51.(册 P56. 3)某人有 5 把钥匙,但只有一把能打开门,他每次取一把钥匙尝试开门,求试到第 3 把钥匙时才打开门的概率 .第 18 章基本统计方法52. (册 P61. 2 )某班级有40 名同学参加打靶训练,他们的成绩如下表所示(单位:环):测验成绩频数[4, 5) 2[5, 6) 3[6, 7)10[7, 8) 15[8, 9) 8[9, 10] 2 求该班同学的成绩 2 区间估计. (精确到)高三总复习题53. (册 P71. 13 )已知11 7 , n N* ,求C8n . C5n C6n 10C7n54.(册 P74. 5)一个球受热膨胀 . 如果它的表面积增加 21%,那么这个球的半径增加多少?55. (册 P74. 6 )求C383n n C321n n(n N* )的值 .56.(册 P75. 8 )以一个正方体的顶点为顶点能组成多少个三棱锥?57. (册 P75. 10 )已知(x lg x1)n的二项展开式中,末三项的二项式系数的和为22,二项式系数最大的项为20000,求实数x 的值.。
上海中学高三数学综合练习(五)

上海中学高三数学综合练习五班级___________ 学号_______ 姓名_______________ 成绩________ 一、填空题:1.f(x)=()x x 2221-+,(x ≥0),则f –1(x)=___________.2.n2n n 3n lim ⎪⎭⎫⎝⎛-∞→=_____________.3.z=1–2i ,则-+iz 2(z+1)=___________.4.已知:f(x)=x 2–4x+8,x ∈[1,a]的最大值为f(a),则a ∈_______.5.tan α=3x ,tan β=3–x ,若α–β=6π,则x=_________.6.{a,b}⊂{0,1,2,3,5},由ax+by=0确定直线和(x+2)2+(y –1)2=1相交的概率为______7.直线l 经过抛物线y 2=4(x –1)的焦点,且与准线的夹角为30o ,则l 的方程为______________________.8.△ABC 中,AB=2a ,BC=a ,则∠A 最大值为__________.9.理科:曲线ρ=cos θ+sin θ与ρcos θ=1的交点极坐标为_____________.文科:工程总时数为__________天,关键路__________________(不必写虚10.平面α内∠AOB=90o ,P ∉α,∠POA=∠POB=60o ,M 、N 是射线OP 上两点,MN=4,则线段MN 在α内射影长为____________.11.已知曲线C :x 2+(k –1)y 2–3ky+2k=0 (k ≠2). 给出下列命题:(1)k=1,C 是抛物线;(2)1<k<2,C 是焦点在y 轴上椭圆;(3)k>2,C 是焦点在x 轴上椭圆;(4)k<1,k ≠0,C 是双曲线. 其中真命题序号是_______________.12.命题:三角形中,顶点与对边中点连线所得三线段交于一点,且分线段长度比为2:1,类比可得四面体中,顶点与所对面的_________连线所得四线段交于一点,且分线段比为_________. 二、选择题:13.若{a n }的前n 项和S n =1+pa n (p ≠0,p ≠1),则{a n }是----------------------------( )A. 等差数列B. 等比数列C. 常数列D. 即非等差,又非等比数列 14.已知:P(t,m)为y=2x 1-图象上一个动点,过点P 作此曲线的切线,其斜率k是t的函数,则函数k=f(t)在(–1,1)上是--------------------------------------------( ) A. 增函数 B. (–1,0]上是增函数,[0,1)上是减函数C. 减函数D. (–1,0]上是减函数,[0,1)上是增函数 15.正方体ABCD −A 1B 1C 1D 1中,P 是面AA 1B 1B 上点,P 到平面A 1B 1C 1D 1距离是P到BC距离的2倍,则P轨迹所在曲线是--------------------------------------( )A. 直线B. 椭圆C. 抛物线D. 双曲线16.f(x)=x 的点称为函数f(x)的不动点,设f(x)、g(x)都有不动点,则下列陈述正确的是----------------------------------------------------------------------------------------( ) A. f(g(x))与f(x)具有相同数目的不动点 B. f(g(x))一定有不动点C. f(g(x))与g(x)具有相同数目的不动点D. f(g(x))可以无不动点三、解答题:17.已知:a>1. 解关于x 的不等式(x+a)(a –x )>0.18.在棱长为1的正方体ABCD −A 1B 1C 1D 1中,E 是A 1B 1中点. (1)求过A 、E 、C 1的截面面积;(2)B 到截面距离.19.已知数列{x n }、{y n },x n+1=n n x 1x 2-+,y n =1x 1x n n +-.(1){y n }是否为等差数列?说明理由;(2)S n 是{y n }前n 项和,T n 是⎭⎬⎫⎩⎨⎧+1x 1n 前n 项和,求nnn T S lim ∞+.20.某公司用300万元买回客船一艘,投入营运后,每月需开支燃油费、维修费、员工工资. 已知每月燃油费7000元,第n 个月的维修费和工资支出为600(n –1)+3000元,如果把购船费和所有支出费用平摊到的每一个月,叫做每月平均消耗,当平均消耗最低时,营运成本最低. (1)设月平均消耗y ,写出y 与n(月)的函数关系; (2)投入营运几个月时,营运成本最低?(3)若第一年纯收入50万,以后每年纯收入按5%递减,则多少年后可收回成本?21.已知△ABC 三个内角满足A 、B 、C 成等差,设x=cos2CA -,f(x)=cosB ⎪⎭⎫ ⎝⎛+C cos 1A cos 1. (1)求f(x)解析式及定义域;(2)讨论函数单调性,并证明;(3)求f(x)值域.22.(1)A(–2,0)、B(2,0),M 满足⋅=0. 求M 轨迹;(2)若(1)中的轨迹按向量(1,–1)平移后恰与x+ky –3=0相切,求k. (3)如图,l 过2222by a x +=1 (a>b>0)长轴顶点A 且与长轴垂直的直线,E 、F 是两焦点,P ∈l ,P 、A 不重合,若∠EPF=α,则有0<α≤arctan b c,类比此结论到2222b y a x -=1 (a>0,b>0),l 是过焦点F 且垂直x 轴的直线,A 、B 是两顶点,P ∈l ,P 、F 不重合,∠APB=α,求α取值范围.答案及错误率 一.填空题1.2log (1x x ≥ (0.4) 2.6e - (0.17) 3.-1+3i (0.06) 4. [3,)+∞ (0.03)5.0.5 (0.06) 6.33()107(0.72) 7.2)y x =- (0.17) 8.30︒ (0.09) 9.)4π(0.09)10. 0.11) 11.○1○2 (0.86) 12.重心,3:1 (0.42) 二.选择题13.B (0.06) 14.C (0.17) 15.B. (0.42) 16.D (0.25)三.解答题17.22(,)(,)a a a -∞-⋃- (0.17)18.(1)2(2)3(0.31) 19.(1)12n n y y +-= (2)lim 2nn ns T →∞=- (0.34)20.(1)3000.970.03y n n=++ (0.14) (2)n=100 (0.14) (3) 7年 (0.6) 21.(1)221(),(1)43222x f x x x x =<<<≤- (0.37)12(2)(减区间 (0.75)(3)1[2,)2∞⋃+∞(-,-) (0.86) 22. 224(1)4, 0.11 20,(0.22)(3)0arctan (0.63)3ax y k k bα+===<≤圆()()。
上海教育版-实验数学教材高三数学第13课时 练习九

第四单元两、三位数除以一位数第13课时练习九教学内容:教材第68页。
教学目标:1、使学生进一步掌握商中间和末尾有 0 的除法计算,提高除法的计算能力。
2、在解决问题过程中体验解题策略的多样性,进一步培养分析和推理的能力。
教学重难点:两、三位数除以一位数计算题不同类型的比较教学准备:多媒体课件教学过程:一、揭示课题这节课我们一起来练习商中间、末尾有 0 的除法。
(板书课题:练习九)二、基础知识训练1、完成练习九第 1 题先说说商是几位数,再指名板演,其余学生独立完成。
提醒学生思考:第 2 小题十位上为什么是 0?第 4 小题个位上为什么是 0?2、练习九第 2 题分组讨论比较。
第一组:这两题商里的 2 个 0 的位置有什么不同?为什么会不同?第二组:这两题的末尾为什么都是 0?为什么第 2 小题有余数?第三组:这两题商里的 0 有什么不同?为什么?三、解决问题1、完成练习九第 3 题读题,说说题意。
题中告诉我们什么?求什么?你准备怎么做?2、完成练习九第 4 题观察表格,你发现挖的天数和每天挖的米数之间有什么关系?(它们的乘积相等,挖的天数越多,每天挖的米数就越多,挖的天数越少,每天挖的米数就越多。
)我作好了到日本本土作战的准备!陶世齐和上面两名抗战老兵相比,陶世齐的军龄时间最短,只有一年零三个月,如果单算但要以当初的目标和任务来说,他却是最远,也是最艰巨的:即要协同美国盟军一道,准备到日本本土作战,一举将这个战争狂人彻底消灭在他的老巢。
说到这里也许有人会问,陶世齐当年有何德何能,怎么会揽到这样一个特有份量的“瓷器”活?!欲知其中原委,这还得从陶世齐的身家说起。
陶家为东晋时期的著名诗人陶渊明的后裔,受先人“不为五斗米折腰”的思想影响,历代后人均不愿入朝为官,情愿务农经商。
至陶世齐的祖父起,陶家在安徽芜湖老家一直经营数家店铺。
正因家中家底殷实,陶世齐才得已出外求学,并先后在芜湖、南京的教会学校里就读,且在校成绩优异,能说较为流利的两国语言。
上海高三数学练习题推荐

上海高三数学练习题推荐在高三阶段,数学是考试科目中的重点之一,对学生来说,做大量的数学练习题是提高自己数学能力和应对考试的有效途径。
本文将推荐几道适合上海高三学生的数学练习题,旨在帮助学生巩固知识、提高解题能力。
一. 函数与方程1. 已知函数 f(x)=3x+2 和 g(x)=-2x^2+5x-1,求两函数的复合函数(f∘g)(x) = f(g(x))。
2. 解方程:2^(x+1) = 8^(log2x)。
二. 三角函数1. 求函数 y=sin(2x) + cos(3x) 的周期和最小正周期。
2. 已知三角形 ABC,其中∠A=30°,AB=AC。
若三角形 ABC 的外接圆半径 r=2,求 BC 的值。
三. 几何1. 已知线段 AB 的中点为 M,且 AM:MB = 1:2。
点 C 在线段 AB 上,且 AC:CB = 2:3。
连接线段 MC,若 MC:CC' = 1:2,求线段 BB':BA。
2. 如图所示,ABCD 是一个平行四边形,点 P、Q 分别在边 AD 和BC 上,且 PQ // AB。
若 PQ = 6 cm,AP = 3 cm,BP = 2 cm,求 CQ 的长度。
四. 概率与统计1. 甲、乙两个队进行篮球赛,已知甲队胜的概率为 0.6,乙队胜的概率为 0.4。
他们进行五局三胜制的比赛,求甲队获胜的概率。
2. 随机变量X 的概率密度函数如下,求该随机变量的期望值E(X)。
f(x) =1.5x, 0 < x < 1x-1, 1 ≤ x < 20, otherwise五. 解析几何1. 在平面直角坐标系中,求由点 A(2,-1) 和点 B(-3,4) 所确定直线的方程。
2. 已知直线 L1: 2x-3y+5=0 和直线 L2: 3x+y-2=0,求它们的交点坐标。
根据上述题目进行适量的练习,可以巩固相关知识点的理解,并提高解题能力。
希望同学们能够利用这些练习题,有针对性地进行练习,为高考取得优异成绩奠定坚实的数学基础。
高等数学c刷题教材推荐

高等数学c刷题教材推荐在高等数学C的学习中,刷题是不可或缺的环节。
通过刷题,我们可以巩固理论知识,提高解题能力,并为日后的应用问题打下坚实基础。
然而,在选择刷题教材时,我们常常会遇到困扰,不知道哪本书更适合自己。
本文将为大家推荐几本高等数学C的刷题教材,供大家参考选择。
1.《高等数学C题型归纳与解题技巧》这本教材是由高等教育出版社出版的,由中国人民大学数学学院教师编写。
该书从高等数学C的各个知识点出发,系统总结了历年高考和大学期间的各类题型,并提供了详细的解题思路和技巧。
该书内容丰富、涵盖广泛,适合用于基础知识的巩固和拓展。
同时,该书还提供了大量的例题和习题,供学生进行练习和巩固。
2.《高等数学C习题精选》这本教材由上海交通大学出版社出版,编写团队是该校数学系的优秀教师。
该书内容紧扣高等数学C的教学大纲,精选了大量习题,包括选择题、填空题、计算题等各种类型。
每道题目都有详细的解析和解题思路,方便学生理解和掌握解题方法。
此外,该书还提供了一些高难度的习题,挑战性强,适合有一定基础的同学进行辅导性学习。
3.《高等数学C典型例题详解》这本教材由清华大学出版社出版,编写团队是清华大学数学教研室的教师。
该书选取了许多高等数学C的典型例题,并对其进行了详细的讲解和解题思路分析。
该书注重培养学生的问题解决能力和思维方式,强调理论和实践的结合。
通过阅读该书,学生可以提高解题的灵活性和准确性,同时也能够对所学知识点有更深入的理解。
综上所述,以上推荐的三本高等数学C刷题教材都各具特色,适合不同层次的学生使用。
同学们可以根据自己的实际情况和学习需求选择适合自己的教材,结合课堂学习,刻苦努力,相信通过刷题学习,定能在高等数学C中取得优异成绩。
希望本文的推荐能够对大家的学习有所帮助。
上海市上海中学高三数学综合练习试卷(共九套)

上海市上海中学高三综合练习上海市上海中学高三综合练习(一)(数学)班级___________学号__________姓名_______________成绩_________________、编辑:苑娜娜一. 填空题1. 定义在R 上的奇函数f(x)以2为周期,则f(1) =___________. 2. 如果复数11++bii(b R ∈)的实部和虚部互为相反数,则b 等于_____________. 3.(理) 若nx )21(+展开式中含3x 项的系数等于含x 项的系数的8倍,则n =______.(文) 若x y x y ≥≥+≤⎧⎨⎪⎩⎪126,则目标函数z x y =+2的最小值为_______________.4.已知0<a ,则关于x 的不等式1|3|>+ax a的解集为__________________.5.点P 是椭圆2212516x y +=上一点,F 1、F 2是椭圆的两个焦点,且∆PF 1F 2的内切圆半径为1,当P 在第一象限内时,P 点的纵坐标为_____________.6.数列{a n }满足:a n =121 .3nn n n ⎧⎪⎪⎨⎪⎪⎩,为奇数,为偶数 ,它的前n 项和记为S n ,则∞→n lim S n =__________.7.某市为加强城市圈的建设,计划对周边如图所示的A 、B 、 C 、D 、E 、F 、G 、H 八个中小城市进行综合规划治理,第 一期工程拟从这八个中小城市中选取三个城市,但要求没 有任何两个城市相邻,则城市A 被选中的概率为________.8.若方程kx 2x 42-=-仅有一个实数根,则k 的取值范围是______________.9. 在△ABC 中,已知|AB|=2,22||1||2BC CA =,则△ABC 面积的最大值为___________. 10.如图为一几何体的的展开图,其中ABCD 是边长为6的正方形,SD=PD =6,CR=SC ,AQ=AP ,点S,D,A,Q 及P ,D,C,R 共线,沿图中虚线将它们折叠,使P ,Q ,R ,S 四点重合,则需要________个这样的几何体,就可以拼成一个棱长为12的正方体.11.若函数y=a x (a>1)和它的反函数的图像与函数y=x1的图像分别交于点A 、B ,若|AB|=22,则a 约等于_____________(精确到0.1).12.老师告诉学生小明说,“若O 为△ABC 所在平面上的任意一点,且有等式cos cos ()||||AB C AC BOP OA AB AC λ=++,则P 点的轨迹必过△ABC 的垂心”,小明进一步思考何时P 点的轨迹会通过△ABC 的外心,得到的条件等式应为OP =_______________________________.(用O,A,B,C 四个点所构成的向量和角A,B,C 的三角函数以及λ表示)二.选择题13.若函数y =cos2x 与y =sin(x +φ)在[0,π2]上的单调性相同,则φ的一个值为( )A. π6B. π4C. π3D. π2 14.在∆ABC 中,A=3π,BC=3,则∆ABC 的周长为 ( ) A.43sin(B+3π)+3 B. 43sin(B+6π)+3C.6sin(B+3π)+3D. 6sin(B+6π)+315.若点M(a,1b )和N(b,1c )都在直线l :x+y=1上,则点P(c,1a ),Q(1c,b)和l 的关系是( )A. P 和Q 都在l 上B. P 和Q 都不在l 上C. P 在l 上,Q 不在l 上D. P 不在l 上,Q 在l 上 16.数列{a n }满足:a 1=14,a 2=15,且a 1a 2+a 2a 3+…+a n a n+1=na 1a n+1对任何的正整数n 都成立,则1297111a a a +++的值为 ( ) A. 5032 B. 5044 C. 5048 D. 5050 三.解答题 1.已知函数),(23cos cos sin 3)(2R x R x x x x f ∈∈+-⋅=ωωωω的最小正周期为π,且当x =6π时,函数有最小值. (1)求f (x )的解析式;(2)作出f (x )在[0,π]范围内的大致图象.2.设虚数z 满足|2z+15|=3|z +10|.(1)计算|z|的值;(2)是否存在实数a ,使z aa z+∈R ?若存在,求出a 的值;若不存在,说明理由.3.如图所示,已知斜三棱柱ABC-A 1B 1C 1的各棱长均为2,侧棱与底面所成角为3π,且侧面ABB 1A 1垂直于底面. (1)判断B 1C 与C 1A 是否垂直,并证明你的结论; (2)求四棱锥B-ACC 1A 1的体积.4.在新的劳动合同法出台后,某公司实行了年薪制工资结构改革。
上海高三数学刷题练习册

上海高三数学刷题练习册一、选择题(每题5分,共20分)1. 已知函数\( f(x) = 2x^3 - 3x^2 + 5x - 1 \),求导后得到的函数是:A. \( 6x^2 - 6x + 5 \)B. \( 6x^2 - 6x + 4 \)C. \( 6x^2 + 6x + 5 \)D. \( 6x^3 - 6x^2 + 5 \)2. 若\( \sin A = \frac{3}{5} \),且\( A \)为锐角,求\( \cos A \)的值:A. \( \frac{4}{5} \)B. \( \frac{1}{5} \)C. \( -\frac{4}{5} \)D. \( -\frac{1}{5} \)3. 已知数列\( \{a_n\} \)的通项公式为\( a_n = 3n - 1 \),求第10项的值:A. 28B. 29C. 30D. 314. 一个圆的半径为5,求该圆的面积:A. 25πB. 50πC. 75πD. 100π二、填空题(每题4分,共16分)5. 若直线\( y = 3x + 2 \)与直线\( y = -2x + 6 \)平行,则它们的斜率之比为_________。
6. 已知\( \log_{10}100 = 2 \),求\( \log_{10}0.01 \)的值。
7. 一个直角三角形的两条直角边分别为3和4,求斜边的长度。
8. 若\( \cos x = \frac{\sqrt{3}}{2} \),且\( x \)在第一象限,求\( \sin x \)的值。
三、解答题(每题8分,共24分)9. 已知函数\( y = x^2 - 4x + 4 \),求该函数的顶点坐标。
10. 已知等差数列的首项为2,公差为3,求前10项的和。
11. 已知一个圆锥的底面半径为4,高为6,求圆锥的体积,若底面半径为\( r \),高为\( h \)。
四、证明题(每题10分,共20分)12. 证明:对于任意实数\( x \),不等式\( 1 + x + x^2 \geq 0 \)恒成立。
高等数学基础题库推荐教材

高等数学基础题库推荐教材高等数学作为大学数学系列课程的重要组成部分,对于培养学生的数学思维和分析解决问题的能力具有重要作用。
为了帮助学生更好地掌握和应用高等数学知识,选择一本合适的教材和题库是至关重要的。
本文将介绍几本优秀的高等数学基础题库推荐教材,供大家参考选择。
第一本推荐的教材是《高等数学基础习题精选》。
该教材由国内知名高校数学系教师编写,结合教学实践经验,针对高等数学基础知识点,精选了大量的习题。
教材内容全面、系统,题目涵盖了数学分析、微积分、线性代数等多个领域。
而且,每个知识点都有一定数量的习题供学生练习,有助于巩固和加深对知识点的理解。
此外,教材还附有详细的解答和解题思路,方便学生自学和复习。
第二本推荐的教材是《高等数学基础习题大全》。
这本教材按照高等数学课程的知识点进行整理,将难度逐渐升级。
教材中的习题设计丰富多样,既包括基础练习题,也包括拓展思考题和应用题。
同时,教材中还穿插了一些数学定理和推导过程的详细解析,有助于学生理解和掌握数学概念。
此外,教材还根据习题的难度设置了不同的分值,有助于学生有针对性地进行练习和复习。
第三本推荐的教材是《高等数学基础题库与解析》。
这本教材以完整的高等数学知识体系为基础,选取了一定数量的经典习题进行解析。
教材中的习题设计精巧,既考察基本的计算能力,又注重培养学生的分析和解决问题的能力。
每个习题均附有详细的解题思路和解析过程,给出了一种解题思路和方法,方便学生学习和参考。
此外,教材还根据各个知识点的重要程度进行了标注,有助于学生分清重点和难点,有针对性地进行复习和强化。
除了以上介绍的几本教材外,还有许多其他优秀的高等数学基础题库推荐教材可供选择。
在选择教材时,学生可以根据自身的学习需求和实际情况进行综合考虑。
同时,也建议学生多做题、多思考,通过反复练习和思考来巩固和加深对高等数学知识的理解。
希望大家能够选择合适的教材,提高自己的高等数学水平。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
A 第14章 空间直线与平面
1. (册P
2. 2)三个平面可以把空间分割成__________________个部分.
2. (册P7. 1)“直线l 垂直于平面α内的无数条直线”是“l α⊥”的___________条件.
3. (册P8. 7)已知△ABC ,点P 是平面△ABC 外一点,点O 是点P 在平面ABC 上的射影,且点O 在△ABC 内.
(1)若点P 到△ABC 的三个顶点的距离相等,则点O 一定是△ABC 的_______心; (2)若点P 到△ABC 的三边所在直线的距离相等,则点O 一定是△ABC 的_______心;
(3)若PA BC ⊥,PB AC ⊥,PC AB ⊥,则点O 一定是△
ABC 的_______心.
4. (册P10. 2)(理科)已知P 是二面角AB αβ--PC α⊥,垂足为C ,PD β⊥,垂足为D ,且3PC =,PD =60CPD ∠=.
(1)求二面角AB αβ--的大小; (2)求CD 的长.
5. (册P21. 8)(理科)如图,已知二面角l αβ--的两个面内各
有一点A 、B ,A 、B 在直线l 的射影分别为点C 、D ,3AC BD ==,而4CD =,5AB =,求二面角l αβ--的大小.
第15章 简单几何体
6. (本P29例6)如图,在正方体1111ABCD A B C D -中,点P 和Q 位于平面11BB C C 上(PQ 与BC 不平行),点R 位于棱11A B 上,作出由P 、Q 、R 三点确定的平面截正方体所得的截面.
7. (本P30. 2)如图,在正方体1111ABCD A B C D -中,E 、F 、H 分别是棱11C D 、1CC 、
AB 上的点,画出过点E 、F 、H 的正方体的截面.
8. (册P25. 2)从一个底面半径和高都是R 的圆柱中,挖去一个以圆柱的上底为底、下底面的中心为顶点的圆锥,得到一个几何体. 如果用一个与圆柱下底面距离等于d 并且平行
于底面的平面去截这个几何体,求截面面积.
9. (册P29. 2)已知正六棱柱最长的一条对角线长为13厘米,侧面积为180平方厘米,求这个棱柱的体积.
10. (册P31. 1)维度为α的纬度圈上有甲乙两地,它们的纬度圈上的弧长等于πcos R α(R 是地球的半径),求甲乙两地的球面距离.
11. (册P32. 2)现有以下三个命题:①底面是平行四边形的四棱柱是平行六面体;②底面是矩形的平行六面体是长方体;③直四棱柱是直平行六面体. 其中真命题的序号是_______. 12. (册P32. 3)如果一个三棱锥的底面是直角三角形,那么这个三棱锥的三个侧面( ) (A )都不是直角三角形 (B )至多只能有一个是直角三角形 (C )至多只能有两个是直角三角形 (D )可能都是直角三角形
13. (册P35. 1)已知长方体1111ABCD A B C D -的高为h ,底面积为P ,对角面11BB D D 的面积为Q ,求它的侧面积.
14. (册P36. 4)设AB 是球O 的直径,50AB =,1O 、2O 是AB 上的两点,平面α、β分别通过点1O 、2O ,且垂直于AB ,截得圆1O 、圆2O ,当圆1O 、圆2O 的面积分别为49π、
400π时,求1O 、2O 两点的距离.
第16章 排列组合与二项式定理
15. (本P50例3)540的不同正约数共有多少个?
16. (本P55例4)求证:11P P P m m m n n n m -++=. 17. (本P55例5)解方程:4321P 140P n n +=.
18. (本P55. 2)1!2!3!100!++++的个位数为__________.
19. (本P60例4)如果从7名运动员中选4名运动员组成接力队,参加4100⨯接力赛,那么甲乙两人都不跑中间两棒的安排方法有多少种?
20. (本P61例6)将a 、b 、c 、d 、e 、f 六个不同元素排成一列,其中a 不排在首位,b 不排在末位,有几种排法?
21. (本P62. 3)A 、B 、C 、D 、E 五人站成一排,如果B 必须站在A 的右边(A 、B 可以不相邻),那么共有多少种不同的排法?
22. (本P64例2)求证:1
11C C 1
m
m n n m n +++=
+. 23. (本P65. 3)解不等式:46
C C n n >.
24. (本P67. 3)求证:122C C 2C C m m m m n n n n --+=++. 25. (本P67. 4)解方程:221818
C C x x +=. 26. (本P71例3)求12
(1)a +的二项展开式中倒数第5项.
27. (本P73例6
)已知n
的二项展开式中,前三项系数成等差数列,求二项展
开式中的所有有理项.
28. (本P74. 3)求55
55被8除所得的余数.
29. (本P75例11)利用二项式定理证明:2
21n n n >++(5n ≥,n ∈N *).
30. (本P76. 4)求证:024
1C C C C 2n n n n n n -+++
+=(n 是偶数).
31. (册P38. 2)要把4封信投入3个信箱,共有多少种不同的投法?(允许将信全部或部分投入某一个信箱)
32. (册P40. 8)已知10P 1095m
=⨯⨯
⨯,求正整数m 的值.
33. (册P42. 3)化简:
123
1
2!3!4!
!
n n -++++
. (n ∈N *,2n ≥) 34. (册P42. 5)求证:1
2
3
1
1231P 2P 3P P P 1n n n n n +++++
+=-. (n ∈N *)
35. (册P43. 3)将8个相同的小球放入编号为1、2、3的三个盒子内,要求每个盒子的球数不小于它的编号数,共有多少种不同的放法?
36. (册P48. 5)在9
(32)x y -的展开式中,求二项式系数的和以及各项系数的和.
37. (册P49. 9)求和:1231C 3C 9C 3C n n
n n n n -+++
+.
38. (册P49. 10)已知n 为大于1的自然数,证明:112n
n ⎛⎫
+> ⎪⎝⎭
.
(册P49. 11)在23n
x x ⎛
⎫- ⎪⎝⎭的二项展开式中,有且只有第五项的二项式系数最大,求
012
111C C C (1)C 24
2
n
n
n
n n n n -+-+-. 39. (册P49. 1)求和:024
98100100100100100100C C C C C -+-
-+.
40. (册P50. 3)在(13)n
x +的二项展开式中,末三项的二项式系数之和等于631. (1)求二项展开式中二项式系数最大的项是第几项; (2)求二项展开式中系数最大的项.
41. (册P50. 4)求77
7715-除以19的余数. 42. (册P50. 5)用两种方法证明:63
2123n n --+能被11整除.
43. (册P50. 6)已知32(1)1n
n
x x ax bx cx +=+
++++(n ∈N *),且:3:1a b =,求
c 的值.
44. (册P50. 1(4))用数字0、1、2、3、4、5可组成没有重复数字的六位数,其中数字2、4排在相邻数位上,满足条件的六位数共有___________个.
45. (册P52. 1)6个人排成一列,其中甲乙两人之间至少有两个人的不同排法种数是___.
第17章 概率论初步
46. (本P90例7改编为2011年高考试题)求随机抽取10个同学中至少有两个同学在同一个月份出生的概率. (精确到0.0001)
47. (册P54. 4)某城镇共有10000辆自行车,牌照编号从00001到10000. 求在此城镇中偶然遇到的一辆自行车,其牌照号码中有数字8的概率.
48. (册P56. 1)将n 间房分给n 个人,每个人都以相等的可能性进入每一间房间,而且每间房间里的人数没有限制,求不出现空房的概率.
49. (册P56. 2)把10本书随机地排在书架上,求其中指定的3本书排在一起的概率. 50. (册P56. 3)某人有5把钥匙,但只有一把能打开门,他每次取一把钥匙尝试开门,求试到第3把钥匙时才打开门的概率.
第18章 基本统计方法
51. (册P61. 2)某班级有40名同学参加打靶训练,他们的成绩如下表所示(单位:环):
求该班同学的成绩2σ区间估计. (精确到0.01)
高三总复习题
52. (册P71. 13)已知
567
117C C 10C n n n -=,n ∈N *,求8C n
. 53. (册P74. 5)一个球受热膨胀. 如果它的表面积增加21%,那么这个球的半径增加多少?
54. (册P74. 6)求383321C C n n n n -++(n ∈N *)的值.
55. (册P75. 8)以一个正方体的顶点为顶点能组成多少个三棱锥? 56. (册P75. 10)已知lg (1)x
n x
+的二项展开式中,末三项的二项式系数的和为22,二项
式系数最大的项为20000,求实数x 的值.
(注:文档可能无法思考全面,请浏览后下载,供参考。
可复制、编制,期待你的好评与关注!)。
