第六章简单超静定问题习题测验选解
第六章简单的超静定问题

第六章简单的超静定问题知识要点1.超静定问题的概念(1)静定问题结构或结构的约束反力或内力均能通过静力学平衡方程求解的问题。
(2)超静定问题结构或构件的约束反力或内力不能仅凭静力学平衡方程全部求解的问题。
(3)超静定次数未知力(约束反力或内力)数超过独立的静力平衡方程书的数目。
(4)多余约束力超静定问题中,多余维持静力平衡所必需的约束(支座或杆件)。
(5)多余未知力与多余(支座或杆件)相应的支座反力或内力。
(6)基本静定系在求解静定结构时,解除多余约束,并代之以多余未知力,从而得到一个作用有荷载和多余未知力的静定结构,称之为原超静定结构的基本体静定系。
2.静不定问题的解题步骤(1) 静力平衡条件——利用静力学平衡条件,列出平衡方程。
(2) 变形相容条件——根据结构或杆间变形后应保持连续的变形相容条件,作出位移图,由位移图的几何关系列出变形间的关系方程。
(3) 物理关系——应用胡克定律列出力与变形间的关系方程。
(4) 将物理关系代入变形相容条件,得补充方程 。
补充方程和静力平衡方程,二者方程数之和正好等于未知数的个数,联立平衡方程和补充方程,求解全部未知数。
习题详解6-1 试作题6-1图(a )所示等直杆的轴力图。
解 解除题6-1图(a )所示等直杆的约束,代之以约束反力,作受力图,如题6-1图(b )所示。
由静力学平衡条件,03,0=-+=∑F F F FB A Y和变形协调条件0=∆+∆+∆DB CD AC 并将()EAa F EA a F F EA a F B DB A CD A AC -=∆-=∆=∆,22,代入式②,可得 联立式①,③,解得45,47F F F F B A == 轴力如图6-1图(c )所示6-2 题6-2图(a )所示支架承受荷载F=10 kN,1,2,3各杆由同一材料制成,其横截面面积分别为232221200,150,100mm A mm A mm A ===。
试求各杆的轴力。
材料力学第六章简单的超静定问题

l1 l2 y AA3 A3 A4 sin 30 tan 30 2 1.039 3.039mm
A
A A4
AA x2 y2 0.6 2 3.039 2 3.1mm
例2
图所示结构,刚性横梁AB由斜杆CD吊在水 平位置上,斜杆CD的抗拉刚度为EA,B点 处受荷载F作用,试求B点的位移δB。
§6-1 超静定问题
静定结构:
约束反力 可由静力平 衡方程全部 求得
超静定结构:结构的强度和刚度均得到提高 约束反力不能全 部由平衡方程求得 超静定次数: 约束反力多于 独立平衡方程的数
独立平衡方程数: 平面任意力系: 3个平衡方程 平面共点力系:
2个平衡方程
平面平行力系:2个平衡方程 共线力系:1个平衡方程
3
B
联立①②③,解得:
D
1 C 2 30 30 3
A
y
A
3FN1 2FN 2 3FN 3
FN1 FN 3 2F
F
FN 1 FN 2 FN 3
y
A
x
FN 3 2FN1 2FN 2
2 FN1 2 F 25.4kN 3 1 127MPa(拉)
FN 1 FN 2 FN 3
y
A
列出平衡方程: FN 1 cos 30 0 FN 2 FN 3 cos 30 0 Fx 0
Fy 0
FN1 sin 30 0 FN 3 sin 30 0 F
FN1 FN 3 2F
x 即:
3FN1 2FN 2 3FN 3
1 2
EA
2000
EA N1 =
6000
《材料力学》第6章-简单超静定问题-习题解
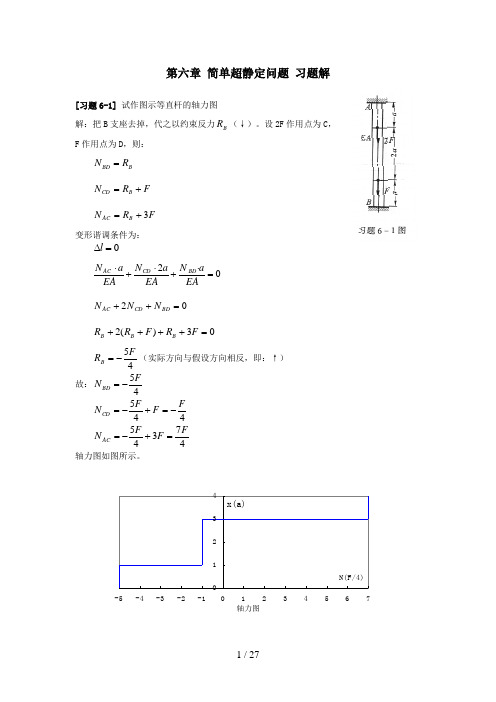
轴力图1234-5-4-3-2-11234567N(F/4)x(a)第六章 简单超静定问题 习题解[习题6-1] 试作图示等直杆的轴力图解:把B 支座去掉,代之以约束反力B R (↓)。
设2F 作用点为C , F 作用点为D ,则:B BD R N = F R N B CD += F R N B AC 3+=变形谐调条件为:0=∆l02=⋅+⋅+⋅EA aN EA a N EA a N BD CD AC 02=++BD CD AC N N N03)(2=++++F R F R R B B B45FR B -=(实际方向与假设方向相反,即:↑) 故:45FN BD-= 445F F F N CD -=+-=47345FF F N AC=+-= 轴力图如图所示。
[习题6-2] 图示支架承受荷载kN F 10=,1,2,3各杆由同一种材料制成,其横截面面积分别为21100mm A =,22150mm A =,23200mm A =。
试求各杆的轴力。
解:以节点A 为研究对象,其受力图如图所示。
∑=0X030cos 30cos 01032=-+-N N N0332132=-+-N N N 0332132=+-N N N (1)∑=0Y030sin 30sin 0103=-+F N N2013=+N N (2)变形谐调条件:设A 节点的水平位移为x δ,竖向位移为y δ,则由变形协调图(b )可知:00130cos 30sin x y l δδ+=∆x l δ=∆200330cos 30sin x y l δδ-=∆03130cos 2x l l δ=∆-∆2313l l l ∆=∆-∆设l l l ==31,则l l 232=223311233EA l N EA lN EA l N ⋅⋅=- 22331123A N A N A N =- 15023200100231⨯=-N N N23122N N N =-21322N N N -= (3)(1)、(2)、(3)联立解得:kN N 45.81=;kN N 68.22=;kN N 54.111=(方向如图所示,为压力,故应写作:kN N 54.111-=)。
材料力学-第六章 简单的超静定问题

变形协调条件:
l1 l 3 cos
F N1
F N3
F N2
l3
l1
A
A
l2
例2.图示AB为刚性梁,1、2两杆的抗拉(压)
刚度均为EA,制造时1杆比原长l短,将1杆装
到横梁后,求两杆内力。
解: 装配后各杆变形 1杆伸长 l1 2杆缩短 l 2 变形协调条件
A
1
l1
4、联解方程
FN 1 F E3 A3 2 cos 2 E1 A 1 cos
FN 3
F E1 A 3 1 1 2 cos E3 A3
●装配应力的计算
装配应力:超静定结构中由于加工误差, 装 配产生的应力。 平衡方程:
FN 1 FN 2
1
3 2
A
l
FN 3 ( FN1 FN 2 ) cos
2、AC和BC材料相同,面积不同,外力作用在 连接界面处,在外力不变的情况下,要使AC上 轴力增加,错误的方法有( )。 A、 增加AC的横截面积 B、 减小BC的横截面积 C、 增加AC的长度 D、 增加BC的长度
A l1 C F B l2
3、AB为等截面杆,横截面面积为A,外力F作 用在中间,则AC和BC上应力分别( )。
2
l 2
B
2( l1 ) l 2
解: 分析AB
A
aF 1 2aF 2 0
F1l 物理方程 l1 EA 变形协调条件
FA
F1
F2
B
F2 l l 2 (缩短) EA
2( l1 ) l 2
4EA 2EA F1 (拉力) F2 (压力) 5l 5l
材料力学土木类第六章简单的超静定问题

第6章 简单的超静定问题
静定结构: 仅靠静力平衡方程就可以求出结构的约束反力或内力
超静定结构(静不定结构): 静力学平衡方程不能求解 超静定结构的未知力的数目多于独立的平衡方程的数目;两者的差值称为超静定的次数
分析:画出受力及变形简图
写出独立平衡方程
一次超静定问题。
l
变形协调条件:原杆两端各自与刚性板固结在一起,故内、外杆的扭转变形相同。即变形协调条件为
代入物理关系(胡克定理),与平衡方程联立,即可求得Ma和Mb。
并可进一步求得杆中切应力如图(内、外两杆材料不同),一般在两杆交界处的切应力是不同的。
按叠加原理:
BB、BM分别为MB、Me引起的在杆端B的扭转角。
线弹性时,物理关系(胡克定理)为
代入上式可解得
MA可平衡方程求得 。
例 图示一长为l 的组合杆,由不同材料的实心圆截面杆和空心圆截面杆套在一起而组成,内、外两杆均在线弹性范围内工作,其扭转刚度分别为GaIpa和GbIpb。当组合杆的两端面各自固结于刚性板上,并在刚性板处受一对扭转力偶矩Me作用时,试求分别作用在内、外杆上的扭转力偶矩。
根据分离体的平衡条件,建立独立的平衡方程;
建立变形协调条件,求补充方程
利用胡克定律,得到补充方程;
联立求解
归纳起来,求解超静定问题的步骤是:
例 一平行杆系,三杆的横截面面积、长度和弹性模量均分别相同,用A、l、E 表示。设AC为一刚性横梁,试求在荷载F 作用下各杆的轴力
解: (1)受力分析--平衡方程
例 设l,2,3杆用铰连接如图,1、2两杆的长度、横截面面积和材料均相同,即l1=l2=l,A1=A2 =A , E1= E2=E;3杆长度为l3 ,横截面面积为A3,弹性模量为E3 ,试求各杆的轴力。
简单的超静定问题

M A Me M B 0
Me MB
A
C
B
2、变形协调方程
B 0
即
BM BM 0
e B
Me
MB
A
C
B
3、补充方程
BM
e
M e a GI p
BM
BM Bl GI p NhomakorabeaM e a M Bl 0 GI p GI p
M ea MB l
4、联立解得
3、物理方程
FN 1l l1 EA FN 3 l l 3 EA FN 2 l l 2 EA
得
FN 1 FN 2 FN 3
F 12 F 3
C′
补充方程 FN 1 FN 3 2FN 2
7F 12
例题3:如图所示结构,杆①、②的刚度为EA,梁BD 为刚体,载荷F=50kN,许用应力[s]160MPa。试确 定各杆的横截面积。 解: 1、确定各杆内力 取横梁为研究对象 平衡方程
FB aEAT
由平衡方程得 FA FB aEAT
例题5:如图所示结构,三杆的刚度均为EA,杆③的长 度比设计长度l短了d。试求装配后各杆的轴力。
A
D
① ③ a a C′ C l2 ②
B
解:对称结构,内力对称 变形协调方程
l1 d l 3 cos a
l
d
l3 l1
lt a1 T l1 a 2 T l 2
A
l1
C
l2
B
约束力产生的变形
l FB FB l1 F l B2 E1 A1 E2 A2
lt
FB
变形协调方程
第六章简单超静定问题共68页

Δ1lΔ2lF EN 1A l11 1E1A F1N cl1oαs
l3
FN3l E3 A3
3
2
1
A
Δ1lΔ2lF EN 1A l11 1E1A F1N cl1oαs
l1 l3
A2 A1
由变形协调方程和物理方程,可得到补充方程。
FN1l FN3l cos E1A1cos E3A3
FN3
FN1
E3A3
超静定次数 ——未知力个数与独立平衡方程数 之差 多余约束 —— 保持结构静定多余的约束
B
D
A
F
B
BC
D
A
D
F
A F
二、求解超静定问题的基本方法
方法1:寻找补充方程法(适用于求解拉压超
静定) 因为未知力个数超过了独立的平衡方程数,必须寻 找补充方程。 寻找补充方程的途径: 利用结构的变形条件
结构受力后变形不是任意的,必须满足以下条件:
例题
两端固支的直杆AB,长度为l ,抗拉刚度为EA, 热膨胀系数为α l。
求:温度升高 t 后0c杆内的应力。
A
B
l
解:
本问题为一次超静定 A
静平衡方程
l
Fx 0 FRAFRB
变形协调方程
l lT lF0
FRA A
物理方程
lT l lt
lF
FRAl EA
联解,得: F RA F RB EA l t
FAFBF
变形条件:
FA
BFBF B0A
A
A
A
物理条件:
a
B
F
Fa EA
F
F
F
B FB
FBl EA
第六章简单的超静定问题

Tl
GI p
补充方程:由几何方程和物理方程得;
解由平衡方程和补充方程组成的方程组。
[例]长为 L=2m 的圆杆受均布力偶 m=20Nm/m 的作用,如图,若杆
的内外径之比为 =0.8 ,外径 D=0.0226m ,G=80GPa,试求固端
反力偶。
解:①杆的受力图如图示, 这是一次超静定问题。 平衡方程为:
所有超静定结构,都是在静定结构上再加一个或几个约束,这些约束对于特定的 工程要求是必要的,但对于保证结构平衡却是多余的,故称为多余约束.
未知力个数与平衡方程数之差,称为超静定次数或静不定次数.
求解超静定问题,需要综合考察结构的平衡,变形协调和物理等三个方面.
超静定问题的方法步骤:
平衡方程; 几何方程——变形协调方程; 物理方程——胡克定律; 补充方程:由几何方程和物理方程得; 解由平衡方程和补充方程组成的方程组。
两杆的横截面面积分别为A钢=1000mm2,A铜=2000mm2。当F=200kN, 且温度升高20℃时,试求1、2杆内的应力。钢杆的弹性模量为E钢=210GPa 线膨胀系数αl钢=12.5×10-6 ℃-1;铜杆的弹性模量为E铜=100GPa,线膨胀 系数αl铜=16.5×10-6 ℃ -1;
1 F1
装配应力——预应力 温度应力
2.拉压超静定问题 一铰接结构如图示,在水平刚性横梁的B端作用有载荷F,
例题 6.1
垂直杆1,2的抗拉压刚度分别为E1A1,E2A2,若横梁AB的自重不计,求 两杆中的内力.
MA 0
1
A
C
2
L1
FN1a FN22a F2a 0
B
变形协调方程
a
a
F
试校核该梁的强度.
简单超静定问题—习题

6-1试作图示等直杆的轴力图。
解:平衡方程:0:3xA B FF F F =+=∑几何方程:00ABACD D AB C B l lll l ∆=∆+∆+∆==∆物理方程:(2)2(2)A AC AAC A C D A C D B ACB AC F l F al E A E AF F l F F al E AE AFlF a lE AE A++-∆==--∆==∆==-补充方程:(32)042A A A B B F a F F a F aE A E A FA E F F -+--==联立求解:7453344A B A A B B F F F F FF F F F F +=⎧⎨-=⎩⎧=⎪⎪⎨⎪=⎪⎩轴力图:如图所示。
F N7F /4 - +F /4 5F /46-2如图所示托架承受载荷10kN F =,等直杆1、2、3由同一材料制成,各杆横截面面积分别为21100mm A =、22150mm A =、23200mm A =。
试求1、2、3轴力。
解:平衡方程(如图所示):oo0:()cos3000:()cos600x D B C y D B F F F F F F F F ⎧=--=⎪⎨=+-=⎪⎩∑∑几何方程(如图所示):123o o13oo 2321o2;;cos(60)cos(90)cos(60)cos(60)1(ctg sin 2cos(60)1(ctg sin 2l l l l l l l l l l θθθθθθθθθ∆∆∆=∆=∆=∆--+⎧∆-==⎪∆⎪∆-∆⇒⎨∆+⎪==∆⎪⎩物理方程: 123oo123;;cos30cos30B C D F l F l F ll l l E A E A E A ∆=∆=∆=补充方程:1323222B D CB DC F F F F F F A A A -=⇒-=联立求解:8.4530kN 2.6795kN 11.5470kN(220(02)2B C B D C D D B C D B F F F F F F F F F F F F ⎧-=⎪+-=⇒⎨⎪-=⎧⎩=⎪=⎨⎪=⎩ll 1 D x6-3如图所示刚性板由四根截面形状、大小及杆长相同的支柱支撑。
06第六章 简单超静定问题(拉压)

补充内容:第六章简单超静定问题§6-1 超静定问题及其解法•一、静定和超静定问题静定问题:约束反力(轴力)可由静力平衡方程求得用平衡方程可求两杆轴力,为静定问题。
§6-2 拉、压超静定问题超静定度(次)数:平面平行力系:2个平衡方程共线力系:1个平衡方程§6-2 拉、压超静定问题拉压超静定结构的求解方法:5、求解方程组得αα3221cos 21cos +==F F F N N α33cos 21+=F F N 1l ∆2l ∆3l ∆§6-2 拉、压超静定问题§6-2 拉、压超静定问题§6-2 拉、压超静定问题o30BC o 30D123§6-2 拉、压超静定问题o30BC o 30D123F§6-2 拉、压超静定问题o30BC o 30D123F拉压超静定问题例 图示刚性梁AB受均布载荷作用,梁在A端铰支,在B点和C点由两根钢杆BD和CE支承。
已知钢杆的横截面面积ADB=200mm2, 例题 6.2 A =400mm2,其许用应力[σ]=170MPa,试校核钢杆的强度。
CE 1)列静力平衡方程 2)变形协调方程1.8L∑MA=0FNCE = 135kN − 3FNBDFNBD × 1.8l 5 3× F × l FNCE= 3∆L− 30kN / m × 3m × 1.56 + FNBD= 3m = 0 NCE 2 ×1m m 2 = × ∆LDB CE NCE 200 × 10 −FNBD × E F400 × 10 −6 m × E mD630kN / mBFNBD = 32.2kNFNCE = 38.4kNALC1m2mEDFBD32.2 × 103 N FNBD = = 161MPa2p [σ ] σ BD = 200mm ADBσ CEB′ FBD1m 2m30kN / mF = NCE ACE38.4 × 103 N = = 96MPa p [σ ] 400mm 2ABCE∆LCE∆ LDB例题 6.3 图示结构中的三角形板可视为刚性板。
材料力学-简单超静定

EA
C
F
B
FRA
b L
F
FRB
a L
F
L
例 图示一长为l 的组合杆,由不同材料的实心圆截
面杆和空心圆截面杆套在一起而组成,内、外两杆
均在线弹性范围内工作,其扭转刚度分别为GaIpa和 GbIpb。组合杆的左端为固定端,右端固结于刚性板 上。当在刚性板处受力偶矩Me作用时,试求分别作 用在内、外杆上的扭矩。
FN1 FN2 FN3 /2
(2) 几何方程
B 1
1
C1 2
A1 l
C 1 3
B
C
A C'
aa
l1l3 Δ FN1l FN3l Δ EA E3A3
二、温度应力
a
t
A
EA
C
L
a
t
A
EA
C
L
b B
b B
静定结构无温度应力
超静定结构 有温度应力
B=0
FB
tL F B L =0
l
A
A
A
F
F
FN3’
(1)
(2)
ΔA1 ΔA2
(F FN3)l
2E1A1 cos2
FN' 3l cos
E3 A3
FN3
12
F E1A1
cos3
E3A3
FN1
FN2
F
2cosE1AE13cAo32s
讨论:1. 刚度引起的受力分配原则 2. 基本结构的不同取法
例2-12 如图所示,三杆的横截面积、长度和弹性
a
b
FAFFB
F
材料力学第五版1课后习题答案

第二章轴向拉伸和压缩2-12-22-32-42-52-62-72-82-9下页2-1试求图示各杆1-1和2-2横截面上的轴力,并作轴力图。
(a)解:;;(b)解:;;(c)解:;。
(d)解:。
返回2-2 试求图示等直杆横截面1-1,2-2和3-3上的轴力,并作轴力图。
若横截面面积,试求各横截面上的应力。
解:返回2-3试求图示阶梯状直杆横截面1-1,2-2和3-3上的轴力,并作轴力图。
若横截面面积,,,并求各横截面上的应力。
解:返回2-4 图示一混合屋架结构的计算简图。
屋架的上弦用钢筋混凝土制成。
下面的拉杆和中间竖向撑杆用角钢构成,其截面均为两个75mm×8mm的等边角钢。
已知屋面承受集度为的竖直均布荷载。
试求拉杆AE和EG横截面上的应力。
解:=1)求内力取I-I分离体得(拉)取节点E为分离体,故(拉)2)求应力75×8等边角钢的面积A=11.5 cm2(拉)(拉)2-5(2-6)图示拉杆承受轴向拉力,杆的横截面面积。
如以表示斜截面与横截面的夹角,试求当,30,45,60,90时各斜截面上的正应力和切应力,并用图表示其方向。
解:2-6(2-8) 一木桩柱受力如图所示。
柱的横截面为边长200mm的正方形,材料可认为符合胡克定律,其弹性模量E=10 GPa。
如不计柱的自重,试求:(1)作轴力图;(2)各段柱横截面上的应力;(3)各段柱的纵向线应变;(4)柱的总变形。
解:(压)(压)返回2-7(2-9)一根直径、长的圆截面杆,承受轴向拉力,其伸长为。
试求杆横截面上的应力与材料的弹性模量E。
解:2-8(2-11)受轴向拉力F作用的箱形薄壁杆如图所示。
已知该杆材料的弹性常数为E,,试求C与D两点间的距离改变量。
解:横截面上的线应变相同因此返回2-9(2-12) 图示结构中,AB为水平放置的刚性杆,杆1,2,3材料相同,其弹性模量E=210GPa,已知,,,。
试求C点的水平位移和铅垂位移。
结构力学第六章题库

第六章 超静定结构计算——位移法一、判断题:1、判断下列结构用位移法计算时基本未知量的数目。
(1) (2) (3)(4) (5) (6)EIEIEIEI2E I EIEIEIEA EA ab E I =E I =E I =244422、位移法求解结构内力时如果P M 图为零,则自由项1P R 一定为零。
3、位移法未知量的数目与结构的超静定次数有关。
4、位移法的基本结构可以是静定的,也可以是超静定的。
5、位移法典型方程的物理意义反映了原结构的位移协调条件。
6、图示结构,当支座B 发生沉降∆时,支座B 处梁截面的转角大小为12./∆l ,方向为顺时针方向,设EI =常数。
7、图示梁之 EI =常数,当两端发生图示角位移时引起梁中点C 之竖直位移为(/)38l θ(向下)。
/2/22l l θθC8、图示梁之EI =常数,固定端A 发生顺时针方向之角位移θ,由此引起铰支端B 之转角(以顺时针方向为正)是-θ/2 。
9、用位移法可求得图示梁B 端的竖向位移为ql EI 324/。
ql二、计算题:10、用位移法计算图示结构并作M 图,各杆线刚度均为i ,各杆长均为 l 。
11、用位移法计算图示结构并作M 图,各杆长均为 l ,线刚度均为i 。
12、用位移法计算图示结构并作M 图,横梁刚度EA →∞,两柱线刚度 i 相同。
213、用位移法计算图示结构并作M 图。
E I =常数。
lll /2l /214、求对应的荷载集度q 。
图示结构横梁刚度无限大。
已知柱顶的水平位移为 ()5123/()EI →。
12m12m8mq15、用位移法计算图示结构并作M 图。
EI =常数。
lll16、用位移法计算图示结构,求出未知量,各杆EI 相同。
4m17、用位移法计算图示结构并作M 图,EI =常数。
18、用位移法计算图示结构并作M 图。
6m2m19、用位移法计算图示结构并作M 图。
qll20、用位移法计算图示结构并作M图。
第六章简单的超静定问题共51页

试校核该梁的强度.
列静力平衡方程
q
Fy 0
A
C
L2
FA
L2
FC
变形协调方程
B
FAF BF CqL 0
MA0
FB
L
qL2
FC 2FBL 2 0
5 qL 4
CqCF C0384 EI Z
FC L3 48 EI Z
7.5kNm0FC来自5 qL 8FB
3 16
qL
FA
3 16
qL
M 7.5kNm max
例题
6.2
点由两根钢杆BD和CE支承。已知钢杆的横截面面积ADB=200mm2, ACE=400mm2,其许用应力[σ]=170MPa,试校核钢杆的强度。
列静力平衡方程 MA0
FNCE 13k5 N 3FNBD
变形协调方程
D
F LN DB 31 C m L CE 3 E k / m 0 N 2 3 m F 0 N 1 1 . 5 0 B F6 m 0 1 Nm D .B 8 2 DlF N E 65 F4 3 NB m CE3 0 D 1 0 F N 0 6 0 m C 2 l E E
F
2m
列静力平衡方程 MA0
F12F2F
变形协调方程2 m F F L1 1 24 mm F 2 L24m
2m A
L2 2L1
4m
F2
1m 2
L1 EF11LA1! gTL1
F2L2 E2A2
L2tTEFL222LA222(EFt11LA1T! L2gTL1)
2 . 1 F 2 8 F 1 2 4 0 1 . 5 1 2 . 5 4 6 . 2 1 2 N 0
a
同济大学结构力学自测题(第六单元位移法解超静定结构)附答案
结构力学自测题(第六单元位移法解超静定结构)姓名 学号一、是 非 题(将 判 断 结 果 填 入 括 弧 :以 O 表 示 正 确 ,以 X 表 示 错 误 )1、图 示 结 构 ,ϕD 和 ∆B 为 位 移 法 基 本 未 知 量 ,有 M i l ql AB B =-682∆// 。
( )lDϕ2、图 a 中 Z 1, Z 2 为 位 移 法 的 基 本 未 知 量 , i = 常 数 , 图 b 是 Z Z 2110== , 时 的 弯 矩 图 , 即 M 2 图 。
( )a b l ( )( )3、图 示 超 静 定 结 构 , ϕD 为 D 点 转 角 (顺 时 针 为 正), 杆 长 均 为 l , i 为 常 数 。
此 结 构 可 写 出 位 移 法 方 程 111202i ql D ϕ+=/ 。
( )二、选 择 题 ( 将 选 中 答 案 的 字 母 填 入 括 弧 内 )1、位 移 法 中 ,将 铰 接 端 的 角 位 移 、滑 动 支 承 端 的 线 位 移 作 为 基 本 未 知 量 :A. 绝 对 不 可 ;B. 必 须;C. 可 以 ,但 不 必 ;D. 一 定 条 件 下 可 以 。
( )2、AB 杆 变 形 如 图 中 虚 线 所 示 , 则 A 端 的 杆 端 弯 矩 为 :A.M i i i l AB A B AB =--426ϕϕ∆/ ;B.M i i i l AB A B AB =++426ϕϕ∆/ ;C.M i i i l AB A B AB =-+-426ϕϕ∆/ ;D.M i i i l AB A B AB =--+426ϕϕ∆/。
( ) ∆A B3、图 示 连 续 梁 , 已 知 P , l ,ϕB , ϕC , 则 :A . M i i BCBC =+44ϕϕ ; B . M i i BC B C =+42ϕϕ ;C . M i Pl BC B =+48ϕ/ ;D . M i Pl BC B =-48ϕ/ 。
第6章简单的超静定问题详解

(3) 建立补充方程
FN1 RA
FN 2 RB
l1
FN1l1 E1 A1
l2
FN 2l2 E2 A2
RAl1 RBl2 0 —— 补充方程 E1A1 E2 A2
RA A P C
B RB
材料力学 任课教师:金晓勤 8
(4) 联立求解
将平衡方程与补充方程联立,求解,可得:
RA RB P
查表知40mm×40mm×4mm等边角钢 Ast 3.086cm2 故 Ast 4Ast 12.34cm2, AW 25 25 625cm2
代入数据,得 FW 0.717F Fst 0.283F
根据角钢许用应力,确定F
st
0.283F Ast
st
F 698kN
根据木柱许用应力,确定F
例: 若管道中,材料的线膨胀系数 12.5106 / C, E 200GPa,
温度升高 T 40C
则
T
RB A
E T
100MPa
材料力学 任课教师:金晓勤 14
2).装配应力
图示超静定杆系结构,中间杆加工 制作时短了Δ。已知1,3杆拉伸刚 度为E1A1 , 2杆为E2A2 ,试求三 杆在D点铰接在一起后各杆的内力。
超静定结构:约束反力不能由平衡方程求得 结构的强度和刚度均得到提高
超静定度(次)数: 约束反力多于独立 平衡方程的数
独立平衡方程数:
平面任意力系: 3个平衡方程
平面共点力系: 2个平衡方程
平面平行力系:2个平衡方程 共线力系:1个平衡方程
材料力学 任课教师:金晓勤 4
6.2 拉压超静定问题
例: 图示构件是由横截面 面积和材料都不相同的 两部分所组成的,在C截 面处受P力作用。试求杆 两端的约束反任课教师:金晓勤 12
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章简单的超静定问题习题选解
[6-5]图示刚性梁受均布荷载作用,梁在 A 端铰支,在B 点和C 点由两根钢杆 BD 和CE 支承。
已知钢杆BD 和CE 的横截面面积A 2
200mm 2和A 400mm 2 , 钢杆的
许用应力[]170MPa ,试校核该钢杆的强度。
[6-1]试作图示等直杆的轴力图 解:把A 支座去掉,代之以约束反力 R A (T)
N A C
R A N CD
R A 2F N BD R A 3F
变形协调条件为: N AC
a N CD 2 a N BD a
E A EA EA
N AC
2N CD N
BD 0
R A 2(R A 2F) R A 3F
7F
R
A
4
故:N AC R A 7F A 4
7F F N CD R A 2F 2F
4 4
7F 5F N BD
R A 3F
3F
4
4
I 0 轴力图如图所示
解:以AB 杆为研究对象,则:
M A 0
2 1.8l
30kN / m
习题6 5图
第六章简单的超静定问题习题选解
3
N1 1 N2 3 (30 3)—0
2
l2 3 l1
3 3凹
EA2 EA1
N2 1.8 3N1
200 400
N1 1.2N2 (2)
⑵代入(1)得:
1.2N2 3N2135
135
N2 32.143(kN)(拉力)
N1 1.2N2 1.2 32.143 38.571(kN) (压力)
按轴力正负号的规定,记作:
N138.571kN ; N232.143kN
强度校核:N2'
N1 3N2135 (1)
变形协调条件:
1
l2 3
/ 30kN / m
N i
A1 38571N
2
400mm
96.4275MPa [] 170MPa,符合强度条件
2 160.715MPa []仃oMPa ,符合强度条件
200mm 2
因此,钢杆符合强度条件,即安全
[6-15(a)]试求图示超静定梁的支反力。
解:把B 支座去掉,代之以约束反力 R B ,则变形协调方程为:
W B 0
W BM e W 冷
查附录IV ,得:
丫 0 得:R A
込(T)
4a
W BM
M e (2a)2
2EI
2M e a 2 EI
W R B
2
R B (2a) 6EI (3 2a 2
a)
8R B a 3 3EI 故, W BM
WR B
2M e a 2
EI
8R B a
3EI
R B
3M e 4a
(负号表示方向向下,即J)
N 2 A
么
习题6 15图
a
B
R
由 M A
0得:M A
—e
2a M e ,M A —(逆时针方向
4a 2a
转动)
[习题6-17]梁AB 因强度和刚度不足,用同一材料和同样截面的短梁
AC 加固,
如图所示。
试求:
(1) 二梁接触处的压力F C ;
(2) 加固后梁AB 的最大弯矩和B 点的挠度减小的百分数。
解: ( 1)求二梁接触处的压力F c
以AB 为研究对象,把C 处的圆柱垫去掉,代之以约束反力 F c (T);以
AC 为研究对象,作用在C 处的力为F c (J)。
F c 与F c 是一对作用与反作用力,
F C F c 。
受力如图所示。
AB 梁在C 处的挠度:
W
CF
F F
6EI (3I 2)
5FI 3 48EI
W c,AB W CF W CF c。
查附录IV 得:
习题6 17图
C
第六章简单的超静定问题习题选解
F C(2)2(3l l)F c l3
W cF C (3 )
c6EI 2 2 24EI
故5Fl3F c l3
故,W c,AB W CF W CF C
c 48 EI 24EI
AC梁在C处的挠度:
变形协调方程:
W C,AB
5Fl3
W C,AC
F c l3F c l3
48EI24 EI 24EI
5F F c F c
482424
5F2F c2F c
5F
F c 51(T)
4
(2)求加固后梁AB的最大弯矩和B点的挠度减小的百分数
①弯矩的变化情况
加固前:M C珂号
B M A Fl max
I
-2
FL
M
图W
C,AC
嗨)3
F c l
3EI 24EI
加固后: M C Fl 2
M max
M A Fl
5F 4
3Fl 8
A
1 2
1 2
3Fl
8
显然, AB 梁的最大弯矩 C M
图
F 2
Fl
减小:
1FI j 50% Fl
(负弯矩只表示AB 梁上侧受拉) ②B 点挠度的变化情况 加固前: W B Fl 3
3EI 加固后: W B
W CF
W CF C
CF C
l_
2
W CF Fl 3 3EI
F C (2)2 W CF C 6EI (3
F c l 3 24EI
CF
C
丄丄 2 2 EI
Feb
2EI ]
F c l 2 8EI
故,
W B
W CF W CF
C
CF
C
l_
2
5F 4 l 3
24EI
5F 4 8EI
l 2
5Fl 3 96EI
5Fl 2 32EI
Fl 3 5FI 3 5FI 2丨
3EI 96EI 32EI 2
39FI 3
192EI
B点挠度减小的百分数为:
3 3 3
FI 39 Fl 25FI
3EI 192 EI 192 EI 25
39% FI364 FI364
3EI 192 EI。
