中考全等三角形复习专题

合集下载

中考数学复习《全等三角形》专题(卷1)

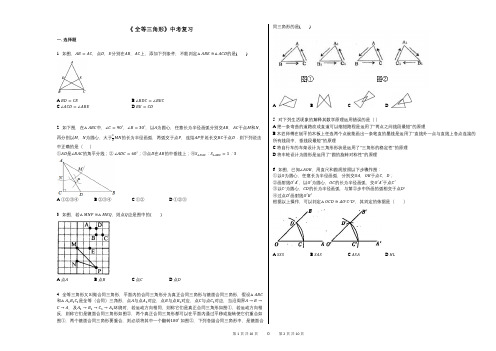
《全等三角形》中考复习一. 选择题1. 如图，AB=AC，点D，E分别在AB，AC上，添加下列条件，不能判定△ABE≅△ACD的是( )A.BD=CEB.∠BDC=∠BECC.∠ACD=∠ABED.BE=CD2. 如下图，在△ABC中，∠C=90∘，∠B=30∘，以A为圆心，任意长为半径画弧分别交AB，AC于点M和N，再分别以M，N 为圆心，大于12MN的长为半径画弧，两弧交于点P ，连结AP 并延长交BC于点D．则下列说法中正确的是（）①AD是∠BAC的角平分线；②∠ADC=60∘；③点D在AB的中垂线上；④S△DAC：S△ABC=1：3.A.①②③④B.②③④C.①②D.①②③3. 如图，若△MNP≅△MEQ，则点Q应是图中的()A.点AB.点BC.点CD.点D4. 全等三角形又叫做合同三角形，平面内的合同三角形分为真正合同三角形与镜面合同三角形，假设△ABC 和△A1B1C1是全等（合同）三角形，点A与点A1对应，点B与点B1对应，点C与点C1对应，当沿周界A→B→C→A，及A1→B1→C1→A1环绕时，若运动方向相同，则称它们是真正合同三角形如图①，若运动方向相反，则称它们是镜面合同三角形如图②，两个真正合同三角形都可以在平面内通过平移或旋转使它们重合如图①，两个镜面合同三角形要重合，则必须将其中一个翻转180∘如图②，下列各组合同三角形中，是镜面合同三角形的是( )A. B. C. D.5. 对下列生活现象的解释其数学原理运用错误的是（）A.把一条弯曲的道路改成直道可以缩短路程是运用了“两点之间线段最短”的原理B.木匠师傅在刨平的木板上任选两个点就能画出一条笔直的墨线是运用了“直线外一点与直线上各点连接的所有线段中，垂线段最短”的原理C.将自行车的车架设计为三角形形状是运用了“三角形的稳定性”的原理D.将车轮设计为圆形是运用了“圆的旋转对称性”的原理6. 如图，已知∠AOB，用直尺和圆规按照以下步骤作图：①以O为圆心，任意长为半径画弧，分别交OA，OB于点C，D；②画射线O′A′，以O′为圆心，OC的长为半径画弧，交O′A′于点C′③以C′为圆心，CD的长为半径画弧，与第②步中所画的弧相交于点D′④过点D′画射线O′B′根据以上操作，可以判定△OCD≅ΔO′C′D′，其判定的依据是（）A.SSSB.SASC.ASAD.HL7. 如图，在扇形OAB中，点C是弧AB上任意一点（不与点A，B重合），CD//OA交OB于点D，点I是△OCD 的内心，连结OI，BI，∠AOB=β，则∠OIB等于()A.180∘−βB.180∘−12β C.90∘+12β D.90∘+β8. 小明不慎将一块三角形的玻璃摔碎成如图所示的四块（即图中标有1，2，3，4的四块），你认为将其中的哪一块带去玻璃店，就能配一块与原来一样大小的三角形玻璃.应该带( )A.第1块B.第2块C.第3块D.第4块二. 填空题三角形具有稳定性，所以要使六边形木架不变形，至少要钉上________根木条．如图，在x、y轴上分别截取OA、OB，使OA=OB，再分别以点A、B 为圆心，以大于12AB的长度为半径画弧，两弧交于点C．若C的坐标为(3a,−a+8)，则a=________.如图，在菱形ABCD中，已知AB=4，∠ABC=60∘，∠EAF=60∘，点E在CB的延长线上，点F在DC的延长线上，有下列结论：①BE=CF；②∠EAB=∠CEF；③△ABE∼△EFC；④若∠BAE=15∘，则点F到BC的距离为2√3−2.正确序号________.如图，△ABC中，点A的坐标为(0, 1)，点C的坐标为(4, 3)，如果要使△ABD与△ABC全等，那么点D的坐标是________．三. 解答题如图，小明用五根宽度相同的木条拼成了一个五边形，已知AE//CD，∠A=12∠C，∠B=120∘.(1)∠D+∠E=________度；(2)求∠A的度数；(3)要使这个五边形木架保持现在的稳定状态，小明至少还需钉上________根相同宽度的木条．根据要求完成下列各题．(1)如图1，在∠AOB的内部有一点P．①过点P画直线PC//OA交OB于点C；②过点P画直线PD⊥OA，垂足为D．(2)如图2，AB⊥BF,CD⊥BF,∠1=∠2，试说明∠3=∠E在下面解答中填空．解：∵AB⊥BF,CD⊥BF（已知），∴∠ABF=∠________=90∘（________），∴AB//CD（________）∵∠1=∠2（已知），∴AB//EF（________），∴CD//EF（平行于同一条直线的两条直线互相平行），∴∠3=∠E（________）如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于点F，且AF= BD，连接BF．(1)线段BD与CD有何数量关系，为什么？(2)当△ABC满足什么条件时，四边形AFBD是矩形？请说明理由．(3)当△ABC满足________条件时，四边形AFBD是正方形？（直接写出结论，不用说明理由）一条大河两岸的A、B处分别立着高压线铁塔，如图所示．假设河的两岸平行，你在河的南岸，请利用现有的自然条件、皮尺和标杆，并结合你学过的全等三角形的知识，设计一个不过河便能测量河的宽度的好办法．（要求，画出示意图，并标出字母，结合图形简要叙述你的方案）参考答案与试题解析一. 选择题1.【答案】D【解析】欲使△ABE≅△ACD，已知AB＝AC，可根据全等三角形判定定理AAS、SAS、ASA添加条件，逐一证明即可．2.【答案】A【解析】①连接NP，MP，根据SSS定理可得△ANP≅△AMP，故可得出结论；②先根据三角形内角和定理求出∠CAB的度数，再由AD是∠BAC的平分线得出∠1=∠2=30∘，根据直角三角形的性质可知∠ADC=60∘；③根据∠1=∠B可知AD=BD，故可得出结论；④先根据直角三角形的性质得出∠2=30∘，CD=12AD，再由三角形的面积公式即可得出结论．3.【答案】D【解析】此题暂无解析4.【答案】B【解析】认真阅读题目，理解真正合同三角形和镜面合同三角形的定义，然后根据各自的定义或特点进行解答．5.【答案】B【解析】根据圆的有关定义、垂线段的性质、三角形的稳定性等知识结合生活中的实例确定正确的选项即可．6.【答案】A【解析】此题暂无解析7.【答案】B 【解析】此题暂无解析8.【答案】B【解析】本题应先假定选择哪块，再对应三角形全等判定的条件进行验证．二. 填空题【答案】3【解析】三角形具有稳定性，所以要使六边形木架不变形需把它分成三角形，即过六边形的一个顶点作对角线，有几条对角线，就至少要钉上几根木条．【答案】2【解析】此题暂无解析【答案】①②【解析】①只要证明△BAE≅△CAF即可判断；②根据等边三角形的性质以及三角形外角的性质即可判断；③根据相似三角形的判定方法即可判断；④求得点F到BC的距离即可判断．【答案】(4, −1)或(−1, 3)或(−1, −1)【解析】因为△ABD与△ABC有一条公共边AB，故本题应从点D在AB的上边、点D在AB的下边两种情况入手进行讨论，计算即可得出答案．三. 解答题【答案】180(2)五边形的内角和为(5−2)×180∘=540∘，由(1)可知，∠D+∠E=180∘，又∠B=120∘，∠A=12∠C.设∠A=x，则∠C=2x，∴∠A+∠B+∠C+∠D+∠E=540∘,即x+120∘+2x+180∘=540∘,解得x=80∘,∴∠A=80∘.2【解析】(1)根据平行线性质，两直线平行同旁内角互补即可得到180∘.先由AE//CD，根据平行线的性质得出∠E+∠D=180∘．再根据∠B=120∘，∠A=12∠C，设∠A=x∘，则∠C=2x∘．利用五边形的内角和为540∘列出方程x+120+2x+180=540，求解即可.根据五边形不具有稳定性，而三角形具有稳定性即可求解．【答案】解：（1）①如图，直线PC即为所求；②如图，直线PD即为所求；（2）解：∵AB⊥BF,CD⊥BF（已知），∴∠ABF=∠CDF=90∘（垂直的定义），∴AB//CD（同位角相等，两直线平行）∵∠1=∠2（已知），∴AB//EF（内错角相等，两直线平行），∴CD//EF（平行于同一条直线的两条直线互相平行），∴∠3=∠E（两直线平行，同位角相等）【解析】此题暂无解析【答案】解：(1)BD=CD．理由如下：依题意得AF // BC，∴∠AFE=∠DCE，∵E是AD的中点，∴AE=DE，在△AEF和△DEC中，{∠AFE=∠DCE，∠AEF=∠DEC，AE=DE，∴△AEF≅△DEC(AAS)，∴AF=CD，∵AF=BD，∴BD=CD；(2)当△ABC满足AB=AC时，四边形AFBD是矩形．理由如下：∵AF // BD，AF=BD，∴四边形AFBD是平行四边形，∵AB=AC，BD=CD，∴∠ADB=90∘，∴四边形AFBD是矩形．AB=AC，∠BAC=90∘【解析】（1）根据两直线平行，内错角相等求出∠AFE=∠DCE，然后利用“角角边”证明△AEF和△DEC全等，根据全等三角形对应边相等可得AF=CD，再利用等量代换即可得证；（2）先利用一组对边平行且相等的四边形是平行四边形证明四边形AFBD是平行四边形，再根据一个角是直角的平行四边形是矩形，可知∠ADB=90∘，由等腰三角形三线合一的性质可知必须是AB=AC．【答案】解：在河南岸AB的垂线BF上取两点C、E，使CE=BE，再定出BF的垂线CD，使A、E、D在同一条直线上，这时测得CD的长就是AB的长．如图所示：【解析】已知等边及垂直，在直角三角形中，可考虑AAS证明三角形全等，从而推出线段相等．。

中考数学考点专题复习三角形与全等三角形

剖析
先看一个事实，如图，将等腰△ABC 的底边 BC 延长线上的任一点和顶点 A 相连，所得的△DAB 和△DAC 无疑是不全等的，由此可知，有两边及其一边的对角对应相等的两个三角形(简称“边边角”)不一定全等．因此，在判定三角形全等时，一定要留心“边边角”，别上当哟．
正解证明：∵EB＝EC，∴∠3＝∠4.又∵∠1＝∠2，∴∠1＋∠3＝ ∠2＋∠4，即∠ABC＝∠ACB，∴AB＝AC.在△AEB和△AEC中， ∵EB＝EC，∠1＝∠2，AB＝AC，∴△AEB≌△AEC(SAS)， ∴∠BAE＝∠CAE
的长可能是下列哪个值( B )
A．11
B．5 C．2 D．1
(2)(2015·巴中)若 a，b，c 为三角形的三边，且 a，b 满足 a2－9＋(b－
2)2＝0，则第三边 c 的取值范围是 1＜c＜5
．
【点评】三角形三边关系性质的实质是“两点之间，线段最短”．根据三角形的三边关系，已知三角形的两边a，b，可确定三角形第三边长c的取值范围|a－b|＜c＜a＋b.
[对应训练] 1．(1)(2014·宜昌)已知三角形两边长分别为3和8，则该三角形第三边的长可能是( )B A．5 B．10 C．11 D．12
(2)(2014·淮安)若一个三角形三边长分别为2，3，x，则x的值可以为___4_．(只需填一个整数)
【例2】 (1)(2014·赤峰)如图，把一块含有30°角(∠A＝30°)的直角三角板ABC的直角顶点放在矩形桌面CDEF的一个顶点C处，桌面的另一个顶点F与三角板斜边相交于点F，如果∠1＝40°，那么 ∠AFE＝( ) D
A．40° B．50° C．60° D．70°
4．(2015·柳州)如图，下列条件中，不能证明△ABC≌△DCB 的是( D )

中考数学复习《全等三角形》专题训练-附带参考答案

中考数学复习《全等三角形》专题训练-附带参考答案一、选择题1．下列选项中表示两个全等的图形的是（）A．形状相同的两个图形B．周长相等的两个图形C．面积相等的两个图形D．能够完全重合的两个图形2．如图，点D、E分别在线段AB、AC上，BE、CD相交于点O，AE＝AD，则不一定能使△ABE≌△ACD的条件是（）A．AB＝AC B．∠B＝∠CC．∠AEB＝∠ADC D．CD＝BE3．如图是用直尺和圆规作已知角的平分线的示意图，则说明∠CAD=∠DAB的依据是（）A．SAS B．ASA C．AAS D．SSS4．如图△ABC≌△DEC，点A和点D是对应顶点，点B和点E是对应顶点，过点A作AF⊥CD，垂足为点F，若∠BCE=65°，则∠CAF的度数为（）A．25°B．30°C．35°D．65°5．如图EF=CF，BF=DF则下列结论不一定正确的是（）A．△BEF≌△DCF B．△ABC≌△ADEC．DC=AC D．AB=AD6．如图，OP平分∠MON，PA⊥ON于点A，点Q是射线OM上的一个动点，若PA=3，则PQ的最小值为（）A．2 B．3 C．4 D．57．如图，CD⊥AB，BE⊥AC，垂足分别为点D，点E，BE、CD相交于点O．∠1＝∠2，则图中全等三角形共有（）A．2对B．3对C．4对D．5对8．如图，AD 是△ABC中∠BAC的平分线，DE⊥AB于点E，△ABC的面积为12，DE =2，AB = 7，则 AC 的长是（）A．3 B．4 C．5 D．6二、填空题9．如图，∠ACD＝∠BCE，BC＝EC，要使△ABC≌△DEC，则可以添加的一个条件是．10．如图所示，在△ABC中，∠C=90°，AB=8，AD是△ABC的一条角平分线．若CD=2，则△ABD的面积为．11．如图，在Rt△ABC中，∠BAC＝90°，分别过点B，C作过点A的直线的垂线BD，若BD＝4cm，CE＝3cm则DE= cm．12．如图，把两根钢条AB，CD的中点连在一起做成卡钳，已知AC的长度是6cm，则工件内槽的宽BD是cm．13．如图，△ABC为等腰直角三角形AC=BC，若A(−3，0)，C(0，2)，则点B的坐标为.三、解答题14．如图所示，线段AC的垂直平分线交线段AB于点D，∠A=50°（1）求证：△ADE≌△CDE．（2）求∠BDC度数．15．如图，已知，EC＝AC，∠BCE＝∠DCA，∠A＝∠E.（1）求证：BC＝DC；（2）若∠A ＝25°，∠D ＝15°，求∠ACB 的度数.16．如图，AB ＝AC ，AD ＝AE ，∠BAC ＝∠DAE.（1）求证：△ABD ≌△ACE ；（2）若∠1＝25°，∠2＝30°，求∠3的度数.17．如图，在ABC 中90C ∠=︒，BD 是ABC ∠的平分线，DE AB ⊥于点E ，点F 在BC 上，连接DF ，且AD DF =． (1)求证：CF AE =；(2)若3AE =，BF=4，求AB 的长．18．如图，∠BAD ＝∠CAE ＝90°，AB ＝AD ，AE ＝AC ，AF ⊥CB ，垂足为F ．(1)求证：△ABC ≌△ADE ；(2)求∠FAE 的度数；(3)求证：CD ＝2BF+DE ．1．D2．D3．D4．A5．C6．B7．C8．C9．AC ＝DC （答案不唯一）10．811．712．613．(2，-1)14．（1）证明：∵DE 是线段AC 的垂直平分线 ∴DA=DC ，AE=CE在△ADE 与△CDE 中：DA=DCAE=CEDE=DE∴△ADE ≌△CDE （SSS ）；（2）解：∵△ADE ≌△CDE ．∴∠DCA=∠A=50°∴∠BDC=∠DCA+∠A=100°15．（1）证明：∵∠BCE ＝∠DCA∴∠BCE +∠ACE ＝∠DCA +∠ECA即∠BCA ＝∠DCE .在△BCA 和△DCE 中{∠BCA =∠DCE AC =EC ∠A =∠E∴△BCA ≌△DCE （ASA ）（2）解：∵△BCA ≌△DCE∴∠B ＝∠D ＝15°.∵∠A ＝25°∴∠ACB ＝180°−∠A −∠B ＝140°.16．（1）证明：∵∠BAC ＝∠DAE∴∠BAC ﹣∠DAC ＝∠DAE ﹣∠DAC∴∠1＝∠EAC在△ABD 和△ACE 中{AB =AC ∠1=∠EAC AD =AE∴△ABD ≌△ACE （SAS ）（2）解：∵△ABD ≌△ACE∴∠ABD ＝∠2＝30°∵∠1＝25°∴∠3＝∠1+∠ABD ＝25°+30°＝55°.17．（1）证明：（1）∵90C ∠=︒∴DC BC ⊥又∵BD 是ABC ∠的平分线DE AB ⊥∴DE DC = 90AED ∠=︒在Rt AED △和Rt FCD △中∵AD DFDE DC =⎧⎨=⎩∴()Rt Rt AED FCD HL ≌△△∴CF AE =．（2）解：由（1）可得3CF AE ==∴437BC BF CF =+=+=∵DE AB ⊥∴90DEB ∠=︒∴DEB C ∠=∠∵BD 是ABC ∠的平分线∴ABD CBD ∠=∠在BED 和BCD △中∵DEB C EBD CBD BD BD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()BED BCD AAS ≌△△ ∴7BE BC ==∴7310AB BE AE =+=+=∴AB 的长为10．18．（1）证明：∵90BAD CAE ∠=∠=︒∴90BAC CAD ∠+∠=︒ 90CAD DAE ∠+∠=︒ ∴BAC DAE ∠=∠在△BAC 和△DAE 中∵AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩∴()BAC DAE SAS ≌△△；（2）解：∵90CAE ∠=︒，AC=AE∴45E ∠=︒由（1）知BAC DAE ≌△△∴45BCA E ∠=∠=︒∵AF BC ⊥∴90CFA ∠=︒∴45CAF ∠=︒∴4590135FAE FAC CAE ∠=∠+∠=︒+︒=︒；（3）证明：延长BF 到G ，使得FG FB = ∵AF BG ⊥∴90AFG AFB ∠=∠=︒在△AFB 和△AFG 中∴BF GF AFB AFG AF AF =⎧⎪∠=∠⎨⎪=⎩∴()AFB AFG SAS ≌△△∴AB AG = ABF G ∠=∠∵BAC DAE ≌△△∴AB AD = CBA EDA ∠=∠ CB=ED ∴AG AD = ABF CDA ∠=∠∴CGA CDA ∠=∠∵45GCA DCA ∠=∠=︒∴在△CGA 和△CDA 中GCA DCA CGA CDA AG AD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()CGA CDA AAS ≌△△∴CG CD =∵22CG CB BF FG CB BF DE BF =++=+=+ ∴2CD BF DE =+．。

初中中考复习之三角形全等（精编含答案）

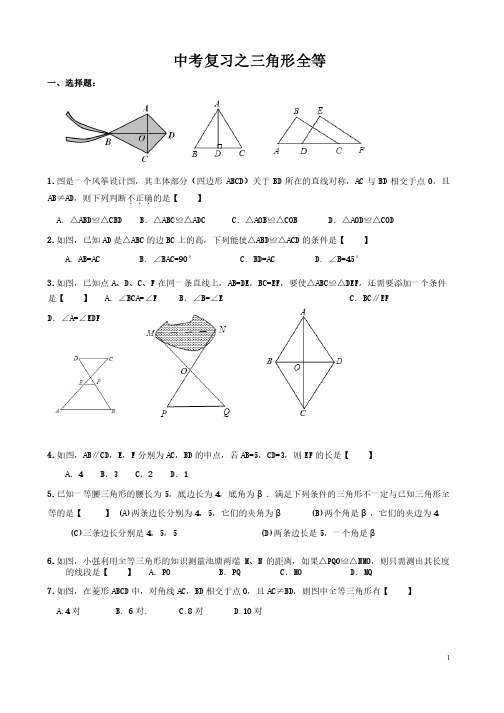
中考复习之三角形全等一、选择题：1.图是一个风筝设计图，其主体部分（四边形ABCD ABCD）关于）关于BD 所在的直线对称，所在的直线对称，AC AC 与BD 相交于点O ，且AB≠AD，则下列判断不正确．．．的是【的是【】】 A ．△ABD≌△CBD ．△ABD≌△CBD B B B．△ABC≌△ADC ．△ABC≌△ADC ．△ABC≌△ADC C C C．△AOB≌△COB ．△AOB≌△COB ．△AOB≌△COB D D D．△AOD≌△COD ．△AOD≌△COD ．△AOD≌△COD2.如图，已知AD 是△ABC 的边BC 上的高，下列能使△ABD≌△ACD 的条件是【的条件是【】】A. AB=ACB. ∠BAC=90°C. BD=AC A. AB=AC B. ∠BAC=90° C. BD=ACD. ∠B=45°D. ∠B=45°D. ∠B=45°3.如图，已知点A 、D 、C 、F 在同一条直线上，在同一条直线上，AB=DE AB=DE AB=DE，，BC=EF BC=EF，要使△ABC≌△DEF，还需要添加一个条件，要使△ABC≌△DEF，还需要添加一个条件是【是【】】 A A．∠BCA=∠F ．∠BCA=∠F ．∠BCA=∠F B B B．∠B=∠E ．∠B=∠E ．∠B=∠EC ．BC∥EF ．BC∥EFD ．∠A=∠EDF ．∠A=∠EDF4.如图，AB∥CD，如图，AB∥CD，E E ，F 分别为AC AC，，BD 的中点，若AB=5AB=5，，CD=3CD=3，则，则EF 的长是【的长是【】】A ．4B ．3C ．2D ．15.已知一等腰三角形的腰长为5，底边长为4，底角为β．满足下列条件的三角形不一定与已知三角形全等的是【等的是【】】 (A) (A)两条边长分别为两条边长分别为4，5，它们的夹角为β (B) (B)两个角是两个角是β，它们的夹边为4(C) (C)三条边长分别是三条边长分别是4，5，5 (D)5 (D)两条边长是两条边长是5，一个角是β6.如图，小强利用全等三角形的知识测量池塘两端M 、N 的距离，如果△PQO≌△NMO，则只需测出其长度的线段是【的线段是【】】 A A．．PO B ．PQ C PQ C．．MO D ．MQ7.如图，在菱形ABCD 中，对角线AC AC，，BD 相交于点O ，且AC≠BD，则图中全等三角形有【AC≠BD，则图中全等三角形有【】】A.4对B. 6对.C.8对D.10对二、填空题：1.在Rt△ABC 中，∠ACB=90°，中，∠ACB=90°，BC=2cm BC=2cm BC=2cm，CD⊥AB，在，CD⊥AB，在AC 上取一点E ，使EC=BC EC=BC，过点，过点E 作EF⊥AC 交CD 的延长线于点F ，若EF=5cm EF=5cm，则，则AE= cm AE= cm．．2.如图所示，如图所示，AB=DB AB=DB AB=DB，∠ABD=∠CBE，请你添加一个适当的条件，∠ABD=∠CBE，请你添加一个适当的条件，∠ABD=∠CBE，请你添加一个适当的条件，，使使ΔABC≌ΔDBE DBE．． ( (只需添只需添加一个即可加一个即可) )3.如图所示，已知点A 、D 、B 、F 在一条直线上，在一条直线上，AC=EF AC=EF AC=EF，，AD=FB AD=FB，要使△ABC≌△FDE，还需添加一个条件，，要使△ABC≌△FDE，还需添加一个条件，这个条件可以是这个条件可以是．．（只需填一个即可）（只需填一个即可）4.如图，点D ，E 分别在线段AB AB，，AC 上，上，BE BE BE，，CD 相交于点O ，AE=AD AE=AD，要使△ABE≌△ACD，需添加一个条，要使△ABE≌△ACD，需添加一个条件是件是（只需一个即可，图中不能再添加其他点或线）（只需一个即可，图中不能再添加其他点或线）．5.如图．点D 、E 在△ABC 的边BC 上，AB=AC AB=AC，，AD=AE AD=AE．．请写出图中的全等三角形请写出图中的全等三角形 ( ( (写出一对即可写出一对即可写出一对即可))．6.如图，己知AC=BD AC=BD，要使△ABC≌△DCB，则只需添加一个适当的条件是，要使△ABC≌△DCB，则只需添加一个适当的条件是，要使△ABC≌△DCB，则只需添加一个适当的条件是 ( ( (填一个即可填一个即可填一个即可) )三、解答题：1.已知：如图，AB AE =，1=2ÐÐ，=B E ÐÐ，求证：BC ED =2.如图，已知AB=DC AB=DC，，DB=AC（1）求证：∠ABD=∠DCA，注：证明过程要求给出每一步结论成立的依据．）求证：∠ABD=∠DCA，注：证明过程要求给出每一步结论成立的依据．（2）在（）在（11）的证明过程中，需要作辅助线，它的意图是什么？）的证明过程中，需要作辅助线，它的意图是什么？3.如图，点D 在AB 上，点E 在AC 上，上，AB=AC AB=AC AB=AC，∠B=∠C．求证：，∠B=∠C．求证：，∠B=∠C．求证：BE=CD BE=CD BE=CD．．4.如图，AB∥CD，以点A 为圆心，小于AC 长为半径作圆弧，分别交AB AB，，AC 于E ，F 两点，再分别以E ，F为圆心，大于12EF 长为半径作圆弧，两条圆弧交于点P ，作射线AP AP，交，交CD 于点M 。

备战2023年中考数学一轮复习考点08 全等三角形

考点08 全等三角形全等三角形主要包括全等图形、全等三角形的概念与性质，全等三角形的判定和角平分线的性质。

在中考中，全等三角形的直接考查主要以选择和填空为主，有时也会以证明的形式考查，难度一般较小；但大多数情况下，全等三角形的知识多作为工具性质与其他几何知识结合，用于辅助证明线段相等、角相等，考查面较广，难度较大，需要考生能够熟练运用全等三角形的性质和判定定理。

一、全等三角形的性质；二、全等三角形的判定；三、角平分线的线的性质。

考向一：全等三角形的性质1.全等三角形的对应边相等，对应角相等；2.全等三角形的周长相等，面积相等；3.全等三角形对应的中线、高线、角平分线、中位线都相等．1．下列四个图形中，属于全等图形的是（）A ．③和④B ．②和③C ．①和③D ．①和②2．下图所示的图形分割成两个全等的图形，正确的是（）A ．B ．C ．D ．3．如图，ABC DBC ∆∆≌，45A ∠=︒，86ACD ∠=︒，则ABC ∠的度数为（）A ．102︒B ．92︒C ．100︒D ．98︒4．如图，将ABC 沿着BC 方向平移6cm 得到DEF △，若AB BC ⊥，10cm AB =，4cm DH =，则四边形HCFD 的面积为（）2cm ．A．40B．24C．48D．645．如图，△ABC≌△ADE，若∠B＝80°，∠E＝30°，则∠C的度数为（）A．80°B．35°C．70°D．30°考向二：全等三角形的判定（一）三角形全等的判定定理：1.边边边定理：有三边对应相等的两个三角形全等（可简写成“边边边”或“SSS”）；2.边角边定理：有两边和它们的夹角对应相等的两个三角形全等（可简写成“边角边”或“SAS”）；3.角边角定理：有两角和它们的夹边对应相等的两个三角形全等（可简写成“角边角”或“ASA”）；4.角角边定理：有两角和它们所对的任意一边对应相等的两个三角形全等（可简写成“角角边”或“AAS”）；5.对于特殊的直角三角形，判定它们全等时，还有HL定理（斜边、直角边定理）：有斜边和一条直角边对应相等的两个直角三角形全等（可简写成“斜边、直角边”或“HL”）．（二）灵活运用定理三角形全等是证明线段相等，角相等的最基本、最常用的方法，这不仅因为全等三角形有很多重要的角相等、线段相等的特征，还在于全等三角形能把已知的线段相等、角相等与未知的结论联系起来．应用三角形全等的判别方法注意以下几点：1. 条件充足时直接应用判定定理在证明与线段或角相等的有关问题时，常常需要先证明线段或角所在的两个三角形全等.这种情况证明两个三角形全等的条件比较充分，只要认真观察图形，结合已知条件分析寻找两个三角形全等的条件即可证明两个三角形全等．2. 条件不足，会增加条件用判定定理此类问题实际是指条件开放题，即指题中没有确定的已知条件或已知条件不充分，需要补充三角形全等的条件．解这类问题的基本思路是：执果索因，逆向思维，即从求证入手，逐步分析，探索结论成立的条件，从而得出答案．3. 条件比较隐蔽时，可通过添加辅助线用判定定理在证明两个三角形全等时，当边或角的关系不明显时，可通过添加辅助线作为桥梁，沟通边或角的关系，使条件由隐变显，从而顺利运用全等三角形的判别方法证明两个三角形全等．常见的几种辅助线添加：①遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题，思维模式是全等变换中的“对折”； ②遇到三角形的中线，倍长中线，使延长线段与原中线长相等，构造全等三角形利用的思维模式是全等变换中的“旋转”；③遇到角平分线，可以自角平分线上的某一点向角的两边作垂线，利用的思维模式是三角形全等变换中的“对折”，所考知识点常常是角平分线的性质定理或逆定理；④过图形上某一点作特定的平分线，构造全等三角形，利用的思维模式是全等变换中的“平移”或“翻转折叠”； ⑤截长法与补短法，具体做法是在某条线段上截取一条线段与特定线段相等，或是将某条线段延长，使之与特定线段相等，再利用三角形全等的有关性质加以说明．这种作法，适合于证明线段的和、差、倍、分之类的题目．1．在如图所示33⨯的小正方形组成的网格中，ABC 的三个顶点分别在小正方形的顶点（格点）上．这样的三角形叫做格点三角形，图中能画出（）个与ABC 全等的格点三角形（不含ABC ）．A ．3B ．4C ．7D ．82．如图，B C ∠=∠，要使ABE ACD △△≌．则添加的一个条件不能是（）A ．ADC AEB ∠=∠ B ．AD AE =C ．AB AC =D ．BE CD =3．一块三角形玻璃不慎被小明摔成了四片碎片（如图所示），小明经过仔细的考虑认为只要带其中的两块碎片去玻璃店，就可以让师傅配一块与原玻璃一样的玻璃．你认为下列四个答案中考虑最全面的是（）A ．带其中的任意两块去都可以B ．带1、4或2、3去就可以了C ．带1、4或3、4去就可以了D ．带1、2或2、4去就可以了4．数学课上，同学们探讨利用不同画图工具画角的平分线的方法．小旭说：我用两块含30°的直角三角板就可以画角平分线．如图，取OM ＝ON ，把直角三角板按如图所示的位置放置，两直角边交于点P ，则射线OP 是∠AOB 的平分线，小旭这样画的理论依据是（）A ．SSAB ．HLC ．ASAD ．SSS5．如图，△ABC ≌△EBD ，∠E =50°，∠D =62°，则∠ABC 的度数是（）A ．68°B ．62°C ．60°D ．50°考向三：角平分线的线的性质1.角的平分线的性质定理：角的平分线上的点到这个角的两边的距离相等.2.角的平分线的判定定理：角的内部到角的两边距离相等的点在角的平分线上.3.三角形的角平分线：三角形角平分线交于一点，且到三边的距离相等.4.与角平分线有关的辅助线：在角两边截取相等的线段，构造全等三角形；在角的平分线上取一点向角的两边作垂线段.1．（2022·重庆八中模拟）下列命题是真命题的是（）A ．三角形的外心到这个三角形三边的距离相等B ．三角形的重心是这个三角形的三条角平分线的交点C ．三角形的三条高线所在的直线一定相交于三角形的内部D ．三角形的任意两边之和大于第三边2．如图，在ABC 中，ABC ∠，ACB ∠的平分线交于点O ，OD BC ⊥于D ，如果25cm AB =，20cm BC =，15cm AC =，且2150cm =ABC S △，那么OD 的长度是（）A ．2cmB ．3cmC ．4cmD ．5cm3．（2022·上海徐汇·二模）如图，两把完全相同的长方形直尺按如图方式摆放，记两把尺的接触点为点P ．其中一把直尺边缘恰好和射线OA 重合，而另一把直尺的下边缘与射线OB 重合，上边缘与射线OA 于点M ，联结OP ．若∠BOP ＝28°，则∠AMP 的大小为（）A ．62°B ．56°C ．52°D ．46°4．工人师傅常用角尺平分一个任意角，具体做法如下：如图，已知AOB ∠是一个任意角，在边,OA OB 上分别取OM ON =，移动角尺，使角尺两边相同的刻度分别与点M N ，重合，则过角尺顶点C 的射线OC 便是AOB ∠的平分线．在证明MOC NOC ≌时运用的判定定理是（）A ．SSSB ．SASC ．ASAD ．AAS5．如图，Rt △ABC 中，∠C =90°，用尺规作图法作出射线AE ，AE 交BC 于点D ，CD =5，P 为AB 上一动点，则PD 的最小值为( )A ．2B ．3C ．4D ．51．下列命题错误的是（）A ．三角形的三条高交于一点B ．三角形的三条中线都在三角形内部C ．直角三角形的三条高交于一点，且交点在直角顶点处D ．三角形的三条角平分线交于一点，且这个交点到三角形三边的距离相等2．如图，已知ABC A BC ''≌，A C BC ''∥，∠C ＝25°，则ABA '∠的度数是（）A ．15°B ．20°C ．25°D ．30°3．（2022·福建·模拟）如图，AD 是AEC △的角平分线，2AC AB =，若4ACD S =，则ABD △的面积为（）A ．3B ．2C ．32D ．14．如图，在Rt ABC 中，90,C BAC ∠=︒∠的平分线交BC 于点D ，DE //AB ，交AC 于点E ，DF AB ⊥于点F ，5,3DE DF ==，则下列结论错误的是（）A ．1BF =B ．3DC = C ．5AE =D ．9AC =5．（2022·河北·石家庄市第四十一中学模拟）如图，已知ABC ，90C ∠=︒，按以下步骤作图：①以点A为圆心，以适当长为半径画弧，分别交边AB ，AC 于点M ，N ；②分别以M ，N 为圆心，以大于12MN 的长为半径画弧，两弧在ABC 的内部相交于点P ；③作射线AP 交BC 于点D ．下列说法一定成立的是（）A ．BD AD =B ．BD CD >C ．>BD AC D ．2BD CD =6．（2022·河南·一模）在以下三个图形中，根据尺规作图的痕迹，能判断射线AD 平分BAC ∠的是（）A ．图2B ．图1与图2C ．图1与图3D ．图2与图37．（2022·山东威海·一模）如图，BD 是△ABC 的角平分线，AE ⊥BD ，垂足为M ．若∠ABC ＝30°，∠C ＝38°，则∠CDE 的度数为（）A ．68°B ．70°C ．71°D ．74°8．（2022·福建三明·模拟）如图，BD 平分∠ABC ，F ，G 分别是BA ，BC 上的点（BF BG ≠），EF EG =，则∠BFE 与∠BGE 的数量关系一定满足的是（）A ．90BFE BGE ∠+∠=B ．180BFE BGE ∠+∠=C ．2BFE BGE ∠=∠D ．90BFE BGE ∠-∠=9．（2022·重庆十八中两江实验中学一模）如图，在ABC 中，AD BC ⊥，垂足为点D ．下列条件中，不一定能推得ABD △与ACD 全等的条件是（）A ．AB AC = B ．BD CD =C ．B DAC ∠=∠D ．BAD CAD ∠=∠ 10．（2022·安徽滁州·二模）如图，OC 为∠AOB 的角平分线，点P 是OC 上的一点，PD ⊥OA 于D ，PE ⊥OB 于E ，F 为OC 上另一点，连接DF ，EF ，则下列结论：①OD ＝OE ；②DF ＝FE ； ③∠DFO ＝∠EFO ；④S △DFP ＝S △EFP ，正确的个数为（）A ．1个B ．2个C ．3个D ．4个11．如图，D 为Rt ABC △中斜边BC 上的一点，且BD AB =，过D 作BC 的垂线，交AC 于E ．若6cm AE =，则DE 的长为 __cm ．12．如图，ABC ∆中，90,6,8ACB AC BC ︒∠===．点P 从A 点出发沿A →C →B 路径向终点B 点运动；点Q 从B 点出发沿B →C →A 路径向终点A 点运动．点P 和Q 分别以1和3的运动速度同时开始运动，两点都要到相应的终点时才能停止运动．在某时刻，分别过P 和Q 作PE l ⊥于E ，QF l ⊥于F ．点P 运动________秒时，PEC ∆与QFC ∆全等．13．如图，在ABC 中，∠BAC ＝90°，AD 是BC 边上的高，BE 是AC 边的中线，CF 是∠ACB 的角平分线，CF 交AD 于点G ，交BE 于点H ，①ABE 的面积＝BCE 的面积；②∠F AG ＝∠FCB ；③AF ＝AG ；④BH ＝CH ．以上说法正确的是_____．14．如图，小虎用10块高度都是4cm 的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板（AC BC =，90ACB ∠=︒），点C 在DE 上，点A 和B 分别与木墙的顶端重合，则两堵木墙之间的距离为______．15．如图，E ABC AD ≅∆∆，BC 的延长线经过点E ，交AD 于F ，105AED ∠=︒，10CAD ∠=︒，50B ∠=︒，则EAB ∠=__︒．16．（2022·黑龙江哈尔滨·三模）如图，在△ABC 中，高AE 交BC 于点E ，若1452ABE C ∠+∠=︒，5CE =，△ABC 的面积为10，则AB 的长为___________．17．（2022·山东济南·三模）如图，正方形ABCD 的边长为3，P 、Q 分别在AB ，BC 的延长线上，且BP=CQ ，连接AQ 和DP 交于点O ，分别与边CD 和BC 交于点F 和E ，连接AE ，以下结论：①AQ ⊥DP ；②AOD S =OECF S 四边形；③OA 2=OE•OP ；④当BP =1时，tan ∠OAE =1316，其中正确的是______．（写出所有正确结论的序号）18．（2022·贵州铜仁·一模）如图，在ABC 中，8BC =，6AC =按下列步骤作图：步骤1：以点C 为圆心，小于AC 的长为半径作弧分别交BC 、AC 于点D 、E ；步骤2：分别以点D 、E 为圆心，大于12DE 的长为半径作弧，两弧交于点M ；步骤3：作射线CM 交AB 于点F ，若 4.5AF =，则AB =______．19．（2022·湖北襄阳·一模）如图，已知AC BD =，A D ∠=∠，添加一个条件______，使AFC DEB △≌△（写出一个即可）．20．如图，在△ABC 中，90ACB ∠=︒，AC ＝8cm ，BC ＝10cm ．点C 在直线l 上，动点P 从A 点出发沿A →C 的路径向终点C 运动；动点Q 从B 点出发沿B →C →A 路径向终点A 运动．点P 和点Q 分别以每秒1cm 和2cm 的运动速度同时开始运动，其中一点到达终点时另一点也停止运动，分别过点P 和Q 作PM ⊥直线l 于M ，QN ⊥直线l 于N ．则点P 运动时间为____秒时，△PMC 与△QNC 全等．21．已知：如图所示，PC PD C D =∠=∠，．求证：PCB PDA ≌．22．如图所示，点E 在线段BC 上，12∠=∠，AD AB AE AC ==，，求证：DE BC =23．（2022·江苏淮安·中考真题）已知：如图，点A 、D 、C 、F 在一条直线上，且AD CF =，AB DE =，BAC EDF ∠=∠．求证：B E ∠=∠．24．如图，己知正方形ABCD，点E是BC边上的一点，连接DE．(1)请用尺规作图法，在CD的延长线上截取线段DF，使=DF CE；（不要求写作法，保留作图痕迹）(2)在（1）的条件下，连接AF．求证：△AFD≌△DEC．25．（2022·陕西延安·二模）如图，已知ABC，请用尺规作图法在BC上求作一点E，使得点E到、的距离相等．（保留作图痕迹，不写作法）AB AC26．如图，已知等边ABC，AD是BC边上的高，请用尺规作图法，在AD上求作一点O，使∠=︒．（保留作图痕迹，不写作法）60BOD，，，与MN分别交于点27．如图，已知直线MN与▱ABCD的对角线AC平行，延长DA DC AB CB，，，．E H G F(1)求证：EF GH =；(2)若FG AC =，试判断AE 与AD 之间的数量关系，并说明理由．28．如图（1）所示，A ，E ，F ，C 在一条直线上，AE ＝CF ，过E ，F 分别作DE ⊥AC ，BF ⊥AC ，若AB ＝CD ，可以得到BD 平分EF ，为什么？若将△DEC 的边EC 沿AC 方向移动，变为图（2）时，其余条件不变，上述结论是否成立？请说明理由．29．如图，已知EB CF ∥，OA ＝OD ，AE ＝DF ．求证：(1)OB=OC ；(2)AB ∥CD ．30．如图，在ABC 中，90ACB ∠=︒，AC BC =，直线MN 经过点C ，且AD MN ⊥于D ，BE MN ⊥于E ．(1)当直线MN 绕点C 旋转到①的位置时，求证：①ADC △≌CEB ；②DE AD BE =+；(2)当直线MN 绕点C 旋转到②的位置时，求证：DE AD BE =-；(3)当直线MN 绕点C 旋转到③的位置时，试问DE 、AD 、BE 具有怎样的数量关系？请直接写出这个等量关系，不需要证明．1．（2022·江苏扬州·中考真题）如图，小明家仿古家具的一块三角形形状的玻璃坏了，需要重新配一块．小明通过电话给玻璃店老板提供相关数据，为了方便表述，将该三角形记为ABC ∆，提供了下列各组元素的数据，配出来的玻璃不一定符合要求的是（）A ．,,AB BC CA B ．,,AB BC B ∠ C ．,,AB AC B ∠D ．,,∠∠A B BC4．（2021·江苏盐城·中考真题）工人师傅常常利用角尺构造全等三角形的方法来平分一个角．如图，在AOB ∠的两边OA 、OB 上分别在取OC OD =，移动角尺，使角尺两边相同的刻度分别与点C 、D 重合，这时过角尺顶点M 的射线OM 就是AOB ∠的平分线．这里构造全等三角形的依据是（）A ．SASB ．ASAC ．AASD ．SSS5．（2022·江苏南通·中考真题）如图，点B 、F 、C 、E 在一条直线上，AB ∥ED ，AC ∥FD ，要使△ABC ≌△DEF ，还需添加一个．．条件是________．（只需添一个）6．（2020·江苏扬州·中考真题）如图，在ABC 中，按以下步骤作图：①以点B 为圆心，任意长为半径作弧，分别交AB 、BC 于点D 、E ．②分别以点D 、E 为圆心，大于12DE 的同样长为半径作弧，两弧交于点F ． ③作射线BF 交AC 于点G ．如果8AB =，12BC =，ABG 的面积为18，则CBG 的面积为________．7．（2022·江苏扬州·中考真题）如图，在ABCD 中，BE 、DG 分别平分ABC ADC ∠∠、，交AC 于点E G 、．(1)求证：,BE DG BE DG =∥；(2)过点E 作EF AB ⊥，垂足为F ．若ABCD 的周长为56，6EF =，求ABC ∆的面积．8．（2020·江苏南京·中考真题）如图，点D 在AB 上，点E 在AC 上，AB =AC ，∠B =∠C ，求证：BD =CE9．（2020·江苏镇江·中考真题）如图，AC 是四边形ABCD 的对角线，∠1＝∠B ，点E 、F 分别在AB 、BC 上，BE ＝CD ，BF ＝CA ，连接EF ．（1）求证：∠D ＝∠2；（2）若EF ∥AC ，∠D ＝78°，求∠BAC 的度数．1．（2022·江苏南京·二模）如图，在ABC 中，点D 在AC 上，BD 平分ABC ∠，延长BA 到点E ，使得BE BC =，连接DE ．若38ADE ∠=︒，则ADB ∠的度数是（）A ．68°B ．69°C ．71°D ．72°2．（2022·江苏常州·一模）如图，已知四边形ABCD 的对角互补，且BAC DAC ∠=∠，15AB =，12AD =．过顶点C 作CE AB ⊥于E ，则AE BE的值为（）A B ．9 C ．6 D ．7．23．（2022·江苏·南通市陈桥中学一模）如图，在锐角三角形ABC 中，AB =4，△ABC 的面积为10，BD 平分∠ABC ，若M 、N 分别是BD 、BC 上的动点，则CM +MN 的最小值为（）A ．4B ．5C ．4.5D ．64．（2022·江苏盐城·一模）如图，点E ，F 在AC 上，AD =BC ，DF =BE ，要使△ADF ≌△CBE ，还需要添加的一个条件是（）A ．∠A =∠CB ．∠D =∠BC ．AD ∥BC D ．DF ∥BE5．（2022·江苏南通·二模）如图，在ABC 中，按以下步骤作图：①以点B 为圆心，任意长为半径作弧，分别交AB ，BC 于点D ，E ；②分别以点D ，E 为圆心，大于12DE 的长为半径作弧，两弧在ABC ∠的内部交于点F ； ③作射线BF ，交AC 于点G ．如果6AB =，9BC =，ABG 的面积为9，则ABC 的面积为______．6．（2022·江苏·模拟）如图，在Rt △ABC 中，∠C ＝90°，∠BAC 的平分线AD 交BC 于点D ，CD ＝2，则点D 到AB 的距离是_________．7．（2022·江苏·南通市陈桥中学一模）如图，在Rt ABC △中，90C ∠=︒，以顶点A 为圆心、适当长为半径画弧，分别交AC 、AB 于点M 、N ，再分别以点M 、N 为圆心，大于12MN 的长为半径画弧，两弧交于点P ，作射线AP 交边BC 于点D ，若4CD =，5AB =，则ABD △的面积是________．8．（2022·江苏·苏州市振华中学校二模）已知：如图，AC BD =，AD BC =，AD ，BC 相交于点O ，过点O 作OE AB ⊥，垂足为E ．求证：(1)ABC BAD ≌．(2)AE BE =．9．（2022·江苏镇江·模拟）如图，∠BAC ＝90°，AB ＝AC ，BE ⊥AD 于点E ，CF ⊥AD 于点F ．(1)求证：△ABE ≌△CAF ；(2)若CF ＝5，BE ＝2，求EF 的长．10．（2022·江苏·宜兴市实验中学二模）如图，在△ABC 中，O 为BC 中点，BD ∥AC ，直线OD 交AC 于点E ．(1)求证：△BDO≌△CEO；(2)若AC=6，BD=4，求AE的长．11．（2022·江苏徐州·模拟）（1）如图1，在四边形ABCD中，AB＝AD，∠B＝∠D＝90°，E、F分别是边BC、CD上的点，且∠EAF＝1∠BAD，线段EF、BE、FD之间的关系是；（不需要证明）2（2）如图2，在四边形ABCD中，AB＝AD，∠B+∠D＝180°，E、F分别是边BC、CD上的点，且∠EAF ∠BAD，（1）中的结论是否仍然成立？若成立，请证明．若不成立，请写出它们之间的数量关系，并＝12证明．（3）如图3，在四边形ABCD中，AB＝AD，∠B+∠D＝180°，E、F分别是边BC、CD延长线上的点，且∠EAF＝1∠BAD，（1）中的结论是否仍然成立？若成立，请证明．若不成立，请写出它们之间的数量关2系，并证明．12．（2022·江苏盐城·一模）【提出问题】如图1，在等边三角形ABC内一点P，P A=3,PB=4,PC=5．求∠APB的度数？小明提供了如下思路：如图2，将△APC绕A点顺时针旋转60°至△AP'B ,则AP'=AP=3,P'C=PB=4,∠P'AC=∠P AB ,所以∠P'AC+∠CAP=∠P AC+∠BAP ,即∠P'AP=∠BAC=60° ,所以△AP'P为等边三角形,所以∠A P'P=60° ,……按照小明的解题思路，易求得∠APB= ；【尝试应用】如图3，在等边三角形ABC外一点P，P A=6,PB=10,PC=8．求∠APC的度数？【解决问题】如图4，平面直角坐标系xoy中，直线AB的解析式为y=－x+b(b>0),在第一象限内一点P，满足PB:PO:P A=1:2:3，则∠BPO= 度（直接写出答案）1．下列四个图形中，属于全等图形的是（）A ．③和④B ．②和③C ．①和③D ．①和②【答案】D【分析】根据全等图形的定义逐一判断即可．【详解】①和②，是全等图形，将①顺时针旋转180°即可和②完全重合，其它两个图形不符合故选D ．2．下图所示的图形分割成两个全等的图形，正确的是（）A ．B ．C ．D ．【答案】B【分析】直接利用全等图形的概念进而得出答案．【详解】解：图形分割成两个全等的图形，如图所示：故选B ．3．如图，ABC DBC ∆∆≌，45A ∠=︒，86ACD ∠=︒，则ABC ∠的度数为（）A ．102︒B ．92︒C ．100︒D ．98︒【答案】B【分析】根据全等三角形的性质得出ACB DCB ∠=∠，求出ACB ∠，根据三角形内角和定理求出即可．【详解】解：ABC DBC ∆∆≌，ACB DCB ∴∠=∠，86ACD ∠=︒， 43ACB ︒∴∠=，45A ∠=︒，18092ABC A ACB ∴︒--∠︒∠=∠=；故选：B ．4．如图，将ABC 沿着BC 方向平移6cm 得到DEF △，若AB BC ⊥，10cm AB =，4cm DH =，则四边形HCFD 的面积为（）2cm ．A ．40B ．24C ．48D ．64【答案】C【分析】根据平移的性质可得ABC ≌DEF △，则四边形HCFD 的面积等于DEFEHCABCEHCABEH SSSSS -=-=梯形即可求解．【详解】解：∵将ABC 沿着BC 方向平移6cm 得到DEF △， ∴ABC ≌DEF △，6BE =cm ， ∴ABC 的面积等于DEF △的面积，又AB BC ⊥，10cm AB =，4cm DH =， ∴1046HE DE DH AB DH =-=-=-=（cm ）， ∴四边形HCFD 的面积等于DEFEHCABCEHCABEH S SSSS -=-=梯形()12AB HE BE =+⋅ ()11066482=+⨯=（2cm ）故选C ．5．如图，△ABC ≌△ADE ，若∠B ＝80°，∠E ＝30°，则∠C 的度数为（）A．80°B．35°C．70°D．30°【答案】D【分析】根据全等三角形的性质即可得到结论．【详解】解：△ABC≌△ADE，∠E＝30°，∠C=∠E＝30°，故选：D．考向二：全等三角形的判定（一）三角形全等的判定定理：1.边边边定理：有三边对应相等的两个三角形全等（可简写成“边边边”或“SSS”）；2.边角边定理：有两边和它们的夹角对应相等的两个三角形全等（可简写成“边角边”或“SAS”）；3.角边角定理：有两角和它们的夹边对应相等的两个三角形全等（可简写成“角边角”或“ASA”）；4.角角边定理：有两角和它们所对的任意一边对应相等的两个三角形全等（可简写成“角角边”或“AAS”）；5.对于特殊的直角三角形，判定它们全等时，还有HL定理（斜边、直角边定理）：有斜边和一条直角边对应相等的两个直角三角形全等（可简写成“斜边、直角边”或“HL”）．（二）灵活运用定理三角形全等是证明线段相等，角相等的最基本、最常用的方法，这不仅因为全等三角形有很多重要的角相等、线段相等的特征，还在于全等三角形能把已知的线段相等、角相等与未知的结论联系起来．应用三角形全等的判别方法注意以下几点：1. 条件充足时直接应用判定定理在证明与线段或角相等的有关问题时，常常需要先证明线段或角所在的两个三角形全等.这种情况证明两个三角形全等的条件比较充分，只要认真观察图形，结合已知条件分析寻找两个三角形全等的条件即可证明两个三角形全等．2. 条件不足，会增加条件用判定定理此类问题实际是指条件开放题，即指题中没有确定的已知条件或已知条件不充分，需要补充三角形全等的条件．解这类问题的基本思路是：执果索因，逆向思维，即从求证入手，逐步分析，探索结论成立的条件，从而得出答案．3. 条件比较隐蔽时，可通过添加辅助线用判定定理在证明两个三角形全等时，当边或角的关系不明显时，可通过添加辅助线作为桥梁，沟通边或角的关系，使条件由隐变显，从而顺利运用全等三角形的判别方法证明两个三角形全等．常见的几种辅助线添加：①遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题，思维模式是全等变换中的“对折”；②遇到三角形的中线，倍长中线，使延长线段与原中线长相等，构造全等三角形利用的思维模式是全等变换中的“旋转”；③遇到角平分线，可以自角平分线上的某一点向角的两边作垂线，利用的思维模式是三角形全等变换中的“对折”，所考知识点常常是角平分线的性质定理或逆定理；④过图形上某一点作特定的平分线，构造全等三角形，利用的思维模式是全等变换中的“平移”或“翻转折叠”；⑤截长法与补短法，具体做法是在某条线段上截取一条线段与特定线段相等，或是将某条线段延长，使之与特定线段相等，再利用三角形全等的有关性质加以说明．这种作法，适合于证明线段的和、差、倍、分之类的题目．的小正方形组成的网格中，ABC的三个顶点分别在小正方形的顶点（格点）上．这样1．在如图所示33的三角形叫做格点三角形，图中能画出（）个与ABC全等的格点三角形（不含ABC）．A．3B．4C．7D．8【答案】C【分析】根据SSS判定两三角形全等．认真观察图形可得答案．【详解】如图所示大正方形上都可作两个全等的三角形，所以共有八个全等三角形，除去ABC 外有7个与ABC 全等的三角形．故选C ．2．如图，B C ∠=∠，要使ABE ACD △△≌．则添加的一个条件不能是（）A ．ADC AEB ∠=∠ B ．AD AE =C ．AB AC =D ．BE CD =【答案】A【分析】根据全等三角形的判定进行解答即可得．【详解】解：在ABE 和ACD 中，AEB ADC A BB C ∠=∠⎧⎪∠=∠⎨⎪∠=∠⎩∴无法证明ABE ACD △△≌，选项A 说法错误，符合题意；在ABE 和ACD 中， A AB C AD AE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴ABE ACD △△≌（AAS ），选项B 说法正确，不符合题意；在ABE 和ACD 中，A A AB AC BD ∠=∠⎧⎪=⎨⎪∠=∠⎩∴ABE ACD △△≌（ASA ），选项C 说法正确，不符合题意；在ABE 和ACD 中， A AB C BE CD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴ABE ACD △△≌（AAS ），选项D 说法正确，不符合题意；故选A ．3．一块三角形玻璃不慎被小明摔成了四片碎片（如图所示），小明经过仔细的考虑认为只要带其中的两块碎片去玻璃店，就可以让师傅配一块与原玻璃一样的玻璃．你认为下列四个答案中考虑最全面的是（）A ．带其中的任意两块去都可以B ．带1、4或2、3去就可以了C ．带1、4或3、4去就可以了D ．带1、2或2、4去就可以了【答案】C【分析】带1、3去，只有两角，没有完整边不能确定三角形，带1、2或2、3去，只有一角，没有完整边，不能确定三角形，带2、4去，有一角，可以延长边还原出原三角形，带3、4可以用“角边角”确定三角形，带1、4可以用“角边角”确定三角形．即可得出答案【详解】解：带1、3去，只有两角，没有完整边不能确定三角形，带1、2或2、3去，只有一角，不能确定三角形，带2、4去，有一角，可以延长边还原出原三角形，带3、4可以用“角边角”确定三角形，带1、4可以用“角边角”确定三角形，所以A 、B 、D 不符合题意，C 符合题，故选：C ．4．数学课上，同学们探讨利用不同画图工具画角的平分线的方法．小旭说：我用两块含30°的直角三角板就可以画角平分线．如图，取OM ＝ON ，把直角三角板按如图所示的位置放置，两直角边交于点P ，则射线OP 是∠AOB 的平分线，小旭这样画的理论依据是（）A ．SSAB ．HLC ．ASAD ．SSS【答案】B【分析】根据题意可得OP OP =，OM ON =，90PMO PNO ∠=∠=︒，根据全等三角形的判定方法，即可求解．【详解】解：根据题意可得OP OP =，OM ON =，90PMO PNO ∠=∠=︒，根据全等三角形的判定方法可得()POM PON HL △≌△ 故选B5．如图，△ABC ≌△EBD ，∠E =50°，∠D =62°，则∠ABC 的度数是（）A ．68°B ．62°C ．60°D ．50°【答案】A【分析】根据三角形内角和定理求出∠EBD ，根据全等三角形的性质解答．【详解】∵∠E ＝50°，∠D ＝62°， ∴∠EBD ＝180°−50°−62°＝68°， ∵△ABC ≌△EBD ， ∴∠ABC ＝∠EBD ＝68°，故选：A ．考向三：角平分线的线的性质1.角的平分线的性质定理：角的平分线上的点到这个角的两边的距离相等.2.角的平分线的判定定理：角的内部到角的两边距离相等的点在角的平分线上.3.三角形的角平分线：三角形角平分线交于一点，且到三边的距离相等.4.与角平分线有关的辅助线：在角两边截取相等的线段，构造全等三角形；在角的平分线上取一点向角的两边作垂线段.1．（2022·重庆八中模拟）下列命题是真命题的是（） A ．三角形的外心到这个三角形三边的距离相等 B ．三角形的重心是这个三角形的三条角平分线的交点 C ．三角形的三条高线所在的直线一定相交于三角形的内部 D ．三角形的任意两边之和大于第三边【答案】D【分析】根据三角形的外心、重心等有关性质，对选项逐个判断即可．【详解】解：A 、三角形的内心到这个三角形三边的距离相等，为假命题，不符合题意； B 、三角形的重心是这个三角形的三条中线的交点，为假命题，不符合题意；C 、只有锐角三角形的三条高线所在的直线相交于三角形的内部，为假命题，不符合题意；D 、三角形的任意两边之和大于第三边，为真命题，符合题意；故选：D2．如图，在ABC 中，ABC ∠，ACB ∠的平分线交于点O ，OD BC ⊥于D ，如果25cm AB =，20cm BC =，15cm AC =，且2150cm =ABC S △，那么OD 的长度是（）A ．2cmB ．3cmC ．4cmD ．5cm【答案】D【分析】作OE AC ⊥交于点E ，作OF AB ⊥交于点F ，连接OA ，证明OD OE OF ==，再利用2150cm =++=ABC BOC AOB AOC S S S S △△△△即可求出OD 的长度．【详解】解：作OE AC ⊥交于点E ，作OF AB ⊥交于点F ，连接OA ，。

中考数学复习专题24全等三角形试题(A卷,含解析)

全等三角形一、选择题 1. (新疆建设兵团，4，5分）如图，在△ABC 和△DEF 中，∠B =∠DEF ，AB =DE ，添加下列一个条件后，仍然不能证明△ABC ≌△DEF ，这个条件是（）A ．∠A =∠DB ．BC =EF C ．∠ACB =∠FD ．AC =DF【答案】D【逐步提示】本题考查了全等三角形的判定方法，解题的关键是熟练掌握全等三角形常见判定方法．注意到题目中给出一组角相等，一组边相等，分别结合四个选项，找到不符号常见判定方法的那个选项．【详细解答】解：选项A 可采用“ASA ”来判定三角形全等，选项B 可采用“SAS ”来判定三角形全等，选项C 可采用“AAS ”来判定三角形全等，选项D 为两边和其中一边的对角不能判定三角形全等，故选择D . 【解后反思】此类问题容易出错的地方是由SSA 就判定三角形全等，从而错选D 选项.三角形全等的判定方法有：SAS ，ASA ，AAS ，SSS ，HL (直角三角形)．【关键词】三角形全等的判定；(浙江金华，6，3分)如图，已知=ABC BAD ∠∠，添加下列条件还不能判定△ABC ≌△BAD 的是( )A. AC=BDB.∠CAB ＝∠DBAC.∠C ＝∠DD.BC=AD 【答案】A【逐步提示】将题目中的条件表示到图形中，再结合图形条件判断已有哪些条件，然后根据三角形全等的判定方法确定正确的选项．【解析】题目中已给出一角相等，图形中有一条公共边，即已有一边及一角对应相等，再需要一边或一角相等即可，A 选项与两已知条件构成SSA 不能确定两个三角形全等；B 选项与两已知条件构成ASA 能确定两个三角形全等；C 选项与两已知条件构成AAS 能确定两个三角形全等；D 选项与两已知条件构成SAS 能确定两个三角形全等，故选择A.【解后反思】对于添加条件从而判断两个全等三角形全等类问题的解题策略：首先理解题目中已存在的条件(包括已知条件及图形条件)，再根据三角形全等的五种判定方法[(1)三边对应相等的两个三角形全等SSS ；(2)两边和它们的夹角对应相等的两个三角形全等SAS ；(3)两角和它们的夹边对应相等的两个三角形全等ASA ；(4)两个角和其中一角的对边对应相等的两个三角形全等AAS ；(5)斜边和一条直角边对应相等的两个直角三角形全等HL]进行综合评判，从而确定需要添加的条件．【关键词】三角形全等的识别 2.3. （四川省广安市，8，3分）下列说法： ①三角形的三条高一定都在三角形内；AB（第6题图）DC②有一个角是直角的四边形是矩形；③有一组邻边相等的平行四边形是菱形；④两边及一角对应相等的两个三角形全等；⑤一组对边平行，另一组对边相等的四边形是平行四边形．其中正确的个数有（）A．1个 B．2个 C．3个 D．4个【答案】A【逐步提示】本题考查了三角形的中线、高线、角平分线的概念，矩形的判定，菱形的判定，全等三角形的判定，平行四边形的判定等，解题的关键是掌握这些概念、定理等．因为直角三角形与钝角三角形的三条高不都在三角形内，故①错；至少有三个角是直角的四边形是才是矩形，故②错；③是菱形的定义，正确；满足④的条件时有可能形成“边边角”的情况，故错误；等腰梯形满足“一组对边平行，另一组对边相等”，但它不是平行四边形，故⑤错误．【详细解答】解：只有③正确，故选择A.【解后反思】要理解三角形“三线”的概念，掌握三角形、平行四边形、矩形、菱形的判定方法，这是正确解题的基础．能画图举反例，以排除不符合条件情形，也是解这类题的基本功，要多思考，勤积累．类似的问题还有：判断下列说法是否正确：（1）一组对边相等且一组对角相等的四边形是平行四边形.解：错误．如图1，作△ABC，使AB＝AC，在BC上取一点D（D点不与B、C重合且BD≠CD），连接AD.再以A为顶点，AD为一边，作∠EAD，使∠EAD＝∠ADC，且AE＝DC，连接DE.由上述画图方法，可知△ADC≌△DAE（SAS）.所以DE＝AC＝AB，∠AED＝∠C＝∠B.即四边形ABCD有一组对边相等（DE＝AB）、一组对角相等（∠AED＝∠B），但却不是平行四边形（另一组对边AE 和BD不平行也不相等）.（2）一组对边相等，且一条对角线平分另一条对角线的四边形是平行四边形.解：错误．如图2，画两条相交直线，交点为O，在其中一条直线上截取OA＝OC，分别过A、C两点向另一条直线作垂线，垂足分别为E、F.在线段OF上取一点D（D点不与O、F重合），连接CD.再在线段OE的延长线上取一点B，使EB＝FD，连接AB.由上述画图方法，易知△COF≌△AOE（AAS），则CF＝AE，由“SAS”可判定△CFD≌△AEB，则CD＝AB.连接AD、BC，则四边形ABCD满足条件，却不是平行四边形.（3）一组对角相等，且连接这一组对角的顶点的对角线被另一条对角线平分的四边形是平行四边形.解：错误．如图，画一个“筝形”ABCD，其中AB＝AD，BC＝DC且AO≠OC，则该“筝形”满足条件，但它不是平行四边形.【关键词】中线、高线、角平分线；矩形的判定；菱形的判定；全等三角形的判定；平行四边形的判定二、填空题1. （山东省枣庄市，17，4分）如图，在△ABC 中，∠C ＝90°，AC ＝BC 2ABC 绕点A 顺时针方向旋转60°到△A ´B ´C ´的位置，连接C ´B ，则C ´B ＝．31【逐步提示】本题考查了旋转、全等三角形、解直角三角形，解题的关键是通过旋转的性质及角度得出△ABB ´为等边三角形．连接BB ´，延长BC ´交AB ´于点H ，根据旋转的性质，对应点到旋转中心的距离相等，可知△ABB ´为等边三角形，然后再证明△ABC ´≌△B ´BC ´，再利用等腰三角形三线合一，证明BH ⊥AB ´，然后分别求HC ´与BH 即可求C ´B ．【详细解答】解：连接BB ´，延长BC ´交AB ´于点H ，∵∠C ＝90°，AC ＝BC 2，∴AB 22AC BC +2，由题意可知：AB ´＝AB ＝2，且∠BAB ´＝60°，∴△ABB ´为等边三角形，∴BB ´＝AB ，∠ABB ´＝60°，又∵BC ´＝BC ´，B´C ´＝AC ´，∴△ABC ´≌△B ´B C ´，∴∠ABC ´＝∠B ´ BC ´＝30°，∴BH ⊥AB ´，且AH ＝12AB ´＝1，∴BH 22AB AH -3AC ´B ´＝90°，AH ＝B ´H ，∴C ´H ＝12AB ´＝1，∴ C ´B ＝BH －C ´H 31 ，故答案为31 .【解后反思】本题考查了旋转的知识，解这类题通常抓住变换前后的全等图形中对应边、对应角相等．当旋转角为60°时，可以得到等边三角形；当旋转角为45°时，可以得到等腰直角三角形．【关键词】三角形全等的识别；全等三角形的性质；等腰三角形的性质；勾股定理；C ´ABHCB ´ABCB ´C ´2. （四川省成都市，12，4分）如图，△ABC ≌△A ´B ´C ´，其中∠A ＝36°，∠C ´＝24°，∠B ＝．【答案】120°．【逐步提示】本题考查了三角形全等的性质及三角形内角和定理，解题的关键是掌握有关的性质．先根据全等三角形对应角相等求出∠C ，再利用三角形内角和定理可求出∠B ．【详细解答】解：∵△ABC ≌△A ´B ´C ´，∴∠C ＝∠C ´＝24°，∴ ∠B ＝180°―∠A ―∠C ＝180°―36°―24°＝120° ，故答案为 120° .【解后反思】全等三角形的性质：全等三角形的对应边相等，全等三角形的对应角相等．【关键词】三角形的内角和；全等三角形的性质三、解答题1. （山东省枣庄市，24，10分）如图，把△EFP 放置在菱形ABCD 中，使得顶点E ，F ，P 分别在线段AB ，AD ，AC 上，EP ＝FP ＝6，EF ＝3，∠BAD ＝60°，AB ＞63⑴求∠EPF 的大小；⑵若AP ＝10，求AE ＋AF ；⑶若△EFP 的三个顶点E ，F ，P 分别在线段AB ，AD ，AC 上运动，请直接写出AP 长的最大值和最小值．【逐步提示】本题考查了菱形的性质、等腰三角形三线合一性及全等三角形等知识，解题的关键是熟练掌握图形的性质和判定，善于转化．⑴过点P 作PG ⊥EF 于G ．根据等腰三角形三线合一性，得∠EPF ＝2∠FPG ，再解Rt △PFG ，利用特殊角三角函数值求∠FPG 的大小，即可得∠EPF ；⑵作PM ⊥AB 于M ，PN ⊥AD 于N ．根据菱形的对角线平分对角的性质，可证明△PME ≌ △PNF ，得ME ＝NF ，再利用三角函数求出AM ＝AN ，通过线段和差得到AE ＋AF 与AM 、AN 的关系，即可求值；⑶当E 、F 分别与A 、B 重合时，AP 取最小值，当EF ⊥AC 时，AP 取最大值．【详细解答】解：⑴如图，过点P 作PG ⊥EF 于G ． ∵PE ＝PF ＝6，PG ⊥EF ，∴FG ＝EG ＝12 EF ＝33FPG ＝∠EPG ＝12∠EPF ．在Rt △FPG 中，sin ∠FPG ＝FG PF333．∴∠FPG ＝60°，∴∠EPF ＝2∠FPG ＝120°．AC BCA ´B ´ABDCFPE⑵作PM ⊥AB 于M ，PN ⊥AD 于N ．∵AC 为菱形ABCD 的对角线，∴∠DAC ＝∠BAC ，AM ＝AN ，PM ＝PN ．在Rt △PME 和Rt △PNF 中，PM ＝PN ，PE ＝PF ， ∴Rt △PME ≌Rt △PNF ．∴ME ＝NF ．又AP ＝10，∠PAM ＝12∠DAB ＝30°， ∴AM ＝AN ＝AP ·cos30°＝10×3＝53． ∴AE ＋AF ＝(AM ＋ME )＋(AN －NF )＝AM ＋AN ＝103．⑶如图，当△EFP 的三个顶E ，F ，P 分别在线段AB ，AD ，AC 上运动时，点P 在P 1，P 2之间运动，易知P 1O ＝P 2O ＝3，AO ＝9，∴AP 的最大值为12，AP 的最小值为6．【解后反思】运动型问题一般是图形在运动中产生函数关系问题或探究几何图形的变化规律问题，这类问题可细分为点动型、线动型、形动型．解答这类问题时，要求对几何元素的运动过程有一个完整、清晰的认识，不管点动、线动还是形动，要善于借助动态思维的观点来分析，不被“动”所迷惑，从特殊情形入手，变中求不变，动中求静，抓住静的瞬间，以静制动，把动态的问题转化为静态的问题来解决，从而找到“动”与“静”的联系，揭示问题的本质，发现运动中的各个变量之间互相依存的函数关系，从而找到解决问题的突破口，也就找到了解决这类问题的途径．【关键词】全等三角形的性质；三角形全等的识别；等腰三角形的性质；特殊角三角函数值的运用；动点题型2. (重庆A ，19，7分)如图，点A ，B ，C ，D 在同一条直线上，CE //DF ，EC =BD ，AC =FD . 求证：AE =FB .【逐步提示】由CE //DF ，可知∠ACE =∠D . 利用“SAS ”可以判定△ACE ≌△FDB ，即可判定AE =FB . 【详细解答】证明：∵CE //DF ，∴∠ACE =∠D . 在△ACE 和△FDB 中，OABDCFP 1EP 2M ABDCFPE N G∵EC=BD，∠ACE=∠D，AC=FD，∴△ACE≌△FDB(SAS).∴AE=FB.【解后反思】利用三角形全等是证明两条线段或两个角相等的重要方法. 证明两个三角形全等必须有一组对应边相等的条件，判定两个三角形全等的方法主要有“SAS”、“ASA”、“AAS”和“SSS”，对于直角三角形，还有“HL”，结合全等三角形的判定方法，可寻找所需要的条件. 当题目中出现平行线时，可根据平行线的性质得到相等的角，还要注意公共线段、公共角、重合线段、重合角在得到相等线段和相等角的作用.【关键词】全等三角形的识别；全等三角形的性质(重庆B，19，7分)如图，在△ABC和△CED中，AB∥CD，AB=CE，AC=CD．求证：∠B=∠E．【逐步提示】根据两直线平行，内错角相等可得∠BAC=∠ECD，再利用“边角边”证明△ABC≌△CED，然后根据全等三角形对应角相等即可证明∠B=∠E．【详细解答】证明：∵AB∥CD，∴∠BAC=∠ECD，在△ABC和△CED中，,,,AB CEBAC ECDAC CD=⎧⎪∠=∠⎨⎪=⎩∴△ABC≌△CED(SAS)，∴∠B=∠E．【解后反思】利用三角形全等是证明两个角或两条线段相等的重要方法. 证明两个三角形全等必须有一组对应边相等的条件，判定两个三角形全等的方法主要有“SAS”、“ASA”、“AAS”和“SSS”，对于直角三角形，还有“HL”，结合全等三角形的判定方法，可寻找所需要的条件. 当题目中出现平行线时，可根据平行线的性质得到相等的角，还要注意公共线段、公共角、重合线段、重合角在得到相等线段和相等角的作用.【关键词】全等三角形的识别；全等三角形的性质3.(重庆B，25，12分)已知△ABC是等腰直角三角形，∠BAC=90°，CD=12BC，DE⊥CE，DE=CE，连接AE，点M 是AE的中点.(1)如图1，若点D在BC边上，连接CM，当AB=4时，求CM的长；(2)如图2，若点D在△ABC的内部，连接BD，点N是BD中点，连接MN，NE，求证MN⊥AE；(3)如图3，将图2中的△CDE绕点C逆时针旋转，使∠BCD=30°，连接BD，点N是BD中点，连接MN，探索MNAC 的值并直接写出结果.EMCBA图1D图2NMEDCBAENMCBA图3D【逐步提示】(1)先证明△ACE是直角三角形，根据CM=12AE，求出AE即可解决问题．(2)如图，延长EN至点F，使NF=EN，连接BF，连接AF.先证明△NBF≌△NDE，可得BF=DE=CE，∠FBN=∠NDE.根据题意可得∠ACE=∠ACB+∠DCE-∠DCB=90°-∠DCB，只要证出∠ABF=90°-∠DCB.即可证明∠ACE=∠ABF，又AB=AC，利用“SAS”可证出△ABF≌△ACE，进而可得∠FAB=∠EAC，所以有∠FAE=∠FAB+∠BAE=∠EAC+∠BAE=∠BAC=90°，又MN是△EAF的中位线.根据三角形的中位线的性质可得MN∥AF，从而∠NME=∠FAE=90°，可证MN⊥AF.(3)如图5，连接DM并延长到点G，使MG=MD，连接AG、BG，延长AG、EC交于点F．可得△AMG≌△EMD，∴AG=DE=EC，∠GAM=∠DEM，∴AG∥DE，∴∠F=∠DEC=90°，∵∠FAC+∠ACF=90°，∠BCD+∠ACF=90°，∴∠FAC=∠BCD=30°∴∠BAG=∠ACE=120°，在△ABG和△CAE中，,,,AB ACBAG ACEAG EC=⎧⎪∠=∠⎨⎪=⎩∴△ABG≌△CAE，∴BG=AE，∵BN=ND，DM=MG，∴MN是△DBG的中位线，∴BG=AE=2MN，设BC=2a，则CD=a，DE=EC=22a，AC=2a，CF=22a，AF=62a，EF=2a，∴AE=22142AF EF+=a，∴MN=144a，∴147442aMNAC a==.【详细解答】(1)解：∵△ABC是等腰直角三角形，∠BAC=90°，AB=4，∴AC=AB=4，BC=42，∠ACB=∠ABC=45°.∵CD=12BC，∴CD=22∵DE⊥CE，DE=CE，∴△CDE是等腰直角三角形，∴∠DCE=∠CDE=45°，∴CE=CD·sin45°=2.∵∠ACE=∠DCE+∠ACB=45°+45°=90°，∴在Rt△ACE中，AE2225AC CE+=∵点M是AE中点，∴CM=12AE5(2)证明：如图4，延长EN至点F，使NF=EN，连接BF，连接AF.∵点N是BD的中点，∴BN=DN.∵∠BNF=∠DNE，∴△NBF≌△NDE.∴BF=DE，∠FBN=∠NDE，∵DE=CE，∴BF=CE.∵∠ACE=∠ACB+∠DCE-∠DCB，∴∠ACE=45°+45°-∠DCB=90°-∠DCB.在△BCD中，∵∠DBC+∠BDC+∠DCB=180°，∠BDC=∠NDE+∠CDE，又∵∠CDE=45°，∴∠DBC+∠NDE=135°-∠DCB.∵∠ABF=∠DBC+∠FBN-∠ABC，∠FBN=∠NDE，∴∠ABF=∠DBC+∠NDE-∠ABC=135°-∠DCB-45°=90°-∠DCB.∴∠ABF=∠ACE.∵AB=AC，∴△ABF≌△ACE.∴∠FAB=∠EAC∵∠BAC=∠BAE+∠EAC=90°，∴∠FAB+∠BAE=90°，即∠FAE=90°.∵点M是AE中点，NF=NE，∴MN是△EAF的中位线.∴MN∥AF.∴∠NME=∠FAE=90°.∴MN⊥AF.(3)解：7 MNAC.【解后反思】本题综合考查全等三角形的判定和性质、勾股定理、三角形的中位线等知识，解题的关键是添加辅助线，构造全等三角形.在几何问题的求解或证明中，全等三角形起着很重要的作用，应该充分利用已知条件和图形找出图中的全等三角形，根据全等三角形对应边、对应角分别相等的性质可实现等边、等角的代换，而当要证明的两线段之间或两角之间没有直接联系时，往往需要通过等量代换适当转换来求解.．【关键词】三角形全等的识别；全等三角形的性质；勾股定理；三角形中位线定理4.5.（四川泸州，18，6分）如图，C是线段AB的中点，CD=BE， CD∥BE.求证：∠D=∠E.【逐步提示】要证明两个不同三角形中的两个角相等，可以证明这两个角所在的两个三角形全等，从而选择合适的判定方法证明两个三角形全等.【详细解答】证明：∵C 是线段AB 的中点，∴AC=CB ，∵CD ∥BE ，∴∠ACD=∠CBE ，在△ACD 和△CBE 中，AC CB ACD CBE CD BE =⎧⎪∠=∠⎨⎪=⎩∴△ACD ≌△CBE, ∴∠D=∠E.【解后反思】证明两个三角形全等，一般情况下是已知两个条件去找第三个全等条件，有以下几种情况：（1）已知两边.⎧⎨⎩找第三边；找两边的夹角；（2）已知两角⎧⎨⎩找其中任意一角的对边找两角的夹边；（3）已知一边及其邻角⎧⎨⎩找任意一角找夹该已知角的边；（4）已知一边及其对角，找余下的任一角. 【关键词】三角形全等的判定方法5. （四川南充，19，8分）已知ΔABN 和ΔACM 位置如图所示，AB =AC ，AD =AE ，∠1=∠2. (1)求证：BD =CE ； (2)求证：∠M =∠N .21O ED MAN【逐步提示】本题考查了全等三角形的判定与性质；解题的关键是证明三角形全等．（1）由SAS 证明△ABD≌△ACE，得出对应边相等即可（2）证出∠BAN=∠CAM，由全等三角形的性质得出∠B=∠C，由AAS 证明△ACM≌△ABN，得出对应角相等即可．【详细解答】解：（1）证明：在△ABD 和△ACE 中，12AB AC AD AE =⎧⎪∠=∠⎨⎪=⎩， ∴△ABD≌△ACE（SAS ）， ∴BD=CE；（2）证明：∵∠1=∠2， ∴∠1+∠DAE=∠2+∠DAE，即∠BAN=∠CAM，由（1）得：△ABD≌△ACE， ∴∠B=∠C，在△ACM 和△ABN 中，C BAC ABCAM BAN∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△ACM≌△ABN（ASA），∴∠M=∠N．已知条件寻找的条件选择的判定方法两角夹边或一角对边ASA或AAS一角及其对边任一角AAS一角及其邻边角的另一边或边的另一邻角或边的对角SA S或ASA或AAS 两边夹角或另一边或直角SAS或SSS或HL 【关键词】全等三角形的性质；三角形全等的识别6（四川省宜宾市，18，6分）如图，已知∠CAB=∠DBA，∠CBD=∠DAC.求证：BC=AD【逐步提示】已知∠CAB=∠DBA，可得AO=BO,因而可证明△BOC≌△AOD,结论成立. 【详细解答】证明：∠CAB=∠DBA，所以AO=BO在△BOC和△AOD 中∠CBD=∠DAC（已知）OB=OA(已证)∠CBD=∠DAC（已证）△BOC≌△AOD（ASA）所以BC=AD【解后反思】除了上面的证明方法外，也可以证明△BAC≌△ABD(ASA)【关键词】全等三角形的性质与判定；等腰三角形的性质与判定。

2025年中考数学总复习+微专题7 全等三角形之六大模型++++课件

39
【解析】(1)∵△ADB与△ADF关于直线AD对称,∴AB=AF,∠BAD=∠FAD,
∵AB=AC,
∴AF=AC,
∵∠FAD+∠FAE=∠DAE=45°,∠BAD+∠CAE=∠CAB-∠DAE=45°,
∴∠FAE=∠CAE,
在△AEF与△AEC中,
=
∠ = ∠ ,
=
∠AOB的平分线,请说明此做法的理由;
拓展实践:(3)小明将研究应用于实践.如图4,校园的两条小路AB和AC,汇聚形成了一个岔路口A,
现在学校要在两条小路之间安装一盏路灯E,使得路灯照亮两条小路(两条小路一样亮),并且路
灯E到岔路口A的距离和休息椅D到岔路口A的距离相等,试问路灯应该安装在哪个位置?请用
4.(2024·淄博沂源县二模 ) 如图 , 点E 在△ABC的外部,点 D 在BC 上,DE 交 AC 于点
F,∠1=∠2=∠3,AB=AD.
求证:△ABC≌△ADE.
14
【证明】∵∠1=∠2=∠3,∠AFE=∠CFD,
∴∠1+∠DAF=∠2+∠DAF,∠C=180°-∠3-∠DFC,∠E=180°-∠2-∠AFE,
∴AE=ED,
∴∠EAD=∠EDA.
30
(2)∵∠AED=∠C=60°,AE=ED,
∴△AED为等边三角形,
∴AE=AD=ED=4,
过A点作AF⊥ED于F,

∴EF= ED=2,

∴AF= − = − =2 ,

∴S△AED= ED·AF= ×4×2

=4 .
∴AP= AM,
∴AB+AN= AM.

2024年中考数学复习+全等三角形课件

3．(2020·衡阳8分)如图，在△ABC中，∠B＝∠C，过BC的中点D作 DE⊥AB，DF⊥AC，垂足分别为点E，F. (1)求证：DE＝DF；
证明：∵DE⊥AB，DF⊥AC，
∴∠BED＝∠CFD＝90° ∵D是BC的中点，∴BD＝CD. 在△BED和△CFD中，
∠BED=∠CFD ∠B=∠C
BD=CD
强调：两角一边一定能判定三角形全等
方法指 ----全等常见的判定思路：引
已知一角一边：找角的邻边找边的邻角找边的对角
已知两边：
找第三边找夹角找直角
已知两角：找夹边
找对边找第三边
方法指引
E
全等与图形的变换：
D
F
G 轴对称
直观发现全等
平移
旋转
通过图形的变换，直观发现全等；发现相等的边、相等的角.
1．(2022·衡阳6分)如图，在△ABC中，AB＝AC，D，E是BC边上的点，且BD＝CE.求证：AD＝AE.
证明：∵AB＝AC， ∴∠B＝∠C.
在△ABD和△ACE中，
AB=AC
∠B=∠C
全等五行
∴△BADB=DC≌E △ACE(SAS)．
∴AD＝AE.
2．(2021·衡阳6分)如图，点A，B，D，E在同一条直线上，AB＝DE， AC∥DF，BC∥EF.求证：△ABC≌△DEF.
4．(2018·衡阳6分)如图，线段AC，BD相交于点E，AE＝DE，BE＝CE. (1)求证：△ABE≌△DCE；(2)当AB＝5时，求CD的长．
（1）证明：在△ABE和△DCE中，
AE=DE
∠AEB=∠DEC
BE=CE
∴△ABE≌△DCE(SAS)．
（2）解：∵△ABE≌△DCE，∴AB＝CD. ∵AB＝5，∴CD＝5.

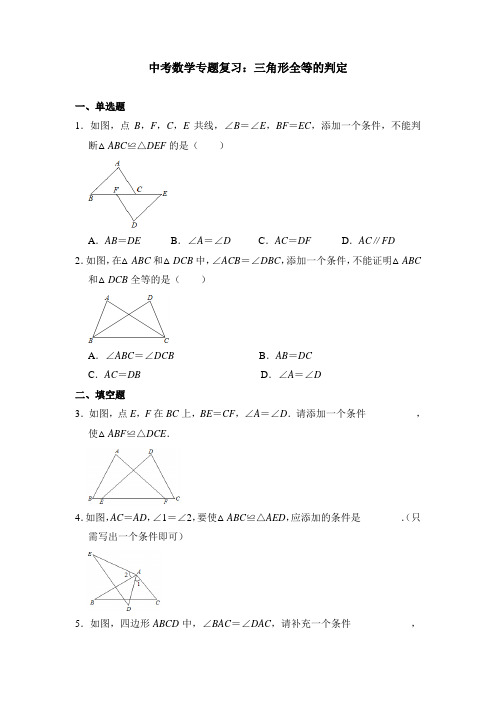
中考数学专题复习：三角形全等的判定

中考数学专题复习：三角形全等的判定一、单选题1．如图，点B，F，C，E共线，∠B＝∠E，BF＝EC，添加一个条件，不能判断△ABC≌△DEF的是（）A．AB＝DE B．∠A＝∠D C．AC＝DF D．AC∥FD2．如图，在△ABC和△DCB中，∠ACB＝∠DBC，添加一个条件，不能证明△ABC 和△DCB全等的是（）A．∠ABC＝∠DCB B．AB＝DCC．AC＝DB D．∠A＝∠D二、填空题3．如图，点E，F在BC上，BE＝CF，∠A＝∠D．请添加一个条件__________，使△ABF≌△DCE．4．如图，AC＝AD，∠1＝∠2，要使△ABC≌△AED，应添加的条件是________．（只需写出一个条件即可）5．如图，四边形ABCD中，∠BAC＝∠DAC，请补充一个条件____________，使△ABC≌△ADC．三、解答题6．如图，已知OA＝OC，OB＝OD，∠AOC＝∠BOD．求证：△AOB≌△COD．7．如图，点A、B、D、E在同一条直线上，AB＝DE，AC∥DF，BC∥EF．求证：△ABC≌△DEF．8．如图，AB∥DE，B，C，D三点在同一条直线上，∠A＝90°，EC⊥BD，且AB＝CD．求证：AC＝CE．9．如图，点D、E分别是AB、AC的中点，BE、CD相交于点O，∠B＝∠C，BD＝CE．求证：（1）OD＝OE；（2）△ABE≌△ACD．10．如图，点E、F在线段BC上，AB∥CD，∠A＝∠D，BE＝CF，证明：AE ＝DF．11．如图，点A，D，B，E在一条直线上，AD＝BE，AC＝DF，AC∥DF．求证：BC＝EF．12．如图，D是△ABC的边AB上一点，CF∥AB，DF交AC于E点，DE＝EF．（1）求证：△ADE≌△CFE；（2）若AB＝5，CF＝4，求BD的长．13．如图，在△ABC中，D是边BC上的点，DE⊥AC，DF⊥AB，垂足分别为E，F，且DE＝DF，CE＝BF．求证：∠B＝∠C．14．已知：如图，AC，DB相交于点O，AB＝DC，∠ABO＝∠DCO．求证：（1）△ABO≌△DCO；（2）∠OBC＝∠OCB．15．如图，BD∥AC，BD＝BC，点E在BC上，且BE＝AC．求证：∠D＝∠ABC．16．如图．已知AB＝DC，∠A＝∠D，AC与DB相交于点O，求证：∠OBC＝∠OCB．17．如图，在四边形ABCD中，AD＝BC，AC＝BD，AC与BD相交于点E．求证：∠DAC＝∠CBD．18．如图，点D在AB上，点E在AC上，AB＝AC，∠B＝∠C，求证：BD＝CE．19．如图，点D在AB上，E在AC上，AB＝AC，∠B＝∠C，求证：AD＝AE．20．如图，树AB与树CD之间相距13m，小华从点B沿BC走向点C，行走一段时间后他到达点E，此时他仰望两棵大树的顶点A和D，且两条视线的夹角正好为90°，EA＝ED．已知大树AB的高为5m，小华行走的速度为1m/s，求小华行走到点E的时间．21．如图，△ABC的两条高AD、BE相交于点H，且AD＝BD，试说明下列结论成立的理由．（1）∠DBH＝∠DAC；（2）△BDH≌△ADC．22．如图，已知：AD＝AB，AE＝AC，AD⊥AB，AE⊥AC．猜想线段CD与BE 之间的数量关系与位置关系，并证明你的猜想．23．如图，已知：AB＝DE且AB∥DE，BE＝CF．求证：（1）∠A＝∠D；（2）AC∥DF．24．如图，在△P AB中，P A＝PB，∠APB＝100°，点M，N，K分别是P A，PB，AB上的点，若MK＝KN，∠MKN＝40°，试判断线段AM，BN与AB之间的数量关系，并说明理由．25．如图，点C、E、B、F在一条直线上，AB⊥CF于B，DE⊥CF于E，AC＝DF，AB＝DE．求证：CE＝BF．26．已知：如图，A、B、C、D在同一直线上，且AE∥DF，AE＝DF，AB＝CD．求证：∠E＝∠F．参考答案1．解：∵BF＝EC，∴BF+FC＝EC+FC，∴BC＝EF，又∵∠B＝∠E，∴当添加条件AB＝DE时，△ABC≌△DEF（SAS），故选项A不符合题意；当添加条件∠A＝∠D时，△ABC≌△DEF（AAS），故选项B不符合题意；当添加条件AC＝DF时，无法判断△ABC≌△DEF，故选项C符合题意；当添加条件AC∥FD时，则∠ACB＝∠DFE，故△ABC≌△DEF（ASA），故选项D不符合题意；故选：C．2．解：在△ABC和△DCB中，∵∠ACB＝∠DBC，BC＝BC，A：当∠ABC＝∠DCB时，△ABC≌△DCB（ASA），故A能证明；B：当AB＝DC时，不能证明两三角形全等，故B不能证明；C：当AC＝DB时，△ABC≌△DCB（SAS），故C能证明；D：当∠A＝∠D时，△ABC≌△DCB（AAS），故D能证明；故选：B．3．解：∵BE＝CF，∴BE+EF＝CF+EF，∴BF＝CE，添加∠B＝∠C，在△ABF和△DCE中，，∴△ABF≌△DCE（AAS），故答案为：∠B＝∠C（答案不唯一）．4．解：∵∠1＝∠2，∴∠1+∠BAD＝∠2+∠BAD，即∠BAC＝∠EAD，∵AC＝AD，∴当添加∠B＝∠E时，可根据“AAS”判断△ABC≌△AED；当添加∠C＝∠D时，可根据“ASA”判断△ABC≌△AED；当添加AB＝AE时，可根据“SAS”判断△ABC≌△AED．故答案为∠B＝∠E或∠C＝∠D或AB＝AE．5．解：添加的条件是AD＝AB，理由是：在△ABC和△ADC中，∴△ABC≌△ADC（SAS），故答案为：AD＝AB（答案不唯一）．6．证明：∵∠AOC＝∠BOD，∴∠AOC﹣∠AOD＝∠BOD﹣∠AOD，即∠COD＝∠AOB，在△AOB和△COD中，，∴△AOB≌△COD（SAS）．7．证明：∵AC∥DF，∴∠CAB＝∠FDE(两直线平行，同位角相等),又∵BC∥EF，∴∠CBA＝∠FED(两直线平行，同位角相等),在△ABC和△DEF中，,8．证明：∵AB∥DE，∴∠B＝∠D，∵EC⊥BD，∠A＝90°，∴∠DCE＝90°＝∠A，在△ABC和△CDE中，，∴△ABC≌△CDE（ASA），∴AC＝CE．9．证明：（1）在△BOD和△COE中，，∴△BOD≌△COE（AAS），∴OD＝OE；（2）∵点D、E分别是AB、AC的中点，∴AD＝BD＝AB，AE＝CE＝AC，∵BD＝CE．∴AD＝AE，AB＝AC，在△ABE和△ACD中，，∴△ABE≌△ACD（SAS）．10．证明：∵AB∥CD，∴∠B＝∠C．在△ABE和△DCF中，∴AE＝DF．11．证明：∵AD＝BE，∴AD+BD＝BE+BD，即AB＝DE，∵AC∥DF，∴∠A＝∠EDF，在△ABC与△DEF中，，∴△ABC≌△DEF（SAS），∴BC＝EF．12．（1）证明：∵CF∥AB，∴∠ADF＝∠F，∠A＝∠ECF．在△ADE和△CFE中，，∴△ADE≌△CFE（AAS）．（2）∵△ADE≌△CFE，∴AD＝CF＝4．∴BD＝AB﹣AD＝5﹣4＝1．13．证明：∵DE⊥AC，DF⊥AB，∴∠BFD＝∠CED＝90°，在△BDF和△CDE中，，∴△BDF≌△CDE（SAS），∴∠B＝∠C．14．证明：（1）在△ABO和△DCO中，，∴△ABO≌△DCO（AAS）；（2）由（1）知，△ABO≌△DCO，∴OB＝OC∴∠OBC＝∠OCB．15．证明：∵BD∥AC，∴∠ACB＝∠EBD，在△ABC和△EDB中，，∴△ABC≌△EDB（SAS），∴∠ABC＝∠D．16．证明：在△AOB与△COD中，，∴△AOB≌△DOC（AAS），∴OB＝OC，∴∠OBC＝∠OCB．17．证明：在△CDA和△DCB中，，∴△CDA≌△DCB（SSS），∴∠DAC＝∠CBD．18．证明：在△ABE与△ACD中，∴△ABE≌△ACD（ASA）．∴AD＝AE．∴AB﹣AD＝AC﹣AE，∴BD＝CE．19．证明：在△ABE与△ACD中，，∴△ACD≌△ABE（ASA），∴AD＝AE（全等三角形的对应边相等）．20．解：∵∠AED＝90°，∴∠AEB+∠DEC＝90°．∵∠ABE＝90°，∴∠A+∠AEB＝90°．∴∠A＝∠DEC，在△ABE和△DCE中∵，∴△ABE≌△ECD（AAS），∴EC＝AB＝5m．∵BC＝13m，∴BE＝8m．∴小华走的时间是8÷1＝8（s）21．证明：（1）∵AD⊥BC，BE⊥AC，∴∠ADC＝∠BEC＝90°，∵∠C＝∠C，∴∠DBH＝∠DAC；（2）∵AD⊥BC∴∠ADB＝∠ADC在△BDH与△ADC中，∴△BDH≌△ADC．22．解：猜想：CD＝BE，CD⊥BE，理由如下：∵AD⊥AB，AE⊥AC，∴∠DAB＝∠EAC＝90°．∴∠DAB+∠BAC＝∠EAC+∠BAC，即∠CAD＝∠EAB，在△ACD和△AEB中，，∴△ACD≌△AEB（SAS），∴CD＝BE，∠ADC＝∠ABE，∵∠AGD＝∠FGB，∴∠BFD＝∠BAD＝90°，即CD⊥BE．23．证明：（1）∵AB∥DE，BE＝CF，∴∠B＝∠DEF，BC＝EF，又AB＝DE，∴△ABC≌△DEF（SAS），∴∠A＝∠D；（2）由（1）知△ABC≌△DEF，∴∠ACB＝∠F，∴AC∥DF．24．解：AM+BN＝AB，理由如下：∵P A＝PB，∠APB＝100°，∴∠A＝∠B＝40°，∴∠AMK+∠AKM＝140°，∵∠MKN＝40°，∴∠AKM+∠BKN＝140°，∴∠AMK＝∠BKN，又∵MK＝KN，∴△AMK≌△BKN（AAS），∴AM＝BK，AK＝BN，∴AB＝AK+BK＝AM+BN．25．证明：在△ABC与△DEB中，，∴△ABC≌△DEB（SSS）∴∠ACB＝∠EBD，∴BF＝CF．26．证明：∵AE∥DF，∴∠A＝∠D，∵AB＝CD，∴AB+BC＝CD+BC，∴AC＝DB，在△EAC和△FDB中，，∴△EAC≌△FDB（SAS），∴∠E＝∠F．。

全等三角形复习专题

全等三角形复习专题一、全等三角形基本概念与性质全等三角形是指能够完全重合的两个三角形，即形状相同和大小相等的三角形。

全等三角形的性质是全等三角形的边、角及其对应线段之间具有一些特殊的数量关系和位置关系。

如全等三角形的对应边相等，对应角相等，对应线段相等，以及全等三角形的中点连线等于其一边。

二、全等三角形的判定全等三角形的判定是全等三角形研究的核心内容，主要有以下五个判定方法：1、边角边定理（SAS）：若两个三角形的两边及其夹角对应相等，则这两个三角形全等。

2、角边角定理（ASA）：若两个三角形的两个角及其夹边对应相等，则这两个三角形全等。

3、边边边定理（SSS）：若两个三角形的三边对应相等，则这两个三角形全等。

4、角角边定理（AAS）：若两个三角形的两个角及其一边对应相等，则这两个三角形全等。

5、斜边直角边定理（HL）：若两个直角三角形的斜边和一条直角边对应相等，则这两个直角三角形全等。

三、全等三角形的应用全等三角形在数学、几何、物理等领域中都有广泛的应用。

如证明线段相等、角相等、平行四边形、矩形、菱形、正方形等几何图形的性质和判定，以及解决一些实际问题等。

四、全等三角形的复习策略1、掌握全等三角形的基本概念和性质，理解判定方法的意义和适用范围。

2、熟练掌握全等三角形的判定方法，能够根据题目条件选择合适的判定方法解决问题。

3、熟悉全等三角形的应用，能够将全等三角形的知识应用到实际问题和数学问题中。

4、多做练习题，熟悉各种题型和解题方法，提高解题能力和思维水平。

5、注意对易错点和难点进行重点复习和强化训练，避免出现常见的错误和失误。

全等三角形动点专题在数学的世界里，全等三角形和动点问题是两个重要的概念。

全等三角形是指两个或两个以上的三角形，它们的边长和角度都相等，可以完全重合。

动点问题则涉及到在给定的图形或轨迹上移动的点，以及这些点的变化和规律。

将这两个概念结合起来，我们可以研究一类非常有趣的数学问题，即全等三角形动点专题。

初三复习专题--全等三角形

•
OA＝OC，EA＝EC，
•
请阐明∠ A＝∠C。
AO C
DB
E
• 分析：欲证明∠A＝ ∠C，有三条思路，一是证明△AOD与△COB全等，而由已知条件不可直接得到，二是连结OE，阐明△AOE与 △COE全等，这条路显而易得， ∠A＝∠C，三是证明 △ABE与△CDE全等，这也是不能直接证明到的，因此应采用第二条思路。
全等三角形
• 一:考纲规定与命题趋势
• 1. 理解并掌握五种识别三角形全等的办法，会灵活的对的选择适宜的识别办法判断两个三角形与否全等。
• 2. 对的运用全等三角形的性质计算三角形中未知的边或角，逐步培养逻辑推理能力和形象思维能力。
• 3. 全等三角形的应用是学习几何证明题的基础，因此它自然是中考必考知识点，同窗们务必学好它。
• 阐明：在解决几何问题的过程中，有时根据条件不能较顺利的得到结论，这时添加必要的辅助线是十分重要的捷径。
• 例3.P是线段AB上一点，△APC与△BPD都是
等边三角形，请你判断：AD与BC相等吗？
试阐明理由。
D
C
AP
B
• 分析：观察图形发现它们所在的三角形全
等，故考虑通过全等来阐明。
• 解：由△APC和△BPD都是等边三角形可知 AP＝PC，BP＝DP，∠APC＝∠BPD＝60°，
变化，结论往往仍然成立，解决大同小异，
要善于抓住规律。
A
A
B
l
3
E
12
D
C
E
①
D
1
l
2
B
C
②
• 例9.如图，等边△ABC的边长为a，在BC的延长线上取点D，使CD＝b，在BA的延长线上取点E，使AE＝a+b，证明EC＝ED。

中考数学专题复习全等三角形(X模型)

中考数学专题复习全等三角形（X模型）学校:___________姓名：___________班级：___________考号：___________评卷人得分一、填空题1．如图，已知AD是ABC的中线，E是AC上的一点，BE交AD于F，AC BF=，24DAC∠=︒，32EBC∠=︒，则ACB=∠__________．评卷人得分二、解答题2．问题背景：课外兴趣小组活动时，老师提出了如下问题：如图1，△ABC中，若AB＝4，AC＝3，求BC边上的中线AD的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长AD到点E，使DE＝AD，则得到△ADC≌△EDB，小明证明△BED≌△CAD用到的判定定理是：（用字母表示）；问题解决：小明发现：解题时，条件中若出现“中点”“中线”字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中．请写出小明解决问题的完整过程；拓展应用：以△ABC的边AB，AC为边向外作△ABE和△ACD，AB＝AE，AC＝AD，∠BAE＝∠CAD＝90°，M是BC中点，连接AM，DE．当AM＝3时，求DE的长．3．如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于F，且AF＝BD，连接BF．（1）求证：D是BC的中点（2）如果AB＝AC，试判断四边形AFBD的形状，并证明你的结论．4．【阅读理解】课外兴趣小组活动时，老师提出了如下问题：如图1，ABC中，若8AB=，6AC=，求BC边上的中线AD的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长AD到点E，使DE AD=，请根据小明的方法思考：（1）由已知和作图能得到ADC△EDB△的理由是______．（2）求得AD的取值范围是______．【感悟】解题时，条件中若出现“中点”“中线”字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中．【问题解决】（3）如图2，在ABC中，点D是BC的中点，点M在AB边上，点N在AC边上，若DM DN⊥，求证：BM CN MN+>．5．如图所示：ABC是等边三角形，D、E分别是AB及AC延长线上的一点，且BD CE=，连接DE交BC于点M．求让：MD ME=6．阅读下面材料【问题情境】课外兴趣小组活动时，老师提出了如下问题：如图△．在△ABC中，若AB=8，AC=6，求BC边上的中线AD取值范围，小明在组内经过合作交流，得到了如下的解决方法：延长AD到点E，使DE=AD，请根据小明方法思考：（1）由已知和作图能得到△ADC△△EDB的理由是（）A．SSS B．SAS C．AAS D．HL（2）由三角形三边的关系可求得AD长的取值范围是（）A．6＜AD＜8B．6≤AD≤8C．1＜AD＜7D．1≤AD≤7【解后感悟】解题时，条件中若出现“中点”“中线”字样可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到一个三角形中．【灵活运用】如图△，AD是△ABC的中线，BE交AC于E，交AD于F，且AE=EF若EF=4，7．阅读下面的题目及分析过程．已知：如图点E是BC的中点，点A在DE上，且AB DC=说明：BAE D ∠=∠分析：说明两个角相等，常用的方法是应用全等三角形或等腰三角形的性质．观察本题中说明的两个角，它们既不在同一个三角形中，而且们所在两个三角形也不全等．因此，要说明BAE D∠=∠，必须添加适当的辅助线，构造全等三角形或等腰三角形，现在提供两种添加辅助线的方法如下：如图△过点C作//CF AB，交DE的延长线于点F．如图△延长DE至点M，使ME DE=，连接BM．（1）请从以上两种辅助线中选择一种完成上题的说理过程．（2）在解决上述问题的过程中，你用到了哪种数学思想？请写出一个．_______________．（3）反思应用：如图，点B是AE的中点，BC BD⊥于点B．请类比（1）中解决问题的思想方法，添加适当的辅助线，判断线段AC DE+与CD之间的大小关系，并说明理由．8．如图，在ABC中，45ABC∠=,AD,BE分别为BC,AC边上的高，连接DE,过点D 作DF DE⊥与点F，G为BE中点，连接AF，DG．（1）如图1，若点F与点G重合，求证：AF DF⊥；（2）如图2，请写出AF与DG之间的关系并证明．9．P为等边△ABC的边AB上一点，Q为BC延长线上一点，且P A＝CQ，连PQ交AC边于D．（1）证明：PD＝DQ．（2）如图2，过P作PE△AC于E，若AB＝6，求DE的长．10．【阅读理解】课外兴趣小组活动时，老师提出了如下问题：如图1，△ABC中，若AB＝8，AC＝6，求BC边上的中线AD的取值范围.小明在组内经过合作交流，得到了如下的解决方法：延长AD到点E，使DE＝AD，请根据小明的方法思考：(1)由已知和作图能得到△ADC△△EDB的理由是_____.A．SSS B．SAS C．AAS D．HL(2)求得AD的取值范围是______.A．6＜AD＜8B．6≤AD≤8C．1＜AD＜7D．1≤AD≤7【感悟】解题时，条件中若出现“中点”“中线”字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中.【问题解决】(3)如图2，AD是△ABC的中线，BE交AC于E，交AD于F，且AE＝EF.求证：AC ＝BF.11．【问题情境】课外兴趣小组活动时，老师提出了如下问题：如图1，△ABC中，若AB＝12，AC＝8，求BC边上的中线AD的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长AD到E，使DE＝AD，连接BE．请根据小明的方法思考：（1）由已知和作图能得到△ADC△△EDB，依据是．A．SSS B．SAS C．AAS D．HL（2）由“三角形的三边关系”可求得AD的取值范围是．解后反思：题目中出现“中点”“中线”等条件，可考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中．【初步运用】如图2，AD是△ABC的中线，BE交AC于E，交AD于F，且AE＝EF．若EF＝3，EC＝2，求线段BF的长．【灵活运用】如图3，在△ABC中，△A＝90°，D为BC中点，DE△DF，DE交AB于点E，DF交AC 于点F，连接EF，试猜想线段BE、CF、EF三者之间的等量关系，并证明你的结论．12．如图，等边三角形ABC中，E是线段AC上一点，F是BC延长线上一点．连接BE，AF．点G是线段BE的中点，BN∥AC，BN与AG延长线交于点N．（1）若∠BAN＝15°，求∠N；（2）若AE＝CF，求证：2AG＝AF．13．（1）【问题情境】课外兴趣小组活动时，老师提出了如下问题：如图△，在△ABC中，AD是△ABC的中线，若AB＝10，AC＝8，求AD的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长AD至点E，使DE＝AD，连接BE．请根据小明的方法思考：△.由已知和作图能得到△ADC△△EDB，依据是________．A．SSS B．SAS C．AAS D．ASA△.由“三角形的三边关系”可求得AD的取值范围是________．解后反思：题目中出现“中点”、“中线”等条件，可考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集中到同一个三角形之中．（2）【学会运用】如图△，AD是△ABC的中线，点E在BC的延长线上，CE=AB, △BAC=△BCA, 求证：AE=2AD．14．如图，等边三角形ABC 中，E 是线段AC 上一点，F 是BC 延长线上一点.连接BE ，AF .点G 是线段BE 的中点，BNAC ，BN 与AG 延长线交于点N .（1）若15BAN ∠=︒，求N ∠；（2）若AE CF =，求证：2AG AF =.15．P 为等边△ABC 的边AB 上一点，Q 为BC 延长线上一点，且P A ＝CQ ，连PQ 交AC 边于D ．（1）证明：PD ＝DQ ．（2）如图2，过P 作PE △AC 于E ，若AB ＝6，求DE 的长．16．数学兴趣小组在活动时，老师提出了这样一个问题：如图1，在ABC 中，AB 8=，AC 6=，D 是BC 的中点，求BC 边上的中线AD 的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长AD 到E ，使DE AD =，请补充完整证明“ADC △EDB ”的推理过程．()1求证：ADC △EDB证明：延长AD 到点E ，使DE AD = 在ADC 和EDB 中AD ED(=已作)，ADC EDB(∠∠=______)，CD BD(=中点定义)，ADC ∴△EDB(______)，()2探究得出AD 的取值范围是______；【感悟】解题时，条件中若出现“中点”“中线”等字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中．【问题解决】()3如图2，ABC 中，B 90∠=，AB 2=，AD 是ABC 的中线，CE BC ⊥，CE 4=，且ADE90∠=，求AE 的长．17．如图，阅读下面的题目及分析过程，并按要求进行证明．已知：如图，E 是BC 的中点，点A 在DE 上，且△BAE=△CDE ．求证：AB=CD ．分析：证明两条线段相等，常用的一般方法是应用全等三角形或等腰三角形的判定和性质，观察本题中要要证AB=CD ，必须添加适当的辅助线，构造全等三角形或等腰三18．如图，点P为等边△ABC的边AB上一点，Q为BC延长线上一点，AP=CQ，PQ交AC于D，(1)求证：DP=DQ；(2)过P作PE△AC于E，若BC=4，求DE的长．19．阅读下面的题目及分析过程，并按要求进行证明．已知：如图，E是BC的中点，点A在DE上，且∠BAE=∠CDE．求证：AB=CD．分析：证明两条线段相等，常用的一般方法是应用全等三角形或等腰三角形的判定和性质，观察本题中要证明的两条线段，它们不在同一个三角形中，且它们分别所在的两个三角形也不全等．因此，要证AB=CD，必须添加适当的辅助线，构造全等三角形或等腰三角形．现给出如下三种添加辅助线的方法，请任意选择其中一种，对原题进行证明．参考答案：1．100°【解析】【分析】延长AD到M，使得DM=AD，连接BM，证△BDM△△CDA（SAS），得BM=AC=BF，△M=△DAC=24°，△C=△DBM，再证△BFM是等腰三角形，求出△MBF的度数，即可解决问题．【详解】解：如图，延长AD到M，使得DM=AD，连接BM，如图所示：在△BDM和△CDA中，DM DABDM CDABD CD=⎧⎪∠=∠⎨⎪=⎩，△△BDM△△CDA（SAS），△BM=AC=BF，△M=△DAC=24°，△C=△DBM，△BF=AC，△BF=BM，△△M=△BFM=24°，△△MBF=180°-△M-△BFM=132°，△△EBC=32°，△△DBM=△MBF-△EBC=100°，△△C=△DBM=100°，故答案为：100°．【点睛】本题考查全等三角形的判定和性质、等腰三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考常考题型．2．问题背景：SAS；问题解决：完整过程见解析；拓展应用：DE＝6．【解析】【分析】问题背景：先判断出BD=CD，由对顶角相等△BDE=△CDA，进而得出△ADC△△EDB （SAS）；问题解决：先证明△ADC△△EDB（SAS），得出BE=AC=3，最后用三角形三边关系即可得出结论；拓展应用：如图2，延长AM到N，使得MN=AM，连接BN，同（1）的方法得出△BMN△△CMA（SAS），则BN=AC，进而判断出△ABN=△EAD，进而判断出△ABN△△EAD，得出AN=ED，即可求解．【详解】问题背景：如图1，延长AD到点E，使DE＝AD，连接BE，△AD是△ABC的中线，△BD＝CD，在△ADC和△EDB中，AD EDCDA BDECD BD=⎧⎪∠=∠⎨⎪=⎩，△△ADC△△EDB（SAS），故答案为：SAS；问题解决：如图1，延长AD到点E，使DE＝AD，连接BE，△AD是△ABC的中线，△BD＝CD，AD EDCDA BDECD BD=⎧⎪∠=∠⎨⎪=⎩，△△ADC△△EDB（SAS），△BE＝AC，在△ABE中，AB﹣BE＜AE＜AB+BE，△AB＝4，AC＝3，△4﹣3＜AE＜4+3，即1＜AE＜7，△DE＝AD，△AD＝12AE，△12＜AD＜72；拓展应用：如图2，延长AM到N，使得MN＝AM，连接BN，由问题背景知，△BMN△△CMA（SAS），△BN＝AC，△CAM＝△BNM，△AC//BN，△AC＝AD，△BN＝AD，△AC//BN，△△BAC+△ABN＝180°，△△BAE＝△CAD＝90°，△△BAC+△EAD＝180°，在△ABN 和△EAD 中，AB EA ABN EAD BN AD =⎧⎪∠=∠⎨⎪=⎩，△△ABN △△EAD （SAS ），△AN ＝DE ，△MN ＝AM ，△DE ＝AN ＝2AM ，△AM ＝3，△DE ＝6．【点睛】此题考查了全等三角形的判定和性质，平行线的判定与性质，补角的性质，掌握倍长中线法，构造全等三角形是解本题的关键．3．（1）见解析；（2）见解析.【解析】【分析】（1）先由AF △BC ，利用平行线的性质可证△AFE =△DCE ，而E 是AD 中点，那么AE =DE ，△AEF =△DEC ，利用AAS 可证△AEF △△DEC ，那么有AF =DC ，又AF =BD ，从而有BD =CD ；（2）四边形AFBD 是矩形．由于AF 平行等于BD ，易得四边形AFBD 是平行四边形，又AB =AC ，BD =CD ，利用等腰三角形三线合一定理，可知AD △BC ，即△ADB =90°，那么可证四边形AFBD 是矩形．【详解】证明：（1）△AF △BC ，△△AFE =△DCE ，△E 是AD 的中点，△AE =DE ，△△AFE ＝△DCE ， ∠AEF∠∠DEC ，AE ＝DE ，△△AEF △△DEC （AAS ），△AF =DC ，△AF =BD ，△BD =CD ，△D 是BC 的中点；（2）四边形AFBD 是矩形．理由： △AB =AC ，D 是BC 的中点，△AD △BC ，△△ADB =90°，△AF =BD ，过A 点作BC 的平行线交CE 的延长线于点F ，即AF △BC ，△四边形AFBD 是平行四边形，又△△ADB =90°，△四边形AFBD 是矩形．【点睛】本题利用了平行线的性质、全等三角形的判定和性质、等量代换、平行四边形的判定、等腰三角形三线合一定理、矩形的判定等知识．4．（1）SAS ；（2）17AD <<；（3）见解析【解析】【分析】（1）根据AD=DE ，△ADC=△BDE ，BD=DC 推出△ADC 和△EDB 全等即可；（2）根据全等得出BE=AC=6，AE=2AD ，由三角形三边关系定理得出8-6＜2AD ＜8+6，求出即可；（3）延长ND 至点E ，使DE DN =，连接BE 、ME ，证明BED △()SAS CND △，得到BE CN =，根据三角形三边关系解答即可．【详解】（1）解：△在△ADC 和△EDB 中，AD DE ADC BDE BD CD =⎧⎪∠=∠⎨⎪=⎩，△△ADC△△EDB （SAS ），故答案为：SAS ；（2）解：△由（1）知：△ADC△△EDB ，△BE=AC=6，AE=2AD ，△在△ABE 中，AB=8，由三角形三边关系定理得：8-6＜2AD ＜8+6，△1＜AD ＜7，故答案为：1＜AD ＜7．（3）证明：延长ND 至点E ，使DE DN =，连接BE 、ME ，如图所示：△点D 是BC 的中点，△BD CD =．在BED 和CND △中，DE DN BDE CDN BD CD =⎧⎪∠=∠⎨⎪=⎩， △BED △()SAS CND △，△BE CN =，△DM DN ⊥，DE DN =，△ME MN =，在BEM △中，由三角形的三边关系得：BM BE ME +>，△BM CN MN +>．【点睛】本题是三角形综合题，主要考查了三角形的中线，三角形的三边关系定理，全等三角形的性质和判定等知识点，主要考查学生运用定理进行推理的能力．5．见详解【解析】【分析】过点D作DE△AC，交BC于点E，根据等边三角形和平行线的性质得△MDE=△MEC，DE=CE，从而证明∆EMD≅∆CME，进而即可得到结论．【详解】过点D作DE△AC，交BC于点E，△ABC是等边三角形，△△B=△ACB=60°，△DE△AC，△△DEB=△ACB=60°，△MDE=△MEC，△BDE是等边三角形，△BD=DE，△BD CE=，△DE=CE，又△△EMD=△CME，△∆EMD≅∆CME，△MD ME=．【点睛】本题主要考查等边三角形的性质和判定定理以及全等三角形的判定和性质定理，添加辅助线，构造等边三角形和全等三角形，是解题的关键．6．(1)B；（2）C；应用：7．【解析】【分析】(1)由已知AD是△ABC的中线，和作图延长AD到点E，使DE=AD，CD=BD,△ADC=△EDB, AD=DE得到△ADC△△EDB(SAS) 即可，(2) 由△ADC△△EDB，则BE=AC=6，AE=2AD，AB=8，在ΔABE中，AB-BE<AE<AB+BE，即则2<2AD<14即可，【灵活运用】延长AD到G，使DG=AD，连接BG，由（1）知△ADC△△GDB，BG=AC=AE+EC=7△G=△DAC可以判定BG△AC，由△BFG=△AFE，得ΔGBF△ΔAEF，由性质BG BF AE EF．【详解】(1)由已知AD是△ABC的中线，和作图延长AD到点E，使DE=AD，CD=BD,△ADC=△EDB, AD=DE得到△ADC△△EDB(SAS)故选择：B，(2) 由△ADC△△EDB，则BE=AC=6，AE=2AD，AB=8，在ΔABE中，AB-BE<AE<AB+BE，即AB-BE=8-6=2，AB+BE=14，则2<2AD<14，1<AD<7故选择：C，灵活运用延长AD到G，使DG=AD，连接BG，由（1）知△ADC△△GDB，BG=AC=AE+EC=7，△G=△DAC，BG△AC，△BFG=△AFE，ΔGBF△ΔAEF，BG BF AE EF=， 744BF =， BF=7．【点睛】本题考查中线加倍问题，由中线加倍，利用SAS 推出三角形全等，把问题转化为三角形中的问题，用三角形的三边关系，确定取值范围，由△ADC △△GDB ，△G=△DAC 可以判定BG△AC ，由△BFG=△AFE ，得ΔGBF△ΔAEF ，用相似三角形的性质解决问题． 7．（1）采用第一种方法，证明见解析（2）转化思想（3）AC+DE ＞CD ，证明见解析【解析】【分析】（1）过点C 作//CF AB ，证明得到△ABE△△FCE ，得到BAE F ∠=∠，再根据AB DC =得到D F =∠∠，故可得到BAE D ∠=∠；（2）此题用到了转化思想；（3）过点E 作//EF AC ，证明得到△ABC△△EBF ，得到AC=EF,连接DF,利用等腰三角形三线合一得到CD=DF ，再根据三角形的三边关系得到EF DE +与DF 之间的大小关系即可求解．【详解】（1）采用第一种方法，过点C 作//CF AB ，交DE 的延长线于点F ．△//CF AB△B ECF ∠=∠,BAE CFE ∠=∠又E 点是BC 中点，△BE=CE△△ABE△△FCE（AAS）△BAE F∠=∠，AB=CF,A,E,F在同一直线上，△AB DC=△D F=∠∠△BAED∠=∠；（2）此题用到了转化思想；故答案为：转化思想；（3）如图，过点E作//EF AC，同（1）理得到△ABC△△EBF，△AC=EF，BC=BF连接DF△BC BD⊥△△CDF是等腰三角形△CD=DF，在△DEF中，EF DE+＞DF故AC+DE＞CD．【点睛】此题主要考查全等三角形的判定与性质，解题的关键是熟知全等三角形的判定方法及等腰三角形的性质．8．(1)详见解析;(2)AF=2DG,且AF△DG,证明详见解析.【解析】【分析】(1) 利用条件先△DAE△△DBF,从而得出△FDE是等腰直角三角形,再证明△AEF是等腰直角三角形,即可.(2) 延长DG至点M,使GM=DG,交AF于点H,连接BM,先证明△BGM△△EGD,再证明△BDM△△DAF即可推出.【详解】解:（1）证明:设BE与AD交于点H..如图，△AD,BE分别为BC,AC边上的高,△△BEA=△ADB=90°.△△ABC=45°,△△ABD是等腰直角三角形.△AD=BD.△△AHE=△BHD,△△DAC=△DBH.△△ADB=△FDE=90°,△△ADE=△BDF.△△DAE△△DBF.△BF=AE,DF=DE.△△FDE是等腰直角三角形.△△DFE=45°.△G为BE中点,△AE=EF.△△AEF是等腰直角三角形.△△AFE=45°.△△AFD=90°,即AF△DF.（2）AF=2DG,且AF△DG.理由:延长DG至点M,使GM=DG,交AF于点H,连接BM,△点G为BE的中点,BG=GE.△△BGM△EGD,△△BGM△△EGD.△△MBE=△FED=45°,BM=DE.△△MBE=△EFD,BM=DF.△△DAC=△DBE,△△MBD=△MBE+△DBE=45°+△DBE.△△EFD=45°=△DBE+△BDF,△△BDF=45°-△DBE.△△ADE=△BDF,△△ADF=90°-△BDF=45°+△DBE=△MBD.△BD=AD,△△BDM△△DAF.△DM=AF=2DG,△FAD=△BDM.△△BDM+△MDA=90°,△△MDA+△FAD=90°.△△AHD=90°.△AF△DG.△AF=2DG,且AF△DG本题考查三角形全等的判定和性质,关键在于灵活运用性质.9．（1）证明见解析；（2）DE＝3．【解析】【分析】（1）过点P作PF△BC交AC于点F；证出△APF也是等边三角形，得出AP=PF=AF=CQ，由AAS证明△PDF△△QDC，得出对应边相等即可；（2）过P作PF△BC交AC于F．同（1）由AAS证明△PFD△△QCD，得出对应边相等FD=CD，证出AE+CD=DE12=AC，即可得出结果．【详解】（1）如图1所示，点P作PF△BC交AC于点F．△△ABC是等边三角形，△△APF也是等边三角形，AP=PF=AF=CQ．△PF△BC，△△PFD=△DCQ．在△PDF和△QDC中，PDF QDCDFP QCDPF QC∠=∠⎧⎪∠=∠⎨⎪=⎩，△△PDF△△QDC（AAS），△PD=DQ；（2）如图2所示，过P作PF△BC交AC于F．△PF△BC，△ABC是等边三角形，△△PFD=△QCD，△APF是等边三角形，△AP=PF=AF．△PE△AC，△AE=EF．△AP=PF，AP=CQ，△PF=CQ．在△PFD和△QCD中，PDF QDCDFP QCDPF QC∠=∠⎧⎪∠=∠⎨⎪=⎩，△△PFD△△QCD（AAS），△FD=CD．△AE =EF ，△EF +FD =AE +CD ，△AE +CD =DE 12=AC ． △AC =6，△DE =3．【点睛】本题考查等边三角形的判定与性质、全等三角形的判定（AAS ）与性质、平行线的性质，熟练掌握等边三角形的性质，解题的关键是掌握等边三角形的判定与性质、全等三角形的判定（AAS ）与性质、平行线的性质，熟练掌握等边三角形的性质．10．(1)B ；(2)C ；(3)证明见解析.【解析】【分析】(1)根据AD ＝DE ，△ADC ＝△BDE ，BD ＝DC 推出△ADC 和△EDB 全等即可；(2)根据全等得出BE ＝AC ＝6，AE ＝2AD ，由三角形三边关系定理得出8﹣6＜2AD ＜8+6，求出即可；(3)延长AD 到M ，使AD ＝DM ，连接BM ，根据SAS 证△ADC△△MDB ，推出BM ＝AC ，△CAD ＝△M ，根据AE ＝EF ，推出△CAD ＝△AFE ＝△BFD ，求出△BFD ＝△M ，根据等腰三角形的性质求出即可.【详解】（1）解：在△ADC 和△EDB 中AD DE ADC BDE BD CD =⎧⎪∠=∠⎨⎪=⎩，△△ADC△△EDB(SAS)，故选B ；（2）解：如图：△由(1)知：△ADC△△EDB，△BE＝AC＝6，AE＝2AD，△在△ABE中，AB＝8，由三角形三边关系定理得：8﹣6＜2AD＜8+6，△1＜AD＜7，故选C.（3）延长AD到M，使AD＝DM，连接BM，△AD是△ABC中线，△CD＝BD，△在△ADC和△MDB中DC DBADC MDBDA DM=⎧⎪∠=∠⎨⎪=⎩△△ADC△△MDB，△BM＝AC，△CAD＝△M，△AE＝EF，△△CAD＝△AFE，△△AFE ＝△BFD ，△△BFD ＝△CAD ＝△M ，△BF ＝BM ＝AC ，即AC ＝BF.【点睛】本题考查了三角形的中线，三角形的三边关系定理，等腰三角形性质和判定，全等三角形的性质和判定等知识点，主要考查学生运用定理进行推理的能力．11．（1）B ；（2）2＜AD ＜10；【初步运用】BF ＝5；【灵活运用】BE 2+CF 2＝EF 2，理由见解析【解析】【分析】（1）根据全等三角形的判定定理解答；（2）根据三角形的三边关系计算；初步运用延长AD 到M ，使AD ＝DM ，连接BM ，证明△ADC △△MDB ，根据全等三角形的性质解答；灵活运用延长ED 到点G ，使DG ＝ED ，连结GF ，GC ，证明△DBE △△DCG ，得到BE ＝CG ，根据勾股定理解答．【详解】解：（1）在△ADC 和△EDB 中，BD=CD BDE=CDA ED=AD ⎧⎪∠∠⎨⎪⎩， △△ADC△△EDB （SAS ），故选B ；（2）△△ADC△△EDB ，△EB=AC=8，在△ABE 中，AB ﹣BE ＜AE ＜AB+BE ，△2＜AD ＜10，故答案为2＜AD ＜10；【初步运用】延长AD 到M ，使AD ＝DM ，连接BM ，△AE ＝EF ．EF ＝3，△AC ＝5，△AD 是△ABC 中线，△CD ＝BD ，△在△ADC 和△MDB 中，BD=CD BDM=CDA DM=DA ⎧⎪∠∠⎨⎪⎩， △△ADC △△MDB ，△BM ＝AC ，△CAD ＝△M ，△AE ＝EF ，△△CAD ＝△AFE ，△△AFE ＝△BFD ，△△BFD ＝△CAD ＝△M ，△BF ＝BM ＝AC ，即BF ＝5；【灵活运用】线段BE 、CF 、EF 之间的等量关系为：BE 2+CF 2＝EF 2．证明：如图3，延长ED 到点G ，使DG ＝ED ，连结GF ，GC ，△ED △DF ，△EF ＝GF ，△D 是BC 的中点，△BD ＝CD ，在△BDE 和△CDG 中， ED=GD BDE=CDG BD=CD ⎧⎪∠∠⎨⎪⎩，△△BDE△△CDG（SAS），△BE＝CG，△△A＝90°，△△B+△ACB＝90°，△△BDE△△CDG，EF＝GF，△BE＝CG，△B＝△GCD，△△GCD+△ACB＝90°，即△GCF＝90°，△Rt△CFG中，CF2+GC2＝GF2，△BE2+CF2＝EF2．【点睛】本题考查全等三角形的判定和性质、三角形三边关系以及勾股定理的应用，掌握全等三角形的判定定理和性质定理是解题的关键．12．（1）45°；（2）见解析【解析】【分析】（1）由等边三角形的性质可知∠ABC＝∠ACB＝60°，由平行线的性质可知∠NBC＝60°，进一步求出∠ABN＝120°，再由三角形内角和定理即可求出∠N的度数；（2）先证△NBG≌△AEG，得到AG＝NG，AE＝BN，再证△ABN≌△ACF，即可推出AF ＝2AG．【详解】解：（1）∵△ABC是等边三角形，∴∠ABC＝∠ACB＝60°，∵AC∥BN，∴∠NBC＝∠ACB＝60°，∴∠ABN＝∠ABC+∠NBC＝120°，∴在△ABN中，∠N＝180°﹣∠ABN﹣∠BAN＝180°﹣120°﹣15°＝45°；（2）∵AC∥BN，∴∠N＝∠GAE，∠NBG＝∠AEG，又∵点G是线段BE的中点，∴BG＝EG，∴△NBG≌△AEG（AAS），∴AG＝NG，AE＝BN，∵AE＝CF，∴BN＝CF，∵∠ACB＝60°，∴∠ACF＝180°﹣∠ACB＝120°，∴∠ABN＝∠ACF，又∵AB＝AC，∴△ABN≌△ACF（SAS），∴AF＝AN，AN，∵AG＝NG＝12∴AF＝2AG．【点睛】本题考查了等边三角形的性质，平行线的性质，三角形内角和定理，全等三角形的判定与性质等，解题的关键是能够熟练运用全等三角形的判定与性质．13．（1）△.B；△. 1＜AD＜9；（2）证明见解析.【解析】【分析】（1）△.根据全等三角形的判定定理解答；△.根据三角形的三边关系定理可得AB−BE＜AE＜AB＋BE，结合BE=AC可确定AE的取值范围，易得AD的取值范围；（2）首先延长AD至M，使DM＝AD，先证明△ABD△△MCD，进而得出MC＝AB，△B ＝△MCD，即可得出△ACM＝△ACE，再证明△ACM△△ACE，即可证明结论．【详解】解：（1）△.在△ADC和△EDB中，BD CDBDE CDA DE AD⎧⎪∠∠⎨⎪⎩＝＝＝，△△ADC△△EDB（SAS），故选B；△.△△ADC△△EDB，△BE=AC，△AB−BE＜AE＜AB＋BE，△AB− AC＜AE＜AB＋AC，即2＜AE＜18，△1＜AD＜9，故答案为1＜AD＜9；（2）延长AD至M，使DM＝AD，△AD是△ABC的中线，△BD＝CD，在△ABD和△MCD中，BD CDADB MDC AD DM⎧⎪∠∠⎨⎪⎩＝＝＝，△△ABD△△MCD（SAS），△MC＝AB，△B＝△MCD，△AB＝CE，△CM＝CE，△△BAC＝△BCA，△△B＋△BAC＝△ACB＋△MCD，即△ACE＝△ACM，在△ACE和△ACM中，AC ACACE ACM CM CE⎧⎪∠∠⎨⎪⎩＝＝＝，△△ACM△△ACE（SAS），△AE＝AM，△AM＝2AD，△AE＝2AD．【点睛】本题考查的是三角形三边关系以及全等三角形的判定和性质，掌握全等三角形的判定定理和性质定理利用倍长中线得出辅助线是解题关键．14．（1）45°；（2）见解析【解析】【分析】（1）由等边三角形的性质可知△ABC=△ACB=60°，由平行线的性质可知△NBC=60°，进一步求出△ABN=120°，再由三角形内角和定理即可求出△N的度数；（2）先证△NBG△△AEG，得到AG=NG，AE=BN，再证△ABN△△ACF，即可推出AF=2AG．【详解】（1）△△ABC是等边三角形，△△ABC=△ACB=60°，△AC△BN，△△NBC=△ACB=60°，△△ABN=△ABC+△NBC=120°，△在△ABN中，△N=180°-△ABN-△BAN=180°-120°-15°=45°；（2）△AC△BN，△△N=△GAE，△NBG=△AEG，又△点G是线段BE的中点，△BG=EG，△△NBG△△AEG（AAS），△AG=NG，AE=BN，△AE=CF，△BN=CF，△△ACB=60°，△△ACF=180°-△ACB=120°，△△ABN=△ACF，又△AB=AC，△△ABN△△ACF（SAS），△AF=AN，△AG=NG=12AN，△AF=2AG．【点睛】考查了等边三角形的性质，平行线的性质，三角形内角和定理，全等三角形的判定与性质等，解题的关键是能够熟练运用全等三角形的判定与性质．15．（1）证明见解析；（2）DE＝3．【解析】【分析】（1）过点P作PF△BC交AC于点F；证出△APF也是等边三角形，得出AP=PF=AF=CQ，由AAS证明△PDF△△QDC，得出对应边相等即可；（2）过P作PF△BC交AC于F．同（1）由AAS证明△PFD△△QCD，得出对应边相等FD=CD，证出AE+CD=DE12=AC，即可得出结果．【详解】（1）如图1所示，点P作PF△BC交AC于点F．△△ABC是等边三角形，△△APF也是等边三角形，AP=PF=AF=CQ．△PF△BC，△△PFD=△DCQ．在△PDF和△QDC中，PDF QDCDFP QCDPF QC∠∠∠∠=⎧⎪=⎨⎪=⎩，△△PDF△△QDC（AAS），△PD=DQ；（2）如图2所示，过P作PF△BC交AC于F．△PF△BC，△ABC是等边三角形，△△PFD=△QCD，△APF是等边三角形，△AP=PF=AF．△PE△AC，△AE=EF．△AP=PF，AP=CQ，△PF=CQ．在△PFD和△QCD中，PDF QDCDFP QCDPF QC∠∠∠∠=⎧⎪=⎨⎪=⎩，△△PFD△△QCD（AAS），△FD=CD．△AE=EF，△EF+FD=AE+CD，△AE+CD=DE 1 2=AC．△AC=6，△DE=3．【点睛】本题考查了等边三角形的判定与性质、等腰三角形的判定与性质、全等三角形的判定与性质、平行线的性质；熟练掌握等边三角形的性质，证明三角形全等是解决问题的关键．16．()1见解析；()21<AD<7；()3AE=6．【解析】【分析】（1）延长AD到点E，使DE=AD，根据SAS定理证明△ADC△△EDB；（2）根据全等三角形的性质、三角形的三边关系计算；（3）延长AD交EC的延长线于F，证明△ABD△△FCD，根据全等三角形的性质解答．【详解】()1延长AD到点E，使DE AD=，在ADC和EDB中，AD ED(=已作)，ADC EDB(∠∠=对顶角相等)，CD BD(=中点定义)，ADC∴△()EDB SAS，故答案为对顶角相等，SAS ；()2ADC △EDB ，BE AC 6∴==，86AE 86-<<+，1AD 7∴<<，故答案为1AD 7<<；()3延长AD 交EC 的延长线于F ，AB BC ⊥，EF BC ⊥，ABD FCD ∠∠∴=，在ABD 和FCD 中，ABD FCD BD CDADB FDC ∠=∠⎧⎪=⎨⎪∠=∠⎩， ABD ∴△FCD ， CF AB 2∴==，AD DF =，ADE 90∠=，AE EF ∴=，EF CE CF CE AB 426=+=+=+=，AE 6∴=．【点睛】本题考查了三角形的三边关系定理和全等三角形的性质和判定，解题关键是熟记全等三角形的判定条件.17．见解析【解析】【详解】试题分析：方法一：如图1中，作BF△DE于点F，CG△DE于点G，先证明△BFE△△CGE，得BF=CG，再证明△ABF△△DCG即可．方法二如图2中，：作CF△AB，交DE的延长线于点F，先证明CF=CD，再证明△ABE△△FCE即可．证明：方法一：如图1中，作BF△DE于点F，CG△DE于点G．△△F=△CGE=90°，在△BFE和△CGE中，，△△BFE△△CGE ．△BF=CG．在△ABF和△DCG中，，△△ABF△△DCG．△AB=CD．方法二如图2中，：作CF△AB，交DE的延长线于点F．△△F=△BAE．又△△ABE=△D，△△F=△D．△CF=CD．在△ABE和△FCE中，，△△ABE△△FCE．△AB=CF．△AB=CD．18．(1)详见解析(2)ED＝2【解析】【分析】（1）过P作PF△BQ，可得△APF为等边三角形，所以AP＝PF，再证△DCQ△△DFP，即可得PD＝DQ；（2）根据等腰三角形三线合一的性质可得AE＝EF，根据全等三角形对应边相等可得FD ＝CD，然后求出2DE=AC，代入数据进行计算即可得解．(1)证明：如图，过点P作PF△BC，则△DPF=△Q，△△ABC为等边三角形，△△APF是等边三角形，△AP=PF，又△AP=CQ，△PF=CQ，在△DPF和△DQC中，DPF QPDF QDCPF CQ∠=∠⎧⎪∠=∠⎨⎪=⎩，△△DPF△△DQC（AAS），△DP=DQ；(2)△△P AF为等边三角形，PE△AC，可得AE＝EF，由（1）知，△DPF△△DQC△FD＝CD，△AC＝AE＋EF＋FD＋CD，△AC＝2EF＋2FD＝2（EF＋FD）＝2ED，△AC＝BC＝4，△2ED＝4，△ED＝2．【点睛】本题考查了等边三角形的性质，全等三角形的判定与性质，等腰三角形三线合一的性质，作辅助线构造出等边三角形和全等三角形是解题的关键，也是本题的难点．19．【解析】【详解】试题分析：方法一：作BF△DE于点F，CG△DE于点G，△△F=△CGE=90°．又△△BEF=△CEG，BE=CE，△△BFE△△CGE．△BF=CG．在△ABF和△DCG中，△△F=△DGC=90°，△BAE=△CDE，BF=CG，△△ABF△△DCG．△AB=CD．方法二：作CF△AB，交DE的延长线于点F，△△F=△BAE．又△△ABE=△D，△△F=△D．△CF=CD．△△F=△BAE，△AEB=△FEC，BE=CE，△△ABE△△FCE．△AB=CF．△AB=CD．方法三：延长DE至点F，使EF=DE，又△BE=CE，△BEF=△CED，△△BEF△△CED．△BF=CD，△D=△F．又△△BAE=△D，△△BAE=△F．△AB=BF．△AB=CD．考点：1．全等三角形的判定与性质；2．阅读理解．。

全等三角形知识点演练(5大核心考点,91题)讲练)2023年中考数学一轮大单元复习

专题4.3 全等三角形考点1：全等形和全等三角形性质例1．（1）（2022秋·江苏连云港·八年级校考阶段练习）下列图标中，不是由全等图形组合成的是（）A．B．C．D．（2）（2023秋·浙江台州·八年级统考期末）如图，△ABC≌△DEF，且∠A=55°，∠B=75°，则∠F=______°．（3）（2022秋·湖南岳阳·八年级校考期中）如图，△ABC≌△DEC，点B、C、D在同一直线上，且BD=12，AC=7，则CE长为____________．知识点训练1．（2023秋·河北邢台·八年级统考期末）与下图全等的图形是（）A．B．C．D．2．（2020秋·江苏常州·八年级常州市清潭中学校考期中）找出下列各组图中的全等图形（）A．②和⑥B．②和⑦C．③和④D．⑥和⑦3．（2022秋·福建龙岩·八年级统考期末）如图，△DBC≌△ECB，且BE与CD相交于点A，下列结论错误的是（）A．BE=CD B．AB=ACC．∠D=∠E D．BD=AE4．（2023秋·四川自贡·八年级统考期末）如图所示，△ABC≌△AEF，∠B=∠E，有以下结论：①AC=AE；②EF=BC；③∠EAB=∠FAC；④∠EFA=∠AFC．其中正确的个数是（）5．（河北省唐山市2022-2023学年八年级上学期期末考试数学试题）如图，△ABC≌△DEC，点B，C，D在同一条直线上，且CE=1，CD=3，则BD的长是（）A．1.5B．2C．3.5D．46．（2023秋·四川南充·八年级统考期末）如图，点A，E，C在同一直线上，△ABC≌△DEC，AE=3，CD=8，则BC的长为（）A．3B．5C．8D．117．（2023秋·天津·八年级统考期末）如图，已知△ABC≌△DEF，CD平分∠BCA，DF与BC交于点G．若∠A=26°，∠CGF=83°，则∠E的度数是（）A．34°B．36°C．38°D．40°8．（2022秋·河南许昌·八年级统考期中）如图所示的图案是由全等的图形拼成的，其中AD=0.8，BC=1.6，则AF=（）9．（2022秋·山东菏泽·八年级统考期中）下列说法正确的是（）A．形状相同的两个三角形全等B．三个角都分别相等的两个三角形全等C．完全重合的两个三角形全等D．所有的等边三角形全等10．（2022秋·山东烟台·七年级统考期中）下列说法：①角是轴对称图形；②等腰三角形有三条对称轴；③关于某直线成轴对称的两个三角形全等；④两个全等三角形一定关于某条直线成轴对称．其中正确的个数是（）A．1个B．2个C．3个D．4个11．（2022秋·江苏宿迁·八年级统考期中）如图所示的网格是由9个相同的小正方形拼成的，图形的各个顶点均为格点，则∠1−∠2−∠3的度数为（）．A．30°B．45°C．55°D．60°12．（2023·福建南平·统考一模）如图，在△ABC中，∠BAC=135°，将△ABC绕点C逆时针旋转得到△DEC，点A，B的对应点分别为D，E．当点A、D、E在同一条直线上时，下列结论不正确．．．的是（）A．△ABC≌△DEC B．AE=AB+CDC．AD=√2AC D．AB⊥AE13．（2021秋·陕西商洛·八年级统考期末）在平面直角坐标系内，点O为坐标原点，A(−4,0)，B(0,3)．若在该坐标平面内有一点P（不与点A、B、O重合）为一个顶点的直角三角形与Rt△ABO全等，且这个以点P 为顶点的直角三角形与Rt△ABO有一条公共边，则所有符合条件的三角形个数为（）A．3个B．4个C．6个D．7个14．（2023秋·云南曲靖·八年级统考期末）如图，在平面直角坐标系中，点A的坐标为(3,0)，点B的坐标为(0,6)，点C在x轴上运动（不与点A重合），点D在y轴上运动（不与点B重合），当以点C、O、D为顶点的三角形与△AOB全等时，则点D的坐标为______．15．（2023秋·江苏镇江·八年级统考期末）如图，△AOD≌△BOC，∠A=30°，∠C=50°，∠AOC=150°，则∠COD=______°．16．（2023秋·四川南充·八年级统考期末）如图，△ABC绕点C旋转得到△DEC，点E在边AB上，若∠B=75°，则∠ACD的度数是_________．考点2：全等三角形的判定及应用例2．（1）（2023秋·山东威海·七年级统考期末）为了测量湖的宽度AB，小明同学先从A点走到点O处，再继续向前走相同的距离到达点C（即OC=OA），然后从点C沿与AB平行的方向，走到与点O，B共线的点D处，测量C，D间的距离就是湖的宽度．下列可以判断△OCD≌△OAB的是（）A．SSS B．SSA C．SAS D．ASA（2）（2023秋·黑龙江齐齐哈尔·八年级统考期末）如图，已知∠CAE=∠DAB，AC=AD，请你再添加一个条件：___________，使△ABC≌△AED．（3）（2023秋·江苏徐州·八年级统考期末）根据下列条件，能确定△ABC（存在且唯一）的是（）A．AB=2，BC=3，AC=6B．AC=4，BC=3，∠A=60°C．AB=5，BC=3，∠B=30°D．∠A=45°，∠B=45°，∠C=90°（4）（2023秋·广东汕头·八年级统考期末）如图，在△ABC中，∠ACB=65°，∠BAC=70°，AD⊥BC于点D，BM⊥AC于点M，AD与BM交于点P，则∠BPC=______．例3（2022秋·浙江宁波·八年级校考期末）如图，在Rt△ABC中，AB=BC，∠ABC=90°，BO⊥AC于点O，P是OC的中点，D是BC延长线上一点，满足PB=PD．(1)求证∠1=∠2；(2)探究CD与AP之间的数量关系，并给出证明．例4．（2023秋·黑龙江齐齐哈尔·八年级统考期末）综合与实践【阅读理解】课外兴趣小组活动时，老师提出了如下问题：如图（1），△ABC中，AB=8，AC=6，求BC边上的中线AD的取值范围，经过组内合作交流．小明得到了如下的解决方法：延长AD到点E，使DE=AD请根据小明的方法思考：(1)由已知和作图得到△ADC≌△EDB的理由是（）A．SSS B．SAS C．AAS D．HL(2)求得AD的取值范围是___________．【感悟】解题时，条件中若出现“中点”、“中线”字样，可以考虑倍长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中．【问题解决】(3)如图（2），AD是△ABC的中线，BE交AC于E，交AD于F，且AE=EF．求证：AC=BF．知识点训练1．（2022秋·浙江温州·八年级校考期中）如图，在Rt△ABC中，∠ACB=90∘,∠ABC=25∘，O为斜边中点，将线段OA绕点O逆时针旋转a(0∘<α<90∘)至OP，若CB=CP，则α的值为（）A．80∘B．65∘C．50∘D．40∘2．（2023秋·山东威海·七年级统考期末）如图，△ABC和△BDE都是等边三角形，点A，D，E在同一条直线上，BE=2，CE=4，则AE=（）A．6B．5C．8D．73．（海南省海口市（部分校）2022-2023学年八年级上学期期末检测数学试题（A））如图，直线l1∥l2∥l3，且l1与l2的距离为1，l2与l3的距离为3，等腰直角△ABC的三个顶点A、B、C分别在直线l2、l1、l3上，∠ACB=90°，则△ABC的面积为（）D．25A．10B．12C．2524．（2022秋·黑龙江双鸭山·八年级统考期末）如图所示的网格是由9个相同的小正方形拼成的，图形的各个顶点均为格点，则∠2+∠3的度数为（）A．30°B．45°C．55°D．60°5．（2022秋·安徽黄山·八年级统考期末）如图，已知等边△ABC和等边△BPE，点P在BC的延长线上，EC的延长线交AP于点M，连接BM，有下列结论：①AP=CE；②∠PME=60°；③MB平分∠AME；④AM+MC=BM，其中正确的结论是（）A．①②③B．①②④C．①③④D．①②③④6．（2022秋·山西吕梁·八年级统考期末）如图，点E，F在线段AC上，AE=CF，AD⊥DF，CB⊥BE，要根据“HL”证明Rt△ADF≌Rt△CBE，则还需添加的一个条件是（）A．AF=CE B．∠A=∠C C．AD=CB D．AD∥BC7．（2023·全国·九年级专题练习）如图，点O为△ABC的内心，∠B=60°，BM≠BN，点M，N分别为AB，BC上的点，且OM=ON．甲、乙、丙三人有如下判断：甲：∠MON=120°；乙：四边形OMBN的面积为定值；丙：当MN⊥BC时，△MON的周长有最小值．则下列说法正确的是（）A．只有甲正确B．只有乙错误C．乙、丙都正确D．只有丙错误8．（2023秋·浙江台州·八年级统考期末）如图，AB与CD相交于点O，且OA=OB，添加下列选项中的一个条件，不能判定△AOC和△BOD全等的是（）A．OC=ODB．∠A=∠BC．AC=BDD．AC∥BD9．（2023秋·浙江台州·八年级统考期末）如图，射线OC为∠AOB的平分线，点M，N分别是边OA，OB上的两个定点，且OM<ON，点P在OC上，满足PM=PN的点P的个数有（）A．0个B．1个C．2个D．无数个10．（2023秋·河南新乡·八年级统考期末）在△ABC和△DEF中，已知AB=DE，∠A=∠D，下列条件：①AC= DF；②∠B=∠E；③∠C=∠F；④BC=EF．其中一定能判定△ABC≌△DEF的个数为（）A．1B．2C．3D．411．（2022秋·四川广安·八年级统考期末）如图，AB=DC，若要用“SSS”证明△ABC≌△DCB，需要补充一个条件，这个条件是__________．12．（2022秋·福建莆田·八年级统考期末）数学社团活动课上，甲乙两位同学玩数学游戏．游戏规则是：两人轮流对△ABC及△A′B′C′的对应边或对应角添加一组等量条件（点A′，B′，C′分别是点A，B，C的对应点），某轮添加条件后，若能判定△ABC与△A′B′C′全等，则当轮添加条件者失败，另一人获胜．1甲AB=A′B′=2cm2乙∠A=∠A′=35°3甲…上表记录了两人游戏的部分过程，则下列说法正确的是___________．（填写所有正确结论的序号）①若第3轮甲添加∠C=∠C′=45°，则甲获胜；②若第3轮甲添加BC=B′C′=3cm，则甲必胜；③若第2轮乙添加条件修改为∠A=∠A′=90°，则乙必胜；④若第2轮乙添加条件修改为BC=B′C′=3cm，则此游戏最多4轮必分胜负．13．（2023秋·山东淄博·七年级统考期末）如图，点C，E，B，F在同一条直线上，AB=DE，AC=DF，BF=CE．说明AC∥DF．14．（2023秋·江苏南京·八年级统考期末）如图AB=AD,CB=CD,AC,BD相交于点E．(1)求证△ABC≅△ADC；(2)求证BE=DE．15．（2022秋·山西吕梁·八年级统考期末）如图，△ABC是等边三角形，点D，E分别在BC，CA的延长线上，且CD=AE．求证：∠D=∠E．16．（2023秋·广东汕头·八年级统考期末）如图，已知点O在等边△ABC的内部，∠AOB=105°，∠BOC=α，以OC为边作等边△COD，连接AD．(1)求证：AD=BO；(2)当α=150∘时，试判断△AOD的形状，并说明理由；17．（2023秋·江苏南京·八年级统考期末）如图，在四边形ABCD中，连接BD，AB∥CD，且AB=CD．(1)求证：△ABD≅△CDB；(2)若AB=BD，∠ABD=48°，求∠C的度数．18．（2023秋·浙江宁波·八年级校考期末）如图，在四边形ABCD中，P为CD边上的一点，BC∥AD．AP、BP 分别是∠BAD、∠ABC的角平分线．(1)若∠BAD=70°，则∠ABP的度数为_______，∠APB的度数为____________；(2)求证：AB=BC+AD；(3)设BP=3a，AP=4a，过点P作一条直线，分别与AD，BC所在直线交于点E、F，若AB=EF，直接写出AE的长（用含a的代数式表示）考点3：角平分线性质定理和逆定理例5.（2023秋·广东汕头·八年级统考期末）如图，DE⊥AB于点E，DF⊥AC于点F，若BD=CD,BE=CF．(1)求证：AD 平分∠BAC ；(2)请猜想AB +AC 与AE 之间的数量关系，并给予证明．例6.（2022秋·湖北武汉·八年级校考期末）如图，在△ABC 中，E 是BC 中垂线上一点，EM ⊥AB 于M ，EN ⊥AC 于N ，BM =CN ．求证：AE 平分∠BAC ．知识点训练1．（2022秋·贵州铜仁·九年级统考期中）如图，在平面直角坐标系中，△OAB 的顶点B 的坐标为(6,0)，OC 平分∠AOB 交AB 于点C ，反比例函数y =k x (x >0)的图象经过点A ，C ．若S △AOC :S △BOC =2:3，则k 的值为（）A ．5√716B ．45√716C ．454D ．916 2．（2023秋·山东济宁·八年级统考期末）如图，Rt △ABC 中，∠C =90°，∠ABC =60°，以顶点B 为圆心、适当长为半径作弧，在边BC 、BA 上截取BE 、BD ；然后分别以点D 、E 为圆心、以大于DE 的长为半径作弧，两弧在∠CBA 内交于点F ；作射线BF 交AC 于点G ．若AC =6，P 为边AB 上一动点，则GP 的最小值为（）A．3B．2C．1D．无法确定3．（2023秋·山东淄博·七年级统考期末）如图，已知AB=AC，∠A=36°，AB的垂直平分线MD交AC于点D，AB于点M，以下结论：①△BCD是等腰三角形；②BD是△ACB的角平分线；③△BCD的周长C△BCD=AC+ BC；④△ADM≌△BCD．正确的有（）A．①③B．①②C．①②③D．③④4．（2023秋·黑龙江牡丹江·八年级统考期末）如图，已知△ABC和△ADE都是等腰直角三角形，∠BAC=∠EAD=90°，BD，CE交于点F，连接AF，下列结论：①BD=CE；②∠AEF=∠ADF；③BD⊥CE；④AF 平分∠CAD；⑤∠AFE=45°，其中结论正确的序号是（）A．①②③④B．①②④⑤C．①③④⑤D．①②③⑤5．（2022秋·福建泉州·八年级统考期末）小明同学在学习了全等三角形的相关知识后发现，只用两把完全相同的长方形直尺就可以作出一个角的平分线．如图：一把直尺压住射线OB，另一把直尺压住射线OA并且与第一把直尺交于点P，小明说：“射线OP就是∠BOA的角平分线．”他这样做的依据是（）A．角的内部到角两边距离相等的点在这个角的平分线上．B．角平分线上的点到角两边的距离相等．C．三角形三个内角的平分线交于同一个点．D．三角形三个内角的平分线的交点到三条边的距离相等．6．（2023秋·河北邢台·八年级统考期末）如图，在△ABC中，∠BAC=60°，角平分线BE，CD相交于点P，若AP=4，AC=6，则S△APC=（）．A．4B．6C．12D．247．（2023秋·江苏泰州·八年级统考期末）已知，如图，△ABC中，∠ABC=48°，∠ACB=84°，点D、E分别在BA、BC延长线上，BP平分∠ABC，CP平分∠ACE，连接AP，则∠PAC的度数为（）A．45°B．48°C．60°D．66°8．（2023秋·河北沧州·八年级统考期末）如图，在△AOB和△COD中，OA=OB,OC=OD,OA<OC,∠AOB=∠COD=108∘，连接AC，BD交于点M，连接OM．甲、乙、丙三人的说法如下，下列判断正确的是（）甲：AC=BD；乙：∠CMD>∠COD；丙：MO平分∠BMCA．乙错，丙对B．甲和乙都对C．甲对，丙错D．甲错，丙对9．（2023秋·重庆大足·八年级统考期末）如图，△ABC的三边AC、BC、AB的长分别是8、12、16，点O是△ABC三条角平分线的交点，则S△OAB:S△OBC:S△OAC的值为（）A．4:3:2B．5:3:2C．2:3:4D．3:4:510．（2022秋·甘肃庆阳·八年级统考期中）庆阳市是传统的中药材生产区，优越的地理气候条件形成了较独特的资源禀赋，孕育了丰富的中药植物资源和优良品种，素有“天然药库”“中药之乡”的美称．如图，三条公路把A、B、C三个盛产中药材的村庄连成一个三角形区域，此地区决定在这个三角形区域内修建一个中药材批发市场，要使批发市场到三条公路的距离相等，则这个批发市场应建在（）A．三角形的三条中线的交点处B．三角形的三条角平分线的交点处C．三角形的三条高的交点处D．以上位置都不对11．（2022秋·海南海口·八年级校联考期末）如图，在△ABC中，∠A=90°，BD平分∠ABC，BC=12，AD=4，则△DBC的面积为__________．12．（2023·湖南衡阳·校考一模）如图所示，点O在一块直角三角板ABC上（其中∠ABC=30°），OM⊥AB于点M，ON⊥BC于点N，若OM=ON，则∠ABO=_______度．13．（2023秋·湖北省直辖县级单位·八年级统考期末）如图，△ABC与△BDE都为等边三角形，连接AE与CD，延长AE交CD于点F，连接FB．给出下面四个结论：①AE=CD；②∠AFC=60°；③BF平分∠EBD；④FB 平分∠EFD.其中所有正确结论的序号是__________．14．（2023春·浙江金华·八年级浙江省义乌市后宅中学校考阶段练习）已知：OP平分∠MON，点A，B分别在边OM，ON上，且∠OAP+∠OBP=180°．(1)如图1，当∠OAP=90°时，求证：OA=OB；(2)如图2，当∠OAP<90°时，作PC⊥OM于点C．求证：①PA=PB；②请直接写出OA，OB，AC之间的数量关系．15．（2022春·广东茂名·八年级统考期中）如图，在Rt△ABC中，∠A=90°，∠B=30°，CM平分∠ACB交AB 于点M，过点M作MN∥BC交AC于点N，若AN=1，求BC的长．考点4：线段垂直平分线性质定理和逆定理例7. (1)（2023秋·浙江宁波·八年级宁波市第七中学校考期末）如图，△ABC中，AB<AC<BC，如果要使用尺规作图的方法在BC上确定一点P，使PA＋PB=BC，那么符合要求的作图痕迹是（）A．B．C．D．(2)（2023秋·云南曲靖·八年级统考期末）如图，在△ABC中，∠BAC=110°，EF是边AB的垂直平分线，垂足为E，交BC于F．MN是边AC的垂直平分线，垂足为M，交BC于N．连接AF、AN则∠FAN的度数是（）A．70B．55C．40D．30(3)（2022秋·新疆乌鲁木齐·八年级校考期末）电信部门要再S区修建一座手机信号发射塔，按照设计要求，发射塔到两个城镇A，B的距离必须相等，到两条高速公路OC，OD的距离也必须相等，则发射塔应建在（）A．∠COD的平分线上任意某点处B．线段AB的垂直平分线上任意某点处C．∠COD的平分线和线段AB的交点处D．∠COD的平分线和线段AB垂直平分线的交点处例8.（2023春·重庆沙坪坝·八年级重庆南开中学校考开学考试）如图，在△ABC中，EF是AB的垂直平分线，AD⊥BC于点D，且D为CE的中点．(1)求证：BE=AC；(2)若∠C=70°，求∠BAC的度数．知识点训练1．（2022秋·海南海口·八年级校联考期末）如图，在△ABC中，DE垂直平分BC，若AB=6，AC=8，则△ABD 的周长等于（）A．11B．13C．14D．162．（2023秋·河南南阳·八年级统考期末）如图，等腰△ABC的底边BC长为6，面积是24，E为腰AB的垂直平分线MN上一动点．点D为BC的中点，则△BDE的周长的最小值为（）A．6B．8C．10D．113．（2023秋·福建泉州·八年级校联考期末）如图，根据尺规作图的痕迹，计算∠α的度数为（）A．56∘B．68∘C．28∘D．34∘4．（2023秋·山东东营·八年级统考期末）如图，平行四边形ABCD的对角线AC、BD交于点O，DE平分∠ADCAB，连接OE．下列结论：①S▱ABCD=AD⋅BC；②DB平分∠CDE；③AO=交AB于点E，∠BCD=60°，AD=12DE；④OE垂直平分BD．其中正确的个数有（）A．1个B．2个C．3个D．4个5．（2022秋·河北石家庄·八年级统考期末）如图，在△ABC中，AB=AC，尺规作图：（1）分别以B，C为圆心，BC长为半径作弧，两弧交于点D；（2）连接AD，BD，CD，AD与BC交于点E，则下列结论中错误的是（）A．△ABD≌△ACD B．△DBE≌△DCEC．△BCD是等边三角形D．BC垂直平分AD6．（2023秋·黑龙江牡丹江·八年级统考期末）如图，在△ABC中，∠ACB=90°，∠A=75°，DE垂直平分AB，交AB于点D，交BC于点E，若BE=8cm，则AC为______cm．7．（2023秋·重庆万州·八年级统考期末）如图，在△ABC中，边AC的垂直平分线交BC于点D，交AC于点E，连接AD，若AD是∠BAC的角平分线，且AB=AD时，则∠B=___________°．8．（2023秋·山东淄博·七年级统考期末）如图，已知AB是线段CD的垂直平分线，垂足为点F．E是AB上的一点，∠CEF=30°，CF=2．试求△CED的周长．9．（2022秋·山西吕梁·八年级统考期末）如图，在△ABC中，AB=BC，EF是AB的垂直平分线，交AB于点E，交BC于点F．(1)按要求作图：作∠ABC的平分线BD，交AC于点D，交EF于点O，连接OA，OC（尺规作图，保留痕迹，不写作法）；(2)求证：点O在BC的垂直平分线上；(3)若∠CBD=20°，求∠COF的度数．10．（2023秋·黑龙江齐齐哈尔·八年级统考期末）如图，∠AOB=30°，M，N分别是射线OA,OB上的动点，OP平分∠AOB，OP=9，则△PMN的周长的最小值为（）C．6D．27A．9B．9211．（2022秋·山东临沂·八年级校考期末）.如图，电信部门要在S区修建一座电视信号发射塔．按照设计要求，发射塔到两个城镇A，B距离必须相等，到两条高速公路m和n的距离也必须相等．发射塔应修建在什么位置？在图上标出它的位置．（保留作图痕迹）12．（2023·全国·九年级专题练习）如图，∠HAB=30°，点B与点C关于射线AH对称，连接AC．D点为射线AH 上任意一点，连接CD．将线段CD绕点C顺时针旋转60°，得到线段CE，连接BE．(1)求证：直线EB是线段AC的垂直平分线；(2)点D是射线AH上一动点，请你直接写出∠ADC与∠ECA之间的数量关系．13．（2023秋·山西运城·九年级统考期末）综合与实践问题情境：课堂上老师展示了一张直角三角形纸片．请同学们进行折纸活动，已知在Rt△ABC中．∠ACB=90°，点D、F分别是BC、AB上的一点．连接DF．(1)如图1．小红将△BDF 沿直线DF 折叠，点B 恰好落在BC 上点E 处，若S △BDF S 四边形ACEF=17，则DEDC的值______．(2)如图2，小明将△BDF 沿直线DF 折叠，点B 落在AC 上点E 处，若FE ⊥AC ，求证：四边形BDEF 是菱形； (3)如图3．小亮将△BDF 沿直线DF 折叠，点B 落在AC 延长线上点E 处，且EF 平分∠AED ，若AC =3，BC =4，求CE 的长．14．（2023秋·江苏南京·八年级统考期末）（1）如图1，在△ABC 中，∠A =30°，∠C =90°．求证BC =12AB ．①补全证明过程．证明：如图2，取AB 中点D ，连接CD ． ∴BD =AD =12AB ．在△ABC 中，∠C =90°， ∴______； ∴CD =BD ．又∠A =30°，∴∠B =90°−∠A =60°． ∴△BCD 为______三角形． ∴BC =BD =12AB ．②请用文字概括①所证明的命题：____________．（2）如图3，某市三个城镇中心D，E，F恰好分别位于一个等边三角形的三个顶点处，在三个城镇中心之间铺设通信光缆，以城镇D为出发点设计了三种连接方案：方案1：DE+EF；方案2：DG+EF（G为EF的中点）；方案3：OD+OE+OF（O为△DEF三边的垂直平分线的交点）．①设DE=6，通过计算，比较三种连接方案中铺设的光缆长度的长短；②不计算，比较三种连接方案中铺设的光缆长度的长短，并说明理由．15．（2023秋·河南洛阳·八年级统考期末）我们已经知道线段是轴对称图形，线段的垂直平分线是线段的对称轴，如图1，直线MN是线段AB的垂直平分线，P是MN上任一点，连接PA、PB，将线段AB沿直线MN对称，我们发现PA与PB完全重合，由此即有：线段垂直平分线的性质定理：线段垂直平分线上的点到线段两端的距离相等．解答下列问题：(1)请你结合图形把已知和求证补充完整，并写出证明过程．已知：如图1，MN⊥AB，垂足为点C，______，点P是直线MN上的任意一点．求证：______．(2)证明：如图2，CD是线段AB垂直平分线，则∠CAD与∠CBD有何关系？请说明理由．考点5：全等三角形的综合问题例9.（2023秋·河南南阳·八年级统考期末）如图，在△ABC中，∠ACB=90°，CE⊥AB于点E，AD=AC，AF平分∠CAB交CE于点F，DF的延长线交AC于点G．(1)求证：DF∥BC；(2)若AE=6，CE=8，求线段GF的长．例10.（2022秋·湖北黄冈·八年级统考期末）已知OM是∠AOB的平分线，点P是射线OM上一定点，点C、D分别在射线OA、OB上，连接PC、PD．(1)如图①，当PC⊥OA，PD⊥OB时，则PC与PD的数量关系是___________；(2)如图②，点C、D在射线OA、OB上滑动，且∠AOB=90∘，当PC⊥PD时，PC与PD在（1）中的数量关系还成立吗？请说明理由．(3)在问题（2）中，若OC+OD=6，则四边形ODPC的面积S是否为定值？若是，请求出该定值，若不是，请说明理由．知识点训练1．（2022秋·河南商丘·八年级统考期中）如图，在△ABC中，∠ABC=90°，D,E分别为边AC,BC上一点，连接BD,DE．已知AB=BE,AD=DE．(1)求证：BD平分∠ABC；(2)若∠A=55°，求证：∠CDE=14∠ADB．2．（2023秋·湖北荆州·八年级统考期末）如图，在△ABC中，BC=2AB，D是AC上一点，∠ABD=20°，E 是BD上一点，EA⊥AB，EB=EC．(1)求证：BD平分∠ABC；(2)求∠DEC的度数．3．（2023秋·重庆长寿·九年级统考期末）在图（1）至图（2）中，直线MN与线段AB相交于点O，∠1=∠2=45°．(1)如图（1），若AO=OB，请写出AO与BD的数量关系和位置关系；(2)将图（1）中的MN绕点O顺时针旋转得到图（2），其中AO=OB．求证：AC=BD，AC⊥BD．4．（2023秋·重庆万州·八年级统考期末）小明在物理课上学习了发声物体的振动实验后，对其作了进一步的探究：在一个支架的横杆点O处用一根细绳悬挂一个小球A，小球A可以自由摆动，如图，OA表示小球静止时的位置．当小明用发声物体靠进小球时，小球从OA摆到OB位置，此时过点B作BD⊥OA于点D，当小球摆到OC位置时，OB与OC恰好垂直（图中的A、B、O、C在同一平面上），过点C作CE⊥OA于点E，测得CE=15cm,AD=2cm．(1)试说明OE=BD；(2)求DE的长．5．（2022秋·海南海口·八年级校联考期末）如图1，在△ABC中，∠BAC=90°，AB=AC，AD⊥BC于点D，∠MDN=90°，将∠MDN绕点D顺时针旋转，它的两边分别交AB、AC于点E、F．(1)求证：△BDE≌△ADF；(2)如图2，若DM=DN，连接BM、NA，求证：BM=AN．6．（2023秋·江苏宿迁·八年级统考期末）如图，已知AC平分∠BAF，CE⊥AB于点E，CF⊥AF于点F，且BC= DC．(1)求证：BE=DF；(2)若AB=21，AD=9，求DF的长．7．（2023秋·广西南宁·九年级统考期末）如图，将矩形ABCD绕点B旋转得到矩形BEFG，点E在AD上，延长DA交GF于点H.(1)求证：△ABE≅△FEH；(2)连接BH，若∠EBC=30°，求∠ABH的度数．8．（2023秋·山东威海·七年级统考期末）在四边形ABDE中，点C是BD边的中点．(1)如图①，AC平分∠BAE，∠ACE=90°，写出线段AE，AB，DE间的数量关系及理由；(2)如图②，AC平分∠BAE，EC平分∠AED，∠ACE=120°，写出线段AB，BD，DE，AE间的数量关系及理由．9．（2022秋·广西柳州·八年级统考期末）在平面直角坐标系中，点O为坐标原点，A(a,0)，B(0,b)，且a，b满足(a−3)2+|b−3|=0，连接AB．(1)求点A，B点的坐标；(2)如图1，动点C从点O出发，以1个单位/秒的速度沿y轴正半轴运动，运动时间为t秒(0<t<3)，连接AC，过点C作CD⊥AC，且CD=CA，点D在第一象限，请用含有t的式子表示点D的坐标；(3)在（2）的条件下，如图2，连接并延长DB交x轴于点E，连接AD和AB，过点B作线段BF交x轴于点F，使得∠OBF=∠DCB，已知此时点F的坐标为(−1,0)，求△ADE的面积．10．（2023秋·福建福州·八年级统考期末）在平面直角坐标系xOy中，点A(0,a)，B(b,0)，C(c,0)，点D在第四象限，其中a>0，b<0，c>0，∠BAC+∠BDC=180°，AC⊥CD．(1)如图1，求证：∠BAO=∠CBD；(2)若|a−c|+b2+6b+9=0，且AB=BD．①如图1，求四边形ACDB的面积；（用含a的式子表示）②如图2，BD交y轴于点E，连接AD，当E关于AD的对称点K落在x轴上时，求CK的长．。

中考数学专题复习全等三角形

∵AE=AC，∠EAD=∠CAD，AD=AD
∴△ADE≌△ADC。DE=CD,∠AED=∠C
∵AB=AC+CD，∴DE=CD=AB-AC=AB-AE=BE
∠B=∠EDB
∠C=∠B+∠EDB=2∠B
12证明：
∵BE‖CF
∴∠E=∠CFM，∠EBM=∠FCM
∵BE=CF
∴△BEM≌△CFM
∴BM=CM
∴AM是△ABC的中线。
9作AG∥BD交DE延长线于G
AGE全等BDE
AG=BD=5
AGF∽CDF
AF=AG=5
所以DC=CF=2
10证明：
做BE的延长线，与AP相交于F点,
∵PA//BC
∴∠PAB+∠CBA=180°，
又∵,AE，BE均为∠PAB和∠CBA的角平分线
∴∠EAB+∠EBA=90°∴∠AEB=90°，EAB为直角三角形
13证明：因为AB=AC，
所以∠EBC=∠DCB
因为BD⊥AC,CE⊥AB
所以∠BEC=∠CDB
BC=CB (公共边)
则有三角形EBC全等于三角形DCB
所以BE＝CD
14
11.证明：∵∠ACB=90°,
∴∠ACD+∠BCE=90°，
而AD⊥MN于D，BE⊥MN于E,
∴∠ADC=∠CEB=90°,∠BCE+∠CBE=90°,
∵CF⊥AD
∴∠ACF+∠DCF=90°
∵∠ACF+∠CAF=90°
∴∠CAF=∠DCF
∵AC=CB∠ACG=∠B
∴△ACG≌△CBE
∴CG=BE
∵∠DCG=∠B CD=BD
∴△CDG≌△BDE

中考数学复习专项之三角形全等 (含答案)

30°AＢＯＣl D 第1题图C A P B D三角形全等一、选择题1、(2022年安徽省模拟六)在△ABC 与△A ′B ′C ′中，已知AB = A ′B ′，∠A =∠A ′，要使△ABC ≌△A ′B ′C ′，还需要增加一个条件，这个条件不正确的是…………【】 A ．AC = A ′C ′ B.BC = B ′C ′ C.∠B =∠B ′ D.∠C =∠C ′．答案：B2、(2022年江苏南京一模)如图，直线上有三个正方形a b c ，，，若a c ，的面积分别为3和4，则b 的面积为（） A ．3 B ．4 C ．5 D ．7 答案：D3．（2022郑州外国语预测卷）如图，两个等圆⊙A 、⊙B 分别与直线l 相切于点C 、D ，连接AB 与直线l 相交于点O ，∠AOB =30°，连接AC 、BD ，若AB =4，则这两个等圆的半径为（） A ．21B ．1C ．3D ．2 答案：B4、（2022河南沁阳市九年级第一次质量检测）如图，把△ABC 绕着点C 顺时针旋转30°，得到△A ′B ′C ，A ′B ′交AC 于点D ，若∠A ′DC ＝90°，则∠A 的度数是【】A.30°B.50°C.60°D.80°C5、（2022年湖北省武汉市中考全真模拟）如图，等腰△ABC 中，AB=AC ，P 为其底角平分线的交点，将△BCP 沿CP 折叠，使B 点恰好落在AC 边上的点D 处，若DA=DP ，则∠A 的度数为( ).A.20°B.30°C.32°D.36°D6、（2022年湖北宜昌调研）如图，AC ，BD 交于点E ，AE=CE ，添加以下四个条件中的一个，其中不能使△ABE ≌△CDE 的条件是（）（A ）BE=DE （B ）AB ∥CD （C ）∠A=∠C （D ）AB=CDabclEABCD答案：D7、（2022年唐山市二模）在锐角△ABC 中，∠BAC =60°，BN 、CM 为高，P 为BC 的中点，连接MN 、MP 、NP ，则结论：①NP =MP ②当∠ABC =60°时，MN ∥BC ③ BN =2AN ④AN︰AB =AM ︰AC ，一定正确的有（）A 、1个B 、2个C 、3个D 、4个答案：C8.（2022年上海闵行区二摸）在△ABC 与△A ′B ′C ′中，已知AB = A ′B ′，∠A =∠A ′，要使△ABC ≌△A ′B ′C ′，还需要增加一个条件，这个条件不正确的是（A ）AC = A ′C ′；（B ）BC = B ′C ′；（C ）∠B =∠B ′；（D ）∠C =∠C ′．答案：B二、填空题1、（2022云南勐捧中学二模）如图，AB CD ，相交于点O ，AO=CO ，试添加一个条件使得AOD COB △≌△，你添加的条件是（只需写一个）．【答案】∠A= ∠C 、∠D= ∠B 、OD=OB （答案不唯一）2．（2022年安徽初中毕业考试模拟卷一）如图，ABC ∆为等边三角形，AQ =PQ ，PR =PS ，PR ⊥AB 于R ，PS ⊥AC 于S ，则四个结论正确的是．（把所有正确答案的序号都填写在横线上）①AP 平分∠BAC ；②AS =AR ；③QP ∥AR ；④BRP ∆≌△QSP ．答案：①②③④三、解答题1、(2022年湖北荆州模拟5)（本题满分8分）将两块斜边长度相等的等腰直角三角纸板如图(1)摆放，若把图(1)中的△BCN 逆时针旋转90°，得到图(2)，图(2)中除△ABC ≌△CED 、△BCN ≌△ACF 外，你还能找到一对全等的三角形吗?写出你的结论并说明理由．AC BDO第1题答案：解：△FCM ≌△NCM ，理由如下： ∵把图中的△BCN 逆时针旋转90°， ∴∠FCN=90°，CN=CF ， ∵∠MCN=45°， ∴∠FCM=90°-45°=45°，在△FCM 和△NCM 中∵CM=CM ，∠FCM=∠NCM ， FC=CN∴△FCM ≌△NCM （SAS ）．2、(2022年湖北荆州模拟6)（本题满分8分）如图，正方形ABCD 和BEFG 在直线AB 的同侧，连接AG 、EC ,易证AG=EC ，现在将正方形BEFG 顺时针旋转30°，那么AG=EC 还成立吗？请作出旋转后的图形，并证明你的结论. 答案：解：成立. 理由如下：在ΔABG 与ΔCBE 中，0120AB CB ABG CBE BG BE =⎧⎪∠=∠=⎨⎪=⎩∴ ΔABG ≌ΔCBE ∴ AG=CE3、(2022年江苏南京一模)（7分）如图， AB =AC ，CD ⊥AB 于D ，BE ⊥AC 于E ，BE 与CD 相交于点O ． (1) 求证：AD =AE ；(2) 连接BC ，DE ，试判断BC 与DE 的位置关系并说明理由．答案：（1）证明：在△ACD 与△ABE 中， ∵∠A =∠A ，∠ADC =∠AEB =90°，AB =AC ， ∴ △ACD ≌△ABE ．…………………… 2分 ∴ AD=AE ． ……………………3分 (2) 互相平行 ……………………4分在△ADE 与△ABC 中， ∵AD=AE ，AB=AC ，∴ ∠ADE=∠AED ,∠ABC=∠ACB ……………6分且 ∠ADE =180－∠A =∠ABC.∴ DE ∥BC ． ……………7分第1题图第2题图第2题解答CACBB第2题图14．（2022年北京房山区一模）如图，点C、B、E在同一条直线上，AB∥DE，∠ACB=∠CDE，AC=CD．求证：AB=CD ．答案：证明：∵AB∥DE∴∠ABC=∠E ------------------------------1分∵∠ACB=∠CDE，AC=CD --------------------- --------3分∴△ABC≌△CED -------------------------4分∴AB=CD--------------------------5分5．（2022年北京房山区一模）（1）如图1，△ABC和△CDE都是等边三角形，且B、C、D三点共线，联结AD、BE相交于点P，求证：BE = AD.（2）如图2，在△BCD中，∠BCD＜120°，分别以BC、CD和BD为边在△BCD外部作等边三角形ABC、等边三角形CDE和等边三角形BDF，联结AD、BE和CF交于点P，下列结论中正确的是（只填序号即可）①AD=BE=CF；②∠BEC=∠ADC；③∠DPE=∠EPC=∠CPA=60°；（3）如图2，在（2）的条件下，求证：PB+PC+PD=BE.答案：(1)证明：∵△ABC和△CDE都是等边三角形∴BC=AC，CE=CD，∠ACB=∠DCE=60°∴∠BCE=∠ACD∴△BCE≌△ACD（SAS）∴BE=AD--------------1分（2）①②③都正确--------------4分（3）证明：在PE上截取PM=PC，联结CM由（1）可知，△BCE≌△ACD（SAS）EDC BA第1题图ADAB∴∠1=∠2设CD 与BE 交于点G ,,在△CGE 和△PGD 中 ∵∠1=∠2，∠CGE =∠PGD∴∠DPG =∠ECG =60°同理∠CPE =60° ∴△CPM 是等边三角形--------------5分 ∴CP =CM ，∠PMC =60° ∴∠CPD =∠CME =120°∵∠1=∠2,∴△CPD ≌△CME （AAS ）---6分 ∴PD =ME∴BE =PB +PM +ME =PB +PC +PD . -------7分即PB+PC+PD=BE .6．（2022年北京龙文教育一模）已知：如图，AB ∥CD ，AB =CD ，点E 、F 在线段AD 上，且AF=DE ．求证：BE =CF ．答案：证明: AF=DE ， ∴ AF-EF=DE –EF ．即 AE=DF ．………………1分AB ∥CD ，∴∠A =∠D ．……2分在△ABE 和△DCF 中， AB =CD ， ∠A =∠D ， AE=DF ．∴△ABE ≌△DCF ．……….4分 ∴ BE =CF ．…………….5分7. （2022年北京龙文教育一模）阅读下面材料：问题：如图①，在△ABC 中， D 是BC 边上的一点，若∠BAD =∠C =2∠DAC =45°，DC =2．求BD 的长．小明同学的解题思路是：利用轴对称，把△ADC 进行翻折，再经过推理、计算使问题得到解决．（1）请你回答：图中BD 的长为；（2）参考小明的思路，探究并解答问题：如图②，在△ABC 中，D 是BC 边上的一点，若∠BAD =∠C =2∠DAC =30°，DC =2，求BD 和AB 的长．FE ACDB第3题图答案：解：（1）22=BD . ……………………………… ………………………1分（2）把△ADC 沿AC 翻折，得△AEC ，连接DE ， ∴△ADC ≌△AEC .∴∠DAC =∠EAC ，∠DCA =∠ECA ， DC ＝EC . ∵∠BAD =∠BCA =2∠DAC =30°， ∴∠BAD =∠DAE =30°，∠DCE =60°.∴△CDE 为等边三角形. ……………………2分 ∴DC ＝DE .在AE 上截取AF ＝AB ，连接DF ， ∴△ABD ≌△AFD . ∴BD ＝DF .在△ABD 中，∠ADB =∠DAC ＋∠DCA =45°， ∴∠ADE =∠AED =75°，∠ABD =105°. ∴∠AFD =105°. ∴∠DFE =75°. ∴∠DFE =∠DEF . ∴DF ＝DE .∴BD ＝DC ＝2. …………………………………………………………………3分作BG ⊥AD 于点G ， ∴在Rt △BDG 中， 2=BG . ……………………………………………4分∴在Rt △ABG 中，22=AB . ……………………………………………5分 8．（2022年北京平谷区一模）已知：如图，AB ∥CD ，AB =EC ，BC =CD . 求证：AC =ED .答案：证明：∵ AB //CD ，∴B DCE ∠=∠．………………… ………………………1分在△ABC 和△ECD 中，= =B DCE AB EC BC CD ∠∠⎧⎪=⎨⎪⎩，，， ∴ △ABC ≌△ECD ． …………………… ………………4分∴ AC =ED ．………………………… ……………………5分9．（2022年北京顺义区一模）已知：如图，CA 平分BCD ∠, 点E 在AC 上，BC EC =，AC DC =．求证：A D ∠=∠．答案：证明：∵CA 平分BCD∠∴ ACB DCE ∠=∠ ……………1分在ABC ∆和DEC ∆中∵BC EC ACB DCE AC DC =⎧⎪∠=∠⎨⎪=⎩……………3分 ∴ABC ∆≌DEC ∆ …………………………………………… 4分 ∴A D ∠=∠ ……………………………………………5分10．（2022年北京平谷区一模）（1）如图(1)，△ABC 是等边三角形，D 、E 分别是 AB 、BC 上的点，且BD CE =，连接AE 、CD 相交于点P . 请你补全图形，并直接写出∠APD 的度数；= （2）如图（2）,Rt △ABC 中，∠B =90°，M 、N 分别是 AB 、BC 上的点，且,AM BC =BM CN =，连接AN 、CM 相交于点P . 请你猜想∠APM = °，并写出你的推理过程.答案：解：（1）60° （2）45° ………………………………..2分证明：作AE ⊥AB 且AE CN BM ==. 可证EAM MBC ∆≅∆. ……………………………..3分 ∴ ,.ME MC AME BCM =∠=∠∵ 90,CMB MCB ∠+∠=︒∴ 90.CMB AME ∠+∠=︒∴ 90.EMC ∠=︒∴ EMC ∆是等腰直角三角形,45.MCE ∠=︒ ……………….5分又△AEC ≌△CAN （s ， a ， s ）∴ .ECA NAC ∠=∠ ∴ EC ∥AN.∴ 45.APM ECM ∠=∠=︒…………………………………………………………………..7分EDCBA第6题图第7题图11.（2022浙江东阳吴宇模拟题）(本题12分) 如图，平面直角坐标系中，点A （0，4），B （3，0），D 、E 在x 轴上，F 为平面上一点，且EF ⊥x 轴，直线DF 与直线AB 互相垂直，垂足为H ，△AOB ≌△DEF ，设BD ＝h 。

2023年中考数学----全等三角形的判定与性质知识回顾与专项练习题(含答案解析)

2023年中考数学----全等三角形的判定与性质知识回顾与专项练习题（含答案解析）知识回顾1.三角形的三边关系：三角形的任意两边之和大于第三边，任意两边之差小于第三边。

三角形的三边一旦确定，这三角形就固定了，这是三角形具有稳定性。

2.三角形的内角和定理：三角形的三个内角之和等于180°。

3.三角形的外角定理：三角形的一个外角等于它不相邻的两个内角之和。

大于它不相邻的任意一个内角。

4.全等三角形的性质：若两个三角形全等，则他们的对应边相等；对应角相等；对应边上的中线相等，高线相等，角平分线也相等；且这两个三角形的周长和面积均相等。

5.全等三角形的判定：①边边边（SSS）：三条边分别对应性相等的两个三角形全等。

②边角边（SAS）：两边及其这两边的夹角对应相等的两个三角形全等。

③角边角（ASA）：两角及其这两角的夹边对应相等的两个三角形全等。

④角角边（AAS）：两角及其其中一角的对边对应相等的两个三角形全等。

⑤直角三角形判定（HL）：直角三角形中斜边与其中任意一直角边分别对应相等的两个直角三角形全等。

全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件。

在应用全等三角形的判定时，要注意三角形间的公共边和公共角，必要时添加适当辅助线构造三角形。

专项练习题（含答案解析）1．已知：如图，∠1＝∠2，∠3＝∠4．求证：AB＝AD．【分析】根据邻补角的定义得出∠ACB＝∠ACD，利用ASA证明△ACB≌△ACD，根据全等三角形的性质即可得解．【解答】证明：∵∠3＝∠4，∴∠ACB＝∠ACD，在△ACB和△ACD中，，∴△ACB≌△ACD（ASA），∴AB＝AD．2．如图，△ABC是等腰三角形，点D，E分别在腰AC，AB上，且BE＝CD，连接BD，CE．求证：BD＝CE．【分析】根据等腰三角形的性质得出∠EBC＝∠DCB，进而利用SAS证明△EBC与△DCB全等，再利用全等三角形的性质解答即可．【解答】证明：∵△ABC∴∠EBC＝∠DCB，在△EBC与△DCB中，，∴△EBC≌△DCB（SAS），∴BD＝CE．3．如图1是小军制作的燕子风筝，燕子风筝的骨架图如图2所示，AB＝AE，AC＝AD，∠BAD＝∠EAC，∠C＝50°，求∠D的大小．【分析】由∠BAD＝∠EAC可得∠BAC＝∠EAD，根据SAS可证△BAC≌△EAD，再根据全等三角形的性质即可求解．【解答】解：∵∠BAD＝∠EAC，∴∠BAD+∠CAD＝∠EAC+∠CAD，即∠BAC＝∠EAD，在△BAC与△EAD中，，∴△BAC≌△EAD（SAS），∴∠D＝∠C＝50°．4．如图，AC平分∠BAD，CB⊥AB，CD⊥AD，垂足分别为B，D．（1）求证：△ABC≌△ADC；（2）若AB＝4，CD＝3，求四边形的面积．【分析】（1）由AC平分∠BAD，得∠BAC＝∠DAC，根据CB⊥AB，CD⊥AD，得∠B＝90°＝∠D，用AAS 可得△ABC≌△ADC；（2）由（1）△ABC≌△ADC，得BC＝CD＝3，S△ABC＝S△ADC，求出S△ABC＝AB•BC＝6，即可得四边形ABCD的面积是12．【解答】（1）证明：∵AC平分∠BAD，∴∠BAC＝∠DAC，∵CB⊥AB，CD⊥AD，∴∠B＝90°＝∠D，在△ABC和△ADC中，，∴△ABC≌△ADC（AAS）；（2）解：由（1）知：△ABC≌△ADC，∴BC＝CD＝3，S△ABC＝S△ADC，∴S△ABC＝AB•BC＝×4×3＝6，∴S△ADC＝6，∴S四边形ABCD＝S△ABC+S△ADC＝12，答：四边形ABCD的面积是12．5．如图，在△ABC中，点D在边BC上，CD＝AB，DE∥AB，∠DCE＝∠A．求证：DE＝BC．【分析】利用平行线的性质得∠EDC＝∠B，再利用ASA证明△CDE≌△ABC，可得结论．【解答】证明：∵DE∥AB，∴∠EDC＝∠B，在△CDE和△ABC中，，∴△CDE≌△ABC（ASA），∴DE＝BC．6．如图，在等边三角形ABC中，点M为AB边上任意一点，延长BC至点N，使CN＝AM，连接MN交AC于点P，MH⊥AC于点H．（1）求证：MP＝NP；（2）若AB＝a，求线段PH的长（结果用含a的代数式表示）．【分析】（1）过点M作MQ∥BC，交AC于点Q，根据等边三角形的性质以及平行线的性质可得∠AMQ＝∠AQM＝∠A＝60°，可得△AMQ是等边三角形，易证△QMP≌△CNP（AAS），即可得证；（2）根据等边三角形的性质可知AH＝HQ，根据全等三角形的性质可知QP＝PC，即可表示出HP的长．【解答】（1）证明：过点M作MQ∥BC，交AC于点Q，如图所示：在等边△ABC中，∠A＝∠B＝∠ACB＝60°，∵MQ∥BC，∴∠AMQ＝∠B＝60°，∠AQM＝∠ACB＝60°，∠QMP＝∠N，∴△AMQ是等边三角形，∴AM＝QM，∵AM＝CN，∴QM＝CN，在△QMP和△CNP中，，∴△QMP≌△CNP（AAS），∴MP＝NP；（2）解：∵△AMQ是等边三角形，且MH⊥AC，∴AH＝HQ，∵△QMP≌△CNP，∴QP＝CP，∴PH＝HQ+QP＝AC，∵AB＝a，AB＝AC，∴PH＝a．7．如图，点A，D，C，F在同一条直线上，AB＝DE，BC＝EF．有下列三个条件：①AC＝DF，②∠ABC ＝∠DEF，③∠ACB＝∠DFE．（1）请在上述三个条件中选取一个条件，使得△ABC≌△DEF．你选取的条件为（填写序号）（只需选一个条件，多选不得分），你判定△ABC≌△DEF的依据是（填“SSS”或“SAS”或“ASA”或“AAS”）；（2）利用（1）的结论△ABC≌△DEF．求证：AB∥DE．【分析】（1）根据SSS ABC≌△DEF，即可解决问题；（2）根据全等三角形的性质可得∠A＝∠EDF，再根据平行线的判定即可解决问题．【解答】（1）解：在△ABC和△DEF中，，∴△ABC≌△DEF（SSS），∴在上述三个条件中选取一个条件，使得△ABC≌△DEF，选取的条件为①，判定△ABC≌△DEF的依据是SSS．故答案为：①，SSS；（答案不唯一）．（2）证明：∵△ABC≌△DEF．∴∠A＝∠EDF，∴AB∥DE．8．在△ABC中，∠ACB＝90°，D为△ABC内一点，连接BD，DC，延长DC到点E，使得CE＝DC．（1）如图1，延长BC到点F，使得CF＝BC，连接AF，EF．若AF⊥EF，求证：BD⊥AF；（2）连接AE，交BD的延长线于点H，连接CH，依题意补全图2．若AB2＝AE2+BD2，用等式表示线段CD与CH的数量关系，并证明．【分析】（1）证明△BCD≌△FCE（SAS），由全等三角形的性质得出∠DBC＝∠EFC，证出BD∥EF，则可得出结论；（2）由题意画出图形，延长BC到F，使CF＝BC，连接AF，EF，由（1）可知BD∥EF，BD＝EF，证出∠AEF＝90°，得出∠DHE＝90°，由直角三角形的性质可得出结论．【解答】（1）证明：在△BCD和△FCE中，，∴△BCD≌△FCE（SAS），∴∠DBC＝∠EFC，∴BD∥EF，∵AF⊥EF，∴BD⊥AF；（2）解：由题意补全图形如下：CD＝CH．证明：延长BC到F，使CF＝BC，连接AF，EF，∵AC⊥BF，BC＝CF，∴AB＝AF，由（1）可知BD∥EF，BD＝EF，∵AB2＝AE2+BD2，∴AF2＝AE2+EF2，∴∠AEF＝90°，∴AE⊥EF，∴BD⊥AE，∴∠DHE＝90°，又∵CD＝CE，∴CH＝CD＝CE．9．如图，在△ABC和△ADE中，AB＝AC，AD＝AE，∠BAC＝∠DAE＝90°，且点D在线段BC上，连CE．（1）求证：△ABD≌△ACE；（2）若∠EAC＝60°，求∠CED的度数．【分析】（1）可利用SAS证明结论；（2）由全等三角形的性质可得∠ACE＝∠ABD，利用等腰直角三角形的性质可求得∠ACE＝∠ABD＝∠AED ＝45°，再根据三角形的内角和定理可求解∠AEC的度数，进而可求可求解【解答】（1）证明：∵∠BAC＝∠DAE＝90°，∴∠BAC﹣∠CAD＝∠DAE﹣∠CAD，即∠BAD＝∠CAE，在△ABD和△ACE中，，∴△ABD≌△ACE（SAS）；（2）解：∵△ABD≌△ACE，∴∠ACE＝∠ABD，∵△ABC和△ADE都是等腰直角三角形，∴∠ACE＝∠ABD＝∠AED＝45°，∵∠EAC＝60°，∴∠AEC＝180°﹣∠ACE﹣∠EAC＝180°﹣45°﹣60°＝75°，∴∠CED＝∠AEC﹣∠AED＝75°﹣45°＝30°．10．如图，在△ABC中（AB＜BC），过点C作CD∥AB，在CD上截取CD＝CB，CB上截取CE＝AB，连接DE、DB．（1）求证：△ABC≌△ECD；（2）若∠A＝90°，AB＝3，BD＝2，求△BCD的面积．【分析】（1）由CD∥AB得∠ABC＝∠ECD，而CD＝CB，CE＝AB，即可根据全等三角形的判定定理“SAS”证明△ABC≌△ECD；（2））由∠A＝90°，根据全等三角形的对应角相等证明∠BED＝∠CED＝∠A＝90°，设BE＝x，由BD2﹣BE2＝CD2﹣EC2＝DE2，列方程（2）2﹣x2＝（3+x）2﹣32，解方程求得符合题意的x的值为2，则BC ＝5，再根据勾股定理求出DE的长，即可求出△BCD的面积．【解答】（1）证明：∵CD∥AB，CD＝CB，CE＝AB，∴∠ABC＝∠ECD，在△ABC和△ECD中，，∴△ABC≌△ECD（SAS）．（2）解：∵∠A＝90°，∴∠CED＝∠A＝90°，∴∠BED＝180°﹣∠CED＝90°，设BE＝x，∵EC＝AB＝3，BD＝2，∴CD＝BC＝3+x，∵BD2﹣BE2＝CD2﹣EC2＝DE2，∴（2）2﹣x2＝（3+x）2﹣32，整理得x2+3x﹣10＝0，解得x1＝2，x2＝﹣5（不符合题意，舍去），∴BE＝2，BC＝3+2＝5，∴DE＝＝＝4，∴S△BCD＝BC•DE＝×5×4＝10，∴△BCD的面积为10．11．如图，在Rt△ABC中，∠BAC＝90°，AB＝AC＝1，D是BC边上的一点，以AD为直角边作等腰Rt △ADE，其中∠DAE＝90°，连接CE．（1）求证：△ABD≌△ACE；（2）若∠BAD＝22.5°时，求BD的长．【分析】（1）由“SAS”可证△ACE；（2）由等腰三角形三角形的性质可得BC的长，由角度关系可求∠ADC＝67.5°＝∠CAD，可得AC＝CD ＝1，即可求解．【解答】（1）证明：∵∠BAC＝90°＝∠DAE，∴∠BAD＝∠CAE，在△ABD和△ACE中，，∴△ABD≌△ACE（SAS）；（2）解：∵∠BAC＝90°，AB＝AC＝1，∴BC＝，∠B＝∠ACB＝45°，∵∠BAD＝22.5°，∴∠ADC＝67.5°＝∠CAD，∴AC＝CD＝1，∴BD＝﹣1．12．如图，已知矩形ABCD中，AB＝8，BC＝x（0＜x＜8），将△ACB沿AC对折到△ACE的位置，AE和CD交于点F．（1）求证：△CEF≌△ADF；（2）求tan∠DAF的值（用含x的式子表示）．【分析】（1）根据矩形的性质得到∠B＝∠D＝90°，BC＝AD，根据折叠的性质得到BC＝CE，∠E＝∠B ＝90°，等量代换得到∠E＝∠D＝90°，AD＝CE，根据AAS证明三角形全等即可；（2）设DF＝a，则CF＝8﹣a，根据矩形的性质和折叠的性质证明AF＝CF＝8﹣a，在Rt△ADF中，根据勾股定理表示出DF的长，根据正切的定义即可得出答案．【解答】（1）证明：∵四边形ABCD是矩形，∴∠B＝∠D＝90°，BC＝AD，根据折叠的性质得：BC＝CE，∠E＝∠B＝90°，∴∠E＝∠D＝90°，AD＝CE，在△CEF与△ADF中，，∴△CEF≌△ADF（AAS）；（2）解：设DF＝a，则CF＝8﹣a，∵四边形ABCD是矩形，∴AB∥CD，AD＝BC＝x，∴∠DCA＝∠BAC，根据折叠的性质得：∠EAC＝∠BAC，∴∠DCA＝∠EAC，∴AF＝CF＝8﹣a，在Rt△ADF中，∵AD2+DF2＝AF2，∴x2+a2＝（8﹣a）2，∴a＝，∴tan∠DAF＝＝．13．如图，△ABC和△DEF，点E，F在直线BC上，AB＝DF，∠A＝∠D，∠B＝∠F．如图①，易证：BC+BE ＝BF．请解答下列问题：（1）如图②，如图③，请猜想BC，BE，BF之间的数量关系，并直接写出猜想结论；（2）请选择（1）中任意一种结论进行证明；（3）若AB＝6，CE＝2，∠F＝60°，S△ABC＝123，则BC＝，BF＝．【分析】（1）根据图形分别得出答案；（2）利用AAS证明△ABC≌△DFE，得BC＝EF，再根据图形可得结论；（3）首先利用含30°角的直角三角形的性质求出BH和AH的长，从而得出BC，再对点E的位置进行分类即可．【解答】解：（1）图②：BC+BE＝BF，图③：BE﹣BC＝BF；（2）图②：∵AB＝DF，∠A＝∠D，∠B＝∠F，∴△ABC≌△DFE（ASA），∴BC＝EF，∵BE＝BC+CE，∴BC+BE＝EF+BC+CE＝BF；图③：∵AB＝DF，∠A＝∠D，∠B＝∠F，∴△ABC≌△DFE（ASA），∴BC＝EF，∵BE＝BF+EF，∴BE﹣BC＝BF+EF﹣BC＝BF+BC﹣BC＝BF；（3）当点E在BC上时，如图，作AH⊥BC于H，∵∠B＝∠F＝60°，∴∠BAH＝30°，∴BH＝3，∴AH＝3，∵S△ABC＝12，∴＝12，∴BC＝8，∵CE＝2，∴BF＝BE+EF＝8﹣2+8＝14；同理，当点E在BC延长线上时，如图②，BF＝BC+BE＝8+10＝18，故答案为：8，14或18．14．△ABC和△ADE都是等边三角形．（1）将△ADE绕点A旋转到图①的位置时，连接BD，CE并延长相交于点P（点P与点A重合），有P A+PB ＝PC（或P A+PC＝PB）成立（不需证明）；（2）将△ADE绕点A旋转到图②的位置时，连接BD，CE相交于点P，连接P A，猜想线段P A、PB、PC 之间有怎样的数量关系？并加以证明；（3）将△ADE绕点A旋转到图③的位置时，连接BD，CE相交于点P，连接P A，猜想线段P A、PB、PC 之间有怎样的数量关系？直接写出结论，不需要证明．【分析】（2）证明△ABD≌△ACE（SAS）和△BAF≌△CAP（SAS），得AF＝AP，∠BAF＝∠CAP，再证明△AFP是等边三角形，最后由线段的和可得结论；（3）如图③，在PC上截取CM＝PB，连接AM，同理可得结论．【解答】解：（2）PB＝P A+PC，理由如下：如图②，在BP上截取BF＝PC，连接AF，∵△ABC、△ADE都是等边三角形，∴AB＝AC，AD＝AE，∠BAC＝∠DAE＝60°，∴∠BAC+∠CAD＝∠CAD+∠DAE，即∠DAB＝∠EAC，∴△ABD≌△ACE（SAS），∴∠ABD＝∠ACE，∵AB＝AC，BF＝CP，∴△BAF≌△CAP（SAS），∴AF＝AP，∠BAF＝∠CAP，∴∠BAC＝∠P AF＝60°，∴△AFP是等边三角形，∴PF＝P A，∴PB＝BF+PF＝PC+P A；（3）PC＝P A+PB，理由如下：如图③，在PC上截取CM＝PB，连接AM，同理得：△ABD≌△ACE（SAS），∴∠ABD＝∠ACE，∵AB＝AC，PB＝CM，∴△AMC≌△APB（SAS），∴AM＝AP，∠BAP＝∠CAM，∴∠BAC＝∠P AM＝60°，∴△AMP是等边三角形，∴PM＝P A，∴PC＝PM+CM＝P A+PB．15．【情境再现】甲、乙两个含45°角的直角三角尺如图①放置，甲的直角顶点放在乙斜边上的高的垂足O处．将甲绕点O 顺时针旋转一个锐角到图②位置．按图②作出示意图，并连接AG，BH，如图③所示，AB交HO于E，AC 交OG于F，通过证明△OBE≌△OAF，可得OE＝OF．请你证明：AG＝BH．【迁移应用】延长GA分别交HO，HB所在直线于点P，D，如图④，猜想并证明DG与BH的位置关系．【拓展延伸】小亮将图②中的甲、乙换成含30°角的直角三角尺如图⑤，按图⑤作出示意图，并连接HB，AG，如图⑥所示，其他条件不变，请你猜想并证明AG与BH的数量关系．【分析】【情境再现】由△OBE≌△OAF，得BE＝AF，OE＝OF，∠BEO＝∠AFO，可证明△BHE≌△AGF （SAS），得BH＝AG；【迁移应用】由△BHE≌△AGF，得∠BHE＝∠AGF，可得∠AGF+∠GPO＝90°，从而∠BHE+∠HPD＝90°，∠HDP＝90°，故DG⊥BH；【拓展延伸】设AB交OH于T，OG交AC于K，根据△ABC，△HOG是含30°角的直角三角形，AO⊥BC，可得OB＝AO，∠OBA＝∠OAC＝30°，∠BOT＝90°﹣∠AOT＝∠AOK，即得△BOT∽△AOK，有＝＝＝，∠BTO＝∠AKO，又OH＝GO，可得＝＝，故△BTH∽△AKG，即得＝＝，BH＝AG．【解答】【情境再现】证明：由阅读材料知△OBE≌△OAF，∴BE＝AF，OE＝OF，∠BEO＝∠AFO，∴∠BEH＝∠AFG，∵OH＝OG，∴OH﹣OE＝OG﹣OF，即EH＝GF，在△BHE和△AGF中，，∴△BHE≌△AGF（SAS），∴BH＝AG；【迁移应用】解：猜想：DG⊥BH；证明如下：由【情境再现】知：△BHE≌△AGF，∴∠BHE＝∠AGF，∵∠HOG＝90°，∴∠AGF+∠GPO＝90°，∴∠BHE+∠GPO＝90°，∵∠GPO＝∠HPD，∴∠BHE+∠HPD＝90°，∴∠HDP＝90°，∴DG⊥BH；【拓展延伸】解：猜想：BH＝AG，证明如下：设AB交OH于T，OG交AC于K，如图：由已知得：△ABC，△HOG是含30°角的直角三角形，AO⊥BC，∴∠AOB＝90°，∴OB＝AO，∠OBA＝∠OAC＝30°，∠BOT＝90°﹣∠AOT＝∠AOK，∴△BOT∽△AOK，∴＝＝＝，∠BTO＝∠AKO，∴OT＝OK，BT＝AK，∠BTH＝∠AKG，∵OH＝GO，∴HT＝OH﹣OT＝GO﹣OK＝（GO﹣OK）＝KG，∴＝＝，∴△BTH∽△AKG，∴＝＝，∴BH＝AG19。

天津市河北区中考《全等三角形》复习练习题及答案

中考数学复习专题练习全等三角形一、选择题：1、如图，已知△ABC≌△ADE，∠D=55°，∠AED=76°，则∠C的大小是（）A．50° B．6O° C．76° D．55°2、如图所示，亮亮书上的三角形被墨迹污染了一部分，很快他就根据所学知识画出一个与书上完全一样的三角形，那么这两个三角形完全一样的依据是（）A．SSS B．SAS C．AAS D．ASA3、如图，小强利用全等三角形的知识测量池塘两端M、N的距离，如果△PQO≌△NMO，则只需测出其长度的线段是( )A．PO B．PQ C．MO D．MQ4、如图，P是等边三角形ABC内的一点，且PA=3，PB=4，PC=5，以BC为边在△ABC外作△BQC△BPA，连接PQ，则以下结论错误的是（）A. △BPQ是等边三角形B. △PCQ是直角三角形C. APB=150°D. APC=135°5、如图，△ABD≌△ACE，∠AEC=110°，则∠DAE的度数为（）A．30° B．40° C．50° D．60°6、如图，点E、F在AC上，AD=BC，DF=BE，要使△ADF≌△CBE，还需要添加一个条件是（）A．AD∥BC B．DF∥BE C．∠D=∠B D．∠A=∠C7、玻璃三角板摔成三块如图，现在到玻璃店在配一块同样大小的三角板，最省事的方法（）A．带①去 B．带②去 C．带③去 D．带①②③去8、如图，在Rt△ABC中，∠C=90°，以顶点A为圆心，适当长为半径画弧，分别交AC，AB于点M，N，再分别以点M，N为圆心，大于MN的长为半径画弧，两弧交于点P，作射线AP交边BC于点D，若CD=4，AB=15，则△ABD的面积是（）A．15 B．30 C．45 D．609、如图，已知△ABC中，∠ABC=45°，AC=4，H是高AD和BE的交点，则线段BH的长度为（）A． B．2 C．5 D．410、如图所示，m∥n，点B，C是直线n上两点，点A是直线m上一点，AB与AC的长不相等，在直线m上另找一点D，使得以点D，B，C为顶点的三角形和△ABC全等，这样的点D（）A．不存在 B．有1个 C．有3个 D．有无数个11、边长为7,24,25的△ABC内有一点P到三边的距离相等，则这个距离是（）A．1 B. 3 C．4 D．612、如图，已知BD为△ABC的角平分线，且BD=BC，E为BD延长线上的一点，BE=BA，过E作EF⊥AB，F为垂足．下列结论：①△ABD≌△EBC；②∠BCE+∠BCD=180°；③AD=AE=EC；④BA+BC=2BF．其中正确的是（）A．①②③ B．①③④ C．①②④ D．①②③④二、填空题：13、如图，AD是△ABC的角平分线，DE⊥AB，垂足为E，若△ABC的面积为9，DE=2，AB=5，则AC长是．14、如图,已知△ABC的周长是21,OB，OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,△ABC面积是．15、如图△ABC≌△ADE,BC延长线交DA于F，交DE于G,∠D=25°,∠E=105°,∠DAC=15°,则∠DGB= ．16、如图，方格纸中△ABC的3个顶点分别在小正方形的顶点（格点）上，这样的三角形叫格点三角形，图中与△ABC全等的格点三角形共有个（不含△ABC）．17、如图，矩形ABCD沿AE折叠，使D点落在BC边上点F处，如果∠BAF=60°，则∠DAE= 度．18、如图所示，△ABC中，∠C=90°，BD是∠ABC的平分线，DE⊥AB于点E，AB=8cm，BC=6cm，S△ABC=14cm2，则DE的长是 cm．19、如图，已知△ABC三个内角的平分线交于点O，点D在CA的延长线上，且DC=BC，AD=AO，若∠BAC=80°，则∠BCA的度数为．20、如图，在等边△ABC中，BD=CE，AD与BE相交于点F，则∠AFE=______．21、如图，在△ABC中（AB＜BC），在BC上截取BD=BA，作∠ABC的平分线与AD相交于点P，连接PC，若△ABC的面积为3，则△BPC的面积为．22、如图，在面积为4的等边△ABC的BC边上有一点D，连接AD，以AD为边作等边△ADE，连接BE．则四边形AEBD的面积是．23、如图，四边形ABCD中，∠BAD=∠C=90°，AB=AD，AE⊥BC于E，若线段AE=5，则S四边形ABCD= ．24、如图，C为线段AE上一动点（不与点A、E重合），在AE同侧分别作正△ABC和正△CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ．以下五个结论：①AD=BE；②PQ∥AE；③AP=BQ；④DE=DP；⑤∠AOB=60°．恒成立的结论有．（把你认为正确的序号都填上）三、简答题:25、如图，在△ABC中，∠ACB=90°，AC=BC，BE⊥CE于点E，AD⊥CE于点D．求证：（1）△BEC≌△CDA；（2）DE=AD﹣BE．26、如图，锐角△ABC中，AD⊥BC于D，BE⊥AC于E，AD与BE相交于F，DF=DC．求证：BF=AC．27、两个大小不同的等腰直角三角形三角板如图①所示放置，图②是由它抽象出的几何图形，B，C，E在同一条直线上，连接DC，（1）请找出图②中的全等三角形，并给予说明（说明：结论中不得含有未标识的字母）；（2）试说明：DC⊥BE．28、如图，画∠AOB=90°，并画∠AOB的平分线OC，将三角尺的直角顶点落在OC的任意一点P上，使三角尺的两条直角边与∠AOB的两边分别相交于点E、F，试猜想PE、PF的大小关系，并说明理由．29、如图所示，在△ABC 中，∠C=90°，AD 是∠BAC 的平分线，DE⊥AB 交 AB于点 E，点 F 在 AC 上，BD=DF.证明：（1）CF=EB;（2）AB=AF+2EB．参考答案1、C.2、D．3、B．4、B.5、B.6、C．7、C．8、B．9、D．10、B．11、B. 12、D．13、答案为：4 14、答案为：31.5．15、答案为：65°16、答案为：7．17、答案为:15．18、答案为：2．19、答案为：60°．20、答案为：60°．21、答案为：．22、答案为：4．23、答案为25．24、答案为：①②③⑤．25、【解答】证明：（1）∵∠ACD+∠BCE=90°，∠ACD+∠CAD=90°，∴∠CAD=∠BCE，在△CDA和△BEC中，，∴△CDA≌△BEC（AAS）；（2）∵△CDA≌△BEC，∴CD=BE，CE=AD，∵DE=CE﹣CD，∴DE=AD﹣BE．26、【解答】证明：∵AD⊥BC，BE⊥AC，∴∠BDF=∠ADC=90°，∠AEF=90°，∵∠AFE+∠CAD+∠AEF=180°，∠FBD+∠BFD+∠BDA=180°，∠AFE=∠BFD，∴∠FBD=∠CAD，在△BDF和△ADC中，∴△BDF≌△ADC（AAS），∴BF=AC27、解：（1）∵△ABC，△DAE是等腰直角三角形，∴AB=AC，AD=AE，∠BAC=∠DAE=90°．∠BAE=∠DAC=90°+∠CAE，在△BAE和△DAC中∴△BAE≌△CAD（SAS）．（2）由（1）得△BAE≌△CAD．∴∠DCA=∠B=45°．∵∠BCA=45°，∴∠BCD=∠BCA+∠DCA=90°，∴DC⊥BE．28、【解答】解：PE=PF，理由是：过点P作PM⊥OA，PN⊥OB，垂足是M，N，则∠PME=∠PNF=90°，∵OP平分∠AOB，∴PM=PN，∵∠AOB=∠PME=∠PNF=90°，∴∠MPN=90°，∵∠EPF=90°，∴∠MPE=∠FPN，在△PEM和△PFN中∴△PEM≌△PFN，∴PE=PF．29、证明：（1）∵ AD是∠BAC的平分线，DE⊥AB，DC⊥AC，∴ DE=DC．又∵ BD=DF，∴ Rt△CDF≌Rt△EDB（HL），∴ CF=EB.（2）∵ AD是∠BAC的平分线，DE⊥AB，DC⊥AC，∴△ADC≌△ADE，∴ AC=AE，∴ AB=AE+BE=AC+EB=AF+CF+EB=AF+2EB．。

微专题全等三角形的六种基本模型-2024年中考数学复习

21
全等三角形的六种基本模型
模型应用
8.如图17， △ 是边长为1的等边三角形， = ，
∠ = 120∘ ，点，分别在，上，且
∠ = 60∘ .求 △ 的周长.
提示：如图16，延长至点，使 = ，连接 .
图6
= ,
在 △ 和 △ 中， ቐ∠ = ∠, ∴ △≌△ SAS .
= ,
∠ = ∠ = 50∘ ．
7
全等三角形的六种基本模型
模型三旋转型
模型剖析
如图7，将三角形绕着公共顶
点旋转一定角度后，两个三角形能
够完全重合，这两个三角形称为旋
图3
在 △ 和△ 中， ∵ ∠ = ∠ ， ∠ = ∠ ， = ，
∴ △ ≌ △ AAS .
∴ = .
4
全等三角形的六种基本模型
模型二对称型
模型剖析
如图4、图5，将所给图形沿某一条直线折叠后，直线两旁的部分能
够完全重合，这两个三角形称为对称型全等三角形，其中重合的顶点就
= ， ∴ △ ≌ △ SAS . ∴ = ，
图17
图16
22
全等三角形的六种基本模型
∠ = ∠. ∵ ∠ = 120∘ ， ∠ = 60∘ ， ∴ ∠ +
∠ = 60∘ . ∴ ∠ + ∠ = 60∘ . ∴ ∠ = ∠ =
∴ ∠ = ∠ + ∠ = 110∘ .
∴ ∠ = ∠ ．
= ,
图9
在 △ 和 △ 中， ቐ∠ = ∠ ， ∴ △ ≌ △ ．
= ,
∴ = ．
11
全等三角形的六种基本模型

中考数学专题《全等三角形》

专题01 全等三角形一、单选题1．（2021·全国）在ABC V 中，B C ∠=∠，与ABC V 全等的三角形有一个角是100︒，那么在ABC V 中与这100︒角对应相等的角是（）A ．A ∠B ．BÐC ．C ∠D ．B Ð或C ∠2．（2021·山西襄汾县·七年级期末）如图，Rt △ABC 沿直角边BC 所在直线向右平移到Rt △DEF ，则下列结论中，错误的是（）A ．BE EC =B ．BC EF =C ．AC DF =D ．ABC DEF △≌△3．（2021·山西七年级期末）下列说法：①两个形状相同的图形称为全等图形；②边、角分别对应相等的两个多边形全等；③全等图形的形状、大小都相同；④面积相等的两个三角形全等．其中正确的是（）A ．①②③B ．①②④C ．①③D ．②③4．（2021·哈尔滨市第四十七中学）如图，ABD BAC ∆∆≌，若AD BC =，则BAD ∠的对应角（）A ．ADB ∠B ．BCD ∠C ．ABC ∠D ．CDA ∠5．（2021·全国八年级课时练习）如图，,40,30ABD CDB ABD CBD ∠=︒∠=︒V V ≌，则C ∠等于（）A ．20︒B ．100︒C ．110︒D ．115︒6．（2021·重庆巴南区·）已知△ABC 的三边的长分别为3，5，7，△DEF 的三边的长分别为3，7，2x ﹣1，若这两个三角形全等，则x 的值是（）A ．3B ．5C ．﹣3D ．﹣57．（2021·大连市第三十四中学八年级月考）如图，ABC A B C '''≅V V ，其中36A ∠=︒，24C '∠=︒，则B ∠=（）A ．150︒B ．120︒C ．90︒D ．60︒8．（2021·全国七年级课时练习）如图，在ABC V 中，D ，E 分别是边AC ，BC 上的点，若ADB EDB EDC V V V ≌≌，则C ∠的度数为（）A ．15︒B ．20︒C ．25︒D ．30°9．（2021·甘肃榆中县·七年级期末）如图，90A B ∠=∠=︒，6AB =，E 、F 分别为线段AB 和射线BD 上的一点，若点E 从点B 出发向点A 运动，同时点F 从点B 出发向点D 运动，二者速度之比为1:2，运动到某时刻同时停止，在射线AC 上取一点G ，使AEG △与BEF V 全等，则AG 的长为（）A ．2B ．3C ．2或3D ．2或610．（2021·全国）如图，锐角△ABC 中，D 、E 分别是AB 、AC 边上的点，△ADC ≌△ADC ′，△AEB ≌△AEB ′，且C ′D //EB ′//BC ，BE 、CD 交于点F ，若∠BAC ＝α，∠BFC ＝β，则（）A ．2α+β＝180°B ．2β﹣α＝180°C ．α+β＝150°D ．β﹣α＝60°11．（2021·全国八年级课时练习）如图，AOB ADC △≌△，点B 和点C 是对应顶点，90O D ∠=∠=︒，记,,OAD ABO ABC ACB αβ∠=∠=∠=∠，当//BC OA 时，α与β之间的数量关系为（）A ．αβ=B ．2αβ=C ．90αβ+=︒D ．2180αβ+=︒12．（2021·河南川汇区·八年级期末）如图，点D ，E ，F 分别在ABC V 的边AB ，BC ，CA 上（不与顶点重合），设BAC α∠=，FED θ∠=．若BED CFE ≌△△，则α，θ满足的关系是（）A ．90αθ+=︒B ．2180αθ+=︒C ．90αθ-=︒D ．2180αθ+=︒第II 卷（非选择题）请点击修改第II 卷的文字说明二、填空题13．（2021·吉林铁西区·八年级期中）如图所示，ABC ECD ≌△△，48A ∠=︒，62D ∠=︒，则图中B Ð的度数是______度．14．（2021·全国八年级课时练习）如图，ABE ACD △≌△，且D ∠与E ∠是对应角，顶点C 与顶点B 对应，若10cm BE =，则CD =__________．15．（2021·全国）如图，长方形ABCD 沿AM 折叠，使D 点落在BC 上的N 点处，AD ＝7cm ，DM ＝5cm ，∠DAM ＝39°，则△ANM ≌△ADM ，AN ＝_____cm ，NM ＝_____cm ，∠NAB ＝_______．17．（2021·浙江东阳市·七年级期末）如图，把一张长方形纸板裁去两个边长为3cm的小正方形和两个全等的小长方形，再把剩余部分（阴影部分）四周折起，恰好做成一个有底有盖的长方体纸盒，纸盒底面长方形的长为3k cm，宽为2k cm，则（1）裁去的每个小长方形面积为___cm2；（用k的代数式表示）（2）若长方体纸盒的表面积是底面积的正整数倍，则正整数k的值为___．18．（2021·山东莱州市·七年级期末）三个全等三角形按如图的形式摆放，则∠1+∠2+∠3的度数等于_______．19．（2021·辽宁本溪市·七年级期末）如图，∠A＝∠B＝90°，AB＝80，点E和点F分别为线段AB和射线BD上的一点，若点E从点B出发向点A运动，同时点F从点B出发向点D运动，点E和点F运动速度之比为2：3，运动到某时刻点E和点F同时停止运动，在射线AC 上取一点G，使△AEG与△BEF全等，则AG的长为________．20．（2021·全国）如图，在△ABC中，AB＝AC＝24厘米，∠B=∠C，BC＝16厘米，点D为AB的中点，点P 在线段BC 上以4厘米/秒的速度由B 点向C 点运动，同时，点Q 在线段CA 上由C 点向A 点运动．当点Q 的运动速度为________厘米/秒时，能够在某一时刻使△BPD 与△CQP 全等．三、解答题21．（2021·全国八年级课时练习）已知：如图，,8cm,5cm ABC DEF BC EC ==V V ≌，求线段CF 的长．22．（2020·铜陵市第二中学八年级月考）如图，ABF V ≌CDE △，已知30B ∠=︒，25DCF ∠=︒，求EFC ∠的度数．23．（2021·河南邓州市·七年级期末）我们已经认识了图形的轴对称、平移和旋转，这是图形的三种基本变换，图形经过这样的变换，虽然位置发生了改变，但图形的形状与大小都不发生变化，反映了图形之间的全等关系．这种运用动态变换研究图形之间的关系的方法，是一种重要而且有效的方法．同学们学完了这些知识后，王老师在黑板上给大家出示了这样的一道题目：（1）如图，△ACB 和△DCE 均为等边三角形，点A 、D 、E 在同一直线上，连接BE ．试说明AD ＝BE ；聪明的小亮很快就找到了解决该问题的方法：请你帮小亮把说理过程补充完整．解：∵△ACB 和△DCE 均为等边三角形，∴CA ＝CB ，CD ＝CE ，∠ACB ＝∠DCE ＝60°，（等边三角形的性质）∴∠ACD ＝（等式的性质）∴△ACD 绕点C 按逆时针方向旋转度，能够与重合∴△ACD ≌ （旋转变换的性质）∴AD ＝BE （）；（2）当同学们把这道题领会感悟后，王老师又在上题基础上追加了一问：试求∠AEB 的度数．聪明的同学们你会解决吗？请写出你的求解过程．（此题不用写推理依据即可）． 24．（2021·全国八年级课时练习）如图，,ABF CDE B ∠V V ≌和D ∠是对应角，AF 和CE 是对应边．（1）写出ABF V 和CDE △的其他对应角和对应边；（2）若30,40B DCF ∠=︒∠=︒，求EFC ∠的度数；（3）若10,2BD EF ==，求BF 的长．25．（2021·河南伊川县·七年级期末）如图，点A、B、C、D在同一直线上，△ACE≌△DBF，AD ＝8，BC＝2．（1）求AC的长；（2）求证：CE∥BF，AE∥DF．⊥于点B，26．（2021·辽宁铁西区·）如图，点B，C，E，F在同一直线上，AB BCCE=．BC=，3DEF ABCV V≌，且6（1）求CF的长；（2）判断DE与EF的位置关系，并说明理由．27．（2021·浙江浙江省·八年级期末）如图，已知正方形ABCD 边长为4cm ，动点M 从点C 出发，沿着射线CD 的方向运动，动点P 从点B 出发，沿着射线BC 的方向运动，连结,BM DP ，（1）若动点M 和P 都以每秒2cm 的速度运动，问t 为何值时DPC △和BCM V 全等？（2）若动点P 的速度是每秒3cm ，动点M 的速度是每秒1.5cm 问t 为何值时DPC △和BCM V 全等？28．（2020·浙江浙江省·）在56⨯的方格纸中，每格的边长为1，请按下列要求画图．（1）在图1中画一个格点ADE V ，使ADE V 与ABC V 全等，且所画格点三角形的顶点均不与点B ，C 重合．（2）在图2中画一个面积为7的格点四边形ABCD ，且BAD ∠为锐角．29．（2021·云南盘龙区·七年级期末）如图，在平面直角坐标系中，O 为坐标原点，ABC V 的边BC 在x 轴上，A 、C 两点的坐标分别为()0,A m ，(),0C n ，()5,0B -，且()231230m n -+-=点P 从B 出发，以每秒1个单位的速度沿射线BO 匀速运动，设点P 运动时间为t ．（1）点A 的坐标为；点C 的坐标为；（2）连接PA ，当POA V 的面积等于ABC V 的面积的一半时，求t 的值；（3）当P 在线段BO 上运动时，在y 轴上是否存在点Q ，使POQ △与AOC △全等？若存在，请直接写出Q 点坐标；若不存在，请说明理由．30．（2021·江苏姑苏区·苏州草桥中学七年级期末）如图，将一副三角板按如图所示的方式放置，其中ABC V 中，90ACB ∠=︒，45BAC ∠=︒，ADE V 中，90ADE ∠=︒，30DAE ∠=︒，AB AD =，点C 在线段AE 上．射线AB '从AB 出发，绕点A 以5︒/秒的速度顺时针旋转；同时，射线DA '从DA 出发，绕点D 顺时针旋转．设射线AB '运动的时间为t 秒（09t <≤），AB '与BC 交于点M ，DA '与AB '交于点N ．（1）若射线DA '旋转的速度为5︒/秒，则AND ∠=________︒；（2）设射线DA '旋转的速度为x ︒/秒，当射线AB '与DA '旋转到某处时，ABM V 与AND △全等，求相应的t 、x 的值．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

全等三角形证明专题
一、平移类型
1、如图，点B、E、C、F在一条直线上，AB∥DE，BE=CF，请添加一个条件，使△ABC≌△DEF．
第1题第2题
2、已知：如图，AB∥DE，AC∥DF，BE=CF．求证：AB=DE．
二、旋转类型
1、如图，已知AB＝AD，∠1＝∠2，要使△ABC≌△ADE，还需添加的条件是（只需填一个）．
第1题第2题
2、平面上有△ACD与△BCE，其中与相交于P点，所示。

若=，=，=，∠ACE=55°，∠BCD=155°，则∠BPD的度数为（）
(A) 110° (B) 125° (C) 130° (D) 155°
3、如图，已知AB=AD，AC=AE，∠1=∠2，求证△ABC≌△ADE.
4、已知：如图，AB=AE，∠1=∠2，∠B=∠E．求证：BC=ED．
5、已知：如图，AB、CD交于O点，CE//DF，CE=DF，AE=BF。

求证：∠ACE=∠BDF。

6、已知：如图，AB、CD交于O点，且OA=OB，OC=OD，过O作直线，交AC于E，交BD于F。

求证：OE=OF。

引申：如上图，若给出的条件是四边形ACBD为平行四边形，O为对角线交点，过O作作直线，交AC于E，交BD于F。

是否还能证明到OE=OF？
7、已知：如图，AB=CD，AD=BC，O是AC中点，OE⊥AB于E，OF⊥DC于F。

求证：OE=OF。

8、两个大小不同的等腰直角三角形三角板如图1所示放置，图2是由它抽象出的几何图形，B、C、E在同
一条直线上，连结DC．
（1）请找出图2中的全等三角形，并给予证明（说明：结论中不得含有未标识的字母）；
（2）证明：．
9、如图7，已知A、B、C在一条直线上，分别以AB、BC为边在AC同侧作等边三角形ABD和等边三角形BCE，AE交BD于点F，DC交BE于点G。

求证：AE=DC，BF=BG；
如图8，如果A、B、C不在一条直线上，那么AE=DC和BF=BG是否仍然成立？并请加以说明。

10、已知： BE⊥
CD，BE＝DE，BC＝DA，求证：△BEC≌△DAE
11、如图，AD⊥BC于D，AD=BD，AC=BE．（1）证明∠BED=∠C；（2）猜想并说明BE和AC有什么数量和位置关系。

三、对称类型
1、如图，和是分别沿着边翻折形成的，若，则
的度数是．
第1题第2题
2、已知：如图，AB⊥BC，AD⊥DC，AB=AD，若E是AC上的一点，求证：EB=ED．
3、如图，在△ABE中，AB＝AE,AD＝AC,∠BAD＝∠EAC, BC、DE交于点O.求证：(1) △ABC≌△AED； (2) OB＝OE .
4、已知：如图，点B、F、C、E在同一直线上，AC、DF相交于点G，AB⊥BE，垂足为B，DE⊥BE，垂足为E，且AB＝DE，BF＝CE．
求证：⑴△ABC≌△DEF；
⑵ GF＝GC．
5、已知：如图，AC⊥OB，BD⊥OA，AC与BD交于E点，若OA=OB，求证：AE=BE。

【综合练习】
1、如图，已知点D为等腰直角△ABC内一点，∠CAD＝∠CBD＝15°，E为AD延长线上的一点，且CE＝CA．
（1）求证：DE平分∠BDC；
（2）若点M在DE上，且DC=DM，求证： ME=BD．
2、如图：在△ABC中，BE、CF分别是AC、AB两边上的高，在BE上截取BD=AC，在CF的延长线上截取CG=AB，连结AD、AG．
（1）求证：；
（2）请你确定△ADG的形状，并证明你的结论．
3、如图，在四边形ABCD中，AD∥BC，E为CD的中点，连结AE、BE，BE⊥AE，延长AE交BC的延长线于点
F.
求证：（1）FC=AD；（2）AB=BC+AD.。

中考全等三角形复习专题

中考数学复习《全等三角形》专题(卷1)

中考数学考点专题复习 三角形与全等三角形

中考数学复习《全等三角形》专题训练-附带参考答案

初中中考复习之三角形全等（精编含答案）

备战2023年中考数学一轮复习考点08 全等三角形

中考数学复习专题24全等三角形试题(A卷,含解析)

2025年中考数学总复习+微专题7 全等三角形之六大模型++++课件

2024年中考数学复习+全等三角形课件

中考数学专题复习：三角形全等的判定

全等三角形复习专题

初三复习专题--全等三角形

中考数学专题复习全等三角形(X模型)

全等三角形知识点演练(5大核心考点,91题)讲练)2023年中考数学一轮大单元复习

中考数学专题复习全等三角形

中考数学复习专项之三角形全等 (含答案)

2023年中考数学----全等三角形的判定与性质知识回顾与专项练习题(含答案解析)

天津市河北区中考《全等三角形》复习练习题及答案

微专题 全等三角形的六种基本模型-2024年中考数学复习

中考数学专题《全等三角形》

中考数学考点专题复习三角形与全等三角形

微专题全等三角形的六种基本模型-2024年中考数学复习