2020年徐汇区西南模范中学初三3月月考卷

合集下载

2019-2020学年上海市徐汇区西南模范中学九年级(上)月考数学试卷试题及答案(9月份)

2019-2020学年上海市徐汇区西南模范中学九年级（上）月考数学试卷（9月份）一．选择题：（本大题共6题，每题4分，满分24分）[每小题只有一个正确选项，在答题纸相应题号的选项上用2B 铅笔正确填涂]1．（4分）已知233m a b =- ，1124n b a =+ ，那么4m n -等于()A ．823a b -B ．443a b -C ．423a b- D ．843a b-2．（4分）如果点D 、E 分别在ABC ∆的边AB 和AC 上，那么不能判定//DE BC 的比例式是()A ．::AD DB AE EC =B ．::BD AB CE AC =C ．::DE BC AD AB=D ．::AB AC AD AE=3．如图，已知123////l l l ，3AB =，2BC =，1CD =，那么下列式子中不成立的是()A ．:5:1EC CG =B ．:1:1EF FG =C ．:3:2EF FC =D ．:3:5EF EG =4．（4分）下列命题中错误的是()A ．相似三角形的周长比等于对应中线的比B ．相似三角形对应高的比等于相似比C ．相似三角形的面积比等于相似比D ．相似三角形对应角平分线的比等于相似比5．（4分）如图，ABC ∆中，点D 在AB 上，点E 在AC 上，若ADE C ∠=∠，则下列等式成立的是()A ．AD AEAB AC=B ．AE ADBC BD=C ．DE AEBC AB=D ．DE ADBC AB=6．如图，在Rt ABC ∆中，90C ∠=︒，5AB =，4BC =．点P 是边AC 上一动点，过点P 作//PQ AB 交BC 于点Q ，D 为线段PQ 的中点，当BD 平分ABC ∠时，AP 的长度为()A ．813B ．1513C ．2513D ．3213二．填空题：（本大题共12题，每题4分，满分48分）[在答题纸相应题号后的空格内直接填写答案]7．（4分）在比例尺为1:20000的地图上，相距4厘米的两地A 、B 的实际距离为米．8．（4分）已知23a b =，则232a b a b-=+．9．（4分）已知点P 是线段AB 的黄金分割点，AP BP >，若4AB =，则BP =．10．（4分）在ABC ∆中，经过重心G 作线段//DE BC 交AB 于D ，交AC 于E ，则:DE BC =．11．（4分）D 、E 是ABC ∆的AB 、AC 边上的点，//DE BC ，2AD =，3DB =， 5.5AC =，则AE =．12．（4分）已知ABC ∆∽△111A B C ，且相似比1123AB A B =，ABC ∆的面积为8，那么△111A B C 的面积为．13．（4分）在ABC ∆中，90ACB ∠=︒，CD AB ⊥，垂足为D ．若2,3ACD CBDS AD CD S ∆∆==则．14．（4分）点E 是ABCD 边AD 上一点，且:3:2AE ED =，CE 交BD 于点O ，则BOBD=．15．（4分）已知ABC ∆中，4AB AC ==，2BC =，把ABC ∆绕点C 旋转，使点B 落在边AB 上的点E ，则AE =．16．（4分）如图，已知ABC ∆中，60BAC ∠=︒，高BE 、CF 交于点D ，则AEFABCS S ∆∆=．17．（4分）如图，ABC ∆中，4AB AC ==，6BC =，点E 、F 在边BC 上，且EAF C ∠=∠，则BF CE =．18．（4分）如图，在ABC ∆中，90C ∠=︒，5AB =，3BC =，点D 、E 分别在AC 、AB 上，且AD BE =．联结DE ，点A 关于直线DE 的对称点为1A ，联结1A E ．若1A E 与ABC ∆的其中一条边垂直，则BE 的长为．三．解答题：（本大题共7题，满分78分）[将下列各题的解答过程，做在答题纸上]19．（10分）如图，已知梯形ABCD 中，//AB DC ，AOB ∆的面积等于9，AOD ∆的面积等于6，7AB =，求CD 的长．20．（10分）如图，AD 是ABC ∆中BC 边上的中线，点E 是AD 的中点，BA a = ，BC b = ，（1）试用向量a，b 表示向量:AE ．（2）在原图上作出BD 在AE 和AC方向上的分向量．21．（10分）如图（1）是夹文件用的铁（塑料）夹子在常态下的侧面示意图．AC ，BC 表示铁夹的两个面，O 点是轴，OD AC ⊥于D ．已知15AD mm =，24DC mm =，10OD mm =．已知文件夹是轴对称图形，试利用图（2），求图（1）中A ，B 两点的距26=）．22．（10分）已知，如图在矩形ABCD 中，AE BD ⊥于点E ，作EP EC ⊥，交AD 于点P ．求证：（1）AEP DEC ∆∆∽；（2）BE AB AE AP = ．23．（12分）如图，点A 在线段BD 上，在BD 的同侧作等腰Rt ABC ∆和等腰Rt ADE ∆，90ABC ADE ∠=∠=︒，CD 与BE 、AE 分别交于点P 、M ．求证：（1）BAE CAD ∆∆∽；（2）22CB CP CM = ．24．（12分）如图，一次函数(0)y kx b k =+≠的图象与x 轴，y 轴分别交于(9,0)A -、(0,6)B ，过点(2,0)C 作直线l 与BC 垂直，点E 在直线l 位于x 轴上方的部分．（1）求一次函数(0)y kx b k =+≠的解析式；（2）求直线l 的解析式；（3）若CBE ∆与ABO ∆相似，求点E 的坐标．25．（14分）如图，ABC ∆中，5AB AC ==，6BC =，点D 、E 分别是边AB 、AC 上的动点（点D 、E 不与ABC ∆的顶点重合），AD 和BE 交于点F ，且AFE ABC ∠=∠．（1）求证：ABD BCE ∆∆∽；（2）设AE x =，AD FD y = ，求y 关于x 的函数关系式，并直接写出x 的取值范围；（3）当AEF ∆是等腰三角形时，求DF 的长度．2019-2020学年上海市徐汇区西南模范中学九年级（上）月考数学试卷（9月份）参考答案与试题解析一．选择题：（本大题共6题，每题4分，满分24分）[每小题只有一个正确选项，在答题纸相应题号的选项上用2B 铅笔正确填涂]1．（4分）已知233m a b =- ，1124n b a =+ ，那么4m n -等于()A ．823a b -B ．443a b -C ．423a b- D ．843a b-【解答】解： 233m a b =- ，1124n b a =+，∴211284(3)4()32232433m n a b b a a b b a a b -=--+=---=-．故选：A ．2．（4分）如果点D 、E 分别在ABC ∆的边AB 和AC 上，那么不能判定//DE BC 的比例式是()A ．::AD DB AE EC =B ．::BD AB CE AC =C ．::DE BC AD AB=D ．::AB AC AD AE=【解答】解：A 、::AD DB AE EC = ，//DE BC ∴，故本选项能判定//DE BC ；B 、::BD AB CE AC = ，//DE BC ∴，故本选项能判定//DE BC ；C 、由::DE BC AD AB =，不能判定//DE BC ；故本选项不能判定//DE BC ；D 、::AB AC AD AE = ，::AB AD AC AE ∴=，//DE BC ∴，故本选项能判定//DE BC ．故选：C ．3．如图，已知123////l l l ，3AB =，2BC =，1CD =，那么下列式子中不成立的是()A ．:5:1EC CG =B ．:1:1EF FG =C ．:3:2EF FC =D ．:3:5EF EG =【解答】解：123////l l l ，::5:1EC CG AC CD ∴==，所以A 选项成立；::3:31:1EF FG AB BD ===，所以B 选项成立；::3:2EF FC AB BC ==，所以C 选项成立；::3:61:2EF EG AB AD ===，所以D 选项不成立．故选：D ．4．（4分）下列命题中错误的是()A ．相似三角形的周长比等于对应中线的比B ．相似三角形对应高的比等于相似比C ．相似三角形的面积比等于相似比D ．相似三角形对应角平分线的比等于相似比【解答】解：A 、相似三角形的周长比与对应中线的比等于相似比，故本选项正确；B 、相似三角形对应高的比等于相似比，故本选项正确；C 、相似三角形的面积比等于相似比的平方，故本选项错误；D 、似三角形对应角平分线的比等于相似比，故本选项正确．故选：C ．5．（4分）如图，ABC ∆中，点D 在AB 上，点E 在AC 上，若ADE C ∠=∠，则下列等式成立的是()A ．AD AEAB AC=B ．AE ADBC BD=C ．DE AEBC AB=D ．DE ADBC AB=【解答】解：ADE C ∠=∠ ，A A ∠=∠，ADE ACB ∴∆∆∽，:::AD AC AE AB DE BC ∴==，故选：C ．6．（4分）如图，在Rt ABC ∆中，90C ∠=︒，5AB =，4BC =．点P 是边AC 上一动点，过点P作//PQ AB交BC于点Q，D为线段PQ的中点，当BD平分ABC∠时，AP的长度为()A．813B．1513C．2513D．3213【解答】解：90C∠=︒，5AB=，4BC=，223AC AB BC∴-=，//PQ AB，ABD BDQ∴∠=∠，又ABD QBD∠=∠，QBD BDQ∴∠=∠，QB QD∴=，2QP QB∴=，//PQ AB，CPQ CAB∴∆∆∽，∴CP CQ PQCA CB AB==，即42345CP QB QB-==，解得，2413CP=，1513AP CA CP∴=-=，故选：B．二．填空题：（本大题共12题，每题4分，满分48分）[在答题纸相应题号后的空格内直接填写答案]7．（4分）在比例尺为1:20000的地图上，相距4厘米的两地A、B的实际距离为800米．【解答】解：设AB的实际距离为xcm，比例尺为1:20000，4:1:20000x∴=，80000800x cm m∴==．故答案为800．8．（4分）已知23a b =，则232a b a b-=+112．【解答】解：设2a k =，3b k =，则2431326612a b k k a b k k --==++．故答案为：112．9．（4分）已知点P 是线段AB 的黄金分割点，AP BP >，若4AB =，则BP =6-【解答】解：点P 是线段AB 的黄金分割点，AP BP >，2AP ∴==，42)6BP AB AP ∴=-=-=-，故答案为：6-．10．（4分）在ABC ∆中，经过重心G 作线段//DE BC 交AB 于D ，交AC 于E ，则:DE BC =2:3．【解答】解：连接AG 并延长到BC 边上一点F ，在ABC ∆中，经过重心G 作线段//DE BC 交AB 于D ，交AC 于E ，ADE ABC ∴∆∆∽，AGE AFC ∆∆∽，∴AG AE AF AC =，AE DEAC BC =，∴DE AGBC AF =，2AG GF = ，∴23DE AG BC AF ==故答案为：2:3．11．（4分）D 、E 是ABC ∆的AB 、AC 边上的点，//DE BC ，2AD =，3DB =， 5.5AC =，则AE =2.2．【解答】解：//DE BC ，::AD DB AE EC ∴=，即2:3:(5.5)AE AE =-，2.2AE ∴=．故答案为2.2．12．（4分）已知ABC ∆∽△111A B C ，且相似比1123AB A B =，ABC ∆的面积为8，那么△111A B C 的面积为18．【解答】解：ABC ∆ ∽△111A B C ，211112:(:)ABC A B C S S AB A B ∆∴= ，即1118:4:9A B C S = ，解得11118A B C S = ．故答案为：18．13．（4分）在ABC ∆中，90ACB ∠=︒，CD AB ⊥，垂足为D ．若2,3ACD CBDS AD CD S ∆∆==则49．【解答】解：90ACB ∠=︒ ，CD AB ⊥，90CDA CDB ∴∠=∠=︒，90A ACD ACD BCD ∠+∠=∠+∠=︒ ，A BCD ∴∠=∠，ACD CBD ∴∆∆∽，∴2224((39ACD CBD S AD S CD ∆∆===，故答案为：49．14．（4分）点E 是ABCD 边AD 上一点，且:3:2AE ED =，CE 交BD 于点O ，则BOBD=57．【解答】解：:3:2AE ED = ，:2:5DE AD ∴=，四边形ABCD 是平行四边形，:2:5DE BC ∴=，四边形ABCD 是平行四边形，//AD BC ∴，DEF BCF ∴∆∆∽，::2:5DE BC OD OB ∴==．∴57BO BD =，故答案为：57．15．（4分）已知ABC ∆中，4AB AC ==，2BC =，把ABC ∆绕点C 旋转，使点B 落在边AB 上的点E ，则AE =3．【解答】解：如图，作AH BC ⊥于H ，CF AB ⊥于F ．AB AC = ，AH BC ⊥，1BH CH ∴==，cos BH BF B AB BC ∠== ，∴142BF =，12BF ∴=，CB CE = ，CF BE ⊥，12BF EF ∴==，413AE AB BE ∴=-=-=，故答案为3．16．（4分）如图，已知ABC ∆中，60BAC ∠=︒，高BE 、CF 交于点D ，则AEF ABC S S ∆∆=14．【解答】解：AB CF ⊥ ，BE AC ⊥，90AEB AFC ∴∠=∠=︒，A A ∠=∠ ，ABE ACF ∴∆∆∽，∴AE AB AF AC =，∴AE AF AB AC=，ABC AEF ∴∆∆∽；在Rt ABE ∆中，60BAC ∠=︒ ，30ABE ∴∠=︒，∴12AE AB =，∴14AEF ABC S S ∆∆=，故答案为：14．17．（4分）如图，ABC ∆中，4AB AC ==，6BC =，点E 、F 在边BC 上，且EAF C ∠=∠，则BF CE = 16．【解答】证明：AEC B BAE EAF BAE BAF ∠=∠+∠=∠+∠=∠ ，又AB AC = ，B C ∴∠=∠，ABF ECA ∴∆∆∽，∴AB BF CE AC=，2BF EC AB AC AB ∴== 4AB = ，16BF CE ∴= ．故答案为：16．18．（4分）如图，在ABC ∆中，90C ∠=︒，5AB =，3BC =，点D 、E 分别在AC 、AB 上，且AD BE =．联结DE ，点A 关于直线DE 的对称点为1A ，联结1A E ．若1A E 与ABC ∆的其中一条边垂直，则BE 的长为53或52或2512．【解答】解：设BE AD x ==，则5AE x =-，90C ∠=︒ ，5AB =，3BC =，4AC ∴=，分三种情况：①1A E AC ⊥时，连接1A D ，如图1所示：则1//A E BC ，由轴对称的性质得：15A E AE x ==-，1A D AD x ==，1DA E BAC ∠=∠，1//A E BC ，AEF ABC ∴∆∆∽，∴EF AE BC AB =，即535EF x -=，3(5)5EF x ∴=-，在Rt △1A DF 中，1A D x =，1cos cos DA E BAC ∠=∠，∴11A F AC A D AB=，即145A F x =，解得：145A F x =，15A E AE x ==- ，∴34(5)555x x x -+=-，解得：53x =；②1A E BC ⊥时，连接1A D ，如图2所示：则1//A E AC ，1A ED ADE ∴∠=∠，由轴对称的性质得：15A E AE x ==-，1A D AD x ==，1A DE ADE ∠=∠，11A DE A ED ∴∠=∠，11A E A D x ∴==，5x x ∴-=，解得：52x =；③1A E AB ⊥时，连接1A D ，作1DP A E ⊥于P ，如图3所示：则//DP AB ，由轴对称的性质得：15A E AE x ==-，1A D AD x ==，1DA E BAC ∠=∠，1sin sin DA E BAC ∴∠=∠，∴1DP BC A D AB=，即35DP x =，解得：35DP x =，//DP AB ，BAC PDF ∴∠=∠，1//A E BC ，cos cos BAC PDF ∴∠=∠，即AC DP AB DF=，3455x DF =，解得：34DF x =，又cos AE AC BAC AF AB ∠== ，∴545x AF -=，5(5)4AF x ∴=-，∴35(5)44x x x +=-，解得：2512x =；综上所述，若1A E 与ABC ∆的其中一条边垂直，则BE 的长为53或52或2512；故答案为：53或52或2512．三．解答题：（本大题共7题，满分78分）[将下列各题的解答过程，做在答题纸上]19．（10分）如图，已知梯形ABCD 中，//AB DC ，AOB ∆的面积等于9，AOD ∆的面积等于6，7AB =，求CD 的长．【解答】解：//AB DC ，∴CD DO AB BO=，⋯（3分）AOB ∆ 的面积等于9，AOD ∆的面积等于6，∴23DO BO =，（3分）∴23CD DO AB BO ==，7AB = ，143CD ∴=．20．（10分）如图，AD 是ABC ∆中BC 边上的中线，点E 是AD 的中点，BA a = ，BC b = ，（1）试用向量a ，b 表示向量:AE 1142b a - ．（2）在原图上作出BD 在AE 和AC 方向上的分向量．【解答】解：（1） AD AB BD =+ ，BD DC =， 12AD a b =-+ ，12AE AD =，∴1142AE b a =- ，故答案为1142b a - ．（2）如图，出BD 在AE 和AC 方向上的分向量分别为BM ，BN ．21．（10分）如图（1）是夹文件用的铁（塑料）夹子在常态下的侧面示意图．AC ，BC 表示铁夹的两个面，O 点是轴，OD AC ⊥于D ．已知15AD mm =，24DC mm =，10OD mm =．已知文件夹是轴对称图形，试利用图（2），求图（1）中A ，B 两点的距离(:26)=．【解答】解：如图，连接AB ，与CO 的延长线交于点E ，夹子是轴对称图形，对称轴是CE ，A 、B 为一组对称点，CE AB ∴⊥，AE EB =．在Rt AEC ∆、Rt ODC ∆中，90AEC ODC ∠=∠=︒ ，OCD ∠是公共角，Rt AEC Rt ODC ∴∆∆∽，∴AE OD AC OC=．又26OC ===，39101526AC OD AE OC ⨯∴=== ，230()AB AE mm ∴==．22．（10分）已知，如图在矩形ABCD中，AE BD⊥于点E，作EP EC⊥，交AD于点P．求证：（1）AEP DEC∆∆∽；（2）BE AB AE AP=．【解答】证明：（1）AE BD⊥，PE EC⊥，90AED PEC∴∠=∠=︒，AEP DEC∴∠=∠，90EAD ADE∠+∠=︒，90ADE CDE∠+∠=︒，EAP EDC∴∠=∠，AEP DEC∴∆∆∽；（2）AEP DEC∆∆∽∴AP AE CD ED=，//AB CD，ABE EDC ∴∠=∠，又EAP EDC∠=∠，又AEB AED∠=∠，AEP BEA∴∆∆∽，∴BE AE AE ED=，∴BE APAE CD=，BE CD AE AP∴=，又AB CD=，BE AB AE AP ∴= ．23．（12分）如图，点A 在线段BD 上，在BD 的同侧作等腰Rt ABC ∆和等腰Rt ADE ∆，90ABC ADE ∠=∠=︒，CD 与BE 、AE 分别交于点P 、M ．求证：（1）BAE CAD ∆∆∽；（2）22CB CP CM = ．【解答】（1）证明：等腰Rt ABC ∆和等腰Rt ADE ∆，90ABC ADE ∠=∠=︒，AC ∴=，AD =，45BAC CAD ∠=∠=︒∴AC AD AB AE=BAC EAD∠=∠ BAE CAD∴∠=∠BAE CAD∴∆∆∽（2）BAE CAD ∆∆ ∽，BEA CDA ∴∠=∠，PME AMD∠=∠ PME AMD∴∆∆∽∴PM ME AM MD=，且PMA DME ∠=∠，PMA EMD ∴∆∆∽，90APD AED ∴∠=∠=︒，18090CAE BAC EAD ∠=︒-∠-∠=︒ ，且ACP ACM ∠=∠，CAP CMA ∴∆∆∽，∴AC CM CP AC=，2AC CP CM ∴= ，AC =22CB CP CM∴= 24．（12分）如图，一次函数(0)y kx b k =+≠的图象与x 轴，y 轴分别交于(9,0)A -、(0,6)B ，过点(2,0)C 作直线l 与BC 垂直，点E 在直线l 位于x 轴上方的部分．（1）求一次函数(0)y kx b k =+≠的解析式；（2）求直线l 的解析式；（3）若CBE ∆与ABO ∆相似，求点E的坐标．【解答】解：（1）一次函数(0)y kx b k =+≠的图象与x 轴，y 轴分别交于(9,0)A -，(0,6)B 两点，∴906k b b -+=⎧⎨=⎩，解得，236k b ⎧=⎪⎨⎪=⎩，∴一次函数y kx b =+的表达式为263y x =+；（2）如图1，直线l 与y 轴的交点为D ，BC l ⊥ ，90BCD BOC ∴∠=︒=∠，OBC OCB OCD OCB ∴∠+∠=∠+∠，OBC OCD ∴∠=∠，BOC COD ∠=∠ ，OBC OCD ∴∆∆∽，∴OB OC OC OD=，(0,6)B ，(2,0)C ，6OB ∴=，2OC =，∴622OD=，23OD ∴=，2(0,3D ∴-，(2,0)C ，设直线l 的函数解析式为y mx n =+，2320n m n ⎧=-⎪⎨⎪+=⎩，得1323m n ⎧=⎪⎪⎨⎪=-⎪⎩∴直线l 的解析式为1233y x =-；（3）CBE ∆ 与ABO ∆相似，∴当1CBE OAB ∆∆∽时，则1CE BCOB AO =，点(9,0)A -、(0,6)B ，点(2,0)C ，9OA ∴=，6OB =，2OC =，90BOD ∠=︒，BC ∴==∴169CE =，解得，13CE =，设点的1E 坐标为12(,33a a -，则22212(2)()33a a =-+-且0a >，解得，6a =，∴点1E 坐标为4(6,3；当2CBE OBA ∆∆∽时，则2CE BCOA BO =，点(9,0)A -、(0,6)B ，点(2,0)C ，9OA ∴=，6OB =，2OC =，90BOD ∠=︒ ，BC ∴==∴296CE =，解得，2CE =，设点的2E 坐标为12(,)33c c -，则22212(2)()33c c =-+-且0c >，解得，11c =，则点2E 坐标为(11,3)；由上可得，E 点坐标为4(6,)3或(11,3)．25．（14分）如图，ABC ∆中，5AB AC ==，6BC =，点D 、E 分别是边AB 、AC 上的动点（点D 、E 不与ABC ∆的顶点重合），AD 和BE 交于点F ，且AFE ABC ∠=∠．（1）求证：ABD BCE ∆∆∽；（2）设AE x =，AD FD y = ，求y 关于x 的函数关系式，并直接写出x 的取值范围；（3）当AEF ∆是等腰三角形时，求DF 的长度．【解答】（1）证明：AFE ABC ∠=∠ ，AFE ABF BAF ∠=∠+∠，ABC ABF CBE ∠=∠+∠，BAD CBE ∴∠=∠，AB AC = ，ABD C ∴∠=∠，ABD BCE ∴∆∆∽．（2）解：BDF ADB ∠=∠ ，DBF BAD ∠=∠，BDF ADB ∴∆∆∽，∴BD DF AD BD=，2BD DF AD ∴= ，ABD BCE ∆∆ ∽，∴DB AB EC BC =，∴556BD x =-，5(5)6BD x ∴=-，2225(5)36y AD DF BD x ∴===- ∴225250625(05)36x x y x -+=<<．（3）解：①如图1中，当AE EF =时，AE EF = ，AFE EAF ∴∠=∠，AFE ABC C ∠=∠=∠ ，DCA ABC EAF ∴∆∆∽∽，∴556DC =，256AD DC ∴==，同法可得65AF x =，2511666BD ∴=-=，2BD DF DA = ，∴12125366DF = ，121150DF ∴=．②如图2中，当FA FE =时，作AH BC ⊥于H ．FA FE = ，FAE FEA ∴∠=∠，ABD BCE ∆∠ ∽，ADB BEC ∴∠=∠，ADC FEA ∴∠=∠，CDA CAD ∴∠=∠，5CD CA ∴==，AB AC = ，AH BC ⊥，3BH CH ∴==，4AH ∴==，532DH ∴=-=，AD ===1BD = ，2BD DF AD = ，1DF ∴= ，10综上所述，121150DF =．。

上海市徐汇区2019-2020学年中考数学三模考试卷含解析

上海市徐汇区2019-2020学年中考数学三模考试卷一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．观察下列图案，是轴对称而不是中心对称的是（）A．B．C．D．2．下列调查中，最适合采用全面调查（普查）的是（）A．对我市中学生每周课外阅读时间情况的调查B．对我市市民知晓“礼让行人”交通新规情况的调查C．对我市中学生观看电影《厉害了，我的国》情况的调查D．对我国首艘国产航母002型各零部件质量情况的调查3．PM2.5是大气压中直径小于或等于0.0000025m的颗粒物，将0.0000025用科学记数法表示为（）A．0.25×10﹣5B．0.25×10﹣6C．2.5×10﹣5D．2.5×10﹣64．二元一次方程组632x yx y+=⎧⎨-=-⎩的解是()A．51xy=⎧⎨=⎩B．42xy=⎧⎨=⎩C．51xy=-⎧⎨=-⎩D．42xy=-⎧⎨=-⎩5．如图，在平面直角坐标系中，点A在第一象限，点P在x轴上，若以P，O，A为顶点的三角形是等腰三角形，则满足条件的点P共有（）A．2个B．3个C．4个D．5个6．计算（x－2）（x+5）的结果是A．x2+3x+7 B．x2+3x+10 C．x2+3x－10 D．x2－3x－107．如图，在平面直角坐标系xOy中，点A（1，0），B（2，0），正六边形ABCDEF沿x轴正方向无滑动滚动，每旋转60°为滚动1次，那么当正六边形ABCDEF滚动2017次时，点F的坐标是（）A ．（2017，0）B ．（2017，12）C ．（2018，3）D ．（2018，0）8．下列解方程去分母正确的是( )A ．由，得2x ﹣1＝3﹣3xB ．由，得2x ﹣2﹣x ＝﹣4C ．由，得2y-15=3yD ．由，得3(y+1)＝2y+69．下列四个图案中，不是轴对称图案的是（）A ．B ．C ．D ．10．如图，等腰直角三角形ABC 位于第一象限，2AB AC ==，直角顶点A 在直线y x =上，其中点A 的横坐标为1，且两条直角边AB ，AC 分别平行于x 轴、y 轴，若反比例函数k y x=的图象与ABC △有交点，则k 的取值范围是（）．A ．12k <<B ．13k ≤≤C ．14k ≤<D ．14k ≤≤11．抛物线y ＝x 2＋2x ＋3的对称轴是( )A ．直线x ＝1B ．直线x ＝－1C ．直线x ＝－2D ．直线x ＝212．在下列四个图案中既是轴对称图形，又是中心对称图形的是（）A ．B ．C ．.D ．二、填空题：（本大题共6个小题，每小题4分，共24分．）13．如图，在平面直角坐标系xOy 中，点A 的坐标为A(1,0)，等腰直角三角形ABC 的边AB 在x 轴的正半轴上，∠ABC=90°，点B 在点A 的右侧，点C 在第一象限。

2024年上海市徐汇区中考三模数学试卷含详解

初三数学摸拟试卷（满分150分，100分钟完成）考生注意：1．本试卷含三个大题，共25题．答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本调研卷上答题一律无效．2．除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤．一、选择题：（本大题共6题，每题4分，满分24分）[每小题只有一个正确选项，在答题纸相应题号的选项上用2B 铅笔正确填涂]1.下列各数中，与112282-相等的是（）A.122B.126C.2D.42.某公司三月份的产值为a 万元，比二月份增长了%m ，那么二月份的产值（单位：万元）为（）A.()1%+a m B.()1%-a m C.1%+a m D.1%-a m 3.下列二次根式里，被开方数中各因式的指数都为1的是（）A.B.C.D.4.如果点C 是线段AB 的中点，那么下列结论正确的是（）A .0AC BC +=uuu r uu u r B.0AC BC -=uuu r uu u r C.0AC BC += D.0AC BC -= 5.某蓄水池的横断面示意图如图所示，分深水区和浅水区，如果以固定的流量把水蓄满蓄水池，下面的图象能大致表示水的深度h 和注水时间t 之间关系的是（）A. B.C. D.6.已知四边形ABCD 中，对角线AC 与BD 相交于点O ，AD BC ∥，下列判断中错误．．的是（）A.如果AB CD =，AC BD =，那么四边形ABCD 是矩形B.如果AB CD ∥，OA OB =，那么四边形ABCD 是矩形C.如果AD BC =，AC BD ⊥，那么四边形ABCD 是菱形D.如果OA OC =，AC BD ⊥，那么四边形ABCD 是菱形二、填空题：（本大题共12题，每题4分，满分48分）[在答题纸相应题号后的空格内直接填写答案]7.当<2x -=________．8.不等式组10260x x -->⎧⎨--≤⎩的整数解是________．9.如果关于x 的方程210ax x -+=有实数根，那么a 的取值范围是________．10.在实数范围内分解因式，2231-+=x y xy ________．11.如果实数x 满足2211210x x x x ⎛⎫+-+-= ⎪⎝⎭，那么1x x +的值是________．12.如果一次函数()211y m x m =-+-的图像一定经过第二、三象限，那么常数m 的取值范围为________．13.某班进行一次班级活动，要在2名男同学和3名女同学中，随机选出2名学生担任主持人，那么选出的2名学生恰好是一男一女的概率是________．14.一斜坡的坡角为α，坡长比坡高多100米，那么斜坡的高为________（用α的锐角三角比表示）．15.在Rt ABC △中，90ACB ∠=︒，点G 是重心，如果3AG =，4BG =，那么CG =________．16.如图，⊙A 和⊙B 的半径分别为5和1，AB ＝3，点O 在直线AB 上，⊙O 与⊙A 、⊙B 都内切，那么⊙O 半径是________．17.如图，在ABC 中，4AB AC ==，1cos 4B =，BD 是中线，将ABC 沿直线BD 翻折后，点A 落在点E ，那么CE 的长为________．18.在一个三角形中，如果一个内角是另一内角的n 倍（n 为整数），那么我们称这个三角形为n 倍三角形．如果一个三角形既是2倍角三角形，又是3倍角三角形，那么这个三角形最小的内角度数为________．三、解答题：（本大题共7题，满分78分）[将下列各题的解答过程，做在答应纸上]19.已知：1-==x y ，求：21122⎛⎫- ⎪⎝⎭x y 值．20.已知点()2,3A m +在双曲线my x=上．（1）求此双曲线的表达式与点A 的坐标；（2）如果点(),5B a a -在此双曲线上，图像经过点A 、B 的一次函数的函数值y 随x 的增大而增大，求此一次函数的解析式．21.已知：如图，在ABC 中，AB AC =，DC BC ⊥，2DC BC ==，90ADB ∠=︒，BD 与AC 相交于点G ．求：（1）AB 的长；（2）AG 的长．22.20个集装箱装满了甲、乙、丙三种商品共120吨，每个集装箱都只装载一种商品，根据下表提供的信息，解答以下问题：商品类型甲乙丙每个集装箱装载量（吨）865每吨价值（万元）121520（1）如果甲种商品装x 个集装箱，乙种商品装y 个集装箱，求y 与x 之间的关系式；（2）如果其中5个集装箱装了甲种商品，求每个集装箱装载商品总价值的中位数．23.已知：如图，在梯形ABCD 中，AD BC ∥，AB CD AD ==，点E 在BA 的延长线上，AE BC =．（1）求证：2BCD AED ∠=∠；（2）当ED 平分BEC ∠时，求证：EBC 是等腰直角三角形．24.如图，抛物线2y ax bx c =++顶点为坐标原点O 、且经过点()3,3A ，直线经过点A 和点()0,6B ．（1）求抛物线与直线的表达式；（2）如果将此抛物线平移，平移后新抛物线的顶点C 在原抛物线上，新抛物线的对称轴与直线AB 在原抛物线的内部相交于点D ，且45COD ∠=︒，求新抛物线的表达式．25.已知：O 的直径8AB B = ，与O 相交于点C 、D ，O 的直径CF 与B 相交于点E ，设B 的半径为x ，OE 的长为y ．（1）如图，当点E 在线段OC 上时，求y 关于x 的函数解析式，并写出定义域；（2）当点E 在直径CF 上时，如果OE 的长为3，求公共弦CD 的长；（3）设B 与AB 相交于G ，试问OEG 能否为等腰三角形？如果能够，请直接写出BC 弧的长度（不必写过程）；如果不能，请简要说明理由初三数学摸拟试卷（满分150分，100分钟完成）一、选择题：（本大题共6题，每题4分，满分24分）[每小题只有一个正确选项，在答题纸相应题号的选项上用2B 铅笔正确填涂]1.下列各数中，与112282-相等的是（）A.122B.126C.2D.4【答案】A【分析】本题考查了幂的乘方逆运算和同底数幂乘法的逆运算，正确运用公式是解题关键．先利用幂的乘方的逆运算将128的底变为2，再通过同底数幂乘法的逆运算变出122，即可计算．【详解】解：()111311111111322222222222822222222222+-=-=-=-=⨯-=，故选：A ．2.某公司三月份的产值为a 万元，比二月份增长了%m ，那么二月份的产值（单位：万元）为（）A.()1%+a mB.()1%-a m C.1%+a m D.1%-a m 【答案】C【分析】本题考查了列代数式，根据“三月份的产值为a 万元，比二月份增长了%m ”，得出答案即可，理解题意、正确列出代数式是解题的关键．【详解】解：∵三月份的产值为a 万元，比二月份增长了%m ，∴二月份的产值()1%1%aa m m =¸+=+，故选：C ．3.下列二次根式里，被开方数中各因式的指数都为1的是（）A.B.C.D.【答案】B【分析】根据二次根式的定义判断即可．【详解】解：A ．x ，y 的指数分别为2，2，此选项错误；B ．22xy +的指数为1，此选项正确；C ．x ＋y 的指数为2，此选项错误；D ．x ，y 的指数分别为1，2．此选项错误；故选：B ．【点睛】本题主要考查了二次根式的定义，分清因数和指数是解答此题的关键．4.如果点C 是线段AB 的中点，那么下列结论正确的是（）A.0AC BC +=uuu r uu u r B.0AC BC -=uuu r uu u r C.0AC BC += D.0AC BC -= 【答案】C【分析】根据点C 是线段AB 的中点，可以判断AC BC =，但它们的方向相反，继而即可得出答案．【详解】解：由题意，∵点C 是线段AB 的中点，∴AC BC= ∵AC 与BC为相反向量，∴0AC BC +=；故选：C ．【点睛】本题考查了平面向量的知识，注意向量包括长度及方向，及0与0的不同．5.某蓄水池的横断面示意图如图所示，分深水区和浅水区，如果以固定的流量把水蓄满蓄水池，下面的图象能大致表示水的深度h 和注水时间t 之间关系的是（）A.B.C. D.【答案】C【分析】首先看图可知，蓄水池的下部分比上部分的体积小，故h 与t 的关系为先快后慢．【详解】根据题意和图形的形状，可知水的最大深度h 与时间t 之间的关系分为两段，每一段h 随t 的增大而增大，增大的速度是先快后慢．故选C ．【点睛】此题考查了函数的图象，根据几何图形的性质确定函数的图象和函数图象的作图能力．要能根据几何图形和图形上的数据分析得出所对应的函数的类型和所需要的条件，结合实际意义画出正确的图象．6.已知四边形ABCD 中，对角线AC 与BD 相交于点O ，AD BC ∥，下列判断中错误．．的是（）A.如果AB CD =，AC BD =，那么四边形ABCD 是矩形B.如果AB CD ∥，OA OB =，那么四边形ABCD 是矩形C.如果AD BC =，AC BD ⊥，那么四边形ABCD 是菱形D.如果OA OC =，AC BD ⊥，那么四边形ABCD 是菱形【答案】A【分析】本题考查了平行四边形、矩形、菱形、正方形的判定，根据平行四边形、矩形、菱形、正方形的判定方法逐项进行分析判定即可得答案．【详解】解：A 、如果AD BC ≠，AD BC ∥，那么四边形ABCD 是梯形，不是平行四边形也就不是矩形，故A 选项错误，符合题意；B 、如果AB CD ∥，AD BC ∥，则四边形ABCD 是平行四边形，则12OA AC =，12OB BD =，因为OA OB =所以AC BD =，那么平行四边形ABCD 是矩形，故B 选项正确，不符合题意；C 、如果AD BC =，AD BC ∥，则四边形ABCD 是平行四边形，又AC BD ⊥，那么平行四边形ABCD 是菱形，故C 选项正确，不符合题意；D 、如果AD BC ∥，OA OC =，则可以证得四边形ABCD 是平行四边形，又AC BD ⊥，那么平行四边形ABCD 是菱形，故D 选项正确，不符合题意，故选A ．二、填空题：（本大题共12题，每题4分，满分48分）[在答题纸相应题号后的空格内直接填写答案]7.当<2x -=________．【答案】12--x【分析】本题考查了二次根式的性质与化简，熟练掌握a =是解题的关键．a =的进行计算即可．12x ==+，∵<2x -，∴11<2022x -++<∴1122x x =+=--．故答案为：12--x ．8.不等式组10260x x -->⎧⎨--≤⎩的整数解是________．【答案】3-，2-【分析】本题考查了解一元一次不等式组，整数解的问题，熟练掌握知识点是解题的关键．写解每一个不等式，再取解集的公共部分，然后即可求解．【详解】解：10260x x -->⎧⎨--≤⎩①②，由①得：1x <-，由②得：3x ≥-，∴原不等式的解集为：31x -≤<-，∴整数解为：3-，2-，故答案为：3-，2-．9.如果关于x 的方程210ax x -+=有实数根，那么a 的取值范围是________．【答案】14a ≤【分析】本题考查了一元二次方程的判别式，根据关于x 的方程210ax x -+=有实数根，得出240b ac ∆=-≥，代入数值进行计算，即可作答．【详解】解：∵关于x 的方程210ax x -+=有实数根，∴()2Δ1410a =--⨯≥，解得14a ≤，故答案为：14a ≤．10.在实数范围内分解因式，2231-+=x y xy ________．【答案】3322⎛⎫⎛⎫+-- ⎪⎪ ⎪⎪⎝⎭⎝⎭xy xy 【分析】本题考查因式分解，二次根式的乘法，熟练掌握公式法进行因式分解是解决本题的关键．根据题意，利用十字相乘因式分解．【详解】解：2231x y xy -+()233322xy xy ⎛⎫⎛⎫+-=-+⨯ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭3322xy xy ⎛⎫⎛⎫+-=-- ⎪⎪ ⎪⎪⎝⎭⎝⎭．11.如果实数x 满足2211210x x x x ⎛⎫+-+-= ⎪⎝⎭，那么1x x +的值是________．【答案】3【分析】本题主要考查了用换元法解一元二次方程、解分式方程，利用完全平方公式把方程变形是解题的关键．利用完全平方公式把方程变形为211230x x x x ⎛⎫⎛⎫+-+-= ⎪ ⎪⎝⎭⎝⎭，利用换元法，设1x m x +=，则2230m m --=，转化为解一元二次方程，求出1x x+可能的值，分别得出分式方程，计算检验是否有解，即可得出答案．【详解】解：∵2211210x x x x ⎛⎫+-+-= ⎪⎝⎭，∴22112230x x xx 骣÷ç++-+-=÷ç÷ç桫，211230x x x x ⎛⎫⎛⎫+-+-= ⎪ ⎝⎭⎝⎭，设1x m x+=，则2230m m --=，因式分解得：()()310m m -+=，∴30m -=或10m +=，解得：3m =或1m =-，当3m =时，则13x x+=，整理得：2310x x -+=，∴439435222b x a -===，解得：1352x +=，2352x -=，经检验，1352x +=，2352x =都是方程13x x +=的解，∴1x x+的值为3；当1m =-时，则11x x+=-，整理得：210x x ++=，241430b ac ∆=-=-=-<，∴11x x+=-时，方程无解．综上所述，1x x+的值为3，故答案为：3．12.如果一次函数()211y m x m =-+-的图像一定经过第二、三象限，那么常数m 的取值范围为________．【答案】1m >-且1m ≠【分析】本题考查一次函数的图像与性质，运用数形结合思想解题是解题的关键，根据“一次函数()211y m x m =-+-的图像一定经过第二、三象限”可知，此图像与x 轴的交点在原点的左边，即与x 轴交点的横坐标小于0，从而得解．【详解】解：∵一次函数()211y m x m =-+-的图像一定经过第二、三象限，∴此图像与x 轴的交点在原点的左边，且10m -≠，即1m ≠，∴此图像与与x 轴交点的横坐标小于0，令()2110y m x m =-+-=，解得：21101m x m m -=-=--<-，解得：1m >-，∴常数m 的取值范围为1m >-且1m ≠，故答案为：1m >-且1m ≠．13.某班进行一次班级活动，要在2名男同学和3名女同学中，随机选出2名学生担任主持人，那么选出的2名学生恰好是一男一女的概率是________．【答案】35##0.6【分析】本题考查的是画树状图法求概率．树状图法适合两步或两步以上完成的事件；用到的知识点为：概率=所求情况数与总情况数之比．先画出树状图得出所有等可能的情况数，再找出符合条件的情况数，然后根据概率公式即可得到答案．【详解】解：根据题意画图如下：共有20种等可能的情况数，选出的2位同学恰好为一男一女的有12种，则主持人是一男一女的概率为123205=．故答案为：35．14.一斜坡的坡角为α，坡长比坡高多100米，那么斜坡的高为________（用α的锐角三角比表示）．【答案】100sin 1sin -αα【分析】本题考查了正弦函数的应用．利用所给角的正弦函数求解．【详解】解：如图所示．由题意得100AB BC =+，∵90C ∠=︒，sin sin A A BC B α==，∴0s n 10i BC BC α+=，整理得100sin 1sin BC αα=-，∴斜坡的高为100sin 1sin -αα米．故答案为：100sin 1sin -αα．15.在Rt ABC △中，90ACB ∠=︒，点G 是重心，如果3AG =，4BG =，那么CG =________．【答案】【分析】本题考查了重心的定义与性质，结合勾股定理，直角三角形斜边中线的性质，关键是掌握重心性质并运用勾股定理列式求解是解题关键．本题先利用重心求出AD 和BE ，再利用勾股定理列式整体法求出AB ，最后利用直角三角形斜边中线性质和重心性质求出CG ．【详解】解：如图，设AG 延长线交BC 于点D ，BG 延长线交AC 于点E ，CG 延长线交AB 于点F ，∵点G 是重心，3AG =，4BG =，∴3922AD AG ==，362BE BG ==，∵90ACB ∠=︒，∴222AD AC CD =+，222BE CE BC =+，∴22222292262BC AC AC BC ⎧⎛⎫⎛⎫=+⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎨⎛⎫⎪=+ ⎪⎪⎝⎭⎩①②，①+②得：22815536444AC BC +=+，化简得：2245AC BC +=，∴22245AB AC BC =+=，∴AB =，∵点G 是重心，90ACB ∠=︒，∴12CF AB ==∴23CG CF ==，．16.如图，⊙A 和⊙B 的半径分别为5和1，AB ＝3，点O 在直线AB 上，⊙O 与⊙A 、⊙B 都内切，那么⊙O 半径是________．【答案】32或92．【分析】根据两圆内切时圆心距=两圆半径之差的绝对值，分两种情况求解即可．【详解】当点O 在点A 左侧时，⊙O 半径r=101922-=,当点O 在点B 右侧时，⊙O 半径r=107322-=.故填92或32.【点睛】此题考查圆与圆之间的位置关系，解题的关键是掌握两圆位置关系与圆心距d ，两圆半径R ，r 的数量之间的联系.17.如图，在ABC 中，4AB AC ==，1cos 4B =，BD 是中线，将ABC 沿直线BD 翻折后，点A 落在点E ，那么CE 的长为________．【答案】6【分析】本题考查三角形的翻折综合计算，涉及三角函数，等腰三角形，平行四边形及勾股定理，能正确进行线段的转换及作辅助线解非直角三角形是解题关键．本题先过点A 作AM BC ⊥于点M ，计算得出AD CD DE BC ===，再证明四边形BCED 是平行四边形，得CE BD =，再在BCD △中求解BD 即可．【详解】解：如图，过点A 作AM BC ⊥于点M ，过点D 作DN BC ⊥于点N ，∵4AB AC ==，∴BM CM =，∵1cos 44BM BM B AB ===，∴1BM CM ==，∴2BC =，∵BD 是中线，∴122CD AD AC ===，由翻折知2AD DE ==，∴AD CD DE BC ===，∴CBD CDB ∠=∠，设DCB α∠=，∴1802CDB α︒-∠=，∴1801809022ADB αα︒-∠=︒-=︒+，由翻折知902EDB ADB α∠=∠=︒+，∴1809022EDC EDB CDB ααα︒-∠=∠-∠=︒+-=，∴EDC DCB ∠=∠，∴DE BC ∥，∴四边形BCED 是平行四边形，∴CE BD =，∵DN BC ⊥，∴1cos cos 24CN CN C B CD ====，∴12CN =，∴13222BN BC CN =-=-=，152DN ==，∴BD ==∴CE BD ==，．18.在一个三角形中，如果一个内角是另一内角的n 倍（n 为整数），那么我们称这个三角形为n 倍三角形．如果一个三角形既是2倍角三角形，又是3倍角三角形，那么这个三角形最小的内角度数为________．【答案】30︒或20︒或18︒或360(11°【分析】根据n 倍三角形的定义结合三角形内角和定理，进行分类讨论计算即可．【详解】设最小的内角为x ︒．分类讨论：①当2倍角为2x ︒，3倍角为3x ︒时，可得：23180x x x ︒+︒+︒=︒，解得30x =．②当2倍角为2x ︒，3倍角为6x ︒时，可得：26180x x x ︒+︒+︒=︒，解得20x =．③当3倍角为3x ︒，2倍角为6x ︒时，可得：36180x x x ︒+︒+︒=︒，解得18x =．④当3x ︒即是2倍角又是三倍角时，即另一个内角为32x ︒，可得：331802x x x ︒+︒+︒=︒，解得36011x =．综上可知，最小的内角为30︒或20︒或18︒或360()11°．【点睛】本题考查三角形内角和定理．理解题干中n 倍三角形的定义以及利用分类讨论的思想是解答本题的关键．三、解答题：（本大题共7题，满分78分）[将下列各题的解答过程，做在答应纸上]19.已知：1-==x y ，求：21122⎛⎫- ⎪⎝⎭x y 值．【答案】2【分析】本题考查了负整数指数幂、分母有理化以及完全平方公式的运算，先整理得出2x =+，2y =-1xy =，再运用完全平方公式展开代入数值，进行计算即可作答．【详解】解：∵1-==x y∴2x =+，2y =1xy=．∴21111122222222212x y x y x y ⎛⎫-=+-=+⨯= ⎪⎝⎭20.已知点()2,3A m +在双曲线m y x=上．（1）求此双曲线的表达式与点A 的坐标；（2）如果点(),5B a a -在此双曲线上，图像经过点A 、B 的一次函数的函数值y 随x 的增大而增大，求此一次函数的解析式．【答案】（1）6y x =-，()2,3A -；（2）1y x 42=-．【分析】（1）把点A （2，m +3）代入m y x =求得m ，即可求出结果；（2）把点B （a ，5-a ）代入m y x =求得a 得到B 点的坐标，根据A 点坐标和函数的增减性排除掉不符合题意的点，再由待定系数法求出一次函数解析式．【详解】解：（1）∵点A （2，m +3）在双曲线m y x=上，∴.32m m +=，解得：m =-6，∴m +3=-3，∴此双曲线的表达式为6y x -=，点A 的坐标为（2，-3）；（2）∵点B （a ，5-a ）在此双曲线6y x -=上，∴6.5a a--=，解得：a =-1或a =6，经检验：1,6a a =-=都是原方程的根，且符合题意，∴点B 的坐标为（-1，6）或（6，-1），∵一次函数的函数值y 随x 的增大而增大，由（1）知A （2，-3），∴点B 的坐标只能为（6，-1），设一次函数的解析式为y =kx +b ，∴3216k b k b -=+⎧⎨-=+⎩，解得：124k b ⎧=⎪⎨⎪=-⎩，∴一次函数的解析式为1y x 42=-．【点睛】本题主要考查了待定系数法求反比例函数解析式和一次函数解析式以及一次函数的性质，熟练掌握待定系数法求解析式是解题的关键．21.已知：如图，在ABC 中，AB AC =，DC BC ⊥，2DC BC ==，90ADB ∠=︒，BD 与AC 相交于点G．求：（1）AB 的长；（2）AG 的长．【答案】（1）AB =（2）AG =【分析】（1）过点A 作AE BC ⊥于E ，交BD 于F ．则45CDB CBD ∠=∠=︒，由勾股定理得，BD =．由AB AC =，AE BC ⊥，可得112BE BC ==，45EFB EBF ∠=︒=∠，则1EF BE ==，45AFD EFB ∠=∠=︒，AD DF =，由勾股定理得，BF =，则AD DF BD BF ==-=，由勾股定理得，AB =，计算求解即可；（2）由题意知，2cos 45DF CD AF ===︒，证明()AAS AGF CGD ≌，则AG CG =，由AG CG +=可求AG ．【小问1详解】解：过点A 作AE BC ⊥于E ，交BD 于F ．∵90BCD ∠=︒，2BC CD ==，∴45CDB CBD ∠=∠=︒，由勾股定理得，BD ==．∵AB AC =，AE BC ⊥，∴112BE BC ==，45EFB EBF ∠=︒=∠，∴1EF BE ==，45AFD EFB ∠=∠=︒，∴45DAF AFD ∠=︒=∠，∴AD DF =，由勾股定理得，BF ==∴AD DF BD BF ==-=由勾股定理得，AB ==∴AB =；【小问2详解】解：由题意知，2cos 45DF CD AF ===︒，又∵45AFG CDG ∠=︒=∠，AGF CGD ∠=∠，∴()AAS AGF CGD ≌，∴AG CG =，∵AG CG +=∴102AG GC ==，∴102AG =．【点睛】本题考查了等腰三角形的判定与性质，勾股定理，余弦，全等三角形的判定与性质等知识．熟练掌握等腰三角形的判定与性质，勾股定理，余弦，全等三角形的判定与性质是解题的关键．22.20个集装箱装满了甲、乙、丙三种商品共120吨，每个集装箱都只装载一种商品，根据下表提供的信息，解答以下问题：商品类型甲乙丙每个集装箱装载量（吨）865每吨价值（万元）121520（1）如果甲种商品装x 个集装箱，乙种商品装y 个集装箱，求y 与x 之间的关系式；（2）如果其中5个集装箱装了甲种商品，求每个集装箱装载商品总价值的中位数．【答案】（1）320y x =-+（2）每个集装箱装载商品总价值的中位数是98万元【分析】本题考查了根据实际问题列函数关系式及中位数，正确认识题中图表及理解题意是解题关键．（1）先列出三种商品装集装箱的个数的式子，再利用三种商品共120吨列式即可；（2）先得出三种商品装载集装箱的个数，再得出20个集装箱装载商品总价值分别是多少，利用中位数定义即可求解．【小问1详解】解：∵甲种商品装x 个集装箱，乙种商品装y 个集装箱，一共20个集装箱，∴丙种商品装()20x y --个集装箱，∴由题意得：()86520120x y x y ++--=，化简得：320y x =-+；【小问2详解】当5x =时，35205y =-⨯+=，20205510x y --=--=，∴甲、乙、丙三种商品装载集装箱个数分别是5、5、10，由表可知每个甲集装箱装载商品总价值为81296⨯=（万元），每个乙集装箱装载商品总价值为61590⨯=（万元），每个丙集装箱装载商品总价值为520100⨯=（万元），∴20个集装箱装载商品总价值有5个90万元，5个96万元，10个100万元，∴这20个数据从小到大排列后第10、11个数据分别是96、100万元，∴每个集装箱装载商品总价值的中位数是96100982+=（万元）．23.已知：如图，在梯形ABCD 中，AD BC ∥，AB CD AD ==，点E 在BA 的延长线上，AE BC =．（1）求证：2BCD AED ∠=∠；（2）当ED 平分BEC ∠时，求证：EBC 是等腰直角三角形．【答案】（1）见解析（2）见解析【分析】（1）连接AC ，由梯形ABCD ，AD BC ∥，可得EAD B ∠=∠，DAC BCA ∠=∠．证明()SAS DEA ACB ≌．则AED BCA ∠=∠．由AD CD =，可得DCA DAC BCA ∠=∠=∠．进而可得22BCD DCA BCA BCA AED ∠=∠+∠==∠．（2）由ED 平分BEC ∠，可得2AEC AED ∠=∠．即AEC BCD ∠=∠，由梯形ABCD ，AD BC ∥，AB CD =，可得EAD B BCD AEC ∠=∠=∠=∠．则CE BC AE ==．证明()SSS AED CED ≌，则ECD EAD B ∠=∠=∠，由180AEC ECD BCD B ∠+∠+∠+∠=︒，可求45AEC ECD BCD B ∠=∠=∠=∠=︒，进而可得90ECB ECD BCD ∠=∠+∠=︒，进而结论得证．【小问1详解】证明：连接AC ，∵梯形ABCD ，AD BC ∥，∴EAD B ∠=∠，DAC BCA ∠=∠．又∵AE BC =，AD AB =，∴()SAS DEA ACB ≌．∴AED BCA ∠=∠．∵AD CD =，∴DCA DAC BCA ∠=∠=∠．∴22BCD DCA BCA BCA AED ∠=∠+∠==∠，∴2BCD AED ∠=∠．【小问2详解】证明：∵ED 平分BEC ∠，∴2AEC AED ∠=∠．∵2BCD AED ∠=∠，∴AEC BCD ∠=∠，∵梯形ABCD ，AD BC ∥，AB CD =，∴EAD B BCD AEC ∠=∠=∠=∠．∴CE BC AE ==．∵AE CE DE DE AD CD ===，，，∴()SSS AED CED ≌，∴ECD EAD B ∠=∠=∠，∵180AEC ECD BCD B ∠+∠+∠+∠=︒，∴45AEC ECD BCD B ∠=∠=∠=∠=︒，∴90ECB ECD BCD ∠=∠+∠=︒，∴EBC 是等腰直角三角形．【点睛】本题考查了等腰梯形的性质，平行线的性质，角平分线，全等三角形的判定与性质，三角形内角和定理，等腰三角形的判定等知识．熟练掌握等腰梯形的性质，平行线的性质，角平分线，全等三角形的判定与性质，三角形内角和定理，等腰三角形的判定是解题的关键．24.如图，抛物线2y ax bx c =++顶点为坐标原点O 、且经过点()3,3A ，直线经过点A 和点()0,6B ．（1）求抛物线与直线的表达式；（2）如果将此抛物线平移，平移后新抛物线的顶点C 在原抛物线上，新抛物线的对称轴与直线AB 在原抛物线的内部相交于点D ，且45COD ∠=︒，求新抛物线的表达式．【答案】（1）抛物线表达式为213y x =，直线的表达式为6y x =-+（2）新抛物线的表达式2133324y x ⎛⎫=-+ ⎪⎝⎭或21335935322y x ⎛--=-+ ⎝⎭【分析】（1）利用待定系数法求解即可；（2）设直线6y x =-+与x 轴交于点E ，求出()6,0E ，设点D 的坐标为(),6m m -+，则点C 的坐标为21,3m m ⎛⎫ ⎪⎝⎭，分①当点D 在线段AB 上时，②当点D 在AB 延长线上时两种情况讨论即可；本题考查二次函数的图象与性质，相似三角形的判定与性质，熟练掌握知识点的应用是解题的关键．【小问1详解】∵抛物线2y ax bx c =++顶点为坐标原点O ，∴0b =，0c =，∵点()3,3A 在二次函数图象上，∴39a =，∴13a =，∴抛物线表达式为213y x =，设直线的表达式为1y kx b =+，∵直线经过点A 和点()0,6B ，∴113306k b k b =+⎧⎨=+⎩，∴116k b =-⎧⎨=⎩，∴直线的表达式为6y x =-+；【小问2详解】设直线6y x =-+与x 轴交于点E ，∴当0y =时，6x =，∴()6,0E ，∴6OE OB ==，∴45EBO ∠=︒，设点D 的坐标为(),6m m -+，∴点C 的坐标为21,3m m ⎛⎫ ⎪⎝⎭，∵CD y ∥轴，∴∠=∠BOD ODC ，当点D 在线段AB 上时，如图，∵45=︒=∠∠DBO COD ，∴∽△△CDO DOB ，∴=CD DO DO OB，∴2=⋅C D D O OB ，∴()2222621236OD m m m m =+-=-+，2163=-+-CD m m ，∴22121236663m m m m ⎛⎫-+=-+-⎪⎝⎭，∴2460m m -=，∵0m ≠，∴32m =，∴点C 的坐标为33,24⎛⎫ ⎪⎝⎭，∴新拋物线的表达式2133324y x ⎛⎫=-+ ⎪⎝⎭，当点D 在AB 延长线上时，延长DC 交x 轴于点H ，在DH 的延长线上截取HF HO =，连接FO ，如图，则45==∠∠∠︒=HFO HOF COD ，662=--=-DF m m m ，∵∠=∠ODF CDO ，∴△∽△CDO ODF ，∴=CD DO DO DF，∴2=⋅C D D O DF ，∴()221212366263m m m m m ⎛⎫-+=--+- ⎪⎝⎭，∴32390--=m m m ，∵0m ≠，∴32±=m （正值不符合题意，舍去），∴点C 的坐标为335935,22⎛-- ⎝⎭．∴新抛物线的表达式2139322y x ⎛--=-+ ⎝⎭．25.已知：O 的直径8AB B = ，与O 相交于点C 、D ，O 的直径CF 与B 相交于点E ，设B 的半径为x ，OE 的长为y ．（1）如图，当点E 在线段OC 上时，求y 关于x 的函数解析式，并写出定义域；（2）当点E 在直径CF 上时，如果OE 的长为3，求公共弦CD 的长；（3）设B 与AB 相交于G ，试问OEG 能否为等腰三角形？如果能够，请直接写出BC 弧的长度（不必写过程）；如果不能，请简要说明理由【答案】（1）()214044y x x =-<≤（21537（3）OEG 能为等腰三角形， BC 的长度为45π或127π【分析】本题主要考查了垂径定理、相似三角形的性质与判定，解直角三角形，圆的基本知识，做题时一定要分析各种情况，不要遗漏．（1）欲求y 关于x 的函数解析式，连接BE ，证明BCE OCB ∽即可；（2）求公共弦CD 的长，作BM CE ⊥，垂足为M ．通过圆的知识得出12BM CD =，转化为求BM 的长；分为两种情况：点E 在线段OC 上时；点E 在线段OF 上时，求出BM 的长；（3）OEG 为等腰三角形，分为两种情况：点E 在线段OC 上时；点E 在线段OF 上时，根据角的关系先求出角的度数，从而求出 BC的长度．【小问1详解】解：连接BE ，∵O 的直径8AB =，∴142OC OB AB ===．∵BC BE OC OB ==，，∴BEC C CBO ∠=∠=∠．∴BCE OCB ∽．∴CE BC CB OC=．∵–4CE OC OE y ==-，∴44y x x -=．∴y 关于x 的函数解析式为()214044y x x =-<≤；【小问2详解】解：如图所所示，当点E 在线段OC 上时，作BM CE ⊥，垂足为M ，∵43OC OE ==，，∴1CE =，∴1122EM CE ==，∴72OM =，∴152B M ===；设两圆的公共弦CD 与AB 相交于H ，则AB 垂直平分CD ．∴sin sin OC COB OB COB B C M H ⋅∠=⋅∠==．∴22CD CH BM ===．当点E 在线段OF 上时，作BM CE ⊥，垂足为M ，∵7OE OC OE =+=，∴1722EM CE ==∴–71322OM EM OE ==-=，∴372B M ==．同理可得2237CD CH BM ===综上所述，CD 1537【小问3详解】解：如图所示，当点E 在线段OC 上时，∵BG BE =，∴BEG BGE ∠=∠，∵180180BEG OEG BGE OGE +≠︒+=︒∠∠，∠∠，∴OEG OGE ≠∠∠，即OE OG ≠；∵180EOB OEB EBG ++=︒∠∠∠，∴180EOB OEG BEG EBG +++=︒∠∠∠∠，又∵180EGO BGE +=︒∠∠，∴EGO EOB OEG EBO =++∠∠∠∠，∴EOG EGO ≠∠∠，即OE GE ≠；当OG EG =时，设2OEG EOG x ==∠∠，∴4BEG BGE OEG EOG x ==+=∠∠∠∠，∴1801808OBE OEB EOB x =︒--=︒-∠∠∠，由（1）得180902BOC BEC OCB CBO x ︒-∠=∠=∠==︒-∠，∴1802CBE BEC BCE x =︒--=∠∠∠，∴1808290x x x ︒-+=︒-，解得18x =︒，∴36BOC ∠=︒，∴ BC 的长为36441805ππ⨯⨯=；如图所示，当点E 在线段OF 上时，同理可证明OG OE OG GE ≠≠，，当OE GE =时，设EOG EGO x ==∠∠，则1802GEO x =︒-∠，∵BG BE =，∴BEG BGE x ==∠∠，∴1801802GBE BGE BEG x =︒--=︒-∠∠∠；∵BC BE =，∴3180BCE BEC BEG GEO x ==-=-︒∠∠∠∠，∴1805406CBE BEC BEC x =︒--=︒-∠∠∠，∵OC OB =，∴3180OBC OCB x ==-︒∠∠，∴318018025406x x x -︒+︒-=︒-，解得5407x ⎛⎫=︒ ⎪⎝⎭，∴ BC 的长为54041271807ππ⨯⨯=；45π或127π．综上所述，OEG能为等腰三角形， BC的长度为。

上海市徐汇区2019-2020学年中考地理三模考试卷含解析

上海市徐汇区2019-2020学年中考地理三模考试卷一、选择题（本题包括25个小题，每小题2分，共50分．在每个小题给出的四个选项中，只有一项是符合题目要求的。

）1．下面为“经纬网示意图”，读图完成下面小题1．M点的经纬度坐标是A．160°E，40°N B．160°E，40°SC．160°W，40°S D．160°W，40°N2．下列各选项说法正确的是A．M点位于N点的西南方向B．M点位于热带，N点位于东半球C．M点位于中纬度，P点位于东半球D．N点位于南温带，四季分明【答案】1．B2．A【解析】【分析】1．读图可知，该图出现180°的经线，此线以东为西经，此线以西为东经；南北纬度的划分都是以赤道为界，赤道以北的纬度称北纬，用符号Ｎ表示；赤道以南为南纬，用符号Ｓ来表示；根据经纬度的变化规律可知，M点的经纬度是160°E，40°S，故答案选B。

2．读图可知，在经纬网地图上，根据经纬线来判断，经线指示南北方向，纬线指示东西方向，M点位于N 点的西南方向，故A正确；M点位于南温带，N点经度是160°W，位于西半球，故B错；M点位于中纬度，P点经度是180°，位于西半球，故C错误；N点位于北温带，四季分明，故D错；故答案选A。

【点睛】该题主要考查的是经纬度的判断、方向的判断、东西半球的判断和五带的判断，要求学生具有较强的读图分析问题的能力。

2．王刚同学的居住地有一口井，每年只有一天有阳光直射井底的现象，王刚同学有可能住在下列哪些省份（）A．台、闽、粤、桂B．滇、黔、粤、闽【答案】C【解析】【分析】【详解】北回归线穿过我国南部的四个省区，自西向东依次是云南省、广西壮族自治区、广东省和台湾省，简称依次是云（滇）、桂、粤、台，只有在以上四个省区中，一年中才会有直射现象，才能在6月22日前后才有阳光直射井底的现象，故选C．【点睛】本题考查我国省区的有关知识．3．我国年降水量空间分布的总趋势是A．从南向北递减B．从西北内陆向东南沿海递C．从东南沿海向西北内陆递减D．从西向东递减【答案】C【解析】【分析】【详解】我国的降水主要受季风的影响，主要依赖从海洋吹来的暖湿气流，暖湿气流大部分沿着东南向西北的方向从东南沿海登陆，随着时间的推移继续向西北移动，所以出现降水是由东南向西北递减，故选C.【点睛】本题考查我国降水的分布规律.4．图例“”表示的是（）A．铁路B．公路C．洲界D．国界【答案】D【解析】【分析】地图上表示各种地理事物的符号叫图例；文字说明，如山脉、河流、国家、城市等的名称，以及标明山高、海深等的数字，叫做注记．【详解】读图可知，图中符号表示国界线．故选D．【点睛】本题考查知识点简单，识记即可．C．径流量的多少D．蒸发量与降水量的多少【答案】D【解析】【分析】【详解】根据降水量与蒸发量的对比状况，我国划分为湿润地区、半湿润地区、半干旱地区和干旱地区。

上海市徐汇区上海市西南模范中学2024-2025学年九年级上学期月考数学试卷(9月份)

上海市徐汇区上海市西南模范中学2024-2025学年九年级上学期月考数学试卷（9月份）一、单选题1．下列条件中，不能确定一个直角三角形的条件是（）A ．已知两条直角边B ．已知两个锐角C ．已知一边和一个锐角D ．已知一条直角边和斜边2．如果ABC V 的三边之比是357::，与它相似的A B C '''V 的最短边为6，那么A B C '''V 的其余两边长的和是（）A ．12B ．19C ．21D ．243．如图，在ABC V 中，∠C ＝90°，设∠A ，∠B ，∠C 所对的边分别为a ，b ，c ，则（）A ．c ＝b sinB B ．b ＝c sin BC ．a ＝b tan BD ．b ＝c tan B 4．下列说法中，正确的是（）A ．有一个角相等的两个菱形必相似B ．有一条边相等的两个矩形必相似C ．有一个角相等的两个等腰三角形必相似D ．有一条边相等的两个等腰三角形必相似5．如图，在ABCD Y 中，M 、N 为对角线BD 上的两点，且::1:2:1BM MN ND ＝，连接AM 并延长交BC 于点E ，连接EN 并延长交AD 于点F ，则:AF FD 的值为（）A ．7:1B ．8:1C ．9:1D ．10:16．如图所示，△ABC 中，AD ⊥BC 于D ，对于下列中的每一个条件：①∠B ＋∠DAC ＝90°；②∠B ＝∠DAC ；③CD ：AD ＝AC ：AB ；④AB 2＝BD ·BC ，其中一定能判定△ABC 是直角三角形的共有（）A ．3个B ．2个C ．1个D ．0个二、填空题7．已知23a b =，则232a b a b -=+． 8．如果两个相似三角形的对应中线的比是5:2，那么它们的周长比是．9．在比例尺为125000:的地图上，相距6cm 的两地A 、B 的实际距离为千米．10．已知点M 是线段AB 的黄金分割点AM BM <（），若4AB =，则BM =．11．在ABC V 中，3,2AB AC ==，分别反向延长AB AC 、到D 、E ，若2AD =，则当AE =时，BC DE ∥．12．已知在ABC V 中，5AB AC ==，8BC =，点G 为重心，那么GA =．13．在以O 为坐标原点的直角坐标平面内有一点()4,3A ，如果AO 与x 轴正半轴的夹角α，那么α的余弦值是．14．在ABC V 中，90ACB ∠=︒，CD AB ⊥于D ．若23AD BD =，则B ∠的余切值为． 15．如图，在平行四边形ABCD 中，E 是线段AB 上一点，连结AC DE 、交于点F ．若23AE EB =，则ADF AEFS S =△△．16．如图，△ABC 中，AB=AC=4，BC =6，点E 、F 在边BC 上，且∠EAF=∠C ，则BF·CE= ．17．如图，四边形ABDC 中，AC 与BD 交于点O ，AC BC =，90ACB ∠=︒，AD BD ⊥于点D ．若258AOB COD S S =V V ，则BC CD=．18．阅读：对于线段MN 与点O （点O 与MN 不在同一直线上），如果同一平面内点P 满足：射线OP 与线段MN 交于点Q ，且12OQ OP =，那么称点P 为点O 关于线段MN 的“准射点”．问题：如图，矩形ABCD 中，3,4AB AD ==，点E 在边AD 上，且1AE =，连接BE ．设点F 是点A 关于线段BE 的“准射点”，且点F 在矩形ABCD 的内部或边上，如果点C 与点F 之间距离为d ，那么d 的取值范围为．三、解答题19．计算：22sin 302cos30tan 60sin 45︒-︒⋅︒⋅︒．20．计算：tan 304cos 45sin 60tan 45︒+︒︒-︒． 21．如图，已知在Rt ABC V 中，90C ∠=︒，3sin 5ABC ∠=，点D 在边BC 上，4BD =，连接AD ，2tan 3DAC∠=．（1）求边AC 的长；（2）求cot BAD ∠的值．22．如图，在ABC V 中，点P 、D 分别在边BC 、AC 上，PA AB ⊥，垂足为点A ，DP BC ⊥，垂足为点P ，AP BP PD CD=．(1)求证：AB AC =；(2)如果5AB =，3CD =，求AP 的长．23．如图，点A 在线段BD 上，在BD 的同侧作等腰Rt △ABC 和等腰Rt △ADE ，∠ABC =∠ADE=90° ，CD 与BE 、AE 分别交于点P 、M ．求证：（1）△BAE ∽△CAD ；（2）2CB 2=CP •CM ．24．如图，在平面直角坐标系中，点A −4,0 、()0,8B ，点C 在第一象限，点D 在线段OB 上，OD t =，90ADC ∠=︒，1tan 2DAC ∠=，CE OD ⊥，垂足为E ，连接AB 、BC ．(1)请直接写出图中与AOD △相似的三角形，直接写出线段CE 、OE 的长（用含t 的代数式表示）；(2)当CBA BAO ∠=∠时，求t 的值；(3)ABC V 的面积是否为定值？若是，请求出这个定值；若不是，请说明理由． 25．已知：如图，在梯形ABCD 中，AD BC ∥，90BAD ∠=︒，2AD =，4AB =，5BC =，在边BC 上任取一点E ，连接AE ，作F E C A E B ∠=∠，FEC ∠的另一边EF 交射线CD 于点F ．(1)求cos C 的值；(2)如图1，当点F 在线段CD 上时，若12=DF CF ，求BE 的长； (3)连接AF ，当AEF △是直角三角形时，直接写出BE 的长．。

上海市徐汇区2019-2020学年中考数学三模试卷含解析

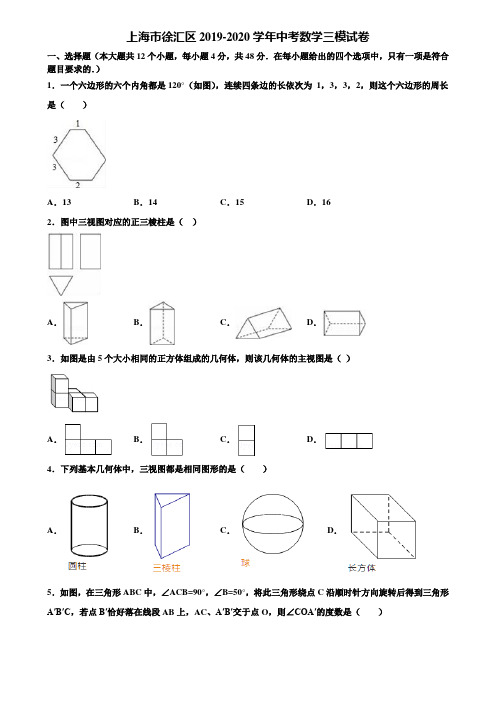
上海市徐汇区2019-2020学年中考数学三模试卷一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．一个六边形的六个内角都是120°（如图），连续四条边的长依次为1，3，3，2，则这个六边形的周长是（）A．13 B．14 C．15 D．162．图中三视图对应的正三棱柱是（）A．B．C．D．3．如图是由5个大小相同的正方体组成的几何体，则该几何体的主视图是（）A．B．C．D．4．下列基本几何体中，三视图都是相同图形的是（）A．B．C．D．5．如图，在三角形ABC中，∠ACB=90°，∠B=50°，将此三角形绕点C沿顺时针方向旋转后得到三角形A′B′C，若点B′恰好落在线段AB上，AC、A′B′交于点O，则∠COA′的度数是（）A ．50°B ．60°C ．70°D ．80°6．函数y=2x -的自变量x 的取值范围是（） A ．x≠2B ．x ＜2C ．x≥2D ．x ＞27．如图，已知▱ABCD 中，E 是边AD 的中点，BE 交对角线AC 于点F ，那么S △AFE ：S 四边形FCDE 为( )A ．1：3B ．1：4C ．1：5D ．1：68．根据中国铁路总公司3月13日披露，2018年铁路春运自2月1日起至3月12日止，为期40天全国铁路累计发送旅客3.82亿人次．3.82亿用科学记数法可以表示为（） A ．3.82×107B ．3.82×108C ．3.82×109D ．0.382×10109．关于二次函数2241y x x =+-，下列说法正确的是（） A ．图像与y 轴的交点坐标为()0,1B ．图像的对称轴在y 轴的右侧C ．当0x <时，y 的值随x 值的增大而减小D ．y 的最小值为-310．若关于x 的方程22(2)0x k x k +-+=的两根互为倒数，则k 的值为( ) A ．±1B ．1C ．－1D ．011．将一块直角三角板ABC 按如图方式放置，其中∠ABC ＝30°，A 、B 两点分别落在直线m 、n 上，∠1＝20°，添加下列哪一个条件可使直线m ∥n( )A ．∠2＝20°B ．∠2＝30°C ．∠2＝45°D ．∠2＝50°12．二次函数y=﹣（x ﹣1）2+5，当m≤x≤n 且mn ＜0时，y 的最小值为2m ，最大值为2n ，则m+n 的值为（） A ．B ．2C ．D ．二、填空题：（本大题共6个小题，每小题4分，共24分．）13．分解因式：32816a a a -+=__________.14．如图，△ABC 内接于⊙O ，AB 是⊙O 的直径，点D 在圆O 上，BD ＝CD ，AB ＝10，AC ＝6，连接OD 交BC 于点E ，DE ＝______．15．如图1，在平面直角坐标系中，将▱ABCD 放置在第一象限，且AB ∥x 轴，直线y ＝﹣x 从原点出发沿x 轴正方向平移，在平移过程中直线被平行四边形截得的线段长度l 与直线在x 轴上平移的距离m 的函数图象如图2，那么ABCD 面积为_____．16．如图，用黑白两种颜色的纸片，按黑色纸片数逐渐增加1的规律拼成如图图案，则第4个图案中有__________白色纸片，第n 个图案中有__________张白色纸片．17．化简：21211x x +=+-_____________. 18．如图，一次函数y 1=kx+b 的图象与反比例函数y 2=mx（x<0）的图象相交于点A 和点B ．当y 1＞y 2＞0时，x 的取值范围是_____．三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．19．（6分）如今，旅游度假成为了中国人庆祝传统春节的一项的“新年俗”，山西省旅发委发布的《2018年“春节”假日旅游市场总结分析报告》中称：山西春节旅游供需两旺，实现了“旅游接待”与“经济效益”的双丰收，请根据图表信息解决问题：（1）如图1所示，山西近五年春节假日接待海内外游客的数量逐年增加，2018年首次突破了“千万”大关，达到万人次，比2017年春节假日增加万人次．（2）2018年2月15日﹣20日期间，山西省35个重点景区每日接待游客数量如下：日期2月15日（除夕）2月16日（初一）2月17日（初二）2月18日（初三）2月19日（初四）2月20日（初五）日接待游客数量（万人次）7.56 82.83 119.51 84.38 103.2 151.55这组数据的中位数是万人次．（3）根据图2中的信息预估：2019年春节假日山西旅游总收入比2018年同期增长的百分率约为，理由是．（4）春节期间，小明在“青龙古镇第一届新春庙会”上购买了A，B，C，D四枚书签（除图案外完全相同）．正面分别印有“剪纸艺术”、“国粹京剧”、“陶瓷艺术”、“皮影戏”的图案（如图3），他将书签背面朝上放在桌面上，从中随机挑选两枚送给好朋友，求送给好朋友的两枚书签中恰好有“剪纸艺术”的概率．20．（6分）在△ABC中，AB=BC=2，∠ABC=120°，将△ABC绕着点B顺时针旋转角a（0°＜a＜90°）得到△A1BC；A1B交AC于点E，A1C1分别交AC、BC于D、F两点．（1）如图1，观察并猜想，在旋转过程中，线段BE与BF有怎样的数量关系？并证明你的结论．（2）如图2，当a=30°时，试判断四边形BC1DA的形状，并证明．（3）在（2）的条件下，求线段DE的长度．21．（6分）已知反比例函数的图象过点A（3，2）．（1）试求该反比例函数的表达式；（2）M（m，n）是反比例函数图象上的一动点，其中0＜m＜3，过点M作直线MB∥x轴，交y轴于点B；过点A作直线AC∥y轴，交x轴于点C，交直线MB于点D．当四边形OADM的面积为6时，请判断线段BM与DM的大小关系，并说明理由．22．（8分）我市某外资企业生产的一批产品上市后30天内全部售完，该企业对这批产品上市后每天的销售情况进行了跟踪调查．其中，国内市场的日销售量y1（万件）与时间t（t为整数，单位：天）的部分对应值如下表所示．而国外市场的日销售量y2（万件）与时间t（t为整数，单位：天）的关系如图所示．（1）请你从所学过的一次函数、二次函数和反比例函数中确定哪种函数能表示y1与t的变化规律，写出y1与t的函数关系式及自变量t的取值范围；（2）分别探求该产品在国外市场上市20天前（不含第20天）与20天后（含第20天）的日销售量y2与时间t所符合的函数关系式，并写出相应自变量t的取值范围；（3）设国内、外市场的日销售总量为y万件，写出y与时间t的函数关系式，并判断上市第几天国内、外市场的日销售总量y最大，并求出此时的最大值．23．（8分）【发现证明】如图1，点E，F分别在正方形ABCD的边BC，CD上，∠EAF=45°，试判断BE，EF，FD之间的数量关系．小聪把△ABE绕点A逆时针旋转90°至△ADG，通过证明△AEF≌△AGF；从而发现并证明了EF=BE+FD．【类比引申】（1）如图2，点E、F分别在正方形ABCD的边CB、CD的延长线上，∠EAF=45°，连接EF，请根据小聪的发现给你的启示写出EF、BE、DF之间的数量关系，并证明；【联想拓展】（2）如图3，如图，∠BAC=90°，AB=AC，点E、F在边BC上，且∠EAF=45°，若BE=3，EF=5，求CF的长．24．（10分）如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C=90°，∠B=∠E=30°.操作发现如图1，固定△ABC，使△DEC绕点C旋转．当点D恰好落在BC边上时，填空：线段DE与AC的位置关系是；②设△BDC的面积为S1，△AEC的面积为S1．则S1与S1的数量关系是．猜想论证当△DEC绕点C旋转到图3所示的位置时，小明猜想（1）中S1与S1的数量关系仍然成立，并尝试分别作出了△BDC和△AEC中BC，CE边上的高，请你证明小明的猜想．拓展探究已知∠ABC=60°，点D是其角平分线上一点，BD=CD=4，OE∥AB交BC于点E（如图4），若在射线BA上存在点F，使S△DCF=S△BDC,请直接写出相应的BF的长25．（10分）. 在一个不透明的布袋中装有三个小球，小球上分别标有数字﹣1、0、2，它们除了数字不同外，其他都完全相同．（1）随机地从布袋中摸出一个小球，则摸出的球为标有数字2的小球的概率为；（2）小丽先从布袋中随机摸出一个小球，记下数字作为平面直角坐标系内点M的横坐标．再将此球放回、搅匀，然后由小华再从布袋中随机摸出一个小球，记下数字作为平面直角坐标系内点M的纵坐标，请用树状图或表格列出点M所有可能的坐标，并求出点M落在如图所示的正方形网格内（包括边界）的概率．26．（12分）某校检测学生跳绳水平，抽样调查了部分学生的“1分钟跳绳”成绩，并制成了下面的频数分布直方图（每小组含最小值，不含最大值）和扇形图（1）D组的人数是人，补全频数分布直方图，扇形图中m＝；（2）本次调查数据中的中位数落在组；（3）如果“1分钟跳绳”成绩大于或等于120次为优秀，那么该校4500名学生中“1分钟跳绳”成绩为优秀的大约有多少人？27．（12分）某高中进行“选科走班”教学改革，语文、数学、英语三门为必修学科，另外还需从物理、化学、生物、政治、历史、地理（分别记为A、B、C、D、E、F）六门选修学科中任选三门，现对该校某班选科情况进行调查，对调查结果进行了分析统计，并制作了两幅不完整的统计图．请根据以上信息，完成下列问题：该班共有学生人；请将条形统计图补充完整；该班某同学物理成绩特别优异，已经从选修学科中选定物理，还需从余下选修学科中任意选择两门，请用列表或画树状图的方法，求出该同学恰好选中化学、历史两科的概率．参考答案一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．） 1．C 【解析】【详解】解:如图所示，分别作直线AB 、CD 、EF 的延长线和反向延长线使它们交于点G 、H 、I ．因为六边形ABCDEF 的六个角都是120°，所以六边形ABCDEF 的每一个外角的度数都是60°．所以AFI BGC DHE GHI V V V V 、、、都是等边三角形．所以31AI AF BG BC ====，． 3317GI GH AI AB BG ∴==++=++=， 7232DE HE HI EF FI ==--=--=， 7124CD HG CG HD ．=--=--= 所以六边形的周长为3+1+4+2+2+3=15；故选C ． 2．A 【解析】【分析】由俯视图得到正三棱柱两个底面在竖直方向，由主视图得到有一条侧棱在正前方，从而求解【详解】解：由俯视图得到正三棱柱两个底面在竖直方向，由主视图得到有一条侧棱在正前方，于是可判定A 选项正确．故选A ．【点睛】本题考查由三视图判断几何体，掌握几何体的三视图是本题的解题关键．3．A【解析】试题分析：观察图形可知，该几何体的主视图是．故选A．考点：简单组合体的三视图．4．C【解析】【分析】根据主视图、左视图、俯视图的定义，可得答案．【详解】球的三视图都是圆，故选C．【点睛】本题考查了简单几何体的三视图，熟记特殊几何体的三视图是解题关键．5．B【解析】试题分析：∵在三角形ABC中，∠ACB=90°，∠B=50°，∴∠A=180°﹣∠ACB﹣∠B=40°．由旋转的性质可知：BC=B′C，∴∠B=∠BB′C=50°．又∵∠BB′C=∠A+∠ACB′=40°+∠ACB′，∴∠ACB′=10°，∴∠COA′=∠AOB′=∠OB′C+∠ACB′=∠B+∠ACB′=60°．故选B．考点：旋转的性质．6．D【解析】【分析】根据被开放式的非负性和分母不等于零列出不等式即可解题.【详解】有意义,解：∵函数x-2∴x-2>0,即x＞2故选D【点睛】本题考查了根式有意义的条件,属于简单题,注意分母也不能等于零是解题关键.7．C【解析】【分析】根据AE∥BC，E为AD中点，找到AF与FC的比，则可知△AEF面积与△FCE面积的比，同时因为△DEC 面积=△AEC面积，则可知四边形FCDE面积与△AEF面积之间的关系．【详解】解：连接CE，∵AE∥BC，E为AD中点，∴12 AE AFBC FC==．∴△FEC面积是△AEF面积的2倍．设△AEF面积为x，则△AEC面积为3x，∵E为AD中点，∴△DEC面积=△AEC面积=3x．∴四边形FCDE面积为1x，所以S△AFE：S四边形FCDE为1：1．故选：C．【点睛】本题考查相似三角形的判定和性质、平行四边形的性质，解题关键是通过线段的比得到三角形面积的关系．8．B【解析】【分析】根据题目中的数据可以用科学记数法表示出来，本题得以解决．【详解】解：3.82亿=3.82×108，故选B．【点睛】本题考查科学记数法-表示较大的数，解答本题的关键是明确科学记数法的表示方法．9．D【解析】分析：根据题目中的函数解析式可以判断各个选项中的结论是否成立，从而可以解答本题．详解：∵y=2x2+4x-1=2（x+1）2-3，∴当x=0时，y=-1，故选项A 错误，该函数的对称轴是直线x=-1，故选项B 错误，当x ＜-1时，y 随x 的增大而减小，故选项C 错误，当x=-1时，y 取得最小值，此时y=-3，故选项D 正确，故选D ．点睛：本题考查二次函数的性质、二次函数的最值，解答本题的关键是明确题意，利用二次函数的性质解答．10．C【解析】【分析】根据已知和根与系数的关系12c x x a =得出k 2=1，求出k 的值，再根据原方程有两个实数根，即可求出符合题意的k 的值．【详解】解：设1x 、2x 是22(2)0x k x k +-+=的两根，由题意得：121=x x ，由根与系数的关系得：212x x k =， ∴k 2=1，解得k=1或−1，∵方程有两个实数根，则222=(2)43440∆--=--+>k k k k ，当k=1时，34430∆=--+=-<，∴k=1不合题意，故舍去，当k=−1时，34450∆=-++=>，符合题意，∴k=−1，故答案为：−1．【点睛】本题考查的是一元二次方程根与系数的关系及相反数的定义，熟知根与系数的关系是解答此题的关键． 11．D【解析】【分析】根据平行线的性质即可得到∠2=∠ABC+∠1，即可得出结论．【详解】∵直线EF∥GH，∴∠2=∠ABC+∠1=30°+20°=50°，故选D．【点睛】本题考查了平行线的性质，熟练掌握平行线的性质是解题的关键．12．D【解析】【分析】由m≤x≤n和mn＜0知m＜0，n＞0，据此得最小值为1m为负数，最大值为1n为正数．将最大值为1n 分两种情况，①顶点纵坐标取到最大值，结合图象最小值只能由x=m时求出．②顶点纵坐标取不到最大值，结合图象最大值只能由x=n求出，最小值只能由x=m求出．【详解】解：二次函数y=﹣（x﹣1）1+5的大致图象如下：．①当m≤0≤x≤n＜1时，当x=m时y取最小值，即1m=﹣（m﹣1）1+5，解得：m=﹣1．当x=n时y取最大值，即1n=﹣（n﹣1）1+5，解得：n=1或n=﹣1（均不合题意，舍去）；②当m≤0≤x≤1≤n时，当x=m时y取最小值，即1m=﹣（m﹣1）1+5，解得：m=﹣1．当x=1时y取最大值，即1n=﹣（1﹣1）1+5，解得：n=52，或x=n时y取最小值，x=1时y取最大值，1m=-（n-1）1+5，n=52，∴m=11 8，∵m＜0，∴此种情形不合题意，所以m+n=﹣1+52=12．二、填空题：（本大题共6个小题，每小题4分，共24分．）13．a(a －4)2【解析】【分析】首先提取公因式a ，进而利用完全平方公式分解因式得出即可．【详解】32816a a a -+22816()4.)(a a a a a =-+=-故答案为：2()4.a a -【点睛】本题主要考查因式分解，熟练掌握提取公因式法和公式法是解题的关键.分解一定要彻底.14．1【解析】【分析】先利用垂径定理得到OD ⊥BC ，则BE=CE ，再证明OE 为△ABC 的中位线得到116322OE AC ==⨯=，入境计算OD−OE 即可．【详解】解：∵BD ＝CD ， ∴¶¶BDCD =， ∴OD ⊥BC ，∴BE ＝CE ，而OA ＝OB ，∴OE 为△ABC 的中位线，∴116322OE AC ==⨯=， ∴DE ＝OD －OE ＝5－3＝1．故答案为1．【点睛】此题考查垂径定理,中位线的性质，解题的关键在于利用中位线的性质求解.15．1【解析】【分析】根据图象可以得到当移动的距离是4时,直线经过点A,当移动距离是7时,直线经过D,在移动距离是1时经过B,则AB=1-4=4,当直线经过D点,设其交AB与E,则DE=22,作DF⊥AB于点F.利用三角函数即可求得DF即平行四边形的高,然后利用平行四边形的面积公式即可求解【详解】解：由图象可知，当移动距离为4时，直线经过点A，当移动距离为7时，直线经过点D，移动距离为1时，直线经过点B，则AB＝1﹣4＝4，当直线经过点D，设其交AB于点E，则DE＝22，作DF⊥AB于点F，∵y＝﹣x于x轴负方向成45°角，且AB∥x轴，∴∠DEF＝45°，∴DF＝EF，∴在直角三角形DFE中，DF2+EF2＝DE2，∴2DF2＝1∴DF＝2，那么ABCD面积为：AB•DF＝4×2＝1，故答案为1．【点睛】此题主要考查平行四边形的性质和一次函数图象与几何变换，解题关键在于利用好辅助线16．13 3n+1【解析】分析：观察图形发现：白色纸片在4的基础上，依次多3个；根据其中的规律得出第n个图案中有白色纸片即可．详解：∵第1个图案中有白色纸片3×1+1=4张第2个图案中有白色纸片3×2+1=7张，第3图案中有白色纸片3×3+1=10张，∴第4个图案中有白色纸片3×4+1=13张第n个图案中有白色纸片3n+1张，故答案为：13、3n+1.点睛：考查学生的探究能力，解题时必须仔细观察规律，通过归纳得出结论.17．11 x-【解析】【分析】根据分式的运算法则即可求解. 【详解】原式=1211 (1)(1)(1)(1)(1)(1)1x xx x x x x x x -++==+-+-+--.故答案为：11 x-.【点睛】此题主要考查分式的运算，解题的关键是熟知分式的运算法则.18．-2<x<-0.5【解析】【分析】根据图象可直接得到y1＞y2＞0时x的取值范围．【详解】根据图象得：当y1＞y2＞0时，x的取值范围是﹣2＜x＜﹣0.5，故答案为﹣2＜x＜﹣0.5.【点睛】本题考查了反比例函数与一次函数的交点问题，熟悉待定系数法以及理解函数图象与不等式的关系是解题的关键．三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．19．（1）1365.45、414.4（2）93.79（3）30%；近3年平均涨幅在30%左右，估计2019年比2018年同比增长约30%（4）1 2【解析】【分析】（1）由图1可得答案；（2）根据中位数的定义求解可得；（3）由近3年平均涨幅在30%左右即可做出估计；（4）根据题意先画出树状图，得出共有12种等可能的结果数，再利用概率公式求解可得．【详解】（1）2018年首次突破了“千万”大关，达到1365.45万人次，比2017年春节假日增加1365.45﹣951.05=414.4万人次．故答案为：1365.45、414.4；（2）这组数据的中位数是84.38+103.22=93.79万人次，故答案为：93.79；（3）2019年春节假日山西旅游总收入比2018年同期增长的百分率约为30%，理由是：近3年平均涨幅在30%左右，估计2019年比2018年同比增长约30%，故答案为：30%；近3年平均涨幅在30%左右，估计2019年比2018年同比增长约30%．（4）画树状图如下：则共有12种等可能的结果数，其中送给好朋友的两枚书签中恰好有“剪纸艺术”的结果数为6，所以送给好朋友的两枚书签中恰好有“剪纸艺术”的概率为12．【点睛】本题考查了列表法与树状图法：利用列表法和树状图法展示所有可能的结果求出n ，再从中选出符合事件A 或B 的结果数目m ，求出概率，也考查了条形统计图与样本估计总体．20．（1）1EA FC =．（2）四边形1BC DA 是菱形.（3）2233．【解析】【分析】（1）根据等边对等角及旋转的特征可得1ABE C BF ≅V V即可证得结论；（2）先根据两组对边分别平行的四边形是平行四边形，再得到邻边相等即可判断结论；（3）过点E 作EG AB ⊥于点G ，解Rt AEG V 可得AE 的长，结合菱形的性质即可求得结果．【详解】（1）1EA FC =．证明：（证法一）AB BC A C =∴∠=∠Q ，．由旋转可知，111,,AB BC A C ABE C BF =∠=∠∠=∠∴1A BF CBE V V ≌．∴BE BF ，=又1AB BC =Q ，∴11A C A B CB ∠=∠=，，即1EA FC =．（证法二）AB BC A C =∴∠=∠Q ，．由旋转可知，1BA BE BC BF -=-，而1EBC FBA ∠=∠∴1A BF CBE ∴≅V V∴BE BF ，=∴1BA BE BC BF -=-即1EA FC =．（2）四边形1BC DA 是菱形.证明：111130,A ABA AC AB ︒∠=∠=∴Q ‖同理1AC BC ‖ ∴四边形1BC DA 是平行四边形.又1AB BC =Q ，∴四边形1BC DA 是菱形（3）过点E 作EG AB ⊥于点E ，则1AG BG ==．在EG AB ⊥中， 233AE = .由（2）知四边形1BC DA 是菱形，∴1AG BG ==．∴2233ED AD AE =-=-．【点睛】解答本题的关键是掌握好旋转的性质，平行四边形判定与性质，的菱形的判定与性质，选择适当的条件解决问题.21．（1）；（2）MB=MD ．【解析】【分析】(1)将A(3，2)分别代入y= ，y=ax 中，得a 、k 的值，进而可得正比例函数和反比例函数的表达式；(2)有S △OMB=S △OAC=×=3 ，可得矩形OBDC 的面积为12；即OC×OB=12 ；进而可得m 、n 的值，故可得BM 与DM 的大小；比较可得其大小关系.【详解】（1）将A（3，2）代入中，得2，∴k=6，∴反比例函数的表达式为．（2）BM=DM，理由：∵S △OMB=S△OAC=×=3，∴S矩形OBDC=S四边形OADM+S△OMB+S△OAC=3+3+6=12，即OC·OB=12，∵OC=3，∴OB=4，即n=4，∴，∴MB=，MD=，∴MB=MD．【点睛】本题考查了待定系数法求反比例函数和正比例函数解析式，反比例函数比例系数的几何意义，矩形的性质等知识.熟练掌握待定系数法是解（1）的关键，掌握反比例函数系数的几何意义是解（2）的关键.22．（1）y1=﹣15t（t﹣30）（0≤t≤30）；（2）∴y2=2(020)4120(2030)t tt t≤<⎧⎨-+≤≤⎩；（3）上市第20天，国内、外市场的日销售总量y最大，最大值为80万件．【解析】【分析】(1)根据题意得出y1与t之间是二次函数关系，然后利用待定系数法求出函数解析式；(2)利用待定系数法分别求出两个函数解析式，从而得出答案；(3)分0≤t＜20、t=20和20≤t≤30三种情况根据y=y1+y2求出函数解析式，然后根据二次函数的性质得出最值，从而得出整体的最值．【详解】解：(1)由图表数据观察可知y1与t之间是二次函数关系，设y1=a（t﹣0）（t﹣30）再代入t=5，y1=25可得a=﹣1 5∴y1=﹣15t（t﹣30）（0≤t≤30）(2)由函数图象可知y2与t之间是分段的一次函数由图象可知：0≤t＜20时，y2=2t，当20≤t≤30时，y2=﹣4t+120，∴y 2=()2(020)41202030t t t t ≤<⎧⎨-+≤≤⎩， (3)当0≤t ＜20时，y=y 1+y 2=﹣15t （t ﹣30）+2t=80﹣15（t ﹣20）2 ，可知抛物线开口向下，t 的取值范围在对称轴左侧，y 随t 的增大而增大，所以最大值小于当t=20时的值80，当20≤t≤30时，y=y 1+y 2=﹣15t （t ﹣30）﹣4t+120=125﹣15（t ﹣5）2 ，可知抛物线开口向下，t 的取值范围在对称轴右侧，y 随t 的增大而减小，所以最大值为当t=20时的值80，故上市第20天，国内、外市场的日销售总量y 最大，最大值为80万件．23．（1）DF=EF+BE ．理由见解析;（2）CF=1．【解析】（1）把△ABE 绕点A 逆时针旋转90°至△ADG ，可使AB 与AD 重合，证出△AEF ≌△AFG ，根据全等三角形的性质得出EF=FG ，即可得出答案；（2）根据旋转的性质的AG=AE ，CG=BE ，∠ACG=∠B ，∠EAG=90°，∠FCG=∠ACB+∠ACG=∠ACB+∠B=90°，根据勾股定理有FG 2=FC 2+CG 2=BE 2+FC 2；关键全等三角形的性质得到FG=EF ，利用勾股定理可得CF.解：（1）DF=EF+BE ．理由：如图1所示，∵AB=AD ，∴把△ABE 绕点A 逆时针旋转90°至△ADG ，可使AB 与AD 重合，∵∠ADC=∠ABE=90°，∴点C 、D 、G 在一条直线上，∴EB=DG ，AE=AG ，∠EAB=∠GAD ， ∵∠BAG+∠GAD=90°，∴∠EAG=∠BAD=90°，∵∠EAF=15°，∴∠FAG=∠EAG ﹣∠EAF=90°﹣15°=15°，∴∠EAF=∠GAF ，在△EAF 和△GAF 中，，∴△EAF ≌△GAF ，∴EF=FG ，∵FD=FG+DG ，∴DF=EF+BE ；（2）∵∠BAC=90°，AB=AC ，∴将△ABE 绕点A 顺时针旋转90°得△ACG ，连接FG ，如图2，∴AG=AE ，CG=BE ，∠ACG=∠B ，∠EAG=90°，∴∠FCG=∠ACB+∠ACG=∠ACB+∠B=90°，∴FG 2=FC 2+CG 2=BE 2+FC 2；又∵∠EAF=15°，而∠EAG=90°，∴∠GAF=90°﹣15°，在△AGF 与△AEF 中，，∴△AEF ≌△AGF ，∴EF=FG ，∴CF 2=EF 2﹣BE 2=52﹣32=16，∴CF=1．“点睛”本题考查了全等三角形的性质和判定，勾股定理，正方形的性质的应用，正确的作出辅助线构造全等三角形是解题的关键，此题是一道综合题，难度较大，题目所给例题的思路，为解决此题做了较好的铺垫．24．解：（1）①DE ∥AC ．②12S S =．（1）12S S =仍然成立，证明见解析；（3）3或2．【解析】【详解】（1）①由旋转可知：AC=DC ，∵∠C=90°，∠B=∠DCE=30°，∴∠DAC=∠CDE=20°．∴△ADC 是等边三角形．∴∠DCA=20°．∴∠DCA=∠CDE=20°．∴DE ∥AC ．②过D 作DN ⊥AC 交AC 于点N ，过E 作EM ⊥AC 交AC 延长线于M ，过C 作CF ⊥AB 交AB 于点F ．由①可知：△ADC 是等边三角形, DE ∥AC ，∴DN=CF,DN=EM ．∴CF=EM ．∵∠C=90°，∠B =30°∴AB=1AC ．又∵AD=AC∴BD=AC ． ∵1211S CF BD S AC EM 22=⋅=⋅， ∴12S S =．（1）如图，过点D作DM⊥BC于M，过点A作AN⊥CE交EC的延长线于N，∵△DEC是由△ABC绕点C旋转得到，∴BC=CE，AC=CD，∵∠ACN+∠BCN=90°，∠DCM+∠BCN=180°-90°=90°，∴∠ACN=∠DCM，∵在△ACN和△DCM中，ACN DCMCMD NAC CD∠∠⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ACN≌△DCM（AAS），∴AN=DM，∴△BDC的面积和△AEC的面积相等（等底等高的三角形的面积相等），即S1=S1；（3）如图，过点D作DF1∥BE，易求四边形BEDF1是菱形，所以BE=DF1，且BE、DF1上的高相等，此时S△DCF1=S△BDE；过点D作DF1⊥BD，∵∠ABC=20°，F1D∥BE，∴∠F1F1D=∠ABC=20°，∵BF1=DF1，∠F1BD=12∠ABC=30°，∠F1DB=90°，∴∠F1DF1=∠ABC=20°，∴△DF1F1是等边三角形，∴DF1=DF1，过点D作DG⊥BC于G，∵BD=CD，∠ABC=20°，点D是角平分线上一点，∴∠DBC=∠DCB=12×20°=30°，BG=12BC=92，∴3∴∠CDF1=180°-∠BCD=180°-30°=150°，∠CDF1=320°-150°-20°=150°，∴∠CDF 1=∠CDF 1， ∵在△CDF 1和△CDF 1中，1212DF DF CDF CDF CD CD ⎧⎪∠⎨⎪⎩＝＝＝， ∴△CDF 1≌△CDF 1（SAS ）， ∴点F 1也是所求的点，∵∠ABC=20°，点D 是角平分线上一点，DE ∥AB ， ∴∠DBC=∠BDE=∠ABD=12×20°=30°，又∵BD=33， ∴BE=12×33÷cos30°=3， ∴BF 1=3，BF 1=BF 1+F 1F 1=3+3=2，故BF 的长为3或2．25．（1）；（2）列表见解析，. 【解析】试题分析：（1）一共有3种等可能的结果总数，摸出标有数字2的小球有1种可能，因此摸出的球为标有数字2的小球的概率为；（2）利用列表得出共有9种等可能的结果数，再找出点M 落在如图所示的正方形网格内（包括边界）的结果数，可求得结果.试题解析：（1）P （摸出的球为标有数字2的小球）=；（2）列表如下：小华小丽 -12-1 （-1，-1）（-1，0）（-1，2） 0（0，-1）（0，0）（0，2）2（2，-1）（2，0）（2，2）共有9种等可能的结果数，其中点M 落在如图所示的正方形网格内（包括边界）的结果数为6， ∴P （点M 落在如图所示的正方形网格内）==.考点：1列表或树状图求概率；2平面直角坐标系.26．（1）16、84°；（2）C ；（3）该校4500名学生中“1分钟跳绳”成绩为优秀的大约有3000（人）【解析】【分析】（1）根据百分比＝所长人数÷总人数，圆心角＝360︒⨯百分比，计算即可；（2）根据中位数的定义计算即可；（3）用一半估计总体的思考问题即可；【详解】（1）由题意总人数610%60÷＝＝人， D 组人数6061419516----＝＝人； B 组的圆心角为143608460︒⨯=︒；（2）根据A 组6人，B 组14人，C 组19人，D 组16人，E 组5人可知本次调查数据中的中位数落在C 组；（3）该校4500名学生中“1分钟跳绳”成绩为优秀的大约有404500300060⨯＝人．【点睛】本题主要考查了数据的统计，熟练掌握扇形图圆心角度数求解方法，总体求解方法等相关内容是解决本题的关键.27．（1）50人；（2）补图见解析；（3）110. 【解析】分析：（1）根据化学学科人数及其所占百分比可得总人数；（2）根据各学科人数之和等于总人数求得历史的人数即可；（3）列表得出所有等可能结果，从中找到恰好选中化学、历史两科的结果数，再利用概率公式计算可得．详解：（1）该班学生总数为10÷20%=50人；（2）历史学科的人数为50﹣（5+10+15+6+6）=8人，补全图形如下：（3）列表如下：化学生物政治历史地理化学生物、化学政治、化学历史、化学地理、化学生物化学、生物政治、生物历史、生物地理、生物政治化学、政治生物、政治历史、政治地理、政治历史化学、历史生物、历史政治、历史地理、历史地理化学、地理生物、地理政治、地理历史、地理由表可知，共有20种等可能结果，其中该同学恰好选中化学、历史两科的有2种结果，所以该同学恰好选中化学、历史两科的概率为21= 2010．点睛：本题考查了列表法与树状图法：利用列表法或树状图法展示所有等可能的结果n，再从中选出符合事件A或B的结果数目m，然后利用概率公式求事件A或B的概率．。

上海西南模范中学2020年中考化学三模试题及答案

上海西南模范中学2020年中考化学三模试题及答案一、选择题（培优题较难）1．下列溶液中无色，且在pH=1时能大量共存的是A．CuSO4NaCl KNO3 B．NaOH NaCl NaNO3C．Na2SO4KCl ZnCl2 D．K2SO4AgNO3 NaCl【答案】C【解析】pH=1的溶液中有大量的H+，大量共存要求物质之间相互交换成分不能结合生成水、气体或沉淀，形成无色溶液要求分析常见离子在水溶液中的颜色，若为无色，符合题意A、物质之间相互交换成分不能结合生成水、气体或沉淀，但Cu2+在水溶液中为蓝色，故A错误．B、NaOH可与酸发生中和反应，故不能共存，所以错误C、物质之间相互交换成分不能结合生成水、气体或沉淀，且离子均为无色，故C正确．D、K2SO4AgNO3生成硫酸银沉淀，故D不正确故选C2．某固体混合物由Mg和MgO组成，取该混合物与19. 6%的稀硫酸恰好完全反应（反应后溶液中无晶体析出），所得溶液蒸发82. 2g水后得到固体的质量为24g，则原混合物中氧元素的质量分数为（）A．16%B．20%C．25%D．40%【答案】C【解析】【详解】镁和稀硫酸反应生成硫酸镁和氢气，氧化镁和稀硫酸反应生成硫酸镁和水，所得溶液蒸发82. 2g水后得到的固体是硫酸镁， 24g硫酸镁中，镁元素的质量为：2424g100% 4.8g120⨯⨯=，硫酸根的质量=42g-4.8g-19.2g，参加反应的硫酸溶液中硫酸的质量=9619.2g100%19.6g98÷⨯=，参加反应的硫酸溶液的质量=19.6g19.6%=100g÷；反应生成的水的质量=82.2g –(100g-19.6g)=1.8g；生成的水中氧元素的质量=161.8g100% 1.6g18⨯⨯=，根据质量守恒定律可知，氧化镁中氧元素的质量=反应生成水中氧元素质量=1.6g。

原混合物中氧元素的质量分数=1.6g100%25%1.6g+4.8g⨯=。

★试卷3套精选★上海市徐汇区某名校2020年中考三模物理试题

C． D．
【答案】B
【解析】AD．两电阻并联，电压表测电源的电压，因电源的电压不变，所以，压力变化时，电压表的示数不变，故AD不符合；
BC．两电阻串联，压力越大时，滑片下移，接入电路中的在变大，电路中的总电阻变大，
由I＝可知，电路中的电流变小，由U＝IR可知，定值电阻两端的电压变小，因串联电路中总电压等于各分电压之和，所以，滑动变阻器两端的电压变大，综上可知，B中电压表并联在滑动变阻器两端符合，C中电压表并联在定值电阻两端不符合。
C． D．
【答案】B
【解析】A．据安培定则判断，该螺线管的右端是N极，左端是S极，故磁感线的方向错误，故A错误；
B．据安培定则判断，该螺线管的左端是N极，右端是S极，且磁感线的方向正确，故B正确；
C．据安培定则判断，该螺线管的右端是N极，左端是S极，故磁感线的方向错误，故C错误；
D．据安培定则判断，该螺线管的左端是N极，右端是S极，故磁感线的方向错误，故D错误；
C．干电池是电源，电源供电时，储存在电源中的化学能转变为电能供给外部电路，故C正确；
D．我们用双手互相摩擦时，需要克服双手之间的摩擦力，这是克服摩擦做功，使双手内能增加，温度升高，将机械能转化为了内能，故D错误．故答案为C．
2．一通电螺线管中的电流方向和其周围磁感线的分布如图所示，其中正确的是
A． B．
4．从微观世界到无垠的宇宙，存在着各种各样的物质，科学家一直在探索．下列科学家中，在实验基础上提出“原子核式结构模型”的是（）
A．阿伏伽德罗B．道尔顿C．汤姆孙D．卢瑟福
【答案】D
【解析】A．1811年，意大利物理学家阿伏加德罗将组成物质的仍能保持其化学性质不变的最小微粒命名为分子；故A错误；
B．1808年，道尔顿继承古希腊朴素原子论和牛顿微粒说，提出原子学说；故B错误

上海西南模范中学2020年中考化学三模试题及答案

上海西南模范中学2020年中考化学三模试题及答案一、选择题（培优题较难）1．除去下列物质中的少量杂质，下列选用试剂或方法正确的是（）A．A B．B C．C D．D【答案】B【解析】【分析】根据原物质和杂质的性质选择适当的除杂剂和分离方法，所谓除杂（提纯），是指除去杂质，同时被提纯物质不得改变，除杂质题至少要满足两个条件：①加入的试剂只能与杂质反应，不能与原物质反应；②反应后不能引入新的杂质。

【详解】A、FeSO4溶液和CuSO4均能与过量的锌粉反应，不但能把杂质除去，也会把原物质除去，不符合除杂原则，故选项所采取的方法错误；B、Na2CO3能与过量稀盐酸反应生成氯化钠、水和二氧化碳，盐酸具有挥发性，再蒸发除去盐酸，能除去杂质且没有引入新的杂质，符合除杂原则，故选项所采取的方法正确。

C、HCl能与过量的Ca（OH）2溶液反应生成氯化钙和水，能除去杂质但引入了新的杂质氢氧化钙（过量的），不符合除杂原则，故选项所采取的方法错误；D、KCl易溶于水，MnO2难溶于水，可采取加水溶解、过滤、蒸发的方法进行分离除杂，故选项所采取的方法错误。

故选B。

【点睛】物质的分离与除杂是中考的重点，也是难点，解决除杂问题时，抓住除杂质的必需条件（加入的试剂只与杂质反应，反应后不能引入新的杂质）是正确解题的关键。

2．下列四个图象，分别对应四种操作过程，其中正确的是（）A．向pH＝2的酸溶液中不断加水B．向NaOH溶液中逐滴加入稀盐酸C．向一定量的水中持续加入食盐（m表示食盐的质量，A%表示溶质质量分数）D．等质量的锌、铁与足量的稀硫酸反应，产生氢气的质量随反应时间t的变化【答案】D【解析】A.溶液的pH小于7，溶液呈酸性，pH越小，酸性越强；溶液的pH大于7，溶液呈碱性，pH越大碱性越强；pH等于7，溶液呈中性。

向pH＝2的酸溶液中不断加水，使溶液的酸性变弱，溶液pH变大，但是始终呈酸性，不会出现pH等于7或pH大于7；B. 向NaOH溶液中逐滴加入稀盐酸，开始是氢氧化钠溶液，pH大于7；随酸的加入，pH不断减小，刚好完全反应pH等于7；酸过量时，溶液呈酸性，pH小于7；C. 向一定量的水中持续加入食盐，开始，随食盐的溶解，溶质的质量分数增大，饱和后，溶质的质量分数不再改变；D. 等质量的锌、铁与足量的稀硫酸反应，锌的活动性比铁强，所以锌先反应完，但是铁比同质量的锌生成氢气多。

2023年上海市徐汇区3月线下中考一模数学含答案

初三数学（考试时间100分钟，满分100分）一、选择题（本大题共6题，每题4分，满分24分）【下列各题的四个选项中，有且只有一个选项是正确的】1．在Rt △ABC 中，∠C ＝90°，AB ＝5，AC ＝4．下列选项中正确的是（）（A ）tan B ＝34；（B ）cot B ＝43；（C ）sin B ＝45；（D ）cos B ＝45． 2．下列命题中假命题是（）（A ）任意两个等腰直角三角形都相似；（B ）任意两个含36°内角的等腰三角形相似；（C ）任意两个等边三角形都相似；（D ）任意两个直角边之比为1：2的直角三角形相似．3．如图，已知////a b c ，32AD DF =，下列选项中错误的是( ) （A ）35AD AF =；（B ）32BC CE =；（C ）23AB EF = ；（D ）35BC BE =． 4．二次函数2(0)y ax bx c a =++≠的图像如图所示，点P 在x 轴的正半轴上，且OP ＝1，下列选项中正确的是（）（A ）0a >；（B ）0c <；（C ）0a b c ++>；（D ）0b <.5．将抛物线212y x =-经过下列平移能得到抛物线()21132y x =-+-的是（）（A ）向右1个单位，向下3个单位；（B ）向左1个单位，向下3个单位；（C ）向右1个单位，向上3个单位；（D ）向左1个单位，向上3个单位．6．如图，点D 在ABC ∆边AB 上，ACD B ∠=∠，点F 是ABC ∆的角平分线AE 与CD 的交点，且AF =2EF ，则下列选项中不正确的是（）（A ）23AD AC =；（B ）23CF BE =；（C ）23DC BC =；（D ）23AD DB =．第4题第3题第6题二、填空题（本大题共12题，每题2分，满分24分）7. 已知43x y =，则x y x y -=+__________． 8．计算：()()1233a b a b ---=___________． 9．两个相似三角形的对应边上的中线之比4 ：5，则这两个三角形面积之比为________．10．大自然巧夺天工，一片树叶也蕴含着“黄金分割”．如图，P 为线段AB 的黄金分割点（AP ＞PB ）如果AB 的长度为8cm ，那么叶片部分AP 的长度是______cm ．11．如图，已知G 为△ABC 的重心，过点G 作BC 的平行线交边AB 和AC 于点D 、E . 设 GB a =，GC b =，试用xa yb +（x 、y 为实数）的形式表示向量=DE ．12.小明和小杰去公园游玩，小明给站在观景台边缘的小杰拍照时，发现他的眼睛、凉亭顶端、小杰的头顶三点恰好在一条直线上（如图所示）．已知小明的眼睛离地面的距离AB 为1.6米，凉亭的高度CD 为6.6米，小明到凉亭的距离BD 为12米，凉亭与观景台底部的距离DF 为42米，小杰身高为1.8米．那么观景台的高度为________米．13．已知点(3,)A m -、(2,)B n -在抛物线422+--=x x y 上，则____m n ．（填“>”、 “=”或“<”）14．小球沿着坡度为i=1：1.5的坡面滚动了13m ，则在这期间小球滚动的水平距离是______m ．15．计算：cos60sin60cot30tan 45︒-︒︒-︒= ． 16．如图，在由正三角形构成的网格图中，A 、B 、C 三点均在格点上，则sin ∠BAC 的值为．17．如图，点E 是矩形ABCD 纸片边CD 上一点，如果沿着AE 折叠矩形纸片，恰好使点D 落在边BC 上的点F 处．已知BF ＝6cm ，tan ∠BAF ＝34，那么折痕AE 的长是．第12题第11题第10题18．规定：如果经过三角形一个顶点的直线把这个三角形分成两个小三角形，其中一个小三角形是等腰三角形，另一个小三角形和原三角形相似，那么符合这样条件的三角形称为“和谐三角形”，这条直线称为这个三角形的“和谐分割线”．例如，如图所示，在Rt ABC ∆中，90C ∠=︒，CA CB =，CD 是斜边AB 上的高，其中ACD ∆是等腰三角形，且BCD ∆和ABC ∆相似，所以ABC ∆是“和谐三角形”，直线CD 为ABC ∆的“和谐分割线”．请依据规定求解问题：已知DEF ∆是“和谐三角形”，42D ∠=︒，当直线EG 是DEF ∆的“和谐分割线”时，F ∠的度数是（写出所有符合条件的情况）．三、解答题（本大题共题，满分78分） 19．如图，在△ABC 中，已知△C ＝90°，sin A ＝135．点D 为边AC 上一点，△BDC ＝45°，AD ＝7，求CD 的长．20．如图，点E 在平行四边形ABCD 的边BC 的延长线上，且2CE BC =，AE 与CD 交于点F ．设AB a =，AD b =．（1）用向量a 、b 表示向量DE ；（2）求作：向量EF 分别在向量EC 、ED 方向上的分向量．（不要求写作法，但要保留作图痕迹，并指出所作图中表示结论的分向量）第19题第20题第18题第17题第16题21．已知二次函数2369y x x =-++．（1）用配方法把二次函数2369y x x =-++化为2()y a x m k =++的形式，并指出这个函数图像的开口方向、对称轴和顶点的坐标；（2）如果将该函数图像向右平移2个单位，所得的新函数的图像与x 轴交于点A B 、（点 A 在点B 左侧），与y 轴交于点C ，顶点为D ，求四边形DACB 的面积．22．如图，是一个放置于水平桌面的平板支架的示意图，底座的高AB 为5cm ，宽MN 为10cm ，点A 是MN 的中点，连杆BC 、CD 的长度分别为18.5cm 和15cm ，△CBA =150°，且连杆BC 、CD 与AB 始终在同一平面内.（1）求点C 到水平桌面的距离；（2）产品说明书提示，若点D 与A 的水平距离超过AN 的长度，则该支架会倾倒. 现将 △DCB 调节为80°，此时支架会倾倒吗？（参考数据：36.020tan ≈︒，75.220cot ≈︒，34.020sin ≈︒，94.020cos ≈︒）第21题第22题23.如图，已知△ABC 是等边三角形，D 、E 分别是边BC 、AC 上的点，且DC BD CE BC ⋅=⋅.在DE 的延长线上取点F ，使得DF =BD ，联结CF .（1）求证：△ADE =60°；（2）求证：CF ∥AB ..24．已知在平面直角坐标系xOy 中，抛物线32++=bx ax y 经过点A (-1，0)、B (4，0)，与y 轴相交于点C .(1) 求抛物线的表达式；(2) 点P 是第一象限内抛物线上的一个动点，过点P 作直线PD x ⊥轴，垂足为点D ，直线PD 与直线BC 相交于点E .① 当CP=CE 时，求点P 的坐标；② 联结AC ，过点P 作直线AC 的平行线，交x 轴于点F ，当△BPF=△CBA 时，求点P 的坐标．第24题25．如图1，已知菱形ABCD 中，点E 在边BC 上，△BFE =△ABC ，AE 交对角线BD 于点F ．（1）求证：△ABF △DBA ；（2）如图2，联结CF ．① 当△CEF 为直角三角形时，求△ABC 的大小；② 如图3，联结DE ．当DE ⊥FC 时，求ABD cos 的值．第25题图1 第25题图2 第25题图32022学年徐汇区初三数学期末学习水平检测试卷参考答案2023.02一．选择题1．C ．2．B ．3．C ．4．D ．5．B ．6．D ．二．填空题7.71． 8．b a 35-． 9．16 ：25． 10．454-． 11．b a 3232+-． 12．3.22． 13．<．14．133． 15．21-． 16．721． 17．55． 18．46322754.︒︒︒︒、、、三、解答题19．解：在Rt△ABC 中，△C ＝90°，sin A ＝135=AB BC ．设BC=k 5，AB=k 13，∴AB=k k k BC AB AC 12)5()13()()(2222=-=-= 在Rt△BCD 中，△C ＝90°，∠BDC ＝45°，∴∠CBD ＝∠BDC ＝45°，∴BC ＝CD ＝k 5．∴AD ＝AC －CD ＝k 7．△AD ＝7，∴7＝k 7，∴1=k ．∴BC ＝CD ＝55=k ． 20．（1）解： ABCD 中，有AD △BE 且AD BC =. AB △DC 且AB DC = △2CE BC =，∴2CE AD =， ∴22AD CE b ==.∴DC AB =a =，∴2DE DC CE a b =+=+（2）作图正确3分，结论正确1分21．（1）223693(2)9y x x x x =-++=--+223(21)123(112)x x x =--+=-++- 函数图像的开口方向向下、对称轴为直线1x =，顶点的坐标为(1,12)；（2）由题意平移后所得的新函数的解析式为2)23(13y x =--+，得到点A (1,0)B 、(5,0)，点C (0,15)-，顶点D (3,12)计算可得四边形DACB 的面积为54.22．解：（1）过点C 作CE ⊥MN 于E ，过点B 作BF ⊥CE 于F .由题意可得，AB =EF =5，∠CBF =60°.在Rt △BFC 中，∠BFC =90°，∠CBF =60°，BC =18.5∴sin ∠CBF==BC CF sin ∠60°23=，即23723CF =，∴4337=CF ∴420337+=CE 答：此时点C 与水平桌面的距离为()420337+厘米.（2）过点C 作CG ∥BF ，过点作DH ⊥CG 于H ，DH 与BF 交于点K. 由题意可知，在Rt △CDH 中，∠CDH =90°，∠DCH =20°，CH =FK ，CD =15. △cos ∠DCH=CD CH ，0.94=15CH ，∴CH =FK =14.1. 在Rt △BFC 中，∠BFC =90°，∠CBF =60°，BC =18.5. ∴cos ∠CBF=BC BF ，5.1821BF =，∴BF=9.25 ∴BK=KF －BF=CH －BF =4.85答：因为BK =4.85＜5，所以支架不会倾倒.23.证明：（1）∵△ABC 是等边三角形，∴∠B =∠ACB =60°，AB =BC .∵DC BD CE BC ⋅=⋅，∴CEBD DC BC = ∴CEBD DC AB =，∴△ABD ∽△DCE . ∴∠BAD =∠CDE∵∠ADC =∠ADE +∠CDE ，∠ADC =∠B +∠BAD ，∴∠ADE =∠B =60°（2）联结AF ，∵AD =AF ，且∠ADF =60°，∴△ADF 是等边三角形，∴∠AFD =60°.∵∠AFD =∠ACB =60°，∠AEF =∠DEC. ∴△AEF ∽△DEC∴ECEF DE AE = ∴EC DE EF AE =,又∵∠AED =∠FEC ，∴△AED ∽△FEC . ∴∠FCA =∠ADF =60°.∵∠B =60°，∠FCB =∠FCA +∠ACB =120°， ∴∠B +∠FCB =180°. ∴CF ∥AB .24.（1）∵抛物线32++=bx ax y 经过点)0,1(-A 、)0,4(B ，∴⎩⎨⎧++=+-=3416030b a b a 解得49,43=-=b a ∴349432++-=x x y（2）过点C 作CH 垂直于PD ，垂足为点H ；∵CP =CE ，CH ⊥PE ，∴PH =HE .∵C (0,3) , B (4,0)，∴OC =3 , OB =4.∵CH ⊥PD ，PD ⊥OB ，CH ∥OB.∴∠HCE =∠CBO.∴tan ∠HCE =tan ∠CBO ，即43==OB OC CH EH . 设CH =4k ，则PH =EH =3k ，PD =HD +HP =O C +HP =3+3k ，∴点P 坐标为（4k ，3+3k ）又∵点P 在抛物线349432++-=x x y 上， ∴3)4(49)4(43332++-=+k k k ，解得k=21，k=0（舍）. ∴)29,2(P .（3）∵PG ∥AC ，∴∠CAB =∠PGB.又∵∠BPG =∠CBA ，∴△PGB ∽△BAC .∵AB =BC=5，∴PF =PB .又∵PD ⊥OB ，∴FD =BD =21FB. ∵点P 在抛物线349432++-=x x y 上，设P （x , 349432++-x x ）,0>x . ∵∠CAB =∠PDB ，∴tan ∠CAB =tan ∠PDB ，即3==AO CO FD PD . 即34349432=-++-xx x ，解得43==x x ，（舍）∴)3,3(P .25．解：（1）证明：∵四边形ABCD 是菱形，∴∠ABC+∠BAD =180°. 又∠BFE+∠AFB =180°且∠ABC =∠BFE ，∴∠AFB=∠BAD.又∠ABD=∠ABD ，∴△ABF ∽△ABD.（2）设∠ABD=α∵四边形ABCD 是菱形，∴AB=AD ，BD 平分∠ABC.∴∠ADB=∠ABD =α，∠CBD=∠ABD =α∴∠ABC=∠CBD+∠ABD =2α.∵△ABF ∽△ABD ，∴∠ADB=∠BAF =α.∴∠AEC=∠BAF+∠ABC =3α∵BA=BC ，∠CBD=∠ABD ，BF=BF , ∴△ABF ≌△CBF .∴∠BCF=∠BAF =α. 在△CEF 中，∠BCF=α，∠AEC =3α，故∠EFC =180°-4α ∵△CEF 是直角三角形∴有以下三种可能的情形：①∠BCF=α=90°，此时∠ABC=2α=180°，不符合题意，应舍去； ②∠AEC =3α=90°，此时∠ABC=2α=60°；③∠EFC =180°-4α=90°，此时4α=90°，∠ABC=2α=45°；综上所述，当△CEF 为直角三角形时，求∠ABC 的大小为60°或45°.（3）联结AC ，交BD 于点O ，记DE 分别交CF 、AC 于点G 、H.∵四边形ABCD 是菱形 ∴AC ⊥BD ∴∠BOC=90°∴∠BCO+∠OBC=90°. ∵DE ⊥CF ∴∠EGC=90°∴∠DEC+∠FCE=90°.又∵∠FCE=∠OBC ∴∠DEC=∠BCO . △HE=HC.∵AD //BC ∴HE HC DE AC= ∴DE=AC ， ∴四边形AECD 为等腰梯形. ∴∠FEC= ∠ECD .又∠BAD= ∠ECD ，∴∠FEC= ∠BAD .又∠FCE= ∠BAF ，∴△EFC ∽△BCF ∽△ABF ∽△ABD..∴∠CFE=∠ECF ,△EF=EC .又DE ⊥FC ，∴DC=DF=BC . 设BF=x ，DC=DF=BC=1，则BD=BF+FD=x +1，∵△ABF ∽△ABD ，∴BF AB AB BD =，即111x x =+，解得BF =.∴BO OD ==∴cos BO ABD AB ∠==.。

徐汇区西南模范中学初三3月月考卷(精选、)

2017年3月西南模范初三测试卷I. Choose the best answer31. What did the teacher ___________ you to __________ at the meeting?A. tell…sayB. ask…speakC. tell…speakD. ask…talk32. I remember ___________ a telephone call to Miss Li last night.A. makeB. to makeC. makingD. made33. Our teacher, together with all the students, __________ morning exercise every day.A. doB. doesC. is doingD. are doing34. The workers in the city ____________ for more than sixteen hours a day in old days.A. are made to workB. are made workC. were made to workD. were made work35. This winter was not too cold. The ice in the river was too thin for us _____________.A. to skate on itB. skating on itC. to skate onD. skating on36. The number of students who ___________ the English club _____________20.A. take part in, isB. join, areC. take part in, areD. join, is37. Mike studies ___________ Mary.A. not so hardly asB. as hardly asC. as hard asD. not as hard as38. They go to see their grandparents ____________ Sunday morning.A. in everyB. everyC. on everyD. in39. We had no ___________ in finding the doctor’s address.A. problemB. troubleC. questionD. matter40. Yesterday I met Miss Li in the street. She told me that she ____________ to Japan twice.A. has beenB. wentC. had beenD. has gone41. Last Teachers’ Day, the teachers received a box ____________ card.A. was filled withB. full ofC. fill withD. fulled with42. He will take part in the beginning ceremony when the new hospital ___________ to the public.A. is openB. is openedC. will openD. will be opened43. – Do you mind my taking this seat?-- ______________.A. Yes, sit down, please.B. Yes, take it, please.C. No, of course not.D. No, you can’t take it.44. He left the meeting early because he had to __________ his son from school.A. pick upB. put upC. take upD. bring up45. Mr. Black didn’t go to work yesterday because he was ill in __________ bed.A. aB. anC. theD. /46. She has made many friends ___________ she came to our school.A. beforeB. afterC. sinceD. until47. I am ___________ your view on spending pocket money. It’s reasonable.A. in favour ofB. in charge ofC. afraid ofD. famous for48. The girl needs some help, _____________?A. does sheB. need sheC. doesn’t sheD. needn’t she49. The characters need strong personalities ____________ will come across in the picture.A. whoB. whichC. whenD. where50. Steam ___________ from the basin after heating the water.A. was seen riseB. was seen to raiseC. was seen raisingD. was seen risingII. Complete the following passage with words or phrases in the box. Each word can only be usedNow satellites are helping to forecast (预报) the weather. They are ______51_______, and they can reach any part of the world. The satellites ______52______ of the atmosphere (大气), because this is where the weather ______53_______. They send these pictures to the weather stations. So meteorologists (气象学家) can see the weather of any part of the world. From the pictures, the scientists can often say _______54______.Today, nearly five hundred weather stations in sixty countries receive satellite pictures. When they receive new pictures, the meteorologists compare them with ______55______. Perhaps they may find that the clouds have changed ______56______. This may mean that the weather on the ground may soon change, too. In their next weather forecast, the meteorologists can say this.So the weather satellites are _____57______ to the meteorologists. Before satellites were invented, the scientists could forecast the weather for about 24 or 48 hours. Now they can make good forecasts for three or five days. Soon, perhaps, they may ______58______ forecast the weather for a week or more ahead (提前).III. Complete the sentences with the given words in their proper forms.59. It’s amazing to see the _____________ areas in France. (scene)60. Do you know the _____________ “Practice makes perfect”? (say)61. He’s old-fashioned and never ___________ his style. (vary)62. Tom and Tim are twins, but they have different _______________. (person)63. He was one of the ____________ artists of his time. (lead)64. We can use sound effects of add ____________. (exciting)65. For _____________, some comic strips have no frame borders. (vary)66. The young man was lucky enough to be still ____________ after the accident. (living)IV. Rewrite the sentences as required67. If she doesn’t come on time, we’ll go without her. (保持原意)We’ll go without her _____________ she _____________ on time.68. The boy was too frightened to say a word. (保持原意)The boy was __________ frightened that he __________ say a word.69. The coat cost Mary nearly a month salary, ___________ ___________? (反义疑问句)70. He was so fat that he couldn’t get through the door. (保持原意)He was not _________ ___________ to get through the door.71. Did the policemen catch the robber? (改被动语态)____________ the robber ____________ by the policemen?72. Noise pollution makes people talk more loudly than before. (保持原意)People have __________ talk more loudly than before ___________ of noise pollution.73. “Has Bob been to London?” Tom asked. (改为宾语从句)Tom asked ___________ Bob ___________ been to London.C. Read the passage and fill in the blanks with proper words.Do you love holidays, but hate the increase in weight that follows? You are not alone. Holidays are happy days with p_____86______ and delicious foods. But many people are worried about the weight that comes with these delicious foods.With proper planning, it is possible to c______87_____ your weight. The idea is to enjoy the holidays but not to eat too much. You don’t have to turn away from the foods that you enjoy. The following advice may be of some help to you.Do not m______88_____ meals. Before you leave home for a party, have a small, low-fat meal or fast food. This may help to keep you from getting too excited before the wonderful foods. Begin with clear soup and fruit or vegetables. A large glass of water before you eat may help you feel full. Use a small plate; a large plate may make you eat m______89______ than enough. Better not have high-fat foods. Choose lean(瘦的) meats. Fill your plate with salad and green vegetables.Try mints (薄荷) and fruits i______90____ you have a sweet tooth. They do not have fat l_____91_____ cream and chocolate.Don’t let exercise take a b______92______ during the holidays. A 20-minute walk after a meal can help you burn off excess calories. (多余的热量)D. Answer the questions (根据短文内容回答下列问题）No matter what happens, I 'll always be there for youIn 1989 an 8.2 earthquake almost flattened America, killing over 30,000 people in less than four minutes. In the midst of utter devastation and chaos, a father left his wife safely at home and rushed to the school where his son was supposed to be, only to discover that the building was as flat as a pancake.After the unforgettably initial shock, he remembered the promise he had made to his son: "No matter what, I'll always be there for you!" And tears began to fill his eyes. As he looked at the pile of ruins that once was the school, it looked hopeless, but he kept remembering his commitment to his son.He began to direct his attention towards where he walked his son to class at school each morning. Remembering his son's classroom would be in the back right corner of the building, he rushed there and started digging through the ruins.As he was digging, other helpless parents arrived, clutching their hearts, saying: "My son!" "Mydaughter!" Other well-meaning parents tried to pull him off what was left of the school, saying: "It's too late! They're all dead! You can't help! Go home! Come on, face reality, there's nothing you can do!"To each parent he responded with one line: "Are you going to help me now?" And then he continued to dig for his son, stone by stone. The fire chief showed up and tried to pull him off the school's ruins saying, "Fires are breaking out, explosions are happening everywhere. You're in danger. We'll take care of it. Go home." To which this loving, caring American father asked, "Are you going to help me now?"The police came and said, "You're angry, anxious and it's over. You're endangering others. Go home. We'll handle it!" To which he replied, "Are you going to help me now?" No one helped. Courageously he went on alone because he needed to know for himself: "Is my boy alive or is he dead?" He dug for eight hours...12 hours...24 hours...36 hours...then, in the 38th hour, he pulled back a large stone and heard his son's voice. He screamed his son's name, "ARMAND!" He heard back, "Dad!?! It's me, Dad! I told the other kids not to worry. I told them that if you were alive, you'd save me and when you saved me, they'd be saved. You promised, No matter what happens, you'll always be there for you! You did it, Dad!" "What's going on in there? How is it?" the father asked."There are 14 of us left out of 33, Dad. We're scared, hungry, thirsty and thankful you're here. When the building collapsed, it made a triangle, and it saved us.""Come out, boy!""No, Dad! Let the other kids out first, cause I know you'll get me! No matter what happens, I know you'll always be there for me!"93.No one knew what would happen,did they ?_______________________________________________94.How many people lost their lives in the Earthquake in less than four minutes?________________________________________________95.Why was the father so insistent that he kept looking for his son ?_______________________________________________96.All of the parents were looking for their children,weren’t they ?_________________________________________________97.What do you think of the story ?__________________________________________________98.How do you feel about the story ?_________________________________________________首字母附加篇The world p_______is growing very fast. In the last 40 years ,it has doubled . By the year 2200, it will be about 10 billion. Our cities will be much bigger. There will be more factories and more roads. We will need more water and other natural r_______. Therefore, we will have serious problems in the future, so we must change the way we use e_______and natural resources now.Every day we throw away millions of tons of rubbish. Half of this is paper that we can use again. An a_______family in Europe or America throws away more than one ton of rubbish each year, but we can r______much of it. If we recycle things, we can save money,energy and resources.A lot of rubbish, however,cannot be recycled. P________and chemicals will not disappear for hundreds of years. They pollute the air, the land and the water. Pollution will be an even bigger problem in the future. Therefore, we must stop using m_______like plastics and chemicals. Many natural resources cannot be r_______. Coal and minerals, for example, will be used up some day.Other resources take a long time to grow, such as trees, or they may not always be a______, such as water. We must learn to use less energy and fewer resources. We also have to find other w_______to make energy . We can find ways to use the sun, the wind and the sea.KeysI. A C B C C D C B B C B B C A D C A C B DII. C G I F E A B HIII. scenic saying varies personalities leading excitement variety aliveIV. unless comes so couldn’t didn’t it thin enough was caught to because if hadC篇pleasant control miss more if like breakD篇93.No,they didn’t94.Over 30000 people95.Because he made the promise to his son that no matter what ,he would always be there for him.96.No ,they weren’t97.it’s moving98.He is a brave boy附加篇：Population resources energy average reducePlastics materials renewable available ways最新文件---------------- 仅供参考--------------------已改成word文本--------------------- 方便更改。

2020年上海市徐汇区中考物理三模试卷(含答案解析)

2020年上海市徐汇区中考物理三模试卷一、单选题（本大题共8小题，共16.0分）1.关于粒子和宇宙，下列说法中错误的是()A. 宇宙是一个有层次的天体结构系统B. 分子间只存在相互作用的吸引力C. 电子的发现揭示了原子是有结构的D. 分子是由原子构成的，分子间有空隙2.声音与我们的生活密切相关，以下有关声现象的说法正确的是()A. 只要物体振动，人就一定会听到声音B. 用超声波可击碎人体内“结石”，说明声波能传递能量C. 市区内“禁鸣喇叭”是在声音传播的过程中减弱噪声D. 用声呐探测海底深度，是因为超声波比次声波在水中的传播速度大3.若水中的鱼能看到岸边的人，它看到的人其实是()A. 变矮了的人的实像B. 变高了的人的实像C. 变矮了的人的虚像D. 变高了的人的虚像4.下列措施中，属于利用电流热效应的是()A. 电视机的后盖有很多孔B. 电饭锅的发热板装在底部C. 与空调器相连的导线很粗D. 电脑的主机中安装微型风扇5.如图所示电路，要使滑动变阻器的滑片P向左滑动时灯泡变亮，变阻器接入电路的方式是()A. C接M，D接NB. C接M，B接NC. A接M，D接ND. A接M，B接N6.下列各图不属于连通器的是()A. 排水管的U形反水弯B. 茶壶C. 盆景自动供水装置D. 锅炉水位计7.如图所示的电路，电源电压保持不变，灯泡L1或L2中有一个发生了短路故障．当开关S闭合时，下列现象中不可能出现的是()A. 电压表无示数，灯L1不发光B. 电压表和电流表都无示数C. 电压表有示数，灯L2不发光D. 电压表和电流表都有示数8.如图所示是甲、乙两种物质的质量和体积的关系图，现用体积相等的甲、乙物质分别制成实心正方体A，B并排放在水平地面上，则A，B对地面的压强之比为()A. 8：1B. 4：1C. 4：3D. 2：1二、填空题（本大题共10小题，共33.0分）9.某款手机电池电压为5V，待机时电流约为10mA，则该款手机待机时的电功率为______W.若该款手机的一块原装电池充满电可供其待机200h，则该电池一次充满电时储存的电能为______ J．10.A、B两车分别从P、Q两点同时同向运动，经过6秒A、B相遇，它们的s−t图象分别如图甲、乙所示，由此可知v A ______ v B((填“>”、“=”或“<”))，P、Q间的距离为 ______m。

上海市徐汇区2019-2020学年中考化学三模考试卷含解析

上海市徐汇区2019-2020学年中考化学三模考试卷一、选择题（本题包括12个小题，每小题3分，共36分．每小题只有一个选项符合题意）1．已知20℃时氯化钠的溶解度为36g，现向50g水中加入20g氯化钠，充分搅拌后能得到20℃时的溶质的质量分数为（）A．40% B．28.6% C．26.5% D．36%【答案】C【解析】【详解】20℃时氯化钠的溶解度为36g，则50g水中加入20g氯化钠后只能溶解18g形成68g饱和溶液，所得溶液的溶质质量分数为185018gg g×100%≈26.5%，故选C。

2．如图表示初中化学常见实验操作，其中正确的是（）A．点燃酒精灯B．检查装置的气密性C．读出液体的体积D．液体的取用【答案】B【解析】试题分析：A、使用酒精灯时要注意“两查、两禁、一不可”，点燃酒精灯要用火柴点燃，禁止用一酒精灯去引燃另一酒精灯，图中所示操作错误；B、检查装置气密性的方法：把导管的一端浸没在水里，双手紧贴容器外壁，若导管口有气泡冒出，装置不漏气；图中所示操作正确；C、量筒读数时视线要与量筒内液体的凹液面的最低处保持水平，图中所示操作错误；D、取用液体药品时，瓶塞要倒放，标签要对准手心，瓶口紧挨；图中所示操作错误。

考点：考查化学仪器的使用及注意事项化学实验操作。

3．成语是我国语言文化的瑰宝。

下列成语的原意中蕴涵化学变化的是（）A．星火燎原B．绳锯木断C．积水成渊D．披荆斩棘【答案】A【解析】【详解】A. 星火燎原就是物质的燃烧，有新物质生成，属于化学变化，选项正确；B. 绳锯木断只是物质的形状发生了变化，没有生成新物质，属于物理变化，选项错误；C. 积水成渊只是水的量增多，没有生成新物质，属于物理变化，选项错误；D. 披荆斩棘只是物质的形状发生改变，没有生成新物质，属于物理变化，选项错误，故选A。

【点睛】物理变化与化学变化的区别在于有没有生成新物质：没有生成新物质的变化属于物理变化，有新物质生成的变化属于化学变化。

上海市徐汇区2019-2020学年中考语文三模试卷含解析

上海市徐汇区2019-2020学年中考语文三模试卷一、选择题1．下列句子没有语病．．．．的一项是（）A．一个人能否成为真正的读者，关键在于青少年时期养成良好的阅读习惯。

B．学校开展“国学课堂”活动，有助于更多同学传承并了解中华优秀传统文化。

C．继美国、法国和芬兰之后，我国成为第四个拥有“生物航油”自主研发技术的国家。

D．走近宽厚里，我禁不住停下脚步驻足欣赏。

2．下列书写完全正确的一项是（）A．侏儒窒息深恶痛极锲而不舍B．叮嘱濡养自惭形秽神采奕奕C．萧索镌刻形消骨立日薄西山D．禁锢恣雎惟妙惟肖翻来复去3．下列有关传统文化常识的表述不正确的一项是（）A．“朋友”一词在传统文化里枝繁叶茂，不同的朋友关系之间有着不同的称谓，如：情谊契合，亲如兄弟的朋友，则称之为“金兰之交”。

B．《陈涉世家》选自我国第一部编年体史书——《史记》，作者是汉朝的司马迁，鲁迅称《史记》为“史家之绝唱，无韵之《离骚》”。

C．古代座次安排也蕴含着丰富的文化。

如：帝王与臣下相对时帝王面南，臣下面北。

宾主之间宴席的四面座位，以东向最尊，次为南向，再次为北向，西向为侍坐。

D．“春蚕到死丝方尽，蜡炬成灰泪始干。

”出自李商隐的《无题》。

这一句诗运用比喻表达了爱情的坚贞。

句中的“丝”喻“思”，含相思之意。

4．下列词语中没有错别字的一项是（）A．取缔褻渎口头禅箪食壶浆妄自菲薄B．搏弈狡點高利贷断章取义心无旁骛C．惬意陨落城皇庙恪尽职守恼羞成怒D．侥幸襁褓震慑力流言斐语分庭抗礼5．下列句子中，没有语病的一项是（）A．《国风美少年》通过年轻人热衷喜爱的方式，呈现和传承国风音乐，推广国风文化。

B．严谨的傅雷多次在家信中向傅聪提出学习要正规化和计划化，生活要科学化的活动。

C．林清玄之所以能创作出如此丰富优美的文学作品，是他重视阅读、观察和思考的原因。

D．世界知名的摇滚马拉松，已成为全世界参赛人数最多、规模最大的马拉松路跑赛事。

二、名句名篇默写6．经典诗文默写(在第(1)-(7)题中，任选五题，在第(8) -(10)题中，任选题。

【精选3份合集】2020-2021学年上海市徐汇区某名校中考数学三月模拟试题

中考数学模拟试卷一、选择题（本题包括10个小题，每小题只有一个选项符合题意）1．如图，AB 是⊙O 的直径，弦CD ⊥AB 于E ，∠CDB=30°，⊙O的半径为3，则弦CD 的长为（）A ．32cmB ．3cmC ．23cmD ．9cm【答案】B【解析】解：∵∠CDB=30°，∴∠COB=60°，又∵3，CD ⊥AB 于点E ，∴3sin 603︒==，解得CE=32cm ，CD=3cm ．故选B ．考点：1．垂径定理；2．圆周角定理；3．特殊角的三角函数值． 2．在围棋盒中有x 颗白色棋子和y 颗黑色棋子，从盒中随机取出一颗棋子，取得白色棋子的概率是25，如再往盒中放进3颗黑色棋子，取得白色棋子的概率变为14，则原来盒里有白色棋子（） A ．1颗B ．2颗C ．3颗D ．4颗【答案】B 【解析】试题解析：由题意得25134x x y x x y ⎧⎪+⎪⎨⎪⎪++⎩＝＝，解得：23x y ⎧⎨⎩＝＝．故选B ．3．学完分式运算后，老师出了一道题“计算：23224x x x x +-++-”. 小明的做法：原式222222(3)(2)26284444x x x x x x x x x x x +--+----=-==----；小亮的做法：原式22(3)(2)(2)624x x x x x x x =+-+-=+-+-=-；小芳的做法：原式32313112(2)(2)222x x x x x x x x x x +-++-=-=-==++-+++．其中正确的是（）A ．小明B ．小亮C ．小芳D ．没有正确的【答案】C 【解析】试题解析：23224x x x x +-++- =()()32222x x x x x +--++- =3122x x x +-++ =3-12x x ++ =22x x ++ =1．所以正确的应是小芳．故选C ．4．下列各数中最小的是（）A ．0B ．1CD ．﹣π【答案】D【解析】根据任意两个实数都可以比较大小．正实数都大于0，负实数都小于0，正实数大于一切负实数，两个负实数绝对值大的反而小即可判断．【详解】﹣π0＜1．则最小的数是﹣π．故选：D ．【点睛】本题考查了实数大小的比较，理解任意两个实数都可以比较大小．正实数都大于0，负实数都小于0，正实数大于一切负实数，两个负实数绝对值大的反而小是关键．5．已知二次函数y ＝x 2﹣4x+m 的图象与x 轴交于A 、B 两点，且点A 的坐标为(1，0)，则线段AB 的长为( ) A ．1B ．2C ．3D ．4 【答案】B【解析】先将点A(1，0)代入y ＝x 2﹣4x+m ，求出m 的值，将点A(1，0)代入y ＝x 2﹣4x+m ，得到x 1+x 2＝4，x 1•x 2＝3，即可解答【详解】将点A(1，0)代入y ＝x 2﹣4x+m ，得到m ＝3，所以y ＝x 2﹣4x+3，与x 轴交于两点，设A(x 1，y 1)，b(x 2，y 2)∴x 2﹣4x+3＝0有两个不等的实数根，∴x 1+x 2＝4，x 1•x 2＝3，∴AB ＝|x 1﹣x 2|＝21212)4x x x x ++（＝2；故选B ．【点睛】此题考查抛物线与坐标轴的交点，解题关键在于将已知点代入.6．某校在国学文化进校园活动中，随机统计50名学生一周的课外阅读时间如表所示，这组数据的众数和中位数分别是（）学生数（人）5 8 14 19 4 时间（小时）6 7 8 9 10 A ．14，9B ．9，9C ．9，8D ．8，9【答案】C【解析】解:观察、分析表格中的数据可得：∵课外阅读时间为1小时的人数最多为11人，∴众数为1．∵将这组数据按照从小到大的顺序排列，第25个和第26个数据的均为2，∴中位数为2．故选C ．【点睛】本题考查（1）众数是一组数据中出现次数最多的数；（2）中位数的确定要分两种情况：①当数据组中数据的总个数为奇数时，把所有数据按从小到大的顺序排列，中间的那个数就是中位数；②当数据组中数据的总个数为偶数时，把所有数据按从小到大的顺序排列，中间的两个数的平均数是这组数据的中位数. 7．如右图,⊿ABC 内接于⊙O ，若∠OAB=28°则∠C 的大小为（）A ．62°B ．56°C ．60°D ．28°【答案】A【解析】连接OB．在△OAB中，OA=OB（⊙O的半径），∴∠OAB=∠OBA（等边对等角）；又∵∠OAB=28°，∴∠OBA=28°；∴∠AOB=180°-2×28°=124°；而∠C=12∠AOB（同弧所对的圆周角是所对的圆心角的一半），∴∠C=62°；故选A8．如图，△ABC中，∠B=55°，∠C=30°，分别以点A和点C为圆心，大于12AC的长为半径画弧，两弧相交于点M，N作直线MN，交BC于点D，连结AD，则∠BAD的度数为（）A．65°B．60°C．55°D．45°【答案】A【解析】根据线段垂直平分线的性质得到AD=DC，根据等腰三角形的性质得到∠C=∠DAC，求得∠DAC=30°，根据三角形的内角和得到∠BAC=95°，即可得到结论．【详解】由题意可得：MN是AC的垂直平分线，则AD=DC，故∠C=∠DAC，∵∠C=30°，∴∠DAC=30°，∵∠B=55°，∴∠BAC=95°，∴∠BAD=∠BAC-∠CAD=65°，故选A．【点睛】此题主要考查了线段垂直平分线的性质，三角形的内角和，正确掌握线段垂直平分线的性质是解题关键．9．如图，排球运动员站在点O 处练习发球，将球从O 点正上方2m 的A 处发出，把球看成点，其运行的高度y （m ）与运行的水平距离x （m ）满足关系式y ＝a （x ﹣k ）2+h ．已知球与D 点的水平距离为6m 时，达到最高2.6m ，球网与D 点的水平距离为9m ．高度为2.43m ，球场的边界距O 点的水平距离为18m ，则下列判断正确的是（）A ．球不会过网B ．球会过球网但不会出界C ．球会过球网并会出界D ．无法确定【答案】C 【解析】分析：（1）将点A(0,2)代入2(6) 2.6y a x =-+求出a 的值；分别求出x=9和x=18时的函数值，再分别与2.43、0比较大小可得．详解：根据题意,将点A(0,2)代入2(6) 2.6y a x =-+，得：36a+2.6=2，解得：160a ，=- ∴y 与x 的关系式为21(6) 2.660y x =--+；当x=9时,()2196 2.6 2.45 2.4360y =--+=>， ∴球能过球网，当x=18时,()21186 2.60.2060y =--+=>， ∴球会出界.故选C.点睛：考查二次函数的应用题，求范围的问题，可以利用临界点法求出自变量的值，根据题意确定范围. 10．－4的绝对值是（）A ．4B ．14C ．－4D ．14- 【答案】A【解析】根据绝对值的概念计算即可.（绝对值是指一个数在坐标轴上所对应点到原点的距离叫做这个数的绝对值.）【详解】根据绝对值的概念可得-4的绝对值为4.【点睛】错因分析：容易题.选错的原因是对实数的相关概念没有掌握，与倒数、相反数的概念混淆.二、填空题（本题包括8个小题）11．在△ABC 中，∠C=90°，若tanA=12，则sinB=______．【答案】255 【解析】分析：直接根据题意表示出三角形的各边，进而利用锐角三角函数关系得出答案．详解：如图所示：∵∠C=90°，tanA=12， ∴设BC=x ，则AC=2x ，故AB=5x ，则sinB=2555AC AB x==. 故答案为：255 ．点睛：此题主要考查了锐角三角函数关系，正确表示各边长是解题关键．12．如图，AB ∥CD ，BE 交CD 于点D ，CE ⊥BE 于点E ，若∠B=34°，则∠C 的大小为________度．【答案】56【解析】解：∵AB ∥CD,34B ∠=，∴34CDE B ∠=∠=，又∵CE ⊥BE ，∴Rt △CDE 中,903456C ∠=-=，故答案为56.13．如图，在平面直角坐标系中，矩形ABCD 的边AB ：BC=3：2，点A （-3，0），B （0，6）分别在x 轴，y 轴上，反比例函数y=k x（x ＞0）的图象经过点D ，且与边BC 交于点E ，则点E 的坐标为__．【答案】（-2，7）．【解析】解：过点D作DF⊥x轴于点F，则∠AOB＝∠DFA＝90°，∴∠OAB+∠ABO＝90°，∵四边形ABCD是矩形，∴∠BAD＝90°，AD＝BC，∴∠OAB+∠DAF＝90°，∴∠ABO＝∠DAF，∴△AOB∽△DFA，∴OA：DF＝OB：AF＝AB：AD，∵AB：BC＝3：2，点A（﹣3，0），B（0，6），∴AB：AD＝3：2，OA＝3，OB＝6，∴DF＝2，AF＝4，∴OF＝OA+AF＝7，∴点D的坐标为：（﹣7，2），∴反比例函数的解析式为：y＝﹣14x①，点C的坐标为：（﹣4，8）．设直线BC的解析式为：y＝kx+b，则b=6-4k+b=8⎧⎨⎩解得：1k=-2b=6⎧⎪⎨⎪⎩∴直线BC的解析式为：y＝﹣12x+6②，联立①②得：x=-2y=7⎧⎨⎩或x=14y=-1⎧⎨⎩（舍去），∴点E的坐标为：（﹣2，7）．故答案为（﹣2，7）．14．亚洲陆地面积约为4400万平方千米，将44000000用科学记数法表示为_____．【答案】4.4×1【解析】分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n 是正数；当原数的绝对值＜1时，n是负数．详解：44000000=4.4×1，故答案为4.4×1．点睛：此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．15．已知23-是一元二次方程240x x c-+=的一个根，则方程的另一个根是________．+【答案】23【解析】通过观察原方程可知，常数项是一未知数，而一次项系数为常数，因此可用两根之和公式进行计算，将3【详解】设方程的另一根为x1，又∵3x13，解得x13．故答案为：23【点睛】解决此类题目时要认真审题，确定好各系数的数值与正负，然后适当选择一个根与系数的关系式求解．16．正五边形的内角和等于______度．【答案】540【解析】过正五边形五个顶点，可以画三条对角线，把五边形分成3个三角形∴正五边形的内角和=3⨯180=540°17．如图是一位同学设计的用手电筒来测量某古城墙高度的示意图．点P处放一水平的平面镜，光线从点A出发经平面镜反射后刚好到古城墙CD的顶端C处，已知AB⊥BD，CD⊥BD，测得AB＝2米，BP＝3米，PD＝15米，那么该古城墙的高度CD是_____米．【答案】10【解析】首先证明△ABP∽△CDP，可得ABBP=CDPD，再代入相应数据可得答案．【详解】如图，由题意可得：∠APE=∠CPE，∴∠APB=∠CPD，∵AB⊥BD，CD⊥BD，∴∠ABP=∠CDP=90°，∴△ABP∽△CDP，∴ABBP =CD PD，∵AB=2米，BP=3米，PD=15米，∴23=15 CD，解得：CD=10米.故答案为10.【点睛】本题考查了相似三角形的应用，解题的关键是熟练的掌握相似三角形的应用.18．如图，AB是⊙O的直径，BD，CD分别是过⊙O上点B，C的切线，且∠BDC＝110°．连接AC，则∠A 的度数是_____°．【答案】4．【解析】试题分析：连结BC，因为AB是⊙O的直径，所以∠ACB＝90°，∠A+∠ABC＝90°，又因为BD，CD分别是过⊙O上点B，C的切线，∠BDC＝440°，所以CD=BD,所以∠BCD＝∠DBC＝4°,又∠ABD＝90°，所以∠A=∠DBC＝4°．考点：4．圆周角定理；4．切线的性质；4．切线长定理．三、解答题（本题包括8个小题）19．某新建火车站站前广场需要绿化的面积为46000米2，施工队在绿化了22000米2后，将每天的工作量增加为原来的1.5倍，结果提前4天完成了该项绿化工程．该项绿化工程原计划每天完成多少米2？该项绿化工程中有一块长为20米，宽为8米的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为56米2，两块绿地之间及周边留有宽度相等的人行通道（如图所示），问人行通道的宽度是多少米？【答案】 (1)2000；(2)2米【解析】（1）设未知数，根据题目中的的量关系列出方程；（2）可以通过平移，也可以通过面积法，列出方程【详解】解：（1）设该项绿化工程原计划每天完成x 米2，根据题意得：4600022000x -﹣46000220001.5x-= 4 解得：x=2000，经检验，x=2000是原方程的解;答：该绿化项目原计划每天完成2000平方米；（2）设人行道的宽度为x 米，根据题意得，（20﹣3x ）（8﹣2x ）=56解得：x=2或x=263（不合题意，舍去）．答：人行道的宽为2米．20．已知抛物线2y x bx c =++过点(0,0)，(1,3)，求抛物线的解析式，并求出抛物线的顶点坐标.【答案】y=2x +2x ；（－1，－1）.【解析】试题分析：首先将两点代入解析式列出关于b 和c 的二元一次方程组，然后求出b 和c 的值，然后将抛物线配方成顶点式，求出顶点坐标.试题解析：将点（0,0）和（1,3）代入解析式得：0{13c b c =++=解得：2{0b c == ∴抛物线的解析式为y=2x +2x ∴y=2x +2x=2(1)x +－1 ∴顶点坐标为（－1，－1）.考点：待定系数法求函数解析式.21．某商场购进甲、乙两种商品，甲种商品共用了2000元，乙种商品共用了2400元.已知乙种商品每件进价比甲种商品每件进价多8元，且购进的甲、乙两种商品件数相同．1（）求甲、乙两种商品的每件进价；2（）该商场将购进的甲、乙两种商品进行销售，甲种商品的销售单价为60元，乙种商品的销售单价为88元，销售过程中发现甲种商品销量不好，商场决定：甲种商品销售一定数量后，将剩余的甲种商品按原销售单价的七折销售；乙种商品销售单价保持不变.要使两种商品全部售完后共获利不少于2460元，问甲种商品按原销售单价至少销售多少件？【答案】()1 甲种商品的每件进价为40元，乙种商品的每件进价为48元；()2甲种商品按原销售单价至少销售20件．【解析】()1设甲种商品的每件进价为x 元，乙种商品的每件进价为（x+8）)元.根据“某商场购进甲、乙两种商品，甲种商品共用了2000元，乙种商品共用了2400元.购进的甲、乙两种商品件数相同”列出方程进行求解即可；()2设甲种商品按原销售单价销售a 件，则由“两种商品全部售完后共获利不少于2460元”列出不等式进行求解即可．【详解】()1设甲种商品的每件进价为x 元，则乙种商品的每件进价为()x 8+元，根据题意得，20002400x x 8=+，解得x 40=，经检验，x 40=是原方程的解，答：甲种商品的每件进价为40元，乙种商品的每件进价为48元；()2甲乙两种商品的销售量为20005040=，设甲种商品按原销售单价销售a 件，则()()()()6040a 600.74050a 8848502460-+⨯--+-⨯≥，解得a 20≥，答：甲种商品按原销售单价至少销售20件．【点睛】本题考查了分式方程的应用，一元一次不等式的应用，弄清题意，找出等量关系列出方程，找出不等关系列出不等式是解题的关键.22．中华文明，源远流长；中华汉字，寓意深广，为了传承优秀传统文化，某校团委组织了一次全校3000名学生参加的“汉字听写”大赛，赛后发现所有参赛学生的成绩均不低于50分．为了更好地了解本次大赛的成绩分布情况，随机抽取了其中200名学生的成绩(成绩x 取整数，总分100分)作为样本进行整理，得到下列不完整的统计图表：50≤x＜60 10 0.0560≤x＜70 30 0.1570≤x＜80 40 n80≤x＜90 m 0.3590≤x≤10050 0.25请根据所给信息，解答下列问题：m＝，n＝；请补全频数分布直方图；若成绩在90分以上(包括90分)的为“优”等，则该校参加这次比赛的3000名学生中成绩“优”等约有多少人？【答案】（1）70，0.2（2）70（3）750【解析】（1）根据题意和统计表中的数据可以求得m、n的值；（2）根据（1）中求得的m的值，从而可以将条形统计图补充完整；（3）根据统计表中的数据可以估计该校参加这次比赛的3000名学生中成绩“优”等约有多少人．【详解】解：（1）由题意可得，m＝200×0.35＝70，n＝40÷200＝0.2，故答案为70，0.2；（2）由（1）知，m＝70，补全的频数分布直方图，如下图所示；（3）由题意可得，该校参加这次比赛的3000名学生中成绩“优”等约有：3000×0.25＝750（人），答：该校参加这次比赛的3000名学生中成绩“优”等约有750人．【点睛】本题考查频数分布直方图、频数分布表、用样本估计总体，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．23．先化简(31a+－a＋1)÷2441a aa-++，并从0，－1，2中选一个合适的数作为a的值代入求值．【答案】1.【解析】试题分析：首先把括号的分式通分化简，后面的分式的分子分解因式，然后约分化简，接着计算分式的乘法，最后代入数值计算即可求解．试题解析：原式=223111(2)a aa a-++⨯+-=2(2)(2)11(2)a a aa a-+-+⨯+-=22aa+--；当a=0时，原式=1．考点：分式的化简求值．24．如图，在五边形ABCDE中，∠C＝100°，∠D＝75°，∠E＝135°，AP平分∠EAB，BP平分∠ABC，求∠P 的度数．【答案】65°【解析】∵∠EAB+∠ABC+∠C+∠D+∠E=（5-2）×180°=540°，∠C=100°，∠D=75°，∠E=135°，∴∠EAB+∠ABC=540°-∠C-∠D-∠E=230°.∵AP平分∠EAB，∴∠PAB=12∠EAB.同理可得，∠ABP=12∠ABC.∵∠P+∠PAB+∠PBA=180°，∴∠P=180°-∠PAB-∠PBA=180°-12∠EAB-12∠ABC=180°-12（∠EAB+∠ABC）=180°-12×230°=65°.25．中央电视台的“朗读者”节目激发了同学们的读书热情，为了引导学生“多读书，读好书”，某校对八年级部分学生的课外阅读量进行了随机调查，整理调查结果发现，学生课外阅读的本书最少的有5本，最多的有8本，并根据调查结果绘制了不完整的图表，如图所示：本数(本) 频数(人数) 频率5 a0.26 18 0.367 14 b8 8 0.16合计c 1(1)统计表中的a=________，b=________，c=________；请将频数分布表直方图补充完整；求所有被调查学生课外阅读的平均本数；若该校八年级共有1200名学生，请你分析该校八年级学生课外阅读7本及以上的人数.【答案】（1）10，0.28，50（2）图形见解析（3）6.4（4）528【解析】分析：（1）首先求出总人数，再根据频率，总数，频数的关系即可解决问题；（2）根据a的值画出条形图即可；（3）根据平均数的定义计算即可；（4）用样本估计总体的思想解决问题即可；详解：（1）由题意c=180.36=50，a=50×0.2=10，b=1450=0.28，c=50；故答案为10，0.28，50；（2）将频数分布表直方图补充完整，如图所示：（3）所有被调查学生课外阅读的平均本数为：（5×10+6×18+7×14+8×8）÷50=320÷50=6.4（本）．（4）该校七年级学生课外阅读7本及以上的人数为：（0.28+0.16）×1200=528（人）．点睛：本题考查频数分布直方图、扇形统计图、样本估计总体等知识，解题的关键是熟练掌握基本概念，灵活运用所学知识解决问题，属于中考常考题型．26．如图，AB为半圆O的直径，AC是⊙O的一条弦，D为BC的中点，作DE⊥AC，交AB的延长线于点F，连接DA．求证：EF为半圆O的切线；若DA＝DF＝63，求阴影区域的面积．（结果保留根号和π）【答案】（1）证明见解析（22736π【解析】（1）直接利用切线的判定方法结合圆心角定理分析得出OD⊥EF，即可得出答案；（2）直接利用得出S△ACD＝S△COD，再利用S阴影＝S△AED﹣S扇形COD，求出答案．【详解】（1）证明：连接OD，∵D为弧BC的中点，∴∠CAD＝∠BAD，∵OA＝OD，∴∠BAD＝∠ADO，∴∠CAD＝∠ADO，∵DE⊥AC，∴∠E＝90°，∴∠CAD+∠EDA＝90°，即∠ADO+∠EDA＝90°，∴OD⊥EF，∴EF为半圆O的切线；（2）解：连接OC与CD，∵DA＝DF，∴∠BAD＝∠F，∴∠BAD＝∠F＝∠CAD，又∵∠BAD+∠CAD+∠F＝90°，∴∠F＝30°，∠BAC＝60°，∵OC＝OA，∴△AOC为等边三角形，∴∠AOC＝60°，∠COB＝120°，∵OD⊥EF，∠F＝30°，∴∠DOF＝60°，在Rt △ODF 中，DF ＝63， ∴OD ＝DF•tan30°＝6，在Rt △AED 中，DA ＝63，∠CAD ＝30°，∴DE ＝DA•sin30°＝33，EA ＝DA•cos30°＝9，∵∠COD ＝180°﹣∠AOC ﹣∠DOF ＝60°，由CO ＝DO ，∴△COD 是等边三角形，∴∠OCD ＝60°，∴∠DCO ＝∠AOC ＝60°，∴CD ∥AB ，故S △ACD ＝S △COD ，∴S 阴影＝S △AED ﹣S 扇形COD ＝216093362360π⨯⨯-⨯＝2736π-．【点睛】此题主要考查了切线的判定，圆周角定理，等边三角形的判定与性质，解直角三角形及扇形面积求法等知识，得出S △ACD ＝S △COD 是解题关键．中考数学模拟试卷一、选择题（本题包括10个小题，每小题只有一个选项符合题意）1．计算(ab2)3的结果是()A．ab5B．ab6C．a3b5D．a3b6【答案】D【解析】试题分析：根据积的乘方的性质进行计算，然后直接选取答案即可．试题解析：（ab2）3=a3•（b2）3=a3b1．故选D．考点：幂的乘方与积的乘方．2．如图所示，直线a∥b，∠1=35°，∠2=90°，则∠3的度数为（）A．125°B．135°C．145°D．155°【答案】A【解析】分析：如图求出∠5即可解决问题．详解：∵a∥b，∴∠1=∠4=35°，∵∠2=90°，∴∠4+∠5=90°，∴∠5=55°，∴∠3=180°-∠5=125°，故选：A．点睛：本题考查平行线的性质、三角形内角和定理，邻补角的性质等知识，解题的关键是灵活运用所学知识解决问题．3．如图，点P是∠AOB内任意一点，OP=5cm，点M和点N分别是射线OA和射线OB上的动点，△PMN 周长的最小值是5cm，则∠AOB的度数是（）．A．25︒B．30︒C．35︒D．40︒【答案】B【解析】试题分析：作点P关于OA对称的点P3,作点P关于OB对称的点P3,连接P3P3,与OA交于点M,与OB交于点N,此时△PMN的周长最小．由线段垂直平分线性质可得出△PMN的周长就是P3P3的长，∵OP=3，∴OP3=OP3=OP=3．又∵P3P3=3，,∴OP3=OP3=P3P3,∴△OP3P3是等边三角形, ∴∠P3OP3=60°，即3（∠AOP+∠BOP）=60°，∠AOP+∠BOP=30°,即∠AOB=30°，故选B．考点：3．线段垂直平分线性质；3．轴对称作图．4．如图，正六边形ABCDEF内接于O，M为EF的中点，连接DM，若O的半径为2，则MD的长度为()A7B5C．2 D．1【答案】A【解析】连接OM、OD、OF，由正六边形的性质和已知条件得出OM⊥OD，OM⊥EF，∠MFO=60°，由三角函数求出OM，再由勾股定理求出MD即可．【详解】连接OM、OD、OF，∵正六边形ABCDEF内接于⊙O，M为EF的中点，∴OM⊥OD，OM⊥EF，∠MFO=60°，∴∠MOD=∠OMF=90°，∴OM=OF•sin∠MFO=2×33，2∴()2222+=+=327OM OD故选A．【点睛】本题考查了正多边形和圆、正六边形的性质、三角函数、勾股定理；熟练掌握正六边形的性质，由三角函数求出OM是解决问题的关键．5．如图，若△ABC内接于半径为R的⊙O，且∠A＝60°，连接OB、OC，则边BC的长为()A．2R B．3R C．2R D．3R【答案】D【解析】延长BO交圆于D，连接CD，则∠BCD=90°，∠D=∠A=60°；又BD=2R，根据锐角三角函数的定义得BC=3R.【详解】解：延长BO交⊙O于D，连接CD，则∠BCD=90°，∠D=∠A=60°，∴∠CBD=30°，∵BD=2R，∴DC=R，∴3，故选D.【点睛】此题综合运用了圆周角定理、直角三角形30°角的性质、勾股定理，注意：作直径构造直角三角形是解决本题的关键.。