立体几何的(向量法)—建系讲义
专题07 立体几何中的向量方法(解析版)

专题07 立体几何中的向量方法【要点提炼】1.直线与平面、平面与平面的平行与垂直的向量方法设直线l 的方向向量为a =(a 1,b 1,c 1),平面α,β的法向量分别为μ=(a 2,b 2,c 2),v =(a 3,b 3,c 3),则 (1)线面平行l ∥α⇔a ⊥μ⇔a ·μ=0⇔a 1a 2+b 1b 2+c 1c 2=0. (2)线面垂直l ⊥α⇔a ∥μ⇔a =k μ⇔a 1=ka 2,b 1=kb 2,c 1=kc 2. (3)面面平行α∥β⇔μ∥v ⇔μ=λv ⇔a 2=λa 3,b 2=λb 3,c 2=λc 3. (4)面面垂直α⊥β⇔μ⊥v ⇔μ·v =0⇔a 2a 3+b 2b 3+c 2c 3=0. 2.直线与直线、直线与平面、平面与平面的夹角计算设直线l ,m 的方向向量分别为a =(a 1,b 1,c 1),b =(a 2,b 2,c 2),平面α,β的法向量分别为μ=(a 3,b 3,c 3),v =(a 4,b 4,c 4)(以下相同). (1)线线夹角设l ,m 的夹角为θ⎝ ⎛⎭⎪⎫0≤θ≤π2,则cos θ=|a ·b ||a ||b |=|a 1a 2+b 1b 2+c 1c 2|a 21+b 21+c 21a 22+b 22+c 22. (2)线面夹角设直线l 与平面α的夹角为θ⎝ ⎛⎭⎪⎫0≤θ≤π2,则sin θ=|cos a ,μ|=|a ·μ||a ||μ|.(3)面面夹角设平面α,β的夹角为θ(0≤θ<π), 则|cos θ|=|cosμ,v|=|μ·v ||μ||v |.考点考向一 利用空间向量证明平行、垂直【典例1】 如图,在四棱锥P -ABCD 中,P A ⊥底面ABCD ,AD ⊥AB ,AB ∥DC ,AD =DC =AP =2,AB =1,点E 为棱PC 的中点.证明:(1)BE ⊥DC ; (2)BE ∥平面P AD ; (3)平面PCD ⊥平面P AD .证明 依题意,以点A 为原点建立空间直角坐标系(如图),可得B (1,0,0),C (2,2,0),D (0,2,0),P (0,0,2).由E 为棱PC 的中点,得E (1,1,1).(1)向量BE →=(0,1,1),DC →=(2,0,0),故BE →·DC →=0. 所以BE ⊥DC .(2)因为AB ⊥AD ,又P A ⊥平面ABCD ,AB ⊂平面ABCD , 所以AB ⊥P A ,P A ∩AD =A ,P A ,AD ⊂平面P AD , 所以AB ⊥平面P AD ,所以向量AB→=(1,0,0)为平面P AD 的一个法向量, 而BE →·AB →=(0,1,1)·(1,0,0)=0,所以BE ⊥AB , 又BE ⊄平面P AD , 所以BE ∥平面P AD .(3)由(2)知平面P AD 的法向量AB →=(1,0,0),向量PD →=(0,2,-2),DC →=(2,0,0),设平面PCD 的法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧n ·PD →=0,n ·DC →=0,即⎩⎨⎧2y -2z =0,2x =0,不妨令y =1,可得n =(0,1,1)为平面PCD 的一个法向量. 且n ·AB →=(0,1,1)·(1,0,0)=0,所以n ⊥AB →. 所以平面P AD ⊥平面PCD .探究提高 1.利用向量法证明平行、垂直,关键是建立恰当的坐标系(尽可能利用垂直条件,准确写出相关点的坐标,进而用向量表示涉及到直线、平面的要素). 2.向量证明的核心是利用向量的数量积或数乘向量,但向量证明仍然离不开立体几何的定理,如在(2)中忽略BE ⊄平面P AD 而致误.【拓展练习1】 如图,在直三棱柱ADE -BCF 中,平面ABFE 和平面ABCD 都是正方形且互相垂直,点M 为AB 的中点,点O 为DF 的中点.证明:(1)OM ∥平面BCF ; (2)平面MDF ⊥平面EFCD .证明 (1)由题意,得AB ,AD ,AE 两两垂直,以点A 为原点建立如图所示的空间直角坐标系A -xyz .设正方形边长为1,则A (0,0,0),B (1,0,0),C (1,1,0),D (0,1,0),F (1,0,1),M ⎝ ⎛⎭⎪⎫12,0,0,O ⎝ ⎛⎭⎪⎫12,12,12.OM →=⎝ ⎛⎭⎪⎫0,-12,-12,BA →=(-1,0,0), ∴OM →·BA →=0,∴OM →⊥BA →. ∵棱柱ADE -BCF 是直三棱柱,∴AB ⊥平面BCF ,∴BA →是平面BCF 的一个法向量, 且OM ⊄平面BCF ,∴OM ∥平面BCF .(2)在第(1)问的空间直角坐标系中,设平面MDF 与平面EFCD 的法向量分别为 n 1=(x 1,y 1,z 1),n 2=(x 2,y 2,z 2).∵DF →=(1,-1,1),DM →=⎝ ⎛⎭⎪⎫12,-1,0,DC →=(1,0,0),CF →=(0,-1,1), 由⎩⎪⎨⎪⎧n 1·DF→=0,n 1·DM →=0,得⎩⎪⎨⎪⎧x 1-y 1+z 1=0,12x 1-y 1=0,令x 1=1,则n 1=⎝ ⎛⎭⎪⎫1,12,-12.同理可得n 2=(0,1,1).∵n 1·n 2=0,∴平面MDF ⊥平面EFCD . 考向二 线线角、线面角的求解【典例2】 (2020·浙江卷)如图,在三棱台ABC -DEF 中,平面ACFD ⊥平面ABC ,∠ACB =∠ACD =45°,DC =2BC .(1)证明:EF ⊥DB ;(2)求直线DF 与平面DBC 所成角的正弦值.(1)证明 如图(1),过点D 作DO ⊥AC ,交直线AC 于点O ,连接OB .图(1)由∠ACD =45°,DO ⊥AC ,得 CD =2CO .由平面ACFD ⊥平面ABC ,得DO ⊥平面ABC , 所以DO ⊥BC .由∠ACB =45°,BC =12CD =22CO ,得BO ⊥BC . 所以BC ⊥平面BDO ,故BC ⊥DB .由ABC -DEF 为三棱台,得BC ∥EF ,所以EF ⊥DB .(2)解 法一 如图(1),过点O 作OH ⊥BD ,交直线BD 于点H ,连接CH .由ABC -DEF 为三棱台,得DF ∥CO ,所以直线DF 与平面DBC 所成角等于直线CO 与平面DBC 所成角.由BC ⊥平面BDO ,得OH ⊥BC ,故OH ⊥平面DBC , 所以∠OCH 为直线CO 与平面DBC 所成角. 设CD =22,则DO =OC =2,BO =BC =2,得BD =6,OH =233,所以sin ∠OCH =OH OC =33.因此,直线DF 与平面DBC 所成角的正弦值为33.法二 由ABC -DEF 为三棱台,得DF ∥CO ,所以直线DF 与平面DBC 所成角等于直线CO 与平面DBC 所成角,记为θ.如图(2),以O 为原点,分别以射线OC ,OD 为y ,z 轴的正半轴,建立空间直角坐标系O -xyz .图(2)设CD =22,由题意知各点坐标如下:O (0,0,0),B (1,1,0),C (0,2,0),D (0,0,2). 因此OC→=(0,2,0),BC →=(-1,1,0),CD →=(0,-2,2). 设平面DBC 的一个法向量为n =(x ,y ,z ),由⎩⎪⎨⎪⎧n ·BC →=0,n ·CD →=0,即⎩⎨⎧-x +y =0,-2y +2z =0,可取n =(1,1,1),所以sin θ=|cos 〈OC →,n 〉|=|OC →·n ||OC →|·|n |=33.因此,直线DF 与平面DBC 所成角的正弦值为33.探究提高 1.异面直线所成的角θ,可以通过两直线的方向向量的夹角φ求得,即cos θ=|cos φ|.2.直线与平面所成的角θ主要通过直线的方向向量与平面的法向量的夹角φ求得,即sin θ=|cos φ|,有时也可分别求出斜线与它在平面内的射影直线的方向向量,转化为求两个方向向量的夹角(或其补角).【拓展练习2】 (2020·全国Ⅱ卷)如图,已知三棱柱ABC -A 1B 1C 1的底面是正三角形,侧面BB 1C 1C 是矩形,M ,N 分别为BC ,B 1C 1的中点,P 为AM 上一点,过B 1C 1和P 的平面交AB 于E ,交AC 于F .(1)证明:AA 1∥MN ,且平面A 1AMN ⊥平面EB 1C 1F ;(2)设O 为△A 1B 1C 1的中心.若AO ∥平面EB 1C 1F ,且AO =AB ,求直线B 1E 与平面A 1AMN 所成角的正弦值.(1)证明 因为侧面BB 1C 1C 是矩形且M ,N 分别为BC ,B 1C 1的中点,所以MN ∥CC 1.又由已知得AA 1∥CC 1,故AA 1∥MN . 因为△A 1B 1C 1是正三角形,所以B 1C 1⊥A 1N . 又侧面BB 1C 1C 是矩形,所以B 1C 1⊥MN . 又A 1N ∩MN =N ,A 1N ,MN ⊂平面A 1AMN , 所以B 1C 1⊥平面A 1AMN .又B 1C 1⊂平面EB 1C 1F , 所以平面A 1AMN ⊥平面EB 1C 1F .(2)解 由已知及(1)得AM ⊥BC ,MN ⊥BC ,AM ⊥MN .以M 为坐标原点,MA →的方向为x 轴正方向,|MB →|为单位长,建立如图所示的空间直角坐标系M -xyz ,则AB =2,AM = 3.连接NP ,AO ∥平面EB 1C 1F ,AO ⊂平面A 1AMN , 平面A 1AMN ∩平面EB 1C 1F =PN ,故AO ∥PN . 又AP ∥ON ,则四边形AONP 为平行四边形,故PM =233,E ⎝ ⎛⎭⎪⎫233,13,0.由(1)知平面A 1AMN ⊥平面ABC .作NQ ⊥AM ,垂足为Q ,则NQ ⊥平面ABC . 设Q (a ,0,0),则 NQ =4-⎝ ⎛⎭⎪⎫233-a2, B 1⎝⎛⎭⎪⎫a ,1,4-⎝ ⎛⎭⎪⎫233-a2. 故B 1E →=⎝ ⎛⎭⎪⎫233-a ,-23,-4-⎝ ⎛⎭⎪⎫233-a 2, |B 1E →|=2103.又n =(0,-1,0)是平面A 1AMN 的一个法向量, 故sin ⎝ ⎛⎭⎪⎫π2-〈n ,B 1E →〉=cos 〈n ,B 1E →〉=n ·B 1E →|n |·|B 1E →|=1010.所以直线B 1E 与平面A 1AMN 所成角的正弦值为1010. 考向三 利用向量求二面角【典例3】 (2020·全国Ⅲ卷)如图,在长方体ABCD -A 1B 1C 1D 1中,点E ,F 分别在棱DD 1,BB 1上,且2DE =ED 1,BF =2FB 1.(1)证明:点C 1在平面AEF 内;(2)若AB =2,AD =1,AA 1=3,求二面角A -EF -A 1的正弦值.解 设AB =a ,AD =b ,AA 1=c .如图,以C 1为坐标原点,C 1D 1→的方向为x 轴正方向, 建立空间直角坐标系C 1-xyz .(1)证明 连接C 1F ,C 1(0,0,0),A (a ,b ,c ),E ⎝ ⎛⎭⎪⎫a ,0,23c ,F ⎝ ⎛⎭⎪⎫0,b ,13c ,EA→=⎝ ⎛⎭⎪⎫0,b ,13c ,C 1F →=⎝ ⎛⎭⎪⎫0,b ,13c ,得EA →=C 1F →, 因此EA ∥C 1F ,即A ,E ,F ,C 1四点共面, 所以点C 1在平面AEF 内.(2)由已知得A (2,1,3),E (2,0,2),F (0,1,1),A 1(2,1,0),AE →=(0,-1,-1),AF →=(-2,0,-2),A 1E →=(0,-1,2),A 1F →=(-2,0,1). 设n 1=(x ,y ,z )为平面AEF 的法向量,则⎩⎪⎨⎪⎧n 1·AE →=0,n 1·AF →=0,即⎩⎨⎧-y -z =0,-2x -2z =0,可取n 1=(-1,-1,1).设n 2为平面A 1EF 的法向量,则⎩⎪⎨⎪⎧n 2·A 1E →=0,n 2·A 1F →=0,同理可取n 2=⎝ ⎛⎭⎪⎫12,2,1.设二面角A -EF -A 1的平面角为α,所以cos α=cos 〈n 1,n 2〉=n 1·n 2|n 1|·|n 2|=-77,则sin α=1-cos2α=42 7,所以二面角A-EF-A1的正弦值为42 7.探究提高 1.二面角的大小可以利用分别在两个半平面内与棱垂直的直线的方向向量的夹角(或其补角)或通过二面角的两个面的法向量的夹角求得,它等于两个法向量的夹角或其补角.2.利用向量法求二面角,必须能判定“所求二面角的平面角是锐角或钝角”,否则解法是不严谨的.【拓展练习3】(2020·沈阳一监)如图,已知△ABC为等边三角形,△ABD为等腰直角三角形,AB⊥BD.平面ABC⊥平面ABD,点E与点D在平面ABC的同侧,且CE∥BD,BD=2CE.点F为AD的中点,连接EF.(1)求证:EF∥平面ABC;(2)求二面角C-AE-D的余弦值.(1)证明取AB的中点为O,连接OC,OF,如图.∵O,F分别为AB,AD的中点,∴OF∥BD且BD=2OF.又CE∥BD且BD=2CE,∴CE∥OF且CE=OF,∴OF綊EC,则四边形OCEF为平行四边形,∴EF∥OC.又OC⊂平面ABC,EF⊄平面ABC,∴EF∥平面ABC.(2)解∵△ABC为等边三角形,O为AB的中点,∴OC⊥AB.∵平面ABC ⊥平面ABD ,平面ABC ∩平面ABD =AB ,BD ⊥AB ,BD ⊂平面ABD ,∴BD ⊥平面ABC .又OF ∥BD ,∴OF ⊥平面ABC .以O 为坐标原点,分别以OA ,OC ,OF 所在的直线为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系.不妨令正三角形ABC 的边长为2,则O (0,0,0),A (1,0,0),C (0,3,0),E (0,3,1),D (-1,0,2),∴AC→=(-1,3,0),AE →=(-1,3,1),AD →=(-2,0,2). 设平面AEC 的法向量为m =(x 1,y 1,z 1),则 ⎩⎪⎨⎪⎧AC →·m =-x 1+3y 1=0,AE →·m =-x 1+3y 1+z 1=0. 不妨令y 1=3,则m =(3,3,0). 设平面AED 的法向量为n =(x 2,y 2,z 2),则 ⎩⎪⎨⎪⎧AD →·n =-2x 2+2z 2=0,AE →·n =-x 2+3y 2+z 2=0. 令z 2=1,得n =(1,0,1). ∴cos 〈m ,n 〉=323×2=64.由图易知二面角C -AE -D 为钝角, ∴二面角C -AE -D 的余弦值为-64. 考向四 利用空间向量求解探索性问题【典例4】 (2020·武汉调研)如图所示,在正方体ABCD -A 1B 1C 1D 1中,点O 是AC 与BD 的交点,点E 是线段OD 1上的一点.(1)若点E 为OD 1的中点,求直线OD 1与平面CDE 所成角的正弦值;(2)是否存在点E ,使得平面CDE ⊥平面CD 1O ?若存在,请指出点E 的位置,并加以证明;若不存在,请说明理由. 解 (1)不妨设正方体的棱长为2.以D 为坐标原点,分别以DA ,DC ,DD 1所在直线分别为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系D -xyz ,则D (0,0,0),D 1(0,0,2),C (0,2,0),O (1,1,0). 因为E 为OD 1的中点, 所以E ⎝ ⎛⎭⎪⎫12,12,1.则OD 1→=(-1,-1,2),DE →=⎝ ⎛⎭⎪⎫12,12,1,DC →=(0,2,0).设p =(x 0,y 0,z 0)是平面CDE 的法向量, 则⎩⎪⎨⎪⎧p ·DE→=0,p ·DC →=0,即⎩⎪⎨⎪⎧12x 0+12y 0+z 0=0,2y 0=0,取x 0=2,则y 0=0,z 0=-1,所以p =(2,0,-1)为平面CDE 的一个法向量. 设直线OD 1与平面CDE 所成角为θ, 所以sin θ=|cos 〈OD 1→,p 〉|=|OD 1→·p ||OD 1→||p |=|-1×2+(-1)×0+2×(-1)|(-1)2+(-1)2+22×22+(-1)2=23015, 即直线OD 1与平面CDE 所成角的正弦值为23015.(2)存在,且点E 为线段OD 1上靠近点O 的三等分点.理由如下. 假设存在点E ,使得平面CDE ⊥平面CD 1O .同第(1)问建立空间直角坐标系,易知点E 不与点O 重合,设D 1E →=λEO →,λ∈[0,+∞),OC →=(-1,1,0),OD 1→=(-1,-1,2). 设m =(x 1,y 1,z 1)是平面CD 1O 的法向量, 则⎩⎪⎨⎪⎧m ·OC →=0,m ·OD 1→=0,即⎩⎨⎧-x 1+y 1=0,-x 1-y 1+2z 1=0,取x 1=1,则y 1=1,z 1=1,所以m =(1,1,1)为平面CD 1O 的一个法向量.因为D 1E →=λEO →,所以点E 的坐标为⎝⎛⎭⎪⎫λ1+λ,λ1+λ,21+λ, 所以DE →=⎝ ⎛⎭⎪⎫λ1+λ,λ1+λ,21+λ. 设n =(x 2,y 2,z 2)是平面CDE 的法向量, 则⎩⎪⎨⎪⎧n ·DE→=0,n ·DC →=0,即⎩⎪⎨⎪⎧λ1+λx 2+λ1+λy 2+21+λz 2=0,2y 2=0,取x 2=1,则y 2=0,z 2=-λ2,所以n =⎝ ⎛⎭⎪⎫1,0,-λ2为平面CDE 的一个法向量. 因为平面CDE ⊥平面CD 1O ,所以m ⊥n . 则m ·n =0,所以1-λ2=0,解得λ=2.所以当D 1E →EO →=2,即点E 为线段OD 1上靠近点O 的三等分点时,平面CDE ⊥平面CD 1O .探究提高 1.空间向量最适合于解决立体几何中的探索性问题,它无需进行复杂的作图、论证、推理,只需通过坐标运算进行判断.但注意空间坐标系建立的规范性及计算的准确性,否则容易出现错误.2.空间向量求解探索性问题:(1)假设题中的数学对象存在(或结论成立)或暂且认可其中的一部分结论;(2)在这个前提下进行逻辑推理,把要成立的结论当作条件,据此列方程或方程组,把“是否存在”问题转化为“点的坐标(或参数)是否有解,是否有规定范围内的解”等.若由此推导出矛盾,则否定假设;否则,给出肯定结论.【拓展练习4】 (2019·北京卷)如图,在四棱锥P -ABCD 中,P A ⊥平面ABCD ,AD ⊥CD ,AD ∥BC ,P A =AD =CD =2,BC =3.E 为PD 的中点,点F 在PC 上,且PF PC =13.(1)求证:CD ⊥平面P AD ; (2)求二面角F -AE -P 的余弦值;(3)设点G 在PB 上,且PG PB =23.判断直线AG 是否在平面AEF 内,说明理由. (1)证明 因为P A ⊥平面ABCD ,CD ⊂平面ABCD ,所以P A ⊥CD . 又因为AD ⊥CD ,P A ∩AD =A ,P A ,AD ⊂平面P AD , 所以CD ⊥平面P AD .(2)解 过点A 作AD 的垂线交BC 于点M . 因为P A ⊥平面ABCD ,AM ,AD ⊂平面ABCD , 所以P A ⊥AM ,P A ⊥AD .建立如图所示的空间直角坐标系A -xyz ,则A (0,0,0),B (2,-1,0),C (2,2,0),D (0,2,0),P (0,0,2).因为E 为PD 的中点, 所以E (0,1,1).所以AE→=(0,1,1),PC →=(2,2,-2),AP →=(0,0,2). 所以PF→=13PC →=⎝ ⎛⎭⎪⎫23,23,-23, 所以AF→=AP →+PF →=⎝ ⎛⎭⎪⎫23,23,43. 设平面AEF 的法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧n ·AE →=0,n ·AF →=0,即⎩⎪⎨⎪⎧y +z =0,23x +23y +43z =0. 令z =1,则y =-1,x =-1. 于是n =(-1,-1,1).又因为平面P AD 的一个法向量为p =(1,0,0), 所以cos 〈n ,p 〉=n ·p |n ||p |=-33.由题知,二面角F -AE -P 为锐角,所以其余弦值为33. (3)解 直线AG 在平面AEF 内,理由如下: 因为点G 在PB 上,且PG PB =23,PB →=(2,-1,-2), 所以PG→=23PB →=⎝ ⎛⎭⎪⎫43,-23,-43, 所以AG→=AP →+PG →=⎝ ⎛⎭⎪⎫43,-23,23. 由(2)知,平面AEF 的一个法向量n =(-1,-1,1), 所以AG →·n =-43+23+23=0.又点A ∈平面AEF ,所以直线AG 在平面AEF 内.【专题拓展练习】一、单选题1.已知三棱锥O -ABC ,点M ,N 分别为AB ,OC 的中点,且,,OA a OB b OC c ===,用,,a b c 表示MN ,则MN 等于( )A .()12b c a +- B .()12a b c ++ C .()12a b c -+D .()12c a b --【答案】D 【详解】MN MA AO ON =++1122BA OA OC =-+ ()1122OA OB OA OC =--+ 111222OA OB OC =--+()12c a b =--. 故选:D2.在棱长为1的正方体1111ABCD A B C D -中,,M N 分别为111,BD B C 的中点,点P 在正方体的表面上运动,且满足MP CN ⊥,则下列说法正确的是( )A .点P 可以是棱1BB 的中点 B .线段MP 3C .点P 的轨迹是正方形D .点P 轨迹的长度为2+5【答案】D 【详解】在正方体1111ABCD A B C D -中,以点D 为坐标原点,分别以DA 、DC 、1DD 方向为x 轴、y 轴、z 轴正方向,建立空间直角坐标系,因为该正方体的棱长为1,,M N 分别为111,BD B C 的中点, 则()0,0,0D ,111,,222M ⎛⎫ ⎪⎝⎭,1,1,12N ⎛⎫⎪⎝⎭,()0,1,0C , 所以1,0,12CN ⎛⎫=⎪⎝⎭,设(),,P x y z ,则111,,222MP x y z ⎛⎫=--- ⎪⎝⎭,因为MP CN ⊥, 所以1110222x z ⎛⎫-+-= ⎪⎝⎭,2430x z +-=,当1x =时,14z =;当0x =时,34z =; 取11,0,4E ⎛⎫ ⎪⎝⎭,11,1,4F ⎛⎫ ⎪⎝⎭,30,1,4G ⎛⎫ ⎪⎝⎭,30,0,4H ⎛⎫ ⎪⎝⎭,连接EF ,FG ,GH ,HE ,则()0,1,0EF GH ==,11,0,2EH FG ⎛⎫==- ⎪⎝⎭, 所以四边形EFGH 为矩形,则0EF CN ⋅=,0EH CN ⋅=,即EF CN ⊥,EH CN ⊥, 又EFEH E =,且EF ⊂平面EFGH ,EH ⊂平面EFGH ,所以CN ⊥平面EFGH , 又111,,224EM ⎛⎫=-⎪⎝⎭,111,,224MG ⎛⎫=- ⎪⎝⎭,所以M 为EG 中点,则M ∈平面EFGH , 所以,为使MP CN ⊥,必有点P ∈平面EFGH ,又点P 在正方体的表面上运动,所以点P 的轨迹为四边形EFGH , 因此点P 不可能是棱1BB 的中点,即A 错; 又1EF GH ==,52EH FG ==,所以EF EH ≠,则点P 的轨迹不是正方形; 且矩形EFGH 的周长为522252+⨯=+,故C 错,D 正确; 因为点M 为EG 中点,则点M 为矩形EFGH 的对角线交点,所以点M 到点E 和点G 的距离相等,且最大,所以线段MP 的最大值为52,故B 错. 3.在空间四边形ABCD 中,AB CD AC DB AD BC ⋅+⋅+⋅=( ) A .-1 B .0 C .1 D .不确定【答案】B 【详解】 如图,令,,AB a AC b AD c ===, 则AB CD AC DB AD BC ⋅+⋅+⋅,()()()a cb b ac c b a =⋅-+⋅-+⋅-,0a c a b b a b c c b c a =⋅-⋅+⋅-⋅+⋅-⋅=.故选:B4.如图,在四棱锥P ABCD -中,底面ABCD 为矩形.PA ⊥底面,2,4ABCD PA AB AD ===.E 为PC 的中点,则异面直线PD 与BE 所成角的余弦值为( )A .35B .3010C .1010D .31010【答案】B 【详解】以A 点为坐标原点,AB 为x 轴,AD 为y 轴,AP 为z 轴建立空间直角坐标系如下图所示:则()2,0,0B ,()1,2,1E ,()002P ,,,()0,4,0D , ()1,2,1BE =-∴,()0,4,2PD =-,设异面直线PD 与BE 所成角为θ,则630cos 10625PD BE PD BEθ⋅===⨯⋅. 5.已知四棱锥,-P ABCD 底面是边长为2的正方形,PAD △是以AD 为斜边的等腰直角三角形,AB ⊥平面PAD ,点E 是线段PD 上的动点(不含端点),若线 AB 段上存在点F (不含端点),使得异面直线PA 与 EF 成30的角,则线段PE 长的取值范围是( )A .202⎛⎫ ⎪ ⎪⎝⎭, B .603⎛⎫⎪ ⎪⎝⎭, C .222⎛⎫⎪ ⎪⎝⎭, D .623,⎛⎫⎪⎝⎭【答案】B 【详解】由PAD △是以AD 为斜边的等腰直角三角形,AB ⊥平面PAD ,取AD 中点G ,建立如图空间直角坐标系,依题意(0,0,0),(1,0,0),(1,0,0),(1,2,0),(0,0,1)G A D B P -,设(1,,0)F y ,,设()()1,0,1,0,DE xDP x x x ===,01x <<,故()1,0,E x x -,()2,,EF x y x =--又()1,0,1PA =-,异面直线PA 与 EF 成30的角,故cos30PA EF PA EF ⋅=⋅︒,即()2223222x y x =-++即()222213y x =--+,01x <<,故220,3y ⎡⎫∈⎪⎢⎣⎭,又02y <<,故60y ⎛∈ ⎝⎭,. 故选:B.6.已知二面角l αβ--,其中平面的一个法向量()1,0,1m =-,平面β的一个法向量()0,1,1n =-,则二面角l αβ--的大小可能为( )A .60︒B .120︒C .60︒或120︒D .30【答案】C 【详解】11cos ,222m n m n m n ⋅-<>===-⨯,所以,120m n <>=,又因为二面角的大小与法向量夹角相等或互补, 所以二面角的大小可能是60或120. 故选:C7.已知向量(,,)x y z a a a a =,(,,)x y z b b b b =,{},,i j k 是空间中的一个单位正交基底.规定向量积的行列式计算:()()(),,yz xy xz y z z y z x x z x y y x xy z yz xyxz xyz ij ka a a a a a ab a b a b i a b a b j a b a b k a a a b b b b b b b b b ⎛⎫⨯=-+-+-==-⎪ ⎪⎝⎭其中行列式计算表示为a b ad bc c d=-,若向量(2,1,4),(3,1,2),AB AC ==则AB AC ⨯=( )A .(4,8,1)---B .(1,4,8)--C .(2,8,1)--D .(1,4,8)---【答案】C 【详解】由题意得()()()()1241+4322+21132,8,1AB AC i j k ⨯=⨯-⨯⨯-⨯⨯-⨯=--, 故选:C.8.长方体1111ABCD A B C D -,110AB AA ==,25AD =,P 在左侧面11ADD A 上,已知P 到11A D 、1AA 的距离均为5,则过点P 且与1A C 垂直的长方体截面的形状为( )A .六边形B .五边形C .四边形D .三角形【答案】B 【详解】以D 为坐标原点建立如图所示的空间直角坐标系,则()()()120,0,5,25,0,10,0,10,0P A C ,()125,10,10AC ∴=--, 设截面与11A D 交于(),0,10Q Q x ,则()20,0,5Q PQ x =-,()12520500Q AC PQ x ∴⋅=---=,解得18Qx =,即()18,0,10Q , 设截面与AD 交于(),0,0M M x ,则()20,0,5M PM x =--,()12520500M AC PM x ∴⋅=--+=,解得22Mx =,即()22,0,0M , 设截面与AB 交于()25,,0N N y ,则()3,,0N MN y =,1253100N AC MN y ∴⋅=-⨯+=,解得7.5Ny =,即()25,7.5,0N , 过Q 作//QF MN ,交11B C 于F ,设(),10,10F F x ,则()18,10,0F QF x =-, 则存在λ使得QF MN λ=,即()()18,10,03,7.5,0F x λ-=,解得22F x =,故F 在线段11B C 上,过F 作//EF QM ,交1BB 于E ,设()25,10,E E z ,则()3,0,10E EF z =--,则存在μ使得EF QM μ=,即()()3,0,104,0,10E z μ--=-,解得 2.5E z =,故E 在线段1BB 上,综上,可得过点P 且与1A C 垂直的长方体截面为五边形QMNEF . 故选:B.9.在四面体ABCD 中,6AB =,3BC =,4BD =,若ABD ∠与ABC ∠互余,则()BA BC BD ⋅+的最大值为( )A .20B .30C .40D .50【答案】B 【详解】设ABD α∠=,可得2ABC πα∠=-,则α为锐角,在四面体ABCD 中,6AB =,3BC =,4BD =, 则()cos cos 2BA BC BD BA BC BA BD BA BC BA BD παα⎛⎫⋅+=⋅+⋅=⋅-+⋅ ⎪⎝⎭()18sin 24cos 30sin αααϕ=+=+,其中ϕ为锐角,且4tan 3ϕ=. 02πα<<,则2πϕαϕϕ<+<+,所以,当2παϕ+=时,()BA BC BD ⋅+取得最大值30.10.已知正方体1111ABCD A B C D -的棱长为1,点E 是底面ABCD 上的动点,则()111CE CA D B -⋅的最大值为( )A .22B .1C .2D .6【答案】B 【详解】以点D 为原点,1,,DA DC DD 为,,x y z 轴建立空间直角坐标系,则111(0,0,1),(1,1,1),(1,0,1),D B A设(,,0)E x y ,其中[],0,1x y ∈,则()()11111,,1,1,1,0CE CA A E x y D B -==--=, 所以111()11CE CA D B x y -⋅=+-≤,等号成立的条件是(1,1,0)E ,故其最大值为1, 故选:B .11.如图,在底面为正方形的四棱锥P-ABCD 中,已知PA ⊥平面ABCD ,且PA =AB .若点M 为PD 中点,则直线CM 与PB 所成角的大小为( )A .60°B .45°C .30°D .90°【答案】C 【详解】如图所示:以A 为坐标原点,以AB ,AD ,AP 为单位向量建立空间直角坐标系A xyz -,设1PA =,则()0,0,0A ,()1,1,0C ,110,,22M ⎛⎫⎪⎝⎭,()0,0,1P ,()1,0,0B , 故()1,0,1PB =-,111,,22MC ⎛⎫=- ⎪⎝⎭,故1132cos ,21111144PB MC PB MC PB MC+⋅===⋅+⋅++, 由异面直线夹角的范围是(]0,90︒︒,故直线CM 与PB 所成角的大小为30. 故选:C.12.如图,在正四面体ABCD 中,,,2BE EC CF FD DG GA ===,记平面EFG 与平面BCD 、平面ACD 、平面ABD ,所成的锐二面角分别为α、β、γ,则( )A .αβγ>>B .αγβ>>C .βαγ>>D .γαβ>>【答案】A【详解】 解:(空间向量法)因为,,2BE EC CF FD DG GA ===,所以E 、F 分别为BC 、CD 的中点,G 为AD 上靠近A 的三等分点,取BD 的中点M ,连接CM ,过A 作AO ⊥平面BCD ,交CM 于点O ,在平面BCD 中过O 作//ON BD ,交CD 于N ,设正四面体ABCD 的棱长为2,则33OM =,233CO =,22222326233OA AC OC ⎛⎫=-=-= ⎪ ⎪⎝⎭, 以O 为原点,OC 为x 轴,ON 为y 轴,OA 为z 轴,建立空间直角坐标系,26A ⎛ ⎝⎭,31,0B ⎛⎫- ⎪ ⎪⎝⎭,23C ⎫⎪⎝⎭,3D ⎛⎫ ⎪⎝⎭,31,02E ⎫-⎪⎝⎭,31,062F ⎛⎫ ⎪⎝⎭,3146,939G ⎛- ⎝⎭,(0,1,0)EF =,53546,8691EG ⎛⎫=- ⎪ ⎪⎝⎭,232633AC ⎛=- ⎝⎭,32633AD ⎛=-- ⎝⎭,3261,33AB ⎛⎫=--- ⎪⎝⎭,设平面EFG 的一个法向量为()1,,n x y z =,则110n EF n EG ⎧⋅=⎪⎨⋅=⎪⎩,即05354606y x y z =⎧⎪⎨+=⎪⎩,不妨令1z =,则18,0,125n ⎛⎫= ⎪ ⎪⎝⎭,同理可计算出平面BCD 、平面ACD 、平面ABD 的一个法向量分别为2(0,0,1)n =,()32,6,1n =,4(22,0,1)n =-,则可得1212517co 1s 5n n n n α⋅==⋅,1313717co 1s 5n n n n β⋅==⋅,14149cos 1751n n n n γ⋅==⋅,所以cos cos cos αβγ<<,又cos y x =在()0.x π∈上递减,所以αβγ>>, 故选:A.13.在正四棱锥P ABCD -中,1PA PB PC PD AB =====,点Q ,R 分别在棱AB ,PC 上运动,当||QR 达到最小值时,||||PQ CQ 的值为( ) A .7010B .355C .3510D .705【答案】A 【详解】以P 在底面的投影O 为坐标原点,建立如图所示的坐标系,设1(,,0)2Q a ,(,,)R m n q因为211(0(,0),22P C -,,112(,22PC =-, 又因为R 在PC 上,PR PC λ=所以(,m m q -=,11(,),22λλ-, 所以R 11(,2222λλ=--+,所以2222111222QR a λλ⎛⎛⎫⎛⎫=--+-+ ⎪ ⎪ ⎝⎭⎝⎭⎝⎭221324a a λλλ=+-++ 因为[]11,,0,122a λ⎡⎤∈-∈⎢⎥⎣⎦设2213()24f a a a λλλ=+-++,2213()24g a a λλλλ=+-++ 对其求导()2f a a λ'=-,1()22g a λλ'=-+当二个导数同时为0时,取最小值,即20a λ-=,1202a λ-+=所以11,36a λ==时取最小值,所以1121,,,1,,02623PQ CQ ⎛⎫⎛⎫=-=- ⎪ ⎪ ⎪⎝⎭⎝⎭ 所以PQCQ==10,所以当||QR 达到最小值时,||||PQ CQ 的值为10. 14.如图所示,正方体1111ABCD A B C D -的棱长为1,E 、F 、G 分别为BC 、1CC 、1BB 的中点,则( )A .直线1D D 与直线AF 垂直B .直线1A G 与平面AEF 平行C .平面AEF 截正方体所得的截面面积为1D .点C 和点G 到平面AEF 的距离相等 【答案】B 【详解】以D 点为坐标原点,DA 、DC 、1DD 为x ,y ,z 轴建系,则(000)D ,,、(100)A ,,、()010C ,,、1(101)A ,,、1(001)D ,,、 1(10)2E ,,、1(01)2F ,,,1(11)2G ,,, 则()1001DD =,,、1112AF ⎛⎫=- ⎪⎝⎭,,,则112DD AF ⋅=, ∴直线1D D 与直线AF 不垂直,A 错误;则11012A G ⎛⎫=- ⎪⎝⎭,,,1102AE ⎛⎫=- ⎪⎝⎭,,,1112AF ⎛⎫=- ⎪⎝⎭,,, 设平面AEF 的法向量为()n x y z =,,,则10021002x y AE n AF n x y z ⎧-+=⎪⎧⋅=⎪⎪⇒⎨⎨⋅=⎪⎪⎩-++=⎪⎩,令2x =,则1y =,2z =,则(212)n =,,,10AG n ⋅=,∴直线1A G 与平面AEF 平行,B 正确; 易知四边形1AEFD 为平面AEF 截正方体所得的截面,且1D F 、DC 、AE 共点于H ,15D H AH ==,12AD =,∴121232(5)()222AD H S ∆=⨯⨯-=,则113948AD HAEFD S S =⋅=四边形,C 错误; (110)AC =-,,,点C 到平面AEF 的距离113AC n d n⋅==, 1012AG ⎛⎫= ⎪⎝⎭,,,点G 到平面AEF 的距离223AG n d n ⋅==,则12d d ≠,D 错误;故选:B .15.如图所示,1111ABCD A B C D -是棱长为6的正方体,E 、F 分别是棱AB 、BC 上的动点,且AE BF =.当1A 、E 、F 、1C 共面时,平面1A DE 与平面1C DF 所成锐二面角的余弦值为( )A .15B .12C .32D .65【答案】B 【详解】以点D 为原点建立如图所示的空间直角坐标系,则1(606)A ,,、(000)D ,,、1(066)C ,,,由题意知:当(630)E ,,、(360)F ,,时,1A 、E 、F 、1C 共面, 设平面1A DE 的法向量为1111()n x y z =,,,1(606)DA =,,,(630)DE =,,, 则1111111660{630n DA x z n DE x y ⋅=+=⋅=+=,取11x =,解得1(121)n =--,,,设平面1C DF 的法向量为2222()n x y z =,,,1(066)DC =,,,(360)DF =,,, 则2122222660{360n DC y z n DF x y ⋅=+=⋅=+=,取22x =,解得2(211)n =-,,,设平面1A DE 与平面1C DF 所成锐二面角为θ,则1212121cos cos 266n n n n n n θ⋅====⋅⋅,, ∴平面1A DE 与平面1C DF 所成锐二面角的余弦值为12, 故选:B.二、解答题16.在三棱柱111ABC A B C -中,1AB AC ==,13AA =AB AC ⊥,1B C ⊥平面ABC ,E 是1B C 的中点.(1)求证:平面1AB C ⊥平面11ABB A ; (2)求直线AE 与平面11AAC C 所成角的正弦值. 【详解】(1)由1B C ⊥平面ABC ,AB 平面ABC ,得1AB B C ⊥,又AB AC ⊥,1CB AC C =,故AB ⊥平面1AB C ,AB 平面11ABB A ,故平面11ABB A ⊥平面1AB C .(2)以C 为原点,CA 为x 轴,1CB 为z 轴,建立如图所示空间直角坐标系, 则()0,0,0C ,()1,0,0A ,()1,1,0B 又2BC =113BB AA ==故11CB =,()10,0,1B ,10,0,2E ⎛⎫⎪⎝⎭,()1,0,0CA = ()111,1,1AA BB ==--,11,0,2AE ⎛⎫=- ⎪⎝⎭设平面11AAC C 的一个法向量为(),,n x y z =,则100n CA n AA ⎧⋅=⎪⎨⋅=⎪⎩,即00x x y z =⎧⎨--+=⎩,令1y =,则1z =, ()0,1,1n =, 设直线AE 与平面11AAC C 所成的角为θ,故1102sin 1214n AE n AEθ⋅===⨯+,即直线AE 与平面11AAC C 所成角的正弦值为1010.17.如图1,矩形ABCD 中,3AB BC =,将矩形ABCD 折起,使点A 与点C 重合,折痕为EF ,连接AF 、CE ,以AF 和EF 为折痕,将四边形ABFE 折起,使点B 落在线段FC 上,将CDE △向上折起,使平面DEC ⊥平面FEC ,如图2.(1)证明:平面ABE ⊥平面EFC ;(2)连接BE 、BD ,求锐二面角A BE D --的正弦值. 【详解】(1)证明:在平面ABCD 中,AF =FC ,BF +FC 3AB , 设3AB a =,则3BC a =,设BF =x ,在BAF △中,()22233x a a x +=-,解得x a =,则2AF FC a ==, 因为点B 落在线段FC 上,所以BC DE a ==,所以BE FC ⊥, 又AB BF ⊥即AB CF ⊥,AB BE B =,,AB BE ⊂平面ABE ,所以CF ⊥平面ABE ,由CF ⊂平面EFC 可得平面ABE ⊥平面EFC ;(2)以F 为原点,FC 为x 轴,过点F 平行BE 的方向作为作y 轴,过点F 垂直于平面EFC 的方向作为z 轴,建立如图所示空间直角坐标系,则()()()()2,0,0,0,0,0,3,0,,0,0C a F E a a B a ,()0,3,0BE a =, 易得平面ABE 的一个法向量为()2,0,0FC a =,作DG EC ⊥于G , 因为平面DEC ⊥平面FEC ,所以DG ⊥平面EFC ,则5334a G a ⎛⎫ ⎪ ⎪⎝⎭,53334a a D a ⎛ ⎝⎭,13334a a BD a ⎛= ⎝⎭,设平面DBE 的一个法向量为(),,n x y z =,则3013330442n BE ay a an BD ax y z ⎧⋅==⎪⎨⋅=++=⎪⎩,令3z =(3n =-, 因为12239cos ,13239n FC n FC a n FC⋅--===⋅⋅,所以锐二面角A -BE -D 223913113⎛⎫--= ⎪ ⎪⎝⎭. 18.如图,在三梭柱111ABC A B C -中,侧面11AA B B ,11AAC C 均为菱形,12AA =,1160ABB ACC ∠=∠=︒,D 为AB 的中点.(Ⅰ)求证:1//AC 平面1CDB ;(Ⅱ)若60BAC ∠=︒,求直线1AC 与平面11BB C C 所成角的正弦值. 【详解】解:(Ⅰ)连结1BC ,与1B C 交于点O ,连结OD , 四边形11BB C C 是平行四边形,O 为1B C 中点,D 为AB 中点,得1//AC OD ,又OD ⊂平面1CDB ,故1//AC 平面1CDB ;(Ⅱ)方法一:由12AB AC ==,12AC AB ==,且O 为1B C ,1BC 的中点, 得1AO BC ⊥,1AO B C ⊥,11B C BC =, 又1BC ,1CB 为平面11BB C C 内两条相交直线,得AO ⊥平面11BB C C ,故1AC B ∠即为直线1AC 与平面11BB C C 所成的角; 由60BAC ∠=︒,2AB AC ==,2BC =,得四边形11BB C C 为菱形,又11B C BC =,故四边形11BB C C 为正方形,122BC =则1ABC 为等腰直角三角形,且12BAC π∠=,故14AC B π∠=,12sin 2AC B ∠=, 因此,直线1AC 与平面11BB C C 所成角的正弦值为22.方法二:以D 为原点,分别以射线DB ,1DB ,CD 为x 轴,y 轴,z 轴的正半轴,建立空间直角坐标系O xyz -,则()0,0,0D ,()1,0,0A -,()1,0,0B ,()13,0A -,()13,0B , 由60BAC ∠=︒,2AB AC ==,ABC 为正三角形, 故CD AB ⊥,又1B D AB ⊥,所以AB ⊥平面1CDB , 设()0,,C y z ,由2CA =,123CA =,得(22223,38,y z y z ⎧+=⎪⎨+=⎪⎩即36,3y z ⎧=⎪⎪⎨⎪=⎪⎩,故3260,33C ⎛- ⎝⎭, 由11B C BC ,得12326C ⎛- ⎝⎭,所以12326AC ⎛= ⎝⎭,()11,3,0BB =-,3261,,33BC ⎛⎫=-- ⎪ ⎪⎝⎭; 设平面11BB C C 的一个法向量为()111,,n x y z =,由10,0,n BB n BC ⎧⋅=⎨⋅=⎩得1111130,33260,x y x y z ⎧-=⎪⎨+-=⎪⎩可取()3,1,2n =,设直线1AC 与平面11BB C C 所成角为θ, 则1112sin cos ,2AC n AC n AC nθ⋅===, 因此,直线1AC 与平面11BB C C 所成角的正弦值为22. 19.如图,在三棱柱111ABC A B C -中,侧面11ABB A 和11BCC B 都是正方形,平面11ABB A ⊥平面11BCC B ,,D E 分别为1BB ,AC 的中点.(1)求证://BE 平面1A CD .(2)求直线1B E 与平面1A CD 所成角的正弦值. 【详解】(1)证明:取1A C 中点F ,连接DF ,EF , ∵,E F 分别为1,AC A C 的中点,∴1//EF AA ,且112EF AA =,又四边形11ABB A 是正方形,∴11//BB AA 且11BB AA =, 即1//EF BB 且112EF BB =,又∵D 为1BB 中点,∴//EF BD 且EF BD =,所以四边形EFDB 为平行四边形,所以//BE DF ,又BE ⊄平面1A CD ,DF ⊂平面1A CD ,所以//BE 平面1A CD .(2)由题意,1,,BA BC BB 两两垂直,所以以B 为原点建立如图所示的空间直角坐标系,设12BA BC BB ===,则11(0,2,0),(1,0,1),(2,0,0),(0,1,0),(0,2,2)B E C D A . ,11(1,2,1),(2,1,0),(2,2,2)B E CD AC =-=-=-,设平面 1A CD 的法向量为(),,m x y z =, 则100AC m CD m ⎧⋅=⎨⋅=⎩,即222020x y z x y -++=⎧⎨-+=⎩,得()1,2,1m =- 设直线1B E 与平面1A CD 所成角为θ,1111412sin cos ,366B E m B E mB E mθ, 所以直线1B E 与平面1A CD 所成角的正弦值为23.。
( 人教A版)2-1:3.2立体几何中的向量方法第1课时空间向量与平行关系课件 (共31张PPT)

解析:(1)∵a=(1,-3,-1),b=(8,2,2) ∴a·b=8-6-2=0,∴a⊥b,∴l1⊥l2. (2)∵u=(1,3,0),v=(-3,-9,0), ∴v=-3u,∴u∥v,∴α∥β. (3)∵a=(1,-4,-3),u=(2,0,3), ∴a与u既不共线,也不垂直, ∴l与平面α斜交.
[证明] 如图所示建立空间直角坐标系D-xyz,则有D(0,0,0), A(2,0,0),C(0,2,0),C1(0,2,2),E(2,2,1),F(0,0,1), B1(2,2,2), 所以F→C1=(0,2,1),D→A=(2,0,0),A→E=(0,2,1).
(1)设n1=(x1,y1,z1)是平面ADE的法向量, 则n1⊥D→A,n1⊥A→E, 即nn11··DA→→EA==22yx11+=z01,=0,
设平面SCD的法向量为n=(1,y,z), 则n·D→C=(1,y,z)·(1,2,0)=1+2y=0, ∴y=-12. 又n·D→S=(1,y,z)·(-1,0,2)=-1+2z=0, ∴z=12. ∴n=1,-12,12即为平面SCD的一个法向量.
探究三 利用空间向量证明平行关系 [典例3] 已知正方体ABCD-A1B1C1D1的棱长为2,E,F分别是BB1,DD1的中 点,求证: (1)FC1∥平面ADE; (2)平面ADE∥平面B1C1F.
G→En=(x,y,z)是平面EFG的法向量,
n·G→E=0, 则n·G→F=0.
∴--2xx-+y+y+2zz==00,.
∴xy==zz., ∴n=(z,z,z),令z=1,此时n=(1,1,1), 所以平面EFG的一个法向量为(1,1,1).
播下一个行动,收获一种习惯;播下一种习惯,收获一种性格;播下一种性格,收获一种命运。思想会变成语言,语言会变成行动,行动会变成习惯,习惯会变成性格。性格会影响人生!习惯不加以抑 制,会变成生活的必需品,不良的习惯随时改变人生走向。人往往难以改变习惯,因为造习惯的就是自己,结果人又成为习惯的奴隶!人生重要的不是你从哪里来,而是你到哪里去。当你在埋头工作的 时侯,一定要抬头看看你去的方向。方向不对,努力白费!你来自何处并不重要,重要的是你要去往何方,人生最重要的不是所站的位置,而是所去的方向。人只要不失去方向,就永远不会失去自己! 这个世界唯一不变的真理就是变化,任何优势都是暂时的。当你在占有这个优势时,必须争取主动,再占据下一个优势,这需要前瞻的决断力,需要的是智慧!世上本无移山之术,惟一能移山的方法就 是:山不过来,我就过去。人生最聪明的态度就是:改变可以改变的一切,适应不能改变的一切!亿万财富不是存在银行里,而是产生在人的思想里。你没找到路,不等于没有路,你想知道将来要得到 什么,你必须知道现在应该先放弃什么!命运把人抛入最低谷时,往往是人生转折的最佳期。谁能积累能量,谁就能获得回报;谁若自怨自艾,必会坐失良机人人都有两个门:一个是家门,成长的地方; 一个是心门,成功的地方。能赶走门中的小人,就会唤醒心中的巨人!要想事情改变,首先自己改变,只有自己改变,才可改变世界。人最大的敌人不是别人,而是自己,只有战胜自己,才能战胜困难! 1、烦恼的时候,想一想到底为什么烦恼,你会发现其实都不是很大的事,计较了,就烦恼。我们要知道,所有发生的一切都是该发生的,都是因缘。顺利的就感恩,不顺利的就忏悔,然后放下。“雁 渡寒潭,雁过而潭不留影;风吹疏竹,风过而竹不留声。”修行者的心境,就是“过而不留”。忍得住孤独;耐得住寂寞;挺得住痛苦;顶得住压力;挡得住诱惑;经得起折腾;受得起打击;丢得起面 子;担得起责任;1提得起精神。闲时多读书,博览凝才气;众前慎言行,低调养清气;交友重情义,慷慨有人气;困中善负重,忍辱蓄志气;处事宜平易,不争添和气;对已讲原则,坚持守底气;淡 泊且致远,修身立正气;居低少卑怯,坦然见骨气;卓而能合群,品高养浩气淡然于心,自在于世间。云淡得悠闲,水淡育万物。世间之事,纷纷扰扰,对错得失,难求完美。若一心想要事事求顺意, 反而深陷于计较的泥潭,不能自拔。若凡事但求无愧于心,得失荣辱不介怀,自然落得清闲自在。人活一世,心态比什么都重要。财富名利毕竟如云烟,心情快乐才是人生的至宝。我们的梦想在哪里? 在路上,在脚踏实地的道路上;我们的期待在哪里?在路上,在勤劳勇敢的心路上;我们的快乐在哪里?在路上,在健康阳光的大道上;我们的朋友在哪里?在心里,在真诚友谊的宽道上!珍惜每一分 钟,对自己负责;善于发现看问题的角度;不满足于现状,别自我设限;勇于承认错误;不断反省自己,向周围的成功者学习;不轻言放弃。做事要有恒心;珍惜你所拥有的,不要感叹你失去或未得到; 学会赞美;不找任何借口。与贤人相近,则可重用;与小人为伍,则要当心;只满足私欲,贪图享乐者,则不可用;处显赫之位,任人唯贤,秉公办事者,是有为之人;身处困境之人,不做苟且之事, 则可重任;贫困潦倒时,不取不义之财者,品行高洁;见钱眼开者,则不可用。人最大的魅力,是有一颗阳光的心态。韶华易逝,容颜易老,浮华终是云烟。拥抱一颗阳光的心态,得失了无忧,来去都 随缘。心无所求,便不受万象牵绊;心无牵绊,坐也从容,行也从容,故生优雅。一个优雅的人,养眼又养心,才是魅力十足的人。容貌乃天成,浮华在身外,心里满是阳光,才是永恒的美。意逐白云 飞,心随流水宁。心无牵挂起,开阔空净明。幸福并不复杂,饿时,饭是幸福,够饱即可;渴时,水是幸福,够饮即可;裸时,衣是幸福,够穿即可;穷时,钱是幸福,够用即可;累时,闲是幸福,够 畅即可;困时,眠是幸福,够时即可。爱时,牵挂是幸福,离时,回忆是幸福。人生,由我不由天,幸福,由心不由境。心是一个人的翅膀,心有多大,世界就有多大。很多时候限制我们的,不是周遭 的环境,也不是他人的言行,而是我们自己。人心如江河,窄处水花四溅,宽时水波不兴。世间太大,一颗心承载不起。生活的最高境界,一是痛而不言,二是笑而不语。无论有多少委屈,一笑而泯之。 人生的幸福在于祥和,生命的祥和在于宁静,宁静的心境在于少欲。无意于得,就无所谓失去,无所谓失去,得失皆安谧。闹市间虽见繁华,却有名利争抢;田园间无争,却有柴米之忧烦;世外桃源祥 和升平,最终不过梦一场。心静,则万象皆静。知足者常在静中邂逅幸福。顺利人生,善于处理关系;普通人生,只会使用关系;不顺人生,只会弄僵关系。为人要心底坦荡,不为虚名所累;做事要头 脑清醒,不为假象所惑。智者,以别人惨痛的教训警示自己;愚者,用自己沉重的代价唤醒别人。对人多一份宽容,多一份爱心;对事多一份认真,多一份责任;对己多一点要求,多一点警醒。傲不可 长,志不可满,乐不可极,警醒自己。静能生慧。让心静下来,你才能看淡一切。静中,你才会反观自己,知道哪些行为还需要修正,哪些地方还需要精进,在静中让生命得到升华洗礼,在自观中走向 觉悟。让心静下来,你才能学会放下。你放下了,你的心也就静了。心不静,是你没有放下。静,通一切境界。人与人的差距,表面上看是财富的差距,实际上是福报的差距;表面上看是人脉的差距, 实际上是人品的差距;表面上看是气质的差距,实际上是涵养的差距;表面上看是容貌的差距,实际上是心地的差距;表面上看是人与人都差不多,内心境界却大不相同,心态决定命运。知恩感恩,是 很重要的一件事。因为当一个人具有感恩的心,心会常常欢喜,总是觉得很满足,一个不感恩不满足的人,总是会觉得欠缺、饥渴。一个常感恩的人,会觉得自己很幸运,有时候其实没什么道理,但他 这样一想、一感恩,就变得很快乐。这种感恩的心,对自己其实是有很大利益。压力最大的时候,效率可能最高;最忙碌的时候,学的东西可能最多;最惬意的时候,往往是失败的开始;寒冷到了极致, 太阳就要光临。成长不是靠时间,而是靠勤奋;时间不是靠虚度,而是靠利用;感情不是靠缘分,而是靠珍惜;金钱不是靠积攒,而是靠投资;事业不是靠满足,而是靠踏实。知恩感恩,是很重要的一 件事。因为当一个人具有感恩的心,心会常常欢喜,总是觉得很满足,一个不感恩不满足的人,总是会觉得欠缺、饥渴。一个常感恩的人,会觉得自己很幸运,有时候其实没什么道理,但他这样一想、 一感恩,就变得很快乐。这种感恩的心,对自己其实是有很大利益。压力最大的时候,效率可能最高;最忙碌的时候,学的东西可能最多;最惬意的时候,往往是失败的开始;寒冷到了极致,太阳就要 光临。成长不是靠时间,而是靠勤奋;时间不是靠虚度,而是靠利用;感情不是靠缘分,而是靠珍惜;金钱不是靠积攒,而是靠投资;事业不是靠满足,而是靠踏实。以平常心观不平常事,则事事平常。 在危险面前,平常心就是勇敢;在利诱面前,平常心就是纯洁;在复杂的环境面前,平常心就是保持清醒智慧。平常心不是消极遁世,而是一种境界,一种积极的人生。不仅要为成功而努力,更要为做 一个有价值的人而努力。命运不是机遇,而是选择;命运不靠等待,全靠争取。成熟就是学会在逆境中保持坚强,在顺境时保持清醒。时间告诉你什么叫衰老,回忆告诉你什么叫幼稚。只有在我们不需 要外来的赞许时,心灵才会真的自由。你没那么多观众,别那么累。温和对人对事。不要随意发脾气,谁都不欠你的。现在很痛苦,等过阵子回头看看,会发现其实那都不算事。和对自己有恶意的人绝 交。人有绝交,才有至交学会宽容伤害自己的人,因为他们很可怜,各人都有自己的难处,大家都不容易。学会放弃,拽的越紧,痛苦的是自己。低调,取舍间,必有得失。不要试图给自己找任何借口, 错误面前没人爱听那些借口。慎言,独立,学会妥协的同时,也要坚持自己最基本的原则。付出并不一定有结果。坚持可能会导致失去更多过去的事情可以不忘记,但一定要放下。活得轻松,任何事都 作一个最好的打算和最坏的打算。做一个简单的人,踏实而务实。不沉溺幻想。不庸人自扰。不说谎话,因为总有被拆穿的一天。别人光鲜的背后或者有�
高中数学《立体几何中的向量方法(一)》课件

抓住3个考点
突破3个考向
⇔_v_∥__u_.
③设平面 α 和 β 的法向量分别为 u1 和 u2,则 α⊥β⇔_u_1⊥__u__2
⇔u__1·_u_2=__0__=0.
抓住3个考点
突破3个考向
揭秘3年高考
3.点面距的求法
如图,设 AB 为平面 α 的一条斜线段,
n
为平面
α
的法向量,则 →
B
到平面
α
|AB·n|
的距离 d=___|n_|___.
→→ 故 cos〈B→E,C→D〉=|BB→EE|·|CC→DD|=
3 2 12+h2× 5
= 10+3 20h2,
所以
10+3 20h2=cos
30°=
3, 2
解得
h=
1100,即
AE=
10 10 .
抓住3个考点
突破3个考向
揭秘3年高考
用向量法解答这类题要做到以下几点: ①建系要恰当,建系前必须证明图形中有从同一点出发 的三条两两垂直的直线,如果图中没有现成的,就需进 行垂直转化;②求点的坐标及有关计算要准确无误,这 就需要在平时加强训练;③步骤书写要规范有序.
抓住3个考点
突破3个考向
揭秘3年高考
解 取 AC 的中点 O,连接 OS、OB. ∵SA=SC,AB=BC, ∴AC⊥SO,AC⊥BO. ∵平面 SAC⊥平面 ABC,平面 SAC∩平面 ABC=AC, ∴SO⊥平面 ABC, 又∵BO⊂平面 ABC,∴SO⊥BO.
如图所示,建立空间直角坐标系 O-xyz,则 B(0,2 3,0),C(- 2,0,0),S(0,0,2 2),M(1, 3,0),N(0, 3, 2). ∴C→M=(3, 3,0),M→N=(-1,0, 2),M→B=(-1, 3,0).
高中数学第三章空间向量与立体几何3.2立体几何中的向量方法3.2.2利用向量解决平行、垂直问题讲义

3.2.2 利用向量解决平行、垂直问题1.用向量方法证明空间中的平行关系(1)证明线线平行设直线l,m的方向向量分别是a=(a1,b1,c1),b=(a2,b2,c2),则l∥m⇔□01a∥b⇔□02 a=λb⇔□03a1=λa2,b1=λb2,c1=λc2(λ∈R).(2)证明线面平行设直线l的方向向量为a=(a1,b1,c1),平面α的法向量为u=(a2,b2,c2),则l∥α⇔□04a⊥u⇔□05a·u=0⇔□06a1a2+b1b2+c1c2=0.(3)证明面面平行①设平面α,β的法向量分别为u=(a1,b1,c1),v=(a2,b2,c2),则α∥β⇔□07u∥v⇔u=λv⇔□08a1=λa2,b1=λb2,c1=λc2(λ∈R).②由面面平行的判定定理,要证明面面平行,只要转化为相应的线面平行、线线平行即可.2.用向量方法证明空间中的垂直关系(1)证明线线垂直设直线l1的方向向量u1=(a1,b1,c1),直线l2的方向向量u2=(a2,b2,c2),则l1⊥l2⇔□09u1⊥u2⇔□10u1·u2=0⇔□11a1a2+b1b2+c1c2=0.(2)证明线面垂直设直线l的方向向量是u=(a1,b1,c1),平面α的法向量v=(a2,b2,c2),则l⊥α⇔□12 u∥v⇔□13u=λv(λ∈R)⇔□14a1=λa2,b1=λb2,c1=λc2(λ∈R).(3)证明面面垂直若平面α的法向量u=(a1,b1,c1),平面β的法向量v=(a2,b2,c2),则α⊥β⇔□15u ⊥v⇔□16u·v=0⇔□17a1a2+b1b2+c1c2=0.1.判一判(正确的打“√”,错误的打“×”)(1)若两直线方向向量的数量积为0,则这两条直线一定垂直相交.( )(2)若一直线与平面垂直,则该直线的方向向量与平面内的所有直线的方向向量的数量积为0.( )(3)两个平面垂直,则其中一平面内的直线的方向向量与另一平面内的直线的方向向量垂直.( )答案 (1)× (2)√ (3)×2.做一做(请把正确的答案写在横线上)(1)若直线l 1的方向向量为u 1=(1,3,2),直线l 2上有两点A (1,0,1),B (2,-1,2),则两直线的位置关系是________.(2)若直线l 的方向向量为a =(1,0,2),平面α的法向量为n =(-2,0,-4),则直线l 与平面α的位置关系为________.(3)已知两平面α,β的法向量分别为u 1=(1,0,1),u 2=(0,2,0),则平面α,β的位置关系为________.(4)若平面α,β的法向量分别为(-1,2,4),(x ,-1,-2),并且α⊥β,则x 的值为________.答案 (1)垂直 (2)垂直 (3)垂直 (4)-10探究1 利用空间向量解决平行问题例1 已知正方体ABCD -A 1B 1C 1D 1的棱长为2,E ,F 分别是BB 1,DD 1的中点,求证: (1)FC 1∥平面ADE ; (2)平面ADE ∥平面B 1C 1F .[证明] (1)如图所示,建立空间直角坐标系Dxyz ,则有D (0,0,0),A (2,0,0),C 1(0,2,2),E (2,2,1),F (0,0,1),B 1(2,2,2), 所以FC 1→=(0,2,1),DA →=(2,0,0),AE →=(0,2,1).设n 1=(x 1,y 1,z 1)是平面ADE 的法向量,则n 1⊥DA →,n 1⊥AE →, 即⎩⎪⎨⎪⎧n 1·DA →=2x 1=0,n 1·AE →=2y 1+z 1=0,得⎩⎪⎨⎪⎧x 1=0,z 1=-2y 1,令z 1=2,则y 1=-1,所以n 1=(0,-1,2). 因为FC 1→·n 1=-2+2=0,所以FC 1→⊥n 1.又因为FC 1⊄平面ADE ,所以FC 1∥平面ADE . (2)因为C 1B 1→=(2,0,0),设n 2=(x 2,y 2,z 2)是平面B 1C 1F 的一个法向量. 由n 2⊥FC 1→,n 2⊥C 1B 1→,得 ⎩⎪⎨⎪⎧n 2·FC 1→=2y 2+z 2=0,n 2·C 1B 1→=2x 2=0,得⎩⎪⎨⎪⎧x 2=0,z 2=-2y 2.令z 2=2,得y 2=-1,所以n 2=(0,-1,2), 因为n 1=n 2,所以平面ADE ∥平面B 1C 1F . 拓展提升利用向量法证明平行问题的两种途径(1)利用三角形法则和平面向量基本定理实现向量间的相互转化,得到向量的共线关系; (2)通过建立空间直角坐标系,借助直线的方向向量和平面的法向量进行平行关系的证明.【跟踪训练1】 在长方体ABCD -A 1B 1C 1D 1中,AB =4,AD =3,AA 1=2,P ,Q ,R ,S 分别是AA 1,D 1C 1,AB ,CC 1的中点.求证:PQ ∥RS .证明 证法一:以D 为原点,DA ,DC ,DD 1所在直线分别为x 轴、y 轴、z 轴,建立如图所示的空间直角坐标系Dxyz .则P (3,0,1),Q (0,2,2),R (3,2,0),S (0,4,1), PQ →=(-3,2,1),RS →=(-3,2,1),∴PQ →=RS →,∴PQ →∥RS →,即PQ ∥RS . 证法二:RS →=RC →+CS →=12DC →-DA →+12DD 1→,PQ →=PA 1→+A 1Q →=12DD 1→+12DC →-DA →,∴RS →=PQ →,∴RS →∥PQ →,即RS ∥PQ . 探究2 利用空间向量解决垂直问题例2 如图,在四棱锥E -ABCD 中,AB ⊥平面BCE ,CD ⊥平面BCE ,AB =BC =CE =2CD =2,∠BCE =120°.求证:平面ADE ⊥平面ABE .[证明] 取BE 的中点O ,连接OC ,则OC ⊥EB , 又AB ⊥平面BCE .∴以O 为原点建立空间直角坐标系Oxyz .如图所示.则由已知条件有C (1,0,0),B (0,3,0),E (0,-3,0),D (1,0,1),A (0,3,2). 设平面ADE 的法向量为n =(a ,b ,c ),则n ·EA →=(a ,b ,c )·(0,23,2)=23b +2c =0,n ·DA →=(a ,b ,c )·(-1,3,1)=-a +3b +c =0.令b =1,则a =0,c =-3, ∴n =(0,1,-3).∵AB ⊥平面BCE ,∴AB ⊥OC ,又OC ⊥EB ,且EB ∩AB =B ,∴OC ⊥平面ABE , ∴平面ABE 的法向量可取为m =(1,0,0). ∵n ·m =(0,1,-3)·(1,0,0)=0, ∴n ⊥m ,∴平面ADE ⊥平面ABE . 拓展提升利用向量法证明几何中的垂直问题的两条途径(1)利用三角形法则和平面向量基本定理实现向量间的相互转化,得到向量的垂直关系. (2)通过建立空间直角坐标系,借助直线的方向向量和平面的法向量进行证明.证明线面垂直时,只需直线的方向向量与平面的法向量平行或直线的方向向量与平面内两相交的直线的方向向量垂直.在判定两个平面垂直时,只需求出这两个平面的法向量,再看它们的数量积是否为0.【跟踪训练2】 如右图所示,在正方体ABCD -A 1B 1C 1D 1中,E ,F 分别是BB 1,D 1B 1的中点.求证:EF ⊥平面B 1AC .证明 证法一:设AB →=a ,AD →=c ,AA 1→=b ,则EF →=EB 1→+B 1F →=12(BB 1→+B 1D 1→)=12(AA 1→+BD →)=12(AA 1→+AD →-AB →)=12(-a +b +c ),∵AB 1→=AB →+AA 1→=a +b .∴EF →·AB 1→=12(-a +b +c )·(a +b )=12(b 2-a 2+c ·a +c ·b ) =12(|b |2-|a |2+0+0)=0. ∴EF →⊥AB 1→,即EF ⊥AB 1,同理,EF ⊥B 1C . 又AB 1∩B 1C =B 1, ∴EF ⊥平面B 1AC .证法二:设正方体的棱长为2,以DA ,DC ,DD 1所在直线分别为x 轴、y 轴、z 轴建立如图所示的直角坐标系,则A (2,0,0),C (0,2,0),B 1(2,2,2),E (2,2,1),F (1,1,2).∴EF →=(1,1,2)-(2,2,1) =(-1,-1,1).AB 1→=(2,2,2)-(2,0,0)=(0,2,2),AC →=(0,2,0)-(2,0,0)=(-2,2,0),∴EF →·AB 1→=(-1,-1,1)·(0,2,2)=(-1)×0+(-1)×2+1×2=0.EF →·AC →=(-1,-1,1)·(-2,2,0)=2-2+0=0, ∴EF →⊥AB 1→,EF →⊥AC →, ∴EF ⊥AB 1,EF ⊥AC . 又AB 1∩AC =A , ∴EF ⊥平面B 1AC .证法三:同法二得AB 1→=(0,2,2),AC →=(-2,2,0), EF →=(-1,-1,1).设面B 1AC 的法向量n =(x ,y ,z ), 则AB →1·n =0,AC →·n =0,即⎩⎪⎨⎪⎧2y +2z =0,-2x +2y =0,取x =1,则y =1,z =-1,∴n =(1,1,-1),∴EF →=-n ,∴EF →∥n ,∴EF ⊥平面B 1AC . 探究3 与平行、垂直有关的探索性问题例3 如图,在三棱锥P -ABC 中,AB =AC ,D 为BC 的中点,PO ⊥平面ABC ,垂足O 落在线段AD 上,已知BC =8,PO =4,AO =3,OD =2.(1)证明:AP ⊥BC ;(2)在线段AP 上是否存在点M ,使得平面AMC ⊥平面BMC ?若存在,求出AM 的长;若不存在,请说明理由.[解] (1)证明:如图,以O 为原点,以射线OD 为y 轴的正半轴,射线OP 为z 轴的正半轴,建立空间直角坐标系Oxyz .则O (0,0,0),A (0,-3,0),B (4,2,0),C (-4,2,0),P (0,0,4), AP →=(0,3,4),BC →=(-8,0,0),由此可得AP →·BC →=0,所以AP →⊥BC →,即AP ⊥BC .(2)假设存在满足题意的M ,设PM →=λPA →,λ≠1,则PM →=λ(0,-3,-4).BM →=BP →+PM →=BP →+λPA →=(-4,-2,4)+λ(0,-3,-4)=(-4,-2-3λ,4-4λ),AC →=(-4,5,0).设平面BMC 的法向量n 1=(x 1,y 1,z 1), 平面APC 的法向量n 2=(x 2,y 2,z 2). 由⎩⎪⎨⎪⎧BM →·n 1=0,BC →·n 1=0,得⎩⎪⎨⎪⎧-4x 1-(2+3λ)y 1+(4-4λ)z 1=0,-8x 1=0,即⎩⎪⎨⎪⎧x 1=0,z 1=2+3λ4-4λy 1,可取n 1=⎝ ⎛⎭⎪⎫0,1,2+3λ4-4λ.由⎩⎪⎨⎪⎧AP →·n 2=0,AC →·n 2=0,即⎩⎪⎨⎪⎧3y 2+4z 2=0,-4x 2+5y 2=0,得⎩⎪⎨⎪⎧x 2=54y 2,z 2=-34y 2,可取n 2=(5,4,-3),由n 1·n 2=0,得4-3×2+3λ4-4λ=0,解得λ=25,故PM →=⎝ ⎛⎭⎪⎫0,-65,-85,AM →=AP →+PM →=⎝ ⎛⎭⎪⎫0,95,125,所以AM =3.综上所述,存在点M 符合题意,AM =3. 拓展提升利用向量解决探索性问题的方法对于探索性问题,一般先假设存在,利用空间坐标系,结合已知条件,转化为代数方程是否有解的问题,若有解满足题意则存在,若没有满足题意的解则不存在.【跟踪训练3】 如图,直三棱柱ABC -A 1B 1C 1中,AC =3,BC =4,AB =5,AA 1=4.(1)求证:BC 1⊥平面AB 1C ;(2)在AB 上是否存在点D ,使得AC 1∥平面CDB 1.解 (1)证明:由已知AC =3,BC =4,AB =5,因而△ABC 是∠ACB 为直角的直角三角形,由三棱柱是直三棱柱,则CC 1⊥平面ABC ,以CA ,CB ,CC 1分别为x ,y ,z 轴建立空间直角坐标系,从而CA →=(3,0,0),BC 1→=(0,-4,4),则BC 1→·CA →=(0,-4,4)·(3,0,0)=0,则BC 1→⊥AC →,所以BC 1⊥AC .又四边形BCC 1B 1为正方形,因而BC 1⊥B 1C .又∵B 1C ∩AC =C ,∴BC 1⊥平面AB 1C .(2)假设存在点D (x ,y,0),使得AC 1∥平面CDB 1,CD →=(x ,y,0),CB 1→=(0,4,4), 设平面CDB 1的法向量m =(a ,b ,c ),则⎩⎪⎨⎪⎧m ·CD →=0,m ·CB 1→=0,即⎩⎪⎨⎪⎧xa +yb =0,4b +4c =0.令b =-x ,则c =x ,a =y ,所以m =(y ,-x ,x ),而AC 1→=(-3,0,4),则AC 1→·m =0,得-3y +4x =0.① 由D 在AB 上,A (3,0,0),B (0,4,0)得x -3-3=y4,即得4x +3y =12,② 联立①②可得x =32,y =2,∴D ⎝ ⎛⎭⎪⎫32,2,0,即D 为AB 的中点. 综上,在AB 上存在点D ,使得AC 1∥平面CDB 1,点D 为AB 的中点.1.利用向量证明线线平行的两种思路一是建立空间直角坐标系,通过坐标运算,利用向量平行的坐标表示证明;二是用基底思路,通过向量的线性运算,利用共线向量定理证明.2.向量法证明线线垂直的方法用向量法证明空间中两条直线相互垂直,其主要思路是证明两条直线的方向向量相互垂直.具体方法为:(1)坐标法:根据图形的特征,建立适当的空间直角坐标系,准确地写出相关点的坐标,表示出两条直线的方向向量,证明其数量积为0.(2)基向量法:利用向量的加减运算,结合图形,将要证明的两条直线的方向向量用基向量表示出来.利用数量积运算说明两向量的数量积为0.3.向量法证明线面垂直的方法(1)向量基底法,具体步骤如下:①设出基向量,用基向量表示直线的方向向量;②找出平面内两条相交直线的方向向量并分别用基向量表示;③分别计算直线的方向向量与平面内两条相交直线的方向向量的数量积.(2)坐标法,具体方法如下:方法一:①建立空间直角坐标系;②将直线的方向向量用坐标表示;③将平面内任意两条相交直线的方向向量用坐标表示;④分别计算直线的方向向量与平面内两条相交直线的方向向量的数量积.方法二:①建立空间直角坐标系;②将直线的方向向量用坐标表示;③求平面的法向量;④说明平面的法向量与直线的方向向量平行.4.证明面面垂直的两种思路一是证明其中一个平面过另一个平面的垂线,即转化为线面垂直;二是证明两平面的法向量垂直.1.已知线段AB的两端点坐标为A(9,-3,4),B(9,2,1),则线段AB与坐标平面( ) A.xOy平行B.xOz平行C.yOz平行D.yOz相交答案 C解析 因为AB →=(9,2,1)-(9,-3,4)=(0,5,-3),所以AB ∥平面yOz .2.若两个不同平面α,β的法向量分别为u =(1,2,-1),v =(-3,-6,3),则( ) A .α∥β B .α⊥βC .α,β相交但不垂直D .以上均不正确 答案 A解析 ∵v =-3u ,∴α∥β.3.已知直线l 与平面α垂直,直线l 的一个方向向量为u =(1,-3,z ),向量v =(3,-2,1)与平面α平行,则z 等于( )A .3B .6C .-9D .9 答案 C解析 ∵l ⊥α,v 与平面α平行,∴u ⊥v ,即u ·v =0,∴1×3+3×2+z ×1=0,∴z =-9.4.在三棱锥P -ABC 中,CP ,CA ,CB 两两垂直,AC =CB =1,PC =2,在如图所示的空间直角坐标系中,下列向量中是平面PAB 的法向量的是( )A.⎝⎛⎭⎪⎫1,1,12 B .(1,2,1) C .(1,1,1) D .(2,-2,1) 答案 A解析 PA →=(1,0,-2),AB →=(-1,1,0),设平面PAB 的一个法向量为n =(x ,y,1),则x -2=0,即x =2;-x +y =0,即y =x =2.所以n =(2,2,1).因为⎝⎛⎭⎪⎫1,1,12=12n ,所以A正确.5.在棱长为1的正方体ABCD -A 1B 1C 1D 1中,M 为棱BB 1的中点,在棱DD 1上是否存在点P ,使MD ⊥平面PAC?解 如图,建立空间直角坐标系,则A (1,0,0),C (0,1,0),D (0,0,0),M ⎝⎛⎭⎪⎫1,1,12.假设存在P (0,0,x )满足条件,则PA →=(1,0,-x ),AC →=(-1,1,0).设平面PAC 的法向量为n =(x 1,y 1,z 1),则由⎩⎪⎨⎪⎧ PA →·n =0,AC →·n =0,得⎩⎪⎨⎪⎧ x 1-xz 1=0,-x 1+y 1=0.令x 1=1得y 1=1,z 1=1x ,即n =⎝ ⎛⎭⎪⎫1,1,1x , 由题意MD →∥n ,由MD →=⎝⎛⎭⎪⎫-1,-1,-12,得x =2, ∵正方体棱长为1,且2>1,∴棱DD 1上不存在点P ,使MD ⊥平面PAC .。
第八章第六节立体几何中的向量方法课件共18张PPT

A.-
10 10
B.-210
C.210
D.
10 10
D [建立如图所示的空间直角坐标系 D-xyz,
设 DA=1,A(1,0,0),C(0,1,0),E(0,12 ,1),
则A→C =(-1,1,0),D→E =(0,12 ,1),
设异面直线 DE 与 AC 所成的角为 θ,
则 cos θ=|cos〈A→C
(2)点到平面的距离 如图所示,已知 AB 为平面 α 的一条斜线段,n 为平面 α 的法向量,则 B 到平面 α 的距离为|B→O |=|A→B|n·| n| .
直线的方向向量与平面的法向量的确定 (1)直线的方向向量:l 是空间一直线,A,B 是直线 l 上任意两点,则称A→B 为直线 l 的方向向量,与A→B 平行的任意非零向量也是直线 l 的方向向量.
,D→E
〉|=
10 10
.]
4.(选修 2-1P113 习题 T9 改编)如图所示,在空间直角坐标系中,有一 棱长为 a 的正方体 ABCD-A′B′C′D′,A′C 的中点 E 与 AB 的中点 F 的 距离为________.
解析: 由图易知 A(a,0,0),B(a,a,0),C(0,a,0),A′(a,0, a),所以 F(a,a2 ,0),E(a2 ,a2 ,所成的角是这两个平面所成的角.( )
(4) 两 异 面 直 线 夹 角 的 范 围 是 0,π2 , 直 线 与 平 面 所 成 角 的 范 围 是
0,π2 ,二面角的范围是[0,π].(
)
答案: (1)× (2)× (3)× (4)√
2.已知两平面的法向量分别为 m=(0,1,0),n=(0,1,1),则两平面
所以 EF= (a-a2)2+(a2-a2)2+(0-a2)2
立体几何中的向量方法-人教版高中数学

知识图谱-利用向量方法求线线角与线面角-利用向量方法求二面角-利用向量方法求距离直线与直线的夹角直线与平面的夹角向量法求二面角含有参数的二面角求法点到点线面的距离线与线面的距离第03讲_立体几何中的向量方法错题回顾利用向量方法求线线角与线面角知识精讲一.用向量方法求线线角与线面角1.两条异面直线所成的角(1)定义:设是两条异面直线,过空间任一点作直线,则与所夹的锐角或直角叫做所成的角;(2)范围:两异面直线所成的角的取值范围是;(3)向量求法:设直线的方向向量为,其夹角为,则有.2.直线与平面所成的角(1)定义:直线与平面所成的角,是指直线与它在这个平面内的射影所成的角;(2)斜线和它在平面内的射影所成的角,是斜线和这个平面内所有直线所称角中最小的角;(3)范围:直线和平面所成角的取值范围是;(4)向量求法:设直线的方向向量为,平面的法向量为,直线与平面所成的角为,与的夹角为,则有或,此外还可以根据定义得到直线与平面所成的角如下图:.三点剖析一.方法点拨1.在用向量法求两条直线的夹角时,如果两条直线方向向量的夹角余弦值是负数时,则取绝对值,要正数,因为两条直线的夹角范围是.2.在用向量法求直线与平面的夹角时,如果算出的是负值时,则线面角的正弦值也需要取正值.题模精讲题模一直线与直线的夹角例1.1、已知是异面直线,,且,则所成的角是( )B、A、C、D、例1.2、如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,A B=,BC=1,PA=2,E为PD的中点.(Ⅰ)求直线AC与PB所成角的余弦值;(Ⅱ)在侧面PAB内找一点N,使NE⊥面PAC,并求出N点到AB和AP的距离.例1.3、如图所示,正四面体的高的中点为的中点为.(1)求证:两两垂直;(2)求.题模二直线与平面的夹角例2.1、若斜线段的长度是它在平面内的射影长的倍,则与所成角的正切值为__________.例2.2、直三棱柱中,底面是等腰直角三角形,,侧棱,分别是的中点,点在平面上的射影是.求与平面所成角的大小(结果用正弦值表示).例2.3、已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=AC=AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.(Ⅰ)证明:CM⊥SN;(Ⅱ)求SN与平面CMN所成角的大小.例2.4、如图,在三棱锥中,底面,,为的中点,为的中点,,.(1)求证:平面;(2)求与平面成角的正弦值;(3)设点在线段上,且,平面,求实数的值.随堂练习随练1.1、若异面直线的方向向量分别是,则异面直线与的夹角的余弦值等于( )A、B、C、D、随练1.2、在棱长为1的正方体中,分别是的中点,在棱上,且,的中点,应用空间向量方法求解下列问题。
选修2-1课件3.2.2_立体几何中的向量方法(全面)

D1 C1
B1
依据向量的加法法则, AC1 AB AD AA1
进行向量运算
A1 D A 图1
B
C
AC1 ( AB AD AA1 ) 2
2 2 2
2
AB AD AA1 2( AB AD AB AA1 AD AA1 )
1 1 1 2(cos60 cos60 cos60) 6 所以 | AC1 | 6
空间“距离”问题(1)
一、复习引入
用空间向量解决立体几何问题的“三步曲”。 (1)建立立体图形与空间向量的联系,用空间向
量表示问题中涉及的点、直线、平面,把立体几
何问题转化为向量问题;(化为向量问题)
(2)通过向量运算,研究点、直线、平面之间的 位置关系以及它们之间距离和夹角等问题; (进行向量运算) (3)把向量的运算结果“翻译”成相应的几何意 义。 (回到图形)
P
n
A
O
这个结论说明,平面外一点到平面的距离为:连结此点与平面 上的任一点(常选择一个特殊点)的向量与该平面的法向量数量积的 绝对值与该法向量模长的商.
练习(用向量法求距离): 1.如图, ABCD 是矩形, PD 平面 ABCD , PD DC a , AD 2a , M 、N 分别是 AD 、PB 的中点,求点 A 到平面 MNC 的距离.
z
G
C
1 1 n ( , ,1) ,BE (2,0,0) A 3 3 | n BE| 2 11 d . 11 n
E
y
B
2 11 答:点 B 到平面 EFG 的距离为 . 11
空间“距离”问题(2)
空间向量之立体几何建系和求点坐标(共24张PPT)

建系方法4 练习1
已知斜三棱柱ABC A1B1C1, BCA 90, AC BC 2, A1在底面ABC上的射影 恰好为AC的中点D,又知BA1 AC1,建立合适的空间直角坐标系 并确定各点坐标。
A1
C1
B1
造“墙角”
A
D
C
B
敬请各位教师批评指正
投影点,坐标是否好写。如果可以则直接确定了横纵坐标,而竖 坐标为该点到底面的距离。
以上两个类型已经可以囊括大多数几何体中的点, 但总还有一些特殊点,那么就要用到第三个方法:
基础知识:
3、需要计算的点 ① 中点坐标公式: ② 利用向量关系进行计算(先设再求):向量坐标化后,向量的 关系也可转化为坐标的关系,进而可以求出一些位置不好的点的坐
建系方法2例题
二、利用线面垂直关系构建空间直角坐标系(转化为墙角模型) 例2 如图,在四棱锥P-ABCD中,底面ABCD为正方形,且边
长为2a,棱PD⊥底面ABCD,PD=2b,取各侧棱的中点E,F,G, H,写出点E,F,G,H的坐标.
找“墙角”
建系方法2练习1
练1.在三棱锥P ABC中,PA 平面ABC, BAC 90, D, E, F分别是棱AB, BC,CD的中点,AB AC 1, PA 2, 试建立适当的空间直角坐标系并确定各点坐标。
基础知识:
(二)坐标的书写:建系之后要能够
快速准确的写出点的坐标,按照特点
可以分为两3大类 1、能够直接写出坐标的点:
• F
(1)坐标轴上的点
(2)底面上的点:
x
点P的位置
原点O
x轴上A
z
•C
•E
1
O• • B
2019版数学(理)培优增分一轮全国经典版培优讲义:第7章 第7讲立体几何中的向量方法 含答案

第7讲立体几何中的向量方法板块一知识梳理·自主学习[必备知识]考点1直线的方向向量和平面的法向量1.直线的方向向量直线l上的向量e或与e共线的向量叫做直线l的方向向量,显然一条直线的方向向量有无数个.2.平面的法向量如果表示向量n的有向线段所在直线垂直于平面α,则称这个向量垂直于平面α,记作n⊥α,此时向量n叫做平面α的法向量.显然一个平面的法向量也有无数个,且它们是共线向量.3.设直线l,m的方向向量分别为a,b,平面α,β的法向量分别为u,v,则l∥m⇔a∥b⇔a=k b,k∈R;l⊥m⇔a⊥b⇔a·b=0;l∥α⇔a⊥u⇔a·u=0;l⊥α⇔a∥u⇔a=k u,k∈R;α∥β⇔u∥v⇔u=k v,k∈R;α⊥β⇔u⊥v⇔u·v=0.考点2空间向量与空间角的关系1.两条异面直线所成角的求法设两条异面直线a,b的方向向量分别为a,b,其夹角为θ,则cosφ=|cosθ|=|a·b||a||b|错误!其中φ为异面直线a,b所成的角,范围是.2.直线和平面所成角的求法如图所示,设直线l的方向向量为e,平面α的法向量为n,直线l与平面α所成的角为φ,两向量e与n的夹角为θ,则有sinφ=|cosθ|=错误!,φ的取值范围是错误!.3.求二面角的大小(1)如图①,AB,CD是二面角α-l-β的两个半平面内与棱l 垂直的直线,则二面角的大小θ=〈错误!,错误!〉.(2)如图②③,n1,n2分别是二面角α-l-β的两个半平面α,β的法向量,则二面角的大小θ满足cosθ=cos<n1,n2>或-cos<n1,n2>.取值范围是[0,π].考点3求空间的距离1.点到平面的距离如图,设AB为平面α的一条斜线段,n为平面α的法向量,则点B到平面α的距离d=错误!.2.线面距、面面距均可转化为点面距进行求解.[必会结论]1.直线的方向向量的确定:l是空间一直线,A,B是l上任意两点,则错误!及与错误!平行的非零向量均为直线l的方向向量.2.平面的法向量的确定:设a,b是平面α内两不共线向量,n为平面α的法向量,则求法向量的方程组为错误![考点自测]1.判断下列结论的正误.(正确的打“√”,错误的打“×”)(1)直线的方向向量是唯一确定的.()(2)两条不重合的直线l1和l2的方向向量分别为v1=(1,0,-1),v2=(-2,0,2),则l1与l2的位置关系是平行.()(3)已知错误!=(2,2,1),错误!=(4,5,3),则平面ABC的单位法向量是n0=±错误!。
68.立体几何讲义3:求方向向量、求法向量、建系、求点的坐标 课件-2021届高三数学一轮复习

A1
C1
B1
A
D
C
B
ቤተ መጻሕፍቲ ባይዱ
题目 5:如图,在等腰梯形 ABCD 中, AB∥CD , AD DC CB 1,ABC 60 , CF 平面 ABCD ,且CF 1,建立适当的直角坐标系并确定各点坐标。 F
题目 6:已知四边形 ABCD 满足 AD∥BC,BA AD DC 1 BC a ,E 是 BC 中点, D 2
等边三角形,侧面 ABB1A1 为菱形且BAA1 60o , E, F 分别为 BB1 和C1B1 的中点,
建立适当的直角坐标系并求向量C1B1 的坐标。
五、怎样设点的坐标
题目 10:已知斜三棱柱 ABC A1B1C1,BCA 90 , AC BC 2, A1 在底面 ABC 上的 射影恰为 AC 的中点 D ,又知BA1 AC1 ,建立如下图所示的坐标系并确定各点坐标。
立体几何讲义3:垂直问题
一、求直线的方向向量和平面的法向量
题目 1:已知点 A2,4,6, B3,0,2 ,求直线AB 的一个方向向量。
题目 2:已知点 A0,0,0, B1, 2,0,C 2,1,3 ,求平面 ABC 的一个法向量。
二、不同建系法的比较
题目 3:如图 1,在三棱柱 ABC A1B1C1 中, H 是正方形 AA1B1B 的中心,
将 BAE 翻折成 B1AE ,使得平面 B1AE 平面 AECD , F 为B1D 中点,建立适当的直 A
角坐标系并确定各点坐标。
B'
A
D
F
A
D
B
E
C
E
C
C B
三、求点的坐标
题目 7:已知四棱锥 P ABCD 的底面是菱形,对角线 AC, BD 交于点O,OA 4, OB 3, OP 4 ,且OP 平面 ABCD ,点 M 为 PC 的三等分点(靠近P ),建立适当的直角坐
【课件】高二数学复习课件:用空间向量解决立体几何问题中的建系策略 (共24张PPT) - 最新

与△ABD 都是边长为 2 的等
边三角形.
(1)证明:PB⊥CD.
(2)求二面角 A-PD-C 的
余弦值.
z
O xE
y
类型三:造“墙角”
例 3.如图,四棱锥 P-
ABCD 中,∠ABC=∠BAD
=90°,BC=2AD,△PAB
与△B⊥CD.
(2)求二面角 A-PD-C 的
BC1 存在点
D,使得
AD⊥A1B,并求
BD BC1
的值.
真题 5(辽宁卷)如图,AB 是圆的直径,PA 垂直圆所在的平面,C 是圆上的点.
(1)求证:平面 PAC⊥平面 PBC; (2)若 AB=2,AC=1,PA=1,求证:二面
角 C-PB-A 的余弦值.
真题 6(新课标 1)如图,三棱柱 ABC-A1B1C1 中,CA=CB,AB=A A1,∠BA A1=60°.
余弦值.
z
O xE
y
类型三:造“墙角”
●题型分析 造墙角:通过作辅助线并加以证明,“造”出“墙角”,从而可建系.
类型四:找“直角”
例 4.(大纲全国卷)如图,四棱锥 P-ABCD 中,底面 ABCD 为菱形,PA⊥底面 ABCD, AC=2 2,PA=2,E 是 PC 上的一点,PE=2EC.
(1)证明:PC⊥平面 BED; (2)设二面角 A-PB-C 为 90°,求 PD 与平面 PBC 所成角的大小.
余弦值;
(3)证明:在线段 BC1 存在点 D,
使得
AD⊥A1B,并求
BD BC1
的值.
类型二:找“墙角”
●题型分析
1.需要证明AB,AC,AA1两两垂直,坐标和向量容易得到.
2.第(1)小题不适合向量法.
3.2立体几何中的向量方法(二)

A A1 B1 H D B C D1 C1
AC = ( AB + BC )2 = 1 + 1 + 2cos 60° = 3 ∴
2
AC = 3
AA1 AC = AA1 ( AB + BC ) = AA1 AB + AA1 BC = cos 60° + cos 60° = 1.
顶点A为端点的三条棱长都相等, 顶点 为端点的三条棱长都相等,且它们彼此的夹角 为端点的三条棱长都相等 都是60° 都是 °,那么以这个顶点为端点的晶体的对角线的 长与棱长有什么关系? 长与棱长有什么关系? 如图1,不妨设 解:如图 不妨设 如图
AB = AA1 = AD = 1 , A1 ∠BAD = ∠BAA1 = ∠DAA1 = 60°
的一个法向量. ∴ n = (4, 3, 6) 是平面 ABC 的一个法向量.
方法小结
3
问题:如何求平面的法向量 问题 如何求平面的法向量? 如何求平面的法向量
⑴设平面的法向量为 n = ( x , y , z )
找出(求出) ⑵找出(求出)平面内的两个不共线的向量的 坐标 a = ( a1 , b1 , c1 ), b = ( a2 , b2 , c2 )
∴ cos ∠A1 AC = AA1 AC | AA1 | | AC | = 1 3
∴
6 sin ∠A1 AC = 3
∴
如何用向量法求点到平面的距离? 如何用向量法求点到平面的距离
6 6 ∴ 所求的距离是 . A1 H = AA1 sin ∠A1 AC = 3 3
12
如何用向量法求点到平面的距离? 如何用向量法求点到平面的距离
空间向量之立体几何建系和求点坐标(共24张PPT)

xOy面内D yOz面内E zOx面内F
坐标形式 (x,y,0)
(0,y,z)
(x,0,z)
基础知识:
2、空间中在底面投影为特殊位置的点:
如果 A' x1, y1, z 在底面的投影为 A x2, y2,0 ,那么x1 x2, y1 y2
(即点与投影点的横纵坐标相同) 由这条规律出发,在写空间中的点坐标时,可看一下在底面的
建系方法2练习2 练2.如图,已知四棱锥P ABCD的底面是菱形,对角线AC, BD交于点O, OA 4,OB 3,OP 4,且OP 平面ABCD,点M为PC的三等分点(靠近P), 建立适当的直角坐标系并求各点坐标。
找“墙角”
14
建系方法2练习3
练3.如图,在等腰梯形ABCD中,AB // CD, AD DC CB 1, ABC 60,CF 平面ABCD,且CF 1,建立适当的直角坐标系 并确定各点坐标。
找“墙角”
建系方法2练习5
真题(辽宁卷)如图,AB 是圆的直径,PA 垂 直圆所在的平面,C 是圆上的点.
(1)求证:平面 PAC⊥平面 PBC; (2)若 AB=2,AC=1,PA=1,求证:二面
角 C-PB-A 的余弦值.
造“墙角”
建系方法3例题
三、利用面面垂直关系构建空间直角坐标系(转化为墙角模型) 例3.在四棱锥V-ABCD中,底面ABCD是边长为2的正方形,侧面VAD 是正三角形,平面VAD⊥底面ABCD.点P、H分别是线段VC、AD的 中点.试建立空间直角坐标系并写出P、V、A、B、C、D的坐标.
互相垂直,EF // BD, ED BD, AD 2, EF ED 1, 试建立合适的 空间直角坐标系并确定各点的坐标
立体几何(向量法)—建系讲义

立体几何(向量法)—建系引入空间向量坐标运算,使解立体几何问题避免了传统方法进行繁琐的空间分析,只需建立空间直角坐标系进行向量运算,而如何建立恰当的坐标系,成为用向量解题的关键步骤之一.所谓“建立适当的坐标系”,一般应使尽量多的点在数轴上或便于计算。
一、利用共顶点的互相垂直的三条线构建直角坐标系例1(2012高考真题重庆理19)(本小题满分12分 如图,在直三棱柱111C B A ABC - 中,AB=4,AC=BC=3,D 为AB 的中点(Ⅰ)求点C 到平面11ABB A 的距离;(Ⅱ)若11AB A C ⊥求二面角 的平面角的余弦值.【答案】解:(1)由AC =BC ,D 为AB 的中点,得CD ⊥AB 。
又CD ⊥AA 1,故CD ⊥面A 1ABB 1,所以点C 到平面A 1ABB 1的距离为CD =错误!=错误!.(2)解法一:如图,取D 1为A 1B 1的中点,连结DD 1,则DD 1∥AA 1∥CC 1。
又由(1)知CD ⊥面A 1ABB 1,故CD ⊥A 1D ,CD ⊥DD 1,所以∠A 1DD 1为所求的二面角A 1-CD -C 1的平面角.因A 1D 为A 1C 在面A 1ABB 1上的射影,又已知AB 1⊥A 1C ,由三垂线定理的逆定理得AB 1⊥A 1D ,从而∠A 1AB 1、∠A 1DA 都与∠B 1AB 互余,因此∠A 1AB 1=∠A 1DA ,所以Rt △A 1AD ∽Rt △B 1A 1A .因此错误!=错误!,即AA 错误!=AD ·A 1B 1=8,得AA 1=2错误!.从而A1D=错误!=2错误!。
所以,在Rt△A1DD1中,cos∠A1DD1=错误!=错误!=错误!。
解法二:如图,过D作DD1∥AA1交A1B1于点D1,在直三棱柱中,易知DB,DC,DD1两两垂直.以D为原点,射线DB,DC,DD1分别为x轴、y轴、z轴的正半轴建立空间直角坐标系D-xyz.设直三棱柱的高为h,则A(-2,0,0),A1(-2,0,h),B1(2,0,h),C(0,错误!,0),C1(0,错误!,h),从而错误!=(4,0,h),错误!=(2,错误!,-h).由错误!⊥错误!,有8-h2=0,h=2错误!。
立体几何中的向量方法(一)

x − 2 y − 4z = 0 , 2 x − 4 y − 3z = 0
⇒ x = 2 y , z = 0.
取y = 1
【反思感悟】 反思感悟】
用待定系数法求平面的法向量, 用待定系数法求平面的法向量,关键是在 平面内找两个不共线的向量,列出方程组, 平面内找两个不共线的向量,列出方程组, 取其中一组解(非零向量)即可. 取其中一组解(非零向量)即可.
【方法探讨】 方法探讨】
证明线面 平行问题,可以有 三个途径,一是 在平面ODC1 内找一向量与B1C共线;二是说明 B1C与平面ODC1的两个不共线的向量共面;三是 证明B1C与平面ODC1的法向量垂直.
例:求证:如果一个平面经过另一个平面的 求证: 一条垂线,那么这两个平面互相垂直。 一条垂线,那么这两个平面互相垂直。
线面平行 l ∥ α ⇔ a ⊥ u ⇔ a ⋅ u = 0 ;
面面平行 α ∥ β ⇔ u ∥ v ⇔ u = kv.
注意:这里的线线平行包括线线重合,线 注意:这里的线线平行包括线线重合, 面平行包括线在面内,面面平行包 面平行包括线在面内,面面平行包 括面面重合. 括面面重合.
三、用方向向量和法向量判定位置关系
对于平面 对于平面 α 上的任 存在有序 有序实数 一点 P ,存在有序实数 对 ( x , y ) ,使得
P
b
α O
a
OP = xa + yb
二、平面的法向量 (1)定义 (1)定义 如果表示向量 n的有向线段所在直线垂 直于平面 α ,则称这个向量垂直于平面 α ,记 记 作 n⊥ α ,如果 n ⊥α ,那么向量 n 叫做平面
立体几何中的向量方法( 立体几何中的向量方法(一)
前面, 前面,我们把
立体几何—建系讲义

立体几何(向量法)—建系引入空间向量坐标运算,使解立体几何问题避免了传统方法进行繁琐的空间分析,只需建立空间直角坐标系进行向量运算,而如何建立恰当的坐标系,成为用向量解题的关键步骤之一.所谓“建立适当的坐标系”,一般应使尽量多的点在数轴上或便于计算。
一、利用共顶点的互相垂直的三条线构建直角坐标系例1(2012高考真题重庆理19)(本小题满分12分 如图,在直三棱柱111C B A ABC - 中,AB=4,AC=BC=3,D 为AB 的中点(Ⅰ)求点C 到平面11ABB A 的距离;(Ⅱ)若11AB A C ⊥求二面角 的平面角的余弦值.【答案】解:(1)由AC =BC ,D 为AB 的中点,得CD ⊥AB .又CD ⊥AA 1,故CD ⊥面A 1ABB 1,所以点C 到平面A 1ABB 1的距离为CD =BC 2-BD 2= 5.(2)解法一:如图,取D 1为A 1B 1的中点,连结DD 1,则DD 1∥AA 1∥CC 1.又由(1)知CD ⊥面A 1ABB 1,故CD ⊥A 1D ,CD ⊥DD 1,所以∠A 1DD 1为所求的二面角A 1-CD -C 1的平面角.因A 1D 为A 1C 在面A 1ABB 1上的射影,又已知AB 1⊥A 1C ,由三垂线定理的逆定理得AB 1⊥A 1D ,从而∠A 1AB 1、∠A 1DA 都与∠B 1AB 互余,因此∠A 1AB 1=∠A 1DA ,所以Rt △A 1AD ∽Rt △B 1A 1A .因此AA 1AD =A 1B 1AA 1,即AA 21=AD ·A 1B 1=8,得AA 1=2 2.从而A 1D =AA 21+AD 2=2 3.所以,在Rt △A 1DD 1中, cos ∠A 1DD 1=DD 1A 1D =AA 1A 1D =63.解法二:如图,过D 作DD 1∥AA 1交A 1B 1于点D 1,在直三棱柱中,易知DB ,DC ,DD 1两两垂直.以D 为原点,射线DB ,DC ,DD 1分别为x 轴、y 轴、z 轴的正半轴建立空间直角坐标系D -xyz .设直三棱柱的高为h ,则A (-2,0,0),A 1(-2,0,h ),B 1(2,0,h ),C (0,5,0),C 1(0,5,h ),从而AB 1→=(4,0,h ),A 1C →=(2,5,-h ).由AB 1→⊥A 1C →,有8-h 2=0,h =2 2. 故DA 1→=(-2,0,22),CC 1→=(0,0,22),DC →= (0,5,0).设平面A 1CD 的法向量为m =(x 1,y 1,z 1),则m ⊥DC →,m ⊥DA 1→,即 ⎩⎨⎧5y 1=0,-2x 1+22z 1=0,取z 1=1,得m =(2,0,1),设平面C 1CD 的法向量为n =(x 2,y 2,z 2),则n ⊥DC →,n ⊥CC 1→,即⎩⎨⎧5y 2=0,22z 2=0, 取x 2=1,得n =(1,0,0),所以 cos 〈m ,n 〉=m·n |m ||n |=22+1·1=63. 所以二面角A 1-CD -C 1的平面角的余弦值为63.二、利用线面垂直关系构建直角坐标系例 2.如图所示,AF 、DE 分别是圆O 、圆1O 的直径,AD 与两圆所在的平面均垂直,8AD =.BC 是圆O 的直径,6AB AC ==,//OE AD .(I)求二面角B AD F --的大小; (II)求直线BD 与EF 所成的角的余弦值. 19.解:(Ⅰ)∵AD 与两圆所在的平面均垂直,∴AD⊥AB, AD⊥AF,故∠BAD 是二面角B —AD —F 的平面角, 依题意可知,ABCD 是正方形,所以∠BAD=450. 即二面角B —AD —F 的大小为450;(Ⅱ)以O 为原点,BC 、AF 、OE 所在直线为坐标轴,建立空间直角坐标系(如图所示),则O (0,0,0),A (0,23-,0),B (23,0,0),D (0,23-,8),E (0,0,8),F (0,23,0)所以,)8,23,0(),8,23,23(-=--=FE BD10828210064180||||,cos =⨯++=•>=<FE BD FE BD EF BD 设异面直线BD 与EF 所成角为α,则1082|,cos |cos =><=EF BD α直线BD 与EF 所成的角为余弦值为8210.三、利用图形中的对称关系建立坐标系例3(2013年重庆数学(理))如图,四棱锥P ABCD -中,PA ABCD ⊥底面,2,4,3BC CD AC ACB ACD π===∠=∠=,F 为PC 的中点,AF PB ⊥.(1)求PA 的长; (2)求二面角B AF D --的正弦值.【答案】解:(1)如图,联结BD 交AC 于O ,因为BC =CD ,即△BCD 为等腰三角形,又AC 平分∠BCD ,故AC ⊥BD .以O 为坐标原点,OB →,OC →,AP →的方向分别为x 轴,y 轴,z 轴的正方向,建立空间直角坐标系O -xyz ,则OC =CD cos π3=1,而AC =4,得AO =AC -OC =3.又OD =CD sinπ3=3,故A (0,-3,0),B (3,0,0),C (0,1,0),D (-3,0,0).因P A ⊥底面ABCD ,可设P (0,-3,z ),由F 为PC 边中点,得F ⎝⎛⎭⎫0,-1,z 2,又AF →=⎝⎛⎭⎫0,2,z 2,PB →=(3,3,-z ),因AF ⊥PB ,故AF →·PB →=0,即6-z 22=0,z =23(舍去-23),所以|P A →|=2 3.(2)由(1)知AD →=(-3,3,0),AB →=(3,3,0),AF →=(0,2,3).设平面F AD 的法向量为1=(x 1,y 1,z 1),平面F AB 的法向量为2=(x 2,y 2,z 2).由1·AD →=0,1·AF →=0,得⎩⎨⎧-3x 1+3y 1=0,2y 1+3z 1=0,因此可取1=(3,3,-2). 由2·AB →=0,2·AF →=0,得⎩⎨⎧3x 2+3y 2=0,2y 2+3z 2=0,故可取2=(3,-3,2). 从而向量1,2的夹角的余弦值为 cos 〈1,2〉=n 1·n 2|n 1|·|n 2|=18.故二面角B -AF -D 的正弦值为378.四、利用正棱锥的中心与高所在直线,投影构建直角坐标系 例4-1(2013大纲版数学(理))如图,四棱锥P ABCD -中,902,ABC BAD BC AD PAB ∠=∠==∆,与PAD ∆都是等边三角形.(I)证明:;PB CD ⊥ (II)求二面角A PD C --的余弦值.【答案】解:(1)取BC 的中点E ,联结DE ,则四边形ABED 为正方形. 过P 作PO ⊥平面ABCD ,垂足为O . 联结OA ,OB ,OD ,OE .由△P AB 和△P AD 都是等边三角形知P A =PB =PD ,所以OA =OB =OD ,即点O 为正方形ABED 对角线的交点, 故OE ⊥BD ,从而PB ⊥OE .因为O 是BD 的中点,E 是BC 的中点,所以OE ∥CD .因此PB ⊥CD .(2)解法一:由(1)知CD ⊥PB ,CD ⊥PO ,PB ∩PO =P , 故CD ⊥平面PBD .又PD ⊂平面PBD ,所以CD ⊥PD .取PD 的中点F ,PC 的中点G ,连FG . 则FG ∥CD ,FG ⊥PD .联结AF ,由△APD 为等边三角形可得AF ⊥PD . 所以∠AFG 为二面角A -PD -C 的平面角. 联结AG ,EG ,则EG ∥PB . 又PB ⊥AE ,所以EG ⊥AE .设AB =2,则AE =22,EG =12PB =1,故AG =AE 2+EG 2=3,在△AFG 中,FG =12CD =2,AF =3,AG =3.所以cos ∠AFG =FG 2+AF 2-AG 22·FG ·AF =-63.解法二:由(1)知,OE ,OB ,OP 两两垂直.以O 为坐标原点,OE →的方向为x 轴的正方向建立如图所示的空间直角坐标系O -xyz .设|AB →|=2,则A (-2,0,0),D (0,-2,0), C (22,-2,0),P (0,0,2),PC →=(22,-2,-2),PD →=(0,-2,-2), AP →=(2,0,2),AD →=(2,-2,0). 设平面PCD 的法向量为1=(x ,y ,z ),则 1·PC →=(x ,y ,z )·(22,-2,-2)=0,1·PD →=(x ,y ,z )·(0,-2,-2)=0,可得2x -y -z =0,y +z =0.取y =-1,得x =0,z =1,故1=(0,-1,1). 设平面P AD 的法向量为2=(m ,p ,q ),则 2·AP →=(m ,p ,q )·(2,0,2)=0, 2·AD →=(m ,p ,q )·(2,-2,0)=0,可得m +q =0,m -p =0.取m =1,得p =1,q =-1,故2=(1,1,-1). 于是cos 〈,2〉=n 1·n 2|n 1||n 2|=-63. 例4-2如图1-5,在三棱柱ABC -A 1B 1C 1中,已知AB =AC =AA 1=5,BC =4,点A 1在底面ABC 的投影是线段BC 的中点O .(1)证明在侧棱AA 1上存在一点E ,使得OE ⊥平面BB 1C 1C ,并求出AE 的长; (2)求平面A 1B 1C 与平面BB 1C 1C 夹角的余弦值.图1-5【答案】解:(1)证明:连接AO ,在△AOA 1中,作OE ⊥AA 1 于点E ,因为AA 1∥BB 1,所以OE ⊥BB 1.因为A 1O ⊥平面ABC ,所以A 1O ⊥BC . 因为AB =AC ,OB =OC ,所以AO ⊥BC , 所以BC ⊥平面AA 1O . 所以BC ⊥OE ,所以OE ⊥平面BB 1C 1C ,又AO =AB 2-BO 2=1,AA 1=5, 得AE =AO 2AA 1=55.(2)如图,分别以OA ,OB ,OA 1所在直线为x ,y ,z 轴,建立空间直角坐标系,则A (1,0,0),B (0,2,0),C (0,-2,0),A 1(0,0,2),由AE →=15AA 1→得点E 的坐标是⎝ ⎛⎭⎪⎫45,0,25, 由(1)得平面BB 1C 1C 的法向量是OE→=⎝ ⎛⎭⎪⎫45,0,25,设平面A 1B 1C 的法向量=(x ,y ,z ),由⎩⎪⎨⎪⎧·AB →=0,n ·A 1C →=0得⎩⎨⎧-x +2y =0,y +z =0,令y =1,得x =2,z =-1,即=(2,1,-1),所以 cos 〈OE →,〉=OE →·n |OE →|·|n |=3010.即平面BB 1C 1C 与平面A 1B 1C 的夹角的余弦值是3010三、利用面面垂直关系构建直角坐标系 例5(2012高考真题安徽理18)(本小题满分12分)平面图形ABB 1A 1C 1C 如图1-4(1)所示,其中BB 1C 1C 是矩形,BC =2,BB 1=4,AB=AC=2,A1B1=A1C1= 5.图1-4现将该平面图形分别沿BC和B1C1折叠,使△ABC与△A1B1C1所在平面都与平面BB1C1C垂直,再分别连接A1A,A1B,A1C,得到如图1-4(2)所示的空间图形.对此空间图形解答下列问题.(1)证明:AA1⊥BC;(2)求AA1的长;(3)求二面角A-BC-A1的余弦值.【答案】解:(向量法):(1)证明:取BCB1C1的中点分别为D和D1,连接A1D1,DD1,AD.由BB1C1C为矩形知,DD1⊥B1C1,因为平面BB1C1C⊥平面A1B1C1,所以DD1⊥平面A1B1C1,又由A1B1=A1C1知,A1D1⊥B1C1.故以D1为坐标原点,可建立如图所示的空间直角坐标系D1-xyz.由题设,可得A1D1=2,AD=1.由以上可知AD⊥平面BB1C1C,A1D1⊥平面BB1C1C,于是AD∥A1D1.所以A (0,-1,4),B (1,0,4),A 1(0,2,0),C (-1,0,4),D (0,0,4). 故AA 1→=(0,3,-4),BC →=(-2,0,0),AA 1→·BC →=0, 因此AA 1→⊥BC →,即AA 1⊥BC . (2)因为AA 1→=(0,3,-4), 所以||AA 1→=5,即AA 1=5. (3)连接A 1D ,由BC ⊥AD ,BC ⊥AA 1,可知BC ⊥平面A 1AD ,BC ⊥A 1D ,所以∠ADA 1为二面角A -BC -A 1的平面角.因为DA →=(0,-1,0),DA 1→=(0,2,-4),所以 cos 〈DA →,DA 1→〉=-21×22+(-4)2=-55. 即二面角A -BC -A 1的余弦值为-55.(综合法)(1)证明:取BC ,B 1C 1的中点分别为D 和D 1,连接A 1D 1,DD 1,AD ,A 1D .由条件可知,BC ⊥AD ,B 1C 1⊥A 1D 1, 由上可得AD ⊥面BB 1C 1C ,A 1D 1⊥面BB 1C 1C . 因此AD ∥A 1D 1,即AD ,A 1D 1确定平面AD 1A 1D . 又因为DD 1∥BB 1,BB 1⊥BC ,所以DD 1⊥BC . 又考虑到AD ⊥BC ,所以BC ⊥平面AD 1A 1D , 故BC ⊥AA 1.(2)延长A 1D 1到G 点,使GD 1=AD ,连接AG . 因为AD 綊GD 1,所以AG 綊DD 1綊BB 1. 由于BB 1⊥平面A 1B 1C 1,所以AG ⊥A 1G .由条件可知,A 1G =A 1D 1+D 1G =3,AG =4, 所以AA 1=5.(3)因为BC ⊥平面AD 1A 1D ,所以∠ADA 1为二面角A -BC -A 1的平面角. 在Rt △A 1DD 1中,DD 1=4,A 1D 1=2,解得 sin ∠D 1DA 1=55,cos ∠ADA 1=cos ⎝ ⎛⎭⎪⎫π2+∠D 1DA 1=-55.即二面角A -BC -A 1的余弦值为-55.。
高考试题中空间向量与立体几何建系问题专题探究ppt课件

A
A(0,0,2 3),B(0,0,0),C( 3,1,0),D(0,2,0)
33
M
F(2 3,0,0),M( , , 3),F(2 3,0,0) 22
B o
设 n ( x , y , z ) 是平面 MCB 一个法向量则
BA ( 0 , 0 , 2 3 ), BC ( 3 ,1 , 0 ).
一、空间直角坐标系的建立及空间 中点的坐标确定方法
•1、空间直角坐标系的建立方法:
在空间中取原点0,从原点0引三条两两垂直
的直线做为坐标轴,最后选定某个长度作为
单位长度。如右图
z
o
x
y
2、空间中点的坐标的确定方法
对于空间任意M一 ,点 求它的坐标: M分过别点做 个平面分别x垂 , y,直 z轴,平面与三个交 坐点 标轴 分别为 P,Q,R,在其相应轴上坐x标 ,y,依 z, 为 则(x, y, z)叫P的空间坐标,P(记 x, y作 , z), 三个数值P的 叫横坐标,纵坐坐 标标 ,。 竖
C1 B1
E1
D
E
A
R
F
C B
解(1): AB 4, BCCD 2, F为棱AB中点
BF BCCF, BCF为正三角形, ABCD
z
为等腰梯形,BACABC60。,取AF中
D1
点M,连DM,则DM AB,DMCD,以DM为x A1
例1、(2010 江西数理 17)如图, BCD 与A
MCD 都是边长为 2的正三角形,平
面MCD 平面 BCD , AB 平面 BCD ,
已知 AB 2 3.
M
(1)求点 A到平M 面B的 C 距离;
B
D
立体几何中的建系设点讲解学习
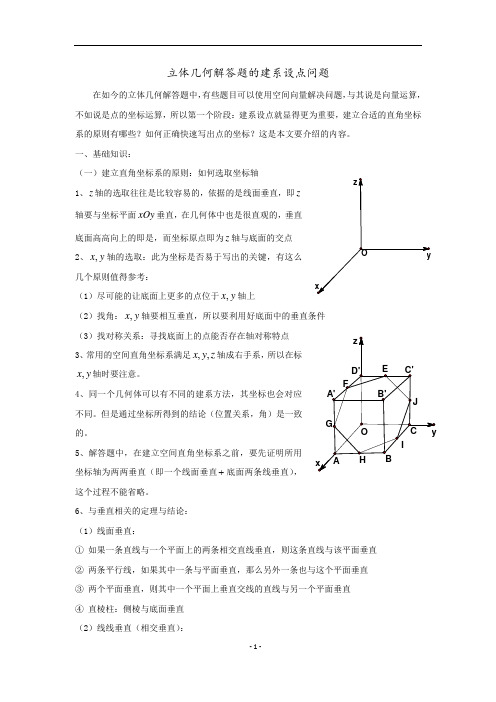
(2)对于一条线段上的某点分线段成比例,可以利用向量关系将该点坐标计算出来
由这条规律出发,在写空间中的点时,可看下在底面的投影ቤተ መጻሕፍቲ ባይዱ,坐标是否好写。如果可以则直接确定了横纵坐标,而竖坐标为该点到底面的距离。例如:正方体中的 点,其投影为 ,而 所以 ,而其到底面的距离为 ,故坐标为
以上两个类型已经可以囊括大多数几何体中的点,但总还有一些特殊点,那么就要用到第三个方法:
3、需要计算的点
(3)找对称关系:寻找底面上的点能否存在轴对称特点
3、常用的空间直角坐标系满足 轴成右手系,所以在标 轴时要注意。
4、同一个几何体可以有不同的建系方法,其坐标也会对应不同。但是通过坐标所得到的结论(位置关系,角)是一致的。
5、解答题中,在建立空间直角坐标系之前,要先证明所用坐标轴为两两垂直(即一个线面垂直 底面两条线垂直),这个过程不能省略。
二、典型例题:
例1:在三棱锥 中, 平面 , , 分别是棱 的中点, ,试建立适当的空间直角坐标系并确定各点坐标
例2:在长方体 中, 分别是棱 上的点, , ,建立适当的直角坐标系并写出点的坐标。
例3:如图,在等腰梯形 中, , , 平面 ,且 ,建立适当的直角坐标系并确定各点坐标。
小炼:建立坐标系的最重要的条件就是线面垂直(即 轴),对于 轴的选取,如果没有已知线段,可以以垂足所在的某一条直线为坐标轴,然后作这条轴的垂线来确定另一条轴。
例4:已知四边形 满足 , 是 中点,将 翻折成 ,使得平面 平面 , 为 中点
思路:在处理翻折问题时,首先要确定在翻折的过程中哪些量与位置关系不变,这些都是作为已知条件使用的。
例5:如图,已知四棱锥 的底面是菱形,对角线 交于点 ,且 平面 ,点 为 的三等分点(靠近 ),建立适当的直角坐标系并求各点坐标
高中数学讲义立体几何中的建系设点问题
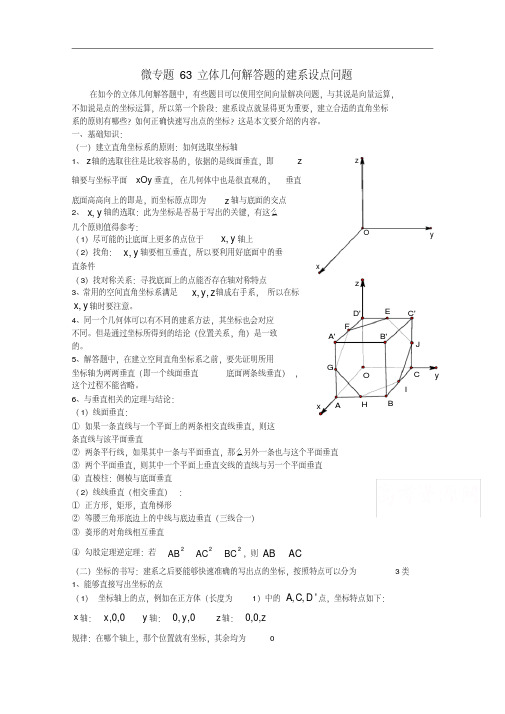
OyxzF E GHIJ O yxzA'C'BB'C D'A微专题63 立体几何解答题的建系设点问题在如今的立体几何解答题中,有些题目可以使用空间向量解决问题,与其说是向量运算,不如说是点的坐标运算,所以第一个阶段:建系设点就显得更为重要,建立合适的直角坐标系的原则有哪些?如何正确快速写出点的坐标?这是本文要介绍的内容。
一、基础知识:(一)建立直角坐标系的原则:如何选取坐标轴1、z 轴的选取往往是比较容易的,依据的是线面垂直,即z轴要与坐标平面xOy 垂直,在几何体中也是很直观的,垂直底面高高向上的即是,而坐标原点即为z 轴与底面的交点2、,x y 轴的选取:此为坐标是否易于写出的关键,有这么几个原则值得参考:(1)尽可能的让底面上更多的点位于,x y 轴上(2)找角:,x y 轴要相互垂直,所以要利用好底面中的垂直条件(3)找对称关系:寻找底面上的点能否存在轴对称特点3、常用的空间直角坐标系满足,,x y z 轴成右手系,所以在标,x y 轴时要注意。
4、同一个几何体可以有不同的建系方法,其坐标也会对应不同。
但是通过坐标所得到的结论(位置关系,角)是一致的。
5、解答题中,在建立空间直角坐标系之前,要先证明所用坐标轴为两两垂直(即一个线面垂直底面两条线垂直),这个过程不能省略。
6、与垂直相关的定理与结论:(1)线面垂直:①如果一条直线与一个平面上的两条相交直线垂直,则这条直线与该平面垂直②两条平行线,如果其中一条与平面垂直,那么另外一条也与这个平面垂直③两个平面垂直,则其中一个平面上垂直交线的直线与另一个平面垂直④直棱柱:侧棱与底面垂直(2)线线垂直(相交垂直):①正方形,矩形,直角梯形②等腰三角形底边上的中线与底边垂直(三线合一)③菱形的对角线相互垂直④勾股定理逆定理:若222ABACBC ,则ABAC(二)坐标的书写:建系之后要能够快速准确的写出点的坐标,按照特点可以分为3类1、能够直接写出坐标的点(1)坐标轴上的点,例如在正方体(长度为1)中的,,'A C D 点,坐标特点如下:x 轴:,0,0x y 轴:0,,0y z 轴:0,0,z规律:在哪个轴上,那个位置就有坐标,其余均为(2)底面上的点:坐标均为,,0x y ,即竖坐标0z ,由于底面在作立体图时往往失真,所以要快速正确写出坐标,强烈建议在旁边作出底面的平面图进行参考:以上图为例:则可快速写出,H I 点的坐标,位置关系清晰明了111,,0,,1,022H I2、空间中在底面投影为特殊位置的点:如果'11,,A x y z 在底面的投影为22,,0A x y ,那么1212,x x y y (即点与投影点的横纵坐标相同)由这条规律出发,在写空间中的点时,可看下在底面的投影点,坐标是否好写。
最新-2021届高考数学理科1轮复习课件:第八章 立体几何 第7讲 立体几何中的向量方法 精品

A.π6
B.π4
π
π
C.3
D.2
【解析】 以 O 为坐标原点建系如图,
则
A(0,1,0),A1(0,1,1),B1
23,12,1,
C
23,-12,0.
所以A→A1=(0,0,1),B→1C=(0,-1,
-1),
所以 cos〈A→A1,B→1C〉=A|A→→AA11·||BB→→11CC| =0×1×0+002×+((--11))+2+1×((--1)1)2 =- 22, 所以〈A→A1,B→1C〉=34π, 所以异面直线 B1C 与 AA1 所成的角为π4.故选 B.
m·A→C=0, 设平面 ACC1A1 的一个法向量为 m=(x,y,z),则由m·C→C1=0
得x-+xy+=03,z=0,取 m=( 3,- 3,1).
所以 cos〈B→1D,m〉=B|B→→ 11DD·||mm|
=
0× 3+1×(- 02+12+(- 3)2×
3()+3)(2-+(3-)×31)2+12=
A→O=V→O-V→A=12V→D-V→A=16(b+c-5a), 所以|D→M|= 16(-2a-2b+c)2=12, |A→O|= 16(b+c-5a)2= 22, D→M·A→O=16(-2a-2b+c)·16(b+c-5a)=14. 设 DM 与 AO 所成的角是 θ,
所以 cos θ=||DD→→MM|··A|→A→OO||= 22,所以 θ=45°.
取 x=1,则 m=(1,-1,0).设直线 PD 与平面 PAC 所成
的角为 α,所以 sin
α=|cos〈P→D,m〉|=||PP→→DD·|·|mm||=
2 5×
2
=
510,因为 α∈0,π2 ,所以 cos
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立体几何(向量法)—建系引入空间向量坐标运算,使解立体几何问题避免了传统方法进行繁琐的空间分析,只需建立空间直角坐标系进行向量运算,而如何建立恰当的坐标系,成为用向量解题的关键步骤之一.所谓“建立适当的坐标系” ,一般应使尽量多的点在数轴上或便于计算。
一、利用共顶点的互相垂直的三条线构建直角坐标系例1(2012 高考真题重庆理19 )(本小题满分12 分如图,在直三棱柱ABC A1B1C1中,AB=4,AC=BC=,3 D 为AB的中点Ⅰ)求点C到平面A1ABB1的距离;(Ⅱ)若AB1 A1C 求二面角的平面角的余弦值.【答案】解:(1)由AC=BC,D为AB的中点,得CD⊥AB.又CD⊥AA1,故CD⊥面A1ABB1,所以点 C 到平面A1ABB1 的距离为CD=BC2-BD2= 5.(2)解法一:如图,取D1 为A1B1的中点,连结DD1,则DD1∥AA1∥CC1.又由(1)知CD⊥面A1ABB1,故CD⊥A1D,CD⊥DD1,所以∠ A1DD 1为所求的二面角A1-CD-C1 的平面角.因A1D 为A1C 在面A1ABB1 上的射影,又已知AB1⊥A1C,由三垂线定理的逆定理得AB1⊥A1D,从而∠ A1AB1、∠A1DA 都与∠ B1AB互余,因此∠ A1AB1=∠A1DA,所以Rt△A1AD∽Rt△B1A1A.因此A A A D1=A A1A B1,即AA21=AD·A1B1=8,得AA1=2 2.从而 A 1D = AA 12+ AD 2=2 3. 所以,在 Rt △A 1DD 1 中, DD 1=AA1 = 6.A 1D =A 1D =3 .解法二:如图,过 D 作 DD 1∥AA 1交A 1B 1于点 D 1,在直三棱柱中,易知DB , DC ,DD 1两两垂直.以 D 为原点,射线 DB ,DC ,DD 1分别为 x 轴、y轴、z 轴 的正半轴建立空间直角坐标系 D -xyz.设直三棱柱的高为 h ,则 A (-2,0,0),A 1(-2,0,h ),B 1(2,0,h ), C(0, 5,0),C 1(0, 5,h ),从而 A →B 1=(4,0,h ),A →1C =(2, 5,- h ). 由A →B 1⊥ A →1C ,有 8- h 2=0,h =2 2.故D →A 1= (-2,0,2 2),C →C 1=(0,0,2 2),D →C = (0, 5,0). 设平面 A 1CD 的法向量为 m =(x 1, y 1,z 1),则 m ⊥D →C ,m ⊥D →A 1,即5y 1=0,-2x 1+ 2 2z 1= 0,取 z 1= 1,得 m = ( 2,0,1),设平面 C 1CD 的法向量为 n = (x 2,y 2, z 2),则 n ⊥D →C ,n ⊥C →C 1,即5y 2=0, 2 2z 2= 0,取 x 2=1,得 n = (1,0,0),所以m ·n2 6cos 〈 m , n 〉= = = .|m ||n | 2+ 1·1 3所以二面角 A 1-CD -C 1 的平面角的余弦值为 6.、利用线面垂直关系构建直角坐标系cos ∠A 1DD1例 2. 如图所示, AF 、 DE 分别是圆 O 、圆 O 1 的直径,AD 8. BC 是圆 O 的直径, AB AC 6, OE // AD . (I ) 求二面角 B AD F 的大小;(II ) 求直线 BD 与EF 所成的角的余弦值 . 19. 解:( Ⅰ) ∵A D 与两圆所在的平面均垂直 ,∴AD ⊥AB, AD ⊥AF,故∠BAD 是二面角 B — AD —F 的平面角, 依题意可知, ABCD 是正方形,所以∠ BAD = 450. 即二面角 B —AD —F 的大小为 450;( Ⅱ) 以 O 为原点, BC 、AF 、OE 所在直线为坐标轴,建立空间直角坐标系(如图所示) ,则 O0,0,0),A (0, 3 2 ,0), B ( 3 2,0,0),D (0, 3 2,8),E (0,0,8),F 0,3 2 ,0)所以, BD ( 3 2, 3 2,8), FE (0, 3 2,8)82设异面直线 BD 与 EF 所成角为 ,则cos |cos BD,EF | 直线 BD 与 EF 所成的10三、利用图形中的对称关系建立坐标系例 3 (2013年重庆数学(理) )如图,四棱锥 P ABCD 中, PA 底面ABCD ,BC CD 2,AC 4, ACB ACD , F 为 PC 的中点, AF PB .3(1) 求 PA 的长 ; (2) 求二面角 B AF D 的正弦值 .AD 与两圆所在的平面均垂直,cos BD,EFBD FE |BD ||FE |0 18 64 100 8282 10角为余弦值为8210解:(1)如图,联结 BD 交AC 于 O ,因为 BC = CD ,即△ BCD 为等腰三角形,又 AC 平分∠ BCD , 故 AC ⊥BD.以 O 为坐标原点, O →B ,O →C ,A →P 的方向分别为 x 轴, y 轴, z 轴的正方向,建立空间直角坐标系 O - xyz ,则OC = CDcos 3π= 1,而 AC =4,得AO =AC -OC =3.又 OD =CD sin 3π= 3,故 A (0,-3,0),B ( 3,0, 0), C (0, 1, 0), D ( - 3,0,0).因 PA ⊥底面 ABCD ,可设 P (0,-3,z ),由 F 为 PC 边中点, 得F 0,- 1,2z ,又A →F = 0, 2, z 2 ,P →B =( 3,3,- z ),因 AF ⊥ PB ,故A →F ·P →B = 0,即 6-z 2=0,z =2 3(舍去- 23),所以 |P →A|= 2 3.(2)由(1)知 A →D =(- 3,3,0),A →B =( 3,3,0),A →F =(0,2, 3).设平面 FAD 的法 向量为 1= (x 1,y 1,z 1),平面 FAB 的法向量为 2=(x 2,y 2,z 2).→→由 1·AD = 0,1·AF =0,得 - 3x 1+ 3y 1= 0,因此可取2y 1+ 3z 1= 0,由 2·AB =0, 2·AF =0,得1=(3, 3,- 2).答案】3x2+3y2=0,故可取2=(3-3,2).2y2+3z2=0,从而向量1,2 的夹角的余弦值为cos〈1,2〉n1·n 2 1|n1| |·n2|=8故二面角 B -AF - D 的正弦值为 3 7.8四、利用正棱锥的中心与高所在直线,投影构建直角坐标系 例 4-1(2013 大纲版数学(理) )如图, 四棱锥 P ABCD 中, ABC BAD 90,BC 2AD, PAB 与 PAD 都是等边三角形(I) 证明:PB CD; (II) 求二面角 A PD C 的余弦值 .【答案】 解: (1)取 BC 的中点 E ,联结 DE ,则四边形 ABED 为正方形. 过 P 作 PO ⊥平面 ABCD ,垂足为 O. 联结 OA ,OB , OD ,OE.由△ PAB 和△ PAD 都是等边三角形知 PA = PB = PD , 所以 OA =OB =OD ,即点 O 为正方形 ABED 对角线的交点, 故OE ⊥BD ,从而 PB ⊥ OE.因为 O 是 BD 的中点, E 是 BC 的中点,所以 OE ∥CD.因此 PB ⊥CD.(2)解法一:由 (1)知 CD ⊥PB ,CD ⊥PO ,PB ∩PO =P , 故 CD ⊥平面 PBD.又 PD? 平面 PBD ,所以 CD ⊥PD. 取 PD 的中点 F ,PC 的中点 G ,连 FG. 则 FG ∥CD ,FG ⊥PD.联结AF ,由△ APD 为等边三角形可得 AF ⊥PD. 所以∠ AFG 为二面角 A -PD -C 的平面角. 联结 AG , EG ,则 EG ∥PB. 又 PB ⊥ AE ,所以 EG ⊥ AE.设 AB = 2,则 AE =2 2, EG =2PB =1, 故 AG = AE 2+EG 2= 3,1在△AFG 中, FG = 21CD = 2,AF = 3,AG =3.所以 cos ∠ AFG = 2 2 2FG 2+AF 2-AG 2=2·FG ·AF=解法由 (1)知, OE ,OB , OP 两两垂直.以O 为坐标原点, OE 的方向为 x 轴的正方向建立如图所示的空间直角坐标系O -xyz.6.3.设|A→B|=2,则A(-2,0,0),D(0,-2,0),C(2 2,-2,0),P(0,0,2),P→C=(2 2,-2,-2),P→D =(0,-2,-2),A→P=( 2,0,2),A→D=( 2,-2,0).设平面PCD 的法向量为1=(x,y,z),则1·P→C=(x,y,z)·(2 2,-2,-2)=0,1·P→D=(x,y,z)·(0,-2,-2)=0,可得2x-y-z=0,y+z=0.取y=-1,得x=0,z=1,故1=(0,-1,1).设平面PAD 的法向量为2=(m,p,q),则2·A→P=(m,p,q)·( 2,0,2)=0,2·A→D =(m,p,q)·( 2,-2,0)=0,可得m+q=0,m-p=0.取m=1,得p=1,q=-1,故2=(1,1,-1).于是cos〈,2〉=n1·n 2 6 |n1||n2|=- 3 .例4-2 如图1-5,在三棱柱ABC-A1B1C1 中,已知AB=AC=AA1=5,BC=4,点A1在底面ABC的投影是线段BC 的中点O.(1)证明在侧棱AA1 上存在一点E,使得OE⊥平面BB1C1C,并求出AE 的长;(2)求平面A1B1C 与平面BB1C1C 夹角的余弦值.图1- 5【答案】解:(1)证明:连接AO,在△ AOA1 中,作OE⊥AA1 于点E,因为AA1∥ BB1,所以OE⊥BB1.因为 A 1O ⊥平面 ABC ,所以 A 1O ⊥ BC. 因为 AB = AC , OB =OC ,所以AO ⊥BC ,所以 BC ⊥平面 AA 1O. 所以 BC ⊥OE ,所以 OE ⊥平面 BB 1C 1C ,又 AO = AB 2-BO 2=1,AA 1= 5,(2)如图,分别以 OA ,OB ,OA 1所在直线为 x ,y ,z 轴,建立空间直角坐标系,则 A(1,0,0),B(0,2,0),C(0,-2,0), A 1(0,0,2),由A →E =51A →A 1得点 E 的坐标是 54, 0, 25 ,由(1)得平面 BB 1C 1C 的法向量是 O →E = (x ,y ,z),·A →B =0, - x +2y =0, 由得n ·A →1C =0y +z =0,令 y =1,得 x =2,z =- 1,即= (2,1,-1),所以cos 〈O →E ,〉= O →→E ·n= 1300.|O →E| ·|n | 10即平面 BB 1C 1C 与平面 A 1B 1C 的夹角的余弦值是 1300三、利用面面垂直关系构建直角坐标系例 5(2012 高考真题安徽理 18)(本小题满分 12分)平面图形 ABB 1A 1C 1C 如图 1-4(1)所示,其中 BB 1C 1C 是矩形, BC =2,BB 1得 AE = AO 2AA 15.5.设平面 A 1B 1C 的法向量== 4, AB =AC = 2,A 1B 1=A 1C 1=5.图 1- 4现将该平面图形分别沿 BC 和B 1C 1折叠,使△ ABC 与△ A 1B 1C 1所在平面都 与平面 BB 1C 1C 垂直,再分别连接 A 1A ,A 1B ,A 1C ,得到如图 1-4(2)所示的空间 图形.对此空间图形解答下列问题.(1)证明: AA 1⊥BC ; (2)求 AA 1 的长;(3)求二面角 A -BC -A 1 的余弦值.【答案】由 BB 1C 1C 为矩形知,DD 1⊥B 1C 1,因为平面 BB 1C 1C ⊥平面 A 1B 1C 1,所以 DD 1⊥平面 A 1B 1C 1,又由 A 1B 1=A 1C 1 知,A 1D 1⊥B 1C 1.故以 D 1 为坐标原点,可建立如图所示的空间直角坐标系 D 1-xyz. 由题设,可得 A 1D 1=2,AD = 1.由以上可知 AD ⊥平面 BB 1C 1C ,A 1D 1⊥平面 BB 1C 1C ,于是 AD ∥ A 1D 1.解: (向量法 ):(1)证明:B C 的中点分别为 D 和 取 BC ,D 1,连接 A 1D 1,DD 1,AD.所以 A (0,- 1,4),B (1,0,4),A 1(0,2,0),C (-1,0,4),D(0,0,4).故A →A 1=(0,3,-4),B →C =(-2,0,0),A →A 1·B →C =0, 因此 A →A 1⊥B →C ,即 AA 1⊥BC.(2)因为A →A 1=(0,3,- 4),所以 |A →A 1|=5,即 AA 1=5.(3)连接 A 1D ,由 BC ⊥AD ,BC ⊥AA 1,可知 BC ⊥平面 A 1AD ,BC ⊥A 1D ,所 以∠ ADA 1 为二面角 A -BC -A 1的平面角.因为D →A =(0,-1,0),D →A 1=(0,2,-4),所以(综合法)(1)证明:取 BC ,B 1C 1 的中点分别为 D 和 D 1,连接 A 1D 1,DD 1, AD ,A 1D.由条件可知, BC ⊥AD , B 1C 1⊥A 1D 1, 由上可得 AD ⊥面 BB 1C 1C , A 1D 1⊥面 BB 1C 1C. 因此 AD ∥A 1D 1,即 AD ,A 1D 1 确定平面 AD 1A 1D. 又因为DD 1∥BB 1,BB 1⊥BC ,所以 DD 1⊥BC. 又考虑到 AD ⊥ BC ,所以 BC ⊥平面 AD 1A 1D , 故 BC ⊥ AA 1.(2)延长 A 1D 1到 G 点,使 GD 1=AD ,连接 AG.因为 AD 綊 GD 1,所以 AG 綊 DD 1 綊 BB 1. 由于 BB 1⊥平面 A 1B 1C 1,所以 AG ⊥ A 1G.cos 〈D →A ,D →A 1〉 2=- 51× 22+ -42=-5 即二面角 A -BC -A 1 的余弦值为- 5.5.实用标准文案精彩文档由条件可知, A 1G =A 1D 1+D 1G =3, AG =4, 所以 AA 1= 5.(3)因为 BC ⊥平面 AD 1A 1D ,所以∠ ADA 1 为二面角 A -BC -A 1 的平面角. 在 Rt △A 1DD 1 中,DD 1=4,A 1D 1=2,解得即二面角 A -BC -A 1 的余弦值为- 55. sin ∠ D 1DA 15, 5, cos ∠ADA 1∠ D 1DA 1 =- 55.。
