信息在计算机中的存储形式
信息存取处理和传递的形式

信息存取处理和传递的形式
在计算机内部,一切信息的存取、处理和传递的形式是二进制。
二进制是一种数制,它使用0和1两个数码来表示信息。
计算机内部的所有数据都采用二进制编码,主要包括以下几个方面:
1. 存储:计算机内部使用二进制来存储数据,如文本、图像、声音等。
数据在存储器中以补码的形式存储,便于进行运算和处理。
2. 运算:计算机内部采用二进制运算,包括加法、减法、乘法、除法等。
二进制运算规则简单,有利于简化计算机硬件结构,提高运算速度。
3. 处理:计算机内部对输入的信息进行处理,如数据清洗、格式转换、算法执行等。
处理过程中,二进制数据在各个模块之间传递,经过一系列操作后,生成输出结果。
4. 传递:计算机内部采用二进制编码的方式进行数据传输,如在总线、接口等部件之间传输。
传递过程中,数据按照二进制编码的形式从一个部件传输到另一个部件。
总之,在计算机内部,一切信息的存取、处理和传递的形式都是二进
制。
这是因为二进制具有可行性、易行性、简单性、可靠性和逻辑性等优点,便于实现计算机硬件结构和进行高效的数据运算和处理。
1.2 信息在计算机中的存储形式

②
用乘2取整法将小数部分(0.6875)10转换为二进制形式: 2 …… 整数部分为1 高位
0. 6875 ×
1.3750 0. 3750
×
2
…… 整数部分为0
0. 7500 0. 7500
×
2
…… 整数部分为1 即:(0.6875)10 = (0.1011)2
1. 5000 0. 5000 × 2
点阵数越大,分辨率越高,字形越美观,但占用的存储空
间越多。
希腊字母、标点、序号等)
③ 汉字机内码
汉字机内码,也称汉字内码,是指汉字在计算机中存储、加 工、处理时所用的代码。 汉字机内码以汉字交换码为基础,在得到汉字交换码后,将 汉字交换码的每个最高位置加1,就得到了汉字机内码。
汉字两字节的机内码和国标码有一个对应关系:
国标码+8080(H)=机内码 例如:“重”字国标码是3122(H),它的机内码是: 3122(H)+8080(H)=B1A2(H)
② 二进制数
二进制数的数码为0、1共2个,
进数规则为逢二进一,
借一当二。
③ 八进制数
八进制数的数码为0、1、2、3、4、5、6、 7共8个。 进数规则为逢八进一,
借一当八。
④ 十六进制数
十六进制数的数码为0、1、2、3、4、5、6、7、 8、9、A、B、C、D、E、F共16个,其中数码A、B、C、 D、E、F分别代表十进制数中的10、11、12、13、14、 15。 进数规则为逢十六进一, 借一当十六。
送的一串二进制数,其英文名为“Word”。
• 字长:是CPU 一次处理数据的实际位数,是衡量计算
机性能的一个重要指标。字长越长,一次可处理的数据
计算机中所有信息采用的存储方式是

计算机中所有信息采用的存储方式是计算机中所有信息采用的存储方式是什么?在计算机中,所有的信息都是以二进制的形式存储的。
二进制是一种由0和1组成的数字系统,也是计算机能够理解和处理的唯一语言。
计算机内部的存储器、硬盘、固态硬盘以及各种外部存储设备都是以二进制的方式来存储和访问数据。
二进制存储是因为计算机的存储器由一系列的存储单元组成,每个存储单元只能存储一个位(bit)的信息,而一个位只能是0或者1。
这是由于计算机使用的电子元件只有两个状态,即通电和断电,因而只能表示二进制的数字。
每8个位组成一个字节(byte),一个字节可以表示256种不同的状态,可以用来表示不同的字符、数字或者其他类型的数据。
计算机中的存储方式可以大致分为主存储器(RAM)和辅助存储器(硬盘、固态硬盘等)。
主存储器是计算机的内存,用于临时存储正在被处理的程序和数据,具有读写的功能。
而辅助存储器则是用于永久存储数据和程序的设备,可以长时间保存数据而不会丢失。
辅助存储器具有较大的容量和较慢的访问速度,相比之下,主存储器则容量相对较小但访问速度更快。
除了存储器之外,计算机中的信息还可以通过各种输入输出设备进行存储和传输。
例如,通过键盘输入的信息可以被计算机接收并临时存储在内存中,在需要时可以通过显示器输出到屏幕上显示出来。
另外,计算机中的数据也可以通过网络传输到其他计算机上,实现数据共享和远程访问。
计算机中信息的存储方式对计算机的运行和数据的处理起着至关重要的作用。
正确的存储方式可以提高计算机的运行效率和数据的安全性。
因此,在设计和使用计算机系统时,需要合理选择存储设备和存储器的类型,以满足不同的需求和应用场景。
综上所述,计算机中所有信息采用的存储方式是二进制。
通过各种存储设备和存储器,计算机可以有效地存储和处理不同类型的数据,实现各种各样的应用和功能。
信息的存储和传输是计算机的核心功能之一,也是计算机科学和技术发展的重要基础。
计算机信息表示与存储

计算机的信息表示与存储1.计算机中的信息单位2.数制及数制转换3.计算机中的数4.编码和文本1. 计算机中的信息单位计算机中采用二进制编码:在冯·诺依曼型计算机中,计算机的内部都是采用二进制的形式来存储信息的。
二进制位(bit):是计算机中最小的信息单位,只有“0”和“1”两种状态。
二进制表示信息的优点:1)易于物理实现2)二进制数运算简单3)机器可靠性高4)通用性强位、字节位(bit):位是度量数据的最小单位,表示一位二进制数字。
字节(Byte):一个字节是8位(bit)二进制,是存放一个英文字母的基本宽度,也是计算机描述信息存储容量的基本单位。
1 Byte = 8 bit一个字节可以表示28=256 种状态K(千)字节1KB = 1024 Byte=210M(兆)字节1MB = 1024 KB =220G(吉)字节1GB = 1024 MB =230T(太)字节1TB = 1024 GB =240字、字长字(word):计算机内部进行信息处理的基本单位。
计算机可以同时处理的二进制数的位数。
字长:一个字所包含的二进制位数。
字长是计算机硬件设计的一个指标,它代表了机器的精度,字长越长,处理速度越快。
字长一般是字节的整数倍。
例:PC486是32位;奔腾机是64位。
2. 数制及数制转换十进制数由0~9共十个数字符号构成,基数是10。
10的i 次幂称为该位的权。
运算原则:逢十进一,借一当十。
如:9+1=10;4+5=9;11-5=6;6783461071081031041021012.=⨯+⨯+⨯+⨯+⨯--基数权数码二进制数由0、1两个数字符号构成,基数是2。
运算原则:逢二进一,借一当二。
如:0+0=0; 0+1=1;1+0=1; 1+1=10;(计数满2向高位进一)0-0=0;1-1=0;1-0=1;八进制数由0~7共八个数字符号构成,基数是8。
运算原则:逢八进一,借一当八。
如:7+1=10;2+5=7;11-5=4;注意:八进制数中不能出现8、9两个数字是错误的。
了解电脑系统的数据存储方式

了解电脑系统的数据存储方式数据存储是计算机系统中至关重要的一部分,它涉及到将信息保存在计算机内存中的过程。
了解电脑系统的数据存储方式对于我们更好地理解计算机的工作原理和优化计算机程序都非常有帮助。
本文将介绍几种常见的数据存储方式,包括内存存储、硬盘存储以及固态硬盘存储。
一、内存存储内存存储是计算机系统中最常见的数据存储方式之一。
它是计算机的主要工作空间,用于存储正在运行的程序和临时数据。
内存存储是易失性存储器,当计算机断电时,其中的数据将丢失。
内存的工作原理是通过电子元件(通常是DRAM)将信息以二进制形式存储在地址上。
二、硬盘存储硬盘存储是计算机系统中常用的非易失性存储介质。
硬盘由多个盘片组成,每个盘片上有覆盖着磁性物质的碟片。
数据以磁性形式存储在磁盘上,通过磁头进行读取和写入操作。
硬盘存储的数据可以长期保存,即使计算机断电也不会丢失。
硬盘存储的速度相对较慢,但容量较大,适合长期存储大量数据。
在现代计算机中,常见的硬盘接口有SATA和SAS,它们通过数据线将硬盘与主板连接起来,实现数据的读写。
三、固态硬盘存储固态硬盘(SSD)是一种采用闪存存储芯片进行数据存储的新型存储设备。
它与传统硬盘相比具有更快的读写速度、更低的能耗和更高的抗震性能。
固态硬盘没有机械部件,因此也没有机械故障的风险,更加耐用可靠。
固态硬盘的工作原理是基于快速电子存储技术,数据以电荷状态进行存储。
与传统硬盘相比,固态硬盘在数据读取速度上有着明显优势,可以大大提升计算机的性能。
四、其他存储方式除了内存存储、硬盘存储和固态硬盘存储,还有一些其他的数据存储方式。
例如光盘(CD、DVD)和闪存卡(SD卡、U盘)等,它们广泛用于存储和传输数据。
光盘以激光技术读取磁性材料上的信息,光盘存储的数据相对较大,但读写速度较慢。
闪存卡则采用闪存技术进行数据存储,具有速度快、体积小、易携带等优点。
不同的存储方式在不同的场景和需求下有各自的应用。
例如,内存存储用于运行程序和存储临时数据,硬盘存储用于长期存储大量数据,而固态硬盘存储则适用于需要高速读写和频繁访问的场合。
数据在计算机内的存贮形式和数据的表示方法

1010 12 A 10
1011 13 B 11
⑶ 权位。一个数字放在不同的数位上,表示的大小是不一样的,例如数字6放在0位(个位)上,其大小为6,即6*10^0,放在1位(十位)上,表示60,即6*10^1;也就是说一个数字放在不同的数位上,其大小是该数字乘一个固定的数值,这个固定的数值叫权位;
权位 = 基数^n|m
十进制数有十个基本数码0、1、2、3、4、5、6、7、8、9,进位原则是逢10进1,基数为10,依照这个规律,二进制数的数码为0和1,进位原则是逢2进1,基数为2。十进制与二进制的表示方法如下。
1、数字化编码的概念
所谓编码,就是采用少量的基本符号,按照一定的组合原则,表示大量复杂多样的信息。基本符号的种类和这些符号的组合规则是一切信息编码的两大要素。例如用26个英文字母表示英文词汇,用10个阿拉伯数码表示数字等,就是典型的编码例子。在计算机中,广泛采用的是只用“0”和“1”两个基本符号组成的二进制码。
⑸ 地址 每个字节有一个“地址”,只有通过地址才能找到某个存贮单元,并从中取数或向其存贮数据。计算机的整个内存被划分成若干个存储单元,每个存储单元可存放8位二进制数。即,每个存储单元是用来存放数据或程序代码的。为了能有效地存取该单元内存储的内容,每个单元必须有唯一的编号来标识,这个编号称为地址。
十六进制 A C 3 7
⑵ 运算规则简单。例如,一位二进制数的加法运算和一位二进制数的乘法运算规则为:
0+0=0 0×0=0
0+1=1+0=1 0×1=1×0=0
十进制与二 5 6 7 8 9
二进制数 0 1 10 11 100 101 110 111 1000 1001
计算机中信息的存储(非常齐全)

ASCII含义:因为1位二进制数可以表示(2=)2种状态:0、1;而2位二进制数可以表示(2=)4种状态:00、01、10、11;依次类推,7位二进制数可以表示(2=)128种状态,每种状态都唯一地编为一个7位的二进制码,对应一个字符(或控制码),这些码可以排列成一个十进制序号0~127。
所以,7位ASCII码是用七位二进制数进行编码的,可以表示128个字符。
第0~32号及第127号(共34个)是控制字符或通讯专用字符,如控制符:LF(换行)、CR(回车)、FF(换页)、DEL(删除)、BS(退格)、BEL(振铃)等;通讯专用字符:SOH(文头)、EOT(文尾)、ACK(确认)等;第33~126号(共94个)是字符,其中第48~57号为0~9十个阿拉伯数字;65~90号为26个大写英文字母,97~122号为26个小写英文字母,其余为一些标点符号、运算符号等。
注意:在计算机的存储单元中,一个ASCII码值占一个字节(8个二进制位),其最高位(b7)用作奇偶校验位。
所谓奇偶校验,是指在代码传送过程中用来检验是否出现错误的一种方法,一般分奇校验和偶校验两种。
奇校验规定:正确的代码一个字节中1的个数必须是奇数,若非奇数,则在最高位b7添1;偶校验规定:正确的代码一个字节中1的个数必须是偶数,若非偶数,则在最高位b7添1。
一个ASCll码由8位二进制数码组成的。
其中,用于表达字符的二进制码有7个,最后一个用于检测错误,或空闲不用。
存储器单元内容是储存器单元里面储存的二进制数据。
如0100011存储器单元地址是由十六进制数指向存储器某个特定的单元。
如0FFE2A一个是实实在在的数据,一个是指向该数据的地址计算机信息存储单元的结构数据必须首先在计算机内被表示,然后才能被计算机处理。
计算机表示数据的部件主要是存储设备;而存储数据的具体单位是存储单元;因此,了解存储单元的结构是十分必要的。
(1)"位"(Bit):是计算机中最小的信息单位。
计算机中所有信息的存储都采用

计算机中所有信息的存储都采用
计算机中所有信息的存储,采用的是数字信号的方式。
数字信号是一种能够被数字设备识别并存储的信号,它常见于计算机中的数据传输、音频传输等领域。
这种信号是一种离散的信号,即将连续的波形信号离散化后得到的信号。
数字信号的存储方式,通常是将输入的模拟信号经过采样和量化的过程后,转换成数字信号,再存储在计算机的磁盘中。
具体的过程如下:
首先,要对输入的模拟信号进行采样,即将连续的信号在某一时间间隔内进行取样,以离散的形式表示。
采样的间隔越小,采集到的数据就越准确,但是占用的存储空间也相应增大。
然后,将采集到的信号进行量化。
量化是将采样后的信号离散化,并将其转换为数字信号的过程。
通过指定一个预定的区间,将连续的信号分割成许多个离散的区间,每个区间的大小相同。
量化的结果就是每个区间的采样值,它是一个离散的数字,用于表示输入信号在该区间内的振幅。
最后,将经过采样和量化后的数字信号按照一定的格式存储在计算机的磁盘中。
由于数字信号是离散的,并且采样率和量化精度都是固定的,因此它的存储是非常规律的,可以按照一定的格式进行组织和存储。
除了数字信号,计算机中还有许多其他类型的数据和信息需要存储,例如文本、图像、视频等等。
这些数据的存储方式也都不一样,但是都采用了数字化的方法进行处理和存储。
因此,数字化技术是计算机中所有信息存储的基础。
它不仅可以使信息高效地存储和传输,而且还可以有效地提高信息处理的效率。
计算机数据存储

计算机数据存储,通常被称为存储或记忆体,是一种技术,包括计算机组件和用于保存数字数据的记录媒体。
这是一个核心功能和计算机的基本组成部分。
在当代的用法中,内存通常是读写的半导体存储随机存取存储器中,通常是DRAM(动态RAM)或其他形式的快,但临时存储。
存储由存储设备及其媒体不能直接访问由CPU,(二次或三级存储),典型的硬盘驱动器,光盘驱动器,和其他设备比RAM慢,但是非易失性(保持断电时的内容)。
[ 1 ]从历史上看,存储器被称为核心,主存储器,实存储器或存储设备的内部记忆体,而被称为辅助存储器,外部存储器或辅助/周边存储。
的区别是计算机的体系结构的基础。
的区别也反映了内存和大容量存储设备,它已经模糊了的历史使用情况的长期存储的一个重要和显着的技术差别。
然而,本文采用了传统的命名。
许多不同形式的存储,各种自然现象的基础上,已经发明了。
到目前为止,还没有实际的通用存储介质存在,并且所有的存储形式也存在一些缺点。
因此,计算机系统通常包含数种存储,每个个别的目的。
一个现代化的数字电脑表示使用二进制数字系统的数据。
位,或二进制数位,每一个都具有1或0的值的字符串可以被转换成文本,数字,图片,音频,和几乎任何其他形式的信息。
存储的最常见的单位是字节,等于8位。
一块的信息可以由任何计算机或设备的存储空间是足够大以容纳的二进制表示的信息片,或仅仅数据处理。
例如,莎士比亚全集,在打印约1250页,可存储约五兆字节(4000万位)每个字符一个字节。
定义组件的计算机的中央处理单元(CPU,或简单的处理器),因为它操作数据,执行计算,并控制其他元件。
在最常用的电脑架构,CPU由两个主要部分组成:控制单元和算术逻辑单元(ALU)。
前者控制的CPU和存储器之间的数据流;后者执行对数据的算术和逻辑运算。
如果没有一个显着的内存量,电脑将仅仅是能够进行固定操作,并立即输出结果。
这将不得不重新配置,以改变其行为。
这是可以接受的设备,如台计算器,数字信号处理器,以及其他专业设备。
信息在计算机中的存储形式

信息在计算机中的存储形式人类用文字、图表、数字表达和记录着世界上各种各样的信息,便于人们用来处理和交流。
现在可以把这些信息都输入到计算机中,由计算机来保存和处理。
前面提到,当代冯·诺依曼型计算机都使用二进制来表示数据,现在我们所要讨论的就是用二进制来表示这些数据。
一、计算机中的数据经过收集、整理和组织起来的数据,能成为有用的信息。
数据是指能够输入计算机并被计算机处理的数字、字母和符号的集合。
平常所看到的景象和听到的事实,都可以用数据来描述。
可以说,只要计算机能够接受的信息都可叫数据。
(一)计算机中数据的单位计算机数据的表示经常用到以下几个概念。
在计算机内部,数据都是以二进制的形式存储和运算的。
1. 位二进制数据中的一个位(bit)简写为b,音译为比特,是计算机存储数据的最小单位。
一个二进制位只能表示0或1两种状态,要表示更多的信息,就要把多个位组合成一个整体,一般以8位二进制组成一个基本单位。
2. 字节字节是计算机数据处理的最基本单位,并主要以字节为单位解释信息。
字节(Byte)简记为B,规定一个字节为8位,即1B=8bit。
每个字节由8个二进制位组成。
一般情况下,一个ASCII码占用一个字节,一个汉字国际码占用两个字节。
3. 字一个字通常由一个或若干个字节组成。
字(Word)是计算机进行数据处理时,一次存取、加工和传送的数据长度。
由于字长是计算机一次所能处理信息的实际位数,所以,它决定了计算机数据处理的速度,是衡量计算机性能的一个重要指标,字长越长,性能越好。
4. 数据的换算关系1Byte=8bit,1KB=1024B,1MB=1024KB,1GB=1024MB,1TB=1024GB。
计算机型号不同,其字长是不同的,常用的字长有8、16、32和64位。
一般情况下,IBM PC/XT的字长为8位,80286微机字长为16位,80386/80486微机字长为32位,Pentium 系列微机字长为64位。
计算机中的数据表示与存储方式有哪些

计算机中的数据表示与存储方式有哪些计算机是数字化处理信息的工具,而数据就是这些信息的基本单位。
计算机中的数据表示与存储方式是非常重要的,不同的数据表示方式和存储方式对于计算机的运行和数据处理都有着直接的影响。
本文将介绍计算机中常见的数据表示方式和存储方式,并探讨它们的特点和应用。
一、数据表示方式数据在计算机中的表示方式可以分为两种:二进制表示和十六进制表示。
1. 二进制表示二进制表示是计算机中最基本、最常用的数据表示方式,二进制是一种只包含0和1的数字方式。
计算机中的所有数据都是以二进制形式存储和处理的。
二进制表示具有以下特点:(1)简单明了:由于只有两个数位,所以二进制表示更加简单和直观。
(2)易于电子器件实现:计算机中的电子器件一般都是以开关形式工作,而开关只有两种状态,与二进制数据对应非常方便。
(3)高可靠性:二进制表示可以有效地减小误差和噪声带来的影响,提高数据的可靠性。
(4)计算机底层的数据表示方式:计算机的中央处理器(CPU)内部的数据处理单元,以及内存、存储器等硬件设备,都是以二进制的方式来进行数据表示和处理的。
2. 十六进制表示十六进制表示是二进制表示的一种衍生形式,它一共有16个符号,分别是0~9和A~F,其中A~F分别表示10~15。
十六进制表示常用于计算机程序的调试和表示内存地址。
十六进制表示具有以下特点:(1)简化了复杂的二进制:由于二进制比较长,所以通过十六进制可以简化二进制的表示,提高编程和调试的效率。
(2)易于转换:十六进制和二进制之间可以很容易地进行转换,方便计算机程序编写和调试。
二、数据存储方式数据在计算机中的存储方式主要包括字节序和存储器结构两种方式。
1. 字节序字节序是指在计算机内存中对于多字节数据如何进行存储和访问的方式。
常见的字节序有大端序和小端序两种方式。
大端序(Big Endian)是指将数据的高位字节存储在低地址位,而低位字节存储在高地址位,类似于人们读书的习惯,从左到右。
信息在计算机中的存储形式

信息在计算机中的存储形式计算机作为现代信息技术的核心工具,承载着海量的信息。
信息在计算机中的存储形式对于数据的传输和处理至关重要。
本文将探讨信息在计算机中的存储形式,包括二进制表示、字节和位、数据类型和数据结构等方面。
一、二进制表示在计算机中,信息以二进制形式进行存储。
二进制由0和1两个数字组成,可用于表示任何数据和指令。
计算机根据电压高低来表示0和1,高电压表示1,低电压表示0。
这种二进制表示方式使得计算机能够高效地处理和运算信息。
二、字节和位计算机存储和处理信息的基本单位是字节(byte)。
一个字节由8个二进制位(bit)组成,每个二进制位代表一个0或1。
字节是计算机中最小的可寻址的单位,它能够表示256种不同的值,如0~255。
字节可以用于存储字符、数字、图像、音频等各种类型的信息。
三、数据类型在计算机中,信息以不同的数据类型进行存储。
常见的数据类型包括整数、浮点数、字符、布尔值等。
不同的数据类型占用不同的存储空间,如整数一般占用4个字节,浮点数占用8个字节。
数据类型的选择和使用能够有效地提高计算机存储和处理信息的效率。
四、数据结构数据结构是指将数据组织起来以便于存储和操作的方式。
常见的数据结构包括数组、链表、栈、队列、树、图等。
数据结构的选择和设计直接影响到信息在计算机中的存储和处理效率。
合理选择和设计数据结构能够提高计算机程序的性能。
五、非易失性存储器信息的存储除了在计算机内存中进行,还需要在计算机关机后能够保持不丢失。
这时就需要使用非易失性存储器(non-volatile memory),如硬盘、固态硬盘(SSD)、光盘等。
非易失性存储器能够长期存储大量的信息,保证了信息的持久性和可靠性。
六、虚拟存储器虚拟存储器是一种计算机内存管理技术,它将计算机内存和硬盘空间组合起来使用。
虚拟存储器能够将已用的内存空间释放出来,从而提高计算机的运行效率。
虚拟存储器对于大规模的数据处理和计算非常重要,能够有效地利用计算机的存储资源。
计算机信息的储存

计算机信息的储存计算机信息的储存是指将数据存储在计算机系统中,以便后续使用和处理。
随着计算机技术的不断发展,储存方式也在不断演变和完善。
本文将介绍计算机信息储存的几种主要方式及其特点。
一、主存储器主存储器是计算机中最常用的储存方式之一,用于临时存储正在进行中的程序和数据。
主存储器是计算机的内存,以芯片的形式存在。
它具有容量大、读写速度快等特点,是计算机的重要组成部分。
主存储器分为静态随机存取存储器(SRAM)和动态随机存取存储器(DRAM)。
SRAM读取速度快、功耗低,但价格昂贵;DRAM则容量大、价格便宜,但读取速度较慢。
主存储器不仅是数据储存的地方,也是CPU执行指令的地方,因此对计算机的性能和速度起着重要的影响。
二、辅助存储器辅助存储器是计算机中用于长期储存数据和程序的设备,主要包括硬盘、光盘、磁带等。
与主存储器相比,辅助存储器容量更大,但读写速度相对较慢。
其中,硬盘是计算机最主要的辅助存储设备。
它通过磁头在盘片上记录和读取数据。
硬盘的容量大,可以存储大量的数据,而且价格相对较低。
光盘是另一种常见的辅助存储设备,它使用激光技术读取信息。
光盘容量较小,但具有可擦写、便携等优点,适合存储音视频等多媒体资料。
磁带则主要用于大规模数据的备份和存档,在数据安全性和存储成本上有一定的优势。
三、缓存存储器缓存存储器是位于主存储器和CPU之间的一层高速缓存,用于提高计算机的读取速度。
缓存存储器的容量较小,但读写速度非常快。
缓存存储器分为一级缓存和二级缓存。
一级缓存位于CPU内部,容量较小,读写速度非常快,可以存储最经常使用的数据和指令;二级缓存位于CPU外部,容量较大,读写速度也比主存储器快。
缓存存储器的作用是利用空间换时间的原理来提高计算机的运行速度。
通过在CPU和主存储器之间增加一层缓存,可以减少CPU等待数据的时间,从而提高计算效率。
四、云存储随着云计算技术的发展,云存储逐渐成为一种流行的储存方式。
计算机中数据的表达形式

计算机中数据的表达形式数据在计算机中是以不同的形式进行表达和存储的。
这些形式可以是数字、文本、图像、音频等等。
本文将介绍计算机中常见的数据表达形式,并对其特点和应用进行分析。
1. 数字形式数字是计算机中最基本的数据类型之一。
计算机使用二进制来表示数字,其中0和1分别表示逻辑的假和真。
在计算机中,数字可以用不同的进制进行表示,如二进制、十进制、十六进制等。
数字的表达形式可以用于计算、存储和传输数据。
例如,在计算机中进行数值计算时,可以使用数字形式进行操作。
2. 文本形式文本是计算机中用于表示语言文字的数据形式。
计算机使用字符编码来表示不同的字符,如ASCII码、Unicode等。
文本可以用于存储和处理各种类型的信息,如文章、代码、日志等。
在计算机中,文本通常以字符串的形式进行表达和处理。
例如,在编程中,可以使用文本形式来表示和处理程序代码。
3. 图像形式图像是计算机中用于表示视觉信息的数据形式。
计算机使用像素来表示图像的各个点。
图像可以是二维的,也可以是三维的。
在计算机中,图像可以用于图像处理、图像识别、计算机视觉等领域。
例如,在数字摄影中,图像可以用于存储和显示照片。
4. 音频形式音频是计算机中用于表示声音信息的数据形式。
计算机使用采样来表示声音的波形。
音频可以是单声道的,也可以是立体声的。
在计算机中,音频可以用于音频处理、音频识别、语音合成等领域。
例如,在音乐播放器中,音频可以用于存储和播放音乐。
5. 视频形式视频是计算机中用于表示连续图像序列的数据形式。
计算机使用帧来表示视频的各个图像。
视频可以是单个帧的连续播放,也可以是多个帧的连续播放。
在计算机中,视频可以用于视频处理、视频压缩、视频传输等领域。
例如,在在线视频网站中,视频可以用于存储和播放视频内容。
6. 数据库形式数据库是计算机中用于存储和管理数据的系统。
数据库可以用于存储和查询各种类型的数据,如文本、图像、音频等。
在计算机中,数据库可以用于数据的持久化和共享。
信息在计算机中的表示方法

信息在计算机中的表示方法信息在计算机中的表示方法是计算机科学领域中的重要概念之一。
计算机通过不同的方式来表示和存储信息,以便能够进行处理和计算。
本文将介绍一些常用的信息表示方法,包括二进制、十进制、十六进制以及ASCII码。
一、二进制表示法二进制是计算机系统中最常用的信息表示方法。
二进制只包含两个数字,即0和1,也被称为“0/1码”或“二码”。
在计算机中,所有的数据以二进制形式存储和处理。
例如,数字“10”的二进制表示为“1010”。
二进制的优点是能够更直接地与计算机内部的电路进行对应,从而使计算机更高效地处理数据。
同时,二进制表示法也非常简洁,只需使用两个数字即可表示任意数据。
二、十进制表示法十进制是我们日常生活中最常用的数字表示方法。
十进制有十个数字,即0到9,是一种基于十的数制系统。
在计算机中,十进制数需要转换为二进制数才能被计算机理解和处理。
十进制的优点在于它更符合人们的思维方式,便于人们直观地理解和计算。
然而,与二进制相比,十进制的表示方式更占用存储空间,并需要更多的计算资源。
三、十六进制表示法十六进制是一种基于十六的数制系统,它使用了0到9的十个数字和A到F的六个字母。
十六进制广泛应用于计算机科学和工程领域,特别是在编程和网络通信中。
十六进制的优点在于它既比二进制更简洁,又比十进制更易于计算。
在计算机中,十六进制数经常用于表示内存地址、颜色代码等。
例如,颜色代码"#FF0000"表示红色。
四、ASCII码ASCII码(American Standard Code for Information Interchange,美国信息交换标准代码)是一种常用的字符编码标准。
它定义了128个字符的编码方式,包括数字、字母、标点符号和控制字符等。
ASCII码使用七位二进制数来表示一个字符,可以方便地转换为二进制形式进行存储和处理。
例如,字符“A”的ASCII码为65(二进制表示为01000001)。
计算机中信息的存储与进制数的转换

学案——数据的存储与进制转换学习目标:1.了解计算机的存储单位2.掌握不同进制数之间的关系。
学习难点:不同进制数之间的转换学习重点:1. 计算机中数据的存储单位及其换算2. 不同进制数之间的转换教学方法:对比讲解,演示讲述。
教学工具:多媒体教室课时安排:1课时教学过程:信息在计算机中的存储形式人类用文字、图表、数字表达和记录着世界上各种各样的信息,便于人们用来处理和交流。
现在可以把这些信息都输入到计算机中,由计算机来保存和处理。
前面提到,当代冯·诺依曼型计算机都使用二进制来表示数据,现在我们所要讨论的就是用二进制来表示这些数据。
一、计算机中的数据经过收集、整理和组织起来的数据,能成为有用的信息。
数据是指能够输入计算机并被计算机处理的数字、字母和符号的集合。
平常所看到的景象和听到的事实,都可以用数据来描述。
可以说,只要计算机能够接受的信息都可叫数据。
(一)计算机中数据的单位计算机数据的表示经常用到以下几个概念。
在计算机内部,数据都是以二进制的形式存储和运算的。
1. 位二进制数据中的一个位(bit)简写为b,音译为比特,是计算机存储数据的最小单位。
一个二进制位只能表示0或1两种状态,要表示更多的信息,就要把多个位组合成一个整体,一般以8位二进制组成一个基本单位。
2. 字节字节是计算机数据处理的最基本单位,并主要以字节为单位解释信息。
字节(Byte)简记为B,规定一个字节为8位,即1B=8bit。
每个字节由8个二进制位组成。
一般情况下,一个ASCII码占用一个字节,一个汉字国际码占用两个字节。
3. 字一个字通常由一个或若干个字节组成。
字(Word)长是计算机进行数据处理时,一次存取、加工和传送的数据长度。
由于字长是计算机一次所能处理信息的实际位数,所以,它决定了计算机数据处理的速度,是衡量计算机性能的一个重要指标,字长越长,性能越好。
4. 数据的换算关系计算机存储单位一般用B,KB,MB,GB,TB,EB,ZB,YB,BB 来表示,它们之间的关系是:位 bit(比特)(Binary Digits):存放一位二进制数,即 0 或 1,最小的存储单位。
计算机——信息表示及存储
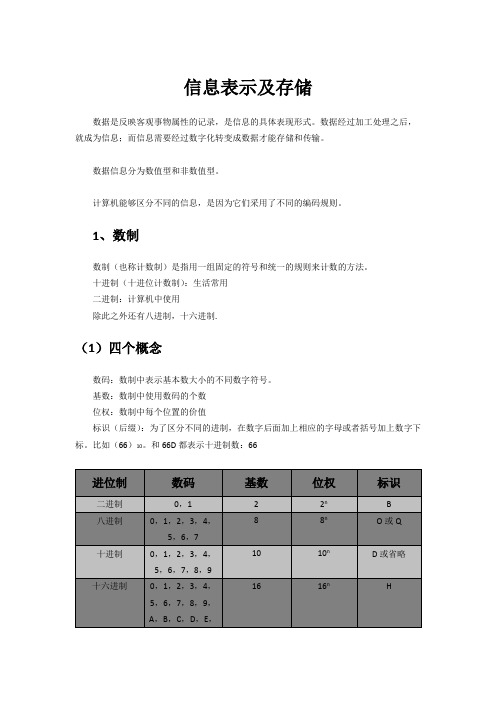
信息表示及存储数据是反映客观事物属性的记录,是信息的具体表现形式。
数据经过加工处理之后,就成为信息;而信息需要经过数字化转变成数据才能存储和传输。
数据信息分为数值型和非数值型。
计算机能够区分不同的信息,是因为它们采用了不同的编码规则。
1、数制数制(也称计数制)是指用一组固定的符号和统一的规则来计数的方法。
十进制(十进位计数制):生活常用二进制:计算机中使用除此之外还有八进制,十六进制.(1)四个概念数码:数制中表示基本数大小的不同数字符号。
基数:数制中使用数码的个数位权:数制中每个位置的价值标识(后缀):为了区分不同的进制,在数字后面加上相应的字母或者括号加上数字下标。
比如(66)10。
和66D都表示十进制数:66规则:进位规则,多进制就满多少进!借位规则,多少进制(向高位)借一位就当多少十进制下:8+2=10 10-3=7 9+2=11八进制下:6+2=10 6+3=11 10-2=6二进制下:1+1=10 10- |=|十六进制下:8+2=A 11-2= F 8+8=10练习:判断102B 1Q ABCDF H 是否正确(××√)6+3=11判断几进制(八进制)(2)进制转换①十进制→R进制整数:除以R反向取余小数:乘以R正向取整(取整变0)例:20.625 D=10100.101 B二进制66.5 D=102.4 Q八进制30.5 D=1E.8 H十六进制练习:29.125 D=11101.001 B二进制②R进制→十进制乘权求和法:每一位的值乘以对应的价值(位权)标位数时注意两点:①从个位开始标,小数和整数方开②位权是0指数开始例:10110.011 B=22.375 D10110.011=1*2⁴+0*2³+1*2²+1*2¹+0*2⁰+0*2⁻¹+1*2⁻²+1*2⁻³=16+0+4+2+0+0+1/4+1/8=22.37516.6 Q=14.75 D16.6=1*81+6*80+6*8-1=8+6+3/4=14.758A.4 H = 138.25 D8A.4=8*161+A*160+4*16-1=128+A+1/4=138.25练习:1010.101B=10.625D1010.101=1*23+0*22+1*21+0*20+1*2-1+0*2-2+1*2-3 =8+0+2+0+1/2+0+1/8=10.625③8421拼素法:二进制→十进制例:25D=11001 B25=16+8+1=1100110110B =22D10110=16+4+2=22练习:1011B=11D1011=8+2+1=1135 D = 1000 1135=32+2+1=100011④二进制→八进制/十六进制分组转换法:二进制→八进制:3位转成1位二进制→+六进制:4位转成1位注意两点:①以小数点为界,整数和小数方开②整数位数不够在前面添0,小数位数不够在后面添0.例:10101,1B=25.4Q10101.1=010 101 . 100= 2 5 . 4=25.4110l01.1101 B= 35. D H110101.1101=0011 0101 . 1101= 3 5 . D=35.D练习:110001,11B=61.6Q110001. 11=110 001. 11O=6 1 . 6=61. 6⑤八进制/十六进制→二进制还组转换法:八进制→二进制:1位还成3位(4 2 1)十六进制→二进制:1位还成4位(8 4 2 1)例:16.32Q =1110.01101 B1=001 6=110 . 3=011 2=010=00110.011010F.3DH = 1111.00 111101 BF=15=1101 . 3=0011 D=13=1101=1101.00111101练习:ABC.DH=101010111100.1101 BA=10=1010 B=11=1011 C=12=1100 . D=13=1101=101010111100.1101⑥八进制←→十六进制以二进制为桥八进制(十六进制)→二进制→十六进制(八进制)例:56.3Q=2E.6H①Q→B (1→3) ②B→H (4→1)5=101 101110.0116=110 0010=23=011 1110=E0110=6练习:3D.2H=75.1Q①H→B (1→4) ②B→Q (3→1)3=0011 00111101.0010D=13=1101 111=72=0010 101=5001=1⑦小数点位移对于二进制,小数点左移几位数变为原来的R-n倍。
计算机中信息的表示及存储形式

计算机中信息的表⽰及存储形式计算机内部均采⽤⼆进制来表⽰各种信息。
⼀、数的位置计数法及进制的概念①数制只采⽤R个基本符号——基R数制,R称为数制的“基数”。
②数制中每⼀位(e.g.⼗进制的个⼗百千位等)对应的单位称为“权”,权即以R为底的幂。
③每⼀位数的数值=数码×权,数码为0~R-1。
⼆、数制之间的转换① R转⼗按权展开求和。
②⼗转R整数部分采⽤除基数取余法,⼩数部分采⽤乘基数取整法。
【个⼈理解】⼩数部分权值的指数为负——R-1,除相当于乘以R。
可带⼊公式:数值=数码×权,数码即为待求量。
三、计算机中数的表⽰(定点数,原码,反码,补码)①计算机中数据分为数值数据和⾮数值数据,数值数据分为⽆符号数和有符号数。
⽆符号数多⽤于表⽰字符、地址以及逻辑值等。
有符号数的最⾼位作为符号位,“0”表⽰正,“1”表⽰负,即把符号数值化,这样的数称为“机器数”,机器数对应的原来有正负号的数称为“真值”。
有符号数分为定点数和浮点数。
定点数分为定点整数(纯整数)和定点⼩数(纯⼩数)。
②机器数三种表⽰形式——原码、反码、补码原码:整数X的原码为,符号位为0表⽰正,为1表⽰负,数值部分就是X的绝对值的⼆进制数。
反码:正数的反码与原码相同;对负数,符号位不变,其数值位(X的绝对值位)按位取反。
补码:正数补码与原码相同,对负数,符号位不变,数值位(X的绝对值位)按位取反后在最低位加1。
补码运算简单⽅便,符号位可作为数据的⼀位参与运算,不必单独处理,且最后结果的符号位仍然有效。
四、计算机中实数的浮点表⽰①实数X的浮点形式(科学表⽰法)若采⽤⼆进制表⽰为:X=±M×2±E,M为X的尾数,采⽤⼆进制纯⼩数形式(0.xxxxx),代表X的全部有效数字,其位数反映了数据的精度。
E为X的阶码,表⽰2的⼏次⽅,通常采⽤⼆进制整数形式,决定了数的范围。
M和E都可以是正数或者负数,即阶码和尾数都是带符号的数,可以采⽤不同的码制表⽰法,例如尾数可以⽤原码或补码表⽰,阶码⽤补码表⽰。
第3章-计算机中信息的表示与存储

2. 非十进制数转换为十进制数
非十进制数转换为十进制数采用“按权展开法”,即先把各位 非十进制数按权展开,写成多项式,然后计算十进制结果。
例如:写出(1101.01)2, (237)8,(10D)16的十进制数。
3. 二进制与八、十六进制数的转换
二进制数与八进制数,以及十六进制数存在着倍数的关系,例如
位权的表示法是指,数字的总个数为基数,每个数字都要乘以基 数的幂次,而该幂次由每个数所在的位置决定。排列方式是以小 数点为界,整数部分自右向左分别为0次幂、1次幂、2次幂、……, 小数部分自左向右分别为负1次幂、负2次幂、负3次幂、……。
2. 常用的进位记数制
(1)十进制 所使用的数码有10个,即0、1、2、…、9,基数为10 ,各位的位
2. 浮点数
小数点位置浮动变化的数称为浮点数。对十进制来说,浮点数是以10 的n次方表示的数。例如,十进制数245.78, 使用浮点表示法为 0.24578×103。其中0.24578为一个定点数,3表示小数点向右移动3位。 当浮点数采用指数形式表示时,指数部分称为“阶码”,小数部分称 为“尾数”。尾数和阶码有正负之分,例如,二进制数“-0.00111”, 浮点表示为“-0.111×2-2”,这里尾数(-0.111)和阶码(-2)都是 负数。尾数的符号表示数的正负,阶码的符号则表明小数点的实际位 置。
例如,求十进制数“+5”与“-5”的反码。 若用一个字节表示,将十进制数5转化为二进制数为00000101。 因为“+5”是正数,转化为二进制数的原码为00000101,所以
反码与原码相同,( +5 )反=00000101;
正数 +0 +1 +2 +3 +4 +5 +6 +7
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.工作可靠
在计算机中,用两个状态代表两个数据,数字传输和处理方便、简单、不容易出错,因而电路更加可靠。
3.简化运算
在计算机中,二进制运算法则很简单。例如:
相加减的速度快,求积规则有3个,求和规则也只有3个。
4.逻辑性强
二进制只有两个数码,正好代表逻辑代数中的“真”与“假”,而计算机工作原理是建立在逻辑运算基础上的,逻辑代数是逻辑运算的理论依据。用二进制计算具有很强的逻辑性。
0011
0100
01
0110
0111
1000
1001
10
1011
1100
1101
1110
11八进制
10
11
12
13
14
15
16
17十六进制89A
B C D
E
F
十进制的特点如下:
(1)有10个数码:
0、1、
2、3、
4、5、
6、7、
8、9。
(2)基数:10。
(3)逢十进一(加法运算),借一当十(减法运算)。
(4)按权展开式。对于任意一个n位整数和m位小数的十进制数D,均可按权展开为:
101
D=D
n-1·10n-1+D
n-2·10n-2+„+D
1·10+D
0·10+D
1·81+O
0·80+O-Leabharlann ·8–1+„+O–m·8-m
例:
(5346)
8相当于十进制数为:
5×83+3×82+4×81+6×80=
(2790)
10
4.十六进制(Hexadecimal notation)
十六进制有如下特点:
(1)有16个数码:
0、1、
2、3、
4、5、
6、7、
8、9、
A、B、
C、D、
10、11、
12、13、14和15,这是国际上通用的表示法。
例:
十六进制数(4C4D)
16代表的十进制数为:
4×163+C×162+4×161+D×160=
(19533)
10
二进制数与其他数之间的对应关系如表1所示。
表1几种常用进制之间的对照关系
十进制89
10
11
12
13
14
15二进制
00
0001
0010
(一)计算机中数据的单位
计算机数据的表示经常用到以下几个概念。在计算机内部,数据都是以二进制的形式存储和运算的。
1.位
二进制数据中的一个位(bit)简写为b,音译为比特,是计算机存储数据的最小单位。
一个二进制位只能表示0或1两种状态,要表示更多的信息,就要把多个位组合成一个整体,一般以8位二进制组成一个基本单位。
由于技术原因,计算机内部一律采用二进制,而人们在编程中经常使用十进制,有时为了方便还采用八进制和十六进制。理解不同计数制及其相互转换是非常重要的。
(二)进位计数制
在计算机中,二进制并不符合人们的习惯,但是计算机内部却采用二进制表示信息,其主要原因有如下4点:
1.电路简单
在计算机中,若采用十进制,则要求处理10种电路状态,相对于两种状态的电路来说,是很复杂的。而用二进制表示,则逻辑电路的通、断只有两个状态。例如:
例如,一台微机,内存为256MB,软盘容量为
1.44MB,硬盘容量为80GB,则它实际的存储字节数分别为:
内存容量=256×1024×1024B=6B
软盘容量=
1.44×1024×1024B=
.44B
硬盘容量=80×1024×1024×1024B=920B
如何表示正负和大小,在计算机中采用什么计数制,是学习计算机的一个重要问题。数据是计算机处理的对象,在计算机内部,各种信息都必须通过数字化编码后才能进行存储和处理。
E、F。
(2)基数:16。
(3)逢十六进一(加法运算),借一当十六(减法运算)。
(4)按权展开式。对于任意一n位整数和m位小数的十六进制数D,均可按权展开为:
D=H
n-1·16n-1+„+H
1·161+H
0·160+H
-1·16–1+…+H
–m·16-m
在16个数码中,
A、B、
C、D、E和F这6个数码分别代表十进制的
-1·10–+„+D
–m·10–m例:
将十进制数
456.24写成按权展开式形式为:
456.24=4×102+5×101+6×100+2×10-1+4×10-2
2.二进制(Binary notation)
二进制有如下特点:
(1)有两个数码:
0、1。
(2)基数:2。
(3)逢二进一(加法运算),借一当二(减法运算)。
数码:
一个数制中表示基本数值大小的不同数字符号。例如,八进制有8个数码:
0、1、
2、3、
4、5、
6、7。
基数:
一个数值所使用数码的个数。例如,八进制的基数为8,二进制的基数为2。
位权:
一个数值中某一位上的1所表示数值的大小。例如,八进制的123,1的位权是64,2的位权是8,3的位权是1。
1.十进制(Decimal notation)
人类用文字、图表、数字表达和记录着世界上各种各样的信息,便于人们用来处理和交流。现在可以把这些信息都输入到计算机中,由计算机来保存和处理。前面提到,当代冯·诺依曼型计算机都使用二进制来表示数据,现在我们所要讨论的就是用二进制来表示这些数据。
一、计算机中的数据
经过收集、整理和组织起来的数据,能成为有用的信息。数据是指能够输入计算机并被计算机处理的数字、字母和符号的集合。平常所看到的景象和听到的事实,都可以用数据来描述。可以说,只要计算机能够接受的信息都可叫数据。
(二)计算机中常用的几种计数制
用若干数位(由数码表示)的组合去表示一个数,各个数位之间是什么关系,即逢“几”进位,这就是进位计数制的问题。也就是数制问题。数制,即进位计数制,是人们利用数字符号按进位原则进行数据大小计算的方法。通常是以十进制来进行计算的。另外,还有二进制、八进制和十六进制等。
在计算机的数制中,要掌握3个概念,即数码、基数和位权。下面简单地介绍这3个概念。
(4)按权展开式。对于任意一个n位整数和m位小数的二进制数D,均可按权展开为:
D=B
n-1·2n-1+B
n-2·2n-2+„+B
1·21+B
0·20+B
-1·2–1
+…+B
–m·2-m
例:
把(
11001.101)
2写成展开式,它表示的十进制数为:
1×24+1×23+0×22+0×21+1×20+1×2-1+0×2-2+1×2-3=(
25.625)
10
3.八进制(Octal notation)
八进制的特点如下:
(1)有8个数码:
0、1、
2、3、
4、5、
6、7。
(2)基数:8。
(3)逢八进一(加法运算),借一当八(减法运算)。
(4)按权展开式。对于任意一个n位整数和m位小数的八进制数D,均可按权展开为:
D=O
n-1·8n-1+„+O
4.数据的换算关系
1Byte=8bit,1KB=1024B,1MB=1024KB,1GB=1024MB,1TB=1024GB。
计算机型号不同,其字长是不同的,常用的字长有
8、16、32和64位。一般情况下,IBM PC/XT的字长为8位,80286微机字长为16位,微机字长为32位,Pentium系列微机字长为64位。
2.字节
字节是计算机数据处理的最基本单位,并主要以字节为单位解释信息。字节(Byte)简记为B,规定一个字节为8位,即1B=8bit。每个字节由8个二进制位组成。一般情况下,一个ASCII码占用一个字节,一个汉字国际码占用两个字节。
3.字
一个字通常由一个或若干个字节组成。字(Word)是计算机进行数据处理时,一次存取、加工和传送的数据长度。由于字长是计算机一次所能处理信息的实际位数,所以,它决定了计算机数据处理的速度,是衡量计算机性能的一个重要指标,字长越长,性能越好。
