五年级数学解题能力展示初赛试题

合集下载

五年级数学解题能力展示初赛试题(无答案)

五年级组初试试卷一、填空题（每题8分，共40分）1. 计算12345678910⨯+⨯+⨯+⨯+⨯的结果是。

2. 十二月份共有31天，如果某年12月1日是星期一，那么该年12月19日是星期。

3. 如图的等腰梯形上底长度等于3，下底长度等于9，高等于4。

这个等腰梯形的周长等于。

4. 某乐团女生人数是男生人数的2倍；若调走24名女生，那么男生人数是女生人数的2倍。

该乐团原有男女学生一共人。

5. 规定12010203=+=※...，232349=0+0+0=0※....，54567826=0+0+0+0=※.....，如果15165a =※.，那么a 等于。

二、填空题（每题10分，共50分）6. 从如图正方体的顶点A 沿正方体的棱到顶点B ，每个顶点恰好经过一次，一共有种不同的走法。

7. 在如图每个方框中填入一个数字，使得乘法竖式成立。

那么，两个乘数的和是。

8. 两个正方形如图放置，图中的每个三角形都是等腰直角三角形；若其中较小正方形的边长为12cm ，那么较大正方形的面积是 cm 2。

9. 如图的5×5的表格中有6个字母，请沿格线将右图分割为6个面积不同的小长方形（含正方形），使得每个长方形中恰好有一个字母，且每个字母都在小长方形角上的方格中。

若这六个字母分别等于它所在小长方形的面积，那么五位数ABCDE = 。

10. 一个村庄有2011个小矮人，他们每个人不是戴红帽子，就是戴蓝帽子。

戴红帽子时说真话；戴1蓝帽子时说假话。

他们可以改变帽子的颜色。

某一天，他们恰好每两人都见了一次面，并且都说对方戴蓝帽子。

这一天他们总共最少改变了次帽子的颜色。

三、填空题（每题12分，共60分）11. 如图，一个长方形被分成8个小长方形，其中长方形A 、B 、C 、D 、E 的周长分别是26厘米、28厘米、30厘米、32厘米、34厘米，那么大长方形的面积最大是平方厘米。

12. 如图是一个6×6的方格表，将数字1~6填入空白方格中，使得每一行、每一列数字1~6都只恰好出现一次，方格表还被粗线划分成了6块区域，每个区域数字1~6也恰好都只出现一次，那么最下面的一行6个数字组成的6位数是。

2012五年级数学解题能力展示初赛试题+详解

E、F、G、H 代表 1～8 中不同的数字（不同的字母代表不同的数字）．那么四位数 ABCD ＝． H
12. 有一个 6×6 的正方形，分成 36 个 1×1 的正方形．选出其
中一些 1×1 的正方形并画出它们的对角线，使得所画出的任何两条对角线都没有公共点，那么最多可以画出角线．条对
8. 今天是 2011 年 12 月 17 日，在这个日期中有 4 个 1、2 个 2、1 个 0、1 个 7．用这 8 个
数字组成若干个合数再求和（每个数字恰用一次，首位数字不能为 0，例如 21110 与 217 的和是 21327），这些合数的和的最小值是．
1/8
【杯赛真题】 · 【迎春杯】 · 【五年级】 · 【初赛】
4. 在右图中，共能数出
知识点：几何计数难度：★★ 答案：40
个三角形．
解：按组成三角形的块数来分类．
3/8
【杯赛真题】 · 【迎春杯】 · 【五年级】 · 【初赛】
一块的三角形：16；两块的三角形：16；三块的三角形：8．所以，三角形一共 16＋16＋8＝40（个）
二．填空题（每小题 10 分，共 40 分） 5. 一个电子钟表上总把日期显示为八位数，如 2011 年 1 月 1 日显示为 20110101．如果 2011
． E F A
2. 在右图中，BC = 10，EC = 6，直角三角形 EDF 的面积比直角三 D
角形 FAB 的面积小 5．那么长方形 ABCD 的面积是． C
3. 龙腾小学五年级共有四个班．五年级一班有学生 42 人，五年级二
班是一班人数的年级共有
B
6 5 ，五年级三班是二班人数的，五年级四班是三班人数的 1.2 倍．五 7 6

2010五年级数学解题能力展示初赛试题+详解

．
答案：30 简答：
1 1 1 1 6 （） 12 （） 19 33 21 7 22 2 3 3 4 1 7 19 33 21 7 22 30
2. 小张有 200 支铅笔，小李有 20 支钢笔．每次小张给小李 6 支铅笔，小李还给小张 1 支
6. 甲、乙两车同时从 A 城市出发驶向距离 300 千米远的 B 城市.已知甲车比乙车晚出发 1
个小时，但提前 1 个小时到达 B 城市.那么，甲车在距离 B 城市_________千米处追上乙车．
7. 已知一个五位回文数等于 45 与一个四位回文数的乘积（即 abcba＝45×deed）,那么这
个五位回文数最大的可能值是_________．
1/7
【杯赛真题】 · 【迎春杯】 · 【五年级】 · 【初赛】
8. 从 1，2，3· · · ，9，10 中选出若干个数，使得 1，2，3， · · · ，19，20 这 20 个数中的每
个数都等于某个选出的数（可以相等）的和.那么，至少需要选出_________个数．
2010个 2009
5. 一个等差数列的第 3 项是 14，第 18 项是 23，那么这个数列的前 2010 项中有
项是整数．答案：402 简答：等差数列的公差等于
23 14 3 ．这个等差数列的前两项不是整数，第 n n 3 18 3 5
3 项等于 14 n - 3 ．当 n 除以 5 余 3 时，第 n 项是整数．3—2010 中一共有 402 个数 5
1 小时
甲车追上乙车的地点乙车甲车
A
1 小时
于是，甲车在距离 B 城市 150 千米处追上乙车．
7. 已知一个五位回文数等于 45 与一个四位回文数的乘积（即 abcba 45 deed ），则这个

五年级数学解决问题能力竞赛试题

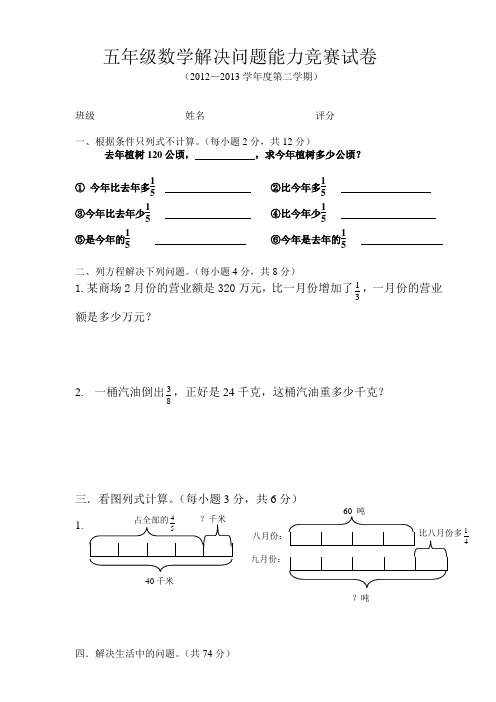
五年级数学解决问题能力竞赛试卷（2012—2013学年度第二学期）班级______________ 姓名_________________ 评分______________一、根据条件只列式不计算。

（每小题2分，共12分）去年植树120公顷，，求今年植树多少公顷？① 今年比去年多15 ②比今年多15③今年比去年少15 ④比今年少15⑤是今年的15 ⑥今年是去年的15二、列方程解决下列问题。

（每小题4分，共8分）1.某商场2月份的营业额是320万元，比一月份增加了31，一月份的营业额是多少万元？2.一桶汽油倒出83，正好是24千克，这桶汽油重多少千克？三．看图列式计算。

（每小题3分，共6分） 1.四．解决生活中的问题。

（共74分）40千米？吨41九月份：1、一个无盖长方体水箱，长2米，宽8分米，高6分米，做成这个水箱需铁皮多少平方分米？最多装水几升？（4分）2、粉刷80平方米墙面，要刷2次，在无损耗的情况下，每平米需涂料0.6升，第2次粉刷用了第1次粉刷的85，在实际粉刷中损耗约5升涂料，共需准备多少升？（4分）3、做一个长7厘米，宽4厘米，高6厘米的长方形框架，至少需要多长的铁丝？（接头处忽略不计）（4分）4、同乐学校五年级有科技书300本,科技书的本数是故事书的53,文艺书的本数是故事书的52,文艺书有多少本? （4分）5、人的血液约占人体重的131，血液中大约32是水，文文的体重是39千克，她的血液里大约含水多少千克？（4分）6、某电视机厂五月份生产电视机16万台，六月份比五月份减产81，六月份生产多少万台？（4分）7、学校图书馆新购一批图书，其中科技书240本，科技书比文艺书多51，文艺书有多少本？（4分）8、加工一批零件，第一天加工200个，第二天加工250个，两天共加工了这批零件的53，这批零件共多少个？（4分）9、一台电视机原价4500元，现在降价51，这台电视机现价多少钱？（4分）10、同学们采集树种，第一天采集了35 千克，第二天比第一天多采了16 千克，第二天采集了多少千克的树种？（4分）11、仓库有化肥3400吨，第一次取出总量的41，第二次取出总量的103，还剩多少吨？（4分）12、小军过生日，妈妈买来一个蛋糕，切了31给小军。

2020年“春笋杯”数学解题能力展示初赛试卷(五年级)(5)

2013年“迎春杯”数学解题能力展示初赛试卷（五年级）一、填空题（共3小题，每小题8分，满分24分）1．（8分）算式999999999﹣88888888+7777777﹣666666+55555﹣4444+333﹣22+1的计算结果的各位数字之和是．2．（8分）如图竖式中，使得乘积最小的两个乘数和是．3．（8分）把1﹣8这8个数字放到一个正方体的八个顶点处，然后在每条棱的中点处写上这条棱的两个顶点处所写的数的平均数，如果上底面的四个中点和下底面的四个中点上写的数都是整数，那么另外四个中点处所写的数中，有不是整数．二、填空题（共3小题，每小题12分，满分36分）4．（12分）如图，在等腰直角三角形ABC中，斜边AB上有一点D，已知CD＝5，BD比AD长2，那么三角形ABC的面积是．5．（12分）如图，7×7的表格中，每格填入一个数字，使得相同的数字所在的方格都连在一起（相连的两个方格必须有公共边），现在已经给出了1，2，3，4，5各两个，那么，表格中所有数的和是．12533421546．（12分）甲、乙两人从A地步行去B地．乙早上6：00出发，匀速步行前往；甲早上8：00才出发，也是匀速步行．甲的速度是乙的速度的2.5倍，但甲每行进半小时都需要休息半小时．甲出发后经过分钟才能追上乙．三、填空题（每小题15分，满分75分）7．（15分）五支足球队伍比赛，每两个队伍之间比赛一场：胜者得3分，负者得0分，平局各得1分，比赛完毕后，发现各队得分均不超过9分，且恰有两只队伍同分，设五支队伍的得分从高到低依次为A、B、C、D、E（有两个字母表示的数是相同的），若恰好是15的倍数，那么此次比赛中共有多少场平局？8．（15分）由2013个边长为1的小正三角形拼成的四边形中，周长的最小值是．9．（15分）如图，正六边形ABCDEF的面积为1222，K、M、N分别AB，CD，EF的中点，那么三角形PQR的边长是．10．（15分）一个自然数恰有9个互不相同的约数，其中3个约数A，B，C满足：①A+B+C＝79②A×A＝B×C那么，这个自然数是．11．（15分）有一个奇怪的四位数（首位不为0），它是完全平方数，它的数字和也是完全平方数，用这个四位数除以它的数字和得到的结果还是完全平方数，并且它的约数个数还恰好等于它的数字和，那当然也是完全平方数，如果这个四位数的各位数字互不相同，那么这个四位数是多少？2013年“迎春杯”数学解题能力展示初赛试卷（五年级）参考答案与试题解析一、填空题（共3小题，每小题8分，满分24分）1．（8分）算式999999999﹣88888888+7777777﹣666666+55555﹣4444+333﹣22+1的计算结果的各位数字之和是45．【解答】解：由于计算过程没有出现进位借位，故结果各位数字之和就是式中各数的各位数字之和相加减，原式＝9×9﹣8×8+7×7﹣6×6+5×5﹣4×4+3×3﹣2×2+1×1（mod10）＝（9+8）（9﹣8）+（7+6）（7﹣6）+…+（3+2）（3﹣2）+1＝9+8+7+6+5+4+3+2+1＝45，故答案为45．2．（8分）如图竖式中，使得乘积最小的两个乘数和是160．【解答】解：（1）积的最高位是2，可以得出前面两次算出的积的最高位都是1，再由此推出第一个乘数的第一位是1，最后一位是3；（2）根据积的个位是1，可以知道两个乘数的个位数字的积的末尾是1，结合上第一个乘数的个位是3，就能确定第二个乘数的个位是7；（3）因为第一个乘数乘第二个乘数的十位数字得到的是一百多，也就能确定第二个乘数的十位数字是1；（4）根据第一个乘数乘7的积是一千零几，可以推出第一个乘数的十位数字是4．故这题中两个乘数是143和17，第一次算出的积是1001，第二次的积是143，最后的积是2431．因此这两个乘数的和是143+17＝160．3．（8分）把1﹣8这8个数字放到一个正方体的八个顶点处，然后在每条棱的中点处写上这条棱的两个顶点处所写的数的平均数，如果上底面的四个中点和下底面的四个中点上写的数都是整数，那么另外四个中点处所写的数中，有4个不是整数．【解答】解：奇偶性问题1～8八个数4奇4偶，上下两组各4个数同时满足相邻和为偶数，唯一情况为上下另组数分别同奇同偶．即上面4个为奇数，下面4个为偶数或者上面4个为偶数，下面4个为奇数．所以上下4组数和都是奇数，即它们的平均数都不是整数．所以有4个不是整数．故答案为4个．二、填空题（共3小题，每小题12分，满分36分）4．（12分）如图，在等腰直角三角形ABC中，斜边AB上有一点D，已知CD＝5，BD比AD长2，那么三角形ABC的面积是24．【解答】解：作CE⊥AB于E．∵CA＝CB，CE⊥AB，∴CE＝AE＝BE，∵BD﹣AD＝2，∴BE+DE﹣（AE﹣DE）＝2，∴DE＝1，在Rt△CDE中，CE2＝CD2﹣DE2＝24，＝•AB•CE＝CE2＝24，∴S△ABC故答案为245．（12分）如图，7×7的表格中，每格填入一个数字，使得相同的数字所在的方格都连在一起（相连的两个方格必须有公共边），现在已经给出了1，2，3，4，5各两个，那么，表格中所有数的和是150．1253342154【解答】解：首先理解题目，找出唯一填法的空格，例如第一行第一个1，与其唯一相邻的空白空格必须为1，以此类推，第二行第一个5也具有唯一相邻空格．逆推得出唯一图形．相加求和为150．黑豆网https://黑豆网是国内不错的在线观看电影的网站，涵盖电影，电视剧，综艺，动漫等在线观看资源！金马医药招商网:##金马医药招商网是专业提供医药代理招商的资讯信息发布平台，医药代理招商网即医药视频招商网或医药火爆招商网这里提供专业的医药代理招商服务。

数学解题能力展示五年级真题汇编0712

5.如图，7×7 的表格中，每格填入一个数字，使得相同的数字所在的方格都连在一起（相连的两个方格必须有公共边），现在已经给出了 1，2，3，4，5 各两个，那么，表格中所有数的和是________。
-4-
指南针小升初
6.甲、乙两人从 A 地步行去 B 地。乙早上 6:00 出发，匀速步行前往；甲早上 8:00 才出发，也是匀速步行。甲的速度是乙的速度的 2.5 倍，但甲每行进半小时都需要休息半小时。甲出发后经过________分钟才能追上乙。
三、填空题Ⅲ（每题12 分，共48 分）
-6-
指南针小升初
9.甲、乙两人分别从AB两地同时出发，相向而行。第一次迎面相遇在距离B地100米处，相遇后甲的速度提高到原来的 2倍；甲到 B 后立即调头，追上乙时，乙还有 50米才到A。那么，AB间的路程长________米。 10.在右图中，线段AE、FG将长方形ABCD分成了四块；已知其中两块的面积分别是 2 cm2、 11cm2，且E 是 BC 的中点， O是AE的中点；那么长方形ABCD的面积是________cm2。
-7-
指南针小升初
2011 年“数学解题能力展示”读者评选活动五年级组初试试题
一、填空题（每题8分，共40分） 1.算式 1 2 3 4 5 6 7 8 9 10 的计算结果是________。
2.十二月份共有 31天，如果某年 12月 1 日是星期一，那么该年 12月 19日是星期 ________。(星期一至星期日用数字1至7表示) 3.如图的等腰梯形上底长度等于3，下底长度等于9，高等于4，那么这个等腰梯形的周长等于________。 4.某乐团女生人数是男生人数的2倍，若调走24名女生，则男生人数是女生人数的2 倍，那么该乐团原有男女学生一共有________人。 5.规定 1※2=0.1+0.2=0.3 , 2※3=0.2+0.3+0.4=0.9 , 5※4=0.5+0.6+0.7+0.8=2.6 。如果 a ※15=16.5，那么 a 等于________。

2014数学解题能力展示五年级初赛真题

（B）图 2
（C）图 3
（D）图 4 ）辆这样
一辆大卡车一次可以装煤 2.5 吨，现在要一次运走 48 吨煤，那么至少需要（的大卡车. （A）18 （B）19 （C）20 （D）21
4.
已知 a 、 b 、 c 、（D）四个数的平均数是 12.345， a > b > c >（D），那么 b （（A）大于 12.345 （C）等于 12.345 （B）小于 12.345 （D）无法确定
7.
在下列算式的空格中填入互不相同的数字： □□□□ □□□□□ 2014 .其中五个一位数的和最大是（（A）15 （B）24 ）（C）30 （D）35 ）
8.
已知 4 个质数的积是它们和的 11 倍，则它们的和为（（A）46 （B）47 （C）48
（D）没有符合条件的数
9.
为了减少城市交通拥堵的情况，某城市拟定从 2014 年 1 月 1 日起开始试行新的限行规则，规定尾号为 1、6 的车辆周一、周二限行，尾号 2、7 的车辆周二、周三限行，尾号 3、8 的车辆周三、周四限行，尾号 4、9 的车辆周四、周五限行，尾号 5、0 的车辆周五、周一限行，周六、周日不限行．由于 1 月 31 日是春节，因此，1 月 30 日和 1 月 31 日两天不限行．已知 2014 年 1 月 1 日是周三并且限行，那么 2014 年 1 月份（多．（A）1、6 （B）2、7 （C）4、9 （D）5、0 ）是不）组尾号可出行的天数最
13. 甲、乙两人比赛折返跑，同时从 A 出发，到达 B 点后，立即返回，先回到 A 点的人获胜．甲先到达 B 点，在距离 B 点 24 米的地方遇到乙．相遇后，甲的速度减为原来的一半，乙的速度保持不变．在距离终点 48 米的地方，乙追上甲．那么，当乙到达终点时，甲距离终点还有 __________米． A. 6 B. 8 C. 12 D. 16

第五届数学节《五年级数学解题能力大赛试题及答案》

武汉市光谷第三小学教育集团第五届数学节五年级数学解题能力大赛竞赛题学校：班级：姓名：分数：一、填空：（每空2分，共36分）1、小林家住在三楼，他每上一层楼要走14级台阶，小林从一楼走到三楼要走（）级台阶。

2、一件毛衣102元，比一副手套的5倍还多12元，一副手套（）元。

3、小张有2元和5元的人民币共34张，总值110元，问2元的人民币有（）张；5元的人民币有（）张。

4、5.08、10.008、15.0008、（）。

5、小英4次语文测验的平均成绩是89分，第5次测验得了94分。

她5次测验的平均成绩是( )分。

6、用5、5、5、1四个数字组成一个算式，使其结果为24。

算式是。

7、1、一个三位小数，四舍五入后是5.70，那么原来这个三位小数最大是( )，最小是( )。

8、3÷7的商的小数点后的第1995个数字是( )。

9、一个小数去掉小数点后比原数大229.68，这个小数是( )。

10、甲数减去乙数等于36.63，甲数的小数点向左移动两位就等于乙数，甲乙两数各是( )，( )。

11、一道减法算式，被减数加减数再加差的和是647，又知减数比差的3倍多17，减数是( )。

12、小红做一道乘法题时，错把乘数112看成121，这样算的积比正确积多450，正确的积是( )。

13、长方形的长与宽都扩大5倍，它的周长扩大( )倍，而面积增加( )倍。

14、学校举行篮球比赛，裁判员抛银币来决定谁开球，出现正面的可能性和反面的可能性是（）。

二、简算:（每题7分，共14分）7.29×4.6+46×1.271 2.01＋2.02＋2.03＋2.04＋……＋2.49＋2.5二、应用题：（每题10分，共50分）1、一架飞机从甲地到乙地，原计划每分钟飞行9千米，现在按每分钟12千米的速度飞行，结果比原计划提前半小时到达。

甲、乙两地相距多少千米？2、一列火车长140米，每秒钟行驶20米，全车通过汉江上一座长420米的大桥，需要多长时间？3、为鼓励居民节约用水，自来水公司规定：每户每月用水15吨以内（含15吨）每吨1.2元收费，超过15吨的部分按每吨3.5元收费。

2020年“春笋杯”数学解题能力展示初赛试卷(五年级)(4)

金马医药招商网:## 金马医药招商网是专业提供医药代理招商的资讯信息发布平台，医药代理招商网即医药视频招商网或医药火爆招商网这里提供专业的医药代理招商服务。
科技新闻网:## 科技新闻网每天更新最新科技新闻,这里有最权威的科技新闻资料,我们是国内外最新的科技新闻网。
所以 AB 间的路程为： 100×（1.5+1）＝100×2.5 ＝250（米）答：A、B 间的路程长 250 米． 10．（12 分）在图中，线段 AE、FG 将长方形 ABCD 分成了四块；已知其中两块的面积分别是 2 平方厘米、11 平方厘米，且 E 是 BC 的中点，O 是 AE 的中点；那么长方形 ABCD 的面积是 28 平方厘米．
中不同的数字（不同的字母代表不同的数字），那么四位数＝
．
12．（12 分）有一个 6×6 的正方形，分成 36 个 1×1 的正方形．选出其中一些 1×1 的正方
形并画出它们的对角线，使得所画出的任何两条对角线都没有公共点，那么最多可以画
出
条对角线．
第 2页（共 9页）
2012 年“迎春杯”数学解题能力展示初赛试卷（五年级）
若五个队的积分是 4～8，则总分是 30，从而没有平局，每个队得分都是 3 的倍数，矛盾．
所以五个队的积分是 3～7，则总分是 25，共平 5 场，A+B+C+D+E＝2×5＝10，
第一名得 7 分，共 4 场，只能是胜 2，平 1，负 1，所以 A＝1，
第三名得 5 分，共 4 场，只能是胜 1，平 2，负 1，所以 C＝2，
＝ 13213 ．
【解答】解：五支足球队比赛，共赛＝10 场，每场两队得分和为 2 或 3，所以总分为
20～30 之间．

五年级数学竞赛初赛试题及答案小学数学五年级下册奥数试题及答案人教版

五年级数学竞赛初赛试题及答案小学数学五年级下册奥数试题及答案人教版五年级数学竞赛初赛试题（满分120分）一、计算题（能用简便方法计算的，要用简便算法。

每题4分，共12分。

）2.77×13+255×999+510二、填空题（1～9题每空4分，10～12题每空3分，共54分。

）1.a=8.8+8.98+8.998+8.9998+8.99998，a的整数部分是____。

2.1995的约数共有____。

3.等式“学学×好好+数学=1994”，表示两个两位数的乘积，再加上一个两位数，所得的和是1994。

式中的“学、好、数”3个汉字各代表3个不同数字，其中“数”代表____。

4.如图1，“好、伙、伴、助、手、参、谋”这7个汉字代表1～7这7个数字。

已知3条直线上的3个数相加、2个圆圈上3个数相加所得的5个和都相等。

图中间的“好”代表____。

5.农民叔叔阿根想用20块长2米、宽1.2米的金属网建一个靠墙的长方形鸡窝（如图2）。

为了防止鸡飞出，所建鸡窝高度不得低于2米。

要使所建的鸡窝面积最大，BC的长应是米。

7.小胡和小涂计算甲、乙两个两位数的乘积，小胡看错了甲数的个位数字，计算结果为1274；小涂看错了甲数的十位数字，计算结果为819。

甲数是____。

8.1994年“世界杯”足球赛中，甲、乙、丙、丁4支队分在同一小组。

在小组赛中，这4支队中的每支队都要与另3支队比赛一场。

根据规定：每场比赛获胜的队可得3分；失败的队得0分；如果双方踢平，两队各得1分。

已知：（1）这4支队三场比赛的总得分为4个连续奇数；（2）乙队总得分排在第一；（3）丁队恰有两场同对方踢平，其中有一场是与丙队踢平的。

根据以上条件可以推断：总得分排在第四的是____队。

9.一块空地上堆放了216块砖（如图3），这个砖堆有两面靠墙。

现在把这个砖堆的表面涂满石灰，被涂上石灰的砖共有____块。

10.南方某城市的一家企业有90％的员工是股民，80％的员工是“万元户”，60％的员工是打工仔。

解题能力展示初赛五级(Word解析)

2013“数学解题能力展示”读者评选活动笔试试题小学五年级（2012年12月22日）一、填空题（每小题8分，共24分）1．算式999999999888888887777777666666555554444333221-+-+-+-+的计算结果的各位数字之和是___________．2．如图竖式中，使得乘积最小的两个乘数和是___________．213×3．把1～8这8个数字放到一个正方体的八个顶点处，然后在每条棱的中点处写上这条棱的两个顶点处所写的数的平均数．如果上底面的四个中点和下底面的四个中点上写的数都是整数，那么另外四个中点处所写的数中，有___________个不是整数．二、填空题（每小题12分，共36分）4．如图，在等腰直角三角形ABC中，斜边AB上有一点D．已知=5CD，BD比AD长２，那么三角形ABC 的面积是___________．DC BA5．如图，77⨯的表格中，每格填入一个数字，使得相同的数字所在的方格都连在一起（相连的两个方格必须有公共边），现在已经给出了1，2，3，4，5各两个，那么，表格中所有数的和是___________．6．甲、乙两人从A 地步行去B 地，乙早上6：00出发，匀速步行前往；甲早上8:00才出发，也是匀速步行．甲的速度是乙的速度的2．5倍，但甲每行进半小时都需要休息半小时，那么甲出发后经过________分钟才能追上乙．三、填空题（每小题15分，共60分）7．五支足球队伍比赛，每两个队伍之间比赛一场；胜者得3分，负者得0分，平局各得1分．比赛完毕后，发现各队得分均不超过9分，且恰有两支队伍同分．设五支队伍的得分从高到低依次为A 、B 、C 、D 、E （有两个字母表示的数是相同的）．若ABCDE 恰好是15的倍数，那么此次比赛中共有______场平局．8．由2013个边长为1的小正三角形拼成的四边形中，周长的最小值是__________．9．如图，正六边形ABCDEF 的面积为1222，K 、M 、N 分别AB 、CD 、EF 的中点，那么三角形PQR 的面积是___________．N MK R Q PF EDCBA10．一个自然数恰有9个互不相同的约数，其中有3个约数A 、B 、C 满足：①79A B C ++= ②A A B C ⨯=⨯那么，这个自然数是___________．11．有一个奇怪的四位数（首位不为0），它是完全平方数，它的数字和也是完全平方数，用这个四位数除以它的数字和得到的结果还是完全平方数，并且它的约数个数还恰好等于它的数字和，那当然也是完全平方数，如果这个四位数的各位数字互不相同，那么这个四位数是__________．2013“数学解题能力展示”读者评选活动笔试试题小学五年级参考答案1 2 3 4 545 160 4 24 1506 7 8 9 10 11 330 3 127 141 4412601部分解析一、填空题（每小题8分，共24分）1．算式999999999888888887777777666666555554444333221-+-+-+-+的计算结果的各位数字之和是___________．【考点】计算【难度】☆☆【答案】45【解析】方法一：多位数计算，算出结果918273645，求得各位数字和为45．方法二：由于计算过程没有产生进位或借位，故结果的数字和是99887766554433221145⨯-⨯+⨯-⨯+⨯-⨯+⨯-⨯+⨯=2．如图竖式中，使得乘积最小的两个乘数和是___________．213×【考点】数字谜【难度】☆☆☆【答案】160【解析】首先判断出第一，第二，第三，第四排第一个数均为1（如图1）11111213×73A11111213×进而求出两个乘数的末尾数字（如图2），这时经测试发现A可取4和5，由题意要求最小则两个乘数分别为143和17，求和得160．3．把1～8这8个数字放到一个正方体的八个顶点处，然后在每条棱的中点处写上这条棱的两个顶点处所写的数的平均数．如果上底面的四个中点和下底面的四个中点上写的数都是整数，那么另外四个中点处所写的数中，有___________个不是整数．【考点】奇偶性【难度】☆☆【答案】4【解析】奇偶性问题1～8八个数4奇4偶，上下两组各4个数同时满足相邻和为偶数，唯一情况为上下另组数分别同奇同偶．即上面4个为奇数，下面4个为偶数或者上面4个为偶数，下面4个为奇数．所以上下4组数和都是奇数，即它们的平均数都不是整数．所以有4个不是整数．二、填空题（每小题12分，共36分）4．如图，在等腰直角三角形ABC中，斜边AB上有一点D．已知=5CD，BD比AD长２，那么三角形ABC 的面积是___________．ADC B 【考点】几何【难度】☆☆☆【答案】24【解析】等腰直角三角形，面积等于斜边高的平方．ADEC B过C点做斜边AB的垂线，交AB于点E，由于2BD ADDE=-=得到1根据勾股定理，22222=-=-=5124CE CD DE所以24S =ABC5．如图，77⨯的表格中，每格填入一个数字，使得相同的数字所在的方格都连在一起（相连的两个方格必须有公共边），现在已经给出了1，2，3，4，5各两个，那么，表格中所有数的和是___________．【考点】数阵图【难度】☆☆☆☆ 【答案】150【解析】首先理解题目，找出唯一填法的空格，例如第一行第一个1，与其唯一相邻的空白空格必须为1，以此类推，第二行第一个5也具有唯一相邻空格．逆推得出唯一图形．相加求和为150．44444444444445555555333333333333332222221111111116．甲、乙两人从A 地步行去B 地，乙早上6：00出发，匀速步行前往；甲早上8:00才出发，也是匀速步行．甲的速度是乙的速度的2．5倍，但甲每行进半小时都需要休息半小时，那么甲出发后经过________分钟才能追上乙．【考点】行程问题【难度】☆☆☆ 【答案】330【解析】有休息间隔的追及问题和工程问题，直接用平均的速度进行计算容易产生错误．此题可列表解决，假设甲一小时走5米，乙一小时走2米，列表如下：时间甲（米）乙（米）时间甲（米）乙（米） 0小时 0 4 3小时 7．5 10 0．5小时 2．5 5 3．5小时 10 11 1小时 2．5 6 4小时 10 12 1．5小时 5 7 4．5小时 12．5 13 2小时 5 8 5小时 12．5 14 2．5小时7．595．5小时1515观察得5．5小时恰好追上（如果这时间超过了乙，就要用具体追及公式计算追及时间）5.560=330⨯（分钟）三、填空题（每小题15分，共60分）7．五支足球队伍比赛，每两个队伍之间比赛一场；胜者得3分，负者得0分，平局各得1分．比赛完毕后，发现各队得分均不超过9分，且恰有两支队伍同分．设五支队伍的得分从高到低依次为A 、B 、C 、D 、E （有两个字母表示的数是相同的）．若ABCDE 恰好是15的倍数，那么此次比赛中共有______场平局．【考点】逻辑推理【难度】☆☆☆☆☆ 【答案】3【解析】体育比赛得分问题，首先算出比赛一共10场，总分在20到30分之间．五位数ABCDE 是15的倍数，利用整除性可知，E 可为0或者5，考虑到E 最小，如果5E =，总分最小为 8+7+6+5+5=31分，不成立，所以=0E ，即第五名4场全负积0分．第五名负四场，则平局最多为6场，总分最少为24分．又考虑到分数和为3的倍数，总分可能情况为30，27，24．对三种情况分别讨论：（1）总分30分：即无平局情况，那么前四名队伍得分只可能为9，6，3分．不能在只有两个重复的情况下凑出30．所以总分30分情况不存在．（2）总分27分：经测试，存在9+8+5+5=27，满足题目分数要求，且四个队7场胜3场负，恰好满足第五队的4场负，所以此为一解，比赛3场平局．（3）总分24分：在24分情况下，只有前四名只能各胜1场平2场，但不满足只有两队得分相同．所以总分24分情况不存在．综上，唯一存在总分27分情况下，比赛中共有3场平局．8．由2013个边长为1的小正三角形拼成的四边形中，周长的最小值是__________．【考点】几何【难度】☆☆☆☆☆ 【答案】127【解析】正三角形组成两种四边形，平行四边形和梯形．平行四边形要求偶数个三角形，而此题为2013个正三角形，所以一定构成梯形．那么在构造的梯形中，相邻层数间都差2个三角形，且都是奇数个，则可以构造一个梯形：第一次层有：21a +个三角形；最后一层有21b +个三角形，则有层数为1b a -+层．利用等差数列求和公式得：(2121)(1)22013a b b a +++⨯-+÷= 化简得(1)(1)2013b a b a ++⨯-+=再考虑这个梯形上底长：a ；下底长1b +；腰为：1b a -+；则周长可列为：33b a -+ 由于2013=31161⨯⨯，考虑到要想周长最小，即b 尽量大，a 尽量小取161b a ++=，133b a -+=，得14a =，46b =．带入得最小周长33127b a --=．9．如图，正六边形ABCDEF 的面积为1222，K 、M 、N 分别AB 、CD 、EF 的中点，那么三角形PQR 的面积是___________．N MK R Q PF EDCBA【考点】几何【难度】☆☆☆☆☆ 【答案】141【解析】如图延长BA 和EF 交于点O ，并连接AE ，ON M K RQ PF EDCBA由正六边形的性质，我们可知13ABCM CDEN EFAK S S S ===六边形面积根据容斥原理，重叠部分三个三角形面积和等于阴影部分面积，且因为对称，AKP ∆，CMQ ∆，ENR ∆三个三角形是一样的，有KP RN =，AP ER =，RP PQ =，13AK OK =，则34EN EO =，34KP AP =，由鸟头定理可知道3KP AP RP PQ ⨯⨯=⨯ 综上可得：322PR KP RE ==，那么由三角形AEK 是六边形面积的16，且14123APK AKE S S ∆∆=⨯++，14726APK ABCDEF S S ∆=⨯=，所以阴影面积为473=141⨯10．一个自然数恰有9个互不相同的约数，其中有3个约数A 、B 、C 满足：①79A B C ++= ②A A B C ⨯=⨯那么，这个自然数是___________．【考点】数论【难度】☆☆☆☆☆ 【答案】441【解析】一个自然数N 恰有9个互不相同的约数，则可得22N x y =⨯，或者8N x =，（1）当8N x =，则九个约数分别是：23456781,,,,,,,,x x x x x x x x ，其中有3个约数A 、B 、C 且满足A A B C ⨯=⨯，不可能．（2）当22N x y =⨯，则九个约数分别是：2222221,,,,,,,,x y x xy y x y xy x y ，其中有3个约数A 、B 、C 且满足A A B C ⨯=⨯，① A x =，1B =，2C x =，则2179x x ++=，无解． ② A xy =，1B =，22C x y =，则22179xy x y ++=，无解． ③ A xy =，B x =，2C xy =，则279xy x xy ++=，无解．④ A xy =，2B x =，2C y =，则2279xy x y ++=,解得：37x y =⎧⎨=⎩，则2237441N =⨯=．⑤ 2A x y =，22B x y =，2C x =，则222279x y x y x ++=，无解．11．有一个奇怪的四位数（首位不为0），它是完全平方数，它的数字和也是完全平方数，用这个四位数除以它的数字和得到的结果还是完全平方数，并且它的约数个数还恰好等于它的数字和，那当然也是完全平方数，如果这个四位数的各位数字互不相同，那么这个四位数是__________．【考点】数论【难度】☆☆☆☆☆【答案】2601【解析】四位数中，各个位数不重复的情况下，和可以为9，16，25．且因为完全平方数的约数为奇数个，则可以是9，25两种情况．9的情况下，该数为223a=，得符合要求四位数2601．a⨯形式，因为a为质数，经测试可取1725的情况下，该数为445a⨯形式，故a取任何质数不能满足条件．所以符合题意要求的四位数为2601．。

“数学解题能力展示”读者评选活动五年级组初赛试卷(无答案)

用心爱心专心 1“数学解题能力展示”读者评选活动五年级组初赛试卷（无答案）（测评时间：2007年12月2日9：00—10：30；满分150）一、填空题Ⅰ（每题8分，共40分）1. 小华在计算3.69除以一个数时，由于商的小数点向右多点了一位，结果得24.6，这道题的除数是。

（1.5）2. 右图中平行四边形的面积是1080m 2，则平行四边形的周长为 m 。

（216）3. 当a = 时，下面式子的结果是0？当a = 时，下面式子的结果是1？（9；7）（36－4a ）÷84. 箱子里装有同样数量的乒乓球和羽毛球。

每次取出5个乒乓球和3个羽毛球，取了几次之后，乒乓球恰好没有了，羽毛球还有6个，则一共取了次，原来有乒乓球和羽毛球各个。

（3；15）5. 在右边的竖式中，相同字母代表相同数字，不同字母代表不同数字，则四位数tavs = 。

（1038）二、填空题Ⅱ（每题10分，共50分）6. 一个五位数恰好等于它各位数字和的2007倍，则这个五位数是。

（36126或54189）7. 一个等腰直角三角形和一个正方形如图摆放，①、②、③这三块的面积分别是2、8、58，则④、⑤这两块的面积差是。

（8）8. 在纸上写着一列自然数1，2，…，98，99。

一次操作是指将这列数中最前面的三个数划去，然后把这三个数的和写在数列的最后面。

例如第一次操作后得到4，5，…，98，99，6；而第二次操作后得到7，8，…，98，99，6，15。

这样不断进行下去，最后将只剩下一个数，则最后剩下的数是。

（4950）①④②③⑤本资料来自于资源最齐全的２１世纪教育网21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。

奥数2012迎春杯数学解题能力展示初赛五年级试卷及答案

一、填空题（每小题 8 分，共 32 分） 1. 算式 101×2012×121÷1111÷503 的计算结果是＿＿＿＿。解析：
2. 在右图中，BC=10,EC=6,直角三角形 EDF 的面积比直角三角形 FAB 的面积小 5.那么长方形 ABCD 的面积是＿＿＿＿。
解析：
3. 龙腾小学五年级共有四个班。五年级一班有 42 人，五年级二班是一班人数的 6/7，五年级三班是二班人数的 5/6，五年级四班是三班人数的 1.2 倍。五年级共有＿＿＿＿人。
解析：
4. 在右图中，共能数出＿＿个三角形。
解析：
二、填空题（每小题 10 分，共 40 分）
5. 一个电子钟表上总把日期显示为八位数，如 2011 年 1 月 1 日显示为 20110101。如果 2011 年最后
一个能被 101 整除的日子是，那么＝＿＿＿＿。
解析：
-1-
试题
6. 在右图的除法竖式中，被除数是＿＿＿＿。
解析：
12. 有一个 6×6 的正方形，分成 36 个 1×1 的正方形。选出其中一些 1×1 的正方开并画出它们的对角线，使得所画出的任何两条对角线都没有公共点，那么最多可以画出＿＿＿＿条对角线。
解析：
-4-
试题
2012“数学解题能力展示”读者评选活动
五年级组初试试卷
（评测时间：2011 年 12 月 17 日 9：00——10：00）
学生诚信协议：活动期间，我确定没有就所涉及的问题或结论，与任何人、用任何方式交流或讨论，我确定以下的答案均为我个人独立完成的成果。否则愿接受本次成绩无效的处罚。
我同意遵守以上协议签名＿＿＿＿＿＿
10. 在右图中，线段 AE、FG 将长方形 ABCD 分成了四块；书籍其中两块的面积分别是、,且 E 是 BC 的中点，O 是 AE 的中点，那么长方形 ABCD 的面积是＿＿＿＿.

“数学解题能力展示”五年级组初试试卷

2010年“数学解题能力展示”五年级组初试试卷试题一、填空题I1、计算：6x(1/2—1/3)+12x(1/3+1/4)+19—33+21—7+22=（）2、小张有200支铅笔，小李有20支钢笔，每次小张给小李6支铅笔，小李还给小张1支钢笔，经过________次这样的交换后，小张手中铅笔的数量是小李手中钢笔数量的11倍。

3、在长方形ABCD中，BE=5，EC=4，CF=4，FD=1，如图所示，那么△AEF的面积为（）4、2009x2009x……2009 的个位数字是______.2010个2009二、填空题II5、一个等差数列的第3项是14，第18项是23，那么这个数列的前2010项中有___项是整数。

6、甲、乙两车同时从A城市出发驶向距离300千米远的B城市。

已知甲车比乙车晚出发1个小时，但提前1个小时到达B城市。

那么，甲车在距离B城市千米处追上乙车。

7、已知一个五位回文数等于45与一个四位回文数的乘积（即abcda =45xdeed）,那么这个五位回文数最大的可能值是___ 。

8、请从1，2，3……，9，10中选出若干个数，使得1，2，3……，19，20这20个数中的每个数都等于某个选出的数或某两个选出的数（可以相等）的和。

那么，至少需要选出____个数。

三、填空题III9、如图，请沿虚线将7x7的方格表分割成若干个长方形，使得每个长方形中恰好包含一个数字，并且这个数字就是长方形的面积，那么第四列的7个小方格分别属于个不同长方形。

10、九个大小相等的小正方形拼成了右图。

现从点A走到点B，每次只能沿着小正方形的对角线从一个顶点到另一个顶点，不允许走重复路线（如图的虚线就是一种走法），那么从点A走到点B共有__________ 种不同的走法。

11如图，等腰直角三角形DEF的斜边在等腰直角三角形ABC AE、AD、AF，于是整个图形被分成五块小三角形。

图中已标出其中三块的面积，那么△ABC的面积是_____。

2021年五年级数学解决问题能力竞赛试卷及答案最全面

17 — 18 学年第一学期五年级数学解决问题能力竞赛卷班级姓名成绩一、填空。

（50 分，每空 5分）1、暑假里 ,兄弟两人去池塘边钓鱼,哥哥比弟弟多钓了20 条,哥哥钓地条数又正好为弟弟地 3 倍,哥哥钓了 ( )条,弟弟钓了 ( )条。

2、“十·一”假期，妈妈买一台洗衣机花了2508元，还买了一台冰箱，冰箱比洗衣机便宜365 元，买这两样电器共用了（）元钱。

3、五年级学生组成一个正方形方队表演团体操，共8 行，每行 8 人，后来由于服装不够，只好去掉一行一列，共去掉了（）个学生。

4 、小红到商店买铅笔与钢笔，全部地钱可以买 6 支铅笔与 3 支钢笔，或者10支铅笔与 2 支钢笔，如果全部买铅笔，可以买（）支。

）米。

（得数5、一幢大楼有23 层，每层高2.84米，这幢大楼约高（保留整数）6、西山小学本学期新购置课桌椅，买来 5 张桌子与 9 把椅子，共用1040 元。

）元，每把椅子（）元。

已知这种桌椅一套160 元，每张桌子（7 、一座楼房每上一层要走16 个台阶，到小英家要走64 个台阶，他家住（）楼。

8 、小明从家到学校大约 1.2 千米，他每天往返两次，一周（按 5 天）要走（）千米。

二、解决问题（ 5×8+1× 10=50分）1 、一个足球 70.5 元，学校想购买16 个， 1000 元够吗？如果不够，还应准备多少钱？2、一艘轮船从A港开往 B港，计划每小时行20 千米，实际每小时比计划多行 2.4 千米，这样行了 4.5 小时后，离B港还有 11 千米，求 AB两港相距多少千米？3、新强买了 1 枝钢笔与 1 本笔记本共用 3.6 元，向伟买了同样地 1 枝钢笔与 4 本笔记本共用了10.5 元，钢笔与笔记本地单价各为多少元？4、星期天小明去外婆家，全程 2 千米，他10 分钟走了800 米。

按这样地速度，他从上午9:00 出发，什么时候到达外婆家？5、有一堆砂子，第一次用去一半又0.5 吨，第二次用去剩下地一半又0.5吨，第三次用去第二次剩下地一半又0.5 吨，最后还剩下 6 吨，这堆砂子原来有多少吨？6、某停车场收费标准为：（1） 1 小时内收 2.5 元。

五年级学生数学能力初赛试题

五年级学生数学能力初赛试题一、看清题目，巧思妙算。

（30分）1、直接写得数(4分)2.4×5= 0.125×32= 0.32－0.22= 20÷0.01=4.7+3= 48÷0.16= 63-63÷21 = 1.6×4÷1.6×4= 2、估算（4分）7.99×8.1≈ 203÷4.2≈ 29.98-9.8≈ 795+203≈632÷69 ≈ 149×31≈ 31.8÷3.8≈ 1608-696≈3、用合适的方法计算。

（14分，最后两题6分）1600+8400÷4÷25 25×(40+8)×12568.59-8.62+78.62+31.41 87.58－（17.58－9.6）63.2×2.5+6.32×75 999×22.22＋333×33.344、求未知数X。

（8分）5.8－0.25x=3.8 5x-8+12=643.5x-x=40 18x-28=4x+84二、用心思考，正确填写。

30分（1-5题每空1分，其余每空2分）1、4.05升=（）毫升 1500平方米=( )公顷2、用1、0、8这三个数字组成一些三位数，这些三位数中含有因数2的数有（）个，含有因数3的数有（）个，含有因数5的数有（）个。

3、一个三位小数，四舍五入到百分位后是3.60，那么这个三位小数最大是（），最小是（）。

4、一个三角形的三个内角中，最大的一个角不能小于（）度。

5、观察下列算式，寻找规律填数。

2+4=2×3 2+4+6=3×4 2+4+6+8=4×52+4+6+8+10+……+50=（）×（）6、一个物体由若干个小正方体拼成，从正面、左面和上面看分别是这个物体至少由（）个小正方体拼成。

五年级数学 解题能力展示初赛试题