聚类分析ppt课件
合集下载
聚类分析及其应用实例ppt课件

在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
Outlines
聚类的思想 常用的聚类方法 实例分析:层次聚类
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
3. 实例分析:层次聚类算法
定义:对给定的数据进行层次的分解
第4 步
➢
凝聚的方法(自底向上)『常用』
思想:一开始将每个对象作为单独的
第3 步
一组,然后根据同类相近,异类相异 第2步 的原则,合并对象,直到所有的组合
并成一个,或达到一个终止条件。 第1步
a, b, c, d, e c, d, e d, e
X3 Human(人) X4 Gorilla(大猩猩) X5 Chimpanzee(黑猩猩) X2 Symphalangus(合趾猿) X1 Gibbon(长臂猿)
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
离差平方和法( ward method ):
各元素到类中心的欧式距离之和。
Gp
Cluster P
Cluster M
Cluster Q
D2 WM Wp Wq
G q
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
凝聚的层次聚类法举例
Gp G q
Dpq max{ dij | i Gp , j Gq}
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
Outlines
聚类的思想 常用的聚类方法 实例分析:层次聚类
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
3. 实例分析:层次聚类算法
定义:对给定的数据进行层次的分解
第4 步
➢
凝聚的方法(自底向上)『常用』
思想:一开始将每个对象作为单独的
第3 步
一组,然后根据同类相近,异类相异 第2步 的原则,合并对象,直到所有的组合
并成一个,或达到一个终止条件。 第1步
a, b, c, d, e c, d, e d, e
X3 Human(人) X4 Gorilla(大猩猩) X5 Chimpanzee(黑猩猩) X2 Symphalangus(合趾猿) X1 Gibbon(长臂猿)
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
离差平方和法( ward method ):
各元素到类中心的欧式距离之和。
Gp
Cluster P
Cluster M
Cluster Q
D2 WM Wp Wq
G q
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
凝聚的层次聚类法举例
Gp G q
Dpq max{ dij | i Gp , j Gq}
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
聚类分析 ppt课件
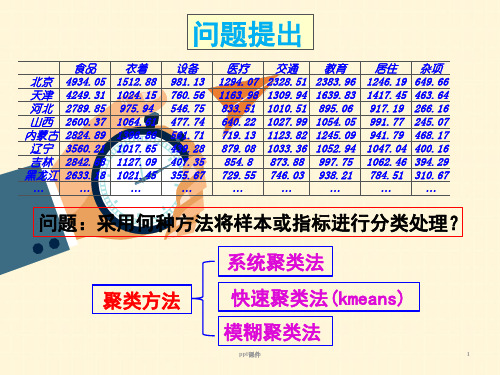
(2)相关系数
(3)距离和相关系数转换
di2j 1Ci2j
ppt课件
9
7.3 系统聚类法
1.基本思想 n个样本分成n类 计算任何两类距离 最小距离归为1类
整个过程画成聚类图
最短距离
最长距离 取
距 类平均法
离
方
重心法
法
中心距离法
离差平方和法 (Ward法)
ppt课件
10
2.系统聚类法计算公式
(1)最短距离法
…
教育 2383.96 1639.83 895.06 1054.05 1245.09 1052.94 997.75 938.21
…
居住 杂项
1246.19 649.66
1417.45 463.64
917.19 266.16
991.77 245.07
941.79 468.17
1047.04 400.16
0 0 0
0
结论:六种系统聚类法的并类原则和过程完全相同, 不同之处在于类与类之间的距离定义不同。
ppt课件
15
(7)程序实现
hc<-hclust(dist(X),method="single") #最短距离法 cbind(hc$merge,hc$height) #分类过程 plot(hc) #聚类图
[,1] [,2] [,3] [1,] -4 -5 1 [2,] -1 1 1.414 [3,] -2 2 4.123 [4,] -3 3 4.123
…
设备 981.13 760.56 546.75 477.74 561.71 439.28 407.35 355.67
…
医疗 1294.07 1163.98 833.51 640.22 719.13 879.08 854.8 729.55
(3)距离和相关系数转换
di2j 1Ci2j
ppt课件
9
7.3 系统聚类法
1.基本思想 n个样本分成n类 计算任何两类距离 最小距离归为1类
整个过程画成聚类图
最短距离
最长距离 取
距 类平均法
离
方
重心法
法
中心距离法
离差平方和法 (Ward法)
ppt课件
10
2.系统聚类法计算公式
(1)最短距离法
…
教育 2383.96 1639.83 895.06 1054.05 1245.09 1052.94 997.75 938.21
…
居住 杂项
1246.19 649.66
1417.45 463.64
917.19 266.16
991.77 245.07
941.79 468.17
1047.04 400.16
0 0 0
0
结论:六种系统聚类法的并类原则和过程完全相同, 不同之处在于类与类之间的距离定义不同。
ppt课件
15
(7)程序实现
hc<-hclust(dist(X),method="single") #最短距离法 cbind(hc$merge,hc$height) #分类过程 plot(hc) #聚类图
[,1] [,2] [,3] [1,] -4 -5 1 [2,] -1 1 1.414 [3,] -2 2 4.123 [4,] -3 3 4.123
…
设备 981.13 760.56 546.75 477.74 561.71 439.28 407.35 355.67
…
医疗 1294.07 1163.98 833.51 640.22 719.13 879.08 854.8 729.55
聚类分析 PPT课件
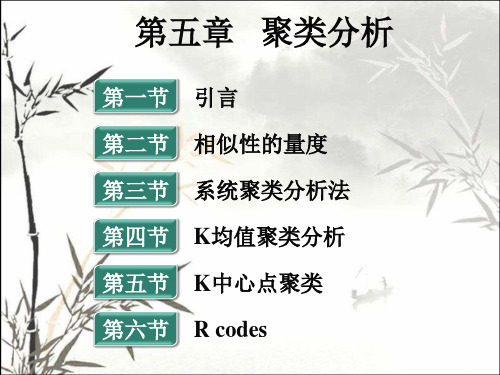
(f) (f) p dij f 1 ij d (i, j) (f) p f 1 ij
f is binary or nominal: dij(f) = 0 if xif = xjf , or dij(f) = 1 otherwise f is ordinal Compute ranks rif and Treat zif as interval-scaled
x1 x2 x3 x4
x1 0 3.61 5.1 4.24
x2 0 5.1 1
x3
x4
5
0 5.39
0
第二节 相似性的量度
一 样品相似性的度量
二 变量相似性的度量
含名义变量样本相似性度量
例: 学员资料包含六个属性:性别(男或女);外语语种
(英、日或俄);专业(统计、会计或金融);职业(教师 或非教师);居住处(校内或校外);学历(本科或本科以 下) 现有两名学员: X1=(男,英,统计,非教师,校外,本科)′ X2=(女,英,金融,教师,校外,本科以下)′ 对应变量取值相同称为配合的,否则称为不配合的 记配合的变量数为m1,不配合的变量数为m2,则样本之间 的距离可定义为
第五章 聚类分析
第一节 第二节 第三节 第四节 第五节 引言 相似性的量度 系统聚类分析法 K均值聚类分析 K中心点聚类
第六节
R codes
第一节 引言
“物以类聚,人以群分” 无监督分类聚类分析 分析如何对样品(或变量)进行量化分类的 问题 Q型聚类—对样品进行分类 R型聚类—对变量进行分类
用他们的序代替xif
zif
rif 1 M f 1
10
混合型属性
A database may contain all attribute types Nominal, symmetric binary, asymmetric binary, numeric, ordinal 可以用加权法计算合并的影响
f is binary or nominal: dij(f) = 0 if xif = xjf , or dij(f) = 1 otherwise f is ordinal Compute ranks rif and Treat zif as interval-scaled
x1 x2 x3 x4
x1 0 3.61 5.1 4.24
x2 0 5.1 1
x3
x4
5
0 5.39
0
第二节 相似性的量度
一 样品相似性的度量
二 变量相似性的度量
含名义变量样本相似性度量
例: 学员资料包含六个属性:性别(男或女);外语语种
(英、日或俄);专业(统计、会计或金融);职业(教师 或非教师);居住处(校内或校外);学历(本科或本科以 下) 现有两名学员: X1=(男,英,统计,非教师,校外,本科)′ X2=(女,英,金融,教师,校外,本科以下)′ 对应变量取值相同称为配合的,否则称为不配合的 记配合的变量数为m1,不配合的变量数为m2,则样本之间 的距离可定义为
第五章 聚类分析
第一节 第二节 第三节 第四节 第五节 引言 相似性的量度 系统聚类分析法 K均值聚类分析 K中心点聚类
第六节
R codes
第一节 引言
“物以类聚,人以群分” 无监督分类聚类分析 分析如何对样品(或变量)进行量化分类的 问题 Q型聚类—对样品进行分类 R型聚类—对变量进行分类
用他们的序代替xif
zif
rif 1 M f 1
10
混合型属性
A database may contain all attribute types Nominal, symmetric binary, asymmetric binary, numeric, ordinal 可以用加权法计算合并的影响
聚类分析(共8张PPT)
第4页,共8页。
聚类分析
三、聚类分析中的测度与标准化
在聚类分析技术的发展过程中,形成了很多种测度相似性的方法。每一种方法 都从不同的角度测度了研究对象的相似性。
在数据采集过程中,一般可以用三种方式采集数据:二分类型数据、等级类型 数据和连续类型数据。在进行聚类分析时可以根据不同的数据特点采用相应的测度 方法。
尽量避免绝对数据。
研究个案 A B C
受教育年限 10 16 6
年收入(万元) 2
1.5 1
年收入(元) 20000 15000 10000
A、B、C在不同距离单位时的距离图
A
B
B
10.01
C
A
10000
C
单位:万元
第6页,共8页。
单位:元
聚类分析
四、常用两种聚类分析方法
1.快速聚类法
快速聚类过程是初始分类的有效方法。适用于大容量样本的情形,由用户指定须聚类的 类数之后,系统采用标准迭代算法进行运算,把所有的个案归并在不同的类中。
m维空间中点与点之间的某种距离就可用来描述样品之间的亲疏程度。 而聚类分析则较常使用于将变量属性相似程度较高的观察值,加以分类,使类与类间的异质性达到最大,而同一类的几个观察值同质性很高。 ③对数据进行变换处理,(如标准化或规格化);
mm维维空 空间间中中点点与与点点实之之际间间的的应某某用种种距距时离离,就就可可两用用者来来描描的述述主样样品品要之之差间间的的别亲亲在疏疏程程于度度因。。子分析是针对“变量”予以分组,而聚类分析 按照这种方则法是不断将进“行合观并察,直值到个把所体有”的样予品以合为分一组个,大类亦为即止。因子分析时,根据因变量(题项)间关系密切与 四⑦、最常 后用绘两制否种系,聚统类聚将分类变析谱方系量法图予,按以不分同的类分(类标分准为或不几同个的层分类面原因则,子得)出不;同而的分聚类类结果分。析则较常使用于将变量属性相似 从数据结构程和度统计较形高式上的看观,因察子值分析,是加一种以“横分向类合并,”的使方类法,与聚类类分间析的则是异一质种“性纵向达合到并”最的方大法,。 而同一类的几个观察值 适每用一于 种大方容法同量都质样从本不性的同很情的形角高,度。由测用度户了指研定究须对聚象类的的相类似数性之。后,系统采用标准迭代算法进行运算,把所有的个案归并在不同的类中。 研究学生学业差异、因教师素教分学水析平:等等横,向都需简要化对研,究聚对象类进分行分析类:。纵向分组
聚类分析
三、聚类分析中的测度与标准化
在聚类分析技术的发展过程中,形成了很多种测度相似性的方法。每一种方法 都从不同的角度测度了研究对象的相似性。
在数据采集过程中,一般可以用三种方式采集数据:二分类型数据、等级类型 数据和连续类型数据。在进行聚类分析时可以根据不同的数据特点采用相应的测度 方法。
尽量避免绝对数据。
研究个案 A B C
受教育年限 10 16 6
年收入(万元) 2
1.5 1
年收入(元) 20000 15000 10000
A、B、C在不同距离单位时的距离图
A
B
B
10.01
C
A
10000
C
单位:万元
第6页,共8页。
单位:元
聚类分析
四、常用两种聚类分析方法
1.快速聚类法
快速聚类过程是初始分类的有效方法。适用于大容量样本的情形,由用户指定须聚类的 类数之后,系统采用标准迭代算法进行运算,把所有的个案归并在不同的类中。
m维空间中点与点之间的某种距离就可用来描述样品之间的亲疏程度。 而聚类分析则较常使用于将变量属性相似程度较高的观察值,加以分类,使类与类间的异质性达到最大,而同一类的几个观察值同质性很高。 ③对数据进行变换处理,(如标准化或规格化);
mm维维空 空间间中中点点与与点点实之之际间间的的应某某用种种距距时离离,就就可可两用用者来来描描的述述主样样品品要之之差间间的的别亲亲在疏疏程程于度度因。。子分析是针对“变量”予以分组,而聚类分析 按照这种方则法是不断将进“行合观并察,直值到个把所体有”的样予品以合为分一组个,大类亦为即止。因子分析时,根据因变量(题项)间关系密切与 四⑦、最常 后用绘两制否种系,聚统类聚将分类变析谱方系量法图予,按以不分同的类分(类标分准为或不几同个的层分类面原因则,子得)出不;同而的分聚类类结果分。析则较常使用于将变量属性相似 从数据结构程和度统计较形高式上的看观,因察子值分析,是加一种以“横分向类合并,”的使方类法,与聚类类分间析的则是异一质种“性纵向达合到并”最的方大法,。 而同一类的几个观察值 适每用一于 种大方容法同量都质样从本不性的同很情的形角高,度。由测用度户了指研定究须对聚象类的的相类似数性之。后,系统采用标准迭代算法进行运算,把所有的个案归并在不同的类中。 研究学生学业差异、因教师素教分学水析平:等等横,向都需简要化对研,究聚对象类进分行分析类:。纵向分组
聚类分析详解ppt课件

以上我们对例6.3.1采用了多种系统聚类法进行聚类,其结果 都是相同的,原因是该例只有很少几个样品,此时聚类的过 程不易有什么变化。一般来说,只要聚类的样品数目不是太 少,各种聚类方法所产生的聚类结果一般是不同的,甚至会 有大的差异。从下面例子中可以看到这一点。
动态聚类法(快速聚类)
(4) 对D1 重复上述对D0 的两步得 D2,如此下去 直至所有元素合并成一类为止。
如果某一步Dm中最小的元素不止一个,则称此现 象为结(tie),对应这些最小元素的类可以任选一对 合并或同时合并。
27
二、最长距离法
类与类之间的距离定义为两类最远样品间的距离, 即
DKL
max
iGK , jGL
聚类分析应注意的问题
(1)所选择的变量应符合聚类的要求
如果希望依照学校的科研情况对高校进行分类,那么可以 选择参加科研的人数、年投入经费、立项课题数、支出经 费、科研成果数、获奖数等变量,而不应选择诸如在校学 生人数、校园面积、年用水量等变量。因为它们不符合聚 类的要求,分类的结果也就无法真实地反映科研分类的情 况。
主要内容
引言 聚类分析原理 聚类分析的种类 聚类分析应注意的问题 聚类分析应用 聚类分析工具及案例分析
聚类分析的种类
(1)系统聚类法(也叫分层聚类或层次聚类) (2)动态聚类法(也叫快速聚类) (3)模糊聚类法 (4)图论聚类法
系统聚类法
对比
常用的系统聚类方法
一、最短距离法 二、最长距离法 三、中间距离法 四、类平均法 五、重心法 六、离差平方和法(Ward方法)
对比
k均值法的基本步骤
(1)选择k个样品作为初始凝聚点,或者将所有样品分成k 个初始类,然后将这k个类的重心(均值)作为初始凝聚点。
聚类分析法ppt课件全

8/21/2024
25
1.2.2 动态聚类分析法
1.2 聚类分析的种类
(3)分类函数
按照修改原则不同,动态聚类方法有按批修改法、逐个修改法、混合法等。 这里主要介绍逐步聚类法中按批修改法。按批修改法分类的原则是,每一步修 改都将使对应的分类函数缩小,趋于合理,并且分类函数最终趋于定值,即计 算过程是收敛的。
8/21/2024
23
1.2.2 动态聚类分析法
1.2 聚类分析的种类
(2)初始分类 有了凝聚点以后接下来就要进行初始分类,同样获得初始分类也有不同的
方法。需要说明的是,初始分类不一定非通过凝聚点确定不可,也可以依据其 他原则分类。
以下是其他几种初始分类方法: ①人为分类,凭经验进行初始分类。 ②选择一批凝聚点后,每个样品按与其距离最近的凝聚点归类。 ③选择一批凝聚点后,每个凝聚点自成一类,将样品依次归入与其距离
8/21/2024
14
1.2 聚类分析的种类
(2)系统聚类分析的一般步骤 ①对数据进行变换处理; ②计算各样品之间的距离,并将距离最近的两个样品合并成一类; ③选择并计算类与类之间的距离,并将距离最ቤተ መጻሕፍቲ ባይዱ的两类合并,如果累的个
数大于1,则继续并类,直至所有样品归为一类为止; ④最后绘制系统聚类谱系图,按不同的分类标准,得出不同的分类结果。
8/21/2024
18
1.2 聚类分析的种类
(7)可变法
1 2 D kr
2 (8)离差平方和法
(D k 2 pD k 2 q)D p 2q
D k 2 rn n ir n n p i D i2 pn n ir n n q iD i2 qn rn in iD p 2 q
8/21/2024
机器学习之聚类分析(PPT48页)

间中两点间的距离公式。 两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的
欧氏距离:
聚类的相似性度量
2. 曼哈顿距离(Manhattan Distance) 想象你在曼哈顿要从一个十字路口开车到另外一个十字
路口,驾驶距离是两点间的直线距离吗?显然不是,除非 你能穿越大楼。实际驾驶距离就是这个“曼哈顿距离”, 也称为城市街区距离(City Block distance)。 两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的曼 哈顿距离
密度聚类——DBSCAN
3)密度直达:如果xi位于xj的ε-邻域中,且xj是核心对象,则称xi由xj密 度直达。注意反之不一定成立, 除非且xi也是核心对象。
4)密度可达:对于xi和xj,如果存在样本序列p1,p2,...,pT满足 p1=xi,pT=xj且pt+1由pt密度直达,则称xj由xi密度可达。密度可达满足传递 性。此时序列中的传递样本p1,p2,...,pT−1均为核心对象,因为只有核心 对象才能使其他样本密度直达。 5)密度相连:对于xi和xj,如果存在核心对象样本xk,使xi和xj均由xk密度 可达,则称xi和xj密度相连。
什么是聚类?
• “物以聚类,人以群分” • 所谓聚类,就是将相似的事物聚集在一 起,而将不相似
的事物划分到不同的类别的过程,是数据分析之中十分 重要的一种手段。
什么是聚类?
•在图像分析中,人们希望将图像分割成具有类似性质的 区域 •在文本处理中,人们希望发现具有相同主题的文本子集 •在顾客行为分析中,人们希望发现消费方式类似的顾客 群,以便制订有针对性的客户管理方式和提高营销效率
G1
G2
欧氏距离:
聚类的相似性度量
2. 曼哈顿距离(Manhattan Distance) 想象你在曼哈顿要从一个十字路口开车到另外一个十字
路口,驾驶距离是两点间的直线距离吗?显然不是,除非 你能穿越大楼。实际驾驶距离就是这个“曼哈顿距离”, 也称为城市街区距离(City Block distance)。 两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的曼 哈顿距离
密度聚类——DBSCAN
3)密度直达:如果xi位于xj的ε-邻域中,且xj是核心对象,则称xi由xj密 度直达。注意反之不一定成立, 除非且xi也是核心对象。
4)密度可达:对于xi和xj,如果存在样本序列p1,p2,...,pT满足 p1=xi,pT=xj且pt+1由pt密度直达,则称xj由xi密度可达。密度可达满足传递 性。此时序列中的传递样本p1,p2,...,pT−1均为核心对象,因为只有核心 对象才能使其他样本密度直达。 5)密度相连:对于xi和xj,如果存在核心对象样本xk,使xi和xj均由xk密度 可达,则称xi和xj密度相连。
什么是聚类?
• “物以聚类,人以群分” • 所谓聚类,就是将相似的事物聚集在一 起,而将不相似
的事物划分到不同的类别的过程,是数据分析之中十分 重要的一种手段。
什么是聚类?
•在图像分析中,人们希望将图像分割成具有类似性质的 区域 •在文本处理中,人们希望发现具有相同主题的文本子集 •在顾客行为分析中,人们希望发现消费方式类似的顾客 群,以便制订有针对性的客户管理方式和提高营销效率
G1
G2
聚类分析法ppt课件

7
(2)计算样品的距离。
d ij xi x j yi y j
8
G1
D(0)
G2 G3
G4
G5
G1 G2 G3 G4 G5
0 0.34 1.37 1.34 1.33
0 1.03 1 1.67
0 0.63 1.3
0 0.67
0
9
(3)找出D(0)非对角线上的最小元素, 将其对应的两个类合并为一个新类。
0 0.63 1.30 0 0.67
0
19
0
D(2)
1.37 0
1.67 1.30
0
20
0 1.67
D(3)
0
21
G1 G2 G3 G4 G5
0.4
0.8 1.2 1.6 2.0
聚类距离
பைடு நூலகம்22
G1 G2 G3 G4 G5
0.2 0.4 0.6 0.8 1.0
G1 G2 G3 G4 G5
0.4
0.8
1.2
1.6
2.0
聚类距离
聚类距离
23
某村对5个地块就其土壤质地和土壤有机 质含量进行了评估,结果如下。请分别 使用最长距离法和最短距离法对这5个地 块进行聚类分析,要求分为两类。
地块 A
B
C
D
E
质地 8
3
6
6
4
有机质 5
7
4
9
7
含量
24
聚类分析法
Cluster Analysis
1
聚类分析
将具有相似(similarity)性质(或距离)的 个体(样本)聚为一类,具有不同性质 的个体聚为不同的类。
聚类分析-基因芯片ppt课件

样品之间的距离和类与类之间的距离,然后将距离 最近的两类合并成一个新类,计算新类与其他类的 距离;重复进行两个最近类的合并,每次减少一类, 直至所有的样品合并为一类。
常用的系统聚类方法
❖ 一、最短距离法 ❖ 二、最长距离法 ❖ 三、中间距离法 ❖ 四、类平均法 ❖ 五、重心法 ❖ 六、离差平方和法(Ward方法)
❖ 最短距离法、最长距离法、可变法、类平均法、可 变类平均法和离差平方和法都具有单调性,但中间 距离法和重心法不具有单调性。
类的个数
❖ 如果能够分成若干个很分开的类,则类的个数就比 较容易确定;反之,如果无论怎样分都很难分成明 显分开的若干类,则类个数的确定就比较困难了。
❖ 确定类个数的常用方法有: 1.给定一个阈值T。 2.观测样品的散点图。 3.使用统计量。包括R:2 统计量,半偏R2 统计量, 伪F 统计量和伪t2 统计量。
一、最短距离法
❖ 定义类与类之间的距离为两类最近样品间的距离, 即
DKL
min
iGK , jGL
dij
最短距离法的聚类步骤
❖ (1) 规定样品之间的距离,计算 n 个样品的距离矩
阵 D0 ,它是一个对称矩阵。
❖ ❖
(合 (23))并选计成择算一新D个类0新中G类的M 与,最任记小一为元类G素MG,,J 设之即为间G距MDK离L ,G的K则递将G推LG公K 和式为GL
❖ (3)重复步骤(2),直至所有的样品都不能再分配为止。
❖ 最终的聚类结果在一定程度上依赖于初始凝聚点或 初始分类的选择。经验表明,聚类过程中的绝大多 数重要变化均发生在第一次再分配中。
例6.4.2
❖ 对例6.3.3使用k均值法进行聚类,聚类前对各变量作 标准化变换,聚类结果如下:
常用的系统聚类方法
❖ 一、最短距离法 ❖ 二、最长距离法 ❖ 三、中间距离法 ❖ 四、类平均法 ❖ 五、重心法 ❖ 六、离差平方和法(Ward方法)
❖ 最短距离法、最长距离法、可变法、类平均法、可 变类平均法和离差平方和法都具有单调性,但中间 距离法和重心法不具有单调性。
类的个数
❖ 如果能够分成若干个很分开的类,则类的个数就比 较容易确定;反之,如果无论怎样分都很难分成明 显分开的若干类,则类个数的确定就比较困难了。
❖ 确定类个数的常用方法有: 1.给定一个阈值T。 2.观测样品的散点图。 3.使用统计量。包括R:2 统计量,半偏R2 统计量, 伪F 统计量和伪t2 统计量。
一、最短距离法
❖ 定义类与类之间的距离为两类最近样品间的距离, 即
DKL
min
iGK , jGL
dij
最短距离法的聚类步骤
❖ (1) 规定样品之间的距离,计算 n 个样品的距离矩
阵 D0 ,它是一个对称矩阵。
❖ ❖
(合 (23))并选计成择算一新D个类0新中G类的M 与,最任记小一为元类G素MG,,J 设之即为间G距MDK离L ,G的K则递将G推LG公K 和式为GL
❖ (3)重复步骤(2),直至所有的样品都不能再分配为止。
❖ 最终的聚类结果在一定程度上依赖于初始凝聚点或 初始分类的选择。经验表明,聚类过程中的绝大多 数重要变化均发生在第一次再分配中。
例6.4.2
❖ 对例6.3.3使用k均值法进行聚类,聚类前对各变量作 标准化变换,聚类结果如下:
聚类分析专题教育课件

❖ 由距离来构造相同系数总是可能旳,如令
cij
1 1 dij
这里dij为第i个样品与第j个样品旳距离,显然cij满足 定义相同系数旳三个条件,故可作为相同系数。
❖ 距离必须满足定义距离旳四个条件,所以不是总能 由相同系数构造。高尔(Gower)证明,当相同系 数矩阵(cij)为非负定时,如令
dij 2 1 cij
0
2
0
5
3
D(2) G7
0 3
G5 0 G5 0
表
D(3)
G6
G8
G6
0
G8
4
0
其中G6= G1∪G2
图6.3.2 最短距离法树形图
二、最长距离法
❖ 类与类之间旳距离定义为两类最远样品间旳 , jGL
dij
图6.3.3 最长距离法: DKL=d15
❖ 最长距离法与最短距离法旳并类环节完全相同,只 是类间距离旳递推公式有所不同。
注:
❖ 假如某一步D(m)中最小旳元素不止一种,相应这些 最小元素旳类能够同步合并。
❖ 因为最短距离法是用两类之间近来样本点旳距离来 聚旳,所以该措施不适合对分离得很差旳群体进行 聚类
❖ D(0)等均为对称阵 ❖ 一般距离采用绝对距离或欧氏距离
❖ 例6.3.1 设有五个样品,每个只测量了一种指标, 分别是1,2,6,8,11,试用最短距离法将它们分 类。
❖ 递推公式:
DMJ maxDKJ , DLJ
❖ 对例采用最长距离法,其树形图如图所示,它与图 有相同旳形状,但并类旳距离要比图大某些,仍提 成两类为宜。
图6.3.4 最长距离法树形图
三、中间距离法
❖ 类与类之间旳距离既不取两类近来样品间旳距离,也不取两 类最远样品间旳距离,而是取介于两者中间旳距离,称为中
聚类分析ppt课件

第七章 聚类分析
第一节 引言 第二节 相似性的量度 第三节 系统聚类分析法 第四节 K均值聚类分析 第五节 两步聚类分析
1
第一节 引言
什么是聚类分析? ❖ 聚类分析是根据“物以类聚”的道理,对样本或指
标进行分类的一种多元统计分析方法,它们讨论的 对象是大量的样本,要求能合理地按各自的特性进 行合理的分类,没有任何模式可供参考或依循,即 在没有先验知识的情况下进行的。
1.明考夫斯基距离
p
dij (q) (
X ik X jk )q 1/ q
k 1
明考夫斯基距离简称明氏距离。
(7.1)
13
按q的取值不同又可分成下面的几个式子
(1)绝对距离( q 1)
p
dij (1) X ik X jk k 1
பைடு நூலகம்
(7.2)
(2)欧氏距离( q 2)
p
dij (2) (
X ik X jk )2 1/ 2
22
第三节 系统聚类分析法
一 系统聚类的基本思想 二 类间距离与系统聚类法
23
一、系统聚类的基本思想
❖ 系统聚类的基本思想是:距离相近的样品(或变量)先聚成 类,距离相远的后聚成类,过程一直进行下去,每个样品( 或变量)总能聚到合适的类中。系统聚类过程是:假设总共 有n个样品(或变量),第一步将每个样品(或变量)独自 聚成一类,共有n类;第二步根据所确定的样品(或变量) “距离”公式,把距离较近的两个样品(或变量)聚合为一 类,其它的样品(或变量)仍各自聚为一类,共聚成n 1类 ;第三步将“距离”最近的两个类进一步聚成一类,共聚成 n 2类;……,以上步骤一直进行下去,最后将所有的样品 (或变量)全聚成一类。为了直观地反映以上的系统聚类过 程,可以把整个分类系统画成一张谱系图。所以有时系统聚 类也称为谱系分析。除系统聚类法外,还有有序聚类法、动 态聚类法、图论聚类法、模糊聚类法等。
第一节 引言 第二节 相似性的量度 第三节 系统聚类分析法 第四节 K均值聚类分析 第五节 两步聚类分析
1
第一节 引言
什么是聚类分析? ❖ 聚类分析是根据“物以类聚”的道理,对样本或指
标进行分类的一种多元统计分析方法,它们讨论的 对象是大量的样本,要求能合理地按各自的特性进 行合理的分类,没有任何模式可供参考或依循,即 在没有先验知识的情况下进行的。
1.明考夫斯基距离
p
dij (q) (
X ik X jk )q 1/ q
k 1
明考夫斯基距离简称明氏距离。
(7.1)
13
按q的取值不同又可分成下面的几个式子
(1)绝对距离( q 1)
p
dij (1) X ik X jk k 1
பைடு நூலகம்
(7.2)
(2)欧氏距离( q 2)
p
dij (2) (
X ik X jk )2 1/ 2
22
第三节 系统聚类分析法
一 系统聚类的基本思想 二 类间距离与系统聚类法
23
一、系统聚类的基本思想
❖ 系统聚类的基本思想是:距离相近的样品(或变量)先聚成 类,距离相远的后聚成类,过程一直进行下去,每个样品( 或变量)总能聚到合适的类中。系统聚类过程是:假设总共 有n个样品(或变量),第一步将每个样品(或变量)独自 聚成一类,共有n类;第二步根据所确定的样品(或变量) “距离”公式,把距离较近的两个样品(或变量)聚合为一 类,其它的样品(或变量)仍各自聚为一类,共聚成n 1类 ;第三步将“距离”最近的两个类进一步聚成一类,共聚成 n 2类;……,以上步骤一直进行下去,最后将所有的样品 (或变量)全聚成一类。为了直观地反映以上的系统聚类过 程,可以把整个分类系统画成一张谱系图。所以有时系统聚 类也称为谱系分析。除系统聚类法外,还有有序聚类法、动 态聚类法、图论聚类法、模糊聚类法等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2章
2.1 聚类分析概述 2.2 相似性度量 2.3 系统聚类 2.4 K-Means聚类
聚类分析是多元分析的主要方法之一,主要用来 对大量的样品或变量进行分类。
同一类别内的个体具有尽可能高的同质性。 类别之间应具有尽可能高的异质性。
聚类的实质
根据样品(变量)间的亲疏关系将样品(变量)分为 类,相近的归为一类,差别较大的归为另一类。所获 得的分类应有一定的意义。
区域发展水平:根据经济及社会发展水平把全国各地 市(县)分类 产品市场细分:按照消费者的需求特征分成不同的细 分市场 客户分类:银行根据贷款者的收入水平、抵押状况、 信用记录对信息,对贷款者的资信分类并给予相应的 贷款额度
根据分类的方法:
系统/层次聚类(hierarchical clustering )
7
8
8
3
6
8
6
9
7
4
3
2
3
4
4
5
2
3
2
3
2
相关测度更大程度上反映了案例在聚类变量上变化模式的 相似性,变量值大小的差异对其影响不大,也被称为形状 测度。
相关测度的缺点在于忽视了变量值大小的差异,高度相关
的两个样本提供的信息可能相差甚远。
聚类分析的大部分应用中更重视变量值大小的差异,而不
是值的变化模式,以此相关测度在聚类分析中的应用并不
马氏距离既排除了各指标间相关性的干扰,并不受各指 标量纲的影响。
和相关测度不同,距离测度更侧重于变量值 的大小,
不考虑案例在聚类上的变化模式,认为靠得近的案例
为相似案例
距离测度:欧式距离
案例
1
2
3
2
8.72
3
7.21
2.83
4
3.74
9.90
9.38
5
4.24
2.75
10.86
按照距离
越近,相
聚类分析的一般规则
亲疏关系的判别:相似性与距离(不相似性) 将相似性较大的点或距离较小的点归为同一类 将相似性较小的点或距离较大的点归为不同类
根据分类的对象
样品/记录聚类(clustering for cases/individuals) 指标/变量聚类(clustering for variables)
p
[ (xik x jk )2 ]1 2 k 1
x2
x12
①
两样品p个指标值之
d21 (x21 x11)2 (x22 x12 )2 差平方和的平方根
x22- x12
x22
x21- x2
②
x2
x21
欧式距离是最广泛使 用的距离指标。
x1
两样品p个指标值绝对差的最大值
dij ()
k
连续变量和分类变量在聚类时常用的测量方式不同。
连续变量一般采用欧氏平方距离 分类变量一般用卡方作为距离指标 多数传统聚类方法只能使用其中单一各类的变量进行
分析 数据中如果同时有这两类变量,可考虑只采用连续变
量进行分析;或者将分类变量转换成虚拟变量的形式, 按照连续变量进行分析
xik
x jk
,称为切比雪夫(Chebychey)距离
各指标同等对待(权数相同),不能反映各指标 变异程度上的差异
距离的大小与各指标的观测单位有关,有时会出 现不合理结果
没有考虑指标之间的相关性
当各指标的测量值相差悬殊时,可以先对数据标 准化,然后用标准化后的数据计算距离。
di2j (Xi X j )' 1(Xi X j ) 其中为p维随机向量的协方差矩阵
max
1k p
xik
x jk
两样品p个指标值绝对差 的q次幂总和的q次方根
p
dij [
1
xik x jk q ]q
k 1
p
当q 1,dij (1) xik x jk ,为绝对距离; k 1
当q 2,即为欧氏距离;
当q
,dij ()
max
1k p
聚类分析过程基本上与分布理论和显著性检验无 关,一般不从样本推断总体。
聚类分析可通过将众多个体聚集成几个类别而简 化数据,可作为其他多元统计的预备过程。
聚类分析主要用于探索性的研究,最终的解需要 研究者的主观判断和后续分析。
聚类分析的解完全依赖于所选择的聚类变量,增 删变量对于聚类解会产生实质性影响。
在m维空间中定义点与点的距离,距离越近的点, 相似程度越高,越可能归为一类。
dij满足下列条件
dij≥0 dii =0 dij = dji dij ≤ dik + dkj
两样品p个指标值绝对差的总和
p
dij (1) xik x jk k 1
dij (xi1 x j1)2 (xi2 x j2 )2 (xip x jp )2
开始将样品/指标各视为一类,根据类与类之间的距离/相 似程度,将最相似的类加以合并,再计算新类与其他类之 间的相似程度,并选择最相似的类加以合并,每合并一次 就减少一类,不断重复,直到所有样本/指标都合并为一类。
快速/K-均值/动态聚类(k-means clustering)
开始按照一定方法选取一批聚类的中心,让样品向最近 的聚心凝聚,然后按最近距离原则不断修改不合理分类, 直到合理为止。
4
似度越高
的原则,2
和3归为一
类,1、4、
5归为一类。
2.83
关联测度用于度量聚类变量为分类变量的相似性。
简单匹配系数
对于二分类变量,关联测度是要估计研究对象在回答这些问 题时的一致程度。
简单匹配系数是两个案例在所有聚类变量上答案相同的情况 出现的频率。
在聚类分析技术的发展过程中,形成了很多种测度相 似性的方法,主要分为三类:
相关测度 距离测度 关联测度
应用最广泛的相关测度是皮尔逊相关系数(Pearson
correlation),聚类分析中用它来测量案例之间的
相似程度。
原始数据
案例
变量
x1
x2
x3
X4
x5
1
2
5
3
6
4
2
8
7
普遍。
相关测度:相关系数
案例
1
2
3
4
2
0.00
3
0.97
0.14
4
0.19
0.76
017
0.91
-0.22
样品间的亲疏关系通常用距离描述
Block距离 欧式距离 明氏距离 切比雪夫距离 马氏距离 兰氏距离
距离的定义:
距离测度的出发点是把每个案例看成是m维空间中 (m 为变量个数)的一个点。
2.1 聚类分析概述 2.2 相似性度量 2.3 系统聚类 2.4 K-Means聚类
聚类分析是多元分析的主要方法之一,主要用来 对大量的样品或变量进行分类。
同一类别内的个体具有尽可能高的同质性。 类别之间应具有尽可能高的异质性。
聚类的实质
根据样品(变量)间的亲疏关系将样品(变量)分为 类,相近的归为一类,差别较大的归为另一类。所获 得的分类应有一定的意义。
区域发展水平:根据经济及社会发展水平把全国各地 市(县)分类 产品市场细分:按照消费者的需求特征分成不同的细 分市场 客户分类:银行根据贷款者的收入水平、抵押状况、 信用记录对信息,对贷款者的资信分类并给予相应的 贷款额度
根据分类的方法:
系统/层次聚类(hierarchical clustering )
7
8
8
3
6
8
6
9
7
4
3
2
3
4
4
5
2
3
2
3
2
相关测度更大程度上反映了案例在聚类变量上变化模式的 相似性,变量值大小的差异对其影响不大,也被称为形状 测度。
相关测度的缺点在于忽视了变量值大小的差异,高度相关
的两个样本提供的信息可能相差甚远。
聚类分析的大部分应用中更重视变量值大小的差异,而不
是值的变化模式,以此相关测度在聚类分析中的应用并不
马氏距离既排除了各指标间相关性的干扰,并不受各指 标量纲的影响。
和相关测度不同,距离测度更侧重于变量值 的大小,
不考虑案例在聚类上的变化模式,认为靠得近的案例
为相似案例
距离测度:欧式距离
案例
1
2
3
2
8.72
3
7.21
2.83
4
3.74
9.90
9.38
5
4.24
2.75
10.86
按照距离
越近,相
聚类分析的一般规则
亲疏关系的判别:相似性与距离(不相似性) 将相似性较大的点或距离较小的点归为同一类 将相似性较小的点或距离较大的点归为不同类
根据分类的对象
样品/记录聚类(clustering for cases/individuals) 指标/变量聚类(clustering for variables)
p
[ (xik x jk )2 ]1 2 k 1
x2
x12
①
两样品p个指标值之
d21 (x21 x11)2 (x22 x12 )2 差平方和的平方根
x22- x12
x22
x21- x2
②
x2
x21
欧式距离是最广泛使 用的距离指标。
x1
两样品p个指标值绝对差的最大值
dij ()
k
连续变量和分类变量在聚类时常用的测量方式不同。
连续变量一般采用欧氏平方距离 分类变量一般用卡方作为距离指标 多数传统聚类方法只能使用其中单一各类的变量进行
分析 数据中如果同时有这两类变量,可考虑只采用连续变
量进行分析;或者将分类变量转换成虚拟变量的形式, 按照连续变量进行分析
xik
x jk
,称为切比雪夫(Chebychey)距离
各指标同等对待(权数相同),不能反映各指标 变异程度上的差异
距离的大小与各指标的观测单位有关,有时会出 现不合理结果
没有考虑指标之间的相关性
当各指标的测量值相差悬殊时,可以先对数据标 准化,然后用标准化后的数据计算距离。
di2j (Xi X j )' 1(Xi X j ) 其中为p维随机向量的协方差矩阵
max
1k p
xik
x jk
两样品p个指标值绝对差 的q次幂总和的q次方根
p
dij [
1
xik x jk q ]q
k 1
p
当q 1,dij (1) xik x jk ,为绝对距离; k 1
当q 2,即为欧氏距离;
当q
,dij ()
max
1k p
聚类分析过程基本上与分布理论和显著性检验无 关,一般不从样本推断总体。
聚类分析可通过将众多个体聚集成几个类别而简 化数据,可作为其他多元统计的预备过程。
聚类分析主要用于探索性的研究,最终的解需要 研究者的主观判断和后续分析。
聚类分析的解完全依赖于所选择的聚类变量,增 删变量对于聚类解会产生实质性影响。
在m维空间中定义点与点的距离,距离越近的点, 相似程度越高,越可能归为一类。
dij满足下列条件
dij≥0 dii =0 dij = dji dij ≤ dik + dkj
两样品p个指标值绝对差的总和
p
dij (1) xik x jk k 1
dij (xi1 x j1)2 (xi2 x j2 )2 (xip x jp )2
开始将样品/指标各视为一类,根据类与类之间的距离/相 似程度,将最相似的类加以合并,再计算新类与其他类之 间的相似程度,并选择最相似的类加以合并,每合并一次 就减少一类,不断重复,直到所有样本/指标都合并为一类。
快速/K-均值/动态聚类(k-means clustering)
开始按照一定方法选取一批聚类的中心,让样品向最近 的聚心凝聚,然后按最近距离原则不断修改不合理分类, 直到合理为止。
4
似度越高
的原则,2
和3归为一
类,1、4、
5归为一类。
2.83
关联测度用于度量聚类变量为分类变量的相似性。
简单匹配系数
对于二分类变量,关联测度是要估计研究对象在回答这些问 题时的一致程度。
简单匹配系数是两个案例在所有聚类变量上答案相同的情况 出现的频率。
在聚类分析技术的发展过程中,形成了很多种测度相 似性的方法,主要分为三类:
相关测度 距离测度 关联测度
应用最广泛的相关测度是皮尔逊相关系数(Pearson
correlation),聚类分析中用它来测量案例之间的
相似程度。
原始数据
案例
变量
x1
x2
x3
X4
x5
1
2
5
3
6
4
2
8
7
普遍。
相关测度:相关系数
案例
1
2
3
4
2
0.00
3
0.97
0.14
4
0.19
0.76
017
0.91
-0.22
样品间的亲疏关系通常用距离描述
Block距离 欧式距离 明氏距离 切比雪夫距离 马氏距离 兰氏距离
距离的定义:
距离测度的出发点是把每个案例看成是m维空间中 (m 为变量个数)的一个点。
