反比例函数与相似的综合
中考反比例函数与几何综合
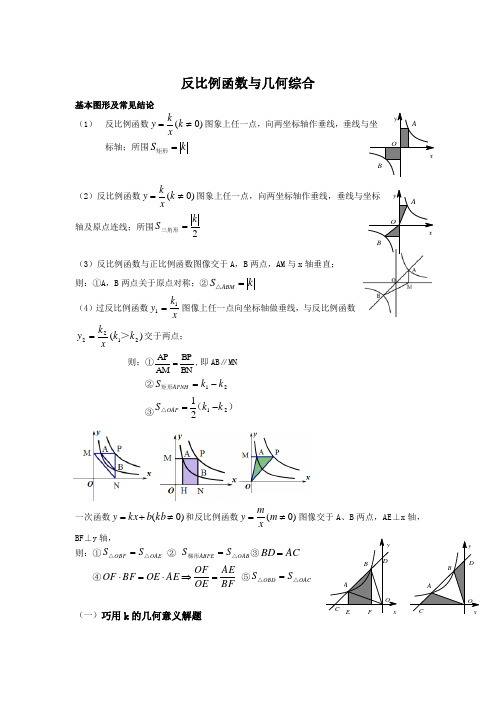
Oy xBAABxy O反比例函数与几何综合基本图形及常见结论 (1) 反比例函数)0(≠=k xky 图象上任一点,向两坐标轴作垂线,垂线与坐标轴;所围k S =矩形(2)反比例函数)0(≠=k xky 图象上任一点,向两坐标轴作垂线,垂线与坐标轴及原点连线;所围2k S =三角形(3)反比例函数与正比例函数图像交于A ,B 两点,AM 与x 轴垂直; 则:①A ,B 两点关于原点对称;②k S ABM =△(4)过反比例函数xk y 11=图像上任一点向坐标轴做垂线,与反比例函数)(2122k k xk y >=交于两点; 则:①BNBP AM AP =,即AB ∥MN②21k k S APNH -=矩形③)(△2121k k S OAP -=一次函数)0(≠+=kb b kx y 和反比例函数)0(≠=m xmy 图像交于A 、B 两点,AE ⊥x 轴,BF ⊥y 轴,则:①OAE OBF S S △△= ② OAB ABFE S S △梯形=③AC BD =④BFAEOE OF AE OE BF OF =⇒⋅=⋅ ⑤OACOBD S S △△=(一)巧用k 的几何意义解题y x ABO CDy xDC F EO B A例1.函数y=和y=在第一象限内的图象如图,点P 是y=的图象上一动点,PC ⊥x 轴于点C ,交y=的图象于点B .给出如下结论:①△ODB 与△OCA 的面积相等;②PA 与PB 始终相等;③四边形PAOB 的面积大小不会发生变化;④CA=AP .其中所有正确结论的序号是________。
迁移练习1(1).如图,双曲线)0x (k>=xy 经过Rt △OAB 斜边OB 的中点D ,与AB 交于点C .若△OBC 面积为3,则k =_______迁移练习1(2)..双曲线)0x (k>=xy 经过矩形OABC 边AB 的中点F ,交BC 于点E ; 若梯形OEBA 的面积为9,则k=________。
(完整版)初中数学反比例函数知识点及经典例

04
利用相似三角形求解线段长度或角度大小
通过相似三角形的性质,我们可以建立 比例关系,从而求解未知线段长度或角 度大小。
解方程求解未知量。
具体步骤
根据相似比建立等式关系。
确定相似三角形,找出对应边或对应角 。
经典例题讲解和思路拓展
例题1
解题思路
例题2
解题思路
已知直角三角形ABC中, ∠C=90°,AC=3,BC=4,将 △ABC沿CB方向平移2个单位 得到△DEF,若AG⊥DE于点G ,则AG的长为____反比例函数$y = frac{m}{x}$的图像经过点$A(2,3)$,且与直线$y = -x + b$相 交于点$P(4,n)$,求$m,n,b$的
值。
XXX
PART 03
反比例函数与不等式关系 探讨
REPORTING
一元一次不等式解法回顾
一元一次不等式的定义
01
在材料力学中,胡克定律指出弹簧的 伸长量与作用力成反比。这种关系同 样可以用反比例函数来描述。
牛顿第二定律
在物理学中,牛顿第二定律表明物体 的加速度与作用力成正比,与物体质 量成反比。这种关系也可以用反比例 函数来表示。
经济学和金融学领域应用案例分享
供需关系
在经济学中,供需关系是决定商品价 格的重要因素。当供应量增加时,商 品价格下降;反之,供应量减少时, 商品价格上升。这种供需关系可以用 反比例函数来表示。
XXX
PART 02
反比例函数与直线交点问 题
REPORTING
求解交点坐标方法
方程组法
将反比例函数和直线的方程联立 ,解方程组得到交点坐标。
图像法
在同一坐标系中分别作出反比例 函数和直线的图像,找出交点并 确定其坐标。
【玩转压轴题】必考3:相似三角形的综合(原卷版)-浙教版2022年初三数学期末压轴题精选汇编

【玩转压轴题】必考3:相似三角形的综合(原卷版)一、单选题1.如图,C 是线段AB 上的任一点,分别以,,AB AC BC 为直径在线段AB 同侧作半圆,则这三个半圆周围成的图形被阿基米德称为“鞋匠刀形”(即图中阴影部分).当“鞋匠刀形”的面积等于以BC 为直径的半圆的面积时,过C 作CD AB ⊥,交圆周于点D ,连结BD ,则CD 与BC 的比值为( )A .12B C .13D 2.如图,在△ABC 中,∠CAB =45°,以其三边为边向外作正方形,连接GC 并延长交BH 于点L ,过点C 作CK ⊥DE 于点K .若L 为BH 中点,则GL CK 的值为( )A .1B .98C D3.如图,矩形ABCD 中,6,8AB BC ==.点E 、F 分别为边BC 、AD 上一点,连接EF ,将矩形ABCD 沿着EF 折叠,使得点A 落到边CD 上的点A '处,且2DA A C '=',则折痕EF 的长度为( )A .B .CD 4.如图,在ABC 中,AE 和BD 是高,45ABE ∠=︒,点F 是AB 的中点,BD 与FE AE、分别交于点,G H ,CAE ABD ∠=∠.有下列结论:①FD FE =;②2BH CD =;③22BD BH BE ⋅=;④43ABC BCDFS S =△四边形.其中正确的有( )A .①③B .②④C .①②③D .①②④5.如图,E ,F ,G ,H 分别是矩形ABCD 四条边上的点,连结EG ,HF 相交于点O ,//EG AD ,//FH AB ,矩形BFOE ∽矩形OGDH ,连结AC 交EG ,FH 于点P ,Q .下列一定能求出BPQ ∆面积的条件是( )A .矩形BFOE 和矩形OGDH 的面积之差B .矩形ABCD 与矩形BFOE 的面积之差C .矩形BFOE 和矩形FCGO 的面积之差D .矩形BFOE 和矩形EOHA 的面积之差6.如图,在ABC 中,90ACB ∠=︒,以ABC 的各边为边分别作正方形ACDE ,正方形BCFG 与正方形ABMN ,AN 与FG 相交于点H ,连结NF 并延长交AE 于点P ,且2NF FP =.记ABC 的面积为1S ,FNH △的面积为2S ,若1221S S -=,则BC 的长为( )A .6B .C .8D .97.如图,将边长为6的正六边形ABCDEF 沿HG 折叠,点B 恰好落在边AF 的中点上,延长B C ''交EF 于点M ,则C M '的长为( )A .1B .65C .56D .958.如图,等腰Rt ABC 中,90BAC AD BC ∠=︒⊥,于D ,ABC ∠的平分线分别交AC AD 、于E F 、两点,M 为EF 的中点,延长AM 交BC 于点N ,连接DM MC 、下列结论:①DF DN =;②ABE MBN ≌;③ CMN 是等腰三角形;④AE CN =,其中正确的是( )A .①②B .①④C .①③D .②③9.勾股定理有着悠久的历史,它曾引起很多人的兴趣.1955年希腊发行了以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在Rt ABC 中,()90,,BAC AC a AB b a b ∠=︒==<.如图所示作矩形HFPQ ,延长CB 交HF 于点G .若正方形BCDE 的面积等于矩形BEFG 面积的3倍,则ab的值为( )A B C D 35210.如图,在正方形ABCD 中,对角线AC ,BD 相交于点O ,点E 在DC 边上,且2CE DE =,连接AE 交BD 于点G ,过点D 作DF AE ⊥,连接OF 并延长,交DC 于点P ,过点O 作⊥OQ OP 分别交AE ,AD 于点N ,H ,交BA 的延长线于点Q ,现给出下列结论:①45AFO ∠=︒;②2N P O D H H =⋅;③Q OAG ∠=∠;④OG DG =.其中正确的结论有( )A .①③B .②④C .①②③D .①②③④二、填空题11.如图,在矩形ABCD 中,6AB =,8AD =.连接BD ,DBC ∠的角平分线BE 交DC 于点E ,现把BCE 绕点B 逆时针旋转,记旋转后的BCE 为BC E ''△.当射线BE '和射线BC '都与线段AD 相交时,设交点分别为F ,G .若BFD △为等腰三角形,则线段DG 长为______.12.如图,点D 是等边ABC 边BC 上一点,将等边ABC 折叠,使点A 与点D 重合,折痕为EF (点E 在边AB 上).(1)当点D 为BC 的中点时,:AE EB =__; (2)当点D 为BC 的三等分点时,:AE EB =__.13.小明想设计一款如图1所示的喷水壶,于是他绘制了如图2所示的设计图,壶身的主视图呈矩形ABCD ,壶把手呈圆弧状,圆心O 落在AD 上,圆弧交CD 于点E .支撑架HF 所在直线恰好经过O .壶嘴GI 的端点I 恰好在AD 所在直线上.已知258cm,4cm,cm, 6.5cm 12AD DE AF HF FG =====,则半径AO 的长为________cm ,壶嘴GI 的长度为________cm .14.如图,AB 是半圆O 的直径.点C 在半径OA 上,过点C 做CD AB ⊥交半圆O 于点D .以,CD CA 为边分别向左、下作正方形,CDEF CAGH .过点B 作GH 的垂线与GH 的延长线交于点I ,M 为HI 的中点.记正方形,CDEF CAGH ,四边形BCHI 的面积分别为123,,S S S .(1)若:2:3AC BC =,则12S S 的值为_______;(2)若D ,O ,M 在同一条直线上,则123S S S +的值为______.15.四个全等的直角三角形如图摆放成一个风车的形状,形成正方形ABCD 和正方形IJKL .若BF 平分∠ABK ,AF :FK =5:3,风车周长为面积和是___.16.用一张正方形纸片折成一个“小蝌蚪”图案(如图1).如图2,正方形ABCD 的边长为2,等腰直角ACE 的斜边AE 过点D .点F 为CE 边上一点,连结AF 交CD 于点G ,将AEF 沿AF 对称得AE F ',AE '与BC 交于点H .当//FE CD '时,E FA '∠=______︒;当点G 为CD 的中点时,则CF 的长为______.17.如图,点A C 、分别是x 轴、y 轴正半轴上的点,矩形ABCO 的边,AB BC 分别交函数ky x=(0,0,x k k >≠为常数)的图象于点,P Q ,连接PQ . (1)若P 为AB 中点,则BQBC=___. (2)若把BPQ ∆沿PQ 翻折,点B 恰好落在x 轴上的点E ,且6,2OE EA ==,则k =___.18.如图,在ABCD 中,E 是BC 边上的中点,AP CD ⊥于点P ,将ABE △沿AE 翻折,点B 的对称点B '落在AP 上,延长EB '恰好经过点D ,若4AB =,则折痕AE 的长为________.19.如图,点A ,B 分别是反比例函数(0,0)a y a x x =>>和(0,0)by b x x=<<图象上的点,且//AB x 轴,点C 在x 轴的正半轴上,连接AC 交反比例函数(0,0)ay a x x=>>的图象于点D ,已知20BOD S =△,8COD S =△,2AD CD =,则-a b 的值为______.20.如图1是护眼台灯,该台灯的活动示意图如图2所示.灯柱6cm BC ,灯臂AC 绕着支点C 可以旋转,灯罩呈圆弧形(即弧AD 和弧EF ).在转动过程中,AD (EF )总是与桌面BH 平行.当AC BH ⊥时,51cm AB =.DM MH ⊥,测得42cm DM =(点M 在墙壁MH 上,且MH BH ⊥);当灯臂AC 转到CE 位置时,FN MH ⊥,测得15cm FN =,则点E 到桌面的距离为______cm .若此时点C ,F ,M 在同一条直线上,弧EF 的最低点到桌面BH 的距离为31cm ,则弧EF 所在圆的半径为_____cm (保留一位小数).三、解答题 21.特例感知(1)如图,已知在Rt ABC 中,90BAC ∠=︒,AB AC =,取BC 边上中点D ,连结AD ,点E 为AB 边上一点,连结DE ,作DF DE ⊥交AC 于点F ,求证BE AF =;探索发现(2)如图,已知在Rt ABC 中,90BAC ∠=︒,3AB AC ==,取BC 边上中点D ,连结AD ,点E 为BA 延长线上一点,1AE =,连结DE ,作DF DE ⊥交AC 延长线于点F ,求AF 的长;类比迁移(3)如图,已知在ABC 中,120BAC ∠=︒,4AB AC ==,取BC 边上中点D ,连结AD ,点E 为射线BA 上一点(不与点A 、点B 重合),连结DE ,将射线DE 绕点D 顺时针旋转30°交射线CA 于点F ,当4AE AF =时,求AF 的长.22.(证明体验)(1)如图1,AD 为ABC 的角平分线,60ADC ∠=︒,点E 在AB 上,AE AC =.求证:DE 平分ADB ∠.(思考探究)(2)如图2,在(1)的条件下,F 为AB 上一点,连结FC 交AD 于点G .若FB FC =,2DG =,3CD =,求BD 的长.(拓展延伸)(3)如图3,在四边形ABCD 中,对角线AC 平分,2BAD BCA DCA ∠∠=∠,点E 在AC上,EDC ABC ∠=∠.若5,2BC CD AD AE ===,求AC 的长. 23.(推理)如图1,在正方形ABCD 中,点E 是CD 上一动点,将正方形沿着BE 折叠,点C 落在点F 处,连结BE ,CF ,延长CF 交AD 于点G .(1)求证:BCE CDG △△≌. (运用)(2)如图2,在(推理)条件下,延长BF 交AD 于点H .若45HD HF =,9CE =,求线段DE 的长. (拓展)(3)将正方形改成矩形,同样沿着BE 折叠,连结CF ,延长CF ,BF 交直线AD 于G ,两点,若AB k BC =,45HD HF =,求DEEC的值(用含k 的代数式表示).24.在Rt ABC 中,90ACB ∠=︒,点D 在直线AC 上,连结BD ,以BD 为边作等腰直角BDE (点E 在直线BD 右侧),连结CE .(1)如图1,若45A ∠=︒,且点D 在AC 边上,求证:ABD CBE ∽△△; (2)如图2,若045A ︒<∠<︒,且12BC =,5CD =,求CE 的长;(3)如图3,若点D 在AC 的延长线上,BD ,CE 相交于点F ,设CDF 的面积为1S ,BEF 的面积为2S ,BCF △的面积为3S ,则2123122BC S S S =-+,请说明理由.25.如图,四边形ABCD 是矩形,20AB =,10BC =,以CD 为一边向矩形外部作等腰直角CDG ,90G ∠=︒.点M 在线段AB 上,且AM a =,点P 沿折线AD DG -运动,点Q 沿折线BC CG -运动(P ,Q 与点G 不重合),在运动过程中终保持//PQ AB .设PQ 与AB 之间的距离为x ,四边形AMQP 的面积为y .(1)若12a =,回答下列问题:①当点P 在线段AD 上时,若四边形AMQP 的面积为48,则x =______. ②求整个运动过程中,y 关于x 的函数解析式,并求出y 的最大值;(2)如图2,若点P 在线段DG 上时,要使四边形AMQP 的面积始终不小于50,求a 的取值范围.26.如图1,在矩形ABCD 中,动点P 沿着边AB 从点A 运动到点B ,同时动点Q 沿着边BC ,CD 从点B 运动到点D .它们同时到达终点,若点Q 的运动路程x 与线段BP 的长,满足487y x =-+,BD 与PQ 交于点E . (1)求AB ,BC 的长.(2)如图2.当Q 在CD 上时,求BEDE. (3)将矩形沿着PQ 折叠,点B 的对应点为点F ,连结EF ,当EF 所在直线与BCD △的一边垂直时,求BP 的长.27.如图1,在ABC 中,90A ∠=︒,当点P 从点A 出发,沿着AB 方向匀速运动到点B 时,点Q 恰好从点B 出发,沿着BC 方向匀速运动到点C ,连结PQ ,记,AP x CQ y ==,已知554y x =-+.(1)求AB和BC的长.(2)当BPQ是以PQ为腰的等腰三角形时,求x的值.(3)如图2,直线l是线段PQ的垂直平分线.①若直线l过点B,交AC于点D,请判断四边形BQDP的形状,并说明理由;②A'是点A关于直线l的对称点,若点A'落在ABC的内部,请直接写出x的取值范围.28.如图,四边形ABCD为边长等于7的菱形,其中∠B=60°,点E在对角线AC上,且AE=1,点F在射线CB上运动,连接EF,作∠FEG=60°,交DC延长线于点G.(1)当点F与B点重合时,试判断△EFG的形状,并说明理由;(2)以点B为原点,BC所在的直线为x轴建立平面直角坐标系,当CF=10时,平面内是否存在一点M,使得以点M、E、F、G为顶点的四边形与菱形ABCD相似?若存在,求M的坐标,若不存在,说明理由;(3)记点F关于直线AB的轴对称点为点N,若点N落在∠EDC的内部(不含边界),求CF的取值范围.29.如图,在△ABC中,AC=BC=tan∠CAB=12,P为AC上一点,PD⊥AB交AB于点E,AD⊥AC交PD于点D,连结BD,CD,CD交AB于点Q.(1)若CD⊥BC,求证:△AED∽△QCB;(2)若AB平分∠CBD,求BQ的长;(3)连结PQ并延长交BD于点M.①当点P是AC的中点时,求tan∠BQM的值②当PM平行于四边形ADBC中的某一边时,求BMDM的值.30.如图,已知AB是⊙O的弦,OB=1,C是弦AB上的任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接AD.设∠B=α,∠ADC=β.(1)求∠BOD的度数(用含α,β的代数式表示);(2)若α=30°,当AC的长度为多少时,以点A、C、D为顶点的三角形与B、C、O 为顶点的三角形相似?请写出解答过程.(3)若α=β,连接AO,记△AOD、△AOC、△COB的面积分别为S1,S2,S3,如果S2是S1和S3的比例中项,求OC的长.。
数学反比例函数知识点总结

数学反比例函数知识点总结数学反比例函数知识反比例函数主要考察三个方面1)反比例函数图像的性质;2)求反比例函数解析式;3)K的几何性质的应用。
以上几点考察基本上都是和一次函数,相似,全等,方程,圆,三角函数,勾股定理等知识相结合考察,单一命题的机会比较少同时题目也比较简单。
本专题主要针对B卷类近几年考到的填空题做出总结,让同学们能够从多角度,多方位的训练。
反比例函数的定义如果两个变量x,y之间的对应关系可以表示成y=k/x(k为常数,k≠0)的形式,那么称y是x的反比例函数。
y是x的反比例函数?函数表达式为y=k/x 或y=kxˉ1或xy=k(k为常数,k≠0)。
反比例专题我们总结出六类常考题型:1)由反比例函数k的几何意义转化出三角形或梯形之间面积的等量关系题型。
2)由反比例函数和一次函数相交形成的线段等量关系题型。
3)由反比例函数和一次函数相交求交点坐标的题型。
4)反比例函数与相似三角形综合考察求k或线段比题型。
5)反比例函数图像的分布与k之间的关系题型6)反比例函数与三角函数,方程(组)等有关的问题。
数学反比例函数知识2反比例性质1规律:反比函数与一次函数(与正比例函数相交,交点关于原点对称)相交,求线段数量关系时,切记“原点O到两交点的距离是相等的”若给出反比函数解析式,那么最终求得的结果的过程肯定要转化成关于“k”的几何意义。
2规律:一次函数与反比函数相交且两函数解析式都未知,此时一次函数所在直线与交点分别于x轴,y轴做垂线的交点所连接的线段是相互平行的,同时一次函数与反比函数的交点到一次函数与x轴,y轴的交点的距离是相等的。
3规律:题目中给出线段比例和四边形的面积求k 问题,利用同底等高三角形面积与高之间的关系,面积与k之间的关系。
求出k(此时不用具体求出点坐标)。
4规律:有中点时利用中点坐标公式,再根据反比函数上任何一点处的几何意义都相同的思想转化出面积问题。
5规律:若反比例函数图像经过多个点,那么在这几点处的几何意义是相同的。
反比例函数常见几何模型归纳(七大模型)(解析版)-初中数学
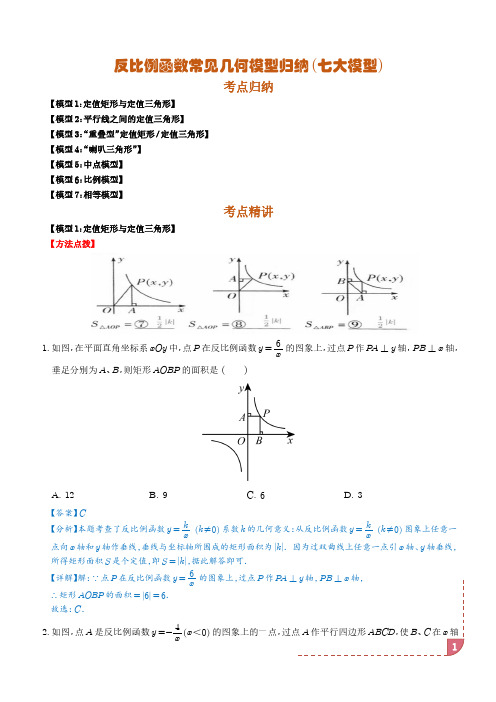
反比例函数常见几何模型归纳(七大模型)考点归纳【模型1:定值矩形与定值三角形】【模型2:平行线之间的定值三角形】【模型3:“重叠型”定值矩形/定值三角形】【模型4:“喇叭三角形”】【模型5:中点模型】【模型6:比例模型】【模型7:相等模型】考点精讲【模型1:定值矩形与定值三角形】【方法点拨】1.如图,在平面直角坐标系xOy 中,点P 在反比例函数y =6x的图象上,过点P 作P A ⊥y 轴,PB ⊥x 轴,垂足分别为A 、B ,则矩形AOBP 的面积是()A.12B.9C.6D.3【答案】C【分析】本题考查了反比例函数y =k x k ≠0 系数k 的几何意义:从反比例函数y =kxk ≠0 图象上任意一点向x 轴和y 轴作垂线,垂线与坐标轴所围成的矩形面积为k .因为过双曲线上任意一点引x 轴、y 轴垂线,所得矩形面积S 是个定值,即S =k ,据此解答即可.【详解】解:∵点P 在反比例函数y =6x的图象上,过点P 作P A ⊥y 轴,PB ⊥x 轴,∴矩形AOBP 的面积=6 =6.故选:C .2.如图,点A 是反比例函数y =-4x <0 的图象上的一点,过点A 作平行四边形ABCD ,使B 、C 在x 轴上,点D 在y 轴上,则平行四边形ABCD 的面积为()A.2B.4C.6D.8【答案】B【分析】本题考查了反比例函数y =k x k ≠0 系数k 的几何意义:从反比例函数y =kxk ≠0 图象上任意一点向x 轴和y 轴作垂线,垂线与坐标轴所围成的矩形面积为k .作AH ⊥OB 于H ,根据平行四边形的性质得AD ∥OB ,则S 平行四边形ABCD =S 矩形AHOD ,再根据反比例函数y =kxk ≠0 系数k 的几何意义得到S 矩形AHOD =-4 =4,所以有S 平行四边形ABCD =4.【详解】解:作AH ⊥OB 于H ,如图,∵四边形ABCD 是平行四边形,∴AD ∥OB ,∴S 平行四边形ABCD =S 矩形AHOD ,∵点A 是反比例函数y =-4xx <0 的图象上的一点,∴S 矩形AHOD =-4 =4,∴S 平行四边形ABCD =4.故选:B .3.如图,A 、B 是反比例函数y =kx(k ≠0)的图象上两点,点C 、D 、E 、F 分别在坐标轴上,若正方形OCAD 的面积为6,则矩形OEBF 的面积为.【答案】6【分析】本题主要考查反比例函数中比例系数k 的几何意义和函数图象的对称性,难易程度适中,是中考较常见的考查点.根据双曲线的图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的四边形的面积S 的关系即S =k ,进行解答即可.【详解】解:∵S 正方形OCAD =OD ⋅OC =x A ⋅y A =k =6,∴S 长方形OCAD =OE ⋅OF =x B ⋅y B =k =6.故答案为:6.4.如图是反比例函数y =-4x在第二象限内的图象,则图中矩形BCOA 的面积为.【答案】4【分析】根据矩形的面积公式S 矩形BCOA =AB ⋅BC =a ⋅b =ab ,再根据反比例函数的性质解答即可.本题考查了矩形的面积公式,反比例函数的性质,熟练运用反比例函数的性质是解题的关键.【详解】解:设点B a ,b ,∵四边形BCOA 是矩形,∴AB =a ,BC =b ,∴S 矩形BCOA =AB ⋅BC =a ⋅b =ab ,∵点B 在反比例函数y =-4x在图象上,∴a ⋅b =-4,∴a ⋅b =4,∴S 矩形BCOA =ab =4;故答案为4.【模型2:平行线之间的定值三角形】【方法点拨】5.如图,是反比例函数y =5x 和y =-9x在x 轴上方的图象,x 轴的平行线AB 分别与这两个函数图象相交于点A ,B ,则△AOB 的面积是()A.7B.14C.18D.28【答案】A【分析】本题考查了反比例函数k 的几何意义,利用反比例函数的比例系数的几何意义直接写出答案即可.【详解】解:∵x 轴的平行线AB 分别与这两个函数图象相交于点A .B ,∴AB ⊥y 轴,∵点A 、B 在反比例函数y =5x 和y =-9x 的x 轴上方的图象上,∴S △AOB =S △COB +S △AOC =12(5+9)=7,故选:A .6.已知反比例函数y =-6x x <0 与y =2xx >0 的图象如图所示,过y 轴正半轴上的任意一点P 作x 轴的平行线,分别与这两个函数的图象交于M ,N 两点.若点A 是x 轴上的任意一点,连接MA ,NA ,则S △AMN 等于.【答案】4【分析】本题考查了反比例函数k 的几何意义,连接MO ,NO ,根据MN ∥x 轴可得,S △AMN =S △OMN ,进而即可求解.【详解】解:如图所示,连接MO ,NO ,∵MN ∥x 轴∴S △AMN =S △OMN =S △POM +S △PON =-62+22=4故答案为:4.7.如图,在函数y =2x x >0 的图象上任取一点A ,过点A 作y 轴的垂线交函数y =-8xx <0 的图象于点B ,连接OA 、OB ,则△AOB 的面积是.【答案】5【分析】根据反比例函数系数k 的几何意义进行计算即可.理解反比例函数系数k 的几何意义是正确解答的关键.【详解】解:如图,∵点A 在函数y =2xx >0 的图象上,∴S △AOC =12×2=1,又∵点B 在反比例函数y =-8xx <0 的图象上,∴S △BOC =12×8=4,∴S △AOB =S △AOC +S △BOC =1+4=5,故答案为:5.8.如图,B 、C 两点分别在函数y =5x (x >0)和y =-1x(x <0)的图象上,线段BC ⊥y 轴,点A 在x 轴上,则△ABC 的面积为.【答案】3【分析】设B m ,n ,则mn =5,结合BC ⊥y 轴,得到C -1n ,n ,计算BC =m --1n =m +1n,根据平行线间的距离处处相等,得到△ABC 的面积为1BC ·y B =1m +1×n 计算即可.本题考查了反比例函数的性质,平行线间距离处处相等,熟练掌握反比例函数的性质是解题的关键.【详解】设B m ,n ,根据题意,得mn =5,∵BC ⊥y 轴,∴C -1n ,n ,∴BC =m --1n =m +1n,根据平行线间的距离处处相等,得到△ABC 的面积为12BC ·y B =12m +1n ×n =12mn +1 =3,故答案为:3.【模型3:“重叠型”定值矩形/定值三角形】【方法点拨】9.如图,点A 在反比例函数y =1x 的图像上,点B 在反比例函数y =3x的图像上,且AB ∥x 轴,点C .D 在x 轴上,若四边形ABCD 为长方形,则它的面积为.【答案】2【分析】此题考查了反比例函数的系数k 的几何意义.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.首先延长BA 交y 轴于点E ,易得四边形ADOE 与四边形BCOE 是矩形,又由点A 在反比例函数y =1x 的图像上,点B 在反比例函数y =3x的图像上,即可得S 矩形ADOE =1,S 矩形BCOE =3,继而求得答案.【详解】解:延长BA 交y 轴于点E ,∵四边形ABCD 为矩形,且AB ∥x 轴,点C 、D 在x 轴上,∴AE ⊥y 轴,∴四边形ADOE 与四边形BCOE 是矩形,∵点A 在反比例函数y =1x 的图像上,点B 在反比例函数y =3x的图像上,∴S 矩形ADOE =1,S 矩形BCOE =3,∴S 矩形ABCD =S 矩形BCOE -S 矩形ADOE =3-1=2.故答案为:2.10.如图,点A 、B 分别是反比例函数y =3xx >0 的图象上两点,分别过点A 、B 向坐标轴作垂线,四边形ACEG 的面积记作S 1,四边形BFDG 的面积记作S 2,则S 1S 2(填>、<或=).【答案】=【分析】本题考查了反比例系数k 的几何意义,在反比例函数y =kx图像中任取一点,过这一个点向x 轴和y 轴分别作垂线,与坐标轴围成的矩形的面积是定值k ,在反比例函数的图像上任意一点作坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是12k ,且保持不变.根据反比例函数解析式中k 的几何意义可知S 矩形ACOD =S 矩形BEOF =3,设S 矩形DOEG =m ,得出S 1=3-m ,S 2=3-m ,即可得出答案.【详解】解:∵A ,B 两点在反比例函数y =3xx >0 的图像上,∴S 矩形ACOD =S 矩形BEOF =3,设S 矩形DOEG =m ,∴S 1=3-m ,S 2=3-m ,∴S 1=S 2.故答案为:=.11.如图,平行于x 轴的直线l 与函数y =6x (x >0)和y =2x(x >0)的图象分别相交于A ,B 两点,分别连接AO 、BO ,则△ABO 的面积为.【答案】2【分析】本题考查反比例函数图象上点的坐标特征,k 的几何意义,设l 交y 轴于点M ,根据反比例函数k 的几何意义,得出S △ABO =S △AOM -S △BOM =2,即可求解.【详解】解:如图,设l 交y 轴于点M ,∵S △AOM =3,S △BOM =1,则S △ABO =S △AOM -S △BOM =2,故答案为:2.12.如图,点A 在双曲线y =1x 上,点B 在双曲线y =3x上,且AB ∥x 轴,则△ABO 的面积是.【答案】1【分析】本题主要考查了反比例函数比例系数的几何意义,延长BA 交y 轴于C ,则AB ⊥y 轴,根据反比例函数比例系数的几何意义可得S △AOC =12,S △BOC =32,则S △AOB =S △BOC -S △AOC =1.【详解】解:如图所示,延长BA 交y 轴于C ,∵AB ∥x 轴,∴AB ⊥y 轴,∵点A 在双曲线y =1x 上,点B 在双曲线y =3x上,∴S △AOC =12,S △BOC =32,∴S △AOB =S △BOC -S △AOC =1,故答案为:1.【模型4:“喇叭三角形”】【方法点拨】13.如图,点A ,B ,在反比例函数y =4x的图象上,连接OA ,OB ,分别过点A ,B 作x 轴的垂线,垂足分别为M ,N ,图中两块阴影部分面积分别为S 1、S 2;若S 1=1,则AMBN=.【答案】2【分析】本题考查的是反比例函数系数k 的几何意义,熟知在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积为12|k |是解答此题的关键.利用k 的几何意义求出△OAM 、△OBN 的面积,然后求出△OCM 的面积,利用相似三角形的性质得到S △OCM S △OBN =OM ON 2即可求解.【详解】解:设OB 交AM 于点C ,∵分别过点A ,B 作x 轴的垂线,垂足分别为M ,N ,∴S △OAM =S △OBN =2,∴S △OCM =S △OAM -S 1=2-1=1,又∵AM ∥BN ,∴△OCM ∽△OBN ,∴S △OCM S △OBN =OM ON2=12,∴OM ON=22,又∵OM ⋅AM =ON ⋅BN ,∴AM BN =ON OM =2.故答案为:214.如图是一个反比例函数(x >0)的图象,点A (2,4)在图象上,AC ⊥x 轴于C ,当点A 运动到图象上的点B (4,2)处,BD ⊥x 轴于D ,△AOC 与△BOD 重叠部分的面积为()A.1B.2C.34D.13【答案】A【解答】解:如图所示:∵点A (2,4),点B (4,2),AC ⊥x 轴于C ,BD ⊥x 轴于D ,∴点C 的坐标为(2,0),点D 的坐标为(4,0),AC ∥BD ,∴△OCE ∽△ODB ,∴OC OD =CE DB ,即24=CE 2解得CE =1,∴S △OCE OC ⋅CE 2=2×12=1,即△AOC 与△BOD 重叠部分的面积为1.故选:A .15.如图,过反比例函数y =9x(x >0)的图象上任意两点A 、B 分别作x 轴的垂线,垂足分别为C 、D ,连接OA 、OB ,设△AOC 和△BOD 的面积分别是S 1、S 2,比较它们的大小,可得()A.S 1>S 2B.S 1=S 2C.S 1<S 2D.大小关系不能确定【答案】B 【解答】解:由于A 、B 均在反比例函数y =9x 的图象上,且AC ⊥x 轴,BD ⊥x 轴,则S 1=92;S 2=92.故S 1=S 2.故选:B .16.如图,在第一象限内,点P (2,3),M (a ,2)是双曲线y =k x (k ≠0)上的两点,P A ⊥x 轴于点A ,MB ⊥x 轴于点B ,P A 与OM 交于点C ,则△OAC 的面积为()A.32B.43C.2D.83【答案】B 【解答】解:把P (2,3),M (a ,2)代入y =k x得k =2×3=2a ,解得k =6,a =3,设直线OM 的解析式为y =mx ,把M (3,2)代入得3m =2,解得m =23,所以直线OM 的解析式为y =23x ,当x =2时,y =23×2=43,所以C 点坐标为(2,43),所以△OAC 的面积=12×2×43=43.故选:B .【方法点拨】条件:A /B 两点分别位y =k x上不同两点,延长AB 交x 轴与点F ,B 位AF 的中点结论:①▲ACF ~▲BDF ,且相似比为BF AF =12。
押浙江卷第15-16题(反比例函数、相似三角形、四边形)(原卷版)-备战2024年中考数学临考题押题

押浙江卷第15-16题(反比例函数、相似三角形、四边形)押题方向一:反比例函数2023年浙江真题考点命题趋势2023年温州卷第15题反比例函数的应用从近几年浙江各地中考来看,反比例函数在填空题中主要考查反比例函数的应用与反比例函数系数k 的几何意义,属于稍难题,有时候作为填空题的压轴题考查;预计2024年浙江卷还将继续重视反比例函数系数k 的几何意义。
2023年衢州卷、绍兴卷第15题、宁波卷第16题反比例函数系数k的几何意义1.(2023•温州)在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,加压后气体对汽缸壁所产生的压强p (kPa )与汽缸内气体的体积V (mL )成反比例,p 关于V 的函数图象如图所示.若压强由75kPa 加压到100kPa ,则气体体积压缩了mL .2.(2023•绍兴)如图,在平面直角坐标系xOy 中,函数(k 为大于0的常数,x >0)图象上的两点A (x 1,y 1),B (x 2,y 2),满足x 2=2x 1,△ABC 的边AC ∥x 轴,边BC ∥y 轴,若△OAB 的面积为6,则△ABC 的面积是.3.(2023•衢州)如图,点A ,B 在x 轴上,分别以OA ,AB 为边,在x 轴上方作正方形OACD ,ABEF ,反比例函数y =(k >0)的图象分别交边CD ,BE 于点P ,Q .作PM ⊥x 轴于点M ,QN ⊥y 轴于点N .若OA =2AB ,Q 为BE 的中点,且阴影部分面积等于6,则k 的值为.4.(2023•宁波)如图,点A ,B 分别在函数y =(a >0)图象的两支上(A 在第一象限),连结AB 交x轴于点C .点D ,E 在函数y =(b <0,x <0)图象上,AE ∥x 轴,BD ∥y 轴,连结DE ,BE .若AC=2BC ,△ABE 的面积为9,四边形ABDE 的面积为14,则a ﹣b 的值为,a 的值为.1.||A PB O A P B O A P B O S S S k 111222333===矩形矩形矩形2.||△△△P A O P A O P A O k S S S 112233===21.如图,在△OAB 中,边OA 在y 轴上.反比例函数y =(x >0)的图象恰好经过点B ,与边AB 交于点C .若BC =3AC ,S △OAB =10.则k 的值为.2.如图,直角坐标系中,▱AOBC 的顶点B 在x 轴的正半轴上,A ,C 在第一象限.反比例函数y =(x >0)的图象经过点A ,与BC 交于点D ,AE ⊥x 轴于点E ,连结DE 并延长交AO 的延长线于点F ,反比例函数y =(x <0)的图象经过点F ,连结BF ,则△BDF 的面积为.3.如图,矩形ABCD 的顶点D 在反比例函数的图象上,顶点B ,C 在x 轴上,对角线AC 的延长线交y 轴于点E ,连接BE ,若△BCE 的面积是2,则k 的值为.4.如图,Rt△ABC顶点A落在y轴上,斜边上的中线CD⊥x轴于点D,O为坐标原点,反比例函数经过直角顶点C,若△BCD的面积为5,则k的值为.5.如图,AB平行于x轴,点A在函数y=(x>0)的图象上,点B在函数y=(x<0)的图象上,BC∥AO,若四边形AOBC的面积为,则实数k的值为.6.如图,点A为反比例函数y=(x>0)上一点,连结AO并延长交反比例函数y=(x<0)于点B,且k2=9k1.点C在y轴正半轴上,连结CA并延长交x轴于点E,连结BC交x轴于点F,若=4,S△COB=10,则△COF的面积为.7.如图,点A,B在反比例函数y=(x>0)的图象上,点C在反比例函数y=(x>0)的图象上,连接AC,BC,且AC∥x轴,BC∥y轴,AC=BC.若点A的横坐标为2,则k的值为.8.如图,点A在反比例函数y=(x>0)的图象上,点B在反比例函数y=(x<0)的图象上,AB∥x 轴,AB=2.(1)若点A的坐标为(,2),则a+b的值是.(2)若点C在反比例函数y=(x>0)的图象上,点D在反比例函数y=(x<0)的图象上,CD ∥AB,CD=3,AB与CD之间的距离为1,则a﹣b的值是.9.如图,直线AB与反比例函数的图象相交于A,B两点,与y轴相交于点C,点D是x轴负半轴上的一点,连结CD和AD,AD交y轴于点E,且AC=AE,若,△CDE的面积为6,则k 的值为.押题方向二:相似三角形2023年浙江真题考点命题趋势2023年湖州卷第15题相似三角形的应用从近几年浙江各地中考来看,对相似三角形的应用及相似三角形的综合考查经常会出现在填空题的压轴题,整体稍有难度;预计2024年浙江卷在填空题中还将继续重视相似三角形的综合的考查。
初中数学中考复习 备战2020年中考数学一轮专项复习——反比例函数综合问题(含详细解答)

备战2020年中考数学一轮专项复习——反比例函数综合问题一、反比例函数的概念:知识要点:1、一般地,形如 y = x k ( k 是常数, k = 0 ) 的函数叫做反比例函数。
注意:(1)常数 k 称为比例系数,k 是非零常数;(2)解析式有三种常见的表达形式:(A )y = xk (k ≠ 0) ; (B )xy = k (k ≠ 0); (C )y=kx -1(k ≠0) 二、反比例函数的图象和性质:知识要点:1、形状:图象是双曲线。
2、位置:(1)当k>0时,双曲线分别位于第一、三象限内;(2)当k<0时, 双曲线分别位于第二、四象限内。
3、增减性:(1)当k>0时,y = xk (k ≠ 0)为减函数,y 随x 的增大而减小; (2)当k<0时,y = xk (k ≠ 0)为增函数,y 随x 的增大而增大。
4、变化趋势:双曲线无限接近于x 、y 轴,但永远不会与坐标轴相交5、对称性:(1)对于双曲线本身来说,它的两个分支关于直角坐标系原点成中心对称;(2)对于k 取互为相反数的两个反比例函数(如:y =x 6 和y = x 6 )来说,它们是关于x 轴,y 轴成轴对称。
一、选择题:1.下列函数,①y =2x ,②y =x ,③y =x ﹣1,④y =是反比例函数的个数有( ) A .0个 B .1个 C .2个 D .3个【分析】根据反比例函数的定义,反比例函数的一般式是(k ≠0)判定则可. 【解析】①y =2x 是正比例函数;②y =x 是正比例函数;③y =x ﹣1是反比例函数;④y=不是反比例函数,是反比例关系;所以共有1个.故选:B.2.(2019•济南)函数y=﹣ax+a与y=(a≠0)在同一坐标系中的图象可能是()A.B.C.D.【解析】a>0时,﹣a<0,y=﹣ax+a在一、二、四象限,y=在一、三象限,无选项符合.a<0时,﹣a>0,y=﹣ax+a在一、三、四象限,y=(a≠0)在二、四象限,只有D符合;故选:D.3.如图,过原点的直线l与反比例函数y=﹣的图象交于M,N两点,根据图象猜想线段MN的长的最小值是()A.B.2C.2 D.1【分析】设N的横坐标是a,则纵坐标是﹣,利用a即可表示出ON的长度,然后根据不等式的性质即可求解.【解析】设N的横坐标是a,则纵坐标是﹣.则OM=ON=≥.则MN的最小值是2.故选:B.4.(2019•阜新)如图,点A在反比例函数y=(x>0)的图象上,过点A作AB⊥x轴,垂足为点B,点C在y 轴上,则△ABC的面积为()A.3 B.2 C.D.1【解析】连结OA,如图,∵AB⊥x轴,∴OC∥AB,∴S△OAB=S△CAB,而S△OAB=|k|=,∴S△CAB=,故选:C.5.(2019•遵义)如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为4,2,反比例函数y=(x>0)的图象经过A,B两点,若菱形ABCD的面积为2,则k的值为()A.2 B.3 C.4 D.6【解析】过点A作x轴的垂线,交CB的延长线于点E,∵A,B两点在反比例函数y=(x>0)的图象,且纵坐标分别为4,2,∴A(,4),B(,2),∴AE=2,BE=k﹣k=k,∵菱形ABCD的面积为2,∴BC×AE=2,即BC=,∴AB=BC=,在Rt△AEB中,BE==1∴k=1,∴k=4.故选:C.6.如图,在菱形ABOC中,∠ABO=120°,它的一个顶点C在反比例函数y=的图象上,若将菱形向下平移2个单位,点A恰好落在函数图象上,则该反比函数的表达式为()A.y=﹣B.y=﹣C.y=﹣D.y=﹣【分析】点C作CD⊥x轴于D,设菱形的边长为a,根据菱形的性质和三角函数分别表示出C,以及点A向下平移2个单位的点,再根据反比例函数图象上点的坐标特征得到方程组求解即可.【解析】过点C作CD⊥x轴于D,设菱形的边长为a,在Rt△CDO中,OD=a•cos60°=a,CD=a•sin60°=a,则C(﹣a,a),点A向下平移2个单位的点为(﹣a﹣a,a﹣2),即(﹣a,a﹣2),则,解得.故反比例函数解析式为y=﹣.故选:B.7.(2019•淄博)如图,△OA1B1,△A1A2B2,△A2A3B3,…是分别以A1,A2,A3,…为直角顶点,一条直角边在x 轴正半轴上的等腰直角三角形,其斜边的中点C1(x1,y1),C2(x2,y2),C3(x3,y3),…均在反比例函数y =(x>0)的图象上.则y1+y2+…+y10的值为()A.2B.6 C.4D.2【解析】过C1、C2、C3…分别作x轴的垂线,垂足分别为D1、D2、D3…其斜边的中点C1在反比例函数y=,∴C(2,2)即y1=2,∴OD1=D1A1=2,设A1D2=a,则C2D2=a此时C2(4+a,a),代入y=得:a(4+a)=4,解得:a=,即:y2=,同理:y3=,y 4=,……∴y1+y2+…+y10=2+++……=,故选:A.8.如图,已知点A,B在双曲线y=(x>0)上,AC⊥x轴于点C,BD⊥y轴于点D,AC与BD交于点P,P 是AC的中点.若△ABP的面积为4,则k的值为().A.16 B.8 C.4 D.24【分析】由△ABP的面积为4,知BP•AP=8.根据反比例函数y=中k的几何意义,知本题k=OC•AC,由反比例函数的性质,结合已知条件P是AC的中点,得出OC=BP,AC=2AP,进而求出k的值.【解答】解:∵△ABP 的面积为•BP •AP =4,∴BP •AP =8,∵P 是AC 的中点,∴A 点的纵坐标是B 点纵坐标的2倍,又∵点A 、B 都在双曲线y =(x >0)上,∴B 点的横坐标是A 点横坐标的2倍,∴OC =DP =BP ,∴k =OC •AC =BP •2AP =16.故选A.二、填空题:9.(2019山西)如图,在平面直角坐标系中,点O 为坐标原点,菱形ABCD 的顶点B 在x 轴的正半轴上,点A 坐标为(-4,0),点D 的坐标为(-1,4),反比例函数)0(>=x xk y 的图象恰好经过点C ,则k 的值为 .【解析】过点D 作DE ⊥AB 于点E ,则AD=5,∵四边形ABCD 为菱形,∴CD=5∴C (4,4),将C 代入x k y =得:44k =,∴16=k10.(2019遂宁中考 第15题 4分)如图,在平面直角坐标系中,矩形OABC 的顶点O 落在坐标原点,点A 、点C 分别位于x 轴,y 轴的正半轴,G 为线段OA 上一点,将△OCG 沿CG 翻折,O 点恰好落在对角线AC 上的点P 处,反比例函数y =经过点B .二次函数y =ax 2+bx +c (a ≠0)的图象经过C (0,3)、G 、A 三点,则该二次函数的解析式为 .(填一般式)【解析】点C (0,3),反比例函数y =经过点B ,则点B (4,3),则OC =3,OA =4,∴AC =5,设OG =PG =x ,则GA =4﹣x ,PA =AC ﹣CP =AC ﹣OC =5﹣3=2, 由勾股定理得:(4﹣x )2=4+x 2,解得:x =,故点G (,0),将点C 、G 、A 坐标代入二次函数表达式得:,解得:,故答案为:y =x 2﹣x +3. 11.如图,已知点(1,3)在函数y =kx (x >0)的图象上,正方形ABCD 的边BC 在x 轴上,点E 是对角线BD 的中点,函数y =kx(x >0)的图象又经过A ,E 两点,则点E 的横坐标为____.【解析】 把(1,3)代入到y =kx,得k =3, 所以函数解析式为y =3x. 设A (a ,b ),根据图象和题意可知,点E ⎝ ⎛⎭⎪⎫a +b 2,b 2.因为y =3x 的图象经过A ,E ,所以分别把点A 和E 代入到函数解析式中得 ab =3,①b 2⎝ ⎛⎭⎪⎫a +b 2=3,② 由②得ab 2+b 24=3,把①代入得32+b 24=3, 即b 2=6,解得b =±6,因为A 在第一象限,所以b >0,所以b = 6.把b =6代入①求得a =62, 所以点E 的横坐标为a +b 2= 6.故答案为 6. 12.如图,Rt △AOB 中,∠OAB =90°,∠OBA =30°,顶点A 在反比例函数y =图象上,若Rt △AOB 的面积恰好被y 轴平分,则进过点B 的反比例函数的解析式为 .【分析】分别过A 、B 作AE ⊥x 轴于E ,BD ⊥y 轴交AE 于F .设A (a ,b ),则ab =﹣4.根据两角对应相等的两三角形相似,得出△OAE ∽△ABF ,由相似三角形的对应边成比例,则BD 、OD 都可用含a 、b 的代数式表示,从而求出B 的坐标,进而得出结果.【解析】分别过A 、B 作AE ⊥x 轴于E ,BD ⊥y 轴交AE 于F .设A (a ,b ).∵顶点A 在反比例函数y =图象上,∴ab=﹣4.∵∠OAB=90°,∠OAE=90°﹣∠BAF=∠ABF,∠OEA=∠BFA=90°,∴△OAE∽△ABF,∴OA:AB=OE:AF=AE:BF,在Rt△AOB中,∠AOAB=90°,∠OBA=30°,∴OA:AB=1:,∴﹣a:AF=b:BF=1:,∴AF=﹣,BF=b,∵Rt△AOB的面积恰好被y轴平分,∴AC=BC,∴BD=DF=BF=﹣a,OD=AE+AF=b﹣a,∴b=﹣a,∴A(﹣b,b),B(b,b﹣)∴﹣b•b=﹣4,∴b2=,∴k=b(b﹣)=b2﹣ab=10,故答案为:10.13.如图, △OAP ,△ABQ 是等腰直角三角形,点P ,Q 在反比例函数y =4x (x >0)上,直角顶点A ,B 均在x 轴上,则点Q 的坐标为 .【解析】 ∵△OAP 是等腰直角三角形,∴PA =OA .∴设P 点的坐标是(a ,a ),把(a ,a )代入解析式y =4x,解得a =2(a =-2舍去), ∴P 的坐标是(2,2),∴OA =2,∵△ABQ 是等腰直角三角形,∴BQ =AB ,∴可以设Q 的纵坐标是b ,∴横坐标是b +2,把Q 的坐标代入解析式y =4x, 得b =4b +2,∴b =5-1(b =-5-1舍去),∴点Q 的坐标为(5+1,5-1).14.(2019•毕节市)如图,在平面直角坐标中,一次函数y =﹣4x +4的图象与x 轴、y 轴分别交于A 、B 两点.正方形ABCD 的顶点C 、D 在第一象限,顶点D 在反比例函数y =(k ≠0)的图象上.若正方形ABCD 向左平移n 个单位后,顶点C 恰好落在反比例函数的图象上,则n 的值是 .【解析】过点D 作DE ⊥x 轴,过点C 作CF ⊥y 轴,∵AB ⊥AD ,∴∠BAO =∠DAE ,∵AB =AD ,∠BOA =∠DEA ,∴△ABO ≌△DAE (AAS ),∴AE =BO ,DE =OA ,易求A (1,0),B (0,4),∴D (5,1),∵顶点D 在反比例函数y =上,∴k =5,∴y =,易证△CBF ≌△BAO (AAS ),∴CF =4,BF =1,∴C (4,5),∵C 向左移动n 个单位后为(4﹣n ,5),∴5(4﹣n )=5,∴n =3,故答案为3;三、解答题15.如图,一次函数y =kx +2的图象与反比例函数y =m x的图象在第一象限的交点为P .PA 垂直x 轴于点A .PB 垂直y 轴于点B .函数y =kx +2的图象分别交x 轴,y 轴于点C ,D .已知DB =2OD ,△PBD 的面积S △PBD =4.(1)求点D 的坐标;(2)求k ,m 的值;(3)写出当x >0时,使一次函数y =kx +2的值大于反比例函数y =m x的值的x 的取值范围.【解析】(1)在y =kx +2中,令x =0,得y =2,所以点D (0,2).(2)因为OD =2,DB =2OD =4,由S △PBD =4,可得BP =2,而OB =OD +DB =6,所以点P (2,6).将P (2,6)分别代入y =kx +2与y =mx,可得 k =2,m =12.(3) 由图象可知,当x >0时,使一次函数y =kx +2的值大于反比例函数y =mx的值的x 的取值范围是x >2.16.(2019遂宁中考 第23题 10分)如图,一次函数y =x ﹣3的图象与反比例函数y ═(k ≠0)的图象交于点A 与点B (a ,﹣4).(1)求反比例函数的表达式;(2)若动点P 是第一象限内双曲线上的点(不与点A 重合),连接OP ,且过点P 作y 轴的平行线交直线AB于点C,连接OC,若△POC的面积为3,求出点P的坐标.【解析】(1)将B(a,﹣4)代入一次函数y=x﹣3中得:a=﹣1∴B(﹣1,﹣4)将B(﹣1,﹣4)代入反比例函数y═(k≠0)中得:k=4∴反比例函数的表达式为y=;(2)如图:设点P的坐标为(m,)(m>0),则C(m,m﹣3)∴PC=|﹣(m﹣3)|,点O到直线PC的距离为m∴△POC的面积=m×|﹣(m﹣3)|=3解得:m=5或﹣2或1或2∵点P不与点A重合,且A(4,1)∴m≠4又∵m>0∴m=5或1或2∴点P的坐标为(5,)或(1,4)或(2,2).17.(2019•河池)在平面直角坐标系中,矩形ABCD的顶点坐标为A(0,0),B(6,0),C(6,8),D(0,8),AC,BD交于点E.(1)如图(1),双曲线y=过点E,直接写出点E的坐标和双曲线的解析式;(2)如图(2),双曲线y=与BC,CD分别交于点M,N,点C关于MN的对称点C′在y轴上.求证△CMN~△CBD,并求点C′的坐标;(3)如图(3),将矩形ABCD向右平移m(m>0)个单位长度,使过点E的双曲线y=与AD交于点P.当△AEP为等腰三角形时,求m的值.【解析】(1)如图1中,∵四边形ABCD是矩形,∴DE=EB,∵B(6,0),D(0,8),∴E(3,4),∵双曲线y=过点E,∴k1=12.∴反比例函数的解析式为y=.(2)如图2中,∵点M,N在反比例函数的图象上,∴DN•AD=BM•AB,∵BC=AD,AB=CD,∴DN•BC=BM•CD,∴=,∴=,∴=,∵∠MCN=∠BCD,∴△MCN∽△BCD,∴∠CNM=∠CDB,∴MN∥BD,∴△CMN∽△CBD.∵B(6,0),D(0,8),∴直线BD的解析式为y=﹣x+8,∵C,C′关于MN对称,∴CC′⊥MN,∴CC′⊥BD,∵C(6,8),∴直线CC′的解析式为y=x+,∴C′(0,).(3)如图3中,①当AP=AE=5时,∵P(m,5),E(m+3,4),P,E在反比例函数图象上,∴5m=4(m+3),∴m=12.②当EP=AE时,点P与点D重合,∵P(m,8),E(m+3,4),P,E在反比例函数图象上,∴8m=4(m+3),∴m=3.③显然PA≠PE,若相等,则PE∥x轴,显然不可能.综上所述,满足条件的m的值为3或12.18.“六一”儿童节,小文到公园游玩.看到公园的一段人行弯道MN(不计宽度)如图,它与两面互相垂直的围墙OP,OQ之间有一块空地MPOQN(MP⊥OP,NQ⊥OQ),他发现弯道MN上任意一点到两边围墙的垂线段与围墙所围成的矩形的面积都相等.比如:A,B,C是弯道MN上的三点,矩形ADOG、矩形BEOH、矩形CFOI 的面积相等.爱好数学的他建立了平面直角坐标系(如图),图中三块阴影部分的面积分别记为S1,S2,S3,并测得S2=6(单位:平方米),OG=GH=HI.(1)求S1和S3的值;(2)设T(x,y)是弯道MN上的任一点,写出y关于x的函数解析式;(3)公园准备对区域MPOQN内部进行绿化改造,在横坐标、纵坐标都是偶数的点处种植花木(区域边界上的点除外),已知MP=2米,NQ=3米.问一共能种植多少棵花木?【解析】(1)∵矩形ADOG 、矩形BEOH 、矩形CFOI 的面积相等,∴弯道为反比例函数图象的一部分.设反比例函数的解析式为y =k x (k ≠0),OG =GH =HI =a ,则AG =k a ,BH =k 2a ,CI =k 3a .所以S 2=k 2a •a -k 3a•a =6,解得k =36.所以S 1=k a •a -k 2a •a =12k =12×36=18,S 3=k 3a •a =13k =13×36=12;(2)由(1)得,弯道的函数解析式为y =36x .∵T(x ,y)是弯道MN 上的任一点,∴y =36x ;(3)∵MP =2,NQ =3,∴GM =362=18,OQ =363=12.∵在横坐标、纵坐标都是偶数的点处种植花木(区域边界上的点除外),∴当x =2时,y =18,可以种8棵;当x =4时,y =9,可以种4棵;当x =6时,y =6,可以种2棵;当x =8时,y =4.5,可以种2棵;当x =10时,y =3.6,可以种1棵.故一共可以种8+4+2+2+1=17(棵)花木.19、如图,已知反比例函数k y x=与一次函数y x b =+的图象在第一象限相交于点(1,4)A k -+. (1)试确定这两个函数的表达式;(2)求出这两个函数图象的另一个交点B 的坐标,并根据图象写出使反比例函数的值大于一次函数的值的x 的取值范围.【解析】(1)∵已知反比例函数k y x =经过点(1,4)A k -+,∴41k k-+=,即4k k -+= ∴2k =∴A(1,2) ∵一次函数y x b =+的图象经过点A(1,2),∴21b =+∴1b =∴反比例函数的表达式为2y x=, 一次函数的表达式为1y x =+。
非学科数学学培训 相似三角形判定与性质综合(资料附答案)
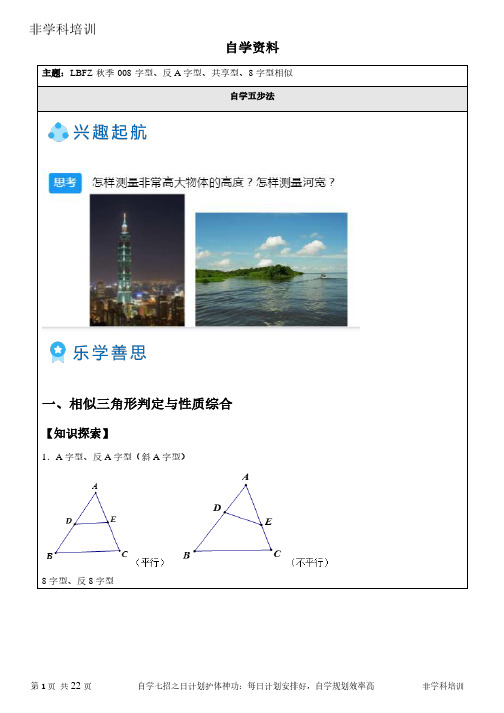
自学资料一、相似三角形判定与性质综合【知识探索】1.A字型、反A字型(斜A字型)8字型、反8字型第1页共22页自学七招之日计划护体神功:每日计划安排好,自学规划效率高非学科培训2.共享性:【错题精练】例1.如图,△ABC中,D边BC上一点,E是CD的中点,且∠ACD=∠ABE,已知AC=2,设AB=x,AD=y,则y与x满足的关系式为()A. xy=4;B. 2xy−y2=4;C. xy−y2=4;D. x2+xy−2y2=4.【答案】B例2.如右图,AD//CB,AB与CD相交于点E,过点B的直线交CD于点F,交AD于点G,若BEAE =23,BF GF =85,EF=2,则DF的长为()第2页共22页自学七招之以背代诵掌:高效记忆有妙招,以背代诵效果好非学科培训A. 72; B. 257;C. 185; D. 4.【答案】B例3.如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为()A. 4;B. 6;C. 4√2;D. 4√3.【答案】C例4.如图,在△ABC中,点D在边AB上,过点D作DE∥BC交AC于点E,DF∥AC交BC于点F,若AE:DF=2:3,则BF:BC的值是()A. 23; B. 35;C. 12; D. 25.【答案】B例5.如图,在平行四边形ABCD中,E是DC上的点,DE:EC=3:2,连接AE交BD于点F,则SΔDEF:SΔBAF:S四边形BCEF= .第3页共22页自学七招之举一反三剑:总结归纳典型题,多种解法开脑洞非学科培训【答案】9:25:48例6.如图,在△ABC中,D,E分别是AB,AC上的点,AF平分∠BAC,交DE于点G,交BC 于点F.若∠AED=∠B,且AG:GF=3:2,则DE:BC=.【答案】3:5例7.如图,在△ABC中,点D,E分别在边AB,AC上,∠ACD=∠B,DE∥BC.(1)求证:△ADE∽△ACD;(2)若DE=6,BC=10,求线段CD的长.【解答】(1)证明:∵∠ACD=∠B,又∵∠DAC=∠CAB,∴△ACD∽△ABC,∵DE∥BC,∴△ABC∽△ADE,∴△ADE∽△ACD;(2)解:∵DE∥BC,∴∠EDC=∠DCB,∵∠ACD=∠B,即∠ECD=∠B,∴△EDC∽△DCB,∴CDBC =DECD,即CD2=BC⋅DE,∵DE=6,BC=10,第4页共22页自学七招之以背代诵掌:高效记忆有妙招,以背代诵效果好非学科培训∴CD2=BC⋅DE=60,解得:CD=2√15.【答案】(1)略;(2)2√15.例8.如图,在△ABC中,AD、BE是中线,它们相交于点F,EG∥BC,交AD于点G.(1)求证:△FGE∽△FDB;(2)求AGDF的值.【解答】(1)解:由题意知:∵EG∥BC,∴∠GEF=∠FBD,∵∠BFD=∠GFE,∠GEF=∠FBD,∴△FGE∽△FDB;(2)解:∵AD、BE分别是三角形的中线,∴BD=CD,AE=EC,∵EG∥BC,∴EG是△ADC的中位线,∴EG=12CD,∵△EFG∽△BDF,∴EGBD =FGFD=12,∴DF=23DG,∵EG是△ADC的中位线,∴AG=DG,∴DF=23AG,∴AG:DF=3:2=32.【答案】(1)略;(2)32.第5页共22页自学七招之举一反三剑:总结归纳典型题,多种解法开脑洞非学科培训例9.如图,等边△ABC中,点D是BC上任意点,以AD为边作∠ADE=∠ADF=60∘,分别交AC,AB于点E,F.(1)求证:AD2=AE×AC;(2)已知BC=2,设BD的长为x,AF的长为y,求y关于x的函数表达式;(3)若四边形AFDE的外接圆直径为13√312,求y与x的值.【解答】(1)解:在等边△ABC中∠B=∠C=60∘∵∠ADE=60∘∴∠ADE=∠ACD,∠DAE=∠CAD,∴△ADE=△ACD∴ADAE =ACAD∴AD2=AE×AC;(2)解:∵∠B=∠ADF,∠DAF∠BAD∴△DAF∽△BAD∴DABA =AFAD∴AD2=AF×AB∴△DAF∽△BAD由(1)知AD2=AE×AC,且AB=AC∴AE=AF∵∠B=∠C=∠ADE且∠BAD+∠B=∠ADE+∠CDE ∴∠BAD=∠CDE∴△ABD∽△DCE∴ABBD =DCCE∵BC=2,BD=x,AF=y∴AB=2,CD=2−x,CE=2−y∴2x =2−x2−y∴y=12x2−x+2(0≤x≤2);第6页共22页自学七招之以背代诵掌:高效记忆有妙招,以背代诵效果好非学科培训第7页 共22页自学七招之举一反三剑:总结归纳典型题,多种解法开脑洞非学科培训(3)解:连接EF ,AF =AE ,∠EAF =60∘∠EDF =120∘则△AEF 为等边三角形 ∴四边形AFDE 的外接圆即为等边三角形△AEF 的外接圆 ∵四边形AFDE 的外接圆直径为13√312∴AF =EF =138∴当y =138时,x 1=12,x2=32.【答案】(1)略;(2)y =12x 2−x +2(0≤x ≤2);(3)当y =138时,x 1=12,x 2=32.例10.已知:如图,点D 是等腰直角△ABC 的重心,其中∠ACB =90∘,将线段CD 绕点C 逆时针旋转90°得到线段CE ,连结DE ,若△ABC 的周长为6,则△DCE 的周长为( )A. 2√2;B. 2√3;C. 4;D. 3√2.【答案】A例11.如图,△ABC 是等边三角形,D ,E 在BC 边所在的直线上,且BC 2=BD ⋅CE . (1)求∠DAE 的度数.(2)求证:AD 2=DB ⋅DE .【解答】(1)解: ∵△ABC 是等边三角形,∴∠ABC =∠ACB =60∘,AB =AC =BC , ∴∠ABD =∠ACE , ∵BC 2=BD ⋅CE , ∴AB ⋅AC =BD ⋅CE ,即ABBD =CEAC,∴△ABD∽△ECA;∴∠DAB=∠E,∴∠DAE=∠DAB+∠BAC+∠EAC=120∘(2)证明:∵∠DAE=∠ADB=120∘,∠D=∠D,∴△ABD∽△EAD∴ADDE =BDAD,∴AD2=DB⋅DE.【答案】(1)∠DAE=120∘;(2)略.例12.如图使用卡钳测量容器内径的示意图,现量得卡钳上A、D两端点的距离为6cm,AOBO =DOCO=47,求容器的内径BC.【解答】解:∵AOBO =DOCO又∵∠AOD=∠BOC ∴△AOD∽△BOC∴ADBC =AOBO=DOCO=47∵AD=6cm∴BC=212cm【答案】BC=212cm.例13.如图,在△ABC中,∠A=36∘,AC=AB=2,将△ABC绕点B逆时针方向旋转得到△DBE,使点E在边AC上,DE交AB于点F,则△AFE与△DBF的面积之比等于()第8页共22页自学七招之以背代诵掌:高效记忆有妙招,以背代诵效果好非学科培训A. √5−1;2;B. √5−14C. 3−√5;2D. 3−√5.4【答案】C例14.如图,已知在Rt△OAC中,O为坐标原点,直角顶点C在x轴的正半轴上,反比例函数y=k(k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若△OCD∽△ACO,则直线OA的x解析式为.【答案】y=2x例15.如图:在⊙O中,经过⊙O内一点P有一条弦AB,且AP=4,PB=3,过P点另有一动弦CD,连接AC,DB.设CP=x,PD=y.(1)求证:△ACP∽△DBP;(2)写出y关于x的函数解析式;(3)若CD=8时,求S△ACP:S△DBP的值.第9页共22页自学七招之举一反三剑:总结归纳典型题,多种解法开脑洞非学科培训【解答】(1)证明:∵∠C=∠B,∠A=∠D,∴△ACP∽△DBP.(2)解:由(1)可得:CP⋅PD=AP⋅PB,即xy=12.∴y=12x.(3)解:由题意得{xy=12x+y=8.由②得y=8−x.代入①得x(8−x)=12.得x1=2,x2=6.∴CP=2,PD=6或CP=6,PD=2.S△ACP:S△DBP=CP2:BP2=22:32=4:9或S△ACP:S△DBP=CP2:BP2=62:32=4:1.【答案】(1)略;(2)y=12x;(3)4:1.【举一反三】1.如图,在直角△ABC中,∠ACB=90∘,AC=3,BC=4,且点D,D分别在BC,AB上,连结AD和CE交于点H,若BDCD =2,AHDH=1,则BE的长为.【答案】154.第10页共22页自学七招之以背代诵掌:高效记忆有妙招,以背代诵效果好非学科培训2.在平行四边形ABCD中,E为AB上的一点,连结CE,P为CE的中点,过P作直线MN分别交边AD,BC于点M,N,若EA:EB=5:4,则且PM:PN=.【答案】723.已知,如图,△ABC中,AB=2,BC=4,D为BC边上一点,BD=1.(1)求证:△ABD∽△CBA;(2)在原图上作DE∥AB交AC与点E,请直接写出另一个与△ABD相似的三角形,并求出DE的长.【解答】(1)∵AB=2,BC=4,BD=1,∴ABBC =24=12,BD AB =12,∴ABBC =BDAB,∵∠ABD=∠CBA,∴△ABD∽△CBA;(2)∵DE∥AB,∴△CDE∽△CBA,∴△ABD∽△CDE,∴DE=1.5.【答案】(1)见解答;(2)DE=1.5.4.如图,在平行四边形ABCD中,∠BCD和∠ABC的平分线分别交AD于E,G两点,CE,BG相交于点O.(1)求证:AG=DE;(2)已知AB=4,AD=5,求OEOC的值;(3)求四边形ABOE的面积与△BOC的面积之比.【解答】(1)证明:BG平分∠ABC,CE平分∠BCD∴∠ABG=∠CBG,∠BCE∠DCE∵AD∥BC∴∠CBG=∠AGB,∠BCE=∠CED∴AB=AG,CD=DE∵AB=CD∴AG=DE;(2)解:∵AB=4,AD=5∴AG=DG=4,AE=AD−DE=1,GD=AD−AG=1∴EG=AD−AE−DG=3∵AD∥BC∴OEOC =EGBC=35;(3)解:连接AO,设SΔOEG=9a∵AD∥BC,∴△OEG∽△OCB∴SΔOEG:SΔOBC=9:25∴SΔOBC=25a∵AE:EG=1:3∴SΔOAE:SΔOEG=1:3∴SΔOAE=3a∴SΔOAG=12a∵SΔOAB:SΔOAG=OB:OG=5:3∴SΔOAB=20a∴S四边形ABOE=SΔOAB+SΔOAE=23a∴S四边形ABOE:SΔOBC=23a:25a=23:25.【答案】(1)略;(2)35;(3)23∶25.5.如图,在△ABC中,点D、E分别在AB、AC上,DE∥BC,若AD=2,DB=1,△ADE、△ABC的面积分别为S1、S2,则S1的值为()S2;A. 23B. 1;2;C. 49D. 2.【答案】C6.如图,在△ABC中,AC=4,BC=2,点D是边AB上一点,CD将△ABC分成△ACD和△BCD,若△ACD是以AC为底的等腰三角形,且△BCD与△BAC相似,则CD的长为..【答案】4√337.如图,在△ABC中,EF∥CD,DE∥BC.(1)求证:AF:FD=AD:DB;(2)若AB=15,AD:BD=2:1,求DF的长.【解答】(1)证明:∵EF∥CD,∴AFFD =AEEC,∵DE∥BC,∴ADBD =AEEC,∴AF:FD=AD:DB;(2)解:∵AD:BD=2:1,∴BD=12AD,∴AD+12AD=15,∴AD=10,∵AF:FD=AD:DB,∴AF:FD=2:1,∴AF=2DF,∵AF+DF=10,∴2DF+DF=10,∴DF=103.【答案】(1)略;(2)DF=103.8.在△ABC中,点D、E分别在AB、AC上,∠AED=∠B,如果AE=2,△ADE的面积为4,四边形BCED的面积为5,那么AB的长为.【答案】3.9.如图,ABCD中,AC,BD交于点O,BC=6,OE=2,BO=4.(1)求证△DEF∽△BEC;(2)求AF的长.【解答】(1)证明:∵∠FDE=∠CBE,∠DFE=∠BCE,∠DEF=∠BEC,∴△DEF∽△BEC;(2)解:∴OB=OD=4,AD∥BC,AD=BC=18,∵OE=2,∴DE=4−2=2,∵AD∥BC,∴△DFE∽△BCE,∴DF+BC=DE+BE,∴DF+18=24+2,∴DF=6,∴AF=18−6=12.【答案】(1)略;(2)12.10.如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90∘,E为AB的中点,连接CE、DE.AC 与DE相交于点F.(1)求证:△ADF∽△CEF;的值.(2)若AD=4,AB=6,求ACAF【解答】(1)证明:∵∠ACB=90∘,E为AB的中点,∴AE=CE,∴∠EAC=∠ACE,∵AC平分∠DAB,∴∠DAC=∠CAB,∴∠DAC=∠ACE,∴AD∥CE,∴△ADF∽△CEF;(2)解:∵E为AB的中点,∴CE=12AB=AE,∴∠EAC=∠ECA;∵∠DAC=∠CAB,∴∠DAC=∠ECA,∴CE∥AD;∴△AFD∽△CFE,∴AD:CE=AF:CF;∵CE=12AB=3,AD=4,∴AFCF =ADCE=43,∴ACAF =74.【答案】(1)略;(2)ACAF =74.11.如图,矩形ABCD中,AB=4,BC=3,将△ABC沿AC折叠,点B落到E点,此时AE交CD于F,则AF:EF=()A. 24:7;B. 25:7;C. 2:1;D. 3:1.【答案】B12.如图,B、C、D在同一直线上,△ABC和△DCE都是等边三角形,且在直线BD的同侧,BE交AD于F,BE交AC于M,AD交CE于N.(1)求证:AD=BE;(2)求证:△ABF∽△ADB.【解答】(1)证明:∵△ABC与△DCE都是等边三角形,∴AC=BC,CD=CE,∠ACB=∠DCE=60∘.∴∠ACB+∠ACE=∠ACE+∠DCE,即∠BCE=∠ACD.在△BCE和△ACD中,{BC=AC∠BCE=∠ACDCD=CE,∴△BCE≌△ACD(SAS),∴AD=BE;(2)证明:由(1)知:△BCE≌△ACD,∴∠CBE=∠CAD,又∵∠BMC=∠AMF,∴∠AFB=∠ACB=60∘=∠ABC,又∵∠BAF=∠BAD,∴△ABF∽△ADB.【答案】(1)略;(2)略.13.在梯形ABCD中,AB∥CD,点E在线段DA上,直线CE与BA的延长线交于点G.(1)求证:△CDE∽△GAE;(2)当DE:EA=1:2时,过点E作EF∥CD交BC于点F且CD=4,EF=6,求AB的长.【解答】(1)证明:∵梯形ABCD,AB∥CD,∴∠CDE=∠GAE,∠DCE=∠EAG.∴△CDE∽△GAE.(2)证明:由(1)△CDE∽△GAE,∴DE:EA=DC:GA.∵DE:EA=1:2,CD=4,∴GA=8,CE:CG=1:3.又∵EF∥CD,AB∥CD,∴EF∥GB.∴△CEF∽△CGB.∴CE:CG=EF:GB.∵EF=6,∴GB=18.∴AB=GB−GA=18−8=10.【答案】(1)略;(2)10.14.如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D.求证:(1)D是BC的中点;(2)△BEC∽△ADC.【解答】(1)证明:∵AB为⊙O的直径,∴∠BDA=90∘∴AD⊥BC,∵AB=AC,∴BD=CD,∴D是BC的中点;(2)证明:AB=AC,∴∠C=∠ABD,∵AB为⊙O的直径,∴∠ADB=∠BEC=90∘,∴△BEC∽△ADC.【答案】(1)略;(2)略.1.如图,在△ABC中,AB=8,AC=6,点D在边AB上,AD=4.5,△ABC的角平分线AE交CD于点F.(1)求证:△ACD∽△ABC;(2)求AFAE的值.【解答】(1)证明:ADAC =ACAB,∵∠BAC=∠CAD,∴△ACD∽△ABC (2)解:∵△ACD∽△ABC,AE是∠BAC的角平分线,∴AFAE =ACAB=34.【答案】(1)略;(2)AFAE =ACAB=34.2.从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.(1)如图1,在△ABC中,CD为角平分线,∠A=40∘,∠B=60∘,求证:CD为△ABC的完美分割线;(2)在△ABC中,∠A=48∘,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数;(3)如图2,△ABC中,AC=2,BC=√2,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.【解答】(1)证明:如图1中,∵∠A=40∘,∠B=60∘,∴∠ACB=80∘,∴△ABC不是等腰三角形,∵CD平分∠ACB,∴∠ACD=∠BCD=12∠ACB=40∘,∴∠ACD=∠A=40∘,∴△ACD为等腰三角形,∵∠DCB=∠A=40∘,∠CBD=∠ABC,∴△BCD∽△BAC,∴CD为△ABC的完美分割线;(2)解:①当AD=CD时,如图2,∠ACD=∠A=48∘,∵△BDC∽△BCA,∴∠BCD=∠A=48∘,∴∠ACB=∠ACD+∠BCD=96∘;②当AD=AC时,如图3中,∠ACD=∠ADC=180∘−48∘2=66∘,∵△BDC∽△BCA,∴∠BCD=∠A=48∘,∴∠ACB=∠ACD+∠BCD=114∘;③当AC=CD时,如图4中,∠ADC=∠A=48∘,∵△BDC∽△BCA,∴∠BCD=∠A=48∘,∵∠ADC>∠BCD,矛盾,舍弃.∴∠ACB=96∘或114°;(3)解:由已知AC=AD=2,∵△BCD∽△BAC,∴BCBA =BDBC,设BD=x,∴(√2)2=x(x+2),∵x>0,∴x=√3−1,∵△BCD∽△BAC,∴,∴CD=√3−1√2×2=√6−√2.【答案】(1)略;(2)略;(3)√6−√2.3.已知,如图,△ABC中,AB=2,BC=4,D为BC边上一点,BD=1.(1)求证:△ABD∽△CBA;(2)在原图上作DE∥AB交AC与点E,请直接写出另一个与△ABD相似的三角形,并求出DE的长.【解答】(1)证明:∵AB=2,BC=4,BD=1,∴ABBC =24=12,BDAB=12,∴ABBC =BDAB,∵∠ABD=∠CBA,∴△ABD∽△CBA;(2)解:∵DE∥AB,∴△CDE∽△CBA,∴△ABD∽△CDE,∴DE=1.5.【答案】(1)略;(2)1.5.4.如图,正方形ABCD的对角线AC、BD相交于点O,E是BC中点,DE交AC于F,若DE=12,则EF等于()第21页共22页自学七招之举一反三剑:总结归纳典型题,多种解法开脑洞非学科培训A. 8;B. 6;C. 4;D. 3.【答案】C第22页共22页自学七招之以背代诵掌:高效记忆有妙招,以背代诵效果好非学科培训。
(2021年整理)中考数学狙击重难点系列专题27----反比例函数与三角形综合(含答案)

案)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整版)中考数学狙击重难点系列专题27----反比例函数与三角形综合(含答案))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整版)中考数学狙击重难点系列专题27----反比例函数与三角形综合(含答案)的全部内容。
角形综合(含答案)编辑整理:张嬗雒老师尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布到文库,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是我们任然希望 (完整版)中考数学狙击重难点系列专题27--——反比例函数与三角形综合(含答案)这篇文档能够给您的工作和学习带来便利。
同时我们也真诚的希望收到您的建议和反馈到下面的留言区,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请下载收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为 <(完整版)中考数学狙击重难点系列专题27—--—反比例函数与三角形综合(含答案)> 这篇文档的全部内容。
反比例函数与三角形综合1. 如图,在平面直角坐标系中,反比例函数y= (x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )A. 6B. 10C. 2D。
22。
如图,在反比例函数y= 的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y= 的图象上运动,若tan∠CAB=2,则k的值为()A. ﹣3 B. ﹣6 C。
反比例函数与几何的综合应用(教案)

四、教学流程
(一)导入新课(用时5分钟)
同学们,今天我们将要学习的是《反比例函数与几何的综合应用》这一章节。在开始之前,我想先问大家一个问题:“你们在日常生活中是否遇到过需要根据面积或比例来求解问题的情况?”比如,我们如何根据已知的长和宽来求解矩形的面积。这个问题与我们将要学习的内容密切相关。通过这个问题,我希望能够引起大家的兴趣和好奇心,让我们一同探索反比例函数在几何问题中的奥秘。
3.重点难点解析:在讲授过程中,我会特别强调反比例函数的性质和图像,以及它在几何问题中的应用这两个重点。对于难点部分,比如反比例函数与一次函数的交点求解,我会通过具体例题和逐步解析来帮助大家理解。
(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与反比例函数在几何问题中应用相关的实际问题。
三、教学难点与重点
1.教学重点
(1)反比例函数的定义及其性质:反比例函数的定义,图像特点,以及其在实际中的应用。
举例:y = k/x(k≠0),解释k的取值对函数图像的影响,如k>0时图像位于一、三象限,k<0时图像位于二、四象限。
(2)反比例函数与其他函数的交点问题:分析反比例函数与一次函数、二次函数的交点情况,掌握求解方法。
(二)新课讲授(用时10形如y = k/x(k≠0)的函数,它的图像是一条经过原点的曲线。反比例函数在解决与比例相关的问题时非常重要。
2.案例分析:接下来,我们来看一个具体的案例。这个案例将展示如何利用反比例函数来求解矩形的面积,以及它如何帮助我们解决实际问题。
此外,我在课堂上尝试引导同学们提出问题、分析问题并解决问题,目的是培养他们的独立思考能力。但从实际情况来看,同学们在这一方面的表现还不够理想。因此,我计划在接下来的教学中,进一步加强这方面的训练,鼓励同学们敢于提问、善于提问。
初中锐角三角形和反比例函数和相似

初中锐角三角形和反比例函数和相似首先,让我们从锐角三角形开始。
锐角三角形是指一个三角形的所有内角都小于90度的三角形。
在初中数学中,我们通常会学习三角函数以及它们在锐角三角形中的应用。
而锐角三角形的三个重要的三角函数分别是正弦函数(sin)、余弦函数(cos)和正切函数(tan)。
通过这些函数,我们可以计算出在锐角三角形中任意一个角的正弦、余弦和正切值。
接下来,让我们来探索一下反比例函数。
在数学中,我们常常会遇到一种函数形式,即y与x之间满足y与x的乘积恒定的关系。
这种函数关系被称为反比例函数。
具体而言,对于一个反比例函数,可以用y=k/x的形式来表示,其中k是常数。
反比例函数的图像通常是一个双曲线。
首先,我们来看一下锐角三角形的一个重要性质,即三角比例恒等式。
对于一个任意锐角三角形ABC,我们有以下三个比例恒等式:sin A / a = sin B / b = sin C / ccos A / a = cos B / b = cos C / ctan A / a = tan B / b = tan C / c其中,A、B、C分别表示三角形的内角,a、b、c分别表示与这些角相对的边的长度。
这些比例恒等式表明,在锐角三角形中,角的正弦、余弦和正切值与它们相对的边的比值相等。
现在,让我们来引入反比例函数。
对于一个反比例函数y=k/x,我们可以将k理解为一个比例常数。
现在,我们来看一下,在锐角三角形的三角比例恒等式中,比例常数k与锐角的正弦、余弦和正切值之间的关系。
首先,考虑正弦函数sin。
根据三角比例恒等式sin A / a = sin B / b = sin C / c,我们可以将它表示为:sin A = kasin B = kbsin C = kc其中k为比例常数。
我们可以看到,k与a、b、c之间的关系正好是反比例函数y=k/x的形式。
同样地,我们也可以利用三角比例恒等式来推导出余弦函数和正切函数与反比例函数之间的关系。
“反比例函数与相似三角形问题”的复习课课例分析

“反比例函数与相似三角形问题”的复习课课例分析作者:吴博思来源:《课程教育研究》2020年第52期【中图分类号】G633.6 【文献标识码】A 【文章编号】2095-3089(2020)52-0085-02一、教学背景分析笔者吴博思老师在深圳市九年级数学教研会上为全市初中数学老师上了一节中考专题复习示范课。
反比例函数是在学生学习了一次函数、二次函数的基础上开始学习的,反比例函数的教学一方面丰富了用函数思想分析问题、解决问题的经验,也为学生构建数学模型奠定了基础,在中学数学体系中占有重要的地位。
作为九年级第一轮复习课,学生已经学过了《反比例函数》和《相似三角形》全章的知识,掌握了反比例函数的概念、图像、性质,初步具有对反比例函数的有关问题进行合作探究的意识与能力,会用反比例函数的知识解决一些简单问题。
为了与时下的中考热点相结合,为大家提供一节有价值的复习课,笔者所在的备课组全体老师全力以赴、共同研究,经过反复几轮的备课、上课、评课等磨课活动,最终成功地展示了一节“反比例函数与相似三角形”的高效复习课。
下面笔者谈谈这节课的教学设计与反思,希望给同行一点启发。
二、教学设计分析设计分析:初中阶段最重要的三个相似三角形数学模型分别是“A字型”、“一线三等角模型”、“双垂直模型”,也是学生思维重要的切入口。
通过三道热身训练,让学生捕捉到反比函数当中隐藏的相似三角形的模型,通过辅助线的添加能够进一步呈现模型。
设计的目的就是抓住学生的心灵,激发学生的思维,为接下来的问题引入埋下伏笔,突出反比例函数与相似三角形结合的教学意图,顺理成章引出本节课的课题——反比例函数与相似三角形问题。
本环节注重夯实知识点,对于反比例函数与相似三角形的综合应用采用启发式教学,通过课前热身的训练指导学生进行知识的自我整理、自我质疑,通过自我挑战,达到自我提高的目标。
本环节将由学生自行探索题目中所蕴含的相似三角形模型,一方面可培养学生的表达能力,另一方面又能培养及时归纳总结的好习惯。
函数与相似三角形结合典型试题

函数与相似三角形结合典型试题1、已知反比例函数y =m-2/x( x<0)的图象经过点A (-2,3),过点A 作直线AC 与函数y =m-2/x 的图象交于点B ,与x 轴交于点C ,且AB =2BC .(1)求m 的值及点B 的坐标:(2)求△AOB 的面积.2、如图,在△ABC 中,AB =AC =10,BC =12,AM ∥BC ,点P 在线段BC 上以每秒2个单位的速度由B 点向C 点运动,点Q 在线段BA 上以每秒1个单位的速度由B 点向A 点运动,在运动中,始终保持∠QPD =∠B ,且PD 交AC 于点E ,交AM 于点D ,当P 点运动到C 点时,Q 点随之停止运动.设运动时间为t (秒).(1)当t =4秒时,试证明:△BPQ ≌△CEP ; (2)设△BPQ 的面积为S ,求S 与t 之间的函数关系式;(3)当t 为何值时?使得S ∆ADE/S ∆CPE=1/4.3、如图,在直角梯形ABCD 中,∠D=90°,AB=10cm,BC=6cm ,AB ∥CD,AC ⊥BC, F 点以2cm/s 的速度在线段AB 上由A 向B 匀速运动,点E 同时以1cm/s 的速度在线段BC 上由B 向C 匀速运动,设运动的时间为t (0<t <5).(1)求证:⊿ACD ∽⊿BAC ;(2)求DC 的长(3)当t 为何值时,⊿FEB 与⊿ABC 相似?4、如图,已知△ABC 中,AB =AC =2,∠A =90°,O 为AB 边上移动,动点F 在AC 边上移动. (1)点E ,F 的移动过程中,△OEF 是否能成为∠EOF =45°的等腰三角形?若能,求BE 的长;若不能,请说明理由;(2)当∠EOF =45°时,设BE =x ,CF =y ,求y 与x 之间的函数解析式,并写出x 的取值范围.5、如图,在矩形ABCD 中,已知AB =2,BC =3,点E 为AD 边上一动点(不与A 、D 重合),连结CE ,作EF ⊥CE 交AB 边于F(1)求证:△AEF ∽△DCE ;(2)当△ECF ∽△AEF 时,求AF 的长;(3)在点E 的运动过程中,AD 边上是否存在异于点E 的点G ,使△AGF ∽△DCG 成立?若存在,请猜想点G 的位置,并给出证明;若不存在,请说明理由.6、如图1,已知,CE 是Rt △ABC 的斜边AB 上的高,点P 是CE 的延长线上任意一点,BG ⊥AP ,求证:(1)△AEP ∽△DEB ; (2) CE 2=ED·EP 。
相似与反比例综合题练习(含答案)

相似与反比例综合题练习(含解析)一.选择题(共12小题)1.如图所示,已知双曲线y=(x<0)和y=(x>0),直线OA与双曲线y=交于点A,将直线OA向下平移与双曲线y=交于点B,与y轴交于点P,与双曲=6,=,则k=()线y=交于点C,S△ABCA.﹣6 B.﹣4 C.6 D.42.如图,点A在反比例函数y=(k≠0)的图象上,且点A是线段OB的中点,点D为x轴上一点,连接BD交反比例函数图象于点C,连接AC,若BC:CD=2:1,S△ADC=.则k的值为()A.B.16 C.D.103.如图,O为坐标原点,点C在x轴上.四边形OABC为菱形,D为菱形对角线AC与OB的交点,反比例函敬y=在第一象限内的图象经过点A与点D,若菱形OABC的面积为24,则点A的坐标为()A.(1,6)B.(,5)C.(2,4)D.(3,3)4.如图,平面直角坐标系中,矩形OABC的边与函数y=(x>0)图象交于E,F两点,且F是BC的中点,则四边形ACFE的面积等于()A.4 B.6 C.8 D.不能确定5.如图,点A是反比例函数y=(x>0)的图象上一点,过点A作直线y=﹣x 的垂线,垂足为点B,再过点A作AC⊥AB交y=(x>0)的图象于点C,若△ABC是等腰三角形,则点B的坐标是()A.(﹣,)B.(﹣,)C.(﹣2,2)D.(﹣3,3)6.如图,菱形四边形ABCD的四个顶点分别在反比例函数y=,y=﹣的图象上,若该菱形的面积为78,则这个菱形的边长为()A.B.C.13 D.137.如图,已知A,B为反比例函数y1=图象上两点,连接AB,线段AB经过点O,C是反比例函数y2=(k<0)在第二象限内的图象上一点,当△CAB是以AB 为底的等腰三角形,且=时,k的值为()A.﹣ B.﹣3 C.﹣4 D.﹣8.已知,直线y=k1x(k1>0)与反比例函数y=图象交于点A、B两点,以AB 为边作等边△ABC,随着k1的取值不同,点C在反比例函数y=运动,则k2的值是()A.﹣2B.﹣3C.﹣6 D.﹣39.如图,反比例函数y=上有一点A,连接并延长OA,使得OA=AB,过点B作x轴的垂线,分别交反比例函数和x轴于点C、点D.若CD=,∠B=60°,则△AOD的面积为()A.9 B.10C.11D.1210.如图,△ABC是等边三角形,顶点C在y轴的负半轴上,点A(1,),点B在第一象限,经过点A的反比例函数y=(x>0)的图象恰好经过顶点B,则△ABC的边长为()A.3 B.2 C.4 D.311.如图,以矩形OABC的顶点O为坐标原点建立平面直角坐标系,使点A、C 分别在x轴、y轴的正半轴上,双曲线y=(x>0)的图象经过BC的中点D,且与AB交于点E.过OC边上一点F,把△BCF沿直线BF翻折,使点C落在点C′处(点C′在矩形OABC内部),且C′E∥BC,若点C′的坐标为(2,3),则k的值为()A.B.C.D.12.如图,A、B、C是反比例函数y=(k<0)图象上三点,作直线l,使A、B、C到直线l的距离之比为3:1:1,则满足条件的直线l共有()A.4条 B.3条 C.2条 D.1条二.解答题(共8小题)13.如图,∠C=90°,点A、B在∠C的两边上,CA=30,CB=20,连接AB.点P 从点B出发,以每秒4个单位长度的速度沿BC的方向运动,到点C停止.当点P与B、C两点不重合时,作PD⊥BC交AB于点D,作DE⊥AC于点E.F为射线CB上一点,使得∠CEF=∠ABC.设点P运动的时间为x秒.(1)用含有x的代数式表示CE的长.(2)求点F与点B重合时x的值.(3)当点F在线段CB上时,设四边形DECP与四边形DEFB重叠部分图形的面积为y(平方单位).求y与x之间的函数关系式.14.如图,射线AM平行于射线BN,AB⊥BN,且AB=3,C是射线BN上的一个动点,连接AC,作CD⊥AC,且CD=AC,过C作CE⊥BN交AD于点E,设BC 长为t.(1)AC长为,△ACD的面积为(用含有t的代数式表示);(2)求点D到射线BN的距离(用含有t的代数式表示);(3)是否存在点C,使△ACE为等腰三角形?若存在,请求出此时BC的长度;若不存在,请说明理由.15.如图,四边形ABCD中,AD=CD,∠DAB=∠ACB=90°,过点D作DE⊥AC,垂足为F,DE与AB相交于点E.(1)求证:AB•AF=CB•CD;(2)已知AB=15cm,BC=9cm,P是线段DE上的动点.设DP=x cm,梯形BCDP 的面积为ycm2.①求y关于x的函数关系式.②y是否存在最大值?若有求出这个最大值,若不存在请说明理由.16.如图,在矩形ABCD(AB<AD)中,将△ABE沿AE对折,使AB边落在对角线AC上,点B的对应点为F,同时将△CEG沿EG对折,使CE边落在EF所在直线上,点C的对应点为H.(1)证明:AF∥HG(图(1));(2)证明:△AEF∽△EGH(图(1));(3)如果点C的对应点H恰好落在边AD上(图(2)).求此时∠BAC的大小.17.如(a)图,在平面直角坐标系中,点A坐标为(12,0),点B坐标为(6,8),点C为OB的中点,点D从点O出发,沿△OAB的三边按逆时针方向以2个单位长度/秒的速度运动一周.(1)点C坐标是,当点D运动8.5秒时所在位置的坐标是;(2)设点D运动的时间为t秒,试用含t的代数式表示△OCD的面积S,并指出t为何值时,S最大;(3)点E在线段AB上以同样速度由点A向点B运动,如(b)图,若点E与点D同时出发,问在运动5秒钟内,以点D,A,E为顶点的三角形何时与△OCD 相似?(只考虑以点A、O为对应顶点的情况)18.如图,在平面直角坐标系中,点A,B坐标分别为(8,4),(0,4),点C,D在x轴上,C(t,0),D(t+3,0)(0<t≤5),过点D作x轴的垂线交线段AB 于点E,交OA于点G,连接CE交OA于点F(1)请用含t的代数式表示线段AE与EF的长;(2)若当△EFG的面积为时,点G恰在的图象上,求k的值;(3)若存在点Q(0,2t)与点R,其中点R在(2)中的的图象上,以A,C,Q,R为顶点的四边形是平行四边形,求R点的坐标.19.如图,点A(m,m+1),B(m+3,m﹣1)都在反比例函数的图象上.(1)求m,k的值;(2)求三角形ABO的面积.20.如图,将透明三角形纸片PAB的直角顶点P落在第四象限,顶点A、B分别落在反比例函数y=图象的两支上,且PB⊥x于点C,PA⊥y于点D,AB分别与x轴,y轴相交于点E、F.已知B(1,3).(1)k=;(2)试说明AE=BF;(3)当四边形ABCD的面积为时,求点P的坐标.相似与反比例练习参考答案与试题解析一.选择题(共12小题)1.如图所示,已知双曲线y=(x<0)和y=(x>0),直线OA与双曲线y=交于点A,将直线OA向下平移与双曲线y=交于点B,与y轴交于点P,与双曲线y=交于点C,S△ABC=6,=,则k=()A.﹣6 B.﹣4 C.6 D.4【解答】解:设A(x a,y a),B(x b,y b),C(x c,y c),则有x a y a=x b y b=5,x c y c=k,∵OA∥BC∴=,整理得到:y a x b﹣y a x c=x a y b﹣x a y c①过点A作AF⊥x轴于点F,BE⊥x轴于点E,CD⊥x轴于点D,∵S△ABC =S梯形AFEB+S梯形BEDC﹣S梯形AFDC=6∴(AF+BE)×EF+(BE+CD)×DE﹣(AF+CD)×DF=6代入坐标可得到:(y a+y b)(x b﹣x a)+(y b+y c)(x c﹣x b)﹣(y a+y c)(x c﹣x a)=6,整理得:y a x b﹣x a y b+y b x c﹣y c x b﹣y a x c+x a y c=6,②①②联立得:y b x c﹣y c x b=12,③由=,可得:=,即x b=x c,∴y b==,代入③得:10+x c y c=12,解得:x c y c=4,即k=﹣4.故选:B.2.如图,点A在反比例函数y=(k≠0)的图象上,且点A是线段OB的中点,点D为x轴上一点,连接BD交反比例函数图象于点C,连接AC,若BC:CD=2:1,S△ADC=.则k的值为()A.B.16 C.D.10【解答】解:作AE⊥OD于E,CF⊥OD于F.∵BC:CD=2:1,S△ADC=,∴S△ACB=,∵OA=OB,∴B(2m,2n),S△AOC =S△ACB=,∵A、C在y=上,BC=2CD,∴C(m,n),∵S△AOC =S△AOE+S梯形AEFC﹣S△OCF=S梯形AEFC,∴•(n+n)×m=,∴mn=16,故选:B.3.如图,O为坐标原点,点C在x轴上.四边形OABC为菱形,D为菱形对角线AC与OB的交点,反比例函敬y=在第一象限内的图象经过点A与点D,若菱形OABC的面积为24,则点A的坐标为()A.(1,6)B.(,5)C.(2,4)D.(3,3)【解答】解:作AE⊥OC于E,DF⊥OC于F.设A(a,b).∵四边形ABCO是菱形,∴AD=DC,∵AE∥DF,∴EF=FC,∴DF=AE=b∵反比例函敬y=在第一象限内的图象经过点A与点D,∴D (2a ,b ),∴OE=EF=FC=a ,∴OA=OC=3a ,∴AE==2a ,∵OC•AE=24, ∴3a•2a=24, ∴a 2=4,∵a >0,∴a=2,∴A (2,4), 故选:C .4.如图,平面直角坐标系中,矩形OABC 的边与函数y=(x >0)图象交于E ,F 两点,且F 是BC 的中点,则四边形ACFE 的面积等于( )A .4B .6C .8D .不能确定【解答】解:连接OF 、OB 、OE .∵四边形ABCO 是矩形,∴S △ABO =S △BCO ,∵BF=CF ,∴S △CFO =S △BFO ,∵E 、F 在y=(x >0)上,∴S △AEO =S △FCO =S △ABO ,∴AE=EB ,∵BF=CF ,∴EF ∥AC ,∴△BEF ∽△BAC , ∴=,∵S 矩形ABCO =16,∴S △BEF =×8=2,∴S 四边形ACFE =8﹣2=6,故选:B .5.如图,点A 是反比例函数y=(x >0)的图象上一点,过点A 作直线y=﹣x 的垂线,垂足为点B ,再过点A 作AC ⊥AB 交y=(x >0)的图象于点C ,若△ABC 是等腰三角形,则点B 的坐标是( )A .(﹣,)B .(﹣,)C .(﹣2,2)D .(﹣3,3)【解答】解:由题意,△ABC 是等腰直角三角形,BC ∥x 轴,设B (a ,﹣a ), ∵AC ∥OB ,∴AC ⊥直线y=x ,∴A 、C 关于直线y=x 对称,作OH ⊥AC 于H ,则四边形ABOH 是矩形,∴AH=HC=OB,AB=2OB,∴A(﹣a,﹣3a),∴3a2=6,∴a2=2,∵a<0,∴a=﹣,∴B(﹣,),故选:A.6.如图,菱形四边形ABCD的四个顶点分别在反比例函数y=,y=﹣的图象上,若该菱形的面积为78,则这个菱形的边长为()A.B.C.13 D.13【解答】解:根据对称性可知,反比例函数y=,y=﹣的图象是中心对称图形,菱形是中心对称图形,∴菱形ABCD的对角线AC与BD的交点即为原点O.如图:作DM⊥x轴于M,CN⊥x轴于N.连接OD,OC.∵DO ⊥OC ,∴∠DOM +∠CON=90°,∠CON +∠OCN=90°,∴∠DOM=∠OCN ,∵∠DMO=∠CNO=90°,∴△DOM ∽△OCN ,∵S △DOM =2,S △OCN =, ∴()2=,∴可以假设OD=2k ,OC=3k ,∵S 菱形ABCD =4••2k•3k=78,∴k=, ∴CD==k=,故选:B .7.如图,已知A ,B 为反比例函数y 1=图象上两点,连接AB ,线段AB 经过点O ,C 是反比例函数y 2=(k <0)在第二象限内的图象上一点,当△CAB 是以AB 为底的等腰三角形,且=时,k 的值为( )A.﹣ B.﹣3 C.﹣4 D.﹣【解答】解:如图作AE⊥x轴于E,CF⊥x轴于F.连接OC.∵A、B关于原点对称,∴OA=OB,∵AC=BC,OA=OB,∴OC⊥AB,∴∠CFO=∠COA=∠AEO=90°,∵∠COF+∠AOE=90°,∠AOE+∠EAO=90°,∴∠COF=∠OAE,∴△CFO∽△OEA,∴=()2,∵CA:AB=5:8,AO=OB,∴CA:OA=5:4,∴CO:OA=3:4,∴=()2=,∵S△AOE=2,=,∴S△COF∴=,∵k<0,∴k=﹣,故选:A.。
微专题4 反比例函数的综合应用++课件+2025年九年级中考数学总复习人教版(山东)

①当AC,BO为对角线时,AC,BO的中点重合,∴
,
+4=0+0
=
解得
,
= −
经检验,t=4,k=-16符合题意,
此时点C的坐标为(4,-4);
25
②当CB,AO为对角线时,CB,AO的中点重合,
+=+
∴
,
+0=4+0
= −
解得
,
= −
经检验,t=-4,k=-16符合题意,
所以S△AOB=S△AOM+S△BOM= ×2×3+ ×2×1=4.
因为正比例函数图象与反比例函数图象都是中心对称图形,且坐标原点是对称中
心,
所以点B和点C关于点O成中心对称,所以BO=CO,所以S△ABC=2S△AOB=8.
17
类型2
求特殊三角形或特殊四边形
【思维切入】
1.动点三角形的形状问题:
∵点A(m,4)在y=2x+2上,
∴2m+2=4,∴m=1,
∴点A的坐标为(1,4),
∵点A(1,4)在y= 上,∴4= ,∴k2=4,∴y= .
8
(2)如图,连接DE,过点B作BF垂直于y轴,垂足为F,
联立
= +
=
= 1 = −2
,解得
,
,
= 4 = −2
3.动点四边形的问题转化为动点三角形问题:
动点菱形问题转化为动点等腰三角形问题;
动点矩形问题转化为动点直角三角形问题.
人教版九年级数学下册第27章《相似》测试带答案解析

人教版九年级数学下册第27章《相似》测试带答案解析学校:___________姓名:___________班级:___________考号:___________一、单选题(本大题12个小题,每小题4分,共48分)1.下列选项中的两个图形一定相似的是()A.两个等边三角形B.两个矩形C.两个菱形D.两个等腰梯形2.如图,D,E是△ABC边上的两个点,请你再添加一个条件,使得△ABC∽△AED,则下列选项不成立的是()A.ABAE =ACADB.ABAE=BCDEC.∠C=∠ADE D.∠B=∠AED3.如图,△ABC中,点D、E分别在AB、AC上,DE∥BC,DB=2AD,则S△ADE:S△ABC =()A.19B.14C.16D.134.如图,在平面直角坐标系中,C为△AOB的OA边上一点,AC:OC=1:2,过C作CD∥OB 交AB于点D,C、D两点纵坐标分别为1、3,则B点的纵坐标为()5.如图,东汉末年数学家刘徽利用青朱出入图,证明了勾股定理,“勾自乘为朱方,股自乘为青方,令出入相补,各从其类”.若CE=4,DE=2,则正方形BFGH的面积为()A.15 B.25 C.100 D.1176.如图,在平面直角坐标系中,以A(0,1)为位似中心,在y轴右侧作△ABC放大2倍后的位似图形△AB'C,若点B的坐标为(﹣1,3),则点B的对应点B'的坐标为()A.(2,﹣4)B.(1,﹣4)C.(2,﹣3)D.(1,﹣3)7.如图,在△ABC和△AED中,∠CAB=∠DAE=36°,AB=AC、AE=AD,连接CD,连接BE并延长交AC,AD于点F、G.若BE恰好平分∠ABC,则下列结论:①DE=GE;②CD∥AB;③∠ADC=∠AEB;④BF =CF•AC.其中正确的个数为()A.1个B.2个C.3个D.4个(k>0,x>0)的图象上,x过点A 8.如图,在平面直角坐标系中,点A、B在函数y=kx作x轴的垂线,与函数y=−kx(x>0)的图象交于点C,连结BC交x轴于点D.若点A 的横坐标为1,BC=3BD,则点B的横坐标为()A.32B.2C.52D.39.如图,已知△ABC.(1)以点A为圆心,以适当长为半径画弧,交AC于点M,交AB于点N.(2)分别以M,N为圆心,以大于12MN的长为半径画弧,两弧在∠BAC的内部相交于点P.(3)作射线AP交BC于点D.(4)分别以A,D为圆心,以大于12AD的长为半径画弧,两弧相交于G,H两点.(5)作直线GH,交AC,AB分别于点E,F.依据以上作图,若AF=2,CE=3,BD=32,则CD的长是()A.910B.1 C.94D.410.如图,在菱形ABCD中,对角线AC与BD相交于点O,在BC的延长线上取一点E,连接OE交CD于点F.已知AB=5,CE=1,则CF的长是()A.23B.34C.35D.5711.如图,已知点A(0,4),B(4,1),BC⊥x轴于点C.点P为线段OC上一点,且PA⊥PB.则点P的坐标为()A.(1,0)B.(1.5,0)C.(1.8,0)D.(2,0)12.如图,在平面直角坐标系中,矩形ABCD的顶点A在第一象限,B,D分别在y轴上,AB交x轴于点E,AF⊥x轴,垂足为F.若OE=3,EF=1.以下结论正确的个数是()①OA=3AF;②AE平分∠OAF;③点C的坐标为(−4,−√2);④BD=6√3;⑤矩形ABCD 的面积为24√2.A.2个B.3个C.4个D.5个二、填空题(本大题4个小题,每小题4分,共16分)13.如图,在△ABC中,点D在AB边上,点E在AC边上,请添加一个条件_________,使△ADE∽△ABC.14.如图,数学兴趣小组利用硬纸板自制的Rt△ABC来测量操场旗杆MN的高度,他们通过调整测量位置,并使边AC与旗杆顶点M在同一直线上,且Rt△ABC与△AEM在同一个平面内.已知AC=0.8米,BC=0.5米,目测点A到地面的距离AD=1.5米,到旗杆的水平距离AE=20米,则旗杆MN的高度为_____米.15.如图,将菱形ABCD绕点A逆时针旋转到菱形AB′C′D′的位置,使点B′落在BC上,B′C′与CD交于点E,若AB=5,BB′=3则CE的长为________.(x<0)16.如图,点A在x轴的负半轴上,点B在y轴的正半轴上,反比例函数y=kx的图象经过线段AB点的中点C,△ABO的面积为1,则k的值是______.三、解答题(共9个小题,17、18每小题8分,19-25每小题10分,共86分)17.如图,在Rt△ABC中,CD是斜边AB上的高.求证:△ACD∽△ABC.18.已知:如图ΔABC三个顶点的坐标分别为A(−2,−2)、B(−3,−4)、C(−1,−4),正方形网格中,每个小正方形的边长是1个单位长度.(1)以点C为位似中心,在网格中画出△A1B1C,使△A1B1C与ΔABC的位似比为2:1,并直接写出点A1的坐标______;(2)△A1B1C的面积为______.19.如图,△ABC在坐标平面内,三个顶点的坐标分别为A(0,4),B(2,2),C(4,6)(正方形网格中,每个小正方形的边长为1).(1)以点O为位似中心,在第三象限画出△A1B1C1,使△A1B1C1与△ABC位似,且位似比为1:2;(2)画出将线段AB绕点A顺时针旋转90°所得的线段AB2,并求出点B旋转到点B2所经过的路径长.20.在平面直角坐标系中,已知△ABC的三个顶点的坐标分别是A(2,2),B(4,0),C(4,−4).(1)画出△ABC向左平移6个单位长度后得到的△A1B1C1(2)在y轴右侧画出以点O为位似中心,将△ABC缩小为原来12后得到的△A2B2C2 21.如图,四边形ABCD内接于圆O,AB是直径,点C是BD̂的中点,延长AD交BC的延长线于点E.(1)求证:CE=CD;(2)若AB=3,BC=√3,求AD的长.22.如图,AB是⊙O的直径,点C是⊙O上异于A、B的点,连接AC、BC,点D在BA的延长线上,且∠DCA=∠ABC,点E在DC的延长线上,且BE⊥DC.(1)求证:DC是⊙O的切线;(2)若OAOD =23,BE=3,求DA的长.23.如图,一次函数y=−x−2的图象与y轴交于点A,与反比例函数y=−3x(x<0)的图象交于点B.(1)求点B的坐标;(2)点C是线段AB上一点(不与点A、B重合),若ACBC =12,求点C的坐标.24.如图,AC与BD交于点O,OA=OD,∠ABO=∠DCO,E为BC延长线上一点,过点E作EF//CD,交BD的延长线于点F.(1)求证△AOB≌△DOC;(2)若AB=2,BC=3,CE=1,求EF的长.25.如图,DP是⊙O的切线,D为切点,弦AB//DP,连接BO并延长,与⊙O交于点C,与DP交于点E,连接AC并延长,与DP交于点F,连接OD.(1)求证:AF//OD;(2)若OD=5,AB=8,求线段EF的长.参考答案:1.A【分析】根据相似图形的概念进行判断即可;【详解】解:A、两个等边三角形,三个角都是60°∴它们是相似图形,符合题意;B、两个矩形四个角都是90°,但对应边的比不一定相等∴它们不是相似图形,不符合题意;C、两个菱形角不一定相等∴它们不是相似图形,不符合题意;D、两个等腰梯形对应边的比不一定相等,∴它们不是相似图形;故选:A.【点睛】本题考查的是相似图形的判断,掌握形状相同的图形称为相似图形是解题的关键.2.B【分析】根据题意,已知一个公共角相等,所以再添加一组角相等,或者夹这个角的两边对应成比例即可判断两三角形相似,据此即可求解.【详解】解:已知∠BAC=∠EAD,A. ABAE =ACAD,两边成比例,夹角相等,可证明△ABC∽△AED,不符合题意,B. ABAE =BCDE,不能证明△ABC∽△AED,符合题意,C. ∠C=∠ADE加上条件∠BAC=∠EAD,可证明△ABC∽△AED,不符合题意,D. ∠B=∠AED加上条件∠BAC=∠EAD,可证明△ABC∽△AED,不符合题意,故选:B.【点睛】本题考查了相似三角形的判定,掌握相似三角形的判定定理是解题的关键.3.A【分析】根据DE∥BC得到△ADE∽△ABC,再结合相似比是AD:AB=1:3,因而面积的比是1:9.【详解】解:如图:∵DE∥BC,∴∠ADE=∠ABC,∠AED=∠ACB∴△ADE∽△ABC,∵DB=2AD∴AD:DB=1:2,∴AD:AB=1:3,∴S△ADE:S△ABC=1:9.故选:A.【点睛】本题考查的是相似三角形的判定与性质,熟知相似三角形面积的比等于相似比的平方是解答此题的关键.4.C【分析】根据CD∥OB得出ACAO =CDOB,根据AC:OC=1:2,得出ACAO=13,根据C、D两点纵坐标分别为1、3,得出OB=6,即可得出答案.【详解】解:∵CD∥OB,∴ACAO =CDOB,∵AC:OC=1:2,∴ACAO =13,∵C、D两点纵坐标分别为1、3,∴CD=3−1=2,∴2OB =13,解得:OB=6,∴B点的纵坐标为6,故C正确.故答案为:6.【点睛】本题主要考查了平行线的性质,平面直角坐标系中点的坐标,根据题意得出ACAO=CD OB =13,是解题的关键.5.D【分析】先求出BC=AD=AB=CD=6,证明△DEF∽△CEB,求出DF=3,则AF=AD+DF=9,由勾股定理得到BF2=AF2+AB2=117,则正方形BFGH的面积为117.【详解】解:∵CE=4,DE=2,∴CD=DE+CE=6,∴BC=AD=AB=CD=6,∵AD∥BC,∴△DEF∽△CEB,∴DFBC =DECE,即DF6=24,∴DF=3,∴AF=AD+DF=9,∴BF2=AF2+AB2=117,∴正方形BFGH的面积为117,故选D.【点睛】本题主要考查了相似三角形的性质与判定,正方形性质,勾股定理,熟知相关知识是解题的关键.6.C【分析】过点A作x轴的平行线DD′,作BD⊥DD′于D,作B′D′⊥DD′于D′,设出B点坐标(x,y),分别表示出AD,BD,A′D′,B′D′,根据位似比列出等式,求解即可解决问题.【详解】解:如图所示,过点A作x轴的平行线DD′,作BD⊥DD′于D,作B′D′⊥DD′于D′,设B′(x,y),则BD=3﹣1=2,AD=1,B′D′=﹣y+1,AD′=x,∵△ABC与△A′B′C的位似比为1:2,∴BDB′D′=ADAD′=12,即2−y+1=1x=12解得:x=2,y=﹣3,∴点B′得坐标为(2,﹣3).故选:C.【点睛】本题考查位似图形的性质,懂得利用位似图形的相似比求解是解题的关键.7.C【分析】利用SAS证明△DAC≌△EAB可得∠ADC=∠AEB,可判断③正确;由全等三角形的性质,三角形的内角和定理及等腰三角形的性质可求解∠ACB的度数,利用角平分线的定义求得∠ACD=∠ABE=36°,即可得∠ACD=∠CAB,进而可证明CD∥AB,即可判断②正确;根据已知条件可求出∠BCF=∠BFC=72°,从而可以得出BC=BF,证明△ABC∽△BFC,即可证明BF2=CF⋅AC,可判断④正确,无法证明DE=GE,即可判断①错误,进而可求解.【详解】∵∠CAB=∠DAE=36°,∴∠CAB−∠CAE=∠DAE−∠CAE,即∠DAC=∠EAB,∵在△DAC和△EAB中{AD=AE∠DAC=∠EABAC=AB,∴△DAC≌△EAB(SAS),∴∠ADC=∠AEB,AC=AB,∠ACD=∠ABE,故③正确;∴∠ACB=∠ABC,∵∠CAB=∠DAE=36°,∴∠ACB=∠ABC=(180°−36°)÷2=72°,∵BE平分∠ABC,∴∠ABE=∠CBE=36°,∴∠ACD=∠ABE=36°,∵∠DCA=∠CAB=36°,∴CD∥AB,故②正确;∵∠BFC=180°−∠ACB−∠CBE=180°−72°−36°=72°,∴∠BFC=∠BCF=72°,∴BF=BC,∵∠BAC=∠CBF=36°,∠ACB=∠BCF,∴△ACB∽△BCF,∴ACBC =BCCF,∴BC2=CF⋅AC,即BF2=CF⋅AC,故④正确;根据题目中的已知条件无法证明DE=GE,故①错误;综上分析可知,正确的个数为3个,故C正确.故选:C.【点睛】本题主要考查全等三角形的判定与性质,平行线的判定,角平分线的定义,三角形的内角和定理,等腰三角形的判定和性质,证明△DAC≌△EAB是解题的关键.8.B【分析】首先设出A的坐标,根据题意得出C的坐标,表示出CE的长度,过点B作BF垂直x轴,证明△CED∼△BFD,由题目条件BC=3BD得出相似比,代换出点B的纵坐标,即可求出B的横坐标.【详解】设点A的坐标为(1,k),设AC与x轴的交点为E,过点B作BF⊥x轴,垂足为F,如图:∵点C在函数y=−kx(x>0)的图象上,且AC⊥x轴,∴C的坐标为(1,−k),∴EC=k,∵BF⊥x轴,CE⊥x轴,∴△CED∼△BFD,∴BFCE =BDCD,又∵BC=3BD,∴BDCD =12,∴BFCE =12=BFk,即BF=12k,∴点B的纵坐标为12k,代入反比例函数解析式:y=kx当y=12k时,x=k12k=2,∴B点的横坐标是2,故选:B.【点睛】本题考查反比例函数及相似三角形,解题关键是将线段比转化为两个相似三角形的相似比,由相似三角形的对应边得出点的坐标.9.C【分析】首先根据题意可知AD平分∠BAC,EF垂直平分AD,再证明四边形AEDF为菱形,可知AE,然后根据平行线分线段成比例得CDDB =CEEA,再代入数值求出答案.【详解】由作法得AD平分∠BAC,EF垂直平分AD,∴∠EAD=∠F AD,EA=ED,F A=FD.∵EA=ED,∴∠EAD=∠EDA,∴∠F AD=∠EDA,∴DE∥AF,同理可得AE∥DF,∴四边形AEDF为平行四边形,而EA=ED,∴四边形AEDF为菱形,∴AE=AF=2.∵DE∥AB,∴CDDB =CEEA,即CD32=32,∴CD=94.故选:C.【点睛】本题主要考查了尺规作角平分线,作线段垂直平分线,特殊平行四边形的判定,平行线分线段成比例等,根据两直线平行列出比例式是解题的关键.10.D【分析】作OG∥CD交BC于点G,根据平行线分线段成比例定理证明BG=CG,根据菱形的性质可得OB=OD,则GO是△BCD的中位线,可求出BG、CG和OG的长,再求出GE 的长,由CF∥GO可得△ECF∽△EGO,根据相似三角形的对应边成比例即可求出CF的长.【详解】解:如图,作OG∥CD交BC于点G,∵四边形ABCD 是菱形,且AB =5,∴BC =CD =AB =5,OB =OD ,∴BG CG =BO DO =1 ,∴BG =CG =12BC =52 ,∴GO 是△BCD 的中位线∴GO =12CD =52,GO ∥CD ∵CE =1,∴GE =CG +CE =52+1=72,∵CF ∥GO ,∴∠ECF =∠EGO∵∠E =∠E∴△ECF ∽△EGO ,∴CF GO =CE GE ,∴CF =GO•CE GE =52×172=57, ∴CF 的长为57,故选:D .【点睛】此题考查菱形的性质、平行线分线段成比例定理、三角形的中位线定理、相似三角形的判定与性质等知识,正确地作出所需要的辅助线是解题的关键.11.D【分析】先证△AOP ∽△PCB ,设OP =x ,CP =4-x ,得出44-x =x 1,解方程即可.【详解】解:∵BC ⊥OC ,∴∠BCP =90°,∠PBC +∠BPC =90°,∵PA⊥PB∴∠APB=90°,∠APO+∠BPC=90°,∴∠APO=∠PBC∵∠AOP=90°,∴∠AOP=PCB=90°,∴△AOP∽△PCB,∴OACP =OPCB,设OP=x,CP=4-x,4 4-x =x1,整理得x2−4x+4=0,解得x=2,经检验4-x=4-2=2≠0,∴x=2是原方程的解∴点P(2,0).故选择D.【点睛】本题考查图形与坐标,三角形相似判定与性质,可化为一元二次方程的分式方程,掌握图形与坐标,三角形相似判定与性质,可化为一元二次方程的分式方程是关键.12.C【分析】根据相似三角形的判定得出△EOB∽△EFA,利用相似三角形的性质及已知OE,EF 的值即可判断结论①;由①分析得出的条件,结合相似三角形、矩形的性质(对角线)即可判断结论②;根据直角坐标系上点的表示及结论①OA=3AF,利用勾股定理建立等式求解可得点A坐标,再根据关于原点对称的点的坐标得出点D坐标,即可判断结论③;由③可知AF=√2,进而得出OA的值,根据矩形的性质即可判断结论④;根据矩形的性质及④可知BD=6√2,利用三角形的面积公式求解即可判断结论⑤.【详解】解:∵矩形ABCD的顶点A在第一象限,AF⊥x轴,垂足为F,∴∠EOB=∠EFA=90°,AC=BD,OD=OA=OB=OC.∵∠AEF=∠BEO,∴△EOB∽△EFA.∵OE=3,EF=1,∴EFEO =AFOB=AFOA=13,即OA=3AF.(①符合题意)∵OA=OB,△EOB∽△EFA,∴∠OAB=∠OBA,∠EAF=EBO.∴∠OAB=∠EAF.∴AE平分∠OAF.(②符合题意)∵OF=OE+EF=3+1=4,∴点A的横坐标为4.∵OA=3AF,∴9AF2−AF2=OF2,即8AF2=16.∴AF=√2,点A的纵坐标为√2.∴A(4,√2).∵点A与点C关于原点对称,∴C(−4,−√2).(③符合题意)∵OA=3AF=3√2,∴BD=OD+OB=2OA=6√2.(④不符合题意)∵S矩形ABCD=S△BCD+S△BAD=2S△BAD,∴S矩形ABCD =2×12×6√2×4=24√2.(⑤符合题意)∴结论正确的共有4个符合题意.故选:C.【点睛】本题考查矩形与坐标的综合应用.涉及矩形的性质,相似三角形的判定与性质,勾股定理,直角坐标系上点的表示,关于原点对称的点的坐标,三角形的面积公式等知识点.矩形的对角线相等且互相平分;两角分别相等的两个三角形相似;相似三角形对应角相等,对应边成比例;两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点的对称点位P′(−x,−y).灵活运用相关知识点,通过已知条件建立等式关系是解本题的关键.13.∠ADE=∠B(答案不唯一).【分析】已知有一个公共角,则可以再添加一个角从而利用有两组角对应相等的两个三角形相似来判定或添加夹此角的两边对应成比例也可以判定.【详解】解∶∵∠A=∠A,∴根据两角相等的两个三角形相似,可添加条件∠ADE=∠B或∠AED=∠C证△ADE∽△ABC相似;根据两边对应成比例且夹角相等,可添加条件ADAB =AEAC证△ADE∽△ABC相似.故答案为∶∠ADE=∠B(答案不唯一).【点睛】此题考查了本题考查了相似三角形的判定,解题的关键是掌握相似三角形的判定方法.14.14【分析】利用相似三角形的性质求出EM,利用矩形的性质求出EN,可得结论.【详解】解:∵∠CAB=∠EAM,∠ACB=∠AEM=90°,∴△ACB∽△AEM,∴ACAE =BCEM,∴0.820=0.5EM,∴EM=12.5,∵四边形ADNE是矩形,∴AD=EN=1.5米,∴MN=ME+EN=12.5+1.5=14(米).故旗杆MN的高度为14米,故答案为:14.【点睛】本题考查相似三角形的应用,矩形的性质等知识,解题的关键是正确寻找相似三角形解决问题.15.158【分析】过C作CF∥C′D′交B′C′于F,根据菱形和旋转的性质求得△ABB′∽△B′FC,△ABB′≌△ADD′,可得CF和C′D的长,再由△CFE∽△DC′E求得CE和DE的比即可解答;【详解】解:如图,过C作CF∥C′D′交B′C′于F,AB ′C ′D ′是菱形,则AB ′∥C ′D ′,∴CF ∥AB ′,∴∠B ′FC =∠AB ′F ,∠B ′CF =∠AB ′B ,∵∠AB ′C ′=∠B ,∴∠B ′FC =∠B ,∴△ABB ′∽△B ′FC ,∴AB ′∶B ′C =BB ′∶FC ,AB ′=5,BB ′=3,则B ′C =2,∴FC =65,由旋转性质可得∠BAB ′=∠DAD ′,∵AB =AB ′=AD =AD ′,∴△ABB ′≌△ADD ′,∴BB ′=DD ′=3,∴DC ′=2,∵CF ∥C ′D ′,∴△CFE ∽△DC ′E ,∴CF ∶DC ′=CE ∶DE =65∶2=3∶5,∴CE =DC ×38=158; 故答案为:158; 【点睛】本题考查了菱形的性质,旋转的性质,相似三角形的判定和性质等知识;掌握相似三角形的判定和性质是解题关键.16.−12 【分析】取AO 的中点为M ,取BO 的中点为N ,连接CM ,CN .根据三角形中位线定理,平行线的的性质,矩形的判定定理确定四边形CMON 是矩形,根据相似三角形的判定定理和性质求出△ACM 和△CBN 的面积,进而求出矩形CMON 的面积,再根据反比例函数比例系数k 的几何意义求解即可.【详解】解:如下图所示,取AO 的中点为M ,取BO 的中点为N ,连接CM ,CN .∵C是AB中点,M是AO中点,N是BO中点,∴CM是△ABO中位线,CN是△ABO中位线,AMAO =12,BNBO=12,∴CM∥BO,CN∥AO,∴△ACM∽△ABO,△CBN∽△ABO,∠AMC=∠AOB=90°,∠CNB=∠AOB=90°,∴S△ACMS△ABO =(AMAO)2=14,S△CBNS△ABO=(BNBO)2=14,∠CNO=90°,∠CMO=90°,∴四边形CMON是矩形,∵△ABO的面积是1,∴S△ACM=14S△ABO=14,S△CBN=14S△ABO=14,∴S矩形CMON=S△ABO−S△ACM−S△CBN=12,∵反比例函数y=kx(x<0)的图象经过线段AB点的中点C,∴k=−12,故答案为:−12.【点睛】本题考查反比例函数比例系数k的几何意义,三角形中位线定理,平行线的性质,矩形的判定定理,相似三角形的判定定理和性质,综合应用这些知识点是解题关键.17.见解析【分析】根据两个角相等的两个三角形相似进行证明即可.【详解】证明:如图,∵在Rt△ABC中,CD是斜边AB上的高∴∠ADC=∠ACB=90°∵∠A是公共角∴△ACD∽△ABC.【点睛】本题考查了相似三角形的判定,解题关键是熟练掌握相似三角形的判定定理,准确运用进行推理证明.18.(1)作图见解析;(−3,0)(2)8【分析】(1)延长CA到A1使AA1=CA,延长CB到B1使BB1=CB,从而得到△A1B1C;然后写出点A1的坐标;(2)利用面积公式直接进行求解即可.【详解】(1)解:如图,△A1B1C为所作;点A1的坐标为(−3,0);(2)解:由图可知:S△A1B1C =12B1C⋅A1B=12×4×4=8.【点睛】本题考查位似三角形的作图,解题的关键是:熟练掌握位似三角形的定义:如果两个三角形不仅是相似三角形,而且每组对应点的连线交于一点,对应边互相平行,那么这两个三角形叫做位似三角形.19.(1)见解析(2)√2π【分析】(1)把A、B、C点的横纵坐标都乘以−12得到A1、B1、C1的坐标,然后描点即可;(2)利用网格特点和旋转的性质画出点B的对应点B2,从而得到AB2,然后利用弧长公式计算点B旋转到点B2所经过的路径长.(1)解:∵△ABC在坐标平面内,三个顶点的坐标分别为A(0,4),B(2,2),C(4,6)△A1B1C1与△ABC位似,且位似比为1:2;∴A1(0,−2),B1(−1,−1),C1(−2,−3),如图所示,△A1B1C1即为所求,(2)如图,AB2即为所求,∵AB=√22+22=2√2,=√2π∴点B旋转到点B2所经过的路径长为=90×π×2√2180【点睛】本题考查了求弧长,旋转的性质,位似变换作图,在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k,掌握以上知识是解题的关键20.(1)见解析(2)见解析【分析】(1)根据平移的性质作图即可;(2)根据位似的性质作图,由图可得出答案.【详解】(1)解:如图,△A1B1C1为所作;(2)解:如图,△A2B2C2为所作;.【点睛】本题考查了作图-位似变换:先确定位似中心;再分别连接并延长位似中心和能代表原图的关键点;接着根据位似比,确定能代表所作的位似图形的关键点;然后顺次连接上述各点,得到放大或缩小的图形.也考查了平移变换.21.(1)见解析(2)1【分析】(1)连接AC,根据圆周角推论得∠ACB=∠ACE=90°,根据点C是BD̂的中点得∠CAE=∠CAB,CD=CB,用ASA证明△ACE≌△ACB,即可得;(2)根据题意和全等三角形的性质得AE=AB=3,根据四边形ABCD内接于圆O和角之间的关系得∠CDE=∠ABE,即可得ΔEDC∽ΔEBA,根据相似三角形的性质得DEBE =CDAB,即可得(1)证明:如图所示,连接AC,∵AB为直径,∴∠ACB=∠ACE=90°,又∵点C是BD̂的中点∴∠CAE =∠CAB ,CD =CB ,在△ACE 和△ACB 中,{∠ACE =∠ACB AB =AC ∠CAE =∠CAB∴ΔACE ≅ΔACB(ASA),∴CE =CB ,∴CE =CD ;(2)解:∵ΔACE ≅ΔACB ,AB =3,∴AE =AB =3,又∵四边形ABCD 内接于圆O ,∴∠ADC +∠ABC =180°,又∵∠ADC +∠CDE =180°,∴∠CDE =∠ABE ,又∵∠E =∠E ,∴ΔEDC ∽ΔEBA ,∴DE BE =CD AB , 即:2√3=√33, 解得:DE =2,∴AD =AE −DE =1.【点睛】本题考查相似三角形的判定和性质,全等三角形的判定和性质,圆周角定理,理解相关性质定理,正确添加辅助线是解题关键.22.(1)见解析(2)910【分析】(1)连接OC ,先根据等腰三角形的性质可得∠1=∠2,再根据圆周角定理可得∠ACB =∠1+∠3=90°,从而可得∠OCD =90°,然后根据圆的切线的判定定理即可得证;(2)设OA =OB =OC =2x ,则OD =3x ,AD =x,BD =5x ,再根据相似三角形的判定证出△DCO ∼△DEB ,然后根据相似三角形的性质求出x 的值,由此即可得出答案.(1)证明:如图,连接OC,∵OC=OB,∴∠1=∠2,∵AB是⊙O的直径,∴∠ACB=∠1+∠3=90°,∴∠2+∠3=90°,∵∠ACD=∠2,∴∠ACD+∠3=90°,即∠OCD=90°,∴DC⊥OC,又∵OC是⊙O的半径,∴DC是⊙O的切线.(2)解:∵OAOD =23,∴设OA=OB=OC=2x,则OD=3x,∴AD=OD−OA=3x−2x=x,BD=OB+OD=5x,∵CO⊥DC,BE⊥DC,∴BE∥CO,∴△DCO∼△DEB,∴ODBD =OCBE,即3x5x=2x3,解得x=910,∴DA=x=910.【点睛】本题考查了圆的切线的判定定理、圆周角定理、相似三角形的判定与性质等知识点,熟练掌握圆的切线的判定定理和相似三角形的判定定理是解题关键.23.(1)(−3,1)(2)(−1,−1)【分析】(1)由两函数交点的求解方法可得:联立一次函数与反比例函数解析式,求解交点坐标即可.(2)过点C 、B 分别作CD 、BE 垂直于y 轴于D 、E ,易证△ACD ∽△ABE ,根据对应线段成比例以及点C 在直线AB 上,即可求解.【详解】(1)解:∵一次函数和反比例函数交于点B ,∴{y =−x −2y =−3x ,解得:{x 1=−3y 1=1 ,{x 2=1y 2=−3, ∵x <0∴B(−3,1) ;(2)解:如图,过点C 、B 分别作CD 、BE 垂直于y 轴于D 、E ,∴CD ∥BE ,∴∠ACD =∠ABE,∠ADC =∠AEB ,∴△ACD ∽△ABE ,∴AC AB =CD BE , ∵AC BC =12, ∴AC AB=13 , ∴CD BE =AC AB =13,由(1)得:BE =3,∴CD =1 ,∵C 不与点A 、B 重合,点C 是线段AB 上一点,∴C 的横坐标为-1,将其代入直线y =−x −2,可得:y =−1 ,∴C(−1,−1) .【点睛】本题考查了一次函数和反比例函数图象与性质,交点问题,一次函数和坐标轴交点以及一次函数图象上的点的坐标特点,三角形相似的判定与性质,牢固掌握一次函数和二次函数图象与性质是解题的关键.24.(1)证明见解析;(2)EF=83【分析】(1)直接利用“AAS”判定两三角形全等即可;(2)先分别求出BE和DC的长,再利用相似三角形的判定与性质进行计算即可.【详解】解:(1)∵OA=OD,∠ABO=∠DCO,又∵∠AOB=∠DOC,∴△AOB≌△DOC(AAS);(2)∵△AOB≌△DOC(AAS),AB=2,BC=3,CE=1∴AB=DC=2,BE=BC+CE=3+1=4,∵EF//CD,∴△BEF∽△BCD,∴EFCD =BEBC,∴EF2=43,∴EF=83,∴EF的长为83.【点睛】本题考查了全等三角形的判定与性质、平行线分线段成比例的推论、相似三角形的判定与性质等,解决本题的关键是牢记相关概念与公式,能结合图形建立线段之间的关联等,本题较基础,考查了学生的几何语言表达和对基础知识的掌握与应用等.25.(1)见解析(2)83【分析】(1)延长DO交AB于点H,根据切线的性质得到OD⊥DP,根据圆周角定理得到∠BAC=90°,根据平行线的判定定理证明结论;(2)根据垂径定理求出AH、BH,根据勾股定理求出OH,根据相似三角形的性质计算即可.(1)证明:延长DO交AB于点H,∵DP是⊙O的切线,∴OD⊥DP,∵AB//DP,∴HD⊥AB,∵BC为⊙O的直径,∴∠BAC=90°,∴AF//OD;(2)∵OH⊥AB,AB=8,∴BH=AH=4,∴OH=√OB2−BH2=√52−42=3,∵BH//ED,∴△BOH∽△EOD,∴BHED =OHOD,即4ED=35,解得:ED=203,∵∠BAC =90°,DH ⊥AB ,DH ⊥DP ,∴四边形AFDH 为矩形,∴DF =AH =4,∴EF =ED ﹣DF =203﹣4=83.【点睛】本题考查的是切线性质、相似三角形的判定和性质、矩形的判定和性质,掌握圆的切线垂直于经过切点的半径是解题的关键.。
反比例函数背景下的全等、相似问题(解析版)-2023年中考数学重难点解题大招复习讲义-函数

例题精讲考点1反比例函数与全等三角形综合问题【例1】.如图,把一个等腰直角三角形放在平面直角坐标系中,∠ACB=90°,点C(﹣1,0),点B在反比例函数y=的图象上,且y轴平分∠BAC,则k的值是________解:如图,过点B作BD⊥x轴于D,在OA上截取OE=OC,连接CE,∵点C(﹣1,0),∴CO=1,∴CO=EO=1,∴∠CEO=45°,CE=,∵△BAC为等腰直角三角形,且∠ACB=90°,∴BC=AC,∠OCA+∠DCB=90°,∠CAB=45°,∵∠OCA+∠OAC=90°,∴∠OAC=∠BCD,在△OAC和△DCB中,∴△OAC≌△DCB(AAS),∴AO=CD,OC=BD=1,∵y轴平分∠BAC,∴∠CAO=22.5°,∵∠CEO=∠CEA+∠OAC=45°,∴∠ECA=∠OAC=22.5°,∴CE=AE=,∴AO=1+=CD,∴DO=,∴点B坐标为(,﹣1),∵点B在反比例函数y=的图象上,∴k=﹣1×=﹣,变式训练【变1-1】.如图,在平面直角坐标系中,Rt△ABC的斜边AB在x轴上,点C在y轴上,∠BAC=30°,点A的坐标为(﹣3,0),将△ABC沿直线AC翻折,点B的对应点D 恰好落在反比例函数的图象上,则k的值为()A.B.﹣2C.4D.﹣4解:如图,过点D作DE⊥y轴于点E.由对称可知CD=BC,易证△DCE≌△BCO(AAS),∴CE=CO,DE=OB,∵∠BAC=30°,OA=3∴OC=OA=,∠OCB=30°,∴OB=OC=1,∴DE=OB=1,CE=OC=,OE=2,|k|=DE•OE=1×2=2,∵反比例函数图象在第二象限,∴k=﹣2,故选:B.【变1-2】.如图,点A是反比例函数y=图象上的一动点,连接AO并延长交图象的另一支于点B.在点A的运动过程中,若存在点C(m,n),使得AC⊥BC,AC=BC,则m,n满足_______(填等量关系)解:如图,连接OC,过点A作AE⊥x轴于点E,过点C作CF⊥y轴于点F,∵由直线AB与反比例函数y=的对称性可知A、B点关于O点对称,∴AO=BO.又∵AC⊥BC,AC=BC,∴CO⊥AB,CO=AB=OA,∵∠AOE+∠AOF=90°,∠AOF+∠COF=90°,∴∠AOE=∠COF,又∵∠AEO=90°,∠CFO=90°,∴△AOE≌△COF(AAS),∴OE=OF,AE=CF,∵点C(m,n),∴CF=﹣m,cF=n,∴OE=﹣m,AE=n,∴A(﹣m,n),∵点A是反比例函数y=图象上,∴﹣mn=4,即mn=﹣4,考点2反比例函数与相似三角形综合问题【例2】.如图,在平面直角坐标系中,四边形AOBD的边OB与x轴的正半轴重合,AD∥OB,DB⊥x轴,对角线AB,OD交于点M.已知AD:OB=2:3,△AMD的面积为4.若反比例函数y=的图象恰好经过点M,则k的值为()A.B.C.D.12解:过点M作MH⊥OB于H.∵AD∥OB,∴△ADM∽△BOM,∴=()2=,=4,∵S△ADM=9,∴S△BOM∵DB⊥OB,MH⊥OB,∴MH∥DB,∴===,∴OH=OB,=×S△OBM=,∴S△MOH∵=,∴k=,故选:B.变式训练【变2-1】.如图,已知第一象限内的点A在反比例函数y=上,第二象限的点B在反比例函数y=上,且OA⊥OB,=,则k的值为()A.B.﹣C.﹣D.﹣3解:作AC⊥x轴于点C,作BD⊥x轴于点D.则∠BDO=∠ACO=90°,则∠BOD+∠OBD=90°,∵OA⊥OB,∴∠BOD+∠AOC=90°,∴∠BOD=∠AOC,∴△OBD∽△AOC,∴=()2=()2=,=×4=2,又∵S△AOC=,∴S△OBD∴k=﹣.故选:B.【变2-2】.如图,Rt△ABC的直角边BC在x轴正半轴上,斜边AC边上的中线BD反向延=8,则k等于长线交y轴负半轴于E,双曲线的图象经过点A,若S△BEC ()A.8B.16C.24D.28解:∵BD为Rt△ABC的斜边AC上的中线,∴BD=DC,∠DBC=∠ACB,又∠DBC=∠EBO,∴∠EBO=∠ACB,又∠BOE=∠CBA=90°,∴△BOE∽△CBA,∴=,即BC×OE=BO×AB.=8,即BC×OE=2×8=16=BO×AB=|k|.又∵S△BEC又由于反比例函数图象在第一象限,k>0.所以k等于16.故选:B.【变2-3】.如图,在等腰△AOB中,AO=AB,顶点A为反比例函数y=(x>0)图象上一点,点B在x轴的正半轴上,过点B作BC⊥OB,交反比例函数y=的图象上于点C,连接OC交AB于点D,若△BCD的面积为2,则k的值为()A.18B.20C.22D.21解:如图,过点A作AF⊥OB交x轴于F,交OC于点E,∵OA=AB,AF⊥OB,∴OF=FB=OB,∵BC⊥OB,∴AF∥BC,∴△ADE∽△BDC,,∴BC=2EF,设OF=a,则OB=2a,∴A(a,),C(2a,),∴AF=,BC=,∴AF=2BC=4EF,AE=AF﹣EF=3EF,∵△ADE∽△BDC,∴,∴=()2=,∵△BCD的面积为2,=,∴S△ADE∴=,∵=,∴EC=OE,∴=,∴=,=,∴S△AOE∵==,∴==,=S△AOE=×=10,∴S△AOF∴|k|=10,∵k>0,∴k=20.故选:B.1.如图,AB⊥x轴,B为垂足,双曲线y=(x>0)与△AOB的两条边OA,AB分别相交于C,D两点,OC=CA,且△ABC的面积为3,则k等于()A.4B.2C.3D.1解:连接BC,过点C作CM⊥OB于M,∵OC=CA,即=,∴==,又∵△ABC的面积为3,=,∴S△OBC又∵CM∥AB,∴==,∴==,=S△OBC==|k|,∴S△OMC∵k>0,∴k=1,故选:D.2.如图,在△ABC中,AB=AC,点A在反比例函数y=(k>0,x>0)的图象上,点B,C在x轴上,OC=OB,延长AC交y轴于点D,连接BD,若△BCD的面积等于1,则k的值为()A.3B.2C.D.4解:作AE⊥BC于E,连接OA,∵AB=AC,∴CE=BE,∵OC=OB,∴OC=BC=×2CE=CE,∵AE∥OD,∴△COD∽△CEA,∴=()2=4,∵△BCD的面积等于1,OC=OB,=S△BCD=,∴S△COD=4×=1,∴S△CEA∵OC=CE,=S△CEA=,∴S△AOC=+1=,∴S△AOE=k(k>0),∵S△AOE∴k=3,故选:A.3.如图所示,Rt△AOB中,∠AOB=90°,顶点A,B分别在反比例函数y=(x>0)与y=﹣(x<0)的图象上,则tan∠BAO的值为()A.B.C.D.解:作AC⊥x轴于C,BD⊥x轴于D,如图,∵顶点A,B分别在反比例函数y=(x>0)与y=﹣(x<0)的图象上,=×|1|=,S△BOD=×|﹣5|=,∴S△AOC∵∠AOB=90°,∴∠BOD+∠AOC=90°,∵∠AOC+∠OAC=90°,∴∠OAC=∠BOD,而∠ACO=∠BDO,∴△AOC∽△OBD,∴=()2==,∴=,在Rt△AOB中,tan∠BAO==,故选:B.4.如图,函数y=﹣(x<0)的图象经过Rt△ABO斜边OB的中点D,与直角边AB相交于C,连接AD.若AD=3,则△ABO的周长为()A.12B.6+C.6+2D.6+2解:如图,过点D作DE⊥AO于E,∵点D是BO的中点,∴AD=BD=DO=3,∴BO=6,∵DE⊥AO,AB⊥AO,∴AB∥DE,∴,∴AB=2DE,AO=2EO,=DE×EO=,∵S△DEO=AB×AO=2,∴S△ABO∵AB2+AO2=OB2=36,∴(AB+AO)2=36+8,∴AB+AO=2,∴△ABO的周长=AO+BO+AB=6+2,故选:D.5.如图,长方形ABCD的顶点A、B均在y轴的正半轴上,点C在反比例函数y=(x>0)的图象上,对角线DB的延长线交x轴于点E,连接AE,已知S△ABE=1,则k的值是()A.1B.C.2D.4解:延长DC与x轴交于点F,∵ABCD是矩形,∴AD=BC,AD∥BC∥OE,∴△ABD∽△OBE,∴=,即:AD•OB=AB•OE,=1=AB•OE,又∵S△ABE∴AD•OB=AB•OE=2=BC•OB,=BC•OB=2=|k|,即:S矩形OBCF∴k=2或k=﹣2(舍去),故选:C.6.如图,直线y=x+2与反比例函数y=的图象在第一象限交于点P,若OP=,则k的值为3.解:设点P(m,m+2),∵OP=,∴=,解得m1=1,m2=﹣3(不合题意舍去),∴点P(1,3),∴3=,解得k=3.故答案为:3.7.已知一次函数y=2x+4的图象分别交x轴、y轴于A、B两点,若这个一次函数的图象与一个反比例函数的图象在第一象限交于点C,且AB=2BC,则这个反比例函数的表达式为y=.解:∵一次函数y=2x+4的图象分别交x轴、y轴于A、B两点,∴A(﹣2,0),B(0,4),过C作CD⊥x轴于D,∴OB∥CD,∴△ABO∽△ACD,∴==,∴CD=6,AD=3,∴OD=1,∴C(1,6),设反比例函数的解析式为y=,∴k=6,∴反比例函数的解析式为y=.故答案为:y=.8.在平面直角坐标系xOy中,点A,B在反比例函数y=(x>0)的图象上,且点A与点B关于直线y=x对称,C为AB的中点,若AB=4,则线段OC的长为2.解:设A(t,),∵点A与点B关于直线y=x对称,∴B(,t),∵AB=4,∴(t﹣)2+(﹣t)2=42,即t﹣=2或t﹣=﹣2,解方程t﹣=﹣2,得t=﹣﹣2(由于点A在第一象限,所以舍去)或t=﹣+2,经检验,t=﹣+2,符合题意,∴A(﹣+2,+2),B(+2,﹣+2),∵C为AB的中点,∴C(2,2),∴OC==2.故答案为2.9.如图,△OMN是边长为10的等边三角形,反比例函数y=(x>0)的图象与边MN、OM分别交于点A、B(点B不与点M重合).若AB⊥OM于点B,则k的值为9.解:过点B作BC⊥x轴于点C,过点A作AD⊥x轴于点D,如图,∵△OMN是边长为10的等边三角形,∴OM=ON=MN=10,∠MON=∠M=∠MNO=60°设OC=b,则BC=,OB=2b,∴BM=OM﹣OB=10﹣2b,B(b,b),∵∠M=60°,AB⊥OM,∴AM=2BM=20﹣4b,∴AN=MN﹣AM=10﹣(20﹣4b)=4b﹣10,∵∠AND=60°,∴DN==2b﹣5,AD=AN=2b﹣5,∴OD=ON﹣DN=15﹣2b,∴A(15﹣2b,2b﹣5),∵A、B两点都在反比例函数y=(x>0)的图象上,∴k=(15﹣2b)(2b﹣5)=b•b,解得b=3或5,当b=5时,OB=2b=10,此时B与M重合,不符题意,舍去,∴b=3,∴k=b•b=9,故答案为:9.10.如图,在Rt△ABC中,∠ABC=90°,C(0,﹣3),CD=3AD,点A在反比例函数y=图象上,且y轴平分∠ACB,求k=.解:过A作AE⊥x轴,垂足为E,∵C(0,﹣3),∴OC=3,∵∠AED=∠COD=90°,∠ADE=∠CDO∴△ADE∽△CDO,∴,∴AE=1;又∵y轴平分∠ACB,CO⊥BD,∴BO=OD,∵∠ABC=90°,∴∠OCD=∠DAE=∠ABE,∴△ABE∽△DCO,∴设DE=n,则BO=OD=3n,BE=7n,∴,∴n=∴OE=4n=∴A(,1)∴k=.故答案为:.11.如图,矩形OABC的两边落在坐标轴上,反比例函数y=的图象在第一象限的分支过AB的中点D交OB于点E,连接EC,若△OEC的面积为12,则k=12.解:如图,过点D、E分别作x轴的垂线,垂足分别为F、G,=S矩形OADF=2S△OEG=k,则S△OBC又∵EG∥BC,∴△OEG∽△OBC,∴=()2=2,∴=,∴=,∴==,∴=,∴k=12.故答案为12.12.如图,在平面直角坐标系中,∠OAB=60°,∠AOB=90°,反比例函数y1=的图象经过点A,反比例函数y2=﹣的图象经过点B,则m的值为1.解:作BH⊥x轴,垂足为H,AM⊥y轴,垂足为M,∵∠OAB=60°,∠AOB=90°,∴△BHO∽△AMO,∴,令OM=a,则BH=,代入反比例函数y2=﹣得:x=,∴OH=,得:AM=,∴,又∵AM•OM=m,∴m=1.故答案为1.13.如图,线段OA与函数y=(x>0)的图象交于点B,且AB=2OB,点C也在函数y =(x>0)图象上,连结AC并延长AC交x轴正半轴于点D,且AC=3CD,连结BC,若△BCD的面积为3,则k的值为.解:如图,分别过点A,B,C作x轴的垂线,垂足分别为M,E,F.∴BE∥CF∥AM,∴OB:OA=BE:AM=OE:OM=1:3,CD:AD=DF:DM=CF:AM=1:4,设点B的坐标为(a,b),∴OE=a,BE=b,∴AM=3BE=3b,OM=3OE=3a,∴CF=AM=b,∴C(a,b),∴OF=a,∴FM=OM﹣OF=a,∴DF=FM=a,∴OD=OM﹣DF﹣FM=a.∵△BCD的面积为3,∴△ABC的面积=3×△BCD的面积=9,∴△ABD的面积=12.∴△BOD的面积=×△ABD的面积=6.∴•OD•BE=a×b=6.解得k=ab=.故答案为:.14.如图,在平面直角坐标系中,点A、B在函数y=(k>0,x>0)的图象上,过点A作x轴的垂线,与函数y=﹣(x>0)的图象交于点C,连接BC交x轴于点D.若点A的横坐标为1,BC=3BD,则点B的横坐标为2.解:作BE⊥x轴于E,∴AC∥BE,∴△CDF∽△BDE,∴==,∵BC=3BD,∴==,∴CF=2BE,DF=2DE,设B(,b),∴C(1,﹣2b),∵函数y=﹣(x>0)的图象交于点C,∴﹣k=1×(﹣2b)=﹣2b,∴k=2b,∴B的横坐标为==2,故答案为:2.15.如图,在△ABC中,边AB在x轴上,边AC交y轴于点E.反比例函数y=(x>0)=6,则k=的图象恰好经过点C,与边BC交于点D.若AE=CE,CD=2BD,S△ABC.解:如图,作CM⊥AB于点M,DN⊥AB于点N,设C (m ,),则OM =m ,CM =,∵OE ∥CM ,AE =CE ,∴==1,∴AO =m ,∵DN ∥CM ,CD =2BD ,∴===,∴DN =,∴D 的纵坐标为,∴=,∴x =3m ,即ON =3m ,∴MN =2m ,∴BN =m ,∴AB =5m ,∵S △ABC =6,∴5m •=6,∴k =.故答案为:.16.如图,A 为反比例函数(其中x >0)图象上的一点,在x 轴正半轴上有一点B ,OB =4.连接OA ,AB ,且OA =AB =2.过点B 作BC ⊥OB ,交反比例函数(其中x >0)的图象于点C ,连接OC 交AB 于点D ,则的值为.解:过点A作AH⊥x轴,垂足为点H,AH交OC于点M,如图所示.∵OA=AB,AH⊥OB,∴OH=BH=OB=2,∴AH===6,∴点A的坐标为(2,6).∵A为反比例函数(其中x>0)图象上的一点,∴k=2×6=12.∵BC⊥x轴,OB=4,点C在反比例函数y=上,∴BC=3.∵AH∥BC,OH=BH,∴MH=BC=,∴AM=AH﹣MH=.∵AM∥BC,∴△ADM∽△BDC,∴,故答案为.17.如图,已知菱形ABCD的对角线相交于坐标原点O,四个顶点分别在双曲线y=和y=(k<0)上,=,平行于x轴的直线与两双曲线分别交于点E,F,连接OE,OF,则△OEF的面积为.解:作AM⊥x轴于M,DN⊥x轴于N,∵四边形ABCD是菱形,∴AC⊥BD,∴∠AOM+∠DON=∠ODN+DON=90°,∴∠AOM=∠ODN,∵∠AMO=∠OND=90°,∴△AOM∽△ODN,∴=()2,∵A点在双曲线y=,=,=×4=2,=,∴S△AOM∴=()2,=,∴S△ODN∵D点在双曲线y=(k<0)上,∴|k|=,∴k=﹣9,∵平行于x轴的直线与两双曲线分别交于点E,F,=+=,∴S△OEF故答案为.18.如图,已知直线l:y=﹣x+4分别与x轴、y轴交于点A,B,双曲线(k>0,x>0)与直线l不相交,E为双曲线上一动点,过点E作EG⊥x轴于点G,EF⊥y轴于点F,分别与直线l交于点C,D,且∠COD=45°,则k=8.解:点A、B的坐标分别为(4,0)、(0,4),即:OA=OB,∴∠OAB=45°=∠COD,∠ODA=∠ODA,∴△ODA∽△CDO,∴OD2=CD•DA,设点E(m,n),则点D(4﹣n,n),点C(m,4﹣m),则OD2=(4﹣n)2+n2=2n2﹣8n+16,CD=(m+n﹣4),DA=n,即2n2﹣8n+16=(m+n﹣4)×n,解得:mn=8=k,故答案为8.19.如图,平行四边形ABCD的顶点C在y轴正半轴上,CD平行于x轴,直线AC交x轴=2,于点E,BC⊥AC,连接BE,反比例函数y=(x>0)的图象经过点D,已知S△BCE 则k的值是4.解:(解法一)过点D作DF⊥x轴于点F,如图所示.∵四边形ABCD是平行四边形,∴BC∥AD,BC=AD.又∵BC⊥AC,∴DA⊥AC.∵CD平行于x轴,∴∠ACD=∠CEO.∵CO⊥OE,DA⊥AC,∴∠ECO=∠D.设点D的坐标为(m,)(m>0),则CD=m,OC=DF=.在Rt△CAD中,CD=m,∠CAD=90°,AD=m•cos∠D.在Rt△COE中,OC=,∠COE=90°,CE==.S△BCE=CE•BC=•m•cos∠D=k=2,解得:k=4;(解法二)设点D的坐标为(m,n)(m>0,n>0),则CD=m,OC=n,∵CD∥x轴,∴∠ACD=∠OEC.∵四边形ABCD为平行四边形,BC⊥AC,∴DA⊥AC,AD=BC,∴∠DAC=∠COE=90°,∴△COE∽△DAC,∴=,即=,∴mn=BC•CE.=BC•CE=2,∵S△BCE=4.∴mn=2S△BCE∵点D在反比例函数y=(x>0)的图象上,∴k=mn=4.故答案为:4.20.如图,A为反比例函数y=(其中x>0)图象上的一点,在x轴正半轴上有一点B,OB=4.连接OA,AB,且OA=AB.过点B作BC⊥OB,交反比例函数y=(其中x>0)的图象于点C,连接OC交AB于点D,则的值为.解:过点A作AH⊥x轴,垂足为H,AH交OC于点M,如图,∵OA=AB,AH⊥OB,∴OH=BH=OB=×4=2,A(2,),C(4,),∵AH∥BC,∴MH=BC=,∴AM=AH﹣MH=﹣=,∵AM∥BC,∴△ADM∽△BDC,∴==.21.如图,点A在反比例函数第一象限内图象上,点B在反比例函数第三象限内图象上,AC⊥y轴于点C,BD⊥y轴于点D,交于点E,若BO=CE,则k的值为.解:过点A作AP⊥x轴于点P,过点B作BQ⊥x轴于点Q,∵AC=BD=,∴点A的横坐标为,点B的横坐标为﹣,∵点A在反比例函数第一象限内图象上,点B在反比例函数第三象限内图象上,∴点A的纵坐标为6,点B的纵坐标为﹣3,∵AC⊥y轴,BD⊥y轴,∴CD=AP+BQ=9,OD=3,AC∥BD,∴∠CAE=∠DBE,∠ACE=∠BDE,∴△ACE≌△BDE(AAS),∴CE=DE=CD=,∵BO=CE,∴BO=,在Rt△BOD中,由勾股定理可得BD2+OD2=OB2,即,解得k=或k=﹣(舍去),故答案为:.22.如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O,AE⊥BC于E点,交BD于M点,反比例函数的图象经过线段DC的中点N,若BD=4,则ME的长为.解:在菱形ABCD中,AB=BC,BD⊥AC,OB=OD==2,∠ABC=2∠OBC,∴点D(0,2),设点C(m,0),∵点N为CD的中点,∴点,∵反比例函数的图像经过点N,∴,解得:,即点,∴,∴,,∴∠OBC=30°,∴∠ABC=60°,∴△ABC为等边三角形,∴,∵AE⊥BC,∴,∴.故答案为:.23.如图,平面坐标系中,AB交矩形ONCM于E、F,若=(m>1),且双曲线y==S1,S△OEF=S2,用含m的代数式表示.也过E、F两点,记S△CEF解:过点F作FG⊥y轴于点G,如图所示:∵CM⊥y轴,FG⊥y轴,∴CM∥FG,MC=FG,∴△BME∽△BGF,∴===,设点C的坐标为(a,b),则E(,b),F(a,),∴S1=×(a﹣)•(b﹣)=ab;S2=a•b﹣•﹣•﹣ab=ab.∴=.24.如图,在平面直角坐标系中,点P、Q在函数y=(x>0)的图象上,PA、QB分别垂直x轴于点A、B,PC、QD分别垂直y轴于点C、D.设点P的横坐标为m,点Q的纵坐标为n,△PCD的面积为S1,△QAB的面积为S2.(1)当m=2,n=3时,求S1、S2的值;(2)当△PCD与△QAB全等时,若m=3,直接写出n的值.解:(1)∵当m=2时,y==6,∴P(2,6).∵PA⊥x轴,PC⊥y轴,∴PC=OA=2,PA=OC=6.∵当m=3时,x==4,∴Q(4,3).∵QB⊥x轴,QD⊥y轴,∴DQ=OB=4,QB=OA=3,∴CD=OC﹣OD=3,AB=OB﹣OA=2,∴S1=CD•CP=×3×2=3,S2=AB•QB=×2×3=3.(2)∵m=3,∴P(3,4),∴PC=OA=3,当△PCD≌△QBA时,∵QB=PC=3,∴n=3;当△PCD≌△ABQ时,∵PC=OA=3,∴AB=PC=3,∴OB=OA+AB=3+3=6.∵点Q在反比例函数y=的图象上,∴y==2,∴n=2.综上所述,n=2或3.25.如图,一次函数y=k1x+b的图象与反比例函数y=的图象相交于A(1,2)、B(﹣2,n)两点.(1)求一次函数和反比例函数的解析式;(2)根据图象,直接写出满足k1x+b>的x的取值范围;:S△BOP=1:4,求点P的坐标.(3)若点P在线段AB上,且S△AOP解:(1)∵反比例函数y=经过A(1,2),∴k2=1×2=2,∴反比例函数解析式为y=,∵B(﹣2,n)在反比例函数y=的图象上,∴n==﹣1,∴B(﹣2,﹣1),∵直线y=k1x+b经过A(1,2),B(﹣2,﹣1),∴,解得,∴一次函数的解析式为y=x+1;(2)观察图象,k1x+b>的x的取值范围是﹣2<x<0或x>1;(3)设P(x,x+1),:S△BOP=1:4,∵S△AOP∴AP:PB=1:4,即PB=4PA,∴(x+2)2+(x+1+1)2=16[(x﹣1)2+(x+1﹣2)2],解得x1=,x2=2(舍去),∴P点坐标为(,).26.如图,在矩形OABC中,OA=3,OC=5,分别以OA、OC所在直线为x轴、y轴,建立平面直角坐标系,D是边CB上的一个动点(不与C、B重合),反比例函数y=(k >0)的图象经过点D且与边BA交于点E,连接DE.(1)连接OE,若△EOA的面积为2,则k=4;(2)连接CA、DE与CA是否平行?请说明理由;(3)是否存在点D,使得点B关于DE的对称点在OC上?若存在,求出点D的坐标;若不存在,请说明理由.解:(1)连接OE,如图1,∵Rt△AOE的面积为2,∴k=2×2=4.(2)连接AC,如图1,设D(x,5),E(3,),则BD=3﹣x,BE=5﹣,=,∴,又∵∠B=∠B,∴△BDE∽△BCA,∴∠BED=∠BAC,∴DE∥AC.(3)假设存在点D满足条件.设D(x,5),E(3,),则CD=x,BD=3﹣x,BE=5﹣,AE=.作EF⊥OC,垂足为F,如图2,易证△B′CD∽△EFB′,∴,即=,∴B′F=,∴OB′=B′F+OF=B′F+AE=+=,∴CB′=OC﹣OB′=5﹣,在Rt△B′CD中,CB′=5﹣,CD=x,B′D=BD=3﹣x,由勾股定理得,CB′2+CD2=B′D2,(5﹣)2+x2=(3﹣x)2,解这个方程得,x1=1.5(舍去),x2=0.96,∴满足条件的点D存在,D的坐标为D(0.96,5).27.如图,点A和点E(2,1)是反比例函数y=(x>0)图象上的两点,点B在反比例函数y=(x<0)的图象上,分别过点A、B作y较的垂线,垂足分别为点C、D,AC =BD,连接AB交y轴于点F.(1)求k;(2)设点A的横坐标为a,点F的纵坐标为m,求证:am=﹣2.(3)连接CE、DE,当∠CED=90°时,求A的坐标.(1)解:∵点E(2,1)是反比例函数y=(x>0)图象上的点,∴k=1×2=2;(2)证明:∵点A的横坐标为a,∴点A的纵坐标为,∵AC=BD,∴B(﹣a,﹣),∵AC∥BD,∴∠CAF=∠DBF,∠ACF=∠BDF,∵AC=BD,∴△ACF≌△BDF(ASA),∴CF=DF,∴m=﹣,∴am=﹣2;(3)解:∵∠CED=90°,CF=DF,∴CD=2EF,∴=2,由(2)知,=﹣m,∴﹣4m=2,解得m=1或﹣,当m=1时,a=﹣2(舍去),当m=﹣时,a=,∴A(,).28.已知在平面直角坐标系xOy中,点A是反比例函数y=(x>0)图象上的一个动点,连结AO,AO的延长线交反比例函数y=(k>0,x<0)的图象于点B,过点A作AE⊥y轴于点E.(1)如图1,过点B作BF⊥x轴,于点F,连接EF.①若k=1,求证:四边形AEFO是平行四边形;②连结BE,若k=4,求△BOE的面积.(2)如图2,过点E作EP∥AB,交反比例函数y=(k>0,x<0)的图象于点P,连结OP.试探究:对于确定的实数k,动点A在运动过程中,△POE的面积是否会发生变化?请说明理由.(1)①证明:设点A的坐标为(a,),则当点k=1时,点B的坐标为(﹣a,﹣),∴AE=OF=a,∵AE⊥y轴,∴AE∥OF,∴四边形AEFO是平行四边形;②解:过点B作BD⊥y轴于点D,如图1,∵AE⊥y轴,∴AE∥BD,∴△AEO∽△BDO,∴,∴当k=4时,,即,=2S△AOE=1;∴S△BOE(2)不改变.理由如下:过点P作PH⊥x轴于点H,PE与x轴交于点G,设点A的坐标为(a,),点P的坐标为(b,),则AE=a,OE=,PH=﹣,∵四边形AEGO是平行四边形,∴∠EAO=∠EGO,AE=OG,∵∠EGO=∠PGH,∴∠EAO=∠PGH,又∵∠PHG=∠AEO,∴△AEO∽△GHP,∴,∵GH=OH﹣OG=﹣b﹣a,∴,∴﹣k=0,解得,∵a,b异号,k>0,∴,=×OE×(﹣b)=×(﹣b)=﹣,∴S△POE∴对于确定的实数k,动点A在运动过程中,△POE的面积不会发生变化.。
中考数学压轴题专题复习——反比例函数的综合及答案

中考数学压轴题专题复习——反比例函数的综合及答案一、反比例函数1.如图,反比例函数y= 的图象经过点A(﹣1,4),直线y=﹣x+b(b≠0)与双曲线y= 在第二、四象限分别相交于P,Q两点,与x轴、y轴分别相交于C,D两点.(1)求k的值;(2)当b=﹣2时,求△OCD的面积;(3)连接OQ,是否存在实数b,使得S△ODQ=S△OCD?若存在,请求出b的值;若不存在,请说明理由.【答案】(1)解:∵反比例函数y= 的图象经过点A(﹣1,4),∴k=﹣1×4=﹣4;(2)解:当b=﹣2时,直线解析式为y=﹣x﹣2,∵y=0时,﹣x﹣2=0,解得x=﹣2,∴C(﹣2,0),∵当x=0时,y=﹣x﹣2=﹣2,∴D(0,﹣2),∴S△OCD= ×2×2=2(3)解:存在.当y=0时,﹣x+b=0,解得x=b,则C(b,0),∵S△ODQ=S△OCD,∴点Q和点C到OD的距离相等,而Q点在第四象限,∴Q的横坐标为﹣b,当x=﹣b时,y=﹣x+b=2b,则Q(﹣b,2b),∵点Q在反比例函数y=﹣的图象上,∴﹣b•2b=﹣4,解得b=﹣或b= (舍去),∴b的值为﹣.【解析】【分析】(1)根据反比例函数的图象上点的坐标特征易得k=﹣4;(2)当b=﹣2时,直线解析式为y=﹣x﹣2,则利用坐标轴上点的坐标特征可求出C(﹣2,0),D(0,﹣2),然后根据三角形面积公式求解;(3)先表示出C(b,0),根据三角形面积公式,由于S△ODQ=S△OCD,所以点Q和点C到OD的距离相等,则Q的横坐标为(﹣b,0),利用直线解析式可得到Q(﹣b,2b),再根据反比例函数的图象上点的坐标特征得到﹣b•2b=﹣4,然后解方程即可得到满足条件的b的值.2.已知点A,B分别是x轴、y轴上的动点,点C,D是某个函数图象上的点,当四边形ABCD(A,B,C,D各点依次排列)为正方形时,我们称这个正方形为此函数图象的“伴侣正方形”.例如:在图1中,正方形ABCD是一次函数y=x+1图象的其中一个“伴侣正方形”.(1)如图1,若某函数是一次函数y=x+1,求它的图象的所有“伴侣正方形”的边长;(2)如图2,若某函数是反比例函数(k>0),它的图象的“伴侣正方形”为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数的解析式;(3)如图3,若某函数是二次函数y=ax2+c(a≠0),它的图象的“伴侣正方形”为ABCD,C,D中的一个点坐标为(3,4),请你直接写出该二次函数的解析式.【答案】(1)解:(I)当点A在x轴正半轴、点B在y轴负半轴上时:正方形ABCD的边长为.(II)当点A在x轴负半轴、点B在y轴正半轴上时:设正方形边长为a,易得3a= ,解得a= ,此时正方形的边长为.∴所求“伴侣正方形”的边长为或(2)解:如图,作DE⊥x轴,CF⊥y轴,垂足分别为点E、F,易证△ADE≌△BAO≌△CBF.∵点D的坐标为(2,m),m<2,∴DE=OA=BF=m,∴OB=AE=CF=2﹣m.∴OF=BF+OB=2,∴点C的坐标为(2﹣m,2).∴2m=2(2﹣m),解得m=1.∴反比例函数的解析式为y=(3)解:实际情况是抛物线开口向上的两种情况中,另一个点都在(3,4)的左侧,而开口向下时,另一点都在(3,4)的右侧,与上述解析明显不符合a、当点A在x轴正半轴上,点B在y轴正半轴上,点C坐标为(3,4)时:另外一个顶点为(4,1),对应的函数解析式是y=﹣ x2+ ;b、当点A在x 轴正半轴上,点 B在 y轴正半轴上,点D 坐标为(3,4)时:不存在,c、当点A 在 x 轴正半轴上,点 B在 y轴负半轴上,点C 坐标为(3,4)时:不存在d、当点A在x 轴正半轴上,点B在y轴负半轴上,点D坐标为(3,4)时:另外一个顶点C为(﹣1,3),对应的函数的解析式是y= x2+ ;e、当点A在x轴负半轴上,点B在y轴负半轴上,点C坐标为(3,4)时,另一个顶点D的坐标是(7,﹣3)时,对应的函数解析式是y=﹣ x2+ ;f、当点A在x轴负半轴上,点B在y轴负半轴上,点C坐标为(3,4)时,另一个顶点D 的坐标是(﹣4,7)时,对应的抛物线为y= x2+ ;故二次函数的解析式分别为:y= x2+ 或y=﹣ x2+ 或y=﹣ x2+ 或y= x2+【解析】【分析】(1)先正确地画出图形,再利用正方形的性质确定相关点的坐标从而计算正方形的边长.(2)因为ABCD为正方形,所以可作垂线得到等腰直角三角形,利用点D(2,m)的坐标表示出点C的坐标,可求出m的值,即可得到反比例函数的解析式.(3)由抛物线开口既可能向上,也可能向下.当抛物线开口向上时,正方形的另一个顶点也是在抛物线上,这个点既可能在点(3,4)的左边,也可能在点(3,4)的右边,过点(3,4)向x轴作垂线,利用全等三角形确定线段的长即可确定抛物线上另一个点的坐标;当抛物线开口向下时也是一样地分为两种情况来讨论,即可得到所求的结论.3.【阅读理解】对于任意正实数a、b,因为≥0,所以≥0,所以≥2 ,只有当时,等号成立.【获得结论】在≥2 (a、b均为正实数)中,若为定值,则≥2 ,只有当时,有最小值2 .(1)根据上述内容,回答下列问题:若 >0,只有当 =________时,有最小值________.(2)【探索应用】如图,已知A(-3,0),B(0,-4),P为双曲线(>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.【答案】(1)1;2(2)解:设P(x,),则C(x,0),D(0,),∴CA=x+3,BD= +4,∴S四边形= CA×BD= (x+3)( +4),化简得:S=2(x+ )+12.∵x>0,>0,∴x+ ≥2 ABCD=6,只有当x= ,即x=3时,等号成立,∴S≥2×6+12=24,∴四边形ABCD的面积有最小值24,此时,P(3,4),C(3,0),D(0,4),AB=BC=CD=DA=5,∴四边形ABCD是菱形.【解析】【解答】解:(1)根据题目所给信息可知m+ ≥2 ,且当m= 时等号,∴当m=1时,m+ ≥2,即当m=1时,m+ 有最小值2.故答案为:1,2;【分析】(1)此题是一道阅读题,根据题中所给的信息可知:,只有当m=时等号成立,一个正数只有1和它的倒数相等,从而得出答案;(2)根据双曲线上点的坐标特点设出P点的坐标,根据垂直于坐标轴上的点的坐标特点表示出C,D两点的坐标,从而表示出AC,BD的长,根据对角线互相垂直的四边形的面积等于两对角线积的一半建立出S与x的函数关系式,根据题干提供的信息得出得出,只有在,即x=3时,等号成立,从而得出S的最小值,从而得出P,C,D三点的坐标,进而算出AB=BC=CD=DA=5,根据四边相等的四边形是菱形得出结论。
反比例函数与相似三角形综合

反比例函数与相似三角形如图,点A 在第一象限内,点B 在x 轴正半轴上,反比例函数x k y =)0(>k 的图象与直线OA 交于点C 、E 两点,与直线AB 交于点D ,若AB AO =. 求证:AE AC AD ⋅=2.方法一:(面积+相似)证: 作如图所示的辅助线,∵AB AO =,C 、D 在反比例函数x ky =上,∴BDG OCH S S 四边形=∆.∴ OAF ABF ADG OCH S S S S ∆∆∆∆==+.∴1=+∆∆∆∆OAFADG OAF OCHS S S S .∵ CH ∥AF ,∴ OCH ∆∽OAF ∆,则2)(OAOCS S OAF OCH =∆∆.同理2)(OAADS S OAF ADG =∆∆.∴12222=+OA AD OA OC ,则222OC OA AD -=.∴ ))((2OC OA OC OA AD -+=.由反比例函数的对称性知:OC OE =,∴AE AC AD ⋅=2.F G H 比方法一图方法二:(解析法+相似):证: 作如图所示的辅助线;设),(n m C ,),(t s D , 由对称性知),(n m E --. 易求得直线CD 的解析式为t n x ms k y ++-=; 易求得直线DE 的解析式为n t x ms k y -+=. 可求得),0(t n F +,),0(n t G -.∴ n GH FH ==,则DG DF =. ∴DGF DFG ∠=∠.∴DNM ONG DMN ∠=∠=∠.∵AB AO =,∴ AOB ABO ∠=∠.由三角形的外角定理知:E BDM ADC ∠=∠=∠. ∵A A ∠=∠,∴ ADC ∆∽AED ∆,则AD ACAE AD =.∴ AE AC AD ⋅=2.方法三:(三角函数+相似):证: 作如图所示的辅助线;∵AB AO =, ∴ AOB ABO ∠=∠.∵DF ∥OB ,∴ ABO ADF ∠=∠,同理AOB AEH ∠=∠. ∴AEH ADF ∠=∠. 设点),(m km D ,点),(n kn C ,由对称性得),(n kn E --.∴mn n m k m k n k CF )(-=-=,n m DF -=.在CDF Rt ∆中,mn kDF CF CDF ==∠tan ,同理mn kDEH =∠tan .∴DEH CDF ∠=∠.∴AED ADC ∠=∠.∵A A ∠=∠,∴∴ ADC ∆∽AED ∆,则AD ACAE AD=.∴ AE AC AD ⋅=2.FG H NM H F方法四:(见何国平老师的解法)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
反比例函数与相似的综合题型一利用平行线构造A型或X型相似1.(2020•鞍山一模)如图,点A在双曲线y=3x上,点B在双曲线y=kx(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=32CD,则k的值为152.【解析】解:设点A的坐标为(a,3a ),则点B的坐标为(ak3,3a),∵AB∥x轴,∴∠BAC=∠ODC,∠ACB=∠DCO,∴ABOD =ACDC,∵AC=32CD,∴ABDO=32,∵OD=a,∴AB=1.5a,∴点B的横坐标是2.5a,∴2.5a=ak3,解得,k=152,故答案为:152.2.(220•黔东南州)如图,已知点A,B分别在反比例函数y1=−2x和y2=kx的图象上,若点A是线段OB的中点,则k的值为﹣8.【解析】解:设A(a,b),则B(2a,2b),∵点A在反比例函数y1=−2x的图象上,∴ab=﹣2;∵B点在反比例函数y2=kx的图象上,∴k=2a•2b=4ab=﹣8.故答案是:﹣8.题型二 利用平行线构造相似3.(2020•柯桥区一模)如图,已知B 、A 分别在反比例函数y =−9x,y =k x上,当AO ⊥BO 时,BO :AO =3:4,则k = 16 .【解析】解:设点A 的坐标为(a ,ka),点B 的坐标为(b ,−9b ),作BC ⊥x 轴于点C ,作AD ⊥x 轴于点D ,∵∠AOB =90°,∠BOC +∠OBC =90°,∴∠BOC +∠AOD =90°,∴∠BOC =∠OAD ,∵∠BCO =∠ODA =90°,BO :AO =3:4,∴△BOC ∽△OAD ,∴OCAD=BC OD=OB AO,即−bk a=−9ba=34,解得,k =16,故答案为:16.4.(2020•历下区期中)如图,在平面直角坐标系中,等边三角形OAB 的顶点A 的坐标为(5,0),顶点B 在第一象限,函数y =kx (x >0)的图象分别交边OA 、AB 于点C 、D .若OC =2AD ,则k = 4√3【解析】解:如图,过C 作CE ⊥x 轴于E ,过D 作DF ⊥x 轴于F ,则∠CEO =∠DF A =90°,又∵∠COE =∠DAF =60°,∴△COE ∽△DAF ,又∵OC =2AD ,∴DF =12CE ,AF =12OE ,设OE =a ,则CE =√3a ,∴AF =12a ,DF =√32a ,∴C (a ,√3a ),D (5−12a ,√32a ), ∵函数y =k x(x >0)的图象分别交边OA 、AB 于点C 、D ,∴a •√3a =(5−12a )•√32a ,解得a =2, ∴C (2,2√3),∴k =2×2√3=4√3,故答案为4√3.5.(2020•如东县一模)如图,点A (1,n )和点B 都在反比例函数y =kx (x >0)的图象上,若∠OAB =90°,OA AB=23,则k 的值是 2 .【解析】解:如图,过A 作AC ⊥x 轴,过B 作BD ⊥AC 于D ,则∠ACO =∠BDA =90°,OC =1,AC =n ,∵∠BAO =90°,∴∠CAO +∠BAC =∠ABD +∠BAC =90°,∴∠CAO =∠DBA ,∴△AOC ∽△BAD ,∴AD OC=BD AC=AB OA,即AD 1=BD n=32,∴AD =32,BD =32n ,∴B (1+32n ,n −32),∵k =1×n =(1+32n )(n −32),解得n =2或n =﹣0.5(舍去),∴k =1×2=2故答案为:2.6.(2020•泗阳县一模)如图,点A在反比例函数y=3x(x>0)上,以OA为边作正方形OABC,边AB交y轴于点P,若PB:P A=2:1,则正方形OABC的边长AB=√10.【解析】解:由题意可得,OA=AB,设AP=a,则BP=2a,OA=3a,设点A的坐标为(m,3m),作AE⊥x轴于点E,∵∠P AO=∠OEA=90°,∠POA+∠AOE=90°,∠AOE+∠OAE=90°,∴∠POA=∠OAE,∴△POA∽△OAE,∴APAO =OEEA,即a3a=m3m,解得,m=1或m=﹣1(舍去),∴点A的坐标为(1,3),∴OA=√10,故答案为:√10.巩固练习1.(2020•滨州模拟)如图,点A在双曲线y=4x上,点B在双曲线y=kx(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为12.【解析】解:设点A的坐标为(a,4a ),则点B的坐标为(ak4,4a),∵AB∥x轴,AC=2CD,∴∠BAC=∠ODC,∵∠ACB=∠DCO,∴△ACB∽△DCO,∴ABOD =ACDC,∴ABOD=21,∵OD=a,则AB=2a,∴点B的横坐标是3a,∴3a=ak4,解得,k=12,故答案为:12.2.(2020•岳麓区校级模拟)如图,已知第一象限内的点A在反比例函数y=4x上,第二象限的点B在反比例函数y=kx上,且OA⊥OB,OBOA=34,则k的值为−94.【解析】解:作AC⊥x轴于C,BD⊥x轴于D,如图,∵OA⊥OB,∴∠BOD+∠AOC=90°,∵∠BOD+∠OBD=90°,∴∠AOC=∠OBD,∴Rt△OBD∽Rt△AOC,∴S△OBDS△AOC=(OBOA)2=(34)2=916,∵S△OBD=12|k|,S△AOC=12×4=2,∴12|k|2=916,而k<0,∴k=−94.故答案为−94.3.(2020•洛宁县期中)已知反比例函数y=kx(k<0)的图象上有两点A(x1,y1)、B(x2,y2),且有x1<x2<0,则y1和y2的大小关系是y1<y2.【解析】解:∵反比例函数y=kx(k<0)的k<0,可见函数位于二、四象限,∵x1<x2<0,可见A(x1,y1)、B(x2,y2)位于第二象限,由于在二四象限内,y随x的增大而增大,∴y1<y2.故答案为y1<y2.4.(2020•渝中区校级月考)如图,△ABC 是等边三角形,顶点C 在y 轴的负半轴上,点A (1,5√32),点B 在第一象限,经过点A 的反比例函数y =kx(x >0)的图象恰好经过顶点B ,则△ABC 的边长为 2√7 .【解析】如图延长AB 到D ,使得AB =BD ,连接CD ,作AH ⊥y 轴于H ,DE ⊥y 轴于E .设C (0,c ). ∵△ABC 是等边三角形,∴AB =AC =BC ,∵AB =BD ,∴BA =BC =BD ,∴△ACD 是直角三角形, ∵∠CAD =60°,∴DC =√3AC ,∵∠ACD =∠AHC =∠DEC =90°,∴∠ACH +∠DCE =90°,∵∠ECD +∠CDE =90°,∴∠ACH =∠CDE ,∴△ACH ∽△CDE ,∴AH EC=HC DE=AC CD=√33, ∵A (1,5√32),∴AH =1,CH =5√32−c ,∴EC =√3,DE =152−√3c ,∴D (152−√3c ,c −√3), ∵BA =BD ,∴B (17−2√3c4,3√3−2√3c4), ∵A 、B 在y =kx上,∴5√32=17−2√3c 4×3√3−2√3c4, 整理得:4√3c 2﹣16c ﹣11√3=0,解得c =−√32或11√36(舍弃),∴C (0,−√32), ∴AC =2+CH 2=√12+(3√3)2=2√7,故答案为2√7.5.(2020•碑林区校级一模)如图,反比例函数y=kx,(k>0)经过正方形ABCD的顶点C,D,若正方形的边长为4,则k的值为16.【解析】解:作CE⊥x轴于E,DF⊥y轴于F,如图,设A(0,m),B(n,0),∵四边形ABCD为正方形,∴BC=BA,∠ABC=90°,∵∠ABO+∠CBE=90°,∠ABO+∠OAB=90°,∴∠CBE=∠OAB,而∠AOB=∠BEC,∴△AOB≌△BEC(AAS),∴OA=BE=m,OB=CE=n,∴C(m+n,n),同理方法可证明△AOB≌△DF A(AAS),∴OA=DF=m,OB=AF=n,∴D(m,m+n),∵反比例函数y=kx,(k>0)经过正方形ABCD的顶点C,D,∴m(m+n)=(m+n)n,∴m=n,∵OA2+OB2=AB2,∴m2+n2=42,即m2+m2=16,解得m=2√2,∴C(4√2,2√2),∴k=4√2×2√2=16.故答案为16.6.(2020•深圳)如图,在Rt△ABC中,∠ABC=90°,C(0,﹣3),CD=3AD,点A在反比例函数y=kx图象上,且y轴平分∠ACB,求k=4√77.【解析】解:过A作AE⊥x轴,垂足为E,∵C(0,﹣3),∴OC=3,∵∠AED =∠COD =90°,∠ADE =∠CDO ∴△ADE ∽△CDO ,∴AE CO=DE OD=AD CD=13,∴AE =1;又∵y 轴平分∠ACB ,CO ⊥BD ,∴BO =OD ,∵∠ABC =90°,∴∠OCD =∠DAE =∠ABE ,∴△ABE ~△COD ,∴AEOD=BE OC设DE =n ,则BO =OD =3n ,BE =7n ,∴13n=7n3,∴n =√77∴OE =4n =4√77∴A (4√77,1)∴k =4√77×1=4√77.故答案为:4√77.。
