轴心受压铝合金构件的稳定系数
轴心受压构件的稳定系数
1
2
3
4
5
6
7
8
9
0
10
20
30
40
50
60
70
80
90
100
110
120
130
140
150
160
170
180
190
200
1.000
0.984
0.937
0.848
0.766
0.690
0.618
0.552
0.493
0.439
0.394
0.359
0.328
0.299
0.272
0.248
0.227
0.208
0.322
0.288
0.259
0.234
0.212
0.193
0.176
0.162
0.149
0.137
0.127
0.996
0.978
0.946
0.910
0.870
0.823
0.769
0.707
0.641
0.575
0.511
0.453
0.402
0.357
0.318
0.285
0.256
0.232
0.210
0.202
0.184
0.169
0.155
0.143
0.132
1.000
0.989
0.963
0.929
0.891
0.847
0.797
0.739
0.675
0.608
0.542
0.481
0.426
a类截面的轴心压杆稳定系数

a类截面的轴心压杆稳定系数A类截面的轴心压杆稳定系数是指压杆在轴向压力作用下的稳定性能。
它反映了压杆在轴向压力下的抗弯刚度和稳定性能。
具体计算轴心压杆的稳定系数需要考虑截面形状、材料特性、截面尺寸等因素,因此在具体设计中需要进行详细的结构分析和计算。
一般情况下,轴心压杆稳定系数可以通过以下公式计算:
NCr = π²EI / L²
其中,NCr为轴心压杆的临界压力,E为材料的弹性模量,I为截面的惯性矩,L为压杆的有效长度。
这个公式是基于欧拉公式推导而来,用于判断压杆在轴向压力作用下是否稳定。
当实际的轴向压力小于轴心压杆的临界压力时,压杆可以保持稳定;当实际轴向压力大于或等于临界压力时,压杆可能会产生屈曲失稳现象。
需要注意的是,轴心压杆稳定系数只是判断稳定性的一个指标,具体的设计应考虑材料强度、安全系数、实际应用条件等因素,以确保压杆的安全可靠性。
对于特定的工程结构和要求,可能需要使用更为复杂的分析方法和公式进行稳定性计算。
因此,在实际设计中,应该遵循相关的设计规范和标准,同时与专业的结构工程师合作,进行详细的结构分析和计算。
1/ 1。
轴心受压构件的稳定性计算

轴心受压构件的稳定性计算7.2.1 除可考虑屈服后强度的实腹式构件外,轴心受压构件的稳定性计算应符合下式要求:式中:φ——轴心受压构件的稳定系数(取截面两主轴稳定系数中的较小者),根据构件的长细比(或换算长细比)、钢材屈服强度和表7.2.1-1、表7.2.1-2的截面分类,按本标准附录D采用。
表7.2.1-1 轴心受压构件的截面分类(板厚t<40mm)注:1 a*类含义为Q235钢取b类,Q345、Q390、Q420和Q460钢取a类;b*类含义为Q235钢取c类,Q345、Q390、Q420和Q460钢取b类;2 无对称轴且剪心和形心不重合的截面,其截面分类可按有对称轴的类似截面确定,如不等边角钢采用等边角钢的类别;当无类似截面时,可取c类。
表7.2.1-2 轴心受压构件的截面分类(板厚t≥40mm)7.2.2 实腹式构件的长细比λ应根据其失稳模式,由下列公式确定:1 截面形心与剪心重合的构件:1) 当计算弯曲屈曲时,长细比按下列公式计算:式中:l0x、l0y——分别为构件对截面主轴x和y的计算长度,根据本标准第7.4节的规定采用(mm);i x、i y——分别为构件截面对主轴x和y的回转半径(mm)。
2) 当计算扭转屈曲时,长细比应按下式计算,双轴对称十字形截面板件宽厚比不超过15εk者,可不计算扭转屈曲。
式中:I0、I t、I w——分别为构件毛截面对剪心的极惯性矩(m m4)、自由扭转常数(m m4)和扇性惯性矩(m m6),对十字形截面可近似取I w=0;I w——扭转屈曲的计算长度,两端铰支且端截面可自由翘曲者,取几何长度l;两端嵌固且端部截面的翘曲完全受到约束者,取0.5l(mm)。
2 截面为单轴对称的构件:1) 计算绕非对称主轴的弯曲屈曲时,长细比应由式(7.2.2-1)、式(7.2.2-2)计算确定。
计算绕对称主轴的弯扭屈曲时,长细比应按下式计算确定:式中:y s——截面形心至剪心的距离(mm);i0——截面对剪心的极回转半径,单轴对称截面i20=y2s+i2x+i2y(mm);λz——扭转屈曲换算长细比,由式(7.2.2-3)确定。
轴心受压构件的稳定系数

附录B 轴心受压构件的稳定系数B.0.1 轴心受压构件的稳定系数ϕ应按下式计算:2212ηλϕλ++= (B.0.1-1) 式中 η —— 构件的几何缺陷系数,应按下式计算:()0λλαη-= (B.0.1-2) 对于T6类合金:0.22α=,00.15λ=;对于非T6类合金:0.35α=,00.05λ=。
λ —— 相对长细比,应按下式计算:λ= (B.0.1-3) e A —— 有效毛截面面积(mm 2);cr N —— 基于毛截面的欧拉临界力(N ),应按下式计算: 2cr 20x xEI N l π= (B.0.1-4)0x l —— 构件对截面主轴的计算长度(mm ); x I —— 构件毛截面对其主轴的惯性矩(mm 4)。
B.0.2 对于存在局部焊接的轴心受压构件,其局部焊接稳定系数haz ϕ应按下式计算:2haz haz 2haz 12ηλϕλ++= (B.0.2-1) 式中 haz λ —— 局部焊接相对长细比,应按下式计算:haz λ= (B.0.2-2)u,e A —— 有效焊接截面面积(mm 2);cr N —— 基于毛截面的欧拉临界力(N ); u f —— 铝合金材料的极限抗拉强度最小值(N/mm 2)。
B.0.3 单轴对称截面的轴心受压构件,对非对称轴的相对长细比x λ仍应按式(B.0.1-3)计算(或局部焊接下,haz x λ按式(B.0.2-2)),但对对称轴应取计及扭转效应的下列换算相对长细比y ωλ代替y λ(或局部焊接下y λ代替,haz y λ): yωλ= ,haz y ωλ= (B.0.3-1)式中 y N ω—— 基于毛截面的单轴对称截面弯扭屈曲临界力(N ),应按下式计算:0021y y N y ω-⎣⎦ (B.0.3-2)y N —— 基于毛截面的对y 轴的欧拉临界力(N ),应按下式计算: 2y 2y EA N πλ= (B.0.3-3)y λ —— 构件绕对称轴的长细比;N ω—— 基于毛截面的扭转屈曲临界力(N ),应按下式计算: 2t 2201EI N GI i l ωωωπ⎛⎫=+ ⎪⎝⎭(B.0.3-4)I ω —— 毛截面扇性惯性矩(mm 4); t I —— 毛截面抗扭惯性矩(mm 4); l ω —— 扭转屈曲计算长度(mm ),应按附表C 中表C-1的规定进行计算;G —— 铝合金材料的剪切模量(N/mm 2),应按下式计算: 2(1)E G ν=+ (B.0.3-5)E —— 弹性模量;ν—— 泊松比;0i —— 截面对剪心的极回转半径(mm ),应按下式计算:0i = (B.0.3-6)x y i i , —— 构件毛截面对其主轴x 轴和y 轴的回转半径(mm ); 00x y , —— 截面剪心坐标(mm )。
B94-实际轴心受压构件整体稳定计算公式

x
x
x
x
格构式
y
x
y
x
y
x
x
x
x 焊接,翼缘为 轧制或剪切边
b类
c类
y
y
y
y
焊接,翼缘为轧
y 焊接,板件
x
制或剪切边 x
宽厚比≤20
c类
c类
轴心受压构件截面分类(板厚t≥40mm)
截面形式
对x轴
b x
y
h
轧制工字形 或H形截面
t<80mm
b类
t≥80mm
c类
y
x
x
y
焊接工字 形形截面
翼缘为焰切边
b类
y
边
轧制等 边角钢
对x轴
y x
y
xx
x
y
x
x
y
y
y
y
y
b类
y 轧制、焊接
x
x
轧制或 焊接
x
板件宽厚比
大于20
y x
y
x 轧制截面和翼 缘为焰切边的 焊接截面
y
x
y
x 焊接,板件 边缘焰切
对y轴 b类
轴心受压构件截面分类(板厚t<40mm)
截面形式
对x轴 对y轴
y
y
y
y
y
x
x
x
x
x
焊接
y
y
y
y
b类 b类
计算 l0
i
据
截面类型
查表
得到
代入公 式验算
N f
A
如何提高轴心受压构件整体稳定性 ?
由公式 N f 及 l0
附录1 轴心受压构件的稳定系数
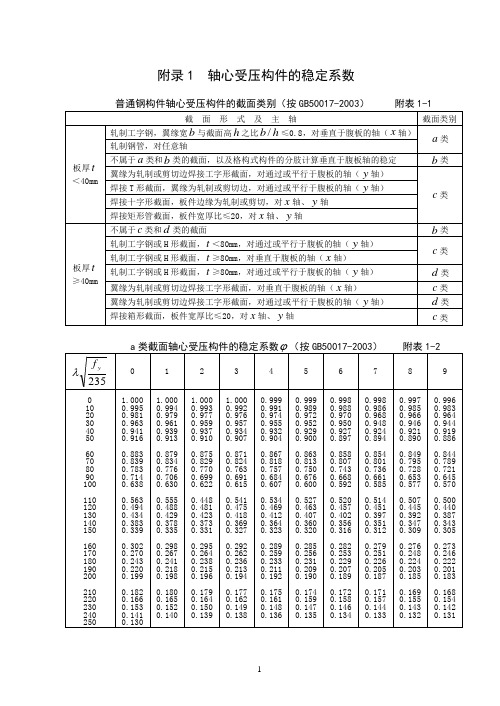
附录1 轴心受压构件的稳定系数普通钢构件轴心受压构件的截面类别(按GB50017-2003) 附表1-1截 面 形 式 及 主 轴截面类别板厚t <40mm轧制工字钢,翼缘宽b 与截面高h 之比h b /≤0.8,对垂直于腹板的轴(x 轴) a 类轧制钢管,对任意轴不属于a 类和b 类的截面,以及格构式构件的分肢计算垂直于腹板轴的稳定b 类翼缘为轧制或剪切边焊接工字形截面,对通过或平行于腹板的轴(y 轴) c 类焊接T 形截面,翼缘为轧制或剪切边,对通过或平行于腹板的轴(y 轴) 焊接十字形截面,板件边缘为轧制或剪切,对x 轴、y 轴 焊接矩形管截面,板件宽厚比≤20,对x 轴、y 轴 板厚t ≥40mm不属于c 类和d 类的截面b 类轧制工字钢或H 形截面,t <80mm ,对通过或平行于腹板的轴(y 轴) c 类轧制工字钢或H 形截面,t ≥80mm ,对垂直于腹板的轴(x 轴)轧制工字钢或H 形截面,t ≥80mm ,对通过或平行于腹板的轴(y 轴) d 类 翼缘为轧制或剪切边焊接工字形截面,对垂直于腹板的轴(x 轴)c 类 翼缘为轧制或剪切边焊接工字形截面,对通过或平行于腹板的轴(y 轴)d 类 焊接箱形截面,板件宽厚比≤20,对x 轴、y 轴c 类a 类截面轴心受压构件的稳定系数ϕ(按GB50017-2003) 附表1-2235yf λ0 1 2 3 4 5 6 7 8 9 0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 210 220 230 240 2501.000 0.995 0.981 0.963 0.941 0.916 0.883 0.839 0.783 0.714 0.638 0.563 0.494 0.434 0.383 0.339 0.302 0.270 0.243 0.220 0.199 0.182 0.166 0.153 0.141 0.1301.000 0.994 0.979 0.961 0.939 0.913 0.879 0.834 0.776 0.706 0.630 0.555 0.488 0.429 0.378 0.335 0.298 0.267 0.241 0.218 0.198 0.180 0.165 0.152 0.1401.000 0.993 0.977 0.959 0.937 0.910 0.875 0.829 0.770 0.699 0.622 0.448 0.481 0.423 0.373 0.331 0.295 0.264 0.238 0.215 0.196 0.179 0.164 0.150 0.1391.000 0.992 0.976 0.957 0.934 0.907 0.871 0.824 0.763 0.691 0.615 0.541 0.475 0.418 0.369 0.327 0.292 0.262 0.236 0.213 0.194 0.177 0.162 0.149 0.1380.999 0.991 0.974 0.955 0.932 0.904 0.867 0.818 0.757 0.684 0.607 0.534 0.469 0.412 0.3640.323 0.289 0.259 0.233 0.211 0.192 0.175 0.161 0.148 0.1360.999 0.989 0.972 0.952 0.929 0.900 0.863 0.813 0.750 0.676 0.600 0.527 0.463 0.407 0.360 0.320 0.285 0.256 0.231 0.209 0.190 0.174 0.159 0.147 0.1350.998 0.988 0.970 0.950 0.927 0.897 0.858 0.807 0.743 0.668 0.592 0.520 0.457 0.402 0.356 0.316 0.282 0.253 0.229 0.207 0.189 0.172 0.158 0.146 0.1340.998 0.986 0.968 0.948 0.924 0.894 0.854 0.801 0.736 0.661 0.585 0.514 0.451 0.397 0.351 0.312 0.279 0.251 0.226 0.205 0.187 0.171 0.157 0.144 0.1330.997 0.985 0.966 0.946 0.921 0.890 0.849 0.795 0.728 0.653 0.577 0.507 0.445 0.392 0.347 0.309 0.276 0.248 0.224 0.203 0.185 0.169 0.155 0.143 0.1320.996 0.983 0.964 0.944 0.919 0.886 0.844 0.789 0.721 0.645 0.570 0.500 0.440 0.387 0.343 0.305 0.273 0.246 0.222 0.201 0.183 0.168 0.154 0.142 0.131235y f λ0 1 2 3 4 5 6 7 8 9 0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 210 220 230 240 2501.000 0.992 0.970 0.936 0.899 0.8560.807 0.751 0.688 0.6210.5550.493 0.437 0.387 0.345 0.3080.276 0.249 0.225 0.204 0.1860.170 0.156 0.144 0.133 0.1231.000 0.991 0.967 0.932 0.895 0.8520.802 0.745 0.681 0.614 0.5490.487 0.432 0.383 0.341 0.3040.273 0.246 0.223 0.202 0.1840.169 0.155 0.143 0.1321.000 0.989 0.963 0.929 0.891 0.8470.797 0.739 0.675 0.608 0.5420.481 0.426 0.378 0.337 0.3010.270 0.244 0.220 0.200 0.1830.167 0.154 0.142 0.1310.999 0.987 0.960 0.925 0.887 0.8420.791 0.732 0.668 0.601 0.5360.475 0.421 0.374 0.333 0.2980.267 0.241 0.218 0.198 0.1810.166 0.153 0.141 0.1300.999 0.985 0.957 0.922 0.882 0.8380.786 0.726 0.661 0.594 0.5290.470 0.416 0.370 0.329 0.2950.265 0.239 0.216 0.197 0.1800.165 0.151 0.140 0.1290.998 0.983 0.953 0.918 0.878 0.8330.780 0.720 0.655 0.588 0.5230.464 0.411 0.365 0.326 0.2910.262 0.236 0.214 0.195 0.1780.163 0.150 0.138 0.1280.997 0.981 0.950 0.914 0.874 0.8280.774 0.714 0.648 0.581 0.5170.458 0.406 0.361 0.322 0.2880.259 0.234 0.212 0.193 0.1760.162 0.149 0.137 0.1270.996 0.978 0.946 0.910 0.870 0.8230.769 0.707 0.641 0.575 0.5110.453 0.402 0.357 0.318 0.2850.256 0.232 0.210 0.191 0.1750.160 0.148 0.136 0.1260.995 0.976 0.943 0.906 0.865 0.8180.763 0.701 0.635 0.568 0.5050.447 0.397 0.353 0.315 0.2820.254 0.229 0.208 0.190 0.1730.159 0.146 0.135 0.1250.994 0.973 0.939 0.903 0.861 0.8130.757 0.694 0.628 0.561 0.4990.442 0.392 0.349 0.311 0.2790.251 0.227 0.206 0.188 0.1720.158 0.145 0.134 0.124c 类截面轴心受压构件的稳定系数ϕ(按GB50017-2003) 附表1-4235y f λ0 1 2 3 4 5 6 7 8 9 0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 210 220 230 240 2501.000 0.992 0.966 0.902 0.8390.775 0.709 0.648 0.578 0.517 0.463 0.419 0.379 0.342 0.309 0.280 0.254 0.230 0.210 0.192 0.176 0.162 0.150 0.138 0.128 0.1191.000 0.990 0.959 0.896 0.833 0.768 0.702 0.636 0.572 0.511 0.458 0.415 0.375 0.339 0.306 0.277 0.251 0.228 0.208 0.190 0.175 0.161 0.148 0.137 0.1271.000 0.988 0.953 0.890 0.826 0.762 0.695 0.629 0.566 0.505 0.454 0.411 0.371 0.335 0.303 0.274 0.249 0.226 0.206 0.189 0.173 0.159 0.147 0.136 0.1260.999 0.986 0.947 0.884 0.820 0.755 0.689 0.623 0.559 0.500 0.449 0.407 0.367 0.332 0.300 0.271 0.246 0.224 0.205 0.187 0.172 0.158 0.1460.135 0.1250.999 0.983 0.940 0.877 0.814 0.748 0.682 0.616 0.553 0.494 0.445 0.403 0.364 0.328 0.297 0.269 0.244 0.222 0.203 0.186 0.170 0.157 0.145 0.134 0.124 0.998 0.981 0.934 0.871 0.807 0.742 0.676 0.610 0.547 0.488 0.441 0.399 0.360 0.325 0.294 0.266 0.242 0.220 0.201 0.184 0.169 0.156 0.144 0.133 0.1240.997 0.978 0.928 0.865 0.801 0.735 0.669 0.604 0.541 0.483 0.436 0.395 0.356 0.322 0.291 0.264 0.239 0.218 0.199 0.182 0.168 0.154 0.143 0.132 0.1230.996 0.976 0.921 0.858 0.794 0.729 0.662 0.597 0.535 0.477 0.432 0.391 0.353 0.319 0.288 0.261 0.237 0.216 0.197 0.181 0.166 0.153 0.142 0.131 0.1220.995 0.973 0.915 0.852 0.788 0.722 0.656 0.591 0.529 0.472 0.428 0.387 0.349 0.315 0.285 0.258 0.235 0.214 0.196 0.179 0.165 0.152 0.140 0.130 0.1210.993 0.970 0.909 0.846 0.781 0.715 0.649 0.584 0.523 0.467 0.423 0.383 0.346 0.312 0.282 0.256 0.233 0.212 0.194 0.178 0.163 0.151 0.139 0.129 0.120235y f λ0 1 2 3 4 5 6 7 8 90 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 2001.000 0.984 0.937 0.848 0.766 0.690 0.618 0.552 0.493 0.439 0.394 0.359 0.328 0.299 0.272 0.248 0.227 0.208 0.191 0.176 0.1621.000 0.981 0.927 0.840 0.759 0.683 0.612 0.546 0.487 0.434 0.390 0.356 0.325 0.296 0.270 0.246 0.225 0.206 0.189 0.1740.999 0.978 0.918 0.831 0.751 0.675 0.605 0.540 0.481 0.429 0.387 0.353 0.322 0.293 0.267 0.244 0.223 0.204 0.188 0.1730.999 0.974 0.909 0.823 0.743 0.668 0.598 0.534 0.476 0.424 0.383 0.350 0.319 0.290 0.265 0.242 0.221 0.203 0.186 0.1710.998 0.969 0.900 0.815 0.735 0.661 0.591 0.528 0.470 0.419 0.380 0.346 0.316 0.288 0.262 0.240 0.219 0.201 0.184 0.170 0.996 0.965 0.891 0.807 0.728 0.654 0.585 0.522 0.465 0.414 0.376 0.343 0.313 0.285 0.260 0.237 0.217 0.199 0.183 0.1680.994 0.960 0.883 0.799 0.720 0.646 0.578 0.516 0.460 0.410 0.373 0.340 0.310 0.282 0.258 0.235 0.215 0.197 0.181 0.1670.992 0.955 0.874 0.790 0.712 0.639 0.572 0.510 0.454 0.405 0.370 0.337 0.307 0.280 0.255 0.233 0.213 0.196 0.180 0.1660.990 0.949 0.865 0.782 0.705 0.632 0.565 0.504 0.449 0.401 0.366 0.334 0.304 0.277 0.253 0.231 0.212 0.194 0.178 0.1640.987 0.944 0.857 0.774 0.697 0.625 0.559 0.498 0.444 0.397 0.363 0.331 0.301 0.275 0.251 0.229 0.210 0.192 0.177 0.163Q235钢冷弯薄壁型钢轴心受压构件的稳定系数ϕ(按50018-2002) 附表1-6λ0 1 2 3 4 5 6 7 8 90 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 210 220 230 240 250 1.000 0.974 0.947 0.918 0.886 0.852 0.818 0.775 0.722 0.661 0.588 0.516 0.452 0.396 0.349 0.308 0.274 0.245 0.220 0.199 0.180 0.164 0.150 0.138 0.127 0.117 0.997 0.971 0.944 0.915 0.882 0.849 0.814 0.770 0.716 0.654 0.580 0.509 0.446 0.391 0.344 0.305 0.271 0.213 0.218 0.197 0.179 0.163 0.149 0.137 0.126 0.995 0.968 0.941 0.912 0.879 0.846 0.810 0.765 0.710 0.648 0.573 0.502 0.440 0.386 0.340 0.301 0.268 0.240 0.216 0.195 0.177 0.161 0.148 0.136 0.125 0.992 0.966 0.938 0.909 0.875 0.843 0.806 0.760 0.704 0.641 0.566 0.496 0.434 0.381 0.336 0.298 0.265 0.237 0.214 0.193 0.175 0.160 0.146 0.135 0.124 0.989 0.963 0.936 0.906 0.872 0.839 0.802 0.755 0.698 0.634 0.558 0.489 0.428 0.376 0.332 0.294 0.262 0.235 0.211 0.191 0.174 0.159 0.145 0.133 0.123 0.987 0.960 0.933 0.903 0.868 0.836 0.797 0.750 0.692 0.626 0.551 0.483 0.423 0.371 0.328 0.291 0.259 0.232 0.209 0.189 0.172 0.157 0.144 0.132 0.122 0.984 0.958 0.930 0.899 0.864 0.832 0.793 0.744 0.686 0.618 0.544 0.476 0.417 0.367 0.324 0.287 0.256 0.230 0.207 0.188 0.171 0.156 0.143 0.131 0.121 0.981 0.955 0.927 0.896 0.861 0.829 0.789 0.739 0.680 0.611 0.537 0.470 0.412 0.362 0.320 0.284 0.253 0.227 0.205 0.186 0.169 0.154 0.141 0.130 0.120 0.979 0.952 0.924 0.893 0.858 0.825 0.784 0.733 0.673 0.603 0.530 0.464 0.406 0.357 0.316 0.281 0.251 0.225 0.203 0.184 0.167 0.153 0.140 0.129 0.119 0.976 0.949 0.921 0.889 0.855 0.822 0.779 0.728 0.667 0.595 0.523 0.458 0.401 0.353 0.312 0.277 0.248 0.223 0.201 0.182 0.166 0.152 0.139 0.128 0.118λ0 1 2 3 4 5 6 7 8 90 10 20 30 40 5060 70 80 90 100110 120 130 140 150160 170 180 190 200 210 220 230 240 250 1.0000.9710.9400.9060.8670.8290.7770.7100.6320.5500.4750.4050.3470.3000.2610.2290.2030.1810.1620.1460.1320.1200.1090.1000.0920.0850.9970.9680.9370.9020.8640.8240.7710.7030.6230.5420.4670.3980.3420.2960.2580.2270.2010.1790.1600.1440.1300.1190.1080.0990.0910.9940.9650.9340.8980.8600.8190.7650.6950.6150.5350.4600.3920.3370.2920.2550.2240.1980.1770.1580.1430.1290.1180.1070.0980.0910.9910.9620.9300.8940.8570.8150.7590.6880.6070.5270.4520.3860.3320.2880.2510.2210.1960.1750.1570.1410.1280.1160.1060.0980.0900.9880.9590.9270.8900.8530.8100.7520.6800.5990.5190.4450.3800.3270.2840.2480.2180.1940.1730.1550.1400.1270.1150.1060.0970.0890.9850.9560.9240.8860.8490.8050.7460.6720.5910.5120.4380.3750.3220.2800.2450.2160.1910.1710.1530.1380.1260.1140.1050.0960.0880.9820.9520.9200.8820.8450.8000.7390.6640.5830.5040.4310.3690.3180.2760.2420.2130.1890.1690.1520.1370.1240.1130.1040.0950.0880.9790.9490.9170.8780.8410.7940.7320.6560.5740.4970.4240.3630.3130.2720.2380.2100.1870.1670.1500.1360.1230.1120.1030.0940.0870.9760.9460.9130.8740.8370.7890.7250.6480.5660.4890.4180.3580.3090.2690.2350.2080.1850.1650.1490.1340.1220.1110.1020.0940.0860.9730.9430.9090.8700.8330.7830.7180.6400.5580.4820.4110.3520.3040.2650.2320.2050.1830.1630.1470.1330.1210.1100.1010.0930.086附录2 普通受弯钢构件稳定系数一、焊接工字形和轧制H 型钢等截面简支梁焊接工字形和轧制H 型钢等截面简支梁的整体稳定系数应按下式计算:y b y x y b b f h t W Ah 2354.414320212⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛+⋅=ηλλβϕ (附2-1) 式中 b β——梁整体稳定等效弯矩系数,根据荷载的形式和作用位置按附表2-1选用;y λ——梁的侧向长细比,y y i l /1=λ;1l ——梁的侧向计算长度,取受压翼缘侧向支承点间的距离;y i ——梁毛截面对y 轴的回转半径; A ——梁的毛截面面积; h ——梁的截面高度;x W ——梁受压翼缘边缘纤维的毛截面抵抗矩;y f ——钢材的屈服强度;b η——截面不对称影响系数:双轴对称焊接工字形截面(附图2-1a 、d )的b η=0;单轴对称焊接工字形截面:加强受压翼缘(附图2-1b ))12(8.0-=b b αη,加强受拉翼缘(附图2-1c )的12-=b b αη;b α——受压翼缘与全截面侧向惯性矩比值,yb I II I I 1211=+=α;1I 、2I ——受压翼缘和受拉翼缘对y 轴的惯性矩。
铝合金圆管轴心受压构件稳定系数的试验研究

结构得到了越来越广泛的应用 ! 早在 !# 世纪 D# 年 代, 欧美等国就建造了许多铝合金结构, 而我国对铝 合金结构的研究和应用起步较晚, 尤其是对长细比 较大 ( 的轴心受压构件的研究就更为 ! G "D# H !##) 少见 ! 因此, 对网格结构中最常用的铝合金圆管型截
械锯断后, 将两端截面磨平, 使两端截面尽可能地与 构件轴线垂直 $ 另一方面为确保端截面与两端支座 有效接触, 需要在端截面处设置加载板 $ 传统的加载 板做法为在端截面处加焊一钢板, 由于试件直径及 壁厚均较小, 在端截面处加焊钢板作为加载板质量 不易得到保证, 且会产生较大的焊接残余变形 $ 为 此, 采用机械咬合的方法, 在试件端部两端设置向心 滚动轴承 (如图 ’) , 这样既保证了试件的有效接触 面, 又避免了试件产生残余变形 $ 试验是在 )"" 4 的长柱压力试验机上进行的, 所 有试件均采用正位试验 $ 为了使试件两端的边界条 件与铰接一致, 在试件上下两端均设置了双向十字 刀口支座 $ 若在试件两端设置球形铰支座, 其接触面 摩擦阻力大, 所得极限承载力偏大且不真实, 因而未 予采用 $ 安装试件时, 对试件进行了几何对中, 尽量
第 !" 卷
第"期
!##$ 年 % 月
长安大学学报 (建筑与环境科学版) (8)9/: ; <*32): =924*94 <>262’*) &’()*+, ’- ./+*0’ +* 1*234)5267
ቤተ መጻሕፍቲ ባይዱ
?’, : !"
@’ : "
A+) : !##$
轴心受压构件的稳定系数

附录1 轴心受压构件的稳定系数

附录1 轴心受压构件的稳定系数普通钢构件轴心受压构件的截面类别(按GB50017-2003) 附表1-1截 面 形 式 及 主 轴截面类别板厚t <40mm轧制工字钢,翼缘宽b 与截面高h 之比h b /≤0.8,对垂直于腹板的轴(x 轴) a 类轧制钢管,对任意轴不属于a 类和b 类的截面,以及格构式构件的分肢计算垂直于腹板轴的稳定b 类翼缘为轧制或剪切边焊接工字形截面,对通过或平行于腹板的轴(y 轴) c 类焊接T 形截面,翼缘为轧制或剪切边,对通过或平行于腹板的轴(y 轴) 焊接十字形截面,板件边缘为轧制或剪切,对x 轴、y 轴 焊接矩形管截面,板件宽厚比≤20,对x 轴、y 轴 板厚t ≥40mm不属于c 类和d 类的截面b 类轧制工字钢或H 形截面,t <80mm ,对通过或平行于腹板的轴(y 轴) c 类轧制工字钢或H 形截面,t ≥80mm ,对垂直于腹板的轴(x 轴)轧制工字钢或H 形截面,t ≥80mm ,对通过或平行于腹板的轴(y 轴) d 类 翼缘为轧制或剪切边焊接工字形截面,对垂直于腹板的轴(x 轴)c 类 翼缘为轧制或剪切边焊接工字形截面,对通过或平行于腹板的轴(y 轴)d 类 焊接箱形截面,板件宽厚比≤20,对x 轴、y 轴c 类a 类截面轴心受压构件的稳定系数ϕ(按GB50017-2003) 附表1-2235yf λ0 1 2 3 4 5 6 7 8 9 0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 210 220 230 240 2501.000 0.995 0.981 0.963 0.941 0.916 0.883 0.839 0.783 0.714 0.638 0.563 0.494 0.434 0.383 0.339 0.302 0.270 0.243 0.220 0.199 0.182 0.166 0.153 0.141 0.1301.000 0.994 0.979 0.961 0.939 0.913 0.879 0.834 0.776 0.706 0.630 0.555 0.488 0.429 0.378 0.335 0.298 0.267 0.241 0.218 0.198 0.180 0.165 0.152 0.1401.000 0.993 0.977 0.959 0.937 0.910 0.875 0.829 0.770 0.699 0.622 0.448 0.481 0.423 0.373 0.331 0.295 0.264 0.238 0.215 0.196 0.179 0.164 0.150 0.1391.000 0.992 0.976 0.957 0.934 0.907 0.871 0.824 0.763 0.691 0.615 0.541 0.475 0.418 0.369 0.327 0.292 0.262 0.236 0.213 0.194 0.177 0.162 0.149 0.1380.999 0.991 0.974 0.955 0.932 0.904 0.867 0.818 0.757 0.684 0.607 0.534 0.469 0.412 0.3640.323 0.289 0.259 0.233 0.211 0.192 0.175 0.161 0.148 0.1360.999 0.989 0.972 0.952 0.929 0.900 0.863 0.813 0.750 0.676 0.600 0.527 0.463 0.407 0.360 0.320 0.285 0.256 0.231 0.209 0.190 0.174 0.159 0.147 0.1350.998 0.988 0.970 0.950 0.927 0.897 0.858 0.807 0.743 0.668 0.592 0.520 0.457 0.402 0.356 0.316 0.282 0.253 0.229 0.207 0.189 0.172 0.158 0.146 0.1340.998 0.986 0.968 0.948 0.924 0.894 0.854 0.801 0.736 0.661 0.585 0.514 0.451 0.397 0.351 0.312 0.279 0.251 0.226 0.205 0.187 0.171 0.157 0.144 0.1330.997 0.985 0.966 0.946 0.921 0.890 0.849 0.795 0.728 0.653 0.577 0.507 0.445 0.392 0.347 0.309 0.276 0.248 0.224 0.203 0.185 0.169 0.155 0.143 0.1320.996 0.983 0.964 0.944 0.919 0.886 0.844 0.789 0.721 0.645 0.570 0.500 0.440 0.387 0.343 0.305 0.273 0.246 0.222 0.201 0.183 0.168 0.154 0.142 0.131235y f λ0 1 2 3 4 5 6 7 8 9 0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 210 220 230 240 2501.000 0.992 0.970 0.936 0.899 0.8560.807 0.751 0.688 0.6210.5550.493 0.437 0.387 0.345 0.3080.276 0.249 0.225 0.204 0.1860.170 0.156 0.144 0.133 0.1231.000 0.991 0.967 0.932 0.895 0.8520.802 0.745 0.681 0.614 0.5490.487 0.432 0.383 0.341 0.3040.273 0.246 0.223 0.202 0.1840.169 0.155 0.143 0.1321.000 0.989 0.963 0.929 0.891 0.8470.797 0.739 0.675 0.608 0.5420.481 0.426 0.378 0.337 0.3010.270 0.244 0.220 0.200 0.1830.167 0.154 0.142 0.1310.999 0.987 0.960 0.925 0.887 0.8420.791 0.732 0.668 0.601 0.5360.475 0.421 0.374 0.333 0.2980.267 0.241 0.218 0.198 0.1810.166 0.153 0.141 0.1300.999 0.985 0.957 0.922 0.882 0.8380.786 0.726 0.661 0.594 0.5290.470 0.416 0.370 0.329 0.2950.265 0.239 0.216 0.197 0.1800.165 0.151 0.140 0.1290.998 0.983 0.953 0.918 0.878 0.8330.780 0.720 0.655 0.588 0.5230.464 0.411 0.365 0.326 0.2910.262 0.236 0.214 0.195 0.1780.163 0.150 0.138 0.1280.997 0.981 0.950 0.914 0.874 0.8280.774 0.714 0.648 0.581 0.5170.458 0.406 0.361 0.322 0.2880.259 0.234 0.212 0.193 0.1760.162 0.149 0.137 0.1270.996 0.978 0.946 0.910 0.870 0.8230.769 0.707 0.641 0.575 0.5110.453 0.402 0.357 0.318 0.2850.256 0.232 0.210 0.191 0.1750.160 0.148 0.136 0.1260.995 0.976 0.943 0.906 0.865 0.8180.763 0.701 0.635 0.568 0.5050.447 0.397 0.353 0.315 0.2820.254 0.229 0.208 0.190 0.1730.159 0.146 0.135 0.1250.994 0.973 0.939 0.903 0.861 0.8130.757 0.694 0.628 0.561 0.4990.442 0.392 0.349 0.311 0.2790.251 0.227 0.206 0.188 0.1720.158 0.145 0.134 0.124c 类截面轴心受压构件的稳定系数ϕ(按GB50017-2003) 附表1-4235y f λ0 1 2 3 4 5 6 7 8 9 0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 210 220 230 240 2501.000 0.992 0.966 0.902 0.8390.775 0.709 0.648 0.578 0.517 0.463 0.419 0.379 0.342 0.309 0.280 0.254 0.230 0.210 0.192 0.176 0.162 0.150 0.138 0.128 0.1191.000 0.990 0.959 0.896 0.833 0.768 0.702 0.636 0.572 0.511 0.458 0.415 0.375 0.339 0.306 0.277 0.251 0.228 0.208 0.190 0.175 0.161 0.148 0.137 0.1271.000 0.988 0.953 0.890 0.826 0.762 0.695 0.629 0.566 0.505 0.454 0.411 0.371 0.335 0.303 0.274 0.249 0.226 0.206 0.189 0.173 0.159 0.147 0.136 0.1260.999 0.986 0.947 0.884 0.820 0.755 0.689 0.623 0.559 0.500 0.449 0.407 0.367 0.332 0.300 0.271 0.246 0.224 0.205 0.187 0.172 0.158 0.1460.135 0.1250.999 0.983 0.940 0.877 0.814 0.748 0.682 0.616 0.553 0.494 0.445 0.403 0.364 0.328 0.297 0.269 0.244 0.222 0.203 0.186 0.170 0.157 0.145 0.134 0.124 0.998 0.981 0.934 0.871 0.807 0.742 0.676 0.610 0.547 0.488 0.441 0.399 0.360 0.325 0.294 0.266 0.242 0.220 0.201 0.184 0.169 0.156 0.144 0.133 0.1240.997 0.978 0.928 0.865 0.801 0.735 0.669 0.604 0.541 0.483 0.436 0.395 0.356 0.322 0.291 0.264 0.239 0.218 0.199 0.182 0.168 0.154 0.143 0.132 0.1230.996 0.976 0.921 0.858 0.794 0.729 0.662 0.597 0.535 0.477 0.432 0.391 0.353 0.319 0.288 0.261 0.237 0.216 0.197 0.181 0.166 0.153 0.142 0.131 0.1220.995 0.973 0.915 0.852 0.788 0.722 0.656 0.591 0.529 0.472 0.428 0.387 0.349 0.315 0.285 0.258 0.235 0.214 0.196 0.179 0.165 0.152 0.140 0.130 0.1210.993 0.970 0.909 0.846 0.781 0.715 0.649 0.584 0.523 0.467 0.423 0.383 0.346 0.312 0.282 0.256 0.233 0.212 0.194 0.178 0.163 0.151 0.139 0.129 0.120235y f λ0 1 2 3 4 5 6 7 8 90 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 2001.000 0.984 0.937 0.848 0.766 0.690 0.618 0.552 0.493 0.439 0.394 0.359 0.328 0.299 0.272 0.248 0.227 0.208 0.191 0.176 0.1621.000 0.981 0.927 0.840 0.759 0.683 0.612 0.546 0.487 0.434 0.390 0.356 0.325 0.296 0.270 0.246 0.225 0.206 0.189 0.1740.999 0.978 0.918 0.831 0.751 0.675 0.605 0.540 0.481 0.429 0.387 0.353 0.322 0.293 0.267 0.244 0.223 0.204 0.188 0.1730.999 0.974 0.909 0.823 0.743 0.668 0.598 0.534 0.476 0.424 0.383 0.350 0.319 0.290 0.265 0.242 0.221 0.203 0.186 0.1710.998 0.969 0.900 0.815 0.735 0.661 0.591 0.528 0.470 0.419 0.380 0.346 0.316 0.288 0.262 0.240 0.219 0.201 0.184 0.170 0.996 0.965 0.891 0.807 0.728 0.654 0.585 0.522 0.465 0.414 0.376 0.343 0.313 0.285 0.260 0.237 0.217 0.199 0.183 0.1680.994 0.960 0.883 0.799 0.720 0.646 0.578 0.516 0.460 0.410 0.373 0.340 0.310 0.282 0.258 0.235 0.215 0.197 0.181 0.1670.992 0.955 0.874 0.790 0.712 0.639 0.572 0.510 0.454 0.405 0.370 0.337 0.307 0.280 0.255 0.233 0.213 0.196 0.180 0.1660.990 0.949 0.865 0.782 0.705 0.632 0.565 0.504 0.449 0.401 0.366 0.334 0.304 0.277 0.253 0.231 0.212 0.194 0.178 0.1640.987 0.944 0.857 0.774 0.697 0.625 0.559 0.498 0.444 0.397 0.363 0.331 0.301 0.275 0.251 0.229 0.210 0.192 0.177 0.163Q235钢冷弯薄壁型钢轴心受压构件的稳定系数ϕ(按50018-2002) 附表1-6λ0 1 2 3 4 5 6 7 8 90 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 210 220 230 240 250 1.000 0.974 0.947 0.918 0.886 0.852 0.818 0.775 0.722 0.661 0.588 0.516 0.452 0.396 0.349 0.308 0.274 0.245 0.220 0.199 0.180 0.164 0.150 0.138 0.127 0.117 0.997 0.971 0.944 0.915 0.882 0.849 0.814 0.770 0.716 0.654 0.580 0.509 0.446 0.391 0.344 0.305 0.271 0.213 0.218 0.197 0.179 0.163 0.149 0.137 0.126 0.995 0.968 0.941 0.912 0.879 0.846 0.810 0.765 0.710 0.648 0.573 0.502 0.440 0.386 0.340 0.301 0.268 0.240 0.216 0.195 0.177 0.161 0.148 0.136 0.125 0.992 0.966 0.938 0.909 0.875 0.843 0.806 0.760 0.704 0.641 0.566 0.496 0.434 0.381 0.336 0.298 0.265 0.237 0.214 0.193 0.175 0.160 0.146 0.135 0.124 0.989 0.963 0.936 0.906 0.872 0.839 0.802 0.755 0.698 0.634 0.558 0.489 0.428 0.376 0.332 0.294 0.262 0.235 0.211 0.191 0.174 0.159 0.145 0.133 0.123 0.987 0.960 0.933 0.903 0.868 0.836 0.797 0.750 0.692 0.626 0.551 0.483 0.423 0.371 0.328 0.291 0.259 0.232 0.209 0.189 0.172 0.157 0.144 0.132 0.122 0.984 0.958 0.930 0.899 0.864 0.832 0.793 0.744 0.686 0.618 0.544 0.476 0.417 0.367 0.324 0.287 0.256 0.230 0.207 0.188 0.171 0.156 0.143 0.131 0.121 0.981 0.955 0.927 0.896 0.861 0.829 0.789 0.739 0.680 0.611 0.537 0.470 0.412 0.362 0.320 0.284 0.253 0.227 0.205 0.186 0.169 0.154 0.141 0.130 0.120 0.979 0.952 0.924 0.893 0.858 0.825 0.784 0.733 0.673 0.603 0.530 0.464 0.406 0.357 0.316 0.281 0.251 0.225 0.203 0.184 0.167 0.153 0.140 0.129 0.119 0.976 0.949 0.921 0.889 0.855 0.822 0.779 0.728 0.667 0.595 0.523 0.458 0.401 0.353 0.312 0.277 0.248 0.223 0.201 0.182 0.166 0.152 0.139 0.128 0.118λ0 1 2 3 4 5 6 7 8 90 10 20 30 40 5060 70 80 90 100110 120 130 140 150160 170 180 190 200 210 220 230 240 250 1.0000.9710.9400.9060.8670.8290.7770.7100.6320.5500.4750.4050.3470.3000.2610.2290.2030.1810.1620.1460.1320.1200.1090.1000.0920.0850.9970.9680.9370.9020.8640.8240.7710.7030.6230.5420.4670.3980.3420.2960.2580.2270.2010.1790.1600.1440.1300.1190.1080.0990.0910.9940.9650.9340.8980.8600.8190.7650.6950.6150.5350.4600.3920.3370.2920.2550.2240.1980.1770.1580.1430.1290.1180.1070.0980.0910.9910.9620.9300.8940.8570.8150.7590.6880.6070.5270.4520.3860.3320.2880.2510.2210.1960.1750.1570.1410.1280.1160.1060.0980.0900.9880.9590.9270.8900.8530.8100.7520.6800.5990.5190.4450.3800.3270.2840.2480.2180.1940.1730.1550.1400.1270.1150.1060.0970.0890.9850.9560.9240.8860.8490.8050.7460.6720.5910.5120.4380.3750.3220.2800.2450.2160.1910.1710.1530.1380.1260.1140.1050.0960.0880.9820.9520.9200.8820.8450.8000.7390.6640.5830.5040.4310.3690.3180.2760.2420.2130.1890.1690.1520.1370.1240.1130.1040.0950.0880.9790.9490.9170.8780.8410.7940.7320.6560.5740.4970.4240.3630.3130.2720.2380.2100.1870.1670.1500.1360.1230.1120.1030.0940.0870.9760.9460.9130.8740.8370.7890.7250.6480.5660.4890.4180.3580.3090.2690.2350.2080.1850.1650.1490.1340.1220.1110.1020.0940.0860.9730.9430.9090.8700.8330.7830.7180.6400.5580.4820.4110.3520.3040.2650.2320.2050.1830.1630.1470.1330.1210.1100.1010.0930.086附录2 普通受弯钢构件稳定系数一、焊接工字形和轧制H 型钢等截面简支梁焊接工字形和轧制H 型钢等截面简支梁的整体稳定系数应按下式计算:y b y x y b b f h t W Ah 2354.414320212⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛+⋅=ηλλβϕ (附2-1) 式中 b β——梁整体稳定等效弯矩系数,根据荷载的形式和作用位置按附表2-1选用;y λ——梁的侧向长细比,y y i l /1=λ;1l ——梁的侧向计算长度,取受压翼缘侧向支承点间的距离;y i ——梁毛截面对y 轴的回转半径; A ——梁的毛截面面积; h ——梁的截面高度;x W ——梁受压翼缘边缘纤维的毛截面抵抗矩;y f ——钢材的屈服强度;b η——截面不对称影响系数:双轴对称焊接工字形截面(附图2-1a 、d )的b η=0;单轴对称焊接工字形截面:加强受压翼缘(附图2-1b ))12(8.0-=b b αη,加强受拉翼缘(附图2-1c )的12-=b b αη;b α——受压翼缘与全截面侧向惯性矩比值,yb I II I I 1211=+=α;1I 、2I ——受压翼缘和受拉翼缘对y 轴的惯性矩。
轴心受压构件的稳定系数(纵向弯曲系数)

轴心受压构件的稳定系数,即纵向弯曲系数,在结构设计和分析中扮演着非常重要的角色。
它是用来描述构件在受压状态下的稳定性能,并在设计中扮演着至关重要的作用。
在本篇文章中,我将从深度和广度两方面对轴心受压构件的稳定系数进行全面评估,并据此撰写一篇有价值的文章。
让我们来了解一下轴心受压构件的基本概念。
轴心受压构件是指在受压状态下轴心受力的构件,例如混凝土柱、钢柱等。
在设计和分析中,我们需要考虑构件在受压状态下的稳定性能,以确保结构的安全可靠。
而轴心受压构件的稳定系数,即纵向弯曲系数,就是用来描述构件在受压状态下的稳定性能的重要参数之一。
在实际的设计和分析中,我们需要根据构件的几何形状、材料性质、受力条件等因素来计算轴心受压构件的稳定系数。
稳定系数的大小直接影响着构件在受压状态下的稳定性能,因此在设计中需要进行综合考虑并进行合理设计。
在计算稳定系数时,我们需要考虑构件的截面形状、长细比、材料的本构关系等因素。
在满足构件受压强度的前提下,稳定系数的大小应该尽可能大,以确保构件在受压状态下的稳定性能。
我们需要通过合理的截面设计、优化材料选用等方式来提高稳定系数,以满足结构的设计要求。
除了计算稳定系数外,我们还需要对轴心受压构件在受力状态下的稳定性进行全面的评估。
在实际的设计和分析中,我们需要考虑构件在受压状态下的整体稳定性、局部稳定性以及稳定性的失效模式等因素,以确保结构的安全可靠。
轴心受压构件的稳定系数在结构设计和分析中扮演着非常重要的角色。
在设计过程中,我们需要综合考虑构件的几何形状、材料性质、受力条件等因素,通过合理的计算和优化设计来提高稳定系数,以确保构件在受压状态下的稳定性能。
我们还需要对构件在受力状态下的整体稳定性、局部稳定性等进行全面的评估,以保证结构的安全可靠。
希望通过本篇文章的阐述,能够帮助你更深入地理解轴心受压构件的稳定系数这一重要概念。
个人观点和理解方面,在实际的工程实践中,轴心受压构件的稳定系数的计算和优化设计是非常复杂的,需要全面考虑构件的各项参数。
工字型铝合金轴心受压构件中美设计规范对比

s t r u c t u r e s ” ( G B 5 1 M2 9 -2 0 0 7 ) , “ T e c h n i c n o f r d e s i g n a n d c o n s t uc r t i o n o f l a u m i n u m— l a l o y s r e t i c u l a t e d s t uc r t u r e s ” ( D G J 0 8
a l u mi n u m a l l o y me mb e r u n d e r a x i a l l y l o a d
T A N J i n t a o , Z H A N G We i , T A N G X u e f e n g , Z HU Q i a n g , F E N G Q i a o r o n g
( S h a n g h a i H a o r o n g S t r u c t u r a l E n g i n e e i r n g D e s i g n C o . , L t d . , S h a n g h a i 2 0 1 9 0 0 , C h i n a )
第4 O卷
第 1 期
四川建筑科学研 究
S i c h u a n B u i l d i n g S c i e n c e 61
2 0 1 4年 2月
工字型铝合 金轴 心受压构件 中美设 计规 范对 比
谭金涛 , 张 伟 , 汤 雪锋 , 朱 强 , 冯 巧容
( 上海 浩荣 建筑工程结构设计事务所 有限公司 , 上海 2 0 1 9 0 0 )
关键词 : 铝合金 ; 轴心受压 ; 稳定 系数 ; 弹性屈 曲应力 ; 长细比与宽厚 比; 规 范对 比 中图分类号 : T U 3 9 5 文献标 志码 : A 文章编号 : 1 0 0 8—1 9 3 3 ( 2 0 1 4 ) 0 1~ 0 6 1— 0 4
截面轴心受压构件稳定系数的εk

截面轴心受压构件稳定系数的εk下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!截面轴心受压构件稳定系数的εk在结构设计中,截面轴心受压构件的稳定性是一个重要的考虑因素。
铝合金稳定承载力计算

1铝合金角钢构件稳定系数计算
铝合金角钢构件为非焊接单轴对称截面的轴心受压构件,稳定性计算方法如下:
N
f A
ϕ≤
e as ϕηηϕ
=
1)e η修正系数,对需考虑板件局部屈曲的截面进行修正: 强硬化的角钢的自由外伸宽厚比限值:
5b
t
≤ε= 加劲肋修正系数1η=,不均匀受压局部稳定系数=1k '。
当宽厚比大于限值时,需计算有效厚度:
12210.221e t t ααλλ=-≤,同时需满足21e t t λ
≤
强硬化的角钢120.9αα==,
板件的换算柔性系数λ=
受压板件的弹性临界屈曲应力:()
22
212(1)/cr k E b t πσν=
-⋅
铝合金弹性模量E=70000,泊松比0.3ν=。
2)as η截面非对称系数: 强硬化的角钢:max min
y y h
φ-=
max min
y y h φ-=,其中y max 及y min 为截面最外边缘到截面形心的距离,max min y y ≥,
h 为截面高度,max min h y y =+。
3)ϕ稳定系数:
()(){}
1/22222211142ϕηληλλλ⎛⎫⎡⎤=++-++- ⎪⎢⎥⎣⎦⎝⎭
,且1ϕ≤,
考虑初始弯曲和初偏心的系数:()0ηαλλ=-, 对于强化角钢构件0.35α=,00.1λ=,
相对长细比:λλπ⎛= ⎝ 2铝合金角钢稳定系数对比
2
稳定系数
长细比。
轴心受压构件稳定系数表(GB50017)

0.572
0.511
0.458
0.695
0.629
0.566
0.505
0.454
0.689
0.623
0.559
0.500
0.449
0.682
0.616
0.553
0.494
0.445
0.676
0.610
0.547
0.488
0.441
0.669
0.604
0.541
0.483
0.436
0.662
附录D 轴心受压构件的稳定系数
板厚t<
40mm
板厚t≥
40mm
普通钢构件轴心受压构件的截面类别(按GB50017-2017) 附表1-1
截 面 形 式 及 主 轴
轧制工字钢,翼缘宽b与截面高h之比hb/≤0.8,对垂直于腹板的轴(x轴)
轧制钢管,对任意轴
不属于a类和b类的截面,以及格构式构件的分肢计算垂直于腹板轴的稳定
0.374
0.333
0.298
0.470
0.416
0.370
0.329
0.295
0.464
0.411
0.365
0.326
0.291
0.458
0.406
0.361
0.322
0.288
0.453
0.402
0.357
0.318
0.285
0.447
0.397
0.353
0.315
0.282
0.442
0.392
0.690
1
1.000
0.981
0.927
0.840
幕墙立柱设计 轴心受压稳定系数

幕墙立柱设计轴心受压稳定系数5.7 立柱设计5.7.1 立柱截面的主要受力部分的厚度,应符合下列规定:1 铝合金型材截面主要受力部分的厚度不应小于3mm,采用螺纹受力连接时螺纹连接部位截面的厚度不应小于螺钉的公称直径;2 钢型材截面主要受力部分的厚度不应小于3.5mm;3 偏心受压的立柱,截面宽厚比应符合本规范第5.6.1条的规定。
5.7.2 上下立柱之间应有不小于15mm的缝隙,并应采用芯柱连结。
芯柱总长度不应小于400mm。
芯柱与立柱应紧密接触。
芯柱与下柱之间应采用不锈钢螺栓固定。
5.7.3 立柱与主体结构的连接可每层设一个支承点,也可设两个支承点;在实体墙面上,支承点可加密。
5.7.4 每层设一个支承点时,立柱应按简支单跨梁或铰接多跨梁计算;每层设两支承点时,立柱应按双跨梁或双支点铰接多跨梁计算。
5.7.5 立柱上端应悬挂在主体结构上,宜设计成偏心受拉构件,其轴力应考虑幕墙板材、横梁以及立柱的重力荷载值。
5.7.6 偏心受拉的幕墙立柱截面承载力应符合下式要求:5.7.7 偏心受压的幕墙立柱截面承载力应符合下式要求:5.7.8 轴心受压柱的稳定系数应按表5.7.8采用。
5.7.9 偏心受压的幕墙立柱,其长细比可按下式计算:λ=L/i(5.7.9)式中λ——立柱长细比;L——构件侧向支承点之间的距离(mm);i——截面回转半径(mm)。
立柱长细比不应大于150。
5.7.10 立柱由风荷载标准值和地震作用标准值产生的挠度u应按本规范第5.7.4条的规定计算,并应符合下列要求:1 当跨度不大于7.5m的立柱:1)铝合金型材:u≤1/180(5.7.10-1)u≤20mm2)钢型材:u≤1/300(5.7.10-2)u≤15mm2 当跨度大于7.5m的钢立柱:u≤1/500(5.7.10-3)式中u——挠度;l——支承点间的距离(mm)。
5.7.11 立柱应采用螺栓与角码连接,并再通过角码与预埋件或钢构件连接。
铝合金轴心受压构件的稳定性研究与数值模拟

铝合金轴心受压构件的稳定性研究与数值模拟翟希梅;吴海;王誉瑾;范峰【摘要】To provide reliable verification and guidance forexperiments,numerical simulations of 17 high-strength aluminum alloy columns in compression were conducted using ABAQUS and the results were compared with experimental results.Factors which influenced simulation results,including meshes size,thickness of end plates,initial imperfection and material properties were analyzed.3D full integration continuum element C3D20 and Ramberg-Osgood model for stress-strain relationship were adopted in simulation.The simulation results show that the relative errors of buckling load between experiments and simulations are under 12%;the meshes size and thickness of end plates have a negligible influence on stability coefficient,and the existence of end plates rarely influence mechanical properties of specimens with hinge supports;as initial geometric imperfection ascends and the parameter n of aluminum alloy descends,the value of stability coefficient decreases;buckling loads of specimens obviously increases as proof stress f0.2increases,especially for specimens with small slenderness ratio.%为了给试验提供可靠的依据与指导,采用有限元软件ABAQUS对17根6082-T6型高强铝合金轴心受压构件进行数值模拟,并与试验结果进行对比分析.对影响有限元计算结果的各项因素,包括网格划分与尺寸、端板厚度、初弯曲大小和材料参数进行分析.有限元模型采用完全积分形式的20节点实体单元,铝合金应力应变关系采用Ramberg-Osgood模型.结果显示:采用三维实体单元C3D20进行的数值模拟与试验的屈曲荷载相对误差控制在12%以内;通常的轴向网格尺寸与端板厚度对构件稳定系数的影响可忽略不计,支座处端板的存在基本不会影响构件的铰支受力状态;稳定系数随初弯曲幅值的增大而降低,随材性参数n值的增大而提高;随着名义屈服强度f0.2的增大,构件的屈曲荷载也随之增大,且增幅在长细比λ越小时更为显著.【期刊名称】《哈尔滨工业大学学报》【年(卷),期】2011(043)012【总页数】6页(P1-6)【关键词】铝合金;轴压;数值模拟;稳定系数;屈曲【作者】翟希梅;吴海;王誉瑾;范峰【作者单位】哈尔滨工业大学土木工程学院,哈尔滨150090;哈尔滨工业大学土木工程学院,哈尔滨150090;哈尔滨工业大学土木工程学院,哈尔滨150090;哈尔滨工业大学土木工程学院,哈尔滨150090【正文语种】中文【中图分类】TU395铝合金结构的发展始于20世纪30年代,以其高强、轻质、耐腐蚀等优点被广泛应用于建筑领域.但由于铝合金材料弹性模量较低,因此构件的失稳问题显得尤为突出.欧洲、美国于20世纪70年代各自建立了设计规范[1-2],目前,我国刚刚推出铝合金结构设计规范[3],然而针对部分型号铝合金的设计大多参考国外规范,其适用性仍有待研究.本文利用有限元软件ABAQUS对H型、箱型截面的6082-T6型高强铝合金轴心受压构件进行数值模拟,并与构件试验结果进行比较,对影响有限元计算结果的各项因素,包括网格的划分与尺寸、端板厚度、初弯曲大小和材料参数进行分析,提供了较为合理、有效的铝合金轴压构件的有限元数值模拟方法.由于实际的铝合金构件并非理想直杆,为极值点失稳问题,影响其失稳模式的主要因素为初始缺陷,初始缺陷包括残余应力与初始弯曲,本文研究的挤压成型的高强铝合金构件,其残余应力很小,可以忽略不计[4-5].初弯曲可以分解为无穷多种模态形状的组合[6],但构件通常以一阶模态失稳为主.如果二、三阶模态为局部屈曲,则构件的失稳形式中还会伴随相应的局部屈曲.因此对各构件先按理想直杆进行模态分析,取其一阶模态形状并将其初弯曲幅值调整到L/1 000(L为构件长度),如果二、三阶模态为局部屈曲形式,则初始缺陷中要相应引入局部屈曲模态,然后基于大变形理论进行非线性分析.对屈曲一类不稳定问题,当力-位移平衡路径出现下降段时,切线刚度变为负值,牛顿-拉普森迭代将出现收敛困难,因此多采用改进的牛顿-拉普森方法或弧长法[7],本文采用的是弧长法,整个有限元屈曲问题求解流程见图1.Ramberg-Osgood模型是目前广泛使用的分析模型,且与本文研究的高强铝合金构件的材性本构关系曲线吻合较好,Ramberg-Osgood[8]模型的表达式为式中E与f0.2分别为材料的弹性模量与名义屈服强度,采用 Steinhardt[9]建议,取 n=f0.2/10,该值与本文铝合金试件的材性试验结果吻合较好.采用三维实体单元进行有限元模拟,为避免线性单元模拟弯曲时单元刚度过大导致的剪力自锁,和采用减缩积分时积分点过少而产生的沙漏问题[10],本文采用完全积分下的三维20节点二阶单元C3D20来模拟高强铝合金构件在轴心受压下的力学行为.有限元模型中的单元类型、本构关系模型及6082-T6型铝合试件的材性试验参数见表1.本文涉及的所有试件皆在MTS电液伺服压力机上完成,试验时,构件两端各用一个钢板槽,通过向内浇注高强石膏将H型或箱型构件固定住,钢槽底面单向开槽,以模拟单向铰支,试件两端支座及试验装置见图2、3.位移计和应变片测点位置见图4、5.由于单向铰支构件的端部应力较小,石膏一般不会出现裂缝,因此在有限元模型中将试件端部的钢板及石膏简化为钢材质,并按线弹性体的应力-应变关系处理.本文针对H型、箱型2种截面共17根试验构件[11]进行数值模拟.模拟所用构件长度均为实测值,因此对同一种名义尺寸的构件模拟结果略有差异,数值模拟与试验关于屈曲荷载及破坏模式的比较见表2.模拟结果显示:17根构件的破坏形式与试验结果一致,全部以整体弯曲失稳为主,其中箱型试件F1-1、F1-2和F1-3还伴随局部失稳现象.在数值模拟时,上述3个试件的二、三阶失稳模态为局部屈曲,因此在初始缺陷的引入中包括整体与局部屈曲2种形式,其中局部屈曲幅值ωd 采用 Walker[12]提出的公式式中:t为构件截面厚度,σcr为弹性局部屈曲应力,可以通过模态分析得到.由表2可知,试验与模拟结果关于屈曲荷载的相对误差控制在12.41%内.以构件I3-1为例,部分测点实测值与数值模拟的位移与应变结果见图6、7.数值模拟与试验结果的对比说明,两者在荷载-位移曲线以及试件局部测点的应变变化方面皆显示了良好的一致性,说明本文的铝合金轴压构件的数值模拟在单元选取、参数设置及网格划分等方面是适用的.通常情况下网格尺寸越小,计算精度越高,但机时增加,为此进行了构件及支座端板的网格尺寸敏感性分析.考虑到铝合金构件腹板和翼缘的厚度很小,一般在10 mm以内,可将其在腹板和翼缘厚度方向上划分为2个单元,同时尽量保证构件横截面内(XZ平面,见图8)的单元格为正方形或接近正方形.另外,两端支座处端板上位于构件截面之外的网格对结果影响很小,可以采用较粗糙网格.为确定构件沿轴向(Y向)的网格尺寸,进行了稳定系数φ对网格尺寸的敏感性分析,稳定系数的计算公式为式中:N、f0.2、A分别为屈曲荷载、名义屈服强度、构件截面面积.针对4种不同的长细比构件,沿构件轴向(Y向)的网格尺寸分别按 10、20、30、40、50 mm 计算了构件的稳定系数,结果见图9.构件稳定系数结果几乎不受轴向网格尺寸的影响,所有相对误差控制在0.05%以内.为减少计算时间,本文轴向网格尺寸采用50 mm.试验中通过石膏将构件固定在钢槽内,而在有限元模拟时将石膏与钢槽底板共同简化为钢材质的端板.试验中采用的钢槽底板与石膏的总厚度一般在40 mm左右,本文分析了上下刀口间距保持不变,但端板厚度分别为 0、10、20、30、40 mm 5种情况对φ的影响,结果见图10,其中端板厚度为0意味着理想铰支状态,可以看到,不同正则化长细比下数值模拟结果几乎不受端板厚度的影响,相对误差控制在0.8%以内,说明试验时采用的单向铰支座方法能够保证试件接近理想铰支状态,不会带来较大误差.国内外规范针对铝合金轴心受压构件,均采用与Perry公式形式相同的设计公式[1-3]式中:φP为柏利公式推导的稳定系数;为正则化长细比为相对初弯曲;ν0为初弯曲幅值,一般表示为长度的函数,ν0=L/m,m为系数,例如中国钢结构设计规范中m取1 000;ρ为截面核心距.由于相对初弯曲η一般表示为长度的函数,即与正则化长细比有关,为方便进一步分析,将相对初弯曲作如下变换式中i为截面绕弯曲轴的回转半径.对式(7)和有限元模拟得到的稳定系数进行对比,见图11.为进一步验证本文数值模拟结果与柏利公式的一致性以及了解初始弯曲对有限元结果的影响,对式(7)中参数α求偏导数,α中包含了初始弯曲的因素,并引入参数K,得将式(8)用三维视图表示,见图12,此时α∈(0,1],∈(0,4],即属于通常的初弯曲与正则化长细比范围内.当α→0→1时,K的绝对值趋近于最大,即这种情况下利用柏利公式会得到最大的稳定系数.为验证数值模拟结果是否也存在此规律,对相同截面尺寸及不同长细比和初弯曲情况下的H型构件进行数值模拟,见图13,图中曲线表明:对同一长细比构件,稳定系数随初弯曲幅值增大而减小;当接近1时,初弯曲幅值对稳定系数的影响更明显,例如当=1.188时,稳定系数由0.672(ν0=L/8 000)降低至0.525(ν0=L/500),降低了27.98%,因此初弯曲幅值对数值模拟结果的影响与理论推导类似.本文应力应变关系采用Ramber-Osgood模型,如式(1)所示,并通过材性试验确定了式(1)中高强铝合金6082-T6本构关系中的3个参数,即弹性模量E、名义屈服强度f0.2和指数n.由于轴压试验构件的材料特性与材性试验试件之间存在差异,对本构关系中几个参数分别进行分析可以得到材料参数的影响规律,有利于分析误差产生的原因.从材性试验中了解到,构件的E一般比较稳定,因此材料的离散性主要反映在n与f0.2上.首先考虑f0.2不变,n值决定了图14中曲线的切线模量,当n值越大,本构关系模型越接近理想弹塑性,反之n值越小,本构关系模型越接近完全线弹性体,但同时弹性模量也大幅度降低.图14中,由于假定f0.2不变,应力应变曲线近似相交于应力值为f0.2处,各当应力小于f0.2时,n值越大,同一应变所对应的应力越大,即构件达到相同变形所需施加的荷载越大.而构件弯曲失稳时,屈曲荷载所对应截面上的最大应力一般小于f0.2,因此对同一几何尺寸构件,n值越大,屈曲荷载越大.同理,在荷载-位移曲线的下降区段,n值越大,同一变形所对应的荷载越小,即荷载下降越快.本文进行了构件在通常的n值范围(n=10~50)情况下的数值模拟,见图15.对同一构件,随n值增大,稳定系数略有增加,当接近1时,n值对稳定系数的影响更明显,例如当=1.188时,稳定系数由0.555(n=10)提高到0.586(n=50),增长了5.51%.6082-T6材料的f0.2一般为270~350 MPa,在弹性模量保持不变的情况下,f0.2的增加意味着本构曲线中弹性段的增长,见图16.本文针对4种长细比构件在不同f0.2情况下进行数值模拟,f0.2对屈曲荷载的影响见图17,可以看到,对λ相同的构件,屈曲荷载随f0.2增大而增大,且屈曲荷载的增幅随λ的减小而增大,例如当λ=108.82时,屈曲荷载从60.78 kN(f0.2=270)提高到了61.78kN(f0.2=350),仅提高了1.64%,而当λ=29.84时,屈曲荷载从278.07kN(f0.2=270)提高到了355.54 kN(f0.2=350),增长了27.86%.1)采用3维实体单元C3D20模拟两端单向铰支H型及箱型高强铝合金轴压构件,其有限元结果在构件变形曲线及屈曲荷载方面与试验实测值吻合良好,最大误差控制在12%.2)轴向网格尺寸和端板厚度对构件的稳定承载力结果影响很小,可忽略不计.3)试验时采用的钢板槽与石膏结合的单向铰支座方法能够保证试件接近理想铰支状态,不会带来较大误差.4)稳定系数随初弯曲幅值的增大而降低,当为1.0时,初弯曲对构件的稳定系数影响最大.5)随着Ramber-Osgood模型中的材性参数n的增大,构件的稳定系数有所提高,且提高程度在为1.0时最为显著,约为5.5%;随着f0.2的增大,构件的屈曲荷载也随之增大,且增幅在λ越小时越显著.范峰(1971—),男,教授,博士生导师.【相关文献】[1]Eurocode 9:BS EN1999-1-1.Design of aluminum structures-general structure rules [S].Brussels:European Committee for Standardization,2007.[2]The Aluminum Association.Specification for aluminum structures[S].6thed.Washington D C:The Aluminum Association,1994.[3]GB50429铝合金结构设计规范[S].北京:中华人民共和国建设部,2007.[4]MAZZOLANI F M.Resid ual stress tests on French profiles 63×63×4 in aluminum alloys,Doc 16-74-3[R].Brussels:ECCS Committee,1974.[5]MAZZOLANI F M.Residual stress tests alu-alloy Austrian profiles,Doc 16-75-1 [R].Brussels:ECCS Committee,1975.[6]陈骥.钢结构稳定理论与设计[M].2版.北京:科学出版社,2003.[7]ABAQUS analysis user's manual:version 6.9.1[M].[S.l.]:ABAQUS Inc,2009.[8]RAMBERG W,OSGOOD W R.Description of stressstrain curves by three parameters,NACA TN-902[R].Washington D C:National Advisory Committee for Aeronautics,1943. [9]STEINHARDT O.Aluminum constructions in civil engineering[J].Aluminum,1971,47:131-139.[10]庄茁,张帆,岺松.ABAQUS非线性有限元分析与实例[M].北京:科学出版社,2005. [11]ZHAI Ximei,WANG Yujin,WU Hai,et al.Research on stability of high strength aluminum alloy columns loaded by axial compressive load[J].Advanced Materials Research,2011,168/169/170:1915 -1920.[12]WALKER A C.Design and analysis of cold-formed sections[M].New York:Wiley,1975.。
