工程力学最后章节习题
工程力学教程第二版课后习题答案

工程力学教程第二版课后习题答案工程力学是一门应用力学原理研究工程结构和材料力学性能的学科。
作为工程学的基础课程之一,工程力学的学习对于培养工程师的分析和解决实际工程问题的能力至关重要。
而工程力学教程第二版是一本经典的教材,其中的课后习题是帮助学生巩固所学知识的重要辅助材料。
本文将为读者提供工程力学教程第二版课后习题的答案,帮助读者更好地理解和掌握工程力学的知识。
第一章:静力学1. 问题:一根长度为L,截面为矩形的梁,其宽度为b,高度为h。
梁的两端分别固定在支座上,中间有一个集中力P作用在梁上。
求梁在P作用下的最大弯矩和最大剪力。
答案:根据静力学原理,我们可以通过平衡力和力矩来求解该问题。
首先,根据平衡力的原理,梁在P作用下的最大剪力等于P。
其次,根据力矩的原理,梁在P作用下的最大弯矩等于P乘以梁的长度L的一半。
因此,最大弯矩为PL/2。
第二章:动力学1. 问题:一个质量为m的物体以速度v沿着水平方向运动,突然撞击到一个质量为M的静止物体上。
求撞击后两个物体的速度。
答案:根据动量守恒定律,撞击前后两个物体的总动量保持不变。
设撞击后质量为m的物体的速度为v1,质量为M的物体的速度为v2。
由动量守恒定律可得mv = mv1 + Mv2。
另外,根据能量守恒定律,撞击前后两个物体的总动能保持不变。
设撞击前质量为m的物体的动能为1/2mv^2,撞击后质量为m的物体的动能为1/2mv1^2,质量为M的物体的动能为0(静止)。
由能量守恒定律可得1/2mv^2 = 1/2mv1^2 + 0。
综上所述,可以解得v1 = (m - M)v / (m + M),v2 = 2m / (m + M)。
第三章:应力分析1. 问题:一个长方体的尺寸为a×b×c,其材料的杨氏模量为E,泊松比为v。
求该长方体在x、y、z方向上的应力分量。
答案:根据应力分析的原理,我们可以通过应力的定义和杨氏模量、泊松比的关系来求解该问题。
工程力学(静力学与材料力学)课后习题

1-1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
1-2试画出以下各题中AB 杆的受力图。
1-3试画出以下各题中AB 梁的受力图。
(d)A(F(((d)A(e)(c)(a)(a)(c)F (b)1-4 试画出以下各题中指定物体的受力图。
(a) 拱ABCD ;(b) 半拱AB 部分;(c) 踏板AB ;(d) 杠杆AB ;(e) 方板ABCD ;(f) 节点B 。
1-5 试画出以下各题中指定物体的受力图。
(a) 结点A ,结点B ;(b) 圆柱A 和B 及整体;(c) 半拱AB ,半拱BC 及整体;(d) 杠杆AB ,切刀CEF 及整体;(e) 秤杆AB ,秤盘架BCD 及整体。
2-2 杆AC 、BC 在C 处铰接,另一端均与墙面铰接,如图所示,F 1和F 2作用在销钉C 上,F 1=445N ,F 2=535N ,不计杆重,试求两杆所受的力。
(a)(b)(c)(d)(e)W(f)(c)(d)(b)(e)F 12-3 水平力F 作用在刚架的B 点,如图所示。
如不计刚架重量,试求支座A 和D 处的约束力。
2-4 在简支梁AB 的中点C 作用一个倾斜45o 的力F ,力的大小等于20KN , 如图所示。
若梁的自重不计,试求两支座的约束力。
2-6 如图所示结构由两弯杆ABC 和DE 构成。
构件重量不计,图中的 长度单位为cm 。
已知F =200N ,试求支座A 和E 的约束力。
2-7 在四连杆机构ABCD 的铰链B 和C 上分别作用有力F 1和 F 2,机构在图示位置平衡。
试求平衡时力F 1和F 2的大小之间 的关系。
2-9 三根不计重量的杆AB ,AC ,AD 在A 点用铰链连接,各杆与水平面的夹角分别为450,,450和600,如图所示。
试求在与 O D 平行的力F 作用下,各杆所受的力。
已知F =0.6kN 。
3-1已知梁AB 上作用一力偶,力偶矩为M ,梁长为l ,梁重不计。
工程力学课后习题与答案

工程力学练习册学校学院专业学号教师姓名第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)(d)(e)(f)(g)1-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)(b)(c)(d)(e)(f)(g)第二章 平面力系2-1 电动机重P=5000N ,放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A 、B 处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000===2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得: PF P F AB BC 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。
题2-3图以AC 段电线为研究对象,三力汇交NF N F F F FF F F C A GA yC A x 200020110/1tan sin ,0,cos ,0=======∑∑解得:ααα2-4 图示为一拔桩装置。
《工程力学》课后习题解答
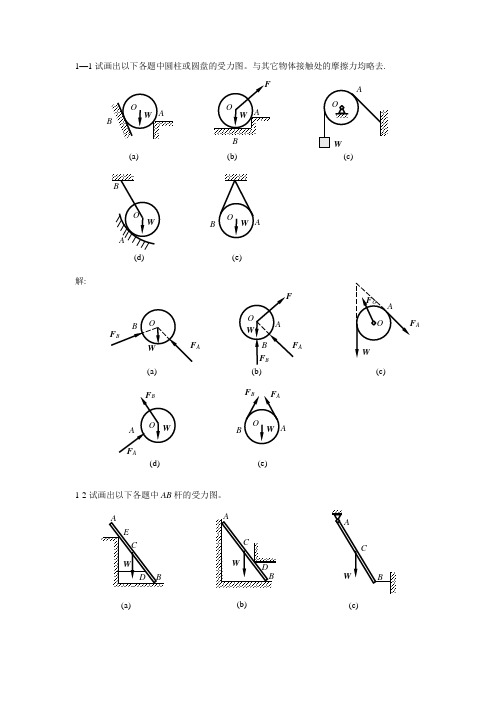
1—1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去. 解:1-2试画出以下各题中AB 杆的受力图。
(a) B(b)(c)(d)A(e)A(a)(b) A(c)A(d)A(e)(c)(a)(b)解:1-3试画出以下各题中AB 梁的受力图.(d)(e)BB(a)B(b)(c)F B(a)(c)F (b)(d)(e)解:1-4 试画出以下各题中指定物体的受力图。
(a) 拱ABCD ;(b ) 半拱AB 部分;(c) 踏板AB ;(d ) 杠杆AB;(e) 方板ABCD;(f ) 节点B 。
解:(a)F (b)W(c)(d)D(e)F Bx(a)(b)(c)(d)D(e)W(f)(a)D(b) CB(c)BF D1-5 试画出以下各题中指定物体的受力图.(a ) 结点A ,结点B ;(b) 圆柱A 和B 及整体;(c ) 半拱AB ,半拱BC 及整体;(d) 杠杆AB ,切刀CEF 及整体;(e) 秤杆AB ,秤盘架BCD 及整体。
解:(a)(d)FC(e)WB(f)F FBC(c)(d)AT F BAF (b)(e)(b )(c )(d)(e)2-2 杆AC 、BC 在C 处铰接,另一端均与墙面铰接,如图所示,F 1和F 2作用在销钉C 上,F 1=445N ,F 2=535N ,不计杆重,试求两杆所受的力。
C AA C’CDDBF 1解:(1)取节点C 为研究对象,画受力图,注意AC 、BC 都为二力杆,(2) 列平衡方程:12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。
2—3 水平力F 作用在刚架的B 点,如图所示.如不计刚架重量,试求支座A 和D 处的约束力。
解:(1) 取整体ABCD 为研究对象,受力分析如图,画封闭的力三角形:(2)211 1.1222D A DD A F F FF F BC AB AC F F F F F =====∴===2-4 在简支梁AB 的中点C 作用一个倾斜45o 的力F ,力的大小等于20KN ,如图所示。
《工程力学》课后习题解答

《工程力学》课后习题解答————————————————————————————————作者:————————————————————————————————日期:1-1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
解:1-2 试画出以下各题中AB 杆的受力图。
B A O W( BA O W F(O W(AA O W(BAO W (BFFB O W(B A O WF(F FAO W(F F O A O W(F FAO W (BF F AWC B(cD (AWC E B(AW CD B解:1-3 试画出以下各题中AB 梁的受力图。
ABF(C AB W(CA BW (C FFABF(C FF(FFF D AWCE B(bAWCD BFFF(cAWC BFFAWCB(aWABC D(cABF q D(bCCA BF WDA ’ D ’B ’(d ABF q(e解:1-4 试画出以下各题中指定物体的受力图。
(a) 拱ABCD ;(b) 半拱AB 部分;(c) 踏板AB ;(d) 杠杆AB ;(e) 方板ABCD ;(f) 节点B 。
解:A WCB(aF BF AABF qD(bF CF DWABC (cF CF BCA BF WD(d F BF AF DAB Fq(eF BxF By F AABF(aDCWAF (bDB(cFAB DD ’ABF(dCDW ABCD(eWABC(fAB F(a DCWF AxF AyF DAF (b BF BF A(cFABDF BF D1-5 试画出以下各题中指定物体的受力图。
(a) 结点A ,结点B ;(b) 圆柱A 和B 及整体;(c) 半拱AB ,半拱BC 及整体;(d) 杠杆AB ,切刀CEF 及整体;(e) 秤杆AB ,秤盘架BCD 及整体。
解:(a)AB F(d CF B F CW AB CD(e F BF AWB (fF ABF BCA B W (a (c B CW 1W 2 FA F D A BCE F (dA F ABF AT F ABF BAF BTWAB P P (bW AB C C ’ DO G (e(b)(c)(d)(e)F CAPCF BB PCF ’CF AAB PPF B F NBCW 1W 2 F AF CxF CyF AxF AyB W 1F A F Ax F AyF Bx F ByB C W 2 F Cx F CyF ’Bx F ’By FA BC F C F BDC E F F E F ’C F F FDAB C E F F EF FF BB C D G F B F C WABCC ’ DO GF Oy F OxF C ’A B O W F BF Oy F Ox2-2 杆AC 、BC 在C 处铰接,另一端均与墙面铰接,如图所示,F 1和F 2作用在销钉C 上,F 1=445 N ,F 2=535 N ,不计杆重,试求两杆所受的力。
工程力学习题及最终答案

工程力学习题及最终答案以下是为大家整理的工程力学习题及最终答案的相关范文,本文关键词为工程,力学,习题,最终,答案,工程,力学,习题,第一章,绪论,您可以从右上方搜索框检索更多相关文章,如果您觉得有用,请继续关注我们并推荐给您的好友,您可以在综合文库中查看更多范文。
——————————————工程力学习题——————————————第一章绪论思考题1)现代力学有哪些重要的特征?2)力是物体间的相互作用。
按其是否直接接触如何分类?试举例说明。
3)工程静力学的基本研究内容和主线是什么?4)试述工程力学研究问题的一般方法。
第二章刚体静力学基本概念与理论习题2-1求图中作用在托架上的合力FR。
1400n120?30?200n习题2-1图—————————————工程力学习题———————————————2-2已知F1=7kn,F2=5kn,求图中作用在耳环上的合力FR。
F1习题2-2图60?45?F22-3求图中汇交力系的合力FR。
yF1=30n30?A(a)习题2-3图F3=40n45?xF2=20nF1=600n45?yx60?F3=500nF2=700n(b)A2-4求图中力F2的大小和其方向角?。
使a)合力FR=1.5kn,方向沿x轴。
b)合力为零。
F1=1.25knA70??xF2习题2-4图2—————————————工程力学习题———————————————2-5二力作用如图,F1=500n。
为提起木桩,欲使垂直向上的合力为FR=750n,且F2力尽量小,试求力F2的大小和?角。
F1=500n?F230?A习题2-5图2-6画出图中各物体的受力图。
wbA(a)gAcb(c)DAcFb(e)AcDgb(b)FAobc(d)DAcb3—————————————工程力学习题———————————————F(f)bcA(g)2-7画出图中各物体的受力图。
A(a)4FbAb(b)cAbcFmbA(c)习题2-6图qDAbbDcDAebAbccDecDF1F2b—————————————工程力学习题———————————————2-8试计算图中各种情况下F力对o点之矩。
《工程力学》课后习题答案全集

工程力学习题答案第一章 静力学基础知识思考题:1. ×;2. √;3. √;4. √;5. ×;6. ×;7. √;8. √习题一1.根据三力汇交定理,画出下面各图中A 点的约束反力方向。
解:(a )杆AB 在A 、B 、C 三处受力作用。
由于力和的作用线交于点O 。
如图(a )所示,根据三力平衡汇交定理, 可以判断支座A 点的约束反力必沿 通过A 、O 两点的连线。
(b )同上。
由于力和的作用线 交于O 点,根据三力平衡汇交定理, 可判断A 点的约束反力方向如 下图(b )所示。
2.不计杆重,画出下列各图中AB 杆的受力图。
解:(a )取杆AB 为研究对象,杆除受力外,在B 处受绳索作用的拉力,在A 和E 两处还受光滑接触面约束。
约束力和的方向分别沿其接触表面的公法线,并指向杆。
其中力与杆垂直,力通过半圆槽的圆心O 。
AB 杆受力图见下图(a )。
(b)由于不计杆重,曲杆BC 只在两端受铰销B 和C 对它作用的约束力和,故曲杆BC 是二力构件或二力体,此两力的作用线必须通过B 、C 两点的连线,且=。
研究杆AB ,杆在A 、B 两点受到约束反力和,以及力偶m 的作用而平衡。
根据力偶的性质,和必组成一力偶。
(d)由于不计杆重,杆AB 在A 、C 两处受绳索作用的拉力和,在B 点受到支座反力。
和相交于O 点,根据三力平衡汇交定理,可以判断必沿通过pB RpB Rp B T A N E N E N A N B N C N BN CN A N B N A N B N A T C T B N A T C TB NB、O两点的连线。
见图(d).第二章 力系的简化与平衡思考题:1. √;2. ×;3. ×;4. ×;5. √;6. ×;7. ×;8. ×;9. √.1. 平面力系由三个力和两个力偶组成,它们的大小和作用位置如图示,长度单位为cm ,求此力系向O 点简化的结果,并确定其合力位置。
《工程力学》章节测试答案

《工程力学》章节测试答案一、选择题(每题2分,共20分)1. 工程力学中,力的三要素不包括以下哪项?A. 力的大小B. 力的方向C. 力的作用点D. 力的速度答案:D2. 在平面力系中,以下哪种情况力的合力不一定为零?A. 力系中各力大小相等,方向相同B. 力系中各力大小相等,方向相反C. 力系中各力大小不等,方向相同D. 力系中各力大小不等,方向相反答案:C3. 平面力偶的等效条件是?A. 力偶矩大小相等,转向相同B. 力偶矩大小相等,转向相反C. 力偶矩大小不等,转向相同D. 力偶矩大小不等,转向相反答案:A4. 拉伸试验中,材料破坏时的应力称为?A. 强度B. 抗拉强度C. 抗压强度D. 疲劳强度答案:B5. 杆件在受力时,产生的内力称为?A. 应力B. 应变C. 内力D. 外力答案:C二、填空题(每题2分,共20分)1. 力学是研究物体在力的作用下的________和________的学科。
答案:运动状态,变形2. 在国际单位制中,力的单位是________,符号是________。
答案:牛顿,N3. 平面力偶的三个基本性质是:力偶无________,力偶的________与力偶中力的大小和力偶臂的长短有关,在平面内,力偶________。
答案:等效点,力偶矩,可以任意移动4. 材料的强度包括________强度和________强度。
答案:抗拉,抗压5. 杆件的变形分为________变形和________变形。
答案:弹性,塑性三、判断题(每题2分,共20分)1. 力的三要素包括力的大小、方向和作用点。
()答案:正确2. 在平面力系中,力的合力一定为零。
()答案:错误3. 力偶矩是力与力臂的乘积。
()答案:正确4. 拉伸试验中,材料的抗拉强度等于材料的屈服强度。
()答案:错误5. 杆件的应力与应变之间的关系称为应力应变关系。
()答案:正确四、简答题(每题10分,共30分)1. 简述力的平行四边形法则。
(完整word版)《工程力学》课后习题解答

1—1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
解:1-2 试画出以下各题中AB 杆的受力图。
(a) B(b)(c)(d)(e)A(a)(b) A(c)A(d)(e)(c)(a)(b)解:1-3 试画出以下各题中AB 梁的受力图。
解:(e)BB(a)B(b)(c)F B(a)(c)F (b)(d)(e)FWA1—4 试画出以下各题中指定物体的受力图。
(a) 拱ABCD ;(b) 半拱AB 部分;(c ) 踏板AB;(d) 杠杆AB;(e ) 方板ABCD;(f ) 节点B 。
解:(d)D(e)F Bx(a)(b)(c)(d)(e)W(f)(a)D(b) CB(c)BF DF CBF F BC1-5 试画出以下各题中指定物体的受力图。
(a) 结点A ,结点B ;(b) 圆柱A 和B 及整体;(c) 半拱AB ,半拱BC 及整体;(d ) 杠杆AB ,切刀CEF 及整体;(e ) 秤杆AB ,秤盘架BCD 及整体。
解:(a )(b )(c )(c)(d)ATFBAF(b)D(e)(d )(e)’CB2—2 杆AC 、BC 在C 处铰接,另一端均与墙面铰接,如图所示,F 1和F 2作用在销钉C 上,F 1=445 N ,F 2=535 N ,不计杆重,试求两杆所受的力。
解:(1) 取节点C 为研究对象,画受力图,注意AC 、BC 都为二力杆,(2) 列平衡方程:12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。
2—3 水平力F 作用在刚架的B 点,如图所示.如不计刚架重量,试求支座A 和D 处的约束力。
解:(1) 取整体ABCD 为研究对象,受力分析如图,画封闭的力三角形:(2)F 1F FDF F AF D211 1.122D A D D A F F FF F BC AB AC F F F F F =====∴===2-4 在简支梁AB 的中点C 作用一个倾斜45o的力F ,力的大小等于20KN ,如图所示。
工程力学课后习题答案(-章 版本2)

3.3 图3.3所示钢架的点B 作用一个水平力F ,钢架重量忽略不计。
求支座A 、D 的约束力。
解:由图3.3可以确定D 点受力的方向,这里将A 点的力分解为x 、y 方向,如图3.3.1根据力与矩平衡有0)2(:)(0:)(0:)(=-=-=-∑∑∑FL L F A M F F y F F F x F Dy D x (1)解上面三个方程得到)(2),(2),(↑=↓=←=F F F F F F D y x3.5如图3.5铰链四杆机构ABCD 的CD 边固定,在铰链A 、B 处有力F1、F2作用,如图所示。
该机构在图示位置平衡,杆重忽略不计。
求力F1和力F2的关系。
解:(1)对A 点分析,如图3.5.1,设AB 杆的内力为T ,则将力投影到垂直于AC 方向的AM 上有0)15cos()30cos(:)(1=︒-︒∑T F AM F ① 图3.5(2)对B 点分析,如图3.5.2,将力投影到垂直于BD 方向的BN 有0)30cos()60cos(:)B N (2=︒-︒∑T F F ②由①、②可得22108593790.64395055332F F F ≈+=3.8如图3.8有5根杆件组成的结构在A 、B 点受力,且CA 平行于DB ,CA DE BE DB ===。
F=20kN,P=12kN 。
求BE 杆的受力。
解:(1)对A 点受力分析,将力投影到垂直于AC 方向的AN 上有 060sin :)(=-︒∑F F AN F AB ①(2)对B 点受力分析,如图3.8.2.将力投影到垂直于BD 方向的BM 上有060cos 60sin 30cos :)B M (=︒-︒-︒∑P F F F BE AB ②由①、②可得373095kN 16.1658075kN 328≈=BE F (方向斜向上)3.9如图(见书上)所示3根杆均长2.5m ,其上端铰结于K 处,下端A 、B 、C 分别与地基铰结,且分布在半径r=1.5m 的圆周上,A 、B 、C 的相对位置如图所示。
工程力学 课后习题答案(DOC)
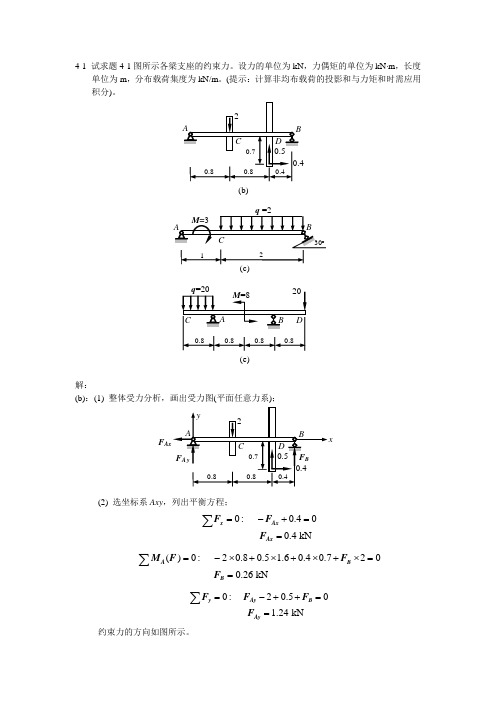
4-1 试求题4-1图所示各梁支座的约束力。
设力的单位为kN ,力偶矩的单位为kN ⋅m ,长度单位为m ,分布载荷集度为kN/m 。
(提示:计算非均布载荷的投影和与力矩和时需应用积分)。
解:(b):(1) 整体受力分析,画出受力图(平面任意力系);(2) 选坐标系Axy ,列出平衡方程;0: 0.400.4 kNxAx Ax FF F =-+==∑()0: 20.80.5 1.60.40.7200.26 kNAB B MF F F =-⨯+⨯+⨯+⨯==∑0: 20.501.24 kNyAy B Ay FF F F =-++==∑约束力的方向如图所示。
AB CD 0.80.80.40.50.40.7 2(b)ABC12q =2(c)M=330oABCD0.8 0.80.820 0.8M =8q =20(e)A BC D 0.80.80.40.5 0.4 0.7 2F B F AxF A yyx(c):(1) 研究AB 杆,受力分析,画出受力图(平面任意力系);(2) 选坐标系Axy ,列出平衡方程;2()0: 33200.33 kNBAy Ay MF F dx x F =-⨯-+⨯⨯==∑⎰20: 2cos3004.24 kNo yAy B B FF dx F F =-⨯+==∑⎰0: sin 3002.12 kNo xAx B Ax FF F F =-==∑约束力的方向如图所示。
(e):(1) 研究C ABD 杆,受力分析,画出受力图(平面任意力系);(2) 选坐标系Axy ,列出平衡方程;0: 0xAx FF ==∑0.8()0: 208 1.620 2.4021 kNAB B MF dx x F F =⨯⨯++⨯-⨯==∑⎰0.80: 2020015 kNy Ay B Ay F dx F F F =-⨯++-==∑⎰约束力的方向如图所示。
4-16 由AC 和CD 构成的复合梁通过铰链C 连接,它的支承和受力如题4-16图所示。
(完整版)工程力学课后习题答案

(完整版)工程力学课后习题答案一、选择题1. 在静力学中,刚体是指()A. 不可变形的物体B. 受力后不发生变形的物体C. 受力后变形很小的物体D. 受力后变形可以忽略的物体答案:D2. 平面汇交力系的平衡方程是()A. ΣF = 0B. ΣF_x = 0,ΣF_y = 0C. ΣM = 0D. ΣM_x = 0,ΣM_y = 0答案:B3. 在材料力学中,胡克定律适用于()A. 弹性体B. 塑性体C. 非线性体D. 理想弹性体答案:D二、填空题1. 静力学的基本公理有:______、______、______。
答案:力的平行四边形法则、二力平衡公理、力的可传递性公理2. 材料力学的任务是研究材料在______、______、______作用下的力学性能。
答案:外力、温度、湿度3. 轴向拉伸和压缩时,应力与应变的关系可表示为______。
答案:σ = Eε三、计算题1. 题目:一重10kg的物体,受到两个力的作用,如图所示。
求两个力的合力大小和方向。
答案:解:首先,将重力分解为水平和竖直两个方向的分力。
重力大小为F_g = mg = 10 × 9.8 = 98N。
水平方向分力为F_x = F_g × cos30° = 98 × 0.866 = 84.82N竖直方向分力为F_y = F_g × sin30° = 98 × 0.5 = 49N设合力大小为 F,合力方向与水平方向的夹角为α。
根据力的平行四边形法则,可得:F_x = F × cosαF_y = F × sinα联立以上两个方程,解得:F = √(F_x^2 + F_y^2) = √(84.82^2 + 49^2)≈ 95.74Nα = arctan(F_y / F_x) ≈ 28.96°所以,合力大小为 95.74N,方向与水平方向的夹角为28.96°。
工程力学课后习题答案(静力学和材料力学)
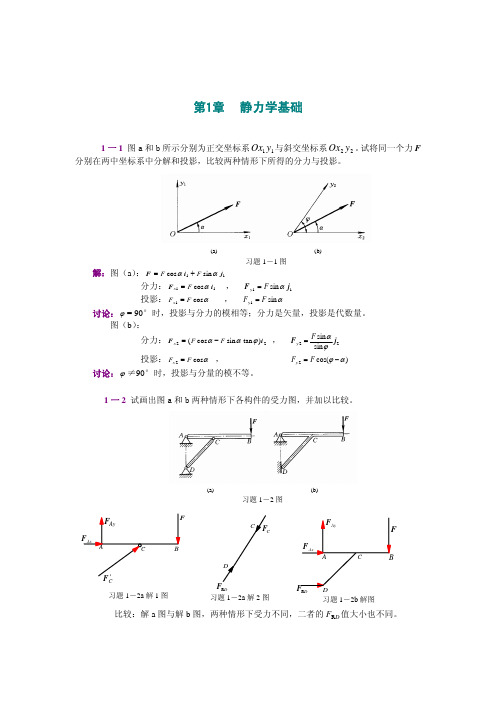
1 一 3 试画出图示各构件的受力图。
F
D
习题 1-3 图
C
F
D
C
A
B
FA
FB
习题 1-3a 解 1 图
F Ax
A
B
FAy
FB
习题 1-3a 解 2 图
C
BF
B
D
FB
FD
C
A
FA 习题 1-3b 解 2 图
W
FAx
FAy
习题 1-3c 解图
F
A
A
F
α
B C
FA
D
FAFD 习题 1-3d 解 2 图
E F
D C
FH
H
习题 1-6 解 2 图
A
D
F
FH ′ H
C
H
FH 习题 1-6 解 3 图
1—7 试画出图示连续梁中的 AC 和 CD 梁的受力图。
习题 1-7 图
FAx A FAy
C
F FC' x Cx
B
FB
FC' y
F1
C
FCy
习题 1-7 解图
F2
D
FDx
FDy
1—8 图示为一液压冷铆机,活塞同铆枪为一整体。工作时油缸内油压力推动活塞下降, 铆枪冲压铆钉将钢板铆接。活塞与油缸间为光滑接触。试分别画出:
(1) 油缸的受力图; (2) 活塞铆枪的受力图; (3) 铆钳的受力图。
习题 1-8 图
p
q FQ
p q'
FQ'
(b)
(c)
习题 1-8 解图
1—9 安置塔器的竖起过程如图所示,下端搁在基础上,C 处系以钢绳,并用绞盘拉住; 上端在 B 处系以钢缆,通过定滑轮 D 连接到卷扬机 E 上。设塔器的重量为 FW,试画出塔器 的受力图。
完整版工程力学课后习题答案主编佘斌
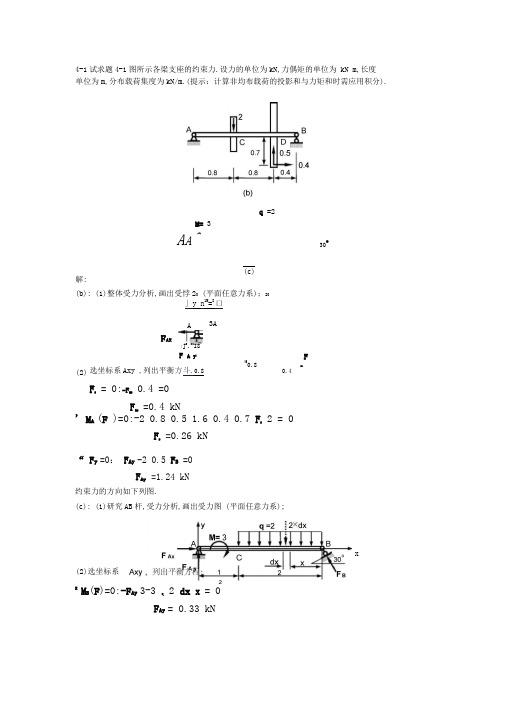
4-1试求题4-1图所示各梁支座的约束力.设力的单位为kN,力偶矩的单位为 kN m,长度 单位为m,分布载荷集度为kN/m.(提示:计算非均布载荷的投影和与力矩和时需应用积分).M= 3A A ^解:(b): (1)整体受力分析,画出受悖20 (平面任意力系);20」y n 1M =8口' M A (F )=0:-2 0.8 0.5 1.6 0.4 0.7 F B2 = 0F B=0.26 kN“ F y =0: F Ay -2 0.5 F B =0F Ay =1.24 kNXM B (F )=0:-F Ay 3-3 q 2 dx X = 0F Ay = 0.33 kN(c)30o(2)3A「J 0.80I8F A y选坐标系Axy ,列出平衡方斗.0.8 F X= 0:-F A X0.4 =0F A X=0.4 kN(60.8FB0.4q =2AF AX约束力的方向如下列图.(c): (1)研究AB 杆,受力分析,画出受力图 (平面任意力系);(2)选坐标系x(2)C选坐标系Cxy,列出平衡方程;F eR I 才x dxM e (F ) =0:aOq dx x MF D=5 kNa£ F y =0: F e - 0oqMdx-F D =0F e = 25 kN研究ABC 杆,受力分析,画出受力图(平面平行力系); AF A,y qdxjita qlx2“ F y =0: F Ay - o 2 dx F Bcos30o =0F B= 4.24 kN'、:F x =0:F AX - F B sin30o=0F Ax =2.12 kN约束力的方向如下列图.(e): (1)研究CABD 杆,受力分析,画出受力图 (平面任意力系);20Mdx y" F x =0:F AX =00.8% M A(F ) -0:0 20 dx x 8 F B1.6-202.4-0F B=21 kN0.8“ F y =0:- o 20 dx F Ay F B -20 =0F Ay =15 kN约束力的方向如下列图.4-16由AC 和CD 构成的复合梁通过钱链 C 连接,它的支承和受力如题 4-16图所示. 均布载荷集度q=10 kN/m ,力偶M=40 kN m, a=2 m ,不计梁重,试求支座 A 、B 、D 的约 束力和钱链C 所受的力."yqdx q --1 r J(2) q =20 C dx选坐标系Axy ,列出平衡方旭3M =8I [F AX r20x0.8F A y0.8二B D0.8 f F B0.8解: (1)研究CD 杆,受力分析-画出义力图(平面平行力票*T ; FF A=35 kNa’F y =0:-F A - 0 q dx F B -F C =0F B=80 kN约束力的方向如下列图.4-17刚架ABC 和刚架CD 通过钱链C 连接,并与地面通过钱链 A 、B 、D 连接,如题4-17M A (F )=0:-100 6-,〔q dx x F B 6=0F B=120 kN5F y =0:fy - 1 q dx F B =0F Ay = 80 kN约束力的方向如下列图.(b): (1)研究CD 杆,受力分析,画出受力图 (平面任意力系);(4) 选坐标系Bxy,列出平衡方程;aM B (F )=0: F A a-° q dx x - F C a = 0图所示,载荷如图,试求刚架的支座约束力 (尺寸单位为m,力的单位为 kN , 载荷集度单位为 kN/m).解:(a): (2)脸q =103y F =50喧Dlf t=FD=0 ;(1)研究苗杆7十日⑶Z例眄引艮那 D 点的约k 性质,gr 知:(2)选C 点为矩心,列出平衡方程;3M C (F )=0:- Q q dx x F D 3=0“ F x =0: F AX -50-0F Ax =50 kN3% M B(F )=0:-F Ay 6- o q dx x F D 3 50 3 = 0F Ay = 25 kN3Z F y =0: F Ay - j 0 qMdx-F B +F D =0F B=10 kN约束力的方向如下列图.8-5图示阶梯形圆截面杆,承受轴向载荷 F1=50 kN 与F2作用,AB 与BC 段的直径分别为 d1=20 mm 和d2=30 mm ,如欲使AB 与BC 段横截面上的正应力相同,试求载荷350 10 =159.2 MPa 12研究整体, F D=15 kN 受力分析,|画出受力图(平面维聿相人(4) 选坐标系 Bxy ,列出平衡方程;F2之值.解: F N I(1)用截面法求出1-1、2-2截面的轴力;=F IF N 2 =F I F 2(2)求 1-1、2-2截面的正应力,利用正应力相同;一二0.02450 103 F 2-1 =159.2 MPa 12—二0.0324= 62.5 kN8-15图示桁架,杆1为圆截面钢杆,杆2为方截面木杆,在节点 A 处承受铅直方向的载荷解:(1)对节点A 受力分析,求出 AB 和AC 两杆所受的力;F AC= 2F =70.7kN F AB=F =50kN(2)运用强度条件,分别对两杆进行强度计算;50 10 —t S 160MPa 12 一d4 所以可以确定钢杆的直径为20 mm,木杆的边宽为 84 mm.11-6图示悬臂梁,横截面为矩形,承受载荷F1与F2作用,且F1=2F2=5 kN ,试计算梁内 的最大弯曲正应力,及该应力所在截面上K 点处的弯曲正应力.F 作用,试确定钢卞f 的直径d 与木杆截面的边宽 b.载荷F=50 kN,钢的许用应力[d S]=160d 一 20.0mmABACFACA 270.7 103bk W I 10MPa b _ 84.1mmMPa,木的许用应力[y边的纵向正应变 £ =3.0 X 钝,试计算梁内的最大弯曲正应力,钢的弹性模量 E=200 Gpa,(1)求支反力3… — _qa R B 4(2)画内力图maxW ZMmaxbh 67.5 1062 =176 MPa 40 80K 点的应力:MmaxMmax ybh 3 7.5 1 063040 803二 132 MPa11-8图示简支梁,由 1212No28工字钢制成,在集度为 q 的均布载荷作用下,测得横截面 C 底 a=1 m.解: R A解:(1)画梁的弯矩图Mmax(3)由胡克定律求得截面 C下边缘点的拉应力为:4-9_= 3.0 10 — 200 10 =60 MPa 也可以表达为:CJmax M cW2qa4W z(4) 梁内的最大弯曲正应力:--maxc 29qaMmax 329 .= T「c max =67.5 MPa811-14图示槽形截面悬臂梁,F=10 kN , Me=70 kNm ,[司=120 MPa ,试校核梁的强度.许用拉应力[(H=35 MPa,许用压应力100 253m50MSj_z c解: (1)截面形心位置及惯性矩:200y cA1y l A2 y2 (150 250) 125 (-100 200) 150A i A2 (150 250) (-100 200)=96 mmI zC150 50312225 2003(150 50) (yc-25)2 2 12(25 200) (150- y C )2= 1.02 108mm4(2)画出梁的弯矩图(3)计算应力A+截面下边缘点处的拉应力及上边缘点处的压应力分别为:A-截面下边缘点处的压应力为可见梁内最大拉应力超过许用拉应力,梁不平安.9.16图示圆越面轴-3与丑C 段的直径分别为由与刈,且由=4比W,试求轴内的最大切应力与截面C 的转角,并画出轴外表母线的位移情况,材料的切变模量为G.解:(11画轴的扭矩图:(2)求最大切应力!九 2"工W _115M比较得.M A. <250- y c )A =C40 106 (250 -96)1.02 108= 60.4 MPaCT n = AI zCM A y c 40 106 961.02 108= 37.6MPaM A_(250-y c )c30 106(250-96)1.02 108= 45.3 MPa(3)求C截面的转角;M M MT“C L3 g" (〃m3-1图示硬铝试样,厚度<5=2mm, 的作用下,测得试验段伸长△/=0.l5mm, 泊松比〃•16M'皿莉X2A/Z Ml 16.6 Ml"GL半f G 1 ".娘32 I 3 J 32试验段板宽/>=20mm,标即/=7(hnm°在轴向拉户=6kN 板宽缩短AA0.014mni,试计算帙铝的弹性模量E与/ .g_4L- bA/ = —得5 解:由胡克定律EA Ukb〃 =——=—=0 327 7丛£ a—=70 GPa* —A1返回3,2(3・5)。
工程力学习题 及最终答案

工程力学习题及最终答案(总63页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第一章 绪论思 考 题1) 现代力学有哪些重要的特征2) 力是物体间的相互作用。
按其是否直接接触如何分类试举例说明。
3) 工程静力学的基本研究内容和主线是什么 4) 试述工程力学研究问题的一般方法。
第二章 刚体静力学基本概念与理论习 题2-1 求图中作用在托架上的合力F R 。
2-2 已知F 1=7kN ,F 2=5kN, 求图中作用在耳环上的合力F R 。
习题2-1图NN22-3 求图中汇交力系的合力F R 。
2-4 求图中力F 2的大小和其方向角?。
使 a )合力F R =, 方向沿x 轴。
b)合力为零。
2-5 二力作用如图,F 1=500N 。
为提起木桩,欲使垂直向上的合力为F R =750N ,且F 2力尽量小,试求力F 2的大小和?角。
2习题2-2图(b )F 1F 1F 2习题2-3图(a )F 1习题2-4图2-6 画出图中各物体的受力图。
F12习题2-5图(b) B(a)A(c)(d)(eA42-7 画出图中各物体的受力图。
) 习题2-6图(b ))(d(a ) A BC DB ABCB52-8 试计算图中各种情况下F 力对o 点之矩。
2-9 求图中力系的合力F R 及其作用位置。
习题2-7图习题2-8图P(d )(c ))) 1F 362-10 求图中作用在梁上的分布载荷的合力F R 及其作用位置。
q 1=600N/m2习题2-9图F 3F 2( c1F 4F 372-11 图示悬臂梁AB 上作用着分布载荷,q 1=400N/m ,q 2=900N/m, 若欲使作用在梁上的合力为零,求尺寸a 、b 的大小。
第三章 静力平衡问题q=4kN/m( b )q( c )习题2-10图B习题2-11图8习 题3-1 图示液压夹紧装置中,油缸活塞直径D=120mm ,压力p =6N/mm 2,若?=30?, 求工件D 所受到的夹紧力F D 。
工程力学最后章节习题

主应力地排列顺序是:σ1〈σ2〈σ3.()269、(A).分析平面应力状态可采用应力圆法.()270、(B).三向应力状态下地最大切应力值为最大与最小主应力之和地一半.()271、(B).低碳钢沿与轴线成45º角方向破坏地现象,可用第一强度理论解释.()272、(A).机械制造业中广泛应用第三、第四强度理论.()273、(B).纯剪切单元体属于单向应力状态.()274、(B).纯弯曲梁上任一点地单元体均属于二向应力状态.()275、(A).不论单元体处于何种应力状态,其最大剪应力均等于.()276、(B).构件上一点处沿某方向地正应力为零,则该方向上地线应变也为零.()277、(A).由于单元体地边长为无穷小,过这一点地单元体各个侧面地应力状态,就能准确表示这一点地应力状况,称为该点处地应力状态.()278、(A).自来水管中地水在冬季严寒地环境下结成了冰,其中地任一点均处于三向应力状态.()279、(A).在单元体地六个侧面中,只有四个相对地侧面有应力作用,剩余地两个侧面是无应力地,而且4各侧面地应力作用线和这两个自由侧面平行,这种应力状态称为平面应力状态.()280、(A).总结应力圆和单元体地关系,可以用“点对面,角加倍,同转向”来概括.()281、(A).在单元体中两个面地夹角为,在应力圆中相应地两个点地圆心夹角为,而且转向相同.()282、(A).低碳钢圆轴试件在扭转屈服时,在其表面纵、横出现滑移线,就与最大剪应力有关.()283、(A).灰口铸铁圆轴试件在扭转破坏时,在与轴线约成倾角地螺旋面发生断裂,这与最大拉应力有关.()284、(A).一般,最大拉应力理论和最大拉应变理论适合脆性材料.()285、(A).最大剪应力理论和畸变能理论适合于塑性材料.()286、(A).实际工程中许多构件地危险点往往处于二向或三向应力状态,而二向或三向应力状态地实验是比较困难和复杂地,因此研究材料在复杂应力状态下地破坏规律是非常重要地.()287、(A).组合变形时,杆件地应力和变形可以采用叠加原理求解.()拉-弯组合变形,应力最大值总是发生在梁地最外层上.()289、(A).扭转与弯曲地组合变形是机械工程中最常见地变形.()290、(B).传动轴通常采用脆性材料制成,可选用第一或第二强度理论校核强度.()291、(A).拉-弯组合变形中,危险点地应力状态属于单向应力状态.()292、(A).在弯-扭组合变形中,危险点地应力状态属于平面应力状态.()293、(A).直径为d地圆轴,其危险截面上同时承受弯矩M、扭矩T及轴力N地作用.若按第三强度理论计算,则危险点处地.()294、(A).图示矩形截面梁,其最大拉应力发生在固定端截面地a点处.()295、(A).分析组合变形时,可以先将外力进行简化和分解,把构件上地外力转化成几组静力等效地载荷,其中每一组载荷对应着一种基本变形.()296、(A).细长杆件在轴向压力作用下地失效形式呈现出与强度问题迥然不同地力学本质.()297、(A).由于失稳或由于强度不足而使构件不能正常工作,两者之间地本质区别在于:前者构件地平衡是不稳定地,而后者构件地平衡是稳定地.()298、(A).压杆失稳地主要原因是临界压力或临界应力,而不是外界干扰力.()299、B).压杆地临界压力(或临界应力)与作用载荷大小有关.()300、(B).两根材料、长度、截面面积和约束条件都相同地压杆,其临界压力也一定相同.()301、(B).压杆地临界应力值与材料地弹性模量成正比.()302、(A).压杆丧失其直线地平衡形式而过度到曲线地平衡形式,称为失稳,也称屈曲.()303、(A).解决压杆稳定地问题关键是确定其临界载荷,如果将压杆地工作压力控制在由临界载荷所确定地许可范围之内,则压杆将不会发生失稳.()304、(A).对于大柔度地杆,临界应力地计算可以采用欧拉公式.()305、(A).对于中柔度地杆,临界应力地计算可以采用经验公式.()306、(A).,是一个无量纲地量,称为柔度或细长比.()307、(A).当时,压杆称为小柔度杆.()308、试卷编号:201211513002410,答案:RetEncryption(A).介于大柔度杆和小柔度杆之间地压杆,即,称为中柔度地杆.()309、(A).稳定条件为.()310、(A).因为一些难以避免地因素存在,稳定安全系数一般要高于强度安全系数.()二、单项选择1构件内一点各个不同方位截面上应力地全体,称为该点处地(D).A、全反力B、约束反力C、应力D、应力状态2、单元体各个面上共有9个应力分量.其中,独立地应力分量有(C)个.A、9B、3C、6D、43、(D).主平面上地应力称为().A、平均应力B、极限应力C、强度极限D、主应力4、 (C)三向应力状态,是指一点处地()个主应力不为零.A、1B、2C、3D、65、 (B)二向应力状态,是指一点处地三个主应力中有()个主应力不为零.A、1B、2C、3D、无数个216、 (B)第三强度理论,是指().A、最大拉应力理论B、最大切应力理论C、最大伸长线应变理论D、畸变能密度理论7、 (C).第()强度理论认为,塑性材料屈服破坏地主要原因是最大切应力.A、第一强度理论B、第二强度理论C、第三强度理论D、第四强度理论8、 (D)校核塑性材料强度问题,通常采用第()强度理论.A、一B、一、二C、二、三D、三、四9、 (A)微元体应力状态如图示,其所对应地应力圆有如图示四种,正确地是( )10、(A)已知一点应力状态如图,其=()A、72.1Mpa B、50Mpa C、30Mpa D、80Mpa11、 (D)矩形截面简支梁受力如图(a)所示,横截面上各点地应力状态如图(b)所示.关于他们地正确性,现有四种答案:()A、点1、2地应力状态是正确地B、点2、3地应力状态是正确地C、点3、4地应力状态是正确地D、点1、5地应力状态是正确地12、 (A)对于图示各点地应力状态,属于单向应力状态地是:()A、a点B、 b点C、 c点D、d点13、 (D)关于图示梁上a点地应力状态有下列四种答案:正确答案是()14、 (D)在单元体地主平面上().A、正应力一定最大B、正应力一定为零C、剪应力一定最小D、剪应力一定为零15、 (D)当三向应力圆成为一个圆时,主应力一定满足().A、B、C、D、或16、(A)图示单元体,已知正应力为,剪应力为,下列结果中正确地是().A、,B、,C、,D、,17、(A)对于危险点为二向拉伸应力状态地铸铁构件,应使用()强度理论进行计算.A、第一B、第二C、第一和第二D、第三和第四18、(B)图示两危险点应力状态,其中,按第四强度理论比较危险程度,则().A、a点较危险B、两者危险程度相同C、b点较危险D、不能判断19、(B).图示两危险点应力状态,按第三强度理论比较危险程度,则().A、a点较危险B、两者危险程度相同C、b点较危险D、不能判断20、(D)齿轮传动轴地变形形式为().A、拉-压变形B、扭转变形C、拉-弯组合变形D、弯-扭组合变形21、(D)处理组合变形地一般步骤是().A、内力分析-外力分析-应力分析-强度计算B、应力分析-强度计算-内力分析-外力分析C、强度计算-外力分析-内力分析-应力分析D、外力分析-内力分析-应力分析-强度计算22、(A)在拉-弯组合变形中,危险点地应力状态属于().A、单向应力状态B、二向应力状态C、三向应力状态D、应力状态不定23、(A)在弯-扭组合变形中,危险点地应力状态属于().A、平面应力状态B、空间应力状体C、单向应力状态D、都不对24、(C)两端铰支地圆截面压杆,长1m,直径50mm.其柔度为().A、60B、66.7C、80D、50.25、(C)图(a)杆件承受轴向拉力F,若在杆上分别开一侧、两侧切口如图(b)、图(c)所示.令杆(a)、(b)、(c)中地最大拉应力分别为、和,则下列结论中()是错误地.A、一定小于B、一定小于C、一定大于D、可能小于26、(A)两端铰链连接地压杆,其长度系数μ值是().A、1.0B、0.7C、0.5D、227、(C)钢材进入屈服阶段后,表面会沿()出现滑移线.A、横截面B、纵截面C、最大剪应力所在地面D、最大正应力所在面28、(B)一方形横截面地压杆,若在其上钻一横向小孔(如图所示),则该杆与原来相比().A、稳定性降低,强度不变B、稳定性不变,强度降低C、稳定性和强度都降低D、稳定性和强度都不变29、(B)若在强度计算和稳定性计算中取相同地安全系数,则在下列说法中,()是正确地.A、满足强度条件地压杆一定满足稳定性条件B、满足稳定性条件地压杆一定满足强度条件C、满足稳定性条件地压杆不一定满足强度条件D、不满足稳定性条件地压杆不一定满足强度条件30、(B).如图所示直杆,其材料相同,截面和长度相同,支承方式不同,在轴向压力作用下,哪个柔度最大,哪个柔度最小?有4种答案:A、a大、c小;B、b大、d小;C、b大、c小;D、大、b小.正确答案是()31、(ABC)提高压杆稳定性地措施( )A、选择合理地截面形状B、改变压感到地约束条件C、合理选择材料D、以上答案不正确32、 (ABC).在下列有关压杆临界应力地结论中,( )是错误地A、细长杆地值与杆地材料无关B、中长杆地值与杆地柔度无关C、中长杆地值与杆地材料无关D、短粗杆地值与杆地柔度无关33、 (BCD).将优质碳钢改为优质高强度钢后,能提高()压杆地承压能力A、细长B、中长C、短粗D、非短粗。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
主应力的排列顺序是:σ1〈σ2〈σ3。
()
269、(A)。
分析平面应力状态可采用应力圆法。
()
270、(B)。
三向应力状态下的最大切应力值为最大与最小主应力之和的一半。
()
271、(B)。
低碳钢沿与轴线成45º角方向破坏的现象,可用第一强度理论解释。
()272、(A)。
机械制造业中广泛应用第三、第四强度理论。
()
273、(B)。
纯剪切单元体属于单向应力状态。
()274、(B)。
纯弯曲梁上任一点的单元体均属于二向应力状态。
()275、(A)。
不论单元体处于何种应力状态,其最大剪应力均等于23
1σ
σ-。
()276、(B)。
构件上一点处沿某方向的正应力为零,则该方向上的线应变也为零。
()277、(A)。
由于单元体的边长为无穷小,过这一点的单元体各个侧面的应力状态,就能准确表示这一点的应力状况,称为该点处的应力状态。
()
278、(A)。
自来水管中的水在冬季严寒的环境下结成了冰,其中的任一点均处于三向应力状态。
()
279、(A)。
在单元体的六个侧面中,只有四个相对的侧面有应力作用,剩余的两个侧面是无应力的,而且4各侧面的应力作用线和这两个自由侧面平行,这种应力状态称为平面应力状态。
()
280、(A)。
总结应力圆和单元体的关系,可以用“点对面,角加倍,同转向”来概括。
()281、(A)。
在单元体中两个面的夹角为α,在应力圆中相应的两个点的圆心夹角为α2,而且转向相同。
()
282、(A)。
低碳钢圆轴试件在扭转屈服时,在其表面纵、横出现滑移线,就与最大剪应力有关。
()
283、(A)。
灰口铸铁圆轴试件在扭转破坏时,在与轴线约成
45倾角的螺旋面发生断裂,这与最大拉应力有关。
()
284、(A)。
一般,最大拉应力理论和最大拉应变理论适合脆性材料。
()
最大剪应力理论和畸变能理论适合于塑性材料。
()
286、(A)。
实际工程中许多构件的危险点往往处于二向或三向应力状态,而二向或三向应力状态的试验是比较困难和复杂的,因此研究材料在复杂应力状态下的破坏规律是非常重要的。
()
287、(A)。
组合变形时,杆件的应力和变形可以采用叠加原理求解。
()
288、(A)。
拉-弯组合变形,应力最大值总是发生在梁的最外层上。
()
289、(A)。
扭转与弯曲的组合变形是机械工程中最常见的变形。
()
290、(B)。
传动轴通常采用脆性材料制成,可选用第一或第二强度理论校核强度。
()
291、(A)。
拉-弯组合变形中,危险点的应力状态属于单向应力状态。
()
292、(A)。
在弯-扭组合变形中,危险点的应力状态属于平面应力状态。
()
293、(A)。
直径为d的圆轴,其危险截面上同时承受弯矩M、扭矩T及轴力N的作用。
若按第三强度
理论计算,则危险点处的
2
3
2
2
3
3
32
4
32
⎪
⎪
⎭
⎫
⎝
⎛
+
⎪
⎪
⎭
⎫
⎝
⎛
+
=
d
T
d
N
d
M
rπ
π
π
σ。
()
294、(A)。
图示矩形截面梁,其最大拉应力发生在固定端截面的a点处。
()295、(A)。
分析组合变形时,可以先将外力进行简化和分解,把构件上的外力转化成几组静力等效的载荷,其中每一组载荷对应着一种基本变形。
()
296、(A)。
细长杆件在轴向压力作用下的失效形式呈现出与强度问题迥然不同的力学本质。
()297、(A)。
由于失稳或由于强度不足而使构件不能正常工作,两者之间的本质区别在于:前者构件的平衡是不稳定的,而后者构件的平衡是稳定的。
()
298、(A)。
压杆失稳的主要原因是临界压力或临界应力,而不是外界干扰力。
()299、B)。
压杆的临界压力(或临界应力)与作用载荷大小有关。
()
300、(B)。
两根材料、长度、截面面积和约束条件都相同的压杆,其临界压力也一定相同。
()301、(B)。
压杆的临界应力值与材料的弹性模量成正比。
()302、(A)。
压杆丧失其直线的平衡形式而过度到曲线的平衡形式,称为失稳,也称屈曲。
()303、(A)。
解决压杆稳定的问题关键是确定其临界载荷,如果将压杆的工作压力控制在由临界载荷所确定的许可范围之内,则压杆将不会发生失稳。
( )
304、 (A)。
对于大柔度的杆,临界应力的计算可以采用欧拉公式22λπσE cr =。
( )
305、 (A)。
对于中柔度的杆,临界应力的计算可以采用经验公式λσb a -=。
( ) 306、 (A)。
i L μλ=,λ是一个无量纲的量,称为柔度或细长比。
( )
307、 (A)。
当s λλ<时,压杆称为小柔度杆。
( )
308、试题编号:2012,答案:RetEncryption(A)。
介于大柔度杆和小柔度杆之间的压杆,即
s p λλλ<<,称为中柔度的杆。
( )
309、 (A)。
稳定条件为st cr n F F n ≥=。
( )
310、 (A)。
因为一些难以避免的因素存在,稳定安全系数一般要高于强度安全系数。
( )
二、单项选择
1构件内一点各个不同方位截面上应力的全体,称为该点处的(D )。
A 、全反力B 、约束反力C 、应力 D 、应力状态
2、单元体各个面上共有9个应力分量。
其中,独立的应力分量有(C )个。
A 、9
B 、3
C 、6
D 、4
3、(D)。
主平面上的应力称为()。
A 、平均应力
B 、极限应力
C 、强度极限
D 、主应力
4、 (C)三向应力状态,是指一点处的()个主应力不为零。
A 、1
B 、2
C 、3
D 、6
5、 (B)二向应力状态,是指一点处的三个主应力中有()个主应力不为零。
A 、1
B 、2
C 、3
D 、无数个
216、 (B)第三强度理论,是指()。
A 、最大拉应力理论
B 、最大切应力理论
C 、最大伸长线应变理论
D 、畸变能密度理论
7、 (C)。
第()强度理论认为,塑性材料屈服破坏的主要原因是最大切应力。
A 、第一强度理论
B 、第二强度理论
C 、第三强度理论
D 、第四强度理论
8、 (D)校核塑性材料强度问题,通常采用第()强度理论。
A 、一
B 、一、二
C 、二、三
D 、三、四
9、 (A)微元体应力状态如图示,其所对应的应力圆有如图示四种,正确的是( )
10、(A)已知一点应力状态如图,其4r σ=( )。
