高中数学必修三习题：第一章1.3算法案例(附答案)

合集下载

人教A版高中数学必修三1-3-1 辗转相除法与更相减损术、秦九韶算法

用更相减损术求 294 和 84 的最大公约数时，第一步是 ________．
[答案] 用 2 约简 [解析] 由于 294 和 84 都是偶数，先用 2 约简．
2．秦九韶算法 (1)概念：求多项式 f(x)＝anxn＋an－1xn－1＋…＋a1x＋a0 的值时，常用秦九韶算法，这种算法的运算次数较少，是多项式求值比较先进的算法，其实质是转化为求 n 个__一__次__多项式的值，共进行_n_次乘法运算和_n_次加法运算．其过程是：
[答案] C
3．更相减损术的理论依据是( ) A．每次操作所得的两数和前两数具有相同的最小公倍数 B．每次操作所得的两数和前两数具有相同的最大公约数 C．每次操作所得的两数和前两数的最小公倍数不同 D．每次操作所得的两数和前两数的最大公约数不同
[答案] B
4．用秦九韶算法计算f(x)＝3x6＋4x5＋5x4＋6x3＋7x2＋
3．求满足1＋
1 22
＋
1 32
＋…＋
1 n2
>106的最小正整数n，要求
设计算法画出其程序框图，编写程序．
[答案]
由于事先不知道循环的次数，故可用WHILE语句编写程序如下：
新课引入
秦朝末年，楚汉相争．一次，韩信率 1500 名将士与楚王大将李锋交战．苦战一场，楚军不敌，败退回营，汉军也死伤四五百人，于是韩信整顿兵马返回大本营．当行至一山坡，忽有后军来报，说有楚军骑兵追来．只见远方尘土飞扬，杀声震天．汉军本来已十分疲惫，这时队伍大哗．韩信骑马到坡顶，见来敌不足五百骑，便急速点兵迎敌．
这样的问题，也有人称为“韩信点兵”．它形成了一类问题，也就是初等数论中解同余式．这类问题的有解条件和解题方法被称为“中国剩余定理”，这是由中国人首先提出的．

高中人教版数学必修3课本练习-习题参考答案

高中数学必修③课本练习,习题参考答案第一章算法初步1.1算法与程序框图1.1.1算法的概念（p5)1. 解；第一步：输入任意正实数r，第二步：计算第三步：输出圆的面积S2. 解；第一步：给定一个大于l的正整数；第二步：令；第三步：用除，得到余数；第四步：判断“”是否成立，若成立，则i是n的因数；否则，i不是n的因数；第五步：使的值增加l，仍用表示，即令；第六步，判断“”是否成立．若是，则结束算法；否则，返回第三步1.1.2程序框图与算法的基本逻辑（P19）1.解；算法步骤：第一步，给定精确地d，令i=1第二步，取出的到小数点后第i位的不足近似值，记为a；取出的到小数点后第i位的过剩近似值，记为b,第三步，计算第四步，若m<d，则执行第五步；否则，将i的值增加1，返回第二步.第五步，输出程序框图如下图所示：1.1算法与程序框图（P20）解；题目：在国内寄平信（外埠），每封信的质量x （克）不超过60克时的邮费（单位：分）标准为，试写出计算邮费的算法并画出程序框图。

算法如下：第一步，输入质量数x 。

第二步，判断是否成立，若是，则输出y=120，否则执行第三步。

第三步，判断是否成立，若是，则输出y=240，否则，输出y=360，算法结束。

程序框图如下图所示：（注释：条件结构）2.解：算法如下：第一步，i=1,S=0.第二步，判断是否成立，若成立，则执行第三步，否则，执行第四步。

第三步，，i=i+1，返回第二步。

第四步，输出S.程序框图如下图所示：（注释：循环结构）3. 解：算法如下：第一步，输入人数x，设收取的卫生费为y元。

第二步，判断x>3是否成立，若不成立，y=5，输出y；否则，输出y.程序框图如下图所示：（注释：条件结构）1. 解：分析：我们设计对于一般的二元一次方程组（其中）的通用算法：第一步,,得（即） (3)第二步，解（3），得 (4)第三步，将（4）代入（1），得，因此，只要输入相应的未知数的系数和常数项，就能计算出方程组的解，即可以输出x、y的值，用顺序结构即可。

人教A版高中数学必修三练习：第一章算法初步1.3算法案例含答案

分层训练·进阶冲关A组基础练( 建议用时 20 分钟)1.在对 16 和 12 求最大条约数时 , 整个操作如下:16-12=4,12-4=8,8-4=4.由此能够看出12 和 16 的最大条约数是( A )A.4B.12C.16D.82. 在 m=nq+r(0≤r<n) 中, 若 k 是 n,r 的条约数 , 则 k m,n 的条约数.( A)A. —定是B. 不必定是C.必定不是D.不可以确立3.相关展转相除法以下说法正确的选项是 ( C ) A.它和更相减损术同样是求多项式值的一种方法B. 基本步骤是用较大的数m除以较小的数 n 获得除式 m=nq+r,直至 r<n 为止C.基本步骤是用较大的数m除以较小的数 n 获得除式 m=nq+r(0≤r<n),频频进行 , 直到 r=0 为止D.以上说法皆错4. 已知 7 163=209×34+57,209=57×3+38,57=38×1+19,38=19×2. 根据上述一系列等式 , 可确立 7 163 和 209 的最大条约数是( C )A.57B.3C.19D.345. 把 389 化为四进制数 , 则该数的末位是( A )A.1B.2C.3D.46. 用秦九韶算法求n 次多式 f(x)=a n x n+a n-1 x n-1 +⋯+a1x+a0的 , 当 x=x0 , 求f(x 0) 需要算乘方、乘法、加法的次数分 ( C )A.,n,nB.n,2n,nC.0,n,nD.0,2n,n7. 用更相减求36 与 134 的最大公数 , 第一步先除以2,获得 18与 67 .8.用相除法求 294 和 84 的最大公数 , 需要做除法的次数是2 .9. 三位七制数表示的最大的十制数是342 .10.秦九韶是我国南宋期的数学家 , 普州 ( 四川省安岳 ) 人, 他在所著的《数九章》中提出的多式求的秦九韶算法 , 到现在还是比先的算法 , 如所示的程序框出了利用秦九韶算法求某多式的一个例 . 若入 n,x 的分 3,3, 出 v 的48 .11.将 1234(5)化八制数 .【分析】先将 1234 (5)化十制数 :1234 (5) =1 ×5 3 +2 ×5 2 +3 ×5 1+4 ×5 0 =194.再将十制数 194 化八制数 :因此 1234 (5) =302 (8) .12. 用秦九韶算法计算多项式f(x)=x 6-12x 5+60x4 -160x 3+240x2-192x+64,当 x=2 时的值 .【分析】将 f(x) 改写为f(x)=(((((x-12)x+60)x-160)x+240)x-192)x+64, v0 =1,v 1 =1×2-12=-10,v 2 =-10×2+60=40,v 3 =40×2-160=-80,v 4 =-80×2+240=80,v 5 =80×2-192=-32,v 6 =-32×2+64=0.因此f(2)=0,即x=2 时,原多项式的值为0.B组提高练( 建议用时 20 分钟)13.以下各数中最小的数为 ( A )A.101011(2)B.1210(3)C.110(8)D.68(12)14.《九章算术》是中国古代的数学专著 , 此中的一段话“可半者半之 , 不行半者 , 副置分母、子之数 , 以少减多 , 更相减损 , 求其等也 , 以等数约之”用程序框图表示如图, 那么这个程序的作用是( B )A. 求两个正数 a,b 的最小公倍数B. 求两个正数 a,b 的最大公数C.判断此中一个正数能否能被另一个正数整除D.判断两个正数 a,b 能否相等15.用秦九韶算法求多式 f(x)=1+2x+x 2-3x 3+2x4在 x=-1 的 ,v 2的果是( D)A.-4B.-1C.5D.616.396 与 270 的最大公数与最小公倍数分18,5 940 .17.已知一个 k 制的数 123(k)与十制的数 38 相等 , 求 k 的 .【分析】由 123 (k) =1 ×k 2 +2 ×k 1 +3 ×k 0=k 2 +2k+3,得 k 2+2k+3=38, 因此 k 2 +2k-35=0,因此 k=5或k=-7(舍),因此 k=5.18. 用秦九韶算法求多式f(x)=12+35x-8x 2+79x3+6x4+5x5+3x6, 当 x=-4 ,v 4的 .【分析】依照秦九韶算法有v 0 =a 6 =3,v 1 =v 0x+a 5 =3 ×(-4)+5=-7,v2=v 1 x+a 4 =-7×(-4)+6=34,v3=v 2 x+a 3 =34×(-4)+79=-57,v4=v 3 x+a 2=-57×(-4)+(-8)=220.C 培 ( 建用 15 分 )19.程序框 , 利用秦九韶算法算多式 f(x)=a n x n+a n-1 x n-1 +⋯+a1x+a0的 , 当 x=x0, 框中 A 填入a n-k.20. 三个数 168,54,264 的最大条约数为 6 .封闭 Word 文档返回原板块。

人教版高中数学必修三第一章算法初步1.3算法案例 (教师版)【个性化辅导含答案】-教育文档

算法案例__________________________________________________________________________________ __________________________________________________________________________________1．理解算法案例的算法步骤和程序框图.2．引导学生得出自己设计的算法程序.3. 体会算法的基本思想，提高逻辑思维能力，发展有条理地思考与数学表达能力.1．求两个正整数最大公约数的算法(1)更相减损之术(等值算法)用两数中较大的数减去较小的数，再用差数和较小的数构成新的一对数，再用大数减小数，以同样的操作一直做下去，直到产生一对相等的数，这个数就是最大公约数．(2)用“等值算法”求最大公约数的程序while a ＝a －b b ＝b －a end2．割圆术用圆内接正多边形面积逐渐逼近圆的面积的算法是计算圆周率的一种方法．3.秦九韶算法:把一个n 次多项式f (x )＝a n x n ＋a n －1x n －1＋…＋a 1x ＋a 0改写成如下形式：f (x )＝a n x n ＋a n －1x n －1＋…＋a 1x ＋a 0＝(a n x n －1＋a n －1x n －2＋…＋a 1)x ＋a 0＝((a n x n －2＋a n －1x n －3＋…＋a 2)x ＋a 1)x ＋a 0＝(…((a n x ＋a n －1)x ＋a n －2)x ＋…＋a 1)x ＋a 0求多项式的值时，首先计算最内层括号内一次多项式的值，然后由内向外逐层计算一次多项式的值．这样通过一次式的反复运算，逐步得出高次多项式的值的方法称作秦九韶算法。

观察上述秦九韶算法中的n 个一次式可见，只要令⎩⎨⎧+==--kn k k n a x v v a v 10其中n k ,,2,1 =就得到了一个递推关系。

(人教a版)必修三同步课件：1.3算法案例

故加法次数要减少一次，为5－1＝4.故选D.
要点三进位制
例3 (1)把二进制数1110011(2)化为十进制数．
(2)将8进制数314706(8)化为十进制数．
解
(1)1110011(2)＝1×26＋1×25＋1×24＋0×23＋0×22＋
1×21＋1＝115. (2)314706(8)＝3×85＋1×84＋4×83＋7×82＋0×81＋6×80 ＝104902.所以，化为十进制数是104902.
所以80与36的最大公约数为4.
要点二
例2
秦九韶算法
已知一个5次多项式为f(x)＝4x5＋2x4＋3.5x3－2.6x2＋1.7x－0.8，用秦九韶算法求这个
多项式当x＝5时的值．
解
将f(x)改写为f(x)＝((((4x＋2)x＋3.5)x－2.6)x＋1.7)x－
0.8，由内向外依次计算一次多项式当x＝5时的值： v0＝4；
2．注意：当多项ห้องสมุดไป่ตู้中n次项不存在时，可将第n次项看作0· xn.
跟踪演练2
用秦九韶算法计算f(x)＝6x5－4x4＋x3－2x2－9x，需要加法(或减法)与乘法运算 ( )
的次数分别为
A．5，4 B．5，5 C．4，4 D．4，5 答案 D
解析
n次多项式需进行n次乘法；若各项均不为零，则需进
行n次加法，缺一项就减少一次加法运算．f(x)中无常数项，
v2x＋an－3
vn－1x＋a0 n个一次多项式
4．进位制
运算方便进位制是人们为了_____和_________ k进一”就是k进制，k进计数而约定的记数系统，“满
制的基数是k.把十进制转化为k进制数时，通常用除k取余法．

高中数学算法案例-进位制(公开课)教案新人教A版必修3

必修3第一章1.3算法案例:案例3进位制[教学目标]：（1）了解各种进位制与十进制之间转换的规律，会利用各种进位制与十进制之间的联系进行各种进位制之间的转换。

（2）学习各种进位制转换成十进制的计算方法，研究十进制转换为各种进位制的除k 去余法，并理解其中的数学规律。

[教学重点]各进位制表示数的方法及各进位制之间的转换[教学难点]除k取余法的理解[情感态度价值观] 学生通过合作完成任务，领悟十进制，二进制的特点，了解计算机与二进制的联系，进一步认识到计算机与数学的联系,培养他们的合作精神和严谨的态度。

[教学方法] 讲解法、尝试法、归纳法、讨论法、[教学用具]多媒体电脑[学法] 学习各种进位制特点的同时探讨进位制表示数与十进制表示数的区别与联系，熟悉各种进位制表示数的方法，从而理解十进制转换为各种进位制的除k取余法。

[教学过程]一、创设情景，揭示课题辗转相除法和更相减损术，是求两个正整数的最大公约数的算法，秦九韶算法是求多项式的值的算法，将这些算法转化为程序，就可以由计算机来完成相关运算。

人们为了计数和运算方便，约定了各种进位制，本节课我们来共同学习《进位制》你都了解那些进位制？比如说？在日常生活中，我们最熟悉、最常用的是十进位制，据说这与古人曾以手指计数有关；由于计算机的计算与记忆元件特点，计算机上通用的是二进位制；一周七天是七进位；一年十二个月〔生肖、一打〕是十二进制；旧式的称是十六进制；〔老称一斤为16两，故而有了半斤八两之说〕、24进制〔节气〕一小时六十分、角度的单位是六十进位制。

二进制是有德国数学家莱布尼兹发明的。

第一台计算机ENIAC〔埃尼阿克〕用的就是十进制。

计算机之父冯·诺伊曼研究后，提出改进意见，用二进制替代十进制。

主要原因①二进制只有0和1两个数字，要得到两种不同稳定状态的电子器件很容易，而且制造简单，可靠性高；②各种计数法中，二进制运算规那么简单。

如：十进制乘法叫九九表，二进制只有4句。

2018年高中数学人教A版必修3第1章算法初步1.3.2习题含解析

人教版2018-2019学年高中数学必修 3习题第2课时进位制课时过关能力提升13.33 ⑷是（）A.十进制数 C.三进制数2•下列写法正确的是 A.858（8）B.865（7）C.121（3）D.68（6）解析:k 进制中各位上的数字均小于k,故A,B,D 错误•3•已知k 进制数32501 （k ）,则k 不可能是（）A.5B.6C.7D.84.101（2）转化为十进制数是（）A.2B.5C.20D.1012105.下列各数中最大的是（）A.110（2）B.18C.16（8）D.20（5）解析：| 110（2）=1 X22+ 1 X21 + 0疋0= 6;16（8）=1 ^81+6X8°= 14;20（5）= 2^51+0X5°= 10.则最大数是答案：|B6.312⑷化为十进制数后的个位数字是_________ . 2107.把十进制数93化为二进制数为 _______ 解析］以2作为除数相应得出的除法算式为、基础巩固B.四进制数 D.二进制数18.I即93=1011101 (2) 答案：| 1011101 (2)8.二进制数中的最大四位数化为十进制数是_____________解析：最大的四位二进制数是 1111（2），化为十进制数为1怎3+ 1怎2+ 1 >2+1 = 15. 答案：| 159•把98（5）转化为九进制数为 __________ .—鞘---------- 11o解析：98（5）= 9拓 +8拓=53,故 98（5）=58（9）. 答案:58（9）10.求将127（8）化为六进制数时，最高数位上的数字• 解：T 127（沪1 X82+2 X8+7=87,「. 127（8）=223（6）.解析:3|血殛3] 63 A 21 0 3TT Q 3]T 10 1答案：|D3.已知k 进制数132与十进制数30相等，那么k 等于（）A.-7B.4C.-7 或 4D.7解析：|由题意得1乂2+3 *+2 >°=30，即k 2+ 3k-28=0,解得k=4或k=- 7（舍）.故选B. 答案：B 4.计算机中常用的十六进制是逢16进1的数制，采用数字0— 9和字母A — F 共16个记数符号，这些十八进制 0 1 2 3 4 56789 A B C D E F 十进制0 1 2 3 4 5 6 7 8 9101112131415例如，用十六进制表示：E+D = 1B ，则A X B = （） A.6EB.72C.5FD.B0•••127（ 8）化为六进制数后的最高数位上的数字是 2.二、能力提升11.01（9）化为十进制数为（） A.9B.11C.82解析：101（9）=1 X92+0 X91+1 >90= 82. 答案：|C2.把十进制数189化为三进制数，则末位数是（D.1010 25.21（7）+ 個4）= ___ .1010★ 6.古时候，当边境有敌人入侵时，守边的官兵通过在烽火台上点火向国内报告.如图，烽火台上点火表示二进制数1,不点火表示数字0,约定二进制数对应十进制的单位是 1 000,请你计算一下，这组烽火台表示有 ___________________ 名敌人入侵.解析:：由题图可知这组烽火台表示的二进制数为11011,它表示的十进制数为11011（2）= 27,因为对应十进制的单位是1000，所以入侵敌人的人数为27000.答案 :|27 0007.已知175（8）=120+r,求正整数r. 解：|175（8）=1 X82+7 X81 + 5 X8°=125,••• 125=120+r. ••• r= 5,即所求正整数r 为5.★ 8.已知44（紆=36把67（k）转化为十进制数. 解：|由题意得36=4>k1 + 4>k0,^ k= 8.故67（k）= 67（8）=6 4+7 X°=55.。

高中数学必修三课后习题答案

高中数学必修三课后习题答案第一章算法初步 1．1算法与程序框图练习（P5） 1、算法步骤：第一步，给定一个正实数r .第二步，计算以r 为半径的圆的面积2S r π=.第三步，得到圆的面积S .2、算法步骤：第一步，给定一个大于1的正整数n .第二步，令1i =.第三步，用i 除n ，等到余数r .第四步，判断“0r =”是否成立. 若是，则i 是n 的因数；否则，i 不是n 的因数. 第五步，使i 的值增加1，仍用i 表示.第六步，判断“i n >”是否成立. 若是，则结束算法；否则，返回第三步.练习（P19）算法步骤：第一步，给定精确度d ，令1i =.的到小数点后第i 位的不足近似值，赋给a 的到小数点后第i 位的过剩近似值，赋给b . 第三步，计算55b am =-.第四步，若m d <，则得到5a；否则，将i 的值增加1，仍用i 表示.返回第二步. 第五步，输出5a.程序框图：习题1.1 A 组（P20）1、下面是关于城市居民生活用水收费的问题.为了加强居民的节水意识，某市制订了以下生活用水收费标准：每户每月用水未超过7 m 3时，每立方米收费1.0元，并加收0.2元的城市污水处理费；超过7m 3的部分，每立方收费1.5元，并加收0.4元的城市污水处理费.设某户每月用水量为x m 3，应交纳水费y 元，那么y 与x 之间的函数关系为 1.2,071.9 4.9,7x x y x x ≤≤⎧=⎨->⎩我们设计一个算法来求上述分段函数的值.算法步骤：第一步：输入用户每月用水量x .第二步：判断输入的x 是否不超过7. 若是，则计算 1.2y x =；若不是，则计算 1.9 4.9y x =-.第三步：输出用户应交纳的水费y .程序框图：2、算法步骤：第一步，令i =1，S=0.第二步：若i ≤100成立，则执行第三步；否则输出S. 第三步：计算S=S+i 2.第四步：i = i +1，返回第二步.程序框图：3、算法步骤：第一步，输入人数x ，设收取的卫生费为m 元.第二步：判断x 与3的大小. 若x >3，则费用为5(3) 1.2m x =+-⨯；若x ≤3，则费用为5m =.第三步：输出m .程序框图：B 组 1、算法步骤：第一步，输入111222,,,,,a b c a b c ..第二步：计算21121221b c b c x a b a b -=-.第三步：计算12211221a c a c y ab a b -=-.第四步：输出,x y .程序框图：INPUT “a ，b=”；a ，bsum=a+b diff=a －b pro=a*b quo=a/bPRINT sum ，diff ，pro ，quoEND2、算法步骤：第一步，令n =1第二步：输入一个成绩r ，判断r 与6.8的大小. 若r ≥6.8，则执行下一步；若r<6.8，则输出r ，并执行下一步.第三步：使n 的值增加1，仍用n 表示.第四步：判断n 与成绩个数9的大小. 若n ≤9，则返回第二步；若n >9，则结束算法.程序框图：说明：本题在循环结构的循环体中包含了一个条件结构.1．2基本算法语句练习（P24） 1、程序：2、程序：3、程序：练习（P29） 1、程序：INPUT “a ，b ，c=”；a ，b ，cIF a+b>c AND a+c>b AND b+c>a THEN PRINT “Yes.” ELSEPRINT “No.” END IF INPUT “a ，b ，c=”；a ，b ，cp=(a+b+c)/2 s=SQR(p*(p －a) *(p －b) *(p －c)) PRINT “s=”；s END INPUT “F=”；F C=(F －32)*5/9 PRINT “C=”；C END4、程序： INPUT “a ，b ，c=”；a ，b ，csum=10.4*a+15.6*b+25.2*c PRINT “sum =”；sum END2、本程序的运行过程为：输入整数x . 若x 是满足9<x <100的两位整数，则先取出x 的十位，记作a ，再取出x 的个位，记作b ，把a ，b 调换位置，分别作两位数的个位数与十位数，然后输出新的两位数. 如输入25，则输出52. 34练习（P32） 1 2习题1.2 A 组（P33）1、1(0)0(0)1(0)x x y x x x -+<⎧⎪==⎨⎪+>⎩23、程序：习题1.2 B 组（P33） 1、程序：23 41．3算法案例练习（P45） 1、（1）45；（2）98；（3）24；（4）17. 2、2881.75.3、2200811111011000=（），820083730=（）习题1.3 A 组（P48） 1、（1）57；（2）55. 2、21324.3、（1）104；（2）7212（）（3）1278；（4）6315（）.4、习题1.3 B 组（P48）1、算法步骤：第一步，令45n =，1i =，0a =，0b =，0c =.第二步，输入()a i .第三步，判断是否0()60a i ≤<. 若是，则1a a =+，并执行第六步. 第四步，判断是否60()80a i ≤<. 若是，则1b b =+，并执行第六步. 第五步，判断是否80()100a i ≤≤. 若是，则1c c =+，并执行第六步. 第六步，1i i =+. 判断是否45i ≤. 若是，则返回第二步.2、如“出入相补”——计算面积的方法，“垛积术”——高阶等差数列的求和方法，等等. 第二章复习参考题A组（P50）1、（1）程序框图：程序：1、（2）程序框图：程序：2、见习题1.2 B组第1题解答.INPUT “x=”；x IF x<0 THENy=0ELSEIF x<1 THENy=1ELSEy=xEND IFEND IFPRINT “y=”；y ENDINPUT “x=”；x IF x<0 THENy=（x＋2）＾2 ELSEIF x=0 THENy=4ELSEy=（x－2）＾2 END IFEND IFPRINT “y=”；y END34、程序框图：程序：INPUT “t=0”；t IF t<0 THEN PRINT “Please input again.”ELSE IF t>0 AND t<=180 THENy=0.2ELSEIF （t －180） MOD 60＝0 THENy=0.2＋0.1*（t-180）／60ELSEy=0.2＋0.1*（（t-180）＼60＋1）END IFEND IFPRINT “y=”；yEND IF END INPUT “n=”；n i=1 S=0WHILE i<=n S=S+1／i i=i+1 WENDPRINT “S=”；S END5、（1）向下的运动共经过约199.805 m （2）第10次着地后反弹约0.098 m （3）全程共经过约299.609 m 第二章复习参考题B 组（P35）1、 2、3、算法步骤：第一步，输入一个正整数x 和它的位数n . 第二步，判断n 是不是偶数，如果n 是偶数，令2n m =;如果n 是奇数，令12n m -=. 第三步，令1i =i=100 sum=0 k=1 WHILE k<=10 sum=sum+i i=i ／2 k=k+1 WEND PRINT “（1）”；sum PRINT “（2）”；i PRINT “（3）”；2*sum －100 ENDINPUT “n=”；n IF n MOD 7=0 THEN PRINT “Sunday ” END IF IF n MOD 7=1 THEN PRINT “Monday ” END IF IF n MOD 7=2 THEN PRINT “Tuesday ” END IF IF n MOD 7=3 THEN PRINT “Wednesday ” END IF IF n MOD 7=4 THEN PRINT “Thursday ” END IF IF n MOD 7=5 THEN PRINT “Friday ” END IF IF n MOD 7=6 THEN PRINT “Saturday ” END IF END第四步，判断x 的第i 位与第(1)n i +-位上的数字是否相等. 若是，则使i 的值增加1，仍用i 表示；否则，x 不是回文数，结束算法.第五步，判断“i m >”是否成立. 若是，则n 是回文数，结束算法；否则，返回第四步.第二章统计 2．1随机抽样练习（P57）1、.况之间有误差. 如抽取的部分个体不能很好地代表总体，那么我们分析出的结果就会有偏差. 2、（1）抽签法：对高一年级全体学生450人进行编号，将学生的名字和对应的编号分别写在卡片上，并把450张卡片放入一个容器中，搅拌均匀后，每次不放回地从中抽取一张卡片，连续抽取50次，就得到参加这项活动的50名学生的编号. （2）随机数表法：第一步，先将450名学生编号，可以编为000,001， (449)第二步，在随机数表中任选一个数. 例如选出第7行第5列的数1（为了便于说明，下面摘取了附表的第6～10行）.16 22 77 94 39 49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 64 84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76 63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79 33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54 57 60 86 32 44 09 47 27 96 54 49 17 46 09 62 90 52 84 77 27 08 02 73 43 28第三步，从选定的数1开始向右读，得到一个三位数175，由于175<450，说明号码175在总体内，将它取出；继续向右读，得到331，由于331<450，说明号码331在总体内，将它取出；继续向右读，得到572，由于572>450，将它去掉. 按照这种方法继续向右读，依次下去，直到样本的50个号码全部取出，这样我们就得到了参加这项活动的50名学生. 3、用抽签法抽取样本的例子：为检查某班同学的学习情况，可用抽签法取出容量为5的样本. 用随机数表法抽取样本的例子：部分学生的心理调查等.抽签法能够保证总体中任何个体都以相同的机会被选到样本之中，因此保证了样本的代表性.4、与抽签法相比，随机数表法抽取样本的主要优点是节省人力、物力、财力和时间，缺点是所产生的样本不是真正的简单样本. 练习（P59）1、系统抽样的优点是：（1）简便易行；（2）当对总体结构有一定了解时，充分利用已有信息对总体中的个体进行排队后再抽样，可提高抽样调查；（3）当总体中的个体存在一种自然编号（如生产线上产品的质量控制）时，便于施行系统抽样法.系统抽样的缺点是：在不了解样本总体的情况下，所抽出的样本可能有一定的偏差. 2、（1）对这118名教师进行编号；（2）计算间隔1187.37516k==，由于k不是一个整数，我们从总体中随机剔除6个样本，再来进行系统抽样. 例如我们随机剔除了3,46,59,57,112,93这6名教师，然后再对剩余的112位教师进行编号，计算间隔7k=；（3）在1～7之间随机选取一个数字，例如选5，将5加上间隔7得到第2个个体编号12，再加7得到第3个个体编号19，依次进行下去，直到获取整个样本.3、由于身份证（18位）的倒数第二位表示性别，后三位是632的观众全部都是男性，所以这样获得的调查结果不能代表女性观众的意见，因此缺乏代表性.练习（P62）1、略2、这种说法有道理，因为一个好的抽样方法应该能够保证随着样本容量的增加，抽样调查结果会接近于普查的结果. 因此只要根据误差的要求取相应容量的样本进行调查，就可以节省人力、物力和财力.3、可以用分层抽样的方法进行抽样. 将麦田按照气候、土质、田间管理水平的不同而分成不同的层，然后按照各层麦田的面积比例及样本容量确定各层抽取的面积，再在各层中抽取个体（这里的个体是单位面积的一块地）.习题2.1 A组（P63）1、产生随机样本的困难：（1）很难确定总体中所有个体的数目，例如调查对象是生产线上生产的产品.（2）成本高，要产生真正的简单随机样本，需要利用类似于抽签法中的抽签试验来产生非负整值随机数.（3）耗时多，产生非负整数值随机数和从总体中挑选出随机数所对的个体都需要时间.2、调查的总体是所有可能看电视的人群.学生A的设计方案考虑的人数是：上网而且登录某网址的人群，那些不能上网的人群，或者不登录某网址的人群就被排除在外了. 因此A方案抽取的样本的代表性差.学生B的设计方案考虑的人群是小区内的居民，有一定的片面性. 因此B方案抽取的样本的代表性差.学生C的设计方案考虑的人群是那些有电话的人群，也有一定的片面性. 因此C方案抽取的样本的代表性.所以，这三种调查方案都有一定的片面性，不能得到比较准确的收视率.3、（1）因为各个年级学习任务和学生年龄等因素的不同，影响各年级学生对学生活动的看法，所以按年级分层进行抽样调查，可以得到更有代表性的样本.（2）在抽样的过程中可能遇到的问题如敏感性问题：有些学生担心提出意见对自己不利；又如不响应问题：由于种种原因，有些学生不能发表意见；等等.（3）前面列举的两个问题都可能导致样本的统计推断结果的误差.（4）为解决敏感性问题，可以采用阅读与思考栏目“如何得到敏感性问题的诚实反应”中的方法设计调查问卷；为解决不响应问题，可以事先向全体学生宣传调查的意义，并安排专人负责发放和催收调查问卷，最大程度地回收有效调查问卷.4、将每一天看作一个个体，则总体由365天组成. 假设要抽取50个样本，将一年中的各天按先后次序编号为0～364天用简单随机抽样设计方案：制作365个号签，依次标上0～364. 将号签放到容器内充分搅拌均匀，从容器中任意不放回取出50个号签. 以签上的号码所对应的那些天构成样本，检测样本中所有个体的空气质量.用系统抽样设计抽样方案：先通过简单随机抽样方法从365天中随机抽出15天，再把剩下的350天重新按先后次序编号为0～349. 制作7个分别标有0～7的号签，放在容器中充分搅拌均匀. 从容器中任意取出一个号签，设取出的号签的编号为a，则编号为7(050)a k k +≤<所对应的那些天构成样本，检测样本中所有个体的空气质量.显然，系统抽样方案抽出的样本中个体在一年中排列的次序更规律，因此更好实施，更受方案的实施者欢迎.5、田径队运动员的总人数是564298+=（人），要得到28人的样本，占总体的比例为27.于是，应该在男运动员中随机抽取256167⨯=（人），在女运动员中随机抽取281612-=（人）.这样我们就可以得到一个容量为28的样本.6、以10为分段间隔，首先在1～10的编号中，随机地选取一个编号，如6，那么这个获奖者奖品的编号是：6,16,26,36,46.7、说明：可以按年级分层抽样的方法设计方案. 习题2.1 B 组（P64）1、说明：可以按年级分层抽样的方法设计方案，调查问卷由学生所关心的问题组成. 例如：（1）你最喜欢哪一门课程？（2）你每月的零花钱平均是多少？（3）你最喜欢看《新闻联播》吗？（4）你每天早上几点起床？（5）你每天晚上几点睡觉？要根据统计的结果和具体的情况解释结论,主要从引起结论的可能原因及结论本身含义来解释.2、说明：这是一个开放性的题目，没有一个标准的答案. 2．2用样本估计总体练习（P71） 1、说明：由于样本的极差为364.41362.51 1.90-=，取组距为0.19，将样本分为10组. 可以按照书上的方法制作频率分布表、频率分布直观图和频率折线图. 2、说明：此题目属于应用题，没有标准的答案.3、茎叶图为：由该图可以看出30名工人的日加工零件个数稳定在120件左右. 练习（P74）这里应该采用平均数来表示每一个国家项目的平均金额，因为它能反应所有项目的信息. 但平均数会受到极端数据2000万元的影响，所以大多数项目投资金额都和平均数相差比较大.练习（P79）1、甲乙两种水稻6年平均产量的平均数都是900，但甲的标准差约等于23.8，乙的标准差约等于41.6，所以甲的产量比较稳定.2、（1）平均重量496.86x ≈，标准差 6.55s ≈.（2）重量位于(,)x s x s -+之间有14袋白糖，所占的百分比约为66.67％.3、（1）略. （2）平均分19.25x ≈，中位数为15.2，标准差12.50s ≈.这些数据表明这些国家男性患该病的平均死亡率约为19.25，有一半国家的死亡率不超过15.2，15.2x >说明存在大的异常数据，值得关注. 这些异常数据使标准差增大. 习题2.2 A 组（P81） 1、（1）茎叶图为：（2）汞含量分布偏向于大于1.00 ppm 的方向，即多数鱼的汞含量分布在大于1.00 ppm 的区域. （3）不一定. 因为我们不知道各批鱼的汞含量分布是否都和这批鱼相同. 即使各批鱼的汞含量分布相同，上面的数据只能为这个分布作出估计，不能保证平均汞含量大于1.00 ppm. （4）样本平均数 1.08x ≈，样本标准差0.45s ≈.（5）有28条鱼的汞含量在平均数与2倍标准差的和（差）的范围内.2比较短，所以在这批棉花中混进了一些次品.3、说明：应该查阅一下这所大学的其他招生信息，例如平均数信息、最低录取分数线信息等. 尽管该校友的分数位于中位数之下，而中位数本身并不能提供更多录取分数分布的信息.在已知最低录取分数线的情况下，很容易做出判断；在已知平均数小于中位数很多，则说明最低录取分数线较低，可以推荐该校友报考这所大学，否则还要获取其他的信息（如标准差的信息）来做出判断. 4、说明：（1）对，从平均数的角度考虑；（2）对，从标准差的角度考虑；（3）对，从标准差的角度考虑；（4）对，从平均数和标准差的角度考虑； 5、（1）不能. 因为平均收入和最高收入相差太多，说明高收入的职工只占极少数. 现在已知知道至少有一个人的收入为50100x =万元，那么其他员工的收入之和为4913.55010075ii x==⨯-=∑（万元）每人平均只有1.53. 如果再有几个收入特别高者，那么初进公司的员工的收入将会很低. （2）不能，要看中位数是多少.（3）能，可以确定有75％的员工工资在1万元以上，其中25％的员工工资在3万元以上.（4）收入的中位数大约是2万. 因为有年收入100万这个极端值的影响，使得年平均收入比中位数高许多.6、甲机床的平均数=1.5x 甲，标准差=1.2845s 甲；乙机床的平均数 1.2z y =，标准差0.8718z s =. 比较发现乙机床的平均数小而且标准差也比较小，说明乙机床生产出的次品比甲机床少，而且更为稳定，所以乙机床的性能较好. 7、（1）总体平均数为199.75，总体标准差为95.26. （2）可以使用抓阄法进行抽样. 样本平均数和标准差的计算结果和抽取到的样本有关. （3）（4）略习题2.2 B 组（P82）1、（1）由于测试1T 的标准差小，所以测试1T 结果更稳定，所以该测试做得更好一些. （2）由于2T 测出的值偏高，有利于增强队员的信心，所以应该选择测试2T .2、说明：此题需要在本节开始的时候就布置，先让学生分头收集数据，汇总所收集的数据才能完成题目.2．3变量间的相关关系练习（P85）1、从已经掌握的知识来看，吸烟会损害身体的健康. 但除了吸烟之外，还有许多其他的随机因素影响身体健康，人体健康是很多因素共同作用的结果. 我们可以找到长寿的吸烟者，也更容易发现由于吸烟而引发的患病者，所以吸烟不一定引起健康问题. 但吸烟引起健康问题的可能性大，因此“健康问题不一定是由吸烟引起的，所以可以吸烟”的说法是不对的.2、从现在我们掌握的知识来看，没有发现根据说明“天鹅能够带来孩子”，完全可能存在既能吸引天鹅和又使婴儿出生率高的第3个因素（例如独特的环境因素），即天鹅与婴儿出生率之间没有直接的关系，因此“天鹅能够带来孩子”的结论不可靠.而要证实此结论是否可靠，可以通过试验来进行. 相同的环境下将居民随机地分为两组，一组居民和天鹅一起生活（比如家中都饲养天鹅），而另一组居民的附近不让天鹅活动，对比两组居民的出生率是否相同. 练习（P92）1、当0x =时，147.767y =，这个值与实际卖出的热饮杯数150不符，原因是：线性回归方程中的截距和斜率都是通过样本估计的，存在随机误差，这种误差可以导致预测结果的偏差；即使截距和斜率的估计没有误差，也不可能百分之百地保证对应于x ，预报值y 能够等于实际值y . 事实上：y bx a e =++. （这里e 是随机变量，是引起预报值y 与真实值（1）散点图如下： y 之间的误差的原因之一，其大小取决于e 的方差.）2、数据的散点图为：从这个散点图中可以看出，鸟的种类数与海拔高度应该为正相关（事实上相关系数为0.793）. 但是从散点图的分布特点来看，它们之间的线性相关性不强. 习题2.3 A 组（P94）1、教师的水平与学生的学习成绩呈正相关关系. 又如，“水涨船高”“登高望远”等.2、（3）基本成正相关关系，即食品所含热量越高，口味越好.（4）因为当回归直线上方的食品与下方的食品所含热量相同时，其口味更好. 3、（1）散点图如下：（2）回归方程为：0.66954.933y x =+.（2）回归直线如下图所示：（3）加工零件的个数与所花费的时间呈正线性相关关系. 4、（1）散点图为：（2）回归方程为：0.546876.425y x =+.（3）由回归方程知，城镇居民的消费水平和工资收入之间呈正线性相关关系，即工资收入水平越高，城镇居民的消费水平越高. 习题2.3 B 组（P95） 1、（1）散点图如下：（2）回归方程为： 1.44715.843y x =-.（3）如果这座城市居民的年收入达到40亿元，估计这种商品的销售额为42.037y ≈（万元）. 2、说明：本题是一个讨论题，按照教科书中的方法逐步展开即可.第二章复习参考题A 组（P100）1、A .2、（1）该组的数据个数，该组的频数除以全体数据总数；（2）nmN. 3、（1）这个结果只能说明A 城市中光顾这家服务连锁店的人比其他人较少倾向于选择咖啡色，因为光顾连锁店的人使一种方便样本，不能代表A 城市其他人群的想法. （2）这两种调查的差异是由样本的代表性所引起的. 因为A 城市的调查结果来自于该市光顾这家服装连锁店的人群，这个样本不能很好地代表全国民众的观点.4、说明：这是一个敏感性问题，可以模仿阅读与思考栏目“如何得到敏感性问题的诚实反应”来设计提问方法.5、表略. 可以估计出句子中所含单词的分布，以及与该分布有关的数字特征，如平均数、标准差等.6、（1）可以用样本标准差来度量每一组成员的相似性，样本标准差越小，相似程度越高. （2）A 组的样本标准差为 3.730A S ≈，B 组的样本标准差为11.789B S ≈. 由于专业裁判给分更符合专业规则，相似程度应该高，因此A 组更像是由专业人士组成的.7、（1）中位数为182.5，平均数为217.1875.（2）这两种数字特征不同的主要原因是，430比其他的数据大得多，应该查找430是否由某种错误而产生的. 如果这个大数据的采集正确，用平均数更合适，因为它利用了所有数据的信息；如果这个大数据的采集不正确，用中位数更合适，因为它不受极端值的影响，稳定性好. 8、（1）略.（2）系数0.42是回归直线的斜率，意味着：对于农村考生，每年的入学率平均增长0.42％.（3）城市的大学入学率年增长最快. 说明：（4）可以模仿（1）（2）（3）的方法分析数据.第二章复习参考题B 组（P101）1、频率分布如下表：从表中看出当把指标定为17.46千元时，月65％的推销员经过努力才能完成销售指标.2、（1）数据的散点图如下：（2）用y 表示身高，x 表示年龄，则数据的回归方程为 6.31771.984y x =+. （3）在该例中，斜率6.317表示孩子在一年中增加的高度.（4）每年身高的增长数略. 3～16岁的身高年均增长约为6.323 cm. （5）斜率与每年平均增长的身高之间之间近似相等.第三章概率3．1随机事件的概率练习（P113） 1、（1）试验可能出现的结果有3个，两个均为正面、一个正面一个反面、两个均为反面. （2）通过与其他同学的结果汇总，可以发现出现一个正面一个反面的次数最多，大约在50次左右，两个均为正面的次数和两个均为反面的次数在25次左右. 由此可以估计出现一个正面一个反面的概率为0.50，出现两个均为正面的概率和两个均为反面的概率均为0.25. 2、略 3、（1）例如：北京四月飞雪；某人花两元钱买福利彩票，中了特等奖；同时抛10枚硬币，10枚都正面朝上.（2）例如：在王府井大街问路时，碰到会说中文的人；去烤鸭店吃饭的顾客点烤鸭；在1～1000的自然数任选一个数，选到的数大于1. 练习（P118）1、说明：例如，计算机键盘上各键盘的安排，公交线路及其各站点的安排，抽奖活动中各奖项的安排等，其中都用到了概率. 学生可能举出各种各样的例子，关键是引导他们正确分析例子中蕴涵的概率思想.2、通过掷硬币或抽签的方法，决定谁先发球，这两种方法都是公平的. 而猜拳的方法不太公平，因为出拳有时间差，个人反应也不一样.3、这种说法是错误的. 因为掷骰子一次得到2是一个随机事件，在一次试验中它可能发生也可能不发生. 掷6次骰子就是做6次试验，每次试验的结果都是随机的，可能出现2也可能不出现2，所以6次试验中有可能一次2都不出现，也可能出现1次，2次，…，6次. 练习（P121）1、0.72、0.6153、0.44、D5、B 习题3.1 A 组（P123） 1、D . 2、（1）0；（2）0.2；（3）1.3、（1）430.067645≈；（2）900.140645≈；（3）7010.891645-≈.4、略5、0.136、说明：本题是想通过试验的方法，得到这种摸球游戏对先摸者和后摸者是公平的结论. 最好把全班同学的结果汇总，根据两个事件出现的频率比较近，猜测在第一种情况下摸到红球的概率为110，在第二种下也为110. 第4次摸到红球的频率与第1次摸到红球的频率应该相差不远，因为不论哪种情况，第4次和第1次摸到红球的概率都是1 10.习题3.1 B组（P124）1、D.2、略. 说明：本题是为了学生根据实际数据作出一些推断. 一般我们假定每个人的生日在12个月中哪一个月是等可能的，这个假定是否成立，引导学生通过收集的数据作出初步的推断.3．2古典概率练习（P130）1、110. 2、17. 3、16.练习（P133）1、38，38.2、（1）113；（2）1213；（3）14；（4）313；（5）0；（6）213；（7）12；（8）1.说明：模拟的方法有两种.（1）把1～52个自然数分别与每张牌对应，再用计算机做模拟试验.（2）让计算机分两次产生两个随机数，第一次产生1～4的随机数，代表4个花色；第二次产生1～13的随机数，代表牌号.3、（1）不可能事件，概率为0；（2）随机事件，概率为49；（3）必然事件，概率为1；（4）让计算机产生1～9的随机数，1～4代表白球，5～9代表黑球.4、（1）16；（2）略；（3）应该相差不大，但会有差异. 存在差异的主要原因是随机事件在每次试验中是否发生是随机的，但在200次试验中，该事件发生的次数又是有规律的，所以一般情况下所得的频率与概率相差不大.习题3.2 A组（P133）1、游戏1：取红球与取白球的概率都为12，因此规则是公平的.游戏2：取两球同色的概率为13，异色的概率为23，因此规则是不公平的.游戏3：取两球同色的概率为12，异色的概率为12，因此规则是公平的.2、第一位可以是1～9这9个数字中的一个，第二位可以是0～9这10个数字中的一个，所以（1）190；（2）18919090-=；（3）9919010-=3、（1）0.52；（2）0.18.4、（1）12；（2）16；（3）56；（4）16.5、（1）25；（2）825.6、（1）920；（2）920；（3）12.习题3.2 B组（P134）1、（1）13；（2）14.2、（1）35；（2）310；（3）910.说明：（3）先计算该事件的对立事件发生的概率会比较简单.3、具体步骤如下：①建立概率模型. 首先要模拟每个人的出生月份，可用1,2,…,11,12表示月份，用产生取整数值的随机数的办法，随机产生1～12之间的随机数. 由于模拟的对象是一个有10个人的集体，故把连续产生的10个随机数作为一组模拟结果，可模拟产生100组这样的结果.②进行模拟试验. 可用计算器或计算机进行模拟试验.如使用Excel软件，可参看教科书125页的步骤，下图是模拟的结果：其中，A,B,C,D,E,F,G,H,I,J的每一行表示对一个10人集体的模拟结果. 这样的试验一共做了100次，所以共有100行，表示随机抽取了100个集体.③统计试验的结果. K,L,M,N列表示统计结果. 例如，第一行前十列中至少有两个数相同，表示这个集体中至少有两个人的生日在同一月. 本题的难点是统计每一行前十列中至少有两个数相同的个数. 由于需要判断的条件态度，所以用K,L,M三列分三次完成统计.其中K列的公式为“=IF(OR(A1=B1，A1=C1，A1=D1，A1=E1，A1=F1，A1=G1，A1=H1，A1=I1，A1=J1，B1=C1，B1=D1，B1=E1，B1=F1，B1=G1，B1=H1，B1=I1，B1=J1，C1=D1，C1=E1，C1=F1，C1=G1，C1=H1，C1=I1，C1=J1，D1=E1，D1=F1，D1=G1，D1=H1，D1=I1，D1=J1)，1，0)”，L列的公式为“=IF(OR(E1=F1，E1=G1，E1=H1，E1=I1，E1=J1，F1=G1，F1=H1，F1=I1，F1=J1，G1=H1，G1=I1，G1=J1，H1=I1，H1=J1，I1=J1)，1，0)”，M列的公式为“=IF(OR(K1=1，L1=1)，1，0)”，M列的值为1表示该行所代表的10人集体中至少有两个人的生日在同一个月. N1表示100个10人集体中至少有两个人的生日在同一个月的个数，其公式为“=SUM(M$1：M$100)”. N1除以100所得的结果0.98，就是用模拟方法计算10人集体中至少有两个人的生日在同一个月的概率的估计值. 可以看出，这个估计值很接近1.3．3几何概率。

2014-2015学年高中数学(人教版必修三)课时训练第一章 1.3.3 算法综合问题(习题课)

上图是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图，则图中判断框应填________，输出的s＝________(注：框图中的赋值等号“＝”也可以
写成“←”或“：＝”)．
解析：由题意该程序框图是求该 6 名队员在最近三场比赛中投进三分球的总数．故判断框应填： i≤6？或 i<7？，输出 s 为 a1＋a2＋a3＋a4＋a5＋a6. 答案：i<7？(或 i≤6？)
栏目链接
正解：把条件“i>＝100”修改为“i>100”．

点评：避免以上错误的关键是对循环控制条件进行检验．对一个循环语句的检验，不可能像执行循环体那样一次一次地去检验．如例4，循环次数达100次，若检验循环
栏目链接
100次是不可取的．对循环的检验可分为两步进行：首先，
(
1．在赋值语句中，“N＝N＋1”的说法正确的是 C )
A．没有意义的
B．N与N＋1相等
C．将N的原值加1再赋给N，N的值增加1 D．无法运行
2．在算法当中，有时需要进行判断，判断的结果决 B 定后面的步骤，像这样的结构称为( )
栏 ห้องสมุดไป่ตู้ 链接
A．顺序结构
B．条件结构

3．已知一个三角形的三边长分别是 a，b，c，利用公 a＋b＋c 其中p＝计式 S＝－－－ 2 算面积，设计一个算法，其框图只需( B ) A．条件结构 B．顺序结构

跟踪训练
1．求正数 a 平方根近似值的一种算法思路是这样的：第一步，确定平方根的首次近似值：a1 (a1 可以任取一个正数)． a 第二步，由代数式 b1＝求出 b1. a1 a1＋b1 第三步，取二者的算术平均值 a2＝为第二次近似值． 2 a 第四步，由方程 b2＝求出 b2 . a2 a2＋b2 第五步，取算术平均值 a3＝作为第三次近似值． 2 „„ 反复进行上述步骤，直到获得满足误差在 0.1 以内的数为止．请依照上述思路，画出相应的算法流程图．

人教版高中数学必修三第一章算法初步1.3算法案例 (教师版)【个性化辅导含答案】

人教版高中数学必修三第一章算法初步1.3算法案例（教师版）【个性化辅导含答案】算法案例____________________________________________ __________________________________________________________________________________ ______________________________________1．理解算法案例的算法步骤和程序框图.2．引导学生得出自己设计的算法程序.3. 体会算法的基本思想，提高逻辑思维能力，发展有条理地思考与数学表达能力.1．求两个正整数最大公约数的算法(1)更相减损之术(等值算法)用两数中较大的数减去较小的数，再用差数和较小的数构成新的一对数，再用大数减小数，以同样的操作一直做下去，直到产生一对相等的数，这个数就是最大公约数．(2)用“等值算法”求最大公约数的程序while a＝a－b b＝b－a end2．割圆术用圆内接正多边形面积逐渐逼近圆的面积的算法是计算圆周率的一种方法．3.秦九韶算法:初赋值v ＝a n ，用v ＝v *x ＋a n －i 实现递推循环，i 的初值为1，i ＝i ＋1记录循环次数，i ≤n 控制何时结束循环输出v .f (x )的系数a k 用一个循环语句实现输入。

（2）f (x )＝a n x n ＋a n －1xn －1＋…＋a 1x ＋a 0当x ＝x 0时，求函数值f (x 0)的算法设计。

程序框图：（3）用秦九韶算法将一个多项式(n 次)的至多()21+n n 次乘法和n 次加法运算减少为至多n 次乘法和n次加法运算，大大提高了运算效率。

类型一用更相减损术求两个正整数的最大公约数例1：求80和36的最大公约数．[解析] 当大数减小数的差等于小数时停止减法，较小的数就是两数的最大公约数．[答案] 80－36＝44，44－36＝8，36－8＝28，28－8＝20，20－8＝12，12－8＝4，8－4＝4.∴80和36的最大公约数是4.练习1：用更相减损之术分别求下列两组数的最大公约数：(1)78与36； (2)1 515与600.[答案] (1)(78,36)→(42,36)→(6,36)→(6,30)→(6,24)→(6,18) →(6,12)→(6,6)，故78与36的最大公约数为6.(2)1 515－600＝915,915－600＝315,600－315＝285,315－285＝30,285－30＝255,255－30＝225,225－30＝195,195－30＝165,165－30＝135,135－30＝105,105－30＝75,75－30＝45,45－30＝15,30－15＝15，故1 515与600的最大公约数是15.类型二用辗转相除法求两个正整数的最大公约数例2：用辗转相除法求546与429的最大公约数.[解析] 用辗转相除法求最大公约数步骤较少，而更相减损术虽然步骤较长，但运算简单．[答案] 546＝1×429＋117，429＝3×117＋78，117＝1×78＋39，78＝2×39，故546与429的最大公约数为39.练习1：用辗转相除法求288和123的最大公约[答案] 288＝2×123＋42，123＝2×42＋39，42＝1×39＋3，39＝13×3，故3就是288和123的最大公约数.练习2：用辗转相除法求355和60的最大公约数．[答案] 355＝5×60＋55，60＝1×55＋5，55＝11×5，故5就是355和60的最大公约数.类型三用秦九韶算法求多项式的值例3：用秦九韶算法求多项式f(x)＝x5＋0.11x3－0.15x－0.04当x＝0.3时的值．[解析](1)用秦九韶算法求多项式的值，首先要将多项式改写，然后由内向外逐次计算. 由于下一次计算要用到上一次的结果，故应认真、细心，确保每个中间结果的准确性．(2)当多项式中有几项不存在时，可将这几项的系数看成是0，即0×x n.[答案]将f(x)写为：f(x)＝x5＋0×x4＋0.11x3＋0×x2－0.15x－由秦九韶算法的递推公式，得v0＝1，v1＝v0×0.3＋0＝0.3，v2＝v1×0.3＋0.11＝0.2，v3＝v2×0.3＋0＝0.06，v＝v3×0.3－0.15＝－0.132，4v5＝v4×0.3－0.04＝－0.079 6，所以当x＝0.3时，多项式的值为－0.079 6.练习1：已知函数f(x)＝x3－2x2－5x＋6，用秦九韶算法求f(10)的值．[答案] 由秦九韶法，得f(x)＝x3－2x2－5x＋6＝(x2－2x－5)x＋6＝((x－2)x－5)x＋6，当x＝10时，f(10)＝((10－2)×10－5)×10＋6＝(8×10－5)×10＋6＝75×10＋6＝756.练习2：已知函数f(x)＝x3－2x2＋5x＋6，用秦九韶算法求f(10)的值．[答案] 由秦九韶法，得f(x)＝x3－2x2＋5x＋6＝(x2－2x＋5)x＋6＝((x－2)x＋5)x＋6，当x＝10时，f(10)＝((10－2)×10＋5)×10＋6＝(8×10＋5)×10＋6＝85×10＋6＝856.练习3：已知多项式f(x)＝3x5－2x2－5x4＋3x3＋x，则f(2)＝________.[答案] 34f(x)＝3x5－2x2－5x4＋3x3＋x＝3x5－5x4＋3x3－2x2＋x＝((((3x－5)x＋3)x－2)x＋1)x，v0＝3，v1＝3×2－5＝1，v2＝1×2＋3＝5，v3＝5×2－2＝8，v4＝8×2＋1＝17，v5＝17×2＝34.∴当x＝2时，多项式的值为34.类型四求三个正整数的最大公约数例4：求三个数324、243、270的最大公约数．[解析] 求三个数的最大公约数，可先求两数的最大公约数a，然后求a与第三个数的最大公约数b，则b为所求的三数的最大公约数．该题解法可推广到求多个数的最大公约数．[答案] 324＝243×1＋81,243＝81×3＋0，则324与243的最大公约数为a＝81.又270＝81×3＋27,81＝27×3＋0，则324,243,270的最大公约数为27.练习1：求324,243和135的最大公约数．[答案] (324,243)―→(81,243)―→(81,162)―→(81,81)则324与243最大公约数为81.又(81,135)―→(81,54)―→(27,54)―→(27,27)，则81与135的最大公约数为27，∴324、243、135的最大公约数为27.类型五求两个正整数的最小公倍数例5：求375、85的最小公倍数[解析] 求两个正整数的最小公倍数，即利用它们的积除以它们的最大公约数．本题求法可推广到求多个数的情况．[答案] 先求最大公约数，375＝85×4＋35,85＝35×2＋15,35＝15×2＋5,15＝5×3＋0.∴375与85的最大公约数是5，∴375与85的最小公倍数是(375×85)÷5＝6 375.练习1：求80与36的最小公倍数．[答案] 先求最大公约数．80＝36×2＋836＝8×4＋4＝8＝4×2＋0∴80与36的最大公约数为4.∴80与36的最小公倍数是(80×36)÷4＝720.1．秦九韶算法与直接计算相比较，下列说法错误的是( )A．秦九韶算法与直接计算相比，大大节省乘法的次数，使计算量减少，并且逻辑结构简单B．秦九韶算法减少做乘法的次数，在计算机上也就加快了计算的速度C．秦九韶算法减少做乘法的次数，在计算机上也就降低了计算的速度D．秦九韶算法避免对自变量x单独做幂的计算，而是与系数一起逐次增长幂次，从而可提高计算的精度[答案] C2．用圆内接正多边形逼近圆，因而得到的圆周率总是________π的实际值．( )A．大于等于B．小于等于C．等于D．小于[答案] D3．用更相减损之术求88与24的最大公约数为( )A．2 B．7C．8 D．12[答案] C4．三个数72,120,168的最大公约数是________．[答案] 245．用秦九韶算法计算f(x)＝9x6＋3x5＋4x4＋6x3＋x2＋8x＋1，当x＝3时的值，需要进行________次乘法和________次加法运算．[答案] 6 66．已知f(x)＝x5＋x3＋x2＋x＋1，求f(3)的值．[答案] f(x)＝((((x＋0)x＋1)x＋1)x＋1)x＋1，v1＝1×3＋0＝3，v2＝3×3＋1＝10，v3＝10×3＋1＝31，v4＝31×3＋1＝94，v5＝94×3＋1＝283，∴f(3)＝((((3＋0)×3＋1)×3＋1)×3＋1)×3＋1＝283.____________________________________________ _________________________________________________________________________________ _____________________________________基础巩固一、选择题1．在秦九韶算法中用到的一种方法是()A．消元B．递推C．回代D．迭代[答案] B[解析]秦九韶算法中用到的是递推法．2．用更相减损术求294和84的最大公约数时，需要做减法的次数为()A．2 B．3C．4 D．5[答案] C[解析](84,294)→(84,210)→(84,126)→(84,42)→(42,42)，一共做了4次减法．3．用秦九韶算法求多项式f(x)＝x3－3x2＋2x－11的值时，应把f(x)变形为()A．x3－(3x＋2)x－11 B．(x－3)x2＋(2x－11)C．(x－1)(x－2)x－11 D．((x－3)x＋2)x－11[答案] D[解析]f(x)＝x3－3x2＋2x－11＝((x－3)x＋2)x －11，故选D.4．用“等值算法”可求得204与85的最大公约数是()A．15 B．17C．51 D．85[答案] B[解析]204－85＝119,119－85＝34,85－34＝51,51－34＝17,34－17＝17，∴204和85的最大公约数是17，故选B.5．根据递推公式⎩⎨⎧v 0＝a n v k ＝v k －1x ＋a n －k ，其中k ＝1,2，…，n ，可得当k ＝2时，v 2的值为( )A ．v 2＝a n x ＋a n －1B ．v 2＝(a n x ＋a n －1)x ＋a n －2C ．v 2＝(a n x ＋a n －1)xD ．v 2＝a n x ＋a n －1x[答案] B[解析] 根据秦九韶算法知，v 2＝v 1x ＋a n －2，v 1＝a n x ＋a n －1，故选B.6．用秦九韶算法求多项式f (x )＝0.5x 5＋4x 4－3x 2＋x －1，当x ＝3时的值时，先算的是( )A ．3×3B ．0.5×35C ．0.5×3＋4D ．(0.5×3＋4)×3[答案] C[解析] 把多项式表示成如下形式：f(x)＝((((0.5x＋4)x＋0)x－3)x＋1)x－1，按递推方法，由内往外，先算0.5x＋4的值，故选C.二、填空题7．117与182的最大公约数等于________．[答案]13[解析] (117,182)→(117,65)→(52,65)→(52,13)→(39,13)→(26, 13)→(13,13)，所以其最大公约数为13.8．245与75两数的最小公倍数为________．[答案] 3 675[解析]先求245与75的最大公约数．(245,75)→(170,75)→(95,75)→(20,75)→(55,20) →(35,20)→(15,20)→(5,15)→(10,5)→(5,5)．故245与75的最大公约数为5，∴245与75的最小公倍数为245×75÷5＝3 675.三、解答题9．利用更相减损之术求319和261的最大公约数．[解析]319－261＝58,261－58＝203,203－58＝145,145－58＝87,87－58＝29,58－29＝29.即(319,261)→(261,58)→(203,58)→(145,58)→(87,58)→( 58,29)→(29,29)．故319与261的最大公约数是29.能力提升一、选择题1．用秦九韶算法求多项式f(x)＝12＋35x－8x2＋79x3＋6x4＋5x5＋3x6在x＝－4的值时，v4的值为()A．－57 B．220C．－845 D．3 392[答案] B[解析]由秦九韶算法，得v0＝3，v1＝3×(－4)＋5＝－7，v2＝－7×(－4)＋6＝34，v3＝34×(－4)＋79＝－57，v4＝－57×(－4)－8＝220.2．三个数390、455、546的最大公约数是() A．65 B．91C．26 D．13[答案] D[解析]对于三个数求最大公约数时，先求其中两个数的最大公约数，再用此公约数与第三个数求出最大公约数，此时就是三个数的最大公约数.3．已知f(x)＝4x5＋3x4＋2x3－x2－x－12，用秦九韶算法求f(－2)等于()A．－1972B．1972C ．1832D ．－1832[答案] A [解析] ∵f (x )＝((((4x ＋3)x ＋2)x －1)x －1)x －12， ∴f (－2)＝((((4×(－2)＋3)×(－2)＋2)×(－2)－1)×(－2)－1)×(－2)－12＝－1972. 4．用“更相减损之术”求120与75的最大公约数时，需要做减法运算的次数为( )A ．6B ．5C ．4D ．3 [答案] C[解析] ∵(120,75)→(45,75)→(45,30)→(15,30)→(15,15)，∴120与75的最大公约数是15，共进行4次减法运算．二、填空题5．4 830与3 289的最大公约数为________．[答案]23[解析](4 830,3 289)→(1 541,3 289)→(1 541，1 748)→(1 541,207)→(1 334,207)→(1 127,207)→(920,207)→(713,207)→(506,207)→(299,20 7)→(92,207)→(92,115)→(92,23)→(69,23)→(46,23)→(23,23)．6．用秦九韶算法求多项式f(x)＝7x5＋5x4＋10x3＋10x2＋5x＋1当x＝－2时的值的算法：①第一步，x＝－2.第二步，f(x)＝7x5＋5x4＋10x3＋10x2＋5x＋1.第三步，输出f(x)．②第一步，x＝－2.第二步：f(x)＝((((7x＋5)x＋10)x＋10)x＋5)x＋1.第三步，输出f(x)．③需要计算5次乘法、5次加法．④需要计算9次乘法、5次加法．以上说法中正确的是________(填序号)．[答案]②③[解析]①是直接求解，并不是秦九韶算法，故①错．对于一元n次多项式，应用秦九韶算法需要运用n次乘法和n次加法，故③正确．三、解答题7．求1 356和2 400的最小公倍数．[解析](1 356,2 400)→(1 356,1 044)→(312，1 044)→(312,732)→(321,420)→(312，108)→(204,108)→(96,108)→(96,12)→…→(12,12)．∴1 356和2 400的最大公约数为12.∴1 356和2 400的最小公倍数为(2 400×1 356)÷12＝271 200.8．用秦九韶算法求多项式f(x)＝2＋0.35x＋1.8x2－3x3＋6x4－5x5＋x6在x＝－1时的值时，令v0＝a6，v1＝v0x＋a5，…，v t＝v5x＋a0，求v3的值．[解析]f(x)＝(((((x－5)x＋6)x－3)x＋1.8)x＋0.35)x＋2，v0＝1，v1＝v0x－5＝－6，v2＝v1x＋6＝－6×(－1)＋6＝12，v3＝v2x－3＝－15.9．有甲、乙、丙三种溶液，质量分别为147 g,343 g,133 g，现要将它们分别全部装入小瓶中，每个小瓶装入液体的质量相同，则每个小瓶最多装多少溶液？[解析]每个小瓶内溶液的质量应是147,343,133三种溶液质量的公约数，最大质量即是其最大公约数.先求147和343的最大公约数．343－147＝196,196－147＝49,147－49＝98,98－49＝49，所以147和343的最大公约数是49.再求49和133的最大公约数．133－49＝84,84－49＝35,49－35＝14，35－14＝21,21－14＝7,14－7＝7，所以49和133的最大公约数是7.所以147,343,133的最大公约数是7，即每个小瓶最多装7 g溶液．。

人教A版高中数学必修三练习：第一章算法初步1.3 算法案例含答案

分层训练·进阶冲关A组基础练(建议用时20分钟)1.在对16和12求最大公约数时,整个操作如下:16-12=4,12-4=8,8-4=4.由此可以看出12和16的最大公约数是( A )A.4B.12C.16D.82.在m=nq+r(0≤r<n)中,若k是n,r的公约数,则k m,n的公约数.( A )A.—定是B.不一定是C.一定不是D.不能确定3.有关辗转相除法下列说法正确的是 ( C )A.它和更相减损术一样是求多项式值的一种方法B.基本步骤是用较大的数m除以较小的数n得到除式m=nq+r,直至r<n 为止C.基本步骤是用较大的数m除以较小的数n得到除式m=nq+r(0≤r<n),反复进行,直到r=0为止D.以上说法皆错4.已知7 163=209×34+57,209=57×3+38,57=38×1+19,38=19×2.根据上述一系列等式,可确定7 163和209的最大公约数是( C )A.57B.3C.19D.345.把389化为四进制数,则该数的末位是 ( A )A.1B.2C.3D.46.用秦九韶算法求n次多项式f(x)=a n x n+a n-1x n-1+…+a1x+a0的值,当x=x0时,求f(x0)需要算乘方、乘法、加法的次数分别为 ( C )A.,n,nB.n,2n,nC.0,n,nD.0,2n,n7.用更相减损术求36与134的最大公约数时,第一步应为先除以2,得到18与67.8.用辗转相除法求294和84的最大公约数时,需要做除法的次数是2.9.三位七进制数表示的最大的十进制数是342.10.秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例.若输入n,x的值分别为3,3,则输出v的值为48.11.将1234(5)转化为八进制数.【解析】先将1234(5)转化为十进制数:1234(5)=1×53+2×52+3×51+4×50=194.再将十进制数194转化为八进制数:所以1234(5)=302(8).12.用秦九韶算法计算多项式f(x)=x6-12x5+60x4-160x3+240x2-192x+64,当x=2时的值.【解析】将f(x)改写为f(x)=(((((x-12)x+60)x-160)x+240)x-192)x+64, v0=1,v1=1×2-12=-10,v2=-10×2+60=40,v3=40×2-160=-80,v4=-80×2+240=80,v5=80×2-192=-32,v6=-32×2+64=0.所以f(2)=0,即x=2时,原多项式的值为0.B组提升练(建议用时20分钟)13.下列各数中最小的数为 ( A )A.101011(2)B.1210(3)C.110(8)D.68(12)14.《九章算术》是中国古代的数学专著,其中的一段话“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也,以等数约之”用程序框图表示如图,那么这个程序的作用是( B )A.求两个正数a,b的最小公倍数B.求两个正数a,b的最大公约数C.判断其中一个正数是否能被另一个正数整除D.判断两个正数a,b是否相等15.用秦九韶算法求多项式f(x)=1+2x+x2-3x3+2x4在x=-1时的值,v2的结果是 ( D )A.-4B.-1C.5D.616.396与270的最大公约数与最小公倍数分别为18,5 940.17.已知一个k进制的数123(k)与十进制的数38相等,求k的值. 【解析】由123(k)=1×k2+2×k1+3×k0=k2+2k+3,得k2+2k+3=38,所以k2+2k-35=0,所以k=5或k=-7(舍),所以k=5.18.用秦九韶算法求多项式f(x)=12+35x-8x2+79x3+6x4+5x5+3x6,当x=-4时,v4的值.【解析】依据秦九韶算法有v0=a6=3,v1=v0x+a5=3×(-4)+5=-7,v2=v1x+a4=-7×(-4)+6=34,v3=v2x+a3=34×(-4)+79=-57,v4=v3x+a2=-57×(-4)+(-8)=220.C组培优练(建议用时15分钟)19.阅读程序框图,利用秦九韶算法计算多项式f(x)=a n x n+a n-1x n-1+…+a1x+a0的值,当x=x0时,框图中A处应填入a n-k.20.三个数168,54,264的最大公约数为6.关闭Word文档返回原板块。

高中数学第一章算法初步1.3.3进位制练习(含解析)新人教A版必修3

高中数学第一章算法初步1.3.3进位制练习（含解析）新人教A版必修3知识点一进位制的概念1．关于进制的说法，正确的个数为( )①“几进制”的数，其基数就是几，就“满几进一”；②计算机采用的进制一般都是二进制；③各种进制的数之间可以相互转化；④任何进制的数都必须在右下角标明基数．A．2 B．3 C．4 D．1答案 B解析①②③都是正确的，④中说法不对，因为十进制数一般省略基数．2．以下给出的各数中不可能是八进制数的是( )A．312 B．10110 C．82 D．7457答案 C解析八进制数只用到数字0，1，2，…，7，不会出现数字8．知识点二不同进位制间的转化3．将数30012(4)转化为十进制数为( )A．524 B．774 C．256 D．260答案 B解析30012(4)＝3×44＋0×43＋0×42＋1×41＋2×40＝774．4．已知10b1(2)＝a02(3)，则a＋b的值为________．答案 2解析10b1(2)＝1×20＋b×21＋0×22＋1×23＝9＋2b．a02(3)＝2×30＋0×31＋a×32＝9a＋2，因为10b1(2)＝a02(3)，b∈{0，1}，a∈{0，1，2}，且9＋2b＝9a＋2，所以a＝b＝1，所以a＋b＝2．5．把下列各数转换成十进制数．(1)101101(2)；(2)2102(3)；(3)4301(6)．解(1)101101(2)＝1×25＋0×24＋1×23＋1×22＋0×2＋1＝45．(2)2102(3)＝2×33＋1×32＋2＝65．(3)4301(6)＝4×63＋3×62＋1＝973．易错点对进位制转换的方法掌握不牢致错6．把十进制数48化为二进制数．易错分析由于基础知识，基本方法掌握不牢而错将结果写成11(2)．正解如下图所示，得48＝110000(2)．一、选择题1．将二进制数110101(2)转换成十进制数是( )A．105 B．54 C．53 D．29答案 C解析按照二进制数转换成十进制数的方法，可得十进制数是53．2．已知k进制数132与十进制数30相等，则k的值为( )A．－7或4 B．－7C．4 D．以上都不对答案 C解析132(k)＝1×k2＋3×k＋2＝k2＋3k＋2，所以k2＋3k＋2＝30，解得k＝4或k＝－7(舍去)，所以k＝4．3．如图是把二进制的数11111(2)化成十进制数的一个程序框图，则判断框内应填入的条件是( )A．i≤4? B．i≤5? C．i＞4? D．i＞5?答案 A解析11111(2)＝1×20＋1×21＋1×22＋1×23＋1×24＝2×(2×(2×(2×1＋1)＋1)＋1)＋1．(秦九韶算法)11111(2)＝31＝2×15＋1＝2×(2×7＋1)＋1＝2×(2×(2×3＋1)＋1)＋1＝2×(2×(2×(2×1＋1)＋1)＋1)＋1．故选A．4．下列各数中最小的数是( )A．101010(2) B．210(8)C．1001(16) D．81答案 A解析101010(2)＝1×25＋0×24＋1×23＋0×22＋1×21＋0×20＝42，210(8)＝2×82＋1×81＋0×80＝136，1001(16)＝1×163＋0×162＋0×16＋1×160＝4097，故选A．5．计算机中常用十六进制，采用数字0～9和字母A～F共16个计数符号，与十进制的对应关系如下表：例如用十六进制表示D＋E＝1B，则(2×F＋1)×4＝( )A．6E B．7C C．5F D．B0答案B解析(2×F＋1)×4用十进制可以表示为(2×15＋1)×4＝124，而124＝16×7＋12，所以用十六进制表示为7C，故选B．二、填空题6．若六进制数13m502(6)化为十进制数为12710，则m＝________．答案 4解析根据将k 进制数转化为十进制数的方法有13m502(6)＝1×65＋3×64＋m×63＋5×62＋0×61＋2＝12710，解得m ＝4．7．(1)三位四进制数中的最大数等于十进制数的是________；(2)把389化为四进制数，则该数的末位是________．答案 (1)63 (2)1解析 (1)本题主要考查算法案例中进位制的原理．三位四进制数中的最大数为333(4)，则333(4)＝3×42＋3×41＋3＝63．(2)解法一：由389＝4×97＋1，97＝4×24＋1，24＝4×6＋0，6＝4×1＋2，1＝4×0＋1，389化为四进制数的末位是第一个除法代数式中的余数1．解法二：以4作为除数，相应的除法算式如图所示，所以389＝12011(4)．显然该数的末位是1．8．已知三个数12(16)，25(7)，33(4)，则它们按由小到大的顺序排列为________．答案 33(4)<12(16)<25(7)解析将三个数都化为十进制数，则12(16)＝1×16＋2＝18，25(7)＝2×7＋5＝19，33(4)＝3×4＋3＝15，∴33(4)<12(16)<25(7)．三、解答题9．若二进制数100y011(2)(y ＝0或1)和八进制数x03(8)(0≤x≤8，x ∈N )相等，求x ＋y 的值．解 ∵100y 011(2)＝1×26＋y ×23＋1×21＋1＝67＋8y ，x 03(8)＝x ×82＋3＝64x ＋3，∴8y ＋67＝64x ＋3， y 可取0或1，x 可取1，2，3，4，5，6，7，当y ＝0时，x ＝1；当y ＝1时，64x ＋3＝75，x ＝98，不符合题意，∴x ＋y ＝1． 10．古时候，当边境有敌人来犯时，守边的官兵通过在烽火台上点火向境内报告，如下图所示，烽火台上点火表示数字1，未点火表示数字0，约定二进制数对应的十进制数的单位是1000，请你计算一下，这组烽火台表示有多少敌人入侵？解由题图可知这组烽火台表示的二进制数为11011(2)，它表示的十进制数为1×24＋1×23＋0×22＋1×21＋1×20＝27，由于二进制数对应的十进制数的单位是1000，所以入侵的敌人的数目为27×1000＝27000．。

高中数学人教A版必修3课件：1.3 算法案例

1.3 算法案例
题型1 辗转相除法与更相减损术
4．分别用辗转相除法和更相减损术求36和80的最大公约数．
解
辗转相除法：
80＝36×2＋8，36＝8×4＋4，8＝4×2.
故36和80的最大公约数是4.
更相减损术：
80－36＝44，44－36＝8，36－8＝28，28－8＝20，
20－8＝12，12－8＝4，8－4＝4.
解析
111÷2＝55……1，55÷2＝27……1，27÷2＝13……1，13÷2＝6……1， 6÷2＝3……0，3÷2＝1……1，1÷2＝0……1，故111(10)＝1101111(2)．故选C.
1.3 算法案例
题型3 进位制
11．把十进制数189化为四进制数，则末位数字是( B )
A．0
B．1
1.3 算法案例
刷基础
题型3 进位制
13．十六进制数与十进制数的对应如下表：
十六进 1 2 3 4 5 6 7 8 9 10 A B C D E F 制数十进制 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 数
例如：A＋B＝11＋12＝16＋7＝F＋7＝17(16)，所以A＋B的值用十六进制表示就等于17(16)．
f(x)＝anxn＋an－1xn－1＋…＋a1x＋a0的具体函数值，运用常规方法计算出结果最多需要n次加法和
n(n 2
1)
次乘法，而运用秦九韶算法由内而外逐层计算一次多项式的值的算法至多需要n次加法和n次乘法．对于计
算机来说，做一次乘法运算所用的时间比做一次加法运算要长得多，所以此算法极大地缩短了CPU运算的
A．2
B．3
C．4
D．5

高中数学必修三1.3算法案例-辗转相除法

解：1）先求1734与816的最大公约数
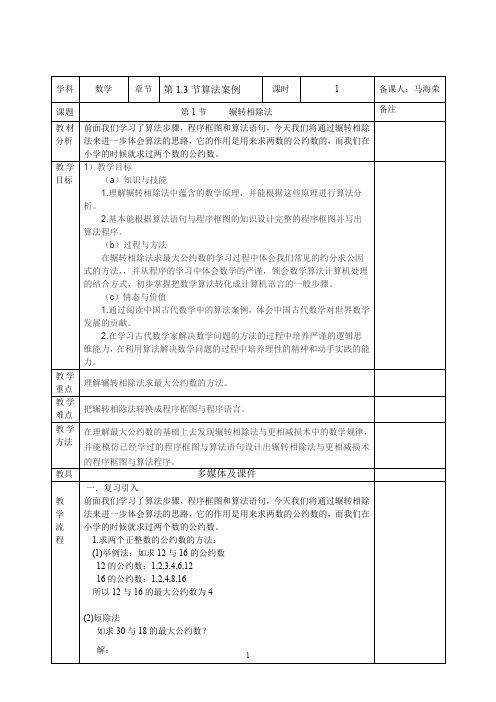
1734=816×2＋102
816=102×8
2）再求102与1343的最大公约数
1343=102×13＋17
102=17×6
所以17为102与1343的最大公约数
所以17为1734、816、1343这三个数的最大公约数
板
书
设
计
第1.3节算法案例-----辗转相除法
............................... ................................... ...............
课后作业
P45练习：1.
P48习题1.3A组：1.
课
后
反
思
1.辗转相除法的思想2.辗转相除法算法框图3.例题讲解
................................ ................................... ...............
............................... ................................... ...............
2.基本能根据算法语句与程序框图的知识设计完整的程序框图并写出算法程序。
（b）过程与方法
在辗转相除法求最大公约数的学习过程中体会我们常见的约分求公因式的方法，，并从程序的学习中体会数学的严谨，领会数学算法计算机处理的结合方式，初步掌握把数学算法转化成计算机语言的一般步骤。
（c）情态与价值
1.通过阅读中国古代数学中的算法案例，体会中国古代数学对世界数学发展的贡献。
PRINT m
END
课堂练习：1.求两数4081与20723的最大公约数.

高中数学人教A版必修3第一章1.3算法案例课件

去
9－ 3= 6
6 － 3 = 3 减数与差相等
3×2=6
78与36的最大公约数为6.
更相减损术
问题6.根据更相减损术的过程，设计求两个正整数m，n最大公约数的算法，需要用到什么逻辑结构？为什么？
第一步：任意给定两个正整算法分析：
数，判断它们是否都是偶数。第一步，给定两个正整数m，n(m>n).
更相减损术
例2. 用更相减损术求78与36的最大公约数.
解： 78与36都是偶数
“可半”
78 ÷ 2 = 39 36 ÷ 2 = 18
“可半者半之”
除完
39 － 18 = 21 大减小 21 － 18 = 3
再
18 － 3 = 15
乘
15 － 3 = 12
“更相减损”（辗转相减）
回
12 － 3 = 9
2 18 30 3 9 15 35
18与30的最大公约数为2 3 6 .
问题1. 求8251与6105的最大公约数. 可以使用短除法吗？
困难：两数比较大、公约数不易视察。（辗转相除法、更相减损术）
知问
思考1：辗转相除法与更相减损术可以用来解决什么问题？可以解决求两个正整数最大公约数的任何问题。
《九章算术》——更相减损术
“可半者半之，不可半者，副置分母、子之数，以少减多，更相减损，求其等也，以等数约之。”
《九章算术》
刘徽
《九章算术》其作者已不可考，现今流传的大多是在三国时期刘徽为《九章》所作的注本。它是中国古代第一部数学专著，系统总结了战国、秦、汉时期的数学成绩，收录了246个数学问题及其解法，是当时世界上最简练有效的应用数学，它的出现标志中国古代数学形成了完整的体系。

高中数学人教A版必修三第一章1.3.3进位制-算法案例课件

把89化为五进制的数.
5 89 5 17 53
0
余数
4 2 3
∴ 89=324(5)
练习：把3282化为16进制的数.
10
11
12
13
14
15
A
B
C
D
E
F
思考你会把三进制数10221(3)化为二进制数吗?
解:第一步:先把三进制数化为十进制数: 10221(3)=1×34+0×33+2×32+2×31+1×30
51
把89化为二进制的数.
2 89
2 44 2 22 2 11 25
22 21
0
余数
1 0 0 1 1 0 1
把算式中各步所得的余数从下到上排列,得到
89=1011001(2) 可以用2连续去除89或所得商(一直到商为0为止),然后取余数---除2取余法.
这种方法也可以推广为把十进制数化为k进制数的算法,称为除k取余法.
=81+18+6+1=106. 第二步:再把十进制数化为二进制数:
106=1101010(2). ∴10221(3)=106=110就是几，基数都是大于1的数.
按照十进制数的运算规则计算出结果，结果就是十进制下该数的大小了.
1.3算法案例
进位制
十进制数3721中的3表示3个千,7表示7个百,2表示2个十,1表示1个一,从而它可以写成下面的形式:
3721=3×103+7×102+2×101+1×100.
同理: 3421(5)= 3×53+4×52+2×51+1×50.
每一位上的数都是整数.

人教版高中数学必修三知识讲解,巩固练习(教学资料,补习资料)：专题1.3 算法案例

知识1．求两个正整数的最大公约数的算法（1）辗转相除法①定义：辗转相除法是用于求_____________的最大公约数的一种算法，这种算法是由欧几里得在公元前300年左右首先提出的，因而又叫欧几里得算法．就是对于给定的两个正整数，用较大的数除以较小的数，若余数不为零，则将余数和较小的数构成一对新数，继续上面的除法，直到余数为零，则这时较小的数就是原来两个数的最大公约数． ②算法步骤用辗转相除法求两个正整数的最大公约数，其算法步骤如下：第一步，给定两个正整数,m n ．第二步，计算m 除以n 所得的余数r ．第三步，,m n n r ==．第四步，若0r =，则,m n 的最大公约数等于m ；否则，返回第二步． ③程序框图如图所示：④程序如下：INPUT m ，n DOr=m MOD n m=n n=rPRINT m END或INPUT m ，nr=1 While r>0 r=m MOD n m=n n=rPRINT m END（2）更相减损术①定义：中国古代的数学专著《九章算术》中记载着“更相减损术”，即“可半者半之，不可半者，副置分母、子之数，以少减多，更相减损，求其等也．以等数约之．” ②算法步骤第一步，任意给定两个正整数，判断它们是否都是偶数．若是，用2约简；若不是，执行第二步．第二步，以较大的数减去较小的数，接着把所得的差与较小的数比较，并以大数减小数．继续这个操作，直到所得的数相等为止，则这个数(等数)或这个数与约简的数的乘积就是所求的最大公约数． ③程序框图④程序如下：INPUT “a ，b=”;a ，b WHILE a≠b r=a-bIF b>r THEN a=b b=r ELSE a=r END IF WEND PRINT b END2．秦九韶算法（1）定义及原理：把一个n 次多项式1110()n n n n f a x a x x a x a --=++⋅⋅⋅++改写成如下形式：2110()((()))n n n f a x a x x a x a x a --=⋅⋅⋅+++⋅⋅+⋅+．求多项式的值时，首先计算最内层括号内一次多项式的值，即11n n v a x a -=+，然后由内向外逐层计算一次多项式的值，即212323,n n v v x a v v x a --=+=+，…，10n n v v x a -=+，这种求n 次多项式()f x 的值的方法叫做秦九韶算法．（2）秦九韶算法程序化的可行性探讨：观察秦九韶算法中的n 个一次式，可见计算k v 时要用到1k v -的值，若令0n v a =，我们可以得到下面的递推公式：0____________(1,2,,)n k v a v k n =⎧⎨==⋅⋅⋅⎩．这是一个在秦九韶算法中反复执行的步骤，可以用循环结构来实现．（3）算法步骤第一步，输入多项式次数n 、最高次项的系数n a 和x 的值．第二步，将v 的值初始化为n a ，将i 的值初始化为n －1．第三步，输入i 次项的系数i a ．第四步，,1i v vx a i i =+=-．第五步，判断i是否大于或等于0．若是，则返回第三步；否则，输出多项式的值v．（4）程序框图如图所示：（5）程序如下：INPUT “n=”；nINPUT “an=”；aINPUT “x=”；xv=ai=n-1WHILE i>=0PRINT “i=”；iINPUT “ai=”；av=v*x+ai=i-1WENDPRINT vEND3．进位制（1）定义：进位制是人们为了计数和运算方便而约定的记数系统，约定满二进一，就是二进制；满十进一，就是十进制；满六十进一，就是六十进制；等等．也就是说，“满几进一”就是几进制，几进制的基数就是几．一般地，若k 是一个大于1的整数，那么以k 为基数的k 进制数可以表示为一串数字连写在一起的形式：1210()110110(,,,,,0<,0,,,)n n n k n n n n a a a a a a a a a a k a a a k ----⋅⋅⋅⋅⋅⋅∈<≤⋅⋅⋅<N ．说明：①若一个数为十进制数，其基数可以省略不写．②若是其他进位制的数，在没有特别说明的前提下，其基数必须写出，常在数的右下角标明基数．（2）将k 进制数转化为十进制数 ①算法步骤：计算k 进制数a 的右数第i 位数字i a 与1i k -的乘积1i i a k -⋅，再将其累加，这是一个重复操作的步骤．所以，可以用循环结构来构造算法，算法步骤如下：第一步，输入,a k 和n 的值．第二步，将b 的值初始化为0，i 的值初始化为1．第三步，1,1i i b b a k i i -=+⋅=+．第四步，判断i n >是否成立．若是，则执行第五步；否则，返回第三步．第五步，输出b 的值． ②程序框图如图所示：③程序如下：INPUT “a ，k ，n=”；a ，k ，n b=0 i=1 t=a MOD 10 DOb=b+t*k^(i-1) a=a\10 t=a MOD 10 i=i+1LOOP UNTIL i>n PRINT b END（3）将十进制数转化为k 进制数 ①转化方法：十进制数化为k 进制数用____________，即先把十进制数a 除以k ，商为0q ，余数为0r ，再把0q 除以k ，商为1q ，余数为1r ，…，反复进行这种除法，直到商1n q -除以k 所得的商为0，余数是n r ，即1n n q r -=为止，此时将所有余数按从右到左排列就得到所要求的k 进制数10()n n k r r r -⋅⋅⋅． ②算法步骤：第一步，给定十进制正整数a 和转化后的数的基数k ．第二步，求出a 除以k 所得的商q ，余数r ．第三步，把得到的余数依次从右到左排列．第四步，若0q ≠，则a q =，返回第二步；否则，输出全部余数r 排列得到的k 进制数． ③程序框图如图所示：④程序如下：INPUT “a ，k=”；a ，k b=0 i=0 DO q=a\k r=a MOD k b=b+r*10^i i=i+1 a=qLOOP UNTIL q=0 PRINT b END知识参考答案： 1．（1）两个正整数2．（2）1k n k v x a --+3．（3）①除k 取余法重点重点辗转相除法、更相减损术、秦九韶算法、进位制难点用秦九韶算法求多项式的值，进位制间的转换易错易对秦九韶算法中的运算次数理解错误1．辗转相除法与更相减损术辗转相除法与更相减损术有着相同的算法依据，但要注意运算过程的差别．两者的区别是：（1）辗转相除法进行的是除法运算，即辗转相除，更相减损术进行的是减法运算，即辗转相减，但其实质都是一个不断的递推过程．（2）辗转相除法，下一次进行相除时，由上一次的除数和余数直接相除即可．而更相减损术下一次相减前必须有一个判断大小的过程，以区别谁做被减数．注意：用更相减损术求两正整数的最大公约数时，若两数为偶数，可先约去2，这时莫忘记求得的相等两数乘以约简的数才是所求的最大公约数．【例1】用辗转相除法和更相减损术求840与1764的最大公约数．【答案】840与1764的最大公约数是84．【解析】辗转相除法：1764=840×2+84，840=84×10+0，∴840与1764的最大公约数是84．更相减损术：1764–840=924，924–840=84，840–84=756，756–84=672，672–84=588，588–84=504， 504–84=420， 420–84=336， 336–84=252， 252–84=168， 168–84=84，∴840与1764的最大公约数是84．【例2】利用辗转相除法求3869与6497的最大公约数．【答案】3869与6497的最大公约数为73．【名师点睛】辗转相除法计算次数少，而更相减损术计算次数多，但是更相减损术每一步的计算都是减法，比做除法运算要简单一些，所以一般当数较小时考虑用更相减损术，当数较大时考虑用辗转相除法． 2．秦九韶算法秦九韶算法的实质是：求多项式1110()n n n n f a x a x x a x a --=++⋅⋅⋅++的值时，转化为求n 个一次多项式的值，共进行n 次乘法运算和n 次加法运算．这种算法的运算次数较少，是多项式求值比较先进的算法．【例3】用秦九韶算法计算多项式f （x ）=12+35x –8x 2+79x 3+6x 4+5x 5+3x 6在x =–4时的值时，V 3的值为A ．–845B ．220C ．–57D ．34【答案】C【解析】∵多项式f （x ）=12+35x –8x 2+79x 3+6x 4+5x 5+3x 6=（（（（（3x +5）x +6）x +79）x –8）x +35）x +12，当x =–4时，∴v 0=3，v 1=3×（–4）+5=–7，v 2=–7×（–4）+6=34，v 3=34×（–4）+79=–57．故选C ．【例4】用秦九韶算法计算函数f （x ）=2x 4+3x 3+5x –4在x =2时的函数值．【答案】62【名师点睛】利用秦九韶算法计算多项式的值的策略：（1）正确地将多项式改写，若在多项式中有几项不存在，可将这些项的系数看成0，即把这些项看做0n x ⨯．（2）由内向外逐次计算．（3）每一步计算结果准确，由于下一次计算用到上一次计算的结果，应认真、细致地计算每一步． 3．进位制把一个非十进制数转化为另一种非十进制数，通常是把这个数先转化为十进制数，然后再利用除k 取余法，把十进制数转化为k 进制数．【例5】将八进制数127（8）化为十进制数．【答案】87【解析】()21081271828786416787=⨯+⨯+⨯=++=．【例6】已知一个k 进制的数123（k ）与十进制的数38相等，求k 的值．【答案】5【解析】将转化为十进制，()210212312323k k k k k k =⨯+⨯+⨯=++，由题意，得k 2+2k +3=38，所以k 2+2k –35=0，所以k =5或k =–7（舍）所以k =5．【名师点睛】除k 取余法的两个关注点：①要连续除：用k 连续去除十进制数或所得的商，直到商为零为止． ②若是其他进位制的数，在没有特别说明的前提下，其基数必须写出，常在数的右下角标明基数．基础训练1．秦九韶算法的先进性主要体现在减少运算次数，下列说法正确的是A ．可以减少加法运算次数B ．可以减少乘法运算次数C ．同时减少加法和乘法的运算次数D ．加法次数和乘法次数都有可能减少2．用秦九韶算法求多项式652()7632f x x x x =+++，当4x =时的值，先算的是A ．4×4=16B ．7×4=28C ．4×4×4=64D ．7×4+6=343．把十进制的23化成二进制数是A ．00 110（2）B ．10 111（2）C ．10 1111（2）D ．11 101（2）4．若十进制数26等于k 进制数32，则k 等于A ．4B ．5C ．6D ．85．用更相减损术求294和84的最大公约数时，需要做减法的次数是A ．3B ．4C ．5D ．66．1 037和425的最大公约数是A ．51B ．17C ．9D ．37．已知多项式54321()4322f x x x x x x =++---，用秦九韶算法求(2)f -等于 A ．1972-B ．1972C ．1832D ．1832-8．用更相减损术求156与91的最大公约数时，需要做减法的次数是__________． 9．将45（6）改写成十进制数为__________．10．用秦九韶算法计算多项式5432()54321f x x x x x x =+++++当4x =时的值时，乘法运算的次数为__________．11．用更相减损术求288与153的最大公约数．12．用秦九韶算法求多项式5432()3532f x x x x x x =-+-+当2x =时的值．能力提升13．在下列四个数中，最小的数是A ．(9)85B ．(6)210C ．(4)1000D ．(2)11111114．用秦九韶算法计算多项式65432()256238103f x x x x x x x =+++-+-当4x =-时的值时，3v 的值为A ．742-B ．49-C ．18D ．18815．若98与63的最大公约数为a ，二进制数(2)110011化为十进制数为b ，则a b +=A ．53B ．54C ．58D ．6016．用更相减损术求123和48的最大公约数是A ．3B ．7C ．9D ．1217．计算机是将信息转换成二进制处理，二进制即“逢二进一”，如(2)1101表示二进制数．将它转化成十进制形式是32101212021213⨯+⨯+⨯+⨯=，那么将二进制数1611111个（2）转换成十进制形式是A ．217-2B ．216-2C ．216-1D ．215-118．在下列各数中，最大的数是A ．(9)85B ．(6)210C ．(4)1000D ．(2)1111119．完成进位制之间的转化：(5)413=__________(7)． 20．（1）把八进制数()87341化为十进制数；（2）把1285化为16进制数．21．先将412（5）化成十进制的数，然后用“除k取余法”再化成七进制的数．22．用辗转相除法和更相减损术求261与319的最大公约数．参考答案1 2 3 4 5 6 7 13 14 15 16 17 18B D B D B B A D BC A C B 1．【答案】B【解析】通过对秦九韶算法的理解，可知它的主要作用是减少乘法的次数，将原来的乘法次数由(1)2n n减少到n，而对加法没有影响．故选B．2．【答案】D3．【答案】B【解析】23÷2=11…1，11÷2=5…1，5÷2=2…1，2÷2=1…0，1÷2=0…1，故23（10）=10111（2）．故选B．4．【答案】D【解析】由题意知，10 2632k k =⨯+⨯，解得8k =．故选D ． 5．【答案】B【解析】()()()()()294,84210,84126,8484,4242,42→→→→． 6．【答案】B【解析】∵1 037＝425×2＋187，425＝187×2＋51，187＝51×3＋34，51＝34×1＋17，34＝17×2，即1 037和425的最大公约数是17． 7．【答案】A【解析】∵1()((((43)2)1)1)2f x x x x x x =++---，∴197(2)2f -=-．8．【答案】5【解析】求最大公约数的过程如下：1569165-=，916526-=，652639-=，392613-=，261313-=．故13是最大公约数，共进行了5次减法运算． 9．【答案】29（10）【解析】由于45（6）=4×61+5×60=29（10）．故答案为：29（10）． 10．【答案】5【解析】5432((((54)3)2)1()54321)1f x x x x x x x x x x x =++++++++++=，不难发现要经过5次乘法，5次加法运算． 11．【答案】详见解析．【解析】288－153＝135，153－135＝18，135－18＝117，117－18＝99，99－18＝81，81－18＝63，63－18＝45，45－18＝27，27－18＝9，18－9＝9．因此288与153的最大公约数为9． 12．【答案】详见解析．13．【答案】D【解析】因为(9)8589577=⨯+=，2(6)210261678=⨯+⨯=，3(4)10001464=⨯=，543210(2)11111122222263=+++++=，所以最小的数是(2)111111．故选D ．14．【答案】B【解析】65432()256238103f x x x x x x x =+++-+- (((((25)6)23)8)10)3x x x x x x =+++-+-，则010212,52(4)53,63(4)618v v v x v v x ==+=⨯-+=-=+=-⨯-+=，322318(4)v v x =+=⨯-2349+=-，故选B ． 15．【答案】C【解析】∵9816335=⨯+，6313528=⨯+，351287=⨯+，2874=⨯，∴98和63的最大公约数是7，即7a =．二进制数(2)110011化为十进制数为54321012120202121251⨯+⨯+⨯+⨯+⨯+⨯=，即51b =，则58a b +=．故选C ． 16．【答案】A【解析】123-48=75，75-48=27，48-27=21，27-21=6，21-6=15，15-6=9，9-6=3，6-3=3，所以123和48的最大公约数是3． 17．【答案】C【解析】161111个（2）1514016=12+12++12=21⨯⨯⨯-．18．【答案】B19．【答案】213【解析】∵012(5)41335154535425108=⨯+⨯+⨯=++⨯=，012108371727=⨯+⨯+⨯，∴(7)(5)421313=．20．【答案】（1）3809；（2）()16505．【解析】（1）()87341=3210783848183809⨯+⨯+⨯+⨯=；（2）用16连续去除1285，直到商为0为止，所得到的余数依次从右向左排列，就得到()161285505=． 21．【答案】详见解析．【解析】412（5）=2×50+1×51+4×52=2+5+4×25=107， ∵107=7×15+2， 15=7×2+1， 2=7×0+2．∴把5进制的数412（5）化为7进制是212（7）． 22．【答案】详见解析．【解析】辗转相除法： 319＝261×1＋58， 261＝58×4＋29， 58=29×2，所以261与319的最大公约数为29．。

人教版数学必修三练习1.3算法案例

1.3算法案例一、基础过关1．下列各进制数中值最小的是() A．85(9)B．210(6)C．1 000(4)D．111 111(2)2．把189化为三进制数，则末位数是() A．0 B．1 C．2 D．33．已知一个k进制的数132与十进制的数30相等，那么k等于() A．7或4 B．－7C．4 D．都不对4．四位二进制数能表示的最大十进制数是() A．4 B．64 C．255 D．155．七进制数中各个数位上的数字只能是______中的一个．6．已知三个数12(16)，25(7)，33(4)，将它们按由小到大的顺序排列为________．7．已知1 0b1(2)＝a02(3)，求数字a，b的值．8．古时候，当边境有敌人来犯时，守边的官兵通过在烽火台上举火向国内报告，如图，烽火台上点火，表示数字1，不点火表示数字0，约定二进制数对应的十进制的单位是1 000，请你计算一下，这组烽火台表示约有多少敌人入侵？二、能力提升9．已知44(k)＝36，把67(k)转化为十进制数为() A．8 B．55 C．56 D．6210．计算机中常用的十六进制是逢16进1的计数制，采用数字0～9和字母A～F共16个计数符号，这些符号与十进制的数的对应关系如下表：十六进制0123456789 A B C D E F十进0123456789101112131415A．6E B．72 C．5F D．8011．10 303(4)和235(7)化为十进制数分别为______，_______.12．把五进制数1 234(5)转化为十进制数，再把它转化为八进制数．三、探究与拓展13．分别用算法步骤、程序框图、程序语句表示把k进制数a(共有n位数)转化成十进制数b.1.答案 D2.答案 A解析将189除以3得余数为0，所以189化为三进制数的末位数为0.3.答案 C解析132(k)＝1×k2＋3×k＋2＝k2＋3k＋2，∴k2＋3k＋2＝30，即k2＋3k－28＝0，解得k＝4或k＝－7(舍去)．4.答案 D解析由二进制数化为十进制数的过程可知，当四位二进制数为1 111时表示的十进制数最大，此时，1 111(2)＝15.5.答案0、1、2、3、4、5、6解析“满几进一”就是几进制．∵是七进制．∴满七进一，根本不可能出现7或比7大的数字，所以各个数位上的数字只能是0、1、2、3、4、5、6中的一个．6.答案33(4)<12(16)<25(7)解析将三个数都化为十进制数.12(16)＝1×16＋2＝18,25(7)＝2×7＋5＝19，33(4)＝3×4＋3＝15，∴33(4)<12(16)<25(7)．7.解∵1 0b1(2)＝1×23＋b×2＋1＝2b＋9，a02(3)＝a×32＋2＝9a＋2，∴2b＋9＝9a＋2，即9a－2b＝7.∵a∈{1,2}，b∈{0,1}，∴当a ＝1时，b ＝1符合题意，当a ＝2时，b ＝112不合题意， ∴a ＝1，b ＝1.8.解由图可知从左到右的五个烽火台，表示二进制数的自左到右五个数位，依题意知这组烽火台表示的二进制数是11 011，改写为十进制为：11 011(2)＝1×24＋1×23＋0×22＋1×21＋1×20＝16＋8＋2＋1＝27(10)．又27×1 000＝27 000，所以这组烽火台表示边境约有27 000个敌人来犯．9.答案 B解析由题意得，36＝4×k 1＋4×k 0，所以k ＝8.则67(k )＝67(8)＝6×81＋7×80＝55.10.答案 A解析 A ×B 用十进制可以表示为10×11＝110，而110＝6×16＋14，所以用十六进制表示为6E .11.答案 307 124解析 10 303(4)＝1×44＋3×42＋3×40＝307.235(7)＝2×72＋3×71＋5×70＝124(10)．12.解 1 234(5)＝1×53＋2×52＋3×51＋4×50＝194(10)．因为，所以1 234(5)＝194(10)＝302(8)．13.解算法步骤：第一步，输入a ，k ，n 的值．第二步，赋值b ＝0，i ＝1.第三步，b ＝b ＋a i ·k i －1，i ＝i ＋1.第四步，判断i >n 是否成立．若是，则执行第五步；否则，返回第三步．第五步，输出b 的值．程序框图：程序语句：INPUT “a,k,n=”;a,k,n b=0i=1t=a MOD 10DOb=b+t*k＾(i-1)a=a\\10t=a MOD 10i=i+1LOOP UNTIL i>n PRINT bEND。

人教版高中数学必修三第一章算法初步13算法案例教师版个性化辅导含答案教育文档

算法案例__________________________________________________________________________________ __________________________________________________________________________________ 1．理解算法案例的算法步骤和程序框图.2．引导学生得出自己设计的算法程序.3. 体会算法的基本思想，提高逻辑思维能力，发展有条理地思考与数学表达能力.1．求两个正整数最大公约数的算法(1)更相减损之术(等值算法)用两数中较大的数减去较小的数，再用差数和较小的数构成新的一对数，再用大数减小数，以同样的操作一直做下去，直到产生一对相等的数，这个数就是最大公约数．(2)用“等值算法”求最大公约数的程序while b＝b－aend a＝a－b2．割圆术用圆内接正多边形面积逐渐逼近圆的面积的算法是计算圆周率的一种方法．3.秦九韶算法:axaxaaxfx＋…＋＝＋nn－1nfxaxaxaxa 把一个＋次多项式＋…＋(＋)＝改写成如下形式：nn011－nn－1(＋)nn0－11nn－2－1axaxaxa )＋＝(＋…＋＋nn01－1nn－3－2axaxaxaxa )＋)＝((＋＋…＋＋nn0－112axaxaxaxa＋＋…＋)＋＋)) ＝(…((nnn02－11－求多项式的值时，首先计算最内层括号内一次多项式的值，然后由内向外逐层计算一次多项式的值．这样通过一次式的反复运算，逐步得出高次多项式的值的方法称作秦九韶算法。

v?a?n0k?1,2, ,n就得到个一次式可见，只要令其中观察上述秦九韶算法中的n?v?vx?a?n1k?kk?了一个递推关系。

这个递推关系是一个反复执行的步骤，可用循环语句来实现。

理解秦九韶算法的关键：一是弄清算法原理是加法对乘法的分配律，二是弄清算法设计中递推关系是一个反复执行的运算，故用循环语句来实现。

高中数学必修三习题：第一章1.3算法案例含答案

第一章算法初步1.3算法事例A 级基础稳固一、选择题1．以下说法中正确的个数为()①展转相除法也叫欧几里得算法；②展转相除法的基本步骤是用较大的数除以较小的数；③求最大条约数的方法除展转相除法以外，没有其余方法；④编写展转相除法的程序时，要用到循环语句．A．1B．2C．3D．4分析：依照展转相除法可知，①②④正确，③错误．答案： C2．用更相减损术求48 和 132 的最大条约数时，需做减法的次数是() A．2B．3C．4D．5分析： 132－ 48＝ 84， 84－48＝ 36， 48－36＝ 12， 36－ 12＝ 24， 24－ 12＝ 12.答案： D3．若用秦九韶算法求多项式f (x) ＝ 45－x2＋2 当x＝ 3 时的值，则需要做乘法运算和x加减法运算的次数分别为 ()A．4，2 B ． 5，3 C ．5，2 D ．6， 2分析： f ( x)＝4x5－ x2＋2＝((((4x) x) x－1)x) x＋2，因此需要做5次乘法运算和 2 次加减运算．答案： C4．已知一个k进制的数123 与十进制的数38 相等，那么k等于 ()A．7或 5B．－ 7C． 5D．都不对分析： (123)( k ) ＝1×k2＋2×k＋3＝k2＋2k＋3，因此 k2＋2k＋3＝38，即 k2＋2k－35＝0.解得 k＝5或 k＝－7(舍去)．答案： C5．已知 44＝ 36，把 67( k)转变为十进制数为 ()( k)A． 8B． 55 C． 56D． 62分析：当题意得，36＝4×k1＋4×k0，因此k＝ 8.则 67( k)＝ 67(8)＝6×81＋7×80＝ 55.答案： B二、填空题6．用秦九韶算法求 f ( x)＝2x3＋ x－3当 x＝3时的值 v2＝________．分析： f ( x)＝((2 x＋0) x＋1) x－3，v0＝2；v1＝2×3＋0＝6；v2＝6×3＋1＝19.答案： 197．已知函数 f ( x)＝ x3－2x2－5x＋6，用秦九韶算法，则 f (10)＝________．分析： f ( x)＝ x3－2x2－5x＋6＝( x2－2x－5) x＋6＝[( x－2) x－5] x＋6.当 x＝10时， f (10)＝[(10－2)×10－5]×10＋6＝(8×10－5)×10＋6＝75×10＋6＝756.答案： 7568．已知 1 0 b1(2)＝a02(3)，则 ( a，b) ＝ ________．分析：由于 1 0 b1(2)＝1×23＋b×2＋ 1＝ 2b＋ 9，2a02(3)＝a×3＋2＝9a＋2，因此 2b＋ 9＝ 9a＋ 2，即 9a－ 2b＝ 7.由于 a∈{1，2}， b∈{0，1}，因此当 a＝1时， b＝1切合题意，11当 a＝2时， b＝2不合题意，因此 a＝1，b＝1.因此( a，b)＝(1，1)．答案： (1 ，1)三、解答题9．分别用展转相除法和更相减损术求261， 319 的最大条约数．解：展转相除法：319＝261×1＋ 58，261＝58×4＋ 29，58＝29×2.因此 319 与 261 的最大条约数是29.更相减损术：319－ 261＝58，261－ 58＝203，203－ 58＝145，145－ 58＝87，87－ 58＝ 29，58－ 29＝ 29，因此 319 与 261 的最大条约数是29.10．已知函数f ( x) ＝x3－ 3x2－4x＋ 5，试用秦九韶算法求 f (2)的值．解：依据秦九韶算法，把多项式改写成以下形式：f (x) ＝x3－ 3x2－4 ＋5＝(x2－ 3x－ 4)x＋ 5＝x(( x－ 3) x－4) x＋ 5.把 x＝2代入函数式得f (2)＝((2－3)×2－4)×2＋5＝－7.B 级能力提高1．m是一个正整数，关于两个正整数a， b，假如 a－ b 是 m的倍数，则称a， b 对模 m 同余，用符号ab(MOD m)表示，则以下各式中不正确的为()A． 127(MOD 5)B． 2110(MOD 3)C． 3420(MOD 2)D． 477(MOD 40)分析：逐个考证，关于A， 12－ 7＝5 是 5 的倍数；关于B， 21－ 10＝ 11 不是 3 的倍数；关于 C， 34－ 20＝ 14 是 2 的倍数；关于D， 47－ 7＝ 40 是 40 的倍数．答案： B2． 324， 243， 135 三个数的最大条约数是________．分析： 324＝243×1＋ 81，243＝81×3，因此 243 与 324 的最大条约数是81.又 135＝81×1＋ 54，81＝54×1＋ 27，54＝27×2＋ 0，因此 135 与 81 的最大条约数是27.答案： 273．已知三个数12(16)，25(7)，33(4)，将它们按由小到大的次序摆列为________________ ．分析：将三个数都化为十进制数．12(16)＝1×16＋ 2＝ 18， 25(7)＝2×7＋ 5＝ 19，33(4)＝3×4＋ 3＝ 15，因此 33(4)＜ 12(16)＜25(7)．答案： 33(4)＜ 12(16)＜ 25(7)。