2020届高三一轮总复习:课时跟踪训练23
【人教版】红对勾2020届高考一轮数学(理)复习:课时作业23

第五章数列课时作业30数列的概念与简单表示法1.(2019·青岛模拟)数列1,3,6,10,15,…的一个通项公式是(C)A.a n=n2-(n-1) B.a n=n2-1n n+1n n-1 C.a n=D.a n=2 2解析:设此数列为{a n},则由题意可得a1=1,a2=3,a3=6,a4=10,a5=15,…仔细观察数列1,3,6,10,15,…可以发现:1=1,3=1+2,6=1+2+3,10=1+2+3+4,…n n+1所以第n项为1+2+3+4+5+…+n=,2n n+1所以数列1,3,6,10,15,…的通项公式为a n=.22.(2019·长沙模拟)已知数列的前4 项为2,0,2,0,则依此归纳该数列的通项不可能是(C)A.a n=(-1)n-1+1 B.a n=Error!nπC.a n=2sin D.a n=cos(n-1)π+12nπ解析:对n=1,2,3,4 进行验证,a n=2sin 不合题意.23.(2019·广东茂名模拟)S n是数列{a n}的前n项和,且∀n∈N*都有2S n=3a n+4,则S n=(A)A .2-2×3nB .4×3nC .-4×3n -1D .-2-2×3n -1解 析:∵2S n =3a n +4,∴2S n =3(S n -S n -1)+4(n ≥2),变形为 S n - 2=3(S n -1-2),又 n =1 时,2S 1=3S 1+4,解得 S 1=-4,∴S 1-2=- 6.∴数列{S n -2}是等比数列,首项为-6,公比为 3.∴S n -2=-6×3n-1,可得 S n =2-2×3n ,故选 A.1+a n4.(2019·河北石家庄一模)若数列{a n }满足 a 1=2,a n +1= ,1-a n则 a 2 018 的值为( B )A .2B .-311C .-D.2 3 1+a n 1+a 1 解析:∵a 1=2,a n +1= ,∴a 2= =-3, 1-a n 1-a 11 1同理可得:a 3=- ,a 4= ,a 5=2,……,可得 a n +4=a n ,2 3则 a 2 018=a 504×4+2=a 2=-3.故选 B.5.(2019·广东广州一模)已知数列{a n }满足 a 1=2,2a n a n +1=a 2n +1, a n -1设 b n = ,则数列{b n }是( D ) a n +1A .常数列B .摆动数列C .递增数列D .递减数列 1 1 解析:∵2a n a n +1=a 2n +1,∴a n +1= ,a n +2( a n)11 a n + -12( a n)a n -1 a n +1-1 a n -12∵b n = ,∴b n +1= ===b ,2na n+1 a n+1+1 1 1 a n+1 2a n++12(a n)∴b-b n=b2n-b n=b n(b n-1),n+12-1 1∵a=2,b1==,12+1 3Earlybird1 1 1 1 1=(2,∴b3=2=4,b4=2=8,∴b22 43 )[(3)](3)[(3)](3)}是递减数列,故选D.∴数列{bn6.在数列{a n}中,a1=1,a2=2,若a n+2=2a n+1-a n+2,则a n=(C)1 2 6A. n2-n+B.n3-5n2+9n-45 5 5C.n2-2n+2 D.2n2-5n+4解析:由题意得(a n+2-a n+1)-(a n+1-a n)=2,因此数列{a n+1-a n}是以1 为首项,2 为公差的等差数列,a n+1-a n=1+2(n-1)=2n-1,当n≥2 时,a n=a1+(a2-a1)+(a3-a2)+…+(a n-a n-1)=1+1+1+2n-3n-13+…+(2n-3)=1+=(n-1)2+1=n2-2n+2,2又a1=1=12-2×1+2,因此a n=n2-2n+2(n∈N*),故选C.7.(2019·河北保定一模)已知函数f(x)=Error!若数列{a n}满足a n=f(n)(n∈N*),且{a n}是递增数列,则实数a的取值范围是(C) A.(1,3) B.(1,2]24C.(2,3) D.[,3)11解析:∵数列{a n}是递增数列,f(x)=Error!a n=f(n)(n∈N*),∴3-a>0,a>1 且f(10)<f(11),∴1<a<3 且10(3-a)-6<a2,解得2<a<3,故实数a的取值范围是(2,3),故选C.a n8.已知数列{a n}满足a n+1=a n+2n,且a1=33,则的最小值为n(C)A.21 B.1021 17C. D.2 2Earlybird解析:由已知条件可知,当n≥2 时,a n=a1+(a2-a1)+(a3-a2)+…+(a n-a n-1)=33+2+4+…+2(n-1)=n2-n+33,又n=1 时,a1=33 满足此式.a n33所以=n+-1.n na n33令f(n)==n+-1,n n则f(n)在[1,5]上为减函数,在[6,+∞)上为增函数.53 21又f(5)=,f(6)=,则f(5)>f(6),5 2a n21故f(n)=的最小值为.n 29.在一个数列中,如果∀n∈N*,都有a n a n+1a n+2=k(k为常数),那么这个数列叫做等积数列,k叫做这个数列的公积.已知数列{a n}是等积数列,且a1=1,a2=2,公积为8,则a1+a2+a3+…+a12=28__.解析:依题意得数列{a n}是周期为3 的数列,且a1=1,a2=2,a3=4,因此a1+a2+a3+…+a12=4(a1+a2+a3)=4×(1+2+4)=28.n2 10.(2019·成都质检)在数列{a n}中,a1=1,a n=a n-1(n≥2,n2-12nn∈N*),则a n=.n+1a n n2 n2解析:由题意知==.a n-1 n2-1 n-1n+1a2 a3 a n所以a n=a1×××…×a1 a2 a n-122 32 n2=1×××…×=22-1 32-1 n2-122 ×32 ×42 ×…×n22-1×2+1×3-1×3+1×4-1×4+1×…×n-1×n+1Earlybird22 ×32 ×42 ×…×n2 2n==.1 ×3 ×2 ×4 ×3 ×5 ×…×n-1×n+1n+1111.数列{a n}的通项公式为a n=(2n+1)(n-1,则数列{a n}的2 )1最大项为.21 1=(2n+3)(n+1-(2n+1) n解析:a n+1-a n2 )(2)1 1-2n+1](n=2n+3×[ 2 )23 1-2n+1](n=n+[ 2 )21 1 1 1-n)(2 ) 2 (2) 2a n<0,所以a n+1<a n,所以a1>a2>a3>…>a n>a n+1>…,所以数列1{a n}的最大项为a1=.212.(2019·山东青岛调研)已知S n是数列{a n}的前n项和,S n=3×2n-3,其中n∈N*.(1)求数列{a n}的通项公式;(2)数列{b n}为等差数列,T n为其前n项和,b2=a5,b11=S3,求T n 的最值.解:(1)由S n=3×2n-3,n∈N*得,(ⅰ)当n=1 时,a1=S1=3×21-3=3.(ⅱ)当n≥2 时,a n=S n-S n-1=(3×2n-3)-(3×2n-1-3)=3×(2n -2n-1)=3×2n-1(*).又当n=1 时,a1=3 也满足(*)式.所以,对任意n∈N*,都有a n=3×2n-1.(2)设等差数列{b n}的首项为b1,公差为d,由(1)得b2=a5=3×25-1=48,b11=S3=3×23-3=21.由等差数列的通项公式得EarlybirdError!解得Error!所以b n=54-3n.可以看出b n随着n的增大而减小,令b n≥0,解得n≤18,所以T n有最大值,无最小值,且T18(或T17)为前n项和T n的最大18b1+b18值,T18==9×(51+0)=459.213.(2019·黄冈质检)已知数列{x n}满足x n+2=|x n+1-x n|(n∈N*),若x1=1,x2=a(a≤1,a≠0),且x n+3=x n对于任意的正整数n均成立,则数列{x n}的前2 017 项和S2 017=(D)A.672 B.673C.1 342 D.1 345解析:∵x1=1,x2=a(a≤1,a≠0),∴x=|x2-x1|=|a-1|=1-a,3∴x+x2+x3=1+a+(1-a)=2,1又x n+3=x n对于任意的正整数n均成立,}的周期为3,所以数列{x n}的前2 017 项和S2 017=S672×3∴数列{xn=672×2+1=1 345.故选D.+114.(2019·河南郑州一中模拟)数列{a n}满足:a1=1,且对任意的1 1 1 1m,n∈N*,都有a m+n=a m+a n+mn,则+++…+=(D)a1 a2 a3 a2 0182 017 2 018A. B.2 018 2 0194 034 4 036C. D.2 018 2 019解析:∵a1=1,且对任意的m,n∈N*都有a m+n=a m+a n+mn,∴a n+1=a n+n+1,即a n+1-a n=n+1,用累加法可得a n=a1 +n-1n+2n n+1=,2 2Earlybird1 2 1 1∴==2 ,-n n+1(n+1)a n n1 1 1 1∴+++…+=a1 a2 a3 a2 0181 1 1 1 1 4 0362(=,故选D.2 019)1-+-+…+-2 23 2 018 2 01915.设{a n}是首项为1 的正项数列,且(n+1)a n+2 1-na2n+a n+1·a n=10(n=1,2,3,…),则它的通项公式a n=.n解析:因为(n+1)a n+2 1-na2n+a n+1·a n=0,所以(a n+1+a n)[(n+1)a n+1-na n]=0,又因为a n>0,故(n+1)a n+1-na n=0,a n+1 n a2 1 a3 2 a4 3即=,故=,=,=,…a n n+1 a1 2 a2 3 a3 4a n n-1=,a n-1 na n 1 1把以上各式分别相乘得=,即a n=.a1 n n16.(2019·宝安中学等七校联考)已知{a n}是递增数列,其前n项和为S n,a1>1,且10S n=(2a n+1)(a n+2),n∈N*.(1)求数列{a n}的通项a n;(2)是否存在m,n,k∈N*,使得2(a m+a n)=a k成立?若存在,写出一组符合条件的m,n,k的值;若不存在,请说明理由.解:(1)由10a1=(2a1+1)(a1+2),1得2a21-5a1+2=0,解得a1=2 或a1=.2又a1>1,所以a1=2.因为10S n=(2a n+1)(a n+2),所以10S n=2a2n+5a n+2.故10a n+1=10S n+1-10S n=2a n+2 1+5a n+1+2-2a2n-5a n-2,整理,得2(a n+2 1-a2n)-5(a n+1+a n)=0,Earlybird即(a n+1+a n)[2(a n+1-a n)-5]=0.因为{a n}是递增数列且a1=2,5所以a n+1+a n≠0,因此a n+1-a n=.25所以数列{a n}是以2 为首项,为公差的等差数列.25 1所以a n=2+(n-1)=(5n-1).2 2(2)满足条件的正整数m,n,k不存在,理由如下:假设存在m,n,k∈N*,使得2(a m+a n)=a k,1则5m-1+5n-1=(5k-1),23整理,得2m+2n-k=,(*)5显然,(*)式左边为整数,所以(*)式不成立.故满足条件的正整数m,n,k不存在.。
2020版高考数学一轮复习课时跟踪检测一集合含解析

课时跟踪检测(一) 集合一、题点全面练1.已知集合M={|2+-2=0},N={0,1},则M∪N=( )A.{-2,0,1} B.{1}C.{0} D.∅解析:选A 集合M={|2+-2=0}={|=-2或=1}={-2,1},N={0,1},则M∪N={-2,0,1}.故选A.2.设集合A={|2--2<0},集合B={|-1<≤1},则A∩B=( )A.[-1,1] B.(-1,1]C.(-1,2) D.[1,2)解析:选B ∵A={|2--2<0}={|-1<<2},B={|-1<≤1},∴A∩B={|-1<≤1}.故选B.3.设集合M={|=2+1,∈},N={|=+2,∈},则( )A.M=N B.M⊆NC.N⊆M D.M∩N=∅解析:选B ∵集合M={|=2+1,∈}={奇数},N={|=+2,∈}={整数},∴M⊆N.故选B.4.设集合U={1,2,3,4,5},A={2,4},B={1,2,3},则图中阴影部分所表示的集合是( )A.{4} B.{2,4}C.{4,5} D.{1,3,4}解析:选A 图中阴影部分表示在集合A中但不在集合B中的元素构成的集合,故图中阴影部分所表示的集合是A∩(∁U B)={4},故选A.5.(2018·湖北天门等三地3月联考)设集合A={1,2,3},B={4,5},M={|=a+b,a ∈A,b∈B},则M中元素的个数为( )A.3 B.4C.5 D.6解析:选B a∈{1,2,3},b∈{4,5},则M={5,6,7,8},即M中元素的个数为4,故选B.二、专项培优练(一)易错专练——不丢怨枉分1.已知集合M ={|y =lg(2-)},N ={y |y =1-x +x -1},则( ) A .M ⊆N B .N ⊆M C .M =ND .N ∈M解析:选B ∵集合M ={|y =lg(2-)}=(-∞,2),N ={y |y =1-x +x -1}={0},∴N ⊆M .故选B.2.(2019·皖南八校联考)已知集合A ={(,y )|2=4y },B ={(,y )|y =},则A ∩B 的真子集个数为( )A .1B .3C .5D .7解析:选B 由⎩⎨⎧ x 2=4y ,y =x 得⎩⎨⎧ x =0,y =0或⎩⎨⎧x =4,y =4,即A ∩B ={(0,0),(4,4)}, ∴A ∩B 的真子集个数为22-1=3.3.已知集合P ={y |y 2-y -2>0},Q ={|2+a +b ≤0}.若P ∪Q =R ,且P ∩Q =(2,3],则a +b =( )A .-5B .5C .-1D .1解析:选A 因为P ={y |y 2-y -2>0}={y |y >2或y <-1}.由P ∪Q =R 及P ∩Q =(2,3],得Q =[-1,3],所以-a =-1+3,b =-1×3,即a =-2,b =-3,a +b =-5,故选A.4.已知集合M =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x =k π4+π4,k ∈Z ,集合N =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x =k π8-π4,k ∈Z ,则( )A .M ∩N =∅B .M ⊆NC .N ⊆MD .M ∪N =M解析:选B由题意可知,M=⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x =2k +48-π4,k ∈Z =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x =2n π8-π4,n ∈Z ,N =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x =2k π8-π4或x =2k -18-π4,k ∈Z ,所以M ⊆N ,故选B.5.(2018·安庆二模)已知集合A ={1,3,a },B ={1,a 2-a +1},若B ⊆A ,则实数a =( )A .-1B .2C .-1或2D .1或-1或2解析:选C 因为B ⊆A ,所以必有a 2-a +1=3或a 2-a +1=a . ①若a 2-a +1=3,则a 2-a -2=0,解得a =-1或a =2. 当a =-1时,A ={1,3,-1},B ={1,3},满足条件; 当a =2时,A ={1,3,2},B ={1,3},满足条件. ②若a 2-a +1=a ,则a 2-2a +1=0,解得a =1,此时集合A ={1,3,1},不满足集合中元素的互异性,所以a =1应舍去. 综上,a =-1或2.故选C.6.(2018·合肥二模)已知A =[1,+∞),B =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ∈R| 12a ≤x ≤2a -1,若A ∩B ≠∅,则实数a 的取值范围是( )A .[1,+∞)B.⎣⎢⎡⎦⎥⎤12,1 C .⎣⎢⎡⎭⎪⎫23,+∞D .(1,+∞)解析:选A因为A ∩B ≠∅,所以⎩⎨⎧2a -1≥1,2a -1≥12a ,解得a ≥1.(二)难点专练——适情自主选7.(2018·日照联考)已知集合M =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x| x 216+y 29=1,N =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫y | x 4+y 3=1,则M ∩N =( )A .∅B .{(4,0),(3,0)}C .[-3,3]D .[-4,4]解析:选D 由题意可得M ={|-4≤≤4},N ={y |y ∈R},所以M ∩N =[-4,4].故选D.8.(2019·河南八市质检)在实数集R 上定义运算*:*y =·(1-y ).若关于的不等式*(-a )>0的解集是集合{|-1≤≤1}的子集,则实数a 的取值范围是( )A.[0,2] B.[-2,-1)∪(-1,0]C.[0,1)∪(1,2] D.[-2,0]解析:选D 依题意可得(1-+a)>0.因为其解集为{|-1≤≤1}的子集,所以当a≠-1时,0<1+a≤1或-1≤1+a<0,即-1<a≤0或-2≤a<-1.当a=-1时,(1-+a)>0的解集为空集,符合题意.所以-2≤a≤0.9.已知集合A={|3≤3≤27},B={|log2>1}.(1)分别求A∩B,(∁R B)∪A;(2)已知集合C={|1<<a},若C⊆A,求实数a的取值范围.解:(1)∵3≤3≤27,即31≤3≤33,∴1≤≤3,∴A={|1≤≤3}.∵log2>1,即log2>log22,∴>2,∴B={|>2}.∴A∩B={|2<≤3}.∴∁R B={|≤2},∴(∁R B)∪A={|≤3}.(2)由(1)知A={|1≤≤3},C⊆A.当C为空集时,满足C⊆A,a≤1;当C为非空集合时,可得1<a≤3.综上所述,实数a的取值范围是(-∞,3].。
2020版高考数学(理)新创新一轮复习通用版课时跟踪检测(一)集合

课时跟踪检测(一) 集合1 •已知集合M = {x|x2+ x—2 = 0}, N = {0,1},贝V M U N =( )A• {—2,0,1} B. {1}C • {0} D• ?解析:选A 集合M = {x|x2+ x —2 = 0} = {x|x =—2 或x= 1} = { —2,1}, N = {0,1},则M U N = { —2,0,1}.故选A.2. (2018 浙江高考)已知全集U = {1,2,3,4,5} , A = {1,3},则?u A=( )A. ?B. {1,3}C • {2,4,5} D. {1,2,3,4,5}解析:选 C ••• U= {1,2,3,4,5} , A= {1,3},二?u A= {2,4,5} •3.(2019 衡水模拟)已知集合A={x|y= x2—2x}, B= {y|y= x2+ 1},贝V An B =( )A • [1 ,+s ) B. [2 ,+s )C. ( — s, 0] U [2,+^ )D. [0,+s )解析:选B 由于集合A= {x|y= x2—2x}表示的是函数y= x2—2x的定义域,所以由x2—2x > 0可知集合A = {x|x< 0或x> 2}.集合B= {y|y= x2+ 1}表示的是函数y= x2+1的值域,因此B= {y|y> 1}.••• A n B= [2, + s).故选B.4. (2019河北五个一名校联考)若集合A= {x|3 + 2x —x2>0},集合B = {x|2x<2},则A n B 等于()A. (1,3)B. ( — s, —1)C • (—1,1)D • (—3,1)解析:选C 依题意,可求得 A = (—1,3), B= (—s, 1),• A n B= (—1,1).5. (2019 浙江五校联考)设全集U = R,集合A = {x|x> 3}, B = {x|0< x<5},则(?U A) n B =( )A. {x|0<x<3}B. {x|0< x w 3}C. {x|0<x w 3}D. {x|0< x<3}解析:选 D 由题意得?U A = {x|x<3},所以(?U A) n B= {x|0w x<3},故选 D.6. (2019 长沙模拟)已知集合A= {1,2,3} , B= {x|x2—3x + a = 0, a€ A},若A n B M ?, 则a的值为()A. 1B. 2C . 3D . 1 或2解析:选B 当a= 1时,x2—3x+ 1 = 0,无整数解,贝U An B= ?;当a= 2时,B = {1,2}, . n . U. n . UA nB = {1,2}工?;当 a = 3时,B = ?, A A B = ?.因此实数 a = 2.7.(2019 资阳模拟)设全集 U = R ,集合 A = {x|x 2— 2x — 3<0} , B = {x|x - 1> 0},则图中阴 影部分所表示的集合为()A. {x|x <— 1 或 x > 3}B. {x|x<1 或 x > 3}C. {x|x < 1}D. {x|x <— 1}解析:选D 图中阴影部分表示集合 U B = {x|x> — 1},二?U (A U B)= {x|x < — 1},故选 D.8. (2019石家庄重点高中毕业班摸底则 M A N =() A . ?C . [ — 2,2] 解析:选D 因为集合 M = {x|— 3< x w 3}, N = R ,所以M A N = [ — 3,3],故选D.9.设集合 A = {x|y = Ig(— x 2+ x + 2)} , B = {x|x — a>0},若 A ? B ,则实数 a 的取值范围 是()A . ( — rn,— 1)B . ( — m, — 1]C . ( — m,— 2)D . ( — m,— 2]解析:选 B 因为集合 A = {x|y = Ig(— x 2+ x + 2)} = {x|— 1<x<2}, B = {x|x>a},因为 A ? B ,所以 a < — 1.10.已知全集 U = {x|— 1<x<9} , A = {x|1<xva} , A 是U 的子集,若 A M ?,贝U a 的取值 范围是( )A . {a|a<9}B . {a|a w 9}C . {a|a > 9}D . {a|1<a w 9} 解析:选D 由题意知,集合 A M ?,所以a>1,又因为A 是U 的子集,故需a w 9,所 以a 的取值范围是{a|1<a w 9}.U (A U B),又 A = {x|— 1vx<3} , B = {x|x > 1}A2 2 r 、)已知集合 M = { x 氏 + \ = 1 },N 1j , B . {(3,0), (0,2)} D . [ — 3,3]11. 定义集合M与N的新运算:M ® N = {x|x € M或x€ N且x?M A N},则(M ® N) ® N =( ) . n . UC. MD. N解析:选C 按定义,M ® N表示图中的阴影部分,两圆内部的公共部分表示M A N.(M ® N)® N 应表示x€ M ® N 或x € N 且x? (M ® N)nN的所有x的集合,(M ® N)n N表示N上的阴影部分,因此(M ® N)® N = M.12. 某班共40人,其中24人喜欢篮球运动,16人喜欢乒乓球运动,6人这两项运动都不喜欢,则喜欢篮球运动但不喜欢乒乓球运动的人数为()A. 17B. 18C. 19D. 20解析:选B 记全集U为该班全体同学,喜欢篮球运动的记作集合A,喜欢乒乓球运动的记作集合B,则喜欢篮球但不喜欢乒乓球运动的记作A n ?U B(如图),故有18人.13. 设A= {1,4,2x}, B= {1, x },若B? A,贝U x= _________ .解析:由B? A,贝U x2= 4 或x2= 2x.得x= d2或x= 0,当x=- 2 时,A= {1,4, - 4}, B= {1,4},符合题意;当x= 2时,贝V 2x = 4,与集合的互异性相矛盾,故舍去;当x= 0时, A= {1,4,0} , B= {1,0},符合题意.综上所述,x=-2 或x= 0.答案:—2或014. 设集合A = {x|x + m>0}, B= {x| —2<x<4},全集U= R,且(?u A)n B= ?,则实数m的取值范围为__________ .解析:由已知A= {x|x> —m},「. ?U A= {x|x<—m}. v B = {x|—2<x<4} , (?u A)n B= ?, •••—m W—2, 即卩m> 2.「. m 的取值范围为{m|m> 2}.答案:{m|m> 2}15. ______________________________________________ 对于任意两集合A, B,定义A—B = {x|x € A且x?B}, A* B= (A—B) U但—A),记A= {y|y>0}, B = {x|—3< x W 3},贝U A*B = ___________________________________________________________ .解析:由题意知A—B= {x|x>3} , B— A = {x|—3W x<0},所以A*B= [ —3,0)U (3, + ).答案:[—3,0)U (3,+s )16. 设[x]表示不大于x的最大整数,集合A = {x|x2—2[x] = 3}, B=1 xgv2x<8 :则A n BAw解析:1因为不等式8<2x<8的解为一3<x<3 ,所以B = ( —3,3).若x € A n B ,则所以[x]只可能取值一3, —2, —1,0,1,2.若[x] W —2,则x2= 3 + 2[x]<0,没x2—2[x] = 3,—3<x<3,有实数解;若[x]=—1,贝U x2= 1,得x=—1;若[x] = 0,贝U x2= 3,没有符合条件的解;若[x] = 1,则x2= 5,没有符合条件的解;若[x] = 2,则x2= 7,有一个符合条件的解,x = 7.因此,A n B= {- 1, 7}.答案:{-1, .7}17. (2019 南阳模拟)若集合A= {(x, y)|x2+ mx-y+ 2= 0, x€ R}, B={(x, y)|x—y+ 1 =0,0W x w 2},当A n B M ?时,求实数m的取值范围.解:•••集合A = {(x, y)|x2+ mx—y+ 2 = 0, x€ R} = {(x, y)|y= x2+ mx + 2, x€ R} , B ={(x, y)|x—y+ 1= 0,0< x< 2} = {(x, y)|y= x + 1,0< x w 2},l y= x2+ mx+ 2,2••• A n B M ?等价于方程组在X € [0,2]上有解,即x2+ mx+ 2= x + 1ly= x +1在[0,2]上有解,即x2+ (m—1)x+ 1 = 0在[0,2]上有解,显然x= 0不是该方程的解,1从而问题等价于—(m—1) = x + -在(0,2]上有解.又•••当x€ (0,2]时,1+ x>2(当且仅当丄=x,即x= 1 时取“ =”),•一(m —1)>2, • m w —1,即m的取值范围为(一g,—1].18. 已知集合A= {x|x2—3x+ 2= 0}, B = {x|x2+ 2(a+ 1)x+ a2—5= 0}.(1) 若A n B= {2},求实数a的值;(2) 若A U B= A,求实数a的取值范围.解:(1) •/ A = {x|x2—3x+ 2= 0} = {1,2}, A n B = {2},•2€ B,2 是方程x2+ 2(a+ 1)x+ a2—5= 0 的根,•a2+ 4a + 3= 0, a=—1 或a=—3.经检验a的取值符合题意,故 a =— 1 或a=— 3.(2) •/ A U B= A, • B? A.当B= ?时,由△= 4(a+ 1)2—4(a2—5)<0 ,解得a<—3;当B M ?时,由B= {1}或B = {1,2},可解得a€ ?;由B= {2},可解得a = — 3.综上可知,a的取值范围是(―^ ,—3].。
【人教版】2020高考政治一轮总复习:必修二单元课时跟踪练合集(含答案)

第一单元公民的政治生活第一课生活在人民当家作主的国家课时跟踪练一、选择题1、2017年《政府工作报告》指出,县级政府要建立基本生活保障协调机制,切实做好托底工作,使困难群众心里有温暖、生活有奔头。
提出这一要求的根本原因在于( )①在我国人民是国家的主人②我国的民主是全民的民主③我国是人民当家作主的国家④我国的民主具有广泛性A、①②B、③④C、①③D、②④解析:中华人民共和国是工人阶级领导的、以工农联盟为基础的人民民主专政的社会主义国家。
人民民主专政的本质是人民当家作主,①③符合题意。
民主具有鲜明的阶级性,没有全民的民主,②是错误的;人民民主的优点:广泛性和真实性。
广泛性表现在:民主主体和民主权利的广泛。
真实性表现在:人民当家作主的权利有制度、法律和物质的保障;广大人民的利益得到日益充分的实现,④不符合题意;故本题答案选C。
答案:C2、有一种感动,叫做“祖国带我回家”,2017年暑期,一部名为《战狼2》的电影火遍了大江南北,点燃了国人的爱国热情,让人们重新将目光投向近些年来的一系列撤侨行动。
“中国护照的含金量不仅仅在于它能帮你免签去多少个国家和地区,更在于危急时刻来临时,祖国能带你回家!”这是身为中国公民的自豪,也是“外交为民”最好的写照。
中国全力保护海外公民安全是因为( )①人民民主专政的本质是人民当家作主②我国的人民民主具有真实性③公民的国家意识和民主意识不断增强④民主是专政的前提和基础A、①②B、①③C、②④D、③④解析:人民民主专政的本质是人民当家作主,因而我国要保护公民安全,①正确;我国的人民民主具有真实性,国家要保障海外公民安全,②正确;公民的国家意识和民主意识不断增强并不是我国全力保护海外公民的原因,③不选;我国全力保护海外公民与专政无关,④不选,故本题答案选择A。
答案:A3、2018年3月5日至20日,第十三届全国人民代表大会第一次会议在北京举行。
2017年12月中旬至2018年1月,全国35个选举单位共选举产生了2 980名十三届全国人大代表。
2020版高考语文一轮复习课时作业23(含解析)

309教育网309教育资源库课时作业 23一、对点专练(一)阅读下面的文字,完成后面的题目。
独木舟之道[美]西格德·F.奥尔森①移动的独木舟颇像一叶风中摇曳的芦苇。
宁静是它的一部分,还有拍打的水声,树中的鸟语和风声。
荡舟之人是独木舟的一部分,从而也与它所熟悉的山水融为一体。
从他将船桨浸入水中的那一刻起,他便与它一起漂流,独木舟在他的手下服服帖帖,完全依照他的意愿而行。
船桨是他延长的手臂,一如手臂是他身体的器官。
划独木舟的感觉与在一片绝好的雪坡上滑雪几近相同,带着那种轻快如飞的惬意、小舟灵活敏捷,任你摆布;划独木舟还有一种与大地和睦相处、融为一体的感觉。
然而,对于一个划独木舟的人而言,最重要的莫过于当他荡起船桨时所体验的那种欢乐。
②掌控独木舟需要平衡,要使小舟与灵活摇摆的身体成为一体。
当每次划桨的节律与独木舟本身前进的节律相吻合时,疲劳便被忘却,还有时间来观望天空和岸上的风景,不必费力,也不必去考虑行驶的距离。
此时,独木舟随意滑行,划桨就如同呼吸那样毫无意识,悠然自得。
倘若你幸而划过一片映照着云影的平静水面,或许还会有悬在天地之间的感觉,仿佛不是在水中而是在天上荡舟。
③如果风起浪涌,你必须破浪前进,则另有一番奋战的乐趣。
每一道席卷而来的浪头都成为要被挫败的敌手。
顶风破浪的一天——巧妙地躲过一个又一个小岛,沿着狂风肆虐的水域下风处的岸边艰难行进,猛然再冲进激荡的水流和狂风之中,如此这般,周而复始——可以确保你晚上睡得香,做个好梦。
在独木舟上,你是独自一人在用自己的体魄、机智和勇气来与狂风暴雨抗争。
这就是为什么当经过一天的搏斗之后,终于在能挡风避雨的悬崖的背风处支起帐篷,竖起独木舟晾干,烧着晚饭时,心中会油然升起那种只有划独木舟的人才会有的得意之情。
乘风破浪需要的不只是划桨的技巧,而且要凭直觉判断出浪的规模势头,要知道它们在身后如何破碎。
荡舟之人不仅要熟悉他的独木舟及其路数,还要懂得身后涌起的波涛意味着什么。
2020届高三数学(文)一轮总复习课时跟踪检测 算法初步Word版含答案
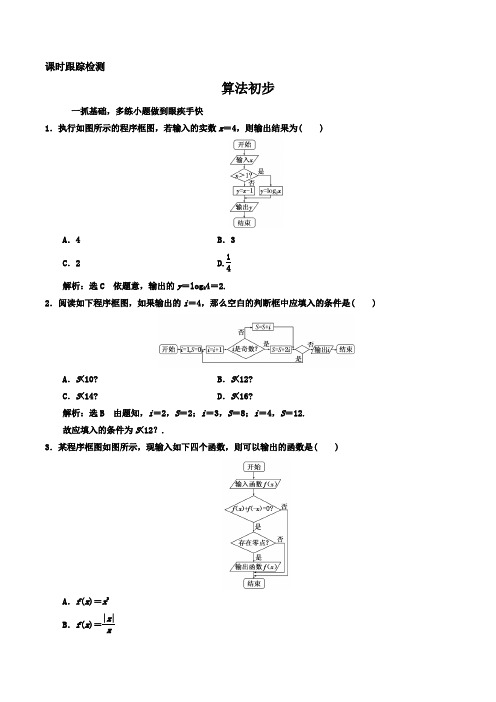
课时跟踪检测算法初步1.执行如图所示的程序框图,若输入的实数x =4,则输出结果为( )A .4B .3C .2D.14解析:选C 依题意,输出的y =log 24=2.2.阅读如下程序框图,如果输出的i =4,那么空白的判断框中应填入的条件是( )A .S <10?B .S <12?C .S <14?D .S <16?解析:选B 由题知,i =2,S =2;i =3,S =8;i =4,S =12. 故应填入的条件为S <12?.3.某程序框图如图所示,现输入如下四个函数,则可以输出的函数是( )A .f (x )=x 2B .f (x )=|x |xC.f(x)=e x-e-x e x+e-xD.f(x)=1+sin x+cos x 1+sin x-cos x解析:选C 由框图可知输出函数为奇函数且存在零点,依次判断各选项,A为偶函数,B不存在零点,均不符合,对于C,由于f(-x)=e-x-e xe-x+e x=-f(x),即函数为奇函数,且存在零点为x=0,对于D,由于其定义域不关于原点对称,故其为非奇非偶函数.4.执行如图所示的程序框图,如果输入的t∈[-1,3],则输出的s属于( )A.[-3,4] B.[-5,2]C.[-4,3] D.[-2,5]解析:选A 当-1≤t<1时,s=3t,则s∈[-3,3).当1≤t≤3时,s=4t-t2.函数在[1,2]上单调递增,在[2,3]上单调递减.∴s∈[3,4].综上知s∈[-3,4].5.执行如图所示的程序框图,则输出S的值为( )A.3 B.-6C.10 D.-15解析:选D 第一次执行程序,得到S=0-12=-1,i=2;第二次执行程序,得到S=-1+22=3,i=3;第三次执行程序,得到S=3-32=-6,i=4;第四次执行程序,得到S =-6+42=10,i =5; 第五次执行程序,得到S =10-52=-15,i =6, 到此结束循环,输出的S =-15.二保高考,全练题型做到高考达标1.(2019·北京东城模拟)如图给出的是计算12+14+16+18+…+1100的一个程序框图,其中判断框内应填入的条件是( )A .i <50?B .i >50?C .i <25?D .i >25?解析:选B 因为该循环体需要运行50次,i 的初始值是1,间隔是1,所以i =50时不满足判断框内的条件,而i =51时满足判断框内条件,所以判断框内的条件可以填入i >50?. 2.(2019·郑州模拟)执行如图所示的程序框图,输出的S 值是( )A.22B .-1C .0D .-1-22解析:选D 由程序框图可知n =1,S =0;S =cos π4,n =2;S =cos π4+cos 2π4,n =3; 这样依次循环,一直到S =cos π4+cos2π4+cos 3π4+…+cos 2 014π4=251⎝⎛⎭⎪⎫cosπ4+cos 2π4+…+cos 8π4+cos π4+cos 2π4+…+cos 6π4=251×0+22+0+⎝ ⎛⎭⎪⎫-22+(-1)+⎝ ⎛⎭⎪⎫-22+0 =-1-22,n =2 015. 3.(2019·全国卷Ⅱ)下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a ,b 分别为14,18,则输出的a =( )A .0B .2C .4D .14解析:选B a =14,b =18.第一次循环:14≠18且14<18,b =18-14=4; 第二次循环:14≠4且14>4,a =14-4=10; 第三次循环:10≠4且10>4,a =10-4=6; 第四次循环:6≠4且6>4,a =6-4=2; 第五次循环:2≠4且2<4,b =4-2=2; 第六次循环:a =b =2, 跳出循环,输出a =2,故选B.4.(2019·安徽皖南八校三联)如图所示是用模拟数方法估计椭圆x 24+y 2=1的面积S 的程序框图,则图中空白框内应填入( )A .S =N500B .S =M500C .S =4N500D .S =4M500解析:选D 从0到2产生的2 000个随机数中,落入椭圆内部或边界的有M 个,则M2 000=S44,故S =4M 500. 5.如图(1)是某县参加2 016年高考的学生身高条形统计图,从左到右的各条形表示的学生人数依次记为A 1,A 2,…,A 10(如A 2表示身高(单位:cm)在[150,155)内的学生人数).图(2)是统计图(1)中身高在一定范围内学生人数的一个程序框图.现要统计身高在160~180 cm(含160 cm ,不含180 cm)的学生人数,则在流程图中的判断框内应填写( )A .i <6?B .i <7?C .i <8?D .i <9?解析:选C 统计身高在160~180 cm 的学生人数,则求A 4+A 5+A 6+A 7的值.当4≤i ≤7时,符合要求.6.某程序框图如图所示,则该程序运行后输出的s 值为________.解析:根据程序框图,所求的值可以通过逐次循环求得,i =5,s =1;i =4,s =2×1+1=3;i =3,s =7;i =2,s =15;i =1,s =31,循环结束,故输出的s =31.答案:317.(2019·江西八校联考)执行如图所示的程序框图,输出的s 是________.解析:第一次循环:i =1,s =1;第二次循环:i =2,s =-1;第三次循环:i =3,s =2;第四次循环:i =4,s =-2,此时i =5,执行s =3×(-2)=-6.答案:-68.(2019·黄冈模拟)数列{a n }满足a n =n ,阅读如图所示的程序框图,运行相应的程序,若输入n =5,a n =n ,x =2的值,则输出的结果v =________.解析:该程序框图循环4次,各次v 的值分别是14,31,64,129,故输出结果v =129. 答案:1299.(2019·安徽高考)执行如图所示的程序框图(算法流程图),输出的n 为________.解析:执行第一次判断:|a -1.414|=0.414>0.005,a =32,n =2;执行第二次判断:|a-1.414|=0.086>0.005,a=75,n=3;执行第三次判断:|a-1.414|=0.014>0.005,a=1712,n=4;执行第四次判断:|a-1.414|<0.005,输出n=4.答案:410.给出以下10个数:5,9,80,43,95,73,28,17,60,36.要求把大于40的数找出来并输出.试画出该问题的程序框图.解:程序框图如下:三上台阶,自主选做志在冲刺名校1.执行如图所示的程序框图,若输入的a的值为3,则输出的i=( )A.4 B.5C.6 D.7解析:选C 第1次循环,得M=100+3=103,N=1×3=3,i=2;第2次循环,得M=103+3=106,N=3×3=9,i=3;第3次循环,得M=106+3=109,N=9×3=27,i=4;第4次循环,得M=109+3=112,N=27×3=81,i=5;第5次循环,得M =112+3=115,N =81×3=243,i =6, 此时M <N ,退出循环,输出的i 的值为6.2.执行如图所示的程序框图,若输入x =9,则输出y =________.解析:第一次循环:y =5,x =5;第二次循环:y =113,x =113;第三次循环:y =299,此时|y -x |=⎪⎪⎪⎪⎪⎪299-113=49<1,故输出y =299. 答案:2993.某篮球队6名主力队员在最近三场比赛中投进的三分球个数如表格所示:统计该6名队员在最近三场比赛中投进的三分球总数的程序框图如图所示. (1)试在判断框内填上条件; (2)求输出的s 的值.解:(1)依题意,程序框图是统计6名队员投进的三分球的总数. ∴判断框内应填条件“i ≤6?”.(2)6名队员投进的三分球数分别为a 1,a 2,a 3,a 4,a 5,a 6. 故输出的s =a 1+a 2+…+a 6.。
(江苏专版)2020版高考数学(理)一轮复习:课时跟踪检测(12套,含答案)

( )5 25
25
则 g(t)max=g 2 = 8 ,所以 a≥ 8 ;
( ) 1 5 1 5 25 t+ 记 h(t)=2t2+2t=2 2 2- 8 ,
则 h(t)min=h(2)=7,所以 a≤7, 25
综上所述, 8 ≤a≤7.
[ ] 25 ,7 所以实数 a 的取值范围是 8 .
三上台阶,自主选做志在冲刺名校
3 k+α=2.
3 答案:2
2.(2019·连云港调研)若函数 f(x)=-x2+2(a-1)x+2 在(-∞,4)上为增函数,
则 a 的取值范围是________.
解析:∵f(x)=-x2+2(a-1)x+2 的对称轴为 x=a-1,
f(x)=-x2+2(a-1)x+2 在(-∞,4)上为增函数,
=2x+b 的“关联区间”是[-3,0],则 b 的取值范围是________.
1 解析:由题意设 m(x)=f(x)-g(x)=3x3-x2-3x-b, 则 m′(x)=x2-2x-3,
由 m′(x)=0,得 m=-1 或 m=3.
∵f(x)与 g(x)在[-3,0]上是“关联函数”,
∴x=-1 是函数 m(x)在[-3,0]上的极大值,同时也是最大值.
________.
解析:不等式 x2-4x-2-a>0 在区间(1,4)内有解等价于 a<(x2-4x-2)max, 令 f(x)=x2-4x-2,x∈(1,4),
所以 f(x)<f(4)=-2,所以 a<-2.
答案:(-∞,-2)
4.(2018·泰州中学调研)已知 f(x)是定义在 R 上的奇函数,当 x<0 时,f(x)
1.(2019·金陵中学期中)设 f(x)与 g(x)是定义在同一区间[a,b]上的两个函数,若
2020届高考数学(理科)总复习课时跟踪练(三十三)等差数列及其前n项和

课时跟踪练(三十三)A 组 基础巩固1.[一题多解]已知数列{a n }是等差数列,a 1+a 7=-8,a 2=2,则数列{a n }的公差d 等于( )A .-1B .-2C .-3D .-4解析:法一由题意可得⎩⎨⎧a 1+(a 1+6d )=-8,a 1+d =2,解得a 1=5,d =-3.法二 a 1+a 7=2a 4=-8,所以a 4=-4, 所以a 4-a 2=-4-2=2d ,所以d =-3. ★答案★:C2.[一题多解](2016·全国卷Ⅰ)已知等差数列{a n }前9项的和为27,a 10=8,则a 100=( )A .100B .99C .98D .97解析:法一 因为{a n }是等差数列,设其公差为d , 所以S 9=92(a 1+a 9)=9a 5=27,所以a 5=3.又因为a 10=8,所以⎩⎨⎧a 1+4d =3,a 1+9d =8,所以⎩⎨⎧a 1=-1,d =1.所以a 100=a 1+99d =-1+99×1=98.故选C. 法二 因为{a n }是等差数列,所以S9=92(a1+a9)=9a5=27,所以a5=3.在等差数列{a n}中,a5,a10,a15,…,a100成等差数列,且公差d′=a10-a5=8-3=5.故a100=a5+(20-1)×5=98.故选C.★答案★:C3.(2019·太原模拟)已知等差数列{a n}的前n项和为S n,若a2+a3+a10=9,则S9=()A.3 B.9 C.18 D.27解析:设等差数列{a n}的首项为a1,公差为d.因为a2+a3+a10=9,所以3a1+12d=9,即a1+4d=3,所以a5=3,所以S9=9×(a1+a9)2=9×2a52=27.故选D.★答案★:D4.(2019·汕头模拟)已知等差数列{a n}的前n项和为S n,a1=9,S9 9-S55=-4,则S n取最大值时的n为()A.4 B.5 C.6 D.4或5解析:由{a n}为等差数列,得S99-S55=a5-a3=2d=-4,即d=-2,由于a 1=9,所以a n =-2n +11,令a n =-2n +11<0,得n >112,又因为n ∈N *,所以S n 取最大值时的n 为5,故选B. ★答案★:B5.(2019·合肥质量检测)中国古诗词中,有一道“八子分绵”的数学名题:“九百九十六斤绵,赠分八子作盘缠,次第每人多十七,要将第八数来言”.题意是:把996斤绵分给8个儿子作盘缠,按照年龄从大到小的顺序依次分绵,年龄小的比年龄大的多17斤绵,那么第8个儿子分到的绵是( )A .174斤B .184斤C .191斤D .201斤解析:用a 1,a 2,…,a 8表示8个儿子按照年龄从大到小得到的绵数,由题意得数列a 1,a 2,…,a 8是公差为17的等差数列,且这8项的和为996,所以8a 1+8×72×17=996,解得a 1=65.所以a 8=65+7×17=184,即第8个儿子分到的绵是184斤.故选B.★答案★:B6.在等差数列{a n }中,公差d =12,前100项的和S 100=45,则a 1+a 3+a 5+…+a 99=________.解析:因为S 100=1002(a 1+a 100)=45,所以a 1+a 100=0.9.a 1+a 99=a 1+a 100-d =0.4,则a 1+a 3+a 5+…+a 99=502(a 1+a 99)=502×0.4=10.★答案★:107.(2019·莆田质量检测)已知数列{a n }满足a 1=1,a n -a n +1=2a n a n+1,则a 6=________.解析:将a n -a n +1=2a n a n +1两边同时除以a n a n +1可得1a n +1-1a n =2.所以⎩⎨⎧⎭⎬⎫1a n 是以1a 1=1为首项,2为公差的等差数列,所以1a 6=1a 1+5×2=11,即a 6=111.★答案★:1118.设S n 是等差数列{a n }的前n 项和,S 10=16,S 100-S 90=24,则S 100=________.解析:依题意,S 10,S 20-S 10,S 30-S 20,…,S 100-S 90依次成等差数列,设该等差数列的公差为d .又S 10=16,S 100-S 90=24,因此S 100-S 90=24=16+(10-1)d =16+9d ,解得d =89,因此S 100=10S 10+10×92d =10×16+10×92×89=200.★答案★:2009.(2016·全国卷Ⅱ)等差数列{a n }中,a 3+a 4=4,a 5+a 7=6. (1)求{a n }的通项公式;(2)设b n =[a n ],求数列{b n }的前10项和,其中[x ]表示不超过x 的最大整数,如[0.9]=0,[2.6]=2.解:(1)设数列{a n }首项为a 1,公差为d ,由题意得⎩⎨⎧2a 1+5d =4,a 1+5d =3,解得⎩⎪⎨⎪⎧a 1=1,d =25.所以{a n }的通项公式为a n =2n +35.(2)由(1)知,b n =⎣⎢⎢⎡⎦⎥⎥⎤2n +35.当n =1,2,3时,1≤2n +35<2,b n =1;当n =4,5时,2≤2n +35<3,b n =2;当n =6,7,8时,3≤2n +35<4,b n =3;当n =9,10时,4≤2n +35<5,b n =4.所以数列{b n }的前10项和为1×3+2×2+3×3+4×2=24. 10.已知等差数列的前三项依次为a ,4,3a ,前n 项和为S n ,且S k =110.(1)求a 及k 的值;(2)设数列{b n }的通项公式b n =S nn ,证明:数列{b n }是等差数列,并求其前n 项和T n .(1)解:设该等差数列为{a n },则a 1=a ,a 2=4,a 3=3a , 由已知有a +3a =8,得a 1=a =2,公差d =4-2=2, 所以S k =ka 1+k (k -1)2·d =2k +k (k -1)2×2=k 2+k .由S k =110,得k 2+k -110=0,解得k =10或k =-11(舍去),故a =2,k =10. (2)证明:由(1)得S n =n (2+2n )2=n (n +1),则b n =S nn=n +1,故b n +1-b n =(n +2)-(n +1)=1,即数列{b n }是首项为2,公差为1的等差数列, 所以T n =n (2+n +1)2=n (n +3)2.B 组 素养提升11.(2019·河南普通高中毕业班高考适应性考试)已知等差数列{a n }的前n 项和为S n (n ∈N *),且a n =2n +λ,若数列{S n }(n ≥5,n ∈N *)为递增数列,则实数λ的取值范围为( )A .(-3,+∞)B .(-10,+∞)C .(-11,+∞)D .(-12,+∞)解析:在等差数列{a n }中,由a n =2n +λ,得a 1=2+λ,d =2,所以S n =na 1+n (n -1)2d =n (2+λ)+2n (n -1)2=n 2+(λ+1)n ,其图象的对称轴方程为n =-λ+12,要使数列{S n }在{n |n ≥5,n ∈N *}内为递增数列,则-λ+12<112,即λ>-12,故选D.★答案★:D12.设数列{a n }的前n 项和为S n ,若S nS 2n为常数,则称数列{a n }为“吉祥数列”.已知等差数列{b n }的首项为1,公差不为0,若数列{b n }为“吉祥数列”,则数列{b n }的通项公式为( )A .b n =n -1B .b n =2n -1C .b n =n +1D .b n =2n +1解析:设等差数列{b n }的公差为d (d ≠0),S nS 2n=k ,因为b 1=1,则n +12n (n -1)d =k ⎣⎢⎡⎦⎥⎤2n +12×2n (2n -1)d ,即2+(n -1)d =4k +2k (2n -1)d , 整理得(4k -1)dn +(2k -1)(2-d )=0. 因为对任意的正整数n 上式均成立, 所以(4k -1)d =0,(2k -1)(2-d )=0, 解得d =2,k =14,所以数列{b n }的通项公式为b n =2n -1. ★答案★:B13.(2019·中山一中统测)设S n 是数列{a n }的前n 项和,且a 1=-1,a n +1=S n S n +1,则S n =________.解析:因为a n +1=S n +1-S n ,a n +1=S n S n +1, 所以S n +1-S n =S n S n +1.因为S n ≠0,所以1S n -1S n +1=1,即1S n +1-1S n=-1.又1S 1=-1,所以⎩⎨⎧⎭⎬⎫1S n 是首项为-1,公差为-1的等差数列. 所以1S n =-1+(n -1)×(-1)=-n ,所以S n =-1n .★答案★:-1n14.(2019·北京海淀区模拟)已知{a n }是各项为正数的等差数列,S n 为其前n 项和,且4S n =(a n +1)2.(1)求a 1,a 2的值及{a n }的通项公式;(2)求数列⎩⎨⎧⎭⎬⎫S n -72a n 的最小值. 解:(1)因为4S n =(a n +1)2,所以当n =1时,4a 1=(a 1+1)2,解得a 1=1, 所以当n =2时4(1+a 2)=(a 2+1)2, 解得a 2=-1或a 2=3,因为{a n }是各项为正数的等差数列,所以a 2=3. 所以{a n }的公差d =a 2-a 1=2,所以{a n }的通项公式为a n =a 1+(n -1)d =2n -1. (2)因为4S n =(a n +1)2,所以S n =(2n -1+1)24=n 2,所以S n -72a n =n 2-72(2n -1)=n 2-7n +72=⎝ ⎛⎭⎪⎫n -722-354,所以当n =3或n =4时,S n -72a n 取得最小值-172.感谢您的下载!快乐分享,知识无限!由Ruize收集整理!。
2020年数学新高考一轮复习(理)课时跟踪检测(一)集合

课时跟踪检测(一) 集合一抓基础,多练小题做到眼疾手快1. (2019浙江考前热身联考)已知集合M = {x|y= .2x—x2}, N = {x|—1 v x v 1},贝U M U N =( )A. [0,1)B. (—1,2)C . (—1,2]D . ( — s, 0] U (1,+s )解析:选C 法一:易知M = {x|0W x w 2},又N = {x| —1v x v 1},所以M U N= (—1,2].故选C.法二:取x= 2,贝U 2€ M,所以2€ M U N,排除A、B;取x= 3,贝U 3? M,3 ?N,所以3?M U N,排除D,故选C.2. (2019 浙江三地联考)已知集合P= {x||x|v 2}, Q= {x|—1 w x w 3},贝U P n Q=( )A. [—1,2)B. (—2,2)C. (—2,3]D. [ —1,3]解析:选 A 由凶v 2,可得一2v x v 2,所以P= {x|—2v x v 2},所以P n Q= [—1,2).3. (2018嘉兴期末测试)已知集合P= {x|x v 1}, Q= {x|x>0},则()A. P? QB. Q? PD. ?R P ? QC. P?? R Q解析:选D 由已知可得?R P = [1,+ s),所以?R P? Q故选D.4 . (2018浙江吴越联盟第二次联考)已知集合M = {0,1,2,3,4} , N= {2,4,6} , P= M n N ,则P的子集有_________个.解析:集合M = {0,1,2,3,4} , N = {2,4,6} , P = M n N = {2,4},则P 的子集有?, {2} , {4}, {2,4},共 4 个.答案:45.已知集合A= {x|x> 3} ,B = {x|x> m},且A U B = A,则实数m的取值范围是 __________ .解析:因为集合 A = {x|x> 3}, B = {x|x> m},且A U B= A,■ ■ ■ ] ] ■ # ■ ■ 所以B? A,如图所示,所以m> 3. '答案:[3 ,+s )二保咼考,全练题型做到咼考达标1. (2019 杭州七校联考)已知集合A= {x|x2> 1} , B= {x|(x2—1)(x2—4)= 0},则集合A n B 中的元素个数为()B. 2D. 4解析:选 B A= {x|x v—1 或x> 1}, B= {—2, —1,1,2} , A n B = {—2,2},故选 B.2. (2019 浙江六校联考)已知集合 U = {x|y = $}, A = {x|y = log g x}, B = {y|y =- 2x }则 A H (?u B)=()A . ?B . RC . {x|x > 0}D . {0}解析:选C由题意得,u = R, A = {x|x > 0},因为y =— 2x v 0,所以B = {y|y v 0},所以?u B = {x|x > 0},故 A H (?u B) = {x|x > 0}.故选 C.3. (2019 永康模拟)设集合 M = {x|x 2— 2x — 3 >0}, N = {x|— 3 v x v 3},则( )A . M ? NB . N ? MC . M U N = RD . M H N = ?解析:选 C 由 x 2— 2x — 3 > 0,解得 x > 3 或 x < — 1,所以 M = {x|x < — 1 或 x > 3}, 所以M U N = R .4. (2019宁波六校联考)已知集合A = {x|x 2— 3x v 0}, B = {1, a},且A H B 有4个子集, 则实数a 的取值范围是()B . (0,1) U (1,3)C . (0,1)D . ( — s, 1)U (3,+^ )解析:选B •/ A H B 有4个子集,••• A H B 中有2个不同的元素,二a € A ,A a 2— 3av 0,解得0v a v 3且1,即实数a 的取值范围是(0,1) U (1,3),故选B.r'2一 x5. (2018 镇海中学期中)若集合 M = x y = lg --------------------------------------------------------------------------- : N = {x|x v 1},贝V M U N =()A . (0,1) C . ( — s, 2)r2 一 x解析:选C 集合M = x y = IgJ^ =(—s, 2).故选 C.6.设集合 A = {x|x 2— x — 2W 0}, B = {x|x v 1,且 x € Z },贝V A H B = ______ .解析:依题意得 A = {x|(x + 1)(x — 2)W 0} = {x|— 1 W x < 2},因此 A H B = {x|— 1W x v 1, x € Z }= { — 1,0}.答案:{ — 1,0}7. (2018 嘉兴二模)已知集合 A = {x|— 1W x W 2},B = {x|x 2— 4x W 0},则 A U B = ______ , A H (?R B) = _______ .解析:因为 B = {x|x 2— 4x W 0} = {x|0W x W 4},所以 A U B = {x|— 1 W x W 4};因为?R B = {x|xv 0 或 x > 4},所以 A H (?R B) = {x|— 1W x v 0}.A . (0,3)B . (0,2) M U N = {x|x v 2}D . (0 ,+s )N = {x|x v答案:{x|— 1 W x W 4} {x|— 1 W x v 0}8. 设集合A = {(x, y)|y> |x—2|, x> 0}, B = {(x, y)|y W—x+ b}, A H B 丰?.(1)b的取值范围是⑵若(x, y)€ A n B,且x+ 2y的最大值为9,贝U b的值是____________解析:由图可知,当y=—x往右移动到阴影区域时,才满足条件,所以b>2;要使z= x+ 2y取得最大值,则过点(0, b),有0 +92b= 9? b= 2.答案:(1)[2, +^ ) (2)|9.已知集合A= {x|4W 2x w 16}, B= [a, b],若A? B,则实数a—b的取值范围是又因为B? A,m> 3,所以—2m w- 2,m —4> 1,②当一2m > m—4, 即m v f时, A= {x|m —4v x v —2m},4综上所述,实数 m 的取值范围为 —’,一2 u [5,+^). (2)由(1)知,B = {x|— 2 v x v 1}. 当A = ?时,m =扌,符合题意.4当A H ?时,m H 孑.34① 当一2m v m — 4,即卩 m >-时,A = {x|— 2m v x v m — 4},3 又因为A A B = ?,所以一2m A 1或者m —4 W — 2, 1 4即m W — 一或者m W 2,所以一v m W 2.2 34② 当一2m > m — 4,即卩 m v 3时,A = {x|m — 4v x v — 2m},3 又因为 A A B = ?,所以 m —4 A 1或者一2m W — 2, 即m A 5或者m A 1,所以1 W m v 一. 3综上所述,实数 m 的取值范围为[1,2]. 三上台阶,自主选做志在冲刺名校3= 1,xy € S ”,则当 b = 1, 时,b + c + d 等于()宀bB .— 1 D . i解析:选B •/ S = {a , b , c , d},由集合中元素的互异性可知当 a = 1时,b =— 1, c 2 =—1 ,「• c = ±,由“对任意 x , y € S ,必有 xy € S ” 知 ± € S ,「. c = i , d =— i 或 c =— i , d =i ,••• b + c + d = (— 1) + 0=— 1.2.对于集合 M , N ,定义 M — N = {x|x € M ,且 x?N}, M ® N = (M — N)U (N — M),设 A = ix x A — 9,x € R ,, B = {x|x v 0, x € R},贝U A ® B =()所以 m< 3,—2m > 1,m — 4W — 2,广 4m v 3, 叫m < 1m — 2,m1所以m W —亍1•对于复数 a , b , c , d ,若集合S = {a , b , c , d}具有性质“对任意x , y € S,必有A r 9 / B「9「4A. 14,0丿B.「4, 0丿C. —g,— 4 U [0,+s )D.—g,— 9 U (0,+s )9解析:选 C 依题意得A— B = {x|x》0, x€ R}, B—A= {x x V —:, x€ R F,故A® B I4, =—g,—9 U [0, + g).故选C.3•已知函数f(x)= x —3——1的定义域为集合A,且B= {x € Z|2V x V 10}, C= {x寸7 —x€ R|x v a 或x> a +1}.(1) 求:A 和(?R A)Q B;(2) 若A U C= R,求实数a的取值范围.解:⑴要使函数f(x) = x—3—十“―,寸7 —x应满足x—3> 0,且7—x>0,解得3< x V 7,则A= {x|3< x v 7},得到?R A= {x|x v 3 或x > 7},而B= {x€ Z|2V x v 10} = {3,4,5,6,7,8,9},所以(?R A)A B= {7,8,9}.(2)C= {x € R|x v a 或x> a+ 1},要使A U C= R,则有 a > 3,且 a + 1v 7,解得3< a v 6.故实数a的取值范围为[3,6).解析:集合A= {x|4W 2x W 16} = {X|2*123W 2x< 24}= {x|2< x< 4} =[2,4],因为A? B,所以a w 2, b> 4,所以a—b< 2 —4 =—2,即实数a—b的取值范围是(一^,—2].答案:(—a, —2]r1 一x10.已知集合A= {x|(x + 2m)(x—m+ 4)v 0},其中m€ R,集合B = c x >0'•| x I 2—j(1) 若B? A,求实数m的取值范围;(2) 若A n B= ?,求实数m的取值范围.1 一x解:(1)集合B= x x+2> 0 = {x|— 2 V X V 1}.当A= ?时,m= f,不符合题意.4当A M ?时,m z ;.34①当一2m V m—4,即卩m>一时,A= {x|—2m v x v m—4},3又因为B? A,4m> 3,即“ 所以m> 5. m > 1, m> 5,。
2020版高考物理一轮复习:全套课时跟踪检测(Word版,含答案)

机械运动与物理模型第1节描述运动的基本概念一、质点、参考系1.质点(1)定义:用来代替物体的有质量的点。
(2)条件:物体的大小和形状对研究的问题的影响可以忽略不计。
[注1](3)实质:质点是一种理想化的模型,实际并不存在。
2.参考系(1)定义:在描述物体的运动时,用来做参考的物体。
(2)参考系的选取[注2]①参考系的选取是任意的,既可以是运动的物体,也可以是静止的物体,但被选为参考系的物体应认为是静止的,通常选地面为参考系。
②对于同一物体,选择不同的参考系时观察运动结果一般不同。
③比较两物体的运动情况时,必须选同一参考系。
二、位移、速度1.位移和路程(1)二者的定义(2)二者的区别和联系2(1)平均速度:物体发生的位移与发生这段位移所用时间的比值,即v =x t,是矢量,其方向就是对应位移的方向。
(2)瞬时速度:运动物体在某一时刻或经过某一位置的速度,是矢量。
[注3](3)速率:瞬时速度的大小,是标量。
三、加速度[注4]1.物理意义:描述物体速度变化快慢的物理量。
2.定义式:a =Δv Δt,单位为m/s 2。
3.方向:加速度为矢量,方向与速度变化量的方向相同。
【注解释疑】[注1] 不以“大小”论质点①大的物体不一定不能看成质点;②小的物体不一定能看成质点。
[注2] 不能选自身为参考系。
[注3] 在实际问题中,只要时间足够短,平均速度可认为等于瞬时速度,如光电门问题。
[注4] 速度变化快慢、速度变化率、加速度三者含义相同,速度变化快,也就是速度变化率大,加速度大。
[深化理解]1.质点的辨识物体能否看成质点,关键不在物体本身,而是要看研究的问题,同一个物体在不同情况下有时可看成质点,有时则不能。
2.“速度”的理解“速度”一词在不同情境下可能表示瞬时速度、平均速度、速率、平均速率,解决具体问题时需要加以区分。
3.平均速度和平均速率平均速度是位移与所用时间的比值,平均速率是路程与所用时间的比值,所以平均速率不是平均速度的大小。
2020届高三数学(文)一轮总复习课时跟踪检测 数列的概念与简单表示法Word版含答案

课时跟踪检测数列的概念与简单表示法一抓基础,多练小题做到眼疾手快1.(2019·宝鸡一检)设数列{a n }的前n 项和S n =n 2+n ,则a 4的值为( )A .4B .6C .8D .10解析:选C a 4=S 4-S 3=20-12=8.2.数列1,23,35,47,59,…的一个通项公式a n =( ) A.n 2n +1B.n 2n -1C.n 2n -3D.n 2n +3解析:选B 由已知得,数列可写成11,23,35,…,故通项为n 2n -1. 3.(2019·哈尔滨二模)下列说法正确的是( )A .数列1,-2,3,-4,…是一个摆动数列B .数列-2,3,6,8可以表示为{-2,3,6,8}C .{a n }和a n 是相同的概念D .每一个数列的通项公式都是唯一确定的解析:选A 对于A ,摆动数列是指从第2项起,有些项大于它的前一项,有些项小于它的前一项的数列,故A 正确;数列与数集是不同的,故B 错误;{a n }和a n 是不同的概念,{a n }表示数列a 1,a 2,a 3,…,a n ,而a n 表示的是这个数列的第n 项,故C 错误;每一个数列的通项公式并不都是唯一确定的,故D 错误.4.(2019·黄冈月考)已知数列{a n }的前n 项和为S n =n 2-2n +2,则数列{a n }的通项公式为( )A .a n =2n -3B .a n =2n +3C .a n =⎩⎪⎨⎪⎧ 1,n =1,2n -3,n ≥2D .a n =⎩⎪⎨⎪⎧1,n =1,2n +3,n ≥2 解析:选C 当n =1时,a 1=S 1=1,当n ≥2时,a n =S n -S n -1=2n -3,由于n =1时a 1的值不适合n ≥2的解析式,故通项公式为C.5.(2019·杭州三模)数列{a n }定义如下:a 1=1,当n ≥2时,a n=⎩⎨⎧ 1+a n 2,n 为偶数,1a n -1,n 为奇数,若a n =14,则n 的值为( )A .7B .8C .9D .10解析:选C 因为a 1=1,所以a 2=1+a 1=2,a 3=1a 2=12,a 4=1+a 2=3,a 5=1a 4=13,a 6=1+a 3=32,a 7=1a 6=23,a 8=1+a 4=4,a 9=1a 8=14,所以n =9.二保高考,全练题型做到高考达标1.数列0,1,0,-1,0,1,0,-1,…的一个通项公式是a n 等于( )A.(-1)n +12B .cos n π2C .cos n +12πD .cos n +22π 解析:选D 令n =1,2,3,…,逐一验证四个选项,易得D 正确.2.数列{a n }满足a n +a n +1=12(n ∈N *),a 2=2,S n 是数列{a n }的前n 项和,则S 21为( ) A .5B.72C.92D.132解析:选B ∵a n +a n +1=12,a 2=2, ∴a n =⎩⎪⎨⎪⎧-32,n 为奇数,2, n 为偶数.∴S 21=11×⎝⎛⎭⎫-32+10×2=72. 3.(2019·石家庄二模)在数列{a n }中,已知a 1=2,a 2=7,a n +2等于a n a n +1(n ∈N *)的个位数,则a 2 015=( )A .8B .6C .4D .2 解析:选D 由题意得:a 3=4,a 4=8,a 5=2,a 6=6,a 7=2,a 8=2,a 9=4,a 10=8;所以数列中的项从第3项开始呈周期性出现,周期为6,故a 2 015=a 335×6+5=a 5=2.4.设曲线y =x n +1(n ∈N *)在点(1,1)处的切线与x 轴的交点的横坐标为x n ,令a n =lg x n ,则a 1+a 2+…+a 99=( )A .100B .2C .-2D .-100解析:选C 因为y ′=(n +1)x n ,所以曲线y =x n +1在点(1,1)处的切线斜率为n +1,切线方程为y -1=(n +1)(x -1),令y =0,得x n =1-1n +1=n n +1.则a n =lg x n =lg n n +1,所以a 1+a 2+…+a 99=lg ⎝⎛⎭⎫12×23×…×99100=lg 1100=-2. 5.(2019·北京海淀区期末)若数列{a n }满足:a 1=19,a n +1=a n -3(n ∈N *),则数列{a n }的前n 项和数值最大时,n 的值为( )A .6B .7C .8D .9解析:选B ∵a 1=19,a n +1-a n =-3,∴数列{a n }是以19为首项,-3为公差的等差数列,∴a n =19+(n -1)×(-3)=22-3n .设{a n }的前k 项和数值最大,则有⎩⎪⎨⎪⎧ a k ≥0,a k +1≤0k ∈N *,∴⎩⎪⎨⎪⎧22-3k ≥0,22-3(k +1)≤0, ∴193≤k ≤223, ∵k ∈N *,∴k =7.∴满足条件的n 的值为7.6.在数列-1,0,19,18,…,n -2n 2,…中,0.08是它的第____________项. 解析:令n -2n 2=0.08,得2n 2-25n +50=0, 即(2n -5)(n -10)=0.解得n =10或n =52(舍去). 答案:107.(2019·浙江瑞安三校联考)已知数列{a n }满足:a 4n -3=1,a 4n -1=0,a 2n =a n ,n ∈N *,则a 2 013=________,a 2 016=________.解析:由题意可得a 2 013=a 4×504-3=1,a 2 016=a 1 008=a 504=a 252=a 126=a 63=a 4×16-1=0. 答案:1 08.在一个数列中,如果∀n ∈N *,都有a n a n +1a n +2=k (k 为常数),那么这个数列叫做等积数列,k 叫做这个数列的公积.已知数列{a n }是等积数列,且a 1=1,a 2=2,公积为8,则a 1+a 2+a 3+…+a 12=________.解析:依题意得数列{a n }是周期为3的数列,且a 1=1,a 2=2,a 3=4,因此a 1+a 2+a 3+…+a 12=4(a 1+a 2+a 3)=4×(1+2+4)=28.答案:289.已知S n 为正项数列{a n }的前n 项和,且满足S n =12a 2n +12a n (n ∈N *). (1)求a 1,a 2,a 3,a 4的值;(2)求数列{a n }的通项公式.解:(1)由S n =12a 2n +12a n (n ∈N *),可得 a 1=12a 21+12a 1,解得a 1=1; S 2=a 1+a 2=12a 22+12a 2,解得a 2=2; 同理,a 3=3,a 4=4.(2)S n =12a 2n +12a n ,① 当n ≥2时,S n -1=12a 2n -1+12a n -1,② ①-②得(a n -a n -1-1)(a n +a n -1)=0.由于a n +a n -1≠0,所以a n -a n -1=1,又由(1)知a 1=1,故数列{a n }是首项为1,公差为1的等差数列,故a n =n .10.已知数列{a n }的通项公式是a n =n 2+kn +4.(1)若k =-5,则数列中有多少项是负数?n 为何值时,a n 有最小值?并求出最小值;(2)对于n ∈N *,都有a n +1>a n ,求实数k 的取值范围. 解:(1)由n 2-5n +4<0,解得1<n <4.因为n ∈N *,所以n =2,3,所以数列中有两项是负数,即为a 2,a 3.因为a n =n 2-5n +4=⎝⎛⎭⎫n -522-94, 由二次函数性质,得当n =2或n =3时,a n 有最小值,其最小值为a 2=a 3=-2.(2)由a n +1>a n 知该数列是一个递增数列,又因为通项公式a n =n 2+kn +4,可以看作是关于n 的二次函数,考虑到n ∈N *,所以-k 2<32,即得k >-3. 所以实数k 的取值范围为(-3,+∞).三上台阶,自主选做志在冲刺名校1.已知{a n }满足a n +1=a n +2n ,且a 1=33,则a n n的最小值为( ) A .21B .10 C.212 D.172解析:选C 由已知条件可知,当n ≥2时, a n =a 1+(a 2-a 1)+(a 3-a 2)+…+(a n -a n -1) =33+2+4+…+2(n -1)=n 2-n +33,又n =1时,a 1=33满足此式.所以a n n =n +33n-1. 令f (n )=a n n =n +33n-1,则f (n )在[1,5]上为减函数, 在[6,+∞)上为增函数,又f (5)=535,f (6)=212, 则f (5)>f (6),故f (n )=a n n 的最小值为212. 2.(2019·天水一模)已知数列{a n }中,a 1=1,且a n +a n +1=2n .求数列{a n }的通项公式.解:∵a n +a n +1=2n ,①∴a n +1+a n +2=2n +1,② ②-①,得a n +2-a n =2n ,由a 1=1,a 1+a 2=2,得a 2=1.当n 为奇数时,a n =(a n -a n -2)+(a n -2-a n -4)+…+(a 3-a 1)+a 1 =2n -2+2n -4+…+2+1 =13×2n +13; 当n 为偶数时,a n =(a n -a n -2)+(a n -2-a n -4)+…+(a 4-a 2)+a 2 =2n -2+2n -4+…+22+1 =13×2n -13. 故a n =⎩⎨⎧ 13×2n +13,n 为奇数,13×2n -13,n 为偶数.。
2020届高考总复习数学(文科)课时跟踪练(三十三)

课时跟踪练(三十三)A 组基础巩固i . (20佃湖北调考)设等比数列{a n }中, a 2 = 2, a 2 + a 4 + a 6 = i4, 则公比q =()A . 3 B. 士. 3C . 2 D.士. 2a i q = 2,解析: 由题意得解得q 2= 2,a i q + a i q + a i q 5= i4,所以q = 士 2,故选D. 答案:D2.[—题多解](20佃成都二诊)在等比数列{a n }中,已知a 3 = 6, a 3+ 85+ 87= 78,贝卩 a 5=() A . 12 B . 18 C . 24D . 36解析:法一 设等比数列{a n }的公比为q ,则有a 3+a 3q 2+ a 3q 4= 6+ 6q 2 + 6q 4= 78,解得 q 2= 3,所以决=a 3q 2= 18,故选 B.设等比数列{a n }的首项为a i ,公比为q ,则由题意有_!_a i= 2,解得 q =± 3,所以 a 5 = a i q =i8-答案:B法二阳=6,4§a i q 2 + a i q 4 + a i q 6 = 78,3. (20i9菏泽模拟)等比数列{a n}中,a2,盹是方程x2+ 6x+ 2 = 0的两个实数根,则警的值为()a9A. 2B.—2或2C・ 2 D. —2解析:因为a2, a ie是方程X2+6X+ 2= 0的根,所以a2+ a ie= —a?a i6 6, a2 a ie = 2,所以a2<0, a ie<0,即a i>0, q<0 或a i<0, q>0,所以二a9 =a9= 士a2a ie= 士2•故选 B.答案:B4. 已知各项均为正数的等比数列{a n}中,a4与a i4的等比中项为2 2,则2a7+ a ii的最小值为()A. i6B. 8C. 2 2D. 4解析:因为a4与a i4的等比中项为2 2,所以a4 a i4= a7 a ii= (2 2)2= 8,所以2a7 + a ii》2材2a7a ii = 22x 8 = 8,所以2a7 + a ii的最小值为8.答案:B*5. 已知数列{a n}满足loga n +1 = log3a n+ i(n€ N ),且a2+ d + a e =9,贝S logi(a5 + a?+ a?)的值是()3i A. —5 B.—-5解析:因为 log 3a n + 1= log 3a n +1, 所以a n +1 = 3a n •又由题意知a n >0 , 所以数列{a n }是公比q =3的等比数列. 因为 a 5+a 7+a 9 = q 3(a 2 + a 4+a 6),所以 Iog1(a 5 + a ? + 诙)=Iog1(9 x 33)= Iog135= — 5.3 3 3 答案:A6. _________________________________________________ 在等比数列{a n }中,若 a 1 a 5= 16, au = 8,贝S a 6 = _________ . 解析:由题意得,a 2 a 4 = a 1 a 5= 16,所以a 2= 2,所以q 2 = :4= 4,所以 a 6 = a 4q 2 = 32.a 2 答案:327. 在各项均为正数的等比数列{a n }中,若a m a m +2= 2a m + 1(m € N *),数列{a n }的前n 项积为T n ,且T ?m +1= 128,则m 的值为 _______ ,解牛析:因为 a m a m +2 = 2a m +1,所以 a m +1 = 2a m +1,即 a m +1 = 2, 即{a n }为常数列.又 T 2m +1 = (a m +1)2m +1,由 2叫1 = 128,得 m = 3.答案:3a 2 +8. (2019 合肥二测)已知数列{a n }中,a 1 = 2,且严 =4佃+1 — a n )(n a n*€ N ),则其前9项的和S 9 = ________ .解析:a n +1a n4(a n +1—a n )可得 a n +1 — 4a n + 1a n + 4a n = 0,即(a n + 1—2a n)2 = 0,即a n+1= 2a n,又a1 = 2,所以数列{a n}是首项和公比都是答案:1 0229. (2016全国卷I )已知{a n }是公差为3的等差数列,数列{b n } 、卄1满足 b = 1, b 2= 3, a n b n +1 + b n +1 = ng.(1) 求{a n }的通项公式; (2) 求{b n }的前n 项和.1解:(1)由已知,a 1 b a + b 2 = b i , b 1 = 1, b 2=3,得 a 1 = 2,所以数列{a n }是首项为2,公差为3的等差数列,通项公式为a n =3n — 1.(2)由(1)知 a n b n +1 + b n +1 = nb n ,得 b n +1= 3 , 1因此{b n }是首项为1,公比为3的等比数列.记{b n }的前n 项和为S n ,解:(1)因为点(a n , a n +1)在直线y = x + 2上, 所以 a n +1 = a n +2,所以 a n +1 — a n = 2,所以数列{a n }是等差数列,公差为2,又a 1= 1,所以a n = 1+2(n2的等比数列,则其前 9项的和S g =2 (1 — 29)1 — 2=210 — 2= 1 022. 则S n =1—1n 1 31-31 2X 3n — 1—1)= 2n—1.n (1 + 2n —1)⑵数列{a n}的前n项和S n=------2= n2.等比数列{b n}中,b1= a1= 1, b2 = a2 = 3,所以q= 3.所以b n= 3n-1・1 —3n 3n—1所以数列{b n}的前n项和T n= 1 —3 = 2T n<S n可化为2< n2,又n€ N*,所以n= 1或2.故适合条件T n<S n的所有n的值为1, 2.B组素养提升11.数列{a n}中,已知对任意n€ N*, d + a? + a3+…+ a n= 3n—1,则a1 + a2+ 82+・・・+82等于( )A. (3n—1)2B・2(9n—1)C. 9n— 1D.4(3n—1)解析:因为a“ + a2+…+ a n= 3n—1, n€ N*,当n》2 时,a“ + a2 +…+ a n—1= 31 — 1—1,所以当n> 2 时,a n= 3n—3n-1= 2 3n-1, 又n= 1时,a i = 2适合上式,所以a n= 2 3n_ 1, 故数列{a2}是首项为4,公比为9的等比数列,4 (1-9n) 1因此a“ + a2+…+ a n = = o(9 —1).1 - 9 2答案:B12. (2019河南六市联考)若正项递增等比数列{a n }满足1 + (a 2 — a 4)+ X a s — a 5)= 0(入€ R),贝卩a 6 +入7的最小值为( )A . — 2B . — 4C . 2D . 4解析:因为{a n }是正项递增的等比数列, 所以 a 1>0, q>1,由 1 + (a 2 — a 4)+ 牝3—a 5)= 0, 得 1 + (a 2 — a 4)+ 入値2 — a 4)= 0,1所以1 +入q,a4—a2所以a 6 +入力=a 6(1 +入)=a 6 =:a 4—a 2 q — 1=[(q2- 1)+ 1]2 = (q 2 -1) + 2+ 21广 2q — 1+ 2=4(q 2 —1>0),当且仅当q = 2时取等号,所以a 6+入a 勺最小值为4•故选D. 答案:D心1)q 2—1q 2—113. (2019佛山质量检测)数列{a n }满足a i + 3a 2 +…+ (2n — 1)a n=3— -^^―, n € N *,贝S a “ + a 2+…+ a n = _____________2n + 3 解析:因为 a “ + 3a 2 +…+ (2n — 1)a n = 3 — ?n ,2n — 1 1两式相减得(2n — 1)a n = 2* (n >2), a n = 2n (n >2),5 1 1 *当 n = 1 时,a 1 = 3— 2= 2,适合上式,所以 a n = 2n (n € N ),1— 2因此 a i + a 2 +…+ a n =答案:1 — f n14.已知数列{a n }满足 a 1 = 5, a 2= 5,為+1 = a *+ 6a “-1(n >2). (1)求证:{a n +1 + 2a n }是等比数列;⑵求数列{a n }的通项公式.(1)证明:因为 a n +1 = a n + 6a n - 1(n >2),所以 a n +1 + 2a n = 3a n + 6a n —1 = 3(a n + 2a n - 1)(n 》2). 因为 a 1 = 5, a 2= 5,所以 a 2 + 2a “= 15, 所以 a n + 2a n — 1^0(n >2),所以 a 1 + 3a 2 + …+ (2 n — 3)a n -1 = 3—2n + 12“— 1(n > 2),=1 21a n +1 + 2a n所以-------- =3(n> 2),a n + 2a n—1所以数列{a n+1 + 2a n}是以15为首项,3为公比的等比数列.(2)解:由(1)得a n+1 + 2a n = 15X 3n-1= 5X 3n,则a n +1 = —2a n + 5x 3 ,所以a n+1 —3n+1=-2(a n —3n).又因为a1 — 3 = 2,所以a n—3—0,所以{a n —3n}是以2为首项,—2为公比的等比数列.所以a n—3n= 2X ( —2)n-1,即a n = 2X (—2)n—1+ 3n.10. (2019惠州三调)已知数列{a n}中,点(a n, a n+1)在直线y= x + 2上,且首项a1= 1.(1) 求数列{a n}的通项公式;(2) 数列{a n}的前n项和为S n,等比数列{b n}中,6=站,b = a?, 数列{b n}的前n项和为T n,请写出适合条件T n< S n的所有n的值.。
2020届高三数学(文)一轮复习课时跟踪训练:第一章 集合与常用逻辑用语 课时跟踪训练2 Word版含解析.doc

课时跟踪训练(二)[基础巩固] 一、选择题1.(2017·安徽马鞍山模拟)命题“若△ABC有一内角为π3,则△ABC的三个内角成等差数列”的逆命题()A.与原命题同为假命题B.与原命题的否命题同为假命题C.与原命题的逆否命题同为假命题D.与原命题同为真命题[解析]原命题显然为真,原命题的逆命题为“若△ABC的三个内角成等差数列,则△ABC有一内角为π3”,它是真命题.故选D.[答案] D2.(2017·河北唐山二模)已知a,b为实数,则“a3<b3”是“2a<2b”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件[解析]由于函数y=x3,y=2x在R上单调递增,所以a3<b3⇔a<b ⇔2a<2b,即“a3<b3”是“2a<2b”的充要条件.故选C.[答案] C3.(2016·山东卷)已知直线a,b分别在两个不同的平面α,β内,则“直线a和直线b相交”是“平面α和平面β相交”的() A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件[解析]由题意得,直线a和直线b相交⇒平面α和平面β相交,反之,由“平面α和平面β相交”不能推出“直线a 和直线b 相交”,故“直线a 和直线b 相交”是“平面α和平面β相交”的充分不必要条件,故选A.[答案] A4.(2015·安徽卷)设p :1<x <2,q :2x >1,则p 是q 成立的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件D .既不充分也不必要条件 [解析] q :2x >1⇔x >0,且(1,2)(0,+∞),所以p 是q 的充分不必要条件.故选A.[答案] A5.已知p :(a -1)2≤1,q :∀x ∈R ,ax 2-ax +1≥0,则p 是q 成立的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 [解析] 由(a -1)2≤1解得0≤a ≤2, ∴p :0≤a ≤2.当a =0时,ax 2-ax +1≥0对∀x ∈R 恒成立;当a ≠0时,由⎩⎨⎧a >0Δ=a 2-4a ≤0得0<a ≤4, ∴q :0≤a ≤4.∴p 是q 成立的充分不必要条件.故选A. [答案] A6.(2018·昆明三中、玉溪一中统考)已知条件p :|x -4|≤6;条件q :(x -1)2-m 2≤0(m >0),若p 是q 的充分不必要条件,则m 的取值范围是( )A .[21,+∞)B .[9,+∞)C .[19,+∞)D .(0,+∞)[解析] 条件p :-2≤x ≤10,条件q :1-m ≤x ≤m +1,又因为p 是q 的充分不必要条件,所以有⎩⎪⎨⎪⎧ 1-m ≤-21+m >10或⎩⎪⎨⎪⎧1-m <-21+m ≥10解得m ≥9.故选B.[答案] B 二、填空题7.(2017·北京卷)能够说明“设a ,b ,c 是任意实数.若a >b >c ,则a +b >c ”是假命题的一组整数a ,b ,c 的值依次为________.[解析] 要使该命题为假命题,只需证a >b >c 时,a +b ≤c (a ,b ,c ∈R )为真命题,所以c <b <a <0.不妨取a =-2,b =-3,c =-4(不唯一),经检验,符合题意.[答案] -2,-3,-4(答案不唯一)8.(2017·湖北百校联考)命题“若x ≥1,则x 2-4x +2≥-1”的否命题为____________________.[解析] 由否命题的定义可知,命题“若x ≥1,则x 2-4x +2≥-1”的否命题为“若x <1,则x 2-4x +2<-1”.[答案] 若x <1,则x 2-4x +2<-19.(2018·河北保定期中)已知命题p :x 2+2x -3>0;命题q :x >a ,且綈q 的一个充分不必要条件是綈p ,则a 的取值范围是________.[解析] p :由x 2+2x -3>0,得x <-3或x >1.由綈q 的一个充分不必要条件是綈p ,可知綈p 是綈q 的充分不必要条件,等价于q 是p 的充分不必要条件.又q :x >a ,故a ≥1.[答案] [1,+∞)10.(2017·山东威海教学质量检测)下列命题:①“全等三角形的面积相等”的逆命题;②“若ab =0,则a =0”的否命题;③“正三角形的三个角均为60°”的逆否命题.其中真命题的序号是________.[解析] ①“全等三角形的面积相等”的逆命题为“面积相等的两个三角形全等”,显然该命题为假命题;②“若ab =0,则a =0”的否命题为“若ab ≠0,则a ≠0”,而由ab ≠0可得a ,b 都不为零,故a ≠0,所以②是真命题;③因为原命题“正三角形的三个角均为60°是真命题,故其逆否命题也是真命题.故填②③.[答案] ②③[能力提升]11.(2017·全国卷Ⅰ)设有下面四个命题 p 1:若复数z 满足1z ∈R ,则z ∈R ; p 2:若复数z 满足z 2∈R ,则z ∈R ; p 3:若复数z 1,z 2满足z 1z 2∈R ,则z 1=z -2; p 4:若复数z ∈R ,则z -∈R . 其中的真命题为( ) A .p 1,p 3 B .p 1,p 4 C .p 2,p 3D .p 2,p 4[解析] 设复数z =a +b i(a ,b ∈R ).p 1:1z =1a +b i =a a 2+b 2-b a 2+b 2i ∈R ,则b =0,∴z ∈R ,是真命题;p 2:z 2=(a +b i)2=a 2-b 2+2ab i ∈R ,则2ab =0,所以a =0或b =0.所以z 为实数或纯虚数,是假命题;p 3:设z 1=-2+i ,z 2=2+i ,则z 1z 2∈R ,但z 1≠z -2,是假命题; p 4:z ∈R ,所以b =0,∴z -∈R ,是真命题.故选B. [答案] B12.(2017·河北衡水中学第三次调研)△ABC 中,“角A ,B ,C 成等差数列”是“sin C =(3cos A +sin A )cos B ”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件[解析] 由角A ,B ,C 成等差数列,得B =π3;由sin C =(3cos A +sin A )cos B ,得sin(A +B )=(3cos A +sin A )cos B ,化简得cos A sin ⎝ ⎛⎭⎪⎫B -π3=0,所以A =π2或B =π3,所以“角A ,B ,C 成等差数列”是“sin C =(3cos A +sin A )cos B ”的充分不必要条件,故选A.[答案] A13.(2017·吉林长春一模)设a ,b 都是非零向量,则使a |a |=b |b |成立的充分条件是( )A .|a |=|b|且a ∥bB .a =-bC .a ∥bD .a =2b[解析] 对于A ,当a ∥b 且|a |=|b |时,可能有a =-b ,此时a |a |≠b|b |;对于B ,当a =-b 时,a |a |≠b |b |;对于C ,当a ∥b 时,a |a |与b|b |可能不相等;对于D ,当a =2b 时,a |a |=2b |2b |=b |b |.综上所述,使a |a |=b|b |成立的充分条件是a =2b ,选D.[答案] D14.(2017·贵州贵阳月考)以下四个命题中,真命题的个数是( )①“若a +b ≥2,则a ,b 中至少有一个不小于1”的逆命题;②存在正实数a ,b ,使得lg(a +b )=lg a +lg b ;③“所有奇数都是素数”的否定是“至少有一个奇数不是素数”;④在△ABC 中,A <B 是sin A <sin B 的充分不必要条件.A .0B .1C .2D .3[解析] ①中,令a =2,b =-3,则a +b <2,故逆命题是假命题;②中,令a =b =2,lg(a +b )=lg a +lg b 成立,故命题②是真命题;③中,根据命题否定的规则,可以判定命题③是真命题;④中,在△ABC 中,A <B ⇔sin A <sin B ,是充要条件,故命题④是假命题.综上,真命题的个数为2.故选C.[答案] C15.设p :|4x -3|≤1;q :x 2-(2a +1)x +a (a +1)≤0,若綈p 是綈q 的必要不充分条件,求实数a 的取值范围.[解] 设A ={x ||4x -3|≤1}, B ={x |x 2-(2a +1)x +a (a +1)≤0},易知A =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪12≤x ≤1,B ={x |a ≤x ≤a +1}.由綈p 是綈q 的必要不充分条件,从而p 是q 的充分不必要条件,即AB ,∴⎩⎨⎧a ≤12,a +1>1或⎩⎨⎧a <12,a +1≥1,所求实数a 的取值范围是⎣⎢⎡⎦⎥⎤0,12. [延伸拓展](2017·湖北荆、荆、襄、宜四地七校联盟联考)已知函数f (x )=ax 2-4ax -ln x ,则f (x )在(1,3)上不单调的一个充分不必要条件是( )A .a ∈⎝⎛⎭⎪⎫-∞,16B .a ∈⎝⎛⎭⎪⎫-12,+∞C .a ∈⎝ ⎛⎭⎪⎫-12,16D .a ∈⎝ ⎛⎭⎪⎫12,+∞[解析] f ′(x )=2ax -4a -1x ,f (x )在(1,3)上不单调,则f ′(x )=2ax -4a -1x =0在(1,3)上有解.此方程可化为2ax 2-4ax -1=0,设其解为x 1,x 2,则x 1+x 2=2,因此方程的两解不可能都大于1,所以其在(1,3)中只有一解,其充要条件是(2a -4a -1)·(18a -12a -1)<0,解得a <-12或a >16.因此选项D 是满足要求的一个充分不必要条件.故选D.[答案] D。
浙江专版2020版高考数学一轮复习课时跟踪检测一集合含解析

课时跟踪检测(一)集合一抓基础,多练小题做到眼疾手快1.(2019·浙江考前热身联考)已知集合M={x|y=2x-x2},N={x|-1<x<1},则M∪N=( )A.[0,1) B.(-1,2)C.(-1,2] D.(-∞,0]∪(1,+∞)解析:选C 法一:易知M={x|0≤x≤2},又N={x|-1<x<1},所以M∪N=(-1,2].故选C.法二:取x=2,则2∈M,所以2∈M∪N,排除A、B;取x=3,则3∉M,3∉N,所以3∉M∪N,排除D,故选C.2.(2019·浙江三地联考)已知集合P={x|||x<2},Q={x|-1≤x≤3},则P∩Q=( )A.[-1,2) B.(-2,2)C.(-2,3] D.[-1,3]解析:选A 由|x|<2,可得-2<x<2,所以P={x|-2<x<2},所以P∩Q=[-1,2).3.(2018·嘉兴期末测试)已知集合P={x|x<1},Q={x|x>0},则( )A.P⊆Q B.Q⊆PC.P⊆∁R Q D.∁R P⊆Q解析:选D 由已知可得∁R P=[1,+∞),所以∁R P⊆Q.故选D.4.(2018·浙江吴越联盟第二次联考)已知集合M={0,1,2,3,4},N={2,4,6},P=M∩N,则P的子集有________个.解析:集合M={0,1,2,3,4},N={2,4,6},P=M∩N={2,4},则P的子集有∅,{2},{4},{2,4},共4个.答案:45.已知集合A={x|x≥3},B={x|x≥m},且A∪B=A,则实数m的取值范围是________.解析:因为集合A={x|x≥3},B={x|x≥m},且A∪B=A,所以B⊆A,如图所示,所以m≥3.答案:[3,+∞)二保高考,全练题型做到高考达标1.(2019·杭州七校联考)已知集合A={x|x2>1},B={x|(x2-1)(x2-4)=0},则集合A∩B中的元素个数为( )A.1 B.2C.3 D.4解析:选B A={x|x<-1或x>1},B={-2,-1,1,2},A∩B={-2,2},故选B.2.(2019·浙江六校联考)已知集合U={x|y=3x},A={x|y=log9x},B={y|y=-2x}则A∩(∁U B)=( )A.∅ B.RC.{x|x>0} D.{0}解析:选C 由题意得,U=R,A={x|x>0},因为y=-2x<0,所以B={y|y<0},所以∁U B={x|x≥0},故A∩(∁UB )={x |x >0}.故选C.3.(2019·永康模拟)设集合M ={x |x 2-2x -3≥0},N ={x |-3<x <3},则( ) A .M ⊆N B .N ⊆M C .M ∪N =RD .M ∩N =∅解析:选C 由x 2-2x -3≥0,解得x ≥3或x ≤-1,所以M ={x |x ≤-1或x ≥3},所以M ∪N =R.4.(2019·宁波六校联考)已知集合A ={x |x 2-3x <0},B ={1,a },且A ∩B 有4个子集,则实数a 的取值范围是( )A .(0,3)B .(0,1)∪(1,3)C .(0,1)D .(-∞,1)∪(3,+∞)解析:选B ∵A ∩B 有4个子集,∴A ∩B 中有2个不同的元素,∴a ∈A ,∴a 2-3a <0,解得0<a <3且a ≠1,即实数a 的取值范围是(0,1)∪(1,3),故选B.5.(2018·镇海中学期中)若集合M =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪y =lg2-xx ,N ={x |x <1},则M ∪N =( ) A .(0,1) B .(0,2) C .(-∞,2)D .(0,+∞)解析:选C 集合M =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪y =lg2-xx ={x |0<x <2},N ={x |x <1}.M ∪N ={x |x <2}=(-∞,2).故选C. 6.设集合A ={x |x 2-x -2≤0},B ={x |x <1,且x ∈Z},则A ∩B =________.解析:依题意得A ={x |(x +1)(x -2)≤0}={x |-1≤x ≤2},因此A ∩B ={x |-1≤x <1,x ∈Z}={-1,0}. 答案:{-1,0}7.(2018·嘉兴二模)已知集合A ={x |-1≤x ≤2},B ={x |x 2-4x ≤0},则A ∪B =________,A ∩(∁R B )=________. 解析:因为B ={x |x 2-4x ≤0}={x |0≤x ≤4},所以A ∪B ={x |-1≤x ≤4};因为∁R B ={x |x <0或x >4},所以A ∩(∁RB )={x |-1≤x <0}.答案:{x |-1≤x ≤4} {x |-1≤x <0}8.设集合A ={(x ,y )|y ≥|x -2|,x ≥0},B ={(x ,y )|y ≤-x +b },A ∩B ≠∅. (1)b 的取值范围是________;(2)若(x ,y )∈A ∩B ,且x +2y 的最大值为9,则b 的值是________. 解析:由图可知,当y =-x 往右移动到阴影区域时,才满足条件,所以b ≥2;要使z =x +2y 取得最大值,则过点(0,b ),有0+2b =9⇒b =92.答案:(1)[2,+∞) (2)929.已知集合A ={x |4≤2x≤16},B =[a ,b ],若A ⊆B ,则实数a -b 的取值范围是________.解析:集合A ={x |4≤2x≤16}={x |22≤2x ≤24}={x |2≤x ≤4}=[2,4],因为A ⊆B ,所以a ≤2,b ≥4,所以a -b ≤2-4=-2,即实数a -b 的取值范围是(-∞,-2].答案:(-∞,-2]10.已知集合A ={x |(x +2m )(x -m +4)<0},其中m ∈R ,集合B =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪1-xx +2>0. (1)若B ⊆A ,求实数m 的取值范围; (2)若A ∩B =∅,求实数m 的取值范围.解:(1)集合B =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪1-x x +2>0={x |-2<x <1}. 当A =∅时,m =43,不符合题意.当A ≠∅时,m ≠43.①当-2m <m -4,即m >43时,A ={x |-2m <x <m -4},又因为B ⊆A ,所以⎩⎪⎨⎪⎧ m >43,-2m ≤-2,m -4≥1,即⎩⎪⎨⎪⎧m >43,m ≥1,m ≥5,所以m ≥5.②当-2m >m -4,即m <43时,A ={x |m -4<x <-2m },又因为B ⊆A ,所以⎩⎪⎨⎪⎧m <43,-2m ≥1,m -4≤-2,即⎩⎪⎨⎪⎧m <43,m ≤-12,m ≤2,所以m ≤-12.综上所述,实数m 的取值范围为⎝ ⎛⎦⎥⎤-∞,-12∪[5,+∞). (2)由(1)知,B ={x |-2<x <1}. 当A =∅时,m =43,符合题意.当A ≠∅时,m ≠43.①当-2m <m -4,即m >43时,A ={x |-2m <x <m -4},又因为A ∩B =∅,所以-2m ≥1或者m -4≤-2, 即m ≤-12或者m ≤2,所以43<m ≤2.②当-2m >m -4,即m <43时,A ={x |m -4<x <-2m },又因为A ∩B =∅,所以m -4≥1或者-2m ≤-2, 即m ≥5或者m ≥1,所以1≤m <43.综上所述,实数m 的取值范围为[1,2]. 三上台阶,自主选做志在冲刺名校1.对于复数a ,b ,c ,d ,若集合S ={a ,b ,c ,d }具有性质“对任意x ,y ∈S ,必有xy ∈S ”,则当⎩⎪⎨⎪⎧a =1,b 2=1,c 2=b时,b +c +d 等于( )A .1B .-1C .0D .i解析:选B ∵S ={a ,b ,c ,d },由集合中元素的互异性可知当a =1时,b =-1,c 2=-1,∴c =±i,由“对任意x ,y ∈S ,必有xy ∈S ”知±i∈S ,∴c =i ,d =-i 或c =-i ,d =i ,∴b +c +d =(-1)+0=-1.2.对于集合M ,N ,定义M -N ={x |x ∈M ,且x ∉N },M ⊕N =(M -N )∪(N -M ),设A =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ≥-94,x ∈R ,B ={x |x <0,x ∈R},则A ⊕B =( )A.⎝ ⎛⎭⎪⎫-94,0B.⎣⎢⎡⎭⎪⎫-94,0C.⎝⎛⎭⎪⎫-∞,-94∪[0,+∞) D.⎝⎛⎦⎥⎤-∞,-94∪(0,+∞) 解析:选C 依题意得A -B ={x |x ≥0,x ∈R},B -A =⎩⎨⎧x ⎪⎪⎪⎭⎬⎫x <-94,x ∈R ,故A ⊕B =⎝⎛⎭⎪⎫-∞,-94∪[0,+∞).故选C.3.已知函数f (x )=x -3-17-x 的定义域为集合A ,且B ={x ∈Z|2<x <10},C ={x ∈R|x <a 或x >a +1}. (1)求:A 和(∁R A )∩B ;(2)若A ∪C =R ,求实数a 的取值范围. 解:(1)要使函数f (x )=x -3-17-x ,应满足x -3≥0,且7-x >0,解得3≤x <7, 则A ={x |3≤x <7}, 得到∁R A ={x |x <3或x ≥7},而B ={x ∈Z|2<x <10}={3,4,5,6,7,8,9}, 所以(∁R A )∩B ={7,8,9}.(2)C={x∈R|x<a或x>a+1},要使A∪C=R,则有a≥3,且a+1<7,解得3≤a<6.故实数a的取值范围为[3,6).。
2020高考复习物理名师教学课件课后跟踪训练23

课后跟踪训练(二十三)[基础巩固]1.(多选)(2018·河南南阳质检)下列关于力的冲量和动量的说法中正确的是()A.物体所受的合外力为零,它的动量一定为零B.物体所受的合外力做的功为零,它的动量变化量一定为零C.物体所受的合外力的冲量为零,它的动量变化量一定为零D.物体所受的合外力不变,它的动量变化率不变[解析]物体所受的合外力为零,物体可能处于静止状态,也可能做匀速直线运动,故其动量不一定为零,A错误;物体所受的合外力做的功为零,有可能合外力垂直于速度方向,不改变速度大小,只改变速度方向,而动量是矢量,所以其动量变化量有可能不为零,B 错误;根据动量定理I=Δp可知,物体所受的合外力的冲量为零,则其动量变化量一定为零,C正确;根据Ft=Δp⇒F=Δp可得物体所受t的合外力不变,则其动量变化率不变,D正确.[答案]CD2.(2018·山东枣庄期末联考)质量为60 kg的建筑工人不慎从高空跌下,由于弹性安全带的保护,使他悬挂起来;已知弹性安全带的缓冲时间是1.2 s,安全带长5 m,不计空气阻力影响,g取10 m/s2,则安全带所受的平均冲力的大小为()A.100 N B.500 NC.600 N D.1100 N[解析] 在安全带产生拉力的过程中,人受重力和安全带的拉力作用做减速运动,此过程的初速度就是自由落体运动的末速度,所以有v 0=2gh =2×10×5 m/s =10 m/s ,根据动量定理,取竖直向下为正方向,有mg ·t -F ·t =0-m v 0,解得F =mg +m v 0t =600 N +60×101.2N =1100 N ,故选D.[答案] D3.放在水平面上的物体,用水平推力F 推它t 秒,物体始终不动,则在这t 秒内,关于合力的冲量与摩擦力冲量的大小,下列说法正确的是( )A .合力的冲量及摩擦力的冲量均为0B .合力的冲量及摩擦力的冲量大小均为FtC .合力的冲量为0,摩擦力的冲量大小为FtD .合力的冲量大小为Ft ,摩擦力的冲量为0[解析] 用水平力F 推物体t 秒,物体不动,说明合外力为0;水平方向静摩擦力与力F 平衡,则合力的冲量为0;摩擦力冲量的大小为Ft ,方向与F 方向相反,故C 项正确.[答案] C4.从高处跳到低处时,为了安全,一般都是让脚尖着地,这样做是为了( )A .减小冲量B .减小动量的变化量C .增大与地面的冲击时间,从而减小冲力D.增大人对地面的压强,起到安全作用[解析]脚尖先着地,接着逐渐到整只脚着地,延长了人落地时动量变化所用的时间,由动量定理可知,人落地动量变化量一定,这样就减小了地面对人的冲力,故C正确.[答案] C5.(2018·全国卷Ⅱ)高空坠物极易对行人造成伤害.若一个50 g 的鸡蛋从一居民楼的25层坠下,与地面的碰撞时间约为2 ms,则该鸡蛋对地面产生的冲击力约为()A.10 N B.102 NC.103 N D.104 N[解析]对鸡蛋受力分析,由动量定理得Ft-mgt=m v-0,根据动能定理知mgh=12,又h=24×3 m,联立解得F=1.0×103 N,2m vC正确.[答案] C6.如图1所示,物体A和B用轻绳相连接,挂在轻弹簧下静止不动,A的质量为m,B的质量为M,当连接A、B的绳突然断开后,物体A上升经某一位置时的速度大小为v.这时,物体B的下落速度大小为u,如图2所示.在这段时间里,弹簧的弹力对物体A的冲量为()A.m v B.m v-MuC.m v+Mu D.m v+mu[解析]由题意可知,虽然整个过程所用的时间可以直接求出,但弹簧的弹力是一变力,要求它的冲量只能用动量定理来计算.以物体A为研究对象,取竖直向上为正方向,根据动量定理有:(F-mg)t =m v.①在t时间内,物体B做自由落体运动,则:t=ug.②由①②两式得弹力的冲量Ft=m v+mu.所以正确的选项为D.[答案] D7.(多选)(2018·武汉调研)如图所示,两个质量相等的物体在同一高度沿倾角不同的两个光滑斜面由静止开始自由下滑,不计空气阻力,在它们到达斜面底端的过程中()A.重力的冲量相同B.斜面弹力的冲量不同C.斜面弹力的冲量均为零D.合力的冲量不同[解析]设斜面高度为h,倾角为θ,物体质量为m,可求得物体滑至斜面底端的速度大小为v=2gh,所用时间t=1sinθ2hg.由冲量定义可求得重力的冲量大小为I G=mgt=m2ghsinθ,方向竖直向下,故A错误;斜面弹力的冲量大小为I N=mg cosθ·t=m2ghtanθ,方向垂直斜面向上,B正确,C错误;合力的大小为mg sinθ,I合=mg sinθ·t =m2gh,方向沿斜面向下(与合力方向相同),即合力冲量的大小相同,方向不同,故D正确.[答案]BD8.蹦床是运动员在一张绷紧的弹性网上蹦跳、翻滚并做各种空中动作的运动项目.一个质量为60 kg的运动员,从离水平网面3.2 m 高处自由下落,着网后沿竖直方向蹦回到离水平网面5.0 m高处.已知运动员与网接触的时间为1.2 s.若把这段时间内网对运动员的作用力当作恒力处理,求此力的大小.(g取10 m/s2)[解析]将运动员看作质量为m的质点,从高h1处下落,刚接触网时速度的大小v1=2gh1(竖直向下).弹跳后到达的高度为h2,刚离网时速度的大小v2=2gh2(竖直向上).选竖直向上为正方向.由动量定理得(F-mg)·Δt=m[v2-(-v1)]由以上各式解得F=mg+m 2gh2+2gh1Δt代入数据得F=1.5×103 N[答案] 1.5×103 N[能力提升]9.(多选)(2018·陕西摸底)某人身系弹性绳自高空P点自由下落,a点是弹性绳的原长位置,c是人所能到达的最低点,b是人静止悬挂时的平衡位置.若把由P点到a点过程称为过程Ⅰ,由a点到c 点过程称为过程Ⅱ,不计空气阻力,下列说法正确的是()A.过程Ⅰ中人的动量的改变量等于重力的冲量B.过程Ⅱ中人的动量的减少量等于过程Ⅰ中重力的冲量的大小C.过程Ⅱ中人的动能逐渐减小到零D.过程Ⅱ中人的机械能的减少量等于过程Ⅰ中重力做功的大小[解析]根据动量定理可知过程Ⅰ中人的动量的改变量等于重力的冲量,选项A正确;过程Ⅱ中动量的减少量等于过程Ⅰ中重力的冲量的大小,选项B正确.从a到b的过程中,人的重力大于绳的弹力,从b到c的过程中,人的重力小于绳的弹力,故过程Ⅱ中人的动能先增大再减小,选项C错误;过程Ⅱ中机械能的减少量等于过程Ⅰ和过程Ⅱ中重力做功的大小,选项D错误.[答案]AB10.(多选)(2018·衡水中学调研)如图所示,可看作质点的物体从光滑固定斜面的顶端a点以某一初速度水平抛出,落在斜面底端b点,运动时间为t,合外力做功为W1,合外力的冲量大小为I1.若物体从a 点由静止释放,沿斜面下滑,物体经过时间2t到达b点,合外力做功为W2,合外力的冲量大小为I2.不计空气阻力,下列判断正确的是()A.W1∶W2=1∶1B.I1∶I1=1∶2C .斜面与水平面的夹角为30°D .物体水平抛出到达b 点时速度方向与水平方向的夹角为60°[解析] 设a 、b 之间的竖直高度为h ,物体做平抛运动时只受重力,从a 点到b 点合外力做功为W 1=mgh .若物体从a 点由静止释放,沿斜面下滑,只有重力做功,合外力做功为W 2=mgh ,选项A 正确.设斜面与水平面的夹角为θ,根据牛顿第二定律,mg sin θ=ma 0,解得a 0=g sin θ,根据平抛运动规律,h =12gt 2,斜面长度L =h sin θ,L =12a 0(2t )2,联立解得θ=30°,选项C 正确.根据冲量定义,物体从光滑固定斜面的顶端a 点以某一初速度水平抛出,落在斜面底端b 点,运动时间为t ,合外力的冲量大小为I 1=mgt .物体从a 点由静止释放,沿斜面下滑,所受的合外力为mg sin θ=0.5mg ,物体经过时间2t 到达b 点,合外力的冲量大小为I 2=0.5mg ×2t =mgt ,所以I 1∶I 2=1∶1,选项B 错误.物体从a 点水平抛出到达b 点时,根据平抛运动规律,L cos θ=v x t ,L sin θ=12gt 2,竖直分速度v y =gt ,物体水平抛出到达b 点时速度方向与水平方向的夹角的正切值tan α=v y v x,联立解得tan α=2tan θ=233,所以物体水平抛出到达b 点时速度方向与水平方向的夹角小于60°,选项D 错误.[答案] AC11.(2018·广东汕头期末)水龙头打开后,水柱以大小为v 0的速度竖直向下稳定喷出,将一平板水平放置在靠近水龙头处,水柱冲击平板后,在竖直方向水的速度变为零,在水平方向朝四周均匀散开,此时水对平板的冲击力为F 0.将平板向下平移至距离水龙头h 处,水流出后经过时间t 落在平板上,此时水对平板的冲击力变为2F 0.忽略空气阻力,下列关系式正确的是( )A .h =v 202gB .h =v 20gC .t =v 0gD .t =(2-1)v 0g [解析] 设Δt 时间内喷出的水的质量为m ,在Δt 时间内水的速度变成0,选取向下为正方向,由动量定理可得-F 0·Δt =0-m v 0,将平板向下平移至距离水龙头h 处,Δt 时间内喷出的水流出后经过时间t 落在平板上,仍然会在Δt 时间内与平板作用后速度变成0,则-2F 0·Δt =0-m v ,又有v =v 0+gt ,联立解得v =2v 0,则h =3v 202g,t =v 0g ,C 正确.[答案] C12.(2018·山西太原期末)在我国很多地方都建有钟楼,每逢重大节日都会进行撞钟仪式.如图所示,在大钟旁用钢丝吊着质量为m 的撞锤(可视为质点),其悬点O 与撞锤重心的距离为L ,撞锤静止时恰好与大钟相接触.光滑轻质定滑轮与O 等高,跨过定滑轮的轻质细绳一端连在撞锤上,另一端自然下垂.某次撞钟时,抓住绳子的自由端往下拉至α=37°时静止,此时连接撞锤的两根绳恰好成直角,然后突然松手,撞锤摆动后撞击大钟发出声音.(不计空气阻力,取sin37°=0.6,cos37°=0.8)求:(1)撞锤被拉起静止时,人对绳的拉力是多大;(2)撞锤撞击大钟前的瞬间,钢丝的弹力是多大;(3)若撞锤撞击大钟后速度变为0,大钟对撞锤的冲量是多大.[解析] (1)撞锤被拉起静止时,撞锤受力平衡,可得 F 1=mg cos37°=0.8mg(2)从静止释放到撞锤撞击大钟前的瞬间,由动能定理得mg (L -L sin37°)=12m v 2 撞锤撞击大钟前的瞬间,为圆周运动的最低点,则F -mg =m v 2L联立解得v =45gL ,F =1.8mg (3)规定向右为正方向,对撞锤运用动量定理,有I =0-m v解得I =-m 45gL 大钟对撞锤的冲量大小为m 45gL ,方向水平向左.4 [答案](1)0.8mg(2)1.8mg(3)m5gL。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时跟踪训练(二十三)Ⅰ.单词拼写/用所给词的正确形式填空1.It was a fair __________ (贸易)—I got a pleasure, and she had yet another tasty treat. [答案] trade2.Leaping on a __________ (狭窄的) balance beam is not easy.[答案] narrow3.Students are __________ (禁止) to smoke at school.[答案] forbidden4.The old man often tells us many __________ (传奇故事), which makes us happy.[答案] legends5.He lives in a __________ (遥远的) mountain village.[答案] remote6.__________ (surround) by trees, the school looks more beautiful.[答案] Surrounded7.The train soon disappeared in the __________ (distant).[答案] distance8.Switzerland is a __________ (mountain) country, which is very beautiful.[答案] mountainous9.The weather in this region is __________ (vary) and you should prepare well.[答案] varied10.__________ (nature), all the boys like sports.[答案] NaturallyⅡ.完成句子1.因特网的发明注定要改变我们相互交流的方式。
The invention of the Internet ______________ the way we communicate with each other. [答案] is to change2.只要你按时还,我就借给你一些书。
I'll lend you some books ________________ them on time.[答案] only if you return3.一周至少打扫一次房间。
Rooms will be cleaned ________________.[答案] once at least4.我们家乡的工厂每年生产成百上千万的玩具火车,他们大多数被卖往国外。
The factory in our hometown produces millions of toy trains every year, ________________.[答案] most of them sold abroad5.有时你就看到一些乞丐利用人们的善良赚钱。
Sometimes you can see beggars ________________ people's kindness to make money.[答案] take advantage ofⅢ.阅读理解A(2017·云南昆明高三两区七校模拟)With fresh, pollution-free air, amazing scenery, glorious lakes and a range of activities to keep you entertained, the following mountain destinations are good choices for you.Firstly, it's Gstaad in Switzerland. If your expectations are rather high, then you've come to the right place. As a destination where world royalty and celebrities go for holiday, Gstaad is not only among the crème_de_la_crème of winter break destinations, but perfect for summer too. With glorious farmland and amazing scenery, not to mention some of the best cafes and restaurants in Europe, the mix of alpine complete quietness and simple luxury makes this one of the best mountain areas to visit.The region offers a wide variety of excellent 5-star hotels too, including Le Grand Bellevue, a fascinating design, golf and wellness hotel located in the middle of an idyllic (田园的) park. The hotel's unique spa offers an indoor and outdoor salt-water pool, a sauna center, and various massages and treatments. Guests can take part in accompanied walks in the mountains, too.Secondly, it's Deer Valley in Utah, US. Settled at the base of the Wasatch Mountains, Deer Valley is an alpine ski resort in the Wasatch Range. It is famous for its upscale facilities and consistently ranks among the top ski resorts in North America. Deer Valley was also one of the sites during the 2002 Winter Olympics, hosting the freestyle moguls (雪上特技), aerial, and alpine slalom (障碍滑雪) events. It regularly holds competitions for the International Ski Federation, too.One of the best places to stay here is the St Regis resort. The resort's contemporary rooms are equipped with fiat-screen TVs, sound stereos and Wi-Fi. It also features ski-in, ski -out access.语篇解读:本文介绍了两个适合滑雪的度假胜地:瑞士的格施塔德(Gstaad)和美国的麓谷(Deer Valley)。
在这些地方你可以享受世界上最美好的山林假日。
1.The purpose of the opening paragraph is to __________.A. entertain readersB.introduce the topicC.show an ideal lifestyleD.praise the natural scenery[解析] 推理判断题。
根据第一段可知,文章开头从描写自然美景入手,为下文介绍两处度假胜地做铺垫,起到引入话题的作用。
[答案] B2.What does the underlined part “crème de la crème” in Paragraph 2 mean?A.Best. B.Magic.C.Imagination. D.Expectation.[解析] 词义猜测题。
根据第二段中的“not only... but perfect for summer too"可知,格施塔德不仅仅是冬季最好的度假胜地之一,而且也是夏季很完美的去处。
故答案为A项。
[答案] A3.What attracts visitors most in Deer Valley may be that __________.A.it is a place for international competitionsB.it is a good place to watch sunriseC.it is a wonderful skiing placeD.it is a historic site[解析] 细节理解题。
根据第四段和第五段可知,比较而言,美国的麓谷(Deer Valley)最吸引人的是这里的高山滑雪场。
[答案] C4.The passage can be considered as an introduction to __________.A.two mountain holiday resortsB.5-star hotels in traveling destinationsC.amazing scenery of two mountain areasD.world-famous restaurants in traveling destinations[解析] 主旨大意题。
通读全文可知,文章主要介绍了两处山区的度假旅游胜地。
[答案] AB(2017·福建省福州市高中毕业班质量检测)Booking a trip on an online travel site is convenient, but comes with its own set of problems.◆They know who's going to spend more.Last year, US travel research company Orbitz tracked people's online activities to test out whether Mac users spend more on travel than PC users. It turned out that on average, Mac users lay out $20~30 more per night on hotels. As a result, online travel sites show these users more expensive travel options first. To avoid paying more, sort results by price.◆Their software doesn't always link the hotel's system.A guaranteed reservation is almost impossible to come by anywhere—the risk of your flight or hotel being overbooked increases with third party providers. The middleman's soft ware isn't immune (不受影响的) to system errors, so always call the hotel or airline to make sure your booking is processed.◆You could miss out on loyalty (忠诚)points.Third party providers can get between you and frequent flyers miles or points. Many hotel loyalty programs don't recognize external sites, while others award only minimum points without special offers, like double points on hotel stays.◆Don't be fooled by packages: Often, they're low-end items grouped together.Ever noticed how travel sites recommend a hotel, a rental car, and tour packages all in one click? These deals usually feature travel that no one wants, like flights with multiple layovers (中途停留). Check the fine_print.◆Once your trip is purchased, you're on your own.An online travel agency can't provide assistance the same way an agent can if a flight is cancelled or a room is substandard. Basically, when you arrive at the airport or hotel, you're just another customer who booked at the lowest rate.语篇解读:本文是一篇应用文。
