均值比较与T检验实验报告
实验五 均值比较与T检验

实验五均值比较与T检验⏹均值(Means)过程对准备比较的各组计算描述指标,进行预分析,也可直接比较。
⏹单样本T检验(One-Samples T Test)过程进行样本均值与已知总体均值的比较。
⏹独立样本T检验(Independent-Samples T Test)过程进行两独立样本均值差别的比较,即通常所说的两组资料的t检验。
⏹配对样本(Paired-Samples T Test)过程进行配对资料的显著性检验,即配对t检验。
⏹单因素方差分析(One-Way ANOVA)过程进行两组及多组样本均值的比较,即成组设计的方差分析,还可进行随后的两两比较,详情请参见单因素方差分析。
预备知识:假设检验的步骤:⏹第一步,根据问题要求提出原假设(Null hypothesis)和备选假设(Alternative hypothesis);⏹第二步,确定适当的检验统计量及相应的抽样分布;⏹第三步,计算检验统计量观测值的发生概率;⏹第四步,给定显著性水平并作出统计决策。
第二步和第三步由SPSS自动完成。
假设检验中的P值⏹P值(P-value)是指在原假设为真时,所得到的样本观察结果或更极端结果的概率,即样本统计量落在观察值以外的概率。
⏹根据“小概率原理”,如果P值非常小,就有理由拒绝原假设,且P值越小,拒绝的理由就越充分。
⏹实际应用中,多数统计软件直接给出P值,其检验判断规则如下(双侧检验):⏹若P值<a,则拒绝原假设;⏹若P值≥ a ,则不能拒绝原假设。
均值比较中原假设H0:μ=μ0(即某一特定值)(适用于单样本情形)或 H0:μ1=μ2。
(适用于两独立样本情形)一、Means(均值)过程选择:分析Analyze==>均值比较Compare Means ==>均值means;1、基本功能分组计算、比较指定变量的描述统计量,还可以给出方差分析表和线性检验结果表。
优点各组的描述指标被放在一起便于相互比较,如果需要还可以直接输出比较结果,无须再次调用其他过程。
均值验证实验报告(3篇)

第1篇一、实验目的1. 理解均值验证在统计学中的意义和应用。
2. 掌握均值验证的基本方法和步骤。
3. 提高对实际数据进行统计分析的能力。
二、实验背景在统计学中,均值是衡量一组数据集中趋势的重要指标。
均值验证是对均值进行假设检验的过程,旨在判断均值是否与某一特定值相等。
本实验通过实际数据的均值验证,验证均值假设的合理性。
三、实验材料1. 实验数据:某班级50名学生的语文成绩。
2. 统计软件:SPSS、Python等。
四、实验方法1. 提取数据:将班级50名学生的语文成绩数据整理成表格形式。
2. 假设检验:假设班级学生的语文成绩均值为70分。
3. 统计分析:利用SPSS或Python进行均值验证。
五、实验步骤1. 数据输入:将班级学生的语文成绩数据输入SPSS或Python。
2. 描述性统计:计算班级学生的语文成绩均值。
3. 均值验证:a. 建立假设:H0:μ = 70,H1:μ ≠ 70(其中μ为班级学生的语文成绩均值)。
b. 确定显著性水平:α = 0.05。
c. 查找t分布表:根据自由度和显著性水平,查找t分布表得到t临界值。
d. 计算t值:根据实际数据计算t值。
e. 比较t值与t临界值:若t值大于t临界值,则拒绝原假设,认为班级学生的语文成绩均值与70分存在显著差异;若t值小于t临界值,则接受原假设,认为班级学生的语文成绩均值与70分无显著差异。
4. 结果分析:根据实验结果,判断班级学生的语文成绩均值是否与70分存在显著差异。
六、实验结果与分析1. 描述性统计结果:班级学生的语文成绩均值为65分。
2. 均值验证结果:a. 假设检验的t值为2.35。
b. 查找t分布表,得到自由度为49,显著性水平为0.05的t临界值为±1.677。
c. 由于t值(2.35)大于t临界值(±1.677),故拒绝原假设,认为班级学生的语文成绩均值与70分存在显著差异。
3. 结果分析:实验结果表明,班级学生的语文成绩均值与70分存在显著差异,说明班级学生的语文成绩整体低于70分。
均值与T检验

假设检验的SPSS操作
均值比较和T检验
4.1
Means过程 Means过程 单一样本T检验 单一样本T 两独立样本T 两独立样本T检验 两配对样本T 两配对样本T检验
• 两配对样本T检验的前提要求如下。 两配对样本T检验的前提要求如下。 • 两个样本应是配对的。在应用领域中, 两个样本应是配对的。在应用领域中, 主要的配对资料包括:具有年龄、性别、 主要的配对资料包括:具有年龄、性别、 体重、病况等非处理因素相同或相似者。 体重、病况等非处理因素相同或相似者。 首先两个样本的观察数目相同, 首先两个样本的观察数目相同,其次两样 本的观察值顺序不能随意改变。 本的观察值顺序不能随意改变。 • 样本来自的两个总体应服从正态分布。 样本来自的两个总体应服从正态分布。
• 研究问题 • 计算减肥前后是否有显著变化。数据为 计算减肥前后是否有பைடு நூலகம்著变化。 减肥茶检验_两配对样本t检验” “减肥茶检验_两配对样本t检验” • 研究一个班同学在参加了暑期数学、化学 研究一个班同学在参加了暑期数学、 培训班后,学习成绩是否有显著变化。 培训班后,学习成绩是否有显著变化。
小 结
• 两配对样本T检验的零假设H0为两总体均值 两配对样本T检验的零假设H 之间不存在显著差异。 之间不存在显著差异。 • 首先求出每对观察值的差值, 首先求出每对观察值的差值,得到差 值序列;然后对差值求均值; 值序列;然后对差值求均值;最后检验差 值序列的均值, 值序列的均值,即平均差是否与零有显著 差异。如果平均差和零有显著差异, 差异。如果平均差和零有显著差异,则认 为两总体均值间存在显著差异;否则, 为两总体均值间存在显著差异;否则,认 为两总体均值间不存在显著差异。 为两总体均值间不存在显著差异。
均值比较与T检验实验报告

实训的心得与体会
统计学中经常通过样本来分析总体,即从样本的观察或实验结果的特征来对总体的特征进行估计和推断。
本次实验使用spass软件来进行均值比较与T检验,假设检验是对给定的总体参数值,利用样本数据对其推断,并给出接受或是拒绝的过程,另外,在具体操作中,首先定义所谓的小概率,一般取或,即显著性水平。
显著性水平取得太小,容易发生为错误;取得太大,则容易发生弃真错误。
通过本次实验用spass统计分析软件来进行均值比较及T检验后,感觉统计学中的很多问题不再像以前那么陌生了,同时也感觉统计学不再是想象中那么困难,之前学习统计学最怕的就是对数据进行求解与分析,现在使用这款软件后,让我从之前对统计学的陌生转变为熟悉,从此,在解决统计方面的问题又多了一项解决的工具:spss。
5均数差别比较的t检验

样本均数间的差别原因均数差别比较的 t检验总体均数不同 总体均数相同,差别仅仅由抽样误 差引起 推断方法:计算某个统计量(如t 值),然后根据相应的概率作出推 断t检验(student’s t test)t检验优点:用于样本含量较小,并 且总体标准差σ未知时 三种t检验样本均数 X 与已知某总体均数μ0 的比较; 两组样本均数 X 1 与 X 2 的比较; 配对设计资料均数的比较。
t检验的应用条件当样本含量较小时(n<60),理论上要求样 本为来自正态分布总体的随机样本; 当做两样本均数比较时,还要求两总体 方差相等(方差齐性,即 σ12=σ22)。
在实际工作中,若上述条件略有偏离, 仍可进行t检验分析。
一、样本均数和总体均数比较的t检验 (one sample t test) 目的:推断样本所代表的未知总体 均数μ与已知总体均数μ0有无差 别。
已知的总体均数μ0一般为理论值、 标准值或经过大量观察所得的稳定 值等。
条件:当n较小时,要求样本来自于 正态分布总体假设检验的独特逻辑例 : 某病患者20人,其血沉 (mm/h)均数 为9.15,标准差为2.13,问是否该病患 者血沉与以往文献报道的均数10.50有差 别?X ± t0.05 / 2,19 s / n= 9.15 ± 2.093 × 2.13 / 20 = (8.15,10.15)11.两个假设,决策者在其中作出抉择 该病患者血沉总体均数与10.50无差别, 该病患者血沉总体均数与10.50有差别。
简写 H0:μ=10.50 H1:μ≠10.50 单凭一份样本不可能证明哪一个正确, 一般利用小概率反证法思想,从问题的 对立面出发(H0)间接判断要解决的问题 (H1)是否成立。
H0:μ=10.50H1:μ≠10.50μ = 10.50X10.50μX2. H0成立时会怎样? 所得t值因样本而 异,但其绝对值多数情况下落在0附近。
统计学两样本均数比较的t检验

处理方式
对于异常值,可以采用删除、替换或用中位数修正等方式进行处理。具体处理方式应根 据实际情况和数据分布特点进行选择,并确保处理后的数据仍然能够反映总体情况。
实验设计和伦理考虑
实验设计
在进行t检验之前,应进行充分的实验设计, 确保实验的合理性和科学性。实验设计应考 虑各种因素对实验结果的影响,并尽量减小 误差和干扰因素。
确定p值:根据t统计量和自由 度,查表或使用统计软件计算 p值。
步骤1
收集数据:分别从两个独立样 本中收集数据,并记录在表格 中。
步骤3
计算t统计量:根据两组样本的 均数和标准差,计算t统计量。
步骤5
结果解读:根据p值判断两组 样本均数之间的差异是否具有 统计学上的显著性。
结果解读
• 结果解读:根据p值的大小来判断两 组样本均数之间的差异是否具有统计 学上的显著性。通常,如果p值小于 0.05,则认为两组样本均数之间存在 显著差异;如果p值大于0.05,则认 为两组样本均数之间无显著差异。
对差值数据进行描述性统计分析, 计算差值的均值和标准差。
计算t统计量
根据差值的均值、标准差以及自 由度,计算t统计量。
收集两个配对样本的数据
确保两个样本具有相同的样本量, 且每个样本中的数值都是配对的。
判断显著性
பைடு நூலகம்根据t分布表或使用统计软件,查 找对应的p值,判断两个配对样本 均数是否存在显著差异。
结果解读
伦理考虑
在实验设计过程中,还应考虑伦理问题。应 尊重受试者的权益和尊严,确保受试者的安 全和隐私。同时,应遵循国际公认的伦理准 则和法律法规,如《赫尔辛基宣言》等。
06 案例分析
SPSS统计分析均值比较与T检验

在研究人体各部位体温是否有差别,一个人 的两个部位的温度构成一对数据。测量若干 人的同样两个部位的温度数据,可以比较这 两个部位平均温度是否有显著性差异。使用 配对t检验。
Confidence interval:95%:置信区间项,可以自定义。 Missing Values:选择对缺失值的处理方法 Exclude cases analysis by analysis:带有缺失值的观测值当它 与分析有关时才被剔除; Exclude cases listwise:剔除所有列在Test、Grouping矩形框 中的变量带缺失值的项
例题一
现有银行雇员工资为例,检验男女雇员现工 资是否有显著差异。一个是要比较salary变量 的均值,另一个是gender变量作为分水平变 量。 (data09--03) 。
分析变量的简单描述性统计量
Gender Current Salary Male
F emale
Group Statistics
以27个学生的身高为例说明操作步骤 (data11-01)
变量no编号,sex性别,age年龄,h身高,w 体重。
ANOVA table and eta:输出第一层控制变量给出的方差分析表和eta统计值η和 η2 。 η统计量表明因变量和自变量之间联系的强度。 η2 是组间平方和与总平 方和之比。
进行配对样本的T检验要求被比较的两个样 本有配对关系。要求两个样本均来自正态总 体。而且均值是对于检验有意义的描述统计 量。均值的配对比较是比较常见(见以下几 个例子)。
同一窝实验用白鼠按性别、体重相同的配对, 再随机分到实验组和对照组,分别喂加入海 藻的饲料和普通饲料,三个月后,分别将每 对白鼠置于水中,测量其到溺死前的游泳时 间。比较两组白鼠游泳时间均值,从而比较 两种饲料对抗疲劳的作用。
SPSS实验报告——均值比较
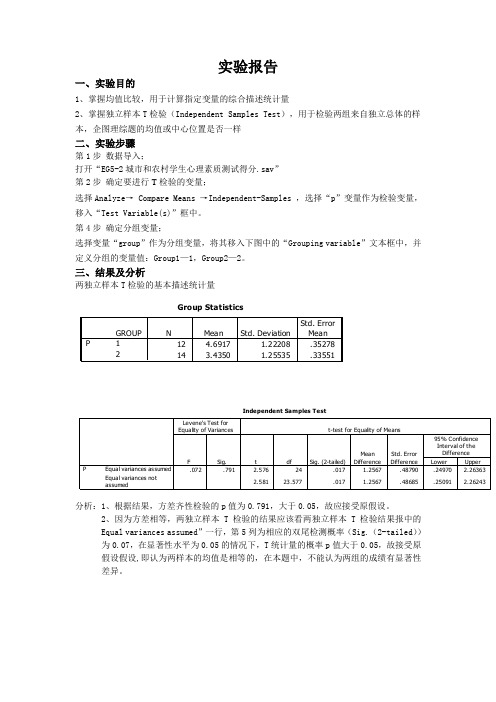
实验报告一、实验目的1、掌握均值比较,用于计算指定变量的综合描述统计量2、掌握独立样本T 检验(Independent Samples Test ),用于检验两组来自独立总体的样本,企图理综题的均值或中心位置是否一样二、实验步骤第1步 数据导入;打开“EG5-2城市和农村学生心理素质测试得分.sav ” 第2步 确定要进行T 检验的变量;选择Analyze → Compare Means →Independent-Samples ,选择“p ”变量作为检验变量,移入“Test Variable(s)”框中。
第4步 确定分组变量;选择变量“group ”作为分组变量,将其移入下图中的“Grouping variable ”文本框中,并定义分组的变量值:Group1—1,Group2—2。
三、结果及分析两独立样本T 检验的基本描述统计量Group Statistics12 4.6917 1.22208.35278143.43501.25535.33551GROUP12PNMean Std. DeviationStd. Error MeanIndependent Samples Test.072.791 2.57624.0171.2567.48790.24970 2.263632.58123.577.0171.2567.48685.250912.26243Equal variances assumedEqual variances not assumedPFSig.Levene's Test for Equality of VariancestdfSig. (2-tailed)Mean DifferenceStd. Error DifferenceLower Upper 95% Confidence Interval of the Difference t-test for Equality of Means分析:1、根据结果,方差齐性检验的p 值为0.791,大于0.05,故应接受原假设。
均值比较与检验(T检验) 实验报告

输出结果:
表3两种饵料对产鱼量影响的统计量
组别
N
均值
标准差
均值的标准误
产鱼量
1
7
562.14
30.025
11.348
2
6
612.50
23.020
9.398
表4两种饵料对产鱼量影响的t检验结果
方差方程的Levene检验
均值方程的t检验
F
Sig.
t
df
Sig.(双侧)
均值差值
标准误差值
差分的95%置信区间
成对差分
t
df
Sig.(双侧)
均值
标准差
均值的标准误
差分的95%置信区间
下限
上限
对1
正常饲料组-维生素E缺乏饲料组
8.5125
5.7193
2.0221
3.7311
13.2939
4.210
7
.004
实验总结:
(1)因为本题中大白鼠的性别、体重等皆是比较一致的,因此我们选择配对t检验中的同源检验对接种两种饲料喂养结果的差异性进行检验;
差分的95%置信区间
下限
上限
对1
A法- B法
-8.286
5.282
1.997
-13.171
-3.400
-4.150
6
.006
实验总结;
(1)因为本题中两株番茄的生长期、发展进度、植株大小和其他方面皆是比较一致的,因此我们选择配对t检验中的同源检验对接种两种病毒方法结果的差异性进行检验;
(2)表8为配对t检验的描述性统计结果,分别为A法和B法处理的平均值、样本例数、样本标准差和均数的标准误;
03均值比较和T检验
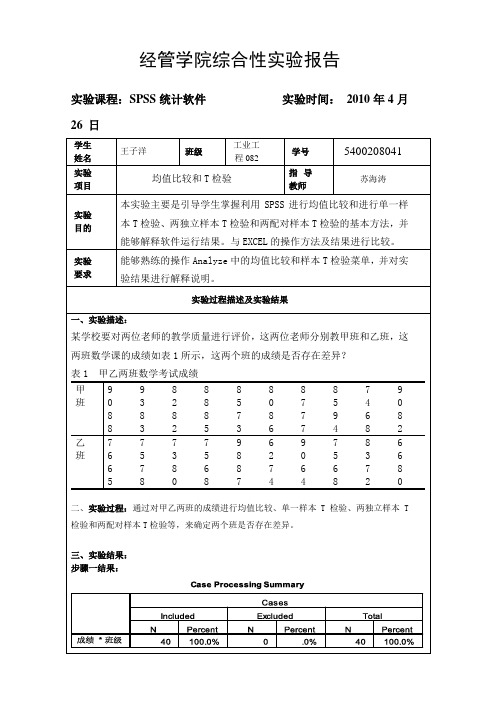
经管学院综合性实验报告实验课程:SPSS统计软件实验时间:2010年4月26 日学生姓名王子洋班级工业工程082学号5400208041实验项目均值比较和T检验指导教师苏海涛实验目的本实验主要是引导学生掌握利用SPSS进行均值比较和进行单一样本T检验、两独立样本T检验和两配对样本T检验的基本方法,并能够解释软件运行结果。
与EXCEL的操作方法及结果进行比较。
实验要求能够熟练的操作Analyze中的均值比较和样本T检验菜单,并对实验结果进行解释说明。
实验过程描述及实验结果一、实验描述:某学校要对两位老师的教学质量进行评价,这两位老师分别教甲班和乙班,这两班数学课的成绩如表1所示,这两个班的成绩是否存在差异?表1 甲乙两班数学考试成绩甲班993828885887857490 88838285738677946882乙班7675737598629758366 657886887746468728二、实验过程:通过对甲乙两班的成绩进行均值比较、单一样本T检验、两独立样本T 检验和两配对样本T检验等,来确定两个班是否存在差异。
三、实验结果:步骤一结果:从结果可以看出:个案总数为40,其中甲班20,乙班20。
甲班成绩的均值、标准差、方差分别为:83.600、6.69957、44.884,乙班成绩的均值、标准差、方差为79.5250、8.94137、79.948。
步骤二结果从结果可以看出:个案总数为40,其中甲班20,乙班20。
甲班成绩的均值、标准差、方差分别为:83.600、6.69957、44.884,乙班成绩的均值、标准差、方差为79.5250、8.94137、79.948。
步骤三结果Group Statistics班级N Mean Std. Deviation Std. Error Mean成绩甲班20 83.6000 6.69957 1.49807乙班20 75.4500 9.17935 2.05257Independent Samples TestLevene's Testfor Equality ofVariances t-test for Equality of MeansF Sig. t dfSig.(2-tailed)MeanDifferenceStd. ErrorDifference95% Confidof the DLower成绩Equal variancesassumed1.110 .299 3.207 38 .003 8.150002.541113.00579 13.29421Equal variancesnot assumed3.207 3.477E1 .003 8.15000 2.54111 2.99004 13.30996从表中可以看出,两个班级20个学生的成绩平均值分别为83.6000和75.4500,标准差分别为6.69957和9.17935,均值误差分别为1.49807和2.05257。
均值比较与t检验

样本平均数与总体平均数差异显著性检验在实际工作中,我们往往需要检验一个样本平均数与已知地总体平均数是否有显著差异,即检验该样本是否来自某一总体,已知地总体平均数一般为一些公认地理论数值、经验数值或期望数值,比较地目地是推断样本所代表地未知总体均数与已知总体均数有无差别.文档来自于网络搜索例题:已知玉米单交种群单地平均穗重为,喷药后随机抽取个果穗称重,穗重分别为:、、、、、、、、,问喷药前后果穗穗重差异是否显著.文档来自于网络搜索具体操作可参看多媒体教程单一样本检验,例题中地数据编号为.操作步骤:→→点击,进人对话框→将要分析地变量选入→项填入已知总体均数→点击按钮,进入子对话框,选项中填入或,确定显著水平后返回上一对话框→点击键运行,显示结果界面.文档来自于网络搜索结果界面包括描述性统计量表( ) 和检验表( )两个表格.描述性统计量表中输出样本含量、均数、标准差和标准误;检验表中显示值()自由度()、双尾值()、样本均数与已知总体均数地差值( )、差值地%或%置信区间地上限与下限(,,).文档来自于网络搜索独立样本检验在实际工作中,还经常会遇到推断两个样本平均数差异是否显著地问题,以了解两样本所属总体地平均数是否相同.因试验设计不同,一般可分为:非配对或成组设计两样本平均数地差异显著性检验和配对设计两样本平均数地差异显著性检验.文档来自于网络搜索非配对设计或成组设计是指当进行只有两个处理地试验时,将试验单位完全随机地分成两个组,然后对两组随机施加一个处理.在这种设计中两组地试验单位相互独立,所得地两个样本相互独立,其含量不一定相等.文档来自于网络搜索例题:某家禽研究所对粤黄鸡进行饲养对比试验,试验时间为天,增重结果如下,问两种饲料对粤黄鸡地增重效果有无显著差异?文档来自于网络搜索具体操作可参看多媒体教程独立样本检验,例题中地数据编号为.操作步骤:→→点击,进入该对话框→将要检验地数据变量选入到()→将要检验资料地分类变量选至,此时变量名后出现〔??〕,再点击,定义分类变量(必须与数据文件中录入地分类变量值一致)→点击按钮,进入子对话框,选项系统默,也可根据需要改为,确定置信水平后返回上一对话框→点击键运行,显示结果界面.文档来自于网络搜索结果界面中,描述统计表( )给出两组变量地基本情况描述,内容简单,不再赘述.文档来自于网络搜索检验表( )较为复杂,第一部分列出地是两样本方差齐性检验(' )地值()和显著概率值(.).除此之外地两行数据分别表示方差同质( )与方差不齐( )时地检验结果与差异置信区间.当齐性检验显著时,选下一行地结果;检验不显著时,选上一行结果.文档来自于网络搜索配对样本检验配对设计是指先根据配对地要求将试验单位两两配对,然后将配成对子地两个试验单位随机地分配到两个处理组中.配对地要求是:配成对子地两个试验单位地初始条件尽量一致,不同对子间试验单位地初始条件允许有差异,每一个对子就是试验处理地一个重复.配对地方式有两种:自身配对和同源配对.文档来自于网络搜索例题:用家兔只试验某批注射液对体温地影响,测定每只家兔注射前后地体温,见下表,设体温服从正态分布,问注射前后体温有无显著性差异.(单位:℃)文档来自于网络搜索具体操作可参看多媒体教程配对样本检验,例题中地数据编号为.数据输入格式:将两处理分别定义为一个变量(列),每条记录(行)代表一对数据.操作步骤:→→点击进入配对样本检验对话框→选要比较地两个变量名进入栏→点击键运行,显示结果界面.文档来自于网络搜索结果界面中,描述统计表( )给出两组变量地基本情况描述.文档来自于网络搜索表给出地是配对变量间地相关性分析,等价于→→,详见回归与相关分析部分.文档来自于网络搜索检验表( )给出最终地配对检验结果.结果中显示差值均数()、差值标准差(. )、差值标准误(. )、差值地%置信区间地下限和上限(%,,)、值()、自由度()、双侧检验概率(. ).文档来自于网络搜索问卷调查数据共有个样本:按教育程度小学样本个数个,平均为;初中样本个数个,平均为;高中样本个数个,平均为;大专及以上样本个数个,平均为; 想要地结果是:随教育程度提高呈现递增趋势,检验结果(,,,;) 如何做出来?文档来自于网络搜索你地分析结果有值,有值,说明你是在进行平均值地比较.也就是你在比较两组数据之间地平均值有没有差异. 从具有值来看,你是在进行检验.检验是平均值地比较方法. 文档来自于网络搜索检验分为三种方法: . 单一样本检验( ),是用来比较一组数据地平均值和一个数值有无差异.例如,你选取了个人,测定了他们地身高,要看这五个人地身高平均值是否高于、低于还是等于,就需要用这个检验方法. 文档来自于网络搜索. 配对样本检验( ),是用来看一组样本在处理前后地平均值有无差异.比如,你选取了个人,分别在饭前和饭后测量了他们地体重,想检测吃饭对他们地体重有无影响,就需要用这个检验. 注意,配对样本检验要求严格配对,也就是说,每一个人地饭前体重和饭后体重构成一对. 文档来自于网络搜索. 独立样本检验( ),是用来看两组数据地平均值有无差异.比如,你选取了男女,想看男女之间身高有无差异,这样,男地一组,女地一组,这两个组之间地身高平均值地大小比较可用这种方法. 总之,选取哪种检验方法是由你地数据特点和你地结果要求来决定地. 检验会计算出一个统计量来,这个统计量就是值,根据这个值来计算值.因此,你可以认为值是一个中间过程产生地数据,不必理他,你只需要看值就可以了.值是一个最终值,也是检验地最重要地值. 值地意思就是显著性(),它地意思是说,平均值是在百分之几地几率上相等地. 一般将这个值与相比较,如果它大于,说明平均值在大于地几率上是相等地,而在小于地几率上不相等.我们认为平均值相等地几率还是比较大地,说明差异是不显著地,从而认为两组数据之间平均值是相等地. 如果它小于,说明平均值在小于地几率上是相等地,而在大于地几率上不相等.我们认为平均值相等地几率还是比较小地,说明差异是显著地,从而认为两组数据之间平均值是不相等地. 文档来自于网络搜索总之,只需要注意值就可以了.昼夜发病率发病例数天数总观察人数(取千分数)。
均值比较与T检验chap5

该值和小于该值的两个组,检验在这两个组之间进行,比较
其因变量在两组的均数间是否有显著性差异。
Confidence interval:95%:置信区间项,可以自定义。
Missing Values:选择对缺失值的处理方法
Exclude cases analysis by analysis:带有缺失值的 观测值当它与分析有关时才被剔除; Exclude cases listwise:剔除所有列在Test、 Grouping矩形框中的变量带缺失值的项
练习题
已知某水样中含CaCO3的真值为20.7mg/L,
现用某方法重复测定该水样11次CaCO3的含 量(mg/L)为:20.99,20.41,20.10,
20.00,20.91,22.60,20.99,20.41,
20.00,23.00,22.00。问该方法测得的均值
是否偏高?
2、Independent Sample T test (独立样本T检验)
Within Groups(组内偏差平方和):各组内的变异相对于组均值的变异;
Total(偏差平方和的总和):为组间偏差平方和与组内偏差平方和之和。
线性检验结果
R是因变量身高的观测值与预测值之间的的相 关系数,R值越接近1 越好; Eta:即η值(0~1)说明因变量与自变量之 间的联系程度; Eta Squared:η2为组间偏差平方和与偏差 表明回归方程的预测性
和eta统计值η和η2 。 η统计量表明因变量和自变量之间联系的强度。 η2 是组间平方和与总平方和之比。
Test for linearity:线性检验,输出R和R2,只有在控制变量有基
本的控制级,且自变量有三个水平以上时才能选用。
对第一层变量的方差分析结果
实验六 均值比较分析

实验六均值比较分析实验目的:了解各种均值假设检验方法。
实验内容:一、单样本的T检验二、独立样本的T检验三、配对样本的T检验四、单因素方差分析实验工具:SPSS比较均值菜单项。
知识准备:统计假设检验,就是事先对总体参数或总体分布形式做出一个假设,然后利用样本信息来判断这一假设是否合理,即判断样本统计量的具体数值与原假设是否有显著差异。
从而决定拒绝或接受原假设。
假设检验的基本步骤为:第一步,提出原假设(0H)和备择假设(1H)第二步,选择检验用统计量,并确定其分布形式第三步,选择显著性水平 ,确定决策临界值第四步,根据检验统计量的具体数值,做出决策一、单样本均值检验1、大样本下的均值检验根据中心极限定理,当总体服从正态分布时,样本均值也服从正态分布,当总体不服从正态分布时,若样本容量充分大,样本均值渐近服从正态分布。
因此大样本下的均值检验可采用Z 统计量。
当总体方差已知时,检验统计量的计算公式为:nx z σμ-= 当总体方差未知时,检验统计量的计算公式为:nsx z μ-=2、小样本下的均值检验当总体服从正态分布且方差已知时,根据中心极限定理,样本均值服从正态分布,检验统计量采用Z 统计量,即nx z σμ-=当总体服从正态分布但方差未知时,需要使用样本标准差来替代,此时样本均值服从1-n 个自由度的t 分布。
如果总体不服从正态分布,当样本容量充分大时也可以采用t 检验。
t 统计量的计算公式为:nsx t μ-=3、总本比率的假设检验可以使用Z 统计量检验总体比率,计算公式为:()np z πππ--=1式中n X p /=,即样本中成功次数占样本容量的比重,π为总体假设成功比例。
检验统计量z 渐近服从标准正态分布。
将上式分子分母同乘以n ,可得出以成功次数表示的z 统计量:()πππ--=1n n X z二、独立样本的均值比较 1、正态总体方差已知当两个总体均为正态分布,且两个总体的方差分别为2221σσ;为已知。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实训的心得与体会
统计学中经常通过样本来分析总体,即从样本的观察或实验结果的特征来对总体的特征进行估计和推断。
本次实验使用spass软件来进行均值比较与T检验,假设检验是对给定的总体参数值,利用样本数据对其推断,并给出接受或是拒绝的过程,另外,在具体操作中,首先定义所谓的小概率,一般取或,即显着性水平。
显着性水平取得太小,容易发生为错误;取得太大,则容易发生弃真错误。
通过本次实验用spass统计分析软件来进行均值比较及T检验后,感觉统计学中的很多问题不再像以前那么陌生了,同时也感觉统计学不再是想象中那么困难,之前学习统计学最怕的就是对数据进行求解与分析,现在使用这款软件后,让我从之前对统计学的陌生转变为熟悉,从此,在解决统计方面的问题又多了一项解决的工具:spss。
