第三节 一维势箱中的粒子
第三章 一维势场中的粒子 new 2(1) 量子力学教学课件

第3章 一维势场中的粒子@ Quantun 第6页
定理 2 对应于能量E,总可找到方程(1)的一组实解, 凡是属于E的任何解,均可表示为这一组实解的线性叠加 。 证明: 假设ψ(x)是方程(1)的对应于E的一个解,若是实 解,则归到实解集合中去。若是复解,按定理 1, ψ*(x) 也必是方程属于E的一个解,则它们的叠加
两边除以
( x ,y ,z ) X ( x ) Y ( y ) Z ( z )
1 2d 2 1 2d 2 1 2 d 2
X 2 d 2 X x V 1 ( x ) Y 2 d 2 Y y V 2 ( y ) Z 2 d 2 Z z V 3 ( z ) E
第3章 一维势场中的粒子@ Quantum Mechanics
Fang Jun 第8页
空间反射算符P 定义为Pψ(x) = ψ(-x),按定理 3,若 V(-x) = V(x),则ψ(-x)和ψ(x)都是对应E的量子态。若对 应E,方程(1)的解无简并,则解必具有确定的宇称,即 偶宇称 Pψ(x) = ψ(-x)= ψ(x),或者 奇宇称 Pψ(x) = ψ(-x)= -ψ(x)。 证明: 由于无简并, Pψ(x) = ψ(-x) = Cψ(x) P2ψ(x) = P Cψ(x) = C2ψ(x), P2ψ(x) = ψ(x), 则有C2=1,C = ±1。 若能级有简并,能量本征态不一定具有确定宇称。
2 [
2
d2 dx 2
V1 ( x )] X ( x )
Ex X (x)
2 [
2
d2 dy 2
V2 ( y )]Y ( y )
E yY ( y )
2 [
2
d2 dz 2
V3 ( z )] Z ( z )
势箱中的粒子的薛定谔方程及其解
三.量子力学处理问题的一般方法
1. 2. 3. 写出体系的哈密顿算符[H](主要是势能算符); 写出Sch.方程; 解Sch.方程.解Sch.方程和通常解微分方程差不 多,解Sch.方程时,把 Ψ 当作未知函数E 作为参 数看待. 4. 由所得Ψi就可知道体系的几率分布以及体系的其 它物理性质.
1 4
第一章习题 6 7 9 11 12 18 21
�
1 2 X (x) 1 2Y ( y) 1 2 Z (z) 8π 2 m + + = 2 (Ex + Ey + Ez ) 2 2 2 X (x) x Y ( y) y Z (z) z h
因为x,y,z是三个变数,要满足上式,必须下列三式同时成立
d 2 X ( x) 8π 2 mE x + X ( x) = 0 2 2 dx h 2 8π 2 mE y d Y ( y) + Y ( y) = 0 2 2 dy h
长,宽,高分别为a,b,c 的三维势箱,Sch.方程为
2 2 2 [ 2 ( 2 + 2 + 2 ) + V ( x, y, z )]ψ ( x, y, z ) = Eψ ( x, y, z ) y 8π m x z h2
设
Ψ(x,y,z)=X(x)Y(y)Z(z) E = E x + Ey + E z 8π 2 m 代入Sch.方程,并以X(x)Y(y)Z(z)除之,两边乘 2 h
通式 R2N-(CH=CH-)rCH=NR2+
E h[(r + 3) 2 (r + 2) 2 ] h(2r + 5) = = ν= 2 h 8ml 8ml 2
8ml 2 c 3.30l 2 3.30(248r + 565) 2 = = λ = c/ν = pm h(2r + 5) 2r + 5 2r + 5
高二物理竞赛课件:一维势场中的粒子

l
8
(3):
p x x p̂ x n x dx
1
0
1
0
*
n
2
nx ih d 2
nx
sin
sin
dx
l
l 2 dx l
l
nih l
nx
nx
2 sin
cos
dx 0
l
l
l 0
9
经典物理无法理解势垒贯穿。
sin
sin
dx
0
0
l
l
l
l
l
l
1 cos 2n x
2
2
nx
l dx
x sin 2
dx
x
0
l
l 0
2
l
l
1 x2
l2
l
2
l
l
0
l
2nx l
l
x sin
0
2n
l
2n
2nx
∵E=T+V,T=E-V<0,不可能 . 本节介绍量子
力学如何解释势垒贯穿,以及如何计算穿过势垒的几率。
Eபைடு நூலகம்
应用:
1973年: 固体中的隧道效应,
V0
-a/2
0
a/2
半导体中的隧道效应.
约朔夫森, 江琦, 迦埃非.
1986年: 设计世界上第一架电子显微镜,设计隧
道效应显微镜.
鲁斯卡, 宾尼(德国),罗雷尔因(瑞士).
结构化学1-3

x
★ 根据边界条件确定方程的特解
因为必须是连续的,即 (0)= (l)=0,故有
(0) c1 cos(0) c2 sin(0) 0
c1 0 c2 0
(l) c2 sin 2m El 0
2m E l n n 1, 2,3
n2π22 n2h2 E 2ml 2 8ml 2
2πx
)dx
a0
a
a0 a
a
a0
a
例:函数 ( x) 2
2 sin πx 3 aa
2 sin 2πx aa
是不是一维势箱中
粒子的一种可能的状态?如果是,其能量有没有确定值?
如有,其值是多少?如果没有确定值,其平均值是多少?
解:
a
*dx
8
asin2( πx )dx 24
解:
a
*
Hˆ dx
0
E *(Hˆ )d *d
0a 2
2 sin πx 3 aa
2 a
sin
2πx a
h2 8π2m
d2 dx 2
2
2 sin πx 3 aa
2 a
sin
2πx a
dx
h2
4ma2
0a 2
sin
2πx a
h2 8π2m
d2 dx 2
2
2 sin πx 3 aa
2 a
sin
2πx a
h2 8π2m
π2 a2
2
2 πx 4π2
sin a
第三章 箱中的粒子

1 1 sin ni t sin n j t cos[( ni n j )t ] cos[( ni n j )t ] 2 2
j dx 于是: i *
2
0
1 2 1 cos[(ni n j )t ]dt cos[(ni n j )t ]dt 2 0 2
1/ 2
c2e
i ( 2mE )1 / 2 x /
(2mE) x /
II c1e c2e
i
i
由于:
e cos i sin
(c1 c2 ) cos i(c1 c2 ) sin A cos B sin
i
则: II c1 cos ic1 sin c2 cos ic2 sin
2
上述方程为常系数二阶线齐次方程,其辅助方程为:
s 2 2m E 2 0
此,上式可写为:
s 2mE
1
1
此处能量E为势能(为零)加上动能,所以为正的,因
s i 2mE
代入常系数二阶线齐次方程的通解公式,得:
II c1e
暂令: 则:
i ( 2mE )1 / 2 x /
1 1/ 2 1 1/ 2 A cos[ ( 2 mE ) x ] B sin[ ( 2 mE ) x] 于是: II
下面利用边界条件求任意常数A与B。
由于波函数是连续的,其值不会发生突跃。
若ψ在x=0点连续,则ψI和ψII在x=0处必趋于同一值,即:
lim I lim II
一维势箱波函数的正交归一性
对于一维势箱中特定的波函数Ψi,其量子数为ni,则:
箱中的粒子专业知识课件

3.2 一维自由粒子
一种自由粒子意味着不受任何旳力。对于一种自由粒子,
不论x旳值是什么,势能保持恒定。因为能级零点旳选 用是任意旳,我们可令V(X)=0,薛与 旳定一 方谔维 程方势一程箱样中(能粒除够子边记作:
界条件外)
d 2
dx2
2m 2
E
0所以,其通解为:c e c e i(2mE)1/ 2 x / 1
dx l
III
dx 1
B 2 l sin2 ( nx )dx 1 B 2 l
0
l
2
B
2
1/
2
(B为满足绝对值旳任何数)
l
II
( 2)1/2 sin( nx ),
l
l
n 1,2,3
波函数和概率密度旳图形表达
正弦函数
n=4
n=3 n=2 n=1
波函数
概率密度
n=4
n=3
n=2 n=1
0
x
0
x
经典力学:若粒子能量不小于势垒,则全部粒子飞越 势垒继续迈进;反之,则全部粒子被势垒档回来,没有 粒子能穿过势垒。 量子力学:若粒子能量不小于势垒,除了大部分经过 还有少部分为势垒所反射;虽然粒子能量不不小于势垒, 仍有一定数量旳粒子穿透势垒,这就是微观粒子特有旳 量子效应--隧道效应。
将上述整个空间分为3个区域,相应旳波函数分别为 ψ1,ψ2,ψ3,满足Schrodinger方程:
i(2mE )1/ 2 x / 2
c e c e i(2mE)1/ 2 x / 1
i(2mE )1/ 2 x / 2
问题:边界条件?
假设当x趋于±∞时Ψ将保持有限是合理旳。若E不大于 零,那么边界条件将被破坏,因为E<0,有:
高二物理竞赛课件:一维势场中的粒子(1)

在继续阐述量子力学基本原理之前,先用
Schrodinger 方程来处理一类简单的问题——
一维定态问题。其好处有四:
1. 有助于具体理解已学过的基本原理;
2. 有助于进一步阐明其他基本原理;
3. 处理一维问题,数学简单,从而能对结果进
行细致讨论, 量子体系的许多特征都可以在
′ − ′=C
对于束缚态(bound state指粒子局限在有限空间中,即
无限远处找到粒子的概率为零)则有′ − ′=0
ℏ
−
+ =
(1)
定理7: 设粒子在规则势场V(x)
{V(x)无奇点}
中运动,如存在束缚态,则必定是不简并的。
这些一维问题中展现出来;
4. 一维问题还是处理各种复杂问题的基础。
2
一维薛定谔方程
ℏ
ℏ , = −
+ (, )
对定态,具有能量 E
, = ()−/ℏ
一维粒子的能量本征方程:
ℏ
−
+ =
റ , 称为奇宇称
在一维情况下,宇称的奇偶性与函数的奇偶性是一致的。
定理3的推论
U(-x)=U(x),如果对应某能量E,方程(1)
的解无简并,则解必有确定的宇称。
7
ℏ
−
定理4
证:
+ =
(1)
设 U(-x)=U(x),则对应任何一个能量本征值E总
可以找到方程(1)的一组解(每个解都有确定
如果 是实解,就可以将其归为实解集合。
1-3一维势箱1
Chapter 1
教四220 © 2011.09
量子尺寸效应
能级差与粒子质量成反比,与粒子运动范围的平方成反 比。这表明量子化是微观世界的特征。
由此定性地看更复杂的三维体系就不难理解:普通金属费
米能级附近的准连续能级在纳米颗粒中会变为离散能级,而
G.Binnig, H.Rohrer, E.Ruska 1986年诺贝尔物理学奖
三维势箱中 运动的粒子
五、量子力学处理微观体系的一般步骤
1. 根据体系的物理条件写出势能函数,进一步写出哈密 敦算符及薛定鄂方程。
2. 解薛定鄂方程,根据边界条件求得Ψn和En。 3. 描绘Ψn,Ψn2的图形,讨论它们的分布特点。 4. 由所得的Ψn,求各个对应状态的各种力学量的数值,
了解体系的性质。
I Ψ= 0 V= ∞
II
Ψ=?
m
V= 0
0
III
Ψ= 0
V= ∞
一维无限
l
深势阱x
一维势箱数学表达式
0
V=
0<X<l
∞ X≤0 和 X≥ l
Chapter 1
教四220 © 2011.09
一维势箱模型
一个质量为 m 的粒子在一维 X 方向上运动,局 限在 X = 0 到 X = l 之间。在此范围内(Ⅱ区)V = 0,但在边界和区域外面 V = ∞。由于外面势能过大 ,粒子跑不出去,即:粒子在Ⅰ、Ⅲ区内出现的几率为 零,Ψ= 0。这样的体系称为一维势箱,是一个抽象的 模型。但可描述微观体系基本运动形式-平动等体系。
Chapter 1
教四220 © 2011.09
大学物理 12.6 一维势场中的粒子剖析

把特解代入,得关于R、A、B、S的四个代数 方程。解出S,可近似地求出穿透系数:
T T0 e
2a 2 m(U 0 E )
量子隧道效应的应用: 隧道二极管,金属场致发射,核的 衰变,… (1)原子核的 衰变
238
U
35MeV 库仑势能
U
234
Th + He
4
E 4.25MeV
空腔内壁的分子可以看成带电简谐振子,在 一定温度下这些简谐振子所发射的各种频率的 能量子,在空腔内就形成了辐射场。 简谐振子是一个十分有用的振动模型,可用 于原子核中质子和中子的振动、分子中原子的振 动、固体晶格点阵上原子的振动。固体晶格点阵 上原子振动的能量就可以用能量子来描述,这时 的能量子称为声子。
在状态(x,0)上测量能量,能测到的值为
1 5 1 E 0 h , E 2 2 h h 2 2 2
测到E0的概率:1/3;测到E2的概率:2/3;它 们分别等于展开式中相应展开系数的模方。
1 2 11 测量值的平均值: E E0 E 2 h 3 3 6
1 一维简谐振子的势能函数: U ( x) m 2 x 2 2
1 1 En n h n , n 0,1,2, 2 2
零点能:h/2; 能量子:h
可以证明,在光照下带电简谐振子的跃迁只 能发生在相邻能级之间,即一次跃迁只能发射 或吸收一个能量子。
通过隧道效应射出
对不同的核,算出的衰 变概率和实验一致。
0 R
4.25MeV
r
核力势能
(2)扫描隧道显微镜(STM) (Scanning Tunneling Microscopy) 1986年诺贝尔物理学奖: 毕宁(G.Binning) 罗尔(Rohrer) 发明STM
1-3在维势箱中运动的粒子-结构化学课件

2.建立薛定谔方程 需要将薛定谔方程用变数分离法分解成三个一维的微分方程, 然后分别求解,最后由
x y z
x, y, z n x n y n z
E Ex E y Ez
分别求得体系的完全波函数和能级。
§1-3 在一维势箱中运动的粒子
(2)写出薛定谔方程 边界条件:
* a a i j i j d 0
因ai a j, 故 i* j d i dx ij
* i * j
0, 当i j 正交性 ij 1, 当i j 归一性
§1-3 在一维势箱中运动的粒子
三个波函数对应三种不同的运动状态,但对应同一个能量
值,称三个状态为简并态,简并度为3。
定义:象这样一个能级有两个或两个以上的状态与之对应, 则称此能级为简并能级,相应的状态(波函数)为简并态,
简并态的数目为简并度。
2 n
x ~ x 作图,范围
0 xl
n=4
n=3
n=2 n=1
波函数
几率密度
§1-3 在一维势箱中运动的粒子
波函数可以有正负变化,但几率密度总是非负的。 节点: 除边界条件 x 节点数:
0, x l 外其余各处 x 0 的点称为节点。
n 1
一般来说,节点越多的状态,波长越短,频率越高,能量越高。 当 n 很大时,将分辨不清箱中各处几率密度的变化,这就是 说,高量子态时趋于经典的均一的几率密度分布。
在一定条件下,如果粒子的活动范围扩大(即 l 增大), 相应的能量降低,如有机共轭分子中的离域效应。
§1-3 在一维势箱中运动的粒子
(2) 零点能
h2 E1 零点能即基态能量,任何微观粒子的零点能不为零, 8ml 2 (3) 相邻能级间的能差
第三节 一维势箱中的粒子

2
2 l 1 cos (nx/l) 2 nx x sin dx x dx u cos nudu l 0 l l 0 2 2
l 2
cos nu
1
u sin nu n
2 2 1x 2nx l 2nx l l x sin cos l 2 2n l 2n l 0 2
( l ) B sin( 2 m E
sin
l )0
由此 A=0
B不能为0 (否则波函数处处为0)
l 2mE 0
2 mE
l
n ( n 0, 1, 2, )
En
n h 8 ml
2
2 2
将En代入(x),得:
( n 1, 2 ,3 ) nx ( x ) B sin
六、三维势箱中运动的粒子
三维势箱的定态Schrödinger方程为 2 h ( 2 ) ( x , y , z ) E ( x , y , z ) 2 2 2 8 m x y z 由于粒子在三个方向的运动是独立的,因此:
( x , y , z ) ( x ) ( y ) ( z )
2
nx cos l l
n 2 4 l h
2
2
2
n h nx sin 2 l l 4l
2 2
n
E
P
2 x
2m
n h 8ml
2
2 2
五、量子力学处理微观体系的一般步骤
①根据体系的物理条件,写出势能函数,进而写出 Schrödinger方程; ②解方程,由边界条件和品优波函数条件确定归一 化因子及En,求得n ③描绘n, n*n等图形,讨论其分布特点; ④用力学量算符作用于n,求各个对应状态各种力 学量的数值,了解体系的性质; ⑤联系实际问题,应用所得结果。
一维势箱中粒子的薛定谔方程及其解.pdf

8ml 2
若将一个电子束缚于l =10-8cm的势箱中,能级差为:
E
(2n
1)
8
(6.6 1027 )2 9.11028 (108 )2
(2n 1) 37.60eV
能级分立明显
若将一个质量为m=1g的物体束缚于l =1cm的势箱中,
能级差为:
E (2n 1) (6.6 1027 )2 811
3、示例:
i* j
dx
l 0
2 sin( nix )
l
l
2 sin( n jx )dx
l
l
2 l sin( nix ) sin( n jx )dx
l0
l
l
(ni n j )
1
l
l 0
cos(ni
n
j
)
x
l
cos(ni
n
j
)
x
l
dx
三、能级公式的意义:
En
n2h2 8ml 2
⑴受束缚的粒子其能量必须是量子化的,即边界条 件迫使能量量子化(一维势箱中的量子化是解方程 自然得到的,而非象旧量子论是人为附加的.) ⑵相邻两能级差:
E En1 En
(n 1)2 h2 n2h2 (2n 1)h2
8ml 2 8ml 2
能级变化可认
(2n 1) 3.431042 eV
为是连续的
⑶En≠0. ∵n≠0, 否则(x) 0
n=1——基态——最低能量: E h2 称为“零点能”——表明运动的永恒性
8ml 2
⑷对于给定的n:
l
1-3一维势箱1
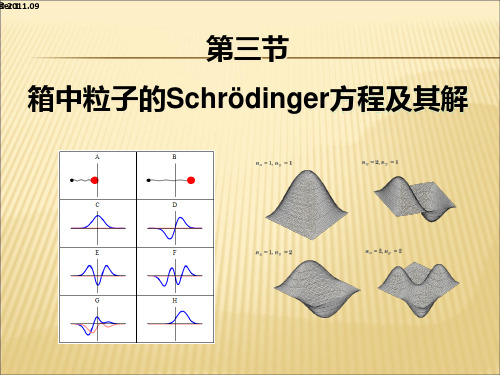
h2 0 Bsin
h2 0
Acos(0) Bsin(0) 0
∵ sin(0)= 0 cos(0)≠ 0 ∴ A = 0 (A≠0那部分解不符合边界条件,舍去)
解SCHRÖDINGER方程
因此 B ≠ 0
(x) B sin
8 2mE
h2
x
如果B = 0 则意味着Ψ到处恒等于0,不是非零解。
第三节 箱中粒子的Schrödinger方程及其解
这一节在量子力学的基本假设的基础上,以 一维势箱为例,说明如何用量子力学方法处理微 观体系的步骤,在讨论中所获得的信息可帮助了 解原子、分子内的电子运动。
注意:如何确定势能函
数,如何考虑界条件,得 到有关“量子化”的信息
一、一维势箱模型及SCHRÖDINGER方程
∴ n = 1,2,3,…
由归一化条件
解Schrödinger方程
(x) B sin nx
l
l
2
0 dτ 1
l B2 sin 2 nπ xdx 1
0
l
解Schrödinger方教四2程20 ©2011.09
B 2 l sin 2 nπxdx Chapter 1
0
l
H Ψ EΨ
-
h2 8π 2m
d 2Ψ(x) dx 2
EΨ
(x)
或 d 2Ψ 8π 2m EΨ 0
dx 2
h2
ቤተ መጻሕፍቲ ባይዱ
二、解SCHRÖDINGER 方程
d 2Ψ 8π 2m dx2 h2 EΨ 0
Schrödinger方程是二阶常系数线性齐次微分方程 (二阶齐次方程)。其通解为:
第三章 箱中的粒子

limψ I = limψ II
x →0
−1
x →0
0 = lim A cos[h (2mE )
x →0
{
1/ 2
x] + B sin[h (2mE )
−1
1/ 2
x]
}
A=0
2π 则: ψ II = B sin[ (2mE )1/ 2 x] h
运用x=l处的连续条件, 运用 处的连续条件,得: 处的连续条件
1 dψ ψ= 2 ∞ dx
2
于是,箱外的波函数为零, 于是,箱外的波函数为零,即:
ψ I = 0, ψ III = 0
V(x)= 区II,势能V为零。其薛定谔方程为: II,势能V为零。其薛定谔方程为: V(x)= II I V(x)= 0 III
d ψ II 2m + 2 Eψ II = 0 2 dx h
2π 1/ 2 B sin[ (2mE ) l ] = 0 h
(B不能为零,否则波函数处处为零,将有一个空箱) 不能为零,否则波函数处处为零,将有一个空箱 不能为零
2π 所以: 所以: sin[ (2mE )1/ 2 l ] = 0 h
在0,±π,±2π,±3π,…时,正弦函数为零。则: , , , , 时 正弦函数为零。
只有上式中的能量值才能使ψ满足在 处连续的边界条件 只有上式中的能量值才能使 满足在x=l处连续的边界条件,并 满足在 处连续的边界条件, 且可以看出箱中粒子的能量是量子化的,有一大于零的极小值, 且可以看出箱中粒子的能量是量子化的,有一大于零的极小值, 这与经典的结果相反(可以存在任何非负能量) 这与经典的结果相反(可以存在任何非负能量)。
(i=j) =)
那么, 对应于不同能级的波函数时( ) 那么 , 对应于不同能级的波函数时 ( i≠j) 上述积分的 值是多少? 值是多少?即:
一维势箱中粒子的波函数

一维势箱中粒子的波函数
一维势箱是量子力学中一种比较基础的模型,通常被用来研究粒子在有限空间内的运动情况。
本文将介绍一维势箱中粒子的波函数。
一维势箱是一个长度为L的无限深势阱,也就是说当粒子在势箱内部时,势能为零,当粒子处于势箱外部时,势能为无穷大。
这样的势场约束了粒子只能在势箱内部运动,此外无处可去。
为了求解一维势箱中粒子的波函数,我们可以利用薛定谔方程。
根据波粒二象性,一个粒子可以看作是一个波包,如果用y(x,t)表示粒子的波函数,则粒子的能量E与角频率w的关系为E=hw,其中h为普朗克常数。
而薛定谔方程可以表示为:
i(h/2π)·∂y(x,t)/∂t=(-h^2/2m)·∂^2y(x,t)/∂x^2
式子中,i是虚数单位,m为粒子的质量。
这个方程可以看做是描述粒子在一维势箱中的运动情况的基本方程。
对这个方程进行数学求解,我们可以得到一维势箱中粒子的波函数:
y(x,t)=Asin(nπx/L)·exp(-i(Et/h))
式中,A为归一化因子,n为正整数,代表是势箱内的第n个能级。
此外,由于一维势箱中的边界条件,波函数必须满足在x=0和x=L 处的边界条件。
总的来说,一维势箱中粒子的波函数与粒子的能量以及势场的形状密切相关。
对于能级有限的势场,可以通过求解薛定谔方程,得到粒子的波函数。
通过对波函数的分析,我们可以了解粒子在一维势箱中的运动和行为。
一维势箱中粒子的最大德布罗意波长

一维势箱中粒子的最大德布罗意波长量子力学是一门探究原子和分子行为的学科,其中粒子的波动性质是其研究的核心。
而德布罗意波长则是表征粒子波动特性的物理量,它在一维势箱中的最大值更是具有重要的物理意义。
一维势箱是一种理想模型,它能够清晰而简洁地展现物质的量子力学性质。
当一个粒子被限制在能够容纳其的一维势箱内时,其波函数必须满足一些特殊的条件。
首先,波函数必须为零,当粒子离开势箱的两端时;其次,波函数必须是正弦曲线的形式,在势箱内部的位置与时间的关系上。
由于波函数的存在,粒子被视为是一种波动现象,而德布罗意波长就是描述这种波动特性的物理量。
它是一个粒子的普朗克常数除以其动量得到的值,即λ = h/p,其中h是普朗克常数,p是粒子的动量。
在一维势箱中,粒子的动量p是由其波长λ决定的:p = h/λ。
因此,当粒子在势箱内的波长变短时,其动量就必须变大。
但由于势箱的尺寸是固定的,因此存在一定的限制。
当粒子的波长λ等于势箱长度L时,它的动量也就达到了最大值。
因此,一维势箱中粒子的最大德布罗意波长为L。
这个结论对于量子力学的研究具有重要的物理意义。
它代表着粒子所具有的最大分辨率,即这个粒子最小的特征大小。
在现代科技中,可以应用于许多地方,例如扫描电子显微镜等高分辨率科学设备的研制。
除此之外,这一论断也为量子力学提供了更深入的理解。
由于波函数的存在,粒子的特殊行为被更好地解释了。
波函数是波动性的载体,它描述了粒子的位置、动量、角动量等各种物理属性。
在势箱中的波函数示范了波动性质的极限,这对于探究粒子的本质具有重要的意义。
总之,一维势箱中粒子的最大德布罗意波长,是量子力学中的一个重要概念,它展示了波动性质在量子世界中的重要性。
也因此,科学家们对这一原理的理解深化,不断应用于科学探索中,以期更好地理解自然界。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C
C
4/9E 4/9 1ll Fra bibliotek域键l
1/9E1
3l 离域键
四、求体系的各种物理量
1、粒子在箱中的平均位置
ˆ ˆ 本 值 只 求 均 : 由 x = x , xψn ≠ cψn, x无 征 , 能 平 值 于ˆ
x = ∫ ψ xψndx = ∫
0 * n
l
l
0
2 nπx 2 nπx sin x sin dx l l l l
n 2h 2 = 8 ml 2
( n = 1,2,3 ⋅ ⋅ ⋅ ⋅ ⋅ ⋅) nπx ψ ( x) = B sin
l
由波函数的归一化条件求常数B:
nπx B2 l 2nπx 2 2 ∫0 ψ ( x) dx = B ∫0 sin l dx = 2 ∫0 (1 − cos l )dx 2 2 B l 2nπ l B = [x − sin x 0] = l =1 l 2 2nπ 2
ψ ( x , y , z ) = ψ ( x ) ⋅ ψ ( y ) ⋅ψ ( z )
三维势箱中粒子运动的波函数: 三维势箱中粒子运动的波函数
E = Ex + E y + Ez
8 ψ = abc
2
1/ 2
nyπy nxπx nzπz sin sin sin a b c
三维势箱能级表达式: 三维势箱能级表达式:
第三节 一维势箱中运动的粒子
一、一维势箱模型
V=0 V=∞ 0<x<l(Ⅱ区) x≤0,x≥l(Ⅰ 、Ⅲ区,ψ=0)
Ⅰ V=∞ Ⅱ V=0 Ⅲ V=∞
二、Schr dinger方程求解 Schrödinger dinger方程求解
d − 2 ψ = Eψ 2 8π m dx
d2ψ 8π 2mE 即 , 2 + ψ =0 2 dx h
例:丁二烯的离域效应
C C C C E1 C C
•丁二烯的离域效应: =2× E定=2×2h2⁄8ml2=4E1 E离=2h2/8m(3l)2+ 2×22h2/8m(3l)2 =(10/9)E1 •势箱长度的增加,使分 势箱长度的增加, 势箱长度的增加 子能量降低,更稳定。 子能量降低,更稳定。
π4 4
l 2 l
2 B=± l
习惯上取 B = 2
l
∴ψ ( x) =
nπx 2 sin l l
(n=1,2,3….)
一维势箱粒子的Schr dinger 一维势箱粒子的Schrödinger Schr
结果如下: 结果如下:
∴ψ ( x) =
2 nπx sin l l
(0 < x < l )
En
n 2h 2 = 8 ml 2
2 2 l
(2)粒子动量的x轴分量px
ˆ ˆ 可以验证,Px 也无本征值,即 Px ψ n ≠ cψ n
* ˆ Px = ∫ ψ n Pxψ n dx 0 l
2 l nπx ih d nπx = − ∫ sin sin dx 0 l l 2π dx l ih l nπx nπx = − ∫ sin d sin 0 πl l l
ψ (0) = A cos 0 + B sin 0 = 0
ψ (l ) = B sin( 2 mE
s in
l )=0 h
A=0 B 为0 ( 则 数处处为0 数处处为0)
l 2mE = 0 h
l 2mE = nπ (n = 0,±1,±2,⋅ ⋅ ⋅ ⋅ ⋅⋅) h
En
将En代入ψ(x),得:
2 l π 2 l 1−cos( πx/l) 2n 2 n x = ∫ xsin dx = ∫ x dx ∫ u cos nudu = 12 cos nu + 1 u sin nu 0 0 n n l l 2 l
1 x l 2nπx l 2nπx l xsin = − − cos = l 2 2nπ l 2nπ l 2 0
★ 受一定势能场束缚的粒子的共同特征
1、粒子可以存在多种运动状态,它们可由ψ1,ψ2,…,ψn等描述; 2、能量量子化; 3、存在零点能; 4、没有经典运动轨道,只有几率分布; 5、存在节点,节点越多,能量越高。
量子效应
当∆En=(2n+1)h2/8ml2中m、l增大到宏观数量时,能级间隔 变小,能量变为连续,量子效应消失。
六、三维势箱中运动的粒子
三维势箱的定态Schr dinger Schrödinger Schr 为
∂ ∂ ∂ − 2 ( 2 + 2 + 2 )ψ ( x, y, z ) = Eψ ( x, y, z ) 8π m ∂x ∂y ∂z h2
由于粒子在三个方向的运动是独立的,因此 由于粒子在三个方向的运动是独立的,因此:
(n = 1,2,3 ⋅ ⋅ ⋅ ⋅ ⋅ ⋅)
三、结果讨论
(1)粒子在势箱中没有经 典的运动轨道,而是以不同 的几率密度出现在箱内各点。
0
n=3 n=3 E3 0 ψ*ψ n=2 n=2
(2)在量子力学中,能量
是量子化的;而经典力学 中,箱内粒子的能量是连 续的。 (3)零点能。按经典力学 基态能量为零,按量子力学 零点能为h2/8ml2>0;
称为简并能级。相应的状态为简并态, 称为简并能级。相应的状态为简并态,简并态的数目为简 并度。 并度。
ih sin 2 (nπx / l) =− =0 πl 2 x =0
x =l =l
(3)粒子的动量平方px2值
2 x
h2 h 2 d 2 2 nπx ˆ p ψn = − 2 2 sin = − 2 4π 4π dx l l
=
d nπ dx l
2 2 2 nx ny nz h E= + 2 + 2 nx, y, z均 非 整 n n 为 零 数 2 8m a b c
若a=b=c,则:
h 2 2 2 E= nx + n y + nz 2 8ma
2
(
)
♣简并能级:一个能级有两个或两个以上状态与其相对应, 简并能级:一个能级有两个或两个以上状态与其相对应,
2 nπx cos l l
nh h nπ 2 nπx • sin = 2 ψn l l 4π 2 l 4l
2 2
2
2
P2 n2h2 E= x = 2m 8ml2
五、量子力学处理微观体系的一般步骤
①根据体系的物理条件,写出势能函数,进而写出 Schrödinger方程; ②解方程,由边界条件和品优波函数条件确定归一 化因子及En,求得ψn ③描绘ψn, ψn*ψn等图形,讨论其分布特点; ④用力学量算符作用于ψn,求各个对应状态各种力 学量的数值,了解体系的性质; ⑤联系实际问题,应用所得结果。
ψ
0
E2 0 n=1 n=1 E1 0
0
(4)ψ可正可负,ψ=0称节 点,节点数随量子数增加而 增加,共有n-1个节点,节点 越多,能量越高。
0
x
l
0
x
l
(5)波函数的正交归一性
l
∫ ψ ψ n dx = 0(m ≠ n)
0 ∗ m
(正交)
ψ ψ n dx = 1(m = n) ∫
0 ∗ m
l
(归一)
h
2
2
0
l
x
此方程为二阶常系数线性齐次微分方程,方程的通解为:
2mE 2mE ψ(x) = Acos x + Bsin x h h
h (h = ) 2π
可以看出,任何一组A、B和E的数值都可确定一个ψ, 即可得到方程的一个解,但A、B和E所确定的解要满足 波函数的三个条件。
根据品优波函数的连续性和单值性条件,x=0和x=l 时,ψ=0 根据品优波函数的连续性和单值性条件,
