八年级数学上册第11章平面直角坐标系111平面内点的坐标第2课时图形与坐标作业新版沪科版
2022八年级数学上册第11章平面直角坐标系11.2图形在坐标系中的平移课件新版沪科版28

A.(-1,-1)
B.(1,0)
C.(-1,0)
D.(3,0)
6.【中考·台州】如图,已知一个直角三角板的直角顶点 与原点重合,另两个顶点 A,B 的坐标分别为(-1, 0),(0, 3).现将该三角板向右平移使点 A 与点 O 重合,得到三角形 OCB′,则点 B 的 对应点 B′的坐标是( C ) A.(1,0) B .( 3, 3) C .(1, 3) D .(-1, 3)
第11章 平面直角坐标系
11.2 图形在坐标系中的平移
提示:点击 进入习题
1A 2B 3A 4D 5C
6C 7D 8C 9B 10 (1,1)
答案显示
提示:点击 进入习题
11 见习题 12 见习题 13 见习题 14 见习题
答案显示
1.【中考·大连】在平面直角坐标系中,将点P(3,1) 向下平移2个单位长度,得到的点P′的坐标为( A )
7.如图,若图①中点 P 的坐标为83,2,则它在图②中
的对应点 P1 的坐标为( D )
A.(3,2)
B.83,1
C.1,131
D.131,1
8.【中考·海南】如图,在平面直角坐标系中,三角
形ABC位于第一象限,点A的坐标是(4,3),把
三角形ABC向左平移6个单位长度,得到三角形
A1B1C1,则点B1的坐标是( C )
谢谢观赏
You made my day!
解:如图①,由图可得虎山(0,0)、 熊猫馆(3,2)、鸟岛(-1,3)、狮子 馆(-2,-2)、猴园(3,-1).
(2)若以猴园为原点,水平向右为x轴正方向、铅直 向上为y轴正方向建立平面直角坐标系,写出各 景点的坐标.
解:如图②,由图可得 虎山(-3,1)、熊猫馆(0,3)、 鸟岛(-4,4)、狮子馆(-5,-1)、 猴园(0,0).
八年级数学上册第11章平面直角坐标系11.1平面内点的坐标2图形与坐标授课课件新版沪科版2

例 5 〈一题多解〉如图, 三角形ABC,角形ABC的面积.
导引:因为三边均不平行于坐标轴,所以我们 无法直接求边长,也无法求高,利用分 割法不易求解,因此需另想方法.根据 平面直角坐标系的特点,可以将三角形 ABC围在一个梯形或长方形中.
2
2
2
2
14312729.
2
2
2
感悟新知
归纳
知2-讲
此题运用了割补法,对于平面直角坐标系中的三 角 形,可以通过作垂线,运用割补法转化为能求出面积 的图形,通过这些图形面积的和差关系来求原三角形的 面积.
感悟新知
知2-练
1.如图在5×4的方格纸中,每个小正方形的边长 为1,点O,A,B在方格线的交点(格点)上.在 第四象限内的格点上找点C,使三角形ABC的 面积为3,那么这样的点C共有B( )
感悟新知
知2-练
解:过点A作x轴的垂线,过点B作y轴的垂线,过点C分别作x轴、
y轴的垂线,交于D,E,F三点,如下图.
方法一: S 三 角 形 A B C S 长 方 形 C D E F
S S S 直角三角形ACD
直角三角形ABE
直角三角形BCF
CDDE1ADCD1AEBE1BFCF
2
2
2
5 71 3 51 4 3 1 2 72 9.
222
2
感悟新知
知2-练
方法二: S三角形ABC S 梯形BCDE S直角三角形ACD S直角三角形ABE
1(BECD)DE1ADCD1AEBE1(35)7
2
2
2
2
13514329.
2
2
2
方法三:S三角形ABC S 梯形CAEF S直角三角形ABE S 直角三角形BCF
八年级上册 数学 课件 11.1平面内点的坐标

B
-1
-2
-3
12 3 4 x C
探究1
想已一知各想点:的(坐2,3)与
y
( 点标 坐 点吗3,标的,2系请位?)中在置表找直:示出角同一个
5 4
平A(面2,内3)的点 与B(有3,序2)实C数(对 !2DE,((一-411,),一--3对2))应 -4
( -2,1 )ห้องสมุดไป่ตู้3 2
· C 1 -3 -2 -1 0
-1
-2
· -3
D ( -4,- 3 ) -4
( 2,3 )
A
··B ( 3,2 )
12345 x
·E ( 1,- 2 )
探究2 各象限内点的坐标有何特征?
y
陈浩 江珊 陶颖 2
(-,+)
余庆 航
饶磊
陈胜 1
李潇 冯洁 吴昊
(+,+)
姚悦
陶魏 琪
陈恩 浩
-3 -2 -1 O
12
3
X
董佳 程
王超
方琴 -1
平面内点的坐标
1 1 6陈浩
2
余庆航
2
江珊
饶磊
讲台
3
陶颖
陈胜
4
李潇
5
冯洁
吴昊
姚悦
陶魏琪
陈恩浩
行数
3
董佳程
王超
方琴
4
张媛
季佳鑫
汪文昊
列 数
陈煜
饶徐珍
汪信
王文博
胡雪菲
陈曦贤
生活中的数学
回顾旧知
1.什么是数轴? 2.数轴上的点与 ?一一对应
实数
3.写出数轴上A、B、C各点所对应的数.
沪科版(2012)初中数学八上 11.1 平面直角坐标系 平面内点的坐标 课件

思考如何确定空间中一个点的位置,提出方案并相 互交流。
谢谢!
【老师寄语】
不忘初心,砥砺前行,在人生 的坐标系中画出辉煌的图像!
1、概念:在平面内画两条互相垂直、原点重合
的数轴,组成平面直角坐标系.
5
y
5 4 3 2
4
1
水平的数轴叫x轴或横轴; 习惯上取向右方向为正方向
3
-4 -3 -2 -1-O1 -2
2
-3
竖直的数轴叫y轴或纵轴;
1
-4
习惯上取向上方向为正方向
x轴与y轴的交点-叫4 平面-3直角-坐2 标系-1的原-O1点. 1 2 3
小游戏
请两位同学 (1)一位同学在平面直角坐标系中指点, 另一位说坐标; (2)交换后,一位同学说坐标,另一位在坐 标系中指点。
比一比哪一组说的又快又准确!
二 点的坐标y5
、
4
3
N(0,2)2
.Q ·P
在X轴上点 的特征: (a,0) 在Y轴上点 的特征:
1
M(3,0) (0,b)
-4 -3 -2 -1 0 -1
你能根据地图说 出合肥65中的位
置吗?
你能说出这个同学在教室中的 位置吗?
6 5
4 3
2 1
1
2
3
45
纵列 讲桌
横 排
6
第十一章 平面直角坐标系
11.1 平面内点的坐标
复习
在直线上如何确定点的位置呢?
P
· A
原点
B
•
•
-3 -2 -1 0 1 2 3 4
数轴上的点 一一对应 实数
6
5
4
横 排
201X年秋八年级数学上册 第11章 平面直角坐标系 11.1 平面内点的坐标 第2课时 图形与坐标

编辑ppt
13
13.在平面直角坐标系xOy中,对于任意三点A,B,C的“矩面积”,给出如下定 义:“水平底”a:任意两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差 的最大值,则“矩面积”S=ah.例如:三点坐标分别为A( 1,2 ),B( 3,1 ),C( 2,-2 ),则“水平底”a=5,“铅垂高”h=4,“矩面积”S=ah=20.根据所 给定义解决下列问题: ( 1 )若已知点D( 1,2 ),E( -2,1 ),F( 0,6 ),则这3点的“矩面积”= 15 ;
为( -3,-2 ),后来墨墨不小心在该图洒上了墨水,如图所示,点C的坐标看不清了,但他记得
线段AC与y轴平行,则点C的坐标为 ( C )
A.( 2,1 )
B.( 1,2 ) C.( 2,-1 )D.( -1,2 )
【变式拓展】已知点A( 0,4 ),B点在x轴上,AB与坐标轴围成的三角形面积为2,
编辑ppt
15
感谢亲观看此幻灯片,此课件部分内容来源于网络, 如有侵权请及时联系我们删除,谢谢配合!
第11章 平面直角坐标系
编辑ppt
1
11.1 平面内点的坐标
编辑ppt
2
第2课时 图形与坐标
编辑ppt
3
知识点1 通过找点、连线、观察,确定图形的大致形状
1.经过两点A( 2,3 ),B( -4,3 )作直线AB,则直线AB ( A ) A.平行于x轴 B.平行于y轴 C.经过原点 D.无法确定 2.在平面直角坐标系内顺次连接下列各点,不能得到正方形的是 (C) A.( -2,2 ),( 2,2 ),( 2,-2 ),( -2,-2 ),( -2,2 ) B.( 0,0 ),( 2,0 ),( 2,2 ),( 0,2 ),( 0,0 ) C.( 0,0 ),( 0,2 ),( 2,-2 ),( -2,0 ),( 0,0 ) D.( -1,-1 ),( -1,1 ),( 1,1 ),( 1,-1 ),( -1,-1 )
八年级数学上册第11章平面直角坐标系11.1平面内点的坐标第2课时坐标平面内的图形教案新版沪科版

第2课时坐标平面内的图形◇教学目标◇【知识与技能】1.能正确地画出平面直角坐标系;2.在给定的平面直角坐标系中,会根据坐标描出点的位置.【过程与方法】1.经历画坐标系、描点、连线、看图以及由点找坐标等过程,发展学生的数形结合思想,培养学生的合作交流能力;2.通过由点确定坐标到根据坐标描点的转化过程,进一步培养学生的转化意识.【情感、态度与价值观】将现实的题材呈现给学生,揭示平面直角坐标系与现实世界的联系.◇教学重难点◇【教学重点】能够根据点的坐标确定平面内点的位置.【教学难点】体会点的坐标与点到坐标轴的距离之间的关系.◇教学过程◇一、情境导入由点找坐标是已知点在平面直角坐标系中的位置,根据这点在方格纸上对应的x轴、y 轴上的数字写出它的坐标,反过来,已知坐标,在平面直角坐标系中找点,你能找到吗?二、合作探究典例在图中的平面直角坐标系中描出下列各组点,并将各组内的点用线段依次连接起来.(1)(-6,5),(-10,3),(-9,3),(-3,3),(-2,3),(-6,5);(2)(-9,3),(-9,0),(-3,0),(-3,3);(3)(3.5,9),(2,7),(3,7),(4,7),(5,7),(3.5,9);(4)(3,7),(1,5),(2,5),(5,5),(6,5),(4,7);(5)(2,5),(0,3),(3,3),(3,0),(4,0),(4,3),(7,3),(5,5).观察所得的图形,你觉得它像什么?[解析]如图所示,这个图形像一栋“房子”,旁边还有一棵“大树”.在图中的平面直角坐标系中描出下列各组点,并将各组内的点用线段依次连接起来观察所得的图形,看一看像什么?(1)(2,0),(4,0),(6,2),(6,6),(5,8),(4,6),(2,6),(1,8),(0,6),(0,2),(2,0);(2)(1,3),(2,2),(4,2),(5,3);(3)(1,4),(2,4),(2,5),(1,5),(1,4);(4)(4,4),(5,4),(5,5),(4,5),(4,4);(5)(3,3).[解析]如图所示,看起来像“猫脸”.在图中的平面直角坐标系中描出下列各组点,并将各组内的点用线段依次连接起来,观察所得的图形,看一看像什么?(1)(0,0),(1,3),(2,0),(3,3),(4,0);(2)(0,3),(1,0),(2,3),(3,0),(4,3).[解析]如图所示,观察所得的图形,分别像字母“M”和“W”,合起来看像“活动门”.三、板书设计坐标平面内的图形坐标平面内的图形在坐标平面内描点作图坐标平面内图形面积的计算建立适当的直角坐标系描述图形的位置◇教学反思◇引导学生去学习找点的位置和它们的坐标之间的关系,形成数形结合的思想,用数字特征去描述它们之间的关系.。
2022秋八年级数学上册第11章平面直角坐标系11.2图形在坐标系中的平移授课课件新版沪科版

单位长度.根据点的坐标的变化规律,由
A(1,2),B(3,1),C(4,1),D(5,2),E(3,2),F(3,4),
G(2,3),可确定平移后各对应点的坐标,根据原图的连接方式
连接即可得到平移后的图形.
感悟新知
知2-练
解: A,B,C,D,E,F,G平移后对应点的坐标分别为
A′(-5,-3),B′(-3,-4),C′(-2,-4),D′(-1, -3),E′(-3,-3),F′(-3,-1),G′(-4,-2), 描出这些对应点并按原来的顺序连接起来,可得平移 后的图形,如图.
感悟新知
归纳
点的平移与点的坐标变化规律:
知1-讲
在平面直角坐标系中,将点(x,y)向右或左平移a(a>
0)个单位,可以得到对应点(x+a,y)或(x-a,y);将点(x,
y)向上或下平移b(b>0)个单位,可以得到对应点(x,y+b)
或(x,y-b).简记为:左、右平移,横变纵不变,“右加
左减”;上、下平移,纵变横不变,“上加下减”.
感悟新知
知1-练
1 (中考·广西)如图,在平面直角坐标系中,将点M(2,
1)向下平移2个单位得到点N,则点N的坐标为( )
A.(2,-1) B.(2,3)
C.(0,1)
D.(4,1)
2 (中考·大连)在平面直角坐标系中,将点P(3,2)向右 平移2个单位,所得的点的坐标是( ) A.(1,2) B.(3,0) C.(3,4) D.(5,2)
情况,即可得到图形上各点坐标的变化情况; (2)平移时,因为图形上各点的变化情况相同,所以已知图
感悟新知
知2-讲
要点精析: (1)图形的平移首先应转化为图形顶点的平移,再按照点
华坪县师院附中八年级数学上册 第11章 平面直角坐标系 11.1 平面内点的坐标 第2课时 坐标平面

12.1 平面内点的坐标第2课时坐标平面内的图形学习目标:1、通过找点、连线、观察,确定图形的大致形状并能计算图形的面积.2、会根据实际情况建立适当的坐标系.3、通过点的位置关系探索坐标之间的关系以及根据坐标之间的关系探索点的位置关系,体会平面直角坐标系在实际中的应用.学习重点::会根据实际情况建立适当的坐标系,用平面直角坐标系表示具体的地理位置.学习难点:通过点的位置关系探索坐标之间的关系以及根据坐标之间的关系探索点的位置关系一、学前准备1.在平面直角坐标系中描出A(5,1),A→B→C→A将所描出的点连接起来;说出得到的是什么图形;并计算它的面积.2.如图,矩形ABCD的长与宽分别是6,4标。
3.(1)写出坐标:A( ),B( ),C( ),D( )(2)对称点的坐标特点:点A与点B关于____轴对称, 两个点的横坐标_____,纵坐标互为________点A与点C关于____轴对称, 两个点的纵坐标_____,横坐标互为________点A与点D关于______对称, 两个点的横、纵坐标分别互为________(3)平面直角坐标系中的点到坐标轴的距离:点P(x,y)到x轴的距离是_____,到y轴的距离是______.练一练:1.已知点P关于x轴的对称点P1的坐标是(2,3),那么点P关于原点的对称点P2的坐标是()A.(-3,-2)B.(2,-3)C.(-2,-3)D.(-2,3)2.点A(2,3)到x轴的距离为;点B(-4,0)到y轴的距离为;预习疑难摘要_________________________________________________________________________________________________________________________________________________________________________________________________________ 二、探究活动(一)师生探究·解决问题例1. 在平面直角坐标系中描出A(-1,2), B(-2,-1),C(2,-1),D(3,2)各点,并按次序A→B→C→D→A将所描出的点连接起来; 说出得到的是什么图形;并计算它的面积.例2.适当的直角坐标系,并写出各点的坐标。
【精品推荐】2020年秋八年级数学上册第11章平面直角坐标系11.2平面内点的坐标第2课时课件新版沪科版

7.如图,A点、B点的坐标分别是(-2,0)和(2,0). (1)请你在图中描出下列各点:C(0,5)、D(4,5)、E(-4,-5)、F(0,-5); (2)连接AC、CD、DB、BF、FE、EA,并写出图中的任意一组平行线.
解:(1)如答图所示; (2)如答图,平行线有:AB∥CD∥EF,CE∥DF.
谢谢观看,敬请指导
天平两臂平衡,表示两边的物体质量相等;两臂不平衡,表示两边物体的质量不相等。让学生在天平平衡的直观情境中体会等式,符合学生的认知特点。例1在天平图下方呈现“=”,让学生用等式表达天平两边物体质量的相等关系,从中体会等式的含义。教材使用了“质量”这个词,是因为天平与其他的秤不同。习惯上秤计量物体有多重,天平计量物体的质量是多少。教学时不要把质量说成重量,但不必作过多的解释。 例2继续教学等式,教材的安排有三个特点: 第一,有些天平的两臂平衡,有些天平两臂不平衡。根据各个天平的状态,有时写出的是等式,有时写出的不是等式。学生在相等与不等的比较与感受中,能进一步体会等式的含义。第二,写出的四个式子里都含有未知数,有两个是含有未知数的等式。这便于学生初步感知方程,为教学方程的意义积累了具体的素材。第三,写四个式子时,对学生的要求由扶到放。圆圈里的关系符号都要学生填写,学生在选择“=”“>”或“<”时,能深刻体会符号两边相等与不相等的关系;符号两边的式子与数则逐渐放手让学生填写,这是因为他们以前没有写过含有未知数的等式与不等式。
形像( C )
A.树
B.房子
C.雨伞
D.电灯
10.在坐标平面内有三点A(-1,1)、B(1,1)、C(1,-1),那么以A、B、C三点画正来自形,则第四点D的坐标为( D )
A.(2,2)
八年级数学上册第11章平面直角坐标系11.1平面内点的坐标2图形与坐标教学设计新版沪科版2
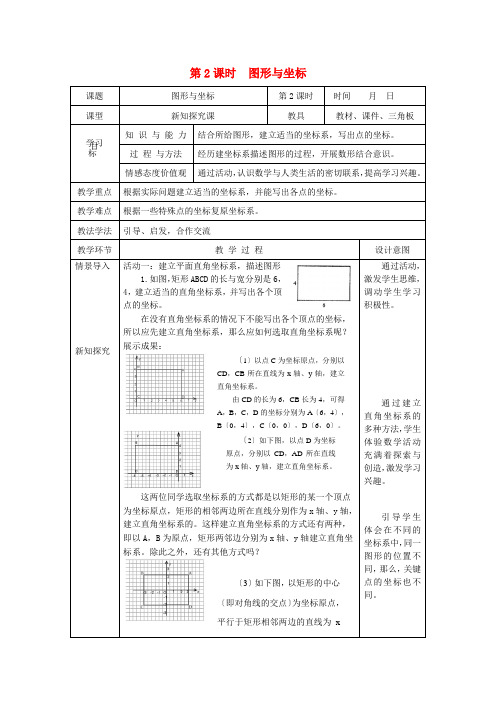
第2课时图形与坐标课题图形与坐标第2课时时间月日课型新知探究课教具教材、课件、三角板学习目标知识与能力结合所给图形,建立适当的坐标系,写出点的坐标。
过程与方法经历建坐标系描述图形的过程,开展数形结合意识。
情感态度价值观通过活动,认识数学与人类生活的密切联系,提高学习兴趣。
教学重点根据实际问题建立适当的坐标系,并能写出各点的坐标。
教学难点根据一些特殊点的坐标复原坐标系。
教法学法引导、启发,合作交流教学环节教学过程设计意图情景导入新知探究活动一:建立平面直角坐标系,描述图形1.如图,矩形ABCD的长与宽分别是6,4,建立适当的直角坐标系,并写出各个顶点的坐标。
在没有直角坐标系的情况下不能写出各个顶点的坐标,所以应先建立直角坐标系,那么应如何选取直角坐标系呢?展示成果:这两位同学选取坐标系的方式都是以矩形的某一个顶点为坐标原点,矩形的相邻两边所在直线分别作为x轴、y轴,建立直角坐标系的。
这样建立直角坐标系的方式还有两种,即以A,B为原点,矩形两邻边分别为x轴、y轴建立直角坐标系。
除此之外,还有其他方式吗?通过活动,激发学生思维,调动学生学习积极性。
通过建立直角坐标系的多种方法,学生体验数学活动充满着探索与创造,激发学习兴趣。
引导学生体会在不同的坐标系中,同一图形的位置不同,那么,关键点的坐标也不同。
〔1〕以点C为坐标原点,分别以CD,CB所在直线为x轴、y轴,建立直角坐标系。
由CD的长为6,CB长为4,可得A,B,C,D的坐标分别为A〔6,4〕,B〔0,4〕,C〔0,0〕,D〔6,0〕。
〔2〕如下图,以点D为坐标原点,分别以CD,AD所在直线为x轴、y轴,建立直角坐标系。
〔3〕如下图,以矩形的中心〔即对角线的交点〕为坐标原点,平行于矩形相邻两边的直线为x稳固训练归纳小结〔4〕把上图中的横坐标逐渐向上、下移动,纵坐标左、右移动,那么可得到不同的坐标系,从而得到A,B,C,D四点的不同坐标。
从刚刚我们讨论的情况看,大家能发现什么?建立直角坐标系有多种方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2课时图形与坐标
知识要点基础练
知识点1通过找点、连线、观察,确定图形的大致形状
1.经过两点A(2,3),B(-4,3)作直线AB,则直线AB(A)
A.平行于x轴
B.平行于y轴
C.经过原点
D.无法确定
2.在平面直角坐标系内顺次连接下列各点,不能得到正方形的是(C)
A.(-2,2),(2,2),(2,-2),(-2,-2),(-2,2)
B.(0,0),(2,0),(2,2),(0,2),(0,0)
C.(0,0),(0,2),(2,-2),(-2,0),(0,0)
D.(-1,-1),(-1,1),(1,1),(1,-1),(-1,-1)
知识点2坐标系中图形的面积问题
3.如图,在平面直角坐标系中,平行四边形ABCD的顶点A,B,C,D的坐标分别是(0,0),(5,0),(7,4),(2,4),则这个四边形的面积为(D)
A.6
B.8
C.12
D.20
4.如图,在平面直角坐标系中,A(2,3),B(4,0),则三角形AOB的面积为6.
知识点3根据实际情况建立适当的坐标系求解问题
5.如图,在方格纸上有A,B两点,若以点B为原点建立平面直角坐标系,则点A的坐标为(4,3);若以点A为原点建立平面直角坐标系,则点B的坐标为(A)
A.(-4,-3)
B.(-4,3)
C.(4,-3)
D.(4,3)
6.如图,正方形ABCD的边长为6.
(1)如果以点A为原点,AB所在的直线为x轴,建立平面直角坐标系,那么y轴是哪条线?
(2)写出正方形的顶点A,B,C,D的坐标.
(3)请另建立一个平面直角坐标系,并写出此时正方形的顶点A,B,C,D的坐标.
解:(1)AD所在直线.
(2)A(0,0),B(6,0),C(6,6),D(0,6).
(3)略.
综合能力提升练
7.如图,在平面直角坐标系中,点A,B,C的坐标分别为A(2,3),B(5,0),C(4,1),则三角形AOC的面积为(A)
A.5
B.10
C.15
D.75
8.在网格图中有一个面积为10的三角形ABC,三角形ABC的三个顶点均在网格的格点上,墨墨在网格图中建立了适当的平面直角坐标系,并知道点A的坐标为(2,3),点B的坐标为(-3,-2),后来墨墨不小心在该图洒上了墨水,如图所示,点C的坐标看不清了,但他记得线段AC与y轴平行,则点C的坐标为(C)
A.(2,1)
B.(1,2)
C.(2,-1)
D.(-1,2)
【变式拓展】已知点A(0,4),B点在x轴上,AB与坐标轴围成的三角形面积为2,则B点坐标是(1,0)或(-1,0).
9.若线段AB平行于x轴,AB长为5,且点A的坐标为(4,5),则点B的坐标为(-1,5)或(9,5).
10.(1)如图,若以火车站为坐标原点,建立平面直角坐标系,超市的坐标为(2,-3),则市场的坐标为(4,3),文化宫的坐标为(-3,1);
(2)如图,若已知医院的坐标为(1,-1),宾馆的坐标为(5,3),请根据题目条件画出适合的平面直角坐标系,并直接写出体育馆的坐标(-1,4).
解:(2)图略.
11.在平面直角坐标系中描出下列各点,并将各点用线段依次连接起来.
A(-2,-1),B(2,-1),C(2,2),D(3,2),E(0,3),F(-3,2),G(-2,2),A(-2,-1).根据图形回答下列问题:
(1)观察所得图形,你觉得像什么?
(2)线段FD和x轴有什么位置关系?点F和点D的坐标有什么特点?
解:(1)如图所示,图形像一个房子的图案.。
