刚架结构的有限元法
有限元之平面刚架

第二节 平面刚架有限元法的直接法
由叠加原理很容易得到如下关系式
EA EA ui − uj l l 12EI 6EI 12EI 6EI Vi = 3 vi + 2 θi − 3 vj + 2 θ j l l l l 6EI 4EI 6EI 2EI θi − 2 vj + θj Mi = 2 vi + l l l l EA EA Uj = − ui + uj l l 12EI 6EI 12EI 6EI Vj = − 3 vi − 2 θi + 3 vj − 2 θ j l l l l 6EI 2EI 6EI 4EI θi − 2 vj + θj Mj = 2 vi + l l l l Ui =
根据分块的性质,(2-2)可写成
e Fi e K ii e = e F j K ji e K ij δ ie e e K jj δ j
e K ij 是节点j的位移 δ e 对节点i的节点力 Fi e的影响系数子矩阵。 j
(2-2)
第二节 平面刚架有限元法的直接法
(2) [K]e具有分块性 我们来观察单元刚度矩阵的结构,其数学表达式如下:
EA l U i 0 V i M i 0 U = EA j − l V j M j 0 0 0 0 6EI l2 4EI l 0 − EA l 0 0 EA l 0 0 0 0 6EI l2 2EI l 0 u i vi θ i u j v j θ j
第二章 有限元法的直接方法
第一节 有限元法的思路
我们以压杆问题为例来说 明有限元法的基本思路。图示 结构,我们将杆件看成是连接 三个节点的两个单元,首先看 单元①,由材料力学公式
结构分析的有限元法-第三章

式中
H 1 u B A yH v
(3.32)
而
H 0 u H 0 v 0 0 0 0 1 0 0 2 0 6x
(3.33)
单元刚度矩阵
再次应用式(2.70),并进行一系列的积分运算,可以得出单元刚度矩阵的显式如下:
l
K
e
E d A B B d x
0 1 l
Av
1
2 l
0 0 1 l 2 1 l
(3.21)
MATLAB不仅可以进行数值运算,也能进行符号运算。如式(3.20)中的矩 阵Au和Av的求逆运算,我们可以在MATLAB的命令窗口下输入 >> syms L >> Au = [ 1 0 1 L ] ; >> Av = [ 1 0 0 0 0 1 0 0 1 L L^2 L^3 0 1 2*L 3*L^2] ; 第一句是定义符号变量L,后面定义两个矩阵Au和Av。然后我们再输入下 面求逆的命令 >> inv(Au) ans = 0 1 1 [ 1, 0] Au [ -1/L, 1/L] 1 l 1 l >> inv(Av) ans = 0 0 1 [ 1, 0, 0, 0] 0 1 0 1 [ 0, 1, 0, 0] A v 2 2 3 l 2 l 3 l [ -3/L^2, -2/L, 3/L^2, -1/L] 3 2 3 1 l 2 l [ 2/L^3, 1/L^2, -2/L^3, 1/L^2] 2 l
根据材料力学的有关知识,我们可以立刻写出杆单元的结点位移与结点力 之间的关系为
FNi EA l (u i u j ) FNj EA l (u j u i )
有限元法概述

(2)MSC/NASTRAN。 MSC/NASTRAN是在原NAST RAN基础上进行大量改进后的系统软件,主要包括MS C.Patran并行框架式有限元前后处理及分析系统、 MS C.GS-Mesher快速有限元网格、 MSC.MARC非线性有 限元软件等。其中MSC.MARC具有较强的结构分析能
.
5.在产品制造或工程施工前预先发现潜在的问题; 6. 模拟各种试验方案,减少试验时间和经费; 7. 进行机械事故分析,查找事故原因。
轴承强度分析
.
汽车碰撞实验
.
刹车制动时地盘的应力分析
.
钢板精轧机热轧制分析
.
三维椭圆封头开孔补强
.
水轮机叶轮的受力分析模拟
.
人体股骨端受力分析
.
半导体芯片温度场的数值仿真
知量时称为混合法。 位移法易于实现计算自动化,所以,在有限单元法
中位移法应用范围最广。
.
2、有限元法的发展
有限单元法基本思想的提出,可以追溯到Courantl在1 943年的工作,他第一次尝试应用定义在三角形区域上的 分片连续函数和最小位能原理相结合,来求解St·Venant 扭转问题。相继一些应用数学家、物理学家和工程师由于 各种原因都涉足过有限单元的概念。
.
4、有限元的特点
(1) 概念清楚,容易理解。可以在不同的专业背景和水平 上建立起对该方法的理解。从使用的观点来讲,每个人的 理论基础不同,理解的深度也可以不同,既可以通过直观的 物理意义来学习,也可以从严格的力学概念和数学概念推 导。
钢架结构有限元分析

Workbench 的无缝连接,将 UG 环境中建立的 CAD 模型
直接导入 ANSYS Workbench 环境中进行有限元分析。
在 ANSYS Workbench 的 simulation 模块中,定义钢
架结构材料为碳钢,材料性
能为:弹性模量 2×105MPa,
泊 松 比 0.3, 屈 服 应 力
1 钢架结构有限元分析思路
2 有限元模型的建立
钢架结构由钢板、角钢焊接而成,起着承载外力的作
(1)建模软件和分析平台介绍
用。使用常规的设计计算方法,难以直观了解其在使用过
采用的 UG 是一套基于 Windows 平台上的参数化 3D 实
程中的变形和受力情况。随着 CAD 和 CAE 技术的不断 体 模 型 构 建 软 件 , 有 限 元 分 析 则 是 基 于 ANSYS
235MPa, 屈 服 极 限
380MPa。 运 用 自 由 网 格 划
分技术,对所建立的几何模
型进行有限元网格划分,划
分网格后单元数为 27338,
节点数为 65165,建立的有
限元模型如图 3 所示。
图 3 钢架结构有限元模型
(3)荷载及边界条件 在 ANSYS Workbench
静强度分析环境中,零部件
Abstract:The 3D model of steel structure is established by using UG in the computer, on the base of the circum stances of ANSYS Workbench, the stress and strain of steel structure are calculated under the applied force, the results indicate that the intensity of this steel structure is enough, thus it provides a valuable reference for design of steel structure. Key words:steel structure; finite element; UG; ANSYS workbench
刚架的有限元分析

刚架的有限元分析有限元分析(Finite Element Analysis,FEA)是一种数值模拟方法,用于解决物体结构、材料、流体等的力学问题。
它将复杂的结构分解成小的、简单的单元,并在每个单元上建立适当的数学模型,最终求解全局问题。
有限元分析的步骤包括:前处理、求解和后处理。
前处理阶段主要包括几何建模、网格划分和单元属性定义等;求解阶段则是通过建立合适的方程组并求解,得到所需的物理量;后处理阶段则是对求解结果进行可视化和分析。
在进行有限元分析时,首先需要对结构进行几何建模。
几何建模的目的是准确描述结构的形状和尺寸。
可以使用CAD软件对结构进行建模,也可以简单地使用几何参数描述结构。
在建模过程中,需要考虑结构的实际工作状态、边界条件和加载情况等。
接下来,需要对结构进行网格划分。
网格划分是将结构分解成小的、简单的单元,以便进行数学建模和计算。
常用的单元包括三角形单元、四边形单元和六面体单元等。
网格划分的精度和密度会影响到最终的求解精度和计算时间。
每个单元都需要定义适当的属性,如材料特性、边界条件和加载情况等。
材料特性包括弹性模量、杨氏模量、泊松比等,它们决定了材料在受力时的变形特性。
边界条件包括约束边界和加载边界,它们描述了结构的边界条件和约束情况。
建立了合适的数学模型后,就可以求解得到所需的物理量了。
通常,求解的过程是通过建立合适的方程组来实现的。
方程组的形式取决于问题的类型和边界条件。
可以使用有限元法、有限差分法或其他数值方法来求解方程组。
求解过程通常需要借助计算机进行,计算时间与问题的复杂度和求解精度有关。
最后,需要对求解结果进行后处理,包括结果的可视化和分析。
常用的后处理工具包括绘图软件和数据分析软件。
可视化结果可以帮助理解结构的行为和变形情况,进而优化设计。
数据分析则可以帮助提取结构的关键参数和性能指标,为结构的工作提供参考依据。
总结起来,有限元分析是一种强大的工程技术手段,可以帮助工程师解决复杂的结构和材料力学问题。
有限元分析第4章 平面问题有限单元法1

6
P
3
4 5
4
2
位移协调条件:各单元共享节点的位移相等 节点平衡条件:各节点单元内力与节点外力构成平衡力系
最终数学模型: K Q
基本概念
单元(element) 节点 (node)
回顾
单元节点位移 (node displacement)
单元节点内力 (node force)
单元刚度矩阵 (element stiffness matrix)
e
bx u by v
d
S
e p
px u py v dS
代入
u v
N
e
{} [B]{ }e
{ } [S]{ }e
得
内力虚功=
e x x y y xy xy d
T d
cj
y)v j
(am
bmx
cm y)vm ]
二、平面问题三角形单元分析
三角形单元形函数
形函数
u x,
y
1 2A
[(ai
bi x
ci
y)ui
(a j
bj x
cj
y)u j
(am
bm x
cm
y)um ]
v x,
y
1 2A
[(ai
bi x
ci
y)vi
(a j
插值系数的确定:待定系数法
ui a1 a2 xi a3 yi u j a1 a2 x j a3 y j um a1 a2 xm a3 ym
第二章-杆和梁结构的有限元法案例

第二章
杆和梁结构的有限元法
§2.1.2 弹簧系统分析
注意: 上述弹簧系统的分析求解原理和过程就是有限元 法求解连续体力学问题时对离散后系统的分析求 解原理和过程。
第二章
杆和梁结构的有限元法
§2.1.2 弹簧系统分析
例题1:弹簧系统
已知条件:
求:(a) 系统总刚度矩阵 (b) 节点2,3的位移
单元特性
系统平衡方程
第二章 杆和梁结构的有限元法
KD F
2)单元方程扩大相加法 单元特性
F1 f11
相加
F2 f 21 f12 F3 f 22
系统节点 平衡条件
引入系统节点平衡条件
KD F
系统节点平衡方程
第二章 杆和梁结构的有限元法
2.2 杆单元和平面桁架
杆单元
2.2.1 一维等截面 杆单元
fi k f j k
第二章
k ui k u j
f kd
杆和梁结构的有限元法
2、弹簧系统的集成 1)列节点平衡方程法
F1 f11 F2 f 21 f12 F3 f 22
系统节点 平衡条件
F1 k1u1 k1u2 F2 k1u1 ( k1 k2 )u2 k2u3 F3 k2u2 k2u3
第二章 杆和梁结构的有限元法
k k k
k k
fi k f j k
k ui k u j
kii k k ji
kij k jj
§2.1.2 弹簧系统分析
求解一个弹簧系统:
1)各单元的特性分别为:
第二章 杆和梁结构的有限元法
第二讲 平面刚架结构的有限元方法

陈 乐 生
( 福州大学机械工程及 自 动化学院) 刚架结构在 工程上很多见 , 比如建 筑工程 中 的框架结构、 梁, 桥 机械行 业 中起 重设备 、 轴类零 中称之为刚架结构 , 如果问题 可 以简化为平 面结 构, 就称之为平面刚架。图 l 就是简单 的平面刚架 结构的 3 个例子 。
\ ●●● ●●● _ 、、
\ ●● ●●● ●_、、
(. ) 13
12 整体坐标系的单元刚度矩 阵 . 从上面的讨论可以看出 , 13 式相对于各个 (. ) 单元局部坐标系 , 换句话说 , 由于各个单元 的和方 向并不一致 , 因此 , 各个单元的节点力 和节点位移 方向的描述也不一致 , 为了对节点力和节点位移
分量 , 时 也 具 有 3个 节 点 力 分 量 , 见 图 2, 同 参 因
这里 , 是参 数 、 凡 字母 上 面带 “ ” 均 表示 相 一 者 对 自身坐标 系 , 下文 亦如 此 , 不再 重 复 。
此 , ( . ) 中, 在 1 1式 节点力与节 点位移 向量可 以分 别写作 :
,,..一 .... ,... ..... . . 一 一,.. ....._ ,..一 ...一 一/ , . . .
的具体表达式可以采用叠加原理得到 :
ol 盟 — 裔 垦 ol — —
。 半 。 半
一 一 一 一 一 一
l
图 2 典 型 半 面 刚 架 单 兀
设单元两个节点 的编码为 l2 这是该单元节 、, 点的局部码 。显然 , 每个杆单 元只有两个节点 , 因 此, 所有单元 的节 点局部码 均为 l2 、 。但是 , 每个 节点还有其在整 个结构 中的编码 , 我们称之为节
第六章 刚架结构的有限单元法

0 1 2 − l 1 l2
0 0 3 l2 2 − 3 l
]
0 0 1 − l 1 l2
3 x2 2 x3 = 1− 2 + 3 l l
根据 {δ
2 x2 x3 x− + 2 l l
3 x2 2 x3 − 3 2 l l
x2 x3 − − 2 l l
[
vj θ j 0
]
T
= [ A2 ] {a y }
0 a3 a 1 0 0 4 2 3 l l l a5 2 1 2l 3l a6
(6-6)
由(6-5)、(6-6)求得:
{ a x } = [ A1 ]
式中逆阵
−1
~ }, {u
如刚架结构每个构件横截面主惯性轴之一和刚架所承受的载荷 都在同一个平面内,则称这种刚架结构为平面刚架。 一.平面梁单元的位移模式 在平面刚架中任取一般结点为i , j的单元,由于此单元可以有轴 向位移、横向位移、转角,其变形与梁的变形相同,故亦称为梁单 元。
选取右手坐标系ixyz作为局部坐标系,且使x轴与梁单元的轴线重合, 而使y轴和z轴为梁横截面的主惯性轴方向。由于平面刚架结构所受 外载荷都作用在xiy平面内。故梁单元处于轴向拉压和平面弯曲的组 合变形状态(因单元两端刚性联接)。结点i和j在局部坐标下所受 的结点力(梁元端点内力;其中包括中间载荷产生的梁元端点内力) 为轴向力
~ { a }= [ A ] { v }
−1 y 2
(6-7)
[ A1 ]
−1
1 0 = 1 1, −l l
[ A2 ]
−1
1 0 3 =− 2 l 2 l3
谭继锦有限元法课件之七 4.4刚架的有限元分析

第4章 杆梁结构的有限元法
平面刚架中各单元的轴向大多不相同 平面刚架中各单元的轴向大多不相同, 为了进行单元分析,需要对每个单元建立局 部坐标系 坐标原点置于节点i, 部坐标系。坐标原点置于节点 i 单元的轴线为 x轴,i端截面的形心主惯性轴为y轴和z轴,它 们构成右手坐标系 如图4-4 们构成右手坐标系,如图 4 4所示。 所示 局部坐标系约定为从整体编号小的节点 到大号码节点的方向。任一节点有3个自由度: 轴向位移、横向位移和绕z轴的转角。相应的 节点力分量为:轴向力、剪力和弯矩。轴向 拉压杆单元的刚度矩阵式(4-10 0),梁单元 刚度矩阵式为(4-28)。将两式扩展成6×6 的矩阵,叠加形成平面刚架在局部坐标系下 的单元刚度矩阵。
2
第4章 杆梁结构的有限元法
即: AE l 0 0 e K AE l 0 0 0 12EI l3 6EI l2 0 12EI l3 6EI l2 0 6EI l2 4EI l 0 6EI l2 2EI l AE l 0 0 AE l 0 0 0 12EI l3 6EI l2 0 12EI l3 6EI l2 ui 0 6EI vi 2 l 2EI i l 0 u j 6EI v 2 l j 4EI l j
i1 0 i1 0 0 0
0 0 0 0 0 0
i1 0
0 0
3 3 i1 i2 0 i2 4 4 3 1 0 i2 0 i2 4 4 3 3 i2 i2 4 4 3 1 i2 i2 4 4
0 0 u1 R1x 3 3 i2 i2 v R1 y 4 4 1 R2 x u2 3 1 i2 i2 R 4 4 v2 2 y 3 3 u3 R3 x i2 i2 4 4 R3 y v3 3 1 i2 i2 4 4 0 0
结构有限元法(绪论)

有限单元法的应用 有限单元法在应用上已远远超过了原来的范围。
它已由弹性力学平面问题扩展到空间问题和板壳问题, 能对原子能反应堆、拱坝、飞机、船体、涡轮叶片等 复杂结构进行应力分析;它已出平衡问题扩展到稳定 问题与动力问题,由弹性问题扩展到弹塑性与粘弹性 问题,由结构的应力分析扩展到结构的优化设计。除 此,它在流体力学、热传导、磁场、建筑声学、 生物力学等等方面部有不同程度的应用。
近几十年来,随着电子计算机的高速化和普遍化, 有限元继续不断地向更加广阔、更加深入的方面发展。
有限单元法的发展借助于两个重要工具,在理论 推导方面,采用了矩阵方法,在实际计算中,采用了 电子计算机。有限元、矩阵、计算机是三位一体的。 由于有了现代化的、先进的计算工具,使得有限单元 法近年来以惊人的速度骤然崛起。
又有效的数值方法。
有限单元法的发展历史 有限单元法最初是在五十年代作为处理固体力学
问题的方法出现的。 追溯历史,早在一九四三年,库兰特(courant)已
应用了“单元”概念。在一九五六年,特纳(Turner) 等人把刚架位移法的解题思路,推广应用于弹性力学 平面问题。他们把连续体划分成一个个三角形的和矩 形的单元,单元中位移函数首先采用了近似表达式, 推导了单元刚度矩阵,建立了单元结点位移与结点力 之间的单元刚度方程。
即物体在引起形变的外力被除去以后,能够完 全恢复其原来的形状,这种性质称为“弹性”。如 果材料又服从虎克定律,即外力与变形之间的关系 成正比,这种弹性就叫做“线性弹性”。在这一假 定下的物体只能发生线性弹性变形。
(2)假设物体是连续的 这假设认为整个物体的体积都被组成这个物体
的物质所填满,而不留下任何空隙。这样物体中应 力、应变和位移等等物理量就可看成是连续的,因 而我们就可用坐标的连续函数来表示它们的变化规 律。
第2章杆件结构的有限元法_直接刚度法
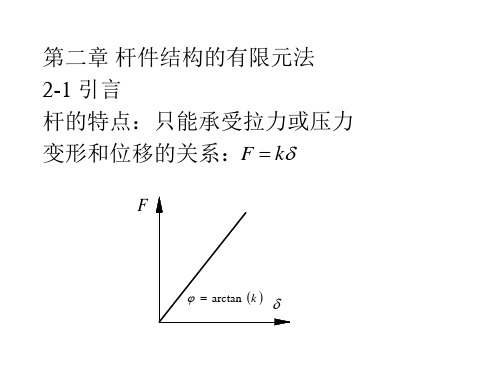
对于弹簧2-3(2单元)
F2( 2) 1800 − 1800 u 2 ( 2) = u F3 − 1800 1800 3
对于弹簧3-4(3单元)
F3( 3) 1500 − 1500 u 2 ( 3) = u F4 − 1500 1500 3
上式可以简写为 {F} = [K ]{δ } 上述过程可以用节点力平衡来完成。 为此,先写出单元的节点位移和节点力向 量的关系式: F1( e1 ) k1 − k1 u1 ( e1 ) = u F2 − k1 k1 2 F2( e2 ) k 2 − k 2 u2 ( e2 ) = u F3 − k 2 k 2 3
F 2 = 10 kN
F 3 = 20 kN
F1
F4
1
k1
2
k2
3
k3
4
三弹簧受力系统
解: (1)单元分划 一个弹簧为一个单元,一共3个单元,4个节点。 (2)形成每个单元的刚度矩阵 对于弹簧1-2(1单元)
F1(1) 1200 − 1200 u1 (1) = u F2 − 1200 1200 2
用下,发生与杆长垂直方向的位移。
(3) 局部坐标系和总体坐标系的关系 为了根据节点的力平衡条件建立杆系总体刚度矩 阵,必须将局部坐标系下的单元刚度矩阵转换到 总体坐标系下。
y
(e Fy(e ) 2
F
(e) y1
2
Fx(1e )
o
o
ϕ
F22 = (k1 + k 2 )u 2
F12 = −k1u2
F32 = −k 2u2
第2章_有限元法的直接刚度法_平面刚架

0 0 1 0 0
0 0 0 cos 0
0 0 0 sin cos 0
0 sin
0 ui 0 vi 0 i u 0 j 0 v j 1 j
i 0 i 分块形式为 0 j j
{
单元:6个 节点:4个
结构自由度
{ 4 3 12
的矩阵。
每个节点3个自由度
个自由度
结构的整体刚度矩阵是一个
12 12
二、单元刚度矩阵 1、单元的节点力、节点位移 任取一个单元,设单元号为 e,两个节点分别为i、j。 局部坐标:局部坐标只对 该单元有效,每一个单元 有一个局部坐标。以下对 该单元所进行的分析都在 这个局部坐标系下进行。 在局部坐标系下,两个 节点的节点位移为:
6 EI l 2 f 2 EI i l i 6 EI f j 2 l j 4 EI l
(3)刚架单元的节点力和节点位移之间的关系——单元刚度矩阵 刚架单元的所有节点力和节点位移之间的关系为:
EA 0 l 12EI Ti 0 q l3 i 6 EI 0 2 mi l EA T j 0 qj l 12EI 0 m j l3 6 EI 0 l2 0 6 EI l2 4 EI l 0 6 EI l2 2 EI l EA l 0 0 EA l 0 0 0 12EI l3 6 EI 2 l 0 12EI l3 6 EI 2 l 6 EI i 2 l f 2 EI i i l j 0 f j 6 EI 2 l j 4 EI l 0
有限元法课后习题答案

1、有限元是近似求解一般连续场问题的数值方法2、有限元法将连续的求解域离散为若干个子域,得到有限个单元,单元和单元之间用节点连接3、直梁在外力的作用下,横截面的内力有剪力和弯矩两个.4、平面刚架结构在外力的作用下,横截面上的内力有轴力、剪力、弯矩.5、进行直梁有限元分析,平面刚架单元上每个节点的节点位移为挠度和转角6、平面刚架有限元分析,节点位移有轴向位移、横向位移、转角。
7、在弹性和小变形下,节点力和节点位移关系是线性关系。
8、弹性力学问题的方程个数有15个,未知量个数有15个。
9、弹性力学平面问题方程个数有8,未知数8个。
10、几何方程是研究应变和位移之间关系的方程11、物理方程是描述应力和应变关系的方程12、平衡方程反映了应力和体力之间关系的13、把经过物体内任意一点各个截面上的应力状况叫做一点的应力状态14、9形函数在单元上节点上的值,具有本点为_1_.它点为零的性质,并且在三角形单元的任一节点上,三个行函数之和为_1_15、形函数是_三角形_单元内部坐标的_线性_函数,他反映了单元的_位移_状态16、在进行节点编号时,同一单元的相邻节点的号码差尽量小.17、三角形单元的位移模式为_线性位移模式_-18、矩形单元的位移模式为__双线性位移模式_19、在选择多项式位移模式的阶次时,要求_所选的位移模式应该与局部坐标系的方位无关的性质为几何_各向同性20、单元刚度矩阵描述了_节点力_和_节点位移之间的关系21、矩形单元边界上位移是连续变化的1. 诉述有限元法的定义答:有限元法是近似求解一般连续场问题的数值方法2. 有限元法的基本思想是什么答:首先,将表示结构的连续离散为若干个子域,单元之间通过其边界上的节点连接成组合体。
其次,用每个单元内所假设的近似函数分片地表示求解域内待求的未知厂变量。
3. 有限元法的分类和基本步骤有哪些答:分类:位移法、力法、混合法;步骤:结构的离散化,单元分析,单元集成,引入约束条件,求解线性方程组,得出节点位移。
刚架结构有限元

对于梁的弯曲问题,由材料力学知识可知,应力-应变相当于内力矩与曲率关系, 近似表达式为:
d 2w M EI 2 dx
x, y EI 62 123x
L L
4 6x L L2
6 12 x L2 L3
w1 2 6 x z1 2 DB e L L w2 z 2
以上两式写成矩阵形式
6 L 12 6 L w1 Fy1 12 M 2 2 Z 1 EI 6 L 4 L 6 L 2 L z 2 Fy 2 L3 12 6 L 12 6 L w2 2 2 M Z 2 6 L 2 L 6 L 4 L z 2
T T T
任一点处虚位移引起的虚应变为 * x, y ,该处应力为 x, y
T
e*
F
T e
* 内应力所做的功(单位体积上的应变能)为: Wint x, y x, y
虚位移引起的虚应变同样成立:
x, y B
第三章 刚架结构的有限元法
直接刚度法推导梁单元有限元格式
Fy1 y
w1
Fy 2
w2
z1
1 L
x z2
2
M z1
M z1
平面刚架结构 — 梁单元
F
y1
M Z1
Fy 2
M Z 2
T
T
w1 Z 1
w2 Z 2
由结构力学可知:梁所受弯矩与变形之间的关系,列方程
6 EI 4 EI 6 EI 2 EI M z1 2 w1 z1 2 w2 z 2 L L L L M z 2 6 EI w1 2 EI z1 6 EI w2 4 EI z 2 2 2 L L L L
5第5讲空间杆件结构的有限元法

l2
l
0
0
0
0
wi
0
2EI z l
xi
yi
zi
0
0
0
0
u
j
0
12EI y l3
0 0
0
6EI y l2
6EI l2
z
v
j
w
j
0
xj
M yj 0
M zj
0
0
0
0 GJ 0
0
l
0
6EIy 0 2EIy
0
l2
l
6EI z
0
0
0
2EI z
0
第一节 局部坐标系下的单元分析
图 2-1 所示为空间刚架中的任一
杆件单元。选取局部坐标系时,去
形心轴为 x 轴,横截面的主轴分
别为坐标系的 y 轴和 z 轴。 x、y、z
轴的方向按右手定则确定。这样,
单元在 x y 平面内的位移与 xz
平面内的位移是彼此独立的。设杆截面面积为 A,在 xz 平面内的抗弯刚
l2 0
0
0 4EI z
l 0 6EIz l2 0
0
0 2EI z
l
EA l 0
0 12EI z
l3
0
0
0
0
0
0
0 6EIz l2
EA
0
l
0
12EI z
l3
0
0
0
0
0
0
0 6EIz l2
0
0 12EI y
l3 0 6EI y l2 0
0
0 12EI y
l3 0 6EI y l2 0
刚架的非节点载荷等效解析

非节点载荷的等效是有限元法求解的关键步骤之一,尤其是刚架,但是由于很多教材上给出的解法相对比较难,不利于学生理解,本文主要运用“力――位移”之间的关系来讲述,从而使复杂问题简单化,更有利于学生掌握有限元法,尤其是对于参加机电一体化专业参加全国自学考试的学生可以起积极有效的作用。
非节点载荷力――位移等效自学考试一、非节点载荷在杆系结构中,对于刚架结构,承受的载荷既可能作用在节点上,也可能不直接作用在节点上,而作用在杆单元的其余点上,称为非节点载荷。
对于非节点载荷的处理是有限元中列出总体平衡方程的关键,处理的办法就是把非节点载荷移植到节点上,教材上给出了两个步骤:(1)载荷移植原理;(2)固定端反力和反力矩的计算,需要用到材料力学中的公式。
但是对于很多自学者而言,在学有限元法之前,根本没接触到材料力学,或者力学部分基础比较薄弱,这样理解起来就很难,杆的方向发生变化后,就不知道该如何等效了,并且从历年的考试中看出,考试时也没有给出固定端反力和反力矩的计算公式。
简单的说非节点载荷的处理就是要等效到节点上,等效的含义就是作用在非节点上的效果和作用在节点上的效果应该是一样的。
二、非节点载荷等效分析下面以常见的几种非节点载荷分析一下等效到节点上后的情况。
(1)集中力集中力的形式大体上有两类,一类是垂直作用到杆上的力,另一类是平行于杆的力。
就这两种形式的力分别分析,但仅限于分析作用一个力的情况,多个力的情况和这类似。
a.当作用在杆上有一个与杆垂直向下的力f,在这个力f的作用下,会使整个杆产生与力方向f相同方向的位移(包括节点i和节点j),同时会使节点i产生顺时针角位移,会使节点i产生逆时针角位移(角位移的方向可以根据力f对节点i和j产生的力矩的方向进行判断)。
因此,去掉集中力后,两个节点的位移应该还得有,所以就必须在节点i上加上与原力f方向相同的力f?i,在i处加上一个能使i产生顺时针位移的顺时针弯矩m?i,节点j同理.一般自学考试中,集中力f都是作用在中点,则等效后i和j节点的弯矩大小为fl/8,载荷大小为f/2,且等效后两力的大小相等,方向相同,弯矩的大小相等,方向相反,方向根据具体情况判断。
2-2 平面刚架问题的有限元法

2014-5-19
2
Institute of Mechanical Engineering and Automation
一 结构离散
梁单元离散,各杆有局部坐标系,方向为杆的轴 线方向。结构的刚度方程是在统一的坐标系(总体 坐标系)中建立并求解,因此需将单元局部坐标各 量转换到总体坐标系中。 取杆件与杆件交点、集中力作用点、杆件与支承 的交点为节点。相邻两节点间的杆件段是单元。节 点编号时力求单元两端点号差最小。
K F
经约束处理消除[K]的奇异后,求得位移{δ}e。从而 求得局部坐标下的位移
T
' e e
2014-5-19
e
14
Institute of Mechanical Engineering and Automation
例2-2 变截面梁 • 有一变截面梁,一端固定,另一端铰支。梁长 为2l,固支端的截面尺寸为b×1.6h,铰支端的 截面尺寸为b×h。梁上作用均布载荷p0。求梁 端的约束反力。
3
1 6 3l 2 2 3l l 6 3l 3 3l 2l 2
2014-5-19
18
Institute of Mechanical Engineering and Automation
• 荷载等效结点力向量
{Fd }(1) p0 l / 2 p0 l 2 / 12 1 p0 l / 2 2 2 p0 l / 12
e
2014-5-19
2 3 4 vi i v j j
T
T
(2-24)
4
Institute of Mechanical Engineering and Automation
三角形刚架结构的有限元法分析-PB

三角形刚架结构的有限元法分析PB02005015 徐叶松如图所示,等腰直角三角形如刚架结构,斜边长度为2L ,所有横截面同为半径为R 的实心圆,材料弹性系数为E 。
已给出单元和节点编号,平面坐标系原点位于节点①处,x 方向指向节点②。
节点①固支,节点②承受集中力P ,方向沿-y 方向。
材料的密度为ρ,考虑自重影响。
用有限元方法求出节点②和③的位移及节点①的支反力/力矩,具体包括:写出局部坐标系下刚架单元刚度矩阵,坐标变换矩阵,组装成总体刚度方程,结合外载和边界条件求解。
其中:32,0.01, 2.011,8.03/,500.L m R m E e Pa e kg m p N ρ=====解:结构平衡方程为{}[]{}F K D =,其中[]K 为刚度矩阵,[]D 为节点位移向量{}[]111222333TD u v u v u v θθθ=1、 将刚架离散为3个杆元,编号为⑴、⑵、⑶;3个节点,编号为①、②、③。
并建立各杆元的局部坐标系oxy 。
2、 计算各杆元的刚度矩阵3232223232220000126126006462000012612600626400e EAEA ll EI EIEI EI l l l l EI EI EI EI l l l l K EAEA L L EIEI EI EI l l l l EI EI EI EI l lll ⎡⎤-⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥-⎢⎥⎡⎤=⎢⎥⎣⎦⎢⎥-⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦ 其中各杆元的EA 及EI 均相同,l 为各杆元的长度,杆元⑴为2L ,杆元⑵、,代入即可得各杆元得刚度矩阵(1)(2)(3)eeeK K K ⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦、、。
为将局部坐标系中得到的刚度矩阵eK ⎡⎤⎣⎦转换到平面坐标系,设坐标转换矩阵为[]T ,则有 [][]Te e K T K T ⎡⎤⎡⎤=⎣⎦⎣⎦坐标系oxyz 的基本单位向量为,,i j k ;坐标系ox yz 的基本单位向量为,i j k ,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
F F F F
* T e 1 e* 2 T e 2 e* n T e n e* T e
外力虚功
节点虚位移 向量
内力虚功
T T
Wint * ( x, y ) ( x, y ) B e
求单元应力
应力应变关系
( x, y) D ( x, y) D B e
以矩阵形式表达
6 12 x ( x, y ) EI 2 3 L L 4 6x L L2 6 12 x 3 L2 L w1 2 6 x z1 2 L L w2 z2
2
以矩阵形式表达
0 1 ( x, y) 0 0 2 6 x 2 3
7
2012/5/24
求单元应变
节点位移表示的单元应变
几何矩阵
( x, y) C B e
单元应变 节点位移
6
2012/5/24
单元中任一点的位移和节点位移关系
位移模式 形函数
{ ( x, y)} [ f ( x, y)] {} A { e }
1
单元上任 意点位移
节点位移
求单元应变
应变是位移函数的微分
( x, y) d
w 2 2 6 3 x dx 2
2012/5/24
刚架结构的有限元法
刚架结构的有限元法
直接刚度法推导梁单元有限元格式 位移函数—虚功原理推导梁单元有限元格式
1
2012/5/24
直接刚度法推导梁单元有限元格式
梁单元 梁单元定义—两端刚性连接的杆件 梁单元和杆单元的区别 梁单元节点力和位移 梁单元力和变形关系
8
2012/5/24
求节点力和节点位移
虚功原理
系统保持平衡的充要条件是外力在虚位移上所做的 功等于相应内力在虚位移上所做的功 刚体虚位移原理 弹性体虚位移原理
求节点力和节点位移
虚位移原理应用于刚体
平衡关系
PA A PB B 0
9
2012/5/24
求节点力和节点位移
位移法简介
i EI / l
2
2012/5/24
直接刚度法推导梁单元有限元格式
梁单元静力平衡关系式
M z1 M z2 L )( 12 EI 6EI 12 EI 6EI ) w1 ( 2 ) z1 ( 3 ) w2 ( 2 ) z2 L3 L L L
Fy1 Fy2 (
选择位移函数
位移函数表达式
以矩阵形式表示
0 w 1 x x 2 x 3 1 ( x, y) 2 z 0 1 2 x 3 x 2 3 f ( x, y)
矩阵形式表示的节点力和变形表达式
Fy1 6 L 12 6 L w1 12 M 6 L 4 L2 6 L 2 L2 z1 EI z1 3 F w 12 6 L 12 6 L L y 2 2 2 2 M 6 L 2 L 6 L 4 L z2 z2 e e e F K
单元中任一点的位移和节点位移关系
已知单元节点处的位移值
x 0, w1 0 ; z1 1 x L, w2 0 1 L 2 L2 3 L3
2
z 1 2 2 L 3 3 L2
表达成矩阵形式
0 1 0 1 2 2 3 / L 3 3 2/ L 0 w1 1 0 0 z1 A 2 / L 3 / L 1 / L w2 1 / L2 2 / L 1 / L2 z2 0 0
D B
* T e
弹性矩阵 几何矩阵
求节点力和节点位移
积分
T V
V
e Wintdv B
D B dv W F
* T e e* T e ext
T e
节点虚位移是任意的,因此
F B D Bdv
直接刚度法推导梁单元有限元格式
梁单元在整体坐标下的形式
[ K e ] [T ]T [ K e ] [T ]
直接刚度法推导有限元格式
从单元受力(力矩)和位移之间的关系导出
3
2012/5/24
虚功原理推导梁单元有限元格式
步骤
写出节点的位移、节点力向量 选择适当的位移函数 求单元中任意点的位移和节点位移关系 求单元应变——单元位移—节点位移的关系 求应力——应变—节点位移间的关系 求节点力与节点位移关系 节点位移与应力关系
虚位移原理应用于弹性体
在外力作用下,处于平衡状态的弹性体,当发生约 束允许的任意微小虚位移时,外力在虚位移上所做 的功等于虚位移发生时引起的弹性体的应变能增量, 即整个体积内应力在虚应变上所做的功
U W 0
求节点力和节点位移
10
2012/5/24
求节点力和节点位移
Wext 1e
选择位移函数
ቤተ መጻሕፍቲ ባይዱ
位移函数表达式
通过节点位移表达单元上任意点的位移 w ( x, y) z w 0 1 x 2 x 2 3 x3
z
dw 1 2 2 x 3 3 x 2 dx
5
2012/5/24
{
6 EI 4 EI 6 EI 2 EI M z1 2 w1 z 2 w2 z L L 1 L L 2 6 EI 2 EI 6 EI 4 EI M z2 2 w1 z1 2 w2 z2 L L L L
单元分析
单元分析过程
4
2012/5/24
选择位移函数
有限元法中,载荷的移置、应力矩阵和刚度矩 阵的建立依赖于位移函数 位移函数满足的条件
位移函数必须能反映单元的刚体位移 位移函数必须能反映单元的常量应变 位移函数应尽量反映位移的连续性
反映刚体位移和常量应变是必要条件,反映相 邻单元的位移连续性是充分条件
e
V
单元刚度矩阵
11
2012/5/24
空间梁单元的定向
梁单元定向目的—确定梁的主惯性轴 梁单元定向的步骤
12
