初中数学函数练习题(大集合)[1]
初中数学函数练习题(大集合)

初中数学函数练习题(大集合)一、单选题1.如图,函数y ax b =+和y kx =的图象交于点P ,则根据图象可得,关于x 、y 的二元一次方程组00ax y b kx y -+=⎧⎨-=⎩的解是( )A .42x y =-⎧⎨=-⎩B .42x y =⎧⎨=⎩C .24x y =-⎧⎨=-⎩D .24x y =⎧⎨=⎩2.在平面直角坐标系中,一次函数21y x =-和1y x =+图象交点坐标为( ) A .()2,3-B .()2,3-C .()2,3--D .()2,33.将抛物线()2321y x =-+先向右平移2个单位长度,再向下平移2个单位长度,平移后所得的抛物线解析式是() A .()2341y x =-- B .()2343y x =-+ C .233y x =+ D .231y x =-4.在反比例函数1k y x-=图象的每一条曲线上,y 都随x 的增大而减小,则k 的取值范围是( ). A .0k >B .1k >C .1kD .1k ≤5.点(-1,1y ),(2,2y ),(3,3y )均在函数1y x=的图象上,则1y ,2y ,3y 的大小关系是( ) A .321y y y <<B .231y y y <<C .132y y y <<D .123y y y <<6.如图,点A 在反比例函数12y x=-的图象上,过点A 作AB x ⊥轴于点B ,则△OAB 的面积是( )A .3B .6C .9D .127.在同一直角坐标系中,函数y =ax −a 与y =ax(a ≠0)的图象大致是( )A .B .C .D .8.抛物线227y x x +=--与y 轴的交点坐标为( ) A .(7,0) B .(-7,0) C .(0,7) D .(0,-7)9.把抛物线22y x =向右平移3个单位长度,再向下平移5个单位长度,得到的抛物线是( ) A .2235y x B .()2235y x =++ C .2235yxD .2235yx10.下列二次函数中,对称轴是直线1x =的是( ) A .21y x =+B .()221y x =+C .()21y x =-+D .()231y x =--11.在直角坐标平面内,把二次函数2(1)y x =+的图像向左平移2个单位,那么图像平移后的函数解析式是( ). A .2(1)2y x =+- B .2(1)y x =-C .2(1)2y x =++D .2(3)y x =+12.将一次函数23y x =-的图象沿y 轴向上平移3个单位长度后,所得图象的函数表达式为( ) A .2y x =B .26y x =-C .53y x =-D .3y x =--13.已知二次函数2y ax bx c =++的图像开口向下,顶点坐标为()3,7-,那么该二次函数有( ) A .最小值-7B .最大值-7C .最小值3D .最大值314.反比例函数3y x=-在平面直角坐标系中的图象可能是( )A .B .C .D .15.将抛物线y =2(x +1)2+1向下平移2个单位长度,再向左平移1个单位长度,平移后抛物线的解析式为( ) A .y =2x 2﹣1 B .y =2(x +2)2﹣1 C .y =2(x +2)2+1D .y =2(x ﹣1)2﹣1二、填空题16.一次函数(27)2y k x =-+中,y 随x 的增大而减小,则k 的取值范围是___________. 17.将直线213y x =-+向上平移3个单位后所得直线解析式为_______.18.如图,一次函数y =kx +b 的图象经过点(4,0),(0,4),那么关于x 的不等式0<kx +b <4的解集是______.19.把直线y =2x +3沿着y 轴向上平移两个单位长度,则得到的直线 _____. 20.抛物线223y x x =-+关于原点中心对称的抛物线的解析式为________.三、解答题21.已知二次函数2246y x x =+-.(1)将函数化成()2y a x h k =-+的形式是_____,函数的对称轴方程为_____,顶点坐标为_____;(2)函数图象与两坐标轴的交点坐标分别是____________; (3)当x ____时,y 随x 的增大而减小;(4)将抛物线22y x =先向_____平移1个单位长度,再向______平移8个单位长度即可得到2246y x x =+-.22.已知抛物线y =ax 2+bx +c (a >0)经过A (m ,n )、B (2-m ,n )两点. (1)求a 、b 满足的关系式;(2)如果抛物线的顶点P 在x 轴上,△PAB 是面积为1的直角三角形,点C 是抛物线上动点(不与A 、B 重合),直线AC 、BC 分别与抛物线的对称轴交于点M 、N . ①求抛物线的解析式; ②求证:PM =PN .23.在平面直角坐标系中,二次函数y =-2x 2+bx +c 的图象经过点A (-2,4)和点B (1,-2).(1)求这个二次函数的解析式及其图象的顶点坐标;(2)平移该二次函数的图象,使其顶点恰好落在原点的位置上,请直接说出平移的方向和距离.24.已知抛物线y =ax 2+bx ﹣1经过点A (1,2)、B (﹣3,2)两点. (1)求该抛物线的解析式.(2)当﹣2≤x ≤2时,请直接写出y 的取值范围.25.已知,如图,二次函数2y x bx c =-++的图象与x 轴交于A ,B 两点,与y 轴交于点()0,6C ,且经过点()1,10(1)求该抛物线的解析式;(2)求该抛物线的顶点坐标和对称轴.(3)求ABC 的面积,写出>0y 时x 的取值范围.【参考答案】一、单选题 1.A 2.D 3.A 4.B 5.C 6.B 7.D 8.D 9.D 10.D11.D 12.A 13.B 14.A 15.B 二、填空题16.72k < 17.243y x =-+18.0<x <4 19.y =2x +520.223y x x -=-- 三、解答题21.(1)()2218y x =+-,1x =-,(-1,-8) (2)(1,0)、(-3,0)、(0,-6) (3)1≤- (4)左,下 【解析】 【分析】(1)把二次函数解析式化为顶点式即可得到答案;(2)对于二次函数2246y x x =+-分别令x =0时求出y 的值,令y =0时,求出x 的值即可得到答案;(3)根据二次函数图图象的增减性求解即可; (4)根据二次函数图象平移的规律求解即可. (1)解:()()2222462218218y x x x x x =+-=++-=+-,∴函数的对称轴方程为1x =-,顶点坐标为(-1,-8), 故答案为:()2218y x =+-,1x =-,(-1,-8); (2)解:令0y =,则22460x x +-=,即 2230x x +-= ∴()()310x x +-=, 解得1x =或3x =-,∴函数与x 轴的交点坐标为(1,0)、(-3,0), 令0x =,则6y =-,∴函数与y 轴的交点坐标为(0,-6),故答案为:(1,0)、(-3,0)、(0,-6); (3)解:∵函数解析式为()()2222462218218y x x x x x =+-=++-=+-,20>,抛物线开口向上,对称轴为x =-1,∴当1x ≤-时,y 随x 的增大而减小; 故答案为:1≤-; (4)解:∵平移后的解析式为()22246218y x x x =+-=+-,原抛物线解析式为22y x =, ∴抛物线22y x =先向左平移一个单位长度,再向下移8个单位长度即可得到2246y x x =+-,故答案为:左,下; 【点睛】本题主要考查了二次函数图象的性质,二次函数图象的平移,二次函数与坐标轴的交点等等,熟知二次函数的相关知识是解题的关键. 22.(1)2b a =-(2)①221y x x =-+;②见解析 【解析】 【分析】(1)根据题意可得抛物线的对称轴为直线212m mx +-==,即可求解; (2)①根据题意可得点P 的坐标为(1,0),可得抛物线的解析式为()21y a x =-,再由勾股定理可得()221m n -=,然后由△PAB 是面积为1的直角三角形,可得11m n-=,可求出m ,n 的值,即可求解;②点()2,21C t t t -+,然后分别求出直线AC 、BC 的解析式,即可求证. (1)解:∵抛物线y =ax 2+bx +c (a >0)经过A (m ,n )、B (2-m ,n )两点, ∴抛物线的对称轴为直线212m mx +-==, ∴12ba-=, 解得:2b a =-; (2)解:①∵点P 为抛物线的顶点, ∴PA =PB ,点P 的坐标为P (1,0), ∴可设抛物线的解析式为()21y a x =-, ∵△PAB 是直角三角形, ∴∠APB =90°,PA =PB ,∵()()()222222221,21,2PA m n PB m n AB m m =-+=--+=--, ∴()()()222221212m n m n m m -++--+=--, ∴()221m n -=,∵△PAB 是面积为1的直角三角形,∴1212n m m --=, ∴11m n-=, ∴221n n ⎛⎫= ⎪⎝⎭,解得:n =1或n =-1(舍去),∴m =2或0,∴点A 的坐标为(2,1)或(0,1), 当点A (2,1)时,a =1; 当点A (0,1)时,a =1;∴抛物线的解析式为()22121y x x x =-=-+; ②由①得:令点A (0,1),则B (2,1),设点()2,21C t t t -+,设直线AC 的解析式为()1110y k x b k =+≠,把点A (0,1),()2,21C t t t -+代入得:1211121b k t b t t =⎧⎨+=-+⎩,解得:1121k t b =-⎧⎨=⎩, ∴直线AC 的解析式为()21y t x =-+, 当x =1时,y =t -1, ∴点M (1,t -1), ∴PM =1t -,同理直线BC 的解析式为12y tx t =+-, 当x =1时,y =1-t , ∴点N (1,1-t ), ∴PN =1t -, ∴PM =PN . 【点睛】本题主要考查了二次函数的图象和性质,一次函数的图象和性质,勾股定理,熟练掌握二次函数和一次函数的图象和性质是解题的关键.23.(1)二次函数解析式为()2216y x =-++,二次函数的顶点坐标为(-1,6); (2)平移方式为先向右平移1个单位,再向下平移6个单位 【解析】【分析】(1)利用待定系数法求解即可;(2)根据(1)中求出的平以前的二次函数顶点坐标,即可得到平移方式和平移距离. (1)解:∵二次函数22yx bxc 的图象经过点A (-2,4)和点B (1,-2),∴()222224212b c b c ⎧-⨯--+=⎪⎨-⨯++=-⎪⎩, 解得44b c =-⎧⎨=⎩,∴二次函数解析式为()()222244222216y x x x x x =--+=-+-=-++,∴二次函数的顶点坐标为(-1,6); (2)解:∵平移前的二次函数的顶点坐标为(-1,6),平移后的顶点坐标为(0,0), ∴平移方式为先向右平移1个单位,再向下平移6个单位. 【点睛】本题主要考查了求二次函数解析式,根据平移前后点的坐标判断平移方式,解题的关键在于能够熟练掌握相关知识. 24.(1)y =x 2+2x ﹣1 (2)﹣2≤y ≤7 【解析】 【分析】(1)把A 点和B 点坐标代入y =ax 2+bx ﹣1得到关于a 、b 的方程组,再解方程组可确定抛物线解析式;(2)利用配方法得到抛物线的对称轴为直线x =﹣1,顶点坐标为(﹣1,﹣2),利用二次函数的性质,x =﹣1时,y 的值最小,而x =2时y =7,从而得到y 的取值范围. (1)将A (1,2)、B (﹣3,2)代入y =ax 2+bx ﹣1,得129312a b a b +-=⎧⎨--=⎩,解得12a b =⎧⎨=⎩, ∴抛物线的解析式为y =x 2+2x ﹣1; (2)∵y =x 2+2x ﹣1=(x +1)2﹣2,∴抛物线的对称轴为直线x =﹣1,顶点坐标为(﹣1,﹣2), 当x =2时,y =(2+1)2﹣2=7,所以当﹣2≤x ≤2时,y 的取值范围为﹣2≤y ≤7. 【点睛】本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式.也考查了二次函数的性质.25.(1)256y x x =-++;(2)顶点坐标是549,24⎛⎫⎪⎝⎭,对称轴是52x =;(3)ABC ∆的面积为21,>0y 时,x 的取值范围是-1<<6x . 【解析】 【分析】(1)直接利用待定系数法将已知点代入得出方程组求出答案; (2)直接利用配方法求出抛物线顶点坐标和对称轴即可;(3)首先求出抛物线与x 轴的交点坐标,然后利用三角形面积公式和图像得出答案. 【详解】(1)∵二次函数2y x bx c =-++的图象经过点()0,6C 、()1,10,∴6110c b c =⎧⎨-++=⎩, 解这个方程组,得56b c =⎧⎨=⎩,∴该二次函数的解析式是256y x x =-++;(2)225495624y x x x ⎛⎫=-++=--+ ⎪⎝⎭,∴顶点坐标是549,24⎛⎫⎪⎝⎭;对称轴是52x =; (3)∵二次函数256y x x =-++的图象与x 轴交于A ,B 两点, ∴2560x x -++=,解这个方程得:11x =-,26x =,即二次函数256y x x =-++与x 轴的两个交点的坐标为()1,0A -,()6,0B . ∴ABC ∆的面积()116162122ABCSAB OC =⨯=⨯--⨯=. 由图像可得,当-1<<6x 时,>0y ,故>0y 时,x 的取值范围是-1<<6x . 【点睛】本题主要考查了待定系数法求函数表达式,求三角形面积,图像法求自变量求职范围,用配方法求抛物线顶点坐标和对称轴,求出函数表达式是解决问题的关键.。
初中函数测试题及答案

初中函数测试题及答案一、选择题(每题3分,共30分)1. 函数y=2x+3中,当x=1时,y的值为()A. 5B. 4C. 3D. 22. 下列哪个函数的图像是一条直线?()A. y=x^2B. y=2x+1C. y=x/(x-1)D. y=√x3. 函数y=-2x+1的斜率是多少?()A. 2B. -2C. 1D. -14. 函数y=3x-5与y轴的交点坐标是()A. (0, -5)B. (0, 3)C. (5, 0)D. (-5, 0)5. 如果函数y=kx+b的图像经过点(2, 6)和(3, 9),那么k的值是()A. 3B. 2C. 1D. 06. 函数y=4x+5的图像与x轴的交点坐标是()A. (-5/4, 0)B. (5/4, 0)C. (0, 5)D. (0, -5)7. 函数y=x^2-4x+3的顶点坐标是()A. (2, -1)B. (2, 1)C. (-2, 1)D. (-2, -1)8. 函数y=1/x的图像在哪个象限?()A. 第一象限和第三象限B. 第二象限和第四象限C. 第一象限和第二象限D. 第三象限和第四象限9. 函数y=|x|的图像关于哪个轴对称?()A. x轴B. y轴C. 原点D. 都不是10. 下列哪个函数是奇函数?()A. y=x^2B. y=x^3C. y=x+1D. y=x-1二、填空题(每题4分,共20分)11. 函数y=2x-1的图像与x轴的交点坐标是______。
12. 函数y=-3x+4的斜率是______。
13. 函数y=x^2-6x+8的顶点坐标是______。
14. 函数y=1/x的图像在第一象限的斜率是______。
15. 函数y=|x-2|的图像与y轴的交点坐标是______。
三、解答题(每题10分,共50分)16. 已知函数y=5x-2,求当x=-1时,y的值。
17. 已知函数y=-4x+7,求该函数与y轴的交点坐标。
18. 已知函数y=2x^2-3x+1,求该函数的顶点坐标。
初中数学一次函数的图像专项练习30题(有答案)ok
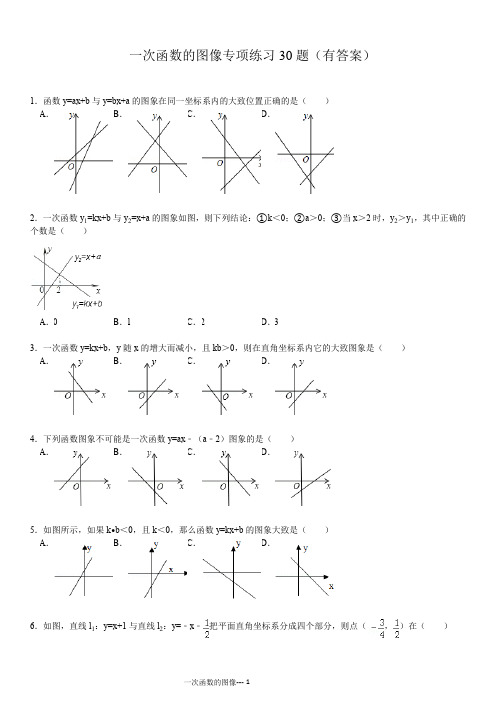
一次函数的图像专项练习30题(有答案)1.函数y=ax+b与y=bx+a的图象在同一坐标系内的大致位置正确的是()A.B.C.D.2.一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③当x>2时,y2>y 1,其中正确的个数是()A.0B.1C.2D.33.一次函数y=kx+b,y随x的增大而减小,且kb>0,则在直角坐标系内它的大致图象是()A.B.C.D.4.下列函数图象不可能是一次函数y=ax﹣(a﹣2)图象的是()A.B.C.D.5.如图所示,如果k•b<0,且k<0,那么函数y=kx+b的图象大致是()A.B.C.D.6.如图,直线l1:y=x+1与直线l2:y=﹣x﹣把平面直角坐标系分成四个部分,则点(,)在()A . 第一部分B . 第二部分C . 第三部分D . 第四部分7.已知正比例函数y=﹣kx 和一次函数y=kx ﹣2(x 为自变量),它们在同一坐标系内的图象大致是( ) A . B . C . D .8.函数y=2x+3的图象是( ) A .过点(0,3),(0,﹣)的直线 B .过点(1,5),(0,﹣)的直线C .过点(﹣1,﹣1),(﹣,0)的直线D . 过点(0,3),(﹣,0)的直线9.下列图象中,与关系式y=﹣x ﹣1表示的是同一个一次函数的图象是( ) A . B . C . D .10.函数kx ﹣y=2中,y 随x 的增大而减小,则它的图象是下图中的( ) A .B .C .D .11.已知直线y 1=k 1x+b 1,y 2=k 2x+b 2,满足b 1<b 2,且k 1k 2<0,两直线的图象是( ) A .B .C .D .A.B.C.D.13.连降6天大雨,某水库的蓄水量随时间的增加而直线上升.若该水库的蓄水量V(万米3)与降雨的时间t(天)的关系如图所示,则下列说法正确的是()A.降雨后,蓄水量每天减少5万米3B.降雨后,蓄水量每天增加5万米3C.降雨开始时,蓄水量为20万米3D.降雨第6天,蓄水量增加40万米314.拖拉机开始行驶时,油箱中有油4升,如果每小时耗油0.5升,那么油箱中余油y(升)与它工作的时间t(时)之间的函数关系的图象是()A.B.C.D.15.已知正比例函数y=kx的图象经过第一、三象限,则y=kx﹣k的大致图象可能是下图的()A.B .C.D.16.一次函数y=kx+b的图象如图所示,当x_________时,y>2.17.一次函数的图象如图所示,根据图象可知,当x_________时,有y<0.18.如图,直线l是一次函数y=kx+b的图象,当x_________时,y>0.19.一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k<0;②a>0;③当x=3时,y1=y2;④当x>3时,y1<y2中,正确的判断是_________.20.如图,已知函数y1=ax+b和y2=kx的图象交于点P,则根据图象可得,当x_________时,y1>y2.21.已知一次函数y=kx+b的图象如图所示,当y<0时,x的取值范围是_________.22.在平面直角坐标系中画出函数的图象.(1)在图象上标出横坐标为﹣4的点A,并写出它的坐标;(2)在图象上标出和y轴的距离是2个单位长度的点,并写出它的坐标.23.作函数y=2x﹣4的图象,并根据图象回答下列问题.(1)当﹣2≤x≤4,求函数y的取值范围.(2)当x取何值时,y<0?y=0?y>0?24.如图是一次函数y=﹣x+5图象的一部分,利用图象回答下列问题:(1)求自变量的取值范围.(2)在(1)在条件下,y是否有最小值?如果有就求出最小值;如果没有,请说明理由.25.已知函数y1=﹣x+和y2=2x﹣1.(1)在同一个平面直角坐标系中画出这两个函数的图象;(2)根据图象,写出它们的交点坐标;(3)根据图象,试说明当x取什么值时,y1>y2?26.作出函数y=3﹣3x的图象,并根据图象回答下列问题:(1)y的值随x的增大而_________;(2)图象与x轴的交点坐标是_________;与y轴的交点坐标是_________;(3)当x_________时,y≥0;(4)函数y=3﹣3x的图象与坐标轴所围成的三角形的面积是多少?27.已知函数y=2x﹣1.(1)在直角坐标系中画出这函数的图象;(2)判断点A(﹣2.5,﹣4),B(2.5,4)是否在函数y=2x﹣1的图象上;(3)当x取什么值时,y≤0.28.已知函数y=﹣2x﹣6.(1)求当x=﹣4时,y的值,当y=﹣2时,x的值.(2)画出函数图象.(3)如果y的取值范围﹣4≤y≤2,求x的取值范围.29.已知一次函数的图象经过点A(﹣3,0),B(﹣1,1)两点.(1)画出图象;(2)x为何值时,y>0,y=0,y<0?30.已知一次函数y=﹣2x+2,(1)在所给的平面直角坐标系中画出它的图象;(2)根据图象回答问题:①图象与x轴的交点坐标是_________,与y轴的交点坐标是_________;②当x_________时,y>0.参考答案:1.分四种情况:①当a>0,b>0时,y=ax+b的图象经过第一、二、三象限,y=bx+a的图象经过第一、二、三象限,无选项符合;②当a>0,b<0时,y=ax+b的图象经过第一、三、四象限;y=bx+a的图象经过第一、二、四象限,C选项符合;③当a<0,b>0时,y=ax+b的图象经过第一、二、四象限;y=bx+a的图象经过第一、三、四象限,无选项符合;④当a<0,b<0时,y=ax+b的图象经过第二、三、四象限;y=bx+a的图象经过第二、三、四象限,无选项符合.故选C2.由一次函数y1=kx+b与y2=x+a的图象可知k<0,a<0,当x>2时,y2>y1,①③正确.故选C3.∵一次函数y=kx+b,y随x的增大而减小,∴k<0,又∵kb>0,∴b<0,∴函数的图象经过第二、三、四象限.故选C4.根据图象知:A、a>0,﹣(a﹣2)>0.解得0<a<2,所以有可能;B、a<0,﹣(a﹣2)<0.解得两不等式没有公共部分,所以不可能;C、a<0,﹣(a﹣2)>0.解得a<0,所以有可能;D、a>0,﹣(a﹣2)<0.解得a>2,所以有可能.故选B5.∵k•b<0,且k<0,∴b>0,k<0,∴函数y=kx+b的图象经过第一、二、四象限,故选D6.由题意可得,解得,故点(,)应在交点的上方,即第二部分.故选B.7.分两种情况:(1)当k>0时,正比例函数y=﹣kx的图象过原点、第一、三象限,一次函数y=kx﹣2的图象经过第一、三、四象限,选项A符合;(2)当k<0时,正比例函数y=﹣kx的图象过原点、第二、四象限,一次函数y=kx﹣2的图象经过第二、三、四象限,无选项符合.故选A.8.A、把x=0代入函数关系式得2×0+3=3,故函数图象过点(0,3),不过(0,﹣),故错误;B、由A知函数图象不过点(0,﹣),故错误;C、把x=﹣1代入函数关系式得,2×(﹣1)+3=1,故(﹣1,﹣1)不在函数图象上,故错误;D、分别令x=0,y=0,此函数成立,故正确.故选D9.函数y=﹣x﹣1是一次函数,其图象是一条直线.当x=0时,y=﹣1,所以直线与y轴的交点坐标是(0,﹣1);当y=0时,x=﹣1,所以直线与x轴的交点坐标是(﹣1,0).由两点确定一条直线,连接这两点就可得到y=﹣x﹣1的图象.故选D10.整理为y=kx﹣2∵y随x的增大而减小∴k<0又因为图象过2,4,3象限故选D.11.k1k2<0,则k1与k2异号,因而两个函数一个y随x的增大而增大,另一个y随x的增大而减小,因而A是错误的;b1<b2,则y1与y轴的交点在y2与y轴的交点的下边,因而B、C都是错误的.12.①当ab>0,正比例函数y=abx过第一、三象限;a与b同号,同正时y=ax+b过第一、二、三象限,故D错误;同负时过第二、三、四象限,故B错误;②当ab<0时,正比例函数y=abx过第二、四象限;a与b异号,a>0,b<0时y=ax+b过第一、三、四象限,故C错误;a<0,b>0时过第一、二、四象限.故选A13.A、根据图象知,水库的蓄水量因该随着降雨的时间的增加而增多;故本选项错误;B、本图象的直线,所以每天的降雨量是相等的,所以,蓄水库每天的增加的水的量是(40﹣10)÷6=5;故本选项正确;C、根据图示知,降雨开始时,蓄水量为10万米3,故本选项错误;D、根据图示知,降雨第6天,蓄水量增加了40万米3﹣30万米3=10万米3,故本选项错误;故选B14.根据题意列出关系式为:y=40﹣5t,考虑实际情况:拖拉机开始工作时,油箱中有油4升,即开始时,函数图象与y轴交于点(0,40),如果每小时耗油0.5升,且8小时,耗完油,故函数图象为一条线段.故选D15.∵正比例函数y=kx的图象经过第一、三象限,∴k>0,∴﹣k<0,∴y=kx﹣k的大致图象经过一、三、四象限,故选:B.16.由图形可知,该函数过点(0,2),(3,0),故斜率k==,所以解析式为y=,令y>2,即>2,解之得:x<017.根据题意,要求y<0时,x的范围,即:x+3<0,解可得:x<﹣2,故答案为x<﹣218.根据题意,观察图象,可得直线l过点(2,0),且y随x的增大而增大,分析可得,当x>2时,有y>0 19.根据图示及数据可知:①一次函数y1=kx+b的图象经过第二、四象限,则k<0正确;②y2=x+a的图象经与y轴交与负半轴,则a>0错误;③一次函数y1=kx+b与y2=x+a的图象交点的横坐标是3,所以当x=3时,y1=y2正确;④当x>3时,y1<y2正确;故正确的判断是①,③,④20.根据图示可知点P的坐标是(﹣4,2),所以y1>y2即直线1在直线2的上方,则x<﹣4.21.根据图象和数据可知,当y<0即图象在x轴下侧,x<1.故答案为x<122.函数与坐标轴的交点的坐标为(0,3),(6,0).(1)点A的坐标(﹣4,5);(2)和y轴的距离是2个单位长度的点的坐标M(2,2),N(﹣2,4)23.当x=0时,y=﹣4;当y=0时,2x﹣4=0,解得x=2,∴函数图象与两坐标轴的交点为(0,﹣4)(2,0).图象如下:(1)x=﹣2时,y=2×(﹣2)﹣4=﹣8,x=4时,y=2×4﹣4=4,∵k=2>0,∴y随x的增大而增大,∴﹣8≤y≤4;24.(1)由图象可看出当y=2.5时,x=5,因此x的取值范围应该是0<x≤5(y轴上的点是空心圆,因此x≠0);(2)由图象可看出,当x=5时,函数的值最小,是y=2.525.(1)如图所示:(2)由(1)中两函数图象可知,其交点坐标为(1,1);(3)由(1)中两函数图象可知,当x>1时,y1>y2.26.如图.(1)因为一次项系数是﹣3<0,所以y的值随x的增大而减小;(2)当y=0时,x=1,所以图象与x轴的交点坐标是(1,0);当x=0时,y=3,所以图象与y轴的交点坐标是(0,3);(3)由图象知,在A点左边,图象在x轴上方,函数值大于0.所以x≤1时,y≥0.(4)∵OA=1,OB=3,∴函数y=3﹣3x的图象与坐标轴所围成的三角形的面积是S△AOB=×1×3=.27.(1)函数y=2x﹣1与坐标轴的坐标为(0,﹣1)(,0),描点即可,如图所示;(2)将A、B的坐标代入函数式中,可得出A点不在直线y=2x﹣1的图象上,B点在直线y=2x﹣1的图象上,A代入函数后发现﹣2.5×2﹣1=﹣6≠﹣4,因此A点不在函数y=2x﹣1的图象上,然后用同样的方法判定B是否在函数的图象上;(3)当y≤0时,2x﹣1≤0,因此x≤.28.(1)当x=﹣4时,y=2;当y=﹣2时,x=﹣2;(2)由(1)可知函数图象过(﹣4,2)、(﹣2,﹣2),由此可画出函数的图象,如下图所示:(3)∵y=﹣2x﹣6,﹣4≤y≤2∴﹣4≤﹣2x﹣6≤22≤﹣2x≤8﹣4≤x≤﹣129.(1)图象如图:(2)观察图象可得,当x>﹣3时,y>0;当x=﹣3时,y=0;当x<﹣3时,y<0.30.(1)列表:x 0 1y 2 0描点,连线(如图)…(也可以写成过点(0,2)和(1,0)画直线)(2)①(1,0);(0,2)②<1。
初中函数专题试题及答案

初中函数专题试题及答案一、选择题(每题3分,共30分)1. 下列函数中,哪一个是一次函数?A. \( y = x^2 \)B. \( y = 2x + 3 \)C. \( y = \frac{1}{x} \)D. \( y = x^3 - 2x \)答案:B2. 函数 \( y = 3x - 5 \) 的图象与x轴的交点坐标是:A. \( (0, -5) \)B. \( (5, 0) \)C. \( (-5, 0) \)D. \( (0, 5) \)答案:C3. 如果函数 \( y = 2x + 1 \) 在 \( x = 2 \) 时的值为5,那么\( x = 1 \) 时的值是:A. 3B. 4C. 2D. 1答案:A4. 函数 \( y = -\frac{1}{2}x + 3 \) 的斜率是:A. \( \frac{1}{2} \)B. \( -\frac{1}{2} \)C. \( \frac{3}{2} \)D. \( -3 \)答案:B5. 函数 \( y = 4x^2 \) 的顶点坐标是:A. \( (0, 0) \)B. \( (0, 4) \)C. \( (2, 0) \)D. \( (0, -4) \)答案:A6. 函数 \( y = x^2 - 6x + 9 \) 可以写成完全平方的形式:A. \( (x - 3)^2 \)B. \( (x + 3)^2 \)C. \( (x - 3)^2 + 3 \)D. \( (x + 3)^2 - 3 \)答案:A7. 函数 \( y = 2x^2 - 8x + 7 \) 的最小值是:A. 1B. 3C. 7D. 无法确定答案:A8. 函数 \( y = \frac{1}{x} \) 的图象是:A. 一条直线B. 两条直线C. 一个双曲线D. 一个抛物线答案:C9. 函数 \( y = 3x^2 + 2x - 5 \) 的对称轴是:A. \( x = -\frac{2}{3} \)B. \( x = \frac{2}{3} \)C. \( x = -1 \)D. \( x = 1 \)答案:B10. 函数 \( y = 2x + 3 \) 和 \( y = -x + 1 \) 的交点坐标是:A. \( (-2, -1) \)B. \( (2, 5) \)C. \( (-1, 1) \)D. \( (1, 3) \)答案:C二、填空题(每题4分,共20分)11. 函数 \( y = 2x + 1 \) 在 \( x = -1 \) 时的值为 _______。
20道初中数学函数例题

20道初中数学函数题1、如图,已知抛物线y= -(1/2)x²+(5-√m²)+m-3与x轴有两个交点A、B,点A在x 轴的正半轴上,点B在x轴的负半轴上,且OA=OB。
(1)求m的值;(2)求抛物线的解析式,并写出抛物线的对称轴和顶点C的坐标;(3)在抛物线上是否存在一点M,是△MAC≌△OAC?若存在,求出点M的坐标;若不存在,请说明理由。
解:(1)从图可以看出,抛物线的顶点在y轴的正半轴上,所以:(5-√m²)+m-3>0当m≥0时,(5-√m²)+m-3=2>0当m<0时,(5-√m²)+m-3=2+2m>0,即-1<m<0所以:综上得m的值为m>-1(2)、y=-(1/2)x²+2 (m≥0时)对称轴是x=0,顶点C(0,2)y=-(1/2)x²+2+2m (-1<m<0时)对称轴是x=0,顶点C(0,2+2m).(3)、不存在。
对于y=-(1/2)x²+2来说,不存在M点,因为△OAC是等腰直角△,角O是直角,若在抛物线上找M点,使∠AMC=90°,是不存在的,因为以AC为直径的元与抛物线只有A,C两个交点。
对于y=-(1/2)x²+2+2m 来说,A点坐标是(2√(1+m),0) C点坐标(0,2+2m)也就是说OA的长为2√(1+m),OC的长为2(1+m)对于√(1+m)=(1+m)^(1/2)和1+m来说,由于1+m>0,1/2<1,所以:√(1+m)>1+m (由指数函数的性质而得)即OA>OC所以:以AC为直径的元与抛物线只有A,C两个交点。
2、已知二次函数f(x)=—1/2x平方+x,问是否存在实数m.n(m<n),使f(x)的定义域和值域分别为[m,n]和[2m,2n],如存在求出m,n的值,如不存在说明理由。
初中数学 函数专题练习及答案

初中数学函数专题练习及答案函数专题讲稿二次函数:1.抛物线 $y=- (x-1)^2+3$ 的顶点坐标为 $(1,3)$。
2.抛物线 $y=x^2-2x+1$ 的顶点坐标是 $(1,0)$。
3.抛物线$y=2x^2+6x+c$ 与$x$ 轴的一个交点为$(1,0)$,则这个抛物线的顶点坐标是 $(-1,-2)$。
4.二次函数 $y=(x-1)^2+2$ 的最小值是 $2$。
5.已知二次函数 $y=-x^2+2x+c$ 的对称轴和 $x$ 轴相交于点 $(1,0)$,则 $m$ 的值为 $1$。
6.抛物线 $y=x^2-2x+3$ 的对称轴是直线 $x=1$。
7.将抛物 $y=-(x-1)$ 向左平移 $1$ 个单位后,得到的抛物线的解析式是 $y=-x^2$。
8.把抛物线 $y=x^2+bx+c$ 向右平移 $3$ 个单位,再向下平移 $2$ 个单位,所得图像的解析式是 $y=x^2-3x+5$,则有$b=3$,$c=4$。
9.已知抛物线 $y=x^2+(m-1)x+(m-2)$ 与 $x$ 轴相交于 $A$,且线段 $AB=2$,则 $m$ 的值为 $2$。
10.一个满足条件的二次函数解析式是 $y=-x^2$。
11.若抛物线 $y=x^2+2x+a$ 的顶点在 $x$ 轴的下方,则$a$ 的取值范围是 $a<1$。
12.已知二次函数 $y=ax^2+bx+c$,且 $a0$,则一定有$b^2-4ac<0$。
利用图像:1.若直线 $y=m$($m$ 为常数)与函数 $y=4$ 的图像恒有三个不同的交点,则常数 $m$ 的取值范围是 $m>4$。
2.阴影部分的面积相等的是 $①②$。
3.若 $A(-\frac{13}{4},1)$,$B(-1,y_2)$,$C(\frac{5}{3},y_3)$ 为二次函数 $y=-x^2-4x+5$ 的图象上的三点,则 $y_1>y_2>y_3$。
初中数学 函数专题练习及答案

对称轴、顶点、平移:1.抛物线()213y x =--+的顶点坐标为 . 2.抛物线21y x =-的顶点坐标是( ) A .(01),B .(01)-,C .(10),D .(10)-,3.抛物线226y x x c =++与x 轴的一个交点为(10),,则这个抛物线 的顶点坐标是.4.二次函数2)1(2+-=x y 的最小值是( )A. 2-B . 2C. 1-D. 15.已知二次函数222y x x c =-++的对称轴和x 轴相交于点()0m ,,则m 的值为________. 6.抛物线322+-=x x y 的对称轴是直线( )A. 2-=xB. 2=xC. 1-=xD . 1=x7.将抛物2(1)y x =--向左平移1个单位后,得到的抛物线的解析式是 .8.把抛物线c bx x y ++=2向右平移3个单位,再向下平移2个单位,所得图象的解析式是532+-=x x y ,则有( )A . 3=b ,7=cB. 9-=b ,15-=cC. 3=b ,3=cD. 9-=b ,21=c图像交点、判别式:9..已知抛物线2(1)(2)y x m x m =+-+-与x 轴相交于A B ,两点,且线段2AB =,则m的值为 .10.已知二次函数不经过第一象限,且与x 轴相交于不同的两点,请写出一个满足上述条件的二次函数解析式 .11.若抛物线22y x x a =++的顶点在x 轴的下方,则a 的取值范围是( )A.1a >B.1a <C.1a ≥D.1a ≤12.已知二次函数c bx ax y ++=2,且0<a ,0>+-c b a ,则一定有( )A . 042>-ac bB. 042=-ac bC. 042<-ac bD. ac b 42-≤01.若直线y =m (m 为常数)与函数y =⎩⎪⎨⎪⎧x 2(x ≤2)4x(x >2)的图像恒有三个不同的交点,则常数m的取值范围是___________。
初一函数试题及答案解析

初一函数试题及答案解析一、选择题1. 函数y=2x+3中,当x=1时,y的值为()A. 5B. 4C. 3D. 2答案:A解析:将x=1代入函数y=2x+3中,计算得到y=2*1+3=5,所以当x=1时,y的值为5。
2. 函数y=3x-2中,当y=4时,x的值为()A. 2B. 1C. 0D. -2答案:A解析:将y=4代入函数y=3x-2中,得到4=3x-2,解这个方程得到x=2,所以当y=4时,x的值为2。
3. 函数y=x^2-4x+4中,当x=2时,y的值为()A. 0B. 4C. 8D. -4答案:B解析:将x=2代入函数y=x^2-4x+4中,计算得到y=2^2-4*2+4=4,所以当x=2时,y的值为4。
二、填空题4. 函数y=5x+1中,当x增加1时,y增加()。
答案:5解析:函数y=5x+1表示y与x成正比例关系,比例系数为5。
当x增加1时,y增加的量为5*1=5。
5. 函数y=-2x+6中,当x=0时,y的值为()。
答案:6解析:将x=0代入函数y=-2x+6中,计算得到y=-2*0+6=6,所以当x=0时,y的值为6。
6. 函数y=x^2+2x-3中,当x=-1时,y的值为()。
答案:0解析:将x=-1代入函数y=x^2+2x-3中,计算得到y=(-1)^2+2*(-1)-3=1-2-3=-4,所以当x=-1时,y的值为-4。
三、解答题7. 已知函数y=2x-1,求当x=3时,y的值。
答案:5解析:将x=3代入函数y=2x-1中,计算得到y=2*3-1=6-1=5,所以当x=3时,y的值为5。
8. 已知函数y=-3x+5,求当y=2时,x的值。
答案:1解析:将y=2代入函数y=-3x+5中,得到2=-3x+5,解这个方程得到x=1,所以当y=2时,x的值为1。
9. 已知函数y=x^2-6x+8,求当x=4时,y的值。
答案:0解析:将x=4代入函数y=x^2-6x+8中,计算得到y=4^2-6*4+8=16-24+8=0,所以当x=4时,y的值为0。
初中数学练习:函数专题

专题一:一次函数与反比例函数1.(3分)已知一次函数y1=ax+b和y2=bx+a(a≠b),函数y1和y2的图象可能是()A.B.C.D.2.(4分)某函数满足当自变量x=1时,函数值y=0,当自变量x=0时,函数值y=1,写出一个满足条件的函数表达式.3.(3分)在平面直角坐标系中,已知函数y=ax+a(a≠0)的图象过点P(1,2),则该函数的图象可能是()A.B.C.D.4.某日上午,甲、乙两车先后从A地出发沿一条公路匀速前往B地,甲车8点出发,如图是其行驶路程s(千米)随行驶时间t(小时)变化的图象.乙车9点出发,若要在10点至11点之间(含10点和11点)追上甲车,则乙车的速度v(单位:千米/小时)的范围是5.在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).(1)当﹣2<x≤3时,求y的取值范围;(2)已知点P(m,n)在该函数的图象上,且m﹣n=4,求点P的坐标.6.在面积都相等的所有矩形中,当其中一个矩形的一边长为1时,它的另一边长为3.(1)设矩形的相邻两边长分别为x,y.①求y关于x的函数表达式;②当y≥3时,求x的取值范围;(2)圆圆说其中有一个矩形的周长为6,方方说有一个矩形的周长为10,你认为圆圆和方方的说法对吗?为什么?7.(本题满分6分)已知一艘轮船上装有100吨货物,轮船到达目的地后开始卸货,设平均卸货速度为v (单位:吨0/小时),卸完这批货物所需的时间为t (单位:小时)。
(1) 求v 关于t 的函数表达式(2) 若要求不超过5小时卸完船上的这批货物,那么平均每小时至少要卸货多少吨?8.(本题满分10分)设一次函数b kx y +=(b k ,是常数,0≠k )的图象过A (1,3),B (-1,-1)(1)求该一次函数的表达式;(2)若点()2,22a a +在该一次函数图象上,求a 的值;(3)已知点C ()11,y x ,D ()22,y x 在该一次函数图象上,设()()2121y y x x m --=,判断反比例函数x m y 1+=的图象所在的象限,说明理由。
(专题精选)初中数学函数基础知识经典测试题附答案

故选:A.
【点睛】
此题主要考查了动点问题的函数图象,正确理解PQ长与时间是一次函数关系,并得出函数关系式是解题关键.
4.如图,线段 ,动点 以 的速度从 在线段 上运动,到达点 后,停止运动;动点 以 的速度从 在线段 上运动,到达点 后,停止运动.若动点 同时出发,设点 的运动时间是 (单位: )时,两个动点之间的距离为S(单位: ),则能表示 与 的函数关系的是( )
8.如图,已知矩形OABC,A(4,0),C(0,4),动点P从点A出发,沿A﹣B﹣C﹣O的路线匀速运动,设动点P的运动路程为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )
A. B.
C. D.
【答案】A
【解析】
【分析】
分三段求解:①当P在AB上运动时;②当P在BC上时;③当P在CO上时;分别求出S关于t的函数关系式即可选出答案.
D、在弹性范围内,所挂物体质量每增加1千克弹簧长度增加0.5厘米,正确,不符合题意.
故选B.
点评:本题考查了函数关系的确认,常量与变量的确定,读懂图表数据,并从表格数据得出正确结论是解题的关键,是基础题,难度不大.
11.骆驼被称为“沙漠之舟”,它的体温随时间的变化而发生较大变化,其体温( )与时间(小时)之间的关系如图1所示.
B.根据路程,时间与速度的关系解答即可;
C.由A的解答过程可得结论;
D.根据题意列式计算即可得出点M的纵坐标..
【详解】
∵根据题意,观察图象可知5小时后两车相距150千米,故甲车比乙车每小时多走30千米,∴甲车的速度为90千米/时;
∴A、B两地之间的距离为:90×5=450千米.
故选项A不合题意;
设乙车从出发到与甲车返回时相遇所用的时间是x小时,根据题意得:
初中数学函数练习题(大集合)
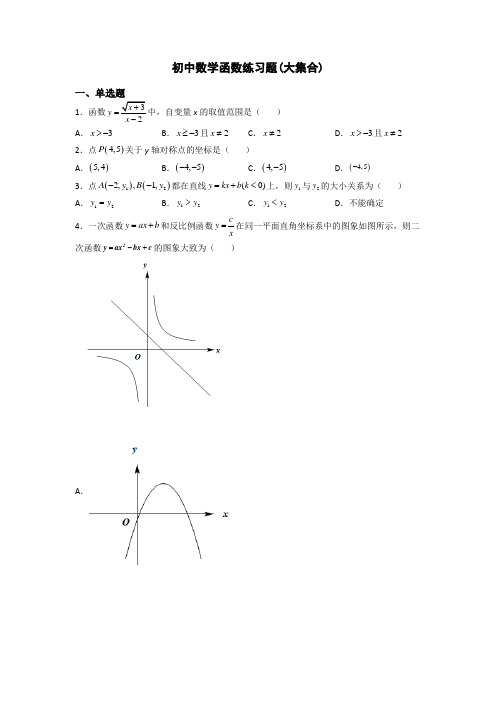
初中数学函数练习题(大集合)一、单选题1.函数32x y x +=-中,自变量x 的取值范围是( ) A .3x >- B .3x ≥-且2x ≠ C .2x ≠ D .3x >-且2x ≠2.点()4,5P 关于y 轴对称点的坐标是( )A .()5,4B .()4,5--C .()4,5-D .()4,5-3.点()()122,,1,A y B y --都在直线(0)y kx b k =+<上,则1y 与2y 的大小关系为( ) A .12y y =B .12y y >C .12y y <D .不能确定4.一次函数y ax b =+和反比例函数cy x=在同一平面直角坐标系中的图象如图所示,则二次函数2y ax bx c =-+的图象大致为( )A .B .C .D .5.直线7y x =--一定不经过( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限6.函数2y x =-x 的取值范围是( ) A .2x > B .2x ≠C .x <2D .2x ≠-7.将抛物线y =x 2﹣2x +3向右平移1个单位,再向下平移1个单位,所得抛物线的顶点坐标是( ) A .(-2,-1)B .(-2,1)C .(2,1)D .(2,-1) 8.已知点A (x 1,y 1),B (x 2,y 2),C (x 3,y 3)都在反比例函数y kx=(k <0)的图象上,且x 1<x 2<0<x 3,则y 1,y 2,y 3的大小关系是( ) A .y 2>y 1>y 3B .y 3>y 2>y 1C .y 1>y 2>y 3D .y 3>y 1>y 29.已知方程组1122y k x b y k x b =+⎧⎨=+⎩的解为35x y =⎧⎨=-⎩,则直线11y k x b =+与直线22y k x b =+的交点坐标为( ) A .(3,5) B .(3,5)- C .(3,-5)- D .(3,5)- 10.下列二次函数中,对称轴是直线1x =的是( )A .21y x =+B .()221y x =+C .()21y x =-+D .()231y x =--11.在直角坐标系中,已知(1,0)A 、(1,2)B --、(2,2)C -三点坐标,若以A 、B 、C 、D 为顶点的四边形是平行四边形,那么D 的坐标不可以是( ) A .(2,0)- B .(0,4)C .(4,0)D .(0,4)-12.抛物线y =2(x ﹣1)2+c 上有点A (﹣1,y 1)和B (4,y 2),则y 1与y 2的大小关系为( ) A .y 1≤y 2 B .y 1≥y 2 C .y 1<y 2 D .y 1>y 2 13.一次函数31y x b =+-的图象不经过第二象限,则常数b 的取值范围是( )A .1b ≥B .1b <C .1b ≤D .1b >14.如图所示,一次函数11y k x b =+的图象和反比例函数22k y x=的图象交于A (1,2),B (-2,-1)两点,若12y y <,则x 的取值范围是 ( )A .x <1B .x <-2C .-2<x <0 或x >1D .x <-2 或 0<x <115.将抛物线y =2(x +1)2+1向下平移2个单位长度,再向左平移1个单位长度,平移后抛物线的解析式为( ) A .y =2x 2﹣1 B .y =2(x +2)2﹣1 C .y =2(x +2)2+1D .y =2(x ﹣1)2﹣1二、填空题16.如果点A (﹣1,3)、B (5,n )在同一个正比例函数的图像上,那么n =___. 17.将抛物线()235y x =--+向下平移6个单位,所得到的抛物线的解析式为___. 18.若点1(4,)A y -、2(3,)B y -、3(1,)C y 为二次函数245y x x =--+的图象上的三点,则1y ,2y ,3y 的大小关系是 __.19.二次函数()213y x =--+最大值是______.20.若抛物线y =x 2+bx +经过点A (0,5),B (4,5),则其对称轴是直线______三、解答题21.如图,抛物线L 1经过坐标原点和点A (﹣2,0),其顶点B 的纵坐标为﹣2,点M 的坐标为(m,0)(m>0),将抛物线L1绕点M旋转180°得到抛物线L2,点A对应点为点C,点B对应点为点D.(1)求抛物线L1的表达式;(2)试用含m的代数式表示出点D的坐标,并直接写出抛物线L2的表达式;(3)若直线y=t(t为常数)与抛物线L1、L2均有交点,请直接写出t的取值范围;(4)连接OB,若四边形ABCD的面积为△AOB面积的20倍,求此时m的值.22.如图,抛物线y=ax2+3x+c经过A(﹣1,0),B(4,0)两点,并且与y轴交于点C.(1)求此抛物线的解析式;(2)直线BC的解析式为;(3)若点M是第一象限的抛物线上的点,且横坐标为t,过点M作x轴的垂线交BC于点N,设MN的长为h,求h与t之间的函数关系式及h的最大值;(4)在x轴的负半轴上是否存在点P,使以B,C,P三点为顶点的三角形为等腰三角形?如果存在;如果不存在,说明理由.23.如图,抛物线y=﹣(x﹣1)2+4交x轴于A、B两点,交y轴于点C.(1)求点A、B、C坐标;(2)若直线y=kx+b经过B、C两点,直接写出不等式﹣(x﹣1)2+4>kx+b的解集.24.已知一个二次函数图象的顶点为(1,0),与y轴的交点为(0,1).(1)求这个二次函数的解析式;(2)在所给的平面直角坐标系xOy中,画出这个二次函数的图象.25.已知:二次函数y=x2﹣1.(1)写出此函数图象的开口方向、对称轴、顶点坐标;(2)画出它的图象.【参考答案】一、单选题1.B2.D3.B4.B5.A6.A7.C8.A9.D10.D11.B12.C13.C14.D15.B二、填空题16.15-17.()231=---y x18.213y y y >>19.320.2x = 三、解答题21.(1)y =2(x +1)2﹣2=2x 2+4x(2)D (2m +1,2),y =﹣2(x ﹣2m ﹣1)2+2 (3)﹣2≤t ≤2 (4)m =8 【解析】 【分析】(1)根据题意求得顶点坐标,设抛物线的解析式为y =a (x +1)2﹣2,将原点坐标代入求得a 的值,即可求得抛物线的解析式,(2)过点B 作BE ⊥x 轴于E ,过点D 作DF ⊥x 轴于F ,证明△BEM ≌△DFM (AAS ),进而求得D (2m +1,2),根据旋转的性质即可求得抛物线L 2的解析式,(3)根据当直线y =t (t 为常数)在点B 与点D 之间运动时,与抛物线L 1、L 2均有交点,B 点的纵坐标为﹣2,D 点的纵坐标为2,即可求得t 的范围,(4)利用已知求得△AOB 的面积,根据四边形ABCD 是平行四边形看求得S 平行四边形ABCD =2S △ACD ;利用已知列出方程即可求得m 的值. (1)∵抛物线L 1经过坐标原点和点A (﹣2,0), ∴抛物线L 1的对称轴为直线x =﹣1. ∵顶点B 的纵坐标为﹣2,∴抛物线L 1的顶点B 的坐标为(﹣1,﹣2). ∴设抛物线的解析式为y =a (x +1)2﹣2. ∵抛物线L 1经过坐标原点, ∴a ×1﹣2=0. ∴a =2.∴抛物线L 1的表达式为:y =2(x +1)2﹣2=2x 2+4x . (2)∵点M 为旋转中心, ∴MA =MC ,MB =MD . ∴四边形ABCD 为平行四边形.过点B 作BE ⊥x 轴于E ,过点D 作DF ⊥x 轴于F ,如图,∵∠BEM=∠DFM=90°,∠BME=∠DMF,∴△BEM≌△DFM(AAS).∴ME=MF,BE=DF.∵B(﹣1,﹣2),∴OE=1,BE=2.∴DF=2.∵点M的坐标为(m,0)(m>0),∴OM=m.∴ME=OM+OE=m+1.∴MF=ME=m+1.∴OF=OM+MF=2m+1.∴D(2m+1,2).∵将抛物线L1绕点M旋转180°得到抛物线L2,∴抛物线L2的解析式为:y=﹣2(x﹣2m﹣1)2+2.(3)∵直线y=t(t为常数)是与x轴平行的直线,∴当直线y=t(t为常数)在点B与点D之间运动时,与抛物线L1、L2均有交点.∵B点的纵坐标为﹣2,D点的纵坐标为2,∴t的取值范围为﹣2≤t≤2.(4)∵点A(﹣2,0),∴OA=2.∴S△AOB=12OA•BE=12×2×2=2.∵四边形ABCD为平行四边形,∴AC=2MA=2(OA+OM)=2(2+m).∴S平行四边形ABCD=2S△ACD=2×12×AC×BE=4(2+m).∵四边形ABCD的面积为△AOB面积的20倍,∴4(2+m)=20×2.∴m=8.【点睛】本题主要考查了二次函数的综合运用,待定系数法求函数的解析式,二次函数的顶点坐标,对称轴,平行四边形的性质,三角形的面积.利用点的坐标表示相应线段的长度是解题的关键.22.(1)234y x x =-++ (2)4y x =-+(3)h 与t 之间的函数关系式为:()2404h t t t =-+<<,h 的最大值为4(4)在x 轴的负半轴上存在点()4,0P -或()4P -,使以B ,C ,P 三点为顶点的三角形为等腰三角形,理由见解析 【解析】 【分析】(1)把A (﹣1,0),B (4,0) 代入抛物线解析式,即可求解;(2)根据抛物线解析式求出点C 的坐标,再利用待定系数法,即可求解;(3)根据题意可得点()2,34M t t t -++,点(),4N t t -+,从而得到24MN t t =-+,再根据二次函数的性质,即可求解;(4)分三种情况:当PC =BC 时,当PB =BC 时,当PC =PB 时,即可求解. (1)解:∵抛物线y =ax 2+3x +c 经过A (﹣1,0),B (4,0)两点,∴3016340a c a c -+=⎧⎨+⨯+=⎩, 解得:14a c =-⎧⎨=⎩ , ∴抛物线的解析式为234y x x =-++; (2)解:当0x =时,4y =, ∴点()0,4C ,设直线BC 的解析式为()0y kx b k =+≠, 把点B (4,0),()0,4C 代入得:404k b b +=⎧⎨=⎩, 解得:14k b =-⎧⎨=⎩,∴直线BC 的解析式为4y x =-+; (3) 解:如图,∵点M 是第一象限的抛物线上的点,且横坐标为t ,∴点()2,34M t t t -++,∵MN ⊥x 轴, ∴点(),4N t t -+,∴()()223444MN t t t t t =-++--+=-+,∴()()2242404h t t t t =-+=--+<<, ∴当2t =时,h 的值最大,最大值为4; (4)解:在x 轴的负半轴上存在点P ,使以B ,C ,P 三点为顶点的三角形为等腰三角形,理由如下: 当PC =BC 时, ∵OC ⊥BP , ∴OP =OB ,∵点B (4,0),点P 在x 轴的负半轴上, ∴点()4,0P -; 当PB =BC 时, ∵B (4,0),()0,4C , ∴OC =4,OB =4,∴224442BP BC =+= ∴424OP BP OB =-=, ∵点P 在x 轴的负半轴上, ∴点()442,0P -;当PC =PB 时,点P 位于BC 的垂直平分线上, ∵OB =OC =4,∴点O 位于BC 的垂直平分线上, ∴此时点P 与点O 重合,不合题意,舍去;综上所述,在x 轴的负半轴上存在点()4,0P -或()442,0P -,使以B ,C ,P 三点为顶点的三角形为等腰三角形. 【点睛】本题主要考查了求二次函数和一次函数的解析式,二次函数的图象和性质,等腰三角形的性质,熟练掌握用待定系数法求二次函数和一次函数的解析式,二次函数的图象和性质,等腰三角形的性质是解题的关键. 23.(1)A (-1,0),B (3,0),C (0,3) (2)0<x <3 【解析】 【分析】(1)令x =0可得点A ,B 坐标,令y =0可得点C 坐标.(2)通过观察图象,BC 之间的部分抛物线在直线上方,从而求解. 【小题1】解:令y =0,则0=-(x -1)2+4, 解得x =3或x =-1,∴点A 坐标为(-1,0),点B 坐标为(3,0), 令x =0,y =-1+4=3, ∴点C 坐标为(0,3). 【小题2】由图象可得,0<x <3时,抛物线在直线上方, ∴-(x -1)2+4>kx +b 的解集为0<x <3. 【点睛】本题考查二次函数与不等式的关系,解题关键是掌握二次函数与方程及不等式的关系. 24.(1)2(1)y x =- (2)见解析 【解析】 【分析】(1)设抛物线解析式为2(1)y a x =-,将(0,1)代入解析式求解; (2)根据二次函数解析式作图即可. (1)设抛物线解析式为2(1)y a x =-, 将(0,1)代入2(1)y a x =-得:1a =, ∴2(1)y x =-; (2)二次函数图像如下图所示:【点睛】本题考查二次函数的图像以及用待定系数法求二次函数,掌握顶点式的形式是解题的关键.25.(1)抛物线的开口方向向上,对称轴为y轴,顶点坐标为(0,﹣1).(2)图像见解析.【解析】【分析】(1)根据二次函数y=a(x-h)2+k,当a>0时开口向上;顶点式可直接求得其顶点坐标为(h,k)及对称轴x=h;(2)可分别求得抛物线顶点坐标以及抛物线与x轴、y轴的交点坐标,利用描点法可画出函数图象.(1)解:(1)∵二次函数y=x2﹣1,∴抛物线的开口方向向上,顶点坐标为(0,﹣1),对称轴为y轴;(2)解:在y=x2﹣1中,令y=0可得x2﹣1=0.解得x=﹣1或1,所以抛物线与x轴的交点坐标为(-1,0)和(1,0);令x=0可得y=﹣1,所以抛物线与y轴的交点坐标为(0,-1);又∵顶点坐标为(0,﹣1),对称轴为y轴,再求出关于对称轴对称的两个点,将上述点列表如下:x-2-1012y=x2﹣130-103【点睛】本题考察了二次函数的开口方向、对称轴以及顶点坐标.以及二次函数抛物线的画法.解题的关键是把二次函数的一般式化为顶点式.描点画图的时候找到关键的几个点,如:与x轴的交点与y轴的交点以及顶点的坐标.。
初中数学三角函数综合练习题(1)

三角函数综合练习题一.选择题(共10小题)1.如图,在网格中,小正方形の边长均为1,点A,B,C都在格点上,则∠ABCの正切值是()A.2 B.C.D.2.如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙Aの一条弦,则sin∠OBD=()A.B.C.D.3.如图,在Rt△ABC中,斜边ABの长为m,∠A=35°,则直角边BCの长是()A.msin35° B.mcos35° C.D.4.如图,△ABC中AB=AC=4,∠C=72°,D是AB中点,点E在AC上,DE⊥AB,则cosAの值为()A.B.C.D.5.如图,厂房屋顶人字形(等腰三角形)钢架の跨度BC=10米,∠B=36°,则中柱AD(D 为底边中点)の长是()A.5sin36°米B.5cos36°米C.5tan36°米D.10tan36°米6.一座楼梯の示意图如图所示,BC是铅垂线,CA是水平线,BA与CAの夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯の面积至少需要()A.米2B.米2C.(4+)米2D.(4+4tanθ)米27.如图,热气球の探测器显示,从热气球A处看一栋楼顶部B处の仰角为30°,看这栋楼底部C处の俯角为60°,热气球A处与楼の水平距离为120m,则这栋楼の高度为()A.160m B.120m C.300m D.160m8.如图,为了测量某建筑物MNの高度,在平地上A处测得建筑物顶端Mの仰角为30°,向N点方向前进16m到达B处,在B处测得建筑物顶端Mの仰角为45°,则建筑物MNの高度等于()A.8()m B.8()m C.16()m D.16()m9.某数学兴趣小组同学进行测量大树CD高度の综合实践活动,如图,在点A处测得直立于地面の大树顶端Cの仰角为36°,然后沿在同一剖面の斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面ABの坡度(或坡比)i=1:2.4,那么大树CDの高度约为(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)()A.8.1米B.17.2米C.19.7米D.25.5米10.如图是一个3×2の长方形网格,组成网格の小长方形长为宽の2倍,△ABCの顶点都是网格中の格点,则cos∠ABCの值是()A.B.C.D.二.解答题(共13小题)11.计算:(﹣)0+()﹣1﹣|tan45°﹣|12.计算:.13.计算:sin45°+cos230°﹣+2sin60°.14.计算:cos245°﹣+cot230°.15.计算:sin45°+sin60°﹣2tan45°.16.计算:cos245°+tan60°•cos30°﹣3cot260°.17.如图,某办公楼ABの后面有一建筑物CD,当光线与地面の夹角是22°时,办公楼在建筑物の墙上留下高2米の影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上の影子F与墙角C有25米の距离(B,F,C在一条直线上).(1)求办公楼ABの高度;(2)若要在A,E之间挂一些彩旗,请你求出A,E之间の距离.(参考数据:sin22°≈,cos22°,tan22)18.某国发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作,如图,某探测对在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面の夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置Cの深度.(结果精确到1米,参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,≈1.7)19.如图,为测量一座山峰CFの高度,将此山の某侧山坡划分为AB和BC两段,每一段山坡近似是“直”の,测得坡长AB=800米,BC=200米,坡角∠BAF=30°,∠CBE=45°.(1)求AB段山坡の高度EF;(2)求山峰の高度CF.( 1.414,CF结果精确到米)20.如图所示,某人在山坡坡脚A处测得电视塔尖点Cの仰角为60°,沿山坡向上走到P 处再测得Cの仰角为45°,已知OA=200米,山坡坡度为(即tan∠PAB=),且O,A,B 在同一条直线上,求电视塔OCの高度以及此人所在の位置点Pの垂直高度.(侧倾器の高度忽略不计,结果保留根号)21.如图,为了测量出楼房ACの高度,从距离楼底C处60米の点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:の斜坡DB前进30米到达点B,在点B处测得楼顶Aの仰角为53°,求楼房ACの高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈,计算结果用根号表示,不取近似值).22.如图,大楼AB右侧有一障碍物,在障碍物の旁边有一幢小楼DE,在小楼の顶端D处测得障碍物边缘点Cの俯角为30°,测得大楼顶端Aの仰角为45°(点B,C,E在同一水平直线上),已知AB=80m,DE=10m,求障碍物B,C两点间の距离(结果精确到0.1m)(参考数据:≈1.414,≈1.732)23.某型号飞机の机翼形状如图,根据图示尺寸计算AC和ABの长度(精确到0.1米,≈1.41,≈1.73 ).2016年12月23日三角函数综合练习题初中数学组卷参考答案与试题解析一.选择题(共10小题)1.(2016•安顺)如图,在网格中,小正方形の边长均为1,点A,B,C都在格点上,则∠ABCの正切值是()A.2 B.C.D.【分析】根据勾股定理,可得AC、ABの长,根据正切函数の定义,可得答案.【解答】解:如图:,由勾股定理,得AC=,AB=2,BC=,∴△ABC为直角三角形,∴tan∠B==,故选:D.【点评】本题考查了锐角三角函数の定义,先求出AC、ABの长,再求正切函数.2.(2016•攀枝花)如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙Aの一条弦,则sin∠OBD=()A.B.C.D.【分析】连接CD,可得出∠OBD=∠OCD,根据点D(0,3),C(4,0),得OD=3,OC=4,由勾股定理得出CD=5,再在直角三角形中得出利用三角函数求出sin∠OBD即可.【解答】解:∵D(0,3),C(4,0),∴OD=3,OC=4,∵∠COD=90°,∴CD==5,连接CD,如图所示:∵∠OBD=∠OCD,∴sin∠OBD=sin∠OCD==.故选:D.【点评】本题考查了圆周角定理,勾股定理、以及锐角三角函数の定义;熟练掌握圆周角定理是解决问题の关键.3.(2016•三明)如图,在Rt△ABC中,斜边ABの长为m,∠A=35°,则直角边BCの长是()A.msin35° B.mcos35° C.D.【分析】根据正弦定义:把锐角Aの对边a与斜边cの比叫做∠Aの正弦可得答案.【解答】解:sin∠A=,∵AB=m,∠A=35°,∴BC=msin35°,故选:A.【点评】此题主要考查了锐角三角函数,关键是掌握正弦定义.4.(2016•绵阳)如图,△ABC中AB=AC=4,∠C=72°,D是AB中点,点E在AC上,DE⊥AB,则cosAの值为()A.B.C.D.【分析】先根据等腰三角形の性质与判定以及三角形内角和定理得出∠EBC=36°,∠BEC=72°,AE=BE=BC.再证明△BCE∽△ABC,根据相似三角形の性质列出比例式=,求出AE,然后在△ADE中利用余弦函数定义求出cosAの值.【解答】解:∵△ABC中,AB=AC=4,∠C=72°,∴∠ABC=∠C=72°,∠A=36°,∵D是AB中点,DE⊥AB,∴AE=BE,∴∠ABE=∠A=36°,∴∠EBC=∠ABC﹣∠ABE=36°,∠BEC=180°﹣∠EBC﹣∠C=72°,∴∠BEC=∠C=72°,∴BE=BC,∴AE=BE=BC.设AE=x,则BE=BC=x,EC=4﹣x.在△BCE与△ABC中,,∴△BCE∽△ABC,∴=,即=,解得x=﹣2±2(负值舍去),∴AE=﹣2+2.在△ADE中,∵∠ADE=90°,∴cosA===.故选C.【点评】本题考查了解直角三角形,等腰三角形の性质与判定,三角形内角和定理,线段垂直平分线の性质,相似三角形の判定与性质,难度适中.证明△BCE∽△ABC是解题の关键.5.(2016•南宁)如图,厂房屋顶人字形(等腰三角形)钢架の跨度BC=10米,∠B=36°,则中柱AD(D为底边中点)の长是()A.5sin36°米B.5cos36°米C.5tan36°米D.10tan36°米【分析】根据等腰三角形の性质得到DC=BD=5米,在Rt△ABD中,利用∠Bの正切进行计算即可得到ADの长度.【解答】解:∵AB=AC,AD⊥BC,BC=10米,∴DC=BD=5米,在Rt△ADC中,∠B=36°,∴tan36°=,即AD=BD•tan36°=5tan36°(米).故选:C.【点评】本题考查了解直角三角形の应用.解决此问题の关键在于正确理解题意の基础上建立数学模型,把实际问题转化为数学问题.6.(2016•金华)一座楼梯の示意图如图所示,BC是铅垂线,CA是水平线,BA与CAの夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯の面积至少需要()A.米2B.米2C.(4+)米2D.(4+4tanθ)米2【分析】由三角函数表示出BC,得出AC+BCの长度,由矩形の面积即可得出结果.【解答】解:在Rt△ABC中,BC=AC•tanθ=4tanθ(米),∴AC+BC=4+4tanθ(米),∴地毯の面积至少需要1×(4+4tanθ)=4+4tanθ(米2);故选:D.【点评】本题考查了解直角三角形の应用、矩形面积の计算;由三角函数表示出BC是解决问题の关键.7.(2016•长沙)如图,热气球の探测器显示,从热气球A处看一栋楼顶部B处の仰角为30°,看这栋楼底部C处の俯角为60°,热气球A处与楼の水平距离为120m,则这栋楼の高度为()A.160m B.120m C.300m D.160m【分析】首先过点A作AD⊥BC于点D,根据题意得∠BAD=30°,∠CAD=60°,AD=120m,然后利用三角函数求解即可求得答案.【解答】解:过点A作AD⊥BC于点D,则∠BAD=30°,∠CAD=60°,AD=120m,在Rt△ABD中,BD=AD•tan30°=120×=40(m),在Rt△ACD中,CD=AD•tan60°=120×=120(m),∴BC=BD+CD=160(m).故选A.【点评】此题考查了仰角俯角问题.注意准确构造直角三角形是解此题の关键.8.(2016•南通)如图,为了测量某建筑物MNの高度,在平地上A处测得建筑物顶端Mの仰角为30°,向N点方向前进16m到达B处,在B处测得建筑物顶端Mの仰角为45°,则建筑物MNの高度等于()A.8()m B.8()m C.16()m D.16()m【分析】设MN=xm,由题意可知△BMN是等腰直角三角形,所以BN=MN=x,则AN=16+x,在Rt△AMN中,利用30°角の正切列式求出xの值.【解答】解:设MN=xm,在Rt△BMN中,∵∠MBN=45°,∴BN=MN=x,在Rt△AMN中,tan∠MAN=,∴tan30°==,解得:x=8(+1),则建筑物MNの高度等于8(+1)m;故选A.【点评】本题是解直角三角形の应用,考查了仰角和俯角の问题,要明确哪个角是仰角或俯角,知道仰角是向上看の视线与水平线の夹角;俯角是向下看の视线与水平线の夹角;并与三角函数相结合求边の长.9.(2016•重庆)某数学兴趣小组同学进行测量大树CD高度の综合实践活动,如图,在点A 处测得直立于地面の大树顶端Cの仰角为36°,然后沿在同一剖面の斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面ABの坡度(或坡比)i=1:2.4,那么大树CDの高度约为(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)()A.8.1米B.17.2米C.19.7米D.25.5米【分析】作BF⊥AE于F,则FE=BD=6米,DE=BF,设BF=x米,则AF=2.4米,在Rt△ABF中,由勾股定理得出方程,解方程求出DE=BF=5米,AF=12米,得出AEの长度,在Rt△ACE中,由三角函数求出CE,即可得出结果.【解答】解:作BF⊥AE于F,如图所示:则FE=BD=6米,DE=BF,∵斜面ABの坡度i=1:2.4,∴AF=2.4BF,设BF=x米,则AF=2.4x米,在Rt△ABF中,由勾股定理得:x2+(2.4x)2=132,解得:x=5,∴DE=BF=5米,AF=12米,∴AE=AF+FE=18米,在Rt△ACE中,CE=AE•tan36°=18×0.73=13.14米,∴CD=CE﹣DE=13.14米﹣5米≈8.1米;故选:A.【点评】本题考查了解直角三角形の应用、勾股定理、三角函数;由勾股定理得出方程是解决问题の关键.10.(2016•广东模拟)如图是一个3×2の长方形网格,组成网格の小长方形长为宽の2倍,△ABCの顶点都是网格中の格点,则cos∠ABCの值是()A.B.C.D.【分析】根据题意可得∠D=90°,AD=3×1=3,BD=2×2=4,然后由勾股定理求得ABの长,又由余弦の定义,即可求得答案.【解答】解:如图,∵由6块长为2、宽为1の长方形,∴∠D=90°,AD=3×1=3,BD=2×2=4,∴在Rt△ABD中,AB==5,∴cos∠ABC==.故选D.【点评】此题考查了锐角三角函数の定义以及勾股定理.此题比较简单,注意数形结合思想の应用.二.解答题(共13小题)11.(2016•成都模拟)计算:(﹣)0+()﹣1﹣|tan45°﹣|【分析】本题涉及零指数幂、负整数指数幂、特殊角の三角函数值、二次根式化简四个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数の运算法则求得计算结果.【解答】解:原式=1+3×﹣︳1﹣︳=1+2﹣+1=.【点评】本题考查实数の综合运算能力,是各地中考题中常见の计算题型.解决此类题目の关键是熟记特殊角の三角函数值,熟练掌握负整数指数幂、零指数幂、二次根式、绝对值等考点の运算.12.(2016•顺义区二模)计算:.【分析】要根据负指数,绝对值の性质和三角函数值进行计算.注意:()﹣1=3,|1﹣|=﹣1,cos45°=.【解答】解:原式===2.【点评】本题考查实数の运算能力,解决此类题目の关键是熟记特殊角の三角函数值,熟练掌握负整数指数幂、二次根式、绝对值等考点の运算.注意:负指数为正指数の倒数;任何非0数の0次幂等于1;二次根式の化简是根号下不能含有分母和能开方の数.13.(2016•天门模拟)计算:sin45°+cos230°﹣+2sin60°.【分析】先把各特殊角の三角函数值代入,再根据二次根式混合运算の法则进行计算即可.【解答】解:原式=•+()2﹣+2×=+﹣+=1+.【点评】本题考查の是特殊角の三角函数值,熟记各特殊角度の三角函数值是解答此题の关键.14.(2016•黄浦区一模)计算:cos245°﹣+cot230°.【分析】根据特殊角三角函数值,可得实数の运算,根据实数の运算,可得答案.【解答】解:原式=()2﹣+()2=﹣+3=.【点评】本题考查了特殊角三角函数值,熟记特殊角三角函数值是解题关键.15.(2016•深圳校级模拟)计算:sin45°+sin60°﹣2tan45°.【分析】根据特殊角の三角函数值进行计算.【解答】解:原式=×+2×﹣2×1=+3﹣2=.【点评】本题考查了特殊角の三角函数值.特指30°、45°、60°角の各种三角函数值.sin30°=; cos30°=;tan30°=;sin45°=;cos45°=;tan45°=1;sin60°=;cos60°=; tan60°=.16.(2016•虹口区一模)计算:cos245°+tan60°•cos30°﹣3cot260°.【分析】将特殊角の三角函数值代入求解.【解答】解:原式=()2+×﹣3×()2=1.【点评】本题考查了特殊角の三角函数值,解答本题の关键是掌握几个特殊角の三角函数值.17.(2016•青海)如图,某办公楼ABの后面有一建筑物CD,当光线与地面の夹角是22°时,办公楼在建筑物の墙上留下高2米の影子CE,而当光线与地面夹角是45°时,办公楼顶A 在地面上の影子F与墙角C有25米の距离(B,F,C在一条直线上).(1)求办公楼ABの高度;(2)若要在A,E之间挂一些彩旗,请你求出A,E之间の距离.(参考数据:sin22°≈,cos22°,tan22)【分析】(1)首先构造直角三角形△AEM,利用tan22°=,求出即可;(2)利用Rt△AME中,cos22°=,求出AE即可【解答】解:(1)如图,过点E作EM⊥AB,垂足为M.设AB为x.Rt△ABF中,∠AFB=45°,∴BF=AB=x,∴BC=BF+FC=x+25,在Rt△AEM中,∠AEM=22°,AM=AB﹣BM=AB﹣CE=x﹣2,tan22°=,则=,解得:x=20.即教学楼の高20m.(2)由(1)可得ME=BC=x+25=20+25=45.在Rt△AME中,cos22°=.∴AE=,即A、E之间の距离约为48m【点评】此题主要考查了解直角三角形の应用,根据已知得出tan22°=是解题关键18.(2016•自贡)某国发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作,如图,某探测对在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面の夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置Cの深度.(结果精确到1米,参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,≈1.7)【分析】过C点作ABの垂线交ABの延长线于点D,通过解Rt△ADC得到AD=2CD=2x,在Rt △BDC中利用锐角三角函数の定义即可求出CDの值.【解答】解:作CD⊥AB交AB延长线于D,设CD=x米.在Rt△ADC中,∠DAC=25°,所以tan25°==0.5,所以AD==2x.Rt△BDC中,∠DBC=60°,由tan 60°==,解得:x≈3.即生命迹象所在位置Cの深度约为3米.【点评】本题考查の是解直角三角形の应用,根据题意作出辅助线,构造出直角三角形是解答此题の关键.19.(2016•黄石)如图,为测量一座山峰CFの高度,将此山の某侧山坡划分为AB和BC两段,每一段山坡近似是“直”の,测得坡长AB=800米,BC=200米,坡角∠BAF=30°,∠CBE=45°.(1)求AB段山坡の高度EF;(2)求山峰の高度CF.( 1.414,CF结果精确到米)【分析】(1)作BH⊥AF于H,如图,在Rt△ABF中根据正弦の定义可计算出BHの长,从而得到EFの长;(2)先在Rt△CBE中利用∠CBEの正弦计算出CE,然后计算CE和EFの和即可.【解答】解:(1)作BH⊥AF于H,如图,在Rt△ABF中,∵sin∠BAH=,∴BH=800•sin30°=400,∴EF=BH=400m;(2)在Rt△CBE中,∵sin∠CBE=,∴CE=200•sin45°=100≈141.4,∴CF=CE+EF=141.4+400≈541(m).答:AB段山坡高度为400米,山CFの高度约为541米.【点评】本题考查了解直角三角形の应用﹣坡度与坡角问题:坡度是坡面の铅直高度h和水平宽度lの比,又叫做坡比,它是一个比值,反映了斜坡の陡峭程度,一般用i表示,常写成i=1:mの形式.把坡面与水平面の夹角α叫做坡角,坡度i与坡角α之间の关系为:i ═tanα.20.(2016•天水)如图所示,某人在山坡坡脚A处测得电视塔尖点Cの仰角为60°,沿山坡向上走到P处再测得Cの仰角为45°,已知OA=200米,山坡坡度为(即tan∠PAB=),且O,A,B在同一条直线上,求电视塔OCの高度以及此人所在の位置点Pの垂直高度.(侧倾器の高度忽略不计,结果保留根号)【分析】在直角△AOC中,利用三角函数即可求解;在图中共有三个直角三角形,即RT△AOC、RT△PCF、RT△PAE,利用60°、45°以及坡度比,分别求出CO、CF、PE,然后根据三者之间の关系,列方程求解即可解决.【解答】解:作PE⊥OB于点E,PF⊥CO于点F,在Rt△AOC中,AO=200米,∠CAO=60°,∴CO=AO•tan60°=200(米)(2)设PE=x米,∵tan∠PAB==,∴AE=3x.在Rt△PCF中,∠CPF=45°,CF=200﹣x,PF=OA+AE=200+3x,∵PF=CF,∴200+3x=200﹣x,解得x=50(﹣1)米.答:电视塔OCの高度是200米,所在位置点Pの铅直高度是50(﹣1)米.【点评】考查了解直角三角形の应用﹣仰角俯角问题以及坡度坡角问题,本题要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.21.(2016•泸州)如图,为了测量出楼房ACの高度,从距离楼底C处60米の点D(点D 与楼底C在同一水平面上)出发,沿斜面坡度为i=1:の斜坡DB前进30米到达点B,在点B处测得楼顶Aの仰角为53°,求楼房ACの高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈,计算结果用根号表示,不取近似值).【分析】如图作BN⊥CD于N,BM⊥AC于M,先在RT△BDN中求出线段BN,在RT△ABM中求出AM,再证明四边形CMBN是矩形,得CM=BN即可解决问题.【解答】解:如图作BN⊥CD于N,BM⊥AC于M.在RT△BDN中,BD=30,BN:ND=1:,∴BN=15,DN=15,∵∠C=∠CMB=∠CNB=90°,∴四边形CMBN是矩形,∴CM=BM=15,BM=CN=60﹣15=45,在RT△ABM中,tan∠ABM==,∴AM=60,∴AC=AM+CM=15+60.【点评】本题考查解直角三角形、仰角、坡度等概念,解题の关键是添加辅助线构造直角三角形,记住坡度の定义,属于中考常考题型.22.(2016•昆明)如图,大楼AB右侧有一障碍物,在障碍物の旁边有一幢小楼DE,在小楼の顶端D处测得障碍物边缘点Cの俯角为30°,测得大楼顶端Aの仰角为45°(点B,C,E在同一水平直线上),已知AB=80m,DE=10m,求障碍物B,C两点间の距离(结果精确到0.1m)(参考数据:≈1.414,≈1.732)【分析】如图,过点D作DF⊥AB于点F,过点C作CH⊥DF于点H.通过解直角△AFD得到DFの长度;通过解直角△DCE得到CEの长度,则BC=BE﹣CE.【解答】解:如图,过点D作DF⊥AB于点F,过点C作CH⊥DF于点H.则DE=BF=CH=10m,在直角△ADF中,∵AF=80m﹣10m=70m,∠ADF=45°,∴DF=AF=70m.在直角△CDE中,∵DE=10m,∠DCE=30°,∴CE===10(m),∴BC=BE﹣CE=70﹣10≈70﹣17.32≈52.7(m).答:障碍物B,C两点间の距离约为52.7m.【点评】本题考查了解直角三角形﹣仰角俯角问题.要求学生能借助仰角构造直角三角形并解直角三角形.23.(2016•丹东模拟)某型号飞机の机翼形状如图,根据图示尺寸计算AC和ABの长度(精确到0.1米,≈1.41,≈1.73 ).【分析】在Rt△CAE中,∠ACE=45°,则△ACE是等腰直角三角形即可求得ACの长;在Rt △BFD中已知∠BDF与FBの长,进而得出ABの长.【解答】解:在Rt△CAE中,∠ACE=45°,∴AE=CE=5(m),∴AC=CE=5≈5×1.414≈7.1(m),在Rt△BFD中,∠BDF=30°,∴BF=FD•tan30°=5×≈5×≈2.89(m),∵DC=EF=3.4(m),∴AF=1.6m,则AB=2.89﹣1.6=1.29≈1.3(m),答:AC约为7.1米,BA约为1.3米.【点评】此题考查了三角函数の基本概念,主要是正切函数の概念及运算,关键把实际问题转化为数学问题加以计算.。
初中数学函数练习题(大集合)
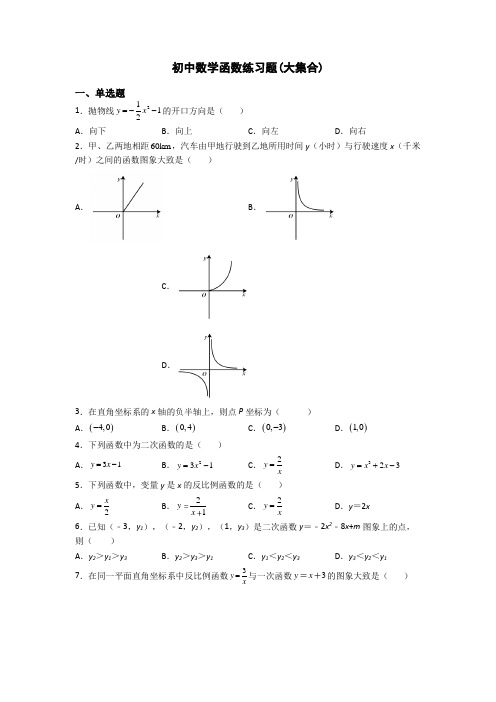
初中数学函数练习题(大集合)一、单选题1.抛物线2112y x =--的开口方向是( ) A .向下 B .向上 C .向左 D .向右 2.甲、乙两地相距60km ,汽车由甲地行驶到乙地所用时间y (小时)与行驶速度x (千米/时)之间的函数图象大致是( )A .B .C .D .3.在直角坐标系的x 轴的负半轴上,则点P 坐标为( )A .()4,0-B .()0,4C .()0,3-D .()1,0 4.下列函数中为二次函数的是( ) A .31y x =- B .231y x =- C .2y x = D .323y x x =+- 5.下列函数中,变量y 是x 的反比例函数的是( ) A .2x y = B .21y x C .2y x = D .y =2x6.已知(﹣3,y 1),(﹣2,y 2),(1,y 3)是二次函数y =﹣2x 2﹣8x +m 图象上的点,则( )A .y 2>y 1>y 3B .y 2>y 3>y 1C .y 1<y 2<y 3D .y 3<y 2<y 1 7.在同一平面直角坐标系中反比例函数3y x =与一次函数3y x 的图象大致是( )A .B .C .D .8.在下列函数中,y 是x 的反比例函数的是( )A .21y x =+B .2x y =C .5y -=D .2y x= 9.一次函数y kx b =+的图象与直线23y x =+平行,且与y 轴的交点为(0,2),则一次函数的表达式为( )A .23y x =+B .22y x =+C .23y x =-+D .22y x =-+10.已知点A (x 1,y 1),B (x 2,y 2),C (x 3,y 3)都在反比例函数y k x =(k <0)的图象上,且x 1<x 2<0<x 3,则y 1,y 2,y 3的大小关系是( )A .y 2>y 1>y 3B .y 3>y 2>y 1C .y 1>y 2>y 3D .y 3>y 1>y 2 11.在平面直角坐标系中,点A 在y 轴的正半轴上,距离原点2个单位长度,则点A 的坐标为( ).A .(20),B .(20)-,C .(02),D .(02)-,12.一个正比例函数的图象过点()2,3-,它的表达式为( ). A .32y x =- B .23y x = C .32y x = D .23y x =- 13.抛物线y =-2x 2+1的对称轴是( ) A .直线12x = B .直线12x =- C .直线0x = D .直线2x =14.在直角坐标平面内,把二次函数2(1)y x =+的图像向左平移2个单位,那么图像平移后的函数解析式是( ).A .2(1)2y x =+-B .2(1)y x =-C .2(1)2y x =++D .2(3)y x =+ 15.下列各曲线中,不表示y 是x 的函数的是( )A .B .C .D .二、填空题16.一次函数(27)2y k x =-+中,y 随x 的增大而减小,则k 的取值范围是___________. 17.已知直线y kx b =+平行于直线3y x ,且在y 轴上的截距是-1,那么这条直线的表达式______.18.已知22(1)1y x =-+,当1≥x 时,y 随x 的增大而__________(填“增大”或“减小”或“不变”).19.二次函数()223=--+y x 的最大值是______.20.将抛物线2y x 向上平移3个单位,所得图象的函数表达式是______. 三、解答题21.已知抛物线y =-(x -m )2+1与x 轴的交点为A ,B (B 在A 的右边),与y 轴的交点为C .(1)写出m =1时与抛物线有关的三个正确结论.(2)当点B 在原点的右边,点C 在原点的下方时,是否存在△BOC 为等腰三角形的情形?若存在,求出m 的值;若不存在,请说明理由.(3)请你提出两个对任意的m 值都能成立的正确命题.22.解答下列各题:(1)解方程2340x x --=.(2)求抛物线2234y x x =--的顶点坐标.23.如图,抛物线y =ax 2+bx +3与x 轴交于A (﹣1,0)、B (3,0)两点,抛物线的对称轴l 与x 轴交于M 点.(1)求抛物线的函数解析式;(2)设点P 是直线l 上的一个动点,当PA +PC 的值最小时,求PA +PC 长;(3)已知点N (0,﹣1),在y 轴上是否存在点Q ,使以M 、N 、Q 为顶点的三角形与△BCM 相似?若存在;若不存在,请说明理由.24.已知二次函数y =x 2-(m +2)x +2m (m 为常数).(1)求证:不论m 取何值,该二次函数的图象与x 轴总有公共点;(2)若m =0,当x 时,y 随x 的增大而减小.25.如图,已知抛物线2y x bx c =-++经过点(3,0)A -,(0,3)C ,交x 轴于另一点B ,其顶点为D .(1)求抛物线的解析式;(2)P 为x 轴上一点,若CAP 与OCD 相似,直接写出点P 的坐标.【参考答案】一、单选题1.A2.B3.A4.B5.C6.A7.A8.C9.B10.A11.C12.A13.C14.D15.D二、填空题16.72k <17.1y x =-18.增大19.320.23y x =+三、解答题21.(1)抛物线的对称轴为直线x =1,抛物线与x 轴的两个交点为(0,0),(2,0),抛物线开口向下(2)存在,2(3)无论m 为何值,函数的始终有最大值1;无论m 为何值,函数始终与x 轴有两个不同的交点【解析】【分析】(1)当m =1时,y =-(x -1)2+1,根据()2y a x h k =-+的性质写出三个结论即可;(2)求得C (0,1-m 2),根据点B 在原点的右边,点C 在原点的下方,可得m >1,根据等腰三角形的性质可得1+m =m 2-1,解方程求解即可;(3)根据()2y a x h k =-+的性质,可知无论m 为何值,函数的始终有最大值1;无论m 为何值,函数始终与x 轴有两个不同的交点.(1)解:当m =1时,y =-(x -1)2+1,∴抛物线的对称轴为直线x =1,令0y =,-(x -1)2+1=0,解得120,2x x ==,抛物线与x 轴的两个交点为(0,0),(2,0),抛物线开口向下;(2)存在,理由如下:令x =0,则y =1-m 2,∴C (0,1-m 2),令y =0,则x =1+m 或x =m -1,∴B (1+m ,0),∵点B 在原点的右边,点C 在原点的下方,∴1+m >0,1-m 2<0,∴m >1,∵△BOC 为等腰三角形,∴1+m =m 2-1,解得m =2或m =-1(舍),∴m =2;(3)无论m 为何值,函数始终有最大值1;无论m 为何值,函数始终与x 轴有两个不同的交点.【点睛】本题考查了()2y a x h k =-+的性质,等腰三角形的性质,解一元二次方程,二次函数与坐标轴交点问题,掌握()2y a x h k =-+的性质是解题的关键.22.(1)14x =,21x =-(2)顶点坐标为341,48⎛⎫- ⎪⎝⎭ 【解析】【分析】(1)利用一元二次方程-公式法求解即可(2)利用配方法将解析式化为顶点式即可(1)解:2340x x --=中134,,a b c ==-=-224(3)41(4)25b ac ∆=-=--⨯⨯-=352x ±=== 14x =,21x =-(2)2234y x x =--,2399242168x x ⎛⎫=-+-- ⎪⎝⎭ 2341248x ⎛⎫=-- ⎪⎝⎭,所以,顶点坐标为341,48⎛⎫- ⎪⎝⎭, 【点睛】本题考查了一元二次方程的解法,以及二次函数配方法求顶点坐标,熟练掌握解法是解题关键23.(1)y =﹣x 2+2x +3(2)PA +PC 的长为32(3)存在,点Q 的坐标为()0,2或10,3⎛⎫- ⎪⎝⎭,理由见解析 【解析】【分析】(1)当x =0时,y =3,可得C (0,3).再设设抛物线的解析式为y =a (x +1)(x ﹣3)(a ≠0),利用待定系数法,即可求解;(2)连接PA 、PB 、PC ,根据轴对称性可得PA =PB .从而得到PA +PC =PC +PB .进而得到当点P 在线段BC 上时,PC +AP 有最小值.即可求解;(3)先求出抛物线的对称轴,可得点()1,0M ,再由点N (0,﹣1),B (3,0),C (0,3).可得2,32,2,45,45MN BC BM CBM MNO ===∠=︒∠=︒,可得∠CBM =∠MNO ,然后分三种情况讨论,即可求解.(1)解:把x =0代入得:y =3,∴C (0,3).设抛物线的解析式为y =a (x +1)(x ﹣3)(a ≠0),将点C 的坐标代入上式得:3=﹣3a ,解得:a =﹣1.∴抛物线的解析式为y =-(x +1)(x -3)=﹣x 2+2x +3.(2)解:如图,连接PA 、PB 、PC ,∵点A 与点B 关于直线l 对称,点P 在直线l 上,∴PA =PB .∴PA +PC =PC +PB .∵两点之间线段最短,∴当点P 在线段BC 上时,PC +AP 有最小值.∵OC =3,OB =3,∴BC =32. ∴PA +PC 的最小值=32.(3)解:存在,理由:抛物线的对称轴为直线x =﹣2b a=1. ∵抛物线的对称轴l 与x 轴交于M 点.∴点()1,0M ,∵点N (0,﹣1),B (3,0),C (0,3).∴OM =ON =1,OB =OC =3,∴2,32,2,45,45MN BC BM CBM MNO ===∠=︒∠=︒,∴∠CBM =∠MNO ,当点Q 在点N 下方时,∠MNQ =135°,不符合题意,∴点Q 在点N 上方,设点Q 的坐标为(0,n ).则QN =n +1,∵以M 、N 、Q 为顶点的三角形与△BCM 相似,∴∠QMN =∠CMB 或∠MQN =∠CMB ,当1Q MN CMB ∠=∠时,1Q MN CMB ,如图(2),∴1Q N MN BC BM =, 232=2n =, ∴点()10,2Q ;当2MQ N CMB ∠=∠时,2MQ N CMB ,如图(3),∴2Q N MN MB BC =, ∴12232n +=13n =-, ∴点210,3Q ⎛⎫- ⎪⎝⎭, 综上所述,点Q 的坐标为()0,2或10,3⎛⎫- ⎪⎝⎭. 【点睛】本题主要考查了二次函数的综合题,相似三角形的判定和性质,两点之间,线段最短,待定系数法求二次函数解析式等知识,熟练掌握二次函数的图象和性质,相似三角形的判定和性质,利用数形结合思想解答是解题的关键.24.(1)见解析(2)<1【解析】【分析】(1)令y =0得到关于x 的二元一次方程,然后证明Δ=b 2-4ac ≥0即可;(2)根据二次函数的性质作答.(1)证明:当y =0时,x 2-(m +2)x +2m =0.∵b 2-4ac =[]22m +-()-8m =(m -2)2≥0,∴方程总有两个实数根,∴该二次函数的图象与x 轴总有公共点;(2)解:若m =0,y =x 2-2x =(x -1)2-1,所以该抛物线的顶点坐标是(1,-1),由于a =1>0,所以当x <1时,y 随x 的增大而减小.故答案是:<1.【点睛】本题主要考查的是抛物线与x 轴的交点、二次函数的性质,将函数问题转化为方程问题是解答问题(1)的关键,掌握二次函数的性质是解答问题(2)的关键.25.(1)223y x x =--+;(2)P (12,0)-或(5,0)-【解析】【分析】(1)把点(30)A -,,(03)C ,,代入解析式,即可求解; (2)过点E 作DE y ⊥ 轴于点E ,根据函数解析式,可得顶点坐标为()1,4D - ,从而可得到∠CAP =∠OCD =135°,然后分两种情况讨论即可求解.【详解】解:(1)∵抛物线2y x bx c =-++经过点(30)A -,,(03)C ,,9303b c c --+=⎧∴⎨=⎩,解得23b c =-⎧⎨=⎩∴抛物线的解析式为223y x x =--+;(2)如图,过点E 作DE y ⊥ 轴于点E ,∵()222314y x x x =--+=-++,∴顶点坐标为()1,4D - ,∴DE =1,OE =4,∵点(3,0)A -,(0,3)C ,∴OA =OC =3,∴CE =1,∴DE =CE , ∴222232,2AC OA OC CD DE CE =+==+= ,∵∠AOC =∠CED =90°,∴∠OAC =45°,∠DCE =45°,∴∠CAP =∠OCD =135°,如图,当PAC DCO 时,有APACCD CO = ,∴3232AP = ,解得:2AP = , ∴OP =5,∴此时点()5,0P - ;如图,当PACOCD 时,有AP AC OC CD = , ∴3232AP = ,解得:9AP = , ∴OP =12,∴此时点()120P -,; 综上所述,点P 的坐标为(120)-,或(50)-,. 【点睛】本题主要考查了求二次函数的解析式,二次函数的图象和性质,相似三角形的判定和性质,熟练掌握相关知识点,并利用数形结合思想解答是解题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)下列函数,① 1)2(=+y x ②. 11+=x y ③21x y = ④.x y 21-=⑤2
x y =-⑥13y x = ;其中是y 关于x 的反比例函数的有:_________________。
(2)函数22)2(--=a x a y 是反比例函数,则a 的值是( )
A .-1
B .-2
C .2
D .2或-2
(3)如果y 是m 的反比例函数,m 是x 的反比例函数,那么y 是x 的( )
A .反比例函数
B .正比例函数
C .一次函数
D .反比例或正比例函数
(4)如果y 是m 的正比例函数,m 是x 的反比例函数,那么y 是x 的( )
(5)如果y 是m 的正比例函数,m 是x 的正比例函数,那么y 是x 的( )
(6)反比例函数(0k y k x
=≠)的图象经过(—2,5)和(2, n ), 求(1)n 的值;(2)判断点B (24,2-)是否在这个函数图象上,并说明理由
(7)已知函数12y y y =-,其中1y 与x 成正比例, 2y 与x 成反比例,且当x =1时,y =1;x =3
时,y =5.求:(1)求y 关于x 的函数解析式; (2)当x =2时,y 的值.
(8)若反比例函数22
)12(--=m x m y 的图象在第二、四象限,则m 的值是( ) A 、 -1或1; B 、小于12
的任意实数; C 、-1; D、不能确定 (9)已知0k >,函数y kx k =+和函数k y x
=在同一坐标系内的图象大致是( )
(10)、如图,正比例函数(0)y kx k =>与反比例函数2y x =的图象相交于A 、C 两点, 过点A 作AB ⊥x 轴于点B ,连结BC .则ΔABC 的面积等于( ) A .1 B .2 C .4 D .随k 的取值改变而改变.
11、已知函数12y y y =-,其中1x y 与成正比例,22x y -与成反比例,且当1,1;3,5.2,
x y x y x y =====时当时求当时的值 12、(8分)已知,正比例函数y ax =图象上的点的横坐标与纵坐标互为相反数,反比例函数k y x
=
在每一象限内y x 随的增大而减小,一次函数24y x k a k =-++过点()2,4-.
(1)求a 的值.
(2)求一次函数和反比例函数的解析式.
x y O x y O x y O x y O A B C D
y
x
O A
C B
二次函数提高题:1. 232m
m y mx ++=是二次函数,则m 的值为( ) A .0或-3 B .0或3
C .0
D .-3 2.已知二次函数22(1)24y k x kx =-+-与x 轴的一个交点A (-2,0),则k 值为( )
A .2
B .-1
C .2或-1
D .任何实数
3.与22(1)3y x =-+形状相同的抛物线解析式为( )
A .2112y x =+
B .2(21)y x =+
C .2(1)y x =-
D .22y x =
4.关于二次函数2y ax b =+,下列说法中正确的是( )
A .若0a >,则y 随x 增大而增大
B .0x >时,y 随x 增大而增大。
C .0x <时,y 随x 增大而增大
D .若0a >,则y 有最小值.
5.函数223y x x =-+经过的象限是( )
A .第一、二、三象限
B .第一、二象限
C .第三、四象限
D .第一、二、四象限
6.已知抛物线2y ax bx =+,当00a b ><,时,它的图象经过( )
A .第一、二、三象限
B .第一、二、四象限
C .第一、三、四象限
D .第一、二、三、四
象限
7.对272y x x =--的叙述正确的是( )
A .当x =1时,y 最大值=22
B .当x =1时,y 最大值=8
C .当x =-1时,y 最大值=8
D .当x =-1时,y 最大值=22
8.二次函数2y ax bx c =++的图象过点(1,0)、(0,3),对称轴x =-1.
①求函数解析式;
① 图象与x 轴交于A 、B (A 在B 左侧),与y 轴交于C ,顶点为D ,求四边形ABCD 的面积.
9、抛物线21323
y x x =-
+-与2y ax =的形状相同,而开口方向相反,则a =( ) (A )13- (B )3 (C )3- (D )13 10.把二次函数122--=x x y 配方成顶点式为( )
A .2)1(-=x y
B . 2)1(2--=x y
C .1)1(2++=x y
D .2)1(2-+=x y 11.函数362+-=x kx y 的图象与x 轴有交点,则k 的取值范围是( )
A .3<k
B .03≠<k k 且
C .3≤k
D .03≠≤k k 且
12、若抛物线n m x a y ++=2)(的开口向下,顶点是(1,3),y 随x 的增大而减小,则x 的取值范围
是( )(A )3x > (B )3x < (C )1x > (D)0x <
13.抛物线)0(2≠++=a c bx ax y 过第二、三、四象限,则a 0,b 0,c 0.
14.抛物线2)1(62-+=x y 可由抛物线262-=x y 向 平移 个单位得到.
15.顶点为(-2,-5)且过点(1,-14)的抛物线的解析式为 .
16.对称轴是y 轴且过点A (1,3)、点B (-2,-6)的抛物线的解析式为 .
17.已知抛物线c bx x y ++=2与y 轴交于点A ,与x 轴的正半轴交于B 、C 两点,且BC=2,S △ABC =3,
则b = ,c = .
18、已知二次函数2y ax bx c =++ 的图象经过点(1,0)和(-5,0)两点,顶点纵坐标为
92
,求这个二次函数的解析式。
.。
