理论力学习题解答第九章
《理论力学》第9章作业

第九章 作业解答参考9-2 图示A 、B 两物体的质量分别为m 1 与m 2 ,二者间用一绳子连接,此绳跨过一滑轮,滑轮半径为r 。
如在开始时,两物体的高度差为h ,而且m 1 > m 2 ,不计滑轮质量。
求由静止释放后,两物体达到相同的高度时所需的时间。
解:分别取重物m 1、m 2为研究对象,它们的受力和运动情况如右下图所示,则此两物体在铅垂方向上的运动方程分别为:()()111122221 2m a m g F m a F m g =-=- 由于不计滑轮质量,因此有:1212=F F a a a ==,且:代入⑴⑵式解得:1212m m a g m m -=+ a 为常数,说明两物体以相等的加速度相向作匀加速运动设两物体由静止释放至达到相同高度所经历的时间为t则有: 212122h s s at === 将1212m m a g m m -=+代入,解得: ()()1212m m h t gm m +=⋅- 即:由静止释放后,两物体达到相同高度所经历的时间为:()()1212m m h t g m m +=⋅- 9-7 图示质量为10 t 的物体随同跑车以v 0 = 1.0 m/s 的速度沿桥式吊车的桥架移动,今因故急刹车,物体由于惯性绕悬挂点C 向前摆动。
绳长l = 5 m ,求:⑴ 刹车时绳子的张力;⑵ 最大摆角φ 的大小。
解:⑴ 取物体为研究对象,由题意可知,刹车时,物体将作圆周运动,其此时的受力和运动情况如右中图所示;由题意可知: 20n v a l= 则其在铅垂方向的运动方程为: 20T v m F mg l=- 因此: ()()2203T 3 1.010109.85 10010N 100kN v F m g l ⎛⎫⎛⎫=+=⨯⨯+ ⎪ ⎪⎝⎭⎝⎭=⨯=⑵ 设物体至最大摆角时物体上升了h (如右下图所示),则有:cos l h l ϕ-= 由于刹车之后,物体的运动中只有重力做功,因此其机械能守恒 故有:20/2mv mgh =,即: 202v h g= 则: 220 1.0cos 110.98980229.85v gl ϕ=-=-≈⨯⨯ 即: 1cos 0.989808.192ϕ-=≈︒故:刹车时绳子的张力为100 kN ,最大摆角φ 约为 8.192°。
理论力学第七版答案解析第九章

9-10 在瓦特行星传动机构中,平衡杆O 1A 绕O 1轴转动,并借连杆AB 带动曲柄OB ;而曲柄OB 活动地装置在O 轴上,如图所示。
在O 轴上装有齿轮Ⅰ,齿轮Ⅱ与连杆AB 固连于一体。
已知:r 1=r 2=0.33m ,O 1A =0.75m ,AB =1.5m ;又平衡杆的角速度O 1=6rad/s 。
求当=60°且=90°时,曲柄OB 和齿轮Ⅰ的角速度。
题9-10图【知识要点】 Ⅰ、Ⅱ两轮运动相关性。
【解题分析】 本题已知平衡杆的角速度,利用两轮边缘切向线速度相等,找出ωAB ,ωOB 之间的关系,从而得到Ⅰ轮运动的相关参数。
【解答】 A 、B 、M 三点的速度分析如图所示,点C 为AB 杆的瞬心,故有 ABA O CA v A AB ⋅⋅==21ωω ωω⋅=⋅=A O CD v AB B 123所以 s rad r r v BOB /75.321=+=ωs rad r v CM v MAB M /6,1==⋅=I ωω 9-12 图示小型精压机的传动机构,OA =O 1B =r =0.1m ,EB =BD =AD =l =0.4m 。
在图示瞬时,OA ⊥AD ,O 1B ⊥ED ,O 1D 在水平位置,OD 和EF 在铅直位置。
已知曲柄OA 的转速n =120r/min ,求此时压头F 的速度。
题9-12图【知识要点】 速度投影定理。
【解题分析】 由速度投影定理找到A 、D 两点速度的关系。
再由D 、E 、F 三者关系,求F 速度。
【解答】 速度分析如图,杆ED 与AD 均为平面运动,点P 为杆ED 的速度瞬心,故 v F = v E = v D由速度投影定理,有A D v v =⋅θcos可得 s ll r n r v v A F /30.1602cos 22m =+⋅⋅==πθ 9-16 曲柄OA 以恒定的角速度=2rad/s 绕轴O 转动,并借助连杆AB 驱动半径为r 的轮子在半径为R 的圆弧槽中作无滑动的滚动。
理论力学课后答案9
四川大学 建筑与环境学院 力学科学与工程系 魏泳涛
w.
kh
a ,方向向上。 2
da
w.
co
我在沙滩上写上你的名字,却被浪花带走了;我在云上写上你的名字,却被风儿带走了;于是我在理论力 学的习题答案上写上我的名字.
我在沙滩上写上你的名字,却被浪花带走了;我在云上写上你的名字,却被风儿带走了;于是我在理论力 学的习题答案上写上我的名字.
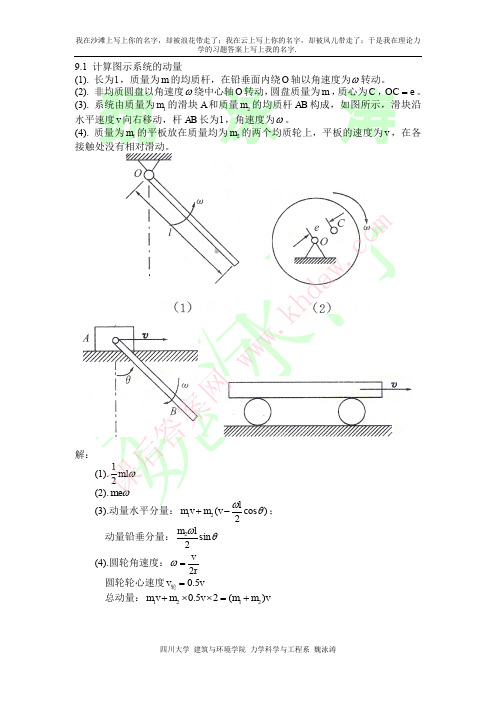
9.9 图示一凸轮导板机构。半径为 r 的偏心圆轮 O 以匀角速度 绕轴 O 转动,偏 心距 OO e ,导板 AB 重 FW 。当导板在最低位置时,弹簧的压缩量为 。要使 导板在运动过程中始终不离开轮轴,试求弹簧的刚度系数。
魏
泳
涛
m
课
后
答
四川大学 建筑与环境学院 力学科学与工程系 魏泳涛
案
网
ww
w.
kh
而 A 点坐标为 xA 2l cos S y A 2l sin 化简后 y2 ( x A l cos ) 2 A l 2 4
da
w.
co
解: 由于在水平方向上质心运动守恒。由于系统初始静止,因此系统质心位置始 终保持不变。 由图知 xC l cos l cos S
魏
泳
涛
m
ae 即为 AB 的加速度。
当 0 时, AB 处于最高位置,其加速度为 2e 。弹簧的压缩量为 2e 。 AB 受力图如下。
课
后
答
案
网
ww
T FW N k ( 2e) FW N
要保持接触,则应该有
理论力学谢传锋第九章习题解答
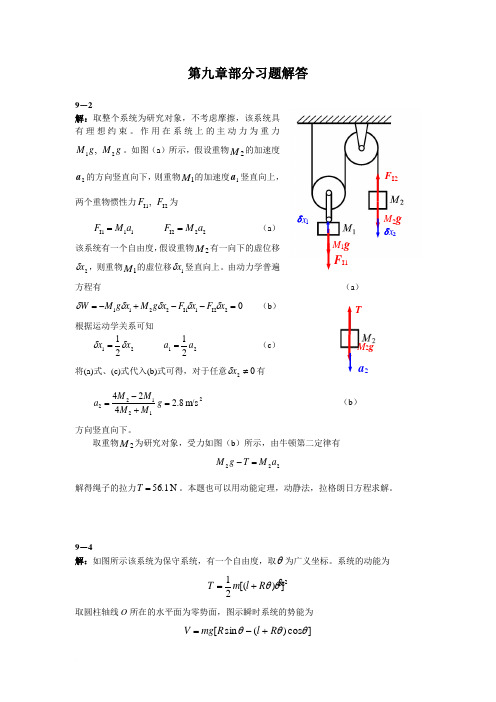
第九章部分习题解答9-2解:取整个系统为研究对象,不考虑摩擦,该系统具有理想约束。
作用在系统上的主动力为重力g M g M 21,。
如图(a )所示,假设重物2M 的加速度2a 的方向竖直向下,则重物1M 的加速度1a 竖直向上,两个重物惯性力I2I1,F F 为11I1a M F = 22I2a M F =(a )该系统有一个自由度,假设重物2M 有一向下的虚位移2x δ,则重物1M 的虚位移1x δ竖直向上。
由动力学普遍方程有 (a )02I21I12211=--+-=x F x F x g M x g M W δδδδδ (b )根据运动学关系可知2121x x δδ=2121a a =(c )将(a)式、(c)式代入(b)式可得,对于任意02≠x δ有212122m/s 8.2424=+-=g M M M M a (b )方向竖直向下。
取重物2M 为研究对象,受力如图(b )所示,由牛顿第二定律有222a M T g M =-解得绳子的拉力N 1.56=T 。
本题也可以用动能定理,动静法,拉格朗日方程求解。
9-4解:如图所示该系统为保守系统,有一个自由度,取θ为广义坐标。
系统的动能为2])[(21θθ R l m T +=取圆柱轴线O 所在的水平面为零势面,图示瞬时系统的势能为]cos )(sin [θθθR l R mg V +-=M 1gM 2gF I2F I1δx 2δx 1M 2gT a 2拉格朗日函数V T L -=,代入拉格朗日方程0)(=∂∂-∂∂θθL L dt d 整理得摆的运动微分方程为0sin )(2=+++θθθθg R R l 。
9-6解:如图所示,该系统为保守系统,有一个自由度,取弧坐标s 为广义坐标。
系统的动能为221S m T =取轨线最低点O 所在的水平面为零势面,图示瞬时系统的势能为mgh V =由题可知b s ds dh 4sin ==ϕ,因此有b s d b s h So8s 42==⎰。
理论力学答案完整版(清华大学出版社)9

F1 = F1(sinϑ i − cosϑ j) , F2 = F2i
点 A 和 B 的坐标及其变分为
rA = −(l1 − l2 )cosϑ i + (l1 + l2 )sinϑ j
,
rB = −2l1 cosϑ i
δrA = (l1 − l2 )sinϑ ⋅δϑ i + (l1 + l2 )cosϑ ⋅δϑ j ,
Fδ re − G1δ ra = 0 按速度合成定理,虚位移存在如下关系:δ ra = δ re tan β ,于是
(a)
题 9-9 图
导出 F = G1 tan β .
(2)水平面有摩擦时,当水平力 F 较小,斜面 D 有向左运动趋势,此时摩擦力方向向右,
临界平衡时,虚功方程为
(F + ) Fmax δ re − G1δ ra = 0 , 其中 Fmax = (G1 + G2 ) f 。求得: F ≥ G1 tan β − (G1 + G2 ) f .
i =1
解题要领 1) 对于自由度不为零的系统,求其平衡时主动力满足的关系可用虚功原理. 2) 对于自由度为零的系统,为求其约束力,可以依次解除一个约束,使自由度为 1,即将
此约束力作为主动力应用虚功原理. 3) 独立的坐标变分个数与系统的自由度相同,可以用解析或虚速度的方法建立不独立的坐
标变分满足的关系.
三 广义坐标表示的虚位移原理
广义坐标:确定质点系位形的独立坐标。
虚功原理的广义坐标表述:受理想约束的质点系,其平衡的充分必要条件是系统所有与广义
坐标对应的广义力为零
Qj = 0 ( j = 1,2,L, m)
∑ 其中
Qj
=
理论力学第三版 (洪嘉振) 答案第9章

1
9-1C 如图所示,均质摆杆的质量为 m,杆长为 2l。摆杆的铰 O 上有一驱动约束,驱动规律为 ϕ1 = θ − ω t ,θ为常数。试 (1)建立系统带拉格朗日乘子的封闭的动力学方程; (2)解出拉格朗日乘子。
r y O r y1
φ1
x
洪嘉振等《理论力学》第 3 版习题详解
2
&12 cos ϕ1 ⎞ & ⎞ ⎛ − lϕ x ⎛ 1 0 l sin ϕ1 ⎞⎛ & ⎟ ⎜ ⎟⎜ 1 ⎟ ⎜ &12 sin ϕ1 ⎟ &1 ⎟ = ⎜ − lϕ y ⎜ 0 1 − l cos ϕ1 ⎟⎜ & ⎟ ⎜0 0 ⎟⎜ ϕ ⎟ ⎜ ⎜ ⎟ 1 0 ⎝ ⎠⎝ &&1 ⎠ ⎝ ⎠
系统带拉格朗日乘子的动力学方程
⎛ ⎜m 0 ⎜ ⎜0 m ⎜0 0 ⎜ ⎝ ⎞ &⎞ ⎛ 0 ⎟⎛ & 1 0 0 ⎞⎛ λ1 ⎞ ⎛ 0 ⎞ x ⎟⎜ ⎟ ⎜ ⎟ ⎟⎜ ⎟ ⎜ &⎟+⎜ y 0 ⎟⎜ & 0 1 0 ⎟⎜ λ2 ⎟ = ⎜ − mg ⎟ ml 2 ⎟⎜ ϕ ⎟ ⎜ ⎟⎜ ⎟ ⎜ ⎟ ⎟⎝ &&1 ⎠ ⎝ − l cos ϕ1 l sin ϕ1 1 ⎠⎝ λ3 ⎠ ⎝ 0 ⎠ 3 ⎠
得拉格朗日乘子 λ 的表达式
⎛ ⎜ m ⎛ λ1 ⎞ ⎜ ⎟ ⎜ = − λ 0 ⎜ 2⎟ ⎜ ⎜λ ⎟ ⎜ lm cos ϕ ⎝ 3⎠ ⎜ 1 ⎝
0 m 0 0 ml 2 3
− lm sin ϕ1
⎞ &⎞ ⎛ ⎟⎛ & 0 x ⎞ ⎟ ⎟⎜ ⎟ ⎜ & & + − y mg ⎟ ⎟⎜ ⎟ ⎜ ⎟ ⎜ mgl sin ϕ ⎟ ⎟⎜ & & ϕ 1⎠ ⎟⎝ ⎠ ⎝ ⎠
理论力学(机械工业出版社)第九章质点动力学习题解答

习 题9-1 如图9-9所示,一质量为700kg 的载货小车以v=1.6m/s 的速度沿缆车轨道下降,轨道的倾角a=15°,运动总阻力系数f =0.015;求小车匀速下降时缆索的拉力。
又设小车的制动时间为t=4s ,在制动时小车作匀减速运动,试求此时缆绳的拉力。
图9-90sin 1T =-+αmg F F)cos (sin cos sin sin 1T αααααf mg fmg mg F mg F -=-=-=N 1676)15cos 015.015(sin 8.9700=︒⨯-︒⨯⨯=2m/s 4.0406.1=-=amamg F F =-+αsin 2TN19564.07001676sin 1T 2T =⨯+=+=+-=ma F ma F mg F α9-2 小车以匀加速度a 沿倾角为a 的斜面向上运动,如图9-10所示。
在小车的平顶上放一重W 的物块,随车一同运动,试问物块与小车间的摩擦因数μ应为多少?图9-10y 方向0s i n c o s c o s N =--αααF W Fαμαt a n t a n N N F W F W F +=+= αμt a n 1N -=W Fx 方向ma W F F =-+αααsin cos sin NmaW F F =-+ααμαsin cos sin N N a g W W F =-+ααμαsin )cos (sin N a g W W W=-+-ααμααμsin )cos (sin tan 1 g a=--+ααμαμαsin tan 1cos sing a=-+-+αμααμααμαtan 1sin tan sin cos sin g a =-+αμαααμtan 1sin tan cos g a =-αμαμtan 1cos /1 g a =-αμαμsin cos 1 )sin (cos αμαμ-=g ag a a +=ααμsin cos 分析得 g a a +≥ααμsin cos9-3 如图9-11所示,在曲柄滑道机构中,滑杆与活塞的质量为50kg ,曲柄长300mm ,绕O 轴匀速转动,转速为n=120r/min 。
《理论力学》第九章_质点动力学_习题解

AC
g l AC
( cos )
F
n
TAC W cos man W an g
W an g
TAC W cos TAC W cos
W W 2 a n W cos l AC AC g g
初瞬时, AC 0 ,故: TAC W cos (2)求小球 A 运动到铅垂位置时,AC 绳中的拉力 小球运动到铅垂位置时,由上一步骤可知:
dx 9 cos(2t )d (2t ) dt
2
dx 9 sin(2t ) C1 dt
x 9 sin(2t ) C1
x |t 0 x0 9 sin(2 0) C1 C1 0
dx 9 sin(2t ) dt 9 x sin(2t )d (2t ) 2 9 x cos(2t ) C 2 2 9 9 x |t 0 x0 cos(2 0) C 2 C 2 4.5(m) C 2 (m) 0.04(m) 2 2
y
v0
30 0
1m
地面
v x v0 cos 30 0 dx 13 3 dt 2 x 13 3 t C1 2
13 3 (m / s ) 2
mg
O
x
x |t 0
13 3 0 C1 C1 0 2
x
13 3 t 2
v y v0 sin 30 0 gt 6.5 9.8t
x
y
5
[习题 9-4] 通过光滑圆环 C 的绳索将物体 A 与 B 相连,已知 m A 7.5kg , mB 6.0kg , 物体 A 与水平面的摩擦因素 f 0.6 , 在图示瞬时, 物体 B 具有朝右上方的速度 v B 2m / s 。 若在此时突然剪断墙与物体间的绳子,求该瞬时物体 A 的加速度 a A 解: (1)求 AB 间绳子的拉力 以 B 为研究对象,其受力如图所示。
理论力学(刘又文 彭献)答案第9章

∑ FQx =
δWF (x) δx
=
−k1xδx − (δx tanα )(m2 δx
+
m3 )g
=
−k1x − (m2
+ m3)g
tan α
令 δx = 0, δ y ≠ 0 ,则
∑ δWF ( y)
=
−k2
⎛ ⎜ ⎝
y
−
m3 g k2
⎞ ⎟ δy ⎠
−
m3 gδy
质量,试求系统对应于广义坐标 x 、ϕ 的广义力。
x
A
ϕ
θ
mg
B
图 9.2
答:系统自由度为 2。令虚位移 δx ≠ 0 , δϕ = 0 ,则
∑ δWF (x) = mg sinθ δx
故
∑ FQx =
δWF (x) = mg sinθ δx
令虚位移 δx = 0, δϕ ≠ 0 ,则
∑ δWF (ϕ )
10.对于受完整而非理想约束的系统,只要把非理想约束解除,代之以约束
力,并视其为主动力,则仍能应用拉格朗日方程。对吗?
答:对。当主动力全为非有势力时,采用上述第一种形式的拉氏方程;当主
动力中既有势力,又有非有势力,则采用第三种形式的拉格朗日方程。
11. 如图 9.5 所示,均质杆 AB 的质量为 m、长为 l,用光滑铰链铰结于不计
−
1 2
ar
=
0
(1)
令 δϕ = 0 , δx ≠ 0 ,则
−
G1 g
a1δx
−
G2 g
a1δx
+
G2 g
ar
cosθ
δx
=
南航理论力学习题答案9(1)

第九章刚体的平面运动1.平面运动刚体相对其上任意两点的( )。
① 角速度相等,角加速度相等② 角速度相等,角加速度不相等③ 角速度不相等,角加速度相等④ 角速度不相等,角加速度不相等正确答案:①2.在图示瞬时,已知O 1A = O 2B ,且O 1A 与O 2 B 平行,则( )。
① ω1 = ω2,α1 = α2② ω1≠ω2,α1 = α2③ ω1 = ω2,α1 ≠α2④ ω1≠ω2,α1 ≠α2正确答案:③3.设平面图形上各点的加速度分布如图①~④所示,其中不可能发生的是( )。
正确答案:②4.刚体平面运动的瞬时平动,其特点是( )。
① 各点轨迹相同;速度相同,加速度相同② 该瞬时图形上各点的速度相同③ 该瞬时图形上各点的速度相同,加速度相同④ 每瞬时图形上各点的速度相同正确答案:②5.某瞬时,平面图形上任意两点A 、B 的速度分别v A 和v B ,如图所示。
则此时该两点连线中点C 的速度v C 和C 点相对基点A的速度v CA 分别为( )和( )。
① v C = v A + v B ② v C = ( v A + v B )/2③ v C A = ( v A - v B )/2 ④ v C A = ( v B - v A )/2正确答案:② ④α1α2 ①②③④6.平面图形上任意两点A 、B 的加速度a A 、a B 与连线AB 垂直,且a A ≠ a B ,则该瞬时,平面图形的角速度ω和角加速度α应为( )。
① ω≠0,α ≠0② ω≠0,α = 0③ ω = 0,α ≠0④ ω = 0,α = 0正确答案:③7.平面机构在图示位置时,AB 杆水平,OA 杆鉛直。
若B 点的速度v B ≠0,加速度τB a = 0,则此瞬时OA 杆的角速度ω和角加速度α为( )。
① ω = 0,α ≠0② ω≠0,α = 0③ ω = 0,α = 0④ ω≠0,α ≠0正确答案:②8.在图示三种运动情况下,平面运动刚体的速度瞬心:(a )为( );(b )为( );(c )为( )。
理论力学第九章习题
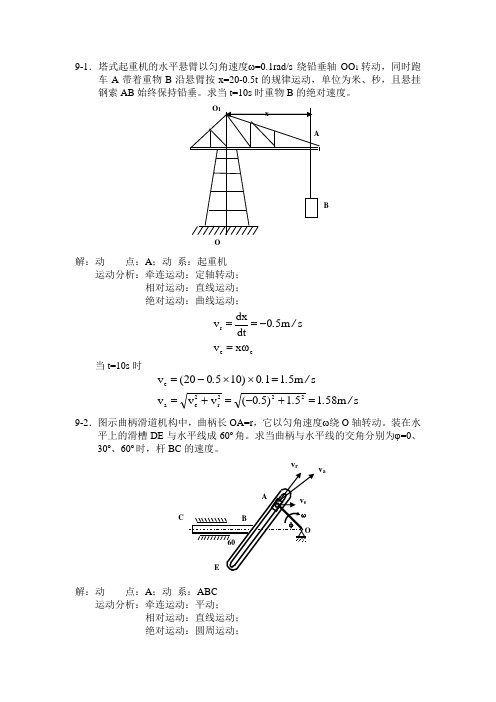
9-1.塔式起重机的水平悬臂以匀角速度ω=0.1rad/s 绕铅垂轴OO 1转动,同时跑车A 带着重物B 沿悬臂按x=20-0.5t 的规律运动,单位为米、秒,且悬挂钢索AB 始终保持铅垂。
求当t=10s 时重物B 的绝对速度。
解:动 点:A ;动 系:起重机运动分析:牵连运动:定轴转动; 相对运动:直线运动; 绝对运动:曲线运动;ee r ωx v sm 50dtdx v =-==/.当t=10s 时sm 58151)50(v v v s m 5110)105020(v 222r 2e a e /.../...=+-=+==⨯⨯-=9-2.图示曲柄滑道机构中,曲柄长OA=r ,它以匀角速度ω绕O 轴转动。
装在水平上的滑槽DE 与水平线成60o 角。
求当曲柄与水平线的交角分别为ϕ=0、30o 、60o 时,杆BC 的速度。
解:动 点:A ;动 系:ABC 运动分析:牵连运动:平动; 相对运动:直线运动; 绝对运动:圆周运动;OBC v rv a由正弦定理得:()()()12030φv v φ90v 30φv 120v ae rea sin sin sin sin sin -=-=-=当ϕ=0o 时, ωr 33v e -=当ϕ=30o 时, 0v e = 当ϕ=60o 时, ωr 33v e =9-3.图示曲柄滑道机构中,杆BC 为水平,而杆DE 保持铅垂。
曲柄长OA=10cm ,以匀角速度ω=20rad/s 绕O 轴转动,通过滑块A 使杆BC 作往复运动。
求当曲柄与水平线的交角分别为ϕ=0、30o 、90o 时,杆BC 的速度。
解:动 点:A ;动 系:BDC 运动分析:牵连运动:平动;相对运动:直线运动; 绝对运动:圆周运动;φv v s cm 200ωr v a e a sin /===当ϕ=0o 时, 0v e =;当ϕ=30o 时, s cm 100v e /=; 当ϕ=90o 时, s cm 200v e /=9-4.矿砂从传送带A 落到另一传送带B 的绝对速度为v 1=4m/s ,其方向与铅垂线成30o 角。
理论力学课后习题答案 第9章 动量矩定理及其应用)

习题9-2图习题20-3图习题20-3解图OxF Oy F gm Ddα第9章 动量矩定理及其应用9-1 计算下列情形下系统的动量矩。
1. 圆盘以ω的角速度绕O 轴转动,质量为m 的小球M 可沿圆盘的径向凹槽运动,图示瞬时小球以相对于圆盘的速度v r 运动到OM = s 处(图a );求小球对O 点的动量矩。
2. 图示质量为m 的偏心轮在水平面上作平面运动。
轮心为A ,质心为C ,且AC = e ;轮子半径为R ,对轮心A 的转动惯量为J A ;C 、A 、B 三点在同一铅垂线上(图b )。
(1)当轮子只滚不滑时,若v A 已知,求轮子的动量和对B 点的动量矩;(2)当轮子又滚又滑时,若v A 、ω已知,求轮子的动量和对B 点的动量矩。
解:1、2s m L O ω=(逆)2、(1))1()(Remv e v m mv p A A C +=+==ωRv me J R e R mv J e R mv L A A A C C B)()()(22-++=++=ω(2))(e v m mv p A C ω+==ωωωω)()()())(()(2meR J v e R m me J e R e v m J e R mv L A A A A C C B +++=-+++=++=9-2 图示系统中,已知鼓轮以ω的角速度绕O 轴转动,其大、小半径分别为R 、r ,对O 轴的转动惯量为J O ;物块A 、B 的质量分别为m A 和m B ;试求系统对O 轴的动量矩。
解:ω)(22r m R m J L B A O O ++=9-3 图示匀质细杆OA 和EC 的质量分别为50kg 和100kg ,并在点A 焊成一体。
若此结构在图示位置由静止状态释放,计算刚释放时,杆的角加速度及铰链O 处的约束力。
不计铰链摩擦。
解:令m = m OA = 50 kg ,则m EC = 2m 质心D 位置:(设l = 1 m) m 6565===l OD d 刚体作定轴转动,初瞬时ω=0l mg lmg J O ⋅+⋅=22α222232)2(212131ml ml l m ml J O =+⋅⋅+=即mgl ml 2532=α2rad/s 17.865==g l α gl a D 362565t =⋅=α 由质心运动定理: Oy D F mg a m -=⋅33t4491211362533==-=mg g mmg F Oy N (↑) 0=ω,0n=D a , 0=Ox F习题9-1图(a)v (b)(b ) 习题9-5解图习题9-5图J 9-4 卷扬机机构如图所示。
清华大学-理论力学-习题解答-9-09

! sin ϕ − z ! cos ϕ ) x = 2ω ( y !! !! ! y = −2ω x sin ϕ !! ! cos ϕ z = − g + 2ω x
! (0) = 0,y ! (0) = v0 cos α,z ! (0) = v0 sin α 。 初始条件为: x(0) = y (0) = z (0) = 0;x
(1)
将 ω = 0 代入(1)式,得到零次近似项:
x0 = 0 !! y0 = 0 !! !! z0 = − g !0 (0) = 0,y ! 0 (0) = v0 cos α,z !0 (0) = v0 sin α 得: 积分上式,并由初始条件 x0 (0) = y0 (0) = z0 (0) = 0;x !0 = 0 x ! 0 = v0 cos α y z !0 = − gt + v0 sin α !! ! 将上式代入公式 r 1 = − gk − 2ω × r0 ,可得第一次近似项: !! r1 = − gk + 2ω (v0 sin ϕ cos α − v0 cos ϕ sin α + gt cos ϕ )i
1 x1 = ω (v0 sin ϕ cos பைடு நூலகம் − v0 cos ϕ sin α )t 2 + ω gt 3 cos ϕ 3
故经过时间 t 后,炮弹偏东的距离为 ω v0 t 2 sin(ϕ − α ) + ω gt 3 cos ϕ 。
(word完整版)理论力学习题解答第九章

9-1在图示系统中,均质杆OA 、AB 与均质轮的质量均为m ,OA 杆的长度为1l ,AB 杆的长度为2l ,轮的半径为R ,轮沿水平面作纯滚动。
在图示瞬时,OA 杆的角速度为ω,求整个系统的动量.ω125ml ,方向水平向左题9-1图 题9-2图9-2 如图所示,均质圆盘半径为R ,质量为m ,不计质量的细杆长l ,绕轴O 转动,角速度为ω,求下列三种情况下圆盘对固定轴的动量矩: (a )圆盘固结于杆;(b )圆盘绕A 轴转动,相对于杆OA 的角速度为ω-; (c )圆盘绕A 轴转动,相对于杆OA 的角速度为ω。
(a )ω)l R (m L O 222+=;(b )ω2ml L O =;(c )ω)l R (m L O 22+= 9-3水平圆盘可绕铅直轴z 转动,如图所示,其对z 轴的转动惯量为z J 。
一质量为m 的质点,在圆盘上作匀速圆周运动,质点的速度为0v ,圆的半径为r ,圆心到盘中心的距离为l 。
开始运动时,质点在位置0M ,圆盘角速度为零。
求圆盘角速度ω与角ϕ间的关系,轴承摩擦不计。
9-4如图所示,质量为m 的滑块A ,可以在水平光滑槽中运动,具有刚性系数为k 的弹簧一端与滑块相连接,另一端固定。
杆AB 长度为l ,质量忽略不计,A 端与滑块A 铰接,B 端装有质量1m ,在铅直平面内可绕点A 旋转.设在力偶M 作用下转动角速度ω为常数.求滑块A 的运动微分方程。
t l m m m x m m kxωωsin 2111+=++9-5质量为m,半径为R的均质圆盘,置于质量为M的平板上,沿平板加一常力F。
设平板与地面间摩擦系数为f,平板与圆盘间的接触是足够粗糙的,求圆盘中心A点的加速度。
9-6均质实心圆柱体A 和薄铁环B 的质量均为m ,半径都等于r ,两者用杆AB 铰接,无滑动地沿斜面滚下,斜面与水平面的夹角为θ,如图所示。
如杆的质量忽略不计,求杆AB 的加速度和杆的内力.θsin 74g a =; 9-7均质圆柱体A 和B 的质量均为m ,半径为r ,一绳缠在绕固定轴O 转动的圆柱A 上,绳的另一端绕在圆柱B 上,如图所示.摩擦不计。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
理论力学习题解答第九章
题9-2图9-2 如图所示,均质圆盘半径为R,质量为m ,不计质量的细杆长,绕轴O转动,角速度为,求下列三种情况下圆盘对固定轴的动量矩:(a)圆盘固结于杆;(b)圆盘绕A轴转动,相对于杆OA的角速度为;(c)圆盘绕A轴转动,相对于杆OA的角速度为。
(a);(b);(c)9-3水平圆盘可绕铅直轴转动,如图所示,其对轴的转动惯量为。
一质量为m的质点,在圆盘上作匀速圆周运动,质点的速度为,圆的半径为r,圆心到盘中心的距离为。
开始运动时,质点在位置,圆盘角速度为零。
求圆盘角速度与角间的关系,轴承摩擦不计。
9-4如图所示,质量为m的滑块A,可以在水平光滑槽中运动,具有刚性系数为k的弹簧一端与滑块相连接,另一端固定。
杆AB长度为l,质量忽略不计,A端与滑块A铰接,B端装有质量,在铅直平面内可绕点A旋转。
设在力偶M作用下转动角速度为常数。
求滑块A的运动微分方程。
9-5质量为m ,半径为R的均质圆盘,置于质量为M的平板上,沿平板加一常力F。
设平板与地面间摩擦系数为f,平板与圆盘间的接触是足够粗糙的,求圆盘中心A点的加速度。
9-6均质实心圆柱体A和薄铁环B的质量均为m,半径都等于r,两者用杆AB铰接,无滑动地沿斜面滚下,斜面与水平面的夹角为,如图所示。
如杆的质量忽略不计,求杆AB的加速度和杆的内力。
;9-7均质圆柱体A和B的质量均为
m,半径为r,一绳缠在绕固定轴O转动的圆柱A上,绳的另一端绕在圆柱B上,如图所示。
摩擦不计。
求:(1)圆柱体B下落时质心的加速度;(2)若在圆柱体A上作用一逆时针转向,矩为M 的力偶,试问在什么条件下圆柱体B的质心加速度将向上。
9-8平面机构由两匀质杆AB,BO组成,两杆的质量均为m,长度均为l,在铅垂平面内运动。
在杆AB上作用一不变的力偶矩M,从图示位置由静止开始运动。
不计摩擦,试求当A即将碰到铰支座O时A 端的速度。
9-9长为l、质量为m的均质杆OA以球铰链O固定,并以等角速度绕铅直线转动,如图所示。
如杆与铅直线的夹角为,求杆的动能。
题9-9图题9-10图9-10物质量为,沿楔状物D的斜面下降,同时借绕过滑车C的绳使质量为的物体B上升,如图所示。
斜面与水平成角,滑轮和绳的质量和一切摩擦均略去不计。
求楔状物D作用于地板凸出部分E的水平压力。
9-11鼓轮重,对轮心点的回转半径为,物块重,均质圆轮半径为,重为,在倾角为的斜面上只滚动不滑动,其中,,弹簧刚度系数为,绳索不可伸长,定滑轮质量不计。
在系统处于静止平衡时,给轮心以初速度,求轮沿斜面向上滚过距离时,轮心的速度vB。
解:轮作平面运动,物块作平动①代入已知数据得:同理取平衡位置为各物体重力势能的零位置,有:为确定,考虑静平衡时,及轮,由,得:由,有:代入①,有解得:题9-11图9-12 均质棒AB的质量为,其两端悬挂在两条平行绳上,棒处在水平位置,如图所
示。
设其中一绳突然断了,试用刚体平面运动方程求此瞬时另一绳的张力。
9-13图示机构中,物块
A、B的质量均为,两均质圆轮
C、D的质量均为,半径均为。
C轮铰接于无重悬臂梁CK上,D为动滑轮,梁的长度为,绳与轮间无滑动。
系统由静止开始运动,求:(1)A物块上升的加速度;(2)HE段绳的拉力;(3)固定端K处的约束反力。
;;题9-13图题9-14图9-14匀质细杆,长为,放在铅直面内与水平面成角,杆的端靠在光滑的铅直墙上,端放在光滑的水平面上,杆由静止状态在重力作用下倒下。
求:(1)杆在任意位置时的角速度和角加速度;(2)当杆的端脱离墙时,杆与水平面所成的角多大?9-15鼓轮重,置于水平面上,外半径,轮轴半径,对质心轴的回转半径。
缠绕在轮轴上的软绳水平地连于固定点,缠在外轮上的软绳水平地跨过质量不计的定滑轮,吊一重物,重。
鼓轮与水平面之间的动摩擦系数为0、4,求轮心的加速度。
解:分别取轮和重物为研究对象,轮作平面运动,设其角加速度为,轮心加速度,由题知,物加速度对轮列平面运动微分方程:
(1)(2)即:
(3)对重物:,即:
(4)(2)代入(3)式,有:
(5):
(6)(5)+(6):
题9-15图题9-16图9-16 三根匀质细杆的长均为,质量均为,铰接成一等边三角形,在铅垂平面内悬挂在固定铰接支座上。
在图示瞬时处的铰链销钉突然脱落,系统由静止进入运动,试求销钉脱落的瞬时,(1)杆的角加速度;(2)杆的角加速度。
解:(1)取为研究对象,杆长为,质量为,依刚体转动微分方程:∵ ∴ (顺时针)(2)分别取,为研究对象::(1):
(2)(3)(4)由(2)得:
(5)由(4)得:
(6)将(5),(6)式代入(1)式,化简后得:
(7)将(6)式代入(3)式,化简得:
(8)解(7)与(8)式得:(逆时针)将值代入(7)解得:(顺时针)9-17图示匀质细长杆AB,质量为m,长度为l,在铅垂位置由静止释放,借A端的水滑轮沿倾斜角为的轨道滑下。
不计摩擦和小滑轮的质量,试求刚释放时点A的加速度。
习题9-17图解:图(a),初瞬时,以A为基点,则即(1)(2)由平面运动微分方程:(a)∴(3)(4)即(5)解(2)、(4)、(5)联立,得(6)由(1)、(3),得(6)代入,得题9-17图题9-18图9-18匀质细长杆AB,质量为m,长为l,CD = d,与铅垂墙间的夹角为,D棱是光滑的。
在图示位置将杆突然释放,试求刚释放时,质心C的加速度和D处的约束力。
习题9-18图解:初始静止,杆开始运动瞬时,必沿支承处
切向,即沿AB方向,所以此时沿AB方向,如图(a),以D为基点:由(1)由AB作平面运动:(2)(a)(3)(4)由(3),解(1)、(2)、(4)联立9-19匀质杆AB,质量为m、长为L,两端均以速度v0下落,且这时杆与铅垂线的夹角为。
假设碰撞以后杆将绕A点作定轴转动。
试求:(1)碰撞前后的能量损失;(2)B点与水平面即将接触时的速度。
解:动量矩守恒:倒下着地时:得:
题9-19图题9-20图9-20匀质圆柱体的质量m =10kg、半径r =30cm,沿水平轨道以匀速v0 =2m/s作纯滚动时,碰到高h =6cm的障碍。
设恢复系数e = 0,A处有足够的摩擦力,试求:(1)碰撞结束时圆柱体的角速度;(2)使圆柱能超过障碍的v0的大小;(3)碰撞时动能的损失;(4)碰撞冲量的水平及竖直分量。
解:由对A点冲量矩守恒:得:9-21两根相同的均质直杆在B处铰接并铅垂静止地悬挂在铰链C处,如图所示。
设每杆长l=1、2m,质量m=4kg。
现在下端A处作用一个冲量为I=14Ns的水平碰撞力,求碰撞后BC杆的角速度。
(顺时针)题9-21图题9-22图9-22 质量为0、2kg的垒球以水平方向的速度km/h打在一质量为2、4kg的匀质木棒上,木棒的一端用细绳悬挂于天花板上。
若恢复系数为0、5,求碰撞后棒两端
A、B的速度。
