数值计算课后答案2
(湖南大学-曾金平《数值计算方法》课后题答案)

1习题一1.设x>0相对误差为2%,4x的相对误差。
解:由自变量的误差对函数值引起误差的公式:(())(())'()()()()f x xf x f x xf x f xδδ∆=≈得(1)()f x=11()()*2%1%22x xδδδ≈===;(2)4()f x x=时444()()'()4()4*2%8%xx x x xxδδδ≈===2.设下面各数都是经过四舍五入得到的近似数,即误差不超过最后一位的半个单位,试指出他们各有几位有效数字。
(1)12.1x =;(2)12.10x =;(3)12.100x =。
解:由教材9P关于1212.m nx a a a bb b=±型数的有效数字的结论,易得上面三个数的有效数字位数分别为:3,4,53.用十进制四位浮点数计算(1)31.97+2.456+0.1352;(2)31.97+(2.456+0.1352)哪个较精确?解:(1)31.97+2.456+0.1352≈21((0.3197100.245610)0.1352)fl fl⨯+⨯+=2(0.3443100.1352)fl⨯+=0.3457210⨯(2)31.97+(2.456+0.1352)21(0.319710(0.245610))fl fl≈⨯+⨯= 21(0.3197100.259110)fl⨯+⨯=0.3456210⨯易见31.97+2.456+0.1352=0.345612210⨯,故(2)的计算结果较精确。
4.计算正方形面积时,若要求面积的允许相对误差为1%,测量边长所允许的相对误差限为多少?2解:设该正方形的边长为x,面积为2()f x x=,由(())(())'()()()()f x xf x f x xf x f xδδ∆=≈解得(())()()'()f x f xxxf xδδ≈=2(())(())22f x x f xx xδδ==0.5%5.下面计算y的公式哪个算得准确些?为什么?(1)已知1x<<,(A)11121xyx x-=-++,(B)22(12)(1)xyx x=++;(2)已知1x>>,(A)y=,(B)y=;(3)已知1x<<,(A)22sin xyx=,(B)1cos2xyx-=;(4)(A)9y=(B)y=解:当两个同(异)号相近数相减(加)时,相对误差可能很大,会严重丧失有效数字;当两个数相乘(除)时,大因子(小除数)可能使积(商)的绝对值误差增大许多。
数值计算方法课后习题答案

第一章 绪论(12)1、设0>x ,x 的相对误差为δ,求x ln 的误差。
[解]设0*>x 为x 的近似值,则有相对误差为δε=)(*x r ,绝对误差为**)(x x δε=,从而x ln 的误差为δδεε=='=*****1)()(ln )(ln x x x x x , 相对误差为****ln ln )(ln )(ln x x x x rδεε==。
2、设x 的相对误差为2%,求n x 的相对误差。
[解]设*x 为x 的近似值,则有相对误差为%2)(*=x r ε,绝对误差为**%2)(x x =ε,从而nx 的误差为nn x x nxn x x n x x x **1***%2%2)()()()(ln *⋅=='=-=εε,相对误差为%2)()(ln )(ln ***n x x x nr==εε。
3、下列各数都是经过四舍五入得到的近似数,即误差不超过最后一位的半个单位,试指出它们是几位有效数字:1021.1*1=x ,031.0*2=x ,6.385*3=x ,430.56*4=x ,0.17*5⨯=x 。
[解]1021.1*1=x 有5位有效数字;0031.0*2=x 有2位有效数字;6.385*3=x 有4位有效数字;430.56*4=x 有5位有效数字;0.17*5⨯=x 有2位有效数字。
4、利用公式(3.3)求下列各近似值的误差限,其中*4*3*2*1,,,x x x x 均为第3题所给的数。
(1)*4*2*1x x x ++; [解]3334*4*2*11***4*2*1*1005.1102110211021)()()()()(----=⨯=⨯+⨯+⨯=++=⎪⎪⎭⎫ ⎝⎛∂∂=++∑x x x x x f x x x e nk k k εεεε;(2)*3*2*1x x x ;[解]52130996425.010********.2131001708255.01048488.2121059768.01021)031.01021.1(1021)6.3851021.1(1021)6.385031.0()()()()()()()()(3333334*3*2*1*2*3*1*1*3*21***3*2*1*=⨯=⨯+⨯+⨯=⨯⨯+⨯⨯+⨯⨯=++=⎪⎪⎭⎫⎝⎛∂∂=-------=∑x x x x x x x x x x x f x x x e n k k kεεεε;(3)*4*2/x x 。
数值计算方法与算法第三版课后习题答案

数值计算方法与算法第三版课后习题答案1. 矩阵乘法问题描述给定两个矩阵A和B,尺寸分别为n×m和m×p,求矩阵A 和矩阵B的乘积矩阵C,尺寸为n×p。
算法实现import numpy as npdef matrix_multiplication(A, B):n, m = A.shapem, p = B.shapeC = np.zeros((n, p))for i in range(n):for j in range(p):for k in range(m):C[i][j] += A[i][k] * B[k][j] return C示例A = np.array([[1, 2], [3, 4]])B = np.array([[5, 6], [7, 8]])C = matrix_multiplication(A, B)print(C)输出结果:[[19. 22.][43. 50.]]2. 数值积分问题描述给定一个函数f(x),以及积分区间[a, b],求函数f(x)在区间[a, b]上的定积分值∫abf(x)dx。
算法实现简单的数值积分算法是采用小梯形法,将区间[a, b]均分成n个子区间,然后计算每个子区间的面积,最后将这些子区间面积相加得到定积分值。
def numerical_integration(f, a, b, n):h = (b - a) / nintegral =0for i in range(n):x1 = a + i * hx2 = a + (i +1) * hintegral += (f(x1) + f(x2)) * h /2 return integral示例import mathf =lambda x: math.sin(x)a =0b = math.pin =100result = numerical_integration(f, a, b, n) print(result)输出结果:1.99983550388744363. 非线性方程求解问题描述给定一个非线性方程f(x) = 0,求方程的根x。
数值计算方法课后习题答案(李庆扬等) (修复的)

,。
第一章 绪论(12)1、设0>x ,x 的相对误差为δ,求x ln 的误差。
[解]设0*>x 为x 的近似值,则有相对误差为δε=)(*x r ,绝对误差为**)(x x δε=,从而x ln 的误差为δδεε=='=*****1)()(ln )(ln x xx x x , 相对误差为****ln ln )(ln )(ln x x x x rδεε==。
2、设x 的相对误差为2%,求n x 的相对误差。
[解]设*x 为x 的近似值,则有相对误差为%2)(*=x r ε,绝对误差为**%2)(x x =ε,从而nx 的误差为nn x x nxn x x n x x x **1***%2%2)()()()(ln *⋅=='=-=εε,相对误差为%2)()(ln )(ln ***n x x x nr==εε。
3、下列各数都是经过四舍五入得到的近似数,即误差不超过最后一位的半个单位,试指出它们是几位有效数字:1021.1*1=x ,031.0*2=x ,6.385*3=x ,430.56*4=x ,0.17*5⨯=x 。
[解]1021.1*1=x 有5位有效数字;0031.0*2=x 有2位有效数字;6.385*3=x 有4位有效数字;430.56*4=x 有5位有效数字;0.17*5⨯=x 有2位有效数字。
4、利用公式(3.3)求下列各近似值的误差限,其中*4*3*2*1,,,x x x x 均为第3题所给的数。
(1)*4*2*1x x x ++;[解]3334*4*2*11***4*2*1*1005.1102110211021)()()()()(----=⨯=⨯+⨯+⨯=++=⎪⎪⎭⎫ ⎝⎛∂∂=++∑x x x x x f x x x e nk k k εεεε;(2)*3*2*1x x x ;[解]52130996425.010********.2131001708255.01048488.2121059768.01021)031.01021.1(1021)6.3851021.1(1021)6.385031.0()()()()()()()()(3333334*3*2*1*2*3*1*1*3*21***3*2*1*=⨯=⨯+⨯+⨯=⨯⨯+⨯⨯+⨯⨯=++=⎪⎪⎭⎫⎝⎛∂∂=-------=∑x x x x x x x x x x x f x x x e n k k kεεεε;(3)*4*2/x x 。
数值计算方法习题答案(第二版)(绪论)

数值分析(p11页)4 试证:对任给初值x 0,0)a >的牛顿迭代公式112(),0,1,2,......k ak k x x x k +=+= 恒成立下列关系式:2112(1)(,0,1,2,....(2)1,2,......kk k x k x x k x k +-=-=≥=证明:(1)(21122k k k k k kx a x x x x +-⎫⎛-=+==⎪ ⎝⎭(2) 取初值00>x ,显然有0>k x ,对任意0≥k ,a a x a x x a x x k k k k k ≥+⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛+=+2121216 证明:若k x 有n 位有效数字,则n k x -⨯≤-110218, 而()k k k k k x x x x x 288821821-=-⎪⎪⎭⎫⎝⎛+=-+ nnk k x x 2122110215.22104185.28--+⨯=⨯⨯<-∴>≥ 1k x +∴必有2n 位有效数字。
8 解:此题的相对误差限通常有两种解法. ①根据本章中所给出的定理:(设x 的近似数*x 可表示为m n a a a x 10......021*⨯±=,如果*x 具有l 位有效数字,则其相对误差限为()11**1021--⨯≤-l a x x x ,其中1a 为*x 中第一个非零数)则7.21=x ,有两位有效数字,相对误差限为025.010221111=⨯⨯≤--x x e 71.22=x ,有两位有效数字,相对误差限为025.010221122=⨯⨯≤--x x e 3 2.718x =,有两位有效数字,其相对误差限为:00025.010221333=⨯⨯≤--x e x ②第二种方法直接根据相对误差限的定义式求解 对于7.21=x ,0183.01<-e x∴其相对误差限为00678.07.20183.011≈<-x e x 同理对于71.22=x ,有003063.071.20083.022≈<-x e x 对于718.23=x ,有00012.0718.20003.033≈<-x e x备注:(1)两种方法均可得出相对误差限,但第一种是对于所有具有n 位有效数字的近似数都成立的正确结论,故他对误差限的估计偏大,但计算略简单些;而第二种方法给出较好的误差限估计,但计算稍复杂。
《数值计算方法》课后题答案(湖南大学-曾金平)

习题一1.设x >0相对误差为2%,4x 的相对误差。
解:由自变量的误差对函数值引起误差的公式:(())(())'()()()()f x xf x f x x f x f x δδ∆=≈得(1)()f x =11()()*2%1%22x x δδδ≈===;(2)4()f x x =时444()()'()4()4*2%8%x x x x x xδδδ≈===2.设下面各数都是经过四舍五入得到的近似数,即误差不超过最后一位的半个单位,试指出他们各有几位有效数字。
(1)12.1x =;(2)12.10x =;(3)12.100x =。
解:由教材9P 关于1212.m nx a a a bb b =±型数的有效数字的结论,易得上面三个数的有效数字位数分别为:3,4,53.用十进制四位浮点数计算 (1)31.97+2.456+0.1352; (2)31.97+(2.456+0.1352)哪个较精确?解:(1)31.97+2.456+0.1352 ≈21((0.3197100.245610)0.1352)fl fl ⨯+⨯+ =2(0.3443100.1352)fl ⨯+=0.3457210⨯(2)31.97+(2.456+0.1352)21(0.319710(0.245610))fl fl ≈⨯+⨯ = 21(0.3197100.259110)fl ⨯+⨯ =0.3456210⨯易见31.97+2.456+0.1352=0.210⨯,故(2)的计算结果较精确。
4.计算正方形面积时,若要求面积的允许相对误差为1%,测量边长所允许的相对误差限为多少?解:设该正方形的边长为x ,面积为2()f x x =,由(())(())'()()()()f x xf x f x x f x f x δδ∆=≈解得(())()()'()f x f x x xf x δδ≈=2(())(())22f x x f x x xδδ==0.5%5.下面计算y 的公式哪个算得准确些?为什么?(1)已知1x <<,(A )11121xy x x-=-++,(B )22(12)(1)x y x x =++; (2)已知1x >>,(A )y=,(B )y =; (3)已知1x <<,(A )22sin x y x =,(B )1cos 2xy x-=;(4)(A)9y =(B )y =解:当两个同(异)号相近数相减(加)时,相对误差可能很大,会严重丧失有效数字;当两个数相乘(除)时,大因子(小除数)可能使积(商)的绝对值误差增大许多。
数值计算课后习题答案

习 题 一 解 答1.取3.14,3.15,227,355113作为π的近似值,求各自的绝对误差,相对误差和有效数字的位数。
分析:求绝对误差的方法是按定义直接计算。
求相对误差的一般方法是先求出绝对误差再按定义式计算。
注意,不应先求相对误差再求绝对误差。
有效数字位数可以根据定义来求,即先由绝对误差确定近似数的绝对误差不超过那一位的半个单位,再确定有效数的末位是哪一位,进一步确定有效数字和有效数位。
有了定理2后,可以根据定理2更规范地解答。
根据定理2,首先要将数值转化为科学记数形式,然后解答。
解:(1)绝对误差:e(x)=π-3.14=3.14159265…-3.14=0.00159…≈0.0016。
相对误差:3()0.0016()0.51103.14r e x e x x-==≈⨯有效数字:因为π=3.14159265…=0.314159265…×10,3.14=0.314×10,m=1。
而π-3.14=3.14159265…-3.14=0.00159…所以│π-3.14│=0.00159…≤0.005=0.5×10-2=21311101022--⨯=⨯所以,3.14作为π的近似值有3个有效数字。
(2)绝对误差:e(x)=π-3.15=3.14159265…-3.14=-0.008407…≈-0.0085。
相对误差:2()0.0085()0.27103.15r e x e x x--==≈-⨯有效数字:因为π=3.14159265…=0.314159265…×10,3.15=0.315×10,m=1。
而π-3.15=3.14159265…-3.15=-0.008407…所以│π-3.15│=0.008407……≤0.05=0.5×10-1=11211101022--⨯=⨯所以,3.15作为π的近似值有2个有效数字。
(3)绝对误差:22() 3.14159265 3.1428571430.0012644930.00137e x π=-=-=-≈-相对误差:3()0.0013()0.4110227r e x e x x--==≈-⨯有效数字:因为π=3.14159265...=0.314159265 (10)22 3.1428571430.3142857143107==⨯,m=1。
数值分析答案第二章参数估计习题

f(x)= () { > − ex λ ) λ 0λ ( x解: λe , x ≥ 0
第二章 参数估计 1.设母体X具有负指数分布,它的分布密度 −λ x 为 λe , x ≥ 0 f(x)= 0, x < 0 其中 λ > 0 。试用矩法求的估计量。 解:x e(λ ) f(x)=
0
1
θ −1
dx =
θ θ +1
X 估计EX
X ∴θ = 1− X
1 e 5.设母体X的密度为 f ( x) = 2σ
−
x
σ
, −∞ < x < ∞
试求 σ 的最大似然估计;并问所得估计量是 否的无偏估计. ∑x x n 解: n 1 −σ 1 n − σ
i
L = ∏ f ( xi ) = ∏
i =1 i =1
ln L = n ln θ + (θ − 1)∑ ln xi
i
0, 其他 n
i =1
( θ >0 )
n i =1
d ln L n ^= − n = + ∑ ln xi = 0,∴θ θ i dθ ∑ ln xi
i
2矩法估计
EX =
用
X 用估计EX
+∞
−∞
∫ x ⋅ f ( x)dx = ∫ x ⋅θ ⋅ x
2
给定置信概率1−α 即
P ( x − uα
2
σ/ n
,有 uα ,使
2
P{ u ≤ uα } = 1 − α
数值计算方法(宋岱才版)课后答案

第一章 绪论一 本章的学习要求(1)会求有效数字。
(2)会求函数的误差及误差限。
(3)能根据要求进行误差分析。
二 本章应掌握的重点公式(1)绝对误差:设x 为精确值,x *为x 的一个近似值,称e x x **=-为x *的绝对误差。
(2)相对误差:r e e x***=。
(3)绝对误差限:e x x ε***==-。
(4)相对误差限:r x x xxεε*****-==。
(5)一元函数的绝对误差限:设一元函数()()()0,df f x f x dx εε***⎛⎫==⋅ ⎪⎝⎭则。
(6)一元函数的相对误差限:()()1r df f x dx f εε****⎛⎫=⋅ ⎪⎝⎭。
(7)二元函数的绝对误差限:设一元函数()()(),0,f f x y f y y εε***⎛⎫∂==⋅ ⎪∂⎝⎭则。
(8)二元函数的相对误差限:()()()1r f f f x y x y f εεε******⎡⎤⎛⎫∂∂⎛⎫⎢⎥=⋅+⋅ ⎪ ⎪∂∂⎝⎭⎢⎥⎝⎭⎣⎦。
三 本章习题解析1. 下列各数都是经过四舍五入得到的近似值,(1)试指出它们有几位有效数字,(2)分别估计1123A X X X ***=及224X A X **=的相对误差限。
12341.1021,0.031,385.6,56.430x x x x ****====解:(1)1x *有5位有效数字,2x *有2位有效数字,3x *有4位有效数字,4x *有5位有效数字。
(2)1111123231312123,,,,A A AA x x x x x x x x x x x x ∂∂∂====∂∂∂由题可知:1A *为1A 的近似值,123,,x x x ***分别为123,,x x x 近似值。
所以()()111rA A Aεε***=()()()12311111123A A A x x x A X X X εεε*******⎡⎤⎢⎥=++⎢⎥⎢⎥⎣⎦⎛⎫⎛⎫⎛⎫∂∂∂ ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭43123131212311111010100.215222x x x x x x x x x **-**-**-***⎡⎤=⨯⨯+⨯⨯+⨯⨯=⎢⎥⎣⎦()222222424441,,,X A Ax A X x x x x ∂∂===-∂∂则有同理有2A *为2A 的近似值,2x *,4x *为2x ,4x 的近似值,代入相对误差限公式:()()222rA A Aεε***=()()24212224A A X X A X X εε*****⎡⎤⎢⎥=+⎢⎥⎢⎥⎣⎦⎛⎫⎛⎫∂∂ ⎪ ⎪∂∂⎝⎭⎝⎭()33542224411*********X X X X X **--***⎡⎤⎢⎥=⨯⨯+⨯⨯=⎢⎥⎣⎦2. 正方形的边长大约为100cm ,怎样测量才能使其面积误差不超过21cm ? 解:设正方形的边长为x ,则面积为2S x =,2dsx dx=,在这里设x *为边长的近似值,S *为面积的近似值:由题可知:()()1ds s x dx εε***=≤⎛⎫ ⎪⎝⎭即:()21x x ε**⋅≤ 推出:()10.005200xcm ε*≤=。
数值计算课后规范标准答案2
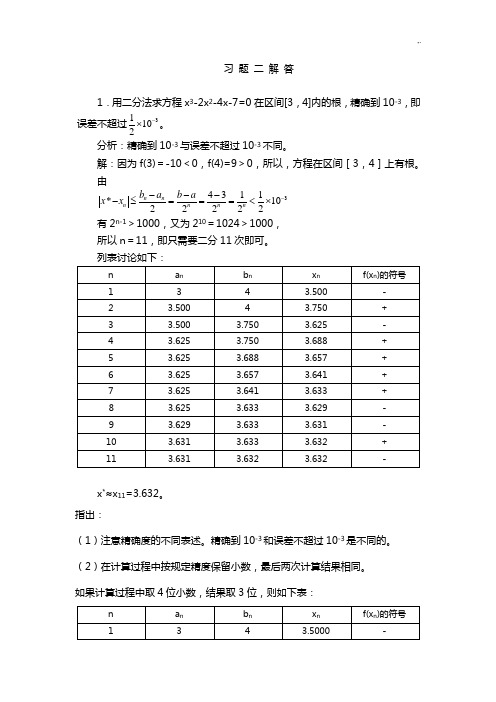
习 题 二 解 答1.用二分法求方程x 3-2x 2-4x-7=0在区间[3,4]内的根,精确到10-3,即误差不超过31102-⨯。
分析:精确到10-3与误差不超过10-3不同。
解:因为f(3)=-10<0,f(4)=9>0,所以,方程在区间[3,4]上有根。
由34311*1022222n n n n n n b a b a x x -----≤===<⨯ 有2n-1>1000,又为210=1024>1000, 所以n =11,即只需要二分11次即可。
x *≈x 11=3.632。
指出:(1)注意精确度的不同表述。
精确到10-3和误差不超过10-3是不同的。
(2)在计算过程中按规定精度保留小数,最后两次计算结果相同。
如果计算过程中取4位小数,结果取3位,则如下表:(3)用秦九韶算法计算f(x n )比较简单。
1*.求方程x 3-2x 2-4x-7=0的隔根区间。
解:令32247y x x x =---, 则2344322()()y x x x x '=--=+-当23443220()()y x x x x '=--=+-=时,有12223,x x =-=。
函数单调区间列表分析如下:因为214902150327(),()y y -=-<=-<,所以方程在区间223(,)-上无根; 因为21490327()y -=-<,而函数在23(,)-∞-上单调增,函数值不可能变号,所以方程在该区间上无根;因为2150()y =-<,函数在(2,+∞)上单调增,所以方程在该区间上最多有一个根,而(3)=-10<0,y(4)=9>0,所以方程在区间(3,4)有一个根。
所以,该方程有一个根,隔根区间是(3.4)。
2.证明1sin 0x x --=在[0,1]内有一个根,使用二分法求误差不大于41102-⨯的根,需要迭代多少次?分析:证明方程在指定区间内有一个根,就是证明相应的函数在指定区间有至少一个零点。
天津大学《数值计算方法》在线作业二答案

A.按模最大
B.按模最小
C.全部
D.任意一个
?
正确答案:B
8. ()是利用函数的值求自变量的值。
A.三次样条插值
B.反插值
C.分段插值
D.爱尔米特插值
?
正确答案:B
9. A.
B.
C.
D.
?
正确答案:B
10.梯形公式是求解常微分方程的()阶方法。
《数值计算方法》在线作业二
一,单选题
1. A. 1
B. 2
C. 0
D. 3
?
正确答案:A
2.设f(-1)=1,f(0)=3,f(2)=4,则抛物插值多项式中x2的系数为()。
A. -0.5
B. 0.5
C. 2
D. -2
?
正确答案:A
3.求解一阶常微分方程初值问题的梯形公式为()步法。
A.多
B. 2
C. 3
A.错误
B.正确
?
正确答案:A
8.高斯-塞德尔迭代法一定比雅可比迭代法收敛快。()
A.错误
B.正确
?
正确答案:A
9. A.错误
B.正确
?
正确答案:A
10.逐次超松弛迭代法是高斯-赛.正确
?
正确答案:B
A. 2
B. 4
C. 3
D. 5
?
正确答案:A
二,判断题
1.梯形方法是一种隐式的多步法。()
A.错误
B.正确
?
正确答案:A
2.求解微分方程初值问题的向后Euler法是隐式方法。()
A.错误
B.正确
现代数值计算方法习题解答

现代数值计算方法习题答案习 题 一1、解:根据绝对误差限不超过末位数的半个单位,相对误差限为绝对误差限除以有效数字本身,有效数字的位数根据有效数字的定义来求.因此49×10-2:E = 0.005; r E= 0.0102; 2位有效数字. 0.0490 :E = 0.00005;r E = 0.00102; 3位有效数字. 490.00 :E = 0.005; r E = 0.0000102;5位有效数字. 2、解:722= 3.1428 …… , π = 3.1415 …… ,取它们的相同部分3.14,故有3位有效数字.E= 3.1428 - 3.1415 = 0.0013 ;r E = 14.3E = 14.30013.0 = 0.00041. 3、解:101的近似值的首位非0数字1α= 1,因此有 |)(*x E r |)1(10121−−××=n < = 21× 10-4, 解之得n > = 5,所以 n = 5 . 4、证:)()(1)()(1)(*11**11**x x x nx E x n x E n n n−=≈−−)(11)()(1)()(*****11****x E nx x x n x x x x nx x E x E r nnnn n r =−=−≈=− 5、解:(1)因为=204.4721…… , 又=)(*x E |*x x −| = |47.420−| = 0.0021 < 0.01, 所以 =*x4.47. (2)20的近似值的首位非0数字1α = 4,因此有|)(*x E r |)1(10421−−××=n < = 0.01 , 解之得n > = 3 .所以,=*x 4.47. 6、解:设正方形的边长为x ,则其面积为2x y =,由题设知x 的近似值为*x = 10 c m .记*y 为y 的近似值,则)(20)(20)(2)(*****x E x x x x x y E =−=−= < = 0.1,所以)(*x E< = 0.005 c m . 7、解:因为)()(*1x x nx x E n n −≈−,所以n x nE x x x n xx E x E r nn nr 01.0)()()(*==−≈=. 8、解:9、证:)()()(**t gtE t t gt S S S E =−≈−=t t E gt t t gt S S S S E r )(22/)()(2**=−≈−= 由上述两式易知,结论. 10、解:代入求解,经过计算可知第(3)个计算结果最好.11、解:基本原则为:因式分解,分母分子有理化、三角函数恒等变形…… (1)通分;(2)分子有理化;(3)三角函数恒等变形.12、解: 因为20=x ,41.1*0=x ,所以|*00x x −| < = δ=×−21021于是有|*11x x −| = |110110*00+−−x x | = 10|*00x x −| < =δ10|*22x x −| = |110110*11+−−x x | = 10|*11x x −| < =δ210类推有 |*1010x x −| < =810102110×=δ 即计算到10x ,其误差限为δ1010,亦即若在0x 处有误差限为δ,则10x 的误差将扩大1010倍,可见这个计算过程是不稳定的.习 题 二1、 解:只用一种方法. (1)方程组的增广矩阵为:−−−−11114423243112M M M → −−−−1010411101110112M M M →−−−11041001110112M M M → 31=x , 12=x , 13=x . (2)方程组的增广矩阵为:−−−−−−017232221413M M M → −−247210250413M M M → −−147200250413M M M → 21=x , 12=x, 2/13=x . (3)适用于计算机编程计算.2、 解:第一步:计算U 的第一行,L 的第一列,得611=u 212=u 113=u 114−=u3/1/112121==u a l 6/1/113131==u a l 6/1/114141−==u a l第二步:计算U 的第二行,L 的第二列,得3/1012212222=−=u l a u 3/213212323=−=u l a u 3/114212424=−=u l a u 5/1/)(2212313232=−=u u l a l 10/1/)(2212414242=−=u u l a l第三步:计算U 的第三行,L 的第三列,得10/37233213313333=−−=u l u l a u 10/9243214313434−=−−=u l u l a u 37/9/)(33234213414343−=−−=u u l u l a l第四步:计算U 的第四行,得370/9553443244214414444−=−−−=u l u l u l a u从而,−−−−3101141101421126 =−−137/910/16/1015/16/10013/10001−−−370/95500010/910/37003/13/23/1001126 由b LY =, 解得Y =(6,-3,23/5,-955/370)T . 由Y UX = , 解得X =(1,-1,1,-1)T . 3、(1)解:首先检验系数矩阵的对称正定性,这可以通过计算其各阶顺序主子式是否大于零来判断. 11a = 3 > 0,2223= 2 > 0, 301022123 = 4 > 0,所以系数矩阵是对称正定的.记系数矩阵为A ,则平方根法可按如下三步进行:第一步 分解:A = L L T . 由公式计算出矩阵的各元素:311=l 33221=l 3622=l 3331=l 3632−=l 233=l 因此, L =−23633036332003. 第二步 求解方程组LY = b . 解得Y = (335,36,2)T . 第三步 求解方程组L T X = Y . 解得X =(0,2,1)T .(2)解:首先检验系数矩阵的对称正定性,这可以通过计算其各阶顺序主子式是否大于零来判断.11a = 3 > 0,2223= 2 > 0, 1203022323 = 6 > 0,所以系数矩阵是对称正定的.记系数矩阵为A ,则平方根法可按如下三步进行:第一步 分解:A = L L T . 由公式计算出矩阵的各元素:311=l 33221=l 3622=l 331=l 632−=l 333=l因此, L =−363036332003 . 第二步 求解方程组LY = b . 解得Y = (335,66−,33)T. 第三步 求解方程组L T X = Y . 解得X = (1,21,31)T. 4、解: 对1=i , 2111==a d ;对2=i , 121−=t , 2121−=l ,252−=d ; 对3=i , 131=t , 2732=t ,2131=l , 5732−=l ,5273=d .所以数组A 的形式为:−−−=527572102521002A 求解方程组LY = b . 解得Y = (4,7,569)T .求解方程组DL T X = Y . 解得X = (910,97,923)T .5、解:(1)设A = LU =1010000000000010010015432l l l l5432106000000000600006006u u u u u 计算各元素得: 51=u ,512=l , 1952=u , 1953=l , 19653=u , 65194=l , 652114=u , 211655=l , 2116655=u .求解方程组LY = d . 解得Y = (1,51−,191,651−,211212)T.求解方程组UX = Y . 解得X = (6651509,6651145,665703,665395−,665212)T.(2)设A = LU =100100132l l3211001u u u 计算各元素得:51=u ,512=l ,5242=u ,2453=l ,241153=u . 求解方程组LY = d . 解得Y = (17,553,24115)T. 求解方程组UX = Y . 解得X = (3,2,1)T . 6、证:(1)(2)相同. 因为此方程组的系数矩阵为严格对角占优矩阵,所以雅可比迭代法和相应的高斯-赛德尔迭代法都收敛. (1)雅可比迭代公式:7107271)(3)(2)1(1+−−=+k k k x x x14141)(3)(1)1(2+−−=+k k k x x x329292)(2)(1)1(3+−−=+k k k x x x高斯-赛德尔迭代公式:7107271)(3)(2)1(1+−−=+k k k x x x14141)(3)1(1)1(2+−−=++k k k x x x329292)1(2)1(1)1(3+−−=+++k k k x x x(2)雅可比迭代公式:545152)(3)(2)1(1+−=+k k k x x x 525351)(3)(1)1(2++−=+k k k x x x 5115152)(2)(1)1(3++=+k k k x x x 高斯-赛德尔迭代公式:545152)(3)(2)1(1+−=+k k k x x x 525351)(3)1(1)1(2++−=++k k k x x x5115152)1(2)1(1)1(3++=+++k k k x x x7、(1)证:因为此方程组的系数矩阵为严格对角占优矩阵,所以雅可比迭代法和相应的高斯-赛德尔迭代法都收敛。
数值计算课后全部答案(整合)
目录第一章-----------------------------------------1 第二章-----------------------------------------4 第三章-----------------------------------------9 第四章-----------------------------------------15 第五章-----------------------------------------20 第六章-----------------------------------------27 第七章-----------------------------------------30第一章数值计算中的误差习题一1.1 下列各近似数的绝对误差限是最末位的半个单位,试指出它们各有几位有效数字。
1x =-3.105 , 2x =0.001, 3x =0.100, 4x =253.40, 5x =5000, 6x =5⨯310.答案:4,1,3,6,4,1.1.2 设100>*x >10,x 是*x 的有五位有效数字的的近似数,求x 的绝对误差限。
答案:当10<x<100时,因为有5位有效数字,所以绝对误差限为0.005. 1.3 求下列各近似数的相对误差限和有效数字位数: 1) 123x x x ++,2) 124x x x 3) 24x x 答案:()10.0005e x ≤()20.0005e x ≤()30.0005e x ≤ ()40.005e x ≤ ()50.5e x ≤ ()60.5e x ≤1)()()()()123123e x x x e x e x e x ++=++≤()()()123e x e x e x ++3221.5100.15100.510---≤⨯=⨯≤⨯2123()0.1510x x x ε-++=⨯123123123()()0.0004993...0.0004994r x x x e x x x x x x ε++++==≤++123x x x ++=-3.004 精确到小数点后两位,所以有三位有效数字。
数值计算方法答案第2版 Doc2

Generated by Foxit PDF Creator © Foxit Software http://www.foxiห้องสมุดไป่ตู้ For evaluation only.
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
数值计算方法丁丽娟课后习题答案

数值计算方法丁丽娟课后习题答案【篇一:北京理工大学数值计算方法大作业数值实验1】)书p14/4分别将区间[?10,10]分为100,200,400等份,利用mesh或surf命令画出二元函数的三维图形。
z=|??|+ ??+?? +??++??【matlab求解】[x,y]=meshgrid(-10:0.1:10);a=exp(-abs(x));b=cos(x+y);c=1./(x.^2+y.^2+1);z=a+b+c;mesh(x,y,z);[x,y]=meshgrid(-10:0.05:10);a=exp(-abs(x));b=cos(x+y);c=1./(x.^2+y.^2+1);z=a+b+c;mesh(x,y,z);[x,y]=meshgrid(-10:0.025:10); a=exp(-abs(x));b=cos(x+y);c=1./(x.^2+y.^2+1);z=a+b+c;mesh(x,y,z);(二)书p7/1.3.2数值计算的稳定性(i)取= ??c语言程序—不稳定解 +=ln1.2,按公式=?? (n=1,2,…) #includestdio.h#includeconio.h#includemath.hvoid main(){float m=log(6.0)-log(5.0),n;int i;i=1;printf(y[0]=%-20f,m); while(i20){n=1/i-5*m;printf(y[%d]=%-20f,i,n);m=n;i++;if (i%3==0) printf(\n); }getch();}(ii) c语言程序—稳定解≈??[ ??+?? +?? ??+??按公式 =??(??)#includestdio.h#includeconio.h#includemath.hvoid main(){float m=(1/105.0+1/126.0)/2,n; k=n,n-1,n-2,…)(【篇二:北京理工大学数值计算方法大作业数值实验4】 p260/1考纽螺线的形状像钟表的发条,也称回旋曲线,它在直角坐标系中的参数方程为= ?????????????????? ?? ??????????= ?????????????? ??曲线关于原点对称,取a=1,参数s的变化范围[-5,5],容许误差限分别是,,和。
数值计算方法课后习题答案吕同富

数值计算方法课后习题答案吕同富【篇一:《数值计算方法》(二)课程教学大纲】txt>课程编号: l124008课程类别:专业必修学分数: 3 学时数:48 适用专业:信息与计算科学应修(先修)课程:数学分析、高等代数一、本课程的地位和作用数值分析(二)为数值分析课程的第二部分,它是信息与计算科学专业的一门专业必修课。
主要内容包括函数最佳逼近、数值积分、数值微分、常微分方程数值解法。
通过本课程的学习,学生将初步具备用计算机去有效地解决实际问题的能力。
二、本课程的教学目标通过本课程的学习,使学生了解和掌握求解函数最佳逼近、数值积分、数值微分、常微分方程等问题所涉及的各种常用的数值计算方法、数值方法的构造原理及适用范围。
本课程坚持理论与实践教学并重的原则,理论上主要讲述求解函数最佳逼近、数值积分、数值微分、常微分方程等问题的基本理论和基本方法。
与此同时,通过上机实验加深学生对各种计算方法的理解,为今后用计算机去有效地解决实际问题打下基础。
三、课程内容和基本要求(“*”记号标记难点内容,“▽”记号标记重点内容,“▽*”记号标记既是重点又是难点的内容)第六章函数最佳逼近 1.教学基本要求(1)理解:几类常用的正交多项式。
(2)掌握:最佳一致逼近和最佳平方逼近。
(3)掌握:曲线拟合的最小二乘法。
2.教学内容(1)*正交多项式。
(2)▽*最佳一致逼近。
(3)▽最佳平方逼近。
(4)正交多项式的逼近性质。
(5)▽曲线拟合的最小二乘法。
第七章数值积分 1.教学基本要求(1)理解:机械求积公式的基本思想、插值型求积公式的特点。
(2)掌握:newton-cotes求积公式、复合求积公式。
(3)掌握:romberg求积公式、gauss求积公式。
2.教学内容(1)*机械求积公式。
(2)▽newton-cotes求积公式。
(3)▽复合求积公式。
(4)变步长求积公式。
(5)▽romberg求积公式。
(6)▽*gauss求积公式第八章数值微分 1.教学基本要求(1)了解:数值微分的中点法。
最新数值计算课后答案2
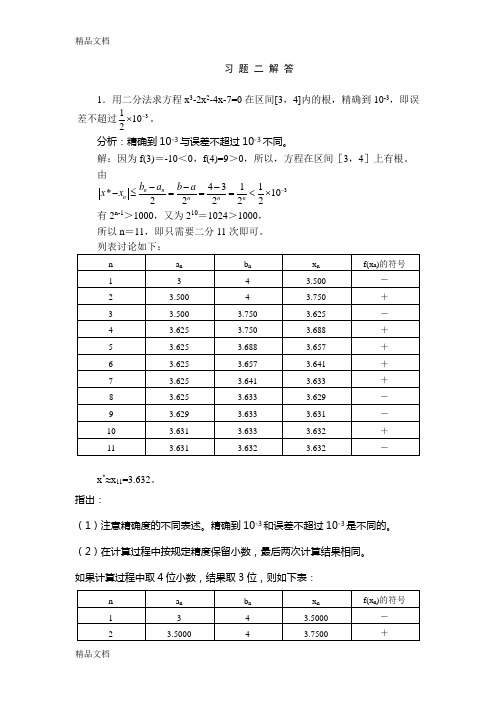
习 题 二 解 答1.用二分法求方程x 3-2x 2-4x-7=0在区间[3,4]内的根,精确到10-3,即误差不超过31102-⨯。
分析:精确到10-3与误差不超过10-3不同。
解:因为f(3)=-10<0,f(4)=9>0,所以,方程在区间[3,4]上有根。
由34311*1022222n n n n n n b a b a x x -----≤===<⨯ 有2n-1>1000,又为210=1024>1000, 所以n =11,即只需要二分11次即可。
x *≈x 11=3.632。
指出:(1)注意精确度的不同表述。
精确到10-3和误差不超过10-3是不同的。
(2)在计算过程中按规定精度保留小数,最后两次计算结果相同。
如果计算过程中取4位小数,结果取3位,则如下表:(3)用秦九韶算法计算f(x n )比较简单。
1*.求方程x 3-2x 2-4x-7=0的隔根区间。
解:令32247y x x x =---, 则2344322()()y x x x x '=--=+-当23443220()()y x x x x '=--=+-=时,有12223,x x =-=。
因为214902150327(),()y y -=-<=-<,所以方程在区间223(,)-上无根;因为21490327()y -=-<,而函数在23(,)-∞-上单调增,函数值不可能变号,所以方程在该区间上无根;因为2150()y =-<,函数在(2,+∞)上单调增,所以方程在该区间上最多有一个根,而(3)=-10<0,y(4)=9>0,所以方程在区间(3,4)有一个根。
所以,该方程有一个根,隔根区间是(3.4)。
2.证明1sin 0x x --=在[0,1]内有一个根,使用二分法求误差不大于41102-⨯的根,需要迭代多少次?分析:证明方程在指定区间内有一个根,就是证明相应的函数在指定区间有至少一个零点。
数值计算与MATLAB方法课后答案

第一章习题1. 序列满足递推关系,取及试分别计算,从而说明递推公式对于计算是不稳定的。
n1 1 0.01 0.00012 0.01 0.0001 0.0000013 0.0001 0.000001 0.000000014 0.000001 0.0000000110-105 0.00000001 10-10n1 1.000001 0.01 0.0000992 0.01 0.000099 -0.000099013 0.000099 -0.00009901-0.010000994 -0.00009901 -0.01000099-1.00015 -0.01000099-1.0001初始相差不大,而却相差那么远,计算是不稳定的。
2. 取y0=28,按递推公式,去计算y100,若取(五位有效数字),试问计算y100将有多大误差?y100中尚留有几位有效数字?解:每递推一次有误差因此,尚留有二位有效数字。
3.函数,求f(30)的值。
若开方用六位函数表,问求对数时误差有多大?若改用另一等价公式计算,求对数时误差有多大?设z=ln(30-y),,y*, |E(y)| 10-4z*=ln(30-y*)=ln(0.0167)=-4.09235若改用等价公式设z=-ln(30+y),,y*, |E(y)|⨯10-4z*=-ln(30+y*)=-ln(59.9833)=-4.094074.下列各数都按有效数字给出,试估计f的绝对误差限和相对误差限。
1)f=sin[(3.14)(2.685)]设f=sin xyx*=3.14, E(x)⨯10-2, y*=2.685, E(y)⨯10-3,sin(x*y*)=0.838147484, cos(x*y*)=-0.545443667⨯(-0.5454) ⨯⨯10-2+3.14(-0.5454) ⨯⨯10-3|⨯10-2⨯10-2|E r(f)| ⨯10-2⨯10-2<10-22)f=(1.56)设f = x y ,x*=1.56, E(x)⨯10-2, y*=3.414, E(y)⨯10-3,⨯⨯⨯10-2⨯⨯⨯10-3|⨯⨯⨯10-2⨯⨯⨯10-3|=0.051|E r(f)| =0.01125.计算,利用下列等式计算,哪一个得到的结果最好,为什么?6.下列各式怎样计算才能减少误差?7. 求方程x2-56x+1=0的二个根,问要使它们具有四位有效数字,至少要取几位有效数字?如果利用伟达定理, 又该取几位有效数字呢?解一:若要取到四位有效数字,如果利用伟达定理,解二:由定理二,欲使x1,x2有四位有效数字,必须使由定理一知,∆至少要取7位有效数字。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习 题 二 解 答1.用二分法求方程x 3-2x 2-4x-7=0在区间[3,4]内的根,精确到10-3,即误差不超过31102-⨯。
分析:精确到10-3与误差不超过10-3不同。
解:因为f(3)=-10<0,f(4)=9>0,所以,方程在区间[3,4]上有根。
由34311*1022222n n n n n n b a b a x x -----≤===<⨯ 有2n-1>1000,又为210=1024>1000, 所以n =11,即只需要二分11次即可。
x *≈x 11=3.632。
指出:(1)注意精确度的不同表述。
精确到10-3和误差不超过10-3是不同的。
(2)在计算过程中按规定精度保留小数,最后两次计算结果相同。
如果计算过程中取4位小数,结果取3位,则如下表:(3)用秦九韶算法计算f(x n )比较简单。
1*.求方程x 3-2x 2-4x-7=0的隔根区间。
解:令32247y x x x =---, 则2344322()()y x x x x '=--=+-当23443220()()y x x x x '=--=+-=时,有12223,x x =-=。
因为214902150327(),()y y -=-<=-<,所以方程在区间223(,)-上无根;因为21490327()y -=-<,而函数在23(,)-∞-上单调增,函数值不可能变号,所以方程在该区间上无根;因为2150()y =-<,函数在(2,+∞)上单调增,所以方程在该区间上最多有一个根,而(3)=-10<0,y(4)=9>0,所以方程在区间(3,4)有一个根。
所以,该方程有一个根,隔根区间是(3.4)。
2.证明1sin 0x x --=在[0,1]内有一个根,使用二分法求误差不大于41102-⨯的根,需要迭代多少次?分析:证明方程在指定区间内有一个根,就是证明相应的函数在指定区间有至少一个零点。
解:令()1sin f x x x =--,因为(0)10sin 010,(1)11sin1sin10f f =--=>=--=-<, 则(0)(1)0f f <,由零点定理,函数f(x)在[0,1]区间有一个根。
由41011*1022222n n n n n n b a b a x x -----≤===<⨯ 有2n-1>10000,又为210=1024,213=8192<10000,214=16384>10000 所以n =15,即需要二分15次。
指出:要证明的是有一个解而不是唯一解,因此不必讨论单调性。
3.试用迭代公式10220,1210k k k x x x x +==++,求方程32210200x x x ++-=的根,要求精确到510-。
分析:精确到510-即误差不超过51102-⨯解:令32()21020f x x x x =++-指出:精确到510-可以从两个方面判定。
第一,计算过程中取小数到510-位,最后两个计算结果相同,终止计算。
第二,计算过程中取小数到610-,当511102k k x x -+-<⨯终止计算。
本题采用第一种方法。
4.将一元非线性方程20cos x x e -=写成收敛的迭代公式,并求其在005.x =附近的根,要求精确到210-。
解:20cos x x e -=改写为222110cos cos cos x x xx xx e e e=⇒=⇒-=,则 21cos xxx x e =+-,设 21cos ()xxg x x e=+- 有 22224111)sin cos (sin cos )()()xxx xxx xe xe x x g x e e e π+--+'=+=-=-在005.x =处,因为05054051096151..)(.).g e π+'=-=<所以迭代法121cos ()kkk k x x g x x e +=+-在005.x =的邻域内收敛。
列表迭代如下:此时0692069000614.cos ..e -=。
5.为求方程3210x x --=在015.x =附近的一个根,设将方程改为下列等价形式,并建立相应的迭代公式:12213223121121111121111311(),;(),();(),.()k kk kk k x x x x x x x x x x x x +++=+=+=+=+==--迭代公式迭代公式迭代公式 试分析每种迭代公式的收敛性,并取一种公式求出具有4位有效数字的近似值。
解:(1)因为211x x =+,所以迭代函数为211()g x x=+,则23212()()()g x x x x --'''===-,3322152151153375(.)...g -'=-⨯==<满足局部收敛性条件,所以迭代公式1211k k x x +=+具有局部收敛性。
(2)因为1231()x x =+,所以迭代函数为1231()()g x x =+,则12122332231221213331()()()()x g x x x x x x --'=+=+=+,22321515045613115.(.).(.)g ⨯'==<+满足局部收敛性条件,所以迭代公式12311()k kx x +=+具有收敛性。
(3)因为1211()x x =-,所以迭代函数为1211()()g x x =-,则13122111122()()()g x x x ---'=--=--,32321115151141412205(.)(.)..g -'=-==>⨯不满足收敛性条件,所以迭代公式11211()k k x x +=-不具有收敛性。
用迭代公式1211k k x x +=+列表计算如下:所以,方程的近似根为1465*.x ≈。
6.设23()()x x C x ϕ=+-,应如何取C 才能使迭代公式1()k k x x ϕ+=具有局部收敛性?解:设C 为常数,因为23()()x x C x ϕ=+-,所以12()x Cx ϕ'=+,要使迭代公式具有局部收敛性,需00121()x Cx ϕ'=+<,此时即有01121Cx -<+<,也即010Cx -<<。
即只要C 取满足如上条件的常数,就可以使得迭代公式具有局部收敛性。
指出:本题的一般形式为:设()()x x Cf x ϕ=+,应如何取C 才能使迭代公式1()k k x x ϕ+=具有局部收敛性?显然,()()x x Cf x ϕ=+是迭代格式1()k k x x ϕ+=相应的迭代函数,因此该迭代格式要求解的方程是()()()0x x x x Cf x f x ϕ=⇒=+⇒=。
也就是说,这是如何选择C ,构造一个求解方程f(x)=0的收敛的迭代格式的问题。
因为()()x x Cf x ϕ=+,所以()1()x Cf x ϕ''=+, 要使迭代格式收敛,需()1()1x Cf x ϕ''=+< 解之得2()0Cf x '-<<,即C 与()f x '异号,且()2Cf x '<。
下面的讨论利用了本题的特殊条件,求出了具体的结果:因为23()()x x C x ϕ=+-,所以当2(3)x x C x =+-时,有2(3)0C x -=,则x =23()()x x C x ϕ=+-的不动点为*x =。
而12()x Cx ϕ'=+, 根据局部收敛性定理,当1210c ϕ'=+<⇒<<;当(12(10C c ϕ'=+<⇒<<时,迭代格式收敛到 7.用牛顿法求方程3310x x --=在初始值02x =邻近的一个正根,要求3110k k x x -+-<。
解: 因为3310x x --=所以有3()31f x x x =--,相应的迭代公式为3312231213333k k k k k k k x x x x x x x +--+=-=-- 取x 0=2为迭代的初始近似值。
迭代的结果列表如下:因为33210.0001102x x --=<⨯,符合计算的精度要求,所以*3 1.8794x x ≈=。
8.用牛顿法解方程10c x -=,导出计算数c 的倒数而不用除法的一种简单的迭代公式。
用此公式求0.324的倒数,设初始值03x =,要求计算有5位有效数字。
解:对于方程10c x -=,有1()f x c x =-,相应的迭代公式为212121kk k k k kc x x x x cx x +-=-=--。
应用该迭代公式求0.324的倒数,列表计算如下所以1308640324..≈。
指出:如果将方程10c x-=改写为等价的10cx -=,则有1()f x cx =-,相应的迭代公式为111k k k cx x x c c+-=-=无法展开迭代。
9.设a 的迭代公式,并求极限limk解:设a 为正实数,n 为自然数,由牛顿法,方程0()n f x x a =-=的解为11111()()(1)1[(1)]k k k k n n n k k k k n n k kn k n kk n kf x x x f x x a nx x a x nx nx n x a nxa n x n x +----=-'--+=-=-+==-+由此,则111111[(1)][(1)]lim 1[(1)(1)]1[(1)(1)]1[((1)()lim n k n k k k k k n k k nk k n k k a n x n x ax n a n x n a n x a n n x n --→∞----→∞-+-+==--+-=--+-=---=111]2(1)(1)(1)lim 22lim n n k kk k a n a n x x -++→∞→∞-⨯---====指出:本题中,表面上是k →∞的问题,但实际上却是k x 的问题,1,k k x x +才是极限过程中实际的变量。
本质上。
本题实际上是求极限11111[(1)][(1)]lim 1[(1)]n k n k k k k k n x a n x n x ax n x ax ----+-+==-+=由于讨论的是0型不定式,且不定式的分母上有2次的“0”因子,因此两次应用罗必塔法则。
解二:首先证明一个定理:定理:设**()0,()0f x f x '=≠,又设f(x)在*x 的某个邻域内具有连续的二阶导数,则牛顿迭代法具有局部收敛性,且有。
