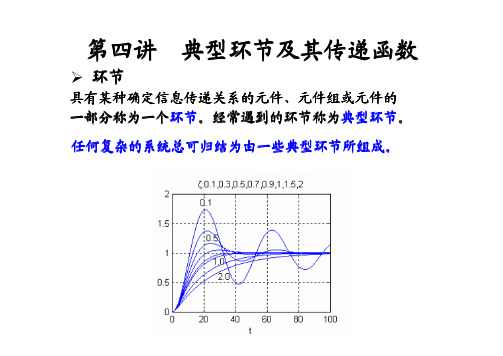
第二章-传递函数(第四讲)
合集下载
第4讲 典型环节
� 典型环节示例 � 比例环节
输出量不失真、无惯性、快速地跟随输入量，两者成 比例关系。
其运动方程为：xo(t)=Kxi(t)
xo(t)、xi(t)——分别为环节的输出量和输入量； K——比例系数，等于输出量与输入量之比。
比例环节的传递函数为： X o ( s) G( s) = =K X i ( s)
传递函数： G ( s ) = K τ 2 s 2 + 2ξ τs + 1
(
)
式中，τ——时间常数 ξ——阻尼比，对于二阶微分环节， 0<ξ<1 K——比例系数
系统数学模型 第二章 � 积分环节
输出量正比于输入量对时间的积分。 运动方程为： xo (t ) = 1 ∫ t xi (t )dt 0
T
车初始位置距平衡点1.0，则所建立模型如图示。
F c k 系统微分方程 ̇ ̇= − x ̇− x x m m m
若外力输入F=0，仿真所得示 波器窗口小车位移随时间变 化的轨迹如图。
F
为0
初值为1
第二章 系统数学模型
质量—弹簧—阻尼系统
F
F如下图 系统输入 系统输入F
系统输出 x如下图所示 系统输出x
微分环节的输出是输入的导数，即输出反映了 输入信号的变化趋势，从而给系统以有关输入 变化趋势的预告。因此， 微分环节常用来改善 变化趋势的预告。因此，微分环节常用来改善 控制系统的动态性能。
第二章 系统数学模型
� 二阶微分环节 运动方程：
⎡ 2 d2 ⎤ d xo (t ) = K ⎢τ x (t ) + 2ξ τ xi (t ) + xi (t )⎥, 0 < ξ < 1 2 i dt ⎣ dt ⎦
输出量不失真、无惯性、快速地跟随输入量，两者成 比例关系。
其运动方程为：xo(t)=Kxi(t)
xo(t)、xi(t)——分别为环节的输出量和输入量； K——比例系数，等于输出量与输入量之比。
比例环节的传递函数为： X o ( s) G( s) = =K X i ( s)
传递函数： G ( s ) = K τ 2 s 2 + 2ξ τs + 1
(
)
式中，τ——时间常数 ξ——阻尼比，对于二阶微分环节， 0<ξ<1 K——比例系数
系统数学模型 第二章 � 积分环节
输出量正比于输入量对时间的积分。 运动方程为： xo (t ) = 1 ∫ t xi (t )dt 0
T
车初始位置距平衡点1.0，则所建立模型如图示。
F c k 系统微分方程 ̇ ̇= − x ̇− x x m m m
若外力输入F=0，仿真所得示 波器窗口小车位移随时间变 化的轨迹如图。
F
为0
初值为1
第二章 系统数学模型
质量—弹簧—阻尼系统
F
F如下图 系统输入 系统输入F
系统输出 x如下图所示 系统输出x
微分环节的输出是输入的导数，即输出反映了 输入信号的变化趋势，从而给系统以有关输入 变化趋势的预告。因此， 微分环节常用来改善 变化趋势的预告。因此，微分环节常用来改善 控制系统的动态性能。
第二章 系统数学模型
� 二阶微分环节 运动方程：
⎡ 2 d2 ⎤ d xo (t ) = K ⎢τ x (t ) + 2ξ τ xi (t ) + xi (t )⎥, 0 < ξ < 1 2 i dt ⎣ dt ⎦
2.2-6传递函数
s zi (i 1, 2 m)是N (s) 0的根，称为传递 函数的零点，s pi (i 1, 2 n)是D(s) 0的根 是传递函数的极点。
因为组成系统的元部件或多或少存在惯 性，所以G(s)的分母阶次大于等于分子阶 次，即 n,是m有理真分式，若 ,我们m 就 n 说这是物理不可实现的系统。
c(t)
a1
d dt
c(t
)
a0c(t
)
bm
dm dt m
r(t)
bm1
d m1 dt m1
r(t)
b1
d dt
r(t)
b0r(t
)
y(t)为系统的输出，r(t)为系统输入，则零 初始条件下，对上式两边取拉氏变换，得到 系统传递函数为：
G(s)
Y (s) R(s)
bmsm ansn
bm1sm1 an1sn1
一、传递函数的定义和概念
以上一节RLC电路的微分方程为例：
LC
d
2uC (t) dt 2
RC
duC (t) dt
uC
(t )
ur
(t )
设初始状态为零，对上式进行拉氏变换，得到：
LCs2Uc (s) RCsUc (s) Uc (s) Ur (s) （LCs2 RCs 1）Uc (s) Ur (s)
例 电枢控制式直流电动机
电枢回路： ur Ri Eb
[Ur (s) Eb (s)] / R I (s)
电枢反电势：Eb ce m
ce m (s) Eb (s)
电磁力矩： Mm cmi
cm I (s) Mm (s)
力矩平衡： Jmm fmm Mm Mm (s) /(Jm s fm ) m (s)
I1 ( s )
因为组成系统的元部件或多或少存在惯 性，所以G(s)的分母阶次大于等于分子阶 次，即 n,是m有理真分式，若 ,我们m 就 n 说这是物理不可实现的系统。
c(t)
a1
d dt
c(t
)
a0c(t
)
bm
dm dt m
r(t)
bm1
d m1 dt m1
r(t)
b1
d dt
r(t)
b0r(t
)
y(t)为系统的输出，r(t)为系统输入，则零 初始条件下，对上式两边取拉氏变换，得到 系统传递函数为：
G(s)
Y (s) R(s)
bmsm ansn
bm1sm1 an1sn1
一、传递函数的定义和概念
以上一节RLC电路的微分方程为例：
LC
d
2uC (t) dt 2
RC
duC (t) dt
uC
(t )
ur
(t )
设初始状态为零，对上式进行拉氏变换，得到：
LCs2Uc (s) RCsUc (s) Uc (s) Ur (s) （LCs2 RCs 1）Uc (s) Ur (s)
例 电枢控制式直流电动机
电枢回路： ur Ri Eb
[Ur (s) Eb (s)] / R I (s)
电枢反电势：Eb ce m
ce m (s) Eb (s)
电磁力矩： Mm cmi
cm I (s) Mm (s)
力矩平衡： Jmm fmm Mm Mm (s) /(Jm s fm ) m (s)
I1 ( s )
机电控制基础 第二章第四节传递函数
G(s) b0 b0
b0
b0
a0 a0 sn an1 sn1 ... a1 s 1
an
an
an
m1
m2
( k s 1)
(
2 l
s
2
2
l
s
1)
G(s) K
k 1 v n1
s
l 1 n2
(Ti s 1)
(T
2 j
s
2
2Tj
s
1)
i 1
j 1
2.4、控制系统的复域模型—传递函数
例1 已知
10
2.4、控制系统的复域模型—传递函数
4．积分环节
微分方程 传递函数
t
c(t) K 0 r(t)dt
G(s) C(s) K R(s) s
例6：液压缸 输入：流量q(t) 输出：活塞位移y(t)
q(t) A dy(t) dt
y(t)
1 A
q(t)dt
Y (s) 1 Q(s) As
G(s) Y(s) 1 Q(s) As
Ts 1
s 2 2 s 1
n2
n
e s
7
2.4、控制系统的复域模型—传递函数
1．比例环节
运动学方程
c(t) Kr(t)
传递函数
G(s) C(s) K R(s)
例3： 测速发电机 输入：角速度ω 输出：电压u
u(t) Kt(t)
G(s)
U (s) (s)
Kt
2.4、控制系统的复域模型—传递函数
（3） 画出对应的零极点图； （4） 求系统的单位脉冲响应；
(3) 如图所示
(4)
k(t)
L1[G ( s )]
传递函数求法
y(t) K x(t)dt
2）传递函数
G(s) X C (s) K X r (s) s
x(t) R
-+
y(t)
+
3) 输入输出变化曲线
4）结构图
Ur C
U R (s)
K
c (s)
s
0
t
4、微分环节
1）数学表达式
y(t)
K
dx(t) dt
＋x(t）
Xr (s)
1i sC R
=
K
(T1S (T1S
1)(T2 S 1)(T2S
1)(Tm S 1)(Tm S
1) 1)
=
K
(T1S (T1S
1)(T2 S 1)(T2S
1)(Tm S 1)(Tm S
1) 1)
二、 传递函数的性质
1 .线性定常系统或元件的微分方程与传递函数一一对 应，它们是在不同域对同一系统或元件的描述。
－自然振荡角频率
R RC LC R LC －振荡环节阻尼比
2n L
2L
2
i Xc
输入量单位阶跃响应时，则 对上式拉氏反变换，求输出响应得
X C (s)
s2
n2 2ns
n2
xc (t) 1 e2 nt
1 2nt 1 2
tan1
b0sm b1sm1 bm1s bm a0sn a1sn1 an1s an
G(s)
传递函数的两种表达形式：
1)
G(s)
Xc (s) Xr (s)
b0sm b1sm1 bm1s bm a0sn a1sn1 an1s an
自动控制原理课件第4次课 传递函数、结构图
• 一阶微分环节: G ( s ) s 1 • 振荡环节 : • 延迟环节
2 n 1 G( s) 2 2 2 T s 2Ts 1 s 2n s n 2
G ( s ) e s
哈尔滨工程大学自动化学院
20
自动控制原理
第二章 控制系统的数学模型
注意： 环节是根据微分方程划分的，不是具体的物理 装置或元件。 一个环节往往由几个元件之间的运动特性共同 组成。
哈尔滨工程大学自动化学院
12
自动控制原理
第二章 控制系统的数学模型
Part 2-4-2 传递函数的零点和极点
b0 s m b1s m 1 bm 1s bm an 1s an M (s) N (s)
M (s) b0 s m b1s m1 ... bm1s bm
系统(或环节) 的输入量 系统(或环节) 的输出量
X r ( s)
X c ( s) X r ( s)G( s)
X c (s)
哈尔滨工程大学自动化学院
7
自动控制原理
第二章 控制系统的数学模型
系统传递函数的一般形式 设线性定常系统由n阶线性定常微分方程描述：
d d d a0 n c(t ) a1 n1 c(t ) an1 c(t ) an c(t ) dt dt dt m m 1 d d d b0 m r (t ) b1 m1 r (t ) bm1 r (t ) bm r (t ) dt dt dt
哈尔滨工程大学自动化学院
6
自动控制原理
第二章 控制系统的数学模型
Part 2-4-1 传递函数的定义和性质
定义：在零初始条件(输入量施加于系统之前，系统处于
2传递函数
通过Laplace变换，将微分方程的解简化为关于S的代数方程，并得到 输出的Laplace变换C(s)后，反变换得到微分方程的时间域解C(t)。
二、传递函数
传递函数表征了系统的动态性能，而且可以用来研究系统结构和参数 变化对系统性能的影响，是经典控制理论中最重要的数学模型之一。
1．传递函数定义 在线性系统中，当初始条件为零时，系统输出的Laplace变换象 函数与输入的Laplace变换象函数之比，称为系统的传递函数。
★当极点既有互异的实数根、共轭复数根，又有重实数根、重复数 根时，自由运动的模态形式将是上述几种形式的线性组合。
（2）极点位置决定了自由运动模态的收敛性，从而决定了各模态的 稳定性和快速性，并影响系统响应的快速性 ●从响应模态来看，e pit、eit cos it、t m1e pit、t m-1eit cos it ，只要 pi 0、 i 0 ，则其模态就会随着时间t的增长而衰减，最终消失。系 统响应的自由运动分量（即能得到稳态响应）能够消失的称为稳定系 统，因此系统的稳定性由其全部极点的位置来决定。
e
★当极点出现复数重根，如m重复数根 pi i ji 时，自由运动 的模态形式将出现： it it m-1 i t
e cos it，te cos it， ，t e cos it
t t t
或 e i sin it，te i sin it， ，t m-1e i sin it
系统的初始条件为零。 传递函数与系统的初始状态无关
传递函数只能适用于线性系统，另外对输入输出进行Laplace变换时，
设线性时不变系统的微分方程为：
d nc d n-1c dc d mr d m-1r dr a0 n a1 n-1 an-1 an c b0 m b1 m-1 bm-1 bm r dt dt dt dt dt dt
自动控制原理》第二章传递函数
中国矿业大学信电学院
Z (S ) 自动控制原理 X (S )
17
二、系统方框图的等效变换和化简
补充结论：控制系统方块图简化的原则
1. 利用串联、并联和反馈的结论进行简化 2. 变成大闭环路套小闭环路 3. 解除交叉点（同类互移）
比较点移向比较点：比较点之间可以互移 引出点移向引出点：引出点之间可以互移 注：比较点和引出点之间不能互移
注意：进行相加减的量，必须具有相同的量纲。
中国矿业大学信电学院
自动控制原理
3
一、控制系统方框图的组成
(4) 引出点（分支点、测量点） 表示信号测量或引出的位置
R ( s)
X (s)
G1(s)
G2 (s)
C (s)
分支点示意图
X ( s)
特别要注意：同一位置 引出的信号大小和性质
完全一样。
中国矿业大学信电学院
方框图（结构图）的四要素：
自动控制原理
R(s)
C(s)
G(s)
(a)
R(s) + R(s) C(s) C(s)
(b)
c(t)
r(t)
C(s)
R(s)
C(s)
(c)
(d )
（1）方框（方块）:表示输入到输出单向传输间 的函数关系。
r(t)
R (s )
G( s )
c(t)
C (s )
信号线
方框
图2- 11 方框图中的方框
G4
R(s)
-
A
G1
G2
-B
H1
G3 H2
C C(s)
中国矿业大学信电学院
自动控制原理
22
二、系统方框图的等效变换和化简
第二章 传递函数
第二章 传递函数
2．根据系统微分方程对系统进行分类 1）线性系统：方程只包含变量X0(t)、Xi(t) 的各阶导数 a．线性定常系统：an…a0 ；bm…b0为常数 b．线性时变系统：an…a0 ；bm…b0为时间的函数 2）非线性系统：方程中含有非X0(t)、Xi(t) 各阶导数的其它函数形式
第二章 传递函数
解：由 KVL 有：
di u1 = Ri + L + u2 dt 1 du2 = i dt i=C , u2 C dt
R
L i(t)
C
u1(t)
u2(t)
消去中间变量i ：
du2 d 2 u2 + L C 2 + u2 U1 = R C dt dt
写成微分方程标准形式：
LC d 2 u2 dt
2
a n x(0n)( t ) + a n -1 x(0n 1)( t ) + L + a0 x0( t )
= bm x(i m)( t ) + bm -1 x( m -1)( t ) + L + b0 xi( t )
i
式中：a n…a 0, b m…b 0 均为常系数
x 0 (t)为系统输出量，x i(t)为系统输入量
R 2 C 2 ) u 2 ( t ) + Hu 2 ( t ) = u (t )
.
此结果错误
第二章 传递函数
四、非线性微分方程线性化
1．系统由单变量非线性函数所描述 y= f (x) y(t):输出 x(t):输入
df 1 d2 f Dx + Dx 2 f ( x) = f ( x0 ) + dx x 2! dx 2 0 x0 1 d3 f + 3! dx 3 D x 3 + LL
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
传递函数为： 式中，—微分环节的时间常数
无负载时
式中， Kt为电机常数。
测速发电机
无源微分网络
显然，无源微分网络包括有惯性环节和微分环节，称之为 惯性微分环节，只有当|Ts|<<1时，才近似为微分环节。 除了上述微分环节外，还有一类一阶微分环节， 其传递函 数为：
积分环节
输出量正比于输入量对时间的积分。
输出量不失真、无惯性地跟随输入量，两者成比例关系。
齿轮传动副
运算放大器
一阶惯性环节 凡运动方程为一阶微分方程
形式的环节称为惯性环节。其传递函数为：
K—环节增益（放大系数）； T—时间常数，表征环节的惯性，
和环节结构参数有关
弹簧-阻尼器组成的环节
微分环节 输出量正比于输入量的微分。
运动方程为：
Table 2.2 等效弹簧系数
传递函数求解示例 质量-弹簧-阻尼系统的传递函数
所有初始条件均为零时，其拉氏变换为：
按照定义，系统的传递函数为：
Table 2.3 复阻抗说明
R-L-C无源电路网络的传递函数
所有初始条件均为零时，其拉氏变换为：
几点结论 传递函数是复数 s 域中的系统数学模型，其参数仅取决 于系统本身的结构及参数，与系统的输入形式无关。 传递函数通过系统输入量与输出量之间的关系来描述 系统的固有特性。即以系统外部的输入－输出特性来描 述系统的内部特性。 若输入给定，则系统输出特性完全由传递函数G(s) 决 定，即传递函数表征了系统内在的固有动态特性。
含共轭复数极点的情况
含多重极点的情况 设F(s)存在r个重极点-p0，其余极点均不同，则
= 式中，Ar+1，…，An利用前面的方法求解。
五、传递函数及其典型环节传递函数
传递函数的概念和定义
在零初始条件下，线性定常系统输出量的拉氏变换 与引起该输出的输入量的拉氏变换之比。
零初始条件： t<0时，输入量及其各阶导数均为0； 输入量施加于系统之前，系统处于稳定的工作状态， 即t < 0 时，输出量及其各阶导数也均为0；
典型环节及其传递函数
线性系统传递函数的零、极点表达式
假设系统有b个实零点，c 对复零点，d 个实极点， e对复极点和v个零极点 可见
b+2c = m v+d+2e = n
对于实零点 成如下形式：
和实极点
，其因式可以变换
对于复零点对 可以变换成如下形式：
和
，其因式
式中，
对于复极点对 变换成如下形式：
特征方程、零点和极点
特征方程 令：
则： N(s)=0称为系统的特征方程，其根称为系统的特征根。 特征方程决定着系统的动态特性。N(s)中s的最高阶次 等于系统的阶次。
零点和极点 将G(s)写成下面的形式
系统传递函数的极点就是系统的特征根。 零点和极点的数值完全取决于系统的结构参数。
零、极点分布图 将传递函数的零、 极点表示在复平面上 的图形称为传递函数 的零、极点分布图。 零点用“O”表示， 极点用“×”表示。
和
，其因式可以
于是，系统的传递函数可以写成：
为系统静态放大倍数。
环节的分类 比例环节： 一阶微分环节： 二阶微分环节： 积分环节： 惯性环节：
振荡环节：
典型环节示例 比例环节 其运动方程为：xo(t)=Kxi(t)
xo(t)、xi(t)—分别为环节的输出和输入量； K—比例系数，等于输出量与输入量之比。
的零极点分布图
脉冲响应函数 初始条件为0时，系统在单位脉冲输入作用下的输 出响应的拉氏变换为 Y (s) G(s) X (s) G(s)
即 y(t ) L1[Y (s)] L1[G(s)] g (t )
g(t)称为系统的脉冲响应函数（权函数）。 系统的脉冲响应函数与传递函数包含关于系统动态 特性的相同信息。
四、拉氏变换和拉氏反变换
L [ t 1( t )]
L[ 1 2 t 1( t )]
1 s
2
1 s
3
性质 微分定理 积分定理
as
延时定理
L [ f ( t a ) 1( t a )] e
F (s)
衰减定理 初值定理
终值定理
拉氏反变换
只含有实数极点的情况
设线性定常系统的微分方程为
则零初始条件下，系统传递函数为
它有以下特点： 比微分方程简单，通过拉氏变换，实数域复杂的微积分运 算已经转化为简单的代数运算；
输入典型信号时，其输出与传递函数有一定对应关系，当 输入是单位脉冲函数时，输入的象函数为1，其输出象函数 与传递函数相同； 令传递函数中的s=jω，则系统可在频率域内分析（详见第 四章）； G（s）的零极点分布决定系统动态特性。
运动方程为：
传递函数为： 式中，T—积分环节的时间常数。
如：有源积分网络
二阶振荡环节 运动方程为：
传递函数：
式中，T—振荡环节的时间常数 ζ—阻尼比，对于振荡环节，0<ζ<1
K—比例系数
ωn称为无阻尼固有角频率。
式中，
当
质量-弹簧-阻尼系统
时，为振荡环节。
作业: 2-1， 2-2， 2-9(b)， 2-10(a) ，2-11(c)， 2-19
无负载时
式中， Kt为电机常数。
测速发电机
无源微分网络
显然，无源微分网络包括有惯性环节和微分环节，称之为 惯性微分环节，只有当|Ts|<<1时，才近似为微分环节。 除了上述微分环节外，还有一类一阶微分环节， 其传递函 数为：
积分环节
输出量正比于输入量对时间的积分。
输出量不失真、无惯性地跟随输入量，两者成比例关系。
齿轮传动副
运算放大器
一阶惯性环节 凡运动方程为一阶微分方程
形式的环节称为惯性环节。其传递函数为：
K—环节增益（放大系数）； T—时间常数，表征环节的惯性，
和环节结构参数有关
弹簧-阻尼器组成的环节
微分环节 输出量正比于输入量的微分。
运动方程为：
Table 2.2 等效弹簧系数
传递函数求解示例 质量-弹簧-阻尼系统的传递函数
所有初始条件均为零时，其拉氏变换为：
按照定义，系统的传递函数为：
Table 2.3 复阻抗说明
R-L-C无源电路网络的传递函数
所有初始条件均为零时，其拉氏变换为：
几点结论 传递函数是复数 s 域中的系统数学模型，其参数仅取决 于系统本身的结构及参数，与系统的输入形式无关。 传递函数通过系统输入量与输出量之间的关系来描述 系统的固有特性。即以系统外部的输入－输出特性来描 述系统的内部特性。 若输入给定，则系统输出特性完全由传递函数G(s) 决 定，即传递函数表征了系统内在的固有动态特性。
含共轭复数极点的情况
含多重极点的情况 设F(s)存在r个重极点-p0，其余极点均不同，则
= 式中，Ar+1，…，An利用前面的方法求解。
五、传递函数及其典型环节传递函数
传递函数的概念和定义
在零初始条件下，线性定常系统输出量的拉氏变换 与引起该输出的输入量的拉氏变换之比。
零初始条件： t<0时，输入量及其各阶导数均为0； 输入量施加于系统之前，系统处于稳定的工作状态， 即t < 0 时，输出量及其各阶导数也均为0；
典型环节及其传递函数
线性系统传递函数的零、极点表达式
假设系统有b个实零点，c 对复零点，d 个实极点， e对复极点和v个零极点 可见
b+2c = m v+d+2e = n
对于实零点 成如下形式：
和实极点
，其因式可以变换
对于复零点对 可以变换成如下形式：
和
，其因式
式中，
对于复极点对 变换成如下形式：
特征方程、零点和极点
特征方程 令：
则： N(s)=0称为系统的特征方程，其根称为系统的特征根。 特征方程决定着系统的动态特性。N(s)中s的最高阶次 等于系统的阶次。
零点和极点 将G(s)写成下面的形式
系统传递函数的极点就是系统的特征根。 零点和极点的数值完全取决于系统的结构参数。
零、极点分布图 将传递函数的零、 极点表示在复平面上 的图形称为传递函数 的零、极点分布图。 零点用“O”表示， 极点用“×”表示。
和
，其因式可以
于是，系统的传递函数可以写成：
为系统静态放大倍数。
环节的分类 比例环节： 一阶微分环节： 二阶微分环节： 积分环节： 惯性环节：
振荡环节：
典型环节示例 比例环节 其运动方程为：xo(t)=Kxi(t)
xo(t)、xi(t)—分别为环节的输出和输入量； K—比例系数，等于输出量与输入量之比。
的零极点分布图
脉冲响应函数 初始条件为0时，系统在单位脉冲输入作用下的输 出响应的拉氏变换为 Y (s) G(s) X (s) G(s)
即 y(t ) L1[Y (s)] L1[G(s)] g (t )
g(t)称为系统的脉冲响应函数（权函数）。 系统的脉冲响应函数与传递函数包含关于系统动态 特性的相同信息。
四、拉氏变换和拉氏反变换
L [ t 1( t )]
L[ 1 2 t 1( t )]
1 s
2
1 s
3
性质 微分定理 积分定理
as
延时定理
L [ f ( t a ) 1( t a )] e
F (s)
衰减定理 初值定理
终值定理
拉氏反变换
只含有实数极点的情况
设线性定常系统的微分方程为
则零初始条件下，系统传递函数为
它有以下特点： 比微分方程简单，通过拉氏变换，实数域复杂的微积分运 算已经转化为简单的代数运算；
输入典型信号时，其输出与传递函数有一定对应关系，当 输入是单位脉冲函数时，输入的象函数为1，其输出象函数 与传递函数相同； 令传递函数中的s=jω，则系统可在频率域内分析（详见第 四章）； G（s）的零极点分布决定系统动态特性。
运动方程为：
传递函数为： 式中，T—积分环节的时间常数。
如：有源积分网络
二阶振荡环节 运动方程为：
传递函数：
式中，T—振荡环节的时间常数 ζ—阻尼比，对于振荡环节，0<ζ<1
K—比例系数
ωn称为无阻尼固有角频率。
式中，
当
质量-弹簧-阻尼系统
时，为振荡环节。
作业: 2-1， 2-2， 2-9(b)， 2-10(a) ，2-11(c)， 2-19