神经网络在数据拟合方面的应用
神经网络算法的优缺点与适用场景分析

神经网络算法的优缺点与适用场景分析随着信息技术的迅猛发展,神经网络算法在人工智能和机器学习领域中扮演着至关重要的角色。
本文将探讨神经网络算法的优缺点,并分析其适用场景,以帮助读者更好地理解这一复杂而强大的工具。
## 优点### 1. 高度适应性神经网络算法以其高度适应性而闻名。
它们能够自动学习和适应不同类型的数据,包括图像、文本、语音等。
这种适应性使得神经网络在各种领域中表现出色,如图像识别、自然语言处理和语音识别。
### 2. 非线性建模神经网络允许非线性建模,这意味着它们可以处理复杂的关系和模式。
传统的线性模型在处理非线性数据时效果不佳,而神经网络可以更好地捕捉数据中的非线性关系,从而提高了预测和分类的准确性。
### 3. 分布式表示神经网络使用分布式表示来表示数据特征。
这意味着每个神经元(或节点)不仅仅代表一个单一特征,而是与多个特征相关联。
这有助于提高特征的抽象性和泛化能力,使得神经网络在处理大规模数据时效果显著。
### 4. 自动特征提取神经网络可以自动从原始数据中提取特征,无需手动工程特征。
这减轻了数据预处理的负担,使模型更容易构建,并能够更好地适应不同数据集。
### 5. 高度并行化神经网络的计算可以高度并行化,利用GPU等硬件加速设备可以加快训练速度。
这对于处理大规模数据集和复杂模型非常有利。
## 缺点### 1. 数据需求量大神经网络通常需要大量的数据来训练,特别是在深度学习领域。
如果数据不足,模型容易过拟合,导致性能下降。
### 2. 训练时间长深度神经网络的训练时间通常较长,尤其是在使用大型数据集和复杂模型时。
这会导致计算成本上升,因此需要适当的硬件支持。
### 3. 超参数选择困难神经网络有许多超参数需要调整,如学习率、层数、神经元数量等。
选择合适的超参数通常需要经验和实验,因此可能会耗费时间。
### 4. 解释性差神经网络通常被认为是黑盒模型,难以解释其内部工作机制。
这对于一些应用,如医疗诊断或金融风险分析,可能不够可接受。
如何利用神经网络进行预测分析(Ⅰ)

神经网络是一种模仿人脑神经元之间相互连接的数学模型,可以用来进行复杂的数据处理和预测分析。
利用神经网络进行预测分析是一种常见的应用,可以用于股票价格预测、天气预测、人口增长预测等多个领域。
本文将探讨如何利用神经网络进行预测分析,并介绍一些常用的方法和技巧。
1. 数据收集在利用神经网络进行预测分析之前,首先需要收集相关的数据。
数据可以来自各种渠道,如历史数据、实时数据、传感器数据等。
例如,如果要预测股票价格,可以收集历史的股票交易数据;如果要预测天气,可以收集气象局的观测数据。
数据的质量和数量对预测结果有很大的影响,因此在收集数据时需要尽量确保数据的完整性和准确性。
2. 数据预处理在收集到数据后,需要对数据进行预处理以便神经网络进行分析。
数据预处理包括数据清洗、数据标准化、数据归一化等步骤。
数据清洗是指去除数据中的噪声和异常值,以确保数据的质量;数据标准化是指将数据按照一定的规则进行转换,使得数据具有统一的尺度和分布;数据归一化是指将数据按照一定的比例进行缩放,以便神经网络更好地学习和训练。
3. 神经网络模型选择选择合适的神经网络模型是进行预测分析的关键一步。
常用的神经网络模型包括前馈神经网络、循环神经网络、卷积神经网络等。
不同的神经网络模型适用于不同的预测分析任务,需要根据具体的问题选择合适的模型。
例如,对于时间序列数据的预测分析,循环神经网络通常是一个较好的选择;对于图像识别和语音识别等任务,卷积神经网络通常是更合适的模型。
4. 数据分割和训练在选择了合适的神经网络模型之后,需要将数据分割成训练集和测试集,并对神经网络进行训练。
训练集用于训练神经网络模型,测试集用于评估模型的性能。
在训练神经网络时,需要选择合适的优化算法和损失函数,以使得神经网络能够更好地拟合数据并进行预测分析。
5. 参数调整和模型评估在训练神经网络模型过程中,需要对模型的参数进行调整,并对模型的性能进行评估。
参数调整包括学习率的选择、隐藏层节点数的选择等。
在Matlab中使用神经元网络进行数据拟合的技巧

在Matlab中使用神经元网络进行数据拟合的技巧在Matlab中使用神经网络进行数据拟合的技巧引言:在现代数据科学领域中,数据拟合是一项非常重要的任务。
数据拟合可以理解为通过数学模型来拟合已知的数据,以便更好地理解和预测未知的数据。
在数据拟合方法中,神经网络被广泛应用。
神经网络是一种模拟生物神经网络的人工智能方法,以其灵活性和强大的拟合能力受到了广大研究者的青睐。
在本文中,将探讨如何在Matlab中使用神经网络进行数据拟合,并分享一些技巧和经验。
一、Matlab中的神经网络工具箱Matlab提供了强大的神经网络工具箱,使得我们能够轻松地构建并训练神经网络模型。
该工具箱包含了多种神经网络类型,如前馈神经网络、递归神经网络等,并提供了丰富的功能和参数调整选项。
在使用神经网络进行数据拟合之前,首先需要导入神经网络工具箱,并了解一些基本的函数和工具。
二、数据准备和预处理在进行数据拟合之前,我们需要准备和预处理原始数据,以确保数据的完整性和准确性。
数据准备的过程包括数据收集、数据清洗、数据变换等。
在Matlab中,可以使用一些内置函数和工具箱来帮助我们进行数据准备和预处理。
例如,可以使用Matlab的数据导入工具箱来导入和预览数据,使用数据清洗工具箱来清洗和去除异常值,使用数据变换方法来调整数据的规模和分布。
三、神经网络模型设计神经网络模型的设计是数据拟合中的重要步骤。
在设计模型时,需要选择适当的网络结构和参数设置。
常见的网络结构包括单层感知器、多层感知器、径向基函数网络等。
在选择网络结构时,需要考虑数据的特点和需求,以及模型的复杂度和计算效率。
此外,还需要确定模型的激活函数、误差函数和学习算法等参数。
这些参数的选择将直接影响到模型的拟合效果和性能。
在Matlab中,可以使用图形化界面或编程的方式来构建和调整神经网络模型。
四、神经网络的训练和验证神经网络的训练是数据拟合过程中的核心步骤。
训练过程通过不断调整网络的权重和偏置值,使得网络能够逼近目标函数。
大数据分析中的卷积神经网络算法应用

大数据分析中的卷积神经网络算法应用随着物联网技术不断进步和智能化浪潮的兴起,数据量在不断膨胀。
如何更好地处理、分析这些庞大的数据量,将其中有价值的信息提取出来,成为了当前亟待解决的问题。
而大数据分析技术就是解决这个问题的重要手段之一。
在大数据分析技术中,卷积神经网络算法的应用越来越受到重视。
一、卷积神经网络算法介绍卷积神经网络是一个可以自动学习和提取特征的神经网络模型。
它结构复杂、理论丰富,广泛应用于图像、语音等信号处理领域,具有良好的分类、识别能力。
相比传统方法,它能够更好地模拟人类视觉和听觉系统的工作过程。
卷积神经网络的核心是卷积层、池化层和全连接层。
其中卷积层和池化层可以有效地减少模型复杂度和参数量,全连接层是整个网络的输出层,可以输出分类或回归结果。
二、卷积神经网络在大数据分析中的应用1. 图像识别卷积神经网络在图像识别领域的应用比较广泛。
在大数据分析中,通过使用卷积神经网络,可以训练模型进行图片分类、定位和检测等任务。
卷积神经网络的局部连接和共享参数的特点,使得对于图像中位置的变化,可以具有一定的不变性,能够更好地学习图像的特征,提高识别的准确性。
2. 自然语言处理卷积神经网络在自然语言处理中的应用也比较广泛。
在大数据分析中,卷积神经网络可以用于文本分类、情感分析、问答系统等任务。
卷积神经网络的卷积层可以提取文本中的n-gram特征,对于文本中的局部结构特征有很好的捕获能力。
而卷积神经网络的全连接层则可以输出文本的分类结果。
3. 信号处理信号处理是大数据分析的一个重要领域,而卷积神经网络在这个领域的应用也是不可或缺的。
卷积神经网络可以用于音频分类、音频分割、语音识别等任务。
卷积神经网络的卷积层可以对音频信号的时域和频域进行特征提取和抽象,对于音频数据的局部信息和全局信息都能够较好地进行处理。
三、卷积神经网络算法的优缺点1. 优点(1) 卷积神经网络具有良好的特征提取能力,能够从庞大的数据中自动识别,提取有效的特征进行分类等任务。
人工神经网络的基本原理和应用

人工神经网络的基本原理和应用概述人工神经网络是一种受到人脑神经元启发的计算模型。
它由许多高度互连的处理单元(神经元)组成,这些神经元之间通过连接强度(权值)相互通信。
人工神经网络能够通过学习和训练,自动调整权值和拓扑结构,从而实现某种特定任务。
基本原理人工神经网络的基本原理是模拟生物神经元的工作方式。
每个神经元接收一组输入信号,并根据这些输入信号的权值和激活函数的输出,产生一个输出信号。
这个输出信号又可以作为其他神经元的输入信号,从而实现信息的传递和处理。
人工神经网络通常由多层神经元组成,包括输入层、隐藏层和输出层。
输入层接收外部输入信号,隐藏层和输出层对输入信号进行处理和转换。
隐藏层和输出层之间的连接强度(权值)通过训练过程进行学习和调整,以实现预期的输出结果。
应用领域人工神经网络在各个领域都有广泛的应用,包括但不限于以下几个方面:1.图像识别–人工神经网络可用于图像识别任务,如人脸识别、物体识别等。
通过训练大量图像数据,神经网络可以学习到图像中的特征,并通过对输入图像进行处理,达到准确分类和识别的目的。
2.自然语言处理–人工神经网络在自然语言处理方面也有着广泛的应用。
它可以用于语音识别、情感分析、机器翻译等任务。
通过训练大量文本数据,神经网络可以学习到单词和语义之间的关联,从而实现对自然语言的理解和处理。
3.预测和分类–人工神经网络可以通过训练历史数据,对未来事件进行预测。
例如,它可以用于股票市场预测、天气预报等领域。
此外,神经网络还可用于数据分类,如垃圾邮件过滤、疾病诊断等任务。
4.控制与优化–人工神经网络在控制与优化领域也有着广泛应用。
它可以用于自动驾驶车辆、工业生产优化、智能电网调度等控制系统中,通过学习和训练,实现自动控制和优化的目标。
优势与挑战人工神经网络相比传统的算法有一些明显的优势,但同时也面临一些挑战。
优势•并行处理能力:神经网络的并行处理能力可以加快训练和推理的速度。
•自适应学习:神经网络可以通过训练和反馈机制,自动学习和调整权值,适应输入数据的变化。
报告中非线性数据分析和拟合的方法

报告中非线性数据分析和拟合的方法一、引言非线性数据分析和拟合是数据科学中的重要任务,它广泛应用于各个领域,包括经济学、生物学、工程学等。
在这些领域中,许多现象都不能用简单的线性模型进行描述,因此需要采用更为复杂的非线性模型进行分析和拟合。
本篇报告将着重介绍几种常用的非线性数据分析和拟合的方法。
二、多项式拟合法多项式拟合是一种简单但有效的非线性数据拟合方法。
该方法通过采用多项式函数来对数据进行拟合,其中函数的系数可由最小二乘法来确定。
多项式拟合的优点在于简单易用,在任何编程环境下都可以轻松实现。
然而,多项式拟合也存在一些问题,比如过度拟合、局部最小和数据不平滑等。
针对这些问题,可以通过选择适当的多项式阶数、引入正则化项或将数据进行平滑处理来解决。
三、非线性回归法非线性回归是一种更为灵活多样的非线性数据分析方法。
与多项式拟合不同,非线性回归不仅考虑多项式函数,还可以使用各种其他非线性函数。
对于给定的数据集,非线性回归的目标是找到最佳拟合函数,使其能够最好地解释数据中的变化。
非线性回归通常需要一些数值优化算法来确定最佳参数估计。
这些算法包括梯度下降法、Levenberg-Marquardt算法等。
四、局部加权回归法局部加权回归是一种基于样本点周围信息的非线性数据拟合方法。
它利用距离加权来对不同样本点进行不同程度的拟合权重,从而在拟合过程中更加关注靠近目标点的数据。
这种方法克服了全局模型的刚性问题,并能够更好地适应数据中的局部变化。
局部加权回归方法相对简单,但在处理大规模数据集时会面临一定的挑战,需要采用一些高效的近似算法来提高计算速度。
五、神经网络方法神经网络是一种强大的非线性数据建模和拟合工具。
它通过构建多层神经元网络来学习数据之间的复杂非线性关系。
神经网络可以包含多个隐藏层和大量的参数,可以应对各种复杂的数据模式。
神经网络的训练通常使用反向传播算法,该算法可以通过最小化误差函数来调整网络参数,使其拟合数据。
基于神经网络的激光扫描数据拟合

() £一
一 V
() 5
1 激光 扫描 仪的 误差分 析
影响激光扫描精度 的 因素有很 多 , 大致 可分 为 3类 : 器误 仪
3 基于 B P神 经 网络 的拟合
神经网络具有大规模并行 、 布式存储 和处理 、 分 自组 织 、 自适
特 差 、 目标 物体反射 面有关 的误差 、 与 外界 环境条 件。仪器误 差是 应和 自学 习能力 , 别适 合 处理 需要 同时考 虑许 多 因素 和条 件 不精确和模糊信息 。因此 , 神经网络被广泛应用于测量领域。 仪器本身性能缺陷造成 的测 量误差 , 括激 光测距 的误 差 、 包 扫描 的 , 角度测量 的误差 ; 目标物 体反 射面有关 的误差 主要包括 目标物 与 针对 可能存 在偶 然误差 或系统误 差 的数据 , 中采 用 B 文 P神
2 B P神经 网络
程 中的参数进行 附值 。此处 , 取平 面坐 标 (2, i作 为训练 样 选 3 Y) 18 9 5年 , u l r, Ce ad提 出了 B R me atMc ll h ln P网络学 习算 法 , 实 本 , 高程 H 为神经 网络 的期望输 出。 现 了 Misy的多 层 网 络 设 想 。 B nk P神 经 网 络 是 一 个 多 层 前 馈 型 神经 网络 , 网络由输入层 、 该 隐含层和输 出层 组成 , 隐含层 可 以为 单层或者多层 , 同层神经元之 间相互独立 。 设神经 网络 的输 入 向量 为 X=[ x 一, , 望输 出为 期 d=[ 一, I , d d T 输入层 与隐含层 的权 为 w , 其维数 为 ×S 阈 , 值为 0 , 维数为 S ; ×1 隐含层 与输 出层的权 为 w 其维数 为 S , × m, 阈值为 0 , 2维数为 m×1其 中, S m 分别 为输入层 、 , , 和 隐含 层和输出层的神经元节点数 。神经网络正向传输的计算过程如下 : 隐含层的输出计算 公式为1 : J ,
《神经网络基础知识》word版

实验十二: 神经网络及其在数据拟合中的应用(设计性实验)一、实验目的1.了解神经网络的基本知识。
2.学会用matlab神经网络工具箱进行数据拟合。
3.通过实例学习matlab神经网络工具箱的应用。
二、实验原理人工神经网络是在对复杂的生物神经网络研究和理解的基础上发展起来的。
我们知道, 人脑是由大约个高度互连的单元构成, 这些单元称为神经元, 每个神经元约有个连接。
仿照生物的神经元, 可以用数学方式表示神经元, 引入人工神经元的概念, 并由神经元的互连可以定义出不同种类的神经网络。
1.神经网络的概念及结构单个人工神经元的数学表示形式如图1所示。
其中, 为一组输入信号, 它们经过权值加权后求和, 再加上阈值, 则得出的值。
可以认为该值为输入信号与阈值所构成的广义输入信号的线性组合。
该信号经过传输函数可以得出神经元的输出信号。
图1由若干个神经元相互连接, 则可以构成一种网络, 称为神经网络。
由于连接方式的不同, 神经网络的类型也不同。
这里仅介绍前馈神经网络, 因为其权值训练中采用误差逆向传播的方式, 所以这类神经网络更多地称为反向传播(back propagation)神经网络, 简称BP神经网络。
BP网的基本结构如下图所示:MATLAB的神经网络工具箱提供了现成的函数和神经网络类, 可以使用newff()函数来建立一个前馈的BP神经网络模型。
newff()的具体调用格式如下:net=newff(x,y,[h1,h2,…,hk],{f1,f2,…,fk})其中, x为输入向量, y为输出(目标)向量。
[h1,h2,…,hk]是一个行向量, 用以存储神经网络各层的节点数, 该向量的大小等于神经网络隐层的层数。
{f1,f2,…,fk}为一个元胞数组, 由若干个字符串构成, 每个字符串对应于该层的传输函数类型。
当这些参数设定好后, 就建立了一个神经网络数据对象net, 它的一些重要属性在下表给出。
2.神经网络的训练和泛化若建立了神经网络模型net, 则可以调用train()函数对神经网络参数进行训练。
基于小波分析的神经网络在混凝土测强曲线拟合中的应用

数据拟合的智能方法

数据拟合的智能方法
数据拟合是指根据已知的数据点,通过建立数学模型来预测未知数据点的值。
在现代科学和工程领域,数据拟合是一项重要的任务,它可以帮助我们理解数据之间的关系,进行预测和优化。
随着人工智能和机器学习技术的不断发展,越来越多的智能方法被应用于数据拟合中。
这些方法包括神经网络、决策树、支持向量机、回归分析等。
这些方法利用大量的数据和复杂的算法来寻找数据之间的模式和规律,从而进行准确的数据拟合。
其中,神经网络作为一种模仿人脑神经元网络的计算模型,被广泛应用于数据拟合中。
通过多层神经元的连接和权重调整,神经网络可以学习复杂的非线性关系,从而实现高精度的数据拟合。
另外,支持向量机也是一种智能方法,它通过找到数据点之间的最优超平面来进行数据拟合。
支持向量机在处理高维数据和非线性数据拟合方面具有很好的效果,被广泛应用于模式识别、数据分类和回归分析等领域。
除了传统的机器学习方法,近年来深度学习技术也在数据拟合
中展现出强大的能力。
深度学习通过构建多层次的神经网络结构,可以处理大规模数据,并实现更加复杂的数据拟合任务。
总的来说,数据拟合的智能方法为我们提供了更加精确和高效的数据分析工具,帮助我们更好地理解和利用数据。
随着人工智能技术的不断发展,相信智能方法在数据拟合领域将会有更广泛的应用和更深入的研究。
解读测绘数据处理中的数据拟合方法

解读测绘数据处理中的数据拟合方法数据拟合是测绘数据处理中常用的一种方法,通过拟合函数将观测数据与理论模型相匹配,从而得到更加准确的测量结果。
在实际的测绘工作中,数据拟合方法有广泛的应用,可以用来处理地面形变、地壳运动等测绘数据。
本文将深入探讨几种常见的数据拟合方法,并分析它们的优缺点。
一、直线拟合方法直线拟合是最简单、最常见的一种数据拟合方法。
它假设观测数据服从线性关系,通过最小二乘法将数据点与一条直线相拟合。
直线拟合方法常用于测量直线路径上的地面形变、高程变化等情况。
但是,直线拟合方法对于曲线路径上的数据处理效果较差,容易引入较大的误差。
二、多项式拟合方法多项式拟合是一种常用的非线性数据拟合方法。
它通过多项式函数来逼近观测数据,可以更好地拟合曲线路径上的数据。
多项式拟合方法具有灵活性强、适用范围广的特点,可以适应不同类型的测绘数据。
但是,多项式拟合方法容易出现过拟合的情况,即在训练数据集上表现良好,但在未知数据上的预测效果较差。
三、指数拟合方法指数拟合是一种常用的非线性数据拟合方法,它通过指数函数来逼近观测数据。
指数拟合方法常用于处理地壳运动、地球重力场等测绘数据。
指数函数具有较强的曲线拟合能力,可以较好地拟合非线性变化的数据。
但是,指数拟合的结果较为复杂,需要进行较为复杂的数学计算。
四、样条插值方法样条插值是一种常用的数据拟合方法,它通过插值函数来逼近观测数据。
样条插值方法可以有效地处理非连续、离散的测绘数据,适用于对地面形状、高程变化等进行精细化处理。
样条插值方法具有较高的精度和稳定性,但是计算复杂度较高,需要消耗较大的计算资源。
五、神经网络拟合方法神经网络是一种模仿人脑神经元结构和功能的数据拟合方法。
通过多层神经元之间的连接和权重调整,可以实现对高维、非线性的测绘数据进行拟合。
神经网络拟合方法具有较高的拟合能力和预测精度,可以适应复杂的测绘数据处理需求。
但是,神经网络拟合方法的训练过程较为复杂,需要消耗较长的时间和计算资源。
神经网络中的过拟合问题研究与应用

神经网络中的过拟合问题研究与应用神经网络发展至今已经成为了人工智能领域的核心技术之一。
神经网络的强大之处在于它能够模仿人类的神经系统的工作方式,从而能够拟合各种不同的数据集和模型。
然而,在神经网络中存在一个严重的问题,那就是过拟合问题。
过拟合(Overfitting)是指模型在训练集上的表现非常好,但在测试集上的表现却很差。
本文将介绍神经网络中的过拟合问题以及一些应对策略。
# 过拟合的原因过拟合的原因有很多种,本文我们只讨论其中几种:模型复杂度过高、数据量过小、数据分布不均匀。
首先,如果我们训练出来的模型过于复杂,就会导致模型严重过拟合。
因为神经网络能够拟合的函数集合是非常大的,而我们所选择的模型只是其中的一个子集。
如果我们的模型比真实函数集合要复杂的话,就容易训练出对训练集过拟合的模型。
其次,如果训练数据量太少,也会导致过拟合。
因为过少的数据量不能很好地代表整个数据集的分布,导致训练出来的模型只是对训练数据过度拟合了,而不能很好地泛化到测试集上。
最后,数据分布不均匀也是导致过拟合的原因之一。
比如在分类任务中,如果某一类的数据比其他类数据量要小很多,那么在训练过程中就很难让模型很好地理解这一类数据,导致在测试时,这一类数据分类的精度很差。
# 解决过拟合问题的方法有很多种方法可以解决过拟合问题,本文将介绍其中几种:正则化、早停、数据增强、dropout、迁移学习。
首先,正则化是一种常用的防止过拟合方法。
正则化的本质是通过在损失函数中添加关于模型参数的惩罚项来减小模型的复杂度。
常见的正则化方法包括L1正则化和L2正则化。
L1正则化能够让模型参数变得稀疏,即能够让一部分模型参数值变为0,从而让模型变得更简单;而L2正则化能够让模型参数的大小变得更小,使得模型的复杂度降低。
正则化方法能够有效地防止过拟合,但是需要在实际应用中进行调参。
其次,早停是一种常用的迭代式模型防止过拟合的方法。
早停的本质是在模型训练过程中,当验证集误差不再下降时停止训练,从而避免了模型对训练集的过拟合。
最小二乘法和神经网络的应用

最小二乘法和神经网络的应用最小二乘法和神经网络是两种常用的数学与计算机科学领域的算法。
它们在不同的问题领域中有着广泛的应用。
本文将分析最小二乘法和神经网络的原理,并探讨它们在实际应用中的优点和局限性。
一、最小二乘法最小二乘法是一种经典的数值优化方法,用于拟合数据和解决线性方程组。
其基本思想是通过最小化误差的平方和来求得最优解。
最小二乘法常用于回归分析和曲线拟合等问题中。
在回归分析中,我们希望通过一组自变量来预测因变量的值。
最小二乘法可以通过求解线性方程组,建立自变量和因变量之间的数学模型。
通过最小化拟合点与真实数据点之间的误差,我们可以得到最佳的拟合曲线。
最小二乘法还可以应用于解决过完备线性方程组的问题。
过完备线性方程组指的是方程数量大于未知数的数量。
最小二乘法可以通过找到满足方程组的近似解,使得误差最小化。
最小二乘法在实际应用中具有许多优点。
首先,它是一种简单而直观的方法,可以通过解析求解或者数值计算得到结果。
其次,最小二乘法对于数据中的噪声具有一定的鲁棒性,能够减小噪声对拟合结果的影响。
此外,最小二乘法还可以通过引入正则化项进行约束,避免过拟合问题。
然而,最小二乘法也存在一些局限性。
首先,它对于非线性问题的求解能力有限。
在非线性问题中,最小二乘法得到的拟合结果可能并不是最优的。
另外,最小二乘法对于异常点较为敏感,可能会导致拟合曲线受到异常点的影响。
二、神经网络神经网络是一种基于生物神经系统的计算模型,具有强大的非线性建模和拟合能力。
神经网络由多个神经元组成,通过不同层次之间的连接来实现信息传递和处理。
神经网络的核心组件是神经元,它可以接收多个输入并产生一个输出。
神经元通过激活函数对输入进行非线性变换,从而实现对复杂模式的学习和表示。
神经网络通常采用前向传播的方式进行训练,通过调整网络的权重和偏置来最小化损失函数。
神经网络在许多领域中取得了显著的应用成果。
在图像识别领域,深度卷积神经网络(CNN)已成为最先进的技术。
线性分类器与神经网络在数据处理方面的应用
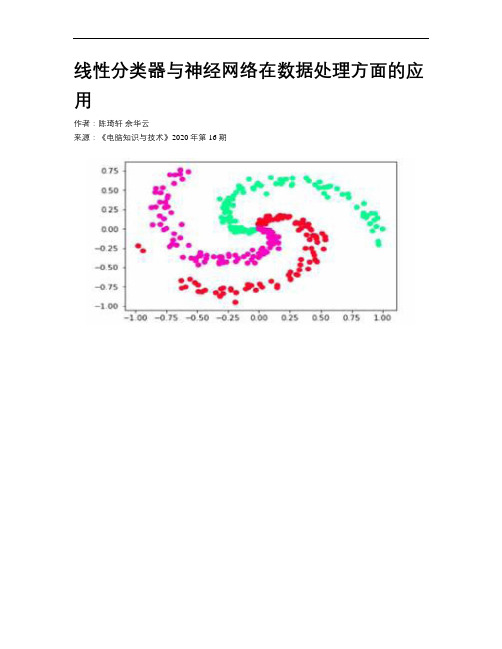
线性分类器与神经网络在数据处理方面的应用作者:陈琦轩余华云来源:《电脑知识与技术》2020年第16期摘要:在机器学习诞生之时起,线性回归分类器便体现出优越的性能,然而,随着时代的进步,每类训练样本数量增大,线性分类器的速度变得很慢,也凸显了线性分类的一个致命弱点:对大样本数据束手无策。
即当用于训练的样本数量大于样本的维数时,线性分类器会无法工作。
解决的办法之一是对分类器作局部化处理从而对数据进行筛选,避免大样本数据问题的出现。
然而,随着神经网络的兴起,对于大样本数据的处理,也有了更多的新兴的处理办法。
关键词:机器学习;线性回归分类器;局部化处理;神经网络;大样本数据中图分类号:TP391; ; 文献标识码:A文章编号:1009-3044(2020)16-0198-021局部线性回归分类器在机器学习领域中,分类的目的是指将具有相似特征的对象聚集在一起。
而一个线性分类器会透过特征的线性组合来做出分类决定,以达到此种目的。
对象的特征通常被描述为特征值,而在向量中则描述为特征向量。
1.1 Softmax线性回归Softmax是除SVM(支持向量机)外,另一种常见的线性分类模型,是逻辑回归推广的一种形式。
Softmax作为线性分类器的一种,可以从两个方面来研究它:评分函数,也有人称之为目标函数(score function)和损失函数(loss function)。
1.1.1 Score functionScore function: f(xi;W;b)=Wxi+b。
Softmax的评分函数与多类别支持向量机是一样的,都是“线性分类器”的一种,既然都是线性分类器,其计算目标的公式必定是经典的线性公式。
其中,Softmax对目标的解释:转换为概率分布。
分类器将目标向量看成是没有归一化处理的对数概率分布。
经过转化以后得到相对应类的概率。
例如,三个数字1、2、3,取max每次都会取到3,但是把它们映射成三个概率,取到3的概率最大,但也有取到其他两个数的可能,三个概率和为1,这就是Softmax 值。
神经网络的原理和实际应用

神经网络的原理和实际应用神经网络是一种模拟人脑结构的计算模型,具有深度学习和模式识别等强大功能,已经广泛应用于语音识别、图像识别、自然语言处理、医学诊断和金融分析等众多领域。
本文将介绍神经网络的原理和实际应用,探讨其优缺点和未来发展趋势。
一、神经网络的原理神经网络由一系列神经元、连接和激活函数组成,可以分为输入层、隐藏层和输出层。
输入层接收外部数据输入,隐藏层处理数据特征提取和汇聚,输出层产生最终结果输出。
神经元之间的连接具有不同的权重,决定了信息传递的强度和方向,激活函数根据输入的加权和产生输出。
通过不断迭代训练,神经网络可以学习到复杂的特征和规律,具有非线性映射和自适应性等优势。
二、神经网络的实际应用1. 语音识别:神经网络可以将语音信号转化为文字识别结果,实现自然语言处理和交互式应用。
例如,苹果的Siri和微软的Cortana等智能助手就是基于神经网络实现的。
2. 图像识别:神经网络可以识别图像中的物体、场景和情感等信息,实现图像分类、目标跟踪和安防监控等功能。
例如,谷歌的TensorFlow和Facebook的Caffe等深度学习框架就是用于图像识别的。
3. 自然语言处理:神经网络可以分析文本数据中的语义和句法关系,实现文本分类、文本生成和机器翻译等应用。
例如,IBM 的Watson和谷歌的Translate等机器翻译系统就采用了神经网络的方法。
4. 医学诊断:神经网络可以通过学习医学图像和数据,辅助医生判断疾病类型和严重程度,实现医学影像分析和病理诊断等任务。
例如,阿里巴巴的AI医生和IBM的Watson for Health等健康应用就启用了神经网络技术。
5. 金融分析:神经网络可以对金融市场的历史数据进行分析和预测,实现股票交易、信用评估和风险控制等应用。
例如,高盛的纪元神经网络交易系统和花旗银行的风险管理系统等金融领域的创新应用都利用了神经网络的优势。
三、神经网络的优缺点神经网络具有以下优势:1. 非线性映射:神经网络可以建立复杂的非线性关系,从而更真实地反映数据之间的内在联系。
神经网络算法在数据挖掘中的应用与优化

神经网络算法在数据挖掘中的应用与优化神经网络算法是现今数据挖掘领域中的一种非常热门的算法,该算法模拟了人脑的神经网络结构,利用大量数据的训练过程,不断地调整神经元之间的连接权重,从而使得神经元的输出结果更加准确地预测出实际情况。
在实际的数据挖掘中,神经网络算法被广泛应用于金融、医疗、教育等领域,能够快速准确地从海量复杂的数据中提取有用的信息,得出有意义的结论。
本文将介绍神经网络算法在数据挖掘中的应用和优化,为读者深入了解神经网络算法提供参考。
一、神经网络算法在数据挖掘中的应用随着互联网、物联网等技术的迅速发展,我们已经进入了信息时代。
在此过程中,大数据也成为了一个普遍存在的概念,而数据挖掘就是应对大数据的一种有效手段。
数据挖掘的核心就是从海量数据中挖掘出有用的信息,用以指导决策和行动。
而神经网络算法就是其中一种较为常用的算法。
在实际的数据挖掘中,神经网络算法可以应用于以下几个领域。
1. 金融领域在金融领域中,神经网络算法可以应用于风险评估。
例如,如何对申请贷款的客户进行评估,以决定是否应该给予该客户贷款。
神经网络算法可以利用客户的信用记录、财务状况、个人背景等信息,通过建立一个神经网络模型来预测该客户的还款能力。
这样,金融机构可以准确地评估客户的信用风险,从而降低不良贷款的风险。
2. 医疗领域在医疗领域中,神经网络算法可以应用于病理诊断。
例如,如何利用医学影像等数据提高病理诊断的准确性。
神经网络算法可以训练出一个基于影像特征的神经网络模型,来实现对肿瘤的自动检测和辅助诊断。
这样,医生可以更加快速、准确地判断患者病情,为治疗提供更好的指导和建议。
3. 教育领域在教育领域中,神经网络算法可以应用于学生行为预测。
例如,如何利用学生的行为数据、成绩等信息对其进行分析和预测,以提高教育教学质量。
神经网络算法可以对数据进行处理和分析,训练出一个能够预测学生行为的神经网络模型,以便在教学中针对学生的实际情况制定个性化的教学方案,提高学生的学习成绩。
BP神经网络拟合区域似大地水准面的应用分析

W ANG n,M A w y n Bi Xi i g,W ANG e —i W nl
( o e i Da aPr c s i g Ce t r Ge d t t o e sn n e 。Na in l m iit a i n o u v y n c t a o Ad n sr t fS r e i g,M a p n n o n o ma i n,Xi a 1 0 4 o p ig a d Ge i f r t o ’ n 7 0 5 ,Ch n ) i a
d c h eibl y Th eiin y f rfti g t e q a ie i t e r ln t r sd su s d Two u et er l i t . a i ed fce c o it h u sg o d wih BP n u a ewo k i ic s e . n
的一个重要因素。国内外学者 已将 函数模 型逼 近和统
丰硕的研究成果…州 4 。但 B P神经网络容易陷入局部 极小值 , 这对拟合计算将造成一定影响 。
Ab ta t BP n u a e wo k i s d t a e h y t m a i e r r n o d r t m p o e t e a c r c f sr c : e r ln t r s u e o we k n t e s s e tc r o s i r e o i r v h c u a y o q a i e i o h y t m a i e r r n t e d t f u sg o d f rt e s s e t r o s i h a ao c GPS a d lv l n h a a o r v t u sg od ma e n e e d t ed t f a i q a i e i y r — a g y
神经网络算法在数据分析中的应用

神经网络算法在数据分析中的应用一、引言数据分析作为一门学科,通过对大量数据的收集、整理、处理和分析,从中提取出对决策和问题解决有用的信息。
随着人工智能技术的发展,神经网络算法逐渐成为数据分析领域中的热门技术。
本文将从神经网络算法的基本原理、常见应用案例以及未来发展趋势等方面,探讨神经网络算法在数据分析中的应用。
二、神经网络算法基本原理神经网络算法源于对生物神经系统的模拟,通过模拟人脑中的神经元之间的连接和传递信息的过程,实现对数据的分析和处理。
神经网络由多层次的神经元组成,每个神经元与其他神经元之间通过权重相连。
在数据分析中,神经网络通过学习和调整权重,以逼近或拟合输入和输出之间的关系。
三、神经网络算法在数据分析中的应用案例1. 金融风险预测在金融领域,神经网络算法被广泛运用于风险预测。
通过对金融市场的历史数据进行分析,神经网络可以学习到金融市场的复杂动态,并能够识别潜在的风险事件。
例如,神经网络可以根据历史数据的变化情况,预测未来股市的波动情况,帮助投资者制定合理的投资策略。
2. 医疗诊断神经网络算法在医疗领域的应用也非常广泛。
通过对大量的医学数据进行分析,神经网络可以根据患者的症状和病历信息,辅助医生进行疾病诊断。
例如,神经网络可以通过学习已有的病例,判断患者是否患有某种疾病,并可以预测疾病的发展情况,帮助医生制定更精确的治疗方案。
3. 图像识别神经网络在图像识别领域的应用是最为知名的。
通过对大量的训练图像进行学习,神经网络可以识别和分类图像中的各种物体。
例如,神经网络可以识别人脸、车辆、动物等常见的物体,并可以应用于视频监控、人脸识别、自动驾驶等领域。
四、神经网络算法的优势与挑战1. 优势神经网络算法具有较强的自适应能力,能够根据数据的特点自动调整模型的参数。
此外,神经网络算法还适用于处理大规模数据集,并具有较强的容错性。
与传统的统计学方法相比,神经网络算法能够处理非线性关系,更适合处理复杂的数据分析问题。
基于深度神经网络的大规模数据处理与分析

基于深度神经网络的大规模数据处理与分析在当今信息爆炸的时代,大规模数据处理和分析成为了科学研究、商业应用和社会发展的关键挑战之一。
随着互联网的普及和计算技术的发展,我们正在迎来一个数据时代,海量的数据被生成并积累,需要以快速、准确、高效的方式进行处理和分析。
为了应对这一挑战,深度神经网络成为了处理和分析大规模数据的一种非常有力的工具。
深度神经网络是一种模拟人脑神经网络的技术,通过多层神经元的连接和学习来提取数据的特征和模式。
与传统的机器学习算法相比,深度神经网络具有更强大的抓取数据特征的能力,并且可以自动学习复杂的模式和关系。
在大规模数据处理和分析中,深度神经网络可以发挥多重作用。
首先,它可以用于数据的预处理和清洗。
数据预处理是将原始数据进行清洗、标准化和转换的过程,以便更好地适应分析模型的要求。
深度神经网络可以通过自动化的方式进行特征提取和数据转换,从而减少了手动处理数据的工作量和错误的可能性。
其次,深度神经网络可以用于数据的分类和聚类。
数据分类是将数据按照一定的标准进行划分,以便更好地理解和分析数据的属性和特征。
深度神经网络通过学习数据的特征和模式,可以将数据进行有意义的分类,从而帮助我们更好地理解数据背后的规律和关系。
数据聚类是将相似的数据归为一类,以便更好地理解和利用数据的相似性和差异性。
深度神经网络可以通过学习数据的相似性和差异性,将数据进行有效的聚类,从而有助于数据的进一步分析和利用。
此外,深度神经网络可以用于数据的预测和预测建模。
数据预测是根据已有的历史数据和模型,对未来的数据进行预测和估计。
深度神经网络可以学习数据的历史模式和趋势,在未来的预测上具有一定的准确性和可信度。
数据建模是根据已有的数据和模型,构建适合描述和解释数据的模型。
深度神经网络可以学习数据的复杂模式和关系,从而生成适合数据的模型,帮助我们更好地理解和解释数据的属性和特征。
值得注意的是,深度神经网络在大规模数据处理和分析中并非没有挑战。
神经网络中的过拟合

神经⽹络中的过拟合先说下⼀般对原始数据的划分为什么分为训练集、验证集、测试集三个部分?train data的作⽤是训练模型,validation data的作⽤是对模型的超参数进⾏调节,为什么不直接在test data上对参数进⾏调节?因为如果在test data上来调节参数,那么随着训练的进⾏,我们的⽹络实际上就是在⼀点⼀点地向我们的test data过度拟合,导致最后得到的test data的指标参考意义下降。
⾸先明确我们训练神经⽹络模型的⽬标是使得其在未知数据上也有很好的拟合能⼒(⼀般测试集充当未知数据的⾓⾊),所以如何直观的判断模型是否过拟合了?如果模型在训练集上有良好的表现,但是在测试集上表现却没那么好,很可能就是过拟合了。
那么在神经⽹络中该如何解决过拟合问题?根据问题解决问题(⼀)数据⽅⾯导致的过拟合1.训练数据集过⼩导致过拟合如果数据集过⼩,由于神经⽹络中的参数过多,这时很容易就导致过拟合,此时应该增⼤训练数据,或者选⽤别的更合适的模型。
2.训练数据不均衡导致过拟合如果训练数据不均衡,显然模型会趋向于拟合数据较多的⼀类,因为它提供的信息更多,这种情况应该⾸先考虑的是均衡数据、数据增强等,具体可以参照如何处理数据不均衡问题。
(⼆)由模型导致的过拟合如果数据相对均衡且训练数据⾜够仍出现过拟合,应该从模型⾓度着⼿1.简化模型简化模型最直接的⼿段是减少模型层数或者减⼩模型中隐层节点的个数。
L1正则化:L1正则化倾向于使得接近于0的参数变成0,这样就相当于减少了参数,模型⾃然变得更简单。
L2正则化:L2正则化加快了参数的减⼩速度,参数⼩模型能够拟合的数据变少且拟合的刚刚好(这个法则也叫做奥卡姆剃⼑),过拟合的可能性就降低。
此外参数过多使得⽹络能够拟合更多的数据,且为了拟合⼀些数据,这些数据中特有的⼀些特征可能相应的参数就很⼤,很容易导致过拟合,简化模型、减⼩权值从⽽防⽌过拟合。
2.提取更泛化的表征神经⽹络可以理解为⼀个⾮线性多元函数簇,训练神经⽹络是为了很好的完成输⼊到输出的映射,且模型的泛化能⼒⾜够好,这就需要提取鲁棒的表征产⽣过拟合使得模型泛化性降低,说明抽取的表征泛化性不够强。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
神经网络在数据拟合方面的应用摘要本文将讲述人工神经网络及其数据拟合中的应用。
人工神经网络是从信息处理角度对人脑神经元网络进行抽象,建立某种简单模型,按不同的连接方式组成不同的网络。
它在模式识别、智能机器人、自动控制、预测估计、生物、医学、经济等领域得到广泛的应用。
本文主要研究神经网络在数据拟合中的应用,通过对背景、基础知识及其神经网络的相关理论,推出神经网络的发展历程及其模型,最后得出神经网络在数据拟合中的算法的设计与实现。
本文通过实例介绍了用神经网络来进行数据拟合处理的方法。
关键词:人工神经网络; 拟合; 径向基结构; MATLABAbstractThis paper will describe the application of artificial neural network and its data fitting. Artificial neural network is a kind of simple model, which is based on the information processing point of view of the human brain neural network to establish a simple model. The different connection ways form different networks. It is widely used in pattern recognition, intelligent robot, automatic control, prediction and estimation, biology, medicine, economy and so on. This paper studied the neural network in the data fitting application. By the background, basic knowledge and neural network theory, we introduced the development process of neural network and its models, and finally we got the design and implementation of algorithm of neural network in data fitting. This paper introduced the method of using neural network to fit the data through an example.Key Words:Curve fitting; Surface fitting; Least-squares method; Engineering applications目录摘要................................................................错误!未定义书签。
Abstract...........................................................错误!未定义书签。
第1章绪论 (1)1.1 课题国内外研究动态,课题研究背景及意义 (1)1.1.1国内外的研究现状 (1)1.1.2课题研究的意义 (2)1.2 研究主要成果 (2)1.3发展趋势 (3)1.4研究的基本内容 (4)1.5论文的主要工作及结构安排 (4)第2章神经网络概述2.1 神经网络基础知识 (5)2.1.1 人工神经元模型 (5)2.1.2 神经网络结构 (5)2.1.3 神经网络结构工作方式 (6)2.1.4 神经网络的训练与泛化 (7)2.2 径向基网络结构与应用 (7)2.3 例题详解 (7)2.3.1 例1 (7)2.3.2 例2 (11)第3章数据拟合的基本理论 (12)3.1 最小二乘曲线拟合 (12)3.1.1 多项式拟合 (14)3.1.2 正交多项式作最小二乘拟合的原理 (14)3.1.3 非线性最小二乘拟合 (16)3.2 多元最小二乘拟合 (18)3.3 最小二乘法的另一种数学表达 (19)3.4 本章小结 (21)第4章数据拟合应用实例 (22)4.1 数据拟合在物理实验中的应用 (22)4.1.1 多项式拟合 (22)4.1.2 指数拟合 (22)4.2 数据拟合在塔机起重量方面的应用 (24)4.2.1 工程原理 (24)4.2.2 应用实例 (24)4.3 数据拟合在换热器方面的应用 (26)4.3.1 工程原理 (26)4.3.2 应用实例 (28)4.4 数据拟合在起重力矩方面的应用 (31)4.4.1工程原理 (31)4.4.2 模型估计算法的研究 (31)4.4.3 应用实例 (32)4.5 数据拟合在轮辋逆向设计工程中的应用 (33)4.5.1 工程原理 (34)4.5.2 参数拟合算法 (35)4.5.3 轴截面圆半径的拟合算法 (35)4.6 数据拟合在其他实际工程中的应用 (36)4.6.1 数据拟合在神经网络设计开发中的应用 (37)4.6.2 数据拟合在透气性测试方面的应用 (37)4.7 本章小结 (37)第5章结论 (38)参考文献 (39)第1章绪论1.1 课题国内外研究动态,课题研究背景及意义在科技飞速发展的今天数学也早已成为众多研究的基础学科。
尤其是在这个信息量巨大的时代,实际问题中国得到的中离散数据的处理也成为数学研究和应用领域中的重要的课题。
1.1.1 国内外的研究现状数据拟合的研究和应用主要是面对各种工程问题,有着系统的研究和很大的发展。
通过研究发展使得数据拟合有着一定的理论研究基础。
但是,由于现实问题的复杂性,数据拟合还拥有很好的研究空间,还有很多能够优化和创新的问题需要去研究和探索。
各种算法的改进和应用以及如何得到合适的模型一直是一个比较热门的研究领域。
其中北京系统工程研究所对模糊方法在知识发现中应用;北京大学对数据立方体代数的研究;华中理工大学、复旦大学对关联规则算法的优化和改造;数据拟合出现于20世纪80年代后期,90年代有了突飞猛进的发展,例如对银行或商业上经常发生的诈骗行为进行预测;1.1.2 课题研究的意义对实验数据进行拟合是为了得到符合数据的函数关系,从而能更好地理解数据背后的数学、物理意义。
进而对实验的各个参数有更深入的理解,能分析出各个参数对实验结果的影响。
研究和发展数据拟合理论,发掘各种数据拟合的优化方案。
根据离散的数据,我们想要得到连续的函数或更加密集的离散方程与已知数据相吻合。
1.2 研究主要成果作为数据拟合的最基本也是应用最广泛的方法,最小二乘法有了很大的发展。
在工程实际应用和实验中,我们经常采用实验的方法寻找变量间的相互关系。
但是,当观测到的数据较多时,一般情况下使用插值多项式来求近似函数是不现实的。
根据多元函数线性回归理论,使用曲线拟合最小二乘法来寻求变量之间的函数关系能够很好的解决这个问题。
而且我们对它在实际应用中产生各方面的需求有着各种研究。
例如:基于于均差最小二乘拟合方程形式的研究、数据拟合函数的最小二乘积分法、非线性最小二乘法等各种方法已经在工程中得到了应用。
高斯-马尔科夫定理:在给定经典线性回归的假定下,最小二乘估计量是在实际工程问题中,如何由测量的离散数据设计和确定最优的拟合曲线?其关键在于选择适当类型的拟合曲线,一些时候根据专业的知识和我们的经验就可以确定拟合曲线类型;但是当我们在对拟合曲线一无所知的情况下,可以先绘制离散数据的粗略图形,也许能够从中观测出拟合曲线的类型;或者对数据进行多种可能较好的曲线类型的拟合,并且计算出它们的均方误差,利用数学实验的方法找出最小二乘法意义下误差最小的拟合函数。
1.3 发展趋势应用高次隐式多项式曲线和曲面为各个领域的数据进行可视化建模还没有广泛的研究。
用隐式多项式曲线来描述数据点集合的轮廓有天然的优势,在数据点集合轮廓的拟合过程中,为业务信息建模所具有的优点,其它建模方法根本无法比拟,这主要是因为隐式多项式曲线有着精确的表达能力,隐式多项式曲线的参数完全取决于它的次数和系数,解析式明确,操纵和使用方便,它还具有着天然的。
机相关软件解数据拟合问题也已经成为了不可缺少的步骤。
1.4 研究的基本内容数据拟合理论体系的研究:研究数据拟合的基本理论,了解并掌握数据拟合的基本理论和方法。
通过阅读参考文献和有关资料,学习数据拟合的重要意义以及目前关于数据拟合问题的研究现状。
并对目前数据拟合的各种方法的特点做出概述。
其特点进行分析和总结。
1.5 论文的主要工作及结构安排由上可知,论文将从数据拟合发展过程、特点、基本方法以及数据拟合在工程实际中的应用实例对数据拟合进行全面、深入地研究,在此基础上,归纳总结数据拟合在工程问题中的各种应用,并对其进行理论分析。
具体内容安排如下:(1)第2章主要介绍了神经网络的基础知识及一些简单应用。
(2)第3章主要从理论的角度研究数据拟合的基本思想,方法。
分别从处理两个变量之间关系的曲线拟合基本理论和多元函数拟合的基本理论两个大的方面进行研究细分。
(3)第4章主要通过工程实际中的应用实例,利用数据拟合的基本理论也分别从曲线拟合在工程实际中的应用实例和多元函数拟合在工程实际中的应用实例进行归纳并进行分析。
第2章 神经网络概述2.1神经网络基础知识2.1.1人工神经元模型。
2.1.3神经网络结构工作方式神经网络的工作过程主要分为两个阶段: 第。
所以我们知道,神经网络要解决的问题是通过已知数据,反复训练神经网络,得到加权量和阀值,使得神经网络的计算输出信号 与实际期望输出信号误差最小。
一种较适合的方式就是使得误差的平方和最小,即iy ∑∑==-N l mi li livw yy11,2)^ˆ(m in其中上标N 为样本组数。
对于w v 采用共轭梯度法来搜索最优值。
给出权值和的初值和,则可以通过下面的递推算法修正权值MATLAB 里利用newff()函数来建立前馈的神经网络模型,其调用格式为, 分别为列向量,存储各个样本输入数据的最小值和最大值,第二个输入变量是一个行向量,将神经网络的节点数输入,单元的个数是隐层的层数;第三个输入变量为单元数组。
2.1.4神经网络的训练与泛化建立了神经网络模型net ,则可以调用train ()函数对神经网络参数进行训练。
im()函数进行泛化,得出这些输入点处的输出矩阵 。
2.2径向基网络结构与应用径向基网络是一类特殊的神经网络结构。
隐层的传输函数为径向基函数,输出的传输函数为线性函数,则此结构的网络称为径向基网络。
