(完整版)向量积数量积
空间向量的数量积运算完整版课件

设∠AOB=∠BOC=∠AOC=θ,
又设O→A=a,O→B=b,O→C=c,
则|a|=|b|=|c|.
2分
又O→G=12(O→M+O→N)=12[12O→A+12(O→B+O→C)]
=14(a+b+c),
B→C=c-b. ∴O→G·B→C=14(a+b+c)·(c-b)
数量 特别地:a·a=|a|2或|a|= a·a
积的 性质
(3)若θ为a,b的夹角,则cos θ=
a·b |a||b|
.
(4)|a·b|≤|a|·|b|.
想一想:类比平面向量,你能说出a·b的几何意义吗? 提示 数量积a·b等于a的长度|a|与b在a的方向上的投影 |b|·cos θ的乘积.
名师点睛
所以O→A·B→C=O→A·A→C-O→A·A→B
=|O→A||A→C|cos〈O→A,A→C〉-|O→A||A→B|cos〈O→A,A→B〉
=8×4×cos 135°-8×6×cos 120°
=-16 2+24.
所以 cos〈O→A,B→C〉=O|→O→AA·||B→B→CC|=24-8×165
2=3-52
1.空间向量夹角的理解 (1)任意两个空间向量均是共面的,故空间向量夹角范围 同两平面向量夹角范围一样,即[0,π]; (2)空间向量的夹角在[0,π]之间,但空间两异面直线夹角
π 在(0, 2 ]内,利用向量求两异面直线夹角时注意转化,两
异面直线的夹角余弦值一定为非负数.
2.平面向量与空间向量数量积的关系 由于空间任意两个向量都可以转化为共面向量,所以空间 两个向量的夹角的定义和取值范围、两个向量垂直的定义 和表示符号、向量的模的概念和表示符号、以及运算律等 都与平面向量相同.
向量数量积的定义

对于任意两个非零向量$vec{a}$和$vec{b}$,有$cos{langlevec{a}, vec{b}rangle} = frac{vec{a} cdot vec{b}}{|vec{a}| |vec{b}|}$。
证明
向量数量积的坐标表示的证明
利用向量的坐标表示和点积的定义,通过代数运算 证明。
向量数量积与模的关系的证明
利用向量的模的定义和点积的性质,通过代数运算 证明。
向量数量积与角度的关系的证明
利用向量的点积的性质和三角函数的性质,通过代 数运算证明。
04
向量数量积的应用
在物理中的应用
描述速度和加速度
向量数量积可以用来描述物理中 的速度和加速度,通过计算速度 和加速度的向量数量积,可以得 出物体运动的方向和速度变化的 快慢。
02
向量数量积的计算
计算公式
定义
两个向量$vec{A} = (a_1, a_2, ..., a_n)$和$vec{B} = (b_1, b_2, ..., b_n)$的数量积定义为$vec{A} cdot vec{B} = a_1b_1 + a_2b_2 + ... + a_nb_n$。
几何意义
向量长度和夹角
向量的数量积可以用来计算向量的长度和夹角,从而确定两个向量 的相似性和关系。
向量投影
在数学中,向量的投影是一个重要的概念,可以通过向量的数量积 来计算,从而确定一个向量在另一个向量上的投影。
在其他领域的应用
计算机图形学
在计算机图形学中,向量的数量积可以用来描述二维图形和三维模型的方向和旋转,从而实现图形的旋转、缩 放和平移等变换。
定理
向量数量积的坐标表示
向量的数量积

数量积可以用于计算向量的长度或模长,即$|vec{A}| = sqrt{vec{A} cdot vec{A}}$。
向量投影
数量积可以用于计算一个向量在另一个向量上的投影长度,即 $text{Proj}_{vec{B}} (vec{A}) = frac{vec{A} cdot vec{B}}{|vec{B}|}$。
定义
向量可以用箭头表示,箭 头的长度代表模长,箭头 的指向代表方向。
表示方法
在平面上,向量可以用有 方向的线段表示;在空间 中,向量可以用有方向的 箭头表示。
注意事项
向量表示法直观易懂,但 无法直接计算数量积,需 要转换为代数法或几何法 进行计算。
03
CHAPTER
向量数量积的坐标表示
坐标表示
定义
积和向量的模。
05
CHAPTER
向量数量积的物理意义
力的合成与分解
力的合成
向量数量积可以用于表示力的合成效果,当两个力同时作用于一个物体时,其效果可以由这两个力的 向量数量积来描述。
力的分解
在物理中,一个力可以分解为两个或多个分力,这些分力的大小和方向可以通过向量数量积来计算。
动量与冲量
动量
物体的动量定义为质量与速度的向量数 量积,即质量乘以速度的大小和方向。
THANKS
谢谢
标量积
数量积的结果是一个标量,而不是向量。
无方向性
数量积不具有方向性,即$vec{A} cdot vec{B} = vec{B} cdot vec{A}$。
性质
交换律
数量积满足交换律,即$vec{A} cdot vec{B} = vec{B} cdot vec{A}$。
分配律
向量的数量积

向量的数量积向量的数量积是线性代数中的一个重要概念,也是向量运算中的一种常用运算。
它可以帮助我们计算向量之间的夹角、判断向量是否垂直等问题。
本文将详细介绍向量的数量积的定义、性质以及应用。
一、定义在二维空间或三维空间中,我们可以用向量来表示有方向和大小的量。
设有两个向量A和B,向量A的坐标表示为(A1,A2,A3),向量B的坐标表示为(B1,B2,B3),则向量A和向量B的数量积定义为:A·B=|A||B|cosθ,其中|A|表示向量A的长度,|B|表示向量B的长度,θ表示向量A和向量B之间的夹角。
二、性质1. 交换律:A·B=B·A2. 结合律:(kA)·B=A·(kB)=k(A·B),其中k为实数3. 分配律:(A+B)·C=A·C+B·C三、计算方法1. 若向量A和向量B的坐标分别为(A1,A2,A3)和(B1,B2,B3),则A·B=A1B1+A2B2+A3B3。
2. 若向量A和向量B的坐标形式为A=a1i+a2j+a3k和B=b1i+b2j+b3k,其中i,j,k分别是坐标轴上的单位向量,则A·B=a1b1+a2b2+a3b3。
四、应用1. 判断向量是否垂直:如果向量A·B的结果为0,则向量A和向量B垂直;如果向量A·B的结果大于0,则向量A和向量B之间的夹角为锐角;如果向量A·B的结果小于0,则向量A和向量B之间的夹角为钝角。
2. 计算向量的模长:|A|=√(A·A)3. 计算向量的夹角:cosθ=(A·B)/(|A||B|)4. 计算向量的投影:向量A在向量B上的投影记作projBA=(A·B)/|B|总结:本文详细介绍了向量的数量积的定义、性质和应用。
向量的数量积是一种常用的向量运算,可以帮助我们计算向量之间的夹角、判断向量是否垂直等问题。
平面向量的数量积和向量积推导

平面向量的数量积和向量积推导平面向量的数量积和向量积是向量运算中常用的两个操作。
它们在几何学、物理学等领域中有广泛的应用。
本文将对平面向量的数量积和向量积进行推导和说明。
一、平面向量的数量积数量积(也称为点积或内积)是两个向量的乘积的数量表示。
设有两个平面向量a和b,它们的数量积为:a ·b = |a| * |b| * cosθ其中,|a|和|b|分别表示向量a和b的模长,θ表示a和b之间的夹角。
由此可见,数量积的结果是一个实数。
它有以下几个性质:1. 交换律:a · b = b · a2. 分配律:(a + b) · c = a · c + b · c3. 数乘结合律:(k * a) · b = k * (a · b) = a · (k * b)二、平面向量的向量积向量积(也称为叉积或外积)是两个向量的乘积的向量表示。
设有两个平面向量a和b,它们的向量积为:a ×b = |a| * |b| * sinθ * n其中,|a|和|b|分别表示向量a和b的模长,θ表示a和b之间的夹角,n表示与a和b均垂直的单位向量。
向量积的结果是一个向量,它的方向垂直于平面,由右手法则确定。
由此可见,向量积具有以下几个性质:1. 反交换律:a × b = - (b × a)2. 分配律:(a + b) × c = a × c + b × c3. 数乘结合律:(k * a) × b = k * (a × b) = a × (k * b)三、数量积和向量积之间的关系数量积和向量积之间存在一个重要的关系,即向量积的模长等于数量积的模长和夹角的正弦值的乘积:|a × b| = |a| * |b| * sinθ此外,还可以通过向量积来求得两个向量之间的夹角θ:cosθ = (a · b) / (|a| * |b|)四、应用举例1. 面积计算:对于平行四边形,以两边为相邻边的一条对角线为底,可以使用向量积求得其面积。
向量的数量积运算的所有公式

向量的数量积运算的所有公式1.定义:设向量a=(a1,a2,a3)和向量b=(b1,b2,b3),则a与b的数量积定义为:a·b=a1b1+a2b2+a3b32.单位向量:如果向量a是一个单位向量,则a与任何向量b的数量积等于b在a的方向上的投影长度。
3.平行向量:如果两个向量a和b平行,则它们的数量积为:a ·b = ,a,,b,cosθ其中,a,和,b,分别表示向量的模(长度),θ表示a和b之间的夹角。
4.正交向量:如果两个向量a和b互相垂直(夹角为90度),则它们的数量积为:a·b=05.向量的模:设向量a=(a1,a2,a3),则a的模定义为:a,=√(a1^2+a2^2+a3^2向量的模也可以表示为向量的数量积与自身的开方,即:a,=√(a·a6.向量的投影长度:设向量a与向量b之间的夹角为θ,则向量b 在a的方向上的投影长度为:proj_a(b) = ,b,cosθ投影长度也可以表示为数量积与向量a的模的商,即:proj_a(b) = (a · b) / ,a7.向量的夹角:设向量a和b之间的夹角为θ,则夹角的余弦可以表示为向量的数量积与两个向量模的商,即:cosθ = (a · b) / (,a,,b,)从该公式可以推导出两个向量夹角的正弦和余弦。
8.柯西-施瓦茨不等式:对于任意两个向量a和b,有:a·b,≤,a,当且仅当a和b共线时,等号成立。
9.向量的数量积的性质:-交换律:a·b=b·a-结合律:(c*a)·b=c*(a·b),其中c是一个标量-分配律:(a+b)·c=a·c+b·c这些公式是向量的数量积运算中的一些重要性质和公式。
它们在向量运算、物理学、几何学等领域具有广泛的应用。
第三节向量的数量积与向量积

第三节 向量的数量积与向量积
一、两向量的数量积 二、两向量的向量积
一、两向量的数量积
1.数量积的定义及其性质 规定两向量 a , b 的正方向之间不超过 180º的 夹角为向量 a 与 b 的夹角,记作 (a , b) ,或 (b , a). 若有一质点在常力 (大小与方向均不变) F 的作
坐标面上,所以 z = 0 . 又因为 b 是单位向量 且与 a 垂
直,所以 b 1, a b 0, 即有
z 0
x
2
y2
z2
1,
4x 3 y 7z 0.
解之得
x3 , y4,z0
5
5
故所求向量 b 3 i 4 j 或 b 3 i 4 j .
(2) c 垂直于 a,b 所确定的平面,它的正方 向由右手法则确定,则称向量 c 为 a 与 b 的向量 积,记为 a × b,即
c=a×b. 因此向量积也称为叉积.
由向量积的定义可知,a ×b 的模等于以 a、b 为邻边的平行四边形面积.
向量积具有下列运算规律:
a b b a;
c = a×b
a b a b sin ( a ,b ) 0, 因此 a b = 0.
反之,当 a、b 为非零向量,且 a b = 0 时,则
a b sin (a , b) = 0. 因为a 0, b 0.
所以 sin (a , b) = 0. 从而断定 (a , b) = 0 或 , 即 a // b . 当 a ,b 中至少有一个为零向量时,我 们规定零向量与任何向量平行. 这样,两个向量 平行的充要条件是这两个向量的向量积为 0 .
两向量的数量积汇总
c = ab b
(1) | c | = | a | | b | sin
a
(2) c 与a、b所在的平面垂直, (即 c a且c b). c 的指向按右手规则从 a 转向 b 来确定. 则将向量c 称为 a 与 b 的向量积, 记作: a b. 即: c=ab 注: 向量积的模的几何意义. 以a、b为邻边的平行四边形, 其面积等于| a | | b |sin, 所以a b的模, 等于以a、b为邻边的平行四边形的面积.
即
ab
2
例如: i、j、k 互相垂直, 所以 ij=jk=ik =0
例1: 如图, 利用数量积证明三角形的余弦定理 | c |2 = | a |2 + | b |2 2 | a | | b |cos
b c
证: 由于c = a b , 于是
a
| c |2 = | a b |2 = (a b) (a b) = a a + b b 2 a b
由 | a | 0, | b | 0, 得
= 0或 = . 所以 a 与 b 平行
例如: i i = j j = k k = 0 ij=k
ji=k
jk=i
kj=i i j
ki=j
ik=j
k
三、向量积的坐标表示式
设 a ={ax, ay , az},
2
1. 定义: 设有两个向量 a、b, 它们的夹角为,
将数值|a||b|cos 称为a与b的数量积, 记作 a b.
即: 注1: 于是 注2: 例如: a b = |a| |b| cos | b | cos = Prjab | a |cos = Prjba
8.2向量的数量积与向量积

a ⋅ b = axbx + ayby + azbz
数量积的坐标表达式
a⋅b , a ⋅ b =| a || b | cosθ ⇒ cos θ = | a || b | axbx + ayby + azbz cosθ = 2 2 2 2 2 2 ax + ay + az bx + by + bz
M1 M 2 =
2
M 1 P + M 1Q + M 1 R
2 2
2
| a |= a x + a y + a z 向量模的坐标表示式
2 2
向量方向余弦的坐标表示式 当
a x + a y + a z ≠ 0 时,
2 2 2
cos α = cos β =
cos γ =
ax a x + a y + az ay
符合右手系法则. 向量积也称为“叉积” c 符合右手系法则. 向量积也称为“叉积”、
“外积” “外积”. 外积 关于向量积的说明: 关于向量积的说明:
(1) a × a = 0.
(∵θ = 0 ⇒ sinθ = 0)
( a ≠ 0, b ≠ 0 )
( 2) a // b ⇐⇒ a × b = 0.
向量积符合下列运算规律: 向量积符合下列运算规律: (1) a × b = − b × a . ) (2)分配律: ( a + b ) × c = a × c + b × c . )分配律: 为实数: (3)若λ 为实数: (λa ) × b = a × (λb ) = λ (a × b ). )
向量的数量积与向量积运算详解

向量的数量积与向量积运算详解向量是线性代数中的一个重要概念,可以用来描述物理量的大小和方向。
在向量运算中,我们主要涉及两个操作:数量积和向量积。
这两个操作在不同的应用领域中有着广泛的应用,比如物理学、工程学等等。
在本文中,我们将会详细解释和探讨向量的数量积和向量积运算。
首先我们来介绍向量的数量积,也叫点积或内积。
数量积是指两个向量按照一定规则进行运算得到一个标量的运算。
设有两个向量A和B,分别表示为A=(a1, a2, a3)和B=(b1, b2, b3),则向量A和B的数量积表示为A·B,计算方式为A·B = a1b1 + a2b2 + a3b3。
这个计算方式可以用于计算向量的模长、夹角以及求解垂直关系等等。
它的计算结果是一个标量,表示两个向量之间的相关性。
数量积有一些重要的性质。
首先,数量积是可交换的,即A·B = B·A。
其次,数量积满足分配律,即A·(B+C) = A·B + A·C。
此外,如果A·B = 0,则称向量A和B垂直或正交。
接下来我们介绍向量的向量积,也叫叉积或外积。
向量积是指两个向量按照一定规则进行运算得到一个新的向量的运算。
设有两个向量A和B,分别表示为A=(a1, a2, a3)和B=(b1, b2, b3),则向量A和B的向量积表示为A×B,其结果是一个新的向量C=(c1, c2, c3)。
向量C的坐标c1、c2、c3的计算方式如下:c1 = a2b3 - a3b2,c2 = a3b1 - a1b3,c3 = a1b2 - a2b1。
向量积的计算方式与数量积有些相似,但结果是一个向量而不是一个标量。
向量积在几何学和物理学中有着广泛应用,比如计算平面的法向量、计算力矩等等。
向量积的结果是一个垂直于原来两个向量所在平面的向量,其模长等于以这两个向量为邻边的平行四边形的面积。
向量积也有一些重要的性质。
向量的数量积与向量积的计算与性质

向量的数量积与向量积的计算与性质向量是高中数学中的一个重要概念,它不仅在几何学中具有重要意义,也在物理学等学科中有广泛应用。
本文将探讨向量的数量积与向量积的计算方法以及它们的性质。
一、向量的数量积的计算数量积,又称点积或内积,是指两个向量的数量上的乘积。
对于两个向量A和B,在数量上的计算方法为A·B=|A||B|cosθ,其中|A|和|B|分别表示向量A和B的模,θ表示两个向量之间的夹角。
例如,假设有向量A(3, 4)和向量B(1, 2),要计算它们的数量积。
首先,计算向量A和向量B的模,分别为|A|=√(3²+4²)=5和|B|=√(1²+2²)=√5。
然后,计算夹角θ的余弦值cosθ=(A·B)/(|A||B|)=(3*1+4*2)/(5*√5)=0.95。
因此,向量A和向量B的数量积为A·B=5*√5*0.95=4.24。
二、向量积的计算向量积,又称叉积或外积,是指两个向量的向量上的乘积。
对于两个向量A和B,在向量上的计算方法为A×B=|A||B|sinθn,其中|A|和|B|表示向量A和B的模,θ表示两个向量之间的夹角,n表示垂直于平面的单位向量。
例如,假设有向量A(3, 4)和向量B(1, 2),要计算它们的向量积。
首先,计算向量A和向量B的模,分别为|A|=√(3²+4²)=5和|B|=√(1²+2²)=√5。
然后,计算夹角θ的正弦值sinθ=sinθ=(A×B)/(|A||B|)=(3*2-4*1)/(5*√5)=0.6。
最后,计算n的值,垂直于A和B的平面可以取z轴正方向,所以n=(0, 0, 1)。
因此,向量A 和向量B的向量积为A×B=5*√5*0.6*(0, 0, 1)=(0, 0, 6)。
三、向量的数量积和向量积的性质1. 交换律:向量的数量积满足交换律,即A·B=B·A;而向量的向量积不满足交换律,即A×B=-B×A。
空间向量的数量积和向量积

空间向量的数量积和向量积空间向量是三维空间中的矢量,有数量积和向量积两种运算。
一、数量积数量积,也称为点积或内积,是指两个向量之间进行的一种运算,结果是一个标量。
数量积的计算方法是将两个向量的对应分量相乘,并将乘积相加。
设有两个向量A = (A1, A2, A3)和A = (A1, A2, A3),它们的数量积表示为A·A。
计算公式如下:A·A = A1A1 + A2A2 + A3A3数量积有以下几个重要性质:1. 交换律:A·A = A·A2. 结合律:(AA)·A = A(A·A) = A·(AA),其中A为常数。
3. 分配律:A·(A + A) = A·A + A·A数量积可以用来计算向量之间的夹角和向量的投影。
夹角公式如下:cos A = A·A / (│A││A│)其中,A为A和A之间的夹角,│A│和│A│分别为向量A和A的模。
二、向量积向量积,也称为叉积或外积,是指两个向量之间进行的一种运算,结果是一个新的向量。
向量积的计算方法是利用行列式,将原向量和单位向量按照一定的顺序排列成矩阵,然后计算该矩阵的行列式。
设有两个向量A = (A1, A2, A3)和A = (A1, A2, A3),它们的向量积表示为A×A。
计算公式如下:A×A = (A2A3 - A3A2, A3A1 - A1A3, A1A2 - A2A1)向量积有以下几个重要性质:1. 反交换律:A×A = -A×A2. 分配律:A×(A + A) = A×A + A×A向量积的模可以表示为:│A×A│ = │A││A│sinA其中,A为A和A之间的夹角,│A×A│为向量积的模。
向量积可以用来计算以两个向量为邻边所构成的平行四边形的面积,并且垂直于这两个向量的方向。
空间向量的数量积与向量积

空间向量的数量积与向量积空间向量是在三维空间中具有大小和方向的量,可以表示为一个有序的三元组( x, y, z )。
向量的数量积和向量积是两个重要的运算,它们在物理学、工程学以及其他科学领域中经常被使用。
一、空间向量的数量积空间向量的数量积是指两个向量之间的数乘运算,表示为A·B。
假设有两个向量A和B,它们的数量积的定义如下:A·B = |A|·|B|·cosθ其中,|A|和|B|分别代表向量A和B的模长,θ表示两个向量之间的夹角。
数量积具有以下特性:1. A·B = B·A,即数量积的结果与向量的顺序无关。
2. 如果两个向量的数量积为零,即A·B = 0,则它们垂直于彼此,夹角为90°。
3. 如果两个向量的数量积大于零,即A·B > 0,则它们夹角小于90°,即锐角。
4. 如果两个向量的数量积小于零,即A·B < 0,则它们夹角大于90°,即钝角。
数量积的应用:1. 求解向量的夹角可以利用数量积的公式求解两个向量之间的夹角。
根据公式A·B = |A|·|B|·cosθ,可以通过已知的向量和夹角的模长计算出夹角的值。
2. 判定向量的垂直和平行关系如果向量A·B = 0,则可以判定向量A和B垂直。
如果向量A·B ≠ 0,则可以判定向量A和B不垂直。
3. 计算向量的投影通过数量积的计算,可以求一个向量在另一个向量上的投影。
投影是指一个向量在另一个向量上的映射。
二、空间向量的向量积空间向量的向量积是指两个向量之间的叉乘运算,表示为A×B。
假设有两个向量A和B,它们的向量积的定义如下:A×B = |A|·|B|·sinθ·n其中,|A|和|B|分别代表向量A和B的模长,θ表示两个向量之间的夹角,n是一个垂直于A和B所在平面的单位向量。
空间向量的数量积最完美版课件

02 空间向量向量的数量积定义为它们的 模长之积与它们夹角的余弦值的乘积 ,记作a·b。
当两个向量垂直时,它们的数量积为 0;当两个向量同向时,它们的数量 积为它们的模长之积。
空间向量的数量积最 完美版课件
目录
CONTENTS
• 空间向量的数量积定义 • 空间向量的数量积运算 • 空间向量的数量积的应用 • 空间向量的数量积的习题解析 • 空间向量的数量积的扩展知识
01 空间向量的数量积定义
定义
空间向量的数量积定义为两个向量的模长之积与它们夹角的 余弦值的乘积,记作:$mathbf{a} cdot mathbf{b} = |mathbf{a}| times |mathbf{b}| times cos theta$。
题目8: 已知空间向量 $overset{longrightarrow}{a} = (x,y,z)$, $overset{longrightarrow}{b} = (x + y - z,y - x - z,z - x - y)$,且 $overset{longrightarrow}{a}$与 $overset{longrightarrow}{b}$的数 量积为$0$,求$x^{2} + y^{2} + z^{2}$的值。
高级习题解析
题目7: 已知空间向量 $overset{longrightarrow}{a} = (x,y,z)$, $overset{longrightarrow}{b} = ( 2y + z,x + y, - x + z)$,且 $overset{longrightarrow}{a}$与 $overset{longrightarrow}{b}$的数 量积为$5$,求$x^{2} + y^{2} + z^{2}$的值。
平面向量的数量积和向量积的计算

平面向量的数量积和向量积的计算平面向量是应用广泛的数学工具之一,在物理、工程学和计算机科学等领域都有重要的应用。
在平面向量的运算中,数量积和向量积是两个重要的计算方法。
本文将介绍平面向量的数量积和向量积的计算方法及其应用。
一、数量积的计算方法数量积(又称点积或内积)是两个向量的乘积与两个向量之间夹角的余弦值的乘积。
对于平面向量A(x1, y1)和B(x2, y2),它们的数量积可以通过以下公式计算:A·B = |A| * |B| * cosθ其中,“·”表示数量积,“|A|”表示向量A的模长,“|B|”表示向量B的模长,θ表示向量A与向量B之间的夹角。
例如,对于向量A(3,-2)和向量B(5,4),它们的数量积可以计算如下:A·B = |A| * |B| * cosθ= √(3^2 + (-2)^2) * √(5^2 + 4^2) * cosθ= √13 * √41 * cosθ二、向量积的计算方法向量积(又称叉积或外积)是两个向量的乘积与两个向量所在平面的法向量的模长的乘积。
对于平面向量A(x1, y1)和B(x2, y2),它们的向量积可以通过以下公式计算:A×B = |A| * |B| * sinθ * n其中,“×”表示向量积,“|A|”表示向量A的模长,“|B|”表示向量B的模长,θ表示向量A与向量B之间的夹角,n是垂直于A和B所在平面的单位法向量。
例如,对于向量A(3,-2)和向量B(5,4),它们的向量积可以计算如下:A×B = |A| * |B| * sinθ * n= √(3^2 + (-2)^2) * √(5^2 + 4^2) * sinθ * n= √13 * √41 * sinθ * n三、数量积和向量积的应用1. 数量积:数量积在很多物理应用中起到重要的作用。
例如,在力学中,当两个力的夹角为零时,数量积表示力的乘积,可以用来计算功和能量;当两个力的夹角为90°时,数量积为零,表示两个力垂直,可以用来判断力的正交性。
平面向量的数量积与向量积

平面向量的数量积与向量积一、平面向量的数量积1.定义:两个非零向量a和b的点积(数量积)定义为a·b=|a||b|cosθ,其中θ为a和b之间的夹角,|a|和|b|分别为向量a和b的模长。
(1)交换律:a·b=b·a(2)分配律:a·(b+c)=a·b+a·c(3)数乘律:λa·b=(λa)·b=λ(a·b)(4)共线向量的性质:若向量a与向量b共线,则a·b=03.数量积的应用:(1)求向量的夹角:cosθ=(a·b)/(|a||b|)(2)判断向量垂直:若a·b=0,则向量a与向量b垂直(3)计算向量的模长:|a|=√(a·a)二、平面向量的向量积1.定义:两个非零向量a和b的向量积(叉积)定义为a×b=|a||b|sinθn,其中θ为a和b之间的夹角,n为垂直于a和b所在平面的单位法向量。
(1)交换律:a×b=b×a(2)与数量积的关系:|a×b|=|a||b|sinθ(3)数乘律:λa×b=(λa)×b=λ(a×b)(4)垂直性:a×b与a、b垂直,即(a×b)·a=0,(a×b)·b=03.向量积的应用:(1)求向量的夹角:sinθ=|a×b|/(|a||b|)(2)判断向量平行:若a×b=0,则向量a与向量b平行(3)计算平行四边形的面积:S=|a×b|(4)求力矩:力矩M=r×F,其中r为力的作用点到转轴的向量,F为力向量三、数量积与向量积的区别与联系(1)数量积是基于两个向量的夹角和模长计算的,而向量积是基于两个向量的夹角和模长计算的垂直于它们所在平面的向量。
(2)数量积是一个标量,而向量积是一个向量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(4) a a | a |2 或 | a | a a
(5) | a b || a | | b |
cos a b
|a||b|
2、判断下列各题是否正确
(1)若a=0,则对任意向量b,有a·b=0------
(2)若a≠0,且a·b=0,则b=0 ------------------(3)对任意向量a有a2=│a│2 ---------------(4)若a≠0且a·b=a·c,则b=c -------------------
注意:数量积运算不满足结合律
探究:数量积的运算律
证明运算律(3) (a b) c a c b c
A
a
θ2
b
B
θ1
θ O
c A1
B1 C
练习3:
已知 a,b为任意向量 求(1)(a b)2 (2)(a b) (a b)
平面向量数量积的常用公式
2
2
(1)(a b)2 a 2a b b
2
2
(2)(a b)(a b) a b
练 习4: 已 知 a 3 , b 2 , a 与 b 的夹 角为60
求 (1): (a 2b)2
(2) :| a 2b | (3) : (a 2b) (a 3b)
练习5:已知 a 5 , b 4, a 与 b(且 a 与 b 不共线),当且仅当k为何值时, 向量 a kb 与a kb 互相垂直?
2
求:a b及a
解:a2=a . a = a a cos α
a
2
|
a
|2
= a a cos 0 =a2
| a |
a
2
=52=25
变式:已知| a | 5 , | b | 4,且ab 5求a 与b的夹角余弦.
cos a b
|a||b|
夹角公式
根据定义思考下列各题:
设a , b 是非零向量,e 是与 b 方向相同的单位向量,
规定:零向量与任一向量的数量积为0
0·a=0
练习1:已知a 5 , b 4, a 与 b 的夹角 120 ,
2
求:a b及a
解:a b | a | | b | cos
5 4 cos120o 54( 1)
2 10 思考: 平面向量的数量积与差向量、和 向量的区别是什么?
练习1:已知a 5 , b 4, a 与 b 的夹角 120 ,
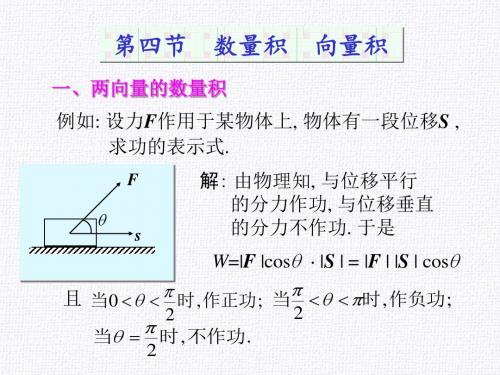
F θ
O
A
位移S
问:一个物体在力F 的作用下产生的位移s,那么力F 所做的功应当怎样计算?
力F做的功:W = |F||s|cos,是F与s的夹角。
定义:已知两个非零向量a和b,他们的夹角为θ,我 们把数量│a││b│cosθ叫做a与b的数量积 (或内积),记作a·b,即
a·b=│a││b│cosθ
小结: (1)向量的数量积的定义及几何意义. (2)向量数量积的5条性质. (3)向量数量积的运算律。
a b 的几何意义: 向 量a 与b的 数 量 积a b等 于a的 长 度 与
b在a的 方 向 上 的 投 影| b | cos的 积
平面向量数量积的运算律
(1)a b b a (交换律)
(2)( a) b (a b) a (b) (数乘结合律)
(3)(a b) c a c b c (分配律)
向量的夹角
已知两个非零向量 a 和 b , 作OA a ,OB b则AOB (0 ) 叫做向量 a 和 b 的夹角。
B
θ
O
A
判断下面两个向量的夹角大小:
a
a
a
┐b
b
b
(1)
( 2)
(3)
a
a
60O
b (4)
120O
b
注意在两向量的夹角定义中,两向量必须是同起点的. 范围0≤≤180
(√)
(× ) (√ ) (× )
如图:作出| b | cos ,并说出它的几何意义
B
B
B
b
b
b
θ ┐a O B1 A
┐ θ a ┓θ
a
B1 O A O (B1) A
(1)
(2)
(3)
| b | cos 叫 做b在a方 向 上 的 投 影 ;
| a | cos 叫 做a在b方 向 上 的 投 影
是 a , e 的夹角,则
(1) a e 和 e a 的关系是: a e e a | a |b的关系是: a b 0 a b
(3) 当 a 与 b 同向时,a b | a | | b |
当 a 与 b 反向时,a b | a | | b |
