【高中数学】线面角的最小性

合集下载

高二数学空间角——线线角与线面角

(2)法一如图 1，取 PB 中点 F，连接 EF，AF，
则 EF∥BC，从而∠AEF(或其补角)是异面直线
BC 与 AE 所成的角．
在△AEF 中，由于 EF＝ 2，AF＝ 2，
F
AE＝12PC＝2.
则△AEF 是等腰直角三角形，
所以∠AEF＝π4.
因此，异面直线 BC 与 AE 所成的角的大小是π4.
因为 PD＝ 22＋2 22＝2 3，CD＝2，所以三角形 PCD 的面积为12×2×2 3＝2 3.
求异面直线所成的角
【例 1】如图，在四棱锥 P-ABCD 中，底面 ABCD 是矩形，PA⊥底面
ABCD，E 是 PC 的中点．已知 AB＝2，AD＝2 2，PA＝2.求： (1)三角形 PCD 的面积． (2)异面直线 BC 与 AE 所成的角的大小．
n0＝±13，－23，23.( )
(3)已知 a＝(－2，－3,1)，b＝(2,0,4)，c＝(－4，－6,2)，则 a∥c，a⊥b.( )
2.空间角
(4)两异面直线夹角的范围是0，π2，直线与平面所成角的范围是0，π2，
二面角的范围是[0，π]．( ) (5)已知向量 m，n 分别是直线 l 和平面 α 的方向向量、法向量，若 cos〈m，n〉＝－12，则 l 与 α 所成的角为 150°.( ) (6)在如图所示的正方体 ABCD-A1B1C1D1 中，异面直线 A1B 与 B1C 所成角的大小为 60°.( )
ABCD，E 是 PC 的中点．已知 AB＝2，AD＝2 2，PA＝2.求： (1)三角形 PCD 的面积． (2)异面直线 BC 与 AE 所成的角的大小．
规律方法
z
本题可从两个不同角度求异面直线所成的

高中数学新教材《8.6.2 线面角》公开课优秀课件(好用)

心.
2、如图，三棱锥 A－SBC 中，∠BSC＝90°，∠ASB＝∠ASC＝60°，SA＝SB＝ SC.求直线 AS 与平面 SBC 所成的角．
解：∵∠ASB＝∠ASC＝60°，SA＝SB＝SC ∴△ASB 与△SAC 都是等边三角形．∴AB＝AC. 如图，取 BC 的中点 D，连接 AD，SD，则 AD⊥BC.设 SA＝a，
在 Rt△ASD 中，SD＝AD＝ 22a，所以∠ASD＝45°，即直线 AS 与平面 SBC 所成的角为 45°.
作业
课本163页13题
谢谢指导！
解析：由图可知，直线 BD1 与平面 ABCD 所成的角为
∠D1
BD，由条件可知
tan∠D1BD＝DD1BD＝2
4
＝ 2
2.
，BC＝ 2，PA⊥平面 ABCD，PA ＝1，则 PC 与平面 ABCD 所成的角是________．
解析：由题意知∠PCA 为 PC 与平面 ABCD 所成的角．
提示：能．
例在正方体ABCD-A1B1C1D1中. 求直线A1B和平面A1B1CD所成的角.
D1 A1
D A
C1 B1
O C
B
课堂小结
本节课你有哪些收获？
达标测试
1、过三角形 ABC 所在平面 α 外一点 P，作 PO⊥α，垂足为 O，连接 PA，PB，
PC，若 PA=PB=PC，则点 O 是三角形 ABC 的
斜线PA在平面内的射影
斜线PA与平面所成的角为PAB
2.平面的垂线与平面所成的角为 3.一条直线与平面平行或在平面内，则这条直线与平面所成的角为
一条直线与平面所成的角的取值范围是
跟踪训练 1.如图，若正四棱柱 ABCD －A1B1C1D1 的底面边长为 2，

2023年高考全国乙卷数学(理)真题(解析版)

2023年普通高等学校招生全国统一考试理科数学一、选择题1.设z =2+i1+i 2+i5，则z =()A.1-2iB.1+2iC.2-iD.2+i【答案】B 【解析】【分析】由题意首先计算复数z 的值，然后利用共轭复数的定义确定其共轭复数即可.【详解】由题意可得z =2+i 1+i 2+i 5=2+i 1-1+i =i 2+i i2=2i -1-1=1-2i ，则z=1+2i.故选：B .2.设集合U =R ，集合M =x x <1 ，N =x -1<x <2 ，则x x ≥2 =()A.∁U M ∪NB.N ∪∁U MC.∁U M ∩ND.M ∪∁U N【答案】A 【解析】【分析】由题意逐一考查所给的选项运算结果是否为x |x ≥2 即可.【详解】由题意可得M ∪N =x |x <2 ，则∁U M ∪N =x |x ≥2 ，选项A 正确；∁U M =x |x ≥1 ，则N ∪∁U M =x |x >-1 ，选项B 错误；M ∩N =x |-1<x <1 ，则∁U M ∩N =x |x ≤-1 或x ≥1 ，选项C 错误；∁U N =x |x ≤-1 或x ≥2 ，则M ∪∁U N =x |x <1 或x ≥2 ，选项D 错误；故选：A .3.如图，网格纸上绘制的一个零件的三视图，网格小正方形的边长为1，则该零件的表面积为()A.24B.26C.28D.30【答案】D 【解析】【分析】由题意首先由三视图还原空间几何体，然后由所得的空间几何体的结构特征求解其表面积即可.【详解】如图所示，在长方体ABCD -A 1B 1C 1D 1中，AB =BC =2，AA 1=3，点H ,I ,J ,K 为所在棱上靠近点B 1,C 1,D 1,A 1的三等分点，O ,L ,M ,N 为所在棱的中点，则三视图所对应的几何体为长方体ABCD -A 1B 1C 1D 1去掉长方体ONIC 1-LMHB 1之后所得的几何体，该几何体的表面积和原来的长方体的表面积相比少2个边长为1的正方形，其表面积为：2×2×2 +4×2×3 -2×1×1 =30.故选：D .4.已知f (x )=xe xe ax -1是偶函数，则a =()A.-2B.-1C.1D.2【答案】D 【解析】【分析】根据偶函数的定义运算求解.【详解】因为f x =xe x e ax-1为偶函数，则f x -f -x =xexe ax -1--x e-xe -ax -1=x e x -e a -1xe ax -1=0，又因为x 不恒为0，可得e x -e a -1 x=0，即e x =e a -1x，则x =a -1 x ，即1=a -1，解得a =2.故选：D .5.设O 为平面坐标系的坐标原点，在区域x ,y 1≤x 2+y 2≤4 内随机取一点，记该点为A ，则直线OA 的倾斜角不大于π4的概率为()A.18B.16C.14D.12【解析】【分析】根据题意分析区域的几何意义，结合几何概型运算求解.【详解】因为区域x ,y |1≤x 2+y 2≤4 表示以O 0,0 圆心，外圆半径R =2，内圆半径r =1的圆环，则直线OA 的倾斜角不大于π4的部分如阴影所示，在第一象限部分对应的圆心角∠MON =π4，结合对称性可得所求概率P =2×π42π=14.故选：C .6.已知函数f (x )=sin (ωx +φ)在区间π6,2π3 单调递增，直线x =π6和x =2π3为函数y =f x 的图像的两条对称轴，则f -5π12 =()A.-32B.-12C.12D.32【答案】D 【解析】【分析】根据题意分别求出其周期，再根据其最小值求出初相，代入x =-5π12即可得到答案.【详解】因为f (x )=sin (ωx +φ)在区间π6,2π3单调递增，所以T 2=2π3-π6=π2，且ω>0，则T =π，w =2πT =2，当x =π6时，f x 取得最小值，则2⋅π6+φ=2k π-π2，k ∈Z ，则φ=2k π-5π6，k ∈Z ，不妨取k =0，则f x =sin 2x -5π6 ，则f -5π12 =sin -5π3 =32，7.甲乙两位同学从6种课外读物中各自选读2种，则这两人选读的课外读物中恰有1种相同的选法共有()A.30种B.60种C.120种D.240种【答案】C 【解析】【分析】相同读物有6种情况，剩余两种读物的选择再进行排列，最后根据分步乘法公式即可得到答案.【详解】首先确定相同得读物，共有C 16种情况，然后两人各自的另外一种读物相当于在剩余的5种读物里，选出两种进行排列，共有A 25种，根据分步乘法公式则共有C 16⋅A 25=120种，故选：C .8.已知圆锥PO 的底面半径为3，O 为底面圆心，PA ，PB 为圆锥的母线，∠AOB =120°，若△PAB 的面积等于934，则该圆锥的体积为()A.πB.6πC.3πD.36π【答案】B 【解析】【分析】根据给定条件，利用三角形面积公式求出圆锥的母线长，进而求出圆锥的高，求出体积作答.【详解】在△AOB 中，∠AOB =120°，而OA =OB =3，取AC 中点C ，连接OC ,PC ，有OC ⊥AB ,PC ⊥AB ，如图，∠ABO =30°，OC =32,AB =2BC =3，由△PAB 的面积为934，得12×3×PC =934，解得PC =332，于是PO =PC 2-OC 2=332 2-32 2=6，所以圆锥的体积V =13π×OA 2×PO =13π×(3)2×6=6π.9.已知△ABC 为等腰直角三角形，AB 为斜边，△ABD 为等边三角形，若二面角C -AB -D 为150°，则直线CD 与平面ABC 所成角的正切值为()A.15B.25C.35D.25【答案】C 【解析】【分析】根据给定条件，推导确定线面角，再利用余弦定理、正弦定理求解作答.【详解】取AB 的中点E ，连接CE ,DE ，因为△ABC 是等腰直角三角形，且AB 为斜边，则有CE ⊥AB ，又△ABD 是等边三角形，则DE ⊥AB ，从而∠CED 为二面角C -AB -D 的平面角，即∠CED =150°，显然CE ∩DE =E ,CE ,DE ⊂平面CDE ，于是AB ⊥平面CDE ，又AB ⊂平面ABC ，因此平面CDE ⊥平面ABC ，显然平面CDE ∩平面ABC =CE ，直线CD ⊂平面CDE ，则直线CD 在平面ABC 内的射影为直线CE ，从而∠DCE 为直线CD 与平面ABC 所成的角，令AB =2，则CE =1,DE =3，在△CDE 中，由余弦定理得：CD =CE 2+DE 2-2CE ⋅DE cos ∠CED =1+3-2×1×3×-32=7，由正弦定理得DE sin ∠DCE =CDsin ∠CED，即sin ∠DCE =3sin150°7=327，显然∠DCE 是锐角，cos ∠DCE =1-sin 2∠DCE =1-3272=527，所以直线CD 与平面ABC 所成的角的正切为35.故选：C10.已知等差数列a n 的公差为2π3，集合S =cos a n n ∈N * ，若S =a ,b ，则ab =()A.-1B.-12C.0D.12【解析】【分析】根据给定的等差数列，写出通项公式，再结合余弦型函数的周期及集合只有两个元素分析、推理作答.【详解】依题意，等差数列{a n }中，a n =a 1+(n -1)⋅2π3=2π3n +a 1-2π3，显然函数y =cos 2π3n +a 1-2π3的周期为3，而n ∈N ∗，即cos a n 最多3个不同取值，又{cos a n |n ∈N ∗}={a ,b }，则在cos a 1,cos a 2,cos a 3中，cos a 1=cos a 2≠cos a 3或cos a 1≠cos a 2=cos a 3，于是有cos θ=cos θ+2π3 ，即有θ+θ+2π3 =2k π,k ∈Z ，解得θ=k π-π3,k ∈Z ，所以k ∈Z ，ab =cos k π-π3 cos k π-π3 +4π3 =-cos k π-π3 cos k π=-cos 2k πcos π3=-12.故选：B11.设A ，B 为双曲线x 2-y 29=1上两点，下列四个点中，可为线段AB 中点的是()A.1,1B.-1,2C.1,3D.-1,-4【答案】D 【解析】【分析】根据点差法分析可得k AB ⋅k =9，对于A 、B 、D ：通过联立方程判断交点个数，逐项分析判断；对于C ：结合双曲线的渐近线分析判断.【详解】设A x 1,y 1 ,B x 2,y 2 ，则AB 的中点M x 1+x 22,y 1+y 22，可得k AB =y 1-y 2x 1-x 2,k =y 1+y 22x 1+x 22=y 1+y 2x 1+x 2，因为A ,B 在双曲线上，则x 21-y 219=1x 22-y 229=1，两式相减得x 21-x 22-y 21-y 229=0，所以k AB ⋅k =y 21-y 22x 21-x 22=9.对于选项A ：可得k =1,k AB =9，则AB :y =9x -8，联立方程y =9x -8x 2-y 29=1 ，消去y 得72x 2-2×72x +73=0，此时Δ=-2×72 2-4×72×73=-288<0，所以直线AB 与双曲线没有交点，故A 错误；对于选项B ：可得k =-2,k AB =-92，则AB :y =-92x -52，联立方程y =-92x -52x 2-y 29=1，消去y 得45x 2+2×45x +61=0，此时Δ=2×45 2-4×45×61=-4×45×16<0，所以直线AB 与双曲线没有交点，故B 错误；对于选项C ：可得k =3,k AB =3，则AB :y =3x由双曲线方程可得a =1,b =3，则AB :y =3x 为双曲线的渐近线，所以直线AB 与双曲线没有交点，故C 错误；对于选项D ：k =4,k AB =94，则AB :y =94x -74，联立方程y =94x -74x 2-y 29=1，消去y 得63x 2+126x -193=0，此时Δ=1262+4×63×193>0，故直线AB 与双曲线有交两个交点，故D 正确；故选：D .12.已知⊙O 的半径为1，直线PA 与⊙O 相切于点A ，直线PB 与⊙O 交于B ，C 两点，D 为BC 的中点，若PO =2，则PA ⋅PD的最大值为()A.1+22B.1+222C.1+2D.2+2【答案】A 【解析】【分析】由题意作出示意图，然后分类讨论，利用平面向量的数量积定义可得PA ⋅PD =12-22sin 2α-π4 ，或PA ⋅PD =12+22sin 2α+π4 然后结合三角函数的性质即可确定PA ⋅PD的最大值.【详解】如图所示，OA =1,OP =2，则由题意可知:∠APO =45°，由勾股定理可得PA =OP 2-OA 2=1当点A ,D 位于直线PO 异侧时，设∠OPC =α,0≤α≤π4，则：PA ⋅PD =|PA |⋅|PD |cos α+π4=1×2cos αcos α+π4=2cos α22cos α-22sin α =cos 2α-sin αcos α=1+cos2α2-12sin2α=12-22sin 2α-π4 0≤α≤π4，则-π4≤2α-π4≤π4∴当2α-π4=-π4时，PA ⋅PD 有最大值1.当点A ,D 位于直线PO 同侧时，设∠OPC =α,0≤α≤π4，则：PA ⋅PD =|PA |⋅|PD |cos α-π4=1×2cos αcos α-π4=2cos α22cos α+22sin α =cos 2α+sin αcos α=1+cos2α2+12sin2α=12+22sin 2α+π40≤α≤π4，则π4≤2α+π4≤π2∴当2α+π4=π2时，PA ⋅PD 有最大值1+22.综上可得，PA ⋅PD 的最大值为1+22.【点睛】本题的核心在于能够正确作出示意图，然后将数量积的问题转化为三角函数求最值的问题，考查了学生对于知识的综合掌握程度和灵活处理问题的能力.二、填空题13.已知点A 1,5 在抛物线C ：y 2=2px 上，则A 到C 的准线的距离为.【答案】94【解析】【分析】由题意首先求得抛物线的标准方程，然后由抛物线方程可得抛物线的准线方程为x =-54，最后利用点的坐标和准线方程计算点A 到C 的准线的距离即可.【详解】由题意可得：5 2=2p ×1，则2p =5，抛物线的方程为y 2=5x ，准线方程为x =-54，点A 到C 的准线的距离为1--54 =94.故答案为：94.14.若x ，y 满足约束条件x -3y ≤-1x +2y ≤93x +y ≥7，则z =2x -y 的最大值为.【答案】8【解析】【分析】作出可行域，转化为截距最值讨论即可.详解】作出可行域如下图所示：z =2x -y ，移项得y =2x -z ，联立有x -3y =-1x +2y =9，解得x =5y =2，设A 5,2 ，显然平移直线y =2x 使其经过点A ，此时截距-z 最小，则z 最大，代入得z =8，故答案为：8.15.已知a n 为等比数列，a 2a 4a 5=a 3a 6，a 9a 10=-8，则a 7=.【解析】【分析】根据等比数列公式对a 2a 4a 5=a 3a 6化简得a 1q =1，联立a 9a 10=-8求出q 3=-2，最后得a 7=a 1q ⋅q 5=q 5=-2.【详解】设a n 的公比为q q ≠0 ，则a 2a 4a 5=a 3a 6=a 2q ⋅a 5q ，显然a n ≠0，则a 4=q 2，即a 1q 3=q 2，则a 1q =1，因为a 9a 10=-8，则a 1q 8⋅a 1q 9=-8，则q 15=q 5 3=-8=-2 3，则q 3=-2，则a 7=a 1q ⋅q 5=q 5=-2，故答案为：-2.16.设a ∈0,1 ，若函数f x =a x +1+a x 在0,+∞ 上单调递增，则a 的取值范围是.【答案】5-12,1 【解析】【分析】原问题等价于f x =a x ln a +1+a x ln 1+a ≥0恒成立，据此将所得的不等式进行恒等变形，可得1+a a x ≥-ln aln 1+a ，由右侧函数的单调性可得实数a 的二次不等式，求解二次不等式后可确定实数a 的取值范围.【详解】由函数的解析式可得f x =a x ln a +1+a x ln 1+a ≥0在区间0,+∞ 上恒成立，则1+a x ln 1+a ≥-a x ln a ，即1+a a x ≥-ln aln 1+a在区间0,+∞ 上恒成立，故1+a a 0=1≥-ln aln 1+a，而a +1∈1,2 ，故ln 1+a >0，故ln a +1 ≥-ln a 0<a <1即a a +1 ≥10<a <1 ，故5-12≤a <1，结合题意可得实数a 的取值范围是5-12,1.故答案为：5-12,1.三、解答题17.某厂为比较甲乙两种工艺对橡胶产品伸缩率的处理效应，进行10次配对试验，每次配对试验选用材质相同的两个橡胶产品，随机地选其中一个用甲工艺处理，另一个用乙工艺处理，测量处理后的橡胶产品的伸缩率，甲、乙两种工艺处理后的橡胶产品的伸缩率分别记为x i ，y i (i =1,2,⋅⋅⋅10)，试验结果如下试验序号i 12345678910伸缩率x i545355525754545659545312541868伸缩率y i536527543530560533522550576536记z i =x i -y i (i =1,2,⋯,10)，记z 1，z 2，⋯，z 10的样本平均数为z，样本方差为s 2，(1)求z ，s 2；(2)判断甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率是否有显著提高(如果z ≥2s 210，则认为甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率有显著提高，否则不认为有显著提高).【答案】(1)z =11，s 2=61；(2)认为甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率有显著提高.【解析】【分析】(1)直接利用平均数公式即可计算出x ,y ，再得到所有的z i 值，最后计算出方差即可；(2)根据公式计算出2s 210的值，和z 比较大小即可.【小问1详解】x =545+533+551+522+575+544+541+568+596+54810=552.3，y =536+527+543+530+560+533+522+550+576+53610=541.3，z =x -y=552.3-541.3=11，z i =x i -y i 的值分别为:9,6,8,-8,15,11,19,18,20,12，故s 2=(9-11)2+(6-11)2+(8-11)2+(-8-11)2+(15-11)2+0+(19-11)2+(18-11)2+(20-11)2+(12-110=61【小问2详解】由(1)知:z=11，2s 210=2 6.1=24.4，故有z ≥2s 210,所以认为甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率有显著提高.18.在△ABC 中，已知∠BAC =120°，AB =2，AC =1.(1)求sin ∠ABC ；(2)若D 为BC 上一点，且∠BAD =90°，求△ADC 的面积.【答案】(1)21 14；(2)310.【解析】【分析】(1)首先由余弦定理求得边长BC的值为BC=7，然后由余弦定理可得cos B=5714，最后由同角三角函数基本关系可得sin B=21 14；(2)由题意可得S△ABDS△ACD=4，则S△ACD=15S△ABC，据此即可求得△ADC的面积.【小问1详解】由余弦定理可得：BC2=a2=b2+c2-2bc cos A=4+1-2×2×1×cos120°=7，则BC=7，cos B=a2+c2-b22ac=7+4-12×2×7=5714，sin B=1-cos2B=1-2528=2114.【小问2详解】由三角形面积公式可得S△ABDS△ACD=12×AB×AD×sin90°12×AC×AD×sin30°=4，则S△ACD=15S△ABC=15×12×2×1×sin120°=310.19.如图，在三棱锥P-ABC中，AB⊥BC，AB=2，BC=22，PB=PC=6，BP，AP，BC的中点分别为D，E，O，AD=5DO，点F在AC上，BF⊥AO.(1)证明：EF⎳平面ADO；(2)证明：平面ADO⊥平面BEF；(3)求二面角D-AO-C的正弦值.【答案】(1)证明见解析；(2)证明见解析；(3)22.【解析】【分析】(1)根据给定条件，证明四边形ODEF 为平行四边形，再利用线面平行判定推理作答.(2)由(1)的信息，结合勾股定理的逆定理及线面垂直、面面垂直的判定推理作答.(3)由(2)的信息作出并证明二面角的平面角，再结合三角形重心及余弦定理求解作答.【小问1详解】连接DE ,OF ，设AF =tAC ，则BF =BA +AF =(1-t )BA +tBC ，AO =-BA +12BC ，BF ⊥AO ，则BF ⋅AO =[(1-t )BA +tBC ]⋅-BA +12BC =(t -1)BA 2+12tBC 2=4(t -1)+4t =0，解得t =12，则F 为AC 的中点，由D ,E ,O ,F 分别为PB ,PA ,BC ,AC 的中点，于是DE ⎳AB ,DE =12AB ,OF ⎳AB ,OF =12AB ，即DE ⎳OF ,DE =OF ，则四边形ODEF 为平行四边形，EF ⎳DO ,EF =DO ，又EF ⊄平面ADO ,DO ⊂平面ADO ，所以EF ⎳平面ADO .ABCDEO P【小问2详解】由(1)可知EF ⎳OD ，则AO =6,DO =62，得AD =5DO =302，因此OD 2+AO 2=AD 2=152，则OD ⊥AO ，有EF ⊥AO ，又AO ⊥BF ,BF ∩EF =F ，BF ,EF ⊂平面BEF ，则有AO ⊥平面BEF ，又AO ⊂平面ADO ，所以平面ADO ⊥平面BEF .【小问3详解】过点O 作OH ⎳BF 交AC 于点H ，设AD ∩BE =G ，由AO ⊥BF ，得HO ⊥AO ，且FH =13AH ，又由(2)知，OD ⊥AO ，则∠DOH 为二面角D -AO -C 的平面角，因为D ,E 分别为PB ,PA 的中点，因此G 为△PAB 的重心，即有DG =13AD ,GE =13BE ，又FH =13 AH ，即有DH =32GF ，cos ∠ABD =4+32-1522×2×62=4+6-PA 22×2×6，解得PA =14，同理得BE =62，于是BE 2+EF 2=BF 2=3，即有BE ⊥EF ，则GF 2=13×622+622=53，从而GF =153，DH =32×153=152，在△DOH 中，OH =12BF =32,OD =62,DH =152，于是cos ∠DOH =64+34-1542×62×32=-22，sin ∠DOH =1--222=22，所以二面角D -AO -C 的正弦值为22.ABCD EFGH OP20.已知椭圆C ：y 2a 2+x 2b 2=1a >b >0 的离心率为53，点A -2,0 在C 上.(1)求C 的方程；(2)过点-2,3 的直线交C 于点P ，Q 两点，直线AP ，AQ 与y 轴的交点分别为M ，N ，证明：线段MN 的中点为定点.【答案】(1)y 29+x 24=1(2)证明见详解【解析】【分析】(1)根据题意列式求解a ,b ,c ，进而可得结果；(2)设直线PQ 的方程，进而可求点M ,N 的坐标，结合韦达定理验证y M +y N2为定值即可.【小问1详解】由题意可得b =2a 2=b 2+c 2e =c a =53，解得a =3b =2c =5，所以椭圆方程为y 29+x 24=1.【小问2详解】由题意可知：直线PQ 的斜率存在，设PQ :y =k x +2 +3,P x 1,y 1 ,Q x 2,y 2 ，联立方程y =k x +2 +3y 29+x 24=1，消去y 得：4k 2+9 x 2+8k 2k +3 x +16k 2+3k =0，则Δ=64k 22k +3 2-644k 2+9 k 2+3k =-1728k >0，解得k <0，可得x 1+x 2=-8k 2k +34k 2+9,x 1x 2=16k 2+3k 4k 2+9，因为A -2,0 ，则直线AP :y =y 1x 1+2x +2 ，令x =0，解得y =2y 1x 1+2，即M 0,2y 1x 1+2,同理可得N 0,2y 2x 2+2，则2y 1x 1+2+2y 2x 2+22=k x 1+2 +3x 1+2+k x 2+2 +3x 2+2=kx 1+2k +3 x 2+2 +kx 2+2k +3 x 1+2 x 1+2 x 2+2=2kx 1x 2+4k +3 x 1+x 2 +42k +3x 1x 2+2x 1+x 2 +4=32k k 2+3k 4k 2+9-8k 4k +3 2k +34k 2+9+42k +316k 2+3k 4k 2+9-16k 2k +34k 2+9+4=10836=3，所以线段PQ 的中点是定点0,3 .【点睛】方法点睛：求解定值问题的三个步骤(1)由特例得出一个值，此值一般就是定值；(2)证明定值，有时可直接证明定值，有时将问题转化为代数式，可证明该代数式与参数(某些变量)无关；也可令系数等于零，得出定值；(3)得出结论．21.已知函数f(x)=1x +aln(1+x).(1)当a=-1时，求曲线y=f x 在点1,f1处的切线方程；(2)是否存在a，b，使得曲线y=f1x关于直线x=b对称，若存在，求a，b的值，若不存在，说明理由.(3)若f x 在0,+∞存在极值，求a的取值范围.【答案】(1)ln2x+y-ln2=0；(2)存在a=12,b=-12满足题意，理由见解析.(3)0,12.【解析】【分析】(1)由题意首先求得导函数的解析式，然后由导数的几何意义确定切线的斜率和切点坐标，最后求解切线方程即可；(2)首先求得函数的定义域，由函数的定义域可确定实数b的值，进一步结合函数的对称性利用特殊值法可得关于实数a的方程，解方程可得实数a的值，最后检验所得的a,b是否正确即可；(3)原问题等价于导函数有变号的零点，据此构造新函数g x =ax2+x-x+1ln x+1，然后对函数求导，利用切线放缩研究导函数的性质，分类讨论a≤0，a≥12和0<a<12三中情况即可求得实数a的取值范围.【小问1详解】当a=-1时，f x =1x-1ln x+1，则f x =-1x2×ln x+1+1x-1×1x+1，据此可得f1 =0,f 1 =-ln2，函数在1,f1处的切线方程为y-0=-ln2x-1，即ln2x+y-ln2=0.【小问2详解】由函数的解析式可得f1x=x+aln1x+1，函数的定义域满足1x+1=x+1x>0，即函数的定义域为-∞,-1∪0,+∞，定义域关于直线x=-12对称，由题意可得b=-12，由对称性可知f-12+m=f-12-mm>12，取m=32可得f1 =f-2，即a+1ln2=a-2ln 12，则a+1=2-a，解得a=12，经检验a=12,b=-12满足题意，故a=12,b=-12.即存在a=12,b=-12满足题意.【小问3详解】由函数的解析式可得f x =-1 x2ln x+1+1x+a1x+1，由f x 在区间0,+∞存在极值点，则f x 在区间0,+∞上存在变号零点;令-1 x2ln x+1+1x+a1x+1=0，则-x+1ln x+1+x+ax2=0，令g x =ax2+x-x+1ln x+1，f x 在区间0,+∞存在极值点，等价于g x 在区间0,+∞上存在变号零点，g x =2ax-ln x+1,g x =2a-1 x+1当a≤0时，g x <0，g x 在区间0,+∞上单调递减，此时g x <g0 =0，g x 在区间0,+∞上无零点，不合题意;当a≥12，2a≥1时，由于1x+1<1，所以g x >0,g x 在区间0,+∞上单调递增，所以g x >g 0 =0，g x 在区间0,+∞上单调递增，g x >g0 =0，所以g x 在区间0,+∞上无零点，不符合题意；当0<a<12时，由gx =2a-1x+1=0可得x=12a-1，当x∈0,12a-1时，g x <0，g x 单调递减，当x∈12a-1,+∞时，g x >0，g x 单调递增，故g x 的最小值为g12a-1=1-2a+ln2a，令m x =1-x+ln x0<x<1，则m x =-x+1x>0，函数m x 在定义域内单调递增，m x <m1 =0，据此可得1-x+ln x<0恒成立，则g 12a-1=1-2a +ln2a <0，令h x =ln x -x 2+x x >0 ，则hx =-2x 2+x +1x ，当x ∈0,1 时，h x >0,h x 单调递增，当x ∈1,+∞ 时，h x <0,h x 单调递减，故h x ≤h 1 =0，即ln x ≤x 2-x (取等条件为x =1)，所以g x =2ax -ln x +1 >2ax -x +1 2-x +1 =2ax -x 2+x ，g 2a -1 >2a 2a -1 -2a -1 2+2a -1 =0，且注意到g 0 =0，根据零点存在性定理可知:g x 在区间0,+∞ 上存在唯一零点x 0.当x ∈0,x 0 时，g x <0，g x 单调减，当x ∈x 0,+∞ 时，g x >0，g x 单调递增，所以g x 0 <g 0 =0.令n x =ln x -12x -1x ，则n x =1x -121+1x 2=-x -1 22x2≤0，则n x 单调递减，注意到n 1 =0，故当x ∈1,+∞ 时，ln x -12x -1x <0，从而有ln x <12x -1x，所以g x =ax 2+x -x +1 ln x +1 >ax 2+x -x +1 ×12x +1 -1x +1=a -12 x 2+12，令a -12 x 2+12=0得x 2=11-2a，所以g 11-2a>0，所以函数g x区间0,+∞ 上存在变号零点，符合题意.综合上面可知:实数a 得取值范围是0,12.【点睛】(1)求切线方程的核心是利用导函数求切线的斜率，求函数的导数要准确地把函数拆分成基本初等函数的和、差、积、商，再利用运算法则求导，合函数求导，应由外到内逐层求导，必要时要进行换元.(2)根据函数的极值(点)求参数的两个要领：①列式:根据极值点处导数为0和极值这两个条件列方程组，利用待定系数法求解;②验证:求解后验证根的合理性.本题中第二问利用对称性求参数值之后也需要进行验证.四、选做题【选修4-4】(10分)22.在直角坐标系xOy 中，以坐标原点O 为极点，x 轴正半轴为极轴建立极坐标系，曲线C 1的极坐标方程为ρ=2sin θπ4≤θ≤π2，曲线C 2：x =2cos αy =2sin α (α为参数，π2<α<π).(1)写出C 1的直角坐标方程；(2)若直线y =x +m 既与C 1没有公共点，也与C 2没有公共点，求m 的取值范围.【答案】(1)x 2+y -1 2=1,x ∈0,1 ,y ∈1,2 (2)-∞,0 ∪22,+∞ 【解析】【分析】(1)根据极坐标与直角坐标之间的转化运算求解，注意x ,y 的取值范围；(2)根据曲线C 1,C 2的方程，结合图形通过平移直线y =x +m 分析相应的临界位置，结合点到直线的距离公式运算求解即可.【小问1详解】因为ρ=2sin θ，即ρ2=2ρsin θ，可得x 2+y 2=2y ，整理得x 2+y -1 2=1，表示以0,1 为圆心，半径为1的圆，又因为x =ρcos θ=2sin θcos θ=sin2θ,y =ρsin θ=2sin 2θ=1-cos2θ，且π4≤θ≤π2，则π2≤2θ≤π，则x =sin2θ∈0,1 ,y =1-cos2θ∈1,2 ，故C 1:x 2+y -1 2=1,x ∈0,1 ,y ∈1,2 .【小问2详解】因为C 2:x =2cos αy =2sin α(α为参数，π2<α<π)，整理得x 2+y 2=4，表示圆心为O 0,0 ，半径为2，且位于第二象限的圆弧，如图所示，若直线y =x +m 过1,1 ，则1=1+m ，解得m =0；若直线y =x +m ，即x -y +m =0与C 2相切，则m2=2m >0 ，解得m =22，若直线y=x +m 与C 1,C 2均没有公共点，则m >22或m <0，即实数m 的取值范围-∞,0 ∪22,+∞ .【选修4-5】(10分)23.已知f x =2x +x -2 .(1)求不等式f x ≤6-x 的解集；(2)在直角坐标系xOy 中，求不等式组f (x )≤yx +y -6≤0所确定的平面区域的面积.【答案】(1)[-2,2]；(2)6.【解析】【分析】(1)分段去绝对值符号求解不等式作答.(2)作出不等式组表示的平面区域，再求出面积作答.【小问1详解】依题意，f (x )=3x -2,x >2x +2,0≤x ≤2-3x +2,x <0，不等式f (x )≤6-x 化为：x >23x -2≤6-x或0≤x ≤2x +2≤6-x 或x <0-3x +2≤6-x ，解x >23x -2≤6-x，得无解；解0≤x ≤2x +2≤6-x ，得0≤x ≤2，解x <0-3x +2≤6-x ，得-2≤x <0，因此-2≤x ≤2，所以原不等式的解集为：[-2,2]小问2详解】作出不等式组f (x )≤yx +y -6≤0表示的平面区域，如图中阴影△ABC，由y =-3x +2x +y =6，解得A (-2,8)，由y =x +2x +y =6 , 解得C (2,4)，又B (0,2),D (0,6)，所以△ABC 的面积S △ABC =12|BD |×x C -x A =12|6-2|×|2-(-2)|=8.。

第1章 1.2.3 直线与平面的夹角-人教B版(2021)高中数学选择性必修第一册讲义

直线与平面的夹角学习目标核心素养1．理解斜线和平面所成的角的定义，体会夹角定义的唯一性、合理性．2．会求直线与平面的夹角．(重点、难点)通过学习空间线面角，提升数学运算、逻辑推理素养．1．直线和平面所成的角2．最小角定理3．用空间向量求直线与平面的夹角如果v 是直线l 的一个方向向量，n 是平面α的法向量，设直线l 与平面α所成角的大小为θ，则θ＝π2－〈v ，n 〉或θ＝〈v ，n 〉－π2，特别地cos θ＝sin〈v ，n 〉或sin θ＝|cos 〈v ，n 〉|．[提示] 不是．直线和平面的夹角为⎪⎪⎪⎪⎪⎪π2－〈s ，n 〉．1．思考辨析(正确的打“√”，错误的打“×”) (1)直线与平面的夹角不是锐角就是直角． ( ) (2)斜线与它在平面内的射影所成的角是锐角． ( ) (3)斜线与平面的夹角为[0,90°]． ( ) (4)直线与平面的夹角为[0,90°]．( )[答案] (1)× (2)√ (3)× (4)√[提示] (1)× 错误，角的度数还可以是零度． (2)√ 根据线面角的定义知正确． (3)× 斜线与平面的夹角为(0,90°)． (4)√ 正确．2．若直线l 的方向向量与平面α的法向量的夹角等于120°，则直线l 与平面α所成的角等于( )A ．120°B ．60°C ．30°D ．以上均错C [设直线l 与平面α所成的角为θ，则sin θ＝|cos 120°|＝12，又∵0≤θ≤90°，∴θ＝30°．]3．已知向量m ，n 分别为直线l 和平面α的方向向量、法向量，若cos 〈m ，n 〉＝－32，则直线l 与平面α所成的角为________．60° [设直线l 与平面α所成的角为θ，则sin θ＝|cos 〈m ，n 〉|＝32．又∵θ∈[0,90°]，∴θ＝60°．]4．在正方形ABCD -A 1B 1C 1D 1中，CB 1与平面AA 1C 1C 所成角的大小为________．30°[如图，连接B1D1交A1C1于O，连接OC，因为几何体是正方体，所以OB1⊥平面AA1C1C，所以∠B1CO是CB1与平面AA1C1C所成角，设正方体的棱长为1，则OB1＝22，CB1＝2，sin∠B1CO＝222＝12，可得∠B1CO＝30°．即CB1与平面AA1C1C所成角的大小为30°．]公式cos θ＝cos θ1·cos θ2的应用AOC ＝60°，OA＝OB＝OC＝a，BC＝2a，求OA与平面α所成的角．[解]法一：∵OA＝OB＝OC＝a，∠AOB＝∠AOC＝60°，∴AB＝AC＝a．又∵BC＝2a，∴AB2＋AC2＝BC2．∴△ABC 为等腰直角三角形．同理△BOC 也为等腰直角三角形．取BC 中点为H ，连接AH ，OH ， ∴AH ＝22a ，OH ＝22a ，AO ＝a ， AH 2＋OH 2＝AO 2．∴△AHO 为等腰直角三角形．∴AH ⊥OH ．又∵AH ⊥BC ，OH ∩BC ＝H ， ∴AH ⊥平面α．∴OH 为AO 在α平面内的射影，∠AOH 为OA 与平面α所成的角．在Rt △AOH 中，∴sin ∠AOH ＝AH AO ＝22． ∴∠AOH ＝45°．∴OA 与平面α所成的角为45°．法二：∵∠AOB ＝∠AOC ＝60°， ∴OA 在α内的射影为∠BOC 的平分线，作∠BOC 的角平分线OH 交BC 于H ．又OB ＝OC ＝a ，BC ＝2a ，∴∠BOC ＝90°．得cos ∠AOH ＝cos ∠AOB cos ∠BOH＝22，∴OA 与平面α所成的角为45°．[跟进训练]1．如图所示，在四棱锥P-ABCD中，ABCD是正方形，PD⊥平面ABCD．若∠PBC＝60°，求直线PB与平面ABCD所成的角θ．[解]由题意得∠CBD＝45°，∠PBD即为直线PB与平面ABCD所成的角θ．用定义法解决直线与平面的夹角问题[[提示]寻找直线与平面的夹角，即准确确定直线在平面内的投影．[提示]①若直线与平面平行或直线在平面内，则直线与平面的夹角为0°；②若直线与平面垂直，则直线与平面的夹角为π2；③若直线与平面相交但不垂直，设直线与平面的交点为O，在直线上任取异于O点的另一点P，过P作平面的垂线P A，A为垂足，则OA即为直线在平面内的投影，∠AOP即为直线与平面的夹角，然后通过解三角形求出直线与平面夹角的大小．【例2】如图所示，在三棱锥P-ABC中，P A⊥平面ABC，P A＝AB，∠ABC ＝60°，∠BCA＝90°．(1)求证：BC⊥平面P AC；(2)若D为PB的中点，试求AD与平面P AC夹角的正弦值．[思路探究](1)证明BC和平面P AC内的两条相交直线垂直．(2)作出AD在平面P AC内的射影后，构造三角形求解．[解](1)因为P A⊥平面ABC，BC⊂平面ABC，所以P A⊥BC．又∠BCA＝90°，所以AC⊥BC，又AC⊂平面P AC，P A⊂平面P AC，P A∩AC＝A，所以BC⊥平面P AC．(2)取PC的中点E，连接DE．因为D为PB的中点，所以DE∥BC，所以DE⊥平面P AC．连接AE，则AE是AD在平面P AC内的投影，所以∠DAE是直线AD与平面P AC的夹角．设P A＝AB＝a，在直角三角形ABC中．因为∠ABC＝60°，∠BCA＝90°，所以BC＝a2，DE＝a4，在直角三角形ABP中，AD＝22a，所以sin∠DAE＝DEAD＝a422a＝24．即AD与平面P AC夹角的正弦值为24．1．(变问法)若本例条件不变，问题(2)改为：D为PB上的一点，且BD＝13PB，试求AD与平面P AC夹角的正弦值．[解]由已知BC⊥AC，BC⊥P A，AC∩P A＝A，所以BC⊥平面P AC，BC⊥PC，过PB的三等分点D作DE∥BC，则DE⊥平面P AC，连接AE，AD，则∠DAE为AD与平面P AC的夹角，不妨设P A＝AB＝1，因为∠ABC＝60°，所以BC＝12，DE＝23×12＝13，PB＝2，BD＝23．即AD与平面P AC夹角的正弦值为55．[解]由例题(1)知BC⊥平面P AC，所以平面P AC⊥平面PBC．过A作AE⊥PC．所以AE⊥平面PBC．连接ED，则∠ADE为AD与平面PBC的夹角．设P A＝2a，AB＝2a，所以PB＝22a．故AD＝2a．在△APC中，AP＝2a，所以PC＝3a2＋4a2＝7a，设∠ACP＝θ，＝3a×2a7a＝237a＝2217a，所以sin∠ADE＝AEAD＝221a72a＝427．即AD与平面PBC夹角的正弦值为427．用定义法求直线与平面的夹角找直线在平面内的射影，充分利用面面垂直的性质及解三角形知识可求得夹角(或夹角的某一三角函数值)．用向量求直线与平面所成的角1111，CC1＝2，点M是A1B1的中点．(1)求证：B 1C ∥平面AC 1M ；(2)求AA 1与平面AC 1M 所成角的正弦值．[解] (1)证明：在直三棱柱A 1B 1C 1-ABC 中，AC ⊥BC ，AC ＝BC ＝1，CC 1＝2，点M 是A 1B 1的中点．以C 为原点，建立如图所示空间直角坐标系，则B 1(0,1,2)，C (0,0,0)，A (1,0,0)，C 1(0,0,2)，A 1(1,0,2)，M ⎝ ⎛⎭⎪⎫12，12，2，B 1C →＝(0，－1，－2)，AC 1→＝(－1,0,2)， AM →＝⎝ ⎛⎭⎪⎫－12，12，2，设平面AC 1M 的法向量n ＝(x ，y ，z )，则⎩⎨⎧n ·AC 1→＝－x ＋2z ＝0，n ·AM →＝－12x ＋12y ＋2z ＝0，取z ＝1，得n ＝(2，－2,1)，∴B 1C ∥平面AC 1M ．(2)AA 1→＝(0,0,2)，平面AC 1M 的法向量n ＝(2，－2,1)，设AA 1与平面AC 1M 所成角为θ，则AA 1与平面AC 1M 所成角的正弦值： sin θ＝|AA 1→·n ||AA 1→|·|n |＝22×3＝13，所以AA 1与平面AC 1M 所成角的正弦值为13．用向量法求线面角的步骤(1)建立空间直角坐标系； (2)求直线的方向向量AB →； (3)求平面的法向量n ；(4)计算：设线面角为θ，则sin θ＝|n ·AB →||n |·|AB →|．[跟进训练]2．已知棱台ABC -A 1B 1C 1，平面AA 1C 1C ⊥平面A 1B 1C 1，∠B 1A 1C 1＝60°，∠A 1B 1C 1＝90°，AA 1＝AC ＝CC 1＝A 1C 12，D ，E 分别是BC 和A 1C 1的中点．(1)证明：DE ⊥B 1C 1；(2)求DE 与平面BCC 1B 1所成角的余弦值．[解] (1)证明：过点A 作AO ⊥平面A 1B 1C 1，交A 1C 1于点O ，连接B 1O ，设AA 1＝AC ＝CC 1＝A 1C 12＝2，则A 1O ＝1，A 1B 1＝2，∴B 1O ⊥A 1C 1，B 1O ＝3，以O 为原点，建立如图所示空间直角坐标系，则B ⎝ ⎛⎭⎪⎫32，12，3，C (0,2，3)，D ⎝ ⎛⎭⎪⎫34，54，3，E ()0，1，0，B 1(3，0,0)，C 1(0,3,0)，DE →＝⎝ ⎛⎭⎪⎫－34，－14，－3，B 1C 1→＝(－3，3,0)，(2)CB 1→＝(3，－2，－3)，CC 1→＝(0,1，－3)，设平面BCC 1B 1的法向量n ＝(x ，y ，z )，则⎩⎨⎧n ·CB 1→＝3x －2y －3z ＝0，n ·CC 1→＝y －3z ＝0，取y ＝3，得n ＝(3，3，1)， DE →＝⎝ ⎛⎭⎪⎫－34，－14，－3，设DE 与平面BCC 1B 1所成角为θ，则sin θ＝|DE →·n ||DE →|·|n |＝4313．∴cos θ＝1－⎝⎛⎭⎪⎫43132＝1113． ∴DE 与平面BCC 1B 1所成角的余弦值为1113．1．知识：掌握线面角的概念以及最小角定理．2．方法：(转化思想)利用空间向量求角的基本思路是把空间角转化为求两个向量之间的关系．首先要找出并利用空间直角坐标系或基向量(有明显的线面垂直关系时尽量建系)表示出向量，其次理清要求角和两个向量夹角之间的关系．1．若直线l 与平面α所成角为π3，直线a 在平面α内，且与直线l 异面，则直线l 与直线a 所成角的取值范围是( )A ．⎣⎢⎡⎦⎥⎤0，2π3B ．⎣⎢⎡⎦⎥⎤π2，2π3C ．⎣⎢⎡⎦⎥⎤π3，2π3D ．⎣⎢⎡⎦⎥⎤π3，π2D [由最小角定理知直线l 与直线a 所成的最小角为π3，又l ，a 为异面直线，则所成角的最大值为π2．]2．已知长方体ABCD -A 1B 1C 1D 1中，AB ＝BC ＝4，CC 1＝2，则直线BC 1和平面DBB 1D 1所成角的正弦值为( )A ．32B ．52C ．105D ．1010C [连接A 1C 1交B 1D 1于O 点，由已知得C 1O ⊥B 1D 1，且平面BDD 1B 1⊥平面A 1B 1C 1D 1，∴C 1O ⊥平面BDD 1B 1，连接BO ，则BO 为BC 1在平面BDD 1B 1上的射影，∠C 1BO 即为所求．C 1O ＝12×42＋42＝22，BC 1＝42＋22＝25，∴sin ∠C 1BO ＝C 1O BC 1＝2225＝105．]3．若平面α的一个法向量为(1,1,1)，直线l 的方向向量为(0,3,4)，则l 与α所成角的正弦值为________．7315 [设l 与平面α所成的角为θ，则sin θ＝|1×0＋1×3＋1×4|3×02＋32＋42＝73×25＝7315．]4．在正三棱锥P -ABC 中，P A ＝4，AB ＝3，则侧棱P A 与底面ABC 所成角的正弦值为________．154 [如图，在正三棱锥P -ABC 中，P A ＝4，AB ＝3，设P 在底面上的射影为O ，则O 为△ABC 的中心，由已知求得AO ＝1，又P A ＝4， ∴PO ＝42－12＝15．∴sin ∠P AO ＝PO P A ＝154．即侧棱P A 与底面ABC 所成角的正弦值为154．]5．在正四棱锥S -ABCD 中，O 为顶点在底面上的射影，P 为侧棱SD 的中点，且SO ＝OD ，求直线BC 与平面P AC 所成的角．[解] 以O 为原点建立空间直角坐标系O -xyz ，设OD ＝SO ＝OA ＝OB ＝OC ＝a ，则A (a,0,0)，B (0，a,0)， C (－a ，0,0)， P ⎝ ⎛⎭⎪⎫0，－a 2，a 2，从而CA →＝(2a,0,0)，AP →＝⎝ ⎛⎭⎪⎫－a ，－a 2，a 2，CB →＝(a ，a,0)．设平面P AC 的一个法向量为n ，可求得n ＝(0,1,1)，则cos 〈CB →，n 〉＝CB →·n |CB →||n |＝a 2a 2·2＝12．所以直线BC 与平面P AC 所成的角为90°－60°＝30°．。

高中数学空间中线线角,线面角,面面角成法原理与求法思路

DBA C α空间中线线角，线面角，面面角成法原理与求法思路空间中各种角包括：异面直线所成的角、直线与平面所成的角以及二面角。

1、异面直线所成的角（1）异面直线所成的角的范围是2,0(π。

求两条异面直线所成的角的大小一般方法是通过平行移动直线，把异面问题转化为共面问题来解决。

具体步骤如下：①利用定义构造角，可固定一条，平移另一条，或两条同时平移到某个特殊的位置，顶点选择在特殊的位置上；②证明作出的角即为所求的角；③利用解三角形来求角。

简称为“作，证，求” 2、线面夹角直线与平面所成的角的范围是]2,0[π。

求直线和平面所成的角用的是射影转化法。

具体步骤如下：（若线面平行，线在面内，线面垂直，则不用此法，因为角度不用问你也知道）①找过斜线上一点与平面垂直的直线；②连结垂足和斜足，得出斜线在平面的射影，确定出所求的角； ③把该角置于三角形中计算。

也是简称为“作，证，求”注：斜线和平面所成的角，是它和平面内任何一条直线所成的一切角中的最小角，即若θ为线面角，β为斜线与平面内任何一条直线所成的角，则有θβ≤；（这个证明，需要用到正弦函数的单调性，请跳过。

在右图的解释为 BAD CAD ∠>∠））2.1确定点的射影位置有以下几种方法：①斜线上任意一点在平面上的射影必在斜线在平面的射影上；②如果一个角所在的平面外一点到角的两边距离相等，那么这一点在平面上的射影在这个角的平分线上；已知：如图，BAC ∠在一个平面α内，,,PN AC PM AB PN PM ⊥⊥且＝（就是点P 到角两边的距离相等）过P 作PO α⊥（说明点O 为P 点在面α内的射影）求证：OAN OAM ∠∠＝（OAN OAM ∠∠＝，所以AO 为BAC ∠的角平分线，所以点O 会在BAC ∠的角平分线上）证明： PA ＝PA ，PN ＝PM ，90PNA PMA ∠∠︒＝＝PNA PMA ∴∆≅∆（斜边直角边定理） AN AM ∴＝①(PO NO MO PN PM α⊥⎫⇒=⎬⎭斜线长相等推射影长相等）＝ O AN AM AO AO AMO ANO NAO MAO OM N ⎫⎪⇒∆≅∆⇒∠∠⎬⎪⎭＝＝＝＝所以，点P 在面的射影为BAC ∠的角平分线上。

横看成岭侧成峰远近高低各不同——2020年高考数学浙江卷第19题线面角问题的多角度分析

数理化解题研究2021年第01期总第494期横看成岭侧成峰远近高低各不同2020年高考数学浙江卷第19题线面角问题的多角度分析章显联(浙江省绍兴鲁迅高级中学312000)摘要：本文对2020年高考数学浙江卷第19题线面角问题进行多角度分析：非坐标形式的向量法(基底法)、三余弦定理法、等体积法、纯几何法、空间直角坐标系法.给出了复习的两个建议：关注最小，秒杀线面；重视非坐标形式的向量法.关键词：非坐标形式的向量法；线面角；两个原理中图分类号:G632 文献标识码：A 文章编号：1008 -0333(2021)01 -0036 -04一、典型考题所成角为0 ,由已知，得0C 与平面DBC 所成角也为0.由公式，得例1（2020年浙江第19题）如图1,在三棱台ABC-DEF 中，平面 ACFD 丄平面 ABC , /ACB - /ACD -45°,DC -2B C.(1) 证明：EF 丄DB ；(2) 求直线DF 与平面DBC 所成角的正弦值.本题主要考查空间直线互相垂直的判定和性质，以及直线与平面所成角的几何计算问题，考查了空间想象能力和思维能力，平面与空间互相转化能力,几何计算能力，以及逻辑推理能力，本题属综合性较强的中档题.笔者认为此题无论图1是试题难度、试题背景、命题立意,还是对数学核心素养的考查，都很到位,可谓简约不简单.它也是一道解题训练的优质题,横看成岭侧成峰，很有研究价值.解法1非坐标形式的向量法(基底法)过点D 作D0丄AC 于点0,以｛ C B ，C B ,CD ｝为基底. 不妨设 DC - 2B C -2,贝V DB - 3 , C0 - 2 , / 0CB -：,/0CD - n , /DCB - n ,设平面DBC 的法向量为n - %-CD -0,（• C B -0 得｛2% + y + 4z - 0,% + y + z - 0.C O + y C B + zC B ，贝V 由所以n - -3 C0 +2 B + CD.设直线DF 与平面DBC解法2三余弦定理法过点D 作D0丄AC 于点0,由已知,得0在平面DBC 的射影H 在/DCB 的角平分线上,设直线DF 与平面DBC 所成角为0,由已知,得0C 与平面DBC 所成角也为0.由三余弦定理，得 cos n - cos n • cos 0,cos 0 - f •463所以sin 0 -耳.解法3等体积法.过点D 作D0丄AC 于点0,设直线DF 与平面DBC 所成角为0,由已知，得0C 与平面DBC 所成角也为0.由 % - DBC 二 % - 0BC ，解得 h 二专,sin 0 二豊二专.解法4坐标形式的向量法以0为原点,0D 为Z 轴,0C 为Y 轴,在平面ABC 内, 过点0作0C 垂线为Z 轴，易求D ,C ,B 坐标，从而求得平面DBC 的法向量，利用线面角公式sin 0 - 3 •解法5纯几何法分析(1)题根据已知条件，作DH 丄AC ,根据面面垂直，可得DH 丄BC ,进一步根据直角三角形的知识可判断收稿日期：2020 -10 -05作者简介:章显联(1972. 12 -)，男，浙江省龙港人，本科，中学高级教师，从事高中数学教学研究.—36—2021年第01期总第494期数理化解题研究出厶BHC是直角三角形，且Z HBC_90°,则HB丄BC,从而可证出BC丄面DHB,最后根据棱台的定义有EF〃BC,根据平行线的性质可得EF丄DB.（2）题可先设BC_1,根据解直角三角形可得BH_1,HC_2,DH_2,DC_2,DB_3,然后找到CH与面DBC的夹角即为Z HCG,根据棱台的特点可知DF与面DBC所成角与CH与面DBC的夹角相图2等，通过计算乙HCG的正弦值，即可得到DF与面DBC所成角的正弦值.二、考题赏析本题建系有些困难,不存在明显的过同一点的两两垂直的直线.这种情况下，非坐标形式的向量法（基底法）显得更实用.本题解法以｛CO,C B,CD｝为基底，因为它们不共面长度可求,且它们的夹角也可求.应用此法，可使求解过程更自由.若CO,C B,CD是单位向量且两两垂直,就是通常的坐标形式的向量法了.坐标形式的向量法可以看作是非坐标形式的向量法的一种特殊情形.解法2中0在平面DBC的射影H在Z DCB的角平分线上，利用三余弦定理可求出0C与平面DBC所成角.B图4三正弦定理（最大角定理）设二面角M-AB-N的度数为Y,在平面M上有一条射线AC,它和棱AB所成的角为0,和平面N所成的角为//a,贝V sin a_si叩•sin y.（为了力便于记忆，我们约定:0为线棱角,a为线面角，Y为二面角）证明如图4,C0丄平面N,0B丄AB,BC丄AB,0C△0BC,△0AC,△ABC均为直角三角形,sin y_,si叩_BCBCAC，sin a_器，易得sin a_sin S•sin y.说明由sin a_sin S•sin y且sin S W1,知sin a W sin y,a W y，所以二面角的半平面M内的任意一条直线与另一个半平面N所成的线面角不大于二面角,即二面角是线面角中最大的角.若平面斜线上异于斜足的点在平面上的射影不易确定，则可转换为其他点如是操作或利用等体积法求出垂线段的长，利用公式sin O_h求得.如本题解法3.其实不管是纯几何法还是坐标形式的向量法,都能解决线面角问题，高考试题的参考答案一贯都是纯几何法与坐标形式的向量法,每种方法的学习都可促进学生能力的提高,只是各有侧重.如解法4与解法5.三余弦定理（最小角定理或爪子定理）设点A为平面a上一点，过点A的斜线在平面a上的射影为B0,BC为平面a上的任意直线,那E么Z ABC,乙0BC,乙0BA三、复习建议三角的余弦关系为cosZ ABC图3_cos Z0BC•cos Z0BA.即斜线与平面内一条直线夹角0的余弦值等于斜线与平面所成角a的余弦值乘以射影与平面内直线夹角O的余弦值,cos0_cos a-cos O.（为了便于记忆,我们约定:0为斜线角,a为线面角,O为射影角）证明如图3,^0AB,△0BC,△ABC均为直角三角形,cosQ BCAB，cosaB0AB，cosO B0，易知cosQ_cos a•cos O，得证.说明这三个角中，角0是最大的,其余弦值最小,等于另外两个角的余弦值之积.斜线与平面所成角a是斜线与平面内所有直线所成角中最小的角.1.紧扣最小，秒杀线面在研究空间角的最值与求值问题时，我们应关注最大角与最小角定理,三余弦公式与三正弦公式.这样的考查在近几年的学考、高考试题中已多次出现：例2（2019年浙江高考第8题）设三棱锥V-ABC 的底面是正三角形,侧棱长均相等,P是棱VA上的点（不含端点）.记直线PB与直线AC所成的角为a,直线PB与平面ABC所成的角为S,二面角P-AC-B的平面角为Y，则（）.A.S<Y,a<yB.S<a,0<yC.S<a,y<aD.a<0,y<0解法1由最小角原理，得S<a，记二面角V-AB-C的平面角为y'（显然y_y'），由最大角原理，得S<y，故选B.解法2（特殊位置）取V-ABC为正四面体,P是棱VA上的中点，算出a,0,y的正弦值，可得选项B.例3（2018年浙江高考第8题）已知四棱锥S-ABCD的底面是正方形，侧棱长均相等,E是线段—37—数理化解题研究2021年第01期总第494期AB上的点（不含端点）,设SE与BC所成的角为O],SE 与平面ABCD所成的角为O2,二面角S-AB-C的平面角为O3,则（）•A.O1W O2W O3B.O3W O2W O1C.O1W O3W O2D.O2W O3W O1解法1作出三个角，通过定量计算得出答案为D.解法2由最小角与最大角原理知：O1M O2,O3M O2,故选D.例4（2014年浙江高考第17题）如图5,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练.已知点A到墙面的距离为AB,某目标点P沿墙面的射击线CM-移动，此人为了准确瞄准目标点P,需计算由点A观察点P的仰角O的大小•若AB=15m,图5AC=25m,Z BCM=30°,贝卩tan O的最大值解析由线面角W面面角,求tan O的最大值转化为求二面角M-AC-Q的平面角•易求最大值为5j•例5（2018年11月浙江学考）四边形ABCD为矩形，沿AC将A ADC翻折成A AD'C.设二面角D'-AB-C 的平面角为O,直线AD'与BC所成的角为O1,直线AD'与平面ABC所成的角为O2,当O为锐角时，有（）•A.O2W O1W OB.O2W O W O1C.O1W O2W OD.O W O2W O1解析由最小角原理，得O1M O2,由最大角原理，得O M O2,下面比较O]与O的大小即可•故选B.例6（2018年全国高考n卷理科第20题）如图6,在三棱锥P-ABC中,AB=BC=22,PA=PB=PC=4,0为AC的中点•（1）证明：PO丄平面ABC；（2）若点M在棱BC上,且二面角M-PA-C为30°,求PC与平面图6PAM所成角的正弦值.解析（1）略.（2）由题意，知线棱角Z CPA=60°,二面角M-PA-C为30°，由三正弦定理，得sin a=sin60°sin30°=例7（2009年浙江高考理科第17题）如图7,在长方形ABCD中,AB=2,BC=1,E为DC的中点，F为线段EC（端点除外）上一动点•现将△AFD沿AF折起,使平面—38—ABD丄平面ABC.在平面ABD内过点D作DK丄AB,K为垂足•设AK=£,则t的取值范围是•」___E.$____C d/一A B A K B图7解析由三余弦定理及已知，得cos Z DAF= cosZ DAK・cosZ BAF,又Z DAF+Z BAF二;，则cos Z DAK=tan Z BAF.在Rt△DAK中t=cos Z DAB,因此t=tanZ BAF,又由折叠前的图形，知0<Z CAB<Z BAFn<Z EAB=；.4所以tan Z CAB<tan Z BAF<tan Z EAB.所以1<t<1.考查这类空间角的大小是命题者难以割舍的情结,其本质是考查线面角与面面角定义的合理性,是考查学生数学核心素养的有效途径•2.非坐标形式的向量法非坐标形式的向量法比坐标形式的向量法应用更自由，更广泛•相比较纯几何法可避免令人深感畏惧的辅助线的添加技巧等.当然,解题方法中的选择也是当用则用，不分彼此,有时多种方法可揉合于同一道题中,特别是向量与几何的紧密联系与转化•应用非坐标形式的向量法解题的基本步骤：（1）会选基底.只需要不共面的三条线段长度可求，且它们的夹角也可求即可.（2）会表示•会用基底表示其他向量,一般只涉及向量的三角形式及其推广（闭合回路）,数乘与平行,数量积与垂直两个定理•特别是要掌握好平面法向量的求法，方法可参考高考真题解法1•（3）会用公式•运算过程中无论是平面向量还是空间向量操作完全一致，运用的公式与坐标形式的向量法一致.笔者尝试用非坐标形式的向量法研究高考数学卷，发现非坐标向量法作为解答立体几何的方法有着诸多的可取之处.例8（2018年浙江高考第19题）如图8,已知多面体ABCA1B1C1中，A1A,B1B,C1C均垂直于平面ABC, Z ABC=120°,A1A=4,C1C=1,AB=BC=B1B=2.（1）证明:AB】丄平面A]B]C]；（2）求直线AC】与平面ABB]所成的角的正弦值.解析以｛BA,B C,B—｝为基底，可证明（1）,也可求2021年第01期总第494期数理化解题研究得直线AC]与平面ABB1所成的角的正弦值为晋•例9(2019年浙江高考第19题)如图9,已知三棱柱ABC-A1B1C1,平面A1ACC1丄平面ABC,/ABC-90°,/BAC-30°,A1A二A1C-AC,E,F分别是AC,A]B]的中点(1)证明：EF丄BC；(2)求直线EF与平面A1BC所成角的余弦值.解析以｛E b]c B,C B｝为基底,可证明(1)，也可求得直线EF与平面A]BC所成角的余弦值是3•我们研究的向量是自由向图9量，运用非坐标形式的向量法无需考虑建立空间直角坐标系所需要的特殊要求,使解题过程更自由•例10(2009年浙江高考理科第17题)如图10,在长方形ABCD中,AB-2,BC-1,E为DC的中点,F为线段EC(端点除外)上一动点•现将△AFD沿AF折起，使平面ABD丄平面ABC.在平面ABD内过点D作DK丄AB,K为垂足•设AK-t，则t的取值范围是•图10解析以｛K4,KD,KF｝为基底，设DF-m,抓住折叠过程中的不变量AD-1,AB-2,由于平面ABD丄平面ABC,DK丄AB,从而DK丄平面ABC.由DF二D A+AF二d K+k A+AF，得m2二(d K+K4+AF)2.化简,得mt-1,即t——.由1<m<2,得<t<1.m2利用非坐标形式的向量法进行的上述解答,化动为静，简捷别致，令人耳目一新.例11(2000年全国高考理科第18题)如图11,已知平行六面体ABCD-A1B1C1D1的底面ABCD是菱形，且/C1CB-/C1CD-/BCD-60°.(1)证明：C]C丄BD；3(2)假定CD-2,CC]-3，记Bi Ai图11面C]BD为a,面CBD为0,求二面角a-BD-0的平面角的余弦值；(3)当CD的值为多少时，能使A]C丄平面C]BD?请给出证明.解析以｛Cc1，CD,C B｝为基底，则CA]-C c]+CD+CB.(1)由BD-CD-CB,得C2C・BD-0,所以C2C丄BD.(2)易知平面a的法向量为C B；--8CC]+CD+C B，所以平面S的法向量为n--4CC]+CD+C B,从而求得a-D-S的平面角的余弦值为3•(3)当CD-1时,能使A]C丄平面C]BD.设CD-2,可证A]C丄BD,再由A]C丄BC2求得CC2-2.例12(2015年浙江省高考理科第13题)如图12,三棱锥A-BCD中，AB二AC二BD二CD-3,AD-BC-2,点M,N分别是AD,BC的中点，则异面直线AN,CM所成的角的余弦值是•解析以｛BA,BC,BD｝为基底，在△ABD,由余弦定理得cos图12/ABD-7,同理得cos/CBD-[,cos/ABC-[,BA・933B C-2,BA・B D-7,B C・BD-2.用基底表示A N,C M,AN--BA+2BC,C M-2(BD+BA-2BC),异面直线AN,CM所成的角的余弦值是简]CM-T•平面向量仅是空间向量的一种特殊情形•“平面向量”可向“空间向量”自然转化.用向量方法求解空间角度与距离问题,为某些位置关系的判断问题创立了一种新的方法•在向量的运算中,要注意数形结合,灵活运用图形的几何意义、向量的几何意义去解题.《新课程标准(2017年版)》对空间向量的应用提出了更多、更高的要求,可见非坐标形式的向量法用于解决立体几何问题,完全符合新课程标准对学生的要求•如何使非坐标形式的向量法成为学生解决立体几何问题的又一个通用的好方法,还需要我们建一步地探索与总结•参考文献:[1]章显联.高考复习要注意回归教材[J].数理化解题研究，2020(13)：15-18.[责任编辑:李璟]—39—。

浅谈线线角、线面角、面面角的定义方式及其中蕴含的数学基本思想

浅谈线线角、线面角、面面角的定义方式北京市顺义区第九中学101300高中阶段在学习空间线、面位置关系的时候，会给出线线角、线面角及面面角的定义，本文以角形成的定义方式及蕴含的基本思想为主，进行研究。

1、直线与直线所成的角：（1）共面：同一平面内的两直线所成角，是利用两直线位置关系，平行、重合所成角为0度，如果相交就取交线所构成的锐角（或直角）。

（2）异面：如图所示，已知两条异面直线a和b,经过空间任一点O分别作直线a′∥a，b′∥b，我们把直线a′与b′所成的角叫做异面直线a与b所成的角（或夹角）。

θ定义方式：是发生定义法（即构造定义方式）定义中的“空间中任取一点O”，意味着：角的大小与O 点选取的位置无关；通过平移把异面直线所成角转化成两相交直线，是将空间图形问题转化成平面图形问题的定义方式，体现了定义的纯粹性和完备性。

2、直线和平面所成的角：如图，一条直线和一个平面相交，但不与这个平面垂直，这条直线叫做这个平面的斜线，斜线和平面的交点A叫做斜足.过斜线上斜足以外的一点P向平面引垂线PO，过垂足O和斜足A的直线AO叫做斜线在这个平面上的射影.平面的一条斜线和它在平面上的射影所成的角，叫做这条直线和这个平面所成的角。

规定：一条直线垂直于平面，我们说它们所成的角是直角；一条直线和平面平行，或在平面内，我们说它们所成的角是0°的角。

3、面面所成的角：(1)在二面角的棱l上任取一点O，以该点O为垂足，在半平面和内分别作垂直于棱l的射线OA和OB，则射线OA和OB构成的角称为二面角的平面角.( 2)作二面角的平面角的方法方法一：(定义法)在二面角的棱上找一个特殊点，在两个半平面内分别作垂直于棱的射线．如图所示，∠AOB为二面角αaβ的平面角．方法二：(垂线法)过二面角的一个面内一点作另一个平面的垂线，过垂足作棱的垂线，连接该点与垂足，利用线面垂直可找到二面角的平面角或其补角．如图所示，∠ACB为二面角αmβ的平面角．4、线线、线面、面面所成角的定义方式线线、线面、面面所成角的定义方式是“属加种差定义法”。

【高中数学】8.5考点3 线面角、二面角的求法

高考真题（2019•浙江卷）如图，已知三棱柱，平面平面,，分别是的中点.（1）证明：；（2）求直线与平面所成角的余弦值.【解析】（1）如图所示，连结，等边中，，则，平面ABC ⊥平面，且平面ABC ∩平面，由面面垂直的性质定理可得：平面，故，由三棱柱的性质可知，而，故，且，由线面垂直的判定定理可得：平面，111ABC A B C -11A AC C ⊥ABC 90ABC ∠=︒1130,,,BAC A A AC AC E F ∠=︒==11,AC AB EF BC ⊥EF 1A BC 11,A E BE 1AAC △AE EC =-18%11A ACC 11A ACC AC =1A E ⊥ABC 1A E BC ⊥11A B AB ∥AB BC ⊥11A B BC ⊥1111A B A E A =BC ⊥11A B E结合⊆平面，故.（2）在底面ABC 内作EH ⊥AC ，以点E 为坐标原点，EH ,EC ,方向分别为x ,y ,z 轴正方向建立空间直角坐标系.设，则，，据此可得：，由可得点的坐标为，利用中点坐标公式可得：，由于，故直线EF 的方向向量为：设平面的法向量为，则：，据此可得平面的一个法向量为，此时，EF 11A B E EFBC ⊥1EA E xyz -1EH =AE EC ==11AA CA ==3BC AB ==()()()130,,,,0,0,3,22A B A C ⎛⎫⎪ ⎪⎝⎭11AB A B =1B 132B ⎛⎫ ⎪⎝⎭34F ⎛⎫⎪⎝⎭()0,0,0E 34EF ⎛⎫=⎪⎝⎭1A BC (),,m x y z =()()133,,,,330222233,,,02222m A B x y z x y z m BC x y z xy ⎧⎛⎫⋅=⋅-=+-=⎪ ⎪ ⎪⎪⎝⎭⎨⎛⎫⎪⋅=⋅-=-+= ⎪⎪ ⎪⎝⎭⎩1A BC ()1,3,1m =34EF ⎛⎫=⎪⎝⎭4cos ,55EF m EF m EF m⋅===⨯设直线EF 与平面所成角为，则. 【答案】（1）证明见解析；（2）.（2019•浙江卷）设三棱锥的底面是正三角形，侧棱长均相等，是棱上的点（不含端点），记直线与直线所成角为，直线与平面所成角为，二面角的平面角为，则（） A ． B ． C ． D ．【解析】方法1：如图为中点，在底面的投影为，则在底面投影在线段上，过作垂直，易得，过作交于，过作，交于，则，则，即，，即，综上所述，答案为B ．方法2：由最小角定理，记的平面角为（显然）由最大角定理，故选B ．方法3：（特殊位置）取为正四面体，为中点，易得1A BC θ43sin cos ,,cos 55EF m θθ===35V ABC -P VA PB AC αPB ABC βP AC B --γ,βγαγ<<,βαβγ<<,βαγα<<,αβγβ<<G AC V ABC O P D AO D DE AE //PE VG P //PF AC VG F D //DH AC BG H ,,BPF PBD PED α=∠β=∠γ=∠cos cos PF EG DH BDPB PB PB PBα===<=βαβ>tan tan PD PDED BDγ=>=βy >ββα<V AB C --γ'γ'=γβ<γ'=γV ABC -P VAB ．【答案】B（2019•天津卷（理））如图，平面，，.（Ⅰ）求证：平面；（Ⅰ）求直线与平面所成角的正弦值；（Ⅰ）若二面角的余弦值为，求线段的长.【解析】依题意，可以建立以A 为原点，分别以的方向为x 轴，y 轴，z 轴正方向的空间直角坐标系（如图），可得.cos sin sin α=⇒α=β=γ=AE ⊥ABCD ,CF AE AD BC ∥∥,1,2AD AB AB AD AE BC ⊥====BF ∥ADE CE BDE E BD F --13CF ,,AB AD AE ()()()()()0,0,0,1,0,0,1,2,0,0,1,0,0,0,2A B C D E设，则.（Ⅰ）依题意，是平面ADE 的法向量，又，可得，又因为直线平面，所以平面. （Ⅱ）依题意，，设为平面BDE 的法向量，则，即，不妨令z =1，可得，因此有.所以，直线与平面所成角的正弦值为. （Ⅲ）设为平面BDF 的法向量，则，即.不妨令y =1，可得. 由题意，有，解得. 经检验，符合题意｡所以，线段的长为. 【答案】（Ⅰ）见证明；（Ⅱ）（Ⅲ）（2019•全国III 卷（理））图1是由矩形ADEB ，RtⅠABC 和菱形BFGC 组成的一个平面图形，其中AB =1，BE =BF =2，∠FBC =60°，将其沿AB ，BC 折起使得BE 与BF 重合，连结DG ，如图2. （1）证明：图2中的A ，C ，G ，D 四点共面，且平面ABC ⊥平面BCGE ；()0CF h h =>()1,2,F h ()1,0,0AB =()0,2,BF h =0BF AB ⋅=BF ⊄ADE BF ∥ADE (1,1,0),(1,0,2),(1,2,2)BD BE CE =-=-=--(),,n x y z =00n BD n BE ⎧⋅=⎨⋅=⎩020x y x z -+=⎧⎨-+=⎩()2,2,1n =4cos ,9||||CE n CE n CE n ⋅〈〉==-CE BDE 49(),,m x y z =00m BD m BF ⎧⋅=⎨⋅=⎩020x y y hz -+=⎧⎨+=⎩21,1,m h ⎛⎫=-⎪⎝⎭41cos ,332m n m n m n-⋅===⨯87h =CF 874987（2）求图2中的二面角B−CG−A 的大小.【解析】（1）证：，，又因为和粘在一起.，A ，C ，G ，D 四点共面.又.平面BCGE ，平面ABC ，平面ABC 平面BCGE ，得证.（2）过B 作延长线于H ，连结AH ，因为AB 平面BCGE ，所以而又，故平面，所以.又因为所以是二面角的平面角，而在中，又因为故，所以而在中,，即二面角的度数为.【答案】（1）见详解；（2） .（2019•北京卷（理））如图，在四棱锥P –ABCD 中，P A ⊥平面ABCD ，AD ⊥CD，AD ∥BC ，P A =AD =CD =2，BC =3．E 为PD 的中点，点F 在PC 上，且．（Ⅰ）求证：CD ⊥平面P AD ；（Ⅱ）求二面角F–AE–P 的余弦值；（Ⅲ）设点G 在PB 上，且．判断直线AG 是否在平面AEF 内，说明理由． //AD BE //BF CG E F ∴//AD CG ,AB BE AB BC ⊥⊥AB ∴⊥AB ⊂∴⊥BH GC ⊥⊥AB GC ⊥BH GC ⊥GC ⊥HAB AH GC ⊥BH GC ⊥BHA ∠B CG A --BHC △90BHC ∠=60FBC ∠=60BCH ∠=sin 603BH BC ==ABH 90ABH ∠=tan 3AB BHA BH ∠===B CG A --303013PF PC =23PG PB =【解析】（Ⅰ）由于P A ⊥平面ABCD ，CD 平面ABCD ，则P A ⊥CD ，由题意可知AD ⊥CD ，且P A ∩AD =A ，由线面垂直的判定定理可得CD ⊥平面P AD ．（Ⅱ）以点A 为坐标原点，平面ABCD 内与AD 垂直的直线为x 轴，AD ,AP 方向为y 轴，z 轴建立如图所示的空间直角坐标系，易知：，由可得点F 的坐标为，由可得，设平面AEF 的法向量为：，则，据此可得平面AEF 的一个法向量为：，⊂A xyz-()()()()0,0,0,0,0,2,2,2,0,0,2,0A P C D 13PF PC =224,,333F ⎛⎫ ⎪⎝⎭12PE PD =()0,1,1E (),,m x y z =()()()224224,,,,0333333,,0,1,10m AF x y z x y z m AE x y z y z ⎧⎛⎫⋅=⋅=++=⎪ ⎪⎝⎭⎨⎪⋅=⋅=+=⎩()1,1,1m =-很明显平面AEP 的一个法向量为，，二面角F -AE -P 的平面角为锐角，故二面角F -AE -P. （Ⅲ）易知，由可得，则，注意到平面AEF 的一个法向量为：，其且点A 在平面AEF 内，故直线AG 在平面AEF 内. 【答案】（Ⅰ）见解析；（Ⅱ）；（Ⅲ）见解析.（2019•全国I 卷（理））如图，直四棱柱ABCD–A 1B 1C 1D 1的底面是菱形，AA 1=4，AB =2，∠BAD =60°，E ，M ，N 分别是BC ，BB 1，A 1D 的中点．（1）证明：MN ∥平面C 1DE ；（2）求二面角A -MA 1-N 的正弦值．【解析】（1）连接，()1,0,0n =1cos ,3m n m n m n⋅<>===⨯⨯()()0,0,2,2,1,0P B -23PG PB =422,,333G ⎛⎫- ⎪⎝⎭422,,333AG ⎛⎫=-⎪⎝⎭()1,1,1m =-0m AG ⋅=3ME 1B C，分别为，中点为的中位线且又为中点，且且四边形为平行四边形，又平面，平面平面（2）设，由直四棱柱性质可知：平面四边形为菱形则以为原点，可建立如下图所示的空间直角坐标系：则：，，，D （0，-1,0）取中点，连接，则四边形为菱形且为等边三角形M E 1BB BC ME ∴1B BC ∆1//ME B C ∴112ME B C =N 1A D 11//A D B C 1//ND B C ∴112ND B C =//ME ND ∴∴MNDE //MN DE ∴MN ⊄1C DE DE 1C DE //MN ∴1C DE ACBD O =11111AC B D O =1OO ⊥ABCD ABCD AC BD ∴⊥O )A()0,1,2M )14A 1,,222N ⎛⎫-⎪ ⎪⎝⎭AB FDF 01,2F ⎫⎪⎪⎝⎭ABCD 60BAD ∠=BAD ∴∆DFAB ∴⊥又平面，平面平面，即平面为平面的一个法向量，且设平面的法向量，又，，令，二面角【答案】（1）见解析；（2.（2019•全国II 卷（理））如图，长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形，点E 在棱AA 1上，BE ⅠEC 1.（1）证明：BE Ⅰ平面EB 1C 1；（2）若AE =A 1E ，求二面角B –EC –C 1的正弦值.【解析】分析：（1）利用长方体的性质，可以知道侧面，利用线面垂直的性质可以证明出，这样可以利用线面垂直的判定定理，证明出平面；1AA ⊥ABCD DF ⊂ABCD 1DFAA ∴⊥DF ⊥∴11ABB A DF ⊥1AMA DF ∴1AMA 33,,022DF ⎛⎫= ⎪⎪⎝⎭1MA N (),,n x y z =()13,1,2MA =-33,022MN ⎛⎫=-⎪ ⎪⎝⎭132033022n MA x y z n MN x y ⎧⋅=-+=⎪∴⎨⋅=-=⎪⎩x 1y =1z =-()3,1,1n ∴=-3cos ,515DF n DF n DF n⋅∴<>===⋅10sin ,5DF n ∴<>=∴1A MA N --11B C ⊥11A B BA 11B C EB ⊥BE ⊥11EB C（2）以点坐标原点，以分别为轴，建立空间直角坐标系，设正方形的边长为，，求出相应点的坐标，利用，可以求出之间的关系，分别求出平面、平面的法向量，利用空间向量的数量积公式求出二面角的余弦值的绝对值，最后利用同角的三角函数关系，求出二面角的正弦值.详解：证明（1）因为是长方体，所以侧面，而平面，所以又，，平面，因此平面；（2）以点坐标原点，以分别为轴，建立如下图所示的空间直角坐标系，，因为，所以，所以，，设是平面的法向量，所以，设是平面的法向量，所以， B 1,,BC BA BB ,,x y z ABCD a 1B B b =1BE EC ⊥,a b EBC 1ECC 1B EC C --1B EC C --1111ABCD A B C D -11B C ⊥11A B BA BE ⊂11A B BA 11BE B C ⊥1BE EC ⊥1111B C EC C ⋂=111,B C EC ⊂11EB C BE ⊥11EB C B 1,,BC BA BB ,,x yz 1(0,0,0),(,0,0),(,0,),(0,,)2b B C a C a b E a 1BE EC ⊥2210(0,,)(,,)002224b b b BE EC a a a a b a ⋅=⇒⋅-=⇒-+=⇒=(0,,)E a a 1(,,),(0,0,2),(0,,)EC a a a CC a BE a a =--==111(,,)m x y z =BEC 111110,0,(0,1,1)0.0.ay az m BE m ax ay az m EC +=⎧⎧⋅=⇒⇒=-⎨⎨--=⋅=⎩⎩222(,,)n x y z =1ECC 2122220,0,(1,1,0)0.0.az n CC n ax ay az n EC =⎧⎧⋅=⇒⇒=⎨⎨--=⋅=⎩⎩二面角的余弦值的绝对值为，所以二面角. 【答案】（1）证明见解析；（2高考数学：试卷答题攻略一、“六先六后”，因人因卷制宜。

高中数学选择性必修第一册《第1章空间向量与立体几何》单元测试卷(3)(含解析)

高中数学选择性必修第一册《第1章空间向量与立体几何》单元测试卷(3)一、解答题（本大题共8小题，共96.0分）1.如图，已知四棱锥P−ABCD的底面是直角梯形，∠ABC=∠BCD=90°，AB=BC=PB=PC=2CD=2，侧面PBC⊥底面ABCD，点M在AB上，且AM：MB=1：2，E为PB的中点．(1)求证：CE//平面ADP；(2)求证：平面PAD⊥平面PAB；(3)棱AP上是否存在一点N，使得平面DMN⊥平面ABCD，若存在，求出AN的值；若不存在，请说NP明理由．2.如图，在四棱锥P−ABCD中，已知棱AB，AD，AP两两垂直且长度DC．分别为1，2，2，AB//CD，AB=12(1)若PC中点为M，证明：BM//平面PAD；(2)求点A到平面PCD的距离．3.在如图所示的四棱锥P−ABCD中，底面ABCD是边长为2的正方形，△PAD是正三角形，平面PAD⊥平面ABCD．(1)求平面PAB与平面PCD所成锐二面角的大小；(2)设E为PB上的动点，直线CE与平面PAB所成的角为θ，求sinθ的最大值．4.(本题满分10分)如图，已知四棱锥底面为菱形，平面，，分别是、的中点．(1)证明：(2)设，若为线段上的动点，与平面所成的最大角的正切值为，求此时异面直线AE和CH所成的角．5.如图，在三棱锥P−ABC中，平面PAC⊥平面ABC，PA⊥AC，AB=BC=CA=AP=2，G是△ABC重心，E是线段PC上一点，且CE=λCP．(1)当EG//平面PAB时，求λ的值；(2)当直线CP与平面ABE所成角的正弦值为√42时，求λ的值．76.在四棱锥P−ABCD中，∠ABC=∠ACD=90°，∠BAC=∠CAD=60°，PA⊥平面ABCD，直线PC与平面ABCD所成角为45°，AB=2．(Ⅰ)求四棱锥P−ABCD的体积V；(Ⅱ)若E为PC的中点，求证：平面ADE⊥平面PCD．7.如图所示，矩形ABED所在的平面垂直于△ABC所在的平面，AC⊥BC，G，F分别是EC，BD的中点．(1)求证：GF//平面ABC；(2)求证：直线AC⊥平面BEC．8.如图，在四棱锥P−ABCD中，AB//CD，CD⊥BC，PC=AB=2BC=2，PA=PB=√3BC．(1)求证：平面PAB⊥平面ABCD；(2)若二面角D−PB−C的正切值为√6，求PD与平面ABCD所成角的余弦值．【答案与解析】1.答案：(1)证明：取棱AP中点F，连接DF，EF．∵EF为△PAB的中位线，∴EF//AB，且EF=12AB∵CD//AB，且CD=12AB，∴EF//CD，且EF=CD，∴四边形EFDC为平行四边形，∴CE//DF，∵DF⊂平面ADP，CE⊄平面ADP，∴CE//平面ADP;(2)证明：由(1)可得CE//DF∵PC=BC，E为PB的中点，∴CE⊥PB∵AB⊥BC，平面PBC⊥平面ABCD，平面PBC∩平面ABCD=BC，AB⊂平面ABCD，∴AB⊥平面PBC，又∵CE⊂平面PBC，∴AB⊥CE，又∵CE⊥PB，AB∩PB=B，AB，PB⊂平面PAB，∴CE⊥平面PAB，∵CE//DF，∴DF⊥平面PAB，又∵DF⊂平面PAD，∴平面PAD⊥平面PAB；(3)解：存在，ANNP =47．证明：取BC中点O，连结AO交MD于Q，连结NQ，在平面ABCD中由已知计算可得AQQO =47，∴ANNP =AQQO，∴NQ//OP，∵O为等腰△PBC底边上的中点，∴PO⊥BC，∵PBC ⊥底面ABCD ，PO ⊂平面PBC ，平面PBC ∩平面ABCD =BC ， ∴PO ⊥平面ABCD ，∴NQ ⊥平面ABCD ， ∵NQ ⊂平面DMN ，∴平面DMN ⊥平面ABC ．解析：(1)取棱AP 中点F ，连接DF ，EF ，证明四边形EFDC 为平行四边形，可得CE//DF ，即可证明CE//平面ADP ；(2)证明CE ⊥平面PAB ，利用CE//DF ，可得DF ⊥平面PAB ，即可证明平面PAD ⊥平面PAB ； (3)存在，ANNP =47ANNP =47，取BC 中点O ，连结AO 交MD 于Q ，连结NQ ，证明NQ ⊥平面ABCD ，即可得出结论．本题考查线面垂直、线面平行，面面垂直，考查学生分析解决问题的能力，属于中档题． 2.答案：(1)证明：分别以AB ，AD ，AP 所在直线为x 轴，y 轴，z 轴建立空间直角坐标系如图所示，因为AB ，AD ，AP 的长度分别为1，2，2，且AB =12DC ，则A(0,0，1)，B(1,0，0)，D(0,2，0)，P(0,0，2)，C(2,2，0)，又M 是PC 的中点，所以M(1,1，1)，所以BM ⃗⃗⃗⃗⃗⃗ =(0,1,1)，由已知可得平面PAD 的一个法向量为n ⃗ =(1,0,0)，则BM ⃗⃗⃗⃗⃗⃗ ⋅n ⃗ =0×1+1×0+1×0=0，所以BM ⃗⃗⃗⃗⃗⃗ ⊥n ⃗ ，又BM ⊄平面PAD ，所以BM//平面PAD ；(2)解：设平面PDC 的法向量为m ⃗⃗⃗ =(x,y,z)，因为CD ⃗⃗⃗⃗⃗ =(−2,0,0),PD ⃗⃗⃗⃗⃗ =(0,2,−2)，则有{m ⃗⃗⃗ ⋅CD ⃗⃗⃗⃗⃗ =0m ⃗⃗⃗ ⋅PD ⃗⃗⃗⃗⃗ =0，即{−2x =02y −2z =0，令y =1，则x =0，z =1，故m ⃗⃗⃗ =(0,1,1)，又AD⃗⃗⃗⃗⃗⃗ =(0,2,0)，所以点A 到平面PCD 的距离d =|AD ⃗⃗⃗⃗⃗⃗ ⋅m ⃗⃗⃗ |m ⃗⃗⃗ ||=|√2|=√2．解析：(1)建立空间直角坐标系，求出所需点的坐标，求出直线BM 的方向向量BM ⃗⃗⃗⃗⃗⃗ 和平面PAD 的法向量n ⃗ ，证明BM ⃗⃗⃗⃗⃗⃗ ⋅n ⃗ =0即可；(2)利用待定系数法求出平面PDC 的法向量，求出AD ⃗⃗⃗⃗⃗⃗ 的坐标，然后利用点到直线的距离公式求解即可．本题考查了空间向量在立体几何中的应用，对于空间中的线线、线面、面面以及空间距离和空间角问题，建立空间直角坐标系，转化为空间向量问题是常用的方法，属于中档题．3.答案：解：取AD 的中点O ，取BC 的中点F ，连接OP ，OF ，因为底面ABCD 是正方形，∴OF ⊥AD ，∵△PAD 是正三角形，O 为AD 的中点，∴OP ⊥AD ，又因为平面PAD ⊥平面ABCD ，平面PAD ∩平面ABCD =AD ，OP ⊂平面PAD ， ∴OP ⊥平面ABCD ，以{OF ⃗⃗⃗⃗⃗ ,OD ⃗⃗⃗⃗⃗⃗ ,OP ⃗⃗⃗⃗⃗ }为正交基底建立如图所示空间直角坐标系O −xyz. …………………(2分) (1)P(0,0,√3)，A(0,−1,0)，B(2,−1,0)，则AB ⃗⃗⃗⃗⃗ =(2,0,0)，AP ⃗⃗⃗⃗⃗ =(0,1,√3)，设m⃗⃗⃗ =(x,y,z)为平面PAB 的一个法向量，则{m ⃗⃗⃗ ⋅AB ⃗⃗⃗⃗⃗ =2x =0m ⃗⃗⃗ ⋅AP ⃗⃗⃗⃗⃗ =y +√3z =0，则x =0，令z =1，得y =−√3，m ⃗⃗⃗ =(0,−√3,1)，…………(4分)P(0,0,√3)，C(2,1，0)，D(0,1，0)，则DC ⃗⃗⃗⃗⃗ =(2,0,0)，DP ⃗⃗⃗⃗⃗ =(0,−1,√3)，设n⃗ =(a,b,c)为平面PCD 的一个法向量，则{n ⃗ ⋅DC ⃗⃗⃗⃗⃗ =2a =0n ⃗ ⋅DP ⃗⃗⃗⃗⃗ =−b +√3c =0，则a =0，令c =1，得b =√3，n ⃗ =(0,√3,1)，……………(6分) ∴cos <m ⃗⃗⃗ ,n ⃗ >=m ⃗⃗⃗ ⋅n ⃗⃗|m ⃗⃗⃗ ||n ⃗⃗ |=−22×2=−12，又<m ⃗⃗⃗ ,n ⃗ >∈[0,π]，∴<m ⃗⃗⃗ ,n ⃗ >=2π3，∴面PAB 与平面PCD 所成锐二面角的大小为π3. …………………(8分) (2)设BE⃗⃗⃗⃗⃗ =λBP ⃗⃗⃗⃗⃗ ，λ∈[0,1]，则BE ⃗⃗⃗⃗⃗ =λ(−2,1,√3)=(−2λ,λ,√3λ)，则CE ⃗⃗⃗⃗⃗ =CB ⃗⃗⃗⃗⃗ +BE ⃗⃗⃗⃗⃗ =(0,−2,0)+(−2λ,λ,√3λ)=(−2λ,λ−2,√3λ)，因为直线CE 与平面PAB 所成的角为θ， ∴sinθ=|cos <CE ⃗⃗⃗⃗⃗ ,m ⃗⃗⃗ >|=|CE ⃗⃗⃗⃗⃗ ⋅m ⃗⃗⃗ ||CE ⃗⃗⃗⃗⃗ ||m ⃗⃗⃗ |=√3(λ−2)+√3λ|√(−2λ)2+(λ−2)2+(√3λ)2×2………………(10分)=√3√8λ2−4λ+4=√32√2(λ−14)2+78≤√3√72=√427，当且仅当λ=14时取等号，故求sinθ的最大值为√427. …………………(12分)解析：取AD 的中点O ，取BC 的中点F ，连接OP ，OF ，以{OF ⃗⃗⃗⃗⃗ ,OD ⃗⃗⃗⃗⃗⃗ ,OP ⃗⃗⃗⃗⃗ }为正交基底建立如图所示空间直角坐标系O −xyz ．(1)求出平面PAB 的一个法向量，平面PCD 的一个法向量，利用空间向量的数量积求解面PAB 与平面PCD 所成锐二面角的大小．(2)设BE⃗⃗⃗⃗⃗ =λBP ⃗⃗⃗⃗⃗ ，λ∈[0,1]，求出CE ⃗⃗⃗⃗⃗ ，利用空间向量的数量积求解直线CE 与平面PAB 所成的角的正弦函数值的表达式，然后求解sinθ的最大值．本题考查二面角的平面角以及直线与平面所成角的求法，考查空间想象能力，转化思想以及计算能力，是中档题．4.答案：.(1)证明：见解析；(2)异面直线所成角300解析：试题分析：(I)根据题意可得：△ABC 为正三角形，所以AE ⊥BC ，又因为BC//AD ，所以AE ⊥AD.又PA ⊥AE ，且PA ∩AD =A ，所以AE ⊥平面PAD ，进而可得答案； (Ⅱ)先根据条件由(1)知AE ⊥平面PAD ，则∠EHA 为EH 与平面PAD 所成的角.在Rt △EAH 中，AE =，所以当AH 最短时，∠EHA 最大进而得到异面直线的所成的角。

(压轴题)高中数学必修五第二章《解三角形》检测题(答案解析)(3)

一、选择题1．在锐角ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c ．若22212a b c =+，则tan A 的取值范围是（） A ．)3,⎡+∞⎣B ．()3,+∞C ．()2,+∞D ．[)2,+∞2．在△ABC 中，若2223a c b ab -+=，则C ＝( )． A ．45°B ．30°C ．60°D ．120°3．设,,a b c 分别是ABC 中,,A B C ∠∠∠所对边的边长，则直线sin 0x A a y c ⋅+⋅+=与sin sin 0b x y B C ⋅-⋅+=位置关系是（） A ．平行B ．重合C ．垂直D ．相交但不垂直4．如图，某船在A 处看见灯塔P 在南偏东15方向，后来船沿南偏东45的方向航行30km 后，到达B 处，看见灯塔P 在船的西偏北15方向，则这时船与灯塔的距离是：A ．10kmB ．20kmC ．3kmD ．53km5．设ABC 的内角A ，B ，C 的对边分别是a ，b ，c .已知2cos 0b a C -=，()sin 3sin A A C =+，则2bca =（） A 7 B 14 C ．23D 66．如果等腰三角形的周长是底边长的5倍，那么顶角的余弦值是 A ．518B ．34C 3D ．787．在ABC ∆中，角A B C ，，的对边分别是a b c ，，，若sin 3cos 0b A a B -=，且三边a b c ，，成等比数列，则2a cb+的值为（）A ．24B ．22C ．1D ．28．已知ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，2b =，45B =︒，若三角形有两解，则a 的取值范围是（） A ．2a >B ．02a <<C ．222a <<D ．223a <<9．正三棱锥P ABC -中，若6PA =，40APB ∠=︒，点E 、F 分别在侧棱PB 、PC 上运动，则AEF 的周长的最小值为（） A ．36sin 20︒ B ．62C ．12D ．6310．在△ABC 中，a 2tanB =b 2tanA ，则△ABC 是（）A ．等腰三角形B ．直角三角形C ．等腰直角三角形D ．等腰或直角三角形11．如图，测量河对岸的塔高AB 时，选与塔底B 在同一水平面内的两个测点C 与D .现测得15BCD ∠=︒，45BDC ∠=︒，302CD m =，并在点C 测得塔顶A 的仰角为30，则塔高AB 为( )A ．302mB ．203mC ．60mD ．20m12．已知a 、b 、c 分别是ABC 内角A 、B 、C 的对边，sin sin 3sin A B C +=，cos cos 2a B b A +=，则ABC 面积的最大值是（）A ．2B ．2C ．3D ．23二、填空题13．ABC 中，D 是边BC 上的点，满足90BAD ∠=︒，30DAC ∠=︒，4BD CD =.则sin sin BC=______. 14．ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，ABC 的面积2228a b c S +-=，D为线段BC 上一点．若ABD △为等边三角形，则tan DAC ∠的值为___________． 15．如图，在ABC 中，角C 的平分线交AB 于D 且CD AD =.若3AC =，2BC =，则AB =________16．在ABC 中，60,12,183ABCA b S=︒==，则sin sin sin a b cA B C____________.17．在锐角ABC 中，内角A 、B 、C 的对边分别是,,a b c ，若()231a b b a +-=，1c =，则3a b -的取值范围是______.18．在ABC 中，已知24cos 2sin a C c B =+，22b =，则ABC 面积的最大值是__________.19．太阳光线照于地面，与地面成角02παα⎛⎫<<⎪⎝⎭.调整木棍角度可改变其在水平地面的影子长度.则长度为d 的木棍在水平地面的影子最长为______.20．如图，在ABC 中，点D 是边BC 上的一点，1DC =，2AC =，3BD =，120BAD ∠=︒，则AB 的长为________.三、解答题21．在ABC 中，a ，b ，c 分别为角A ，B ，C 的对边，且3bcos A c ⋅=. （1）求角B ；（2）若ABC 的面积为3BC 边上的高1AH =，求b ，c . 22．在ABC 中，内角A ，B ，C 的对边依次为a ，b ，c ，221sin cos 22A B C +-=．（1）求角C ；（2）若2c =，4A π=，求ABC 的面积．23．已知ABC ∆的内角,,A B C 的对边分别为,,a b c ，且4B π=．（1）请从下面两个条件中选择一个作为已知条件，求sin A 的值； ①5b =，2c =；②3a =，2c =.注：如果选择多个条件分别解答，则按第一个解答计分. （2）若5b =，3a c +=，求ABC 的面积．24．在ABC 中，它的内角A ，B ，C 的对边分别为a ，b ，c ，且23B π=，6b =. （Ⅰ）若2cos cos 3A C =，求ABC 的面积；（Ⅱ）试问111a c+=能否成立？若能成立，求此时ABC 的周长；若不能成立，请说明理由.25．已知ABC 中角A ，B ，C 所对的边分别为a ，b ，c ，满足()sin 2sin sin A B A C -=-.（1）求B ；（2）若点D 为BC 上一点，2DC =，π6C =，DE 平分ADC ∠交AC 于点E ，7ADE CDE S S =△△，求BD .26．ABC 的内角A ，B ，C 的对边分别为a ，b ，c ()3sin 2cos b A a B =+. （1）求角B ；（2）若3b =，且ABC 311a c +的值.【参考答案】***试卷处理标记，请不要删除一、选择题 1．B【分析】根据题中条件，由三角形的余弦定理、正弦定理和两角和的正弦公式，化简可得tan 3tan A B =，再由两角和的正切公式，以及锐角三角形的定义，可得tan 0A >，tan 0C >，解不等式可得所求范围．【详解】因为22212a b c =+，由余弦定理可得，2222cos a b c bc A =+-，则222212cos 2b c b c bc A +=+-，可得4cos c b A =，由正弦定理可得：sin 4sin cos C B A =，可得sin()sin cos sin cos 4sin cos A B A B B A B A +=+=，化为3sin cos sin cos B A A B =，在锐角ABC 中，cos 0A ≠，cos 0B ≠，则tan 3tan A B =，又21tan tan tan tan 3tan tan()11tan tan 1tan 3A AA B C A B A B A ++=-+=-=---，由tan 0A >，tan 0C >，可得211tan 03A -<，解得tan A >，故选：B ．【点睛】本题考查三角形的正弦定理和余弦定理的运用，以及两角和的三角函数公式，考查方程思想和化简运算能力，属于中档题．2．B解析：B 【分析】根据余弦定理，可以求出C 角的余弦值，进而根据C 为三角形内角，解三角方程可以求出C 角．【详解】∵222a c b -+=，∴22222a b c cosC ab +-==. 又∵C 为三角形内角 ∴30C =︒. 故选B ．本题考查余弦定理的应用，属基础题．3．C解析：C 【解析】,,a b c 分别是ABC 中,,A B C ∠∠∠所对边的边长，则直线sin 0x A a y c ⋅+⋅+=斜率为：sin Aa-， sin sin 0b x y B C ⋅-⋅+=的斜率为：sin bB， ∵sin sin A ba B -=﹣1，∴两条直线垂直．故选C ．4．C解析：C 【分析】在ABP ∆中，利用正弦定理求出BP 得长，即为这时船与灯塔的距离，即可得到答案．【详解】由题意，可得30PAB PBA ∠=∠=，即30,120AB APB =∠=，在ABP ∆中，利用正弦定理得30sin 30sin120PB ==即这时船与灯塔的距离是km ，故选C ．【点睛】本题主要考查了正弦定理，等腰三角形的判定与性质，以及特殊角的三角函数值的应用，其中熟练掌握正弦定理是解答本题的关键，着重考查了推理与运算能力，属于基础题．5．D解析：D 【分析】根据正弦定理把角化边，可得3a b =，进一步得到2cos 3C =，然后根据余弦定理，可得c =，最后可得结果.【详解】在ABC ∆中，sin sin a b A B=，由()sin 3sin()3sin 3sin A A C B B π=+=-=，所以3a b =①，又2cos 0b a C -=②，由①②可知：2cos 3C =，又2222cos 23a b c C ab +-==③，把①代入③化简可得：c =，则23bc a b ==，故选：D. 【点睛】本题考查正弦定理、余弦定理的综合应用，难点在于将c 用b 表示，当没有具体数据时，可以联想到使用一个参数表示另外两个参数，属于中档题.6．D解析：D 【解析】设顶角为C ，∵l=5c ， ∴a=b=2c ，由余弦定理得：222222447cos 22228a b c c c c C ab c c +-+-===⨯⨯．故答案为D.7．C解析：C 【分析】先利用正弦定理边角互化思想得出3B π=，再利余弦定理1cos 2B =以及条件2b ac =得出a c =可得出ABC ∆是等边三角形，于此可得出2a cb+的值．【详解】sin cos 0b A B =，由正弦定理边角互化的思想得sin sin cos 0A B A B =，sin 0A >，sin 0B B ∴=，tan B ∴=，则3B π=.a 、b 、c 成等比数列，则2b ac =，由余弦定理得222221cos 222a cb ac ac B ac ac +-+-===，化简得2220a ac c -+=，a c ∴=，则ABC ∆是等边三角形，12a cb+∴=，故选C ．【点睛】本题考查正弦定理边角互化思想的应用，考查余弦定理的应用，解题时应根据等式结构以及已知元素类型合理选择正弦定理与余弦定理求解，考查计算能力，属于中等题．8．C解析：C 【分析】直接利用正弦定理计算得到答案.【详解】根据正弦定理：sin sin 22a b A B==，故sin 22A =，三角形有两解，故2sin 1222A <=<，解得222a <<. 故选：C. 【点睛】本题考查了利用正弦定理解三角形，意在考查学生的计算能力和转化能力.9．D解析：D 【分析】画出正三棱锥P ABC -侧面展开图，将问题转化为求平面上两点间的距离最小值问题，不难求得结果．【详解】将三棱锥由PA 展开，如图，正三棱锥P ABC -中，40APB ∠=︒，则图中1120APA ∠=︒，当点A 、E 、F 、1A 位于同一条直线上时，AEF ∆的周长最小，故1AA 为AEF ∆的周长的最小值，又1PA PA =，1PAA ∴∆为等腰三角形，6PA =，16PA ∴=，22166266cos12063AA ∴=+-⨯⨯⨯︒=，AEF ∴∆的最小周长为：63．故选：D ．【点睛】本题考查的知识点是棱锥的结构特征，其中将三棱锥的侧面展开，将空间问题转化为平面上两点之间的距离问题，是解答本题的关键．10．D解析：D 【分析】根据正弦定理22tan ta in n s sin B B A A =⋅⋅，化简得到sin 2sin 2A B =，得到答案. 【详解】22tan tan a B b A =，故22tan ta in n s sin B B A A =⋅⋅，即sin 2sin 2A B =.故22A B =或22A B π+=，即A B =或2A B π+=.故选：D . 【点睛】本题考查了正弦定理判断三角形形状，意在考查学生的计算能力.11．D解析：D 【分析】由正弦定理确定BC 的长，再tan30AB BC 求出AB ．【详解】15BCD ∠=︒，45BDC ∠=︒120CBD由正弦定理得：sin120sin 45BC302sin 45203sin120BC3tan 3020320ABBC故选D【点睛】本题是正弦定理的实际应用，关键是利用正弦定理求出BC ，属于基础题．12．B解析：B 【分析】由cos cos 2a B b A +=，利用余弦定理代入化简解得2c =，再根据sin sin 3sin A B C +=，利用正弦定理得到36a b c +==，即62CA CB AB +=>=，得到点C 的轨迹是以A ，B 为焦点的椭圆，再利用椭圆的焦点三角形求解. 【详解】∵cos cos 2a B b A +=，∴222222222a c b b c a a b ac bc+-+-⋅+⋅=，∴2c =，∵sin sin 3sin A B C += ∴36a b c +==，即62CA CB AB +=>=，∴点C 的轨迹是以A ，B 为焦点的椭圆，其中长半轴长3，短半轴长22，以AB 为x 轴，以线段AB 的中点为原点，建立平面直角坐标系，其方程为22198x y ，如图所示：则问题转化为点C 在椭圆22198x y 上运动求焦点三角形的面积问题．当点C 在短轴端点时，ABC 的面积取得最大值，最大值为22故选：B ．【点睛】本题主要考查正弦定理，余弦定理以及椭圆焦点三角形的应用，还考查了转化求解问题的能力，属于中档题.二、填空题13．【分析】直接利用三角形的面积建立等量关系进一步利用正弦定理的应用求出结果【详解】解：中D 是边上的点满足所以又因为则则故答案为：【点睛】本题考查了正弦定理三角形面积计算公式及其性质考查了推理能力与计算解析：12【分析】直接利用三角形的面积建立等量关系，进一步利用正弦定理的应用求出结果．【详解】解：ABC 中，D 是边BC 上的点，满足90BAD ∠=︒，30DAC ∠=︒，4BD CD =，所以1sin 90221sin 302ABD ACD ABAD S AB S ACAC AD ⋅︒==⋅⋅︒△△，又因为4ABD ACD S BD S CD ==△△，则24AB BD AC CD ==，则sin 1sin 2B AC C AB ==. 故答案为：12.【点睛】本题考查了正弦定理、三角形面积计算公式及其性质，考查了推理能力与计算能力，属于中档题．14．【分析】由及三角形面积公式余弦定理可得又利用两角差的正切公式展开计算即可【详解】因为所以由三角形面积公式及余弦定理得所以又为等边三角形所以故答案为：【点睛】本题考查正余弦定理在解三角形中的应用涉及到解析：853-+【分析】由2228a b c S +-=及三角形面积公式，余弦定理可得1tan 2C =，又()tan tan 60DAC C ︒∠=-，利用两角差的正切公式展开计算即可.【详解】因为2228a b c S +-=, 所以，由三角形面积公式及余弦定理得12cos sin 28ab C ab C =，所以tan C =sin 1cos 2C C =，又ABD △为等边三角形，所以()tan tan 60DAC C ︒∠=-=3tan 23185313tan 23C C --==-+++．故答案为：853-+【点睛】本题考查正余弦定理在解三角形中的应用，涉及到两角差的正切公式，三角形面积公式，考查学生的数学运算求解能力，是一道中档题.15．【分析】不妨令易知然后在中利用正弦定理求出的值最后在中利用正弦定理可求出的值【详解】解：在中角的平分线交于且设则即整理得所以：结合得即显然是锐角所以再由得：解得故答案为：【点睛】本题考查正弦定理三角 10【分析】不妨令A α∠=，易知ACD BCD α∠==，3B πα∠=-，然后在ABC 中，利用正弦定理，求出sin α，cos α的值，最后在ABC 中，利用正弦定理，可求出AB 的值．【详解】解：在ABC 中，角C 的平分线交AB 于D ，且CD AD =．设A α∠=，则ACD BCD α∠==，3B πα∠=-， ∴sin sin AC BC B A =∠∠，即32sin(3)sin παα=-，整理得2sin33sin αα=，所以：2(sin cos2cos sin 2)3sin ααααα+=，结合sin 0α≠得222(2cos 12cos )3αα-+=，即258cos α=，显然α是锐角，所以106cos αα= ∴15sin 22sin cos ααα==．再由ABC 得：2sin sin 2AB αα=，∴615= 解得10AB ． 10【点睛】本题考查正弦定理，三角恒等变换的知识方法在解题中的作用，属于中档题． 16．【分析】根据三角形面积公式以及余弦定理求解即可【详解】由余弦定理可知故答案为：【点睛】本题主要考查了三角形面积公式以及余弦定理的应用属于中档题解析：12【分析】根据三角形面积公式以及余弦定理求解即可.【详解】11sin 1222ABC S bc A c ==⨯=△6c ∴=由余弦定理可知a =12sin sin sin sin a b c a A B C A ++∴===++ 故答案为：12【点睛】本题主要考查了三角形面积公式以及余弦定理的应用，属于中档题.17．【分析】根据结合余弦定理可得再根据正弦定理将化简成关于的三角函数表达式再根据锐角求得的取值范围结合三角函数的性质求解值域即可【详解】因为故所以又锐角故由正弦定理所以又锐角故解得即故故答案为：【点睛】解析：(【分析】根据()21a b b +=，结合余弦定理可得6C π=b -化简成关于A 的三角函数表达式，再根据锐角ABC 求得A 的取值范围，结合三角函数的性质求解值域即可.【详解】因为()21a b b +=，1c =，故222c a b =+.所以222cos 2a b c C ab +-===.又锐角ABC ，故6C π=. 由正弦定理，12sin sin sin sin 6a b c A B C π====，)52sin 2sin 6b A B A A π⎤⎛⎫-=-=-- ⎪⎥⎝⎭⎦112sin cos 2cos 2sin 22226A A A A A A π⎫⎛⎫⎛⎫=--=-=-⎪ ⎪ ⎪⎪ ⎪⎝⎭⎭⎝⎭.又锐角ABC ，故02062A A ππππ⎧<<⎪⎪⎨⎪<--<⎪⎩，解得32A ππ<<，即663A πππ<-<.(2sin 6b A π⎛⎫-=-∈ ⎪⎝⎭.故答案为：(【点睛】本题主要考查了正余弦定理在解三角形中的应用、边角互化求取值范围的问题，需要将所给的边的表达式利用正弦定理转换为角的表达式，同时结合角度的范围求解.属于中档题. 18．【分析】根据已知条件利用边角互化即可求得再由余弦定理结合均值不等式即可求得的最大值则面积的最大值可解【详解】因为故可得即则又因为故可得又故可得由余弦定理可得即当且仅当时取得等号故故答案为：【点睛】本解析：)21 【分析】根据已知条件，利用边角互化即可求得B ，再由余弦定理，结合均值不等式，即可求得ac 的最大值，则面积的最大值可解.【详解】4cos sin C B =，b =，=+，即sinA sinBcosC sinCsinB =+则cosBsinC sinCsinB =，又因为sin 0C ≠，故可得1tanB =，又()0,B π∈，故可得4B π=.由余弦定理可得222222(2b a c accosB a c ac =+-+≥--=,即(42ac ≤+，当且仅当a c =时取得等号.故()11cos 4221222ABC S ac B =≤⨯⨯+=△.故答案为：)21 【点睛】本题考查利用正余弦定理以及均值不等式求三角形面积的最值，属综合中档题. 19．【分析】太阳光与水平面所成的角是不变量设利用正弦定理公式可得影子长为是不变量且确定只需要最大计算即可得出结果【详解】光线照于地面与地面成角调整木棍角度可改变其在水平地面的影子长度则长度为如图所示：设解析：sin d α 【分析】太阳光与水平面所成的角是不变量, 设BAC θ∠=，利用正弦定理公式可得， ()sin sin d AC αθα=+影子长为()sin sin d AC θαα+=，α是不变量，且sin α确定,只需要()sin θα+最大，计算即可得出结果.【详解】光线照于地面，与地面成角02παα⎛⎫<< ⎪⎝⎭.调整木棍角度可改变其在水平地面的影子长度.则长度为d ，如图所示：AB d =，C α=，设BAC θ∠=，影子长为AC ,根据正弦定理：()sin sin d AC αθα=+，则()sin sin d AC θαα+=，因为α是不变量，且sin α确定,只需要()sin θα+最大,故有2πθα+=，此时，木棍在水平地面的影子最长为sin d α. 故答案为：sin d α【点睛】本题考查了线面角中的最小角定理，还考查了学生们的空间想象能力及把生活中的实例用数学的思想加以解释的能力，即建模能力．20．【分析】在两个三角形中利用余弦定理建立等量关系式整理得出结合题中所给的条件利用余弦定理建立等量关系式求得结果【详解】因为所以可得在△中所以整理得出所以所以故答案为：【点睛】该题考查的是有关解三角形的 67 【分析】在两个三角形中，利用余弦定理，建立等量关系式，整理得出2AB AD =，结合题中所给的条件，利用余弦定理建立等量关系式，求得结果.【详解】因为cos cos ADB ADC ∠=-∠，所以2229142321AD AB AD AD AD+-+-=-⨯⨯⨯⨯，可得2AB AD =，在△ABD 中，2222cos BD AD AB AD AB BAD =+-⨯⨯∠，所以22192()422AB AB AB AB =+-⨯⨯⨯-，整理得出2794AB =，所以2367AB =，所以7AB =，故答案为：7. 【点睛】该题考查的是有关解三角形的问题，涉及到的知识点有余弦定理解三角形，属于简单题目.三、解答题21．（1）6π；（2）b =2c =. 【分析】（1）化角为边，化简得222c a b +-=，再利用余弦定理求角B ；（2）由正弦定理算出c ，由面积公式算出a ，由余弦定理计算b 中即可.【详解】解：（1）因为cos b A c =-，所以2222b c a b c bc +-⋅=-，所以22222b c a c +-=-，即222c a b +-=.由余弦定理可得222cos 2c a b B ac +-==，因为(0,)B π∈，所以6B π=.（2）由正弦定理可得sin sin 22sin sin 6AH AH AHB c B ππ∠===. 因为ABC的面积为11sin 22ac B a ==，解得a = 由余弦定理可得2222cos b a c ac B =+-=48422282+-⨯⨯=，则b =【点睛】在处理三角形中的边角关系时，一般全部化为角的关系，或全部化为边的关系．题中若出现边的一次式一般采用到正弦定理，出现边的二次式一般采用到余弦定理．应用正、余弦定理时，注意公式变式的应用．解决三角形问题时，注意角的限制范围．22．（1）2C π=或3C π=；（2或1．【分析】（1）利用二倍角余弦公式可得22cos cos C C -=-，从而可得cos 0C =或1cos 2C =，即求.（2）由（1）知3C π=或2C π=，当3C π=时，利用正弦定理求出,a b ，再根据三角形的面积公式即可求解；当2C π=时，根据直角三角形即可求解. 【详解】（1）由221sin cos 22A B C +-=，得222sin 2cos 12A B C +-=，化简得222cos 12sin2A B C +-=-，即()22cos cos C A B -=+，即22cos cos C C -=-，即()cos 2cos 10C C -=，解得cos 0C =或2cos 10C -=．即cos 0C =或1cos 2C =．又0C π<<，所以2C π=或3C π=．（2）由（1）得3C π=或2C π=，当3C π=时，由正弦定理sin sin sin a b c A B C ==得，sin sin c a A C =⋅=3， 2sinsin 34c b B C ππ⎛⎫=⋅=- ⎪⎝⎭ 22sin cos cos sin3434ππππ⎫=-⎪⎭122223⎛⎫=⨯--⨯= ⎪⎝⎭⎦，故113sin 223323ABC S ab C +==⨯⨯=△；当2C π=时，由2c =，4A π=，得4B π=，a b ==因此11122ABC S ab ===△．综上，ABC 的面积是33+或1．23．（121- 【分析】（1）选择条件①，由余弦定理求出3a =，再由正弦定理即可求出；选择条件②，由余弦定理求出b =（2）由余弦定理结合已知条件可求出4ac =-，再由面积公式即可求出.【详解】（1）选择条件①由余弦定理2222cos b a c ac B =+-得2230a a --=，解得3a =.由正弦定理sin sin b a B A =得sin sin 10a B Ab ==. 选择条件②由余弦定理2222cos 5b a c ac B =+-=得b =由正弦定理sin sin b a B A =得sin sin a B A b ==.（2）由余弦定理2222cos b a c ac B =+-得225a c =+，所以25()(29(2a c ac ac =+-+=-+，得4ac =-所以1sin 12ABC S ac B ==.24．（ⅠⅡ）不能成立，理由见解析. 【分析】（Ⅰ）由于3A C π+=，cos()cos cos sin sin A C A C A C +=-，得1sin sin 6A C =，结合正弦定理与面积公式可得结果；（Ⅱ）假设111a c+=能成立，得a c ac +=，由余弦定理，2222cos b a c ac B =+-可得3ac =，结合基本不等式判断即可.【详解】（Ⅰ）由23B π=，得3A C π+=，cos()cos cos sin sin A C A C A C +=-，即1cos cos sin sin 2A C A C =-. 又∵2cos cos 3A C =，∴1sin sin 6A C =.∵sin sin a c A C===∴a A =，c C =.∴1sin 4sin sin sin 2ABC S A C B A B C =⋅⋅⋅=△14623=⨯⨯=. （Ⅱ）假设111a c+=能成立，∴a c ac +=. 由余弦定理，2222cos b a c ac B =+-，∴226a c ac =++.∴2()6a c ac +-=，∴2()60ac ac --=，∴3ac =或-2（舍），此时3a c ac +==.不满足a c +≥，∴111a c +=不成立. 【点睛】解三角形的基本策略：一是利用正弦定理实现“边化角”，二是利用余弦定理实现“角化边”. 25．（1）π4；（2）4+. 【分析】（1）根据两角和差公式展开化简可得cos 2B =，从而得解；（2）根据面积比及题中边长可得AD =ABC中，由ππsin sin 64BAC ⎛⎫∠=+= ⎪⎝⎭BD . 【详解】（1）∵()sin sin A B A C -=-，∴()sin cos cos sin sin cos cos sin A B A B A A B A B -=-+，∴2sin cos A B A .∵sin 0A >，∴cos B =. ∵()0,πB ∈，∴π4B =. （2）∵1sin 2ADE S AD DE ADE =⋅∠△， 1sin 2CDE S CD DE CDE =⋅∠△，2CD =，∴AD =在ACD △中，设AC x =，由余弦定理得24428x x +-=，即2240x --=，解得43x (舍负).在ABC中，ππsin sin 64BAC ⎛⎫∠=+= ⎪⎝⎭由正弦定理得sin 6πsin 4BAC BC AC ∠==+∴4BD =+【点睛】思路点睛：本题考查正弦定理、余弦定理、三角形的面积公式，解题中要注意条件与结论之间的联系，确定选用的公式与顺序．出现多个三角形时，要从条件较多的三角形入手求解.．26．（1）2π3；（2【分析】（1）利用正弦定理的边角互化以及辅助角公式即可求解.（2）根据三角形的面积公式可得2ac =，再利用余弦定理可得a c +=.【详解】解：（1sin (2cos )A a B =+，sin sin (2cos )A B A B =+.∵(0π)A ∈，，∴sin 0A >，∴cos 2B B -=，∴π2sin 26B ⎛⎫-= ⎪⎝⎭， ∴ππ62B -=，∴2π3B =. （2）因为ABC S =，∴12πsin 23ac =，∴2ac =. 又∵22222cos ()b a c ac B a c ac =+-=+-，∴a c +=∴11a c a c ac ++==.。

点线面角高一的知识点

点线面角高一的知识点在高中数学学科中，点、线、面和角是最基本的几何概念之一。

它们是我们探索和研究空间几何性质的基石。

本文将重点介绍高一学生需要掌握的关于点、线、面和角的重要知识点。

一、点（Point）点是几何学中最基本的概念，通常用字母表示，例如点A、点B等。

点没有大小和方向，它只是空间中的一个位置。

点可以通过坐标来描述，如平面直角坐标系中的点P(x, y)。

二、线（Line）线可以看作由无数个点按一定规律排列而成，它没有宽度和厚度。

直线是由无数个点按一定方向延伸而成，可以用字母表示，例如直线l。

直线上的两点可以确定一条唯一的直线。

曲线是由无数个点按复杂的运动轨迹得到的，它可以弯曲和闭合。

三、面（Plane）面是由无数个点按一定规律排列而成的，它有无限的长和宽，但没有厚度。

平面可以看作由无数条平行直线按一定间隔排列而成。

平面可以用大写字母表示，例如平面α、平面β等。

平面上有无数个点，通过三个不共线的点可以确定一个唯一的平面。

四、角（Angle）角是由两条射线共同起点所组成的图形。

射线的起点称为角的顶点，两条射线称为角的边。

角可以用字母表示，例如角∠ABC。

角的大小通常用度数、弧度或比例来衡量。

例如，一个直角的度数为90°，一个周角（完全转角）的度数为360°。

五、点、线、面和角的关系点可以构成线，两个点可以确定一条唯一的直线。

线可以在平面上移动，形成平面。

两条相交的直线可以形成一个角。

通过点、线、面和角的基本关系，我们可以研究和解决与空间几何相关的问题，如两条直线是否平行、直线与平面的关系、角的性质等。

六、点、线、面和角的性质1. 点的性质：点在空间中只占据一个位置，无大小和方向。

2. 线的性质：线无宽度和厚度，可以无限延伸。

两点可以确定一条直线，两直线可以相交、平行或重合。

3. 面的性质：面有无限长和宽，但没有厚度。

三个不共线的点可以确定一个平面，两平面可以相交、平行或重合。

高中数学立体几何线面角公式

高中数学立体几何线面角公式【原创版】目录1.高中数学立体几何的概述2.线面角的概念和求解方法3.线面角公式及其应用4.立体几何问题的解题技巧和常用公式5.总结正文【高中数学立体几何的概述】高中数学立体几何是欧氏空间几何的一个分支，它是我们在平面几何基础上向三维空间延伸的学习内容。

立体几何主要包括空间向量在立体几何中的应用、立体测绘、线面角、面面角、异面直线所成角等知识点。

这些知识点与我们生活中的空间关系密切相关，因此学习立体几何有助于培养我们的空间想象能力和思维能力。

【线面角的概念和求解方法】线面角是指一条直线与一个平面之间的夹角。

求解线面角的方法通常有两种：一种是通过作图法，过线上的一点做面的垂线，交点记作 A，线与面的另一个交点为 B，线上的那点（就是刚过线上一点的那个点）记作C，CAB 就是线面角；另一种是通过向量法，利用线向量与面法向量的点积求解线面角的余弦值，从而得到线面角的大小。

【线面角公式及其应用】线面角的余弦值公式为：cos<a,b> = (A·B) / (|A|·|B|)，其中 A、B 为向量，|A|、|B|为向量的模。

线面角的正弦值公式为：sin<a,b> = |A·B| / (|A|·|B|)。

在求解立体几何问题时，我们可以利用这些公式计算线面角的余弦值和正弦值，从而更好地理解和解决相关问题。

【立体几何问题的解题技巧和常用公式】在解决立体几何问题时，我们需要注意以下几点：1.建立正确的空间几何图形，以便于理解和解决问题；2.利用空间向量进行坐标运算，如加法、减法、数乘等；3.利用线面角、面面角、异面直线所成角等概念，以及相关公式求解问题；4.注意问题的对称性和特殊情况，以便于简化问题和快速求解。

【总结】高中数学立体几何是学习空间几何知识的重要组成部分，掌握线面角、面面角等概念及其公式，可以帮助我们更好地理解和解决立体几何问题。

(常考题)人教版高中数学选修一第一单元《空间向量与立体几何》检测卷(包含答案解析)(1)

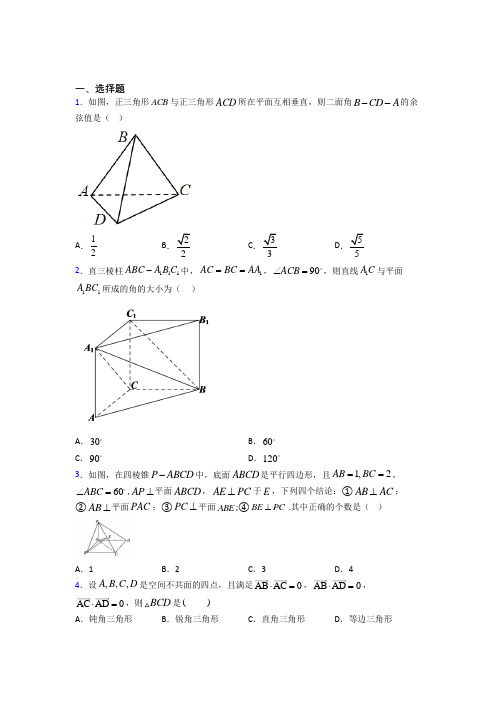
一、选择题1．如图，正三角形ACB 与正三角形ACD 所在平面互相垂直，则二面角B CD A --的余弦值是（）A ．12B ．22C ．33D ．552．直三棱柱111ABC A B C -中，1AC BC AA ==，90ACB ∠=，则直线1A C 与平面11A BC 所成的角的大小为（）A ．30B ．60C ．90D ．1203．如图，在四棱锥P ABCD -中，底面ABCD 是平行四边形，且1,2AB BC ==，60ABC ∠=,AP ⊥平面ABCD ，AE PC ⊥于E ，下列四个结论：①AB AC ⊥；②AB ⊥平面PAC ；③PC ⊥平面ABE ;④BE PC ⊥ .其中正确的个数是（）A ．1B ．2C ．3D ．44．设,,,A B C D 是空间不共面的四点，且满足AB AC 0⋅=，AB AD 0⋅=，AC AD 0⋅=，则BCD 是( )A ．钝角三角形B ．锐角三角形C ．直角三角形D ．等边三角形5．已知()1,1,2P -，()23,1,0P 、()30,1,3P ，则向量12PP 与13PP 的夹角是（） A ．30B ．45C ．60D ．906．如图，在四面体A BCD -中，已知AD a →→=，AB b →→=，AC c →→=，12BE EC →→=，则DE →等于（）A ．2133a b c →→→-++B ．2133a b c →→→++ C ．2133a b c →→→-+ D ．2133a b c →→→-+7．在一直角坐标系中，已知(1,6),(3,8)A B --，现沿x 轴将坐标平面折成60︒的二面角，则折叠后,A B 两点间的距离为（） A ．241B ．41C ．17D ．2178．在直三棱柱111ABC A B C -中，120ABC ∠=，1AB BC CC ==，则异面直线1AB 与1BC 所成角的余弦值为（）A ．34-B ．34-C ．34D ．349．在底面为锐角三角形的直三棱柱111ABC A B C -中，D 是棱BC 的中点，记直线1B D 与直线AC 所成角为1θ，直线1B D 与平面111A B C 所成角为2θ，二面角111C A B D --的平面角为3θ，则（） A ．2123,θθθθ<<B ．2123 ,θθθθ><C ．2123 ,θθθθD ．2123 ,θθθθ>>10．如图，平行六面体中1111ABCD A B C D -中，各条棱长均为1，共顶点A 的三条棱两两所成的角为60°，则对角线1BD 的长为（）A ．1B ．2C ．3D ．211．以下四个命题中正确的是（）A ．空间的任何一个向量都可用其他三个向量表示B ．若{},,a b c 为空间向量的一组基底，则{},,a b b c c a +++构成空间向量的另一组基底 C ．ABC ∆为直角三角形的充要条件是0AB AC ⋅=D ．任何三个不共线的向量都可构成空间向量的一个基底12．已知A ，B ，C 三点不共线，O 是平面ABC 外一点，下列条件中能确定点M 与点A ，B ，C 一定共面的是（） A ．OM OA OB OC =++ B ．23OM OA OB OC =++ C ．111222OM OA OB OC =++ D ．111333OM OA OB OC =++ 13．如图，四个棱长为1的正方体排成一个正四棱柱，AB 是一条侧棱，()1,2,,8i P i =是上底面上其余的八个点，则()1,2,,8i AB AP i ⋅=⋅⋅⋅的不同值的个数为（）A ．8B ．4C ．2D ．1二、填空题14．如图，在棱长为2的正方体1111ABCD A B C D -中，E 为BC 的中点，点P 在底面ABCD 上移动，且满足11B P D E ⊥，则线段1B P 的长度的最大值为______15．已知向量()()0,1,1,4,1,0,29a b a b λ=-=+=，且0λ>，则λ=____________．16．如图：二面角α﹣l ﹣β等于120°，A 、B 是棱l 上两点，AC 、BD 分别在半平面α、β内，AC ⊥l ，BD ⊥l ，AB ＝AC ＝BD ＝1，则CD 的长等于__．17．已知正三棱锥P ABC -的侧棱长为2020，过其底面中心O 作动平面α交线段PC 于点S ，交,PA PB 的延长线于,M N 两点，则111PS PM PN++的取值范围为__________18．设空间任意一点O 和不共线三点A B C ，，，且点P 满足向量关系OP xOA yOB zOC =++，若,,,P A B C 四点共面，则x y z ++=______．19．已知向量(1,2,1)a =-，(2,2,0)b =-，则a 在b 方向上的投影为________． 20．已知A(1,2,0)，B(0,1，－1)，P 是x 轴上的动点，当0AP BP ⋅=取最小值时，点P 的坐标为__________．21．ABC ∆的三个顶点分别是(1,1,2)A -，(5,6,2)B -，(1,3,1)C -，则AC 边上的高BD 长为__________．22．在平行六面体1111ABCD A B C D -中，12AB AD AA ===，90BAD ∠=，1160BAA DAA ∠=∠=，则异面直线1AB 与1BC 所成角的余弦值是________．23．已知向量()2,1,3a =-，31,,2b k ⎛⎫=-- ⎪⎝⎭，若向量a 、b 的夹角为钝角，则实数k 的取值范围是__________．24．已知(2,1,3)a →=-，(4,2,)b x →=-，(1,,2)c x →=-，若a b c →→→⎛⎫+⊥ ⎪⎝⎭，是x =________.25．如图，在正四棱锥V ABCD -中，二面角V BC D --为60°，E 为BC 的中点.已知F 为直线VA 上一点，且F 与A 不重合，若异面直线BF 与VE 所成角为60°，则VFVA=_____________.26．已知直线l 的一个方向向量为()2,8,1m =--，平面α的一个法向量为1,,22n t ⎛⎫= ⎪⎝⎭，且//l α，则实数t =______.【参考答案】***试卷处理标记，请不要删除一、选择题 1．D 解析：D 【分析】取AC 的中点E ，连接BE,DE,证明BE 垂直于平面ACD ，以点E 为原点建立空间直角坐标系，分别求出平面BCD 和平面CDA 的法向量，利用空间向量公式即可求出所求二面角的余弦. 【详解】如图示，取AC 中点E ，连结BE 、DE ，在正三角形ACB 与正三角形ACD 中， BE ⊥AC ，DE ⊥AC ，因为面ACB ⊥面ACD ，面ACB 面=ACD AC ，所以BE ⊥面ADC ,以E 为原点，ED 为x 轴正方向，EC 为y 轴正方向，EB 为z 轴正方向，建立空间直角坐标系，设AC =2，则())()()(0,0,0,3,0,0,0,1,0,0,1,0,3E DC A B -,平面ACD 的一个法向量为(3EB = 而()()0,1,3,3,1,0CB CD =-=-，设(),,n x y z =为面BCD 的一个法向量，则：·0·0n CB n DC ⎧=⎨=⎩即 3030y z y x ⎧-+=⎪⎨-+=⎪⎩，不妨令x =1，则()1,3,1n = 设二面角B CD A --的平面角为θ，则θ为锐角，所以35cos |cos ,||||||||35EB n EB n EB n θ⋅====⨯.故选：D向量法解决立体几何问题的关键： (1)建立合适的坐标系； (2)把要用到的向量正确表示； (3)利用向量法证明或计算.2．A解析：A 【分析】以点C 为坐标原点，CA 、CB 、1CC 所在直线分别为x 、y 、z 轴建立空间直角坐标系，利用空间向量法可求得直线1A C 与平面11A BC 所成的角. 【详解】在直三棱柱111ABC A B C -中，1CC ⊥平面ABC ，又90ACB ∠=，以点C 为坐标原点，CA 、CB 、1CC 所在直线分别为x 、y 、z 轴建立空间直角坐标系，如下图所示：设11AC BC AA ===，则()11,0,1A 、()0,1,0B 、()0,0,0C 、()10,0,1C ， ()111,0,0A C =-，()10,1,1=-BC ，()11,0,1=--AC ，设平面11A BC 的法向量为(),,n x y z =，由11100n AC x n BC y z ⎧⋅=-=⎪⎨⋅=-+=⎪⎩，可得0x y z =⎧⎨=⎩，令1y =，可得0x =，1z =，所以，平面11A BC 的一个法向量为()0,1,1n =，1111cos ,222n A C n A C n A C⋅<>==-⨯⋅，所以，直线1A C 与平面11A BC 所成角的正弦值为12，则直线1A C 与平面11A BC 所成角为30.故选：A.方法点睛：计算线面角，一般有如下几种方法：（1）利用面面垂直的性质定理，得到线面垂直，进而确定线面角的垂足，明确斜线在平面内的射影，即可确定线面角；（2）在构成线面角的直角三角形中，可利用等体积法求解垂线段的长度h ，从而不必作出线面角，则线面角θ满足sin hlθ=（l 为斜线段长），进而可求得线面角；（3）建立空间直角坐标系，利用向量法求解，设a 为直线l 的方向向量，n 为平面的法向量，则线面角θ的正弦值为sin cos ,a n θ=<>.3．D解析：D 【详解】已知1260AB BC ABC ==∠=︒，，，由余弦定理可得2222cos60AC AB BC AB BC =+-︒3=，所以22AC AB +2BC =，即AB AC ⊥，①正确；由PA ⊥平面ABCD ，得AB PA ⊥，所以AB ⊥平面PAC ，②正确；AB ⊥平面PAC ，得AB ⊥PC ，又AE PC ⊥，所以PC ⊥平面ABE ，③正确；由PC ⊥平面ABE ，得PC BE ⊥，④正确，故选D ．4．B解析：B 【分析】由0AB AC ⋅=，0AB AD ⋅=，0AC AD ⋅=，可得()()20BC BD AC AB AD AB AB ⋅=--=>，B ∠是锐角，同理可得D ∠，C ∠都是锐角，从而可得结果．【详解】因为0AB AC ⋅=，0AB AD ⋅=，0AC AD ⋅=，所以()()220BC BD AC AB AD AB AC AD AC AB AB AD AB AB ⋅=--=⋅-⋅-⋅+=>，cos 0BC BD B BC BD⋅∴=>⋅，故B ∠是锐角，同理0CB CD ⋅>，0DC DB ⋅>，可得D ∠，C ∠都是锐角，故BCD 是锐角三角形，故选B ．【点睛】本题主要考查向量的数量积的运算以及向量运算的三角形法则，属于中档题．判断三角形的形状有两种基本的方法：①看三角形的角；②看三角形的边.5．D解析：D 【分析】设向量12PP 与13PP 的夹角为θ，计算出向量12PP 与13PP 的坐标，然后由12131213cos PP PP PP PP θ⋅=⋅计算出cos θ的值，可得出θ的值.【详解】设向量12PP 与13PP 的夹角为θ， ()()()123,1,01,1,22,2,2PP =--=-，()()()130,1,31,1,21,2,1PP =--=-，则12131213cos 0PP PP PP PP θ⋅==⋅，所以，90θ=，故选D.【点睛】本题考查空间向量的坐标运算，考查利用向量的坐标计算向量的夹角，考查计算能力，属于中等题.6．A解析：A 【分析】利用向量三角形法则与向量共线定理可得：DE BE BD →→→=-，13BE BC →→=，BC AC AB →→→=-，BD AD AB →→→=-，代入即可得出．【详解】解：已知AD a →→=，AB b →→=，AC c →→=，12BE EC →→=，利用向量三角形法则和向量共线定理得出：DE BE BD →→→=-，13BE BC →→=，BC AC AB →→→=-，BD AD AB →→→=-， ∴112()()333DE AC AB AD AB c a b →→→→→→→→=---=-+，即：2133DE a b c →→→→=-++. 故选：A. 【点睛】本题考查向量的三角形法则和向量基本定理的应用，考查了推理能力．7．D解析：D画出图形，作,AC CD BD CD ⊥⊥，则6,8,4AC BD CD ===，可得0,0AC CD BD CD ⋅=⋅=，沿x 轴将坐标平面折成60︒的二面角，故两异面直线,CA DB所成的角为60︒，结合已知，即可求得答案. 【详解】如图为折叠后的图形，其中作,AC CD BD CD ⊥⊥则6,8,4AC BD CD ===，∴0,0AC CD BD CD ⋅=⋅=沿x 轴将坐标平面折成60︒的二面角∴两异面直线,CA DB 所成的角为60︒．可得：.cos6024CA DB CA DB ︒⋅=⋅= 故由AB AC CD DB =++ 得22||||AB AC CD DB =++2222+22AC CD DB AC CD CD DB AC DB +++⋅⋅+⋅=2222+22AC CD DB AC CD CD DB CA DB +++⋅⋅-⋅=36166448=++-68=||17AB ∴=故选：D. 【点睛】本题考查了立体几何体中求线段长度，解题的关键是作图和掌握空间向量的距离求解公式，考查了分析能力和空间想象能力，属于中档题.8．C解析：C 【分析】作出图形，分别取AC 、11A C 的中点O 、1O ，连接OB 、1OO ，然后以点O 为坐标原点，OA 、OB 、1OO 所在直线分别为x 、y 、z 轴建立空间直角坐标系，设12AB BC CC ===，利用空间向量法可求出异面直线1AB 与1BC 所成角的余弦值.设12AB BC CC ===，分别取AC 、11A C 的中点O 、1O ，连接OB 、1OO ，在直三棱柱111ABC A B C -中，四边形11AAC C 为平行四边形，则11//AC A C 且11AC A C =，O 、1O 分别为AC 、11A C 的中点，所以，11//AO AO 且11AO A O =，所以，四边形11AAO O 为平行四边形，11//OO AA ∴，1AA ⊥底面ABC ，1OO ∴⊥底面ABC ，AB BC =，O 为AC 的中点，OB AC ∴⊥，以点O 为坐标原点，OA 、OB 、1OO 所在直线分别为x 、y 、z 轴建立空间直角坐标系O xyz -，由于120ABC ∠=，则()3,0,0A、()0,1,0B 、()10,1,2B 、()13,0,2C -，()13,1,2AB =-，()13,1,2BC =--， 1111113cos ,42222AB BC AB BC AB BC ⋅===⨯⋅，因此，异面直线1AB 与1BC 所成角的余弦值为34. 故选：C.【点睛】本题考查利用空间向量法求异面直线所成角的余弦值，考查计算能力，属于中等题.9．A解析：A 【分析】以A 为坐标原点，建立空间直角坐标系，写出点的坐标，分别求出直线的方向向量以及平面的法向量，通过向量法即可求得各个角度的余弦值，再结合余弦函数的单调性即可判断. 【详解】由题可知，直三棱柱111ABC A B C -的底面为锐角三角形，D 是棱BC 的中点，设三棱柱111ABC A B C -是棱长为2的正三棱柱，以A 为原点，在平面ABC 中，过A 作AC 的垂线为x 轴，AC 为y 轴，1AA 为z 轴，建立空间直角坐标系，则1(0,0,2)A ，1(3,1,2)B ，(0,2,0)C ，33,022D ⎛⎫⎪ ⎪⎝⎭，(0,0,0)A ， (0,2,0)AC =，131,222B D ⎛⎫=-- ⎪ ⎪⎝⎭，11(3,1,0)A B =，因为直线1B D 与直线AC 所成的角为1θ，10,2πθ⎛⎤∈ ⎥⎝⎦，111||cos ||||25θ⋅∴==⋅B D AC B D AC ，因为直线1B D 与平面111A B C 所成的角为2θ，20,2πθ⎡⎤∈⎢⎥⎣⎦，平面111A B C 的法向量()0,0,1n =，121||sin ||5∣θ⋅∴==⋅B D n B D n ，222cos 155θ⎛⎫∴=-= ⎪⎝⎭，设平面11A B D 的法向量(,,)m a b c =，则1113031202m A B a b m B D b c ⎧⋅=+=⎪⎨⋅=-+-=⎪⎩，取3a =33,3,2m ⎛⎫=--⎪⎝⎭，因为二面角111C A B D --的平面角为3θ，由图可知，其为锐角，33||2cos ||57m n m n θ⋅∴===⋅∣，231cos cos cos θθθ>>，由于cos y θ=在区间(0,)π上单调递减，故231θθθ<<，则2123,θθθθ<<. 故选：A . 【点睛】本题考查利用向量法研究空间中的线面角以及二面角，属综合基础题.10．B解析：B 【分析】在平行六面体中1111ABCD A B C D -中，利用空间向量的加法运算得到11BD BA BB BC =++，再根据模的求法，结合各条棱长均为1，共顶点A 的三条棱两两所成的角为60°，由()()2211BD BA BB BC =++222111222BA BB BC BA BB BC BA BB BC =+++⋅+⋅+⋅求解.【详解】在平行六面体中1111ABCD A B C D -中，因为各条棱长均为1，共顶点A 的三条棱两两所成的角为60°，所以111111cos120,11cos6022BA BB BA BC BC BB ⋅=⋅=⨯⨯=-⋅=⨯⨯=，所以11BD BA BB BC =++，所以()()2211BD BA BB BC =++，222111222BA BB BC BA BB BC BA BB BC =+++⋅+⋅+⋅，113+22+2222⎛⎫=⨯-⨯⨯= ⎪⎝⎭，所以12BD =故选：B 【点睛】本题主要考查空间向量的运算以及向量模的求法，还考查了运算求解的能力，属于中档题.11．B解析：B 【分析】根据空间向量基底的定义：任何三个不共面的向量都可构成空间向量的一组基底，逐一分析A ，B ，D 可判断这三个结论的正误；根据向量垂直的充要条件，及直角三角形的几何特征，可判断C 的真假. 【详解】对A ，空间的任何一个向量都可用其他三个不共面的向量表示，A 中忽略三个基底不共面的限制，故A 错误；对B ，若{},,a b c 为空间向量的一组基底，则,,a b c 三个向量互不共面；则,,a b b c c a +++，也互不共面，故{,,}a b b c c a +++可又构成空间向量的一组基底，故B 正确；对C ，0AB AC ABC ⋅=⇔∆的A ∠为直角ABC ⇒∆为直角三角形，但ABC ∆为直角三角形时，A ∠可能为锐角，此时0AB AC ⋅>，故C 错误；对D ，任何三个不共面的向量都可构成空间向量的一组基底，三个向量不共线时可能共面，故D 错误；故选：B ．【点睛】本题以命题的真假判断为载体考查空间向量的基底概念、向量垂直的充要条件，考查对概念的理解与应用，属基础题．12．D解析：D 【分析】首先利用坐标法，排除错误选项，然后对符合的选项验证存在,λμ使得AM AB AC λμ=+，由此得出正确选项.【详解】不妨设()()()()0,0,0,1,0,1,0,0,1,0,1,1O A B C .对于A 选项，()1,1,3OM OA OB OC =++=，由于M 的竖坐标31>，故M 不在平面ABC 上，故A 选项错误.对于B 选项，()231,3,6OM OA OB OC =++=，由于M 的竖坐标61>，故M 不在平面ABC 上，故B 选项错误. 对于C 选项，111113,,222222OM OA OB OC ⎛⎫=++= ⎪⎝⎭，由于M 的竖坐标312>，故M 不在平面ABC 上，故C 选项错误. 对于D 选项，11111,,133333OM OA OB OC ⎛⎫=++= ⎪⎝⎭，由于M 的竖坐标为1，故M 在平面ABC 上，也即,,,A B C M 四点共面.下面证明结论一定成立：由111333OM OA OB OC =++，得()()1133OM OA OB OA OC OA -=-+-，即1133AM AB AC =+，故存在13λμ==，使得AM AB AC λμ=+成立，也即,,,A B C M 四点共面.故选：D.【点睛】本小题主要考查空间四点共面的证明方法，考查空间向量的线性运算，考查数形结合的数学思想方法，考查化归与转化的数学思想方法，属于中档题.13．D解析：D 【分析】根据平面向量运算法则可知2i i AB AP AB AB BP ⋅=+⋅，由线面垂直性质可知0i AB BP ⋅=，从而得到21i AB AP AB ⋅==，进而得到结果. 【详解】()2i i i AB AP AB AB BP AB AB BP ⋅=⋅+=+⋅AB ⊥平面286BP P P i AB BP ∴⊥ 0i AB BP ∴⋅= 21i AB AP AB ∴⋅== 则()1,2,,8i AB AP i ⋅=⋅⋅⋅的不同值的个数为1个故选：D 【点睛】本题考查向量数量积的求解问题，关键是能够利用平面向量线性运算将所求向量数量积转化为已知模长的向量和有垂直关系向量的数量积的运算问题，考查了转化与化归的思想.二、填空题14．3【分析】以为原点以分别为轴轴轴正方向建立空间直角坐标系设根据则可得从而点在底面内的轨迹为一条线段从而可得答案【详解】以为原点以分别为轴轴轴正方向建立空间直角坐标系则设则由则即则当时设所以点在底面内解析：3 【分析】以D 为原点，以,,DA DC DD '分别为x 轴，y 轴，z 轴正方向建立空间直角坐标系，设(),,0P x y ，根据11B P D E ⊥，则110PB ED ⋅=，可得220x y +-=，从而点P 在底面ABCD 内的轨迹为一条线段AF ,从而可得答案. 【详解】以D 为原点，以,,DA DC DD '分别为x 轴，y 轴，z 轴正方向建立空间直角坐标系，则()()()112,2,2,1,2,0,0,0,2B E D ，设(),,0P x y ，则02,02x y ≤≤≤≤()12,2,2PB x y =--，()11,2,2ED =--由11B P D E ⊥，则110PB ED ⋅=，即()22240x y -+⨯-+=，则220x y +-= 当0x =时，1y =,设()0,1,0F所以点P 在底面ABCD 内的轨迹为一条线段AF , 所以()()2221224548B P x y y y =-+-+=-+，则01y ≤≤又二次函数2548t y y =-+的对称轴为25，当01y ≤≤时，当1y =时，1B P 有最大值3. 故答案为：3【点睛】关键点睛：本题考查根据垂直关系得出动点的轨迹从而求线段的长度的最值，解答的关键是建立坐标系，利用向量根据11B P D E ⊥，则110PB ED ⋅=，可得220x y +-=，从而点P 在底面ABCD 内的轨迹为一条线段AF ，可得01y ≤≤，从而可出答案，属于中档题.15．3【分析】利用向量的坐标运算求得求出根据空间向量模的公式列方程求解即可【详解】因为所以可得因为解得故答案为3解析：3 【分析】利用向量的坐标运算求得求出()4,1,a b λλλ+=-，根据空间向量模的公式列方程求解即可. 【详解】因为()()0,1,1,4,1,0,29a b a b λ=-=+=，所以()4,1,a b λλλ+=-，可得()2216129λλ+-+=，因为0λ>，解得3λ=，故答案为3.16．2【分析】求CD 的长即为由向量的加法可得利用向量的数量积运算即可得出答案【详解】∵AB 是棱l 上两点ACBD 分别在半平面αβ内AC ⊥lBD ⊥l 因为所以因为所以故答案为：2【点睛】本题主要考查空间向量的解析：2 【分析】求CD 的长即为CD ，由向量的加法可得CD CA AB BD =++，利用向量的数量积运算即可得出答案. 【详解】∵A 、B 是棱l 上两点，AC 、BD 分别在半平面α、β内，AC ⊥l ，BD ⊥l ，0,0∴⋅=⋅=CA AB BD AB ，,60︒<>=CA BD因为1AB AC BD ===，所以111cos602︒⋅=⨯⨯=CA BD ，因为CD CA AB BD =++，所以2()12=++==CD CA AB BD故答案为：2 【点睛】本题主要考查空间向量的加法，减法及几何意义和空间向量的数量积，考查了运算求解能力和转化的数学思想，属于一般题目.17．【分析】设则根据空间四点共面的条件又四点共面则即得出答案【详解】设则由为底面中心又因为四点共面所以且所以即即故答案为：【点睛】本题考查空间四点共面的条件的应用属于中档题解析：32020⎧⎫⎨⎬⎩⎭【分析】设,,PM x PN y PS z ===,则111333zPAPB PCPO PM PN PS xy =⨯⋅+⨯⋅+⨯⋅,根据空间四点共面的条件，又,,,S M N O 四点共面，则202020202020+1333zx y +=，即得出答案. 【详解】设,,PM x PN y PS z ===. 则PA PA PM x=⋅,PB PB PN y=⋅,PC PC PS z=⋅.由O 为底面ABC 中心, ()2132PO PA AO PA AB AC =+=+⨯+ ()()133PA PB PCPA PB PA PC PA ++⎡⎤=+-+-=⎣⎦ 111333z PA PB PCPM PN PS x y =⨯⋅+⨯⋅+⨯⋅ 333zPA PB PC PM PN PS x y=⋅+⋅+⋅ 又因为,,,S M N O 四点共面,所以+1333zPA PB PC xy+=且2020PA PB PC ===.所以202020202020+1333z x y +=，即1113+z 2020x y += 即11132020PS PM PN ++=. 故答案为：32020⎧⎫⎨⎬⎩⎭.【点睛】本题考查空间四点共面的条件的应用，属于中档题.18．【分析】先根据不共线三点用平面向量基底表示;再根据平面向量基本定理表示求和即得结果【详解】因为四点共面三点不共线所以因为因为是任意一点故可不共面所以故故答案为：1【点睛】本题考查用基底表示向量以及平解析：1【分析】先根据不共线三点A B C ，，，用平面向量基底AB AC ，表示PA ;再根据平面向量基本定理表示,,x y z ，求和即得结果. 【详解】因为,,,P A B C 四点共面，三点A B C ，，不共线，所以,,,m n R PA mAB nAC ∃∈=+()(),(1)OA OP m OB OA n OC OA OP m n OA mOB nOC -=-+-∴=++--因为OP xOA yOB zOC =++，因为O 是任意一点，故,,OA OB OC 可不共面，所以1,,x m n y m z n =++=-=-，故1x y z ++=. 故答案为：1 【点睛】本题考查用基底表示向量以及平面向量基本定理应用，考查基本分析求解能力，属基础题.19．【分析】根据向量投影的计算公式计算出在方向上的投影【详解】依题意在方向上的投影为【点睛】本小题主要考查向量在另一个向量上的投影的计算考查空间向量的数量积的坐标运算属于基础题解析：【分析】根据向量投影的计算公式，计算出a 在b 方向上的投影. 【详解】依题意a 在b 方向上的投影为()22222a b b⋅===-+-.【点睛】本小题主要考查向量在另一个向量上的投影的计算，考查空间向量的数量积的坐标运算，属于基础题.20．(00)【分析】设P(x00)求出·＝x(x －1)＋2＝(x －)2＋再利用二次函数求出函数的最小值和此时点P 的坐标【详解】设P(x00)则＝(x －1－20)＝(x －11)·＝x(x －1)＋2＝(x －解析：(12，0,0) 【分析】设P (x,0,0)，求出·＝x (x －1)＋2＝(x －)2＋，再利用二次函数求出函数的最小值和此时点P 的坐标. 【详解】设P (x,0,0)，则＝(x －1，－2,0)，＝(x ，－1,1)，·＝x (x －1)＋2＝(x －)2＋， ∴当x ＝时，·取最小值，此时点P 的坐标为(，0,0)．故答案为(12，0,0) 【点睛】(1)本题主要考查空间向量的坐标表示和数量积的计算，意在考查学生对这些知识的掌握水平和分析推理能力.(2) 111222121212(,,),(,,),a x y z b x y z a b x x y y z z ==⋅=++.21．5【解析】分析：设则的坐标利用求得即可得到即可求解的长度详解：设则所以因为所以解得所以所以点睛：(1)应用平面向量基本定理表示向量的实质是利用平行四边形法则或三角形法则进行向量的加减或数乘运算(2)解析：5 【解析】分析：设AD AC λ=，则,OD BD 的坐标，利用BD AC ⊥，求得45λ=-，即可得到 912(4,,)55BD =-，即可求解BD 的长度. 详解：设AD λAC =，则()()()OD OA λAC 1,1,2λ0,4,31,14λ,23λ=+=-+-=-+-，所以()BD OD OB 4,54λ,3λ=-=-+-，因为BD AC ⊥，所以()BD AC 0454λ9λ0⋅=+++=，解得4λ5=-，所以912BD 4,,55⎛⎫=- ⎪⎝⎭，所以()222912BD 4555⎛⎫⎛⎫=-++= ⎪ ⎪⎝⎭⎝⎭.点睛：(1)应用平面向量基本定理表示向量的实质是利用平行四边形法则或三角形法则进行向量的加、减或数乘运算.(2)用向量基本定理解决问题的一般思路是：先选择一组基底，并运用该基底将条件和结论表示成向量的形式，再通过向量的运算来解决.22．【分析】利用表示向量利用空间向量数量积计算出即可得解【详解】如下图所示：所以因此异面直线与所成角的余弦值是故答案为：【点睛】方法点睛：求异面直线所成角的余弦值方法如下：一是几何法：作—证—算；二是向解析：23【分析】利用AB 、AD 、1AA 表示向量1AB 、1BC ，利用空间向量数量积计算出11cos ,AB BC <>，即可得解.【详解】如下图所示：11AB AB AA =+，111BC BC BB AD AA =+=+，()222222111111122cos AB AB AA AB AA AB AA AB AA AB AA BAA =+=++⋅=++⋅∠22212222122=++⨯⨯=，123AB ∴= ()222222111111122cos BC AD AA AD AA AD AA AD AA AD AA DAA =+=++⋅=++⋅∠22212222122=++⨯⨯=，123BC ∴= ()()21111111AB BC AB AA AD AA AB AD AB AA AD AA AA ⋅=+⋅+=⋅+⋅+⋅+222111111cos cos 22282AB AA BAA AD AA DAA AA =⋅∠+⋅∠+=⨯⨯+=，所以，()111121182cos ,323AB BC AB BC AB BC ⋅<>===⋅，因此，异面直线1AB 与1BC 所成角的余弦值是23. 故答案为：23. 【点睛】方法点睛：求异面直线所成角的余弦值，方法如下：一是几何法：作—证—算；二是向量法：把角的求解转化为向量运算，应注意体会两种方法的特点，“转化”是求异面直线所成角的关键，一般地，异面直线的夹角的余弦值为cos ,m nm n m n ⋅<>=⋅.23．【分析】根据向量夹角为钝角可知且解不等式可求得结果【详解】由题意可知：且解得：且即本题正确结果：【点睛】本题考查向量夹角的相关问题的求解易错点是忽略夹角为的情况造成出现增根解析：1311,,222⎛⎫⎛⎫-+∞ ⎪ ⎪⎝⎭⎝⎭【分析】根据向量夹角为钝角，可知cos ,0a b <><且cos ,1a b <>≠-，解不等式可求得结果.【详解】由题意可知：132cos ,014k a b a b a b --⋅<>==<⋅且13cos ,1k a b --<>=≠- 解得：132k >-且12k ≠，即1311,,222k ⎛⎫⎛⎫∈-+∞ ⎪ ⎪⎝⎭⎝⎭本题正确结果：1311,,222⎛⎫⎛⎫-+∞ ⎪ ⎪⎝⎭⎝⎭【点睛】本题考查向量夹角的相关问题的求解，易错点是忽略夹角为π的情况，造成出现增根. 24．-4【分析】由题可知可得运用向量数量积的坐标运算即可求出【详解】解：根据题意得解得：故答案为：【点睛】本题考查空间向量垂直的数量积关系运用空间向量数量积的坐标运算考查计算能力解析：-4【分析】由题可知，a b c →→→⎛⎫+⊥ ⎪⎝⎭，可得0a b c →→→⎛⎫+= ⎪⎝⎭，运用向量数量积的坐标运算，即可求出x ．【详解】解：根据题意得， ()2,1,3a b x →→+=-+ a b c →→→⎛⎫+⊥ ⎪⎝⎭， ∴22(3)0a b c x x →→→⎛⎫+=--++= ⎪⎝⎭，解得：4x =-．故答案为：4-．【点睛】本题考查空间向量垂直的数量积关系，运用空间向量数量积的坐标运算，考查计算能力． 25．11【分析】由题意建立空间直角坐标系由二面角的定义得出从而写出的坐标由向量共线的性质设利用向量的加法得出由异面直线与所成角利用向量法得出的值从而得出的值【详解】取的中点G 与的交点为以O 为坐标原点分别解析：11【分析】由题意建立空间直角坐标系，由二面角的定义得出60OEV ∠=︒，从而写出,,,V E B A 的坐标，由向量共线的性质设(1)VF VA λλ=≠，利用向量的加法得出BF ，由异面直线BF 与VE 所成角，利用向量法得出λ的值，从而得出VF VA 的值. 【详解】取AB 的中点G ，AC 与DB 的交点为O ，以O 为坐标原点，分别以,,OG OE OV 为,,x y z 轴的正方向，建立空间直角坐标系O xyz -，设2AB =因为二面角V BC D --为60°，所以60OEV ∠=︒则()()()()0,0,3,0,1,0,1,1,0,1,1,0V E B A -()()()1,1,3,1,1,3,0,1,3VA VB VE =--=-=-.设(1)VF VA λλ=≠，则()1,1,33BF VF VB λλλ=-=----+从而22||cos ,cos 60||||24(1)(1)BF VE BF VE BF VE λλ⋅===︒-++ 整理得210110λλ+-=，解得1λ=(舍)，11λ=-故11VF VA=. 故答案为：11【点睛】本题主要考查了已知面面角，线线角求参数，属于中档题.26．-1【解析】【分析】由直线的一个方向向量为平面的一个法向量为得到由此能求出的值【详解】∵直线的一个方向向量为平面的一个法向量为∴解得故答案为：【点睛】本题考查实数值的求法考查直线的方向向量平面的法向解析：-1【解析】【分析】由直线l 的一个方向向量为m ，平面α的一个法向量为n ，//l α，得到 0m n ⋅=，由此能求出t 的值．【详解】∵直线l 的一个方向向量为()2,8,1m =--，平面α的一个法向量为1,,22n t ⎛⎫= ⎪⎝⎭，//l α，∴2420m n t ⋅=--+=，解得1t =-，故答案为：1-．【点睛】本题考查实数值的求法，考查直线的方向向量、平面的法向量等基础知识，考查运算与求解能力，考查化归与转化思想，是基础题．。

高中数学直线与平面的夹角知识点解析

3 达标检测
PART THREE
1.已知向量m，n分别是直线l的方向向量和平面α的法向量，若cos〈m，n〉
＝－ 12，则l与α所成的角为
√A.30°
B.60°
C.120°
D.150°
解析设l与α所成的角为θ，则 sin θ＝|cos〈m，n〉|＝21.
∴θ＝30°.
12345
2.正方体ABCD—A1B1C1D1中，直线BC1与平面A1BD所成的角的正弦值为
第三章 §3.2 直线的方向向量与直线的向量方程
3.2.3 直线与平面的夹角 3.2.4 二面角及其度量
学习目标
XUEXIMUBIAO
1.理解斜线和平面所成的角的定义，体会夹角定义的唯一性、合理性. 2.会求直线与平面的夹角θ. 3.掌握二面角的概念，二面角的平面角的定义，会找一些简单图形中的二面角的平面角. 4.掌握求二面角的基本方法、步骤.
思考辨析判断正误
SIKAOBIANXIPANDUANZHENGWU
1.直线与平面所成的角α与该直线的方向向量与平面的法向量的夹角β互余.( × ) 2.二面角的大小范围是 0，π2 .( × ) 3.二面角的大小等于其两个半平面的法向量的夹角的大小.( × )
2 题型探究
PART TWO
(2)求二面角E—BC—A的余弦值.
素养评析试题以一个面为正方形的五面体为载体，分层设计问题，由浅入深，给不同基础的考生提供了想象的空间和展示才华的平台.第(1)问侧重对立体几何中线面垂直、面面垂直等基础知识的考查，题目比较简单.求解第 (2)问的关键是充分运用直观想象，把握图形的结构特征，构建空间直角坐标系，并针对运算问题，合理选择运算方法，设计运算程序，解决问题.

高中数学立体几何线面角公式

高中数学立体几何线面角公式
一、高中立体几何线面角的概念
在高中立体几何中，线面角是指一条直线与一个平面所成的最小角。

这个概念帮助我们更好地理解空间中线与面的关系，以及如何计算它们之间的角度。

二、线面角公式及其推导
1.线面角公式
线面角公式如下：
α= β + γ
其中，α表示线面角，β 表示直线与平面内的直线所成的角度，γ 表示平面内的直线与平面所成的角度。

2.推导
根据空间几何中的知识，我们知道：
β+ γ = 180°
因此，
α= 180° - γ
这样，我们就得到了线面角的计算公式。

三、线面角公式的应用
线面角公式在解决立体几何问题时非常有用，例如：
1.判断直线与平面是否垂直：若线面角为90°，则直线与平面垂直。

2.计算线面角的大小：根据线面角公式，求得线面角α的值。

3.求解空间几何中的角度和：利用线面角公式，可以计算出空间中多个角度之和。

四、总结与练习
线面角公式是高中立体几何中的重要知识点，理解和掌握这个公式，能够帮助我们更好地解决实际问题。

通过下面的练习，巩固所学知识：
1.已知直线l与平面α所成角为30°，直线l与平面β所成角为45°，求直线l与平面α、β的夹角。

2.一平面与直线l垂直，直线l与另一平面β成60°，求平面α与β之间的夹角。

02 教学设计_直线与平面的夹角(第1课时)(2)

1.2.3 直线与平面的夹角(1)本节课选自《2019人教B 版高中数学选择性必修第一册》第一章《空间向量与立体几何》，本节主要学习直线与平面的夹角。

学生在学习了异面直线所成角的概念，对空间角的问题有了一定的经验，线面角的问题，依然按照将空间问题化为平面问题、将立体几何问题化为空间向量运算问题的基本思路展开。

为培养学生直观想象、数学抽象、逻辑推理、数学建模和数学运算的核心素养提供舞台。

1.教学重点：利用空间向量求直线与平面所成的角问题.2.教学难点：线面角的概念多媒体一、情境导学日常生活中，很多场景中都有直线与平面成一定角度的形象，例如如图1所示，握笔写字时，如果把笔抽象成直线，把纸抽象成平面，则直线与平面呈一定角度；如图2所示，地球仪的地轴（即旋转轴）与赤道所在的平面垂直，并且与水平桌面呈一定角度，那么怎样来刻画直线与平面所成的角呢？二、探究新知问题1：如图所示，设l是平面α的一条斜线，m是平面α内的任意一条直线. 能否将m与l所成的角定义为直线l与平面α所成的角？如果不能，该怎样规定直线l与平面α所成的角？1.直线与平面所成的角1.判断(1)直线与平面所成的角就是该直线与平面内的直线所成的角. ()(2)若直线与平面相交,则该直线与平面所成角的范围为0,π2 . ()答案:(1)×(2)×2.直线与平面的夹角的取值范围是什么?斜线与平面的夹角的取值范围是什么?],斜线与平面的夹提示:直线与平面的夹角的取值范围是[0,π2).角的取值范围是(0,π2问题2：如图所示，设AO是平面α的一条斜线段，O为斜足，A′为A在平面α内的射影，而OM是平面α内的一条射线，A′M ⊥OM记∠OAA′=θ1，∠A′OM=θ2, ∠A OM =θ（1）从直观上判断θ1与θ2的大小关系；（2）说明AM⊥OM是否成立，探究θ1，θ2，θ三者之间的等量关系2.最小角定理(1)线线角、线面角的关系式如图,设OA是平面α的一条斜线段,O为斜足,B为A在平面α内的射影,OM是平面α内的一条射线.θ是OA与OM所成的角,θ1是OA与OB所成的角,θ2是OB与OM所成的角.则有cos θ=cos θ1cos θ2.(2)最小角定理平面的斜线与平面所成的角,是斜线和这个平面内所有直线所成角中最小的角.3. 已知平面α内的角∠APB=60°,射线PC与P A,PB所成角均为135°,则PC与平面α所成角的余弦值是()A.-√63B.√63C.√33D.-√33解析:设PC与平面α所成的角为θ,由最小角定理知cos 45°=cos θcos 30°,∴cos θ=√63.答案:B4.将公式cos θ=cos θ1cos θ2中角的余弦值换成正弦值是否成立?提示:不成立.只有在特定的条件下能相等.也只能是数值上的相等,不具有等式的一般性结论.问题3：如果v是直线l的一个方向向量，n是平面α的一个法向量,设直线l与平面α所成角的大小为θ，通过作图讨论θ与<v,n >的关系3.用空间向量求直线与平面的夹角如果v 是直线l 的一个方向向量,n 是平面α的一个法向量,设直线l 与平面α所成角的大小为θ,则有 (1)θ=π2-<v ,n >,θ=<v ,n >-π2;(2)cos θ=sin <v ,n >,sin θ=|cos <v ,n >|.5.判断：直线与平面所成的角等于直线的方向向量与该平面法向量夹角的余角.( ) 答案:×例1 已知ABCD −A ′B ′C ′D ′是正方体，求B ′D ′与平面A ′BCD ′所成角的大小。

2019北师大版高中数学必修二§6.1.1.1空间中的线面角与面面角(补充)精品课件

（2）证明: 证明某平面角就是线面角。空间角转化为平面角
（3）计算: 通常在直角三角形中计算，或用公式计算。
O

： (4)解题技巧线线角找平行,线面角找射影
l
A
B
一．二面角的概念
1、半平面：平面内的一条直线，把这个平面分成两部分，每一部分都叫做半平面。
2、二面角：
从一条直线引出的两个半平面所组成的图形叫做二面角。这条直线叫做二面角的棱，这两个半平面叫做二面角的面。
O
B
A
①二面角的平面角与点（或垂直平面）的位置无任何关系，只与二面角的张角大小有关。
②二面角就是用它的平面角来度量的。一个二面角的平面角多大，我们就说这个二面角是多少度的二面角。
二面角的平面角必须满足：
1）角的顶点在棱上
二面
2）角的两边分别在两个面内
角 3）角的边都要垂直于二面角的棱
C1
A1
B1
A1C与平面A1D1DA所成角是：∠ 。
D C
A1C与平面A1B1C1D1所成角是：∠ 。
A
B
【例1】已知正方体的棱长为a，(1)求直线AB1和平面A1B1C1D1所成的角；
【例2】已知正方体的棱长为a，(2)求直线DB1和平面A1B1C1D1所成的角；
练习1:在正方体ABCD-A1B1C1D1中，E是 A1D1的中点，求EB和平面ABCD所成角的大小。
的平

面
A
A
角
l

O
B
O B
哪个对?怎么画才对?
10
1.定义法

二根据定义作出来 A
面角的
2.垂面法作与棱垂直的平面与

高中数学同步教学课件直线与平面的夹角

∴cos∠C1DC＝
2＝ 2
22，
2
又0°≤∠C1DC≤90°，∴∠C1DC＝45°.
1234
4.若平面 α 的一个法向量为 n＝(－ 3，1,1)，直线 l 的一个方向向量为 a
1 ＝( 3，1,1)，则 l 与 α 所成角的正弦值为__5___.
由题设l与α所成的角为θ，
可得 sin θ＝|cos〈n，a〉|＝||nn|·|aa||
反思感利用线面角定义，求线面角即求斜线与它在平面内的射影悟
所成的角，所以找该斜线在平面内的射影是关键，而要找
射影关键是找垂线，所以求线面角的关键是找平面的垂线.
跟踪训练 1 在正四棱柱ABCD－A1B1C1D1中，AA1＝2AB，则直线CD与
25 平面BCD1所成角的正弦值等于___5___.
＝
－
|－3＋1＋1| 32＋1＋1×
32＋1＋1＝15.
1234
五
课时对点练
基础巩固
1.已知向量m，n分别是直线l的方向向量和平面α的法向量，若cos〈m，n〉
＝－ 1 ，则l与α所成的角为 2
√A.30°
B.60°
C.120°
D.150°
设 l 与 α 所成的角为 θ，则 sin θ＝|cos〈m，n〉|＝12. 又0°≤θ≤90°，∴θ＝30°.
(5)代入公式sin
θ＝|cos〈a，n〉|＝
|a·n| |a||n|
；(6)回归几何问题.
例 3 如图，已知三棱锥P－ABC中，PA⊥平面ABC，
AB⊥AC，PA＝AC＝
1 2
AB，N为AB上一点，AB＝4AN，
M，S分别为PB，BC的中点.
(1)证明：CM⊥SN；

【高中数学】线面角的最小性

高二数学 空间角——线线角与线面角

高中数学新教材《8.6.2 线面角》公开课优秀课件(好用)

2023年高考全国乙卷数学(理)真题(解析版)

第1章 1.2.3 直线与平面的夹角-人教B版(2021)高中数学选择性必修第一册讲义

高中数学 空间中线线角,线面角,面面角成法原理与求法思路

横看成岭侧成峰 远近高低各不同——2020年高考数学浙江卷第19题线面角问题的多角度分析

浅谈线线角、线面角、面面角的定义方式及其中蕴含的数学基本思想

【高中数学】8.5考点3 线面角、二面角的求法

高中数学选择性必修第一册《第1章 空间向量与立体几何》单元测试卷(3)(含解析)

(压轴题)高中数学必修五第二章《解三角形》检测题(答案解析)(3)

点线面角高一的知识点

高中数学立体几何线面角公式

(常考题)人教版高中数学选修一第一单元《空间向量与立体几何》检测卷(包含答案解析)(1)

高中数学直线与平面的夹角知识点解析

高中数学立体几何线面角公式

02 教学设计_直线与平面的夹角(第1课时)(2)

2019北师大版高中数学必修二§6.1.1.1空间中的线面角与面面角(补充)精品课件

高中数学同步教学课件 直线与平面的夹角

高二数学空间角——线线角与线面角

高中数学空间中线线角,线面角,面面角成法原理与求法思路

横看成岭侧成峰远近高低各不同——2020年高考数学浙江卷第19题线面角问题的多角度分析

高中数学选择性必修第一册《第1章空间向量与立体几何》单元测试卷(3)(含解析)

高中数学同步教学课件直线与平面的夹角