中考数学专题训练--函数综合题

合集下载

2023年九年级数学下册中考数学专题训练：角度问题(二次函数综合)【含答案】

2023年九年级数学下册中考数学专题训练：角度问题（二次函数综合）一、解答题1．如图，直线y ＝x ﹣3与x 轴、y 轴分别交于B 、C 两点，抛物线y ＝x 2+bx +c 经过B 、C ，且与x 轴另一交点为49A ，连接AC ．(1)求抛物线的解析式；(2)点E 在抛物线上，连接EC ，当∠ECB +∠ACO ＝45°时，求点E 的横坐标；(3)点M 从点A 出发，沿线段AB 由A 向B 运动，同时点N 从点C 出发沿线段CA 由C 向A 运动，M ，N 的运动速度都是每秒1个单位长度，当N 点到达A 点时，M ，N 同时停止运动，问在坐标平面内是否存在点D ，使M ，N 运动过程中的某些时刻t ，以A ，D ，M ，N 为顶点的四边形为菱形？若存在，直接写出t 的值；若不存在，说明理由．2．已知抛物线y=ax ²+bx +c 经过点A （-6，0）、B （2，0）和C （0，3），点D 是该抛物线在第四象限上的一个点，连接 AD 、AC 、CD ，CD 交x 轴于E ．（1）求这个抛物线的解析式；（2）当S △DAE =S △ACD 时，求点 D 的坐标；14（3）在（2）的条件下，抛物线上是否存在点P ，使得△PAD 中的一个角等于2∠BAD ?若存在，直接写出点P 的坐标；若不存在，请说明理由．3．如图1，直线y =ax ²+4ax +c 与x 轴交于点A （-6，0）和点B ，与y 轴交于点C ，且OC =3OB(1)直接写出抛物线的解析式及直线AC 的解析式；(2)抛物线的顶点为D ，F 为抛物线在第四象限的一点，直线AF 解析式为，求∠CAF -∠CAD 的度数．123y x =--(3)如图2，若点P 是抛物线上的一个动点，作PQ ⊥y 轴垂足为点Q ，直线PQ 交直线AC 于E ，再过点E 作x 轴的垂线垂足为R ，线段QR 最短时，点P 的坐标及QR 的最短长度．4．已知顶点为A (2，一1)的抛物线与y 轴交于点B ，与x 轴交于C 、D 两点，点C 坐标(1，O )；(1)求这条抛物线的表达式；(2)连接AB 、BD 、DA ，求cos ∠ABD 的大小；(3)点P 在x 轴正半轴上位于点D 的右侧，如果∠APB =45°，求点P 的坐标．5．如图1，抛物线与x 轴交于A ，B 两点（点A 在点B 的左侧），与y 轴交于点C ，过点C()2102y x bx c c =++<作轴，与抛物线交于另一点D ，直线与相交于点M ．CD x ∥BC AD(1)已知点C 的坐标是，点B 的坐标是，求此抛物线的解析式；()04-，()40，(2)若，求证：；112b c =+AD BC ⊥(3)如图2，设第（1）题中抛物线的对称轴与x 轴交于点G ，点P 是抛物线上在对称轴右侧部分的一点，点P 的横坐标为t ，点Q 是直线上一点，是否存在这样的点P ，使得是以点G 为直角顶点的直角三角形，且满足BC PGQ △，若存在，请直接写出t 的值；若不存在，请说明理由．GQP OCA ∠=∠6．抛物线与x 轴相交于A ，B 两点（点A 在点B 的左侧），与y 轴的正半轴相交于点C ，点D 为223y ax ax a =--抛物线的顶点，点O 为坐标原点．(1)若是直角三角形，求抛物线的函数表达式；ABC (2)王亮同学经过探究认为：“若，则”，王亮的说法是否正确？若你认为正确，请加以证明：a<02∠=∠DCB ABC 若是错误的，说明理由；(3)若第一象限的点E 在抛物线上，四边形面积的最大值为，求a 的值．ABEC 2547．如图，抛物线经过，两点，与x 轴交于另一点A ，点D 是抛物线的顶点．22y ax ax c =++(1,0)B (0,3)C(1)求抛物线的解析式及点D 的坐标；(2)如图1，点E 在抛物线上，连接并延长交x 轴于点F ，连接，若是以为底的等腰三角形，求DE BD BDF BD 点E 坐标．(3)如图2，连接、，在抛物线上是否存在点M ，使，若存在，求出M 点的坐标；若不存AC BC ACM BCO ∠=∠在，请说明理由．8．抛物线的顶点坐标为，与x 轴交于点两点，与y 轴交于点C ，点M 是抛物线上的动2y ax bx c =++(1,4),(3,0)A B 点．(1)求这条抛物线的函数表达式；(2)如图1，若点M 在直线BC 上方抛物线上，连接AM 交BC 于点E ，求的最大值及此时点M 的坐标；MEAE (3)如图2，已知点，是否存在点M ，使得？若存在，求出点M 的坐标；若不存在，请说明理(0,1)Q 1tan 2MBQ ∠=由．9．如图，一次函数y ＝x﹣2的图象与x 轴交于点A ，与y 轴交于点B ，点D 的坐标为（﹣1，0），二次函数12y ＝ax 2+bx+c （a≠0）的图象经过A ，B ，D 三点．（1）求二次函数的解析式；（2）如图1，已知点G （1，m ）在抛物线上，作射线AG ，点H 为线段AB 上一点，过点H 作HE ⊥y 轴于点E ，过点H 作HF ⊥AG 于点F ，过点H 作HM ∥y 轴交AG 于点P ，交抛物线于点M ，当HE•HF 的值最大时，求HM 的长；（3）在（2）的条件下，连接BM ，若点N 为抛物线上一点，且满足∠BMN ＝∠BAO ，求点N 的坐标．10．已知二次函数．()20y ax bx c a =++>（1）若，，求方程的根的判别式的值；12a =2b c ==-20ax bx c ++=（2）如图所示，该二次函数的图像与x 轴交于点、，且，与y 轴的负半轴交于点C ，()1,0A x ()2,0B x 120x x <<点D 在线段OC 上，连接AC 、BD ，满足，．ACO ABD ∠=∠1b c x a -+=①求证：；AOC DOB ≅ ②连接BC ，过点D 作于点E ，点在y 轴的负半轴上，连接AF ，且，DE BC ⊥()120,F x x -ACO CAF CBD ∠=∠+∠求的值．1cx 11．如图，在平面直角坐标系中，已知抛物线的图象与x 轴交于点A ，B 两点，点A 坐标为，243y ax x c =-+()3,0点B 坐标为，与y 轴交于点C ．()1,0-(1)求抛物线的函数解析式；(2)若将直线绕点A 顺时针旋转，交抛物线于一点P ，交y 轴于点D ，使，求直线函数解析AC BAP BAC ∠=∠AP 式；(3)在（2）条件下若将线段平移（点A ，C 的对应点M ，N ），若点M 落在抛物线上且点N 落在直线上，求AC AP 点M 的坐标．12．在平面直角坐标系中，抛物线与轴交于点和点（点在点的左侧），与轴交212y x bx c =-++x (2,0)A -B A B y 于点．(0,3)C （1）求抛物线的表达式；的坐标，并直接写出此时直线的表达式．D DC （3）在（2）的条件下，点为轴右侧抛物线上一点，过点作直线的垂线，垂足为，若，E y E DC P ECP DAB ∠=∠请直接写出点的坐标．E 13．已知函数y ＝（n 为常数）．22()1()222x nx n x n n n x x x n ⎧-++≥⎪⎨++<⎪⎩(1)当n ＝5时，①点P （4，b ）在此函数图象上，求b 的值．②求此函数的最大值．(2)当n ＜0时，作直线x ＝n 与x 轴交于点P ，与该函数图象交于点Q ，若∠POQ ＝45°，求n 的值．23(3)若此函数图象上有3个点到直线y ＝2n 的距离等于2，求n 的取值范围．14．如图，已知抛物线y ＝ax 2+4（a ≠0）与x 轴交于点A 和点B （2，0），与y 轴交于点C ，点D 是抛物线在第一象限的点．（1）当△ABD 的面积为4时，①求点D 的坐标；②联结OD ，点M 是抛物线上的点，且∠MDO ＝∠BOD ，求点M 的坐标；（2）直线BD 、AD 分别与y 轴交于点E 、F ，那么OE +OF 的值是否变化，请说明理由．15．如图，已知，抛物线经过A 、B 两点，交y 轴于点C ．点P 是第一象限内抛物线(2,0),(3,0)A B -24y ax bx =++上的一点，点P 的横坐标为m ．过点P 作轴，垂足为点M ，PM 交BC 于点Q ．过点P 作，垂足PM x ⊥PN BC ⊥为点N ．(1)求抛物线的函数表达式；(2)请用含m 的代数式表示线段PN 的长，并求出当m 为何值时PN 有最大值，最大值是多少？(3)连接PC ，在第一象限的抛物线上是否存在点P ，使得？若存在，请直接写出m 的值；若290BCO PCN ∠+∠=︒不存在，请说明理由．16．如图1，在平面直角坐标系中．抛物线与x 轴交于和，与y 轴交于点C ，连接22y ax bx =++(4,0)A -(1,0)B ．,AC BC(1)求该抛物线的解析式；(2)如图2，点M 为直线上方的抛物线上任意一点，过点M 作y 轴的平行线，交于点N ，过点M 作x 轴的AC AC 平行线，交直线于点Q ，求周长的最大值；AC MNQ △(3)点P 为抛物线上的一动点，且，请直接写出满足条件的点P 的坐标．45ACP BAC ∠=︒-∠17．抛物线经过A （-1，0）、C （0，-3）两点，与x 轴交于另一点B ．23y ax bx a =+-（1）求此抛物线的解析式；（2）已知点D 在第四象限的抛物线上，求点D 关于直线BC 对称的点D’的坐标;(m,-m-1)（3）在（2）的条件下，连结BD ，问在x 轴上是否存在点P ，使，若存在，请求出P 点的坐标；PCB CBD ∠=∠若不存在，请说明理由.参考答案：1．(1)y ＝x 2﹣x ﹣34913(2)或1543916(3)存在，t ＝或或754415845222．（1）；（2）；（3）P 点坐标为综上所述：2134y x x =--+(21)D -+-1P，、、、(617-）2P (-5.00.，175)()3 3.47, 3.48P -4(220P -)5P ，．(14.22,33.30)--6(9.74,30.47)P -3．(1)抛物线的解析式为y =-x ²-2x +6，直线BC 的解析式为y =x +612(2)45°(3)点P 的坐标为（，3）或（，3），QR 的最短长度为4．（1）y =x 2﹣4x +3；（23）P （3+，0）5．(1)2142y x x =--(2)11(3)t =t =6．(1)2=y x (2)王亮的说法正确(3)23a =-7．(1)抛物线的解析式为：，223y x x =--+(1,4)D -(2)720(,39E -(3)存在，或()4,5M --57(,)24M -8．(1)；223y x x =-++(2)；；916315,24⎛⎫ ⎪⎝⎭(3)存在；或（0，3）829,749⎛⎫-- ⎪⎝⎭9．（1）y ＝x 2﹣x﹣2；（2）2；（3）(1，﹣3)或(﹣，)12325317910．（1）（2）①1；②=2=8∆1c x 11．(1)224233y x x =--(2)223y x =-+(3)或或()3,8-104,3⎛⎫ ⎪⎝⎭102,3⎛⎫- ⎪⎝⎭12．（1）；（2）D (2，2)，；（3点E 的坐标为(1，3)或211322y x x =-++132y x =-+(，)113179-13．(1)①b =；②此函数的最大值为；92458(2)n 的值是-或-；15232(3)或423n -<<-463n <<-6n =+14．（1）①；②；（2）不变化，值为8)2D ()2M 15．(1)222433y x x =-++(2)，当时，有最大值22655PN m m =-+32m =910答案第3页，共3页(3)存在，74m =16．(1)213222y x x =--+(2)6+(3)或()5,3--2375,749⎛⎫- ⎪⎝⎭17．（1）2y x 2x 3=--（2）（0，-1）（3）（1,0）（9,0）答案第4页，共1页。

中考数学专题五函数应用问题综合题(解析版全国适用)

函数实际问题综合题一、一次函数+二次函数应用问题例题（2020·湖北随州·中考真题）2020年新冠肺炎疫情期间.部分药店趁机将口罩涨价.经调查发现某药店某月（按30天计）前5天的某型号口罩销售价格p （元/只）和销量q （只）与第x 天的关系如下表：第x 天1 2 3 4 5 销售价格p （元/只）2 3 4 5 6 销量q （只）7075808590店从第6天起将该型号口罩的价格调整为1元/只．据统计.该药店从第6天起销量q （只）与第x 天的关系为2280200q x x =-+-（630x ≤≤.且x 为整数）.已知该型号口罩的进货价格为0.5元/只．（1）直接写出．．．．该药店该月前5天的销售价格p 与x 和销量q 与x 之间的函数关系式. （2）求该药店该月销售该型号口罩获得的利润W （元）与x 的函数关系式.并判断第几天的利润最大.（3）物价部门为了进一步加强市场整顿.对此药店在这个月销售该型号口罩的过程中获得的正常利润之外的非法所得部分处以m 倍的罚款.若罚款金额不低于2000元.则m 的取值范围为______．【答案】（1）1p x =+.15x ≤≤且x 为整数.565q x =+.15x ≤≤且x 为整数.（2）22135655,152240100,630x x x x W x x x x ⎧++⎪=⎨⎪-+-⎩且为整数且为整数.第5天时利润最大.（3）85m ．【解析】【分析】（1）根据表格数据.p 是x 的一次函数.q 是x 的一次函数.分别求出解析式即可. （2）根据题意.求出利润w 与x 的关系式.再结合二次函数的性质.即可求出利润的最大值．（3）先求出前5天多赚的利润.然后列出不等式.即可求出m 的取值范围．【详解】（1）观察表格发现p 是x 的一次函数.q 是x 的一次函数. 设p=k 1x+b 1.将x=1.p=2.x=2.p=3分别代入得：1111232k b k b =+⎧⎨=+⎩. 解得：1111k b =⎧⎨=⎩. 所以1p x =+.经验证p=x+1符合题意. 所以1p x =+.15x ≤≤且x 为整数. 设q=k 2x+b 2.将x=1.q=70.x=2.q=75分别代入得：222270752k b k b =+⎧⎨=+⎩. 解得：22565k b =⎧⎨=⎩. 所以565q x =+.经验证565q x =+符合题意. 所以565q x =+.15x ≤≤且x 为整数. （2）当15x ≤≤且x 为整数时.(10.5)(565)W x x =+-+213565522x x =++. 当630x ≤≤且x 为整数时.()2(10.5)280200W x x =--+-240100x x =-+-.即有22135655,152240100,630x x x x W x x x x ⎧++⎪=⎨⎪-+-⎩且为整数且为整数. 当15x ≤≤且x 为整数时.售价.销量均随x 的增大而增大. 故当5x =时.495W =最大（元）当630x ≤≤且x 为整数时.2240100(20)300W x x x =-+-=--+ 故当20x时.300W =最大（元）.由495300>.可知第5天时利润最大．（3）根据题意.前5天的销售数量为：7075808590400q =++++=（只）. ∴前5天多赚的利润为：(270375480585690)140016504001250W =⨯+⨯+⨯+⨯+⨯-⨯=-=（元）.∴12502000m ≥. ∴85m. ∴m 的取值范围为85m ．【点睛】此题考查二次函数的性质及其应用.一次函数的应用.不等式的应用.也考查了二次函数的基本性质.另外将实际问题转化为求函数最值问题.从而来解决实际问题．练习题1．（2021·山东青岛·中考真题）科研人员为了研究弹射器的某项性能.利用无人机测量小钢球竖直向上运动的相关数据．无人机上升到离地面30米处开始保持匀速竖直上升.此时.在地面用弹射器（高度不计）竖直向上弹射一个小钢球（忽路空气阻力）.在1秒时.它们距离地面都是35米.在6秒时.它们距离地面的高度也相同．其中无人机离地面高度1y （米）与小钢球运动时间x （秒）之间的函数关系如图所示.小钢球离地面高度2y （米）与它的运动时间x （秒）之间的函数关系如图中抛物线所示．（1）直接写出1y 与x 之间的函数关系式. （2）求出2y 与x 之间的函数关系式.（3）小钢球弹射1秒后直至落地时.小钢球和无人机的高度差最大是多少米？【答案】（1）1530y x =+.（2）22540y x x =-+.（3）70米【解析】【分析】（1）先设出一次函数的解析式.再用待定系数法求函数解析式即可. （2）用待定系数法求函数解析式即可.（3）当1＜x ≤6时小钢球在无人机上方.因此求y 2-y 1.当6＜x ≤8时.无人机在小钢球的上方.因此求y 1-y 2.然后进行比较判断即可．【详解】解：（1）设y 1与x 之间的函数关系式为y 1=kx +b'. ∵函数图象过点（0.30）和（1.35）.则'35'30k b b +=⎧⎨=⎩. 解得5'30k b =⎧⎨=⎩. ∴y 1与x 之间的函数关系式为1530y x =+．（2）∵6x =时.1563060y =⨯+=. ∵2y 的图象是过原点的抛物线.∴设22y ax bx =+.∴点()1,35.()6,60在抛物线22y ax bx =+上．∴3536660a b a b +=⎧⎨+=⎩.即35610a b a b +=⎧⎨+=⎩. 解得540a b =-⎧⎨=⎩. ∴22540y x x =-+．答：2y 与x 的函数关系式为22540y x x =-+．（3）设小钢球和无人机的高度差为y 米. 由25400x x -+=得10x =或28x =. ①16x <≤时.21y y y =-2540530x x x =-+-- 253530x x =-+-27125524x ⎛⎫=--+⎪⎝⎭. ∵50a =-<.∴抛物线开口向下. 又∵16x <≤. ∴当72x =时.y 的最大值为1254. ②68x <≤时.12y y y =-2530540x x x =++- 253530x x =-+27125524x ⎛⎫=--⎪⎝⎭. ∵50a =>.∴拋物线开口向上. 又∵对称轴是直线72x =. ∴当72x >时.y 随x 的增大而增大. ∵68x <≤.∴当8x =时.y 的最大值为70． ∵125704<. ∴高度差的最大值为70米．答：高度差的最大值为70米．【点睛】本题考查了二次函数以及一次函数的应用.关键是根据根据实际情况判断无人机和小钢球的高度差．2．（2021·辽宁盘锦·中考真题）某工厂生产并销售A .B 两种型号车床共14台.生产并销售1台A 型车床可以获利10万元.如果生产并销售不超过4台B 型车床.则每台B 型车床可以获利17万元.如果超出4台B 型车床.则每超出1台.每台B 型车床获利将均减少1万元．设生产并销售B 型车床x 台．（1）当4x >时.完成以下两个问题： ①请补全下面的表格：A 型B 型车床数量/台 ________ x每台车床获利/万元10________70万元.问：生产并销售B 型车床多少台？（2）当0＜x ≤14时.设生产并销售A .B 两种型号车床获得的总利润为W 万元.如何分配生产并销售A .B 两种车床的数量.使获得的总利润W 最大？并求出最大利润．【答案】（1）①14x -.21x -.②10台.（2）分配产销A 型车床9台、B 型车床5台.或产销A 型车床8台、B 型车床6台.此时可获得总利润最大值170万元【解析】【分析】（1）①由题意可知.生产并销售B 型车床x 台时.生产A 型车床（14-x ）台.当4x >时.每台就要比17万元少（4x -）万元.所以每台获利17(4)x --.也就是（21x -）万元. ②根据题意可得根据题意：(21)10(14)70x x x ---=然后解方程即可. （2）当0≤x ≤4时.W ＝10(14)x -＋17x ＝7140x +.当4＜x ≤14时. W ＝2( 5.5)170.25x --+.分别求出两个范围内的最大值即可得到答案. 【详解】解：（1）当4x >时.每台就要比17万元少（4x -）万元所以每台获利17(4)x --.也就是（21x -）万元 ①补全表格如下面：A 型B 型车床数量/台 14x -x每台车床获利/万元1021x -由B 型可获得利润为(21)x x -万元.根据题意：(21)10(14)70x x x ---=. 2312100x x -+=.(21)(10)0x x --=.∵0≤x ≤14. ∴10x =.即应产销B 型车床10台. （2）当0≤x ≤4时. 当0≤x ≤4 A 型 B 型车床数量/台 14x -x每台车床获利/万元 1017 利润10(14)x -17x该函数值随着x 的增大而增大.当x 取最大值4时.W 最大1＝168（万元）. 当4＜x ≤14时. 当4＜x ≤14 A 型 B 型车床数量/台 14x -x每台车床获利/万元1021x -利润10(14)x - (21)x x -则＝＋＝211140x x -++＝( 5.5)170.25x --+.当5x =或6x =时（均满足条件4＜x ≤14）.W 达最大值W 最大2＝170（万元）. ∵W 最大2＞ W 最大1.∴应分配产销A 型车床9台、B 型车床5台.或产销A 型车床8台、B 型车床6台.此时可获得总利润最大值170万元．【点睛】本题主要考查了一元二次方程的实际应用.一次函数和二次函数的实际应用.解题的关键在于能够根据题意列出合适的方程或函数关系式求解.3．（2021·辽宁锦州·中考真题）某公司计划购进一批原料加工销售.已知该原料的进价为6.2万元/t .加工过程中原料的质量有20%的损耗.加工费m （万元）与原料的质量x （t ）之间的关系为m ＝50＋0.2x .销售价y （万元/t ）与原料的质量x （t ）之间的关系如图所示．（1）求y 与x 之间的函数关系式.（2）设销售收入为P （万元）.求P 与x 之间的函数关系式.（3）原料的质量x 为多少吨时.所获销售利润最大.最大销售利润是多少万元？（销售利润＝销售收入﹣总支出）．【答案】（1）1y 204x =-+.（2）21165P x x =-+.（3）原料的质量为24吨时.所获销售利润最大.最大销售利润是3265万元【解析】【分析】（1）利用待定系数法求函数关系式.（2）根据销售收入＝销售价×销售量列出函数关系式.（3）设销售总利润为W .根据销售利润＝销售收入﹣原料成本﹣加工费列出函数关系式.然后根据二次函数的性质分析其最值．【详解】解：（1）设y 与x 之间的函数关系式为y kx b +＝. 将（20.15）.（30.12.5）代入. 可得：20153012.5k b k b +=⎧⎨+=⎩. 解得：1420k b ⎧=-⎪⎨⎪=⎩. ∴y 与x 之间的函数关系式为1y 204x =-+.（2）设销售收入为P （万元）.∴()2411120%2016545P xy x x x x ⎛⎫=-=⨯-+=-+ ⎪⎝⎭.∴P 与x 之间的函数关系式为21165P x x =-+.（3）设销售总利润为W .∴()216.216 6.2500.25W P x m x x x x =--=-+--+.整理.可得：()22148132650245555W x x x =-+-=--+. ∵﹣15＜0.∴当24x ＝时.W 有最大值为3265. ∴原料的质量为24吨时.所获销售利润最大.最大销售利润是3265万元．【点睛】本题考查了二次函数的实际应用.涉及了数形结合的数学思想.熟练掌握待定系数法求解析式是解决本题的关键．4．（2021·湖北荆门·中考真题）某公司电商平台.在2021年五一长假期间.举行了商品打折促销活动.经市场调查发现.某种商品的周销售量y （件）是关于售价x （元/件）的一次函数.下表仅列出了该商品的售价x .周销售量y .周销售利润W （元）的三组对应值数据． x 40 70 90 y1809030W 3600 4500 2100.（2）若该商品进价a （元/件）.售价x 为多少时.周销售利润W 最大？并求出此时的最大利润.（3）因疫情期间.该商品进价提高了m （元/件）（0m >）.公司为回馈消费者.规定该商品售价x 不得超过55（元/件）.且该商品在今后的销售中.周销售量与售价仍满足（1）中的函数关系.若周销售最大利润是4050元.求m 的值．【答案】（1）3300y x =-+.（2）售价60元时.周销售利润最大为4800元.（3）5m = 【解析】【分析】（1）①依题意设y=kx+b.解方程组即可得到结论.（2）根据题意得(3300)()W x x a =-+-.再由表格数据求出20a =.得到2(3300)(20)3(60)4800W x x x =-+-=--+.根据二次函数的顶点式.求出最值即可.（3）根据题意得3(100)(20)(55)W x x m x =----.由于对称轴是直线60602mx =+>.根据二次函数的性质即可得到结论．【详解】解：（1）设y kx b =+.由题意有401807090k b k b +=⎧⎨+=⎩.解得3300k b =-⎧⎨=⎩. 所以y 关于x 的函数解析式为3300y x =-+. （2）由（1）(3300)()W x x a =-+-.又由表可得： 3600(340300)(40)a =-⨯+-.20a ∴=.22(3300)(20)336060003(60)4800W x x x x x ∴=-+-=-+-=--+．所以售价60x =时.周销售利润W 最大.最大利润为4800. （3）由题意3(100)(20)(55)W x x m x =----. 其对称轴60602mx =+>.055x ∴<时上述函数单调递增. 所以只有55x =时周销售利润最大.40503(55100)(5520)m ∴=----． 5m ∴=．【点睛】本题考查了二次函数在实际生活中的应用.重点是掌握求最值的问题．注意：数学应用题来源于实践.用于实践.在当今社会市场经济的环境下.应掌握一些有关商品价格和利润的知识.总利润等于总收入减去总成本.然后再利用二次函数求最值．5．（2021·辽宁营口·中考真题）某商家正在热销一种商品.其成本为30元/件.在销售过程中发现随着售价增加.销售量在减少．商家决定当售价为60元/件时.改变销售策略.此时售价每增加1元需支付由此产生的额外费用150元．该商品销售量y （件）与售价x （元/件）满足如图所示的函数关系.（其中4070x ≤≤.且x 为整数）（1）直接写出y 与x 的函数关系式.（2）当售价为多少时.商家所获利润最大.最大利润是多少？【答案】（1）10700406052006070x x y x x -+≤≤⎧=⎨-<≤⎩.（2）当售价为70元时.商家所获利润最大.最大利润是4500元【解析】【分析】（1）利用待定系数法分段求解函数解析式即可.（2）分别求出当4060x ≤≤时与当6070x <≤时的销售利润解析式.利用二次函数的性质即可求解．【详解】解：（1）当4060x ≤≤时.设11y k x b =+. 将()40,300和()60,100代入.可得11113004010060k b k b =+⎧⎨=+⎩.解得1110700k b =-⎧⎨=⎩.即10700y x =-+. 当6070x <≤时.设22y k x b =+. 将()70,150和()60,100代入.可得22221507010060k b k b =+⎧⎨=+⎩.解得225200k b =⎧⎨=-⎩.即5200y x =-. ∴10700406052006070x x y x x -+≤≤⎧=⎨-<≤⎩. （2）当4060x ≤≤时.销售利润()()22301010002100010504000w y x x x x =⋅-=-+-=--+.当50x =时.销售利润有最大值.为4000元. 当6070x <≤时.销售利润()()()2230150605500150005502500w y x x x x x =⋅---=-+=-+.该二次函数开口向上.对称轴为50x =.当6070x <≤时位于对称轴右侧. 当70x =时.销售利润有最大值.为4500元. ∵45004000>.∴当售价为70元时.商家所获利润最大.最大利润是4500元．【点睛】本题考查一次函数的应用、二次函数的性质.根据图象列出解析式是解题的关键． 6．（2021·湖南郴州·中考真题）某商店从厂家以每件2元的价格购进一批商品.在市场试销中发现.此商品的月销售量y （单位：万件）与销售单价x （单位：元）之间有如下表所示关系：x… 4.0 5.0 5.5 6.5 7.5 … y…8.06.05.03.01.0…（1）根据表中的数据.在图中描出实数对(,)x y 所对应的点.并画出y 关于x 的函数图象. （2）根据画出的函数图象.求出y 关于x 的函数表达式. （3）设经营此商品的月销售利润为P （单位：万元）． ①写出P 关于x 的函数表达式.②该商店计划从这批商品获得的月销售利润为10万元（不计其它成本）.若物价局限定商品的销售单价不得超过．．．．进价的200%.则此时的销售单价应定为多少元？【答案】（1）图象见详解.（2）216y x =-+.（3）①222032P x x =-+-.②销售单价应定为3元．【解析】【分析】（1）由题意可直接进行作图.（2）由图象可得y 与x 满足一次函数的关系.所以设其关系式为y kx b =+.然后任意代入表格中的两组数据进行求解即可.（3）①由题意易得()2P x y =-.然后由（2）可进行求解.②由①及题意可得22203210x x -+-=.然后求解.进而根据销售单价不得超过进价的200％可求解．【详解】解：（1）y 关于x 的函数图象如图所示：（2）由（1）可设y 与x 的函数关系式为y kx b =+.则由表格可把()()4,8,5,6代入得：4856k b k b +=⎧⎨+=⎩.解得：216k b =-⎧⎨=⎩. ∴y 与x 的函数关系式为216y x =-+. （3）①由（2）及题意可得：()()()22221622032P x y x x x x =-=--+=-+-.∴P 关于x 的函数表达式为222032P x x =-+-. ②由题意得：2200x ≤⨯％.即4x ≤. ∴22203210x x -+-=. 解得：123,7x x ==.∴3x=.答：此时的销售单价应定为3元．【点睛】本题主要考查二次函数与一次函数的应用.熟练掌握二次函数与一次函数的应用是解题的关键．7．（2021·四川南充·中考真题）超市购进某种苹果.如果进价增加2元/千克要用300元.如果进价减少2元/千克.同样数量的苹果只用200元．（1）求苹果的进价．（2）如果购进这种苹果不超过100千克.就按原价购进.如果购进苹果超过100千克.超过部分购进价格减少2元/千克．写出购进苹果的支出y（元）与购进数量x（千克）之间的函数关系式．（3）超市一天购进苹果数量不超过300千克.且购进苹果当天全部销售完．据统计.销售单价z（元/千克）与一天销售数量x（千克）的关系为112100z x=-+．在（2）的条件下.要使超市销售苹果利润w（元）最大.求一天购进苹果数量．（利润＝销售收入-购进支出）【答案】（1）苹果的进价为10元/千克.（2）10(100)8200(100)x xyx x≤⎧=⎨+>⎩.（3）要使超市销售苹果利润w最大.一天购进苹果数量为200千克．【解析】【分析】（1）设苹果的进价为x元/千克.根据等量关系.列出分式方程.即可求解.（2）分两种情况：当x≤100时. 当x＞100时.分别列出函数解析式.即可.（3）分两种情况：若x≤100时.若x＞100时.分别求出w关于x的函数解析式.根据二次函数的性质.即可求解．【详解】解：（1）设苹果的进价为x元/千克.由题意得：30020022x x=+-.解得：x=10.经检验：x=10是方程的解.且符合题意.答：苹果的进价为10元/千克.（2）当x≤100时.y=10x.当x＞100时.y=10×100+（10-2）×（x-100）=8x+200.∴10(100)8200(100)x x y x x ≤⎧=⎨+>⎩. （3）若x ≤100时.w =zx -y =21112102100100x x x x x ⎛⎫-+-=-+ ⎪⎝⎭=()21100100100x --+. ∴当x =100时.w 最大=100. 若x ＞100时.w =zx -y =()2111282004200100100x x x x x ⎛⎫-+-+=-+- ⎪⎝⎭=()21200200100x --+. ∴当x =200时.w 最大=200.综上所述：当x =200时.超市销售苹果利润w 最大.答：要使超市销售苹果利润w 最大.一天购进苹果数量为200千克．【点睛】本题主要考查分式方程、一次函数、二次函数的实际应用.根据数量关系.列出函数解析式和分式方程.是解题的关键．8．（2021·湖北十堰·中考真题）某商贸公司购进某种商品的成本为20元/kg .经过市场调研发现.这种商品在未来40天的销售单价y （元/kg ）与时间x （天）之间的函数关系式为：0.2530(120)35(2040)x x y x +≤≤⎧=⎨<≤⎩且x 为整数.且日销量()kg m 与时间x （天）之间的变化规律符合一次函数关系.如下表：时间x （天） 1 3 6 10 …日销量()kg m 142 138 132 124 …（1）m 与x 的函数关系为___________.（2）哪一天的销售利润最大？最大日销售利润是多少？（3）在实际销售的前20天中.公司决定每销售1kg 商品就捐赠n 元利润（4n <）给当地福利院.后发现：在前20天中.每天扣除捐赠后的日销售利润随时间x 的增大而增大.求n 的取值范围．【答案】（1）2144m x =-+.（2）第16天销售利润最大.最大为1568元.（3）1.75＜n ＜4 【解析】【分析】（1）设m kx b =+.将()1142,.()3138,代入.利用待定系数法即可求解. （2）分别写出当120x ≤≤时与当2040x <≤时的销售利润表达式.利用二次函数和一次函数的性质即可求解.（3）写出在前20天中.每天扣除捐赠后的日销售利润表达式.根据二次函数的性质可得对称轴16220n +≤.求解即可．【详解】解：（1）设m kx b =+.将()1142,.()3138,代入可得： 1421383k b k b =+⎧⎨=+⎩.解得2144k b =-⎧⎨=⎩. ∴2144m x =-+. （2）当120x ≤≤时.销售利润()()()212021440.2530201615682W my m x x x =-=-++-=--+. 当16x =时.销售利润最大为1568元. 当2040x <≤时.销售利润20302160W my m x =-=-+. 当21x =时.销售利润最大为1530元.综上所述.第16天销售利润最大.最大为1568元. （3）在前20天中.每天扣除捐赠后的日销售利润为：()()()21'200.2510214416214401442W my m nm x n x x n x n =--=+--+=-+++-.对称轴为直线x ═16+2n .∵在前20天中.每天扣除捐赠后的日销售利润随时间x 的增大而增大.且x 只能取整数.故只要第20天的利润高于第19天. 即对称轴要大于19.5 ∴16+2n ＞19.5. 求得n ＞1.75.又∵n ＜4. ∴n 的取值范围是：1.75＜n ＜4. 答：n 的取值范围是1.75＜n ＜4．【点睛】本题考查二次函数与一次函数的实际应用.掌握二次函数与一次函数的性质是解题的关键．9．（2021·江苏扬州·中考真题）甲、乙两汽车出租公司均有50辆汽车对外出租.下面是两公司经理的一段对话：甲公司经理：如果我公司每辆汽车月租费3000元.那么50辆汽车可以全部租出．如果每辆汽车的月租费每增加50元.那么将少租出1辆汽车．另外.公司为每辆租出的汽车支付月维护费200元．乙公司经理：我公司每辆汽车月租费3500元.无论是否租出汽车.公司均需一次性支付月维护费共计1850元．．．②月利润=月租车费-月维护费.③两公司月利润差=月利润较高公司的利润-月利润较低公司的利润．在两公司租出的汽车数量相等的条件下.根据上述信息.解决下列问题：（1）当每个公司租出的汽车为10辆时.甲公司的月利润是_______元.当每个公司租出的汽车为_______辆时.两公司的月利润相等. （2）求两公司月利润差的最大值.（3）甲公司热心公益事业.每租出1辆汽车捐出a 元()0a >给慈善机构.如果捐款后甲公司剩余的月利润仍高于乙公司月利润.且当两公司租出的汽车均为17辆时.甲公司剩余的月利润与乙公司月利润之差最大.求a 的取值范围．【答案】（1）48000.37.（2）33150元.（3）50150a << 【解析】【分析】（1）用甲公司未租出的汽车数量算出每辆车的租金.再乘以10.减去维护费用可得甲公司的月利润.设每个公司租出的汽车为x 辆.根据月利润相等得到方程.解之即可得到结果. （2）设两公司的月利润分别为y 甲.y 乙.月利润差为y .同（1）可得y 甲和y 乙的表达式.再分甲公司的利润大于乙公司和甲公司的利润小于乙公司两种情况.列出y 关于x 的表达式.根据二次函数的性质.结合x 的范围求出最值.再比较即可.（3）根据题意得到利润差为()25018001850y x a x =-+-+.得到对称轴.再根据两公司租出的汽车均为17辆.结合x 为整数可得关于a 的不等式180016.517.5100a-<<.即可求出a 的范围．【详解】解：（1）()50105030001020010-⨯+⨯-⨯⎡⎤⎣⎦=48000元.当每个公司租出的汽车为10辆时.甲公司的月利润是48000元. 设每个公司租出的汽车为x 辆.由题意可得：()5050300020035001850x x x x -⨯+-=-⎡⎤⎣⎦. 解得：x =37或x =-1（舍）.∴当每个公司租出的汽车为37辆时.两公司的月利润相等.（2）设两公司的月利润分别为y 甲.y 乙.月利润差为y . 则y 甲=()50503000200x x x -⨯+-⎡⎤⎣⎦. y 乙=35001850x -.当甲公司的利润大于乙公司时.0＜x ＜37. y =y 甲-y 乙=()()5050300020035001850x x x x -⨯+---⎡⎤⎣⎦ =25018001850x x -++. 当x =1800502--⨯=18时.利润差最大.且为18050元. 当乙公司的利润大于甲公司时.37＜x ≤50. y =y 乙-y 甲=()3500185050503000200x x x x ---⨯++⎡⎤⎣⎦ =25018001850x x --. ∵对称轴为直线x =1800502--⨯=18. 当x =50时.利润差最大.且为33150元. 综上：两公司月利润差的最大值为33150元.（3）∵捐款后甲公司剩余的月利润仍高于乙公司月利润.则利润差为25018001850y x x ax =-++-=()25018001850x a x -+-+.对称轴为直线x =1800100a-. ∵x 只能取整数.且当两公司租出的汽车均为17辆时.月利润之差最大. ∴180016.517.5100a-<<. 解得：50150a <<．【点睛】本题考查了二次函数的实际应用.二次函数的图像和性质.解题时要读懂题意.列出二次函数关系式.尤其（3）中要根据x 为整数得到a 的不等式．10．（2018·湖北荆门·中考真题）随着龙虾节的火热举办.某龙虾养殖大户为了发挥技术优势.一次性收购了10000kg 小龙虾.计划养殖一段时间后再出售．已知每天养殖龙虾的成本相同.放养10天的总成本为166000.放养30天的总成本为178000元．设这批小龙虾放养t 天后的质量为akg.销售单价为y 元/kg.根据往年的行情预测.a 与t 的函数关系为a=()()1000002010080002050t t t ⎧≤≤⎪⎨+<≤⎪⎩.y 与t 的函数关系如图所示．（1）设每天的养殖成本为m 元.收购成本为n 元.求m 与n 的值. （2）求y 与t 的函数关系式.（3）如果将这批小龙虾放养t 天后一次性出售所得利润为W 元．问该龙虾养殖大户将这批小龙虾放养多少天后一次性出售所得利润最大？最大利润是多少？（总成本=放养总费用+收购成本.利润=销售总额﹣总成本）【答案】（1）m=600.n=160000.（2）()()316020513220505t t y t t ⎧+≤≤⎪⎪=⎨⎪-+<≤⎪⎩.（3）该龙虾养殖大户将这批小龙虾放养25天后一次性出售所得利润最大.最大利润是108500元. 【解析】【详解】【分析】（1）根据题意列出方程组.求出方程组的解得到m 与n 的值即可. （2）根据图象.分类讨论利用待定系数法求出y 与P 的解析式即可.（3）根据W=ya ﹣mt ﹣n.表示出W 与t 的函数解析式.利用一次函数与二次函数的性质求出所求即可．【详解】（1）依题意得1016600030178000m n m n +=⎧⎨+=⎩ . 解得：600160000m n =⎧⎨=⎩. （2）当0≤t≤20时.设y=k 1t+b 1.由图象得：111162028b k b =⎧⎨+=⎩. 解得：113516k b ⎧=⎪⎨⎪=⎩ ∴y=35t+16.当20＜t≤50时.设y=k 2t+b 2.由图象得：222220285022k b k b +=⎧⎨+=⎩.解得：221532k b ⎧=-⎪⎨⎪=⎩. ∴y=﹣15t+32.综上.()()3160t 205y 13220t 505t t ⎧+≤≤⎪⎪=⎨⎪-+<≤⎪⎩. （3）W=ya ﹣mt ﹣n.当0≤t≤20时.W=10000（35t+16）﹣600t ﹣160000=5400t.∵5400＞0.∴当t=20时.W 最大=5400×20=108000.当20＜t≤50时.W=（﹣15t+32）（100t+8000）﹣600t ﹣160000=﹣20t 2+1000t+96000=﹣20（t ﹣25）2+108500. ∵﹣20＜0.抛物线开口向下. ∴当t=25.W 最大=108500. ∵108500＞108000.∴当t=25时.W 取得最大值.该最大值为108500元．【点睛】本题考查了二次函数的应用.具体考查了待定系数法确定函数解析式.利用二次函数的性质确定最值.熟练掌握二次函数的性质是解本题的关键．二、一次函数+反比例函数应用问题例题（2021·广东深圳·中考真题）探究：是否存在一个新矩形.使其周长和面积为原矩形的2倍、12倍、k 倍．（1）若该矩形为正方形.是否存在一个正方形.使其周长和面积都为边长为2的正方形的2倍？_______（填“存在”或“不存在”）．（2）继续探究.是否存在一个矩形.使其周长和面积都为长为3.宽为2的矩形的2倍？同学们有以下思路：设新矩形长和宽为x 、y .则依题意10x y +=.12xy =.联立1012x y xy +=⎧⎨=⎩得210120x x -+=.再探究根的情况：根据此方法.请你探究是否存在一个矩形.使其周长和面积都为原矩形的12倍.如图也可用反比例函数与一次函数证明1l ：10y x =-+.2l ：12y x=.那么.①是否存在一个新矩形为原矩形周长和面积的2倍？_______． ②请探究是否有一新矩形周长和面积为原矩形的12.若存在.用图像表达. ③请直接写出当结论成立时k 的取值范围：．【答案】（1）不存在.（2）①存在.②不存在.见解析.③2425k 【解析】【分析】（1）直接求出边长为2的正方形周长与面积.再求出周长扩大2倍即边长扩大2倍时正方形的面积.比较是否也为2倍即可.（2）①依题意根据一元二次方程根的情况判断即可.②设新矩形长和宽为x 、y .则依题意52x y +=.3xy =.联立.求出关于x 、y 的一元二次方程.判断根的情况.③设新矩形长和宽为x 和y .则由题意5x y k +=.6xy k =.同样列出一元二次方程.利用根的判别式进行求解即可．【详解】（1）边长为2的正方形.周长为8.面积为4.当周长为其2倍时.边长即为4.面积为16.即为原来的4倍.故不存在. （2）①存在.∵210120x x -+=的判别式0∆>.方程有两组正数解.故存在. 从图像来看.1l ：10y x =-+.2l ：12y x=在第一象限有两个交点.故存在. ②设新矩形长和宽为x 、y .则依题意52x y +=.3xy =.联立523x y xy ⎧+=⎪⎨⎪=⎩得25302x x -+=. 因为∆<0.此方程无解.故这样的新矩形不存在.从图像来看.1l ：52y x =-+.2l ：3y x =在第一象限无交点.故不存在.③2425k. 设新矩形长和宽为x 和y .则由题意5x y k +=.6xy k =. 联立56x y k xy k +=⎧⎨=⎩得2560x kx k -+=.225240k k ∆=-.故2425k ．【点睛】本题考查了一元二次方程的应用.根的判别式．需要认真阅读理解题意.根据题干过程模仿解题．练习题1．（2021·浙江台州·中考真题）电子体重科读数直观又便于携带.为人们带来了方便．某综合实践活动小组设计了简易电子体重秤：制作一个装有踏板（踏板质量忽略不计）的可变电阻R 1. R 1与踏板上人的质量m 之间的函数关系式为R 1＝km ＋b （其中k .b 为常数.0≤m ≤120）.其图象如图1所示.图2的电路中.电源电压恒为8伏.定值电阻R 0的阻值为30欧.接通开关.人站上踏板.电压表显示的读数为U 0 .该读数可以换算为人的质量m . 温馨提示：①导体两端的电压U .导体的电阻R .通过导体的电流I .满足关系式I ＝UR. ②串联电路中电流处处相等.各电阻两端的电压之和等于总电压．（1）求k .b 的值.（2）求R 1关于U 0的函数解析式. （3）用含U 0的代数式表示m .（4）若电压表量程为0~6伏.为保护电压表.请确定该电子体重秤可称的最大质量．【答案】（1）2402b k =⎧⎨=-⎩.（2）1024030R U =-.I （3）0120135m U =-.（4）该电子体重秤可称的最大质量为115千克．【解析】【分析】（1）根据待定系数法.即可求解.（2）根据“串联电路中电流处处相等.各电阻两端的电压之和等于总电压”.列出等式.进而即可求解.（3）由R 1＝12-m ＋240.1024030R U =-.即可得到答案. （4）把06U =时.代入0480540m U =-.进而即可得到答案．【详解】解：（1）把（0.240）.（120.0）代入R 1＝km ＋b .得2400120bk b =⎧⎨=+⎩.解得：2402b k =⎧⎨=-⎩. （2）∵001830U U R -=. ∴1024030R U =-. （3）由（1）可知：2402b k =⎧⎨=-⎩. ∴R 1＝2-m ＋240. 又∵1024030R U =-. ∴024030U -=2-m ＋240.即：0120135m U =-. （4）∵电压表量程为0~6伏. ∴当06U =时.1201351156m =-= 答：该电子体重秤可称的最大质量为115千克．【点睛】本题主要考查一次函数与反比例函数的实际应用.熟练掌握待定系数法.是解题的关键． 2．（2021·安徽·中考真题）已知正比例函数(0)y kx k =≠与反比例函数6y x=的图象都经过点A （m .2）．（1）求k .m 的值.（2）在图中画出正比例函数y kx =的图象.并根据图象.写出正比例函数值大于反比例函数值时x 的取值范围．【答案】（1）,k m 的值分别是23和3.（2）30x -<<或3x > 【解析】【分析】（1）把点A （m .2）代入6y x=求得m 的值.从而得点A 的坐标.再代入(0)y kx k =≠求得k 值即可.（2）在坐标系中画出y kx =的图象.根据正比例函数(0)y kx k =≠的图象与反比例函数6y x=图象的两个交点坐标关于原点对称.求得另一个交点的坐标.观察图象即可解答．【详解】（1）将(,2)A m 代入6y x=得62m =.3m ∴=.(3,2)A ∴.将(3,2)A 代入y kx =得23k =.23k ∴=. ,k m ∴的值分别是23和3．（2）正比例函数23y x =的图象如图所示.∵正比例函数(0)y kx k =≠与反比例函数6y x=的图象都经过点A （3.2）. ∴正比例函数(0)y kx k =≠与反比例函数6y x=的图象的另一个交点坐标为（-3.-2）. 由图可知：正比例函数值大于反比例函数值时x 的取值范围为30x -<<或3x >．【点睛】本题是正比例函数与反比例函数的综合题.利用数形结合思想是解决问题的关键． 3．（2020·广西柳州·中考真题）如图.平行于y 轴的直尺（部分）与反比例函数my x=（x ＞0）的图象交于A 、C 两点.与x 轴交于B 、D 两点.连接AC .点A 、B 对应直尺上的刻度分别为5、2.直尺的宽度BD ＝2.OB ＝2．设直线AC 的解析式为y ＝kx +b ．（1）请结合图象.直接写出： ①点A 的坐标是 . ②不等式mkx b x+>的解集是 . （2）求直线AC 的解析式．。

中考数学专题专练--二次函数与一次函数的综合

中考数学专题专练--二次函数与一次函数的综合1．如图，二次函数y＝- 34x2+94x+3的图象与x轴交于点A、B（B在A右侧），与y轴交于点C．（1）求点A、B、C的坐标；（2）求△ABC的面积．2．如图，已知抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=﹣1，且抛物线经过A （1，0），C（0，3）两点，与x轴相交于点B．（1）求抛物线的解析式；（2）在抛物线的对称轴x=﹣1上找一点M，使点M到点A的距离与到点C的距离之和最小，求出点M的坐标；（3）设点P为抛物线的对称轴x=﹣1上的一个动点，求使△BPC为直角三角形的点P的坐标．3．如图，抛物线y=x2 +bx+c与x轴交于A（﹣1，0），B（2，0）两点．（1）求该抛物线的解析式；（2）设（1）中的抛物线上有一个动点P，当点P在该抛物线上滑动到什么位置时，满足S△P AB=6，并求出此时P点的坐标．4．如图，抛物线y1=a(x-1)2+4与x轴交于A(-1，0)。

（1）求该抛物线所表示的二次函数的表达式；（2）一次函数y2=x+1的图象与抛物线相交于A，C两点，过点C作CB垂直于x 轴于点B，求△ABC的面积。

5．如图，已知直线y=-3x+3与x轴交于点A，与y轴交于点C，抛物线y=ax2+bx+c经过点A和点C，对称轴为直线I：x=-1，该抛物线与x轴的另一个交点为B。

（1）求此抛物线的解析式；（2）点P在抛物线上且位于第二象限，求△PBC的面积最大值及点P的坐标。

（3）点M在此抛物线上，点N在对称轴上，以B、C、M、N为顶点的四边形能否为平行四边形？若能，写出所有满足要求的点M 的坐标；若不能，请说明理由。

6．如图，直线y=-x+2与抛物线y=ax 2交于A ，B 两点，点A 坐标为(1，1)。

（1）水抛物线的函数表达式：（2）连结OA ，OB ，求△AOB 的面积。

7．已知抛物线y=ax 2+bx+c 的顶点P(1，-1)，且过Q(5，3)。

2023年中考九年级数学高频考点专题训练--二次函数与一元二次方程

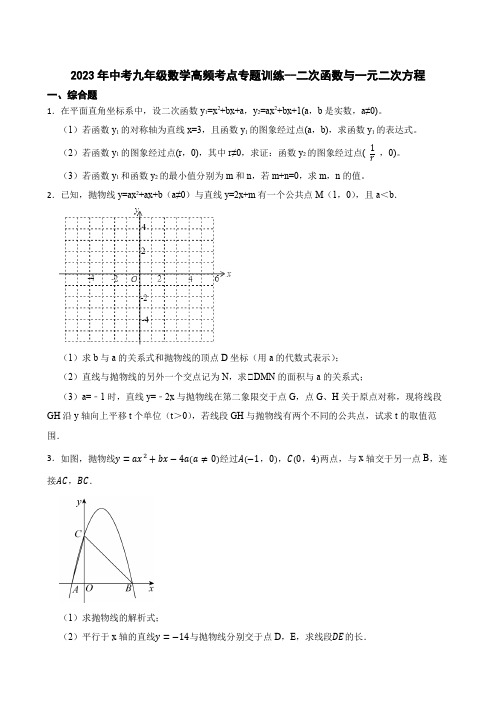
2023年中考九年级数学高频考点专题训练--二次函数与一元二次方程一、综合题1．在平面直角坐标系中，设二次函数y1=x2+bx+a，y2=ax2+bx+1(a，b是实数，a≠0)。

（1）若函数y1的对称轴为直线x=3，且函数y1的图象经过点(a，b)，求函数y1的表达式。

（2）若函数y1的图象经过点(r，0)，其中r≠0，求证：函数y2的图象经过点( 1r，0)。

（3）若函数y1和函数y2的最小值分别为m和n，若m+n=0，求m，n的值。

2．已知，抛物线y=ax2+ax+b（a≠0）与直线y=2x+m有一个公共点M（1，0），且a＜b．（1）求b与a的关系式和抛物线的顶点D坐标（用a的代数式表示）；（2）直线与抛物线的另外一个交点记为N，求△DMN的面积与a的关系式；（3）a=﹣1时，直线y=﹣2x与抛物线在第二象限交于点G，点G、H关于原点对称，现将线段GH沿y轴向上平移t个单位（t＞0），若线段GH与抛物线有两个不同的公共点，试求t的取值范围．3．如图，抛物线y=ax2+bx−4a(a≠0)经过A(−1，0)，C(0，4)两点，与x轴交于另一点B，连接AC，BC．（1）求抛物线的解析式；（2）平行于x轴的直线y=−14与抛物线分别交于点D，E，求线段DE的长．4．如图1，抛物线C1：y＝ax2+bx+1的顶点坐标为D（1，0）且经过点（0，1），将抛物线C1向右平移1个单位，向下平移1个单位得到抛物线C2，直线y＝x+c，经过点D交y轴于点A，交抛物线C2于点B，抛物线C2的顶点为P．（1）求抛物线C1的解析式；（2）如图2，连结AP，过点B作BC△AP交AP的延长线于C，设点Q为抛物线上点P至点B 之间的一动点，连结BQ并延长交AC于点F，①当点Q运动到什么位置时，S△PBD×S△BCF＝8？②连接PQ并延长交BC于点E，试证明：FC（AC+EC）为定值．5．十一黄金周期间，某商场销售一种成本为每件60元的服装，规定销售期间销售单价不低于成本单价，且获利不得高于45%，经试销发现，销售量y（件）与销售单价x（元）符合一次函数y=-x+120（1）销售单价定为多少元时，该商场获得的利润恰为500元？（2）设该商场获得利润为W元，试写出利润W与销售单价x之间的关系式；销售单价定为多少元时，商场可获得最大利润，最大利润是多少？6．如图，抛物线y＝x2+bx+c经过点A（－1，0），B（3，0）.请解下列问题：（1）求抛物线的解析式；（2）点E（2，m）在抛物线上，抛物线的对称轴与x轴交于点H，点F是AE中点，连接FH，求线段FH的长.7．已知二次函数y=x2−2mx+2m−1．（1）求证：二次函数的图象与x轴总有交点；（2）若二次函数的图象与x轴的一个交点为原点，求方程x2−2mx+2m−1=0的解．8．某运动器材批发市场销售一种篮球，每个篮球进价为50元，规定每个篮球的售价不低于进价，经市场调查，每月的销售量y（个）与每个篮球的售价x（元）满足一次函数关系，部分数据如下表：（1）求y与x之间的函数关系式；（不需求自变量x的取值范围）（2）该批发市场每月想从这种篮球销售中获利8000元，又想尽量多给客户实惠，应如何给这种篮球定价？（3）物价部门规定，该篮球的每个利润不允许高于进货价的50%，设销售这种篮球每月的总利润为w（元），那么销售单价定为多少元可获得最大利润？最大利润是多少？9．如图，已知：P（-1，0），Q（0，-2）.（1）求直线PQ的函数解析式；（2）如果M（0，m）是线段OQ上一动点，抛物线y=ax2+bx+c(a≠0)经过点M和点P，①求抛物线y=ax2+bx+c与x轴另一交点N的坐标（用含a，m的代数式表示）；②若PN= 12是，抛物线y=ax2+bx+c有最大值m+1，求此时a的值；③若抛物线y=ax2+bx+c与直线PQ始终都有两个公共点，求a的取值范围.10．已知二次函数y=ax2+bx+3(a≠0)的最小值为1，图象上一点的坐标为(2，3)。

初三中考数学函数综合题含答案

初三中考数学函数综合题含答案一、单选题1．函数32x y x +=-中，自变量x 的取值范围是（） A ．3x >-B ．3x ≥-且2x ≠C ．2x ≠D ．3x >-且2x ≠2．如图，函数y ax b =+和y kx =的图象交于点P ，则根据图象可得，关于x 、y 的二元一次方程组0ax y b kx y -+=⎧⎨-=⎩的解是（）A ．42x y =-⎧⎨=-⎩B ．42x y =⎧⎨=⎩C ．24x y =-⎧⎨=-⎩D ．24x y =⎧⎨=⎩3．若反比例函数1k y x-=，当0x >时，y 随x 的增大而减小，则k 的取值范围是（） A ．1k >B ．1k <C ．1k >-D ．1k <-4．将抛物线()2321y x =-+先向右平移2个单位长度，再向下平移2个单位长度，平移后所得的抛物线解析式是（） A ．()2341y x =-- B ．()2343y x =-+ C ．233y x =+D ．231y x =-5．抛物线213y x =的开口方向、对称轴分别是（）A ．向上，x 轴B ．向上，y 轴C ．向下，x 轴D ．向下，y 轴 6．二次函数y ＝x 2＋6x ＋4的对称轴是（） A ．x ＝6B ．x ＝﹣6C ．x ＝﹣3D ．x ＝47．下列y 关于x 的函数中，一次函数为（） A ．()2y a x b =-+B ．()211y k x =++C ．2y x=D ．221y x =+8．一次函数y kx b =+的图象与直线23y x =+平行，且与y 轴的交点为(0,2)，则一次函数的表达式为（） A ．23y x =+B ．22y x =+C ．23y x =-+D ．22y x =-+9．已知抛物线y ＝ax 2＋bx ＋c （a ≠0）的顶点为（2，4），有以下结论：①当a >0时，b 2－4ac >0；②当a >0时，ax 2＋bx ＋c≥4；③若点（-2，m ）,（3，n ）在抛物线上，则m <n ；④若关于x 的一元二次方程ax 2＋bx ＋c ＝0的一根为－1，则另一根为5．其中正确的是（） A ．①②B ．①④C ．②③D ．②④10．已知点A （x 1，y 1），B （x 2，y 2），C （x 3，y 3）都在反比例函数y kx=（k ＜0）的图象上，且x 1＜x 2＜0＜x 3，则y 1，y 2，y 3的大小关系是（） A ．y 2＞y 1＞y 3 B ．y 3＞y 2＞y 1 C ．y 1＞y 2＞y 3 D ．y 3＞y 1＞y 211．已知y =kx +b ，当x =2时，y =-2；当x =3时，y =0．则（）A ．k =2，b =-6B ．k =-6，b =2C ．k =-2，b =6D ．k =-2，b =-612．抛物线y ＝﹣2（x ﹣3）2﹣4的顶点坐标是（）A ．（﹣3，4）B ．（﹣3，﹣4）C ．（3，﹣4）D ．（3，4）13．将一次函数23y x =-的图象沿y 轴向上平移3个单位长度后，所得图象的函数表达式为（） A ．2y x = B ．26y x =- C ．53y x =- D ．3y x =-- 14．二次函数22(3)1y x =-+-的顶点坐标是（）A ．(31)， B ．(13)-， C ．(3,1)-D ．(3,1)--15．已知A （﹣11,3y ），B （﹣21,2y ），C （1，y 3）是一次函数y ＝b ﹣3x 的图象上三点，则y 1、y 2、y 3的大小关系为（） A ．y 3＜y 1＜y 2B ．y 3＜y 2＜y 1C ．y 1＜y 2＜y 3D ．y 2＜y 1＜y 3二、填空题16．一次函数(27)2y k x =-+中，y 随x 的增大而减小，则k 的取值范围是___________． 17．将直线213y x =-+向上平移3个单位后所得直线解析式为_______．18．已知点(2,)A m 在一次函数53y x =+的图象上，则m 的值是__．19．已知一次函数(1)2y m x m =-+-的图象经过平面直角坐标系中的第一、三、四象限，那么m 的取值范围是______．20．若函数y ＝（m ﹣2）x +|m |﹣2是正比例函数，则m ＝_____．三、解答题21．如图，抛物线y ＝ax 2+3x +c 经过A (﹣1，0)，B (4，0)两点，并且与y 轴交于点C ．(1)求此抛物线的解析式； (2)直线BC 的解析式为；(3)若点M 是第一象限的抛物线上的点，且横坐标为t ，过点M 作x 轴的垂线交BC 于点N ，设MN 的长为h ，求h 与t 之间的函数关系式及h 的最大值；(4)在x 轴的负半轴上是否存在点P ，使以B ，C ，P 三点为顶点的三角形为等腰三角形？如果存在；如果不存在，说明理由．22．如图，抛物线y ＝ax 2+bx +3与x 轴交于A （﹣1，0）、B （3，0）两点，抛物线的对称轴l 与x 轴交于M 点．(1)求抛物线的函数解析式；(2)设点P 是直线l 上的一个动点，当PA +PC 的值最小时，求PA +PC 长；(3)已知点N （0，﹣1），在y 轴上是否存在点Q ，使以M 、N 、Q 为顶点的三角形与△BCM 相似？若存在；若不存在，请说明理由．23．已知二次函数222y x x m =-+-的图象与x 轴有交点，求非负整数m 的值． 24．已知抛物线y ＝12x 2﹣x ﹣32与x 轴交于点A ，点B （点A 在点B 左侧）． (1)求点A ，点B 的坐标；(2)用配方法求该抛物线的顶点C 的坐标，判断△ABC 的形状，并说明理由；(3)在抛物线的对称轴上是否存在点P ，使以点O 、点C 、点P 为顶点的三角形构成等腰三角形？若存在，请直接写出点P 的坐标；若不存在，请说明理由． 25．已知抛物线222y x mx m =--．(1)求证：对任意实数m ，抛物线与x 轴总有交点． (2)若该抛物线与x 轴交于1,0A ，求m 的值．【参考答案】一、单选题 1．B 2．A3．A 4．A 5．B 6．C 7．B 8．B 9．D 10．A 11．A 12．C 13．A 14．D 15．A 二、填空题16．72k < 17．243y x =-+18．1319．2m >20．-2三、解答题21．(1)234y x x =-++ (2)4y x =-+(3)h 与t 之间的函数关系式为：()2404h t t t =-+<<，h 的最大值为4(4)在x 轴的负半轴上存在点()4,0P -或()4P -，使以B ，C ，P 三点为顶点的三角形为等腰三角形，理由见解析【解析】【分析】（1）把A (﹣1，0)，B (4，0) 代入抛物线解析式，即可求解；（2）根据抛物线解析式求出点C 的坐标，再利用待定系数法，即可求解；（3）根据题意可得点()2,34M t t t -++，点(),4N t t -+，从而得到24MN t t =-+，再根据二次函数的性质，即可求解；（4）分三种情况：当PC =BC 时，当PB =BC 时，当PC =PB 时，即可求解． (1)解：∵抛物线y ＝ax 2+3x +c 经过A (﹣1，0)，B (4，0)两点，∴3016340a c a c -+=⎧⎨+⨯+=⎩，解得：14a c =-⎧⎨=⎩， ∴抛物线的解析式为234y x x =-++； (2)解：当0x =时，4y =， ∴点()0,4C ，设直线BC 的解析式为()0y kx b k =+≠，把点B (4，0)，()0,4C 代入得：404k b b +=⎧⎨=⎩，解得：14k b =-⎧⎨=⎩，∴直线BC 的解析式为4y x =-+； (3) 解：如图，∵点M 是第一象限的抛物线上的点，且横坐标为t ，∴点()2,34M t t t -++，∵MN ⊥x 轴， ∴点(),4N t t -+，∴()()223444MN t t t t t =-++--+=-+，∴()()2242404h t t t t =-+=--+<<， ∴当2t =时，h 的值最大，最大值为4； (4)解：在x 轴的负半轴上存在点P ，使以B ，C ，P 三点为顶点的三角形为等腰三角形，理由如下：当PC =BC 时， ∵OC ⊥BP ， ∴OP =OB ，∵点B (4，0)，点P 在x 轴的负半轴上， ∴点()4,0P -；当PB =BC 时， ∵B (4，0)，()0,4C ， ∴OC =4，OB =4，∴BP BC ==∴4OP BP OB =-=， ∵点P 在x 轴的负半轴上，∴点()4P -；当PC =PB 时，点P 位于BC 的垂直平分线上， ∵OB =OC =4，∴点O 位于BC 的垂直平分线上， ∴此时点P 与点O 重合，不合题意，舍去；综上所述，在x 轴的负半轴上存在点()4,0P -或()4P -，使以B ，C ，P 三点为顶点的三角形为等腰三角形．【点睛】本题主要考查了求二次函数和一次函数的解析式，二次函数的图象和性质，等腰三角形的性质，熟练掌握用待定系数法求二次函数和一次函数的解析式，二次函数的图象和性质，等腰三角形的性质是解题的关键． 22．(1)y ＝﹣x 2+2x +3(2)PA +PC 的长为(3)存在，点Q 的坐标为()0,2或10,3⎛⎫- ⎪⎝⎭，理由见解析【解析】【分析】（1）当x ＝0时，y ＝3，可得C （0，3）．再设设抛物线的解析式为y ＝a （x +1）（x ﹣3）（a ≠0），利用待定系数法，即可求解；（2）连接PA 、PB 、PC ，根据轴对称性可得PA ＝PB ．从而得到PA +PC ＝PC +PB ．进而得到当点P 在线段BC 上时，PC +AP 有最小值．即可求解；（3）先求出抛物线的对称轴，可得点()1,0M ，再由点N （0，﹣1），B （3，0），C （0，3）．可得2,45,45MN BC BM CBM MNO ===∠=︒∠=︒，可得∠CBM =∠MNO ，然后分三种情况讨论，即可求解． (1)解：把x ＝0代入得：y ＝3， ∴C （0，3）．设抛物线的解析式为y ＝a （x +1）（x ﹣3）（a ≠0），将点C 的坐标代入上式得：3＝﹣3a ，解得：a ＝﹣1．∴抛物线的解析式为y ＝-（x +1）（x -3）=﹣x 2+2x +3． (2)解：如图，连接PA 、PB 、PC ，∵点A 与点B 关于直线l 对称，点P 在直线l 上， ∴PA ＝PB ． ∴PA +PC ＝PC +PB ． ∵两点之间线段最短，∴当点P 在线段BC 上时，PC +AP 有最小值． ∵OC ＝3，OB ＝3， ∴BC ＝32∴PA +PC 的最小值＝32 (3)解：存在，理由：抛物线的对称轴为直线x ＝﹣2ba＝1． ∵抛物线的对称轴l 与x 轴交于M 点． ∴点()1,0M ，∵点N （0，﹣1），B （3，0），C （0，3）． ∴OM =ON =1，OB =OC =3，∴2,32,2,45,45MN BC BM CBM MNO ===∠=︒∠=︒， ∴∠CBM =∠MNO ，当点Q 在点N 下方时，∠MNQ =135°，不符合题意， ∴点Q 在点N 上方，设点Q 的坐标为（0，n ）．则QN =n +1， ∵以M 、N 、Q 为顶点的三角形与△BCM 相似， ∴∠QMN =∠CMB 或∠MQN =∠CMB ，当1Q MN CMB ∠=∠时，1Q MNCMB ，如图（2），∴1Q N MNBC BM=， ∴12232n +=，解得：2n =， ∴点()10,2Q ；当2MQ N CMB ∠=∠时，2MQ NCMB ，如图（3），∴2Q N MN MB BC=， ∴12232n +=13n =-，∴点210,3Q ⎛⎫- ⎪⎝⎭，综上所述，点Q 的坐标为()0,2或10,3⎛⎫- ⎪⎝⎭．【点睛】本题主要考查了二次函数的综合题，相似三角形的判定和性质，两点之间，线段最短，待定系数法求二次函数解析式等知识，熟练掌握二次函数的图象和性质，相似三角形的判定和性质，利用数形结合思想解答是解题的关键． 23．0或1或2或3 【解析】【分析】根据二次函数y =x 2-2x +m -2的图象与x 轴有交点，根据Δ≥0列出m 的不等式，求出m 的取值范围即可．【详解】解：∵二次函数y =x 2-2x +m -2的图象与x 轴有交点， ∴Δ=4-4（m -2）≥0， ∴m ≤3， ∵m 为非负整数， ∴m =0或1或2或3．【点睛】本题主要考查了抛物线与x 轴交点的知识，解答本题的关键是根据二次函数y =x 2-2x +m -2的图象与x 轴有交点列出m 的不等式，此题难度不大． 24．(1)A （-1，0），B （3，0）(2)点C 的坐标为（1，-2），ABC 为等腰直角三角形，理由见解析(3)点P 的坐标为（1，2），2)，(1,2)或3(1,)4-【解析】【分析】（1）把0y =代入到21322y x x =--得，213022x x --=，解得13x =，21x =-，又因为点A 在点B 的左侧，即可得；（2）21322y x x =--配方得21(1)22y x =--，即可得点C 的坐标为（1，-2），根据点A ，B ，C 的坐标得4AB =，AC ，BC =AC =BC ，又因为2224+=，所以222AC BC AB +=，即可得90ACB ∠=︒，从而得出ACB △是等腰直角三角形；（3）当点P 与点C 关于x 轴对称时，OC =OP ，OCP △为等腰三角形，即可得点P 的坐标（1，2），当CO CP =时，CP =，即可得点P 的坐标为2)或(1,2)，当OP CP =时，点P 在OC 的垂直平分线上，设点(1,)P a ，点P 交x 轴于点D ，在Rt ODP 中，根据勾股定理得，222(2)1a a +=+，解得34a =-，即可得点P 的坐标为3(1,)4-，综上，即可得． (1)解：把0y =代入到21322y x x =--得， 213022x x --= 2230x x --= (3)(1)0x x -+=解得13x =，21x =-， ∵点A 在点B 的左侧，∴A （-1，0），B （3，0）． (2) 解：21322y x x =-- =21(3)2x x -- =21(1)22x x -+- =21(1)22x --∴点C 的坐标为（1，-2），ABC 为等腰直角三角形，理由如下：∵A （-1，0），B （3，0），C （1，-2）， ∴3(1)4AB =--=，22(11)(02)8AC =----=， 22(31)(02)8BC =---=，∴AC =BC ， ∵222(8)(8)4+=， ∴222AC BC AB +=， ∴90ACB ∠=︒，∴ACB △是等腰直角三角形． (3)解：当点P 与点C 关于x 轴对称时，OC =OP ，OCP △为等腰三角形， ∴点P 的坐标为（1，2）；当CO CP =时，22(10)(20)5CP =-+-=， ∴点P 的坐标为(1,52)-或(1,52)--；当OP CP =时，点P 在OC 的垂直平分线上，设点(1,)P a ，如图所示，点P 交x 轴于点D ，在Rt ODP 中，根据勾股定理得，222(2)1a a +=+，22441a a a ++=+34a =- ∴点P 的坐标为3(1,)4-；综上，点P 的坐标为（1，2），2)，(1,2)或3(1,)4-．【点睛】本题考查了二次函数与三角形的综合，解题的关键是掌握二次函数的性质，等腰三角形的判定与性质．25．(1)见解析(2)122,1m m =-=【解析】【分析】（1）令0y =，得到关于x 的一元二次方程，根据一元二次方程根的判别式判断即可；（2）令1x =，0y =，解一元二次方程即可求得m 的值(1)令0y =，则有2220x mx m --=222890m m m ∆=+=≥即，对于任意实数方程2220x mx m --=总有两个实数根，∴对任意实数m ，抛物线与x 轴总有交点．(2)解：∵抛物线222y x mx m =--与x 轴交于1,0A ，∴202m m =--解得122,1m m =-=【点睛】本题考查了二次函数与坐标轴交点问题，掌握一元二次方程根的判别式以及解一元二次方程是解题的关键．。

(中考试题)初中数学专题训练-函数

函数一．选择题（共20小题）1．（2014•射阳县校级模拟）若点P（a，a﹣b）在第四象限，则点Q（b，﹣a）在（）A．第四象限B．第三象限C．第二象限D．第一象限2．（2012•翁源县校级模拟）函数的自变量x的取值范围是（）A．x≥1B．x≥﹣1或x≠﹣3C．x≥﹣1 D．x≥﹣1且x≠﹣33．（2017春•姜堰区校级月考）如图，在物理实验课上，小明用弹簧秤将铁块A 从完全置身水槽外，到匀速向下放入盛有水的水槽中，直至铁块完全浸入水面下的一定深度，则图能反映弹簧秤的读数y（单位：N）与铁块下降的高度x（单位：cm）之间的函数关系的大致图象是（）A．B ．C．D．4．（2012•山西模拟）一辆汽车和一辆摩托车分别从A，B两地去同一城市，它们离A地的路程随时间变化的图象如图所示．则下列结论错误的是（）初中数学A．摩托车比汽车晚到1h B．A，B两地的路程为20kmC．摩托车的速度为45km/h D．汽车的速度为60km/h 5．（2011•大同校级模拟）有一个附有进出水管的容器，每单位时间进、出的水量都是一定的．设从某一时刻开始5分钟内只进水不出水，在接着的2分钟内只出水不进水，又在随后的15分钟内既进水又出水，刚好将该容器注满．已知容器中的水量y升与时间x分之间的函数关系如图所示．则在第7分钟时，容器内的水量为（）升．A．15B．16C．17D．18 6．（2016•阳泉模拟）如图1，E为矩形ABCD边AD上一点，点P从点B沿折线BE﹣ED﹣DC运动到点C时停止，点Q从点B沿BC运动到点C时停止，它们运动的速度都是1cm/s．若点P、Q同时开始运动，设运动时间为t（s），△BPQ的面积为y（cm）2．已知y与t的函数关系图象如图2，则下列结论错误的是（）A．AE=6cmB．sin∠EBC=0.8C．当0＜t≤10时，y=0.4t2D．当t=12s时，△PBQ是等腰三角形7．如图，在Rt△ABC中，∠ACB=90°，∠ABC=60°，AB=4，D是AB边上的一个动点（不与点A，B重合），过点D作CD的垂线交射线CA于点E．设AD=x，CE=y，则下列图象中，能表示与的函数关系的图象大致是（）A．B．C．D．8．（2016春•新洲区期末）若一次函数y=（1﹣m）x|m|﹣1+3的函数值y随x的增大而增大，则m的取值为（）A．2B．1C．﹣2D．﹣1 9．（2014•泗县校级模拟）函数y=（m+1）x﹣（4m﹣3）的图象在第一、二、四象限，那么m的取值范围是（）A．B．C．m＜﹣1D．m＞﹣110．（2014•永嘉县校级模拟）已知点（﹣4，y1），（2，y2）都在直线y=﹣x+2上，则y1，y2大小关系是（）A．y1＞y2B．y1=y2C．y1＜y2D．不能比较11．（2012春•翠屏区校级期中）直线y=kx+3与x轴的交点是（1，0），则k的值是（）A．3B．2C．﹣2D．﹣312．（2014•泗县校级模拟）如果是方程组的解，则一次函数y=mx+n的解析式为（）A．y=﹣x+2B．y=x﹣2C．y=﹣x﹣2D．y=x+2 13．（2014•白云区校级模拟）根据下表中，反比例函数的自变量x与函数y的对应值，可得p的值为（）x﹣21y3pA．3B．1C．﹣2D．﹣614．一次函数y=kx+b（b＞0）与反比例函数y=在同一直角坐标系下的大致图象为（）A．B．C．D．15．（2014•泗县校级模拟）若反比例函数y=（2m﹣1）的图象在第二，四象限，则m的值是（）A．﹣1或1B．小于的任意实数C．﹣1D．不能确定16．（2014•泗县校级模拟）如图，A为反比例函数图象上一点，AB⊥x轴于=3，则k的值为（）点B，若S△AOBA．3B．6C．D．无法确定17．（2014•鼓楼区校级模拟）已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出以下结论：①因为a＞0，所以函数y有最大值；②该函数的图象关于直线x=﹣1对称；③当x=﹣2时，函数y的值等于0；④当x=﹣3或x=1时，函数y的值都等于0．其中正确结论的个数是（）A．4B．3C．2D．1 18．（2014•磐石市校级模拟）已知函数y=ax2+bx+c的图象如图所示，那么能正确反映函数y=ax+b图象的只可能是（）A．B．C．D．19．（2014•溧水县校级模拟）二次函数y=ax2+bx+c（a、b、c为常数且a≠0）中的x与y的部分对应值如下表：x﹣3﹣2﹣1012345y1250﹣3﹣4﹣30512给出了结论：（1）二次函数y=ax2+bx+c有最小值，最小值为﹣4；（2）若y＜0，则x的取值范围为0＜x＜2；（3）二次函数y=ax2+bx+c的图象与x轴有两个交点，且它们分别在y轴两侧．则其中正确结论的个数是（）A．0B．1C．2D．320．对二次函数进行配方，其结果及顶点坐标是（）A．B．C．D．二．填空题（共20小题）21．根据点所在位置填表（图）点的位置横坐标符号纵坐标符号第一象限第二象限第三象限第四象限22．（2015秋•灯塔市期末）坐标平面内的点与是一一对应的．23．（2017秋•昌平区校级期中）从甲地向乙地打长途电话，按时间收费，3分钟内收费2.4元，每加1分钟加收1元，若时间t≥3（分）时，电话费y（元）与t（分）之间的函数关系式是．24．（2014•新泰市校级模拟）函数y=中，自变量x的取值范围是；函数中，自变量x的取值范围是．25．（2012秋•合肥期末）根据图中所示的程序计算变量y的值，若输入自变量x 的值为，则输出的结果是．26．（2016春•西和县校级月考）用描点法画函数图象的一般步骤是、、．27．（2014•无棣县校级模拟）如图（单位：m ），等腰三角形ABC 以2米/秒的速度沿直线L 向正方形移动，直到AB 与CD 重合．设x 秒时，三角形与正方形重叠部分的面积为ym 2．则y 与x 的关系式为，当重叠部分的面积是正方形面积的一半时，三角形移动时间是．28．（2015秋•深圳校级期中）函数的三种表示方式分别是．29．（2017•和平区校级模拟）当m=时，函数y=（m +3）x 2m +1+4x ﹣5（x≠0）是一次函数．30．（2014•泗县校级模拟）已知函数y=2x ﹣3，当x 时，y ≥0；当x时，y ＜5．31．一次函数y=kx +b 的图象与性质k 、b 的符号k ＞0，b ＞0k ＞0，b ＜0k ＜0，b ＞0k ＜0，b ＜0图象的大致位置经过象限第象限第象限第象限第象限性质y 随x 的增大而y 随x 的增大而y 随x 的增大而y 随x 的增大而32．（2014•射阳县校级模拟）如图，点A （﹣3，4）在一次函数y=﹣3x ﹣5的图象上，图象与y 轴的交点为B ，那么△AOB 的面积为．33．（2014秋•路北区期末）如图，⊙A和⊙B都与x轴和y轴相切，圆心A和圆心B都在反比例函数y=的图象上，则图中阴影部分的面积等于．34．若正方形OABC的顶点B和正方形ADEF的顶点E都在函数的图象上．若正方形OABC的面积为1，则k的值为；点E的坐标为．35．（2008春•通城县期中）反比例函数y=的图象经过点（﹣，5）和（a，﹣3），则a=．36．（2014•泗县校级模拟）已知y﹣2与x成反比例，当x=3时，y=1，则y与x 的函数关系式为．37．二次函数y=2x2﹣4x+5的对称轴方程是x=；当x=时，y有最小值是．38．已知二次函数y=ax2+bx+c的图象与x轴交于点（﹣1，0），（x1，0），且1＜x1＜2，与y轴的正半轴的交点在（0，1）的下方．下列结论：①a﹣b+c=0，②0＜b＜﹣a，③a+c＞0，④a﹣b+1＞0，其中正确结论的个数是个．39．（2014•射阳县校级模拟）已知抛物线y=ax2+bx+c（a＞0）的对称轴为直线x=1，且经过点（﹣1，y1），（2，y2），试比较y1和y2的大小：y1y2．（填“＞”，“＜”或“=”）40．（2014•大石桥市校级模拟）将二次函数y=x2的图象向右平移一个单位长度，再向上平移3个单位长度所得的图象解析式为．三．解答题（共10小题）41．已知点M（3a+8，﹣1﹣a），分别根据下列条件求出点M的坐标．（1）点M在x轴上；（2）点M在一、三象限角平分线上；（3）点M在第四象限，并且a为最小自然数；（4）N点坐标为（﹣3，6），并且直线MN∥y轴．42．在平面直角坐标系中，已知点A（﹣3，4），点B（﹣1，﹣2），点C（1，2），O是坐标原点．（1）求△AOB的面积；（2）求△ABC的面积．43．求下列函数自变量x的取值范围．（1）y=﹣x2﹣5x+6；（2）y=；（3）y=；（4）y=．44．已知一次函数y=（m+2）x+2﹣n，求：（1）y随x的增大而增大，m的取值范围；（2）函数的图象与y轴的交点在x轴的下方时，m，n的取值范围；（3）m，n为何值时图象与坐标轴交于原点；（4）函数的图象经过第一、二、三象限，m，n的取值范围．45．（2016•阳泉模拟）已知方程x2+mx+n=0的两根是直角三角形的两个锐角的余弦．（1）求证：m2=2n+1；（2）若P（m，n）是一次函数y=x﹣图象上的点，求点P的坐标．46．（2014•浙江模拟）如图，直线AB与x轴交于点A（1，0），与y轴交于点B （0，﹣2）．（1）求直线AB的解析式；（2）若直线AB上的点C在第一象限，且S=2，求点C的坐标．△OBC47．（2016•阳泉模拟）如图所示，矩形OABC的顶点A，C分别在x，y轴的正半轴上，点D为对角线OB的中点，点E（6，n）在边AB上，反比例函数y=（k ≠0）在第一象限内的图象经过点D，E，且tan∠BOA=．（1）求边AB的长；（2）求反比例函数的表达式和n的值．48．如图所示，直线y=2x+3与双曲线y=相交于A，B两点，与轴交于点C，且△OCA的面积为1.5．（1）求双曲线y=的解析式；（2）若点D，B关于原点对称，一动点P沿着x轴运动，则|PA﹣PD|是否有最大值？如果有，请确定点P的位置；如果没有，请说明理由．49．（2014•溧水县校级模拟）已知：二次函数y=ax2+bx+c（a≠0）中的x，y满足下表：x…﹣10123…y…0﹣3﹣4﹣3m…（1）求m的值；（2）根据上表求y＞0时的x的取值范围；（3）若A（p，y1），B（p+1，y2）两点都在该函数图象上，且p＜1，试比较y1与y2大小．50．如图，在平面直角坐标系中，矩形OABC四个顶点的坐标分别为O（0，0），A（0，3），B（6，3），C（6，0），抛物线过y=ax2+bx+c（a≠0）点A．（1）求c的值；（2）若a=﹣1，且抛物线与矩形有且只有三个交点，A，D，E，求△ADE的面积S的最大值．第11页（共11页）。

一次函数综合题(解析版)--2024年中考数学压轴题专项训练

一次函数综合题通用的解题思路：(1)一次函数与几何图形的面积问题首先要根据题意画出草图，结合图形分析其中的几何图形，再求出面积．(2)一次函数的优化问题通常一次函数的最值问题首先由不等式找到x 的取值范围，进而利用一次函数的增减性在前面范围内的前提下求出最值．(3)用函数图象解决实际问题从已知函数图象中获取信息，求出函数值、函数表达式，并解答相应的问题．1(2024•鼓楼区一模)如图，直线y =-3x +6与⊙O 相切，切点为P ，与x 轴y 轴分别交于A 、B 两点．⊙O 与x 轴负半轴交于点C ．(1)求⊙O 的半径；(2)求图中阴影部分的面积．【分析】(1)由OP =OA ⋅sin60°，即可求解；(2)由图中阴影部分的面积=S 扇形COP -S ΔPOC ，即可求解．【解答】解：(1)对于直线y =-3x +6，令y =-3x +6=0，则x =23，即OA =23，由一次函数的表达式知，OB =6，则tan ∠BAC =OB AO =623=3，则∠BAC =60°连接OP ，则OP ⊥AB ，则OP =OA ⋅sin60°=23×32=3；(2)过点P 作PH ⊥AC 于点H ，∵∠POH =30°，则∠POC =150°，PH =12OP =32，则图中阴影部分的面积=S 扇形COP -S ΔPOC =150°360°×π×32-12×3×32=15π-94．【点评】本题考查了一次函数和圆的综合运用，涉及到圆切线的和一次函数的性质，解直角三角形，面积的计算等，综合性强，难度适中．2(2023•宿豫区三模)如图①，在平面直角坐标系中，直线l 1:y =x +1与直线l 2:x =-2相交于点D ，点A 是直线l 2上的动点，过点A 作AB ⊥l 1于点B ，点C 的坐标为(0,3)，连接AC ，BC ．设点A 的纵坐标为t ，ΔABC 的面积为s ．(1)当t =2时，求点B 的坐标；(2)s 关于t 的函数解析式为s =14t 2+bt -54t -1或t 5 a t +1 t -5 (-1<t <5)，其图象如图②所示，结合图①、②的信息，求出a 与b 的值；(3)在直线l 2上是否存在点A ，使得∠ACB =90°，若存在，请求出此时点A 的坐标；若不存在，请说明理由．【分析】(1)解法一：先根据t =2可得点A (-2,2)，因为B 在直线l 1上，所以设B (x ,x +1)，利用y =0代入y =x +1可得G 点的坐标，在Rt ΔABG 中，利用勾股定理列方程可得点B 的坐标；解法二：根据可以使用y =x +1与x 轴正半轴夹角为45度来解答；(2)先把(7,4)代入s =14t 2+bt -54中计算得b 的值，计算在-1<t <5范围内图象上一个点的坐标值：当t =2时，根据(1)中的数据可计算此时s =94，可得坐标2,94，代入s =a (t +1)(t -5)中可得a 的值；(3)存在，设B (x ,x +1)，如图5和图6，分别根据两点的距离公式和勾股定理列方程可解答．【解答】解：(1)解法一：如图1，连接AG ，当t =2时，A (-2,2)，设B (x ,x +1)，在y =x +1中，当x =0时，y =1，∴G (0,1)，∵AB ⊥l 1，∴∠ABG =90°，∴AB 2+BG 2=AG 2，即(x +2)2+(x +1-2)2+x 2+(x +1-1)2=(-2)2+(2-1)2，解得：x 1=0(舍)，x 2=-12，∴B -12，12；解法二：如图1-1，过点B 作BE ⊥x 轴于E ，过点A 作AH ⊥BE 于H ，当x =0时，y =1，当y =0时，x +1=0，则x =-1，∴OF =OG =1，∵∠GOF =90°，∴∠OGF =∠OFG =45°，∴BE =EF ，∵∠ABD =90°，∴∠ABH =∠BAH =45°，∴ΔABH 是等腰直角三角形，∴AH =BH ，当t =2时，A (-2,2)，设B (x ,x +1)，∴x +2=2-(x +1)，∴x =-12，∴B -12，12 ；(2)如图2可知：当t =7时，s =4，把(7,4)代入s =14t 2+bt -54中得：494+7b -54=4，解得：b =-1，如图3，过B 作BH ⎳y 轴，交AC 于H ，由(1)知：当t =2时，A (-2,2)，B -12，12 ，∵C (0,3)，设AC 的解析式为：y =kx +n ，则-2k +n =2n =3 ，解得k =12n =3 ，∴AC 的解析式为：y =12x +3，∴H -12，114，∴BH =114-12=94，∴s=12BH⋅|x C-x A|=12×94×2=94，把2,9 4代入s=a(t+1)(t-5)得：a(2+1)(2-5)=94，解得：a=-1 4；(3)存在，设B(x,x+1)，当∠ACB=90°时，如图5，∵∠ABD=90°，∠ADB=45°，∴ΔABD是等腰直角三角形，∴AB=BD，∵A(-2,t)，D(-2,-1)，∴(x+2)2+(x+1-t)2=(x+2)2+(x+1+1)2，(x+1-t)2=(x+2)2，x+1-t=x+2或x+1-t=-x-2，解得：t=-1(舍)或t=2x+3，RtΔACB中，AC2+BC2=AB2，即(-2)2+(t-3)2+x2+(x+1-3)2=(x+2)2+(x+1-t)2，把t=2x+3代入得：x2-3x=0，解得：x=0或3，当x=3时，如图5，则t=2×3+3=9，∴A(-2,9)；当x=0时，如图6，此时，A(-2,3)，综上，点A的坐标为：(-2,9)或(-2,3)．【点评】本题考查二次函数综合题、一次函数的性质、等腰直角三角形的判定和性质、三角形的面积、两点间距离公式等知识，解题的关键是灵活运用所学知识解决问题．3(2023•溧阳市一模)如图1，将矩形AOBC放在平面直角坐标系中，点O是原点，点A坐标为(0,4)，点B坐标为(5,0)，点P是x轴正半轴上的动点，连接AP，ΔAQP是由ΔAOP沿AP翻折所得到的图形．(1)当点Q落在对角线OC上时，OP=　165　；(2)当直线PQ经过点C时，求PQ所在的直线函数表达式；(3)如图2，点M是BC的中点，连接MP、MQ．①MQ的最小值为；②当ΔPMQ是以PM为腰的等腰三角形时，请直接写出点P的坐标．【分析】(1)通过Q 点在OC 上，可以通过∠BOC 的三角函数和∠OAP 的三角函数来导出对应的边的关系，求得结果；(2)通过直角ΔAQC 中，得到QC 的长度，然后通过OP =PQ =x ，可以在Rt ΔBCP 中，得到对应的x 值然后求出结果；(3)通过QA =OA =4，可得出Q 点的运动轨迹，是以A 点为圆心，4为半径长度的圆弧，从而可知，MA 的连线上的Q 点为最短的MQ 长度，通过分类讨论，PM =PQ ，PM =QM ，PQ =QM 来求得对应的P 的坐标．【解答】解：(1)如图1，∵∠OAP +∠AOE =90°，∠BOC +∠AOE =90°，∴∠OAP =∠BOC ，又∵∠AOP =∠OBC =90°，∴ΔOAP ∽ΔBOC ，∴OP BC =OA OB ，即OP 4=45，∴OP =165，故答案为：165；(2)如图，∵AQ ⊥PQ ，∴∠AQC =90°，∴QC =AC 2-AQ 2=52-42=3，∵AQ =AO =4，设OP =PQ =x ，则CP =3+x ，PB =5-x ，∴CP 2=BP 2+BC 2，(3+x )2=(5-x )2+42，x =2，∴P 点的坐标为(2,0)，将P (2,0)和C (5,4)代入y =kx +b 中，0=2k +b 4=5k +b ，解得：k =43b =-83，∴PQ 所在直线的表达式为：y =43x -83；(3)如图，①∵AQ =AO =4，∴Q 点的运动轨迹，是以A 为圆心，4为半径的圆弧，∴MQ 的最小值在AM 的连线上，如图，MQ ′即为所求，∵M 是BC 中点，CM =12BC =2，∴AM =52+22=29，MQ ′=MA -AQ ′=29-4，故答案为：29-4；②如图，设OP =PQ =x ，BP =5-x ，∴PM 2=(5-x )2+22=x 2-10x +29，当PM =PQ 时，PM 2=PQ 2，∴x 2-10x +29=x 2，x =2910，∴P 2910，0，当MP =MQ 时，如图，若点Q 在AC 上，则AQ =OA =4，∵MP =MQ ，MB =MC ，∠PBM =∠QCM ，∴ΔPMB ≅ΔQMC (HL )，∴PB =QC ，QC =AC -AQ =5-4=1，∴PB =1，∴OP =BO -PB =5-1=4，∴P (4,0)；若点Q 在AC 上方时，由对称性可知OM =MQ ，∵MQ =MQ ，∴MO =MP ，∴P (10,0)；当MQ =PQ 时，不符合题意，不成立，故P 点坐标为P 2910，0或P (4,0)或(10,0)．【点评】本题考查一次函数的图象及应用，通过一次函数坐标图象的性质，三角函数的性质，全等三角形的性质和勾股定理，来求得对应的解．4(2022•启东市模拟)我们知道一次函数y =mx +n 与y =-mx +n (m ≠0)的图象关于y 轴对称，所以我们定义：函数y =mx +n 与y =-mx +n (m ≠0)互为“M ”函数．(1)请直接写出函数y =2x +5的“M ”函数；(2)如果一对“M ”函数y =mx +n 与y =-mx +n (m ≠0)的图象交于点A ，且与x 轴交于B ，C 两点，如图所示，若∠BAC =90°，且ΔABC 的面积是8，求这对“M ”函数的解析式；(3)在(2)的条件下，若点D 是y 轴上的一个动点，当ΔABD 为等腰三角形时，请求出点D 的坐标．【分析】(1)根据互为“M ”函数的定义，直接写出函数y =2x +5的“M ”函数；(2)现根据已知条件判断ΔABC 为等腰直角三角形，再根据互为“M ”函数的图象关于y 轴对称，得出OA =OB =OC ，再根据函数解析式求出点A 、B 、C 的坐标，再根据ΔABC 的面积是8求出m 、n 的值，从而求出函数解析式；(3)ΔABD 为等腰三角形，分以A 为顶点，以B 为顶点，以D 为顶点三种情况讨论即可．【解答】(1)解：根据互为“M ”函数的定义，∴函数y =2x +5的“M ”函数为y =-2x +5；(2)解：根据题意，y =mx +n 和y =-mx +n 为一对“M 函数”．∴AB =AC ，又∵∠BAC =90°，∴ΔABC 为等腰直角三角形，∴∠ABC =∠ACB =45°，∵OB =OC ，∴∠BAO =∠CAO =45°，∴OA =OB =OC ，又∵S ΔABC =12×BC ×AO =8且BC =2AO ，∴AO =22，∵A 、B 、C 是一次函数y =mx +n 与y =-mx +n (m ≠0)的图象于坐标轴的交点，∴A (0,n )，B -n m ，0 ，C n m ，0，∵OA =OB =n ，∴n m=22，∴m =1，∴y =x +22和y =-x +22；(3)解：根据等腰三角形的性质，分情况，∵AO =BO =22，∴AB =4，由(2)知，A (0，22)，B (-22，0)，C (22，0)，∴①以A 为顶点，则AB =AD ，当点D 在点A 上方时，AD =22+4，当点D 在点A 下方时，AD =22-4，∴D 1(0，22+4)，D 2(0，22-4)，②以B 为顶点，则BA =BD ，此时点D 在y 轴负半轴，∴D 3(0,-22)，③以D 为顶点，则DA =DB ，此时D 为坐标原点，∴D 4(0,0)．∴D 点坐标为D 1(0，22+4)，D 2(0，22-4)，D 3(0,-22)，∴D 4(0,0)．【点评】本题考查一次函数的综合应用，以及新定义、等腰三角形的性质等知识，关键是理解新定义，用新定义解题．5(2024•新北区校级模拟)如图①，动点P 从矩形ABCD 的顶点A 出发，以v 1的速度沿折线A -B -C 向终点C 运动；同时，一动点Q 从点D 出发，以v 2的速度沿DC 向终点C 运动，当一个点到达终点时，另一个点也停止运动．点E 为CD 的中点，连接PE ，PQ ，记ΔEPQ 的面积为S ，点P 运动的时间为t ，其函数图象为折线MN -NF 和曲线FG (图②)，已知，ON =4，NH =1，点G 的坐标为(8,0)．(1)点P 与点Q 的速度之比v 1v 2的值为　85　；AB AD的值为；(2)如果OM =15．①求线段NF 所在直线的函数表达式；②求FG 所在曲线的函数表达式；③是否存在某个时刻t ，使得S ≥154？若存在，求出t 的取值范围：若不存在，请说明理由．【分析】(1)由函数图象可知t =3时，Q 与E 重合，t =4时，P 与B 重合，t =6时，P 与C 重合，则Q 的速度v 2=DE 4，P 的速度v 1=AB 4，从而得出答案；(2)①当t =0时，P 与A 重合，Q 与D 重合，此时S ΔADE =2，可得AD =BC =DE =15，AB =CD =53AD =10，从而得出点P 与Q 的速度，即可得出点F 的坐标，利用待定系数法可得答案；②设FG 所在的曲线的数解析式为S =a (t -6)2+k (a ≠0)，把F 5,154，G (8,0)代入解析式求得a ，k 值即可求解答；③利用待定系数法求出直线MN 的函数解析式，当S =154时，可得t 的值，根据图象可得答案．【解答】解：(1)∵ON =4，NH =1，G (8,0)，∴N (4,0)，H (5,0)，由图象可知：t =4时，Q 与E 重合，t =5时，P 与B 重合，t =8时，P 与C 重合，∴Q 的速度v 2=DE 4，P 的速度v 1=AB 5，∵四边形ABCD 是矩形，∴AB =CD ，AD =BC ，∵E 为CD 的中点，∴DE =12CD =12AB ，∴v 1v 2=AB5DE 4=AB 5⋅4DE =85，∵P 从A 到B 用了5秒，从B 到C 用了3秒，∴AB =5v 1，BC =3v 1，∴AB =53BC ，∴AB :AD 的值为53，故答案为：85，53；(2)①∵OM =15，∴M (0,15)，由题知，t =0时，P 与A 重合，Q 与D 重合，∴S ΔEPQ =12AD ⋅DE =15，∵AB :AD =53，DE =12AB ，∴DE =56AD ，∴12AD ⋅56AD =15，∴AD =BC =6(舍去负值)，∴AB =CD =53AD =10，∴v 2=DE 4=54，当t =5时，DQ =v 2t =54×5=254，∴QE =DQ -DE =254-5=54，此时P 与B重合，∴S ΔEPQ =12EQ ⋅BC =12×54×6=154，∴F 5,154 ，设直线NF 的解析式为S =kt +b (k ≠0)，将N (4,0)与F 5,154 代入得：4k +b =05k +b =154，∴k =154b =-15 ，∴线段NF 所在直线的函数表达式为S =154t -15(4<t ≤5)；②设FG所在的曲线的数解析式为S=1254t-5(16-2t)=-54t2+15t-40，∴FG所在的曲线的函数解析式为S=-54t2+15t-40(5≤t≤8)；③存在，分情况讨论如下：当Q在DE上，P在AB上时，∵直线MN经过点M(0,15)，N(4,0)，可求得直线MN的解析式为S=-54t+15(0≤t≤4)，当s=154时，-154t+15=154，∴x=3，∵s随x的增大而减小，∴当0≤x≤3时，S≥154，当Q在CE上，P在BC上时，直线NF的解析式为S=154t-15(4<t≤5)；由F5,15 4知：当t=5时，S=154，当S=154时，-54t2+15t-40=154，∴t=7或5，由图象知：当5≤x≤7，x的取值范围为0≤t≤3或5≤t≤7．【点评】本题是一次函数综合题，主要考查了待定系数法求函数解析式，三角形的面积，矩形的性质等知识，理解函数图象中每一个拐点的意义是解题的关键．6(2024•梁溪区校级模拟)在平面直角坐标系xOy 中，二次函数y =-ax 2+3ax +4a 的图象与x 轴交于A 、B 两点(点A 在点B 的左侧)，与y 轴正半轴交于点C ，直线y =12x 交于第一象限内的D 点，且ΔABC 的面积为10．(1)求二次函数的表达式；(2)点E 为x 轴上一点，过点E 作y 轴的平行线交线段OD 于点F ，交抛物线于点G ，当GF =5OF 时，求点G 的坐标；(3)已知点P (n ,0)是x 轴上的点，若点P 关于直线OD 的对称点Q 恰好落在二次函数的图象上，求n 的值．【分析】(1)在y =-ax 2+3ax +4a 中，令y =0得A (-1,0)，B (4,0)，根据ΔABC 的面积为10，即得OC =4，C (0,4)，用待定系数法即得二次函数的表达式为y =-x 2+3x +4；(2)设E (m ,0)，则F m ,12m ，G (m ,-m 2+3m +4)，由GF =5OF ，可得-m 2+52m +4=5×52m ，即可解得G (2,6)；(3)连接PQ 交直线OD 于K ，过Q 作QT ⊥x 轴于T ，设Q (r ,s )，可得K n +r 2，s 2 ，即得s 2=12×n +r 2，n +r =2s ①，又r 2+s 2=n 2，(n +r )(n -r )=s 2②，可解得r =35n ，s =45n ，故Q 35n ，45n ，代入y =-x 2+3x +4得45n =-35n 2+3×35n +4，解得n =5或n =-209．【解答】解：(1)如图：在y =-ax 2+3ax +4a 中，令y =0得-ax 2+3ax +4a =0，解得x =4或x =-1，∴A (-1,0)，B (4,0)，∴AB =5，∵ΔABC 的面积为10，∴12AB ⋅OC =10，即12×5⋅OC =10，∴OC =4，∴C (0,4)，把C (0,4)代入y =-ax 2+3ax +4a 得：4a =4，∴a =1，∴二次函数的表达式为y =-x 2+3x +4；(2)如图：设E (m ,0)，则F m ,12m ，G (m ,-m 2+3m +4)，∴OF =m 2+12m 2=52m ，GF =-m 2+3m +4-12m =-m 2+52m +4，∵GF =5OF ，∴-m 2+52m +4=5×52m ，解得m =2或m =-2(舍去)，∴G (2,6)；(3)连接PQ 交直线OD 于K ，过Q 作QT ⊥x 轴于T ，如图：∵P (n ,0)关于直线对称点为Q ，∴OQ =OP =|n |，K 是PQ 中点，设Q (r ,s )，∴K n +r 2，s 2，∵K 在直线y =12x 上，∴s 2=12×n +r 2，整理得：n +r =2s ①，∵OT 2+QT 2=OQ 2，∴r 2+s 2=n 2，变形得：(n +r )(n -r )=s 2②，把①代入②得：2s (n -r )=s 2，∵s ≠0，∴n -r =s2③，由①③可得r =35n ，s =45n ，∴Q 35n ，45n ，∵Q 在抛物线y =-x 2+3x +4上，∴45n =-35n 2+3×35n +4，解得n =5或n =-209，答：n 的值为5或-209．【点评】本题考查一次函数、二次函数综合应用，涉及待定系数法，三角形面积，对称变换等知识，解题的关键是用含n 的代数式表示Q 的坐标．7(2023•邗江区校级一模)如图1，在平面直角坐标系中，直线l :y =-33x +43分别与x 轴、y 轴交于点A 点和B 点，过O 点作OD ⊥AB 于D 点，以OD 为边构造等边ΔEDF (F 点在x 轴的正半轴上)．(1)求A 、B 点的坐标，以及OD 的长；(2)将等边ΔEDF ，从图1的位置沿x 轴的正方向以每秒1个单位的长度平移，移动的时间为t (s )，同时点P 从E 出发，以每秒2个单位的速度沿着折线ED -DF 运动(如图2所示)，当P 点到F 点停止，ΔDEF 也随之停止．①t =3或6(s )时，直线l 恰好经过等边ΔEDF 其中一条边的中点；②当点P 在线段DE 上运动，若DM =2PM ，求t 的值；③当点P 在线段DF 上运动时，若ΔPMN 的面积为3，求出t 的值．【分析】(1)把x =0，y =0分别代入y =-33x +43，即可求出点A 、B 的坐标，求出∠BAO =30°，根据直角三角形的性质，即可得出OD =12OA =6；(2)①当直线l 分别过DE 、DF 、EF 的中点，分三种情况进行讨论，得出t 的值，并注意点P 运动的最长时间；②分点P 在直线l 的下方和直线l 上方两种情况进行讨论，求出t 的值即可；③分点P 在DN 之间和点P 在NF 之间两种情况进行讨论，求出t 的值即可．【解答】解：(1)令x =0，则y =43，∴点B 的坐标为(0,43)，令y =0，则-33x +43=0，解得x =12，∴点A 的坐标为(12,0)，∵tan ∠BAO =OB OA=4312=33，∴∠BAO =30°，∵OD ⊥AB ，∴∠ODA =90°，∴ΔODA 为直角三角形，∴OD =12OA =6；(2)①当直线l 过DF 的中点G 时，∵ΔDEF 为等边三角形，∴∠DFE =60°，∵∠BAO =30°，∴∠FGA =60°-30°=30°，∴∠FGA =∠BAO ，∴FA =FG =12DF =3，∴OF =OA -FA =9，∴OE =OF -EF =9-6=3，∴t =3；当l 过DE 的中点时，∵DE ⊥l ，DG =EG ，∴直线l 为DE 的垂直平分线，∵ΔDEF 为等边三角形，∴此时点F 与点A 重合，∴t =12-61=6；当直线l 过EF 的中点时，运动时间为t =12-31=9；∵点P 从运动到停止用的时间为：6+62=6，∴此时不符合题意；综上所述，当t =3s 或6s 时，直线l 恰好经过等边ΔEDF 其中一条边的中点，故答案为：3或6；②∵OE =t ，AE =12-t ，∠BAO =30°，∴ME =6-t2，∴DM =DE -EM =t2，∵EP =2t ，∴PD =6-2t ，当P 在直线l 的下方时，∵DM =23DP ，∴t 2=23(6-2t )，解得：t =2411；当P 在直线l 的上方时，∵DM =2DP ，∴t2=2(6-2t )，解得t =83；综上所述：t 的值为2411或83；③当3<t ≤6时，∵∠D =60°，∠DMN =90°，DM =t2，∴∠DNM =90°-60°=30°，∴MN =DM ×tan60°=32t ，DN =2DM =2×t2=t ，∵DP =2t -6，∴PN =DN -DP =t -(2t -6)=6-t ，∵∠DNM =30°，∴边MN 的高h =12PN =3-12t ，∵ΔPMN 的面积为3，∴12×32t 3-12t =3，整理得：t 2-6t +8=0，解得t =2(舍)或t =4当点P 在NF 之间时，∵∠D =60°，∠DMN =90°，DM =t2，∴∠DNM =90°-60°=30°，∴MN =DM ×tan60°=32t ，DN =2DM =2×t2=t ，∵DP =2t -6，∴PN =DP -DN =2t -6-t =t -6，∵∠DNM =30°，∴∠FNA =∠DNM =30°，∴边MN 的高h =12PN =12t -3，∵ΔPMN 的面积为3，∴12×32t 12t -3 =3，解得t =3+17(舍)或t =3-17(舍)，综上所述，t 的值为4s ．【点评】本题主要考查了一次函数的性质、等边三角形的性质、直角三角形的性质、利用三角函数解直角三角形，熟练掌握含30°的直角三角形的性质并注意进行分类讨论是解题的关键．8(2023•武进区校级模拟)在平面直角坐标系xOy 中，对于任意两点P 1(x 1，y 1)与P 2(x 2，y 2)的“非常距离”，给出如下定义：若|x 1-x 2|≥|y 1-y 2|，则点P 1与点P 2的“非常距离”为|x 1-x 2|；若|x 1-x 2|<|y 1-y 2|，则点P 1与点P 2的“非常距离”为|y 1-y 2|．例如：点P 1(1,2)，点P 2(3,5)，因为|1-3|<|2-5|，所以点P 1与点P 2的“非常距离”为|2-5|=3，也就是图1中线段P 1Q 与线段P 2Q 长度的较大值(点Q 为垂直于y 轴的直线P 1Q 与垂直于x 轴的直线P 2Q 交点)．(1)已知点A -12，0，B 为y 轴上的一个动点，①若点A 与点B 的“非常距离”为2，写出一个满足条件的点B 的坐标；②直接写出点A 与点B 的“非常距离”的最小值；(2)已知C 是直线y =34x +3上的一个动点，①如图2，点D 的坐标是(0,1)，求点C 与点D 的“非常距离”的最小值及相应的点C 的坐标；②如图3，E 是以原点O 为圆心，1为半径的圆上的一个动点，求点C 与点E 的“非常距离”的最小值及相应的点E 与点C 的坐标．【分析】(1)①根据点B 位于y 轴上，可以设点B 的坐标为(0,y )．由“非常距离”的定义可以确定|0-y |=2，据此可以求得y 的值；②设点B 的坐标为(0,y )．因为-12-0 ≥|0-y |，所以点A 与点B 的“非常距离”最小值为-12-0 =12；(2)①设点C 的坐标为x 0，34x 0+3 ．根据材料“若|x 1-x 2|≥|y 1-y 2|，则点P 1与点P 2的“非常距离”为|x 1-x 2|”知，C 、D 两点的“非常距离”的最小值为-x 0=34x 0+2，据此可以求得点C 的坐标；②根据“非常距离”的定义，点E 在过原点且与直线y =34x +3垂直的直线上，且C 与E 的横纵坐标差相等时，点C 与点E 的“非常距离”取最小值，据此求出C 与E 的坐标及“非常距离”的最小值．【解答】解：(1)①∵B 为y 轴上的一个动点，∴设点B 的坐标为(0,y )．∵-12-0 =12≠2，∴|0-y |=2，解得，y =2或y =-2；∴点B 的坐标是(0,2)或(0,-2)；②点A 与点B 的“非常距离”的最小值为12．(2)①如图2，当点C 与点D 的“非常距离”取最小值时，需要根据运算定义“若|x 1-x 2|≥|y 1-y 2|，则点P 1与点P 2的“非常距离”为|x 1-x 2|”解答，此时|x 1-x 2|=|y 1-y 2|．即AC =AD ，∵C 是直线y =34x +3上的一个动点，点D 的坐标是(0,1)，∴设点C 的坐标为x 0，34x 0+3 ，∴-x 0=34x 0+2，此时，x 0=-87，∴点C 与点D 的“非常距离”的最小值为：|x 0|=87，此时C -87，157；②如图3，当点E 在过原点且与直线y =34x +3垂直的直线上，且CF =EF 时，点C 与点E 的“非常距离”最小，设E (x ,y )(点E 位于第二象限)．则y x=-43x 2+y 2=1 ，解得x =-35y =45，故E -35，45．设点C 的坐标为x 0，34x 0+3 ，-35-x 0=34x 0+3-45，解得x0=-8 5，则点C的坐标为-8 5，95，点C与点E的“非常距离”的最小值为1．【点评】本题考查了一次函数综合题．对于信息给予题，一定要弄清楚题干中的已知条件．本题中的“非常距离”的定义是正确解题的关键．9(2023•海安市一模)对于平面直角坐标系xOy中的图形W和点P，给出如下定义：F为图形W上任意一点，将P，F两点间距离的最小值记为m，最大值记为M，称M与m的差为点P到图形W的“差距离”，记作d(P,W)，即d(P,W)=M-m，已知点A(2,1)，B(-2,1)(1)求d(O,AB)；(2)点C为直线y=-1上的一个动点，当d(C,AB)=1时，点C的横坐标是　(2-5)或(5-2，)　；(3)点D为函数y=x+b(-2≤x≤2)图象上的任意一点，当d(D,AB)≤2时，直接写出b的取值范围．【分析】(1)画出图形，根据点P到图形W的“差距离”的定义即可解决问题．(2)如图2中，设C(m,-1)．由此构建方程即可解决问题．(3)如图3中，取特殊位置当b=6时，当b=-4时，分别求解即可解决问题．【解答】解：(1)如图1中，∵A(2,1)，B(-2,1)，∴AB⎳x轴，∴点O到线段AB的最小距离为1，最大距离为5，∴d(O,AB)=5-1．(2)如图2中，设C(m,-1)．当点C在y轴的左侧时，由题意AC-2=1，∴AC=3，∴(2-m)2+22=9，∴m=2-5或2+5(舍弃)，∴C(2-5，-1)，当点C在y轴的右侧时，同法可得C(5-2，-1)，综上所述，满足条件的点C的坐标为(2-5，-1)或(5-2，-1)．故答案为：(2-5，-1)或(5-2，-1)．(3)如图3中，当b=6时，线段EF:y=x+6(-2≤x≤2)上任意一点D，满足d(D,AB)≤2，当b=-4时，线段E′F′:y=x-4(-2≤x≤2)上任意一点D′，满足d(D′,AB)≤2，观察图象可知：当b≥6或b≤-4时，函数y=x+b(-2≤x≤2)图象上的任意一点，满足d(D,AB)≤2．【点评】本题属于一次函数综合题，考查了一次函数的性质，点P到图形W的“差距离”的定义等知识，解题的关键是理解题意，学会利用参数解决问题，学会寻找特殊位置解决问题，属于中考创新题型．10(2022•姑苏区校级模拟)平面直角坐标系xOy中，对于任意的三个点A、B、C，给出如下定义：若矩形的任何一条边均与某条坐标轴平行，且A，B，C三点都在矩形的内部或边界上，则称该矩形为点A，B，C的“三点矩形”．在点A，B，C的所有“三点矩形”中，若存在面积最小的矩形，则称该矩形为点A，B，C的“最佳三点矩形”．如图1，矩形DEFG，矩形IJCH都是点A，B，C的“三点矩形”，矩形IJCH是点A，B，C的“最佳三点矩形”．如图2，已知M(4,1)，N(-2,3)，点P(m,n)．(1)①若m=2，n=4，则点M，N，P的“最佳三点矩形”的周长为18，面积为；②若m=2，点M，N，P的“最佳三点矩形”的面积为24，求n的值；(2)若点P在直线y=-2x+5上．①求点M，N，P的“最佳三点矩形”面积的最小值及此时m的取值范围；②当点M，N，P的“最佳三点矩形”为正方形时，求点P的坐标；(3)若点P(m,n)在抛物线y=ax2+bx+c上，当且仅当点M，N，P的“最佳三点矩形”面积为12时，-2≤m≤-1或1≤m≤3，直接写出抛物线的解析式．【分析】(1)①利用“最佳三点矩形”的定义求解即可，②利用“最佳三点矩形”的定义求解即可；(2)①利用“最佳三点矩形”的定义求得面积的最小值为12，②由“最佳三点矩形”的定义求得正方形的边长为6，分别将y=7，y=-3代入y=-2x+5，可得x分别为-1，5，点P的坐标为(-1,7)或(4,-3)；(3)利用“最佳三点矩形”的定义画出图形，可分别求得解析式．【解答】解：(1)①如图，画出点M，N，P的“最佳三点矩形”，可知矩形的周长为6+6+3+3=18，面积为3×6=18；故答案为：18，18．②∵M(4,1)，N(-2,3)，∴|x M-x N|=6，|y M-y N|=2．又∵m=2，点M，N，P的“最佳三点矩形”的面积为24．∴此矩形的邻边长分别为6，4．∴n=-1或5．(2)如图，①由图象可得，点M，N，P的“最佳三点矩形”面积的最小值为12；分别将y=3，y=1代入y=-2x+5，可得x分别为1，2；结合图象可知：1≤m≤2；②当点M，N，P的“最佳三点矩形”为正方形时，边长为6，分别将y=7，y=-3代入y=-2x+5，可得x分别为-1，4；∴点P的坐标为(-1,7)或(4,-3)；(3)设抛物线的解析式为y=ax2+bx+c，经过点(-1,1)，(1,1)，(3,3)，∴a -b +c =1a +b +c =19a +3b +c =3，a =14b =0c =34，∴y =14x 2+34，同理抛物线经过点(-1,3)，(1,3)，(3,1)，可求得抛物线的解析式为y =-14x 2+134，∴抛物线的解析式y =14x 2+34或y =-14x 2+134．【点评】本题主要考查了一次函数的综合题，涉及点的坐标，正方形及矩形的面积及待定系数法求函数解析式等知识，解题的关键是理解运用好“最佳三点矩形”的定义．11(2022•太仓市模拟)如图①，动点P 从矩形ABCD 的顶点A 出发，以v 1的速度沿折线A -B -C 向终点C 运动；同时，一动点Q 从点D 出发，以v 2的速度沿DC 向终点C 运动，当一个点到达终点时，另一个点也停止运动．点E 为CD 的中点，连接PE ，PQ ，记ΔEPQ 的面积为S ，点P 运动的时间为t ，其函数图象为折线MN -NF 和曲线FG (图②)，已知，ON =3，NH =1，点G 的坐标为(6,0)．(1)点P 与点Q 的速度之比v 1v 2的值为　32　；AB :AD 的值为；(2)如果OM =2．①求线段NF 所在直线的函数表达式；②是否存在某个时刻t ，使得S ≥23？若存在，求出t 的取值范围；若不存在，请说明理由．【分析】(1)由函数图象可知t =3时，Q 与E 重合，t =4时，P 与B 重合，t =6时，P 与C 重合，则Q 的速度v 2=DE 3，P 的速度v 1=AB4，从而得出答案；(2)①当t =0时，P 与A 重合，Q 与D 重合，此时S ΔADE =2，可得AD =BC =DE =2，AB =CD =2AD =4，从而得出点P 与Q 的速度，即可得出点F 的坐标，利用待定系数法可得答案；②利用待定系数法求出直线MN 的函数解析式，当S =23时，可得t 的值，根据图象可得答案．【解答】解：(1)∵ON =3，NH =1，G (6,0)，∴N (3,0)，H (4,0)，由图象可知：t =3时，Q 与E 重合，t =4时，P 与B 重合，t =6时，P 与C 重合，∴Q 的速度v 2=DE 3，P 的速度v 1=AB4，∵四边形ABCD 是矩形，∴AB =CD ，AD =BC ，∵E 为CD 的中点，∴DE =12CD =12AB ，∴v 1v 2=AB4DE 3=AB 4⋅3DE =AB 4⋅312AB =32，∵P 从A 到B 用了4秒，从B 到C 用了2秒，∴AB =4v 1，BC =2v 1，∴AB =2BC ，∴AB :AD 的值为2，故答案为：32,2；(2)①∵OM =2，∴M (0,2)，由题知，t =0时，P 与A 重合，Q 与D 重合，∴S ΔEPQ =12AD ⋅DE =2，∵AB :AD =2，∴AD =DE =12AB ，∴12AD 2=2，∴AD =BC =DE =2，AB =CD =2AD =4，∴v 2=DE 3=23，当t =4时，DQ =v 2t =23×4=83，∴QE =DQ -DE =83-2=23，此时P 与B 重合，∴S ΔEPQ =12EQ ⋅BC =12×23×2=33，∴F 4,23，设直线NF 的解析式为S =kx +b (k ≠0)，将N (3,0)与F 4,23 代入得：3k +b =04k +b =23 ，∴k =23b =-2，∴线段NF 所在直线的函数表达式为S =23x -2(3<x ≤4)；②存在，分情况讨论如下：当Q 在DE 上，P 在AB 上时，∵直线MN 经过点M (0,2)，N (3,0)，同理求得直线MN 的解析式为S =-23x +2(0≤x ≤3)，当s =23时，-23x +2=2，∴x =2，∵s随x的增大而减小，∴当0≤x≤2时，S≥23，当Q在CE上，P在AB上时，直线NF的解析式为S=23x-2(3<x≤4)，由F4,2 3知：当x=4时，S=23，当Q在CE上，P在BC上时，SΔEPQ=12EQ⋅CP，∵DQ=v2t=23t，∴EQ=DQ-DE=23t-2，∵v1=AB4=44=1，∴AB+BP=v1t=t，∵AB+BC=4+2=6，∴CP=6-t，∴S=1223t-2(6-t)=-13t2+3t-6(4<x≤6)，当S=23时，-13t2+3t-6=23，∴t=4或5，由图象知：当4<x≤5时，S≥2 3，综上，S≥23时，x的取值范围为0≤x≤2或4≤x≤5．【点评】本题是一次函数综合题，主要考查了待定系数法求函数解析式，三角形的面积，矩形的性质等知识，理解函数图象中每一个拐点的意义是解题的关键．12(2022•邗江区校级一模)在平面直角坐标系xOy中，对于点P和线段ST，我们定义点P关于线段ST的线段比k=PSST(PS<PT)PTST(PS≥PT) ．(1)已知点A(0,1)，B(1,0)．①点Q(2,0)关于线段AB的线段比k=　22　；②点C(0,c)关于线段AB的线段比k=2，求c的值．(2)已知点M(m,0)，点N(m+2,0)，直线y=x+2与坐标轴分别交于E，F两点，若线段EF上存在点使得这一点关于线段MN的线段比k≤14，直接写出m的取值范围．【分析】(1)①求出QA、QB、AB，根据线段比定义即可得到答案；②方法同①，分c>0和c≤0讨论；(2)分两种情况，画出图象，根据线段比定义，分别在M(N)为“临界点”时列出不等式，即可得到答案．【解答】解：(1)①∵A(0,1)，B(1,0)，Q(2,0)，∴AB=2，QA=5，QB=1，根据线段比定义点Q(2,0)关于线段AB的线段比k=QBAB=22；故答案为：22；②∵A (0,1)，B (1,0)，C (0,c )，∴AB =2，AC =|1-c |，BC =1+c 2，AC 2=1+c 2-2c ，BC 2=1+c 2，当c >0时，AC 2<BC 2，即AC <BC ，由C (0,c )关于线段AB 的线段比k =2可得：|1-c |2=2，解得c =3或c =-1(舍去)，∴c =3，当c ≤0时，AC 2≥BC 2，即AC ≥BC ，由C (0,c )关于线段AB 的线段比k =2可得：1+c 22=2，解得c =3(舍去)或c =-3，∴c =-3，综上所述，点C (0,c )关于线段AB 的线段比k =2，c =3或c =-3；(2)∵直线y =x +2与坐标轴分别交于E ，F 两点，∴E (-2,0)，F (0,2)，∵点M (m ,0)，点N (m +2,0)，∴MN =2，N 在M 右边2个单位，当线段EF 上的点到N 距离较小时，分两种情况：①当M 、N 在点E 左侧时，如图：线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14，∴NE MN≤14，即-2-(m +2)2≤14，解得：m ≥-92，②当N 在E 右侧，M 在E 左侧时，过M 作MG ⊥EF 于G ，如图：线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14，∴GM MN ≤14，即GM 2≤14，∴GM ≤12，而E (-2,0)，F (0,2)，∴∠FEO =45°，∴ΔHEM 时等腰直角三角形，∴GM =22EM ，∴22EM ≤12，即22[(m +2)-(-2)]≤12，解得m ≤-4+22，∴线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14，线段EF 上的点到N 距离较小时，-92≤m ≤-4+22，当线段EF 上的点到M 距离较小时，也分两种情况：①当N 在E 右侧，M 在E 左侧时，如图：线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14，∴ME MN≤14，即-2-m 2≤14，解得m ≥-52，②当M 、N 在点E 右侧时，过M 作MH ⊥EF 于H ，如图：线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14，∴HM MN ≤14，即HM 2≤14，∴HM ≤12，而E (-2,0)，F (0,2)，∴∠FEO =45°，∴ΔHEM 时等腰直角三角形，∴HM =22EM ，∴22EM ≤12，即22[m -(-2)]≤12，解得：m ≤-2+22，∴线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14，线段EF 上的点到M 距离较小时，-52≤m ≤-2+22，综上所述，线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14，则-92≤m ≤-4+22或-52≤m ≤-2+22．【点评】本题考查一次函数应用，解题的关键是读懂线段比的定义，找出“临界点”列不等式．13(2022•泰州)定义：对于一次函数y 1=ax +b 、y 2=cx +d ，我们称函数y =m (ax +b )+n (cx +d )(ma +nc ≠0)为函数y 1、y 2的“组合函数”．(1)若m =3，n =1，试判断函数y =5x +2是否为函数y 1=x +1、y 2=2x -1的“组合函数”，并说明理由；(2)设函数y 1=x -p -2与y 2=-x +3p 的图像相交于点P ．①若m +n >1，点P 在函数y 1、y 2的“组合函数”图像的上方，求p 的取值范围；②若p ≠1，函数y 1、y 2的“组合函数”图像经过点P ．是否存在大小确定的m 值，对于不等于1的任意实数p ，都有“组合函数”图像与x 轴交点Q 的位置不变？若存在，请求出m 的值及此时点Q 的坐标；若不存在，请说明理由．【分析】(1)由y =5x +2=3(x +1)+(2x -1)，可知函数y =5x +2是函数y 1=x +1、y 2=2x -1的“组合函数”；(2)①由y =x -p -2y =-x +3p得P (2p +1,p -1)，当x =2p +1时，y =m (2p +1-p -2)+n (-2p -1+3p )=(p-1)(m +n )，根据点P 在函数y 1、y 2的“组合函数”图象的上方，有p -1>(p -1)(m +n )，而m +n >1，可得p <1；②由函数y 1、y 2的“组合函数” y =m (x -p -2)+n (-x +3p )图象经过点P ，知p -1=m (2p +1-p -2)+n (-2p -1+3p )，即(p -1)(1-m -n )=0，而p ≠1，即得n =1-m ，可得y =(2m -1)x +3p -(4p +2)m ，令y =0得(2m -1)x +3p -(4p +2)m =0，即(3-4m )p +(2m -1)x -2m =0，即可得m =34时，“组合函数”图象与x 轴交点Q 的位置不变，Q (3,0)．【解答】解：(1)函数y =5x +2是函数y 1=x +1、y 2=2x -1的“组合函数”，理由如下：∵3(x +1)+(2x -1)=3x +3+2x -1=5x +2，∴y =5x +2=3(x +1)+(2x -1)，∴函数y =5x +2是函数y 1=x +1、y 2=2x -1的“组合函数”；(2)①由y =x -p -2y =-x +3p得x =2p +1y =p -1 ，∴P (2p +1,p -1)，∵y 1、y 2的“组合函数”为y =m (x -p -2)+n (-x +3p )，∴x =2p +1时，y =m (2p +1-p -2)+n (-2p -1+3p )=(p -1)(m +n )，∵点P 在函数y 1、y 2的“组合函数”图象的上方，∴p -1>(p -1)(m +n )，∴(p -1)(1-m -n )>0，∵m +n >1，∴1-m -n <0，∴p -1<0，∴p <1；②存在m =34时，对于不等于1的任意实数p ，都有“组合函数”图象与x 轴交点Q 的位置不变，Q (3,0)，理由如下：由①知，P (2p +1,p -1)，∵函数y 1、y 2的“组合函数”y =m (x -p -2)+n (-x +3p )图象经过点P ，∴p -1=m (2p +1-p -2)+n (-2p -1+3p )，∴(p -1)(1-m -n )=0，∵p ≠1，∴1-m -n =0，有n =1-m ，∴y =m (x -p -2)+n (-x +3p )=m (x -p -2)+(1-m )(-x +3p )=(2m -1)x +3p -(4p +2)m ，令y =0得(2m -1)x +3p -(4p +2)m =0，变形整理得：(3-4m )p +(2m -1)x -2m =0，∴当3-4m =0，即m =34时，12x -32=0，∴x =3，∴m =34时，“组合函数”图象与x 轴交点Q 的位置不变，Q (3,0)．【点评】本题考查一次函数综合应用，涉及新定义，函数图象上点坐标的特征，一次函数与一次方程的关系等，解题的关键是读懂“组合函数“的定义．14(2024•钟楼区校级模拟)在同一平面内，具有一条公共边且不完全重合的两个全等三角形，我们称这两个三角形叫做“共边全等”．(1)下列图形中两个三角形不是“共边全等”是③；AB，点E、F分别在AC、BC边(2)如图1，在边长为6的等边三角形ABC中，点D在AB边上，且AD=13上，满足ΔBDF和ΔEDF为“共边全等”，求CF的长；(3)如图2，在平面直角坐标系中，直线y=-3x+12分别与直线y=x、x轴相交于A、B两点，点C是OB 的中点，P、Q在ΔAOB的边上，当以P、B、Q为顶点的三角形与ΔPCB“共边全等”时，请直接写出点Q 的坐标．【分析】(1)由于第③个图不符合共边要求，所以图③即为答案；(2)DF为两个全等三角形的公共边，由于F点在BC边上，E在AC边上，两个三角形的位置可以如图②，在公共边异侧，构成一个轴对称图形，也可以构成一个平行四边形(将图③的两条最长边重合形成)，分两类讨论，画出图形，按照图②构图，会得到一个一线三等角模型，利用相似，列出方程来解决，按照平行四边形构图，直接得到ΔADE为等边三角形，计算边长即可求得；(3)由题目要求，可以知道两个全等三角形的公共边为PB边，由于要构成ΔPCB，所以P点只能在OA和OB边上，当P在OA边上，两个三角形可以在PB同侧，也可以在PB异侧，当在PB异侧构图时，可以得到图3和图4，在图3中，当在PB同侧构图时，可以得到图6，当P在OB边上时，Q只能落在OA上，得到图7，利用已知条件，解三角形，即可求出Q点坐标．【解答】解：(1)①②均符合共边全等的特点，只有③，没有公共边，所以③不符合条件，∴答案是③；(2)①如图1，当ΔBDF≅ΔEFD，且是共边全等时，∠BFD=∠EDF，∴DE⎳BC，∵ΔABC是等边三角形，∴ΔADE是等边三角形，AB=2，∵AD=13∴DE=AE=BF=2，∴CF=BC-BF=4，②如图2，当ΔBDF≅ΔEDF，且是共边全等时，BD=DE=6-AD=4，∠DEF=∠B=60°，EF=BF，∴∠AED+∠FEC=120°，又∠AED+∠EDA=120°，。

初三中考数学函数综合题含答案

初三中考数学函数综合题含答案一、单选题1．已知点A （1，y 1），B （2，y 2）在抛物线y =（x +1）2+2上，则下列结论正确的是（）． A ．122y y >> B ．212y y >> C ．122y y >>D ．212y y >>2．抛物线y ＝14（x ﹣6）2+3的顶点坐标是（）A ．（6，﹣3）B ．（6，3）C ．（﹣6，3）D ．（﹣6，﹣3） 3．抛物线y =2（x -1）2-3的顶点坐标是（） A ．()1,3-- B ．()1,3- C ．()1,3- D ．()1,3 4．一次函数y ＝－2x ＋5的图像不经过的象限是（）A ．一B ．二C ．三D ．四 5．将函数y ＝2x 的图象向上平移4个单位后，下列各点在平移后的图象上的是（） A ．()1,5 B ．()0,4 C ．()1,3- D ．()2,3- 6．在直角坐标系的x 轴的负半轴上，则点P 坐标为（）A ．()4,0-B ．()0,4C ．()0,3-D ．()1,0 7．直线7y x =--一定不经过（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限8．下列各点中，在反比例函数2y x=-图象上的是-（）A ．(21)，B ．233⎛⎫⎪⎝⎭， C ．(21)--， D ．(12)-，9．已知点()11,A x y ，()22,B x y 在直线()0y kx b k =+≠上，当12x x <时，12y y >，且0kb <，则直线()0y kx b k =+≠在平面直角坐标系中的图象大致是（）A ．B ．C ．D ．10．下列一次函数中，y 随x 的增大而减小的是（） A ．y ＝x ﹣3 B ．y ＝1﹣x C ．y ＝2x D ．y ＝3x +2 11．下列二次函数中，对称轴是直线1x =的是（）A ．21y x =+B ．()221y x =+C ．()21y x =-+D ．()231y x =--12．反比例函数y ＝2x的图象位于（）A ．第一、三象限B ．第二、三象限C ．第一、二象限D ．第二、四象限13．如图，△ABC 中，点B ，C 是x 轴上的点，且A （3，2），以原点O 为位似中心，作△ABC 的位似图形△A ′B ′C ′，且△ABC 与A ′B ′C ′的相似比是1：2，则点A ′的坐标是（）A ．（﹣6，﹣4）B ．（﹣1.5，﹣1）C ．（1.5，1）或（﹣1.5，﹣1）D ．（6，4）或（﹣6，﹣4）14．已知点P （a ，a ﹣1）在平面直角坐标系的第四象限，则a 的取值范围在数轴上可表示为（） A ．B ．C ．D ．15．要得到抛物线()2321y x =-++可以将抛物线232y x =-+（） A ．先向右平移2个单位，再向上平移1个单位 B ．先向右平移2个单位，再向下平移1个单位C ．先向左平移2个单位，再向上平移1个单位D ．先向左平移2个单位，再向下平移1个单位二、填空题16．已知点(),P m n 在一次函数1y x =+的图象上，则n m -=______．17．已知某函数图像过点（－1，1），写出一个符合条件的函数表达式：______．18．将一次函数123=+y x 向上平移5个单位长度后得到直线AB ，则平移后直线AB 对应的函数表达式为______．19．将抛物线22(3)y x m =-+向右平移3个单位，再向上平移1个单位后恰好经过点(2,3)，则m 值是 __．20．若抛物线y =x 2+bx +经过点A （0，5），B （4，5），则其对称轴是直线______三、解答题21．已知抛物线y ＝－（x －m ）2＋1与x 轴的交点为A ，B （B 在A 的右边），与y 轴的交点为C ．(1)写出m ＝1时与抛物线有关的三个正确结论．(2)当点B 在原点的右边，点C 在原点的下方时，是否存在△BOC 为等腰三角形的情形？若存在，求出m 的值；若不存在，请说明理由． (3)请你提出两个对任意的m 值都能成立的正确命题．22．在平面直角坐标系xOy 中，点()11,A x y ，()22,B x y 在抛物线()2210y ax ax a =-+>上，其中12x x < (1)求抛物线的对称轴；(2)若122x x a +=-，比较1y 与2y 的大小关系，并说明理由．23．如图，在平面直角坐标系中，二次函数243y ax x =+-图象的顶点是A ，与x 轴交于B ，C 两点，与y 轴交于点D ．点B 的坐标是()1,0．(1)求A ，C 两点的坐标，并根据图象直接写出当0y >时x 的取值范围；(2)将图象向上平移m 个单位后，二次函数图象与x 轴交于E ，F 两点，若6EF =，求m 的值．24．一抛物线以()1,9-为顶点，且经过x 轴上一点()4,0-，求该抛物线解析式及抛物线与y 轴交点坐标．25．已知抛物线y ＝（x ﹣1）2+k 与y 轴相交于点A (0，﹣3)，点P 为抛物线上的一点． (1)求此抛物线的解析式；(2)若点P 的横坐标为2，则点P 到x 轴的距离为．【参考答案】一、单选题 1．D 2．B 3．C 4．C 5．B 6．A 7．A 8．D 9．C 10．B 11．D 12．A 13．D 14．C 15．D 二、填空题 16．117．y ＝-x （答案不唯一） 18．y =13x +719．-3020．2x = 三、解答题21．(1)抛物线的对称轴为直线x =1，抛物线与x 轴的两个交点为（0，0），（2，0），抛物线开口向下 (2)存在，2(3)无论m 为何值，函数的始终有最大值1；无论m 为何值，函数始终与x 轴有两个不同的交点【解析】【分析】（1）当m =1时，y =-（x -1）2+1，根据()2y a x h k =-+的性质写出三个结论即可；（2）求得C （0，1-m 2），根据点B 在原点的右边，点C 在原点的下方，可得m ＞1，根据等腰三角形的性质可得1+m =m 2-1，解方程求解即可；（3）根据()2y a x h k =-+的性质，可知无论m 为何值，函数的始终有最大值1；无论m为何值，函数始终与x 轴有两个不同的交点． (1)解：当m =1时，y =-（x -1）2+1， ∴抛物线的对称轴为直线x =1，令0y =，-（x -1）2+1=0，解得120,2x x ==，抛物线与x 轴的两个交点为（0，0），（2，0），抛物线开口向下； (2)存在，理由如下：令x =0，则y =1-m 2， ∴C （0，1-m 2），令y =0，则x =1+m 或x =m -1， ∴B （1+m ，0），∵点B 在原点的右边，点C 在原点的下方， ∴1+m ＞0，1-m 2＜0， ∴m ＞1，∵△BOC 为等腰三角形， ∴1+m =m 2-1，解得m =2或m =-1（舍）， ∴m =2； (3)无论m 为何值，函数始终有最大值1；无论m 为何值，函数始终与x 轴有两个不同的交点．【点睛】本题考查了()2y a x h k =-+的性质，等腰三角形的性质，解一元二次方程，二次函数与坐标轴交点问题，掌握()2y a x h k =-+的性质是解题的关键． 22．(1)直线1x = (2)12y y >，见解析【解析】【分析】（1）将解析式整理成顶点式，直接写出对称轴；（2）方法一：利用作差法，将12y y -表示出来，再进行判断正负，据此判断大小即可；方法二：判断12,y y 距离对称轴的大小，根据函数增减性判断． (1)解：∵()222111y ax ax a x a =-+=--+， ∴抛物线的对称轴为直线1x = (2)方法一：()()221211222121y y ax ax ax ax -=-+--+，()()22122122ax ax ax ax =-+-，()()12122a x x x x =-+-， ()212a x x =--，∵0a >，12x x <， ∴120y y ->，即12y y >，方法二：∵0a >，122x x a +=-， ∴122x x +<， ∴1212x x +<，又∵抛物线对称轴是直线1x =，开口向上，且12x x <， ∴1211x x ->-， ∴12y y >．【点睛】本题主要考查二次函数中系数的运用，以及比较函数值的大小，熟练掌握二次函数的基础运算是解题的关键．23．(1)(2,1)A ，(3,0)C ，当0y >时，13x <<． (2)8m = 【解析】【分析】（1）利用待定系数法求出a ，再求出点C 的坐标即可解决问题．（2）由题意得抛物线的解析式为243y x x m =-+-+，设二次函数图象与x 轴交于1(E x ，0)，2(F x ，0)两点，则124x x +=，123x x m =-，由12|6|x x -=可得出答案．(1)解：把(1,0)B 代入243y ax x =+-，得043a =+-，解得1a =-，2243(2)1y x x x ∴=-+-=--+，)1(2,A ∴，对称轴为直线2x =，B ，C 关于2x =对称，(3,0)C ∴，∴当0y >时，13x <<．(2)解：抛物线向上平移m 个单位，可得抛物线的解析式为243y x x m =-+-+，设二次函数图象与x 轴交于1(E x ，0)，2(F x ，0)两点，则124x x +=，123x x m =-，12||6x x ∴-=，212()36x x ∴-=，21212()436x x x x ∴+-=，164(3)36m ∴-⨯-=，8m ∴=．【点睛】本题考查了抛物线与x 轴的交点，二次函数的性质和二次函数图象上点的坐标特征，解决问题的关键是能够把二次函数的一般形式化为顶点式． 24．y =﹣x 2-2x ＋8；抛物线与y 轴交点为()0,8 【解析】【分析】知道顶点和抛物线上一点，可以用抛物线的顶点式求答；【详解】解：设抛物线解析式为()2y a x h k =-+，依题意1h =-，9k =，将()4,0-代入()219y a x =++中，得099a =+，解得1a =-，∴抛物线解析式为()219y x =-++，即y =﹣x 2-2x ＋8；令0x =，则8y =，∴抛物线与y 轴交点为()0,8．【点睛】本题考查待定系数法求二次函数的解析式；在知道顶点坐标的时候，利用顶点式求二次函数解析式十分方便． 25．(1)223y x x =-- (2)3 【解析】【分析】（1）把点A (0，﹣3)，代入抛物线解析式，即可求解；（2）根据抛物线()214y x =--的对称轴为直线1x =，可得点P 和点A (0，﹣3)关于直线1x =对称，从而得到点的纵坐标为-3，即可求解．(1)解：∵抛物线y ＝（x ﹣1）2+k 与y 轴相交于点A (0，﹣3)， ∴()2301k -=-+，解得：4k =-，∴此抛物线的解析式为()221423y x x x =--=--； (2)解：∵抛物线()214y x =--的对称轴为直线1x =， ∴点P 和点A (0，﹣3)关于直线1x =对称， ∴点的纵坐标为-3， ∴点P 到x 轴的距离为3．【点睛】本题主要考查了求二次函数的解析式，利用抛物线的对称性求函数值，熟练掌握利用待定系数法求函数解析式的步骤是解题的关键．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

中考数学专题训练函数综合题专题1．如图，一次函数b kx y +=与反比例函数x y 4=的图像交于A 、B 两点，其中点A 的横坐标为1，又一次函数b kx y +=的图像与x 轴交于点()0,3-C . （1）求一次函数的解析式；（2）求点B 的坐标.2．已知一次函数y=（1-2x ）m+x+3图像不经过第四象限，且函数值y 随自变量x 的减小而减小。

（1）求m 的取值范围；（2）又如果该一次函数的图像与坐标轴围成的三角形面积是4.5 ，求这个一次函数的解析式。

3. 如图，在平面直角坐标系中，点O 为原点，已知点A 的坐标为（2，2），点B 、C 在x 轴上，BC =8，AB=AC ，直线AC 与y 轴相交于点D ．（1）求点C 、D 的坐标；（2）求图象经过B 、D 、A 三点的二次函数解析式及它的顶点坐标．4．如图四，已知二次函数223y ax ax =-+的图像与x 轴交于点A ，点By C 点为D ，直线DC 的函数关系式为y kx b =+，又tan 1OBC∠=．（1）求二次函数的解析式和直线DC 的函数关系式；（2）求ABC △的面积．（图四）5．已知在直角坐标系中，点A 的坐标是（-3，1），将线段OA 绕着点O 顺时针旋转90°得到OB . (1)求点B 的坐标； (2)求过A 、B 、O 三点的抛物线的解析式； (3)设点B 关于抛物线的对称轴的对称点为C ，求△ABC 的面积。

6．如图，双曲线x y 5=在第一象限的一支上有一点C （1，5），过点C 的直线)0(>+-=k b kx y 与x轴交于点A （a ，0）、与y 轴交于点B .(1)求点A 的横坐标a 与k 之间的函数关系式；(2)当该直线与双曲线在第一象限的另一交点D 的横坐标是9时，求△COD 的面积.7．在直角坐标系中，把点A （－1，a ）（a 为常数）向右平移4个单位得到点A '，经过点A 、A '的抛物线2y ax bx c =++与y 轴的交点的纵坐标为2．（1）求这条抛物线的解析式；（2）设该抛物线的顶点为点P ，点B为)1m ，（，且3<m ，若△ABP 是等腰三角形，求点B的坐标。

8．在直角坐标平面内，O 为原点，二次函数2y x bx c =-++的图像经过A （-1，0）和点B （0，3），顶点为P 。

（1）求二次函数的解析式及点P 的坐标；（2）如果点Q 是x 轴上一点，以点A 、P 、Q 为顶点的三角形是直角三角形，求点Q 的坐标。

x图79．如图，在平面直角坐标系xOy 中，抛物线212y xbx c=-++经过点(1,3)A ，(0,1)B ．（1）求抛物线的表达式及其顶点坐标；（2）过点A 作x 轴的平行线交抛物线于另一点C ， ①求△ABC 的面积；②在y 轴上取一点P ，使△ABP 与△ABC 相似，求满足条件的所有P 点坐标．10．在平面直角坐标系xOy 中，将抛物线22y x =沿y 轴向上平移位，平移后抛物线的顶点坐标记作A ，直线3x =与平移后的抛物线相交于B ，与直线OA 相交于C ．（1）求△ABC 面积；（2）点P 在平移后抛物线的对称轴上，如果△ABP 与△ABC 相似，求所有满足条件的P 点坐标．11．如图，直线OA 与反比例函数的图像交于点A(3，3)，向下平移直线OA ，与反比例函数的图像交于点B(6，m)与y 轴交于点C ．（1）求直线BC 的解析式；（2）求经过A 、B 、C （3）设经过A 、B 、C 三点的二次函数图像的顶点为D ，对称轴与x 数的对称轴上是否存在一点P ，使以O 、E 、P 为顶点的三角形与△BCD 坐标；若不存在，请说明理由．图8（图16）12．二次函数图像过A （2，1）B （0，1）和C （1，-1）三点。

（1）求该二次函数的解析式；（2）该二次函数图像向下平移4个单位，向左平移2个单位后，原二次函数图像上的A 、B 两点相应平移到A 1、B 1处，求∠BB 1A 1的余弦值。

13．如图，在直角坐标系中，直线421+=x y 与x 轴、y 轴分别交于A 、B 两点，过点A 作CA ⊥AB ，CA ＝52,并且作CD ⊥x 轴. (1) 求证:△ADC ∽△BOA (2) 若抛物线c bx x y ++-=2经过B 、C 两点. ①求抛物线的解析式； ②该抛物线的顶点为P ，M 是坐标轴上的一个点，若直线PM 与y 轴的夹角为30°，请直接写出点M 的坐标.14．如图，已知二次函数y =ax 2-2ax +3（a <0）的图像与x 轴的负半轴交于点A ，与y 轴的正半轴交于点B ，顶点为P ，且OB =3OA ，一次函数y =kx +b 的图像经过点A 、点B ．（1）求一次函数的解析式；（2）求顶点P 的坐标；（3）平移直线AB 使其过点P ，如果点M 在平移后的直线上，且tan ∠OAM =23，求点M 的坐标．15．如图16，在平面直角坐标中，四边形OABC 是等腰梯形，CB∥OA，OA=7，AB=4，∠COA=60°，点P 为x 轴上的—个动点，但是点P 不与点0、点A 重合．连结CP ， D 点是线段AB 上一点，连结PD. (1)求点B 的坐标；(2)当∠C PD=∠OAB，且ABBD =85，求这时点P 的坐标.B AB O x y P （第15题图）16. 如图，二次函数c bx x y ++-=241的图像经过点()()4,4,0,4--B A，且与y 轴交于点C .（1）试求此二次函数的解析式；（2）试证明：CAO BAO ∠=∠（其中O 是原点）；（3）若P 是线段AB 上的一个动点（不与A 、B 重合），过P 作y 轴的平行线，分别交此二次函数图像及x 轴于Q 、H 两点，试问：是否存在这样的点P ，使QH PH 2=？若存在，请求出点P的坐标；若不存在，请说明理由.17．如图，在平面直角坐标系中，矩形ABOC 的边BO 在x 轴正半轴上，边CO 在y 轴的正半轴上，且322==OB AB ，，矩形ABOC 绕点O 逆时针旋转后得到矩形EFOD ，且点A 落在y 轴上的E 点，点B 的对应点为点F ，点C 的对应点为点D . (1)求F 、E 、D 三点的坐标；（2）若抛物线c bx ax y ++=2经过点F 、E 、D ，求此抛物线的解析式；（3）在x 轴上方的抛物线上求点Q 的坐标，使得三角形QOB 的面积等于矩形ABOC 的面积？18．如图，在平面直角坐标系xOy 中，O 为原点，点A 、C 的坐标分别为（2，0）、（1，33）. 将△AOC 绕AC 的中点旋转180°，点O 落到点B 的位置，抛物线x ax y 322-=经过点A ，点D 是该抛物线的顶点.（1）求证：四边形ABCO 是平行四边形；（2）求a 的值并说明点B 在抛物线上；（3）若点P 是线段OA 上一点，且∠APD=∠OAB ，求点P 的坐标；(4) 若点P 是x 轴上一点，以P 、A 、D 为顶点作平行四边形，该平行四边形的另一顶点在y 轴上，写出点P 的坐标.BCA xyOABCDEFx y O19．已知，矩形OABC 在平面直角坐标系中位置如图所示，A 的坐标)0,4(，C 的坐标)20(-，，直线xy 32-=与边BC 相交于点D ，(1)求点D 的坐标；(2)抛物线c bx ax y++=2经过点A 、D 、O ，求此抛物线的表达式；(3)在这个抛物线上是否存在点M ，使O 、D 、A 、M 为顶点的四边形是梯形？若存在，请求出所有符合条件的点 M20．如图，在平面直角坐标系中，直线343+-=x y 分别与x 轴、y 轴交于点A 和点B ．二次函数c ax ax y +-=42的图象经过点B 和点C （-1，0），顶点为P .（1）求这个二次函数的解析式，并求出P 点坐标；（2）若点D 在二次函数图象的对称轴上，且AD ∥BP ，求PD 的长；x32-参考答案1、解：（1）由点A 在反比例函数图像上，则414==y ，—（1分）又点()4,1A 与()0,3-C 在一次函数图像上，则⎩⎨⎧+-=+=b k bk 304，—（2分）解得⎩⎨⎧==31b k . （1分） ∴一次函数解析式为3+=x y .——（1分）（2）由⎪⎩⎪⎨⎧=+=x y x y 43,———（2分）消元得0432=-+x x ,—（1分）解得1,421=-=x x （舍去）,——（1分） ∴点B 的坐标是()1,4--.——（1分）2．解：（1）∵一次函数y=（1-2x ）m+x+3 即y=（1-2m ）x+m+3 图像不经过第四象限且函数值y 随自变量x 的减小而减小 ∴ 1-2m>0 ， m+3≥0, (2分） ∴ ………（2分）根据题意，得：函数图像与y 轴的交点为（0，m+3），与x 轴的交点为 …（1分）则 ………（1分）解得m=0 或 m=-24（舍） …（1分）∴一次函数解析式为：y=x+3……（1分） 3．解：（1）过点A 作AE ⊥x 轴，垂足为点E ．……1′∵点A 的坐标为（2，2）， ∴点E 的坐标为（2，0）．…1′∵AB=AC ，BC =8， ∴BE=CE ， ………1′ 点B 的坐标为（-2，0），……1′ 点C 的坐标为（6，0）．…1′ 设直线AC 的解析式为：y kx b =+（0k ≠），将点A 、C得到： 132y x =-+．…1′ ∴点D 的坐标为（0，3）． ……1′（3）设二次函数解析式为：2y ax bx c =++（0a ≠）， ∵ 图象经过B 、D 、A 三点， ∴4230,423 2.a b a b -+=⎧⎨++=⎩…2′解得：1,21.2a b ⎧=-⎪⎪⎨⎪=⎪⎩……1∴此二次函数解析式为：211322y x x =-++……1′ 顶点坐标为（12，38）． …………1′4．解：(1) tan 1OBC ∠=，∴OB=OC=3, ∴B （3,0） ………（2分）将B （3,0）代入223y ax ax =-+ 0963a a =-+，∴1a =- ……（1∴223y x x =-++；∴2(1)4y x =--+…（1分） ∴D(1,4)，A(-1,0) …（将D(1,4)代入3y kx =+，∴1k =，3y x =+ ……………（2分）(2)14362ABC S ∆=⨯⨯= …………………（4分）213<≤-m ⎪⎭⎫⎝⎛-+0,123m m ()293m 213m 21=+⋅-+⋅m（图八）5．解：（1）过点A 作AH ⊥x 轴，过点B 作BM ⊥y 轴，由题意得OA=OB,∠AOH=∠BOM, ∴△AOH ≌△BOM-------------1分∵A 的坐标是（-3，1）， ∴AH=BM=1,OH=OM=3 ∴B 点坐标为（1，3）---------2分（2）设抛物线的解析式为y=ax 2+bx+c则⎪⎩⎪⎨⎧==+-=++01393c c b a c b a --------3分得0,613,65===c b a ∴抛物线的解析式为x x y 613652+=-----2分（3）对称轴为1013-=x -------1分 ∴C 的坐标为(3,518-)--------1分∴ 5232)5181(2121=⋅+⋅=⋅⋅=∆BC ABC h BC S --------------2分6．解：（1）∵点C （1，5）在直线)0(>+-=k b kx y 上， ∴b k +⋅-=15， ∴5+=k b ，…1′ ∴5++-=k kx y .…1′∵点A （a ，0）在直线5++-=k kx y 上， ∴50++-=k ka .…1′ ∴15+=k a .………1′（2）∵直线与双曲线在第一象限的另一交点D 的横坐标是9，设点D （9，y ），………1′ ∴95=y . ∴点D （9，95）.……1′ 代入5++-=k kx y，可解得：95=k ，………1′95095+-=x y . ………1′ 可得：点A （10，0），点B （0，950）. ………2′∴BOCAODAOB COD S S S S ∆∆∆∆--= =1950219510219501021⨯⨯-⨯⨯-⨯⨯ …1′=)1110(95021--⨯ = )1110(95021--⨯ = 9200 =9222.……1′7．解：（1）设抛物线的解析式为2y ax bx c =++ 点A （－1，a ）（a 为常数）向右平移4个单位得到点 A '（3，a ）…………（1分） ∵抛物线与y 轴的交点的纵坐标为2 ∴2=c …………（1分）∵ 图像经过点A （－1，a ）、A '（3，a ） ∴⎩⎨⎧=++=++a c b a a c b a 9…（1分）解得⎩⎨⎧=-=21b a ……（2分）∴222++-=x x y …………………（1分）（2）由222++-=x x y =()312+--x 得P(1，3) 52=AP ……………（1分） ∵△ABP 是等腰三角形,点B 的坐标为)1m ，（,且3<m （Ⅰ）当AP=PB 时， 52=PB ，即 523=-m …（1分） ∴523-=m ……（1分）（Ⅱ）当AP=AB 时 ()()()()22221113111m --+--=--+--解得5,3-==m m ……（1分） 3=m 不合题意舍去， ∴5-=m ………（1分）（Ⅲ）当PB=AB 时()()()()2222111311m m --+--=-+-解得21=m ………（1分）综上：当523-=m 或-5或21时，△ABP 是等腰三角形.8．解：（1）由题意，得103b c c --+=⎧⎨=⎩ （2分）解得2b =，3c = （1分）∴二次函数的解析式是223y x x =-++ （1分） ()222314y x x x =-++=--+， ∴点P 的坐标是（1，4）（2分）（2） P （1，4），A （-1，0）∴2AP =20．（1分）设点Q 的坐标是（x ，0） ∠PAQ =90°不合题意则()221AQ x =-，()22116PQ x =-+ （1分）当∠AQP =90°时，222AQ PQ AP +=，()()22111620x x ++-+=，解得11x =，21x =-（舍去） ∴点Q 的坐标是（1，0）（2分）当∠APQ =90°时，222AP PQ AQ +=，()()22201161x x +-+=+，解得9x =，∴点Q 的坐标是（9，0）（2分）综上所述，所求点P 的坐标是（1，0）或（9，0）．9．解：（1）将(1,3)A ，(0,1)B ，代入212y x bx c=-++，解得52b =，1c =． …………2分 ∴抛物线的解析式为211225y x x =-++．………1分 ∴顶点坐标为(,)53328．……1分（2）①由对称性得(4,3)C ．……1分 ∴1231413ABC S =--=．…1分②将直线AC 与y 轴交点记作D ， ∵12ADBDBD CD ==，∠CDB 为公共角，∴△ABD ∽△BCD ． ∴∠ABD =∠BCD ．………1分1°当∠PAB =∠ABC时，PBAB ACBC=，∵BC ==AB ==3AC =∴32PB =，∴1(0,5)2P ． …………2分2°当∠PAB =∠BAC时，PBAB BCAC=，， ∴310PB =， ∴2(0,13)3P ．……2分综上所述满足条件的P 点有5(0,)2，13(0,)3． …………1分10．解：平移后抛物线的解析式为22(2)1y x =-+．……2分 ∴A 点坐标为（2，1），……1分设直线OA 解析式为y kx =，将A （2，1）代入得12k =，直线OA 解析式为12y x=，将3x =代入12y x =得32y =，∴C 点坐标为（3，32）．…………1分将3x =代入22(2)1y x =-+得3y =， ∴B 点坐标为（3，3）．…1分 ∴ABC34S=…2分（2）∵PA ∥BC ，∴∠PAB =∠ABC 1°当∠PBA =∠BAC 时，PB ∥AC ，∴四边形PACB 是平行四边形，∴32PA BC ==．…1分 ∴15(2,)2P ． …1分得29-=b…（1分）所以，直线BC 的解析式为29-=x y … （1分）(2)由直线29-=x y 得点C(0，29-)，设经过A 、B 、C 三点的二次函数的解析式为292-+=bx ax y将A 、B 两点的坐标代入292-+=bx ax y ，得⎪⎪⎩⎪⎪⎨⎧=-+=-+232963632939b a b a … （1分）解得⎪⎩⎪⎨⎧=-=421b a （1分）所以，抛物线的解析式为294212-+-=x x y ………（1分）（3）存在把294212-+-=x x y 配方得27)4(212+--=x y ，所以得点D(4，27)，对称轴为直线4=x …（1分）得对称轴与x 轴交点的坐标为E(4，0). ………（1分）由BD=8，BC=72，CD=80,得222BD BC CD +=，所以，∠DBC=90 ……（1分）又∠PEO=90，若以O 、E 、P 为顶点的三角形与△BCD 相似，则有：① DB PE BC OE =即22264PE = 得34=PE ，有1P (4，34) ，2P (4，34-) ② BC PEDB OE =即26224PE = 得12=PE ，有3P(4，12) ，4P (4，12-). …（3分）所以，点P 的坐标为 (4，34) ， (4，34-)， (4，12) ， (4，12-).12．（1）设y=ax 2+bx+c … 1’，代入A 、B 、C 坐标得⎪⎩⎪⎨⎧'++=-=++=311241 c b a cc b a 解得'1142 ⎪⎩⎪⎨⎧=-==c b a得142+-=x x y … 1’ （2）BB 1=52 … 1’ cos ∠BB 1A 1=55 … 3’13．(1) ∵CD ⊥AB ∴∠BAC ＝90° ∴∠BAO ＋∠CAD ＝90°………（1分）∵CD ⊥x 轴 ∴∠CDA ＝90° ∴∠C ＋∠CAD ＝90°……（1分）∴∠C ＝∠BAO ……（1分）又∵∠CDO ＝∠AOB ＝90° ∴△ADC ∽△BOA …………（1分） (2)①由题意得，A(－8，0)，B(0，4) …（1分） ∴OA ＝8，OB ＝4，AB ＝54……（1分） ∵△ADC ∽△BOA ，CA ＝52 ∴AD ＝2，CD ＝4 ∴C(－10，4) ……（1分）将B(0，4)，C(－10，4)代入c bx x y ++-=2⎩⎨⎧=+--=4101004c b c ∴⎩⎨⎧-==104b c ∴4102+--=x x y ………（1分）③ M(0，3529+)，M(0，3529-) M(53329--,0)，M(53329-,0) ……（4分）14．解：（1）y =ax 2-2ax +3，当0=x 时,3=y ∴)3,0(B ……… (1分) ∴3=OB ，又OB =3OA ， ∴1=AO ∴)0,1(-A ………（2分）设直线AB 的解析式b kx y +=⎩⎨⎧==+-30b b k ，解得 3=k ，3=b∴直线AB 的解析式为33+=x y ．……… (1分) （2）)0,1(-A ， ∴320++=a a ，∴1-=a ∴322++-=x x y 4)1(2+--=x …(2分)∴抛物线顶点P 的坐标为（1，4）．………… (1分) （3）设平移后的直线解析式m x y +=3 点P 在此直线上，∴m +=34， 1=m∴平移后的直线解析式13+=x y ………… (1分) 设点M 的坐标为)13,(+x x ，作ME x ⊥轴-若点M 在x 轴上方时， 13+=x ME ，1+=x AE在Rt △AME 中，由11323tan ++===∠x x AE ME OAM ，∴31=x ……(1分) ∴)2,31(M ……(1分) 若点M 在x 轴下方时， 13--=x ME ，x AE +=1在Rt △AME 中，由x x AE ME OAM +--===∠11323tan ，∴95-=x ∴)32,95(--M …… (1分) 综上所述： M 的坐标是)2,31(或)32,95(--……（1分）15．解：（1）作BQ ⊥x 轴于Q. ∵四边形OABC 是等腰梯形， ∴∠BAQ =∠COA =60° 在Rt △BQA 中，BA =4， BQ =AB ·sin ∠BAO =4×sin60°=32…（1分） AQ =AB ·cos ∠BAO =4×cos60°=2，……（1分） ∴OQ=OA －AQ=7－2=5 点B 在第一象限内，∴点B 的坐标为（5，32）……(1分) （2）∵∠CPA =∠OCP +∠COP 即∠CPD +∠DPA =∠COP +∠OCP 而∠CPD =∠OAB=∠COP =60° ∴∠OCP =∠APD ……（1分） ∵∠COP =∠PAD ……（1分）∴△OCP ∽△APD ……（1分） ∴AP OCAD OP =，∴OP ·AP =OC ·AD ……(1分)∵85=AB BD∴BD =85AB=25，AD=AB －BD=4－25=23∵AP =OA －OP =7－OP ∴OP （7－OP ）=4×23 …（1分）解得OP =1或6∴点P 坐标为（1，0）或（6，0）…………（2分）16、解：（1）∵点()0,4A 与()4,4--B 在二次函数图像上，∴⎩⎨⎧+--=-++-=c b c b 444440，解得⎪⎩⎪⎨⎧==221c b ，∴二次函数解析式为221412++-=x x y .————（2+1+1分）（2）过B 作x BD ⊥轴于点D ，由（1）得()2,0C ，———（1分）则在AOC Rt ∆中，2142tan ===∠AO CO CAO ，又在ABD Rt ∆中，2184tan ===∠AD BD BAD ，———（1分） ∵BAD CAO ∠=∠tan tan ，—（1分） ∴BAO CAO ∠=∠.———（1分）（3）由()0,4A 与()4,4--B ，可得直线AB 的解析式为221-=x y ，—（1分）设()44,221, x x x P -⎪⎭⎫ ⎝⎛-，则⎪⎭⎫ ⎝⎛++-22141,2x x x Q ， ∴22141,2122212++-=-=-=x x QH x x PH . ∴2214122122++-=-x x x .——（1分）当4212122++-=-x x x ，解得 4,121=-=x x （舍去），∴⎪⎭⎫ ⎝⎛--25,1P .———（1分）当4212122--=-x x x ，解得 4,321=-=x x （舍去），∴⎪⎭⎫ ⎝⎛--27,3P .———（1分）综上所述，存在满足条件的点，它们是⎪⎭⎫ ⎝⎛--25,1与⎪⎭⎫⎝⎛--27,3.17．解：（1）联结AO ,矩形ABOC 322==OB AB ，40=∴A ---------------（1分）矩形ABOC 绕点O 逆时针旋转后得到矩形EFOD ,A 落在y 轴上的点E4==∴EO AO )4,0(E ∴ ----------------(1分)过D 点作DH ⊥X 轴于H ，AOB DOH ABO DHO ∠=∠∠=∠, ， DHO ∆∴∽ABO ∆AO DOOB HO AB DH ==∴4,2,32,2====AO DO OB AB 3,1==∴OH DH )1,3(-∴D ----------------(1分) 同理求得)3,3(F ∴-------------(1分)（2）因为抛物线c bx ax y ++=2经过点F 、E 、D ⎪⎩⎪⎨⎧+-=++=∴43314333b a b a求得：4,33,32==-=c b a --（3分）所求抛物线为：433322++-=x x y -（1分）（3）因为在x 轴上方的抛物线上有点Q ，使得三角形QOB 的面积等于矩形ABOC 的面积设三角形QOB 的OB 边上的高为h ，则3223221⨯=⨯⨯h ，所以4=h --------------（1分）因为点Q 在x 轴上方的抛物线上, )4,(x Q ∴23.0,433324212==++-=∴x x x x ------（1分）所以Q 的坐标是)4,0(或)4,23(------------------（2分）18．（1）证明：∵△AOC 绕AC 的中点旋转180°，点O 落到点B 的位置， ∴△ACO ≌△CAB . ………1′ ∴AO=CB ，CO=AB ，……1′ ∴四边形ABCO 是平行四边形. …………1′（2）解：∵抛物线x ax y 322-=经过点A ，点A 的坐标为（2，0），……1′ ∴0344=-a ，解得：3=a . …1′ ∴x x y 3232-=.∵四边形ABCO 是平行四边形， ∴OA ∥CB .∵点C 的坐标为（1，33），…………1′ ∴点B 的坐标为（3，33）. ………1′把3=x 代入此函数解析式，得：333639332332=-=⨯-⨯=y . ∴点B 的坐标满足此函数解析式，点B 在此抛物线上. …1′ ∴顶点D 的坐标为（1，-3）. …1′（3）联接BO ，过点B 作BE ⊥x 轴于点E ，过点D 作DF ⊥x 轴于点F . tan ∠BOE =3，tan ∠DAF=3， ∴tan ∠BOE=tan ∠DAF . ∴∠BOE=∠DAF . …1′ ∵∠APD=∠OAB ， ∴△APD ∽△OAB . ……1′设点P 的坐标为（x ，0）， ∴OB AD OA AP =， ∴6222=-x ，解得：34=x ………1′ ∴点P 的坐标为（34，0）.（4）)0,1(1P ，)0,1(2-P ，3(3,0)P ………2′19．解：（1） D 在BC 上，BC ∥x 轴，C(D （x ，-2）---------（1分）D在直线xy 32-=上 ∴3322=-=-x x------（2分） ∴D （3，-2）-----（1分）（2）抛物线c bx ax y ++=2经过点A 、D 、O ∴⎪⎩⎪⎨⎧-=++==++23900416c b a c c b a 解得：⎪⎪⎪⎩⎪⎪⎪⎨⎧=-==03832c b a ------（3分）所求的二次函数解析式为x x y 38322-=----（1分）（3）假设存在点M ，使O 、D 、A 、M 为顶点的四边形是梯形①若以OA 为底，BC ∥x 轴，抛物线是轴对称图形 ∴点M 的坐标为（21-，）--------（1分） ②若以OD 为底，过点A 作OD 的平行线交抛物线为点M直线OD 为x y 32-= ∴直线AM 为3832+-=x y ∴=+-3832x xx 38322- 解得：4,121=-=x x （舍去） ∴点M 的坐标为（310,1-）----------（2分） ③ 若以AD 为底，过点O 作AD 的平行线交抛物线为点M直线AD 为82-=x y ∴直线OM 为x y 2= ∴=x 2xx 38322- 解得：0,721==x x （舍去） ∴点M 的坐标为（14,7）-----------（1分）∴综上所述，当点M 的坐标为（21-，）、（310,1-）、（14,7）时以O 、D 、A 、M 为顶点的四边形是梯形第2520.解：（1）因为直线343+-=x y 分别与x 轴、y 轴交于点A 和点B ．由,0=x 得3=y ，0=y ，得4=x ，所以)0,4(A )3,0(B ………1分把)0,1(-C )3,0(B 代入c ax ax y +-=42中，得 ⎩⎨⎧=++=043c a a c ，解得⎪⎩⎪⎨⎧-==533a c ……2分 ∴这个二次函数的解析式为3512532++-=x x y ……1分527)2(532+--=x y ，P 点坐标为P )527,2( ………1分（２）设二次函数图象的对称轴与直线343+-=x y 交于E 点，与x 轴交于F 点把2-=x 代入343+-=x y 得，23=y ， ∴)23,2(E ， ∴103923527=-=PE ………1分 ∵PE//OB ，OF=AF ， ∴AE BE = ∵AD ∥BP ，∴DE PE =，5392==PE PD …2分。