中考数学压轴题、几何证明题
2023年 九年级数学中考复习 几何图形变换综合压轴题 专题训练(含答案)

2023年春九年级数学中考复习《几何图形变换综合压轴题》专题训练(附答案)1.如图,△ABC和△ECD都是等边三角形,直线AE,BD交于点F.(1)如图1,当A,C,D三点在同一直线上时,∠AFB的度数为,线段AE与BD的数量关系为.(2)如图2,当△ECD绕点C顺时针旋转α(0°≤α<360°)时,(1)中的结论是否还成立?若不成立,请说明理由;若成立,请就图2给予证明.(3)若AC=4,CD=3,当△ECD绕点C顺时针旋转一周时,请直接写出BD长的取值范围.2.如图1,在Rt△ABC中,∠BAC=90°,AB=AC,D、E两点分别在AC、BC上,且DE∥AB,将△CDE绕点C按顺时针方向旋转,记旋转角为α.(1)问题发现:当α=0°时,的值为;(2)拓展探究:当0°≤α<360°时,若△EDC旋转到如图2的情况时,求出的值;(3)问题解决:当△EDC旋转至A、B、E三点共线时,若CE=5,AC=4,直接写出线段AD的长.3.已知:如图1,线段AD=5,点B从点A出发沿射线AD方向运动,以AB为底作等腰△ABC,使得AC=BC=AB.(1)如图2,当AB=10时,求证:CD⊥AB;(2)当△BCD是以BC为腰的等腰三角形时,求BC的长;(3)当AB>5时,在线段BC上是否存在点E,使得△BDE与△ACD全等,若存在,求出BC的长;若不存在,请说明理由;(4)作点A关于直线CD的对称点A′,连接CA′当CA′∥AB时,CA′=(请直接写出答案).4.如图1,在△ABC中,AE⊥BC于点E,AE=BE,D是AE上的一点,且DE=CE,连接BD,CD.(1)试判断BD与AC的位置关系是:;数量关系是:;(2)如图2,若将△DCE绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由;(3)如图3,若将(2)中的等腰直角三角形都换成等边三角形,其他条件不变.①试猜想BD与AC的数量关系为:;②你能求出BD与AC的夹角度数吗?如果能,请直接写出夹角度数;如果不能,请说明理由.5.如图,平面直角坐标系中O为原点,Rt△ABC的直角顶点A在y轴正半轴上,斜边BC 在x轴上,已知B、C两点关于y轴对称,且C(﹣8,0).(1)请直接写出A、B两点坐标;(2)动点P在线段AB上,横坐标为t,连接OP,请用含t的式子表示△POB的面积;(3)在(2)的条件下,当△POB的面积为24时,延长OP到Q,使得PQ=OP,在第一象限内是否存在点D,使得△OQD是等腰直角三角形,如果存在,求出D点坐标;如果不存在,请说明理由.6.如图1,已知△ABC中,∠ACB=90°,AC=BC=6,点D在AB边的延长线上,且CD =AB.(Ⅰ)求BD的长度;(Ⅱ)如图2,将△ACD绕点C逆时针旋转α(0°<α<360°)得到△A'CD'.①若α=30°,A'D'与CD相交于点E,求DE的长度;②连接A'D、BD',若旋转过程中A'D=BD'时,求满足条件的α的度数.(Ⅲ)如图3,将△ACD绕点C逆时针旋转α(0°<α<360°)得到△A'CD',若点M 为AC的中点,点N为线段A'D'上任意一点,直接写出旋转过程中线段MN长度的取值范围.7.如图①,将两个等腰直角三角形纸片OAB和OCD放置在平面直角坐标系中,点O(0,0),点A(0,+1),点B(+1,0),点C(0,1),点D(1,0).(Ⅰ)求证:AC=BD;(Ⅱ)如图②,现将△OCD绕点O顺时针方向旋转,旋转角为α(0°<α<180°),连接AC,BD,这一过程中AC和BD是否仍然保持相等?说明理由;当旋转角α的度数为时,AC所在直线能够垂直平分BD;(Ⅲ)在(Ⅱ)的情况下,将旋转角α的范围扩大为0°<α<360°,那么在旋转过程中,求△BAD的面积的最大值,并写出此时旋转角α的度数.(直接写出结果即可)8.在△ABC中,AB=AC,∠BAC=α,过点A作直线l平行于BC,点D是直线l上一动点,连接CD,射线DC绕点D顺时针旋转α交直线AB于点E.(1)如图1,若α=60°,当点E在线段AB上时,请直接写出线段AC,AD,AE之间的数量关系,不用证明;(2)如图2,若α=60°,当点E在线段BA的延长线上时,(1)中的结论是否成立?若成立,请证明;若不成立,请写出正确结论,并证明.(3)如图3,若α=90°,BC=6,AD=,请直接写出AE的长.9.有一根直尺短边长4cm,长边长10cm,还有一块锐角为45°的直角三角形纸板,它的斜边长为16cm,如图甲,将直尺的短边DE与直角三角形纸板的斜边AB重合,且点D 与点A重合.将直尺沿射线AB方向平移,如图乙,设平移的长度为xcm,且满足0≤x ≤12,直尺和三角形纸板重叠部分的面积为Scm2.(1)当x=0cm时,S=;当x=12cm时,S=.(2)当0<x<8(如图乙、图丙),请用含x的代数式表示S.(3)是否存在一个位置,使重叠部分面积为28cm2?若存在求出此时x的值.10.如图①,C为线段BD上的一点,BC≠CD,分别以BC,BD为边在BD的上方作等边△ABC和等边△CDE,连接AE,F,G,H分别是BC,AE,CD的中点,连接FG,GH,FH.(1)△FGH的形状是;(2)将图①中的△CDE绕点C顺时针旋转,其他条件不变,(1)的结论是否成立?结合图②说明理由;(3)若BC=2,CD=4,将△CDE绕点C旋转一周,当A,E,D三点共线时,直接写出△FGH的周长.11.已知,射线AB∥CD,P是直线AC右侧一动点,连接AP,CP,E是射线AB上一动点,过点E的直线分别与AP,CP交于点M,N,与射线CD交于点F,设∠BAP=∠1,∠DCP=∠2.(1)如图1,当点P在AB,CD之间时,求证:∠P=∠1+∠2;(2)如图2,在(1)的条件下,作△PMN关于直线EF对称的△P'MN,求证:∠3+∠4=2(∠1+∠2);(3)如图3,当点P在AB上方时,作△PMN关于直线EF对称的△P'MN,(1)(2)的结论是否仍然成立,若成立,请说明理由;若不成立,请直接写出∠P,∠1,∠2之间数量关系,以及∠3,∠4与∠1,∠2之间数量关系.12.(1)如图1,平面直角坐标系中A(0,a),B(a,0)(a>0).C为线段AB的中点,CD⊥x轴于D,若△AOB的面积为2,则△CDB的面积为.(2)如图2,△AOB为等腰直角三角形,O为直角顶点,点E为线段OB上一点,且OB=3OE,C与E关于原点对称,线段AB交x轴于点D,连CD,若CD⊥AE,试求的值.(3)如图3,点C、E在x轴上,B在y轴上,OB=OC,△BDE是以B为直角顶点的等腰直角三角形,直线CB、ED交于点A,CD交y轴于点F,试探究:是否为定值?如果是定值,请求出该定值;如果不是,请求出其取值范围.13.在△ABC中,AB=AC,∠BAC=90°.(1)如图1,点P,Q在线段BC上,AP=AQ,∠BAP=15°,求∠AQB的度数;(2)点P,Q在线段BC上(不与点B,C重合),AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.①依题意将图2补全;②用等式表示线段BP,AP,PC之间的数量关系,并证明.14.【问题背景】如图1,在Rt△ABC中,AB=AC,D是直线BC上的一点,将线段AD绕点A逆时针旋转90°至AE,连接CE,求证:△ABD≌△ACE;【尝试应用】如图2,在图1的条件下,延长DE,AC交于点G,BF⊥AB交DE于点F,求证:FG=AE;【拓展创新】如图3,A是△BDC内一点,∠ABC=∠ADB=45°,∠BAC=90°,BD =,直接写出△BDC的面积为.15.在平面直角坐标系中,A(a,0),B(0,b)分别是x轴负半轴和y轴正半轴上一点,点C与点A关于y轴对称,点P是x轴正半轴上C点右侧一动点.(1)当2a2+4ab+4b2+2a+1=0时,求A,B的坐标;(2)当a+b=0时,①如图1,若D与P关于y轴对称,PE⊥DB并交DB延长线于E,交AB的延长线于F,求证:PB=PF;②如图2,把射线BP绕点B顺时针旋转45o,交x轴于点Q,当CP=AQ时,求∠APB的大小.16.已知:在Rt△ABC中,∠C=90°,∠B=30°,BC=6,左右作平行移动的等边三角形DEF的两个顶点E、F始终在边BC上,DE、DF分别与AB相交于点G、H.(1)如图1,当点F与点C重合时,点D恰好在斜边AB上,求△DEF的周长;(2)如图2,在△DEF作平行移动的过程中,图中是否存在与线段CF始终相等的线段?如果存在,请指出这条线段,并加以证明;如果不存在,请说明理由;(3)假设C点与F点的距离为x,△DEF与△ABC的重叠部分的面积为y,求y与x的函数关系式,并写出定义域.17.在△ABC中,∠C=90°,AC=2,BC=2,点D为边AC的中点(如图),点P、Q 分别是射线BC、BA上的动点,且BQ=BP,联结PQ、QD、DP.(1)求证:PQ⊥AB;(2)如果点P在线段BC上,当△PQD是直角三角形时,求BP的长;(3)将△PQD沿直线QP翻折,点D的对应点为点D',如果点D'位于△ABC内,请直接写出BP的取值范围.18.定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.(1)已知点M,N是线段AB的勾股分割点,若AM=2,MN=3,求BN的长.(2)如图2,在等腰直角△ABC中,AC=BC,∠ACB=90°,点M,N为边AB上两点满足∠MCN=45°,求证:点M,N是线段AB的勾股分割点;阳阳同学在解决第(2)小题时遇到了困难,陈老师对阳阳说:要证明勾股分割点,则需设法构造直角三角形,你可以把△CBN绕点C逆时针旋转90°试一试.请根据陈老师的提示完成第(2)小题的证明过程.19.问题背景如图(1),△ABD,△AEC都是等边三角形,△ACD可以由△AEB通过旋转变换得到,请写出旋转中心、旋转方向及旋转角的大小.尝试应用如图(2),在Rt△ABC中,∠ACB=90°,分别以AC,AB为边,作等边△ACD和等边△ABE,连接ED,并延长交BC于点F,连接BD.若BD⊥BC,求的值.拓展创新如图(3),在Rt△ABC中,∠ACB=90°,AB=2,将线段AC绕点A顺时针旋转90°得到线段AP,连接PB,直接写出PB的最大值.20.【教材呈现】如图是苏科版九年级下册数学教材第92页的第17题.一块直角三角形木板,它的一条直角边AC长为1.5m,面积为1.5m2.甲乙两人分别按图1、图2把它加工成一个正方形的桌面,请说明哪个正方形的面积较大.【解决问题】(1)记图1、图2中的正方形面积分别为S1,S2,则S1S2.(填“>”、“<”或“=”).【问题变式】若木板形状是锐角三角形A1B1C1.某数学兴趣小组继续思考:按图3、图4、图5三种方式加工,分别记所得的正方形面积为S3、S4、S5,哪一个正方形的面积最大呢?(2)若木板的面积S仍为1.5m2.小明:记图3中的正方形为“沿B1C1边的内接正方形”,图4中的正方形为“沿A1C1边的内接正方形”,依此类推.以图3为例,求“沿B1C1边的内接正方形DEFG”的面积.设EF =x ,B 1C 1=a ,B 1C 1边上的高A 1H =h ,则S =ah .由“相似三角形对应高的比等于相似比”易得x =;同理可得图4、图5中正方形边长,再比较大小即可.小红:若要内接正方形面积最大,则x 最大即可;小莉:同一块木板,面积相同,即S 为定值,本题中S =1.5,因此,只需要a +h 最小即可.我们可以借鉴以前研究函数的经验,令y =a +h =a +=a +(a >0).下面来探索函数y =a +(a >0)的图象和性质.①根据如表,画出函数的图象:(如图6)a… 1 2 3 4 … y … 12 9 6 4 3 3 4 4…②观察图象,发现该函数有最小值,此时a 的取值 ;A .等于2;B .在1~之间;C .在~之间;D .在~2之间.(3)若在△A 1B 1C 1中(如图7),A 1B 1=5,A 1C 1=,高A 1H =4.①结合你的发现,得到S 3、S 4、S 5的大小关系是 (用“<”连接). ②小明不小心打翻了墨水瓶,已画出最大面积的内接正方形的△A 1B 1C 1原图遭到了污损,请用直尺和圆规帮他复原△A 1B 1C 1.(保留作图痕迹,不写作法)参考答案1.解:(1)∵△ABC是等边三角形,∴AC=BC,∠BAC=∠ACB=60°,∵△ECD是等边三角形,∴CE=CD,∠DCE=60°,∴∠ACB=∠DCE=60°,∴∠ACB+∠BCE=∠DCE+∠BCE,即∠ACE=∠BCD,在△ACE和△BCD中,,∴△ACE≌△BCD(SAS),∴AE=BD,∠CAE=∠CBD,在△ABF中,∠AFB=180°﹣(∠BAF+∠ABF)=180°﹣(∠BAF+∠CBF+∠ABC)=180°﹣(∠BAC+∠ABC)=180°﹣(60°+60°)=60°,∴∠AFB=60°,故答案为:∠AFB=60°,AE=BD;(2)(1)中结论仍成立,证明:∵△ABC是等边三角形,∴AC=BC,∠BAC=∠ACB=60°,∵△ECD是等边三角形,∴CE=CD,∠DCE=60°,∴∠ACB=∠DCE=60°,∴∠ACB+∠BCE=∠DCE+∠BCE,即∠ACE=∠BCD,在△ACE和△BCD中,,∴△ACE≌△BCD(SAS),∴AE=BD,∠CAE=∠CBD,∵∠AFB+∠CBD=∠ACB+∠CAE,∴∠AFB=∠ACB,∵∠ACB=60°,∴∠AFB=60°;(3)在△BCD中,BC+CD>BD,BC﹣CD<BD,∴点D在BC的延长线上时,BD最大,最大为4+3=7,当点D在线段BC上时,BD最小,最小为4﹣3=1,∴1≤BD≤7,即BD长的取值范围为1≤BD≤7.2.解:(1)∵∠BAC=90°,AB=AC,∴△ABC为等腰直角三角形,∠B=45°,∵DE∥AB,∴∠DEC=∠B=45°,∠CDE=∠A=90°,∴△DEC为等腰直角三角形,∴cos∠C==,∵DE∥AB,∴==,故答案为:;(2)由(1)知,△BAC和△CDE均为等腰直角三角形,∴==,又∠BCE=∠ACD=α,∴△BCE∽△ACD,∴==,即=;(3)①如图3﹣1,当点E在线段BA的延长线上时,∵∠BAC=90°,∴∠CAE=90°,∴AE===3,∴BE=BA+AE=4+3=7;由(2)知,=.故AD=.②如图3﹣2,当点E在线段BA上时,AE===3,∴BE=BA﹣AE=4﹣3=1,由(2)知,=.故AD=.综上所述,AD的长为或,故答案为:或.3.解:(1)如图2中,∵AB=10,AD=5,∴AD=DB,∵CA=CB,AD=DB,∴CD⊥AB.(2)如图1中,当AB<AD时,BC=BD.设AB=10k,则AC=BC=6k,∵AD=5,∴10k+6k=5,∴k=,∴BC=6k=.如图1﹣1中,当AB>AD时,BC=BD,同法可得10k﹣6k=5,解得k=,∴BC=6k=,综上所述,BC的值为或.(3)如图3﹣1中,当△ADC≌△BED时,BD=AC=BC,由(2)可知,BC=.如图3﹣2中,当△ADC≌△BCE时,点E与C重合,此时AB=10k=10,∴k=1,BC=6k=6.综上所述,BC的值为或6.(4)如图3中,当CA′∥AB时,∵CA′∥AB,∴∠ADC=∠A′CD,由翻折可知,∠A′CD=∠ACD,∴∠ACD=∠ADC,∴AC=AD=5,∴CA′=CA=5.故答案为5.4.解:(1)结论:BD=AC,BD⊥AC.理由:延长BD交AC于F.∵AE⊥CB,∴∠AEC=∠BED=90°.在△AEC和△BED中,,∴△AEC≌△BED(SAS),∴AC=BD,∠CAE=∠EBD,∵∠AEC=90°,∴∠ACB+∠CAE=90°,∴∠CBF+∠ACB=90°,∴∠BFC=90°,∴AC⊥BD,故答案为:BD⊥AC,BD=AC.(2)如图2中,不发生变化,设DE与AC交于点O,BD与AC交于点F.理由是:∵∠BEA=∠DEC=90°,∴∠BEA+∠AED=∠DEC+∠AED,∴∠BED=∠AEC,在△BED和△AEC中,,∴△BED≌△AEC(SAS),∴BD=AC,∠BDE=∠ACE,∵∠DEC=90°,∴∠ACE+∠EOC=90°,∵∠EOC=∠DOF,∴∠BDE+∠DOF=90°,∴∠DFO=180°﹣90°=90°,∴BD⊥AC;(3)①如图3中,结论:BD=AC,理由是:∵△ABE和△DEC是等边三角形,∴AE=BE,DE=EC,∠BEA=∠DEC=60°,∴∠BEA+∠AED=∠DEC+∠AED,∴∠BED=∠AEC,在△BED和△AEC中,,∴△BED≌△AEC(SAS),∴BD=AC,故答案为:BD=AC.②能;设BD与AC交于点F,由①知,△BED≌△AEC,∴∠BDE=∠ACE,∴∠DFC=180°﹣(∠BDE+∠EDC+∠DCF)=180°﹣(∠ACE+∠EDC+∠DCF)=180°﹣(60°+60°)=60°,即BD与AC的夹角中的锐角的度数为60°.5.解:(1)∵B、C两点关于y轴对称,且C(﹣8,0),∴点B(8,0),BO=CO,又∵AO⊥BC,∴AC=AB,∵∠CAB=90°,AC=AB,CO=BO,∴AO=CO=BO=8,∴点A(0,8);(2)如图1,过点P作PM⊥OB于M,∵点P的横坐标为t,∴OM=t,∴MB=8﹣t,∵∠CAB=90°,AC=AB,∴∠ABO=45°,∴∠BPM=∠ABO=45°,∴PM=MB=8﹣t,∴S△POB=×OB×PM=×8×(8﹣t)=32﹣4t;(3)∵△POB的面积为24,∴32﹣4t=24,∴t=2,∴点P(2,6),如图2,当点Q为直角顶点时,过点Q作HG⊥y轴,过点D作DG⊥HG于点G,∵PQ=OP,点P(2,6),∴点Q(4,12),∵∠OQD=90°=∠OHQ=∠QGD,∴∠OQH+∠DQG=90°=∠OQH+∠HOQ,∴∠HOQ=∠GQD,又∵OQ=QD,∴△OHQ≌△QGD(AAS),∴OH=QG=12,HQ=GD=4,∴HG=16,∴点D(16,8);当点D为直角顶点时,过点Q作HG⊥y轴,过点D作DG⊥HG于点G,过点D作DN ⊥y轴于N,同理可求△QDG≌△ODN,∴ON=QG,DN=DG,∵DN=QG+HQ=4+QG,DG=HN=12﹣ON,∴ON=QG=4,DN=DG=8,∴点D(8,4),综上所述:点D(16,8)或(8,4).6.解:(Ⅰ)如图1,过点C作CH⊥AB于H,∵∠ACB=90°,AC=BC=6,CH⊥AB,∴AB=CD=6,CH=BH=AB=3,∠CAB=∠CBA=45°,∴DH===3,∴BD=DH﹣BH=3﹣3;(Ⅱ)①如图2,过点E作EF⊥CD'于F,∵将△ACD绕点C逆时针旋转α(0°<α<360°)得到△A′CD′,∴CD=CD'=6,∠DCD'=30°=∠CDA=∠CD'A',∴CE=D'E,又∵EF⊥CD',∴CF=D'F=3,EF=,CE=2EF=2,∴DE=DC﹣CE=6﹣2;②如图2﹣1,∵∠ABC=45°,∠ADC=30°,∴∠BCD=15°,∴∠ACD=105°,∵将△ACD绕点C逆时针旋转α(0°<α<360°)得到△A′CD′,∴AC=A'C,CD=CD',∠ACA'=∠DCD'=α,∴CB=CA',又∵A′D=BD′,∴△A'CD≌△BCD'(SSS),∴∠A'CD=∠BCD',∴105°﹣α=15°+α,∴α=45°;如图2﹣2,同理可证:△A'CD≌△BCD',∴∠A'CD=∠BCD',∴α﹣105°=360°﹣α﹣15°,∴α=225°,综上所述:满足条件的α的度数为45°或225°;(Ⅲ)如图3,当A'D'⊥AC时,N是AC与A'D'的交点时,MN的长度最小,∵∠A'=45°,A'D'⊥AC,∴∠A'=∠NCA'=45°,∴CN=A'N=3,∵点M为AC的中点,∴CM=AC=3,∴MN的最小值=NC﹣CM=3﹣3;如图4,当点A,点C,点D'共线,且点N与点D'重合时,MN有最大值,此时MN=CM+CN=6+3,∴线段MN的取值范围是3﹣3≤MN≤6+3.7.解:(Ⅰ)∵点A(0,+1),点B(+1,0),点C(0,1),点D(1,0),∴OA=+1,OB=+1,OC=1,OD=1,∴AC=OA﹣OC=+1﹣1=,BD=+1﹣1=,∴AC=BD;(Ⅱ)由题意知,OA=OB,OC=OD,∠AOB=∠COD=90°,∴∠AOC=∠AOB﹣∠COB=90°﹣∠COB,∠BOD=∠COD﹣∠COB=90°﹣∠COB,∴∠AOC=∠BOD,∴△AOC≌△BOD(SAS),∴AC=BD,∠OAC=∠OBD,如图1(注:点C在x轴上,为了不要出现误解,点C没画在x轴上),延长AC交BD 于D,连接BC,在Rt△AOB中,OA=OB,∴∠OAB=∠OBA=45°,∴∠CAB+∠ABD=∠OAB﹣∠OAC+∠ABO+∠BOD=∠OAB+∠OBA=90°,∴AC⊥BD,∵AC垂直平分BD,∴CD=BC,设点C的坐标为(m,n),∴m2+n2=1①,由旋转知,CD==,∵B(+1,0),[m﹣(+1)]2+n2=2②,联立①②解得,m=1,n=0,∴点C在x轴上,∴旋转角为∠AOC=90°,故答案为:90°;(Ⅲ)如图2,∵OA=OB=+1,∴AB=OA=2+,过点O作OH⊥AB于H,∴S△AOB=OA•OB=AB•OH,∴OH====,过点D作DG⊥AB于G,S△ABD=AB•DG=(2+)DG,要使△ABD的面积最大,则DG最大,由旋转知,点D是以O为圆心,1为半径的圆上,∴点D在HO的延长线上时,DG最大,即DG的最大值为D'H=OD'+OH=1+=,∴S△ABD最大=AB•D'H=(2+)×=,在Rt△AOB中,OA=OB,OH⊥AB,∴∠BOH=45°,∴旋转角∠BOD'=180°﹣45°=135°.8.解:(1)AC=AE+AD.证明:连接CE,∵线段DC绕点D顺时针旋转α交直线AB于点E,α=60°,∵AB=AC,∠BAC=60°,∴CB=CA=AB,∠ACB=60°,∵AD∥BC,∴∠DAF=∠ACB=60°,∵∠FDC=∠EAF=60°,∠AFE=∠DFC,∴△AFE∽△DFC,∴,∴,∵∠AFD=∠EFC,∴△AFD∽△EFC,∴∠DAF=∠FEC=60°,∴△DEC是等边三角形,∴CD=CE,∠ECD=60°,∴∠BCE=∠ACD,∴△BCE≌△ACD(SAS),∴BE=AD,∴AB=AE+BE=AE+AD,∴AC=AE+AD;(2)不成立,AD=AC+AE.理由如下:在AC的延长线上取点F,使AF=AD,连接DF,当α=60°时,∠BAC=∠EDC=60°,∵AB=AC,∴△ABC是等边三角形,∴AB=AC=BC∠BCA=60°,∵l∥BC,∴∠DAC=∠BCA=60°,∠EAD=∠ABC=60°,∵AF=AD,∴∠ADF=∠AFD=60°,AD=FD=AF,∴∠EDC=∠ADF=60°,∴∠EDC﹣∠ADC=∠ADF﹣∠ADC,即∠EDA=∠CDF,∵AD=FD,∠EAD=∠AFD=60°,∴△EAD≌△CFD(ASA),∴AE=CF,∴AD=AF=AC+CF=AC+AE;(3)AE的长为或.当点E在线段AB上,过点D作直线l的垂线,交AC于点F,如图3所示.∵△ABC中,∠BAC=90°,AC=AB,∴∠ACB=∠B=45°.∵直线l∥BC,∴∠DAF=∠ACB=45°.∵FD⊥直线l,∴∠DAF=∠DF A=45°.∴AD=FD.∵∠EDC=∠ADF=90°,∴∠ADE=∠FDC.由(1)可知DC=DE,∴△ADE≌△FDC(SAS),∴AE=CF.∵AD=,∴AF=2,∵BC=6,∴AC=AB=3,∴AE=AC﹣AF=3﹣2.当点E在线段AB的延长线上时,如图4所示.过点D作直线l的垂线,交AB于点M,同理可证得△ADC≌△MDE(SAS),∴AC=EM=3,∵AD=,∴AM=2,∴EM+AM=3+2.综合以上可得AE的长为3+2或3﹣2.9.解:(1)当x=0cm时,S=4×4÷2=8cm2;当x=12cm时,S=4×4÷2=8cm2.故答案为:8cm2;8cm2.(2)①当0<x<4时,∵△CAB为等腰直角三角形,∴∠CAB=45°,∴△ADG和△AEF都是等腰直角三角形,∴AD=DG=x,AE=EF=x+4,∴梯形GDEF的面积=×(GD+EF)×DE=×(x+x+4)×4=4x+8.②如图所示:过点C作CM⊥AB于点M.当4<x<8时,梯形GDMC的面积=(GD+CM)×DM=(x+8)(8﹣x)=﹣x2+32,梯形CMEF的面积=(EF+CM)×ME=[16﹣(x+4)+8][(x+4)﹣8]=(20﹣x)(x﹣4)=﹣x2+12x﹣40,S=梯形GDMC的面积+梯形CMEF的面积=(﹣x2+32)+(﹣x2+12x﹣40)=﹣x2+12x ﹣8.综合以上可得,S=.(3)当0<x<4时s最大值小于24,当x=4时,S=24cm2,所以当S=28cm2时,x必然大于4,即﹣x2+12x﹣8=28,解得x1=x2=6,当x=6cm时,阴影部分面积为28cm2.当8<≤12时,由对称性可知s的最大值也是小于24,不合题意舍去.∴当x=6cm时,阴影部分面积为28cm2.10.解:(1)∵△ABC和△CDE都是等边三角形,∴∠B=∠DCE=60°,AB=BC,CE=CD,∴CE∥AB,∵BC≠CD,∴CE≠AB,∴四边形ABCE是梯形,∵点F,G分别是BC,AE的中点,∴FG是梯形ABCE的中位线,∴FG∥AB,∴∠GFC=60°,同理:∠GHB=60°,∴∠FGH=180°﹣∠GFC﹣∠GHB=60°=∠GFC=∠GHB,∴△FGH是等边三角形,故答案为:等边三角形;(2)成立,理由如下:如图1,取AC的中点P,连接PF,PG,∵△ABC和△CDE都是等边三角形,∴AB=BC,CE=CD,∠BAC=∠ACB=∠ECD=∠B=60°,又F,G,H分别是BC,AE,CD的中点,∴FP=AB,FC=BC,CH=CD,PG=CE,PG∥CE,PF∥AB,∴FP=FC,PG=CH,∠GPC+∠PCE=180°,∠FPC=∠BAC=60°,∠PFC=∠B=60°,∴∠FPG=∠FPC+∠GPC=60°+∠GPC,∠GPC=180°﹣∠PCE,∴∠FCH=360°﹣∠ACB﹣∠ECD﹣∠PCE=360°﹣60°﹣60°﹣(180°﹣∠GPC)=60°+∠GPC,∴∠FPG=∠FCH,∴△FPG≌△FCH(SAS),∴FG=FH,∠PFG=∠CFH,∴∠GFH=∠GFC+∠CFH=∠GFC+∠PFG=∠PFC=60°,∴△FGH为等边三角形;(3)①当点D在AE上时,如图2,∵△ABC是等边三角形,∴∠ACB=60°,AC=BC=2,∵△CDE是等边三角形,∴∠CED=∠CDE=60°,CE=CD=DE=4,过点C作CM⊥AE于M,∴DM=EM=DE=2,在Rt△CME中,根据勾股定理得,CM===2,在Rt△AMC中,根据勾股定理得,AM===4,∴AD=AM﹣DM=4﹣2=2,∵∠ACB=∠DCE=60°,∴∠ACB﹣∠DCB=∠DCE﹣∠DCB,∴∠ACD=∠BCE,连接BE,在△ACD和△BCE中,,∴△ACD≌△BCE(SAS),∴BE=AD=2,∠ADC=∠BEC,∵∠ADC=180°﹣∠CDE=120°,∴∠BEC=120°,∴∠BEA=∠BEC﹣∠CED=60°,过点B作BN⊥AE于N,∴∠BNE=90°,在Rt△BNE中,∠EBN=90°﹣∠BEA=30°,∴EN=BE=1,∴BN=EN=,DN=DE﹣EN=3,连接BD,根据勾股定理得,BD===2,∵点H是CD的中点,点F是BC的中点,∴FH是△BCD的中位线,∴FH=BD=,由(2)知,△FGH是等边三角形,∴△FGH的周长为3FH=3,②当点D在AE的延长线上时,如图3,同①的方法得,FH=,∴△FGH的周长为3FH=3,即满足条件的△FGH的周长为3或3.11.(1)证明:如图1中,过点P作PT∥AB.∵AB∥CD,AB∥PT,∴AB∥PT∥CD,∴∠1=∠APT,∠2=∠CPT,∴∠APC=∠APT+∠CPT=∠1+∠2.(2)证明:如图2中,连接PP′.∵∠3=∠MPP′+∠MP′P,∠4=∠NPP′+∠NP′P,∠APC=∠MP′N,∴∠3+∠4=2∠APC,∵∠APC=∠1+∠2,∴∠3+∠4=2(∠1+∠2).(3)结论不成立.结论是:∠P=∠2﹣∠1,∠4﹣∠3=2(∠2﹣∠1).理由:如图3中,设PC交AB于E,AP交NP′于F.∵AB∥CD,∴∠PEB=∠2,∵∠PEB=∠1+∠P,∴∠2=∠P+∠1,∴∠P=∠2﹣∠1.∵∠4=∠P+∠PFN,∠PFN=∠3+∠P′,∠P=∠P′,∴∠4=∠P+∠3+∠P,∴∠4﹣∠3=2∠P=2(∠2﹣∠1),∴∠4﹣∠3=2(∠2﹣∠1).12.解:(1)∵A(0,a),B(a,0)(a>0),∴OA=a,OB=a,∵△AOB的面积为2,∴S△AOB=×a×a=2,∴a=2(负值舍去),∴A(0,2),B(2,0),∵C为线段AB的中点,∴C(1,1),∴OD=BD=CD=1,∴S△CDB=×1×1=.故答案为:.(2)连AC,过点D作DM⊥BC于M,∵△AOB是等腰直角三角形,∴AO⊥BO,AO=BO,∠B=∠OAB=45°,又CO=EO,∴AO是CE的垂直平分线,∴AE=AC,不妨设AE、CD交于F,AO、CD交于G,∴∠CGA=∠OAE+∠AFC=∠OCD+∠COA,∵∠AFC=∠COA=90°,∴∠OAE=∠OCD=∠OAC,又∵∠CAD=∠CAO+∠OAB=∠OCD+∠B=∠CDA,∴CD=CA=EA,∴△AOE≌△CMD(AAS),∴OE=DM,∴===3,∴=2;(3)=2,理由如下:作点C关于y轴的对称点N,连接BN,作DM∥BC交y轴于M,∵OB=OC=ON,∠BON=90°,∴△BON等腰直角三角形,∴∠BNO=∠BMD=45°,∴∠MBD=∠OBE+∠DBE=∠OBE+∠BOE=∠BEN,又∵BD=BE,∴△BMD≌△ENB(AAS),∴EN=BM,BN=DM=BC,又∵∠BFC=∠DFM,∠BCF=∠FDM,∴△BCF≌△MDF(AAS),∴BF=MF,∴CO﹣EO=NO﹣EO=NE=BM=2BF,即=2.13.解:(1)∵在△ABC中,AB=AC,∠BAC=90°,∴∠B=∠C=45°,∵∠APQ是△ABC的一个外角,∴∠APQ=∠B+∠BAP,∵∠BAP=15°,∴∠APQ=60°,∵AP=AQ,∴∠APQ=∠AQB=60°.(2)①图形如图2所示.②解:结论:PC2+BP2=2AP2.理由:连接MC.∵AB=AC,∠BAC=90°,∴∠B=∠ACB=45°,∵AP=AQ,∴∠APQ=∠AQP,∴∠BAP=∠CAQ,∴△ABP≌△ACQ(SAS),∴BP=CQ,∵点Q关于直线AC的对称点为M,∴AQ=AM,CQ=CM,∠CAM=∠CAQ,∠ACM=∠ACQ=45°,∴AP=AM,∠B=∠ACM=45°,∠BAP=∠CAM,BP=CM,∴∠BAC=∠P AM=90°,在Rt△APM中,AP=AM,∠P AM=90°,∴PM=,∵∠ACQ=∠ACM=45°,∴∠PCM=90°,在Rt△PCM中,∠PCM=90°,∴PC2+CM2=PM2,∴PC2+BP2=2AP2.14.【问题背景】证明:如图1,∵∠BAC=∠DAE=90°,∴∠DAB=∠EAC,在△ABD和△ACE中,,∴△ABD≌△ACE(SAS).【尝试应用】证明:如图2,过点D作DK⊥DC交FB的延长线于K.∵DK⊥CD,BF⊥AB,∴∠BDK=∠ABK=90°,∵AB=AC,∠BAC=90°,∴∠ABC=∠ACB=45°,∴∠DBK=∠K=45°,∴DK=DB,∵△ABD≌△ACE,∴∠ABD=∠ACE=135°,DB=EC=DK,∴∠ECG=45°,∵BF⊥AB,CA⊥AB,∴AG∥BF,∴∠G=∠DFK,在△ECG和△DKF中,,∴△ECG≌△DKF(AAS),∴DF=EG,∵DE=AE,∴DF+EF=AE,∴EG+EF=AE,即FG=AE.【拓展创新】解:如图3中,过点A作AE⊥AD交BD于E,连接CE..∵∠ADB=45°,∠DAE=90°,∴△ADE与△ABC都是等腰直角三角形,同法可证△ABD≌△ACE,∴CE=BD=2,∵∠AEC=∠ADB=45°,∴∠CED=∠CEB=90°,∴S△BDC=•BD•CE=×2×2=6.故答案为:6.15.解:(1)∵2a2+4ab+4b2+2a+1=0,∴(a+2b)2+(a+1)2=0,∵(a+2b)2≥0 (a+1)2≥0,∴a+2b=0,a+1=0,∴a=﹣1,b=,∴A(﹣1,0)B(0,).(2)①证明:如图1中,∵a+b=0,∴a=﹣b,∴OA=OB,又∵∠AOB=90°,∴∠BAO=∠ABO=45°,∵D与P关于y轴对称,∴BD=BP,∴∠BDP=∠BPD,设∠BDP=∠BPD=α,则∠PBF=∠BAP+∠BP A=45°+α,∵PE⊥DB,∴∠BEF=90°,∴∠F=90o﹣∠EBF,又∠EBF=∠ABD=∠BAO﹣∠BDP=45°﹣α,∴∠F=45o+α,∴∠PBF=∠F,∴PB=PF.②解:如图2中,过点Q作QF⊥QB交PB于F,过点F作FH⊥x轴于H.可得等腰直角△BQF,∵∠BOQ=∠BQF=∠FHQ=90°,∴∠BQO+∠FQH=90°,∠FQH+∠QFH=90°,∴∠BQO=∠QFH,∵QB=QF,∴△FQH≌△QBO(AAS),∴HQ=OB=OA,∴HO=AQ=PC,∴PH=OC=OB=QH,∴FQ=FP,又∠BFQ=45°∴∠APB=22.5°.16.解:(1)在Rt△ABC中,∠C=90°,∠B=30°,BC=6,∴AC=2,∠A=60°,∵△DEF是等边三角形,∴∠DCE=60°,∴∠ACD=30°,∴∠ADC=90°,∴CD=AC=3,∴△DEF的周长=9;(2)解:结论:CF=DG.理由:∵BC=6,EF=DF=DE=3,∴CF+BE=BC﹣EF=6﹣3=3,∵△DEF是等边三角形,∴∠DEF=60°,∵∠DEF=∠B+∠EGB,∴∠B=∠EGB=∠DGE=30°,∴EG=BE,∵EG+DG=CF+BE=3,∴CF=DG;(3)∵S△DEF=×32=,S△DGH=•GH•DH=•x•x=x2,y=S△DFE﹣S△DHG=﹣x2(0≤x≤3).17.解:(1)在Rt△ABC中,AC=2,BC=2,根据勾股定理得,AB===4,∴=,∵BQ=BP,∴=,∴,∵∠QBP=∠CBA,∴△BPQ∽△BAC,∴∠BQP=∠ACB=90°,∴PQ⊥AB;(2)∵点D是AC的中点,∴AD=CD=AC=1,由(1)知,PQ⊥AB,∴∠AQP=90°,∴∠PQD<90°,∵△PQD是直角三角形,∴①当∠DPQ=90°时,如图1,在Rt△ABC中,AC=2,AB=4,∴sin∠ABC==,∴∠ABC=30°,∴∠QPB=90°﹣∠ABC=60°,∴∠DPC=90°﹣∠BPQ=30°,∴CP===,∴BP=BC﹣CP=,②当∠PDQ=90°时,∴∠ADQ+∠PDC=90°,如图2,过Q作QE⊥AC于E,∴∠DEQ=90°=∠ACB,∴∠ADQ+∠DQE=90°,∴∠DQE=∠PDC,∴△EQD∽△CDP,∴,∴,设BP=t,则CP=BC﹣BP=2﹣t,在Rt△BQP中,BQ=BP cos30°=t,∴AQ=AB﹣BQ=4﹣t,在Rt△AEQ中,QE=AQ cos30°=(4﹣t)•=2﹣t,AE=AQ=2﹣t,∴DE=AD﹣AE=t﹣1,∴,∴t=或t=(大于2,舍去)∴BP=;即BP=或;(3);理由:如图3,①当点D'恰好落在边BC上时,由折叠知,PD'=PD,PQ⊥DD',由(1)知,PQ⊥AB,∴DD'∥AB,∴∠DD'C=∠ABC=30°,∴CD'=CD=,设BP=m,则CP=BC﹣BP=2﹣m,∴DP=D'P=CD'﹣CP=m﹣,在Rt△CDP中,根据勾股定理得,DP2=CP2+CD2,∴(m﹣)2=(2﹣m)2+1,∴m=,②当点D'落在D时,即PQ过点D,在Rt△CDP'中,∠P'=90°﹣∠DD'P'=30°,∴CP'===,∴BP'=BC+CP'=,综上:.18.(1)解:当MN最长时,BN===;当BN最长时,BN===,综合以上可得BN的长为或;(2)证明:如图,把△CBN绕点C逆时针旋转90°,得到△CAN',连接MN',∴△AN'C≌△BNC,∴CN'=CN,∠ACN'=∠BCN,∠CBN=∠CAN',∵∠MCN=45°,∴∠N'CA+∠ACM=∠ACM+∠BCN=45°,∴∠MCN'=∠BCM,∴△MN'C≌△MNC(SAS),∴MN'=MN,∵AC=BC,∠ACB=90°,∴∠B=∠CAM=45°,∴∠CAN'=45°,∴∠MAN'=∠CAN'+∠CAM=45°+45°=90°,在Rt△MN'A中,AN'2+AM2=N'M2,∴BN2+AM2=MN2,∴点M,N是线段AB的勾股分割点.19.问题背景解:∵△ABD,△AEC都是等边三角形,∴∠BAD=60°,∠CAE=60°,AD=AB,AC=AE,∴∠BAD+∠BAC=∠CAE+∠BAC,∴∠DAC=∠BAE,∴△ACD≌△AEB(SAS),∴△ACD可以由△AEB绕点A顺时针旋转60°得到,即旋转中心是点A,旋转方向是顺时针,旋转角是60°;尝试应用∵△ACD和△ABE都是等边三角形,∴AC=AD,AB=AE,∠CAD=∠BAE=60°,∴∠CAB=∠DAE,∴△ADE≌△ACB(SAS),∴∠ADE=∠ACB=90°,DE=CB,∵∠ADE=90°,∴∠ADF=90°,∵∠ADC=∠ACD=60°,∴∠DCF=∠CDF=30°,∴CF=DF,∵BD⊥BC,∴∠BDF=30°,∴BF=DF,设BF=x,则CF=DF=2x,DE=3x,∴;拓展创新∵∠ACB=90°,∴点C在以AB为直径的圆上运动,取AB的中点D,连接CD,∴CD=AB=1,如图,过点A作AE⊥AB,且使AE=AD,连接PE,BE,∵将线段AC绕点A顺时针旋转90°得到线段AP,∴∠P AC=90°,P A=AC,∵∠EAD=90°,∴∠P AE=∠CAD,∴△CAD≌△P AE(SAS),∴PE=CD=1,∵AB=2,AE=AD=1,∴BE===,∴BP≤BE+PE=+1,当且仅当P、E、B三点共线时取等号,∴BP的最大值为+1.20.解:(1)由AC长为1.5m,△ABC的面积为1.5m2,可得BC=2m,如图①,设加工桌面的边长为xcm,∵DE∥CB,∴△ADE∽△ACB,∴=,即=,解得:x=;如图②,设加工桌面的边长为ym,过点C作CM⊥AB,分别交DE、AB于点N、M,∵AC=1.5m,BC=2m,∴AB===2.5(m),∵△ABC的面积为1.5m2,∴CM=m,∵DE∥AB,∴△CDE∽△CAB,∴=,即=,解得:y=,∴x>y,即S1>S2,故答案为:>.(2)①函数图象如图6所示:②观察图象,发现该函数有最小值,此时a的取值~2之间.故选D.(3)①由(2)可知,S5<S4<S3.故答案为:S5<S4<S3.②如图7,△A1B1C1即为所求作.。
中考数学几何压轴题及答案及答案

中考数学几何压轴题及答案一、解答题(共30小题)1.观察猜想(1)如图①,在Rt△ABC中,∠BAC=90°,AB=AC=3,点D与点A重合,点E在边BC上,连接DE,将线段DE绕点D顺时针旋转90°得到线段DF,连接BF,BE与BF的位置关系是,BE+BF=;探究证明(2)在(1)中,如果将点D沿AB方向移动,使AD=1,其余条件不变,如图②,判断BE与BF的位置关系,并求BE+BF的值,请写出你的理由或计算过程;拓展延伸(3)如图③,在△ABC中,AB=AC,∠BAC=α,点D在边BA的延长线上,BD=n,连接DE,将线段DE绕着点D顺时针旋转,旋转角∠EDF=α,连接BF,则BE+BF的值是多少?请用含有n,α的式子直接写出结论2.在△ABC的边BC上取B′、C′两点,使∠AB′B=∠AC′C=∠BAC(1)如图1中∠BAC为直角,∠BAC=∠AB′B=∠AC′C=90°(点B′与点C′重合),则△ABC∽△B'BA∽△C'AC,,,进而可得AB2+AC2=;(2)如图2中当∠BAC为锐角,图3中∠BAC为钝角时(1)中的结论还成立吗?若不成立,则AB2+AC2等于什么(用含用BC和B′C′的式子表示)?并说明理由(3)若在△ABC中,AB=5,AC=6,BC=9,请你先判断出△ABC的类型,再求出B′C′的长3.(1)问题发现如图1,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=45°,点D是线段AB上一动点,连接BE填空:①的值为;②∠DBE的度数为.(2)类比探究如图2,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,点D是线段AB上一动点,连接BE.请判断的值及∠DBE的度数,并说明理由;(3)拓展延伸如图3,在(2)的条件下,将点D改为直线AB上一动点,其余条件不变,取线段DE 的中点M,连接BM、CM,若AC=2,则当△CBM是直角三角形时,线段BE的长是多少?请直接写出答案.4.(1)问题发现:如图①,在△ABC中,∠BAC=90°,AB=AC,点D是BC的中点,以点D为顶点作正方形DFGE,使点A、C分别在DE和DF上,连接BE、AF.则线段BE 和AF数量关系.(2)类比探究:如图②,保持△ABC固定不动,将正方形DFGE绕点D旋转α(0°<α≤360°),则(1)中的结论是否成立?如果成立,请证明;如果不成立,请说明理由.(3)解决问题:若BC=DF=2,在(2)的旋转过程中,连接AE,请直接写出AE的最大值.5.如图,在平行四边形ABCD中,AC与BD交于点O,以点O为顶点的∠EOF的两边分别与边AB、AD交于点E、F,且∠EOF与∠BAD互补.(1)若四边形ABCD是正方形,则线段OE与OF有何数量关系?请直接写出结论;(2)若四边形ABCD是菱形,那么(1)中的结论是否成立?若成立,请画出图形并给出证明;若不成立,请说明理由;(3)若AB:AD=m:n,探索线段OE与OF的数量关系,并证明你的结论.6.如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.(1)证明与推断:①求证:四边形CEGF是正方形;②推断:的值为:(2)探究与证明:将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由;(3)拓展与运用:正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2,则BC=.7.如图1,在△ABC中,AB=AC=2,∠BAC=120°,点D、E分别是AC、BC的中点,连接DE.定理:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.探索发现:图1中,的值为;的值为.(2)拓展探完若将△CDE绕点C逆时针方向旋转一周,在旋转过程中的大小有无变化?请仅就图2的情形给出证明.(3)问题解决当△CDE旋转至A,D,E三点共线时,直接写出线段BE的长.8.已知△ABC是边长为4的等边三角形,边AB在射线OM上,且OA=6,点D是射线OM上的动点,当点D不与点A重合时,将△ACD绕点C逆时针方向旋转60°得到△BCE,连接DE,设OD=m.(1)问题发现如图1,△CDE的形状是三角形.(2)探究证明如图2,当6<m<10时,△BDE的周长是否存在最小值?若存在,求出△BDE周长的最小值;若不存在,请说明理由.(3)解决问题是否存在m的值,使△DEB是直角三角形?若存在,请直接写出m的值;若不存在,请说明理由.9.等腰直角三角形ABC和等腰直角三角形ADE中,∠BAC=∠DAE=90°,AB=4,AE=2,其中△ABC固定,△ADE绕点A作360°旋转,点F、M、N分别为线段BE、BC、CD 的中点,连接MN、NF.问题提出:(1)如图1,当AD在线段AC上时,则∠MNF的度数为,线段MN 和线段NF的数量关系为;深入讨论:(2)如图2,当AD不在线段AC上时,请求出∠MNF的度数及线段MN和线段NF的数量关系;拓展延伸:(3)如图3,△ADE持续旋转过程中,若CE与BD交点为P,则△BCP面积的最小值为.10.四边形是我们在学习和生活中常见的图形,而对角线互相垂直的四边形也比较常见,比如筝形、菱形、图1中的四边形ABCD等.它们给我们的学习和生活带来了很多的乐趣和美感.(1)如图2,在四边形ABCD中,AB=AD,CB=CD,则AC与BD的位置关系是,请说明理由.(2)试探究图1中四边形ABCD的两组对边AB,CD与BC,AD之间的数量关系,请写出证明过程.(3)问题解决:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG 和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5,求GE的长.11.问题发现:如图(1)在Rt△ABC和Rt△BDE中,∠A=∠DEB=30°,BC=BE=6,Rt△BDE绕点B逆时针旋转,H为CD的中点,当点C与点E重合时,BH与AE的位置关系为,BH与AE的数量关系为;问题证明:在Rt△BDE绕点B旋转的过程中,(1)中的结论是否仍然成立?若成立,请就图(2)的情形给出证明若不成立,请说明理由;拓展应用:在Rt△BDE绕点B旋转的过程中,当DE∥BC时,请直接写出BH2的长.12.如图1,菱形ABCD与菱形GECF的顶点C重合,点G在对角线AC上,且∠BCD=∠ECF=60°,(1)问题发现的值为;(2)探究与证明将菱形GECF绕点C按顺时针方向旋转α角(0°<α<60°),如图2所示,试探究线段AG与BE之间的数量关系,并说明理由;(3)拓展与运用:菱形GECF在旋转过程中,当点A,G,F三点在一条直线上时,如图3所示连接CG并延长,交AD于点H,若CE=2,GH=,则AH的长为.13.如图,在Rt△ABC中,∠ACB=90°,=,CD⊥AB于点D,点E是直线AC上一动点,连接DE,过点D作FD⊥ED,交直线BC于点F.(1)探究发现:如图1,若m=n,点E在线段AC上,则=;(2)数学思考:①如图2,若点E在线段AC上,则=(用含m,n的代数式表示);②当点E在直线AC上运动时,①中的结论是否仍然成立?请仅就图3的情形给出证明;(3)拓展应用:若AC=,BC=2,DF=4,请直接写出CE的长.14.如图,已知点E是射线BC上的一点,以BC、CE为边作正方形ABCD和正方形CEFG,连接AF,取AF的中点M,连接DM、MG(1)如图1,判断线段DM和GM的数量关系是,位置关系是;(2)如图2,在图中的正方形CEFG绕点C逆时针旋转的过程中,其他条件不变,(1)中的结论是否成立?说明理由;(3)已知BC=10,CE=2,正方形CEFG绕点C旋转的过程中,当A、F、E共线时,直接写出△DMG的面积.15.在Rt△ABC中,∠ACB=90°,AB=,AC=2,过点B作直线m∥AC,将△ABC绕点C顺时针旋转得到△A′B′C(点A,B的对应点分别为A',B′),射线CA′,CB′分别交直线m于点P,Q.(1)如图1,当P与A′重合时,求∠ACA′的度数;(2)如图2,设A′B′与BC的交点为M,当M为A′B′的中点时,求线段PQ的长;(3)在旋转过程中,当点P,Q分别在CA′,CB′的延长线上时,试探究四边形P A'B′Q的面积是否存在最小值.若存在,求出四边形P A′B′Q的最小面积;若不存在,请说明理由.16.如图(1),在等边三角形ABC中,点D,E分别在边AB,AC上,AD=AE,连接BE,CD,点M,N,P分别是BE,CD,BC的中点,连接DE,PM,PN,MN.(1)观察猜想,图(1)中△PMN是(填特殊三角形的名称)(2)探究证明,如图(2),△ADE绕点A按逆时针方向旋转,则△PMN的形状是否发生改变?并就图(2)说明理由.(3)拓展延伸,若△ADE绕点A在平面内自由旋转,AD=2,AB=6,请直接写出△PMN 的周长的最大值.17.已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE,设∠BAD=α,∠CDE=β,(1)如图1,若点D在线段BC上,点E在线段AC上.∠ABC=60°,∠ADE=70°,则α=°;β=°.(2)如图2,若点D在线段BC上,点E在线段AC上,则α,β之间有什么关系式?说明理由.(3)是否存在不同于(2)中的α,β之间的关系式?若存在,请写出这个关系式(写出一种即可),说明理由;若不存在,请说明理由.18.问题提出:(1)如图1,在四边形ABCD中,连接AC、BD,AB=AD,∠BAD=∠BCD=90°,将△ABC绕点A逆时针旋转90°,得到△ADE,点B的对应点落在点D,点C的对应点为点E,可知点C、D、E在一条直线上,则△ACE为三角形,BC、CD、AC的数量关系为;探究发现:(2)如图2,在⊙O中,AB为直径,点C为的中点,点D为圆上一个点,连接AD、CD、AC、BC、BD,且AD<BD,请求出CD、AD、BD间的数量关系.拓展延伸:(3)如图3,在等腰直角三角形ABC中,点P为AB的中点,若AC=13,平面内存在一点E,且AE=10,CE=13,当点Q为AE中点时,PQ=.19.已知△ABC中,CA=CB,0°<∠ACB≤90°,点M、N分别在边CA,CB上(不与端点重合),BN=AM,射线AG∥BC交BM延长线于点D,点E在直线AN上,EA=ED.(1)【观察猜想】如图1,点E在射线NA上,当∠ACB=45°时,①线段BM与AN的数量关系是;②∠BDE的度数是;(2)【探究证明】如图2点E在射线AN上,当∠ACB=30°时,判断并证明线段BM与AN的数量关系,求∠BDE的度数;(3)【拓展延伸】如图3,点E在直线AN上,当∠ACB=60°时,AB=3,点N是BC 边上的三等分点,直线ED与直线BC交于点F,请直接写出线段CF的长.20.如图①,在正方形ABCD和正方形AB'C'D'中,AB=2,AB'=,连接CC’(1)问题发现:.(2)拓展探究:将正方形AB'C'D'绕点A逆时针旋转,记旋转角为θ,连接BB',试判断:当0°≤θ<360°时,的值有无变化?请仅就图②中的情形给出你的证明;(3)问题解决:请直接写出在旋转过程中,当C,C′,D'三点共线时BB′的长.21.如图1,在正方形ABCD中,点O是对角线BD的中点.(1)观察猜想将图1中的△BCD绕点O逆时针旋转至图2中△ECF的位置,连接AC,DE,则线段AC与DE的数量关系是,直线AC与DE的位置关系是.(2)类比探究将图2中的△ECF绕点O逆时针旋转至图3的位置,(1)中的结论是否成立?并说明理由.(3)拓展延伸将图2中的△ECF在平面内旋转,设直线AC与DE的交点为M,若AB=4,请直接写出BM的最大值与最小值.22.如图1,点B在直线l上,过点B构建等腰直角三角形ABC,使∠BAC=90°,且AB=AC,过点C作CD⊥直线l于点D,连接AD.(1)小亮在研究这个图形时发现,∠BAC=∠BDC=90°,点A,D应该在以BC为直径的圆上,则∠ADB的度数为°,将射线AD顺时针旋转90°交直线l于点E,可求出线段AD,BD,CD的数量关系为;(2)小亮将等腰直角三角形ABC绕点B在平面内旋转,当旋转到图2位置时,线段AD,BD,CD的数量关系是否变化,请说明理由;(3)在旋转过程中,若CD长为1,当△ABD面积取得最大值时,请直接写AD的长.23.如图1,将三角板放在正方形ABCD上,使三角板的直角顶点E与正方形ABCD的顶点A重合,三角板的一边交CD于点F.另一边交CB的延长线于点G.(1)观察猜想:线段EF与线段EG的数量关系是;(2)探究证明:如图2,移动三角板,使顶点E始终在正方形ABCD的对角线AC上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理由:(3)拓展延伸:如图3,将(2)中的“正方形ABCD”改为“矩形ABCD”,且使三角板的一边经过点B,其他条件不变,若AB=a、BC=b,求的值.24.如图1,在Rt△ABC中,∠B=90°,AB=2,BC=1,点D,E分别是边BC,AC的中点,连接DE.将△EDC绕点C按顺时针方向旋转,记旋转角为α.(1)问题发现①当α=0°时,=;②当α=180°时,=.(2)拓展探究试判断:当0°≤α<360°时,的大小有无变化?请仅就图2的情况给出证明.(3)问题解决当△EDC旋转至A、B、E三点共线时,直接写出线段BD的长.25.在△ABC中,AD为BC边上的中线,E为AD上一动点,设DE=nEA,连接CE并延长,交AB于点F.(1)尝试探究如图(1),当∠BAC=90°,∠B=30°,DE=EA时,BF,BA之间的数量关系是;(2)类比延伸如图(2),当△ABC为锐角三角形,DE=EA时,(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由;(3)拓展迁移如图(3),当△ABC为锐角三角形,DE=nEA时,请直接写出BF,BA之间的数量关系.26.古希腊数学家毕达哥拉斯认为:“一切平面图形中最美的是圆”.请研究如下美丽的圆.如图,线段AB是⊙O的直径,延长AB至点C,使BC=OB,点E是线段OB的中点,DE ⊥AB交⊙O于点D,点P是⊙O上一动点(不与点A,B重合),连接CD,PE,PC.(1)求证:CD是⊙O的切线;(2)小明在研究的过程中发现是一个确定的值.回答这个确定的值是多少?并对小明发现的结论加以证明.27.定义:三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角.(1)如图1,∠E是△ABC中∠A的遥望角,若∠A=α,请用含α的代数式表示∠E.(2)如图2,四边形ABCD内接于⊙O,=,四边形ABCD的外角平分线DF交⊙O 于点F,连结BF并延长交CD的延长线于点E.求证:∠BEC是△ABC中∠BAC的遥望角.(3)如图3,在(2)的条件下,连结AE,AF,若AC是⊙O的直径.①求∠AED的度数;②若AB=8,CD=5,求△DEF的面积.28.【性质探究】如图,在矩形ABCD中,对角线AC,BD相交于点O,AE平分∠BAC,交BC于点E.作DF⊥AE于点H,分别交AB,AC于点F,G.(1)判断△AFG的形状并说明理由.(2)求证:BF=2OG.【迁移应用】(3)记△DGO的面积为S1,△DBF的面积为S2,当=时,求的值.【拓展延伸】(4)若DF交射线AB于点F,【性质探究】中的其余条件不变,连结EF,当△BEF的面积为矩形ABCD面积的时,请直接写出tan∠BAE的值.29.如图,已知AC为正方形ABCD的对角线,点P是平面内不与点A,B重合的任意一点,连接AP,将线段AP绕点P顺时针旋转90°得到线段PE,连接AE,BP,CE.(1)求证:△APE∽△ABC;(2)当线段BP与CE相交时,设交点为M,求的值以及∠BMC的度数;(3)若正方形ABCD的边长为3,AP=1,当点P,C,E在同一直线上时,求线段BP 的长.30.如图1和图2,在△ABC中,AB=AC,BC=8,tan C=.点K在AC边上,点M,N 分别在AB,BC上,且AM=CN=2.点P从点M出发沿折线MB﹣BN匀速移动,到达点N时停止;而点Q在AC边上随P移动,且始终保持∠APQ=∠B.(1)当点P在BC上时,求点P与点A的最短距离;(2)若点P在MB上,且PQ将△ABC的面积分成上下4:5两部分时,求MP的长;(3)设点P移动的路程为x,当0≤x≤3及3<x≤9时,分别求点P到直线AC的距离(用含x的式子表示);(4)在点P处设计并安装一扫描器,按定角∠APQ扫描△APQ区域(含边界),扫描器随点P从M到B再到N共用时36秒.若AK=,请直接写出点K被扫描到的总时长.参考答案与试题解析一.解答题(共30小题)1.【解答】解:(1)如图①中,∵∠EAF=∠BAC=90°,∴∠BAF=∠CAE,∵AF=AE,AB=AC,∴△BAF≌△CAE,∴∠ABF=∠C,BF=CE,∵AB=AC,∠BAC=90°,∴∠ABC=∠C=45°,∴∠FBE=∠ABF+∠ABC=90°,BC=BE+EC=BE+BF,故答案为:BF⊥BE,BC.(2)如图②中,作DH∥AC交BC于H.∵DH∥AC,∴∠BDH=∠A=90°,△DBH是等腰直角三角形,由(1)可知,BF⊥BE,BF+BE=BH,∵AB=AC=3,AD=1,∴BD=DH=2,∴BH=2,∴BF+BE=BH=2;(3)如图③中,作DH∥AC交BC的延长线于H,作DM⊥BC于M.∵AC∥DH,∴∠ACB=∠H,∠BDH=∠BAC=α,∵AB=AC,∴∠ABC=∠ACB∴∠DBH=∠H,∴DB=DH,∵∠EDF=∠BDH=α,∴∠BDF=∠HDE,∵DF=DE,DB=DH,∴△BDF≌△HDE,∴BF=EH,∴BF+BE=EH+BE=BH,∵DB=DH,DM⊥BH,∴BM=MH,∠BDM=∠HDM,∴BM=MH=BD•sin.∴BF+BE=BH=2n•sin.2.【解答】解:(1)如图1中,∵△ABC∽△B'BA∽△C'AC,∴=,=,∴AB2=BB′×BC,AC2=CC′×BC,∴AB2+AC2=BC(BB′+CC′)=BC×BC=BC2,故答案为BC2.(2)不成立.理由:如图2中当∠BAC为锐角时,BB′+CC′﹣B′C′=BC,且△ABC∽△B'BA∽△C'AC,∴∴=,=,∴AB2=BB′×BC,AC2=CC′×BC,∴AB2+AC2=BC(BB′+CC′)=BC2+BC•B′C′.图3中∠BAC为钝角时,BB′+CC′+B′C′=BC.AB2+AC2=BC(BB′+CC′)=BC2﹣BC•B′C′.(3)当AB=5,AC=6,BC=9时,则AB2+AC2<BC2,可知△ABC为钝角三角形,由图3可知:AB2+AC2=BC2﹣BC•B′C′,∴52+62=92﹣9B′C′,∴B′C′=.3.【解答】解:(1)∵∠ACB=∠DCE=90°,∠CAB=∠CDE=45°,∴∠ABC=∠CAB=45°=∠CDE=∠CED,∴AC=BC,CD=CE,∵∠ACB=∠DCE=90°,∴∠ACD=∠BCE,在△ACD和△BCE中,,∴△ACD≌△BCE(SAS),∴BE=AD,∠CAB=∠CBE=45°,∴∠DBE=∠ABC+∠CBE=90°,=1,故答案为:1,90°(2),∠DBE=90°理由如下:∵∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,∴∠ACD=∠BCE,∠CED=∠ABC=30°∴tan∠ABC=tan30°==∵∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,∴Rt△ACB∽Rt△DCE∴∴,且∠ACD=∠BCE∴△ACD∽△BCE∴=,∠CBE=∠CAD=60°∴∠DBE=∠ABC+∠CBE=90°(3)若点D在线段AB上,如图,由(2)知:=,∠ABE=90°∴BE=AD∵AC=2,∠ACB=90°,∠CAB=90°∴AB=4,BC=2∵∠ECD=∠ABE=90°,且点M是DE中点,∴CM=BM=DE,∵△CBM是直角三角形∴CM2+BM2=BC2=(2)2,∴BM=CM=∴DE=2∵DB2+BE2=DE2,∴(4﹣AD)2+(AD)2=24∴AD=+1∴BE=AD=3+若点D在线段BA延长线上,如图同理可得:DE=2,BE=AD∵BD2+BE2=DE2,∴(4+AD)2+(AD)2=24,∴AD=﹣1∴BE=AD=3﹣综上所述:BE的长为3+或3﹣4.【解答】解:(1)∵△ABC中,∠BAC=90°,AB=AC,点D是BC的中点,∴AD=BD=DC,∠BDA=90°,∵四边形DFGE是正方形,∴DE=DF,∠EDF=90°,∴∠BDE=∠ADF=90°,在△BDE和△ADF中,,∴△BDE≌△ADF(SAS),∴BE=AF故答案为:BE=AF;(2)成立;理由如下:当正方形DFGE在BC的上方时,如图②所示,连接AD,∵在Rt△ABC中,AB=AC,D为斜边BC的中点,∴AD=BD,AD⊥BC,∴∠ADE+∠EDB=90°,∵四边形DFGE为正方形,∴DE=DF,且∠EDF=90°,∴∠ADE+∠ADF=90°,∴∠BDE=∠ADF,在△BDE和△ADF中,,∴△BDE≌△ADF(SAS),∴BE=AF;当正方形DFGE在BC的下方时,连接AD,如图③所示:∵∠BDE=∠BDF+90°,∠ADF=∠BDF+90°,∴∠BDE=∠ADF,在△BDE和△ADF中,,∴△BDE≌△ADF(SAS),∴BE=AF;综上所述,(1)中的结论BE=AF成立;(3)在△ADE中,∵AE<AD+DE,∴当点A、D、E共线时,AE取得最大值,最大值为AD+DE.如图④所示:则AD=BC=1,DE=DF=2,∴AE=AD+DE=3,即AE的最大值为3.5.【解答】解:(1)如图1,过点O作OM⊥AB于M,ON⊥AD于N,∴∠OME=∠ONF=90°,∴∠BAD+∠MON=180°,∵∠BAD+∠EOF=180°,∴∠MON=∠EOF,∴∠EOM=∠FON,∵O是正方形ABCD的对角线的交点,∴∠BAO=∠DAO,∵OM⊥AB,ON⊥AD,∴OM=ON,∴△OME≌△ONF(AAS)∴OE=OF;(2)(1)的结论成立;理由:如图2,过点O作OM⊥AB于M,ON⊥AD于N,∴∠OME=∠ONF=90°,∴∠BAD+∠MON=180°,∵∠BAD+∠EOF=180°,∴∠MON=∠EOF,∴∠EOM=∠FON,∵O是菱形ABCD的对角线的交点,∴∠BAO=∠DAO,∵OM⊥AB,ON⊥AD,∴OM=ON,∴△OME≌△ONF(AAS)∴OE=OF;(3)如图3,过点O作OG⊥AB于G,OH⊥AD于H,∴∠OGE=∠OHF=90°,∴∠BAD+∠GOH=180°,∵∠BAD+∠EOF=180°,∴∠GOH=∠EOF,∴△EOG∽△FOH,∴,∵O是▱ABCD的对角线的交点,∴S△AOB=S△AOD,∵S△AOB=AB•OG,S△AOD=AD•OH,∴AB•OG=AD•OH,∴=,∴.6.【解答】解:(1)①∵四边形ABCD是正方形,∴∠BCD=90°,∠BCA=45°,∵GE⊥BC、GF⊥CD,∴∠CEG=∠CFG=∠ECF=90°,∴四边形CEGF是矩形,∠CGE=∠ECG=45°,∴EG=EC,∴四边形CEGF是正方形;②由①知四边形CEGF是正方形,∴∠CEG=∠B=90°,∠ECG=45°,∴=,GE∥AB,∴==,故答案为:;(2)连接CG,由旋转性质知∠BCE=∠ACG=α,在Rt△CEG和Rt△CBA中,=cos45°=、=cos45°=,∴==,∴△ACG∽△BCE,∴==,∴线段AG与BE之间的数量关系为AG=BE;(3)∵∠CEF=45°,点B、E、F三点共线,∴∠BEC=135°,∵△ACG∽△BCE,∴∠AGC=∠BEC=135°,∴∠AGH=∠CAH=45°,∵∠CHA=∠AHG,∴△AHG∽△CHA,∴==,设BC=CD=AD=a,则AC=a,则由=得=,∴AH=a,则DH=AD﹣AH=a,CH==a,∴=得=,解得:a=3,即BC=3,故答案为:3.7.【解答】解:(1)如图1,连接AE,∵AB=AC=2,点E分别是BC的中点,∴AE⊥BC,∴∠BEC=90°,∵AB=AC=2,∠BAC=120°,∴∠B=∠C=30°,在Rt△ABE中,AE=AB=1,根据勾股定理得,BE=∵点E是BC的中点,∴BC=2BE=2,∴==,∵点D是AC的中点,∴AD=CD=AC=1,∴==,故答案为:,;(2)无变化,理由:由(1)知,CD=1,CE=BE=,∴=,,∴=,由(1)知,∠ACB=∠DCE=30°,∴∠ACD=∠BCE,∴△ACD∽△BCE,∴,(3)当点D在线段AE上时,如图2,过点C作CF⊥AE于F,∠CDF=180°﹣∠CDE=60°,∴∠DCF=30°,∴DF=CD=,∴CF=DF=,在Rt△AFC中,AC=2,根据勾股定理得,AF==,∴AD=AF+DF=,由(2)知,,∴BE=AD=当点D在线段AE的延长线上时,如图3,过点C作CG⊥AD交AD的延长线于G,∵∠CDG=60°,∴∠DCG=30°,∴DG=CD=,∴CG=DG=,在Rt△ACG中,根据勾股定理得,AG=,∴AD=AG﹣DG=,由(2)知,,∴BE=AD=即:线段BE的长为或.8.【解答】解:(1)证明:∵将△ACD绕点C逆时针方向旋转60°得到△BCE,∴∠DCE=60°,DC=EC,∴△CDE是等边三角形;故答案为:等边;(2)存在,当6<t<10时,由旋转的性质得,BE=AD,∴C△DBE=BE+DB+DE=AB+DE=4+DE,由(1)知,△CDE是等边三角形,∴DE=CD,∴C△DBE=CD+4,由垂线段最短可知,当CD⊥AB时,△BDE的周长最小,此时,CD=2,∴△BDE的最小周长=CD+4=2+4;(3)存在,①∵当点D与点B重合时,D,B,E不能构成三角形,∴当点D与点B重合时,不符合题意,②当0≤m<6时,由旋转可知,∠ABE=60°,∠BDE<60°,∴∠BED=90°,由(1)可知,△CDE是等边三角形,∴∠DEB=60°,∴∠CEB=30°,∵∠CEB=∠CDA,∴∠CDA=30°,∵∠CAB=60°,∴∠ACD=∠ADC=30°,∴DA=CA=4,∴OD=OA﹣DA=6﹣4=2,∴m=2;③当6<m<10时,由∠DBE=120°>90°,∴此时不存在;④当m>10时,由旋转的性质可知,∠DBE=60°,又由(1)知∠CDE=60°,∴∠BDE=∠CDE+∠BDC=60°+∠BDC,而∠BDC>0°,∴∠BDE>60°,∴只能∠BDE=90°,从而∠BCD=30°,∴BD=BC=4,∴OD=14,∴m=14,综上所述:当m=2或14时,以D、E、B为顶点的三角形是直角三角形.9.【解答】解:(1)如图1中,连接DB,MF,CE,延长BD交EC于H.∵AC=AB,AE=AD,∠BAD=∠CAE=90°,∴△BAD≌△CAE(SAS),∴BD=EC,∠ACE=∠ABD,∵∠ABD+∠ADB=90°,∠ADB=∠CDH,∴∠ADH+∠DCH=90°,∴∠CHD=90°,∴EC⊥BH,∵BM=MC,BF=FE,∴MF∥EC,MF=EC,∵CM=MB,CN=ND,∴MN∥BD,MN=BD,∴MN=MF,MN⊥MF,∴∠NMF=90°,∴∠MNF=45°,NF=MN.故答案为:45°(2):如图2中,连接MF,EC,BD.设EC交AB于O,BD交EC于H.∵AC=AB,AE=AD,∠BAD=∠CAE=90°,∴∠BAD=∠CAE,∴△BAD≌△CAE(SAS),∴BD=EC,∠ACE=∠ABD,∵∠AOC+∠ACO=90°,∠AOC=∠BOH,∴∠OBH+∠BOH=90°,∴∠BHO=90°,∴EC⊥BD,∵BM=MC,BF=FE,∴MF∥EC,MF=EC,∵CM=MB,CN=ND,∴MN∥BD,MN=BD,∴MN=MF,MN⊥MF,∴∠NMF=90°,∴∠MNF=45°,NF=MN.(3):如图3中,如图以A为圆心AD为半径作⊙A.当直线PB与⊙A相切时,此时∠CBP的值最小,点P到BC的距离最小,即△BCP的面积最小,∵AD=AE,AB=AC,∠BAC=∠DAE=90°,∴∠BAD=∠CAE,∴△BAD≌△CAE(SAS),∴∠ACE=∠ABD,BD=EC,∵∠ABD+∠AOB=90°,∠AOB=∠CPO,∴∠CPB=90°,∵PB是⊙A的切线,∴∠ADP=90°,∵∠DPE=∠ADP=∠DAE=90°,∴四边形ADPE是矩形,∵AE=AD,∴四边形ADPE是正方形,∴AD=AE=PD=PE=2,BD=EC==2,∴PC=2﹣2,PB=2+2,∴S△BCP的最小值=×PC×PB=(2﹣2)(2+2)=4.10.【解答】(1)解:AC⊥BD,理由如下:连接AC、BD,如图2所示:∵AB=AD,∴点A在线段BD的垂直平分线上,∵CB=CD,∴点C在线段BD的垂直平分线上,∴直线AC是线段BD的垂直平分线,∴AC⊥BD,故答案为:AC⊥BD;(2)解:AD2+BC2=AB2+CD2;理由如下:如图1,已知四边形ABCD中,AC⊥BD,设BD、AC相交于E,∵AC⊥BD,∴∠AED=∠AEB=∠BEC=∠CED=90°,由勾股定理得,AD2+BC2=AE2+DE2+BE2+CE2,AB2+CD2=AE2+BE2+CE2+DE2,∴AD2+BC2=AB2+CD2;(3)解:如图3,连接CG、BE,∵四边形ACFG和四边形ABDE是正方形,∴AC=AG,AB=AE,∠CAG=∠BAE=90°,∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,在△GAB和△CAE中,,∴△GAB≌△CAE(SAS),∴∠ABG=∠AEC,又∠AEC+∠AME=90°,∴∠ABG+∠AME=90°,即CE⊥BG,由(2)得,CG2+BE2=CB2+GE2,在Rt△ABC中,AC=4,AB=5,根据勾股定理得,BC2=52﹣42=9,∵CG和BE分别是正方形ACFG和正方形ABDG的对角线,∴CG2=42+42=32,BE2=52+52=50,∴GE2=CG2+BE2﹣CB2=32+50﹣9=73,∴GE=.11.【解答】解:问题发现:如图1中,结论:AE=2BH,AE⊥BH.理由:在Rt△ABC中,∵BC=6,∠A=30°,∴AE=2BC=12,在Rt△CDB中,∵∠DCB=30°,∴CD==4,∵CH=DH,∴BH=CD=2,∴==2,∴AE=2BH.故答案为AE⊥BH,AE=2BH.问题证明:如图2中,(1)中结论成立.理由:延长BH到F使得HF=BH,连接CF.设AE交BF于O.∵CH=DH,BH=HF,∠CHF=∠BHD,∴△CHF≌△DHB(SAS),∴BD=CF,∠F=∠DBH,∴CF∥BD,∵AB=BC,BE=BD,∴BE=CF,∴==,∵CF∥BD,∴∠BCF+∠CBD=180°,∵∠ABC+∠DBE=∠ABD+∠CBD+∠CBD+∠CBE=∠CBD+∠ABE=180°,∴∠BCF=∠ABE,∴△ABE∽△BCF,∴∠CBF=∠BAE,==,∴AE=BF=2BH,∵∠CBF+∠ABF=90°,∴∠ABF+∠BAE=90°,∴∠AOB=90°,∴BH⊥AE.拓展应用:如图3﹣1中,当DE在BC的下方时,延长AB交DE于F.∵DE∥BC∴∠ABC=∠BFD=90°,由题意BC=BE=6,AB=6,BD=2,DE=4,∵•BD•BE=•DE•BF,∴BF==3,∴EF=BF=3,∴AF=6+3,∴AE2=AF2+EF2=(6+3)2+(3)2=144+36.∵AE=2BH,∴AE2=12BH2,∴BH2=12+3如图3﹣2中,当DE在BC的上方时,同法可得AF=6﹣3,EF=3,∴BH2==(=12﹣3.12.【解答】解:(1)如图1中,作EH⊥CG于H.∵四边形ECFG是菱形,∠ECF=60°,∴∠ECH=∠ECF=30°,EC=EG,∵EH⊥CG,∴GH=CG,∴=cos30°=,∴=2•=,∵EG∥CD,AB∥CD,∴GE∥AB,∴==.故答案为.(2)结论:AG=BE.理由:如图2中,连接CG.∵四边形ABCD,四边形ECFG都是菱形,∠ECF=∠DCB=60°,∴∠ECG=∠EGC=∠BCA=∠BAC=30°,∴△ECG∽△BCE,∴=,∵∠ECB=∠GCA,∴△ECB∽△GCA,∴==,∴AG=BE.(3)如图3中,∵∠AGH=∠CGF=30°.∠AGH=∠GAC+∠GCA,又∵∠DAC=∠HAG+∠GAC=30°,∴∠HAG=∠ACH,∵∠AHG=∠AHC,∴△HAG∽△HCA,∴HA:HC=GH:HA,∴AH2=HG•HC,∴FC=2,CG=CF,∴GC=2,∵HG=,∴AH2=HG•HC=•3=9,∵AH>0,∴AH=3.故答案为3.13.【解答】解:(1)当m=n时,即:BC=AC,∵∠ACB=90°,∴∠A+∠ABC=90°,∵CD⊥AB,∴∠DCB+∠ABC=90°,∴∠A=∠DCB,∵∠FDE=∠ADC=90°,∴∠FDE﹣∠CDE=∠ADC﹣∠CDE,即∠ADE=∠CDF,∴△ADE∽△CDF,∴,∵∠A=∠DCB,∠ADC=∠BDC=90°,∴△ADC∽△CDB,∴=1,∴=1(2)①∵∠ACB=90°,∴∠A+∠ABC=90°,∵CD⊥AB,∴∠DCB+∠ABC=90°,∴∠A=∠DCB,∵∠FDE=∠ADC=90°,∴∠FDE﹣∠CDE=∠ADC﹣∠CDE,即∠ADE=∠CDF,∴△ADE∽△CDF,∴,∵∠A=∠DCB,∠ADC=∠BDC=90°,∴△ADC∽△CDB,∴,∴②成立.如图,∵∠ACB=90°,∴∠A+∠ABC=90°,又∵CD⊥AB,∴∠DCB+∠ABC=90°,∴∠A=∠DCB,∵∠FDE=∠ADC=90°,∴∠FDE+∠CDE=∠ADC+∠CDE,即∠ADE=∠CDF,∴△ADE∽△CDF,∴,∵∠A=∠DCB,∠ADC=∠BDC=90°,∴△ADC∽△CDB,∴,∴.(3)由(2)有,△ADE∽△CDF,∵=,∴=,∴CF=2AE,在Rt△DEF中,DE=2,DF=4,∴EF=2,①当E在线段AC上时,在Rt△CEF中,CF=2AE=2(AC﹣CE)=2(﹣CE),EF=2,根据勾股定理得,CE2+CF2=EF2,∴CE2+[2(﹣CE)]2=40∴CE=2,或CE=﹣(舍)而AC=<CE,∴此种情况不存在,②当E在AC延长线上时,在Rt△CEF中,CF=2AE=2(AC+CE)=2(+CE),EF=2,根据勾股定理得,CE2+CF2=EF2,∴CE2+[2(+CE)]2=40,∴CE=,或CE=﹣2(舍),③如图1,当点E在CA延长线上时,CF=2AE=2(CE﹣AC)=2(CE﹣),EF=2,根据勾股定理得,CE2+CF2=EF2,∴CE2+[2(CE﹣)]2=40,∴CE=2,或CE=﹣(舍)即:CE=2或CE=.14.【解答】解:(1)如图1,延长GM交AD于H,∵AD∥GF,∴∠GFM=∠HAM,在△FMG和△AMH中,,∴△FMG≌△AMH(ASA),∴HM=GM,AH=FG,∵AD=CD,AH=FG=CG,∴DH=DG,∵∠HDG=90°,HM=GM,∴DM=MG,DM⊥MG,故答案为DM=MG,DM⊥MG.(2)结论成立:DM=MG,DM⊥MG,理由:如图2中,延长GM使得MH=GM,连接AH、DH、DG,延长AD交GF的延长线于N,交CD于O.∵AM=MF,∠AMH=∠FMG,MH=MG,∴△AMH≌△FMG(SAS),∴AH=GF=CG,∠AHM=∠FGM,∴AH∥GN,∴∠HAD=∠N,∵∠ODN=∠OGC=90°,∠DON=∠GOC,∴∠N=∠OCG,∴∠HAD=∠DCG,∵AH=CG,AD=CD,∴△HAD≌△GCD(SAS),∴DH=DG,∠HDA=∠CDG,∴∠HDG=∠ADC=90°,∴△HDG是等腰直角三角形,∵MH=MG,∴DM⊥GH,DM=MH=MG,(3)①如图3﹣1中,连接AC.在Rt△ABC中,AC==10,在Rt△ACE中,AE==14,∴AF=AE=EF=14﹣2=12,∴FM=AM=AF=6,在Rt△MGF中,MG==2,∴S△DMG=×2×2=20,②如图3﹣2中,连接AC.同法可得AE=14,AF=16,FM=8,MG==2,∴S△DMG=×2×2=34,综上所述,满足条件的△DMG的面积为20或34.15.【解答】解:(1)由旋转可得:AC=A'C=2,∵∠ACB=90°,AB=,AC=2,∴BC=,∵∠ACB=90°,m∥AC,∴∠A'BC=90°,∴cos∠A'CB==,∴∠A'CB=30°,∴∠ACA'=60°;(2)∵M为A'B'的中点,∴∠A'CM=∠MA'C,由旋转可得,∠MA'C=∠A,∴∠A=∠A'CM,∴tan∠PCB=tan∠A=,∴PB=BC=,∵∠PCQ=∠PBC=90°,∴∠BQC+∠BPC=∠BCP+∠BPC=90°,∴∠BQC=∠BCP=∠A,∴tan∠BQC=tan∠A=,∴BQ=BC×=2,∴PQ=PB+BQ=;(3)∵S四边形P A'B′Q=S△PCQ﹣S△A'CB'=S△PCQ﹣,∴S四边形P A'B′Q最小,即S△PCQ最小,∴S△PCQ=PQ×BC=PQ,法一:(几何法)取PQ的中点G,∵∠PCQ=90°,∴CG=PQ,即PQ=2CG,当CG最小时,PQ最小,∴CG⊥PQ,即CG与CB重合时,CG最小,∴CG min=,PQ min=2,∴S△PCQ的最小值=3,S四边形P A'B′Q=3﹣;法二(代数法)设PB=x,BQ=y,由射影定理得:xy=3,∴当PQ最小时,x+y最小,∴(x+y)2=x2+2xy+y2=x2+6+y2≥2xy+6=12,当x=y=时,“=”成立,∴PQ=+=2,∴S△PCQ的最小值=3,S四边形P A'B′Q=3﹣.16.【解答】解:(1)结论:△PMN是等边三角形.理由:如图1中,∵△ABC是等边三角形,∴AB=AC,∠ABC=∠ACB=60°,∵AD=AE,∴BD=EC,∵PB=PC,CN=ND,BM=EM,∴PN∥BD,PM∥EC,PN=BD,PM=EC,∴PM=PN,∠NPC=∠ABC=60°,∠MPB=∠ACB=60°,∴∠MPN=60°,∴△PMN是等边三角形,故答案为等边三角形.(2)△PMN的形状不发生改变,仍为等边三角形,理由如下:如图2中,连接BD,CE.由旋转可得∠BAD=∠CAE,∵△ABC是等边三角形,∴AB=AC,∠ACB=∠ABC=60°又∵AD=AE,∴△ABD≌△ACE(SAS),∴BD=CE,∠ABD=∠ACE,∵M是BE的中点,P是BC的中点,∴PM是△BCE的中位线,∴PM=,且PM∥CE.同理可证PN=BD且PN∥BD,∴PM=PN,∠MPB=∠ECB,∠NPC=∠DBC,∴∠MPB+∠NPC=∠ECB+∠DBC=(∠ACB+∠ACE)+(∠ABC﹣∠ABD)=∠ACB+∠ABC=120°,∴∠MPN=60°,∴△PMN是等边三角形.(3)∵PM=EC,∴当EC最大时,等边△PMN的周长最大,∵EC≤AE+AC,∴EC≤8,∴PM≤4,∴PM的最大值为4,∴△PMN的周长的最大值为12.17.【解答】解:(1)∵AB=AC,∠ABC=60°,∴∠BAC=60°,∵AD=AE,∠ADE=70°,∴∠DAE=180°﹣2∠ADE=40°,∴α=∠BAD=60°﹣40°=20°,∴∠ADC=∠BAD+∠ABD=60°+20°=80°,∴β=∠CDE=∠ADC﹣∠ADE=10°,故答案为:20,10;(2)设∠ABC=x,∠AED=y,∴∠ACB=x,∠AED=y,在△DEC中,y=β+x,在△ABD中,α+x=y+β=β+x+β,∴α=2β;(3)①当点E在CA的延长线上,点D在线段BC上,如图1设∠ABC=x,∠ADE=y,∴∠ACB=x,∠ACE=y,在△ABD中,x+α=β﹣y,在△DEC中,x+y+β=180°,∴α=2β﹣180°,②当点E在CA的延长线上,点D在CB的延长线上,如图2,同①的方法可得α=180°﹣2β.18.【解答】解:(1)由旋转变换的性质可知,∠CAE=90°,AC=AE,∴△ACE为等腰直角三角形,∴CE=AC,∵CE=CD+DE=CD+BC,∴BC+CD=AC,故答案为:等腰直角;BC+CD=AC;(2)延长CO交⊙O于E,连接AE、BE、DE,则∠CDE=90°,∵点C为的中点,∴点E为的中点,∴EA=EB,∵AB为⊙O的直径,∴∠ADB=90°,由(1)得,DE=(AD+BD),由勾股定理得,CD2=CE2﹣DE2=AD2+BD2﹣(AD+BD)2=(AD﹣BD)2,∴CD=(BD﹣AD);(3)如图3,当点E在直线AC的左侧时,连接CQ、PC,∵CA=CB,点P为AB的中点,∴CP⊥AB,∵CA=CE,点Q为AE中点,∴CQ⊥AE,AQ=QE=AE=5,∴由勾股定理得,CQ==12,由(1)得,AQ+CQ=PQ,。
2023年九年级数学中考专题:几何探究压轴题

2023年九年级数学中考专题:几何探究压轴题一、解答题1.如图,在ABC 中,4AC =,3BC =,90ACB ∠=︒,D 是边AC 上一动点(不与点A 、C 重合),CE BD ⊥,垂足为E ,交边AB 于点F .(1)当点D 是边AC 中点时,求DE ,EC 的值;(2)设CD x =,AF y =,求y 关于x 的函数关系式,并写出定义域;(3)当EFD △与EFB △相似时,求线段CD 的长.2.【温故知新】黄金分割是一种最能引起美感的分割比例,具有严格的比例性、艺术性、和谐性,蕴藏着丰富的美学价值.我们知道:如图1,点C 把线段AB 分成两部分,如果BC AC AC AB=,那么称点C 为线段AB 的黄金分割点.(1)【问题发现】如图1,点C 为线段AB 的黄金分割点,且AC BC >,若2AB =,请直接写出CB 的值是__________.(2)【问题探究】如图2,在Rt ABC △中,90C ∠=︒,2AC =,1BC =,在BA 上截取BD BC =,再在AC 上截取AE AD =,则AE AC的值为__________. (3)【问题解决】如图3,用边长为6的正方形纸片进行如下操作:对折正方形ABDE 得折痕MN ,连接EN ,将AE 折叠到EN 上,点A 对应点H ,得折痕CE ,试说明:C 是AB 的黄金分割点.3.定义:若连接三角形一个顶点和对边上一点的线段能把该三角形分成一个等腰三角形和一个直角三角形,我们称这条线段为该三角形的智慧线,这个三角形叫做智慧三角形.(1)如图1,在智慧三角形ABC 中,AD BC ⊥,AD 为该三角形的智慧线,1CD =,则BD 长为_____,B ∠的度数为_____.(2)如图2,ABC 为等腰直角三角形,90BAC ∠︒=,2AB =,F 是斜边BC 延长线上一点,连接AF ,以AF为直角边作等腰直角三角形AFE (点A ,F ,E 按顺时针排列),90EAF ∠=︒, CF =AE 交BC 于点D ,连接EC ,EB .当2BDE BCE ∠=∠时,求线段ED 的长;(3)如图3,ABC 中,5AB AC ==,BC =BCD △是智慧三角形,且AC 为智慧线,求BCD △的面积.4.【问题提出】如图1,在等边三角形ABC 内部有一点P ,3PA=,4PB =,5PC =,求APB ∠的度数.(1)【尝试解决】将APC △绕点A 逆时针旋转60︒,得到AP B '△,连接PP ',则APP '为等边三角形. ∵3P P PA '==,4PB =,5P B PC '==,∴222=P P PB P B ''+∴BPP '为三角形∴APB ∠的度数为.(2)【类比探究】如图2,在等边三角形ABC 外部有一点P ,若∠BP A =30°,求证222PA PB PC +=.(3)【联想拓展】如图3,在ABC 中,90BAC ∠︒=,AB AC =.点P 在直线BC 上方且45APB ∠︒=,PC BC ==求PA 的长.5.已知正方形 ABCD 和正方形 CEFG ,连接 AF 交 BC 于点 O ,点 P 是 AF 的中点,过点 P 作 PH DG ⊥ 于 H ,2CD =,1CG =.(1)如图1,点 D ,C ,G 在同一直线上,点 E 在 BC 边上,求 PH 的长;(2)把正方形 CEFG 绕着点C 逆时针旋转 ()0180αα<<.①如图2,当点E 落在AF 上时,求CO 的长;②如图3,当DG =PH 的长.6.在ABC ∆中,点E 为AC 边上一动点,以CE 为边在CE 上方作等边CEN .(1)如图1,EN 与AB 交于点P ,连接PC ,若tan A =,1AE =,5CN =,求PC 的长: (2)如图2.当N 与B 重合时,在BC 上取一点D ,过点D 作DF AC ∥,连接BF ,EF ,过C 作CH EF ⊥交EF 于点H ,若30FBC DFE ︒∠-∠=,求证:CH BF +=;(3)如图3,若BC AB ⊥,且4AB BC ==,过点B 作BQ AC ∥,I 为射线.BQ 上一动点,取AC 中点M ,连接MI ,过点B 作BK MI ⊥交M 于点K ,连接NK ,直接写出NK 的最小值.7.问题情境:如图1,在Rt △ABC 和Rt △BEF 中,∠ACB =∠EFB =90°,AC =3,BC =4,且M ,N 分别为AE ,CF 的中点.(1)猜想证明:如图2,将Rt △BEF 绕点B 按逆时针方向旋转90°,其他条件不变.试判断54AM CN =是否成立?若成立,请写出证明过程;若不成立,请说明理由.(2)解决问题:如图3,将图2中的Rt △BEF 沿BF 所在直线折叠得到Rt BE F ',连接AE ',CF ,并分别取它们的中点P ,H ,连接CP ,FP ,PH .①试判断CP 与FP 之间的数量关系,并说明理由.②若AB =2BE ',BC =2BF ,请直接写出PH 的长.8.【方法尝试】(1)如图1,矩形ABFC 是矩形ADGE 以点A 为旋转中心,按逆时针方向旋转90︒所得的图形,CB ED 、分别是它们的对角线.则CB 与ED 数量关系________,位置关系________.【类比迁移】(2)如图2,在Rt ABC 和Rt ADE △中,90,9,6,3,2BAC DAE AC AB AE AD ∠=∠=︒====.将DAE 绕点A 在平面内逆时针旋转,设旋转角BAE ∠为()0360αα︒<︒,连接,CE BD .请判断线段CE 和BD 的数量关系和位置关系,并说明理由;【拓展延伸】(3)如图3,在Rt ABC 中,90,6ACB AB ∠=︒=,过点A 作AP BC ∥,在射线AP 上取一点D ,连结CD,使得3tan4ACD∠=,请求写出线段BD的最大值.9.如图①,在正方形ABCD中,点N、M分别在边BC、CD上,连接AM、AN、MN.∠MAN=45°,将△AMD 绕点A顺时针旋转90°,点D与点B重合,得到△ABE.易证:△ANM≌△ANE,从而得DM+BN=MN.【实践探究】(1)在图①条件下,若CN=6,CM=8,则正方形ABCD的边长是______.(2)如图②,点M、N分别在边CD、AB上,且BN=DM.点E、F分别在BM、DN上,∠EAF=45°,连接EF,猜想三条线段EF、BE、DF之间满足的数量关系,并说明理由.(3)【拓展应用】如图③,在矩形ABCD中,AB=6,AD=8,点M、N分别在边DC、BC上,连接AM,AN,已知∠MAN=45°,BN=2,求DM的长.10.小圆同学对图形旋转前后的线段之间、角之间的关系进行了拓展探究.(1)猜测探究:在△ABC中,AB=AC,M是平面内任意一点,将线段AM绕点A按顺时针方向旋转与∠BAC 相等的角度,得到线段AN,连接NB.①如图1,若M是线段BC上的任意一点,请直接写出∠NAB与∠MAC的数量关系是,NB与MC的数量关系是;②如图2,点E是AB延长线上点,若M是∠CBE内部射线BD上任意一点,连接MC,(1)中结论是否仍然成立?若成立,请给予证明,若不成立,请说明理由.(2)拓展应用:如图3,在△A 1B 1C 1中,A 1B 1=8,∠A 1B 1C 1=60°,∠B 1A 1C 1=75°,P 是B 1C 1上的任意点,连接A 1P ,将A 1P 绕点A 1按顺时针方向旋转75°,得到线段A 1Q ,连接B 1Q .求线段B 1Q 长度的最小值. 11.如图,在Rt ABC △中,90BAC ∠=︒,AB AC =,D 为AC 边上一点,连接BD ,作AP BD ⊥于点P ,过点C 作CE AC ⊥交AP 延长线于点E .(1)如图1,求证:AD CE =;(2)如图2,以AD ,BD 为邻边作ADBF ,连接EF 交BC 于点G ,连接AG ,①求证:AG EF ⊥;②若点D 为AC 中点,EF 、AB 交于点H ,求BH AB的值. 12.如图1,在ABC 中,90ACB ∠=︒,D 为AC 边上的一点,过点D 作DE AB ⊥,垂足为E ,连接BD ,P 为BD 中点,连接PC ,PE .(1)求证:PC PE =;(2)将图1中ADE 绕着点A 顺时针旋转如图2的位置,其他条件不变,(1)中的结论是否成立?若成立,请证明:若不成立,请说明理由;(3)若10AB =,6AD =,30BAC DAE ∠=∠=︒,在平面内,将Rt ADE △绕点A 旋转一周,当A ,C ,E 三点共线时,请直接写出PCE 的面积.13.如图1,在直角坐标系中,点()2,0A ,点()0,2C ,点D ,点E 分别为OA ,OC 的中点,ODE 绕原点O 顺时针旋转α角(090α︒<<︒)得11OD E ,射线1CD ,1AE 相交于点F .(1)求证:11OCD OAE △≌△;(2)如图2,在ODE 旋转过程中,当点1D 恰好落在线段CE 上时,求AF 的长;(3)如图3,在旋转α角从090α︒≤≤︒逐渐增大ODE 旋转过程中,求点F 的运动路线长.14.已知ABC 为等边三角形,边长为4,点D 、E 分别是BC 、AC 边上一点,连接AD 、BE .AE CD =.(1)如图1,若2AE =,求BE 的长度;(2)如图2,点F 为AD 延长线上一点,连接BF 、CF ,AD 、BE 相交于点G ,连接CG ,已知60,∠=︒=EBF CE CG ,求证:2+=BF GE CF ;(3)如图3,点P 是ABC 内部一动点,顺次连接PA PB PC 、、++的最小值.15.【问题提出】(1)如图1,在ABC 中,90C ∠=︒,BD 平分ABC ∠交AC 于点D ,设CD 的长为m ,点D 到边AB 的距离为n ,则m _______n ;(填“>”“<”或“=”)【问题探究】(2)如图2,在梯形ABCD 中,90A ∠=︒,AD BC ∥,(201AB =,BD 为对角线,且45BDC ∠=︒,求BCD △面积的最小值;【问题解决】(3)某景点有一个形状为菱形ABCD 的草坪,如图3,AB ==60B ∠︒,现欲将该草坪扩建为BEF △,使得点E 、F 分别在BA 、BC 的延长线上,且边EF 经过点D ,为了节省成本,要求扩建后的草坪面积(BEF △的面积)尽可能小,问BEF △的面积是否存在最小值?若存在,求出其最小值;若不存在,请说明理由.16.综合与实践:数学课外小组研究了两个问题,请你帮助解答.问题一:如图1,在矩形ABCD 中,6AB =,8AD =,E ,F 分别为AB ,AD 边的中点,四边形AEGF 为矩形,连接CG .问题二:数学小组对图形的旋转进行了拓展研究,如图4,在平行四边形ABCD 中,=60B ∠︒,6AB =,8AD =,E ,F 分别为AB ,AD 边的中点,四边形AEGF 为平行四边形,连接CG .数学小组发现DF 与CG 仍然存在着特定的数量关系.(1)请直接写出CG 的长是______.如图2,当矩形AEGF 绕点A 旋转(如顺时针旋转)至点G 落在边AB 上时,DF =______,CG =______,DF 与CG 之间的数量关系是______.(2)当矩形AEGF 绕点A 旋转至如图3的位置时,(1)中DF 与CG 之间的数量关系是否还成立?并说明理由.(3)如图5,当平行四边形ABCD 绕点A 旋转(如顺时针旋转),其它条件不变时,数学小组发现DF 与CG 仍然存在着这一特定的数量关系.请你直接写出这个特定的数量关系是______.17.如图,在四边形ABCD 中,AD ∥BC ,∠ABC =90°,AD =CD ,O 是对角线AC 的中点,连接BO 并延长交边AD 或边CD 于点E .(1)如图1,当点E 在AD 上时,连接CE ,求证:四边形ABCE 是矩形.(2)如图2,当点E 在CD 上时,当AC =4,BC =3时,求DAC S △与OBC S的比值.(3)若DE =2,OE =3,直接写出CD 的长.18.已知在正方形ABCD 中,E 是BC 边上一动点,作点B 关于AE 的对称点F ,BF 交AE 于点G ,连结DF .(1)如图1,求DFB ∠的度数;(2)如图2,过点D 作DM BF ⊥交BF 的延长线于点M ,连结,CM CF .若DF CM =,试探究四边形DFCM 的形状,并说明理由;(3)如图3,连结BD ,在AG 上截取=GT GB ,点P ,Q 分别是,AD BD 上的动点.若正方形ABCD 的面积为32,直接写出PTQ 周长的最小值.。
济南市中考数学几何综合压轴题易错专题

济南市中考数学几何综合压轴题易错专题一、中考数学几何综合压轴题1.如图1,已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.(1)证明:四边形CEGF是正方形;(2)探究与证明:将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图2所示,试探究线段AG 与BE之间的数量关系,并说明理由;(3)拓展与运用:正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图3所示,当B,E,F三点在一条直线上时,延长CG交AD于点H,若AG=6,GH=22,求BC的长.解析:(1)证明见解析;(2)AG2BE,理由见解析;(3)5【分析】(1)先说明GE⊥BC、GF⊥CD,再结合∠BCD=90°可证四边形CEGF是矩形,再由∠ECG=45°即可证明;(2)连接CG,证明△ACG∽△BCE,再应用相似三角形的性质解答即可;(3)先证△AHG∽△CHA可得AG GH AHAC AH CH==,设BC=CD=AD=a,则AC2,求出AH=23a,DH=13a,10,最后代入AG AHAC CH=即可求得a的值.【详解】(1)∵四边形ABCD是正方形,∴∠BCD=90°,∠BCA=45°,∵GE⊥BC、GF⊥CD,∴∠CEG=∠CFG=∠ECF=90°,∴四边形CEGF是矩形,∠CGE=∠ECG=45°,∴EG=EC,∴四边形CEGF是正方形.(2)结论:AG2;理由:连接CG,由旋转性质知∠BCE =∠ACG =α,在Rt △CEG 和Rt △CBA 中,CE CG =cos45°2,2cos 45CB CA ︒== , ∴2CE CA CG CB=, ∴△ACG ∽△BCE , ∴2AG CA BE CB == ∴线段AG 与BE 之间的数量关系为AG 2;(3)∵∠CEF =45°,点B 、E 、F 三点共线,∴∠BEC =135°,∵△ACG ∽△BCE ,∴∠AGC =∠BEC =135°,∴∠AGH =∠CAH =45°,∵∠CHA =∠AHG ,∴△AHG ∽△CHA , ∴AG GH AH AC AH CH==, 设BC =CD =AD =a ,则AC 2a , 则由AG GH AC AH =222a = ∴AH =23a , 则DH =AD ﹣AH =13a ,2210CH CD DH =+=, ∴AG AH AC CH =23210a a = , 解得:a =5BC =5【点睛】本题属于四边形综合题,主要考查相似形的判定和性质、正方形的性质等知识点,解题的关键是正确寻找相似三角形解决问题并利用参数构建方程解决问题.2.(1)(问题背景)如图1,在Rt ABC 中,90BAC ∠=︒,AB AC =,D 是直线BC 上的一点,将线段AD 绕点A 逆时针旋转90°至AE ,连接CE ,求证:ABD ACE △≌△;(2)(尝试应用)如图2,在(1)的条件下,延长DE ,AC 交于点G ,BF AB ⊥交DE 于点F .求证:2FG AE =;(3)(拓展创新)如图3,A 是BDC 内一点,45ABC ADB ∠=∠=︒,90BAC ∠=︒,3BD =,直接写出BDC 的面积为_____________.解析:(1)见解析;(2)见解析;(3)32【分析】(1)【问题背景】如图1,根据SAS 证明三角形全等即可.(2)【尝试应用】如图2,过点D 作DK ⊥DC 交FB 的延长线于K .证明△ECG ≌△DKF (AAS ),推出DF =EG ,再证明FG =DE =2AE 即可.(3)【拓展创新】如图3中,过点A 作AE ⊥AD 交BD 于E ,连接CE .利用全等三角形的性质证明CE =BD ,CE ⊥BD ,再根据三角形面积公式即可求解.【详解】(1)【问题背景】证明:如图1,∵90BAC DAE ∠=∠=︒,∴DAB EAC ∠=∠,在ABD △和ACE 中,AD AE DAB EAC AB AC =⎧⎪∠=∠⎨⎪=⎩, ∴()ABD ACE SAS △≌△.(2)【尝试应用】证明:如图2,过点D 作DK DC ⊥交FB 的延长线于K .∵DK CD ⊥,BF AB ⊥,∴90BDK ABK ∠=∠=︒,∵AB AC =,90BAC ∠=︒,∴45ABC ACB ∠=∠=︒,∴45DBK K ∠=∠=︒,∴DK DB =,∵ABD ACE △≌△,∴135ABD ACE ∠=∠=︒,DB EC DK ==,∴45ECG ∠=︒,∵BF AB ⊥,CA AB ⊥,∴AG BF ∥,∴G DFK ∠=∠,在ECG 和DKF △中,ECG K G DFK CE KD ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴()ECG DKF AAS ≌△△,∴DF EG =, ∵2DE AE =,∴2DF EF AE +=,∴2EG EF AE +=,即2FG AE =.(3)【拓展创新】如图3中,过点A 作AE AD ⊥交BD 于E ,连接CE .∵45ADB ∠=︒,90DAE ∠=︒,∴ADE 与ABC 都是等腰直角三角形,同法可证ABD ACE △≌△, ∴3CE BD ==, ∵45AEC ADB ∠=∠=︒,∴90CED CEB ∠=∠=︒, ∴11333222BDC S BD CE =⋅⋅=⨯⨯=△. 故答案为:32. 【点睛】 本题属于几何变换综合题,考查了等腰直角三角形的判定和性质,全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考压轴题.3.[初步尝试](1)如图①,在三角形纸片ABC 中,∠ACB =90°,将△ABC 折叠,使点B 与点C 重合,折痕为MN ,则AM 与BM 的数量关系为 ;[思考说理](2)如图②,在三角形纸片ABC 中,AC =BC =6,AB =10,将△ABC 折叠,使点B 与点C 重合,折痕为MN ,求AM BM 的值; [拓展延伸](3)如图③,在三角形纸片ABC 中,AB =9,BC =6,∠ACB =2∠A ,将△ABC 沿过顶点C 的直线折叠,使点B 落在边AC 上的点B ′处,折痕为CM .①求线段AC 的长;②若点O 是边AC 的中点,点P 为线段OB ′上的一个动点,将△APM 沿PM 折叠得到△A ′PM ,点A 的对应点为点A ′,A ′M 与CP 交于点F ,求PF MF的取值范围. 解析:(1)AM =BM ;(2)169;(3)①AC =152;②310≤PF FM ≤34. 【分析】 (1)利用平行线分线段成比例定理解决问题即可.(2)利用相似三角形的性质求出BM ,AM 即可.(3)①证明△BCM ∽△BAC ,推出BC BM CM AB BC AC== 由此即可解决问题.②证明△PFA ′∽△MFC ,推出'PF PA FM CM =,因为CM =5,推出'5PF PA FM =即可解决问题. 【详解】 解:(1)如图①中,∵△ABC 折叠,使点B 与点C 重合,折痕为MN ,∴MN 垂直平分线段BC ,∴CN =BN ,∵∠MNB =∠ACB =90°,∴MN ∥AC ,∵CN =BN ,∴AM =BM .故答案为:AM =BM .(2)如图②中,∵CA =CB =6,∴∠A =∠B ,由题意MN 垂直平分线段BC ,∴BM =CM ,∴∠B =∠MCB ,∴∠BCM =∠A ,∵∠B =∠B ,∴△BCM ∽△BAC ,∴BC BM BA BC =, ∴6106BM =, ∴BM =185, ∴AM =AB ﹣BM =10﹣183255=,∴321651895AM BM ==; (3)①如图③中,由折叠的性质可知,CB =CB ′=6,∠BCM =∠ACM ,∵∠ACB =2∠A ,∴∠BCM =∠A ,∵∠B =∠B ,∴△BCM ∽△BAC ,∴BC BM CM AB BC AC == ∴696BM =, ∴BM =4,∴AM =CM =5,∴659AC=, ∴AC =152. ②如图③﹣1中,∵∠A =∠A ′=∠MCF ,∠PFA ′=∠MFC ,PA =PA ′,∴△PFA ′∽△MFC ,∴PF PA FM CM'=, ∵CM =5,∴5PF PA FM '=, ∵点P 在线段OB 上运动,OA =OC =154,AB ′=152﹣6=32, ∴32≤PA ′≤154, ∴310≤PF FM ≤34. 【点睛】本题属于几何变换综合题,考查了相似三角形的判定和性质,解直角三角形,等腰三角形的判定和性质,平行线分线段成比例定理等知识,解题的关键是正确寻找相似三角形解决问题,属于中考压轴题.4.定义:有一组对角互补的四边形叫做“对补四边形”,例如,四边形ABCD 中,若180A C ∠+∠=︒或180B D ∠+∠=︒,则四边形ABCD 是“对补四边形”.(概念理解)(1)如图1,四边形ABCD 是“对补四边形”.①若::3:2:1A B C ∠∠∠=,则D ∠=________;②若90B ∠=︒.且3,2AB AD ==时.则22CD CB -=_______;(拓展提升)(2)如图,四边形ABCD 是“对补四边形”,当AB CB =,且12EBF ABC ∠=∠时,图中,,AB CF EF 之间的数量关系是 ,并证明这种关系; (类比应用)(3)如图3,在四边形ABCD 中,,AB CB BD =平分ADC ∠;①求证:四边形ABCD 是“对补四边形”;②如图4,连接AC ,当90ABC ∠=︒,且12ACDABC S S =时,求tan ACD ∠的值. 解析:(1)①90︒,②5;(2)AE CF EF +=,理由见解析;(3)①见解析,②23【分析】(1)①根据“对补四边形”的定义,结合::3:2:1A B C ∠∠∠=,即可求得答案; ②根据“对补四边形”的定义,由90B ∠=︒,得D ∠90=︒,再利用勾股定理即可求得答案;(2)延长EA 至点K ,使得AK CF =,连接BK ,根据“对补四边形”的定义,可证明ABK CBF △≌△,继而证明BEK BEF △≌△,从而可得结论; (3)①过点B 作BM AD ⊥于点M ,BN AC ⊥于点N ,则90BMA BNC ∠=∠=︒,可证Rt ABM Rt CBN △≌△,进而可证四边形ABCD 是“对补四边形”; ②设,AD a DC b ==,则tan a ACD b ∠=根据222AC a b =+,再运用12ACD ABC S S =建立方程,解方程即可求得tan ACD ∠.【详解】(1)::3:2:1A B C ∠∠∠=,设3,2,A x B x C x ∠=∠=∠=,根据“对补四边形”的定义,180A C ∠+∠=︒,即3180x x +=︒,解得45x =︒,290B x ∴∠==︒,180B D ∠+∠=︒,90D ∴∠=︒.故答案为:90︒.②如图1,连接AC ,90B ∠=︒,180B D ∠+∠=︒,90D ∴∠=︒,在Rt ABC 中22BC AC AB =-,在Rt ADC 中222CD AC AD =-,22222222()CD CB AC AD AC AB AB AD ∴-=---=-, 3,2AB AD ==,2222325CD CB ∴-=-=,故答案为:5.(2)AE CF EF +=,理由如下:如图2,延长EA 至点K ,使得AK CF =,连接BK ,四边形ABCD 是“对补四边形”, ∴180BAD C ∠+∠=︒, 180BAK BAD ∠+∠=︒,∴BAK C ∠=∠,,AK CF AB CB ==, ∴()ABK CBF SAS △≌△, ∴,ABK CBF BK BF ∠=∠=, ∴ABK ABF CBF ABF ∠+∠=∠+∠, 即KBF ABC ∠=∠, 12EBF ABC ∠=∠, ∴12EBF KBF ∠=∠, ∴EBK EBF ∠=∠, ,BK BF BE BE ==,∴()BEK BEF SAS △≌△, ∴EK EF =,∴AE CF AE AK EK EF +=+==, 即AE CF EF +=,故答案为:AE CF EF +=. (3)①证明:如图3,过点B 作BM AD ⊥于点M ,BN AC ⊥于点N ,则90BMA BNC ∠=∠=︒, BD 平分ADC ∠, BM BN ∴=,AB CB =,()Rt ABM Rt CBN HL ∴△≌△,BAM C ∴∠=∠, 180BAM BAD ∠+∠=︒,180C BAD ∴∠+∠=︒,BAD ∴∠与C ∠互补,∴四边形ABCD 是“对补四边形”;②由①可知四边形ABCD 是“对补四边形”, 180ABC ADC ∴∠+∠=︒,90ABC ∠=︒,90ADC ∴∠=︒,设AD a DC b ==,,则22222AC AD CD a b =+=+, AB BC =,2222211()22AB BC AC a b ∴===+, 1122ACD S AD CD ab ∴=⋅=△, 222111()224ABC S AB BC AB a b =⋅==+△,12ACD ABCS S=, 22112=12()4ab a b ∴+,整理得:2()410a ab b-⨯+=,解得:2ab= 在Rt ABC 中,tan a ACD b∠=,∴tan ACD∠=2.【点睛】本题考查了勾股定理,四边形内角和定理,全等三角形的性质与判定,解一元二次方程,三角函数的定义等知识,熟练掌握勾股定理和全等三角形的判定和性质,准确理解新定义是解题的关键. 5.情境观察:将矩形ABCD 纸片沿对角线AC 剪开,得到△ABC 和△A′C′D ,如图1所示.将△A′C′D 的顶点A′与点A 重合,并绕点A 按逆时针方向旋转,使点D 、A (A′)、B 在同一条直线上,如图2所示.观察图2可知:与BC相等的线段是▲,∠CAC′= ▲ °.问题探究:如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q. 试探究EP与FQ之间的数量关系,并证明你的结论.拓展延伸:如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H. 若AB=k AE,AC=k AF,试探究HE与HF之间的数量关系,并说明理由.解析:情境观察:AD(或A′D),90问题探究:EP=FQ. 证明见解析结论: HE=HF. 证明见解析【详解】情境观察AD(或A′D),90问题探究结论:EP=FQ.证明:∵△ABE是等腰三角形,∴AB=AE,∠BAE=90°.∴∠BAG+∠EAP=90°.∵AG⊥BC,∴∠BAG+∠ABG=90°,∴∠ABG=∠EAP.∵EP⊥AG,∴∠AGB=∠EPA=90°,∴Rt△ABG≌Rt△EAP. ∴AG=EP.同理AG=FQ. ∴EP=FQ拓展延伸结论: HE=HF.理由:过点E作EP⊥GA,FQ⊥GA,垂足分别为P、Q.∵四边形ABME是矩形,∴∠BAE=90°,∴∠BAG+∠EAP=90°.AG⊥BC,∴∠BAG+∠ABG=90°,∴∠ABG=∠EAP.∵∠AGB=∠EPA=90°,∴△ABG∽△EAP,同理△ACG∽△FAQ,∵AB= k AE,AC= kAF,∴EP=FQ.∵∠EHP=∠FHQ,∴Rt△EPH≌Rt△FQH. ∴HE=HF6.我们定义:有一组邻角相等的凸四边形叫做“等邻角四边形”(1)概念理解:请你根据上述定义举一个等邻角四边形的例子;(2)问题探究;如图1,在等邻角四边形ABCD中,∠DAB=∠ABC,AD,BC的中垂线恰好交于AB边上一点P,连结AC,BD,试探究AC与BD的数量关系,并说明理由;(3)应用拓展;如图2,在Rt△ABC与Rt△ABD中,∠C=∠D=90°,BC=BD=3,AB=5,将Rt△ABD绕着点A 顺时针旋转角α(0°<∠α<∠BAC)得到Rt△AB′D′(如图3),当凸四边形AD′BC为等邻角四边形时,求出它的面积.解析:(1)矩形或正方形;(2)AC=BD,理由见解析;(3)10417或12﹣372.【分析】(1)矩形或正方形邻角相等,满足“等邻角四边形”条件;(2)AC=BD,理由为:连接PD,PC,如图1所示,根据PE、PF分别为AD、BC的垂直平分线,得到两对角相等,利用等角对等角得到两对角相等,进而确定出∠APC=∠DPB,利用SAS得到三角形ACB与三角形DPB全等,利用全等三角形对应边相等即可得证;(3)分两种情况考虑:(i)当∠AD′B=∠D′BC时,延长AD′,CB交于点E,如图3(i)所示,由S四边形ACBD′=S△ACE﹣S△BED′,求出四边形ACBD′面积;(ii)当∠D′BC=∠ACB=90°时,过点D′作D′E⊥AC于点E,如图3(ii)所示,由S四边形ACBD′=S△AED′+S矩形ECBD′,求出四边形ACBD′面积即可.【详解】(1)矩形或正方形;(2)AC=BD,理由为:连接PD,PC,如图1所示:∵PE是AD的垂直平分线,PF是BC的垂直平分线,∴PA=PD,PC=PB,∴∠PAD=∠PDA,∠PBC=∠PCB,∴∠DPB=2∠PAD,∠APC=2∠PBC,即∠PAD=∠PBC,∴∠APC=∠DPB,∴△APC≌△DPB(SAS),∴AC=BD;(3)分两种情况考虑:(i)当∠AD′B=∠D′BC时,延长AD′,CB交于点E,如图3(i)所示,∴∠ED′B=∠EBD′, ∴EB=ED′,设EB=ED′=x , 由勾股定理得:42+(3+x )2=(4+x )2, 解得:x=4.5, 过点D ′作D′F ⊥CE 于F , ∴D′F ∥AC , ∴△ED′F ∽△EAC , ∴D F ED AC AE ''=, 即4.544 4.5D F '=+, 解得:D′F=3617, ∴S △ACE =12AC×EC=12×4×(3+4.5)=15;S △BED′=12BE×D′F=12×4.5×3617=8117, 则S 四边形ACBD′=S △ACE ﹣S △BED′=15﹣8117=10417; (ii )当∠D′BC=∠ACB=90°时,过点D′作D′E ⊥AC 于点E , 如图3(ii )所示,∴四边形ECBD′是矩形, ∴ED′=BC=3,在Rt △AED′中,根据勾股定理得:7, ∴S △AED′=12AE×ED′=12737S 矩形ECBD′=CE×CB=(47)×3=12﹣7, 则S 四边形ACBD′=S △AED′+S 矩形ECBD′37+12﹣737【点睛】此题是四边形综合题,主要考查了“等邻角四边形”的理解,三角形,四边形的内角和定理,角平分线的意义,勾股定理,旋转的性质,相似三角形的性质和判定,理解“等邻角四边形”的定义是解本题的关键,分类讨论是解本题的难点,是一道中考常考题.7.如图所示,在△ABC 中,AB BC =,D 、E 分别是边AB 、BC 上的动点,且BD BE =,连结AD 、AE ,点M 、N 、P 分别是CD 、AE 、AC 的中点,设B α∠=.(1)观察猜想 ①在求MNCE的值时,小明运用从特殊到一般的方法,先令60α=︒,解题思路如下: 如图1,先由,AB BC BD BE ==,得到CE AD =,再由中位线的性质得到PM PN =,60NPM ∠=︒,进而得出△PMN 为等边三角形,∴12MN NP CE CE ==. ②如图2,当90α=︒,仿照小明的思路求MNCE的值; (2)探究证明 如图3,试猜想MNCE的值是否与()0180αα︒<<︒的度数有关,若有关,请用含α的式子表示出MNCE,若无关,请说明理由; (3)拓展应用如图4,2,36AC B =∠=︒,点D 、E 分别是射线AB 、CB 上的动点,且AD CE =,点M 、N 、P 分别是线段CD 、AE 、AC 的中点,当1BD =时,请直接写出MN 的长. 解析:(1)②2MN CE =2)MN CE 的值与α的度数有关,sin 2MN CE α=;(3)MN 的长55-35+ 【分析】(1)②先根据线段的和差求出AD CE =,再根据中位线定理、平行线的性质得出,45PM PN APN CPM =∠=∠=︒,从而可得出90NPM ∠=︒,然后根据等腰直角三角形的性质即可得;(2)参照题(1)的方法,得出PMN 为等腰三角形和NPM ∠的度数,再利用等腰三角形的性质即可求出答案;(3)分两种情况:当点D 、E 分别是边AB 、CB 上的动点时和当点D 、E 分别是边AB 、CB 的延长线上的动点时,如图(见解析),先利用等腰三角形的性质与判定得出,ABC BCE CAB AFC ∠=∠∠=∠,再根据相似三角形的判定与性质得出BC 、CE 的长,由根据等腰三角形的三线合一性得出1,182BP AC CBP ABC ⊥∠=∠=︒,从而可得sin18︒的值,最后分别利用(2)的结论即可得MN 的长. 【详解】 (1)②,AB BC BD BE ==∴AD CE = ,90AB BC B =∠=︒∴ABC 为等腰直角三角形,45ACB CAB ∠=∠=︒∵点M 、N 、P 分别是CD 、AE 、AC 的中点 11//,,//,22PN CE PN CE PM AD PM AD ∴==,45,45PM PN APN ACB CPM CAB ∴=∠=∠=︒∠=∠=︒∴18090NPM APN CPM ∠=︒-∠-∠=︒ ∴PMN 为等腰直角三角形,∴222MN PN CE == 即22MN CE =; (2)MNCE的值与α的度数有关,求解过程如下: 由(1)可知,PM PN =,即PMN 为等腰三角形180180NPM APN CPM ACB CAB B α∠=︒-∠-∠=︒-∠-∠=∠=如图5,作PH MN ⊥ 则11,222NH MN NPH NPM α=∠=∠= 在Rt NPH 中,sin NHNPH PN∠=,即12sin 122MN CE α=则sin 2MN CE α=;(3)依题意,分以下两种情况: ①当点D 、E 分别是边AB 、CB 上的动点时如图6,作ACB ∠的角平分线交AB 边于点F ,并连结BP2,36,AC ABC AB AC =∠=︒=72ACB CAB ∴∠=∠=︒136,722ACE BCE ACB AFC ABC BCE ∴∠=∠=∠=︒∠=∠+∠=︒,ABC BCE CAB AFC ∴∠=∠∠=∠2BF CF AC ∴===,ACF ABC ~AF ACAC AB∴=,即2AC AF AB =⋅ 设==AB BC x ,则2AF AB BF x =-=- 22(2)x x ∴=-解得15x 或15x =-(不符题意,舍去)即15BC =+1515CE BC BE BC BD ∴=-=-=+-=由(2)可知,36sin sin182MN CE ︒==︒ sin185sin18MN CE ∴=⋅︒=︒点P 是AC 上的中点1,182BP AC CBP ABC ∴⊥∠=∠=︒,112CP AC ==(等腰三角形的三线合一)在Rt CBP 中,sin CP CBP BC ∠=,即151sin18415-︒==+51555sin18544MN --∴=︒=⨯=②如图7,当点D 、E 分别是边AB 、CB 的延长线上的动点时 同理可得:15BC =+15125CE BC BE BC BD ∴=+=+=++=+5135sin18(25)44MN CE -+∴=⋅︒=+⨯=综上,MN 的长为554-或354+.【点睛】本题考查了中位线定理、平行线的性质、相似三角形的判定与性质、等腰三角形的性质、解直角三角形等知识点,较难的是题(3),依据题意,正确分两种情况,并结合题(2)的结论是解题关键.8.()1问题发现如图①,正方形,ABCD DEFG 、将正方形DEFG 绕点D 旋转,直线AE CG 、交于点,P 请直接写出线段AE 与CG 的数量关系是 ,位置关系是 _;()2拓展探究如图②,矩形,2,2,ABCD DEFG AD DE AB DG ==、将矩形DEFG 绕点D 旋转,直线,AE CG 交于点,P ()1中线段关系还成立吗/若成立,请写出理由;若不成立,请写出线段AE CG 、的数量关系和位置关系,并说明理由;()3解决问题在()2的条件下,24,28,AD DE AB DG ====矩形DEFG 绕D 点旋转过程中,请直接写出当点P 与点G 重合时,线段AE 的长,解析:()1,AE CG AE CG =⊥;()()21中数量关系不成立,位置关系成立.1,2AE AE CG CG =⊥,理由见解析;()32565【分析】(1)证明△ADE ≌△CDG (SAS ),可得AE =CG ,∠DAG =∠DCG ,再由直角三角形两个锐角互余即可证得AE ⊥CG ;(2)先证明△ADE ∽△CDG ,利用相似三角形的性质证明即可.(3)先通过作图找到符合题意的两种情况,第一种情况利用勾股定理求解即可;第二种情况借助相似三角形及勾股定理计算即可. 【详解】(1),AE CG AE CG =⊥;理由如下:由题意知在正方形ABCD DEFG 、中,90EDG ADC ∠=∠=︒,,AD DC DE DG ==, EDG GDA ADC GDA ∴∠+∠=∠+∠EDA GDC ∴∠=∠在△ADE 与△CDG 中,AD DC ADE CDG DE DG =⎧⎪∠=∠⎨⎪=⎩∴△ADE ≌△CDG (SAS ) ∴AE CG =,DEA DGC ∠=∠ ∵对顶角相等,∴,DEA EDG DGC GPE ∠+∠=∠+∠ 90.GPE ∴∠=AE CG ∴⊥.(2)(1)中数量关系不成立,位置关系成立.即:1,2AE AE CG CG =⊥ 理由如下:由题意知在矩形ABCD DEFG 、中,90EDG ADC ∠=∠=︒,EDG GDA ADC GDA ∴∠+∠=∠+∠EDA GDC ∴∠=∠2,2AD DE AB DG ==,2AD DC .EDAGDC ∴ 12AE CG ∴=,DEA DGC ∠=∠ ∵对顶角相等∴,DEA EDG DGC GPE ∠+∠=∠+∠90.GPE ∴∠=AE CG ∴⊥.综上所述:1,2AE AE CG CG =⊥ (3)如图1,当点G 、P 在点A 处重合时,连接AE ,则此时∠ADE =∠GDE =90°∴在Rt △ADE 中,AE =22224225AD DE +=+= ,如图1,当点G 、P 重合时, 则点A 、E 、G 在同一直线上,∵AD =DG =4,∴∠DAG =∠DGA ,∵∠ADC =∠AGP =90°,∠AOD =∠COG ,∴∠DAG =∠COG ,∴∠DGA =∠COG ,又∵∠GDO =∠CDG ,∴△GDO ∽△CDG ,∴DO DG OG DG DC CG==48CG ∴DO =2,CG =2OG ,∴OC =DC -DO =8-2=6,∵在Rt △COG 中,OG 2+GC 2=OC 2,∴OG 2+(2OG )2=62,∴OG =655(舍负), ∴CG =1255, 由(2)得:12AE CG = ∴AE =655, 综上所述,AE 的长为25或655. 【点睛】本题综合考查了全等三角形及相似三角形的判定及性质,以及勾股定理的应用,根据题意画出符合题意的图形是解决本题的关键.9.[问题解决](1)如图1.在平行四边形纸片ABCD (AD >AB )中,将纸片沿过点A 的直线折叠,使点B 落在AD 上的点B '处,折线AE 交BC 于点E ,连接B 'E .求证:四边形ABEB '是菱形.[规律探索](2)如图2,在平行四边形纸片ABCD (AD >AB )中,将纸片沿过点P 的直线折叠,点B 恰好落在AD 上的点Q 处,点A 落在点A ′处,得到折痕FP ,那么△PFQ 是等腰三角形吗?请说明理由.[拓展应用](3)如图3,在矩形纸片ABCD (AD >AB )中,将纸片沿过点P 的直线折叠,得到折痕FP ,点B 落在纸片ABCD 内部点B '处,点A 落在纸片ABCD 外部点A '处,A B ''与AD 交于点M ,且A 'M =B 'M .已知:AB =4,AF =2,求BP 的长.解析:(1)证明见解析;(2)是,理由见解析;(3)422.【分析】(1)由平行线的性质和翻折可推出CEB ABE '∠=∠,即//AB B E '.故四边形ABEB '是平行四边形,再由翻折可知AB AB '=,即证明平行四边形ABEB '是菱形.(2)由翻折和平行线的性质可知BPF QPF ∠=∠,BPF QFP ∠=∠,即得出QPF QFP ∠=∠,即PFQ △是等腰三角形.(3)延长PB '交AD 于点G ,根据题意易证()FA M GB M ASA ''≅,得出结论2A F B G AF ''===,FM GM =.根据(2)同理可知PFG △为等腰三角形,即FG =PG .再在Rt A FM '中,FM =2PG FG FM ===2PB PB PG B G ''==-=.【详解】(1)由平行四边形的性质可知//AD BC ,∴AB E CEB ''∠=∠,由翻折可知AB E ABE '∠=∠,∴CEB ABE '∠=∠,∴//AB B E '.∴四边形ABEB '是平行四边形.再由翻折可知AB AB '=,∴四边形ABEB '是菱形.(2)由翻折可知BPF QPF ∠=∠,∵//AD BC ,∴BPF QFP ∠=∠,∴QPF QFP ∠=∠,∴QF =QP ,∴PFQ △是等腰三角形.(3)如图,延长PB '交AD 于点G ,根据题意可知90FA M GB M ''∠=∠=︒,在FA M '和GB M '中,90FA M GB M A M B M FMA GMB ''''∠=∠''=︒⎧⎪=⎨⎪∠=∠⎩, ∴()FA M GB M ASA ''≅,∴2A F B G AF ''===,FM GM =.根据(2)同理可知PFG △为等腰三角形.∴FG =PG .∵2A F AM '==,∴在Rt A FM '中,FM =∴2FG FM ==∴PG =∴2PB PB PG B G ''==-=.【点睛】本题为矩形的折叠问题.考查矩形的性质,折叠的性质,平行线的性质,菱形的判定,等腰三角形的判定和性质,全等三角形的判定和性质以及勾股定理,综合性强.掌握折叠的性质和正确的连接辅助线是解答本题的关键.10.(1)探究发现:下面是一道例题及解答过程,请补充完整:如图①在等边△ABC内部,有一点P,若∠APB=150°,求证:AP2+BP2=CP2证明:将△APC绕A点逆时针旋转60°,得到△AP’B,连接PP’,则△APP’为等边三角形∴∠APP’=60° ,PA=PP’ ,PC=∵∠APB=150°,∴∠BPP’=90°∴P’P2+BP2= ,即PA2+PB2=PC2(2)类比延伸:如图②在等腰△ABC中,∠BAC=90°,内部有一点P,若∠APB=135°,试判断线段PA,PB,PC之间的数量关系,并证明.(3)联想拓展:如图③在△ABC中,∠BAC=120°,AB=AC,点P在直线AB上方,且∠APB=60°,满足(kPA)2+PB2=PC2(其中k>0),请直接写出k的值.解析:(1)P’B,P’B2;(2)2PA2+PB2=PC2,见解析;(3)3【分析】(1)根据旋转的性质和勾股定理直接写出即可.(2)将△APC绕A点逆时针旋转90°,得到△AP′B,连接PP′,论证PP′=2PA,再根据勾股定理代换即可.(3)将△APC 绕A点顺时针旋转120°得到△AP′B,连接PP′,过点A作AH⊥PP′,论证3,再根据勾股定理代换即可.【详解】(1)PC=P’B,P’P2+BP2=P’B2(2)关系式为:2PA2+PB2=PC2证明:将△APC 绕A 点逆时针旋转90°,得到△AP’B ,连接PP’,则△APP’为等腰直角三角形,∴∠APP’=45°,PP’=2PA ,P C=P’B ,∵∠APB=135°,∴∠BPP’=90°,∴P’P 2+BP 2=P’B 2,∴2PA 2+PB 2=PC 2.(3)k=3将△APC 绕点A 顺时针旋转120°得到△AP’B ,连接PP’,过点A 作AH ⊥PP’,可得303,APP PP PA PC P B '︒''∠===60APB ︒∠=90BPP '︒∴∠=222P P BP P B ''∴+=222(3)PA PB PC ∴+=222()kPA PB PC +=3k ∴=【点睛】本题考查了旋转三角形的问题,掌握旋转的性质、勾股定理是解题的关键.11.如图1,在等腰三角形ABC 中,120,,A AB AC ∠==点D E 、分别在边AB AC 、上,,AD AE =连接,BE 点M N P 、、分别为DE BE BC 、、的中点.(1)观察猜想图1中,线段NM NP 、的数量关系是____,MNP ∠的大小为_____;(2)探究证明把ADE 绕点A 顺时针方向旋转到如图2所示的位置,连接,MP BD CE 、、判断MNP △的形状,并说明理由;(3)拓展延伸把ADE 绕点A 在平面内自由旋转,若1,3AD AB ==,请求出MNP △面积的最大值. 解析:(1)相等,60;(2)MNP △是等边三角形,理由见解析;(3)MNP △面积的3【分析】(1)根据"120,,A AB AC ∠==,AD AE =点M N P 、、分别为DE BE BC 、、的中点",可得MN //BD ,NP //CE ,根据三角形外角和定理,等量代换求出MNP ∠.(2)先求出ABD ACE △≌△,得出ABD ACE ∠=∠,根据MN //BD ,NP //CE ,和三角形外角和定理,可知MN=PN ,再等量代换求出MNP ∠,即可求解.(3)根据BD AB AD ≤+,可知BD 最大值,继而求出MNP △面积的最大值.【详解】()1由题意知:AB=AC ,AD=AE ,且点M N P 、、分别为DE BE BC 、、的中点, ∴BD=CE ,MN //BD ,NP //CE ,MN=12BD ,NP=12EC∴MN=NP又∵MN //BD ,NP //CE ,∠A=120︒,AB=AC ,∴∠MNE=∠DBE ,∠NPB=∠C ,∠ABC=∠C=30根据三角形外角和定理,得∠ENP=∠NBP+∠NPB∵∠MNP=∠MNE+∠ENP ,∠ENP=∠NBP+∠NPB ,∠NPB=∠C ,∠MNE=∠DBE ,∴∠MNP=∠DBE+∠NBP+∠C=∠ABC+∠C =60. ()2MNP 是等边三角形.理由如下:如图,由旋转可得BAD CAE ∠=∠ 在ABD 和ACE 中AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩()ABD ACE SAS ∴≌BD CE ABD ACE ,=∠=∠∴.点M N 、分别为DE BE 、的中点,MN ∴是EBD △的中位线,12MN BD ∴=且//MN BD 同理可证12PN CE =且//PN CE ,MN PN MNE DBE NPB ECB ,∴=∠=∠∠=∠MNE DBE ABD ABE ACE ABE ∠=∠=∠+∠=∠+∠ENP EBP NPB EBP ECB ∠=∠+∠=∠+∠MNP MNE ENP ACE ABE EBP ECB ∴∠=∠+∠=∠+∠+∠+∠60ABC ACB =∠+∠=︒.在MNP △中∵∠MNP=60︒,MN=PNMNP ∴是等边三角形.()3根据题意得:BD AB AD ≤+即4BD ≤,从而2MN ≤MNP △的面积212MN ==. ∴MNP △【点睛】本题主要考查了三角形中点的性质、三角形相似的判定定理、三角形外角和定理以及图形旋转的相关知识;正确掌握三角形相似的判定定理、三角形外角和定理以及图形旋转的相关知识是解题的关键.12.在△ABC 中,AD 为BC 边上的中线,E 为AD 上一动点,设DE =nEA ,连接CE 并延长,交AB 于点F .(1)尝试探究:如图1,当∠BAC =90°,∠B =30°,DE =EA 时,BF ,BA 之间的数量关系是 ;(2)类比延伸:如图2,当△ABC 为锐角三角形,DE =EA 时,(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由;(3)拓展迁移:如图3,当△ABC 为锐角三角形,DE =nEA 时,请直接写出BF ,BA 之间的数量关系.解析:(1)23BF AB =;(2)仍然成立,见解析;(3)221BF n AB n =+ 【分析】 (1)尝试探究:过点D 作DMCF ,交AB 于M ,可证BDM BCF ∽, ,AFE AMD ∽ ,可得11,22BD BM AE AF BC BF AD AM ==== ,可证BM MF AF ==, 可得BF ,BA 之间的数量关系; (2)类比延伸:过点D 作DMCF ,交AB 于M ,可证BDM BCF ∽,AFE AMD ∽,可得11,22BD BM AE AF BC BF AD AM ====,可证BM MF AF ==,可得BF BA ,之间的数量关系; (3)拓展迁移:过点D 作DMCF ,交AB 于M ,由平行线分线段成比例可得BM MF FM nAF =,=,可得22AB nAF AF BF nAF +=,=,即可求BF BA ,之间的数量关系.【详解】解:(1)尝试探究如图,过点D 作DM CF ,交AB 于M∵AD 是中线,AE DE =∴1122BD CD BC AE AD ==,= ∵DM CF ,∴BDM BCF ∽,AFE AMD ∽ ∴11,22BD BM AE AF BC BF AD AM ==== ∴22BF BM AM AF =,=∴BM MF AF FM =,=∴BM MF AF ==∴23BF AB =(2)类比延伸:结论仍然成立,理由如下:如图,过点D 作DM CF ,交AB 于M∵AD 是中线,AE DE = ∴1122BD CD BC AE AD ==,= ∵DM CF ,∴BDM BCF ∽,AFE AMD ∽ ∴11,22BD BM AE AF BC BF AD AM ==== ∴22BF BM AM AF =,=∴BM MF AF FM =,=∴BM MF AF ==∴23BF AB = (3)拓展迁移 如图,过点D 作DMCF ,交AB 于M∵DM FC ,且BD CD =∴1BD BM DC FM== ∴BM MF =∵DM CF DE nEA ,=∴1AE AF DE FM n== ∴FM nAF =∴BM MF nAF ==∴2AB nAF AF += 2BF nAF = ∴221BF n AB n =+ 【点睛】本题主要考查了相似三角形的判定和性质综合,根据题干条件作出辅助线并得到对应的相似三角形是解决本题的关键.13.在Rt ABC 中,9072ACB AB AC ∠=︒==,,,过点B 作直线m AC ∥,将ABC 绕点C 顺时针旋转得到A B C '''(点A B ,的对应点分别为A B '',).(1)问题发现如图1,若P 与A 重合时,则ACA '∠的度数为____________;(2)类比探究:如图2,设AB 与BC 的交点为M ,当M 为A B ''的中点时,求线段PQ 的长;(3)拓展延伸在旋转过程中,当点P Q ,分别在CA CB '',的延长线上时,试探究四边形PA B O ''的面积是否存在最小值.若存在,直接写出四边形PA B O ''的最小面积;若不存在,请说明理由.解析:(1)60︒;(2)72;(3)33 【分析】(1)由旋转可得:AC=A'C=2,进而得到3∠A'BC=90°,可得3cos BC A CB A C ''∠==,即可得到∠A'CB=30°,∠ACA'=60°; (2)根据M 为A'B'的中点,即可得出∠A=∠A'CM ,进而得到332PB ==,依据tan ∠Q=tan ∠33,进而得出PQ=PB+BQ=72; (3)依据S 四边形PA'B′Q =S △PCQ -S △A'CB '=S △PCQ 3S 四边形PA'B′Q 最小,即S △PCQ 最小,而S △PCQ =123,利用几何法或代数法即可得到S △PCQ 的最小值=3,S 四边形PA'B′Q =3-3 【详解】解:(1)由旋转可得:2AC A C ''==,90,7,2ACB AB AC ∠=︒==,3BC ∴90ACB ∠=︒,m AC ∥,90A BC '∴∠=︒,cos BC A CB A C '∴∠==' 30A CB '∴∠=︒,60ACA ∴'∠=︒.(2)M 为A B ''的中点,A CM MA C ''∴∠=∠,山旋转可得,MA C A '∠=∠,A A CM '∴∠=∠,tan tan PCB A ∴∠-∠32PB ∴==,tan tan BQC PCB ∠=∠=2BQ BC ∴===, 72PQ PB BQ ∴=+=;(3)S 四边形PA B Q PCQ A CB PCQ S S S ''''==-△△△S ∴四边形PA B Q ''最小即PCQ S 最小,12PCQ S PQ BC ∴=⨯⨯=△, 取PQ 的中点C ,90PQC ∠=︒,12CC PQ '∴=,即2PQ CC '=, 当CG 最小时,PQ 最小,CG PQ ∴⊥,即CG 与CB 正合时,CG 最小,min CG ∴=min PQ =,PCQ S ∴△的最小值3=, S 四边形PA B Q ''=3【点睛】此题考查四边形综合题,旋转的性质,解直角三角形以及直角三角形的性质的综合运用,解题关键在于掌握旋转变换中,对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.14.小明研究了这样一道几何题:如图1,在ABC 中,把AB 绕点A 顺时针旋转()0180a a ︒<<︒得到AB ',把AC 绕点A 逆时针旋转β得到AC ',连接B C ''.当180a β+=︒时,请问AB C ''△边B C ''上的中线AD 与BC 的数量关系是什么?以下是他的研究过程:特例验证:(1)①如图2,当ABC 为等边三角形时,猜想AD 与BC 的数量关系为AD =_______BC ;②如图3,当90BAC ∠=︒,8BC =时,则AD 长为________. 猜想论证:(2)在图1中,当ABC 为任意三角形时,猜想AD 与BC 的数量关系,并给予证明.拓展应用:(3)如图4,在四边形ABCD ,90C ∠=︒,120A B ∠+∠=︒,123BC =6CD =,63DA =P ,使PDC △与PAB △之间满足小明探究的问题中的边角关系?若存在,请画出点P 的位置(保留作图痕迹,不需要说明)并直接写出PDC △的边DC 上的中线PQ 的长度;若不存在,说明理由.解析:(1)①12;②4,(2)12AD BC =;理由见解析,(3)存在;313【分析】(1)①首先证明ADB '∆是含有30的直角三角形,可得1122AD AB BC '==,即可解决问题;②首先证明BAC B AC ''∆∆≌,根据直角三角形斜边中线定理即可解决问题. (2)AD 与BC 的数量关系为12AD BC =,如图5,延长AD 到M ,使AD DM =,连接B M '、C M ',先证四边形AC MB ''是平行四边形,再证明BAC AB M '∆∆≌,即可解决问题.(3)存在,如图6,延长AD 交BC 的延长线于M ,作BE AD ⊥于E ,做直线BC 的垂直平分线交BE 于P ,交BC 于F ,连接PA 、PD 、PC ,作PDC ∆的中线PQ ,连接DF 交PC 于O ,先证明PA PD =,PB PC =,再证明+180APD BPC ∠∠=︒,即可得出结论,再在Rt PDQ ∆中,根据勾股定理,即可求出PQ 的长.【详解】(1)①如图2,∵ABC ∆是等边三角形,把AB 绕点A 顺时针旋转α得到AB ',把AC 绕点A 逆时针旋转β得到AC ',∴===AB AC BC AB AC ''=,又∵AD 是AB C ''△边B C ''上的中线,∴=DB DC '',∴AD B C ''⊥,即90ADB '∠=︒,∵60BAC ∠=︒,180BAC B AC ''∠+∠=︒,∴120B AC ''∠=︒,∴=30B C ''∠∠=︒,∴在ADB '∆中,90ADB '∠=︒,30B '∠=︒, ∴1122AD AB BC '==.故答案为:12. ②如图3,∵90BAC ∠=︒,+=180BAC B AC ''∠∠︒,∴==90BAC B AC ''∠∠︒,即ABC ∆和AB C ''∆为直角三角形,∵把AB 绕点A 顺时针旋转α得到AB ',把AC 绕点A 逆时针旋转β得到AC ', ∴=AB AB ',=AC AC ',∴在ABC ∆和AB C ''∆中,===AB AB BAC B AC AC AC '''∠'⎧⎪∠⎨⎪⎩∴BAC B AC ''∆∆≌,∴=BC B C '',∵AD 是AB C ''△边B C ''上的中线,AB C ''∆为直角三角形,∴1122AD B B C C ''==, 又∵8BC =, ∴11=8=422AD BC =⨯. 故答案为:4. (2)12AD BC =, 如图5,延长AD 到M ,使AD DM =,连接B M '、C M ',图5∵=B D DC '',AD DM =,∴四边形AC MB ''是平行四边形,∴AC B M AC ''==,∵+=180BAC B AC ''∠∠︒,+=180B AC AB M '''∠∠︒,∴=BAC AB M '∠∠,∵=AB AB ',∴在BAC ∆和AB M '∆中,==AC B M BAC AB M AB AB ''=⎧'⎪∠∠⎨⎪⎩∴BAC AB M '∆∆≌,∴BC AM =, ∴12AD BC =. (3)存在,如图6,延长AD 交BC 的延长线于M ,作BE AD ⊥于E ,作直线BC 的垂直平分线交BE 于P ,交BC 于F ,连接PA 、PD 、PC ,作PDC ∆的中线PQ ,连接DF 交PC 于O ,图6∵+=120A B ∠∠︒,∴=180=60M A B ∠︒-∠-∠︒, ∵=90C ∠︒,∴=180=30MDC M MCD ∠︒-∠-∠︒,在Rt DCM ∆中,∵=6CD ,=90DCM ∠︒,=30MDC ∠︒, ∴3CM =43DM =60M ∠︒, 在Rt BEM ∆中,∵=90BEM ∠︒,143BM BC CM =+==30MDC ∠︒,∴1732EM BM ==, ∴33DE EM DM =-= ∵=63AD ∴=AE DE ,∵BE AD ⊥,∴PA PD =,PB PC =,在Rt CDF ∆中,∵=6CD ,=63CF∴tan 3CDF ∠=∴60CDF CPF =︒=∠∠,∴FCP CFD ∆∆≌,∴CD PF =,∵//CD PF ,∴四边形CDPF 是矩形,∴=90CDP ∠︒,∴=60ADP ADC CDP ∠∠-∠=︒,∴ADP ∆是等边三角形,∴==63PA PD AD =∵=60BPF CPF ∠∠=︒,∴120BPC ∠=︒,∴+180APD BPC ∠∠=︒,∴PDC ∆与PAB ∆之间满足小明探究的问题中的边角关系,在Rt PDQ ∆中,∵=90PDQ ∠︒,63PD PA AD ===,132DQ CD ==, ∴()2222=363313PQ DQ DP +=+=.【点睛】 本题考查了三角形的综合问题.掌握全等三角形的性质以及判定定理、直角三角形斜边中线定理、解直角三角形、勾股定理、中线的性质是解题的关键.在处理三角形的边旋转问题时,旋转前后边长不变,根据已知角度变化,求得线段之间关系.在证明某点是否存在问题时,先假设这点存在,能求出相关线段或坐标,即证实存在性.15.《函数的图象与性质》拓展学习片段展示:(问题)如图①,在平面直角坐标系中,抛物线y=a (x ﹣2)2﹣经过原点O ,与x 轴的另一个交点为A ,则a= .(操作)将图①中抛物线在x 轴下方的部分沿x 轴折叠到x 轴上方,将这部分图象与原抛物线剩余部分的图象组成的新图象记为G ,如图②.直接写出图象G 对应的函数解析式. (探究)在图②中,过点B (0,1)作直线l 平行于x 轴,与图象G 的交点从左至右依次为点C ,D ,E ,F ,如图③.求图象G 在直线l 上方的部分对应的函数y 随x 增大而增大时x 的取值范围.(应用)P 是图③中图象G 上一点,其横坐标为m ,连接PD ,PE .直接写出△PDE 的面积不小于1时m 的取值范围. 解析:【问题】:a=;【操作】:y=;【探究】:当1<x <2或x >2+时,函数y 随x 增大而增大;【应用】:m=0或m=4或m≤2﹣或m≥2+. 【详解】 试题分析:【问题】:把(0,0)代入可求得a 的值;【操作】:先写出沿x 轴折叠后所得抛物线的解析式,根据图象可得对应取值的解析式;【探究】:令y=0,分别代入两个抛物线的解析式,分别求出四个点CDEF 的坐标,根据图。
几何最值问题-2023年中考数学压轴题专项训练(全国通用)(解析版)

12023年中考数学压轴题专项训练1.几何最值问题一、压轴题速练1一、单选题1(2023·山东烟台·模拟预测)如图,在矩形ABCD 中,AB =8,AD =4,点E 是矩形ABCD 内部一动点,且∠BEC =90°,点P 是AB 边上一动点,连接PD 、PE ,则PD +PE 的最小值为()A.8 B.45 C.10 D.45-2【答案】A【分析】根据∠BEC =90°得到点的运动轨迹,利用“将军饮马”模型将PE 进行转化即可求解.【详解】解:如图,设点O 为BC 的中点,由题意可知,点E 在以BC 为直径的半圆O 上运动,作半圆O 关于AB 的对称图形(半圆O '),点E 的对称点为E 1,连接O 'E 1,则PE =PE 1,∴当点D 、P 、E 1、O '共线时,PD +PE 的值最小,最小值为DE 1的长,如图所示,在Rt △DCO '中,CD =8,CO '=6,∴DO '=82+62=10,又∵O 'E 1=2,∴DE 1=DO '-O 'E 1=8,即PD +PE 的最小值为8,故选:A .【点睛】本题考查线段和最短问题、轴对称的性质、勾股定理及圆周角定理,利用“将军饮马”模型将PE 进行转化时解题的关键.2(2023·安徽黄山·校考模拟预测)如图,在平面直角坐标系中,二次函数y =32x 2-32x -3的图象与x 轴交于点A ,C 两点,与y 轴交于点B ,对称轴与x 轴交于点D ,若P 为y 轴上的一个动点,连接PD ,则12PB +PD 的最小值为()2A.334B.32C.3D.543【答案】A【分析】作射线BA ,作PE ⊥BA 于E ,作DF ⊥BA 于F ,交y 轴于P ,可求得∠ABO =30°,从而得出PE =12PB ,进而得出PD +12PB =PD +EP ,进一步得出结果.【详解】解:如图,作射线BA ,作PE ⊥BA 于E ,作DF ⊥BA 于F ,交y 轴于P ,抛物线的对称轴为直线x =--322×32=12,∴OD =12,当x =0时,y =-3,∴OB =3,当y =0时,32x 2-32x -3=0,∴x 1=-1,x 2=2,∴A (-1,0),∴OA =1,∵tan ∠ABO =OA OB =13=33,∴∠ABO =30°,∴PE =12PB ,∴12PB +PD =PD +PE ≥DF ,当点P 在P 时,PD +PE 最小,最大值等于DF ,在Rt △ADF 中,∠DAF =90°-∠ABO =60°,AD =OD +PA =12+1=32,∴DF =AD ⋅sin ∠DAE =32×32-334,∴12PB +PD 最小=DF =334,故选:A .【点睛】本题以二次函数为背景,考查了二次函数与一元二次方程之间的关系,解直角三角形等知识,解决问题的关键是用三角函数构造12PB .3(2023秋·浙江金华·九年级统考期末)如图,正方形ABCD 的边长为4,点E 是正方形ABCD 内的动点,点P 是BC 边上的动点,且∠EAB =∠EBC .连结AE ,BE ,PD ,PE ,则PD +PE 的最小值为()3A.213-2B.45-2C.43-2D.215-2【答案】A【分析】先证明∠AEB =90°,即可得点E 在以AB 为直径的半圆上移动,设AB 的中点为O ,作正方形ABCD 关于直线BC 对称的正方形CFGB ,则点D 的对应点是F ,连接FO 交BC 于P ,交半圆O 于E ,根据对称性有:PD =PF ,则有:PE +PD =PE +PF ,则线段EF 的长即为PE +PD 的长度最小值,问题随之得解.【详解】解:∵四边形ABCD 是正方形,∴∠ABC =90°,∴∠ABE +∠EBC =90°,∵∠EAB =∠EBC ,∴∠EAB +∠EBA =90°,∴∠AEB =90°,∴点E 在以AB 为直径的半圆上移动,如图,设AB 的中点为O ,作正方形ABCD 关于直线BC 对称的正方形CFGB ,则点D 的对应点是F ,连接FO 交BC 于P ,交半圆O 于E ,根据对称性有:PD =PF ,则有:PE +PD =PE +PF ,则线段EF 的长即为PE +PD 的长度最小值,E∵∠G =90°,FG =BG =AB =4,∴OG =6,OA =OB =OE =2,∴OF =FG 2+OG 2=213,∴EF =OF -OE =213-2,故PE +PD 的长度最小值为213-2,故选:A .【点睛】本题考查了轴对称-最短路线问题,正方形的性质,勾股定理,正确的作出辅助线,得出点E 的运动路线是解题的关键.4(2022秋·安徽池州·九年级统考期末)如图,Rt △ABC 中,∠C =90°,AC =4,BC =3,点P 为AC 边上的动点,过点P 作PD ⊥AB 于点D ,则PB +PD 的最小值为()4 A.154 B.245 C.5 D.203【答案】B【分析】作点B 关于AC 的对称点B ,过点B 作B D ⊥AB 于点D ,交AC 于点P ,点P 即为所求作的点,此时PB +PD 有最小值,连接AB ,根据对称性的性质,可知:BP =B P ,△ABC ≅△AB C ,根据S △ABB =S △ABC +S △AB C =2S △ABC ,即可求出PB +PD 的最小值.【详解】解:如下图,作点B 关于AC 的对称点B ,过点B 作B D ⊥AB 于点D ,交AC 于点P ,连接AB ,点P 即为所求作的点,此时PB +PD 有最小值,根据对称性的性质,可知:BP =B P ,在Rt △ABC 中,∠ACB =90°,AC =4,BC =3,∴AB =AC 2+BC 2=5,根据对称性的性质,可知:△ABC ≅△AB C ,∴S △ABB =S △ABC +S △ABC =2S △ABC ,即12×AB ⋅B D =2×12BC ⋅AC ,∴5B D =24,∴B D =245,故选:B .【点睛】本题考查了轴对称一最短路线问题,解题的关键是掌握轴对称的性质.5(2023秋·甘肃定西·八年级校考期末)如图所示,在△ABC 中,∠ABC =68°,BD 平分∠ABC ,P 为线段BD 上一动点,Q 为 边AB 上一动点,当AP +PQ 的值最小时,∠APB 的度数是()A.118°B.125°C.136°D.124°【答案】D【分析】先在BC 上截取BE =BQ ,连接PE ,证明△PBQ ≌△PBE SAS ,得出PE =PQ ,说明AP +PQ =AP +PE ,找出当A 、P 、E 在同一直线上,且AE ⊥BC 时,AP +PE 最小,即AP +PQ 最小,过点A 作AE ⊥BC 于点E ,交BD 于点P ,根据三角形外角的性质可得答案.【详解】解:在BC 上截取BE =BQ ,连接PE ,如图:∵BD 平分∠ABC ,∠ABC =68°,∴∠ABD =∠CBD =12∠ABC =34°,∵BP =BP ,∴△PBQ ≌△PBE SAS ,∴PE =PQ ,∴AP +PQ =AP +PE ,∴当A 、P 、E 在同一直线上,且AE ⊥BC 时,AP +PE 最小,即AP +PQ最小,过点A作AE ⊥BC 于点E ,交BD 于点P ,如图:∵∠AEB =90°,∠CBD =34°,∴∠APB =∠AEB +∠CBD =124°.故选:D .5【点睛】本题主要考查了角平分线的定义,三角形全等的判定和性质,垂线段最短,三角形内角和定理与三角形的外角的性质,解题的关键是找出使AP +PQ 最小时点P 的位置.6(2022秋·重庆沙坪坝·八年级重庆市凤鸣山中学校联考期末)如图,E 为正方形ABCD 边AD 上一点,AE =1,DE =3,P 为对角线BD 上一个动点,则PA +PE 的最小值为()A.5B.42C.210D.10【答案】A【分析】连接EC 交BD 于P 点,根据“两点之间线段最短”,可知PA +PE 的最小值即为线段EC 的长,求出EC 的长即可.【详解】连接EC ,交BD 于P 点∵四边形ABCD 为正方形∴A 点和C 点关于BD 对称∴PA =PC∴PA +PE =PC +PE =EC根据“两点之间线段最短”,可知PA +PE 的最小值即为线段EC 的长.∵AE =1,DE =3∴AD =4∴DC =4∴CE =DE 2+CD 2=32+42=5∴PA +PE 的最小值为5故选:A【点睛】本题主要考查了正方形的性质和两点之间线段最短,这是一个将军饮马模型.熟练掌握正方形的性质并且能够识别出将军饮马模型是解题的关键.7(2023春·湖南张家界·八年级统考期中)如图,正方形ABCD 的边长为4,点M 在DC 上,且DM =1,N 是AC 上一动点,则DN +MN 的最小值为()A.4B.42C.25D.5【答案】D【分析】由正方形的对称性可知点B 与D 关于直线AC 对称,连接BM 交AC 于N ′,N ′即为所求在Rt △BCM 中利用勾股定理即可求出BM 的长即可.【详解】∵四边形ABCD 是正方形,∴点B 与D 关于直线AC 对称,6连接BD ,BM 交AC 于N ′,连接DN ′,∴当B 、N 、M 共线时,DN +MN 有最小值,则BM 的长即为DN +MN 的最小值,∴AC 是线段BD 的垂直平分线,又∵CD =4,DM =1∴CM =CD -DM =4-1=3,在Rt △BCM 中,BM =CM 2+BC 2=32+42=5故DN +MN 的最小值是5.故选:D .【点睛】本题考查的是轴对称-最短路线问题及正方形的性质,先作出D 关于直线AC 的对称点,由轴对称及正方形的性质判断出D 的对称点是点B 是解答此题的关键.8(2022秋·浙江杭州·九年级杭州外国语学校校考开学考试)如图,在平面直角坐标系中,二次函数y =-x 2+bx +3的图像与x 轴交于A 、C 两点,与x 轴交于点C (3,0),若P 是x 轴上一动点,点D 的坐标为(0,-1),连接PD ,则2PD +PC 的最小值是()A.4B.2+22C.22D.32+232【答案】A【分析】过点P 作PJ ⊥BC 于J ,过点D 作DH ⊥BC 于H ,根据2PD +PC =2PD +22PC =2PD +PJ ,求出DP +PJ 的最小值即可解决问题.【详解】解:连接BC ,过点P 作PJ ⊥BC 于J ,过点D 作DH ⊥BC 于H .∵二次函数y =-x 2+bx +3的图像与x 轴交于点C (3,0),∴b =2,∴二次函数的解析式为y =-x 2+2x +3,令y =0,-x 2+2x +3=0,解得x =-1或3,∴A (-1,0),令x =0,y =3,∴B (0,3),∴OB =OC =3,∵∠BOC =90°,∴∠OBC =∠OCB =45°,∵D(0,-1),∴OD =1,BD =4,∵DH ⊥BC ,∴∠DHB =90°,设DH =x ,则BH =x ,∵DH 2+BH 2=BD 2,7∴x =22,∴DH =22,∵PJ ⊥CB ,∴∠PJC =90°,∴PJ =22PC ,∴2PD +PC =2PD +22PC =2PD +PJ ,∵DP +PJ ≥DH ,∴DP +PJ ≥22,∴DP +PJ 的最小值为22,∴2PD +PC 的最小值为4.故选:A .【点睛】本题考查了二次函数的相关性质,以及等腰直角三角形的判定和性质,垂线段最短等知识,得到∠OBC =∠OCB =45°,PJ =22PC 是解题的关键.9(2022·山东泰安·统考中考真题)如图,四边形ABCD 为矩形,AB =3,BC =4.点P 是线段BC 上一动点,点M 为线段AP 上一点.∠ADM =∠BAP ,则BM 的最小值为()A.52 B.125 C.13-32 D.13-2【答案】D【分析】证明∠AMD =90°,得出点M 在O 点为圆心,以AO 为半径的圆上,从而计算出答案.【详解】设AD 的中点为O ,以O 点为圆心,AO 为半径画圆∵四边形ABCD 为矩形∴∠BAP +∠MAD =90°∵∠ADM =∠BAP∴∠MAD +∠ADM =90°∴∠AMD =90°∴点M 在O 点为圆心,以AO 为半径的圆上连接OB 交圆O 与点N∵点B 为圆O 外一点∴当直线BM 过圆心O 时,BM 最短∵BO 2=AB 2+AO 2,AO =12AD =2∴BO 2=9+4=13∴BO =13∵BN =BO -AO =13-2故选:D .【点睛】本题考查直角三角形、圆的性质,解题的关键是熟练掌握直角三角形和圆的相关知识.810(2022·河南·校联考三模)如图1,正方形ABCD 中,点E 是BC 的中点,点P 是对角线AC 上的一个动点,设AP =x ,PB +PE =y ,当点P 从A 向点C 运动时,y 与x 的函数关系如图2所示,其中点M 是函数图象的最低点,则点M 的坐标是()A.42,35B.22,35C.35,22D.35,42【答案】A【分析】根据图像,当P 与C 重合时,PB +PE =9即CB +CE =9,从而确定正方形的边长为6,根据将军饮马河原理,连接DE 交AC 于点G ,当点P 与点G 重合时,PE +PB 最小,且为DE 的长即点M 的纵坐标,利用相似三角形,计算AG 的长即为横坐标.【详解】如图,根据图像,当P 与C 重合时,PB +PE =9即CB +CE =9,∵点E 是BC 的中点,∴BC =6,连接DE 交AC 于点G ,当点P 与点G 重合时,PE +PB 最小,且为DE 的长即点M 的纵坐标,∵四边形ABCD 是正方形,AB =6,∴CE ∥AD ,AC =62+62=62,DE =62+32=35,∴△CGE ∽△AGD ,∴CG AG =CE AD =12,∴AC AG=32,∴AG =42,故点M 的坐标为(42,35),故A 正确.故选:A .【点睛】本题考查了正方形的性质,三角形相似的判定和性质,函数图像信息的获取,将军饮马河原理,熟练掌握正方形的性质,灵活运用三角形相似,构造将军饮马河模型求解是解题的关键.2二、填空题11(2023春·江苏宿迁·九年级校联考阶段练习)如图,矩形ABCD ,AB =4,BC =8,E 为AB 中点,F 为直线BC 上动点,B 、G 关于EF 对称,连接AG ,点P 为平面上的动点,满足∠APB =12∠AGB ,则DP 的最小值.【答案】210-22【分析】由题意可知,∠AGB =90°,可得∠APB =12∠AGB =45°,可知点P 在以AB 为弦,圆周角∠APB =45°的9圆上,(要使DP 最小,则点P 要靠近蒂点D ,即点P 在AB 的右侧),设圆心为O ,连接OA ,OB ,OE ,OP ,OD ,过点O 作OQ ⊥AD ,可知△AOB 为等腰直角三角形,求得OA =22AB =22=OP ,AQ =OQ =22OA =2,QD =AD -AQ =6,OD =OQ 2+QD 2=210,再由三角形三边关系可得:DP ≥OD -OP =210-22,当点P 在线段OD 上时去等号,即可求得DP 的最小值.【详解】解:∵B 、G 关于EF 对称,∴BH =GH ,且EF ⊥BG∵E 为AB 中点,则EH 为△ABG 的中位线,∴EH ∥AG ,∴∠AGB =90°,∵∠APB =12∠AGB ,即∠APB =12∠AGB =45°,∴点P 在以AB 为弦,圆周角∠APB =45°的圆上,(要使DP 最小,则点P 要靠近蒂点D ,即点P 在AB 的右侧)设圆心为O ,连接OA ,OB ,OE ,OP ,OD ,过点O 作OQ ⊥AD ,则OA =OB =OP ,∵∠APB =45°,∴∠AOB =90°,则△AOB 为等腰直角三角形,∴OA =22AB =22=OP ,又∵E 为AB 中点,∴OE ⊥AB ,OE =12AB =AE =BE ,又∵四边形ABCD 是矩形,∴∠BAD =90°,AD =BC =8,∴四边形AEOQ 是正方形,∴AQ =OQ =22OA =2,QD =AD -AQ =6,∴OD =OQ 2+QD 2=210,由三角形三边关系可得:DP ≥OD-OP =210-22,当点P 在线段OD 上时去等号,∴DP 的最小值为210-22,故答案为:210-22.【点睛】本题考查轴对称的性质,矩形的性质,隐形圆,三角形三边关系,正方形的判定及性质,等腰直角三角形的判定及性质,根据∠APB =12∠AGB =45°得知点P 在以AB 为弦,圆周角∠APB =45°的圆上是解决问题的关键.12(2023春·江苏连云港·八年级期中)如图,在边长为8的正方形ABCD 中,点G 是BC 边的中点,E 、F 分别是AD 和CD 边上的点,则四边形BEFG 周长的最小值为.【答案】2410【分析】作点G 关于CD 的对称点G ,作点B 关于AD 的对称点B ,连接B G ,根据两点之间线段最短即可解决问题.【详解】作点G 关于CD 的对称点G ,作点B 关于AD 的对称点B ,连接B G∵EB =EB ,FG =FG ,∴BE +EF +FG +BG =B E +EF +FG +BG ,∵EB +EF +FG ≥B G ,∴四边形BEFG 的周长的最小值=BG +B G ,∵正方形ABCD 的边长为8∴BG =4,BB =16,BG =12,∴B G =162+122=20,∴四边形BEFG 的周长的最小值为=4+20=24.故答案为:24.【点睛】本题考查轴对称求线段和的最短问题,正方形的性质,勾股定理,解题的关键是学会利用轴对称解决最短问题.13(2022·湖南湘潭·校考模拟预测)如图,菱形草地ABCD 中,沿对角线修建60米和80米两条道路AC <BD ,M 、N 分别是草地边BC 、CD 的中点,在线段BD 上有一个流动饮水点P ,若要使PM +PN 的距离最短,则最短距离是米.【答案】50【分析】作M 关于BD 的对称点Q ,连接NQ ,交BD 于P ,连接MP ,当P 点与P 重合时,MP +NP =MP +NP =NQ 的值最小,根据菱形的性质和勾股定理求出BC 长,即可得出答案.【详解】解:作M 关于BD 的对称点Q ,连接NQ ,交BD 于P ,连接MP ,当P 点与P 重合时,MP +NP =MP +NP =NQ 的值最小,∵四边形ABCD 是菱形,∴AC ⊥BD ,∠QBP =∠MBP ,即Q 在AB 上,∵MQ ⊥BD ,∴AC ∥MQ ,∴M 为BC 中点,∴Q 为AB 中点,∵N 为CD 中点,四边形ABCD 是菱形,∴BQ ∥CD ,BQ =CN ,∴四边形BQNC 是平行四边形,∴NQ =BC ,设AC 与BD 的交点为点O ,∵四边形ABCD 是菱形,∴AC ⊥BD,OC =12AC =30米,OB =12BD =40米,∴BC =OB 2+OC 2=50米,∴PM +PN 的最小值是50米.故答案为:50.11【点睛】本题考查了轴对称-最短路线问题,平行四边形的性质和判定,菱形的性质,勾股定理的应用,解此题的关键是能根据轴对称找出P 的位置.14(2023春·江苏·九年级校考阶段练习)如图,正方形ABCD 的边长为4,⊙B 的半径为2,P 为⊙B 上的动点,则2PC -PD 的最大值是.【答案】2【分析】解法1,如图:以PD 为斜边构造等腰直角三角形△PDM ,连接MC ,BD ,连接PM 、DM ,推得2PC -PD=2PC -22PD =2PC -PM ,因为PC -PM ≤MC ,求出MC 即可求出答案.解法2:如图:连接BD 、BP 、PC ,在BD 上做点M ,使BM BP =24,连接MP ,证明△BMP ∼△BPD ,在BC 上做点N ,使BN BP=12,连接NP ,证明△BNP ∼△BPC ,接着推导出2PC -PD =22MN ,最后证明△BMN ∼△BCD ,即可求解.【详解】解法1如图:以PD 为斜边构造等腰直角三角形△PDM ,连接MC ,BD ,∴∠PDM =45,DM =PM =22PD ,∵四边形ABCD 正方形∴∠BDC =45°,DB DC=2又∵∠PDM =∠PDB +MDB ,∠BDC =∠MDB +MDC∴∠PDB =∠MDC在△BPD 与△MPC 中∠PDB =∠MDC ,DB DC=DP DM =2∴△BPD ∼△MPC∴PB MC=2∵BP =2∴MC =2∵2PC -PD =2PC-22PD =2PC -PM ∵PC -PM ≤MC ∴2PC -PD =2PC -PM ≤2MC =2故答案为:2.解法2如图:连接BD 、BP 、PC根据题意正方形ABCD 的边长为4,⊙B 的半径为2∴BP =2,BD =BC 2+CD 2=42+42=42∵BP BD =242=2412在BD 上做点M ,使BM BP=24,则BM =22,连接MP 在△BMP 与△BPD 中∠MBP =∠PBD ,BP BD =BM BP∴△BMP ∼△BPD∴PM PD =24,则PD =22PM ∵BP BC =24=12在BC 上做点N ,使BN BP=12,则BN =1,连接NP 在△BNP 与△BPC 中∠NBP =∠PBC ,BN BP =BP PC∴△BNP ∼△BPC∴PN PC=12,则PC =2PN ∴如图所示连接NM ∴2PC -PD =2×2PN -22PM =22PN -PM ∵PN -PM ≤NM ∴2PC -PD =22PN -PM ≤22NM在△BMN 与△BCD 中∠NBM=∠DBC ,BM BC =224=28,BN BD =142=28∴BM BC=BN BD ∴△BMN ∼△BCD∴MN CD=28∵CD =4∴MN =22∴22MN =22×22=2∴2PC -PD ≤22NM =2故答案为:2.【点睛】本题考查正方形的性质,相似三角形,勾股定理等知识,难度较大,熟悉以上知识点运用是解题关键.15(2023秋·广东广州·九年级统考期末)如图,四边形ABCD 中,AB ∥CD ,AC ⊥BC ,∠DAB =60°,AD =CD =4,点M 是四边形ABCD 内的一个动点,满足∠AMD =90°,则△MBC 面积的最小值为.【答案】63-4【分析】取AD 的中点O ,连接OM ,过点M 作ME ⊥BC 交BC 的延长线于点E ,过点O 作OF ⊥BC 于F ,交CD 于G ,则OM +ME ≥OF ,通过计算得出当O ,M ,E 三点共线时,ME 有最小值,求出最小值即可.【详解】解:如图,取AD 的中点O ,连接OM ,过点M 作ME ⊥BC 交BC 的延长线于点E ,过点O 作OF ⊥BC 于F ,交CD 于G ,则13OM +ME ≥OF ,∵AB ∥CD ,∠DAB =60°,AD =CD =4,∴∠ADC =120°,∵AD =CD ,∴∠DAC =30°,∴∠CAB =30°,∵AC ⊥BC ,∴∠ACB =90°∴∠B =90°-30°=60°,∴∠B =∠DAB ,∴四边形ABCD 为等腰梯形,∴BC =AD =4,∵∠AMD =90°,AD =4,OA =OD ,∴OM =12AD =2,∴点M 在以点O 为圆心,2为半径的圆上,∵AB ∥CD ,∴∠GCF =∠B =60°,∴∠DGO =∠CGF =30°,∵OF ⊥BC ,AC ⊥BC ,∴∠DOG =∠DAC =30°=∠DGO ,∴DG =DO =2,∴OG =2OD ⋅cos30°=23,GF =3,OF =33,∴ME ≥OF -OM =33-2,∴当O ,M ,E 三点共线时,ME 有最小值33-2,∴△MBC 面积的最小值为=12×4×33-2 =63-4.【点睛】本题考查了解直角三角形、隐圆、直角三角形的性质等知识点,点M 位置的确定是解题关键.16(2023春·全国·八年级专题练习)如图,在等边△ABC 中,BD ⊥AC 于D ,AD =3cm .点P ,Q 分别为AB,AD 上的两个定点且BP =AQ =1cm ,点M 为线段BD 上一动点,连接PM ,QM ,则PM +QM 的最小值为cm .【答案】5【分析】如图所示,作点P 关于BD 的对称点P ,且点P 在BC 上,则PM +QM =P M+QM ,当P ,M ,Q 在同一条直线上时,有最小值,证明四边形PP QA 是平行四边形,P Q =AP =AB -BP ,由此即可求解.【详解】解:如图所示,作点P 关于BD 的对称点P ,∵△ABC 是等边三角形,BD ⊥AC ,∴∠ABD =∠DBC =12∠ABC =12×60°=30°,14∴点P 在BC 上,∴P M =PM ,则PM +QM =P M +QM ,当P ,M ,Q 在同一条直线上时,有最小值,∵点P 关于BD 的对称点P ,∠ABD =∠DBC =30°,∴PP ⊥BM ,BP =BP =1cm ,∴∠BP P =60°,∴△BPP 是等边三角形,即∠BP P =∠C =60°,∴PP ∥AC ,且PP =AQ =1cm ,∴四边形PP QA 是平行四边形,∴P Q =AP =AB -BP ,在Rt △ABD 中,∠ABD =30°,AD =3,∴AB =2AD =2×3=6,∴AP =P Q =P M +QM =PM +QM =AB -BP =6-1=5,故答案为:5.【点睛】本题主要考查动点与等边三角形,对称-最短路径,平行四边形的判定和性质的综合,理解并掌握等边三角形得性质,对称-最短路径的计算方法,平行四边形的判定和性质是解题的关键.17(2022秋·山东菏泽·九年级校考阶段练习)如图,在周长为12的菱形ABCD 中,DE =1,DF =2,若P 为对角线AC 上一动点,则EP +FP 的最小值为.【答案】3【分析】作F 点关于BD 的对称点F ,连接EF 交BD 于点P ,则PF =PF ,由两点之间线段最短可知当E 、P 、F 在一条直线上时,EP +FP 有最小值,然后求得EF 的长度即可.【详解】解:作F 点关于BD 的对称点F ,则PF =PF ,连接EF '交BD 于点P .∴EP +FP =EP +F P .由两点之间线段最短可知:当E 、P 、F '在一条直线上时,EP +FP 的值最小,此时EP +FP =EP +F P =EF .∵四边形ABCD 为菱形,周长为12,∴AB =BC =CD =DA =3,AB ∥CD ,∵AF =2,AE =1,∴DF =AE =1,∴四边形AEF D 是平行四边形,∴EF =AD =3.∴EP +FP 的最小值为3.故答案为:3.【点睛】本题主要考查的是菱形的性质、轴对称--路径最短问题,明确当E 、P 、F 在一条直线上时EP +FP 有最小值是解题的关键.18(2023春·上海·八年级专题练习)如图,直线y =x +4与x 轴,y 轴分别交于A和B ,点C 、D 分别为线段AB 、OB 的中点,P 为OA 上一动点,当PC +PD 的值最小时,点P 的坐标为.15【答案】(-1,0)【分析】直线y =x +4与x 轴,y 轴分别交于A 和B ,可求出点A ,B 的坐标,点C 、D 分别为线段AB 、OB 的中点,可求出点C 、D 的坐标,作点C 关于x 轴的对称点C ,连接C D 与x 轴的交点就是所求点P 的坐标.【详解】解:直线y =x +4与x 轴,y 轴分别交于A 和B ,∴当y =0,x =-4,即A (-4,0);当x =0,y =4,即B (0,4),∵点C 、D 分别为线段AB 、OB 的中点,∴C (-2,2),D (0,2),如图所示,过点C 关于x 轴的对称点C,∴C (-2,-2),∴直线C D 的解析式为:y =2x +2,当y =0,x =-1,即P (-1,0),故答案为:(-1,0).【点睛】本题主要考查一次函数与最短线段的综合,掌握对称中最短线段的解题方法是解题的关键.19(2023秋·黑龙江鸡西·九年级统考期末)如图,抛物线y =x 2-4x +3与x 轴分别交于A ,B两点(点A 在点B 的左侧),与y 轴交于点C ,在其对称轴上有一动点M ,连接MA ,MC ,AC ,则△MAC 周长的最小值是.【答案】32+10【分析】根据“将军饮马”模型,先求出A 1,0 ,B 3,0 ,C 0,3 ,由二次函数对称性,A ,B 关于对称轴对称,从而C △MAC =CA +CM +MA =CA +CM +MB ,AC =OA 2+OC 2=10,则△MAC 周长的最小值就是CM +MB 的最小值,根据两点之间线段最短即可得到CM +MB 的最小值为C ,M ,B 三点共线时线段CB 长,从而得到CB =OC 2+OB 2=32,即可得到答案.【详解】解:∵抛物线y =x 2-4x +3与x 轴分别交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,16∴当y =0时,0=x 2-4x +3解得x =1或x =3,即A 1,0 ,B 3,0 ;当x =0时,y =3,即C 0,3 ,由二次函数对称性,A ,B 关于对称轴对称,即MA =MB ,∴C △MAC =CA +CM +MA =CA +CM +MB ,∵AC =OA 2+OC 2=10,∴△MAC 周长的最小值就是CM +MB 的最小值,根据两点之间线段最短即可得到CM +MB 的最小值为C ,M ,B 三点共线时线段CB 长,∵CB =OC 2+OB 2=32,∴△MAC 周长的最小值为CA +CB =32+10,故答案为:32+10.【点睛】本题考查动点最值问题与二次函数综合,涉及“将军饮马”模型求最值、二次函数图像与性质、解一元二次方程、勾股定理求线段长等知识,熟练掌握动点最值的常见模型是解决问题的关键.20(2023秋·浙江温州·九年级校考期末)如图所示,∠ACB =60°,半径为2的圆O 内切于∠ACB.P 为圆O 上一动点,过点P 作PM 、PN 分别垂直于∠ACB 的两边,垂足为M 、N ,则PM +2PN 的取值范围为.【答案】6-23≤PM +2PN ≤6+23【分析】根据题意,本题属于动点最值问题-“阿氏圆”模型,首先作MH ⊥NP 于H ,作MF ⊥BC 于F ,如图所示,通过代换,将PM +2PN 转化为PN +12PM =PN +HP =NH ,得到当MP 与⊙O 相切时,MF 取得最大值和最小值,分两种情况,作出图形,数形结合解直角三角形即可得到相应最值,进而得到取值范围.【详解】解:作MH ⊥NP 于H ,作MF ⊥BC 于F ,如图所示:∵PM ⊥AC ,PN ⊥CB ,∴∠PMC =∠PNC =90°,∴∠MPN =360°-∠PMC -∠PNC -∠C =120°,∴∠MPH =180°-∠MPN =60°,∴HP =PM ⋅cos ∠MPH =PM ⋅cos60°=12PM ,∴PN +12PM =PN +HP =NH ,∵MF =NH ,∴当MP 与⊙O 相切时,MF 取得最大和最小,①连接OP ,OG ,OC ,如图1所示:可得:四边形OPMG 是正方形,∴MG =OP =2,在Rt △COG 中,CG =OG ⋅tan60°=23,∴CM =CG +GM =2+23,在Rt △CMF 中,MF =CM ⋅sin60°=3+3,∴HN =MF =3+3,即PM +2PN =212PM +PN =2HN =6+23;②连接OP ,OG ,OC ,如图2所示:可得:四边形OPMG 是正方形,17∴MG =OP =2,由上同理可知:在Rt △COG 中,CG =OG ⋅tan60°=23,∴CM =CG -GM =23-2,在Rt △CMF 中,MF =CM ⋅sin60°=3-3,∴HN =MF =3-3,即PM +2PN =212PM +PN =2HN =6-23,∴6-23≤PM +2PN ≤6+23.故答案为:6-23≤PM +2PN ≤6+23.【点睛】本题考查动点最值模型-“阿氏圆”,难度较大,掌握解决动点最值问题的方法,熟记相关几何知识,尤其是圆的相关知识是解决问题的关键.3三、解答题21(2022春·江苏·九年级专题练习)综合与探究如图,已知抛物线y =ax 2+bx +4经过A -1,0 ,B 4,0 两点,交y 轴于点C .(1)求抛物线的解析式,连接BC ,并求出直线BC 的解析式;(2)请在抛物线的对称轴上找一点P ,使AP +PC 的值最小,此时点P 的坐标是;(3)点Q 在第一象限的抛物线上,连接CQ ,BQ ,求出△BCQ 面积的最大值.【答案】(1)y =-x 2+3x +4;y =-x +4(2)32,52(3)8【分析】(1)将A -1,0 ,B 4,0 两点,代入抛物线解析式,可得到抛物线解析式,从而得到C 0,4 ,再设直线BC 的解析式为y =kx +b k ≠0 ,把点B 、C 的坐标代入,即可求解;(2)连接BC ,PB ,根据题意可得A 、B 关于抛物线的对称轴直线x =32对称,从而得到当P 在直线AB 上三点共线时,AP +CP 的值最小,把x =32代入直线BC 的解析式,即可求解;(3)过Q 作QD ⊥x 轴,交BC 于D ,设Q d ,-d 2+3d +4 ,其中0≤d ≤4,则D d ,-d +4 ,可得QD =-d 2+4d ,从而得到S ΔBCQ =12OB ×QD =-2d -2 2+8,即可求解;【详解】(1)解:(1)∵抛物线y =ax 2+bx +4经过A -1,0 ,B 4,0 两点,∴a -b +4=016a +4b +4=0,解得:a =-1b =3 ,18∴抛物线的解析式为y =-x 2+3x +4;∵抛物线与y 轴的交点为C ,∴C 0,4 ,设直线BC 的解析式为y =kx +b k ≠0 ,把点B 、C 的坐标代入得:4k +b =0b =4 ,解得:k =-1b =4 ,∴直线BC 的解析式为y =-x +4;(2)如图,连接BC ,PB ,∵y =-x 2+3x +4=-x -32 2+74,∴抛物线的对称轴为直线x =32,根据题意得:A 、B 关于抛物线的对称轴直线x =32对称,∴AP =BP ,∴AP +CP =BP +CP ≥BC ,即当P 在直线AB 上时,AP +CP 的值最小,∴当x =32时,y =-32+4=52,∴P 32,52 ,故答案是:32,52 ;(3)过Q 作QD ⊥x 轴,交BC 于D ,设Q d ,-d 2+3d +4 ,其中0≤d ≤4,则D d ,-d +4 ,∴QD =-d 2+3d +4 --d +4 =-d 2+4d ,∵B 4,0 ,∴OB =4,∴S ΔBCQ =12OB ×QD =-2d 2+8d =-2d -2 2+8,当d =2时,S ΔBCQ 取最大值,最大值为8,∴△BCQ 的最大面积为8;【点睛】本题主要考查了二次函数的图像和性质,利用数形结合思想和分类讨论思想是解题的关键.22(2023秋·江苏淮安·八年级统考期末)如图1,直线AB :y =-x +6分别与x ,y 轴交于A ,B 两点,过点B 的直线交x 轴负半轴于点C -3,0 .(1)请直接写出直线BC 的关系式:(2)在直线BC 上是否存在点D,使得S △ABD =S △AOD 若存在,求出点D 坐标:若不存请说明理由;(3)如图2,D 11,0 ,P 为x 轴正半轴上的一动点,以P 为直角顶点、BP 为腰在第一象限内作等腰直角三角形△BPQ ,连接QA ,QD .请直接写出QB -QD 的最大值:.19【答案】(1)y =2x +6(2)当D 185,665 或D -185,-65时,S △ABD =S △AOD (3)37【分析】(1)根据直线AB 与y 轴的交点,可求出点B 的坐标,再用待定系数法即可求解;(2)设D (a ,2a +6),分别用含a 的式子表示出出S △AOD ,S △ABD ,由此即可求解;(3)△BPQ 是等腰直角三角形,设P (m ,0)(m >0),可表示出QB ,再证Rt △BOP ≌Rt △PTQ (AAS ),如图所示,当点B ,R ,Q 在一条直线上时,QB -QD 的值最大,最大值为BR 的值,可求得点R 的坐标,根据勾股定理即可求解.【详解】(1)解:∵直线AB :y =-x +6分别与x ,y 轴交于A ,B 两点,令x =0,则y =6,∴B (0,6),且C -3,0 ,设直线BC 的解析式为y =kx +b ,∴b =6-3k +b =0,解得,k =2b =6 ,∴直线BC 的解析式为y =2x +6,故答案为:y =2x +6.(2)解:由(1)可知直线BC 的解析式为y =2x +6,直线AB 的解析式为y =-x +6,∴A (6,0),B (0,6),C (-3,0),∴OA =6,BO =6,OC =3,如图所示,点D 在直线BC 上,过点D 作DE ⊥x 轴于E ,∴设D (a ,2a +6),E (a ,0),∴S △ABC =12AC ·OB =12×(6+3)×6=27,S △ADC =12AC ·DE =12×(6+3)×a =92a ,S △AOD =12OA ·DE =12×6×a =3a ,∴S △ABD =S △ABC -S △ADC =27-92a ,若S △ABD =S △AOD ,则27-92a =3a ,当a >0时,27-92a =3a ,解得,a =185,即D 185,665 ;当a <0时,27+92a =-3a ,解得,a =-185,即D -185,-65 ;综上所述,当D 185,665 或D -185,-65时,S △ABD =S △AOD .(3)解:已知A (6,0),B (0,6),D (11,0),设P (m ,0)(m >0),∴在Rt △BOP 中,OB =6,OP =m ,∵△BPQ 是等腰直角三角形,∠BPQ =90°,∴BP =QP ;如图所示,过点Q 作QT ⊥x 轴于T ,20在Rt △BOP ,Rt △PTQ 中,∠BOP =∠PTQ =90°,∠BPO +∠QPA =∠QPA +∠PQT =90°,∴∠BPO =∠PQT ,∴∠BPO =∠PQT∠BOP =∠PTQ BP =QP,∴Rt △BOP ≌Rt △PTQ (AAS ),∴OP =TQ =m ,OB =PT =6,∴AT =OP +PT -OA =m +6-6=m ,∴AT =QT ,且QT ⊥x 轴,∴△ATQ 是等腰直角三角形,∠QAT =45°,则点Q 的轨迹在射线AQ 上,如图所示,作点D 关于直线AQ 的对称点R,连接QR ,BR ,AR ,A (6,0),B (0,6),D (11,0),∵△ATQ 是等腰直角三角形,即∠QAT =45°,根据对称性质,∴∠QAR =45°,∴RA ⊥x 轴,且△DQA ≌△RQA ,∴AR =AD =11-6=5,则R (6,5),如图所示,当点B ,R ,Q 在一条直线上时,QB -QD 的值最大,最大值为BR 的值;∴由勾股定理得:BR =62+(6-5)2=37,故答案为:37.【点睛】本题主要考查一次函数,几何的综合,掌握待定系数法求解析式,将军饮马问题,等腰直角三角形的性质,勾股定理是解题的关键.23(2023春·重庆沙坪坝·九年级重庆八中校考阶段练习)△ABC 中,∠B =60°.(1)如图1,若AC >BC ,CD 平分∠ACB 交AB 于点D ,且AD =3BD .证明:∠A =30°;(2)如图2,若AC <BC ,取AC 中点E ,将CE 绕点C 逆时针旋转60°至CF ,连接BF 并延长至G ,使BF =FG ,猜想线段AB 、BC 、CG 之间存在的数量关系,并证明你的猜想;(3)如图3,若AC =BC ,P 为平面内一点,将△ABP 沿直线AB 翻折至△ABQ ,当3AQ +2BQ +13CQ 取得最小值时,直接写出BPCQ的值.【答案】(1)见解析(2)BC =AB +CG ,理由见解析(3)213+33913【分析】(1)过点D 分别作BC ,AC 的垂线,垂足为E ,F ,易得DE =DF ,由∠B =60°,可得DE =DF =32BD ,由AD =3BD ,求得sin A =DE AD=12,可证得∠A =30°;(2)延长BA ,使得BH =BC ,连接EH ,CH ,易证△BCH 为等边三角形,进而可证△BCF ≌△HCE SAS ,可得BF =HE ,∠BFC =∠HEC ,可知∠AEH =∠CFG ,易证得△AEH ≌△CFG SAS ,可得AH =CG ,由BC =BH =AB +AH =AB +CG 可得结论;(3)由题意可知△ABC 是等边三角形,如图,作CM ⊥CA ,且CM =32CA ,作CN ⊥CQ ,且CN =32CQ ,可得CM CA=CN CQ =32,QN =CQ 2+CN 2=132CQ ,可知△ACQ ∽△MCN ,可得MN =32AQ ,由3AQ +2BQ +13CQ =232AQ +BQ +132CQ =2MN +BQ +QN ≥2BM 可知点Q ,N 都在线段BM 上时,3AQ +2BQ+13CQ 有最小值,过点C 作CR ⊥BM ,过点M 作MT ⊥BC 交BC 延长线于T ,可得CR =CQ ⋅sin ∠CQN =313CQ ,QR =CQ ⋅cos ∠CQN =213CQ ,可证△CBR ∽△MBT ,得BR CR =BT MT ,设BC =a 由等边三角形的性质,可得CM =32a ,进而可得CT =CM ⋅cos30°=334a ,MT =CM ⋅sin30°=34a ,结合BR CR=BTMT 可得:BQ +213CQ 313CQ =a +334a 34a ,可得BQ CQ =213+33913,由翻折可知,BP =BQ ,可求得BP CQ的值.【详解】(1)证明:过点D 分别作BC ,AC 的垂线,垂足为E ,F ,∵CD 平分∠ACB ,DE ⊥BC ,DF ⊥AC ,∴DE =DF ,又∵∠B =60°,∴DE =BD ⋅sin60°=32BD ,则DE =DF =32BD ,又∵AD =3BD ,∴sin A =DE AD =32BD3BD=12,∴∠A =30°;(2)BC =AB +CG ,理由如下:延长BA ,使得BH =BC ,连接EH ,CH ,∵∠ABC =60°,BH =BC ,∴△BCH 为等边三角形,∴CB =CH ,∠BCH =60°,∵CE 绕点C 逆时针旋转60°至CF ,∴CE =CF ,∠ECF =60°,则∠BCH -∠ACB =∠ECF -∠ACB ,∴∠ECH =∠FCB ,∴△BCF ≌△HCE SAS ,∴BF =HE ,∠BFC =∠HEC ,则∠AEH =∠CFG ,∵BF =FG ,∴BF =HE =FG ,又∵E 为AC 中点,∴AE =CE =CF ,∴△AEH ≌△CFG SAS ,∴AH =CG ,∴BC =BH =AB +AH =AB +CG ;(3)∵∠ABC =60°,AC =BC ,∴△ABC 是等边三角形,如图,作CM ⊥CA ,且CM =32CA ,作CN ⊥CQ ,且CN =32CQ ,则CM CA=CN CQ =32,QN =CQ 2+CN 2=132CQ ,∴sin ∠CQN =CN QN =313,cos ∠CQN =CQ QN =213,则∠ACM =∠QCN =90°,∴∠ACM -∠ACN =∠QCN -∠ACN ,则∠ACQ =∠MCN∴△ACQ ∽△MCN ,∴MN AQ =CM CA=32,即:MN =32AQ ,∴3AQ +2BQ +13CQ =232AQ +BQ +132CQ =2MN +BQ +QN ≥2BM即:点Q ,N 都在线段BM 上时,3AQ +2BQ +13CQ 有最小值,如下图,过点C 作CR ⊥BM ,过点M 作MT ⊥BC 交BC 延长线于T ,则∠BRC =∠BTM =90°,CR =CQ ⋅sin ∠CQN =313CQ ,QR =CQ ⋅cos ∠CQN =213CQ ,又∵∠CBR =∠MBT ,∴△CBR ∽△MBT ,∴BR CR=BT MT ,∵△ABC 是等边三角形,设BC =a ∴∠ACB =60°,AC =BC =a ,则CM =32a ,∵∠ACM =90°,∴∠MCT =30°,则CT =CM ⋅cos30°=334a ,MT =CM ⋅sin30°=34a ,则由BR CR=BT MT 可得:BQ +213CQ 313CQ =a +334a34a ,整理得:133BQ CQ +23=4+333,得BQ CQ=213+33913,由翻折可知,BP =BQ ,∴BP CQ =BQ CQ=213+33913.【点睛】本题属于几何综合,考查了解直角三角形,等边三角形的判定及性质,全等三角形的判定及性质,相似三角形的判定及性质,旋转的性质以及费马点问题,掌握费马点问题的解决方法,添加辅助线构造全等三角形和相似三角形是解决问题的关键.24(2023春·江苏·八年级专题练习)定义:既相等又垂直的两条线段称为“等垂线段”,如图1,在Rt △ABC 中,∠A =90°,AB =AC ,点D 、E 分别在边AB 、AC 上,AD =AE ,连接DE 、DC ,点M 、P 、N 分别为DE 、DC 、BC 的中点,且连接PM 、PN .(1)观察猜想线段PM 与PN 填(“是”或“不是”)“等垂线段”.(2)△ADE 绕点A 按逆时针方向旋转到图2所示的位置,连接BD ,CE ,试判断PM 与PN 是否为“等垂线段”,并说明理由.(3)拓展延伸把△ADE 绕点A 在平面内自由旋转,若DE =2,BC =4,请直接写出PM 与PN 的积的最大值.。
中考数学几何压轴题(有关三角形、四边形)的综合专题(含答案解析)
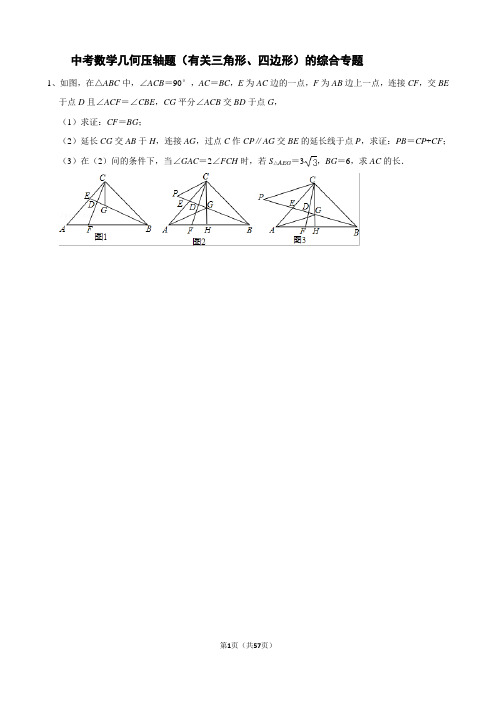
中考数学几何压轴题(有关三角形、四边形)的综合专题1、如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的一点,F为AB边上一点,连接CF,交BE于点D且∠ACF=∠CBE,CG平分∠ACB交BD于点G,(1)求证:CF=BG;(2)延长CG交AB于H,连接AG,过点C作CP∥AG交BE的延长线于点P,求证:PB=CP+CF;(3)在(2)问的条件下,当∠GAC=2∠FCH时,若S△AEG=3,BG=6,求AC的长.2、[问题背景]如图1所示,在△ABC中,AB=BC,∠ABC=90°,点D为直线BC上的一个动点(不与B、C重合),连结AD,将线段AD绕点D按顺时针方向旋转90°,使点A旋转到点E,连结EC.[问题初探]如果点D在线段BC上运动,通过观察、交流,小明形成了以下的解题思路:过点E作EF⊥BC 交直线BC于F,如图2所示,通过证明△DEF≌△,可推证△CEF是三角形,从而求得∠DCE=.[继续探究]如果点D在线段CB的延长线上运动,如图3所示,求出∠DCE的度数.[拓展延伸]连接BE,当点D在直线BC上运动时,若AB=,请直接写出BE的最小值.3、(2019秋•锦江区校级期末)在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线.(1)如图1,求证:AD=2DC.(2)如图2,作∠CBD的角平分线交线段CD于点M,若CM=1,求△DBM的面积;(3)如图3,过点D作DE⊥AB于点E,点N是线段AC上一点(不与C、D重合),以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G,试探究线段ND,DG与AD之间的数量关系,并说明理由.4、(2019•镇平县三模)如图1,已知直角三角形ABC,∠ACB=90°,∠BAC=30°,点D是AC边上一点,过D作DE⊥AB于点E,连接BD,点F是BD中点,连接EF,CF.(1)发现问题:线段EF,CF之间的数量关系为;∠EFC的度数为;(2)拓展与探究:若将△AED绕点A按顺时针方向旋转α角(0°<α<30°),如图2所示,(1)中的结论还成立吗?请说明理由;(3)拓展与运用:如图3所示,若△AED绕点A旋转的过程中,当点D落到AB边上时,AB边上另有一点G,AD=DG=GB,BC=3,连接EG,请直接写出EG的长度.5、(2017春•西城区校级期末)如图1,在等腰△ABC中,AB=AC,∠BAC=a,点P是线段AB的中点,点E是线段CB延长线上一点,且PE=PC,将线段PC绕点P顺时针旋转α得到PD,连接BD.(1)如图2,若α=60°,其他条件不变,先补全图形,然后探究线段BD和BC之间的数量关系,并说明理由.(2)如图3,若α=90°,其他条件不变,探究线段BP、BD和BC之间的等量关系,并说明理由.6、【发现问题】如图1,已知△ABC,以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE.请你以A为直角顶点、AC为腰,向△ABC外作等腰直角△ACD(不写作法,保留作图痕迹).连接BD、CE.那么BD与CE的数量关系是BD=CE.【拓展探究】如图2,已知△ABC,以AB、AC为边向外作正方形AEFB和正方形ACGD,连接BD、CE,试判断BD与CE之间的数量关系,并说明理由.【解决问题】如图3,有一个四边形场地ABCD,∠ADC=60°,BC=15,AB=8,AD=CD,求BD的最大值.7、(1)如图1,点C为线段AB外一个动点,已知AB=a,AC=b.当点C位于BA的延长线上时,线段BC取得最大值,则最大值为(用含a,b的式子表示);(2)如图2,点C为线段AB外一个动点,若AB=10,AC=3,分别以AC,BC为边,作等边三角形ACD和等边三角形BCE,连接AE,DB.①求证:AE=DB;②请直接写出线段AE的最大值;(3)如图3,AB=6,点M为线段AB外一个动点,且AM=2,MB=MN,∠BMN=90°,请直接写出线段AN的最大值.8、【初步探索】(1)如图1:在四边形ABC中,AB=AD,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且EF =BE+FD,探究图中∠BAE、∠F AD、∠EAF之间的数量关系.小王同学探究此问题的方法是:延长FD到点G,使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是;【灵活运用】(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且EF=BE+FD,上述结论是否仍然成立,并说明理由;【拓展延伸】(3)如图3,已知在四边形ABCD中,∠ABC+∠ADC=180°AB=AD,若点E在CB的延长线上,点F在CD的延长线上,如图3所示,仍然满足EF=BE+FD,请写出∠EAF与∠DAB的数量关系,并给出证明过程.9、(2018•大东区一模)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与点B、点C重合),连接OC、OP,将线段OP绕点P逆时针旋转60°,得到线段PQ,连接BQ.(1)如图1,当点P在线段BC上时,请直接写出线段BQ与CP的数量关系.(2)如图2,当点P在CB延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;(3)如图3,当点P在BC延长线上时,若∠BPO=45°,AC=,请直接写出BQ的长.10、模型发现:同学们知道,三角形的两边之和大于第三边,即如图1,在△ABC中,AB+AC>BC.对于图1,若把点C看作是线段AB外一动点,且AB=c,AC=b,则线段BC的长会因为点C的位置的不同而发生变化.因为AB、AC的长度固定,所以当∠BAC越大时,BC边越长.特别的,当点C位于时,线段BC的长取得最大值,且最大值为(用含b,c的式子表示)(直接填空).模型应用:点C为线段AB外一动点,且AB=3,AC=2,如图2所示,分别以AC,BC为边,作等边三角形ACD 和等边三角形BCE,连接BD,AE.(1)求证:BD=AE.(2)线段AE长的最大值为.模型拓展:如图3,在平面直角坐标系中,点A是y轴正半轴上的一动点,点B是x轴正半轴上的一动点,且AB =8.若AC⊥AB,AC=3,试求OC长的最大值.11、已知:△ABC中,∠ACB=90°,AC=BC.(1)如图1,点D在BC的延长线上,连AD,过B作BE⊥AD于E,交AC于点F.求证:AD=BF;(2)如图2,点D在线段BC上,连AD,过A作AE⊥AD,且AE=AD,连BE交AC于F,连DE,问BD与CF有何数量关系,并加以证明;(3)如图3,点D在CB延长线上,AE=AD且AE⊥AD,连接BE、AC的延长线交BE于点M,若AC =3MC,请直接写出的值.12、已知在△ABC中,AB=AC,射线BM、BN在∠ABC内部,分别交线段AC于点G、H.(1)如图1,若∠ABC=60°,∠MBN=30°,作AE⊥BN于点D,分别交BC、BM于点E、F.①求证:∠1=∠2;②如图2,若BF=2AF,连接CF,求证:BF⊥CF;(2)如图3,点E为BC上一点,AE交BM于点F,连接CF,若∠BFE=∠BAC=2∠CFE,求的值.13、已知,△ABC中,AB=AC,∠BAC=90°,E为边AC任意一点,连接BE.(1)如图1,若∠ABE=15°,O为BE中点,连接AO,且AO=1,求BC的长;(2)如图2,F也为AC上一点,且满足AE=CF,过A作AD⊥BE交BE于点H,交BC于点D,连接DF交BE于点G,连接AG;①若AG平分∠CAD,求证:AH=AC;②如图3,当G落在△ABC外时,若将△EFG沿EF边翻折,点G刚好落在AB边上点P,直接写出AG与EF的数量关系.14、如图所示,Rt△ABC中,∠ACB=90°,E为AC中点,作ED⊥AC交AB于D,连接CD;(1)如图1,求证:AB=2CD;(2)如图2,作CF⊥AB交AB于F,点G为CF上一点,点H为DE延长线上一点,分别连接AH、GH,若∠AHG=2∠B,求证:AH=GH;(3)如图3,在(2)的条件下,连接DG,且有DE=BF,∠EDG=90°,若AC=6,求AH的长度.15、【问题情境】一节数学课后,老师布置了一道课后练习题:如图:已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,点E、F分别在A和BC上,∠1=∠2,FG⊥AB于点G,求证:△CDE≌△EGF.(1)阅读理解,完成解答本题证明的思路可用下列框图表示:根据上述思路,请你完整地书写这道练习题的证明过程;(2)特殊位置,证明结论若CE平分∠ACD,其余条件不变,求证:AE=BF;(3)知识迁移,探究发现如图,已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,若点E是DB的中点,点F在直线CB上且满足EC=EF,请直接写出AE与BF的数量关系.(不必写解答过程)16、在正方形ABCD和等腰直角△BGF中,∠BGF=90°,P是DF的中点,连接PG、PC.(1)如图1,当点G在BC边上时,延长GP交DC于点E.求证:PG=PC;(2)如图2,当点F在AB的延长线上时,(1)中的结论是否成立?请证明你的结论;(3)如图3,若四边形ABCD为菱形,且∠ABC=60°,△BGF为等边三角形,点F在CB的延长线上时,线段PC、PG又有怎样的数量关系,请直接写出你的结论,并画出论证过程中需要添加的辅助线.17、在△ABC中,∠BAC=60°,点D、E分别在边AC、AB上,AD=AE,连接CE、BD相交于点F,且∠BEC=∠ADF,连接AF.(1)如图1,连接ED,求证:∠ABD=∠CED;(2)如图2,求证:EF+FD=AF;(3)如图3,取BC的中点G,连接AG交BD于点H,若∠GAC=3∠ABD,BH=7,求△ABH的面积.18、点D,E分别在△ABC的边AC,BD上,BD,CE交于点F,连接AF,∠F AE=∠F AD,FE=FD.(1)如图1,若∠AEF=∠ADF,求证:AE=AD;(2)如图2,若∠AEF≠∠ADF,FB平分∠ABC,求∠BAC的度数;(3)在(2)的条件下,如图3,点G在BE上,∠CFG=∠AFB若AG=6,△ABC的周长为20,求BC长.中考数学几何压轴题(有关三角形、四边形)的综合专题参考答案1、如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的一点,F为AB边上一点,连接CF,交BE于点D且∠ACF=∠CBE,CG平分∠ACB交BD于点G,(1)求证:CF=BG;(2)延长CG交AB于H,连接AG,过点C作CP∥AG交BE的延长线于点P,求证:PB=CP+CF;(3)在(2)问的条件下,当∠GAC=2∠FCH时,若S△AEG=3,BG=6,求AC的长.证明:(1)如图1,∵∠ACB=90°,AC=BC,∴∠A=45°,∵CG平分∠ACB,∴∠ACG=∠BCG=45°,∴∠A=∠BCG,在△BCG和△CAF中,∵,∴△BCG≌△CAF(ASA),∴CF=BG;(2)如图2,∵PC∥AG,∴∠PCA=∠CAG,∵AC=BC,∠ACG=∠BCG,CG=CG,∴△ACG≌△BCG,∴∠CAG=∠CBE,∵∠PCG=∠PCA+∠ACG=∠CAG+45°=∠CBE+45°,∠PGC=∠GCB+∠CBE=∠CBE+45°,∴∠PCG=∠PGC,∴PC=PG,∵PB=BG+PG,BG=CF,∴PB=CF+CP;(3)解法一:如图3,过E作EM⊥AG,交AG于M,∵S△AEG=AG•EM=3,由(2)得:△ACG≌△BCG,∴BG=AG=6,∴×6×EM=3,EM=,设∠FCH=x°,则∠GAC=2x°,∴∠ACF=∠EBC=∠GAC=2x°,∵∠ACH=45°,∴2x+x=45,x=15,∴∠ACF=∠GAC=30°,在Rt△AEM中,AE=2EM=2,AM==3,∴M是AG的中点,∴AE=EG=2,∴BE=BG+EG=6+2,在Rt△ECB中,∠EBC=30°,∴CE=BE=3+,∴AC=AE+EC=2+3+=3+3.解法二:同理得:∠CAG=30°,AG=BG=6,如图4,过G作GM⊥AC于M,在Rt△AGM中,GM=3,AM===3,∵∠ACG=45°,∠MGC=90°,∴GM=CM=3,∴AC=AM+CM=3+3.2、[问题背景]如图1所示,在△ABC中,AB=BC,∠ABC=90°,点D为直线BC上的一个动点(不与B、C重合),连结AD,将线段AD绕点D按顺时针方向旋转90°,使点A旋转到点E,连结EC.[问题初探]如果点D在线段BC上运动,通过观察、交流,小明形成了以下的解题思路:过点E作EF⊥BC 交直线BC于F,如图2所示,通过证明△DEF≌△ADB,可推证△CEF是等腰直角三角形,从而求得∠DCE=135°.[继续探究]如果点D在线段CB的延长线上运动,如图3所示,求出∠DCE的度数.[拓展延伸]连接BE,当点D在直线BC上运动时,若AB=,请直接写出BE的最小值.解:[问题初探]如图2,过点E作EF⊥BC交直线BC于F,∴∠DFE=90°=∠ABD,∴∠EDF+∠DEF=90°,由旋转知,AD=DE,∠ADE=90°,∴∠ADB+∠EDF=90°,∴∠ADB=∠DEF,∴△ABD≌△DFE(AAS),∴BD=EF,DF=AB,∵AB=BC,∴BC=DF,∴BD=CF,∴EF=CF,∴△CEG是等腰直角三角形,∴∠ECF=45°,∴∠DCE=135°,故答案为:ADB,等腰直角,135;[继续探究]如图3,过点E作EF⊥BC于F,∴∠DFE=90°=∠ABD,∴∠EDF+∠DEF=90°,由旋转知,AD=DE,∠ADE=90°,∴∠ADB+∠EDF=90°,∴∠ADB=∠DEF,∴△ABD≌△DFE(AAS),∴BD=EF,DF=AB,∵AB=BC,∴BC=DF,∴BD=CF,∴EF=CF,∴△CEG是等腰直角三角形,∴∠ECF=45°,∴∠DCE=45°;[拓展延伸]如图4,在△ABC中,∠ABC=90°,AB=BC=,∴∠ACB=45°当点D在射线BC上时,由[问题初探]知,∠BCM=135°,∴∠ACM=∠BCM﹣∠ACB=90°,当点D在线段CB的延长线上时,由[继续探究]知,∠BCE=45°,∴∠ACN=∠ACB+∠BCM=90°,∴点E是过点C垂直于AC的直线上的点,∴当BE⊥MN时,BE最小,∵∠BCE=45°,∴∠CBE=45°=∠BCE,∴BE=CE,∴BE最小=BC=,即:BE的最小值为.3、在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线.(1)如图1,求证:AD=2DC.(2)如图2,作∠CBD的角平分线交线段CD于点M,若CM=1,求△DBM的面积;(3)如图3,过点D作DE⊥AB于点E,点N是线段AC上一点(不与C、D重合),以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G,试探究线段ND,DG与AD之间的数量关系,并说明理由.证明:(1)如图1,过点D作DE⊥AB,∵BD是△ABC的角平分线,DE⊥AB,∠ACB=90°,∴DC=DE,∵∠A=30°,DE⊥AB,∴AD=2DE,∴AD=2DC;(2)如图2,过点M作ME∥BD,∵∠ACB=90°,∠A=30°,∴∠ABC=60°,∵BD是△ABC的角平分线,∴∠ABD=∠DBC=30°,∵BM平分∠CBD,∴∠CBM=15°=∠DBM,∵ME∥BD,∴∠MEC=∠CBD=30°,∠EMB=∠DBM=∠MBE,∴ME=BE,∵∠MEC=30°,∠C=90°∴CE=MC=,ME=2MC=2=BE,∴BC=+2,∵∠CBD=30°,∠C=90°,∴BC=CD,∴CD=1+,∴DM=,∴△DBM的面积=××(+2)=1+;(3)若点N在CD上时,AD=DG+DN,理由如下:如图3所示:延长ED使得DW=DN,连接NW,∵∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于点E,∴∠ADE=∠BDE=60°,AD=BD,∵DN=DW,且∠WDN=60°∴△WDN是等边三角形,∴NW=DN,∠W=∠WND=∠BNG=∠BDN=60°,∴∠WNG=∠BND,在△WGN和△DBN中,∴△WGN≌△DBN(SAS),∴BD=WG=DG+DN,∴AD=DG+DN.(3)若点N在AD上时,AD=DG﹣DN,理由如下:如图4,延长BD至H,使得DH=DN,连接HN,由(1)得DA=DB,∠A=30°.∵DE⊥AB于点E.∴∠2=∠3=60°.∴∠4=∠5=60°.∴△NDH是等边三角形.∴NH=ND,∠H=∠6=60°.∴∠H=∠2.∵∠BNG=60°,∴∠BNG+∠7=∠6+∠7.即∠DNG=∠HNB.在△DNG和△HNB中,∴△DNG≌△HNB(ASA).∴DG=HB.∵HB=HD+DB=ND+AD,∴DG=ND+AD.∴AD=DG﹣ND.4、如图1,已知直角三角形ABC,∠ACB=90°,∠BAC=30°,点D是AC边上一点,过D作DE⊥AB于点E,连接BD,点F是BD中点,连接EF,CF.(1)发现问题:线段EF,CF之间的数量关系为EF=CF;∠EFC的度数为120°;(2)拓展与探究:若将△AED绕点A按顺时针方向旋转α角(0°<α<30°),如图2所示,(1)中的结论还成立吗?请说明理由;(3)拓展与运用:如图3所示,若△AED绕点A旋转的过程中,当点D落到AB边上时,AB边上另有一点G,AD=DG=GB,BC=3,连接EG,请直接写出EG的长度.解:(1)如图1中,∵DE⊥AB,∴∠BED=90°,∵∠BCD=90°,BF=DF,∴FE=FB=FD=CF,∴∠FBE=∠FEB,∠FBC=∠FCB,∴∠EFC=∠EFD+∠CFD=∠FBE+∠FEB+∠FBC+∠FCB=2(∠FBE+∠FBC)=2∠ABC=120°,故答案为:EF=CF,120°.(2)结论成立.理由:如图2中,取AB的中点M,AD的中点N,连接MC,MF,ED,EN,FN.∵BM=MA,BF=FD,∴MF∥AD,MF=AD,∵AN=ND,∴MF=AN,MF∥AN,∴四边形MFNA是平行四边形,∴NF=AM,∠FMA=∠ANF,在Rt△ADE中,∵AN=ND,∠AED=90°,∴EN=AD=AN=ND,同理CM=AB=AM=MB,在△AEN和△ACM中,∠AEN=∠EAN,∠MCA=∠MAC,∵∠MAC=∠EAN,∴∠AMC=∠ANE,又∵∠FMA=∠ANF,∴∠ENF=∠FMC,在△MFC和△NEF中,,∴△MFC≌△NEF(SAS),∴FE=FC,∠NFE=∠MCF,∵NF∥AB,∴∠NFD=∠ABD,∵∠ACB=90°,∠BAC=30°,∴∠ABC=60°,△BMC是等边三角形,∠MCB=60°∴∠EFC=∠EFN+∠NFD+∠DFC=∠MCF+∠ABD+∠FBC+∠FCB=∠ABC+∠MCB=60°+60°=120°.(3)如图3中,作EH⊥AB于H.在Rt△ABC中,∵∠BAC=30°,BC=3,∴AB=2BC=6,在Rt△AED中,∠DAE=30°,AD=2,∴DE=AD=1,在Rt△DEH中,∵∠EDH=60°,DE=1,∴EH=ED•sin60°=,DH=ED•cos60°=,在Rt△EHG中,EG==.5、如图1,在等腰△ABC中,AB=AC,∠BAC=a,点P是线段AB的中点,点E是线段CB延长线上一点,且PE=PC,将线段PC绕点P顺时针旋转α得到PD,连接BD.(1)如图2,若α=60°,其他条件不变,先补全图形,然后探究线段BD和BC之间的数量关系,并说明理由.(2)如图3,若α=90°,其他条件不变,探究线段BP、BD和BC之间的等量关系,并说明理由.解:(1)BC=2BD,理由:如图2,连接CD,由旋转可得,CP=DP,∠CPD=60°,∴△CDP是等边三角形,∴∠CDP=60°=∠PCD,又∵P是AB的中点,AB=AC,∠A=60°,∴等边三角形ABC中,∠PCB=30°,CP⊥AB,∴∠BCD=30°,即BC平分∠PCD,∴BC垂直平分PD,∴∠BDC=∠BPC=90°,∴Rt△BCD中,BC=2BD.(2)如图3,取BC中点F,连接PF,∵∠A=90°,AB=AC,∴△ABC是等腰直角三角形,∵P是AB的中点,F是BC的中点,∴PF是△ABC的中位线,∴PF∥AC,∴∠PFB=∠ACB=45°,∠BPF=∠A=90°,∴△BPF是等腰直角三角形,∴BF=BP,BP=PF,∵∠DPC=∠BPF=90°,∴∠BPD=∠FPC,又∵PD=PC,∴△BDP≌△FCP,∴BD=CF,∵BC=BF+FC,∴BC=BD+BP.6、【发现问题】如图1,已知△ABC,以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE.请你以A为直角顶点、AC为腰,向△ABC外作等腰直角△ACD(不写作法,保留作图痕迹).连接BD、CE.那么BD与CE的数量关系是BD=CE.【拓展探究】如图2,已知△ABC,以AB、AC为边向外作正方形AEFB和正方形ACGD,连接BD、CE,试判断BD与CE之间的数量关系,并说明理由.【解决问题】如图3,有一个四边形场地ABCD,∠ADC=60°,BC=15,AB=8,AD=CD,求BD的最大值.【发现问题】解:延长CA到M,作∠MAC的平分线AN,在AN上截取AD=AC,连接CD,即可得到等腰直角△ACD;连接BD、CE,如图1所示:∵△ABE与△ACD都是等腰直角三角形,∴AB=AE,AD=AC,∠BAE=∠CAD=90°,∴∠BAD=∠EAC,在△BAD和△EAC中,,∴△BAD≌△EAC(SAS),∴BD=CE,【拓展探究】解:BD=CE;理由如下:∵四边形AEFB与四边形ACGD都是正方形,∴AB=AE,AD=AC,∠BAE=∠CAD=90°,∴∠BAD=∠EAC,在△BAD和△EAC中,,∴△BAD≌△EAC(SAS),∴BD=CE;【解决问题】解:以AB为边向外作等边三角形ABE,连接CE,如图3所示:则∠BAE=60°,BE=AB=AE=8,∵AD=CD,∠ADC=60°,∴△ACD是等边三角形,∴∠CAD=60°,AC=AD,∴∠CAD+∠BAC=∠BAE+∠BAC,即∠BAD=∠EAC,在△BAD和△EAC中,,∴△BAD≌△EAC(SAS),∴BD=CE;当C、B、E三点共线时,CE最大=BC+BE=15+8=23,∴BD的最大值为23.7、如图1,点C为线段AB外一个动点,已知AB=a,AC=b.当点C位于BA的延长线上时,线段BC取得最大值,则最大值为a+b(用含a,b的式子表示);(2)如图2,点C为线段AB外一个动点,若AB=10,AC=3,分别以AC,BC为边,作等边三角形ACD和等边三角形BCE,连接AE,DB.①求证:AE=DB;②请直接写出线段AE的最大值;(3)如图3,AB=6,点M为线段AB外一个动点,且AM=2,MB=MN,∠BMN=90°,请直接写出线段AN的最大值.(1)解:∵点C为线段AB外一动点,且AC=b,AB=a,∴当点C位于BA的延长线上时,线段BC的长取得最大值,且最大值为AC+AB=a+b,(2)①证明:如图2中,∵△ACD与△BCE是等边三角形,∴CD=AC,CB=CE,∠ACD=∠BCE=60°,∴∠DCB=∠ACE,在△CAD与△EAB中,,∴△CAD≌△EAB(SAS),∴AE=BD.②∵线段AE长的最大值=线段BD的最大值,由(1)知,当线段BD的长取得最大值时,点D在BA的延长线上,∴最大值为AD+AB=3+10=13;(3)如图3中,连接BN,∵将△AMN绕着点M顺时针旋转90°得到△PBM,连接AP,则△APM是等腰直角三角形,∴MA=MP=2,BP=AN,∴P A=2,∵AB=6,∴线段AN长的最大值=线段BP长的最大值,∴当P在线段BA的延长线时,线段BP取得最大值最大值=AB+AP=6+2.8、【初步探索】(1)如图1:在四边形ABC中,AB=AD,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且EF =BE+FD,探究图中∠BAE、∠F AD、∠EAF之间的数量关系.小王同学探究此问题的方法是:延长FD到点G,使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是∠BAE+∠F AD=∠EAF;【灵活运用】(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且EF=BE+FD,上述结论是否仍然成立,并说明理由;【拓展延伸】(3)如图3,已知在四边形ABCD中,∠ABC+∠ADC=180°AB=AD,若点E在CB的延长线上,点F在CD的延长线上,如图3所示,仍然满足EF=BE+FD,请写出∠EAF与∠DAB的数量关系,并给出证明过程.解:(1)∠BAE+∠F AD=∠EAF.理由:如图1,延长FD到点G,使DG=BE,连接AG,根据SAS可判定△ABE≌△ADG,进而得出∠BAE=∠DAG,AE=AG,再根据SSS可判定△AEF≌△AGF,可得出∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF.故答案为:∠BAE+∠F AD=∠EAF;(2)仍成立,理由:如图2,延长FD到点G,使DG=BE,连接AG,∵∠B+∠ADF=180°,∠ADG+∠ADF=180°,∴∠B=∠ADG,又∵AB=AD,∴△ABE≌△ADG(SAS),∴∠BAE=∠DAG,AE=AG,∵EF=BE+FD=DG+FD=GF,AF=AF,∴△AEF≌△AGF(SSS),∴∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF;(3)∠EAF=180°﹣∠DAB.证明:如图3,在DC延长线上取一点G,使得DG=BE,连接AG,∵∠ABC+∠ADC=180°,∠ABC+∠ABE=180°,∴∠ADC=∠ABE,又∵AB=AD,∴△ADG≌△ABE(SAS),∴AG=AE,∠DAG=∠BAE,∵EF=BE+FD=DG+FD=GF,AF=AF,∴△AEF≌△AGF(SSS),∴∠F AE=∠F AG,∵∠F AE+∠F AG+∠GAE=360°,∴2∠F AE+(∠GAB+∠BAE)=360°,∴2∠F AE+(∠GAB+∠DAG)=360°,即2∠F AE+∠DAB=360°,∴∠EAF=180°﹣∠DAB.9、如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与点B、点C重合),连接OC、OP,将线段OP绕点P逆时针旋转60°,得到线段PQ,连接BQ.(1)如图1,当点P在线段BC上时,请直接写出线段BQ与CP的数量关系.(2)如图2,当点P在CB延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;(3)如图3,当点P在BC延长线上时,若∠BPO=45°,AC=,请直接写出BQ的长.解:(1)CP=BQ,理由:如图1,连接OQ,由旋转知,PQ=OP,∠OPQ=60°⊅∴△POQ是等边三角形,∴OP=OQ,∠POQ=60°,在Rt△ABC中,O是AB中点,∴OC=OA=OB,∴∠BOC=2∠A=60°=∠POQ,∴∠COP=∠BOQ,在△COP和△BOQ中,,∴△COP≌△BOQ(SAS),∴CP=BQ,(2)CP=BQ,理由:如图2,连接OQ,由旋转知,PQ=OP,∠OPQ=60°∴△POQ是等边三角形,∴OP=OQ,∠POQ=60°,在Rt△ABC中,O是AB中点,∴OC=OA=OB,∴∠BOC=2∠A=60°=∠POQ,∴∠COP=∠BOQ,在△COP和△BOQ中,,∴△COP≌△BOQ(SAS),∴CP=BQ,(3)如图3,在Rt△ABC中,∠A=30°,AC=,∴BC=AC•tan∠A=,过点O作OH⊥BC,∴∠OHB=90°=∠BCA,∴OH∥AB,∵O是AB中点,∴CH=BC=,OH=AC=,∵∠BPQ=45°,∠OHP=90°,∴∠BPQ=∠PQH,∴PH=OH=,∴CP=PH﹣CH=﹣=,连接BQ,同(1)的方法得,BQ=CP=.10、模型发现:同学们知道,三角形的两边之和大于第三边,即如图1,在△ABC中,AB+AC>BC.对于图1,若把点C看作是线段AB外一动点,且AB=c,AC=b,则线段BC的长会因为点C的位置的不同而发生变化.因为AB、AC的长度固定,所以当∠BAC越大时,BC边越长.特别的,当点C位于线段BA的延长线上时,线段BC的长取得最大值,且最大值为b+c(用含b,c的式子表示)(直接填空)模型应用:点C为线段AB外一动点,且AB=3,AC=2,如图2所示,分别以AC,BC为边,作等边三角形ACD 和等边三角形BCE,连接BD,AE.(1)求证:BD=AE.(2)线段AE长的最大值为5.模型拓展:如图3,在平面直角坐标系中,点A是y轴正半轴上的一动点,点B是x轴正半轴上的一动点,且AB =8.若AC⊥AB,AC=3,试求OC长的最大值.解:当点C位于线段BA的延长线上时,线段BC的长取得最大值,最大值为b+c,故答案为:线段BA的延长线上;b+c;模型应用:(1)证明:∵△ACD、△BCE都是等边三角形,∴CD=CA=AD,CB=CE,∠ACD=60°,∠BCE=60°,∴∠DCB=∠ACE,在△DCB和△ACE中,,∴△DCB≌△ACE(SAS)∴BD=AE;(2)当点D位于线段BA的延长线上时,线段BD的长取得最大值,最大值为AB+AD=AB+AC=3+2=5,∵AE=BD,∴线段AE长的最大值为5,模型拓展:取AB的中点G,连接OG、CG,在Rt△AOB中,G为AB的中点,∴OG=AB=4,在Rt△CAG中,CG===5,当点O、G、C在同一条直线上时,OC最大,最大值为4+5=9.11、已知:△ABC中,∠ACB=90°,AC=BC.(1)如图1,点D在BC的延长线上,连AD,过B作BE⊥AD于E,交AC于点F.求证:AD=BF;(2)如图2,点D在线段BC上,连AD,过A作AE⊥AD,且AE=AD,连BE交AC于F,连DE,问BD与CF有何数量关系,并加以证明;(3)如图3,点D在CB延长线上,AE=AD且AE⊥AD,连接BE、AC的延长线交BE于点M,若AC =3MC,请直接写出的值.(1)证明:如图1中,∵BE⊥AD于E,∴∠AEF=∠BCF=90°,∵∠AFE=∠CFB,∴∠DAC=∠CBF,∵BC=CA,∴△BCF≌△ACD,∴BF=AD.(2)结论:BD=2CF.理由:如图2中,作EH⊥AC于H.∵∠AHE=∠ACD=∠DAE=90°,∴∠DAC+∠ADC=90°,∠DAC+∠EAH=90°,∴∠DAC=∠AEH,∵AD=AE,∴△ACD≌△EHA,∴CD=AH,EH=AC=BC,∵CB=CA,∴BD=CH,∵∠EHF=∠BCF=90°,∠EFH=∠BFC,EH=BC,∴△EHF≌△BCF,∴FH=CF,∴BD=CH=2CF.(3)如图3中,同法可证BD=2CM.∵AC=3CM,设CM=a,则AC=CB=3a,BD=2a,∴==.12、已知在△ABC中,AB=AC,射线BM、BN在∠ABC内部,分别交线段AC于点G、H.(1)如图1,若∠ABC=60°,∠MBN=30°,作AE⊥BN于点D,分别交BC、BM于点E、F.①求证:∠1=∠2;②如图2,若BF=2AF,连接CF,求证:BF⊥CF;(2)如图3,点E为BC上一点,AE交BM于点F,连接CF,若∠BFE=∠BAC=2∠CFE,求的值.(1)①证明:如图1中,∵AB=AC,∠ABC=60°∴△ABC是等边三角形,∴∠BAC=60°,∵AD⊥BN,∴∠ADB=90°,∵∠MBN=30°,∠BFD=60°=∠1+∠BAF=∠2+∠BAF,∴∠1=∠2②证明:如图2中,在Rt△BFD中,∵∠FBD=30°,∴BF=2DF,∵BF=2AF,∴BF=AD,∵∠BAE=∠FBC,AB=BC,∴△BFC≌△ADB,∴∠BFC=∠ADB=90°,∴BF⊥CF(2)在BF上截取BK=AF,连接AK.∵∠BFE=∠2+∠BAF,∠CFE=∠4+∠1,∴∠CFB=∠2+∠4+∠BAC,∵∠BFE=∠BAC=2∠EFC,∴∠1+∠4=∠2+∠4∴∠1=∠2,∵AB=AC,∴△ABK≌CAF,∴∠3=∠4,S△ABK=S△AFC,∵∠1+∠3=∠2+∠3=∠CFE=∠AKB,∠BAC=2∠CEF,∴∠KAF=∠1+∠3=∠AKF,∴AF=FK=BK,∴S△ABK=S△AFK,∴=2.13、已知,△ABC中,AB=AC,∠BAC=90°,E为边AC任意一点,连接BE.(1)如图1,若∠ABE=15°,O为BE中点,连接AO,且AO=1,求BC的长;(2)如图2,F也为AC上一点,且满足AE=CF,过A作AD⊥BE交BE于点H,交BC于点D,连接DF交BE于点G,连接AG;①若AG平分∠CAD,求证:AH=AC;②如图3,当G落在△ABC外时,若将△EFG沿EF边翻折,点G刚好落在AB边上点P,直接写出AG与EF的数量关系.(1)解:如图1中,在AB上取一点M,使得BM=ME,连接ME.在Rt△ABE中,∵OB=OE,∴BE=2OA=2,∵MB=ME,∴∠MBE=∠MEB=15°,∴∠AME=∠MBE+∠MEB=30°,设AE=x,则ME=BM=2x,AM=x,∵AB2+AE2=BE2,∴(2x+x)2+x2=22,∴x=(负根已经舍弃),∴AB=AC=(2+)•,∴BC=AB=+1.方法二:作EH⊥BC于H,求出BH,CH即可解决问题.(2)证明:如图2中,作CP⊥AC,交AD的延长线于P,GM⊥AC于M.∵BE⊥AP,∴∠AHB=90°,∴∠ABH+∠BAH=90°,∵∠BAH+∠P AC=90°,∴∠ABE=∠P AC,在△ABE和△CAP中,,∴△ABE≌△CAP,∴AE=CP=CF,∠AEB=∠P,在△DCF和△DCP中,,∴△DCF≌△DCP,∴∠DFC=∠P,∴∠GFE=∠GEF,∴GE=GF,∵GM⊥EF,∴FM=ME,∵AE=CF,∴AF=CE,∴AM=CM,在△GAH和△GAM中,,∴△AGH≌△AGM,∴AH=AM=CM=AC(3)解:结论:AG=EF.理由:如图3中,作CM⊥AC交AD的延长线于M,连接PG交AC于点O.由(2)可知△ACM≌△BAE,△CDF≌△CDM,∴∠AEB=∠M=∠GEF,∠M=∠CFD=∠GFE,AE=CM=CF,∴∠GEF=∠GFE,∴GE=GF,∵△EFP是由△EFG翻折得到,∴EG=EP=GF=PF,∴四边形EGFP是菱形,∴PG⊥AC,OE=OF,∵AE=CF,∴AO=OC,∵AB∥OP,∴BP=PC,∵PF∥BE,∴EF=CF=AE,∵PB=PC,AO=OC,∴PO=OG=AB,∴AB=PG,AB∥PG,∴四边形ABPG是平行四边形,∴AG∥BC,∴∠GAO=∠ACB=45°,设EO=OF=a,则OA=OG=3a,AG=3a,∴==,∴AG=EF14、如图所示,Rt△ABC中,∠ACB=90°,E为AC中点,作ED⊥AC交AB于D,连接CD;(1)如图1,求证:AB=2CD;(2)如图2,作CF⊥AB交AB于F,点G为CF上一点,点H为DE延长线上一点,分别连接AH、GH,若∠AHG=2∠B,求证:AH=GH;(3)如图3,在(2)的条件下,连接DG,且有DE=BF,∠EDG=90°,若AC=6,求AH的长度.解:(1)∵E为AC中点,作ED⊥AC交AB于D,∴AD=CD,∵∠ACB=90°,∴BC∥DE,∴AD=BD,∴CD=BD,∴AB=2CD;(2)如图2,连接CH,∵点E是AC的中点,∴AE=CE,∵DE⊥AC,∴CH=AH,∴∠ACH=∠CAH,∵∠ACB=90°,∴∠B+∠BAC=90°,∵CF⊥AB,∴∠BAC+∠ACF=90°,∴∠ACF=∠B,∴∠HCG=∠ACH+∠ACF=∠CAH+∠B,∠AHG=2∠B∴在四边形AHGF中,∠AFG+∠FGH+∠AHG+∠F AH=360°,∴∠FGH=360°﹣(∠AFG+∠AHG+∠F AH)=360°﹣(90°+2∠B+∠CAH+∠BAC)=360°﹣(90°+2∠B+∠CAH+90°﹣∠B)=360°﹣(180°+∠B+∠CAH)=180°﹣(∠B+∠CAH),∵∠CGH=180°﹣∠FGH=∠B+∠CAH=∠HCG,∴CH=GH,∵CH=AH,∴AH=GH;(3)如图3,由(1)知,DE∥BC,∴∠B=∠ADE,在△BFC和△DEA中,,∴△BFC≌△DEA,∴BC=AD,∵AD=BD=CD,∴BC=BD=CD,∴△BCD是等边三角形,∴∠B=60°,在Rt△ABC中,AC=6,∴BC=2,AB=4,∵CF⊥BD,∴DF=,CF=3,∵∠BAC=30°,∴∠ADE=60°,∵∠EDG=90°,∠FDG=30°,在Rt△DFG中,DF=,∴FG=1,DG=2,∴CG=CF﹣FG=2过点H作HN⊥CF,由(2)知,CH=GH,∴NG=CG=1,∴FN=NG+FG=2,过点H作HM⊥AB,∴∠FMH=∠NFM=∠HNF=90°,∴四边形NFMH是矩形,∴HM=FN=2,在Rt△DMH中,∠ADE=60°,HM=2,∴DH=,在Rt△HDG中,根据勾股定理得,HG==.15、【问题情境】一节数学课后,老师布置了一道课后练习题:如图:已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,点E、F分别在A和BC上,∠1=∠2,FG⊥AB于点G,求证:△CDE≌△EGF.(1)阅读理解,完成解答本题证明的思路可用下列框图表示:根据上述思路,请你完整地书写这道练习题的证明过程;(2)特殊位置,证明结论若CE平分∠ACD,其余条件不变,求证:AE=BF;(3)知识迁移,探究发现如图,已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,若点E是DB的中点,点F在直线CB上且满足EC=EF,请直接写出AE与BF的数量关系.(不必写解答过程)(1)证明:∵AC=BC,∠ACB=90°,∴∠A=∠B=45°,∵CD⊥AB,∴∠CDB=90°,∴∠DCB=45°,∵∠ECF=∠DCB+∠1=45°+∠1,∠EFC=∠B+∠2=45°+∠2,∠1=∠2,∴∠ECF=∠EFC,∴CE=EF,∵CD⊥AB,FG⊥AB,∴∠CDE=∠EGF=90°,在△CDE和△EGF中,,∴△CDE≌△EGF(AAS);(2)证明:由(1)得:CE=EF,∠A=∠B,∵CE平分∠ACD,∴∠ACE=∠1,∵∠1=∠2,∴∠ACE=∠2,在△ACE和△BEF中,,∴△ACE≌△BEF(AAS),∴AE=BF;(3)AE=BF,作EH⊥BC与H,如图3所示:设DE=x,根据题意得:BE=DE=x,AD=BD=2x,CD=AD=2x,AE=3x,根据勾股定理得:BC=AC=2x,∵∠ABC=45°,EH⊥BC,∴BH=x,∴CH=BC﹣BH=x,∵EC=EF,∴FH=CH=x,∴BF=x﹣x=x,∴=,∴AE=.16、在正方形ABCD和等腰直角△BGF中,∠BGF=90°,P是DF的中点,连接PG、PC.(1)如图1,当点G在BC边上时,延长GP交DC于点E.求证:PG=PC;(2)如图2,当点F在AB的延长线上时,(1)中的结论是否成立?请证明你的结论;(3)如图3,若四边形ABCD为菱形,且∠ABC=60°,△BGF为等边三角形,点F在CB的延长线。
2020年数学中考复习:压轴几何证明题的解法(含答案)

2020年数学中考复习:压轴几何证明题的解法1.(2019.葫芦岛)如图,△ABC 是等腰直角三角形,∠ACB =900,D 是射线CB 上一点(点D 不与点B 重合),以AD 为斜边作等腰直角三角形ADE (点E 和点C 在AB 的同侧),连接CE 。
(1)如图①,当点D 与点C 重合时,直接写出CE 与AB 的位置关系;(2)如图②,当点D 与点C 不重合时,(1)的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;(3)当∠EAC =150时,请直接写出AB CE 的值。
解析:(1)由∠ECA =∠CAB =450,可得EC ∥AB 。
(2)由22=AB AC =AD AE ,且∠EAC =∠DAB ,可得△EAC ∽△DAB 进而得出∠ECA =∠DBA =450=∠CAB ,所以CE ∥AB .(3)此问分两种情况点D 在BC 上,点D 在CB 延长线上。
①当点D 在BC 上时,如图(2),此时∠CAB =150能得出∠CAD =300,这样就有33=AC CD ,也就是BC -DB =33AC ,BC =AC ,所以BD =333-AC 。
又由△EAC ∽△DAB 得21=BD CE ,因此有BD =2CE ,所以可得CE =6623-AC ,又AB =2AC ,因此ABCE =63-3.当D 点在CB 延长线上时,∠CDA =300,解三角形得3AC =3CD 。
CD =BC +BD ,由△AEC ∽△ABD ,可得BD =2AC ,就能得到CE =AC2-13,AB =2AC ,所以2-13=AB CE . 2.(2019.沈阳)思维启迪:(1)如图1,A ,B 两点分别位于一个池塘的两端,小亮想用绳子测量A ,B 间的距离,但绳子不够长,聪明的小亮想出一个办法:先在地上取一个可以直接到达B 点的点C ,连接BC ,取BC 的中点P (点P 可以直接到达A 点),利用工具过点C 作CD ∥AB 交AP 的延长线于点D ,此时测得CD =200米,那么A ,B 间的距离是_200_米。
中考数学全等三角形压轴几何题知识点-+典型题及答案
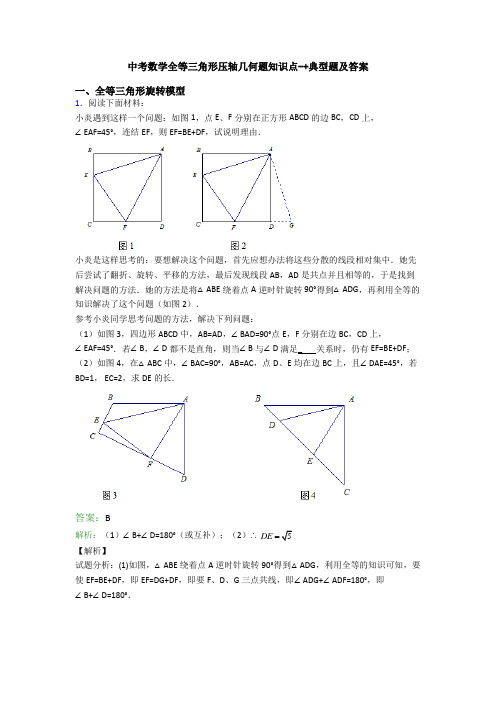
中考数学全等三角形压轴几何题知识点-+典型题及答案一、全等三角形旋转模型1.阅读下面材料:小炎遇到这样一个问题:如图1,点E、F分别在正方形ABCD的边BC,CD上,∠EAF=45°,连结EF,则EF=BE+DF,试说明理由.小炎是这样思考的:要想解决这个问题,首先应想办法将这些分散的线段相对集中.她先后尝试了翻折、旋转、平移的方法,最后发现线段AB,AD是共点并且相等的,于是找到解决问题的方法.她的方法是将△ABE绕着点A逆时针旋转90°得到△ADG,再利用全等的知识解决了这个问题(如图2).参考小炎同学思考问题的方法,解决下列问题:(1)如图3,四边形ABCD中,AB=AD,∠BAD=90°点E,F分别在边BC,CD上,∠EAF=45°.若∠B,∠D都不是直角,则当∠B与∠D满足_ 关系时,仍有EF=BE+DF;(2)如图4,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,若BD=1, EC=2,求DE的长.答案:B解析:(1)∠B+∠D=180°(或互补);(2)∴5DE【解析】试题分析:(1)如图,△ABE绕着点A逆时针旋转90°得到△ADG,利用全等的知识可知,要使EF=BE+DF,即EF=DG+DF,即要F、D、G三点共线,即∠ADG+∠ADF=180°,即∠B+∠D=180°.(2) 把△ABD绕A点逆时针旋转90°至△ACG,可使AB与AC重合,通过证明△AEG≌△AED 得到DE=EG,由勾股定理即可求得DE的长.(1)∠B+∠D=180°(或互补).(2)∵ AB=AC,∴把△ABD绕A点逆时针旋转90°至△ACG,可使AB与AC重合.则∠B=∠ACG,BD=CG,AD=AG.∵在△ABC中,∠BAC=90°,∴∠ACB+∠ACG=∠ACB+∠B=90°于,即∠ECG=90°.∴ EC2+CG2=EG2.在△AEG与△AED中,∠EAG=∠EAC+∠CAG=∠EAC+∠BAD=90°-∠EAD=45°=∠EAD.又∵AD=AG,AE=AE,∴△AEG≌△AED .∴DE=EG.又∵CG=BD,∴ BD2+EC2=DE2.∴5DE=.考点:1.面动旋转问题;2.全等三角形的判定和性质;3.勾股定理.2.我们定义:有一组对角为直角的四边形叫做“对直角四边形”.(1)如图①,四边形ABCD为对直角四边形,∠B=90°,若AB2-AD2=4,求CD2-BC2的值;(2)如图②,四边形ABCD中,∠ABC=90°,AB=BC,若BD平分∠ADC,求证:四边形ABCD为对直角四边形;(3)在(2)的条件下,如图③,连结AC,若35ACDABCSS=,求tan∠ACD的值.答案:A解析:⑴ 4;⑵见解析;⑶tan∠ACD的值为3或13.【分析】(1)利用勾股定理即可解决问题;(2)如图②中,作BE⊥CD于E,BF⊥DA交DA的延长线于F.只要证明∠EBF=90°即可解决问题;(3)如图③中,设AD=x,BD=y.根据35ACDABCSS,构建方程即可解决问题.【详解】解:如图①中,∵四边形ABCD为对直角四边形,∠B=90°,∴∠D=∠B=90°,∴AC2=AB2+BC2=AD2+DC2,∴CD2-BC2=AB2-AD2=4.(2)证明:如图②中,作BE⊥CD于E,BF⊥DA交DA的延长线于F.∵BD平分∠ADC,BE⊥CD,BF⊥AD,∴BE=BF,∵∠BFA=∠BEC=90°,BA=BC ,BF=BE , ∴Rt △BFA ≌Rt △BEC (HL ), ∴∠ABF=∠CBE , ∴∠EBF=∠ABC=90°, ∴ADC=360°-90°-90°-90°=90°, ∵∠ABC=∠ADC=90°,∴四边形ABCD 为对直角四边形. (3)解:如图③中,设AD=x ,BD=y .∵∠ADC=90°, ∴tan ∠ACD=xy,22x y + ∵AB=AC ,∠ABC=90°, ∴222x y + ∵35ACD ABCS S=, ∴()22132154xy x y =+, 整理得:3x 2-10xy+3y 2, ∴3(x y )2-10•xy+3=0, ∴x y =3或13. ∴tan ∠ACD 的值为3或13. 【点睛】本题属于四边形综合题,考查了勾股定理,三角形的面积,全等三角形的判定和性质,角平分线的性质定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用参数,构建方程解决问题,属于中考压轴题.3.如图,△ABC 是边长为4的等边三角形,点D 是线段BC 的中点,∠EDF=120°,把∠EDF绕点D旋转,使∠EDF的两边分别与线段AB、AC交于点E、F.(1)当DF⊥AC时,求证:BE=CF;(2)在旋转过程中,BE+CF是否为定值?若是,求出这个定值;若不是,请说明理由答案:D解析:(1)证明见解析;(2)是,2.【解析】【分析】(1)根据四边形内角和为360°,可求∠DEA=90°,根据“AAS”可判定△BDE≌△CDF,即可证BE=CF;(2)过点D作DM⊥AB于M,作DN⊥AC于N,如图2,易证△MBD≌△NCD,则有BM=CN,DM=DN,进而可证到△EMD≌△FND,则有EM=FN,就可得到BE+CF=BM+EM+CF=BM+FN+CF=BM+CN=2BM=2BD×cos60°=BD=12BC=2.【详解】(1)∵△ABC是边长为4的等边三角形,点D是线段BC的中点,∴∠B=∠C=60°,BD=CD,∵DF⊥AC,∴∠DFA=90°,∵∠A+∠EDF+∠AFD+∠AED=180°,∴∠AED=90°,∴∠DEB=∠DFC,且∠B=∠C=60°,BD=DC,∴△BDE≌△CDF(AAS)(2)过点D作DM⊥AB于M,作DN⊥AC于N,则有∠AMD=∠BMD=∠AND=∠CND=90°.∵∠A=60°,∴∠MDN=360°-60°-90°-90°=120°.∵∠EDF=120°,∴∠MDE=∠NDF.在△MBD 和△NCD 中,BMD CND B CBD CD ∠∠⎧⎪∠∠⎨⎪⎩===, ∴△MBD ≌△NCD (AAS ) BM=CN ,DM=DN . 在△EMD 和△FND 中,EMD FND DM DNMDE NDF ∠∠⎧⎪⎨⎪∠∠⎩===, ∴△EMD ≌△FND (ASA ) ∴EM=FN ,∴BE+CF=BM+EM+CF=BM+FN+CF=BM+CN =2BM=2BD×cos60°=BD=12BC=2. 【点睛】本题主要考查了等边三角形的判定与性质、全等三角形的判定与性质、特殊角的三角函数值等知识,通过证明三角形全等得到BM=CN ,DM=DN ,EM=FN 是解决本题的关键. 4.如图1,在Rt △ABC 中,∠A =90°,AB =AC ,点D ,E 分别在边AB ,AC 上,AD =AE ,连接DC ,点M ,P ,N 分别为DE ,DC ,BC 的中点.(1)观察猜想:图1中,线段PM 与PN 的数量关系是 ,位置关系是 ;(2)探究证明:把△ADE 绕点A 逆时针方向旋转到图2的位置,连接MN ,BD ,CE ,判断△PMN 的形状,并说明理由;(3)拓展延伸:把△ADE 绕点A 在平面内自由旋转,若AD =4,AB =10,请直接写出△PMN 面积的最大值.解析:(1)PM =PN ,PM ⊥PN ;(2)△PMN 是等腰直角三角形.理由见解析;(3)S △PMN 最大=492. 【分析】(1)由已知易得BD CE =,利用三角形的中位线得出12PM CE =,12PN BD =,即可得出数量关系,再利用三角形的中位线得出//PM CE 得出DPM DCA ∠=∠,最后用互余即可得出位置关系;(2)先判断出ABD ACE ∆≅∆,得出BD CE =,同(1)的方法得出12PM BD =,12PN BD =,即可得出PM PN =,同(1)的方法由MPN DCE DCB DBC ACB ABC ∠=∠+∠+∠=∠+∠,即可得出结论;(3)方法1:先判断出MN 最大时,PMN ∆的面积最大,进而求出AN ,AM ,即可得出MN 最大AM AN =+,最后用面积公式即可得出结论.方法2:先判断出BD 最大时,PMN ∆的面积最大,而BD 最大是14AB AD +=,即可得出结论. 【详解】 解:(1)点P ,N 是BC ,CD 的中点,//PN BD ∴,12PN BD =, 点P ,M 是CD ,DE 的中点, //PM CE ∴,12PM CE =, AB AC =,AD AE =, BD CE ∴=, PM PN ∴=, //PN BD ,DPN ADC ∴∠=∠, //PM CE ,DPM DCA ∴∠=∠, 90BAC ∠=︒,90ADC ACD ∴∠+∠=︒,90MPN DPM DPN DCA ADC ∴∠=∠+∠=∠+∠=︒, PM PN ∴⊥,故答案为:PM PN =,PM PN ⊥; (2)PMN ∆是等腰直角三角形. 由旋转知,BAD CAE ∠=∠, AB AC =,AD AE =,()ABD ACE SAS ∴∆≅∆,ABD ACE ∴∠=∠,BD CE =,利用三角形的中位线得,12PN BD =,12PM CE =,PM PN ∴=,PMN ∴∆是等腰三角形,同(1)的方法得,//PM CE , DPM DCE ∴∠=∠,同(1)的方法得,//PN BD ,PNC DBC ∴∠=∠,DPN DCB PNC DCB DBC ∠=∠+∠=∠+∠, MPN DPM DPN DCE DCB DBC ∴∠=∠+∠=∠+∠+∠BCE DBC ACB ACE DBC =∠+∠=∠+∠+∠ ACB ABD DBC ACB ABC =∠+∠+∠=∠+∠, 90BAC ∠=︒,90ACB ABC ∴∠+∠=︒, 90MPN ∴∠=︒,PMN ∴∆是等腰直角三角形;(3)方法1:如图2,同(2)的方法得,PMN ∆是等腰直角三角形,MN ∴最大时,PMN ∆的面积最大, //DE BC ∴且DE 在顶点A 上面, MN ∴最大AM AN =+, 连接AM ,AN ,在ADE ∆中,4AD AE ==,90DAE ∠=︒, 22AM ∴=在Rt ABC ∆中,10AB AC ==,52AN = 22522MN ∴=最大,222111149(72)22242PMN S PM MN ∆∴==⨯=⨯=最大. 方法2:由(2)知,PMN ∆是等腰直角三角形,12PM PN BD ==, PM ∴最大时,PMN ∆面积最大, ∴点D 在BA 的延长线上, 14BD AB AD ∴=+=, 7PM ∴=,2211497222PMN S PM ∆∴==⨯=最大. 【点睛】此题属于几何变换综合题,主要考查了三角形的中位线定理,等腰直角三角形的判定和性质,全等三角形的判断和性质,直角三角形的性质的综合运用;解(1)的关键是判断出12PM CE =,12PN BD =,解(2)的关键是判断出ABD ACE ∆≅∆,解(3)的关键是判断出MN 最大时,PMN ∆的面积最大.5.问题发现:(1)如图1,在等腰直角三角形ABC 中,90C ∠=︒,点O 为AB 的中点,点M 为AC 上一点,将射线OM 顺时针旋转90︒交BC 于点N ,则OM 与ON 的数量关系为____;问题探究:(2)如图2,在等腰三角形ABC 中,120C ∠=︒,点O 为AB 的中点,点M 为AC 上一点,将射线OM 顺时针旋转60︒交BC 于点N ,则OM 与ON 的数量关系是否改变,请说明理由;问题解决:(3)如图3,点O 为正方形ABCD 对角线的交点,点P 为DO 的中点,点M 为直线BC 上一点,将射线OM 顺时针旋转90︒交直线AB 于点N ,若4AB =,当PMN 面积为252时,直接写出线段BN 的长.答案:B解析:(1)OM =ON ;(2)不改变;证明见解析;(3)线段BN 的长为172-或172+【分析】(1)连接,OC ,证明△AOM ≌△CON (ASA )可得结论.(2)数量关系不变.如图2中,过点O 作OK ⊥AC 于K ,OJ ⊥BC 于J ,连接OC .证明△OKM ≌△OJN (AAS )可得结论.(3)如图3中,过点P 作PG ⊥AB 于G ,PH ⊥BC 于H .证明△MOC ≌△NOB (SAS ),推出CM=BN ,设CM=BN=m ,根据S △PMN =252=S △PBM +S △BMN -S △PBN ,构建方程求解即可.当点M 在CB 的延长线上时,同法可求. 【详解】解:(1)如图1中,结论:OM=ON . 理由:连接OC .∵CA=CB,∠ACB=90°,AO=OB,CO=OA=OB,OC⊥AB,∠A=∠B=45°,∠BCO=∠ACO=45°∴∠AOC=∠MON=90°,∴∠AOM=∠CON,∵∠A=∠CON,∴△AOM≌△CON(ASA),∴OM=ON.故答案为:OM=ON.(2)理由:如图2中,过点O作OK⊥AC于K,OJ⊥BC于J,连接OC.∵∠ACB=120°,∠OKC=∠OJC=90°,∠KOJ=60°=∠MON,∴∠MKO=∠NOJ,∵CA=CB,OA=OB,∴OC平分∠ACB,∵OK⊥CA,OJ⊥CB,∴OK=OJ,∵∠OKM=∠OJN=90°,∴△OKM≌△OJN(AAS),∴OM=ON.(3)如图3中,过点P作PG⊥AB于G,PH⊥BC于H.∵四边形ABCD是正方形,AB=AD=4,∠BAD=90°,∴BD=2AB=42, ∴OD=OB=22,PD=OP=2,∴PB=33,∵四边形PGBH 是正方形,∴PG=PH=3,∵∠MON=∠COB=90°,∴∠MOC=∠NOB ,∵OM=ON ,OC=OB ,∴△MOC ≌△NOB (SAS ),∴CM=BN ,设CM=BN=m ,∵S △PMN =252=S △PBM +S △BMN -S △PBN , ∴12•(4+m )•3+12•m•(4+m )12-•m•3=252, ∴整理得:m 2+4m-13=0,解得m=172-或172--(舍去),∴BN=172-.当点M 在CB 的延长线上时,同法可得BN=172+.综上所述,满足条件的BN 的值为172-或172+.【点睛】本题属于四边形综合题,考查了正方形的性质,全等三角形的判定和性质,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会用分类讨论的思想思考问题,学会利用参数构建方程解决问题,属于中考压轴题.6.在ABC 中,,AB AC BAC α=∠=,点P 为线段CA 延长线上一动点,连接PB ,将线段PB 绕点P 逆时针旋转,旋转角为α,得到线段PD ,连接,DB DC .(1)如图1,当60α=︒时,请直接写出线段PA 与线段CD 的数量关系是__________,DCP ∠为______度;(2)如图2,当120α=︒时,写出线段PA 和线段DC 的数量关系,并说明理由;(3)如图2,在(2)的条件下,当23AB =时,求13BP PC +的最小值. 答案:A解析:(1)PA =DC ,60;(2)CD =3PA .理由见详解;(2)3+22【分析】(1)先证明△ABC ,△PBD 是等边三角形,再证明△PBA ≌△DBC ,进而线段PA 与线段CD 的数量关系,利用全等三角形的性质以及三角形内角和等于180°,解决问题即可;(2)证明△CBD ∽△ABP ,可得3CD BC PA AB==,解决问题; (3)过点C 作射线CM ,使得sin ∠ACM =13,过点P 作PN ⊥CM 于点N ,则PN =13PC , 过点B 作BG ⊥BA 于点G ,当点B 、P 、N 共线时,BP +PN 最小,即13BP PC +最小,由BGP CNP ∽,得13GP NP BP CP ==,结合勾股定理求出GP ,从而得CP ,进而即可求解. 【详解】(1)①证明: ∵将线段PB 绕点P 逆时针旋转,旋转角为α,得到线段PD ,∴PB =PD ,∵AB =AC ,PB =PD ,∠BAC =∠BPD =60°,∴△ABC ,△PBD 是等边三角形,∴∠ABC =∠PBD =60°,∴∠PBA =∠DBC ,∵BP =BD ,BA =BC ,∴△PBA ≌△DBC (SAS ),∴PA =DC .设BD 交PC 于点O ,如图1,∵△PBA ≌△DBC ,∴∠BPA =∠BDC ,∵∠BOP =∠COD ,∴∠OBP =∠OCD =60°,即∠DCP =60°.故答案是:PA =DC ,60;(2)解:结论:CD .理由如下:∵AB =AC ,PB =PD ,∠BAC =∠BPD =120°,∴BC =2•AB •cos30°,BD ═2BP •cos30°, ∴BC BDBA BP= ∵∠ABC =∠PBD =30°,∴∠ABP =∠CBD ,∴△CBD ∽△ABP ,∴CD BC PA AB== ∴CD; (3) 过点C 作射线CM ,使得sin ∠ACM =13,过点P 作PN ⊥CM 于点N ,则PN =13PC ,过点B 作BG CA ⊥于点G ,则BG =AB ×sin ∠BAG =3,AG = AB ×cos ∠BAG 当点B 、P 、N 共线时,BP +PN 最小,即13BP PC +最小, ∵∠BGP =∠CNP =90°,∠BPG =∠CPN , ∴BGP CNP ∽, ∴13GP NP BP CP ==,设GP =x ,则AP -x ,BP =3x ,∴()22233x x +=,解得:x∴BPAP∴CP =AC +AP∴13BP PC +最小值13+【点睛】本题属于几何变换综合题,考查了全等三角形的判定和性质,相似三角形的判定和性质,解直角三角形等知识,第(1)(2)题解题的关键是正确寻找全等三角形或相似三角形解决问题,第(3)题的关键是过点C 作射线CM ,使得sin ∠ACM =13,过点P 作PN ⊥CM 于点N .7.如图1,在正方形ABCD 中,点,E F 分别在边,AB AD 上,且AE AF =,延长FD 到点G ,使得DG DF =,连接,,EF GE CE .(特例感知)(1)图1中GE 与CE 的数量关系是______________.(结论探索)(2)图2,将图1中的AEF 绕着点A 逆时针旋转()090αα︒<<︒,连接FD 并延长到点G ,使得DC DF =,连接,,GE CE BE ,此时GE 与CE 还存在(1)中的数量关系吗?判断并说明理由.(拓展应用) (3)在(2)的条件下,若5,32AB AE ==EFG 是以EF 为直角边的直角三角形时,请直接写出GE 的长.答案:G解析:(1) GE 2CE ,(2)存在,证明见解析,(3)25810或16或4.【分析】(1)连接GC,证△CDG≌△CBE,得出△GCE为等腰直角三角形即可;(2)类似(1)的方法,先证△AFD≌△AEB,再证△CDG≌△CBE,得出△GCE为等腰直角三角形即可;(3)根据E、F是直角顶点分类讨论,结合(2)中结论,利用勾股定理求解即可.【详解】解:(1)连接GC,∵AE=AF,AD=AB,∴DF=BE,,∵DG DF∴DG = BE,∵∠GDC=∠B=90°,DC=BC,∴△CDG≌△CBE,∴CE=CG,∠GCD=∠ECB,∵∠ECB+∠DCE=90°,∴∠GCE=∠GCD+∠DCE=90°,∴GE=2CE;故答案为:GE=2CE;(2) 存在,连接GC,∵AE=AF,AD=AB,∠FAE=∠DAB=90°,∴∠FAD=∠EAB,∴△FAD≌△EAB,∴FD=EB=GD,∠FDA=∠EBA,∵∠GDC+∠FDA=90°,∠EBC+∠EBA=90°,∴∠GDC=∠EBC,∵DC=BD,∴△CDG≌△CBE,与(1)同理,GE=2CE;(3)当∠FEG=90°时,如图1,因为∠FEA=∠GEC=45°,所以,A、E、C在一条直线上,∵AB=5,∴AC=52,CE=52-32=22,GE=2EC=4;如图2,E在CA延长线上,同理可得,EC2,GE2EC=16;当∠EFG =90°时,如图3,∠AFD =∠EFG +∠AFE =135°,由(2)得,∠AFD =∠AEB =135°,DF =BE ,所以,B 、E 、F 在一条直线上,作AM ⊥EF ,垂足为M , ∵5,32AB AE ==,∴EF =6,AM =ME =MF =3,224BM AB AM =-=,BE =DF =1,FG =2,22210GE FG EF =+=;如图4,同图3,BE =DF =7,FG =14,EF =6,22258GE FG EF =+=,综上,GE的长为258或210或16或4.【点睛】本题考查了旋转的性质、全等三角形的判定与性质、勾股定理和等腰直角三角形的性质,解题关键是恰当的连接辅助线,构造全等三角形;会分类讨论,结合题目前后联系,解决问题.8.如图,△ABC和△CEF中,∠BAC=∠CEF=90°,AB=AC,EC=EF,点E在AC边上.(1)如图1,连接BE,若AE=3,BE=58,求FC的长度;(2)如图2,将△CEF绕点C逆时针旋转,旋转角为α(0°<α<180°),旋转过程中,直线EF分别与直线AC,BC交于点M,N,当△CMN是等腰三角形时,求旋转角α的度数;(3)如图3,将△CEF绕点C顺时针旋转,使得点B,E,F在同一条直线上,点P为BF 的中点,连接AE,猜想AE,CF和BP之间的数量关系并说明理由.答案:C解析:(1)422)22.5°或45°或112.5°;(3)CF+AE2BP,见解析【分析】(1)利用勾股定理求出AB=AC=7,求出EC=EF=4即可解决问题;(2)分三种情形分别画出图形,利用等腰三角形的性质求解即可;(3)结论:CF+AE2BP.如图3中,过点A作AD⊥AE,利用全等三角形的性质以及等腰直角三角形的性质求解即可.【详解】解:(1)如图1中,在Rt △ABE 中,AB =()2222583497-=-==BF AE ,∴AC =AB =7,∴EF =EC =AC ﹣AE =7﹣3=4,∵∠CEF =90°,EC =EF =3, ∴CF =22224442+=+=EF CE ;(2)①如图2﹣1中,当CM =CN 时,α=∠MCE =∠ECN =12∠ACB =22.5°.如图2﹣2中,当NM =NC 时,α=∠MCN =45°.如图2﹣3中,当CN =CM 时,∠NCE =12∠BCM =67.5°,α=∠ACE =45°+67.5°=112.5°.综上所述,满足条件的α的值为22.5°或45°或112.5°.(3)结论:CF +AE =2BP .理由:如图3中,过点A 作AD ⊥AE ,∴∠DAE =∠BAC =90°,∴∠BAD =∠CAE ,∵∠BAC =∠BEC =90°,∴∠ABP =∠ACE ,∵AB =AC ,∴△ABD ≌△ACE (ASA ),∴BD =EC =EF ,AD =AE ,∴△ADE 是等腰直角三角形,∴DE 2AE ,∵P 是BF 的中点,∴BP =12BF , ∵BP =12BF =12(2EF +DE ),CF 2EF ,DE 2AE , ∴BP =122CF 2AE ), ∴CF +AE 2.【点睛】本题属于几何变换综合题,考查了等腰直角三角形的性质,全等三角形的判定和性质,直角三角形的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题. 9.如图,ABD △和ACE △都是等边三角形.(1)连接CD 、BE 交于点P ,求∠BPD ;(2)连接PA ,判断线段PA 、PB 、PD 之间的数量关系并证明;(3)如图,等腰ABC 中AB =AC ,∠BAC =α(0<α<90),在ABC 内有一点M ,连接MA 、MB 、MC .当MA +MB +MC 最小时,∠ABM = (用含α的式子表示)答案:D解析:(1)60BPD ∠=︒(2)PD PB PA =+,证明见详解(3)1602α︒-【分析】(1)证明()DAC BAE SAS ≅,得ADC ABE ∠=∠,就可以证明60BPD DAB ∠=∠=︒;(2)在DP 上截取PF=PB ,连接BF ,证明()DBF ABP SAS ≅,得DF PA =,即可证明PD PB PA =+;(3)分别以AB 和AC 为边,向两边作等边三角形ABD 和等边三角形ACE ,连接BE 和CD ,交于点M ,连接AM ,此时MA MB MC ++最小,然后利用等腰三角形ADC ,求出ADC ∠的度数,即可得到ABM ∠的度数.【详解】解:(1)∵ABD △和ACE △是等边三角形,∴AD AB =,AC AE =,60DAB CAE ∠=∠=︒,∵DAB BAC CAE BAC ∠+∠=∠+∠,∴DAC BAE ∠=∠,在DAC △和BAE △中,AD AB DAC BAE AC AE =⎧⎪∠=∠⎨⎪=⎩,∴()DAC BAE SAS ≅,∴ADC ABE ∠=∠,∵ADC DAB ABE BPD ∠+∠=∠+∠,∴60BPD DAB ∠=∠=︒;(2)如图,在DP 上截取PF=PB ,连接BF ,∵60BPD ∠=︒,PF PB =,∴PFB △是等边三角形,∴BF BP =,60FBP ∠=︒,∴DBA FBP ∠=∠,∵DBA FBA FBP FBA ∠-∠=∠-∠,∴DBF ABP ∠=∠,在DBF 和ABP △中,DB AB DBF ABP BF BP =⎧⎪∠=∠⎨⎪=⎩,∴()DBF ABP SAS ≅,∴DF PA =,∵PD PF FD =+,∴PD PB PA =+;(3)如图,分别以AB 和AC 为边,作等边三角形ABD 和等边三角形ACE ,连接BE 和CD ,交于点M ,连接AM ,此时MA MB MC ++最小,由(2)中的结论可得MD MA MB =+,则当D 、M 、C 三点共线时MA MB MC ++最小,即CD 的长,由(1)得ADC ABM ∠=∠,∵AD AB AC ==,60DAC α∠=︒+,∴()1806016022ADC αα︒-︒+∠==︒-, ∴1602ABM α∠=︒-,故答案是:1602α︒-.【点睛】本题考查全等三角形的性质和判定,等边三角形的性质,解题的关键是做辅助线构造全等三角形来进行证明求解.10.回答下列问题:(1)(发现)如图1,点A 为线段BC 外一动点,且4BC =,2AB =.填空:线段AC 的最大值为 .图1(2)(应用)点A 为线段BC 外一动点,且3BC =,2AB =,如图2所示,分别以AB ,AC 为边,作等腰直角ABD △和等腰直角ACE ,连接CD ,BE .图2①证明:BE DC =.②求线段BE 的最大值.(3)(拓展)如图3,在平面直角坐标系中,直线l ;4y x =+与坐标轴交于点A 、B 两点,点C 为线段AB 外一动点,且2CB =,以AC 为边作等边ACD △,连接BD ,求线段BD 长的最大值并直接写出此时点C 的横坐标.图3答案:A解析:(1)6(2)①证明见解析.②3+(3)2【分析】(1)根据点A 位于CB 的延长线上时,线段AC 的长取得最大值,即可得到结论;(2) ①由“SAS” 可证△DAC ≌△BAE ,可得BE=DC ;②由于线段长BE 的最大值=线段DC 的最大值,根据(1)中的结论即可得到结果,(3)以BC 为边作等边三角形BCE ,可以证明△ACE ≌△DCB(SAS) ,从而得到BD=AE ,BE=BC ,由AE≤AB+BE ,当且仅当A 、B 、E 三点共线时,AE 取得最大值,即BD 取得最大值,当BD 取得最大值时,①当C 在直线AB 的上方时,过C 作CH ⊥y 轴于H ,作BC 的垂直平分线交BH 于N ,求出CH 的长度,即可求出点C 的横坐标,②当C 在直线AB 的下方时,按同①的方法也可以求出点C 的横坐标.【详解】(1)当A 在选段BC 的延长线上时, max 6AC AB BC =+=.(2)①∵等腰直角AEC 与等腰直角三角形ABD ,∴AD AB =,AE AC =,90DAB EAC ∠=∠=︒,∴DAB BAC EAC BAC ∠+∠=∠+∠,∴DAC EAB ∠=∠,在DAC △和BAE 中,DA BA DAC BAE AB AE =⎧⎪∠=∠⎨⎪=⎩,∴()SAS DAC BAE ≌△△, ∴BE CD =.②由①可知,BE DC =,∵线段BE 的最大值即线段DC 的最大值.在等腰直角ABD △中,BD ==∵CD BC BD ≤+,∴当点D 在CB 的延长线上时, CD取得最大值为3+.∴线段BE的最大值为3+(3)如图,以BC 为边作等边三角形BCE ,则BC CE =,60BCE ∠=︒.∵60ACD ∠=︒,∴ACD ECD BCE ECD ∠-∠=∠-∠,∴ACE DCB ∠=∠.在ACE 与DCB 中,AC DC ACE DCB CE CB =⎧⎪∠=∠⎨⎪=⎩,∴()SAS ACE DCB ≌△△, ∴BD AE =.对于一次函数4y x =+,令0x =,则4y =,∴()0,4B ,令0y =,则4x =-,∴()4,0A -. ∴224442AB =+=,又∵2BE BC ==,∴AE AB BE ≤+,∴当且仅当A 、B 、E 三点共线时,AE 取得最大值,即BD 取得最大值为422+;当BD 取得最大值时,①当C 在直线AB 的上方时过C 作CH y ⊥轴于H ,∵45ABO HBE ∠=∠=︒,60CBE ∠=︒,∴15CBH CBE HBE ∠=∠-∠=︒,作BC 的垂直平分线交BH 于N ,∴CN BN =,15NCB NBC ∠=∠=︒,∴30CNB ∠=︒,在Rt CHN △中,设CH x =.则3HN x =, 2CN x =, ∴2BN x =,∴()32BH HN BN x =+=+, 在Rt BHC △中,22222HC BH BC +==,∴()222322x x ⎡⎤++=⎣⎦, 整理得()227434x x ++=, 223x =-,()12312x =-,()22312x =--(舍), ∴622CH -=, ∴点C 的横坐标为262-. ②当C 在直线AB 的下方时,过C 作CL ⊥y 轴于L ,∵∠ABO=45°,∠CBE=60°,∴∠CBL=180°-∠CBE−∠ABO=75°,∴∠BCL=15°,作BC 的垂直平分线交BL 于M ,∴CM=BM ,∠MCB=∠MBC=15°,∴∠LMB=30°,在Rt △CLB 中,设BL=y .则3,BM=2y ,∴CM=2y ,∴3+2)y ,在Rt △BLC 中,BL 2+CL 2=BC 2=22, ∴)222322y y ⎡⎤+=⎣⎦, 整理得(227434y y ++=, 223y =)12312y =,)22312y =-(舍去), 622BL =∴CL=)32BL 26+所以点C 26+综合以上可得点C 26-26+【点睛】本题是三角形综合题,考查了全等三角形的判.定和性质,等腰直角三角形的性质,最大值问题,旋转的性质正确的作出辅助线构造全等三角形是解题的关键.11.如图1所示,在Rt ABC △中90BAC ∠=︒,AB AC =,2BC =,以BC 所在直线为x 轴,边BC 的垂直平分线为y 轴建立平面直角坐标系,将ABC 绕P 点0,1顺时针旋转.(1)填空:当点B 旋转到y 轴正半轴时,则旋转后点A 坐标为______;(2)如图2所示,若边AB 与y 轴交点为E ,边AC 与直线1y x =-的交点为F ,求证:AEF 的周长为定值;(3)在(2)的条件下,求AEF 内切圆半径的最大值.解析:(1)2,21;(2)见解析;(3)324【分析】(1)作出图形,'''A B C 是ABC 绕 P 点0,1顺时针旋转,点B 旋转到y 轴正半轴时得到的图形,连接 BP ,CP ,根据2BC =,y 轴垂直平分BC , AB AC =,()0,1P -可证得四边形ABPC 是正方形,则有 '''2BP B P AB A B ,'0'21B B P PO ,可得点 A 坐标;(2)作BPQ CPF ∠=∠,交AB 延长线于Q 点,根据四边形ABPC 是正方形,得到90QBP FCP ∠=∠=︒,BP CP =,可证BPQ CPF ASA ≌△△,得BQ CF =,QP FP =,利用ASA 再可证得QPE FPE ≌△△,得QE FE =则AEF 的周长22AB AC =+=(3)设EF m =,AE n =,Rt AEF 的内切圆半径为r ,由(2)可得22AF m n =-则2AE AF EF r +-=22n m n m+---=2m =,当m 最小时,r 最大.得到22222n m n m 整理得:2224220n m n m ,关于n 的一元二次方程有解,即22244220m m 化简得24280m m +-≥,利用二次函数图像可得422m ≥-422m ≤--(不合题意,舍去)可得m 的最小值为42-r 2422324,则有AEF 内切圆半径的最大值为324.【详解】解:(1)如图示,'''A B C 是ABC 绕 P 点0,1顺时针旋转,点B 旋转到y 轴正半轴时得到的图形,连接 BP ,CP ,∵2BC =,y 轴垂直平分BC∴1BO CO ==又∵Rt ABC △中,AB AC =∴1AO =,2AB AC ==∵()0,1P -∴1PO =∴AO BO CO PO ===∴四边形ABPC 是正方形 ∴'''2BPB P AB A B ∴'0'21B B P PO ∴点A 坐标为2,21(2)如图2所示,作BPQ CPF ∠=∠,交AB 延长线于Q 点∵四边形ABPC 是正方形∴90QBP FCP ∠=∠=︒, BP CP =∴BPQ CPF ASA ≌△△∴ BQ CF =,QP FP =∵点F 在直线1y x =-∴45FPE ∠=︒∴ 45BPE FPC ∠+∠=︒∴45BPE BPQ ∠+∠=︒∴45QPE FPE ∠=∠=︒∵EP EP =∴QPE FPE ASA ≌△△∴ QE FE = ∴AEF 的周长AE EF AF AE QE AF =++=++AE BE BQ AF AE BE FC AF =+++=+++22AB AC =+=(3)设EF m =,AE n =,Rt AEF 的内切圆半径为 r ,由(2)可得22AF m n =--则2AE AF EF r +-= 222n m n m +---= 2m =-∴当m 最小时,r 最大.∵在Rt AEF 中,222AE AF EF +=∴22222n m n m 整理得: 2224220n m nm ∵关于n 的一元二次方程有解∴22244220m m∴24280m m +-≥ 利用二次函数图像可得422m ≥-或422m ≤--(不合题意,舍去)∴m 的最小值为422-∴r 的最大值为2422324即AEF 内切圆半径的最大值为324-.【点睛】本题主要考查了一次函数的综合应用以及根的判别式、全等三角形的判定与性质、旋转、三角形内切圆等知识,能熟练应用相关性质是解题关键.12.(1)ABC 和CDE △是两个等腰直角三角形,如图1,其中90ACB DCE ∠=∠=︒,连接AD 、BE ,求证:ACD △≌BCE .(2)ABC 和CDE △是两个含30°的直角三角形,中90ACB DCE ∠=∠=︒,∠=CAB CDE ∠30=︒,CD AC <,CDE △从边CD 与AC 重合开始绕点C 逆时针旋转一定角度()0180αα︒<<︒.①如图2,DE 与BC 交于点F ,交AB 于G ,连接AD ,若四边形ADEC 为平行四边形,求BG AG 的值.②若12AB =,当点D 落在AB 上时,求BE 的长.答案:A解析:(1)见解析;(2)①13BG AG =;【分析】(1)利用SAS 证明即可;(2)①连接CG ,根据平行四边形的性质推出//AD CE ,求出120ADE ∠=︒,得到90ADC ADE CDE ∠=∠-∠=︒,根据30CAB CDE ∠=∠=︒证得A 、D 、G 、C 四点共圆,从而得到90AGC ADC ∠=∠=︒,利用直角三角形中30度角的性质求出AG =,CG =,即可求出答案;②先证明ACD △∽BCE ,由此推出∠DBE=90°,得到DBE 为直角三角形,设BE a =,则AD =,12BD =-,过D 点作DH AC ⊥于H ,利用30A ∠=︒得到sin 302DH AD a =︒=,由ACD α∠=,得到sin 2sin HD CD αα==,由此求出cos30sin CD a DE α==︒,由勾股定理得222DE BE BD =+,即()222222121443sin a a a a α=+-=++-,解方程求出a.【详解】 (1)∵ABC 和CDE △是两个等腰直角三角形,∴AC BC =,CD CE =,ACB DCE ∠=∠,∴∠ACB-∠DCB=∠DCE-∠DCB ,∴ACD BCE ∠=∠, 在ACD △和BCE 中,AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩,∴ACD △≌BCE (SAS ).(2)①连接CG ,如图所示,∵四边形ADEC 为平行四边形,∴//AD CE ,∴180ADE CED ∠+∠=︒,∵90903060CED CDE ∠=︒-∠=︒-︒=︒,∴120ADE ∠=︒,∴90ADC ADE CDE ∠=∠-∠=︒,∵30CAB CDE ∠=∠=︒,∴A 、D 、G 、C 四点共圆,∴90AGC ADC ∠=∠=︒,∵30CAB ∠=︒, ∴12CG AC =,3AG CG =,30BCG ∠=︒, ∴3CG BG =,即33BG CG =, ∴13BG AG =;②∵90ACB DCE ∠=∠=︒,∴ACB DCB DCE DCB ∠-∠=∠-∠,∴ACD BCE ∠=∠,∵30CAB CDE ∠=∠=︒,∴3AC DC BC CE ==, ∴ACD △∽BCE ,∴CAD CBE ∠=∠,∴90DBE DBC CBE DBC CAD ∠=∠+∠=∠+∠=︒, ∴DBE 为直角三角形,设BE a =,∴3AD a =,∴123BD a =,过D 点作DH AC ⊥于H ,30A ∠=︒, 则3sin 302DH AD a =︒=, 又∵ACD α∠=,∴3sin 2sin HD a CD αα==, 又在Rt CDE △中,30∠=︒CDE ,∴cos30sin CD a DE α==︒, ∴在Rt BDE △中,由勾股定理得222DE BE BD =+,即()2222221231443243sin a a a a a a α=+=++-,∴22142431440sin a a α⎛⎫--+= ⎪⎝⎭, 解得22576243576sin 28sin a αα±-=-即222243sin 241sin 8sin 2a ααα+-=- 2222243sin 24cos 123sin 12cos 8sin 24sin 1αααααα++==--, 故BE 的长为22123sin 12cos 4sin 1ααα+-.【点睛】此题考查等腰直角三角形的性质,三角形全等的判定及性质,旋转的性质,平行四边形的性质,四点共圆,含30度角的直角三角形的性质,相似三角形的判定及性质,锐角三角函数,是一道较难的几何综合题.13.在ABC 中,AB AC =,点P 在平面内,连接AP ,并将线段AP 绕A 顺时针方向旋转与BAC ∠相等的角度,得到线段AQ ,连接BQ .(1)如图,如果点P 是BC 边上任意一点.则线段BQ 和线段PC 的数量关系是__________.(2)如图,如果点P 为平面内任意一点.前面发现的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由.请仅以图所示的位置关系加以证明(或说明);(3)如图,在DEF 中,8DE =,60EDF ∠=︒,75DEF ∠=︒,P 是线段EF 上的任意一点,连接DP ,将线段DP 绕点D 顺时针方向旋转60°,得到线段DQ ,连接EQ .请直接写出线段EQ 长度的最小值.答案:B解析:(1)相等;(2)成立,证明见解析;(3)2622-【分析】(1)先判断出∠BAQ=∠CAP ,进而用SAS 判断出△BAQ ≌△CAP ,即可得出结论; (2)结论BQ=PC 仍然成立,理由同(1)的方法;(3)先构造出△DEQ ≌△DHP ,得出EQ=HP ,进而判断出要使EQ 最小,当HP ⊥EF (点P 和点M 重合)时,EQ 最小,最后用解直角三角形即可得出结论.【详解】解:(1)由旋转知:AQ=AP ,∵PAQ BAC ∠=∠,∴PAQ BAP BAC BAP ∠-∠=∠-∠,∴BAQ CAP ∠=∠,∵AB AC =,∴()BAQ CAP SAS ∆≅∆,∴BQ CP =故答案为:相等.(2)BQ PC =仍成立,理由如下:证明:由旋转知:AQ=AP ,∵PAQ BAC ∠=∠,∴PAQ BAP BAC BAP ∠-∠=∠-∠,∴BAQ CAP ∠=∠,∵AB AC =,∴()BAQ CAP SAS ∆≅∆,∴BQ C =P(3)如图:在DF 上取一点H ,使8DH DE ==,连接PH,过点H作HM EF ⊥于M,由旋转知,DQ DP =,60PDQ ∠=︒,∵60EDF ∠=︒,∴PDQ EDF ∠=∠,∴EDQ HDP ∠=∠,∴()DEQ DHP SAS ∆≅∆,∴EQ HP =,要使EQ 最小,则有HP 最小,而点H 是定点,点P 是EF 上的动点,∴当HM EF ⊥(点P 和点M 重合)时,HP 最小,即:点P 与点M 重合,EQ 最小,最小值为HM ,过点E 作EG DF ⊥于G ,在Rt DEG ∆中,8DE =,60EDF ∠=︒,∴30DEG ∠=︒, ∴142DG DE ==, ∴343EG DG ==,在Rt EGF ∆中,753045FEG DEF DEG ∠=∠-∠=︒-︒=︒,∴9045F FEG FEG ∠=︒-∠=︒=∠,43FG EG ==,∴443DF DG FG =+=+,∴4438434FH DF DH =-=+-=-,在Rt HMF ∆中,45F ∠=︒,∴()22434262222HM FH ==-=-, 即:EQ 的最小值为2622-.【点睛】本题考查旋转的性质、最值问题,属于几何变换综合题,掌握全等三角形的证明方法,点到直线的距离等知识为解题关键.14.已知在△ABC 中,AB =AC ,∠BAC =α,直线l 经过点A (不经过点B 或点C ),点C 关于直线l 的对称点为点D ,连接CD ,BD , AD .(1)如图1,①填空:∠ABD ∠ADB (填 >,=,<号).②求∠BDC 的度数(用含α的式子表示).(2)如图2,当α=60°时,过点D 作BD 的垂线与直线l 交于点E ,求证:AE =BD ; (3)如图3,当α=90°时,在直线l 绕点A 旋转过程中,记直线l 与CD 的交点为F . ①若点M 为AC 的中点,连接MF , MF 的长是否会发生变化?若不变,求出MF 的长;若会发生变化,说明理由;②连接BF ,当线段BF 的长取得最大值时,求tan ∠FBC 的值.答案:B解析:(1)①=;②∠BDC =12α;(2)详见解析;(3)①MF 的长在直线l 绕点A 旋转过程中,不会发生变化,MF=1;②13 【分析】(1)①根据点C 关于直线l 的对称点为点D ,得到AD =AC ,且AB =AC ,则AD =AB =AC ,可得∠ADB =∠ABD ;②连接DA ,并延长DA 交BC 于点M ,由①可知AD =AB =AC ,则有∠ADB =∠ABD ,∠ADC =∠ACD ,可以得到∠BAM =2∠ADB ,∠MAC =2∠ADC ,利用∠BAC =∠BAM +∠MAC ,可得12BDC =,(2)连接CE ,根据∠BAC =60°,AB =AC ,得到△ABC 是等边三角形,则有BC =AC ,∠ACB =60°,根据12BDC =,可知∠BDC =30°,则有∠CDE =60°,易证△CDE 是等边三角形,可以得出△BCD ≌△ACE (SAS ),则有BD =AE ;(3)①根据∠AFC =90°,M 为AC 的中点,得到 MF = 12AC =122⨯=1,则可知MF 的长在直线l 绕点A 旋转过程中,不会发生变化,②连接MB ,根据在△BMF 中,BM MF BC ,可知当点M ,点B ,点F 三点共线时,BF 最长,过点M 作MH ⊥BC ,根据∠BAC =90°,AB =AC ,可得BC ,∠ACB =45°,且MH ⊥BC ,则有∠CMH =∠HCM =45°,可得出MC ,根据点M 是AC 中点,得到AC =,∴BC =4HC ,则可求出BH =BC ﹣HC =3HC ,利用tan ∠FBC =3MH HC BH HC=可得出结果. 【详解】解:(1)①ABD ADB ∠=∠.∵点C 关于直线l 的对称点为点D ,∴AD =AC ,且AB =AC ,∴AD =AB =AC ,∴∠ADB =∠ABD .②如图1,连接DA ,并延长DA 交BC 于点M ,∵AD=AB=AC,∴∠ADB=∠ABD,∠ADC=∠ACD.∵∠BAM=∠ADB+∠ABD,∠MAC=∠ADC+∠ACD,∴∠BAM=2∠ADB,∠MAC=2∠ADC,∴∠BAC=∠BAM+∠MAC=2∠ADB+2∠ADC=2∠BDC=α .∴1BDC=.2(2)如图3,连接CE,∵∠BAC=60°,AB=AC,∴△ABC是等边三角形,∴BC=AC,∠ACB=60°,∵1BDC=,2∴∠BDC=30°,∵BD⊥DE,∴∠CDE=60°.∵点C关于直线l的对称点为点D,∴DE=CE,且∠CDE=60°.∴△CDE是等边三角形.∴CD=CE=DE,∠DCE=60°=∠ACB,∴∠BCD=∠ACE,且AC=BC,CD=CE,∴△BCD≌△ACE(SAS).∴BD=AE .(3)①如图4,因为∠AFC=90°,M为AC的中点,∴ MF = 12AC =122⨯=1. ∴MF 的长在直线l 绕点A 旋转过程中,不会发生变化.②法一:如图5,连接MB ,∵在△BMF 中,BM +MF ≥BC∴当点M ,点B ,点F 三点共线时,BF 最长,如图6,过点M 作MH ⊥BC ,∵∠BAC =90°,AB =AC ,∴BC 2AC ,∠ACB =45°,且MH ⊥BC ,∴∠CMH =∠HCM =45°,∴MH =HC ,∴MC 2HC ,∵点M 是AC 中点,∴AC =22HC ,∴BC 2AC =4HC .∴BH =BC ﹣HC =3HC .∴tan ∠FBC =3MH HC BH HC ==13. 【点睛】本题是三角形综合题,考查了全等三角形的判定和性质,等腰三角形的性质,勾股定理,三角形的三边关系,灵活运用相关的性质定理、综合运用知识是解题的关键. 15.如图,在等边三角形ABC 中,点D 是射线CB 上一动点,连接DA ,将线段DA 绕点D逆时针旋转60°得到线段DE ,过点E 作EF ∥BC 交直线AB 于点F ,连接CF .(1)如图1,若点D 为线段BC 的中点,则四边形EDCF 是 ;(2)如图2,若点D 为线段CB 延长线上任意一点,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;(3)若点D 为射线CB 上任意一点,当∠DAB =15°,△ABC 的边长为2时,请直接写出线段BD 的长.答案:A解析:(1)平行四边形;(2)成立,见解析;(3)423-或31-.【分析】(1)证明△ADB ≌△DEO (AAS )和四边形EOBF 为平行四边形,进而求解;(2)证明△OED ≌△DAC (SAS ),则∠EOD =∠ACD =60°=∠ABC ,故OE ∥AB ,进而求解;(3)分点D 在线段BC 上、点D (D ′)在BC 的延长线上两种情况,利用勾股定理和等腰直角三角形的性质分别求解即可.【详解】解:(1)过点E 作DE 的垂线交CB 的延长线于点O ,设BA 交ED 于点R ,∵点D 为线段BC 的中点,则AD ⊥BC 且∠BAD =30°,∵∠ADE =60°,∴∠EDB =∠ADB ﹣ADE =90°﹣60°=30°,∵EF ∥BC ,∴∠EFD =∠ABC =60°,∠FED =∠EDO =30°,∴∠ERF =90°,∴DE ⊥AB ,∵AD =ED ,∠BAD =∠EDO =30°,∠ADB =∠DEO =90°,。
九年级数学中考专题:动态几何综合压轴题

2023年九年级数学中考专题:动态几何综合压轴题1.如图1,在△ABC 中,点P 为BC 边中点,直线a 绕顶点A 旋转.若B 、P 在直线a 的异侧,BM △直线a 于点M ,CN △直线a 于点N ,连接PM 、PN ; (1)延长MP 交CN 于点E (如图2). △求证:△BPM △△CPE ; △求证:PM =PN ;(2)若直线a 烧点A 旋转到图3的位置时,点B 、P 在直线a 的同侧,其它条件不变.此时PM =PN 还成立吗?若成立,请给予证明;若不成立,请说明理由;(3)若直线a 绕点A 旋转到与BC 边平行的位置时,其它条件不变.请直接判断四边形MBCN 的形状及此时PM =PN 还成立吗?(不必说明理由)2.如图△,在Rt ABC △中,90ABC ∠=︒,AB BC =,延长CA 至点E ,作DE CE ⊥交BA 的延长线于点D ,连接CD ,点F 为CD 的中点,连接EF ,BF .(1)直接写出线段EF 和BF 之间的数量关系为______.(2)将ADE 绕A 顺时针旋转到图△的位置,猜想EF 和BF 之间的数量关系,并加以证明;(3)若AC =:5AD BC =,将ADE 绕点A 顺时针旋转,当A ,E ,B 共线时,请直接写出EF 的长.3.如图,O 是正ABC 内一点,OA =3,OB =4,OC =5,将线段BO 以点B 为旋转中心逆时针旋转60°得到线段BO ′,连接AO ′、OO ′, (1)OO ′= .(2)求△AOB 的度数及四边形AOB O '的面积.(3)直接写出AOC AOB S S +△△的值,AOC AOB S S +△△= .4.如图1,在△ABC 中,△C =90°,△ABC =30°,AC =1,D 为△ABC 内部的一动点(不在边上),连接BD ,将线段BD 绕点D 逆时针旋转60°,使点B 到达点F 的位置;将线段AB 绕点B 顺时针旋转60°,使点A 到达点E 的位置,连接AD ,CD ,AE ,AF ,BF ,EF .(1)求证:△BDA △△BFE ;(2)△CD +DF +FE 的最小值为 ; △当CD +DF +FE 取得最小值时,求证:AD △BF .(3)如图2,M ,N ,P 分别是DF ,AF ,AE 的中点,连接MP ,NP ,在点D 运动的过程中,请判断△MPN 的大小是否为定值.若是,求出其度数;若不是,请说明理由.5.已知在ABC 中,O 为BC 边的中点,连接AO ,将AOC 绕点O 顺时针方向旋转(旋转角为钝角),得到EOF ,连接AE ,CF .(1)如图1,当△BAC =90°且AB =AC 时,则AE 与CF 满足的数量关系是 ; (2)如图2,当△BAC =90°且AB ≠AC 时,(1)中的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;(3)如图3,延长AO 到点D ,使OD =OA ,连接DE ,当AO =CF =5,BC =6时,求DE 的长.6.已知,在ABC 中,AB AC =,D 是平面上一点,连接AD ,把AD 绕点A 逆时针旋转至点E ,使DAE BAC ∠=∠.连接DE 并延长,交AB 于点O ,交BC 于点F .连接BD 和CE ,CE 的延长线分别交AB ,BD 于点P ,G .(1)如图1,求证:BGC DAE ∠=∠;(2)如图2,若点F 是BC 的中点,//AD CB ,求证12AE BC =; (3)在(2)的条件下,若G 是BD 的中点,连接,OG FG .当5,3AB AD ==时,请直接写出OFG △的周长.7.【问题探究】(1)如图1,△ABC和△DEC均为等腰直角三角形,△ACB=△DCE=90°,点B,D,E 在同一直线上,连接AD,BD.△请探究AD与BD之间的位置关系?并加以证明.△若AC=BC,DC=CE AD的长.【拓展延伸】(2)如图2,△ABC和△DEC均为直角三角形,△ACB=△DCE=90°,AC BC,CD CE=1.将△DCE绕点C在平面内顺时针旋转,设旋转角△BCD为α(0°≤α<360°),作直线BD,连接AD,当点B,D,E在同一直线上时,画出图形,并求线段AD的长.8.如图1和图2,四边形ABCD中,已知AD=DC,△ADC=90°,点E、F分别在边AB、BC上,△EDF=45°.(1)观察猜想:如图1,若△A、△DCB都是直角,把△DAE绕点D逆时针旋转90°至△DCG,使AD与DC重合,易得EF、AE、CF三条线段之间的数量关系,直接写出它们之间的关系式_____;(2)类比探究:如图2,若△A、△C都不是直角,则当△A与△C满足数量关系_____时,EF、AE、CF三条线段仍有(1)中的关系,并说明理由;(3)解决问题:如图3,在△ABC中,△BAC=90°,AB=AC=D、E均在边BC上,且△DAE=45°,若BD=1,求AE的长.9.如图,在Rt ABC 中,90BAC ∠=︒,AB AC =,点D ,E 分别在边AB ,AC 上,AD AE =,连接DC 、BE ,点P 为DC 的中点.(1)观察图1,猜想线段AP 与BE 的数量关系是______,位置关系是______; (2)把ADE 绕点A 逆时针方向旋转到图2的位置,(1)中的结论是否仍然成立,若成立请证明;若不成立,请写出新的结论并说明理由;(3)把ADE 绕点A 在平面内自由旋转,若6DE =,10BC =,请直接写出线段AP 长的取值范围.10.已知AOB 和△MON 都是等腰直角三角形,△AOB =△MON =90°. (1)如图1:连AM ,BN ,求证:AOM △BON ;(2)若将Rt MON 绕点O 顺时针旋转,当点A ,M ,N 恰好在同一条直线上时,如图2所示,线段OH //BN ,OH 与AM 交点为H ,若OB =4,ON =3,求出线段AM 的长; (3)若将MON 绕点O 顺时针旋转,当点N 恰好落在AB 边上时,如图3所示,MN 与AO 交点为P ,求证:MP 2+PN 2=2PO 2.11.如图1,在Rt ABC △中,90BAC ∠=︒,AB AC =,点D 是BC 边上一动点,连接AD ,把AD 绕点A 顺时针旋转90°,得到AE ,连接DE .(1)如图1所示,若4BC =,在D 点运动过程中,当8tan 11BDE ∠=时,求线段CD 的长.(2)如图2所示,点F 是线段DE 的中点,连接BF 并延长交CA 延长线于点M ,连接DM ,交AB 于点N ,连接CF ,AF ,当点N 在线段CF 上时,求证:AD BF CF +=.(3)如图3,若AB =ABC 绕点A 顺时针旋转得AB C ''△,连接CC ',P 为线段CC '上一点,且CC ''=,连接BP ,将BP 绕点B 顺时针旋转60°得到BQ ,连接PQ ,K 为PQ 的中点,连接CK ,请直接写出线段CK 的最大值.12.已知:如图1,将一块45︒角的直角三角板DEF 与正方形ABCD 的一角重合,连结AF 、CE ,点M 是CE 的中点,连结DM .(1)请你猜想AF 与DM 的数量关系是___________.(2)如图2,把正方形ABCD 绕着点D 逆时针旋转α角(090α︒<<︒). △AF 与DM 的数量关系是否仍成立,若成立,请证明:若不成立,请说明理由;△若60α=︒,且3FDM MDC ∠=∠,求DEDC的值.13.在等腰直角三角形ABC 中,290AC BC ACB ==∠=︒,,点M 为射线CA 上一个动点.过点M 作ME BM ⊥,交射线BA 于E ,将线段BM 绕点B 逆时针旋转90︒得到线段BN ,过点N 作NF BN ⊥交BC 延长线于点F ,连接EF .(1)如图1,当点M 在边AC 上时,线段,,EM EF NF 的数量关系为_______; (2)如图2,当点M 在射线CA 上时,判断线段,,EM EF NF 的数量关系并说明理由; (3)当点M 在射线CA 上运动时,能否存在BEF △为等腰三角形,若不存在,请说明理由;若存在,请直接写出CM 的长.14.如图,等腰Rt CEF 绕正方形ABCD 的顶点C 顺时针旋转,且AB CE EF ==,90CEF ∠=︒.连接AF 与射线BE 交于点G .(1)如图1,当点B 、C 、F 三点共线时,则ABE ∠ FEM ∠(填“>”、“=”或“<”),则AG FG (填“>”、“=”或“<”);(2)如图2,当点B 、C 、F 三点不共线时,求证:AG GF =;(3)若等腰CEF △从图1的位置绕点C 顺时针旋转α(090α︒<≤︒),当直线AB 与直线EF 相交构成的4个角中最小角为30°时,直接写出α的值.15.在菱形ABCD 中,4AB =,60ABC ∠=︒,E 是对角线AC 上一点,F 是线段BC 延长线上一点,且CF AE =,连接BE 、EF .(1)如图1,若E 是线段AC 的中点,求EF 的长;(2)如图2,若E 是线段AC 延长线上的任意一点,求证:BE EF =. (3)如图3,若E 是线段AC 延长线上的一点,12CE AC =,将菱形ABCD 绕着点B 顺时针旋转α︒(0360)α≤≤,请直接写出在旋转过程中DE 的最大值.16.如图,等边三角形ABC 中,D 为AB 边上一点(点D 不与点,A B 重合),连接CD ,将CD 平移到BE (其中点B 和C 对应),连接AE .将BCD △绕着点B 逆时针旋转至BAF △,延长AF 交BE 于点G .(1)连接DF ,求证:BDF 是等边三角形; (2)求证:,,D F E 三点共线;(3)当2BG EG =时,求tan AEB ∠的值.17.ABC 为等边三角形,CD AB ⊥于点D ,点E 为边BC 上一点,点F 为线段CD 上一点,连接EF ,且CE EF =.(1)如图1,若342AB CE ==,,连接BF ,G 为BF 的中点,连接DG ,求线段DG 的长:(2)如图2,将CEF △绕点C 逆时针方向旋转一定的角度得到CMN ,连接BN ,点H为BN 的中点,连接AH HM ,,求证:AH =:(3)如图3,在(2)问的条件下,线段HM 与线段CN 交于点P ,连接AM ,交线段CN 于点Q ,当2CQ PN a ==时,请直接用含a 的式子表示PQ 的长.18.在ABC 中,90ACB ∠=︒.将ABC 绕点C 逆时针旋转一定角度(旋转角度不大于180︒),得到DEC (点D ,E 分别与点A ,B 对应),连接AD ,BE .(1)如图1,当点A ,C ,E 在同一条直线上时,直接写出AD 与BE 的位置关系为__________;(2)如图2,当点D 落在AB 上时,(点D 不与点A 重合),请判断AD 与BE 的位置关系,并证明你的结论;(3)如图3,将ABC 绕点C 逆时针旋转60︒时,延长AD 与直线BC ,BE 分别相交于点F ,G ,连接CG ,试探究线段CG 与DE 之间满足的数量关系,并说明理由.19.如图△,在矩形ABCD 中,1AB =,对角线AC ,BD 相交于点O ,60COD ∠=︒,点E 是线段CD 上一点,连接OE ,将线段OE 绕点O 逆时针旋转60︒得到线段OF ,连接DF .(1)求证:DF CE =;(2)连接EF 交OD 于点P ,求DP 的最大值;(3)如图△,点E 在射线CD 上运动,连接AF ,在点E 的运动过程中,若AF AB =,求OF 的长.20.将等边三角形ABC 如图放置在平面直角坐标系中,8AB =,E 为线段AO 的中点,将线段AE 绕点A 逆时针旋转60°得线段AF ,连接EF . (△)如图1,求点E 的坐标;(△)在图1中,EF 与AC 交于点G ,连接EC ,N 为EC 的中点,连接NG ,求线段NG 的长.请你补全图形,并完成计算;(△)如图2,将AEF △绕点A 逆时针旋转,M 为线段EF 的中点,N 为线段CE 的中点,连接MN ,请直接写出在旋转过程中MN 的取值范围.参考答案:1.(2)成立(3)四边形MBCN的是矩形,PM=PN.2.(1)EF BF=;(2)FE FB=,(33.(1)4;(2)150°,(3)64.(2)(3)是,△MPN=30°.5.(1)AE CF=;(2)成立,(36.(3)47.(1)△AD BD⊥;△4;(2)8.(1)EF=AE+CF;(2)△A+△C=180°;(39.(1)12AP BE=,AP BE⊥;(2)12AP BE=,AP BE⊥仍成立;(3AP≤≤.10.(2;11.(1)3219;(3)312.(1)AF=2DM,(2)△AF=2DM仍然成立;13.(1)结论:EM+EF=FN;(2)结论:EF=EM=FN;(3)2或2+14.(1)=;=;(3)15°或75°15.(1)(3)16.tan AEB∠=17.(1;(318.(1)AD BE⊥;(2)AD BE⊥,(3)CG DE=19.(2)DP的最大值为14;(3)1OF=20.(△)(0,E;(△;(△)44MN≤≤答案第1页,共1页。
初三数学几何压轴题

初三数学几何压轴题
1.请计算一个圆的周长,已知它的半径为5cm。
答案:
圆的周长=2πr=2*π*5cm≈31.42cm。
2.已知一个矩形的长为12cm,宽为8cm,求它的面积和周长。
答案:
面积=长*宽=12cm*8cm=96cm^2。
周长=2(长+宽)=2(12cm+8cm)=2*20cm=40cm。
3.在一个等边三角形中,每个角都是多少度?
答案:
在一个等边三角形中,每个角都是60度。
4.请证明:垂直于同一条直线的两条直线互相垂直。
答案:
假设有两条直线L1和L2,它们都垂直于同一条直线L。
我们需要证明L1与L2互相垂直。
由于L1和L2都垂直于L,所以L1与L的夹角为90度,L2与L的夹角也为90度。
又因为直线与直线相交时,相交的两个夹角互为补角,所以L1与L2相交时的夹角为90度。
因此,L1与L2互相垂直,证毕。
5.请计算一个正六边形的内角和外角之和。
答案:
正六边形的内角和=(6-2)*180度=4*180度=720度。
正六边形的外角和=360度(一圈)。
内角和+外角和=720度+360度=1080度。
6.已知一个梯形的上底长度为6cm,下底长度为12cm,高为8cm,求它的面积。
答案:
面积=(上底+下底)*高/2=(6cm+12cm)*8cm/2=72cm^2。
7.请计算一个球的表面积,已知它的半径为3cm。
答案:
球的表面积=4πr^2=4*π*(3cm)^2≈113.1cm^2。
中考数学几何压轴题及答案及答案

中考数学几何压轴题及答案一、解答题(共30小题)1.观察猜想(1)如图①,在Rt△ABC中,∠BAC=90°,AB=AC=3,点D与点A重合,点E在边BC上,连接DE,将线段DE绕点D顺时针旋转90°得到线段DF,连接BF,BE与BF的位置关系是,BE+BF=;探究证明(2)在(1)中,如果将点D沿AB方向移动,使AD=1,其余条件不变,如图②,判断BE与BF的位置关系,并求BE+BF的值,请写出你的理由或计算过程;拓展延伸(3)如图③,在△ABC中,AB=AC,∠BAC=α,点D在边BA的延长线上,BD=n,连接DE,将线段DE绕着点D顺时针旋转,旋转角∠EDF=α,连接BF,则BE+BF的值是多少?请用含有n,α的式子直接写出结论2.在△ABC的边BC上取B′、C′两点,使∠AB′B=∠AC′C=∠BAC(1)如图1中∠BAC为直角,∠BAC=∠AB′B=∠AC′C=90°(点B′与点C′重合),则△ABC∽△B'BA∽△C'AC,,,进而可得AB2+AC2=;(2)如图2中当∠BAC为锐角,图3中∠BAC为钝角时(1)中的结论还成立吗?若不成立,则AB2+AC2等于什么(用含用BC和B′C′的式子表示)?并说明理由(3)若在△ABC中,AB=5,AC=6,BC=9,请你先判断出△ABC的类型,再求出B′C′的长3.(1)问题发现如图1,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=45°,点D是线段AB上一动点,连接BE填空:①的值为;②∠DBE的度数为.(2)类比探究如图2,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,点D是线段AB上一动点,连接BE.请判断的值及∠DBE的度数,并说明理由;(3)拓展延伸如图3,在(2)的条件下,将点D改为直线AB上一动点,其余条件不变,取线段DE 的中点M,连接BM、CM,若AC=2,则当△CBM是直角三角形时,线段BE的长是多少?请直接写出答案.4.(1)问题发现:如图①,在△ABC中,∠BAC=90°,AB=AC,点D是BC的中点,以点D为顶点作正方形DFGE,使点A、C分别在DE和DF上,连接BE、AF.则线段BE 和AF数量关系.(2)类比探究:如图②,保持△ABC固定不动,将正方形DFGE绕点D旋转α(0°<α≤360°),则(1)中的结论是否成立?如果成立,请证明;如果不成立,请说明理由.(3)解决问题:若BC=DF=2,在(2)的旋转过程中,连接AE,请直接写出AE的最大值.5.如图,在平行四边形ABCD中,AC与BD交于点O,以点O为顶点的∠EOF的两边分别与边AB、AD交于点E、F,且∠EOF与∠BAD互补.(1)若四边形ABCD是正方形,则线段OE与OF有何数量关系?请直接写出结论;(2)若四边形ABCD是菱形,那么(1)中的结论是否成立?若成立,请画出图形并给出证明;若不成立,请说明理由;(3)若AB:AD=m:n,探索线段OE与OF的数量关系,并证明你的结论.6.如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.(1)证明与推断:①求证:四边形CEGF是正方形;②推断:的值为:(2)探究与证明:将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由;(3)拓展与运用:正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2,则BC=.7.如图1,在△ABC中,AB=AC=2,∠BAC=120°,点D、E分别是AC、BC的中点,连接DE.定理:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.探索发现:图1中,的值为;的值为.(2)拓展探完若将△CDE绕点C逆时针方向旋转一周,在旋转过程中的大小有无变化?请仅就图2的情形给出证明.(3)问题解决当△CDE旋转至A,D,E三点共线时,直接写出线段BE的长.8.已知△ABC是边长为4的等边三角形,边AB在射线OM上,且OA=6,点D是射线OM上的动点,当点D不与点A重合时,将△ACD绕点C逆时针方向旋转60°得到△BCE,连接DE,设OD=m.(1)问题发现如图1,△CDE的形状是三角形.(2)探究证明如图2,当6<m<10时,△BDE的周长是否存在最小值?若存在,求出△BDE周长的最小值;若不存在,请说明理由.(3)解决问题是否存在m的值,使△DEB是直角三角形?若存在,请直接写出m的值;若不存在,请说明理由.9.等腰直角三角形ABC和等腰直角三角形ADE中,∠BAC=∠DAE=90°,AB=4,AE=2,其中△ABC固定,△ADE绕点A作360°旋转,点F、M、N分别为线段BE、BC、CD 的中点,连接MN、NF.问题提出:(1)如图1,当AD在线段AC上时,则∠MNF的度数为,线段MN 和线段NF的数量关系为;深入讨论:(2)如图2,当AD不在线段AC上时,请求出∠MNF的度数及线段MN和线段NF的数量关系;拓展延伸:(3)如图3,△ADE持续旋转过程中,若CE与BD交点为P,则△BCP面积的最小值为.10.四边形是我们在学习和生活中常见的图形,而对角线互相垂直的四边形也比较常见,比如筝形、菱形、图1中的四边形ABCD等.它们给我们的学习和生活带来了很多的乐趣和美感.(1)如图2,在四边形ABCD中,AB=AD,CB=CD,则AC与BD的位置关系是,请说明理由.(2)试探究图1中四边形ABCD的两组对边AB,CD与BC,AD之间的数量关系,请写出证明过程.(3)问题解决:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG 和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5,求GE的长.11.问题发现:如图(1)在Rt△ABC和Rt△BDE中,∠A=∠DEB=30°,BC=BE=6,Rt△BDE绕点B逆时针旋转,H为CD的中点,当点C与点E重合时,BH与AE的位置关系为,BH与AE的数量关系为;问题证明:在Rt△BDE绕点B旋转的过程中,(1)中的结论是否仍然成立?若成立,请就图(2)的情形给出证明若不成立,请说明理由;拓展应用:在Rt△BDE绕点B旋转的过程中,当DE∥BC时,请直接写出BH2的长.12.如图1,菱形ABCD与菱形GECF的顶点C重合,点G在对角线AC上,且∠BCD=∠ECF=60°,(1)问题发现的值为;(2)探究与证明将菱形GECF绕点C按顺时针方向旋转α角(0°<α<60°),如图2所示,试探究线段AG与BE之间的数量关系,并说明理由;(3)拓展与运用:菱形GECF在旋转过程中,当点A,G,F三点在一条直线上时,如图3所示连接CG并延长,交AD于点H,若CE=2,GH=,则AH的长为.13.如图,在Rt△ABC中,∠ACB=90°,=,CD⊥AB于点D,点E是直线AC上一动点,连接DE,过点D作FD⊥ED,交直线BC于点F.(1)探究发现:如图1,若m=n,点E在线段AC上,则=;(2)数学思考:①如图2,若点E在线段AC上,则=(用含m,n的代数式表示);②当点E在直线AC上运动时,①中的结论是否仍然成立?请仅就图3的情形给出证明;(3)拓展应用:若AC=,BC=2,DF=4,请直接写出CE的长.14.如图,已知点E是射线BC上的一点,以BC、CE为边作正方形ABCD和正方形CEFG,连接AF,取AF的中点M,连接DM、MG(1)如图1,判断线段DM和GM的数量关系是,位置关系是;(2)如图2,在图中的正方形CEFG绕点C逆时针旋转的过程中,其他条件不变,(1)中的结论是否成立?说明理由;(3)已知BC=10,CE=2,正方形CEFG绕点C旋转的过程中,当A、F、E共线时,直接写出△DMG的面积.15.在Rt△ABC中,∠ACB=90°,AB=,AC=2,过点B作直线m∥AC,将△ABC绕点C顺时针旋转得到△A′B′C(点A,B的对应点分别为A',B′),射线CA′,CB′分别交直线m于点P,Q.(1)如图1,当P与A′重合时,求∠ACA′的度数;(2)如图2,设A′B′与BC的交点为M,当M为A′B′的中点时,求线段PQ的长;(3)在旋转过程中,当点P,Q分别在CA′,CB′的延长线上时,试探究四边形P A'B′Q的面积是否存在最小值.若存在,求出四边形P A′B′Q的最小面积;若不存在,请说明理由.16.如图(1),在等边三角形ABC中,点D,E分别在边AB,AC上,AD=AE,连接BE,CD,点M,N,P分别是BE,CD,BC的中点,连接DE,PM,PN,MN.(1)观察猜想,图(1)中△PMN是(填特殊三角形的名称)(2)探究证明,如图(2),△ADE绕点A按逆时针方向旋转,则△PMN的形状是否发生改变?并就图(2)说明理由.(3)拓展延伸,若△ADE绕点A在平面内自由旋转,AD=2,AB=6,请直接写出△PMN 的周长的最大值.17.已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE,设∠BAD=α,∠CDE=β,(1)如图1,若点D在线段BC上,点E在线段AC上.∠ABC=60°,∠ADE=70°,则α=°;β=°.(2)如图2,若点D在线段BC上,点E在线段AC上,则α,β之间有什么关系式?说明理由.(3)是否存在不同于(2)中的α,β之间的关系式?若存在,请写出这个关系式(写出一种即可),说明理由;若不存在,请说明理由.18.问题提出:(1)如图1,在四边形ABCD中,连接AC、BD,AB=AD,∠BAD=∠BCD=90°,将△ABC绕点A逆时针旋转90°,得到△ADE,点B的对应点落在点D,点C的对应点为点E,可知点C、D、E在一条直线上,则△ACE为三角形,BC、CD、AC的数量关系为;探究发现:(2)如图2,在⊙O中,AB为直径,点C为的中点,点D为圆上一个点,连接AD、CD、AC、BC、BD,且AD<BD,请求出CD、AD、BD间的数量关系.拓展延伸:(3)如图3,在等腰直角三角形ABC中,点P为AB的中点,若AC=13,平面内存在一点E,且AE=10,CE=13,当点Q为AE中点时,PQ=.19.已知△ABC中,CA=CB,0°<∠ACB≤90°,点M、N分别在边CA,CB上(不与端点重合),BN=AM,射线AG∥BC交BM延长线于点D,点E在直线AN上,EA=ED.(1)【观察猜想】如图1,点E在射线NA上,当∠ACB=45°时,①线段BM与AN的数量关系是;②∠BDE的度数是;(2)【探究证明】如图2点E在射线AN上,当∠ACB=30°时,判断并证明线段BM与AN的数量关系,求∠BDE的度数;(3)【拓展延伸】如图3,点E在直线AN上,当∠ACB=60°时,AB=3,点N是BC 边上的三等分点,直线ED与直线BC交于点F,请直接写出线段CF的长.20.如图①,在正方形ABCD和正方形AB'C'D'中,AB=2,AB'=,连接CC’(1)问题发现:.(2)拓展探究:将正方形AB'C'D'绕点A逆时针旋转,记旋转角为θ,连接BB',试判断:当0°≤θ<360°时,的值有无变化?请仅就图②中的情形给出你的证明;(3)问题解决:请直接写出在旋转过程中,当C,C′,D'三点共线时BB′的长.21.如图1,在正方形ABCD中,点O是对角线BD的中点.(1)观察猜想将图1中的△BCD绕点O逆时针旋转至图2中△ECF的位置,连接AC,DE,则线段AC与DE的数量关系是,直线AC与DE的位置关系是.(2)类比探究将图2中的△ECF绕点O逆时针旋转至图3的位置,(1)中的结论是否成立?并说明理由.(3)拓展延伸将图2中的△ECF在平面内旋转,设直线AC与DE的交点为M,若AB=4,请直接写出BM的最大值与最小值.22.如图1,点B在直线l上,过点B构建等腰直角三角形ABC,使∠BAC=90°,且AB=AC,过点C作CD⊥直线l于点D,连接AD.(1)小亮在研究这个图形时发现,∠BAC=∠BDC=90°,点A,D应该在以BC为直径的圆上,则∠ADB的度数为°,将射线AD顺时针旋转90°交直线l于点E,可求出线段AD,BD,CD的数量关系为;(2)小亮将等腰直角三角形ABC绕点B在平面内旋转,当旋转到图2位置时,线段AD,BD,CD的数量关系是否变化,请说明理由;(3)在旋转过程中,若CD长为1,当△ABD面积取得最大值时,请直接写AD的长.23.如图1,将三角板放在正方形ABCD上,使三角板的直角顶点E与正方形ABCD的顶点A重合,三角板的一边交CD于点F.另一边交CB的延长线于点G.(1)观察猜想:线段EF与线段EG的数量关系是;(2)探究证明:如图2,移动三角板,使顶点E始终在正方形ABCD的对角线AC上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理由:(3)拓展延伸:如图3,将(2)中的“正方形ABCD”改为“矩形ABCD”,且使三角板的一边经过点B,其他条件不变,若AB=a、BC=b,求的值.24.如图1,在Rt△ABC中,∠B=90°,AB=2,BC=1,点D,E分别是边BC,AC的中点,连接DE.将△EDC绕点C按顺时针方向旋转,记旋转角为α.(1)问题发现①当α=0°时,=;②当α=180°时,=.(2)拓展探究试判断:当0°≤α<360°时,的大小有无变化?请仅就图2的情况给出证明.(3)问题解决当△EDC旋转至A、B、E三点共线时,直接写出线段BD的长.25.在△ABC中,AD为BC边上的中线,E为AD上一动点,设DE=nEA,连接CE并延长,交AB于点F.(1)尝试探究如图(1),当∠BAC=90°,∠B=30°,DE=EA时,BF,BA之间的数量关系是;(2)类比延伸如图(2),当△ABC为锐角三角形,DE=EA时,(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由;(3)拓展迁移如图(3),当△ABC为锐角三角形,DE=nEA时,请直接写出BF,BA之间的数量关系.26.古希腊数学家毕达哥拉斯认为:“一切平面图形中最美的是圆”.请研究如下美丽的圆.如图,线段AB是⊙O的直径,延长AB至点C,使BC=OB,点E是线段OB的中点,DE ⊥AB交⊙O于点D,点P是⊙O上一动点(不与点A,B重合),连接CD,PE,PC.(1)求证:CD是⊙O的切线;(2)小明在研究的过程中发现是一个确定的值.回答这个确定的值是多少?并对小明发现的结论加以证明.27.定义:三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角.(1)如图1,∠E是△ABC中∠A的遥望角,若∠A=α,请用含α的代数式表示∠E.(2)如图2,四边形ABCD内接于⊙O,=,四边形ABCD的外角平分线DF交⊙O 于点F,连结BF并延长交CD的延长线于点E.求证:∠BEC是△ABC中∠BAC的遥望角.(3)如图3,在(2)的条件下,连结AE,AF,若AC是⊙O的直径.①求∠AED的度数;②若AB=8,CD=5,求△DEF的面积.28.【性质探究】如图,在矩形ABCD中,对角线AC,BD相交于点O,AE平分∠BAC,交BC于点E.作DF⊥AE于点H,分别交AB,AC于点F,G.(1)判断△AFG的形状并说明理由.(2)求证:BF=2OG.【迁移应用】(3)记△DGO的面积为S1,△DBF的面积为S2,当=时,求的值.【拓展延伸】(4)若DF交射线AB于点F,【性质探究】中的其余条件不变,连结EF,当△BEF的面积为矩形ABCD面积的时,请直接写出tan∠BAE的值.29.如图,已知AC为正方形ABCD的对角线,点P是平面内不与点A,B重合的任意一点,连接AP,将线段AP绕点P顺时针旋转90°得到线段PE,连接AE,BP,CE.(1)求证:△APE∽△ABC;(2)当线段BP与CE相交时,设交点为M,求的值以及∠BMC的度数;(3)若正方形ABCD的边长为3,AP=1,当点P,C,E在同一直线上时,求线段BP 的长.30.如图1和图2,在△ABC中,AB=AC,BC=8,tan C=.点K在AC边上,点M,N 分别在AB,BC上,且AM=CN=2.点P从点M出发沿折线MB﹣BN匀速移动,到达点N时停止;而点Q在AC边上随P移动,且始终保持∠APQ=∠B.(1)当点P在BC上时,求点P与点A的最短距离;(2)若点P在MB上,且PQ将△ABC的面积分成上下4:5两部分时,求MP的长;(3)设点P移动的路程为x,当0≤x≤3及3<x≤9时,分别求点P到直线AC的距离(用含x的式子表示);(4)在点P处设计并安装一扫描器,按定角∠APQ扫描△APQ区域(含边界),扫描器随点P从M到B再到N共用时36秒.若AK=,请直接写出点K被扫描到的总时长.参考答案与试题解析一.解答题(共30小题)1.【解答】解:(1)如图①中,∵∠EAF=∠BAC=90°,∴∠BAF=∠CAE,∵AF=AE,AB=AC,∴△BAF≌△CAE,∴∠ABF=∠C,BF=CE,∵AB=AC,∠BAC=90°,∴∠ABC=∠C=45°,∴∠FBE=∠ABF+∠ABC=90°,BC=BE+EC=BE+BF,故答案为:BF⊥BE,BC.(2)如图②中,作DH∥AC交BC于H.∵DH∥AC,∴∠BDH=∠A=90°,△DBH是等腰直角三角形,由(1)可知,BF⊥BE,BF+BE=BH,∵AB=AC=3,AD=1,∴BD=DH=2,∴BH=2,∴BF+BE=BH=2;(3)如图③中,作DH∥AC交BC的延长线于H,作DM⊥BC于M.∵AC∥DH,∴∠ACB=∠H,∠BDH=∠BAC=α,∵AB=AC,∴∠ABC=∠ACB∴∠DBH=∠H,∴DB=DH,∵∠EDF=∠BDH=α,∴∠BDF=∠HDE,∵DF=DE,DB=DH,∴△BDF≌△HDE,∴BF=EH,∴BF+BE=EH+BE=BH,∵DB=DH,DM⊥BH,∴BM=MH,∠BDM=∠HDM,∴BM=MH=BD•sin.∴BF+BE=BH=2n•sin.2.【解答】解:(1)如图1中,∵△ABC∽△B'BA∽△C'AC,∴=,=,∴AB2=BB′×BC,AC2=CC′×BC,∴AB2+AC2=BC(BB′+CC′)=BC×BC=BC2,故答案为BC2.(2)不成立.理由:如图2中当∠BAC为锐角时,BB′+CC′﹣B′C′=BC,且△ABC∽△B'BA∽△C'AC,∴∴=,=,∴AB2=BB′×BC,AC2=CC′×BC,∴AB2+AC2=BC(BB′+CC′)=BC2+BC•B′C′.图3中∠BAC为钝角时,BB′+CC′+B′C′=BC.AB2+AC2=BC(BB′+CC′)=BC2﹣BC•B′C′.(3)当AB=5,AC=6,BC=9时,则AB2+AC2<BC2,可知△ABC为钝角三角形,由图3可知:AB2+AC2=BC2﹣BC•B′C′,∴52+62=92﹣9B′C′,∴B′C′=.3.【解答】解:(1)∵∠ACB=∠DCE=90°,∠CAB=∠CDE=45°,∴∠ABC=∠CAB=45°=∠CDE=∠CED,∴AC=BC,CD=CE,∵∠ACB=∠DCE=90°,∴∠ACD=∠BCE,在△ACD和△BCE中,,∴△ACD≌△BCE(SAS),∴BE=AD,∠CAB=∠CBE=45°,∴∠DBE=∠ABC+∠CBE=90°,=1,故答案为:1,90°(2),∠DBE=90°理由如下:∵∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,∴∠ACD=∠BCE,∠CED=∠ABC=30°∴tan∠ABC=tan30°==∵∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,∴Rt△ACB∽Rt△DCE∴∴,且∠ACD=∠BCE∴△ACD∽△BCE∴=,∠CBE=∠CAD=60°∴∠DBE=∠ABC+∠CBE=90°(3)若点D在线段AB上,如图,由(2)知:=,∠ABE=90°∴BE=AD∵AC=2,∠ACB=90°,∠CAB=90°∴AB=4,BC=2∵∠ECD=∠ABE=90°,且点M是DE中点,∴CM=BM=DE,∵△CBM是直角三角形∴CM2+BM2=BC2=(2)2,∴BM=CM=∴DE=2∵DB2+BE2=DE2,∴(4﹣AD)2+(AD)2=24∴AD=+1∴BE=AD=3+若点D在线段BA延长线上,如图同理可得:DE=2,BE=AD∵BD2+BE2=DE2,∴(4+AD)2+(AD)2=24,∴AD=﹣1∴BE=AD=3﹣综上所述:BE的长为3+或3﹣4.【解答】解:(1)∵△ABC中,∠BAC=90°,AB=AC,点D是BC的中点,∴AD=BD=DC,∠BDA=90°,∵四边形DFGE是正方形,∴DE=DF,∠EDF=90°,∴∠BDE=∠ADF=90°,在△BDE和△ADF中,,∴△BDE≌△ADF(SAS),∴BE=AF故答案为:BE=AF;(2)成立;理由如下:当正方形DFGE在BC的上方时,如图②所示,连接AD,∵在Rt△ABC中,AB=AC,D为斜边BC的中点,∴AD=BD,AD⊥BC,∴∠ADE+∠EDB=90°,∵四边形DFGE为正方形,∴DE=DF,且∠EDF=90°,∴∠ADE+∠ADF=90°,∴∠BDE=∠ADF,在△BDE和△ADF中,,∴△BDE≌△ADF(SAS),∴BE=AF;当正方形DFGE在BC的下方时,连接AD,如图③所示:∵∠BDE=∠BDF+90°,∠ADF=∠BDF+90°,∴∠BDE=∠ADF,在△BDE和△ADF中,,∴△BDE≌△ADF(SAS),∴BE=AF;综上所述,(1)中的结论BE=AF成立;(3)在△ADE中,∵AE<AD+DE,∴当点A、D、E共线时,AE取得最大值,最大值为AD+DE.如图④所示:则AD=BC=1,DE=DF=2,∴AE=AD+DE=3,即AE的最大值为3.5.【解答】解:(1)如图1,过点O作OM⊥AB于M,ON⊥AD于N,∴∠OME=∠ONF=90°,∴∠BAD+∠MON=180°,∵∠BAD+∠EOF=180°,∴∠MON=∠EOF,∴∠EOM=∠FON,∵O是正方形ABCD的对角线的交点,∴∠BAO=∠DAO,∵OM⊥AB,ON⊥AD,∴OM=ON,∴△OME≌△ONF(AAS)∴OE=OF;(2)(1)的结论成立;理由:如图2,过点O作OM⊥AB于M,ON⊥AD于N,∴∠OME=∠ONF=90°,∴∠BAD+∠MON=180°,∵∠BAD+∠EOF=180°,∴∠MON=∠EOF,∴∠EOM=∠FON,∵O是菱形ABCD的对角线的交点,∴∠BAO=∠DAO,∵OM⊥AB,ON⊥AD,∴OM=ON,∴△OME≌△ONF(AAS)∴OE=OF;(3)如图3,过点O作OG⊥AB于G,OH⊥AD于H,∴∠OGE=∠OHF=90°,∴∠BAD+∠GOH=180°,∵∠BAD+∠EOF=180°,∴∠GOH=∠EOF,∴△EOG∽△FOH,∴,∵O是▱ABCD的对角线的交点,∴S△AOB=S△AOD,∵S△AOB=AB•OG,S△AOD=AD•OH,∴AB•OG=AD•OH,∴=,∴.6.【解答】解:(1)①∵四边形ABCD是正方形,∴∠BCD=90°,∠BCA=45°,∵GE⊥BC、GF⊥CD,∴∠CEG=∠CFG=∠ECF=90°,∴四边形CEGF是矩形,∠CGE=∠ECG=45°,∴EG=EC,∴四边形CEGF是正方形;②由①知四边形CEGF是正方形,∴∠CEG=∠B=90°,∠ECG=45°,∴=,GE∥AB,∴==,故答案为:;(2)连接CG,由旋转性质知∠BCE=∠ACG=α,在Rt△CEG和Rt△CBA中,=cos45°=、=cos45°=,∴==,∴△ACG∽△BCE,∴==,∴线段AG与BE之间的数量关系为AG=BE;(3)∵∠CEF=45°,点B、E、F三点共线,∴∠BEC=135°,∵△ACG∽△BCE,∴∠AGC=∠BEC=135°,∴∠AGH=∠CAH=45°,∵∠CHA=∠AHG,∴△AHG∽△CHA,∴==,设BC=CD=AD=a,则AC=a,则由=得=,∴AH=a,则DH=AD﹣AH=a,CH==a,∴=得=,解得:a=3,即BC=3,故答案为:3.7.【解答】解:(1)如图1,连接AE,∵AB=AC=2,点E分别是BC的中点,∴AE⊥BC,∴∠BEC=90°,∵AB=AC=2,∠BAC=120°,∴∠B=∠C=30°,在Rt△ABE中,AE=AB=1,根据勾股定理得,BE=∵点E是BC的中点,∴BC=2BE=2,∴==,∵点D是AC的中点,∴AD=CD=AC=1,∴==,故答案为:,;(2)无变化,理由:由(1)知,CD=1,CE=BE=,∴=,,∴=,由(1)知,∠ACB=∠DCE=30°,∴∠ACD=∠BCE,∴△ACD∽△BCE,∴,(3)当点D在线段AE上时,如图2,过点C作CF⊥AE于F,∠CDF=180°﹣∠CDE=60°,∴∠DCF=30°,∴DF=CD=,∴CF=DF=,在Rt△AFC中,AC=2,根据勾股定理得,AF==,∴AD=AF+DF=,由(2)知,,∴BE=AD=当点D在线段AE的延长线上时,如图3,过点C作CG⊥AD交AD的延长线于G,∵∠CDG=60°,∴∠DCG=30°,∴DG=CD=,∴CG=DG=,在Rt△ACG中,根据勾股定理得,AG=,∴AD=AG﹣DG=,由(2)知,,∴BE=AD=即:线段BE的长为或.8.【解答】解:(1)证明:∵将△ACD绕点C逆时针方向旋转60°得到△BCE,∴∠DCE=60°,DC=EC,∴△CDE是等边三角形;故答案为:等边;(2)存在,当6<t<10时,由旋转的性质得,BE=AD,∴C△DBE=BE+DB+DE=AB+DE=4+DE,由(1)知,△CDE是等边三角形,∴DE=CD,∴C△DBE=CD+4,由垂线段最短可知,当CD⊥AB时,△BDE的周长最小,此时,CD=2,∴△BDE的最小周长=CD+4=2+4;(3)存在,①∵当点D与点B重合时,D,B,E不能构成三角形,∴当点D与点B重合时,不符合题意,②当0≤m<6时,由旋转可知,∠ABE=60°,∠BDE<60°,∴∠BED=90°,由(1)可知,△CDE是等边三角形,∴∠DEB=60°,∴∠CEB=30°,∵∠CEB=∠CDA,∴∠CDA=30°,∵∠CAB=60°,∴∠ACD=∠ADC=30°,∴DA=CA=4,∴OD=OA﹣DA=6﹣4=2,∴m=2;③当6<m<10时,由∠DBE=120°>90°,∴此时不存在;④当m>10时,由旋转的性质可知,∠DBE=60°,又由(1)知∠CDE=60°,∴∠BDE=∠CDE+∠BDC=60°+∠BDC,而∠BDC>0°,∴∠BDE>60°,∴只能∠BDE=90°,从而∠BCD=30°,∴BD=BC=4,∴OD=14,∴m=14,综上所述:当m=2或14时,以D、E、B为顶点的三角形是直角三角形.9.【解答】解:(1)如图1中,连接DB,MF,CE,延长BD交EC于H.∵AC=AB,AE=AD,∠BAD=∠CAE=90°,∴△BAD≌△CAE(SAS),∴BD=EC,∠ACE=∠ABD,∵∠ABD+∠ADB=90°,∠ADB=∠CDH,∴∠ADH+∠DCH=90°,∴∠CHD=90°,∴EC⊥BH,∵BM=MC,BF=FE,∴MF∥EC,MF=EC,∵CM=MB,CN=ND,∴MN∥BD,MN=BD,∴MN=MF,MN⊥MF,∴∠NMF=90°,∴∠MNF=45°,NF=MN.故答案为:45°(2):如图2中,连接MF,EC,BD.设EC交AB于O,BD交EC于H.∵AC=AB,AE=AD,∠BAD=∠CAE=90°,∴∠BAD=∠CAE,∴△BAD≌△CAE(SAS),∴BD=EC,∠ACE=∠ABD,∵∠AOC+∠ACO=90°,∠AOC=∠BOH,∴∠OBH+∠BOH=90°,∴∠BHO=90°,∴EC⊥BD,∵BM=MC,BF=FE,∴MF∥EC,MF=EC,∵CM=MB,CN=ND,∴MN∥BD,MN=BD,∴MN=MF,MN⊥MF,∴∠NMF=90°,∴∠MNF=45°,NF=MN.(3):如图3中,如图以A为圆心AD为半径作⊙A.当直线PB与⊙A相切时,此时∠CBP的值最小,点P到BC的距离最小,即△BCP的面积最小,∵AD=AE,AB=AC,∠BAC=∠DAE=90°,∴∠BAD=∠CAE,∴△BAD≌△CAE(SAS),∴∠ACE=∠ABD,BD=EC,∵∠ABD+∠AOB=90°,∠AOB=∠CPO,∴∠CPB=90°,∵PB是⊙A的切线,∴∠ADP=90°,∵∠DPE=∠ADP=∠DAE=90°,∴四边形ADPE是矩形,∵AE=AD,∴四边形ADPE是正方形,∴AD=AE=PD=PE=2,BD=EC==2,∴PC=2﹣2,PB=2+2,∴S△BCP的最小值=×PC×PB=(2﹣2)(2+2)=4.10.【解答】(1)解:AC⊥BD,理由如下:连接AC、BD,如图2所示:∵AB=AD,∴点A在线段BD的垂直平分线上,∵CB=CD,∴点C在线段BD的垂直平分线上,∴直线AC是线段BD的垂直平分线,∴AC⊥BD,故答案为:AC⊥BD;(2)解:AD2+BC2=AB2+CD2;理由如下:如图1,已知四边形ABCD中,AC⊥BD,设BD、AC相交于E,∵AC⊥BD,∴∠AED=∠AEB=∠BEC=∠CED=90°,由勾股定理得,AD2+BC2=AE2+DE2+BE2+CE2,AB2+CD2=AE2+BE2+CE2+DE2,∴AD2+BC2=AB2+CD2;(3)解:如图3,连接CG、BE,∵四边形ACFG和四边形ABDE是正方形,∴AC=AG,AB=AE,∠CAG=∠BAE=90°,∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,在△GAB和△CAE中,,∴△GAB≌△CAE(SAS),∴∠ABG=∠AEC,又∠AEC+∠AME=90°,∴∠ABG+∠AME=90°,即CE⊥BG,由(2)得,CG2+BE2=CB2+GE2,在Rt△ABC中,AC=4,AB=5,根据勾股定理得,BC2=52﹣42=9,∵CG和BE分别是正方形ACFG和正方形ABDG的对角线,∴CG2=42+42=32,BE2=52+52=50,∴GE2=CG2+BE2﹣CB2=32+50﹣9=73,∴GE=.11.【解答】解:问题发现:如图1中,结论:AE=2BH,AE⊥BH.理由:在Rt△ABC中,∵BC=6,∠A=30°,∴AE=2BC=12,在Rt△CDB中,∵∠DCB=30°,∴CD==4,∵CH=DH,∴BH=CD=2,∴==2,∴AE=2BH.故答案为AE⊥BH,AE=2BH.问题证明:如图2中,(1)中结论成立.理由:延长BH到F使得HF=BH,连接CF.设AE交BF于O.∵CH=DH,BH=HF,∠CHF=∠BHD,∴△CHF≌△DHB(SAS),∴BD=CF,∠F=∠DBH,∴CF∥BD,∵AB=BC,BE=BD,∴BE=CF,∴==,∵CF∥BD,∴∠BCF+∠CBD=180°,∵∠ABC+∠DBE=∠ABD+∠CBD+∠CBD+∠CBE=∠CBD+∠ABE=180°,∴∠BCF=∠ABE,∴△ABE∽△BCF,∴∠CBF=∠BAE,==,∴AE=BF=2BH,∵∠CBF+∠ABF=90°,∴∠ABF+∠BAE=90°,∴∠AOB=90°,∴BH⊥AE.拓展应用:如图3﹣1中,当DE在BC的下方时,延长AB交DE于F.∵DE∥BC∴∠ABC=∠BFD=90°,由题意BC=BE=6,AB=6,BD=2,DE=4,∵•BD•BE=•DE•BF,∴BF==3,∴EF=BF=3,∴AF=6+3,∴AE2=AF2+EF2=(6+3)2+(3)2=144+36.∵AE=2BH,∴AE2=12BH2,∴BH2=12+3如图3﹣2中,当DE在BC的上方时,同法可得AF=6﹣3,EF=3,∴BH2==(=12﹣3.12.【解答】解:(1)如图1中,作EH⊥CG于H.∵四边形ECFG是菱形,∠ECF=60°,∴∠ECH=∠ECF=30°,EC=EG,∵EH⊥CG,∴GH=CG,∴=cos30°=,∴=2•=,∵EG∥CD,AB∥CD,∴GE∥AB,∴==.故答案为.(2)结论:AG=BE.理由:如图2中,连接CG.∵四边形ABCD,四边形ECFG都是菱形,∠ECF=∠DCB=60°,∴∠ECG=∠EGC=∠BCA=∠BAC=30°,∴△ECG∽△BCE,∴=,∵∠ECB=∠GCA,∴△ECB∽△GCA,∴==,∴AG=BE.(3)如图3中,∵∠AGH=∠CGF=30°.∠AGH=∠GAC+∠GCA,又∵∠DAC=∠HAG+∠GAC=30°,∴∠HAG=∠ACH,∵∠AHG=∠AHC,∴△HAG∽△HCA,∴HA:HC=GH:HA,∴AH2=HG•HC,∴FC=2,CG=CF,∴GC=2,∵HG=,∴AH2=HG•HC=•3=9,∵AH>0,∴AH=3.故答案为3.13.【解答】解:(1)当m=n时,即:BC=AC,∵∠ACB=90°,∴∠A+∠ABC=90°,∵CD⊥AB,∴∠DCB+∠ABC=90°,∴∠A=∠DCB,∵∠FDE=∠ADC=90°,∴∠FDE﹣∠CDE=∠ADC﹣∠CDE,即∠ADE=∠CDF,∴△ADE∽△CDF,∴,∵∠A=∠DCB,∠ADC=∠BDC=90°,∴△ADC∽△CDB,∴=1,∴=1(2)①∵∠ACB=90°,∴∠A+∠ABC=90°,∵CD⊥AB,∴∠DCB+∠ABC=90°,∴∠A=∠DCB,∵∠FDE=∠ADC=90°,∴∠FDE﹣∠CDE=∠ADC﹣∠CDE,即∠ADE=∠CDF,∴△ADE∽△CDF,∴,∵∠A=∠DCB,∠ADC=∠BDC=90°,∴△ADC∽△CDB,∴,∴②成立.如图,∵∠ACB=90°,∴∠A+∠ABC=90°,又∵CD⊥AB,∴∠DCB+∠ABC=90°,∴∠A=∠DCB,∵∠FDE=∠ADC=90°,∴∠FDE+∠CDE=∠ADC+∠CDE,即∠ADE=∠CDF,∴△ADE∽△CDF,∴,∵∠A=∠DCB,∠ADC=∠BDC=90°,∴△ADC∽△CDB,∴,∴.(3)由(2)有,△ADE∽△CDF,∵=,∴=,∴CF=2AE,在Rt△DEF中,DE=2,DF=4,∴EF=2,①当E在线段AC上时,在Rt△CEF中,CF=2AE=2(AC﹣CE)=2(﹣CE),EF=2,根据勾股定理得,CE2+CF2=EF2,∴CE2+[2(﹣CE)]2=40∴CE=2,或CE=﹣(舍)而AC=<CE,∴此种情况不存在,②当E在AC延长线上时,在Rt△CEF中,CF=2AE=2(AC+CE)=2(+CE),EF=2,根据勾股定理得,CE2+CF2=EF2,∴CE2+[2(+CE)]2=40,∴CE=,或CE=﹣2(舍),③如图1,当点E在CA延长线上时,CF=2AE=2(CE﹣AC)=2(CE﹣),EF=2,根据勾股定理得,CE2+CF2=EF2,∴CE2+[2(CE﹣)]2=40,∴CE=2,或CE=﹣(舍)即:CE=2或CE=.14.【解答】解:(1)如图1,延长GM交AD于H,∵AD∥GF,∴∠GFM=∠HAM,在△FMG和△AMH中,,∴△FMG≌△AMH(ASA),∴HM=GM,AH=FG,∵AD=CD,AH=FG=CG,∴DH=DG,∵∠HDG=90°,HM=GM,∴DM=MG,DM⊥MG,故答案为DM=MG,DM⊥MG.(2)结论成立:DM=MG,DM⊥MG,理由:如图2中,延长GM使得MH=GM,连接AH、DH、DG,延长AD交GF的延长线于N,交CD于O.∵AM=MF,∠AMH=∠FMG,MH=MG,∴△AMH≌△FMG(SAS),∴AH=GF=CG,∠AHM=∠FGM,∴AH∥GN,∴∠HAD=∠N,∵∠ODN=∠OGC=90°,∠DON=∠GOC,∴∠N=∠OCG,∴∠HAD=∠DCG,∵AH=CG,AD=CD,∴△HAD≌△GCD(SAS),∴DH=DG,∠HDA=∠CDG,∴∠HDG=∠ADC=90°,∴△HDG是等腰直角三角形,∵MH=MG,∴DM⊥GH,DM=MH=MG,(3)①如图3﹣1中,连接AC.在Rt△ABC中,AC==10,在Rt△ACE中,AE==14,∴AF=AE=EF=14﹣2=12,∴FM=AM=AF=6,在Rt△MGF中,MG==2,∴S△DMG=×2×2=20,②如图3﹣2中,连接AC.同法可得AE=14,AF=16,FM=8,MG==2,∴S△DMG=×2×2=34,综上所述,满足条件的△DMG的面积为20或34.15.【解答】解:(1)由旋转可得:AC=A'C=2,∵∠ACB=90°,AB=,AC=2,∴BC=,∵∠ACB=90°,m∥AC,∴∠A'BC=90°,∴cos∠A'CB==,∴∠A'CB=30°,∴∠ACA'=60°;(2)∵M为A'B'的中点,∴∠A'CM=∠MA'C,由旋转可得,∠MA'C=∠A,∴∠A=∠A'CM,∴tan∠PCB=tan∠A=,∴PB=BC=,∵∠PCQ=∠PBC=90°,∴∠BQC+∠BPC=∠BCP+∠BPC=90°,∴∠BQC=∠BCP=∠A,∴tan∠BQC=tan∠A=,∴BQ=BC×=2,∴PQ=PB+BQ=;(3)∵S四边形P A'B′Q=S△PCQ﹣S△A'CB'=S△PCQ﹣,∴S四边形P A'B′Q最小,即S△PCQ最小,∴S△PCQ=PQ×BC=PQ,法一:(几何法)取PQ的中点G,∵∠PCQ=90°,∴CG=PQ,即PQ=2CG,当CG最小时,PQ最小,∴CG⊥PQ,即CG与CB重合时,CG最小,∴CG min=,PQ min=2,∴S△PCQ的最小值=3,S四边形P A'B′Q=3﹣;法二(代数法)设PB=x,BQ=y,由射影定理得:xy=3,∴当PQ最小时,x+y最小,∴(x+y)2=x2+2xy+y2=x2+6+y2≥2xy+6=12,当x=y=时,“=”成立,∴PQ=+=2,∴S△PCQ的最小值=3,S四边形P A'B′Q=3﹣.16.【解答】解:(1)结论:△PMN是等边三角形.理由:如图1中,∵△ABC是等边三角形,∴AB=AC,∠ABC=∠ACB=60°,∵AD=AE,∴BD=EC,∵PB=PC,CN=ND,BM=EM,∴PN∥BD,PM∥EC,PN=BD,PM=EC,∴PM=PN,∠NPC=∠ABC=60°,∠MPB=∠ACB=60°,∴∠MPN=60°,∴△PMN是等边三角形,故答案为等边三角形.(2)△PMN的形状不发生改变,仍为等边三角形,理由如下:如图2中,连接BD,CE.由旋转可得∠BAD=∠CAE,∵△ABC是等边三角形,∴AB=AC,∠ACB=∠ABC=60°又∵AD=AE,∴△ABD≌△ACE(SAS),∴BD=CE,∠ABD=∠ACE,∵M是BE的中点,P是BC的中点,∴PM是△BCE的中位线,∴PM=,且PM∥CE.同理可证PN=BD且PN∥BD,∴PM=PN,∠MPB=∠ECB,∠NPC=∠DBC,∴∠MPB+∠NPC=∠ECB+∠DBC=(∠ACB+∠ACE)+(∠ABC﹣∠ABD)=∠ACB+∠ABC=120°,∴∠MPN=60°,∴△PMN是等边三角形.(3)∵PM=EC,∴当EC最大时,等边△PMN的周长最大,∵EC≤AE+AC,∴EC≤8,∴PM≤4,∴PM的最大值为4,∴△PMN的周长的最大值为12.17.【解答】解:(1)∵AB=AC,∠ABC=60°,∴∠BAC=60°,∵AD=AE,∠ADE=70°,∴∠DAE=180°﹣2∠ADE=40°,∴α=∠BAD=60°﹣40°=20°,∴∠ADC=∠BAD+∠ABD=60°+20°=80°,∴β=∠CDE=∠ADC﹣∠ADE=10°,故答案为:20,10;(2)设∠ABC=x,∠AED=y,∴∠ACB=x,∠AED=y,在△DEC中,y=β+x,在△ABD中,α+x=y+β=β+x+β,∴α=2β;(3)①当点E在CA的延长线上,点D在线段BC上,如图1设∠ABC=x,∠ADE=y,∴∠ACB=x,∠ACE=y,在△ABD中,x+α=β﹣y,在△DEC中,x+y+β=180°,∴α=2β﹣180°,②当点E在CA的延长线上,点D在CB的延长线上,如图2,同①的方法可得α=180°﹣2β.18.【解答】解:(1)由旋转变换的性质可知,∠CAE=90°,AC=AE,∴△ACE为等腰直角三角形,∴CE=AC,∵CE=CD+DE=CD+BC,∴BC+CD=AC,故答案为:等腰直角;BC+CD=AC;(2)延长CO交⊙O于E,连接AE、BE、DE,则∠CDE=90°,∵点C为的中点,∴点E为的中点,∴EA=EB,∵AB为⊙O的直径,∴∠ADB=90°,由(1)得,DE=(AD+BD),由勾股定理得,CD2=CE2﹣DE2=AD2+BD2﹣(AD+BD)2=(AD﹣BD)2,∴CD=(BD﹣AD);(3)如图3,当点E在直线AC的左侧时,连接CQ、PC,∵CA=CB,点P为AB的中点,∴CP⊥AB,∵CA=CE,点Q为AE中点,∴CQ⊥AE,AQ=QE=AE=5,∴由勾股定理得,CQ==12,由(1)得,AQ+CQ=PQ,。
2024年中考数学压轴题(全国通用):以相似为载体的几何综合问题(教师版含解析)

专题 27 以相似为载体的几何综合问题
21.(2022·四川内江·中考真题)如图,在矩形 ABCD 中,AB=6,BC=4,点 M、N 分别在 AB、AD 上,且 MN⊥MC,点 E 为 CD 的中点,连接 BE 交 MC 于点 F.
(1)当 F 为 BE 的中点时,求证:AM=CE; (2)若퐸퐵 =2,求퐴 的值; (3)若 MN∥BE,求퐴 的值.
(1)问题解决:如图①,若
AB//CD,求证:��12
=
�퐶⋅� �퐴⋅�퐵
(2)探索推广:如图②,若퐴퐵与퐶 不平行,(1)中的结论是否成立?若成立,请证明;
若不成立,请说明理由.
(3)拓展应用:如图③,在�퐴上取一点 E,使�퐸 = �퐶,过点 E 作퐸 ∥퐶 交� 于点
F,点 H 为퐴퐵的中点,� 交퐸 于点 G,且� = 2
=
�퐶⋅� �퐴⋅�퐵
=
5�⋅5� 6�⋅9�
∴ 퐸 = � ⋅ sin∠ �퐸,퐵 = �퐵 ⋅ sin∠퐵� ,
∴�△�퐶
=�1=
1 2
�퐶
⋅
�△퐴�퐵=�2=
1 2
�퐴
⋅
퐵
퐸=
1 2
�퐶
⋅
�
⋅ sin∠ �퐸,
=
1 2
�퐴
⋅
�퐵
⋅
sin∠퐵�
,
∵∠DOE=∠BOF,
∴sin∠ �퐸 = sin∠퐵� ;
∴�1
�2
=
12�퐶⋅� ⋅sin∠ �퐸 12�퐴⋅�퐵⋅sin∠퐵�
(3)首先利用同角的余角相等得
∠CBF=
∠CMB,则
中考数学压轴题重难点突破十 几何图形综合题 类型一:与全等三角形有关的问题

∠CRD=12∠ARB=45°.∴∠MON=135°.
此时,P,O,B 在一条直线上,△PAB 为直角三角 PQ= 2PQ,则PQ= 2.
1.如图,在△ABC 和△ADE 中,AB=AC,AD=AE,∠BAC=∠DAE,F 为 BD,CE 的交点. (1)求证:BD=CE; (2)连接 AF,求证:AF 平分∠BFE.
Ⅲ)∵∠EMD=45°,∠DGM=90°, ∴∠DMG=∠GDM,∴DG=GM, 又∵DM=6 2, ∴DG=GM=6, ∵DE=12, ∴EG= ED2-DG2=6 3, ∴EM=GM+EG=6+6 3.
模型二:半角模型
如图,在正方形 ABCD 中,点 E,F 分别在边 BC,CD 上,分别连接 EF, AE,AF,∠EAF=45°.求证: (1)EF=BE+DF; (2)AF 平分∠EFD.
证明:(1)将△ADF 绕点 A 顺时针旋转 90°, 得到△ABG, ∵四边形 ABCD 为正方形, ∴∠BAD=∠D=∠ABC=90°,
出现等顶角,共顶点,等线段就能构造全等型手拉手.
1.(2016·安徽第 23 题 14 分)如图①,A,B 分别在射线 OM,ON 上,且 ∠MON 为钝角.现以线段 OA,OB 为斜边向∠MON 的外侧作等腰直角三角 形,分别是△OAP,△OBQ,点 C,D,E 分别是 OA,OB,AB 的中点. (1)求证:△PCE≌△EDQ; (2)延长 PC,QD 交于点 R. Ⅰ)如图②,若∠MON=150°,求证:△ABR 为等边三角形; Ⅱ)如图③,若△ARB∽△PEQ,求∠MON 的大小和APBQ的值.
(2)Ⅰ)证明:如图②,连接 OR. ∵PR 与 QR 分别为线段 OA 与 OB 的中垂线, ∴AR=OR=BR,∠ARC=∠ORC,∠ORD=∠BRD. 在四边形 OCRD 中, ∠OCR=∠ODR=90°,∠MON=150°, ∴∠CRD=30°. ∴∠ARB=∠ARO+∠BRO =2∠CRO+2∠ORD =2∠CRD=60°. ∴△ABR 为等边三角形.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 17 2
圆的半径为 1 17 或 1 17 10 分
2
2
【例 3】已知两个关于 x 的二次函数 y1 与当 x k 时, y2 17 ;且二次函数 y2 的
图象的对称轴是直 y2, y1 a( x k ) 2 2(k 0), y1 y2 x2 6x 12 线 x 1 . ( 1)求 k 的值; ( 2)求函数 y1, y2 的表达式;
( 3)在同一直角坐标系内,问函数 明理由.
y1 的图象与 y2 的图象是否有交点?请说
解析过程及每步分值 (1)由 y1 a (x k )2 2, y1 y2 x2 6x 12 得 y2 ( y1 y2 ) y1 x2 6x 12 a( x k) 2 2 x2 6x 10 a ( x k ) 2 . 又因为当 x k 时, y2 17 ,即 k 2 6k 10 17 ,
解得 k1 1 ,或 k2 7 (舍去),故 k 的值为 1. (2)由 k 1 ,得 y2 x2 6x 10 a( x 1)2 (1 a)x2 (2 a 6) x 10 a ,
所以函数 y 2 的图象的对称轴为 x
2a 6 , 2(1 a)
于是,有 2a 6
1 ,解得 a 1 ,
2(1 a)
所以 y1 x2 2 x 1, y2 2 x2 4 x 11 .
S, 点 P 的横坐标为 x, 当
4 6 2 S 6 8 2 时 , 求 x 的取值范围 .
解析过程及每步分值 解:( 1)∵ y x 2 4x ( x 2) 2 4
(3)由 y1 (x 1)2 2 ,得函数 y1的图象为抛物线,其开口向下,顶点坐标为
(1,2) ;
由 y2 2 x2 4 x 11 2( x 1)2 9 ,得函数 y2 的图象为抛物线,其开口向上,顶点坐标
为 ( 1,9) ;
故在同一直角坐标系内,函数 y1 的图象与 y2 的图象没有交点.
【例 4】如图 , 抛物线 y x2 4x 与 x 轴分别相交于点 B、 O,它的顶点为 A, 连接 AB,把 AB
8分
9分 10 分
【例2】如图二次函数 y= ax2+ bx+c( a> 0) 与坐标轴交于点 A、B、C 且 OA= 1 OB=OC= 3. ( 1)求此二次函数的解析式. ( 2)写出顶点坐标和对称轴方程. ( 3)点 M、N在 y= ax2+ bx+c 的图像上 ( 点 N 在点 M的右边 ) ,且 MN∥ x 轴,求 以 MN为直径且与 x 轴相切的圆的半径.
所的直线沿 y 轴向上平移 , 使它经过原点 O,得到直线 l, 设 P 是直线 l 上一动点 .
( 1)求点 A 的坐标 ;
( 2)以点 A、B、O、P 为顶点的四边形中 , 有菱形、等腰梯形、直角梯形 , 请分别直接写
出这些特殊四边形的顶点 P 的坐标 ;
( 3 )设以点 A、 B、 O、 P 为顶点的四边形的面积为
解析过程及每步分值
(1)依题意 A( 1,0), B (3,0), C (0, 3) 分别代入 y ax2 bx c ········ 1 分
解方程组得所求解析式为 y x2 2x 3 ···················
4分
(2) y x2 2 x 3 ( x 1)2 4 ······················
5分
顶点坐标 (1, 4) ,对称轴 x 1 ······················
7分
(3)设圆半径为 r ,当 MN 在 x 轴下方时, N 点坐标为 (1 r, r ) ········ 8 分
把 N 点代入 y x2 2x 3 得 r
1 17
··················
2
9分
同理可得另一种情形 r
说明你的理由.
( 3)设 BE=x,△ DEF的面积为 y,请你求出 y 和 x 之间的函数关系式,并求
出当 x 为何值时, y 有最大值,最大值是多少?
A
D
F
M
B
x
E
C
G 图 10
解析过程及每步分值
( 1) 因为四边形 ABCD是平行四边形, 所以 AB DG ··········· 1 分
所以 B GCE , G BFE
5
5
所以 y
1 EF DG
14 3 x[ (10 x) 5]
2
25 5
6 x2
22 x
25
5
·········
配方得: y
6 (x
55) 2
121
.
25 6
6
所以,当 x
55 时, y 有最大值. ·····················
6
最大值为 121 . ······························ 6
因此, △ BEF 与△ CEG 的周长之和等于 BC+ CH+ BH
由 BC= 10, AB= 5, AM=4,可得 CH= 8, BH= 6,
所以 BC+ CH+ BH= 24 ··························
理由二:
由 AB= 5,AM= 4,可知
H
在 Rt △ BEF与 Rt △ GCE中,有:
A
F
EF 4 BE, BF 3 BE , GE 4 EC , GC 3 CE ,
5
5
5
5
M
所以,△
BEF的周长是
12 BE ,
△ ECG的周长是
12 CE
B
xE
5
5
6分
D
C G
又 BE+ CE= 10,因此 BEF 与 CEG 的周长之和是 24. ··········· 6 分
( 3)设 BE= x,则 EF 4 x, GC 3 (10 x)
中考数学例题讲解
【例1】如图 10,平行四边形 ABCD中, AB=5,BC= 10,BC边上的高 AM=4, E
为 BC边上的一个动点(不与 B、C重合).过 E 作直线 AB的垂线,垂足为 F.FE 与 DC的延长线相交于点 G,连结 DE,DF。
(1)求证: ΔBEF∽Δ CEG.
( 2)当点 E 在线段 BC上运动时,△ BEF和△ CEG的周长之间有什么关系?并
所以 △BEF ∽△CEG ························· ( 2) △ BEF 与△ CEG 的周长之和为定值. · ················
3分 4分
理由一: 过点 C作 FG的平行线交直线 AB于 H , 因为 GF⊥ AB,所以四边形 FHCG为矩形.所以
FH= CG,FG= CH
