关于全等三角形的旋转难题93287
初二数学全等三角形旋转模型知识归纳总结及答案

初二数学全等三角形旋转模型知识归纳总结及答案一、全等三角形旋转模型1.ABC △和ADE 都是等腰直角三角形,CE 与BD 相交于点,M BD 交AC 于点,N CE 交AD 于点H .试确定线段BD CE 、的关系.并说明理由.解析:BD CE ⊥且BD CE =【分析】由已知条件可证明BAD CAE ≅△△,再根据全等三角形的性质,得到BD CE ∴= ADB AEC ∠=∠,在AEH △中90AEC AHE ∠+∠=︒,又AHE MHD ∠=∠,可得:90HMD ∠=︒,即可证明BD CE ⊥且BD CE =.【详解】解: ABC 和ADE 是直角三角形BAC DAE ∴∠=∠AB AC =AD AE =则BAC CAD DAE CAD ∠+∠=∠+∠即BAD CAE ∠=∠在BAD 与CAE 中AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩S )AS BAD CAE ∴≅(△△BD CE ∴= ADB AEC ∠=∠在AEH △中90AEC AHE ∠+∠=︒又AHE MHD ∠=∠90ADB MHD ∴∠+∠=︒则MHD 中90HMD ∠=︒,即,BD CE ⊥,综上所述,BD CE ⊥且BD CE =.【点睛】本题主要考查三角形全等的判定方法和性质定理和等腰直角三角形的性质,从复杂的图形中找到全等三角形和“8”字形三角形是解题的关键.2.(1)如图1,在OAB 和OCD 中,OA=OB ,OC=OD ,∠AOB=∠COD=40°,连接AC ,BD 交于点M .求:①AC BD 的值; ②∠AMB 的度数. (2)如图2,在OAB 和OCD 中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC 交BD 的延长线于点M .请判断AC BD的值及∠AMB 的度数,并说明理由; (3)在(2)的条件下,将OCD 点O 在平面内旋转,AC ,BD 所在直线交于点M ,若OD=2,OB=23,请直接写出当点C 与点M 重合时AC 的长.答案:A解析:(1)①1,②40°;(2)AC BD 3∠AMB=90°,见解析;(3)33【分析】 (1)①根据已知条件证明△COA ≌△DOB ,即可证明AC=BD ;②根据△COA ≌△DOB 可得∠CAO=∠DBO ,根据已知条件可得∠OAB+∠ABO=140°,然后在△AMB 中,根据等角的转换即可得到答案;(2)根据已知条件证明△AOC ∽△BOD ,可得∠CAO=∠DBO ,进而可得∠MAB=∠OAB+∠DBO ,最后可得∠AMB=180°-(∠OAB+∠ABM+∠DBO )=90°;(3)分两种情况讨论,根据题(2),同理可得OAC OBD △△,90AMB ∠=︒,3AC BD=,设BD=x ,则3AC x = 用x 表示出AM 、BM 的长,在Rt AMB 中,根据勾股定理222AM BM AB +=列出方程,求解即可.【详解】 解:(1)①如图1,∵∠AOB=∠COD=40°,∴∠COA=∠DOB ,∵OC=OD ,OA=OB ,∴△COA ≌△DOB (SAS ),∴AC=BD , ∴AC BD =1, ②∵△COA ≌△DOB ,∴∠CAO=∠DBO ,∵∠AOB=40°,∴∠OAB+∠ABO=140°,在△AMB 中,∠AMB=180°﹣(∠CAO+∠OAB+∠ABD )=180°﹣(∠DBO+∠OAB+∠ABD )=180°﹣140°=40°,(2)如图2,AC BD=3,∠AMB=90°,理由是:在Rt △COD 中,∠DCO=30°,∠DOC=90°,∴3tan 303OD OC =︒=,同理得:3tan 303OB OA =︒=, ∴OD OB OC OA=, ∵∠AOB=∠COD=90°,∴∠AOC=∠BOD ,∴△AOC ∽△BOD ,∴AC OC BD OD==3,∠CAO=∠DBO , 在△AMB 中,∠AMB=180°﹣(∠MAB+∠ABM )=180°﹣(∠OAB+∠ABM+∠DBO )=90°;(3)AC 的长为23或43.①如图,点C 与点M 重合,同理可得:OAC OBD △△,90AMB ∴∠=︒,3AC BD =设BD=x ,则3AC x =,在Rt ODC 中,30OCD ∠=︒,OD=2,4CD ∴=,在Rt AOB 中,30OAB ∠=︒,33AB ∴=,在Rt AMB 中,222AM BM AB +=,即222(3)(4)(43)x x ++=,解得:x=2或-4(舍),323x =②如图,点C 与点M 重合,同理可得:90AMB ∠=︒,3AC BD =设BD=x ,则3x ,在Rt COD 中, 90OCD ∠=︒,OD=2,4CD ∴=,4BC x =-,在Rt AOB 中,30OAB ∠=︒,3OB =243AB OB ∴==,在Rt AMB 中,222AM BM AB +=, 即222(3)(4)(43)x x +-=,解得:x=4或-2(舍), 343x =综上所述,AC 的长为2343【点睛】本题主要考查三角形的综合运用,涉及全等三角形与相似三角形的性质和判定、勾股定理、解一元一次方程、图形旋转证明、特殊角的三角函数值等知识点,难度较大,第(1)题证明△COA ≌△DOB 是关键,第(2)题证明△AOC ∽△BOD 是关键,第(3)题要特别注意分情况讨论.3.定义:按螺旋式分别延长n 边形的n 条边至一点,若顺次连接这些点所得的图形与原多边形相似,则称它为原图形的螺旋相似图形.例如:如图1,分别延长多边形A 1A 2…A n 的边得A 1′,A 2′,…,A n ′,若多边形A 1′A 2′…A n ′与多边形A 1A 2…An 相似,则多边形A 1′A 2′…A n ′就是A 1A 2…A n 的螺旋相似图形.(1)如图2,已知△ABC 是等边三角形,作出△ABC 的一个螺旋相似图形,简述作法,并给以证明.(2)如图3,已知矩形ABCD ,请探索矩形ABCD 是否存在螺旋相似图形,若存在,求出此时AB 与BC 的比值;若不存在,说明理由.(3)如图4,△ABC 是等腰直角三角形,AC =BC =2,分别延长CA ,AB ,BC 至A′,B′,C′,使△A′B′C′是△ABC 的螺旋相似三角形.若AA′=kAC ,请直接写出BB′,CC′的长(用含k 的代数式表示)答案:A解析:(1)见解析;(2)AB:BC=1;(3)BB′=2k,CC′=k.【分析】(1)如图2中,延长AB到E,延长BC到F,延长CA到D,使得BE=CF=AD,连接EF,DF,DE.则△DEF是△ABC的一个螺旋相似图形,证明△DEF是等边三角形即可解决问题.(2)如图3中,假设存在.四边形EFGH是矩形ABCD的螺旋相似图形,设AB=CD=a,BC=AD=b,BE=DG=x,CF=AH=y.分两种情形,利用相似三角形的性质以及相似矩形的性质,构建关系式证明a=b即可解决问题.(3)如图4中,作B′T⊥CB交CB的延长线于T.设TB=TB′=m,证明△A′CC′≌△A′TB′(ASA),推出A′C=TC′,CC′=TB′=BT,构建关系式推出m=k即可解决问题.【详解】解:(1)如图2中,延长AB到E,延长BC到F,延长CA到D,使得BE=CF=AD,连接EF,DF,DE.则△DEF是△ABC的一个螺旋相似图形.理由:∵△ABC是等边三角形,∴AB=BC=AC,∠CAB=∠ABC=∠ACB,∴∠DAE=∠FCD=∠EBF=120°,∵BE=CF=AD,∴CD=AE=BF,∴△FCD≌△DAE≌△EBF(SAS),∴DF =DE =EF ,∴△DEF 是等边三角形,∴△DEF ∽△ABC ,∴△DEF 是△ABC 的一个螺旋相似图形.(2)如图3中,假设存在.四边形EFGH 是矩形ABCD 的螺旋相似图形,设AB =CD =a ,BC =AD =b ,BE =DG =x ,CF =AH =y .由题意:△BEF ∽△AHE , ∴EF EH =BE AH =BF AE, ∴x y =b y a x++, 当EF HE =BC AB =b a 时,b a =x y =b y a x++, ∴x =b a•y ,ax +x 2=by +y 2, ∴by +22b a•y 2=by +y 2, ∴a 2=b 2,∴a =b ,即AB :BC =1. 当EF EH =AB BC =a b 时.a b =x y =b y a x ++, ∴x =a b•y ,ax +x 2=by +y 2, ∴2a b •y +22a b•y 2=by +y 2, ∴22a b b -•y (1+y b)=0, ∵y ≠0,1+y b≠0,∴a2=b2,∴a=b,即AB:BC=1,综上所述,AB:BC=1.(3)如图4中,作B′T⊥CB交CB的延长线于T.∵AC=BC=2,∠ACB=90°,∴∠ABC=∠CAB=45°,∴∠TBB′=∠ABC=45°,∴∠TB′B=∠TBB′=45°,∴TB=TB′,设TB=TB′=m,∵△A′B′C′是△ABC的螺旋相似三角形,∴A′C′=B′C′,∠A′C′B′=90°,∵∠A′C′C+∠B′C′=90°,∠A′CC+∠C′A′C=90°,∴∠C′A′C=∠B′C′T,∵∠A′CC′=∠T=90°,∴△A′CC′≌△A′TB′(ASA),∴A′C=TC′,CC′=TB′=BT,∴2+2k=2+2m,∴m=k,∴BB′2k,CC′=k.【点睛】本题属于相似形综合题,考查了等边三角形的性质,矩形的性质,等腰直角三角形的判定和性质等知识,解题的关键是理解题意,学会利用参数解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.4.已知:在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合).以AD为边作正方形ADEF,连接CF.(1)如图1,当点D在线段BC上时,请直接写出线段BD与CF的数量关系:;(2)如图2,当点D在线段BC的延长线上时,其它条件不变,若AC=2,CD=1,则CF= ;(3)如图3,当点D在线段BC的反向延长线上时,且点A、F分别在直线BC的两侧,其它条件不变:①请直接写出CF、BC、CD三条线段之间的关系:;②若连接正方形对角线AE、DF,交点为O,连接OC,探究△AOC的形状,并说明理由.答案:B解析:(1)BD=CF ;(2)221;(3)①CD=CF+BC ,②等腰三角形,见解析【分析】(1)△ABC 是等腰直角三角形,利用SAS 即可证明△BAD ≌△CAF ;(2)同(1)相同,利用SAS 即可证得△BAD ≌△CAF ,从而证得BD=CF ,即可得到CF=CD+BC ,然后求出答案;(3)中的①与(1)相同,可证明BD=CF ,又点D 、B 、C 共线,故:CD=BC+CF ; ②由(1)猜想并证明BD ⊥CF ,从而可知△FCD 为直角三角形,再由正方形的对角线的性质判定△AOC 三边的特点,再进一步判定其形状.【详解】解:(1)证明:∵∠BAC=90°,AB=AC ,∴∠ABC=∠ACB=45°,∵四边形ADEF 是正方形,∴AD=AF ,∠DAF=90°,∵∠BAC=∠BAD+∠DAC=90°,∠DAF=∠CAF+∠DAC=90°,∴∠BAD=∠CAF ,在△BAD 和△CAF 中,AB AC BAD CAF AD AF =⎧⎪∠=∠⎨⎪=⎩,∴△BAD ≌△CAF (SAS ),∴BD=CF ,(2)与(1)同理,证△BAD ≌△CAF ;∴BD=CF ,∴CF=BC+CD ,∵AC=AB=2,CD=1, ∴22222BC =+=∴CF=221;(3)①BC 、CD 与CF 的关系:CD=BC+CF理由:与(1)同法可证△BAD ≌△CAF ,从而可得:BD=CF ,即:CD=BC+CF②△AOC是等腰三角形理由:与(1)同法可证△BAD≌△CAF,可得:∠DBA=∠FCA,又∵∠BAC=90°,AB=AC,∴∠ABC=∠ACB=45°,则∠ABD=180°-45°=135°,∴∠ABD=∠FCA=135°∴∠DCF=135°-45°=90°∴△FCD为直角三角形.又∵四边形ADEF是正方形,对角线AE与DF相交于点O,∴OC=12DF,∴OC=OA∴△AOC是等腰三角形.【点睛】本题考查了等腰三角形、正方形的性质及全等三角形的判定与性质等知识点,一般情况下,要证明两条线段相等,就得证明这两条线段所在的两个三角形全等,关键是掌握图形特点挖掘题目所隐含的条件.5.如图1,在等腰Rt△ABC中,∠ABC=90°,AB=BC=6,过点B作BD⊥AC交AC于点D,点E、F分别是线段AB、BC上两点,且BE=BF,连接AF交BD于点Q,过点E作EH⊥AF交AF于点P,交AC于点H.(1)若BF=4,求△ADQ的面积;(2)求证:CH=2BQ;(3)如图2,BE=3,连接EF,将△EBF绕点B在平面内任意旋转,取EF的中点M,连接AM,CM,将线段AM绕点A逆时针旋转90°得线段AN,连接MN、CN,过点N作NR⊥AC 交AC于点R.当线段NR的长最小时,直接写出△CMN的周长.答案:A解析:(1)1.8;(2)证明见解析;(3326335102.【分析】(1)利用等腰直角三角形的性质求出12BD AD CD AC ====积相等和勾股定理分别求出AQ 和QD ,最后利用三角形面积公式即可求解;(2)如图,先作辅助线构造()AEH CFG ASA ∆∆≌,得到AH CG =,再通过转化得到2AH DQ =,最后利用AC ,得到一个相等关系,即()2AH HC BQ QD +=+,利用等式性质即可得到所求;(3)如图,通过做辅助线构造全等三角形确定出当HN ⊥AC ,且N 点位于H 、R 之间时,此时NR 的长最小,接着利用勾股定理和等腰直角三角形的性质,分别求出CM 、MN 、CN 的长,相加即可.【详解】解:6AB BC ==,°90ABC =∠,AC ==∴又∵AC BD ⊥∴BD 平分AC ,且BD 是∠ABC 的角平分线∴12BD AD CD AC ====Q 点到BA 和BC 边的距离相等; ∵4BF =, ∴6342ABQ BFQ S S ∆∆==, ∴32AQ FQ =,∵AF ===∴35AQ AF ==∴QD ===,∴1 1.825ADQ S ∆=⨯⨯=, ∴△ADQ 的面积为1.8.(2)如图,作CG ⊥AC ,垂足为C ,交AF 的延长线于点G ,∴°90ACG =∠∵°45ACB CAB ==∠∠,∴°45GCB CAB ==∠∠,∵EH ⊥AF ,∴°90EAP AEP +=∠∠,又∵°90EAP AFB +=∠∠∴AEP AFB =∠∠,∴AEP CFG =∠∠∵BE BF =,BA BC =∴AE CF =,在AEH ∆和CFG ∆中,AEH CFG AE CFEAH FCG ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()AEH CFG ASA ∆∆≌∴AH CG =;∵BD ⊥AC ,CG ⊥AC ,∴BD ∥CG ,∵D 点是AC 的中点,且BD ∥CG ,∴DQ 是ACG ∆的中位线, ∴12DQ CG =, ∴2DQ CG AH ==; ∵AC =2BD ,∴()2AH HC BQ QD +=+,∵2AH DQ =,∴CH =2BQ .(3)如图①,作AH ⊥AB ,且AH =AB ,∴∠NAH +∠HAM =∠HAM +∠BAM =90°,∴∠BAM =∠NAH ,∵AB =AH ,AM =AN ,∴()ABM AHN SAS ∆∆≌,∴HN =BM ,∵BE =BF =3,∠EBF =90°, ∴EF ==∴由M 点是EF 的中点,可得122BM EF ==,∴2NH =,∴N 点在以H 点为圆心,2为半径的圆上, 如图②,当HN ⊥AC ,且N 点位于H 、R 之间时,此时NR 的长最小,为2NR HR HN HR =-=-, ∵∠BAC =45°,∴∠HAC =45°,∴∠AHN =45°,HR =AR ,∵222HR AR AH +=,∴HR AR ===,∴22NR HR =-=, ∵AC == ∴CR AC AR =-=∴CN AN === ∵∠MAN =90°,AM =AN ,∴MN ==∴∠ABM =45°,∴∠EBM =45°,∴F 点在BA 上,E 点在CB 延长线上,如图,作MP ⊥EC ,垂足为P ,∴1322BP MP EB ===, ∴315622PC PB BC =+=+=,∴2MC ==∴MC MN CN ++=∴△CMN 的周长为3263351022++.【点睛】本题综合考查了等腰直角三角形的性质、全等三角形的判定与性质、旋转的性质、勾股定理、圆等知识,要求学生熟练掌握相关概念并能灵活应用它们,本题的综合性较强,难点在于作辅助线构造全等三角形以及线段之间的关系转化等,考查了学生综合分析和推理论证以及计算的能力,本题属于压轴题,蕴含了数形结合和转化的思想方法等.6.如图.四边形ABCD 、BEFG 均为正方形.(1)如图1,连接AG 、CE ,请直接写出.....AG 和CE 的数量和位置关系(不必证明).(2)将正方形BEFG 绕点B 顺时针旋转β角(0180β︒︒<<),如图2,直线AG 、CE 相交于点M .①AG 和CE 是否仍然满足(1)中的结论?如果是,请说明理由:如果不是,请举出反例:②连结MB ,求证:MB 平分AME ∠.(3)在(2)的条件下,过点A 作AN MB ⊥交MB 的延长线于点N ,请直接写出.....线段CM 与BN 的数量关系.答案:A解析:(1)AG=EC ,AG ⊥EC ;(2)①满足,理由见解析;②见解析;(3)CM=2BN .【分析】(1)由正方形BEFG 与正方形ABCD ,利用正方形的性质得到两对边相等,一对直角相等,利用SAS 得出三角形ABG 与三角形CBE 全等,利用全等三角形的对应边相等,对应角相等得到CE=AG ,∠BCE=∠BAG ,再利用同角的余角相等即可得证;(2)①利用SAS 得出△ABG ≌△CEB 即可解决问题;②过B 作BP ⊥EC ,BH ⊥AM ,由全等三角形的面积相等得到两三角形面积相等,而AG=EC ,可得出BP=BH ,利用到角两边距离相等的点在角的平分线上得到BM 为角平分线;(3)在AN 上截取NQ=NB ,可得出三角形BNQ 为等腰直角三角形,利用等腰直角三角形的性质得到BQ=2BN ,接下来证明BQ=CM ,即要证明三角形ABQ 与三角形BCM 全等,利用同角的余角相等得到一对角相等,再由三角形ANM 为等腰直角三角形得到NA=NM ,利用等式的性质得到AQ=BM ,利用SAS 可得出全等,根据全等三角形的对应边相等即可得证.【详解】解:(1)AG=EC ,AG ⊥EC ,理由为:∵正方形BEFG ,正方形ABCD ,∴GB=BE ,∠ABG=90°,AB=BC ,∠ABC=90°,在△ABG 和△BEC 中,BG BE ABC EBC BA BC =⎧⎪∠=∠⎨⎪=⎩,∴△ABG ≌△BEC (SAS ),∴CE=AG ,∠BCE=∠BAG ,延长CE 交AG 于点M ,∴∠BEC=∠AEM ,∴∠ABC=∠AME=90°,∴AG=EC ,AG ⊥EC ;(2)①满足,理由是:如图2中,设AM 交BC 于O .∵∠EBG=∠ABC=90°,∴∠ABG=∠EBC ,在△ABG 和△CEB 中,AB BC ABG CBE BG EB =⎧⎪∠=∠⎨⎪=⎩,∴△ABG ≌△CEB (SAS ),∴AG=EC ,∠BAG=∠BCE ,∵∠BAG+∠AOB=90°,∠AOB=∠COM ,∴∠BCE+∠COM=90°,∴∠OMC=90°,∴AG ⊥EC .②过B 作BP ⊥EC ,BH ⊥AM ,∵△ABG ≌△CEB ,∴S △ABG =S △EBC ,AG=EC , ∴12EC•BP=12AG•BH , ∴BP=BH ,∴MB 平分∠AME ;(3)2BN ,理由为:在NA 上截取NQ=NB ,连接BQ ,∴△BNQ 为等腰直角三角形,即2BN ,∵∠AMN=45°,∠N=90°,∴△AMN 为等腰直角三角形,即AN=MN ,∴MN-BN=AN-NQ ,即AQ=BM ,∵∠MBC+∠ABN=90°,∠BAN+∠ABN=90°,∴∠MBC=∠BAN ,在△ABQ 和△BCM 中,AQ BM BAN MBC AB BC =⎧⎪∠=∠⎨⎪=⎩,∴△ABQ ≌△BCM (SAS ),∴CM=BQ ,则CM=2BN .【点睛】此题考查了正方形,全等三角形的判定与性质,等腰直角三角形的判定与性质,角平分线的判定,熟练掌握正方形的性质是解本题的关键.7.如图1所示,矩形ABCD 中,点E ,F 分别为边AB ,AD 的中点,将△AEF 绕点A 逆时针旋转α(0°<α≤360°),直线BE 、DF 相交于点P .(1)若AB =AD ,将△AEF 绕点A 逆时针旋转至如图2所示的位置,则线段BE 与DF 的数量关系是 .(2)若AD =nAB (n ≠1),将△AEF 绕点A 逆时针旋转,则(1)中的结论是否仍然成立?若成立,请就图3所示的情况加以证明,若不成立,请写出正确结论,并说明理由. (3)若AB =8,BC =12,将△AEF 旋转至AE ⊥BE ,请算出DP 的长.答案:B解析:(1)BE =DF ;(2)不成立,结论:DF =nBE ;理由见解析(3)634或634【分析】(1)如图2中,结论:BE=DF,BE⊥DF.证明△ABE≌△ADF(SAS),利用全等三角形的性质可得结论;(2)结论:DF=nBE,BE⊥DF,证明△ABE∽△ADF(SAS),利用相似三角形的性质可得结论;(3)分两种情形画出图形,利用相似三角形的性质以及勾股定理求解即可.【详解】解:(1)结论:BE=DF,BE⊥DF,理由:∵四边形ABCD是矩形,AB=AD,∴四边形ABCD是正方形,AE=12AB,AF=12AD,∴AE=AF,∵∠DAB=∠EAF=90°,∴∠BAE=∠DAF,∴△ABE≌△ADF(SAS),∴BE=DF,故答案为:BE=DF;(2)结论不成立,结论:DF=nBE,∵AE=12AB,AF=12AD,AD=nAB,∴AF=nAE,∴AF∶AE=AD∶AB,∴AF∶AE=AD∶AB,∵∠DAB=∠EAF=90°,∴∠BAE=∠DAF,∴△BAE∽△DAF,∴DF∶BE=AF∶AE=n,∠ABE=∠ADF,∴DF=nBE;(3)如图4-1中,当点P在BE的延长线上时,在Rt△AEB中,∵∠AEB=90°,AB=8,AE=12AB=4,∴BE=22AB AE -=43,∵△ABE ∽△ADF ,∴AB AD =BE DF , ∴812=43DF, ∴DF=63,∵四边形AEPF 是矩形,∴AE=PF=4,∴PD=DF-PF=634-;如图4-2中,当点P 在线段BE 上时,同法可得DF=63,PF=AE=4,∴PD=DF +PF=634+,综上所述,满足条件的PD 的值为634-或634+.【点睛】此题考查了矩形的性质,全等三角形的判定及性质,旋转的性质,相似三角形的判定及性质,勾股定理,注意应用分类思想解决问题, 是一道较难的几何综合题.8.在平面直角坐标系中,点A 在y 轴正半轴上,点B 在x 轴负半轴上,BP 平分∠ABO . (1)如图1,点T 在BA 延长线上,若AP 平分∠TAO ,求∠P 的度数;(2)如图2,点C 为x 轴正半轴上一点,∠ABC =2∠ACB ,且P 在AC 的垂直平分线上. ①求证:AP //BC ;②D 是AB 上一点,E 是x 轴正半轴上一点,连接AE 交DP 于H .当∠DHE 与∠ABE 满足什么数量关系时,DP =AE .给出结论并说明理由.答案:D解析:(1)45°;(2)①见解析;②∠DHE +∠ABE =180°,理由见解析【分析】(1)由三角形的外角性质和角平分线的性质可得∠AOB =2∠P =90°,可求解;(2)①过点P 作PE ⊥AB 交BA 延长线于E ,过点P 作PF ⊥BC 于F ,连接PC ,由角平分线的性质可得PE =PF ,由垂直平分线的性质可得PA =PC ,由“HL ”可证Rt △APE ≌Rt △CPF ,可得∠EPA =∠CPF ,由四边形内角和定理可得∠EBF +∠EPF =180°,由角的数量关系可证∠ACB =∠PAC ,由平行线的判定可证AP ∥BC ;②如图3,在OE 上截取ON =OB ,连接AN ,通过证明△ADP ≌△NEA ,可得DP =AE .【详解】解:(1)∵BP 平分∠ABO ,AP 平分∠TAO ,∴∠PBT =12∠ABO ,∠TAP =12∠TAO , ∵∠TAO =∠ABO+∠AOB ,∠TAP =∠P+∠ABP ,∴∠AOB =2∠P =90°,∴∠P =45°;(2)①如图2,过点P 作PE ⊥AB 交BA 延长线于E ,过点P 作PF ⊥BC 于F ,连接PC ,又∵PB 平分∠ABC ,∴PE =PF ,∵P 在AC 的垂直平分线上,∴PA =PC ,∴∠PAC =∠PCA ,在Rt △APE 和Rt △CPF 中,AP PC PE PF =⎧⎨=⎩, ∴Rt △APE ≌Rt △CPF (HL ),∴∠EPA =∠CPF ,∴∠EPF =∠APC ,在四边形BEPF 中,∠EBF+∠BEP+∠EPF+∠PFB =180°,∴∠EBF+∠EPF =180°,∴∠ABC+∠APC =180°,∵∠APC+∠PAC+∠PCA =180°,∴∠ABC =∠PAC+∠PCA =2∠PAC ,∵∠ABC =2∠ACB ,∴∠ACB =∠PAC ,∴AP ∥BC ;②当∠DHE+∠ABE =180°时,DP =AE ,理由如下:如图3,在OE 上截取ON =OB ,连接AN ,∵OB =ON ,AO ⊥BE ,∴AB =AN ,∴∠ABN =∠ANB ,∵AP ∥BE ,BP 平分∠ABE ,∴∠APB =∠PBE =∠ABP ,∠ABN+∠BAP =180°,∴AP =AB ,∴AP =AN ,∵∠ANB+∠ANE =180°,∴∠BAP =∠ANE ,∵∠DHE+∠ABE =180°,∠DHE+∠ABE+∠BDH+∠BEH =360°,∴∠BDH+∠BEH =180°,∵∠ADP+∠BDP =180°,∴∠ADP =∠AEN ,在△ADP 和△NEA 中,DAP ANE ADP AEN AP AN ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADP ≌△NEA (AAS ),∴DP =AE .【点睛】本题是三角形综合题,考查了全等三角形的判定和性质,角平分线的性质,线段垂直平分线的性质,四边形内角和定理等知识,添加恰当辅助线构造全等三角形是本题的关键. 9.在等腰Rt ABC △中,AB AC =、90BAC ∠=︒.(1)如图1,D ,E 是等腰Rt ABC △斜边BC 上两动点,且45DAE ∠=︒,将ABE△绕点A 逆时针旋转90后,得到AFC △,连接DF .①求证:AED AFD ≌.②当3BE =,9CE =时,求DE 的长.(2)如图2,点D 是等腰Rt ABC △斜边BC 所在直线上的一动点,连接AD ,以点A 为直角顶点作等腰Rt ADE △(E 点在直线BC 的上方),当3BD =,9BC =时,求DE 的长.答案:D解析:(1)①证明见解析;②5;(2)35或317【分析】(1)①证明∠DAE=∠DAF=45°即可利用SAS 证明全等;②由①中全等可得DE=DF ,再在Rt △FDC 中利用勾股定理计算即可;(2)连接BE ,根据共顶点等腰直角三角形证明全等,再利用勾股定理计算即可。
全等三角形——旋转问题

G F E D C BA全等三角形——旋转问题一、知识梳理:把图形G 绕平面上的一个定点O 旋转一个角度θ,得到图形G ',这样的由图形G 到G '变换叫做旋转变换,点O 叫做旋转中心,θ叫做旋转角,G '叫做G 的象;G 叫做G '的原象,无论是什么图形,在旋转变换下,象与原象是全等形.很明显,旋转变换具有以下基本性质:①旋转变换的对应点到旋转中心的距离相等; ②对应直线的交角等于旋转角.旋转变换多用在等腰三角形、正三角形、正方形等较规则的图形上,其功能还是把分散的条件相对集中,以便于诸条件的综合与推演.二、典型例题:例1、如图,有四个图案,它们绕中心旋转一定的角度后,都能和原来的图案相互重合,其中有一个图案与其余三个图案旋转的角度不同,它是_____________.及时练习:如图,同学们曾玩过万花筒,它是由三块等宽等长的玻璃片围成的, 其中菱形AEFG 可以看成是把菱形ABCD 以A 为中心_____________。
A .顺时针旋转60°得到B .顺时针旋转120°得到C .逆时针旋转60°得到D .逆时针旋转120°得到例2、如图,C 是线段BD 上一点,分别以BC 、CD 为边在BD 同侧作等边△ABC 和等边△CDE ,AD 交CE 于F ,BE 交AC 于G ,则图中可通过旋转而相互得到的三角形对数有___________。
A .1对B .2对C .3对D .4对KGFEDC BA及时练习:如图,B ,C ,E 三点共线,且ABC ∆与DCE ∆是等边三角形,连结BD ,AE 分别交AC ,DC 于M ,N 点.求证:CM CN =.NMEDCBAP DC B A 例3、如图,四边形ABCD 、DEFG 都是正方形,连接AE 、CG .求证:AE CG =.G FE DCBA及时练习:如图,点C 为线段AB 上一点,ACM ∆、CBN ∆是等边三角形,D 是AN 中点,E 是BM 中点,求证:CDE ∆是等边三角形.M DNECBA例4、如图,等边三角形ABC ∆与等边DEC ∆共顶点于C 点.求证:AE BD =.DECBA及时练习:如图,D 是等边ABC ∆内的一点,且BD AD =,BP AB =,DBP DBC ∠=∠,问BPD ∠的度数是否一定,若一定,求它的度数;若不一定,说明理由.例5、如图,等腰直角三角形ABC 中,90B =︒∠,AB a =,O 为AC 中点,EO OF ⊥.求证:BE BF +为定值. OB ECF A及时练习:如图,正方形OGHK 绕正方形ABCD 中点O 旋转,其交点为E 、F ,求证:AE CF AB +=.54321OHBE DK G CFA例6、E 、F 分别是正方形ABCD 的边BC 、CD 上的点,且45EAF =︒∠,AH EF ⊥,H为垂足,求证:AH AB =.CHF E D B A及时练习:如图,正方形ABCD 的边长为1,点F 在线段CD 上运动,AE 平分BAF ∠交BC 边于点E .⑴求证:AF DF BE =+.⑵设DF x =(01x ≤≤),ADF ∆与ABE ∆的面积和S 是否存在最大值?若存在,求出此时x 的值及S .若不存在,请说明理由.FEDC BA例7、请阅读下列材料:已知:如图1在Rt ABC ∆中,90BAC ∠=︒,AB AC =,点D 、E 分别为线段BC 上两动点,若45DAE ∠=︒.探究线段BD 、DE 、EC 三条线段之间的数量关系.小明的思路是:把AEC ∆绕点A 顺时针旋转90︒,得到ABE '∆,连结E D ', 使问题得到解决.请你参考小明的思路探究并解决下列问题:⑴ 猜想BD 、DE 、EC 三条线段之间存在的数量关系式,并对你的猜想给予证明; ⑵ 当动点E 在线段BC 上,动点D 运动在线段CB 延长线上时,如图2,其它条件不变,⑴中探究的结论是否发生改变?请说明你的猜想并给予证明.图1ABCDE图2AB CDE及时练习:(1)如图,在四边形ABCD 中,AB =AD ,∠B =∠D =90︒,E 、F 分别是边BC 、CD 上的点,且∠EAF=12∠BAD .求证:EF =BE +FD;FED CBA(2) 如图,在四边形ABCD 中,AB =AD ,∠B+∠D =180︒,E 、F 分别是边BC 、CD上的点,且∠EAF=12∠BAD , (1)中的结论是否仍然成立?不用证明.FEDCB A三、课堂练习:1. 如下图,在线段AE 同侧作两个等边三角形ABC ∆和CDE ∆(120ACE ∠<°),点P 与点MPM BC DEA PD CB A 分别是线段BE 和AD 的中点,则CPM ∆是_____________。
初中数学全等三角形旋转模型知识归纳总结含答案

初中数学全等三角形旋转模型知识归纳总结含答案一、全等三角形旋转模型1.如图1,在Rt △ABC 中,∠A =90°,AB =AC ,点D ,E 分别在边AB ,AC 上,AD =AE ,连接DC ,点M ,P ,N 分别为DE ,DC ,BC 的中点.(1)观察猜想:图1中,线段PM 与PN 的数量关系是 ,位置关系是 ;(2)探究证明:把△ADE 绕点A 逆时针方向旋转到图2的位置,连接MN ,BD ,CE ,判断△PMN 的形状,并说明理由;(3)拓展延伸:把△ADE 绕点A 在平面内自由旋转,若AD =4,AB =10,请直接写出△PMN 面积的最大值.解析:(1)PM =PN ,PM ⊥PN ;(2)△PMN 是等腰直角三角形.理由见解析;(3)S △PMN 最大=492. 【分析】(1)由已知易得BD CE =,利用三角形的中位线得出12PM CE =,12PN BD =,即可得出数量关系,再利用三角形的中位线得出//PM CE 得出DPM DCA ∠=∠,最后用互余即可得出位置关系;(2)先判断出ABD ACE ∆≅∆,得出BD CE =,同(1)的方法得出12PM BD =,12PN BD =,即可得出PM PN =,同(1)的方法由MPN DCE DCB DBC ACB ABC ∠=∠+∠+∠=∠+∠,即可得出结论;(3)方法1:先判断出MN 最大时,PMN ∆的面积最大,进而求出AN ,AM ,即可得出MN 最大AM AN =+,最后用面积公式即可得出结论.方法2:先判断出BD 最大时,PMN ∆的面积最大,而BD 最大是14AB AD +=,即可得出结论.【详解】解:(1)点P ,N 是BC ,CD 的中点,//PN BD ∴,12PN BD =, 点P ,M 是CD ,DE 的中点, //PM CE ∴,12PM CE =,AB AC =,AD AE =,BD CE ∴=,PM PN ∴=,//PN BD ,DPN ADC ∴∠=∠,//PM CE ,DPM DCA ∴∠=∠,90BAC ∠=︒,90ADC ACD ∴∠+∠=︒,90MPN DPM DPN DCA ADC ∴∠=∠+∠=∠+∠=︒,PM PN ∴⊥,故答案为:PM PN =,PM PN ⊥;(2)PMN ∆是等腰直角三角形.由旋转知,BAD CAE ∠=∠,AB AC =,AD AE =,()ABD ACE SAS ∴∆≅∆,ABD ACE ∴∠=∠,BD CE =, 利用三角形的中位线得,12PN BD =,12PM CE =, PM PN ∴=,PMN ∴∆是等腰三角形,同(1)的方法得,//PM CE ,DPM DCE ∴∠=∠,同(1)的方法得,//PN BD ,PNC DBC ∴∠=∠,DPN DCB PNC DCB DBC ∠=∠+∠=∠+∠,MPN DPM DPN DCE DCB DBC ∴∠=∠+∠=∠+∠+∠BCE DBC ACB ACE DBC =∠+∠=∠+∠+∠ACB ABD DBC ACB ABC =∠+∠+∠=∠+∠,90BAC ∠=︒,90ACB ABC ∴∠+∠=︒,90MPN ∴∠=︒,PMN ∴∆是等腰直角三角形;(3)方法1:如图2,同(2)的方法得,PMN ∆是等腰直角三角形,MN ∴最大时,PMN ∆的面积最大,//DE BC ∴且DE 在顶点A 上面,MN ∴最大AM AN =+,连接AM ,AN ,在ADE ∆中,4AD AE ==,90DAE ∠=︒,22AM ∴=在Rt ABC ∆中,10AB AC ==,52AN =22522MN ∴=最大,222111149(72)22242PMN S PM MN ∆∴==⨯=⨯=最大. 方法2:由(2)知,PMN ∆是等腰直角三角形,12PM PN BD ==, PM ∴最大时,PMN ∆面积最大,∴点D 在BA 的延长线上,14BD AB AD ∴=+=,7PM ∴=,2211497222PMN S PM ∆∴==⨯=最大. 【点睛】此题属于几何变换综合题,主要考查了三角形的中位线定理,等腰直角三角形的判定和性质,全等三角形的判断和性质,直角三角形的性质的综合运用;解(1)的关键是判断出12PM CE =,12PN BD =,解(2)的关键是判断出ABD ACE ∆≅∆,解(3)的关键是判断出MN 最大时,PMN ∆的面积最大.2.问题提出:(1)如图1,在ABC 中,AB AC BC =≠,点D 和点A 在直线BC 的同侧,BD BC =,90BAC ∠=︒,30DBC ∠=︒,连接AD ,将ABD △绕点A 逆时针旋转90︒得到ACD ',连接BD '(如图2),可求出ADB ∠的度数为______.问题探究:(2)如图3,在(1)的条件下,若BAC α∠=,DBC β∠=,且120αβ+=︒,DBC ABC ∠<∠ ,①求ADB ∠的度数.②过点A 作直线AE BD ⊥,交直线BD 于点E ,7,2BC AD ==.请求出线段BE 的长.答案:A解析:(1)30°;(2)①30︒;②73-【分析】(1)由旋转的性质,得△ABD ≌ACD '∆,则ADB AD C '∠=∠,然后证明BCD '∆是等边三角形,即可得到30ADB AD C '∠=∠=︒;(2)①将ABD △绕点A 逆时针旋转,使点B 与点C 重合,得到'ACD △,连接'BD .与(1)同理证明D BC '∆为等边三角形,然后利用全等三角形的判定和性质,即可得到答案;②由解直角三角形求出3DE =【详解】解:(1)根据题意,∵AB AC BC =≠,90BAC ∠=︒,∴ABC ∆是等腰直角三角形,∴45ABC ACB ∠=∠=︒,∵30DBC ∠=︒,∴15ABD ∠=︒,由旋转的性质,则△ABD ≌ACD '∆,∴ADB AD C '∠=∠,15ABD ACD '∠=∠=︒,BC CD '=,∴60BCD '∠=︒,∴BCD '∆是等边三角形,∴60BD C '∠=︒,BD CD ''=∵AB AC =,AD AD ''=,∴ABD '∆≌ACD '∆,∴30AD B AD C ''∠=∠=︒,∴30ADB AD C '∠=∠=︒;(2)①DBC ABC ∠<∠,60120α︒︒∴<<.如图1,将ABD △绕点A 逆时针旋转,使点B 与点C 重合,得到'ACD △,连接'BD .AB AC =,ABC ACB ∴∠=∠,BAC α∠=, ()111809022ABC αα︒︒∴∠=-=-, 1902ABD ABC DBC αβ︒∴∠=∠-∠=--, 119090180()22D CB ACD ACB αβααβ''︒︒︒∴∠=∠+∠=--+-=-+. 120,αβ︒+=60D CB '︒∴∠=.,BD BC BD CD '==,,BC CD '∴=D BC '∴为等边三角形,D B D C ''∴=,AD B AD C ''∴≌,AD B AD C ''∴∠=∠,1302AD B BD C ''︒∴∠=∠=, 30ADB ︒∴∠=.②如图2,由①知,30ADB ︒∠=,在Rt ADE △中,30,2ADB AD ︒∠==, 3DE ∴=.BCD '是等边三角形,7BD BC '∴==,7BD BD '∴==,73BE BD DE ∴=-=-.【点睛】本题考查了解直角三角形,旋转的性质,全等三角形的判定和性质,等边三角形的判定和性质,等腰直角三角形的性质,以及三角形的内角和定理,解题的关键是熟练掌握所学的知识,正确利用旋转模型进行解题.3.如图,点B ,C ,D 在同一条直线上,△BCF 和△ACD 都是等腰直角三角形,连接AB ,DF ,延长DF 交AB 于点E .(1)如图1,若AD =BD ,DE 是∠ADB 的平分线,BC =1,求CD 的长度;(2)如图2,连接CE ,求证:DE =2CE +AE ;(3)如图3,改变△BCF 的大小,始终保持点在线段AC 上(点F 与点A ,C 不重合).将ED 绕点E 顺时针旋转90°得到EP ,取AD 的中点O ,连接OP .当AC =2时,直接写出OP 长度的最大值.解析:(1)21CD =;(2)证明见解析;(3)22+【分析】 (1)根据等腰直角三角形的性质,求出1FC BC ==,再判断出FA FB =,即可得出结论;(2)先判断出ABC DFC ≅△△,得出BAC CDF ∠=∠,进而判断出ACE DCH ≅△△,得出AE DH =,CE CH =,即可得出结论;(3)先判断出2OE OQ ==,再判断出OED QEP ≅△△,进而求出2PQ OD ==得出结论.【详解】(1)解:BCF 和ACD △都是等腰直角三角形,AC CD ∴=,1FC BC ==,2FB =,AD BD =,DE 是ABD ∆的平分线,DE ∴垂直平分AB ,2FA FB ∴==,21AC FA FC ∴=+=,21CD ∴=;(2)证明:如图2,过点C 作CH CE ⊥交ED 于点H ,BCF 和ACD △都是等腰直角三角形,AC DC ∴=,FC BC =,90ACB DCF ∠=∠=︒;()ABC DFC SAS ∴≅△△,BAC CDF ∴∠=∠,90ECH ∠=︒,90ACE ACH ∴∠+∠=︒,90ACD ∠=︒,90DCH ACH ∴∠+∠=︒,ACE DCH ∴∠=∠.在ACE 和DCH 中,BAC CDF AC DCACE DCH ∠=∠⎧⎪=⎨⎪∠=∠⎩, ()ACE DCH ASA ∴≅△△,AE DH ∴=,CE CH =,2EH CE ∴=.2DE EH DH CE AE =+=+;(3)OP 的最大值是22+解:如图3,连接OE ,将OE 绕点E 顺时针旋转90︒得到EQ ,连接OQ ,PQ ,则2OQ OE =.由(2)知,90AED ABC CDF ABC BAC ∠=∠+∠=∠+∠=︒,在Rt AED △中,点O 是斜边AD 的中点,122222OE OD AD AC ∴===== 2222OQ OE ∴===,在OED 和QEP △中,OE QE OED QEP DE PE =⎧⎪∠=∠⎨⎪=⎩,()OED QEP SAS ∴≅△△,2PQ OD ∴==22OP OQ PQ +=+O 、P 、Q 三点共线时,取“=”号,OP ∴的最大值是22+【点睛】此题是几何变换综合题,主要等腰直角三角形的性质,全等三角形的判定和性质,构造出全等三角形是解本题的关键.4.如图1所示,在Rt ABC △中90BAC ∠=︒,AB AC =,2BC =,以BC 所在直线为x 轴,边BC 的垂直平分线为y 轴建立平面直角坐标系,将ABC 绕P 点0,1顺时针旋转.(1)填空:当点B 旋转到y 轴正半轴时,则旋转后点A 坐标为______;(2)如图2所示,若边AB 与y 轴交点为E ,边AC 与直线1y x =-的交点为F ,求证:AEF 的周长为定值;(3)在(2)的条件下,求AEF 内切圆半径的最大值.解析:(1)2,21;(2)见解析;(3)324【分析】 (1)作出图形,'''A B C 是ABC 绕 P 点0,1顺时针旋转,点B 旋转到y 轴正半轴时得到的图形,连接 BP ,CP ,根据2BC =,y 轴垂直平分BC , AB AC =,()0,1P -可证得四边形ABPC 是正方形,则有 '''2BP B PAB A B ,'0'21B B P PO ,可得点 A 坐标; (2)作BPQ CPF ∠=∠,交AB 延长线于Q 点,根据四边形ABPC 是正方形,得到90QBP FCP ∠=∠=︒,BP CP =,可证BPQ CPF ASA ≌△△,得BQ CF =,QP FP =,利用ASA 再可证得QPE FPE ≌△△,得QE FE =则AEF 的周长22AB AC =+=(3)设EF m =,AE n =,Rt AEF 的内切圆半径为r ,由(2)可得22AF m n =-则2AE AF EF r +-=222n m n m +--=2m =,当m 最小时,r 最大.得到22222n m n m 整理得:2224220nm n m ,关于n 的一元二次方程有解,即22244220m m 化简得24280m m +-≥,利用二次函数图像可得422m ≥-422m ≤--(不合题意,舍去)可得m 的最小值为42-r 2422324,则有AEF 内切圆半径的最大值为324.【详解】解:(1)如图示,'''A B C 是ABC 绕 P 点0,1顺时针旋转,点B 旋转到y 轴正半轴时得到的图形,连接 BP ,CP ,∵2BC =,y 轴垂直平分BC∴1BO CO ==又∵Rt ABC △中,AB AC =∴1AO =,2AB AC ==∵()0,1P -∴1PO =∴AO BO CO PO ===∴四边形ABPC 是正方形 ∴'''2BPB P AB A B ∴'0'21B B P PO ∴点A 坐标为2,21(2)如图2所示,作BPQ CPF ∠=∠,交AB 延长线于Q 点 ∵四边形ABPC 是正方形∴90QBP FCP ∠=∠=︒, BP CP = ∴BPQ CPF ASA ≌△△∴ BQ CF =,QP FP = ∵点F 在直线1y x =-∴45FPE ∠=︒∴ 45BPE FPC ∠+∠=︒ ∴45BPE BPQ ∠+∠=︒∴45QPE FPE ∠=∠=︒ ∵EP EP =∴QPE FPE ASA ≌△△∴ QE FE = ∴AEF 的周长AE EF AF AE QE AF =++=++ AE BE BQ AF AE BE FC AF =+++=+++22AB AC =+=(3)设EF m =,AE n =,Rt AEF 的内切圆半径为 r ,由(2)可得22AF m n =--则2AE AF EF r +-= 222n m n m +---= 2m =-∴当m 最小时,r 最大.∵在Rt AEF 中,222AE AF EF +=∴22222n m n m 整理得: 2224220n m nm ∵关于n 的一元二次方程有解∴22244220m m∴24280m m +-≥ 利用二次函数图像可得422m ≥-或422m ≤--(不合题意,舍去)∴m 的最小值为422-∴r 的最大值为2422324即AEF 内切圆半径的最大值为324-.【点睛】本题主要考查了一次函数的综合应用以及根的判别式、全等三角形的判定与性质、旋转、三角形内切圆等知识,能熟练应用相关性质是解题关键.5.如图1,在△ABC 和△ADE 中,∠DAE=∠BAC ,AD=AE ,AB=AC .(1)求证:△ABD ≌△ACE ;(2)如图2,在△ABC 和△ADE 中,∠DAE=∠BAC ,AD=AE ,AB=AC ,∠ADB=90°,点E 在△ABC 内,延长DE 交BC 于点F ,求证:点F 是BC 中点;(3)△ABC 为等腰三角形,∠BAC=120°,AB=AC ,点P 为△ABC 所在平面内一点,∠APB=120°,AP=2,BP=4,请直接写出 CP 的长.答案:D解析:(1)证明见详解;(2)证明见详解;(3)27或213.【分析】(1)因为∠DAE=∠BAC ,可以得到∠DAB=∠EAC ,因为AD=AE ,AB=AC ,即可得到△ABD ≌△ACE ;(2)连接CE ,延长EF 至点H ,取CF=CH ,连接CH ,由(1)可得△ABD ≌△ACE ,所以∠AEC=90°和CE=BD ,可以推出∠BDF=∠CEF ,再证明△DBF ≌△ECH ,所以BF=CH ,等量代换即可得到BF=FC ,即可解决;(3)点P 在△ABC 内部,将△ABP 逆时针旋转120°,得到ACP ∆',连接PP '和PC ,可以得到△PP C '是直角三角形,利用勾股定理即可求出PC 的值;当点P 在△ABC 外部,将△APB 绕点A 逆时针旋转120︒得到PDC ∆,连接PP '和PC ,过点P 作PD ⊥'CP 于点D ,连接PD 可以得到△PP D ',△PP D '是直角三角形和,利用勾股定理即可求出'DP 及PC 的值.【详解】解:(1)证明:∵∠DAE=∠BAC∴∠DAB=∠EAC∵AD=AE ,AB=AC∴△ABD ≌△ACE(2)证明:连接CE ,延长EF 至点H ,取CF=CH ,连接CH ,如图所示:∵△ADB ≌△AEC∴BD=EC ,∠ADB=∠AEC=90°∵AD=AE∴∠ADE=∠AED∵∠ADE+∠EDB=∠AED+∠CEH=90°∴∠EDB=∠CEH∵CF=CH∴∠CFH=∠CHF∴∠DFB=∠H∵CE=BD∴△DBF ≌△ECH∴BF=CH∴BF=CF∴点F 是BC 的中点(3)当点P 在△ABC 内部,如图所示,将△ABP 逆时针旋转120°,得到ACP ∆',连接PP '和PC∵将△ABP 旋转120°得到ACP ∆'∴∠PAP '=120°,AP='AP =2,BP=CP '=4∴PP '=23,∵∠AP C '=120°,∠AP P '=30°,∴∠PP C '=90°,∴PC=()2223427+=.当点P 在△ABC 外部,如图所示,将△APB 绕点A 逆时针旋转120︒到△'AP C ,过点P 作PD ⊥'CP 于点D ,连接PD , ∵将△ABP 旋转120°得到ACP ∆'∴∠PAP '=120°,AP='AP =2,BP=CP '=4,∴PP '3∵∠AP C '=120°,∠AP P '=30°,∴∠PP C '=150°,∴∠PP D '=30°,在Rt 'PDP 中,1'32PD PP ==, 22''3DP PP PD ∴=-=,''347DC DP P C ∴=+=+=,()222237213PC PD DC ∴=+=+=. 综上所述,27213PC =或【点睛】本题主要考查了全等三角形以及旋转,合理的作出辅助线以及熟练旋转的性质是解决本题的关键.6.如图,直线y=﹣x+c与x轴交于点B(3,0),与y轴交于点C,过点B,C的抛物线y=﹣x2+bx+c与x轴的另一个交点为A.(1)求抛物线的解析式和点A的坐标;(2)P是直线BC上方抛物线上一动点,PA交BC于D.设t=PDAD,请求出t的最大值和此时点P的坐标;(3)M是x轴上一动点,连接MC,将MC绕点M逆时针旋转90°得线段ME,若点E恰好落在抛物线上,请直接写出此时点M的坐标.答案:A解析:(1)y=﹣x2+2x+3,A(﹣1,0);(2)t的最大值为916,此时P(32,154);(3)M 933-,0933+0).【分析】(1)利用待定系数法解决问题即可;(2)连接AC,PC,PB,过点A作AE⊥BC于E,过等P作PF⊥BC于F.设P(m,﹣m2+2m+3).利用相似三角形的性质构建二次函数解决问题即可;(3)过点E作EH⊥x轴于H.设M(m,0),利用全等三角形的性质求出点E的坐标(用m表示),再利用待定系数法解决问题即可.【详解】解:(1)∵直线y=﹣x+c与x轴交于点B(3,0),与y轴交于点C,∴0=﹣3+c,解得c=3,∴C(0,3),∵抛物线经过B,C,∴9303b cc-++=⎧⎨=⎩,解得23bc=⎧⎨=⎩,∴抛物线的解析式为y=﹣x2+2x+3,令y=0,得到﹣x2+2x+3=0,解得x=﹣1或3,∴A(﹣1,0);(2)如图,连接AC,PC,PB,过点A作AE⊥BC于E,过点P作PF⊥BC于F.设P(m,﹣m2+2m+3).∵AE∥PF,∴△PFD∽△AED,∴PDAD =PFAE,∵S△PBC=12•BC•PF,S△ACB=12•BC•AE,∴PDAD =PBCABCSS∆∆,∵S△ABC=12•AB•OC=12×4×3=6,∴t=PDAD =6PBCS∆=211133(23)332226m m m⨯⨯+⨯⨯-++-⨯⨯=﹣14m2+34m=﹣14(m﹣32)2+916,∵﹣14<0,∴m=32时,t有最大值,最大值为916,此时P(32,154);(3)如图,过点E作EH⊥x轴于H,∵∠COM =∠EHM =∠CME =90°,∴∠EMH +∠CMH =90°,∠EMH +∠MEH =90°,∴∠MEH =∠CMO ,∵MC =ME ,∴△COM ≌△MHE (AAS ),∴OC =MH =3,OM =EH ,设M (m ,0),则E (m ﹣3,﹣m ),把E (m ﹣3,﹣m )代入y =﹣x 2+2x +3,可得﹣(m ﹣3)2+2(m ﹣3)+3=﹣m , 整理得,m 2﹣9m +12=0,解得m =9332-或9332+, ∴M (9332-,0)或(9332+,0). 【点睛】本题考查的是二次函数综合题,涉及全等三角形的性质和判定,相似三角形的性质和判定,解题的关键是利用数形结合的思想,在二次函数图象上构造全等三角形或相似三角形,利用几何的性质进行点坐标的求解.7.如图,BC ⊥CA ,BC =CA ,DC ⊥CE ,DC =CE ,直线BD 与AE 交于点F ,交AC 于点G ,连接CF .(1)求证:△ACE ≌△BCD ;(2)求证:BF ⊥AE ;(3)请判断∠CFE 与∠CAB 的大小关系并说明理由.答案:C解析:(1)见解析;(2)见解析;(3)∠CFE =∠CAB ,见解析【分析】(1)根据垂直的定义得到∠ACB =∠DCE =90°,由角的和差得到∠BCD =∠ACE ,即可得到结论;(2)根据全等三角形的性质得到∠CBD =∠CAE ,根据对顶角的性质得到∠BGC =∠AGE ,由三角形的内角和即可得到结论;(3)过C 作CH ⊥AE 于H ,CI ⊥BF 于I ,根据全等三角形的性质得到AE =BD ,S △ACE =S △BCD ,根据三角形的面积公式得到CH =CI ,于是得到CF 平分∠BFH ,推出△ABC 是等腰直角三角形,即可得到结论.【详解】(1)证明:∵BC ⊥CA ,DC ⊥CE ,∴∠ACB =∠DCE =90°,∴∠BCD =∠ACE ,在△BCD 与△ACE 中,BC CA ACD ACE CD CE =⎧⎪∠=∠⎨⎪=⎩,∴△ACE ≌△BCD ;(2)∵△BCD ≌△ACE ,∴∠CBD =∠CAE ,∵∠BGC =∠AGE ,∴∠AFB =∠ACB =90°,∴BF ⊥AE ;(3)∠CFE =∠CAB ,过C 作CH ⊥AE 于H ,CI ⊥BF 于I ,∵△BCD ≌△ACE ,∴ACE BCD AE BD,S S ∆∆==,∴CH =CI ,∴CF 平分∠BFH ,∵BF ⊥AE ,∴∠BFH =90°,∠CFE =45°,∵BC ⊥CA ,BC =CA ,∴△ABC 是等腰直角三角形,∴∠CAB =45°,∴∠CFE =∠CAB .【点睛】角的和差、对顶角的性质这些知识点在证明全等和垂直过程中经常会遇到,需要掌握。
关于全等三角形的旋转难题

扭转之杨若古兰创作已知,如图,三角形ABC是等腰直角三角形,∠ACB=90°,F是AB的中点,直线l经过点C,分别过点A、B作l的垂线,即AD⊥CE,BE⊥CE,(1)如图1,当CE位于点F的右边时,求证:△ADC≌△CEB;(2)如图2,当CE位于点F的左边时,求证:ED=BE-AD;(3)如图3,当CE在△ABC的内部时,试猜测ED、AD、BE之间的数量关系,并证实你的猜测.考点:全等三角形的判定与性质.专题:证实题;探究型.分析:(1)利用同角的余角相等得出∠CAD=∠BCE,进而根据AAS证实△ADC≌△CEB.(2)根据AAS证实△ADC≌△CEB后,得其对应边相等,进而得到ED=BE-AD.(3)根据AAS证实△ADC≌△CEB后,得DC=BE,AD=CE,又有ED=CE+DC,进而得到ED=AD+BE.解答:(1)证实:∵AD⊥CE,BE ⊥CE,∴∠ADC=∠CEB=90°.∵∠ACD+∠ECB=90°,∠CAD+∠ACD=90°,∴∠CAD=∠BCE(同角的余角相等).在△ADC与△CEB中∠ADC=∠CEB ∠CAD=∠BCE AC=BC ,∴△ADC≌△CEB(AAS).(2)证实:∵AD⊥CE,BE⊥CE,∴∠ADC=∠CEB=90°.∵∠ACD+∠ECB=90°,∠CAD+∠ACD=90°,∴∠CAD=∠BCE(同角的余角相等).在△ADC与△CEB中∠ADC=∠CEB ∠CAD=∠BCE AC=BC ,∴△ADC≌△CEB(AAS).∴DC=BE,AD=CE.又∵ED=CD-CE,∴ED=BE-AD.(3)ED=AD+BE.证实:∵AD⊥CE,BE⊥CE,∴∠ADC=∠CEB=90°.∵∠ACD+∠ECB=90°,∠CAD+∠ACD=90°,∴∠CAD=∠BCE(同角的余角相等).在△ADC与△CEB中∠ADC=∠CEB ∠CAD=∠BCE AC=BC ,∴△ADC≌△CEB(AAS).∴DC=BE,AD=CE.又∵ED=CE+DC,∴ED=AD+BE.点评:本题考查了全等三角形的判定和性质;利用全等三角形的对应边相等进行等量交换,证实线段之间的数量关系,这是一种很次要的方法,留意把握3.如图1、图2、图3,△AOB,△COD均是等腰直角三角形,∠AOB=∠COD=90º,(1)在图1中,AC与BD相等吗,有如何的地位关系?请说明理由.(2)若△COD绕点O顺时针扭转必定角度后,到达图2的地位,请问AC与BD还相等吗,还具有那种地位关系吗?为何?(3)若△COD绕点O顺时针扭转必定角度后,到达图3的地位,请问AC与BD还相等吗?还具有上问中的地位关系吗?为何?考点:扭转的性质;全等三角形的判定与性质;等腰直角三角形.分析:(1)根据等腰三角形的两腰相等进行解答.(2)证实△DOB≌△COA,根据全等三角形的对应边相等进行说明.解答:解:(1)相等.在图1中,∵△AOB,△COD均是等腰直角三角形,∠AOB=∠COD=90°,∴OA=OB,OC=OD,∴0A-0C=0B-OD,∴AC=BD;(2)相等.在图2中,0D=OC,∠DOB=∠COA,OB=OA,∴△DOB≌△COA,∴BD=AC.点评:本题考查了等腰三角形的性质、全等三角形的性质和扭转成绩,在扭转的过程中要留意哪些量是不变的,找出图形中的对应边与对应角.4.(2008河南).(9分)复习“全等三角形”的常识时,老师安插了一道功课题:“如图①,已知在△ABC中,AB=AC,P是△ABC内部任意一点,将AP绕A顺时针扭转至AQ,使∠QAP=∠BAC,连接BQ、CP,则BQ=CP.”小亮是个爱动脑筋的同学,他通过对图①的分析,证实了△ABQ≌△ACP,从而证得BQ=CP以后,将点P移到等腰三角形ABC以外,原题中的条件不变,发现“BQ=CP”仍然成立,请你就图②给出证实.考点:全等三角形的判定与性质;等腰三角形的性质.专题:证实题;探究型.分析:此题的两个小题思路是分歧的;已知∠QAP=∠BAC,那么这两个等角同时减去同一个角(2题是加上同一个角),来证得∠QAB=∠PAC;而根据扭转的性质知:AP=AQ,且已知AB=AC,即可由SAS证得△ABQ≌△ACP,进而得出BQ=CP的结论.解答:证实:(1)∵∠QAP=∠BAC,∴∠QAP-∠BAP=∠BAC-∠BAP,即∠QAB=∠CAP;在△BQA和△CPA中,AQ=AP ∠QAB=∠CAP AB=AC ,∴△BQA≌△CPA(SAS);∴BQ=CP.(2)BQ=CP仍然成立,理由如下:∵∠QAP=∠BAC,∴∠QAP+∠PAB=∠BAC+∠PAB,即∠QAB=∠PAC;在△QAB和△PAC中,AQ=AP ∠QAB=∠PAC AB=AC ,∴△QAB≌△PAC(SAS),∴BQ=CP.点评:此题次要考查了等腰三角形的性质和全等三角形的判定和性质;选择并利用三角形全等是准确解答本题的关键.5.(2009山西太原)将一张透明的平行四边形胶片沿对角线剪开,得到图①中的两张三角形胶片ABC△.将这两张三角形胶△≌DEF△和DEF△.且ABC片的顶点B 与顶点E 重合,把DEF △绕点B 顺时针方向扭转,这时候AC 与DF 订交于点O .①当DEF △扭转至如图②地位,点()B E ,C D ,在同不断线上时,AFD ∠与DCA ∠的数量关系是.②当DEF △继续扭转至如图③地位时,(1)中的结论还成立吗?AO 与DO 存在如何的数量关系?请说明理由.点:扭转的性质;全等三角形的判定与性质.专题:探究型.分析:(1)根据外角的性质,得∠AFD=∠D+∠ABC ,∠DCA=∠A+∠ABC ,从而得出∠AFD=∠DCA ;(2)成立.由△ABC ≌△DEF ,可证实∠ABF=∠DEC .则△ABF ≌△DEC ,从而证出∠AFD=∠DCA ;(3)BO ⊥AD .由△ABC ≌△DEF ,可证得点B 在AD 的垂直平分线上,进而证得点O 在AD 的垂直平分线上,则直线BO 是AD 的垂直平分线,即BO ⊥AD .解答:解:(1)∠AFD=∠DCA (或相等). (2)∠AFD=∠DCA (或成立),理由如下:方法一:由△ABC ≌△DEF ,得AB=DE ,BC=EF (或BF=EC ),∠ABC=∠DEF ,∠BAC=∠EDF .∴∠ABC-∠FBC=∠DEF-∠CBF , ∴∠ABF=∠DEC .在△ABF 和△DEC 中, AB=DE ∠ABF=∠DEC BF=EC ∴△ABF ≌△DEC ,∠BAF=∠EDC .∴∠BAC-∠BAF=∠EDF-∠EDC ,∠FAC=∠CDF . ∵∠AOD=∠FAC+∠AFD=∠CDF+∠DCA , ∴∠AFD=∠DCA .方法二:连接AD .同方法一△ABF ≌△DEC ,∴AF=DC .由△ABC ≌△DEF ,得FD=CA .在△AFD ≌△DCA , AF=DC FD=CA AD=DA ∴△AFD ≌△DCA ,∠AFD=∠DCA . (3)如图,BO ⊥AD .方法一:由△ABC ≌△DEF ,点B 与点E 重合, 得∠BAC=∠BDF ,BA=BD . ∴点B 在AD 的垂直平分线上, 且∠BAD=∠BDA .∵∠OAD=∠BAD-∠BAC ,∠ODA=∠BDA-∠BDF , ∴∠OAD=∠ODA .∴OA=OD ,点O 在AD 的垂直平分线上. ∴直线BO 是AD 的垂直平分线,BO ⊥AD .方法二:耽误BO 交AD 于点G ,同方法一,OA=OD . 在△ABO 和△DBO 中, AB=DB BO=BO OA=OD ∴△ABO ≌△DBO ,∠ABO=∠DBO .在△ABG 和△DBG 中, AB=DB ∠ABG=∠DBG BG=BG ∴△ABG ≌△DBG ,∠AGB=∠DGB=90°.∴BO ⊥AD .点评:本题考查了三角形全等的判定和性质和扭转的性质,是基础常识要熟练把握.例1 正方形ABCD 中,E 为BC 上的一点,F 为CD 上的一点,BE+DF=EF ,求∠EAF 的度数.考点:扭转的性质;全等三角形的判定与性质;正方形的性质.分析:耽误EB 使得BG=DF ,易证△ABG ≌△ADFFED CBA(SAS)可得AF=AG,进而求证△AEG≌△AEF可得∠EAG=∠EAF,再求出∠EAG+∠EAF=90°即可解题.解答:解:耽误EB使得BG=DF,在△ABG和△ADF中,由 AB=AD ∠ABG=∠ADF=90° BG=DF ,可得△ABG≌△ADF(SAS),∴∠DAF=∠BAG,AF=AG,又∵EF=DF+BE=EB+BG=EG,AE=AE,∴△AEG≌△AEF(SSS),∴∠EAG=∠EAF,∵∠DAF+∠EAF+∠BAE=90°∴∠EAG+∠EAF=90°,∴∠EAF=45°.答:∠EAF的角度为45°.点评:本题考查了正方形各内角均为直角,考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证∠EAG=∠EAF是解题的关键.∆斜边AB的中点,DN,DM,DN分别交BC,CA于点E,F.A ∠绕点D动弹时,求证DE=DF.(1)当MDN(2)若AB=2,求四边形DECF的面积.考点:扭转的性质;全等三角形的判定与性质;等腰直角三角形.专题:计算题.分析:(1)连CD,根据等腰直角三角形的性质得到CD平分∠ACB,CD⊥AB,∠A=45°,CD=DA,则∠BCD=45°,∠CDA=90°,由∠DM⊥DN得∠EDF=90°,根据等角的余角相等得到∠CDE=∠ADF,根据全等三角形的判定易得△DCE≌△ADF,即可得到结论;(2)由△DCE ≌△ADF ,则S △DCE=S △ADF ,因而四边形DECF 的面积=S △ACD ,由而AB=2可得CD=DA=1,根据三角形的面积公式易求得S △ACD ,从而得到四边形DECF 的面积.解答:解:(1)连CD ,如图, ∵D 为等腰Rt △ABC 斜边AB 的中点,∴CD 平分∠ACB ,CD ⊥AB ,∠A=45°,CD=DA , ∴∠BCD=45°,∠CDA=90°, ∵∠DM ⊥DN , ∴∠EDF=90°, ∴∠CDE=∠ADF , 在△DCE 和△ADF 中,∠DCE=∠DAF DC=DA ∠CDE=∠ADF , ∴△DCE ≌△ADF , ∴DE=DF ;(2)∵△DCE ≌△ADF , ∴S △DCE=S △ADF ,∴四边形DECF 的面积=S △ACD , 而AB=2, ∴CD=DA=1,∴四边形DECF 的面积=S △ACD=1 2 CD •DA=1 2 .点评:本题考查了扭转的性质:扭转前后两图形全等,即对应角相等,对应线段相等,对应点与扭转中间的连线段的夹角等于扭转角.也考查了等腰直角三角形的性质和全等三角形的判定与性质. 1、已知四边形ABCD中,AB AD⊥,BC CD⊥,AB BC=,120ABC =∠,60MBN =∠,MBN ∠绕B 点扭转,它的两边分别交AD DC ,(或它们的耽误(图1) A BCDE FM N(图2)A B CDE FMN(图3)AB CDE F MN线)于E F ,.当MBN ∠绕B 点扭转到AE CF =时(如图1),易证AE CF EF +=.当MBN ∠绕B 点扭转到AE CF ≠时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证实;若不成立,线段AE CF ,,EF 又有如何的数量关系?请写出你的猜测,不需证实.2、(西城09年一模)已知以AB 为一边作正方形ABCD,使P 、D 两点落在直线AB 的两侧.(1)如图,当∠APB=45°时,求AB 及PD 的长;(2)当∠APB 变更,且其它条件不变时,求PD 的最大值,及响应∠APB 的大小.3、在等边ABC ∆的两边AB 、AC 所在直线上分别有两点M 、N ,D 为ABC 外一点,且︒=∠60MDN ,︒=∠120BDC ,BD=DC. 探究:当M 、N 分别在直线AB 、AC 上挪动时,BM 、NC 、MN 之间的数量关系及AMN ∆的周长Q 与等边ABC ∆的周长L 的关系.图1 图2 图3(I )如图1,当点M 、N 边AB 、AC 上,且DM=DN 时,BM 、NC 、MN之间的数量关系是; 此时=L Q ;(II )如图2,点M 、N 边AB 、AC 上,且当DM ≠DN 时,猜测(I )问的两个结论还成立吗?写出你的猜测并加以证实;(III ) 如图3,当M 、N 分别在边AB 、CA 的耽误线上时, 若AN=x ,则Q=(用x 、L 暗示).考点:等边三角形的性质;全等三角形的判定与性质.分析:(1)由DM=DN ,∠MDN=60°,可证得△MDN 是等边三角形,又由△ABC 是等边三角形,CD=BD ,易证得Rt △BDM ≌Rt △CDN ,然后由直角三角形的性质,即可求得BM、NC、MN之间的数量关系BM+NC=MN,此时QL =2 3 ;(2)在CN的耽误线上截取CM1=BM,连接DM1.可证△DBM≌△DCM1,即可得DM=DM1,易证得∠CDN=∠MDN=60°,则可证得△MDN≌△M1DN,然后由全等三角形的性质,即可得结论仍然成立;(3)首先在CN上截取CM1=BM,连接DM1,可证△DBM≌△DCM1,即可得DM=DM1,然后证得∠CDN=∠MDN=60°,易证得△MDN≌△M1DN,则可得NC-BM=MN.解答:解:(1)如图1,BM、NC、MN之间的数量关系 BM+NC=MN.此时 Q L =2 3 .(2分).理由:∵DM=DN,∠MDN=60°,∴△MDN是等边三角形,∵△ABC是等边三角形,∴∠A=60°,∵BD=CD,∠BDC=120°,∴∠BDC=∠DCB=30°,∴∠MBD=∠NCD=90°,∵DM=DN,BD=CD,∴Rt△BDM≌Rt△CDN,∴∠BDM=∠CDN=30°,BM=CN,∴DM=2BM,DN=2CN,∴MN=2BM=2CN=BM+CN;∴AM=AN,∴△AMN是等边三角形,∵AB=AM+BM,∴AM:AB=2:3,∴Q L =2 3 ;(2)猜测:结论仍然成立.(3分).证实:在CN的耽误线上截取CM1=BM,连接DM1.(4分)∵∠MBD=∠M1CD=90°,BD=CD,∴△DBM≌△DCM1,∴DM=DM1,∠MBD=∠M1CD,M1C=BM,∵∠MDN=60°,∠BDC=120°,∴∠M1DN=∠MDN=60°,∴△MDN≌△M1DN,∴MN=M1N=M1C+NC=BM+NC,∴△AMN的周长为:AM+MN+AN=AM+BM+CN+AN=AB+AC,∴Q L =2 3 ;(3)证实:在CN上截取CM1=BM,连接DM1.(4分)可证△DBM≌△DCM1,∴DM=DM1,(5分)可证∠CDN=∠MDN=60°,∴△MDN≌△M1DN,∴MN=M1N,(7分).∴NC-BM=MN.(8分).点评:此题考查了等边三角形,直角三角形,等腰三角形的性质和全等三角形的判定与性质等常识.此题综合性很强,难度较大,解题的关键是留意数形结合思想的利用与辅助线的作法.例8.(2005年马尾)用两个全等的等边三角形△ABC和△ACD拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合,使三角尺的60°角的顶点与点A重合,两边分别与AB,AC重合.将三角尺绕点A按逆时针方向扭转.(1)当三角尺的两边分别与菱形的两边BC,CD订交于点E,F时,(如图13—1),通过观察或测量BE,CF的长度,你能得出什么结论?并证实你的结论;(2)当三角尺的两边分别与菱形的两边BC,CD的耽误线订交于点E,F 时(如图13—2),你在(1)中得到的结论还成立吗?简要说明理由.考点:菱形的性质;三角形的面积;全等三角形的判定与性质;扭转的性质.分析:(1)利用全等三角形的判定得出△ABE≌△ACF即可得出答案;(2)根据已知可以得出∠BAE=∠CAF,进而求出△ABE≌△ACF即可;(3)利用四边形AECF的面积S=S△AEC+S△ACF=S△AEC+S△ABE=S △ABC求出即可.解答:解:(1)得出结论是:BE=CF,证实:∵∠BAC=∠EAF=60°,∴∠BAC-∠EAC=∠EAF-∠EAC,即:∠BAE=∠CAF,又∵AB=AC,∠ABE=∠ACF=60°,∴∠BAE=∠CAF AB=AC ∠ABE=∠ACF ,∴△ABE≌△ACF(ASA),∴BE=CF,(2)还成立,证实:∵∠BAC=∠EAF=60°,∴∠BAC+∠EAC=∠EAF+∠EAC,即∠BAE=∠CAF,又∵AB=AC,∠ABE=∠ACF=60°,即∠BAE=∠CAF AB=AC ∠ABE=∠ACF ,∴△ABE≌△ACF(ASA),∴BE=CF,(3)证实:∵△ABE≌△ACF,∴S△ABE=S△ACF,∴四边形AECF的面积S=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC;而S△ABC=1 2 S菱形ABCD,∴S=1 2 S菱形ABCD.点评:此题次要考查了全等三角形的判定和四边形面积,熟练利用全等三角形判定求出是解题关键.解:(1)BE=CF.证实:在△ABE和△ACF中,∵∠BAE+∠EAC=∠CAF+∠EAC=60°,∴∠BAE=∠CAF.∵AB=AC,∠B=∠ACF=60°,∴△ABE≌△ACF(ASA).∴BE=CF.(2)BE=CF仍然成立. 根据三角形全等的判定公理,同样可以证实△ABE和△ACF扭转型1、如图,正方形ABCD 的边长为1,G 为CD 边上一动点(点G 与C 、D不重合), 以CG 为一边向正方形ABCD 外作正方形GCEF ,连接DE 交BG 的耽误线于H.求证:①△BCG ≌△DCE ② BH ⊥DE考点:正方形的性质;全等三角形的判定与性质;线段垂直平分线的性质.专题:动点型.分析:(1)根据正方形的边的性质和直角可通过SAS 判定△BCG ≌△DCE ,从而利用全等的性质得到∠BGC=∠DEC ;(2)连接BD ,解题关键是利用垂直平分线的性质得出BD=BE ,从而找到BD= 2,CE=BE-BC= 2-1,根据全等三角形的性质求解即可.解答:解:(1)证实:∵四边形ABCD 、GCEF 都是正方形,∴BC=DC ,∠BCG=∠DCE=90°,GC=EC ∴△BCG ≌△DCE (3分) ∴∠BGC=∠DEC (4分) (2)连接BD如果BH 垂直平分DE ,则有BD=BE (6分) ∵BC=CD=1, ∴BD= 2 (8分)∴CE=BE-BC= 2 -1(9分) ∴CG=CE= 2 -1即当CG= 2 -1时,BH 垂直平分DE .(10分)点评:此题次要考查正方形的性质,全等三角形的判定和线段的垂直平分线的性质等几何常识.线段的垂直平分线上的点到线段的两个端点的距离相等.特殊图形的特殊性FED CABG H质要熟练把握.2、两个大小分歧的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B ,C ,E在同一条直线上,连结DC .(1)请找出图2中的全等三角形,并给予证实(说明:结论中不得含有未标识的字母);(2)证实:DC ⊥BE .∠BAE=∠CAD AE=AD∴△ABE ≌△ACD . (2)∵△ABE ≌△ACD , ∴∠ACD=∠ABE=45°.又∵∠ACB=45°,∴∠BCD=∠ACB+∠ACD=90°. ∴DC ⊥BE .点评:此题是一个实际利用成绩,利用全等三角形的性质与判定来解决实际成绩,关键是理解题意,得到所须要的已知条件.3、(1)如图7,点O 是线段AD 的中点,分别以AO 和DO 为边在线段AD 的同侧作等边三角形OAB 和等边三角形OCD ,连结AC 和BD ,订交于点E ,连结BC .求∠AEB 的大小;(2)如图8,ΔOAB 固定不动,坚持ΔOCD 的外形和大小不变,将ΔOCD 绕着点O 扭转(ΔOAB 和ΔOCD 不克不及堆叠),求∠AEB 的大小.4、如图,AE ⊥AB ,AD ⊥AC ,AB=AE ,∠B=∠E ,求证:(1)BD=CE ;(2)BD ⊥CE ..证实:(1)AE ⊥AB ,AD ⊥AC ∠BAE=∠CAD∠BAD=∠CAE .而AB=AE ,∠B=∠E ,∴△ABD ≌△AEC .∴BD=CE .(2)由△ABD ≌△AEC 知∠B=∠E .而∠AGB=∠EGF ,∴∠EFG=∠EAB=90°,∴BD ⊥CE .如图,点O 是线段AD 的中点,分别以AO 和DO 为边在线段AD 的同侧CBO D图7AEBAODCE图8作等边三角形OAB和等边三角形OCD,连接AC和BD,订交于点E,连接BC.求∠AEB的大小.考点:等边三角形的性质;全等三角形的判定与性质.专题:计算题.分析:因为△BOC和△ABO都是等边三角形,可得OD=DC=OC=OB=OA,进而求出∠BDA与∠CAD的大小及关系,则可求解∠AEB.解答:解:∵△DOC和△ABO都是等边三角形,且点O是线段AD的中点,∴OD=DC=OC=OB=OA,∴△ACD≌△DBA,∴∠BDA=∠CAD.又∵∠BDA+∠OBD=∠BOA=60°,而∠ODB=∠OBD,∴∠BDA=30°.∴∠CAD=30°.∵∠AEB=∠BDA+∠CAD,∴∠AEB=60°.点评:本题考查了全等三角形的判定与性质及等边三角形的性质;可环绕结论寻觅全等三角形,应用全等三角形的性质判定线段相等,求得角的度数是准确解答本题的关键.答题:yeyue5、如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.求证:(1)EC=BF;(2)EC⊥BFAB MCF6、 正方形ABCD 中,E 为BC 上的一点,F 为CD 上的一点,BE+DF=EF ,求∠EAF 的度数.考点:扭转的性质;全等三角形的判定与性质;正方形的性质.分析:耽误EB 使得BG=DF ,易证△ABG ≌△ADF (SAS )可得AF=AG ,进而求证△AEG ≌△AEF 可得∠EAG=∠EAF ,再求出∠EAG+∠EAF=90°即可解题.解答:解:耽误EB 使得BG=DF , 在△ABG 和△ADF 中,由 AB=AD ∠ABG=∠ADF=90° BG=DF , 可得△ABG ≌△ADF (SAS ), ∴∠DAF=∠BAG ,AF=AG ,又∵EF=DF+BE=EB+BG=EG ,AE=AE , ∴△AEG ≌△AEF (SSS ), ∴∠EAG=∠EAF ,∵∠DAF+∠EAF+∠BAE=90° ∴∠EAG+∠EAF=90°, ∴∠EAF=45°.答:∠EAF 的角度为45°.点评:本题考查了正方形各内角均为直角,考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证∠EAG=∠EAF 是解题的关键.7、D 为等腰Rt ABC ∆斜边AB 的中点,DM ⊥DN,DM,DN 分别交BC,CA 于点E,F.①当MDN ∠绕点D 动弹时,求证DE=DF. ②若AB=2,求四边形DECF 的面积.10、如图,已知AB=CD=AE=BC+DE=2,∠ABC=∠AED=90°,求五边A形ABCDE 的面积考点:全等三角形的判定与性质.专题:利用题.分析:可耽误DE 至F ,使EF=BC ,可得△ABC ≌△AEF ,连AC ,AD ,AF ,可将五边形ABCDE 的面积转化为两个△ADF 的面积,进而求出结论.解答:解:耽误DE 至F ,使EF=BC ,连AC ,AD ,AF ,∵AB=CD=AE=BC+DE ,∠ABC=∠AED=90°, ∴CD=EF+DE=DF ,在Rt △ABC 与Rt △AEF 中,∵ AB=AE ∠ABC=∠AEF BC=EF ∴Rt △ABC ≌Rt △AEF (SAS ), ∴AC=AF ,在△ACD 与△AFD 中, ∵ AC=AF CD=DF AD=AD ∴△ACD ≌△AFD (SSS ),∴SABCDE=2S △ADF=2×1 2 •DF •AE=2×1 2 ×2×2=4.点评:本题次要考查了全等三角形的判定及性质和三角形面积的计算,应熟练把握 五、扭转例1 正方形ABCD 中,E 为BC 上的一点,F 为CD 上的一点,BE+DF=EF ,求∠EAF 的度数.将三角形ADF 绕点A 顺时针扭转90度,至三角形ABG则GE=GB+BE=DF+BE=EF 又AE=AE ,AF=AG , 所以三角形AEF 全等于AEG所以∠EAF=∠GAE=∠BAE+∠GAB=∠BAE+∠DAF 又∠EAF+∠BAE+∠DAF=90FED CBA所以∠EAF=45度(1)如图1,现有一正方形ABCD,将三角尺的指直角顶点放在A点处,两条直角边也与CB的耽误线、DC分别交于点E、F.请你通过观察、测量,判断AE与AF之间的数量关系,并说明理由.(2)将三角尺沿对角线平移到图2的地位,PE、PF之间有如何的数量关系,并说明理由.(3)如果将三角尺扭转到图3的地位,PE、PF之间是否还具有(2)中的数量关系?如果有,请说明理由.如果没有,那么点P在AC的什么地位时,PE、PF才具有(2)中的数量关系.考点:正方形的性质;全等三角形的判定与性质.专题:几何综合题.分析:(1)证实△ABE≌△ADF可推出AE=AF.(2)本题要借助辅助线的帮忙.过点P作PM⊥BC于M,PN⊥DC于N,证实△PME≌△PNF可推出PE=PF.(3)PE、PF不具有(2)中的数量关系.当点P在AC的中点时,PE,PF 才具有(2)中的数量关系.解答:解:(1)如图1,AE=AF.理由:证实△ABE≌△ADF(ASA)(2)如图2,PE=PF.理由:过点P作PM⊥BC于M,PN⊥DC于N,则PM=PN.由此可证得△PME≌△PNF(ASA),从而证得PE=PF.(3)PE、PF不具有(2)中的数量关系.当点P在AC的中点时,PE、PF才具有(2)中的数量关系.考点:正方形的性质;全等三角形的判定与性质.专题:几何综合题.分析:(1)证实△ABE≌△ADF可推出AE=AF.(2)本题要借助辅助线的帮忙.过点P作PM⊥BC于M,PN⊥DC于N,证实△PME≌△PNF可推出PE=PF.(3)PE、PF不具有(2)中的数量关系.当点P在AC的中点时,PE,PF才具有(2)中的数量关系.解答:解:(1)如图1,AE=AF.理由:证实△ABE≌△ADF(ASA)(2)如图2,PE=PF.理由:过点P作PM⊥BC于M,PN⊥DC于N,则PM=PN.由此可证得△PME≌△PNF(ASA),从而证得PE=PF.(3)PE、PF不具有(2)中的数量关系.当点P在AC的中点时,PE、PF才具有(2)中的数量关系.点评:本题考查的是正方形的性质和全等三角形的判定.例8.(2005年马尾)用两个全等的等边三角形△ABC和△ACD拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合,使三角尺的60°角的顶点与点A重合,两边分别与AB,AC重合.将三角尺绕点A按逆时针方向扭转.(1)当三角尺的两边分别与菱形的两边BC,CD订交于点E,F时,(如图13—1),通过观察或测量BE,CF的长度,你能得出什么结论?并证实你的结论;(2)当三角尺的两边分别与菱形的两边BC,CD的耽误线订交于点E,F时(如图13—2),你在(1)中得到的结论还成立吗?简要说明理由.解:(1)BE=CF.证实:在△ABE 和△ACF 中, ∵∠BAE +∠EAC =∠CAF +∠EAC =60°,∴∠BAE =∠CAF .∵AB =AC ,∠B =∠ACF =60°,∴△ABE ≌△ACF (ASA ).∴BE =CF .(2)BE =CF 仍然成立. 根据三角形全等的判定公理,同样可以证实△ABE 和△ACF1、用两个全等的等边三角形△ABC 和△°角的三角尺与这个菱形叠合,使三角尺的60°角的顶点与点A 重合,两边分别与AB 、AC 重合.将三角尺绕点A 按逆时针方向扭转.(1)当三角尺的两边分别与菱形的两边BC 、CD 订交于点E 、F 时(如图所示),通过观察或测量BE 、CF的长度,你能得出什么结论?并证实你的结论;(2)当三角尺的两边分别与菱形的两边BC 、CD 的耽误线订交于点E 、F 时(如图所示),你在(1)中得到的结论还成立吗?说明理由.6、 已知∠AOB=90°,∠AOB 的平分线OM 上有一点C ,将一个三角板的直角顶点与点C 重合,它的两条直角边分别与OA 、OB 或它们的反向耽误线订交于D 、E.当三角形绕点C 扭转到CD 与OA 垂直时(如图1),易证:CD=CE当三角板绕点C 扭转到CD 与OA 不垂直时,在图2图3这两种情况下,上述结论是否成立,请给予证实,若不成立,请写出你的猜测,不需证实.10、如图,正方形ABCD 的边长为1,G 为CD 边上一动点(点G 与C 、D不重合),以C为一边向正方形ABCD外作正方形GCEF,连接DE交BG的耽误线于H.(1)说明:△BCG≌△DCE;(2)BG与CD有何关系?为何?(3)将正方形GCEF绕点C顺时针扭转,在扭转过程中,(1)、(2)中的结论还成立吗?画出一个图形,直接回答,不必说明理由.如图①,点M为锐角三角形ABC内任意一点,连接AM、绕点B逆时针扭转60°得到BN,连接EN.(1)求证:△AMB≌△ENB;(2)若AM+BM+CM的值最小,则称点M为△ABC的费尔马点.若点M 为△ABC的费尔马点,试求此时∠AMB、∠BMC、∠CMA的度数;(3)小翔受以上启发,得到一个作锐角三角形费尔马点的简便方法:如图②,分别以△ABC的AB、AC为一边向外作等边△ABE和等边△ACF,连接CE、BF,设交点为M,则点M即为△ABC的费尔马点.试说明这类作法的根据.考点:全等三角形的判定与性质;等边三角形的性质.分析:(1)结合等边三角形的性质,根据SAS可证△AMB≌△ENB;(2)连接MN,由(1)的结论证实△BMN为等边三角形,所以BM=MN,即AM+BM+CM=EN+MN+CM,所以当E、N、M、C四点共线时,AM+BM+CM的值最小,从而可求此时∠AMB、∠BMC、∠CMA的度数;(3)根据(2)中费尔马点的定义,又△ABC的费尔马点在线段EC上,同理也在线段BF上.是以线段EC与BF的交点即为△ABC的费尔马点.解答:解:(1)证实:∵△ABE为等边三角形,∴AB=BE,∠ABE=60°.而∠MBN=60°,∴∠ABM=∠EBN.又∵BM=BN,∴△AMB≌△ENB.(2)连接MN.由(1)知,AM=EN.∵∠MBN=60°,BM=BN,∴△BMN为等边三角形.∴BM=MN.∴AM+BM+CM=EN+MN+CM.∴当E、N、M、C四点共线时,AM+BM+CM的值最小.此时,∠BMC=180°-∠NMB=120°;∠AMB=∠ENB=180°-∠BNM=120°;∠AMC=360°-∠BMC-∠AMB=120°.(3)由(2)知,△ABC的费尔马点在线段EC上,同理也在线段BF上.是以线段EC与BF的交点即为△ABC的费尔马点.点评:本题考查全等三角形的判定与性质和等边三角形的性质,是一道综合性的题目难度很大.。
全等三角形旋转模型知识归纳总结附解析

全等三角形旋转模型知识归纳总结附解析一、全等三角形旋转模型1.(课题研究)旋转图形中对应线段所在直线的夹角(小于等于90°的角)与旋转角的关系.(问题初探)线段AB 绕点O 顺时针旋转得到线段CD ,其中点A 与点C 对应,点B 与点D 对应,旋转角的度数为α,且0°<α<180°.(1)如图①,当α=60°时,线段AB 、CD 所在直线夹角(锐角)为 ;(2)如图②,当90°<α<180°时,直线AB 与直线CD 所夹锐角与旋转角α存在怎样的数量关系?请说明理由;(形成结论)旋转图形中,当旋转角小于平角时,对应线段所在直线的夹角与旋转角 .(运用拓广)运用所形成的结论解决问题:(3)如图③,四边形ABCD 中,∠ABC =60°,∠ADC =30°,AB =BC ,CD =3,BD =19,求AD 的长.解析:(1)60°;(2)互补,理由见解析;【形成结论】相等或互补;(310【分析】(1)由旋转的性质可得AB CD =,OA OC =,BO DO =,可证()AOB COD SSS ,可得B D ∠=∠,由三角形内角和定理可求解;(2)由旋转的性质可得AB CD =,OA OC =,BO DO =,可证()AOBCOD SSS ,可得B D ∠=∠,由平角的定义和四边形内角和定理可求解; 【形成结论】由(1)(2)可知对应线段所在直线的所夹锐角角与旋转角:相等或互补;【运用拓广】(3)将BCD ∆绕点B 顺时针旋转60︒,得到BAF ∆,连接FD ,由旋转的性质可得BF BD =,3AF CD ==,由三角形内角和定理可求90FAD ∠=︒,由勾股定理可求解.【详解】解:(1)如图1,延长DC 交AB 于F ,交BO 于E ,α=︒,60∴∠=︒,60BOD线段AB绕点O顺时针旋转得线段CD,=,AB CD=,BO DO∴=,OA OCAOB COD SSS,()B D∴∠=∠,∠=∠,OED BEF,B DBFE EOD,60故答案为:60︒;(2)直线AB与直线CD所夹锐角角与旋转角α互补,理由如下:如图2,延长AB,DC交于点E,线段AB绕点O顺时针旋转得线段CD,=,=,BO DO∴=,OA OCAB CDAOB COD SSS,()ABO D,ABO EBO,180D EBO,180360EBO E D BOD,E BOD,180∴直线AB与直线CD所夹锐角角与旋转角α互补.形成结论由(1)(2)(3)可知:旋转图形中,当旋转角小于平角时,对应线段所在直线的所夹锐角角与旋转角:相等或互补.故答案为:相等或互补.运用拓广(3)如图3,将BCD ∆绕点B 顺时针旋转60︒,得到BAF ∆,连接FD ,延长FA ,DC 交于点E ,∴旋转角60ABC ∠=︒,BCD BAF ,60AED ABC ∴∠=∠=︒,3AF CD ==,BD BF =,30ADC ∠=︒,90FAD AED ADC ,又60FBD ABC ,BF BD =, BFD ∴∆是等边三角形,BF BD DF ,∴在Rt DAF 中,2219910ADDF AF . 【点睛】本题是几何变换综合题,考查了旋转的性质,全等三角形的判定和性质,等边三角形的判定和性质等知识,添加辅助线构造全等三角形是本题的关键.2.问题背景如图(1),在四边形ABCD 中,∠B+∠D =180°,AB =AD ,∠BAD =α,以点A 为顶点作一个角,角的两边分别交BC ,CD 于点E ,F ,且∠EAF 12=α,连接EF ,试探究:线段BE ,DF ,EF 之间的数量关系.(1)特殊情景在上述条件下,小明增加条件“当∠BAD =∠B =∠D =90°时”如图(2),小明很快写出了:BE ,DF ,EF 之间的数量关系为______.(2)类比猜想类比特殊情景,小明猜想:在如图(1)的条件下线段BE ,DF ,EF 之间的数量关系是否仍然成立?若成立,请你帮助小明完成证明;若不成立,请说明理由.(3)解决问题如图(3),在△ABC中,∠BAC=90°,AB=AC=4,点D,E均在边BC上,且∠DAE=45°,若BD2=,请直接写出DE的长.答案:B解析:(1)BE+DF=EF;(2)成立;(3)DE523 =【分析】(1)将△ABE绕点A逆时针旋转90°,得到△ADG,由旋转的性质可得AE=AG,BE=DG,∠BAE=∠DAG,根据∠EAF=12∠BAD可得∠BAE+∠DAF=45°,即可得出∠∠EAF=∠FAG,利用SAS可证明△AFE≌△AFG,可得EF=FG,进而可得EF=BE+FD;(2)将△ABE 绕点A逆时针旋转α得到△ADH,由旋转的性质可得∠ABE=∠ADH,∠BAE=∠DAH,AE=AH,BE=DH,根据∠BAD=α,∠EAF12=α可得∠BAE+∠FAD12=α,进而可证明∠FAH=∠EAF,利用SAS可证明△AEF≌△AHF,可得EF=FH=BE+FD;(3)将△AEC绕点A顺时针旋转90°,得到△AE′B,连接DE′,由旋转的性质可得BE′=EC,AE′=AE,∠C=∠ABE′,∠EAC=∠E′AB,根据等腰直角三角形的性质可得∠ABC=∠ACB=45°,BC=42,即可求出∠E′BD=90°,利用SAS可证明△AEF≌△AHF,可得DE=DE′,利用勾股定理求出DE的长即可的答案.【详解】(1)BE+DF=EF,如图1,将△ABE绕点A逆时针旋转90°,得到△ADG,∵∠ADC=∠B=∠ADG=90°,∴∠FDG=180°,即点F,D,G共线.由旋转可得AE=AG,BE=DG,∠BAE=∠DAG.∵∠BAE+∠DAF=∠BAD﹣∠EAF=90°﹣12∠BAD=90°-45°=45°,∴∠DAG+∠DAF=45°,即∠FAG=45°,∴∠EAF=∠FAG,∴△AFE≌△AFG(SAS),∴EF=FG.又∵FG=DG+DF=BE+DF,∴BE+DF=EF,故答案为BE+DF=EF.(2)成立.如图2,将△ABE绕点A逆时针旋转α得到△ADH,可得∠ABE=∠ADH,∠BAE=∠DAH,AE=AH,BE=DH.∵∠B+∠ADC=180°,∴∠ADH+∠ADC=180°,∴点C,D,H在同一直线上.∵∠BAD=α,∠EAF12=α,∴∠BAE+∠FAD12=α,∴∠DAH+∠FAD12=α,∴∠FAH=∠EAF,又∵AF=AF,∴△AEF≌△AHF(SAS),∴EF=FH=DF+DH=DF+BE;(3)DE523 =,如图3,将△AEC绕点A顺时针旋转90°,得到△AE′B,连接DE′.可得BE′=EC,AE′=AE,∠C=∠ABE′,∠EAC=∠E′AB,在Rt△ABC中,∵AB=AC=4,∠BAC=90°,∴∠ABC=∠ACB=45°,BC=2,∴2,∴∠ABC+∠ABE′=90°,即∠E′BD=90°,∴E′B 2+BD 2=E′D 2.易证△AE′D ≌△AED ,∴DE =DE′,∴DE 2=BD 2+EC 2,即DE 222(2)(32)DE =+-,解得523DE =. 【点睛】本题考查旋转的性质、全等三角形的判定与性质、勾股定理,旋转后不改变图形的大小和形状,并且对应点到旋转中心的距离相等,对应点与旋转中心的连线的夹角等于旋转角,熟练掌握旋转的性质及全等三角形的判定定理是解题关键.3.一位同学拿了两块45︒三角尺MNK ∆,ACB ∆做了一个探究活动:将MNK ∆的直角顶点M 放在ACB ∆的斜边AB 的中点处,设4AC BC ==.(1)如图1所示,两三角尺的重叠部分为ACM ∆,则重叠部分的面积为______,周长为______.(2)将如图1所示中的MNK ∆绕顶点M 逆时针旋转45︒,得到如图2所示,此时重叠部分的面积为______,周长为______.(3)如果将MNK ∆绕M 旋转到不同于如图1所示和如图2所示的图形,如图3所示,请你猜想此时重叠部分的面积为______.(4)在如图3所示情况下,若1AD =,求出重叠部分图形的周长.答案:A解析:(1)4,442+;(2)4,8;(3)4;(4)425+【分析】()1根据4AC BC ==,90ACB ∠=,得出AB 的值,再根据M 是AB 的中点,得出AM MC =,求出重叠部分的面积,再根据AM ,MC ,AC 的值即可求出周长;()2易得重叠部分是正方形,边长为12AC ,面积为214AC ,周长为2.AC ()3过点M 分别作AC 、BC 的垂线MH 、ME ,垂足为H 、.E 求得RtMHD ≌Rt MEG ,则阴影部分的面积等于正方形CEMH 的面积. ()4先过点M 作ME BC ⊥于点E ,MH AC ⊥于点H ,根据DMH EMH ∠∠=,MH ME =,得出Rt DHM ≌Rt EMG ,从而得出HD GE =,CE AD =,最后根据AD 和DF的值,算出DM =. 【详解】解:()14AC BC ==,90ACB ∠=,AB ∴== M 是AB 的中点,AM ∴=45ACM ∠=,AM MC ∴=,∴4=, ∴周长为:44AM MC AC ++==+故答案为4,4+;()2重叠部分是正方形,∴边长为1422⨯=,面积为14444⨯⨯=, 周长为248⨯=.故答案为4,8.()3过点M 分别作AC 、BC 的垂线MH 、ME ,垂足为H 、E , M 是ABC 斜边AB 的中点,4AC BC ==,12MH BC ∴=, 12ME AC =, MH ME ∴=,又90NMK HME ∠∠==,90NMH HMK ∠∠∴+=,90EMG HMK ∠∠+=,HMD EMG ∠∠∴=,在MHD 和MEG 中,HMD GME MH MEDHM MEG ∠=∠⎧⎪=⎨⎪∠=∠⎩, MHD ∴≌()MEG ASA ,∴阴影部分的面积等于正方形CEMH 的面积, 正方形CEMH 的面积是1144422ME MH ⋅=⨯⨯⨯=; ∴阴影部分的面积是4;故答案为4.()4如图所示, 过点M 作ME BC ⊥于点E ,MH AC ⊥于点H ,∴四边形MECH 是矩形,MH CE ∴=,45A ∠=,45AMH ∠∴=,AH MH ∴=,AH CE ∴=,在Rt DHM 和Rt GEM 中,DMH EMG MH MEDHM GEM ∠=∠⎧⎪=⎨⎪∠=∠⎩, Rt DHM ∴≌.Rt GEMGE DH ∴=,AH DH CE GE ∴-=-,CG AD ∴=,1AD =,1.DH ∴=145DM ∴=+=.∴四边形DMGC 的周长为:CE CD DM ME +++2AD CD DM =++425=+【点睛】此题考查了等腰直角三角形,利用等腰直角三角形的性质,等腰直角三角形的面积公式,正方形的面积公式,全等三角形的判定和性质求解.4.如图1,在Rt △ABC 中,∠A =90°,AB =AC ,点D ,E 分别在边AB ,AC 上,AD =AE ,连接DC ,点M ,P ,N 分别为DE ,DC ,BC 的中点.(1)观察猜想:图1中,线段PM 与PN 的数量关系是 ,位置关系是 ;(2)探究证明:把△ADE 绕点A 逆时针方向旋转到图2的位置,连接MN ,BD ,CE ,判断△PMN 的形状,并说明理由;(3)拓展延伸:把△ADE 绕点A 在平面内自由旋转,若AD =4,AB =10,请直接写出△PMN 面积的最大值.解析:(1)PM =PN ,PM ⊥PN ;(2)△PMN 是等腰直角三角形.理由见解析;(3)S △PMN 最大=492. 【分析】(1)由已知易得BD CE =,利用三角形的中位线得出12PM CE =,12PN BD =,即可得出数量关系,再利用三角形的中位线得出//PM CE 得出DPM DCA ∠=∠,最后用互余即可得出位置关系;(2)先判断出ABD ACE ∆≅∆,得出BD CE =,同(1)的方法得出12PM BD =,12PN BD =,即可得出PM PN =,同(1)的方法由MPN DCE DCB DBC ACB ABC ∠=∠+∠+∠=∠+∠,即可得出结论;(3)方法1:先判断出MN 最大时,PMN ∆的面积最大,进而求出AN ,AM ,即可得出MN 最大AM AN =+,最后用面积公式即可得出结论.方法2:先判断出BD 最大时,PMN ∆的面积最大,而BD 最大是14AB AD +=,即可得出结论.【详解】解:(1)点P ,N 是BC ,CD 的中点,//PN BD ∴,12PN BD =, 点P ,M 是CD ,DE 的中点, //PM CE ∴,12PM CE =, AB AC =,AD AE =,BD CE ∴=,PM PN ∴=,//PN BD ,DPN ADC ∴∠=∠,//PM CE ,DPM DCA ∴∠=∠,90BAC ∠=︒,90ADC ACD ∴∠+∠=︒,90MPN DPM DPN DCA ADC ∴∠=∠+∠=∠+∠=︒, PM PN ∴⊥,故答案为:PM PN =,PM PN ⊥;(2)PMN ∆是等腰直角三角形.由旋转知,BAD CAE ∠=∠,AB AC =,AD AE =,()ABD ACE SAS ∴∆≅∆,ABD ACE ∴∠=∠,BD CE =, 利用三角形的中位线得,12PN BD =,12PM CE =, PM PN ∴=,PMN ∴∆是等腰三角形,同(1)的方法得,//PM CE ,DPM DCE ∴∠=∠,同(1)的方法得,//PN BD ,PNC DBC ∴∠=∠,DPN DCB PNC DCB DBC ∠=∠+∠=∠+∠,MPN DPM DPN DCE DCB DBC ∴∠=∠+∠=∠+∠+∠ BCE DBC ACB ACE DBC =∠+∠=∠+∠+∠ACB ABD DBC ACB ABC =∠+∠+∠=∠+∠,90BAC ∠=︒,90ACB ABC ∴∠+∠=︒,90MPN ∴∠=︒,PMN ∴∆是等腰直角三角形;(3)方法1:如图2,同(2)的方法得,PMN ∆是等腰直角三角形,MN ∴最大时,PMN ∆的面积最大,//DE BC ∴且DE 在顶点A 上面,MN ∴最大AM AN =+,连接AM ,AN ,在ADE ∆中,4AD AE ==,90DAE ∠=︒, 22AM ∴=, 在Rt ABC ∆中,10AB AC ==,52AN =,225272MN ∴=+=最大,222111149(72)22242PMN S PM MN ∆∴==⨯=⨯=最大. 方法2:由(2)知,PMN ∆是等腰直角三角形,12PM PN BD ==, PM ∴最大时,PMN ∆面积最大,∴点D 在BA 的延长线上,14BD AB AD ∴=+=,7PM ∴=,2211497222PMN S PM ∆∴==⨯=最大. 【点睛】此题属于几何变换综合题,主要考查了三角形的中位线定理,等腰直角三角形的判定和性质,全等三角形的判断和性质,直角三角形的性质的综合运用;解(1)的关键是判断出12PM CE =,12PN BD =,解(2)的关键是判断出ABD ACE ∆≅∆,解(3)的关键是判断出MN 最大时,PMN ∆的面积最大.5.如图,在ABC 中,,AB AC BAC α=∠=,过A 作AD BC ⊥于点D ,点E 为直线AD 上一动点,把线段CE 绕点E 顺时针旋转α,得到线段EF ,连接FC 、FB ,直线AD 与BF 相交于点G .(1)(发现)如图1,当60α=︒时,填空:①AE BF的值为___________; ②AGB ∠的度数为___________;(2)(探究)如图2,当120α=︒时,请写出AE BF的值及AGB ∠的度数,并就图2的情形给出证明;(3)(应用)如图3,当90α=︒时,若15AB ACE =∠=︒,请直接写出DFG 的面积.答案:G解析:(1)1;60°;(2)3AE BF =,∠G =30°,理由见解析;(3) 【分析】(1)①根据已知条件可以证明三角形ABC 和三角形EFC 都是等边三角形,然后根据等边三角形的性质证明△AEC ≌△BFC ,即BF =AE 从而得出答案;②根据①中的证明∠ABG =90°,∠BAG =30°,从而计算出∠AGB 的度数;(2)根据题目已知条件可以计算出BC =,同理可以证得CF =,再证ECA FCB ∠=∠即△ACE ∽△BCF ,从而得到比值和角的度数;(3)根据第(2)问的计算结论分E 在AD 上和E 在DA 的延长线上分类讨论求解即可.【详解】解:(1)①∵AB =AC ,CE =EF ,∠BAC =∠FEC =60°∴△ABC 和△EFC 都是等边三角形∴∠ACB =∠ECF =60°,AC =CB ,CE =CF∴∠ACE =∠BCF∴△ACE ≌△BCF∴A E =BF ,即1AE BF= ②∵△ACE ≌△BCF∴∠EAC =∠CBF 由①可知△ABC 是等边三角形∴AD 平分∠BAC ,BD ⊥AD∴∠CAE =∠CBF =30°∴∠AGB =∠180°-∠CBF -∠BDG =60°(2)AE BF = ∵AB =AC ,∠BAC =120°,AD ⊥BC∴∠ABD =30°=∠ACB∴22BD AB AC CD === ∴BC =同理∵∠FEC =120°,EF =EC ∴CF =∴BC CF AC CE=,∠ACB =∠ECF =30° ∴△ACE ∽△BCF∴∠CAE =∠CBF∴AE AC BF BC ==∵AD ⊥BC ,∠BAC =120°,∴∠CAE =∠CBF =60°又∵∠BDG =90°∴∠G =30°(3)第一种情况,如图所示,当E 在AD 上时 ∵AB AC ==∠BAC =90°,AD ⊥BC ∴sin 4562BC AD BD CD AB =====∠DAC =45° ∵∠ACE =15° ∴∠CED =∠CAD +∠ACE =60° ∴2tan 60DC DE ==∴AE AD DE =-=BC CF AC CE==,∠ACB =∠ECF =45° 又∵AD ⊥BC ,∠BAC =90°,∴∠CAE =∠CBF =45°∴△ACE ∽△BCF∴BF BC AE AC==∴2BF == ∵∠ADC =∠BDG∴∠G =∠ACB =45°∴BG ==∴2FG BG BF =-=过点D 作DM ⊥BG 交BG 于M ,∵∠G =∠ACB =45°,∠BDG =90°∴=DG BD CD ==∴DM DG == ∴132DFG S FG DM ==△第二种情况:当E 在DA 的延长线上时过点D 作DM ⊥BG 交BG 于M , 同上可证2BF BC AE AC ==,6BG BD ==,3DM = ∵∠ACE =15°,∠DAC =45°∴∠DEC =30° ∵AD ⊥CD ,6CD =∴32tan 30DC DE == ∴=6DG BD CD ==326AE DE AD =-=-∴2623FB AE ==-∴6FG BF BG =+=1332DFG S FG DM ==△ 故答案为:3或33.【点睛】本题主要考查了相似三角形的性质与判定,旋转的性质,三角函数等知识点,解题的关键在于能够熟练的掌握相关知识点.6.如图,点B ,C ,D 在同一条直线上,△BCF 和△ACD 都是等腰直角三角形,连接AB ,DF ,延长DF 交AB 于点E .(1)如图1,若AD =BD ,DE 是∠ADB 的平分线,BC =1,求CD 的长度;(2)如图2,连接CE ,求证:DE =2CE +AE ;(3)如图3,改变△BCF 的大小,始终保持点在线段AC 上(点F 与点A ,C 不重合).将ED 绕点E 顺时针旋转90°得到EP ,取AD 的中点O ,连接OP .当AC =2时,直接写出OP 长度的最大值.解析:(1)21CD =;(2)证明见解析;(3)22+【分析】 (1)根据等腰直角三角形的性质,求出1FC BC ==,再判断出FA FB =,即可得出结论;(2)先判断出ABC DFC ≅△△,得出BAC CDF ∠=∠,进而判断出ACE DCH ≅△△,得出AE DH =,CE CH =,即可得出结论;(3)先判断出2OE OQ ==,再判断出OED QEP ≅△△,进而求出2PQ OD ==得出结论.【详解】(1)解:BCF 和ACD △都是等腰直角三角形,AC CD ∴=,1FC BC ==,2FB =,AD BD =,DE 是ABD ∆的平分线,DE ∴垂直平分AB ,2FA FB ∴==,21AC FA FC ∴=+=,21CD ∴=;(2)证明:如图2,过点C 作CH CE ⊥交ED 于点H ,BCF 和ACD △都是等腰直角三角形,AC DC ∴=,FC BC =,90ACB DCF ∠=∠=︒;()ABC DFC SAS ∴≅△△,BAC CDF ∴∠=∠,90ECH ∠=︒,90ACE ACH ∴∠+∠=︒,90ACD ∠=︒,90DCH ACH ∴∠+∠=︒,ACE DCH ∴∠=∠.在ACE 和DCH 中,BAC CDF AC DCACE DCH ∠=∠⎧⎪=⎨⎪∠=∠⎩, ()ACE DCH ASA ∴≅△△,AE DH ∴=,CE CH =,2EH CE ∴=.2DE EH DH CE AE =+=+;(3)OP 的最大值是22+解:如图3,连接OE ,将OE 绕点E 顺时针旋转90︒得到EQ ,连接OQ ,PQ ,则2OQ OE =.由(2)知,90AED ABC CDF ABC BAC ∠=∠+∠=∠+∠=︒,在Rt AED △中,点O 是斜边AD 的中点,122222OE OD AD AC ∴===== 2222OQ OE ∴===,在OED 和QEP △中,OE QE OED QEP DE PE =⎧⎪∠=∠⎨⎪=⎩,()OED QEP SAS ∴≅△△,2PQ OD ∴==22OP OQ PQ +=+O 、P 、Q 三点共线时,取“=”号,OP ∴的最大值是22+【点睛】此题是几何变换综合题,主要等腰直角三角形的性质,全等三角形的判定和性质,构造出全等三角形是解本题的关键.7.如图.四边形ABCD 、BEFG 均为正方形.(1)如图1,连接AG 、CE ,请直接写出.....AG 和CE 的数量和位置关系(不必证明).(2)将正方形BEFG 绕点B 顺时针旋转β角(0180β︒︒<<),如图2,直线AG 、CE 相交于点M .①AG 和CE 是否仍然满足(1)中的结论?如果是,请说明理由:如果不是,请举出反例:②连结MB ,求证:MB 平分AME ∠.(3)在(2)的条件下,过点A 作AN MB ⊥交MB 的延长线于点N ,请直接写出.....线段CM 与BN 的数量关系.答案:A解析:(1)AG=EC ,AG ⊥EC ;(2)①满足,理由见解析;②见解析;(3)2.【分析】(1)由正方形BEFG 与正方形ABCD ,利用正方形的性质得到两对边相等,一对直角相等,利用SAS 得出三角形ABG 与三角形CBE 全等,利用全等三角形的对应边相等,对应角相等得到CE=AG ,∠BCE=∠BAG ,再利用同角的余角相等即可得证;(2)①利用SAS 得出△ABG ≌△CEB 即可解决问题;②过B 作BP ⊥EC ,BH ⊥AM ,由全等三角形的面积相等得到两三角形面积相等,而AG=EC ,可得出BP=BH ,利用到角两边距离相等的点在角的平分线上得到BM 为角平分线;(3)在AN 上截取NQ=NB ,可得出三角形BNQ 为等腰直角三角形,利用等腰直角三角形的性质得到2BN ,接下来证明BQ=CM ,即要证明三角形ABQ 与三角形BCM 全等,利用同角的余角相等得到一对角相等,再由三角形ANM 为等腰直角三角形得到NA=NM ,利用等式的性质得到AQ=BM ,利用SAS 可得出全等,根据全等三角形的对应边相等即可得证.【详解】解:(1)AG=EC ,AG ⊥EC ,理由为:∵正方形BEFG ,正方形ABCD ,∴GB=BE ,∠ABG=90°,AB=BC ,∠ABC=90°,在△ABG 和△BEC 中,BG BE ABC EBC BA BC =⎧⎪∠=∠⎨⎪=⎩,∴△ABG ≌△BEC (SAS ),∴CE=AG ,∠BCE=∠BAG ,延长CE 交AG 于点M ,∴∠BEC=∠AEM ,∴∠ABC=∠AME=90°,∴AG=EC ,AG ⊥EC ;(2)①满足,理由是:如图2中,设AM 交BC 于O .∵∠EBG=∠ABC=90°,∴∠ABG=∠EBC ,在△ABG 和△CEB 中,AB BC ABG CBE BG EB =⎧⎪∠=∠⎨⎪=⎩,∴△ABG ≌△CEB (SAS ),∴AG=EC ,∠BAG=∠BCE ,∵∠BAG+∠AOB=90°,∠AOB=∠COM ,∴∠BCE+∠COM=90°,∴∠OMC=90°,∴AG ⊥EC .②过B 作BP ⊥EC ,BH ⊥AM ,∵△ABG ≌△CEB ,∴S △ABG =S △EBC ,AG=EC , ∴12EC•BP=12AG•BH , ∴BP=BH ,∴MB 平分∠AME ;(3)CM=2BN ,理由为:在NA 上截取NQ=NB ,连接BQ ,∴△BNQ 为等腰直角三角形,即BQ=2BN ,∵∠AMN=45°,∠N=90°,∴△AMN 为等腰直角三角形,即AN=MN ,∴MN-BN=AN-NQ ,即AQ=BM ,∵∠MBC+∠ABN=90°,∠BAN+∠ABN=90°,∴∠MBC=∠BAN ,在△ABQ 和△BCM 中,AQ BM BAN MBC AB BC =⎧⎪∠=∠⎨⎪=⎩,∴△ABQ ≌△BCM (SAS ),∴CM=BQ ,则CM=2BN .【点睛】此题考查了正方形,全等三角形的判定与性质,等腰直角三角形的判定与性质,角平分线的判定,熟练掌握正方形的性质是解本题的关键.8.问题解决一节数学课上,老师提出了这样一个问题:如图①,点P 是等边ABC 内的一点,6PA =,8PB = ,10PC =.你能求出APB ∠的度数和等边ABC 的面积吗? 小明通过观察、分析、思考,形成了如下思路:如图①将BPC △绕点B 逆时针旋转60°,得到BPA △,连接PP ',可得BPP '是等边三角形,根据勾股定理逆定理可得AP P '是直角三角形,从而使问题得到解决.(1)结合小明的思路完成填空:PP '=_____________,APP '∠=_______________,APB ∠=_____________ ,ABCS= ______________.(2)类比探究Ⅰ如图②,若点P 是正方形ABCD 内一点,1PA = ,2PB =,3PC =,求APB ∠的度数和正方形的面积.Ⅱ如图③,若点P 是正方形ABCD 外一点,3PA = ,1PB =, 11PC =,求APB ∠的度数和正方形的面积.答案:B解析:(1)8,90˚,150˚,25336;(2)Ⅰ135APB ∠=︒, 722ABCD S =+正方形;Ⅱ45APB ∠=︒, 1032ABCD S =-正方形【分析】(1)根据小明的思路,然后利用等腰三角形和直角三角形性质计算即可;(2)Ⅰ将△BPC 绕点B 逆时针旋转90°,得到△BP′A ,连接PP′,求出∠APB 的度数;先利用旋转求出∠PBP'=90°,BP'=BP=2,AP'=CP=3,利用勾股定理求出PP',进而判断出△APP'是直角三角形,得出∠APP'=90°,即可得出结论;过B 作BE ⊥AP 于点E ,然后利用勾股定理求出AB 的长度即可求出正方形面积;Ⅱ将△BPC 绕点B 逆时针旋转90°,得到△BP′A ,连接PP′,求出∠APB 的度数;先利用旋转求出∠PBP'=90°,BP'=BP=2,AP'=CP=3,利用勾股定理求出PP',进而判断出△APP'是直角三角形,得出∠APP'=90°,即可得出结论;过B 作BF ⊥AP 于点F ,然后利用勾股定理求出AB 的长度即可求出正方形面积; 【详解】解:(1)由题易有P BP '∆是等边三角形,AP P '∆是直角三角形 ∴PP '=BP=8,90?APP '=∠,60?P PB '=∠,∴APB ∠=APP '∠+=P PB '∠150˚, 如图1,过B 作BD ⊥AP 于点D∵APB ∠=150° ∴30?BPD =∠在Rt △BPD 中,30?BPD =∠,BP=8 ∴BD=4,PD=43 ∴AD=6+43∴AB 2=AD 2+BD 2=100+483 ∴ABCS=234AB =25336+ (2)Ⅰ.如图2,将△BPC 绕点B 逆时针旋转90°,得到△BP′A ,连接PP′, ∴△ABP'≌△CBP ,∴∠PBP'=90°,BP'=BP=2,AP'=CP=3, 在Rt △PBP'中,BP=BP'=2,∴∠BPP'=45°,根据勾股定理得,PP'=2BP=22, ∵AP=1,∴AP 2+PP'2=1+8=9, ∵AP'2=32=9, ∴AP 2+PP'2=AP'2,∴△APP'是直角三角形,且∠APP'=90°, ∴∠APB=∠APP'+∠BPP'=90°+45°=135°;过B 作BE ⊥AP 于点E , ∵∠APB=135°∴∠BPE=45°∴△BPE 是等腰直角三角形 ∴BE=BP=22BP =2 ∴AE=1+2∴AB 2=AE 2+BE 2=7+22 ∴2722ABCD S AB ==+正方形Ⅱ.如图3,将△BPC 绕点B 逆时针旋转90°,得到△BP′A ,连接PP′, ∴△ABP'≌△CBP ,∴∠PBP'=90°,BP'=BP=1,AP'=CP=11, 在Rt △PBP'中,BP=BP'=1,∴∠BPP'=45°,根据勾股定理得,PP'=2BP=2, ∵AP=3,∴AP 2+PP'2=9+2=11, ∵AP'2=(11)2=11, ∴AP 2+PP'2=AP'2,∴△APP'是直角三角形,且∠APP'=90°, ∴∠APB=∠APP'-∠BPP'=90°-45°=45°.过B 作BF ⊥AP 于点F ∵∠APB=45°∴△BPF 为等腰直角三角形 ∴PF=BF=22BP =22 ∴2 ∴AB 2=AF 2+BF 2=1032-∴21032ABCD S AB ==-正方形【点睛】此题是四边形综合题,主要考查了正方形的性质,旋转的性质,直角三角形的性质和判定,勾股定理,正确作出辅助线是解本题的关键.9.问题:如图(1),点M、N分别在正方形ABCD的边BC、CD上,∠MAN=45°,试判断BM、MN、ND之间的数量关系.(1)研究发现如图1,小聪把△ADN绕点A顺时针旋转90°至△ABG,从而发现BM、MN、DN之间的数量关系为(直接写出结果,不用证明)(2)类比引申如图2,在(1)的条件下,AM、AN分别交正方形ABCD的对角线BD于点E、F.已知EF =5,DF=4.求BE的长.(3)拓展提升如图3,在(2)的条件下,AM、AN分别交正方形ABCD的两个外角平分线于Q、P,连接PQ.请直接写出以BQ、PQ、DP为边构成的三角形的面积.答案:B解析:(1)BM+DN=MN,理由见解析;(2)BE=3;(3)以BQ、PQ、DP为边构成的三角形的面积为36.【分析】(1)结论是:BM+DN=MN,如图1,利用三角形AND旋转90º得三角形ABG,∠DAN=∠BAG,可证∠GAM=∠GAB+∠BAM=∠MAN,利用SAS证△AMN≌△AMG即可;(2)如图2,按同样方法△AFD顺时针旋转90º,使AD与AB重合,得△ABF′,连结EF′,△BEF′是直角三角形,用勾股定理求EF′=5,再证△AEF≌△AEF即可;(3)如图3,由(2)可得BD=12,可求正方形边长,构建△P′AQ,P′B=DP,将△ADP顺时针转90º,AD与AB重合,得△BQP′,连OP′,可证△BQP′是直角三角形,可证PQ=P′Q,再证△ABQ∽△PDA,将△P′BQ面积=12BQ•BP′=12BQ•DP=12AD•AB可求.【详解】(1)如图1,BM+DN=MN,理由如下:∵四边形ABCD 是正方形,∴AB =AD ,∠D =∠ABC =∠BAD =90°, 小聪把△ADN 绕点A 顺时针旋转90°至△ABG ,由旋转可得:BG =DN ,AN =AG ,∠1=∠2,∠ABG =∠D =90°, ∴∠ABG +∠ABM =90°+90°=180°, 因此,点G ,B ,M 在同一条直线上, ∵∠MAN =45°,∴∠2+∠3=∠BAD ﹣∠MAN =90°﹣45°=45°, ∵∠1=∠2, ∴∠1+∠3=45°, ∴∠GAM =∠MAN , ∵AM =AM ,∴△AMN ≌△AMG (SAS ), ∴MN =GM ,∵GM =BM +BG =BM +DN , ∴BM +DN =MN ; 故答案为:BM +DN =MN ;(2)如图2,把△ADF 绕点A 顺时针旋转90°至△ABF ',连接EF ',∴AF ′ =AF ,∠DAF =∠BAF ',∠ABF ′ =∠ADF =45°,BF ′ =DF =4, ∵∠ABE =45°,∴∠EBF ′ =45°+45°=90°, ∵AE =AE ,同理得△EAF ≌△EAF '(SAS ), ∴EF '=EF =5,在Rt △EBF '中,由勾股定理得:BE ()()2222EF +BF 5-4=3''=3;(3)由(2)知:BE =3,EF =5,DF =4, ∴BD =3+4+5=12,由勾股定理得:AB 2+AD 2=BD 2, ∵AB =AD , ∴AB 2=72,如图3,把△ADP 绕点A 顺时针旋转90°至△ABP ',连接BP ′,则∠ABP′=∠ADP ,PD =P ′B ,AP =AP ′,∵AM 、AN 分别交正方形ABCD 的两个外角平分线于Q 、P , ∴∠ADP =∠ABQ =135°, ∴∠DAP +∠APD =45°, ∵∠DAP +∠BAQ =45°, ∴∠BAQ =∠APD , ∴△ADP ∽△QBA , ∴AD PD=BQ AB, ∴BQ •PD =AD •AB =72, ∵∠ABP '=∠ABQ =135°, ∴∠QBP '=360°﹣135°﹣135°=90°, ∴S △BP 'Q =12BQ•BP′=12BQ•DP =12×72=36, ∵AP =AP ',∠PAQ =∠P 'AQ ,AQ =AQ , ∴△QAP ≌△QAP '(SAS ), ∴PQ =P 'Q ,∴以BQ 、PQ 、DP 为边构成的三角形的面积为36. 【点睛】本题是感知,探究,创新新题型,主要考查了学生对正方形的性质,旋转变换,勾股定理及全等三角形与相似三角形的判定方法的综合运用.关键是灵活掌握所学知识,同时会从感知中学到方法,结合下一图形,找到解决问题的方法,以及突破口,在创新中,注意把给出的问题进行转化,利用转化思想来解决.10.如图,在四边形ABCD 中,AB AC =,AD 是对角线,60BAC ∠=︒,4B C ADB BAC ∠+∠+∠=∠,(1)求ADC ∠的度数;(2)若AD BD CD =+,求证:AD 平分BDC ∠;(3)在(2)的条件下,E 、F 分别在AC 、AB 上,连接BE 、CF ,交于点P ,使得BPC BDC ∠=∠,若7BD EF ==,15AD =,求EFP ∆的面积答案:A解析:(1)=60∠︒ADC ;(2)证明见详解;(3)4003129. 【分析】(1)先由四边形内角和得到++300B C BDC ∠∠∠=︒,再由4B C ADB BAC ∠+∠+∠=∠可得答案;(2)把ABD △绕点A 逆时针旋转60︒得到ACE △,由(1)及题意易得D 、C 、E 三点共线,从而得到ADE 是等边三角形,由等边三角形的性质及旋转的性质易得60ADB E ∠=∠=︒,故得证;(3)过点B 、点F 分别作BG ⊥CD ,FH ⊥AC ,分别交CD 的延长线于点G 、AC 于点H ,连接BC ,由(2)及题意易得DC=8,由BPC BDC ∠=∠易得EBC FCA ∠=∠,进而得到AFC CEB △≌△,设AF=CE=x ,根据勾股定理得到AF 、CE 、BC 的长,最后根据BFE BPC 、的面积比等于FP 与PC 的比,进而求解即可. 【详解】(1)解:=60BAC ∠︒,∴++36060300B C BDC ∠∠∠=︒-︒=︒, 又BDC ADB ADC ∠=∠+∠,4B C ADB BAC ∠+∠+∠=∠,∴30024060ADC ∠=︒-︒=︒; (2)证明:把ABD △绕点A 逆时针旋转60︒得到ACE △,由(1)得:∴AD=AE ,BD=CE ,=ADC=60DAE ∠∠︒AD BD CD =+,DE=DC+CE ,∴D 、C 、E 三点共线,∴ADE 是等边三角形,∴60ADB E ∠=∠=︒, ∴60ADB ADC ∠=∠=︒,∴AD 平分BDC ∠; (3)解:过点B 、点F 分别作BG ⊥CD ,FH ⊥AC ,分别交CD 的延长线于点G 、AC 于点H ,连接BC ,由题意及(2)可得:ABC 是等边三角形,120BDC ∠=︒,∴AB=AC=BC ,60BDG ∠=︒,7BD EF ==,15AD =,∴72DG =,32BG =,DC=AD-BD=8, ∴723822GC GD DC =+=+=, 在Rt BGC △中,222273231322BC BG GC ⎛⎫⎛⎫=+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭, 又=120BPC BDC ∠=∠︒,∴18012060PBC PCB ∠+∠=︒-︒=︒,60ECP PCB ∠+∠=︒,∴=ECP EBC ∠∠,=60,FAC BCA AC BC ∠∠=︒=,∴AFC CEB △≌△,∴CE=AF ,设133,1313222CE AF x AE x AH x FH x EH x ==∴=-==∴=-,,,,∴在Rt FHE 中,222FH EH EF +=即22231372x ⎛⎫+-= ⎪⎝⎭⎝⎭,解得125,8x x ==,①当CE=AF=5时,则AE=8,∴111322BECAFCSSAC FH ==⋅=⨯=16944ABEABCBECSSS =-=-=∴BFE ABEAFESSS=-==设BFPEFPBPCEPCSa Sb Sc Sd ====,,,,则有:a cb d FP PC ==∶∶∶,,BFE BFPFEP BEC BPCEPC S SSSSS=+=+,∴BFEBECSSFP PC =∶∶,∴6465BFE BECSS FP PC =∶∶,又1152224FECSCE FH =⋅=⨯⨯=,∴64641291294129EFP FECSS ==⨯=; ②当CE=AF=8时,AE=5,则有:∴111322BEAAFCSSAC FH ==⋅=⨯=,1694CBEABCBECSSS =-==∴654BFEABEAFESSS=-=-=由①可得:25=4104BFEBECSS FP PC =∶∶∶,又11822FECSCE FH =⋅=⨯⨯=∴2525129129EFPFECSS ==⨯=综上所述:129EFPS =. 【点睛】本题主要考查三角形与四边形的综合问题,主要是利用全等三角形、等边三角形、三角形面积比的转换及勾股定理,熟练掌握各个知识点是解题的关键,尤其是第三问的面积转换问题是本题的难点.11.探究:如图①和②,在四边形ABCD中,AB=AD,∠BAD=90°,点E、F分别在BC、CD上,∠EAF=45°.(1)如图①,若∠B、∠ADC都是直角,把ABE△绕点A逆时针旋转90°至△ADG,使AB与AD重合,则能得EF=BE+DF,请写出推理过程;(2)如图②,若∠B、∠D都不是直角,则当∠B与∠D满足数量关系时,仍有EF=BE+DF;(3)拓展:如图③,在ABC中,∠BAC=90°,AB=AC=22,点D、E均在边BC上,且∠DAE=45°.若BD=1,求DE的长.答案:B解析:(1)见解析;(2)∠B+∠D=180°;(3)5 3【分析】(1)根据已知条件证明△EAF≌△GAF,进而得到EF=FG,即可得到答案;(2)先作辅助线,把△ABE绕A点旋转到△ADG,使AB和AD重合,根据(1),要使EF=BE+DF,需证明△EAF≌△GAF,因此需证明F、D、G在一条直线上,即180ADG ADF∠+∠=︒,即180B D∠+∠=︒;(3)先作辅助线,把△AEC绕A点旋转到△AFB,使AB和AC重合,连接DF,根据已知条件证明△FAD≌△EAD,设DE=x,则DF=x,BF=CE=3﹣x,然后再Rt BDF中根据勾股定理即可求出x的值,即DE的长.【详解】(1)解:如图,∵把△ABE绕点A逆时针旋转90°至△ADG,使AB与AD重合,∴AE=AG,∠BAE=∠DAG,BE=DG,∵∠BAD=90°,∠EAF=45°,∴∠BAE+∠DAF=45°, ∴∠DAG+∠DAF=45°, 即∠EAF=∠GAF=45°, 在△EAF 和△GAF 中AF AF EAF GAF AE AG =⎧⎪∠=∠⎨⎪=⎩∴△EAF ≌△GAF (SAS ), ∴EF=GF , ∵BE=DG , ∴EF=GF=BE+DF ; (2)解:∠B+∠D=180°, 理由是:如图,把△ABE 绕A 点旋转到△ADG ,使AB 和AD 重合, 则AE=AG ,∠B=∠ADG ,∠BAE=∠DAG , ∵∠B+∠ADC=180°, ∴∠ADC+∠ADG=180°, ∴F 、D 、G 在一条直线上, 和(1)类似,∠EAF=∠GAF=45°, 在△EAF 和△GAF 中AF AF EAF GAF AE AG =⎧⎪∠=∠⎨⎪=⎩∴△EAF ≌△GAF (SAS ), ∴EF=GF , ∵BE=DG , ∴EF=GF=BE+DF ; 故答案为:∠B+∠D=180°;(3)解:∵△ABC 中,2∠BAC=90°, ∴∠ABC=∠C=45°,由勾股定理得:22AB AC +,如图,把△AEC 绕A 点旋转到△AFB ,使AB 和AC 重合,连接DF . 则AF=AE ,∠FBA=∠C=45°,∠BAF=∠CAE , ∵∠DAE=45°,∴∠FAD=∠FAB+∠BAD=∠CAE+∠BAD=∠BAC ﹣∠DAE=90°﹣45°=45°, ∴∠FAD=∠DAE=45°, 在△FAD 和△EAD 中AD AD FAD EAD AF AE =⎧⎪∠=∠⎨⎪=⎩∴△FAD ≌△EAD , ∴DF=DE , 设DE=x ,则DF=x , ∵BD=1,∴BF=CE=4﹣1﹣x=3﹣x , ∵∠FBA=45°,∠ABC=45°, ∴∠FBD=90°,由勾股定理得:222DF BF BD =+,22(3)1x x =-+,解得:x=53, 即DE=53. 【点睛】本题综合考查三角形的性质和判定、正方形的性质应用、全等三角形的性质和判定、勾股定理等知识,解题关键在于正确做出辅助线得出全等三角形.12.如图,抛物线y =﹣x 2+bx+c 与x 轴交于A ,B 两点,其中A (3,0),B (﹣1,0),与y 轴交于点C ,抛物线的对称轴交x 轴于点D ,直线y =kx+b 1经过点A ,C ,连接CD . (1)求抛物线和直线AC 的解析式:(2)若抛物线上存在一点P ,使△ACP 的面积是△ACD 面积的2倍,求点P 的坐标; (3)在抛物线的对称轴上是否存在一点Q ,使线段AQ 绕Q 点顺时针旋转90°得到线段QA 1,且A 1好落在抛物线上?若存在,求出点Q 的坐标;若不存在,请说明理由.答案:A解析:(1)2y x 2x 3=-++;3y x =-+ ;(2)(﹣1,0)或(4,﹣5);(3)存在;(1,2)和(1,﹣3) 【分析】(1)将点A ,B 坐标代入抛物线解析式中,求出b ,c 得出抛物线的解析式,进而求出点C 的坐标,再将点A ,C 坐标代入直线AC 的解析式中,即可得出结论;(2)利用抛物线的对称性得出BD =AD ,进而判断出△ABC 的面积和△ACP 的面积相等,即可得出结论;(3)分点Q 在x 轴上方和在x 轴下方,构造全等三角形即可得出结论. 【详解】解:(1)把A (3,0),B (﹣1,0)代入y =﹣x 2+bc+c 中,得93010b c b c -++=⎧⎨--+=⎩,∴23b c =⎧⎨=⎩, ∴抛物线的解析式为y =﹣x 2+2x+3, 当x =0时,y =3, ∴点C 的坐标是(0,3),把A (3,0)和C (0,3)代入y =kx+b 1中,得11303k b b +=⎧⎨=⎩,∴113k b =-⎧⎨=⎩∴直线AC 的解析式为y =﹣x+3; (2)如图,连接BC , ∵点D 是抛物线与x 轴的交点, ∴AD =BD , ∴S △ABC =2S △ACD , ∵S △ACP =2S △ACD ,∴S △ACP =S △ABC ,此时,点P 与点B 重合, 即:P (﹣1,0),过B 点作PB ∥AC 交抛物线于点P ,则直线BP 的解析式为y =﹣x ﹣1①,∵抛物线的解析式为y=﹣x2+2x+3②,联立①②解得,1xy=-⎧⎨=⎩或45xy=⎧⎨=-⎩,∴P(4,﹣5),∴即点P的坐标为(﹣1,0)或(4,﹣5);(3)如图,①当点Q在x轴上方时,设AC与对称轴交点为Q',由(1)知,直线AC的解析式为y=﹣x+3,当x=1时,y=2,∴Q'坐标为(1,2),∵Q'D=AD=BD=2,∴∠Q'AB=∠Q'BA=45°,∴∠AQ'B=90°,∴点Q'为所求,②当点Q在x轴下方时,设点Q(1,m),过点A1'作A1'E⊥DQ于E,∴∠A1'EQ=∠QDA=90°,∴∠DAQ+∠AQD=90°,由旋转知,AQ=A1'Q,∠AQA1'=90°,∴∠AQD+∠A1'QE=90°,∴∠DAQ=∠A1'QE,∴△ADQ≌△QEA1'(AAS),∴AD=QE=2,DQ=A1'E=﹣m,∴点A1'的坐标为(﹣m+1,m﹣2),代入y=﹣x2+2x+3中,解得,m=﹣3或m=2(舍),∴Q的坐标为(1,﹣3),∴点Q的坐标为(1,2)和(1,﹣3).【点睛】本题考查的是二次函数的综合题,涉及解析式的求解,与三角形面积有关的问题,三角形“k”字型全等,解题的关键是利用数形结合的思想,设点坐标并结合几何图形的性质列式求解.13.如图1,ABC ∆中,CA CB =,ACB α∠=,D 为ABC ∆内一点,将CAD ∆绕点C 按逆时针方向旋转角α得到CBE ∆,点,AD 的对应点分别为点,BE ,且,,A D E 三点在同一直线上.(1)填空:CDE ∠=______(用含α的代数式表示);(2)如图2,若60α=︒,请补全图形,再过点C 作CF AE ⊥于点F ,然后探究线段CF ,AE ,BE 之间的数量关系,并证明你的结论;(3)如图3,若90α=︒,52AC =ABEC 面积的最大值______. 解析:(1)1802α-;(2)33AE BE =+;证明见解析;(3)21)2. 【分析】(1)由旋转的性质可得CD CE =,DCE α∠=,即可求解;(2)由旋转的性质可得AD BE =,CD CE =,60DCE ∠=︒,可证CDE ∆是等边三角形,由等边三角形的性质可得33DF EF CF ==,即可求解; (3)如图3中,过点C 作CF BE ⊥交BE 的延长线于F ,设AE 交BC 于J .证明90ACJ BEJ,推出点E 在以AB 为直径的圆上运动,即图中BC 上运动,当CEEB 时,四边形ABEC 的面积最大,此时EC EB =,分别求出ABC ∆,BCE ∆的面积即可解决问题.【详解】解:(1)如图1中,将CAD ∆绕点C 按逆时针方向旋转角α得到CBE ∆ACD BCE ∴∆≅∆,DCE α∠= CD CE ∴=1802CDE α︒-∴∠=. 故答案为:1802α︒-. (2)233AE BE CF =+理由如下:如图2中,将CAD ∆绕点C 按逆时针方向旋转角60︒得到CBE ∆ACD BCE ∴∆≅∆AD BE ∴=,CD CE =,60DCE ∠=︒ CDE ∴∆是等边三角形,且CF DE ⊥33DF EF ∴==AE AD DF EF =++23AE BE ∴=+. (3)如图3中,过点C 作CWBE 交BE 的延长线于W ,设AE 交BC 于J .。
初二数学 全等三角形双等腰旋转知识点-+典型题及解析

初二数学 全等三角形双等腰旋转知识点-+典型题及解析一、全等三角形双等腰旋转1.如图,△ABC 和△CEF 中,∠BAC =∠CEF =90°,AB =AC ,EC =EF ,点E 在AC 边上. (1)如图1,连接BE ,若AE =3,BE =58,求FC 的长度;(2)如图2,将△CEF 绕点C 逆时针旋转,旋转角为α(0°<α<180°),旋转过程中,直线EF 分别与直线AC ,BC 交于点M ,N ,当△CMN 是等腰三角形时,求旋转角α的度数; (3)如图3,将△CEF 绕点C 顺时针旋转,使得点B ,E ,F 在同一条直线上,点P 为BF 的中点,连接AE ,猜想AE ,CF 和BP 之间的数量关系并说明理由.答案:(1);(2)22.5°或45°或112.5°;(3)CF +AE =BP ,见解析【分析】 (1)利用勾股定理求出AB =AC =7,求出EC =EF =4即可解决问题; (2)分三种情形分别画出图形,利用等解析:(1)42;(2)22.5°或45°或112.5°;(3)CF +AE =2BP ,见解析【分析】(1)利用勾股定理求出AB =AC =7,求出EC =EF =4即可解决问题;(2)分三种情形分别画出图形,利用等腰三角形的性质求解即可;(3)结论:CF +AE =2BP .如图3中,过点A 作AD ⊥AE ,利用全等三角形的性质以及等腰直角三角形的性质求解即可.【详解】解:(1)如图1中,在Rt △ABE 中,AB ()2222583497-=-==BF AE ,∴AC =AB =7,∴EF =EC =AC ﹣AE =7﹣3=4,∵∠CEF =90°,EC =EF =3, ∴CF 22224442+=+=EF CE(2)①如图2﹣1中,当CM=CN时,α=∠MCE=∠ECN=12∠ACB=22.5°.如图2﹣2中,当NM=NC时,α=∠MCN=45°.如图2﹣3中,当CN=CM时,∠NCE=12∠BCM=67.5°,α=∠ACE=45°+67.5°=112.5°.综上所述,满足条件的α的值为22.5°或45°或112.5°.(3)结论:CF+AE=2BP.理由:如图3中,过点A作AD⊥AE,∴∠DAE=∠BAC=90°,∴∠BAD =∠CAE ,∵∠BAC =∠BEC =90°,∴∠ABP =∠ACE ,∵AB =AC ,∴△ABD ≌△ACE (ASA ),∴BD =EC =EF ,AD =AE ,∴△ADE 是等腰直角三角形,∴DE =2AE , ∵P 是BF 的中点, ∴BP =12BF , ∵BP =12BF =12(2EF +DE ),CF =2EF ,DE =2AE , ∴BP =12(2CF +2AE ), ∴CF +AE =2BP .【点睛】本题属于几何变换综合题,考查了等腰直角三角形的性质,全等三角形的判定和性质,直角三角形的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题. 2.如图,在ABC 中,90BAC ∠=︒,AB AC =,点D 为线段AB 上一点,线段CD 绕点C 逆时针旋转90︒能与线段CE 重合,点F 为AC 与BE 的交点.(1)若52BC =,42CE =,求线段BD 的长;(2)猜想BD 与AF 的数量关系,并证明你猜想的结论;(3)设36CA DA ==,点M 在线段CD 上运动,点N 在线段CA 上运动,运动过程中,DN MN +的值是否有最小值,如果有,请直接写出这个最小值;如果没有,请说明理由.答案:(1),(2)BD=2FA ,证明见解析(3).【分析】(1)由,可求AC ,再根据,求出AD 即可;(2)延长BA 至M,使AM=AB ,连接ME 、MC ,证ME=BD 即可;(3)作点D 关于AC 的对称解析:(1)57-,(2)BD=2FA ,证明见解析(3)6105. 【分析】 (1)由52BC =,可求AC ,再根据42CE =,求出AD 即可;(2)延长BA 至M,使AM=AB ,连接ME 、MC ,证ME=BD 即可;(3)作点D 关于AC 的对称点G ,过点G 作CD 的垂线,垂足为H ,交AC 于点K ,连接AG ,求出GH 即可.【详解】解:(1)由旋转可知,42CE CD ==,∠DCE=90°,∵90BAC ∠=︒,AB AC =,52BC =,∴5AB AC ==,∠ABC=45°,∴2222(42)57AD CD AC =-=-=,∴57BD =-,(2)BD 与AF 的数量关系是:BD=2FA ,证明:延长BA 至M,使AM=AB ,连接ME 、MC ,∵90BAC ∠=︒,∴BC=MC ,∴∠CBA=∠CMA=45°,∴∠ACM=90°,∵∠DCE=90°,∴∠BCD=∠MCE ,∵CD CE =,∴△BCD ≌△MCE ,∴BD=EM ,∠CME=∠CBD=45°,∴∠EMA=90°,∴AF ∥EM ,∴EM=2AF ,即BD=2AF ;(3)作点D 关于AC 的对称点G ,过点G 作CD 的垂线,垂足为H ,交AC 于点K ,连接AG ,由作图可知,当M 、N 与H 、K 重合时,MN+DN 最小,∵∠BAC=90°,∴D 、A 、G 在一条直线上,∵36CA DA ==,∴DA=2,由对称可知,DG=4,∵∠ACD+∠ADC=90°,∠G+∠ADC=90°,∴∠G=∠ACD ,∵tan ∠ACD=13AD AC =, ∴tanG=13DH GH =, 设DH=x ,GH=3x , 222(3)4x x +=,∵x>0,解得x=2105, ∴GH=6105, ∴最小值为6105.【点睛】本题考查了全等三角形,三角函数,勾股定理,中位线等知识,解题关键是恰当的作辅助线,构造全等三角形或最短路径.3.在正方形ABCD 中,对角线AC 、BD 交于点O ,以BC 为斜边作直角三角形BCP ,连接OP .(1)如图所示,易证:2CP BP OP =;(2)当点P 的位置变换到如第二幅图和第三幅图所示的位置时,线段CP 、BP 、OP 之间又有怎样的数量关系?请写出你的猜想,并对第二幅图加以证明.答案:(1)见解析;(2)第二幅图:,第三幅图:【分析】(1)在CP 上截取CE=BP ,连接OE ,记OB 与CP 交于点F ,根据正方形的性质证明,得到是等腰直角三角形,所以有,从而证得;(2)第二幅图的证解析:(1)见解析;(2)第二幅图:2BP CP OP =+,第三幅图:2BP CP OP +=【分析】(1)在CP 上截取CE=BP ,连接OE ,记OB 与CP 交于点F ,根据正方形的性质证明()OCE OBP SAS ≅,得到EOP △是等腰直角三角形,所以有2PE OP =,从而证得2CP CE PE BP OP =+=+;(2)第二幅图的证明过程类似(1)中的证明过程,在BP 上截取BE=CP ,连接OE ,记OC 与BP 交于点F ,证明()OBE OCP SAS ≅,得到OEP 是等腰直角三角形,可以证得2BP CP OP =+;第三幅图的结论是2BP CP OP +=,证明方法一样是构造三角形全等,由()OBE OCP SAS ≅可以证出结论.【详解】解:(1)如图,在CP 上截取CE=BP ,连接OE ,记OB 与CP 交于点F ,∵四边形ABCD 是正方形,∴OB=OC ,90BOC ∠=°,∵BP CP ⊥,∴90BOC BPC ∠=∠=︒,∵OFC PFB ∠=∠,∴OCE OBP ∠=∠,在OCE △和OBP 中,OC OB OCE OBP CE BP =⎧⎪∠=∠⎨⎪=⎩,∴()OCE OBP SAS ≅,∴OE OP =,COE BOP ∠=∠,∵BOC BOE COE ∠=∠+∠,EOP BOE BOP ∠=∠+∠,∴90EOP BOC ∠=∠=︒,∴EOP △是等腰直角三角形, ∴2PE OP =, ∴2CP CE PE BP OP =+=+;(2)第二幅图:2BP CP OP =+,第三幅图:2BP CP OP +=, 证明第二幅图的结论:如图,在BP 上截取BE=CP ,连接OE ,记OC 与BP 交于点F ,同(1)中证明()OCE OBP SAS ≅的过程证明()OBE OCP SAS ≅,同理OEP 是等腰直角三角形,∴2EP OP =,∴2BP BE EP CP OP =+=+;第三幅图的证明过程是:如图,延长PB 至点E ,使BE=CP ,证明()OBE OCP SAS ≅,得到OEP 是等腰直角三角形,∴2EP OP =, ∵EP EB BP CP BP =+=+, ∴2OP CP BP =+.【点睛】本题考查全等三角形的性质和判定,等腰直角三角形的性质和进行的性质,解题的关键是掌握这些性质定理进行证明求解,并且学会构成全等三角形的方法.4.如图,ABC 是等腰直角三角形,90,ACB ∠=︒分别以,AB AC 为直角边向外作等腰直角ABD △和等腰直角,ACE G 为BD 的中点,连接,,CG BE ,CD BE 与CD 交于点F .(1)证明:四边形ACGD 是平行四边形;(2)线段BE 和线段CD 有什么数量关系,请说明理由;(3)已知2,BC =求EF 的长度(结果用含根号的式子表示).答案:(1)见解析;(2)BE=CD ,理由见解析;(3)EF= .【分析】(1)利用等腰直角三角形的性质易得BD=2BC ,因为G 为BD 的中点,可得BG=BC ,由∠CGB=45°,∠ADB=45得AD ∥解析:(1)见解析;(2)BE =CD ,理由见解析;(3)EF 3105【分析】(1)利用等腰直角三角形的性质易得BD=2BC ,因为G 为BD 的中点,可得BG=BC ,由∠CGB=45°,∠ADB=45得AD ∥CG ,由∠CBD+∠ACB=180°,得AC ∥BD ,得出四边形ACGD 为平行四边形;(2)利用全等三角形的判定证得△DAC ≌△BAE ,由全等三角形的性质得BE=CD ;首先证得四边形ABCE 为平行四边形,再利用全等三角形的判定定理得△BCE ≌△CAD ,易得∠CBE=∠ACD ,由∠ACB=90°,易得∠CFB=90°,得出结论.(3)先证明△DBF 是直角三角形,再利用勾股定理进行计算,即可求出答案.【详解】解:(1)∵△ABC 和△ABD 都是等腰直角三角形∴∠CAB =∠ABD = 45°,BDABBC =2BC =2AC∴AC ∥BD又∵G 为BD 的中点,∴BD =2DG ,∴AC =DG ,AC ∥DG∴四边形ACGD 为平行四边形;(2)BE =CD ,理由如下∵△AEC 和△ABD 都是等腰直角三角形AE =AC ,AB =AD∠EAB =∠EAC +∠CAB =90°+45°=135°,∠CAD =∠DAB +∠BAC =90°+45°=135°,∴∠EAB =∠CAD ,在△DAC 与△BAE 中,AD AB CAD EAB AC AE =⎧⎪∠=∠⎨⎪=⎩,∴△DAC ≌△BAE ,∴BE =CD ;(3) ∵△DAC ≌△BAE∴∠AEB=∠ACD又∵∠EAC=90°∴∠EFC=∠DFB=90°∴ △DBF 是直角三角形∵BC,∴BD根据勾股定理得CD, ∴11••22CD BF BC BD = ∴12=12•∴BF∴EF =BE -BF =CD -BF【点睛】 本题主要考查了等腰直角三角形的性质,平行四边形和全等三角形的判定及性质定理,综合运用各种定理是解答此题的关键.5.如图1,在等腰直角三角形ABC 中,动点D 在直线AB (点A 与点B 重合除外)上时,以CD 为一腰在CD 上方作等腰直角三角形ECD ,且90ECD ∠=︒,连接AE .(1)判断AE 与BD 的数量关系和位置关系;并说明理由.(2)如图2,若4BD =,P ,Q 两点在直线AB 上且5EP EQ ==,试求PQ 的长. (3)在第(2)小题的条件下,当点D 在线段AB 的延长线(或反向延长线)上时,判断PQ 的长是否为定值.分别画出图形,若是请直接写出PQ 的长;若不是请简单说明理由. 答案:(1)AE=BD 且AE ⊥BD ;(2)6;(3)PQ 为定值6,图形见解析【分析】(1)由“SAS”可证△ACE ≌△BCD ,可得AE=BD ,∠EAC=∠DBC=45°,可得AE ⊥BD ;(2)由等腰解析:(1)AE=BD 且AE ⊥BD ;(2)6;(3)PQ 为定值6,图形见解析【分析】(1)由“SAS”可证△ACE ≌△BCD ,可得AE=BD ,∠EAC=∠DBC=45°,可得AE ⊥BD ; (2)由等腰三角形的性质可得PA=AQ ,由勾股定理可求PA 的长,即可求PQ 的长; (3)分两种情况讨论,由“SAS”可证△ACE ≌△BCD ,可得AE=BD ,∠EAC=∠DBC ,可得AE ⊥BD ,由等腰三角形的性质可得PA=AQ ,由勾股定理可求PA 的长,即可求PQ 的长.【详解】解:(1)AE=BD ,AE ⊥BD ,理由如下:∵△ABC ,△ECD 都是等腰直角三角形,∴AC=BC ,CE=CD ,∠ACB=∠ECD=90°,∠ABC=∠CAB=45°,∴∠ACE=∠DCB ,且AC=BC ,CE=CD ,∴△ACE ≌△BCD (SAS )∴AE=BD ,∠EAC=∠DBC=45°,∴∠EAC+∠CAB=90°,∴AE ⊥BD ;(2)∵PE=EQ ,AE ⊥BD ,∴PA=AQ ,∵EP=EQ=5,AE=BD=4,∴AQ=22=2516=3--,EQ AE∴PQ=2AQ=6;(3)如图3,若点D在AB的延长线上,∵△ABC,△ECD都是等腰直角三角形,∴AC=BC,CE=CD,∠ACB=∠ECD=90°,∠ABC=∠CAB=45°,∴∠ACE=∠DCB,且AC=BC,CE=CD,∴△ACE≌△BCD(SAS)∴AE=BD,∠CBD=∠CAE=135°,且∠CAB=45°,∴∠EAB=90°,∵PE=EQ,AE⊥BD,∴PA=AQ,∵EP=EQ=5,AE=BD=4,∴AQ=22=2516=3--,EQ AE∴PQ=2AQ=6;如图4,若点D在BA的延长线上,∵△ABC,△ECD都是等腰直角三角形,∴AC=BC,CE=CD,∠ACB=∠ECD=90°,∠ABC=∠CAB=45°,∴∠ACE=∠DCB,且AC=BC,CE=CD,∴△ACE≌△BCD(SAS)∴AE=BD,∠CBD=∠CAE=45°,且∠CAB=45°,∴∠EAB=90°,∵PE=EQ,AE⊥BD,∴PA=AQ,∵EP=EQ=5,AE=BD=4,∴22=2516=3EQ AE--,∴PQ=2AQ=6.【点睛】本题是三角形综合题,考查了全等三角形的判定和性质,等腰三角形的性质,勾股定理等知识,证明AE⊥BD是本题的关键.6.在等腰Rt△ABC中,AB=AC,∠BAC=90°(1)如图1,D,E是等腰Rt△ABC斜边BC上两动点,且∠DAE=45°,将△ABE绕点A逆时针旋转90后,得到△AFC,连接DF①求证:△AED≌△AFD;②当BE=3,CE=7时,求DE的长;(2)如图2,点D是等腰Rt△ABC斜边BC所在直线上的一动点,连接AD,以点A为直角顶点作等腰Rt△ADE,当BD=3,BC=9时,求DE的长.答案:(1)①见解析;②DE=;(2)DE的值为3或3【分析】(1)①先证明∠DAE=∠DAF,结合DA=DA,AE=AF,即可证明;②如图1中,设DE=x,则CD=7﹣x.在Rt△DCF中,由DF2解析:(1)①见解析;②DE=297;(2)DE的值为517【分析】(1)①先证明∠DAE=∠DAF,结合DA=DA,AE=AF,即可证明;②如图1中,设DE=x,则CD=7﹣x.在Rt△DCF中,由DF2=CD2+CF2,CF=BE=3,可得x2=(7﹣x)2+32,解方程即可;(2)分两种情形:①当点E在线段BC上时,如图2中,连接BE.由△EAD≌△ADC,推出∠ABE=∠C=∠ABC=45°,EB=CD=5,推出∠EBD=90°,推出DE2=BE2+BD2=62+32=45,即可解决问题;②当点D在CB的延长线上时,如图3中,同法可得DE2=153.【详解】(1)①如图1中,∵将△ABE绕点A逆时针旋转90°后,得到△AFC,∴△BAE≌△CAF,∴AE=AF,∠BAE=∠CAF,∵∠BAC=90°,∠EAD=45°,∴∠CAD+∠BAE=∠CAD+∠CAF=45°,∴∠DAE=∠DAF,∵DA=DA,AE=AF,∴△AED≌△AFD(SAS);②如图1中,设DE=x,则CD=7﹣x.∵AB=AC,∠BAC=90°,∴∠B=∠ACB=45°,∵∠ABE=∠ACF=45°,∴∠DCF=90°,∵△AED≌△AFD(SAS),∴DE=DF=x,∵在Rt△DCF中, DF2=CD2+CF2,CF=BE=3,∴x2=(7﹣x)2+32,∴x=29,7∴DE=29;7(2)∵BD=3,BC=9,∴分两种情况如下:①当点E在线段BC上时,如图2中,连接BE.∵∠BAC=∠EAD=90°,∴∠EAB=∠DAC,∵AE=AD,AB=AC,∴△EAB≌△DAC(SAS),∴∠ABE=∠C=∠ABC=45°,EB=CD=9-3=6,∴∠EBD=90°,∴DE2=BE2+BD2=62+32=45,∴DE=②当点D在CB的延长线上时,如图3中,连接BE.同理可证△DBE是直角三角形,EB=CD=3+9=12,DB=3,∴DE2=EB2+BD2=144+9=153,∴DE=综上所述,DE的值为.【点睛】本题主要考查旋转变换的性质,三角形全等的判定和性质以及勾股定理,添加辅助线,构造旋转全等模型,是解题的关键.7.感知:如图①,已知正方形ABCD 的边CD 在正方形DEFG 的边DE 上,连结AE 、CG ,易证AED CGD ≌△△.(不需要证明)探究:将图①中正方形DEFG 绕点D 按顺时针方向旋转,使点E 落在BC 边上,如图②.连结AE 、CG ,证明:AE=CG .应用:如图③,正方形ABCD 中,AD =3,点E 在CB 的延长线上,BE =1,DE=DF ,∠EDF =90°.直接写出点F 与点C 的距离.答案:探究:证明见解析;应用:点F 与点C 的距离为.【分析】探究:结合旋转模型,利用“边角边”证明即可得出结论;应用:连接FC ,根据前序问题中的方法证明△AED ≌△CFD ,从而得到CF=AE ,即在Rt解析:探究:证明见解析;应用:点F 与点C 10.【分析】探究:结合旋转模型,利用“边角边”证明AED CGD ≌△△即可得出结论; 应用:连接FC ,根据前序问题中的方法证明△AED ≌△CFD ,从而得到CF =AE ,即在Rt △AED 中求解AE 即可.【详解】探究:证明:在正方形ABCD 和正方形DEFG 中,AD =CD ,DE =DG ,90ADC EDG ∠=∠=︒,∴ADE CDG ∠=∠,∴AED CGD≌△△,∴AE CG=;应用:连接FC,∵∠EDF=∠ADC=90°,∴∠ADE=∠CDF,又∵AD=CD,DE=DF,∴△AED≌△CFD,∴CF=AE,在Rt△AED中,2210AE AB BE=+=,∴点F与点C的距离为10.【点睛】本题考查全等三角形的判定与性质,掌握基本的旋转模型,根据全等三角形的性质求解问题是解题关键.8.[发现]:(1)如图1.在△ABC中,AB=AC,∠BAC=90°,过点A作AH⊥BC于点H,求证:AH=12 BC.[拓展]:(2)如图2.在△ABC和△ADE中,AB=AC,AD=AE,且∠BAC=∠DAE=90°,点D、B、C在同一条直线上,AH为△ABC中BC边上的高,连接CE.则∠DCE的度数为________,同时猜想线段AH、CD、CE之间的数量关系,并说明理由.[应用]:(3)在图3、图4中.在△ABC中,AB=AC,且∠BAC=90°,在同一平面内有一点P,满足PC=1,PB=6,且∠BPC=90°,请求出点A到BP的距离.答案:(1)证明见解析;(2)∠DCE的度数为90°,CE+2AH=CD,理由见解析;(3)或.【分析】发现:根据同角的余角相等可得∠CAH=∠B,根据AAS证明三角形全等,再根据全等三角形的对应边相解析:(1)证明见解析;(2)∠DCE的度数为90°,CE+2AH=CD,理由见解析;(3)5 2或72.【分析】发现:根据同角的余角相等可得∠CAH=∠B,根据AAS证明三角形全等,再根据全等三角形的对应边相等即可得结论;拓展:证明△ADB≌△AEC,即可得∠DCE的度数为90°,线段AH、CD、CE之间的数量关系;应用:如图3,过点A作AH⊥BP于点H,连接AP,过A作AD垂直于AP,交PB于点D,可得△APC≌△ADB,得BD=CP=1,根据DP=BP-BD=6-1=5,AH⊥DP,即可得点A到BP的距离;同理如图4,过点A作AH⊥BP于点H,连接AP,将△APC绕点A顺时针旋转90度到△ADB,可得DP=BP+BD=6+1=7,进而可得点A到BP的距离.【详解】解:发现:(1)证明:∵AH⊥BC,∠BAC=90°,∴∠AHC=90°=∠BAC.∴∠BAH+∠CAH=90°,∠BAH+∠B=90°.∴∠CAH=∠B ,在△ABH 和△CAH 中,CAH B AHC BHA AB CA ∠∠⎧⎪∠∠⎨⎪⎩=== , ∴△ABH ≌△CAH .(AAS ).∴BH=AH ,AH=CH .∴AH=12BC . 拓展:∠DCE 的度数为90°,线段AH 、CD 、CE 之间的数量关系为:CE+2AH=CD ,理由如下:∵∠DAB+∠BAE=90°,∠EAC+∠BAE=90°,∴∠DAB=∠EAC ,∵AD=AE ,AB=AC ,∴△ADB ≌△AEC (SAS ),∴∠ABD=∠ACE ,∵AB =AC ,∠BAC =90°∴∠ABC=∠ACB=45°,∴∠ABD=135°,∴∠DCE=90°;∵D 、B 、C 三点共线,∴DB+BC=CD ,∵DB=CE ,AH=12BC , ∴CE+2AH=CD .应用:点A 到BP 的距离为:52或72. 理由如下:如图3,过点A 作AH ⊥BP 于点H ,连接AP ,作∠PAD=90°,交BP 于点D ,∴∠BAC=∠DAP=90°,∴∠BAD=∠CAP ,∵∠BDA=∠APC=90°+∠APD ,∴△APC ≌△ADB (AAS ),∴BD=CP=1,∴DP=BP-BD=6-1=5,∵AH ⊥DP ,∴AH=12DP=52; 如图4,过点A 作AH ⊥BP 于点H ,作∠PAD=90°,交PB 的延长线于点D ,∴∠BAC=∠DAP=90°,∴∠BAD=∠CAP ,∵∠BAC=90°,∠BPC=90°,∴∠ACP+∠ABP=180°,∴∠ACP=∠ABD ,∵AB=AC ,∴△APC ≌△ADB (AAS ),∴BD=CP=1∴DP=BP+BD=6+1=7.∵AH ⊥DP ,∴AH=12DP=72. 综上所述:点A 到BP 的距离为:52或72. 【点睛】本题考查了三角形综合题,解决本题的关键是掌握全等三角形的判定与性质. 9.在ABC 中,AB AC =,点D 是直线BC 上一点(不与B 、C 重合),以AD 为一边在AD 的右侧作ADE ,使AD AE =,DAE BAC ∠=∠,连接CE .(1)如图,当点D 在线段BC 上,如果90BAC ∠=︒,则BCE ∠=______度.(2)设BAC α∠=,BCE β∠=.①如图,当点D 在线段BC 上移动时,α、β之间有怎样的数量关系?请直接写出你的结论.②如图,当点D 在线段BC 的反向延长线上移动时,α、β之间有怎样的数量关系?请说明理由.答案:(1)90;(2)①,理由见解析;②,理由见解析【分析】(1)由等腰直角三角形的性质可得∠ABC=∠ACB=45°,由“SAS”可证△BAD ≌△CAE ,可得∠ABC=∠ACE=45°,可求∠BC解析:(1)90;(2)①180αβ+=︒,理由见解析;②αβ=,理由见解析【分析】(1)由等腰直角三角形的性质可得∠ABC=∠ACB=45°,由“SAS”可证△BAD ≌△CAE ,可得∠ABC=∠ACE=45°,可求∠BCE 的度数;(2)①由“SAS”可证△ABD ≌△ACE 得出∠ABD=∠ACE ,再用三角形的内角和即可得出结论;②由“SAS”可证△ADB ≌△AEC 得出∠ABD=∠ACE ,再用三角形外角的性质即可得出结论.【详解】(1)∵AB=AC ,∠BAC=90°,∴∠ABC=∠ACB=45°,∵∠DAE=∠BAC ,∴∠BAD=∠CAE ,在△BAD 和△CAE 中AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴△BAD ≌△CAE (SAS )∴∠ABC=∠ACE=45°,∴∠BCE=∠ACB+∠ACE=90°,故答案为:90;(2)①180αβ+=︒.理由:∵∠BAC=∠DAE ,∴∠BAC-∠DAC=∠DAE-∠DAC .即∠BAD=∠CAE .在△ABD 与△ACE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△ACE (SAS ),∴∠B=∠ACE .∴∠B+∠ACB=∠ACE+∠ACB .∵∠ACE+∠ACB=β,∴∠B+∠ACB=β,∵α+∠B+∠ACB=180°,∴α+β=180°;② 当点D 在射线BC 的反向延长线上时,αβ=. 理由如下:∵DAE BAC ∠=∠,∴DAB EAC ∠=∠,在△ABD 与△ACE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴△≌△ADB AEC(SAS), ∴ABD ACE ∠=∠,∵ABD BAC ACB ∠=∠+∠,ACE BCE ACB ∠=∠+∠, ∴BAC ABD ACB ∠=∠-∠,BCE ACE ACB ∠=∠-∠, ∴BAC BCE ∠=∠,即αβ=.【点睛】此题考查了全等三角形的判定和性质,等腰直角三角形的性质,三角形的内角和定理,以及三角形外交的性质,证明△ABD ≌△ACE 是解本题的关键.10.如图,已知Rt △ABC 中,AB=AC=2,点D 为直线BC 上的动点(不与B 、C 重合),以A 为直角顶点作等腰直角三角形ADE (点A ,D ,E 按逆时针顺序排列),连结CE . (1)当点D 在线段BC 上运动时,①求证:BD=CE ;②请探讨四边形ADCE 的面积是否有变化;(2)当点D 在直线BC 上运动时,直接写出CD ,CB 与CE 之间的数量关系.答案:(1)①见解析;②四边形ADCE 的面积不变;(2)当点D 在线段BC 上时,CB=CE +CD ;当点D 在点C 右侧时,CB = CE -CD ;当点D 在点B 左侧时,CB= CD -CE【分析】(1)①根据等腰解析:(1)①见解析;②四边形ADCE 的面积不变;(2)当点D 在线段BC 上时,CB=CE +CD ;当点D 在点C 右侧时,CB = CE -CD ;当点D 在点B 左侧时,CB= CD -CE【分析】(1)①根据等腰直角三角形的性质可得AB=AC ,AD=AE ,∠BAC=∠DAE=90°,从而得出∠BAD=∠CAE ,然后利用SAS 即可证出△BAD ≌△CAE ,从而得出BD=CE ;②根据直角三角形的面积公式即可求出S △ABC ,然后根据全等三角形的性质可得S △BAD =S △CAE ,然后根据S 四边形ADCE =S △CAE +S △ADC 和等量代换即可得出结论;(2)根据点D 的位置分类讨论,分别画出对应的图形,根据(1)①中证全等的方法和全等三角形的性质即可推出结论.【详解】解:(1)①∵△ABC 和△ADE 都是等腰直角三角形∴AB=AC ,AD=AE ,∠BAC=∠DAE=90°∴∠BAD +∠DAC=90°,∠CAE +∠DAC=90°∴∠BAD=∠CAE在△BAD 和△CAE 中AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩∴△BAD ≌△CAE∴BD=CE ;②∵已知Rt △ABC 中,AB=AC=2,∴S △ABC =12AB·AC=2 ∵△BAD ≌△CAE∴S △BAD =S △CAE ∴S 四边形ADCE =S △CAE +S △ADC =S △BAD +S △ADC = S △ABC =2∴四边形ADCE 的面积不变;(2)当点D 在线段BC 上时,如下图所示由(1)①的结论知BD=CE∴CB=BD +CD= CE +CD ;当点D 在点C 右侧时,如下图所示∵△ABC 和△ADE 都是等腰直角三角形∴AB=AC ,AD=AE ,∠BAC=∠DAE=90°∴∠BAD -∠DAC=90°,∠CAE -∠DAC=90°∴∠BAD=∠CAE在△BAD 和△CAE 中AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩∴△BAD ≌△CAE∴BD=CE∴CB=BD -CD= CE -CD ;当点D 在点B 左侧时,如下图所示∵△ABC 和△ADE 都是等腰直角三角形∴AB=AC ,AD=AE ,∠BAC=∠DAE=90°∴∠BAD=∠DAC -90°,∠CAE=∠DAC - 90°∴∠BAD=∠CAE在△BAD 和△CAE 中AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩∴△BAD ≌△CAE∴BD=CE∴CB= CD -BD = CD -CE .综上所述:当点D 在线段BC 上时,CB=CE +CD ;当点D 在点C 右侧时,CB = CE -CD ;当点D 在点B 左侧时,CB= CD -CE .【点睛】此题考查的是等腰直角三角形的性质、全等三角形的判定及性质和三角形的面积公式,掌握等腰直角三角形的性质、全等三角形的判定及性质、分类讨论的数学思想和三角形的面积公式是解决此题的关键.二、全等三角形手拉手模型11.如图,已知ABC 和ADE 均为等腰三角形,AC =BC ,DE =AE ,将这两个三角形放置在一起.(1)问题发现:如图①,当60ACB AED ∠∠︒==时,点B 、D 、E 在同一直线上,连接CE ,则CEB ∠= °,线段BD 、CE 之间的数量关系是 ;(2)拓展探究: 如图②,当90ACB AED ∠∠︒==时,点B 、D 、E 在同一直线上,连接CE ,请判断CEB ∠的度数及线段BD 、CE 之间的数量关系,并说明理由;(3)解决问题:如图③,90ACB AED ∠∠︒==,25AC =,AE =2,连接CE 、BD ,在AED 绕点A 旋转的过程中,当DE BD ⊥时,请直接写出EC 的长.解析:(1)60BD CE ,=;(2)452CEB BD CE ∠︒=,=,理由见解析;(3)CE 的长为2或2【分析】(1)证明ACE ABD ≌,得出CE =BD ,AEC ADB ∠=∠,即可得出结论; (2)证明ACE ABD ∽,得出AEC ADB ∠=∠,BD =,即可得出结论; (3)先判断出BD =,再求出AB =:①当点E 在点D 上方时,先判断出四边形APDE 是矩形,求出AP =DP =AE =2,再根据勾股定理求出,BP =6,得出BD =4;②当点E 在点D 下方时,同①的方法得,AP =DP =AE =1,BP =6,进而得出BD =BP +DP =8,即可得出结论.【详解】解:(1)ABC 为等腰三角形,60AC BC ACB ∠︒=,=,∴ABC 是等边三角形,同理可得ADE 是等边三角形6018012060BAD DAC DAC CAE BAD CAE AD AE AB ACEAC DAB ACE ABD SAS BD CEAEC ADB ADE AEC AED CEBCEB ∠+∠=∠+∠=︒∴∠=∠=⎧⎪=⎨⎪∠∠⎩∴∴=∠=∠=︒-∠=︒∠=∠+∠∴∠=︒=≌()故答案为:60CEB BD CE ∠=︒=;.(2)45CEB BD ∠︒=,,理由如下:在等腰三角形ABC 中,AC =BC ,90ACB ∠︒=,45AB CAB ∴∠︒,= ,同理,45AD ADE DAE ∠∠︒,==, ∴AE AC AD AB =,DAE CAB ∠∠=, EAC DAB ∴∠∠=,ACE ABD ∴∽ ,∴BD AD CE AE==∴AEC ADB BD ∠∠=,,点B 、D 、E 在同一条直线上:180135ADB ADE ∴∠︒-∠︒==135AEC ∴∠︒=45CEB AEC AED ∴∠∠-∠︒==;(3)由(2)知,ACE ABD ∽, 2BD CE ∴=, 在Rt ABC 中,25AC =, 2210AB AC ∴== ,①当点E 在点D 上方时,如图③,过点A 作AP BD ⊥交BD 的延长线于P ,DE BD ⊥,PDE AED APD ∴∠∠∠==,∴四边形APDE 是矩形,AE DE = ,∴矩形APDE 是正方形,2AP DP AE ∴===,在Rt APB △中,根据勾股定理得,226BP AB AP -==,4BD BP AP ∴-==,1222CE BD ∴==; ②当点E 在点D 下方时,如图④同①的方法得,AP =DP =AE =2,BP =6,∴BD =BP +DP =8,122CE BD ∴==4, 综上CE 的长为22或42.【点睛】本题是几何变换的综合题,主要考查了旋转的性质,全等三角形的判定和定理,相似三角形的判定和性质,勾股定理,等边三角形的性质,判断出三角形ACE 和三角形ABD 相似是关键.12.(1)如图①,ABC 和CDE △都是等边三角形,且点B ,C ,E 在一条直线上,连结BD 和AE ,直线BD ,AE 相交于点P .则线段BD 与AE 的数量关系为_____________.BD 与AE 相交构成的锐角的度数为___________.(2)如图②,点B ,C ,E 不在同一条直线上,其它条件不变,上述的结论是否还成立.(3)应用:如图③,点B ,C ,E 不在同一条直线上,其它条件依然不变,此时恰好有30AEC ∠=.设直线AE 交CD 于点Q ,请把图形补全.若2PQ =,则DP =___________.解析:(1)相等,60;(2)成立,证明见解析;(3)见解析,4.【分析】(1)证明△BCD ≌△ACE ,并运用三角形外角和定理和等边三角形的性质求解即可; (2)是第(1)问的变式,只是位置变化,结论保持不变;(3)根据∠AEC=30°,判定AE 是等边三角形CDE 的高,运用前面的结论,把条件集中到一个含有30°角的直角三角形中求解即可.【详解】(1)相等; 60.理由如下:∵ABC 和CDE △都是等边三角形,∴60ACB DCE ︒∠=∠=,BC AC =,DC CE =,∴BCD ACE ∠=∠,在ACE △和BCD △中CB CA BCD ACE CD CE =⎧⎪∠=∠⎨⎪=⎩,∴ACE BCD △≌△.∴BD AE =,BDC AEC ∠=∠.又∵DNA ENC ∠=∠,∴60DPE DCE ︒∠=∠=.(2)成立;理由如下:证明:∵ABC 和CDE △都是等边三角形,∴60ACB DCE ︒∠=∠=,BC AC =,DC CE =,∴BCD ACE ∠=∠,在ACE △和BCD △中CB CA BCD ACE CD CE =⎧⎪∠=∠⎨⎪=⎩,∴ACE BCD △≌△.∴BD AE =,BDC AEC ∠=∠.又∵DNA ENC ∠=∠,∴60DPE DCE ︒∠=∠=.(3)补全图形(如图),∵△CDE 是等边三角形,∴∠DEC=60°,∵∠AEC=30°,∴∠AEC=∠AED ,∴EQ ⊥DQ ,∴∠DQP=90°,根据(1)知,∠BDC=∠AEC=30°,∵PQ=2,∴DP=4.故答案为:4.【点睛】本题是一道猜想证明题,以两线段之间的大小关系为基础,考查了等边三角形的性质,三角形的全等,直角三角形的性质,证明两个手拉手模型三角形全等是解题的关键. 13.如图,两个正方形ABCD 与DEFG ,连结AG ,CE ,二者相交于点H .(1)证明:△ADG ≌△CDE ;(2)请说明AG 和CE 的位置和数量关系,并给予证明;(3)连结AE和CG,请问△ADE的面积和△CDG的面积有怎样的数量关系?并说明理由.解析:(1)答案见解析;(2) AG=CE,AG⊥CE;(3) △ADE的面积=△CDG的面积【分析】(1)利用SAS证明△ADG≌△CDE;(2)利用△ADG≌△CDE得到AG=CE,∠DAG=∠DCE,利用∠DAG+∠AMD=90°得到∠DCE+∠CMG=90°,即可推出AG⊥CE;(3)△ADE的面积=△CDG的面积,作GP⊥CD于P,EN⊥AD交AD的延长线于N,证明△DPG≌△DNE,得到PG=EN,再利用三角形的面积公式分别表示出△ADE的面积,△CDG 的面积,即可得到结论△ADE的面积=△CDG的面积.【详解】(1)∵四边形ABCD与DEFG都是正方形,∴AD=CD,DG=DE,∠ADC=∠EDG=90°,∴∠ADC+∠CDG=∠EDG+∠CDG,∴∠ADG=∠CDE,∴△ADG≌△CDE(SAS),(2)AG=CE,AG⊥CE,∵△ADG≌△CDE,∴AG=CE,∠DAG=∠DCE,∵∠DAG+∠AMD=90°,∠AMD=∠CMG,∴∠DCE+∠CMG=90°,∴∠CHA=90°,∴AG⊥CE;(3)△ADE的面积=△CDG的面积,作GP⊥CD于P,EN⊥AD交AD的延长线于N,则∠DPG=∠DNE=90°,∵∠GDE=90°,∴∠EDN+∠GDN=90°,∵∠PDG+∠GDN=90°,∴∠EDN=∠PDG ,∵DE=DG ,∴△DPG ≌△DNE ,∴PG=EN ,∵△ADE 的面积=12AD EN ⋅,△CDG 的面积=12CD GP ⋅, ∴△ADE 的面积=△CDG 的面积.【点睛】此题考查正方形的性质,三角形全等的判定及性质,利用三角形面积公式求解,根据图形得到三角形全等的条件是解题的关键.14.如图1,ABC ∆是以ACB ∠为直角的直角三角形,分别以AB ,BC 为边向外作正方形ABFG ,BCED ,连结AD ,CF ,AD 与CF 交于点M ,AB 与CF 交于点N .(1)求证:ABD FBC ∆≅∆;(2)如图2,在图1基础上连接AF 和FD ,若6AD =,求四边形ACDF 的面积. 解析:(1)详见解析;(2)18【分析】(1)根据正方形的性质得出BC=BD ,AB=BF ,∠CBD=∠ABF=90°,求出∠ABD=∠CBF ,根据全等三角形的判定得出即可;(2)根据全等三角形的性质得出∠BAD=∠BFC ,AD=FC=6,求出AD ⊥CF ,根据三角形的面积求出即可.【详解】解:(1)四边形ABFG 、BCED 是正方形,AB FB ∴=,CB DB =,90ABF CBD ∠=∠=︒,ABF ABC CBD ABC ∴∠+∠=∠+∠,即ABD CBF ∠=∠在ABD ∆和FBC ∆中,AB FB ABD CBF DB CB =⎧⎪∠=∠⎨⎪=⎩()ABD FBC SAS ∴∆≅∆;图1 图2(2)ABD FBC ∆≅∆,BAD BFC ∴∠=∠,6AD FC ==,180AMF BAD CNA ∴∠=︒-∠-∠ 180()BFC BNF =︒-∠+∠1809090=︒-︒=︒AD CF ∴⊥-ACD ACF DFM ACM ACDF S S S S S ∆∆∆∆∴=++四边形11112222AD CM CF AM DM FM AM CM =⋅+⋅+⋅-⋅ 1133(6)(6)1822CM AM AM CM AM CM =++---⋅= 【点睛】本题考查了正方形的性质,全等三角形的性质和判定,三角形的面积等知识点,能求出△ABD ≌△FBC 是解此题的关键.15.如图1,对角线互相垂直的四边形叫做垂美四边形.(1)概念理解:如图2,在四边形ABCD 中,,AB AD CB CD ==,问四边形ABCD 是垂美四边形吗?请说明理由;(2)性质探究:如图1,四边形ABCD 的对角线,AC BD 交于点O ,AC BD ⊥. 试证明:2222AB CD AD BC +=+;(3)解决问题:如图3,分别以Rt ACB △的直角边AC 和斜边AB 为边向外作正方形ACFG 和正方形ABDE ,连结,,CE BG GE .已知30,1CAB CB ∠=︒=,求GE 的长.解析:(1)是,理由见解析; (2)见解析;(3)13【分析】(1)根据垂直平分线的判定定理证明即可;(2)根据垂直的定义和勾股定理解答即可;(3)根据垂美四边形的性质、勾股定理、结合(2)的结论计算.【详解】解:(1)是AD AB,理由:=∴A在BD的垂直平分线上.=,∵CD CB∴C在BD的垂直平分线上.∴AC垂直平分BD.∴四边形ABCD为垂美四边形.(2)如图2,连接AC和BD,AC BD,222∴=+,AH AO BO222DC CO CO=+,222=+,AD AO DO222=+.BC BO CO222222∴+=+++.AB DC AO BO CO DO222222+=+++.BC AD BO CO AO DO2222∴+=+;AB DC BC AD(3)连接CG、BE,∵∠CAG=∠BAE=90°,∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,在△GAB 和△CAE 中,AG AC GAB CAE AB AE =⎧⎪∠=∠⎨⎪=⎩,∴△GAB ≌△CAE (SAS ),∴∠ABG=∠AEC ,又∠AEC+∠AME=90°,∴∠ABG+∠AME=90°,即CE ⊥BG ,∴四边形CGEB 是垂美四边形,由(2)得,CG 2+BE 2=CB 2+GE 2,∵30,1CAB CB ∠=︒=,∴AC=3,AB=2,CG=6,BE=22,∴GE 2=CG 2+BE 2-CB 2=13,∴GE=13.【点睛】本题考查的是正方形的性质、全等三角形的判定和性质、垂直的定义、勾股定理的应用,正确理解垂美四边形的定义、灵活运用勾股定理是解题的关键.16.如图,△ABC 是等边三角形,AB =4cm . 动点P ,Q 分别从点A 、B 同时出发,动点P 以1cm /s 的速度沿AC 向终点C 运动.动点Q 以2cm /s 的速度沿射线BC 运动.当点P 停止运动时,点Q 也随之停止运动.点P 出发后,过点P 作PE ∥AB 交BC 于点E ,连结PQ ,以PQ 为边作等边三角形PQF ,连结CF ,设点P 的运动时间为t (s )(1)用含t 的代数式表示CQ 的长.(2)求△PCE 的周长(用含t 的代数式表示).(3)求CF 的长(用含t 的代数式表示).(4)当△PQF 的边与BC 垂直时,直接写出t 的值.解析:(1)当0≤t≤2时,CQ=4-2t ;当2<t≤4时,CQ=2t-4;(2)123t -;(3)CF t =;(4)当PQF △的边与BC 垂直时,t 的值为43或83【分析】(1)分Q 在线段BC 上以及射线CD 上两种情况进行讨论即可;(2)根据题意可先证明△PCE 是等边三角形,然后求出PC ,再乘3即可;(3)根据“双等边”模型,可证明△PEQ ≌△PCF ,从而得到CF =EQ ,求出EQ 即可; (4)分PQ ⊥BC 时,和FQ ⊥BC 时,两种情况进行求解即可.【详解】解:(1)根据题意,∵△ABC 是等边三角形,∴4BC AC AB cm ===,∵动点P 以1/cm s 的速度沿AC 向终点C 运动,∴时间的最大值为:414t =÷=(秒),∴04t ≤≤;∵动点Q 以2/cm s 的速度沿射线BC 运动,∴2BQ t =,当02t ≤≤时,42CQ BC BQ t =-=-;当24t <≤时,24CQ BQ BC t =-=-;(2)∵//PE AB ,ABC 是等边三角形,∴∠PEC =∠B =60°,∠EPC =∠A =60°,∵∠ACB =60°,∴△PCE 是等边三角形,∴PC =PE =CE ,∵4PC t =-,∴△PCE 的周长为:3(4)123t t ⨯-=-;(3)如图:∵PQF ∆是等边三角形,∴PQ PF =,∠QPF =60°,∵△PCE 是等边三角形,∴PC =PE ,∠EPC =∠QPF =60°,∴△PEQ ≌△PCF ,∴CF =EQ ,∵EQ BQ BE =-,∵BE AP t ==,2BQ t =,∴2CF EQ t t t ==-=;(4)根据题意,①当PQ ⊥BC 时,如图:∵△PCE 是等边三角形,∴PQ 是高,也是中线,∴42CQ EQ t ==-,∵BE AP t ==,∴(42)(42)4t t t +-+-=, 解得:43t =; ②当FQ ⊥BC 时,如图:∵∠FQC =90°,∠FQP =60°,∴∠PQE =30°,∵∠PCE =60°,∴∠CPQ =30°=∠PQE ,∴PC =CQ ,∵4PC t =-,24CQ t =-,∴424t t -=-, 解得:83t =; 综合上述,当PQF △的边与BC 垂直时,t 的值为43或83. 【点睛】 本题主要考查等边三角形的性质以及全等三角形的判定与性质,熟练掌握“手拉手”的基本模型是解题关键.17.在直线AB 的同一侧作两个等边三角形ABD △和BCE ,连接AE 与CD ,试解决下列问题:(1)求证:AE DC =;(2)求DHA ∠的度数;(3)连接GF ,试判断BGF 形状.解析:(1)见解析;(2)60DHA ∠=︒;(3)BGF 是等边三角形.【分析】(1)从ABD △和BCE ∆是等边三角形中寻找条件证明(SAS)ABE DBC ≌,然后利用全等三角形的性质即可证明;(2)由ABE DBC ≌可得BAE BDC ∠=∠,再由外角的性质可得DHA BAE DCB ∠=∠+∠,然后根据等量代换即可证明;。
全等三角形与旋转问题专题练习

全等三角形与旋转问题专题练习中考要求知识点睛基本知识把图形G绕平面上的一个定点O旋转一个角度θ,得到图形G',这样的由图形G到G'变换叫做旋转变换,点O叫做旋转中心,θ叫做旋转角,G'叫做G的象;G叫做G'的原象,无论是什么图形,在旋转变换下,象与原象是全等形.很明显,旋转变换具有以下基本性质:①旋转变换的对应点到旋转中心的距离相等;②对应直线的交角等于旋转角.旋转变换多用在等腰三角形、正三角形、正方形等较规则的图形上,其功能还是把分散的条件盯对集中,以便于诸条件的综合与推演.重、难点重点:本节的重点是全等三角形的概念和性质以及判定,全等三角形的性质是以后证明三角形问题的基础,也是学好全章的关键。
同时全等三角形的判定也是本章的重点,特别是几种判定方法,尤其是当在直角三角形中时,HL的判定是整个直角三角形的重点难点:本节的难点是全等三角形性质和判定定理的灵活应用。
为了能熟练的应用性质定理及其推论,要把性质定理和推论的条件和结论弄清楚,哪几个是条件,决定哪个结论,如何用数学符号表示,即书写格式,都要在讲练中反复强化【例1】 如图,有四个图案,它们绕中心旋转一定的角度后,都能和原来的图案相互重合,其中有一个图案与其余三个图案旋转的角度不同,它是_____________.【解析】 A【例2】 如图,同学们曾玩过万花筒,它是由三块等宽等长的玻璃片围成的,其中菱形AEFG可以看成是把菱形ABCD 以A 为中心_____________。
A .顺时针旋转60°得到B .顺时针旋转120°得到C .逆时针旋转60°得到D .逆时针旋转120°得到G FE D C BA【解析】 D【例3】 如图,C 是线段BD 上一点,分别以BC 、CD 为边在BD 同侧作等边△ABC 和等边△CDE ,AD 交CE 于F ,BE 交AC 于G ,则图中可通过旋转而相互得到的三角形对数有_____________。
专题01 全等三角形中的手拉手旋转模型(解析版)
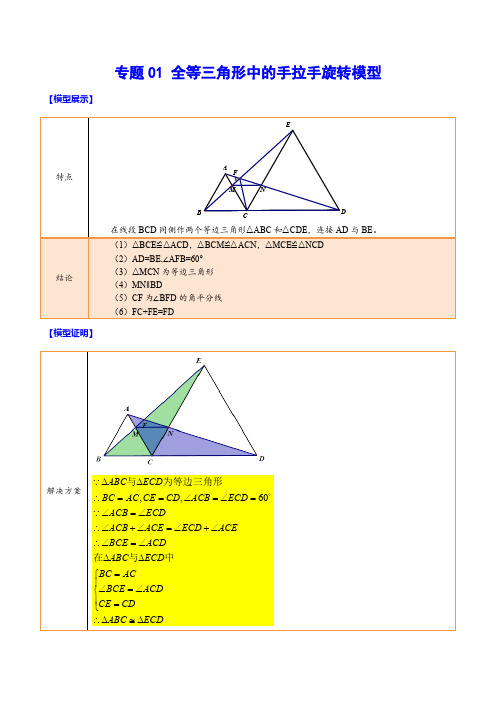
专题01 全等三角形中的手拉手旋转模型【模型展示】【模型证明】ECDABC CD CE ACD BCE AC BC ECD ABC ACD BCE ACE ECD ACE ACB ECDACB ECD ACB CD CE AC BC ECD ABC ∆≅∆∴⎪⎩⎪⎨⎧=∠=∠=∆∆∠=∠∴∠+∠=∠+∠∴∠=∠=∠=∠==∴∆∆中与在为等边三角形与 60,,BDMN NCD MNC NCD MNC MCN MCN MCN CN CM ACN BCM AFB AFM BCM AFM BMC AMF MAF AFM BMC CBM BCM AFM AMF MAF BCM BMC CBM CADCBE ACD BCE ADBE ACD BCE //60606060,60)(180)(180180180∴∠=∠∴=∠=∠∴∆∆∴=∠=∴∆≅∆=∠=∠=∠∴∠=∠∠+∠-=∠∠+∠-=∠∴=∠+∠+∠=∠+∠+∠∠=∠∴∆≅∆=∴∆≅∆为等边三角形为等边三角形即P Q NMFECABD【模型拓展】【题型演练】一、单选题1.如图,在ABCV中,90ABC∠=°,分别以AB,AC为边作等边ABD△和等边ACEV,连结DE,若3AB=,5AC=,则ED=()A.B.C.4D.【答案】C【分析】在Rt△ABC中可直接运用勾股定理求出BC,然后结合“手拉手”模型证得△ABC≌△ADE,即可得到DE=BC,从而求解即可.【详解】解:在Rt△ABC中,AB=3,AC=5,∴由勾股定理得:BC=4,∵ABD △和ACE V 均为等边三角形,∴AB =AD ,AC =AE ,∠BAD =∠CAE =60°,∴∠BAD -∠CAD =∠CAE -∠CAD ,即:∠BAC =∠DAE ,在△ABC 和△ADE 中,AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△ADE (SAS ),∴DE =BC =4,故选:C .【点睛】本题考查全等三角形的判定与性质,勾股定理的应用,掌握全等三角形的判定与性质,熟练运用勾股定理解三角形是解题关键.2.如图,C 为线段AE 上一动点(不与点A ,E 重合),在AE 同侧分别作等边三角形ABC 和等边三角形CDE ,AD 与BE 交于点O ,AD 与BC 交于点P ,BE 与CD 交于点Q ,连结PQ .以下结论错误的是( )A .∠AOB =60°B .AP =BQC .PQ ∥AED .DE =DP【答案】D【分析】利用等边三角形的性质,BC ∥DE ,再根据平行线的性质得到∠CBE =∠DEO ,于是∠AOB =∠DAC +∠BEC =∠BEC +∠DEO =∠DEC =60°,得出A 正确;根据△CQB ≌△CPA (ASA ),得出B 正确;由△ACD ≌△BCE 得∠CBE =∠DAC ,加之∠ACB =∠DCE =60°,AC =BC ,得到△CQB ≌△CPA (ASA ),再根据∠PCQ =60°推出△PCQ 为等边三角形,又由∠PQC =∠DCE ,根据内错角相等,两直线平行,得出C 正确;根据∠CDE =60°,∠DQE =∠ECQ +∠CEQ =60°+∠CEQ ,可知∠DQE ≠∠CDE ,得出D 错误.【详解】解:∵等边△ABC 和等边△CDE ,∴AC =BC ,CD =CE ,∠ACB =∠DCE =60°,∴∠ACB +∠BCD =∠DCE +∠BCD ,即∠ACD =∠BCE,在△ACD 与△BCE 中,AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩,∴△ACD ≌△BCE (SAS ),∴∠CBE =∠DAC ,又∵∠ACB =∠DCE =60°,∴∠BCD =60°,即∠ACP =∠BCQ ,又∵AC =BC ,在△CQB 与△CPA 中,ACP BCQ AC BCPAC CBQ ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△CQB ≌△CPA (ASA ),∴CP =CQ ,又∵∠PCQ =60°可知△PCQ 为等边三角形,∴∠PQC =∠DCE =60°,∴PQ ∥AE ,故C 正确,∵△CQB ≌△CPA ,∴AP =BQ ,故B 正确,∵AD =BE ,AP =BQ ,∴AD -AP =BE -BQ ,即DP =QE ,∵∠DQE =∠ECQ +∠CEQ =60°+∠CEQ ,∠CDE =60°,∴∠DQE ≠∠CDE ,故D 错误;∵∠ACB =∠DCE =60°,∴∠BCD =60°,∵等边△DCE ,∠EDC=60°=∠BCD,∴BC∥DE,∴∠CBE=∠DEO,∴∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°,故A正确.故选:D.【点睛】本题考查了等边三角形的性质、全等三角形的判定与性质,利用旋转不变性,解题的关键是找到不变量.3.如图,在Rt△ABC和Rt△ADE中,∠BAC=∠DAE=90°,AB=AC=5,AD=AE=2,点P,Q,R分别是BC,DC,DE的中点.把△ADE绕点A在平面自由旋转,则△PQR的面积不可能是()A.8B.6C.4D.2【答案】A【分析】连接BD、CE,BD的延长线交CE的延长线于O,AC交BO于H.证明△BAD≌△CAE,然后可推出△PQR是等腰直角三角形,S△PQR=12•PQ2,由AB=5,AD=2可知3≤BD≤7,从而得到32≤PQ≤72,那么9 8≤12•PQ2≤498,即可得出答案.【详解】解:连接BD、CE,BD的延长线交CE的延长线于O,AC交BO于H.∵AB=AC,AD=AE,∠BAC=∠DAE=90°,∴∠BAD=∠CAE,∴△BAD≌△CAE,∴BD=CE,∠ABH=∠OCH,∵∠AHB=∠CHO,∴∠O=∠BAH=90°,∵点P ,Q ,R 分别是BC ,DC ,DE 的中点,∴PQ =12BD ,PQ ∥BO ,QR =12EC ,QR ∥CO ,∵BO ⊥OC ,∴PQ ⊥RQ ,PQ =QR ,∴△PQR 是等腰直角三角形,∴S △PQR =12•PQ 2,∵AB =5,AD =2,∴3≤BD ≤7,∴32≤PQ ≤72,∴98≤12•PQ 2≤498,∴△PQR 的面积不可能是8,故答案为:A .【点睛】本题考查了旋转的性质,等腰直角三角形的性质,全等三角形的判定和性质,三角形的中位线定理,解题的关键是灵活运用所学知识解决问题.4.如图,在ABC V 中,AB AC =,点D 、F 是射线BC 上两点,且AD AF ⊥,若AE AD =,15BAD CAF ∠=∠=°;则下列结论中正确的有( )①CE BF ⊥;②ABD ACE △≌△;③ABC ADCE S S =四边形△;④122BC EF AD CF-=-A .1个B .2个C .3个D .4个【答案】D【分析】由AD ⊥AF ,∠BAD=∠CAF ,得出∠BAC=90°,由等腰直角三角形的性质得出∠B=∠ACB=45°,由SAS 证得△ABD ≌△ACE (SAS ),得出BD=CE ,∠B=∠ACE=45°,S △ABC =S 四边形ADCE ,则∠ECB=90°,即EC ⊥BF ,易证∠ADF=60°,∠F=30°,由含30°直角三角形的性质得出EF=2CE=2BD ,DF=2AD ,则BD=12EF ,由BC-BD=DF-CF ,得出BC-12EF=2AD-CF ,即可得出结果.【详解】∵AD ⊥AF ,∠BAD=∠CAF ,∴∠BAC=90°,∵AB=AC ,∴∠B=∠ACB=45°,在△ABD 和△ACE 中,AB AC BAD CAE AD AE =∠=∠=⎧⎪⎨⎪⎩,∴△ABD ≌△ACE (SAS ),∴BD=CE ,∠B=∠ACE=45°,S △ABC =S 四边形ADCE ,∴∠ECB=90°,∴EC ⊥BF ,∵∠B=45°,∠BAD=15°,∴∠ADF=60°,∴∠F=30°,∴EF=2CE=2BD ,DF=2AD ,∴BD=12EF ,∵BC-BD=DF-CF ,∴BC-12EF=2AD-CF ,∴①、②、③、④正确.故选:D .【点睛】本题考查了全等三角形的判定与性质、等腰直角三角形的性质、含30°角直角三角形的性质、外角的定义等知识,熟练掌握直角三角形的性质、证明三角形全等是解题的关键.5.如图,正ABC V 和正CDE △中,B 、C 、D 共线,且3BC CD =,连接AD 和BE 相交于点F ,以下结论中正确的有( )个①60AFB ∠=° ②连接FC ,则CF 平分BFD ∠ ③3BF DF = ④BF AF FC=+A .4B .3C .2D .1【答案】A【分析】根据“手拉手”模型证明BCE ACD V V ≌,从而得到CBE CAD ∠=∠,再结合三角形的外角性质即可求解60AFB ACB ∠=∠=°,即可证明①;作CM BE ⊥于M 点,CN AD ⊥于N 点,证明CEM CDN V V ≌,结合角平分线的判定定理即可证明②;利用面积法表示BCF △和DCF V 的面积,然后利用比值即可证明③;利用“截长补短”的思想,在AD 上取点Q ,使得FC FQ =,首先判断出FCQ V 为等边三角形,再结合“手拉手”模型推出BCF ACQ V V ≌即可证明④.【详解】解:①∵ABC V 和CDE △均为等边三角形,∴60ACB ECD ∠=∠=°,AC BC =,EC DC =,∴ACB ACE ECD ACE ∠+∠=∠+∠,∴BCE ACD ∠=∠,在BCE V 和ACD △中,BC AC BCE ACDEC DC =⎧⎪∠=∠⎨⎪=⎩∴()BCE ACD SAS V V ≌,∴CBE CAD ∠=∠,∵AFB CBE CDA ∠=∠+∠,ACB CDA CAD ∠=∠+∠,∴60AFB ACB ∠=∠=°,故①正确;②如图所示,作CM BE ⊥于M 点,CN AD ⊥于N 点,则90CME CND ∠=∠=°,∵BCE ACD V V ≌,∴CEM CDN ∠=∠,在CEM V 和CDN △中,CME CND CEM CDNCE CD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()CEM CDN AAS V V ≌,∴CM CN =,∴CF 平分BFD ∠,故②正确;③如图所示,作FP BD ⊥于P 点,∵1122BCF S BF CM BC FP ==V g g ,1122DCF S DF CN CD FP ==V g g ,∴11221122BCFDCF BF CM BC FP S S DF CN CD FP ==V V g g g g ,∵CM CN =,∴整理得:BF BC DF CD=,∵3BC CD =,∴33BF CD DF CD==,∴3BF DF =,故③正确;④如图所示,在AD 上取点Q ,使得FC FQ =,∵60AFB ACB ∠=∠=°,CF 平分BFD ∠,∴120BFD ∠=°,1602CFD BFD ∠=∠=°,∴FCQ V 为等边三角形,∴60FCQ ∠=°,CF CQ =,∵60ACB ∠=°,∴ACB ACF FCQ ACF ∠+∠=∠+∠,∴BCF ACQ ∠=∠,在BCF △和ACQ V 中,BC AC BCF ACQCF CQ =⎧⎪∠=∠⎨⎪=⎩∴()BCF ACQ SAS V V ≌,∴BF AQ =,∵AQ AF FQ =+,FQ FC =,∴BF AF FC =+,故④正确;综上,①②③④均正确;故选:A .【点睛】本题考查等边三角形的判定与性质,全等三角形的判定与性质等,理解等边三角形的基本性质,掌握全等三角形中的辅助线的基本模型,包括“手拉手”模型,截长补短的思想等是解题关键.6.如图,点C 是线段AE 上一动点(不与A ,E 重合),在AE 同侧分别作等边三角形ABC 和等边三角形CDE ,AD 与BE 交于点O ,AD 与BC 交于点P ,BE 与CD 交于点Q ,连接PQ ,有以下5个结论:①AD=BE ;②PQ ∥AE ;③AP=BQ ;④DE=DP ;⑤∠AOB=60°.其中一定成立的结论有( )个A .1B .2C .3D .4【答案】D 【分析】①由于△ABC 和△CDE 是等边三角形,可知AC=BC ,CD=CE ,∠ACB=∠DCE=60°,从而证出△ACD ≌△BCE ,可推知AD=BE;③由△ACD≌△BCE得∠CBE=∠DAC,加之∠ACB=∠DCE=60°,AC=BC,得到△ACP≌△BCQ(ASA),所以AP=BQ;故③正确;②根据②△CQB≌△CPA(ASA),再根据∠PCQ=60°推出△PCQ为等边三角形,又由∠PQC=∠DCE,根据内错角相等,两直线平行,可知②正确;④根据∠DQE=∠ECQ+∠CEQ=60°+∠CEQ,∠CDE=60°,可知∠DQE≠∠CDE,可知④错误;⑤利用等边三角形的性质,BC∥DE,再根据平行线的性质得到∠CBE=∠DEO,于是∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°,可知⑤正确.【详解】①∵等边△ABC和等边△DCE,∴BC=AC,DE=DC=CE,∠DEC=∠BCA=∠DCE=60∘,∴∠ACD=∠BCE,在△ACD和△BCE中,AC=BC,∠ACD=∠BCE,DC=CE,∴△ACD≌△BCE(SAS),∴AD=BE;故①正确;③∵△ACD≌△BCE(已证),∴∠CAD=∠CBE,∵∠ACB=∠ECD=60°(已证),∴∠BCQ=180°-60°×2=60°,∴∠ACB=∠BCQ=60°,在△ACP与△BCQ中,∠CAD=∠CBE,AC=BC,∠ACB=∠BCQ=60°,∴△ACP≌△BCQ(ASA),∴AP=BQ;故③正确;②∵△ACP≌△BCQ,∴PC=QC,∴△PCQ是等边三角形,∴∠CPQ=60∘,∴∠ACB=∠CPQ ,∴PQ ∥AE ;故②正确;④∵AD=BE ,AP=BQ ,∴AD−AP=BE−BQ ,即DP=QE ,∠DQE=∠ECQ+∠CEQ=60°+∠CEQ ,∠CDE=60°,∴∠DQE≠∠CDE ,∴DE≠QE ,则DP≠DE ,故④错误;⑤∵∠ACB=∠DCE=60°,∴∠BCD=60°,∵等边△DCE ,∠EDC=60°=∠BCD ,∴BC ∥DE ,∴∠CBE=∠DEO ,∴∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°.故⑤正确;综上所述,正确的结论有:①②③⑤,错误的结论只有④,故选D .【点睛】本题考查全等三角形的判定和性质,以及等边三角形的判定和性质,此图形是典型的“手拉手”模型,熟练掌握此模型的特点是解题的关键.二、填空题7.如图,ABD △、CDE △是两个等边三角形,连接BC 、BE .若30DBC ∠=°,6BD =,8BC =,则BE =________.【答案】BE =10【分析】连接AC ,根据题意易证△ACD ≌△BED(SAS),根据全等三角形的性质可得AC=BE ,再根据勾股定理求出AC 的值即可得出结论.【详解】如图,连接AC ,∵ABD △、CDE △是两个等边三角形,∴AB=BD=AD=2,CD=DE ,∠ABD=∠ADB=∠CDE=60,∴∠ADB+∠BDC=∠CDE+∠BDC ,∴∠ADC=∠BDE ,在△ACD 与△BDE 中AD BD ADC BDE CD DE =⎧⎪=⎨⎪=⎩∠∠,∴△ACD ≌△BED (SAS ),∴AC=BE ,∵30DBC ∠=°,∴∠ABC=∠ABD+∠DBC=60°+30°=90°,在Rt △ABC 中,AB=6,BC=8,∴10=,∴BE=10,故答案为:10.【点睛】本题考查了等边三角形的性质,全等三角形的判定与性质,勾股定理,孰练的掌握知识点是解题关键.8.如图,△ABC 中,∠C =90°,AC =BC =△ABC 绕点A 顺时针方向旋转60°到△AB 'C '的位置,连接BC ',BC '的延长线交AB '于点D ,则BD 的长为 _____.【分析】连接BB ′,根据旋转的性质可得AB =AB ′,判断出△ABB ′是等边三角形,根据等边三角形的三条边都相等可得AB =BB ′,然后利用“边边边”证明△ABC ′和△B ′BC ′全等,根据全等三角形对应角相等可得∠ABC ′=∠B ′BC ′,延长BC ′交AB ′于D ,根据等边三角形的性质可得BD ⊥AB ′,利用勾股定理列式求出AB ,然后根据等边三角形的性质和等腰直角三角形的性质求出BD .【详解】解:如图,连接BB ′,∵△ABC 绕点A 顺时针方向旋转60°得到△AB ′C ′,∴AB =AB ′,∠BAB ′=60°,∴△ABB ′是等边三角形,∴AB =BB ′,在△ABC ′和△B ′BC ′中,AB BB AC B C BC BC =¢⎧⎪¢=¢¢⎨⎪¢=¢⎩,∴△ABC ′≌△B ′BC ′(SSS ),∴∠ABC ′=∠B ′BC ′30=° ,延长BC ′交AB ′于D ,则BD ⊥AB ′,∵∠C =90°,AC =BC ,∴AB 2=AB ’,∴AD =112AB =∴BD =,【点睛】本题考查了旋转的性质,全等三角形的判定与性质,等边三角形的判定与性质,等腰直角三角形的性质,作辅助线构造出全等三角形并求出BC ′在等边三角形的高上是解题的关键,也是本题的难点.9.如图,ABC V 是边长为5的等边三角形,BD CD =,120BDC ∠=°.E 、F 分别在AB 、AC 上,且60EDF ∠=°,则三角形AEF 的周长为______.【答案】10【分析】延长AB 到N ,使BN =CF ,连接DN ,求出∠FCD =∠EBD =∠NBD =90°,根据SAS 证△NBD ≌△FCD ,推出DN =DF ,∠NDB =∠FDC ,求出∠EDF =∠EDN ,根据SAS 证△EDF ≌△EDN ,推出EF =EN ,易得△AEF 的周长等于AB +AC .【详解】解:延长AB 到N ,使BN =CF ,连接DN ,∵△ABC 是等边三角形,∴∠ABC =∠ACB =60°,∵BD =CD ,∠BDC =120°,∴∠DBC =∠DCB =30°,∴∠ACD =∠ABD =30°+60°=90°=∠NBD ,∵在△NBD 和△FCD 中,BD DC NBD FCD BN CF =⎧⎪∠=∠⎨⎪=⎩,∴△NBD ≌△FCD (SAS ),∴DN =DF ,∠NDB =∠FDC ,∵∠BDC =120°,∠EDF =60°,∴∠EDB +∠FDC =60°,∴∠EDB +∠BDN =60°,即∠EDF =∠EDN ,在△EDN 和△EDF 中,DE DE EDF EDN DN DF =⎧⎪∠=∠⎨⎪=⎩,∴△EDN ≌△EDF (SAS ),∴EF =EN =BE +BN =BE +CF ,即BE +CF =EF .∵△ABC 是边长为5的等边三角形,∴AB =AC =5,∵BE +CF =EF ,∴△AEF 的周长为:AE +EF +AF =AE +EB +FC +AF =AB +AC =10,故答案为:10.【点睛】本题考查了等边三角形性质和判定,等腰三角形的性质,三角形的内角和定理,全等三角形的性质和判定的综合运用.注意掌握辅助线的作法,注意掌握数形结合思想的应用.10.如图,C 为线段AE 上一动点(不与点A 、E 重合),在AE 同侧分别作正△ABC 和正△CDE ,AD 与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ P AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.恒成立的结论有_____.(把你认为正确的序号都填上)【答案】①②③⑤为等边三角形,再证【分析】根据等边三角形的性质及SAS即可证明;根据全等三角形的性质证明MCN明△ACD≌△BCE即可求解.【详解】解:①△ABC和△DCE均是等边三角形,点A,C,E在同一条直线上,∴AC=BC,EC=DC,∠BCE=∠ACD=120°∴△ACD≌△ECB∴AD=BE,故本选项正确,符合题意;②∵△ACD≌△ECB∴∠CBQ=∠CAP,又∵∠PCQ=∠ACB=60°,CB=AC,∴△BCQ≌△ACP,∴CQ=CP,又∠PCQ=60°,∴△PCQ为等边三角形,∴∠QPC=60°=∠ACB,∴PQ P AE,故本选项正确,符合题意;③∵∠ACB=∠DCE=60°,∴∠BCD=60°,∴∠ACP=∠BCQ,∵AC=BC,∠DAC=∠QBC,∴△ACP≌△BCQ(ASA),∴CP=CQ,AP=BQ,故本选项正确,符合题意;④已知△ABC 、△DCE 为正三角形,故∠DCE =∠BCA =60°⇒∠DCB =60°,又因为∠DPC =∠DAC +∠BCA ,∠BCA =60°⇒∠DPC >60°,故DP 不等于DE ,故本选项错误,不符合题意;⑤∵△ABC 、△DCE 为正三角形,∴∠ACB =∠DCE =60°,AC =BC ,DC =EC ,∴∠ACB +∠BCD =∠DCE +∠BCD ,∴∠ACD =∠BCE ,∴△ACD ≌△BCE (SAS ),∴∠CAD =∠CBE ,∴∠AOB =∠CAD +∠CEB =∠CBE +∠CEB ,∵∠ACB =∠CBE +∠CEB =60°,∴∠AOB =60°,故本选项正确,符合题意.综上所述,正确的结论是①②③⑤.三、解答题11.如图,ACB △和ECD V 都是等腰直角三角形,,,CA CB CD CE ACB ==△的顶点A 在ECD V 的斜边DE 上,连接BD .(1)求证:BD AE =.(2)若3cm,6cm AE AD ==,求AC 的长.【答案】(1)证明见解析;(2)AC =.【分析】(1)根据同角的余角相等得出∠BCD=∠ACE ,然后根据SAS 定理证明△BCD ≌△ACE ,从而得出结论;(2)根据全等三角形的性质得出∠BDC=∠AEC ,然后结合等腰直角三角形的性质求得∠BDA 是直角三角形,从而利用勾股定理求解.【详解】(1)∵ACB △和ECD V 都是等腰直角三角形,∴90ACB ECD ∠=∠=°,∴90,90ACD BCD ACD ACE ∠+∠=°∠+∠=°,∴BCD ACE ∠=∠,在BCD △和ACB △中,CB CA BCD ACECD CE =⎧⎪∠=∠⎨⎪=⎩∴()BCD ACE SAS V V ≌,∴BD AE =.(2)∵BCD ACE V V ≌,∴BDC AEC ∠=∠,又∵ECD V 是等腰直角三角形,∴45CDE CED ∠=∠=°,∴45BDC ∠=°,∴90BDC CDE ∠+∠=°,∴BDA ∠是直角三角形,∴22222223645AB BD AD AE AD =+=+=+=,在等腰直角三角形ACB 中,22222AB AC BC AC =+=,∴AC =【点睛】本题考查了全等三角形的判定与性质;证明三角形全等是解决问题的关键.12.如图,A 、B 、C 在同一直线上,且△ABD ,△BCE 都是等边三角形,AE 交BD 于点M ,CD 交BE 于点N ,MN ∥AC ,求证:(1)∠BDN=∠BAM ;(2)△BMN 是等边三角形.【答案】(1)证明过程见详解;(2)证明过程见详解。
初中数学全等三角形旋转模型(讲义及答案)及答案(1)

初中数学全等三角形旋转模型(讲义及答案)及答案(1)一、全等三角形旋转模型1.如图1,在等腰Rt △ABC 中,∠ABC =90°,AB =BC =6,过点B 作BD ⊥AC 交AC 于点D ,点E 、F 分别是线段AB 、BC 上两点,且BE =BF ,连接AF 交BD 于点Q ,过点E 作EH ⊥AF 交AF 于点P ,交AC 于点H .(1)若BF =4,求△ADQ 的面积;(2)求证:CH =2BQ ;(3)如图2,BE =3,连接EF ,将△EBF 绕点B 在平面内任意旋转,取EF 的中点M ,连接AM ,CM ,将线段AM 绕点A 逆时针旋转90°得线段AN ,连接MN 、CN ,过点N 作NR ⊥AC 交AC 于点R .当线段NR 的长最小时,直接写出△CMN 的周长.答案:A解析:(1)1.8;(2)证明见解析;(3)3263351022+. 【分析】(1)利用等腰直角三角形的性质求出1322BD AD CD AC ====积相等和勾股定理分别求出AQ 和QD ,最后利用三角形面积公式即可求解;(2)如图,先作辅助线构造()AEH CFG ASA ∆∆≌,得到AH CG =,再通过转化得到2AH DQ =,最后利用AC ,得到一个相等关系,即()2AH HC BQ QD +=+,利用等式性质即可得到所求;(3)如图,通过做辅助线构造全等三角形确定出当HN ⊥AC ,且N 点位于H 、R 之间时,此时NR 的长最小,接着利用勾股定理和等腰直角三角形的性质,分别求出CM 、MN 、CN 的长,相加即可.【详解】解:6AB BC ==,°90ABC =∠,262AC ==∴又∵AC BD ⊥∴BD 平分AC ,且BD 是∠ABC 的角平分线∴12BD AD CD AC ====Q 点到BA 和BC 边的距离相等; ∵4BF =, ∴6342ABQ BFQ S S ∆∆==, ∴32AQ FQ =,∵AF ===∴355AQ AF ==,∴5QD ===,∴1 1.82ADQ S ∆==, ∴△ADQ 的面积为1.8.(2)如图,作CG ⊥AC ,垂足为C ,交AF 的延长线于点G ,∴°90ACG =∠∵°45ACB CAB ==∠∠,∴°45GCB CAB ==∠∠,∵EH ⊥AF ,∴°90EAP AEP +=∠∠,又∵°90EAP AFB +=∠∠∴AEP AFB =∠∠,∴AEP CFG =∠∠∵BE BF =,BA BC =∴AE CF =,在AEH ∆和CFG ∆中,AEH CFG AE CFEAH FCG ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()AEH CFG ASA ∆∆≌∴AH CG =;∵BD ⊥AC ,CG ⊥AC ,∴BD ∥CG ,∵D 点是AC 的中点,且BD ∥CG ,∴DQ 是ACG ∆的中位线,∴12DQ CG =, ∴2DQ CG AH ==; ∵AC =2BD ,∴()2AH HC BQ QD +=+,∵2AH DQ =,∴CH =2BQ .(3)如图①,作AH ⊥AB ,且AH =AB ,∴∠NAH +∠HAM =∠HAM +∠BAM =90°,∴∠BAM =∠NAH ,∵AB =AH ,AM =AN ,∴()ABM AHN SAS ∆∆≌, ∴HN =BM ,∵BE =BF =3,∠EBF =90°, ∴232EF BE ==∴由M 点是EF 的中点,可得13222BM EF ==, ∴32NH =, ∴N 点在以H 点为圆心,322为半径的圆上, 如图②,当HN ⊥AC ,且N 点位于H 、R 之间时,此时NR 的长最小, 为322NR HR HN HR =-=-, ∵∠BAC =45°,∴∠HAC =45°,∴∠AHN =45°,HR =AR ,∵222HR AR AH +=,∴6322HR AR ===, ∴323222NR HR =-=, ∵262AC AB ==,∴32CR AC AR =-=,∴()22333221022CN AN ⎛⎫==+= ⎪⎝⎭, ∵∠MAN =90°,AM =AN ,∴235MN AN ==,∴∠ABM =45°,∴∠EBM =45°,∴F 点在BA 上,E 点在CB 延长线上,如图,作MP ⊥EC ,垂足为P ,∴1322BP MP EB ===, ∴315622PC PB BC =+=+=, ∴223262MC MP PC =+=, ∴3263351022MC MN CN ++=++, ∴△CMN 的周长为3263351022++.【点睛】本题综合考查了等腰直角三角形的性质、全等三角形的判定与性质、旋转的性质、勾股定理、圆等知识,要求学生熟练掌握相关概念并能灵活应用它们,本题的综合性较强,难点在于作辅助线构造全等三角形以及线段之间的关系转化等,考查了学生综合分析和推理论证以及计算的能力,本题属于压轴题,蕴含了数形结合和转化的思想方法等.2.如图,点B ,C ,D 在同一条直线上,△BCF 和△ACD 都是等腰直角三角形,连接AB ,DF ,延长DF 交AB 于点E .(1)如图1,若AD =BD ,DE 是∠ADB 的平分线,BC =1,求CD 的长度;(2)如图2,连接CE ,求证:DE =2CE +AE ;(3)如图3,改变△BCF 的大小,始终保持点在线段AC 上(点F 与点A ,C 不重合).将ED 绕点E 顺时针旋转90°得到EP ,取AD 的中点O ,连接OP .当AC =2时,直接写出OP 长度的最大值.解析:(1)21CD =;(2)证明见解析;(3)22+【分析】 (1)根据等腰直角三角形的性质,求出1FC BC ==,再判断出FA FB =,即可得出结论;(2)先判断出ABC DFC ≅△△,得出BAC CDF ∠=∠,进而判断出ACE DCH ≅△△,得出AE DH =,CE CH =,即可得出结论;(3)先判断出2OE OQ ==,再判断出OED QEP ≅△△,进而求出2PQ OD ==得出结论.【详解】(1)解:BCF 和ACD △都是等腰直角三角形,AC CD ∴=,1FC BC ==,2FB =,AD BD =,DE 是ABD ∆的平分线,DE ∴垂直平分AB ,2FA FB ∴==,21AC FA FC ∴=+=,21CD ∴=;(2)证明:如图2,过点C 作CH CE ⊥交ED 于点H ,BCF 和ACD △都是等腰直角三角形,AC DC ∴=,FC BC =,90ACB DCF ∠=∠=︒;()ABC DFC SAS ∴≅△△,BAC CDF ∴∠=∠,90ECH ∠=︒,90ACE ACH ∴∠+∠=︒,90ACD ∠=︒,90DCH ACH ∴∠+∠=︒,ACE DCH ∴∠=∠.在ACE 和DCH 中,BAC CDF AC DCACE DCH ∠=∠⎧⎪=⎨⎪∠=∠⎩, ()ACE DCH ASA ∴≅△△,AE DH ∴=,CE CH =,2EH CE ∴=.2DE EH DH CE AE =+=+;(3)OP 的最大值是22+解:如图3,连接OE ,将OE 绕点E 顺时针旋转90︒得到EQ ,连接OQ ,PQ ,则2OQ OE =.由(2)知,90AED ABC CDF ABC BAC ∠=∠+∠=∠+∠=︒,在Rt AED △中,点O 是斜边AD 的中点,122222OE OD AD AC ∴===== 2222OQ OE ∴===,在OED 和QEP △中,OE QE OED QEP DE PE =⎧⎪∠=∠⎨⎪=⎩,()OED QEP SAS ∴≅△△,2PQ OD ∴==22OP OQ PQ +=+O 、P 、Q 三点共线时,取“=”号,OP ∴的最大值是22+【点睛】此题是几何变换综合题,主要等腰直角三角形的性质,全等三角形的判定和性质,构造出全等三角形是解本题的关键.3.如图.四边形ABCD 、BEFG 均为正方形.(1)如图1,连接AG 、CE ,请直接写出.....AG 和CE 的数量和位置关系(不必证明).(2)将正方形BEFG 绕点B 顺时针旋转β角(0180β︒︒<<),如图2,直线AG 、CE 相交于点M .①AG 和CE 是否仍然满足(1)中的结论?如果是,请说明理由:如果不是,请举出反例:②连结MB ,求证:MB 平分AME ∠.(3)在(2)的条件下,过点A 作AN MB ⊥交MB 的延长线于点N ,请直接写出.....线段CM 与BN 的数量关系.答案:A解析:(1)AG=EC ,AG ⊥EC ;(2)①满足,理由见解析;②见解析;(3)2.【分析】(1)由正方形BEFG 与正方形ABCD ,利用正方形的性质得到两对边相等,一对直角相等,利用SAS 得出三角形ABG 与三角形CBE 全等,利用全等三角形的对应边相等,对应角相等得到CE=AG ,∠BCE=∠BAG ,再利用同角的余角相等即可得证;(2)①利用SAS 得出△ABG ≌△CEB 即可解决问题;②过B 作BP ⊥EC ,BH ⊥AM ,由全等三角形的面积相等得到两三角形面积相等,而AG=EC ,可得出BP=BH ,利用到角两边距离相等的点在角的平分线上得到BM 为角平分线;(3)在AN 上截取NQ=NB ,可得出三角形BNQ 为等腰直角三角形,利用等腰直角三角形的性质得到2BN ,接下来证明BQ=CM ,即要证明三角形ABQ 与三角形BCM 全等,利用同角的余角相等得到一对角相等,再由三角形ANM 为等腰直角三角形得到NA=NM ,利用等式的性质得到AQ=BM ,利用SAS 可得出全等,根据全等三角形的对应边相等即可得证.【详解】解:(1)AG=EC ,AG ⊥EC ,理由为:∵正方形BEFG ,正方形ABCD ,∴GB=BE ,∠ABG=90°,AB=BC ,∠ABC=90°,在△ABG 和△BEC 中,BG BE ABC EBC BA BC =⎧⎪∠=∠⎨⎪=⎩,∴△ABG ≌△BEC (SAS ),∴CE=AG ,∠BCE=∠BAG ,延长CE 交AG 于点M ,∴∠BEC=∠AEM ,∴∠ABC=∠AME=90°,∴AG=EC ,AG ⊥EC ;(2)①满足,理由是:如图2中,设AM 交BC 于O .∵∠EBG=∠ABC=90°,∴∠ABG=∠EBC ,在△ABG 和△CEB 中,AB BC ABG CBE BG EB =⎧⎪∠=∠⎨⎪=⎩,∴△ABG ≌△CEB (SAS ),∴AG=EC ,∠BAG=∠BCE ,∵∠BAG+∠AOB=90°,∠AOB=∠COM ,∴∠BCE+∠COM=90°,∴∠OMC=90°,∴AG ⊥EC .②过B 作BP ⊥EC ,BH ⊥AM ,∵△ABG ≌△CEB ,∴S △ABG =S △EBC ,AG=EC , ∴12EC•BP=12AG•BH , ∴BP=BH ,∴MB 平分∠AME ;(3)CM=2BN ,理由为:在NA 上截取NQ=NB ,连接BQ ,∴△BNQ 为等腰直角三角形,即BQ=2BN ,∵∠AMN=45°,∠N=90°,∴△AMN 为等腰直角三角形,即AN=MN ,∴MN-BN=AN-NQ ,即AQ=BM ,∵∠MBC+∠ABN=90°,∠BAN+∠ABN=90°,∴∠MBC=∠BAN ,在△ABQ 和△BCM 中,AQ BM BAN MBC AB BC =⎧⎪∠=∠⎨⎪=⎩,∴△ABQ ≌△BCM (SAS ),∴CM=BQ ,则CM=2BN .【点睛】此题考查了正方形,全等三角形的判定与性质,等腰直角三角形的判定与性质,角平分线的判定,熟练掌握正方形的性质是解本题的关键.4.探究:(1)如图①,在△ABC 中,∠ACB =90°,CD ⊥AB 于点D ,若∠B =28°,则∠ACD 的度数是 .拓展:(2)如图②,∠MCN =90°,射线CP 在∠MCN 的内部,点A 、B 分别存CM 、CN 上,分别过点A 、B 作AD ⊥CP 、BE ⊥CP 于点D 、E ,若AC =CB ,则AD 、DE 、BE 三者间的数量关系为 .请说明理由;应用:(3)如图③,点A 、B 分别在∠MCN 的边CM 、CN 上,射线CP 在∠MCN 的内部,点D 、E 在射线CP 上,连结AD 、BE 、AE ,且使∠MCN =∠ADP =∠BEP .当AC =BC 时,△ ≌△ ;此时如果CD =2DE ,且S △CBE =6,则△ACE 的面积是 .答案:D解析:(1)28° (2)DE =AD ﹣BE ;理由见解析 (3)ACD ;CBE ;9【分析】(1)利用直角三角形的两锐角互余,即可得出结论;(2)利用同角的余角相等判断出∠CAD =∠BCE ,进而判断出△ACD ≌△CBE ,即可得出结论;(3)利用等式的性质判断出∠ADC =∠CEB ,进而判断出△ACD ≌△CBE ,得出S △ACD =S △CBE ,再求出S △ADE =3,即可得出结论.【详解】解:探究:∵CD ⊥AB ,∴∠CDB =90°,∵∠B =28°,∴∠BCD =90°﹣∠B =68°,∵∠ACB =90°,∴∠ACD =90°﹣∠BCD =28°,故答案为:28°;拓展:(2)∵∠MCN =90°,∴∠ACD+∠BCE =90°,∵AD ⊥CP ,BE ⊥CP ,∴∠ADC =∠BEC =90°,∴∠ACD+∠CAD =90°,∴∠CAD =∠BCE ,在△ACD 和△CBE 中,ADC CEB CAD BCE AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ACD ≌△CBE (AAS ),∴CD =BE ,AD =CE ,∴DE =CE ﹣CD =AD ﹣BE ,故答案为:DE =AD ﹣BE ;应用:(3)∵∠MCN =∠ACD+∠BCD ,∠MCN =∠ADP ,∴∠ADP =∠ACD+∠BCD ,∵∠ADP =∠ACD+∠CAD ,∴∠CAD =∠BCE ,∵∠ADP =∠BEP ,∴∠ADC =∠CEB ,在△ACD 和△CBE 中,ADC CEB CAD BCE AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ACD ≌△CBE (AAS ),∴S △ACD =S △CBE ,∵S △CBE =6,∴S △ACD =6,∵CD =2DE ,∴S △ACD =2S △ADE ,∴S △ADE =12S △ACD =3, ∴S △ACE =S △ACD +S △ADE =9,故答案为:ACD ,CBE ,9.【点睛】此题是三角形综合题,主要考查了直角三角形的性质,同角的余角相等,等式的性质,全等三角形的判定和性质,判断出△ACD ≌△CBE 是解本题的关键.5.如图1,在△ABC 和△ADE 中,∠DAE=∠BAC ,AD=AE ,AB=AC .(1)求证:△ABD ≌△ACE ;(2)如图2,在△ABC 和△ADE 中,∠DAE=∠BAC ,AD=AE ,AB=AC ,∠ADB=90°,点E 在△ABC 内,延长DE 交BC 于点F ,求证:点F 是BC 中点;(3)△ABC 为等腰三角形,∠BAC=120°,AB=AC ,点P 为△ABC 所在平面内一点,∠APB=120°,AP=2,BP=4,请直接写出 CP 的长.答案:D解析:(1)证明见详解;(2)证明见详解;(3)27或213.【分析】(1)因为∠DAE=∠BAC ,可以得到∠DAB=∠EAC ,因为AD=AE ,AB=AC ,即可得到△ABD ≌△ACE ;(2)连接CE ,延长EF 至点H ,取CF=CH ,连接CH ,由(1)可得△ABD ≌△ACE ,所以∠AEC=90°和CE=BD ,可以推出∠BDF=∠CEF ,再证明△DBF ≌△ECH ,所以BF=CH ,等量代换即可得到BF=FC ,即可解决;(3)点P 在△ABC 内部,将△ABP 逆时针旋转120°,得到ACP ∆',连接PP '和PC ,可以得到△PP C '是直角三角形,利用勾股定理即可求出PC 的值;当点P 在△ABC 外部,将△APB 绕点A 逆时针旋转120︒得到PDC ∆,连接PP '和PC ,过点P 作PD ⊥'CP 于点D ,连接PD 可以得到△PP D ',△PP D '是直角三角形和,利用勾股定理即可求出'DP 及PC 的值.【详解】解:(1)证明:∵∠DAE=∠BAC∴∠DAB=∠EAC∵AD=AE ,AB=AC∴△ABD ≌△ACE(2)证明:连接CE ,延长EF 至点H ,取CF=CH ,连接CH ,如图所示:∵△ADB ≌△AEC∴BD=EC ,∠ADB=∠AEC=90°∵AD=AE∴∠ADE=∠AED∵∠ADE+∠EDB=∠AED+∠CEH=90°∴∠EDB=∠CEH∵CF=CH∴∠CFH=∠CHF∴∠DFB=∠H∵CE=BD∴△DBF ≌△ECH∴BF=CH∴BF=CF∴点F 是BC 的中点(3)当点P 在△ABC 内部,如图所示,将△ABP 逆时针旋转120°,得到ACP ∆',连接PP '和PC∵将△ABP 旋转120°得到ACP ∆'∴∠PAP '=120°,AP='AP =2,BP=CP '=4∴PP '=23,∵∠AP C '=120°,∠AP P '=30°,∴∠PP C '=90°,∴PC=()2223427+=. 当点P 在△ABC 外部,如图所示,将△APB 绕点A 逆时针旋转120︒到△'AP C ,过点P 作PD ⊥'CP 于点D ,连接PD , ∵将△ABP 旋转120°得到ACP ∆'∴∠PAP '=120°,AP='AP =2,BP=CP '=4,∴PP '3∵∠AP C '=120°,∠AP P '=30°,∴∠PP C '=150°,∴∠PP D '=30°,在Rt 'PDP 中,1'32PD PP ==, 22''3DP PP PD ∴=-=,''347DC DP P C ∴=+=+=,()222237213PC PD DC ∴=+=+=.综上所述,27213PC =或【点睛】本题主要考查了全等三角形以及旋转,合理的作出辅助线以及熟练旋转的性质是解决本题的关键.6.问题:如图(1),点M、N分别在正方形ABCD的边BC、CD上,∠MAN=45°,试判断BM、MN、ND之间的数量关系.(1)研究发现如图1,小聪把△ADN绕点A顺时针旋转90°至△ABG,从而发现BM、MN、DN之间的数量关系为(直接写出结果,不用证明)(2)类比引申如图2,在(1)的条件下,AM、AN分别交正方形ABCD的对角线BD于点E、F.已知EF =5,DF=4.求BE的长.(3)拓展提升如图3,在(2)的条件下,AM、AN分别交正方形ABCD的两个外角平分线于Q、P,连接PQ.请直接写出以BQ、PQ、DP为边构成的三角形的面积.答案:B解析:(1)BM+DN=MN,理由见解析;(2)BE=3;(3)以BQ、PQ、DP为边构成的三角形的面积为36.【分析】(1)结论是:BM+DN=MN,如图1,利用三角形AND旋转90º得三角形ABG,∠DAN=∠BAG,可证∠GAM=∠GAB+∠BAM=∠MAN,利用SAS证△AMN≌△AMG即可;(2)如图2,按同样方法△AFD顺时针旋转90º,使AD与AB重合,得△ABF′,连结EF′,△BEF′是直角三角形,用勾股定理求EF′=5,再证△AEF≌△AEF即可;(3)如图3,由(2)可得BD=12,可求正方形边长,构建△P′AQ,P′B=DP,将△ADP顺时针转90º,AD与AB重合,得△BQP′,连OP′,可证△BQP′是直角三角形,可证PQ=P′Q,再证△ABQ∽△PDA,将△P′BQ面积=12BQ•BP′=12BQ•DP=12AD•AB可求.【详解】(1)如图1,BM+DN=MN,理由如下:∵四边形ABCD 是正方形,∴AB =AD ,∠D =∠ABC =∠BAD =90°,小聪把△ADN 绕点A 顺时针旋转90°至△ABG ,由旋转可得:BG =DN ,AN =AG ,∠1=∠2,∠ABG =∠D =90°,∴∠ABG +∠ABM =90°+90°=180°,因此,点G ,B ,M 在同一条直线上,∵∠MAN =45°,∴∠2+∠3=∠BAD ﹣∠MAN =90°﹣45°=45°,∵∠1=∠2,∴∠1+∠3=45°,∴∠GAM =∠MAN ,∵AM =AM ,∴△AMN ≌△AMG (SAS ),∴MN =GM ,∵GM =BM +BG =BM +DN ,∴BM +DN =MN ;故答案为:BM +DN =MN ;(2)如图2,把△ADF 绕点A 顺时针旋转90°至△ABF ',连接EF ',∴AF ′ =AF ,∠DAF =∠BAF ',∠ABF ′ =∠ADF =45°,B F ′ =DF =4,∵∠ABE =45°,∴∠EBF ′ =45°+45°=90°,∵AE =AE ,同理得△EAF ≌△EAF '(SAS ),∴EF '=EF =5,在Rt △EBF '中,由勾股定理得:BE ()()2222EF +BF 5-4=3''=3;(3)由(2)知:BE=3,EF=5,DF=4,∴BD=3+4+5=12,由勾股定理得:AB2+AD2=BD2,∵AB=AD,∴AB2=72,如图3,把△ADP绕点A顺时针旋转90°至△ABP ',连接BP ′,则∠ABP′=∠ADP,PD=P ′B,AP=AP ′,∵AM、AN分别交正方形ABCD的两个外角平分线于Q、P,∴∠ADP=∠ABQ=135°,∴∠DAP+∠APD=45°,∵∠DAP+∠BAQ=45°,∴∠BAQ=∠APD,∴△ADP∽△QBA,∴AD PD=BQ AB,∴BQ•PD=AD•AB=72,∵∠ABP'=∠ABQ=135°,∴∠QBP'=360°﹣135°﹣135°=90°,∴S△BP'Q=12BQ•BP′=12BQ•DP=12×72=36,∵AP=AP',∠PAQ=∠P'AQ,AQ=AQ,∴△QAP≌△QAP'(SAS),∴PQ=P'Q,∴以BQ、PQ、DP为边构成的三角形的面积为36.【点睛】本题是感知,探究,创新新题型,主要考查了学生对正方形的性质,旋转变换,勾股定理及全等三角形与相似三角形的判定方法的综合运用.关键是灵活掌握所学知识,同时会从感知中学到方法,结合下一图形,找到解决问题的方法,以及突破口,在创新中,注意把给出的问题进行转化,利用转化思想来解决.7.如图,BC⊥CA,BC=CA,DC⊥CE,DC=CE,直线BD与AE交于点F,交AC于点G,连接CF .(1)求证:△ACE ≌△BCD ;(2)求证:BF ⊥AE ;(3)请判断∠CFE 与∠CAB 的大小关系并说明理由.答案:C解析:(1)见解析;(2)见解析;(3)∠CFE =∠CAB ,见解析【分析】(1)根据垂直的定义得到∠ACB =∠DCE =90°,由角的和差得到∠BCD =∠ACE ,即可得到结论;(2)根据全等三角形的性质得到∠CBD =∠CAE ,根据对顶角的性质得到∠BGC =∠AGE ,由三角形的内角和即可得到结论;(3)过C 作CH ⊥AE 于H ,CI ⊥BF 于I ,根据全等三角形的性质得到AE =BD ,S △ACE =S △BCD ,根据三角形的面积公式得到CH =CI ,于是得到CF 平分∠BFH ,推出△ABC 是等腰直角三角形,即可得到结论.【详解】(1)证明:∵BC ⊥CA ,DC ⊥CE ,∴∠ACB =∠DCE =90°,∴∠BCD =∠ACE ,在△BCD 与△ACE 中,BC CA ACD ACE CD CE =⎧⎪∠=∠⎨⎪=⎩,∴△ACE ≌△BCD ;(2)∵△BCD ≌△ACE ,∴∠CBD =∠CAE ,∵∠BGC =∠AGE ,∴∠AFB =∠ACB =90°,∴BF ⊥AE ;(3)∠CFE =∠CAB ,过C 作CH ⊥AE 于H ,CI ⊥BF 于I ,∵△BCD ≌△ACE ,∴ACE BCD AE BD,S S ∆∆==,∴CH =CI , ∴CF 平分∠BFH ,∵BF ⊥AE ,∴∠BFH =90°,∠CFE =45°,∵BC ⊥CA ,BC =CA ,∴△ABC 是等腰直角三角形,∴∠CAB =45°,∴∠CFE =∠CAB .【点睛】角的和差、对顶角的性质这些知识点在证明全等和垂直过程中经常会遇到,需要掌握。
关于全等三角形的旋转难题
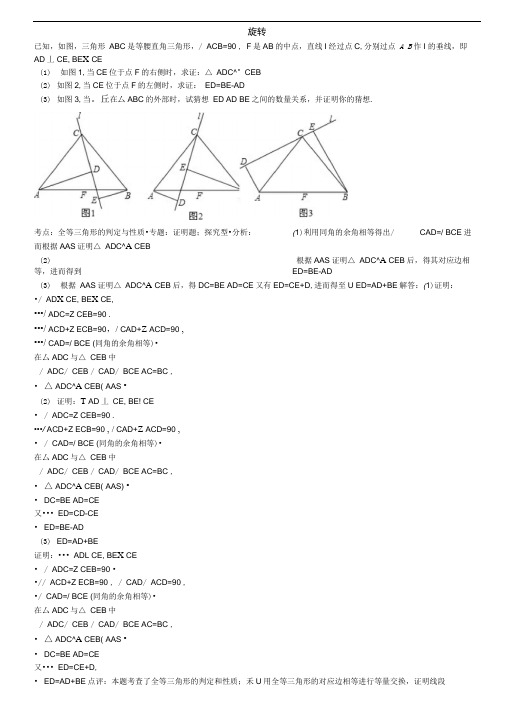
旋转已知,如图,三角形ABC是等腰直角三角形,/ ACB=90 , F是AB的中点,直线I经过点C,分别过点A B作I 的垂线,即AD丄CE, BE X CE(1)如图1,当CE位于点F的右侧时,求证:△ ADC^^ CEB(2)如图2,当CE位于点F的左侧时,求证:ED=BE-AD(3)如图3,当。
丘在厶ABC的外部时,试猜想ED AD BE之间的数量关系,并证明你的猜想.考点:全等三角形的判定与性质•专题:证明题;探究型•分析:(1)利用同角的余角相等得出/ CAD=/ BCE进而根据AAS证明△ ADC^A CEB(2)根据AAS证明△ ADC^A CEB后,得其对应边相等,进而得到ED=BE-AD(3)根据AAS证明△ ADC^A CEB后,得DC=BE AD=CE又有ED=CE+D,进而得至U ED=AD+BE解答:(1)证明:•/ AD X CE, BE X CE,•••/ ADC=Z CEB=90 .•••/ ACD+Z ECB=90,/ CAD+Z ACD=90 ,•••/ CAD=/ BCE (同角的余角相等)•在厶ADC与△ CEB中/ ADC/ CEB / CAD/ BCE AC=BC ,•△ADC^A CEB( AAS •(2)证明:T AD丄CE, BE! CE•/ ADC=Z CEB=90 .•••/ ACD+Z ECB=90 , / CAD+Z ACD=90 ,•/ CAD=/ BCE (同角的余角相等)•在厶ADC与△ CEB中/ ADC/ CEB / CAD/ BCE AC=BC ,•△ADC^A CEB( AAS) ••DC=BE AD=CE又••• ED=CD-CE•ED=BE-AD(3)ED=AD+BE证明:••• ADL CE, BE X CE•/ ADC=Z CEB=90 ••// ACD+Z ECB=90 , / CAD/ ACD=90 ,•/ CAD=/ BCE (同角的余角相等)•在厶ADC与△ CEB中/ ADC/ CEB / CAD/ BCE AC=BC ,•△ADC^A CEB( AAS ••DC=BE AD=CE又••• ED=CE+D,•ED=AD+BE点评:本题考查了全等三角形的判定和性质;禾U用全等三角形的对应边相等进行等量交换,证明线段之间的数量关系,这是一种很重要的方法,注意掌握3. 如图1、图2、图3, △ AOB △ CO[均是等腰直角三角形,/ AOB=/ COD= 90o, (1)在图1中,AC与BD相等吗,有怎样的位置关系?请说明理由。
初二数学 全等三角形双等腰旋转练习题含答案

初二数学 全等三角形双等腰旋转练习题含答案一、全等三角形双等腰旋转1.如图1是实验室中的一种摆动装置,BC 在地面上,支架ABC 是底边为BC 的等腰直角三角形,摆动臂AD 可绕点A 旋转,摆动臂DM 可绕点D 旋转,15AD =,6DM =.(1)在旋转过程中,①当A ,D ,M 三点在同一直线上时,求AM 的长;②当A ,D ,M 三点为同一直角三角形的顶点时,求AM 的长;(2)若摆动臂AD 顺时针旋转90︒,点D 的位置由ABC 外的点1D 转到其内的点2D 处,即1290D AD ︒∠=,连结12D D ,如图2,此时2135AD C ︒∠=,2202CD =2BD 的长.答案:(1)①21或9;②或;(2)【分析】(1)①分两种情形分别求解即可.②显然不能为直角.当为直角时,根据,计算即可,当时,根据,计算即可. (2)连接.首先利用勾股定理求出,再利用全等三角形的解析:(1)①21或9;②3213292)252【分析】(1)①分两种情形分别求解即可.②显然MAD ∠不能为直角.当AMD ∠为直角时,根据222AM AD DM =-,计算即可,当90ADM ∠=︒时,根据222AM AD DM =+,计算即可.(2)连接1CD .首先利用勾股定理求出1CD ,再利用全等三角形的性质证明21BD CD =即可.【详解】解:(1)①由题意可得:21AM AD DM =+=,或9AM AD DM =-=.②显然MAD ∠不能为直角.当AMD ∠为直角时,22222156189AM AD DM =-=-=,321AM ∴=321-当90ADM ∠=︒时,22222156261AM AD DM =+=+=, 293AM ∴=或932-(舍弃).综上所述,满足条件的AM 的值为321或329.(2)如图2中,连接1CD .由题意:1290D AD ∠=︒,1215AD AD ==,2145AD D ∴∠=︒,12152D D =2135AD C ∠=︒,2190CD D ∴∠=︒,()()22221212202152252CD CD D D ∴=+=+=1290BAC D AD ∠=∠=︒,2212BAC CAD D AD CAD ∴∠-∠=∠-∠,21BAD CAD ∴∠=∠,AB AC =,21AD AD =,21()BAD CAD SAS ∴∆≅∆,21252BD CD ∴==.【点睛】本题属于四边形综合题,考查了等腰直角三角形的性质,勾股定理,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.2.如图1,已知ABC 和EFC 都是等边三角形,且点E 在线段AB 上.(1)过点E 作//EG BC 交AC 于点G ,试判断AEG △的形状并说明理由;(2)求证://BF AC ;(3)如图2,若点D 在射线CA 上,且ED EC =,求证:AB AD BF =+.答案:(1)是等边三角形,理由见解析;(2)证明见解析;(3)证明见解析.【分析】(1)如图(见解析),先根据等边三角形的性质可得,再根据平行线的性质可得,然后根据等边三角形的判定即可得;(2)先根解析:(1)AEG △是等边三角形,理由见解析;(2)证明见解析;(3)证明见解析.【分析】(1)如图(见解析),先根据等边三角形的性质可得60BAC ABC ACB ==︒=∠∠∠,再根据平行线的性质可得60AEG ABC ∠=∠=︒,然后根据等边三角形的判定即可得;(2)先根据等边三角形的性质可得,,60AC BC CE CF ACB ECF ==∠=∠=︒,从而可得ACE BCF ∠=∠,再根据三角形全等的判定定理与性质可得60CBF CAE ∠=∠=︒,从而可得CBF ACB ∠=∠,然后根据平行线的判定即可得证;(3)先根据平行线的性质、三角形全等的性质可得,DAE EB AE F BF ∠=∠=,再根据等腰三角形的性质可得D ACE ∠=∠,从而可得D BCF ∠=∠,然后根据三角形的内角和定理可得BEF BCF D ∠=∠=∠,最后根据三角形全等的判定定理与性质可得AD BE =,据此根据线段的和差、等量代换即可得证.【详解】(1)AEG △是等边三角形,理由如下:如图,过点E 作//EG BC 交AC 于点G , ABC 是等边三角形,60BAC ABC ACB ∴∠=∠=∠=︒,60AEG ABC ∴∠=∠=︒, ∴AEG 是等边三角形;(2)ABC 和EFC 是等边三角形,,,60AC BC CE CF ACB ECF ==∠=∠=∴︒,ACB BCE ECF BCE ∴∠-∠=∠-∠,即ACE BCF ∠=∠,在ACE △和BCF △中,AC BC ACE BCF CE CF =⎧⎪∠=∠⎨⎪=⎩,()ACE BCF SAS ∴≅,60CBF CAE ∴∠=∠=︒,CBF ACB ∴∠=∠,//BF AC ∴;(3)由(2)知,//BF AC ,ACE BCF ≅,DAE EBF ∴∠=∠,AE BF =,ED EC =,D ACE ∴∠=∠,由(2)已证:ACE BCF ∠=∠,D BCF ∴∠=∠, ABC 和EFC 是等边三角形,60ABC EFC ∠∴∠==︒,在BEF 中,180120BEF EBC CBF BFE CBF BFE ∠=︒-∠-∠-∠=︒-∠-∠, 在BCF △中,180120BCF EFC CBF BFE CBF BFE ∠=︒-∠-∠-∠=︒-∠-∠, BEF BCF D ∴∠=∠=∠,在ADE 和BEF 中,DAE EBF D BEF AE BF ∠=∠⎧⎪∠=∠⎨⎪=⎩,()ADE BEF AAS ∴≅,AD BE ∴=,AB BE AE AD BF ∴=+=+.【点睛】本题考查了三角形全等的判定定理与性质、等边三角形的性质、平行线的判定与性质、等腰三角形的性质等知识点,较难的是题(3),正确找出两个三角形全等的条件是解题关键.3.如图,ABC 是等腰直角三角形,90,ACB ∠=︒分别以,AB AC 为直角边向外作等腰直角ABD △和等腰直角,ACE G 为BD 的中点,连接,,CG BE ,CD BE 与CD 交于点F .(1)证明:四边形ACGD 是平行四边形;(2)线段BE 和线段CD 有什么数量关系,请说明理由;(3)已知2,BC =求EF 的长度(结果用含根号的式子表示).答案:(1)见解析;(2)BE=CD ,理由见解析;(3)EF= .【分析】(1)利用等腰直角三角形的性质易得BD=2BC ,因为G 为BD 的中点,可得BG=BC ,由∠CGB=45°,∠ADB=45得AD ∥解析:(1)见解析;(2)BE =CD ,理由见解析;(3)EF 3105【分析】(1)利用等腰直角三角形的性质易得BD=2BC ,因为G 为BD 的中点,可得BG=BC ,由∠CGB=45°,∠ADB=45得AD ∥CG ,由∠CBD+∠ACB=180°,得AC ∥BD ,得出四边形ACGD 为平行四边形;(2)利用全等三角形的判定证得△DAC ≌△BAE ,由全等三角形的性质得BE=CD ;首先证得四边形ABCE 为平行四边形,再利用全等三角形的判定定理得△BCE ≌△CAD ,易得∠CBE=∠ACD ,由∠ACB=90°,易得∠CFB=90°,得出结论.(3)先证明△DBF 是直角三角形,再利用勾股定理进行计算,即可求出答案.【详解】解:(1)∵△ABC 和△ABD 都是等腰直角三角形∴∠CAB =∠ABD = 45°,BD 2AB 22BC =2BC =2AC∴AC ∥BD又∵G 为BD 的中点,∴BD =2DG ,∴AC =DG ,AC ∥DG∴四边形ACGD 为平行四边形;(2)BE =CD ,理由如下∵△AEC 和△ABD 都是等腰直角三角形AE =AC ,AB =AD∠EAB =∠EAC +∠CAB =90°+45°=135°,∠CAD =∠DAB +∠BAC =90°+45°=135°,∴∠EAB =∠CAD ,在△DAC 与△BAE 中,AD AB CAD EAB AC AE =⎧⎪∠=∠⎨⎪=⎩,∴△DAC ≌△BAE ,∴BE =CD ;(3) ∵△DAC ≌△BAE∴∠AEB=∠ACD又∵∠EAC=90°∴∠EFC=∠DFB=90°∴ △DBF 是直角三角形∵BC,∴BD根据勾股定理得CD, ∴11••22CD BF BC BD = ∴12=12•∴BF∴EF =BE -BF =CD -BF【点睛】本题主要考查了等腰直角三角形的性质,平行四边形和全等三角形的判定及性质定理,综合运用各种定理是解答此题的关键.4.已知,ABC 中,AB AC =,2BAC α∠=︒,点D 为BC 边中点,连接AD ,点E 为AD 的中点,线段CE 绕点E 顺时针旋转2α︒得到线段EF ,连接FC ,FD . (1)如图1,当60BAC ∠=︒时,请直接写出DF DC的值; (2)如图2,当90BAC ∠=︒时,(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请写出正确的结论,并说明理由;(3)如图3,当2BAC α∠=︒时,请直接写出DF DC的值(用含α的三角函数表示).答案:(1);(2)不成立,,理由见解析;(3).【分析】(1)如图1(见解析),先根据中位线定理得出,再根据旋转的性质、等边三角形的性质得出,,,然后根据三角形全等的判定定理与性质可得,由此即可得出解析:(1)12;(2)不成立,22DF DC =3)sin DF DC α=︒. 【分析】(1)如图1(见解析),先根据中位线定理得出12EG DC =,再根据旋转的性质、等边三角形的性质得出EC FC =,CD CG =,DCF GCE ∠=∠,然后根据三角形全等的判定定理与性质可得DF EG =,由此即可得出答案;(2)如图2(见解析),先根据中位线定理、等腰三角形的三线合一得出90AEM ∠=︒,再根据等腰直角三角形的性质得出ACE BCF ∠=∠,22AC CE BC CF ==,然后根据相似三角形的判定与性质可得CBF CAE ∠=∠,2AE BF =AE AM BF BD =,最后根据相似三角形的判定与性质可得90BFD AEM ∠=∠=︒,据此利用正弦三角函数值即可得;(3)如图3(见解析),参照题(2)的思路,先根据相似三角形的判定与性质得出,90CBF CAE BFD AEN α∠=∠=︒∠=∠=︒,再在Rt BFD 中,利用正弦三角函数值即可得.【详解】(1)如图1,取AC 的中点G ,连接EG ,则12CG AC = 点E 为AD 的中点 EG ∴是ACD 的中位线12EG DC ∴=,即12EG DC =由旋转的性质可知,EC EF =,60FEC ∠=︒CEF ∴是等边三角形60ECF ∴∠=︒,EC FC =AB AC =,60BAC ∠=︒ABC ∴是等边三角形60,ACB AC BC ∴∠=︒=点D 为BC 边中点1122CD BC AC CG ∴=== 60ECF ECD DCF ∠=∠+∠=︒,60ACB ECD GCE ∠=∠+∠=︒DCF GCE ∴∠=∠在DCF 和GCE 中,CD CG DCF GCE FC EC =⎧⎪∠=∠⎨⎪=⎩()DCF GCE SAS ∴≅DF EG ∴=12DF EG DC DC ∴==; (2)不成立,2DF DC =,理由如下: 如图2,连接BF ,取AC 的中点M ,连接EM∵E 是AD 的中点∴//EM BC∴AEM ADC ∠=∠∵AB AC =ABC ∴是等腰三角形∵D 是BC 中点, 2BAC α∠=︒∴AD BC ⊥,12CAD BAC α∠=∠=︒,BD DC = ∴90ADC ∠=︒∴90AEM ∠=︒当90BAC ∠=︒时,则90CEF ∠=︒ABC ∴和CEF △为等腰直角三角形∴45ACB ECF ∠=∠=︒,即45ECD ACE ECD BCF ∠+∠=∠+∠=︒∴ACE BCF ∠=∠,cos 45AC CE BC CF ==︒= ∴ACE BCF ~∴90452CBF CAE α︒∠=∠=︒==︒,2AE AC BF BC ==∵12122AC AM BD BC == ∴AE AM BF BD = ∴BDF AME ~ ∴90BFD AEM ∠=∠=︒在Rt BFD 中,sin DF DF CBF BD DC ∠==,即sin 45DF DC ︒=则2DF DC =; (3)sin DF DCα=︒,求解过程如下: 如图3,连接BF ,取AC 的中点N ,连接EN 参照(2),同理可得:12CAD BAC α∠=∠=︒,BD DC =,90AEN ADC ∠=∠=︒ 当2BAC α∠=︒时,则2CEF α∠=︒AB AC =,EC EF =(旋转的性质)ABC ∴和EFC 为等腰三角形 ∴1(180)902ACB ABC BAC α∠=∠=︒-∠=︒-︒ 1(180)902ECF EFC CEF α∠=∠=︒-∠=︒-︒ 90ACB ECF α∴∠=∠=︒-︒ABC EFC ∴~AC CE BC CF∴= 又,ACB ECD ACE ECF ECD BCF ∠=∠+∠∠=∠+∠∴ACE BCF ∠=∠∴ACE BCF ~∴CBF CAE α∠=∠=︒,AE AC BF BC = ∵1212AC AN AC BD BCBC ==∴AE AN BF BD = ∴BDF ANE ~ ∴90BFD AEN ∠=∠=︒在Rt BFD 中,sin DF DF CBF BD DC ∠== 即sin DF DC α=︒.【点睛】本题考查了等腰三角形的性质、旋转的性质、三角形全等的判定定理与性质、相似三角形的判定与性质等知识点,通过作辅助线,构造全等三角形和相似三角形是解题关键. 5.如图1,在等腰直角三角形ABC 中,动点D 在直线AB (点A 与点B 重合除外)上时,以CD 为一腰在CD 上方作等腰直角三角形ECD ,且90ECD ∠=︒,连接AE .(1)判断AE 与BD 的数量关系和位置关系;并说明理由.(2)如图2,若4BD =,P ,Q 两点在直线AB 上且5EP EQ ==,试求PQ 的长. (3)在第(2)小题的条件下,当点D 在线段AB 的延长线(或反向延长线)上时,判断PQ 的长是否为定值.分别画出图形,若是请直接写出PQ 的长;若不是请简单说明理由. 答案:(1)AE=BD 且AE ⊥BD ;(2)6;(3)PQ 为定值6,图形见解析【分析】(1)由“SAS”可证△ACE ≌△BCD ,可得AE=BD ,∠EAC=∠DBC=45°,可得AE⊥BD;(2)由等腰解析:(1)AE=BD且AE⊥BD;(2)6;(3)PQ为定值6,图形见解析【分析】(1)由“SAS”可证△ACE≌△BCD,可得AE=BD,∠EAC=∠DBC=45°,可得AE⊥BD;(2)由等腰三角形的性质可得PA=AQ,由勾股定理可求PA的长,即可求PQ的长;(3)分两种情况讨论,由“SAS”可证△ACE≌△BCD,可得AE=BD,∠EAC=∠DBC,可得AE⊥BD,由等腰三角形的性质可得PA=AQ,由勾股定理可求PA的长,即可求PQ的长.【详解】解:(1)AE=BD,AE⊥BD,理由如下:∵△ABC,△ECD都是等腰直角三角形,∴AC=BC,CE=CD,∠ACB=∠ECD=90°,∠ABC=∠CAB=45°,∴∠ACE=∠DCB,且AC=BC,CE=CD,∴△ACE≌△BCD(SAS)∴AE=BD,∠EAC=∠DBC=45°,∴∠EAC+∠CAB=90°,∴AE⊥BD;(2)∵PE=EQ,AE⊥BD,∴PA=AQ,∵EP=EQ=5,AE=BD=4,∴,∴PQ=2AQ=6;(3)如图3,若点D在AB的延长线上,∵△ABC,△ECD都是等腰直角三角形,∴AC=BC,CE=CD,∠ACB=∠ECD=90°,∠ABC=∠CAB=45°,∴∠ACE=∠DCB,且AC=BC,CE=CD,∴△ACE≌△BCD(SAS)∴AE=BD,∠CBD=∠CAE=135°,且∠CAB=45°,∴∠EAB=90°,∵PE=EQ,AE⊥BD,∴PA=AQ,∵EP=EQ=5,AE=BD=4,∴,∴PQ=2AQ=6;如图4,若点D在BA的延长线上,∵△ABC,△ECD都是等腰直角三角形,∴AC=BC,CE=CD,∠ACB=∠ECD=90°,∠ABC=∠CAB=45°,∴∠ACE=∠DCB,且AC=BC,CE=CD,∴△ACE≌△BCD(SAS)∴AE=BD,∠CBD=∠CAE=45°,且∠CAB=45°,∴∠EAB=90°,∵PE=EQ,AE⊥BD,∴PA=AQ,∵EP=EQ=5,AE=BD=4,∴AQ=22=2516=3--,EQ AE∴PQ=2AQ=6.【点睛】本题是三角形综合题,考查了全等三角形的判定和性质,等腰三角形的性质,勾股定理等知识,证明AE⊥BD是本题的关键.6.如图,将两块含45°角的大小不同的直角三角板△COD和△AOB如图①摆放,连结AC,BD.(1)如图①,猜想线段AC与BD存在怎样的数量关系和位置关系,请写出结论并证明;(2)将图①中的△COD绕点O顺时针旋转一定的角度(如图②),连结AC,BD,其他条件不变,线段AC与BD还存在(1)中的关系吗?请写出结论并说明理由.(3)将图①中的△COD绕点O逆时针旋转一定的角度(如图③),连结AC,BD,其他条件不变,线段AC与BD存在怎样的关系?请直接写出结论.答案:(1)AC=BD,AC⊥BD,证明见解析;(2)存在,AC=BD,AC⊥BD,证明见解析;(3)AC=BD,AC⊥BD【分析】(1)延长BD交AC于点E.易证△AOC≌△BOD(SAS),可得A解析:(1)AC=BD,AC⊥BD,证明见解析;(2)存在,AC=BD,AC⊥BD,证明见解析;(3)AC=BD,AC⊥BD【分析】(1)延长BD交AC于点E.易证△AOC≌△BOD(SAS),可得AC=BD,∠OAC=∠OBD,由∠ADE=∠BDO,可证∠AED=∠BOD=90º即可;(2)延长BD交AC于点F,交AO于点G.易证△AOC≌△BOD(SAS),可得AC=BD,∠OAC=∠OBD,由∠AGF=∠BGO,可得∠AFG=∠BOG=90º即可;(3)BD交AC于点H,AO于M,可证△AOC≌△BOD(SAS),可得AC=BD,∠OAC=∠OBD,由∠AMH=∠BMO,可得∠AHM=∠BOH=90º即可.【详解】(1)AC=BD,AC⊥BD,证明:延长BD交AC于点E.∵△COD和△AOB均为等腰直角三角形,∴OC=OD,OA=OB,∠COA=∠BOD=90º,∴△AOC≌△BOD(SAS),∴AC=BD,∴∠OAC=∠OBD,∵∠ADE=∠BDO,∴∠AED=∠BOD=90º,∴AC⊥BD;(2)存在,证明:延长BD交AC于点F,交AO于点G.∵△COD和△AOB均为等腰直角三角形,∴OC=OD,OA=OB,∠DOC=BOA=90º,∵∠AOC=∠DOC-∠DOA,∠BOD=∠BOA-∠DOA,∴∠AOC=∠BOD,∴△AOC≌△BOD(SAS),∴AC=BD,∠OAC=∠OBD,∵∠AGF=∠BGO ,∴∠AFG=∠BOG=90º,∴AC ⊥BD ;(3)AC=BD ,AC ⊥BD .证明:BD 交AC 于点H ,AO 于M ,∵△COD 和△AOB 均为等腰直角三角形,∴OC=OD ,OA=OB ,∠DOC=BOA=90º,∵∠AOC=∠DOC+∠DOA ,∠BOD=∠BOA+∠DOA ,∴∠AOC=∠BOD ,∴△AOC ≌△BOD (SAS ),∴AC=BD ,∠OAC=∠OBD ,∵∠AMH=∠BMO ,∴∠AHM=∠BOH=90º,∴AC ⊥BD .【点睛】本题考查三角形旋转变换中对应相等的位置与数量关系,掌握三角形全等的证明方法,及其角度计算是解题关键.7.在ABC 中,AB AC =,点D 是直线BC 上一点(不与B 、C 重合),以AD 为一边在AD 的右侧作ADE ,使AD AE =,DAE BAC ∠=∠,连接CE .(1)如图,当点D 在线段BC 上,如果90BAC ∠=︒,则BCE ∠=______度.(2)设BAC α∠=,BCE β∠=.①如图,当点D 在线段BC 上移动时,α、β之间有怎样的数量关系?请直接写出你的结论.②如图,当点D 在线段BC 的反向延长线上移动时,α、β之间有怎样的数量关系?请说明理由.答案:(1)90;(2)①,理由见解析;②,理由见解析【分析】(1)由等腰直角三角形的性质可得∠ABC=∠ACB=45°,由“SAS”可证△BAD ≌△CAE ,可得∠ABC=∠ACE=45°,可求∠BC解析:(1)90;(2)①180αβ+=︒,理由见解析;②αβ=,理由见解析【分析】(1)由等腰直角三角形的性质可得∠ABC=∠ACB=45°,由“SAS”可证△BAD ≌△CAE ,可得∠ABC=∠ACE=45°,可求∠BCE 的度数;(2)①由“SAS”可证△ABD ≌△ACE 得出∠ABD=∠ACE ,再用三角形的内角和即可得出结论;②由“SAS”可证△ADB ≌△AEC 得出∠ABD=∠ACE ,再用三角形外角的性质即可得出结论.【详解】(1)∵AB=AC ,∠BAC=90°,∴∠ABC=∠ACB=45°,∵∠DAE=∠BAC ,∴∠BAD=∠CAE ,在△BAD 和△CAE 中AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴△BAD ≌△CAE (SAS )∴∠ABC=∠ACE=45°,∴∠BCE=∠ACB+∠ACE=90°,故答案为:90;(2)①180αβ+=︒.理由:∵∠BAC=∠DAE ,∴∠BAC-∠DAC=∠DAE-∠DAC .即∠BAD=∠CAE .在△ABD 与△ACE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△ACE (SAS ),∴∠B=∠ACE .∴∠B+∠ACB=∠ACE+∠ACB .∵∠ACE+∠ACB=β,∴∠B+∠ACB=β,∵α+∠B+∠ACB=180°,∴α+β=180°;② 当点D 在射线BC 的反向延长线上时,αβ=.理由如下:∵DAE BAC ∠=∠,∴DAB EAC ∠=∠,在△ABD 与△ACE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴△≌△ADB AEC(SAS), ∴ABD ACE ∠=∠,∵ABD BAC ACB ∠=∠+∠,ACE BCE ACB ∠=∠+∠,∴BAC ABD ACB ∠=∠-∠,BCE ACE ACB ∠=∠-∠,∴BAC BCE ∠=∠,即αβ=.此题考查了全等三角形的判定和性质,等腰直角三角形的性质,三角形的内角和定理,以及三角形外交的性质,证明△ABD ≌△ACE 是解本题的关键.8.如图,锐角ABC 中,分别以AB 、AC 为边向外作等腰直角ABE △和等腰直角ACD △,使AE AB =,AD AC =,90BAE CAD ∠=∠=︒,连接BD 、CE ,可以通过全等三角形的知识证得BD 与CE 相等.(1)如图,锐角ABC 中分别以AB 、AC 为边向外作等腰ABE △和等腰ACD △,AE AB =,AD AC =,90BAE CAD ∠=∠=︒,连接BD 、CE ,试猜想BD 与CE 的数量关系,并说明理由.(2)如图,在中ABC ,45ACB ∠=︒,以AB 为直角边,A 为直角顶点向外作等腰直角ABD △,连接CD ,若2,3AC BC ==,求CD 的长.(3)如图,在四边形中ABCD ,60,15,8,ADC BC AB AD CD ∠=︒===,求BD 的最大值.答案:(1),证明见解析;(2);(3)23.(1)由等腰三角形的性质解得,继而可证及,再由全等三角形对应边相等解题;(2)过A 作交于点,连接,先证明是等腰直角三角形,得到 ,,再证明,由全解析:(1)BD CE =,证明见解析;(2)13;(3)23.【分析】(1)由等腰三角形的性质解得,,AE AB AD AC BAE CAD ==∠=∠,继而可证EAC BAD ∠=∠及(SAS)EAC BAD ≌,再由全等三角形对应边相等解题;(2)过A 作AE AC ⊥交BC 于点E ,连接DE ,先证明EAC 是等腰直角三角形,得到 AE AC =,DAE BAC ∠=∠,再证明(SAS)DAE BAC ≌,由全等三角形的性质得到3,45DE BC DEA BCA ==∠=∠=︒,接着在等腰直角三角形EAC 中,由勾股定理解得22222EC AC AE AC =+=,最后在Rt DEC △中,由勾股定理即可解得CD 的长; (3)先证明ACD △为等边三角形,再由等边三角形的性质可得,,60AC CD ACD =∠=︒将BCA 绕点C 顺时针旋转60°得到ECD ,连接BE ,由旋转的性质得815DE AB BC EC ====,,继而证明BCE 是等边三角形,由等边三角形的性质得到75BE BC ==,最后根据三角形三边关系解题即可.【详解】解:(1)∵ABE △和ACD △是等腰三角形,,,AE AB AD AC BAE CAD ∴==∠=∠,BAE BAC CAD BAC ∴∠+∠=∠+∠,即:EAC BAD ∠=∠,在EAC 中BAD 中AE AB EAC BAD AC AD =⎧⎪∠=∠⎨⎪=⎩,(SAS)EAC BAD ∴≌,CE BD ∴=;(2)如图(1)所示,过A 作AE AC ⊥交BC 于点E ,连接DE ,45,ACB AE AC ∠=︒⊥,90EAC ∴∠=︒,EAC ∴△是等腰直角三角形,AE AC ∴=, 又ABD 是等腰直角三角形,,90AB AD BAD ∴=∠=︒,90BAD EAC ∴∠=∠=︒,BAD BAE EAC BAE ∴∠+∠=∠+∠,即:DAE BAC ∠=∠,在DAE △和BAC 中,AD AB DAE BAC AE AC =⎧⎪∠=∠⎨⎪=⎩(SAS)DAE BAC ∴≌,3,45DE BC DEA BCA ∴==∠=∠=︒,在等腰直角三角形EAC 中,45AEC ∠=︒,90DEC DEA AEC ∴∠=∠+∠=︒,由勾股定理得:22222EC AC AE AC =+=.在Rt DEC △中,由勾股定理得: 229413CD DE EC =+=+=;(3),60AD CD ADC =∠=︒,∴ACD △为等边三角形,,60AC CD ACD ∴=∠=︒,如图(2)所示,将BCA 绕点C 顺时针旋转60°得到ECD ,连接BE ,由旋转性质可得∶815DE AB BC EC ====,60BCE ∠=︒,∴BCE 是等边三角形,∴75BE BC ==,又∴BE DE BD +≥, 即158BD BE DE ≤+=+,即23BD ≤,∴BD的最大值为23.【点睛】本题考查全等三角形的判定与性质、旋转、勾股定理、等边三角形的判定与性质、三角形三边关系等知识,是重要考点,难度一般,掌握相关知识是解题关键.9.已知Rt△OAB和Rt△OCD的直角顶点O重合,∠AOB=∠COD=90°,且OA=OB,OC=OD.(1)如图1,当C、D分别在OA、OB上时,AC与BD的数量关系是AC BD(填“>”,“<”或“=”)AC与BD的位置关系是AC BD(填“∥”或“⊥”);(2)将Rt△OCD绕点O顺时针旋转,使点D在OA上,如图2,连接AC,BD,求证:AC=BD;(3)现将Rt△OCD绕点O顺时针继续旋转,如图3,连接AC,BD,猜想AC与BD的数量关系和位置关系,并给出证明.答案:(1)=;⊥(2)见解析(3)AC=BD且AC⊥BD;证明见解析【分析】(1)根据等式的性质可得AC与BD的数量关系,根据∠AOB=∠COD=90°,可证AC与BD的位置关系;(2)证解析:(1)=;⊥(2)见解析(3)AC=BD且AC⊥BD;证明见解析【分析】(1)根据等式的性质可得AC与BD的数量关系,根据∠AOB=∠COD=90°,可证AC与BD 的位置关系;(2)证明△OCA≌△ODB,即可得到AC=BD;(3)证明△OCA≌△ODB,可得AC=BD,∠BDO=∠ACO,进而可证∠DEF=90°.【详解】解:(1)∵OA=OB,OC=OD∴OA-OC=OB-OD,∴AC=BD.∵∠AOB=∠COD=90°,∴AO⊥BO,∵C、D分别在OA、OB上,∴AC ⊥BD ;(2)在△OCA 和△ODB 中,90OC OD COA BOD AO BO =⎧⎪∠==⎨⎪=⎩,∴△OCA ≌△ODB ,∴AC=BD ;(3)AC=BD ,AC ⊥BD .理由:∵∠AOB=∠COD=90°,∴∠AOB+∠AOD=∠COD+∠AOD ,∴∠AOC=∠BOD ,在△OCA 和△ODB 中,OC OD COA BOD AO BO =⎧⎪∠=⎨⎪=⎩,∴△OCA ≌△ODB ,∴AC=BD ,∠BDO=∠ACO ,∵∠ACO+∠CFO=90°,∠CFO=∠DFE ,∴∠BDO+∠DFE=90°,∴∠DEF=180°-90°=90°,∴AC ⊥BD .【点睛】本题考查了旋转的性质,等腰直角三角形的性质,全等三角形的判定与性质等知识,掌握全等三角形的判定方法(即SSS 、SAS 、ASA 、AAS 和HL )和全等三角形的性质(即全等三角形的对应边相等、对应角相等)是解题的关键.10.在直线上次取A ,B ,C 三点,分别以AB ,BC 为边长在直线的同侧作正三角形,作得两个正三角形的另一顶点分别为D ,E .(1)如图①,连结CD ,AE ,求证:CD AE =;(2)如图②,若1AB =,2BC =,求DE 的长;(3)如图③,将图②中的正三角形BEC 绕B 点作适当的旋转,连结AE ,若有222DE BE AE +=,试求∠DEB 的度数.答案:(1)见解析;(2);(3)∠DEB =30°.【分析】(1)欲证明CD =AE ,只要证明△ABE ≌△DBC 即可;(2)如图②,取BE 中点F ,连接DF ,首先证明△DBF 是等边三角形,然后证明△BD解析:(1)见解析;(2)3DE =3)∠DEB =30°.【分析】(1)欲证明CD =AE ,只要证明△ABE ≌△DBC 即可;(2)如图②,取BE 中点F ,连接DF ,首先证明△DBF 是等边三角形,然后证明△BDE 是直角三角形,再利用勾股定理计算即可;(3)如图③,连接DC ,先证明△ABE ≌△DBC ,再利用勾股定理的逆定理证明△DEC 是直角三角形,得到∠DEC =90°即可解决问题.【详解】解:(1)∵△ABD 和△ECB 都是等边三角形,∴AD =AB =BD ,BC =BE =EC ,∠ABD =∠EBC =60°,∴∠ABE =∠DBC , 在△ABE 和△DBC 中,AB BD ABE DBC BE BC =⎧⎪∠=∠⎨⎪=⎩,∴△ABE ≌△DBC (SAS ),∴CD =AE ;(2)如图②,取BE 中点F ,连接DF ,∵BD =AB =1,BE =BC =2,∠ABD =∠EBC =60°,∴BF =EF =1=BD ,∠DBF =60°,∴△DBF 是等边三角形,∴DF =BF =EF ,∠DFB =60°,∵∠BFD =∠FED +∠FDE ,∴∠FDE =∠FED =30°∴∠EDB =180°−∠DBE−∠DEB =90°,∴DE =2222213BE BD ;(3)如图③,连接DC ,∵△ABD 和△ECB 都是等边三角形,∴AD =AB =BD ,BC =BE =EC ,∠ABD =∠EBC =60°,∴∠ABE =∠DBC ,在△ABE 和△DBC 中,AB BD ABE DBC BE BC =⎧⎪∠=∠⎨⎪=⎩,∴△ABE ≌△DBC (SAS ),∴AE =DC ,∵DE 2+BE 2=AE 2,BE =CE ,∴DE 2+CE 2=CD 2,∴∠DEC =90°,∵∠BEC =60°,∴∠DEB =∠DEC−∠BEC =30°.【点睛】本题考查了全等三角形的判定和性质、勾股定理以及勾股定理逆定理、等边三角形的性质等知识,寻找全等三角形是解决问题的关键,要学会添加辅助线的方法,属于中考常考题型.二、全等三角形手拉手模型11.(1)如图1,ABC 和DCE 都是等边三角形,且B ,C ,D 三点在一条直线上,连接AD ,BE 相交于点P ,求证:BE AD =.(2)如图2,在BCD 中,若120BCD ∠<︒,分别以BC ,CD 和BD 为边在BCD 外部作等边ABC ,等边CDE △,等边BDF ,连接AD 、BE 、CF 恰交于点P . ①求证:AD BE CF ==;②如图2,在(2)的条件下,试猜想PB ,PC ,PD 与BE 存在怎样的数量关系,并说明理由.解析:(1)详见解析;(2)①详见解析;②PB PC PD BE ++=,理由详见解析【分析】(1)根据等边三角形的性质得出BC=AC ,CE=CD ,∠ACB=∠DCE=60°,进而得出∠BCE=∠ACD ,判断出BCE ACD ≌(SAS ),即可得出结论;(2)①同(1)的方法判断出≌ACD BCE (SAS ),ABD CBF ≌(SAS ),即可得出结论; ②先判断出∠APB=60°,∠APC=60°,在PE 上取一点M ,使PM=PC ,证明CPM △是等边三角形, 进而判断出PCD MCE ≌(SAS ),即可得出结论.【详解】(1)证明:∵ABC 和DCE 都是等边三角形,∴BC=AC ,CE=CD ,∠ACB=∠DCE=60°,∴∠ABC+∠ACE=∠DCE+∠ACE ,即∠BCE=∠ACD ,∴BCE ACD ≌(SAS ),∴BE=AD ;(2)①证明:∵ABC 和DCE 是等边三角形,∴AC=BC ,CD=CE ,∠ACB=∠DCE=60°,∴∠ACB+∠BCD=∠DCE+∠BCD ,即∠ACD=∠BCE ,∴≌ACD BCE (SAS ),∴AD=BE ,同理:ABD CBF ≌(SAS ),∴AD=CF ,即AD=BE=CF ;②解:结论:PB+PC+PD=BE ,理由:如图2,AD 与BC 的交点记作点Q ,则∠AQC=∠BQP ,由①知,≌ACD BCE ,∴∠CAD=∠CBE ,在ACQ 中,∠CAD+∠AQC=180°-∠ACB=120°,∴∠CBE+∠BQP=120°,在BPQ 中,∠APB=180°-(∠CBE+∠BQP )=60°,∴∠DPE=60°,同理:∠APC=60°,60,CPE ∴∠=︒ ∠CPD=120°,在PE 上取一点M ,使PM=PC ,∴CPM △是等边三角形,∴CP CM PM ==,∠PCM=∠CMP=60°,∴∠CME=120°=∠CPD ,∵CDE △是等边三角形,∴CD=CE ,∠DCE=60°=∠PCM ,∴∠PCD=∠MCE ,∴PCD MCE ≌(SAS ),∴PD=ME ,∴BE=PB+PM+ME=PB+PC+PD .【点睛】此题是三角形综合题,主要考查了三角形的内角和定理,等边三角形的性质和判定,全等三角形的判定和性质,构造出全等三角形是解本题的关键.12.在平面直角坐标系中,已知A (3,0),以OA 为一边在第一象限内画正方形OABC ,D (m ,0)为x 轴上的一个动点,以BD 为一边画正方形BDEF (点F 在直线AB 右侧).(1)当m >3时(如图1),试判断线段AF 与CD 的数量关系,并说明理由. (2)当AF=5时,求点E 的坐标;(3)当D 点从A 点向右移动4个单位,求这一过程中F 点移动的路程是多少?解析:(1)AF CD =,理由见解析;(2)点E 的坐标为(7,1)E 或(1,7)E --;(3)这一过程中F 点移动的路程是向上移动4个单位.【分析】(1)先根据正方形的性质得出,,90AB CB BF BD ABC BDF ==∠=∠=︒,再根据角的和差求出CBD ABF ∠=∠,然后根据三角形全等的判定定理与性质即可得;(2)分点D 在点A 的右侧和点D 在点A 的左侧,分别画出图形.①如图1,先利用(1)的结论可得5CD =,再利用勾股定理求出4OD =,从而可得1AD =,然后过点E 作EG x ⊥轴于点G ,根据三角形全等的判定定理与性质可得1,3GE GD ==,从而可得7OG =,由此即可得;②如图2,同①的方法,利用三角形全等的判定定理与性质得出7,3HE HD ==,从而可得1OH =,由此即可得;(3)参照(2)①的方法,求出点F 的坐标,从中可发现点F 的坐标与m 的关系,由此即可得出答案.【详解】(1)AF CD =,理由如下:四边形OABC 和四边形BDEF 都是正方形,,90AB CB BF BD ABC BDF ∴==∠=∠=︒ABC ABD BDF ABD ∴∠+∠=∠+∠,即CBD ABF ∠=∠在BAF △和BCD 中,AB CB ABF CBD BF BD =⎧⎪∠=∠⎨⎪=⎩()BAF BCD SAS ∴≅AF CD ∴=;(2)由题意,分以下两种情况:①如图1,点D 在点A 的右侧四边形OABC 和四边形BDEF 都是正方形,(30)A ,3OC AB OA ∴===,BD DE =,90OAB BDE ∠=∠=︒90ABD ADB GDE ADB ∴∠+∠=∠+∠=︒,即ABD GDE ∠=∠由(1)可知,5AF CD ==在Rt COD中,4OD ===431AD OD OA ∴=-=-=过点E 作EG x ⊥轴于点G在ABD △和GDE △中,90BAD DGE ABD GDE BD DE ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩()ABD GDE AAS ∴≅1,3AD GE AB GD ∴====437OG OD GD ∴=+=+=此时点E 的坐标为(7,1)E②如图2,点D 在点A 的左侧由(1)可知,5AF CD ==在Rt COD 中,2222534OD CD OC =-=-=437AD OD OA ∴=+=+=过点E 作EH x ⊥轴于点H同理可证:ABD HDE ≅7,3AD HE AB HD ∴====431OH OD HD ∴=-=-=此时点E 的坐标为(1,7)E --综上,点E 的坐标为(7,1)E 或(1,7)E --;(3)由题意,只需求出点D 在点A 的右侧,即3m >时,点F 的坐标即可解决问题 如图1,过点F 作FM x ⊥轴于点M由(1)已证:BAF BCD ≅AF CD ∴=,BAF BCD ∠=∠90BAD BCO ∠=∠=︒BAD BAF BCO BCD ∴∠-∠=∠-∠FAM DCO ∴∠=∠在AFM △和CDO 中,90AMF COD FAM DCO AF CD ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩()AFM CDO AAS ∴≅3,MA OC MF OD m ∴====336OM OA MA ∴=+=+=此时点F 的坐标为(6,)F m由此可知,当D 点从A 点向右移动4个单位时,点F 向上移动4个单位即这一过程中F 点移动的路程是向上移动4个单位.【点睛】本题考查了正方形的性质、三角形全等的判定定理与性质、点的坐标变换规律等知识点,较难的是题(2),依据题意,分两种情况讨论,然后分别通过作辅助线,构造全等三角形是解题关键.13.问题发现:如图1,在Rt ABC ∆中,AB AC =,D 为BC 边所在直线上的动点(不与点B 、C 重合),连结AD ,以AD 为边作Rt ADE ∆,且AD AE =,根据BAC CAD CAD DAE ∠+∠=∠+∠,得到BAD CAE ∠=∠,结合AB AC =,AD AE =得出BAD CAE ∆≅∆,发现线段BD 与CE 的数量关系为BD CE =,位置关系为BD CE ⊥;(1)探究证明:如图2,在Rt ABC ∆和Rt ADE ∆中,AB AC =,AD AE =,且点D 在BC 边上滑动(点D 不与点B 、C 重合),连接EC .①则线段BC ,DC ,EC 之间满足的等量关系式为_____;②求证: 2222BD CD AD +=;(2)拓展延伸:如图3,在四边形ABCD 中,45ABC ACB ADC ∠=∠=∠=︒.若13BD cm =,5CD cm =,求AD 的长.解析:(1)①BC =CE+CD ;②见解析;(2)AD =2.【分析】(1)①根据题中示例方法,证明△BAD ≌△CAE ,得到BD =CE ,从而得出BC=CE+CD ; ②根据△BAD ≌△CAE ,得出∠ACE =45°,从而得到∠BCE =90°,则有DE 2=CE 2+CD 2,再根据222DE AD =可得结论;(2)过点A 作AG ⊥AD ,使AG=AD ,连接CG 、DG ,可证明△BAD ≌△CAG ,得到CG =BD ,在直角△CDG 中,根据CD 的长求出DG 的长,再由DG 和AD 的关系求出AD.【详解】解:(1)①如图2,在Rt △ABC 中,AB =AC ,∴∠B =∠ACB =45°,∵∠BAC =∠DAE =90°,∴∠BAC ﹣∠DAC =∠DAE ﹣∠DAC ,即∠BAD =∠CAE ,在△BAD 和△CAE 中,AB AC BAD CAE AD AE =∠=∠=⎧⎪⎨⎪⎩,∴△BAD ≌△CAE (SAS ),∴BD =CE ,∴ BC=BD+CD=CE+CD ,故答案为:BC=BD+CD=CE+CD.②∵△BAD≌△CAE,∴∠B=∠ACE=45°,∵∠ACB=45°,∴∠BCE=45°+45°=90°,∴DE2=CE2+CD2,∵AD=AE,∠DAE=90°,∴22=,DE AD2∴2AD2=BD2+CD2;(3)如图3,过点A作AG⊥AD,使AG=AD,连接CG、DG,则△DAG是等腰直角三角形,∴∠ADG=45°,∵∠ADC=45°,∴∠GDC=90°,同理得:△BAD≌△CAG,∴CG=BD=13,在Rt△CGD中,∠GDC=90°,2222=-=-=,DG CG CD13512∵△DAG是等腰直角三角形,∴22DG AD=,2∴AD2.2【点睛】本题是四边形的综合题,考查的是全等三角形的判定和性质、勾股定理,掌握全等三角形的判定定理和性质定理是解题的关键.14.在菱形ABCD中,∠ABC=60°,P是射线BD上一动点,以AP为边向右侧作等边△APE,连接CE.(1)如图1,当点P在菱形ABCD内部时,则BP与CE的数量关系是,CE与AD的位置关系是.(2)如图2,当点P在菱形ABCD外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由;(3)如图2,连接BE,若AB=23,BE=219,求AP的长.解析:(1)BP=CE,CE⊥AD;(2)结论仍然成立,理由见解析;(3)7【解析】【分析】(1)由菱形ABCD和∠ABC=60°可证△ABC与△ACD是等边三角形,由等边△APE可得AP=AE,∠PAE=∠BAC=60°,减去公共角∠PAC得∠BAP=∠CAE,根据SAS可证得△BAP≌△CAE,故有BP=CE,∠ABP=∠ACE.由菱形对角线平分一组对角可证∠ABP=30°,故∠ACE=30°即CE平分∠ACD,由AC=CD等腰三角形三线合一可得CE⊥AD.(2)结论不变.证明过程同(1).(3)在Rt△AOP中,求出OA,OP即可解决问题.【详解】(1)BP=CE,CE⊥AD.理由:∵菱形ABCD中,∠ABC=60°∴AB=BC=CD=AD,∠ADC=∠ABC=60°∴△ABC、△ACD是等边三角形∴AB=AC,AC=CD,∠BAC=∠ACD=60°∵△APE是等边三角形∴AP=AE,∠PAE=60°∴∠BAC-∠PAC=∠PAE-∠PAC即∠BAP=∠CAE,∴△BAP≌△CAE(SAS)∴BP=CE,∠ABP=∠ACE∵BD平分∠ABC∠ABC=30°∴∠ACE=∠ABP=12∴CE平分∠ACD∴CE⊥AD.故答案为BP=CE,CE⊥AD.(2)结论仍然成立.理由如下:如图,设CE交AD于H,连接AC.∵四边形ABCD是菱形,∠ABC=60°,∴△ABC,△ACD都是等边三角形,∠ABD=∠CBD=30°.∵△APE是等边三角形,∴AB=AC,AP=AE,∠BAC=∠PAE=60°.∴△BAP≌△CAE.∴BP=CE,∠ABP=∠ACE=30°.∵∠CAH=60°,∴∠CAH+∠ACH=90°.∴∠AHC=90°,即CE⊥AD.(3)如图,连接BE,由(2)可知CE⊥AD,BP= CE.在菱形ABCD中,AD∥BC,∴CE⊥BC.∵3,BE=219在Rt△BCE中,22(219)(23)-=8.∴BP=CE=8.∵AC与BD是菱形的对角线,∴∠ABD=12∠ABC=30°,AC⊥BD.∴OA=12322AB AO-,∴OP=BP-BO=5,在Rt△AOP中,22PO AO+1,【点睛】本题考查了菱形的性质,等边三角形的判定和性质,全等三角形的判定和性质,勾股定理.第(2)题的证明过程可由(1)适当转化而得,第(3)题则可直接运用(2)的结论解决问题.15.如图①,在菱形ABCD 中,AC 与BD 交于点O ,13AB =,24BD =,点F 是BD 上一动点(不与点B 重合),将线段AF 绕点A 顺时针旋转60︒得到线段AM .(1)求OA 的长.(2)若点M ,F ,C 在同一条直线上,求证:3AC AM =. (3)如图②,以AB 为边作等边ABE ∆,40AEM S ∆=,求AF 的长.解析:(1)5(2)3AC AM =(3)41【分析】(1)在Rt OAB ∆中,利用勾股定理22OA AB OB =-,求解即可. (2)由四边形ABCD 是菱形,求出△AFM 为等边三角形,∠M=∠AFM=60°,再求出∠MAC=90°,可得∠ACM=30°.(3)求出△MEM ≌△ABF ,利用△AEAM 的面积为40求出BF ,在利用勾股定理22225441AF AO FO =+=+=..【详解】(1)四边形ABCD 是菱形,AC BD ∴⊥,12OB OD BD ==. 24BD =,12OB ∴=在Rt OAB ∆中,13AB =,222213125OA AB OB ∴=-=-=.(2)如图2四边形ABCD 是菱形,BD ∴垂直平分AC ,FA FC ∴=,FAC FCA ∴∠=∠.由已知AF AM =,60MAF ∠=︒.AFM ∆为等边三角形,60M AFM ∴∠=∠=︒.。
数学全等三角形双等腰旋转练习题含答案

数学全等三角形双等腰旋转练习题含答案一、全等三角形双等腰旋转1.如图1,在等腰ABC 中,AB AC =,BAC a ∠=,点P 是线段AB 的中点,将线段PC 绕点P 顺时针旋转α得到PD ,连接BD .(1)如图2,若60α=︒,其他条件不变,先补全图形,然后探究线段BD 和BC 之间的数量关系______(直接写结论,不必说明理由)(2)如图3,若90α=︒,其他条件不变,探究线段BP 、BD 和BC 之间的等量关系,并说明理由.(3)如图4,若120α=︒,其他条件不变,探究线段BP 、BD 和BC 之间的等量关系为______.答案:(1)图形见详解,BC=AB=2BD ;(2)BC=BD+BP ,理由见详解;(3)BC =BD+BP【分析】(1)先补全图形,再连接CD ,可得是等边三角形,从而推出BC 是PD 的垂直平分线,进而即可解析:(1)图形见详解,BC =AB =2BD ;(2)BC =BD 2BP ,理由见详解;(3)BC =BD 3BP【分析】(1)先补全图形,再连接CD ,可得CPD △是等边三角形,从而推出BC 是PD 的垂直平分线,进而即可得到结论;(2)取BC 的中点F ,连接PF ,推出BPF △是等腰直角三角形,从而得BF 2BP ,再证≌,进而即可求解;明BDP FCP≌,可得BD=CF,从而得3PF=3BP=BF,进而即可得到结论.(3)由BDP FCP【详解】解:(1)补全图形如下:BC=2BD,理由如下:连接CD,∵线段PC绕点P顺时针旋转 =60°得到PD,∴CP=DP,∠CPD=60°,∴CPD△是等边三角形,∴∠CDP=∠DCP=60°,∵点P是线段AB的中点,∠A=60°,AB=AC,∠ACB=30°,∴ABC是等边三角形,CP⊥AB,∠BCP=12∴∠BCD=60°-30°=30°,∴BC平分∠PCD,∴BC是PD的垂直平分线,∴BD=PB,即:BC=AB=2BD;(2)取BC的中点F,连接PF,∵∠A=90°,AB=AC,∴ABC是等腰直角三角形,∵P是AB的中点,F是BC的中点,∴PF是ABC的中位线,∴PF∥AC,∴∠PFB=∠ACB=45°,∠BPF=∠A=90°,△是等腰直角三角形,∴BPF∴BF2BP,BP=PF,∵∠DPC=∠BPF=90°,∴∠BPD=∠FPC,又∵PD =PC ,∴BDP FCP ≌,∴BD =CF ,∵BC =BF +FC , ∴BC =BD +2BP ;(3)由第(2)题可知:BDP FCP ≌,∴BD =CF ,∵∠BAC =∠DPC =120°,PF ∥AC ,PF =12AC , 又∵BP =12AB ,AB =AC , ∴3PF =3BP =BF ,∴BC =BF +CF =BD +3BP .【点睛】本题主要考查等腰三角形的性质,全等三角形的判定和性质,等边三角形的判定和性质,添加合适的辅助线,构造全等三角形,是解题的关键.2.已知,ABC 中,AB AC =,2BAC α∠=︒,点D 为BC 边中点,连接AD ,点E 为AD 的中点,线段CE 绕点E 顺时针旋转2α︒得到线段EF ,连接FC ,FD .(1)如图1,当60BAC ∠=︒时,请直接写出DF DC的值; (2)如图2,当90BAC ∠=︒时,(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请写出正确的结论,并说明理由;(3)如图3,当2BAC α∠=︒时,请直接写出DF DC的值(用含α的三角函数表示).答案:(1);(2)不成立,,理由见解析;(3).【分析】(1)如图1(见解析),先根据中位线定理得出,再根据旋转的性质、等边三角形的性质得出,,,然后根据三角形全等的判定定理与性质可得,由此即可得出解析:(1)12;(2)不成立,22DF DC =3)sin DF DC α=︒. 【分析】(1)如图1(见解析),先根据中位线定理得出12EG DC =,再根据旋转的性质、等边三角形的性质得出EC FC =,CD CG =,DCF GCE ∠=∠,然后根据三角形全等的判定定理与性质可得DF EG =,由此即可得出答案;(2)如图2(见解析),先根据中位线定理、等腰三角形的三线合一得出90AEM ∠=︒,再根据等腰直角三角形的性质得出ACE BCF ∠=∠,22AC CE BC CF ==,然后根据相似三角形的判定与性质可得CBF CAE ∠=∠,22AE BF =,从而可得AE AM BF BD =,最后根据相似三角形的判定与性质可得90BFD AEM ∠=∠=︒,据此利用正弦三角函数值即可得;(3)如图3(见解析),参照题(2)的思路,先根据相似三角形的判定与性质得出,90CBF CAE BFD AEN α∠=∠=︒∠=∠=︒,再在Rt BFD 中,利用正弦三角函数值即可得.【详解】(1)如图1,取AC 的中点G ,连接EG ,则12CG AC = 点E 为AD 的中点 EG ∴是ACD 的中位线12EG DC ∴=,即12EG DC = 由旋转的性质可知,EC EF =,60FEC ∠=︒CEF ∴是等边三角形60ECF ∴∠=︒,EC FC =AB AC =,60BAC ∠=︒ABC ∴是等边三角形60,ACB AC BC ∴∠=︒=点D 为BC 边中点1122CD BC AC CG ∴=== 60ECF ECD DCF ∠=∠+∠=︒,60ACB ECD GCE ∠=∠+∠=︒DCF GCE ∴∠=∠在DCF 和GCE 中,CD CG DCF GCE FC EC =⎧⎪∠=∠⎨⎪=⎩()DCF GCE SAS ∴≅DF EG ∴=12DF EG DC DC ∴==; (2)不成立,2DF DC =,理由如下: 如图2,连接BF ,取AC 的中点M ,连接EM∵E 是AD 的中点∴//EM BC∴AEM ADC ∠=∠∵AB AC =ABC ∴是等腰三角形∵D 是BC 中点, 2BAC α∠=︒∴AD BC ⊥,12CAD BAC α∠=∠=︒,BD DC = ∴90ADC ∠=︒∴90AEM ∠=︒当90BAC ∠=︒时,则90CEF ∠=︒ABC ∴和CEF △为等腰直角三角形∴45ACB ECF ∠=∠=︒,即45ECD ACE ECD BCF ∠+∠=∠+∠=︒∴ACE BCF ∠=∠,cos 452AC CE BC CF ==︒= ∴ACE BCF ~ ∴90452CBF CAE α︒∠=∠=︒==︒,2AE AC BF BC ==∵1212AC AM BD BC ==∴AE AM BF BD = ∴BDF AME ~ ∴90BFD AEM ∠=∠=︒在Rt BFD 中,sin DF DF CBF BD DC ∠==,即sin 45DF DC ︒=则2DF DC =; (3)sin DF DC α=︒,求解过程如下: 如图3,连接BF ,取AC 的中点N ,连接EN参照(2),同理可得:12CAD BAC α∠=∠=︒,BD DC =,90AEN ADC ∠=∠=︒ 当2BAC α∠=︒时,则2CEF α∠=︒AB AC =,EC EF =(旋转的性质)ABC ∴和EFC 为等腰三角形 ∴1(180)902ACB ABC BAC α∠=∠=︒-∠=︒-︒ 1(180)902ECF EFC CEF α∠=∠=︒-∠=︒-︒ 90ACB ECF α∴∠=∠=︒-︒ABC EFC ∴~AC CE BC CF∴= 又,ACB ECD ACE ECF ECD BCF ∠=∠+∠∠=∠+∠ ∴ACE BCF ∠=∠ ∴ACE BCF ~∴CBF CAE α∠=∠=︒,AE AC BF BC = ∵1212AC AN AC BD BC BC == ∴AE AN BF BD = ∴BDF ANE ~ ∴90BFD AEN ∠=∠=︒在Rt BFD 中,sin DF DF CBF BD DC ∠== 即sin DF DCα=︒.【点睛】本题考查了等腰三角形的性质、旋转的性质、三角形全等的判定定理与性质、相似三角形的判定与性质等知识点,通过作辅助线,构造全等三角形和相似三角形是解题关键. 3.如图,在ABC ∆中,ABC ∠为锐角,点D 为直线BC 上一动点,以AD 为直角边且在AD 的右侧作等腰直角三角形ADE ,90DAE ∠=︒,AD AE =.(1)如果AB AC =,90BAC ∠=︒.①当点D 在线段BC 上时,如图1,线段CE 、BD 的位置关系为___________,数量关系为_____________②当点D 在线段BC 的延长线上时,如图2,①中的结论是否仍然成立,请说明理由. (2)如图3,如果AB AC ≠,90BAC ∠≠︒,点D 在线段BC 上运动。
初二数学 全等三角形双等腰旋转知识点及练习题附解析

初二数学全等三角形双等腰旋转知识点及练习题附解析一、全等三角形双等腰旋转1.在△ABC中,∠BAC=90°,点E为AC上一点,AB=AE,AG⊥BE,交BE于点H,交BC 于点G,点M是BC边上的点.(1)如图1,若点M与点G重合,AH=2,BC=26,求CE的长;(2)如图2,若AB=BM,连接MH,∠HMG=∠MAH,求证:AM=22HM;(3)如图3,若点M为BC的中点,作点B关于AM的对称点N,连接AN、MN、EN,请直接写出∠AMH、∠NAE、∠MNE之间的角度关系.答案:(1);(2)见解析;(3)∠NAE+2∠MNE=2∠AMH【分析】(1)根据等腰直角三角形的性质以及勾股定理解答即可;(2)根据等腰直角三角形的判定和性质以及全等三角形的判定和性质解答即可;解析:(122)见解析;(3)∠NAE+2∠MNE=2∠AMH【分析】(1)根据等腰直角三角形的性质以及勾股定理解答即可;(2)根据等腰直角三角形的判定和性质以及全等三角形的判定和性质解答即可;(3)根据对称的性质和三角形内角和解答即可.【详解】解:(1)∵∠BAC=90°,AB=AE,∴△BAE为等腰直角三角形,∵AG⊥BE,∴AH是△BAE的中线,∴BE=2AH=4,∵∠BEA=45°,∴∠BEC=135°,在△BCE中,过点C作CD⊥BE交BE的延长线于点D,如图1,∵∠DEC =45°,∴△DEC 是等腰直角三角形,设ED =x ,则DC =x ,CE =2x ,在Rt △BCD 中,BC 2=BD 2+DC 2,即222(26)(4)x x =++ ,∴x 1=1或x 2=﹣5(舍去),∴CE =2;(2)如图2,过H 作HD ⊥HM 交AM 于点D ,连接BD ,∵AB =AE ,∠BAC =90°,∴△ABE 是等腰直角三角形,∵AG ⊥BE ,∴△ABH 为等腰直角三角形,∴BH =AH ,∠BAH =45°,∠BHA =90°,∵AB =BM ,∴∠BAM =∠BMA ,∵∠HMG =∠MAH ,∴∠BAM ﹣∠MAH =∠BMA ﹣∠HMG ,即∠BAH =∠AMH =45°,∵HD ⊥HM ,∴△DHM 为等腰直角三角形,∴DH =HM ,∠DHM =90°,∵∠BHD =∠BHA +∠AHD ,∠AHM =∠DHM +∠AHD ,∴∠BHD =∠AHM ,在△BHD 与△AHM 中,BH AH BHD AHM DH MH =⎧⎪∠=∠⎨⎪=⎩,∴△BHD ≌△AHM (SAS ),∴∠DBH =∠MAH ,BD =AM ,∴∠BHA =∠BDA =90°,∵BA =BM ,∴D 是AM 的中点,∴AM =2DM =HM ,即AM =HM ;(3)∵H 是BE 的中点,M 是BC 的中点,∴MH 是△BCE 的中位线,∴MH ∥CE ,∴∠AMH =∠MAC ,∵∠BAC =90°,∴AM =BM ,∴∠MAB =∠ABM ,∵点B 与点N 关于线段AM 对称,∴∠ABM =∠ANM ,AB =AN ,∴AE =AN ,∴∠AEN =∠ANE ,在△AEN 中,∠NAE +2∠ANE =180°①,∵∠ANE =∠ANM +∠MNE ,∠ABM =∠ANM =∠MAB =90°﹣∠MAC ,∴∠ANE =90°﹣∠MAC +∠MNE ,∴∠ANE =90°﹣∠AMH +∠MNE ②,将②代入①,得:∠NAE +2×(90°﹣∠AMH +∠MNE )=180°,∴∠NAE +180°﹣2∠AMH +2∠MNE =180°,∴∠NAE +2∠MNE =2∠AMH .【点睛】此题考查等腰直角三角形的判定及性质,勾股定理的运用,全等三角形的判定及性质,轴对称的性质,三角形中位线的判定及性质,解一元二次方程,熟练掌握各知识点是解题的关键.2.如图1,已知ABC 和EFC 都是等边三角形,且点E 在线段AB 上.(1)过点E 作//EG BC 交AC 于点G ,试判断AEG △的形状并说明理由;(2)求证://BF AC ;(3)如图2,若点D 在射线CA 上,且ED EC =,求证:AB AD BF =+.答案:(1)是等边三角形,理由见解析;(2)证明见解析;(3)证明见解析.【分析】(1)如图(见解析),先根据等边三角形的性质可得,再根据平行线的性质可得,然后根据等边三角形的判定即可得;(2)先根解析:(1)AEG △是等边三角形,理由见解析;(2)证明见解析;(3)证明见解析.【分析】(1)如图(见解析),先根据等边三角形的性质可得60BAC ABC ACB ==︒=∠∠∠,再根据平行线的性质可得60AEG ABC ∠=∠=︒,然后根据等边三角形的判定即可得;(2)先根据等边三角形的性质可得,,60AC BC CE CF ACB ECF ==∠=∠=︒,从而可得ACE BCF ∠=∠,再根据三角形全等的判定定理与性质可得60CBF CAE ∠=∠=︒,从而可得CBF ACB ∠=∠,然后根据平行线的判定即可得证;(3)先根据平行线的性质、三角形全等的性质可得,DAE EB AE F BF ∠=∠=,再根据等腰三角形的性质可得D ACE ∠=∠,从而可得D BCF ∠=∠,然后根据三角形的内角和定理可得BEF BCF D ∠=∠=∠,最后根据三角形全等的判定定理与性质可得AD BE =,据此根据线段的和差、等量代换即可得证.【详解】(1)AEG △是等边三角形,理由如下:如图,过点E 作//EG BC 交AC 于点G , ABC 是等边三角形,60BAC ABC ACB ∴∠=∠=∠=︒,60AEG ABC ∴∠=∠=︒, ∴AEG 是等边三角形;(2)ABC 和EFC 是等边三角形,,,60AC BC CE CF ACB ECF ==∠=∠=∴︒,ACB BCE ECF BCE ∴∠-∠=∠-∠,即ACE BCF ∠=∠,在ACE △和BCF △中,AC BC ACE BCF CE CF =⎧⎪∠=∠⎨⎪=⎩,()ACE BCF SAS ∴≅,60CBF CAE ∴∠=∠=︒,CBF ACB ∴∠=∠,//BF AC ∴;(3)由(2)知,//BF AC ,ACE BCF ≅,DAE EBF ∴∠=∠,AE BF =,ED EC =,D ACE ∴∠=∠,由(2)已证:ACE BCF ∠=∠,D BCF ∴∠=∠, ABC 和EFC 是等边三角形,60ABC EFC ∠∴∠==︒,在BEF 中,180120BEF EBC CBF BFE CBF BFE ∠=︒-∠-∠-∠=︒-∠-∠, 在BCF △中,180120BCF EFC CBF BFE CBF BFE ∠=︒-∠-∠-∠=︒-∠-∠, BEF BCF D ∴∠=∠=∠,在ADE 和BEF 中,DAE EBF D BEF AE BF ∠=∠⎧⎪∠=∠⎨⎪=⎩,()ADE BEF AAS ∴≅,AD BE ∴=,AB BE AE AD BF ∴=+=+.【点睛】本题考查了三角形全等的判定定理与性质、等边三角形的性质、平行线的判定与性质、等腰三角形的性质等知识点,较难的是题(3),正确找出两个三角形全等的条件是解题关键.3.如图,O 是ABC ∆的外接圆,AC 是O 的直径,点B 是半圆ABC 的中点,点D 是ADC 上一动点(不与点A 、C 重合),连接BD 交AC 于点G .图1 图2(1)如图1,过点B 作//BF AC ,交DA 延长线于点F ,求证:BF 与O 相切;(2)若10AC =,6AD =,求CG 的长;(3)如图2,把DBC ∆沿直线BC 翻折得到EBC ∆,连接AE ,当点D 在ADC 运动时,探究线段AE 、BD 、CD 之间的数量关系,并说明理由. 答案:(1)详见解析;(2);(3),详见解析.【分析】(1)连接,求出,根据得到,问题得证;(2)作交于点,证明,求出CD=8,根据,在中,设,则,,求出,,根据勾股定理即可求出CG ;(3)作解析:(1)详见解析;(2)407;(3)2222AE DB CD =+,详见解析. 【分析】(1)连接OB ,求出OB AC ⊥,根据//BF AC 得到90FBO ∠=︒,问题得证; (2)作GH CD ⊥交CD 于点H ,证明DH GH =,求出CD=8,根据3tan 4ACD ∠=, 在Rt CGH ∆中,设3GH a =,则3DH a =,4CH a =,求出327CH =,247GH =,根据勾股定理即可求出CG ;(3)作BM BE ⊥,使得BM BE =,连接EM ,CM .证明ABE CBM ≅△△,得到AE CM =,证明90CEM ∠=︒,得到222CM EM EC =+,根据数量关系进行代换即可得到2222AE DB CD =+.【详解】证明:(1)连接OB ,O 是ABC 的外接圆,AC 是O 的直径,点B 是半圆ABC 的中点,45BAC ACB ∠∴∠==︒,OB AC ⊥45ABO ∴∠=︒//BF AC45ABF ∴∠=︒90FBO ∴∠=︒BF ∴与O 相切;解:(2)作GH CD ⊥交CD 于点H ,点B 是半圆周ABC 的中点,ADB CDB ∴∠=∠ AC 是O 的直径90ADC ∴∠=︒45CDB ∴∠=︒DH GH ∴=在Rt ACD ∆中,10AC =,6AD =,8CD ∴= 3tan 4ACD ∴∠= 在Rt CGH ∆中,设3GH a =,则3DH a =,4CH a =348a a ∴+=,87a =, 在Rt CGH ∆中,设3GH a =,则3DH a =,4CH a =∴,327CH =,247GH = 在Rt CGH ∆中,22243240777CG ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭图1(3)结论:2222AE DB CD =+作BM BE ⊥,使得BM BE =,连接EM ,CM .90ABC EBM ∠=∠=︒,ABE CBM ∴∠=∠,BA BC=,BE BM=,△△(SAS),∴≅ABE CBM∴=,AE CM∠=∠=∠=︒BEC BDC BEM45∴∠=︒,90CEM222CM EM EC∴=+,=,222∴==,EC CDEM BE BD22222AE DB CD∴=+2图2【点睛】本题为圆的综合题目,考查了圆的性质,切线的判定,利用三角函数求线段的长,勾股定理等知识,综合性较强.解第(2)步关键是添加适当辅助线GH,构造了等腰直角三角形DHG和三边比为3:4:5的直角三角形CGH;解(3)步关键是构造旋转全等,将三条线段转化在同一直角三角形CEM中,得出数量关系后再进行线段的代换.4.在等腰Rt△ABC中,AB=AC,∠BAC=90°(1)如图1,D,E是等腰Rt△ABC斜边BC上两动点,且∠DAE=45°,将△ABE绕点A逆时针旋转90后,得到△AFC,连接DF①求证:△AED≌△AFD;②当BE=3,CE=7时,求DE的长;(2)如图2,点D是等腰Rt△ABC斜边BC所在直线上的一动点,连接AD,以点A为直角顶点作等腰Rt△ADE,当BD=3,BC=9时,求DE的长.答案:(1)①见解析;②DE=;(2)DE的值为3或3【分析】(1)①先证明∠DAE =∠DAF ,结合DA =DA ,AE =AF ,即可证明;②如图1中,设DE =x ,则CD =7﹣x .在Rt △DCF 中,由DF2解析:(1)①见解析;②DE =297;(2)DE 的值为 【分析】(1)①先证明∠DAE =∠DAF ,结合DA =DA ,AE =AF ,即可证明;②如图1中,设DE =x ,则CD =7﹣x .在Rt △DCF 中,由DF 2=CD 2+CF 2,CF =BE =3,可得x 2=(7﹣x )2+32,解方程即可;(2)分两种情形:①当点E 在线段BC 上时,如图2中,连接BE .由△EAD ≌△ADC ,推出∠ABE =∠C =∠ABC =45°,EB =CD =5,推出∠EBD =90°,推出DE 2=BE 2+BD 2=62+32=45,即可解决问题;②当点D 在CB 的延长线上时,如图3中,同法可得DE 2=153.【详解】(1)①如图1中,∵将△ABE 绕点A 逆时针旋转90°后,得到△AFC ,∴△BAE ≌△CAF ,∴AE =AF ,∠BAE =∠CAF ,∵∠BAC =90°,∠EAD =45°,∴∠CAD +∠BAE =∠CAD +∠CAF =45°,∴∠DAE =∠DAF ,∵DA =DA ,AE =AF ,∴△AED ≌△AFD (SAS );②如图1中,设DE =x ,则CD =7﹣x .∵AB =AC ,∠BAC =90°,∴∠B =∠ACB =45°,∵∠ABE =∠ACF =45°,∴∠DCF =90°,∵△AED ≌△AFD (SAS ),∴DE =DF =x ,∵在Rt △DCF 中, DF 2=CD 2+CF 2,CF =BE =3,∴x 2=(7﹣x )2+32,∴x =297, ∴DE =297; (2)∵BD =3,BC =9,∴分两种情况如下:①当点E 在线段BC 上时,如图2中,连接BE .∵∠BAC =∠EAD =90°,∴∠EAB=∠DAC,∵AE=AD,AB=AC,∴△EAB≌△DAC(SAS),∴∠ABE=∠C=∠ABC=45°,EB=CD=9-3=6,∴∠EBD=90°,∴DE2=BE2+BD2=62+32=45,∴DE=35;②当点D在CB的延长线上时,如图3中,连接BE.同理可证△DBE是直角三角形,EB=CD=3+9=12,DB=3,∴DE2=EB2+BD2=144+9=153,∴DE=317,综上所述,DE的值为35或317.【点睛】本题主要考查旋转变换的性质,三角形全等的判定和性质以及勾股定理,添加辅助线,构造旋转全等模型,是解题的关键.5.已知在矩形ABCD中,∠ADC的平分线DE与BC边所在的直线交于点E,点P是线段DE上一定点(其中EP<PD)(1)如图1,若点F在CD边上(不与D重合),将∠DPF绕点P逆时针旋转90°后,角的两边PD、PF分别交射线DA于点H、G.①求证:PG=PF;②探究:DF、DG、DP之间有怎样的数量关系,并证明你的结论.(2)拓展:如图2,若点F在CD的延长线上(不与D重合),过点P作PG⊥PF,交射线DA于点G,你认为(1)中DE、DG、DP之间的数量关系是否仍然成立?若成立,给出证明;若不成立,请写出它们所满足的数量关系式,并说明理由.答案:(1)①详见解析;②DG+DF=DP;(2)不成立,数量关系式应为:DG-DF=DP【解析】【分析】(1)①根据矩形性质证△HPG≌△DPF(ASA),得PG=PF;②由①知,△HPD为等腰直解析:(1)①详见解析;2;(2)不成立,数量关系式应为:DG-2【解析】【分析】(1)①根据矩形性质证△HPG≌△DPF(ASA),得PG=PF;②由①知,△HPD为等腰直角三角形,△HPG≌△DPF,根据直角三角形性质可得2DP;(2)过点P作PH⊥PD 交射线DA于点H,得到△HPD为等腰直角三角形,证△HPG≌△DPF,得HG=DF,DH=DG-HG=DG-DF,2DP.【详解】(1)①∵由矩形性质得∠GPF=∠HPD=90°,∠ADC=90°,∴∠GPH=∠FPD,∵DE平分∠ADC,∴∠PDF=∠ADP=45°,∴△HPD为等腰直角三角形,∴∠DHP=∠PDF=45°,在△HPG和△DPF中,∵PHG PDF PH PDGPH FPD ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△HPG≌△DPF(ASA),∴PG=PF;②结论:2DP,由①知,△HPD为等腰直角三角形,△HPG≌△DPF,∴2DP,HG=DF,∴HD=HG+DG=DF+DG ,∴DG+DF=2DP ;(2)不成立,数量关系式应为:DG-DF=2DP ,如图,过点P 作PH ⊥PD 交射线DA 于点H ,∵PF ⊥PG ,∠GPF=∠HPD=90°,∴∠GPH=∠FPD ,∵DE 平分∠ADC ,且在矩形ABCD 中,∠ADC=90°,∴∠HDP=∠EDC=45°,得到△HPD 为等腰直角三角形,∴∠DHP=∠EDC=45°,且PH=PD ,HD=2DP ,∴∠GHP=∠FDP=180°-45°=135°,在△HPG 和△DPF 中,∵GPH FPD GHP FDP PH PD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△HPG ≌△DPF ,∴HG=DF ,∴DH=DG-HG=DG-DF ,∴DG-DF=2DP .【点睛】考核知识点:矩形性质的运用,等腰直角三角形.综合运用全等三角形判定和等腰直角三角形性质是关键.6.感知:如图①,已知正方形ABCD 的边CD 在正方形DEFG 的边DE 上,连结AE 、CG ,易证AED CGD ≌△△.(不需要证明)探究:将图①中正方形DEFG 绕点D 按顺时针方向旋转,使点E 落在BC 边上,如图②.连结AE 、CG ,证明:AE=CG .应用:如图③,正方形ABCD 中,AD =3,点E 在CB 的延长线上,BE =1,DE=DF ,∠EDF =90°.直接写出点F 与点C 的距离.答案:探究:证明见解析;应用:点F 与点C 的距离为.【分析】探究:结合旋转模型,利用“边角边”证明即可得出结论;应用:连接FC ,根据前序问题中的方法证明△AED ≌△CFD ,从而得到CF=AE ,即在Rt解析:探究:证明见解析;应用:点F 与点C 的距离为10. 【分析】探究:结合旋转模型,利用“边角边”证明AED CGD ≌△△即可得出结论; 应用:连接FC ,根据前序问题中的方法证明△AED ≌△CFD ,从而得到CF =AE ,即在Rt △AED 中求解AE 即可.【详解】探究:证明:在正方形ABCD 和正方形DEFG 中,AD =CD ,DE =DG ,90ADC EDG ∠=∠=︒,∴ADE CDG ∠=∠,∴AED CGD ≌△△,∴AE CG =;应用:连接FC ,∵∠EDF =∠ADC =90°,∴∠ADE =∠CDF ,又∵AD =CD ,DE=DF ,∴△AED ≌△CFD ,∴CF =AE ,在Rt △AED 中,2210AE AB BE =+=,∴点F 与点C 的距离为10.【点睛】本题考查全等三角形的判定与性质,掌握基本的旋转模型,根据全等三角形的性质求解问题是解题关键.7.已知:如图1,AOB 和COD 都是等边三角形.(1)求证:①AC =BD ;②∠APB =60°;(2)如图2,在AOB 和COD 中,OA =OB ,OC =OD ,∠AOB =∠COD =α,则AC 与BD 间的等量关系为 ,∠APB 的大小为答案:(1)①见解析,②见解析;(2)AC =BD ,α【分析】(1)①根据△AOB 和△COD 都是等边三角形,求出∠AOC=∠BOD ,根据SAS 推出△AOC ≌△BOD ,根据全等三角形的性质得出AC=BD ;解析:(1)①见解析,②见解析;(2)AC =BD ,α【分析】(1)①根据△AOB 和△COD 都是等边三角形,求出∠AOC=∠BOD ,根据SAS 推出△AOC ≌△BOD ,根据全等三角形的性质得出AC=BD ;②由△AOC ≌△BOD ,可得∠CAO=∠DBO ,根据三角形内角和可知∠CAO+∠AOB=∠DBO+∠APB ,推出∠APB=∠AOB 即可;(2)根据∠AOB=∠COD=α,求出∠AOC=∠BOD ,根据SAS 推出△AOC ≌△BOD ,根据全等三角形的性质得出AC=BD ,∠CAO=∠DBO ,根据三角形内角和可知∠CAO+∠AOB=∠DBO+∠APB ,推出∠APB=∠AOB 即可.【详解】证明:(1)①∵△AOB 和△COD 都是等边三角形,∴OA=OB ,OC=OD ,∠AOB =∠COD =60°,∴∠AOC =∠BOD ,在△AOC 和△BOD 中,OA OB AOC BOD OC OD =⎧⎪∠=∠⎨⎪=⎩,∴△AOC ≌△BOD (SAS ),∴AC =BD ,∠CAO =∠DBO ,②设AC 与BO 交于E ,∵△AOC ≌△BOD ,∴∠CAO =∠DBO ,∵∠AEO=∠BEP ,∴∠CAO+∠AOB =∠DBO+∠APB ,∴∠APB =∠AOB =60°.(2)AC=BD ,∠A PB=α,理由如下:∵∠AOB=∠COD=α,∴∠AOC=∠BOD ,在△AOC 和△BOD 中,OA OB AOC BOD OC OD =⎧⎪∠=∠⎨⎪=⎩,∴△AOC ≌△BOD ,∴AC=BD ,∠CAO=∠DBO ,设AC 与BO 交于E ,∵∠AEO=∠BEP ,∴∠CAO+∠AOB=∠DBO+∠APB ,∴∠APB=∠AOB=α,故答案为AC=BD ,α.【点睛】本题考查三角形旋转,三角形全等判定与性质,三角形内角和,掌握三角形旋转,三角形全等判定与性质,三角形内角和是解题关键.8.△ABC 中,∠BAC =90°,AB =AC ,点D 为直线BC 上一动点(点D 不与B ,C 重合),以AD 为边在AD 右侧作正方形ADEF ,连接CF .(1)观察猜想:如图1,当点D在线段BC上时,AC,CD,CF之间的数量关系为____________;(将结论直接写在横线上)(2)如图2,当点D在线段CB的延长线上时,(1)中的结论是否仍然成立?若成立,不需证明;若不成立,请你写出正确结论,并说明理由.答案:(1)CD+CF=AC;(2)不成立,CD-CF=AC;理由见解析.【分析】(1)根据正方形的性质可得∠DAF=90°,AD=AF,利用同角的余角相等可得∠BAD=∠CAF,利用SAS可证明△B解析:(1)2AC;(2)不成立,2AC;理由见解析.【分析】(1)根据正方形的性质可得∠DAF=90°,AD=AF,利用同角的余角相等可得∠BAD=∠CAF,利用SAS可证明△BAD≌△CAF,可得CF=BD,即可得出BC=CD+CF,根据等腰直角三角形的性质可得2AC,进而可得答案;(2)同(1)可证明△BAD≌△CAF,可得BD=CF,即可得出CD=BC+CF,根据等腰直角三角形的性质可得2AC,可得2AC,即可得答案.【详解】(1)∵四边形ADEF是正方形,∴∠DAF=90°,AD=AF,∴∠CAF+∠DAC=90°,∵∠BAC=90°,∴∠BAD+∠DAC=90°,∴∠BAD=∠CAF,在△BAD和△CAF中,AB ACBAD CAF AD AF=⎧⎪∠=∠⎨⎪=⎩,∴△BAD≌△CAF,∴CF=BD,∴CD+CF=CD+BD=BC,∵∠BAC=90°,AB=AC,∴BC=2AC,∴CD+CF=2AC.故答案为:CD+CF=2AC(2)不成立,CD-CF=2AC.理由如下:同(1)可证△BAD≌△CAF,∴CF=BD,∴CD=BC+BD=BC+CF,∵BC=2AC,∴CD-CF=2AC.【点睛】本题考查正方形的性质、全等三角形的判定与性质及等腰直角三角形的性质,熟练掌握相关性质及判定定理是解题关键.9.在Rt△ABC中,AB=AC,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转90°得到AE.(1)连接EC,如图①,试探索线段BC,CD,CE之间满足的等量关系,并证明你的结论;(2)连接DE,如图②,求证:BD2+CD2=2AD2(3)如图③,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°,若BD=13,CD=1,则AD的长为▲ .(直接写出答案)答案:(1)BC=DC+EC,理由见解析;(2)见解析;(3)【分析】(1)根据本题中的条件证出△BAD≌△CAE(SAS), 得到BD=CE,再根据条件即可证出结果.(2)由(1)中的条件可得∠解析:(1)BC=DC+EC,理由见解析;(2)见解析;(36【分析】(1)根据本题中的条件证出△BAD≌△CAE(SAS), 得到BD=CE,再根据条件即可证出结果.(2)由(1)中的条件可得∠DCE=∠ACE+∠ACB=90°, 所以CE2+CD2=ED2,可推出BD2+CD2=2ED,再根据勾股定理可得出结果.(3)作AE⊥AD,使AE=AD,连接CE,DE,可推出△BAD≌△CAE(SAS),所以13再根据勾股定理求得DE.【详解】解:(1)结论:BC=DC+EC理由:如图①中,∵∠BAC=∠DAE=90°,∴∠BAC-∠DAC=∠DAE-∠DAC ,即∠BAD=∠CAE,在△BAD 和△CAE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩, ∴△BAD ≌△CAE (SAS );∴BD=CE,∴BC=BD+CD=EC+CD,即:BC=DC+EC.(2)BD 2+CD 2=2AD 2,理由如下:连接CE,由(1)得,△BAD ≌△CAE,∴BD=CE ,∠ACE=∠B,∴∠DCE=∠ACE+∠ACB=90°,∴CE 2+CD 2=ED 2,即:BD 2+CD 2=ED 2;在Rt △ADE 中,AD 2+AE 2=ED 2,又AD=AE,∴ED 2=2AD 2;∴BD 2+CD 2=2AD 2;(3)AD 6(学生直接写出答案).作AE ⊥AD,使AE=AD,连接CE,DE,∵∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,在△BAD与△CAE中,AB=AC,∠BAD=∠CAE,AD=AE.∴△BAD≌△CAE(SAS),∴BD=CE=13,∵∠ADC=45°,∠EDA=45°,∴∠EDC=90°,∴DE2=CE2-CD2=(13)2-12=12,∴DE=23,∵∠DAE=90°,AD2+AE2=DE2,∴AD=6.【点睛】本题属于几何变换综合题,考查了等腰直角三角形的性质,旋转变换,全等三角形的判定和性质,勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.10.如图,已知Rt△ABC中,AB=AC=2,点D为直线BC上的动点(不与B、C重合),以A为直角顶点作等腰直角三角形ADE(点A,D,E按逆时针顺序排列),连结CE.(1)当点D在线段BC上运动时,①求证:BD=CE;②请探讨四边形ADCE的面积是否有变化;(2)当点D在直线BC上运动时,直接写出CD,CB与CE之间的数量关系.答案:(1)①见解析;②四边形ADCE的面积不变;(2)当点D在线段BC 上时,CB=CE+CD;当点D在点C右侧时,CB = CE-CD;当点D在点B左侧时,CB= CD-CE【分析】(1)①根据等腰解析:(1)①见解析;②四边形ADCE 的面积不变;(2)当点D 在线段BC 上时,CB=CE +CD ;当点D 在点C 右侧时,CB = CE -CD ;当点D 在点B 左侧时,CB= CD -CE【分析】(1)①根据等腰直角三角形的性质可得AB=AC ,AD=AE ,∠BAC=∠DAE=90°,从而得出∠BAD=∠CAE ,然后利用SAS 即可证出△BAD ≌△CAE ,从而得出BD=CE ;②根据直角三角形的面积公式即可求出S △ABC ,然后根据全等三角形的性质可得S △BAD =S △CAE ,然后根据S 四边形ADCE =S △CAE +S △ADC 和等量代换即可得出结论;(2)根据点D 的位置分类讨论,分别画出对应的图形,根据(1)①中证全等的方法和全等三角形的性质即可推出结论.【详解】解:(1)①∵△ABC 和△ADE 都是等腰直角三角形∴AB=AC ,AD=AE ,∠BAC=∠DAE=90°∴∠BAD +∠DAC=90°,∠CAE +∠DAC=90°∴∠BAD=∠CAE在△BAD 和△CAE 中AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩∴△BAD ≌△CAE∴BD=CE ;②∵已知Rt △ABC 中,AB=AC=2,∴S △ABC =12AB·AC=2 ∵△BAD ≌△CAE∴S △BAD =S △CAE ∴S 四边形ADCE =S △CAE +S △ADC =S △BAD +S △ADC = S △ABC =2∴四边形ADCE 的面积不变;(2)当点D 在线段BC 上时,如下图所示由(1)①的结论知BD=CE∴CB=BD +CD= CE +CD ;当点D 在点C 右侧时,如下图所示∵△ABC 和△ADE 都是等腰直角三角形∴AB=AC ,AD=AE ,∠BAC=∠DAE=90°∴∠BAD -∠DAC=90°,∠CAE -∠DAC=90°∴∠BAD=∠CAE在△BAD 和△CAE 中AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩∴△BAD ≌△CAE∴BD=CE∴CB=BD -CD= CE -CD ;当点D 在点B 左侧时,如下图所示∵△ABC 和△ADE 都是等腰直角三角形∴AB=AC ,AD=AE ,∠BAC=∠DAE=90°∴∠BAD=∠DAC -90°,∠CAE=∠DAC - 90°∴∠BAD=∠CAE在△BAD 和△CAE 中AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩∴△BAD ≌△CAE∴BD=CE∴CB= CD -BD = CD -CE .综上所述:当点D 在线段BC 上时,CB=CE +CD ;当点D 在点C 右侧时,CB = CE -CD ;当点D 在点B 左侧时,CB= CD -CE .【点睛】此题考查的是等腰直角三角形的性质、全等三角形的判定及性质和三角形的面积公式,掌握等腰直角三角形的性质、全等三角形的判定及性质、分类讨论的数学思想和三角形的面积公式是解决此题的关键.二、全等三角形手拉手模型11.在Rt ABC 中,90BAC ∠=︒,AB AC =.(1)如图1,点D 为BC 边上一点,连接AD ,以AD 为边作Rt ADE △,90DAE ∠=︒,AD AE =,连接EC .直接写出线段BD 与CE 的数量关系为 ,位置关系为 .(2)如图2,点D 为BC 延长线上一点,连接AD ,以AD 为边作Rt ADE △,90DAE ∠=︒,AD AE =,连接EC .①用等式表示线段BC ,DC ,EC 之间的数量关系为 .②求证:2222BD CD AD +=.(3)如图3,点D 为ABC 外一点,且45ADC ∠=︒,若13BD =,5CD =,求AD 的长.解析:(1)BD CE =,BD CE ⊥;(2)①BC DC EC +=,②见解析;(3)62【分析】(1)由等腰直角三角形的性质得到45B ACB ∠=∠=︒,根据题意可知BAC DAC DAE DAC ∠-∠=∠-∠,即BAD CAE ∠=∠,再利用SAS 证明BAD ≌CAE ,可得到BD CE =,45ABC ACE ∠=∠=︒,从而算出BCE ∠的度数,进而得到线段BD 与CE 的位置关系;(2)①根据角度的运算得到BAD CAE ∠=∠,再利用SAS 证得BAD ≌CAE ,得到BD CE =,再根据BD BC CD =+,等量代换即可求出答案;②由①中BAD ≌CAE ,得到BD CE =,ABC ACE ∠=∠,在根据等腰直角三角形的性质即可得出ACE ∠的度数,进而证得90BCE DCE ∠=∠=︒,根据勾股定理得到222AE AD DE +=,222CE CD DE +=,等量代换后得到2222AE AD CE CD +=+,又因为AE AD =,BD CE =,代入即可得出答案;(3)过点A 作AE AD ⊥,并且AE AD =,连接DE ,CE ,得到ADE 是等腰直角三角形,由(2)得BAD ≌CAE ,得到BD CE =,在Rt CDE △中,通过勾股定理求出DE 的长度,在Rt ADE △中又由勾股定理得:222AE AD DE +=,再根据AE AD =,代入数据即可求出AD 的长度.【详解】(1)在Rt ABC 中,90BAC ∠=︒,AB AC =,∴45B ACB ∠=∠=︒,90DAE ∠=︒,∴BAC DAC DAE DAC ∠-∠=∠-∠,即BAD CAE ∠=∠,在BAD 和CAE 中AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴BAD ≌CAE ()SAS ,∴BD CE =,45ABC ACE ∠=∠=︒,∴90BCE ACB ACE ∠=∠+∠=︒,∴BD CE ⊥.故答案为:BD CE =,BD CE ⊥.(2)①90BAC ∠=︒,90DAE ∠=︒,∴BAC CAD DAE CAD ∠+∠=∠+∠,即BAD CAE ∠=∠,在BAD 和CAE 中 AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴BAD ≌CAE ()SAS ,∴BD CE =,BD BC CD =+,∴BC DC EC +=.故答案为:BC DC EC +=.②证明:由①得:BAD ≌CAE ,∴BD CE =,ABC ACE ∠=∠,ABC 和ADE 都是等腰直角三角形,∴45ACE ABC ACB ∠=∠=∠=︒,∴90BCE DCE ∠=∠=︒,在Rt ADE △和Rt ECD △中, 由勾股定理得:222AE AD DE +=,222CE CD DE +=,∴2222AE AD CE CD +=+,AE AD =,BD CE =,∴2222AD BD CD =+,即2222BD CD AD +=.(3)过点A 作AE AD ⊥,并且AE AD =,连接DE ,CE ,如图,∴ADE 是等腰直角三角形,∴45ADE ∠=︒,45ADC ∠=︒,∴90CDE ∠=︒,由(2)中②可知,BAD ≌CAE ,∴BD CE =,13BD =,5CD =,∴13CE =,在Rt CDE △中,由勾股定理得:222DE CD CE +=, ∴2212DE CE CD =-,在Rt ADE △中,由勾股定理得:222AE AD DE +=,∴22144AD =, ∴62AD =【点睛】本题考查了全等三角形的判定和性质,勾股定理,等腰三角形的性质,解题的关键是合理添加辅助线找出两个三角形全等.12.(1)如图1,ABC 和DCE 都是等边三角形,且B ,C ,D 三点在一条直线上,连接AD ,BE 相交于点P ,求证:BE AD =.(2)如图2,在BCD 中,若120BCD ∠<︒,分别以BC ,CD 和BD 为边在BCD 外部作等边ABC ,等边CDE △,等边BDF ,连接AD 、BE 、CF 恰交于点P . ①求证:AD BE CF ==;②如图2,在(2)的条件下,试猜想PB ,PC ,PD 与BE 存在怎样的数量关系,并说明理由.解析:(1)详见解析;(2)①详见解析;②PB PC PD BE ++=,理由详见解析【分析】(1)根据等边三角形的性质得出BC=AC ,CE=CD ,∠ACB=∠DCE=60°,进而得出∠BCE=∠ACD ,判断出BCE ACD ≌(SAS ),即可得出结论;(2)①同(1)的方法判断出≌ACD BCE (SAS ),ABD CBF ≌(SAS ),即可得出结论; ②先判断出∠APB=60°,∠APC=60°,在PE 上取一点M ,使PM=PC ,证明CPM △是等边三角形, 进而判断出PCD MCE ≌(SAS ),即可得出结论.【详解】(1)证明:∵ABC 和DCE 都是等边三角形,∴BC=AC ,CE=CD ,∠ACB=∠DCE=60°,∴∠ABC+∠ACE=∠DCE+∠ACE ,即∠BCE=∠ACD ,∴BCE ACD ≌(SAS ),∴BE=AD ;(2)①证明:∵ABC 和DCE 是等边三角形,∴AC=BC ,CD=CE ,∠ACB=∠DCE=60°,∴∠ACB+∠BCD=∠DCE+∠BCD ,即∠ACD=∠BCE ,∴≌ACD BCE (SAS ),∴AD=BE ,同理:ABD CBF ≌(SAS ),∴AD=CF ,即AD=BE=CF ;②解:结论:PB+PC+PD=BE ,理由:如图2,AD 与BC 的交点记作点Q ,则∠AQC=∠BQP ,由①知,≌ACD BCE ,∴∠CAD=∠CBE ,在ACQ 中,∠CAD+∠AQC=180°-∠ACB=120°,∴∠CBE+∠BQP=120°,在BPQ 中,∠APB=180°-(∠CBE+∠BQP )=60°,∴∠DPE=60°,同理:∠APC=60°,60,CPE∴∠=︒∠CPD=120°,在PE上取一点M,使PM=PC,∴CPM△是等边三角形,∴CP CM PM==,∠PCM=∠CMP=60°,∴∠CME=120°=∠CPD,∵CDE△是等边三角形,∴CD=CE,∠DCE=60°=∠PCM,∴∠PCD=∠MCE,∴PCD MCE≌(SAS),∴PD=ME,∴BE=PB+PM+ME=PB+PC+PD.【点睛】此题是三角形综合题,主要考查了三角形的内角和定理,等边三角形的性质和判定,全等三角形的判定和性质,构造出全等三角形是解本题的关键.13.如图1,已知△ACB和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,以CE、BC 为边作平行四边形CEFB,连CD、CF.(1)如图2,△ADE绕点A旋转一定角度,求证:CD=22CF;(2)如图3,AE=2,AB=26,将△ADE绕A点旋转一周,当四边形CEFB为菱形时,求CF的长.解析:(1)见解析(2)6或4【分析】(1)连接FD,证明△ADC≌△EDF(SAS),推出△DFC为等腰直角三角形即可解决问题;(2)分两种情形分别画出图形,利用(1)中结论求出CD即可解决问题.【详解】(1)解:连接FD,设DE与AC交于点G∵四边形CEFB是平行四边形∴BC∥EF∵AC⊥BC∴EF⊥AC∵AD⊥DE,EF⊥AC,∠DGA=∠CGE∴∠DAC=∠DEF,又∵AD=ED,AC=EF,∴△ADC≌△EDF(SAS),∴DC=DF,∠ADC=∠EDF,即∠ADE+∠EDC=∠FDC+∠EDC,∴∠FDC=∠ADE=90°,∴△DFC为等腰直角三角形,∴CD=2CF;2(2)解:如图,设AE与CD的交点为M,∵四边形CEFB为菱形∴CE=CB∵△ADE、△ACB为等腰直角三角形∴CA=CB∴CE=CA ,∵DE=DA ,∴CD 垂直平分AE , ∵AE=2,AB=26∴DM=EM=12AE=22,AC=BC=22AB=13 ∴CE=13∴CM=22CE EM -=522, ∴CD=DM+CM=32,∵CF=2CD ,∴CF=6;如图,设AE 与CD 的交点为M ,同法可得CD=CM-DM=522-22=2 ∴2CD=4; 综上所述,满足条件的CF 的值为6或4.【点睛】本题属于四边形综合题,考查了等腰直角三角形的性质,平行四边形的性质,菱形的性质,全等三角形的判定和性质等知识点,解题的关键是正确寻找全等三角形解决问题,属于中考压轴题.14.在四边形ABCD 中,对角线AC 、BD 相交于点O ,将COD ∆绕点O 按逆时针方向旋转得到11C OD ∆,旋转角为θ(0°<θ<90°),连接1AC 、1BD ,1AC 与1BD 交于点P .(1)如图1,若四边形ABCD 是正方形.①求证:1AOC ∆≌1BOD ∆.②请直接写出1AC 与1BD 的位置关系.(2)如图2,若四边形ABCD 是菱形,AC=6,BD=9,设11AC =kBD .判断1AC 与1BD 的位置关系,说明理由,并求出k 的值.(3)如图3,若四边形ABCD 是平行四边形,AC=5,BD=10,连接1DD ,设11AC =kBD .请直接写出k 的值和2211AC +(kDD )的值.解析:(1)①证明见解析;②AC 1⊥BD 1;(2)k=23,AC 1⊥BD 1,理由见解析;(3)k=12,AC 12+(kDD 1)2=25 【分析】 (1)①根据正方形与旋转的性质,通过SAS 证明两三角形全等;②由全等三角形的性质得出11AC O BD O ∠=∠,通过证明1190D PC ︒∠=进行求解;(2)根据菱形与旋转的性质得出OC 1=OA ,OD 1=OB ,∠AOC 1=∠BOD 1,进而可证明△AOC 1∽△BOD 1,利用相似三角形的性质进行求解;(3)同(2)的解法相似可求出k 的值,根据旋转的性质得出OD 1=OB=OD ,进而可得出190BD D ︒∠=,利用勾股定理进行求解.【详解】(1)①证明:∵四边形ABCD 是正方形,∴OC=OA=OD=OB ,AC ⊥BD ,∴∠AOB=∠COD=90°,∵△COD 绕点O 按逆时针方向旋转得到△C 1OD 1,∴OC 1=OC ,OD 1=OD ,∠COC 1=∠DOD 1,∴OC 1=OD 1,∠AOC 1=∠BOD 1,在△AOC 1和△BOD 1中,1111OA OB AOC BOD OC OD =⎧⎪∠=∠⎨⎪=⎩,∴△AOC 1≌△BOD 1(SAS );②解:AC 1⊥BD 1,理由如下:∵△AOC 1≌△BOD 1,∴11AC O BD O ∠=∠,∵1111190AC O AC D OD C ︒∠+∠+∠=,∴1111190BD O AC D OD C ︒∠+∠+∠=,即1190D PC ︒∠=,∴AC 1⊥BD 1;(2)解:AC 1⊥BD 1,理由如下: ∵四边形ABCD 是菱形,∴OC=OA=12AC ,OD=OB=12BD ,AC ⊥BD , ∴∠AOB=∠COD=90°, ∵△COD 绕点O 按逆时针方向旋转得到△C 1OD 1, ∴OC 1=OC ,OD 1=OD ,∠COC 1=∠DOD 1, ∴OC 1=OA ,OD 1=OB ,∠AOC 1=∠BOD 1, ∴11OC OA OD OB=, ∴△AOC 1∽△BOD 1,∴∠OAC 1=∠OBD 1,又∵∠AOB=90°,∴∠OAB+∠ABP+∠OBD 1=90°, ∴∠OAB+∠ABP+∠OAC 1=90°, ∴∠APB=90°,∴AC 1⊥BD 1,∵△AOC 1∽△BOD 1, ∴111212AC AC OA AC BD OB BD BD ====69, ∴k=23; (3)解:与(2)一样可证明△AOC 1∽△BOD 1, ∴111212AC AC OA AC BD OB BD BD ===1=2, ∴k=12; ∵△COD 绕点O 按逆时针方向旋转得到△C 1OD 1, ∴OD 1=OD ,而OD=OB ,∴OD 1=OB=OD ,∴△BDD 1为直角三角形,即190BD D ︒∠=, 在Rt △BDD 1中,BD 12+DD 12=BD 2=100,∴(2AC 1)2+DD 12=100,∴AC 12+(kDD 1)2=25.【点睛】本题是四边形的综合题,考查了正方形,菱形,平行四边形的性质,全等三角形的判定与性质,相似三角形的判定与性质,旋转的性质,证明三角形全等或相似是解题的关键,属于中考常考题型.15.已知,在ABC ∆中,90BAC ︒∠=,45ABC ︒∠=,点D 为直线BC 上一动点(点D 不与点B C ,重合),以AD 为边作正方形ADEF ,连接CF .(1)如图①,当点D 在线段BC 上时,求证CF CD BC +=.(2)如图②,当点D 在线段BC 的延长线上时,其他条件不变,请直接写出CF BC CD ,,三条线段之间的关系.(3)如图③,当点D 在线段BC 的反向延长线上,且点A ,F 分别在直线BC 的两侧时,其他条件不变,请直接写出CF BC CD ,,三条线段之间的关系.解析:(1)见解析;(2)CF CD BC -=,见解析;(3)CD CF BC -=,见解析.【分析】(1)△ABC 是等腰直角三角形,利用SAS 即可证明△BAD ≌△CAF ,从而证得CF=BD ,据此即可证得;(2)同(1)相同,利用SAS 即可证得△BAD ≌△CAF ,从而证得BD=CF ,即可得到CF-CD=BC ;(3)同理,证明△BAD ≌△CAF 即可得出结论.【详解】(1)证明:如图1,∵∠BAC=90°,∠ABC=45°,∴∠ACB=∠ABC=45°,∴AB=AC ,∵四边形ADEF 是正方形,∴AD=AF ,∠DAF=90°,∵∠BAD=90°-∠DAC ,∠CAF=90°-∠DAC ,∴∠BAD=∠CAF ,在△BAD 和△CAF 中,AB AC BAD CAF AD AF ⎧⎪∠∠⎨⎪⎩===,∴△BAD ≌△CAF (SAS ),∴BD=CF ,∵BD+CD=BC ,∴CF+CD=BC ;(2)解:CF-CD=BC .理由如下:如图2,∵∠BAD=90°+∠CAD ,∠CAF=90°+∠CAD ,∴∠BAD=∠CAF ,在△BAD 和△CAF 中,AB AC BAD CAF AD AF ⎧⎪∠∠⎨⎪⎩===,∴△BAD ≌△CAF (SAS ),∴BD=CF ,∵BD=BC+CD ,∴CF-CD=BC .(3)CD-CF=BC理由:∵∠BAC=90°,∠ABC=45°,∴∠ACB=∠ABC=45°,∴AB=AC ,∵四边形ADEF 是正方形,∴AD=AF ,∠DAF=90°,∵∠BAD=90°-∠BAF ,∠CAF=90°-∠BAF ,∴∠BAD=∠CAF ,∵在△BAD 和△CAF 中,AB AC BAD CAF AD AF ⎧⎪∠∠⎨⎪⎩=== ∴△BAD ≌△CAF (SAS ),∴BD=CF ,∴CD-BC=CF ,∴CD-CF=BC.【点睛】本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.16.已知:点O 是平行四边形ABCD 两条对角线的交点,点P 是AC 所在直线上的一个动点(点P 不与点A 、C 重合),分别过点A 、C 向直线BP 作垂线,垂足分别为E 、F(1)如图1,当点P 与点O 重合时,求证:OE=OF(2)直线BP 绕点B 逆时针方向旋转,当∠OFE=30︒时,有OE=OF ,如图2,线段CF 、AE 、OE 之间有怎样的数量关系?给出证明.(3)当点P 在图3位置,且∠OFE=30︒时,线段CF 、AE 、OE 之间有怎样的数量关系?(直接写出结论,无需证明.解析:(1)证明见解析;(2)证明见解析;(3)CF=OE-AE.。
初二数学全等三角形旋转模型练习题及答案

初二数学全等三角形旋转模型练习题及答案一、全等三角形旋转模型1.问题背景如图(1),在四边形ABCD中,∠B+∠D=180°,AB=AD,∠BAD=α,以点A为顶点作一个角,角的两边分别交BC,CD于点E,F,且∠EAF12=α,连接EF,试探究:线段BE,DF,EF之间的数量关系.(1)特殊情景在上述条件下,小明增加条件“当∠BAD=∠B=∠D=90°时”如图(2),小明很快写出了:BE,DF,EF之间的数量关系为______.(2)类比猜想类比特殊情景,小明猜想:在如图(1)的条件下线段BE,DF,EF之间的数量关系是否仍然成立?若成立,请你帮助小明完成证明;若不成立,请说明理由.(3)解决问题如图(3),在△ABC中,∠BAC=90°,AB=AC=4,点D,E均在边BC上,且∠DAE=45°,若BD2=DE的长.答案:B解析:(1)BE+DF=EF;(2)成立;(3)DE23 =【分析】(1)将△ABE绕点A逆时针旋转90°,得到△ADG,由旋转的性质可得AE=AG,BE=DG,∠BAE=∠DAG,根据∠EAF=12∠BAD可得∠BAE+∠DAF=45°,即可得出∠∠EAF=∠FAG,利用SAS可证明△AFE≌△AFG,可得EF=FG,进而可得EF=BE+FD;(2)将△ABE 绕点A逆时针旋转α得到△ADH,由旋转的性质可得∠ABE=∠ADH,∠BAE=∠DAH,AE=AH,BE=DH,根据∠BAD=α,∠EAF12=α可得∠BAE+∠FAD12=α,进而可证明∠FAH=∠EAF,利用SAS可证明△AEF≌△AHF,可得EF=FH=BE+FD;(3)将△AEC绕点A顺时针旋转90°,得到△AE′B,连接DE′,由旋转的性质可得BE′=EC,AE′=AE,∠C=∠ABE′,∠EAC=∠E′AB,根据等腰直角三角形的性质可得∠ABC=∠ACB=45°,BC=2,即可求出∠E′BD=90°,利用SAS可证明△AEF≌△AHF,可得DE=DE′,利用勾股定理求出DE的长即可的答案.【详解】(1)BE+DF=EF,如图1,将△ABE绕点A逆时针旋转90°,得到△ADG,∵∠ADC=∠B=∠ADG=90°,∴∠FDG=180°,即点F,D,G共线.由旋转可得AE=AG,BE=DG,∠BAE=∠DAG.∠BAD=90°-45°=45°,∵∠BAE+∠DAF=∠BAD﹣∠EAF=90°﹣12∴∠DAG+∠DAF=45°,即∠FAG=45°,∴∠EAF=∠FAG,∴△AFE≌△AFG(SAS),∴EF=FG.又∵FG=DG+DF=BE+DF,∴BE+DF=EF,故答案为BE+DF=EF.(2)成立.如图2,将△ABE绕点A逆时针旋转α得到△ADH,可得∠ABE=∠ADH,∠BAE=∠DAH,AE=AH,BE=DH.∵∠B+∠ADC=180°,∴∠ADH+∠ADC=180°,∴点C,D,H在同一直线上.∵∠BAD=α,∠EAF1=α,2∴∠BAE+∠FAD1=α,2∴∠DAH+∠FAD1=α,2∴∠FAH=∠EAF,又∵AF=AF,∴△AEF≌△AHF(SAS),∴EF=FH=DF+DH=DF+BE;(3)DE 52=, 如图3,将△AEC 绕点A 顺时针旋转90°,得到△AE′B ,连接DE′.可得BE′=EC ,AE′=AE ,∠C =∠ABE′,∠EAC =∠E′AB , 在Rt △ABC 中,∵AB =AC =4,∠BAC=90°, ∴∠ABC =∠ACB =45°,BC =2, ∴2,∴∠ABC+∠ABE′=90°,即∠E′BD =90°, ∴E′B 2+BD 2=E′D 2. 易证△AE′D ≌△AED , ∴DE =DE′,∴DE 2=BD 2+EC 2,即DE 2222)(32)DE =+, 解得23DE =. 【点睛】本题考查旋转的性质、全等三角形的判定与性质、勾股定理,旋转后不改变图形的大小和形状,并且对应点到旋转中心的距离相等,对应点与旋转中心的连线的夹角等于旋转角,熟练掌握旋转的性质及全等三角形的判定定理是解题关键.2.一位同学拿了两块45︒三角尺MNK ∆,ACB ∆做了一个探究活动:将MNK ∆的直角顶点M 放在ACB ∆的斜边AB 的中点处,设4AC BC ==.(1)如图1所示,两三角尺的重叠部分为ACM ∆,则重叠部分的面积为______,周长为______.(2)将如图1所示中的MNK ∆绕顶点M 逆时针旋转45︒,得到如图2所示,此时重叠部分的面积为______,周长为______.(3)如果将MNK ∆绕M 旋转到不同于如图1所示和如图2所示的图形,如图3所示,请你猜想此时重叠部分的面积为______.(4)在如图3所示情况下,若1AD =,求出重叠部分图形的周长.答案:A解析:(1)4,442+;(2)4,8;(3)4;(4)425+【分析】()1根据4AC BC ==,90ACB ∠=,得出AB 的值,再根据M 是AB 的中点,得出AM MC =,求出重叠部分的面积,再根据AM ,MC ,AC 的值即可求出周长;()2易得重叠部分是正方形,边长为12AC ,面积为214AC ,周长为2.AC()3过点M 分别作AC 、BC 的垂线MH 、ME ,垂足为H 、.E 求得RtMHD ≌Rt MEG ,则阴影部分的面积等于正方形CEMH 的面积.()4先过点M 作ME BC ⊥于点E ,MH AC ⊥于点H ,根据DMH EMH ∠∠=,MH ME =,得出Rt DHM ≌Rt EMG ,从而得出HD GE =,CE AD =,最后根据AD 和DF 的值,算出5DM =.【详解】 解:()14AC BC ==,90ACB ∠=,22224442AB AC BC ∴=++=M 是AB 的中点,22AM ∴=45ACM ∠=, AM MC ∴=,∴22224⨯=,∴周长为:22224442AM MC AC ++==+故答案为4,442+;()2重叠部分是正方形,∴边长为1422⨯=,面积为14444⨯⨯=,周长为248⨯=. 故答案为4,8.()3过点M 分别作AC 、BC 的垂线MH 、ME ,垂足为H 、E ,M 是ABC 斜边AB 的中点,4AC BC ==, 12MH BC ∴=,12ME AC =,MH ME ∴=,又90NMK HME ∠∠==,90NMH HMK ∠∠∴+=,90EMG HMK ∠∠+=,HMD EMG ∠∠∴=, 在MHD 和MEG 中, HMD GME MH MEDHM MEG ∠=∠⎧⎪=⎨⎪∠=∠⎩, MHD ∴≌()MEG ASA ,∴阴影部分的面积等于正方形CEMH 的面积,正方形CEMH 的面积是1144422ME MH ⋅=⨯⨯⨯=; ∴阴影部分的面积是4;故答案为4.()4如图所示, 过点M 作ME BC ⊥于点E ,MH AC ⊥于点H ,∴四边形MECH 是矩形,MH CE ∴=,45A ∠=,45AMH ∠∴=,AH MH ∴=, AH CE ∴=,在Rt DHM 和Rt GEM 中,DMH EMG MH MEDHM GEM ∠=∠⎧⎪=⎨⎪∠=∠⎩, Rt DHM ∴≌.Rt GEM GE DH ∴=,AH DH CE GE ∴-=-, CG AD ∴=, 1AD =, 1.DH ∴=145DM∴=+= . ∴四边形DMGC 的周长为:CE CD DM ME +++ 2AD CD DM =++425=+.【点睛】此题考查了等腰直角三角形,利用等腰直角三角形的性质,等腰直角三角形的面积公式,正方形的面积公式,全等三角形的判定和性质求解.3.我们定义:有一组对角为直角的四边形叫做“对直角四边形”.(1)如图①,四边形ABCD 为对直角四边形,∠B=90°,若AB 2-AD 2=4,求CD 2-BC 2的值; (2)如图②,四边形ABCD 中,∠ABC=90°,AB=BC ,若BD 平分∠ADC ,求证:四边形ABCD 为对直角四边形;(3)在(2)的条件下,如图③,连结AC ,若35ACD ABCSS=,求tan ∠ACD 的值.答案:A解析:⑴ 4;⑵见解析;⑶tan∠ACD的值为3或13.【分析】(1)利用勾股定理即可解决问题;(2)如图②中,作BE⊥CD于E,BF⊥DA交DA的延长线于F.只要证明∠EBF=90°即可解决问题;(3)如图③中,设AD=x,BD=y.根据35ACDABCSS,构建方程即可解决问题.【详解】解:如图①中,∵四边形ABCD为对直角四边形,∠B=90°,∴∠D=∠B=90°,∴AC2=AB2+BC2=AD2+DC2,∴CD2-BC2=AB2-AD2=4.(2)证明:如图②中,作BE⊥CD于E,BF⊥DA交DA的延长线于F.∵BD平分∠ADC,BE⊥CD,BF⊥AD,∴BE=BF,∵∠BFA=∠BEC=90°,BA=BC,BF=BE,∴Rt△BFA≌Rt△BEC(HL),∴∠ABF=∠CBE,∴∠EBF=∠ABC=90°,∴ADC=360°-90°-90°-90°=90°,∵∠ABC=∠ADC=90°,∴四边形ABCD为对直角四边形.(3)解:如图③中,设AD=x,BD=y.∵∠ADC=90°, ∴tan ∠ACD=xy,22x y + ∵AB=AC ,∠ABC=90°, ∴AB=BC=2222x y + ∵35ACD ABCS S=, ∴()22132154xy x y =+, 整理得:3x 2-10xy+3y 2, ∴3(x y )2-10•xy+3=0, ∴x y =3或13. ∴tan ∠ACD 的值为3或13. 【点睛】本题属于四边形综合题,考查了勾股定理,三角形的面积,全等三角形的判定和性质,角平分线的性质定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用参数,构建方程解决问题,属于中考压轴题. 4.问题提出:(1)如图1,在ABC 中,AB AC BC =≠,点D 和点A 在直线BC 的同侧,BD BC =,90BAC ∠=︒,30DBC ∠=︒,连接AD ,将ABD △绕点A 逆时针旋转90︒得到ACD ',连接BD '(如图2),可求出ADB ∠的度数为______. 问题探究:(2)如图3,在(1)的条件下,若BAC α∠=,DBC β∠=,且120αβ+=︒,DBC ABC ∠<∠ , ①求ADB ∠的度数.②过点A 作直线AE BD ⊥,交直线BD 于点E ,7,2BC AD ==.请求出线段BE 的长.答案:A解析:(1)30°;(2)①30︒;②73-【分析】(1)由旋转的性质,得△ABD ≌ACD '∆,则ADB AD C '∠=∠,然后证明BCD '∆是等边三角形,即可得到30ADB AD C '∠=∠=︒;(2)①将ABD △绕点A 逆时针旋转,使点B 与点C 重合,得到'ACD △,连接'BD .与(1)同理证明D BC '∆为等边三角形,然后利用全等三角形的判定和性质,即可得到答案;②由解直角三角形求出3DE =【详解】解:(1)根据题意,∵AB AC BC =≠,90BAC ∠=︒, ∴ABC ∆是等腰直角三角形, ∴45ABC ACB ∠=∠=︒, ∵30DBC ∠=︒, ∴15ABD ∠=︒,由旋转的性质,则△ABD ≌ACD '∆,∴ADB AD C '∠=∠,15ABD ACD '∠=∠=︒,BC CD '=, ∴60BCD '∠=︒, ∴BCD '∆是等边三角形, ∴60BD C '∠=︒,BD CD ''= ∵AB AC =,AD AD ''=, ∴ABD '∆≌ACD '∆, ∴30AD B AD C ''∠=∠=︒, ∴30ADB AD C '∠=∠=︒; (2)①DBC ABC ∠<∠,60120α︒︒∴<<.如图1,将ABD △绕点A 逆时针旋转,使点B 与点C 重合,得到'ACD △,连接'BD .AB AC =,ABC ACB ∴∠=∠, BAC α∠=,()111809022ABC αα︒︒∴∠=-=-,1902ABD ABC DBC αβ︒∴∠=∠-∠=--,119090180()22D CB ACD ACB αβααβ''︒︒︒∴∠=∠+∠=--+-=-+.120,αβ︒+=60D CB '︒∴∠=.,BD BC BD CD '==,,BC CD '∴=D BC '∴为等边三角形, D B D C ''∴=, AD B AD C ''∴≌, AD B AD C ''∴∠=∠,1302AD B BD C ''︒∴∠=∠=,30ADB ︒∴∠=.②如图2,由①知,30ADB ︒∠=,在Rt ADE △中,30,2ADB AD ︒∠==,3DE ∴=.BCD '是等边三角形, 7BD BC '∴==, 7BD BD '∴==,73BE BD DE ∴=-=-.【点睛】本题考查了解直角三角形,旋转的性质,全等三角形的判定和性质,等边三角形的判定和性质,等腰直角三角形的性质,以及三角形的内角和定理,解题的关键是熟练掌握所学的知识,正确利用旋转模型进行解题. 5.问题提出(1)如图①,在ABC 中,AD 是BC 边上的高,若∠BAD =45°,∠DAC =30°,则ABD ACDS S= . 问题探究(2)如图②,在正方形ABCD 中,边长为8,点E 是AB 的中点,作∠EDF =45°,交BC 于点F ,求DEF 的面积. 问题解决(3)如图③,某市为迎接城市运动会,打造融体育、文化、饮食、旅游为一体的综合商业品牌,规划了如图所示的矩形ABCD 观光区,如图,在矩形ABCD 中,AB =16km ,AD =12km ,要求在边AB 上确定一点E 为观光区的南门,在边BC 上确定一点F 为观光区的东门,且∠EDF =30°,同时为了方便市民游览,还要修建一条观光通道FG ,使FG ∥AB ,交DE 于点G (观光带的宽度不计),为了节约成本,要使FG 的长度最小,那么是否存在符合条件的修建方案?若存在,请求出FG 的最小值;若不存在,请说明理由.答案:B解析:3(2)803,(3) 323. 【分析】(1)根据∠BAD =45°,∠DAC =30°,求出BD 、AD 、DC 的关系即可;(2)将△DCF 绕点D 顺时针旋转90°得到△DAG ,可证△DEF ≌△DEG ,得到EF =CF +AE ,求出CF 长即可;(3) 作DM ⊥DF ,交BA 延长线于点M ,作EN ⊥DF 于N ,EH ⊥DM 于H ,作△DME 的外接圆⊙O ,连接OD 、OE 、OM ,作OQ ⊥ME 于Q ,求出△DEF 的面积最小值,再用面积求FG 最小值. 【详解】解:(1)∵AD 是BC 边上的高,若∠BAD =45°,∠DAC =30°, ∴AD =BD ,AD = tan 603DC DC ︒=,12312ABD ACDBD AD S SCD AD ⋅==⋅, (2) 将△DCF 绕点D 顺时针旋转90°得到△DAG , ∵∠DAG =∠C =90°,∠DAE =90°, ∴G 、A 、E 三点共线,由旋转可知,∠FDG =∠CDA =90°,DF =DG , ∴∠GDE =∠FDE =45°,DE =DE , ∴△GDE ≌△FDE , ∴GE =EF , ∴EF =AE +CF ,设EF 为x ,则CF =x -4,BF =12-x ,2224(12)x x +-=,解得,x =203, DEF 的面积=DEG 的面积=120808233⨯⨯=;(3)作DM ⊥DF ,交BA 延长线于点M ,作EN ⊥DF 于N ,EH ⊥DM 于H ,作△DME 的外接圆⊙O ,连接OD 、OE 、OM ,作OQ ⊥ME 于Q , ∵∠FDM =∠CDA =90°, ∴∠ADM =∠CDF , ∵∠C =∠DAM =90°, ∴△ADM ∽△CDF ,∴34MD AD DF DC ==, ∵∠FDE =30°, ∴∠EDM =60°,∵1sin 302EN DE DE =︒=,3sin 602EH DE DE =︒=,∴3EHEN=,1432192DEF DMEDF ENS S DM EH ⋅==⋅,设⊙O 的半径为R , ∵∠MDE =60°, ∴∠MOE =120°, ∠MOQ =60°,3sin 602RMQ OM =︒=,ME =3R ,OQ =12R ,OD +OQ ≥AD , 1122R R +≥,解得,8R ≥, 138122DMES≥⨯⨯⨯,即483DMES ≥,DME S △的最小值为483,DEF S △的最小值为43483649⨯=,1()62DEFDGFEGFSSSFG CF BF FG =+=+=, FG 的最小值为643263=.【点睛】本题考查了全等三角形的判定与性质,相似三角形的判定与性质,三角形的外接圆,解直角三角形等,解题关键是充分理解题意,恰当的构建全等三角形、相似三角形和外接圆. 6.在ABC 中,,AB AC BAC α=∠=,点P 为线段CA 延长线上一动点,连接PB ,将线段PB 绕点P 逆时针旋转,旋转角为α,得到线段PD ,连接,DB DC .(1)如图1,当60α=︒时,请直接写出线段PA 与线段CD 的数量关系是__________,DCP ∠为______度;(2)如图2,当120α=︒时,写出线段PA 和线段DC 的数量关系,并说明理由; (3)如图2,在(2)的条件下,当23AB =13BP PC +的最小值. 答案:A解析:(1)PA =DC ,60;(2)CD 3PA .理由见详解;(232【分析】(1)先证明△ABC ,△PBD 是等边三角形,再证明△PBA ≌△DBC ,进而线段PA 与线段CD 的数量关系,利用全等三角形的性质以及三角形内角和等于180°,解决问题即可;(2)证明△CBD ∽△ABP ,可得3CD BCPA AB== (3)过点C 作射线CM ,使得sin ∠ACM =13,过点P 作PN ⊥CM 于点N ,则PN =13PC ,过点B 作BG ⊥BA 于点G ,当点B 、P 、N 共线时,BP +PN 最小,即13BP PC +最小,由BGP CNP ∽,得13GP NP BP CP ==,结合勾股定理求出GP ,从而得CP ,进而即可求解. 【详解】(1)①证明: ∵将线段PB 绕点P 逆时针旋转,旋转角为α,得到线段PD , ∴PB =PD ,∵AB =AC ,PB =PD ,∠BAC =∠BPD =60°, ∴△ABC ,△PBD 是等边三角形, ∴∠ABC =∠PBD =60°, ∴∠PBA =∠DBC , ∵BP =BD ,BA =BC ,∴△PBA ≌△DBC (SAS ), ∴PA =DC .设BD 交PC 于点O ,如图1,∵△PBA ≌△DBC , ∴∠BPA =∠BDC , ∵∠BOP =∠COD ,∴∠OBP =∠OCD =60°,即∠DCP =60°. 故答案是:PA =DC ,60;(2)解:结论:CD 3.理由如下: ∵AB =AC ,PB =PD ,∠BAC =∠BPD =120°,∴BC =2•AB •cos30°3,BD ═2BP •cos30°3, ∴BC BDBA BP=3 ∵∠ABC =∠PBD =30°, ∴∠ABP =∠CBD , ∴△CBD ∽△ABP , ∴3CD BCPA AB== ∴CD 3;(3) 过点C 作射线CM ,使得sin ∠ACM =13,过点P 作PN ⊥CM 于点N ,则PN =13PC , 过点B 作BG CA ⊥于点G ,则BG =AB ×sin ∠BAG 3=3,AG = AB ×cos ∠BAG 3 当点B 、P 、N 共线时,BP +PN 最小,即13BP PC +最小, ∵∠BGP =∠CNP =90°,∠BPG =∠CPN ,∴BGP CNP ∽, ∴13GP NP BP CP ==, 设GP =x ,则AP 3-x ,BP =3x , ∴()22233x x +=,解得:x 324∴BP =924,AP =3-324,∴CP =AC +AP =23+3-324=33-324,∴13BP PC +最小值=924+13×(33-324)=3+22.【点睛】本题属于几何变换综合题,考查了全等三角形的判定和性质,相似三角形的判定和性质,解直角三角形等知识,第(1)(2)题解题的关键是正确寻找全等三角形或相似三角形解决问题,第(3)题的关键是过点C 作射线CM ,使得sin ∠ACM =13,过点P 作PN ⊥CM 于点N .7.已知等腰三角形底边中点,可以考虑与顶点连接用“三线合一”.请利用上面信息解决以下问题:已知Rt ABC 中,AC BC =,90C ∠=︒,D 为AB 边的中点,90EDF ∠=︒,EDF ∠绕D 点旋转,它的两边分别交AC 、CB (或它们的延长线)于E 、F .(1)当EDF ∠绕D 点旋转到DE AC ⊥于E 时(如图①),求证:12DEF CEF ABC S S S +=△△△; (2)当EDF ∠绕D 点旋转到DE 和AC 不垂直时,在图②和图③这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,DEF S △、CEF S △、ABCS 又有怎样的数量关系?请写出你的猜想,不需要证明.答案:D解析:(1)见解析;(2)图2成立,图3不成立:12DEF CEF ABC S S S -=△△△ 【分析】(1)根据等腰直角三角形和正方形的性质得到AED 、DFB △、EDF 、ECF △为全等的等腰直角三角形,据此即可证明;(2)对于图2:过点D 作DM AC ⊥,DN BC ⊥,根据中位线的性质和等量代换证得MD ND =和MDE NDF ∠=∠,结合90DME DNF ∠=∠=︒,证得DME DNF ∆≅∆,根据全等三角形的性质即可求证;对于图3:根据ASA 证明DME DNF ∆≅∆,根据全等三角形的性质即可求证. 【详解】(1)证明:连接CD∵D 为AB 边的中点,AC BC = ∴AD=CD=BD∴45DAC DCA DCB DBC ∠=∠=∠=∠=︒ 又∵DE AC ⊥,90EDF ∠=︒,90C ∠=︒, ∴四边形ECFD 为矩形 ∴∠CFD=90° 又∵∠DCF=45° ∴CF=DF∴四边形ECFD 是正方形 ∴DE=DF∴DEF CEF DEC DFC S S S S +=+△△△△又∵12DCF DBF ABC S S S +=△△△,且DCF DBF S S =△△ ∴12DEF CEF ABC S S S +=△△△ (2)图2成立,图3不成立对于图2:过点D 作DM AC ⊥,DN BC ⊥,如图2,则90DME DNF MDN ∠=∠=∠=︒又∵90C ∠=︒ ∴DMBC ,DN AC∵D 为AB 边的中点∴根据中位线定理得到:12DN AC =,12MD BC = ∵AC=BC ∴MD=ND ∵90EDF ∠=︒∴90MDE EDN ∠+∠=︒,90NDF EDN ∠+∠=︒ ∴MDE NDF ∠=∠ 在DME ∆与DNF ∆中DME DNFMD NDMDE NDF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴DME DNF ∆≅∆ ∴DME DNF S S ∆∆=∴DEF CEF DMCN DECF S S S S ∆∆==+四边形四边形 ∴12DMCN ABC S S =△ ∴12DEF CEF ABC S S S +=△△△ 对于图3: 连接DC ,在DEC ∆与DBF ∆中135DCE DBF DC DBCDE BDF ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩∴DEC DBF ∆≅∆∴12DEF CFE DBC CFE ABC DBFEC S S S S S S ∆∆∆∆∆==+=+五边形 ∴12DEF CEF ABC S S S ∆∆∆-=. 【点睛】本题考查了全等三角形的判定和性质,中位线的性质,等腰直角三角形的性质,题目较为综合,利用作出的辅助线将不规则的三角形转化为直角三角形进行解决.8.如图1所示,在Rt ABC △中90BAC ∠=︒,AB AC =,2BC =,以BC 所在直线为x 轴,边BC 的垂直平分线为y 轴建立平面直角坐标系,将ABC 绕P 点0,1顺时针旋转.(1)填空:当点B 旋转到y 轴正半轴时,则旋转后点A 坐标为______;(2)如图2所示,若边AB 与y 轴交点为E ,边AC 与直线1y x =-的交点为F ,求证:AEF 的周长为定值;(3)在(2)的条件下,求AEF 内切圆半径的最大值.解析:(1)2,21;(2)见解析;(3)324-【分析】(1)作出图形,'''A B C 是ABC 绕 P 点0,1顺时针旋转,点B 旋转到y 轴正半轴时得到的图形,连接 BP ,CP ,根据2BC =,y 轴垂直平分BC , AB AC =,()0,1P -可证得四边形ABPC 是正方形,则有 '''2BP B PAB A B ,'0'21B B PPO,可得点 A 坐标;(2)作BPQ CPF ∠=∠,交AB 延长线于Q 点,根据四边形ABPC 是正方形,得到90QBP FCP ∠=∠=︒,BP CP =,可证BPQ CPF ASA ≌△△,得BQ CF =,QP FP =,利用ASA 再可证得QPE FPE ≌△△,得QE FE =则AEF 的周长22AB AC =+=(3)设EF m =,AE n =,Rt AEF 的内切圆半径为r ,由(2)可得22AF m n =--则2AE AF EF r +-=22n m n m+---=2m =-,当m 最小时,r 最大.得到22222n m nm 整理得:2224220nm n m,关于n的一元二次方程有解,即22244220m m化简得24280m m +-≥,利用二次函数图像可得422m ≥-或422m ≤--(不合题意,舍去)可得m 的最小值为422-,即r 的最大值为2422324,则有AEF 内切圆半径的最大值为324-.【详解】解:(1)如图示,'''A B C 是ABC 绕 P 点0,1顺时针旋转,点B 旋转到y 轴正半轴时得到的图形,连接 BP ,CP ,∵2BC =,y 轴垂直平分BC∴1BO CO ==又∵Rt ABC △中,AB AC = ∴1AO =,2AB AC ==∵()0,1P - ∴1PO =∴AO BO CO PO === ∴四边形ABPC 是正方形 ∴'''2BP B P AB A B∴'0'21B B PPO∴点A 坐标为2,21(2)如图2所示,作BPQ CPF ∠=∠,交AB 延长线于Q 点 ∵四边形ABPC 是正方形∴90QBP FCP ∠=∠=︒, BP CP = ∴BPQ CPF ASA ≌△△∴ BQ CF =,QP FP =∵点F 在直线1y x =-∴45FPE ∠=︒∴ 45BPE FPC ∠+∠=︒ ∴45BPE BPQ ∠+∠=︒∴45QPE FPE ∠=∠=︒ ∵EP EP =∴QPE FPE ASA ≌△△∴ QE FE =∴AEF 的周长AE EF AF AE QE AF =++=++AE BE BQ AF AE BE FC AF =+++=+++22AB AC =+=(3)设EF m =,AE n =,Rt AEF 的内切圆半径为 r , 由(2)可得22AF m n =-则2AE AF EFr +-=22n m n m+---=2m =∴当m 最小时,r 最大.∵在Rt AEF 中,222AE AF EF +=∴22222n m nm 整理得: 2224220nm nm ∵关于n 的一元二次方程有解∴22244220m m∴24280m m +-≥利用二次函数图像可得422m ≥-或422m ≤--(不合题意,舍去) ∴m 的最小值为422-∴r 的最大值为2422324即AEF 内切圆半径的最大值为324-. 【点睛】本题主要考查了一次函数的综合应用以及根的判别式、全等三角形的判定与性质、旋转、三角形内切圆等知识,能熟练应用相关性质是解题关键. 9.问题解决一节数学课上,老师提出了这样一个问题:如图①,点P 是等边ABC 内的一点,6PA =,8PB = ,10PC =.你能求出APB ∠的度数和等边ABC 的面积吗? 小明通过观察、分析、思考,形成了如下思路:如图①将BPC △绕点B 逆时针旋转60°,得到BPA △,连接PP ',可得BPP '是等边三角形,根据勾股定理逆定理可得AP P '是直角三角形,从而使问题得到解决.(1)结合小明的思路完成填空:PP '=_____________,APP '∠=_______________,APB ∠=_____________ ,ABC S = ______________.(2)类比探究Ⅰ如图②,若点P 是正方形ABCD 内一点,1PA = ,2PB =,3PC =,求APB ∠的度数和正方形的面积.Ⅱ如图③,若点P 是正方形ABCD 外一点,3PA = ,1PB =, 11PC =,求APB ∠的度数和正方形的面积.答案:B解析:(1)8,90˚,150˚,25336;(2)Ⅰ135APB ∠=︒, 722ABCD S =+正方形;Ⅱ45APB ∠=︒, 1032ABCD S =-正方形【分析】(1)根据小明的思路,然后利用等腰三角形和直角三角形性质计算即可;(2)Ⅰ将△BPC 绕点B 逆时针旋转90°,得到△BP′A ,连接PP′,求出∠APB 的度数;先利用旋转求出∠PBP'=90°,BP'=BP=2,AP'=CP=3,利用勾股定理求出PP',进而判断出△APP'是直角三角形,得出∠APP'=90°,即可得出结论;过B 作BE ⊥AP 于点E ,然后利用勾股定理求出AB 的长度即可求出正方形面积;Ⅱ将△BPC 绕点B 逆时针旋转90°,得到△BP′A ,连接PP′,求出∠APB 的度数;先利用旋转求出∠PBP'=90°,BP'=BP=2,AP'=CP=3,利用勾股定理求出PP',进而判断出△APP'是直角三角形,得出∠APP'=90°,即可得出结论;过B 作BF ⊥AP 于点F ,然后利用勾股定理求出AB 的长度即可求出正方形面积; 【详解】解:(1)由题易有P BP '∆是等边三角形,AP P '∆是直角三角形 ∴PP '=BP=8,90?APP '=∠,60?P PB '=∠,∴APB ∠=APP '∠+=P PB '∠150˚, 如图1,过B 作BD ⊥AP 于点D∵APB ∠=150° ∴30?BPD =∠在Rt △BPD 中,30?BPD =∠,BP=8 ∴BD=4,3 ∴3∴AB 2=AD 2+BD 23∴ABCS=234AB =25336 (2)Ⅰ.如图2,将△BPC 绕点B 逆时针旋转90°,得到△BP′A ,连接PP′, ∴△ABP'≌△CBP ,∴∠PBP'=90°,BP'=BP=2,AP'=CP=3, 在Rt △PBP'中,BP=BP'=2,∴∠BPP'=45°,根据勾股定理得,22, ∵AP=1,∴AP 2+PP'2=1+8=9, ∵AP'2=32=9, ∴AP 2+PP'2=AP'2,∴△APP'是直角三角形,且∠APP'=90°, ∴∠APB=∠APP'+∠BPP'=90°+45°=135°;过B 作BE ⊥AP 于点E , ∵∠APB=135° ∴∠BPE=45°∴△BPE 是等腰直角三角形 ∴BE=BP=22BP =2 ∴AE=1+2∴AB 2=AE 2+BE 2=7+22 ∴2722ABCD S AB ==+正方形Ⅱ.如图3,将△BPC 绕点B 逆时针旋转90°,得到△BP′A ,连接PP′, ∴△ABP'≌△CBP ,∴∠PBP'=90°,BP'=BP=1,AP'=CP=11, 在Rt △PBP'中,BP=BP'=1,∴∠BPP'=45°,根据勾股定理得,PP'=2BP=2, ∵AP=3,∴AP 2+PP'2=9+2=11, ∵AP'2=(11)2=11, ∴AP 2+PP'2=AP'2,∴△APP'是直角三角形,且∠APP'=90°, ∴∠APB=∠APP'-∠BPP'=90°-45°=45°.过B 作BF ⊥AP 于点F ∵∠APB=45°∴△BPF 为等腰直角三角形 ∴PF=BF=2BP =2∴AF=AP-PF=3-22∴AB 2=AF 2+BF 2=1032- ∴21032ABCD S AB ==-正方形 【点睛】此题是四边形综合题,主要考查了正方形的性质,旋转的性质,直角三角形的性质和判定,勾股定理,正确作出辅助线是解本题的关键. 10.在等腰Rt ABC △中,AB AC =、90BAC ∠=︒.(1)如图1,D ,E 是等腰Rt ABC △斜边BC 上两动点,且45DAE ∠=︒,将ABE △绕点A 逆时针旋转90后,得到AFC △,连接DF .①求证:AED AFD ≌.②当3BE =,9CE =时,求DE 的长.(2)如图2,点D 是等腰Rt ABC △斜边BC 所在直线上的一动点,连接AD ,以点A 为直角顶点作等腰Rt ADE △(E 点在直线BC 的上方),当3BD =,9BC =时,求DE 的长.答案:D解析:(1)①证明见解析;②5;(2)35或317【分析】(1)①证明∠DAE=∠DAF=45°即可利用SAS 证明全等;②由①中全等可得DE=DF ,再在Rt △FDC 中利用勾股定理计算即可;(2)连接BE ,根据共顶点等腰直角三角形证明全等,再利用勾股定理计算即可。
初二数学全等三角形双等腰旋转 易错题难题学能测试试题

初二数学全等三角形双等腰旋转 易错题难题学能测试试题一、全等三角形双等腰旋转1.如图1是实验室中的一种摆动装置,BC 在地面上,支架ABC 是底边为BC 的等腰直角三角形,摆动臂AD 可绕点A 旋转,摆动臂DM 可绕点D 旋转,15AD =,6DM =.(1)在旋转过程中,①当A ,D ,M 三点在同一直线上时,求AM 的长;②当A ,D ,M 三点为同一直角三角形的顶点时,求AM 的长;(2)若摆动臂AD 顺时针旋转90︒,点D 的位置由ABC 外的点1D 转到其内的点2D 处,即1290D AD ︒∠=,连结12D D ,如图2,此时2135AD C ︒∠=,2202CD =2BD 的长.答案:(1)①21或9;②或;(2)【分析】(1)①分两种情形分别求解即可.②显然不能为直角.当为直角时,根据,计算即可,当时,根据,计算即可. (2)连接.首先利用勾股定理求出,再利用全等三角形的解析:(1)①21或9;②3213292)252【分析】(1)①分两种情形分别求解即可.②显然MAD ∠不能为直角.当AMD ∠为直角时,根据222AM AD DM =-,计算即可,当90ADM ∠=︒时,根据222AM AD DM =+,计算即可.(2)连接1CD .首先利用勾股定理求出1CD ,再利用全等三角形的性质证明21BD CD =即可.【详解】解:(1)①由题意可得:21AM AD DM =+=,或9AM AD DM =-=.②显然MAD ∠不能为直角.当AMD ∠为直角时,22222156189AM AD DM =-=-=,321AM ∴=321-当90ADM ∠=︒时,22222156261AM AD DM =+=+=, 293AM ∴=或932-(舍弃).综上所述,满足条件的AM 的值为321或329.(2)如图2中,连接1CD .由题意:1290D AD ∠=︒,1215AD AD ==,2145AD D ∴∠=︒,12152D D =,2135AD C ∠=︒,2190CD D ∴∠=︒,()()22221212202152252CD CD D D ∴=+=+=,1290BAC D AD ∠=∠=︒,2212BAC CAD D AD CAD ∴∠-∠=∠-∠,21BAD CAD ∴∠=∠,AB AC =,21AD AD =,21()BAD CAD SAS ∴∆≅∆,21252BD CD ∴==.【点睛】本题属于四边形综合题,考查了等腰直角三角形的性质,勾股定理,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.2.如图1,在等腰直角三角形ABC 中,动点D 在直线AB (点A 与点B 重合除外)上时,以CD 为一腰在CD 上方作等腰直角三角形ECD ,且90ECD ∠=︒,连接AE .(1)判断AE 与BD 的数量关系和位置关系;并说明理由.(2)如图2,若4BD =,P ,Q 两点在直线AB 上且5EP EQ ==,试求PQ 的长. (3)在第(2)小题的条件下,当点D 在线段AB 的延长线(或反向延长线)上时,判断PQ 的长是否为定值.分别画出图形,若是请直接写出PQ 的长;若不是请简单说明理由. 答案:(1)AE=BD 且AE ⊥BD ;(2)6;(3)PQ 为定值6,图形见解析【分析】(1)由“SAS”可证△ACE ≌△BCD ,可得AE=BD ,∠EAC=∠DBC=45°,可得AE ⊥BD ;(2)由等腰解析:(1)AE=BD 且AE ⊥BD ;(2)6;(3)PQ 为定值6,图形见解析【分析】(1)由“SAS”可证△ACE ≌△BCD ,可得AE=BD ,∠EAC=∠DBC=45°,可得AE ⊥BD ; (2)由等腰三角形的性质可得PA=AQ ,由勾股定理可求PA 的长,即可求PQ 的长; (3)分两种情况讨论,由“SAS”可证△ACE ≌△BCD ,可得AE=BD ,∠EAC=∠DBC ,可得AE ⊥BD ,由等腰三角形的性质可得PA=AQ ,由勾股定理可求PA 的长,即可求PQ 的长.【详解】解:(1)AE=BD ,AE ⊥BD ,理由如下:∵△ABC ,△ECD 都是等腰直角三角形,∴AC=BC ,CE=CD ,∠ACB=∠ECD=90°,∠ABC=∠CAB=45°,∴∠ACE=∠DCB ,且AC=BC ,CE=CD ,∴△ACE ≌△BCD (SAS )∴AE=BD ,∠EAC=∠DBC=45°,∴∠EAC+∠CAB=90°,∴AE ⊥BD ;(2)∵PE=EQ ,AE ⊥BD ,∴PA=AQ ,∵EP=EQ=5,AE=BD=4,∴,∴PQ=2AQ=6;(3)如图3,若点D 在AB 的延长线上,∵△ABC ,△ECD 都是等腰直角三角形,∴AC=BC ,CE=CD ,∠ACB=∠ECD=90°,∠ABC=∠CAB=45°,∴∠ACE=∠DCB ,且AC=BC ,CE=CD ,∴△ACE ≌△BCD (SAS )∴AE=BD ,∠CBD=∠CAE=135°,且∠CAB=45°,∴∠EAB=90°,∵PE=EQ ,AE ⊥BD ,∴PA=AQ ,∵EP=EQ=5,AE=BD=4,∴AQ=22=2516=3--,EQ AE∴PQ=2AQ=6;如图4,若点D在BA的延长线上,∵△ABC,△ECD都是等腰直角三角形,∴AC=BC,CE=CD,∠ACB=∠ECD=90°,∠ABC=∠CAB=45°,∴∠ACE=∠DCB,且AC=BC,CE=CD,∴△ACE≌△BCD(SAS)∴AE=BD,∠CBD=∠CAE=45°,且∠CAB=45°,∴∠EAB=90°,∵PE=EQ,AE⊥BD,∴PA=AQ,∵EP=EQ=5,AE=BD=4,∴AQ=22=2516=3--,EQ AE∴PQ=2AQ=6.【点睛】本题是三角形综合题,考查了全等三角形的判定和性质,等腰三角形的性质,勾股定理等知识,证明AE⊥BD是本题的关键.3.在等腰Rt△ABC中,AB=AC,∠BAC=90°(1)如图1,D,E是等腰Rt△ABC斜边BC上两动点,且∠DAE=45°,将△ABE绕点A逆时针旋转90后,得到△AFC,连接DF①求证:△AED≌△AFD;②当BE=3,CE=7时,求DE的长;(2)如图2,点D是等腰Rt△ABC斜边BC所在直线上的一动点,连接AD,以点A为直角顶点作等腰Rt△ADE,当BD=3,BC=9时,求DE的长.答案:(1)①见解析;②DE=;(2)DE的值为3或3【分析】(1)①先证明∠DAE=∠DAF,结合DA=DA,AE=AF,即可证明;②如图1中,设DE=x,则CD=7﹣x.在Rt△DCF中,由DF2解析:(1)①见解析;②DE=297;(2)DE的值为517【分析】(1)①先证明∠DAE=∠DAF,结合DA=DA,AE=AF,即可证明;②如图1中,设DE=x,则CD=7﹣x.在Rt△DCF中,由DF2=CD2+CF2,CF=BE=3,可得x2=(7﹣x)2+32,解方程即可;(2)分两种情形:①当点E在线段BC上时,如图2中,连接BE.由△EAD≌△ADC,推出∠ABE=∠C=∠ABC=45°,EB=CD=5,推出∠EBD=90°,推出DE2=BE2+BD2=62+32=45,即可解决问题;②当点D在CB的延长线上时,如图3中,同法可得DE2=153.【详解】(1)①如图1中,∵将△ABE绕点A逆时针旋转90°后,得到△AFC,∴△BAE≌△CAF,∴AE=AF,∠BAE=∠CAF,∵∠BAC=90°,∠EAD=45°,∴∠CAD+∠BAE=∠CAD+∠CAF=45°,∴∠DAE=∠DAF,∵DA=DA,AE=AF,∴△AED≌△AFD(SAS);②如图1中,设DE=x,则CD=7﹣x.∵AB=AC,∠BAC=90°,∴∠B=∠ACB=45°,∵∠ABE=∠ACF=45°,∴∠DCF=90°,∵△AED≌△AFD(SAS),∴DE=DF=x,∵在Rt△DCF中, DF2=CD2+CF2,CF=BE=3,∴x2=(7﹣x)2+32,∴x=29,7∴DE=29;7(2)∵BD=3,BC=9,∴分两种情况如下:①当点E在线段BC上时,如图2中,连接BE.∵∠BAC=∠EAD=90°,∴∠EAB=∠DAC,∵AE=AD,AB=AC,∴△EAB≌△DAC(SAS),∴∠ABE=∠C=∠ABC=45°,EB=CD=9-3=6,∴∠EBD=90°,∴DE2=BE2+BD2=62+32=45,∴DE=35;②当点D在CB的延长线上时,如图3中,连接BE.同理可证△DBE是直角三角形,EB=CD=3+9=12,DB=3,∴DE2=EB2+BD2=144+9=153,∴DE=317,综上所述,DE的值为35或317.【点睛】本题主要考查旋转变换的性质,三角形全等的判定和性质以及勾股定理,添加辅助线,构造旋转全等模型,是解题的关键.4.已知在矩形ABCD中,∠ADC的平分线DE与BC边所在的直线交于点E,点P是线段DE上一定点(其中EP<PD)(1)如图1,若点F在CD边上(不与D重合),将∠DPF绕点P逆时针旋转90°后,角的两边PD、PF分别交射线DA于点H、G.①求证:PG=PF;②探究:DF、DG、DP之间有怎样的数量关系,并证明你的结论.(2)拓展:如图2,若点F在CD的延长线上(不与D重合),过点P作PG⊥PF,交射线DA于点G,你认为(1)中DE、DG、DP之间的数量关系是否仍然成立?若成立,给出证明;若不成立,请写出它们所满足的数量关系式,并说明理由.答案:(1)①详见解析;②DG+DF=DP;(2)不成立,数量关系式应为:DG-DF=DP【解析】【分析】(1)①根据矩形性质证△HPG≌△DPF(ASA),得PG=PF;②由①知,△HPD为等腰直解析:(1)①详见解析;2;(2)不成立,数量关系式应为:DG-2【解析】【分析】(1)①根据矩形性质证△HPG≌△DPF(ASA),得PG=PF;②由①知,△HPD为等腰直角三角形,△HPG≌△DPF,根据直角三角形性质可得2DP;(2)过点P作PH⊥PD 交射线DA于点H,得到△HPD为等腰直角三角形,证△HPG≌△DPF,得HG=DF,DH=DG-HG=DG-DF,2DP.【详解】(1)①∵由矩形性质得∠GPF=∠HPD=90°,∠ADC=90°,∴∠GPH=∠FPD,∵DE平分∠ADC,∴∠PDF=∠ADP=45°,∴△HPD为等腰直角三角形,∴∠DHP=∠PDF=45°,在△HPG和△DPF中,∵PHG PDF PH PDGPH FPD ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△HPG≌△DPF(ASA),∴PG=PF;②结论:DG+DF=2DP ,由①知,△HPD为等腰直角三角形,△HPG≌△DPF,∴HD=2DP,HG=DF,∴HD=HG+DG=DF+DG,∴DG+DF=2DP;(2)不成立,数量关系式应为:DG-DF=2DP,如图,过点P作PH⊥PD交射线DA于点H,∵PF⊥PG,∠GPF=∠HPD=90°,∴∠GPH=∠FPD,∵DE平分∠ADC,且在矩形ABCD中,∠ADC=90°,∴∠HDP=∠EDC=45°,得到△HPD为等腰直角三角形,∴∠DHP=∠EDC=45°,且PH=PD,2DP,∴∠GHP=∠FDP=180°-45°=135°,在△HPG和△DPF中,∵GPH FPDGHP FDP PH PD∠=∠⎧⎪∠=∠⎨⎪=⎩∴△HPG≌△DPF,∴HG=DF,∴DH=DG-HG=DG-DF,∴2DP.【点睛】考核知识点:矩形性质的运用,等腰直角三角形.综合运用全等三角形判定和等腰直角三角形5.在ABC 中,AB AC =,点D 是直线BC 上一点(不与B 、C 重合),以AD 为一边在AD 的右侧作ADE ,使AD AE =,DAE BAC ∠=∠,连接CE .(1)如图,当点D 在线段BC 上,如果90BAC ∠=︒,则BCE ∠=______度.(2)设BAC α∠=,BCE β∠=.①如图,当点D 在线段BC 上移动时,α、β之间有怎样的数量关系?请直接写出你的结论.②如图,当点D 在线段BC 的反向延长线上移动时,α、β之间有怎样的数量关系?请说明理由.答案:(1)90;(2)①,理由见解析;②,理由见解析【分析】(1)由等腰直角三角形的性质可得∠ABC=∠ACB=45°,由“SAS”可证△BAD ≌△CAE ,可得∠ABC=∠ACE=45°,可求∠BC解析:(1)90;(2)①180αβ+=︒,理由见解析;②αβ=,理由见解析【分析】(1)由等腰直角三角形的性质可得∠ABC=∠ACB=45°,由“SAS”可证△BAD ≌△CAE ,可得∠ABC=∠ACE=45°,可求∠BCE 的度数;(2)①由“SAS”可证△ABD ≌△ACE 得出∠ABD=∠ACE ,再用三角形的内角和即可得出结论;②由“SAS”可证△ADB ≌△AEC 得出∠ABD=∠ACE ,再用三角形外角的性质即可得出结论.(1)∵AB=AC ,∠BAC=90°,∴∠ABC=∠ACB=45°,∵∠DAE=∠BAC ,∴∠BAD=∠CAE ,在△BAD 和△CAE 中AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴△BAD ≌△CAE (SAS )∴∠ABC=∠ACE=45°,∴∠BCE=∠ACB+∠ACE=90°,故答案为:90;(2)①180αβ+=︒.理由:∵∠BAC=∠DAE ,∴∠BAC-∠DAC=∠DAE-∠DAC .即∠BAD=∠CAE .在△ABD 与△ACE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△ACE (SAS ),∴∠B=∠ACE .∴∠B+∠ACB=∠ACE+∠ACB .∵∠ACE+∠ACB=β,∴∠B+∠ACB=β,∵α+∠B+∠ACB=180°,∴α+β=180°;② 当点D 在射线BC 的反向延长线上时,αβ=. 理由如下:∵DAE BAC ∠=∠,∴DAB EAC ∠=∠,在△ABD 与△ACE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴△≌△ADB AEC (SAS),∴ABD ACE ∠=∠,∵ABD BAC ACB ∠=∠+∠,ACE BCE ACB ∠=∠+∠,∴BAC ABD ACB ∠=∠-∠,BCE ACE ACB ∠=∠-∠,∴BAC BCE ∠=∠,即αβ=.【点睛】此题考查了全等三角形的判定和性质,等腰直角三角形的性质,三角形的内角和定理,以及三角形外交的性质,证明△ABD ≌△ACE 是解本题的关键.6.△ABC 中,∠BAC =90°,AB =AC ,点D 为直线BC 上一动点(点D 不与B ,C 重合),以AD 为边在AD 右侧作正方形ADEF ,连接CF .(1)观察猜想:如图1,当点D 在线段BC 上时,AC ,CD ,CF 之间的数量关系为____________;(将结论直接写在横线上)(2)如图2,当点D 在线段CB 的延长线上时,(1)中的结论是否仍然成立?若成立,不需证明;若不成立,请你写出正确结论,并说明理由.答案:(1)CD+CF=AC ;(2)不成立,CD-CF=AC ;理由见解析.【分析】(1)根据正方形的性质可得∠DAF=90°,AD=AF ,利用同角的余角相等可得∠BAD=∠CAF ,利用SAS 可证明△B解析:(1)2AC ;(2)不成立,2AC ;理由见解析.【分析】(1)根据正方形的性质可得∠DAF=90°,AD=AF ,利用同角的余角相等可得∠BAD=∠CAF ,利用SAS 可证明△BAD ≌△CAF ,可得CF=BD ,即可得出BC=CD+CF ,根据等腰直角三角形的性质可得2AC ,进而可得答案;(2)同(1)可证明△BAD ≌△CAF ,可得BD=CF ,即可得出CD=BC+CF ,根据等腰直角三角形的性质可得2AC ,可得2AC ,即可得答案.【详解】(1)∵四边形ADEF 是正方形,∴∠DAF=90°,AD=AF ,∴∠CAF+∠DAC=90°,∵∠BAC =90°,∴∠BAD+∠DAC=90°,∴∠BAD=∠CAF ,在△BAD 和△CAF 中,AB AC BAD CAF AD AF =⎧⎪∠=∠⎨⎪=⎩,∴△BAD ≌△CAF ,∴CF=BD ,∴CD+CF=CD+BD=BC ,∵∠BAC=90°,AB=AC ,∴BC=2AC , ∴CD+CF=2AC .故答案为:CD+CF=2AC(2)不成立,CD-CF=2AC .理由如下:同(1)可证△BAD ≌△CAF ,∴CF=BD ,∴CD=BC+BD=BC+CF ,∵BC=2AC ,∴CD-CF=2AC .【点睛】本题考查正方形的性质、全等三角形的判定与性质及等腰直角三角形的性质,熟练掌握相关性质及判定定理是解题关键.7.(1)问题发现:如图①,ABC 与ADE 是等边三角形,且点B ,D ,E 在同一直线上,连接CE ,求BEC ∠的度数,并确定线段BD 与CE 的数量关系.(2)拓展探究:如图②,ABC 与ADE 都是等腰直角三角形,90BAC DAE ∠=∠=︒,且点B ,D ,E 在同一直线上,AF BE ⊥于点F ,连接CE ,求BEC ∠的度数,并确定线段AF ,BF ,CE 之间的数量关系.答案:(1)的度数为,线段与之间的数量关系是;(2).【分析】(1)首先根据和均为等边三角形,可得,,,,据此判断出.然后根据全等三角形的判定方法,判断出≌,即可判断出,.进而判断出∠BEC 的度数为6 解析:(1)BEC ∠的度数为60︒,线段BD 与CD 之间的数量关系是BD CE =;(2)BF CE AF =+.【分析】(1)首先根据ABC 和ADE 均为等边三角形,可得AB AC =,AD AE =,60BAC DAE ∠=∠=︒,60ADE AED ∠=∠=︒,据此判断出BAD CAE ∠=∠.然后根据全等三角形的判定方法,判断出ABD △≌ACE △,即可判断出BD CE =,DBA CEA ∠=∠.进而判断出∠BEC 的度数为60°即可;(2)首先根据ABC 和ADE 均为等腰直角三角形,可得AB AC =,AD AE =,90BAC DAE ∠=∠=︒,45ADE AED ∠=∠=︒,据此判断出BAD CAE ∠=∠.然后根据全等三角形的判定方法,判断出ABD △≌ACE △,即可判断出,BD CE =ADB AEC ∠=∠.进而判断出∠BEC 的度数为90°即可;最后根据90DAE ∠=︒,AD AE =,AF DE ⊥,得到AF DF EF ==于是得到结论.【详解】解:(1)因为ABC 和ADE 均为等边三角形,所以AB AC =,AD AE =,60BAC DAE ∠=∠=︒,60ADE AED ∠=∠=︒, 所以BAC DAC DAE DAC ∠-∠=∠-∠,即BAD CAE ∠=∠.在ABD △和ACE △中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,所以ABD △≌ACE △,所以BD CE =,DBA CEA ∠=∠.因为点B ,D ,E 在同一直线上,所以18060120ADB ∠=︒-︒=︒,所以120AEC ∠=︒,所以1206060BEC AEC AED ∠=∠-∠=︒-︒=︒.综上可得,BEC ∠的度数为60︒,线段BD 与CD 之间的数量关系是BD CE =. (2)因为ABC 和ADE 均为等腰直角三角形,所以AB AC =,AD AE =,90BAC DAE ∠=∠=︒,45ADE AED ∠=∠=︒, 所以BAC DAC DAE DAC ∠-∠=∠-∠,即BAD CAE ∠=∠.在ABD △和ACE △中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,所以ABD △≌ACE △,所以BD CE =,ADB AEC ∠=∠.因为点B ,D ,E 在同一直线上,所以18045135ADB ∠=︒-︒=︒,所以135AEC ∠=︒,所以1354590BEC AEC AED ∠=∠-∠=︒-︒=︒.因为90DAE ∠=︒,AD AE =,AF DE ⊥,易证AF DF EF ==,所以BF BD DF CE AF =+=+.8.在Rt △ABC 中,AB=AC,D 为BC 边上一点(不与点B,C 重合),将线段AD 绕点A 逆时针旋转90°得到AE.(1)连接EC ,如图①,试探索线段BC ,CD ,CE 之间满足的等量关系,并证明你的结论;(2)连接DE ,如图②,求证:BD 2+CD 2=2AD 2(3)如图③,在四边形ABCD 中,∠ABC=∠ACB=∠ADC=45°,若BD=13,CD=1,则AD 的长为 ▲ .(直接写出答案)答案:(1)BC=DC+EC ,理由见解析;(2)见解析;(3)【分析】(1)根据本题中的条件证出△BAD ≌△CAE (SAS ), 得到BD=CE,再根据条件即可证出结果.(2)由(1)中的条件可得∠ 解析:(1)BC=DC+EC ,理由见解析;(2)见解析;(36【分析】(1)根据本题中的条件证出△BAD ≌△CAE (SAS ), 得到BD=CE,再根据条件即可证出结果. (2)由(1)中的条件可得∠DCE=∠ACE+∠ACB=90°, 所以CE 2+CD 2=ED 2,可推出BD 2+CD 2=2ED ,再根据勾股定理可得出结果.(3)作AE ⊥AD,使AE=AD ,连接CE,DE,可推出△BAD ≌△CAE (SAS ),所以13再根据勾股定理求得DE.【详解】解:(1)结论:BC=DC+EC理由:如图①中,∵∠BAC=∠DAE=90°,∴∠BAC-∠DAC=∠DAE-∠DAC ,即∠BAD=∠CAE,在△BAD 和△CAE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩, ∴△BAD ≌△CAE (SAS );∴BD=CE,∴BC=BD+CD=EC+CD,即:BC=DC+EC.(2)BD 2+CD 2=2AD 2,理由如下:连接CE,由(1)得,△BAD ≌△CAE,∴BD=CE ,∠ACE=∠B,∴∠DCE=∠ACE+∠ACB=90°,∴CE 2+CD 2=ED 2,即:BD 2+CD 2=ED 2;在Rt △ADE 中,AD 2+AE 2=ED 2,又AD=AE,∴ED 2=2AD 2;∴BD 2+CD 2=2AD 2; (3)AD 的长为6(学生直接写出答案).作AE ⊥AD,使AE=AD,连接CE,DE,∵∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,在△BAD 与△CAE 中,AB=AC ,∠BAD=∠CAE ,AD=AE.∴△BAD ≌△CAE (SAS ),∴BD=CE=13, ∵∠ADC=45°,∠EDA=45°,∴∠EDC=90°,∴DE 2=CE 2-CD 2=(13)2-12=12,∴DE=23,∵∠DAE=90°,AD 2+AE 2=DE 2,∴AD=6.【点睛】本题属于几何变换综合题,考查了等腰直角三角形的性质,旋转变换,全等三角形的判定和性质,勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.9.在直线上次取A ,B ,C 三点,分别以AB ,BC 为边长在直线的同侧作正三角形,作得两个正三角形的另一顶点分别为D ,E .(1)如图①,连结CD ,AE ,求证:CD AE =;(2)如图②,若1AB =,2BC =,求DE 的长;(3)如图③,将图②中的正三角形BEC 绕B 点作适当的旋转,连结AE ,若有222DE BE AE +=,试求∠DEB 的度数.答案:(1)见解析;(2);(3)∠DEB =30°.【分析】(1)欲证明CD =AE ,只要证明△ABE ≌△DBC 即可;(2)如图②,取BE 中点F ,连接DF ,首先证明△DBF 是等边三角形,然后证明△BD解析:(1)见解析;(2)3DE =3)∠DEB =30°.【分析】(1)欲证明CD =AE ,只要证明△ABE ≌△DBC 即可;(2)如图②,取BE 中点F ,连接DF ,首先证明△DBF 是等边三角形,然后证明△BDE 是直角三角形,再利用勾股定理计算即可;(3)如图③,连接DC ,先证明△ABE ≌△DBC ,再利用勾股定理的逆定理证明△DEC 是直角三角形,得到∠DEC =90°即可解决问题.【详解】解:(1)∵△ABD 和△ECB 都是等边三角形,∴AD =AB =BD ,BC =BE =EC ,∠ABD =∠EBC =60°,∴∠ABE=∠DBC,在△ABE和△DBC中,AB BDABE DBC BE BC=⎧⎪∠=∠⎨⎪=⎩,∴△ABE≌△DBC(SAS),∴CD=AE;(2)如图②,取BE中点F,连接DF,∵BD=AB=1,BE=BC=2,∠ABD=∠EBC=60°,∴BF=EF=1=BD,∠DBF=60°,∴△DBF是等边三角形,∴DF=BF=EF,∠DFB=60°,∵∠BFD=∠FED+∠FDE,∴∠FDE=∠FED=30°∴∠EDB=180°−∠DBE−∠DEB=90°,∴DE =2222213BE BD;(3)如图③,连接DC,∵△ABD和△ECB都是等边三角形,∴AD=AB=BD,BC=BE=EC,∠ABD=∠EBC=60°,∴∠ABE=∠DBC,在△ABE和△DBC中,AB BDABE DBC BE BC=⎧⎪∠=∠⎨⎪=⎩,∴△ABE≌△DBC(SAS),∴AE=DC,∵DE2+BE2=AE2,BE=CE,∴DE2+CE2=CD2,∴∠DEC=90°,∵∠BEC=60°,∴∠DEB=∠DEC−∠BEC=30°.【点睛】本题考查了全等三角形的判定和性质、勾股定理以及勾股定理逆定理、等边三角形的性质等知识,寻找全等三角形是解决问题的关键,要学会添加辅助线的方法,属于中考常考题型.10.ABD ∆和BEP ∆都是等腰直角三角形,90BAD BEP ∠=∠=︒,O 为BD 中点 (1)若P 、E 分别在AB 、BD 上,如图所示,求证:2AP OE =; (2)将如图所示中BEP ∆绕B 点顺时针旋转45︒,如图所示,问(1)中的结论是否仍然成立?请说明理由;(3)将如图所示中BEP ∆绕B 点顺时针旋转到如图所示,问(1)中的结论是否仍然成立?请说明理由.答案:(1)见解析;(2)仍然成立,理由见解析.【解析】【分析】(1)根据等腰三角形的两直角边相等,和勾股定理求得BP 、OB 的值.则易证AP 与OE 的数量关系;(2)将图1中的△BPE 绕B 点顺时针旋解析:(1)见解析;(2)仍然成立,理由见解析.【解析】【分析】(1)根据等腰三角形的两直角边相等,和勾股定理求得BP 、OB 的值.则易证AP 与OE 的数量关系;(2)将图1中的△BPE 绕B 点顺时针旋转45゜,问(1)中的结论成立,通过证明△BOA ∽△BEP ,即可得到问题答案.【详解】(1)证明:∵△ABD 为等腰直角三角形,∠BAD=∠BEP=90゜,∴设AB=AD=a ,则2.又∵点O 为BD 的中点,∴OB=12a .同理,设EP=BE=b ,则b .∴b ,OE=OB-BE=2a-b ,则AP OE ==,∴;(2)∵△BEP 是等腰直角三角形,∴∠B=∠BPE=45°,∵△ABD 是等腰直角三角形,O 是BD 的中点,∴AO ⊥BD ,∴∠BOA=∠BEP=90°,∠BAO=180°-∠BOA-∠B=45°,∴△BOA ∽△BEP ,∵BP BABE BO ==∴BPBABE BO ==∴.方法二(1)连结AO ,过P 作PC AO ⊥,垂足为CABD ∆是等腰直角三角形,90BAD ∠=︒,O 为BD 中点ABO ∴∆是等腰直角三角形 PC AO ⊥APC ∴∆是等腰直角三角形 四边形PCOE 为矩形OE PC ∴=AP =AP ∴=(2)在AB 上取点F ,使AF BE =,连结FO ,FE ,AO由条件知四边形AFEP 为平行四边形 AP FE ∴=AO BO = OAF OBE ∠=∠ FAO EBO ∴∆≅∆FO EO ∴=,AOF BOE ∠=∠ 90FOE ∴∠=︒FE ∴=AP =(3)作MO EO ⊥,且使MO EO =,连结AM ,ME ,AOMOE ∴∆为等腰直角三角形,又AOB ∆为等腰直角三角形AMO BEO ∴∆≅∆ AM BE ∴= 易证AM BE ⊥,AM PE ∥又BE PE =,AM PE ∴= ∴四边形AMEP 为平行四边形AP ME ∴= 在等腰直角三角形MOE中,ME =AP ∴=【点睛】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰直角三角形的判定与性质以及相似三角形的判定和性质,题目的综合性很强难度不小.二、全等三角形手拉手模型11.(1)(探索发现)如图1,正方形ABCD中,点M、N分别是边BC、CD上的点,∠MAN=45°,若将△DAN 绕点A顺时针旋转90°到△BAG位置,可得△MAN≌△MAG,若△MCN的周长为6,则正方形ABCD的边长为.(2)(类比延伸)如图(2),四边形ABCD中,AB=AD,∠BAD=120°,∠B+∠D=180°,点M、N分别在边BC、CD上的点,∠MAN=60°,请判断线段BM,DN,MN之间的数量关系,并说明理由.(3)(拓展应用)如图3,四边形ABCD中,AB=AD=10,∠ADC=120°,点M,N分别在边BC,CD上,连接AM,MN,△ABM是等边三角形,AM⊥AD,DN=531),请直接写出MN的长.解析:(1)3;(2)MN=BM+DN,理由见解析;(3)3【分析】(1)由旋转可知,DN=BG,由全等可知,MN=MG=BM+DN,即△MNC的周长=BC+CD=6,进而解决问题;(2)延长CB至E,使BE=DN,连接AE,证明△MAN≌△MAE,根据全等三角形的性质证明;(3)如图3,把△ABM绕点A逆时针旋转150°至△ADG,连接AN.作NH⊥AD于H,在AH 上取一点K ,使得∠NKH =30°,想办法证明∠MAN =75°=12∠BAD ,再利用(2)中的结论即可解决问题;【详解】解:(1)如图1中,∵△MAN ≌△MAG ,∴MN =GM ,∵DN =BG ,GM =BG +BM ,∴MN =BM +DN ,∵△CMN 的周长为:MN +CM +CN =6,∴BM +CM +CN +DN =6,∴BC +CD =6,∴BC =CD =3,故答案为3.(2)如图2中,结论:MN =NM +DN .延长CB 至E ,使BE =DN ,连接AE ,∵∠ABC +∠D =180°,∠ABC +∠ABE =180°,∴∠D =∠ABE ,在△ABE 和△ADN 中,AB AD ABE D BE DN =⎧⎪∠=∠⎨⎪=⎩,∴△ABE ≌△ADN ,∴AN =AE ,∠DAN =∠BAE ,∵∠BAD =2∠MAN ,∴∠DAN +∠BAM =∠MAN ,∴∠MAN =∠EAM ,在△MAN 和△MAE 中,AN AE MAN MAE AM AM =⎧⎪∠=∠⎨⎪=⎩,∴△MAN ≌△MAE ,∴MN =EM =BE +BM =BM +DN ,即MN =BM +DN ;(3)解:如图3,把△ABM 绕点A 逆时针旋转150°至△ADG ,连接AN .作NH ⊥AD 于H ,在AH 上取一点K ,使得∠NKH =30°在Rt △DHN 中,∵∠NDH =60°,DN =531),∴DH =12DN 5(31)-HN 3=,15532- 在Rt △KNH 中,KN =2HN =15﹣3HK 3HN 15315- ∴AK =AH ﹣HK =15﹣3,∴AK =KN ,∴∠KAN =∠KNA ,∵∠NKH =∠KAN +∠KNA ,∴∠NAK =15°,∴∠MAN =75°=12∠BAD , 由(2)得,MN =BM +DN =10+531)=3(米).【点睛】本题考查的是正方形的性质、旋转变换、全等三角形的判定定理和性质定理、解直角三角形等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.12.已知在ABC 中,AB AC =,过点B 引一条射线BM ,D 是BM 上一点. (问题解决)(1)如图1,若60ABC ︒∠=,射线BM 在ABC ∠内部,60ADB ︒∠=,求证:60BDC ︒∠=.小明同学展示的做法是:在BM 上取一点E 使得AE AD =,通过已知的条件,从而求得BDC ∠的度数,请你帮助小明写出证明过程;(类比探究)(2)如图2,已知30ABC ADB ∠=∠=︒.①当射线BM 在ABC ∠内,求BDC ∠的度数;②当射线BM 在BC 下方,如图3所示,请问BDC ∠的度数会变化吗?若不变,请说明理由,若改变,请求出BDC ∠的度数解析:(1)见解析;(2)①120°;②会变,60°【分析】(1)在BM 上取一点E 使得AE AD =,可证BAE ∆≌CAD ∆,求出∠ADC 的度数,减去∠ADB 的度数即可;(2)在BD 上取一点E ,使得AE AD =,可证BAE ∆≌CAD ∆,求出∠ADC 的度数,减去∠ADB 的度数即可;(3)在DB 延长线上取一点E ,使得AE AD =,按照(2)的方法可求.【详解】证明:(1)在BM 上取一点E 使得AE AD =,∵60ADB ∠=︒,∴ADE ∆为等边三角形,∵,60,AB AC ABC =∠=︒∴ABC ∆为等边三角形,∴60BAE EAC CAD ∠=︒-∠=∠,∴BAE ∆≌CAD ∆(SAS ),∴120ADC AEB ∠=∠=︒,∴1206060BDC ∠=︒-︒=︒;(2)①如图2,在BD 上取一点E ,使得AE AD =,∵30ABC ADB ∠=∠=︒,且AB AC =,∴30,30ABC ACB AED ADE ∠=∠=︒∠=∠=︒,∴120BAC EAD ∠=∠=︒,∴BAE CAD ∠=∠∴BAE ∆≌CAD ∆(SAS ),∴18030150ADC AEB ∠=∠=︒-︒=︒,∴15030120BDC ∠=︒-︒=︒,②会变,如图3,在DB 延长线上取一点E ,使得AE AD =同理可得:BAE ∆≌CAD ∆(SAS ),∴30ADC E ∠=∠=︒,∴303060BDC ADE ADC ∠=∠+∠=︒+︒=︒.【点睛】本题考查了全等三角形的判定与性质,等腰三角形的性质,解题关键是恰当的作辅助线,构造“手拉手”手拉手全等模型,利用全等三角形的性质求角.13.如图,已知四边形ABCD 和四边形CEFG 都是正方形,且AB CE >,连接,BG DE .(1)求证:BG DE =;(2)连接BD ,若CG //BD ,BG BD =,求BDE ∠的度数.解析:(1)见解析;(2)60BDE ∠=︒.【分析】(1)结合正方形的性质利用SAS 证明BCG DCE ∆≅∆,进而可证明结论;(2)连接BE ,通过证明BCG BCE ∆≅∆可得BDE ∆为等边三角形,进而求解.【详解】(1)证明:∵四边形ABCD 和四边形CEFG 是正方形,∴,,90BC DC CG CE BCD GCE ==∠=∠=︒,∴BCD DCG GCE DCG ∠+∠=∠+∠,∴BCG DCE ∠=∠,在BCG ∆和DCE ∆中,BC DC BCG DCE CG CE =⎧⎪∠=∠⎨⎪=⎩∴()BCG DCE SAS ∆≅∆,∴BG DE =;(2)连接BE ,∵//CG BD ,∴45DCG BDC ∠=∠=︒,∴9045135BCG BCD DCG ∠=∠+∠=︒+︒=︒,∵90GCE ∠=︒,∴36036013590135BCE BCG GCE ∠=︒-∠-∠=︒-︒-︒=︒∴BCG BCE ∠=∠.在BCG ∆和BCE ∆中BC BC BCG BCE CG CE =⎧⎪∠=∠⎨⎪=⎩∴()ΔΔBCG BCE SAS ≅,∴BG BE =,∵由(1)可知BG DE =,∴BD BE DE ==,∴BDE ∆为等边三角形,∴60BDE ∠=︒.【点睛】本题主要考查正方形的性质,全等三角形的性质与判定,等边三角形的判定与性质,能证明相关三角形全等是解题的关键.14.在平面直角坐标系中,已知A (3,0),以OA 为一边在第一象限内画正方形OABC ,D (m ,0)为x 轴上的一个动点,以BD 为一边画正方形BDEF (点F 在直线AB 右侧).(1)当m >3时(如图1),试判断线段AF 与CD 的数量关系,并说明理由. (2)当AF=5时,求点E 的坐标;(3)当D 点从A 点向右移动4个单位,求这一过程中F 点移动的路程是多少?解析:(1)AF CD =,理由见解析;(2)点E 的坐标为(7,1)E 或(1,7)E --;(3)这一过程中F 点移动的路程是向上移动4个单位.【分析】(1)先根据正方形的性质得出,,90AB CB BF BD ABC BDF ==∠=∠=︒,再根据角的和差求出CBD ABF ∠=∠,然后根据三角形全等的判定定理与性质即可得;(2)分点D 在点A 的右侧和点D 在点A 的左侧,分别画出图形.①如图1,先利用(1)的结论可得5CD =,再利用勾股定理求出4OD =,从而可得1AD =,然后过点E 作EG x ⊥轴于点G ,根据三角形全等的判定定理与性质可得1,3GE GD ==,从而可得7OG =,由此即可得;②如图2,同①的方法,利用三角形全等的判定定理与性质得出7,3HE HD ==,从而可得1OH =,由此即可得;(3)参照(2)①的方法,求出点F 的坐标,从中可发现点F 的坐标与m 的关系,由此即可得出答案.【详解】(1)AF CD =,理由如下:四边形OABC 和四边形BDEF 都是正方形,,90AB CB BF BD ABC BDF ∴==∠=∠=︒ABC ABD BDF ABD ∴∠+∠=∠+∠,即CBD ABF ∠=∠在BAF △和BCD 中,AB CB ABF CBD BF BD =⎧⎪∠=∠⎨⎪=⎩()BAF BCD SAS ∴≅AF CD ∴=;(2)由题意,分以下两种情况:①如图1,点D 在点A 的右侧四边形OABC 和四边形BDEF 都是正方形,(30)A ,3OC AB OA ∴===,BD DE =,90OAB BDE ∠=∠=︒90ABD ADB GDE ADB ∴∠+∠=∠+∠=︒,即ABD GDE ∠=∠由(1)可知,5AF CD ==在Rt COD中,4OD ===431AD OD OA ∴=-=-=过点E 作EG x ⊥轴于点G在ABD △和GDE △中,90BAD DGE ABD GDE BD DE ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩()ABD GDE AAS ∴≅1,3AD GE AB GD ∴====437OG OD GD ∴=+=+=此时点E 的坐标为(7,1)E②如图2,点D 在点A 的左侧由(1)可知,5AF CD ==在Rt COD中,4OD ===437AD OD OA ∴=+=+=过点E 作EH x ⊥轴于点H同理可证:ABD HDE ≅7,3AD HE AB HD ∴====431OH OD HD ∴=-=-=此时点E 的坐标为(1,7)E --综上,点E 的坐标为(7,1)E 或(1,7)E --;(3)由题意,只需求出点D 在点A 的右侧,即3m >时,点F 的坐标即可解决问题 如图1,过点F 作FM x ⊥轴于点M由(1)已证:BAF BCD ≅AF CD ∴=,BAF BCD ∠=∠90BAD BCO ∠=∠=︒BAD BAF BCO BCD ∴∠-∠=∠-∠FAM DCO ∴∠=∠在AFM △和CDO 中,90AMF COD FAM DCO AF CD ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩()AFM CDO AAS ∴≅3,MA OC MF OD m ∴====336OM OA MA ∴=+=+=此时点F 的坐标为(6,)F m由此可知,当D 点从A 点向右移动4个单位时,点F 向上移动4个单位即这一过程中F 点移动的路程是向上移动4个单位.【点睛】本题考查了正方形的性质、三角形全等的判定定理与性质、点的坐标变换规律等知识点,较难的是题(2),依据题意,分两种情况讨论,然后分别通过作辅助线,构造全等三角形是解题关键.15.如图,P 为等边ABC 的边BC 延长线上的一动点,以AP 为边向上作等边APD △,连接CD .(1)求证:ABP ACD ≌△△;(2)当PC AC =时,求PDC ∠的度数;(3)PDC ∠与PAC ∠有怎样的数量关系?随着点P 位置的变化,PDC ∠与PAC ∠的数量关系是否会发生变化?请说明理由.解析:1)证明见解析;(2)30PDC ∠=︒;(3)PDC PAC ∠=∠;数量关系不变;理由见解析【分析】(1)先根据等边三角形的性质得出∠BAC =∠PAQ =60°,AB =AC ,AP =AQ ,再由SAS 定理即可得出结论;(2)由∠APC=∠CAP ,∠B=∠BAC ,∠B+∠BAC+∠APC+∠CAP=180°,得∠BAP=90°,再结合ABP ACD ≌△△,进而即可求解;(3)设CD 与AP 交于点O ,由ABP ACD ≌△△,得∠ACD=∠APD ,结合∠AOC=∠DOP ,三角形内角和定理,即可得到结论.【详解】(1)证明:∵△ABC 与△APD 是等边三角形,∴∠BAC =∠PAD =60°,AB =AC ,AP =AD ,∴∠BAP =∠DAC ,在△ABP 与△ACD 中,AB AC BAP CAD AP AD ⎧⎪∠∠⎨⎪⎩===,∴ABP ACD ≌△△(SAS );(2)∵PC AC =,∴∠APC=∠CAP ,∵△ABC 是等边三角形,∴∠B=∠BAC=60°,又∵∠B+∠BAC+∠APC+∠CAP=180°,∴∠BAC+∠CAP=12×180°=90°,即:∠BAP=90°, ∴∠APB=90°-60°=30°,∴∠ADC=∠APB=30°,∵△APD 是等边三角形,∴PDC ∠=60°-∠ADC=60°-30°=30°;(3)PDC ∠=PAC ∠,随着点P 位置的变化,PDC ∠与PAC ∠的数量关系不会发生变化,理由如下:设CD 与AP 交于点O ,∵ABP ACD ≌△△,∴∠ACD=∠ABP=60°,∵∠APD=60°,∴∠ACD=∠APD ,又∵∠AOC=∠DOP ,∠AOC+∠ACD+∠PAC=180°,∠DOP+∠APD+∠PDC=180°,∴PDC ∠=PAC ∠.【点睛】本题主要考查全等三角形的判定和性质,等边三角形的性质,直角三角形的判定,熟练掌握全等三角形的判定和性质,是解题的关键.16.问题情境:在自习课上,小雪拿来了如下一道题目(原问题)和合作学习小组的同学们交流,如图①,△ACB 和△∠CDE 均为等腰三角形.CA=CB ,CD=CE ,∠ACB=∠DCE .点A 、D 、E 在同一条直线上,连接BE .求证:∠CDE=∠BCE+∠CBE .问题发现:小华说:我做过一道类似的题目:如图②,△ACB 和△CDE 均为等边三角形,其他条件不变,求∠AEB 的度数.(1)请聪明的你完成小雪的题目要求并直接写出小华的题目要求.拓展研究:(2)如图③,△ACB 和△DCE 均为等腰直角三角形,∠ACB=∠DCE=90°,点A 、D 、E 在同一条直线上,CF 为△DCE 中DE 边上的高,连接BE .请求∠AEB 的度数及线段CF 、AE 、BE 之间的数量关系,并说明理由.解析:(1)证明见解析;∠AEB=60︒;(2)∠AEB=90︒;2AE BE CF =+;理由见解析.【分析】(1)小雪的题目:先利用SAS 证明ADC BEC ≅,再利用全等三角形的性质、三角形外角的性质及等量代换即可得证;小华的题目:先利用SAS 证明ADC BEC ≅,再利用全等三角形的性质得出ADC BEC ∠∠=,然后根据等边三角形的性质求出60CDE CED ∠=∠=︒,最后根据邻补角的概念和角的和与差即可得出答案;(2)根据题意易证ADC BEC ≅,再根据全等三角形的性质及邻补角的概念即可求得 ∠AEB 的度数;然后根据三线合一即可得出CF DF EF ==,最后根据线段的和与差及等量代换即可得出答案.【详解】(1)小雪的题目:证明:ACB DCE ∠=∠ACD BCE ∠∠∴=在ADC 和DCE 中,CA CB ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩()ADC BEC SAS ∴≅△△CAD CBE ∴∠=∠又ACD BCE ∠=∠,CDE CAD ACD ∠=∠+∠CDE CBE BCE ∴∠=∠+∠;小华的题目:解:ACB DCE ∠=∠ ACD BCE ∠∠∴=在ADC 和DCE 中,CA CB ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩()ADC BEC SAS ∴≅△△ADC BEC ∠∠∴= CDE 为等边三角形60CDE CED ∴∠=∠=︒ 又点A 、D 、E 在同一条直线上120ADC BEC ∴∠=∠=︒60AEB BEC CED ∴∠=∠-∠=︒(2)∠AEB=90︒;2AE BE CF =+;理由如下:△ACB 和△DCE 均为等腰直角三角形,,,9045AC BC CD CE ACB DCE CDE CED ∴==∠=∠=︒∠=∠=︒,,ACB DCB DCE DCB ∴∠-∠=∠-∠即ACD BCE ∠=∠在ADC 和DCE 中,CA CB ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩()ADC BEC SAS ∴≅△△,BE AD BEC ADC ∴=∠=∠,点A 、D 、E 在同一直线上18045135ADC ∴∠=︒-︒=︒135BEC ∴∠=︒。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
旋转已知,如图,三角形ABC是等腰直角三角形,∠ACB=90°,F是AB的中点,直线l经过点C,分别过点A、B作l 的垂线,即AD⊥CE,BE⊥CE,(1)如图1,当CE位于点F的右侧时,求证:△ADC≌△CEB;(2)如图2,当CE位于点F的左侧时,求证:ED=BE-AD;(3)如图3,当CE在△ABC的外部时,试猜想ED、AD、BE之间的数量关系,并证明你的猜想.考点:全等三角形的判定与性质.专题:证明题;探究型.分析:(1)利用同角的余角相等得出∠CAD=∠BCE,进而根据AAS证明△ADC≌△CEB.(2)根据AAS证明△ADC≌△CEB后,得其对应边相等,进而得到ED=BE-AD.(3)根据AAS证明△ADC≌△CEB后,得DC=BE,AD=CE,又有ED=CE+DC,进而得到ED=AD+BE.解答:(1)证明:∵AD⊥CE,BE⊥CE,∴∠ADC=∠CEB=90°.∵∠ACD+∠ECB=90°,∠CAD+∠ACD=90°,∴∠CAD=∠BCE(同角的余角相等).在△ADC与△CEB中∠ADC=∠CEB ∠CAD=∠BCE AC=BC ,∴△ADC≌△CEB(AAS).(2)证明:∵AD⊥CE,BE⊥CE,∴∠ADC=∠CEB=90°.∵∠ACD+∠ECB=90°,∠CAD+∠ACD=90°,∴∠CAD=∠BCE(同角的余角相等).在△ADC与△CEB中∠ADC=∠CEB ∠CAD=∠BCE AC=BC ,∴△ADC≌△CEB(AAS).∴DC=BE,AD=CE.又∵ED=CD-CE,∴ED=BE-AD.(3)ED=AD+BE.证明:∵AD⊥CE,BE⊥CE,∴∠ADC=∠CEB=90°.∵∠ACD+∠ECB=90°,∠CAD+∠ACD=90°,∴∠CAD=∠BCE(同角的余角相等).在△ADC与△CEB中∠ADC=∠CEB ∠CAD=∠BCE AC=BC ,∴△ADC≌△CEB(AAS).∴DC=BE,AD=CE.又∵ED=CE+DC,∴ED=AD+BE.点评:本题考查了全等三角形的判定和性质;利用全等三角形的对应边相等进行等量交换,证明线段之间的数量关系,这是一种很重要的方法,注意掌握3.如图1、图2、图3,△AOB,△COD均是等腰直角三角形,∠AOB=∠COD=90º,(1)在图1中,AC与BD相等吗,有怎样的位置关系?请说明理由。
(2)若△COD绕点O顺时针旋转一定角度后,到达图2的位置,请问AC与BD还相等吗,还具有那种位置关系吗?为什么?(3)若△COD绕点O顺时针旋转一定角度后,到达图3的位置,请问AC与BD还相等吗?还具有上问中的位置关系吗?为什么?考点:旋转的性质;全等三角形的判定与性质;等腰直角三角形.分析:(1)根据等腰三角形的两腰相等进行解答.(2)证明△DOB≌△COA,根据全等三角形的对应边相等进行说明.解答:解:(1)相等.在图1中,∵△AOB,△COD均是等腰直角三角形,∠AOB=∠COD=90°,∴OA=OB,OC=OD,∴0A-0C=0B-OD,∴AC=BD;(2)相等.在图2中,0D=OC,∠DOB=∠COA,OB=OA,∴△DOB≌△COA,∴BD=AC.点评:本题考查了等腰三角形的性质、全等三角形的性质以及旋转问题,在旋转的过程中要注意哪些量是不变的,找出图形中的对应边与对应角.4.(2008河南).(9分)复习“全等三角形”的知识时,老师布置了一道作业题:“如图①,已知在△ABC中,AB=AC,P是△ABC内部任意一点,将AP绕A顺时针旋转至AQ,使∠QAP=∠BAC,连接BQ、CP,则BQ=CP.”小亮是个爱动脑筋的同学,他通过对图①的分析,证明了△ABQ≌△ACP,从而证得BQ=CP之后,将点P移到等腰三角形ABC之外,原题中的条件不变,发现“BQ=CP”仍然成立,请你就图②给出证明.考点:全等三角形的判定与性质;等腰三角形的性质.专题:证明题;探究型.分析:此题的两个小题思路是一致的;已知∠QAP=∠BAC,那么这两个等角同时减去同一个角(2题是加上同一个角),来证得∠QAB=∠PAC;而根据旋转的性质知:AP=AQ,且已知AB=AC,即可由SAS证得△ABQ≌△ACP,进而得出BQ=CP的结论.解答:证明:(1)∵∠QAP=∠BAC,∴∠QAP-∠BAP=∠BAC-∠BAP,即∠QAB=∠CAP ; 在△BQA 和△CPA 中,AQ=AP ∠QAB=∠CAP AB=AC , ∴△BQA ≌△CPA (SAS ); ∴BQ=CP .(2)BQ=CP 仍然成立,理由如下: ∵∠QAP=∠BAC ,∴∠QAP+∠PAB=∠BAC+∠PAB , 即∠QAB=∠PAC ; 在△QAB 和△PAC 中,AQ=AP ∠QAB=∠PAC AB=AC , ∴△QAB ≌△PAC (SAS ),∴BQ=CP .点评:此题主要考查了等腰三角形的性质以及全等三角形的判定和性质;选择并利用三角形全等是正确解答本题的关键.5.(2009山西太原)将一张透明的平行四边形胶片沿对角线剪开,得到图①中的两张三角形胶片ABC △和DEF △.且ABC △≌DEF △。
将这两张三角形胶片的顶点B 与顶点E 重合,把DEF △绕点B 顺时针方向旋转,这时AC 与DF 相交于点O .①当DEF △旋转至如图②位置,点()B E ,C D ,在同一直线上时,AFD ∠与DCA ∠的数量关系是 . ②当DEF △继续旋转至如图③位置时,(1)中的结论还成立吗?AO 与DO 存在怎样的数量关系?请说明理由.点:旋转的性质;全等三角形的判定与性质.专题:探究型.分析:(1)根据外角的性质,得∠AFD=∠D+∠ABC ,∠DCA=∠A+∠ABC ,从而得出∠AFD=∠DCA ;(2)成立.由△ABC ≌△DEF ,可证明∠ABF=∠DEC .则△ABF ≌△DEC ,从而证出∠AFD=∠DCA ;(3)BO ⊥AD .由△ABC ≌△DEF ,可证得点B 在AD 的垂直平分线上,进而证得点O 在AD 的垂直平分线上,则直线BO 是AD 的垂直平分线,即BO ⊥AD .解答:解:(1)∠AFD=∠DCA (或相等). (2)∠AFD=∠DCA (或成立),理由如下:方法一:由△ABC ≌△DEF ,得AB=DE ,BC=EF (或BF=EC ),∠ABC=∠DEF ,∠BAC=∠EDF .∴∠ABC-∠FBC=∠DEF-∠CBF , ∴∠ABF=∠DEC .在△ABF 和△DEC 中, AB=DE ∠ABF=∠DEC BF=ECFED CBA∴△ABF ≌△DEC ,∠BAF=∠EDC .∴∠BAC-∠BAF=∠EDF-∠EDC ,∠FAC=∠CDF . ∵∠AOD=∠FAC+∠AFD=∠CDF+∠DCA , ∴∠AFD=∠DCA .方法二:连接AD .同方法一△ABF ≌△DEC , ∴AF=DC .由△ABC ≌△DEF ,得FD=CA .在△AFD ≌△DCA , AF=DC FD=CA AD=DA ∴△AFD ≌△DCA ,∠AFD=∠DCA .(3)如图,BO ⊥AD .方法一:由△ABC ≌△DEF ,点B 与点E 重合, 得∠BAC=∠BDF ,BA=BD . ∴点B 在AD 的垂直平分线上, 且∠BAD=∠BDA .∵∠OAD=∠BAD-∠BAC ,∠ODA=∠BDA-∠BDF , ∴∠OAD=∠ODA .∴OA=OD ,点O 在AD 的垂直平分线上. ∴直线BO 是AD 的垂直平分线,BO ⊥AD .方法二:延长BO 交AD 于点G ,同方法一,OA=OD . 在△ABO 和△DBO 中, AB=DB BO=BO OA=OD ∴△ABO ≌△DBO ,∠ABO=∠DBO .在△ABG 和△DBG 中, AB=DB ∠ABG=∠DBG BG=BG ∴△ABG ≌△DBG ,∠AGB=∠DGB=90°.∴BO ⊥AD .点评:本题考查了三角形全等的判定和性质以及旋转的性质,是基础知识要熟练掌握.例1 正方形ABCD 中,E 为BC 上的一点,F 为CD 上的一点,BE+DF=EF ,求∠EAF 的度数.考点:旋转的性质;全等三角形的判定与性质;正方形的性质.分析:延长EB 使得BG=DF ,易证△ABG ≌△ADF (SAS )可得AF=AG ,进而求证△AEG ≌△AEF 可得∠EAG=∠EAF ,再求出∠EAG+∠EAF=90°即可解题.解答:解:延长EB 使得BG=DF , 在△ABG 和△ADF 中,由 AB=AD ∠ABG=∠ADF=90° BG=DF , 可得△ABG ≌△ADF (SAS ), ∴∠DAF=∠BAG ,AF=AG ,又∵EF=DF+BE=EB+BG=EG ,AE=AE , ∴△AEG ≌△AEF (SSS ), ∴∠EAG=∠EAF ,∵∠DAF+∠EAF+∠BAE=90° ∴∠EAG+∠EAF=90°, ∴∠EAF=45°.答:∠EAF 的角度为45°.点评:本题考查了正方形各内角均为直角,考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证∠EAG=∠EAF 是解题的关键.A例2 D 为等腰Rt ABC ∆斜边AB 的中点,DM ⊥DN,DM,DN 分别交BC,CA 于点E,F 。
(1) 当MDN ∠绕点D 转动时,求证DE=DF 。
(2) 若AB=2,求四边形DECF 的面积。
考点:旋转的性质;全等三角形的判定与性质;等腰直角三角形.专题:计算题.分析:(1)连CD ,根据等腰直角三角形的性质得到CD 平分∠ACB ,CD ⊥AB ,∠A=45°,CD=DA ,则∠BCD=45°,∠CDA=90°,由∠DM ⊥DN 得∠EDF=90°,根据等角的余角相等得到∠CDE=∠ADF ,根据全等三角形的判定易得△DCE ≌△ADF ,即可得到结论;(2)由△DCE ≌△ADF ,则S △DCE=S △ADF ,于是四边形DECF 的面积=S △ACD ,由而AB=2可得CD=DA=1,根据三角形的面积公式易求得S △ACD ,从而得到四边形DECF 的面积.解答:解:(1)连CD ,如图, ∵D 为等腰Rt △ABC 斜边AB 的中点,∴CD 平分∠ACB ,CD ⊥AB ,∠A=45°,CD=DA , ∴∠BCD=45°,∠CDA=90°, ∵∠DM ⊥DN , ∴∠EDF=90°, ∴∠CDE=∠ADF , 在△DCE 和△ADF 中,∠DCE=∠DAF DC=DA ∠CDE=∠ADF , ∴△DCE ≌△ADF , ∴DE=DF ;(2)∵△DCE ≌△ADF , ∴S △DCE=S △ADF ,∴四边形DECF 的面积=S △ACD , 而AB=2, ∴CD=DA=1,∴四边形DECF 的面积=S △ACD=1 2 CD •DA=1 2 .点评:本题考查了旋转的性质:旋转前后两图形全等,即对应角相等,对应线段相等,对应点与旋转中心的连线段的夹角等于旋转角.也考查了等腰直角三角形的性质以及全等三角形的判定与性质. 1、已知四边形ABCD 中,AB AD ⊥,BC CD ⊥,AB BC =,120ABC =o ∠,60MBN =o ∠,MBN ∠绕B 点旋转,它的两边分别交AD DC ,(或它们的延长线)于E F ,.当MBN ∠绕B 点旋转到AE CF =时(如图1),易证AE CF EF +=.当MBN ∠绕B 点旋转到AE CF ≠时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,线段AE CF ,,EF 又有怎样的数量关系?请写出你的猜想,不需证明.(图1) AB CDEFM N(图2)AB CDE FMN(图3)AB C DEF MN2、(西城09年一模)已知:PA=2,PB=4,以AB 为一边作正方形ABCD,使P 、D 两点落在直线AB 的两侧.(1)如图,当∠APB=45°时,求AB 及PD 的长;(2)当∠APB 变化,且其它条件不变时,求PD 的最大值,及相应∠APB 的大小.3、在等边ABC ∆的两边AB 、AC 所在直线上分别有两点M 、N ,D 为ABC V 外一点,且︒=∠60MDN,︒=∠120BDC ,BD=DC.探究:当M 、N 分别在直线AB 、AC 上移动时,BM 、NC 、MN 之间的数量关系及AMN ∆的周长Q 与等边ABC ∆的周长L 的关系.图1 图2 图3(I )如图1,当点M 、N 边AB 、AC 上,且DM=DN 时,BM 、NC 、MN 之间的数量关系是 ; 此时=LQ;(II )如图2,点M 、N 边AB 、AC 上,且当DM ≠DN 时,猜想(I )问的两个结论还成立吗?写出你的猜想并加以证明; (III ) 如图3,当M 、N 分别在边AB 、CA 的延长线上时, 若AN=x ,则Q= (用x 、L 表示).考点:等边三角形的性质;全等三角形的判定与性质.分析:(1)由DM=DN ,∠MDN=60°,可证得△MDN 是等边三角形,又由△ABC 是等边三角形,CD=BD ,易证得Rt △BDM ≌Rt △CDN ,然后由直角三角形的性质,即可求得BM 、NC 、MN 之间的数量关系 BM+NC=MN ,此时 QL =2 3 ;(2)在CN 的延长线上截取CM1=BM ,连接DM1.可证△DBM ≌△DCM1,即可得DM=DM1,易证得∠CDN=∠MDN=60°,则可证得△MDN ≌△M1DN ,然后由全等三角形的性质,即可得结论仍然成立;(3)首先在CN上截取CM1=BM,连接DM1,可证△DBM≌△DCM1,即可得DM=DM1,然后证得∠CDN=∠MDN=60°,易证得△MDN≌△M1DN,则可得NC-BM=MN.解答:解:(1)如图1,BM、NC、MN之间的数量关系BM+NC=MN.此时Q L =2 3 .(2分).理由:∵DM=DN,∠MDN=60°,∴△MDN是等边三角形,∵△ABC是等边三角形,∴∠A=60°,∵BD=CD,∠BDC=120°,∴∠BDC=∠DCB=30°,∴∠MBD=∠NCD=90°,∵DM=DN,BD=CD,∴Rt△BDM≌Rt△CDN,∴∠BDM=∠CDN=30°,BM=CN,∴DM=2BM,DN=2CN,∴MN=2BM=2CN=BM+CN;∴AM=AN,∴△AMN是等边三角形,∵AB=AM+BM,∴AM:AB=2:3,∴Q L =2 3 ;(2)猜想:结论仍然成立.(3分).证明:在CN的延长线上截取CM1=BM,连接DM1.(4分)∵∠MBD=∠M1CD=90°,BD=CD,∴△DBM≌△DCM1,∴DM=DM1,∠MBD=∠M1CD,M1C=BM,∵∠MDN=60°,∠BDC=120°,∴∠M1DN=∠MDN=60°,∴△MDN≌△M1DN,∴MN=M1N=M1C+NC=BM+NC,∴△AMN的周长为:AM+MN+AN=AM+BM+CN+AN=AB+AC,∴Q L =2 3 ;(3)证明:在CN上截取CM1=BM,连接DM1.(4分)可证△DBM≌△DCM1,∴DM=DM1,(5分)可证∠CDN=∠MDN=60°,∴△MDN≌△M1DN,∴MN=M1N,(7分).∴NC-BM=MN.(8分).点评:此题考查了等边三角形,直角三角形,等腰三角形的性质以及全等三角形的判定与性质等知识.此题综合性很强,难度较大,解题的关键是注意数形结合思想的应用与辅助线的作法.例8.(2005年马尾)用两个全等的等边三角形△ABC和△ACD拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合,使三角尺的60°角的顶点与点A重合,两边分别与AB,AC重合.将三角尺绕点A按逆时针方向旋转.(1)当三角尺的两边分别与菱形的两边BC,CD相交于点E,F时,(如图13—1),通过观察或测量BE,CF的长度,你能得出什么结论?并证明你的结论;(2)当三角尺的两边分别与菱形的两边BC,CD的延长线相交于点E,F时(如图13—2),你在(1)中得到的结论还成立吗?简要说明理由.考点:菱形的性质;三角形的面积;全等三角形的判定与性质;旋转的性质.分析:(1)利用全等三角形的判定得出△ABE ≌△ACF 即可得出答案;(2)根据已知可以得出∠BAE=∠CAF ,进而求出△ABE ≌△ACF 即可;(3)利用四边形AECF 的面积S=S △AEC+S △ACF=S △AEC+S △ABE=S △ABC 求出即可.解答:解:(1)得出结论是:BE=CF ,证明:∵∠BAC=∠EAF=60°, ∴∠BAC-∠EAC=∠EAF-∠EAC , 即:∠BAE=∠CAF ,又∵AB=AC ,∠ABE=∠ACF=60°,∴ ∠BAE=∠CAF AB=AC ∠ABE=∠ACF , ∴△ABE ≌△ACF (ASA ), ∴BE=CF , (2)还成立,证明:∵∠BAC=∠EAF=60°, ∴∠BAC+∠EAC=∠EAF+∠EAC , 即∠BAE=∠CAF ,又∵AB=AC ,∠ABE=∠ACF=60°,即 ∠BAE=∠CAF AB=AC ∠ABE=∠ACF , ∴△ABE ≌△ACF (ASA ), ∴BE=CF ,(3)证明:∵△ABE ≌△ACF , ∴S △ABE=S △ACF ,∴四边形AECF 的面积S=S △AEC+S △ACF=S △AEC+S △ABE=S △ABC ; 而S △ABC=1 2 S 菱形ABCD ,∴S=1 2 S 菱形ABCD .点评:此题主要考查了全等三角形的判定以及四边形面积,熟练利用全等三角形判定求出是解题关键. 解:(1)BE =CF .证明:在△ABE 和△ACF 中, ∵∠BAE +∠EAC =∠CAF +∠EAC =60°, ∴∠BAE =∠CAF .∵AB =AC ,∠B =∠ACF =60°,∴△ABE ≌△ACF (ASA ). ∴BE =CF .(2)BE =CF 仍然成立. 根据三角形全等的判定公理,同样可以证明△ABE 和△ACF旋转型1、如图,正方形ABCD 的边长为1,G 为CD 边上一动点(点G 与C 、D 不重合), 以CG 为一边向正方形ABCD外作正方形GCEF ,连接DE 交BG 的延长线于H 。
