随机变量及其分布习题解答
(完整版)多维随机变量及其分布习题及答案

第三章多维随机变量及其分布一、填空题1、随机点落在矩形域的概率为),(Y X ],[2121y y y x x x ≤<≤< .),(),(),(),(21111222y x F y x F y x F y x F -+-2、的分布函数为,则 0 .),(Y X ),(y x F =-∞),(y F3、的分布函数为,则),(Y X ),(y x F =+),0(y x F ),(y x F4、的分布函数为,则),(Y X ),(y x F =+∞),(x F )(x F X5、设随机变量的概率密度为),(Y X ,则.⎩⎨⎧<<<<--=其其042,20)6(),(y x y x k y x f =k 816、随机变量的分布如下,写出其边缘分布.),(Y X 7、设是的联合分布密度,是的边缘分布密度,则1 .),(y x f Y X ,)(x f X X =⎰∞+∞-)(x f X8、二维正态随机变量,和相互独立的充要条件是参数 0.),(Y X X Y =ρXY0123jP ⋅10838308638108182⋅i P 818383819、如果随机变量的联合概率分布为),(Y X YX12316191181231αβ则应满足的条件是 ;若与相互独立,则 , .βα,186=+βαX Y =α184=β18210、设相互独立,,则的联合概率密度Y X ,)1.0(~),1,0(~N Y N X ),(Y X,的概率密度.=),(y x f 22221y x e +-πY X Z +==)(Z f Z 42221x e-π12、 设 ( ξ 、 η ) 的 联 合 分 布 函 数 为则 A =__1___。
()()()()⎪⎩⎪⎨⎧≥≥+-+-+++= y x y x y x A y x F 00,0111111,222二、证明和计算题1、袋中有三个球,分别标着数字1,2,2,从袋中任取一球,不放回,再取一球,设第一次取的球上标的数字为,第二次取的球上标的数字,求的联合分布律.X Y ),(Y X 解: 031}1,1{⋅===Y X P 31131}2,1{=⋅===Y X P 312132}1,2{=⋅===Y X P 312132}2,2{=⋅===Y X P 2、三封信随机地投入编号为1,2,3的三个信箱中,设为投入1号信箱的信数,为投入2X Y 号信箱的信数,求的联合分布律.),(Y X 解:的可能取值为0,1,2,3的可能取值为0,1,2,3X Y331}0,0{===Y X P 333}1,0{===Y X P 3323333}2,0{====C Y X P XY 12103123131331}3,0{===Y X P 333}0,1{===Y X P 3323}1,1{⨯===Y X P3313}2,1{⨯===Y X P 0}3,1{===Y X P 3233}0,2{C Y X P === 333}1,2{===Y X P 0}2,2{===Y X P 0}3,2{===Y X P 331}0,3{===Y X P 0}3,3{}2,3{}1,3{=========Y X P Y X P Y X P X Y123271273273271127327627322732730032710003、设 函 数 F(x , y) = ;问 F(x , y) 是 不 是 某 二 维 随 机 变 量 的⎩⎨⎧≤+>+120121y x y x 联 合 分 布 函 数 ? 并 说 明 理 由 。
概率论与数理统计教程习题(第二章随机变量及其分布)(1)答案

概率论与数理统计练习题系 专业 班 姓名 学号第六章 随机变量数字特征一.填空题1. 若随机变量X 的概率函数为1.03.03.01.02.043211pX-,则=≤)2(X P ;=>)3(X P ;=>=)04(X X P .2. 若随机变量X 服从泊松分布)3(P ,则=≥)2(X P 8006.0413≈--e.3. 若随机变量X 的概率函数为).4,3,2,1(,2)(=⋅==-k c k X P k则=c1516. 4.设A ,B 为两个随机事件,且A 与B 相互独立,P (A )=,P (B )=,则()P AB =____________.() 5.设事件A 、B 互不相容,已知()0.4=P A ,()0.5=P B ,则()=P AB6. 盒中有4个棋子,其中2个白子,2个黑子,今有1人随机地从盒中取出2个棋子,则这2个棋子颜色相同的概率为____________.(13) 7.设随机变量X 服从[0,1]上的均匀分布,则()E X =____________.(12) 8.设随机变量X 服从参数为3的泊松分布,则概率密度函数为 __.(k 33(=,0,1,2k!P X k e k -==L )) 9.某种电器使用寿命X (单位:小时)服从参数为140000λ=的指数分布,则此种电器的平均使用寿命为____________小时.(40000)10在3男生2女生中任取3人,用X 表示取到女生人数,则X 的概率函数为11.若随机变量X 的概率密度为)(,1)(2+∞<<-∞+=x xa x f ,则=a π1;=>)0(X P ;==)0(X P 0 .12.若随机变量)1,1(~-U X ,则X 的概率密度为 1(1,1)()2x f x ⎧∈-⎪=⎨⎪⎩其它13.若随机变量)4(~e X ,则=≥)4(X P ;=<<)53(X P .14..设随机变量X 的可能取值为0,1,2,相应的概率分布为 , ,,则()E X =15.设X 为正态分布的随机变量,概率密度为2(1)8()x f x +-=,则2(21)E X -= 916.已知X ~B (n,p ),且E (X )=8,D (X )=,则n= 。
随机变量及其分布列习题(含解析)
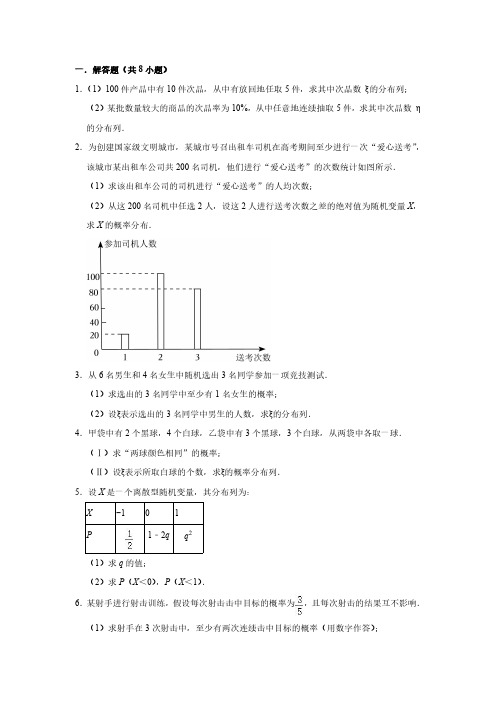
一.解答题(共8小题)1.(1)100件产品中有10件次品,从中有放回地任取5件,求其中次品数ξ的分布列;(2)某批数量较大的商品的次品率为10%,从中任意地连续抽取5件,求其中次品数η的分布列.2.为创建国家级文明城市,某城市号召出租车司机在高考期间至少进行一次“爱心送考”,该城市某出租车公司共200名司机,他们进行“爱心送考”的次数统计如图所示.(1)求该出租车公司的司机进行“爱心送考”的人均次数;(2)从这200名司机中任选2人,设这2人进行送考次数之差的绝对值为随机变量X,求X的概率分布.3.从6名男生和4名女生中随机选出3名同学参加一项竞技测试.(1)求选出的3名同学中至少有1名女生的概率;(2)设ξ表示选出的3名同学中男生的人数,求ξ的分布列.4.甲袋中有2个黑球,4个白球,乙袋中有3个黑球,3个白球,从两袋中各取一球.(Ⅰ)求“两球颜色相同”的概率;(Ⅱ)设ξ表示所取白球的个数,求ξ的概率分布列.5.设X是一个离散型随机变量,其分布列为:X−101P1﹣2q q2(1)求q的值;(2)求P(X<0),P(X<1).6.某射手进行射击训练,假设每次射击击中目标的概率为,且每次射击的结果互不影响.(1)求射手在3次射击中,至少有两次连续击中目标的概率(用数字作答);(2)求射手第3次击中目标时,恰好射击了4次的概率(用数字作答);(3)设随机变量ξ表示射手第3次击中目标时已射击的次数,求ξ的分布列.7.袋中有3个红球,4个黑球,从袋中任取4个球.(1)求红球个数X的分布列;(2)若取到一个红球得2分,取到一个黑球得1分,求得分不小于6分的概率.8.从5名男生和3名女生中任选2人去参加学校组织的“低碳杯”知识抢答赛,用ξ表示选出的女生的人数.(1)求随机变量ξ的分布列;(2)求事件“选出的2学生至少有一女生”的概率.参考答案与试题解析一.解答题(共8小题)1.(1)100件产品中有10件次品,从中有放回地任取5件,求其中次品数ξ的分布列;(2)某批数量较大的商品的次品率为10%,从中任意地连续抽取5件,求其中次品数η的分布列.【解答】解:(1)由题意知ξ的可能取值为0,1,2,3,4,5,每次取出次品的概率为:,相当于5次独立重复实验,ξ~B(5,),P(ξ=0)==0.59059,P(ξ=1)==0.32805,P(ξ=2)==0.07329,P(ξ=3)==0.0081,P(ξ=4)==0.00045,P(ξ=5)==0.00001,∴ξ的分布列为:ξ012345P0.590590.328050.07290.00810.000450.00001(2)由题意知η的可能取值为0,1,2,3,4,5,且η~B(5,0.1),∴η的分布列为:η012345P0.590590.328050.07290.00810.000450.000012.为创建国家级文明城市,某城市号召出租车司机在高考期间至少进行一次“爱心送考”,该城市某出租车公司共200名司机,他们进行“爱心送考”的次数统计如图所示.(1)求该出租车公司的司机进行“爱心送考”的人均次数;(2)从这200名司机中任选2人,设这2人进行送考次数之差的绝对值为随机变量X,求X的概率分布.【解答】解:(1)由统计图得200名司机中送考1次的有20人,送考2次的有100人,送考3次的有80人,∴该出租车公司的司机进行“爱心送考”的人均次数为;(2)从该公司任选两名司机,记“这两人中﹣人送考1次,另一人送考2次”为事件A,“这两人中一人送考2次,另一人送考3次“为事件B,“这两人中﹣人送考1次,另一人送考3次”为事件C,“这两人送考次数相同”为事件D,由题意知X的所有可能取值为0,1,2,,,,所以X的分布列为:X012P3.从6名男生和4名女生中随机选出3名同学参加一项竞技测试.(1)求选出的3名同学中至少有1名女生的概率;(2)设ξ表示选出的3名同学中男生的人数,求ξ的分布列.【解答】解:(1)由意可知,选出的3名同学全是男生的概率为=,∴选出的3名同学中至少有1名女生的概率为P=1﹣=.(2)根据题意,ξ的可能取值为0,1,2,3,P(ξ=0)==,P(ξ=1)==,P(ξ=2)==,P(ξ=3)==,∴ξ的分布列为:ξ0123P4.甲袋中有2个黑球,4个白球,乙袋中有3个黑球,3个白球,从两袋中各取一球.(Ⅰ)求“两球颜色相同”的概率;(Ⅱ)设ξ表示所取白球的个数,求ξ的概率分布列.【解答】解:(I)从甲中取出黑球的概率为,取出白球的概率为,从乙中取出黑球的概率为,取出白球的概率为,故“两球颜色相同”的概率P=.(II)由题意可得,ξ所有可能取值为0,1,2,P(ξ=0)==,P(ξ=1)=,P(ξ=2)=,故ξ的分布列为:ξ012P5.设X是一个离散型随机变量,其分布列为:X−101P1﹣2q q2(1)求q的值;(2)求P(X<0),P(X<1).【解答】解:(1)依题意,得,解得或(舍去),所以.(2)由(1)得,,所以,.6.某射手进行射击训练,假设每次射击击中目标的概率为,且每次射击的结果互不影响.(1)求射手在3次射击中,至少有两次连续击中目标的概率(用数字作答);(2)求射手第3次击中目标时,恰好射击了4次的概率(用数字作答);(3)设随机变量ξ表示射手第3次击中目标时已射击的次数,求ξ的分布列.【解答】解:(1)设事件该射手第i次射击,击中目标为A i,i=1,2,3,则,所以,事件射手在3次射击中,至少有两次连续击中目标可表示为,因为事件,,A1A2A3互斥,所以又事件A1,A2,A3相互独立,所以==;(2)事件射手第3次击中目标时,恰好射击了4次等于事件前3次中恰好击中两次目标且第四次击中目标,又各次击中目标的概率为,所以前3次中恰有两次击中目标的概率为,第四次击中目标的概率为,所以事件射手第3次击中目标时,恰好射击了4次的概率;(3)由已知ξ的取值有3,4,5,⋅⋅⋅,n,⋅⋅⋅,又,,,⋅⋅⋅,,所以随机变量ξ的分布列为:ξ345…n…P……7.袋中有3个红球,4个黑球,从袋中任取4个球.(1)求红球个数X的分布列;(2)若取到一个红球得2分,取到一个黑球得1分,求得分不小于6分的概率.【解答】解:(1)由题意可得,X可能取值为0,1,2,3,P(X=0)=,P(X=1)=,P(X=2)=,P(X=3)=,故X的分布列为:X0123P(2)设得分为Y,则得分Y可以取4,5,6,7,分别对应4个黑球,3黑1红,2黑2红,1黑3红四种情况,P(Y≥6)=P(Y=6)+P(Y=7)=,故得分不小于6分的概率为.8.从5名男生和3名女生中任选2人去参加学校组织的“低碳杯”知识抢答赛,用ξ表示选出的女生的人数.(1)求随机变量ξ的分布列;(2)求事件“选出的2学生至少有一女生”的概率.【解答】解:(1)由题意得ξ的可能取值为0,1,2,P(ξ=0)==,P(ξ=1)==,P(ξ=2)==,∴随机变量ξ的分布列为:ξ012P(2)事件“选出的2学生至少有一女生”的概率为:P=P(ξ=1)+P(ξ=2)==.。
《概率论与数理统计》习题及答案

概率论与数理统计第一部份 习题第一章 概率论基本概念一、填空题1、设A ,B ,C 为3事件,则这3事件中恰有2个事件发生可表示为 。
2、设3.0)(,1.0)(=⋃=B A P A P ,且A 与B 互不相容,则=)(B P 。
3、口袋中有4只白球,2只红球,从中随机抽取3只,则取得2只白球,1只红球的概率 为 。
4、某人射击的命中率为0.7,现独立地重复射击5次,则恰有2次命中的概率为 。
5、某市有50%的住户订晚报,有60%的住户订日报,有80%的住户订这两种报纸中的一种,则同时订这两种报纸的百分比为 。
6、设A ,B 为两事件,3.0)(,7.0)(==B A P A P ,则=)(B A P 。
7、同时抛掷3枚均匀硬币,恰有1个正面的概率为 。
8、设A ,B 为两事件,2.0)(,5.0)(=-=B A P A P ,则=)(AB P 。
9、10个球中只有1个为红球,不放回地取球,每次1个,则第5次才取得红球的概率 为 。
10、将一骰子独立地抛掷2次,以X 和Y 分别表示先后掷出的点数,{}10=+=Y X A {}Y X B >=,则=)|(A B P 。
11、设B A ,是两事件,则B A ,的差事件为 。
12、设C B A ,,构成一完备事件组,且,7.0)(,5.0)(==B P A P 则=)(C P ,=)(AB P 。
13、设A 与B 为互不相容的两事件,,0)(>B P 则=)|(B A P 。
14、设A 与B 为相互独立的两事件,且4.0)(,7.0)(==B P A P ,则=)(AB P 。
15、设B A ,是两事件,,36.0)(,9.0)(==AB P A P 则=)(B A P 。
16、设B A ,是两个相互独立的事件,,4.0)(,2.0)(==B P A P 则=)(B A P 。
17、设B A ,是两事件,如果B A ⊃,且2.0)(,7.0)(==B P A P ,则=)|(B A P 。
随机变量及其分布习题解答

+随机变量及其分布习题解答(共16页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--1第二章 随机变量及其分布1、解:设公司赔付金额为X ,则X 的可能值为; 投保一年内因意外死亡:20万,概率为 投保一年内因其他原因死亡:5万,概率为投保一年内没有死亡:的分布律为:2、一袋中有53、4、5,在其中同时取三只,以X 表示取出的三只球中的最大号码,写出随机变量X 的分布律解:X 可以取值3,4,5,分布律为1061)4,3,2,1,5()5(1031)3,2,1,4()4(1011)2,1,3()3(352435233522=⨯====⨯====⨯===C C P X P C C P X P C C P X P 中任取两球再在号一球为中任取两球再在号一球为号两球为号一球为也可列为下表 X : 3, 4,5 P :106,103,1013、设在15只同类型零件中有2只是次品,在其中取三次,每次任取一只,作不放回抽样,以X 表示取出次品的只数,(1)求X 的分布律,(2)画出分布律的图形.解:任取三只,其中新含次品个数X 可能为0,1,2个.3522)0(315313===C C X P 3512)1(31521312=⨯==C C C X P 351)2(31511322=⨯==C C C X P 再列为下表 X : 0, 1, 2 P : 351,3512,352224、进行重复独立实验,设每次成功的概率为p ,失败的概率为q =1-p (0<p <1)(1)将实验进行到出现一次成功为止,以X 表示所需的试验次数,求X 的分布律.(此时称X 服从以p 为参数的几何分布.)(2)将实验进行到出现r 次成功为止,以Y 表示所需的试验次数,求Y 的分布律.(此时称Y 服从以r, p 为参数的巴斯卡分布.)(3)一篮球运动员的投篮命中率为45%,以X 表示他首次投中时累计已投篮的次数,写出X 的分布律,并计算X 取偶数的概率.解:(1)P (X=k )=q k -1p k=1,2,……(2)Y=r+n={最后一次实验前r+n -1次有n 次失败,且最后一次成功} ,,2,1,0,)(111 ===+=-+--+n p q C p p q C n r Y P r n n n r r n n n r 其中 q=1-p ,或记r+n=k ,则 P {Y=k }= ,1,,)1(11+=----r r k p p C rk r r k (3)P (X=k ) = k -k=1,2…P (X 取偶数)=311145.0)55.0()2(1121===∑∑∞=-∞=k k k k X P5、 一房间有3扇同样大小的窗子,其中只有一扇是打开的.有一只鸟自开着的窗子飞入了房间,它只能从开着的窗子飞出去.鸟在房子里飞来飞去,试图飞出房间.假定鸟是没有记忆的,鸟飞向各扇窗子是随机的.(1)以X 表示鸟为了飞出房间试飞的次数,求X 的分布律.(2)户主声称,他养的一只鸟,是有记忆的,它飞向任一窗子的尝试不多于一次.以Y 表示这只聪明的鸟为了飞出房间试飞的次数,如户主所说是确实的,试求Y 的分布律.(3)求试飞次数X 小于Y 的概率;求试飞次数Y 小于X 的概率. 解:(1)X 的可能取值为1,2,3,…,n ,…P {X=n }=P {前n -1次飞向了另2扇窗子,第n 次飞了出去}=31)32(1⋅-n , n=1,2,……(2)Y 的可能取值为1,2,3 P {Y=1}=P {第1次飞了出去}=31P {Y=2}=P {第1次飞向 另2扇窗子中的一扇,第2次飞了出去} =312132=⨯P {Y=3}=P {第1,2次飞向了另2扇窗子,第3次飞了出去} =31!3!2=3∑∑===<===<==<3231}|{}{}|{}{}{)3(k k k Y Y X P k Y P k Y Y X P k Y P Y X P ⎪⎪⎭⎫⎝⎛==<0}1|{Y Y X P 全概率公式并注意到 278313231313131}{}{32=⎥⎦⎤⎢⎣⎡⨯+⨯+⨯=<==∑=k k X P k Y P }{}|{,k X P k Y Y X P Y X <==<独立即注意到同上,∑======31}|{}{}{k k Y Y X P k Y P Y X P81192743192313131}{}{31=⨯+⨯+⨯====∑=k k X P k Y P故8138){}{1}{==-<-=<Y X P Y X P X Y P 6、一大楼装有5个同类型的供水设备,调查表明在任一时刻t 每个设备使用的概率为,问在同一时刻(1)恰有2个设备被使用的概率是多少0729.0)9.0()1.0()2(322525225=⨯⨯===-C q p C X P (2)至少有3个设备被使用的概率是多少00856.0)1.0()9.0()1.0()9.0()1.0()3(5554452335=⨯+⨯⨯+⨯⨯=≥C C C X P (3)至多有3个设备被使用的概率是多少3225415505)9.0()1.0()9.0(1.0)9.0()3(⨯⨯+⨯⨯+=≤C C C X P99954.0)9.0()1.0(2335=⨯⨯+C(4)至少有一个设备被使用的概率是多少 40951.059049.01)0(1)1(=-==-=≥X P X P7、设事件A 在每一次试验中发生的概率为,当A 发生不少于3次时,指示灯发出信号.(1)进行了5 次独立试验,求指示灯发出信号的概率 .(2)进行了7次独立试验,求指示灯发出信号的概率解: 设X 为 A 发生的次数. 则()0.3,.X B n n=5,7B:“指示等发出信号“① (){}3P B P X =≥55530.30.70.163k k k k C -===∑②(){}3P B P X =≥={}{}7231k P X K P X K ===-=∑∑71622510.70.30.70.30.70.353G G =--⋅⨯-⨯≈ 8、甲、乙二人投篮,投中的概率各为, ,令各投三次.求4(1)二人投中次数相等的概率. 记X 表甲三次投篮中投中的次数 Y 表乙三次投篮中投中的次数由于甲、乙每次投篮独立,且彼此投篮也独立. P (X =Y )=P (X =0, Y=0)+P (X =2, Y=2)+P (X=3, Y=3)= P (X =0) P (Y=0)+ P (X =1) P (Y=1)+ P (X =2) P (Y=2)+ P (X =3) P (Y=3)= 3× 3+ [])3.0(7.0[])4.0(6.0213213⨯⨯⨯⨯⨯C C3223223)6.0(]3.)7.0([]4.0)6.0([+⨯⨯⨯⨯⨯+C C 321.0)7.0(3=⨯(2)甲比乙投中次数多的概率.P (X>Y )=P (X =1, Y=0)+P (X =2, Y=0)+P (X=2, Y=1)+ P (X =3) P (Y=0)+ P (X =3) P (Y=1)+ P (X =3) P (Y=2) =P (X =1) P (Y=0) + P (X =2, Y=0)+ P (X=2, Y=1)+ P (X =3) P (Y=0)+ P (X =3) P (Y=1)+ P (X =3) P (Y=2)=+⨯⨯⨯+⨯⨯⨯82233213)3.0(]4.0)6.0([)3.0(])4.0(6.0[C C 3213223)6.0(])3.0(7.0[]4.0)6.0([+⨯⨯⨯⨯⨯C C321333)6.0(])3.0(7.0[)6.0()3.0(+⨯⨯⨯+⨯C 243.0]3.0)7.0([223=⨯⨯⨯C9、有一大批产品,其验收方案如下,先做第一次检验:从中任取10件,经验收无次品接受这批产品,次品数大于2拒收;否则作第二次检验,其做法是从中再任取5件,仅当5件中无次品时接受这批产品,若产品的次品率为10%,求(1)这批产品经第一次检验就能接受的概率 (2)需作第二次检验的概率(3)这批产品按第2次检验的标准被接受的概率(4)这批产品在第1次检验未能做决定且第二次检验时被通过的概率(5)这批产品被接受的概率解:X 表示10件中次品的个数,Y 表示5件中次品的个数,由于产品总数很大,故X~B (10,),Y~B (5,)(近似服从) (1)P {X =0}=≈(2)P {X ≤2}=P {X =2}+ P {X =1}=581.09.01.09.01.0911082210≈+C C (3)P {Y =0}= 5≈(4)P {0<X ≤2,Y=0} ({0<X ≤2}与{ Y=2}独立) = P {0<X ≤2}P {Y=0}=×≈(5)P {X =0}+ P {0<X ≤2,Y=0} ≈+=510、有甲、乙两种味道和颜色极为相似的名酒各4杯.如果从中挑4杯,能将甲种酒全部挑出来,算是试验成功一次.(1)某人随机地去猜,问他试验成功一次的概率是多少(2)某人声称他通过品尝能区分两种酒.他连续试验10次,成功3次.试问他是猜对的,还是他确有区分的能力(设各次试验是相互独立的.)解:(1)P (一次成功)=701148=C(2)P (连续试验10次,成功3次)= 100003)7069()701(73310=C .此概率太小,按实际推断原理,就认为他确有区分能力.11. 尽管在几何教科书中已经讲过用圆规和直尺三等分一个任意角是不可能的.但每年总有一些“发明者”撰写关于用圆规和直尺将角三等分的文章.设某地区每年撰写此类文章的篇数X 服从参数为6的泊松分布.求明年没有此类文章的概率.解: ().6~πX 6=λ{}0025.01066≈===∴-ee X P12. 一电话交换台每分钟收到呼唤的次数服从参数为4的泊松分布.求(1)每分钟恰有8次呼唤的概率.(2)某一分钟的呼唤次数大于3的概率.()4~πX 4=λ(1){}∑∑∞=∞=--⋅-⋅==899484!!8r r r e r e X P λλ 029771.0021363.0051134.0=-= (2)566530.0}4{}3{=≥=>X P X P13. 某一公安局在长度为t 的时间间隔内收到的紧急呼救的次数X 服从参数为(1/2)t 的泊松分布,而与时间间隔的起点无关(时间以小时计).(1)求某一天中午12时至下午3时没有收到紧急呼救的概率.(2)求某一天中午12时至下午5时至少收到1次紧急呼救的概率.解:2tλ= ()X πλ①32λ= {}3200.2231P X e -===②52λ= {} 2.512.510.918!k k e P X k -∞=≥==∑14、解:~(2)X t π(1)、10t =分钟时16t =小时,6{}131310.2388!1k ee P X k κλ--====(2)、{}00.5P X =≥故()0220.50.346571tt e t -≥⇒≥(小时)所以0.34657*6020.79t ≥≈(分钟) 15、解:{}()(){}10500005000100.001510.0015100.8622k kk P X k P X -=⎛⎫≤=- ⎪⎝⎭≤≈∑ 16、解:{}{}{}011000,0.0001,0.12101110.99530.00470!1!n p np P X P X P X e e λλλλλ--====≥=-=-==--≈-=17、解:设X 服从()01分布,其分布率为{}()11,0,1kk P X k p p k -==-=,求X 的分布函数,并作出其图形.解一:X 0 1 k p1p - p()0,1XX 的分布函数为:()0010111x F x p x x , <⎧⎪=- , ≤<⎨⎪ , ≥⎩718.在区间[]0,a 上任意投掷一个质点,以X 表示这个质点的坐标.设这个质点落在[]0,a 中任意小区间内的概率与这个小区间的长度成正比例,试求X 的分布函数.解:① 当0X <时.{}X x ≤是不可能事件,(){}0F X P X x =≤=②当0x a ≤≤时, {}0P X x kx ≤≤= 而 {}0X a ≤≤是必然事件 {}101P X x ka k a∴≤≤==⇒= {}0x P X x kx a∴≤≤==则 (){}{}{}00x F x P X x P X P X x a=≤=≤+≤≤=③当x a >时,{}X x ≤是必然事件,有(){}1F x P X x =≤=()0001x x F x x a a x a , < ⎧⎪⎪∴ , ≤≤⎨⎪ , >⎪⎩19、以X 表示某商店从早晨开始营业起直到第一顾客到达的等待时间(以分计),X 的分布函数是⎩⎨⎧<≥-=-000,1)(4.0x x e x F x X求下述概率:(1)P {至多3分钟};(2)P {至少4分钟};(3)P {3分钟至4分钟之间};(4)P {至多3分钟或至少4分钟};(5)P {恰好分钟} 解:(1)P {至多3分钟}= P {X ≤3} =2.11)3(--=e F X (2)P {至少4分钟} P (X ≥4) =6.1)4(1-=-e F X(3)P {3分钟至4分钟之间}= P {3<X ≤4}=6.12.1)3()4(---=-e e F F X X (4)P {至多3分钟或至少4分钟}= P {至多3分钟}+P {至少4分钟} =6.12.11--+-e e (5)P {恰好分钟}= P (X ==020、设随机变量X 的分布函数为⎪⎩⎪⎨⎧≥<≤<=.,1,1,ln ,1,0)(e x e x x x x F X ,求(1)P (X<2), P {0<X ≤3}, P (2<X<25);(2)求概率密度f X (x ).解:(1)P (X ≤2)=F X (2)= ln2, P (0<X ≤3)= F X (3)-F X (0)=1,45ln 2ln 25ln )2()25(252(=-=-=<<X X F F X P8(2)⎪⎩⎪⎨⎧<<==其它,0,1,1)(')(e x x x F x f21、设随机变量X 的概率密度)(x f 为(1)⎪⎩⎪⎨⎧≤≤--=其它01112)(2x x x f π(2)⎪⎩⎪⎨⎧≤≤-<≤=其他021210)(x x x x x f求X 的分布函数F (x ),并作出(2)中的f (x )与F (x )的图形.解:(1)当-1≤x ≤1时:21arcsin 111arcsin 211212120)(212121++-=⎥⎦⎤⎢⎣⎡+-=-+=---∞-⎰⎰x πx x πx x x πdx x πdx x F Xx当1<x 时:10120)(11121=+-+=⎰⎰⎰--∞-xdx dx x πdx x F故分布函数为:⎪⎩⎪⎨⎧<≤≤-++--<=x x x πx x πx x F 111121arcsin 11110)(2解:(2)⎰∞-=≤=xdt t f x X P x F )()()(⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰=+-++=<--=-++=≤≤=+=<≤==<∞-∞-∞-∞-122121120010)2(0)(,2122)2(0)(,2120)(,1000)(,0xxxxdt dt t dt t dt x F x xx dt t dt t dt x F x x dt t dt x F x dt x F x 时当时当时当时当故分布函数为⎪⎪⎪⎩⎪⎪⎪⎨⎧<≤≤--<≤<=xx x x x x x x F 212112210200)(22(2)中的f (x )与F (x )的图形如下f (x )(Maxwell)分布,其概率密度为()220xbAx e xf x-⎧⎪ , >=⎨,⎪⎩其它其中2b m kT=,k为Boltzmann常数,T为绝对温度,m是分子的质量.试确定常数A.解: ①()1x dx+∞-∞=⎰即()22xbf x dx Ax e dx-+∞+∞-∞=⎰⎰222xbAb xxe db-+∞⎛⎫=--⎪⎝⎭⎰22200()|222x x xb b bAb Ab Abxd e xe e dx---+∞+∞+∞=-=-+⎰⎰2212002xbAbe dx d x--+∞+∞⎤==⎥⎦⎰1122Ab==221122uduπ+∞-⎛⎫=⎪⎪⎝⎭⎰A∴=②当0t<时,()00tTF t dt-∆=⋅=⎰当0t≥时,()()()2411241xt tT TF t f x dt F t e dt--∞=⋅==⎰⎰2411te-=-()2410,01,0tTtF te t-<⎧⎪∴=⎨⎪- ≥⎩{}{}{}()()501001005010050P T P T P T F F∴<<=<-≤=-50100e e--=-或{}()1005050100P T f t dt<<=⎰50100100241241241501241te dt e e---==-⎰xF (x)923、某种型号的电子的寿命X (以小时计)具有以下的概率密度:⎪⎩⎪⎨⎧>=其它010001000)(2x x x f现有一大批此种管子(设各电子管损坏与否相互独立).任取5只,问其中至少有2只寿命大于1500小时的概率是多少解:一个电子管寿命大于1500小时的概率为32)321(1)1(1000110001)1500(1)1500(15001000150010002=--=⎭⎬⎫⎩⎨⎧--=-=≤-=>⎰x dx x X P X P令Y 表示“任取5只此种电子管中寿命大于1500小时的个数”.则)32,5(~B Y ,{}24323224311132511)31()32()31(1)1()0(1)2(1)2(54155=-=⨯+-=⎭⎬⎫⎩⎨⎧⋅⋅+-==+=-=<-=≥C Y P Y P Y P Y P24、设顾客在某银行的窗口等待服务的时间X (以分计)服从指数分布,其概率密度为:⎪⎩⎪⎨⎧>=-其它,00,51)(5x e x F xX某顾客在窗口等待服务,若超过10分钟他就离开.他一个月要到银行5次.以Y 表示一个月内他未等到服务而离开窗口的次数,写出Y 的分布律.并求P (Y ≥1).解:该顾客“一次等待服务未成而离去”的概率为21051051051)()10(-∞+-∞+-∞+=-===>⎰⎰e edx edx x f X P xx X因此5,4,3,2,1(,)1(5)().,5(~5222=-⎪⎭⎫ ⎝⎛==----k e e k k Y P e B Y kk 即.5167.04833.018677.01)1353363.01(1)389.711(1)1(1)0(1)1(1)1(55552=-=-=--=--=--==-=<-=≥-e Y P Y P Y P 25、设K 在(0,5)上服从均匀分布,求方程02442=+++K xK x 有实根的概率∵K 的分布密度为:⎪⎩⎪⎨⎧<<-=其他50051)(K K f要方程有根,就是要K 满足(4K )2-4×4× (K+2)≥0. 解不等式,得K ≥2时,方程有实根. ∴53051)()2(5522=+==≥⎰⎰⎰∞+∞+dx dx dx x f K P 26、设X ~N ()(1)求P (2<X ≤5),P (-4)<X ≤10),P {|X|>2},P (X>3) ∵ 若X ~N (μ,σ2),则P (α<X ≤β)=φ-⎪⎭⎫ ⎝⎛-σμβφ⎪⎭⎫ ⎝⎛-σμα∴P (2<X ≤5) =φ-⎪⎭⎫ ⎝⎛-235φ⎪⎭⎫ ⎝⎛-232=φ(1)-φ(- =-=P (-4<X ≤10) =φ-⎪⎭⎫⎝⎛-2310φ⎪⎭⎫ ⎝⎛--234=φ-φ(-=-=P (|X |>2)=1-P (|X |<2)= 1-P (-2< P <2 )=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--Φ-⎪⎭⎫ ⎝⎛-Φ-2322321 =1-φ(- +φ(- =1-+=P (X >3)=1-P (X ≤3)=1-φ⎪⎭⎫⎝⎛-233=1-= (2)决定C 使得P (X > C )=P (X ≤C )∵ P (X > C )=1-P (X ≤C )= P (X ≤C ) 得 P (X ≤C )=21=又P (X ≤C )=φ023,5.023=-=⎪⎭⎫⎝⎛-C C 查表可得∴ C =327、某地区18岁的女青年的血压(收缩区,以mm-Hg 计)服从)12,110(2N 在该地区任选一18岁女青年,测量她的血压X .求(1)P (X ≤105),P (100<X ≤120). (2)确定最小的X 使P (X>x ) ≤ .解:3384.06616.01)4167.0(1)4167.0()12110105()105()1(=-=Φ-=-Φ=-Φ=≤X P 5952.017976.021)8333.0(21)65(2)65()65()12110100()12110120()120100(=-⨯=-Φ=-Φ=-Φ-Φ=-Φ--Φ=≤<X P.74.129.74.12974.19110.645.112110.95.0)12110(05.0)12110(1)(1)()2(==+≥⇒≥-≥-Φ⇒≤-Φ-=≤-=>X x x x x x X P x X P 故最小的查表得28、由某机器生产的螺栓长度(cm )服从参数为μ=,σ=的正态分布.规定长度在范围±内为合格品,求一螺栓为不合格的概率是多少设螺栓长度为X P {X 不属于-, + =1-P -<X <+=1-⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡--Φ-⎥⎦⎤⎢⎣⎡-+Φ06.005.10)12.005.10(06.005.10)12.005.10( =1-{φ(2)-φ(-2)}=1-{-} =29、一工厂生产的电子管的寿命X (以小时计)服从参数为μ=160,σ(未知)的正态分布,若要求P (120<X ≤200==,允许σ最大为多少∵ P (120<X ≤200)=80.04040160120160200=⎪⎭⎫ ⎝⎛-Φ-⎪⎭⎫ ⎝⎛Φ=⎪⎭⎫ ⎝⎛-Φ-⎪⎭⎫⎝⎛-Φσσσσ又对标准正态分布有φ(-x )=1-φ(x )∴ 上式变为80.040140≥⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛Φ--⎪⎭⎫ ⎝⎛Φσσ 解出9.040:40≥⎪⎭⎫ ⎝⎛Φ⎪⎭⎫ ⎝⎛Φσσ便得 再查表,得25.31281.140281.140=≤≥σσ30、解:[]{}{}{}223120~(120,2) ~(0,1)2P 118,122P 1181222P 12(10.8413)0.31745(1)0.32042V V N X N V V V X p p -=∉=<⋃>=->=-=⎛⎫∴-= ⎪⎝⎭则p=31、解:0 ,0()0.20.8/30 ,0301 ,30x F x x x x <⎧⎪=+≤<⎨⎪≥⎩32、解:[]()0,()0,01()(1)()0()(1)()()(1)()(1)1f xg x a af x a g x af x a g x dx a f x dx a g x dx a a ∞∞∞-∞-∞-∞≥≥<<∴+-≥+-=+-=+-=⎰⎰⎰且所以()(1)()af x a g x +-为概率密度函数 33、设随机变量X 的分布律为: X :-2, -1, 0, 1, 3P :51,61, 51, 151,3011求Y=X 2的分布律 ∵ Y=X 2:(-2)2 (-1)2 (0)2(1)2(3)2 P : 516151 1513011 再把X 2的取值相同的合并,并按从小到大排列,就得函数Y 的分布律为:∴ Y : 0 1 4 9P : 5115161+ 51301134、设随机变量X 在(0,1)上服从均匀分布 (1)求Y=e X 的分布密度 ∵ X 的分布密度为:⎩⎨⎧<<=为其他x x x f 0101)(Y=g (X ) =e X 是单调增函数 又 X=h (Y )=lnY ,反函数存在 且 α = min [g (0), g (1)]=min (1, e )=1 =βmax [g (0), g (1)]=max (1, e )= e∴ Y 的分布密度为:⎪⎩⎪⎨⎧<<⋅=⋅=为其他y e y yy h y h f y ψ0111|)('|)]([)((2)求Y=-2lnX 的概率密度.∵ Y= g (X )=-2lnX 是单调减函数又 2)(Y e Y h X -== 反函数存在. 且 α = min [g (0), g (1)]=min (+∞, 0 )=0 β=max [g (0), g (1)]=max (+∞, 0 )= +∞∴ Y 的分布密度为:⎪⎩⎪⎨⎧+∞<<=-⋅=⋅=--为其他y y e ey h y h f y ψy y 0021211|)('|)]([)(2235、设X ~N (0,1) (1)求Y=e X 的概率密度 ∵ X 的概率密度是+∞<<∞-=-x e πx f x ,21)(22Y= g (X )=e X 是单调增函数 又 X= h (Y ) = lnY 反函数存在 且 α = min [g (-∞), g (+∞)]=min (0, +∞)=0 β = max [g (-∞), g (+∞)]= max (0, +∞)= +∞ ∴ Y 的分布密度为:⎪⎩⎪⎨⎧+∞<<⋅=⋅=-为其他y y y e πy h y h f y ψy 00121|)('|)]([)(2)(ln 2 (2)求Y=2X 2+1的概率密度.在这里,Y=2X 2+1在(+∞,-∞)不是单调函数,没有一般的结论可用. 设Y 的分布函数是F Y (y ), 则 F Y ( y )=P (Y ≤y )=P (2X 2+1≤y ) =⎪⎪⎭⎫⎝⎛-≤≤--2121y X y P 当y<1时:F Y ( y )=0当y ≥1时:⎰----=⎪⎪⎭⎫ ⎝⎛-≤≤--=212122212121)(y y x y dx e πy X y P y F故Y 的分布密度ψ( y )是:当y ≤1时:ψ( y )= [F Y ( y )]' = (0)' =0当y>1时,ψ( y )= [F Y ( y )]' ='⎪⎪⎭⎫⎝⎛⎰----21212221y y x dx eπ=41)1(21---y ey π(3)求Y=| X |的概率密度. ∵ Y 的分布函数为 F Y ( y )=P (Y ≤y )=P ( | X |≤y ) 当y<0时,F Y ( y )=0当y ≥0时,F Y ( y )=P (| X |≤y )=P (-y ≤X ≤y )=⎰--y yx dx e π2221∴ Y 的概率密度为:当y ≤0时:ψ( y )= [F Y ( y )]' = (0)' =0当y>0时:ψ( y )= [F Y ( y )]' =2222221y y yx e πdx e π---='⎪⎪⎭⎫⎝⎛⎰36、(1)设随机变量X 的概率密度为f (x ),求Y = X 3的概率密度. ∵ Y=g (X )= X 3 是X 单调增函数, 又 X =h (Y ) =31Y ,反函数存在, 且 α = min [g (-∞), g (+∞)]=min (0, +∞)=-∞ β = max [g (-∞), g (+∞)]= max (0, +∞)= +∞ ∴ Y 的分布密度为:ψ( y )= f [h ( h )]·| h' ( y )| = 0,,31)(3231≠+∞<<∞-⋅-y y y y f 但0)0(=ψ(2)设随机变量X 服从参数为1的指数分布,求Y=X 2的概率密度.法一:∵ X 的分布密度为:⎩⎨⎧≤>=-00)(x x e x f xY =x 2是非单调函数当 x<0时 y =x 2 反函数是y x -= 当 x<0时 y =x 2y x =∴ Y ~ f Y (y ) = ))(())(('+'--y y f y y f -y y=⎪⎩⎪⎨⎧≤>=+--00,21210y y e ye yyy法二:)()()()()(~y X P y X P y X y P y Y P y Y F Y -≤-≤=≤<-=≤=⎪⎩⎪⎨⎧≤>-=+--⎰,00,100y y e dx e y y x∴ Y ~ f Y (y ) =⎪⎩⎪⎨⎧≤>-.0,0.0,21y y e y y37、设X 的概率密度为⎪⎩⎪⎨⎧<<=为其他x πx πxx f 002)(2xOyy=x 2求Y =sin X 的概率密度. ∵ F Y ( y )=P (Y ≤y ) = P (sin X ≤y ) 当y<0时:F Y ( y )=0当0≤y ≤1时:F Y ( y ) = P (sin X ≤y ) = P (0≤X ≤arc sin y 或π-arc sin y ≤X ≤π)=⎰⎰-+πy πy dx πx dx πxarcsin 2arcsin 0222当1<y 时:F Y ( y )=1∴ Y 的概率密度ψ( y )为:y ≤0时,ψ( y )=[ F Y ( y )]' = (0 )' = 0 0<y <1时,ψ( y )=[ F Y ( y )]' ='⎪⎭⎫⎝⎛+⎰⎰-πy πydx πx dx πxarcsin 2arcsin 0222=212yπ-1≤y 时,ψ( y )=[ F Y ( y )]' = )1(' = 038、设电流I 是一个随机变量,它均匀分布在9安11安之间.若此电流通过2欧的电阻,在其上消耗22.W I =求W 的概率密度.解:I 在()9,11上服从均匀分布I ∴的概率密度为:()1,1120,q x f x ⎧ <<⎪=⎨⎪ ⎩其它22W I =的取值为162242W <<分布函数 (){}{}2222w w F w P W w P I w P I ⎧⎫=≤=≤=≤⎨⎬⎩⎭()q P Q i f x dx ⎧⎪=<≤=⎨⎪⎩12q q ⎫==⎪⎪⎭()()',1622420,w w w f w F w <<∴== ⎩其它 39、某物体的温度T (o F )是一个随机变量,且有T ~N (,2),试求θ(℃)的概率密度.[已知)32(95-=T θ]法一:∵ T 的概率密度为+∞<<∞-=⨯--t et f t ,221)(22)6.98(2π又 )32(95)(-==T T g θ 是单调增函数. 3259)(+==θθh T 反函数存在.且 α = min [g (-∞), g (+∞)]=min (-∞, +∞)=-∞ β = max [g (-∞), g (+∞)]= max (-∞, +∞)= +∞ ∴ θ的概率密度ψ(θ)为59221|)('|)]([)(4)6.983259(2⋅=⋅=-+-θeπθh θh f θψ +∞<<∞-=--θeπθ,109100)37(812法二:根据定理:若X ~N (α1, σ1),则Y=aX+b ~N (aα1+b, a 2 σ2 ) 由于T ~N (, 2)故 ⎥⎥⎦⎤⎢⎢⎣⎡⨯⎪⎭⎫ ⎝⎛=⎥⎥⎦⎤⎢⎢⎣⎡⨯⎪⎭⎫⎝⎛-⨯-=295,9333295,91606.9895~91609522N N T θ故θ的概率密度为:+∞<<∞-==--⨯⎪⎭⎫ ⎝⎛⨯⎪⎭⎫⎝⎛--θππθψθθ,10929521)(100)37(8129529333222ee。
新教材高中数学习题课二随机变量及其分布新人教A版选择性必修第三册

习题课(二) 随机变量及其分布一、选择题1.已知事件A 发生时,事件B 一定发生,P (A )=13P (B ),则P (A |B )等于( )A.16 B.14 C.13D.12解析:选C 因为P (AB )=P (A )=13P (B ),所以P (A |B )=P AB P B =13.2.甲击中目标的概率是12,如果击中赢10分,否则输11分,用X 表示他的得分,计算X 的均值为( )A .0.5分B .-0.5分C .1分D .5分解析:选B E (X )=10×12+(-11)×12=-0.5.3.已知离散型随机变量ξ的概率分布列如下:ξ 1 3 5 P0.5m0.2则数学期望E (ξ)等于( A .1 B .0.6 C .2+3mD .2.4解析:选D 由题意得m =1-0.5-0.2=0.3, 所以E (ξ)=1×0.5+3×0.3+5×0.2=2.4.4.已知随机变量X ~B ⎝ ⎛⎭⎪⎫6,12,则D (2X +1)等于( ) A .6 B .4 C .3D .9解析:选A 因为D (2X +1)=D (X )×22=4D (X ),D (X )=6×12×⎝ ⎛⎭⎪⎫1-12=32,所以D (2X+1)=4×32=6.5.1号箱中有2个白球和4个红球,2号箱中有5个白球和3个红球,现随机地从1号箱中取出一球放入2号箱,然后从2号箱随机取出一球,则两次都取到红球的概率是( )A.1127 B.1124 C.827D.924解析:选C 设从1号箱取到红球为事件A ,从2号箱取到红球为事件B . 由题意,P (A )=42+4=23,P (B |A )=3+18+1=49, 所以P (AB )=P (B |A )·P (A )=23×49=827,所以两次都取到红球的概率为827.6.一台仪器每启动一次都随机地出现一个5位的二进制数A =(例如:若a 1=a 3=a 5=124A 的各位数中,已知a 1=1,a k (k =2,3,4,5)出现0的概率为13,出现1的概率为23,记X =a 1+a 2+a 3+a 4+a 5,现在仪器启动一次,则E (X )=( )A.83 B.113 C.89D.119解析:选B 法一:X 的所有可能取值为1,2,3,4,5,P (X =1)=C 44⎝ ⎛⎭⎪⎫134⎝ ⎛⎭⎪⎫230=181, P (X =2)=C 34⎝ ⎛⎭⎪⎫133⎝ ⎛⎭⎪⎫231=881, P (X =3)=C 24⎝ ⎛⎭⎪⎫132⎝ ⎛⎭⎪⎫232=827, P (X =4)=C 14⎝ ⎛⎭⎪⎫131⎝ ⎛⎭⎪⎫233=3281, P (X =5)=C 04⎝ ⎛⎭⎪⎫130⎝ ⎛⎭⎪⎫234=1681, 所以E (X )=1×181+2×881+3×827+4×3281+5×1681=113.法二:由题意,X 的所有可能取值为1,2,3,4,5, 设Y =X -1,则Y 的所有可能取值为0,1,2,3,4,因此Y ~B ⎝ ⎛⎭⎪⎫4,23,所以E (Y )=4×23=83, 从而E (X )=E (Y +1)=E (Y )+1=83+1=113.二、填空题7.从1,2,3,4,5中任取2个不同的数,事件A =“取到的2个数之和为偶数”,事件B =“取到的2个数均为偶数”,则P (B |A )=________.解析:P (A )=C 23+C 22C 25=410=25,P (AB )=C 22C 25=110,由条件概率公式,得P (B |A )=P ABP A =11025=14. 答案:148.邮局工作人员整理邮件,从一个信箱中任取一封信,记一封信的质量为X (单位:克),如果P (X <10)=0.3,P (10≤X ≤30)=0.4,那么P (X >30)等于________.解析:根据随机变量的概率分布的性质, 可知P (X <10)+P (10≤X ≤30)+P (X >30)=1, 故P (X >30)=1-0.3-0.4=0.3. 答案:0.39.某种种子每粒发芽的概率都为0.9,现播种了1 000粒,对于没有发芽的种子,每粒需再补种2粒,补种的种子数记为X ,则X 的数学期望为________.解析:种子发芽率为0.9,不发芽率为0.1, 每粒种子发芽与否相互独立,故设没有发芽的种子数为ξ,则ξ~B (1 000,0.1),∴E (ξ)=1 000×0.1=100,故需补种的种子数X 的期望为2E (ξ)=200. 答案: 200 三、解答题10.某一射手射击所得环数X 的分布列如下:X 4 5 6 7 8 9 10 P0.020.040.060.09m0.290.22(1)求m (2)求此射手“射击一次命中的环数≥7”的概率.解:(1)由分布列的性质得m =1-(0.02+0.04+0.06+0.09+0.29+0.22)=0.28. (2)P (射击一次命中的环数≥7)=0.09+0.28+0.29+0.22=0.88.11.随机抽取某中学高一年级若干名学生的一次数学统测成绩,得到样本,并进行统计,已知分组区间和频数是[50,60),2;[60, 70),7;[70,80),10;[80,90),x ;[90,100],2,其频率分布直方图受到破坏,可见部分如图所示,据此解答如下问题.(1)求样本容量及x 的值;(2)从成绩不低于80分的学生中随机选取2人,记2人中成绩不低于90分的人数为ξ,求ξ的数学期望.解:(1)由题意,得分数在[50,60)内的频数为2, 频率为0.008×10=0.08, 所以样本容量n =20.08=25,x =25-(2+7+10+2)=4.(2)成绩不低于80分的人数为4+2=6,成绩不低于90分的人数为2, 所以ξ的所有可能取值为0,1,2,因为P (ξ=0)=C 24C 26=25,P (ξ=1)=C 14C 12C 26=815,P (ξ=2)=C 22C 26=115,所以ξ的分布列为ξ 0 1 2 P25815115所以ξ的数学期望E (ξ)=0×5+1×15+2×15=3.12.经调查统计,网民在网上光顾某淘宝小店,经过一番浏览后,对该店铺中的A ,B ,C 三种商品有购买意向.该淘宝小店推出买一种送5元优惠券的活动.已知某网民购买A ,B ,C 商品的概率分别为23,p 1,p 2(p 1<p 2),至少购买一种的概率为2324,最多购买两种的概率为34.假设该网民是否购买这三种商品相互独立.(1)求该网民分别购买B ,C 两种商品的概率;(2)用随机变量X 表示该网民购买商品所享受的优惠券钱数,求X 的分布列和数学期望. 解:(1)由题意可知至少购买一种的概率为2324,所以一种都不买的概率为1-2324=124,即⎝ ⎛⎭⎪⎫1-23(1-p 1)(1-p 2)=124.① 又因为最多购买两种商品的概率为34,所以三种都买的概率为1-34=14,即23p 1p 2=14.② 联立①②,解得⎩⎪⎨⎪⎧ p 1=12,p 2=34或⎩⎪⎨⎪⎧p 1=34,p 2=12.因为p 1<p 2,所以某网民购买B ,C 两种商品的概率分别为p 1=12,p 2=34.(2)用随机变量X 表示该网民购买商品所享受的优惠券钱数,由题意可得X 的所有可能取值为0,5,10,15.则P (X =0)=124,P (X =5)=23×12×14+13×12×14+13×12×34=14, P (X =10)=23×12×14+23×12×34+13×12×34=1124, P (X =15)=23×12×34=14.所以X 的分布列为则E (X )=0×124+5×14+10×24+15×4=12.。
随机变量及其分布期末练习题及答案

随机变量及其分布期末练习题及答案随机变量及其分布期末练习题及答案1.在事件A 发⽣的概率为p 的伯努利试验中,若以ξ记第r 次A 发⽣时的试验的次数,求ξ的分布。
[解] {}发⽣次试验次⽽第恰好出现了次试验中前A k r A k P k P 11-)(-==ξ),1,(,)1()1(11111 +=-=?-=-------r r k p p Cp p pC rk r r k r k r r k⼩结求离散型随机变量的分布律时,⾸先应该搞清随机变量取可能值时所表⽰的随机事件,然后确定其分布列。
为验证所求分布是否正确,通常可计算⼀下所求得的“分布列”之和是否为1,若不是,则结果⼀定是错误的。
2.设随机变量X 的分布函数为>≤≤<=.1,1;10.0,1)(2x x Ax x x F求(1)A 的值;(2)X 落在)21,1(-及)2,31(内的概率;(3)X 的概率密度函数。
[解] (1)有分布函数的右连续性,在1=x 点处有1)01()1(=+==F A F ,即1=A (2)由分布函数的性质知,41)1()21())21,1((=--=-∈F F X P ;98311)31()2())2,31((2=??-=-=-∈F F X P ;(3)由于)(x F 最多除1=x 和0点外处处可导,且在1,0=x 处连续,若取≤≤><=.10,2;10,0)(x x x x x f 或则0)(≥x f ,且对⼀切x 有?∞-=xdt t f x F )()(,从⽽)(x f 为随机变量X 的密度函数。
3.设),2(~2σN X ,且3.0)42(=<[解] 因为 )0(2)42(3.0Φ-??Φ=<<=σX P 所以 8.05.03.02=+=??Φσ于是 2.0212202)0(=??Φ-=??? ??-Φ=-<-=<σσσσX P X P4.⼀批鸡蛋,优良品种占三分之⼆,⼀般品种占三分之⼀,优良品种蛋重(单位:克))5,55(~21N X ,⼀般品种蛋重)5,45(~22N X 。
概率论与数理统计+第二章+随机变量及其分布+练习题答案

滨州学院《概率论与数理统计》(公共课)练习题第二章 随机变量及其分布一、填空题 10.712设一本书的各页的印刷错误个数X 服从泊松分布律.已知有一个和两个印刷错误的页数相同,则随意抽查的4页中无印刷错误的概率p = 0.0003 .3⎪⎪⎩⎪⎪⎨⎧≥<≤<≤<=≤=.若,;,若;,若;,若 3 1 324544 21 51 1 0 }{)(x x x x x X x F P 4{}12525.032)05.0()02(25.0=-=---=<≤F F X P . 例2.11设随机变量X 的概率密度函数为⎪⎩⎪⎨⎧≤≤≤≤=其它06310)(9231x x x f ;若k 使得32)(=≥k X P ,则k 的取值范围是 . 【[1,3]】例2.13 设X 服从二项分布),(p n B ,且已知)2()1(===X P X P ,)3(2)2(===X P X P ,则)4(=X P = . 【24310】 例2.14若随机变量X 服从正态分布)0)(,(2>σσμN ,且二次方程042=++X y y 无实根的概率是21,则=μ . 【4】2.22 (1)24310;(2)4;(3)2922;(4)649;(5))0(2)1(ln 221)(+∞<<--=y y Y I e y y f π〖选择题〗1 [ C ]2 [ C ]3 [ C ]例2.1 【C 】例2.2 【A 】 例2.3 【B 】例2.5 【A 】例2.16设随机变量X ,Y 相互独立均服从正态分布)4,1(N , 若概率21)1(=<-bY aX P ,则(A)1,2==b a(B) 2,1==b a(C) 1,2=-=b a(D) 2,1-==b a 【A 】例2.18 设X 为随机变量, 若矩阵⎪⎪⎪⎭⎫ ⎝⎛--=01020232X A 的特征根全为实数的概率为0.5, 则(A)X 服从区间[0,2]上的均匀分布 (B) X 服从二项分布B(2, 0.5) (C) X 服从参数为1的指数分布 (D) X 服从标准正态分布 【A 】2.23 (1)A ;(2)B ;(3)C ;(4)C ;(5)B 解答题〗 〖解答题〗例2.30解 不妨假设正立方体容器的边长为1.引进事件:{}0==X A ,即事件A 表示“小孔出现在容器的下底面”.由于小孔出现在正立方体的6个侧面是等可能的,易见 61)(=A P .从而,{}61===)(0A X P P.对于任意x <0,显然()=x F 0;而()610=F .由于小孔出现的部位是随机性,可见对于任意)75.0,0(∈x ,有(){}{}.641646100xx x X X x F +=+=≤<+≤=P P 该式中4x 表示容器的四个侧面x 以下的总面积,而容器6个侧面的总面积为6.对于任意x ≥0.75,显然()1=x F.于是,最后得()⎪⎪⎩⎪⎪⎨⎧≥<≤+<=.若若若 75.0 , 1 , 75.00 , 641, 0 , 0 x x x x x F例2.31(分布函数)解 因X 服从指数分布,且21==λX E (百小时),故分布参数λ=0.5,故X的分布函数为()⎩⎨⎧≤>-=-.,若;,若0 0 0 e 15.0x x x G x 易见,{}1.0min ,X Y=.设)(y F 是Y 的分布函数,则对于y <0,)(y F =0;对于y >0.1,)(y F =1;对于1.00≤≤y ,有{}{}.,y y G y X y X y Y y F 5.0e 1)(}1.0 min{}{)(--==≤=≤=≤=P P P 于是,{}.10 min ,X Y=的分布函数为()⎪⎩⎪⎨⎧≥<≤-<=-.,若,若,,若 1.0 1 , 1.00 e 1 0 0 5.0y y y y F y例2.33解 试验次数X 是一随机变量.为求X 的概率分布,引进事件:j B ={第j 次试验成功}(j =1,2,…,n ).显然P(j B ) = p .而由于试验的独立性,知事件n B B B ,,,21 …相互独立.设试验进行到成功或n 次为止,则X 的可能值为1,2,…,n 且1}1{B X==;对于2≤k ≤n-1,.;;;,111111112111)(}{ )(}1{)12()(}{}{ }{------======-≤≤=======k n k k k n k k q B B n X p B X n k pq B B B k X B B B n X B B B k X P P P P P P于是,X 的概率分布为有限几何分布:⎪⎪⎭⎫ ⎝⎛---1121321~n n q pq pq pq pn n X . 例2.35解 以ν表示抽到的30件产品中不合格品的件数,则ν服从参数为(30,0.02)的二项分布:.;;4545.0}0{1}1{3340.002.098.030}1{5455.098.0}0{2930==-=≥=⨯⨯=====ννννP P P P1) 不合格品不少于两件的概率.1205.002.098.03098.01}1{}0{1}2{2930=⨯⨯--==-=-=≥=ννναP P P2) 在已经发现一件不合格品的条件下,不合格品不少于两件的条件概率{}.2652.0}1{}2{}1{}2,1{12≈≥≥=≥≥≥=≥≥=νννννννβP P P P P 例2.36解 由条件知每台设备出现故障的概率为0.08.以ν表示10台设备中同时出现故障的台数,则ν服从参数为(10,0.08)的二项分布.需要安排的值班人数k 应满足条件:95.0}{≥≤k νP .需要对不同的k 进行试算.首先,设k =1和k =2,相应得{}{}{}{}{}{}.,95.09599.008.092.008.092.01092.021281.008.092.01092.010128210910910≥≈⨯⨯+⨯⨯+==+≤=≤≈⨯⨯+==+==≤C ννννννP P P P P P因此,至少需要安排2个人值班.例2.37解 设X ——一周5个工作日停用的天数;Y ——一周所创利润.X 服从参数为(5,0.2)的二项分布.因此,有.,,,057.0205.0410.0328.01}3{205.08.02.010}2{410.08.02.05}1{328.08.0}0{3245=---=≥=⨯⨯===⨯⨯=====X X X X P P P P一周所创利润Y 是X 的函数:⎪⎪⎩⎪⎪⎨⎧≥-====3.,若2,,若1,,若,,若X X X X Y 2 2 7 0 10 ⎪⎪⎭⎫ ⎝⎛-328.0410.0205.0057.010722~Y . 例2.38(二项分布)解 设n ——至少出现一件不合格品所要生产产品的件数,则n 件产品中不合格品的件数n ν服从参数为(n ,0.01)的二项分布;按题意,n 应满足条件., 0729.29899.0ln 05.0ln 95.099.01}0{1}1{≈≥≥-==-=≥n nn n ννP P 于是,为至少出现一件不合格品的概率超过95%,最少需要298.0729×3≈895分,将近14小时55分.例3.41解 由条件知X +Y 是一日内到过该商店的顾客的人数,服从参数为λ的泊松分布.设X ——一日内到过该商店的顾客中购货的人数.由条件知,在一日内有n 个顾客到过该商店的条件下,购货人数的条件概率分布为{}().;),2,1,0(1m n m p p C n Y X m X mn m m n ≥=-==+=- P由全概率公式可见,对于m =0,1,2,…,有{}{}{}()[]()()()()[]()()[]()()().p mp mk km m n mn m mn nmn mm nmn n mn mm nmn m p m p p k m p p m n m p n p p C n p p Cn Y X n Y X m Xm X λλλλλλλλλλλλλλλ---∞=-∞=--∞=--∞=--∞===-=--=-=⎥⎦⎤⎢⎣⎡-==+=+===∑∑∑∑∑e ! e e ! 1!1e!1!1e!!1ee ! 110P P P于是,一日内到过该商店的顾客中购货的人数X 服从参数为p λ的泊松分布.同理,Y 服从参数为)1(p -λ的泊松分布.例2.44 解 以()t ν表示t =90天内售出的电冰箱台数.可以假设()t ν服从参数为t λ的泊松分布.由条件知()λν77E ==56,从而λ=8(台).这样,()t ν服从参数为t λ=8t 的泊松分布: (){}()() ,2,1,0 e !88===-k k t k t tkνP .随机变量X 的可能值为自然数m =0,1,2,….记t a λ=.由全概率公式,有{}(){}(){}()()()()()()()(), pa m pa a a m k k a m m n mn ammn a n m n m m nmn m pa m pa k qa m pa m n qa m pan a q p C n a n a m X m X ---∞=-∞=--∞=--∞====-=======∑∑∑∑e !e e ! ! e!! e ! e ! 0ννP P P 其中6.390805.0=⨯⨯==t p pa λ.因此返修件数X 服从参数为3.6的泊松分布:{}() ,2,1,0 e !6.36.3===-m m m X m P .例2.47解 由条件知{}{}{}{},⎪⎭⎫ ⎝⎛--≈⎥⎦⎤⎢⎣⎡--⎪⎭⎫ ⎝⎛--=⎭⎬⎫⎩⎨⎧-≤-≤--=≤≤-=≤-≤--=≤--=>-=310821)36(310821310823108310812011 1 025.0a a a X a X a a X a a a X a a X ΦΦΦP P P P P其中()x Φ是标准正态分布函数.由熟知的事实()975.096.1=Φ,可见.;;94.5696.131082 0.975031082≈≈-≈⎪⎭⎫⎝⎛-a a a Φ 例2.48 解 由条件知()210,0~N X.设ν为100次独立重复测量中事件{}6.19 >X 出现的次数,则{}05.096.1106.19 =⎭⎬⎫⎩⎨⎧>=>=X X p P P .易见ν服从参数为(100 , 0.05)的二项分布,近似服从参数为5的泊松分布.因此{}{}{}{}{}().87.05.125115.125105.095.0299100 05.095.010095.012101313555529899100≈++-=---≈⨯⨯⨯-⨯⨯--==-=-=-=<-=≥=----e e e e ννννναP P P P P 〖证明题〗例2.52(分布函数)证明 只需验证)()()(21x bF x aF x F +=满足分布函数的三条基本性质.由条件知a 和b 非负且a +b =1.由于)(1x F 和)(2x F 都是分布函数,可见对于任意,有1)()()(021=+≤+=≤b a x bF x aF x F对于任意实数21x x <,由于)2,1)(()(21=≤i x F x F i i ,可见,)()()()()()(2222112111x F x bF x aF x bF x aF x F =+≤+=即)(x F 单调不减.由)(1x F 和)(2x F 的右连续性,可见)(x F 也右连续.最后,.;1)(lim )(lim )(lim 0)(lim )(lim )(lim 2121=+==+=+∞→+∞→+∞→-∞→-∞→-∞→x F b x F a x F x F b x F a x F x x x x x x于是)()()(21x bF x aF x F +=也是分布函数.例2.53(分布函数) 证明 指数分布函数为)0(e 1)(≥-=-x x F x λ设}{P )(y Y y G ≤=为Y=)(X F 的分布函数.由于分布函数)(x F 的值域为(0,1),可见当0≤y时0)(=y G ;当1≥y 时1)(=y G .设10<<y ,有.y y F y X y y Y y G X =⎪⎭⎫⎝⎛--=⎭⎬⎫⎩⎨⎧--≤=≤-=≤=-)1ln(1)1ln(1}e 1{}{)(λλλP P P 于是,)(y G 是区间(0,1)上的均匀分布函数,从而Y=例2.4 【π2=C ;5)arctan 2(πe】例2.6 连续型随机变量X 的分布函数为:x B A x F arctan )(+=,∞<<∞-x试求:(1)常数A 、B ;(2))11(<<-X P ;(3)随机变量X 的概率密度.【(1)π1,21==B A ;(2)21;(3))1(12x +π】 例2.7 设随机变量X 具有对称的密度函数,即)()(x f x f =-,证明对任意的0>a ,有(1)⎰-=-=-adx x f a F a F 0)(21)(1)((2)1)(2)|(|-=<a F a X P (3) ))(1(2)|(|a F a X P -=>问题3: 已知实际背景, 求随机变量的分布律与分布函数(或密度函数)例2.8 一袋中装有4个球,球上分别记有号码1,2,3,4。
随机变量及其分布方法总结经典习题及解答

随机变量及其分布方法总结经典习题及解答一、离散型随机变量及其分布列1、离散型随机变量:对于随机变量可能取的值,可以按一定次序一一列出,这样的随机变量叫做离散型随机变量。
常用大写英文字母X、Y等或希腊字母ξ、η等表示。
2、分布列:设离散型随机变量ξ可能取得值为:x1,x2,…,x3,…,ξ取每一个值xi(i=1,2,…)的概率为,则称表ξx1x2…xi…PP1P2…Pi…为随机变量ξ的分布列3、分布列的两个性质:⑴Pi≥0,i=1,2,… ⑵P1+P2+…=1、常用性质来判断所求随机变量的分布列是否正确!二、热点考点题型考点一: 离散型随机变量分布列的性质1、随机变量ξ的概率分布规律为P(ξ=n)=(n=1,2,3,4),其中a是常数,则P(<ξ<)的值为A、B、C、D、答案:D考点二:离散型随机变量及其分布列的计算2、有六节电池,其中有2只没电,4只有电,每次随机抽取一个测试,不放回,直至分清楚有电没电为止,所要测试的次数为随机变量,求的分布列。
解:由题知2,3,4,5∵ 表示前2只测试均为没电,∴ ∵ 表示前两次中一好一坏,第三次为坏,∴ ∵ 表示前四只均为好,或前三只中一坏二好,第四个为坏,∴ ∵ 表示前四只三好一坏,第五只为坏或前四只三好一坏第五只为好∴ ∴ 分布列为2345P三、条件概率、事件的独立性、独立重复试验、二项分布与超几何分布1、条件概率:称为在事件A发生的条件下,事件B发生的概率。
2、相互独立事件:如果事件A(或B)是否发生对事件B (或A)发生的概率没有影响,这样的两个事件叫做相互独立事件。
①如果事件A、B是相互独立事件,那么,A与、与B、与都是相互独立事件②两个相互独立事件同时发生的概率,等于每个事件发生的概率的积。
我们把两个事件A、B同时发生记作AB,则有P(AB)= P(A)P(B)推广:如果事件A1,A2,…An相互独立,那么这n个事件同时发生的概率,等于每个事件发生的概率的积。
随机变量及其分布习题解答

随机变量及其分布习题解答第2章随机变量及其分布习题解答⼀.选择题1.若定义分布函数(){}F x P X x =≤,则函数()F x 是某⼀随机变量X 的分布函数的充要条件是( D ).A .0()1F x ≤≤.B .0()1F x ≤≤,且()0,()1F F -∞=+∞=.C .()F x 单调不减,且()0,()1F F -∞=+∞=.D .()F x 单调不减,函数()F x 右连续,且()0,()1F F -∞=+∞=.2.函数()0 212021 0x F x x x <-=-≤A .某⼀离散型随机变量X 的分布函数.B .某⼀连续型随机变量X 的分布函数.C .既不是连续型也不是离散型随机变量的分布函数.D .不可能为某⼀随机变量的分布函数.3.函数()0 0sin 01 x F x x x x ππ=≤( D ).A .是某⼀离散型随机变量的分布函数.B .是某⼀连续型随机变量的分布函数.C .既不是连续型也不是离散型随机变量的分布函数.D .不可能为某⼀随机变量的分布函数.4.设X 的分布函数为1()F x ,Y 的分布函数为2()F x ,⽽12()()()F x aF x bF x =-是某随机变量Z 的分布函数,则, a b 可取( A ).A .32, 55a b ==-.B .2 3a b ==.C .13 , 22a b =-=. D .13 , 22a b ==-. 5.设X 的分布律为⽽(){}F x P X x =≤,则F =( A ).A .0.6.C .0.25.D .0.6.设连续型变量X 的概率密度为()p x ,分布函数为()F x ,则对于任意x 值有( A ).A .(0)0P X ==.B .()()F x p x '=.C .()()P X x p x ==.D .()()P X x F x ==.7.任⼀个连续型的随机变量X 的概率密度为()p x ,则()p x 必满⾜( C ).A .0()1p x ≤≤.B .单调不减.C .()1p x dx +∞-∞=?.D .lim ()1x p x →+∞=.8.为使 x 1()0 1p x x <=≥?成为某个随机变量X 的概率密度,则c 应满⾜( B ).A .1+∞=?.B .11-=?.C .11=.11+∞-=?.9.设随机变量X 的概率密度为2()x p x Ae -=,则A = ( D ).A .2.B .1.C .12.D .14.10.设X 的概率密度函数为1() ,2xp x e x -=-∞<<+∞,⼜{}()F x P X x =≤,则0x <时,()F x =( D ).A .112-e x. B .112xe --. C .12xe -. D .12e x .11.设220()00x cx e x p x cx -??>=??≤?是随机变量X 的概率密度,则常数c ( B ).B .只能是任意正常数.C .仅取1.D .仅取- 1. 12.设连续型随机变量X 的分布函数为()F x ,则112Y X =-分布函数为( D ). A .(22)F y -. B .1(1)22y F -. C .2(22)F y -.D .1(22)F y --.13.设随机变量X 的概率密度为()p x ,12Y X =-,则Y 的分布密度为( A ).A .1122y p -?? ???. B .112y p -??- C .12y p -??-. D .2(12)p y -.14.设随机变量X 的密度函数()p x 是连续的偶函数(即()()p x p x =-),⽽()F x 是X 的分布函数,则对任意实数a 有( C ).A .()()F a F a =-.B .0()1()aF a p x dx -=-.C .01()()2aF a p x dx -=-? . D .()()F a F a -=.⼆.填空题15.欲使2103()103xx e x F x A e x -?-≥为某随机变量的分布函数,则要求x F x Axx x,则必有A =____1/36______.17.从装有4件合格品及1件次品的⼝袋中连取两次,每次取⼀件,取出后不放回,求取出次品数X 的分布律为{0}3/5,{1}2/5P X P X ==== .18.独⽴重复地掷⼀枚均匀硬币,直到出现正⾯为⽌,设X 表⽰⾸次出现正⾯的试验次数,则X的分布列{}P X k ==1111{},1,2,222k kP X k k -??==?== ?.19.设某离散型随机变量X 的分布列是{},1,2,,10kP X k k C===,则C =____55_____.20.设离散型随机变量X 的分布函数是(){}F x P X x =≤,⽤()F x 表⽰概率{}0P X x ==00()(0)F x F x --.21.设X 是连续型随机变量,则{3}P X ==___0____.22.设随机变量X 的分布函数为20,2()(2),231,3x F x x x x(2.54)P X <≤=(4)(2.5)0.75x e x F x e x -?≤??=??->??,则{}1P X <=11e --.24.设连续型随机变量X的分布函数为20()021x xF x x x≥?X 的概率密度()p x=00 ()x x ?≤≤??其它.25.设随机变量X 的分布密度为2(1),(0,1) ()0,(0,1)Ax x x p x x ?-∈=,则常数A =__12____.26.若X的概率密度为()p x ,则31Y X =+的概率密度()Y p y =1133y p -??.27.设电⼦管使⽤寿命的密度函数()2 1001000100x p x x x ?>?=??≤?(单位:⼩时),则在求(1){14}P X <≤;(2)X 的分布函数()F x .解:(1){14}{2}{3}{4}0.30.30.10.7P X P X P X P X <≤==+=+==++=(2)X 的分布函数()F x 为0,00.1,010.3,12()0.6,230.9,341,4x x x F x x x x≤<=≤≥?29. 设连续随机变量X 的概率密度,10(),010,||1c x x p x c x x x +-≤=-≤≤??>?试求: (1)常数c ; (2) 概率{||0.5}P X ≤;(3) X 的分布函数()F x . 解:(1)由01 11()()()21p x dx c x dx c x dx c +∞-∞-==++-=-?,得1c =(2){||0.5}{0.50.5}P X P X ≤=-≤≤00.50.5(1)(1)0.75x dx x dx -=++-=?(3)X 的分布函数为1010,1(1),10()(1)(1),011,1x xx t dt x F x t dt t dt x x --<-??+-≤21,1x x x x x x <-+-≤30.设顾客到某银⾏窗⼝等待服务的时间X (单位:分钟)的概率密度函数为5()50,0xe x p x x -?>?=??≤?某顾客在窗⼝等待,如超过10分钟,他就离开,求他离开的概率. 解:他离开的概率为/5 2101{10}5x P X e dx e +∞--≥==?31.已知随机变量X 的分布函数为()1,x 0211, 02241,2xe F x x x x ?=+≤,求其分布密度()p x .解:()1 021()0240 2xe x p x F x x x ?≥32. 设X 是离散型随机变量,其分布律为(1)求常数a ;(2)23Y X =+的分布律.解:(1)由0.330.10.21a a ++++=得0.1a = (2)由于所以,23Y X =+的分布律为33.设随机变量X 的密度函数为,0()0,0x X e x p x x λλ-?>=?≤?,0λ>,求XY e =的密度函数()Y p y .解:(1)XY e =的分布函数为()()(ln )0,0X XY F y y F y P e y P X y y >?=≤=≤=?≤?(2)XY e =的密度函数()Y p y 为ln 1,ln 0,1(ln )(ln ),01()()0,ln 00,00,10,0y X Y Y e y y p y y y y p y F y y y y y y λλλλ-+?>?'>?>'===?≤=?≤?≤≤。
(完整版)概率论第三章第四章习题及答案

第三章 多维随机变量及其分布
n
解:(1)P{X n} P{X n,Y m}
m0
n e14 (7.14)m (6.86)nm
m0
m!(n m)!
e14 n
n! (7.14)m (6.86)nm
n! m0 m!(n m)!
e14 (7.14 6.86)n 14n e14 , n 0,1,2,
返回主目录
第三章 多维随机变量及其分布
(3)P{Y m | X 20} C2m0 0.51m0.4920m , m 0,1,2, ,20.
P{Y m | X n} Cnm 0.51m0.49nm , m 0,1,2, , n
返回主目录
第三章 多维随机变量及其分布
11.设随机变量(X,Y)的联合概率密度为
0, FU (u) un ,
1,
u 0, 0 u 1,
u 1.
返回主目录
第四章 随机变量的数字特征
U 的密度函数为
nun1, x (0,1),
fU (u)
0,
其他.
0, FU (u) un ,
1,
u 0, 0 u 1,
u 1.
E(U )
ufU (u)du
e14 (7.14)m (6.86)nm m!(n m)!
e
1414n n!
Cnm
7.14 14
m
6.86 14
nm
Cnm 0.51m0.49nm , m 0,1,2, , n
P{X n,Y m} e14 (7.14)m (6.86)nm , m!(n m)!
m 0,1,2, , n; n 0,1,2, .
cxey ,0 x y ,
(完整版)概率论第二章随机变量及其分布答案

概率论与数理统计练习题系 专业 班 姓名 学号第二章 随机变量及其分布(一)一.选择题:1.设X 是离散型随机变量,以下可以作为X 的概率分布是 [ B ](A )1234111124816Xx x x x p (B ) 123411112488X x x x x p (C )1234111123412Xx x x x p(D ) 1234111123412X x x x x p -2.设随机变量ξ的分布列为 01230.10.30.40.2X p )(x F 为其分布函数,则)2(F =[ C ](A )0.2 (B )0.4 (C )0.8 (D )1 二、填空题:1.设随机变量X 的概率分布为0120.20.5X p a ,则a = 0.32.某产品15件,其中有次品2件。
现从中任取3件,则抽得次品数X 的概率分布为 P{X=0}=22/35;P{X=1}=12/35; P{X=2}=1/353.设射手每次击中目标的概率为0.7,连续射击10次,则击中目标次数X 的概率分布为 P{X=k}=k kkC -⨯10103.07.0,10,,0Λ=k 或X~B(10,0.7)三、计算题:1.同时掷两颗骰子,设随机变量X 为“两颗骰子点数之和”求: (1)X 的概率分布; (2)(3)P X ≤; (3)(12)P X >(1) P{X=2}= P{X=12}=1/36; P{X=3}= P{X=11}=1/18;P{X=4}= P{X=10}=1/12; P{X=5}= P{X=9}=1/9;P{X=6}= P{X=8}=5/36;P{X=7}=1/6(2) P{X=2}=1/36; P{X=3}=1/18 (3) P{X>12}=02.产品有一、二、三等品及废品四种,其中一、二、三等品及废品率分别为60%,10%,20%及10%,任取一个产品检查其质量,试用随机变量X 描述检查结果。
概率论解析答案习题解答

第二章 随机变量及其分布I 教学基本要求1、了解随机变量的概念以及它与事件的联系;2、理解随机变量的分布函数的概念与性质;理解离散型随机变量的分布列、连续型随机变量的密度函数及它们的性质;3、掌握几种常用的重要分布:两点分布、二项分布、泊松分布、均匀分布、指数分布、正态分布,且能熟练运用;4、会求简单随机变量函数的分布.II 习题解答A 组1、检查两个产品,用T 表示合格品,F 表示不合格品,则样本空间中的四个样本点为1(,)F F ω=、2(,)T F ω=、3(,)F T ω=、4(,)T T ω=以X 表示两个产品中的合格品数.(1) 写出X 与样本点之间的对应关系;(2) 若此产品的合格品率为p ,求(1)p X =? 解:(1) 10ω→、21ω→、31ω→、42ω→;(2) 12(1)(1)2(1)p X C p p p p ==-=-.2、下列函数是否是某个随机变量的分布函数?(1) 021()2021x F x x x <-⎧⎪⎪=-≤<⎨⎪≥⎪⎩; (2) 21()1F x x =+ ()x -∞<<+∞. 解:(1) 显然()F x 是单调不减函数;0()1F x ≤≤,且()0F -∞=、()1F +∞=;(0)()F x F x +=,故()F x 是某个随机变量的分布函数.(2) 由于()01F +∞=≠,故()F x 不是某个随机变量的分布函数. 3、设X 的分布函数为(1)0()00x A e x F x x -⎧-≥=⎨<⎩求常数A 及(13)p X <≤?解:由()1F +∞=和lim (1)xx A e A -→+∞-=得1A =;(13)(3)(1)(3)(1)p X p X p X F F <≤=≤-≤=- 3113(1)(1)e e e e ----=---=-.4、设随机变量X 的分布函数为200()0111x F x Ax x x ≤⎧⎪=<≤⎨⎪>⎩求常数A 及(0.50.8)p X <≤?解:由(10)(1)F F +=得1A =;(0.50.8)(0.8)(0.5)(0.8)(0.5)p X p X p X F F <≤=≤-≤=- 220.80.50.39=-=.5、设随机变量X 的分布列为()ap X k N==(1,2,,)k N =L 求常数a ?解:由11ii p+∞==∑得11Nk aN ==∑ 1a ⇒=.6、一批产品共有100个,其中有10个次品,求任意取出的5个产品中次品数的分布列? 解:设X 表示5个产品中的次品数,则X 是离散型随机变量,其所有可能取值为0、1、…、5,且0510905100(0)C C p X C ==、1410905100(1)C C p X C ==、2310905100(2)C C p X C ==、3210905100(3)C C p X C ==、4110905100(4)C C p X C ==、5010905100(5)C C p X C ==于是X 的分布列为510905100()k k C C p X k C -== (0,1,,5)k =L . 7、设10件产品中有2件次品,进行连续无放回抽样,直至取到正品为止,以X 表示抽样次数,求(1) X 的分布列; (2) X 的分布函数?解:(1) 由题意知X 是离散型随机变量,其所有可能取值为1、2、3,且84(1)105p X ===、288(2)10945p X ==⨯=、2181(3)109845p X ==⨯⨯=于是X(2) 由(1)可知的分布函数为014125()44234513x x F x x x <⎧⎪⎪≤<⎪=⎨⎪≤<⎪⎪≥⎩.8、设随机变量X 的分布函数为010.211()0.3120.52313x x F x x x x <-⎧⎪-≤<⎪⎪=≤<⎨⎪≤<⎪≥⎪⎩ 求X 的分布列?解:X 9、求在同一时刻(1) 恰有2个设备被使用的概率; (2) 至少有3个设备被使用的概率; (3) 至多有3个设备被使用的概率?解:设X 表示被同时使用的供水设备数,则~(5,0.1)X b (1) 恰有2个设备被使用的概率为2235(2)(0.1)(0.9)0.0729p X C ===;(2) 至少有3个设备被使用的概率为(3)(3)(4)(5)p X p X p X p X ≥==+=+=33244550555(0.1)(0.9)(0.1)(0.9)(0.1)(0.9)0.00856C C C =++=;(3) 至多有3个设备被使用的概率为(3)1(4)(5)p X p X p X ≤=-=-=44550551(0.1)(0.9)(0.1)(0.9)0.99954C C =--=.10、经验表明:预定餐厅座位而不来就餐的顾客比例为20%,如今餐厅有50个座位,但预定给了52位顾客,求到时顾客来到餐厅而没有座位的概率是多少?解:设X 表示预定的52位顾客中不来就餐的顾客数,则~(52,0.2)X b ,由于“顾客来到餐厅没有座位”等价于“52位顾客中至多有1位不来就餐”,于是所求概率为005211515252(1)(0)(1)(0.2)(0.8)(0.2)(0.8)p X p X p X C C ≤==+==+0.0001279=.11、设某城市在一周内发生交通事故的次数服从参数为的泊松分布,求 (1) 在一周内恰好发生2次交通事故的概率; (2) 在一周内至少发生1次交通事故的概率?解:设X 表示该城市一周内发生交通事故的次数,则~(0.3)X P (1) 在一周内恰好发生2次交通事故的概率20.30.3(2)0.03332!p X e -===;(2) 在一周内至少发生1次交通事故的概率00.30.3(1)1(0)10.2590!p X P X e -≥=-==-=.12、设X 服从泊松分布,已知(1)(2)p X p X ===,求(4)p X =? 解:由(1)(2)p X p X ===得22ee λλλλ--=2λ⇒=422(4)0.09024!p X e -⇒===.13、一批产品的不合格品率为,现从中任取40件进行检查,若发现两件或两件以上不合格品就拒收这批产品,分别用以下方法求拒收的概率:(1) 用二项分布作精确计算;(2) 用泊松分布作的似计算?解:设X 表示抽取的40件产品中的不合格品数,则~(40,0.02)X b (1) 拒收的概率为(2)1(0)(1)p X p X p X ≥=-=-=0040113940401(0.02)(0.98)(0.02)(0.98)0.1905C C =--=;(2) 由于400.020.8λ=⨯=,于是拒收的概率为(2)1(0)(1)p X p X p X ≥=-=-= 0.80.810.80.1912e e --≈--=.14、设随机变量X 的密度函数为201()0x x f x ≤≤⎧=⎨⎩其它求X 的分布函数?解:由()()xF x f t dt -∞=⎰得当0x <时()()00xxF x f t dt dt -∞-∞===⎰⎰当01x ≤≤时2200()()02|x xxF x f t dt dt tdt t x -∞-∞==+==⎰⎰⎰当1x >时0121001()()020|1x xF x f t dt dt tdt dt t -∞-∞==++==⎰⎰⎰⎰于是所求分布函数为200()0111x F x x x x <⎧⎪=≤≤⎨⎪>⎩. 15、设随机变量X 的密度函数为212(1)12()0x f x x⎧-≤≤⎪=⎨⎪⎩其它求X 的分布函数?解:由()()xF x f t dt -∞=⎰得当1x <时()()00xxF x f t dt dt -∞-∞===⎰⎰当12x ≤≤时1121111()()02(1)2()|2(2)xxx F x f t dt dt dt t x t t x-∞-∞==+-=+=+-⎰⎰⎰ 当2x >时122121211()()02(1)02()|1xx F x f t dt dt dt dt t t t-∞-∞==+-+=+=⎰⎰⎰⎰于是所求分布函数为011()2(2)1212x F x x x x x <⎧⎪⎪=+-≤≤⎨⎪>⎪⎩. 16、设随机变量X 的密度函数为cos ()220A x x f x ππ⎧-≤≤⎪=⎨⎪⎩其它求(1) 常数A ;(2) X 的分布函数;(3) (0)4p X π<≤?解:(1) 由()1f x dx +∞-∞=⎰得2222220cos 0sin |21dt A xdx dt A x A ππππππ-+∞--∞-++===⎰⎰⎰12A ⇒=; (2) 当2x π<-时()()00xxF x f t dt dt -∞-∞===⎰⎰当22x ππ-≤≤时2221111()()0cos sin |sin 2222x xxF x f t dt dt tdt t x πππ---∞-∞-==+==+⎰⎰⎰当2x π>时22222211()()0cos 0sin |122xx F x f t dt dt tdt dt t ππππππ---∞-∞-==++==⎰⎰⎰⎰ 于是所求分布函数为0211()sin 222212x F x x x x ππππ⎧<-⎪⎪⎪=+-≤≤⎨⎪⎪>⎪⎩;(3) (0)()(0)()(0)444p X p X p X F F πππ<≤=≤-≤=-1111sin sin 0242224π=+--=. 17、设随机变量X 的分布函数为1()ln 11x F x xx e x e<⎧⎪=≤≤⎨⎪>⎩求(1) (03)p X <≤、(2)p X <、(2 2.5)p X <<;(2) X 的密度函数?解:(1) (03)(3)(0)(3)(0)101p X p X p X F F <≤=≤-≤=-=-=(2)(2)(2)(2)ln 2p X p X p X F <=≤-===5(2 2.5)(2 2.5)(2.5)(2)ln 2.5ln 2ln 4p X p X F F <<=<≤=-=-=;(2) 由于在()F x 的可导点处,有()()f x F x '=,于是X 的密度函数为11()0x ef x x⎧≤≤⎪=⎨⎪⎩其它.18、设~(1,6)K U ,求方程210x Kx ++=有实根的概率? 解:由~(1,6)K U 得K 的密度函数为116()5k f k ⎧<<⎪=⎨⎪⎩其它又由于方程210x Kx ++=有实根等价于240K -≥,即||2K ≥,于是方程有实根的概率为22(||2)(2)(2)()()p K p K p K f k dk f k dk -+∞-∞≥=≤-+≥=+⎰⎰621455dk ==⎰. 19、调查表明某商店从早晨开始营业起直至第一个顾客到达的等待时间X (单位:分钟)服从参数为0.4的指数分布,求下述事件的概率(1) X 至多3分钟; (2) X 至少4分钟;(3) X 在3分钟至4分钟之间; (4) X 恰为3分钟?解:(1) X 至多3分钟的概率为0.43 1.2(3)(3)11p X F e e -⨯-≤==-=-;(2) X 至少4分钟的概率为0.44 1.6(4)1(4)1(4)1(1)p X p X F e e -⨯-≥=-<=-=--=;(3) X 在3分钟至4分钟之间的概率为(34)(4)(3)(4)(3)p X p X p X F F ≤≤=≤-<=- 0.440.43 1.2 1.6(1)(1)e e e e -⨯-⨯--=---=-;(4) X 恰为3分钟的概率为(3)0p X ==.20、设~(0,1)X N ,求下列事件的概率( 2.35)p X ≤;( 1.24)p X ≤-;(|| 1.54)p X ≤?解:( 2.35)(2.35)0.9906p X ≤=Φ=;( 1.24)( 1.24)1(1.24)10.89250.1075p X ≤-=Φ-=-Φ=-=; (|| 1.54)( 1.54 1.54)(1.54)( 1.54)p X p X ≤=-≤≤=Φ-Φ- (1.54)[1(1.54)]2(1.54)120.938210.8764=Φ--Φ=Φ-=⨯-=.21、设~(3,4)X N ,(1) 求(25)p X <≤、(||2)p X >、(3)p X >;(2) 确定c ,使得()()p X c p X c >=≤;(3) 若d 满足()0.9p X d >≥,则d 至多为多少?解:(1) 23353(25)()222X p X p ---<≤=≤≤ (1)(0.5)(1)(0.5)10.84130.691510.5328=Φ-Φ-=Φ+Φ-=+-=23323(||2)1(||2)1()222X p X p X p ---->=-≤=-≤≤1(0.5)( 2.5)1(0.5)(2.5)=-Φ-+Φ-=+Φ-Φ10.69150.99380.6977=+-= 333(3)1(3)1()22X p X p X p -->=-≤=-≤ 1(0)10.50.5=-Φ=-=;(2) 由()()p X c p X c >=≤得1()()p X c p X c -≤=≤3330.5()()()222X c c p X c p ---⇒=≤=≤=Φ 3032c c -⇒=⇒=; (3) 由()0.9p X d >≥得3330.9()1()1()1()222X d d p X d p X d p ---≤>=-≤=-≤=-Φ 33()0.11()0.122d d--⇒Φ≤⇒-Φ≤ 33()0.9 1.2820.43622d d d --⇒Φ≥⇒≥⇒≤.22、从甲地飞住乙地的航班,每天上午10:10起飞,飞行时间X 服从均值为4h ,标准差为20min 的正态分布.(1) 该航班在下午2:30以后到达乙地的概率; (2) 该航班在下午2:20以前到达乙地的概率;(3) 该航班在下午1:50至2:30之间到达乙地的概率? 解:(1) 该航班在下午2:30以后到达乙地的概率为240260240240(260)()1(1)202020X X p X p p ---≥=≥=-< 1(1)10.84130.1587=-Φ=-=;(2) 该航班在下午2:20以前到达乙地的概率为240250240(250)()(0.5)0.69152020X p X p --≤=≤=Φ=; (3) 该航班在下午1:50至2:30之间到达乙地的概率为220240240260240(220260)()202020X p X p ---≤≤=≤≤(1)(1)2(1)120.841310.6826=Φ-Φ-=Φ-=⨯-=.23、某地抽样调查结果表明,考生的外语成绩(百分制)近似地服从2(72,)N σ,已知96分以上的人数占总数的%,试求考生的成绩在60分至84分之间的概率?解:设考生的外语成绩为X ,则2~(72,)X N σ 由96分以上的人数占总数的%得0.023(96)p X =>729672240.977(96)()()X p X p σσσ--⇒=≤=≤=Φ242σ⇒=12σ⇒=于是,考生的成绩在60分至84分之间的概率为6072728472(6084)()121212X p X p ---≤≤=≤≤ (1)(1)2(1)120.841310.6826=Φ-Φ-=Φ-=⨯-=.24求cos Y X =的分布列?解:由X于是Y25求2Y X =的分布列?解:由26、设随机变量的密度函数为2311()2X xx f x ⎧-<<⎪=⎨⎪⎩其它求随机变量3Y X =+的密度函数?解:由题意知,当2y ≤时,有()()0Y F y p Y y =≤=当24y <<时,有()()(3)(3)(3)Y X F y p Y y p X y p X y F y =≤=+≤=≤-=-当4y ≥时,有()()1Y F y p Y y =≤=即Y 的分布函数02()(3)2414Y X y F y F y y y ≤⎧⎪=-<<⎨⎪≥⎩于是,Y 的密度函数()()Y Y f y F y '=(3)240X F y y '-<<⎧=⎨⎩其它23(3)2420y y ⎧-<<⎪=⎨⎪⎩其它.27、设随机变量~(0,1)X U ,求随机变量XY e =的密度函数? 解:由题意知,当1y ≤时,有()()0Y F y p Y y =≤=当1y e <<时,有()()()(ln )(ln )X Y X F y p Y y p e y p X y F y =≤=≤=≤=当y e ≥时,有()()1Y F y p Y y =≤=即Y 的分布函数1()(ln )11Y X y F y F y y e y e≤⎧⎪=<<⎨⎪≥⎩于是,Y 的密度函数()()Y Y f y F y '=(ln )10XF y y e'<<⎧=⎨⎩其它110y ey ⎧<<⎪=⎨⎪⎩其它.28、随机变量X 的密度函数为()0xX e x f x x -⎧>=⎨≤⎩ 求随机变量2Y X =的密度函数?解:由于20Y X =≥,故当0y <时,有()()0Y F y p Y y =≤=;当0y ≥时,有2()()()(Y F y p Y y p X y p X =≤=≤=≤≤0()1x X f x dx dx e -===-即Y 的分布函数10()0Y e y F y y ⎧-≥⎪=⎨<⎪⎩于是,Y 的密度函数0()()00Y Y y f y F y y >'==≤⎩.29、设随机变量~(0,1)X N ,试求随机变量||Y X =的密度函数? 解:由于||0Y X =≥,故当0y <时,有()()0Y F y p Y y =≤=; 当0y ≥时,有()()(||)()2()1Y F y p Y y p X y p y X y y =≤=≤=-≤≤=Φ-即Y 的分布函数2()10()00Y y y F y y Φ-≥⎧=⎨<⎩于是,Y 的密度函数()()Y Y f y F y '=2()00y y y 'Φ>⎧=⎨≤⎩22000yy y ->=≤⎩.B 组1、A2、B3、D4、B5、B6、B7、C8、C9、C10、C11、设随机变量X 的分布函数为0111()21232x a x F x a x a b x <-⎧⎪-≤<⎪⎪=⎨-≤<⎪⎪+≥⎪⎩且1(2)2p X ==,求常数a 、b ? 解:由()1F +∞=及()()(0)p X a F a F a ==--得()121(2)(2)(20)()()32F a b p X F F a b a +∞=+=⎧⎪⎨==--=+--=⎪⎩1726a b a b +=⎧⎪⇒⎨+=⎪⎩1656a b ⎧=⎪⎪⇒⎨⎪=⎪⎩.12求常数a ?解:由11ii p+∞==∑得20.5121a a +-+=12a ⇒=±再由11202a a -≥⇒≤,可得12a =-. 13、口袋中有5个球,编号为1、2、3、4、5,从中任取3个,以X 表示取出的3个球中的最大号码.(1) 求X 的分布列; (2) 求X 的分布函数?解:(1) 由题意知X 是离散型随机变量,其所有可能取值为3、4、5,且22351(3)10C p X C ===、23353(4)10C p X C ===、24356(5)10C p X C ===于是X(2) 由(1)可知的分布函数为030.134()0.44515x x F x x x <⎧⎪≤<⎪=⎨≤<⎪⎪≥⎩.14、设随机变量X 的密度函数为||()x af x Ce -= (0)a >求(1) 常数C ;(2) X 的分布函数;(3) (||2)p X <?解:(1) 由()1f x dx +∞-∞=⎰得||0()2221x x aaf x dx C e dx C e dx aC +∞+∞+∞---∞====⎰⎰⎰12C a⇒=; (2) 当0x <时 ||111()()222t t xa a a x x x F x f t dt e dt e dt e a a --∞-∞-∞====⎰⎰⎰当0x ≥时||||0011()()22t t a a xx F x f t dt e dt e dt a a---∞-∞==+⎰⎰⎰ 001111222t t x a a a x e dt e dt e a a ---∞=+=-⎰⎰于是102()1102xa x a e x F x e x -⎧<⎪⎪=⎨⎪-≥⎪⎩;(3) 22211(||2)(22)(2)(2)1122a a a p X p X F F e e e ---<=-<<=--=--=-. 15、设随机变量X 的密度函数为201()0xx f x ≤≤⎧=⎨⎩其它以Y 表示对X 的三次独立重复观察中事件1{}2X ≤出现的次数,求(2)P Y =?解:由题意知:事件1{}2X ≤在一次观察中出现的概率为1112222001()02|4p f x dx dt xdx x -∞-∞==+==⎰⎰⎰ 且~(3,)Y b p ,于是223139(2)()()4464P Y C ===. 16、设顾客在某银行的窗口等待服务的时间X (单位:分钟)服从指数分布,其密度函数为510()5x e x f x x -⎧>⎪=⎨⎪≤⎩某顾客在窗口等待服务,若超过10分钟他就离开.他一个月要到银行5次,以Y 表示一个月内他未等到服务而离开窗口的次数,求(1)p Y ≥?解:由题意知:顾客在窗口等待服务的时间超过10分钟的概率为5521010101()|5x x p f x dx e dx e e +∞+∞--+∞-===-=⎰⎰且~(5,)Y b p ,于是02025255(1)1(0)1()(1)1(1)0.5167P Y P Y C e e e ---≥=-==--=--=.17、设随机变量2~(2,)X N σ且(24)0.3p X <<=,求(0)p X <? 解:由2~(2,)X N σ得224242(24)()()(0)0.3p X p X σσσ---<<=<<=Φ-Φ=2()0.8σ⇒Φ=0222(0)()()1()10.80.2p X p X σσσ-⇒<=<=Φ-=-Φ=-=.18、设随机变量X 的分布函数为()F x ,试求随机变量()Y F X =的密度函数? 解:由于0()1F X ≤≤,故当0Y <时,有()()0Y F y p Y y =≤=; 当01y ≤≤时,有11()()(())(())(())Y F y p Y y p F X y p X F y F F y y --=≤=≤=≤==当1y >时,有()()1Y F y p Y y =≤= 即Y 的分布函数00()0111Y y F y yy y <⎧⎪=≤≤⎨⎪>⎩于是,Y 的密度函数()()Y Y f y F y '=101y <<⎧=⎨⎩其它即随机变量Y 服从区间(0,1)上的均匀分布.。
第2章 随机变量及其分布课后习题答案(高教出版社,浙江大学)

第2章 随机变量及其分布1,设在某一人群中有40%的人血型是A 型,现在在人群中随机地选人来验血,直至发现血型是A 型的人为止,以Y 记进行验血的次数,求Y 的分布律。
解:显然,Y 是一个离散型的随机变量,Y 取k 表明第k 个人是A 型血而前1-k 个人都不是A 型血,因此有116.04.0)4.01(4.0}{--⨯=-⨯==k k k Y P , ( ,3,2,1=k )上式就是随机变量Y 的分布律(这是一个几何分布)。
2,水自A 处流至B 处有3个阀门1,2,3,阀门联接方式如图所示。
当信号发出时各阀门以0.8的概率打开,以X 表示当信号发出时水自A 流至B 的通路条数,求X 的分布律。
设各阀门的工作相互独立。
解:X 只能取值0,1,2。
设以)3,2,1(=i A i记第i个阀门没有打开这一事件。
则)}(){()}({}0{3121321A A A A P A A A P X P ⋃=⋃==)()()()()()()(}{}{}{32131213213121A P A P A P A P A P A P A P A A A P A A P A A P -+=-+= 072.0)8.01()8.01()8.01(322=---+-=,类似有512.08.0)()}({}2{3321321=====A A A P A A A P XP ,416.0}2{}0{1}1{==-=-==X P X P X P ,综上所述,可得分布律为3,据信有20%的美国人没有任何健康保险,现任意抽查15个美国人,以X 表示15个人中无任何健康保险的人数(设各人是否有健康保险相互独立)。
问X 服从什么分布?写出分布律。
并求下列情况下无任何健康保险的概率:(1)恰有3人;(2)至少有2人;(3)不少于1人且不多于3人;(4)多于5人。
解:根据题意,随机变量X 服从二项分布B(15, 0.2),分布律为15,2,1,0,8.02.0)(1515 =⨯⨯==-k C k X P k k k。
(完整版)概率论与数理统计教程习题(第二章随机变量及其分布)(1)答案

概率论与数理统计练习题系 专业 班 姓名 学号第六章 随机变量数字特征一.填空题1. 若随机变量X 的概率函数为1.03.03.01.02.043211pX-,则=≤)2(X P 0.6 ;=>)3(X P 0.1 ;=>=)04(X X P 0.125 .2. 若随机变量X 服从泊松分布)3(P ,则=≥)2(X P 8006.0413≈--e.3. 若随机变量X 的概率函数为).4,3,2,1(,2)(=⋅==-k c k X P k则=c1516. 4.设A ,B 为两个随机事件,且A 与B 相互独立,P (A )=0.3,P (B )=0.4,则()P AB =____________.(0.18)5.设事件A 、B 互不相容,已知()0.4=P A ,()0.5=P B ,则()=P AB 0.16. 盒中有4个棋子,其中2个白子,2个黑子,今有1人随机地从盒中取出2个棋子,则这2个棋子颜色相同的概率为____________.(13) 7.设随机变量X 服从[0,1]上的均匀分布,则()E X =____________.(12) 8.设随机变量X 服从参数为3的泊松分布,则概率密度函数为 __.(k 33(=,0,1,2k!P X k e k -==L )) 9.某种电器使用寿命X (单位:小时)服从参数为140000λ=的指数分布,则此种电器的平均使用寿命为____________小时.(40000)10在3男生2女生中任取3人,用X 表示取到女生人数,则X 的概率函数为11.若随机变量X 的概率密度为)(,1)(2+∞<<-∞+=x x a x f ,则=a π1;=>)0(X P 0.5 ;==)0(X P 0 .12.若随机变量)1,1(~-U X ,则X 的概率密度为 1(1,1)()2x f x ⎧∈-⎪=⎨⎪⎩其它13.若随机变量)4(~e X ,则=≥)4(X P ;=<<)53(X P .14..设随机变量X 的可能取值为0,1,2,相应的概率分布为0.6 , 0.3 ,0.1,则()E X = 0.515.设X为正态分布的随机变量,概率密度为2(1)8()x f x +-=,则2(21)E X -= 916.已知X ~B (n,p ),且E (X )=8,D (X )=4.8,则n= 。
第2章随机变量及其分布习题答案

第2章随机变量及其分布习题答案第⼆章随机变量及其分布§2.1 随机变量的概念与离散型随机变量习题 1. 解: 1112(1)121,.993θθθθ+-++-=∴=±⼜因为≤0)1(2θθ-1≤ , 所以 13θ=.2. 解:设X 表⽰任取3次,取到的不合格品数,则 1)有放回 33()0.20.8,0,1,2,3.k k k P X k C k -=== 即X 的分布律为 X 0 1 2 3 P12564125481251212512)⽆放回 328310(),3,4,5.kkC C P X k k C-===即X 的分布律为 X 0 1 2 P 1571571514. 解:设X 表⽰直⾄取到⽩球为⽌,取球的次数,则其概率分布为X 1 2 3 4P521031531015. 解:由全概率公式得42(2)()(2|)111113().423448k P Y P Xk P Y X k =======++=∑§2.2 0-1分布和⼆项分布习题1. 解:设A 表⽰“10件中⾄少有两件⼀级品”,则P (A )=1()P A -=1=--6.04.04.0911010C 0.9983.2. 解: X 0 1 2 3 4 5P 54.0 6.04.0415C 23256.04.0C 32356.04.0C 4456.40.0C 5 6.00.01024 0.0768 0.2304 0.3456 0.2592 0.077763. 解:设A 表⽰“4个灯泡中⾄少有3个能使⽤1500⼩时以上”,则4. 解:1)设A 表⽰“恰有3粒种⼦发芽”,则003764768.002.098.0)(2335==C A P2)设B 表⽰“⾄少有4粒种⼦发芽”,则=+=544598.002.098.0)(C B P 0.996§2.3 泊松分布习题1. 解:设A 表⽰“⼀页上⾄多有⼀个印刷错误”,则 010.20.20.20.2()(1)(0)(1)0.9820!1!P A P X P X P X ee--=≤==+==+=2.解:1)设X 表⽰5分钟内接到的电话个数,则0,1,2,X = 22(),0,1,2,3,4,5,6.!kP X k e k k -===2)设A 表⽰“5分钟内⾄多接到3个电话”,则∑2!2-ek k=0.8571或4()(3)1(4)1k P A P X P X +∞==≤=-≥=-∑2!2-ek k=(查表)1-0.1429=0.85713.解:1)设A 表⽰“中午12时⾄下午3时没有急症病⼈”, 则~(1.5),X π1.51.5()(0)0.223.0!P A P X e-====2)设B 表⽰“中午12时⾄下午5时⾄少有2个急症病⼈”,则~(2.5),X π12.52.5()(2)1(0)(1)2.5 2.510.7127.0!1!P B P X P X P X ee--=≥=-=-==-§2.4 随机变量的分布函数习题1. 解:1)≥<≤<≤<=2,121,2110,310,0)(x x x x x F312)()(0)(1),221(14)(2),22(14)(1)(2).3P X P X P X P X P X P X P X P X ≤==+==<≤===≤≤==+==2. 解:X 0 1 2 3 4 5P 54.0 6.04.0415C 23256.04.0C 32356.04.0C 4456.40.0C 56.00.01024 0.0768 0.2304 0.3456 0.2592 0.07776≥<≤≤<≤<≤<≤<=515492.04366.03223.021086.01001.000)(x x x x x x x x F <3. 解:X 的分布律为 X -1 0 2 4 P 0.2 0.4 0.3 0.1 §2.5 连续型随机变量习题 1. 解:1)?? =?=?=101231,1)(c dx cx dx x f2)30,0(),011,1x F x x x x=≤)41()21()2141(=-=≤≤F F x P 22219()1()1().33327P X P X F >=-≤=-= 2. 解:1)连续型随机变量的分布函数左连续,则00012l i m ()(0),l i m ()(1),l i m ()(2),10,1,2211,210,,2.2x x x F x F F x F F x F A B C C A B C ---→→→=====----====解得2),01()()2,120,x x f x F x x x <'==-≤其它3)2111117P ()1P ()1F()1().222=-=-= 3. 解:1)12011()2,~(3,),44P A xdx Y B ==则 Y 的概率分布为 Y 0 1 2 3 P642764276496412)设B 表⽰“对X 的三次独⽴重复观测中事件A ⾄多出现两次”,则3163()1()1(3)1().464P B P B P Y =-=-==-= 4.设最⾼洪⽔位为X,河堤⾄少要修c 单位⾼,由题意得:32()1()10.0110.c P X c P X c dx c x>=-≤=-≤?≥?P X dx >==设A 表⽰“3次独⽴观测中⾄少有两次观测值⼤于3”,则223321220()()().33327P A C =+=2. 解:有实根的条件:2(4)44(2)01K 2,K K K -??+≥?≤-≥或所求概率为 3P (K 2.5dx ≥=521)=5 3. 解:1)33001,|1 3.33xxk k kedx ek +∞--+∞=-==?=?即2)23 4.561.5(1.52)3.xP x edx e e ---≤≤=1(200)1,600x P X e dx e--≤==-?设A 表⽰“3只独⽴元件⾄少1只在最初200⼩时内出故障”,则13311)(1)(1)(---=-=-=eeA P A P .§2.7 正态分布习题1. :(1)(0.022.33)(2.33)(0.02)0.99010.50800.4821;P X <<=Φ-Φ=-=解( 1.850.04)(0.04)( 1.85)(0.04)[1(1.85)](0.04)(1.85)10.5160.967810.4838. P X -<<=Φ-Φ-=Φ--Φ=Φ+Φ-=+-= 2. 解:101)(716)(12)(2)(1)3(2)(1)10.97720.841310.8185;X P X P -<<=-<<=Φ-Φ-=Φ+Φ-=+-=10222)(102)()2()120.748610.4972;333x P x P --<=<=Φ-=?-=103)()0.9()0.9,(1.28)0.9,1.28,13.84.3P X αααα-<=?Φ=Φ≈-==反查表得故得3. 解:设X 表⽰螺栓长度,则:10.05(10.050.12)(2)2(2)120.977210.9544.0.06X P X P --<=<=Φ-=?-=4. 解:30(30)()2(1.5)10.8664,2020X P X P ≤=≤=Φ-=设A 表⽰“三次测量中⾄少有⼀次误差的绝对值不超过30cm ”3()1()1(0.1336)0.9976.P A P A =-=-=§2.8 随机变量函数的分布习题 1. 解:1)Y -3 2 5 6 P161 164 167 1642) Z 1 2 3 4 9 P1621641651641612. 解: 3110≤≤?≤≤y x , 当31≤≤y 时,11()();2y Y Y Y y y F y P Y y P X y P X dx f y F y ---=≤=+≤=≤= ='==;当13,y y ≤≥或时Y 的密度函数为零.故Y 的密度函数为1,13()20,Y y f y ?≤≤?=其它22222()2()22()()()(),,()(),.Y X yy yY Y X Y F y P Y y P y P X y dx y R Y f y F y y R µσµσµσµσµ∈'===∈?3.解:因为的分布函数为所以的密度函数为第⼆章随机变量及其分布复习题⼀选择题1. B2. B3. C4. D5. C ⼆填空题 1.22(),0,1,2,;!kP X k e k k -=== 0.592. 27193. ,1,21π==B A2111,,21x R xπ∈+4.,65,61 分布律:X -1 1 2P 611. 解: X 的分布律为 X 1 2 3 4 P643764196476412. 解: X 的分布律为 1(),1,2,3,.k P X k q p k -=== 3. 解:设X 表⽰两次调整之间⽣产的合格品数,则X 的分布律为1()(1),0,1,2,.k P X k p p k -==-=4. 解: X 的概率分布为55()0.250.75,0,1,2,3,4,5.k k kP X k C k -===设A 表⽰“5道选择题⾄少答对两题”,则()1(0)(1)0.3672.P A P X P X =-=-==5. 解:1)⼀天中必须有油船转⾛意味着“X .>3”242(3)0.143;!kk P X ek ∞(查泊松分布表)2) 设设备增加到⼀天能为y 艘油船服务,才能使到达港⼝的90%的油船可以得到服务.则21212()0.910.9!20.1,15 4.!kk y kk y P X y ek ey y k ∞-=+∞-=+≤≥?-≥?≤+≥?≥∑∑反查泊松分布表得6. 解:21)()()31()31(3131=+=+?>dx b ax dx b ax X P X P47,23=-=?b a7.170170170:1)()0.01()()0.99666170(2.33)0.99 2.33184.6X h h P X h P h h ---≥≥?≥解查表得2)(182)P X ≥=1821701()1(2)0.02,6--Φ=-Φ≈设A 表⽰“100个男⼦中与车门碰头⼈数不多于2个”676.002.098.002.098.098.0)(2982100991100100=++=C C A P .8. 解:(1) X 的分布函数为 1,02()11,02xx e x F x e x -?-∞<≤??=??-<<+∞??011(2)P Y P X e dx P Y P X e dx ∞--∞==>===-=≤==故Y的概率分布律为Y-1 1P1/2 1/2Y的分布函数为0,11(),1121,1YyF y yy<-=-≤<≥。
随机变量及其分布习题解答

第2章随机变量及其分布习题解答一.选择题1.若定义分布函数(){}F x P X x =≤,则函数()F x 是某一随机变量X 的分布函数的充要条件是( D ).A .0()1F x ≤≤.B .0()1F x ≤≤,且()0,()1F F -∞=+∞=.C .()F x 单调不减,且()0,()1F F -∞=+∞=.D .()F x 单调不减,函数()F x 右连续,且()0,()1F F -∞=+∞=.2.函数()0 212021 0x F x x x <-⎧⎪⎪=-≤<⎨⎪≥⎪⎩是( A ).A .某一离散型随机变量X 的分布函数.B .某一连续型随机变量X 的分布函数.C .既不是连续型也不是离散型随机变量的分布函数.D .不可能为某一随机变量的分布函数.3.函数()0 0sin 01 x F x x x x ππ<⎧⎪=≤<⎨⎪≥⎩( D ).A .是某一离散型随机变量的分布函数.B .是某一连续型随机变量的分布函数.C .既不是连续型也不是离散型随机变量的分布函数.D .不可能为某一随机变量的分布函数.4.设X 的分布函数为1()F x ,Y 的分布函数为2()F x ,而12()()()F x aF x bF x =-是某随机变量Z 的分布函数,则, a b 可取( A ).A .32, 55a b ==-. B .2 3a b ==.C .13 , 22a b =-=. D .13 , 22a b ==-.5.设X 的分布律为而(){}F x P X x =≤,则F =( A ).A .0.6.B .0.35.C .0.25.D .0.6.设连续型变量X 的概率密度为()p x ,分布函数为()F x ,则对于任意x 值有( A ). A .(0)0P X ==. B .()()F x p x '=. C .()()P X x p x ==.D .()()P X x F x ==.7.任一个连续型的随机变量X 的概率密度为()p x ,则()p x 必满足( C ).A .0()1p x ≤≤. B .单调不减. C .()1p x dx +∞-∞=⎰.D .lim ()1x p x →+∞=.8.为使 x 1()0 1p x x ⎧<⎪=⎨⎪≥⎩成为某个随机变量X 的概率密度,则c 应满足( B ).A .1+∞=⎰.B .11-=⎰.C .11=. D .1+∞-=⎰.9.设随机变量X 的概率密度为2()x p x Ae -=,则A = ( D ).A .2.B .1.C .12. D .14.10.设X 的概率密度函数为1() ,2xp x e x -=-∞<<+∞,又{}()F x P X x =≤,则0x <时,()F x =( D ).A .112-e x. B .112x e --. C .12x e -.D .12e x .11.设220()00x cx e x p x cx -⎧⎪>=⎨⎪≤⎩是随机变量X 的概率密度,则常数c ( B ).A .可以是任意非零常数.B .只能是任意正常数.C .仅取1.D .仅取- 1. 12.设连续型随机变量X 的分布函数为()F x ,则112Y X =-分布函数为( D ). A .(22)F y -. B .1(1)22yF -. C .2(22)F y -. D .1(22)F y --. 13.设随机变量X 的概率密度为()p x ,12Y X =-,则Y 的分布密度为( A ).A .1122y p -⎛⎫ ⎪⎝⎭. B .112y p -⎛⎫- ⎪⎝⎭ C .12y p -⎛⎫- ⎪⎝⎭. D .2(12)p y -. 14.设随机变量X 的密度函数()p x 是连续的偶函数(即()()p x p x =-),而()F x 是X 的分布函数,则对任意实数a 有( C ).A .()()F a F a =-.B .0()1()aF a p x dx -=-⎰.C .01()()2aF a p x dx -=-⎰ . D .()()F a F a -=. 二.填空题15.欲使2103()103xx e x F x A e x -⎧<⎪⎪⎨⎪-≥⎪⎩为某随机变量的分布函数,则要求A =____1_____.16.若随机变量X 的分布函数2()0616x F x Axx x <⎧⎪=≤<⎨⎪≥⎩,则必有A =____1/36______. 17.从装有4件合格品及1件次品的口袋中连取两次,每次取一件,取出后不放回,求取出次品数X 的分布律为{0}3/5,{1}2/5P X P X ==== .18.独立重复地掷一枚均匀硬币,直到出现正面为止,设X 表示首次出现正面的试验次数,则X 的分布列{}P X k ==1111{},1,2,222k kP X k k -⎛⎫⎛⎫==⋅== ⎪⎪⎝⎭⎝⎭.19.设某离散型随机变量X 的分布列是{},1,2,,10kP X k k C===⋅⋅⋅,则C =____55_____.20.设离散型随机变量X 的分布函数是(){}F x P X x =≤,用()F x 表示概率{}0P X x ==00()(0)F x F x --.21.设X 是连续型随机变量,则{3}P X ==___0____.22. 设随机变量X 的分布函数为20,2()(2),231,3x F x x x x <⎧⎪=-≤<⎨⎪≥⎩ ,则(2.54)P X <≤=(4)(2.5)0.75F F -=.23.设随机变量X 的分布函数102()1102xx e x F x e x -⎧≤⎪⎪=⎨⎪->⎪⎩,则{}1P X <=11e --.24.设连续型随机变量X的分布函数为20()021x xF x x x <⎧⎪⎪=≤<⎨⎪⎪≥⎩X 的概率密度()p x=00 ()x x ⎧≤≤⎪⎨⎪⎩其它.25.设随机变量X 的分布密度为2(1),(0,1)()0,(0,1)Ax x x p x x ⎧-∈=⎨∉⎩,则常数A =__12____.26.若X的概率密度为()p x ,则31Y X =+的概率密度()Y p y =1133y p -⎛⎫⎪⎝⎭.27.设电子管使用寿命的密度函数()21001000100x p x x x ⎧>⎪=⎨⎪≤⎩(单位:小时),则在150小时内独立使用的三只管子中恰有一个损坏的概率为_____4/9_____. 三.应用计算题28. 设随机变量X 的分布律为求(1){14}P X <≤;(2)X 的分布函数()F x .解:(1){14}{2}{3}{4}0.30.30.10.7P X P X P X P X <≤==+=+==++=(2)X 的分布函数()F x 为0,00.1,010.3,12()0.6,230.9,341,4x x x F x x x x <⎧⎪≤<⎪⎪≤<=⎨≤<⎪⎪≤<⎪≥⎩29. 设连续随机变量X 的概率密度,10(),010,||1c x x p x c x x x +-≤<⎧⎪=-≤≤⎨⎪>⎩试求: (1)常数c ; (2) 概率{||0.5}P X ≤;(3) X 的分布函数()F x . 解:(1)由0111()()()21p x dx c x dx c x dx c +∞-∞-==++-=-⎰⎰⎰,得1c =(2){||0.5}{0.50.5}P X P X ≤=-≤≤00.50.5(1)(1)0.75x dx x dx -=++-=⎰⎰(3)X 的分布函数为1010,1(1),10()(1)(1),011,1xxx t dt x F x t dt t dt x x --<-⎧⎪+-≤<⎪⎪=⎨⎪++-≤<⎪≥⎪⎩⎰⎰⎰220,11(1),10211(1),0121,1x x x x x x <-⎧⎪⎪+-≤<⎪=⎨⎪--≤<⎪⎪≥⎩30.设顾客到某银行窗口等待服务的时间X (单位:分钟)的概率密度函数为51,0()50,0xe x p x x -⎧>⎪=⎨⎪≤⎩某顾客在窗口等待,如超过10分钟,他就离开,求他离开的概率. 解:他离开的概率为/52101{10}5x P X e dx e +∞--≥==⎰31.已知随机变量X 的分布函数为()1,x 0211, 02241,2xe F x x x x ⎧<⎪⎪⎪=+≤<⎨⎪≥⎪⎪⎩,求其分布密度()p x .解:()1 021()0240 2xe x p x F x x x ⎧<⎪⎪⎪'==≤<⎨⎪≥⎪⎪⎩32. 设X 是离散型随机变量,其分布律为(1)求常数a ;(2)23Y X =+的分布律.解:(1)由0.330.10.21a a ++++=得0.1a = (2)由于所以,23Y X =+的分布律为33.设随机变量X 的密度函数为,0()0,0x X e x p x x λλ-⎧>=⎨≤⎩,0λ>,求XY e =的密度函数()Y p y .解:(1)XY e =的分布函数为(ln ),0()()(ln )0,0X XY F y y F y P e y P X y y >⎧=≤=≤=⎨≤⎩(2)XY e =的密度函数()Y p y 为ln 1,ln 0,1(ln )(ln ),01()()0,ln 00,00,10,0y X Y Y e y y p y y y y p y F y y y y y y λλλλ-+⎧>⎧'>⋅>⎧⎪⎪'===⋅≤=⎨⎨⎨≤⎩⎪⎪≤≤⎩⎩。
第二章 概率论解析答案习题解答

第二章 随机变量及其分布I 教学基本要求1、了解随机变量的概念以及它与事件的联系;2、理解随机变量的分布函数的概念与性质;理解离散型随机变量的分布列、连续型随机变量的密度函数及它们的性质;3、掌握几种常用的重要分布:两点分布、二项分布、泊松分布、均匀分布、指数分布、正态分布,且能熟练运用;4、会求简单随机变量函数的分布.II 习题解答A 组、1、检查两个产品,用T 表示合格品,F 表示不合格品,则样本空间中的四个样本点为1(,)F F ω=、2(,)T F ω=、3(,)F T ω=、4(,)T T ω=以X 表示两个产品中的合格品数.(1) 写出X 与样本点之间的对应关系;(2) 若此产品的合格品率为p ,求(1)p X = 解:(1) 10ω→、21ω→、31ω→、42ω→;(2) 12(1)(1)2(1)p X C p p p p ==-=-.2、下列函数是否是某个随机变量的分布函数(1) 021()2021x F x x x <-⎧⎪⎪=-≤<⎨⎪≥⎪⎩; (2) 21()1F x x =+ ()x -∞<<+∞. :解:(1) 显然()F x 是单调不减函数;0()1F x ≤≤,且()0F -∞=、()1F +∞=;(0)()F x F x +=,故()F x 是某个随机变量的分布函数.(2) 由于()01F +∞=≠,故()F x 不是某个随机变量的分布函数. 3、设X 的分布函数为(1)0()00x A e x F x x -⎧-≥=⎨<⎩求常数A 及(13)p X <≤解:由()1F +∞=和lim (1)xx A e A -→+∞-=得1A =;(13)(3)(1)(3)(1)p X p X p X F F <≤=≤-≤=- 3113(1)(1)e e e e ----=---=-.4、设随机变量X 的分布函数为>200()0111x F x Ax x x ≤⎧⎪=<≤⎨⎪>⎩求常数A 及(0.50.8)p X <≤解:由(10)(1)F F +=得1A =;(0.50.8)(0.8)(0.5)(0.8)(0.5)p X p X p X F F <≤=≤-≤=- 220.80.50.39=-=.5、设随机变量X 的分布列为()ap X k N==(1,2,,)k N =求常数a解:由11ii p+∞==∑得>11Nk a N==∑1a ⇒=.6、一批产品共有100个,其中有10个次品,求任意取出的5个产品中次品数的分布列解:设X 表示5个产品中的次品数,则X 是离散型随机变量,其所有可能取值为0、1、…、5,且0510905100(0)C C p X C ==、1410905100(1)C C p X C ==、2310905100(2)C C p X C ==、3210905100(3)C C p X C ==、4110905100(4)C C p X C ==、5010905100(5)C C p X C ==于是X 的分布列为510905100()k kC C p X k C -== (0,1,,5)k =.7、设10件产品中有2件次品,进行连续无放回抽样,直至取到正品为止,以X 表示抽样次数,求(1) X 的分布列; (2) X 的分布函数\解:(1) 由题意知X 是离散型随机变量,其所有可能取值为1、2、3,且84(1)105p X ===、288(2)10945p X ==⨯=、2181(3)109845p X ==⨯⨯=于是X(2) 由(1)可知的分布函数为014125()44234513x x F x x x <⎧⎪⎪≤<⎪=⎨⎪≤<⎪⎪≥⎩.8、设随机变量X 的分布函数为010.211()0.3120.52313x x F x x x x <-⎧⎪-≤<⎪⎪=≤<⎨⎪≤<⎪≥⎪⎩ 求X 的分布列解:X 的分布列为9、求在同一时刻(1) 恰有2个设备被使用的概率; (2) 至少有3个设备被使用的概率; .(3) 至多有3个设备被使用的概率解:设X 表示被同时使用的供水设备数,则~(5,0.1)X b (1) 恰有2个设备被使用的概率为2235(2)(0.1)(0.9)0.0729p X C ===;(2) 至少有3个设备被使用的概率为(3)(3)(4)(5)p X p X p X p X ≥==+=+=33244550555(0.1)(0.9)(0.1)(0.9)(0.1)(0.9)0.00856C C C =++=;(3) 至多有3个设备被使用的概率为(3)1(4)(5)p X p X p X ≤=-=-=44550551(0.1)(0.9)(0.1)(0.9)0.99954C C =--=.!10、经验表明:预定餐厅座位而不来就餐的顾客比例为20%,如今餐厅有50个座位,但预定给了52位顾客,求到时顾客来到餐厅而没有座位的概率是多少解:设X 表示预定的52位顾客中不来就餐的顾客数,则~(52,0.2)X b ,由于“顾客来到餐厅没有座位”等价于“52位顾客中至多有1位不来就餐”,于是所求概率为005211515252(1)(0)(1)(0.2)(0.8)(0.2)(0.8)p X p X p X C C ≤==+==+0.0001279=.11、设某城市在一周内发生交通事故的次数服从参数为的泊松分布,求 (1) 在一周内恰好发生2次交通事故的概率; (2) 在一周内至少发生1次交通事故的概率解:设X 表示该城市一周内发生交通事故的次数,则~(0.3)X P (1) 在一周内恰好发生2次交通事故的概率20.30.3(2)0.03332!p X e -===;,(2) 在一周内至少发生1次交通事故的概率00.30.3(1)1(0)10.2590!p X P X e -≥=-==-=.12、设X 服从泊松分布,已知(1)(2)p X p X ===,求(4)p X =解:由(1)(2)p X p X ===得22ee λλλλ--=2λ⇒=422(4)0.09024!p X e -⇒===.13、一批产品的不合格品率为,现从中任取40件进行检查,若发现两件或两件以上不合格品就拒收这批产品,分别用以下方法求拒收的概率:(1) 用二项分布作精确计算; (2) 用泊松分布作的似计算 …解:设X 表示抽取的40件产品中的不合格品数,则~(40,0.02)X b (1) 拒收的概率为(2)1(0)(1)p X p X p X ≥=-=-=0040113940401(0.02)(0.98)(0.02)(0.98)0.1905C C =--=;(2) 由于400.020.8λ=⨯=,于是拒收的概率为(2)1(0)(1)p X p X p X ≥=-=-= 0.80.810.80.1912e e --≈--=.14、设随机变量X 的密度函数为201()0x x f x ≤≤⎧=⎨⎩其它求X 的分布函数 *解:由()()xF x f t dt -∞=⎰得当0x <时()()00xxF x f t dt dt -∞-∞===⎰⎰当01x ≤≤时2200()()02|x xxF x f t dt dt tdt t x -∞-∞==+==⎰⎰⎰当1x >时0121001()()020|1x xF x f t dt dt tdt dt t -∞-∞==++==⎰⎰⎰⎰于是所求分布函数为200()0111x F x x x x <⎧⎪=≤≤⎨⎪>⎩. 15、设随机变量X 的密度函数为 ~212(1)12()0x f x x⎧-≤≤⎪=⎨⎪⎩其它求X 的分布函数解:由()()xF x f t dt -∞=⎰得当1x <时()()00xxF x f t dt dt -∞-∞===⎰⎰当12x ≤≤时1121111()()02(1)2()|2(2)xxx F x f t dt dt dt t x t t x-∞-∞==+-=+=+-⎰⎰⎰ 当2x >时122121211()()02(1)02()|1xx F x f t dt dt dt dt t t t-∞-∞==+-+=+=⎰⎰⎰⎰于是所求分布函数为 ·011()2(2)1212x F x x x x x <⎧⎪⎪=+-≤≤⎨⎪>⎪⎩.16、设随机变量X 的密度函数为cos ()220A x x f x ππ⎧-≤≤⎪=⎨⎪⎩其它求(1) 常数A ;(2) X 的分布函数;(3) (0)4p X π<≤解:(1) 由()1f x dx +∞-∞=⎰得2222220cos 0sin |21dt A xdx dt A x A ππππππ-+∞--∞-++===⎰⎰⎰12A ⇒=; (2) 当2x π<-时()()00xxF x f t dt dt -∞-∞===⎰⎰当22x ππ-≤≤时]2221111()()0cos sin |sin 2222xxxF x f t dt dt tdt t x πππ---∞-∞-==+==+⎰⎰⎰当2x π>时22222211()()0cos 0sin |122xx F x f t dt dt tdt dt t ππππππ---∞-∞-==++==⎰⎰⎰⎰ 于是所求分布函数为0211()sin 222212x F x x x x ππππ⎧<-⎪⎪⎪=+-≤≤⎨⎪⎪>⎪⎩;(3) (0)()(0)()(0)444p X p X p X F F πππ<≤=≤-≤=-1111sin sin 0242224π=+--=. 17、设随机变量X 的分布函数为1()ln 11x F x xx e x e<⎧⎪=≤≤⎨⎪>⎩求(1) (03)p X <≤、(2)p X <、(2 2.5)p X <<;(2) X 的密度函数]解:(1) (03)(3)(0)(3)(0)101p X p X p X F F <≤=≤-≤=-=-=(2)(2)(2)(2)ln 2p X p X p X F <=≤-===5(2 2.5)(2 2.5)(2.5)(2)ln 2.5ln 2ln 4p X p X F F <<=<≤=-=-=;(2) 由于在()F x 的可导点处,有()()f x F x '=,于是X 的密度函数为11()0x ef x x⎧≤≤⎪=⎨⎪⎩其它.18、设~(1,6)K U ,求方程210x Kx ++=有实根的概率 解:由~(1,6)K U 得K 的密度函数为116()5k f k ⎧<<⎪=⎨⎪⎩其它又由于方程210x Kx ++=有实根等价于240K -≥,即||2K ≥,于是方程有实根的概率为22(||2)(2)(2)()()p K p K p K f k dk f k dk -+∞-∞≥=≤-+≥=+⎰⎰?621455dk ==⎰. 19、调查表明某商店从早晨开始营业起直至第一个顾客到达的等待时间X (单位:分钟)服从参数为0.4的指数分布,求下述事件的概率(1) X 至多3分钟; (2) X 至少4分钟;(3) X 在3分钟至4分钟之间; (4) X 恰为3分钟解:(1) X 至多3分钟的概率为0.43 1.2(3)(3)11p X F e e -⨯-≤==-=-;(2) X 至少4分钟的概率为0.44 1.6(4)1(4)1(4)1(1)p X p X F e e -⨯-≥=-<=-=--=;?(3) X 在3分钟至4分钟之间的概率为(34)(4)(3)(4)(3)p X p X p X F F ≤≤=≤-<=- 0.440.43 1.2 1.6(1)(1)e e e e -⨯-⨯--=---=-;(4) X 恰为3分钟的概率为(3)0p X ==.20、设~(0,1)X N ,求下列事件的概率( 2.35)p X ≤;( 1.24)p X ≤-;(|| 1.54)p X ≤ 解:( 2.35)(2.35)0.9906p X ≤=Φ=;( 1.24)( 1.24)1(1.24)10.89250.1075p X ≤-=Φ-=-Φ=-=; (|| 1.54)( 1.54 1.54)(1.54)( 1.54)p X p X ≤=-≤≤=Φ-Φ-(1.54)[1(1.54)]2(1.54)120.938210.8764=Φ--Φ=Φ-=⨯-=.&21、设~(3,4)X N ,(1) 求(25)p X <≤、(||2)p X >、(3)p X >;(2) 确定c ,使得()()p X c p X c >=≤;(3) 若d 满足()0.9p X d >≥,则d 至多为多少解:(1) 23353(25)()222X p X p ---<≤=≤≤ (1)(0.5)(1)(0.5)10.84130.691510.5328=Φ-Φ-=Φ+Φ-=+-=23323(||2)1(||2)1()222X p X p X p ---->=-≤=-≤≤ 1(0.5)( 2.5)1(0.5)(2.5)=-Φ-+Φ-=+Φ-Φ10.69150.99380.6977=+-= 333(3)1(3)1()22X p X p X p -->=-≤=-≤ 1(0)10.50.5=-Φ=-=;(2) 由()()p X c p X c >=≤得1()()p X c p X c -≤=≤?3330.5()()()222X c c p X c p ---⇒=≤=≤=Φ3032c c -⇒=⇒=; (3) 由()0.9p X d >≥得3330.9()1()1()1()222X d d p X d p X d p ---≤>=-≤=-≤=-Φ 33()0.11()0.122d d--⇒Φ≤⇒-Φ≤ 33()0.9 1.2820.43622d d d --⇒Φ≥⇒≥⇒≤.22、从甲地飞住乙地的航班,每天上午10:10起飞,飞行时间X 服从均值为4h ,标准差为20min 的正态分布.(1) 该航班在下午2:30以后到达乙地的概率; (2) 该航班在下午2:20以前到达乙地的概率;(3) 该航班在下午1:50至2:30之间到达乙地的概率 *解:(1) 该航班在下午2:30以后到达乙地的概率为240260240240(260)()1(1)202020X X p X p p ---≥=≥=-< 1(1)10.84130.1587=-Φ=-=;(2) 该航班在下午2:20以前到达乙地的概率为240250240(250)()(0.5)0.69152020X p X p --≤=≤=Φ=; (3) 该航班在下午1:50至2:30之间到达乙地的概率为220240240260240(220260)()202020X p X p ---≤≤=≤≤(1)(1)2(1)120.841310.6826=Φ-Φ-=Φ-=⨯-=.23、某地抽样调查结果表明,考生的外语成绩(百分制)近似地服从2(72,)N σ,已知96分以上的人数占总数的%,试求考生的成绩在60分至84分之间的概率解:设考生的外语成绩为X ,则2~(72,)X N σ】由96分以上的人数占总数的%得0.023(96)p X =>729672240.977(96)()()X p X p σσσ--⇒=≤=≤=Φ242σ⇒=12σ⇒=于是,考生的成绩在60分至84分之间的概率为6072728472(6084)()121212X p X p ---≤≤=≤≤ (1)(1)2(1)120.841310.6826=Φ-Φ-=Φ-=⨯-=.24求cos Y X =的分布列解:由X于是Y25求2Y X =的分布列解:由26、设随机变量的密度函数为2311()2X xx f x ⎧-<<⎪=⎨⎪⎩其它求随机变量3Y X =+的密度函数解:由题意知,当2y ≤时,有()()0Y F y p Y y =≤=当24y <<时,有()()(3)(3)(3)Y X F y p Y y p X y p X y F y =≤=+≤=≤-=-当4y ≥时,有()()1Y F y p Y y =≤=¥即Y 的分布函数02()(3)2414Y X y F y F y y y ≤⎧⎪=-<<⎨⎪≥⎩于是,Y 的密度函数()()Y Y f y F y '=(3)240XF y y '-<<⎧=⎨⎩其它23(3)2420y y ⎧-<<⎪=⎨⎪⎩其它.27、设随机变量~(0,1)X U ,求随机变量XY e =的密度函数 解:由题意知,当1y ≤时,有()()0Y F y p Y y =≤=当1y e <<时,有()()()(ln )(ln )X Y X F y p Y y p e y p X y F y =≤=≤=≤=:当y e ≥时,有()()1Y F y p Y y =≤=即Y 的分布函数1()(ln )11Y X y F y F y y e y e≤⎧⎪=<<⎨⎪≥⎩于是,Y 的密度函数()()Y Y f y F y '=(ln )10XF y y e'<<⎧=⎨⎩其它110y ey ⎧<<⎪=⎨⎪⎩其它.28、随机变量X 的密度函数为()0xX e x f x x -⎧>=⎨≤⎩ 求随机变量2Y X =的密度函数~解:由于20Y X =≥,故当0y <时,有()()0Y F y p Y y =≤=;当0y ≥时,有2()()()(Y F y p Y y p X y p X =≤=≤=≤≤0()1x X f x dx dx e -===-即Y 的分布函数10()0Y e y F y y ⎧-≥⎪=⎨<⎪⎩于是,Y 的密度函数0()()00Y Y y f y F y y >'==≤⎩.29、设随机变量~(0,1)X N ,试求随机变量||Y X =的密度函数 解:由于||0Y X =≥,故当0y <时,有()()0Y F y p Y y =≤=;$当0y ≥时,有()()(||)()2()1Y F y p Y y p X y p y X y y =≤=≤=-≤≤=Φ-即Y 的分布函数2()10()00Y y y F y y Φ-≥⎧=⎨<⎩于是,Y 的密度函数()()Y Y f y F y '=2()00y y y 'Φ>⎧=⎨≤⎩22000yy y ->=≤⎩.B 组1、A2、B3、D4、B5、B6、B7、C8、C9、C10、C:11、设随机变量X 的分布函数为0111()21232x a x F x a x a b x <-⎧⎪-≤<⎪⎪=⎨-≤<⎪⎪+≥⎪⎩且1(2)2p X==,求常数a、b解:由()1F+∞=及()()(0)p X a F a F a==--得()121(2)(2)(20)()()32F a bp X F F a b a+∞=+=⎧⎪⎨==--=+--=⎪⎩1726a ba b+=⎧⎪⇒⎨+=⎪⎩1656ab⎧=⎪⎪⇒⎨⎪=⎪⎩.12求常数a解:由11 ii p+∞==∑得20.5121a a+-+=12a⇒=±|再由11202a a-≥⇒≤,可得1a=13、口袋中有5个球,编号为1、2、3、4、5,从中任取3个,以X表示取出的3个球中的最大号码.(1) 求X的分布列;(2) 求X的分布函数解:(1) 由题意知X是离散型随机变量,其所有可能取值为3、4、5,且22351(3)10C p X C ===、23353(4)10C p X C ===、24356(5)10C p X C ===于是X(2) 由(1)可知的分布函数为030.134()0.44515x x F x x x <⎧⎪≤<⎪=⎨≤<⎪⎪≥⎩.14、设随机变量X 的密度函数为||()x af x Ce -= (0)a >-求(1) 常数C ;(2) X 的分布函数;(3) (||2)p X <解:(1) 由()1f x dx +∞-∞=⎰得||()2221x xa a f x dx C e dx C e dx aC +∞+∞+∞---∞====⎰⎰⎰12C a⇒=; (2) 当0x <时 ||111()()222t t xa a a x x x F x f t dt e dt e dt e a a --∞-∞-∞====⎰⎰⎰ 当0x ≥时||||0011()()22t t a a xx F x f t dt e dt e dt a a ---∞-∞==+⎰⎰⎰001111222t t x a a a x e dt e dt e a a ---∞=+=-⎰⎰ 于是102()1102xa x a e x F x e x -⎧<⎪⎪=⎨⎪-≥⎪⎩;(3) 22211(||2)(22)(2)(2)1122a a ap X p X F F e e e ---<=-<<=--=--=-.15、设随机变量X 的密度函数为201()0x x f x ≤≤⎧=⎨⎩其它以Y 表示对X 的三次独立重复观察中事件1{}2X ≤出现的次数,求(2)P Y =解:由题意知:事件1{}2X ≤在一次观察中出现的概率为1112222001()02|4p f x dx dt xdx x -∞-∞==+==⎰⎰⎰ 且~(3,)Y b p ,于是223139(2)()()4464P Y C ===. 16、设顾客在某银行的窗口等待服务的时间X (单位:分钟)服从指数分布,其密度函数为510()5x e x f x x -⎧>⎪=⎨⎪≤⎩某顾客在窗口等待服务,若超过10分钟他就离开.他一个月要到银行5次,以Y 表示一个月内他未等到服务而离开窗口的次数,求(1)p Y ≥解:由题意知:顾客在窗口等待服务的时间超过10分钟的概率为5521010101()|5x x p f x dx e dx e e +∞+∞--+∞-===-=⎰⎰且~(5,)Y b p ,于是02025255(1)1(0)1()(1)1(1)0.5167P Y P Y C e e e ---≥=-==--=--=.17、设随机变量2~(2,)X N σ且(24)0.3p X <<=,求(0)p X < 解:由2~(2,)X N σ得224242(24)()()(0)0.3p X p X σσσ---<<=<<=Φ-Φ=2()0.8σ⇒Φ=0222(0)()()1()10.80.2p X p X σσσ-⇒<=<=Φ-=-Φ=-=.18、设随机变量X 的分布函数为()F x ,试求随机变量()Y F X =的密度函数 解:由于0()1F X ≤≤,故当0Y <时,有()()0Y F y p Y y =≤=; 当01y ≤≤时,有11()()(())(())(())Y F y p Y y p F X y p X F y F F y y --=≤=≤=≤==当1y >时,有()()1Y F y p Y y =≤= 即Y 的分布函数00()0111Y y F y yy y <⎧⎪=≤≤⎨⎪>⎩于是,Y 的密度函数()()Y Y f y F y '=101y <<⎧=⎨⎩其它即随机变量Y 服从区间(0,1)上的均匀分布.。
习题解答 - 第二章 离散型随机变量及其分布律

_
_
_
_
_
_
_
_
11、 一电话交换机每分钟收到的呼叫数服从 λ = 4 的泊松分布。求(1)一分钟内恰好 有 8 次呼叫的概率; (2)一分钟内呼叫数大于 9 次的概率。 解答: 因每分钟受到的呼叫数 ξ
∞
48 −4 e , π (4) , 因此 P{ξ = 8} = 而 P{ξ > 9} = 1 − P{ξ ≤ 9} 8!
什么信号相互独立,所以 A1 , A2 , A3 相互独立。因此 ξ 的分布律为:
P{ξ = 0} = P( A1 ) =
_
_
1 , 2
_
P{ξ = 1} = P( A1 A2 ) = P( A1 ) P ( A2 ) =
_ _ _ _
1 , 4
1 , 8
P{ξ = 2} = P ( A1 A2 A3 ) = P( A1 ) P( A2 ) P( A3 ) =
数 l 使得 l < λ < l + 1 ,则 P{ξ = l} 取得最大;而若存在正整数 l = λ ,则 P{ξ = l − 1} 与
P{ξ = l} 同时达到最大。
16、 设随机变量 ξ
B(2, p),η
B(3, p) ,若 P{ξ ≥ 1} = 5 / 9 ,求 P{η ≥ 1} 。
解答:因 ξ
5 B(3, p) ,所以 = P{ξ ≥ 1} = 1 − P{ξ = 0} = 1 − (1 − p ) 2 ,由此可 9 1 1 3 19 得 p = 。所以 P{η ≥ 1} = 1 − P{η = 0} = 1 − (1 − ) = 。 3 3 27 B(2, p),η
P ( Bi ) = 0.7(i = 1, 2,L) 。由此可知:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 随机变量及其分布1、解:设公司赔付金额为X ,则X 的可能值为; 投保一年内因意外死亡:20万,概率为0.0002 投保一年内因其他原因死亡:5万,概率为0.0010投保一年内没有死亡:0,概率为1-0.0002-0.0010=0.9988 所以X2、一袋中有5X 表示取出的三只球中的最大号码,写出随机变量X 的分布律解:X 可以取值3,4,5,分布律为1061)4,3,2,1,5()5(1031)3,2,1,4()4(1011)2,1,3()3(352435233522=⨯====⨯====⨯===C C P X P C C P X P C C P X P 中任取两球再在号一球为中任取两球再在号一球为号两球为号一球为 也可列为下表 X : 3, 4,5P :106,103,101 3、设在15只同类型零件中有2只是次品,在其中取三次,每次任取一只,作不放回抽样,以X 表示取出次品的只数,(1)求X 的分布律,(2)画出分布律的图形。
解:任取三只,其中新含次品个数X 可能为0,1,2个。
3522)0(315313===C C X P3512)1(31521312=⨯==C C C X P 351)2(31511322=⨯==C C C X P 再列为下表 X : 0, 1, 2P : 351,3512,3522 4、进行重复独立实验,设每次成功的概率为p ,失败的概率为q =1-p (0<p <1) (1)将实验进行到出现一次成功为止,以X 表示所需的试验次数,求X 的分布律。
(此时称X 服从以p 为参数的几何分布。
)(2)将实验进行到出现r 次成功为止,以Y 表示所需的试验次数,求Y 的分布律。
(此时称Y 服从以r, p 为参数的巴斯卡分布。
)(3)一篮球运动员的投篮命中率为45%,以X 表示他首次投中时累计已投篮的次数,写出X 的分布律,并计算X 取偶数的概率。
解:(1)P (X=k )=q k -1p k=1,2,……(2)Y=r+n={最后一次实验前r+n -1次有n 次失败,且最后一次成功},,2,1,0,)(111Λ===+=-+--+n p q C p p q C n r Y P r n n n r r n n n r 其中 q=1-p ,或记r+n=k ,则 P {Y=k }=Λ,1,,)1(11+=----r r k p p C rk r r k (3)P (X=k ) = (0.55)k -10.45 k=1,2…P (X 取偶数)=311145.0)55.0()2(1121===∑∑∞=-∞=k k k k X P 5、 一房间有3扇同样大小的窗子,其中只有一扇是打开的。
有一只鸟自开着的窗子飞入了房间,它只能从开着的窗子飞出去。
鸟在房子里飞来飞去,试图飞出房间。
假定鸟是没有记忆的,鸟飞向各扇窗子是随机的。
(1)以X 表示鸟为了飞出房间试飞的次数,求X 的分布律。
(2)户主声称,他养的一只鸟,是有记忆的,它飞向任一窗子的尝试不多于一次。
以Y 表示这只聪明的鸟为了飞出房间试飞的次数,如户主所说是确实的,试求Y 的分布律。
(3)求试飞次数X 小于Y 的概率;求试飞次数Y 小于X 的概率。
解:(1)X 的可能取值为1,2,3,…,n ,…P {X=n }=P {前n -1次飞向了另2扇窗子,第n 次飞了出去}=31)32(1⋅-n , n=1,2,……(2)Y 的可能取值为1,2,3P {Y=1}=P {第1次飞了出去}=31P {Y=2}=P {第1次飞向 另2扇窗子中的一扇,第2次飞了出去}=312132=⨯P {Y=3}=P {第1,2次飞向了另2扇窗子,第3次飞了出去}=31!3!2=∑∑===<===<==<3231}|{}{}|{}{}{)3(k k k Y Y X P k Y P k Y Y X P k Y P Y X P ⎪⎪⎭⎫ ⎝⎛==<0}1|{Y Y X P 全概率公式并注意到278313231313131}{}{32=⎥⎦⎤⎢⎣⎡⨯+⨯+⨯=<==∑=k k X P k Y P }{}|{,k X P k Y Y X P Y X <==<独立即注意到同上,∑======31}|{}{}{k k Y Y X P k Y P Y X P81192743192313131}{}{31=⨯+⨯+⨯====∑=k k X P k Y P 故8138){}{1}{==-<-=<Y X P Y X P X Y P 6、一大楼装有5个同类型的供水设备,调查表明在任一时刻t 每个设备使用的概率为0.1,问在同一时刻(1)恰有2个设备被使用的概率是多少?0729.0)9.0()1.0()2(322525225=⨯⨯===-C q p C X P (2)至少有3个设备被使用的概率是多少?00856.0)1.0()9.0()1.0()9.0()1.0()3(5554452335=⨯+⨯⨯+⨯⨯=≥C C C X P (3)至多有3个设备被使用的概率是多少?3225415505)9.0()1.0()9.0(1.0)9.0()3(⨯⨯+⨯⨯+=≤C C C X P 99954.0)9.0()1.0(2335=⨯⨯+C(4)至少有一个设备被使用的概率是多少? 40951.059049.01)0(1)1(=-==-=≥X P X P7、设事件A 在每一次试验中发生的概率为0.3,当A 发生不少于3次时,指示灯发出信号。
(1)进行了5 次独立试验,求指示灯发出信号的概率 。
(2)进行了7次独立试验,求指示灯发出信号的概率解: 设X 为 A 发生的次数。
则()0.3,.X B n : n=5,7B:“指示等发出信号“ ① (){}3P B P X =≥55530.30.70.163k k k k C-===∑②(){}3P B P X =≥={}{}7231k P X K P X K ===-=∑∑71622510.70.30.70.30.70.353G G =--⋅⨯-⨯≈ 8、甲、乙二人投篮,投中的概率各为0.6, 0.7,令各投三次。
求 (1)二人投中次数相等的概率。
记X 表甲三次投篮中投中的次数 Y 表乙三次投篮中投中的次数由于甲、乙每次投篮独立,且彼此投篮也独立。
P (X =Y )=P (X =0, Y=0)+P (X =2, Y=2)+P (X=3, Y=3)= P (X =0) P (Y=0)+ P (X =1) P (Y=1)+ P (X =2) P (Y=2)+ P (X =3) P (Y=3)= (0.4)3× (0.3)3+ [])3.0(7.0[])4.0(6.0213213⨯⨯⨯⨯⨯C C 3223223)6.0(]3.)7.0([]4.0)6.0([+⨯⨯⨯⨯⨯+C C 321.0)7.0(3=⨯(2)甲比乙投中次数多的概率。
P (X>Y )=P (X =1, Y=0)+P (X =2, Y=0)+P (X=2, Y=1)+P (X =3) P (Y=0)+ P (X =3) P (Y=1)+ P (X =3) P (Y=2) =P (X =1) P (Y=0) + P (X =2, Y=0)+ P (X=2, Y=1)+ P (X =3) P (Y=0)+ P (X =3) P (Y=1)+ P (X =3) P (Y=2)=+⨯⨯⨯+⨯⨯⨯82233213)3.0(]4.0)6.0([)3.0(])4.0(6.0[C C 3213223)6.0(])3.0(7.0[]4.0)6.0([+⨯⨯⨯⨯⨯C C 321333)6.0(])3.0(7.0[)6.0()3.0(+⨯⨯⨯+⨯C243.0]3.0)7.0([223=⨯⨯⨯C9、有一大批产品,其验收方案如下,先做第一次检验:从中任取10件,经验收无次品接受这批产品,次品数大于2拒收;否则作第二次检验,其做法是从中再任取5件,仅当5件中无次品时接受这批产品,若产品的次品率为10%,求(1)这批产品经第一次检验就能接受的概率 (2)需作第二次检验的概率(3)这批产品按第2次检验的标准被接受的概率(4)这批产品在第1次检验未能做决定且第二次检验时被通过的概率 (5)这批产品被接受的概率解:X 表示10件中次品的个数,Y 表示5件中次品的个数, 由于产品总数很大,故X~B (10,0.1),Y~B (5,0.1)(近似服从) (1)P {X =0}=0.910≈0.349(2)P {X ≤2}=P {X =2}+ P {X =1}=581.09.01.09.01.0911082210≈+C C (3)P {Y =0}=0.9 5≈0.590(4)P {0<X ≤2,Y=0} ({0<X ≤2}与{ Y=2}独立) = P {0<X ≤2}P {Y=0} =0.581×0.590≈0.343(5)P {X =0}+ P {0<X ≤2,Y=0} ≈0.349+0.343=0.69210、有甲、乙两种味道和颜色极为相似的名酒各4杯。
如果从中挑4杯,能将甲种酒全部挑出来,算是试验成功一次。
(1)某人随机地去猜,问他试验成功一次的概率是多少?(2)某人声称他通过品尝能区分两种酒。
他连续试验10次,成功3次。
试问他是猜对的,还是他确有区分的能力(设各次试验是相互独立的。
)解:(1)P (一次成功)=701148=C(2)P (连续试验10次,成功3次)= 100003)7069()701(73310=C 。
此概率太小,按实际推断原理,就认为他确有区分能力。
11. 尽管在几何教科书中已经讲过用圆规和直尺三等分一个任意角是不可能的。
但每年总有一些“发明者”撰写关于用圆规和直尺将角三等分的文章。
设某地区每年撰写此类文章的篇数X 服从参数为6的泊松分布。
求明年没有此类文章的概率。
解: ().6~πX Θ 6=λ{}0025.01066≈===∴-e e X P 12. 一电话交换台每分钟收到呼唤的次数服从参数为4的泊松分布。
求(1)每分钟恰有8次呼唤的概率。
(2)某一分钟的呼唤次数大于3的概率。
()4~πX 4=λ(1){}∑∑∞=∞=--⋅-⋅==899484!!8r r r e r e X P λλ 029771.0021363.0051134.0=-= (2)566530.0}4{}3{=≥=>X P X P13. 某一公安局在长度为t 的时间间隔内收到的紧急呼救的次数X 服从参数为(1/2)t 的泊松分布,而与时间间隔的起点无关(时间以小时计)。
