实验二优选资料连续时间信号卷积运算的MATLAB实现
实验2_连续时间信号的Matlab表示与计算
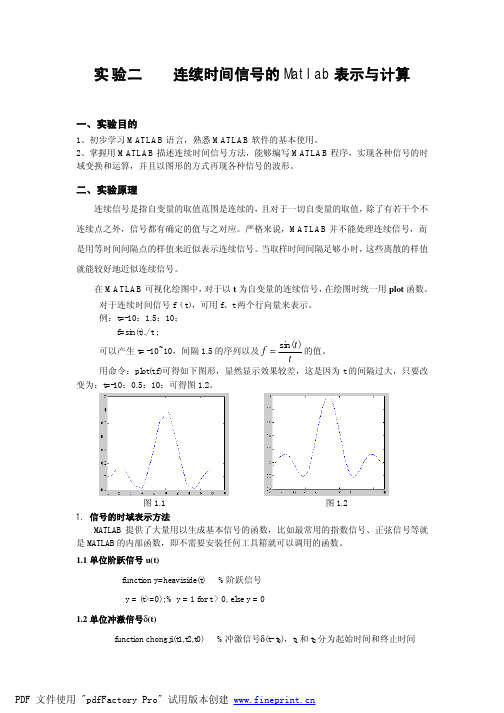
y = rectpuls(t, width)
用以产生一个幅值为 1、宽度为 width、相对于 t=0 点左右对称的矩形波信号。该函数的横 坐标范围由向量 t 决定,是以 t=0 为中心向左右各展开 width/2 的范围。width 的默认值为 1。
用命令:plot(t,f)可得如下图形,显然显示效果较差,这是因为 t 的间隔过大,只要改 变为:t=-10:0.5:10;可得图 1.2。
图 1.1
图 1.2
1. 信号的时域表示方法
MATLAB 提供了大量用以生成基本信号的函数,比如最常用的指数信号、正弦信号等就
是 MATLAB 的内部函数,即不需要安装任何工具箱就可以调用的函数。
1、初步学习 MATLAB 语言,熟悉 MATLAB 软件的基本使用。 2、掌握用 MATLAB 描述连续时间信号方法,能够编写 MATLAB 程序,实现各种信号的时 域变换和运算,并且以图形的方式再现各种信号的波形。
二、实验原理
连续信号是指自变量的取值范围是连续的,且对于一切自变量的取值,除了有若干个不 连续点之外,信号都有确定的值与之对应。严格来说,MATLAB 并不能处理连续信号,而 是用等时间间隔点的样值来近似表示连续信号。当取样时间间隔足够小时,这些离散的样值 就能较好地近似连续信号。
PDF 文件使用 "pdfFactory Pro" 试用版本创建
图 1-5 抽样函数
图 1-6 矩形波信号
周期性矩形波(方波)信号在 MATLAB 中用 square 函数来表示,其调用形式为:
y=square(t,DUTY)
实验2 连续时间信号在MATLAB中运算

实验原理:
信号 f (t)的时移就是将信号数学表达式中的自变量 t
用t t0替换,其中 t0为整实数
信号 f (t)的反折就是将信号数学表达式中的自变量 t
用 t 替换
信号 f (t)的尺度变换就是将信号数学表达式中的自变
量 t 用 at 替t0换
例子1:
function f = unc(t) f = heaviside(t+2)- heaviside(t)+(-t+1).*(heaviside(t)- heaviside(t-1));
实验2 连续时间信号在 MATLAB中的运算
实验目的:
1、学会运用MATLAB进行连续时间信号时移,反 折和尺度变换 2、学会运用MATLAB进行连续信号微分、积分运 算 3、学会运用MATLAB进行连续信号相加、相乘运 算 4、学会运用MATLAB进行连续信号的奇偶分解
一、信号的时移、反折和尺度变换
二、连续时间信号的微分与积分运算
实验原理:
diff ( function,' var iable', n)
int( function,' var iable', a,b)
例子1:
(1) y1 sin(ax2 )
(2) y2 x sin x ln x
clear all syms a x y1 y2 ; y1 = sin(a*x^2) ; y2 = x*sin(x)*log(x); dy1 = diff(y1,'x') ; dy2 = diff(y2) ;
例子3:
(1) y1 (x5 ax2 x )dx
2
(2) y2
1 0
ቤተ መጻሕፍቲ ባይዱ
信号与系统 连续时间信号卷积运算
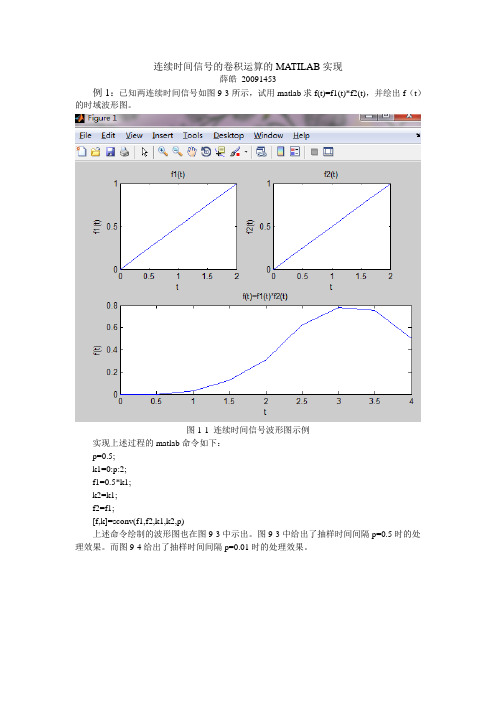
连续时间信号的卷积运算的MATILAB实现薛皓20091453例1:已知两连续时间信号如图9-3所示,试用matlab求f(t)=f1(t)*f2(t),并绘出f(t)的时域波形图。
图1-1 连续时间信号波形图示例实现上述过程的matlab命令如下:p=0.5;k1=0:p:2;f1=0.5*k1;k2=k1;f2=f1;[f,k]=sconv(f1,f2,k1,k2,p)上述命令绘制的波形图也在图9-3中示出。
图9-3中给出了抽样时间间隔p=0.5时的处理效果。
而图9-4给出了抽样时间间隔p=0.01时的处理效果。
图1-2 例1的连续时间信号波形图习题1:已知f1(t)=1(2t 1≤≤),f2(t)=1(3t 2≤≤),用matlab 实现其卷积并绘制出卷积曲线。
解:程序代码如下:>> p=0.01;k1=1:p:2;f1=ones(size(k1)).*(k1>1);k2=2:p:3;f2=ones(size(k2)).*(k2>2);f=conv(f1,f2);f=f*p;k0=k1(1)+k2(1);k3=k1(length(k1))+k2(length(k2));subplot(2,2,1)plot(k1,f1)title('f1(t)')xlabel('t')ylabel('f1(t)')subplot(2,2,2)plot(k2,f2)title('f2(t)')xlabel('t')ylabel('f2(t)')subplot(2,2,3)plot(k,f);h=get(gca,'position');h(3)=2.5*h(3); 0set(gca,'position',h)title('f(t)=f1(t)*f2(t)')xlabel('t')ylabel('f(t)')绘制图形如图2-1所示。
MATLAB实验报告卷积

实验报告学院:机电班级:姓名:学号:实验名称:连续时间信号卷积运算的MATLAB实现1.实验目的:掌握卷积的概念及计算方法2.熟悉通过调用conv()函数求解连续时间信号卷积的数值分析法实验环境:MATLAB 6.5.1软件实验要求:1、已知信号f1(t)=t/2*[ε(t)- ε(t-2)], f2(t)= [ε(t)- ε(t-1)],通过调用conv()函数编程实现卷积计算y(t)= f1(t)* f2(t),画出波形。
2、已知信号f(t)=e-t *ε(t), h(t)= t2 *e-2t *ε(t),y(t)=f(t)* h(t)(1)用符号分析法编程实现计算y(t)的理论解;(2)过调用conv()函数编程实现卷积计算y(t)的数值解并画图实验程序及结果:第一题:M文件(1) function f=uCT(t)f=(t>=0);主程序:k1=0:p:2;k2=0:p:1;f1=k1/2.*[uCT(k1)-uCT(k1-2)]; f2=uCT(k2)-uCT(k2-1);y=conv(f1,f2)*p;k0=k1(1)+k2(1);k3=length(f1)+length(f2)-2; k=k0:p:k3*p+k0;subplot(311)plot(k1,f1);xlabel('t')ylabel('f1(t)')axis([-0.5 2.5 -0.5 1.5])grid onsubplot(312);plot(k2,f2)grid onaxis([-0.5 2.5 -0.5 1.5]) xlabel('t')ylabel('f2(t)')subplot(313)axis([-0.5 4 -0.5 1.5])grid onxlabel('t')ylabel('f1(t)*f2(t)')实验结果:第二题:M文件function f=uCT(t)f=(t>=0);主程序:syms tao>> t=sym('t','positive');>> f=exp(-t);>> h=t^2*exp(-2*t);>> fh_tao=subs(f,t,tao)*subs(h,t,t-tao); >> yt=int(fh_tao,0,t)yt =-(-2*exp(t)+t^2+2*t+2)/exp(t)^2p=0.01;k1=0:p:3;k2=0:p:12;f=exp(-k1).*uCT(k1);h=(k2).^2.*exp(-2.*k2).*uCT(k2);y=conv(f,h)*p;k0=k1(1)+k2(1);k3=length(f)+length(h)-2;k=k0:p:k3*p+k0;subplot(221)plot(k1,f);xlabel('t')ylabel('f(t)')grid onaxis([-0.5 3.5 -0.5 1.5])subplot(222)plot(k2,h);xlabel('t')ylabel('h(t)')grid onaxis([-0.5 11 -0.05 0.2])subplot(223)plot(k,y);grid onxlabel('t')ylabel('f(t)*h(t)数值')axis([-0.5 15 -0.01 0.1])subplot(224)yt =-(-2.*exp(k)+k.^2+2.*k+2)./exp(k).^2; plot(k,yt);grid onxlabel('t')ylabel('f(t)*h(t)理论') axis([-0.5 15 -0.01 0.1]) 实验结果:。
实验一--连续时间信号在Matlab中的运算

实验一连续时间信号在Matlab 中的运算一、实验目的1、学会运用Matlab 进行连续时间信号的时移、反褶和尺度变换。
2、学会运用Matlab 进行连续时间信号相加、相乘、微分、积分和卷积运算。
3、观察并熟悉这些信号的波形和特性。
二、实验原理1、连续时间信号的表示连续信号的表示方法有两种:符号推理法和数值法。
从严格意义上讲,Matlab 数值计算的方法不能处理连续时间信号。
然而,可利用连续信号在等时间间隔点的取样值来近似表示连续信号,即当取样时间间隔足够小时,这些离散样值能被Matlab 处理,并且能较好地近似表示连续信号。
2、信号的时移、反褶和尺度变换信号的平移、反转和尺度变换是针对自变量时间而言的,其数学表达式和波形变换中存在着一定的变化规律。
从数学表达式上来看,信号的上述所有计算都是自变量的替换过程。
所以在使用Matlab 进行连续时间信号的运算时,只需要进行相应的变量代换即可完成相关工作。
3、连续时间信号的微分和积分连续时间信号的微分运算,可使用diff 命令函数来完成,其语句格式为:diff(function, ‘variable ',n) 。
其中,function 表示需要进行求导运算的函数,或者被赋值的符号表达式;variable 为求导运算的独立变量;n 为求导阶数,默认值为一阶导数。
连续时间信号积分运算可以使用int 命令函数来完成,其语句格式为:int(function, ‘variable ',a, b) 。
其中,function 表示被积函数,或者被赋值的符号表达式;variable为积分变量;a为积分下限,b为积分上限,a和b默认时则求不定积分。
4、信号的相加和相乘运算信号的相加和相乘是信号在同一时刻取值的相加和相乘。
因此Matlab 对于时间信号的相加和相乘都是基于向量的点运算。
5、连续信号的卷积运算卷积积分是信号与系统时域分析的重要方法之一。
定义为:f (t) f1(t) f2 (t) -f1( )f2(t )dMatlab 进行卷积计算可通过符号运算方法和数值计算方法实现。
matlab连续函数卷积

matlab连续函数卷积
在matlab中,我们可以使用conv函数实现两个连续函数的卷积运算。
卷积运算是一种数学运算,用于描述两个函数之间的相互影响。
在信号处理、图像处理和控制系统等领域,卷积运算都有广泛的应用。
使用matlab进行连续函数卷积的步骤如下:
1.定义两个连续函数f和g,并将它们存储为向量形式。
2.使用conv函数进行卷积运算,将f和g作为输入参数传递给该函数。
3.将卷积结果存储为一个新的向量。
4.使用plot函数将原始函数和卷积结果进行可视化比较,以便更好地理解两者之间的关系。
需要注意的是,在进行卷积运算时,我们需要对函数进行截断处理,以避免出现无限长的结果。
此外,还需要根据具体情况选择合适的截断长度和采样间隔,以确保计算结果的准确性和稳定性。
- 1 -。
连续信号卷积
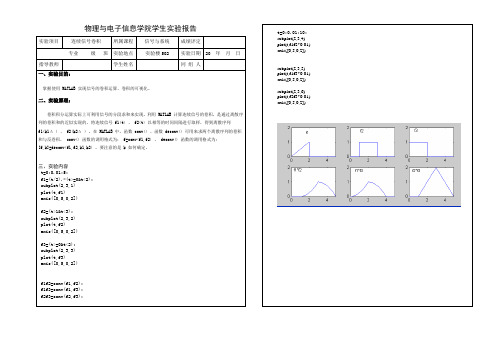
物理与电子信息学院学生实验报告t=0:0.01:10; subplot(2,3,4) plot(t,f1f2*0.01) axis([0,5,0,2])subplot(2,3,5) plot(t,f1f3*0.01) axis([0,5,0,2])subplot(2,3,6) plot(t,f2f3*0.01) axis([0,5,0,2])实验项目连续信号卷积所属课程信号与系统 成绩评定专业 级 班 实验地点 实验楼502实验日期 20 年 月 日 指导教师 学生姓名同 组 人一、实验目的:掌握使用 MATLAB 实现信号的卷积运算、卷积的可视化。
二、实验原理:卷积积分运算实际上可利用信号的分段求和来实现。
利用 MATLAB 计算连续信号的卷积,是通过离散序列的卷积和的近似实现的,将连续信号 f1(t) 、 f2(t) 以相等的时间间隔进行取样,得到离散序列 f1(k1Δ ) 、 f2(k2Δ ) 。
在 MATLAB 中,函数 conv() 、函数 deconv() 可用来求两个离散序列的卷积和与反卷积, conv() 函数的调用格式为: f=conv(f1,f2) 、 deconv() 函数的调用格式为: [f,k]=deconv(f1,f2,k1,k2) 。
要注意的是 k 如何确定。
三、实验内容 t=0:0.01:5;f1=(t/2).*(t>=0&t<2); subplot(2,3,1) plot(t,f1)axis([0,5,0,2])f2=(t>1&t<3); subplot(2,3,2) plot(t,f2)axis([0,5,0,2])f3=(t>=0&t<2); subplot(2,3,3) plot(t,f3)axis([0,5,0,2])f1f2=conv(f1,f2); f1f3=conv(f1,f3); f2f3=conv(f2,f3);四、实验总结(实验中所遇问题的原因分析及解决措施;本实验未解决的问题;对实验的改进;个人的收获等)。
信号的时域表示以及卷积运算(MATLAB)

信号的时域表示【实验目的】利用MATLAB 实现信号的时域表示利用MATLAB 实现图形表示【实验内容(步骤)】软件仿真实验在此部分只需写出代码及相应的注释。
例题实验:clear;%清除工作空间的变量clf;%清除图形clc;%清除命令窗口中的命令t0=-1;%给t0赋值1,作为横轴的最小值tf=5;%给tf赋值5,作为横轴的最大值dt=0.05;%作为冒号表达式的步长t1=0;t=t0:dt:tf; %建立向量Len_t = length(t);%把向量t的长度赋值给Len_tn1 = floor((t1-t0)/dt);%选出t=0在向量t中对应的元素序号x1 = zeros(1,Len_t);%建立一个与t等长的一维零矩阵x1(n1) = 1/dt;%选出t=0在向量t中对应的元素subplot(2,2,1),stairs(t,x1),grid on%把图形窗口分割成2*2的四个部分,第一个部分用stairs函数画出单位冲击函数axis([-1,5,0,22])%控制坐标轴,横轴在-1到5之间,纵轴在0到22之间title('1.冲击信号');%给第一个图形命名% x2 = [zeros(1,n1-1),ones(1,Len_t-n1+1)];% x2 = (t>0);% x2 = 1/2*(sign(t-0)+1);%利用符号函数实现单位阶跃函数x2 = stepfun(t,t1);%建立一个向量x2,当t<t1时,元素都为0,当t>=t1时,元素都为1subplot(2,2,3),stairs(t,x2),grid on%在图形窗口的第三个部分画出单位阶跃函数axis([-1,5,0,1.1]) %设置显示的坐标轴的最大最小值title('2.单位阶跃信号'); %给第二个图形命名alpha = -0.5;%为x3中的alpha赋值omega = 10;%为x3中的omega赋值x3 = exp((alpha+j*omega)*t);%产生了一个复指数信号subplot(2,2,2),plot(t,real(x3)),grid on%在图形窗口的第二部分画出复指数信号的实部title('3.复指数跃信号(实部)'); %命名subplot(2,2,4),plot(t,imag(x3)),grid on%在图形窗口中的第四部分画出复指数信号的虚部title('4.复指数跃信号(虚部)'); %命名【实验结果及分析】图像截图:10HZ和16HZ的周期方波实验:实验步骤:t = linspace(-10,10,100); 产生一百个元素y = (square(t) + 1)./2; y的函数subplot(211); 分割成两块,进入第一块界面plot(t./(2*pi*10),y,'r-');grid on 产生10HZ 的方波axis([0,0.3,-1.2,1.2]);xlabel('t'),ylabel('y1'),title('10Hz');subplot(212); 进入第二块界面plot(t./(2*pi*16),y,'c-');grid on 产生16HZ 的方波axis([0,0.3,-1.2,1.2]);xlabel('t'),ylabel('y2'),title('16Hz');图像截图:连续信号的卷积实验实验步骤:clear %清除Workspace中的变量clc %清除Command Window中的命令uls=ones(1,10); %建立一个1*10的矩阵Length_u = length(uls); %把向量uls的长度赋给Length_uhls = exp(-0.1*(1:15)); %建立一个长度为15的向量hlsLength_h = length(hls); %把向量hls的长度赋给Length_hlmax = max(Length_u,Length_h); %把向量u的长度与向量h的长度中的最大值赋给lmax%if end 语句确定了nh与nu的值,用于下面的向量u与向量h中,保证两者长度相等if Length_u>Length_hnu=0; nh = Length_u - Length_h;elseif Length_u<Length_hnh=0; nu = Length_h - Length_u;elsenu=0; nh=0;end%nh=0 nu=5dt = 0.5;lt = lmax;%把向量u的长度与向量h的长度中的最大值赋给ltu = [zeros(1,lt),uls,zeros(1,nu),zeros(1,lt)];% 建立一个长度为45的向量,uls的值在中间,易于卷积t1 = (-lt+1:2*lt)*dt;%建立了一个长度为45,步长为0.5的向量,从-7到15h = [zeros(1,2*lt),hls,zeros(1,nh)];% 建立一个长度为45的向量,hls的值在末尾一段hf = fliplr(h);%将h进行反褶运算y = zeros(1,3*lt);%建立一个1*45的零矩阵for k = 0:2*lt%设置循环31次p = [zeros(1,k),hf(1:end-k)];%p是长度为45的向量,由向量hf平移k个单位而来y1 = u.*p*dt;%卷积中的相乘yk = sum(y1);%卷积中的积分(求和)y(k+lt+1) = yk;%给y中的元素赋值subplot(4,1,1);stairs(t1,u)%分割图形窗口为4*1,在第一部分画出要进行卷积的函数uaxis([-lt*dt,2*lt*dt,min(u),max(u)]),hold on%设置坐标轴的最值,并让图形等待ylabel('u(t)')%给y轴命名subplot(4,1,2);stairs(t1,p)%在图形窗口的第二部分画出要进行卷积的函数h(k-t)axis([-lt*dt,2*lt*dt,min(p),max(p)])%控制坐标轴的最值ylabel('h(k-t)')%给y轴命名subplot(4,1,3);stairs(t1,y1)%在图形窗口的第三部分画出u(t)*h(k-t)的阶梯状图形axis([-lt*dt,2*lt*dt,min(y1),max(y1)+eps])%控制坐标轴的最值ylabel('s=u*h(k-t)')%给y轴命名subplot(4,1,4);stem(k*dt,yk)%在图形窗口的第四部分画出卷积结果的点状图 axis([-lt*dt,2*lt*dt,floor(min(y)+eps),ceil(max(y+eps))])%控制坐标轴的最值hold on,ylabel('y(k)=sum(s)*dt')%给y轴命名pause(1),%每次循环暂停一秒,方便看清各个图形的变化End图像截图:矩形脉冲信号与锯齿波信号的卷积实验步骤:>> cleardt=0.001; 时间间隔t=0:dt;1; 变化范围f1=(t>0&t<1); 矩形脉冲subplot(311); 分割版面plot(t,f1);grid onxlabel('t'),ylabel('f1'),title('矩形脉冲');axis([-0.3,1.7,0,1.2]);f2=(t>0&t<1).*t; 锯齿波subplot(312);plot(t,f2);grid onxlabel('t'),ylabel('f2'),title('锯齿波');axis([-0.3,1.7,0,1.2]);f3=conv(f1,f2);f3=f3*dt; 实现卷积功能n=length(f1)+length(f2)-2;x=0:dt:n*dt;subplot(313);plot(x,f3);grid onxlabel('x'),ylabel('f3'),title('卷积');axis([-0.3,1.7,0,1.2]);图像截图:。
运用MATLAB进行连续时间信号卷积运算

实验项目名称:运用MATLAB进行连续时间信号卷积运算(所属课程:信号与系统)院系:电子信息与电气工程专业班级:电气工程及其自动化姓名:安永军学号:201002040062实验日期:2012年4月12 号实验地点:A-07-408合作者:张德扬指导老师:李静本实验项目成绩: 教师签字: 日期:一:实验目的1,掌握连续时间信号的基本运算的实现方法。
2,熟悉连续LTI 系统在典型激励信号下的响应及其特征。
3、掌握连续LTI 系统单位冲激响应的求解方法。
4、重点掌握用卷积法计算连续时间系统的零状态响应。
5、熟悉MATLAB 相关函数的调用格式及作用。
6、会用MATLAB 对系统进行时域分析。
二、实验原理1、信号的运算包括:信号的基本运算,包括加、减、乘、除等;信号的时域变换,包括信号的平移、翻转、尺度变换等;两个信号的卷积运算等。
2、连续时间线性时不变系统(LTI )可以用如下的线性常系数差分方程来描述:()(1)()(1)110110()()()()()()()()n n m m n m n n r t r t r t r t e t e t e t e t a a a a b b b b ----++++=++++''其中,n m ≥,系统的初始条件为(0)r -,(0)r -',(0)r -'', (1)(0)n r--。
系统的响应一般包括两个部分,即由当前输入所产生的响应(零状态响应)和由历史输入(初始状态)所产生的响应(零输入响应)。
对于低阶系统,一般可以通过解析的方法得到响应。
但对于高阶系统,手工计算就比较困难,这时MATLAB 强大的计算功能就能比较容易地确定系统的各种响应,如冲激响应、阶跃响应、零输入响应、零状态响应、全响应等。
1)直接求解法在MATLAB 中,要求以系数相量的形式输入系统的微分方程。
因此,在使用前必须对系统的微分方程进行变换,得到其传递函数。
实验二连续时间信号在MATLAB中的运算
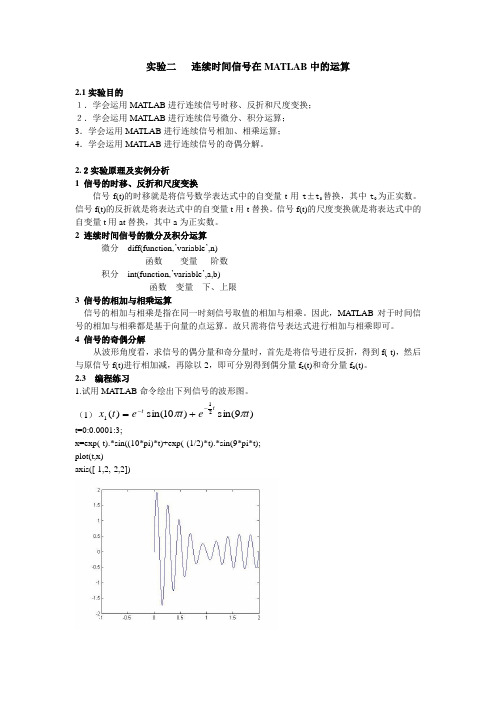
实验二 连续时间信号在MATLAB 中的运算2.1实验目的1.学会运用MATLAB 进行连续信号时移、反折和尺度变换;2.学会运用MATLAB 进行连续信号微分、积分运算;3.学会运用MATLAB 进行连续信号相加、相乘运算;4.学会运用MATLAB 进行连续信号的奇偶分解。
2.2实验原理及实例分析1 信号的时移、反折和尺度变换信号f(t)的时移就是将信号数学表达式中的自变量t 用t ±t 0替换,其中t 0为正实数。
信号f(t)的反折就是将表达式中的自变量t 用-t 替换。
信号f(t)的尺度变换就是将表达式中的自变量t 用at 替换,其中a 为正实数。
2 连续时间信号的微分及积分运算微分 diff(function ,’variable ’,n)函数 变量 阶数积分 int(function ,’variable ’,a,b)函数 变量 下、上限3 信号的相加与相乘运算信号的相加与相乘是指在同一时刻信号取值的相加与相乘。
因此,MATLAB 对于时间信号的相加与相乘都是基于向量的点运算。
故只需将信号表达式进行相加与相乘即可。
4 信号的奇偶分解从波形角度看,求信号的偶分量和奇分量时,首先是将信号进行反折,得到f(-t),然后与原信号f(t)进行相加减,再除以2,即可分别得到偶分量f e (t)和奇分量f o (t)。
2.3 编程练习1.试用MA TLAB 命令绘出下列信号的波形图。
(1))9sin()10sin()(211t e t e t x t t ππ--+=t=0:0.0001:3;x=exp(-t).*sin((10*pi)*t)+exp(-(1/2)*t).*sin(9*pi*t);plot(t,x) axis([-1,2,-2,2])(2) )10cos()(sin )(2t t c t x π=x=sinc(t).*cos(10*pi*t);t=-2:0.01:3;plot(t,x); axis([-2,4,-1,2])2. 已知连续信号f(t)的时域波形如图2-1所示,试用MA TLAB 命令绘出f(t)及其时域变换信号f(-t)、 f(t-1.5)、 f(t+1.5) 、f(0.5t)和 -f(t)的波形。
信号系统MATLAB实验报告

信号与系统实验报告桂林理工大学信息科学与工程学院 电子信息工程实验二 信号及其表示【实验目的】了解各种常用信号的表达方式掌握部分绘图函数【实验内容】一、绘出连续时间信号x(t)=t e 707.0 sin 32t 关于t 的曲线,t 的范围为 0~30s ,并以递增。
MATLAB 源程序为:t=0::30; %对时间变量赋值x=exp*t).*sin(2/3.*t); %计算变量所对应得函数值 plot(t,x);grid; %绘制函数曲线ylabel('x(t)');xlabel('Time(sec)')二、产生周期为的方波。
MATLAB源程序为:Fs=100000;t=0:1/Fs:1;x1=square(2*pi*50*t,20);x2=square(2*pi*50*t,80);subplot(2,1,1),plot(t,x1),axis([0,,,]); subplot(2,1,2),plot(t,x2),axis([0,,,]);三、产生sinc(x)函数波形。
MATLAB源程序为:x=linspace(-4,4);y=sinc(x);plot(x,y)四、绘制离散时间信号的棒状图。
其中x(-1)=-1,x(0)=1,x(1)=2,x(2)=1,x(3)=0,x(4)=-1,其他时间x(n)=0。
MATLAB源程序为:n=-3:5; %定位时间变量x=[0,0,-1,1,2,1,-1,0,0];stem(n,x);grid; %绘制棒状图line([-3,5],[0,0]); %画X轴线xlabel('n');ylabel('x[n]')五、单位脉冲序列δ(n-0n )={00...1...0n n n n =≠直接实现:x=zeros(1,N);x(1,n0)=1;函数实现:利用单位脉冲序列)(0n n -δ的生成函数impseq,即 function[x,n]=impseq(n0,ns,nf)n=[ns:nf];x=[(n-n0)==0];plot(n,x);stem(n,x);输入参数:impseq(0,0,9)——连续图形012345678900.10.20.30.40.50.60.70.80.91输入参数:impseq(0,0,9)——离散图形六、单位阶跃序列ε(n-0n )={00...1...0n n n n ≥<直接实现:n=[ns:nf];x=[(n-n0)>=0];函数实现:利用单位阶跃序列)(0n n -ε的生成函数stepseq ,即 Function[x,n]=stepseq(n0,ns,nf)n=[ns:nf];x=[(n-n0)>=0];plot(n,x);七、实指数序列=,∀)(x n∈,Ranna直接实现:n=[ns:nf]:x=a.^n;函数实现:利用实指数序列n a(的生成函数rexpseq,即n)x=Function[x,n]=rexpseq(a,ns,nf)n=[ns:nf];x=a,^n:八、复指数序列n e n x n j ∀=+,)()(ωδ直接实现:n=[ns:nf];x=exp((sigema+jw)*n);函数实现:利用复指数序列n j e n x )()(ωδ+=的生成函数cexpseq,即 Function[x,n]=cexpseq(sigema,w,ns,nf)n=[ns:nf];x=exp((sigema+j*w)*n);0123456789-3000-2000-1000100020003000400050006000九、正(余)弦序列n wn n x ∀+=),cos()(θ直接实现:n=[ns:nf];x=cos(w*n+sita);函数实现:利用正(余)弦序列x(n)=cos(wn+θ)的生成函数cosswq,即Function[x,n]=cosseq(w,ns,nf,sita)n=[ns:nf];x=cos(w*n+sita);输入参数:cosseq,0,9,30)——连续信号0123456789-0.2-0.15-0.1-0.0500.050.10.150.2输入参数:cosseq,0,9,30)——离散信号0123456789实验三信号的运算【实验目的】了解信号处理的基本操作。
MATLAB信号卷积

利用MATLAB实现信号的时域卷积一.引言MATLAB具有强大的图形处理功能及符号运算功能,为实现信号的可视化以及时域分析提供了强有力的工具,所以我们要利用MATLAB编程辅助分析与计算。
现在我们利用MATLAB 编程辅助计算连续时间信号、离散时间信号的卷积。
我们利用MATLAB编制一个M函数dconv(),该函数可以计算离散序列x1n 和x2n的卷积xn=x1n*x2n,此程序要计算xn,返回xn的非零点对应向量,还将绘制出序列x1n, x2n和xn 的时域波形图;我们要验证并调用这个dconv()函数计算“hn=xn=un-u(n-4)”这两个序列的卷积和运算,并绘制图像。
现在我们再利用MATLAB编制一个计算连续时间信号卷积积分的M函数ddconv(),此函数要计算出两个连续信号f1(t)和f2(t)的卷积积分f (t)的近似值,并绘制f1(t)、f2(t)和f (t)的时域波形图。
编完之后,我们利用ddconv()函数求“et=ut+12-ut-1,ht=12t[ut-ut-2]”这两个连续时间信号的卷积积分运算,并绘制图形。
二.基本原理对于信号的时域卷积有:(1)离散时间信号的卷积和:它的定义为,离散时间信号x1n和x2n的卷积和为:xn=x1n*x2n=m=-∞∞x1(m)x2n-m设序列x1n在区间n1~ n2非零,序列x2n在m1~ m2非零,那么就有xn=x1n*x2n的非零区间就为n1+m1~(n2+m2)并且区间长度为n1+m1-n2+m2+1,则只需计算序列xn的非零区间就可以表示整个序列.那么由上可知,在利用MATLAB的conv()函数的时候就要注意其卷积后的区间长度已经发生变化,在绘制卷积后的图像的时候就要有意识的先减去扩大的区间长度,不然绘制的卷积后的时域图像就是错误的,和横坐标不是正确的对应关系,并且我们在使用conv()函数的时候要先构造x1n和x2n,让它们有限,才能返回序列xn的非零样值时间序列。
实验二连续时间信号卷积运算的MATLAB实现

实验二连续时间信号卷积运算的MATLAB实现实验二连续时间信号卷积运算的M A T L A B实现一.实验目的(1)理解掌握卷积的概念及物理意义。
(2)理解单位冲激响应的概念及物理意义。
二.实验原理三.实验参考程序用MATLAB实现连续信号f1(t)和f2(t)卷积。
首先利用MATLAB实现连续信号卷积的通用函数sconv():function[f,k]=sconv(f1,f2,k1,k2,p);f=conv(f1,f2);f=f*p;k0=k1(1)+k2(1);k3=length(f1)+length(f2)-2;k=k0:p:k3*p;subplot(2,2,1);plot(k1,f1);title('f1(t)');xlabel('t');ylabel('f1(t)');subplot(2,2,2);plot(k2,f2);title('f2(t)');xlabel('t');ylabel('f2(t)');subplot(2,2,3);plot(k,f);h=get(gca,'position');h(3)=*h(3);set(gca,'position',h);title('f(t)=f1(t)*f2(t)');xlabel('t');ylabel('f(t)');例2-1 已知两连续时间信号,试用MATLAB求f(t)=f1(t)*f2(t),并绘出f (t)的时域波形图。
实现上述过程的MATLAB命令如下:p=;k1=0:p:2;f1=*k1;k2=k1;f2=f1;[f,k]=sconv(f1,f2,k1,k2,p);运行程序结果图:而当p=时连续时间信号的波形图为对比上面两幅图可见,当抽样时间p 足够小时,函数sconv()的计算结果就是连续时间卷积)(*)()(21t f t f t f =的较好的数值近似。
连续时间信号在Matlab中的运算

实验二 连续时间信号在Matlab 中的运算一、实验目的1、学会运用Matlab 进行连续时间信号的时移、反褶和尺度变换;2、学会运用Matlab 进行连续时间信号微分、积分运算;3、学会运用Matlab 进行连续时间信号相加、相乘运算;4、学会运用Matlab 进行连续时间信号卷积运算。
二、实验内容1、已知信号的波形(课本P11例题),画出()()()()2332----t f t f t f t f ,,,的波形图。
% 实验二 连续时间信号Matlab 表示%参考:基于Matlab 的信号与系统试验指导 % 参数: % t: 时间变量% pi:matlab 提供常数,3.14161、已知信号的波形(课本P11例题),画出()()()()2332----t f t f t f t f ,,,的波形图。
clear all ;close all ;clct=-5:0.01:5;y1=2*exp(-(t/4).^2);y2=2*exp(-((t-2)/4).^2); y3=2*exp(-(3*t/4).^2); y4=2*exp(-(-t/4).^2);subplot(2,2,1);plot(t,y1);axis([-6,6,0,3]);title('f1(t)'); grid on ;subplot(2,2,2);plot(t,y2);axis([-6,6,0,3]);title('f2(t)'); grid on ;subplot(2,2,3);plot(t,y3);axis([-6,6,0,3]);title('f3(t)'); grid on ;subplot(2,2,4);plot(t,y4);axis([-6,6,0,3]);title('f4(t)'); grid on ;-505123f1(t)-505123f2(t)-505123f3(t)-505123f4(t)2、使用微分命令求xsinxlnx y=关于变量x 的一阶导数;使用积分命令计算不定积分 dx x ax x ⎰⎪⎪⎭⎫ ⎝⎛+-225,定积分()dx x xe x ⎰+1021。
实验二 连续时间信号在MATLAB中的运算

电子信息工程系实验报告课程名称:信号与系统实验项目名称:连续时间信号在MATLAB 中的运算 实验时间:2013-11-22班级:电信112班 姓名: 学号:一、实 验 目 的:1、学会运用MATLAB 进行连续信号的时移、反折和尺度变换;2、学会运用MATLAB 进行连续信号的相加、相乘运算;3、学会运用MATLAB 数值计算方法求连续信号的卷积。
二、实 验 环 境:1、Windows 72、MATLAB 7.1三、实 验 原 理:2.1信号的时移、反折和尺度变换信号的时移、反折和尺度变换是针对自变量时间而言的,其数学表达式与波形变换之间存在一定的变换规律。
信号的时移就是将信号数学表达式中的用替换,其中为正实数。
因此,()f t t 0t t ±0t 波形的时移变换是将原来的波形在时间轴上向左或者向右移动。
为波形()f t 0()f t t +()f t 向左移动;为波形向右移动。
信号的反折就是将表达式中的自变0t 0()f t t -()f t 0t ()f t 量用替换,即变换后的波形是原波形的y 轴镜像。
信号的尺度变换就是将表达式t t -()f t 中的自变量用替换,其中,为正实数。
对应于波形的变换,则是将原来的的波t at a ()f t 形以原点为基准压缩()至原来的,或者扩展()至原来的。
1a >1/a 01a <<1/a 上述可以推广到的情况。
0()f at t ± 2.2 MATLAB 数值计算法求连续时间信号的卷积用MATLAB 分析连续时间信号,可以通过时间间隔取足够小的离散时间信号的数值计算方法来实现。
可调用MATLAB 中的conv( )函数近似地数值求解连续信号的卷积积分。
如果对连续时间信号和进行等时间间隔均匀抽样,则和分别变为离散1()f t 2()f t t ∆1()f t 2()f t 序列和。
其中为整数。
当足够小时,和即为连1()f m t ∆2()f m t ∆m t ∆1()f m t ∆2()f m t ∆续时间信号和。
用MATLAB实现信号的时域卷积

用MATLAB 实现信号的时域卷积摘要:利用抽样方法绘制连续信号和离散信号.编制函数计算连续时间信号,离散时间信号的卷积.关键字:MATLAB ;离散卷积;连续卷积实验原理:卷积运算在信号与系统分析中具有非常重要的意义,是信号与系统分析的基本方法之一.线性是不变系统的零状态响应就可以通过求解驶入激励信号与系统单位冲击响应的卷积运算获得.在连续时间系统中,卷积运算成为卷积积分,表示为在离散时间系统中,卷积运算称为卷积和,表示为:实验任务与实现方法:⑴ 编制计算离散时间序列卷积核的M 函数()dconv ,该函数课计算两离散序列()n x 1和()n x 2的卷积和()()()n x n x n x 21*=.程序计算出卷积和()n x 的同时,还绘制出序列()n x 1、()n x 2和()n x 的时域波形图,并返回()n x 的非零样值点的对应向量.任务〔1〕程序:function dconv<x1,x2,y1,y2>%任意两序列卷积x1=input<'请输入x1='>;x2=input<'请输入x2='>;y1=input<'请输入y1='>;y2=input<'请输入y2='>;subplot<131>,stem<x1,y1>,gridon ,title<'y1'>,axis<[<min<x1>-1>,<max<x1>+1>,<min<y1>-1>,<max<y1>+1>]>subplot<132>,stem<x2,y2>,gridon ,title<'y2'>,axis<[<min<x2>-1>,<max<x2>+1>,<min<y2>-1>,<max<y2>+1>]>%_____________________________________________xmin1=min<x1>;xmax1=max<x1>;xmin2=min<x2>;xmax2=max<x2>;t=<xmax2+xmax1>-<xmin2+xmin1>+1;xx=0:<t-1>;ft=conv<y1,y2>subplot<133>,stem<xx,ft>,grid on ,title<'*'>axis<[<min<xx>+0.5>,<max<xx>+0.5>,<min<ft>-0.5>,<max<ft>+0.5>]>⑵ 调用()dconv 来完成下面两离散序列的卷积和运算,并绘制图形:任务〔2〕程序:function f=ddconv<m1,m2>%-----------------------------%离散序列1t1=m1-5;t2=m1+5;t=t1:t2; %横坐标n=length<t>;tt=t1:m1; %起始到跳变n1=length<tt>;f1=[zeros<1,n1-1>,ones<1,n-n1+1>];%subplot<141>,stem<t,f1>,grid on,title<'阶跃函数序列 u<n-m1> '>,axis<[t1 t2 -0.2 1.5]>%-------------------------------%离散序列2p1=m1-5;p2=m1+5;p=p1:p2; %横坐标z=length<p>;pp=p1:m2; %起始到跳变z1=length<pp>;f2=[zeros<1,z1-1>,ones<1,z-z1+1>];%subplot<142>,stem<p,f2>,grid on,title<'离散阶跃序列 u<n-m2> '>,axis<[p1 p2 -0.2 1.5]>%------------------------------------%两离散序列相减k=min<min<t>,min<p>>:max<max<t>,max<p>>; %共同横坐标s1=zeros<1,length<k>>;s2=s1;s1<find<<k>=min<t>>&<k<=max<t>>==1>>=f1;s2<find<<k>=min<p>>&<k<=max<p>>==1>>=f2;f=s1-s2;subplot<131>,stem<k,f>,grid on,title<'x<n>=u<n>-u<n-4>'>axis<[<min<min<t>,min<p>>-1>,<max<max<t>,max<p>>+1>,<min<f>-0.5>,<max <f>+0.5>]>subplot<132>,stem<k,f>,grid on,title<'h<n>=u<n>-u<n-4>'>axis<[<min<min<t>,min<p>>-1>,<max<max<t>,max<p>>+1>,<min<f>-0.5>,<max <f>+0.5>]>%----------------------------xmin1=min<k>;xmax1=max<k>;xmin2=min<k>;xmax2=max<k>;t=<xmax2+xmax1>-<xmin2+xmin1>+1;xx=0:<t-1>;ft=conv<f,f>subplot<133>,stem<xx,ft>,grid on,title<'h<n>*x<n>'>axis<[<min<xx>+0.5>,<max<xx>+0.5>,<min<ft>-0.5>,<max<ft>+0.5>]>⑶编制计算连续时间信号卷积积分的M函数()sconv,该函数在计算出两信号()t f1和()t f 2的卷积积分()t f的数值近似的同时,还绘制出()t f1、()tf2和()t f的时域波形图. 实现方法:与第〔4〕任务用同一个程序.⑷调用函数()sconv来完成下面两连续时间信号的卷积积分运算,并绘制图形:()()121--⎪⎭⎫⎝⎛+=tutut e,()()()[]221--=tututth任务〔3、4〕程序:function sconv<>%u<t>m1=0;t1=m1-10;t2=m1+10;t=t1:0.01:t2;n=length<t>;tt=t1:0.01:m1;n1=length<tt>;f1=[zeros<1,n1-1>,ones<1,n-n1+1>];%subplot<131>,plot<t,f1>,grid on,title<'ÀëÉ¢½×Ô¾ÐòÁÐ u<t> '>,axis<[t1 t2 -0.2 1.5]>%u<t+1/2>tx1=t-1/2;fx1=f1;%subplot<241>,stairs<tx1,fx1>,grid on,title<' u<t+1/2> '>,axis<[t1 t2 -0.2 1.5]>%u<t-1>tx2=t+1;fx2=f1;%subplot<242>,stairs<tx2,fx2>,grid on,title<' u<t-1> '>,axis<[t1 t2 -0.2 1.5]>k=min<min<tx1>,min<tx2>>:0.01:max<max<tx1>,max<tx2>>;s1=zeros<1,length<k>>;s2=s1;s1<find<<k>=min<tx1>>&<k<=max<tx1>>==1>>=fx1;s2<find<<k>=min<tx2>>&<k<=max<tx2>>==1>>=fx2;e=s1-s2;subplot<131>,stairs<k,e>,grid on,title<'e<t>=u<t+1/2>-u<t-1>'>axis<[<min<min<tx1>,min<tx2>>+5>,<max<max<tx1>,max<tx2>>-5>,<min<e>-0 .5>,<max<e>+0.5>]>tx3=t;fx3=f1;%subplot<243>,stairs<tx3,fx3>,grid on,title<' u<t> '>,axis<[t1 t2 -0.2 1.5]>tx4=t+2;fx4=f1;%subplot<244>,stairs<tx4,fx4>,grid on,title<' u<t-2> '>,axis<[t1 t2 -0.2 1.5]>k1=min<min<tx3>,min<tx4>>:0.01:max<max<tx3>,max<tx4>>;s3=zeros<1,length<k1>>;s4=s1;s3<find<<k1>=min<tx3>>&<k1<=max<tx3>>==1>>=fx3;s4<find<<k1>=min<tx4>>&<k1<=max<tx4>>==1>>=fx4;h=s3-s4;%subplot<236>,stairs<k1,h>,grid on,title<' u<t>-u<t-2>'>%axis<[<min<min<tx3>,min<tx4>>+5>,<max<max<tx3>,max<tx4>>-5>,<min<h>-0.5>,<max<h>+0.5>]>h<t>=1/2*t*[u<t>-u<t-2>]kk1=length<k1>;ont=0:0.01:kk1;ks=min<min<k1>,min<ont>>:0.01:max<max<k1>,max<ont>>;s5=zeros<1,length<ks>>;s6=s5;s5<find<<ks>=min<ont>>&<ks<=max<ont>>==1>>=ont;s6<find<<ks>=min<k1>>&<ks<=max<k1>>==1>>=h;ffu=1/2*<s5.*s6>;subplot<132>,stairs<ks,ffu>,grid on,title<'1/2*t*[u<t>-u<t-2>]'>axis<[-5,5,<min<ffu>-0.5>,<max<ffu>+0.5>]>xmin1=min<k>;xmax1=max<k>;xmin2=min<ks>;xmax2=max<ks>;ttx=<xmax2+xmax1>-<xmin2+xmin1>+0.01;xx=0:0.01:<ttx-0.01>;ft=conv<e,ffu>;subplot<133>,stairs<xx,ft>,grid on,title<'h<n>*x<n>'>axis<[15,55,<min<ft>-0.5>,<max<ft>+0.5>]>实验总结:通过本次实验学会了用MATLAB实现线性系统的时域分析.能自己完成的东西一定要自己独立完成,这样收获的东西才是自己的.。
(完整版)实验二用MATLAB处理连续系统

单位冲击信号δ(t)实验二 用MATLAB 处理连续系统数学模型一、实验目的1. 学会LTI 系统模型的建立;2. 掌握相关函数的调用格式及作用;3. 掌握连续信号的基本运算。
二、实验设备计算机一台,装有MATLAB 软件三、实验原理及基本操作1.典型信号 (1)阶跃信号10()00t u t t >⎧=⎨<⎩ t=-1:0.01:3; f=t>0; plot(t,f);axis([-1,3,-0.2,1.2]); 注:参见函数Heaviside(2)单位冲激信号定义冲激函数function chongji(t1,t2,t0) dt=0.01; t=t1:dt:t2;n=length(t); x=zeros(1,n); x(1,(t0-t1)/dt+1)=1/dt; stairs(t,x);axis([t1,t2,0,1.2/dt])title('单位冲击信号δ(t)')图中调用的是chongji(-1,5,0);可以试着给别的t1,t2,t0,可以得到δ(t-t0)的波形。
注:参见函数dirac2.连续信号的时域基本运算相加、相乘、移位、反折、尺度变换、倒相已知信号)]2()2([)21()(--+⨯+=ttttfεε,用matlab求f(t+2),f(t-2),f(-t),f(2t),-f(t),并绘出时域波形。
syms tf=sym('(t/2+1)*(heaviside(t+2)-heaviside(t-2))') subplot(2,3,1);ezplot(f,[-3,3])title('f(t)')y1=subs(f,t,t+2)subplot(2,3,2),ezplot(y1,[-5,1])title('f(t+2)')y2=subs(f,t,t-2)subplot(2,3,3),ezplot(y2,[-1,5])title('f(t-2)')y3=subs(f,t,-t)subplot(2,3,4),ezplot(y3,[-3,3])title('f(-t)')y4=subs(f,t,2*t)subplot(2,3,5),ezplot(y4,[-2,2])title('f(2t)')y5=-fsubplot(2,3,6),ezplot(y5,[-3,3])title('-f')x=exp(t)y=x(-t)-2020.511.52t f(t)-4-200.511.52t f(t+2)240.511.52t f(t-2)-2020.511.52tf(-t)-20200.511.52tf(2t)-202-2-1.5-1-0.50t-f注:Matlab 提供了函数fliplr()实现信号的左右翻转,其调用格式为y=fliplr(x)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验二连续时间信号卷积运算的M A T L A B实现
一.实验目的
(1)理解掌握卷积的概念及物理意义。
(2)理解单位冲激响应的概念及物理意义。
二.实验原理
三.实验参考程序
用MATLAB实现连续信号f1(t)和f2(t)卷积。
首先利用MATLAB实现连续信号卷积的通用函数sconv():
function[f,k]=sconv(f1,f2,k1,k2,p);
f=conv(f1,f2);
f=f*p;
k0=k1(1)+k2(1);
k3=length(f1)+length(f2)-2;
k=k0:p:k3*p;
subplot(2,2,1);
plot(k1,f1);
title('f1(t)');
xlabel('t');
ylabel('f1(t)');
subplot(2,2,2);
plot(k2,f2);
title('f2(t)');
xlabel('t');
ylabel('f2(t)');
subplot(2,2,3);
plot(k,f);
h=get(gca,'position');
h(3)=*h(3);
set(gca,'position',h);
title('f(t)=f1(t)*f2(t)');
xlabel('t');
ylabel('f(t)');
例2-1 已知两连续时间信号,试用MATLAB求f(t)=f1(t)*f2(t),并绘出f(t)的时域波形图。
实现上述过程的MATLAB命令如下:
p=;
k1=0:p:2;
f1=*k1;
k2=k1;
f2=f1;
[f,k]=sconv(f1,f2,k1,k2,p);
运行程序结果图:
而当p=时连续时间信号的波形图为
对比上面两幅图可见,当抽样时间p 足够小时,函数sconv()的计算结果就是连续时间卷积
)(*)()(21t f t f t f =的较好的数值近似。
四.实验要求
在课本卷积部分课后习题中任选两题,完成信号的卷积运算,绘出波形。
已知两连续时间信号如图所示,使用MATLAB 求()()()12f t f t f t =*,并绘出()f t 的时域波形图。
五.实验心得
通过本次实验我学会使用MATLAB 软件,并用软件实现了的连续时间信号的卷积运算,且进一步理解了卷积的概念和物理意义,对我以后学习卷积知识有了很大的帮助。
