2018上海市初三数学二模-金山区2017学年第二学期初三期中质量检测及评分标准
上海市2018年中考二模数学试卷含答案

2017-2018学年第二学期九年级质量调研考试数 学 试 卷(考试时间100分钟,满分150分)考生注意:1.本试卷含三个大题,共25题.2.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答 题一律无效.3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证 明或计算的主要步骤.一、选择题:(本大题共6题,每题4分,满分24分) 【下列各题的四个选项中,有且只有一个选项是正确的,请选择正确选项的代号并填涂在答题纸的相应位置上】 1.在下列各式中,二次单项式是 (A )21x +;(B )213xy ;(C )2xy ;(D )21()2-.2.下列运算结果正确的是 (A )222()a b a b +=+; (B )2323a a a +=; (C )325a a a ⋅=;(D )112(0)2a a a-=≠. 3.在平面直角坐标系中,反比例函数(0)ky k x=≠图像在每个象限内y 随着x 的增大而减小,那么它的图像的两个分支分别在 (A )第一、三象限; (B )第二、四象限; (C )第一、二象限;(D )第三、四象限.4.有9名学生参加校民乐决赛,最终成绩各不相同,其中一名同学想要知道自己是否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的 (A )平均数;(B )中位数;(C )众数;(D )方差. 5.已知四边形ABCD 是平行四边形,下列结论中不正确的是 (A )当AB = BC 时,四边形ABCD 是菱形; (B )当AC ⊥BD 时,四边形ABCD 是菱形; (C )当∠ABC = 90o 时,四边形ABCD 是矩形;(D )当AC = BD 时,四边形ABCD 是正方形.6.点A 在圆O 上,已知圆O 的半径是4,如果点A 到直线a 的距离是8,那么圆O 与直线a 的位置关系可能是(A )相交; (B )相离; (C )相切或相交; (D )相切或相离.二、填空题:(本大题共12题,每题4分,满分48分) 7.计算:21+2-= ▲ .8.在实数范围内分解因式:243x -= ▲ . 91的解是 ▲ .10.已知关于x 的方程230x x m --=没有实数根,那么m 的取值范围是 ▲ .11.已知直线(0)y kx b k =+≠与直线13y x =-平行,且截距为5,那么这条直线的解析式为 ▲ .12.一个十字路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当小杰过马路时,恰巧是绿灯的概率是 ▲ .13.已知一个40个数据的样本,把它分成6组,第一组到第四组的频数分别是10、5、7、6,第五组的频率是0.1,那么第六组的频数是 ▲ .14.如图,已知在矩形ABCD 中,点E 在边AD 上,且AE = 2ED .设B A a =u u r r ,BC b =uu u r r,那么CE =uu u r ▲ (用a r 、b r的式子表示). 15.如果二次函数2111y a x b x c =++(10a ≠,1a 、1b 、1c 是常数)与2222y a x b x c =++(20a ≠,2a 、2b 、2c 是常数)满足1a 与2a 互为相反数,1b 与2b 相等,1c 与2c 互为倒数,那么称这两个函数为“亚旋转函数”.请直接写出函数232y x x =-+-的“亚旋转函数”为 ▲ .16.如果正n 边形的中心角为2α,边长为5,那么它的边心距为 ▲ .(用锐角α的三角比表示)17.如图,一辆小汽车在公路l 上由东向西行驶,已知测速探头M 到公路l 的距离MN为9米,测得此车从点A 行驶到点B 所用的时间为0.6秒,并测得点A 的俯角为30o ,点B 的俯角为60o .那么此车从A 到B 的平均速度为 ▲ 米/秒.(结果保1.7321.414)18.在直角梯形ABCD 中,AB // CD ,∠DAB = 90o ,AB = 12,DC = 7,5cos 13ABC ∠=,点E 在线段AD 上,将△ABE 沿BE 翻折,点A 恰巧落在对角线BD 上点P 处,那么PD = ▲ .ABDC(第14题图)EABDC(第18题图)AMN (第17题图)l三、解答题:(本大题共7题,满分78分)19.(本题满分10分)120183(1)2cos45+8-+--o.20.(本题满分10分)解方程组:221;20.y xx xy y-=⎧⎨--=⎩21.(本题满分10分,其中第(1)小题4分,第(2)小题6分)已知一次函数24y x=-+的图像与x轴、y轴分别交于点A、B,以AB为边在第一象限内作直角三角形ABC,且∠BAC = 90o,tan ABC∠(1)求点C的坐标;(2)在第一象限内有一点M(1,m),且点MC位于直线AB的同侧,使得ABCABMSS∆∆=2求点M的坐标.22.(本题满分10分)为了响应上海市市政府“绿色出行”的号召,减轻校门口道路拥堵的现状,王强决定改父母开车接送为自己骑车上学.已知他家离学校7.5千米,上下班高峰时段,驾车的平均速度比自行车平均速度快15千米/小时,骑自行车所用时间比驾车所用时间多14小时,求自行车的平均速度?23.(本题满分12分,其中第(1)小题5分,第(2)小题7分)如图,已知在△ABC中,∠BAC=2∠C,∠BAC的平分线AE与∠ABC的平分线BD 相交于点F,FG∥AC,联结DG.(1)求证:BF BC AB BD⋅=⋅;(2)求证:四边形ADGF是菱形.AB E G CFD(第23题图)(第21题图)24.(本题满分12分,其中每小题各4分)如图,已知在平面直角坐标系xOy 中,抛物线22y ax x c =-+与x 轴交于 点A 和点B (1,0),与y 轴相交于点C (0,3). (1)求抛物线的解析式和顶点D 的坐标; (2)求证:∠DAB=∠ACB ;(3)点Q 在抛物线上,且△ADQ 是以AD 为底的等腰三角形,求Q 点的坐标.25.(本题满分14分,其中第(1)小题4分,第(2)、(3)小题各5分)如图,已知在Rt △ABC 中,∠ACB = 90o ,AC =6,BC = 8,点F 在线段AB 上,以点B 为圆心,BF 为半径的圆交BC 于点E ,射线AE 交圆B 于点D (点D 、E 不重合). (1)如果设BF = x ,EF = y ,求y 与x 之间的函数关系式,并写出它的定义域; (2)如果2ED EF =,求ED 的长;(3)联结CD 、BD ,请判断四边形ABDC 是否为直角梯形?说明理由.(第24题图) (备用图)CA (第25题图) CB EF D A参考答案及评分标准一、选择题:(本大题共6题,每题4分,满分24分) 1.C ;2.C ;3.A ;4.B ;5.D ;6.D .二、填空题:(本大题共12题,每题4分,满分48分)7.5; 8.2x x (; 9.1x =; 10.94m <-; 11.153y x =-+;12.512; 13.8; 14.13a b -r r ; 15.2132y x x =+-; 16.5cot 2α(或52tan α);17.17.3; 18.12.三、解答题:(本大题共7题,满分78分) 19.解:原式112+……………………………………(2分+2分+2分+2分)2=.……………………………………………………………………(2分)20.解:由②得:20x y -=,+0x y =…………………………………………(2分)原方程组可化为120y x x y -=⎧⎨-=⎩,10y x x y -=⎧⎨+=⎩………………………………(2分)解得原方程组的解为21x y =-⎧⎨=-⎩,1212x y ⎧=-⎪⎪⎨⎪=⎪⎩…………………………………(5分)∴原方程组的解是21x y =-⎧⎨=-⎩,1212x y ⎧=-⎪⎪⎨⎪=⎪⎩……………………………………(1分)21.解:(1)令0y =,则240x -+=,解得:2x =,∴点A 坐标是(2,0).令0x =,则4y =,∴点B 坐标是(0,4).………………………(1分)∴AB .………………………………(1分)∵90BAC ∠=,1tan 2ABC ∠=,∴AC =过C 点作CD ⊥x 轴于点D ,易得OBA DAC ∆∆∽.…………………(1分) ∴2AD =,1CD =,∴点C 坐标是(4,1).………………………(1分) (2)11522ABC S AB AC ∆=⋅=⨯.………………………………(1分)∵2ABM ABC S S ∆∆=,∴52ABM S ∆=.……………………………………(1分)∵(1M,)m,∴点M在直线1x=上;令直线1x=与线段AB交于点E,2ME m=-;……………………(1分)分别过点A、B作直线1x=的垂线,垂足分别是点F、G,∴AF+BG = OA = 2;……………………………………………………(1分)∴111()222ABM BME AMES S S ME BG ME AF ME BG AF∆∆=+=⋅+⋅=+1152222ME OA ME=⋅=⨯⨯=…………………(1分)∴52ME=,522m-=,92m=,∴(1M,92).……………………(1分)22.解:设自行车的平均速度是x千米/时.………………………………………(1分)根据题意,列方程得7.57.51154x x-=+;……………………………………(3分)化简得:2154500x x+-=;………………………………………………(2分)解得:115x=,230x=-;…………………………………………………(2分)经检验,115x=是原方程的根,且符合题意,230x=-不符合题意舍去.(1分)答:自行车的平均速度是15千米/时.………………………………………(1分)23.证明:(1)∵AE平分∠BAC,∴∠BAC=2∠BAF=2∠EAC.∵∠BAC=2∠C,∴∠BAF=∠C=∠EAC.…………………………(1分)又∵BD平分∠ABC,∴∠ABD=∠DBC.……………………………(1分)∵∠ABF=∠C,∠ABD=∠DBC,∴ABF CBD∆∆∽.…………………………………………………(1分)∴AB BFBC BD=.………………………………………………………(1分)∴BF BC AB BD⋅=⋅.………………………………………………(1分)(2)∵FG∥AC,∴∠C=∠FGB,∴∠FGB=∠F AB.………………(1分)∵∠BAF=∠BGF,∠ABD=∠GBD,BF=BF,∴ABF GBF∆∆≌.∴AF=FG,BA=BG.…………………………(1分)∵BA=BG,∠ABD=∠GBD,BD=BD,∴ABD GBD∆∆≌.∴∠BAD=∠BGD.……………………………(1分)∵∠BAD=2∠C,∴∠BGD=2∠C,∴∠GDC=∠C,∴∠GDC=∠EAC,∴AF∥DG.……………………………………(1分)又∵FG∥AC,∴四边形ADGF是平行四边形.……………………(1分)∴AF=FG.……………………………………………………………(1分)∴四边形ADGF是菱形.……………………………………………(1分)24.解:(1)把B(1,0)和C(0,3)代入22y ax x c=-+中,得9603a cc++=⎧⎨=⎩,解得13ac=-⎧⎨=⎩.……………………………………(2分)∴抛物线的解析式是:223y x x =--+.……………………………(1分) ∴顶点坐标D (-1,4).……………………………………………(1分) (2)令0y =,则2230x x --+=,13x =-,21x =,∴A (-3,0)∴3OA OC ==,∴∠CAO =∠OCA .…………………………………(1分)在Rt BOC ∆中,1tan 3OB OCB OC ∠==.………………………………(1分)∵AC =DCAD =, ∴2220AC DC +=,220AD =;∴222AC DC AD +=,ACD ∆是直角三角形且90ACD ∠=,∴1tan 3DC DAC AC ∠==,又∵∠DAC 和∠OCB 都是锐角,∴∠DAC =∠OCB .…………………(1分) ∴DAC CAO BCO OCA ∠+∠=∠+∠,即DAB ACB ∠=∠.……………………………………………………(1分) (3)令(Q x ,)y 且满足223y x x =--+,(3A -,0),(1D -,4)∵ADQ ∆是以AD 为底的等腰三角形,∴22QD QA =,即2222(3)(1)(4)x y x y ++=++-,化简得:220x y -+=.………………………………………………(1分) 由222023x y y x x -+=⎧⎨=--+⎩,……………………………………………………(1分)解得11x y ⎧=⎪⎪⎨⎪=⎪⎩,22x y ⎧=⎪⎪⎨⎪⎪⎩. ∴点Q的坐标是⎝⎭,⎝⎭.…(2分)25.解:(1)在Rt △ABC 中,6AC =,8BC =,90ACB ∠=∴10AB =.……………………………………………………………(1分) 过E 作EH ⊥AB ,垂足是H ,易得:35EH x =,45BH x =,15FH x =.…………………………(1分)在Rt △EHF 中,222223155EF EH FH x x ⎛⎫⎛⎫=+=+ ⎪ ⎪⎝⎭⎝⎭,∴(08)y x =<<.………………………………………(1分+1分) (2)取ED 的中点P ,联结BP 交ED 于点G∵2ED EF =,P 是ED 的中点,∴EP EF PD ==. ∴∠FBE =∠EBP =∠PBD .∵EP EF=,BP过圆心,∴BG⊥ED,ED =2EG =2DG.…………(1分)又∵∠CEA =∠DEB,∴∠CAE=∠EBP=∠ABC.……………………………………………(1分)又∵BE是公共边,∴BEH BEG∆∆≌.∴35EH EG GD x===.在Rt△CEA中,∵AC = 6,8BC=,tan tan AC CECAE ABCBC AC∠=∠==,∴66339tan822CE AC CAE⨯⨯=⋅∠===.……………………………(1分)∴9169782222BE=-=-=.……………………………………………(1分)∴6672125525ED EG x===⨯=.……………………………………(1分)(3)四边形ABDC不可能为直角梯形.…………………………………(1分)①当CD∥AB时,如果四边形ABDC是直角梯形,只可能∠ABD =∠CDB = 90o.在Rt△CBD中,∵8BC=,∴32cos5CD BC BCD=⋅∠=,24sin5BD BC BCD BE =⋅∠==∴321651025CDAB==,32853245CEBE-==∴CD CE AB BE≠.∴CD不平行于AB,与CD∥AB矛盾.∴四边形ABDC不可能为直角梯形.…………………………(2分)②当AC∥BD时,如果四边形ABDC只可能∠ACD =∠CDB = 90o.∵AC∥BD,∠ACB = 90o,∴∠ACB =∠CBD = 90o.∴∠ABD =∠ACB +∠BCD > 90o.与∠ACD =∠CDB = 90o矛盾.∴四边形ABDC不可能为直角梯形.…………………………(2分)。
2018~2019学年上海市金山区九年级二模数学及参考答案

2018~2019学年上海市金山区九年级二模数学试卷(时间:100分钟,满分:150分)一、选择题(本大题共6题,每小题4分,共24分) 1. 下列实数中,是有理数的是( )(A )π;(B )8;(C )3; (D )37. 2. 不等式组310x x ->⎧⎨-<⎩的解集是( )(A )3x >-; (B )3x <-; (C )1x >; (D )1x <.3. 用换元法解方程:1201x x x x ---=-时,如果设1xy x =-,那么将原方程变形后表示为一元二次方程一般形式的是( )(A )120y y --=; (B )210y y--=; (C )2210y y --=; (D )220y y --=. 4. 数据2、1、0、2-、0、1-的中位数与众数分别是( )(A )0和0;(B )1-和0; (C )0和1; (D )0和2. 5. 下列图形中,是中心对称图形但不是轴对称图形的是( )(A )平行四边形; (B )矩形; (C )菱形; (D )正方形. 6. 已知⊙1O 与⊙2O 内切于点A ,⊙1O 的半径等于5,123O O =,那么2O A 的长等于( ) (A )2;(B )3;(C )8;(D )2或8.二、填空题(每小题4分,共48分) 7. 计算:22a a -÷= . 8. 因式分解:32a a += . 9. 方程:322x -=的解是 . 10. 化简:324a b ()0b ≥的结果是 .11. 已知,反比例函数1k y x-=的图像经过二、四象限,那么k 的取值范围是 . 12. 已知关于x 的一元二次方程20x x m ++=的一个根是1x =,那么这个方程的另一个根是 .13. 从方程20x =,11x -=-,2240x x -+=中,任选一个方程,选出的这个方程无实数解的概率为 . 14. 100克鱼肉中蛋白质的含量如图表,每100克草鱼、鲤鱼、花鲢鱼鱼肉的平均蛋白质含量为16.8克,那么100克鲤鱼肉的蛋白质含量是 克.15. 在ABC △中AB AC =,请你再添加一个条件使得ABC △成为等边三角形,这个条件可以是 (只要写出一个即可). 16. ABCD 中,E 是边BC 上的点,AE 交BD 于点F ,23BE BC =,BE a =u u ur r ,AB b =u u u r r ,那么BD =u u u r(用a r 、b r 表示).17. 如图,飞机于空中A 处观测其正前方地面控制点C 的俯角为30︒,若飞机航向不变,继续向前飞行1000米至B 处时,观测到其正前方地面控制点C 的俯角为45︒,那么该飞机与地面的高度是 米(保留根号).第16题图 第17题图18. 一个正多边形的对称轴共有10条,且该正多边形的半径等于4,那么该正多边形的边长等于 .三.解答题(本大题共7题,满分78分) 19. (本题满分10分)计算:)10123822132-+++.20. (本题满分10分)解方程:212124x x x -=--.21. (本题满分10分,每小题各5分)已知:如图,在Rt ABC △中,90ACB ∠=︒,D 是边AB 的中点,CE CB =,5CD =,3sin 5ABC ∠=. 求:(1)BC 的长; (2)tan E 的值.22. (本题满分10分,每小题各5分)某演唱会购买门票的方式有两种:方式一:若单位赞助广告费10万元,则该单位所购门票的价格为每张0.02万元; 方式二:如图所示.设购买门票x 张,总费用为y 万元,方式一中:总费用=广告赞助费+门票费. (1)求方式一中y 与x 的函数关系式.(2)若甲、乙两个单位分别采用方式一、方式二购买本场演唱会门票共400张,且乙单位购买超过100张,两单位共花费27.2万元,求甲、乙两单位各购买门票多少张?23. (本题满分12分,每小题各6分)已知:如图,菱形ABCD 的对角线AC 与BD 相交于点O ,若CAD DBC ∠=∠. (1)求证:ABCD 是正方形.(2)E 是OB 上一点,DH CE ⊥,垂足为H ,DH 与OC 相交于点F ,求证:OE OF =.24. (本题满分12分,其中第(1)小题4分,第(2)小题8分)已知:抛物线2y x bx c =-++,经过点()1,2A --,()0,1B . (1)求抛物线的关系式及顶点P 的坐标;(2)若点B '与点B 关于x 轴对称,把(1)中的抛物线向左平移m 个单位,平移后的抛物线经过点B ',设此时抛物线顶点为点P '.①求P BB ''∠的大小;②把线段P B ''以点B '为旋转中心顺时针旋转120︒,点P '落在点M 处,设点N 在(1)中的抛物线上,当MNB '△的面积等于63时,求点N 的坐标.25.(本题满分14分,其中第(1)小题4分,第(2)小题10分)如图,在Rt ABC△中,90C∠=︒,16AC=cm,20AB=cm,动点D由点C向点A以每秒1cm速度在边AC上运动,动点E由点C向点B以每秒43cm速度在边BC上运动,若点D,点E从点C同时出发,运动t秒(0t>),联结DE.(1)求证:DCE△∽BCA△;(2)设经过点D、C、E三点的圆为⊙P,①当⊙P与边AB相切时,求t的值;②在点D、点E运动过程中,若⊙P与边AB交于点F、G(点F在点G左侧),联结CP 并延长CP交边AB于点M,当PFM△与CDE△相似时,求t的值.备用图2018~2019学年上海市金山区九年级二模数学试卷参考答案一.选择题(每小题4分,共24分)1.D2.B3.C4.A5.A6.D . 二.填空题(每小题4分,共48分)7.4a ; 8.()22a a +; 9.2x =; 11.1k <;12.2x =-;13.23;14.17.215.60A ∠=o或AB BC =等(答案不唯一); 16. 32a b -r r17.()500 18.2.三.解答题(19—22题,每题10分,23—24题,每题12分,25题14分,共78分)19.解:原式12=+ (8分)12=+; (1分)3= (1分)20. 解:2224x x x +-=-; (4分)260x x +-=; ()()320x x +-=; (2分) 解得:13x =-,22x =; (2分)经检验:22x =为增根舍去 (1分) 所以原方程的解为:3x =-. (1分)21. 解:(1) ∵在Rt ABC ∆中,90ACB ∠=︒,D 是边AB 的中点;∴12CD AB =, (1分) ∵5CD =; ∴10AB =; (1分)∵3sin 5AC ABC AB ∠==; 由10AB =解得6AC =; (1分)∵222BC AC AB += ∴8BC ==. (2分)(2)作EH BC ⊥垂足为H ; (1分)∴90EHC EHB ∠=∠=︒;∵D 是边AB 的中点; ∴12BD CD AB ==; ∴DCB ABC ∠=∠; ∵90ACB ∠=︒; ∴EHC ACB ∠=∠; ∴EHC ∆∽ACB ∆; (1分)∴EH CH ECAC BC AB==; 由8BC =,CE CB =得8CE =,CBE CEB ∠=∠;∴86810EH CH ==解得245EH =,325CH =;328855BH =-=; (2分) ∴tan 3EHCBE BH∠==,即tan 3E =. (1分)22. (1)解:10.0210y x =+. (5分)(2)解:当100x ≥时,设直线解析式为()20y kx b k =+≠,代入点()10010,、()20016,得1010016200k b k b =+⎧⎨=+⎩解得0.064k b =⎧⎨=⎩;∴()20.064100y x x =+≥, (1分) 设甲单位购买门票m 张,乙单位购买门票()400m -张 (1分)根据题意可得:()0.02100.06400427.2m m ++-+= (1分) 解得270m =,得400-130m =; (1分)答:甲、乙两单位购买门票分别为270张和130张. (1分)23.(1)证明:∵四边形ABCD 是菱形,∴//AD BC ,2BAD DAC ∠=∠,2ABC DBC ∠=∠; (2分) ∴180DAB ABC ∠+∠=︒; (1分) ∵CAD DBC ∠=∠;∴BAD ABC ∠=∠, (1分)∴2180BAD ∠=︒; ∴90BAD ∠=︒; (1分) ∴四边形ABCD 是正方形. (1分) (2)证明:∵四边形ABCD 是正方形;∴AC BD ⊥,AC BD =,12CO AC =,12DO BO =; (1分) ∴90COB DOC ∠=∠=︒,CO DO =; (1分)∵DH CE ⊥,垂足为H ;∴90DHE ∠=︒,90EDH DEH ∠+∠=︒; (1分) 又∵90ECO DEH ∠+∠=︒; ∴ECO EDH ∠=∠; (1分) ∴ECO ∆≌FDO ∆; (1分) ∴OE OF =. (1分)24.解:(1)把点()1,2A --,()01B ,代入2y x bx c =-++得211b c c -=--+⎧⎨=⎩解得2c 1b =⎧⎨=⎩∴抛物线的关系式为:221y x x =-++ (2分) 得()212y x =--+; (1分) ∴顶点坐标为()12P ,. (1分) (2)①设抛物线平移后为()2112y x m =--++,代入点()0,1B '-得()2112m -=--+,解得11m =,21m =(舍去);∴(212y x =-+,得顶点()P ' (2分)连结P B ',P B '',作P H y '⊥轴,垂足为H,得P H '=1HB =,2P B '=∵tan P HP BH BH''∠==, (1分) ∴60P BH '∠=︒, ∴18060120P BB ''∠=︒-︒=︒. (1分) ②∵2BB '=,2P B '=即BB P B ''=, ∴30BP B P B B ''''∠=∠=︒;∵线段P B ''以点B '为旋转中心顺时针旋转120︒,点P '落在点M 处; ∴90OB M '∠=︒,B M B P '''= ∴//MB x '轴,B M B P '''==设MNB '∆在B M '边上的高为h,得:2MNB B M hS '∆'⋅==6h =; ∴设()7N a -,或()5N a ,分别代入221y x x =-++得2721a a -=-++ 解得:4a =或2a =-∴()47N -,或()27N --,, 2521a a =-++方程无实数根舍去,∴综上所述:当MNB S '∆=N 的坐标为()47N -,或()27N --,. (2分+2分) 25. (1)证明:由题意得:4,3CD t CE t ==,∵90C ∠=︒,16AC =,20AB =;∴12CB ==,∵1212CD t CE tCB AC ==,;(2分) ∴CD CECB AC=(1分) 又∵90C C ∠=∠=︒ ∴DCE ∆∽BCA ∆. (1分)(2)①连结CP 并延长CP 交AB 于点H , ∵90ACB ∠=︒,∴DE 是⊙P 的直径 即P 为DE 中点,∴12CP DP PE DE ===. (1分) ∴PCE PEC ∠=∠,∵DCE ∆∽BCA ∆,∴CDE B ∠=∠, (1分)∵90CDE CED ∠+∠=︒,∴90B HCB ∠+∠=︒ (1分) ∴CH AB ⊥; (1分) ∵⊙P 与边AB 相切,∴点H 为切点, (1分) CH 为⊙P 的直径, ∵sin CH CB A CA AB ==解得485CH =,∴485DE =sin sin CD CB A CED DE AB =∠==得14425CD =即14425t =. (1分) ②由题意得0t 1640123t <≤⎧⎪⎨<≤⎪⎩解得09t <≤,由①得485CM =,1526CP DE t ==,CM AB ⊥ ∴48556PM t =-,56PF CP t ==,90PMF ∠=︒,∵90ACB PMF ∠=∠=︒ ∴由PFM ∆与CDE ∆相似可得:情况一:PF PM DE CD =得548565653t tt t -=解得:365t =; 36095<≤ 情况二:PF PM DE CE =得54856565433t tt t -=解得:325t =; 32095<≤ ∴综上所述:当PFM ∆与CDE ∆相似时. 325t =或365t = (2分+2分)。
2018上海初三数学二模-浦东新区2017学年第二学期初三教学质量检测及评分标准

2018上海初三数学二模-浦东新区2017学年第二学期初三教学质量检测及评分标准(总10页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--浦东新区2017学年第二学期初三教学质量检测数 学 试 卷(完卷时间:100分钟,满分:150分)考生注意:1.本试卷含三个大题,共25题.答题时,考生务必按答题要求在答题纸...规定的位置上作答,在草稿纸、本试卷上答题一律无效.2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸...的相应位置上写出证明或计算的主要步骤.一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上】1.下列代数式中,单项式是 (A )x1;(B )0; (C )1+x ; (D )x .2.下列代数式中,二次根式n m +的有理化因式可以是 (A )n m +; (B )n m -; (C )n m +;(D )n m -.3.已知一元二次方程0122=-+x x ,下列判断正确的是(A )该方程有两个不相等的实数根; (B )该方程有两个相等的实数根;(C )该方程没有实数根; (D )该方程的根的情况不确定.4.某运动员进行射击测试,共射靶6次,成绩记录如下:,,10,,,10,在下列各统计量中,表示这组数据离散程度的量是 (A )平均数; (B ) 众数; (C ) 方差; (D ) 频率.5.下列y 关于x 的函数中,当0>x 时,函数值y 随x 的值增大而减小的是(A )2x y = ; (B )22+=x y ; (C )3xy = ;(D )xy 1=.6.已知四边形ABCD中,AB=⋅baab232=-224yx312=-x已知正方形的边长为2cm,那么它的半径长是▲ cm.12.某市种植60亩树苗,实际每天比原计划多种植3亩树苗,因此提前一天完成任务,求原计划每天种植多少亩树苗.设原计划每天种植x亩树苗,根据题意可列出关于x的方程▲ .13.近年来,出境旅游成为越来越多中国公民的假期选择.将2017年某小区居民出境游的不同方式的人次情况画成扇形图和条形图,如图1所示.那么2017年该小区居民出境游中跟团游的人数为▲ .14.如图2,在□ABCD中,E是BC中点,AE交BD于点F,如果aAE=,那么AF= ▲ (用向量a表示).15.在南海阅兵式上,某架“直-8”型直升飞机在海平面上方1200米的点A处,测得其到海平面观摩点B的俯角为︒60,此时点A、B之间的距离是▲ 米.16.如图3,已知在梯形ABCD中,AD∥BC,AD=AB=DC=3,BC=6,将△ABD绕着点D逆时针旋转,使点A落在点C处,点B落在点B'处,那么BB'= ▲ .17.如果抛物线C:)0(2≠++=acbxaxy与直线l:)0(≠+=kdkxy都经过y轴上一点P,且抛物线C的顶点Q在直线l上,那么称此直线l与该抛物线C具有“点线和谐”关系.如果直线1+=mxy与抛物线nxxy+-=22具有“点线和谐”关系,那么=+nm▲ .图2图1图3图5 图4 18. 已知1l ∥2l ,1l 、2l 之间的距离是3cm ,圆心O 到直线1l 的距离是1cm ,如果⊙O 与直线1l 、2l 有三个公共点,那么圆O 的半径为 ▲ cm . 三、解答题:(本大题共7题,满分78分) 19.(本题满分10分)计算:1-312127-2-18)(++.20.(本题满分10分)解不等式组⎪⎩⎪⎨⎧+≤-->612163x x x x ,,并把它的解集在数轴(如图4)上表示出来.21.(本题满分10分)如图5,已知AB 是⊙O 的直径,弦CD 交AB 于点E ,30=∠CEA ,OE =4,DE =35.求弦CD 及⊙O 的半径长.22.(本题满分10分,其中第(1)小题5分,第(2)小题5分)某市为鼓励市民节约用气,对居民管道天然气实行两档阶梯式收费.年用天然气量310立方米及以下为第一档;年用天然气量超出310立方米为第二档.某户应交天然气费y (元)与年用天然气量x (立方米)的关系如图6所示,观察图像并回答下列问题:(1)年用天然气量不超过310立方米时,求y 关于x 的函数解析式(不写定义域); (2)小明家2017年天然气费为1029元,求小明家2017年使用天然气量.23.(本题满分12分,其中第(1)小题5分,第(2)小题7分)图6x 1 2 3 4 5 –1 –2 –3 –4 –5 O 图5已知:如图7,在正方形ABCD 中,点E 为边AB 的中点,联结DE .点F 在DE 上,且CF=CD ,过点F 作FG ⊥FC 交AD 于点G . (1)求证:GF=GD ;(2)联结AF ,求证:AF ⊥DE .24.(本题满分12分,每小题4分) 已知平面直角坐标系xOy (如图8),二次函数y =ax 2+bx +4的图像经过A (-2,0)、B (4,0)两点,与y 轴交于点C 点. (1)求这个二次函数的解析式;(2)如果点E 在线段OC 上,且∠CBE =∠ACO ,求点E 的坐标;(3)点M 在y 轴上,且位于点C 上方,点N 在直线BC 上,点P 为上述二次函数图像的对称轴...上的点,如果以C 、M 、N 、P 为顶点的四边形是菱形,求点M 的坐标.25.(本题满分14分,其中第(1)小题4分,第(2)小题5分,第(3)小题5分)如图9,已知在△ABC 中,AB=AC ,21tan =B ,BC =4,点E 是在线段BA 延长线上一点,以点E 为圆心,EC 为半径的圆交射线BC 于点C 、F (点C 、F 不重合),射线EF 与射线AC 交于点P . (1)求证:AC AP AE ⋅=2;yx 1 23 45–1 –2 –3 –4 –5 1 2 3 4 5 –1 –2 –3 –4 –5 O 图8 图7(2)当点F 在线段BC 上,设CF =x ,△PFC 的面积为y ,求y 关于x 的函数解析式及定义域; (3)当21=EF FP 时,求BE 的长.浦东新区2017学年度第二学期初三教学质量检测数学试卷参考答案及评分标准一、选择题:(本大题共6题,每题4分,满分24分) 1.B ; 2.C ; 3.A ; 4.C ; 5.D ; 6.C .二、填空题:(本大题共12题,每题4分,满分48分) 7.22ab ;8.()()y x y x 22-+; 9.5=x ;10.21;11.2;12.136060=+-x x ; 13.24; 14.a 32; 15.3800;16.9;17.0;18.2或4.三、解答题:(本大题共7题,满分78分)19.解:原式23-1-222++=.…………………………………………………(8分)2-23=.………………………………………………………………(2分)20. 解:3611.26x x x x >-⎧⎪-+⎨≤⎪⎩,由①得:62->x .…………………………………………………………(2分)解得3->x .…………………………………………………………(1分)备用图图9①②由②得:11-3+≤x x )(.……………………………………………………(1分)133+≤-x x .……………………………………………………(1分)42≤x .解得2≤x .……………………………………………………………(1分)∴原不等式组的解集为23-≤<x .…………………………………(2分) -44321-1-2-3xO…………………………………(2分)21. 解:OD M CD OM O ,联结于点作过点⊥.……………………………………(1分)∵,︒=∠30CEA∴︒=∠=∠30CEA OEM .…………………………………(1分)在Rt △OEM 中,∵OE =4,∴221==OE OM ,3223430cos =⨯=⋅=︒OE EM .(2分)∵35=DE ,∴33=-=EM DE DM .…………(1分)∵CD OM OM ⊥过圆心,,∴DM CD 2=.…………(2分)∴36=CD .……………………………………………(1分) ∵,,332==DM OM∴在Rt △DOM 中,()313322222=+=+=DM OM OD .……(1分)∴ 弦CD 的长为36,⊙O 的半径长为31.……………………………(1分)22.解:(1)设)0(≠=k kx y .…………………………………………………………(1分)∵)0(≠=k kx y 的图像过点(310,930),……………………………(1分)∴,k 310930=∴3=k .…………………………………………………(2分)∴ x y 3=.…………………………………………………………… (1分)(2)设)0(≠+=k b kx y .………………………………………………………(1分)∵ )0(≠+=k b kx y 的图像过点(310,930)和(320,963),∴ ⎩⎨⎧=+=+63.9320930310b k b k , ∴ ⎩⎨⎧-== 3.93.3b k ,……………………………………………………………(1分)∴933.3-=x y .…………………………………………………………(1分)当3401029933.31029==-=x x y ,解得时,.……………………(1分)答:小明家2017年使用天然气量为340立方米.……………………(1分)23.证明:(1)∵是正方形四边形ABCD ,∴︒=∠90ADC .………(1分)∵FG ⊥FC , ∴∠GFC = 90°. …………………………(1分)∵,CD CF = ∴∠CDF =∠CFD .………………………(1分)∴∠GFC -∠CFD=∠ADC -∠CDE ,即∠GFD =∠GDF .(1分)∴GF =GD .………………………………………………(1分)(2)联结CG .∵,,GD GF CD CF == ∴的中垂线上在线段、点FD C G .……(1分)∴GC ⊥DE ,∴∠CDF +∠DCG= 90°,∵∠CDF +∠ADE= 90°,∴∠DCG =∠ADE .∵是正方形四边形ABCD ,∴AD=DC ,∠DAE =∠CDG= 90°,∴△DAE ≌△CDG .……………………………………………………(1分)∴DG AE =.………………………………………………………… (1分)∵的中点,是边点AB E ∴的中点,是边点AD G∴GF GD AG ==.……………………………………………………(1分)∴,,GFD GDF AFG DAF ∠=∠∠=∠………………………………(1分)∵,︒=∠+∠+∠+∠180GDF GFD AFG DAF ……………………(1分)∴,︒=∠+∠18022GFD AFG∴∠AFD= 90°,即AF ⊥DE .…………………………………………(1分)证法2:(1)联结CG 交ED 于点H .∵是正方形四边形ABCD ,∴︒=∠90ADC .…………………………(1分)∵FG ⊥FC ,∴∠GFC = 90°.……………………………………………(1分)在Rt △C FG 与Rt △CDG 中,⎩⎨⎧==.CG CG CD CF ,…………………………………………………………… (1分)∴Rt△CFG ≌Rt△CDG .………………………………………………(1分)∴GD GF =.…………………………………………………………(1分)(2)∵,,GD GF CD CF == ∴的中垂线上在线段、点FD C G . ……………………………… (1分)∴FH=HD ,GC ⊥DE ,∴∠EDC +∠DCH = 90°,∵∠ADE +∠EDC= 90°,∴∠ADE =∠DCH .……………………………………………………(1分)∵是正方形四边形ABCD ,∴AD=DC =AB ,∠DAE =∠CDG= 90°,∵GDC EAD DC AD DCH ADE ∠=∠=∠=∠,,.∴△ADE ≌△DCG .……………………………………………………(1分)∴DG AE =.…………………………………………………………(1分)∵的中点,是边点AB E ∴的中点,是边点AD G∵的中点,是边点FD H ∴GH 是△AFD 的中位线.………………(1分)∴,AF GH //∴,GHD AFD ∠=∠∵GH ⊥FD ,∴∠GHD = 90°,………………………………………(1分)∴∠AFD = 90°,即AF ⊥DE .………………………………………(1分)24.解:(1)∵ 抛物线42++=bx ax y 与x 轴交于点A (-2,0),B (4,0),∴ ⎩⎨⎧=++=+.04416042-4b a b a ;…………………………………………………(1分)解得⎪⎩⎪⎨⎧==.121-b a ;…………………………………………………………(2分)∴ 抛物线的解析式为421-2++=x x y .……………………………(1分)(2)H BC EH E 于点作过点⊥.在Rt △ACO 中, ∵A (-2,0 4421-02=++==x x y x 时,当,∴ 在Rt△C OB 中,∵∠COB=90°,OC=OB=4,∴2445==∠︒BC OCB ,.∵BC EH ⊥,∴CH=EH .∴在Rt△ACO 中,21tan ==∠CO AO ACO …………………………(1分)∵∠CBE=∠ACO ,∴在Rt△EBH 中,1tan 2EH EBH BH ∠==. 设k BH k k EH 2)0(=>=,则,CH=k ,CE =. ∴243==+=k HB CH CB . ∴,324=k ……………………………………………………………(1分)∴,38=CE ………………………………………………………………(1分)∴,34=EO ∴),(340E .………………………………………………(1分)(3)∵ A (-2,0),B (4,0),∴抛物线的对称轴为直线x =1.………………………………………(1分)①的边时,为菱形当MCNP MC ∴,PN CM //∴∠PNC=∠NCO=45°. ∵点P 在二次函数的对称轴上,∴,的横坐标为点1P 1的横坐标为点N . ∴245sin 1==︒CN . ∵是菱形,四边形MCNP ∴,2==CN CM∴,24+=+=CM OC OM∴)240(+,M .……………………………………………………(1分)②的边时,不存在为菱形当MCPN MC .……………………(1分)③的对角线时,为菱形当MNCP MC,于点交设Q CM NP ∴互相垂直平分,、NP CM∴1==QP NQ .,QC MQ =∵上,在直线点BC N ∠NCM=∠OCB=45°.在Rt △CQN 中,∴∠NCQ =∠CNQ= ∴,1==CQ QN ∴1MQ CQ ==,∴,2=CM ∴,624=+=+=CM OC OM∴ M (0,6).………………………………………………………(1分)∴综上所述)240(+,M 或 M (0,6).25.证明:(1)∵,AC AB =∴∠B=∠ACB . ∵,EC EF =∴∠EFC=∠ECF .…………………………………(1分)∵,BEF B EFC ∠+∠=∠又∵,ACE ACB ECF ∠+∠=∠∴∠BEF=∠ACE .………………………………………………(1分)∵是公共角,EAC ∠∴△AEP ∽△ACE .……………………………………………(1分)∴,AEAPAC AE =∴AC AP AE ⋅=2.……………………………(1分)(2)∵∠B=∠ACB ,∠ECF=∠EFC ,∴△ECB ∽△PFC .∴2⎪⎭⎫⎝⎛=∆∆CB FC S S ECB PFC .………………………………………………(1分) E EH CF H ⊥过点做于点,P M CE HF B A ∵,经过圆心,CF EH EH ⊥∴x FC CH 2121==.∴x BH 214-=.…………………………(1分)在Rt △BEH 中,∵,21tan ==∠BH EH B ∴x EH 41-2=. ∴x x EH BC S ECB 214)412(42121-=-⨯⨯=⋅=∆.…………(1分)∴24214⎪⎭⎫⎝⎛=-x x y .∴)40(32832<<-=x x x y .………………………………………(2分)(3) ①上时,在线段当点BC F ∵,21=EF FP ∴,21==EC PE EF PE ∵△AEP ∽△ACE .∴,ECPEAC AE = ∴12AE AC =.……………………………………………………(1分)M BC AM A ,垂足为点作过点⊥.∵,AC AB =,4=BC ∴,221==BC BM在Rt △ABM 中,∵,21tan =∠B∴1AM AB AC ==,…(1分)∴,25=AE ∴253=BE .………………………………………(1分)②F BC 当点在线段延长线上时,AB FECP∵∠EFC=∠ECF ,EFC FCP P ∠=∠+∠, ECF B BEC ∠=∠+∠.又∵B ACB ACB FCP ∠=∠∠=∠,,∴∠B =∠FCP . ∴∠P =∠BEC . ∵是公共角,EAC ∠∴△AEP ∽△ACE ,∴,ECPEAC AE = ∵,21=EF FP ∴32PE PE EF EC ==,∴32AE AC =………(1分)∴255=BE .………………(1分)综上所述,253=BE.。
上海金山中考二模数学试题含答案

金山区初三中考模拟考试数 学 试 卷(满分150分,考试时间100分钟) 4月一、选择题(共6道小题,每小题4分,共24分)1.14-的绝对值等于……………………………………………………………………( )(A )4(B )4-(C )14(D )14-2.下列计算正确的是……………………………………………………………………( ) (A )248a a a ⋅= (B )224a a a +=;(C )22(2)2a a =;(D )633a a a ÷=.3.二次函数2(1)2y x =--+图象的顶点坐标是……………………………………( ) (A )(1,2) (B )(1,2)- (C )(1,2)--(D )(1,2)-4.众志成城,抗震救灾.某小组7名同学积极捐出自己的零花钱支援灾区,他们捐款的数额分别是(单位:元):50,20,50,30,50,30,120.这组数据的众数和中位数分别是…………………………………………………………………………………( ) (A )120,50(B )50,20 (C )50,30(D )50,505.若一个多边形的内角和等于900,则这个多边形的边数是…………………… ( ) (A )8(B )7(C )6(D )56.在下列命题中,真命题是……………………………………………………………( ) (A )两条对角线相等的四边形是矩形 (B )两条对角线互相垂直的四边形是菱形 (C )两条对角线互相平分的四边形是平行四边形 (D )两条对角线互相垂直且相等的四边形是正方形 二、填空题(共12道小题,每小题4分,共48分) 7.在函数2y x =-中,自变量x 的取值范围是 . 8.分解因式:2x xy -= .9.如果线段AB =4cm ,点P 是线段AB 的黄金分割点,那么较长的线段BP= cm . 102x x -=的根是 . 11.不等式组10230x x -≤⎧⎨+>⎩的整数解为 .12.如果方程2210kx x ++=有两个不等实数根,则实数k 的取值范围是 . 13.点11(,)A x y ,点22(,)B x y 是双曲线2y x=-上的两点,若120x x <<,则1y2y (填“=”、“>”、“<”).14.有三张大小、形状完全相同的卡片,卡片上分别写有数字1、2、3,从这三张卡片中随机同时抽取两张,用抽出的卡片上的数字组成两位数,这个两位数是偶数的概率是 .15.如图,梯形ABCD 中,AB ∥CD ,CD AB 2=,AD a= ,AB b =,请用向量b a、表示向量AC = .16.已知两圆的圆心距为4,其中一个圆的半径长为3,那么当两圆内切时,另一圆的半径为 .17.如图,已知AD 为△ABC 的角平分线,//DE AB 交AC 于E ,如果23AE EC =,那么 ABAC = .18. 在Rt △ABC 中,∠C =90º ,BC =4 ,AC =3,将△ABC 绕着点B 旋转后点A 落在直线BC上的点A ',点C 落在点C '处,那么'tan AAC 的值是 . 三、解答题(共7道小题,共78分)19.(本题满分1010212sin 45(2)321-⎛⎫-+-π- ⎪-⎝⎭20.(本题满分10分)解方程:281242x x x x -=--+ 21.(本题满分10分,第(1)小题满分4分,第(2)小题满分6分)如图,在平行四边形ABCD 中,以点A 为圆心,AB 为半径的圆,交BC 于点E . (1)求证:ABC ∆≌EAD ∆;(2)如果AC AB ⊥,6=AB ,53cos =∠B , 求EC 的长.ECBAB CDABCDEA第15题图第17题图22.(本题满分10分,第(1)(2)小题满分各3分,第(3)小题满分4分)今年3月5日,光明中学组织全体学生参加了“走出校门,服务社会”的活动,活动分为打扫街道、去敬老院服务和到社区文艺演出三项。
上海市各区2017-2018届九年级中考二模数学试卷精选汇编:综合计算专题

上海市各区2018届九年级中考二模数学试卷精选汇编 综合计算宝山区、嘉定区21.(本题满分10分,第(1)小题5分,第(2)小题5分)如图4,在梯形ABCD 中,AD ∥BC ,︒=∠90BAD ,AD AC =. (1)如果BAC ∠︒=∠-10BCA ,求D ∠的度数; (2)若10=AC ,31cot =∠D ,求梯形ABCD 的面积.21.解:(1)∵AD ∥BC∴CAD BCA ∠=∠ …………………1分 ∵BAC ∠︒=∠-10BCA∴BAC ∠︒=∠-10CAD …………………1分 ∵︒=∠90BAD∴BAC ∠︒=∠+90CAD∴︒=∠40CAD …………………1分 ∵AD AC =∴D ACD ∠=∠ …………………1分 ∵︒=∠+∠+∠180CAD D ACD∴︒=∠70D …………………1分(2) 过点C 作AD CH ⊥,垂足为点H ,在Rt △CHD 中,31cot =∠D ∴31cot ==∠CH HD D …………………………1分 设x HD =,则x CH 3=,∵AD AC =,10=AC ∴x AH -=10 在Rt △CHA 中,222AC CHAH =+ ∴22210)3()10(=+-x x∴2=x ,0=x (舍去)∴2=HD …………1分 ∴6=HC ,8=AH ,10=AD ………………1分图4DCB A图4DCBAH∵︒=∠=∠90CHD BAD ∴AB ∥CH∵AD ∥BC ∴四边形ABCH 是平行四边形 ∴8==AH BC ………1分 ∴梯形ABCD 的面积546)810(21)(21=⨯+=⨯+=CH BC AD S ………1分 长宁区21.(本题满分10分,第(1)小题4分,第(2)小题6分)如图,在等腰三角形ABC 中,AB =AC ,点D 在BA 的延长线上,BC =24,135sin =∠ABC . (1)求AB 的长;(2)若AD =6.5,求DCB ∠的余切值.21.(本题满分10分,第(1)小题4分,第(2)小题6分) 解:(1)过点A 作AE ⊥BC ,垂足为点E又∵AB =AC ∴BC BE 21= ∵BC =24 ∴ BE =12 (1分)在ABE Rt ∆中,︒=∠90AEB ,135sin ==∠AB AE ABC (1分)设AE=5k,AB=13k ∵222BE AE AB += ∴1212==k BE ∴1=k , ∴55==k AE , 1313==k AB (2分) (2)过点D 作DF ⊥BC ,垂足为点F ∵AD=6.5,AB=13 ∴BD=AB+AD=19.5∵AE ⊥BC ,DF ⊥BC ∴ ︒=∠=∠90DFB AEB ∴ DF AE //∴BDABBF BE DF AE == 又 ∵ AE =5,BE =12,AB =13, ∴18,215==BF DF (4分) ∴BF BC CF -= 即61824=-=CF (1分) 在DCF Rt ∆中,︒=∠90DFC ,542156cot ===∠DF CF DCB (1分) 崇明区ADB第21题图21.(本题满分10分,第(1)、(2)小题满分各5分)已知圆O 的直径12AB =,点C 是圆上一点,且30ABC ∠=︒,点P 是弦BC 上一动点, 过点P 作PD OP ⊥交圆O 于点D . (1)如图1,当PD AB ∥时,求PD 的长; (2)如图2,当BP 平分OPD ∠时,求PC 的长.21.(本题满分10分,每小题5分)(1)解:联结OD∵直径12AB = ∴6OB OD == ……………………………………1分∵PD OP ⊥ ∴90DPO =︒∠∵PD AB ∥ ∴180DPO POB +=︒∠∠ ∴90POB =︒∠ ……1分 又∵30ABC =︒∠,6OB =∴30OP OB tan =︒= ………………………………………………1分 ∵在Rt POD △中,222PO PD OD += ……………………………1分∴2226PD +=∴PD =……………………………………………………………1分 (2)过点O 作OH BC ⊥,垂足为H ∵OH BC ⊥∴90OHB OHP ==︒∠∠(第21题图1)ABOPCD (第21题图2)OABDPC∵30ABC =︒∠,6OB =∴132OH OB ==,30BH OB cos =︒= ……………………2分 ∵在⊙O 中,OH BC ⊥∴CH BH == ……………………………………………………1分 ∵BP 平分OPD ∠ ∴1452BPO DPO ==︒∠∠ ∴453PH OH cot =︒= ……………………………………………1分∴3PC CH PH =-= ………………………………………1分奉贤区21.(本题满分10分,每小题满分各5分)已知:如图6,在△ABC 中,AB =13,AC=8,135cos =∠BAC ,BD ⊥AC ,垂足为点D ,E 是BD 的中点,联结AE 并延长,交边BC 于点F . (1) 求EAD ∠的余切值; (2) 求BFCF的值. 21、(1)56; (2)58; 黄浦区21.(本题满分10分)如图,AH 是△ABC 的高,D 是边AB 上一点,CD 与AH 交于点E .已知AB =AC =6,cos B =23, AD ∶DB =1∶2.图6ABD EF(1)求△ABC 的面积; (2)求CE ∶DE.21. 解:(1)由AB =AC =6,AH ⊥BC ,得BC =2BH .—————————————————————————(2分) 在△ABH 中,AB =6,cosB =23,∠AHB =90°, 得BH =2643⨯=,AH=2分) 则BC =8,所以△ABC 面积=182⨯=——————————————(1分) (2)过D 作BC 的平行线交AH 于点F ,———————————————(1分)由AD ∶DB =1∶2,得AD ∶AB =1∶3, 则31CE CH BH AB DE DF DF AD ====. ——————————————(4分)金山区21.(本题满分10分,每小题5分)如图5,在矩形ABCD 中,E 是BC 边上的点,AE =BC ,DF ⊥AE ,垂足为F .(1)求证:AF=BE ;(2)如果BE ∶EC=2∶1,求∠CDF 的余切值.21.解:(1)∵四边形ABCD 是矩形,∴AD =BC ,AD ∥BC ,∠B =90°,ABCDFE图5∴∠DAF=∠AEB ,……………………………………………………………………(1分) ∵AE=BC ,DF ⊥AE ,∴AD=AE ,∠ AFD=∠EBA=90°,………………………(2分) ∴△ADF ≌△EAB ,∴AF =EB ,………………………………………………………(2分)(2)设BE =2k ,EC =k ,则AD =BC =AE =3k ,AF =BE =2k ,…………………………(1分)∵∠ADC =90°,∠AFD =90°,∴∠CDF +∠ADF =90°,∠DAF +∠ADF =90°, ∴∠CDF =∠DAF …………………………………………………………………(2分) 在Rt △ADF 中,∠AFD =90°,DF∴cot ∠CDF =cot ∠DAF=5AF DF ==.………………………………(2分) 静安区21.(本题满分10分,第(1)小题满分5分,第(2)小题满分5分)已知:如图,边长为1的正方形ABCD 中,AC 、DB 交于点H .DE 平分∠ADB ,交AC 于点E .联结BE 并延长,交边AD 于点F . (1)求证:DC =EC ; (2)求△EAF 的面积.21.(本题满分10分, 第(1)小题5分,第(2)小题5分)解:(1)∵正方形ABCD ,∴DC=BC=BA=AD , ∠BAD =∠ADC =∠DCB =∠CBA =90° AH=DH=CH=BH , AC ⊥BD ,∴∠ADH =∠HDC =∠DCH =∠DAE = 45°. …………(2分)第21题图H又∵DE 平分∠AD B ∴∠ADE =∠EDH∵∠DAE +∠ADE =∠DEC , ∠EDH +∠HDC =∠EDC …………(1分) ∴∠EDC =∠DEC …………(1分) ∴DC =EC …………(1分) (2)∵正方形ABCD ,∴AD ∥BC , ∴△AFE ∽△CBE ∴2)(ECAE S S CEB AEF =∆∆ ………………………………(1分) ∵AB=BC=DC=EC =1,AC =2,∴AE =12- …………………………(1分)Rt △BHC 中, BH =22BC =22, ∴在△BEC 中,BH ⊥EC , 4222121=⨯⨯=∆BEC S ……………………(2分) ∴2)12(42-=∆AEF S , ∴4423)223(42-=-⨯=∆AEF S …………(1分) 闵行区21.(本题满分10分,其中第(1)小题4分,第(2)小题6分)已知一次函数24y x =-+的图像与x 轴、y 轴分别交于点A 、B ,以AB 为边在第一象限内作直角三角形ABC ,且∠BAC = 90o,1tan 2ABC ∠=.(1)求点C 的坐标;(2)在第一象限内有一点M (1,m ),且点MC 位于直线AB 的同侧,使得ABC ABM S S ∆∆=2求点M 的坐标.21.解:(1)令0y =,则240x -+=,解得:2x =,∴点A 坐标是(2,0).令0x =,则4y =,∴点B 坐标是(0,4).………………………(1分) ∴AB =1分) ∵90BAC ∠=,1tan 2ABC ∠=,∴AC =. (第21题图)过C 点作CD ⊥x 轴于点D ,易得OBA DAC ∆∆∽.…………………(1分) ∴2AD =,1CD =,∴点C 坐标是(4,1).………………………(1分) (2)11522ABC S AB AC ∆=⋅=⨯=.………………………………(1分) ∵2ABM ABC S S ∆∆=,∴52ABM S ∆=.……………………………………(1分) ∵(1M ,)m ,∴点M 在直线1x =上;令直线1x =与线段AB 交于点E ,2ME m =-;……………………(1分) 分别过点A 、B 作直线1x =的垂线,垂足分别是点F 、G ,∴AF +BG = OA = 2;……………………………………………………(1分)∴111()222ABM BME AME S S S ME BG ME AF ME BG AF ∆∆=+=⋅+⋅=+1152222ME OA ME =⋅=⨯⨯=…………………(1分) ∴52ME =,522m -=,92m =,∴(1M ,92).……………………(1分)普陀区21.(本题满分10分)如图7,在Rt △ABC 中,90C ∠=,点D 在边BC 上,DE ⊥AB ,点E 为垂足,7AB =,45DAB ∠=,3tan 4B =. (1)求DE 的长; (2)求CDA ∠的余弦值. 21.解:(1)∵DE ⊥AB ,∴︒=∠90DEA又∵45DAB ∠=,∴AE DE =. ······································································· (1分) 在Rt △DEB 中,︒=∠90DEB ,43tan =B ,∴43=BE DE . ······························ (1分)设x DE 3=,那么x AE 3=,x BE 4=.∵7AB =,∴743=+x x ,解得1=x . ····························································· (2分) ∴3=DE . ············································································································· (1分) (2) 在Rt △ADE 中,由勾股定理,得23=AD . ················································ (1分)ABCDE 图7同理得5=BD . ······································································································ (1分) 在Rt △ABC 中,由43tan =B ,可得54cos =B .∴528=BC . ····················· (1分) ∴53=CD . ············································································································ (1分)∴102cos ==∠AD CD CDA . ················································································ (1分)即CDA ∠青浦区21. (本题满分10分,第(1)、(2)小题,每小题5分)如图5,在Rt △ABC 中,∠C =90°,AC=3,BC =4,∠ABC 的平分线交边AC 于点D ,延长BD 至点E ,且BD=2DE ,联结AE .(1)求线段CD 的长; (2)求△ADE 的面积.21.解:(1)过点D 作DH ⊥AB ,垂足为点H . ································································· (1分)∵BD 平分∠ABC ,∠C =90°,∴DH = DC =x , ·································································································· (1分) 则AD =3-x .∵∠C =90°,AC=3,BC =4,∴AB =5. ····························································· (1分) ∵sin ∠==HD BCBAC AD AB, ∴435=-x x , ·································································································· (1分) ∴43=x . ·········································································································· (1分)(2)1141052233=⋅=⨯⨯=ABD S AB DH . ···························································· (1分)∵BD=2DE , ∴2==ABD ADES BDSDE, ····················································································· (3分) ∴1015323=⨯=ADES. ··················································································· (1分) 松江区ED C BA图521.(本题满分10分, 每小题各5分) 如图,已知△ABC 中,∠B =45°,1tan 2C =, BC =6.(1)求△ABC 面积;(2)AC 的垂直平分线交AC 于点D ,交BC 于 点E. 求DE 的长.21.(本题满分10分, 每小题各5分)解:(1)过点A 作AH ⊥BC 于点H …………1分 在Rt ABC ∆中,∠B =45°设AH =x ,则BH =x ………………………………1分 在Rt AHC ∆中,1tan 2AH C HC == ∴HC=2x ………………………………………………………1分 ∵BC =6∴x+2x =6 得x =2∴AH =2…………………………………………………………1分 ∴162ABC S BC AH ∆=⋅⋅=……………………………………1分(2)由(1)得AH =2,CH=4在Rt AHC ∆中,AC =2分 ∵DE 垂直平分AC ∴12CD AC == ED ⊥AC …………………………………………………1分 在Rt EDC ∆中,1tan 2ED C CD ==……………………………1分 (第21题图)DACE∴DE = ………………………………………………1分 徐汇区21. 如图,在Rt ABC ∆中,90C ∠=︒,3AC =,4BC =,AD 平分BAC ∠交BC 于点D .(1)求tan DAB ∠;(2)若⊙O 过A 、D 两点,且点O 在边AB 上,用尺规作图的方法确定点O 的位置并求出的⊙O 半径.(保留作图轨迹,不写作法)杨浦区21、(本题满分10分,第(1)小题满分3分,第(2)小题满分7分)已知,如图5,在梯形ABCD 中,DC//AB, AD=BC, BD 平分∠ABC ,∠A =600求:(1)求∠CDB 的度数(2)当AD =2时,求对角线BD 的长和梯形ABCD 的面积。
上海市XX区2018年中考二模数学试卷含答案

2017-2018学年第二学期初三数学教学质量检测试卷(考试时间:100分钟 满分:150分)考生注意:1.本试卷含三个大题,共25题.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效.2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸相应位置上写出证明或计算的主要步骤. 一、选择题(本大题共6题, 每题4分, 满分24分)【每题只有一个正确选项, 在答题纸相应题号的选项上用2B 铅笔正确填涂】 1.函数12-=x y 的图像不经过( ▲ )(A ) 第一象限; (B ) 第二象限; (C ) 第三象限; (D ) 第四象限. 2.下列式子一定成立的是( ▲ )(A ) a a a 632=+; (B )428x x x =÷;(C ) aa 121=; (D )6321)(aa-=--. 3.下列二次根式中,2的同类二次根式是( ▲ ) (A )4; (B )x 2; (C )92; (D )12. 4.已知一组数据2、x 、8、5、5、2的众数是2,那么这组数据的中位数是( ▲ ) (A ) 3.5; (B ) 4; (C ) 2; (D )6.5.5.已知圆A 的半径长为4,圆B 的半径长为7,它们的圆心距为d ,要使这两圆没有公共点, 那么d 的值可以取( ▲ )(A ) 11; (B ) 6; (C ) 3; (D )2.6.已知在四边形ABCD 中,AD //BC ,对角线AC 、BD 交于点O ,且AC =BD , 下列四个命题中真命题是( ▲ )(A ) 若AB =CD ,则四边形ABCD 一定是等腰梯形; (B ) 若∠DBC =∠ACB ,则四边形ABCD 一定是等腰梯形; (C ) 若ODCOOB AO =,则四边形ABCD 一定是矩形; (D ) 若AC ⊥BD 且AO =OD ,则四边形ABCD 一定是正方形.二、填空题(本大题共12题, 每题4分, 满分48分) 【在答题纸相应题号后的空格内直接填写答案】 7. 计算:=--︒0)3(30sin ▲ . 8. 方程6+=-x x 的解是 ▲ .9. 不等式组⎪⎩⎪⎨⎧≥-<+-1)12(303x x 的解集是 ▲ .10.已知反比例函数xky =的图像经过点(-2017,2018),当0>x 时,函数值y 随 自变量x 的值增大而 ▲ .(填“增大”或“减小”)11.若关于x 的方程032=--m x x 有两个相等的实数根,则m 的值是 ▲ . 12.在形状为等腰三角形、圆、矩形、菱形、直角梯形的5张纸片中随机抽取一张,抽到中心对称图形的概率是 ▲ .13.抛物线522++=mx mx y 的对称轴是直线 ▲ . 14.小明统计了家里3月份的电话通话清单,按通话时间画出频数分布直方图(如图所示),则通话时间不足10分钟的 通话次数的频率是 ▲ .15.如图,在四边形ABCD 中,点E 、F 分别是边AB 、AD 的中点,BC =15,CD =9,EF =6,∠AFE =50°,则∠ADC 的度数为 ▲ . 16.如图,在梯形ABCD 中,AB //CD ,∠C=90°,BC =CD =4,52=AD ,若a AD =,b DC =,用、表示= ▲ . 17.如果一个三角形有一条边上的高等于这条边的一半,那么我们把这个三角形叫做半高三角形.已知直角三角形ABC是半高三角形,且斜边5=AB ,则它的周长等于 ▲ . 18.如图,在矩形ABCD 中,对角线BD 的长为1,点P 是线段BD上的一点,联结CP ,将△BCP 沿着直线CP 翻折,若点B 落在 边AD 上的点E 处,且EP //AB ,则AB 的长等于 ▲ .第14题图AB CDE F第15题图第16题图DCBA第18题图AB CD三、解答题(本大题共7题, 满分78分)【将下列各题的解答过程, 做在答题纸的相应位置上】 19.(本题满分10分)先化简,再求值:12341311222+-++÷-+-+x x x x x x x ,其中121+=x .20.(本题满分10分)解方程组:⎩⎨⎧=-=-+②12①06522 . ,y x y xy x21.(本题满分10分,第(1)小题4分,第(2)小题6分)如图,在等腰三角形ABC 中,AB =AC ,点D 在BA 的延长线上,BC =24,135sin =∠ABC .(1)求AB 的长;(2)若AD =6.5,求DCB ∠的余切值.22.(本题满分10分,第(1)小题5分,第(2)小题5分)某旅游景点的年游客量y (万人)是门票价格x (元)的一次函数,其函数图像如下图. (1)求y 关于x 的函数解析式;(2)经过景点工作人员统计发现:每卖出一张门票所需成本为20元.那么要想获得年利润11500万元,且门票价格不得高于230元,该年的门票价格应该定为多少元?23.(本题满分12分,第(1)小题5分,第(2)小题7分)如图,在四边形ABCD 中,AD //BC ,E 在BC 的延长线,联结AE 分别交BD 、CD 于点 G 、F ,且AG GF BE AD =.(1)求证:AB //CD ;(2)若BD GD BC ⋅=2,BG =GE ,求证:四边形ABCD 是菱形.ACDB第21题图第22题图ACDEF GB第23题图24.(本题满分12分,第(1)小题4分,第(2)小题3分,第(3)小题5分)如图在直角坐标平面内,抛物线32-+=bx ax y 与y 轴交于点A ,与x 轴分别交于点B (-1,0)、点C (3,0),点D 是抛物线的顶点. (1)求抛物线的表达式及顶点D 的坐标; (2)联结AD 、DC ,求ACD ∆的面积;(3)点P 在直线DC 上,联结OP ,若以O 、P 、C 为顶点的三角形与△ABC 相似,求点P 的坐标.25.(本题满分14分,第(1)小题4分,第(2)小题4分,第(3)小题6分)在圆O 中,C 是弦AB 上的一点,联结OC 并延长,交劣弧AB 于点D ,联结AO 、BO 、AD 、BD . 已知圆O 的半径长为5 ,弦AB 的长为8.(1)如图1,当点D 是弧AB 的中点时,求CD 的长; (2)如图2,设AC =x ,y S S OBDACO=∆∆,求y 关于x 的函数解析式并写出定义域; (3)若四边形AOBD 是梯形,求AD 的长.备用图第24题图OAC BO BA C DBAO2017-2018学年第二学期初三数学参考答案和评分建议一、选择题:(本大题共6题,每题4分,满分24分) 1.B ; 2.D ; 3.C ; 4.A ; 5.D ; 6.C . 二.填空题:(本大题共12题,满分48分) 7.21-; 8.2-=x ; 9.3>x ; 10.增大; 11.43-=m ; 12.53; 13.1-=x ;14.7.0;15.︒140; 16.→→-a b 21; 17.255或535++; 18.215-.三、(本大题共7题,第19、20、21、22每题10分,第23、24每题12分,第25题14分,满分78分)19. (本题满分10分)解:原式= )1)(3()1()1)(1(3112++-⨯-++-+x x x x x x x (3分) =2)1(111+--+x x x (2分) =2)1(11++-+x x x (1分) =2)1(2+x (1分)当12121-=+=x 时,原式=2)1(2+x =2)112(2+- =2)2(2=1 (3分) 20.(本题满分10分)解:方程①可变形为0))(6(=-+y x y x得06=+y x 或0=-y x (2分)将它们与方程②分别组成方程组,得(Ⅰ)⎩⎨⎧=-=+1206y x y x 或(Ⅱ)⎩⎨⎧=-=-120y x y x (2分)解方程组(Ⅰ)⎪⎩⎪⎨⎧-==131136y x , 解方程组(Ⅱ)⎩⎨⎧==11y x (4分) 所以原方程组的解是⎪⎩⎪⎨⎧-==13113611y x , ⎩⎨⎧==1122y x . (2分)另解:由②得12-=x y ③ (1分) 把③代入①,得0)12(6)12(522=---+x x x x (1分)整理得:0619132=+-x x (2分)解得:1,13621==x x (2分)分别代入③,得1,13121=-=y y (2分)所以原方程组的解是⎪⎩⎪⎨⎧-==13113611y x ,⎩⎨⎧==1122y x . (2分)21.(本题满分10分,第(1)小题4分,第(2)小题6分) 解:(1)过点A 作AE ⊥BC ,垂足为点E又∵AB =AC ∴BC BE 21= ∵BC =24 ∴ BE =12 (1分)在ABE Rt ∆中,︒=∠90AEB ,135sin ==∠AB AE ABC (1分)设AE=5k,AB=13k ∵222BE AE AB += ∴1212==k BE∴1=k , ∴55==k AE , 1313==k AB (2分) (2)过点D 作DF ⊥BC ,垂足为点F∵AD=6.5,AB=13 ∴BD=AB+AD=19.5∵AE ⊥BC ,DF ⊥BC ∴ ︒=∠=∠90DFB AEB ∴ DF AE //∴BDABBF BE DF AE == 又 ∵ AE =5,BE =12,AB =13, ∴18,215==BF DF (4分) ∴BF BC CF -= 即61824=-=CF (1分)在DCF Rt ∆中,︒=∠90DFC ,5426cot ===∠DF CF DCB (1分)22.(本题满分10分,第(1)小题5分,第(2)小题5分)解:(1)设)0(≠+=k b kx y ,函数图像过点(200,100), (50,250) (1分)代入解析式得:⎩⎨⎧=+=+25050100200b k b k (2分)解之得:⎩⎨⎧=-=3001b k (1分)所以y 关于x 的解析式为:300+-=x y (1分) (2)设门票价格定为x 元,依题意可得:11500)300)(20(=+--x x (2分) 整理得: 0175003202=+-x x 解之得:x =70或者x =250(舍去) (2分)答:门票价格应该定为70元. (1分) 23.(本题满分12分,第(1)小题5分,第(2)小题7分) 证明:(1)∵BC AD // ∴BG DG BE AD = (2分)∵AG GFBE AD =∴AGGF BG DG = (1分) ∴ CD AB // (2分) (2)∵BC AD //,CD AB //∴四边形ABCD 是平行四边形 ∴BC=AD (1分) ∵ BD GD BC ⋅=2∴ BD GD AD ⋅=2即ADGDBD AD =又 ∵BDA ADG ∠=∠ ∴ADG ∆∽BDA ∆ (1分) ∴ABD DAG ∠=∠∵CD AB // ∴BDC ABD ∠=∠ ∵BC AD // ∴E DAG ∠=∠∵BG =GE ∴E DBC ∠=∠ ∴DBC BDC ∠=∠ (3分) ∴BC=CD (1分) ∵四边形ABCD 是平行四边形 ∴平行四边形ABCD 是菱形. (1分) 24.(本题满分12分,第(1)小题4分,第(2)小题3分,第(3)小题5分) 解:(1) 点B (-1,0)、C (3,0)在抛物线32-+=bx ax y 上∴⎩⎨⎧=-+=--033903b a b a ,解得⎩⎨⎧-==21b a ( 2分)∴抛物线的表达式为322--=x x y ,顶点D 的坐标是(1,-4) ( 2分) (2)∵A (0,-3),C (3,0),D (1,-4) ∴23=AC ,52=CD ,2=AD∴222AD AC CD += ∴︒=∠90CAD ( 2分)∴.32232121=⨯⨯=⋅⋅=∆AD AC S ACD (1分) (3)∵︒=∠=∠90AOB CAD ,2==AOACBO AD , ∴△CAD ∽△AOB ,∴OAB ACD ∠=∠∵OA =OC ,︒=∠90AOC ∴︒=∠=∠45OCA OAC∴ACD OCA OAB OAC ∠+∠=∠+∠,即BCD BAC ∠=∠ ( 1分)若以O 、P 、C 为顶点的三角形与△ABC 相似 ,且△ABC 为锐角三角形 则POC ∆也为锐角三角形,点P 在第四象限由点C (3,0),D (1,-4)得直线CD 的表达式是62-=x y ,设)62,(-t t P (30<<t ) 过P 作PH ⊥OC ,垂足为点H ,则t OH =,t PH 26-=①当ABC POC ∠=∠时,由ABC POC ∠=∠tan tan 得BO AO OH PH =,∴326=-t t ,解得56=t , ∴)518,56(1-P (2分) ②当ACB POC ∠=∠时,由145tan tan tan =︒=∠=∠ACB POC 得1=OHPH ,∴126=-tt,解得2=t ,∴)2,2(2-P ( 2分) 综上得)518,56(1-P 或)2,2(2-P 25.(本题满分14分,第(1)小题4分,第(2)小题4分,第(3)小题6分) 解:(1)∵OD 过圆心,点D 是弧AB 的中点,AB =8,∴OD ⊥AB ,421==AB AC (2分) 在Rt △AOC 中,︒=∠90ACO ,AO =5,∴322=-=AC AO CO (1分)5=OD ,2=-=∴OC OD CD (1分) (2)过点O 作OH ⊥AB ,垂足为点H ,则由(1)可得AH =4,OH =3∵AC =x ,∴|4|-=x CH在Rt △HOC 中,︒=∠90CHO ,AO =5, ∴258|4|322222+-=-+=+=x x x HC HO CO , (1分)∴525882+-⋅-=⋅=⋅==∆∆∆∆∆∆x x x x OD OC BC AC S S S S S S y OBD OBC OBC ACO OBD ACO xx x x 5402582-+-= (80<<x ) (3分)(3)①当OB //AD 时, 过点A 作AE ⊥OB 交BO 延长线于点E ,过点O 作OF ⊥AD ,垂足为点F ,则OF =AE , AE OB OH AB S ABO ⋅=⋅=∆2121 ∴OF OB OH AB AE ==⋅=524 在Rt △AOF 中,︒=∠90AFO ,AO =5,∴5722=-=OF AO AF ∵OF 过圆心,OF ⊥AD ,∴5142==AF AD . (3分)②当OA //BD 时, 过点B 作BM ⊥OA 交AO 延长线于点M ,过点D 作DG ⊥AO ,垂足为点G ,则由①的方法可得524==BM DG , 在Rt △GOD 中,︒=∠90DGO ,DO =5, ∴5722=-=DG DO GO ,518575=-=-=GO AO AG ,在Rt △GAD 中,︒=∠90DGA ,∴622=+=DG AG AD ( 3分)综上得6514或=AD。
上海市各区2017-2018届九年级中考二模数学试卷精选汇编:压轴题专题.docx

上海市各区 2018 届九年级中考二模数学试卷精选汇编:压轴题专题宝山区、嘉定区25.(本分14 分,第( 1)小 4 分,第( 2)小 5 分,第( 3)小 5 分)在 O 中, AO 、 BO 是 O 的半径,点 C 在劣弧 AB 上, OA 10 , AC 12 , AC ∥ OB , AB .(1)如 8,求:AB 平分OAC ;( 2)点M在弦AC的延上,BM ,如果△AMB 是直角三角形,你在如9中画出点 M 的位置并求 CM 的;(3)如10,点D在弦AC上,与点A不重合,OD与弦AB交于点E,点D与点 C 的距离 x ,△OEB的面y,求y与 x 的函数关系式,并写出自量x 的取范.A A AO O D OEC C CB BB891025.(1)明:∵AO 、 BO 是 O 的半径∴ AO BO ⋯⋯⋯⋯1分A∴ OABB ⋯⋯⋯⋯1分O∵AC ∥ OB∴BAC B ⋯⋯⋯⋯1分CB∴OAB BAC ∴ AB 平分OAC8⋯⋯⋯⋯ 1 分(2)解:由意可知BAM 不是直角,所以△ AMB 是直角三角形只有以下两种情况:AMB90 和ABM90①当 AMB90 ,点 M 的位置如9-1⋯⋯⋯⋯⋯ 1 分点 O 作 OH AC ,垂足点 H ∵ OH 心∴ AH HC 1AC 2∵ AC 12∴ AH HC6在 Rt△AHO中,AH2HO 2OA2∵ OA 10∴ OH8∵ AC ∥ OB∴ AMB OBM180∵AMB 90 ∴ OBM 90∴四形 OBMH 是矩形∴OB HM 10∴CM HM HC 4 ⋯⋯⋯⋯⋯2分②当ABM90 ,点 M的位置如 9-2由①可知 AB8 5 ,cos CAB25AB 52在 Rt△ABM中,cos CAB5AM5∴ AM20CM AM AC8⋯⋯⋯⋯⋯ 2 分上所述, CM 的 4 或 8 .明:只要画出一种情况点M 的位置就 1 分,两个点都画正确也(3)点O作OG AB ,垂足点 G由( 1)、( 2)可知,sin OAG sin CAB由( 2)可得:sin CAB5 5∵ OA10 ∴OG 2 5⋯⋯⋯⋯⋯ 1 分∵ AC ∥ OB ∴BE OB⋯⋯⋯⋯⋯ 1 分AE AD又 AE8 5BE ,AD12x , OB10∴BE10∴ BE8051222⋯⋯⋯⋯⋯ 1 分8 5 BE x xAHOCM B9-1AOCMB9-21分 .AD E OGCB10∴ y11805 2 5BE OG22x22∴ y400⋯⋯⋯⋯⋯ 1 分22 x自量 x 的取范0x12⋯⋯⋯⋯⋯ 1 分长宁区25.(本分14 分,第( 1)小 4 分,第( 2)小 4 分,第( 3)小 6 分)在 O 中, C是弦 AB 上的一点,OC 并延,交劣弧AB 于点 D,AO、 BO、AD、 BD. 已知 O 的半径 5 ,弦 AB 的 8.( 1)如 1,当点 D 是弧 AB 的中点,求CD的;( 2)如2,AC=x,SACO y ,求y 关于x 的函数解析式并写出定域;S OBD( 3)若四形AOBD 是梯形,求AD 的.O O OC CA B A B A BD D12用第2525.(本分 14 分,第( 1)小 4 分,第( 2)小 4 分,第( 3)小 6 分)解:( 1)∵ OD 心,点 D 是弧 AB 的中点, AB=8,14( 2 分)∴OD⊥ AB,ACAB2在Rt△ AOC中,ACO 90 ,AO=5,∴ CO AO2AC 23(1分)OD 5 , CD OD OC2( 1 分)(2)过点 O 作 OH⊥AB,垂足为点 H,则由( 1)可得 AH=4,OH=3∵AC=x,∴CH| x 4 |在 Rt△ HOC中,CHO90, AO=5,∴ CO HO 2HC 232 | x 4 |2x28x 25 ,( 1 分)∴ y SACOSACOSOBC AC OC x x28x25SOBDSOBCSOBD BC OD8x5x x28x25( 0 x8)( 3 405x分)(3)①当 OB// AD 时,过点 A 作 AE⊥OB 交 BO 延长线于点 E,过点 O 作 OF⊥ AD,垂足为点 F,则 OF=AE,SABO1AB OH1OB AE∴ AE AB OH24OF 22OB5在Rt△ AOF中,AFO 90 ,AO=5,∴ AF AO 2OF 27∵ OF 过圆心, OF⊥ AD,∴AD 2AF14. (3分)55②当 OA// BD 时,过点 B 作 BM⊥OA 交 AO 延长线于点 M,过点 D 作 DG⊥ AO,垂足为点 G,则由①的方法可得DG BM 24DGO 90,DO=5,,在 Rt△ GOD 中,75718∴ GO DO 2DG 2, AG AO GO 5,555在 Rt△ GAD中,DGA90 ,∴AD AG2DG 26( 3 分)综上得 AD14 或65崇明区25.(本题满分14 分,第 (1)小题4 分,第(2)小题 4 分,第 (3)小题6 分)如图,已知△ ABC 中,AB8 ,BC10 ,AC12 ,D 是AC边上一点,且AB2AD AC ,联结BD,点E、 F 分别是BC、AC 上两点(点 E 不与B、 C 重合),AEF C ,AE与BD 相交于点G.(1)求证:BD 平分ABC ;(2)设BE x ,CF y ,求y 与x 之间的函数关系式;(3)联结FG,当△ GEF是等腰三角形时,求BE的长度.A AD DFGBEC B C(第25 题图)(备用图)25.(分 14 分,第( 1)小 4 分,第( 2)小 4 分,第( 3)小 6 分)( 1)∵AB8 , AC12又∵ AB2AD AC∴ AD16∴ CD121620⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分333∵ AB2AD AC∴ AD ABAB AC又∵∠ BAC 是公共角∴△ ADB∽△ ABC⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分∴∠ABD ∠C ,BDAD BC AB∴ BD 20∴ BD CD∴∠ DBC ∠C⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分3∴∠ABD ∠DBC∴ BD 平分∠ ABC⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分(2)点A作AH∥BC交BD的延于点HAD DH AH 164∵ AH ∥ BC3∴BD BC205 DC3∵ BD20, AH8∴ AD16∴ BH12 ⋯⋯1分CD DH33∵ AH ∥ BC∴ AH HG∴812BG∴ BG12x ⋯1分BE BG x BG x 8∵∠BEF ∠C∠ EFC即∠BEA ∠ AEF∠ C ∠EFC∵∠AEF ∠C∴∠BEA∠EFC又∵∠ DBC ∠C∴△BEG∽△ CFE⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分BE BG x 12x x8∴EC ∴10xCF y∴ y x22x 80⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分12(3)当△GEF是等腰三角形,存在以下三种情况:1°GE GFGE BE2x24⋯⋯⋯ 2 分易CF3,即,得到 BEEF y32°EG EF易 BE CF ,即 x y , BE 5105⋯⋯⋯⋯ 2 分3°FG FEGE BE3x3389⋯⋯⋯ 2 分易CF2,即BEEF y2奉贤区25.(本分 14 分,第 (1)小分 5 分,第 (2) 小分 5分,第 (3)小分 4 分)已知:如 9,在半径 2 的扇形 AOB 中,∠ AOB= 90°,点 C 在半径 OB 上, AC 的垂直平分交OA 于点 D,交弧 AB 于点 E, BE、CD.(1)若 C 是半径 OB 中点,求∠ OCD 的正弦;(2)若 E 是弧 AB 的中点,求:BE 2BO BC ;(3) CE,当△ DCE 是以 CD 腰的等腰三角形,求CD 的.A A AEDO C B O BO B用用9黄浦区25.(本题满分14 分)如图,四边形ABCD 中,∠ BCD =∠ D=90 °, E 是边 AB 的中点 .已知 AD =1,AB =2.(1)设 BC=x, CD=y,求 y 关于 x 的函数关系式,并写出定义域;(2)当∠ B=70 °时,求∠ AEC 的度数;( 3)当△ ACE 为直角三角形时,求边BC 的长 .25. 解:( 1)过 A 作 AH ⊥ BC 于 H ,————————————————————(1 分)由∠ D=∠ BCD =90°,得四边形 ADCH 为矩形 .在△ BAH 中, AB=2,∠ BHA =90°, AH=y , HB = x 1 ,所以 22 y 2x 2(1 分)1 ,—————————————————————— 则 yx 2 2x30 x 3 . ———————————————(2 分)(2)取 CD 中点 T ,联结 TE ,————————————————————(1 分)则 TE 是梯形中位线,得ET ∥ AD ,ET ⊥ CD.∴∠ AET=∠ B=70°. ——————————————————————— ( 1 分)又 AD=AE=1,∴∠ AED =∠ ADE =∠ DET=35°. —————————————————— (1 分)由 ET 垂直平分 CD ,得∠ CET=∠ DET =35°,————————————( 1 分)所以∠ AEC=70°+ 35°=105°. —————————————————— ( 1 分)( 3)当∠ AEC=90°时,易知△ CBE ≌△ CAE ≌△ CAD ,得∠ BCE=30°,则在△ ABH 中,∠ B=60°,∠ AHB =90°, AB=2,得 BH=1,于是 BC=2. —————————————————————— (2 分)当∠ CAE=90°时,易知△ CDA ∽△ BCA ,又 AC BC 2 AB 2 x 2 4 ,ADCA 1x 24117 (舍负)—————(2 分)则x 2xACCB4x2易知∠ ACE< 90°.所以 BC 的 2 或117.——————————————————(1分)2金山区25.(本分14 分,第( 1)小 4 分,第( 2)小 5 分,第( 3)小 5 分)如 9,已知在梯形 ABCD 中, AD ∥ BC,AB=DC=AD=5 ,sin B 3,P 是段 BC 上5一点,以 P 心, PA 半径的⊙ P 与射 AD 的另一个交点Q,射 PQ 与射CD 相交于点 E, BP=x.(1)求△ ABP∽△ ECP;(2)如果点 Q 在段 AD 上(与点 A、 D 不重合),△ APQ 的面 y,求y 关于 x 的函数关系式,并写出定域;(3)如果△ QED 与△ QAP 相似,求 BP 的.EQA D A DBP C B C用925.解:( 1)在⊙ P 中, PA=PQ,∴∠ PAQ =∠ PQA,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)∵AD∥ BC,∴∠ PAQ =∠ APB,∠ PQA =∠ QPC,∴∠ APB =∠ EPC,⋯⋯( 1 分)∵梯形 ABCD中, AD∥BC, AB=DC,∴∠B=∠C,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)∴△ APB∽△ ECP.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)( 2)作 AM ⊥ BC, PN⊥ AD,∵AD∥ BC,∴ AM ∥ PN,∴四形 AMPN 是平行四形,∴AM =PN, AN=MP.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)3在Rt△ AMB 中,∠ AMB=90°, AB=5, sinB= ,5∴AM =3, BM=4,∴ PN=3, PM=AN=x- 4,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)∵PN⊥AQ,∴ AN=NQ,∴ AQ= 2x- 8,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)1AQ PN 1∴ y2x 8 3 ,即 y 3x 12 ,⋯⋯⋯⋯⋯⋯⋯⋯⋯(1分)2132定域是4.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)x2(3)解法一:由△ QED 与△ QAP 相似,∠ AQP=∠ EQD,①如果∠ PAQ=∠ DEQ,∵△ APB∽△ ECP,∴∠ PAB=∠ DEQ,又∵∠ PAQ=∠ APB,∴∠ PAB=∠ APB,∴ BP=BA=5.⋯⋯⋯⋯⋯⋯⋯⋯⋯( 2 分)②如果∠ PAQ=∠ EDQ,∵∠ PAQ=∠ APB,∠ EDQ=∠ C,∠ B=∠ C,∴∠ B=∠ APB,∴ AB=AP,∵ AM⊥ BC,∴ BM=MP=4,∴ BP=8.⋯⋯⋯( 2 分)上所述 BP的 5 或者 8.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)解法二:由△ QAP 与△ QED相似,∠ AQP=∠ EQD,在 Rt△ APN 中,AP PQ32x 42x2 8x25 ,∵QD∥PC,∴EQEP ,QD PC∵△ APB∽△ ECP,∴APEP ,∴ AP EQ ,PB PC PB QDAQ EQ AQ AP2x 8x28x25①如果,∴,即x2x ,QP QD QP PB8x 25解得 x 5 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 2 分)②如果AQDQ ,∴ AQ PB ,即x22x 8x2x,QP QE QP AP8x 258x 25解得 x 8 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 2 分)上所述 BP的 5 或者 8.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)静安区25.(本分 14 分,第( 1)小分 4分,第( 2)小分 6 分,第( 3)小分 4分)如,平行四形ABCD中,已知 AB=6, BC=9,cos ABC 1.角 AC、 BD 交于3点 O.点 P 在 AB 上,⊙ P 点 B,交段 PA于点 E. BP= x.( 1)求 AC 的;A DE OP·( 2) ⊙ O 的半径 y ,当⊙ P 与⊙ O 外切 , 求 y 关于 x 的函数解析式,并写出定 域;( 3) 如果 AC 是⊙ O 的直径,⊙ O 点 E ,求⊙ O 与⊙ P 的 心距OP 的 . ADOBC第 25 题备用图25.(本 分 14 分,第( 1)小 4 分,第( 2)小 6 分,第( 3)小 4 分)解:( 1)作 AH ⊥ BC 于 H ,且 cos1ADABC , AB=6,13O那么 BHAB cos ABC6 2⋯⋯⋯⋯(2 分)E3·PBC=9, HC=9-2=7,BH C第 25 题图 (1)AH 6 2 224 2 ,⋯⋯⋯⋯⋯⋯⋯⋯(1 分)ACAH 2 HC 23249 9 ⋯⋯⋯( 1 分)(2)作 OI ⊥ AB 于 I , PO, AC=BC=9,AO=4.5A D∴∠ OAB=∠ ABC,IOAI 1 Ecos IAOcos∴Rt △ AIO 中,P ·ABC3AOBCH ∴AI=1.5, IO= 2 2 AI 32⋯⋯⋯⋯⋯⋯⋯⋯(第 25 题图 (2)1 分)∴PI=AB-BP-AI=6-x-1.5=9x , ⋯⋯⋯⋯⋯⋯⋯⋯(1 分)2∴ R t △ PIO 中,OP 2PI 2OI 2(3 2) 2 ( 9 x) 2 18 x 29x81 x 2 9x153 ⋯⋯( 1 分)244∵⊙ P 与⊙ O 外切,∴ OPx 2 9 x 153x y4∴ y = x29x 153x 1 4x236x 153 x42⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)∵ 点 P 在 AB 上,⊙ P 点 B,交 段 PA 于点 E .∴定 域: 0<x ≤3⋯⋯⋯⋯( 1 分)(3)由 意得:∵点 E 在 段 AP 上,⊙ O 点 E ,∴⊙ O 与⊙ P 相交∵AO 是⊙ O 半径,且 AO > OI ,∴交点 E 存在两种不同的位置,OE=OA=92① 当 E 与点 A 不重合 , AE 是⊙ O 的弦, OI 是弦心距,∵ AI=1.5,AE =3,∴点 E 是 AB 中点, BE1AB3 , BPPE 3 , PI 3 , IO= 3 222OPPI 2 IO 2 32(3 2 ) 2273 3⋯⋯⋯⋯⋯⋯⋯⋯( 2 分)② 当 E 与点 A 重合 ,点 P 是 AB 中点,点 O 是 AC 中点 , OP1BC9 ⋯⋯( 2 分)22∴ OP 3 3 或9. 2闵行区25.(本 分14 分,其中第( 1)小 4 分,第( 2)、(3)小 各 5 分)如 ,已知在 Rt △ ABC 中,∠ ACB = 90o , AC =6, BC = 8,点 F 在 段 AB 上,以点 B 心, BF 半径的 交 BC 于点 E ,射 AE 交 B 于点 D (点 D 、 E 不重合).( 1)如果BF = x , EF = y ,求 y 与 x 之 的函数关系式,并写出它的定 域;( 2)如果 ED2 EF ,求 ED 的 ;( 3) CD 、 BD , 判断四 形ABDC 是否 直角梯形? 明理由.CDCEA F BA B(第 25 题图)(备用图)25.解:( 1)在 Rt △ ABC 中, AC6 , BC 8 , ACB 90∴ AB10 .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(1 分)E 作 EH ⊥AB ,垂足是 H ,易得: EH3 x , BH4 x , FH 1 x .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)55522在 Rt △EHF 中, EF2EH2FH23 x1x ,5 5∴ y10 x (0 x 8) .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(1 分 +1 分)5(2)取 ED 的中点 P , BP 交 ED 于点 G∵ ED 2 EF , P 是 ED 的中点,∴EP EF PD .∴∠ FBE=∠ EBP=∠ PBD .∵ EP EF , BP 心,∴ BG ⊥ED ,ED =2EG =2DG .⋯⋯⋯⋯( 1 分)又∵∠ CEA=∠ DEB ,∴∠ CAE=∠ EBP=∠ABC .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)又∵ BE 是公共 ,∴BEH ≌ BEG .∴ EH EG3x .GD5在 Rt △CEA 中,∵ AC = 6, BC8 , tan CAEtan ABCAC CE ,BCAC∴ CEAC tanCAE6 6 3 3 9.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)8 22∴BE8 916 97.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(1 分)2 2 2 2∴ ED 2 EG 6 x 6 7 21.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(55 2 5( 3)四 形 ABDC 不可能 直角梯形.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(①当 CD ∥ AB ,如果四 形ABDC 是直角梯形,只可能∠ ABD =∠ CDB = 90o .C D在 Rt △ CBD 中,∵ BC 8 ,E1 分)1 分)∴ CD BC cos BCD32 , 5AF BBDBCsin BCD24BE .53232CD 5 16 CE 81 ∴5AB1025,32 ;BE45∴ CDCE .ABBE∴ CD 不平行于 AB ,与 CD ∥ AB 矛盾.∴四 形 ABDC 不可能 直角梯形.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 2 分)②当 AC ∥BD ,如果四 形 ABDC 是直角梯形,C只可能∠ ACD =∠CDB = 90o .∵ AC ∥ BD ,∠ ACB = 90o ,A∴∠ ACB =∠ CBD = 90o.∴∠ ABD =∠ ACB +∠BCD > 90o .与∠ ACD =∠ CDB = 90o 矛盾.∴四 形ABDC 不可能 直角梯形.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(E DF B2 分)普陀区25.(本 分 14 分)已知 P 是 ⊙O 的直径 BA 延长线上的一个动点,P 的另一边交⊙O 于点C 、D ,两点位于AB 的上方,AB = 6, OP = m ,sin P = 1 3,如图11 所示.另一个半径为6 的 ⊙O 1 经过点 C 、 D ,圆心距 OO 1=n .( 1)当 m =6 时,求线段 CD 的长;( 2)设圆心 O 1 在直线 AB 上方,试用 n 的代数式表示 m ;(3)△ POO 1 在点P 的运动过程中,是否能成为以OO 1 为腰的等腰三角形,如果能,试求出此时n 的值;如果不能,请说明理由.DCPAOBAOB图 11备用图25.解:(1)过点O 作 OH⊥ CD ,垂足为点H,联结 OC .在 Rt △ POH中,∵sin P = 1, PO6 ,∴OH2. ···( 1 分)3∵ AB =6 ,∴ OC =3 . ······( 1 分)由勾股定理得 CH5 . ······( 1 分)∵ OH ⊥ DC ,∴ CD 2CH 2 5 . ·····( 1 分)( 2)在 Rt △ POH 中,∵ sin P = 1 , PO = m ,∴ OH =m. ···( 1 分)33在△ OCH 中, 2=m 2分). ·····(RtCH 93 12在 Rt △ O 1CH 中, CH 2=36 nm. ····( 1 分) 32281. ···( 2 分)可得36m =9 m ,解得 = 3n 2n3m3 2n( 3)△ POO 1 成为等腰三角形可分以下几种情况:● 当圆心 O 1 、 O 在弦 CD 异侧时①OP= OO1,即 m=n ,由 n=3n281解得 n=9 .···(1分) 2n即圆心距等于⊙O 、⊙O1的半径的和,就有⊙O、⊙O1外切不合题意舍去.(1 分)② O1P=OO1,由 ( n m )2m2 (m)2=n ,33解得 m=2n ,即 2 n= 3n281,解得 n=915 .···(1分)332n5● 当圆心O1、 O 在弦 CD 同侧时,同理可得813n2=.m2n∵ POO1是钝角,∴只能是 m= 813n29n ,即 n2n ,解得 n= 5 .·(2分)5综上所述, n的值为95 或915 .55青浦区25.(本题满分14 分,第( 1)小题 4 分,第( 2)小题 6 分,第( 3)小题 4 分)如图 9-1,已知扇形 MON 的半径为 2 ,∠MON =90,点 B 在弧 MN 上移动,联结 BM,作 OD BM,垂足为点 D, C 为线段 OD 上一点,且 OC=BM,联结 BC并延长交半径OM 于点 A,设 OA= x,∠ COM 的正切值为 y.( 1)如图 9-2,当 AB OM 时,求证: AM =AC;( 2)求 y 关于 x 的函数关系式,并写出定义域;( 3)当△ OAC为等腰三角形时,求x 的值 .N N NBBC D CDO A M O A M O M 图 9-1图 9-2备用图25.解:( 1)∵ OD⊥ BM, AB⊥OM ,∴∠ ODM =∠ BAM =90 .° ···( 1 分)∵ ∠ ABM +∠ M =∠ DOM +∠M ,∴∠ ABM =∠DOM.···( 1 分)∵ ∠ OAC=∠BAM, OC =BM,∴△ OAC≌△ ABM,······( 1 分)∴AC =AM .·······( 1 分)(2)过点 D 作 DE// AB,交 OM 于点 E.····( 1 分)∵OB=OM , OD⊥ BM,∴ BD=DM.····( 1 分)∵DE// AB,∴ MD ME,∴ AE= EM,DM AE∵ OM= 2,∴ AE=12 x .····(1分)2∵DE// AB,∴OA OC2DM,·····(1分)OE OD OD∴DMOA , OD2OEx.( 0 x2 )·····(2分)∴ yx 2(3)( i)当 OA=OC 时,∵ DM1BM1OC1x ,222在 Rt△ODM 中,OD OM 2DM 22 1 x2.∵ y DM ,4OD1 xx142142∴2.解得 x,或 x分)1 x2x222(舍).( 224(i i )当 AO=AC时,则∠ AOC=∠ ACO,∵ ∠ ACO>∠ COB,∠ COB =∠ AOC,∴∠ ACO>∠ AOC,∴此种情况不存在.······( 1 分)(ⅲ)当CO=CA 时,则∠ COA=∠ CAO=,∵ ∠ CAO>∠ M ,∠M =90,∴>90,∴> 45,∴BOA290,∵BOA90,∴此种情况不存在.·( 1 分)松江区25.(本题满分 14 分,第( 1)小题 4 分,第( 2)小题每个小题各 5 分)如图,已知 Rt△ ABC 中,∠ ACB=90 °, BC=2,AC=3,以点 C 为圆心、 CB 为半径的圆交 AB 于点 D,过点 A 作 AE∥ CD,交 BC延长线于点 E.(1)求 CE的长;(2) P 是 CE延长线上一点,直线 AP、CD 交于点 Q.①如果△ ACQ∽△ CPQ,求CP的;②如果以点 A 心, AQ 半径的与⊙ C 相切,求 CP的 .A AD DB BC E C E(第 25 题图 )(备用图 )25.(本分 14 分,第( 1)小 4 分,第( 2)小每个小各 5 分)解:( 1)∵ AE∥ CD∴BC DC⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分BE AE∵BC=DC∴B E=AE ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分CE=xAE=BE=x+2∵ ∠ ACB=90°,∴ AC 2CE 2AE 2即 9 x2(x2)2⋯⋯⋯⋯⋯⋯⋯⋯⋯1分5∴ x45即 CE⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分4(2)①∵△ ACQ∽△ CPQ,∠ QAC>∠ P∴∠ ACQ=∠ P⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分又∵ AE∥ CD∴∠ ACQ=∠ CAE∴∠ CAE=∠ P⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分∴△ACE∽△ PCA,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分∴ AC 2CE CP ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分即 32 5 CPADBC E(第 25 题图 )QADBC E P4∴ CP 36⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分55②CP=t,PE t4∵∠ ACB=90°,∴AP 9 t 2∵AE∥ CD∴ AQ EC⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分AP EPAQ 55即4t29t54t 54∴AQ 5t 29⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分4t5若两外切,那么5 t 29AQ14t5此方程无数解⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分若两内切切,那么5 t 29 AQ54t5∴ 15t 240t160解之得t 2041015⋯⋯⋯⋯⋯⋯⋯⋯⋯1分又∵ t54 20410∴ t15⋯⋯⋯⋯⋯⋯⋯⋯⋯1分徐汇区25.已知四形 ABCD 是10的菱形,角 AC 、BD相交于点E,点 C 作 CF ∥DB交AB 延于点F,EF交BC于点H.(1)如1,当EF BC,求AE 的;(2)如 2,以EF直径作⊙O,⊙O点C交CD于点G(点C、G不重合),AE 的 x ,EH的y;①求 y 关于x的函数关系式,并写出定域;③EG ,当DEG 是以 DG 腰的等腰三角形,求AE 的.杨浦区25、(本题满分14 分,第(1)小题 4 分,第(2)小题 6 分,第(3)小题 4 分)如图9,在梯形ABCD中, AD//BC,AB=DC=5,AD=1,BC=9,点P 为边BC上一动点,作PH⊥DC,垂足H 在边DC 上,以点P 为圆心PH 为半径画圆,交射线PB 于点 E.(1)当圆P 过点 A 时,求圆P 的半径;(2)分别联结EH 和EA,当△ABE△ CEH时,以点B 为圆心,r 为半径的圆 B 与圆P 相交,试求圆 B 的半径r 的取值范围;( 3)将劣弧沿直线EH翻折交BC于点F,试通过计算说明线段EH和EF的比值为定值,并求出此定值。
2018年上海金山区初三二模试卷(含答案)

2017学年第二学期初三期中质量检测语文试卷(考试时间100分钟,满分150分)2018.4考生注意:1.本试卷共28题。
2.请将所有答案做在答卷上,做在试卷上一律不计分。
一、文言文(40分)(一)默写(15分)1.僵卧孤村不自哀,。
(《十一月四日风雨大作》)2.草色烟光残照里,。
(《蝶恋花》)3.,莲动下渔舟。
(《山居秋暝》)4.呼嘘毒疠,。
(《捕蛇者说》)5.,皆出酒食。
(《桃花源记》)(二)阅读下面的诗,完成第6—7题(4分)钱塘湖春行白居易孤山寺北贾亭西,水面初平云脚低。
几处早莺争暖树,谁家新燕啄春泥。
乱花渐欲迷人眼,浅草才能没马蹄。
最爱湖东行不足,绿杨阴里白沙堤。
6.《钱塘湖春行》是白居易任哪个地方的刺史时所作?(2分)A.杭州B.苏州C.徐州D.扬州7.下列对诗歌内容理解正确..的一项是()(2分)A.“水面初平”表明湖水丰盈,勾勒出暮春之景。
B.“乱花”写出暮春时节杂花稀少、稀疏的特点。
C.“没马蹄”表明杂草繁茂,把马蹄子都遮住了。
D.“行不足”是因为看不够,表明诗人流连忘返。
(三)阅读下文,完成第8—10题(9分)陈涉世家(节选)吴广素爱人,士卒多为用者。
将尉醉,广故数言欲亡,忿恚尉,令辱之,以激怒其众。
尉果笞广。
尉剑挺,广起,夺而杀尉。
陈胜佐之,并杀两尉。
召令徒属曰:“公等遇雨,皆已失期,失期当斩。
借第令毋斩,而戍死者固十六七。
且壮士不死即已,死即举大名耳,王侯将相宁有种乎!”徒属皆曰:“敬受命。
”乃诈称公子扶苏、项燕,从民欲也。
袒右,称大楚。
为坛而盟,祭以尉首。
陈胜自立为将军,吴广为都尉。
8.《陈涉世家》选自《》,它是我国第一部通史。
(2分)9.用现代汉语翻译下面句子。
(3分)10.。
(4分)(四)阅读下文,完成第11—14题(12分)王沂公①善为文辞,咸平②年间,状元及第,还青州故郡。
府帅闻其归.,乃命父老迎于郊。
公乃易.服,乘小驴,由他门入,谒太守。
守惊曰:“闻君来,已遣人奉迎。
2018上海市初三数学二模-金山区2017学年第二学期初三期中质量检测及评分标准

金山区2017学年第二学期初三期中质量检测数学试卷(满分150分,考试时间100分钟)(2018.4)考生注意:1.本试卷含三个大题,共25题;2.务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效;3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上.】1.下列各数中,相反数等于本身的数是(▲)(A )1-; (B )0; (C )1; (D )2.2.单项式32a b 的次数是(▲)(A )2; (B )3 (C )4; (D )5.3.如果将抛物线22y x =-向上平移1个单位,那么所得新抛物线的表达式是(▲)(A )()221y x =-+; (B )()221y x =--; (C )221y x =--; (D )221y x =-+. 4.如果一组数据1,2,x ,5,6的众数为6,则这组数据的中位数为(▲)(A )1; (B )2 (C )5; (D )6.5.如图1,□ABCD 中,E 是BC 的中点,设AB a =,AD b =,那么向量AE 用向量a 、b 表示为(▲)(A )12a b + ;(B )12a b - ;(C )12a b -+;(D )12a b --. 6.如图2,∠AOB=45°,OC 是∠AOB 的角平分线,PM ⊥OB ,垂足为点M ,PN ∥OB ,PN 与OA 相交于点N ,那么PM PN 的值等于( ▲ ) (A )12; (B)2; (C)2; (D)3. 二、填空题:(本大题共12题,每题4分,满分48分) 【请直接将结果填入答题纸的相应位置】D 图OMNAB C 图P7.因式分解:2a a -= ▲ .8.函数y =的定义域是 ▲ . 9.方程21x x =-的解是 ▲ . 10.一次函数2y x =-+的图像不经过第 ▲ 象限.11.有一枚材质均匀的正方体骰子,它的六个面上分别有1点、2点、…、6点的标记,掷这枚骰子,向上一面出现的点数是素数的概率是 ▲ .12.如果关于x 的一元二次方程240x x k -+=有两个不相等的实数根,那么k 的取值范围是 ▲ .13.如果梯形的中位线长为6,一条底边长为8,那么另一条底边长等于 ▲ .14.空气质量指数,简称AQI ,如果AQI 在0~50空 气质量类别为优,在51~100空气质量类别为良,在101~150空气质量类别为轻度污染,按照某市最 近一段时间的AQI 画出的频数分布直方图如图3所示,已知每天的AQI 都是整数,那么空气质量类别为优和良的天数占总天数的百分比为 ▲ %. 15.一辆汽车在坡度为1:2.4的斜坡上向上行驶 130米,那么这辆汽车的高度上升了 ▲ 米. 16.如果一个正多边形的中心角等于30°,那么这个正多边形的边数是 ▲ .17.如果两圆的半径之比为3:2,当这两圆内切时圆心距为3,那么当这两圆相交时, 圆心距d 的的取值范围是 ▲ . 18.如图4,Rt △ABC 中,∠C =90°,AC =6,BC =8,D 是AB 的中点,P 是直线BC 上一点,把△BDP 沿PD 所在的直线翻折后,点B 落在点Q 处,如果QD ⊥BC ,那么点P 和点B 间的距离等于 ▲ .三、解答题:(本大题共7题,满分78分) 19.(本题满分10分) 计算:21o o 21tan 452sin 60122-⎛⎫-+- ⎪⎝⎭.20.(本题满分10分)解方程组:248x y x xy +=⎧⎨-=⎩.图3A QI AB 图421.(本题满分10分,每小题5分)如图5,在矩形ABCD 中,E 是BC 边上的点,AE =BC ,DF ⊥AE ,垂足为F .(1)求证:AF=BE ; (2)如果BE ∶EC=2∶1,求∠CDF 的余切值.22.(本题满分10分,每小题5分)九年级学生到距离学校6千米的百花公园去春游,一部分学生步行前往,20分钟后另 一部分学生骑自行车前往,设x (分钟)为步行前往的学生离开学校所走的时间,步行 学生走的路程为1y 千米,骑自行车学生骑行的路程为2y 千米,1y 、2y 关于x 的函数 图像如图6所示.(1)求2y 关于x 的函数解析式; (2)步行的学生和骑自行车的学生谁先 到达百花公园,先到了几分钟? 23.(本题满分12分,每小题6分) 如图7,已知AD 是△ABC 的中线, M 是AD 的中点, 过A 点作AE ∥BC ,CM 的延 长线与AE 相交于点E ,与AB 相交于点F . (1)求证:四边形AEBD 是平行四边形; (2)如果AC =3AF ,求证四边形AEBD 是矩形. A B C DF E图5 E A F M B D图Cx (分图624.(本题满分12分,每小题4分)平面直角坐标系xOy 中(如图8),已知抛物线2y x bx c =++经过点A (1,0)和B (3,0), 与y 轴相交于点C ,顶点为P .(1)求这条抛物线的表达式和顶点P 的坐标;(2)点E 在抛物线的对称轴上,且EA =EC ,求点E 的坐标;(3)在(2)的条件下,记抛物线的对称轴为直线MN ,点Q 在直线MN 右侧的抛物线上,∠MEQ =∠NEB ,求点Q 的坐标.25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5 分)如图9,已知在梯形ABCD 中,AD ∥BC ,AB =DC =AD =5,3sin 5B =,P 是线段BC 上 一点,以P 为圆心,PA 为半径的⊙P 与射线AD 的另一个交点为Q ,射线PQ 与射线 CD 相交于点E ,设BP =x .(1)求证△ABP ∽△ECP ;(2)如果点Q 在线段AD 上(与点A 、D 不重合),设△APQ 的面积为y ,求y 关于x 的函数关系式,并写出定义域;(3)如果△QED 与△QAP 相似,求BP 的长.A B P C D Q EA B C D 图9备用图 图8金山区2017学年第二学期初三数学期中质量检测参考答案及评分建议2018.4.19一、选择题:(本大题共6题,每题4分,满分24分)1.B ; 2.C ; 3.D ; 4.C ; 5.A ; 6.B .二.填空题:(本大题共12题,满分48分)7.()1a a -; 8.2x ≥; 9.2x =; 10.三; 11.12; 12.4k <; 13.4; 14.80; 15.50; 16.12; 17.3d 15<<; 18.52或10. 三、(本大题共7题, 第19~22题每题10分, 第23、24题每题12分, 第25题14分, 满分78分) 19.解:原式=124-+…………………………………………………………(8分)14+………………………………………………………………(1分)=5.………………………………………………………………………(1分)20.解:248x y x xy +=⎧⎨-=⎩①②, 由①得:4y x =- ③,…………………………………………………………(2分)把③代入②得:()248x x x --=.………………………………………………(2分)解得:121,1x x ==…………………………………………………(2分)把121,1x x ==,代入③得:121211,33x x y y ⎧⎧==⎪⎪⎨⎨==+⎪⎪⎩⎩,……………………………………………………(4分)21.解:(1)∵四边形ABCD 是矩形,∴AD =BC ,AD ∥BC ,∠B =90°,∴∠DAF=∠AEB ,……………………………………………………………………(1分)∵AE=BC ,DF ⊥AE ,∴AD=AE ,∠ A FD=∠EBA=90°,………………………(2分)∴△ADF ≌△EAB ,∴AF =EB ,………………………………………………………(2分)(2)设BE =2k ,EC =k ,则AD =BC =AE =3k ,AF =BE =2k ,…………………………(1分) ∵∠ADC =90°,∠AFD =90°,∴∠CDF +∠ADF =90°,∠DAF +∠ADF =90°,∴∠CDF =∠DAF …………………………………………………………………(2分)在Rt △ADF 中,∠AFD =90°,DF∴cot ∠CDF =cot ∠DAF=5AF DF ==.………………………………(2分) 22.解:(1)设2y 关于x 的函数关系式是222y k x b =+,根据题意,得:2222200404k b k b +=⎧⎨+=⎩,………………………………………………(2分) 解得:215k =,24b =-,………………………………………………………(2分) ∴2y 关于x 的函数关系式是2145y x =-.……………………………………(1分) (2)设1y 关于x 的函数关系式是11y k x =,根据题意,得:1404k =,∴1110k =, 1y 关于x 的函数关系式是1110y x =,…………………………………………(1分) 当16y =时,60x =,当26y =时,50x =,………………………………(2分)∴骑自行车的学生先到百花公园,先到了10分钟.…………………………(2分)23.证明:(1)∵AE //BC ,∴∠AEM =∠DCM ,∠EAM =∠CDM ,…………………………(1分)又∵AM=DM ,∴△AME ≌△DMC ,∴AE =CD ,………………………………(1分)∵BD=CD ,∴AE =BD .……………………………………………………………(1分)∵AE ∥BD ,∴四边形AEBD 是平行四边形.……………………………………(2分)(2)∵AE //BC ,∴AF AE FB BC=.………………………………………………………(1分)∵AE=BD=CD ,∴12AF AE FB BC ==,∴AB=3AF .……………………………(1分) ∵AC=3AF ,∴AB=AC ,…………………………………………………………(1分)又∵AD 是△ABC 的中线,∴AD ⊥BC ,即∠ADB =90°.……………………(1分)∴四边形AEBD 是矩形.…………………………………………………………(1分)24.解:(1)∵二次函数2y x bx c =++的图像经过点A (1,0)和B (3,0), ∴10930b c b c ++=⎧⎨++=⎩,解得:4b =-,3c =.………………………………………(2分)∴这条抛物线的表达式是243y x x =-+…………………………………………(1分)顶点P 的坐标是(2,-1).…………………………………………………………(1分)(2)抛物线243y x x =-+的对称轴是直线2x =,设点E 的坐标是(2,m ).……(1分)根据题意得: =m=2,……(2分) ∴点E 的坐标为(2,2).……………………………………………………………(1分)(3)解法一:设点Q 的坐标为2(,43)t t t -+,记MN 与x 轴相交于点F .作QD ⊥MN ,垂足为D ,则2DQ t =-,2243241DE t t t t =-+-=-+…………………………………(1分)∵∠QDE=∠BFE=90°,∠QED=∠BEF ,∴△QDE ∽△BFE ,…………………(1分) ∴DQ DE BF EF=,∴224112t t t --+=, 解得11t =(不合题意,舍去),25t =.……………………………………………(1分)∴5t =,点E 的坐标为(5,8).…………………………………………………(1分)解法二:记MN 与x 轴相交于点F .联结AE ,延长AE 交抛物线于点Q ,∵AE=BE , EF ⊥AB ,∴∠AEF=∠NEB ,又∵∠AEF=∠MEQ ,∴∠QEM=∠NEB ,…………………………………………(1分)点Q 是所求的点,设点Q 的坐标为2(,43)t t t -+,作QH ⊥x 轴,垂足为H ,则QH =243t t -+,OH =t ,AH =t -1,∵EF ⊥x 轴,∴EF ∥QH ,∴EF AF QH AH=,∴221431t t t =-+-,……………(1分) 解得11t =(不合题意,舍去),25t =.……………………………………………(1分)∴5t =,点E 的坐标为(5,8).…………………………………………………(1分)25.解:(1)在⊙P 中,PA =PQ ,∴∠PAQ =∠PQA ,……………………………………(1分)∵AD ∥BC ,∴∠PAQ =∠APB ,∠PQA =∠QPC ,∴∠APB =∠EPC ,……(1分)∵梯形ABCD 中,AD ∥BC ,AB =DC ,∴∠B =∠C ,………………………………(1分)∴△APB ∽△ECP .…………………………………………………………………(1分)(2)作AM ⊥BC ,PN ⊥AD ,∵AD ∥BC ,∴AM ∥PN ,∴四边形AMPN 是平行四边形,∴AM =PN ,AN =MP .…………………………………………………………………(1分)在Rt △AMB 中,∠AMB =90°,AB =5,sinB =35, ∴AM =3,BM =4,∴PN =3,PM =AN =x -4,…………………………………………(1分) ∵PN ⊥AQ ,∴AN =NQ ,∴AQ = 2x -8,……………………………………………(1分) ∴()1128322y AQ PN x =⋅⋅=⋅-⋅,即312y x =-,……………………………(1分) 定义域是1342x <<.………………………………………………………………(1分) (3)解法一:由△QED 与△QAP 相似,∠AQP =∠EQD ,①如果∠PAQ =∠DEQ ,∵△APB ∽△ECP ,∴∠PAB =∠DEQ ,又∵∠PAQ =∠APB ,∴∠PAB =∠APB ,∴BP =BA =5.…………………………(2分)②如果∠PAQ =∠EDQ ,∵∠PAQ =∠APB ,∠EDQ =∠C ,∠B =∠C ,∴∠B =∠APB ,∴ AB =AP ,∵AM ⊥BC ,∴ BM =MP =4,∴ BP =8.…………(2分) 综上所述BP 的长为5或者8.………………………………………………………(1分)解法二:由△QAP 与△QED 相似,∠AQP =∠EQD ,在Rt △APN 中,AP PQ === ∵QD ∥PC ,∴EQ EP QD PC=,∵△APB∽△ECP,∴AP EPPB PC=,∴AP EQPB QD=,①如果AQ EQQP QD=,∴AQ APQP PB=x=,解得5x=………………………………………………………………………………(2分)②如果AQ DQQP QE=,∴AQ PBQP AP==解得8x=………………………………………………………………………………(2分)综上所述BP的长为5或者8.………………………………………………………(1分)。
2018上海市初三数学二模-金山区2017学年第二学期初三期中质量检测及评分标准

金山区2017学年第二学期初三期中质量检测数学试卷(满分150分,考试时间100分钟)(2018.4)考生注意:1.本试卷含三个大题,共25题;2.务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效;3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上.】1.下列各数中,相反数等于本身的数是(▲) (A )1-; (B )0; (C )1; (D )2. 2.单项式32a b 的次数是(▲)(A )2; (B )3 (C )4; (D )5.3.如果将抛物线22y x =-向上平移1个单位,那么所得新抛物线的表达式是(▲) (A )()221y x =-+; (B )()221y x =--; (C )221y x =--; (D )221y x =-+.4.如果一组数据1,2,x ,5,6的众数为6,则这组数据的中位数为(▲) (A )1; (B )2 (C )5; (D )6.5.如图1,□ABCD 中,E 是BC 的中点,设AB a =,AD b =, 那么向量AE 用向量a 、b 表示为(▲)E图1(A )12a b + ;(B )12a b - ;(C )12a b -+;(D )12a b --.6.如图2,∠AOB=45°,OC 是∠AOB 的角平分线,PM ⊥OB , 垂足为点M ,PN ∥OB ,PN 与OA 相交于点N ,那么PMPN 的值等于( ▲ ) (A )12; (B(C (D二、填空题:(本大题共12题,每题4分,满分48分) 【请直接将结果填入答题纸的相应位置】 7.因式分解:2a a -= ▲ . 8.函数y =的定义域是 ▲ .9.方程21xx =-的解是 ▲ . 10.一次函数2y x =-+的图像不经过第 ▲ 象限.11.有一枚材质均匀的正方体骰子,它的六个面上分别有1点、2点、…、6点的标记,掷这枚骰子,向上一面出现的点数是素数的概率是 ▲ . 12.如果关于x 的一元二次方程240x x k -+=有两个不相等的实数根,那么k 的取值范围是 ▲ .13.如果梯形的中位线长为6,一条底边长为8,那么另一条底边长等于 ▲ . 14.空气质量指数,简称AQI ,如果AQI 在0~50空 气质量类别为优,在51~100空气质量类别为良,在101~150空气质量类别为轻度污染,按照某市最 近一段时间的AQI 画出的频数分布直方图如图3 所示,已知每天的AQI 都是整数,那么空气质量 类别为优和良的天数占总天数的百分比为 ▲ %.O MNABC 图2P 6图3AQI15.一辆汽车在坡度为1:2.4的斜坡上向上行驶130米,那么这辆汽车的高度上升了 ▲ 米.16.如果一个正多边形的中心角等于30°,那么这个正多边形的边数是 ▲ . 17.如果两圆的半径之比为3:2,当这两圆内切时圆心距为3,那么当这两圆相交时,圆心距d 的的取值范围是 ▲ .18.如图4,Rt △ABC 中,∠C =90°,AC =6,BC =8,D 是AB 的中点,P 是直线BC 上一点,把△BDP 沿PD 所在的直线翻折后,点B 落在点Q 处,如果QD ⊥BC , 那么点P 和点B 间的距离等于 ▲ .三、解答题:(本大题共7题,满分78分) 19.(本题满分10分)计算:21oo21tan 452sin 60122-⎛⎫-+- ⎪⎝⎭.20.(本题满分10分)解方程组:248x y x xy +=⎧⎨-=⎩.21.(本题满分10分,每小题5分)如图5,在矩形ABCD 中,E 是BC 边上的点,AE =BC ,DF ⊥AE ,垂足为F .(1)求证:AF=BE ;A DFC图4(2)如果BE ∶EC=2∶1,求∠CDF 的余切值. 22.(本题满分10分,每小题5分)九年级学生到距离学校6千米的百花公园去春游,一部分学生步行前往,20分钟后另 一部分学生骑自行车前往,设x (分钟)为步行前往的学生离开学校所走的时间,步行学生走的路程为1y的函数 图像如图6所示.(1)求2y 关于x 的函数解析式; (2)步行的学生和骑自行车的学生谁先 到达百花公园,先到了几分钟?23.(本题满分12分,每小题6分)如图7,已知AD 是△ABC 的中线, M 是AD 的中点, 过A 点作AE ∥BC ,CM 的延 长线与AE 相交于点E ,与AB 相交于点F . (1)求证:四边形AEBD 是平行四边形; (2)如果AC =3AF ,求证四边形AEBD 是矩形.E AFMx (分钟)50 60 70 10 20 30 40 图624.(本题满分12分,每小题4分)平面直角坐标系xOy 中(如图8),已知抛物线2y x bx c =++经过点A (1,0)和B (3,0), 与y 轴相交于点C ,顶点为P .(1)求这条抛物线的表达式和顶点P 的坐标; (2)点E 在抛物线的对称轴上,且EA =EC ,求点E 的坐标;(3)在(2)的条件下,记抛物线的对称轴为直线MN ,点Q 在直线MN 右侧的抛物线 上,∠MEQ =∠NEB ,求点Q 的坐标.25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5 分) 如图9,已知在梯形ABCD 中,AD ∥BC ,AB =DC =AD =5,3sin 5B =,P 是线段BC 上一点,以P 为圆心,PA 为半径的⊙P 与射线AD 的另一个交点为Q ,射线PQ 与射线CD 相交于点E ,设BP =x .图8(1)求证△ABP∽△ECP;(2)如果点Q在线段AD上(与点A、D不重合),设△APQ的面积为y,求y关于x的函数关系式,并写出定义域;(3)如果△QED与△QAP相似,求BP的长.ADB C备用图图9金山区2017学年第二学期初三数学期中质量检测参考答案及评分建议2018.4.19一、选择题:(本大题共6题,每题4分,满分24分) 1.B ; 2.C ; 3.D ; 4.C ; 5.A ; 6.B .二.填空题:(本大题共12题,满分48分)7.()1a a -; 8.2x ≥; 9.2x =; 10.三; 11.12; 12.4k <; 13.4; 14.80; 15.50; 16.12; 17.3d 15<<; 18.52或10.三、(本大题共7题, 第19~22题每题10分, 第23、24题每题12分, 第25题14分, 满分78分) 19.解:原式=124-+…………………………………………………………(8分)14+………………………………………………………………(1分)=5-.………………………………………………………………………(1分)20.解:248x y x xy +=⎧⎨-=⎩①②,由①得:4y x =- ③,…………………………………………………………(2分) 把③代入②得:()248x x x --=.………………………………………………(2分)解得:121,1x x ==…………………………………………………(2分)把121,1x x ==,代入③得:121211,33x xy y⎧⎧==⎪⎪⎨⎨==+⎪⎪⎩⎩,……………………………………………………(4分)21.解:(1)∵四边形ABCD是矩形,∴AD=BC,AD∥BC,∠B=90°,∴∠DAF=∠AEB,……………………………………………………………………(1分)∵AE=BC,DF⊥AE,∴AD=AE,∠AFD=∠EBA=90°,………………………(2分)∴△ADF≌△EAB,∴AF=EB,………………………………………………………(2分)(2)设BE=2k,EC=k,则AD=BC=AE=3k,AF=BE=2k,…………………………(1分)∵∠ADC=90°,∠AFD=90°,∴∠CDF+∠ADF=90°,∠DAF+∠ADF=90°,∴∠CDF=∠DAF…………………………………………………………………(2分)在Rt△ADF中,∠AFD=90°,DF∴cot∠CDF=cot∠DAF=5AFDF==.………………………………(2分)22.解:(1)设2y关于x的函数关系式是222y k x b=+,根据题意,得:2222200404k bk b+=⎧⎨+=⎩,………………………………………………(2分)解得:215k=,24b=-,………………………………………………………(2分)∴2y关于x的函数关系式是2145y x=-.……………………………………(1分)(2)设1y关于x的函数关系式是11y k x=,根据题意,得:1404k=,∴1110k=,1y关于x的函数关系式是1110y x=,…………………………………………(1分)当16y=时,60x=,当26y=时,50x=,………………………………(2分)∴骑自行车的学生先到百花公园,先到了10分钟.…………………………(2分)23.证明:(1)∵AE //BC ,∴∠AEM =∠DCM ,∠EAM =∠CDM ,…………………………(1分)又∵AM=DM ,∴△AME ≌△DMC ,∴AE =CD ,………………………………(1分) ∵BD=CD ,∴AE =BD .……………………………………………………………(1分)∵AE ∥BD ,∴四边形AEBD 是平行四边形.……………………………………(2分) (2)∵AE //BC ,∴AF AEFB BC=.………………………………………………………(1分)∵AE=BD=CD ,∴12AF AE FB BC ==,∴AB=3AF .……………………………(1分)∵AC=3AF ,∴AB=AC ,…………………………………………………………(1分)又∵AD 是△ABC 的中线,∴AD ⊥BC ,即∠ADB =90°.……………………(1分) ∴四边形AEBD 是矩形.…………………………………………………………(1分)24.解:(1)∵二次函数2y x bx c =++的图像经过点A (1,0)和B (3,0), ∴10930b c b c ++=⎧⎨++=⎩,解得:4b =-,3c =.………………………………………(2分)∴这条抛物线的表达式是243y x x =-+…………………………………………(1分)顶点P 的坐标是(2,-1).…………………………………………………………(1分)(2)抛物线243y x x =-+的对称轴是直线2x =,设点E 的坐标是(2,m ).……(1分)根据题意得: =解得:m=2,……(2分) ∴点E 的坐标为(2,2).……………………………………………………………(1分) (3)解法一:设点Q 的坐标为2(,43)t t t -+,记MN 与x 轴相交于点F .作QD ⊥MN ,垂足为D ,则2DQ t =-,2243241DE t t t t =-+-=-+…………………………………(1分) ∵∠QDE=∠BFE=90°,∠QED=∠BEF ,∴△QDE ∽△BFE ,…………………(1分)∴DQ DEBF EF=,∴224112t t t --+=, 解得11t =(不合题意,舍去),25t =.……………………………………………(1分) ∴5t =,点E 的坐标为(5,8).…………………………………………………(1分) 解法二:记MN 与x 轴相交于点F .联结AE ,延长AE 交抛物线于点Q ,∵AE=BE , EF ⊥AB ,∴∠AEF=∠NEB ,又∵∠AEF=∠MEQ ,∴∠QEM=∠NEB ,…………………………………………(1分) 点Q 是所求的点,设点Q 的坐标为2(,43)t t t -+,作QH ⊥x 轴,垂足为H ,则QH =243t t -+,OH =t ,AH =t -1, ∵EF ⊥x 轴,∴EF ∥QH ,∴EF AFQH AH=,∴221431t t t =-+-,……………(1分) 解得11t =(不合题意,舍去),25t =.……………………………………………(1分) ∴5t =,点E 的坐标为(5,8).…………………………………………………(1分)25.解:(1)在⊙P 中,PA =PQ ,∴∠PAQ =∠PQA ,……………………………………(1分)∵AD ∥BC ,∴∠PAQ =∠APB ,∠PQA =∠QPC ,∴∠APB =∠EPC ,……(1分)∵梯形ABCD 中,AD ∥BC ,AB =DC ,∴∠B =∠C ,………………………………(1分) ∴△APB ∽△ECP .…………………………………………………………………(1分)(2)作AM ⊥BC ,PN ⊥AD ,∵AD ∥BC ,∴AM ∥PN ,∴四边形AMPN 是平行四边形,∴AM =PN ,AN =MP .…………………………………………………………………(1分)在Rt △AMB 中,∠AMB =90°,AB =5,sinB =35, ∴AM =3,BM =4,∴PN =3,PM =AN =x -4,…………………………………………(1分)∵PN ⊥AQ ,∴AN =NQ ,∴AQ = 2x -8,……………………………………………(1分) ∴()1128322y AQ PN x =⋅⋅=⋅-⋅,即312y x =-,……………………………(1分) 定义域是1342x <<.………………………………………………………………(1分)(3)解法一:由△QED 与△QAP 相似,∠AQP =∠EQD ,①如果∠PAQ =∠DEQ ,∵△APB ∽△ECP ,∴∠PAB =∠DEQ ,又∵∠PAQ =∠APB ,∴∠PAB =∠APB ,∴BP =BA =5.…………………………(2分)②如果∠PAQ =∠EDQ ,∵∠PAQ =∠APB ,∠EDQ =∠C ,∠B =∠C ,∴∠B =∠APB ,∴ AB =AP ,∵AM ⊥BC ,∴ BM =MP =4,∴ BP =8.…………(2分)综上所述BP 的长为5或者8.………………………………………………………(1分)解法二:由△QAP 与△QED 相似,∠AQP =∠EQD ,在Rt△APN中,AP PQ===∵QD∥PC,∴EQ EP QD PC=,∵△APB∽△ECP,∴AP EPPB PC=,∴AP EQPB QD=,①如果AQ EQQP QD=,∴AQ APQP PB=x=,解得5x=………………………………………………………………………………(2分)②如果AQ DQQP QE=,∴AQ PBQP AP==解得8x=………………………………………………………………………………(2分)综上所述BP的长为5或者8.………………………………………………………(1分)。
上海市各区20172018届九年级中考二模数学试卷精选汇编:压轴题专题
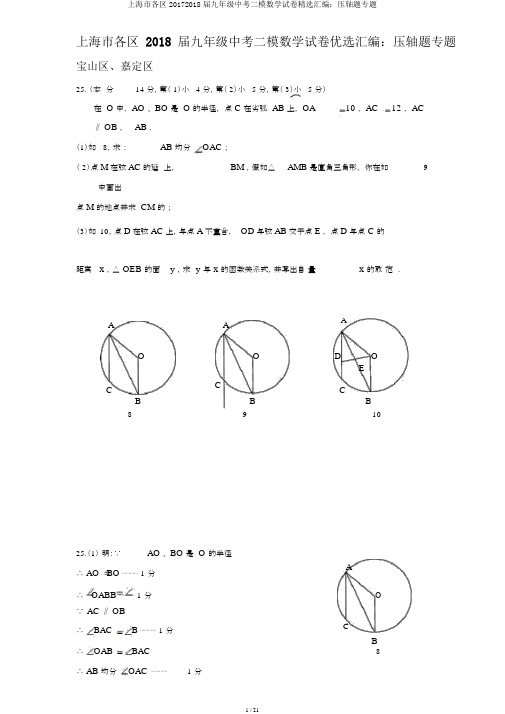
上海市各区 2018 届九年级中考二模数学试卷优选汇编:压轴题专题宝山区、嘉定区25.(本分14 分,第( 1)小 4 分,第( 2)小 5 分,第( 3)小 5 分)在 O 中, AO 、 BO 是 O 的半径,点 C 在劣弧 AB 上, OA 10 , AC 12 , AC∥ OB , AB .(1)如 8,求:AB 均分OAC ;( 2)点M在弦AC的延上,BM ,假如△AMB 是直角三角形,你在如9中画出点 M 的地点并求 CM 的;(3)如10,点D在弦AC上,与点A不重合,OD与弦AB交于点E,点D与点 C 的距离 x ,△OEB的面y,求y与 x 的函数关系式,并写出自量x 的取范.A A AO O D OEC C CB BB891025.(1)明:∵AO 、 BO 是 O 的半径∴ AO BO ⋯⋯⋯⋯1分A∴ OABB ⋯⋯⋯⋯1分O∵AC ∥ OB∴BAC B ⋯⋯⋯⋯1分CB∴OAB BAC ∴ AB 均分OAC8⋯⋯⋯⋯ 1 分(2)解:由意可知BAM 不是直角,因此△ AMB 是直角三角形只有以下两种状况:AMB90 和ABM90①当 AMB90 ,点 M 的地点如9-1⋯⋯⋯⋯⋯ 1 分点 O 作 OH AC ,垂足点 H ∵ OH 心∴ AH HC 1AC 2∵ AC 12∴ AH HC6在 Rt△AHO中,AH2HO 2OA2∵ OA 10∴ OH8∵ AC ∥ OB∴ AMB OBM180∵AMB 90 ∴ OBM 90∴四形 OBMH 是矩形∴OB HM 10∴CM HM HC 4 ⋯⋯⋯⋯⋯2分②当ABM90 ,点 M的地点如 9-2由①可知 AB8 5 ,cos CAB25AB 52在 Rt△ABM中,cos CAB5AM5∴ AM20CM AM AC8⋯⋯⋯⋯⋯ 2 分上所述, CM 的 4 或 8 .明:只需画出一种状况点M 的地点就 1 分,两个点都画正确也(3)点O作OG AB ,垂足点 G由( 1)、( 2)可知,sin OAG sin CAB由( 2)可得:sin CAB5 5∵ OA10 ∴OG 2 5⋯⋯⋯⋯⋯ 1 分∵ AC ∥ OB ∴BE OB⋯⋯⋯⋯⋯ 1 分AE AD又 AE8 5BE ,AD12x , OB10∴BE10∴ BE8051222⋯⋯⋯⋯⋯ 1 分8 5 BE x xAHOCM B9-1AOCMB9-21分 .AD E OGCB10∴ y11805 2 5BE OG22x22∴ y400⋯⋯⋯⋯⋯ 1 分22 x自量 x 的取范0x12⋯⋯⋯⋯⋯ 1 分长宁区25.(本分14 分,第( 1)小 4 分,第( 2)小 4 分,第( 3)小 6 分)在 O 中, C是弦 AB 上的一点,OC 并延,交劣弧AB 于点 D,AO、 BO、AD、 BD. 已知 O 的半径 5 ,弦 AB 的 8.( 1)如 1,当点 D 是弧 AB 的中点,求CD的;( 2)如2,AC=x,SACO y ,求y 对于x 的函数分析式并写出定域;S OBD( 3)若四形AOBD 是梯形,求AD 的.O O OC CA B A B A BD D12用第2525.(本分 14 分,第( 1)小 4 分,第( 2)小 4 分,第( 3)小 6 分)解:( 1)∵ OD 心,点 D 是弧 AB 的中点, AB=8,14( 2 分)∴OD⊥ AB,ACAB2在Rt△ AOC中,ACO 90 ,AO=5,∴ CO AO2AC 23(1分)OD 5 , CD OD OC2( 1 分)(2)过点 O 作 OH⊥AB,垂足为点 H,则由( 1)可得 AH=4,OH=3∵AC=x,∴CH| x 4 |在 Rt△ HOC中,CHO90, AO=5,∴ CO HO 2HC 232 | x 4 |2x28x 25 ,( 1 分)∴ y SACOSACOSOBC AC OC x x28x25SOBDSOBCSOBD BC OD8x5x x28x25( 0 x8)( 3 405x分)(3)①当 OB// AD 时,过点 A 作 AE⊥OB 交 BO 延伸线于点 E,过点 O 作 OF⊥ AD,垂足为点 F,则 OF=AE,SABO1AB OH1OB AE∴ AE AB OH24OF 22OB5在Rt△ AOF中,AFO 90 ,AO=5,∴ AF AO 2OF 27∵ OF 过圆心, OF⊥ AD,∴AD 2AF14. (3分)55②当 OA// BD 时,过点 B 作 BM⊥OA 交 AO 延伸线于点 M,过点 D 作 DG⊥ AO,垂足为点 G,则由①的方法可得DG BM 24DGO 90,DO=5,,在 Rt△ GOD 中,75718∴ GO DO 2DG 2, AG AO GO 5,555在 Rt△ GAD中,DGA90 ,∴AD AG2DG 26( 3 分)综上得 AD14 或65崇明区25.(此题满分14 分,第 (1)小题4 分,第(2)小题 4 分,第 (3)小题6 分)如图,已知△ ABC 中,AB8 ,BC10 ,AC12 ,D 是AC边上一点,且AB2AD AC ,联络BD,点E、 F 分别是BC、AC 上两点(点 E 不与B、 C 重合),AEF C ,AE与BD 订交于点G.(1)求证:BD 均分ABC ;(2)设BE x ,CF y ,求y 与x 之间的函数关系式;(3)联络FG,当△ GEF是等腰三角形时,求BE的长度.A AD DFGBEC B C(第25 题图)(备用图)25.(分 14 分,第( 1)小 4 分,第( 2)小 4 分,第( 3)小 6 分)( 1)∵AB8 , AC12又∵ AB2AD AC∴ AD16∴ CD121620⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分333∵ AB2AD AC∴ AD ABAB AC又∵∠ BAC 是公共角∴△ ADB∽△ ABC⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分∴∠ABD ∠C ,BDAD BC AB∴ BD 20∴ BD CD∴∠ DBC ∠C⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分3∴∠ABD ∠DBC∴ BD 均分∠ ABC⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分(2)点A作AH∥BC交BD的延于点HAD DH AH 164∵ AH ∥ BC3∴BD BC205 DC3∵ BD20, AH8∴ AD16∴ BH12 ⋯⋯1分CD DH33∵ AH ∥ BC∴ AH HG∴812BG∴ BG12x ⋯1分BE BG x BG x 8∵∠BEF ∠C∠ EFC即∠BEA ∠ AEF∠ C ∠EFC∵∠AEF ∠C∴∠BEA∠EFC又∵∠ DBC ∠C∴△BEG∽△ CFE⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分BE BG x 12x x8∴EC ∴10xCF y∴ y x22x 80⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分12(3)当△GEF是等腰三角形,存在以下三种状况:1°GE GFGE BE2x24⋯⋯⋯ 2 分易CF3,即,获得 BEEF y32°EG EF易 BE CF ,即 x y , BE 5105⋯⋯⋯⋯ 2 分3°FG FEGE BE3x3389⋯⋯⋯ 2 分易CF2,即BEEF y2奉贤区25.(本分 14 分,第 (1)小分 5 分,第 (2) 小分 5分,第 (3)小分 4 分)已知:如 9,在半径 2 的扇形 AOB 中,∠ AOB= 90°,点 C 在半径 OB 上, AC 的垂直均分交OA 于点 D,交弧 AB 于点 E, BE、CD.(1)若 C 是半径 OB 中点,求∠ OCD 的正弦;(2)若 E 是弧 AB 的中点,求:BE 2BO BC ;(3) CE,当△ DCE 是以 CD 腰的等腰三角形,求CD 的.A A AEDO C B O BO B用用9黄浦区25.(此题满分14 分)如图,四边形ABCD 中,∠ BCD =∠ D=90 °, E 是边 AB 的中点 .已知 AD =1,AB =2.(1)设 BC=x, CD=y,求 y 对于 x 的函数关系式,并写出定义域;(2)当∠ B=70 °时,求∠ AEC 的度数;( 3)当△ ACE 为直角三角形时,求边BC 的长 .25. 解:( 1)过 A 作 AH ⊥ BC 于 H ,————————————————————(1 分)由∠ D=∠ BCD =90°,得四边形 ADCH 为矩形 .在△ BAH 中, AB=2,∠ BHA =90°, AH=y , HB = x 1 ,因此 22 y 2x 2(1 分)1 ,—————————————————————— 则 yx 2 2x30 x 3 . ———————————————(2 分)(2)取 CD 中点 T ,联络 TE ,————————————————————(1 分)则 TE 是梯形中位线,得ET ∥ AD ,ET ⊥ CD.∴∠ AET=∠ B=70°. ——————————————————————— ( 1 分)又 AD=AE=1,∴∠ AED =∠ ADE =∠ DET=35°. —————————————————— (1 分)由 ET 垂直均分 CD ,得∠ CET=∠ DET =35°,————————————( 1 分)因此∠ AEC=70°+ 35°=105°. —————————————————— ( 1 分)( 3)当∠ AEC=90°时,易知△ CBE ≌△ CAE ≌△ CAD ,得∠ BCE=30°,则在△ ABH 中,∠ B=60°,∠ AHB =90°, AB=2,得 BH=1,于是 BC=2. —————————————————————— (2 分)当∠ CAE=90°时,易知△ CDA ∽△ BCA ,又 AC BC 2 AB 2 x 2 4 ,ADCA 1x 24117 (舍负)—————(2 分)则x 2xACCB4x2易知∠ ACE< 90°.因此 BC 的 2 或117.——————————————————(1分)2金山区25.(本分14 分,第( 1)小 4 分,第( 2)小 5 分,第( 3)小 5 分)如 9,已知在梯形 ABCD 中, AD ∥ BC,AB=DC=AD=5 ,sin B 3,P 是段 BC 上5一点,以 P 心, PA 半径的⊙ P 与射 AD 的另一个交点Q,射 PQ 与射CD 订交于点 E, BP=x.(1)求△ ABP∽△ ECP;(2)假如点 Q 在段 AD 上(与点 A、 D 不重合),△ APQ 的面 y,求y 对于 x 的函数关系式,并写出定域;(3)假如△ QED 与△ QAP 相像,求 BP 的.EQA D A DBP C B C用925.解:( 1)在⊙ P 中, PA=PQ,∴∠ PAQ =∠ PQA,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)∵AD∥ BC,∴∠ PAQ =∠ APB,∠ PQA =∠ QPC,∴∠ APB =∠ EPC,⋯⋯( 1 分)∵梯形 ABCD中, AD∥BC, AB=DC,∴∠B=∠C,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)∴△ APB∽△ ECP.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)( 2)作 AM ⊥ BC, PN⊥ AD,∵AD∥ BC,∴ AM ∥ PN,∴四形 AMPN 是平行四形,∴AM =PN, AN=MP.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)3在Rt△ AMB 中,∠ AMB=90°, AB=5, sinB= ,5∴AM =3, BM=4,∴ PN=3, PM=AN=x- 4,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)∵PN⊥AQ,∴ AN=NQ,∴ AQ= 2x- 8,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)1AQ PN 1∴ y2x 8 3 ,即 y 3x 12 ,⋯⋯⋯⋯⋯⋯⋯⋯⋯(1分)2132定域是4.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)x2(3)解法一:由△ QED 与△ QAP 相像,∠ AQP=∠ EQD,①假如∠ PAQ=∠ DEQ,∵△ APB∽△ ECP,∴∠ PAB=∠ DEQ,又∵∠ PAQ=∠ APB,∴∠ PAB=∠ APB,∴ BP=BA=5.⋯⋯⋯⋯⋯⋯⋯⋯⋯( 2 分)②假如∠ PAQ=∠ EDQ,∵∠ PAQ=∠ APB,∠ EDQ=∠ C,∠ B=∠ C,∴∠ B=∠ APB,∴ AB=AP,∵ AM⊥ BC,∴ BM=MP=4,∴ BP=8.⋯⋯⋯( 2 分)上所述 BP的 5 或许 8.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)解法二:由△ QAP 与△ QED相像,∠ AQP=∠ EQD,在 Rt△ APN 中,AP PQ32x 42x2 8x25 ,∵QD∥PC,∴EQEP ,QD PC∵△ APB∽△ ECP,∴APEP ,∴ AP EQ ,PB PC PB QDAQ EQ AQ AP2x 8x28x25①假如,∴,即x2x ,QP QD QP PB8x 25解得 x 5 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 2 分)②假如AQDQ ,∴ AQ PB ,即x22x 8x2x,QP QE QP AP8x 258x 25解得 x 8 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 2 分)上所述 BP的 5 或许 8.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)静安区25.(本分 14 分,第( 1)小分 4分,第( 2)小分 6 分,第( 3)小分 4分)如,平行四形ABCD中,已知 AB=6, BC=9,cos ABC 1.角 AC、 BD 交于3点 O.点 P 在 AB 上,⊙ P 点 B,交段 PA于点 E. BP= x.( 1)求 AC 的;A DE OP·( 2) ⊙ O 的半径 y ,当⊙ P 与⊙ O 外切 , 求 y 对于 x 的函数分析式,并写出定 域;( 3) 假如 AC 是⊙ O 的直径,⊙ O 点 E ,求⊙ O 与⊙ P 的 心距OP 的 . ADOBC第 25 题备用图25.(本 分 14 分,第( 1)小 4 分,第( 2)小 6 分,第( 3)小 4 分)解:( 1)作 AH ⊥ BC 于 H ,且 cos1ADABC , AB=6,13O那么 BHAB cos ABC6 2⋯⋯⋯⋯(2 分)E3·PBC=9, HC=9-2=7,BH C第 25 题图 (1)AH 6 2 224 2 ,⋯⋯⋯⋯⋯⋯⋯⋯(1 分)ACAH 2 HC 23249 9 ⋯⋯⋯( 1 分)(2)作 OI ⊥ AB 于 I , PO, AC=BC=9,A D∴∠ OAB=∠ ABC,IOAI 1 Ecos IAOcos∴Rt △ AIO 中,P ·ABC3AOBCH ∴, IO= 2 2 AI 32⋯⋯⋯⋯⋯⋯⋯⋯(第 25 题图 (2)1 分)∴PI=AB-BP-AI=6-x-1.5=9x , ⋯⋯⋯⋯⋯⋯⋯⋯(1 分)2∴ R t △ PIO 中,OP 2PI 2OI 2(3 2) 2 ( 9 x) 2 18 x 29x81 x 2 9x153 ⋯⋯( 1 分)244∵⊙ P 与⊙ O 外切,∴ OPx 2 9 x 153x y4∴ y = x29x 153x 1 4x236x 153 x42⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)∵ 点 P 在 AB 上,⊙ P 点 B,交 段 PA 于点 E .∴定 域: 0<x ≤3⋯⋯⋯⋯( 1 分)(3)由 意得:∵点 E 在 段 AP 上,⊙ O 点 E ,∴⊙ O 与⊙ P 订交∵AO 是⊙ O 半径,且 AO > OI ,∴交点 E 存在两种不一样的地点, OE=OA=92① 当 E 与点 A 不重合 , AE 是⊙ O 的弦, OI 是弦心距,∵ ,AE =3,∴点 E 是 AB 中点, BE1AB3 , BPPE 3 , PI 3 , IO= 3 222OPPI 2 IO 2 32(3 2 ) 2273 3⋯⋯⋯⋯⋯⋯⋯⋯( 2 分)② 当 E 与点 A 重合 ,点 P 是 AB 中点,点 O 是 AC 中点 , OP1BC9 ⋯⋯( 2 分)22∴ OP 3 3 或9. 2闵行区25.(本 分14 分,此中第( 1)小 4 分,第( 2)、(3)小 各 5 分)如 ,已知在 Rt △ ABC 中,∠ ACB = 90o , AC =6, BC = 8,点 F 在 段 AB 上,以点 B 心, BF 半径的 交 BC 于点 E ,射 AE 交 B 于点 D (点 D 、 E 不重合).( 1)假如BF = x , EF = y ,求 y 与 x 之 的函数关系式,并写出它的定 域;( 2)假如 ED2 EF ,求 ED 的 ;( 3) CD 、 BD , 判断四 形ABDC 能否 直角梯形? 明原因.CDCEA F BA B(第 25 题图)(备用图)25.解:( 1)在 Rt △ ABC 中, AC6 , BC 8 , ACB 90∴ AB10 .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(1 分)E 作 EH ⊥AB ,垂足是 H ,易得: EH3 x , BH4 x , FH 1 x .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)55522在 Rt △EHF 中, EF2EH2FH23 x1x ,5 5∴ y10 x (0 x 8) .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(1 分 +1 分)5(2)取 ED 的中点 P , BP 交 ED 于点 G∵ ED 2 EF , P 是 ED 的中点,∴EP EF PD .∴∠ FBE=∠ EBP=∠ PBD .∵ EP EF , BP 心,∴ BG ⊥ED ,ED =2EG =2DG .⋯⋯⋯⋯( 1 分)又∵∠ CEA=∠ DEB ,∴∠ CAE=∠ EBP=∠ABC .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)又∵ BE 是公共 ,∴BEH ≌ BEG .∴ EH EG3x .GD5在 Rt △CEA 中,∵ AC = 6, BC8 , tan CAEtan ABCAC CE ,BCAC∴ CEAC tanCAE6 6 3 3 9.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)8 22∴BE8 916 97.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(1 分)2 2 2 2∴ ED 2 EG 6 x 6 7 21.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(55 2 5( 3)四 形 ABDC 不行能 直角梯形.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(①当 CD ∥ AB ,假如四 形ABDC 是直角梯形,只可能∠ ABD =∠ CDB = 90o .C D在 Rt △ CBD 中,∵ BC 8 ,E1 分)1 分)∴ CD BC cos BCD32 , 5AF BBDBCsin BCD24BE .53232CD 5 16 CE 81 ∴5AB1025,32 ;BE45∴ CDCE .ABBE∴ CD 不平行于 AB ,与 CD ∥ AB 矛盾.∴四 形 ABDC 不行能 直角梯形.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 2 分)②当 AC ∥BD ,假如四 形 ABDC 是直角梯形,C只可能∠ ACD =∠CDB = 90o .∵ AC ∥ BD ,∠ ACB = 90o ,A∴∠ ACB =∠ CBD = 90o.∴∠ ABD =∠ ACB +∠BCD > 90o .与∠ ACD =∠ CDB = 90o 矛盾.∴四 形ABDC 不行能 直角梯形.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(E DF B2 分)普陀区25.(本 分 14 分)已知 P 是 ⊙O 的直径 BA 延伸线上的一个动点,P 的另一边交⊙O 于点C 、D ,两点位于AB 的上方,AB = 6, OP = m ,sin P = 1 3,如图11 所示.另一个半径为6 的 ⊙O 1 经过点 C 、 D ,圆心距 OO 1=n .( 1)当 m =6 时,求线段 CD 的长;( 2)设圆心 O 1 在直线 AB 上方,试用 n 的代数式表示 m ;(3)△ POO 1 在点P 的运动过程中,能否能成为以OO 1 为腰的等腰三角形,假如能,试求出此时n 的值;假如不可以,请说明原因.DCPAOBAOB图 11备用图25.解:(1)过点O 作 OH⊥ CD ,垂足为点H,联络 OC .在 Rt △ POH中,∵sin P = 1, PO6 ,∴OH2. ···( 1 分)3∵ AB =6 ,∴ OC =3 . ······( 1 分)由勾股定理得 CH5 . ······( 1 分)∵ OH ⊥ DC ,∴ CD 2CH 2 5 . ·····( 1 分)( 2)在 Rt △ POH 中,∵ sin P = 1 , PO = m ,∴ OH =m. ···( 1 分)33在△ OCH 中, 2=m 2分). ·····(RtCH 93 12在 Rt △ O 1CH 中, CH 2=36 nm. ····( 1 分) 32281. ···( 2 分)可得36m =9 m ,解得 = 3n 2n3m3 2n( 3)△ POO 1 成为等腰三角形可分以下几种状况:● 当圆心 O 1 、 O 在弦 CD 异侧时①OP= OO1,即 m=n ,由 n=3n281解得 n=9 .···(1分) 2n即圆心距等于⊙O 、⊙O1的半径的和,就有⊙O、⊙O1外切不合题意舍去.(1 分)② O1P=OO1,由 ( n m )2m2 (m)2=n ,33解得 m=2n ,即 2 n= 3n281,解得 n=915 .···(1分)332n5● 当圆心O1、 O 在弦 CD 同侧时,同理可得813n2=.m2n∵ POO1是钝角,∴只好是 m= 813n29n ,即 n2n ,解得 n= 5 .·(2分)5综上所述, n的值为95 或915 .55青浦区25.(此题满分14 分,第( 1)小题 4 分,第( 2)小题 6 分,第( 3)小题 4 分)如图 9-1,已知扇形 MON 的半径为 2 ,∠MON =90,点 B 在弧 MN 上挪动,联络 BM,作 OD BM,垂足为点 D, C 为线段 OD 上一点,且 OC=BM,联络 BC并延伸交半径OM 于点 A,设 OA= x,∠ COM 的正切值为 y.( 1)如图 9-2,当 AB OM 时,求证: AM =AC;( 2)求 y 对于 x 的函数关系式,并写出定义域;( 3)当△ OAC为等腰三角形时,求x 的值 .N N NBBC D CDO A M O A M O M 图 9-1图 9-2备用图25.解:( 1)∵ OD⊥ BM, AB⊥OM ,∴∠ ODM =∠ BAM =90 .° ···( 1 分)∵ ∠ ABM +∠ M =∠ DOM +∠M ,∴∠ ABM =∠DOM.···( 1 分)∵ ∠ OAC=∠BAM, OC =BM,∴△ OAC≌△ ABM,······( 1 分)∴AC =AM .·······( 1 分)(2)过点 D 作 DE// AB,交 OM 于点 E.····( 1 分)∵OB=OM , OD⊥ BM,∴ BD=DM.····( 1 分)∵DE// AB,∴ MD ME,∴ AE= EM,DM AE∵ OM= 2,∴ AE=12 x .····(1分)2∵DE// AB,∴OA OC2DM,·····(1分)OE OD OD∴DMOA , OD2OEx.( 0 x2 )·····(2分)∴ yx 2(3)( i)当 OA=OC 时,∵ DM1BM1OC1x ,222在 Rt△ODM 中,OD OM 2DM 22 1 x2.∵ y DM ,4OD1 xx142142∴2.解得 x,或 x分)1 x2x222(舍).( 224(i i )当 AO=AC时,则∠ AOC=∠ ACO,∵ ∠ ACO>∠ COB,∠ COB =∠ AOC,∴∠ ACO>∠ AOC,∴此种状况不存在.······( 1 分)(ⅲ)当CO=CA 时,则∠ COA=∠ CAO=,∵ ∠ CAO>∠ M ,∠M =90,∴>90,∴> 45,∴BOA290,∵BOA90,∴此种状况不存在.·( 1 分)松江区25.(此题满分 14 分,第( 1)小题 4 分,第( 2)小题每个小题各 5 分)如图,已知 Rt△ ABC 中,∠ ACB=90 °, BC=2,AC=3,以点 C 为圆心、 CB 为半径的圆交 AB 于点 D,过点 A 作 AE∥ CD,交 BC延伸线于点 E.(1)求 CE的长;(2) P 是 CE延伸线上一点,直线 AP、CD 交于点 Q.①假如△ ACQ∽△ CPQ,求CP的;②假如以点 A 心, AQ 半径的与⊙ C 相切,求 CP的 .A AD DB BC E C E(第 25 题图 )(备用图 )25.(本分 14 分,第( 1)小 4 分,第( 2)小每个小各 5 分)解:( 1)∵ AE∥ CD∴BC DC⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分BE AE∵BC=DC∴B E=AE ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分CE=xAE=BE=x+2∵ ∠ ACB=90°,∴ AC 2CE 2AE 2即 9 x2(x2)2⋯⋯⋯⋯⋯⋯⋯⋯⋯1分5∴ x45即 CE⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分4(2)①∵△ ACQ∽△ CPQ,∠ QAC>∠ P∴∠ ACQ=∠ P⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分又∵ AE∥ CD∴∠ ACQ=∠ CAE∴∠ CAE=∠ P⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分∴△ACE∽△ PCA,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分∴ AC 2CE CP ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分即 32 5 CPADBC E(第 25 题图 )QADBC E P4∴ CP 36⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分55②CP=t,PE t4∵∠ ACB=90°,∴AP 9 t 2∵AE∥ CD∴ AQ EC⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分AP EPAQ 55即4t29t54t 54∴AQ 5t 29⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分4t5若两外切,那么5 t 29AQ14t5此方程无数解⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分若两内切切,那么5 t 29 AQ54t5∴ 15t 240t160解之得t 2041015⋯⋯⋯⋯⋯⋯⋯⋯⋯1分又∵ t54 20410∴ t15⋯⋯⋯⋯⋯⋯⋯⋯⋯1分徐汇区25.已知四形 ABCD 是10的菱形,角 AC 、BD订交于点E,点 C 作 CF ∥DB交AB 延于点F,EF交BC于点H.(1)如1,当EF BC,求AE 的;(2)如 2,以EF直径作⊙O,⊙O点C交CD于点G(点C、G不重合),AE 的 x ,EH的y;①求 y 对于x的函数关系式,并写出定域;③EG ,当DEG 是以 DG 腰的等腰三角形,求AE 的.杨浦区25、(此题满分14 分,第(1)小题 4 分,第(2)小题 6 分,第(3)小题 4 分)如图9,在梯形ABCD中, AD//BC,AB=DC=5,AD=1,BC=9,点P 为边BC上一动点,作PH⊥DC,垂足H 在边DC 上,以点P 为圆心PH 为半径画圆,交射线PB 于点 E.(1)当圆P 过点 A 时,求圆P 的半径;(2)分别联络EH 和EA,当△ABE△ CEH时,以点B 为圆心,r 为半径的圆 B 与圆P 相交,试求圆 B 的半径r 的取值范围;( 3)将劣弧沿直线EH翻折交BC于点F,试经过计算说明线段EH和EF的比值为定值,并求出此定值。
2018年上海市金山区中考数学二模试卷及参考答案

)
C. 1
D.2
A .2
B.3
C. 4
D.5
3.( 4 分)如果将抛物线
y=﹣
2
2x
向上平移
1 个单位, 那么所得新抛物线的表达式是
(
)
2
A .y=﹣ 2( x+1)
2
B .y=﹣ 2( x﹣ 1)
C. y=﹣ 2x2﹣ 1
D. y=﹣ 2x2+1
4.( 4 分)如果一组数据 1,2, x, 5, 6 的众数为 6,则这组数据的中位数为(
)
A.
B.
C.
D.
二、填空题: (本大题共 12 题,每题 4 分,满分 48 分)【请直接将结果填入答题纸的相应
位置】
7.( 4 分)因式分解: a2﹣ a=
.
8.( 4 分)函数:
的定义域是
.
第 1 页(共 17 页)
9.( 4 分)方程
= 2 的解是
.
10.( 4 分)函数 y=﹣ x+2 的图象不经过第
象限.
11.( 4 分)有一枚材质均匀的正方体骰子,它的六个面上分别有
1 点、 2 点、…、 6 点的标
记,掷一次骰子,向上的一面出现的点数是素数的概率是
.
12.( 4 分)若关于 x 的一元二次方程 x 2﹣ 4x+m= 0 有两个不相等的实数根,则
m 的取值范
围为
.
13.( 4 分)如果梯形的中位线长为 6,一条底边长为 8,那么另一条底边长等于
【解答】 解:根据梯形的中位线定理,得
另一底边长=中位线× 2﹣一底边长= 2× 6﹣ 8=4.
故答案为: 4
2018上海市初三数学二模-金山区2017学年第二学期初三期中质量检测及评分标准

金山区2017学年第二学期初三期中质量检测数学试卷(满分150分,考试时间100分钟)(2018.4)考生注意:1.本试卷含三个大题,共25题;2.务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效;3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上.】1.下列各数中,相反数等于本身的数是(▲)(A )1;(B )0;(C )1;(D )2.2.单项式32a b 的次数是(▲)(A )2;(B )3(C )4;(D )5.3.如果将抛物线22yx 向上平移1个单位,那么所得新抛物线的表达式是(▲)(A )221yx ;(B )221yx ;(C )221yx;(D )221yx.4.如果一组数据1,2,x ,5,6的众数为6,则这组数据的中位数为(▲)(A )1;(B )2(C )5;(D )6.5.如图1,□ABCD 中,E 是BC 的中点,设AB a ,ADb ,那么向量AE 用向量a 、b 表示为(▲)(A )12ab ;(B )12a b ;(C )12a b ;(D )12a b .6.如图2,∠AOB=45°,OC 是∠AOB 的角平分线,PM ⊥OB ,垂足为点M ,PN ∥OB ,PN 与OA 相交于点N ,那么PM PN的值等于(▲ )(A )12;(B )22;(C )32;(D )33.二、填空题:(本大题共12题,每题4分,满分48分)【请直接将结果填入答题纸的相应位置】7.因式分解:2aa▲ .ABDCE图1OMNABC图2P8.函数2y x 的定义域是▲ .9.方程21xx 的解是▲.10.一次函数2y x的图像不经过第▲象限.11.有一枚材质均匀的正方体骰子,它的六个面上分别有1点、2点、…、6点的标记,掷这枚骰子,向上一面出现的点数是素数的概率是▲ .12.如果关于x 的一元二次方程240xx k 有两个不相等的实数根,那么k 的取值范围是▲ .13.如果梯形的中位线长为6,一条底边长为8,那么另一条底边长等于▲ .14.空气质量指数,简称AQI ,如果AQI 在0~50空气质量类别为优,在51~100空气质量类别为良,在101~150空气质量类别为轻度污染,按照某市最近一段时间的AQI 画出的频数分布直方图如图3 所示,已知每天的AQI 都是整数,那么空气质量类别为优和良的天数占总天数的百分比为▲ %.15.一辆汽车在坡度为1:2.4的斜坡上向上行驶130米,那么这辆汽车的高度上升了▲米.16.如果一个正多边形的中心角等于30°,那么这个正多边形的边数是▲.17.如果两圆的半径之比为3:2,当这两圆内切时圆心距为3,那么当这两圆相交时,圆心距d 的的取值范围是▲.18.如图4,Rt △ABC 中,∠C=90°,AC=6,BC=8,D 是AB 的中点,P 是直线BC 上一点,把△BDP 沿PD 所在的直线翻折后,点B 落在点Q 处,如果QD ⊥BC ,那么点P 和点B 间的距离等于▲ .三、解答题:(本大题共7题,满分78分)19.(本题满分10分)计算:21oo21tan452sin 60122.20.(本题满分10分)解方程组:248x y xxy .10 146 天数图3AQI50.5 100.5 150.5ACB图4D21.(本题满分10分,每小题5分)如图5,在矩形ABCD 中,E 是BC 边上的点,AE=BC ,DF ⊥AE ,垂足为F .(1)求证:AF=BE ;(2)如果BE ∶EC=2∶1,求∠CDF 的余切值.22.(本题满分10分,每小题5分)九年级学生到距离学校6千米的百花公园去春游,一部分学生步行前往,20分钟后另一部分学生骑自行车前往,设x (分钟)为步行前往的学生离开学校所走的时间,步行学生走的路程为1y 千米,骑自行车学生骑行的路程为2y 千米,1y 、2y 关于x 的函数图像如图6所示.(1)求2y 关于x 的函数解析式;(2)步行的学生和骑自行车的学生谁先到达百花公园,先到了几分钟?23.(本题满分12分,每小题6分)如图7,已知AD 是△ABC 的中线,M 是AD 的中点,过A 点作AE ∥BC ,CM 的延长线与AE 相交于点E ,与AB 相交于点F .(1)求证:四边形AEBD 是平行四边形;(2)如果AC=3AF ,求证四边形AEBD 是矩形.ABCDFE图5EAFMBD 图7Cy (千米)x (分钟)50 60 7010 20 345630 12 40 图62y 1y24.(本题满分12分,每小题4分)平面直角坐标系xOy 中(如图8),已知抛物线2y xbx c 经过点A (1,0)和B (3,0),与y 轴相交于点C ,顶点为P .(1)求这条抛物线的表达式和顶点P 的坐标;(2)点E 在抛物线的对称轴上,且EA=EC ,求点E 的坐标;(3)在(2)的条件下,记抛物线的对称轴为直线MN ,点Q 在直线MN 右侧的抛物线上,∠MEQ =∠NEB ,求点Q 的坐标.25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题 5 分)如图9,已知在梯形ABCD 中,AD ∥BC ,AB=DC=AD=5,3sin 5B,P 是线段BC 上一点,以P 为圆心,P A 为半径的⊙P 与射线AD 的另一个交点为Q ,射线PQ 与射线CD 相交于点E ,设BP=x .(1)求证△ABP ∽△ECP ;(2)如果点Q 在线段AD 上(与点A 、D 不重合),设△APQ 的面积为y ,求y 关于x 的函数关系式,并写出定义域;(3)如果△QED 与△QAP 相似,求BP 的长.ABPCDQEABCD图9备用图图8金山区2017学年第二学期初三数学期中质量检测参考答案及评分建议2018.4.19一、选择题:(本大题共6题,每题4分,满分24分)1.B ;2.C ;3.D ;4.C ;5.A ;6.B .二.填空题:(本大题共12题,满分48分)7.1a a ;8.2x ;9.2x ;10.三;11.12;12.4k ;13.4;14.80;15.50;16.12;17.3d 15;18.52或10.三、(本大题共7题, 第19~22题每题10分, 第23、24题每题12分, 第25题14分, 满分78分)19.解:原式=3122342…………………………………………………………(8分)=31234………………………………………………………………(1分)=335.………………………………………………………………………(1分)20.解:248x y xxy①②,由①得:4y x③,…………………………………………………………(2分)把③代入②得:248xx x .………………………………………………(2分)解得:1215,15x x …………………………………………………(2分)把1215,15x x ,代入③得:12121515,3535x x y y ,……………………………………………………(4分)21.解:(1)∵四边形ABCD 是矩形,∴AD=BC ,AD ∥BC ,∠B=90°,∴∠DAF=∠AEB ,……………………………………………………………………(1分)∵AE=BC ,DF ⊥AE ,∴AD=AE ,∠AFD=∠EBA=90°,………………………(2分)∴△ADF ≌△EAB ,∴AF =EB ,………………………………………………………(2分)(2)设BE =2k ,EC =k ,则AD=BC =AE =3k ,AF =BE =2k ,…………………………(1分)∵∠ADC =90°,∠AFD =90°,∴∠CDF +∠ADF =90°,∠DAF +∠ADF =90°,∴∠CDF =∠DAF …………………………………………………………………(2分)在Rt △ADF 中,∠AFD =90°,DF =225ADAFk∴cot ∠CDF =cot ∠DAF =22555AF k DFk.………………………………(2分)22.解:(1)设2y 关于x 的函数关系式是222y k x b ,根据题意,得:2222200404k b k b ,………………………………………………(2分)解得:215k ,24b ,………………………………………………………(2分)∴2y 关于x 的函数关系式是2145y x .……………………………………(1分)(2)设1y 关于x 的函数关系式是11y k x ,根据题意,得:1404k ,∴1110k ,1y 关于x 的函数关系式是1110y x ,…………………………………………(1分)当16y 时,60x,当26y 时,50x ,………………………………(2分)∴骑自行车的学生先到百花公园,先到了10分钟.…………………………(2分)23.证明:(1)∵AE //BC ,∴∠AEM=∠DCM ,∠EAM=∠CDM ,…………………………(1分)又∵AM=DM ,∴△AME ≌△DMC ,∴AE =CD ,………………………………(1分)∵BD=CD ,∴AE =BD .……………………………………………………………(1分)∵AE ∥BD ,∴四边形AEBD 是平行四边形.……………………………………(2分)(2)∵AE //BC ,∴AF AE FBBC .………………………………………………………(1分)∵AE=BD=CD ,∴12AF AE FBBC,∴AB=3AF .……………………………(1分)∵AC=3AF ,∴AB=AC ,…………………………………………………………(1分)又∵AD 是△ABC 的中线,∴AD ⊥BC ,即∠ADB =90°.……………………(1分)∴四边形AEBD 是矩形.…………………………………………………………(1分)24.解:(1)∵二次函数2y xbx c 的图像经过点A (1,0)和B (3,0),∴10930b c b c,解得:4b ,3c .………………………………………(2分)∴这条抛物线的表达式是243y xx …………………………………………(1分)顶点P 的坐标是(2,-1).…………………………………………………………(1分)(2)抛物线243y xx 的对称轴是直线2x,设点E 的坐标是(2,m ).……(1分)根据题意得:2222(21)(0)(20)(3)m m ,解得:m=2,……(2分)∴点E 的坐标为(2,2).……………………………………………………………(1分)(3)解法一:设点Q 的坐标为2(,43)t tt ,记MN 与x 轴相交于点F .作QD ⊥MN ,垂足为D ,则2DQt ,2243241DEtt tt …………………………………(1分)∵∠QDE=∠BFE=90°,∠QED=∠BEF ,∴△QDE ∽△BFE ,…………………(1分)∴DQ DEBFEF ,∴224112t tt ,解得11t (不合题意,舍去),25t .……………………………………………(1分)∴5t,点E 的坐标为(5,8).…………………………………………………(1分)解法二:记MN 与x 轴相交于点F .联结AE ,延长AE 交抛物线于点Q ,∵AE=BE ,EF ⊥AB ,∴∠AEF=∠NEB ,又∵∠AEF=∠MEQ ,∴∠QEM=∠NEB ,…………………………………………(1分)点Q 是所求的点,设点Q 的坐标为2(,43)t tt ,作QH ⊥x 轴,垂足为H ,则QH=243tt,OH=t ,AH=t -1,∵EF ⊥x 轴,∴EF ∥QH ,∴EF AF QHAH,∴221431ttt ,……………(1分)解得11t (不合题意,舍去),25t .……………………………………………(1分)∴5t,点E 的坐标为(5,8).…………………………………………………(1分)25.解:(1)在⊙P 中,PA =PQ ,∴∠PAQ =∠PQA ,……………………………………(1分)∵AD ∥BC ,∴∠PAQ =∠APB ,∠PQA =∠QPC ,∴∠APB =∠EPC ,……(1分)∵梯形ABCD 中,AD ∥BC ,AB =DC ,∴∠B =∠C ,………………………………(1分)∴△APB ∽△ECP .…………………………………………………………………(1分)(2)作AM ⊥BC ,PN ⊥AD ,∵AD ∥BC ,∴AM ∥PN ,∴四边形AMPN 是平行四边形,∴AM =PN ,AN=MP .…………………………………………………………………(1分)在Rt △AMB 中,∠AMB=90°,AB =5,sinB=35,∴AM =3,BM=4,∴PN =3,PM=AN=x-4,…………………………………………(1分)∵PN ⊥AQ ,∴AN=NQ ,∴AQ=2x-8,……………………………………………(1分)∴1128322yAQ PNx ,即312y x ,……………………………(1分)定义域是1342x.………………………………………………………………(1分)(3)解法一:由△QED 与△QAP 相似,∠AQP =∠EQD ,①如果∠PAQ =∠DEQ ,∵△APB ∽△ECP ,∴∠PAB =∠DEQ ,又∵∠PAQ =∠APB ,∴∠PAB =∠APB ,∴BP =BA=5.…………………………(2分)②如果∠PAQ =∠EDQ ,∵∠PAQ =∠APB ,∠EDQ =∠C ,∠B =∠C ,∴∠B =∠APB ,∴AB =AP ,∵AM ⊥BC ,∴BM=MP=4,∴BP =8.…………(2分)综上所述BP 的长为5或者8.………………………………………………………(1分)解法二:由△QAP 与△QED 相似,∠AQP =∠EQD ,在Rt △APN 中,22234825AP PQx xx ,∵QD ∥PC ,∴EQ EP QDPC,∵△APB∽△ECP,∴AP EPPB PC,∴AP EQPB QD,①如果AQ EQQP QD,∴AQ APQP PB,即2228825825x x xxx x,解得5x………………………………………………………………………………(2分)②如果AQ DQQP QE,∴AQ PBQP AP,即2228825825x xx x x x,解得8x………………………………………………………………………………(2分)综上所述BP的长为5或者8.………………………………………………………(1分)。
(完整版)2018年金山区二模数学试卷.

金山区2017学年第二学期初三期中质量检测数学试卷(满分150分,考试时间100分钟)(2018.4)考生注意:1.本试卷含三个大题,共25题;2.务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效;3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤. 一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上.】1.下列各数中,相反数等于本身的数是(▲)(A )1-; (B )0; (C )1; (D )2.2.单项式32a b 的次数是(▲)(A )2; (B )3 (C )4; (D )5.3.如果将抛物线22y x =-向上平移1个单位,那么所得新抛物线的表达式是(▲)(A )()221y x =-+; (B )()221y x =--;(C )221y x =--; (D )221y x =-+. 4.如果一组数据1,2,x ,5,6的众数为6,则这组数据的中位数为(▲)(A )1; (B )2 (C )5; (D )6. 5.如图1,□ABCD 中,E 是BC 的中点,设AB a =u u u r r ,AD b =u u u r r ,那么向量AE u u u r 用向量a r 、b r表示为(▲)(A )12a b +r r ;(B )12a b -r r ;(C )12a b -+r r ;(D )12a b --r r .6.如图2,∠AOB=45°,OC 是∠AOB 的角平分线,PM ⊥OB , 垂足为点M ,PN ∥OB ,PN 与OA 相交于点N ,那么PMPN的值等于( ▲ ) (A )12; (B )22; (C )32; (D )33.二、填空题:(本大题共12题,每题4分,满分48分)【请直接将结果填入答题纸的相应位置】7.因式分解:2a a -= ▲ .A B D CE 图1 O MNA BC图2P8.函数2y x =-的定义域是 ▲ .9.方程21xx =-的解是 ▲ . 10.一次函数2y x =-+的图像不经过第 ▲ 象限.11.有一枚材质均匀的正方体骰子,它的六个面上分别有1点、2点、…、6点的标记,掷这枚骰子,向上一面出现的点数是素数的概率是 ▲ . 12.如果关于x 的一元二次方程240x x k -+=有两个不相等的实数根,那么k 的取值范围是 ▲ .13.如果梯形的中位线长为6,一条底边长为8,那么另一条底边长等于 ▲ . 14.空气质量指数,简称AQI ,如果AQI 在0~50空气质量类别为优,在51~100空气质量类别为良, 在101~150空气质量类别为轻度污染,按照某市最 近一段时间的AQI 画出的频数分布直方图如图3 所示,已知每天的AQI 都是整数,那么空气质量类别为优和良的天数占总天数的百分比为 ▲ %. 15.一辆汽车在坡度为1:2.4的斜坡上向上行驶 130米,那么这辆汽车的高度上升了 ▲ 米.16.如果一个正多边形的中心角等于30°,那么这个正多边形的边数是 ▲ . 17.如果两圆的半径之比为3:2,当这两圆内切时圆心距为3,那么当这两圆相交时,圆心距d 的的取值范围是 ▲ .18.如图4,Rt △ABC 中,∠C =90°,AC =6,BC =8,D 是AB 的中点,P 是直线BC 上一点,把△BDP 沿PD 所在的直线翻折后,点B 落在点Q 处,如果QD ⊥BC , 那么点P 和点B 间的距离等于 ▲ .三、解答题:(本大题共7题,满分78分) 19.(本题满分10分)计算:21o o 21tan 452sin 60122-⎛⎫-+- ⎪⎝⎭.20.(本题满分10分) 解方程组:248x y x xy +=⎧⎨-=⎩.1014 6天数图3AQI0 50.5 100.5 150.5A CB图4D21.(本题满分10分,每小题5分)如图5,在矩形ABCD 中,E 是BC 边上的点,AE =BC ,DF ⊥AE ,垂足为F . (1)求证:AF=BE ; (2)如果BE ∶EC=2∶1,求∠CDF 的余切值.22.(本题满分10分,每小题5分)九年级学生到距离学校6千米的百花公园去春游,一部分学生步行前往,20分钟后另 一部分学生骑自行车前往,设x (分钟)为步行前往的学生离开学校所走的时间,步行 学生走的路程为1y 千米,骑自行车学生骑行的路程为2y 千米,1y 、2y 关于x 的函数 图像如图6所示.(1)求2y 关于x 的函数解析式;(2)步行的学生和骑自行车的学生谁先 到达百花公园,先到了几分钟?23.(本题满分12分,每小题6分)如图7,已知AD 是△ABC 的中线, M 是AD 的中点, 过A 点作AE ∥BC ,CM 的延 长线与AE 相交于点E ,与AB 相交于点F .(1)求证:四边形AEBD 是平行四边形;(2)如果AC =3AF ,求证四边形AEBD 是矩形.A B C D F E 图5 E A F M BD 图7Cy (千米)x (分钟)50 60 70 10 20 3 4 5 6 30 12 40 图624.(本题满分12分,每小题4分)平面直角坐标系xOy 中(如图8),已知抛物线2y x bx c =++经过点A (1,0)和B(3,0),与y 轴相交于点C ,顶点为P .(1)求这条抛物线的表达式和顶点P 的坐标; (2)点E 在抛物线的对称轴上,且EA =EC ,求点E 的坐标;(3)在(2)的条件下,记抛物线的对称轴为直线MN ,点Q 在直线MN 右侧的抛物线 上,∠MEQ =∠NEB ,求点Q 的坐标.25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5 分)如图9,已知在梯形ABCD 中,AD ∥BC ,AB =DC =AD =5,3sin 5B =,P 是线段BC 上 一点,以P 为圆心,P A 为半径的⊙P 与射线AD 的另一个交点为Q ,射线PQ 与射线 CD 相交于点E ,设BP =x . (1)求证△ABP ∽△ECP ;(2)如果点Q 在线段AD 上(与点A 、D 不重合),设△APQ 的面积为y ,求y 关于x 的函数关系式,并写出定义域; (3)如果△QED 与△QAP 相似,求BP 的长. A BPC D Q E A BCD图9备用图图8。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∵AD∥BC,∴AM∥PN,∴四边形AMPN是平行四边形,
∴AM=PN,AN=MP.…………………………………………………………………(1分)
在Rt△AMB中,∠AMB=90°,AB=5,sinB= ,
∴AM=3,BM=4,∴PN=3,PM=AN=x-4,…………………………………………(1分)
24.解:(1)∵二次函数 的图像经过点A(1,0)和B(3,0),
∴ ,解得: , .………………………………………(2分)
∴这条抛物线的表达式是 …………………………………………(1分)
顶点P的坐标是(2,-1).…………………………………………………………(1分)
(2)抛物线 的对称轴是直线 ,设点E的坐标是(2,m).……(1分)
根据题意得: ,解得:m=2,……(2分)
∴点E的坐标为(2,2).……………………………………………………………(1分)
(3)解法一:设点Q的坐标为 ,记MN与x轴相交于点F.
作QD⊥MN,垂足为D,
则 , …………………………………(1分)
∵∠QDE=∠BFE=90°,∠QED=∠BEF,∴△QDE∽△BFE,…………………(1分)
九年级学生到距离学校6千米的百花公园去春游,一部分学生步行前往,20分钟后另
一部分学生骑自行车前往,设x(分钟)为步行前往的学生离开学校所走的时间,步行
学生走的路程为 千米,骑自行车学生骑行的路程为 千米, 、 关于 的函数
图像如图6所示.
(1)求 关于 的函数解析式;
(2)步行的学生和骑自行车的学生谁先
(A) ;(B) ;(C) ;(D) .
4.如果一组数据1,2,x,5,6的众数为6,则这组数据的中位数为(▲)
(A)1;(B)2(C)5;(D)6.
5.如图1,□ABCD中,E是BC的中点,设 , ,
那么向量 用向量 、 表示为(▲)
(A) ;(B) ;(C) ;(D) .
6.如图2,∠AOB=45°,OC是∠AOB的角平分线,PM⊥OB,
(2)设BE=2k,EC=k,则AD=BC=AE=3k,AF=BE=2k,…………………………(1分)
∵∠ADC=90°,∠AFD=90°,∴∠CDF+∠ADF=90°,∠DAF+∠ADF=90°,
∴∠CDF=∠DAF…………………………………………………………………(2分)
在Rt△ADF中,∠AFD=90°,DF=
∴cot∠CDF=cot∠DAF= .………………………………(2分)
22.解:(1)设 关于x的函数关系式是 ,
根据题意,得: ,………………………………………………(2分)
解得: , ,………………………………………………………(2分)
∴ 关于x的函数关系式是 .……………………………………(1分)
标记,掷这枚骰子,向上一面出现的点数是素数的概率是▲.
12.如果关于 的一元二次方程 有两个不相等的实数根,
那么 的取值范围是▲.
13.如果梯形的中位线长为6,一条底边长为8,那么另一条底边长等于▲.
14.空气质量指数,简称AQI,如果AQI在0~50空
气质量类别为优,在51~100空气质量类别为良,
∵PN⊥AQ,∴AN=NQ,∴AQ=2x-8,……………………………………………(1分)
∴ ,即 ,……………………………(1分)
定义域是 .………………………………………………………………(1分)
(3)解法一:由△QED与△QAP相似,∠AQP=∠EQD,
①如果∠PAQ=∠DEQ,∵△APB∽△ECP,∴∠PAB=∠DEQ,
21.解:(1)∵四边形ABCD是矩形,∴AD=BC,AD∥BC,∠B=90°,
∴∠DAF=∠AEB,……………………………………………………………………(1分)
∵AE=BC,DF⊥AE,∴AD=AE,∠AFD=∠EBA=90°,………………………(2分)
∴△ADF≌△EAB,∴AF=EB,………………………………………………………(2分)
= .………………………………………………………………………(1分)
20.解: ,
由①得: ③,…………………………………………………………(2分)
把③代入②得: .………………………………………………(2分)
解得: …………………………………………………(2分)
把 ,代入③得:
,……………………………………………………(4分)
点Q是所求的点,设点Q的坐标为 ,
作QH⊥x轴,垂足为H,则QH= ,OH=t,AH=t-1,
∵EF⊥x轴,∴EF∥QH,∴ ,∴ ,……………(1分)
解得 (不合题意,舍去), .……………………………………………(1分)
∴ ,点E的坐标为(5,8).…………………………………………………(1分)
∵AE=BD=CD,∴ ,∴AB=3AF.……………………………(1分)
∵AC=3AF,∴AB=AC,…………………………………………………………(1分)
又∵AD是△ABC的中线,∴AD⊥BC,即∠ADB=90°.……………………(1分)
∴四边形AEBD是矩形.…………………………………………………………(1分)
在101~150空气质量类别为轻度污染,按照某市最
近一段时间的AQI画出的频数分布直方图如图3
所示,已知每天的AQI都是整数,那么空气质量
类别为优和良的天数占总天数的百分比为▲%.
15.一辆汽车在坡度为1:2.4的斜坡上向上行驶
130米,那么这辆汽车的高度上升了▲米.
16.如果一个正多边形的中心角等于30°,那么这个正多边形的边数是▲.
∴ ,∴ ,
解得 (不合题意,舍去), .……………………………………………(1分)
∴ ,点E的坐标为(5,8).…………………………………………………(1分)
解法二:记MN与x轴相交于点F.联结AE,延长AE交抛物线于点Q,
∵AE=BE,EF⊥AB,∴∠AEF=∠NEB,
又∵∠AEF=∠MEQ,∴∠QEM=∠NEB,…………………………………………(1分)
25.解:(1)在⊙P中,PA=PQ,∴∠PAQ=∠PQA,……………………………………(1分)
∵AD∥BC,∴∠PAQ=∠APB,∠PQA=∠QPC,∴∠APB=∠EPC,……(1分)
∵梯形ABCD中,AD∥BC,AB=DC,∴∠B=∠C,………………………………(1分)
∴△APB∽△ECP.…………………………………………………………………(1分)
25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分)
如图9,已知在梯形ABCD中,AD∥BC,AB=DC=AD=5, ,P是线段BC上
一点,以P为圆心,PA为半径的⊙P与射线AD的另一个交点为Q,射线PQ与射线
CD相交于点E,设BP=x.
(1)求证△ABP∽△ECP;
(2)如果点Q在线段AD上(与点A、D不重合),设△APQ的面积为y,
17.如果两圆的半径之比为3:2,当这两圆内切时圆心距为3,那么当这两圆相交时,
圆心距d的的取值范围是▲.
18.如图4,Rt△ABC中,∠C=90°,AC=6,BC=8,D是
AB的中点,P是直线BC上一点,把△BDP沿PD所
在的直线翻折后,点B落在点Q处,如果QD⊥BC,
那么点P和点B间的距离等于▲.
7. ;8. ;9. ;10.三; 11. ;12. ;13.4;
14.80;15.50;16.12;17. ;18. 或10.
三、(本大题共7题,第19~22题每题10分,第23、24题每题12分,第25题14分,满分78分)
19.解:原式= …………………………………………………………(8分)
= ………………………………………………………………(1分)
一、选择题:(本大题共6题,每题4分,满分24分)
【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上.】
1.下列各数中,相反数等于本身的数是(▲)
(A) ;(B)0;(C)1;(D)2.
2.单项式 的次数是(▲)
(A)2;(B)3(C)4;(D)5.
3.如果将抛物线 向上平移1个单位,那么所得新抛物线的表达式是(▲)
到达百花公园,先到了几分钟?
23.(本题满分12分,每小题6分)
如图7,已知AD是△ABC的中线,M是AD的中点,过A点作AE∥BC,CM的延
长线与AE相交于点E,与AB相交于点F.
(1)求证:四边形A形.
24.(本题满分12分,每小题4分)
三、解答题:(本大题共7题,满分78分)
19.(本题满分10分)
计算: .
20.(本题满分10分)
解方程组: .
21.(本题满分10分,每小题5分)
如图5,在矩形ABCD中, 是 边上的点,AE=BC,DF⊥AE,垂足为F.
(1)求证:AF=BE;
(2)如果BE∶EC=2∶1,求∠CDF的余切值.
22.(本题满分10分,每小题5分)
(2)设 关于x的函数关系式是 ,
根据题意,得: ,∴ ,
关于x的函数关系式是 ,…………………………………………(1分)
当 时, ,当 时, ,………………………………(2分)
∴骑自行车的学生先到百花公园,先到了10分钟.…………………………(2分)
23.证明:(1)∵AE//BC,∴∠AEM=∠DCM,∠EAM=∠CDM,…………………………(1分)
垂足为点M,PN∥OB,PN与OA相交于点N,那么 的值等于(▲)
(A) ;(B) ;(C) ;(D) .
