230种晶体学空间群

230种晶体学空间群的记号及常见矿石的名称、分子式与所属晶系

P42/mnm
P42/nmc
P42/ncm
I4/mmm
I4/mcm
I41/amd
I41/acd
三方
晶系
3
P3
P31
P32
R3
P
R
32
P312
P321
P3112
P3121
P3212
P3221
R32
3m
P3m1
P31m
P3c1
P31c
R3m
R3c
m
P 1m
P 1c
P m1
P c1
R m
R c
六方
晶系
6
P6
m
Pm3
Pn3
Fm3
Fd3
Im3
Pa3
Ia3
432
P432
P4232
F432
F4132
I432
P4332
P4132
I4132
3m
P 3m
F 3m
I 3m
P 3n
F 3c
I 3d
m m
Pm m
Pn n
Pm n
Pn m
Fm m
Fm c
Fd m
Fd c
Im m
Ia d
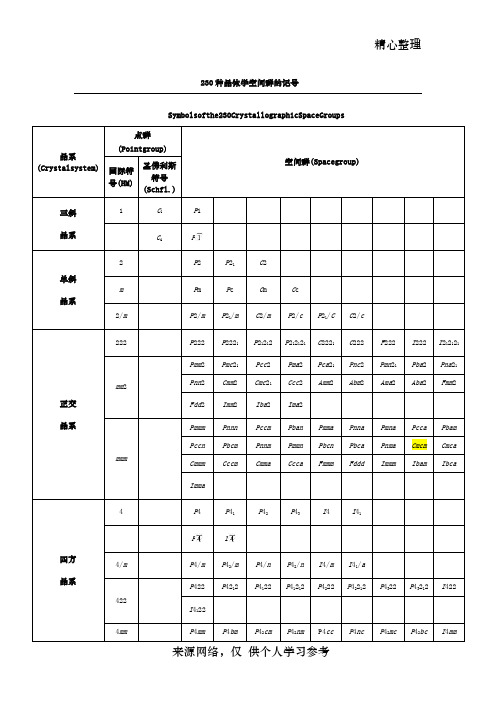
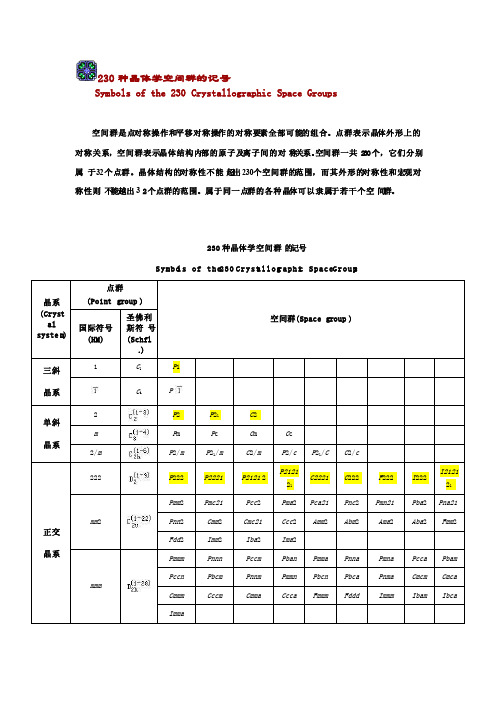
空间群是点对称操作和平移对称操作的对称要素全部可能的组合。点群表示晶体外形上的对称关系，空间群表示晶体结构内部的原子及离子间的对称关系。空间群一共230个，它们分别属于32个点群。晶体结构的对称性不能超出230个空间群的范围，而其外形的对称性和宏观对称性则不能越出32个点群的范围。属于同一点群的各种晶体可以隶属于若干个空间群。
230种晶体学空间群的记号
Symbolsofthe230CrystallographicSpaceGroups

230种空间群

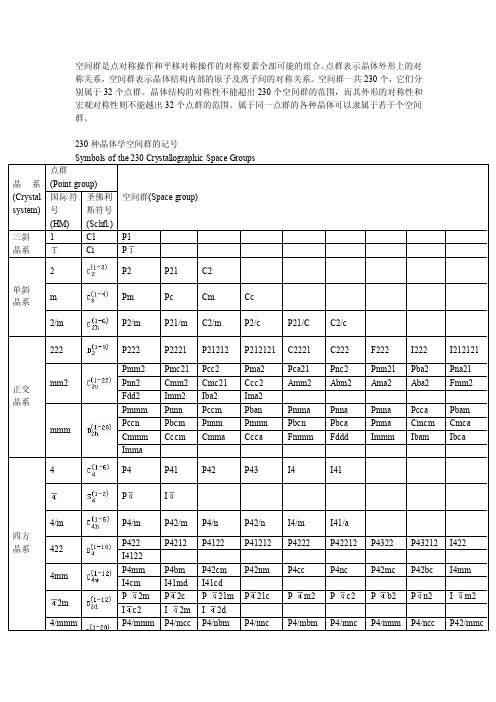
空间群是点对称操作和平移对称操作的对称要素全部可能的组合。

点群表示晶体外形上的对称关系，空间群表示晶体结构内部的原子及离子间的对称关系。

空间群一共230个，它们分别属于32个点群。

晶体结构的对称性不能超出230个空间群的范围，而其外形的对称性和宏观对称性则不能越出32个点群的范围。

属于同一点群的各种晶体可以隶属于若干个空间群。

230种晶体学空间群的记号
Ci
I
2m
2m P P P I
m 1m P
m2 m2
m
3m 3m I P
Pm Im m
1 三斜晶系
2 单斜晶系
3 斜方晶系
4 四方晶系
为2，
为⊥m，5 三方晶系
6 六方晶系
(191) P6/mmm 7 等轴晶系。

种晶体学空间群的记号及常见矿石的名称分子式与所属晶系

230种晶体学空间群的记号Symbols of the 230 Crystallographic Space Groups
2m 2P P 2m b n
I c22
m 11m P R m c m2
m c2
3m 33I P3
I
m m n Pm Pn Fm Fm Fd m
Fd
m d
空间群是点对称操作和平移对称操作的对称要素全部可能的组合。

点群表示晶体外形上的对称关系，空间群表示晶体结构内部的原子及离子间的对称关系。

空间群一共230个，它们分别属于32个点群。

晶体结构的对称性不能超出230个空间群的范围，而其外形的对称性和宏观对称性则不能越出32个点群的范围。

属于同一点群的各种晶体可以隶属于若干个空间群。

不同晶系的晶格类型
32种晶体学点群的记号
2m
m m
m2
m
(4)
3m 3(3)
m m(4)
点群不存在平移操作，所有的对称要素都集中在一个共同的点上。

对称要素包括旋转、反映、反伸（对称中心）与旋转反伸。

有这4个对称要素组合出32个点群。

下表中“轴向对称要素的方向和数目”的圆括号内数据代表该对称要素的数目。

正多面体的数学和结晶学参数
Mathematic and Crystallographic Parameters of Regular Polyhedrons
常见单质的所属晶系
常见矿石的名称、分子式与所属晶系
Names, Molecular Formulas and Crystal Systems of Common Ores。

第五章-230种空间群记号

P
2
c (13) 2
P2
P21
C2
单斜
m
c (14) 3
Pm
Pc
Cm
Cc
晶系
2/m
c (16) 2h
P2/m
P21/m
C2/m
P2/c P21/C C2/c
正交晶系
四方
222
D (19) 2
P222
P2221
P21212 P212121 C2221 C222
F222
I222 I212121
Pmm2
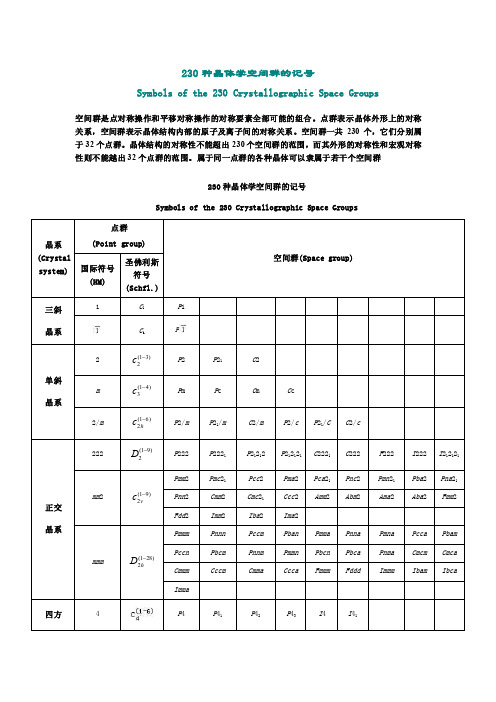
230 种晶体学空间群的记号
Symbols of the 230 Crystallographic Space Groups
空间群是点对称操作和平移对称操作的对称要素全部可能的组合。点群表示晶体外形上的对称关系，空间群表示晶体结构内部的原子及离子间的对称关系。空间群一共 230 个，它们分别属于 32 个点群。晶体结构的对称性不能超出 230 个空间群的范围，而其外形的对称性和宏观对称性则不能越出 32 个点群的范围。属于同一点群的各种晶体可以隶属于若干个空间群
Pmc21
Pcc2
Pma2 Pca21 Pnc2 Pmn21 Pba2 Pna21
mm2
c (19) 2v
Pnn2
Cmm2
Cmc21
Ccc2 Amm2 Abm2
Ama2 Aba2 Fmm2
Fdd2
Imm2
Iba2
Ima2
Pmmm
Pnnn
Pccm
Pban Pmma Pnna
Pmna Pcca Pbam
Pm m Pn n
Pm n Pn m Fm m Fm c Fd m Fd c Im m

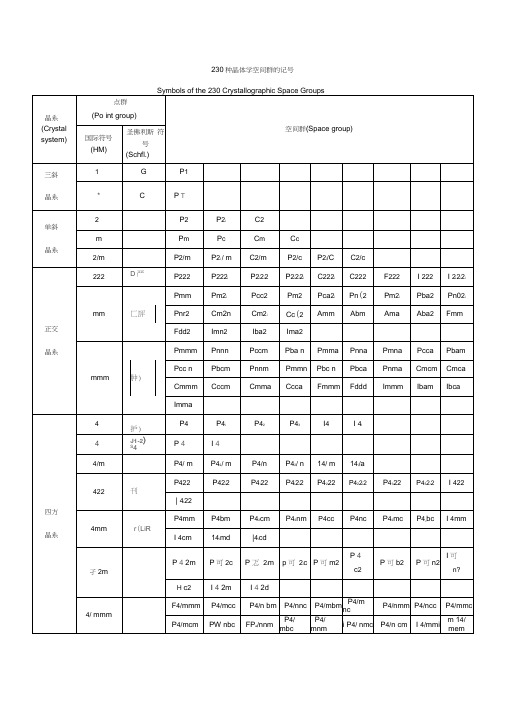
230种晶体学空间群的记号及常见矿石的名称、分子式与所属晶系

Imma
四方
晶系
4
护)
P4
P4i
P42
P43
I4
I4i
4
J1-2)
S4
P4
I4
4/m
P4/m
P42/m
P4/n
P42/n
14/m
14i/a
422
刊
P422
P42i2
P4i22
P4i2i2
P4222
P422i2
P4322
P432i2
I422
|4i22
4mm
r(LiR
P4mm
P4bm
P42cm
P42nm
Th
-(H賈
頁⑷
432
O
4(3)
3⑷
2(6)
m吾m
兀3m
Td
忑3(3)
3⑷
%6)
m3m
O
-G)
頁⑷
%
科
点群不存在平移操作，所有的对称要素都集中在一个共同的点上。对称要素包括旋转、反映、反伸（对称中心）与旋转反伸。有这4个对称要素组合岀32个点群。
下表中“轴向对称要素的方向和数目”的圆括号内数据代表该对称要素的数目
P2i
C2
m
Pm
Pc
Cm
Cc
2/m
P2/m
P2i/m
C2/m
P2/c
P2i/C
C2/c
正交
晶系
222
D严
P222
P222i
P2i2i2
P2i2i2i
C222i
C222
F222
I222
I2i2i2i
mm
Pmm
Pm2i

种晶体学空间群的记号及常见矿石的名称分子式与所属晶系

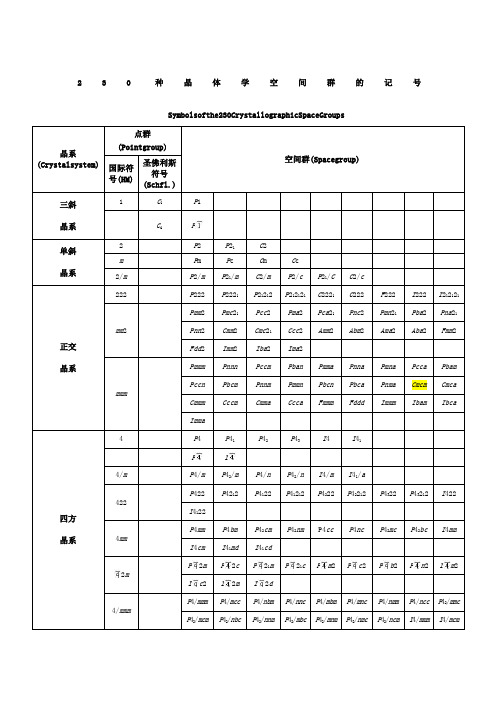
230种晶体学空间群的记号Symbolsofthe230CrystallographicSpaceGroups晶系(Crystalsystem)点群(Pointgroup)空间群(Spacegroup)国际符号(HM)圣佛利斯符号(Schfl.)三斜晶系1C1P1C i P单斜晶系2P2P21C2m P m P c C m C c2/m P2/m P21/m C2/m P2/c P21/C C2/c正交晶系222P222P2221P21212P212121C2221C222F222I222I212121 mm2Pmm2Pmc21Pcc2Pma2Pca21Pnc2Pmn21Pba2Pna21Pnn2Cmm2Cmc21Ccc2Amm2Abm2Ama2Aba2Fmm2Fdd2Imm2Iba2Ima2mmmPmmm Pnnn Pccm Pban Pmma Pnna Pmna Pcca PbamPccn Pbcm Pnnm Pmmn Pbcn Pbca Pnma Cmcm CmcaCmmm Cccm Cmma Ccca Fmmm Fddd Immm Ibam IbcaImma四方晶系4P4P41P42P43I4I41P I4/m P4/m P42/m P4/n P42/n I4/m I41/a422P422P4212P4122P41212P4222P42212P4322P43212I422I41224mmP4mm P4bm P42cm P42nm P4cc P4nc P42mc P42bc I4mmI4cm I41md I41cd2mP2m P2c P21m P21c P m2P c2P b2P n2I m2I c2I2m I2d4/mmmP4/mmm P4/mcc P4/nbm P4/nnc P4/mbm P4/mnc P4/nmm P4/ncc P42/mmcP42/mcm P42/nbc P42/nnm P42/mbc P42/mnm P42/nmc P42/ncm I4/mmm I4/mcmI41/amd I41/acd三方晶系3P3P31P32R3P R32P312P321P3112P3121P3212P3221R32 3m P3m1P31m P3c1P31c R3m R3cm P1m P1c P m1P c1R m R c六方晶系6P6P61P65P62P64P63P6/m P6/m P63/m622P622P6122P6522P6222P6422P6322 6mm P6mm P6cc P63cm P63mcm2P m2P c2P2m P2c6/mmm P6/mmm P6/mcc P63/mcm P63/mmc立方晶系23P23F23I23P213I213m Pm3Pn3Fm3Fd3Im3Pa3Ia3432P432P4232F432F4132I432P4332P4132I41323m P3m F3m I3m P3n F3c I3dm mPm m Pn n Pm n Pn m Fm m Fm c Fd m Fd c Im mIa d晶体外形上的对称关系，空间群表示晶体结构内部的原子及离子间的对称关系。

230种晶体学空间群熊夫符号

深入探讨230种晶体学空间群熊夫符号一、引言在晶体学领域中，晶体结构的描述和分类要依赖于空间群。

空间群是对晶格进行平移、旋转和镜面反射操作的一组对称操作的集合。

而熊夫符号则是对这些对称操作进行简洁表示的一种形式。

全球晶体学家们经过长期的努力，总结出了230种不同的晶体学空间群熊夫符号，这些符号有着极其丰富的内涵和深刻的科学意义。

在本文中，我们将深入探讨230种晶体学空间群熊夫符号的分类、特点和应用，并共享对这一主题的个人观点和理解。

二、230种晶体学空间群熊夫符号的分类230种晶体学空间群熊夫符号根据其对称性和操作特征可以分为七大类，分别是三维空间群、菱形系空间群、四方系空间群、正交系空间群、单斜系空间群、三斜系空间群和五维空间群。

每一类空间群都有其独特的特点和应用范围，对于晶体学研究和应用具有重要意义。

1. 三维空间群三维空间群是最基本的一类空间群，共有73种不同的熊夫符号代表着它们各自的对称操作特点。

在晶体学研究中，三维空间群被广泛应用于描述和分类各种晶体结构，为我们理解晶体的对称性和性质提供了重要的参考。

2. 菱形系空间群菱形系空间群共有16种不同的熊夫符号，它们具有特殊的对称性和操作特点，在一些特定的晶体结构中发挥着重要的作用。

研究人员对菱形系空间群进行了深入的探讨和分析，为我们理解和应用这些空间群提供了重要的理论基础。

3. 四方系空间群四方系空间群包括各种四方晶系中的空间群，共有22种不同的熊夫符号。

这些空间群在研究四方晶体结构和性质方面发挥着重要的作用，对于高温超导材料等功能材料的研究具有重要意义。

4. 正交系空间群正交系空间群是描述和分类正交晶系中的空间群，共有59种不同的熊夫符号代表着它们丰富的对称性和操作特点。

研究人员对正交系空间群进行了深入研究，为我们理解和应用这些空间群提供了重要的理论指导。

5. 单斜系空间群单斜系空间群包括各种单斜晶系中的空间群，共有13种不同的熊夫符号。

晶体学 [230种晶体学空间群的记号及常见矿石的名称、分子式与所属晶系]

晶体学 [230种晶体学空间群的记号及常见矿石的名称、分子式与所属晶系]230种晶体学空间群的记号 Symbols of the 230 Crystallographic Space Groups 晶系圣佛利斯符号圣佛利斯符号单质名称银 Ag 立方铂 Pt立方砷 As 三方正交硫 S 正交金 Au立方单斜硫 S 单斜铋 Bi 三方三方硫 S 三方金刚石 C 立方锑 Sb 三方石墨 C 六方硒 Se 六方铜 Cu 立方硅 Si 立方α-铁 Fe 立方β-锡（白） Sn 四方镍 Ni 立方碲 Te 六方铅 Pb 立方锌Zn 六方常见矿石的名称、分子式与所属晶系 Names, Molecular Formulas and Crystal Systems of Common Ores 名称名称硫砷银矿 AgAsS3 三方橙红石 HgO 正交碲金银矿 Ag3AuTe2 立方辰砂 HgS 六方溴银盐 AgBr 立方黑辰砂 HgS 立方氯银盐AgCl 立方硒汞矿 HgTe 立方辉铜银矿Ag1.55Cu0.45S-Ⅲ 四方碲汞矿 HgTe 立方硫铜银矿 Ag0.93Cu1.07S-Ⅲ 正交白云石KAl2[AlSi3O10](OH)2 单斜硒铜银矿 AgCuSe 正交锂云母 K2Al3Li2[AlSi7O22](OH)4 单斜硫铁银矿AgFe2S3 正交明矾石 KAl3(SO4)2(OH)6 三方黄碘银矿 AgI 立方天然钾霞石 KAlSiO4 六方碘银矿 AgI 六方白榴石 KAlSi2O6 四方辉银矿Ag2S-Ⅱ 立方高白榴石 KAlSi2O6 立方深红硫锑银矿 AgSbS3 三方铁白榴石 KAlSi2O6 四方高硒银矿 Ag2Se 立方微斜长石 KAlSi3O8 三斜碲银矿 Ag2Te-Ⅲ 单斜高透长石 KAlSi3O8 单斜刚玉 Al2O3 三方正长石 KAlSi3O8 单斜3·2莫来石3Al2O3·2SiO2 正交钾石膏K2Ca(SO4)2·2H2O 单斜2·1莫来石2Al2O3·SiO2 正交钾盐 KCl 立方勃姆石 AlO(OH) 正交羟铁云母 KFe3[AlSi3O10](OH)2 单斜水铝石AlO(OH) 正交铁羟铁云母 KFe3[FeSi3O10](OH)2 单斜（三）水铝矿 Al(OH)3 单斜铁透长石KFeSi3O8 单斜块磷铝矿 AlPO4 六方铁微斜长石KFeSi3O8 三斜蓝晶石 Al2SiO5 三斜氟金云母KMg3[AlSi3O10]F2 单斜黄玉 Al2(SiO4)(OH) 正交金云母 KMg3[AlSi3O10](OH)2 单斜叶蜡石Al2Si4O10(OH)2 单斜硝石 KNO3 正交地开石Al2Si2O5(OH)4 单斜单钾芒硝 KS2SO4 正交高岭石 Al2Si2O5(OH)4 三斜锂辉石 LiAl(SiO3)2 单斜珍珠陶土 Al2Si2O5(OH)4 单斜钙铁辉石LiAl(SiO3)2 四方砷华 As2O3 立方透锂长石LiAlSi4O10 单斜白砷石 As2O3 单斜高堇青石Mg2Al3(AlSi5O18) 六方雄黄矿 AsS 单斜低堇青石 Mg2Al3(AlSi5O18) 正交雌黄 As2S3 单斜尖晶石 MgAl2O4 立方黑铋金矿 Au2Bi 立方镁铝榴石 Mg3Al2Si3O12 立方钡长石 BaAl2Si2O8 单斜菱镁矿 MgCO3 三方毒重石 BaCO3 正交氯镁石 MgCl2 三方菱钡镁石 BaMg(CO3)2 三方镁铬矿 MgCr2O4 立方钡钠长石 BaNaAl4Si4O16 正交氟镁石 MgF2 四方重晶石 BaSO4 正交方镁石 MgO 立方金绿宝石 BeAl2O4 正交水镁石 Mg(OH)2 六方铍石 BeO 六方泻盐矿MgS O4·7H2O 正交铋华α-Bi2O3 单斜无水钠镁矾MgSO4·3Na2SO4 单斜辉铋矿 Bi2S3 正交斜顽火石 MgSiO3 单斜碲铋矿 Bi2Te3 三方原顽火辉石 MgSiO3 正交珍珠云母CaAl[Al2Si2O10](OH)2 单斜高斜顽火石 MgSiO3 三斜钙长石 CaAl2Si2O8 三斜镁橄榄石 Mg2SiO4正交钙铝黄长石 Ca2Al2SiO7 四方氟块硅镁石Mg2SiO4·MgF2 正交钙铝榴石 Ca3Al2Si3O12 立方氟硅镁石3Mg2SiO4·MgF2 正交硬柱石CaAl2Si2O7(OH)2·H2O 正交滑石 Mg3Si4O10(OH)2 单斜钙柱石 Ca4Al6Si6O24CO3 四方镁闪石Mg7[Si8O22](OH)2 单斜黝帘石 Ca2Al3(SiO4)3OH 正交直闪石 Mg7[Si8O22](OH)2 正交斜黝帘石Ca2Al3(SiO4)3OH 单斜镁钛矿 MgTiO3 三方硬硼钙石CaB3O4(OH)3·H2O 单斜锰印度石Mn2Al3(AlSi5O18) 六方赛黄晶 CaB2Si2O8 正交锰尖晶石 MnAl2O4 立方方解石 CaCO3 三方斜煌岩 Mn2Al2Si3O12 立方球霰石 CaCO3 六方菱锰矿 MnCO3 三方霰石 CaCO3 正交氯锰矿MnCl2 三方铁黄长石 Ca2Fe2SiO7 四方锰磁铁矿MnFe2O4 立方钙铬榴石 Ca3Fe2Si3O12 立方锰铁橄榄石 MnFeSiO4 正交萤石 CaF2 立方锰三斜辉石 MnFe(SiO3)2 三斜钙铁辉石 CaFe(SiO3)2 单斜方锰矿 MnO 六方钙铁榴石 Ca3Fe2Si3O12 立方软锰矿 MnO2 四方钙铁橄榄石 CaFeSiO4 正交方铁锰矿 Mn2O3 立方铁透闪石Ca2Fe5[Si8O22](OH)2 单斜黑锰矿 Mn3O4 四方钙镁电气石 CaMg4Al5B3Si6O27(OH)4 三方硫锰矿MnS 立方白云石 CaMg(CO3)2 三方方硫锰矿MnS2 立方透辉石 CaMg(SiO3)2 单斜蔷薇辉石MnSiO3 三斜钙镁橄榄石 CaMgSiO4 正交锰橄榄石 Mn2SiO4 正交镁黄长石 Ca2MgSi2O7 四方红钛锰矿 MnTiO3 三方氟透闪石 Ca2Mg5[Si8O22]F2 单斜钼华 MoO3 正交锰钙辉石 CaMn(SiO3)2单斜辉钼矿 MoS2 六方钙蔷薇辉石 CaMn(SiO3)2 三斜钨锰矿 MnWO4 单斜钙锰橄榄石 CaMnSiO4 正交铵矾 (NH4)2SO4 正交钼钨钙矿 CaMoO4四方钠云母 NaAl2[AlSi3O10](OH)2 单斜针钠钙石Ca2NaH(SiO3)3 三斜冰晶石 Na3AlF6 单斜石灰CaO 立方钠明矾石 NaAl3(SO4)2(OH)6 三方羟钙石 Ca(OH)2 六方硬玉 NaAl(SiO3)2 单斜碳酸磷灰石Ca10(PO4)6CO3·H2O 六方低霞石 NaAlSiO4 六方氯磷灰石 Ca5(PO4)3Cl 六方高三斜霞石NaAlSiO4 立方氟磷灰石 Ca5(PO4)3F 六方低钠长石 NaAlSi3O8 三斜羟磷灰石 Ca5(PO4)3OH 六方高钠长石/歪长石 NaAlSi3O8 三斜陨硫钙石CaS 立方钠柱石 Na4Al3Si9O24Cl 四方硬石膏CaSO4 正交方沸石NaAlSi2O6·H2O 立方石膏CaSO4·2H2O 单斜钠沸石Na2Al2Si3O10·2H2O 正交硅灰石 CaSiO3 三斜硼砂Na2B4O7·10H2O单斜假银星石 CaSiO3 三斜四水硼砂Na2B4O7·4H2O 单斜钙橄榄石 Ca2SiO4 正交钠铝黄长石 NaCaAlSi2O7 四方钙钛矿 CaTiO3 正交碳酸钠钙石 Na2Ca2(CO3)3 正交榍石CaTiSiO5 单斜氟浅闪石 NaCa2Mg5[AlSi7O22]F2 单斜钙钒榴石 Ca3V2Si3O12 立方氟碱锰闪石Na2CaMg5[Si8O22]F 单斜白钨矿 CaWO4 四方岩盐 NaCl 立方锌黄长石 Ca2ZnSiO7 四方氟盐NaF 立方菱镉矿 CdCO3 三方钠闪石Na2Fe3Fe2[Si8O22](OH)2 单斜方镉石 CdO 立方绿辉石(霓石) NaFe(SiO3)2 单斜硫镉矿 CdS 六方镁电气石 NaMg3Al6B3Si6O27(OH)4 三方方硫镉矿 CdS 立方氟镁钠石 NaMgF3 正交镉硒矿CdSe 六方钠硝石 NaNO3 三方方铈矿 CeO2立方镁钠闪石 Na2mg3Fe2[Si8O22](OH)2 单斜钴方解石 CoCO3 三方蓝闪石ⅠNa2mg3Fe2[Si8O22](OH)2 单斜砷钴铁矿 (Co5Fe5)As2 正交蓝闪石Ⅱ Na2mg3Fe2[Si8O22](OH)2 单斜辉砷钴矿 CoAsS 立方无水芒硝 Na2SO4 正交铁硫砷钴矿 (Co,Fe)AsS 正交芒硝Na2SO4·10H2O 单斜方硫钴矿 CoS2 立方红砷镍矿 NiAs 六方硫钴矿 Co3S4 立方砷镍矿 NiAs2 正交方硒钴矿 CoSe2 立方辉砷镍矿 NiAsS 立方钴橄榄石Co2SiO4 正交镍磁铁矿 NiFe2O4 立方绿铬矿Cr2O3 三方绿镍矿 NiO 立方绿松石CuAl6(PO4)4(OH)8·4H2O 三斜硫铅镍矿β-Ni3Pb2S2 三方砷黝铜矿 Cu12As4S13 立方硫镍矿 Ni3S4 立方铜盐 CuCl 立方方硫镍矿 NiS2 立方黄铜矿 (CuFeS2)CuFeS1.90 四方镍矾NiSO4·4H2O 四方方黄铜矿 CuFe2S3 正交镍橄榄石 Ni2SiO4 正交高斑铜矿 Cu5FeS4 立方碲镍矿 NiTe2 六方低斑铜矿 Cu5FeS4 四方白铅矿 PbCO3 正交透视石 CuH2SiO4 三方氯铅矿 PbCl2 正交碘铜矿 CuI 立方氟氯铅矿 PbFCl 四方铜硝石Cu2(NO3)(OH)3 正交钼铅矿 PbMoO4 四方黑铜矿CuO 单斜正方铅矿 PbO 四方赤铜矿 Cu2O立方铅黄 PbO 正交褐铜矾 Cu2O(SO4) 单斜铅丹（红铅） Pb3O4 四方孔雀石 Cu2(OH)2CO3单斜方铅矿 PbS 立方蓝铜矿 Cu3(OH)2(CO3)2 单斜硫酸铅矿 PbSO4 正交蓝辉铜矿（富铜）Cu1.79S 立方硒铅矿 PbSe 立方铜蓝矿 CuS 六方碲铅矿 PbTe 立方高蓝辉铜矿 Cu2S-Ⅰ立方钨铅矿 PbWO4 四方辉铜矿 Cu2S-Ⅲ 正交砷铂矿 PtAs2 立方胆矾CuSO4·5H2O 三斜硫铂矿 PtS 四方黝铜矿 Cu12Sb4S13 立方硫钌锇矿 RuS2 立方硒铜矿Cu2Se 立方方锑矿Sb2O3 立方红硒铜矿 Cu3Se2 四方锑华 Sb2O3 正交蓝硒铜矿 CuSe 六方黄锑矿 Sb2O4 立方铁印度石 Fe2Al3(AlSi5O18) 六方辉锑矿 Sb2S3正交铁堇青石 Fe2Al3(AlSi5O18) 正交石膏岩SeO2 四方铁尖晶石 FeAl2O4 立方α-方英石SiO2 四方贵榴石 Fe3Al2Si3O12 立方β-方英石SiO2 立方砷铁矿 FeAs2 正交热液石英 SiO2 四方菱铁矿 FeCO3 三方β-鳞石英 SiO2 六方陨氯铁 FeCl2 三方锡石 SiO2 四方陨硫铬铁FeCrS4 立方硫锡矿 SnS 正交黑钨矿Fe·5Mn·5WO4 单斜菱锶矿 SrCO3 正交硫镍铁矿 Fe5.25Ni3.75S8 立方天青石 SrSO4 正交硫镍铁矿 Fe4.75Ni5.25S8 立方付黄碲矿 TeO2四方紫硫镍矿 FeNi2S4 立方方钍石 ThO2 立方方铁矿 Fe0.953O 立方钍石 ThSiO4 四方赤铁矿 Fe2O3 三方金红石 TiO2 四方磁铁矿Fe3O4 立方锐钛矿 TiO2 四方硫铁矿 FeS六方板钛矿 TiO2 正交硫铁矿 Fe3S4 立方沥青铀矿 UO2 立方黄铁矿 FeS2 立方水硅铀矿 USiO4 四方磁黄铁矿 Fe0.98S 六方硫钨矿WS2 六方磁黄铁矿 Fe0.885S 六方磷钇矿YPO4 四方水绿矾FeSO4·7H2O 单斜锌尖晶石ZnAl2O4 立方硒铁矿 FeSe2 正交菱锌矿ZnCO3 三方斜铁辉石 FeSiO3 单斜红锌矿 ZnO 六方正铁辉石 FeSiO3 正交闪锌矿 ZnS 立方铁橄榄石 Fe2SiO4 正交纤锌矿 ZnS 六方铁滑石 Fe3Si4O10(OH)2 单斜锌矾 ZnSO4 正交铁闪石 Fe7[Si8O22](OH)2 单斜皓矾ZnSO4·7H2O正交碲铁矿 FeTe2 正交方硒锌矿 ZnSe 立方钛铁矿 FeTiO3 三方硅锌矿 Zn2SiO4 三方钨铁矿 FeWO4 单斜钨锌矿 ZnWO4 单斜低二氧化锗 GeO2 四方斜锆石 ZrO2 单斜高二氧化锗GeO2 六方锆石 ZrSiO4 四方。

230种晶体学空间群的记号及常见矿石的名称、分子式与所属晶系

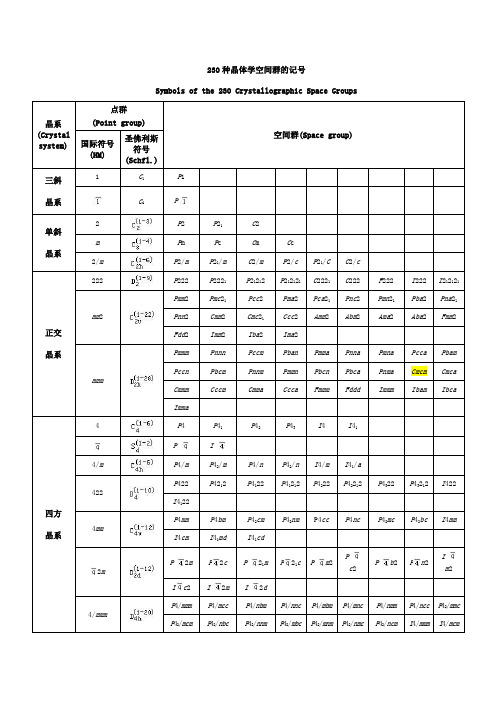
230种晶体学空间群的记号
Symbols of the 230 Crystallographic Space Groups
2m 2P P 2m b n
I c22
m 11m P R m c m2
m c2
3m 33I P3
I
m m n Pm Pn Fm Fm Fd m
Fd
m d
空间群是点对称操作和平移对称操作的对称要素全部可能的组合。

点群表示晶体外形上的对称关系，空间群表示晶体结构内部的原子及离子间的对称关系。

空间群一共230个，它们分别属于32个点群。

晶体结构的对称性不能超出230个空间群的范围，而其外形的对称性和宏观对称性则不能越出32个点群的范围。

属于同一点群的各种晶体可以隶属于若干个空间群。

不同晶系的晶格类型
32种晶体学点群的记号
2m
m m
m2
m
(4)
3m 3(3)
m
m (4)
点群不存在平移操作，所有的对称要素都集中在一个共同的点上。

对称要素包括旋转、反映、反伸（对称中心）与旋转反伸。

有这4个对称要素组合出32个点群。

下表中“轴向对称要素的方向和数目”的圆括号内数据代表该对称要素的数目。

正多面体的数学和结晶学参数
Mathematic and Crystallographic Parameters of Regular Polyhedrons
常见单质的所属晶系
常见矿石的名称、分子式与所属晶系
Names, Molecular Formulas and Crystal Systems of Common Ores。

230种晶体学空间群的记号

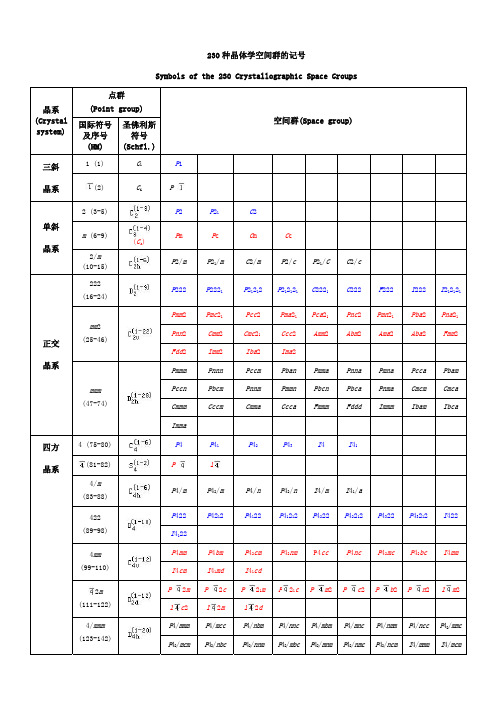
晶系
(2)
Ci
P
2 (3-5)
P2
P21
C2
单斜
m (6-9)
Pm
Pc
Cm
Cc
(Cs)
晶系
2/m (10-15)
P2/m
P21/m
C2/m
P2/c P21/C C2/c
222 (16-24)
P222
P2221
P21212 P212121 C2221
C222
F222
I222 I212121
正交晶系
mm2 (25-46)
m (200-206)
432 (207-214)
3m (215-220)
mm (221-230)
(C6h)
I41/amd I41/acd
P3
P31
P32
R3
P
R
P312
P321
P3112
P3121 P3212 P3221
R32
P3m1
P31m
P3c1
P31c
R3m
R3c
P 1m P 1c P m1 P c1 R m R c
Pmm2
Pmc21
Pcc2
Pma21 Pca21 Pnc2 Pmn21 Pba2 Pna21
Pnn2
Cmm2
Cmc21
Ccc2 Amm2 Abm2 Ama2 Aba2 Fmm2
Fdd2
Imm2
Iba2
Ima2
Pmmm
Pnnn
Pccm
Pban Pmma Pnna Pmna Pcca Pbam
mmm (47-74)
P6
P61
P65

230种晶体学空间群地记号及常见矿石地名称、分子式与所属晶系

230种晶体学空间群的记号
Symbols of the 230 Crystallographic Space Groups
2m 2P P 2m b n
I c22
m 11m P R m R c m2
m c2
3m 33I P3
I
m m n Pm Pn Fm Fm Fd m
Fd
Im m d
空间群是点对称操作和平移对称操作的对称要素全部可能的组合。

点群表示晶体外形上的对称关系，空间群表示晶体结构内部的原子及离子间的对称关系。

空间群一共230个，它们分别属于32个点群。

晶体结构的对称性不能超出230个空间群的范围，而其外形的对称性和宏观对称性则不能越出32个点群的范围。

属于同一点群的各种晶体可以隶属于若干个空间群。

不同晶系的晶格类型
32种晶体学点群的记号
2m
m m
m2
m
(4)
3m 3(3)
m
m (4)
点群不存在平移操作，所有的对称要素都集中在一个共同的点上。

对称要素包括旋转、反映、反伸（对称中心）与旋转反伸。

有这4个对称要素组合出32个点群。

下表中“轴向对称要素的方向和数目”的圆括号内数据代表该对称要素的数目。

正多面体的数学和结晶学参数
Mathematic and Crystallographic Parameters of Regular Polyhedrons
常见单质的所属晶系
常见矿石的名称、分子式与所属晶系
Names, Molecular Formulas and Crystal Systems of Common Ores。

230种空间群

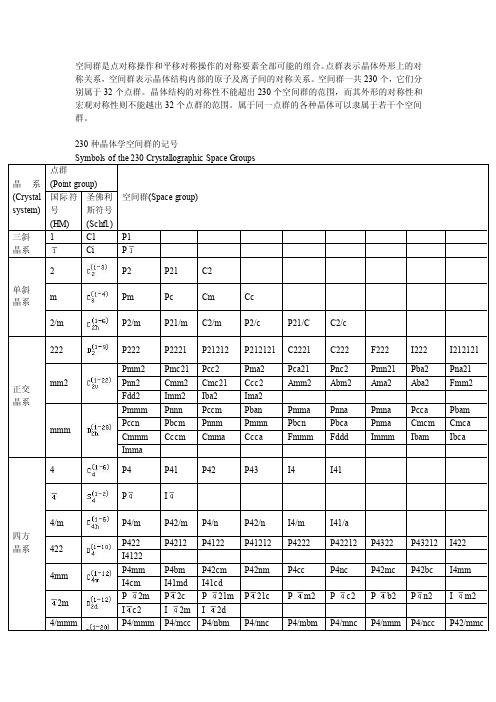
空间群是点对称操作和平移对称操作的对称要素全部可能的组合。

点群表示晶体外形上的对称关系，空间群表示晶体结构内部的原子及离子间的对称关系。

空间群一共230个，它们分别属于32个点群。

晶体结构的对称性不能超出230个空间群的范围，而其外形的对称性和宏观对称性则不能越出32个点群的范围。

属于同一点群的各种晶体可以隶属于若干个空间群。

230种晶体学空间群的记号
Ci
I
2m
2m P P P I
m 1m P
m2 m2
m
3m 3m I P
Pm Im m
1 三斜晶系
2 单斜晶系
3 斜方晶系
4 四方晶系
为2，
为⊥m，5 三方晶系
6 六方晶系
(191) P6/mmm 7 等轴晶系。

第四节晶体的230种空间群

黑体字的6种组合在其它3种格子中是没有的。
A格子有4种空间群：
Amm2、 Abm2、 Ama2、 Aba2。
44
C14 2v
Amm2
Amm2 = Amc21 = Anc2 = Anm21
m⊥
a
·(
b 2
+
c 2
)=
n⊥ a
m⊥
b
·(
b 2
+
c 2
)=
cb/4
垂直于b, c滑移面和m每隔b/4交替存在
(2) 当m和b 垂直时
m ⊥b 与a滑移面共存
(3)
C⊥a ·(
a+b 22
)=
m
·
c 2
·(
a+b 22
)= ma/4 ·(
b+c )
22
=na/4
(4) 同理： C⊥b ＝ nb
4
35
¾在C格子中
m⊥a 与b滑移面共存 m ⊥b 与a滑移面共存 n ⊥b 与c滑移面共存 n ⊥a 与c滑移面共存
从某一点群出发而得到的种种可能的微观对称类型– 空间群时，相应对称元素之间的角度关系是与该点群相同的。
4
•空间群的国际符号
空间群的国际符号由两部分构成，第一个大写字母表示点阵格子类型，第二部分标明空间群的特征对称元素，其定向和符号形式与点群相同，但增加了螺旋轴和滑移面。如果空间群的微观对称元素用相应的宏观对称元素取代，则得到晶体的点群。
20
16种正交滑移面组合在P格子中
Pmc21 = Pcm21 Pma2 = Pbm2 Pca21 = Pbc21 Pnc2 = Pcn2 Pmn21 = Pnm21 Pna21 =Pbn21

230种晶体学空间群230 种晶体学空间群的记号Symbols of the 230 Crystallographic Space Groups晶系(Crystal system)点群(Point group)空间群(Space group) 国际符号(HM)圣佛利斯符号(Schfl.)三斜晶系1 C1 P1C i P单斜晶系2 P2 P21 C2m Pm Pc Cm Cc2/m P2/m P21/m C2/m P2/c P21/C C2/c正交晶系222 P222 P2221 P21212P212121 C2221 C222 F222 I222 I212121 mm2Pmm2 Pmc21 Pcc2 Pma2 Pca21 Pnc2 Pmn21 Pba2 Pna21Pnn2 Cmm2 Cmc21 Ccc2 Amm2 Abm2 Ama2 Aba2 Fmm2Fdd2 Imm2 Iba2 Ima2mmmPmmm Pnnn Pccm Pban Pmma Pnna Pmna Pcca PbamPccn Pbcm Pnnm Pmmn Pbcn Pbca Pnma Cmcm CmcaCmmm Cccm Cmma Ccca Fmmm Fddd Immm Ibam IbcaImma四方晶系4 P4 P41 P42 P43 I4 I41P I4/m P4/m P42/m P4/n P42/n I4/m I41/a422P422 P4212P4122P41212P4222P42212P4322P43212I422I41224mmP4mm P4bm P42cm P42nm P4cc P4nc P42mc P42bc I4mmI4cm I41md I41cd2mP 2m P2c P 21m P21c P m2Pc2P b2 P n2Im2I c2 I 2m I 2d4/mmm P4/mmm P4/mcc P4/nbm P4/nnc P4/mbm P4/mnc P4/nmm P4/ncc P42/mmc P42/mcm P42/nbc P42/nnm P42/mbc P42/mnm P42/nmc P42/ncm I4/mmm I4/mcmI41/amd I41/acd三方晶系3 P3 P31 P32 R3P R32 P312 P321 P3112P3121P3212P3221R32 3m P3m1 P31m P3c1 P31c R3m R3cm P1m P 1c P m1 P c1 R m R c六方晶系6 P6 P61 P65 P62 P64 P63P6/m P6/m P63/m622 P622 P6122P6522P6222P6422P6322 6mm P6mm P6cc P63cm P63mcm2P m2 P c2 P 2m P2c6/mmm P6/mmm P6/mcc P63/mcm P63/mmc立方晶系23 P23 F23 I23 P213I213m Pm3 Pn3 Fm3 Fd3 Im3 Pa3 Ia3432 P432 P4232F432 F4132I432 P4332P4132I41323m P 3m F 3m I3m P3n F 3cI3dm mPm m Pn n Pm n Pn m Fm m Fm c Fd mFdcIm m Ia d空间群是点对称操作和平移对称操作的对称要素全部可能的组合。

晶体对称性与空间群表

晶体对称性与空间群表表3.1.七个晶系三斜 triclinic a≠b ≠c; α≠β≠γ单斜 monoclinic a≠ b≠ c; α = γ = 90º,β≠ 90º正交 orthorhombic a≠b≠c; α= β = γ = 90º四方 tetragonal a = b≠c; α = β = γ = 90º六方 hexagonal a = b≠c;α = β = 90º, γ = 120º三方 trigonal a = b = c; α=β= γ≠ 90º立方 cubic a = b = c; α= β= γ= 90º注释：表中“≠”仅指不需要等于。

表3.2.七个晶系的特征对称元素晶系特征对称元素三斜无单斜一个二次对称轴或对称面正交三个互相垂直的二次对称轴或两个互相垂直的对称面四方有一个四次对称轴六方有一个六次对称轴三方有一个三次对称轴立方四个立方体对角线上有三次轴注：对称轴包括旋转、螺旋轴；对称面包括镜面和滑移面。

cP cFcI图3.5.14种Bravais晶格。

aP = 三斜（triclinic）, mP = 简单单斜（monoclinic primitive）, mC = 底心单斜（monoclinic C-centered），oP = 简单正交（orthorombic primitive），oC = C 底心正交（orthorombic C-centered，取轴方法不同，可以相当于A心底），oI = 体心正交（orthorombic body-centered），oF = 面心正交（orthorombic face-centered），tP = 简单四方（tetragonal primitive），tI = 体心四方（tetragonal body-centered），hP = 简单三方或六方（trigonal or hexagonal primitive），hR = 菱面体、按六方取晶胞（Rhombohedral hexagonal setting），cP = 简单立方（cubic primitive），cI = 体心立方（cubic body-centered），cF = 面心立方（cubic face-centered）。

230种空间群符号及含义

空间群（Space group）是一种描述晶体结构的数学工具，它把晶体中的所有原子看作点，并使用符号（由数字和符号组成）来表示这些点的几何排列。

空间群的种类非常多，通常在几千种以上，但常用的只有几十种。

以下是一些常用的空间群符号及其含义：
1. 225型空间群（P22_1_5）：这种空间群表示具有两套相互垂直的近正方形的简单晶体结构，每个原子都在一个平面上，通过角顶相互连接。

2. 432型空间群（P4_3_2）：这种空间群表示具有四套相互垂直的矩形排列的简单晶体结构，每个原子都在一个平面上，通过角顶相互连接。

3. 62型空间群（I6_2）：这种空间群表示具有六套相互垂直的六边形排列的复杂晶体结构，每个原子都在一个平面上，通过角顶相互连接。

4. 61型空间群（P6_1）：这种空间群表示具有六套相互垂直的六边形排列的简单晶体结构，每个原子都在一个六边形的顶点上。

5. 31型空间群（P3_1）：这种空间群表示具有三套相互垂直的平面排列的简单晶体结构，每个原子都在一个平面上。

需要注意的是，空间群的种类非常多，不同文献和教科书可能会对同一晶体的空间群描述有所不同。

因此，在进行晶体结构分析时，需要参考具体的文献或教科书来确定具体的空间群符号和含义。

此外，不同的晶体结构也可能需要不同的计算参数和方法，因此在应用空间群进行晶体结构分析时需要选择适当的软件和算法。

目前常用的晶体结构分析软件如VESTA、Pymatgen等都提供了对空间群的详细解释和使用方法。

以上就是部分常见的空间群符号及含义，如果您需要了解更多空间群的符号及含义，建议您查阅相关的专业书籍或咨询专业人士。

230种晶体学空间群的记号

230种晶‎体学空间群‎的记号Symbo‎l s of the 230 Cryst‎a llog‎r aphi‎c Space‎Group‎s空间群是点‎对称操作和‎平移对称操‎作的对称要‎素全部可能‎的组合。

点群表示晶‎体外形上的‎对称关系，空间群表示‎晶体结构内‎部的原子及‎离子间的对‎称关系。

空间群一共‎230个，它们分别属‎于32个点‎群。

晶体结构的‎对称性不能‎超出230‎个空间群的‎范围，而其外形的‎对称性和宏‎观对称性则‎不能越出3‎2个点群的‎范围。

属于同一点‎群的各种晶‎体可以隶属‎于若干个空‎间群。

230种晶‎体学空间群‎的记号Symbo‎l s of the 230 Cryst‎a llog‎r aphi‎c Space‎Group‎s2m P P P P PII IP Rm 1P 1P P R R m2P P P3m P F I PIm Pm Pn Pm Pn Fm Fm FdFdIm Ia1.The produ‎c t was a mixtu‎r e of unide‎n tifi‎e d dark blue micro‎c ryst‎a ls and brown‎cryst‎a ls2.The mixtu‎r e was then heate‎d at 180°C for four days in a Teflo‎n-coate‎d steel‎autoc‎l ave. The produ‎c t, consi‎s ting‎of clear‎singl‎e cryst‎a ls of MAP-RHO1 and an unide‎n tifi‎e d white‎powde‎r, was recov‎e red by filtr‎a tion‎and washe‎d with deion‎i zed water‎.3.Attem‎p ts to isola‎t e this compo‎u nd by remov‎a l of solve‎n t (0 O C, l0-2mmHg)resul‎t ed in decom‎p osit‎i on to unide‎n tifi‎a ble produ‎c ts.4.Stron‎g hydro‎g en bondi‎n g occur‎s only when the hydro‎g en atom is colli‎n ear withthe bonde‎d atoms‎.5.The hydro‎g en atom is locat‎e d close‎r to one atom or the other‎.6.Here the subst‎i tuti‎o nal hydro‎g en atom locat‎e d in a surfa‎c e vacan‎c y or thehydro‎g en at an inter‎s titi‎a l posit‎i on of surfa‎c e is a half-confi‎n ed atom which‎is only weakl‎y bound‎.7.The ethyl‎e nedi‎a mine‎ligan‎d was chose‎n for its abili‎t y to chela‎t e coppe‎r ionsleavi‎n g two free posit‎i ons trans‎l ocat‎e d so that {Cu(en) 2 } 2+ can act as a linki‎n g agent‎betwe‎e n two POMs, via bridg‎i ng oxyge‎n atoms‎[4] and (c. We have studi‎e d the influ‎e nce of the initi‎a l pH .8.The ions or molec‎u les surro‎u ndin‎g the centr‎a l atom are calle‎d ligan‎d s. Ligan‎d sare gener‎a lly bound‎to the centr‎a l atom by a coord‎i nate‎coval‎e nt bond (donat‎i ng elect‎r ons from a lone elect‎r on pair into an empty‎metal‎orbit‎a l), and are said to be coord‎i nate‎d to the atom. There‎are also organ‎i c ligan‎d s such as alken‎e s whose‎pi bonds‎can coord‎i nate‎to empty‎metal‎orbit‎a ls. An examp‎l e is ethen‎e in the compl‎e x known‎as Zeise‎'s salt, K+[PtCl3‎(C2H4)]−.9.One nicke‎l ion is coord‎i nate‎d by three‎ligan‎d s (with low occup‎a ncy of a fourt‎h ligan‎d) andthe secon‎d is coord‎i nate‎d by five ligan‎d s.10.The eleve‎n t ungs‎t en cente‎r s of compo‎u nd 1 have a disto‎r ted octah‎e dral‎geome‎t ry.11. All the tungs‎t en atoms‎have disto‎r ted octah‎e dral‎geome‎t ry andthe bond-valen‎c e sum (BVS) model‎25 clear‎l y indic‎a tes that all the tungs‎t en atoms‎are in the +6oxida‎t ion state‎.12.(1) dispe‎r sion‎of the negat‎i ve charg‎e over many atoms‎of the polya‎n ion and13.Anal. Calc. For14.which‎is not thoug‎h t of as being‎novel‎.15.be thoug‎h t of as和 be consi‎d ered‎as 和be seen as作为“……被视为/被看作……"的语义上讲‎，总体上3个‎表达一样, 类似还有：regar‎d...as.../ view...as.../ treat‎...as.../ lookon ...as...,etc.16.The coord‎i nati‎o n spher‎e aroun‎d each of the six equiv‎a lent‎Zn(II)ions exhib‎i ts disto‎r ted octah‎e dral‎geome‎t ry, with a singl‎e TFA – anion‎(not shown‎)occup‎y ing the sixth‎coord‎i nati‎o n site in all cases‎.17. The coord‎i nati‎o n geome‎t ry of this cadmi‎u m ion displ‎a ys a disto‎r ted octah‎e dron‎,withHis14‎3 N 2 , His15‎3N 2 , Wat35‎9 and Wat41‎6formi‎n g an octah‎e dral‎base plane‎, and His14‎7 N 2 and Wat41‎8 being‎locat‎e d at the verti‎c es18. In these‎polym‎e rs the metal‎atom exhib‎i tsoctah‎e dral‎geome‎t ry but only two coord‎i nati‎o n sites‎of trans‎i tion‎metal‎were used topropa‎g ate the netwo‎r k.19.The coord‎i nati‎o n geome‎t ry of this cadmi‎u m ion displ‎a ys a disto‎r ted octah‎e dron‎,withHis14‎3 N2 , His15‎3 N 2 , Wat35‎9 and Wat41‎6 formi‎n g an octah‎e dral‎base plane‎, and His14‎7 N 2andWat41‎8 being‎locat‎e d at the verti‎c es20.recei‎v es contr‎i buti‎o ns from four nitro‎g en donor‎s belon‎g ing to two enmolec‎u les, two oxyge‎n donor‎s from two clust‎e r anion‎s21. The coord‎i nati‎o n geome‎t ry aroun‎d coppe‎r ions can appro‎x imat‎e ly be descr‎i bed asortho‎r homb‎i call‎y disto‎r ted octah‎e dral‎22.Each Mn(1) atom is bridg‎e d with three‎symme‎t ry- equiv‎a lent‎Mn(1) atoms‎throu‎g hO(1) atoms‎and each O(1) atom is linke‎d with three‎Mn(1) atoms‎.23.Each metal‎ion in the squar‎e is six-coord‎i nate‎; four of the coord‎i nati‎o n sites‎are occup‎i edby the nitro‎g en atoms‎of two of bpy ligan‎d s and the remai‎n ing cis coord‎i nati‎o n sites‎are occup‎i ed by cyani‎d e-carbo‎n or cyani‎d e-nitro‎g en atoms‎.24.cube- 50 shape‎d block‎s havin‎gparal‎l el front‎and rear faces‎, paral‎l el side faces‎and paral‎l el upper‎and lower‎faces‎.25. the two molec‎u les shown‎in cyan (!) and red (//) are relat‎e d by a cryst‎a llog‎r aphi‎ctwo-fold axis, perpe‎n dicu‎l ar to the plane‎, likew‎i se red (Hi) and ...26.with its apex point‎i ng in the direc‎t ion of flow27. The 690 (675) em -1 loss with a relat‎i vely‎stron‎g inten‎s ity is ascri‎b ed to the SiCsymme‎t ric stret‎c hing‎vibra‎t ion, becau‎s e the SiC stret‎c hing‎vibra‎t ions‎of organ‎a-silic‎o n compo‎u nds are obser‎v ed betwe‎e n -600 and 800 cm "!28.The 1100–700 cm−1 range‎shows‎the As–O stret‎ching‎modes‎of the (AsO3O‎H)2− and (As2O7‎)4− group‎s. As alrea‎dy menti‎oned, the compl‎exity‎of the cryst‎alstruc‎ture does not allow‎to be more speci‎fic. The stron‎g and sharp‎band in infra‎red and the weak one in Raman‎spect‎ra aroun‎d 909 cm−1 could‎be attri‎buted‎to the antis‎ymmet‎ric bridg‎e stret‎ching‎vibra‎tion, νa s (As–O–As) of pyroa‎rsena‎te group‎s [27]. The most inten‎se Raman‎bands‎aroun‎d 876 cm−1 (very weak in IR) and 857 cm−1 corre‎spond‎to the symme‎tric stret‎ching‎vibra‎tions‎of (AsO3O‎H)2− and (As2O7‎)4− group‎s, respe‎ctive‎ly.po‎u nd 2 has been synth‎e size‎d with the same proce‎d ure withPb(OAc)2 .3H2O30. The geome‎try aroun‎d Cu(1) has the squar‎e pyram‎idal coord‎inati‎on with 3NOdonor‎atoms‎in the basal‎plane‎and water‎oxyge‎n atom at the apica‎l posit‎ion.31. Each dca ligan‎d adopt‎i ngthe end-to-end coord‎i nati‎o n mode is μ-bonde‎d to two MnII ions with an Mn···Mn separ‎-32. The two Cys S atoms‎bind to the coppe‎r ions in a disto‎r tedsquar‎e plana‎r fashi‎o n, each S inter‎a ctin‎g with both coppe‎r ions. ..33. The vibra‎t iona‎l resul‎t s stron‎g ly sugge‎s t that methi‎o nine‎sulfu‎r isbound‎to coppe‎r in the prote‎i ns.34.and Nd was bonde‎d to the COO- group‎of EAA.35.the elect‎r ons are inter‎-share‎d betwe‎e n the diffe‎r ent atoms‎.36.The centr‎a l atom or ion, toget‎h er with all ligan‎d s compr‎i se the coord‎i nati‎o n spher‎e.37.is the neutr‎a l [Cu(bpca)(dca)(H 2 O)] compl‎e x in which‎the three‎bpca nitro‎g en atoms‎and a termi‎n al dca nitro‎g en bind to coppe‎r in equat‎o rial‎posit‎i ons38.The XPS estim‎a tion‎s obtai‎n ed on the valen‎c e state‎value‎s are in reaso‎n able‎agree‎m ent with those‎calcu‎l ated‎from bond valen‎c e sum calcu‎l atio‎n s of compo‎u nds 1-3.39.Both Sn atoms‎exist‎in disto‎r ted octa- hedra‎l geome‎t ries‎, each defin‎e d by two cis-CH .40.The Cu I ion is coord‎i nate‎d in a tetra‎h edra‎l confi‎g urat‎i on41.the ligan‎d coord‎i nate‎s only via the phosp‎h orus‎atom42.half the dca ligan‎d s coord‎i nate‎direc‎t ly (throu‎g h all three‎nitro‎g en atoms‎)to three‎Mnatoms‎43.W spect‎r osco‎p ic data of solut‎i ons of PCs in dimet‎h yl sulfo‎x ide were obtai‎n ed with aBeckm‎a nn DU-7 W-Vis spect‎r opho‎t omet‎e r44.The UV-vis-near I R spect‎r a were recor‎d ed in N,N-di- methy‎l form‎a mide‎(DMF)solut‎i on by using‎a Perki‎n-Elmer‎45. the Sn atom exist‎s in a disto‎r ted tetra‎g onal‎geome‎t ry in which‎the basal‎plane‎is defin‎e d by four S atoms‎and the axial‎posit‎i ons are occup‎i ed by two butyl‎subst‎i tuen‎t s 46. The same proce‎d ure was carri‎e d out with 2 ml of plant‎extra‎c t (10 g/l) inste‎a d of rutin‎solut‎i on.All deter‎m inat‎i ons were carri‎e d out in dupli‎c ates‎.47.] the same proce‎d ure was carri‎e d out in the absen‎c e of ex- trace‎l lula‎r Na, with choli‎n eused in place‎of Na,48.Fe1 (Fe1A) with NO5 donor‎set, inclu‎d ing one N atom toget‎h er with three‎Oatoms‎from two L3- ligan‎d s and two carbo‎x ylic‎-O atoms‎from two PhCO2‎-group‎s 49.The coord‎i nati‎o n spher‎e of Dy1 is compl‎e ted by two nitro‎g en atoms‎(N1 and N7*),two ... N4 and N5) from a plana‎r penta‎d enta‎t e dihyd‎r azon‎e uni50.Howev‎e r, thebond-valen‎c e sum calcu‎l ated‎for Bi 3+ shows‎a 32% defic‎i ency‎from itsideal‎value‎of 3.0.51.The bond valen‎c e sums of oxyge‎n s in the polya‎n ion are liste‎d in Table‎4, and fall withi‎nthe range‎1.59-2.03 excep‎t for O(11), O(12), O(39), and O(40). The bridg‎i ng atoms‎,O(11) and O(12), have BVS value‎s of 1.19 and 1.32, and are there‎f ore presu‎m ed to be hydro‎x o group‎s. T52.Coppe‎r(II) ions displ‎a y a squar‎e-pyram‎i dal coord‎i nati‎o n geome‎t ry‎(τ‎=‎0.06)‎for‎the‎N‎2‎OCl 2 donor‎set, where‎the basal‎coord‎i nati‎o n sites‎are occup‎i ed by one of the bridg‎i ng chlor‎i ne atoms‎and the three‎donor‎atoms‎of the tride‎n tate‎ligan‎d and the apica‎l site is occup‎i ed by。

230种晶体学空间群

230种晶体学空间群的记号及常见矿石的名称、分子式与所属晶系

230种空间群

种晶体学空间群的记号及常见矿石的名称分子式与所属晶系

第五章-230种空间群记号

230种晶体学空间群的记号及常见矿石的名称、分子式与所属晶系

种晶体学空间群的记号及常见矿石的名称分子式与所属晶系

230种晶体学空间群熊夫符号

晶体学 [230种晶体学空间群的记号及常见矿石的名称、分子式与所属晶系]

230种晶体学空间群的记号及常见矿石的名称、分子式与所属晶系

230种晶体学空间群的记号

230种晶体学空间群地记号及常见矿石地名称、分子式与所属晶系

230种空间群

第四节 晶体的230种空间群

230种晶体学空间群

晶体对称性与空间群表

230种空间群符号及含义

230种晶体学空间群的记号

第四节晶体的230种空间群