余切正割余割的图象和性质
三角函数的几何表示

在微积分中,三角函数用于解决与极坐标相关的 问题。
线性代数
在矩阵运算中,三角函数用于计算特征值和特征 向量。
三角函数在金融领域的应用
复利计算
01
在金融领域,复利计算涉及到指数函数和三角函数的结合使用。
期权定价
02
在期权定价模型中,三角函数用于计算期权的价值。
风险管理
03
在风险管理领域,三角函数用于计算风险值(VaR)和压力测试。
三角恒等式是三角函数之间的基本关系式,如sin^2 x + cos^2 x = 1、sin(x+y) 和cos(x+y)分别等于sin x cos y + cos x sin y等。
三角恒等式是三角函数运算的基础,对于简化复杂的三角函数表达式、证明性质 以及解决实际问题非常有用。
THANKS FOR WATCHING
简谐运动
物体在平衡点附近的往复 运动可以用三角函数来描 述。
工程中的三角函数应用
结构设计
在工程中,三角函数常用 于结构设计,如梁的弯曲、 拱桥的设计等。
信号处理
在通信和信号处理中,三 角函数用于频谱分析和滤 波器设计。
测量
在测量领域,三角函数用 于角度和距离的测量。
数学中的三角函数应用
解析几何
在解析几何中,三角函数用于解决与角度和长度 相关的问题。
正割函数的图像
正割函数图像是正弦函数的倒数,其周期为$pi$弧度。
在直角坐标系中,正割函数图像呈现为一个双曲线,随着角度的增加,函数值逐渐减小并趋 近于0。
正割函数图像关于原点对称。
余割函数的图像
余割函数图像是余弦函数的倒数,其周期同样为$pi$ 弧度。
正割函数余割函数

正割函数余割函数正割函数和余割函数是三角函数中的两个概念。
正割函数的记号为sec(x),表示一个角 x 的正切函数的倒数,即 sec(x) =1/cos(x)。
而余割函数的记号为csc(x),表示一个角 x 的正弦函数的倒数,即 csc(x) = 1/sin(x)。
下面将分别介绍正割函数和余割函数的性质和应用。
正割函数的性质:1. 定义域和值域:正割函数的定义域为一切使得cos(x) ≠ 0 的实数,值域为一切实数。
2. 周期性:正割函数的周期为2π,即sec(x+2π) = sec(x)。
3. 奇偶性:正割函数是偶函数,即 sec(-x) = sec(x)。
4. 特殊值:正割函数在x = π/2 + nπ (n为整数) 处无定义,即sec(π/2 + nπ) 不存在。
余割函数的性质:1. 定义域和值域:余割函数的定义域为一切使得sin(x) ≠ 0 的实数,值域为一切实数。
2. 周期性:余割函数的周期为2π,即csc(x+2π) = csc(x)。
3. 奇偶性:余割函数是奇函数,即 csc(-x) = -csc(x)。
4. 特殊值:余割函数在 x = nπ (n为整数) 处无定义,即csc(nπ)不存在。
正割函数和余割函数的应用:1. 三角方程求解:正割函数和余割函数常常用于解三角方程,尤其是在求解关于余弦和正弦的方程时。
2. 几何问题:正割函数和余割函数可在几何问题中用于计算角度和边长之间的关系,尤其是在直角三角形中。
3. 物理学应用:正割函数和余割函数在物理学中的运动学和波动学中经常出现,比如在分析周期运动、波动传播等问题中。
4. 工程应用:在工程中,正割函数和余割函数可用于计算某些结构的强度、稳定性以及电路中的电流、电压等参数。
以上是正割函数和余割函数的相关参考内容,这两个函数是常用的三角函数之一,具有一些特殊性质和应用场景。
分别是-正弦-余弦-正切-余切-正割-余割

不动点
奇 {x∈R〡x≠kπ, k∈Z} (-∞,∞) π
0 N/A N/A ∞ -∞
N/A
kπ+ 0
7
k 是一个整数.
正割
8
性质 奇偶性
定义域
到达域 周期 特定值 当 x=0 当 x=+∞ 当 x=-∞ 最大值 最小值 其他性质 渐近线 根 临界点 拐点 不动点
偶 {x|x≠kπ+π/2, k∈Z} |secx|≥1 2π
同角三角函数间的基本关系式:
·平方关系: sin^2α+cos^2α=1 1+tan^2α=sec^2α 1+cot^2α=csc^2α ·积的关系: sinα=tanα×cosα cosα=cotα×sinα tanα=sinα×secα cotα=cosα×cscα secα=tanα×cscα cscα=secα×cotα ·倒数关系: tanα ·cotα=1
0 N/A N/A ∞ -∞
N/A 无实根 kπ kπ-π/2 0
9
k 是一个整数.
余割
10
性质 奇偶性 定义域 到达域 周期 特定值 当 x=0 当 x=+∞ 当 x=-∞
最大值
最小值
其他性质 渐近线 根 临界点 拐点
奇 {x|x≠kπ,k∈Z} |csc x|≥1 2π
0 N/A N/A ( ,∞) ( ,-∞)
N/A kπ kπ-π/2 kπ 0
余弦
性质 奇偶性 定义域
到达域
周期 特定值 当 x=0 当 x=+∞ 当 x=-∞
偶 (-∞,∞) [-1,1] 2π
0 N/A N/A
3
最大值
(2kπ,1)
最小值 其他性质 渐近线
六种三角函数性质

六种三角函数性质六种三角函数性质、公式三角函数包括。
它包含六种基本函数:正弦、余弦、正切、余切、正割、余割1-1y=sinx-3π2-5π2-7π27π25π23π2π2-π2-4π-3π-2π4π3π2ππ-πoy x1-1y=cosx-3π2-5π2-7π27π25π23π2π2-π2-4π-3π-2π4π3π2ππ-πoy xy=tanx3π2ππ2-3π2-π-π2oyxy=cotx3π2ππ22π-π-π2oyx.反三角函数:arcsinx arccosxarctanx arccotx函数y=sinx y=cosx y=tanx y=cotx 定义域R R{x|x∈R且x≠kπ+2,k∈Z}{x|x∈R且x≠kπ,k∈Z}值[-1,1][-1,1]R Ry=secx的性质:(1)定义域,{x|x≠π/2+kπ,k∈Z}(2)值域,|secx|≥1.即secx≥1或secx≤-1;(3)y=secx是偶函数,即sec(-x)=secx.图像对称于y轴;(4)y=secx是周期函数.周期为2kπ(k∈Z,且k≠0),最小正周期T=2π.(5)正割与余弦互为倒数;余割与正弦互为倒数;(6)正割函数无限趋于直线x=π/2+Kπ;(7) 正割函数是无界函数;(8)正割函数的导数:(secx)′=secx×ta rx;(9正割函数的不定积分:∫secxdx=ln∣se cx+tanx∣+Cy=cscx的性1、定义域:{x|x≠kπ,k∈Z}2、值域:{y|y≤-1或y≥1}3、奇偶性:奇函数4、周期性:最小正周期为2π5、图像:图像渐近线为:x=kπ ,k∈Z 余割函数与正弦函数互为倒数第一部分三角函数公式·两角和与差的三角函数cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)·和差化积[/url]公式:sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]·积化和差[/url]公式:sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]·倍角公式[/url]:sin(2α)=2sinα·cosα=2/(tanα+cotα)cos(2α)=(cosα)^2-(sinα)^2=2(cosα)^2-1=1-2(sinα)^2tan(2α)=2tanα/(1-tan^2α)cot(2α)=(cot^2α-1)/(2cotα)sec(2α)=sec^2α/(1-tan^2α)csc(2α)=1/2*secα·cscα·三倍角公式:sin(3α) = 3sinα-4sin^3α = 4sinα·sin(60°+α)sin(60°-α)cos(3α) = 4cos^3α-3cosα = 4cosα·cos(60°+α)cos(60°-α)tan(3α) = (3tanα-tan^3α)/(1-3tan^2α) = tanαtan(π/3+α)tan(π/3-α)cot(3α)=(cot^3α-3cotα)/(3cot^2α-1)·n倍角公式:sin(nα)=ncos^(n-1)α·sinα-C(n,3)cos^(n-3)α·sin^3α+C(n,5)cos^(n-5)α·sin^5α-…cos(nα)=cos^nα-C(n,2)cos^(n-2)α·sin^2α+C(n,4)cos^(n-4)α·sin^4α-…·半角公式[/url]:sin(α/2)=±√((1-cosα)/2)cos(α/2)=±√((1+cosα)/2)tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinαcot(α/2)=±√((1+cosα)/(1-cosα))=(1+cosα)/sinα=sinα/(1-cosα)sec(α/2)=±√((2secα/(secα+1))csc(α/2)=±√((2secα/(secα-1))·辅助角公式:Asinα+Bcosα=√(A^2+B^2)sin(α+φ)(tanφ=B/A)Asinα+Bcosα=√(A^2+B^2)cos(α-φ)(tanφ=A/B)·万能公式sin(a)= (2tan(a/2))/(1+tan^2(a/2))cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))tan(a)= (2tan(a/2))/(1-tan^2(a/2))·降幂公式sin^2α=(1-cos(2α))/2=versin(2α)/2cos^2α=(1+cos(2α))/2=covers(2α)/2tan^2α=(1-cos(2α))/(1+cos(2α))·三角和的三角函数:sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·si nγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·co sγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)·其它公式·两角和与差的三角函数cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)=sinα/(1-cosα) ·和差化积[/url]公式:sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]·积化和差[/url]公式:sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]·倍角公式[/url]:sin(2α)=2sinα·cosα=2/(tanα+cotα)cos(2α)=(cosα)^2-(sinα)^2=2(cosα)^2-1=1-2(sinα)^2tan(2α)=2tanα/(1-tan^2α)cot(2α)=(cot^2α-1)/(2cotα)sec(2α)=sec^2α/(1-tan^2α)csc(2α)=1/2*secα·cscα·三倍角公式:sin(3α) = 3sinα-4sin^3α = 4sinα·sin(60°+α)sin(60°-α)cos(3α) = 4cos^3α-3cosα = 4cosα·cos(60°+α)cos(60°-α)tan(3α) = (3tanα-tan^3α)/(1-3tan^2α) = tanαtan(π/3+α)tan(π/3-α)cot(3α)=(cot^3α-3cotα)/(3cot^2α-1)·n倍角公式:sin(nα)=ncos^(n-1)α·sinα-C(n,3)cos^(n-3)α·sin^3α+C(n,5)cos^(n-5)α·sin^5α-…cos(nα)=cos^nα-C(n,2)cos^(n-2)α·sin^2α+C(n,4)cos^(n-4)α·sin^4α-…·半角公式[/url]:sin(α/2)=±√((1-cosα)/2)cos(α/2)=±√((1+cosα)/2)tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinαcot(α/2)=±√((1+cosα)/(1-cosα))=(1+cosα)/sinαsec(α/2)=±√((2secα/(secα+1))csc(α/2)=±√((2secα/(secα-1))·辅助角公式:Asinα+Bcosα=√(A^2+B^2)sin(α+φ)(tanφ=B/A)Asinα+Bcosα=√(A^2+B^2)cos(α-φ)(tanφ=A/B)·万能公式sin(a)= (2tan(a/2))/(1+tan^2(a/2))cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))tan(a)= (2tan(a/2))/(1-tan^2(a/2))·降幂公式sin^2α=(1-cos(2α))/2=versin(2α)/2cos^2α=(1+cos(2α))/2=covers(2α)/2tan^2α=(1-cos(2α))/(1+cos(2α))·三角和的三角函数:sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·si nγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·co sγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)·其它公式1+sin(a)=(sin(a/2)+cos(a/2))^2 1-sin(a)=(sin(a/2)-cos(a/2))^2csc(a)=1/sin(a) sec(a)=1/cos(a)cos30=sin60sin30tanα+cotα=2/sin2αtanα-cotα=-2cot21+cos2α=2cos^2α1-cos2α=2sin^2α1+sinα=[sin(α/2)+cos(α/2)]^21+sin(a)=(sin(a/2)+cos(a/2))^2 1-sin(a)=(sin(a/2)-cos(a/2))^2csc(a)=1/sin(a) sec(a)=1/cos(a)cos30=sin60sin30=cos60·推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos^2α1-cos2α=2sin^2α1+sinα=[sin(α/2)+cos(α/2)]^211 / 11。
三角函数公式图像大全2

三角函数公式图像大全2三角函数公式图像大全2三角函数公式和图像是高中数学中的重点内容之一,通过研究三角函数的公式和图像可以深入理解三角函数的性质和特点。
本文将详细介绍常见的三角函数公式和常见的三角函数图像,并提供大量的示意图以帮助读者理解和记忆。
一、三角函数公式1.正弦函数公式:正弦函数是一个周期函数,函数的周期为2π。
① 基本公式:sinθ = y / r,其中θ表示角度,y表示对边的长度,r表示斜边的长度。
② 周期性公式:sin(θ + 2π) = sinθ③ 奇偶性公式:sin(-θ) = -sinθ④ 两角和公式:sin(θ + φ) = sinθ * cosφ + cosθ * sinφ⑤ 两角差公式:sin(θ - φ) = sinθ * cosφ - cosθ * sinφ⑥ 二倍角公式:sin2θ = 2 * sinθ * cosθ2.余弦函数公式:余弦函数也是一个周期函数,函数的周期为2π。
① 基本公式:cosθ = x / r,其中θ表示角度,x表示邻边的长度,r表示斜边的长度。
② 周期性公式:cos(θ + 2π) = cosθ③ 奇偶性公式:cos(-θ)= cosθ④ 两角和公式:cos(θ + φ) = cosθ * cosφ - sinθ * sinφ⑤ 两角差公式:cos(θ - φ) = cosθ * cosφ + sinθ * sinφ⑥ 二倍角公式:cos2θ = cos²θ - sin²θ3.正切函数公式:正切函数也是一个周期函数,函数的周期为π。
① 基本公式:tanθ = y / x,其中θ表示角度,y表示对边的长度,x表示邻边的长度。
② 周期性公式:tan(θ + π) = tanθ③ 奇偶性公式:tan(-θ) = -t anθ④ 两角和公式:tan(θ + φ) = (tanθ + tanφ) / (1 - tanθ * tanφ)⑤ 两角差公式:tan(θ - φ) = (tanθ - tanφ) / (1 + tanθ * tanφ)⑥ 二倍角公式:tan2θ = 2 * tanθ / (1 - tan²θ)二、三角函数图像1.正弦函数图像:正弦函数的图像是一条连续的波浪线,函数的波峰和波谷分别对应于θ=π/2和θ=3π/22.余弦函数图像:余弦函数的图像是一条连续的波浪线,函数的波峰和波谷分别对应于θ=0和θ=π。
正割函数余割函数

正割函数和余割函数引言在数学中,三角函数是一类经典且重要的函数,它们描述了角度与函数值之间的关系。
常见的三角函数包括正弦函数、余弦函数、正切函数以及它们的倒数函数——余弦函数、正割函数和余割函数。
正割函数(Secant Function)正割函数是一个与余弦函数密切相关的函数。
它可以用来表示单位圆上某个角的正弦值的倒数。
正割函数被定义为角θ的余弦值的倒数,用sec(θ)表示。
其数学表达式为:sec(θ) = 1 / cos(θ)在单位圆上,正割函数可以通过求出对应角度的余弦值,再求其倒数得到。
正割函数的定义域为除去余弦函数为零的所有角度。
余割函数(Cosecant Function)余割函数也是一种与正弦函数密切相关的函数。
它可以用来表示单位圆上某个角的正弦值的倒数。
余割函数被定义为角θ的正弦值的倒数,用csc(θ)表示。
其数学表达式为:csc(θ) = 1 / sin(θ)与正割函数类似,余割函数的定义域为除去正弦函数为零的所有角度。
与其它三角函数的关系正割函数和余割函数是三角函数中的倒数函数,它们与正弦函数、余弦函数、正切函数的关系如下:•正割函数与余弦函数的关系:sec(θ) = 1 / cos(θ)•余割函数与正弦函数的关系:csc(θ) = 1 / sin(θ)•正切函数与正割函数的关系:tan(θ) = sin(θ) / cos(θ),可以写作sec(θ) = 1 / cos(θ) = 1 / (1 / tan(θ)) = tan(θ)•余切函数与余割函数的关系:cot(θ) = cos(θ) / sin(θ),可以写作csc(θ) = 1 / sin(θ) = 1 / (1 / cot(θ)) = cot(θ)可以看出,正割函数和余割函数在函数关系上与正弦函数、余弦函数和正切函数密切相关。
特点和图像正割函数和余割函数的特点如下:•定义域:除去余弦函数为零或正弦函数为零的所有角度。
•值域:正割函数的值可以是任意实数,余割函数的值可以是任意实数。
余切正割余割的图象和性质

精心整理曹振卿
一、余切:
余切函数的性质
(1)、定义域:{x|x≠kπ,k∈Z}
(2)、值域:实数集R当x→2kπ时,y→∞;当x→(2k+1)π时,y→-∞;
(3)、奇偶性:奇函数,可由诱导公式cot(-x)=-cotx推出
图像关于原点对称,实际上所有的零点都是它的对称中心
(4)、周期性是周期函数,周期为kπ(k∈Z且k≠0),最小正周期T=π;
(5)、单调性在每一个开区间(kπ,(k+1)π),k∈Z上都是减函数,在整个定义域上不具有单调性。
(6)、对称性中心对称:关于点(kπ/2,0)k∈Z中心对称
二、正割余割:
精心整理
精心整理
粗线是正割函数,细线是余割函数
y=secx的性质:
(1)定义域,{x|x≠π/2+kπ,k∈Z}
(2)值域,|secx|≥1.即secx≥1或secx≤-1;
(3)y=secx是偶函数,即sec(-x)=secx.图像对称于y轴;
(4)y=secx是周期函数.周期为2kπ(k∈Z,且k≠0),最小正周期T=2π.(5)正割与余弦互为倒数;余割与正弦互为倒数;
(6)正割函数无限趋于直线x=π/2+Kπ;
(7)正割函数是无界函数;
精心整理。
三角函数的无穷大

三角函数的无穷大(一)正切函数(y = tan x)1. 函数性质- 正切函数的定义域为x≠ kπ+(π)/(2),k∈ Z。
- 当x趋近于kπ+(π)/(2)(k∈ Z)时,tan x趋近于正无穷或负无穷。
例如,当x 从左侧趋近于(π)/(2)时,tan x的值不断增大,趋近于正无穷;当x从右侧趋近于(π)/(2)时,tan x的值不断减小,趋近于负无穷。
2. 图像特点- 在正切函数的图像上,在x = kπ+(π)/(2)(k∈ Z)处有垂直渐近线。
这是因为函数在这些点处极限为无穷大,函数值在这些点附近无限增大或减小。
(二)余切函数(y=cot x)1. 函数性质- 余切函数的定义域为x≠ kπ,k∈ Z。
- 当x趋近于kπ(k∈ Z)时,cot x趋近于正无穷或负无穷。
例如,当x从左侧趋近于0时,cot x=(cos x)/(sin x),sin x趋近于0且为正,cos x趋近于1,所以cot x趋近于正无穷;当x从右侧趋近于0时,sin x趋近于0且为负,cos x趋近于1,所以cot x趋近于负无穷。
2. 图像特点- 在余切函数的图像上,在x = kπ(k∈ Z)处有垂直渐近线,这是由于函数在这些点处极限为无穷大的缘故。
(三)正割函数(y = sec x=(1)/(cos x))和余割函数(y=csc x=(1)/(sin x))1. 正割函数- 定义域为x≠ kπ+(π)/(2),k∈ Z。
当cos x趋近于0时,sec x趋近于正无穷或负无穷。
例如,当x趋近于(π)/(2)时,cos x趋近于0,sec x=(1)/(cos x)趋近于正无穷(当x从左侧趋近)或负无穷(当x从右侧趋近)。
- 其图像在x = kπ+(π)/(2)(k∈ Z)处有垂直渐近线。
2. 余割函数- 定义域为x≠ kπ,k∈ Z。
当sin x趋近于0时,csc x趋近于正无穷或负无穷。
例如,当x趋近于0时,sin x趋近于0,csc x=(1)/(sin x)趋近于正无穷(当x从右侧趋近)或负无穷(当x从左侧趋近)。
余切正割余割的图象和性质

曹振卿
一、余切:
余切函数的性质
1、定义域:{x|x≠kπ,k∈Z}
2、值域:实数集R当x→2kπ时,y→∞;当x→2k+1π时,y→-∞;
3、奇偶性:奇函数,可由诱导公式cot-x=-cotx推出
图像原点对称,实际上所有的零点都是它的对称中心
4、周期性是周期函数,周期为kπk∈Z且k≠0,最小正周期T=π;
5、单调性在每一个开区间kπ,k+1π,k∈Z上都是减函数,在整个定义域上不具有单调性.
6、对称性中心对称:点kπ/2,0k∈Z中心对称
二、正割余割:
粗线是正割函数,细线是余割函数
y=secx的性质:
1定义域,{x|x≠π/2+kπ,k∈Z}
2值域,|secx|≥1.即secx≥1或secx≤-1;
3y=secx是偶函数,即sec-x=secx.图像对称于y轴;
4y=secx是周期函数.周期为2kπk∈Z,且k≠0,最小正周期T=2π.5正割与余弦互为倒数;余割与正弦互为倒数;
6正割函数无限趋于直线x=π/2+Kπ;
7正割函数是无界函数;。
余割函数知识点归纳总结

余割函数知识点归纳总结余割函数(Cosecant function)是三角函数中的一种,有时也被称为正弦的倒数。
它在数学和物理等学科中有着重要的应用。
本文将对余割函数的定义、性质、图像以及常见的应用进行归纳总结。
一、定义余割函数的定义如下:csc(x) = 1/sin(x)其中,csc(x)表示x的余割值,sin(x)表示x的正弦值。
二、性质1. 定义域和值域:余割函数的定义域为除去正弦函数的零点的全体实数集合,即 D = R \ {kπ | k ∈ Z};值域为实数集合,即 R。
2. 奇偶性:余割函数是奇函数,即满足 csc(-x) = -csc(x)。
3. 周期性:余割函数的周期是π的整数倍,即csc(x + kπ) = csc(x),其中 k ∈Z。
4. 正负性:当正弦函数大于0时,余割函数大于0;当正弦函数小于0时,余割函数小于0。
5. 极值点:余割函数在定义域内不具有极值点。
6. 渐近线:余割函数与x轴交于无穷多个渐近线,即x = kπ,其中 k ∈ Z。
三、图像余割函数的图像表现出频繁的振荡特性,其图像如下所示:【插入余割函数图像】图中每个周期都表现为一个连续的曲线段,延伸到正无穷和负无穷。
与正弦函数类似,余割函数的图像也具有对称性。
四、常见应用1. 物理学中的应用:余割函数在声学、波动学等物理学领域中具有重要的应用,特别是在谐波和共振的研究中。
2. 数学题中的运用:在数学题目中,余割函数经常出现在三角方程的求解过程中,可以通过求解正弦函数的倒数来得到余割函数的值。
3. 数据分析与处理:余割函数也常常用于数据的分析与处理,特别是在周期性数据的振荡特征分析方面。
总结:本文对余割函数的定义、性质、图像以及常见的应用进行了归纳总结。
余割函数作为三角函数家族中的一员,具有独特的特性和广泛的应用领域。
通过了解和熟悉余割函数的知识点,我们可以更好地理解和应用于相关的数学和物理问题中。
余切函数正割函数和余割函数的图形

§餘切函數、正割函數和餘割函數的圖形則函數f 稱為週期函數,而其中最小的p 稱為函數f 的週期。
2.x sec y =,x csc y =的週期為2π,x cot y =的週期為π。
3.週期函數)(x f y =的週期為)0(>P P ,則)0()(≠=k kx f y 的週期為kP 。
4.三角函數)(x f 的週期若為p ,則 (1)k x f +)(與)(x kf 的週期亦為p 。
(2))(b ax f +的週期為||a p 。
※cot ,sec ,csc x x x 之週期:π※下列函數均不是週期函數 (1)y=cot|x| (2)y=csc|x|。
5.六個三角函數的性質:(1)定義域為},,|{Z k k x R x x ∈≠∈π。
(2)值域為R 。
(3)週期為π。
(4)πn x =,Z n ∈時,x cot 沒有意義。
(5)Z k ∈∀,餘切函數在區間πππ+<<k x k 上恆為遞減函數。
(6)直線πn x =,Z n ∈為其漸進線。
(7)因為對於在其定義域的所有x 而言,x x cot )cot(-=-,所以其為奇函數,圖形對稱於原點。
(8)將x y tan =的圖形向左平移2π單位長,在將所得圖形對x軸鏡射,即可得x y cot =的圖形。
※以點Z n n ∈),0,(π為對稱中心,以直線Z n n x ∈+=,2ππ為對稱軸。
2.正割函數x y sec =(1)定義域為},2,|{Z k k x R x x ∈+≠∈ππ。
(2)值域為}11|{-≤≥y y y 或。
(3)週期為π2。
(4)正割函數的遞增遞減區間恰與x y cos =相反。
(5)2ππ+=n x ,Z n ∈時,x sec 沒有意義。
(6)直線2ππ+=n x ,Z n ∈為其漸進線。
(7)因為對於在其定義域的所有x 而言,x x sec )sec(=-,所以其為偶函數,圖形對稱於y 軸。
函数名_正弦_余弦_正切_余切_正割_余割

z
z z 2 z3 zn + + + + + 此时三角函数定义域 1! 2! 3! n!
三角函数的数值符号
正弦 第一,二象限为正, 第三,四象限为负 余弦 第一,四象限为正 正切 第一,三象限为正 第二,三象限为负 第二,四象限为负
三角函数定义域和值域
sin(x),cos(x) 的定义域为 R,值域为 (-1,1) tan(x) 的定义域为 x 不等于
公式四:
利用公式二和公式三可以得到 与 的三角函数值之间的关系:
s i n ) = s n ( i c o s ) = - c o s ( t a n ) = - t a n ( c o t ) = - c o t (
公式五:
利用公式一和公式三可以得到 2 与 的三角函数值之间的关系:
B A +B
2 2
;
cos =
A A 2 +B2
;
B tan = . A
Asin +Bcos = A 2 +B2 cos( - ) ,其中 tan =
A B
·倍角公式:
sin(2 )=2sin cos = 2 (tan +cot )
cos(2 )=cos 2 -sin 2 =2cos 2 -1=1-2sin 2
tan tan tan( + )+tan +tan -tan( + )=0
3
cosx+cos(2x)+...+cos(nx)=
证明: 左边=
[sin(n+1)x+sin(nx)-sinx] 2sinx
三角函数详解大全

三角函数详解大全三角函数是数学中的一种重要函数,用于描述角和边之间的关系。
常见的三角函数包括正弦函数(sin)、余弦函数(cos)、正切函数(tan)以及它们的倒数:余割函数(csc)、正割函数(sec)和余切函数(cot)。
下面对这些三角函数进行详细解释:1. 正弦函数(sin):-定义:在直角三角形中,正弦值表示任意一个锐角的对边与斜边的比值。
-表达式:sinθ= 对边/ 斜边-特点:正弦函数的取值范围为[-1, 1],在0度、90度、180度等特殊角度上有特殊的取值。
2. 余弦函数(cos):-定义:在直角三角形中,余弦值表示任意一个锐角的邻边与斜边的比值。
-表达式:cosθ= 邻边/ 斜边-特点:余弦函数的取值范围也为[-1, 1],在0度、90度、180度等特殊角度上有特殊的取值。
3. 正切函数(tan):-定义:在直角三角形中,正切值表示任意一个锐角的对边与邻边的比值。
-表达式:tanθ= 对边/ 邻边-特点:正切函数的取值范围为全体实数,没有上下限。
4. 余割函数(csc):-定义:余割值是正弦值的倒数,即1除以正弦值。
-表达式:cscθ= 1 / sinθ5. 正割函数(sec):-定义:正割值是余弦值的倒数,即1除以余弦值。
-表达式:secθ= 1 / cosθ6. 余切函数(cot):-定义:余切值是正切值的倒数,即1除以正切值。
-表达式:cotθ= 1 / tanθ这些三角函数在解决几何问题、物理问题、工程问题等方面起着重要的作用。
它们具有周期性、对称性以及一些特殊的性质,可以通过三角函数的图像和性质来进行相关问题的分析和求解。
三角函数公式大全

三角函数公式大全本文主要介绍三角函数公式的大全,包括正弦、余弦、正切、余切、正割、余割、弧度制、角度制等,共计52个公式。
三角函数是初等数学中重要的一部分,以它为基础可以推导出很多数学公式,也是物理、化学等自然科学中常用的数学工具。
1、正弦(sin)与余弦(cos)的关系公式sin θ = cos(90° - θ)cos θ = sin(90° - θ)2、正弦(sin)与余切(ctg)的关系公式sin θ = 1 / ctg θctg θ = 1 / sin θ3、正弦(sin)与正割(sec)的关系公式sin θ = 1 / sec(90° - θ)sec θ = 1 / sin(90° - θ)4、余弦(cos)与正切(tan)的关系公式cos θ = 1 / tan(90° - θ)tan θ = 1 / cos(90° - θ)5、余弦(cos)与余切(cot)的关系公式cos θ = 1 / cot(90° - θ)cot θ = 1 / cos(90° - θ)6、余弦(cos)与余割(cosec)的关系公式c os θ = 1 / cosec(90° - θ)cosec θ = 1 / cos(90° - θ)7、正切(tan)与余切(cot)的关系公式tan θ = 1 / cot θcot θ = 1 / tan θ8、正切(tan)与正割(sec)的关系公式tan θ = 1 / sec(90° - θ)sec θ = 1 / cot(90° - θ)9、正切(tan)与余割(cosec)的关系公式tan θ = 1 / cosec(90° - θ)cosec θ = 1 / cot(90° - θ)10、余切(cot)与正割(sec)的关系公式cot θ = 1 / sec θsec θ = 1 / cot θ11、余切(cot)与余割(cosec)的关系公式cot θ = 1 / cosec(90° - θ)cosec θ = 1 / tan(90° - θ)12、正割(sec)与余割(cosec)的关系公式sec θ = 1 / cosec(90° - θ)cosec θ = 1 / sec(90° - θ)13、正弦(sin)的倒数公式sin(-θ) = -sin θsin(θ ± 360°) = sin θ14、余弦(cos)的倒数公式cos(-θ) = cos θcos(θ ± 360°) = cos θ15、正切(tan)的倒数公式tan(-θ) = -tan θtan(θ ± 180°) = tan θ16、余切(cot)的倒数公式cot(-θ) = -cot θcot(θ ± 180°) = cot θ17、正割(sec)的倒数公式sec(-θ) = sec θsec(θ ± 360°) = sec θ18、余割(cosec)的倒数公式cosec(-θ) = -cosec θcosec(θ ± 360°) = cosec θ19、正弦(sin)的平方公式sin² θ + cos² θ = 11 - sin² θ = cos² θsin² θ = 1 - cos² θ20、余弦(cos)的平方公式sin² θ + cos² θ = 11 - cos² θ = sin² θcos² θ = 1 - sin² θ21、正切(tan)的平方公式tan² θ + 1 = sec² θ1 + cot² θ = cosec² θtan² θ = sec² θ - 122、余切(cot)的平方公式cot² θ + 1 = cosec² θ1 + tan² θ = sec² θcot² θ = cosec² θ - 123、正弦(sin)的角和公式sin(A + B) = sin A cos B + cos A sin Bsin(A - B) = sin A cos B - cos A sin B 24、余弦(cos)的角和公式cos(A + B) = cos A cos B - sin A sin B cos(A - B) = cos A cos B + sin A sin B 25、正弦(sin)的二倍角公式sin 2A = 2 sin A cos A26、余弦(cos)的二倍角公式cos 2A = cos² A - sin² A27、正切(tan)的二倍角公式tan 2A = 2 tan A / (1 - tan² A)28、余切(cot)的二倍角公式cot 2A = (cot² A - 1) / 2 cot A29、正割(sec)的二倍角公式sec 2A = (sec² A + 1) / (2 sec A)30、余割(cosec)的二倍角公式cosec 2A = (cosec² A + 1) / (2 cosec A) 31、正弦(sin)的三倍角公式sin 3A = 3 sin A - 4 sin³ A32、余弦(cos)的三倍角公式cos 3A = 4 cos³ A - 3 cos A33、正切(tan)的三倍角公式tan 3A = (3 tan A - tan³ A) / (1 - 3 tan² A) 34、余切(cot)的三倍角公式cot 3A = (3 cot A - cot³ A) / (3 cot² A - 1) 35、正弦(sin)的四倍角公式sin 4A = 4 sin A cos A (2 cos² A - 1) 36、余弦(cos)的四倍角公式cos 4A = cos² 2A - sin² 2A37、正切(tan)的四倍角公式tan 4A = (4 tan A - 4 tan³ A) / (1 - 6 tan² A + tan⁴ A) 38、余切(cot)的四倍角公式cot 4A = (cot² 2A - 1) / 2 cot 2A39、正弦(sin)的半角公式sin (A/2) = ±√[(1 - cos A) / 2]40、余弦(cos)的半角公式cos (A/2) = ±√[(1 + cos A) / 2]41、正切(tan)的半角公式tan (A/2) = ±√[(1 - cos A) / (1 + cos A)]42、余切(cot)的半角公式cot (A/2) = ±√[(1 + cos A) / (1 - cos A)]43、正割(sec)的半角公式sec (A/2) = ±√[(1 + cos A) / (1 - cos A)]44、余割(cosec)的半角公式cosec (A/2) = ±√[(1 - cos A) / (1 + cos A)]45、正弦(sin)的万能公式a sin x +b cos x = √(a² + b²) sin(x + atan(b/a))46、余弦(cos)的万能公式a cos x -b sin x = √(a² + b²) cos(x + atan(b/a))47、正切(tan)的万能公式a tan x -b cot x = atan[(a sin x - b cos x)/(a cos x + b sin x)]48、余切(cot)的万能公式a cot x -b tan x = atan[(b sin x - a cos x)/(a sin x + b cos x)]49、正割(sec)的万能公式a sec x +b cosec x = 2 √(a² + b²) / [sin(2x + atan(b/a)) + sin(2x - atan(b/a))]50、余割(cosec)的万能公式a cosec x +b sec x = 2 √(a² + b²) / [sin(2x + atan(b/a)) - sin(2x - atan(b/a))]51、弧度制与角度制的转换公式弧度制 = 角度制× π / 180角度制 = 弧度制× 180 / π52、三角函数的图像正弦(sin)的图像:余弦(cos)的图像:正切(tan)的图像:余切(cot)的图像:正割(sec)的图像:余割(cosec)的图像:以上是三角函数公式的大全,通过掌握这些公式可以更深入地了解三角函数的性质和应用,有助于提高数学水平。
三角函数余切,正割,余割和差角,半角,二倍角等公式

三角函数余切,正割,余割和差角,半角,二倍角等公式三角函数余切,正割,余割和差角,半角,二倍角等公式是在数学函数中十分重要的一部分,也是很多数学领域中研究和应用的一块意义重大的基石。
三角函数曲线中存在着余切,正割,余割和差角,半角,二倍角等几种不同的公式,今天我们就来聊聊这三种公式的概念,并讨论它们的区别及应用。
首先我们来了解一下三角函数余切公式。
余切,也叫余切函数,是一种三角函数。
它是对三角函数y=sinθ在各个θ值处取倒数后,得到一个新的函数,即Cotθ。
余切函数也可以写成y=1/sinθ。
由此可见,余切和正弦函数正好相反,因此,余切也被称为正弦的“倒数函数”。
接下来介绍的是三角函数正割公式。
正割函数,也称为正割函数,是三角函数当中的一种,以正割函数表示为y=cosθ。
正割函数是从余弦函数中求倒数得到的函数,因此又称正弦的“倒数函数”。
最后我们来介绍余割与差角,半角,二倍角等公式。
余割函数是一种三角函数,其中余割函数由余切函数和正割函数的乘积得到,表示为y=Cotθ * tanθ=sinθ/cosθ。
差角是指两个给定角(比如θ1和θ2)之间的角度差值。
差角公式可表示为θ=θ2-θ1。
半角是指一个给定角的一半,即θ2=θ1/2,表示为θ2=θ1/2。
而二倍角则是指一个给定角的两倍,即θ2=θ1*2,表示为θ2=θ1*2。
总结一下,以上三角函数余切,正割,余割和差角,半角,二倍角等公式的概念的区别和应用如下:余切:是在三角函数曲线中以余切函数表示的函数,它是对三角函数y=sinθ在各个θ值处取倒数后,得到一个新的函数,即Cotθ。
正割:是一种三角函数,以正割函数表示为y=cosθ,是从余弦函数中求倒数得到的函数,也叫正弦的“倒数函数”。
余割:是一种三角函数,由余切函数和正割函数的乘积得到,表示为y=Cotθ * tanθ=sinθ/cosθ。
差角:是指两个给定角(比如θ1和θ2)之间的角度差值,公式可表示为θ=θ2-θ1。
六种三角函数性质
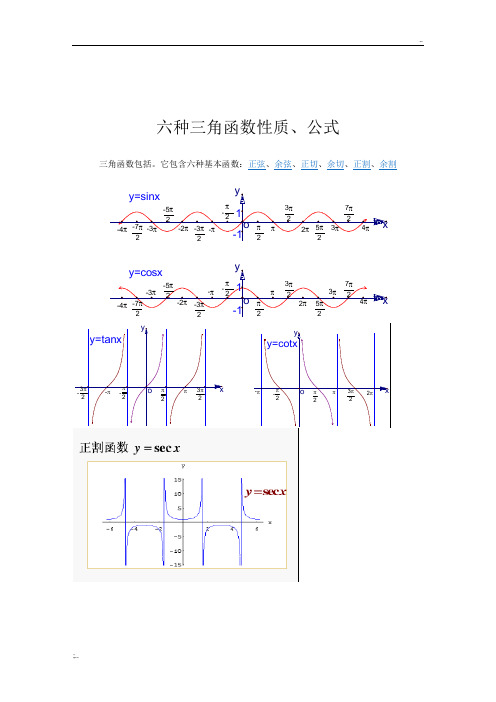
六种三角函数性质、公式三角函数包括。
它包含六种基本函数:正弦、余弦、正切、余切、正割、余割1-1y=sinx-3π2-5π2-7π27π25π23π2π2-π2-4π-3π-2π4π3π2ππ-πoy x1-1y=cosx-3π2-5π2-7π27π25π23π2π2-π2-4π-3π-2π4π3π2ππ-πoyxy=tanx3π2ππ2-3π2-π-π2oyxy=cotx3π2ππ22π-π-π2oyx.反三角函数:arcsinx arccosxarctanx arccotx函数y=sinx y=cosx y=tanx y=cotx定义域R R {x|x∈R且x≠kπ+2π,k∈Z}{x|x∈R且x≠kπ,k∈Z}值域[-1,1]x=2kπ+2π时y max=1x=2kπ-2π时y min=-1[-1,1]x=2kπ时y max=1x=2kπ+π时y min=-1R无最大值无最小值R无最大值无最小值周期性周期为2π周期为2π周期为π周期为π奇偶性奇函数偶函数奇函数奇函数单调性在[2kπ-2π,2kπ+2π]上都是增函数;在在[2kπ-π,2kπ]上都是增函数;在[2kπ,2kπ+π]上都是减函数在(kπ-2π,在(kπ,kπ+π)内都是减函数(k∈Z)y=secx的性质:(1)定义域,{x|x≠π/2+kπ,k∈Z}(2)值域,|secx|≥1.即secx≥1或secx≤-1;(3)y=secx是偶函数,即sec(-x)=secx.图像对称于y轴;(4)y=secx是周期函数.周期为2kπ(k∈Z,且k≠0),最小正周期T=2π.(5)正割与余弦互为倒数;余割与正弦互为倒数;(6)正割函数无限趋于直线x=π/2+Kπ;(7) 正割函数是无界函数;(8)正割函数的导数:(secx)′=secx×tarx;(9正割函数的不定积分:∫secxdx=ln∣secx+tanx∣+Cy=cscx的性1、定义域:{x|x≠kπ,k∈Z}2、值域:{y|y≤-1或y≥1}3、奇偶性:奇函数4、周期性:最小正周期为2π5、图像:图像渐近线为:x=kπ ,k∈Z 余割函数与正弦函数互为倒数第一部分三角函数公式·两角和与差的三角函数cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)·和差化积[/url]公式:sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]·积化和差[/url]公式:sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]·倍角公式[/url]:sin(2α)=2sinα·cosα=2/(tanα+cotα)cos(2α)=(cosα)^2-(sinα)^2=2(cosα)^2-1=1-2(sinα)^2tan(2α)=2tanα/(1-tan^2α)cot(2α)=(cot^2α-1)/(2cotα)sec(2α)=sec^2α/(1-tan^2α)csc(2α)=1/2*secα·cscα·三倍角公式:sin(3α) = 3sinα-4sin^3α = 4sinα·sin(60°+α)sin(60°-α)cos(3α) = 4cos^3α-3cosα = 4cosα·cos(60°+α)cos(60°-α)tan(3α) = (3tanα-tan^3α)/(1-3tan^2α) = tanαtan(π/3+α)tan(π/3-α)cot(3α)=(cot^3α-3cotα)/(3cot^2α-1)·n倍角公式:sin(nα)=ncos^(n-1)α·sinα-C(n,3)cos^(n-3)α·sin^3α+C(n,5)cos^(n-5)α·sin^5α-…cos(nα)=cos^nα-C(n,2)cos^(n-2)α·sin^2α+C(n,4)cos^(n-4)α·sin^4α-…·半角公式[/url]:sin(α/2)=±√((1-cosα)/2)cos(α/2)=±√((1+cosα)/2)tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinαcot(α/2)=±√((1+cosα)/(1-cosα))=(1+cosα)/sinα=sinα/(1-cosα)sec(α/2)=±√((2secα/(secα+1))csc(α/2)=±√((2secα/(secα-1))·辅助角公式:Asinα+Bcosα=√(A^2+B^2)sin(α+φ)(tanφ=B/A)Asinα+Bcosα=√(A^2+B^2)cos(α-φ)(tanφ=A/B)·万能公式sin(a)= (2tan(a/2))/(1+tan^2(a/2))cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))tan(a)= (2tan(a/2))/(1-tan^2(a/2))·降幂公式sin^2α=(1-cos(2α))/2=versin(2α)/2cos^2α=(1+cos(2α))/2=covers(2α)/2tan^2α=(1-cos(2α))/(1+cos(2α))·三角和的三角函数:sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·si nγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·co sγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)·其它公式·两角和与差的三角函数cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)=sinα/(1-cosα) ·和差化积[/url]公式:sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]·积化和差[/url]公式:sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]·倍角公式[/url]:sin(2α)=2sinα·cosα=2/(tanα+cotα)cos(2α)=(cosα)^2-(sinα)^2=2(cosα)^2-1=1-2(sinα)^2tan(2α)=2tanα/(1-tan^2α)cot(2α)=(cot^2α-1)/(2cotα)sec(2α)=sec^2α/(1-tan^2α)csc(2α)=1/2*secα·cscα·三倍角公式:sin(3α) = 3sinα-4sin^3α = 4sinα·sin(60°+α)sin(60°-α)cos(3α) = 4cos^3α-3cosα = 4cosα·cos(60°+α)cos(60°-α)tan(3α) = (3tanα-tan^3α)/(1-3tan^2α) = tanαtan(π/3+α)tan(π/3-α)cot(3α)=(cot^3α-3cotα)/(3cot^2α-1)·n倍角公式:sin(nα)=ncos^(n-1)α·sinα-C(n,3)cos^(n-3)α·sin^3α+C(n,5)cos^(n-5)α·sin^5α-…cos(nα)=cos^nα-C(n,2)cos^(n-2)α·sin^2α+C(n,4)cos^(n-4)α·sin^4α-…·半角公式[/url]:sin(α/2)=±√((1-cosα)/2)cos(α/2)=±√((1+cosα)/2)tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinαcot(α/2)=±√((1+cosα)/(1-cosα))=(1+cosα)/sinαsec(α/2)=±√((2secα/(secα+1))csc(α/2)=±√((2secα/(secα-1))·辅助角公式:Asinα+Bcosα=√(A^2+B^2)sin(α+φ)(tanφ=B/A)Asinα+Bcosα=√(A^2+B^2)cos(α-φ)(tanφ=A/B)·万能公式sin(a)= (2tan(a/2))/(1+tan^2(a/2))cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))tan(a)= (2tan(a/2))/(1-tan^2(a/2))·降幂公式sin^2α=(1-cos(2α))/2=versin(2α)/2cos^2α=(1+cos(2α))/2=covers(2α)/2tan^2α=(1-cos(2α))/(1+cos(2α))·三角和的三角函数:sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·si nγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·co sγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)·其它公式1+sin(a)=(sin(a/2)+cos(a/2))^2 1-sin(a)=(sin(a/2)-cos(a/2))^2csc(a)=1/sin(a) sec(a)=1/cos(a)cos30=sin60sin30tanα+cotα=2/sin2αtanα-cotα=-2cot21+cos2α=2cos^2α1-cos2α=2sin^2α1+sinα=[sin(α/2)+cos(α/2)]^21+sin(a)=(sin(a/2)+cos(a/2))^2 1-sin(a)=(sin(a/2)-cos(a/2))^2 csc(a)=1/sin(a) sec(a)=1/cos(a)cos30=sin60sin30=cos60·推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos^2α1-cos2α=2sin^2α1+sinα=[sin(α/2)+cos(α/2)]^2。
初中数学 什么是角的余割

初中数学什么是角的余割、正割和余切的特殊值角的余割、正割和余切函数是三角函数家族的一部分,它们在数学中有着重要的应用。
在了解这些函数的特殊值之前,我们先来回顾一下正弦、余弦和正切函数的特殊值。
1. 正弦函数的特殊值:正弦函数的图像是一个波动的曲线,它在数学坐标系中以原点为中心上下波动。
正弦函数在某些特定的角度值上有着特殊的函数值。
以下是一些常见的正弦函数的特殊值:- 正弦函数在角度为0度时的函数值为0,即sin(0) = 0。
- 正弦函数在角度为90度时的函数值为1,即sin(90°) = 1。
- 正弦函数在角度为180度时的函数值为0,即sin(180°) = 0。
- 正弦函数在角度为270度时的函数值为-1,即sin(270°) = -1。
- 正弦函数在角度为360度时的函数值为0,即sin(360°) = 0。
2. 余弦函数的特殊值:余弦函数的图像也是一个波动的曲线,它在数学坐标系中以最高点或最低点为中心左右波动。
余弦函数在某些特定的角度值上有着特殊的函数值。
以下是一些常见的余弦函数的特殊值:- 余弦函数在角度为0度时的函数值为1,即cos(0) = 1。
- 余弦函数在角度为90度时的函数值为0,即cos(90°) = 0。
- 余弦函数在角度为180度时的函数值为-1,即cos(180°) = -1。
- 余弦函数在角度为270度时的函数值为0,即cos(270°) = 0。
- 余弦函数在角度为360度时的函数值为1,即cos(360°) = 1。
3. 正切函数的特殊值:正切函数的图像是一条无限延伸的曲线,它在数学坐标系中以原点为中心左右摇摆。
正切函数在某些特定的角度值上有着特殊的函数值。
以下是一些常见的正切函数的特殊值:- 正切函数在角度为0度时的函数值为0,即tan(0) = 0。
- 正切函数在角度为45度时的函数值为1,即tan(45°) = 1。
初中数学 什么是角的余割

初中数学什么是角的余割、正割和余切的奇偶性角的余割、正割和余切函数是三角函数家族的一部分,它们在数学中有着重要的应用。
在了解这些函数的奇偶性之前,我们先来回顾一下正弦、余弦和正切函数的奇偶性。
1. 正弦函数的奇偶性:正弦函数的图像是一个波动的曲线,它在数学坐标系中以原点为中心上下波动。
正弦函数是一个奇函数,也就是说,当角度x为任意实数时,有以下关系成立:sin(-x) = -sin(x)2. 余弦函数的奇偶性:余弦函数的图像也是一个波动的曲线,它在数学坐标系中以最高点或最低点为中心左右波动。
余弦函数是一个偶函数,也就是说,当角度x为任意实数时,有以下关系成立:cos(-x) = cos(x)3. 正切函数的奇偶性:正切函数的图像是一条无限延伸的曲线,它在数学坐标系中以原点为中心左右摇摆。
正切函数是一个奇函数,也就是说,当角度x为任意实数时,有以下关系成立:tan(-x) = -tan(x)有了对正弦、余弦和正切函数奇偶性的了解,我们现在来讨论角的余割、正割和余切函数的奇偶性。
1. 余割函数的奇偶性:余割函数是正弦函数的倒数,即cosec(x) = 1/sin(x)。
根据正弦函数的奇偶性,我们可以推导出余割函数的奇偶性。
当角度x为任意实数时,有以下关系成立:cosec(-x) = 1/sin(-x) = 1/(-sin(x)) = -cosec(x)根据上述推导,我们可以得出结论:余割函数是一个奇函数,即cosec(-x) = -cosec(x)。
2. 正割函数的奇偶性:正割函数是余弦函数的倒数,即sec(x) = 1/cos(x)。
根据余弦函数的奇偶性,我们可以推导出正割函数的奇偶性。
当角度x为任意实数时,有以下关系成立:sec(-x) = 1/cos(-x) = 1/cos(x) = sec(x)根据上述推导,我们可以得出结论:正割函数是一个偶函数,即sec(-x) = sec(x)。
3. 余切函数的奇偶性:余切函数是正切函数的倒数,即cot(x) = 1/tan(x)。
分别是_正弦_余弦_正切_余切_正割_余割

维基百科+k是一个整数.当x=+∞ N/A当x=-∞N/A 最大值(,∞) 最小值(,-∞)其他性质渐近线 N/A 根 无实根临界点 k π-π/2拐点 k π 不动点 0k 是一个整数.反正切反余切反正割反余割百度文库下载分别是正弦余弦正切余切正割余割角θ的所有三角函数(见:函数图形曲线)在平面直角坐标系xOy中,从点O引出一条射线OP,设旋转角为θ,设OP=r,P点的坐标为(x,y)有正弦函数sinθ=y/r余弦函数cosθ=x/r正切函数tanθ=y/x余切函数cotθ=x/y正割函数secθ=r/x余割函数cscθ=r/y(斜边为r,对边为y,邻边为x。
)以及两个不常用,已趋于被淘汰的函数:正矢函数versinθ =1-cosθ余矢函数coversθ =1-sinθ正弦(sin):角α的对边比上斜边余弦(cos):角α的邻边比上斜边正切(tan):角α的对边比上邻边余切(cot):角α的邻边比上对边正割(sec):角α的斜边比上邻边余割(csc):角α的斜边比上对边[编辑本段]同角三角函数间的基本关系式:·平方关系:sin^2α+cos^2α=11+tan^2α=sec^2α1+cot^2α=csc^2α·积的关系:sinα=tanα×cosαcosα=cotα×sinαtanα=sinα×secαcotα=cosα×cscαsecα=tanα×cscαcscα=secα×cotα·倒数关系:tanα ·cotα=1sinα ·cscα=1cosα ·secα=1商的关系:sinα/cosα=tanα=secα/cscαcosα/sinα=cotα=cscα/secα直角三角形ABC中,角A的正弦值就等于角A的对边比斜边,余弦等于角A的邻边比斜边正切等于对边比邻边,·[1]三角函数恒等变形公式·两角和与差的三角函数:cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβta n(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)·三角和的三角函数:sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)·辅助角公式:Asinα+Bcosα=(A²+B²)^(1/2)sin(α+arctan(B/A)),其中sint=B/(A²+B²)^(1/2)cost=A/(A²+B²)^(1/2)tant=B/AAsinα-Bcosα=(A²+B²)^(1/2)cos(α-t),tant=A/B·倍角公式:sin(2α)=2sinα·cosα=2/(tanα+cotα)cos(2α)=cos²(α)-sin²(α)=2cos²(α)-1=1-2sin²(α)tan(2α)=2tanα/[1-tan²(α)]·三倍角公式:sin(3α)=3sinα-4sin³(α)=4sinα·sin(60+α)sin(60-α)cos(3α)=4cos³(α)-3cosα=4cosα·cos(60+α)cos(60-α)tan(3α)=tan a · tan(π/3+a)· tan(π/3-a)·半角公式:sin(α/2)=±√((1-cosα)/2)cos(α/2)=±√((1+cosα)/2)tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinα·降幂公式sin²(α)=(1-cos(2α))/2=versin(2α)/2cos²(α)=(1+cos(2α))/2=covers(2α)/2tan²(α)=(1-cos(2α))/(1+cos(2α))·万能公式:sinα=2tan(α/2)/[1+tan²(α/2)]cosα=[1-tan²(α/2)]/[1+tan²(α/2)]tanα=2tan(α/2)/[1-tan²(α/2)]·积化和差公式:sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]·和差化积公式:sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]·推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos²α1-cos2α=2sin²α1+sinα=(sinα/2+cosα/2)²·其他:sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1)/n]=0cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*(n-1)/n]=0 以及sin²(α)+sin²(α-2π/3)+sin²(α+2π/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0cosx+cos2x+...+cosnx= [sin(n+1)x+sinnx-sinx]/2sinx证明:左边=2sinx(cosx+cos2x+...+cosnx)/2sinx=[sin2x-0+sin3x-sinx+sin4x-sin2x+...+ sinnx-sin(n-2)x+sin(n+1)x-sin(n-1)x]/2sinx (积化和差)=[sin(n+1)x+sinnx-sinx]/2sinx=右边等式得证sinx+sin2x+...+sinnx= - [cos(n+1)x+cosnx-cosx-1]/2sinx证明:左边=-2sinx[sinx+sin2x+...+sinnx]/(-2sinx)=[cos2x-cos0+cos3x-cosx+...+cosnx-cos(n-2)x+cos(n+1)x-cos(n-1)x]/(-2sinx)=- [cos(n+1)x+cosnx-cosx-1]/2sinx=右边等式得证三倍角公式推导sin3a=sin(2a+a)=sin2acosa+cos2asina=2sina(1-sin²a)+(1-2sin²a)sina=3sina-4sin³acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos²a-1)cosa-2(1-sin²a)cosa=4cos³a-3cosasin3a=3sina-4sin³a=4sina(3/4-sin²a)=4sina[(√3/2)²-sin²a]=4sina(sin²60°-sin²a)=4sina(sin60°+sina)(sin60°-sina)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°+a)/2]=4sinasin(60°+a)sin(60°-a)cos3a=4cos³a-3cosa=4cosa(cos²a-3/4)=4cosa[cos²a-(√3/2)²]=4cosa(cos²a-cos²30°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°)/2]}=-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得tan3a=tanatan(60°-a)tan(60°+a)[编辑本段]三角函数的诱导公式公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)=sinαcos(2kπ+α)=cosαtan(2kπ+α)=tanαcot(2kπ+α)=cotα公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotα公式三:任意角α与-α的三角函数值之间的关系:sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotα公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotα公式六:π/2±α及3π/2±α与α的三角函数值之间的关系:sin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanαsin(3π/2+α)=-cosαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-tanαsin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=cotαcot(3π/2-α)=tanα(以上k∈Z)定名法则90°的奇数倍+α的三角函数,其绝对值与α三角函数的绝对值互为余函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
曹振卿
一、余切:
余切函数的性质
(1)、定义域:{x|x≠kπ,k∈Z}
(2)、值域:实数集R当x→2kπ时,y→∞;当x→(2k+1)π时,y→-∞;
(3)、奇偶性:奇函数,可由诱导公式cot(-x)=-cotx推出
图像关于原点对称,实际上所有的零点都是它的对称中心
(4)、周期性是周期函数,周期为kπ(k∈Z且k≠0),最小正周期T=π;
(5)、单调性在每一个开区间(kπ,(k+1)π),k∈Z上都是减函数,在整个定义域上不具有单调性。
(6)、对称性中心对称:关于点(kπ/2,0)k∈Z 中心对称
二、正割余割:
粗线是正割函数,细线是余割函数
y=secx的性质:
(1)定义域,{x|x≠π/2+kπ,k∈Z}
(2)值域,|secx|≥1.即secx≥1或secx≤-1;
(3)y=secx是偶函数,即sec(-x)=secx.图像对称于y轴;
(4)y=secx是周期函数.周期为2kπ(k∈Z,且k≠0),最小正周期T=2π.(5)正割与余弦互为倒数;余割与正弦互为倒数;
(6)正割函数无限趋于直线x=π/2+Kπ;
(7) 正割函数是无界函数;。
