农作物施肥效果分析讲义全
农作物施肥效果分析

农作物施肥效果分析组号:第04组农作物施肥效果分析摘要本文通过MATLAB研究N、P、K对总产量的影响作用,通过最小二乘曲线拟合出各个元素分别对总产量影响的曲线,研究曲线的性质给出改进的措施。
由于研究单个元素对于总产量的影响对于实际应用没有很好的指导作用,所以运用逐步回归法和MATLAB求出各因素对于总产量影响的大小,求出N、P、K共同作用于总产量的关系式,给出更贴合实际的改进。
模型一为分别研究各元素的量与总产量的关系,通过求出N、P、K施肥量分别与总产量的关系式,我们最终得出:对于土豆来说,当N为289.5kg/ha 时,获得最大产量为43.37t/ha;当P超过200kg/ha时增量,产量基本不变;当K为317.5kg/ha时,获得最大产量40.96t/ha。
对于生菜来说,当N为213.7kg/ha时,获得最大产量20.01t/ha;当P大于400kg/ha时,产量基本不变;当K在200kg/ha~400kg/ha时,产量基本不变,而与其他不同的是,在大于400时产量随K施肥量而增加。
模型二为N、P、K三种元素对于产量的综合影响。
对于土豆来说,在N为317.1667kg/ha、P为210.5kg/ha、K为367.5kg/ha时,得到最大产量为39.70998t/ha。
对于生菜来说,在N为169.5kg/ha时、P为198.25kg/ha,N 为500kg/ha时,得到最大产量为33.25459t/ha。
模型三为针对当前市场情况下三种肥料与土豆生菜的价格,建立总利润与成本之间的关系式,通过Lingo得出最优解,从应用价值方面做出了合理的预算与规划。
关键字:回归分析、残差分析、多项式拟合。
1、问题重述与分析本题要求为通过研究N、P、K三种肥料对土豆和生菜的作用,给出反应施肥量与产量关系的模型。
通过对各个肥料进行单因素实验,在其他两种肥料保持在第七个水平不变的情况下,成倍改变另一种肥料的量,给出了各元素施肥量与总产量的数量关系表。
1992年A题农作物施肥效果分析
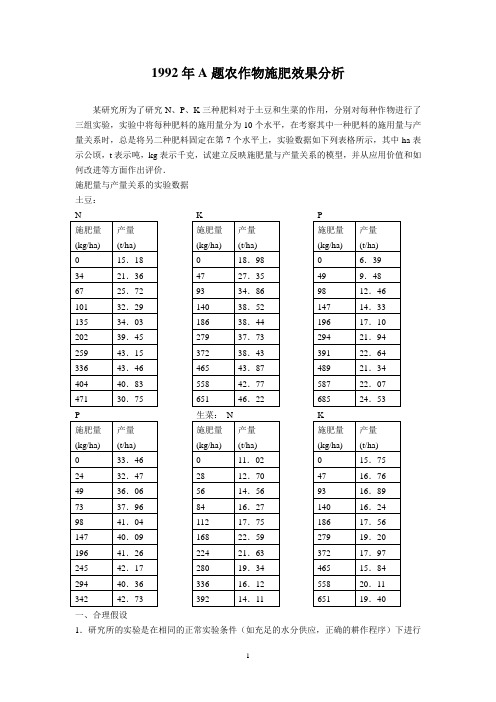
1992年A题农作物施肥效果分析某研究所为了研究N、P、K三种肥料对于土豆和生菜的作用,分别对每种作物进行了三组实验,实验中将每种肥料的施用量分为10个水平,在考察其中一种肥料的施用量与产量关系时,总是将另二种肥料固定在第7个水平上,实验数据如下列表格所示,其中ha表示公顷,t表示吨,kg表示千克,试建立反映施肥量与产量关系的模型,并从应用价值和如何改进等方面作出评价.施肥量与产量关系的实验数据土豆:一、合理假设1.研究所的实验是在相同的正常实验条件(如充足的水分供应,正确的耕作程序)下进行的,产量的变化是由施肥量的改变引起的,产量与施肥量之间满足一定的规律. 2.土壤本身已含有一定数量的氮、磷、钾肥,即具有一定的天然肥力. 3.每次实验是独立进行的,互不影响. 符号说明: W :农作物产量. x :施肥量.N 、P 、K :氮、磷、钾肥的施用量. Tw :农产品价格. Tx :肥料价格.Tn,Tp,Tk :氮、磷、钾肥的价格.a,b,b 0,b 1,b 2,c,c 0,c 1,c ’0,c ’1:常数(对特定肥料,特定农作物而言). 二、问题分析农学规律[2]表明,施肥量与产量满足下图所示关系,它分成三个不同的区段,在第一区段,当施肥量比较小时,作物产量随施肥量的增加而迅速增加,第二区段,随着施肥量的增加,作物产量平缓上升,第三区段,施肥量超过一定限度后,产量反而随施肥量的增加而下降. 图14-1 施肥量与产量的一般关系为考察氮、磷、钾三种肥料对作物的施肥效果,我们以氮、磷、钾的施用量为自变量;土豆和生菜的产量为因变量描点作图.从中看出,氮肥对于作物产量的贡献大致呈指数关系,磷肥对于作物产量的关系大致为分段直线形式,至于钾肥,对土豆而言,大致呈指数关系,对生菜而言,随着施用量的增加,产量的上升幅度很小.这样,我们得到了对施肥效果的定性认识.在长期的实践中,农学家们已经总结出关于作物施肥效果的经验规律,并建立了相应的理论[3].1.Nicklas 和Miller 理论:设h 为达到最高产量时的施肥量,边际产量(即产量W 对施肥量x 的导数)dxdW 与(h-x)成正比例关系.dW/dx=a(h-x),(1) 从而 W=b 0+b 1x+b 2x 2.(2)2.米采利希学说:只增加某种养分时,引起产量的增加与该种养分供应充足时达到的最高产量A 与现在产量W 之差成正比. dW/dx=c(A-W),(3)从而 W=A (1-exp(-cx)).(4)考虑到土壤本身的天然肥力,上式可修正为 W=A (1-exp(-cx+b)).(5)3.英国科学家博伊德发现,在某些情况下,将施肥对象按施肥水平分成几组,则各组的效应曲线就呈直线形式.若按水平分成二组,可以用下式表示:,)x x x (x c c )x x 0(x c c n i 10i 10⎩⎨⎧<≤'+'<≤+(6) 我们假设该研究所的实验是在正常条件下进行的,因而表14-1所示的施肥量与产量的数据应该满足上述规律(对不同肥料,不同作物而言可以满足不同的规律).以这些理论为依据,就可以对作物施肥效果进行回归分析.从实验设计的角度来看,该研究所采用的设计方案是因素轮换法,即在考察每一种肥料的效应时,总将另二种肥料的施用量固定在第7个水平上.采用这种设计方法,无法估算出三种肥料间的交互效应,因此,我们将每组实验看成单因素实验,并根据实验结果,给出反映施肥量与产量关系的一元肥料效应方程及效应曲线. 三、模型与结果我们建立了一元肥料效应回归模型,并在回归分析之前,用Chauvenent 准则进行修正,剔除异常值.根据对问题的初步分析,氮肥的施肥效果应满足Nicklas 和Miller 理论所描述的关系,运用二次多项式回归,得到氮肥对土豆的效应方程:W=14.74+0.197n-0.00034n 2.(7) 氮肥对生菜的效应方程:W=10.23+0.101n-0.00024n 2.(8) 氮肥的效应曲线如图14-2,图14-3所示.磷肥的施用对作物产量的增加表现为分段直线形式,运用线性回归,得到磷肥对土豆的效应方程:⎩⎨⎧≤≤+<≤+=).342p 04.101(p 0059.0968.39),04.101p 0(p 084.0077.32w (9)磷肥对生菜的效应方程:⎩⎨⎧≤≤+<≤+=).685k 54.202(k 00472.0196.20),54.202k 0(k 052.0809.6w (10)磷肥对作物的效应曲线如图14-4,图14-5所示.从钾肥对土豆的实验数据可以看出,当施用量超过一定限度后,产量的增加很不明显,因此用(5)式来描述其施肥效果是合理的,用指数回归分析得到 钾肥对土豆的效应方程:W(k)=42.17(1-exp(-0.01k-0.641)).(11) 对生菜来说,钾肥的施用对产量的影响很小.通过线性回归得到 钾肥对生菜的效应方程:W (k )=16.2269+0.00395k.(12) 钾肥对生菜的效应曲线如图14-6,图14-7所示.可以得到每种肥料的最佳施用量,这无疑为生产提供了极为重要的信息.此外,模型的建立并不依赖于任何特殊条件,这种方法可以适用于任何地区,考察任意一种肥料对于作物产量的效应,具有一定的推广价值.本文没有给出三种肥料用量的最佳组合,因为试验方法本身决定了无法估计肥料的交互效应,因而无法计算最佳施肥比例.如果对实验方法加以改进,可以将我们的模型推广为总效应模型,并根据下列式子(当肥料的边际产量之比等于其价格的反比时,即为肥料施用量的最佳配比)来计算最佳施肥比例:⎪⎪⎩⎪⎪⎨⎧=∂∂∂∂=∂ω∂∂∂.T :T K )k ,p ,n (w :P )k ,p ,n (W ,T :T P)k ,p ,n (:N )k ,p ,n (W p k N p (14) 七、关于交互效应的深入讨论和实验方法的建议 在农业学中[4],可以用三元二次多项式来描述氮、磷、钾三种肥料的综合施肥效果,用下列式子表示:W (N ,P ,K )=B 0+B N N+B P P+B K K+B NN N 2+B PP P 2+B KK K 2+B NP NP+B NK NK+B KP KP . 可以用回归的方法,求出回归系数,但对本题而言,下列处理[1]表明,交互系数是无法确定的,由于所给出的实验全都分布于三条平行于坐标轴的直线上,并且这三条直线交于公共点(n0,p0,k0),以n=N-n0,p=P-p0,k=K-k0作为现的变量,称为相对施肥量,则相对产量W(n,p,k)可表示为w(n,p,k)=b0+b n n+b p p+b k k+b nn n2+b pp p2+b kk k2+b np np+b nk nk+b kp kp.在新的坐标系中,所有的试验点都在坐标轴上,至少有两个坐标为0,这样所有的交叉项全消失了,即不可能由实验结果来确定交互系数,因而试验方法本身注定了交互效应是无法求出的.为估计肥料的交互效应,我们建议该研究所进行正交试验设计[5],将氮、磷、钾肥的用量以第7个水平为中心等问题分为五个水平,作一个五水平三因子的正交表,总共需进行15次实验,将所得数据运用直观分析和方差分析,可以方便地得到氮、磷、钾肥对作物的总效应.试验安排如下.表正交设计表。
数学建模课程设计报告---施肥效果分析

数学建模课程设计报告---施肥效果分析设计报告标题:施肥效果分析一、问题描述:在农作物种植过程中,施肥是提高农作物产量和质量的重要手段之一。
然而,在实际操作中,由于施肥的时间、剂量和方法等因素的不同,施肥效果也会有所差异。
本课程设计旨在通过数学建模的方法,分析施肥对农作物产量的影响,找出最佳施肥方案。
二、问题分析:1. 施肥时间:不同时间段施肥对农作物产量的影响不同,需要确定最佳的施肥时间;2. 施肥剂量:过少的施肥剂量无法满足农作物的生长需要,过多的施肥剂量可能造成浪费和环境污染,需要确定最佳的施肥剂量;3. 施肥方法:不同施肥方法对农作物产量的影响也不同,需要确定最佳的施肥方法;4. 施肥效果评价:需要建立一个评价指标体系来评价不同施肥方案的效果。
三、数学模型的建立:1. 施肥时间模型:假设农作物生长过程分为若干个时期,每个时期的生长速度是不同的。
我们可以建立一个函数来描述农作物在不同施肥时间下的生长速度变化,通过求函数的最大值或最小值来确定最佳的施肥时间。
2. 施肥剂量模型:假设农作物的生长速度与施肥剂量是线性相关的。
建立一个方程,使得农作物的生长速度最大化,然后通过求解该方程来确定最佳的施肥剂量。
3. 施肥方法模型:假设农作物的生长速度与施肥方法有关,可以建立一个函数来描述农作物在不同施肥方法下的生长速度变化。
通过求函数的最大值或最小值来确定最佳的施肥方法。
4. 施肥效果评价模型:建立一个评价指标体系,包括农作物产量、养分利用率、土壤质量等指标,通过加权计算得到一个综合评分来评价不同施肥方案的效果。
四、数据分析与结果验证:根据实际的农作物生长数据和施肥实验数据,进行数据分析,验证所建立的数学模型的有效性和准确性。
五、结论与改进:根据数学模型的分析结果得出最佳的施肥方案,同时提出改进意见和建议,为农作物种植提供科学的施肥指导。
附录:1. 农作物生长数据和施肥实验数据的详细信息;2. 用于建模和计算的数学公式和算法的详细说明;3. 模拟计算和数据分析的代码和程序。
施肥效果分析

施肥效果分析本文研究了营养素对作物的产量的影响,分析了不同营养素对不同作物生长产量的差异,建立了施肥效果模型。
并采用控制变量法和计算机数据拟合法建立了营养素对作物生长影响的模型。
根据研究所所得的营养素与作物产量的数据,运用MATLAB得到营养素与作物产量关系的散点图。
进一步运用拟合工具进行拟合数据,得到多项式的二次,三次函数和正弦函数一项,两项和三项函数。
利用方差比较,得到N在三次多项式时拟合度最好,而P和K 在二次多项式时拟合度最好。
本文最后总结了模型的优点和不足之处,并对施肥效果改进意见。
关键词:散点图,方差比较,拟合方程,控制变量一.问题重述作物生长所需的营养素主要是氮(N)、钾(K)、磷(P)。
为研究三种营养素对作物生长的影响,某作物研究所在该地区选取土豆与生菜做了一定数量的实验,实验过程中当一个营养素的施肥量变化时,总将另二个营养素的施肥量保持在最适宜植物生长状态。
分析数据得出施肥量与产量之间关系,并对所得结果从应用价值与如何改进等方面作出估价。
二.问题分析氮元素可促进植株茎叶的生长,更好的进行光合作用。
磷元素具有一部分促根发育的作用还具有促进开花的作用。
钾元素主要是促进果实的干物质积累,用来膨大果实。
增加产量。
由施肥量与产量的关系表格可得营养素对土豆生菜的产量有明显的促进作用。
根据农业期刊《Biology and fertility of soils》,一般来说,产量W可以用营养素施肥量的多项正弦函数表示,故做拟合曲线并代入试验数据求得关系表达式;同时联想到Logistic函数的导函数曲线为二次多项式(也是随着自变量先增后减),因此作一次二次以及三次多项式拟合,并进行比较。
三.基本假设①每次试验独立且试验条件(如环境条件,种植密度,土壤条件)相同;②由于数据由研究所提供,所以假设试验数据不会出现较大误差;③三种元素的使施用量同作物产量有一定的函数关系,同一种元素对不同作物的作用表现为同一类的函数关系;④忽略土壤中原有的N、P、K对作物生长的影响;⑤三种元素对作物增长的作用是相互独立的;四.名词解释和符号说明名词解释:种植密度:单位面积作物种植量符号说明:①pi(i=1,2,3.....)多项式系数②ai,bi,ci正弦函数各项系数和常数项五.模型建立和求解采用MATLAB2021b中配置的curve fitting tool(曲线拟合工具),直接输入数据,进行曲线拟合。
《农作物施肥技术》PPT课件

13.01.2021
精选ppt
35
有机肥料
有机肥对于作物生长和土壤培肥具有非 常重要的意义。普通的农家肥存在脏、 臭、不卫生、肥效慢、体积大、使用不 方便等缺点,而经过工厂发酵加工和无 害化处理的商品有机肥,就较好地克服 了这些缺点。商品有机肥主要具有以下 作用:
13.01.2021
精选ppt
36
13.01.2021
精选ppt
41
六是改善土壤性能。
如果土壤有机质含量低,沙土就会旱时 起粉尘,涝时易板结,粘土干时坚硬, 湿时泥泞,土壤的物理性能较差,施用 有机肥就会增加土壤有机质,逐步克服 这些弊端,使沙土不是很沙,粘土不是 很粘,从而方便耕作等农事操作,也有 利于作物生长。有机肥的这一作用也是 施用化肥所无法实现的。
13.01.2021
精选ppt
26
追肥:是指在作物生育期中施用的肥料, 它的目的是及时满足作物生育期间,特 别是强度营养期对养分的迫切需要。以 速效化肥为主,化学性质稳定。追肥一 般以氮肥为主,根外喷施也用氮、磷、 钾复合肥,磷钾肥一般以基肥为主。主 要方法有:条施、穴施、塞秧窝,撒施 结合灌水,根外喷施。
15
科学施肥的基本原则或基本要求。
提高作物(包括果树、蔬菜等)的产量 和品质。
13.01.2021
精选ppt
16
提高土壤肥力,用地养地结合。
13.01.2021
精选ppt
17
增加经济效益与社会效益。
13.01.2021
精选ppt
18
不污染土壤、水质和作物。
13.01.2021
精选ppt
19
必须理解的4个基本原理或称基本规律。
育期吸肥百分率分别是:苗期吸钾占2%; 现蕾到始花期吸收钾占9%;始花到盛花 期吸收钾占36%;盛花到吐絮期吸收钾 占42%;吐絮到拔杆吸收钾占11%。
农作物施肥效果分析

农作物施肥效果分析摘要由农作物生长的原理和长期的实践经验可知,氮、磷、钾三种肥料对农作物的生长起到至关重要的作用,其施肥量会影响作物最后的产量,且这三种肥料缺一不可。
究竟肥料的施肥量与产量有怎样的关系?本次实验以土豆和生菜这两种作物为例,研究氮、磷、钾三种肥料的施肥效果。
首先,根据实验数据描出施肥量与产量坐标关系的散点图,建立模型:2y ax bx c =++,在MATLAB 中拟合曲线,求出系数,从而得到N 对土豆的效应方程为:()2111111110.00030.197114.7416f x x x =-++P 对土豆的效应方程为:()2121212120.00010.071932.9161f x x x =-++K 对土豆的效应方程为:()2131313130.00010.075024.4144f x x x =-++N 对生菜的效应方程为:()2212121210.00020.101310.2294f x x x =-++P 对生菜的效应方程为:()2222222220.00010.0606 6.8757f x x x =-++ K 对生菜的效应方程为:()2232323230.00000.005116.2329f x x x =-++将多项式回归模型转化为多元线性回归模型进行检验,效果显著,从而模型成立。
然后,利用已经建立的施肥量与产量关系的模型,固定其中两种肥料的施肥量在第七个水平,建立收益与第三种肥料施肥量关系的模型,如:设土豆每公顷磷肥的施肥量为12x 时的最大利润为12W (元),有()12121212100024259337257000W f x x =⨯--⨯-⨯-当12x =349.5时获得的利润最大,最大利润为:12W =80625.5(元)。
最后通过计算比较,得到土豆的最佳施肥方案为:氮肥317/kg ha ,磷肥196/kg ha ,钾肥372/kg ha ;生菜的最佳施肥方案为:氮肥250.75/kg ha ,磷肥391/kg ha ,钾肥372/kg ha 。
农作物施肥效果分析

关于施肥对农作物生长影响的数学模型摘要:查阅资料,将促进作用分成两类:一种是一开始促进作用随施肥量增大而增大,达到最大值之后促进作用下降。
另一种是一开始促进作用明显,之后将趋于稳定的类型。
整理数据,通过matlab 进行数据拟合得出方程与图像。
分析土豆和生菜两组函数,可以看出氮磷钾肥料对两种作物促进程度不相同。
由此得出施肥量对产量的促进程度与作物种类有关。
但是两组实验,都是氮肥促进程度先上升后下降,磷肥、钾肥的促进程度基本一直上升。
通过查阅资料得出N P K 三种元素之间无相互影响,由此得出初等模型:)()()(z K c y P b x N a W ⨯+⨯+⨯=(其中a b c 为常数)。
进一步考虑,回归系数可能与施肥量有关,由此可以改进得出完善模型:)()()()y ()()('z K z c y P b x N x a W ⨯+⨯+⨯=。
最后,对模型进行分析,所得数据结果与题目所给数据结果接近。
说明完整模型适合农作物施肥效果分析。
在实际生活当中,氮磷钾肥相互之间是有影响的,所以通过类比《龙须草氮磷钾配方施肥的数学模型》【1】中的数学模型,将我们的模型便跟为:k mz ny lx jyz ixz hxy fz ey dx W +---+++++=222''(其中d 、e 、f 、h 、i 、j 、k 、l 、n 、m 都为常数)。
关键字:二次函数 对数函数 回归分析一、问题分析研究所分别对土豆和生菜进行了三组实验,由此研究N、P、K三种肥料对两种作物的作用。
实验中将每种肥料的施用量分为10个水平在考察其中一种肥料的施用量与产量关系是,总是将另外两种肥料固定在第7个水平上(实验数据见附录一)。
增施氮肥对促进植物生长健壮有明显作用。
但是氮肥用量不宜过多,过量施用氮肥时,有延长生长期、贪青晚熟的趋势。
钾与氮磷不同,它不是植物体内有机化合物的成分,钾呈离子状态溶于植物汁液当中,其主要功能与植物新陈代谢有关。
农作物施肥效果分析讲义
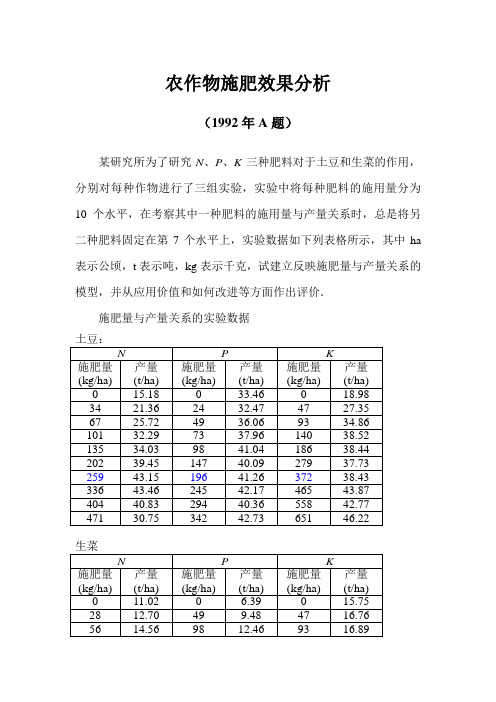
农作物施肥效果分析(1992年A题)某研究所为了研究N、P、K三种肥料对于土豆和生菜的作用,分别对每种作物进行了三组实验,实验中将每种肥料的施用量分为10个水平,在考察其中一种肥料的施用量与产量关系时,总是将另二种肥料固定在第7个水平上,实验数据如下列表格所示,其中ha 表示公顷,t表示吨,kg表示千克,试建立反映施肥量与产量关系的模型,并从应用价值和如何改进等方面作出评价.施肥量与产量关系的实验数据一、符号说明:W:农作物产量.x:施肥量.N、P、K:氮、磷、钾肥的施用量.C W:农产品价格.C N, C P, C K:氮、磷、钾肥的价格.a,b,b0,b1,b2,c,c0,c1,c’0,c’1:常数(对特定肥料,特定农作物而言)二、模型假设1. 研究所的实验是在相同的正常实验条件(如充足的水分供应,正确的耕作程序)下进行的,产量的变化是由施肥量的改变引起的,产量与施肥量之间满足一定的规律。
在实验中,除施肥量,其它影响因子(如环境条件、种植密度等)均处于同等水平。
2. 土壤本身已含有一定数量的氮、磷、钾肥,即具有一定的天然肥力(从数据可以看出,当各种养分的施肥量都为0时,产量并不为0)。
3. 每次实验是独立进行的,且对于N、P、K施用量来说无系统误差,模型的误差项均服从同分布的正态分布。
三、问题分析题目要求建立反映施肥量与产量关系的模型,显然这是一个回归分析的问题,但是什么样的回归模型能体现施肥量与产量之间的关系呢?这就需要从问题的实际背景出发来考察。
一元回归分析理论(1-17页)及其实现(25-30页)农学规律表明,施肥量与产量一般满足这样的关系:它分成三个不同的区段,在第一区段,当施肥量比较小时,作物产量随施肥量的增加而迅速增加,第二区段,随着施肥量的增加,作物产量平缓上升,第三区段,施肥量超过一定限度后,产量反而随施肥量的增加而下降在长期的实践中,农学家们已经总结出关于作物施肥效果的经验规律,并建立了相应的理论1.Nicklas和Miller理论:设h为达到最高产量时的施肥量,边际产量(即产量W对施肥量x的导数)d W/d x与(h-x)成正比例关系,即d W/d x=a(h-x) (1)从而W=b0+b1x+b2x2(2) 2. 米采利希学说:只增加某种养分时,引起产量的增加与该种养分供应充足时达到的最高产量A与现在产量W之差成正比,即dW/d x=c(A-W) (3) 从而W=A(1-exp(-cx))(4) 考虑到土壤本身的天然肥力,上式可修正为W =A (1-exp(-cx +b )) (5)3. 英国科学家博伊德发现,在某些情况下,将施肥对象按施肥水平分成几组,则各组的效应曲线就呈直线形式。
农作物施肥效果分析

农作物施肥效果分析摘要我们通过研究氮、磷、钾三种肥料对土豆和生菜的作用,來建立施肥量与产量关系的模型。
通过回归分析的方法,将所给的数据进行MATLAB L具箱拟合,并利用残差分析的方法,建立反映施肥量与产量关系的模型并检验分析,找到产量的最优解以及氮、磷、钾三种肥料的最优配合比,在耕地面积一定的情况下研究土豆或生菜可以达到得最大收益值。
由此我们建立的土豆产量模型为M = -12.8361 + 0.1903n + 0.0842p + O.O735^-O.OOO3n2一0.0002p2-0.0001k2 生菜产量模型为W2 = -0.4938 + 0.07561? + 0.0234p + 0.0067k 一0.0002??求解得到土豆产量的最值,当n= 317.1667, p = 210.5000, k = 367.5000时,得^imax = 39.71,氮磷钾肥料的最优配合比为1.5:1:1.74, 土豆是喜钾作物。
我们可以得出生菜的最值,当n = 224, p = 685, k= 372时,得w? = 24.53,可以看出生菜是喜磷作物。
在应用方面,为了直观的展示最大的利润以及最优配合比,设计了一个GUI人机交互界而,这样可以清晰明了表示获得的最大收益值。
关键词:回归分析MATLAB拟合残差分析最优配合比GUI人机交互界面一问题重述俗话说“民以食为天”,我们的生活与农作物的供应息息相关。
近年来,随着人口增多,耕地减少,所以化肥对农作物的生长、提高农作物的产量具有重耍的意义。
农作物除了吸收水分和空气屮二氧化碳以获得碳、氢、氧等元素外,还必须从土壤再吸收氮、磷、钾和其他矿质养分,并在太阳能的帮助下合成有机物质,以建造自己的有机机体,但土壤中的常量营养元素氮、磷、钾和其他矿质养分一般不能满足作物生长的需求,需要施用含氮、磷、钾的化肥來补充。
在本问题中,某研究所通过研究氮、磷、钾三种肥料对土豆和生菜的作用,來建立施肥最与产最关系的模型。
农作物施肥效果分析讲义

农作物施肥效果分析讲义
一.引言
农作物施肥是在农作物生长过程中,引入有机或无机肥料进行栽培,以改善土壤肥力,提升作物产量,提高农作物品质的一种栽培技术。
施肥可以增加农作物的产量和品质,并具有一定的经济效益。
因此,施肥是农业的重要组成部分,对提高农业产量、改善环境质量、提高农民收入以及保护农艺品种有重要意义。
二.施肥效果的主要影响因素
1.土壤成分
施肥效果受土壤结构和成分影响较大。
施肥时要充分考虑土壤中酸碱度、矿质养分含量等因素,以适应不同土壤的施肥要求。
携带有效性较强的肥料,其在土壤中的有效性受土壤结构和物理、化学、生物性状影响较大,这也会影响施肥的效果。
2.植物本身的性质
植物对肥料的利用效率有巨大的差异,受植物种类、生长阶段、环境温度、水分条件等因素影响,一些植物对施肥的反应可能会更好。
3.肥料种类
肥料的种类是影响施肥效果的重要因素。
无机肥料可提供养分,而有机肥料可改善土壤结构,获得较好的施肥效果。
同时,各种肥料的组成营养元素也影响施肥的效果,不同营养元素在作物营养需求不同,使用不当容易出现施肥过量等问题。
农作物施肥效果分析

农作物施肥效果分析摘要农作物施肥效果分析本文是对农作物施肥效果进行分析,首先分别就氮肥、磷肥、钾肥对产量的影响做了基本模型,其次基于基本模型用MATLAB对N、P、K对产量的影响做了回归分析模型。
针对氮肥、磷肥、钾肥的施用量,我们考虑三种肥料分别对产量的影响,定义了氮肥、磷肥、钾肥的施用量分别为X1、X2、X3,土豆和生菜的产量分别为Y1、Y2,用excel拟合出方程曲线,通过对基本模型的分析,发现基本模型比较分散,所以建立了回归模型用MATLAB求出回归系数等参数的值,发现和原始数据拟合程度较好,并对该方程求偏导,得出当产量最大时氮肥、磷肥、钾肥的施用量。
针对土豆的经济效益,最后扩展了土豆和生菜的利润模型,来解决何时获得最大经济效益的问题。
根据上述研究,我们认为所建立的模型简单易懂,可以用其在较短的时间内对大量的数据进行处理。
关键字:MATLAB 回归模型曲线拟合一、问题重述某研究所为了研究N、P、K、三种肥料对土豆和生菜的作用,分别对每种作物进行了三组实验,实验中将每种肥料的施用量分为10个水平,在考察其中的一种肥料施用量与产量关系时,总是将另两种肥料固定在第7个水平上,实验数据如下列表格所示,其中ha表示公顷,t表示吨,kg表示千克,试建立反映施用量与产量关系的模型,并从应用价值和如何改进等方面做出评价。
二、基本假设(1)不考虑土壤中原有的N、P、K的影响(2)假设土豆和生菜生长状态相同,即不考虑个体植株间的生长差异(3)假设土豆和生菜在同样的环境下生长,包括阳光,水分,温度湿度等三、符号说明四、问题的分析与准备本题目是为了探究N、P、K三种肥料的施肥量对土豆和生菜的作用,单独一种肥料对土豆和生菜的作用不相同,过量的肥料会造成植株“烧苗”。
所以每种肥料都有一定的施肥量才能保证土豆和生菜的产量最大。
根据所给的表格数据,首先来探究另外两种肥料固定在第七水平时,单独一种肥料对土豆和生菜产量的影响,建立单独一种肥料对产量影响的数学模型,通过MATLAB数学软件进行数据拟合,得到相应的数学模型。
农作物施肥效果分析

农作物施肥效果分析摘要我们通过研究氮、磷、钾三种肥料对土豆和生菜的作用,来建立施肥量与产量关系的模型。
通过回归分析的方法,将所给的数据进行MATLAB工具箱拟合,并利用残差分析的方法,建立反映施肥量与产量关系的模型并检验分析,找到产量的最优解以及氮、磷、钾三种肥料的最优配合比,在耕地面积一定的情况下研究土豆或生菜可以达到得最大收益值。
由此我们建立的土豆产量模型为w1=−12.8361+0.1903n+0.0842p+0.0735k−0.0003n2−0.0002p2−0.0001k2生菜产量模型为w2=−0.4938+0.0756n+0.0234p+0.0067k−0.0002n2求解得到土豆产量的最值,当n=317.1667,p=210.5000,k=367.5000时,得出w1max=39.71,氮磷钾肥料的最优配合比为1.5:1:1.74,土豆是喜钾作物。
我们可以得出生菜的最值,当n=224,p=685,k=372时,得w2=24.53,可以看出生菜是喜磷作物。
在应用方面,为了直观的展示最大的利润以及最优配合比,设计了一个GUI人机交互界面,这样可以清晰明了表示获得的最大收益值。
关键词:回归分析MATLAB拟合残差分析最优配合比GUI人机交互界面一问题重述俗话说“民以食为天”,我们的生活与农作物的供应息息相关。
近年来,随着人口增多,耕地减少,所以化肥对农作物的生长、提高农作物的产量具有重要的意义。
农作物除了吸收水分和空气中二氧化碳以获得碳、氢、氧等元素外,还必须从土壤再吸收氮、磷、钾和其他矿质养分,并在太阳能的帮助下合成有机物质,以建造自己的有机机体,但土壤中的常量营养元素氮、磷、钾和其他矿质养分一般不能满足作物生长的需求,需要施用含氮、磷、钾的化肥来补充。
在本问题中,某研究所通过研究氮、磷、钾三种肥料对土豆和生菜的作用,来建立施肥量与产量关系的模型。
实验中将每种肥料的施用量分为10个水平,在考察其中一种肥料的施用量与产量的关系时,把另两种肥料固定在第7个水平上,通过回归分析的方法,将所给的数据进行MATLAB拟合,从而建立反映施肥量与产量关系的模型,找到产量的最优解以及氮、磷、钾三种肥料的最优配合比,在耕地面积一定的情况下研究土豆和生菜可以达到的最大收益值,并从实际情况出发,评价该模型的优缺点。
农作物施肥效果分析

农作物施肥效果分析第14组赵国欣 20101164刘青海 20100658李莉 201007092011年全国大学生数学建模竞赛论文格式规范●本科组参赛队从A、B题中任选一题,专科组参赛队从C、D题中任选一题。
●论文用白色A4纸单面打印;上下左右各留出至少2.5厘米的页边距;从左侧装订。
●论文第一页为承诺书,具体内容和格式见本规范第二页。
●论文第二页为编号专用页,用于赛区和全国评阅前后对论文进行编号,具体内容和格式见本规范第三页。
●论文题目和摘要写在论文第三页上,从第四页开始是论文正文。
●论文从第三页开始编写页码,页码必须位于每页页脚中部,用阿拉伯数字从“1”开始连续编号。
●论文不能有页眉,论文中不能有任何可能显示答题人身份的标志。
●论文题目用三号黑体字、一级标题用四号黑体字,并居中;二级、三级标题用小四号黑体字,左端对齐(不居中)。
论文中其他汉字一律采用小四号宋体字,行距用单倍行距,打印时应尽量避免彩色打印。
●提请大家注意:摘要应该是一份简明扼要的详细摘要(包括关键词),在整篇论文评阅中占有重要权重,请认真书写(注意篇幅不能超过一页,且无需译成英文)。
全国评阅时将首先根据摘要和论文整体结构及概貌对论文优劣进行初步筛选。
●引用别人的成果或其他公开的资料(包括网上查到的资料) 必须按照规定的参考文献的表述方式在正文引用处和参考文献中均明确列出。
正文引用处用方括号标示参考文献的编号,如[1][3]等;引用书籍还必须指出页码。
参考文献按正文中的引用次序列出,其中书籍的表述方式为:[编号] 作者,书名,出版地:出版社,出版年。
参考文献中期刊杂志论文的表述方式为:[编号] 作者,论文名,杂志名,卷期号:起止页码,出版年。
参考文献中网上资源的表述方式为:[编号] 作者,资源标题,网址,访问时间(年月日)。
●在不违反本规范的前提下,各赛区可以对论文增加其他要求(如在本规范要求的第一页前增加其他页和其他信息,或在论文的最后增加空白页等);从承诺书开始到论文正文结束前,各赛区不得有本规范外的其他要求(否则一律无效)。
农作物施肥效果分析

农作物施肥效果分析摘要本文通过观察实验数据及考虑现实情况,先放弃进行全因素试验,只在部分因素水平下进行试验,观察能否较全面的求出尽可能最大产量对应的N、P、K的施肥量。
即首先进行了忽略相关性,对作物进行单一因素分析,将N肥P肥和K肥三种因素两定一变,通过matlab 软件将散点图汇出并通过最小二乘法拟合最相关的函数图像,分析找到产生最佳产量对应的最佳施肥量,建立出模型一。
鉴于三种营养素有相关性,可能存在1+1>2的效果,我们利用多元回归分析模拟出三元二次函数,并利用matlab编程求出最值,从而进行实验数据检验分析。
关键词:最小二乘法回归分析三元二次函数matlab一、问题重述某研究所为了研究N、P、K三种肥料对于土豆和生菜的作用,分别对每种作物进行了三组实验,实验中将每种肥料的施用量分为10个水平,在考察其中一种肥料的施用量与产量关系时,总是将另二种肥料固定在第7个水平上,实验数据如下列表格所示,其中ha表示公顷,t表示吨,kg表示千克,试建立反映施肥量与产量关系的模型,并从应用价值和如何改进等方面作出评价.表1-1 施肥量对土豆产量的实验数据二、问题的分析在实际生活中,化肥对农作物具有二重性。
结合所学的初等函数,可以使用二次函数对数据进行初步的拟合。
做出数据散点图,利用matlab软件使用最小二乘法拟合找到相关函数,并进行初步的分析和判断。
生活中,考虑到N、P、K肥对农作物的影响,具有1+1>2的效果,所以不能仅仅考虑单一因素对其的影响,还需要进一步进行回归分析。
所以我们队决定拟合三项二次函数,将三者因素结合在一起。
进行数据回归分析和观察,并将模型一中的结果进行相关的检验。
三、建立模型(一)基本假设1.气候、温度等外界自然条件适宜作物生长,且处于稳定的状态。
2.作物水分充足,生长良好,其他营养素(除氮、磷、钾)都充足,不对作物生长造成影响;且忽略所喷洒的农药对作物生长的影响;3.模型一是在单一因素中考虑,认为其他因素对产量的影响达到最大,且N、P、K不相互影响。
施肥效果分析范文

施肥效果分析范文施肥是指农田土壤或植物缺乏一些营养元素时通过人工补充这些营养元素来提高植物生长和产量的一种方法。
正确施肥可以显著改善土壤质量和植物生长状况,提高农作物的产量和品质。
本文将从施肥的类型、作用、施肥效果和施肥技术等方面进行分析。
首先,施肥可以分为有机肥和化肥两种类型。
有机肥主要来自于动植物的有机废弃物,如农家肥、畜禽粪便、厩肥等。
有机肥含有丰富的有机质和微量元素,可以改善土壤结构和保持土壤湿度。
化肥则是人工合成的肥料,主要包括氮肥、磷肥和钾肥等。
化肥中的营养元素比例可以根据植物的需求进行调整。
有机肥和化肥各有其特点,可以根据土壤类型和农作物需求选择合适的施肥类型。
施肥的主要作用是为作物提供营养元素,以促进植物的生长和发育。
氮、磷、钾是植物生长发育的三大主要营养元素,它们分别对植物的叶片、根系和果实的发育起到重要的作用。
氮肥可以促进植物的叶绿素合成,提高光合作用效率;磷肥可以促进根系的生长,增强植物对水分和养分的吸收能力;钾肥可以增加植物的抗病能力和逆境适应性。
除此之外,施肥还可以提供植物的微量元素需求,并调节土壤的酸碱度和供水能力,促进土壤有机质的分解和微生物活动,增强土壤的肥力和保持力。
施肥对作物产量和品质有着显著的影响。
适量的施肥可以提高作物的产量,增加农民的收入。
例如,在水稻种植中,适当添加氮肥可以增加水稻的穗粒数和每穗粒数,从而提高产量;在果树种植中,适量添加钾肥可以增加水果的糖度和口感。
然而,过量的施肥则会导致营养元素的累积和土壤生态环境的破坏,从而适得其反。
因此,施肥的操作要注意施肥量、施肥时间和施肥方式的选择,结合土壤测试结果和农作物的生长需要进行科学施肥。
最后,施肥技术的优化可以进一步提高施肥效果。
第一,要根据作物生长的不同阶段和需求调整施肥方案,例如,在生育初期增加氮肥的供应,促进植物的早期生长;在生育中后期适量添加磷肥和钾肥,提高作物的产量和品质。
第二,要合理选择施肥方式,例如深施、浅施、分施和撒布等,根据不同植物的根系分布和养分吸收规律选择合适的施肥方式,提高养分利用率。
水稻测土配方施肥效果分析

周 奖 鑫
( 贵州省三都水族 自治县周覃镇农业服务中心 贵州 三都 5 5 8 1 0 9 ) 摘 要: 随着我 国农业的迅速 发展, 追求稳产 、 优质 的农 业产品 已是农 业生产者 的共 同 目标。尤其是水稻 的施肥, 这里面 也有较大 的学 问。本 文首先阐述 了测土配方施肥 的概况 , 接着 介绍 了测土 配方施肥技术 的主要 内容 , 介绍水稻 配方施肥 技术 , 最 后采用实 际的 案例, 对其水 稻测土配 方施 肥效果进行 分析 。本文对 从事相关工 作的人员具有 指导与参考价值 。
3 水 稻 测土配 方 施肥技 术
测土配方施肥技术 是按照 土壤测试结果 、 田间试验 、 作物需肥规律 、 农业 生产要求等 , 在合理施用 有机肥的基础 上提出氮 、 磷、 钾、 中量以及 微量 元素等施肥量 与配方 比, 并在适 当的时候 , 使用恰 当的方法应 用科 学的施肥方法。测土配方施肥 技术 包括“ 测土 、 配方 、 供应 、 施肥指导 五 个核心领域 , 八项个重要内容。
_ 8 技 术研 发 该技 术的最大优 点是可 以有 效的解决农 田施肥 与土壤供 肥及作物 3 技术支持 是确保 长期的测土配方施肥的长效性科学性 , 因此需 要进 需肥 之间 的矛盾 , 针对性 的补充作物所 需的短缺的 营养元素 , 能够稳 定 专 注于 田间试验 方法、 土壤测试技 术、 肥料配制 方法 、 数 增产 节本增效 , 提 高农产 品质量, 还能够保 护生态环境 促进农业 可持续 行 技术的研发 , 据 处理方法和其他方面的开发工作, 不断提高测土配方施肥技术水平。 发展 。
关键词 : 农业 ; 测土配方 ; 技术 ; 参 考 价 值
中图分 类号 : S 5 1 1
三都县水稻不同配方施肥效果分析

耕 作 与栽 培
21 00年
第 2 期
三都县水稻不 同配方施肥效果分析
潘洪涛 ,平立燕 ,罗 向琼 ,韦君利
( 贵州省三都县土肥站 ,贵州 三都 摘 要 :为了探 索不 同配方施肥在 三都县水稻 生产 中的应 5 80 ) 51 0 采用“ 4 4 最优 回归设计 , 31” 设氮 、 、 磷 钾三个因素和 0 1 、、 2 3 肥水平 , 1 、施 共 4个处 理 , 2次 重复 , 2 共 8个试 验小 区 。 小 区面积 2 2 区组内各处理随机排列, 4 1, n 各处理小区间打木 桩, 用铁丝拉线连接 , 用农膜包住 , 边缘压人犁底层。重复间 走道 5 c 试验区四周设保护行。小 区设计施肥量见表 1 0 m, 。
的新增纯收入和产投 比在各处理 中处于前列 , 肥料 配方可 其
以取得较好经济效益。
2 2 不 同处 理 的肥 料 利 用情 况 .
从表 3看出 , 氮肥 的利用 率 随着施 肥水 平 的增 高 而降 低 ; 肥的利用率 以中水平最 高, 磷 低水平其 次, 高水平最 低 ;
收 稿 日期 :0 00 —5 2 1-31 第 一作 者 : 涛 (9 1) 男 , 理 农 艺 师 , 事 土 壤 肥 料 技 术 推 广 潘洪 1 8一 , 助 从
佳 施 肥 量 为 5 4 k / 6 , O 的 最 佳 施 肥 量 为 4 5 k / . 1g67 K2 .9 g
表 1 试 验 各 处理 肥 料 用 量
67 , 6 m 最佳产量 5 80 k / 6 ; 2 . 2 g 6 7 N的最大施肥量为 6 3 mz .7
k / 6 m2 P O g 6 7 , 2 2的最 大 施肥 量 为 6 1 k /6 m2K2 的 最 .6  ̄67 , O
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
农作物施肥效果分析
(1992年A题)
某研究所为了研究N、P、K三种肥料对于土豆和生菜的作用,分别对每种作物进行了三组实验,实验中将每种肥料的施用量分为10个水平,在考察其中一种肥料的施用量与产量关系时,总是将另二种肥料固定在第7个水平上,实验数据如下列表格所示,其中ha表示公顷,t表示吨,kg表示千克,试建立反映施肥量与产量关系的模型,并从应用价值和如何改进等方面作出评价.
施肥量与产量关系的实验数据
一、符号说明:
W:农作物产量.
x:施肥量.
N、P、K:氮、磷、钾肥的施用量.
C W:农产品价格.
C N, C P, C K:氮、磷、钾肥的价格.
a,b,b0,b1,b2,c,c0,c1,c’0,c’1:常数(对特定肥料,特定农作物而言)
二、模型假设
1. 研究所的实验是在相同的正常实验条件(如充足的水分供应,正确的耕作程序)下进行的,产量的变化是由施肥量的改变引起的,产量与施肥量之间满足一定的规律。
在实验中,除施肥量,其它影响因子(如环境条件、种植密度等)均处于同等水平。
2. 土壤本身已含有一定数量的氮、磷、钾肥,即具有一定的天然肥力(从数据可以看出,当各种养分的施肥量都为0时,产量并不为0)。
3. 每次实验是独立进行的,且对于N、P、K施用量来说无系统误差,
模型的误差项均服从同分布的正态分布。
三、问题分析
题目要求建立反映施肥量与产量关系的模型,显然这是一个回归分析的问题,但是什么样的回归模型能体现施肥量与产量之间的关系呢?这就需要从问题的实际背景出发来考察。
一元回归分析理论(1-17页)及其实现(25-30页)
农学规律表明,施肥量与产量一般满足这样的关系:它分成三个不同的区段,在第一区段,当施肥量比较小时,作物产量随施肥量的增加而迅速增加,第二区段,随着施肥量的增加,作物产量平缓上升,第三区段,施肥量超过一定限度后,产量反而随施肥量的增加而下降在长期的实践中,农学家们已经总结出关于作物施肥效果的经验规律,并建立了相应的理论
1. Nicklas和Miller理论:
设h为达到最高产量时的施肥量,边际产量(即产量W对施肥量x的导数)d W/d x与(h-x)成正比例关系,即
d W/d x=a(h-x) (1)
从而W=b0+b1x+b2x2 (2) 2. 米采利希学说:
只增加某种养分时,引起产量的增加与该种养分供应充足时达到的最高产量A与现在产量W之差成正比,即
dW/d x=c(A-W) (3)
从而 W =A (1-exp(-cx )) (4) 考虑到土壤本身的天然肥力,上式可修正为
W =A (1-exp(-cx +b )) (5)
3. 英国科学家博伊德发现,在某些情况下,将施肥对象按施肥水平分成几组,则各组的效应曲线就呈直线形式。
若按水平分成二组,可以用下式表示(其中x i 表示分组值):
010
1max (0)
()i i c c x x x c c x x x x +≤<⎧⎪⎨''+≤<⎪⎩ (6) 四、模型与结果
为考察氮、磷、钾三种肥料对作物的施肥效果,我们以氮、磷、钾的施用量为自变量,土豆和生菜的产量为因变量描点作散点图(见图1,图2)。
图1 土豆产量和三种肥料施肥量之间的散点图
图2 生菜产量和三种肥料施肥量之间的散点图
从图中看出,氮肥对于作物产量的贡献大致呈多项式关系,磷肥
对于作物产量的关系大致为分段直线形式,至于钾肥,对土豆而言,大致呈指数关系。
对生菜而言,随着施用量的增加,产量的上升幅度很小.这样,我们得到了对施肥效果的定性认识。
我们建立了一元肥料效应回归模型,并在回归分析之前,用Chauvenent 准则进行修正,剔除异常值.根据对问题的初步分析,氮肥的施肥效果应满足Nicklas 和Miller 理论所描述的关系,运用二次多项式回归,得到
氮肥对土豆的回归方程:W =14.74+0.197N -0.00034N 2 (7) 氮肥对生菜的回归方程:W =10.23+0.101 N -0.00024 N 2 (8) (shifeidata.m )
磷肥的施用对作物产量的增加表现为分段直线形式,运用线性回归,得到
磷肥对土豆的回归方程:
32.0770.084(0101.04)
39.9680.0059(101.04342)P P W P P +≤<⎧=⎨
+≤≤⎩
(9) 磷肥对生菜的回归方程:
6.8090.052(0202.54)20.1960.00472(202.54685)
K K W K K +≤<⎧
=⎨
+≤≤⎩ (10)
从钾肥对土豆的实验数据可以看出,当施用量超过一定限度后,产量的增加很不明显,因此用(5)式来描述其施肥效果是合理的,用指数回归分析得到
钾肥对土豆的回归方程:W =42.17(1-exp(-0.01K -0.641)) (11)
对生菜来说,钾肥的施用对产量的影响很小.通过线性回归得到钾肥对生菜的回归方程:W=16.2269+0.00395K (12) 可以得到每种肥料的最佳施用量,这无疑为生产提供了极为重要的信息.此外,模型的建立并不依赖于任何特殊条件,这种方法可以适用于任何地区,考察任意一种肥料对于作物产量的效应,具有一定的推广价值
五、多元回归模型和交互效应的讨论
从实验设计的角度来看,该研究所采用的设计方案是因素轮换法,即在考察每一种肥料的效应时,总将另二种肥料的施用量固定在第7个水平上. 而此问题中三种肥料用量共同作用于农作物产量,因此仅仅建立一元回归模型是不行的,必须通过多元回归模型来反映虑农作物产量和施肥量之间的关系。
从上述分析可知,农作物产量和各种施肥量之间一般都不能用线性模型来描述,因此有必要考虑非线性回归模型。
此外因为任何光滑的函数都可用足够高阶的多项式来近似,所以针对这个问题,我们可以建立三元多次多项式模型。
又由农业学的经验知,可以采用三元二次多项式来描述.
下面以土豆为例进行说明。
(一)全回归
模型的形式为
()2220N P K NN PP KK NP NK KP E W =B +B N +B P+B K +B N +B P +B K +B NP+B NK +B KP
为了对参数进行估计,对数据进行重新整理后,观测方程为
=+Y X βε
其中130(,,)W W '=Y ,130(,,)e e '=ε,0(,,,,)N NK KP B B B B '=β
可以用回归的方法,求出回归系数,但对本题而言,下列处理表
明,交互系数是无法确定的. 由于所给出的实验全都分布于三条平行于坐标轴的直线上,并且这三条直线交于公共点(n0,p0,k0),以n=N-n0,p=P-p0,k=K-k0作为现的变量,称为相对施肥量,则相对产量W()可表示为:
w(n,p,k)=b 0+b n n+b p p+b k k+b nn n 2+b pp p 2+b kk k 2+b np np+b nk nk+b kp kp 在新的坐标系中,所有的试验点都在坐标轴上,至少有两个坐标为0,这样所有的交叉项全消失了(资料矩阵后三列全为0),即不可能由实验结果来确定交互系数,因而试验方法本身注定了交互效应是无法求出的
(也可从直观的角度看出交互效应是无法从数据计算的。
若b np =0,当n 变为n+δ,则响应变量w(n,p,k)的改变只依赖于n ,而不依赖于其它自变量;反之,若b np 0,当n 变为n+δ,则响应变量w(n,p,k)的改变依赖于n 和其它自变量)
因此我们只能建立不包含交互效应的模型
多元回归分析理论(18-22页)及其实现(30-47页)
22212.83610.19030.08420.07350.00030.00020.0001W =+N +P+K N P K ---- (13)
从输出的相关统计量可知,模型拟合得很好,而且各个参数在显著性水平0.05下都是现在显著的.
为了消除量纲对模型的影响,在建立模型之前,我们最好先对数据进行标准化,即
'()/()
'()/()'()/()'()/()
W W W W N N N N P P P P K K K K σσσσ=-=-=-=- 这样新的模型为
222' 2.82220.4168'0.7583' 1.2589'0.3759'0.1084'0.1546'W =+N +P +K N P K ---- (14)
(二)逐步回归
在回归模型里面,并不是所有的自变量对模型都有显著的影响,这个时候我们就需要通过一些方法来筛选变量,最常用的方法是逐步回归法
逐步回归理论及其实现(逐步回归讲义)
六、实验方法的建议(响应曲面法与设计)
响应曲面法(或RSM 法),是数学方法和统计方法相结合的产物,是用来对所感兴趣的相应受多个变量影响的问题进行建模和分析的,其目的是优化这个响应。
响应和自变量之间是一种函数关系,它们所描绘出来的曲面就叫做响应曲面。
如果曲面有弯曲,一般这种函数关系多采用二阶多项式模型。
RSM 的最终目的是确定系统的最优运行条件或确定因素空间中满足运行规的区域。
本题中为了估计肥料的交互效应,我们通过响应曲面法设计了一个正交试验表,将氮、磷、钾肥的用量以第7个水平为中心等问题分为五个水平,作一个五水平三因子的正交表,总共需进行15次实验,将所得数据运用直观分析和方差分析,可以方便地得到氮、磷、钾肥对作物的总效应.试验安排如下
表 正交设计表
.
.页脚.。
