综合法和分析法 .ppt
合集下载
分析方法与综合方法

⌛️
综合方法的优缺点及适用范围
优点
• 整合事物的内在联系和规律
• 发现新的联系和规律
缺点
• 可能忽视事物的细节和局部
• 需要较高的综合素质和创新能力
适用范围
• 研究事物的整体性和系统性
• 解决复杂问题和创新领域
分析方法与综合方法的综合运用与优化
综合运用
优化
• 在研究过程中,根据需要灵活运用分析方法和综合方法
CREATE TOGETHER
SMART CREATE
分析方法与综合方法:理论应用与实例
01
分析方法与综合方法的基
本概念
分析方法的定义与特点
分析方法是一种深入研究事物内部的方法
• 通过分解、剖析、观察等手段
• 了解事物的本质和规律
• 强调细节和局部
分析方法的特点
• 深入:深入挖掘事物的内在联系
• 细致:关注事物的细节和局部
域
归纳综合方法及其应用
归纳综合方法
应用领域
• 通过归纳手段从具体事物中提炼出一般规律
• 哲学:研究世界观、认识论等
• 如:归纳法、类比法等
• 科学:研究科学方法、科学发现等
• 艺术:研究艺术创作、审美规律等
演绎综合方法及其应用
演绎综合方法
• 通过演绎手段从一般规律推导出具体事物
• 如:演绎法、推理法等
• 员工满意度分析:评估员工满意度、激励措施等
品创新
综合方法在科技创新中的应用
科技创新中的综合方法
• 跨学科研究:整合不同学科的知识和技术,解决复杂问题
• 创新方法论:研究创新过程、创新策略等
• 技术路线图:规划技术发展路径,指导科技创新方向
2.2.1《综合法和分析法》区教研课课件

2
充分条件
思考6:上述证明方法叫做分析法. 一般 地,分析法的基本含义是什么? 从所证结论出发,逐步寻求使它成立的 充分条件,直到归结为判定一个显然成 立的条件(已知条件、定义、公理、定 理、性质、法则等)为止.
分析法又叫“逆推证法”或“执果索因法”, 其基本思想是:由未知探需知,逐步推向 已知.
2
2
2
2
4abc
其左右两边的结构有什么特点? 右边是3个数a,b,c的乘积的4倍,左边 为两项之和,其中每一项都是一个数与 另两个数的平方和之积.
思考2:利用哪个知识点可以沟通两个数 的平方和与这两个数的积的不等关系?
基本不等式 x + y
2 2
2xy
思考3:若已知a>0,b>0,如何利用不 等式性质证明
证明过程中我们要善于观察变形,合理利用已 知条件、定理、公式,把文字语言转化为符号 语言或者图形语言,由因导果!
探究(二):分析法
回顾基本不等式: a + b 2 (a>0,b>0)的证明.
ab 证明 : 要证 2 ab ,
ab
只需证
a b 2 ab
只需证
只需证
a+b-2 ab 0
例1.已知 a, b, c 是不全相等的正数 bc a c a b a b c 求证: 3 a b c
(综合法)
R ∵a,b,c ,
符号语言
b a c a c b 与 , 与 , 与 均为正实数且不能同时相等, a b a c b c b a c a c b 2, + 2 , + 2 , 由重要不等式得: + a b a c b c
2.2直接证明与间接证明
2.2.1 综合法和分析法(1)
充分条件
思考6:上述证明方法叫做分析法. 一般 地,分析法的基本含义是什么? 从所证结论出发,逐步寻求使它成立的 充分条件,直到归结为判定一个显然成 立的条件(已知条件、定义、公理、定 理、性质、法则等)为止.
分析法又叫“逆推证法”或“执果索因法”, 其基本思想是:由未知探需知,逐步推向 已知.
2
2
2
2
4abc
其左右两边的结构有什么特点? 右边是3个数a,b,c的乘积的4倍,左边 为两项之和,其中每一项都是一个数与 另两个数的平方和之积.
思考2:利用哪个知识点可以沟通两个数 的平方和与这两个数的积的不等关系?
基本不等式 x + y
2 2
2xy
思考3:若已知a>0,b>0,如何利用不 等式性质证明
证明过程中我们要善于观察变形,合理利用已 知条件、定理、公式,把文字语言转化为符号 语言或者图形语言,由因导果!
探究(二):分析法
回顾基本不等式: a + b 2 (a>0,b>0)的证明.
ab 证明 : 要证 2 ab ,
ab
只需证
a b 2 ab
只需证
只需证
a+b-2 ab 0
例1.已知 a, b, c 是不全相等的正数 bc a c a b a b c 求证: 3 a b c
(综合法)
R ∵a,b,c ,
符号语言
b a c a c b 与 , 与 , 与 均为正实数且不能同时相等, a b a c b c b a c a c b 2, + 2 , + 2 , 由重要不等式得: + a b a c b c
2.2直接证明与间接证明
2.2.1 综合法和分析法(1)
1.2 综合法与分析法 课件(北师大选修2-2)
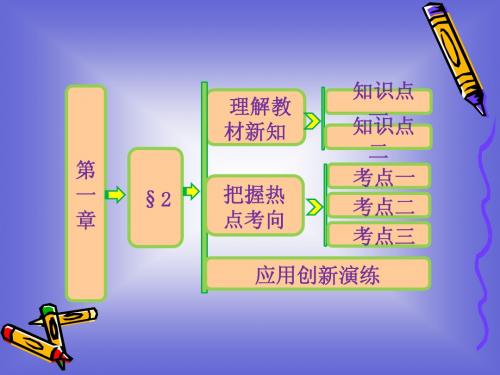
2.已知点P是直角三角形ABC所在平面外的一点,O是斜边 AB的中点,并且PA=PB=PC. 求证:PO⊥平面ABC.
证明:连接OC,如图所示,
∵AB是Rt△ABC的斜边,O是AB的中点, ∴OA=OB=OC. 又∵PA=PB=PC,∴PO⊥AB, 且△POA≌△POC, ∴∠POA=∠POC. ∴∠POC=90°. 即PO⊥AB,PO⊥OC,且AB∩OC=O,所以PO⊥ 平面ABC.
分析法与综合法的优缺点: 综合法和分析法是直接证明的两种基本方法,两种方 法各有优缺点.分析法解题方向较为明确,容易寻找到解
题的思路和方法,缺点是思路逆行,叙述较繁;综合法从
条件推出结论,较简捷地解决问题,但不便于思考.实际 证题时常常两法兼用,先用分析法探索证明途径,然后用 综合法有条理地表述解题过程.
提示:基本不等式.
问题 2:本题证明顺序是什么?
提示:从已知到结论.
综合法
(1)含义:从命题的 条件 出发,利用定义、公理、定理 及运算法则,通过 演绎 推理,一步一步地接近要证明 的 结论 ,直到完成命题的证明的思维方法,称为综合法. (2)思路:综合法用以下的框图表示:
1 2 即证 a +b ≥ (a +b2+2ab),即证 a2+b2≥2ab. 2 因为 a2+b2≥2ab 对一切实数恒成立, 2 所以 a +b ≥ (a+b)成立. 2
2 2
[一点通]
分析法是“执果索因”,一步步寻找结论成
立的充分条件.它是从求证的结论出发,逆着分析,由未
知想需知,由需知逐渐地靠近已知,这种证明的方法关键
AC cos B 1.在△ABC 中,AB= ,证明 B=C. cos C
sin B cos B 证明: 在△ABC 中, 由正弦定理及已知得 = . sin C cos C 于是 sin Bcos C-cos Bsin C=0,即 sin(B-C)=0, 因为-π<B-C<π,从而 B-C=0,所以 B=C.
5.3.2综合法与分析法(1) 课件(人教A版选修4-5)

2 2 2 2 2
例 7 已 知 a , b , c都 是 正 数 , 求 证 : a b c 3 abc , 并 指 出 等 号 成 立 的 条 件 .
3 3 3
5.3.2不等式的证明—综合法和分析法
从已知条件出发, 利用不等式的性质和定理 逐步下推, 推导出所要证明的不等式成立,这种证 明方法叫做综合法。 综合法的思路是“由因导果”. 证明不等式时,有时可以从要证明的不等 式出发,逐步上溯 , 寻求使它成立的充分条件, 直至最后,把要证明的不等式归结为判定条件是 否具备的问题。这种证明的方法叫做分析法。 分析法的思路是“执果索 因”. … A B 综合法: 条件 结论
天才就是百分之一的灵感,百分之九十九的汗水! 书 小 不 学 勤 径,学 徒 伤 悲 作 功! 天 才 在 于 为 奋,努 力 才 能 成功=艰苦的劳动+正确的方法+少谈空话 少 山 有 路 勤习,老 来 海 无 崖 苦成 舟
例1 已 知 a , b都 是 正 数 , 求 证 :
3 3
a b
2
b a
分析法: 结论
B
…
A
条件补Biblioteka 作业(1) 求 证: 1 x
2
1 y
2
2
1 z
2
1 xy
1 yz
1 zx
( 2 ) 求 证: a b ab a b 1
2
( 3 ) 已 知 a , b , c 为 不 全 相 等 的 正 数 , 且 abc 1 . 求证 : a b c 1 a 1 b 1 c
2.
2
例 2 设 a 0 , b 0 , 求 证 : a b a b ab
例 7 已 知 a , b , c都 是 正 数 , 求 证 : a b c 3 abc , 并 指 出 等 号 成 立 的 条 件 .
3 3 3
5.3.2不等式的证明—综合法和分析法
从已知条件出发, 利用不等式的性质和定理 逐步下推, 推导出所要证明的不等式成立,这种证 明方法叫做综合法。 综合法的思路是“由因导果”. 证明不等式时,有时可以从要证明的不等 式出发,逐步上溯 , 寻求使它成立的充分条件, 直至最后,把要证明的不等式归结为判定条件是 否具备的问题。这种证明的方法叫做分析法。 分析法的思路是“执果索 因”. … A B 综合法: 条件 结论
天才就是百分之一的灵感,百分之九十九的汗水! 书 小 不 学 勤 径,学 徒 伤 悲 作 功! 天 才 在 于 为 奋,努 力 才 能 成功=艰苦的劳动+正确的方法+少谈空话 少 山 有 路 勤习,老 来 海 无 崖 苦成 舟
例1 已 知 a , b都 是 正 数 , 求 证 :
3 3
a b
2
b a
分析法: 结论
B
…
A
条件补Biblioteka 作业(1) 求 证: 1 x
2
1 y
2
2
1 z
2
1 xy
1 yz
1 zx
( 2 ) 求 证: a b ab a b 1
2
( 3 ) 已 知 a , b , c 为 不 全 相 等 的 正 数 , 且 abc 1 . 求证 : a b c 1 a 1 b 1 c
2.
2
例 2 设 a 0 , b 0 , 求 证 : a b a b ab
综合法分析法PPT课件

例 3. 已 知 α ,β≠
k π+ π( k 2
Z),且
sinθ+ cosθ = 2sinα
sinθ cosθ = sin 2β
求 证:
1 - tan 2α = 1 - tan 2β . 1 + tan 2α 2(1 + tan 2β )
.
.
用P表示已知条件,定义,定理,公理等,用Q表 示要证的结论,则上述过程可用框图表示为:
A
C
B
因为:SA⊥平面ABC成立 所以. AF⊥SC成立
.
例3:设a,b,c为一个三角形的三边,且s2=2ab,
s = 1(a + b+c), 试证: s < 2a 2
解:欲证s<2a,只需证
s
s2 b
即证b<s,也即证 b 1 (a bc)
2
即证b<a+c
因为a,b,c为一个三角形的三边,所以 b<a+c成立.
b
ab
(a>0,b>0)的证明.
证明:要证;a
+ 2
b
ab
还原成综合法: 证明:
只需证;a+b2 ab
因为;( a b)2 0
只需证;a+b2 ab0 所以 a+b2 ab0
只需证;( a b)2 0
所以 a+b2 ab
因为;( a b)2 0成立
所以 a
+ 2
b
a b成立
所以
a+b 2
a b 成立
.
小结
1.在数学证明中,综合法和分析法是 两种最常用的数学方法,若从已知入手 能找到证明的途径,则用综合法,否则 用分析法.
综合法和分析法 课件

综合法与分析法
1.综合法和分析法是数学中常用的两种直接证明方 法,也是不等式证明中的基本方法.由于两者在证明思路 上存在着明显的互逆性,这里将其放在一起加以认识、学 习,以便于对比研究两种思路方法的特点.
2.所谓综合法,即从已知条件出发,根据不等式的 性质或已知的不等式,逐步推导出要证的不等式.综合法 是“由因及果”.
分析:注意不等式左、右两端的差异,思考 如何脱去左端根号或如何去掉右端的分母
a= b1c<121b+1c,而1a=bc.
证明:法一:因为 a,b,c 是不等正数,且 abc=1,
所以 a+ b+ c=
b1c+
a1c+
1 ab
<121b+1c+121a+1c+121a+1b=1a+1b+1c.
法二:a,b,c 是不等正数,且 abc=1,
设 x,y∈(0,+∞).求证: 12(x+y)2+14(x+y)≥x y+y x.
证明:原不等式⇔2(x+y)2+(x+y)≥4x y+4y x ⇔(x+y)[2(x+y)+1]≥2 xy(2 x+2 y). ∵x+y≥2 xy>0, ∴只需证 2(x+y)+1≥2 x+2 y. 即证(x+14)+(y+14)≥ x+ y.
2
只需证 2ab+ma+b < c , 即证 1+2abm+2m-aab+b<1+mc , 只需证 m2c-abc<2mab+m2(a+b)成立, 只需证 m2[c-(a+b)]<ab(2m+c)成立, ∵a,b,c 分别是△ABC 的三边长,∴a+b>c. 即 c-(a+b)<0,而 m2>0, ∴m2[c-(a+b)]<0. 而 ab(2m+c)>0, ∴m2[c-(a+b)]<ab(2m+c)成立. ∴原不等式成立.
(当且仅当 a=b=c=13时,等式成立)
1.综合法和分析法是数学中常用的两种直接证明方 法,也是不等式证明中的基本方法.由于两者在证明思路 上存在着明显的互逆性,这里将其放在一起加以认识、学 习,以便于对比研究两种思路方法的特点.
2.所谓综合法,即从已知条件出发,根据不等式的 性质或已知的不等式,逐步推导出要证的不等式.综合法 是“由因及果”.
分析:注意不等式左、右两端的差异,思考 如何脱去左端根号或如何去掉右端的分母
a= b1c<121b+1c,而1a=bc.
证明:法一:因为 a,b,c 是不等正数,且 abc=1,
所以 a+ b+ c=
b1c+
a1c+
1 ab
<121b+1c+121a+1c+121a+1b=1a+1b+1c.
法二:a,b,c 是不等正数,且 abc=1,
设 x,y∈(0,+∞).求证: 12(x+y)2+14(x+y)≥x y+y x.
证明:原不等式⇔2(x+y)2+(x+y)≥4x y+4y x ⇔(x+y)[2(x+y)+1]≥2 xy(2 x+2 y). ∵x+y≥2 xy>0, ∴只需证 2(x+y)+1≥2 x+2 y. 即证(x+14)+(y+14)≥ x+ y.
2
只需证 2ab+ma+b < c , 即证 1+2abm+2m-aab+b<1+mc , 只需证 m2c-abc<2mab+m2(a+b)成立, 只需证 m2[c-(a+b)]<ab(2m+c)成立, ∵a,b,c 分别是△ABC 的三边长,∴a+b>c. 即 c-(a+b)<0,而 m2>0, ∴m2[c-(a+b)]<0. 而 ab(2m+c)>0, ∴m2[c-(a+b)]<ab(2m+c)成立. ∴原不等式成立.
(当且仅当 a=b=c=13时,等式成立)
高中数学2.2.1 综合法和分析法

-16-
2.2.1 综合法与分析法
探究一
探究二
探究三
课前篇自主预习 课课堂堂篇篇探探究究学学习习 规范解答 当堂检测
综合法与分析法的综合应用 例3已知a、b、c是不全相等的正数,且0<x<1.
求证:logx������+2������+logx������+2 ������+logx������+2 ������<logxa+logxb+logxc. 分析:解答本题的关键是利用对数运算法则和对数函数性质将题 目转化成整式不等式证明.
①综合法的特点是从“已知”看“未知”,其逐步推理实际上是寻找
已知条件的必要条件.
②综合法从命题的条件出发,利用定义、公理、定理和运算法则,
通过演绎推理,一步一步完成命题的证明.
-3-
2.2.1 综合法与分析法
课前篇自主预习 课堂篇探究学习
【做一做 1】 命题“求证:tan θ+ta1n������ = sin22������”的证明过程“tan
-17-
2.2.1 综合法与分析法
课前篇自主预习 课课堂堂篇篇探探究究学学习习
探究一
探究二
探究三
规范解答 当堂检测
解:要证明 logx������+2������+logx������+2 ������+logx������+2 ������<logxa+logxb+logxc,
只需要证明 logx
①分析法的特点是从“未知”看“需知”,逐步靠拢“已知”,其逐步推
理实际上是寻找使结论成立的充分条件.
②分析法从命题的结论入手,寻求结论成立的条件,直至归结为
数学课件:1.5.2 综合法和分析法

题型一 题型二 题型三
正解:证明:要证 3 + 6 < 4 + 5, 只需证( 3 + 6)2<( 4 + 5)2, 即证 9+2 18 < 9+2 20, 即证 18 < 20, 即证18<20. 因为 18<20 显然成立, 所以 3 + 6 < 4 + 5.
12345
1 设 a,b 为正数,A= ������ + ������,B= ������ + ������, 则A,B 的大小关系是( ) A.A≥B B.A≤B
+
1 ������-������
. 此不等式恒成立的充要条件是n 小于等于(x-
z)
1 ������-������
+
1 ������-������
的最小值.
令 a=x-y,b=y-z,则 a>0,b>0,且 x-z=a+b.
因为可证(a+b)
1 ������
+
1 ������
≥4,当且仅当 a=b,即 x-y=y-z>0 时等号成立,
2bc. Δ=4(b+c)2-4(b2+c2-2bc)=16bc>0. 则f(a)的值可正、可负、可为零,无法确定. 因此,分析题目时,对条件要看清楚,尤其要探寻条件间的限制关
系,以免受到某些思维定式的影响.
题型一 题型二 题型三
用分析法证明不等式
【例 2】
已知
a>b>0,求证:
(������-������)2 8������
只需证明A为真. 已知A为真,故B必为真. 可以简单写成: B⇐B1⇐B2⇐…⇐Bn⇐A.
2.2.1综合法和分析法PPT课件

()
❖ A.既不充分也不必要条件
❖ B.充要条件
❖ C.充分条件
❖ D.必要条件
❖ [答案] D
❖ [解析] ∵②⇒①,但①不一定推出②.故•18 应选D.
2.若 a,b,c∈R,且 ab+bc+ac=1,则下列不等
式成立的是
()
A.a2+b2+c2≥2 B.(a+b+c)2≥3 C.1a+1b+1c≥2 3 D.abc(a+b+c)≤13 ❖ [答案] B
步反推,寻找使当前命题成立的充分条件,
即用分析法证明.
[证明] ∵a>0,b>0,要证
a+ b
b≥ a
a+
b成立,
只需证
a+ b
ba2≥(
a+
b)2 成立,
即证ab2+ba2+2 ab≥a+b+2 ab成立.
•5
即证a3a+bb3≥a+b.
也就是证(a+b)(a2-ab+b2)≥ab(a+b)成立.
要证a+1 b+b+1 c=a+3b+c,
即证a+a+b+b c+a+b+b+c c=3,
也就是a+c b+b+a c=1,
❖ 只需证c(b+c)+a(a+b)=(a+b)(b+c),
❖ 需证c2+a2=ac+b2,
❖ 又△ABC三内角A、B、C成等差数列,故B
=60°,
•11
❖ 由余弦定理,有 ❖ b2=c2+a2-2accos60°,即b2=c2+a2-ac, ❖ 故c2+a2=ac+b2得证. ❖ 综合法: ❖ 证明:∵△ABC三内角A、B、C成等差数列, ❖ ∴B=60°. ❖ 由余弦定理,有b2=c2+a2-2cacos60°, ❖ 得c2+a2=ac+b2, ❖ 等式两边同时加上ab+bc得 ❖ c(b+c)+a(a+b)=(a+b)(b+c),
综合法和分析法 课件

分析法证明.
[规范解答] 要证明 f(x+1)为偶函数,只需证明其对 称轴为直线 x=0.(2 分)
因为 f(x+1)=ax2+(2a+b)x+a+b+c(a≠0)的对称 轴为 x=-2ba-1,所以只需证-2ba-1=0,
即证 b=-2a.(4 分)
由已知,抛物线 f(x+2)的对称轴 x=-2ba-2 与 f(x) 的对称轴 x=-2ba关于 y 轴对称,(8 分)
只需要证明 logxa+2 b·b+2 c·a+2 c<logx (abc).
a+b b+c a+c 由已知 0<x<1,只需证明 2 · 2 · 2 >abc.
a+b
b+c
a+c
由基本不等式得 2 ≥ ab>0, 2 ≥ bc>0, 2
≥ ac>0.又因为 a,b,c 是不全相等的正数,
a+b b+c a+c 所以 2 · 2 · 2 > a2b2c2=abc.
(3)适当调整,回顾反思:解题后回顾解题过程,可 对部分步骤进行调整,并对一些语言进行适当的修饰,反 思总结解题方法的选取.
类型 2 分析法的应用
[典例 2] 设 a,b 为实数,求证:
a2+b2≥
2 2 (a
+b).
证明:当 a+b≤0 时,因为 a2+b2≥0,
所以 a2+b2≥ 22(a+b)成立.
a+b b+c a+c 即 2 · 2 · 2 >abc 成立.
a+b b+c a+c 所以 logx 2 +logx 2 +logx 2 <logx a+logx b+logx c 成立.
温馨提示 运用综合法证明问题的关键是正确运用
相关的定义、定理、公理和已知条件.
2.分析法
(1)定义:从要证明的结论出发,逐步寻求使结论成 立的充分条件,直至最后,把要证明的结论归结为判定 一个明显成立的条件.
[规范解答] 要证明 f(x+1)为偶函数,只需证明其对 称轴为直线 x=0.(2 分)
因为 f(x+1)=ax2+(2a+b)x+a+b+c(a≠0)的对称 轴为 x=-2ba-1,所以只需证-2ba-1=0,
即证 b=-2a.(4 分)
由已知,抛物线 f(x+2)的对称轴 x=-2ba-2 与 f(x) 的对称轴 x=-2ba关于 y 轴对称,(8 分)
只需要证明 logxa+2 b·b+2 c·a+2 c<logx (abc).
a+b b+c a+c 由已知 0<x<1,只需证明 2 · 2 · 2 >abc.
a+b
b+c
a+c
由基本不等式得 2 ≥ ab>0, 2 ≥ bc>0, 2
≥ ac>0.又因为 a,b,c 是不全相等的正数,
a+b b+c a+c 所以 2 · 2 · 2 > a2b2c2=abc.
(3)适当调整,回顾反思:解题后回顾解题过程,可 对部分步骤进行调整,并对一些语言进行适当的修饰,反 思总结解题方法的选取.
类型 2 分析法的应用
[典例 2] 设 a,b 为实数,求证:
a2+b2≥
2 2 (a
+b).
证明:当 a+b≤0 时,因为 a2+b2≥0,
所以 a2+b2≥ 22(a+b)成立.
a+b b+c a+c 即 2 · 2 · 2 >abc 成立.
a+b b+c a+c 所以 logx 2 +logx 2 +logx 2 <logx a+logx b+logx c 成立.
温馨提示 运用综合法证明问题的关键是正确运用
相关的定义、定理、公理和已知条件.
2.分析法
(1)定义:从要证明的结论出发,逐步寻求使结论成 立的充分条件,直至最后,把要证明的结论归结为判定 一个明显成立的条件.
综合法与分析法PPT
例题2
求证 3 + 7 < 2 5.
分析
从待证不等式不易发现证明的出发 点,因此我们直接从待证不等式出发, 分析其成立的充分条件.
证明:
因为 3 + 7和 2 5 都是正数,所以要证
3 + 7 < 2 5,
只需证
( 3 + 7)2 <(2 5)2 .
展开得
10 + 2 21 < 20,
只Hale Waihona Puke 证21 < 5,不等式:a
+ 2
b
ab
(a>0,b>0)的证明.
动动脑
大家想一想, 除了综合法,还有 别的证明方法吗?
证明:要证
a
+ 2
b
ab
只需证:a + b 2 ab
只需证:a + b 2 ab 0
只需证:( a b)2 0
因为:( a b)2 0 成立
所以
a
+ 2
b
ab成立
a2 + c2 - ac = ac,
即 (a - c)2 = 0.
因此
a=c.
从而
A=C.
⑤
由 ② ③ ⑤ ,得
A=B=C= π. 3
所以△ABC为等边三角形.
注意
解决数学问题时,往往要先做语言的转 换,如把文字语言转换成符号语言,或把符 号语言转换成图形语言等.还要通过细致的分 析,把其中的隐含条件明确表示出来.
a(b2+c2)+b(c2+a2)≥4abc
首先,分析待证不等式的特点:不 等式的右端是3个数a,b,c乘积的4倍,左 端为两项之和,其中每一项都是一个数 与另两个数的平方和之积.据此,只要把 两个数的平方和转化为这两个数的积的 形式,就能使不等式左、右两端具有相 同的形式.
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
止,这种证明的方法叫做分析法。其特点是:执果索因,即 要证结果Q,只需证条件P.
类似于综合法,我们也可以用框图来表示分析法。
用Pi表示使所要证明结论成立的充分条件,Q表示所要证明的 结论.则分析法的思路过程,特点用框图表示为:
得到一个明显
Q P1
P1 P2
P2 P3
…
成立的结论
注意:证明最后面的明显成立的条件可以是: 已知条件、定理、定义、公理等
三、例题讲解
例2.在ABC中,设CB a,CA b,
求证 :
SABC
1 2
| a |2| b |2 (a b)2
三、例题讲解
例3.在△ABC中,三个内角A、B、C对应的边分别 为a、b、c,且A、B、C成等差数列,a、b、c成等 比数列,求证△ABC为等边三角形.
分析 •将A,B,C成等差数列,转化为符号
• (3)用分析法证明数学命题时,一定要恰当地用好 “要证”、“只需证”、“即证”等关联词语.
练习:证明不等式:
a
+ 2
b
ab
(a>0,b>0).
综合法
证法1:
因为;( a b)2 0
所以 a + b 2 ab 0
所以 a + b 2 ab
所以
a+b 2
ab 成立
分析法
证法2:要证a;+
2
b
ab
只需证;a + b 2 ab
只需证;a + b 2 ab 0
只需证;( a b)2 0
分析法
综合法和分析法的推证过程如下:
综合法
已知条件 结论
分析法
结论 已知条件
例4.求证:3 7 2 5证明:因为来自3 7和2 5都是正数,所以要证
3 72 5
只需证,( 3 7)2 (2 5)2
只需证:10 2 21 20
只需证: 21 5 只需证:21 25
因为21 25显然成立,所以
则综合法用框图表示为:
P Q1 Q1 Q2 Q2 Q3 … Qn Q
综合法是由一个个推理组成的
二、讲授新课——分析法(逆推证法或执果索因法)
一般地,从要证明的结论出发,逐步寻求推证过程中,使 每一步结论成立的充分条件,直至最后,把要证明的结论归结为 判定一个明显成立的条件(已知条件、定理、定义、公理等)为
2.2.1综合法和分析法(一) ——综合法
一、复习引入
推理
合情推理
(或然性推理)
演绎推理 (必然性推理)
归纳
类比
三段论
(特殊到一般) (特殊到特殊) (一般到特殊)
合情推理得到的结论是不可靠的,需要经过严格 的证明才可以使用。数学中证明的方法有哪些呢?
证明的方法
直接证明
综合法 分析法
间接证明(反证法)
因为;( a b)2 0 成立
a+b
所以
2
ab成立
思考:上述两种证法有什么异同?
相同 都是直接证明
证法1 从已知条件出发,以已知的定义、公理、
不同 定理为依据,逐步下推,直到推出要证明的结论
为止
综合法
证法2 从问题的结论出发,追溯导致结论成立的条
件,逐步上溯,直到使结论成立的条件和已知条件
吻合为止
3 7 2 5成立
反思
在本例中,如果我们从“21<25”出发, 逐步倒推回去,就可以用综合法证出结论.但 由于我们很难想到从“21<25”入手,所以 用综合法比较困难.
• [点评]
• (1)分析法证明不等式的依据是不等式的基本性质、 已知的重要不等式和逻辑推理的基本理论;
• 2)分析法证明思路为:从求证的结论出发,逐步 寻求使结论成立的充分条件,直至把证明的结论 归结为一个明显成立的条件即可。
练习.已知a>0,b>0,求证a(b2+c2)+b(c2+a2)≥4abc
分析: 首先,分析待证不等式的特点:不 等式的右端是3个数a,b,c乘积的4倍, 左端为两项之和,其中每一项都是一个 数与另两个数的平方和之积.据此,只要 把两个数的平方和转化为这两个数的积 的形式,就能使不等式左、右两端具有 相同的形式.
二、讲授新课——综合法(顺推证法或由因导果法)
利用已知条件和某些数学定义、公理、定理等, 经过一系列的推理论证,最后推导出所要证明的结论 成立,这种证明方法叫做综合法。其特点是:“由因导 果” 用P表示已知条件、已有的定义、公理、定理 等,Q表示所要证明的结论.
则综合法用框图表示为:
P Q1 Q1 Q2 Q2 Q3 … Qn Q
2.2.1综合法和分析法(二) ——分析法
一、回顾复习——综合法(顺推证法或由因导果法)
利用已知条件和某些数学定义、公理、定理等, 经过一系列的推理论证,最后推导出所要证明的结论 成立,这种证明方法叫做综合法。其特点是:“由因导 果” 用P表示已知条件、已有的定义、公理、定理 等,Q表示所要证明的结论.
语言就是2B=A+C;
•A,B,C为△ABC的内角,这是一个隐含 条件,即A+B+C=180°;
•a,b,c成等比数列转化为符号语言就是
b2 = ac.
此时,如果能把角和边统一起来,那么就可以进一 步寻找角和边之间的关系,进而判断三角形的形状,余 弦定理正好满足要求.于是,可以用余弦定理进行证明.
证明:由A,B,C成等差数列,有 2B=A+C. ①
因为A,B,C为△ABC的内角,所以 A+B+C=180°. ②
由① ②,得 B = π . ③ 3
由a,b,c成等比数列,有
b2 = ac. ④
注:解决数学问题时,学会语言转换;还要细致,找出隐含条件。
文字语言
图形语言
符号语言
由余弦定理及③,可得
b2 = a2 + c2 - 2accosB = a2 + c2 - ac.
其次,寻找转化的依据及证明中要用的 其他知识:应用不等式x2+y2≥2xy就能实 现转化,不等式的基本性质是证明的依 据.
证明:
∵ b2+c2 ≥ 2bc,a>0 ∴ a(b2+c2) ≥2abc.
又∵ c2+a2 ≥ 2ac,b>0 ∴ b(c2+a2) ≥ 2abc.
∴ a(b2+c2)+b(c2+a2) ≥ 4abc.
再由④,得 a2 + c2 - ac = ac,
即 (a - c)2 = 0.
因此 a=c.
从而 A=C. ⑤
由 ② ③ ⑤ ,得 A = B = C = π . 3
所以△ABC为等边三角形.
四、课堂小结
1.在数学证明中,综合法最常用的数学方法,若从已知 入手能找到证明的途径,则用综合法.
2.综合法的每步推理都是寻找必要条件,在解题表述中 要注意语言的规范性和逻辑性.
类似于综合法,我们也可以用框图来表示分析法。
用Pi表示使所要证明结论成立的充分条件,Q表示所要证明的 结论.则分析法的思路过程,特点用框图表示为:
得到一个明显
Q P1
P1 P2
P2 P3
…
成立的结论
注意:证明最后面的明显成立的条件可以是: 已知条件、定理、定义、公理等
三、例题讲解
例2.在ABC中,设CB a,CA b,
求证 :
SABC
1 2
| a |2| b |2 (a b)2
三、例题讲解
例3.在△ABC中,三个内角A、B、C对应的边分别 为a、b、c,且A、B、C成等差数列,a、b、c成等 比数列,求证△ABC为等边三角形.
分析 •将A,B,C成等差数列,转化为符号
• (3)用分析法证明数学命题时,一定要恰当地用好 “要证”、“只需证”、“即证”等关联词语.
练习:证明不等式:
a
+ 2
b
ab
(a>0,b>0).
综合法
证法1:
因为;( a b)2 0
所以 a + b 2 ab 0
所以 a + b 2 ab
所以
a+b 2
ab 成立
分析法
证法2:要证a;+
2
b
ab
只需证;a + b 2 ab
只需证;a + b 2 ab 0
只需证;( a b)2 0
分析法
综合法和分析法的推证过程如下:
综合法
已知条件 结论
分析法
结论 已知条件
例4.求证:3 7 2 5证明:因为来自3 7和2 5都是正数,所以要证
3 72 5
只需证,( 3 7)2 (2 5)2
只需证:10 2 21 20
只需证: 21 5 只需证:21 25
因为21 25显然成立,所以
则综合法用框图表示为:
P Q1 Q1 Q2 Q2 Q3 … Qn Q
综合法是由一个个推理组成的
二、讲授新课——分析法(逆推证法或执果索因法)
一般地,从要证明的结论出发,逐步寻求推证过程中,使 每一步结论成立的充分条件,直至最后,把要证明的结论归结为 判定一个明显成立的条件(已知条件、定理、定义、公理等)为
2.2.1综合法和分析法(一) ——综合法
一、复习引入
推理
合情推理
(或然性推理)
演绎推理 (必然性推理)
归纳
类比
三段论
(特殊到一般) (特殊到特殊) (一般到特殊)
合情推理得到的结论是不可靠的,需要经过严格 的证明才可以使用。数学中证明的方法有哪些呢?
证明的方法
直接证明
综合法 分析法
间接证明(反证法)
因为;( a b)2 0 成立
a+b
所以
2
ab成立
思考:上述两种证法有什么异同?
相同 都是直接证明
证法1 从已知条件出发,以已知的定义、公理、
不同 定理为依据,逐步下推,直到推出要证明的结论
为止
综合法
证法2 从问题的结论出发,追溯导致结论成立的条
件,逐步上溯,直到使结论成立的条件和已知条件
吻合为止
3 7 2 5成立
反思
在本例中,如果我们从“21<25”出发, 逐步倒推回去,就可以用综合法证出结论.但 由于我们很难想到从“21<25”入手,所以 用综合法比较困难.
• [点评]
• (1)分析法证明不等式的依据是不等式的基本性质、 已知的重要不等式和逻辑推理的基本理论;
• 2)分析法证明思路为:从求证的结论出发,逐步 寻求使结论成立的充分条件,直至把证明的结论 归结为一个明显成立的条件即可。
练习.已知a>0,b>0,求证a(b2+c2)+b(c2+a2)≥4abc
分析: 首先,分析待证不等式的特点:不 等式的右端是3个数a,b,c乘积的4倍, 左端为两项之和,其中每一项都是一个 数与另两个数的平方和之积.据此,只要 把两个数的平方和转化为这两个数的积 的形式,就能使不等式左、右两端具有 相同的形式.
二、讲授新课——综合法(顺推证法或由因导果法)
利用已知条件和某些数学定义、公理、定理等, 经过一系列的推理论证,最后推导出所要证明的结论 成立,这种证明方法叫做综合法。其特点是:“由因导 果” 用P表示已知条件、已有的定义、公理、定理 等,Q表示所要证明的结论.
则综合法用框图表示为:
P Q1 Q1 Q2 Q2 Q3 … Qn Q
2.2.1综合法和分析法(二) ——分析法
一、回顾复习——综合法(顺推证法或由因导果法)
利用已知条件和某些数学定义、公理、定理等, 经过一系列的推理论证,最后推导出所要证明的结论 成立,这种证明方法叫做综合法。其特点是:“由因导 果” 用P表示已知条件、已有的定义、公理、定理 等,Q表示所要证明的结论.
语言就是2B=A+C;
•A,B,C为△ABC的内角,这是一个隐含 条件,即A+B+C=180°;
•a,b,c成等比数列转化为符号语言就是
b2 = ac.
此时,如果能把角和边统一起来,那么就可以进一 步寻找角和边之间的关系,进而判断三角形的形状,余 弦定理正好满足要求.于是,可以用余弦定理进行证明.
证明:由A,B,C成等差数列,有 2B=A+C. ①
因为A,B,C为△ABC的内角,所以 A+B+C=180°. ②
由① ②,得 B = π . ③ 3
由a,b,c成等比数列,有
b2 = ac. ④
注:解决数学问题时,学会语言转换;还要细致,找出隐含条件。
文字语言
图形语言
符号语言
由余弦定理及③,可得
b2 = a2 + c2 - 2accosB = a2 + c2 - ac.
其次,寻找转化的依据及证明中要用的 其他知识:应用不等式x2+y2≥2xy就能实 现转化,不等式的基本性质是证明的依 据.
证明:
∵ b2+c2 ≥ 2bc,a>0 ∴ a(b2+c2) ≥2abc.
又∵ c2+a2 ≥ 2ac,b>0 ∴ b(c2+a2) ≥ 2abc.
∴ a(b2+c2)+b(c2+a2) ≥ 4abc.
再由④,得 a2 + c2 - ac = ac,
即 (a - c)2 = 0.
因此 a=c.
从而 A=C. ⑤
由 ② ③ ⑤ ,得 A = B = C = π . 3
所以△ABC为等边三角形.
四、课堂小结
1.在数学证明中,综合法最常用的数学方法,若从已知 入手能找到证明的途径,则用综合法.
2.综合法的每步推理都是寻找必要条件,在解题表述中 要注意语言的规范性和逻辑性.
