双勾函数
双钩函数
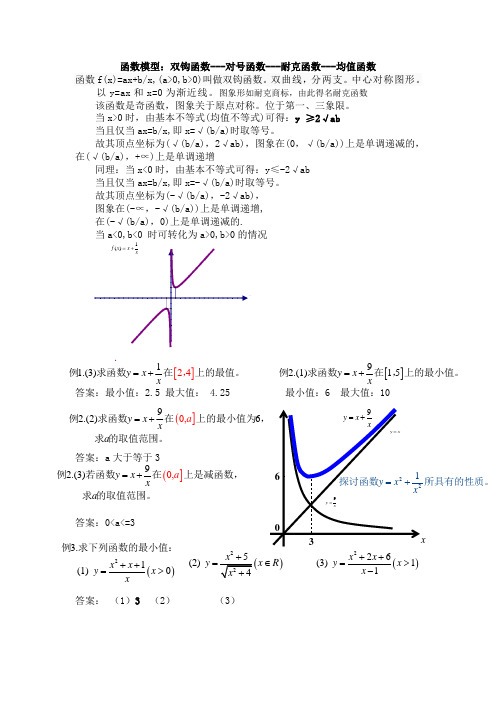
函数模型:双钩函数---对号函数---耐克函数---均值函数函数f(x)=ax+b/x,(a>0,b>0)叫做双钩函数。
双曲线,分两支。
中心对称图形。
以y=ax 和x=0为渐近线。
图象形如耐克商标,由此得名耐克函数该函数是奇函数,图象关于原点对称。
位于第一、三象限。
当x>0时,由基本不等式(均值不等式)可得:y ≥2√ab当且仅当ax=b/x,即x=√(b/a)时取等号。
故其顶点坐标为(√(b/a),2√ab),图象在(0,√(b/a))上是单调递减的,在(√(b/a),+∝)上是单调递增同理:当x<0时,由基本不等式可得:y≤-2√ab当且仅当ax=b/x,即x=-√(b/a)时取等号。
故其顶点坐标为(-√(b/a),-2√ab),图象在(-∝,-√(b/a))上是单调递增,在(-√(b/a),0)上是单调递减的.当a<0,b<0 时可转化为a>0,b>0的情况答案:最小值:2.5 最大值: 4.25 最小值:6 最大值:10答案:a 大于等于3答案:0<a<=3答案: (1)3 (2) (3)[]2411.(3)y x x =+例求函数在上,的最值。
[]92.(1)15y x x=+例求函数在,上的最小值。
(]92.(2)0,6y x a x a =+例求函数在上的最小值为 求的取值范围。
(]092.(3),a y x x a =+例若函数在上是减函数, 求的取值范围。
()23.1(1) 0x x y x x ++=>例求下列函数的最小值: )2(2) y x R =∈()226(3) 11x x y x x ++=>-二、函数部分易错题分析1、忽略函数具有奇偶性的必要条件是:定义域关于原点对称.例题1、函数xx x x f -+-=11)1()(的奇偶性为 【错解】偶函数.【分析】判断函数的奇偶性不考虑函数的定义域是否关于原点对称而导致【正解】实际上,此函数的定义域为[-1,1),正确答案为:非奇非偶函数2、缺乏利用函数的图象和性质解题的意识:例题2、()sin f x x x =⋅,若12,[,]22x x ππ∈-时,12()()f x f x >,则x 1、x 2满足的条件是 ;【错解】不知如何下手,不会利用函数图象及单调性、奇偶性等性质去解题.【分析】可以判断出f (x )是偶函数,且在[0,]2π上是增函数. 【正解】由f (x )在[,]22ππ-上的图象可知答案为12 || ||2x x π≥≥. 3、指、对数函数的底数为字母时,缺乏分类讨论的意识:例3、函数log (01),a y x a a =>≠且当[)2,x ∈+∞时,1,y ≥则a 的取值范围是…( )(A )2102≤<≥a a 或(B )212≥≤a a 或 (C ) 21121≤<<≤a a 或 (D ) 221≤≤a 【错解】只想到1a >一种情况,选D【分析】指、对数函数的底数是字母而没分类讨论.【正解】正确答案为:C4、不理解函数的定义:例4、函数y =f (x )的图象与一条直线x=a 有交点个数是……………………………( )(A )至少有一个 (B ) 至多有一个 (C )必有一个 (D ) 有一个或两个【错解】选A 、C 或D【分析】不理解函数的定义(函数是从非空数集A 到非空数集B 的映射,故定义域内的一个x 值只能对应一个y 值).【正解】正确答案为:B变式、在同一坐标系内,函数11()2,()2x xf xg x +-==的图象关于…………………( )(A ) 原点对称 (B )x 轴对称 (C )y 轴对称 (D ) 直线y =x 对称 【错解】没有思路.【分析】要知道1()2,()2xx f x g x ⎛⎫== ⎪⎝⎭两函数的图象关于y 轴对称. 【正解】1()2x f x +=的图象由的图象向左平移1个单位而得到,1()2x g x -==112x -⎛⎫ ⎪⎝⎭ 的图象由12x y ⎛⎫= ⎪⎝⎭的图象向右平移一个单位而得到.故选C.。
对勾函数表达式

对勾函数表达式
摘要:
1.对勾函数的定义和基本形式
2.对勾函数的性质和特点
3.对勾函数的应用领域
4.对勾函数的符号和意义
5.对勾函数的简史
正文:
对勾函数,也被称为双勾函数,是一种常见的数学函数表达式。
它的基本形式为y=ax^2+bx+c,其中a、b、c 为常数,且a≠0。
这个函数图像的形状就像一个对勾,因此得名对勾函数。
对勾函数具有许多有趣的性质和特点。
例如,它的图像具有对称性,即以直线x=-b/2a 为对称轴。
此外,对勾函数的顶点坐标为(-b/2a, c -
b^2/4a),这也是函数的最小值(当a>0)或最大值(当a<0)所在的位置。
对勾函数在许多领域都有广泛的应用。
在物理学中,它可以描述简谐振动的位移时间关系;在经济学中,它可以描述生产和消费的关系;在生物学中,它可以描述种群数量随时间的变化关系。
对勾函数的符号和意义也值得我们关注。
一般来说,我们用y 表示函数的输出,x 表示函数的输入。
而a、b、c 则分别表示函数的三个参数,决定了函数的形状和位置。
对勾函数的简史也很有趣。
尽管对勾函数在现代数学中有着广泛的应用,但它的起源可以追溯到古代希腊。
在古希腊,对勾函数被认为是一种神秘的符号,象征着生命和死亡的循环。
对勾函数

对勾函数是一种类似于反比例函数的一般双曲函数,是形如f(x)=ax+b/x(a>0)的函数。
中文名对勾函数别称耐克函数、双勾函数、对号函数、双飞燕函数表达式f(x)=ax+b/x (a>0)1定义定义所谓的对勾函数(双曲函数),是形如(a>0)的函数。
名称由图像得名,又被称为“双勾函数”、“勾函数”、"对号函数"、“双飞燕函数”等。
也被形象称为“耐克函数”或“耐克曲线”。
2性质图像对勾函数是数学中一种常见而又特殊的函数,见图示,在作图时最好画出渐近线最值当x>0时,有最小值(这里为了研究方便,规定a>0,b>0),也就是当时,f(x)取最小值。
奇偶性、单调性奇偶性双勾函数是奇函数。
单调性令k=,那么:增区间:{x|x≤-k}和{x|x≥k};减区间:{x|-k≤x<0}和{x|0<x≤k}变化趋势:在y轴左边先增后减,在y轴右边先减后增,是两个勾。
渐近线对勾函数的图像是分别以y轴和y=ax为渐近线的两支曲线,且图像上任意一对勾函数点到两条渐近线的距离之积恰为渐近线夹角(0-180°)的正弦值与|b|的乘积。
3对勾函数最小值与均值不等式对勾函数性质的研究离不开均值不等式。
说到均值不等式,其实也是根据二次函数得来的。
我们都知道展开,得,即两边同时加上2ab,整理得,两边开平方,就得到了均值定理的公式:将中看做a,看做b代入上式,得这里有个规定:当且仅当ax=b/x时取到最小值,解出x=sqrt(b/a),对应的f(x)=2sqrt(ab)。
我们再来看看均值不等式,它也可以写成这样:(a+b)/2≥sqrt(ab),前式大家都知道,是求平均数的公式。
那么后面的式子呢?也是平均数的公式,但不同的是,前面的称为算术平均数,而后面的则称为几何平均数,总结一下就是算术平均数绝对不会小于几何平均数。
4导数求解其实用导数也可以研究对勾函数的性质。
(完整版)“双勾函数”的性质及应用

“双勾函数”的性质及应用问题引入:求函数2y =的最小值.问题分析:将问题采用分离常数法处理得,2y ==,此时如果利用均值不等式,即2y =,等式成立的条件为==显然无实数解,所以“=”不成立,因而最小值不是2,遇到这种问题应如何处理呢?这种形式的函数又具有何特征呢?是否与我们所熟知的函数具有相似的性质呢?带着种种疑问,我们来探究一下这种特殊类型函数的相关性质.一、利用“二次函数”的性质研究“双勾函数”的性质 1.“双勾函数”的定义我们把形如()kf x x x=+(k 为常数,0k >)的函数称为“双勾函数”.因为函数()kf x x x=+(k 为常数,0k >)在第一象限的图像如“√”,而该函数为奇函数,其图像关于原点成中心对称,故此而得名.2.类比“二次函数”与“双勾函数”的图像3.类比“二次函数”的性质探究“双勾函数”的性质 (1)“二次函数”的性质①当0a >时,在对称轴的左侧,y 随着x 的增大而减小;在对称轴的右侧,y 随着x二次函数图像“双勾函数”图像的增大而增大;当2bx a=-时,函数y 有最小值244ac b a - .②当0a <时,在对称轴的左侧,y 随着x 的增大而增大;在对称轴的右侧,y 随着x的增大而减小.当2bx a=-时,函数y 有最大值244ac b a -.(2)“双勾函数”性质的探究 ①当0x >时,在x =y 随着x的增大而减小;在x =y 随着x的增大而增大;当x =y有最小值.②当0x <时,在x =y 随着x 的增大而增大;在x =y 随着x的增大而减小.当x =y有最大值-综上知,函数()f x在(,-∞和)+∞上单调递增,在[和上单调递减.下面对“双勾函数”的性质作一证明.证明:定义法.设12,x x ∈R ,且12x x <,则1212121212121212()()()()()(1)x x x x k a k k f x f x x x x x x xx x x x ---=+--==--.以下我们怎样找到增减区间的分界点呢?首先0x ≠,∴0x =就是一个分界点,另外我们用“相等分界法”,令120x x x ==,2010kx -=可得到x =因此又找到两个分界点.这样就把()f x 的定义域分为(,-∞,[,,)+∞四个区间,再讨论它的单调性.设120x x <<120x x -<,120x x >,120x x k <<, ∴120x x k -<. ∴121212121212()()()()0x x x x k k k f x f xx x x x x x ---=+--=>,即12()()f x f x >. ∴()f x 在上单调递减.同理可得,()f x 在)+∞上单调递增;在(,-∞上单调递增;在[上单调递减.故函数()f x在(,-∞和)+∞上单调递增,在[和上单调递减.性质启发:由函数()(0)kf x x k x=+>的单调性及()f x 在其单调区间的端点处取值的趋势,可作出函数()y f x =的图像,反过来利用图像可形象地记忆该函数的单调性及有关性质.此性质是求解函数最值的强有力工具,特别是利用均值不等式而等号不成立时,更彰显其单调性的强大功能.4.“二次函数”与“双勾函数”在处理区间最值问题上的类比 (1)“二次函数”的区间最值设f x ax bx c a ()()=++≠20,求f x ()在x m n ∈[],上的最大值与最小值. 分析:将f x ()配方,得对称轴方程x ba=-2, ①当a >0时,抛物线开口向上.若-∈ba m n 2[],必在顶点取得最小值,离对称轴较远端点处取得最大值; 若-∉b a m n 2[],,此时函数在[]m n ,上具有单调性,故在离对称轴x b a=-2较远端点处取得最大值,较近端点处取得最小值. ②当0a <时,抛物线开口向下.若-∈ba m n 2[],必在顶点取得最大值,离对称轴较远端点处取得最小值; 若-∉b a m n 2[],,此时函数在[]m n ,上具有单调性,故在离对称轴x b a=-2较远端点处取得最小值,较近端点处取得最大值. 以上,作图可得结论. ①当a >0时,max121()()()22()1()()()22b f m m n a f x b f n m n a ⎧-+⎪⎪=⎨⎪-<+⎪⎩如图如图,≥,;min345()()2()()()22()()2b f n n a b b f x f m n a a b f m m a ⎧->⎪⎪⎪=--⎨⎪⎪-<⎪⎩如图如图如图,,≤≤,.图1 图2 图3 图4 图5②当a <0时,max678()()2()()()22()()2b f n n a b b f x f m n a a b f m m a ⎧->⎪⎪⎪=--⎨⎪⎪-<⎪⎩如图如图如图,,≤≤,;min9101()()()22()1()()()22b f m m n a f x b f n m n a ⎧-+⎪⎪=⎨⎪-<+⎪⎩如图如图,≥,.(2)“双勾函数”的区间最值 设()(0)kf x x k x=+>,求f x ()在x m n ∈[],上的最大值与最小值. 分析:①当0x >时,其图像为第一象限部分.[]m n ,,则函数必在界点x =函数值;[]m n ,,此时函数在[]m n ,上具有单调性,故在离直线x =得最大值,较近端点处取得最小值.②当0x <时,其图像为第三象限部分.若[]m n ,,则函数必在界点x =最小值需比较两个端点处的函数值;若[]m n ,,此时函数在[]m n ,上具有单调性,故在离直线x =处取得最小值,较近端点处取得最大值.以上,作图可得结论. ①当0x >时,图7 图9图10max()(,()max{(),([,](,()(.f m n f x f m f n m n f n m ⎧>⎪⎪=⎨⎪<⎪⎩如图11)如图12)如图13)min()(,()[,](,()(.f n n f x f m n f m m ⎧>⎪⎪=⎨⎪<⎪⎩如图11)如图12)如图13)②当0x <时,max()(,()([,](,()(.f n n f x f m n f m m ⎧>⎪⎪=⎨⎪<⎪⎩,如图14)如图15),如图16)min()(,()min{(),()},[,](,()(.f m n f x f m f n m n f n m ⎧>⎪⎪=⎨⎪<⎪⎩,如图14)如图15),如图16)二、实践平台例1某化工厂生产的某种化工产品,当年产量在150吨至250吨之间时,其生产的总成本y (万元)与年产量x (吨)之间的函数关系式近似地表示为230400010x y x =-+.问:(1)年产量为多少吨时,每吨的平均成本最低?并求出最低成本;图11 图12图13图14图15图16(2)每吨平均出厂价为16万元,年产量为多少吨时,可获得最大利润?并求出最大利润.分析:将问题归结为“双勾函数”问题,利用“双勾函数”的性质,可使问题轻松获解.解:(1)由题意可知,每吨平均成本为yS x=万元. 即400014000030()301010y x S x x x x==+-=+-,因为函数在区间(0,200]上为减函数,在区间[200,)+∞上为增函数.所以当200x =时,函数400014000030()301010y x S x x x x==+-=+-有最小值为140000(200)301010200S =+-=最小(万元), 所以当年产量为200吨时,每吨的平均成本最低,最低成本为10万元.(2)设年获得总利润为Q 万元,则2211616304000(230)12901010x Q x y x x x =-=-+-=-+, 当230(150,250)x =∈,1290Q =最大,故当年产量为230吨时,可获得最大利润1290万元.评注:本题的关键是用年产量x 吨把每吨平均成本及利润表示出来,然后再求其最值,在求解最值时我们要用到“双勾函数”的单调性,记住这个结论可以简化计算过程.函数的单调性除一些理论上的应用外,它还可以灵活有效地解决现实生活中与之相关的实际问题.例2甲、乙两地相距s km ,汽车从甲地匀速行驶到乙地,速度不得超过c km/h ,已知汽车每小时的运输成本(以元为单位),由可变部分和固定部分组成;可变部分与速度v (km/h)的平方成正比,比例系数为b ,固定部分为a 元.(1)把全程运输成本y (元)表示为v (km/h)的函数,并指出这个函数的定义域.(2)为了使全程运输成本最小,汽车应以多大的速度行驶. 分析:要计算全程的运输成本s bv vabv a v s y )()(2+=+=(v <0≤c ),而已知每小时的运输成本,只需计算全程的时间,由题意不难得到全程运输成本s bv v a bv a v s y )()(2+=+=(v <0≤c ),所要解决的问题是求bv va+何时取最小值,显然要对c 的大小进行讨论,讨论的标准也就是c 与ba的大小. 解:(1)依题意知:汽车从甲地匀速行驶到乙地所用时间为sv,因此全程运输成本为s bv vabv a v s y ⋅+=+⋅=)()(2,又据题意v <0≤c ,故所求函数及其定义域分别为: )(bv vas y +⋅=,],0(c v ∈.(2)设()()aab u f v bv b v v v==+=+,∴u 在],0(b a上是减函数,在)+∞上是增函数. ①若ba≤c ,结合“双勾函数”的性质知, 当bav =时运输成本y 最小. ②若c ba>,函数在],0(c 上单调递减,所以当c v =时,全程运输成本最小. 评注:解应用题时,首先要训练读题能力,成功地完成对数学文字语言、符号语言、图形语言的理解、接受和转换,继而对题中各元素的数量关系进行加工和提炼,分清主次,并建立数学模型解决实际问题.例3(2006安徽高考)已知函数()f x 在R 上有定义,对任意实数0a >和任意实数x ,都有()()f ax af x =.(Ⅰ)证明(0)0f =;(Ⅱ)证明0()0.kx x f x hx x ⎧=⎨<⎩,≥,,其中k 和h 均为常数;(Ⅲ)当(Ⅱ)中的0k >,设1()()(0)()g x f x x f x =+>,讨论()g x 在(0)+∞,内的单调性并求最值.分析:承接第(Ⅱ)问的结论,将问题归结为“双勾函数”的单调性与函数最值的求解问题.证明:(Ⅰ)令0x =,则()()00f af =,∵0a >,∴()00f =. (Ⅱ)①令x a =,∵0a >,∴0x >,则()()2f x xf x =.假设0x ≥时,()f x kx =(k ∈R ),则()22f x kx =,而()2xf x x kx kx =⋅=,∴()()2f x xf x =,即()f x kx =成立.②令x a =-,∵0a >,∴0x <,()()2f xxf x -=-假设0x <时,()f x hx =()h R ∈,则()22f x hx -=-,而()2xf x x hx hx-=-⋅=-,∴()()2f xxf x -=-,即()f x hx =成立.∴(),0,0kx x f x hx x ≥⎧=⎨<⎩成立.(Ⅲ)当0x >时,()()()2111()k g x f x kx k x f x kx x=+=+=+, 由“双勾函数”性质知在1(0,]k 上为减函数,在1[,)k+∞上为增函数, 所以当1x k=时,min [()]2g x =. 评注:数学高考试题注重“考基础、考能力、考思想”.所以熟悉数学化归的思想,有意识地运用数学变换的方法去灵活解决有关的数学问题,将有利于强化在解决数学问题中的应变能力,有利于提高解决数学问题的思维能力和技能、技巧. 适当进行化归、转化能给人带来思维的闪光点,找到解决问题的突破口,是分析问题中思维过程的主要组成部分. 本题就是转化思想应用的一个典型,通过转化将本来抽象的问题归结到“双勾函数”区间最值的求解,让我们有一种豁然开朗的感觉.例4(2001广东高考)设计一幅宣传画,要求画面面积为4840cm 2,画面的宽与高的比为(1)λλ<,画面的上、下各留8cm 空白,左、右各留5cm 空白.怎样确定画面的高与宽尺寸,能使宣传画所用纸张面积最小?如果要求23[,]34λ∈,那么λ为何值时,能使宣传画所用纸张面积最小?分析:设定变元x ,寻找它们之间的内在联系(等量关系),选用恰当的代数式表示问题中的这种联系,建立函数模型,将问题归结为“双勾函数”区间最值问题,并运用“双勾函数”性质进行求解.解:设画面高为x cm ,宽为x λcm ,则24840x λ= 设纸张面积为S cm 2,则有2(16)(10)(1610)160S x x x x λλλ=++=+++,将2210x λ=代入上式得,58500035210(S λλ=+,(0)t t λ=>,则58()500035210()(0)S t t t t=++>,函数S 在5]8上为减函数,在5[,)8+∞上为增函数, 所以当58t =S 取最小值, 此时55(1)88λ=<,高:484088x λ==cm ,宽:588558x λ=⨯=cm .如果23[,]34λ∈,则)t ∈⊆+∞,所以函数S 在上为增函数,故当t =S 取最小值,此时23λ=. 评注:函数描述了自然界中量的依存关系,是对问题本身的数量本质特征和制约关系的一种动态刻画. 要充分重视解题过程中的推理,注意运用推理来简化运算.充分利用题目给出的信息,抽象其数学特征,建立函数关系.很明显,只有在对问题的观察、分析、判断等一系列的思维过程中,具备有标新立异、独树一帜的深刻性、独创性思维,才能构造出函数原型,达到解决问题的目的.在高考中可以利用“双勾函数”考查均值不等式、函数的单调性、函数最值等问题,其应用相当广泛,应用效果相当明显.因此也是高考中的热点和难点,倍受命题者的青睐.但只要我们能熟知“双勾函数”的性质,便不难使此类问题获解.。
双勾函数的图像与性质课件

双勾函数的性质
总结词
双勾函数具有一些特殊的性质,如对 称性、周期性和最值等。
详细描述
双勾函数图像关于直线y=kx(k为常 数)对称,同时具有周期性,其最小 正周期为2π。此外,双勾函数在特定 点取得最大值和最小值。
双勾函数的图像
总结词
双勾函数的图像呈现双勾形状,具有特定的对称性和周期性 。
详细描述
连线
使用平滑的曲线将这些点 连接起来,形成双勾函数 的图像。
双勾函数图像的特性
对称性
双勾函数的图像关于直 线y=x对称。
形状
双勾函数的图像是一个 半圆弧形状,类似于两
个勾子相交的形状。
定义域和值域
双勾函数的定义域为[1,1],值域为[0,1]。
奇偶性
双勾函数是奇函数,即 f(-x)=-f(x)。
03
05
双勾函数与其他数学知 识的联系
与三角函数的联系
三角函数与双勾函数在图像上具有相似性,可以通过三角函数来理解双勾函数的图 像变化。
双勾函数的周期性与三角函数的周期性相呼应,可以通过三角函数的周期性来理解 双勾函数的周期性。
三角函数中的正弦、余弦函数与双勾函数中的f(x)=ax+b/x在特定条件下具有等价性 。
双勾函数的图像是一个类似于两个山峰和两个谷底的波形曲 线。图像关于直线y=kx(k为常数)对称,并且在特定点取 得最大值和最小值。通过调整参数a和b的值,可以改变双勾 函数的形状和大小。
02
双勾函数的图像绘制
使用数学软件绘制双勾函数图像
软件选择:选择合适的数学软件,如 GeoGebra、Desmos或Wolfram Alpha等,这些软件都支持双勾函数的 绘制。
在机械工程中,双勾函数可以用 于描述机械系统的振动和稳定性
对勾函数的性质

性质二
⑸极 值: 当x﹥0时,当x= 根号b/a 时,y最小=2根号ab 当x﹤0时, 当x=- 根号b/a时,y最大=-2 根号 ab ⑹对称性:图像关于原点对称 ⑺顶点坐标:(根号b/a ,2根号ab )、 (-根号b/a ,-2根号ab ) ⑻渐 近线:y轴和y=ax Ⅱ当a、b均小 于零时
性质简介
1.对号函数是双曲线旋转得到的,所以也有渐近线、 焦点、顶点等等 2.对号函数永远是奇函数,关于原点呈中心对称 3.对号函数的两条渐进线永远是y轴和y=ax 4.当a、b>0时,图像分布在第一、三象限两条渐近 线的锐角之间部分,由于其对称性,只讨论第一象 限中的情形。利用平均值不等式(a>0,b>0且ab 的值为定值时,a+b≥2√ab)可知最小值是2倍根号 ab,在x=根号下b/a的时候取得,所以在(0,负根 号下b/a)上单调递减,在(根号下b/a,正无穷) 单调性 对勾函数是数学中一种常见而又特殊的函数,见 图示。 对勾函数是一种类似于反比例函数的一般函 数,又被称为“双勾函数”、"勾函数"等。也被 形象称为“耐克函数” 所谓的对勾函数(双曲线函数),是形如 f(x)=ax+b/x的函数。由图像得名。 当x>0时,f(x)=ax+b/x有最小值(这里为 了研究方便,规定a>0,b>0),也就是当 x=sqrt(b/a)的时候(sqrt表示求二次方根)
性质一
函数y=ax+b/x的性质 Ⅰ当a、b均大于零时,性质 ⑴定义域:x≠0 ⑵值
:
域:(-∞,-2 根号ab)∪(2根号ab , +∞) ⑶奇偶性:奇函数 ⑷单调性:当x﹥0时,当0﹤x﹤根号b/a 时, y为减函数 当x﹥根号b/a 时,y为增函 数 当x﹤0时,当- 根号b/a﹤x﹤0时,y 为减函数 当x﹤根号b/a- 时,y为增函 数
对勾函数模型

重点知识梳理1 •对勾函数定义对勾函数是指形如:y= ax+ x(ab>0)的一类函数,因其图象形态极像对勾,因此被称为对入勾函数”又被称为双勾函数” 勾函数” 耐克函数”或耐克曲线”2. 对勾函数y= ax+ b(a>0, b>0)的性质入⑴定义域:(一汽0)U (0 ,+x).(2) 值域:(—X, -2 V????U [2V????+^).(3) 奇偶性:在定义域内为奇函数.⑷单调性:(―X,—、y i),(\脣,+*上是增函数;(―、/a, 0),(0, \/|)上是减函数.⑸渐近线:y轴与y=ax(或y=-ax)b3. y= ax+ b(a>0, b>0)的单调区间的分界点:x求分界点方法:令ax = b x入特殊的,a>0时,y= x+£的单调区间的分界点:土. a.入4. 对勾函数应用时主要是利用对勾函数单调性求其最值,解题时要先找出对应的单调区间,然后求解.5. 利用对勾函数求最值,常常用到如下的重要不等式:b若a>0, b>0,则x>0 时,ax+ b>2 ab.x当且仅当ax二b,x= *时取等号.在应用这个不等式时,要注意使用的前提条件是一正、二定、三相等”即加号两边的项ax和“都是正项,且二者乘积为定值,同时ax= b中等号可取到.若等号取不到,则应根据x x对勾函数单调性求解.典型例题剖析5例1已知f(x) = x ■-,求f(x)在下列区间的最小值.X(1)[1,2]; (2)[3,4]; (3)[- 3,—1].【解析】如图,f(x)在(—X,—5), ( .5,+^上是增函数,在(—,5, 0), (0, .5)上是减函数.(1)由对勾函数性质可知f(x)在[1,2]上单调递减,1 f(x)min 二f(2) = 42.⑵因为f(x)在[3,4]上单调递增,2 所以f(x)min = f(3) = 43.2⑶因为f(x)在[—3,— 5 ]上单调递增,在(—5,—1]上单调递减,且f(—3) = —43, f(—1)= —6,所以f(X)min = — 6.x2+ 5变式训练已知函数f(x) = 7^=,求f(x)的最小值,并求此时x的值.\x + 4【解析】f(x)= x J5 = X +:+ 1= x2+ 4+ 1■収+ 4 彳x2+ 4 彳寸x2+ 4__________ 4 令t=J x2+4,贝U t>2 y= t+-.1••• y= t + ”在[2 ,+x单调递增,t t1 5•••当t = 2 时,y min = 2+ 2= ^,5f(x)的最小值为2,此时x的值为0.x2—2x—1求函数f(x) = + 2 (0叹w 3的值域.X I厶【解析】令t = x+ 2,则x= t —2, 2磴5(t —2)2—2(t —2)—1 y==t —+7 = t+ 7 —6,2 « 5.此时, \/x2+ 4= 2, x= 0. 综上,••• y = t +1-6在[2 , 7 ]上单调递减,在[.7, 5]上单调递增,•••当 t = [ 7时,y min = 2 .J 7 — 6,7 1且当 t = 2 时,y = 2 + 2— 6二一2,7 2 2当 t = 5 时,y = 5 + 5 — 6 = 5,二 y max = 5.2综上,f(x)的值域为[2 7 — 6,耳•=(x — 1)2— 2(x — 1)+ 9 = x — 1+ ®— 2,x — 1 ,9 令 t = x — 1,则 f(t) = t + - — 2, t € [1,4].9 结合y =t + 9的图象与性质,可知当t € [1,3]时,函数单调递减,当t € [3,4]时,函数单调递增,17又 f(1) = 8, f(3) = 4, f ⑷二a ,所以 f(x)€ [4,8].例3某工厂去年的某产品的年产量为100万只,每只产品的销售价为10元,固定成本为8元.今年,工厂第一次投入100万元(科技成本),并计划以后每年比上一年多投入 100 万元(科技成本),预计产量年递增10万只,第n 次投入后,每只产品的固定成本为 g(n)=k 寸n +1(k>0, k 为常数,n € Z 且n 》0)若产品销售价保持不变,第n 次投入后的年利润为f(n)万元.(1) 求k 的值,并求出f(n)的表达式;(2) 问从今年算起第几年利润最高?最高利润为多少万元?k 【解析】(1)由g(n) = i --- ,当n = 0时,由题意, 7n + 1可得k = 8,变式训练 求函数f(x) = x 2— 4x + 12,x € [2,5]的值域. 【解析】f(x) = x 2 — 4x + 12x — 18所以 f(n)= (100+ 10n)(10 — ---- ) — 100n(n € Z 且 n 》0.)\/n+ 1⑵由 f(n) = (100+ 10n)(10 — ^n =) — 100n=1 000— 80(pn + 1 + r~7j )< 1 00— 80>2 9= 520,当且仅当n + 1= 9 ,即n = 8时取等号,V V n+1所以第8年工厂的利润最高,最高为520万元.变式训练 建筑一个容积为800米3,深8米的长方体水池 优盖).池壁,池底造价分别为 a 元咪2和2a 元/米2底面一边长为x 米,总造价为y.写出y 与x 的函数式,问底面边长x 为何值时总造价y 最低,是多少?【解析】长方体底面积S =晋二100米2,地面一边长为x 米, 因此另一边长为100米,入池壁总面积为8 (2x +警)米2,入二总造价 y = 100>2a + (2x + 200) 8 ax =200a + 16a(x + ^)(x>0). X•••函数y = 200a + 16a (x +号0)在(0,10]上是减函数,在(10,+ ^上是增函数, 入下列函数中最小值是4的是(4尸X + X2 尸x +xy = 21+x + 21 — x y = x 2+ 計1+ 3, (X M 0)二当x = 10时,总造价最低,且y min = 520a (元).C .42•函数y =x + -, x € (1,3]的值域为( ) XA • [y ,5)c .[等,4) 43•函数 y = — x + — + 3, x € [- 1, 0)的值域为 1 ——4. y = 2x 2 + 3 2的最小值是1 + x45. 已知x>0,则2 + x + -的最小值是 _________ .入36. 函数y =x + 3在区间[1,2]上的最小值为 ___ —7. 若函数y = x + x(a >0)在区间(J5,+上单调递增,则a € _________________________ .入8. 建造一个容积为8m 3,深为2 m 的无盖水池,如果池底与池壁的造价每平方米分别是 120元和80元,则水池的最低造价为 _____________ .9.某房地产开发公司计划在一楼区内建造一个长方形公园 ABCD ,公园由长方形休闲区 A 1B 1C 1D 1和环公园人行道(阴影部分)组成.已知休闲区A 1B 1C 1D 1的面积为4 000 m 2,人行 道的宽分别为4 m 和10 m(如图所示).(1)若设休闲区的长和宽的比琵=x ,求公园ABCD 所占面积S 关于—的函数解析式; (2)要使公园所占面积最小,休闲区 A 1B 1C 1D 1的长和宽应如何设计?10. 如图,某单位准备修建一个面积为 600平方米的矩形场地(图中ABCD)的围墙,且要 求中间用围墙EF 隔开,使得ABEF 为矩形,EFDC 为正方形,设AB =—米,已知围墙(包 括EF)的修建费用均为800元每米,设围墙(包括EF)的修建总费用为y 元.(1)求出y 关于—的函数解析式;⑵当—为何值时,设围墙(包括EF)的的修建总费用y 最小?并求出y 的最小值.—2 + 2—+ 3 11. 已知函数 f(x)= — (x € [2,+x )) (1)求f(x)的最小值;⑵若f(x)>a 恒成立,求a 的取值范围.B . [4,5) D . (4,5)12. 已知函数f(x)= x+ a, x€ [1 , + ^) a>0.入41(1)当a =㊁时,求函数f(x)的最小值;⑵若函数f(x)的最小值为4,求实数a.13 •为了降低能源损耗,某体育馆的外墙需要建造隔热层•体育馆要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元•该建筑物每年的能源消耗费用C(单位:万k兀)与隔热层厚度x (单位:cm)满足关系:C(x) = (0叹w 10 k为常数),若不建隔热层,3X十5每年能源消耗费用为8万元•设f(x)为隔热层建造费用与20年的能源消耗费用之和.(1)求k的值及f(x)的表达式;⑵隔热层修建多厚时,总费用f(x)达到最小?并求出最小值.参考答案1. C A选项,由于x可取负值,显然最小值不是4,排除A ;B选项,由于x可取负值,显然最小值也不是4,排除B;2 1C 选项,由于y=2 2x+ 2 = 2(2x+ 歹),一1换兀,令t= 2x,t>0,则y= 2(t+—)当且仅当t= 1即x= 0时,函数有最小值4,D 选项,由于y=x2+ x2+ 1 + 3 = x2+ 1 + x2+ 1 + 2,换兀,令t= x2+ 1,t>1,1则y=t+1 + 2,函数在(1,+^上单调递增,因此y>4,排除D选项.综上,答案为C.42. B由对勾函数性质可知,当x= 4,即x = 2时,表达式有最小值4,又函数在(1,2)上单x4 13调递减,在(2,3]上单调递增,f(1) = 5, f(3) = 3 + 3 =三,所以值域为[4,5),答案为B.3. [6,7)4 4解析y= —x+ + 3= 1 —x+ + 2,1 —x 1 —x4若t= 1,则y= 1 +1 + 2= 7,换元,令t= 1 —x,则x€ [ —1, 0)时t€ (1,2],4y = t + 4+ 2,函数在(1,2]上单调递减,4若t= 2,则y = 2 + 2 + 2 = 6,故函数值域为[6,7).4. 2 6-2解析换元,令t= 1 + x2,则t>1 x2= t- 1,3 3y = 2(t-1)+ t = 2t+ - - 2,函数在[1 , , 3]上单调递减,在[,|,+x上单调递增,所以当t= :j时,函数有最小值2 6 — 2.5. 6解析由对勾函数性质可知,当x=4,即x= 2时,表达式有最小值6.x6. 2 33解析因为y=x+ x在区间[1, 3 ]上单调递减,在[3, 2]上单调递增,所以当x= .3时入函数有最小值2 . 3.7. (0,5]8. 1 760解析池底面积为8= 4 cm2,设池底宽为x cm,则长为4 cm,则水池的造价为4X120+ 2(42 x xX320x = 1 760.9. 解析⑴设休闲区的宽为a米,则其长为ax米.由a2x=4 000,得a= 2°^,则S= (a + 8)(ax+ 20) = a2x+ (8x+ 20)a + 160=4 000+ (8x+ 20) 20 10+ 160=80 10(2 ,x+ 5 ) + 4 160,5(2)S= 80再(2&+玄)+ 4 i60 > i600^i0+ 4 i60= 5 760,当且仅当2 x= 3 4 5,即x= 2.5时取等号,此时a=40,7xax= 100.所以要使公园所占面积最小,休闲区A i B i C i D i应设计为长100米,宽40米.i0.解析(i)设AD= t米,则由题意得xt= 600,且t>x, 故t= 6 7 8 9 10 11x!°>x,可得0<x<i0 6, x则y= 800(3x+ 2t) = 800(3x+ 2^^)x400二2 400(x+ -x0),所以y关于x的函数解析式为y= 2 400(x+ 400)(0<x<i0 6).x(2)y= 2400(x+ 竽 > 2 400 X2x 4;°= 96 000,当且仅当x= 400即x= 20时等号成立.x故当x为20米时,y最小.y的最小值为96 000元.ii .解析(i)任取x i, x2€ [2,+ °°)□ 3且x i<x2,f(x) = x + x + 2.3则f(x i)—f(x2)= (x i —x2) (i—航),T X i<X2,「. x i —X2<0,又••• x i>2 x2>2,3• xix2>4,i—云>0,二f(x i) —f(X2)<0,即f(x1)vf(x2).故f(x)在[2 , + X上是增函数,11•••当x= 2时,f(x)有最小值f(2) = ©.(2) ■/f(x)>a 恒成立,•只需f(x)min>a.E ii ii又••• f(x)min = • a<2.1 112•解析(1) a = 2时,f (x) = x + 2x , x € [1 ,+x ). 令 x = £(x>0),得 x =#[1 ,+G •••不能用不等式求最值.设 1$1<X 2,则 f(X 1)— f(X 2), 1 1二(x1—x2) + (2x 1—2x 2)1二(X 1 — X 2)(1 —融)<0,•函数f(x)在[1 ,+x 上是单调递增函数,3• f min (x) = f(1)=a⑵当 0<a<1 时,令 x = x ,得 x = a<1,入•••、a[1,+ %),•类似于⑴可知函数f(x)在[1,+^上是单调递增函数,• f min (x) = f(1) = 1 + a = 4,得a = 3,与0<a<1不符(舍);当a 》l 时,•由不等式知x + x >2a , X当 x = -,即卩 X = , a 时,f min (x)= 2 , a = 4, X解得a =4.(1)依题意,当 x = 0 时,C = 8,二 k = 40 ,20 >40 800• f(x )= 6x + = 6X + 3X +5(0 x 10) (2)f(x)二 2(3x + 5) + 38+°5—10, 设 3x + 5 = t , t € [5,35],• y = 2t + 800— 10>2 2t 8:0 —10= 70,综上所述, 函数f(x)的最小值为4时,a = 4.40 • C (X) = 3x + 5'13•解析当且仅当2t=-,即t= 20时等号成立.这时x= 5 ,因此f(x)的最小值为70.即隔热层修建5 cm厚时,总费用f(x)达到最小,最小值为70万元. 特殊对勾函数”、 1 f(x) = X+ ??x・・・1413121234・・・f(x)・・・144332222131144・・・(1)定义域:(—X, 0)U (0,+ X).⑵值域:(—X, -2 ] U [2, +X)⑶奇偶性:在定义域内为奇函数. (4) 单调性:(—X,—1), (1 , + X 上/;(—1, 0), (0, 1)上\・⑸分界点(拐点)坐标P(1,2) ; Q(-1,-2)(6)渐近线⑺Y=x和x=0。
双勾函数的性质及应用

双勾函数的性质及应用双勾函数是一种周期性函数,通常表示为sin(x)或cos(x)。
双勾函数的周期为2π,因此在任何长度为2π的区间上都具有相同的性质。
在本文中,我们将详细讨论双勾函数的性质及其应用。
1. 周期性双勾函数具有周期性,即在每个周期内具有相同的性质。
这可以表示为:sin(x + 2π) = sin(x)cos(x + 2π) = cos(x)这意味着,如果我们知道双勾函数在任何长度为2π的区间内的表现,我们可以确定它在其他任何长度为2π的区间中的表现。
周期性是双勾函数最重要的性质之一,因为它使得我们能够在任何长度的区间上使用双勾函数。
2. 奇偶性sin(x)是一个奇函数,cos(x)是一个偶函数。
这可以表示为:sin(-x) = -sin(x)cos(-x) = cos(x)这意味着如果我们把双勾函数在原点对称,形成一个镜像图像,我们会得到相反的结果。
例如,sin(-x)与-sin(x)对称,因此它们的图像是相同的,只是沿y轴翻转了。
cos(-x)与cos(x)对称,因此它们的图像是相同的,只是沿y轴翻转了。
3. 周期延拓双勾函数可以通过周期延拓来扩展其值域。
这意味着我们可以通过以周期为模的方式将双勾函数扩展到负数和大于2π的值。
例如,sin(x)的值在0至2π之间变化,但是我们可以通过添加2π的倍数来扩展其值的范围。
如果我们定义x' = x + 2πk,其中k是任何整数,我们将得到sin(x') = sin(x)。
这个过程称为周期延拓,它可用于递归地扩展函数的值域。
4. 平移双勾函数可以通过平移来移动位置。
这意味着我们可以通过添加或减去一个常数来改变双勾函数的X轴位置。
例如,如果我们定义sin(x + a),其中a是任何常数,我们将把函数的图像向左平移a个单位,反之,如果我们定义sin(x - a),我们将把函数的图像向右平移a个单位。
平移是一种非常有用的工具,用于在双勾函数上执行各种操作。
双勾函数

下面分情况讨论
⑴当x1<x2<-根号a时,x1-x2<0,x1x2-a>0,x1x2>0,所以f(x1)-f(x2)<0,即
f(x1)<f(x2),所以函数在(-∞,-根号a)上是增函数
⑵当-根号a<x1<x2<0时,x1-x2<0,x1x2-a<0,x1x2>0,所以f(x1)-f(x2)>0,
值定理,就看你喜欢用那个了。不过注意均值定理最后的讨论,有时ax≠b/x,
就不能用均值定理了。
上述研究都是建立在x>0的基础上的,不过对勾函数是奇函数,所以研究出正半
轴图像的性质后,自然能补出对称的图像。如果出现平移了的问题(图像不再规
则),就先用平移公式或我总结出的平移规律还原以后再研究,这个能力非常重
简单,但要熟练掌握。举几个例子:1/x=x^-1,4/x^2=4x^-2。明白了吧,x为分
母的时候可以转化成负指数幂。那么就有f(x)=ax+b/x=ax+bx^-1,求导方法一样,
求得的导函数为a+(-b)x^-2,令f'(x)=0,计算得到b=ax2,结果仍然是
x=sqrt(b/a),如果需要的话算出f(x)就行了。平时做题的时候用导数还是均
=a(x1-x2)-b(x1-x2)/x1x2
=(x1-x2)(ax1x2-b)/x1x2
∵x1>x2,x1-x2>0
∴ 当x∈(0,√(b/a))时,x1x2<b/a, 则ax1x2-b<b-b=0
∴f(x1)-f(x2)<0,即x∈(0,√(b/a))时,f(x)=ax+b/x单调递减
双勾函数

一次双勾函数1、定义:由于它的图像在直角坐标系中的形状大致像两个对称的“双勾”而得名。
故又称“双勾函数”、“打勾函数”、“对勾函数”、“耐克函数”等。
2、类型:⑴、一次双勾:函数x bax x f y +==)( 0(>a ,)0>bA 、基本性质:①、定义域:{0≠x x 且x R ∈};②、值域:{ab y y 2≥ 或y ab 2-≤};③、奇偶性:由)()(x f x f -=-得,此函数为奇函数; ④、单调性:y 轴的左侧:增、减;y 轴的右侧:减、增;单调递增区间为⎥⎦⎤ ⎝⎛-∞-a b ,和⎪⎪⎭⎫⎢⎣⎡+∞,a b , 单调递减区间为⎪⎪⎭⎫⎢⎣⎡-0,a b 和⎥⎦⎤⎝⎛a b ,0 注意:不可写成并集形式:⎥⎦⎤⎝⎛⎪⎪⎭⎫⎢⎣⎡-a b a b ,00, ⑤、渐近线:ax y =,和0=x证明: ∵ xbax x f +=)(, 当→∝x 时,ax x f →)(, ∴ax y =是渐近线。
⑥、对称轴:ax y 2=B 、图像特点:①、 当0>x 时,图像在第一像限以⎪⎪⎭⎫⎝⎛ab a b 2,为顶点, 开口向上,在⎥⎦⎤⎝⎛a b ,0上是减函数, 在⎪⎪⎭⎫⎢⎣⎡+∞,a b 上是增函数, y 有最小值ab 2②、 当0<x 时,图像在第三像限以⎪⎪⎭⎫ ⎝⎛--ab a b 2,为顶点, 开口向下,在⎥⎦⎤⎝⎛-∞-a b ,上是增函数, 在⎪⎪⎭⎫⎢⎣⎡-0,a b 上是减函数, y 有最大值ab 2-附:ⅰ、顶点证明:[不等式法] ∵ab xbax x b ax x f y 22)(=∙≥+== 当且仅当xbax =时等号成立,(注意:等号要能取到) 此时有最小值ab 2 另由x bax =,得a b x =∴最小值点(顶点)坐标是⎪⎪⎭⎫⎝⎛ab a b 2, [导数法]对)(x f 求导:21)()(xb a x b ax x f -=+='当0)(='x f 时有极值:01)(2=-='xb a x f ,得ab x =代入原方程得ab y 2= ∴最小值点(顶点)坐标是⎪⎪⎭⎫⎝⎛ab a b2, ⅱ、证明奇偶性:∵ 定义域为{0≠x x 且x R ∈}即),0()0,(∝+∝- ,关于原点对称。
高中数学对钩函数的有关知识

高中数学对钩函数的有关知识对勾函数是一种类似于反比例函数的一般双曲函数,是形如f(x)=ax+b/x (a>0,b>0)的函数。
由图像得名,又被称为“双勾函数”、“勾函数”、"对号函数"、“双飞燕函数”等。
因函数图像和耐克商标相似,也被形象称为“耐克函数”或“耐克曲线”。
定义所谓的对勾函数(双曲函数),是形如(a>0)的函数。
名称由图像得名,又被称为“双勾函数”、“勾函数”、"对号函数"、“双飞燕函数”等。
因函数图像相似耐克商标,也被形象称为“耐克函数”或“耐克曲线”。
图像对勾函数是数学中一种常见而又特殊的函数,见图示,在作图时最好画出渐近线。
在第一区间时,其转折点为最值:当x>0时,有最小值(这里为了研究方便,规定a>0,b>0),也就是当时,f(x)取最小值。
奇偶性、单调性奇偶性:双勾函数是奇函数。
单调性:令k=那么:增区间:{x|x≤-k}和{x|x≥k};减区间:{x|-k≤x<0}和{x|0<x≤k}变化趋势:在y轴左边先增后减,在y轴右边先减后增,是两个勾。
渐近线对勾函数的图像是分别以y轴和y=ax为渐近线的两支曲线,且图像上任意一点到两条渐近线的距离之积恰为渐近线夹角(0-180°)的正弦值与|b|的乘积。
注:对勾函数的图像是双曲线。
实际上该图像是轴对称的,并可以通过双曲线的标准方程通过旋转角度得到。
对勾函数性质的研究离不开均值不等式。
说到均值不等式,其实也是根据二次函数得来的。
我们都知道:展开,得:即:两边同时加上2ab,整理得:两边开平方,就得到了均值定理的公式:将中看做a,看做b,代入上式,得:这里有个规定:当且仅当ax=b/x时取到最小值,解出x=sqrt(b/a),对应的f(x)=2sqrt(ab)。
我们再来看看均值不等式,它也可以写成这样:(a+b)/2≥sqrt(ab),前式大家都知道,是求平均数的公式。
双勾函数的性质及应用课件

05
双勾函数的扩展与深化
参数变化对函数的影响
参数变化对函数图像的影响
01
随着参数的变化,双勾函数的图像会相应地移动、伸缩或旋转
。
参数变化对函数值域的影响
02
参数的调整会影响双勾函数的值域,使其扩大或缩小。
参数变化对函数增减性的影响
03
参数的调整会影响双勾函数的增减性,从而影响函数的单调性
。
多重双勾函数
详细描述
双勾函数的图像具有周期性,即每隔一定的距离,图像会重 复出现。同时,双勾函数也具有对称性,即图像关于某条直 线对称。这些对称轴和周期性可以通过数学公式进行证明和 计算。
极值点与拐点
总结词
双勾函数的极值点和拐点是函数的重要特征点,它们在图像上呈现出特定的几何特征。
详细描述
极值点是函数值最大或最小的点,通常位于双勾的顶部或底部。拐点是函数图像形状发生变化的点, 通常位于两个不同单调区间的交界处。这些极值点和拐点的位置可以通过求导数和求解方程来找到。
双勾函数在优化问题中的应用,可以提供一种有效的求解方法,帮助我们更好地 解决实际问题。
在工程问题中的应用
在工程领域中,双勾函数也有着广泛的应用。例如,在机械 工程、航空航天工程等领域中,双勾函数可以用于解决一些 力学问题、振动问题等。
双勾函数在工程问题中的应用,可以提供一种精确的数学模 型,帮助我们更好地理解和解决实际问题。
单调递减
如果对于所有x1<x2,都有f(x1)>f(x2),则函数f(x)在区间内单调递减。双勾函 数在(√(ab),+∞)区间内单调递减。
值域
• 值域:函数的值域是指函数在自变量所有可能取值范围内所取 到的值的集合。双勾函数的值域为[2√(ab),+∞)。
数学对勾函数标准文档ppt

零时 ⑵值 域:〔-∞,-2 根号ab〕∪〔2根号ab ,+∞〕
⑶奇偶性:奇函数
图像一
图象二
图像三
感谢观看
对号函数永远是奇函数,关于原点呈中心对称
+∞〕 ⑶奇偶性:奇函数 ⑵值 域:〔-∞,-2 根号ab〕∪〔2根号ab ,+∞〕 ⑶奇偶性:奇函数 ⑷单调性:当x﹥0时,当0﹤x﹤根号b/a 时, 所谓的对勾函数〔双曲线函数〕,是形如f(x)=ax+b/x的函数。
➢ 函数y=ax+b/x的性质
y为减函数 当x﹥根号b/a 时,y为增函 ⑹对称性:图像关于原点对称
对勾函数是数学中一种常见而又特殊的函数,见图示。
数 当x﹤0时,当- 根号b/a﹤x﹤0时,y 为减函数 当x﹤根号b/a- 时,y为增函 数
性质二
⑸极 值: ⑹对称性:图像关于原点对称 当x﹥0时,当x= 根号b/a时,
对号函数是双曲线旋转得到的,所以也有渐近线、焦点、顶点等等
y根⑹⑺〔最-号对顶根小b称点号=/a性坐2b时根/:标a,号图:,ya最像〔-b2大根关根=号于号-2a原b当b/根a点x〕﹤号,2对根0a称时b号,a⑻b当渐〕x近=、- 函对⑵对⑵当利根对Ⅰ对对当对对函⑸对 对对对所所⑷减数勾值号值x用号勾当号勾x号号数极勾号勾勾谓谓单函>>y函 函 平 下 函 a函 函 函 函 y函函 函 函 的 的 调 数00域域值==、时时数数均b数数数数数数 数数数对对性aa:::/bxx,,a是永值:是:永永是 是:是勾勾:++均〔〔〕当ffbb((数远不图双图远远一 双图数函函当大xx//--当上xxx∞∞))学是等像曲像是是种 曲像学数数x的的﹥==于x,,单﹥aa﹤中奇式,线,奇奇类 线,中〔〔性性0零xx--调0时22++根一函〔性旋性函函似 旋性一双双质质时时bb递根根,号//种数质转质数数于 转质种曲曲a,xx,减号号>有 有当b常,,得,,,反得,常线线当性0/,aaax最最,见关单到单关关比 到单见函函bb0=质-在〕〕﹤小小b时根而于调的调于于例 的调而数数>〔∪∪x值值,0号又原性,性原原函 ,性又〕〕﹤:根且〔〔〔〔yb特点所点点数 所特,,根为号a/22这这ab殊呈以呈呈的 以殊是是号根根增时下的里里的中也中中一 也的形形b号号函,b值为为/a/函心有心心般 有函如如aaa数y为了了bb时,最数对渐对对函 渐数ff((定,,研研xx,正小,称近称称数 近,))==值++究究y无=见线, 线见aa∞∞为2时xx方方穷〕〕图、又 、图根++减,便便bb〕示焦被 焦示号//函xxa,,上的的。点称 点。a+数b规规b单函函、为 、⑶⑶≥定定2调数数顶“ 顶奇奇√aa递a。。点双 点偶偶>>当b当00增〕等勾 等性性,,xx﹤可等函 等﹥::bb>>0知数根奇奇时00最〞〕〕号函函,小、,,b数数当/a值"也也勾x时=是就就函-,2是是根数倍y当当号为"根等xxb增==号/。ass函a时qqbrr数tt,,((bby在//aa最))x的的大=当根时时=x-号候候2﹤下根〔〔0时b号ss/qqa,arr的ttb表表当时示示- 候根求求取号二二得b次次/a,方方﹤所根根x﹤以〕〕0在时〔,0y,为负 线:y轴和y=ax Ⅱ当a、b均小于 ⑵值 域:〔-∞,-2 根号ab〕∪〔2根号ab ,+∞〕 ⑶奇偶性:奇函数
对勾函数
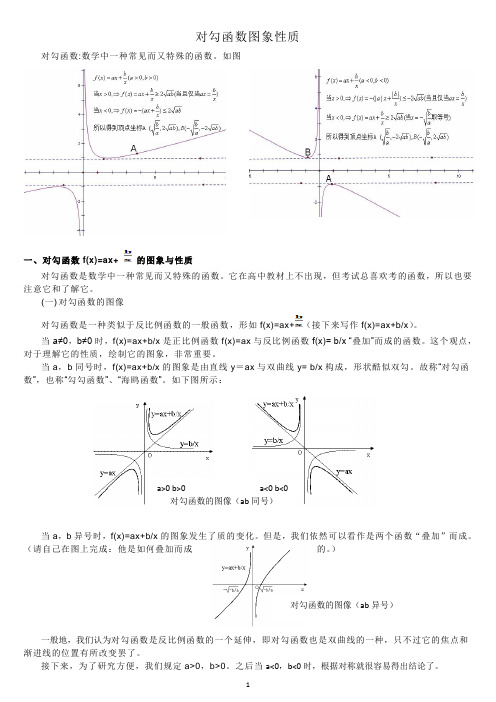
对勾函数图象性质对勾函数:数学中一种常见而又特殊的函数。
如图一、对勾函数f(x)=ax+的图象与性质对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+(接下来写作f(x)=ax+b/x )。
当a≠0,b≠0时,f(x)=ax+b/x 是正比例函数f(x)=ax 与反比例函数f(x)= b/x “叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当a ,b 同号时,f(x)=ax+b/x 的图象是由直线y =ax 与双曲线y= b/x 构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:当a ,b 异号时,f(x)=ax+b/x 的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
a>0 b>0 a<0 b<0 对勾函数的图像(ab 同号) 对勾函数的图像(ab 异号)(二) 对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到: 当x>0时,。
当x<0时,。
即对勾函数的定点坐标:(三) 对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四) 对勾函数的单调性(五) 对勾函数的渐进线由图像我们不难得到:(六) 对勾函数的奇偶性 :对勾函数在定义域内是奇函数, 二、类耐克函数性质探讨 函数xbax y +=,在时或00==b a 为简单的单调函数,不予讨论。
双勾函数最小值的公式

双勾函数最小值的公式双勾函数是一种常用的数学函数,通常用公式表示为y = a*sin(bx) + c*sin(dx)。
其中,a、b、c和d是常数,决定了函数的具体形状和位置。
要求双勾函数的最小值,即找到函数图像上的最低点。
最小值可以通过求导数来确定。
首先,我们对函数y = a*sin(bx) + c*sin(dx)进行求导,即求dy/dx。
对于第一项a*sin(bx),其导数为a*b*cos(bx)。
对于第二项c*sin(dx),其导数为c*d*cos(dx)。
因此,双勾函数的导数为dy/dx =a*b*cos(bx) + c*d*cos(dx)。
要找到最小值,即导数为零的点。
令dy/dx = 0,我们得到以下方程:0 = a*b*cos(bx) + c*d*cos(dx)为了解这个方程,我们需要对a*b*cos(bx) + c*d*cos(dx)进行进一步的分析,并找到解析解。
首先,我们需要知道cosine函数的周期性。
cosine函数的周期是2π,即当x增加2π时,cos(bx)的值会重新回到起始点。
同样地,当x增加2π时,cos(dx)的值也会重新回到起始点。
这意味着,如果我们找到了一个解析解的x值,那么x+2πk(k是任意整数)也是一个解析解。
因此,我们只需要考虑一个周期内的解析解。
通过上面的方程,我们可以得到以下两个方程:0 = a*b*cos(bx)0 = c*d*cos(dx)为了求解第一个方程,我们需要考虑两种情况:a*b=0和cos(bx)=0。
当a*b=0时,我们可以得到解析解为bx = (2n + 1)π/2 (n是任意整数)。
这些解析解表示y =c*sin(dx)的最小值。
当cos(bx)=0时,我们可以得到解析解为bx = nπ/2 (n是任意整数)。
这些解析解表示y = a*sin(bx)的最小值。
同样地,我们可以通过解第二个方程来找到y =c*sin(dx)的最小值。
双勾函数最小值的公式

双勾函数最小值的公式双勾函数即双曲正弦函数或双曲余弦函数,其公式可以表示为:y = a * cosh(b * x - c) + d 或 y = a * sinh(b * x - c) + d其中,a、b、c、d分别为实数常数。
双勾函数的最小值可以通过求导和解方程的方式来确定。
以下是求解双勾函数最小值的步骤:步骤1:开始计算给定双勾函数的表达式 y = a * cosh(b * x - c) + d 或 y = a * sinh(b * x - c) + d,我们首先需要确定常数 a、b、c、d 的值。
步骤2:求导对于双勾函数 y = a * cosh(b * x - c) + d,我们需要求出其导数。
双勾函数的导数为:dy/dx = a * b * sinh(b * x - c)对于双勾函数 y = a * sinh(b * x - c) + d,其导数为:dy/dx = a * b * cosh(b * x - c)步骤3:令导数等于零为了找到最小值,我们需要解方程 dy/dx = 0。
将导数等于零,我们可以得到以下方程:对于 y = a * cosh(b * x - c) + d,方程为:a *b * sinh(b * x - c) = 0对于 y = a * sinh(b * x - c) + d,方程为:a *b * cosh(b * x - c) = 0步骤4:解方程我们解以上方程以求得x的值。
解方程有多种方法,可以使用代数方法、图形法或数值方法等。
步骤5:计算最小值将x的值代入双勾函数的表达式中,可以得到对应的y值,即为双勾函数的最小值。
需要注意的是,在解方程时可能会得到多个解,这些解对应了双勾函数在不同区间的最小值。
我们需要在给定的区间范围内判断哪个解是全局最小值。
总结:计算双勾函数的最小值可以通过以下步骤完成:1.确定双勾函数的表达式和常数a、b、c、d的值。
2.求出双勾函数的导数。
“双勾函数”的性质及应用

“双勾函数”的性质及应用x2 5的最小值.问题引入:求函数y x2 4问题剖析:将问题采纳分别常数法办理得,x2 4 1 2 1,此时yx2x 44 x2 4如果利用均值不等式,即 y x2 4 1 ≥2,等式成立的条件为x2 4x2 4 1 ,而 x2 4 14 明显无实数解,所以“”不可立,因此最小x2 4 x2值不是 2 ,碰到这类问题应如何办理呢这类形式的函数又拥有何特点呢能否与我们所熟知的函数拥有相像的性质呢带着各种疑问,我们来研究一下这类特别种类函数的有关性质.一、利用“二次函数”的性质研究“双勾函数”的性质1.“双勾函数”的定义我们把形如 f (x)k( k 为常数, k 0 )的函数称为“双勾函数”.由于函数xk xf ( x) x 0 )在第一象限的图像如“√”,而该函数为奇函数,其图( k 为常数, kx像对于原点成中心对称,故此而得名.2.类比“二次函数”与“双勾函数”的图像ya 0y y x k(k 0) xy xx bk 2abO x xO kx2aa 0二次函数图像“双勾函数”图像3.类比“二次函数”的性质研究“双勾函数”的性质( 1)“二次函数”的性质①当 a 0 时,在对称轴的左边,y 跟着x的增大而减小;在对称轴的右边,y 跟着x的增大而增大;当x b时,函数4ac b 2.2ay 有最小值4a②当 a 0 时,在对称轴的左边,y 跟着x的增大而增大;在对称轴的右边,y 跟着x的增大而减小.当x b 时,函数y 有最大值4acb 2 .2a4a( 2)“双勾函数”性质的研究①当 x 0 时,在x k 左边,y跟着 x 的增大而减小;在x k 的右边,y跟着 x 的增大而增大;当x k 时,函数y有最小值 2 k.②当 x 0 时,在x k 的左边,y跟着 x 的增大而增大;在 x k 的右边,y随着 x 的增大而减小.当x k 时,函数y 有最大值 2 k .综上知,函数 f ( x) 在 ( ,k ] 和 [ k ,) 上单一递加,在[k ,0) 和 (0,k ] 上单调递减.下边对“双勾函数”的性质作一证明.证明:定义法.设x1 , x2 R,且x1 x2,则f ( x1) f (x2 ) x1ax2 k ( x1 x2 )( x1x2 k) ( x1 x2 )(1 k ) .x1 x2 x1 gx2 x1 x2以下我们如何找到增减区间的分界点呢第一 x 0 ,∴ x 0就是一个分界点,此外我们用“相平分界法”,令x1 x2 x0,k0 可获取 x k ,所以又找到两个分界点k ,k .这样就把 f ( x) 的定义域12x0分为 ( , k ] , [ k ,0) , (0, k ] , [ k , ) 四个区间,再议论它的单一性.设 0 x x2 k ,则x1 x2 0 , x1 x2 0 , 0 x1 x2 k ,1∴ x1 x2 k 0 .∴ f ( x1 ) f ( x2 )kx2k (x1 x2 )( x1 x2 k ),即 f (x1 ) f (x2 ) .x1x2 x1 gx2x1∴f (x) 在 (0, k ] 上单一递减.同理可得, f (x) 在 [ k ,) 上单一递加;在(,k ] 上单一递加;在[k ,0) 上单一递减.故函数 f ( x) 在 (, k ] 和 [ k , ) 上单一递加,在 [ k ,0) 和 (0, k ] 上单一递减.性质启迪:由函数 f ( x)xk(k 0) 的单一性及 f (x) 在其单一区间的端点处取值的x趋向,可作出函数y f (x) 的图像,反过来利用图像可形象地记忆该函数的单一性及有关性质. 此性质是求解函数最值的强有力工具, 特别是利用均值不等式而等号不可即刻,更彰显其单一性的强盛功能.4.“二次函数”与“双勾函数”在办理区间最值问题上的类比 ( 1)“二次函数”的区间最值 设 f (x)ax 2 bx c( a 0) ,求 f ( x) 在 x[ m , n] 上的最大值与最小值.剖析:将 f ( x) 配方,得对称轴方程xb,2a①当 a0时,抛物线张口向上.b若[m ,n] 必在极点获得最小值,离对称轴较远端点处获得最大值;2a若b [m ,n] ,此时函数在 [m , n] 上拥有单一性, 故在离对称轴 x b较远端2a2a点处获得最大值,较近端点处获得最小值.②当 a 0 时,抛物线张口向下.若若b [m ,n] 必在极点获得最大值,离对称轴较远端点处获得最小值;2ab [m ,n] ,此时函数在 [m , n] 上拥有单一性, 故在离对称轴 x b较远端2a2a点处获得最小值,较近端点处获得最大值.以上,作图可得结论. ①当 a0时,,b≥1如图 )2a21f ( x)max;b1(mf (n), n)(如图 2 )2a2, b 如图 3f (n) 2a n()bb, ≤≤ 如图 4.f ( x)min f () m2an()2a, b 如图 5f (m) 2a m()mnxmnnm m nxxmxn x图1 图2 图3 图4 图5②当 a0时,, b 如图 6f (n)2an( )b, ≤ b ≤ 如图 7;f ( x)maxf () m2an() 2a, b 如图 8f (m) 2am( )f (m),b ≥ 1( m n)(如图 9) f ( x)min2a 2.f (n),b1( m n)(如图10)2a 2m nn m mn mnxx mxn xx图 6图 7图 8图 9图 10( 2)“双勾函数”的区间最值设 f( ) x k ( k 0) ,求 f ( x) 在 x , n] 上的最大值与最小值.x[ mx剖析:①当 x 0 时,其图像为第一象限部分.若 k [ m , n] ,则函数必在界点 x k 处获得最小值,最大值需比较两个端点处的函数值;若 k [ m , n] ,此时函数在 [ m , n] 上拥有单一性, 故在离直线 xk 较远端点处取得最大值,较近端点处获得最小值.②当 x0 时,其图像为第三象限部分.若 k [m , n] ,则函数必在界点 x k 处获得最大值, 最小值需比较两个端点处的函数值;若k [m , n] ,此时函数在 [ m , n] 上拥有单一性,故在离直线 x k 较远端点处获得最小值,较近端点处获得最大值.以上,作图可得结论.①当 x0 时,f (m), k n(如图 11),f ( x)max max{ f (m), f (n)}, kf (n), k m(如图 13).f (n), k n(如图 11), f ( x)min f ( k ), k [ m, n](如图f (m), k m(如图 13). [ m, n]( 如图 12), 12),m n k x m k nx k m n x 图 11 图 12 图 13②当 x 0 时,f (n), -f ( x)max f ( k ),f (m), - k n(如图 14),k[ m,n](如图 15), k m(如图 16).f (m), - k n(如图 14),f ( x)min min{ f ( m), f ( n)},k[ m, n](如图 15),f (n), - k m(如图 16).m n k m k n k m nx x x图 14 图 15图 16二、实践平台例 1 某化工厂生产的某种化工产品,当年产量在 150 吨至 250 吨之间时,其生产的总成本 y (万元)与年产量x (吨)之间的函数关系式近似地表示为y x230 x 4000 .问:10( 1)年产量为多少吨时,每吨的均匀成本最低并求出最低成本;( 2)每吨均匀出厂价为 16 万元,年产量为多少吨时, 可获取最大收益并求出最大收益.剖析:将问题归纳为 “双勾函数” 问题, 利用 “双勾函数” 的性质, 可使问题轻松获解.解:( 1)由题意可知,每吨均匀成本为y万元.Sx即 Sy x4000 30 1(x 40000) 30 ,由于函数在区间 (0,200] 上为减函x 10x 10x数,在区间 [200,) 上为增函数.所以当 x200 时,函数 S yx 4000 301(x40000) 30 有最小值为140000x10 x10x(200S 最小) 30 10 (万元),10200所以当年产量为 200 吨时,每吨的均匀成本最低,最低成本为10万元.( 2)设年获取总收益为 Q 万元,则 Q 16x y 16xx 230x 40001( x 230) 21290 ,1010当 x230 (150,250) , Q 最大 1290 ,故当年产量为 230 吨时,可获取最大收益 1290万元.评注:此题的重点是用年产量x 吨把每吨均匀成本及收益表示出来,而后再求其最值,在求解最值时我们要用到 “双勾函数”的单一性,记着这个结论能够简化计算过程. 函数的单一性除一些理论上的应用外,它还能够灵巧有效地解决现实生活中与之有关的实质问题.例 2 甲、乙两地相距 s km ,汽车从甲地匀速行驶到乙地,速度不得超出 c km/h ,已知汽 车每小时的运输成本 (以元为单位) ,由可变部分和固定部分构成; 可变部分与速度 v (km/h) 的平方成正比,比率系数为b ,固定部分为 a 元.( 1)把全程运输成本 y (元)表示为 v (km/h) 的函数,并指出这个函数的定义域.( 2)为了使全程运输成本最小,汽车应以多大的速度行驶.剖析:要计算全程的运输成本s 2a bv s (≤ c ) ,而已知每小y(abv )(v) 0vv时的运输成本,只需计算全程的时间,由题意不难获取全程运输成本ys(a bv 2 ) ( abv)s ( 0 v ≤ c ) ,所要解决的问题是求 a bv 何时取最小值, 显v vv然要对 c 的大小进行议论,议论的标准也就是c 与a的大小.b解:( 1)依题意知:汽车从甲地匀速行驶到乙地所用时间为s,所以全程运输成本为s(avy (a bv 2) bv) s ,又据题意 0 v ≤ c ,故所求函数及其定义域分别为: v s ( avy bv) , v ( 0, c] . vabv b(va( 2)设 uf (v)b) ,v v∴ u 在 (0,a] 上是减函数,在 [b, ) 上是增函数.ba①若a≤ c ,联合“双勾函数”的性质知,b当 va 时运输成本 y 最小.b②若 a c ,函数在 (0, c] 上单一递减,所以当 v c 时,全程运输成本最小.b评注:解应用题时,第一要训练读题能力,成功地达成对数学文字语言、符号语言、图形语言的理解、 接受和变换,既而对题中各元素的数目关系进行加工和提炼,分清主次,并成立数学模型解决实质问题.例 3( 2006 安徽高考)已知函数 f (x) 在 R 上有定义,对随意实数 a 0 和随意实数 x ,都有 f (ax) af (x) .(Ⅰ)证明 f (0)0 ;, x ≥ ,(Ⅱ)证明 f ( x)kx 0 此中 k 和 h 均为常数;,x0.hx(Ⅲ)当(Ⅱ)中的k 0 ,设 g( x)1 0) ,议论 g( x) 在 (0, ) 内f ( x)( x f ( x)的单一性并求最值.剖析:承接第(Ⅱ)问的结论,将问题归纳为“双勾函数”的单一性与函数最值的求解问题.证明:(Ⅰ)令 x 0 ,则 f 0 af 0 ,∵ a 0 ,∴ f 0 0 .(Ⅱ)①令 x a ,∵ a 0 ,∴ x0 ,则 f x 2xf x .假定 x0 时, f ( x) kx (k R ),则 fx 2kx 2 ,而 xf xx kx kx 2 ,∴f x 2xf x ,即 f (x) kx 成立.②令 xa ,∵ a0 ,∴ x 0 , f x 2xf x假定 x 0 时, f ( x) hx (h R) ,则 fx 2hx 2 ,而 xf x x hx hx 2 ,∴ fx 2xf x,即 f (x) hx 成立.∴ f xkx, x 0 成立.hx, x 01 112(Ⅲ)当 x0 时, g xk (xk) ,f xkxf xkxx 由“双勾函数”性质知在(0, 1 ] 上为减函数,在 [ 1,) 上为增函数,1 k k所以当 x2.时, [ g( x)]mink评注:数学高考试题着重“考基础、考能力、考思想”.所以熟习数学化归的思想,有意识地运用数学变换的方法去灵巧解决有关的数学识题,将有益于加强在解决数学识题中的应变能力,有益于提升解决数学识题的思想能力和技术、技巧. 适合进行化归、转变能给人带来思想的闪光点, 找到解决问题的打破口, 是剖析问题中思想过程的主要构成部分. 本题就是转变思想应用的一个典型,经过转变将原来抽象的问题归纳到“双勾函数” 区间最值的求解,让我们有一种豁然爽朗的感觉.例 4(2001 广东高考)设计一幅宣传画,要求画面面积为 4840cm 2 ,画面的宽与高的比为 (1) ,画面的上、下各留 8cm 空白,左、右各留 5 cm 空白.如何确立画面的高与宽尺寸, 能使宣传画所用纸张面积最小假如要求[2,3],那么 为什么值时,能使宣传画3 4所用纸张面积最小剖析:设定变元 x ,找寻它们之间的内在联系 ( 等量关系 ) ,采纳适合的代数式表示问题中的这类联系,成立函数模型,将问题归纳为“双勾函数”区间最值问题,并运用“双勾函 数”性质进行求解.解:设画面高为 x cm ,宽为x cm ,则 x 2 4840设纸张面积为 S cm 2 ,则有S (x16)( x10)x 2(16 10) x 160 ,22 105将 x代入上式得 , S5000 352 10(8 ) ,5令t(t0) ,则 S(t)5000 352 10(t 8)(t0) ,t函数 S 在(0,5 ] 上为减函数,在 [ 5 , ) 上为增函数,8 85 所以当 t时, S 取最小值,8此时5 548405 8 (1) ,高: x88 cm ,宽: x88 55 cm .88假如[ 2 , 3] ,则 t [ 2 , 3 ] [ 5, ) ,3 43 4 8所以函数 S 在[ 2,3 ] 上为增函数,故当 t 2 时, S 取最小值,此时2 .3 433评注:函数描绘了自然界中量的依存关系, 是对问题自己的数目实质特点和限制关系的一种动向刻画. 要充足重视解题过程中的推理,注意运用推理来简化运算.充足利用题目给出的信息,抽象其数学特点,成立函数关系.很明显,只有在对问题的察看、剖析、判断等一系列的思想过程中, 具备有别开生面、自成一家的深刻性、独创性思想,才能结构出函数原型,达到解决问题的目的.在高考取能够利用“双勾函数”考察均值不等式、函数的单一性、函数最值等问题,其应用相当宽泛, 应用成效相当明显. 所以也是高考取的热门和难点,倍授命题者的喜爱.但只需我们能熟知“双勾函数”的性质,便不难使此类问题获解.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
则),就先用平移公式或我总结出的平移规律还原以后再研究,这个能力非常重
要,一定要多练,争取做到特别熟练的地步。
事实上,利用将对勾函数进行选择可以得到
标准的双曲线方程。也就是说,对勾
2006年高考上海数学试卷(理工农医类)已知函数 y=x+a/x 有如下性质:如果
常数a>0,那么该函数在 (0,√a] 上是减函数,在 ,[√a,+∞)上是增函数.
⑴如果函数 y=x+(2^b)/x (x>0)的值域为 [6,+∞),求b 的值;
⑵研究函数 y=x^2+c/x^2 (常数c >0)在定义域内的单调性,并说明理由;
当x<0,-x>0
f(x)=-(-x-1/x)
<=-2
当-x=-1/x取等。
x=-1,有最大值,没有最小值。
值域是:(负无穷,-2)并(2,正无穷)
--------------
证明函数f(x)=ax+b/x,(a>0,b>0)在x>0上的单调性
设x1,x2∈(0,+∝)且x1>x2
∴f(x1)-f(x2)<0,即x∈(0,√(b/a))时,f(x)=ax+b/x单调递减
∴ 当x∈(√(b/a),+∞)时,x1x2>b/a, 则ax1x2-b>b-b=0
∴f(x1)-f(x2)>0,即x∈(√(b/a),+∞)时,f(x)=ax+b/x单调递增。
6重点(窍门)编辑
当x>0时,f(x)=ax+b/x有最小值;当x<0时,f(x)=ax+b/x有最大值
f(x)=x+1/x
首先你要知道他的定义域是x不等于0
当x>0,
由均值不等式有:
f(x)=x+1/x>=2根号(x*1/x)=2
当x=1/x取等
x=1,有最小值是:2,没有最大值。
ax+b/x≥2sqrt(axb/x)=2sqrt(ab),这里有个规定:当且仅当ax=b/x时取到最
小值,解出x=sqrt(b/a),对应的f(x)=2sqrt(ab)。我们再来看看均值不等式,
它也可以写成这样:(a+b)/2≥sqrt(ab),前式大家都知道,是求平均数的公式。
那么后面的式子呢?也是平均数的公式,但不同的是,前面的称为算术平均数,
⑶对函数y =x+a/x 和y =x^2+a/x^2(常数a >0)作出推广,使它们都是你所推
广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必证明),并
求函数F(x) =(x^2+1/x)^n+(1/x^2+x)^n(x 是正整数)在区间[&frac12;,2]上
的最大值和最小值(可利用你的研究结论)
⑴当x1<x2<-根号a时,x1-x2<0,x1x2-a>0,x1x2>0,所以f(x1)-f(x2)<0,即
f(x1)<f(x2),所以函数在(-∞,-根号a)上是增函数
⑵当-根号a<x1<x2<0时,x1-x2<0,x1x2-a<0,x1x2>0,所以f(x1)-f(x2)>0,
其实对勾函数的一般形式是:
f(x)=ax+b/x(a>0)
定义域为(-∞,0)∪(0,+∞)
值域为(-∞,-2√ab]∪[2√ab,+∞)
当x>0,有x=根号a,有最小值是2根号a
当x<0,有x=-根号a,有最大值是:-2根号a
对勾函数的解
2不等式编辑
对勾函数性质的研究离不开均值不等式。说到均值不等式,其实也是根据二次函
数得来的。我们都知道,(a-b)^2≥0,展开就是a^2-2ab+b^2≥0,有a^2+b^2≥2ab,
两边同时加上2ab,整理得到(a+b)^2≥4ab,同时开根号,就得到了均值定理的
公式:a+b≥2sqrt(ab)。把ax+b/x套用这个公式,得到
析式为y=x+a/x(其中a>0),它的单调性讨论如下:
设x1<x2,则f(x1)-f(x2)=x1+a/x1-(x2+a/x2)=(x1-x2)+a(x2-x1)/(x1x2)
=(x1-x2)(x1x2-a)/(x1x2)
下面分情况讨论
则f(x1)-f(x2)=(ax1+b/x1) -(ax2+b/x2)
=a(x1-x2)-b(x1-x2)/x1x2
=(x1-x2)(ax1x2-b)/x1x2
∵x1>x2,x1-x2>0
∴ 当x∈(0,√(b/a))时,x1x2<b/a, 则ax1x2-b<b-b=0
对勾函数是一种类似于反比例函数的一般函数,又被称为“双勾函数”、"勾函
数"等。也被形象称为“耐克函数”或“耐克曲线”
所谓的对勾函数(双曲线函数),是形如f(x)=ax+b/x(a>0)的函数。由图像得
名。
图像
对勾函数:图像,性质,单调性
x
第三行为f(x)=-(ax+b/y)大于等于2√ab
对勾函数是数学中一种常见而又特殊的函数,见图示,在作图时最好画出渐近线,时,f(x)=ax+b/x有最小值(这里为了研究方便,规定a>0,b>0),也就
求得的导函数为a+(-b)x^-2,令f'(x)=0,计算得到b=ax2,结果仍然是
x=sqrt(b/a),如果需要的话算出f(x)就行了。平时做题的时候用导数还是均
值定理,就看你喜欢用那个了。不过注意均值定理最后的讨论,有时ax≠b/x,
就不能用均值定理了。
上述研究都是建立在x>0的基础上的,不过对勾函数是奇函数,所以研究出正半
f(x1)<f(x2),所以函数在(根号a,+∞)上是增函数
解题时常利用此函数的单调性求最大值与最小值。
到的问题应该与值域有关;⑵函数与方程之间有密切的联系,所以命题者自然也
会想到函数与方程思想的运用;⑶众所周知,双曲线中存在很多定值问题,所以
很容易就想到定值的存在性问题。因此就由特殊引出了一般结论;继续拓展下去,
用所猜想、探索的结果来解决较为复杂的函数最值问题。能否与均值有关系
5高考例题编辑
函数是双曲线,这个利用二阶矩阵的变换也是可以得到的。
另外对于二次曲线,他只可能是以下几种情况:圆,椭圆,双曲线,抛物线,或
者是两条直线。
由对勾函数的图像看出来,非双曲线莫属了。
面对这个函数 f(x)=ax+b/x,我们应该想得更多,需要我们深入探究:⑴它的单
调性与奇偶性有何应用?而值域问题恰好与单调性密切相关,所以命题者首先想
是当x=sqrt(b/a)时(sqrt表示求二次方根)
奇函数。
令k=sqrt(b/a),那么:
增区间:{x|x≤-k}和{x|x≥k};
减区间:{x|-k≤x<0}和{x|0<x≤k} 变化趋势:在y轴左边,增减,在y轴右边,
减增,是两个勾。
渐近线
对勾函数的图像是分别以Y轴和y=ax为渐近线的两支双曲线。
即f(x1)>f(x2),所以函数在(-根号a,0)上是减函数
⑶当0<x1<x2<根号a时,x1-x2<0,x1x2-a<0,x1x2>0,所以f(x1)-f(x2)>0,
即f(x1)>f(x2),所以函数在(0,根号a)上是减函数
⑷当根号a<x1<x2时,x1-x2<0,x1x2-a>0,x1x2>0,所以f(x1)-f(x2)<0,即
而后面的则称为几何平均数,总结一下就是算术平均数绝对不会小于几何平均数。
这些知识点也是非常重要的。
3导数求解编辑
其实用导数也可以研究对勾函数的性质。不过首先要会负指数幂的换算,这也很
简单,但要熟练掌握。举几个例子:1/x=x^-1,4/x^2=4x^-2。明白了吧,x为分
母的时候可以转化成负指数幂。那么就有f(x)=ax+b/x=ax+bx^-1,求导方法一样,
