第6章 在Maple中作图
maple绘图

BJUT
4
二维画图----图形参数
7. bnumpoints 设定产生一个函数图形所需的最少样点,格式:
numpoints=n,n=50为默认值。
8. scaling 设置x与y轴的比例。Constrained为等比,
unconstrained为非等比,此为默认值。
目录
➢用Maple画二维函数曲线 ➢三维画图及其它作图 ➢解方程
BJUT
1
二维画图
可直接调用Maple所提供的二维绘图函数plot绘 制二维函数图、参数图、极坐标图、等高线图、不等 式图。其中某些图形的绘制,需要加载程序包plot, 调用相应的函数才能完成。函数plot的调用形式为
plot(f,h,v) plot(f,h,v,option) 其中,f是绘制的函数、表达式或过程,h是x轴 区间, v是y轴区间, option是一些选项。Option 选项主要有以下各种:
4. discont discont设为true时,plot将首先使用函数discont判断输入
是否连续,然后将x轴自动分为几个连续的区间画图,默认是
discont=false.
5. labels 设定坐标轴的标注,格式:labels=[x,y],x与y分别为将为x
与y坐标轴的标注的名称。
6. linestyle 设定所绘线条的线型,格式:linestyle=n,n为1是实线,2
包,并调用函数implicitplot(expr,x=a..b,y=c..d,options)。 with(plots): eq:=(x-1)^2/3+(y-1)^2/4=1; implicitplot(eq,x=-3..3,y=-4..4,scaling=constrained);
第六章 Maple程序设计

第六章Maple程序设计教学目的:学习并掌握计算机代数系统Maple下的算法设计和程序设计原理和方法,包括基本程序结构、子程序求值、程序的嵌套以及程序的调试。
教学要求:掌握算法设计和程序设计原理和基本方法。
重点内容:算法设计,程序设计。
难点内容:算法设计,程序设计。
前面, 我们使用的是Maple 的交互式命令环境. 所谓交互式命令环境, 就是一次输入一条或几条命令, 然后按回车, 这些命令就被执行了, 执行的结果显示在同一个可执行块中. 对于大多数用户来说, 利用交互式命令环境解决问题已经足够了, 但如果要解决一系列同一类型的问题或者希望利用Maple 编写需要的解决特定问题的函数和程序, 以期更加充分地利用Maple 的强大功能, 提高大规模问题的计算效率, 进行一定的程序设计是必要的.程序设计主要包括两个方面: 行为特性的设计与结构特性的设计. 所谓行为特性的设计, 通常是指将解决问题的过程的每一个细节准确地加以定义, 并且还应当将全部的解题过程用某种工具完整地描述出来, 这一过程也称为算法的设计. 而结构特性设计是指为问题的解决确定合适的数据结构.幸运的是, Maple 自身提供了一套编程工具, 即Maple 语言. Maple 语言实际上是由Maple 各种命令以及一些简单的过程控制语句组成的.1编程基础1.1算子所谓算子, 是从一个抽象空间到另一个抽象空间的函数. 在数学上算子的含义通常是函数到函数的映射. 在Maple 中, 算子常用“箭头”记号定义(也称箭头操作符): > f:=x->a*x*exp(x);:= f → x a x e x> g:=(x,y)->a*x*y*exp(x^2+y^2);:= g → (),x y a x y e () + x 2y 2另外, 函数unapply 也可以从表达式建立算子:> unapply(x^2+1,x);→ x + x 21> unapply(x^2+y^2,x,y);→ (),x y + x 2y 2当我们依次把算子f 作用到参数0, a, x^2+a 时即可得平常意义上的函数值:> f:=t->t*sin(t);:= f → t t ()sin t> f(0);> f(a);a ()sin a> f(x^2+a);() + x 2a ()sin + x 2a上述结果是函数作用的例子. 而最后一个结果)sin()(22a x a x ++实际上是算子f 与算子g:=t->t^2+a 复合后再作用到参数x 的结果.从数学上讲, 作用与复合是不同的,它们产生的结果是有区别的, 但在使用它们时, 两者还是有些重叠的. 在Maple 中, 可以依赖于语法把它们区分开:(1) 当复合两个算子时, 结果仍是算子, 两个算子的定义域必须是相容的;(2) 当把一个算子作用于一个参数(参数必须在算子的定义域中)时, 结果是一个表达式;(3) 在Maple 中,函数作用的语法是使用括号( ),如函数f 作用到参数u 写作f(u). 而复合算子的符号是@,多重复合时使用符号@@.通过进一步的例子可以清楚区分作用与复合的功能: f 和g 复合的结果是算子))((:t g f t g f =, 而把这个算子作用到参数x 得到表达式f (g (x )). 例如, )exp(),sin(u u g t t f =+=ϕ, 则))sin(exp(:ϕ+=z z g f 是一个算子, 而))sin(exp()((ϕ+=x x g f 是一个表达式, 因为x 是一个实数. 试比较下述两例: > D(g@f);()@()()D g f ()D f> D(g*h);+ ()D g h g ()D h另外一个应引起注意的问题是算子(函数)与表达式的异同,在第一章2.2.2中曾探讨过函数与表达式的区别,这里再通过几个例子说明其中的微妙差异:> f1:=x^2+1;> f2:=y^2+1;:= f1 + x 21:= f2 + y 21> f3:=f1+f2;:= f3 + + x 22y 2再看下面的例子:> g1:=x->x^2+1;> g2:=y->y^2+1;:= g1 → x + x 21:= g2 → y + y 21> g3:=g1+g2;:= g3 + g1g2与前面例子不同的是,两个算子(函数)g1, g2相加的结果依然是函数名g3,出现这个问题的主要原因是g1与g2分别为x ,y 的函数,Maple 认为它们的定义域不相容. 要得到与前例的结果,只需稍作改动:> g3:=g1(x)+g2(y);:= g3 + + x 22y 2下面的例子想说明生成Maple 函数的两种方式“箭头操作符”及“unapply ”之间微妙的差异:> restart: a:=1: b:=2: c:=3:> a*x^2+b*x+c;+ + x 22x 3> f:=unapply(a*x^2+b*x+c,x);:= f → x + + x 22x 3> g:=x->a*x^2+b*x+c;:= g → x + + a x 2b x c由此可见,f 中的a,b,c 已经作了代换,而g 中则显含a,b,c 。
maple教程

数学实验数学软件Maple使用教程二.Maple工作面maple工作面提示符用来输入maple命令。
提示符[>左边的[号表示所要一起执行的命令区,该区的命令将按先后次序连续一次执行完。
若点击工具栏中T按钮,则提示符箭头消失,变为[号,表示当前为文本输入,工具栏也出现相应的字号字体选择框;常用工具栏中(从左到右)有新建、打开、保存、打印、剪切、复制、粘贴、撤消、Maple输入转换、文体输入转换、增加命令区、撤消分组、建立分组、停止运行及三个显示比例选择x按钮。
点击提示符按钮将增加一个命令区;当将几个命令区及文本输入抹黑,点击建立分组,就会将抹黑部分分在一组,并出现一个分组标志,点击标志可以打开、关闭该组;点击并排的三个x按钮控制显示比例。
三.退出工作面并保存文件1.点击文件菜单exit或键盘alt+F4或点击窗口右上角×,这时系统要提示:是否存盘?点击‘是’,则自动存盘。
如果是第一次使用这个文件,则要出现一个对话框,选择存盘目录并输入文件名称。
2.命令quit done stop 也可退出maple。
注意!这三个退出命令不保存文件,不要随便用。
3.作业中存盘,可以用文件菜单的保存,也可以用工具栏的软盘图标保存。
最好在操作一段后就保存一次,避免意外情况产生损失。
第二章基本命令命令的执行:1.每条命令必须用“:”(执行后不显示)或“;”(执行并显示)结束,否则被认为命令没输完。
2.命令区中“#”号以后为命令注释(不执行)。
3.光标在命令区的任何位置回车,都会依次执行该命令区所有命令。
> 2+3 #没有结束符,执行后会显示警告:语句没输完Warning, incomplete statement or missing semicolon> 2+3; 会输出执行结果> 2+3: 不会输出执行结果,但结果可用作以后计算使用寻求帮助:1.从Help(帮助)菜单按类查找。
2.?后接命令(可以是命令的前几个字母)或help(命令)查找。
Maple入门教程A6- 数据结构

(2.1.1)
(2.1.3)(2.1.4)(2.1.2)
Part 6:数据结构
西希安工程模拟软件(上海)有限公司,2008
6.0 介绍
第六部分:数据结构,学习Maple的数据结构。
6.1 数据结构
Maple 有多种数据结构,提供用于任务的工具。
前面您已经接触了矩阵,其他数据结构包括:列表、集合、序列、数组、表、模块等。
熟悉数据结构和它们之间的区别非常重要,这样可以针对不同的问题选择恰当的结构和操作,这里仅介绍一些最常用的数据结构。
序列
操作步骤
结果
序列是一个用逗号隔开的任意对象集合,一个序列也可以由若干个序列复合而成。
例子:
表示命名 被赋值为一
个序列。
在Maple中,序列是许多数据类型的基础。
特别是,他们出现在函数调用、列表、集合、下标。
使用索引符号提取序列中的元素:指向
序列 s 中的第 个元素。
也可以使用下标符号,,引用第 个元
12a
集合
Array, list, map, seq。
maple教程

读者对象有哪些?
本书适用于高等学校各专业本科生, 以及具有初步的高等数学知识和计算机知识的其他 读者、从事实际工作的工程技术人员、高等中等学校的教师和学生、从事各种理论工作(数 学、物理等)的科学工作者。该书对于从事数学、计算技术、计算机应用等方面的科技人员 及教学人员也是一本极好的参考工具书。
怎样使用本书?
I
目 录
第一篇 第1章 初步篇 Maple 6 起步 ········································································································· 2
1.1 什么是Maple··········································································································· 3 1.2 Maple的结构 ··········································································································· 5 1.3 Maple的功能 ··········································································································· 5 1.3.1 算术 ················································································································ 7 1.3.2 变量和多项式································································································· 9 1.3.3 解方程 ·········································································································· 10 1.3.4 绘图 ·············································································································· 11 1.3.5 表格 ·············································································································· 13 1.3.6 构造文档 ······································································································ 14 1.3.7 在线帮助系统······························································································· 17 1.4 Maple 6 的新特性 ································································································ 18 1.5 本章小结 ··············································································································· 18 第2章 2.1 2.2 2.3 安装与设置 ··········································································································· 19
数学软件Maple使用教程

数学软件Maple使用教程序言一.什么是数学实验?我们都熟悉物理实验和化学实验,就是利用仪器设备,通过实验来了解物理现象、化学物质等的特性。
同样,数学实验也是要通过实验来了解数学问题的特性并解决对应的数学问题。
过去,因为实验设备和实验手段的问题,无法解决数学上的实验问题,所以,一直没有听说过数学实验这个词。
随着计算机的飞速发展,计算速度越来越快,软件功能也越来越强,许多数学问题都可以由计算机代替完成,也为我们用实验解决数学问题提供了可能。
数学实验就是以计算机为仪器,以软件为载体,通过实验解决实际中的数学问题。
二.常用的数学软件目前较流行的数学软件主要有四种:1.MathACD其优点是许多数学符号键盘化,通过键盘可以直接输入数学符号,在教学方面使用起来非常方便。
缺点是目前仅能作数值运算,符号运算功能较弱,输出界面不好。
2.Matlab优点是大型矩阵运算功能非常强,构造个人适用函数方便很方便,因此,非常适合大型工程技术中使用。
缺点是输出界面稍差,符号运算功能也显得弱一些。
不过,在这个公司购买了Maple公司的内核以后,符号运算功能已经得到了大大的加强。
再一个缺点就是这个软件太大,按现在流行的版本5.2,自身有400多兆,占硬盘空间近1个G,一般稍早些的计算机都安装部下。
我们这次没用它主要就是这个原因。
3.Mathematica其优点是结构严谨,输出界面好,计算功能强,是专业科学技术人员所喜爱的数学软件。
缺点是软件本身较大,目前流行的3.0版本有200兆;另一个缺点就是命令太长,每一个命令都要输入英文全名,因此,需要英语水平较高。
4.Maple优点是输出界面很好,与我们平常书写几乎一致;还有一个最大的优点就是它的符号运算功能特别强,这对于既要作数值运算,又要作符号运算时就显得非常方便了。
除此之外,其软件只有30兆,安装也很方便(直接拷贝就可以用)。
所以,我们把它放到学校网上直接调用。
缺点就是目前市面上买不到教材,帮助系统又是英语,为学习带来了不便。
Maple教程第六章Maple绘图

107Maple V Release 5 起步与进阶。
108.和别的语言不同,当我们利用Maple 进行二维或者三维绘图时,Maple 可以自动地决定所需的点数、坐标轴的位置、标尺的数字、图形的颜色等等繁杂的设置,在默认状态下就可以绘制出令人满意的图形。
当然,你也可以自己设定各种不同的绘图设置,比如更改绘图的坐标系(以画出极坐标、球坐标、或柱坐标下的图形),或者绘图的点数。
下面,我们就由浅入深地介绍Maple 中的绘图方法。
6.1 二维基本图形绘制在Maple 中,单变量函数曲线的绘制可以使用函数plot 。
例如,我们需要绘制函数)sin()(32x e x f x π−=在区间[-2,2]上的图形,我们可以这样来实现。
首先用箭头操作符定义函数:然后,调用plot 函数。
键入命令后,所绘制的图形会立即出现在同一个可执行块中。
Maple V Release 5也支持把图形单独绘制在一个窗口中,如图 6.1所示,只需要在菜单Option | Plot Display 选择Window 即可。
一般地,函数plot 的调用格式为plot (f , a..b, options )。
其中,f 是需要绘制的函数,a..b 是自变量的变化范围,options 是可选参数,用它可以控制图形的绘制,我们将在下一节中详细介绍。
除了可以绘制函数的图形外,plot 也可以绘制表达式表示的函数图形,调用格式为plot (expr , x = a..b, options )。
其中,expr 是表达式(相信读者一定知道表达式和函数间的区别了),x 是表达式中的自变量,因为表达式中没有自变量的信息(甚至可以是多变量的表达式),所以必须指定自变量,并用等式形式给出自变量的变化范围。
第六章 Maple绘图。
109.图6.1 在窗口中绘图这些基本的绘图功能,Maple 和其他的树脂绘图工具(比如Matlab 、Origin 等)并没有什么区别。
Maple作图命令详解

Maple作图命令详解在使用Maple进行计算的时候,很多情况下需要对函数进行绘图以便能够进行更深入的研究与说明,那么,在Maple中怎样作图呢?作图的命令有哪些呢?作图有两个软件包。
(1)图形软件包,用with(plots)调入。
(2)图形工具包with(plottools)图形包中有下列作图命令:animate、animate3d 动画;changecoords 改变坐标系;complexplot、complexplot3d复函数图;conformal、contourplot、contourplot3d、coordplot、coordplot3d、cylinderplo柱坐标函数图;densityplot密度图;display、display3d图函数显示;fieldplot、fieldplot3d区域图;gradplot、gradplot3d梯度图;implicitplot、implicitplot3d隐函数图;inequal listcontplot、listcontplot3d listdensityplot、listplot listplot3d、loglogplot、logplot、matrixplot、odeplot微分方程数值解图;pareto pointplot、pointplot3d点图;polarplot极坐标图;polygonplot、polygonplot3d多边形图;polyhedraplot、replot、rootlocus semilogplot、setoptions setoptions3d作图选项设置;spacecurve空间曲线图;sparsematrixplot、sphereplot球坐标图;surfdata textplot、textplot3d、tubeplot工具包中有下列图形工具:arc弧,arrow箭头,circle圆,cone圆锥,cuboid长方体,curve曲线,cutin cutout cylinder 柱,disk圆盘,dodecahedron十二面,ellipse椭圆,ellipticArc椭圆弧,hemisphere半球,hexahedron 六面体,hyperbola双曲线,icosahedron,二十面体,line线段,octahedron八面体,pieslice point点,polygon 多边形,rectangle矩形,semitorus、sphere球,tetrahedron四面体,torus轮Maple绘图示例基本命令(不需调图形包)一元函数曲线作过程函数图x=a..b(中间两点)表示变量x在[a,b]区间。
maple绘图

2*Pi..2*Pi);
三维画图及其它作图
3. 特殊作图 对于无法用解析式表示的多元函数,不能使用函数plot3d绘制,遇到
这种情况,处理的方法同函数plot一样。对隐函数作图,通过加载程序包 plots,调用函数impicitplot3d来绘制。
示多边形与边线Leabharlann 、PATCHNOGRID(只显示色彩而无边界) 10. symbol
设定点的形状:主要有BOX(方块)、CROSS(十字)、 CIRCLE(圆形)、POINT(点)、DIAMONO(菱形)等。
二维画图----图形参数
12. tickmarks 设定坐标轴刻度的数目, 格式: tickmarks=[m,n],m为x轴刻度数,n为y轴 刻度数。
包,并调用函数implicitplot(expr,x=a..b,y=c..d,options)。 with(plots): eq:=(x-1)^2/3+(y-1)^2/4=1; implicitplot(eq,x=-3..3,y=-4..4,scaling=constrained);
参数方程调用形式plot([x(t),y(t),t=a..b],options) 例:作星形线 plot([2*cos(t)^3,2*sin(t)^3,t=-2*Pi..2*Pi],scaling=constrained);
iii、间断函数 例:discont的作用
f:=x->piecewise(x>=0 and x<=1,sqrt(x),x>1,1+x): f(x); plot(f(x),x=0..5,discont=true);
Maple6

(第六章M aple的绘图功能)§6.3 三维图形绘制三绘图原理上,三维图形与二维图形没有本质的区别,但由于涉及到如何在二维的显示设备上表示的问题,在图形学中,三维图形增加了投影方式的选择。
然而在Maple系统中,用户却不需要考虑投影方面的问题,因为几乎所有的三维图形都是以斜投影的方式表示的。
用户可以改变的,只有物体的方向以及视点的远近。
由于三维图形绘制时可以选择的参数同二维图形基本类似,所以在对plot3d函数做基本介绍后,本节的重点将转移到一些plot程序库附带的其他三维图形绘制函数上,比如等高线、密度图等的绘制。
6.3.1 基本三维函数图形的生成由于现实中人们熟知的三维图形一般并非简单函数可以生成的,即使可以表示,也涉及到很多参数的设定,所以在实际三维绘图中,plot3d函数并不像plot函数那样常用。
一般只是用它对三维函数曲线进行绘绘制。
它的使用方法同plot函数几乎完全一样,比如利用简化输入绘制一个三维曲面:> f:=(x,y)->cos(x*y):> plot3d(f,-3..3,-2..2,orientation=[160,50]);之所以称这种输入方法为简化输入,因为我们在输入坐标范围的时候,并不是按照“x=a..b,y=c..d”这种规则形式书写的,而是直接写成“a..b,c..d”的形式。
注意这样的输入方法只对函数变量定义为“x,y”的形式有效,系统会自动将坐标x轴的范围定义为“a..b”,而将y轴定义为“c..d”。
同样,在plot函数中也可以对变量被定义为x的函数使用这种简化输入法。
相对于二维的plot函数,plot3d在坐标轴的形式,曲线、曲面的式样等一些方面有新的参数。
在上例中使用的orientation参数就是其中之一,它可以确定用户的观察角度。
“[ ]”中的数值分别对应三维工具栏中θ角与ϕ角。
由于这些参数同plot 函数中的参数大同小异,本节不再讲述。
Maple数据图形功能介绍

Maple 2022 中的绘图数据操作更加简便。
它的全新命令可以使用各种 2-D 和 3-D 的图形和动画来显示多种数值数据。
数据图形命令也可以与右击鼠标的下拉菜单中“图形”命令结合使用。
一个命令控制不同的图形:使用图形命令,通过简单指定你所需要的图形类型就能生成各种各样的图形。
作为这个命令的快捷方式,可以通过右击命令条中矩阵的下拉菜单选择“图形”——“数据图形”命令来选择你想要显示的数据类型。
Maple 绘图命令示例利用 Maple 绘图命令绘制的物体表面图形利用 Maple 绘图命令绘制的 3-D 图形利用 Maple 绘图命令绘制的密度图形全新的直观调用序列并且支持相同的数据类型数据图形命令可以调用序列,这使得生成图形时不用将你的数据转换到右边的表格中。
此外,在实例中调用 2 个或者更多序列会更加容易。
对数据的标注也可以是一个目录、向量、矩阵或者是箭头。
Maple 支持相同的数据类型在 2-D 点状图中调用序列可以使一个 x 值生成不同的 y 值图形集合变得很容易。
Maple 调用序列使一个 x 值生成不同的 y 值在 3-D 图面调用序列可以根据网格中 z 轴的数值联合调整 x 轴和 y 轴的值。
Maple 3-D 图中根据x、y 值生成 z 值2-D 点状图的更多功能利用数据绘图命令可以使用不少功能,使用这些功能你可以改变 2-D 点图的外观。
挪移一个点状图,为了能够更好地看到动画效果,右击鼠标选择“动画”——“演示”。
Maple 2-D 图的更多功能数据绘图会自动给不同的数据集合添加不同的颜色,但是如果你指定了一个单独的颜色,就会浮现不同的标识将这个数据集区分开来。
Maple 2-D 图中用不同的标识区分图形调色板功能可以改变选中的默认颜色。
Maple 2-D 图中用不同的颜色区分图形统计图数据绘图命令可以生成各种各样的统计图形并且能够将 Quandl 数据集合可视化。
Maple 2-D 图统计图示例比如统计图中的条形图和区域图都是可以的:Maple 2-D 图中的区域图示例Quandl 数据集合也是可以绘图的。
maple教程

读者对象有哪些?
本书适用于高等学校各专业本科生, 以及具有初步的高等数学知识和计算机知识的其他 读者、从事实际工作的工程技术人员、高等中等学校的教师和学生、从事各种理论工作(数 学、物理等)的科学工作者。该书对于从事数学、计算技术、计算机应用等方面的科技人员 及教学人员也是一本极好的参考工具书。
怎样使用本书?
系统要求 ··············································································································· 20 安装Maple 6·········································································································· 20 设置Maple 6·········································································································· 23 2.2.1 内核模式 ······································································································ 23 2.2.2 初始化 ·········································································································· 26 2.4 本章小结 ··············································································································· 27 第3章 3.1 Maple 6运行界面 ································································································· 28
学习如何使用Maple进行数学建模和计算

学习如何使用Maple进行数学建模和计算Maple是一款强大的数学软件,广泛应用于数学建模和计算上。
本文将介绍如何使用Maple进行数学建模和计算,并按照类别将其分为以下章节进行讲解。
第一章:Maple的基本操作在开始学习Maple之前,我们首先需要了解Maple的基本操作。
我们可以通过打开Maple软件,新建一个工作表开始操作。
在Maple中,我们可以进行基本的计算,如加法、减法、乘法和除法。
此外,Maple还支持各种数学函数和运算符的使用,如三角函数、指数函数和积分等。
第二章:使用Maple进行代数运算代数运算是数学建模的重要一环。
Maple可以进行代数表达式的简化,如合并同类项、展开式子和因式分解等。
此外,Maple还支持方程的求解和变量的替换,可以帮助我们轻松地解决代数问题。
第三章:使用Maple进行微积分计算微积分是数学建模和计算中的关键内容。
Maple可以进行函数的微分和积分计算。
我们可以通过使用Maple的微分函数对函数进行微分,并得到导数的表达式。
同样地,Maple也提供了积分函数,可以帮助我们求解各种类型的不定积分和定积分。
第四章:使用Maple进行数值计算在实际的数学建模和计算中,很多问题无法通过解析方法求解,而需要采用数值计算的方法。
Maple提供了丰富的数值计算函数,如求解方程组、数值积分和数值微分等。
我们可以使用这些函数快速解决实际问题,并得到数值结果。
第五章:使用Maple进行图形绘制数据的可视化对于数学建模和计算来说至关重要。
Maple可以绘制各种类型的函数图像和数据图表。
我们可以通过调用绘图函数,设置绘图参数和数据,得到漂亮的图形结果。
此外,Maple还支持图像的导出和保存,方便我们将图形结果用于报告和展示。
第六章:使用Maple进行数据分析数据分析是数学建模和计算的重要一环。
Maple提供了丰富的数据处理和分析函数,如数据拟合、统计分析和回归分析等。
我们可以通过调用这些函数,输入原始数据,得到数据的分析结果和统计性质。
maple绘图

BJUT
三维画图及其它作图
1. 使用plot3d
函数plot3d是三维绘图的重要函数,调用形式如下: style=s:设定绘图的方式,s为:
目录
➢用Maple画二维函数曲线 ➢三维画图及其它作图 ➢解方程
BJUT
二维画图
可直接调用Maple所提供的二维绘图函数plot绘 制二维函数图、参数图、极坐标图、等高线图、不等 式图。其中某些图形的绘制,需要加载程序包plot, 调用相应的函数才能完成。函数plot的调用形式为
plot(f,h,v) plot(f,h,v,option) 其中,f是绘制的函数、表达式或过程,h是x轴 区间, v是y轴区间, option是一些选项。Option 选项主要有以下各种:
iii、间断函数 例:discont的作用
f:=x->piecewise(x>=0 and x<=1,sqrt(x),x>1,1+x): f(x); plot(f(x),x=0..5,discont=true);
BJUT
二维画图
ⅳ、散点作图 例:作出y=x,y=-2,x=1,x=-1的图形。利用plot函数直接表示x=1,x=-1
定视角的最佳方式是用鼠标拖动图形) projection=r 设定投影的模式:NORMAL,
ORTHOGONAL Shading=x 设CALE,NONE. Lightmodel=x 光照模式:none,light1,light2,light3
使用dsolve函数: Dsolve(<方程>,<函数>,[implicit]);
maple画图命令

maple画图命令1 二维图形制作Maple所提供的二维绘图指令plot可以绘制二维的函数图、参数图、极坐标图、等高线图、不等式图,等等. 这些绘图指令有些已经内嵌在其核心程序里, Maple启动时即被装入,直接调用函数命令即可,有些则需要使用with(plots)调用plots函数库才能完成.1.1 基本二维绘图指令plot (f(x), x=xmin .. xmax);plot (f(x), x=xmin .. xmax, y=ymin .. ymax);plot ([f1(x), f2(x), …], x=xmin .. xmax);plot (f(x), x=xmin .. xmax, option);其中,xmin..xmax为x的变化范围,ymin..ymax为y(即f(x))的变化范围. option选项参数主要有:axes:设定坐标轴的显示方式, 一般有FRAME(坐标轴在图形的左边与下面)、BOXED(坐标轴围绕图形)、NORMAL(一般方式显示)或NONE(无)color:设定图形所要涂的颜色(可选用也可自设)coords:指定绘图时所用的坐标系(笛卡尔坐标系(cartesian,默认)、极坐标系(polar)、双极坐标系(bipolar)、logarthmic(对数坐标系)等discont:设定函数在不是否用线段连接起来(discont=true则不连接, 默认是discont=false) labels:设定坐标轴的名称(labels=[x, y], x与y分别为x与y坐标轴的名称)linestyle:设定所绘线条的线型(linestyle=n, n为1是实线, 2为点, 3为虚线, 4为虚线与点交错)numpoints:设定产生一个函数图形所需的最少样点scaling:设置x与y轴的比例(unconstrained非约束,constrained约束,比例为1:1)style:设定图形的显示样式(LINE(线形)、POINT(点)、PATCH(显示多边形与边线)、PA TCHNOGRID(只显示色彩而无边界) symbol:设定点的格式(主要有BOX(方块)、CROSS(十字)、CIRCLE(圆形)、POINT(点)、DIAMOND(菱形)等几项)thickness:设定线条的粗细(0、1、2、3几种参数, 数值越大线条越粗)tickmarks:设定坐标轴刻度的数目(设定tickmarks=[m, n], 则x 轴刻度为m, y轴为n)title:定义图形的标题(要用" "把标题引起来)view:设定屏幕上图形显示的最大坐标和最小坐标,缺省是整个曲线下面通过一些实例学习:> plot(sin(1/x),x=-0.1..0.1,title="y=sin(1/x)",axes=normal);> plot(1/(2*sin(x)),x=-10..10,y=-30..30);试比较下述三图的效果:> plot(tan(x),x=-2*Pi..2*Pi);> plot(tan(x),x=-2*Pi..2*Pi, y=-5..5);> plot(tan(x),x=-2*Pi..2*Pi, y=-5..5,discont=true);(此处命令discont=true的作用是去除垂直渐近线)> plot(sin(cos(6*x))/x, x=0..15*Pi, y=-0.6..0.5, axes=NONE);> plot(Zeta(x),x=-3..3,y=-3..3,discont=true);除了绘制基本的函数图之外, plot还可绘制自定义函数的图形, 也可以同时绘制多个函数图. > f:=x->sin(x)+cos(x)^2;plot(f(x),x=0..16);> plot([sin(x),sin(x^2),sin(x^3/10)],x=-2*Pi..2*Pi);利用seq指令产生一个由函数所组成的序列, 并将此函数的序列赋给变量, 然后将函数序列绘于同一张图上.> f:=x->sin(x)+cos(x);fs:=seq(f(x)^(n-1)+f(x)^n,n=1..4):plot([fs],x=0..20);> f:=x->x*ln(x^2):g:=x->ln(x):plot({f,g},0..2,-1.5..1.5);也可以直接把seq指令放在plot里来绘出一系列的函数图.> plot([seq(f(x)^(2/n),n=1..3)],x=0..10);1.2 二维参数绘图更多情况下,我们无法把隐函数化成显函数的形式, 因而plot指令无法在二维的平面里直接绘图. 但是, 在某些情况下, 我们可以把平面上的曲线f(x, y)化成x=x(t), y=y(t)的形式, 其中t为参数(parameter). 据此即可绘图, 其命令格式如下:plot ([x(t), y(t), t=tmin .. tmax]);plot ([x(t), y(t), t=tmin .. tmax], xmin .. xmax, y=ymin .. ymax);plot ([x(t), y(t), t=tmin .. tmax], scaling=CONSTRAINED);plot ([[x1(t), y1(t), t1=t1min .. t1max], [x2(t), y2(t), t2=t2min .. t2max],…]);> plot([t*exp(t),t,t=-4..1],x=-0.5..1.5,y=-4..1);> plot([sin(t),cos(t),t=0..2*Pi]);> plot([sin(t),cos(t),t=0..2*Pi],scaling=CONSTRAINED);上述两上语句都是绘制圆的命令, 但由于后者指定的x、y坐标的比例为1:1, 所以才得到了一个真正的圆, 而前者由于比例不同, 则像个椭圆. 下面则是内摆线的图形:> x:=(a,b)->(a-b)*cos(t)+b*cos((a-b)*t/b);> y:=(a,b)->(a-b)*sin(t)-b*sin((a-b)*t/b);当a=1, b=0.58时,(x(a,b), y(a,b))图形绘制命令为:> plot ([x(1,0.58), y(1,0.58), t=0..60*Pi], scaling=CONSTRAINED);再作a, b取其它值时的情形:> plot([x(2,1.2),y(2,1.2),t=0..6*Pi],scaling=CONSTRAINED);> plot([x(2,8),y(2,8),t=0..16*Pi],scaling=CONSTRAINED);> plot([x(2,12),y(2,12),t=0..16*Pi],scaling=CONSTRAINED);下面再看同时绘制多个图形的情形.> plot([[cos(3*t),sin(2*t),t=0..2*Pi],[sin(t),cos(3*t),t=0..2*Pi]]);1.3 数据点绘图如果所绘的图形是间断性的数据, 而不是一个连续的函数, 那么我们可以把数据点绘在x-y 坐标系中, 这就是所谓的数据点绘图. 其命令格式如下:plot([[x1, y1], [x2, y2], …], style=point);plot([[x1, y1], [x2, y2], …] );> data1:=seq([2*n,n^3+1],n=1..10):plot([data1],style=point);> data2:=seq([n,1+(-1)^n/n],n=1..15):plot([data2],style=point,view=[0..20,0..2]);> data3:=seq([t*cos(t/3),t*sin(t/3)],t=1..30):plot([data3],style=point);1.4 其它坐标系作图由于所研究的问题的特殊性,常常需要选用不同的坐标系, 在Maple中除笛卡尔坐标系(cartesian, 也称平面直角坐标系, 默认)外,还提供了polar(极坐标系)、elliptic(椭圆坐标系)、bipolar(双极坐标系)、maxwell(麦克斯韦坐标系)、logarithmic(双数坐标系)等14种二维坐标系,其中最常用的是极坐标系。
MAPLE绘图
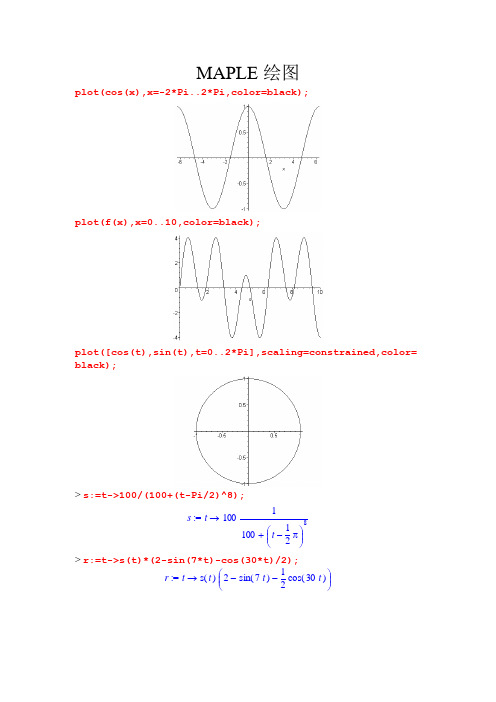
MAPLE 绘图plot(cos(x),x=-2*Pi..2*Pi,color=black);plot(f(x),x=0..10,color=black);plot([cos(t),sin(t),t=0..2*Pi],scaling=constrained,color=black);> s:=t->100/(100+(t-Pi/2)^8);:= s → t 1001+ 100⎛⎝ ⎫⎭⎪⎪- t 12π8> r:=t->s(t)*(2-sin(7*t)-cos(30*t)/2); := r → t ()s t ⎛⎝ ⎫⎭⎪⎪ - - 2()sin 7t 12()cos 30tMaple:polarplot([r(t),t,t=-Pi/2..3/2*Pi],axes=none,color=black);> plot([seq(sin(n*x^3)/n,n=1..3)],x=-2..2,color=black);> with(plots);Warning, the name changecoords has been redefinedanimate animate3d animatecurve arrow changecoords complexplot complexplot3d [,,,,,,, ,,,,,, conformal conformal3d contourplot contourplot3d coordplot coordplot3d,,,,,,, cylinderplot densityplot display display3d fieldplot fieldplot3d gradplot,,,,,, gradplot3d implicitplot implicitplot3d inequal listcontplot listcontplot3d,,,,,,,, listdensityplot listplot listplot3d loglogplot logplot matrixplot odeplot pareto ,,,,,, pointplot pointplot3d polarplot polygonplot polygonplot3d polyhedra_supported ,,,,,,, polyhedraplot replot rootlocus semilogplot setoptions setoptions3d spacecurve,,,,,] sparsematrixplot sphereplot surfdata textplot textplot3d tubeplot>implicitplot(y^2=x^3-1*x+8,x=-10..10,y=-10..10,grid=[100, 100],color=black);>implicitplot(y^2=x^3-2*x+8,x=-10..10,y=-10..10,grid=[100, 100],color=black);>implicitplot(y^2=x^3-3*x+8,x=-10..10,y=-10..10,grid=[100, 100],color=black);>implicitplot(y^2=x^3-4*x+8,x=-10..10,y=-10..10,grid=[100,100],color=black);>implicitplot(y^2=x^3-5*x+8,x=-10..10,y=-10..10,grid=[100, 100],color=black);>implicitplot(y^2=x^3-6*x+8,x=-10..10,y=-10..10,grid=[100, 100]);>implicitplot(y^2=x^3-7*x+8,x=-10..10,y=-10..10,grid=[100, 100],color=black);>implicitplot(y^2=x^3-8*x+8,x=-10..10,y=-10..10,grid=[100, 100],color=black);>implicitplot(y^2=x^3-9*x+8,x=-10..10,y=-10..10,grid=[100, 100],color=black);>implicitplot(y^2=x^3-10*x+8,x=-10..10,y=-10..10,grid=[100 ,100],color=black);>implicitplot(y^2=x^3-11*x+8,x=-10..10,y=-10..10,grid=[100 ,100],color=black);>implicitplot(y^2=x^3-40*x+8,x=-10..10,y=-10..10,grid=[100 ,100],color=black);>MAPLE在图论中的应用with(networks):G:=complete(25);draw(G);proc():=G xGRAPH`11`,option;if thenprocname_Edges{}()=x_Edges :=elif thentable symmetricprocname_EdgeIndex() =x_EdgeIndex :=()tableelif thenprocname_Head()()=x_Head :=elif thentableprocname_Tail()=x_Tail :=()tableelif thenprocname_Eweight()()x_Eweight :==tableelif thenprocname_Ends()()=x_Ends :=procname_Vertices{}elif thenx_Vertices :==()table sparse elif thenprocname_Vweight()()=x_Vweight :=elif thentableprocnam e_Ancestor()=x_Ancestor :=()tableelif thenprocnam e_Daughter()()=x_Daughter :=table elif thenprocnam e_Neighbors()x_Neighbors :==()SIMPLEelif then''procnam e_Status{}=x_Status :=()elif thenprocnam e_Emaxname0=()x_Emaxname :=procname argsels e()return ''end ifend proc> with(networks):G:=complete(20);draw(G);:=proc()G xGRAPH`12`option;,procname_Edges{}if then()x_Edges :==table symmetric elif thenprocname_EdgeIndex()()x_EdgeIndex :==tableelif thenprocname_Head()()=x_Head :=tableelif thenprocname_Tail()()=x_Tail :=tableelif thenprocname_Eweight()()x_Eweight :==tableelif thenprocname_Ends()()x_Ends :==procname_Vertices{}elif then()=x_Vertices :=table sparse elif thenprocname_Vweight()()=x_Vweight :=elif thentableprocnam e_Ancestor()=x_Ancestor :=()tableelif thenprocnam e_Daughter()()=x_Daughter :=table elif thenprocnam e_Neighbors()x_Neighbors :==()SIMPLEelif then''procnam e_Status{}=x_Status :=()elif thenprocnam e_Emaxname0=()x_Emaxname :=procname argsels e()return ''end ifend proc。
[转载]maple之绘图篇~by
![[转载]maple之绘图篇~by](https://img.taocdn.com/s3/m/8b95a038cec789eb172ded630b1c59eef8c79af6.png)
[转载]maple之绘图篇~by zn~原⽂地址:maple之绘图篇~by zn~作者:ctrle如何设置maple中坐标轴的格式,look for help ?tickmarks还有⼀个问题尚未解决,就是maple中legend的位置只能放在“上下左右”四个位置,能不能⾃由放置legend哎,真费解啊,期待⾼⼈解决/maple 作图选项(图像中字体、字号等的设置)选项设置格式取值范围说明adaptive adaptive= true还有false⾃适应,取消axes axes=normal frame, boxed,normal, none坐标轴设置,四种axesfont axesfont=[family,style,size]参看plot,options 设置刻度线标号字形color color=n参看plot,color设置图象颜⾊coords coords=name polar (极坐标)参看plot[coords]选择作图所⽤坐标系discont discont=false还有true是否在间断点⽤垂直线连接filled filled=false还有true是否在图象和x轴之间填充font font=[family,style,size ]参看plot,options 设置图象中⽂字部分的字形labels labels=[x,y] 标记坐标轴labeldirections labeldirections=[x,y]horizontal, vertical设置坐标轴的⽅向Labelfont labelfont=[family,style,size ] 设置坐标轴标记的字形legend legend=s s是元素与曲线条数相同的表加⼊图例linestyle linestyle=11-4对应实线,点线,虚线和点划线设置图象线的类型numpoints numpoints =50正整数设置作图区间的分点数resolution resolution=200正整数设置图象的⽔平分辨率sample sample =[x1,..,xk]⾃变量的取值选定作图是必须取的点scaling scaling=unconstrained constrained x轴与y轴单位的⽐style,style=line point, 参看plot,options设置图象点之间的连接⽅式symbol symbol=point box, cross, circle设置图象中点的类型symbolsize symbolsize=10正整数,单位:吋/72设置图象中点的⼤⼩thickness thickness=01, 2, 3设置图象中线的厚度tickmarks tickmarks =[m,n]正整数或default设置图象中坐标轴标号个数title title =”…n…”n⽤作题⽬中的换⾏作图象标题titlefont titlefont[family,style,size ]参看plot,options 设置图象标题⽂字字形view view =[x1..x2, y1 ..y2] 设置图象坐标选取范围xtickmarks xtickmarks =n正整数设置横坐标轴标号个数Plotting Options (English help)The style of the displayed graph may be controlled with a number of plotting options embedded in the plotting command. For instance the command> plot3d(x^2+y^2, x=-1..1, y=-1..1, style=wireframe, grid=[15,15]);displays the graph in wireframe using a 15x15 grid. (Dynagraph's default action is to display the graph as a solid surface using an (invisible) grid of 25x25.)All options take the form option=value. These can be supplied to the plotting command in any order, separated by commas. The following list describes all the options recognized by dynagraph. These form a subset of options available in Maple. The listing below has been obtained mostly by cut-and-paste from Maple's online help. The options pointsize and the option values x_gridlines and y_gridlines are specific to dynagraph and do not exist in Maple.Option values which are keywords, such as WIREFRAME or HELVETICA can be typed either in all uppercase or all lowercase. Therefore axesfont=[HELVETICA,10] and axesfont=[helvetica,10] are equivalent. In the listing below only the uppercase variants are shown.Alphabetical listing of all optionsaxes=fThis option specifies how the axes are to be drawn, where f is one of BOXED, NORMAL, FRAME, and NONE.Default: axes=NONERemark: In this release of dynagraph all axes options other than NONE are treated as synonymous with BOXED. This may be fixed in future releases.axesfont=lThis option defines the font for the labels on the tick marks of the axes, specified in the same manner as font.Default: axesfont=[HELVETICA,10]color=colornamePrescribes a solid color for the object. Colorname may be any color name recognizable by the X server, such as "red" or "MidnightBlue", or an RGB specification such as "#009000". It must be quoted if it contains non-alphanumericcharacters. For the convenience of our continental friends, colour is provided as a synonym to color.contours=nThis option specifies the number of contours in a contour plot.Default: contours=10coords=cThis option specifies the coordinate system to be used, where c is one of CARTESIAN, SPHERICAL, CYLINDRICAL,Z_CYLINDRICAL.Default: coords=CARTESIANfont=fontspecThis option defines the font for text objects in the plot. Fontspec is a list of the form [family,style,size], where family is one of TIMES, COURIER, HELVETICA, and SYMBOL. For TIMES, style may be one of ROMAN, BOLD, ITALIC or BOLDITALIC. ForHELVETICA and COURIER style may be omitted or select one of BOLD, OBLIQUE, or BOLDOBLIQUE. SYMBOL does not accepta style option. The final value, size, is the point size to be used.Default: font=[HELVETICA,10]grid=[m,n]This option specifies the dimensions of the rectangular grid to use to represent a surface.Default: grid=[25,25]gridstyle=xThis option specifies the type of mesh which is drawn to represent the surface. The value of x is one of RECTANGULAR, TRIANGULAR, X_GRIDLINES, Y_GRIDLINES. (XY_GRIDLINES is also provided as a synonym for RECTANGULAR.) Note that these options set the mesh style but do not cause the mesh to be drawn. The drawing of the mesh is determined by the value of the style option described below.Default: gridstyle=RECTANGULARlabelfont=lThis option defines the font for the labels on the axes of the plot, specified in the same manner as font.Default: labelfont=[HELVETICA,12]labels=[x,y,z]This option specifies labels for the axes. The values of x, y, and z must be strings. The default label for the x and y axesare the names of the variables for the x and y axes and no label on the z axis. Labels are shown only when thecoords=CARTESIAN is in effect.linewidth=nSame as thickness=nnumpoints=nWhen plotting a surface this option specifies the minimum total number of points to be generated (default 625 = 25^2).Plot3d will use a rectangular grid of dimensions ~= sqrt(n). When plotting a spacecurve or a tube, this option specifies the number of points to use along the curve or along the axis of the tube. The default is 60.orientation=[longitude,colatitude]This option sets the viewing position at a point at infinity along the ray given by the spherical coordinates(longitude,colatitude), looking towards the origin.Default: orientation=[45,45]pointsize=nThis option defines the size (in pixels) of points drawn in the plots. n should be an integer from 0 to 10. 0 selects the default pointsize.Default: pointsize=3scaling=sThis option specifies whether the surface should be scaled so that it fits the screen with axes using a relative orabsolute scaling, where s is either UNCONSTRAINED or CONSTRAINED. The dynagraph graphics window is initially set to scaling=CONSTRAINED. The user may toggle the CONSTRAINED/UNCONSTRAINED button at will. Subsequent graphs will obey the button's setting unless specified otherwise on the command line.shading=sThis option specifies how the surface is colored, where s is one of XYZ, XY, Z, ZGREYSCALE, ZHUE, NONE.Default: shading=XYZstyle=sThis specifies how the surface is to be drawn, where s is one of POINT, HIDDEN, PATCH, WIREFRAME, CONTOUR,PATCHNOGRID, PATCHCONTOUR, or LINE.Default: style=PATCHNOGRIDRemark: LINE is synonymous with WIREFRAMEthickness=nThis option defines the thickness (in pixels) of lines in the plots. n should be an integer from 0 to 10. 0 selects the default thickness.Default: thickness=1tickmarks=[l,n,m]This option specifies reasonable numbers no less than l, n and m should be marked along the x-axis, y-axis, and z-axis, respectively. Each tickmarks value must be a positive integer or zero, in which case no tickmarks will drawn on the corresponding axis.Default: tickmarks=[5,5,5]title=tThis option specifies a title for the plot. The value of t must be a string. The two-character sequence n (that is, abackslash followed by n) acts as a line break within the title string, thus making multi-line titles possible. Each line of a multi-line title is horizontally centered within the window.Default: no titletitlefont=lThis option defines the font for the title of the plot, specified in the same manner as font.Default: titlefont=[HELVETICA,BOLDOBLIQUE,14]tuberadius=rThis sets the radius of the tube in a tubeplot.Default: tuberadius=1.0tubepoints=nThis sets the number of points to use for drawing each cross-section of a tubeplot. Note that the circular cross section will appear to have only n-1 equally-spaced points on its circumference, because the first and last points coincide.Default: tubepoints=16view=zmin..zmax or view=[xmin..xmax,ymin..ymax,zmin..zmax]This option indicates the minimum and maximum coordinates of the surface to be displayed on the screen.Default: displays the entire surface/~rouben/dynagraph/index.html。
Maple6-ch6-绘图7页word

第六章M aple的绘图功能Maple之所以在欧美流行,一个重要的原因就是它简单但功能强大的图形绘制函数,以及它内建的大量的特殊函数,要以灵活、方便的实现用户所预期的功能。
§6.1 绘图功能概述可以将Maple的绘图函数简单表示为:函数名(“公式、数据”,“变量范围”,“函数参数”)6.1.1 二维图形工作环境设置在普通的编辑状态,用户是看不见Maple中同绘图相关的菜单与工具栏的,如果用户工作簿中利用函数生成了一个二维图形,并使用鼠标选中系统生成的图形,则Maple的菜单及工具条上就会出现如图所示粉红色椭圆线圈着的新菜单与工具栏。
新增菜单栏各选项与对应的工具栏的作用如下:1.Style菜单主要提供参曲线的线型、点、线宽等属性的设置选项。
包括的选项有:Line: 使用“线条”方式显示图形(对应工具栏上的图标)。
Point: 使用“点”方式显示图形(对应工具栏上的图标)。
Patch: 使用带网格的多边形填充图形(对就着工具栏中按钮)。
Patch o/w grid: 使用无网格多边形填充图形(对着工具栏中的按钮)。
练习:用以上“Style”菜单栏中各种选项观察正弦曲线变化时的表现形式。
2.L egend菜单(图例菜单)例如:在同一坐标系下作正弦与余弦的图形并给出图例。
解(1)作图:> plot([sin(x), cos(x)], x=-Pi..Pi,color=[red,blue], style=[point,line]);(2)选“Legend-Edit Legend”菜单:选中菜单,出现两个可选项:“Show Legend”与“Edit Legend”。
若选后者则有填入不同曲线所代表的函数即可得2.Axes菜单----可用工具按钮给出不同坐标原点下的坐标系等3.Projection----选择坐标轴是否按等比例显示,默认为不按,即Unconstrained 4.Export----将所选择图形对象另存为其他图形对象,常用的格式有“JPG”、“GIF”、“BMP”等Windwos中的常见格式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第6章 Maple 中作图6.1 二维函数作图命令plot6.1.1 二维函数作图用plot 命令可以画出一元函数在指定区间上的二维函数图形。
其用法有plot (函数,变量名) plot (函数,范围,选项)范围和选项均可省略,缺省时系统自动选取最佳设置。
最简单的plot 语句为plot(f(x),x=a..b) 画出f(x)在区间[a,b]上的图像,其中f 可为过程或表达式。
例:画出函数x x f sin )(1=在区间),(∞−∞上的图形。
> plot(sin(x)/x,x=-infinity..infinity);例:画出分段函数⎪⎩⎪⎨⎧>−≤≤−−<−−=ππππππx x x x x x x f )(sin )(21在区间]6,6[−上的图像。
> f:=x->piecewise(x<-Pi,-x-Pi,x<=Pi and x>=-Pi,sin(x),x>Pi,(x-Pi)/2):plot(f(x),x=-6..6);6.1.2 plot 选项 6.1.3 参数方程作图用plot 函数画参数曲线的一般形式为plot ([x(t),y(t),t=a..b],选项) 或plot ([[x(t),y(t),t=a..b],[u(t),v(t),t=c..d]],选项)在一个坐标系中同时画两条参数曲线。
例 :画参数曲线]2,0[sin cos 1π∈⎩⎨⎧=+=t t y tx ,。
> plot([1+cos(t),sin(t),t=0..2*Pi]);6.1.4 特殊坐标系下作图plot 通常画的是直角坐标下的函数图像,通过设置coords 选项,plot 也可以画出特殊坐标下的函数图像。
例如,画出极坐标下函数b t a t r r ≤≤=,)(的图形可用命令plot(r(t),t=a..b,coords=polar) 或 plot([r(t),t,t=a..b],coords=polar)在6.3小节中,还将给出plots 程序包中画特殊坐标系下的函数图像的命令,例如polarplot(r(t),t=a..b)例 :特殊坐标系下的函数图像。
> plot([cos(6*x),x,x=0..2*Pi],coords=polar);> plot(cos(6*t),t=-Pi..Pi,coords=bipolar); # 双极坐标6.2 三维函数作图plot3d6.2.1 三维函数作图画二元函数f(x,y)的三维图像可用plot3d 命令plot3d(f(x,y),x=a..b,y=c..d,选项)与plot 函数相似,plot3d 的选项可有可无,项数可多可少。
plot3d 的部分选项的名称和功能的细节请看6.2.3小节。
例:画出函数ππ≤≤−++=y x yx y x f ,cos sin 11),(44,的图像。
> plot3d(1/(1+sin(x)^4+cos(y)^4),x=-Pi..Pi,y=-Pi..Pi);例:画出球面与锥面所围立体及其表面。
> plot3d([sqrt(8-x^2-y^2),sqrt(x^2+y^2)],x=-2..2,y=-2..2);6.2.2 三维参数方程作图用plot3d 命令画三维参数曲面()),(),,(),,(t s z t s y t s x 的一般形式为plot3d([x(s,t),y(s,t),z(s,t)],s=a..b,t=c..d) plot3d([f,g,h],a..b,c..d)其中x 、y 、z 是关于s 和t 的表达式,f 、g 、h 是有两个参数的过程。
例:画出参数曲面ππ≤≤≤≤⎪⎩⎪⎨⎧===y x yx y x w y x x y x v yx x y x u 020sin ),(cos cos ),(cos sin ),(,。
> plot3d([x*sin(x)*cos(y),x*cos(x)*cos(y),x*sin(y)], x=0..2*Pi,y=0..Pi,labels=['u','v','w']);例:用球坐标作图。
> plot3d(cos(x^2)*sin(y),x=-2*Pi..2*Pi,y=-Pi..Pi, coords=spherical, numpoints=10000);6.3 plots 程序包在plots 包中有56个画图命令和选项设置命令,在本节中只能列出部分命令。
动画演示命令animate 、animate3d 和animatecurve 在6.4节中,绘制微分方程数值解的函数图像的命令odeplot 在第5章中。
> with(plots);Warning, the name changecoords has been redefined [animate, animate3d, animatecurve, arrow, changecoords, complexplot, complexplot3d, conformal, conformal3d, contourplot, contourplot3d, coordplot, coordplot3d, cylinderplot, densityplot, display, display3d, fieldplot, fieldplot3d, gradplot, gradplot3d, graphplot3d, implicitplot, implicitplot3d, inequal, interactive, interactiveparams, listcontplot, listcontplot3d, listdensityplot, listplot, listplot3d, loglogplot, logplot, matrixplot, multiple, odeplot, pareto, plotcompare, pointplot, pointplot3d, polarplot, polygonplot, polygonplot3d, polyhedra_supported, polyhedraplot, replot, rootlocus, semilogplot, setoptions, setoptions3d, spacecurve, sparsematrixplot, surfdata, textplot, textplot3d, tubeplot]z 等值线图contourplot (函数,范围,选项) contourplot3d (函数,范围,选项)例:函数))sin(cos()(22y x x f +=的等值线图。
> contourplot(sin(cos(x^2+y^2)),x=-10..10,y=-10..10,filled=true); contourplot3d(sin(cos(x^2+y^2)),x=-10..10,y=-10..10,filled=true);z密度图densityplot(函数,范围,选项)z向量场图fieldplot(向量场,范围,选项)fieldplot3d(向量场,范围,选项)例:画二维向量场> fieldplot([sin(2*x*y),cos(2*x-y)],x=-2..2,y=-2..2,axes=boxed);z梯度图gradplot(函数,范围,选项)gradplot3d(函数,范围,选项)例:画三维梯度图。
> gradplot3d(x^2+y^2+z^2,x=-1..1,y=-1..1,z=-1..1,axes=boxed);z 隐函数作图implicitplot (方程,范围,选项) implicitplot3d (方程,范围,选项)画出函数222zy x =+的图形。
> implicitplot3d(x^2+y^2=z^2,x=-1..1,y=-1..1,z=-1..1); 画出函数3333)1(1+++=+++z y x z y x 的图形。
> implicitplot3d(x^3+y^3+z^3+1=(x+y+z+1)^3, x=-2..2, y=-2..2, z=-2..2, style=patchnogrid, numpoints=10000);z 数据点列作图z 复函数作图6.4 动画演示动画命令animateanimate(f(x,t),x=a..b,t=c..d)animate 函数在plots 程序包中,使用前要先调出plots 程序包。
例:动画演示sin(x)图像。
> with(plots);> animate(sin(x-t),x=-2*Pi..2*Pi,t=0..10,scaling=constrained);例:红点沿着蓝色曲线滑动。
> curve:=plot(sin(x),x=0..10,color=blue):> animate(pointplot,[[t,sin(t)],symbol=circle,symbolsize=10], t=0..10,color=red,background=curve);例:用函数图形做动画背景。
> fg:=animate(plot3d,[sin(x*y*t),x=-Pi..Pi,y=-Pi..Pi],t=-1..1): bg:=plot3d(x-y,x=-Pi..Pi,y=-Pi..Pi): display(fg,bg);。
