(完整版)Mathematica——常微分方程、拉氏变换与级数实验
实验七 用Mathematica解常微分方程

实验七 用Mathematica 解常微分方程实验目的:掌握用Mathematica 软件求微分方程通解与特解的方法的语句和方法。
实验过程与要求:教师利用多媒体组织教学,边讲边操作示范。
实验的内容:一、求微分方程的通解在Mathematica 系统中用DSolve 函数求解微分方程,基本格式为:DSolve [微分方程,未知函数名称,未知函数的自变量]实验1 求微分方程x y 2='的通解.解 In[1]:= DSolve[y '[x ]==2x ,y [x ],x ]Out[1]=实验2 求微分方程x xe y y y 2323=+'-''的通解.解 In[2]:= DSolve[y ''[x ]-3y '[x ]+2y [x ]==(3x )Exp[2x ],y [x ],x ]Out[2]=实验3 求微分方程x y y sin 23='+''的通解.解 In[3]:=DSolve[y ''[x ]+3y '[x ]==2Sin[x ],y [x ],x ]Out[3]=其中方程中的等号应连输2个“=”,二阶导数记号应连输两个单引号.二、求微分方程的特解在Mathematica 系统中求特解的函数仍为DSolve ,而基本格式为:DSolve [{微分方程,初始条件},未知函数名称,未知函数的自变量]实验4 解微分方程0,20=+='=x y y x y .解 In[4]:=DSolve[{y '[x ]==2x +y [x ],y [0]==0},y [x ],x ]Out[4]=实验用笔算和机算两种方法求解下列微分方程:x xe y y y x x xy y x y y y e y y 43332.43.3cos 244.26.1=-'-''++='=+'-''=-'0,)1.(60)0(,sec tan .50=='+==-'=x x x y e y y e y x x y y。
mathematica数学实验报告

mathematica数学实验报告本次实验使用Mathematica进行数学建模实验,主要包括以下内容:三角函数、极限和导数、积分和微分方程。
一、三角函数1. 三角函数的绘制使用Mathematica的Plot函数绘制正弦函数和余弦函数的图像。
代码:Plot[{Sin[x], Cos[x]}, {x, -2 Pi, 2 Pi},PlotStyle -> {Blue, Red}, PlotTheme -> "Web"]结果:在x趋近于4时的极限。
代码:Limit[x^2/(4 - x), x -> 4]结果:82. 求函数的导数使用Mathematica的D函数计算函数x^3 - 3x的导数。
代码:D[x^3 - 3x, x]结果:3 x^2 - 3三、积分和微分方程1. 求定积分使用Mathematica的Integrate函数计算函数e^x * cos(x)在0到π/2之间的定积分。
代码:Integrate[E^x * Cos[x], {x, 0, Pi/2}]结果:1/2 (1 + E^(π/2))2. 解微分方程使用Mathematica的DSolve函数求解微分方程y''(x) + 4y(x) = 0。
代码:DSolve[y''[x] + 4 y[x] == 0, y[x], x]结果:y[x] -> C[1] Cos[2 x] + C[2] Sin[2 x]本次实验使用Mathematica进行数学建模实验,主要包括三角函数的绘制、求三角函数的值,函数的极限、导数,积分和微分方程等内容。
数学实验 Mathematic实验十 微分方程

天水师范学院数学与统计学院实验报告实验项目名称微分方程所属课程名称数学实验实验类型微积分实验实验日期2011.11.23班级学号姓名成绩【实验目的】1.掌握用Mathematica求微分方程及方程组解的方法;2.学习求微分方程近似解的欧拉折线法.【实验原理】1.求解微分方程的命令DSolve.对于可以用积分方法求解的微分方程和微分方程组,可用Dsolve 命令来求其通解或特解.例DSolve[y''[x]+y'[x]-2*y[x]==0,y[x],x]如果要求初值问题,输入DSolve[{y''[x]+4y'[x]+3y[x]0,y[0]0,y'[0] 10},y[x],x]2.求微分方程数值解的命令NDSolve.对于不可以用积分方法求解的微分方程初值问题,可以用NDsolve命令NDSolve[{y'[x] y[x]^2+x^3,y[0] 0.5},y[x],{x,0,1.5}] 【实验环境】Mathematic 4【实验过程】(实验步骤、记录、数据、分析)1.欧拉折线法.例10.1 用欧拉折线法解初值问题. Clear[x ,y ,dx ,f]; x[0]=0; dx=0.1; y[0]=1;x[n_]:=x[n]=x[n-1]+dx ;y[n_]:=y[n]=y[n-1]+(1+y[n-1])*dx ; euler=Table[{x[n],y[n]},{n ,0,10}]; zhx=TableForm[euler ,TableHeadings {None ,{"x","y(Euler)"}}]Clear[g1,g2,y1,g3]; g1=Graphics[Line[euler]]; g2=ListPlot[euler]; y1[x_]=2Exp[x]-1;g3=Plot[y1[x],{x ,0,1}]; Show[g1,g2,g3,Axes True] Table[y1[x[n]]-y[n],{n ,1,10}] 2.用DSolve 命令解微分方程.例10.2 求微分方程22xxe xy y -=+'的通解.Clear[x ,y];DSolve[y'[x]+2x*y[x]x*Exp[-x^2],y[x],x]例l0.3 求微分方程0xxy y e '+-=在初始条件(1)2y e =下的特解. Clear[x ,y];DSolve[{x*y'[x]+y[x]-Exp[x]0,y[1]2E},y[x],x]例10.4 求微分方程x e y y y x 2cos 52=+'-''的通解. Clear[x ,y];DSolve[y''[x]-2y'[x]+5y[x]==Exp[x]*Cos[2x],y[x],x]//Simplify例10.5 (*example10.5*). Clear[x ,y ,t];DSolve[{x'[t]+x[t]+2y[t]==Exp[t],y'[t]-x[t]-y[t]==0,x[0]==1,y[0]==0},{x[t],y[t]},t]//Simplify 3.用NDSolve 命令求微分方程的近似解.例10.6 求初值问题:(1)(1)0,(1.2)1xy y xy y y '++-==在区间[1.2,4]上的近似解并作图.f1=NDSolve[{(1+x*y[x])*y[x]+(1-x*y[x])*y'[x]==0,y[1.2]==1},y ,{x ,1.2,4}]Plot[Evaluate[y[x]/.f1],{x ,1.2,4}] y[1.6]/.f1例10.7 求范德波尔方程2(1)0,(0)0,(0)0.5y y y y y y ''''+-+===-在区间[0,20]上的近似解.Clear[x ,y];NDSolve[{y''[x]+(y[x]^2-1)*y'[x]+y[x]==0,y[0]==0,y'[0]==-0.5},y,{x,0,20}];Plot[Evaluate[y[x]/.%],{x,0,20}]【实验结论】(结果)1.用Mathematica求微分方程及方程组解的方法;2.学习求微分方程近似解的欧拉折线法.附录1:源程序实验十微分方程第一题(1)Clear[x,y];DSolve[y''[x]+6*y'[x]+13*y[x]0,y[x],x] y x3x C2Cos2x3x C1Sin2x(2)Clear[x,y];DSolve[D[y[x],{x,4}]+2*y''[x]+y[x]0,y[x],x]//S implifyy x C2x C4Cos x C1x C3Sin x(3)Clear[x,y];DSolve[D[y[x],{x,4}]-2*y'''[x]+y''0,y[x],x]y x C1x C2x2C32x C4x3y 12(4)Clear[x,y];DSolve[y''[x]-2*y'[x]+5*y[x]Exp[x]*Sin[2*x],y[ x],x]y xx C2Cos2x x C1Sin2x18x Cos2x2Sin2x12x Cos2x x218Sin4x(5)Clear[x,y];DSolve[y''[x]-6*y'[x]+9*y[x](x+1)*Exp[3*x],y[x ],x]y x 163x3x2x36C16x C2第二题(1)Clear[x,y];DSolve[{y''[x]+4y'[x]+29y[x]0,y[0]0,y'[0]1 5},y[x],x]y x32x Sin5x(2)Clear[x,y];DSolve[{y''[x]-y[x]4*x*Exp[x],y[0]0,y'[0]1 },y[x],x]y x 12x222x22x x22x x2(3)Clear[x,y];DSolve[{y''[x]+y[x]+Sin[2x]0,y[Pi]1,y'[Pi] 1},y[x],x]y x133Cos x Sin x Sin 2x第三题Clear[x,y];DSolve[{(x^2-1)y'[x]+2*x*y[x]-Cos[x]0,y[0]1},y[x],x]y x1Sin x 1x 2Clear[x,y];g1=NDSolve[{(x^2-1)*y'[x]+2*x*y[x]-Cos[x]0,y[0]1},y,{x,0,1}]y InterpolatingFunction 0.,1.,Plot[Evaluate[y[x]/.g1],{x,0,1}]0.20.40.60.812468Graphics第四题Clear[x,y,t];DSolve[{x'[t]+5*x[t]+y[t]Exp[x],y'[t]-x[t]-3*y [t]Exp[2*x]},{x[t],y[t]},t]//Simplifyx t1210115t45t15t x15t15t2x7215t15415C115C2715415C115C2,y t1210115t15t15t x75t15t2x715C115415C2 7215t15C115415C2第五题Clear[x,y,t];DSolve[{x'[t]+3*x[t]-y[t]0,y'[t]-8*x[t]+y[t] 0,x[0]==1,y[0]4},{x[t],y[t]},t]x t t,y t4t第六题Clear[x,y];DSolve[x^2*y''[x]+x*y'[x]-4*y[x]x^3,y[x],x]y x x35C1x2x2C2第七题Clear[x,y];NDSolve[{y''[x]+x*y'[x]+y[x]0,y[1]0,y'[2]5 },y,{x,0,4}]y InterpolatingFunction0.,4.,Plot[Evaluate[y[x]/.%],{x,0,4}]50403020101234 Graphics附录2:实验报告填写说明1.实验项目名称:要求与实验教学大纲一致。
Mathematica在常微分方程实验中的应用

Mathematica在常微分方程中的应用是高等数学教学的一个实验教学环节,是高等数学课程标准中的一项基本内容。
由于求解常微分方程的过程与导数、微分和不定积分有着密切关系,因此解微分方程成为高等数学教学的一个难点。
Mathematica能很方便快捷地求出常微分方程的各种类型的解,几乎覆盖了人工求解的全部范围,功能十分强大。
用Mathematica求微分方程的数值解也很方便,且有利于作出方程解即未知函数的图形。
用拉普拉斯变换解微分方程也是一件轻而易举的事。
一、用Mathematica解常微分方程在Mathematica中使用DS olve[]命令可以求各类常微分方程的解。
求微分方程的解就是求出的函数的解析式。
在Mathematica系统中,微分方程中未知函数用y[x]表示,其导数或微分用y′[x]、y″[x]等表示。
Mathematica语法也就是方程形式及各项参数的表述方式十分严格,不允许有丝毫错误(若出错计算机会作出警示)。
(一)求微分方程的通解Mathematica系统中求解微分方程命令的输入格式如下:DSolve[eqn,y[x],x],求微分方程eqn的通解y[x],其中自变量是x。
[1]实验一:解下列常微分方程:(1)y′=2yx+1+(x+1)52,(2)dydx+2xy=xe-x2解:In[1]:=DSolve[y′[x]==2y[x]/(x+1)+(x+1)^(5/2),y[x],x]Out[1]=y[x]→23(1+x)7/2+(1+x)2c[1→→]→→In[2]:=DSolve[y′[x]+2xy[x]=xE^(-x^2),y[x],x]Out[2]={{y[x]→12e-x2x2+e-x2C[1]}}Out[1]和Out[2]分别是所给两个微分方程的通解。
式中的C[1]是通解中的任意常数,其中C为大写字母。
上述命令也可以输入为:DSolve[D[y[x]]+2x y[x] ==x E^(-x^2),y[x],x]。
(完整版)Mathematica——常微分方程、拉氏变换与级数实验

创3.5 常微分方程、拉氏变换与级数实验[学习目标]1. 会用Mathematica 求解微分方程(组);2. 能用Mathematica 求微分方程(组)的数值解;3. 会利用Mathematica 进行拉氏变换与逆变换;4. 能进行幕级数和傅里叶级数的展开。
一、常微分方程(组)Mathematica 能求常微分方程(组)的准确解,能求解的类型大致覆盖了人工求解的范围, 功能很强。
但不如人灵活(例如在隐函数和隐方程的处理方面),输出的结果与教材上的答 案可能在形式上不同。
另外,Mathematica 求数值解也很方便,且有利于作出解的图形。
在本 节中,使用Laplace 变换解常微分方程(组)的例子也是十分成功的,过去敬而远之的方法 如今可以轻而易举的实现了。
求准确解的函数调用格式如下: DSolve[eqn ,y[x] ,x] 求方程 eqn 的通解 y(x ),其中自变量是X 。
DSolve[{eqn ,y[x o ]= =y 0},y[x],x] 的特解y (x )。
DSolve[{eqn1,eqn2,—},{y 1 [x],y 2[x],…},x]求方程组的通解。
DSolve[{equ1,…,y 1[x 0]= =y 10,…},{y 1[x],y 2[x],…},x] 求方程组的特解。
说明:应当特别注意,方程及各项参数的表述方式很严格,容易出现输入错误。
微分方 程的表示法只有通过例题才能说清楚。
例1 解下列常微分方程(组):52(1) y 斗(x 1)2,(2) y - y 3 ,(3)x 1(x x ) y解:In[1]: =DSolve[y ' [x]= =2y[x]/ (x+1) + (x+1) A (5/2),y[x],x]Out[1]=y[x] i (1 x)7/2 (1 x)2c[1]In[2]: =DSolve[y ' [x]= = (1+y[xF2 ) /((x+xA3 ) y[x]),y[x],x]求满足初始条件y ( x o ) = y o(4)的通解及满足初始条件y (0) =0, z (0) =1的特解。
Mathematica数学实验[2]
![Mathematica数学实验[2]](https://img.taocdn.com/s3/m/c62bcb08f12d2af90242e6d9.png)
数 学 实 验
Experiments in Mathematics
主讲教师: 刘强国 Cell phone: 159 8418 4369 E-mail: mathsuse@
Limit[f,x->a] Limit[f,x->a ,Direction->1] Limit[f,x->x0,Direction->-1] 例:求下列极限。
求极限 求左极限 求右极限
sin x lim x →0 x
lim
x → (π / 2
( x→∞
lim 1 +
1 x x
)
tanx
)-
x → ( π/2 ) +
给出一组方程,求所有可能的解,其格式为
Reduce[{lhs1= =lhs1, lhs2= =lhs2},{x,y}] 例如 Reduce 2 a x - y == 2, x2 - b x y + y == 7 , x, y
8 @
8D <<
5
Solve: 给通解舍特解; 解以代换式给出; Reduce: 给所有解 ( 通解+特解 ); 解以逻辑式给出 Solve[k*x+b==0,x] Reduce[k*x+b==0,x]
1
四川理工学院 理学院 数学实验中心
数学实验
第二讲 Mathematica在高等数学中的应用
> > > >
• • • •
解方程(组) 极限、微分、积分 数列求和、求积、级数 解微分方程组
常微分方程拉氏变换法求解常微分方程课件

求解得到的代数方程,得到$F(s)$的表达式。
解出常微分方程的解
要点一
反变换求解
通过反拉氏变换将$F(s)$还原为$f(t)$,从而得到常微分方 程的解。
要点二
验证解的正确性
将得到的解代入原常微分方程进行验证,确保解的正确性。
06
总结与展望
总结
拉氏变换法的优势
拉氏变换法在求解常微分方程时 具有明显的优势,它可以将复杂 的微分方程转化为代数方程,大 大简化了求解过程。
通过逐一求解一阶常微分方程,拉氏变换法可以应用于高阶微分方程的求解。
拉氏变换法的缺点
计算量大
在应用拉氏变换法求解常微分方程时,需要进行复 杂的积分和代数运算,计算量较大。
对初值条件敏感
对于某些常微分方程,初值条件的微小变化可能导 致拉氏变换法的失效。
不易理解
拉氏变换法的概念较为抽象,不易被初学者理解。
与其他方法的结合
可以考虑将拉氏变换法与其他数值方法或解析方法结合,以更有效 地求解各种类型的微分方程。
实际应用价值
随着科学技术的不断发展,常微分方程在各个领域的应用越来越广 泛,因此拉氏变换法在实际应用中也将发挥更大的作用。
感谢观 看
THANKS
信号处理中,拉氏变换法可以用于分析信号的滤波、调制 和解调等过程,优化信号处理效果。
04
拉氏变换法的优缺点
拉氏变换法的优点
求解过程简化
拉氏变换法可以将复杂的常微分方程转化为简 单的代数方程,从而简化了求解过程。
适用于多种初值条件
拉氏变换法可以处理多种初值条件,使得该方 法具有更广泛的适用性。
可应用于高阶微分方程
拉氏变换法求解一阶常微分方程
实验四利用Mathematica解方程实验目的:学会正确使用Solve和FindRoot及

此方法的理论依据是解方程的弦截法。
方程求解情况比较复杂,有时上述方法不能解决, 则需要其它方法。
三、用DSolve解微分方程
1.命令格式
DSolve[{微分方程,初始条件},未知函数,自变 量]
NDSolve[方程,未知函数,{自变量,a,b}]可求得 微分方程或方程组在自变量指定取值范围内的数值 解
y(0) 6, y(0) 2的0, y,(0在) 20 处的数值x 解0.4
二、应用部分
(1) 找出方程exsinx-xcos2x=0最靠近原点的五个根.
(2)方程y″+9y=0的一条积分曲线通过点(π,-1),且在该 点和直线y+1=x-π相切,求这条曲线的方程.
(3)一垂直悬挂的弹簧,其下有一质量为m的重物,平衡 位置时弹簧伸长a,如果将物体向下拉开一段距离b, 然后放开,物体就在平衡位置上下振动,求其运动规 律x=x(t).
6先观察fxsinxcosx的图形然后选择一个初始点去求解并且根据图形确定
实验四 利用Mathematica解方程
实验目的:学会正确使用Solve和FindRoot及 DSolve解各类方程 预备知识:
(一)理解方程(方程组)的代数解法 (二)解方程的牛顿切线法及弦截法 (三)微分方程相关知识 (四)Mathematica中解各类方程及方程
(二)从初始值开始搜索方程或方程组的解: FindRoot[方程(方程组),{未知元,初值}](4) 解方程:sinxe2x-cosx=0 (三)在界定范围内搜索方程或方程组的解: FindRoot[方程(方程组),{未知元,初值1, 初值2}] (5)解方程:sinxe2x-cosx=0 (6)先观察f(x)=sinx-cosx的图形,然后选择 一个初始点去求解,并且根据图形确定在某个区 间中搜索它的零点
用Mathematica进行级数运算

\确定收敛半径为∞,收敛域为(-∞,+∞)
10
algebra\symboblic.m。 Sum[(-1)^(n+1)*x^n/n,{n,1,Infinity}] \求级数的和,输出结果为Log[1+x] 还可确定收敛域,只需要执行下列各条命令: Clear[f,a,b,n] f[x_] :=(-1)^(n+1)*x^n/n; a[n_]:=(-1)^(n+1) /n; b=Limit[a[n]/a[n+1],n->Infinity]; Print[“R=”,Abs[b]] \确定收敛半径为1 Sum[f[1],{n,1,Infinity}] \确定原级数在x=1处收敛于
12
直接画图,在使用时,可以将其转换为多项式,然 后再计算。需使用命令:
Normal[Series] 如:a=Series[1/(1-x),{x,0,5}],结果为
1 x x2 x3 x4 x5 O x 6
b=Normal[a],结果为
2345
1xx x x x
8
二、边学边做
1.求和 (1)algebra\symboblic.m。 Sum[n*2^n,{n,1,6}] \求有限项的和,输出结果为642 (2)algebra\symboblic.m。 Sum[1/(n*(n+1)),{n,1,Infinity}] \求级数的和,输出结
Log[2] Sum[f[-1],{n,1,Infinity}] \确定原级数在x=-1处发散 因而原级数收敛域为(-1,1]
《数学实验》实验报告——用Mathematica软件解微分方程

Out[1]= In[2]:= s1=LaplaceTransform[1,t,s]
1
Out[2]= s In[3]:= x''[0]=x'[0]=x[0]=0;Solve[f1 s1,LaplaceTransform[x[t],t,s]]
3
Out[3]= In[4]:= Out[4]= 上例中的 LaplaceTransform[x[t],t,s]就是教材中的 X(s) ,In[3]解出 X(s) , 其余过程与教科书完全相同。
例 5 求微分方程ቤተ መጻሕፍቲ ባይዱ:
x 2 x y 2 y 0 t x y 2 x 2e 满足条件 x(0)=3,x′(0)=2,y(0)=0 的特解。
In[1]:= f1=LaplaceTransform[ {x''[t] - 2x'[t] - y'[t] + 2y[t],x'[t] + y'[t] - 2x[t]},t,s]
例2 求常微分方程 y′= x2 + y2,满足初始条件 y(0)= 0 的数值解 例3 求函数 t 5 和 et sint 的拉氏变换 例 4 用拉氏变换解微分方程:
x + 3x″+ 3x′+ x = 1 满足条件 x″(0) = x′(0) = x(0) = 0 的解。
例 5 求微分方程组:
《数学实验》实验报告
班级 试验 内容 **** 学号 **** 姓名 试验 类别 **** 成绩 试验 时间
用 Mathematica 软件解微分方程
自选试验
试验问题:
例1 求解下列微分方程: 1) 2) 3)
y 2 (1 y) (2 y) 2
常微分方程拉氏变换法求解常微分方程全文

拉普拉斯变换法用于求解常微分方程的基本思路:
对常微分方程进行拉氏变换法,得代数方程,求解 再反变换获取原方程的解
问题: 1. 什么是拉氏变换 2. 拉氏变换的基本性质 3. 什么是拉氏逆变换 4. 如何用拉氏变换求解微分方程
2
1拉普拉斯变换定义(简称拉氏变换)
对于在 [0, ) 上有定义的函数 f (t)
sx0(n2)
x (n1) 0
16
x(n) a1x(n1) an1x an x f (t)
给(4.32)两端施行Laplace Transform
sn
X
(s)
s n1 x0
sn2 x0
sx0(n2)
x (n1) 0
a1[s n1 X
(s)
sn2 x0
s n3 x0
x (n2) 0
]
an1[sX (s) x0 ] an X (s) F (s)
F (s) test f (t)dt
0
F (n) (s) (1)n t nest f (t)dt
0
F (n) (s) (1)n L[tn f (t)]
10
§3 拉普拉斯逆变换 已知象函数,求原函数
L1[F (s)] f (t)
也具有线性性质
L1[c1F1(s) c2F2 (s)] c1L1[F1(s)] c2L1[F2 (s)]
(sn a1sn1 an1s an ) X (s) F (s) B(s)
X (s) F(s) B(s) A(s)
x(t) L1[ X (s)] L1[ F (s) B(s)] A(s)
17
用拉氏变换求微分方程实例
例5 求 dx x e2t 满足初始条件 x(0) 0的特解
(完整版)Mathematica入门教程含习题与答案

Mathematica入门教程第1篇第1章MATHEMATICA概述 (3)1.1 M ATHEMATICA的启动与运行 (3)1.2 表达式的输入 (4)1.3 M ATHEMATICA的联机帮助系统 (6)第2章MATHEMATICA的基本量 (8)2.1 数据类型和常数 (8)2.2 变量 (10)2.3 函数 (11)2.4 表 (14)2.5 表达式 (17)2.6 常用的符号 (19)2.7 练习题 (19)第2篇第3章微积分的基本操作 (20)3.1 极限 (20)3.2 微分 (20)3.3 计算积分 (22)3.4 无穷级数 (24)3.5 练习题 (24)第4章微分方程的求解 (26)4.1 微分方程解 (26)4.2 微分方程的数值解 (26)4.3 练习题 (27)第3篇第5章MATHEMATICA的基本运算 (28)5.1 多项式的表示形式 (28)5.2 方程及其根的表示 (29)5.3 求和与求积 (32)5.4 练习题 (33)第6章函数作图 (35)6.1 基本的二维图形 (35)6.2 二维图形元素 (40)6.3 基本三维图形 (42)6.4 练习题 (46)第4篇第7章MATHEMATICA函数大全 (48)7.1 运算符和一些特殊符号,系统常数 (48)7.2 代数计算 (49)7.3 解方程 (50)7.4 微积分 (50)7.5 多项式函数 (51)7.6 随机函数 (52)7.7 数值函数 (52)7.8 表相关函数 (53)7.9 绘图函数 (54)7.10 流程控制 (57)第8章MATHEMATICA程序设计 (59)8.1 模块和块中的变量 (59)8.2 条件结构 (61)8.3 循环结构 (63)8.4 流程控制 (65)8.5 练习题 (67)--------------习题与答案在68页-------------------第1章Mathematica概述1.1 Mathematica的启动与运行Mathematica是美国Wolfram研究公司生产的一种数学分析型的软件,以符号计算见长,也具有高精度的数值计算功能和强大的图形功能。
(完整版)Mathematica求解方程(组)、级数

方程(组)与级数的Mathematica 求解[学习目标]1. 能用Mathematica 求各种方程(组)的数值解和近似解;2. 能对常见函数进行幂级数的展开。
一、 求解简单方程(组)数学里的方程是带有变量的等式。
一般地说,一个或一组方程总是对于方程中出现的变量的可能取值范围增加了一些限制。
所谓求解方程就是设法把方程对于变量取值的限制弄清楚,最好的结果是用不含变量的表达式把变量的值表示出来。
在这个系统里,方程也用含有变量的等式表示,要注意的是在这里等号用连续的两个等号(==)表示。
方程的两端可以是任何数学表达式。
用户可以自己操作Mathematica 系统去求解方程,例如使用移项一类的等价变换规则对方程加以变形、对方程的两端进行整理、把函数作用于方程的两端等等。
系统也提供了一些用于求解方程的函数。
1、 求方程的代数解最基本的方程求解函数是Solve ,它可以用于 求解方程(主要是多项式方程)或方程组。
Solve 有两个参数,第一个参数是一个方程,或者是由若干个方程组的表(表示一个方程组);第二个参数是要求解的变量或变量表。
例如,下面的式子对于变量X 求解方程016x x x 234=+--:In[1]:=Solve[x^4-x^3-6x^2+1==0,x]输入了这个表达式,系统立刻就能计算出方程的四个根,求出的解都是精确解(代数根)。
对于一般的多项式,这样得出的解常常是用根式描述的复数。
方程的解被表示成一个表,表中是几个子表,每一个子表的形式都是{x->...},箭头后面是方程的一个解。
Solve 也可以求解多变量的方程或者方程组:In[2]:=Solve[{x-2y==0,x^2-y==1},{x,y}]这个表达式求解方程组: x y x y -=-=⎧⎨⎩2012.有时求解方程会得到非常复杂的解。
例如将上面的第一个方程稍加变形,所得到的解的表达式就会变得很长:In[3]:=Solve[x^4-x^3-6x^2=2==0,x]这个表达式求出的解的表达式非常长,以至一个计算机屏幕显示不下。
Mathematica用法III

对于非多项式函数,Solve也可以进行求解。 用函数Solve也可以求联立方程组的解。
求解方程组时,我们也可以先定义方程组,再用 Solve命令调用已经定义的方程组进行求解。
在上例中,N元的方程组实际被定义为一个包含N个 元素的列表,表中的每个元素是一个方程(逻辑语句)。
Dt[f,x]
计算f的全微商,所有变量依赖于x
D[f,x,Constants->{a}] 计算f的全微商,设a不依赖于x
SetAttributes [a,Constant]
设a为常数
简单举几个例子:
4、积分
在Mathematica中,用函数Integrate求不定积分和
定积分,用NIntegrate求数值积分,格式如下:
函数FindRoot的缺点是,一次运算只能得到距离起 始点最近的一个解;而且,如果选定的起始点位置不合 适,有可能迭代过程不收敛,从而得不出解。比如:
关于如何选点确保迭代收敛的知识,我们会在后续 的课程中详加说明。现在我们的常用做法是,如果要用 FindRoot求解,就先用Plot命令画出函数图线,观察解 的大概位置,然后在附近选择起始点。如下所示:
2、求极限 Mathematica计算极限的命令是Limit,它的用法如下:
Limit[f,x->x0]
当x->x0时求f的极限
Limit[f,x->x0,Direction->1] 当x->x0时求f的左极限
Limit[f,x->x0,Direction->-1] 当x->x0时求f的右极限
趋向的点x0可以是常数,也可以是+∞,-∞,例如:
由图可知,函数在 0至2.2之间和x轴有两 个交点。所以我们在用 FindRoot命令求根时起 始点可以选在交点附近。
《数学实验》实验报告——用Mathematica使行初等变换化简矩阵
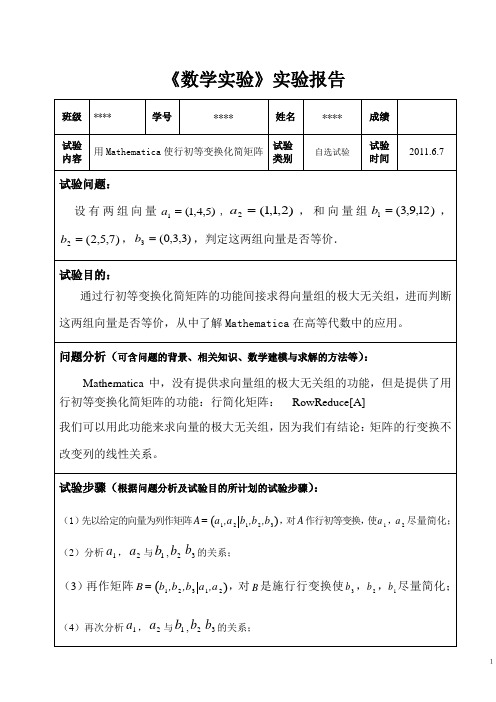
b3 的关系;
(3)再作矩阵 B = (b1 , b 2 , b 3 a 1 ,a 2 ) ,对 B 是施行行变换使 b3 ,b 2 ,b1 尽量简化;
' ' '
b ∴ 1
2a1 a2 , b2 a1 a2 , b3 a1 a2
b3 能用 a1 , a2 表示。
' '
∴ b1 , b2
'
' ' ' a b b a 2 b b 1 1 2 2 2 1 又 ,
∴ a1
b1 b2 , a2 2b2 b1
自选试验
2011.6.7
试验问题: 设 有 两 组 向 量 a1 (1,4,5) , a2 (1,1,2) , 和 向 量 组 b1 (3,9,12) ,
b2 (2,5,7) , b3 (0,3,3) ,判定这两组向量是否等价.
试验目的: 通过行初等变换化简矩阵的功能间接求得向量组的极大无关组,进而判断 这两组向量是否等价,从中了解 Mathematica 在高等代数中的应用。 问题分析(可含问题的背景、相关知识、数学建模与求解的方法等) : Mathematica 中,没有提供求向量组的极大无关组的功能,但是提供了用 行初等变换化简矩阵的功能:行简化矩阵: RowReduce[A] 我们可以用此功能来求向量的极大无关组,因为我们有结论:矩阵的行变换不 改变列的线性关系。 试验步骤(根据问题分析及试验目的所计划的试验步骤) :
微积分基础实验报告mathematica

微积分基础实验报告mathematica 微积分基础实验报告【实验⽬的】1.验证Sinx 的泰勒级数;2.了解函数的升降情况以及求零点和极值;3.了解正弦函数的叠加图像;4.了解⽆极限的函数例;5.了解⽆穷积分;6.通过⽆穷⼤数列求⾃然对数e 【实验要求】1.观察多项式函数、、的图像逼进正弦曲线的情况。
2.观察函数及其导函数的图像,了解图像的升降情况以及凹凸情况,求出零点与极值。
3.观察函数与的图像,了解随着k 的增⼤,图像的变化。
4.(1)绘制函数在区间x [-1,1]上的图像,观察图像当x>0时的变化情况。
(2)在函数中取3000个点,绘制散点图。
观察这些点的分布。
5.绘制函数与的图像,观察当n 增加时p(x)向sinx 逼近的现象。
63x x y -=120653x x x y +-=!7!5!3753x x x x y -+-=63x x y -=21'2x y -k k kx y 1sin xy 1sin=∈x y sin =∏=-=nk k x x x p 1222)1()(π6.(1)通过计算与的值,观察这些值的变化趋势。
(2)绘制,与y=e 的图像,观察当x 增⼤时图像的⾛向。
(3)计算的近似值,观察这些近似值对e 的逼近情况。
【实验内容】(主要包含问题分析、计算过程、实验结果等,按课程要求完成)问题的分析(1)分别⽤不同颜⾊的曲线绘制出区间上正弦曲线以及多项式函数、、的图像。
(2)根据理论知识可知,多项式项数越多越接近正弦曲线的图像。
(1)分别⽤不同颜⾊的曲线绘制出区间上函数及其导函数的图像。
(2)当y ’<0时,函数下降,当y ’>0时函数上升,当y ’=0时,函数图像存在极值。
当y ’上升时,函数图像为凸函数,当y ’下降时,函数图像为凹图像。
当y ’取极值时,函数图像出现拐点。
(3)通过图像得出零点近似值,以及函数极⼩值的近似值,通过编程n nn a )11(+=1)11(++=n n n A x x y 10)1011(+=110)1011(++=x x y ∑∞=+=1!1=120653x x x y +-=!7!5!3753x x x x y -+-=]4,4[-∈x 63x x y -=21'2x y -=得出精确的零点与极值。
mathematica

第二讲微分方程实验一、实验目的现实世界的运动规律,很多都是用微分方程模型来描述,大到天体运动,小到基本粒子的运动,无一不是如此.因此、微分方程在力学、物理学、各种工程技术科学、生物生态学以及经济学等领域都有非常重要的应用.这里涉及两类问题,一类是如何将实际问题转化为微分方程模型,另一类是如何求出方程的解.本实验将借助Mathematica研究与一阶常微分方程相关的几个问题,让我们了解几类微分方程模型、利用Mathematica求解微分方程的方法及如何直观演示方程解的几何形态.二、基本理论让我们首先复习一阶微分方程(组)的几个概念以及利用Mathematica求微分方程解的方法.对于一阶微分方程,(1)若存在定义在某区间内的可微函数满足,则称为方程(1)的解,所对应的曲线称为方程的解曲线(或积分曲线),它直观反映了方程解的变化.若解满足条件(2)则称为满足初始条件(2)的特解,此时解曲线经过点.同样,对于一阶微分方程组,(3)若存在定义在某区间内的可微函数满足则称为方程组(2)的解,若还满足,(4)则称为满足初始条件(4)的特解.曲线(5)称为方程组(3)解的相轨线,而解曲线是三维空间中的曲线(6)若方程(3)在无穷区间内有解,且满足解的存在唯一性条件,则(3)的解对应一个动力系统.研究动力系统在无穷远处的变化性态是非常有意义的事情.若方程(1)的解或方程组(3)的解能用初等函数表示,则称其为各自方程的解析解.我们在微分方程的求解理论中了解了求方程解的一些方法,利用Mathematica 也可以完成求解过程.首先让我们回顾一下Mathematica中用于求微分方程通解和特解的函数及其用法. DSolve[y'[x] f[x,y[x]],y[x],x]--求方程(1)的通解DSolve[{y'[x] f[x,y[x]],y[x0] y0},y[x],x]--求方程(1)在初始条件(3)下的特解DSolve[{x'[t] f[t,x[t],y[t]],y'[t] g[t,x[t],y[t]]},{x[t],y[t]},t]--求方程组(4)的通解DSolve[{x'[t] f[t,x[t],y[t]],y'[t] g[t,x[t],y[t]],[t0] x0,y[t0] y0},{x[t],y[t]},t]--求方程组(4)在初始条件(6)下的特解NDSolve[{y'[x]==f[x,y[x]],y[x0] y0},y[x],{x,x0,x1}]--求方程(1)在初始条件(3)下数值解NDSolve[{x'[t] f[t,x[t],y[t]],y'[t] g[t,x[t],y[t]],x[t0] x0,y[t0] y0},{x[t],y[t]},{t,t0,t1}]--求方程组(4)在初始条件(6)下的数值解特别提示在微分方程求解的操作中,一定要将未知函数y写成y[x]或y[t]的形式!另外,用NDSolve求方程的数值解时,其输出形式是插值函数InterpolatingFunction.例1 利用Mathematica求微分方程的通解及在初始条件下的特解.MathematicaDSolve[y'[x]==(1+x^2) y[x],y[x],x]DSolve[{y'[x]==(1+x^2) y[x],y[0]==1},y[x],x]运算结果分别为:在实际问题中,我们往往要利用方程的解,如画出解曲线的图形,那么如何将上述结果变为可用的形式?我们可以利用替换的方式将方程解的表达式转化为表的形式:y[x]/.DSolve[y'[x]==(1+x^2) y[x],y[x],x]y[x]/.DSolve[{y'[x]==(1+x^2) y[x],y[0]==1},y[x],x]运算结果为:此时可以通过对表的操作引用方程的解.例2 利用Mathematica求微分方程组通解和在初始条件下的特解.DSolve[{x'[t] 3x[t]-2y[t],y'[t] 2x[t]-y[t]},{x[t],y[t]},t]DSolve[{x'[t] 3x[t]-2y[t],y'[t] 2x[t]-y[t], x[0] 1,y[0] 0},{x[t],y[t]},t]运算结果为:但多数情况下没有这么幸运,经常碰到的情形是方程不存在解析解,或者我们能人工求解Mathematica却无能为力.读者不妨尝试一下用上面的方法求黎卡提(Riccati)方程和方程组的解,观察会发生怎样的情形.你会看到第一个方程的一个形式非常复杂的解,实际上,它是用特殊函数来表示的,而非通常的初等函数,因此已不是方程的解析解.而对于第二个方程组,正确地输入以后,运行所得到的结果与输入同样的形式,什么也没有做!也许你对Mahematica的能力产生了怀疑,实际上我们即使不能求得解析解,借助它来研究方程解的性质.在这一章中,我们将介绍如何描绘微分方程所确定的线素场,如何得到方程的几何和数值近似解,同时给出微分方程在实际问题中的几个有趣的应用.三、实验内容问题一:磁场的分布--微分方程的线素场如果你手中有一个条形磁铁和少许铁质粉末,你便可以通过实验了解在磁铁周围的平面内的磁场分布情况,下面我们讨论与此相关的问题.微分方程告诉了我们这样的信息,在平面上某区域内一点处,解曲线的斜率为.我们在区域内的有限个点处作从该点出发的短线段,使其斜率为函数在该点的值,这些线段构成的集合称为微分方程的线素场(line element field)或方向场(directional field),由于每一线段均与方程的解曲线相切,因此当线段长度很短时,它们是解曲线的局部近似,所以线素场可以反映解的变化趋势,当所选取的点俞密,这种变化趋势俞明显.那么,如何用Mathematica来绘制方程的线素场呢?让我们来寻找解决问题的方法.首先我们作出从点出发,斜率为且长度为的线段.我们只需在过且斜率为的直线上找到一点,使与的距离为,利用 Mathematica 解方程且取其中一组解即可.Mathematica程序(ch2-ex1.nb)运算结果为:因此利用基本图形Line便可做出所需线段,例如给定,即a=1;b=2;h=1;k=1/2;Graphics[Line[{{a,b},{x[a,b,h,k],y[a,b,h,k]}}]]//Show输出结果为:下面我们生成微分方程的线素场.首先取函数定义域中的闭矩形区域,将区间和分别等分和等分,得区域的一个划分,即区域的网格图,将网格的每个交点作为小线段的出发点,这样便得到方程分布在区域中的线素场.我们结合前面画线段的方法,可以编写如下Mathematica程序模块. Mathematica程序(ch2-ex2.nb)ClearAll[f,h]directionalField[f_,{x_,xmin_,xmax_},{y_,ymin_,ymax_},{m_,n_,h_},opts___]:=Module[{s,s1,x,y,a,b,k,i,j,lines},s=Solve[{y-b==k (x-a),(x-a)^2+(y-b)^2==h^2},{x,y}]//Simplify;s1=Flatten[s];x[a_,b_,k_]=x/.s1[[4]];y[a_,b_,k_]=y/.s1[[3]];h1=(xmax-xmin)/m;h2=(ymax-ymin)/n;a=xmin+i h1;b=ymin+j h2;k=f/.{x->a,y->b};lines=T able[Line[{{a,b},{x[a,b,k],y[a,b,k]}}],{i,0,m},{j,0,n}];Show[Graphics[lines],opts,Axes->Automatic,AspectRatio->Automatic]]通过上述程序模块,我们可以对具体的方程描绘它的线素场,让我们看两个例子.f[x_,y_]:=x^2+y^2-1directionalField[f[x,y],{x,-2,2},{y,-2,2},{20,20,0.1}]运行结果:f[x_,y_]:=3/2Sign[y] Abs[y]^(1/3)directionalField[f[x,y],{x,-2,2},{y,-2,2},{20,20,0.1}]运行结果:最后,我们观察一个实际问题的线素场,可以看到其几何描述的正好与实际情形相吻合.在平面和处分别放置两个正、负单位电荷,则它们在平面上产生一磁场. 从微分方程教材中,获知描述磁场强度的微分方程为其中对具体的,我们可以作出磁场的分布图.Mathematica程序(ch2-ex3.nb)a=2;P[x_,y_]:=(x+a)/((x+a)^2+y^2)^(3/2)-(x-a)/((x-a)^2+y^2)^(3/2)Q[x_,y_]:=y/((x+a)^2+y^2)^(3/2)-y/((x-a)^2+y^2)^(3/2)f[x_,y_]:=Q[x,y]/P[x,y]directionalField[f[x,y],{x,-3,3},{y,-3,3},{20,20,0.15},Graphics[{RGBColor[1,0,0],PointSize[0.03],Point[{-2,0}],Point[{2,0}]}]]运行结果:这里我们看到在程序模块directionalField中定义变量opt给我们带来了方便,通过它我们可以丰富线素场图,如上面画出两个点电荷的位置,使得到的图形更形象,读者可以在有关的教材中寻找更多的例子.问题二:炮弹飞行的轨迹--欧拉方法在炮弹发射时,我们如何知道炮弹在空中飞行中的轨迹? 假设你拥有一架高速照相机,你可以将炮弹飞行的过程记录下来.但冲洗出来的照片并不是一条连续的轨线,而是炮弹在不同位置的离散图象,不过这已足够让我们了解炮弹的飞行轨迹了,只要照相机的速度有足够的快.前面我们已经知道很多情况下我们不能求出微分方程的解析解,但如照相一样,我们只要在解曲线上找到一连串的点,也可以获知解曲线的形状. 在前面的实验中我们了解了描绘一阶常微分方程线素场的方法,由线素场我们可大概了解解曲线的走势,但它并不能较准确地反映每一条解曲线的几何形状,如何在不能求出方程的解析解的情况下,能将解曲线比较精确地描绘出来?欧拉为我们提供了一个方法,其原理是先通过差分将一阶常微分方程化为差分方程(即代数方程),然后考虑代数方程的解(点列),将这些点顺次连接起来,变得到解曲线的近似图形.考虑初值问题由导数的定义知,当时,,因此上述方程可改写成,或取一列点,记,则有,我们称该方程为差分方程,称为差分步长,一般来说,越小,所求得的点列越反映微分方程解的实际情况,这种处理微分方程的方法称为欧拉(Euler)方法.首先,我们给出用欧拉方法求微分方程近似解的Mathematica程序.Mathematica程序(ch2-ex4.nb)ClearAll[f]euler[f_,{x_,x0_,x1_,h_},{y_,y0_},opt___]:=Module[{points},y[0]=y0;x[n_]:=x0+n h;y[n_]:=y[n-1]+ h f/.{x->x[n-1],y->y[n-1]}//N;m=Floor[(x1-x0)/h];points=T able[{x[n],y[n]},{n,0,m}];ListPlot[points,opt]]我们取,运行下面的程序f[x_,y_]:=3/2 Sign[y] Abs[y]^(1/3)euler[f[x,y],{x,0,1,0.1},{y,1/2},AxesOrigin->{0,0},PlotRange->{{-2.2,2.2},{-2.2,2.2}},PlotStyle->{RGBColor[1,0,0],PointSize[0.02]},AspectRatio->Automatic]运行结果:结合实验一中的线素场,我们可以看到欧拉方法所得解与线素场的一致性.Mathematica程序(ch2-ex5.nb)f1=euler[f[x,y],{x,0,1,0.1},{y,1/2},AxesOrigin->{0,0},PlotRange->{{-2.2,2.2},{-2.2,2.2}},PlotStyle->{RGBColor[1,0,0],PointSize[0.02]},AspectRatio->Automatic,DisplayFunction->Identity];f2=directionalField[f[x,y],{x,-2,2},{y,-2,2},{20,20,0.1}, DisplayFunction->Identity]Show[f1,f2,DisplayFunction->$DisplayFunction]运行结果:另外,我们可以将方程的解析解与欧拉方法所得到的近似解进行比较,让我们以初值问题为例作出解析解和近似解的图形.Mathematica程序(ch2-ex6.nb)Clear[y]f[x_,y_]=Sin[x]+y;s=DSolve[{y'[x]==f[x,y[x]],y[0]==1},y[x],x];p1=Plot[y[x]/.s[[1]],{x,0,2},DisplayFunction->Identity];p2=euler[f[x,y],{x,0,2,0.2},{y,1},PlotStyle->{RGBColor[1,0,0],PointSize[0.02]},DisplayFunction->Identity];Show[p1,p2,DisplayFunction->$DisplayFunction];运行结果:上面介绍的欧拉方法可以改进,使得到的结果更精确,基本想法是取两个斜率的平均值,即我们通过具体例子比较改进前后的欧拉方法的计算结果和精确解的结果,请读者考虑初值问题编写出获得上述结果的Mathematica程序.问题三:黄土高原上的沟壑--最陡下降法也许你去过西北的黄土高原,也许从各种媒体上了解那里的景象,到处是沟壑交错,这主要是由于长年雨水的冲刷而形成的. 你也许会想到,这些沟壑的分布走向与地形有关,如果你手中有一张当地的地形图,你会发现这些沟壑往往是垂直穿过所倚山峦的等值线,下面我们将用数学的理论给出解释.假设山坡可以用函数来表示,且坡面是光滑的,若落在山坡上的雨水没有渗透,则它应往最陡的方向往下流动,现在我们确定流动的路线.我们考虑路线在山脚所在平面(即平面)投影,设投影曲线方程为,则由方向导数和梯度的意义,可建立方程(7)以该投影曲线为准线作母线垂直于z轴的柱面,则该柱面与坡面的交线便是雨水在坡面流下的路线.下面我们给出计算实例.设山坡是上半椭球面,雨水落下的位置为,我们利用Mathematica完成上面的任务,分下面几步进行:(1)求投影曲线方程.设,为为其在平面的投影曲线方程,解初值问题(7)便求得投影曲线方程.不妨设在第一卦限.(2)求出投影曲线的自变量的变化范围.解方程组,解得正解,则得变化范围为.(3)描绘雨水下流路线及投影曲线,并从不同的角度观察图形.Mathematica程序(ch2-ex7.nb)quickestdescent[{a_, b_, c_}, {x0_, y0_}, {h1_, h2_}, opt___]:=Module[{f, fx, fy, g, ellipsoid, s, t, r, l, p, d, descentroad, projection, generator, y},f[x_, y_]:=c Sqrt[1-x^2/a^2-y^2/b^2];fx[x_, y_]:=D[f[x, y], x];fy[x_, y_]:=D[f[x, y], y];g[x_, y_]=fy[x, y]/fx[x, y];ellipsoid=ParametricPlot3D[{a Sin[u] Cos[v], b Sin[u] Sin[v], c Cos[u]},{u, 0, Pi/2}, {v, 0, 2Pi}, DisplayFunction->Identity];s=DSolve[{y'[x]==g[x,y[x]], y[x0]==y0}, y[x], x];y[x]=y[x]/. s[[1,1]];Print["y(x)= ", y[x]];t=Solve[{f[x,y]==0, y==y[x]/. s[[1,1]]}, {x, y}];For[i=1, i<=Length[t], i++, r=x/.t[[i,1]]; If[Im[r]==0&&r>0, l=r]];p=T able[{x, y[x]/. s[[1,1]], 0}, {x, x0, l, h1}];projection=Graphics3D[{RGBColor[1,0,0], Thickness[0.015], Line[p]}];d=T able[{x, y[x]/. s[[1,1]], f[x, y[x]/. s[[1,1]]]}, {x, x0, l, h1}];descentroad=Graphics3D[{RGBColor[1,0,0],Thickness[0.015], Line[d]}];generator=T able[Graphics3D[{RGBColor[0, 1, 0],Line[{{x, y[x]/. s[[1,1]], 0}, {x, y[x]/.s[[1,1]], f[x, y[x]/.s[[1,1]]]}}]}], {x, x0, l, h2}]; startpoint=Graphics3D[{PointSize[0.03], RGBColor[1,0,0],Point[{x0, y0, f[x0, y0]}]}]; Show[projection, ellipsoid, startpoint, descentroad, generator,PlotRange->{{-a,a},{0,b},{0,c}},opt]]给出具体参数,便可得到非常直观得结果.例如x0=0.1;y0=1.5;a=3;b=6;c=3;f1=quickestdescent[{a,b,c},{x0,y0},{0.001,0.2},ViewPoint->{1,-2,1},DisplayFunction->Identity,Boxed->False]f2=quickestdescent[{a,b,c},{x0,y0},{0.001,0.2},ViewPoint->{1,2,1},DisplayFunction->Identity,Boxed->False]f3=quickestdescent[{a,b,c},{x0,y0},{0.001,0.2},ViewPoint->{-1,-2,0.7},DisplayFunction->Identity,Boxed->False]Show[GraphicsArray[{f1,f2,f3}]]运行结果:问题四:战争能爆发吗?--微分方程的稳定性两国势均力敌的军事力量互相制约,能保证相互之间的和平共处,一旦某一国的军事力量无限扩张,便会对另一国构成威胁,爆发战争的机会大大增加.在建立两国军备竞争的数学模型之前,让我们观察几类微分方程的渐近性态,掌握了解方程变化趋势的几何方法.例1 考虑方程的解在平衡点附近的性态.Mathematica程序(ch2-ex8.nb)Clear[x,y,s,data]s=T able[NDSolve[{x'[t]==-x[t]-y[t],y'[t]==x[t]-3y[t],x[0]==x0,y[0]==0},{x,y},{t,0,20}],{x0,-1,1,0.2}];a={x,y}/.s;x[i_]:=a[[i,1,1]]y[i_]:=a[[i,1,2]]orbit=T able[ParametricPlot[{x[i][t],y[i][t]},{t,0,20},PlotRange->{{-0.8,0.8},{-0.2,0.2}},PlotStyle->{RGBColor[1,0,0],Thickness[0.01]},DisplayFunction->Identity],{i,1,10}];Show[orbit,DisplayFunction->$DisplayFunction];运行结果:此时,在不同初值下的轨线趋于平衡点,称平衡点是稳定的.我们还可以通过下面的数值得到相应的结果.Mathematica程序(ch2-ex9.nb)Clear[x,y,s,data]s=T able[NDSolve[{x'[t]==-x[t]-y[t],y'[t]==x[t]-3y[t],x[0]==x0,y[0]==0},{x,y},{t,0,20}],{x0,-1,1,0.2}];a={x,y}/.s;x[i_]:=a[[i,1,1]]y[i_]:=a[[i,1,2]]data=Table[{t,x[1][t],y[1][t]},{t,0,20,1}];GridBox[Join[{{"t","x(t),x(0)=-1","y(t),y(0)=0"}},data],ColumnLines->T rue,RowLines->T rue,ColumnSpacings->{3,5}]//DisplayForm运行结果:从上述数据表格中我们发现,随着的增加,和均趋于零,这与前面的图形正好吻合.是否这一类方程的解都具有如此性质,我们不妨再看一个例子.例2考虑方程的解在平衡点附近的性态.Mathematica程序(ch2-ex10.nb)Clear[x,y,s,data]s=T able[NDSolve[{x'[t]==x[t]-y[t],y'[t]==2x[t]+y[t],x[0]==a,y[0]==0},{x,y},{t,0,20}],{a,-1,1,0.2}];a={x,y}/.s;x[i_]:=a[[i,1,1]]y[i_]:=a[[i,1,2]]data=Table[ParametricPlot[{x[i][t],y[i][t]},{t,0,20},PlotRange->{{-20,20},{-20,20}},PlotStyle->{RGBColor[1,0,0],Thickness[0.01]},DisplayFunction->Identity],{i,1,10}];Show[data,DisplayFunction->$DisplayFunction];运行结果:此时当增大时,将无限远离平衡点,这时我们称原点是非稳定的平衡点,同样也可以用数据加以说明.Mathematica程序(ch2-ex11.nb)Clear[x,y,s,data]s=T able[NDSolve[{x'[t]==x[t]-y[t],y'[t]==2x[t]+y[t],x[0]==a,y[0]==0},{x,y},{t,0,20}],{a,-1,1,0.2}];a={x,y}/.s;x[i_]:=a[[i,1,1]]y[i_]:=a[[i,1,2]]data=Table[{t,x[1][t],y[1][t]},{t,0,20,1}];GridBox[Join[{{"t","x(t),x(0)=-1","y(t),y(0)=0"}},data],ColumnLines->T rue,RowLines->T rue,ColumnSpacings->{3,5}]//DisplayForm运行结果:现在我们回到开始的问题.一个国家的军事力量与该国的军队数量、武器装备和经济实力等因素有关,我们将甲乙两国的军事力量量化为和.一般来说,影响军事力量增加的速度有三个方面:(1)对方国家的军事力量可以刺激本国军事力量的发展;(2)本国已有的军事力量会对本国继续扩军产生抑制作用;(3)本国人民、军队对对方国人民、军队产生仇视的程度会增加本国扩军.综合上面的因素可以建立如下微分方程组,其中为正常数,和是对对方国的敌视程度,为简单我们设它们为常数和.设,解方程得平衡点.可以证明:(1)当时,平衡点是稳定的,此时由于甲、乙两国的军事力量趋于和,所以在这一时期内两国会和平相处;(2)当时,平衡点是不稳定的,此时由于一方的军事扩张,可能形成战争的威胁.下面我们同过具体的数据进行模拟.如1909年到1914年,德奥匈联盟与法俄联盟的军备竞争,双方扩军与抑制的情形是k=l=0.9, = =0.2, -kl=0.04-0.81<0 ,取g=h=0,此时的平衡点(0,0)是不稳定的,双方不能和平相处,两个军事集团最终爆发了第一次世界大战.假设在开始两国的军事力量各为x(0)=0.1,y(0)=0.05,则经过一段时间后,两国的军事格局将发生变化,下面的轨线图和数据表格说明变化的具体情形.Mathematica程序(ch2-ex12.nb)Clear[x,y,s,k,l,a,b,data]k=l=0.9;a=b=0.2;s=NDSolve[{x'[t]==-a x[t]+k y[t],y'[t]==l x[t]-b y[t],x[0]==0.1,y[0]==0.05},{x,y},{t,0,10}];a={x,y}/.s;data=Table[{t,a[[1,1]][t],a[[1,2]][t]},{t,0,10}];ParametricPlot[{a[[1,1]][t],a[[1,2]][t]},{t,0,10},PlotStyle->{RGBColor[1,0,0],Thickness[0.01]}]GridBox[Join[{{"t","x(t),x(0)=0.1","y(t),y(0)=0.05"}},data],ColumnLines->T rue,RowLines->T rue,ColumnSpacings->{3,5}]//DisplayForm运行结果:从上面的计算结果我们看到,尽管开始时军事力量较弱,但经过几年的时间,各自的军事实力得到飞速增长,这时很可能由于某一因素而触发战争.另外,我们还观察到一个有趣的现象,尽管当初彼此的实力相差悬殊,但由于相互竞争,使其军事力量很快趋于一致,这也许对双方形成一种新的制约,在一般情况下,任何一方不敢轻易挑起事端而引发战争. 四、思考题1.画出方程的方向场.从图中你是否猜出一个解,这个解的图形是直线吗?在同一张图上画出你猜的解和方向场.2.用欧拉法解.在同一幅图上画出和的解曲线.3.一条鲨鱼在发现血腥味时,总是沿血腥味最浓的方向追寻.在海面上实验表明,如果把坐标原点取在血源处,在海面上建立直角坐标系,那么点处的浓度(每百万份水中所含血的份数)的近似值为.求鲨鱼从点发向血源前进的路线.(要求画出的等值线图和在不同的起始点处鲨鱼的前进路线图)4.设轴以及是河岸,河水以匀速朝轴负方向流动,小船从处入河以相对于河水的速度直接朝原点行驶,求船行驶的路线.问满足什么条件才能使小船到达彼岸?船在何处登陆?(要求就不同情形画出小船行进的路线图)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
创3.5 常微分方程、拉氏变换与级数实验[学习目标]1. 会用Mathematica 求解微分方程(组);2. 能用Mathematica 求微分方程(组)的数值解;3. 会利用Mathematica 进行拉氏变换与逆变换;4. 能进行幕级数和傅里叶级数的展开。
一、常微分方程(组)Mathematica 能求常微分方程(组)的准确解,能求解的类型大致覆盖了人工求解的范围, 功能很强。
但不如人灵活(例如在隐函数和隐方程的处理方面),输出的结果与教材上的答 案可能在形式上不同。
另外,Mathematica 求数值解也很方便,且有利于作出解的图形。
在本 节中,使用Laplace 变换解常微分方程(组)的例子也是十分成功的,过去敬而远之的方法 如今可以轻而易举的实现了。
求准确解的函数调用格式如下: DSolve[eqn ,y[x] ,x] 求方程 eqn 的通解 y(x ),其中自变量是X 。
DSolve[{eqn ,y[x o ]= =y 0},y[x],x] 的特解y (x )。
DSolve[{eqn1,eqn2,—},{y 1 [x],y 2[x],…},x]求方程组的通解。
DSolve[{equ1,…,y 1[x 0]= =y 10,…},{y 1[x],y 2[x],…},x] 求方程组的特解。
说明:应当特别注意,方程及各项参数的表述方式很严格,容易出现输入错误。
微分方 程的表示法只有通过例题才能说清楚。
例1 解下列常微分方程(组):52(1) y 斗(x 1)2,(2) y - y 3 ,(3)x 1(x x ) y解:In[1]: =DSolve[y ' [x]= =2y[x]/ (x+1) + (x+1) A (5/2),y[x],x]Out[1]=y[x] i (1 x)7/2 (1 x)2c[1]In[2]: =DSolve[y ' [x]= = (1+y[xF2 ) /((x+xA3 ) y[x]),y[x],x]求满足初始条件y ( x o ) = y o(4)的通解及满足初始条件y (0) =0, z (0) =1的特解。
Out[2]={{ y[x]},{y[x]In[3]: =DSolve[{y ' [x]= =z[x] , z ' [x]= = -y[x]},{y[x] , z[x]} , x]Out[3]={{y[x] — C[1]Cos[x]+ C[2]Sin[x],z[x] — C[2]Cos[x]- C[1]Si n[x]}}In[4]: =DSolve[{y ' [x]= =z[x] , z ' [x]= = -y[x] , y[0]= =0 , z[0]= =1},{y[x] , z[x]} , x]Out[4]={{y[x] — Sin[x], z[x] — Cos[x]}}提示:认真观察上例,可以从中学习输入格式,未知函数总带有自变量,等号用连续键 入两个等号表示,这两点由于不习惯会出错!导数符号用键盘上的撇号,连续两撇表示二阶 导数,这与习惯相同。
自变量、未知量、初始值的表示法与普通变量相同。
说明:输出结果总是尽量用显式解表出,有时反而会使表达式变得复杂,这与教科书的 习惯不同。
当求显式解遇到问题时,会给出提示。
通解中的任意常数用C[1],C[2],…例2 求解下列微分方程:x22I 'y (x 5)e,(2) x (y)1,(3) y xyy[x],x]In[2]: =Simplify[%]1Out[2]={{ y[x] e x ( 20x 3 x 4 24C[1] 24xC[2] 24x 2C[3])}}24Out[3]={{ y[x] ^x .1 x 2A rcS *n[x]C[1]},2 2{y[x]1x..1 x 2C [1]}}2 2ln[4]: =DSolve[Sqrt[y ' [x]] = = x y[x] ,y[x],x]3 Out[4]={{ y[x] 厂}} x C[1]说明:由以上可以看出对方程的类型并无限制,但是输出的答案未必符合习惯,例如第 一个方程的答案需要化简,有时即使化简后也未必与教材上的答案一致。
1 x 22x x5x 23x e x5x —ex-— 2223Out[1]={{ y[x]15 34-e x 上 - e x C[1] e x xC[2] e x x 2C[3]}} 2 3 4表示。
解: In[1]: =DSolve[ y [x] +3y " [x] +3y[x] + y[x]==(x - 5) Exp[-x],(1) y3y 3y In[3]: =DSolve[x A 2 + y [x]A 2 = = 1,y[x],x]例3求微分方程法2xy xe"的通解解:In[1]: =DSolve[y [x]+2x y[x]= = x E A (帜八2),y[x],x]1 2 _ 2°u t[1]={{y[x]-尹x eX C[1]}}这就是所给微分方程的通解。
式中的C[1]是通解中的任意常数。
上述命令也可以输入为:DSolve[D[y[x]] + 2x y[x]= =x E A(- x A2), y[x] , x]。
例4 求微分方程xy + y - e x = 0在初始条件y|x=i = 2e下的特解。
解:In[1]: =DSolve[x*y [x]+y[x]-EAx= =0 ,y[1]= =2E,y[x],x]xe eOut[1]= {{y[x]-——}}x二、常微分方程(组)的数值解函数NDSolve用于求给定初值条件或边界条件的常微分方程(组)的近似解,其调用格式如下:NDSolve[eqns, {y 1, y2,…}, {x , xmin , xmax}] 求常微分方程(组)的近似解。
其中微分方程和初值条件的表示法如同DSolve,未知函数仍有带自变量和不带自变量两种形式,通常使用后一种更方便。
初值点x o可以取在区间[xmin , xmax]上的任何一点处,得到插值函数InterpolatingFunction[domain, table]类型的近似解,近似解的定义域domain—般为[domain, table],也有可能缩小。
例5 求常微分方程y' = x2 + y2,满足初始条件y (0)= 0的数值解。
解:In[1]: =s1=NDSolve[{y ' [x]= =xA2+y[x]A2 , y[0]= =0},y, {x , -2, 2}]Out[1]={{y —InterpolatingFunction[{{-2. , 2.}} , < >]}}In[2]: = y=y / . s1[[1]]Out[2]=InterpolatingFunction[{{-2. , 2.}}, < >]ln[3]: =Plot[y[x] , {x , -2 , 2} , AspectRatio-Automatic ,PlotRange-{-1.5 , 1.5}]Out[3]= -Graphics-上例中包含许多值得学习的实用内容,其中第二项参数使用y而不是y[x],比用y[x]好。
如果求解区间改为{x , -3 , 3},就会出现警告提示,实际得不到[-3 , 3]上的解。
Out[1]表明返回的解放在一个表中,不便使用,实际的解就是插值函数:In terpolatingF ln[2]的结果是 例6 求常微unction[{{-2. ,2.}}, < >]用y 表示解函数的名子,因此In[3]顺利画出解曲线如图13-43所示。
枚分方程组:1 3 x yx x 3 y x满足初始条件x (0) =0, y (0) =1的数值解。
解:In[1]: =$仁NDSolve[{x ' [t]= = y[t] - (x[t]A 3/3 - x[t]), y ' [t]= = - x[t] , x[0]= =0 , y[0]==1}, {x , y}, {t , -15, 15}]Out[1]={{x f InterpolatingFunction[{{-15. , 15.}}, < >],y — InterpolatingFunction[{{-15. , 15.}} , < >]}}In[2]: = x=x / . s1[[1 , 1]]y=y / . s1[[1 , 2]]Out[2]=lnterpolatingFunction[{{-15. , 15.}}, < >] Out[3]=lnterpolatingFunction[{{-15. , 15.}}, < >] ln[4]: =ParametricPlot[{x[t] , y[t]} , {t , -15 , 15},Out[3]= -Graphics-说明:上例是求一个著名方程组的近似解,其中 In[2]也可以改用一个赋值式{x , y}={x , y} / . Flatten[s1],一次得到两个函数。
通过求数值解容易得到它的相图,In[4]绘制了解的相轨 线如图13-44所示,图中表明原点是奇点,极限环的形状也已经得到。
为了应付复杂的情况,需要设置可选参数:MaxStepsWorki ngPrecisio n 参见数值积分部分的介绍 AccuracyGoal 计算结果的绝对误差 Precisi on Goal计算结果的相对误差 最大步数。
Starti ngStepSize 初始步长。
以上可选参数的默认值都为Automatic,其中AccuracyGoal和PrecisionGoal的默认值比WorkingPrecision小10,当解趋于0时应将AccuracyGoal取成Infinity。
对于常微分方程,最大步长默认值为1000。
这个函数也可以解偏微分方程,最大步长默认值为200。
例7 解下列微分方程(组):1(1)y — i,满足初始条件y (0)=1的特解;4yx 3x 3y(2)y xz 26.5x y,满足初始条件x(0)=z(0)=0, y(0)=1 的特解。
z xy z解:In[1]: =NDSolve[{y ' [x]= =l/4y[x] ,y[0]= =1},y,{x,1},AccuracyGoal—20,PrecisionGoa220,WorkingPrecision —25] Out[1]={{y —In terpolat ingFun cti on[{{0,1.000000000000000000000000000}}, < >]}In[2]: =y[1] / . %Out[2]={0.968912424710644784118519 +0.24740395925452292962341091}ln[3]: =NDSolve[{x ' [t]= = -3 (x[t] -y[t]),y' [t] = = -x[t] z[t]+36.5x[t] -y[t],z' [t] = = x[t] y[t]- z[t],x[0] = = z[0] = = 0,y[0]= =1},{x,y,z},{t,0,20},MaxSteps—3000]Out[3]={{x —InterpolatingFunction[{{0. ,20.}},< >],y—InterpolatingFunction[{{0. ,20.}},< >],z—InterpolatingFunction[{{0.,20.}},< >]}},ln[4]: =ParametricPlot3D[Evaluate[{x[t],y[t],z[t]} / . %],{t,0,20},PlotPoints —1000]图13-45 3维相轨线Out[3]= -Graphics3D-说明:以上范例中ln[1]取高精度,而且是复系数方程。
