mathematica数学实验报告 实验二
13级数学(3)班,高继红,201370010307

数学实验报告二题目:利用Mathematica计算圆周率π的值学院:数学与统计学院专业:数学与应用数学班级: 2013级数学三班学生姓名:高继红学号: 201370010307指导教师:张贵仓数学实验报告(二)一.实验题目:圆周率π的计算二.实验目的:1.用多种方法计算圆周率错误!未找到引用源。
的值;2.通过实验来说明各种方法的优劣;三.实验环境:在Windows 环境,利用Mathematica7.0这个数学软件四.实验内容1.运用数值积分法来近似计算π的值;2.运用泰勒级数来近似计算π的值;3.利用蒙特卡洛(Monte Carlo )法来近似计算π的值。
五.实验方法1.数值积分法 利用公式⎰+=102114dx x π设分点x 1,x 2,…x n-1将积分区间[0,1]分成n 等分。
所有的曲边梯形的宽度都是h=1/n 。
记yi=f(xi).则第i 个曲边梯形的面积A 近似地等于梯形面积,即:A=(y(i-1)+yi)h/2。
将所有这些梯形面积加起来就得到:A ≈2/n[2(y 1+y 2+…y n-1)+y 0+y n ]利用Mathematica 编程计算上式:n=5000;Y[x]:=4/(1+x*x);s1=(sum[y[k/n],{k,1,n-1}]+(y[0]+y[1])/2)/n;s2=(y[0]+y[1]+2*sum[y[k/n],{k,1,n-1}]+4*sum[y[(k-1/2)/n],{k,1,n}])/(6*n);Print[{N[s1,20],N[s2,30],N[Pi,30]}]实验结果:{0.00020000000000000000000 (sum[y[0.00020000000000000000000 k], {k,1.0000000000000000000,4999.0000000000000000}]+0.50000000000000000000 (y[0]+y[1.0000000000000000000])),0.0000333333333333333333333333333333(4.00000000000000000000000000000 sum[y[0.000200000000000000000000000000000(-0.500000000000000000000000000000+k)],{k,1.00000000000000000000000000000,5000.00000000000000000000000000}]+2.00000000000000000000000000000sum[y[0.000200000000000000000000000000000 k],{k,1.00000000000000000000000000000,4999.00000000000000000000000000}]+y[0]+y[1.00000000000000000000000000000]),3.14159265358979323846264338328}以上s1,s2分别是用梯形公式和辛普森公式计算出的 ,最后一句中的N[s1,20]表示s1的前20位准确有效数字组成的近似值,N[Pi,30]是 的前 位有效数字组成的近似值。
mathematica数学实验报告

mathematica数学实验报告本次实验使用Mathematica进行数学建模实验,主要包括以下内容:三角函数、极限和导数、积分和微分方程。
一、三角函数1. 三角函数的绘制使用Mathematica的Plot函数绘制正弦函数和余弦函数的图像。
代码:Plot[{Sin[x], Cos[x]}, {x, -2 Pi, 2 Pi},PlotStyle -> {Blue, Red}, PlotTheme -> "Web"]结果:在x趋近于4时的极限。
代码:Limit[x^2/(4 - x), x -> 4]结果:82. 求函数的导数使用Mathematica的D函数计算函数x^3 - 3x的导数。
代码:D[x^3 - 3x, x]结果:3 x^2 - 3三、积分和微分方程1. 求定积分使用Mathematica的Integrate函数计算函数e^x * cos(x)在0到π/2之间的定积分。
代码:Integrate[E^x * Cos[x], {x, 0, Pi/2}]结果:1/2 (1 + E^(π/2))2. 解微分方程使用Mathematica的DSolve函数求解微分方程y''(x) + 4y(x) = 0。
代码:DSolve[y''[x] + 4 y[x] == 0, y[x], x]结果:y[x] -> C[1] Cos[2 x] + C[2] Sin[2 x]本次实验使用Mathematica进行数学建模实验,主要包括三角函数的绘制、求三角函数的值,函数的极限、导数,积分和微分方程等内容。
高数实验报告 (2)
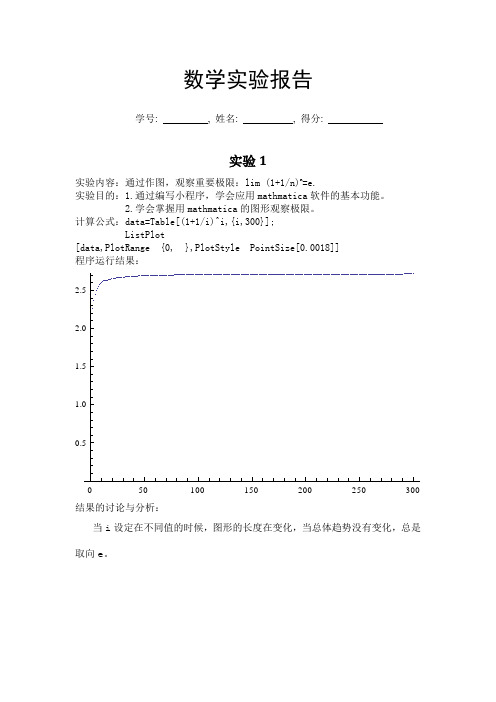
数学实验报告学号: , 姓名: , 得分:实验1实验内容:通过作图,观察重要极限:lim (1+1/n)n=e.实验目的:1.通过编写小程序,学会应用mathmatica软件的基本功能。
2.学会掌握用mathmatica的图形观察极限。
计算公式:data=Table[(1+1/i)^i,{i,300}];ListPlot[data,PlotRange {0, },PlotStyle PointSize[0.0018]]程序运行结果:结果的讨论与分析:当i设定在不同值的时候,图形的长度在变化,当总体趋势没有变化,总是取向e。
实验2实验内容:设数列{Xn}由下列递推关系式给出:x1=1/2,xn+1=xn2+xn(n=1,2………)观察数列1/(x1+1)+ 1/(x2+1) +…….+1/(xn+1)的极限。
实验目的和意义:1:掌握mathmatica数学实验的基本用法。
2:学会利用mathmatica 编程求数列极限。
3:了解函数与数列的关系。
计算公式:f[x_]:=x^2+x;xn=0.5;g[x_,y_]:=y+1/(1+x);y n=0;For[n=1,n 15,n++,xN=xn;yN=yn;xn=N[f[x N]];yn=N[g[xN,yN]]];Print[" y30=",yn]程序运行结果:y30= 2.结果与讨论:这个实验,当yn中n趋向无穷大的时候,能够更加接近极限,当取30以上时候,2就是极限值。
实验3实验内容:已知函数:f(x)=1/(x2+2x+c)(-5<=x<=4),作出并比较当c 取不同的值的时候(-1,0,1,2,3),并从图上观察出极值点,驻点,单调区间,凹凸区间和渐进线。
实验目的:1.通过实验掌握如何用mathmatica作图。
2.学会观察图像来求函数的相关数据。
计算公式:f[x_]=1/(x2+2 x+(-1))Plot[f[x],{x,-5,4},GridLines Automatic,Frame True,PlotStyle RGBColor[1,0,0]]f[x_]=1/(x2+2 x+(0))Plot[f[x],{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0]]f[x_]=1/(x2+2 x+(2))Plot[f[x],{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0]]f[x_]=1/(x2+2 x+(3))Plot[f[x],{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0]]f[x_]=1/(x2+2 x+(3))Plot[f[x],{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0]]程序运行结果:结果的讨论与分析:不同的c,函数的形态有较大的不同,也就是原方程=0什么情况下有解的问题,根据图像很容易的得到驻点,拐点,等相关信息。
数学实验报告2-圆周率的计算-mathematica

数学实验报告实验序号: 2 日期: 2016年月日实验结果报告及实验总结:一、数值积分法计算π因为单位圆的半径为1,它的面积等于π,所以只要计算出单位圆的面积,就算出了π。
在坐标轴上画出以圆点为圆心,以1为半径的单位圆,则这个单位圆在第一象限的部分是一个扇形,而且面积是单位圆的1/4,于是,我们只要算出此扇形的面积,便可以计算出π。
而且单位的精度可能会影响计算的结果,下面将给出不同的n计算所得结果并讨论差异。
1.当n=1000时命令:n=1000;y[x_]:=4/(1+x*x);s1=(Sum[y[k/n],{k,1,n-1}]+(y[0]+y[1])/2)/n;s2=(y[0]+y[1]+2*Sum[y[k/n],{k,1,n-1}]+4*Sum[y[(k-1/2)/n],{k,1,n}])/( 6*n);Print[{N[s1,20],N[s2,30],N[Pi,30]}];结果如下:2.当n=5000时命令:n=5000;y[x_]:=4/(1+x*x);s1=(Sum[y[k/n],{k,1,n-1}]+(y[0]+y[1])/2)/n;s2=(y[0]+y[1]+2*Sum[y[k/n],{k,1,n-1}]+4*Sum[y[(k-1/2)/n],{k,1,n}]) /(6*n);Print[{N[s1,20],N[s2,30],N[Pi,30]}];运行结果:3.当n=10000时命令:n=10000;y[x_]:=4/(1+x*x);s1=(Sum[y[k/n],{k,1,n-1}]+(y[0]+y[1])/2)/n;s2=(y[0]+y[1]+2*Sum[y[k/n],{k,1,n-1}]+4*Sum[y[(k-1/2)/n],{k,1,n}])/( 6*n);Print[{N[s1,20],N[s2,30],N[Pi,30]}];Plot[{4(1-x*x)},{x,0,1}]运行结果:4. 结果分析:当数值积分法得到 的近似值为3.8,可以看出,用这种方法计算所得到的 值是相当精确的,n 越大,计算出来的扇形面积的近似值就越接近 的准确值。
mathematica实验报告

mathematica实验报告《使用Mathematica进行实验报告:探索数学的奥秘》Mathematica是一款强大的数学软件,它不仅可以进行数学计算和图形绘制,还可以进行数据分析和模拟实验。
在本实验报告中,我们将使用Mathematica来探索数学的奥秘,展示其强大的功能和应用。
首先,我们将使用Mathematica进行数学计算。
通过输入数学表达式和方程式,我们可以快速地进行数值计算和符号运算。
Mathematica还提供了丰富的数学函数和算法,可以帮助我们解决复杂的数学问题,如微积分、线性代数和离散数学等。
其次,我们将利用Mathematica进行图形绘制。
通过输入函数表达式和参数设置,我们可以绘制出各种数学图形,如函数图像、曲线图和三维图形等。
Mathematica还提供了丰富的绘图工具和选项,可以帮助我们定制和美化图形,使其更加直观和具有艺术感。
接下来,我们将利用Mathematica进行数据分析。
通过输入数据集和统计方法,我们可以进行数据的可视化和分析,帮助我们发现数据的规律和趋势。
Mathematica还提供了丰富的数据处理和建模工具,可以帮助我们进行数据挖掘和预测分析,为决策和规划提供有力的支持。
最后,我们将利用Mathematica进行模拟实验。
通过输入模型和参数设置,我们可以进行各种科学和工程问题的模拟实验,帮助我们理解和预测实际现象。
Mathematica还提供了丰富的模拟工具和仿真方法,可以帮助我们进行虚拟实验和验证假设,为科学研究和工程设计提供有力的工具支持。
总之,Mathematica是一款强大的数学软件,它可以帮助我们探索数学的奥秘,解决数学问题,展示数学图形,分析数学数据,进行数学模拟实验,为科学研究和工程应用提供有力的支持。
希望本实验报告可以激发更多人对数学和科学的兴趣,让我们一起来探索数学的奥秘吧!。
mathematica实验报告

mathematica实验报告Mathematica 实验报告一、实验目的本实验旨在深入了解和掌握 Mathematica 软件的基本功能和操作方法,通过实际的案例和问题解决,提升运用 Mathematica 进行数学计算、数据分析、图形绘制以及编程的能力。
二、实验环境操作系统:Windows 10Mathematica 版本:121三、实验内容与步骤(一)数学计算1、基本运算在 Mathematica 中,直接输入数学表达式进行计算,例如:计算 2+ 3 4 的结果,输入`2 + 3 4` ,得到结果 14。
2、函数计算使用内置函数进行复杂的数学运算,如计算正弦函数`SinPi / 6`的值,结果为 05。
(二)数据分析1、数据导入通过`Import` 函数导入外部数据文件,如 CSV 格式的数据文件。
假设我们有一个名为`datacsv` 的文件,包含两列数据`x` 和`y` ,使用`data = Import"datacsv"`即可将数据导入。
2、数据处理对导入的数据进行处理,如计算平均值、方差等统计量。
可以使用`Meandata` 计算平均值,`Variancedata` 计算方差。
(三)图形绘制1、二维图形绘制简单的函数图形,如`PlotSinx, {x, 0, 2 Pi}`绘制正弦函数在`0` 到`2 Pi` 区间的图形。
2、三维图形绘制三维图形,如`Plot3Dx^2 + y^2, {x, -2, 2},{y, -2, 2}`绘制一个抛物面。
(四)编程实践1、定义函数使用`Function` 关键字定义自己的函数,例如定义一个计算阶乘的函数`factorialn_ := Ifn == 0, 1, n factorialn 1` 。
2、循环结构使用`For` 循环和`While` 循环实现重复操作,例如使用`For`循环计算 1 到 10 的和,`sum = 0; Fori = 1, i <= 10, i++, sum += i; sum` 。
mathematica实验报告(符号计算)

1.表达式的运算
(1)化简: ;
(2)展开多项式: ;
(3)分解因式: ;
2.求函数的极限:(1) ;(2) ;(3) .
3.求导数:(1) ,求 ;(2) ,求 .
4.求积分: .
5.将 在 点,展开至 。
6.求和式与积式:(1) ;(2) .
7.求解方程 .
8.求微分方程:
四、程序、命令与结果
2.运行结果()A准确,表现效果好;B正确;C部分结果不准确;D有较严重错误.
3.其它问题______________________________________________________________________.
4.综合评定()A优秀;B良好;C合格;D不合格;E有明显抄袭或雷同现象.
结果:
(2)命令:Limit[(Tan[x])^Tan[2*x],xPi/4]
结果:
(3)命令:Limit[Exp[1/x],Direction0]
结果:
三、(1)命令:
结果:
(2)命令:
结果:
成绩评定:1.程序、命令()A准确、简洁、效率高;B命令基本准确,ቤተ መጻሕፍቲ ባይዱ有少量问题;C部分命令有问题;
D许多命令都有问题或错误.
一、
(1)命令:
P=(x-2)*(x^2+2*x+4)+(x+5)*(x^2-5*x+25);
Simplify[P]
结果:
(2)命令:P=(a+b)^3;
Expand[P]
结果:
(3)命令:P=x^5-x;
Factor[P]
结果:
二、
(1)命令:Limit[((x+m)/(x-n))^x,xInfinity]
数学实验mathmaticas

t3=ParametricPlot3D[{u,v,0},{u,-0.5, 1}, {v,-0.5,1},AxesLabel->{“x”,“y”,“z”},PlotPoints->50,
DisplayFunction->Identity];
Show[t1, t2, t3, DisplayFunction -> $DisplayFunction];
三、程序设计
1.实验对象:
输入命令:
t1 = ParametricPlot3D[{Sin[u]*Cos[v], Sin[u]*Sin[v], Cos[u]}, {u,
0, \[Pi]/2}, {v, 0, 2*\[Pi]}, PlotPoints -> 30,
DisplayFunction -> Identity];
t2 = ParametricPlot3D[{(0.5 + 0.5*Cos[u]), 0.5*Sin[u], v}, {u, 0,
2*\[Pi]},{v,-1,1}, PlotPoints->30,
DisplayFunction -> Identity];
t3 = ParametricPlot3D[{u, v, 0}, {u, -1, 1}, {v, -1, 1}, PlotPoints -> 30,
Show[g1,g2,DisplayFunction -> $DisplayFunction]]
五、程序运行结果
六、结果的讨论和分析
有图像可以看出,逼近函数f(x)的效果随n的增大而越来越好。通过实验,更直观的感受到傅里叶级数在函数模拟上的广泛用途。
迭代——方程求解(mathematica数学实验报告)

0,1称为(f、迭代法函数的迭代是数学研究中的一个非常重要的思想工具,哪怕是对一个相当简单的函数进行迭代,都可以产生异常复杂的行为,并由此而衍生了一些崭新的学科分支,如分.同时,迭代在各种数值计算算法以及其它学科领域的诸多算法中处于核心的本实验的基本理论是分形几何学程序运行如下:练习2:利用迭代公式1(),0,1,...()n n g x x x n g x +=-=' 得到()^32g x x =-的迭代序列,其中01x =,10n =,程序运行如下:练习3:对给定的矩阵M ,数组f 和初始向量0x ,由迭代公式1n n x Mx f +=+得到的迭代序列如下:练习4:利用迭代公式11()x L D A X D b --=-+将方程组⎪⎩⎪⎨⎧=++=++11111111.......................................b x a x a b x a x a n nn n n n 即Ax b =改成多种等价形式x Mx f =+做迭代,观察其收敛状况。
给定(){}1,2,2,(1,1,1),(2,2,1)A =-与(){}2,1,1,(1,1,1),(1,1,2)A =--,运行结果如下:练习5:同练习4,给定(){}1,2,2,(1,1,1),(2,2,1)A =-与(){}2,1,1,(1,1,1),(1,1,2)A =--,利用迭代公式111()()x I L Ux I L D b ---=-+-对方程组Ax b =做迭代。
程序运行如下:实验结果和结果分析:对于书上给出的例题程序,要实际上机亲自操作一次,从而了解不同命令的不同作用,对于相似的命令要区分明白他们的不同之处。
这一章小的命令比较多,也比较杂,需要分门别类区分开,并且分别运行一下。
书后的练习题离不开前面的例题,要在掌握好例题的情况下,多练习一些习题,加深记忆。
Mathematica 在迭代法解方程组非常方。
Mathematica基础数学实验(2)

设父亲身高为x, 儿子 身高为y. 显然, y与x有关系, 但这种关系并不是确定的, 即父亲身高x相同时其儿 子身高 y并不是确定的, 也 就是说, y 除受 x这一主要 素的影响外 , 还受到诸多随机因素的影响. 这种关系被 因 称为相关关系.
70 70
69 68 67
66
65
62
64
66
68
70
72
74
在一般情况下, y为随机变量, 而 x为可控制或可 精确观察的变量, 如年龄, 身高, 温度, 压力, 时间等, 因 此不把x看作随机变量. 由于y为随机变量, 则对于x的每一个确定的值, 有 它的分布. 若 y 的数学期望 Ey 存在, 则 Ey 取值随 x 的 取值而定, 因此Ey是 x 的函数, 记作(x), 称(x)为 y 关 于 x 的回归. 由于(x)的大小在一定程度上反映在 x 处随机变 量 y 的观测值的大小, 因此, 如果能通过一组样本来估 计(x), 则在一定条件下我们就能解决如下问题: (1)在给定的置信度下, 估计出当 x 取某一确定值 时, 随机变量 y 的取值范围, 即所谓预测问题; (2)在给定的置信度下, 控制自变量 x 的取值范围, 使 y在给定范围内取值, 即所谓控制问题.
简单介绍回归分析的数学原理和方法; 通过实例讨论如何选择不同类型的模型; 对软件得到的结果进行分析, 对模型进行改进.
例1:F.Galton断言:儿子的身高会受父亲身高的 影响, 但身高偏离父代平均水平的父亲, 其儿子身高有 回归子代平均水平的趋势. K.Pearson给出了如下样本(单位: 英吋):
Mathematica数学实验[2]
![Mathematica数学实验[2]](https://img.taocdn.com/s3/m/c62bcb08f12d2af90242e6d9.png)
数 学 实 验
Experiments in Mathematics
主讲教师: 刘强国 Cell phone: 159 8418 4369 E-mail: mathsuse@
Limit[f,x->a] Limit[f,x->a ,Direction->1] Limit[f,x->x0,Direction->-1] 例:求下列极限。
求极限 求左极限 求右极限
sin x lim x →0 x
lim
x → (π / 2
( x→∞
lim 1 +
1 x x
)
tanx
)-
x → ( π/2 ) +
给出一组方程,求所有可能的解,其格式为
Reduce[{lhs1= =lhs1, lhs2= =lhs2},{x,y}] 例如 Reduce 2 a x - y == 2, x2 - b x y + y == 7 , x, y
8 @
8D <<
5
Solve: 给通解舍特解; 解以代换式给出; Reduce: 给所有解 ( 通解+特解 ); 解以逻辑式给出 Solve[k*x+b==0,x] Reduce[k*x+b==0,x]
1
四川理工学院 理学院 数学实验中心
数学实验
第二讲 Mathematica在高等数学中的应用
> > > >
• • • •
解方程(组) 极限、微分、积分 数列求和、求积、级数 解微分方程组
数分数学建模实验报告2

实验报告(Mathematica)【实验名称】利用MATHEMATICA作图【实验目的】1. 掌握用MATHEMATICA作二维图形,熟练作图函数Plot、ParametricPlot 等应用,对图形中曲线能做简单的修饰。
2. 掌握用MATHEMATICA做三维图形,对于一些二元函数能做出其等高线图等,熟练函数Plot3D,ParametricPlot的用法。
【实验原理】1.二维绘图命令:二维曲线作图:Plot[fx,{x,xmin,xmax}],二维参数方程作图:ParametricPlot[{fx,fy},{t,tmin,tmax}] 2.三维绘图命令:三维作图plot3D[f,{x,xmin,xmax},{y,ymin,ymax}],三维参数方程作图:ParameticaPlot3D[{fx,fy,fz},{t,tmin,tmax}]【实验内容】(含基本步骤、主要程序清单及异常情况记录等)5.作出以下参数方程所描述的图形.x=4costy=3sint (0≤t≤2π);6.作出以下极坐标方程所描述的图形.r=4cos3θ7.作出函数z=sin(π x2+y2)的图形.8.作出以下三维图形椭球面x=R1cosu cosvy=R2cosu sinvz=R3sinu,u∈ −π2,π2, v∈0,2π,R1,R2,R3自行给定;【实验结果】5.6.7.8.的图分别如下。
【总结与思考】MATHEMATICA作图的常见错误:General::spell1: Possible spelling error。
因为在MATHEMATICA中作图函数大小写有区别,如例4中的ParametricPlot3D 函数中两个字母P都要大写,若将其中的一个写成小写p,则将提示以上拼写错误Possible spelling error。
实验二 Mathematica软件操作(2)

If[条件,表达式] If[条件,表达式] 条件
If[条件表达式,表达式1,表达式2] If[条件表达式,表达式1,表达式2] 条件表达式 1,表达式
当条件为Ture时将表达式1 当条件为Ture时将表达式1的值作为 Ture时将表达式 整个语句的值;当条件为False False时 整个语句的值;当条件为False时, If[条件 表达式1,表达式2,表达式3] 条件, 1,表达式2,表达式 If[条件,表达式1,表达式2,表达式3] 将表达式2的值作为整个语句的值; 将表达式2的值作为整个语句的值; 当条件为unknown时将表达式3 unknown时将表达式 当条件为unknown时将表达式3的值作 为整个语句的值
的驻点。 例 4 求函数 f ( x ) = 2 x 3 − 6 x 2 − 18 x + 7 的驻点。
(2)循环控制结构 Do[循环体 {k,k0,k1,d}] 循环体, 循环体 重复执行循环体,循环变量 从 变化 重复执行循环体,循环变量k从k0变化 步长为d. 到k1步长为 . 步长为
例 5 计算
例 6 已知给定 ε = 10−4 ,求 N,使当 n>N 时, ,
1 <ε 2 n
。
For[初始表达式 条件表达式 步长表达式 循环体 初始表达式,条件表达式 步长表达式,循环体 初始表达式 条件表达式,步长表达式 循环体]
对条件表达式进行检验, 对条件表达式进行检验,若为真时则继续 执行循环体,否则终止循环. k的初始值为k0, 的初始值为k0 执行循环体,否则终止循环. k的初始值为k0, k++表示循环控制变量 的值加1. 表示循环控制变量k k++表示循环控制变量k的值加1.
mathematica 实验报告

Mathematica实验报告引言Mathematica是一款功能强大的数学软件,广泛应用于数学、科学和工程等领域。
本实验报告旨在介绍Mathematica软件的使用方法,并通过一系列实例演示其在数学问题求解中的应用。
实验步骤步骤一:安装和启动Mathematica首先,我们需要下载并安装Mathematica软件。
根据操作系统的不同,可以从官方网站或其他可靠来源获取安装文件。
安装完成后,双击启动Mathematica软件。
步骤二:创建新的NotebookMathematica使用Notebook作为工作环境,可以将其类比为一个电子文档。
在Mathematica启动后,点击“File”菜单,选择“New”并选择“Notebook”,即可创建一个新的Notebook。
步骤三:编写代码在Notebook中,我们可以编写Mathematica代码。
Mathematica的代码由一系列的函数、变量和运算符组成。
以下是一个简单的示例代码,用于计算平方根:a = 9;Sqrt[a]在上述代码中,我们首先定义了变量a的值为9,然后使用Sqrt函数计算变量a的平方根。
要执行代码,可以按下“Shift” + “Enter”键,Mathematica将输出计算结果。
步骤四:编辑和运行代码在Mathematica中,可以随时编辑和运行代码。
例如,我们可以更改变量a的值,并重新计算平方根。
只需修改代码为:a = 16;Sqrt[a]然后再次按下“Shift” + “Enter”键,Mathematica将根据新的变量a的值重新计算平方根。
步骤五:绘制图表Mathematica还提供了强大的绘图功能,可以可视化数据和函数。
以下是一个简单的示例代码,用于绘制正弦函数的图表:Plot[Sin[x], {x, 0, 2Pi}]在上述代码中,我们使用Plot函数绘制了正弦函数在0到2π范围内的图表。
执行代码后,Mathematica将显示出相应的图表。
mathematica 实验报告

mathematica 实验报告Mathematica 实验报告引言:Mathematica 是一款强大的数学软件,它能够帮助用户进行各种数学计算、数据分析和可视化等工作。
本实验报告将介绍我在使用 Mathematica 进行实验时的一些经验和心得。
一、实验目的本次实验的目的是通过使用 Mathematica,掌握其基本操作和功能,了解其在数学计算和数据处理方面的应用。
二、实验步骤1. 安装和启动 Mathematica首先,我在官方网站下载了 Mathematica 的安装包,并按照提示完成了安装。
然后,我启动了 Mathematica 软件,进入了主界面。
2. 基本操作在主界面中,我发现 Mathematica 提供了一个强大的交互式界面,用户可以通过键入命令和运行代码来实现各种功能。
我尝试了一些基本操作,比如进行简单的数学计算、定义变量和函数等。
3. 数据处理和分析Mathematica 提供了丰富的数据处理和分析功能,使得用户可以轻松处理和分析各种数据。
我使用了一些内置的函数和工具,对一些实验数据进行了处理和分析。
例如,我使用了 ListPlot 函数绘制了一些实验数据的散点图,并使用了Fit 函数进行了数据拟合。
4. 可视化Mathematica 还提供了强大的可视化功能,用户可以通过绘制图表和图形来展示数据和结果。
我使用了 Plot 函数绘制了一些函数的图像,并使用了 Graphics 函数绘制了一些几何图形。
5. 编程和自动化Mathematica 具有强大的编程功能,用户可以编写自己的函数和程序来实现复杂的计算和操作。
我尝试了一些简单的编程,比如编写了一个计算斐波那契数列的函数。
此外,我还了解到 Mathematica 支持自动化操作,可以通过编写脚本和批处理文件来实现自动化的计算和分析。
三、实验结果与分析通过使用 Mathematica,我成功完成了实验的各项任务,并取得了一些令人满意的结果。
《数学实验》实验报告——用Mathematica软件解微分方程

例1
求解下列微分方程: 1)
y 2 (1 y) (2 y) 2
In[1]:= DSolve[(y[x]^2)(1-y'[x]) (2-y'[x])^2,y[x],x] Out[1]=
书中结果为: y x c 1/( x c) ,其中 c 为任意常数。 y z 2) z y In[1]:= DSolve[{y'[x] z[x],z'[x] -y[x]},{y[x],z[x]},x] Out[1]= {{y[x]C[1] Cos[x]+C[2] Sin[x],z[x]C[2] Cos[x]-C[1] Sin[x]}} 3)
中 1 2 3 为任意常数。 例 2 求常微分方程 y′= x2 + y2,满足初始条件 y(0)= 0 的数值解。 In[1]:= s1=NDSolve[{y'[x]==x^2+y[x]^2,y[0]==0},y,{x,-2,2}] Out[1]= {{yInterpolatingFunction[{{-2.,2.}},<>]}} In[2]:= y=y/.s1[[1]] Out[2]= InterpolatingFunction[{{-2.,2.}},<>] In[3]:= Plot[y[x],{x,-2,2},AspectRatioAutomatic,PlotRange{-1.5,1.5}]
例1 求解下列微分方程: 1) 2) 3)
y 2 (1 y) (2 y) 2
y z z y y 3 y 3 y y ( x 5)e x
例2 求常微分方程 y′= x2 + y2,满足初始条件 y(0)= 0 的数值解 例3 求函数 t 5 和 et sint 的拉氏变换 例 4 用拉氏变换解微分方程:
高数下册实验报告02

实验一一、实验题目作出各种标准二次曲面的图形。
二、实验目的和意义1.学习利用mathematical绘制空间几何图形;2.观察空间曲线和空间曲面图形的特点,加强几何的直观性;三、计算公式1.椭球面方程:x sin cossin sin(0,02)cosay bz cθφθφθπφπθ=⎧⎪=≤≤≤≤⎨⎪=⎩;2.单叶双曲面方程:sec cossec sin(0,02)tanx ay bz cθφθφθπφπθ=⎧⎪=≤≤≤≤⎨⎪=⎩;3.双叶双曲面方程:tan costan sin(0,02)secx ay bz cθφθφθπφπθ=⎧⎪=≤≤≤≤⎨⎪=⎩;4.双曲抛物面:22x ttypz u=⎧⎪⎪=⎨⎪⎪=⎩;5.二次锥面:2cossin(02)x ty t tz kπ⎧=⎪⎪=≤≤⎨⎪=⎪⎩6.椭圆抛物面:2cossin(02)x ty t tz kπ⎧=⎪⎪=≤≤⎨⎪=⎪⎩四、程序设计1、椭球面:a=1,b=2,c=4,ParametricPlot3D[{Cos[u]*Cos[v], 2*Cos[u]*Sin[v], 4*Sin[u]}, {u,0,2*Pi}, {v,0,2*Pi}, PlotPoints→30]2、单叶双曲面:a=1,b=2,c=4,ParametricPlot3D[{Sec[u]*Cos[v],2*Sec[u]*Sin[v],4*Tan[u]}, {u,0,2Pi},{v,0,Pi}, PlotPoints→30]:3、双曲抛物面:Plot3D[x*x-y*y,{x,-2,2}, {y,-2,2}]4、二次锥面:ParametricPlot3D[{2*u*Cos[v], 1.5*u*Sin[v], 1.2*u}, {u, -2, 2}, {v, 0, 2Pi}, PlotPoints→30]五、程序运行结果六、结果的讨论和分析1、通过mathematical作出了各种二次曲面的空间图形,从而加深了对各种二次曲面的理解和体会;2、做二次曲面时需要根据曲面的方程选择适当的表示方法:一般式方程法或参数方程法,恰当的表示能够使作图更方便有效。
综合数学实验报告(mathematica)

综合数学实验报告(mathematica)数学综合实验报告学院:数学与统计学院专业:数学与应用数学姓名:##########学号:##########班级:##########综合实验实验一:观察数列极限一、实验目的利用数形结合的方法观察数列的极限,可以从点图上看出数列的收敛性,以及近似地观察出数列的收敛值;通过编程可以输出数列的任意多项值,以此来得到数列的收敛性。
通过此实验对数列极限概念的理解形象化、具体化。
二.实验环境学校机房,Mathematica 4.0软件三、实验的基本理论和方法1、Mathematica中常用的函数及函数调用的方法;2、对Fabonacci数列、调和级数以及3n+1问题规律的掌握。
四、实验内容及步骤设为实数列,为定数.若对任给的正数,总存在正整数,使得当时有,则称数列收敛于定数称为数列的极限,并记作或。
下面,我们以求为例进行实验,程序编写及运行如下:程序运行结果如下:五、实验结果和结果分析由运行结果和图像可知,发现在时,函数值无限靠近2.7左右。
实验二:函数图像绘制一、实验目的通过函数图形来认识函数,运用函数的图形来观察和分析函数的有关性态,建立数形结合的思想。
二.实验环境学校机房,Mathematica 4.0软件三、实验的基本理论和方法1、Mathematica中常用绘图函数Plot在绘制一元函数时的方法;2、函数迭代法的基本理论以及在Mathematica中的使用。
四、实验内容及步骤1、求的所有根(先画图再求解)。
2、求方程与的根。
3、求下列各题的解。
(1);(2),求;(3)(精确到17位有效数字);(4);(5)将在处展开(最高次幂为8);(6),求。
4、作sinx的n阶Taylor展开(n=10,30,60)并比较图像5、已知函数,作出并比较当分别取-1,0,1,2,3时的图形,并从图形上观察极值点、驻点、单调区间、凹凸区间以及渐近线。
在mathematica中输入下面语句:Do[Plot[1/(x^2+2x+c),{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0]],{c,-1,3}]程序运行结果如下:实验结果和结果分析观察图可得:第一幅图:极大值点为,驻点为,单调区间为增、,减、,凸区间为、,凹区间为,渐近线为水平,垂直, .第二幅图:极大值点为,驻点为,单调区间为增、,减、,凸区间为、,凹区间.第三幅图:没有极值点,没有驻点,单调增区间为,单调减区间为,凸区间为、.第四、五幅图:极大值点为,驻点为,单调区间为增,减,凸区间为、.实验三:泰勒公式与函数逼近一、实验目的利用Mathematica计算函数的各阶泰勒多项式,并通过绘制曲线图形,根据图形观察泰勒展开的误差,进一步掌握泰勒展开与函数逼近的思想,并对泰勒公式与原函数作出比较。
数学应用软件实验报告(mathematica实验程序)2
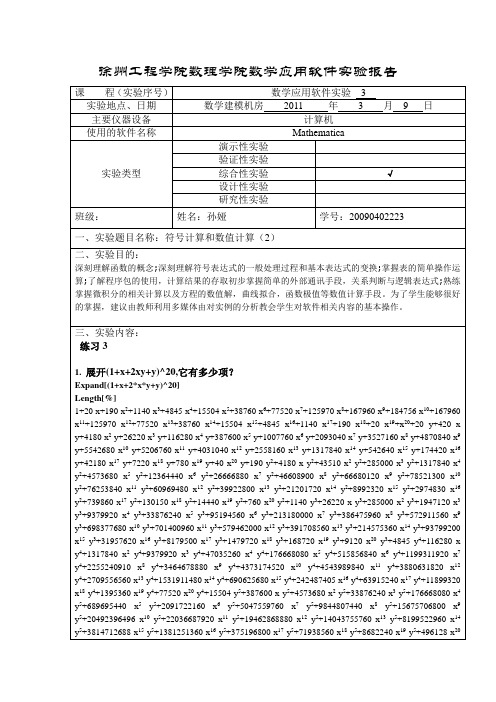
徐州工程学院数理学院数学应用软件实验报告课程(实验序号)数学应用软件实验 3 实验地点、日期数学建模机房2011 年 3 月9 日主要仪器设备计算机使用的软件名称Mathematica实验类型演示性实验验证性实验综合性实验√设计性实验研究性实验班级:姓名:孙娅学号:20090402223一、实验题目名称:符号计算和数值计算(2)二、实验目的:深刻理解函数的概念;深刻理解符号表达式的一般处理过程和基本表达式的变换;掌握表的简单操作运算;了解程序包的使用,计算结果的存取初步掌握简单的外部通讯手段,关系判断与逻辑表达式;熟练掌握微积分的相关计算以及方程的数值解,曲线拟合,函数极值等数值计算手段。
为了学生能够很好的掌握,建议由教师利用多媒体由对实例的分析教会学生对软件相关内容的基本操作。
三、实验内容:练习31. 展开(1+x+2xy+y)^20,它有多少项?Expand[(1+x+2*x*y+y)^20]Length[%]1+20 x+190 x2+1140 x3+4845 x4+15504 x5+38760 x6+77520 x7+125970 x8+167960 x9+184756 x10+167960 x11+125970 x12+77520 x13+38760 x14+15504 x15+4845 x16+1140 x17+190 x18+20 x19+x20+20 y+420 x y+4180 x2 y+26220 x3 y+116280 x4 y+387600 x5 y+1007760 x6 y+2093040 x7 y+3527160 x8 y+4870840 x9 y+5542680 x10y+5206760 x11y+4031040 x12y+2558160 x13y+1317840 x14y+542640 x15y+174420 x16 y+42180 x17y+7220 x18y+780 x19y+40 x20y+190 y2+4180 x y2+43510 x2y2+285000 x3y2+1317840 x4 y2+4573680 x5y2+12364440 x6y2+26666880 x7y2+46608900 x8y2+66680120 x9y2+78521300 x10 y2+76253840 x11y2+60969480 x12y2+39922800 x13y2+21201720 x14y2+8992320 x15y2+2974830 x16 y2+739860 x17 y2+130150 x18y2+14440 x19 y2+760 x20 y2+1140 y3+26220 x y3+285000 x2 y3+1947120 x3 y3+9379920 x4y3+33876240 x5y3+95194560 x6y3+213180000 x7y3+386475960 x8y3+572911560 x9 y3+698377680 x10 y3+701400960 x11 y3+579462000 x12 y3+391708560 x13 y3+214575360 x14 y3+93799200 x15y3+31957620 x16y3+8179500 x17y3+1479720 x18y3+168720 x19y3+9120 x20y3+4845 y4+116280 x y4+1317840 x2y4+9379920 x3y4+47035260 x4y4+176668080 x5y4+515856840 x6y4+1199311920 x7 y4+2255240910 x8y4+3464678880 x9y4+4373174520 x10y4+4543989840 x11y4+3880631820 x12 y4+2709556560 x13 y4+1531911480 x14 y4+690625680 x15 y4+242487405 x16 y4+63915240 x17 y4+11899320 x18 y4+1395360 x19 y4+77520 x20 y4+15504 y5+387600 x y5+4573680 x2 y5+33876240 x3 y5+176668080 x4 y5+689695440 x5y5+2091722160 x6y5+5047559760 x7y5+9844807440 x8y5+15675706800 x9 y5+20492396496 x10y5+22036687920 x11y5+19462868880 x12y5+14043755760 x13y5+8199522960 x14 y5+3814712688 x15 y5+1381251360 x16 y5+375196800 x17 y5+71938560 x18 y5+8682240 x19 y5+496128 x20y5+38760 y6+1007760 x y6+12364440 x2y6+95194560 x3y6+515856840 x4y6+2091722160 x5 y6+6586060440 x6y6+16491449760 x7y6+33358367640 x8y6+55054936560 x9y6+74554588680 x10 y6+82999113600 x11y6+75841498200 x12y6+56582235600 x13y6+34135350600 x14y6+16399045920 x15 y6+6127645920 x16y6+1716602880 x17y6+339227520 x18y6+42170880 x19y6+2480640 x20y6+77520 y7+2093040 x y7+26666880 x2 y7+213180000 x3 y7+1199311920 x4 y7+5047559760 x5 y7+16491449760 x6 y7+42835691520 x7 y7+89846842800 x8 y7+153696500880 x9 y7+215632422720 x10y7+248584159200 x11 y7+235095291600 x12 y7+181435172400 x13 y7+113164471200 x14 y7+56175023040 x15 y7+21676452480 x16 y7+6267336960 x17y7+1277529600 x18y7+163722240 x19y7+9922560 x20y7+125970 y8+3527160 x y8+46608900 x2y8+386475960 x3y8+2255240910 x4y8+9844807440 x5y8+33358367640 x6 y8+89846842800 x7 y8+195370274190 x8 y8+346388778840 x9 y8+503527535940 x10 y8+601227096600 x11 y8+588701269650 x12 y8+470190583200 x13 y8+303365992800 x14 y8+155702951040 x15 y8+62090109120 x16 y8+18542784000 x17 y8+3902046720 x18 y8+515973120 x19 y8+32248320 x20 y8+167960 y9+4870840 x y9+66680120 x2y9+572911560 x3y9+3464678880 x4y9+15675706800 x5y9+55054936560 x6 y9+153696500880 x7 y9+346388778840 x8y9+636450324120 x9 y9+958623134040 x10y9+1185753090600 x11y9+1202454193200 x12y9+994336636800 x13y9+663992908800 x14y9+352587006720 x15 y9+145407674880 x16y9+44889661440 x17y9+9760491520 x18y9+1332930560 x19y9+85995520 x20 y9+184756 y10+5542680 x y10+78521300 x2y10+698377680 x3y10+4373174520 x4y10+20492396496 x5 y10+74554588680 x6 y10+215632422720 x7 y10+503527535940 x8 y10+958623134040 x9 y10+1496053026468 x10y10+1917246268080 x11y10+2014110143760 x12y10+1725059381760 x13y10+1192873418880 x14 y10+655756687872 x15 y10+279883169280 x16 y10+89392343040 x17 y10+20101452800 x18 y10+2837852160 x19 y10+189190144 x20 y10+167960 y11+5206760 x y11+76253840 x2 y11+701400960 x3 y11+4543989840 x4 y11+22036687920 x5 y11+82999113600 x6 y11+248584159200 x7 y11+601227096600 x8 y11+1185753090600 x9y11+1917246268080 x10y11+2545801296480 x11y11+2771110230720 x12y11+2459144014080 x13 y11+1761757969920 x14y11+1003245235200 x15y11+443478896640 x16y11+146665359360 x17 y11+34140221440 x18 y11+4987740160 x19 y11+343982080 x20 y11+125970 y12+4031040 x y12+60969480 x2 y12+579462000 x3y12+3880631820 x4y12+19462868880 x5y12+75841498200 x6y12+235095291600 x7 y12+588701269650 x8y12+1202454193200 x9y12+2014110143760 x10y12+2771110230720 x11 y12+3125924387040 x12y12+2875098969600 x13y12+2134935528960 x14y12+1260135352320 x15 y12+577341672960 x16 y12+197875691520 x17 y12+47727513600 x18 y12+7223623680 x19 y12+515973120 x20 y12+77520 y13+2558160 x y13+39922800 x2y13+391708560 x3y13+2709556560 x4y13+14043755760 x5 y13+56582235600 x6 y13+181435172400 x7 y13+470190583200 x8 y13+994336636800 x9 y13+1725059381760 x10y13+2459144014080 x11y13+2875098969600 x12y13+2741484257280 x13y13+2110905569280 x14 y13+1292175298560 x15y13+614047703040 x16y13+218296320000 x17y13+54613770240 x18 y13+8573091840 x19y13+635043840 x20y13+38760 y14+1317840 x y14+21201720 x2y14+214575360 x3 y14+1531911480 x4y14+8199522960 x5y14+34135350600 x6y14+113164471200 x7y14+303365992800 x8 y14+663992908800 x9y14+1192873418880 x10y14+1761757969920 x11y14+2134935528960 x12 y14+2110905569280 x13y14+1686031472640 x14y14+1070961745920 x15y14+528237404160 x16 y14+194958458880 x17 y14+50644746240 x18 y14+8255569920 x19 y14+635043840 x20 y14+15504 y15+542640 x y15+8992320 x2y15+93799200 x3y15+690625680 x4y15+3814712688 x5y15+16399045920 x6 y15+56175023040 x7y15+155702951040 x8y15+352587006720 x9y15+655756687872 x10 y15+1003245235200 x11y15+1260135352320 x12y15+1292175298560 x13y15+1070961745920 x14 y15+706248130560 x15 y15+361816227840 x16 y15+138757079040 x17 y15+37467586560 x18 y15+6350438400 x19y15+508035072 x20y15+4845 y16+174420 x y16+2974830 x2y16+31957620 x3y16+242487405 x4 y16+1381251360 x5y16+6127645920 x6y16+21676452480 x7y16+62090109120 x8y16+145407674880 x9y16+279883169280 x10y16+443478896640 x11y16+577341672960 x12y16+614047703040 x13 y16+528237404160 x14y16+361816227840 x15y16+192656424960 x16y16+76840304640 x17 y16+21591490560 x18y16+3810263040 x19y16+317521920 x20y16+1140 y17+42180 x y17+739860 x2 y17+8179500 x3y17+63915240 x4y17+375196800 x5y17+1716602880 x6y17+6267336960 x7 y17+18542784000 x8 y17+44889661440 x9 y17+89392343040 x10 y17+146665359360 x11y17+197875691520 x12y17+218296320000 x13y17+194958458880 x14y17+138757079040 x15y17+76840304640 x16 y17+31901614080 x17y17+9338880000 x18y17+1718353920 x19y17+149422080 x20y17+190 y18+7220 x y18+130150 x2y18+1479720 x3y18+11899320 x4y18+71938560 x5y18+339227520 x6y18+1277529600 x7 y18+3902046720 x8y18+9760491520 x9y18+20101452800 x10y18+34140221440 x11y18+47727513600 x12 y18+54613770240 x13 y18+50644746240 x14 y18+37467586560 x15 y18+21591490560 x16 y18+9338880000 x17 y18+2851471360 x18y18+547880960 x19y18+49807360 x20y18+20 y19+780 x y19+14440 x2y19+168720 x3 y19+1395360 x4 y19+8682240 x5 y19+42170880 x6 y19+163722240 x7 y19+515973120 x8 y19+1332930560 x9 y19+2837852160 x10y19+4987740160 x11y19+7223623680 x12y19+8573091840 x13y19+8255569920 x14 y19+6350438400 x15y19+3810263040 x16y19+1718353920 x17y19+547880960 x18y19+110100480 x19 y19+10485760 x20y19+y20+40 x y20+760 x2y20+9120 x3y20+77520 x4y20+496128 x5y20+2480640 x6 y20+9922560 x7y20+32248320 x8y20+85995520 x9y20+189190144 x10y20+343982080 x11y20+515973120 x12y20+635043840 x13y20+635043840 x14y20+508035072 x15y20+317521920 x16y20+149422080 x17 y20+49807360 x18 y20+10485760 x19 y20+1048576 x20 y204412.利用mathematica计算下列不定积分(1)Integrate[x^2*Cos[x^3],x]Sin[x3]/3(2)Integrate[1/(x^2+a^2)^4,x](33 a5 x+40 a3 x3+15 a x5+15 (a^2+x^2)3 ArcTan[x/a])/(48 a7 (a^2+x^2)3)(3)Integrate[(Sin[x])^10,x](63 x)/256-105/512 Sin[2 x]+15/256 Sin[4 x]-(15 Sin[6 x])/1024+(5 Sin[8 x])/2048-Sin[10 x]/51203.拟合曲线Clear[fx,fy,biao,nb,ft,ft1,t1]fy[y_]:=Log[y]fx[x_]:=xbiao={{0.4,1.75},{0.5,1.34},{0.6,1.00},{0.7,0.74}};nb=Table[{fx[biao[[i,1]]],fy[biao[[i,2]]]},{i,1,4}];ft=Fit[nb,{1,x},x];ft1=Exp[ft]t1=Plot[ft1,{x,0,1.0},AxesLabel→{"x","y"},PlotStyle→{RGBColor[1,0,0]}]t2=ListPlot[biao,PlotStyle→{RGBColor[0,0,1],PointSize[0.04]}]Show[t1,t2,PlotRange→{0,2}]©1.71895 -2.87483 x0.20.40.60.8 1.0x 12345y0.450.500.550.600.650.701.01.21.41.60.20.40.60.8 1.0x 0.51.01.52.0y四、总结及心得体会:数据拟合比较复杂,需要多次调试多次运行,数据拟合的程序相对较前面的比较繁复,在做数据拟合的时候应该仔细分析好思路,充分理解,再写程序。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学实验报告
实
验
二
学院:数学与统计学院
班级:信息与计算科学(1)班
姓名:郝玉霞
学号:201171020107
实验二
一、实验名称:π的计算
二、实验目的:首先在Mathematica环境中用多种方法计算圆周率π的值,通过
实验来体会各种方法的区别,比较各种方法的优劣,接着尝试自己提出新的
方法来计算圆周率π的值。
三、实验环境:学校机房,Mathematica软件。
四、实验的基本理论和方法
1、用Mathematica绘图函数Plot绘制圆周率π;
2、计算圆周率π的数值积分法、泰勒级数法、蒙特卡罗法,并且利用特定
的公式来计算圆周率π。
五、实验的内容和步骤及实验的结果和结果分析
步骤一、数值积分法计算π
因为单位圆的半径为1,它的面积等于π,所以只要计算出单位圆的面积,就算出了π。
在坐标轴上画出以圆点为圆心,以1为半径的单位圆,则这个单位圆在第一象限的部分是一个扇形,而且面积是单位圆的1/4,于是,我们只要算出此扇形的面积,便可以计算出π。
当n=5000时;
语句:
n=5000;y[x_]:=4/(1+x*x);
s1=(Sum[y[k/n],{k,1,n-1}]+(y[0]+y[1])/2)/n;
s2=(y[0]+y[1]+2*Sum[y[k/n],{k,1,n-1}]+4*Sum[y[(k-1/2)/n],{k,1,n}])/(6*n);
Print[{N[s1,20],N[s2,30],N[Pi,30]}];
实验结果:
3.1415926469231265718,3.14159265358979323846264334
3.14159265358979323846264338328
当n=10000时;
语句:
n=10000;y[x_]:=4/(1+x*x);
s1=(Sum[y[k/n],{k,1,n-1}]+(y[0]+y[1])/2)/n;
s2=(y[0]+y[1]+2*Sum[y[k/n],{k,1,n-1}]+4*Sum[y[(k-1/2)/n],{k,1,n}])/(6*n);
Print[{N[s1,20],N[s2,30],N[Pi,30]}];
Plot[{4(1-x*x)},{x,0,1}]
实验结果:
3.1415926519231265718,3.14159265358979323846264338
3.14159265358979323846264338328
图1 1/4个单位圆
结果分析:当数值积分法得到π的近似值为3.14159265358979323846264338328, 可以看出,用这种方法计算所得到的π值是相当精确的,n 越大,计算出来的扇形面积的近似值就越接近π的准确值。
步骤二、泰勒级数法计算π 利用反正切函数的泰勒级数
+--+-+-=--1
2)1(53a r c t a n 1
2153k x x x x x
k k 来计算π。
语句:T[x_,n_]:=Sum[(-1)^k*x^(2k+1)/(2k+1),{k,0,n}]; N[4*T[1,20000],20]//Timing
T[x_,n_]:=Sum[(-1)^k*x^(2k+1)/(2k+1),{k,0,n}]; Print[N[4*(T[1/2,260]+T[1/3,170]),150]]; Print[N[16*(T[1/5,110]-4*T[1/239,30]),150]]; Print[N[Pi,150]]
实验结果:
9.14Second,3.1416426510898869
3.14159265358979323846264338327950288419716939937510582494459230781640628620899862803482534211706798214808651230664709384460955058223172535940813
2.89054809346530980659035048572237571973428548091718877376781907690970580083540220107847652474250068362104652048128394634092219187032819003167814
3.14159265358979323846264338327950288419716939937510582494459230781640628620899862803482534211706798214808651230664709384460955058223172535940813
结果分析:从实验过程可以看出,这种方法花费的时间很长。
原因是当x=1时得到的arctan1的展开式收敛太慢。
要使泰勒级数收敛得快,容易想到,应当使x
的绝对值小于1,最好是远比1小。
例如,因为11
arctan1arctan arctan 23
=+,所
以我们可以计算出11
arctan ,arctan 23
的值,从而得到arctan1的值。
这样,就使得
收敛速度加快。
改进后可以看出,泰勒级数法得到的结果比数值分析法精确到小数点后更多位。
步骤三、蒙特卡罗法计算π
在数值分析法中,我们利用求单位圆的1/4面积来得到/4π,从而得到π。
单位圆的1/4是一个扇形,它是边长为1的单位正方形的一部分,单位正方形的面积11S =。
只要能够求出扇形的面积S 在正方形的面积中所占的比例1/k S S =,就能立即得到S ,从而得到π的值。
下面的问题归结为如何求k 的值,这就用到了一种利用随机数来解决此种问题的蒙特卡罗法,其原理就是
在正方形中随机的投入很多点,是所投的每个点落在正方形中每一个位置的机会均等,看其中有多少个点落在扇形内。
降落在扇形内的点的个数m 与所投店的总数n 的比可以近似的作为k 的近似值。
语句:
n=10000;p={}; Do[m=0;
Do[x=Random[];y=Random[]; If[x^2+y^2<=1,m++],{k,1,n}];
AppendTo[p,N[4m/n]],{t,1,10}];
Print[p];
Sum[p[[t]],{t,1,10}]/10 实验结果:
3.1528,3.1472,3.1276,3.134,3.1384,3.1516,3.1424,3.1664,3.1436,3.1
3.14668
结果分析:
从运行结果来看,蒙特卡罗法的计算结果为3.14668,虽然精确度不太高,但运行时间短,在很多场合下,特别是在对精确度要求不高的情况下很有用的。
步骤四、针对步骤三提出疑问:步骤三中我们发现当n=10000时,蒙特卡罗法的计算结果为3.14668,精确度不太高,那么对n 取不同的值,所得结果的精确度
会不会有变化?假如有变化,会有什么变化呢?
猜想:对n 取不同的值,所得结果的精确度应该会有变化,且当n 值越大,所得结果越精确。
现令n=1000;
语句:
n=1000;p={}; Do[m=0;
Do[x=Random[];y=Random[]; If[x^2+y^2<=1,m++],{k,1,n}];
AppendTo[p,N[4m/n]],{t,1,10}];
Print[p];
Sum[p[[t]],{t,1,10}]/10 实验结果:
3.16,3.132,3.08,3.156,3.144,3.184,3.156,3.116,3.092,3.
3.
令n=100000; 语句:
n=100000;p={}; Do[m=0;
Do[x=Random[];y=Random[]; If[x^2+y^2<=1,m++],{k,1,n}];
AppendTo[p,N[4m/n]],{t,1,10}];
Print[p];
Sum[p[[t]],{t,1,10}]/10 实验结果:
3.14,3.13172,3.13692,3.13752,3.140923.13852,3.13976,3.14572,3.14028,3.14
3.1
结果分析:
从运行结果来看,虽然蒙特卡罗法的计算结果的精确度不太高,但对n 取不同的值,所得结果的精确度有变化,且当n 值越大,所得结果越精确,这与我们的猜想完全一致。
步骤五、利用麦琴给出
239
1
arctan 51arctan
44
-=π
,推出π
=4(239
1
arctan
51arctan
4 )。
对比以上方法,这种简单的直接用公式求的π的方法要简单得多,所以用处更广。
