图论中的圈与块
第一章(图论的基本概念)
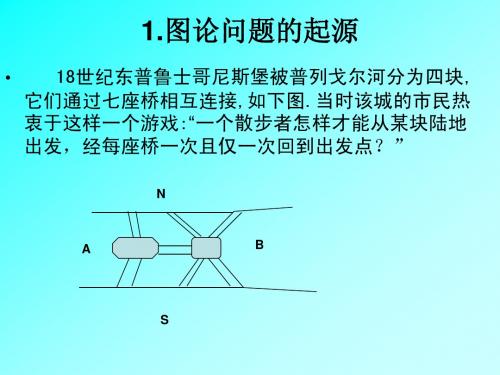
第二节 图的顶点度和图的同构(4)
图序列:简单图的度序列. (d1, d 2 , , d p )(d1 d 2 d p ) 定理4 非负整数序列 是图序列当 p 且仅当 d i 是偶数,并且对一切整数k, 1 k p 1, 有
i 1
第二节 图的顶点度和图的同构(1)
定义1 设G是任意图,x为G的任意结点,与结点x关联的 边数(一条环计算两次)称为x的度数.记作deg(x)或d(x). 定义2 设G为无向图,对于G的每个结点x,若d(x)=K,则 称G为K正则的无向图.设G为有向图,对于G的每个结点 x,若d+(x)=d-(x), 则称G为平衡有向图.在有向图G中, 若 (G) (G) (G) (G) K , 则称G为K正则有向图. 定理1(握手定理,图论基本定理)每个图中,结点度数的 总和等于边数的二倍,即 deg(x) 2 E .
•
A
N
S
B
欧拉的结论 • 欧拉指出:一个线图中存在通过每边一次仅一次 回到出发点的路线的充要条件是: • 1)图是连通的,即任意两点可由图中的一些边连 接起来; • 2)与图中每一顶点相连的边必须是偶数. • 由此得出结论:七桥问题无解. 欧拉由七桥问题所引发的研究论文是图论的开 篇之作,因此称欧拉为图论之父.
xV
定理2 每个图中,度数为奇数的结点必定是偶数个.
第二节 图的顶点度和图的同构(2)
• 定理3 在任何有向图中,所有结点入度之和等于所有结 点出度之和. • 证明 因为每条有向边必对应一个入度和出度,若一个结 点具有一个入度或出度,则必关联一条有向边,因此,有向 图中各结点的入度之和等于边数,各结点出度之和也等 于边数. • 定义 度序列,若V(G)={v1,v2,…,vp},称非负整数序列 (d(v1),d(v2),…,d(vp))为图G的度序列.
图论知识点

图论知识点摘要:图论是数学的一个分支,它研究图的性质和应用。
图由节点(或顶点)和连接这些节点的边组成。
本文将概述图论的基本概念、类型、算法以及在各种领域的应用。
1. 基本概念1.1 节点和边图由一组节点(V)和一组边(E)组成,每条边连接两个节点。
边可以是有向的(指向一个方向)或无向的(双向连接)。
1.2 路径和环路径是节点的序列,其中每对连续节点由边连接。
环是一条起点和终点相同的路径。
1.3 度数节点的度数是与该节点相连的边的数量。
对于有向图,分为入度和出度。
1.4 子图子图是原图的一部分,包含原图的一些节点和连接这些节点的边。
2. 图的类型2.1 无向图和有向图无向图的边没有方向,有向图的每条边都有一个方向。
2.2 简单图和多重图简单图是没有多重边或自环的图。
多重图中,可以有多条边连接同一对节点。
2.3 连通图和非连通图在无向图中,如果从任意节点都可以到达其他所有节点,则称该图为连通的。
有向图的连通性称为强连通性。
2.4 树树是一种特殊的连通图,其中任意两个节点之间有且仅有一条路径。
3. 图的算法3.1 最短路径算法如Dijkstra算法和Bellman-Ford算法,用于在加权图中找到从单个源点到所有其他节点的最短路径。
3.2 最大流最小割定理Ford-Fulkerson算法用于解决网络流中的最大流问题。
3.3 匹配问题如匈牙利算法,用于解决二分图中的匹配问题。
4. 应用4.1 网络科学图论在网络科学中有广泛应用,如社交网络分析、互联网结构研究等。
4.2 运筹学在运筹学中,图论用于解决物流、交通网络优化等问题。
4.3 生物信息学在生物信息学中,图论用于分析蛋白质相互作用网络、基因调控网络等。
5. 结论图论是数学中一个非常重要和广泛应用的领域。
它不仅在理论上有着深刻的内涵,而且在实际应用中也发挥着关键作用。
随着科技的发展,图论在新的领域中的应用将会不断涌现。
本文提供了图论的基础知识点,包括概念、图的类型、算法和应用。
图论中的r-圈策略

图论中的r-圈策略图论中的r-圈策略冯跃峰本文中所指的r-圈是由r条互异的边构成的一个圈,记为Cr。
众所周知,图论中涉及圈的定理通常只指存在某种圈,但并不能确定圈的具体长度。
若要找r-圈,则可采用以下扩充策略。
为叙述问题方便,我们先给出如下的定义:两条有公共顶点的边组成的图称为“2-链”,公共顶点称为2-链的中心,另两个顶点称为2-链的端点。
类似定义t-链。
一般地说,寻找图G中的r-圈,有以下4种常用策略。
(1)由一条“2-链”扩充:取2-链ABC,然后由两端点A、C向两边扩展成更长的链,最后在两端点的邻域中找公共点,或邻域中各取一个点相连。
(2)由一条边扩充:取边AB,然后由两端点A、B向两边扩展成更长的链,最后在两端点的邻域中找公共点,或邻域中各取一个点相连。
(3)由中间点扩充:取两个中间点A、B,在边AB(可能是虚边)两侧分别扩充。
(4)由两条t-链拼合:令每条t-链与其两个端点对应,证明有2条t-链对应同一个“2点组”,则这2条t-链拼合成一个长为2t的圈。
值得指出的是,当r不同时,找r-圈的技巧又略有不同,我们以典型的圈C3、C4为例。
找三角形仅有2种常用策略:(i)由一条“2-链”扩充:取点A为“2-链”中心,证明A的邻域中有2点相邻(通常用到“邻域分块”、“充分条件分类”等技巧);(ii)由一条边扩充:适当取边AB,证明两端点A、B的邻域有公共点,即|D(A)∩D(B)|≥1。
找四边形有4种策略:(i)由一条“2-链”扩充:取点A为“2-链”中心,证明有一个异于A的点向A的邻域引出两条边(与邻域中两个点相邻);(ii)由一条边扩充:取边AB,证明A邻域中一点与B邻域中一点相邻;(iii)由点对扩充:取两点A、B,证明A、B的邻域有2个公共点,即|D(A)∩D(B)|≥2;(4)由两条2-链拼合:令每条2-链与其两个端点对应,证明有两条2-链对应同一个“2点组”,则这两条2-链拼合成一个四边形。
图论及其应用

图和子图 图和简单图图 G = (V, E), 其中 V = {νv v v ,......,,21} V ---顶点集, ν---顶点数E = {e e e 12,,......,ε}E ---边集, ε---边数例。
左图中, V={a, b,......,f}, E={p,q, ae, af,......,ce, cf} 注意, 左图仅仅是图G 的几何实现(代表), 它们有无穷多个。
真正的 图G 是上面所给出式子,它与顶点的位置、边的形状等无关。
不过今后对两者将经常不加以区别。
称 边 ad 与顶点 a (及d) 相关联。
也称 顶点 b(及 f) 与边 bf 相关联。
称顶点a 与e 相邻。
称有公共端点的一些边彼此相邻,例如p 与af 。
环(loop ,selfloop ):如边 l 。
棱(link ):如边ae 。
重边:如边p 及边q 。
简单图:(simple graph )无环,无重边 平凡图:仅有一个顶点的图(可有多条环)。
一条边的端点:它的两个顶点。
记号:νε()(),()().G V G G E G ==。
习题1.1.1 若G 为简单图,则εν≤⎛⎝ ⎫⎭⎪2 。
1.1.2 n ( ≥ 4 )个人中,若每4人中一定有一人认识其他3人,则一定有一 人认识其他n-1人。
同构在下图中, 图G 恒等于图H , 记为 G = H ⇔ V (G)=V(H), E(G)=E(H)。
图G 同构于图F ⇔ V(G)与V(F), E(G)与E(F)之间各存在一一对应关系,且这二对应关系保持关联关系。
记为 G ≅F 。
注 往往将同构慨念引伸到非标号图中,以表达两个图在结构上是否相同。
de f G = (V, E)y z w cG =(V , E )w cyz H =(V ’, E ’)’a ’c ’y ’e ’z ’F =(V ’’, E ’’)注 判定两个图是否同构是NP-hard 问题。
完全图(complete graph) Kn空图(empty g.) ⇔ E = ∅ 。
图论-图的基本概念

证明:按每个顶点的度来计数边,每条边恰数了两次。 推论 1.1.1 任何图中,奇度顶点的个数总是偶数(包括 0)。 4. 子图
子图(subgraph):如果 V (H ) ⊆ V (G) 且 E(H ) ⊆ E(G) ,则称图 H 是 G 的子图,记为 H ⊆G。
生成子图(spanning subgraph): 若 H 是 G 的子图且V (H ) = V (G) ,则称 H 是 G 的生成子图。
这便定义出一个图。
2. 图的图示
通常,图的顶点可用平面上的一个点来表示,边可用平面上的线段来表示(直的或曲的)。 这样画出的平面图形称为图的图示。
例如,例 1.1.1 中图的一个图示为
v1
v2
e1
e6 e5
e2
e4
v5
e7
v3
e3 v4
注:(1)由于表示顶点的平面点的位置的任意性,同一个图可以画出形状迥异的很多图示。
图论块

不可分图
定义:不含割点的非平凡连通图。
定理5.7:阶至少为3的图是不可分的当且 仅当任意两个顶点都位于某个圈上。
证明:[反证法]充分性,设图G阶数至少为3,且任意 两个顶点位于某一个圈上,则这两个顶点是连通的, G当然是连通的,若G不可分,G必包含一个割点v, 设u,w分别为G-v中两个不同连通分支上的点,知u, w位于某个圈C上,则C上有两条u—w路,其中至少 一条不包含v由定理5.3知与假设矛盾,因此G不含割 点,是不可分的。
必要性证明:设G是一个阶至少为3的不可分图,假设G存在一些顶点对, 使得它们不在同一个圈上,在所有这样的顶点对中找到两个顶点u,v 使得它们的距离最小,即d(u,v)最小。假设d(u,v)=1,则 uv∈E(G).通过观察不难发现uv位于一个圈上。因而d(u,v) =k>=2.设P:u=v0,v1,…,vk-1,vk=v是G中一个长度为k的u—v路。由 于d(u,vk-1)=k-1<k,则存在一个包含u和vk-1的圈C。由假设,v不 在C上。由于vk-1不是G的割点,且u和v是与vk-1不同的两个顶点,由 定理5.4,则存在一条不包含vk-1的u—v路Q。由于u位于C上,因此考 虑Q中第一个位于C上的顶点是有意义的,记该顶点为x。设Q′为Q的 v—x子路,P′为C上包含u的vk-1-x路。(若x≠u, 则 P′是唯一的 )然而, 由v到邻点uk-1,再沿P′到x,最后Q′到v所构成的圈C′包含u和v,从而导致
推论5.9 非平凡连通图G的任意两个不同图的块B1和B2具有下 面的性质:
(1)B1,B2是边不相交的。 (2)B1,B2至多有一个公共顶点。 (3)若B1,B2有一个公共顶点v,则v是G的割点。 证明: 由定理5.8.得,任意两个不同的块是边不相交的。下面证明(2)。假设B1,B2 有两个不同的公共顶点u,v,因为B1,B2均是G的连通子图,所以在B1,中存在一 条u-v路P′,在B2中存在一条u-v路P″。此外,由于B1和B2是边不相交的, 则P′和P″也是边不相交的,设w是P′和P″的在u之后的第一公共顶点 (w=v)P′的u-w子路Q′和P′ 的u-w子路Q″构成了G的一个圈,该圈包含了 B1的边e1和B2的边e2,因此,e1 e2 在G的同一个块中,这显然不成立。(3) 设G的两个块B1和B2有一个公共顶点v,则v关联B1中的边e1=vv1和B2中的边 e2=vv2。假设v不是G的割点,则存在一条不包含v的v1-v2路,因此,P与v,e1, e2构成一个包含e1 e2的圈,由于e1 e2属于不同块,故不成立。
图论中的圈与块,无向图的最小环

浙江省2006年集训讲义
29
嗅探器(4)
题目要求的点一定是图中的割点,但是图中 的割点不一定题目要求的点。如上图中的蓝 色点,它虽然是图中的割点,但是割掉它之 后却不能使a和b不连通 由于a点肯定不是我们所求的点,所以可以以 a为根开始DFS遍历整张图。 对于生成的DFS树,如果点v是割点,如果以 他为根的子树中存在点b,那么该点是问题所 求的点。
2011-1-28 浙江省2006年集训讲义 17
DFS算法
父子边用黑色标记,返祖边用红色标记 如下图,除掉返祖边之后,我们可以把它看 作一棵DFS树
1 2 3 4 5
6
7
2011-1-28
浙江省2006年集训讲义
18
割点
G是连通图,v∈V(G),G – v 不再连通,则称 v是G的割顶。
2011-1-28
结点个数N≤100000 边数M≤1000000
2011-1-28
浙江省2006年集训讲义
32
关键网线(2)
朴素算法: 枚举每条边,删除它,然后判断是否有独立 出来的连通区域内没有A属性或者没有B属性。 复杂度O(M2) 当然,这个复杂度太大了!
2011-1-28
浙江省2006年集训讲义
33
关键网线(3)
2011-1-28 浙江省2006年集训讲义 15
块及其相关知识
DFS算法 割点 (一般对于无向图而言) 割边 (一般对于无向图而言) 块(一般对于无向图而言) 强连通子图(一般对于有向图而言)
2011-1-28
浙江省2006年集训讲义
16
DFS算法
1973年,Hopcroft和Tarjan设计了一个有效的DFS算法 PROCEDURE DFS(v); begin inc(sign); dfn[v] := sign; //给v按照访问顺序的先后标号为sign for 寻找一个v的相邻节点u if 边uv没有被标记过 then begin 标记边uv; 给边定向v→u; 如果u被标记过,记uv为父子边,否则记uv为返祖边 if u未被标记 then DFS(u); end; end;
图论第三章

是G 的顶点割。
-3-
图论及其应用第三章 (2)k 顶点割:含有k 个元素的顶点割。 注:1)1 顶点割与割点是两个不同的概念。
u
{u} 是1 顶点割,但 u 不是割点
v
v 是割点,但 {v} 不是1 顶点割
2)G 连通且无环,则 v 是割点
(G v ) (G )
{v} 是1顶点割
-10-
图论及其应用第三章 (2)k 边割 {e}为1 边割 {e}为割边。
(3)G 的连通度 (G ) 定义如下:
min{ k | G 有 k 边割 }, G 是非平凡图 (G ) 0, G 是平凡图
注: 1) (G ) 0
G 平凡或不连通
2)G 是含有割边的连通图
( n ≥l )
(G ) 1 (G xy ) (G )
(G ) 1 (G x )
-14-
图论及其应用第三章 三. 连通度的基本结果
。 证明:(1)先证 。 若G 平凡或不连通,则
定理3.1
0
-17-
图论及其应用第三章
例5
G
(G ) ( 2 ), (G ) ( 3 ), (G ) ( 4 )
-18-
图论及其应用第三章 例6
A 4-edge-connected graph G such that G-{x1, x2, x3, x4} is connected
-19-
(G ) 1
-11-
图论及其应用第三章 3) (G ) k 0 G 的k 边割均为键
(4)k 连通图:若 (G ) k ,则称G 为k 边连通图 的。 注第三章 例4 1、分别找G1和G2两个边割; 2、给出它们的边连通度。 v2 v1 v5 v6 v9 v 7 v8 v4 G1 v3 v1 v3 G 2 v8 v2 v4 v5 v6 v7
图论重要结论

定理1: 图G= (V, E)中所有顶点的度的和等于边数m 的2倍,即: 推论1 在任何图中,奇点个数为偶数。
推论2 正则图的阶数和度数不同时为奇数 。
定理2 若n 阶简单图G 不包含Kl+1,则G度弱于某个完全 l 部图 H ,且若G 具有与H 相同的度序列,则: 定理3 设T 是(n, m)树,则: 偶图判定定理: 定理4 图G 是偶图当且仅当G 中没有奇回路。
敏格尔定理: 定理5(1) 设x 与y 是图G 中的两个不相邻点,则G 中分离点x 与y 的最小点数等于独立的(x, y)路的最大数目; (2)设x 与y 是图G 中的两个不相邻点,则G 中分离点x 与y 的最小边数等于G 中边不重的(x, y)路的最大数目。
欧拉图、欧拉迹的判定: 定理6 下列陈述对于非平凡连通图G 是等价的:(1) G 是欧拉图;(2) G 的顶点度数为偶数; (3) G 的边集合能划分为圈。
推论: 连通非欧拉图G 存在欧拉迹当且仅当G 中只有两个顶点度数为奇数。
H 图的判定: 定理7 (必要条件) 若G 为H 图,则对V(G)的任一非空顶点子集S ,有:定理8 (充分条件) 对于n ≧3的单图G ,如果G 定理9 (充分条件) 对于n ≧3的单图G ,如果G 邻顶点u 与v ,有: 定理10 (帮迪——闭包定理) 图G 是H 图当且仅当它的闭包是H 图。
定理11(Chv átal ——度序列判定法) 设简单图G 的度序列是(d1,d2,…,dn), 这里,d1≦d2≦…≦dn,并且n ≧3.若对任意的m<n/2,或者 dm>m,或者dn -m ≧ n -m,则G 是定理12 设G 是n 阶单图。
若n ≧3且 则G 是H 图;并且,具有n 个顶点 H 图只有C1,n 以及C2,5.定理13 (Hall 存在饱和X 每个顶点推论:若G 是k (k>0)正则偶图,则G 存在完美匹配。
定理14 (哥尼,1931) 在偶图中,最大匹配的边数等于最小覆盖的顶点数。
图论及其应用第三章答案(电子科大)

习题三:● 证明:是连通图G 的割边当且仅当V(G)可划分为两个子集V1和V2,使对任意及, G 中的路必含. 证明:充分性: 是的割边,故至少含有两个连通分支,设是其中一个连通分支的顶点集,是其余分支的顶点集,对12,u V v V ∀∈∀∈,因为中的不连通,而在中与连通,所以在每一条路上,中的必含。
必要性:取12,u V v V ∈∈,由假设中所有路均含有边,从而在中不存在从与到的路,这表明不连通,所以e 是割边。
●3.设G 是阶大于2的连通图,证明下列命题等价:(1)G 是块 (2)G 无环且任意一个点和任意一条边都位于同一个圈上;(3)G 无环且任意三个不同点都位于同一条路上。
: 是块,任取的一点,一边,在边插入一点,使得成为两条边,由此得到新图,显然的是阶数大于3的块,由定理,中的u,v 位于同一个圈上,于是中u 与边都位于同一个圈上。
: 无环,且任意一点和任意一条边都位于同一个圈上,任取的点u ,边e ,若在上,则三个不同点位于同一个闭路,即位于同一条路,如不在上,由定理,的两点在同一个闭路上,在边插入一个点v ,由此得到新图,显然的是阶数大于3的块,则两条边的三个不同点在同一条路上。
:连通,若不是块,则中存在着割点,划分为不同的子集块,,,无环,12,x v y v ∈∈,点在每一条的路上,则与已知矛盾,是块。
●7.证明:若v 是简单图G 的一个割点,则v 不是补图的割点。
证明:是单图的割点,则有两个连通分支。
现任取, 如果不在的同一分支中,令是与处于不同分支的点,那么,与在的补图中连通。
若在的同一分支中,则它们在的补图中邻接。
所以,若是的割点,则不是补图的割点。
● 12.对图3——20给出的图G1和G2,求其连通度和边连通度,给出相应的最小点割和最小边割。
解:()12G κ= 最小点割 {6,8}1()2G λ= 最小边割{(6,5),(8,5)}()25G κ= 最小点割{6,7,8,9,10}2()5G λ= 最小边割{(2,7)…(1,6)}●13.设H 是连通图G 的子图,举例说明:有可能k(H)> k(G).解: 通常.eH整个图为,割点左边的图为的的子图,,则.。
图论中的圈与块.

表示,删除u和v之间的连边之后,u和v之间 的最短路 最小环则是min(u,v) + e(u,v) 时间复杂度是EV2
2018/9/8
浙江省2006年集训讲义
13
一个错误的算法
预处理出任意两点之间的最短路径,记作
min(u,v) 枚举三个点w,u,v,最小环则是min(u,w) + min(w,v) + e(u,v)的最小值 如果考虑min(u,w)包含边u-v的情况? 讨论:是否有解决的方法?
1973年,Hopcroft和Tarjan设计了一个有效的DFS算法 PROCEDURE DFS(v); begin inc(sign); dfn[v] := sign; //给v按照访问顺序的先后标号为sign for 寻找一个v的相邻节点u if 边uv没有被标记过 then begin 标记边uv; 给边定向v→u; 如果u被标记过,记uv为父子边,否则记uv为返祖边 if u未被标记 then DFS(u); end; end;
最小生成树 根据刚才提到的MST的另类做法,我们反向 处理它的每个操作,也就是先删除所有要删 的边,然后再逆向添边并回答min(u,v) 于是该问题就可以用另类MST算法解决了
2018/9/8
浙江省2006年集训讲义
8
水管局长(5)
这里涉及到一些图与树的存储操作,如何在
O(N)的时间内找到环上最大边,并维护一棵 最小生成树呢? 如果采取邻接表的存储方式来记录一棵最小 生成树,从添加的边的某个点开始遍历整棵 树,寻找出环上的最大边,虽然理论复杂度 是O(N)的,但是有很多的冗余
图论中的圈与块
图论经典问题
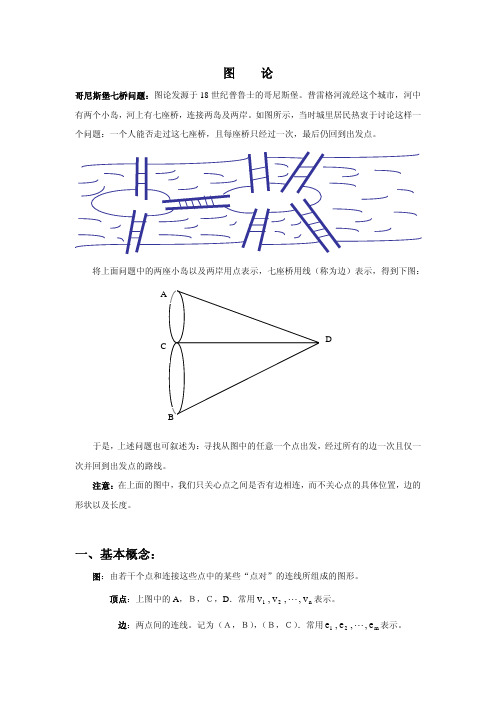
图 论哥尼斯堡七桥问题:图论发源于18世纪普鲁士的哥尼斯堡。
普雷格河流经这个城市,河中有两个小岛,河上有七座桥,连接两岛及两岸。
如图所示,当时城里居民热衷于讨论这样一个问题:一个人能否走过这七座桥,且每座桥只经过一次,最后仍回到出发点。
将上面问题中的两座小岛以及两岸用点表示,七座桥用线(称为边)表示,得到下图:于是,上述问题也可叙述为:寻找从图中的任意一个点出发,经过所有的边一次且仅一次并回到出发点的路线。
注意:在上面的图中,我们只关心点之间是否有边相连,而不关心点的具体位置,边的形状以及长度。
一、基本概念:图:由若干个点和连接这些点中的某些“点对”的连线所组成的图形。
顶点:上图中的A ,B,C,D .常用表示。
n 21 v , , v , v 边:两点间的连线。
记为(A,B),(B,C).常用表示。
m 21e , , e , e次:一个点所连的边数。
定点v的次记为d(v).图的常用记号:G=(V,E),其中,}{v V i =,}{e E i =子图:图G的部分点和部分边构成的图,成为其子图。
路:图G中的点边交错序列,若每条边都是其前后两点的关联边,则称该点边序列为图G的一条链。
圈(回路):一条路中所含边点均不相同,且起点和终点是同一点,则称该路为圈(回路)。
有向图:,其中(,)G N A =12{,,,}k N n n n = 称为的顶点集合,A a 称为G 的弧集合。
G {(,)ij i j }n n ==若,则称为的前驱, 为n 的后继。
(,)ij i j a n n =i n j n j n i 赋权图(网络):设是一个图,若对G 的每一条边(弧)都赋予一个实数,称为边的权,。
记为。
G (,,)G N E W =两个结论:1、图中所有顶点度数之和等于边数的二倍; 2、图中奇点个数必为偶数。
二、图的计算机存储:1. 关联矩阵简单图:,对应(,)G N E =N E ×阶矩阵()ik B b =10ik i k b ⎧=⎨⎩点与边关联否则简单有向图:,对应(,)G N A =N A ×阶矩阵()ik B b =110ik ik ik a i b a i ⎧⎪=−⎨⎪⎩弧以点为尾弧以点为头否则2. 邻接矩阵简单图:,对应(,)G N E =N N ×阶矩阵()ij A a =10ij i j a ⎧=⎨⎩点与点邻接否则简单有向图:,对应(,)G N A =N N ×阶矩阵()ij A a =10ij i ja ⎧=⎨⎩有弧从连向否则5v 34v01010110100101011110101000110111101065432166654321⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=×v v v v v v A v v v v v v3. 权矩阵:简单图:,对应(,)G N E =N N ×阶矩阵()ij A a =ij ij i j a ω⎧=⎨∞⎩点与点邻接否则123456781234567802130654.5061002907250473080 v v v v v v v v v v v v v v v v 48∞∞∞∞⎡⎤⎢⎥∞∞∞∞∞⎢⎥⎢⎥∞∞∞∞∞⎢⎥∞∞∞∞∞⎢⎥⎢⎥∞∞∞∞⎢⎥∞∞∞∞⎢⎥⎢⎥∞∞∞∞⎢⎥∞∞∞∞∞∞⎢⎥⎣⎦三、图的应用:例:如图,用点代表7个村庄,边上的权代表村庄之间的路长,现在要在这7个村庄中布电话线,如何布线,使材料最省?分析:需要将图中的边进行删减,使得最终留下的图仍然连通,并且使总的权值最小。
图论中的圈与块(共79张PPT)精选

程序代码
PROCEDURE DFS(v);
begin
inc(sign); dfn[v] := sign; //给v按照访问顺序的先后标号为sign
lowlink[v] := sign; //给lowlink[v]赋初始值
for 寻找一个v的相邻(xiānɡ lín)节点u
if 边uv没有被标记过 then
1:询问某两个点之间的min(u,v)
2:删除一条边
你的任务是对于每个询问,输出min(u,v)的值。 (WC2006)
2024/2/27
5
第五页,共79页。
水管局长(2)
数据范围约定 结点个数N≤1000 图中的边数M≤100000 询问(xúnwèn)次数Q≤100000 删边次数D≤5000
32
第三十二页,共79页。
关键(guānjiàn)网线(2)
朴素算法: 枚举每条边,删除它,然后判断是否有独立
出来的连通区域内没有A属性或者(huòzhě)没 有B属性。复杂度O(M2) 当然,这个复杂度太大了!
2024/2/27
33
第三十三页,共79页。
关键(guānjiàn)网线(3)
a
b
2024/2/27
27
第二十七页,共79页。
嗅探器(2)
数据范围(fànwéi)约定 结点个数N≤100 边数M≤N*(N-1)/2
2024/2/27
28
第二十八页,共79页。
嗅探器(3)
朴素算法: 枚举每个点,删除它,然后(ránhòu)判断a和
b是否连通,时间复杂度O(NM) 如果数据范围扩大,该算法就失败了!
8
第八页,共79页。
水管局长(5)
图论总结(超强大)解读

1.图论Graph Theory1.1.定义与术语Definition and Glossary1.1.1.图与网络Graph and Network1.1.2.图的术语Glossary of Graph1.1.3.路径与回路Path and Cycle1.1.4.连通性Connectivity1.1.5.图论中特殊的集合Sets in graph1.1.6.匹配Matching1.1.7.树Tree1.1.8.组合优化Combinatorial optimization1.2.图的表示Expressions of graph1.2.1.邻接矩阵Adjacency matrix1.2.2.关联矩阵Incidence matrix1.2.3.邻接表Adjacency list1.2.4.弧表Arc list1.2.5.星形表示Star1.3.图的遍历Traveling in graph1.3.1.深度优先搜索Depth first search (DFS)1.3.1.1.概念1.3.1.2.求无向连通图中的桥Finding bridges in undirected graph1.3.2.广度优先搜索Breadth first search (BFS)1.4.拓扑排序Topological sort1.5.路径与回路Paths and circuits1.5.1.欧拉路径或回路Eulerian path1.5.1.1.无向图1.5.1.2.有向图1.5.1.3.混合图1.5.1.4.无权图Unweighted1.5.1.5.有权图Weighed —中国邮路问题The Chinese post problem1.5.2.Hamiltonian Cycle 哈氏路径与回路1.5.2.1.无权图Unweighted1.5.2.2.有权图Weighed —旅行商问题The travelling salesman problem1.6.网络优化Network optimization1.6.1.最小生成树Minimum spanning trees1.6.1.1.基本算法Basic algorithms1.6.1.1.1.Prim1.6.1.1.2.Kruskal1.6.1.1.3.Sollin(Boruvka)1.6.1.2.扩展模型Extended models1.6.1.2.1.度限制生成树Minimum degree-bounded spanning trees1.6.1.2.2.k小生成树The k minimum spanning tree problem(k-MST)1.6.2.最短路Shortest paths1.6.2.1.单源最短路Single-source shortest paths1.6.2.1.1.基本算法Basic algorithms1.6.2.1.1.1. ..................................................................................................... D ijkstra1.6.2.1.1.2. .......................................................................................... B ellman-Ford1.6.2.1.1.2.1.....................................Shortest path faster algorithm(SPFA)1.6.2.1.2.应用Applications1.6.2.1.2.1. ........................... 差分约束系统System of difference constraints1.6.2.1.2.2. .......................... 有向无环图上的最短路Shortest paths in DAG1.6.2.2.所有顶点对间最短路All-pairs shortest paths1.6.2.2.1.基本算法Basic algorithms1.6.2.2.1.1. ....................................................................................... F loyd-Warshall1.6.2.2.1.2. .................................................................................................... Johnson 1.6.3.网络流Flow network1.6.3.1.最大流Maximum flow1.6.3.1.1.基本算法Basic algorithms1.6.3.1.1.1. ........................................................................ Ford-Fulkerson method1.6.3.1.1.1.1.......................................................... E dmonds-Karp algorithm1.6.3.1.1.1.1.1. ................................................... M inimum length path1.6.3.1.1.1.1.2. ........................................... Maximum capability path1.6.3.1.1.2. ............................................... 预流推进算法Preflow push method1.6.3.1.1.2.1.................................................................................. P ush-relabel1.6.3.1.1.2.2........................................................................... Relabel-to-front1.6.3.1.1.3. .......................................................................................... Dinic method1.6.3.1.2.扩展模型Extended models1.6.3.1.2.1. ............................................................................... 有上下界的流问题1.6.3.2.最小费用流Minimum cost flow1.6.3.2.1.找最小费用路Finding minimum cost path1.6.3.2.2.找负权圈Finding negative circle1.6.3.2.3.网络单纯形Network simplex algorithm1.6.4.匹配Matching1.6.4.1.二分图Bipartite Graph1.6.4.1.1.无权图-匈牙利算法Unweighted - Hopcroft and Karp algorithm1.6.4.1.2.带权图-KM算法Weighted –Kuhn-Munkres(KM) algorithm1.6.4.2.一般图General Graph1.6.4.2.1.无权图-带花树算法Unweighted - Blossom (Edmonds)1.图论Graph Theory1.1. 定义与术语Definition and Glossary1.1.1.图与网络Graph and Network二元组(),V E称为图(graph)。
与图论相关的算法

广度优先搜索
procedure bfs(i:integer); var p:arcptr;
closed,open:integer; q:array[1..maxn] of integer; begin 访问并处理顶点i; map[i].visited:=true; 顶点i进入队列q; closed:=0; open:=1; repeat
编号都不超过k的路径。 递推公式:
t(k)[i,j]= t(k-1)[i,j] or (t(k-1)[i,k] and t(k-1)[k,j])
Johnson算法
Johnson算法常用于求顶点个数较多的稀 疏图的每对点间最短路问题。
感兴趣的同学请参阅《国际信息学奥林 匹克竞赛指导——实用算法的分析与程 序设计》
inc(closed); v:=q[closed]; p:=map[v].firstarc; while p<>nil do begin
if map[p^.v].visited=false then begin 访问并处理顶点q^.v; map[q^.v].visited=true; inc(open); q[open]:=q^.v; end;
q:=q^.nextarc; end; until closed=open; end;
计算连通分支数
count:=0; for i:=1 to n do
map[i].visited:=false; for i:=1 to n do
if map[i].visited=false do begin inc(count); dfs(i); end;
2013电子科大研究生图论考试 附答案

1电子科技大学研究生试卷(考试时间: 至 ,共__2_小时)课程名称 图论及其应用 教师 学时 60 学分 教学方式 讲授 考核日期_2013__年_6__月__20__日 成绩 考核方式: (学生填写)一.填空题(每空2分,共20分)1. n 阶k 正则图G 的边数m =_____。
2.4个顶点的不同构单图的个数为________。
3.完全偶图,r s K (,2r s ≥且为偶数),则在其欧拉环游中共含____条边。
4.高为h 的完全2元树至少有_______片树叶。
5. G 由3个连通分支124,,K K K 组成的平面图,则其共有_______个面。
6. 设图G 与5K 同胚,则至少从G 中删掉_______条边,才可能使其成为可平面图。
7. 设G 为偶图,其最小点覆盖数为α,则其最大匹配包含的边数为________。
8. 完全图6K 能分解为________个边不重合的一因子之并。
9. 奇圈的边色数为______。
10. 彼得森图的点色数为_______。
二.单项选择(每题3分,共15分) 1.下面说法错误的是( )学 号 姓 名 学 院…………………… 密……………封……………线……………以……………内……………答…… ………题……………无……………效……………………2(A) 图G 中的一个点独立集,在其补图中的点导出子图必为一个完全子图;(B) 若图G 连通,则其补图必连通; (C) 存在5阶的自补图; (D) 4阶图的补图全是可平面图. 2.下列说法错误的是( ) (A) 非平凡树是偶图;(B) 超立方体图(n 方体,1n ≥)是偶图; (C) 存在完美匹配的圈是偶图; (D) 偶图至少包含一条边。
3.下面说法正确的是( )(A) 2连通图一定没有割点(假定可以有自环); (B) 没有割点的图一定没有割边;(C) 如果3阶及其以上的图G 是块,则G 中无环,且任意两点均位于同一圈上;(D) 有环的图一定不是块。
离散数学中路径与圈知识点详解

离散数学中路径与圈知识点详解离散数学是计算机科学中的重要基础学科之一,路径与圈是其中的核心概念之一。
在这篇文章中,我们将详细解释路径与圈的概念和相关知识点,以帮助读者更好地理解和应用离散数学中的路径与圈。
一、路径的定义与性质在图论中,路径是指由图中的顶点和边所构成的序列。
形式化地说,路径可以定义为一个顶点的非空序列,其中顶点之间通过边相连。
路径的长度等于路径中边的数量。
路径具有以下性质:1. 路径可以是有向的或无向的,具体取决于图的类型。
2. 在有向图中,路径可以是有向边的序列,顶点之间按照边的方向顺序相连。
3. 在无向图中,路径可以是顶点的序列,顶点之间通过边相连,但没有方向之分。
4. 路径的长度可以通过统计路径中的边数来计算。
二、圈的定义与性质在图论中,圈是指起点和终点相同的路径。
圈也被称为环或回路。
形式化地说,圈可以定义为一个顶点的非空序列,其中起点和终点相同,而且路径中除起点和终点之外的顶点是互不相同的。
圈具有以下性质:1. 圈可以是有向的或无向的,具体取决于图的类型。
2. 在有向图中,圈是有向边的序列,起点和终点相同。
3. 在无向图中,圈是顶点的序列,起点和终点相同,且路径中除起点和终点之外的顶点不重复。
4. 圈的长度等于圈中边的数量。
三、路径与圈在离散数学中的应用路径与圈在离散数学中有广泛的应用,特别是在图论、网络分析和算法设计中。
以下是路径与圈常见的应用场景:1. 最短路径问题:在给定图中寻找两个顶点之间的最短路径。
最短路径算法,如迪杰斯特拉算法和弗洛伊德算法,就是基于路径的概念来设计的。
2. 图的连通性:路径与圈可以帮助我们判断一个图是否连通,即是否存在路径或圈连接图中的所有顶点。
3. 图的环路检测:通过检测图中是否存在圈,可以判断图是否有环。
在拓扑排序和关键路径分析中,环路检测是一个重要的步骤。
4. 调度问题:路径与圈可以用来解决任务调度问题,如在工厂中优化生产流程,或在计算机网络中优化数据传输路径等。
图论入门篇

实现细节
1. if (d[v] == -1) dfs(v);
//树边, 递归遍历
2. else if (f[v] == -1) show(“B”); //后向边
3. else if (d[v] > d[u]) show(“F”); // 前向边
3. begin read(n); for i:=1 to n do begin new(head[i]); head[i]^.key:=i; head[i]^.next:=nil; end; read(m); s:=0; for i:=1 to m do begin read(edgex[i],edgey[i]); new(p); p^.key:=edgey[i]; p^.next:=head[edgex[i]]; head[edgex[i]]:=p; end; fillchar(f,sizeof(f),true); fillchar(instack,sizeof(instack),false); top:=0;time:=0; for i:=1 to n do if f[i] then tarjan(i); fillchar(s1,sizeof(s1),0);
非连通图有多个连通分量(connected component, cc), 每个连通分量是一个 极大连通子图(maximal connected subgraph)
完全图和补图
完全图:N个顶点的图,有N(N-1)/2个节点 对于(u,v), 若邻接则改为非邻接, 若非邻接则改为邻接, 得到的图为原图的补
int j; DFN[i]=LOW[i]=++Dindex; instack[i]=true; Stap[++Stop]=i; for (edge *e=V[i];e;e=e->next) {
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016/4/10
浙江省2006年集训讲义
9
水管局长(6)
这里我们采取父亲表示法来存储一棵最小生
成树,如图所示:
如果被删边在 现在添加入一条红色的边 B到LCA(A,B){A AB 和 我们根据被删边所在的位置来决 定 B 的最近公共祖先 AB的定向 }的那条路径上, 则定义AB的方向为B->A,即A是 B的父亲,并将被删边到B的这条 路径上的所有边反向(同理可得被 删边在A到LCA(A,B)的那条路径 上的情况)
a
b
2016/4/10
浙江省2006年集训讲义
27
嗅探器(2)
数据范围约定
结点个数N≤100 边数M≤N*(N-1)/2
2016/4/10
浙江省2006年集训讲义
28
嗅探器(3)
朴素算法:
枚举每个点,删除它,然后判断a和b是否连
通,时间复杂度O(NM) 如果数据范围扩大,该算法就失败了!
浙江省2006年集训讲义 22
2016/4/10
割边
G是连通图,e∈E(G),G – e 不再连通,则称
e是G的割边,亦称做桥。
2016/4/10
浙江省2006年集训讲义
23
求割边的算法
与割点类似的,我们定义lowlink和dfn。父子
边e=u→v ,当且仅当lowlink[v] > dfn[u]的时 候,e是割边。 我们可以根据割点算法的证明类似的证明割 边算法的正确性。
2016/4/10 浙江省2006年集训讲义 34
关键网线(4)
下图中,蓝色的边表示题目要求的边,黄色
的边表示虽然是图中的割边,但不是题目要 求的边。 A
B B A A A B
2016/4/10
A
A
A
A
35
浙江省2006年集训讲义
块
没有割点的图叫2-连通图,亦称做块,G中成
2016/4/10
浙江省2006年集训讲义
14
改进算法
在floyd的同时,顺便算出最小环
g[i][j]=i,j之间的边长 dist:=g; for k:=1 to n do begin for i:=1 to k-1 do for j:=i+1 to k-1 do answer:=min(answer,dist[i][j]+g[i][k]+g[k][j]); for i:=1 to n do for j:=1 to n do dist[i][j]:=min(dist[i][j],dist[i][k]+dist[k][j]); 算法证明? end;
33
关键网线(3)
正如嗅探器一样,题目要求的边一定是原图
中的割边,但是原图中的割边却不一定是题 目中要求的边。 设A种属性总共有SUMA个,B中属性总共有 SUMB个。和嗅探器类似的,如果边e=u→v 是割边,且以v为根的子树中,A种属性的数 目为0或者为SUMA,或者B种属性的数目为0 或者为SUMB,那么e就是题目要求的边。
2016/4/10
浙江省2006年集训讲义
29
嗅探器(4)
题目要求的点一定是图中的割点,但是图中
的割点不一定题目要求的点。如上图中的蓝 色点,它虽然是图中的割点,但是割掉它之 后却不能使a和b不连通 由于a点肯定不是我们所求的点,所以可以以 a为根开始DFS遍历整张图。 对于生成的DFS树,如果点v是割点,如果以 他为根的子树中存在点b,那么该点是问题所 求的点。
11
最小环问题
虽然涉及到要求最小环的题目并不多
(Ural1004 Sightseeing trip),但是下面介绍 的一些求最小环的算法也会对你有一定的启 示意义
有向带权图的最小环问题(直接用floyd算法可解) 无向带权图的最小环问题
2016/4/10
浙江省2006年集训讲义
12
朴素算法
2016/4/10 浙江省2006年集训讲义
证明?
21
程序代码
PROCEDURE DFS(v); begin inc(sign); dfn[v] := sign; //给v按照访问顺序的先后标号为sign lowlink[v] := sign; //给lowlink[v]赋初始值 for 寻找一个v的相邻节点u if 边uv没有被标记过 then begin 标记边uv; 给边定向v→u; if u未被标记过 then begin DFS(u); //uv是父子边,递归访问 lowlink[v] := min(lowlink[v],lowlink[u]); if lowlink[u] >= dfn[v] then v是割点 end else lowlink[v] := min(lowlink[v],dfn[u]); //uv是返祖边 end; end;
浙江省2006年集训讲义
三个定理
定理1:DFS中,e=ab是返祖边,那么要么a
是b的祖先,要么a是b的后代子孙。
证明?
定理2:DFS中,e=uv是父子边,且dfn[u]>1,
lowlink[v]≥dfn[u],则u是割点。
证明?
定理3:DFS的根r是割点的充要条件是:至
少有2条以r为尾(从r出发)的父子边
浙江省2006年集训讲义 15
2016/4/10
块及其相关知识
DFS算法
割点 (一般对于无向图而言) 割边 (一般对于无向图而言)
块(一般对于无向图而言)
强连通子图(一般对于有向图而言)
2016/4/10
浙江省2006年集训讲义
16
DFS算法
浙江省2006年集训讲义
19
求割点的算法
我们通过DFS把无向图定向成有向图,定义
每个顶的一个lowlink参数,lowlink[v]表示沿v 出发的有向轨能够到达的点u中,dfn[u]的值 的最小值。(经过返祖边后则停止)
1.1 2.1 3.2 4.2 5.2
6.1
2016/4/10
7.7
20
2016/4/10
浙江省2006年集训讲义
24
程序代码
PROCEDURE DFS(v); begin inc(sign); dfn[v] := sign; //给v按照访问顺序的先后标号为sign lowlink[v] := sign; //给lowlink[v]赋初始值 for 寻找一个v的相邻节点u if 边uv没有被标记过 then begin 标记边uv; 给边定向v→u; if u未被标记过 then begin DFS(u); //uv是父子边,递归访问 lowlink[v] := min(lowlink[v],lowlink[u]); if lowlink[u] > dfn[v] then vu是割边 end else lowlink[v] := min(lowlink[v],dfn[u]); //uv是返祖边 end; end;
根据kruskal算法可以知道,最小生成树上的
连接两点之间的唯一路径一定是最大边最小 的 那么,只要维护一棵图的最小生成树,那么 就可以在O(N)的时间内回答每一个min(u,v) 的询问 不断的删边然后维护最小生成树?
2016/4/10
浙江省2006年集训讲义
7
水管局长(4)
通过删边的形式我们似乎很难维护一张图的
B
2016/4/10 浙江省2006年集训讲义 10Βιβλιοθήκη A小H的聚会(1)
给定每个节点的度限制,求在满足所有度限
制的条件下的最大生成树。(NOI2005) 这是一道提交答案式的题目,对于后面的几 个较大的数据,用另类MST算法对你的解进 行调整也能取得不错的效果!
2016/4/10
浙江省2006年集训讲义
浙江省2006年集训讲义 17
2016/4/10
DFS算法
父子边用黑色标记,返祖边用红色标记
如下图,除掉返祖边之后,我们可以把它看
作一棵DFS树
1 2 3 4 5
6
7
2016/4/10
浙江省2006年集训讲义
18
割点
G是连通图,v∈V(G),G – v 不再连通,则称
v是G的割顶。
2016/4/10
令e(u,v)表示u和v之间的连边,再令min(u,v)
表示,删除u和v之间的连边之后,u和v之间 的最短路 最小环则是min(u,v) + e(u,v) 时间复杂度是EV2
2016/4/10
浙江省2006年集训讲义
13
一个错误的算法
预处理出任意两点之间的最短路径,记作
min(u,v) 枚举三个点w,u,v,最小环则是min(u,w) + min(w,v) + e(u,v)的最小值 如果考虑min(u,w)包含边u-v的情况? 讨论:是否有解决的方法?
边,并删除新生成的环上的最大边。
1
10 7 5
3
算法证明? 2
2016/4/10
浙江省2006年集训讲义
4
水管局长(1)
给定一张带权无向连通图,定义max(p)为路
径p上的最大边,min(u,v)为连接u和v的所有 路径中,max(p)的最小值。动态的做如下两 个操作:
1:询问某两个点之间的min(u,v) 2:删除一条边
最小生成树 根据刚才提到的MST的另类做法,我们反向 处理它的每个操作,也就是先删除所有要删 的边,然后再逆向添边并回答min(u,v) 于是该问题就可以用另类MST算法解决了
