立体几何平行证明题教程文件

合集下载

用空间向量证(解)立体几何题之——证明线面平行ppt 人教课标版

通过本例的练习，同学们要进一步掌握平面法向量的求法：即用平面内的两个相交向量与假设的法向量求数量积等于0，利用解方程组的方法求出平面法向量(在解的过程中可令其中一个未知数为某个数)。
( 1 , 1 , 1 ) 同理可得平面 CB1D 1的法向量为m
例4.在正方体ABCDA1B1C1D1中，E、F、 G、H分别是A1B1、 B1C1、C1D1、D1A1的中点. 求证：平面AEH∥平面BDGF
例3.在正方体ABCDA1B1C1D1中，求证： A 1 平面A1BD∥平面CB1D1
平行四边形A1BCD1 A1B∥D1C 平行四边形DBB1D1 B1D1∥BD
D1
B1
C1
D A B
C
于是平面A1BD∥平面CB1D1
证明：建立如图所示的空间直角坐标系o-xyz 设正方形边长为1， A1 ( 1 ,0 , 1 ) 则向量 DA 1
C N B
再见
•
• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •
46．凡事不要说＂我不会＂或＂不可能＂，因为你根本还没有去做！ 47．成功不是靠梦想和希望，而是靠努力和实践． 48．只有在天空最暗的时候，才可以看到天上的星星． 49．上帝说：你要什么便取什么，但是要付出相当的代价． 50．现在站在什么地方不重要，重要的是你往什么方向移动。 51．宁可辛苦一阵子，不要苦一辈子． 52．为成功找方法，不为失败找借口． 53．不断反思自己的弱点，是让自己获得更好成功的优良习惯。 54．垃圾桶哲学：别人不要做的事，我拣来做！ 55．不一定要做最大的，但要做最好的． 56．死的方式由上帝决定，活的方式由自己决定！ 57．成功是动词，不是名词！ 28、年轻是我们拼搏的筹码，不是供我们挥霍的资本。 59、世界上最不能等待的事情就是孝敬父母。 60、身体发肤，受之父母，不敢毁伤，孝之始也；立身行道，扬名於后世，以显父母，孝之终也。——《孝经》 61、不积跬步，无以致千里；不积小流，无以成江海。——荀子《劝学篇》 62、孩子：请高看自己一眼，你是最棒的！ 63、路虽远行则将至，事虽难做则必成！ 64、活鱼会逆水而上，死鱼才会随波逐流。 65、怕苦的人苦一辈子，不怕苦的人苦一阵子。 66、有价值的人不是看你能摆平多少人，而是看你能帮助多少人。 67、不可能的事是想出来的，可能的事是做出来的。 68、找不到路不是没有路，路在脚下。 69、幸福源自积德，福报来自行善。 70、盲目的恋爱以微笑开始，以泪滴告终。 71、真正值钱的是分文不用的甜甜的微笑。 72、前面是堵墙，用微笑面对，就变成一座桥。 73、自尊，伟大的人格力量；自爱，维护名誉的金盾。 74、今天学习不努力，明天努力找工作。 75、懂得回报爱，是迈向成熟的第一步。 76、读懂责任，读懂使命，读懂感恩方为懂事。 77、不要只会吃奶，要学会吃干粮，尤其是粗茶淡饭。 78、技艺创造价值，本领改变命运。 79、凭本领潇洒就业，靠技艺稳拿高薪。 80、为寻找出路走进校门，为创造生活奔向社会。 81、我不是来龙飞享福的，但，我是为幸福而来龙飞的！ 82、校兴我荣，校衰我耻。 83、今天我以学校为荣，明天学校以我为荣。 84、不想当老板的学生不是好学生。 85、志存高远虽励志，脚踏实地才是金。 86、时刻牢记父母的血汗钱来自不易，永远不忘父母的养育之恩需要报答。 87、讲孝道读经典培养好人，传知识授技艺打造能人。 88、知技并重，德行为先。 89、生活的理想，就是为了理想的生活。 —— 张闻天 90、贫不足羞，可羞是贫而无志。 —— 吕坤

方法技巧专题05 立体几何中平行与垂直证明(解析版)

方法技巧专题5 立体几何中平行与垂直证明解析版一、立体几何中平行与垂直知识框架cc∥∥b a ba ∥⇒ 二、立体几何中的向量方法【一】“平行关系”常见证明方法 1.1 直线与直线平行的证明1.1.1 利用某些平面图形的特性：如平行四边形的对边互相平行等 1.1.2 利用三角形中位线性质1.1.3 利用空间平行线的传递性（即公理4）：平行于同一条直线的两条直线互相平行。

1.1.4 利用直线与平面平行的性质定理：如果一条直线与一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行。

1.1.5 利用平面与平面平行的性质定理：如果两个平行平面同时和第三个平面相交，那么它们的交线平行．1.1.6 利用直线与平面垂直的性质定理：垂直于同一个平面的两条直线互相平行。

1.1.7 利用平面内直线与直线垂直的性质：在同一个平面内，垂直于同一条直线的两条直线互相平行。

1.1.8 利用定义：在同一个平面内且两条直线没有公共点 1.2 直线与平面平行的证明1.2.1 利用直线与平面平行的判定定理：平面外的一条直线与此平面内的一条直线平行，则该直线与此平面平行。

αbaabαβ ba a =⋂⊂βαβα∥ba ∥⇒b a b a ////⇒⎪⎭⎪⎬⎫==γβγαβα βα⊥⊥b a ba ∥⇒b∥a b a αα⊂⊄α∥a ⇒αab1.2.2 利用平面与平面平行的性质推论：两个平面互相平行，则其中一个平面内的任一直线平行于另一个平面。

1.2.3 利用定义：直线在平面外，且直线与平面没有公共点 1.3 平面与平面平行的证明1.3.1 利用平面与平面平行的判定定理：一个平面内的两条相交直线与另一个平面平行，则这两个平面平行。

1.3.2 利用某些空间几何体的特性：如正方体的上下底面互相平行等1.3.3 利用定义：两个平面没有公共点 1.例题【例1】如图，已知菱形ABCD ，其边长为2，60BAD ∠=，ABD ∆绕着BD 顺时针旋转120得到PBD ∆，M 是PC 的中点．（1）求证：//PA 平面MBD ；（2）求直线AD 与平面PBD 所成角的正弦值．证明（1）连结AC 交BD 于点O ，连结OM 在菱形ABCD 中，O 为AC 中点，M 为PC 的中点∴OM 为∆APC 的中位线，∴OM ∥AP ---------------（利用1.1.2中位线性质）又OM ⊂面MBD ，且PA ⊄面MBD∴//PA 平面MBD ----------------（利用1.2.1直线与平面平行的判定定理）【例2】已知四棱锥P-ABCD ，底面ABCD 是60=∠A 、边长为a 的菱形，又ABCD PD 底⊥，且PD=CD ，点M 、N 分别是棱AD 、PC 的中点．βαaβαα∥⊂a β∥a ⇒ααββ////∩⊂⊂b a P b a b a =αβ//⇒αβbaP证明：DN//平面PMB。

方法技巧专题05立体几何中平行与垂直证明

方法技巧专题05立体几何中平行与垂直证明平行与垂直证明是立体几何中的重要内容之一，本文将介绍一些方法和技巧用于解决平行与垂直的证明问题。

一、平行性的证明方法：1.公共光线法：如果两条直线分别与第三条直线相交，在相交点处的两个对应的内角相等，则这两条直线是平行的。

例如，如果直线AB和CD都与直线EF相交，在交点F处的∠AFC=∠DFB，则AB，CD。

2.反证法：假设AB和CD不平行，然后通过构造形式，证明得到矛盾。

例如，如果直线AB和CD不平行，则可以证明存在一条直线EF与这两条直线分别相交于F和G，且所形成的内角∠FAG=π/2-∠DAF≠π/2，则与直线EF平行，这是与已知条件矛盾的，所以AB，CD。

3.平行线性质法：利用平行线的性质来证明其他线段平行。

例如，根据平行线的交角性质可证明，如果一条直线与一对平行线之一形成等于直角的角，则与另一条平行线也形成等于直角的角。

二、垂直性的证明方法：1.垂直线性质法：利用垂直线的性质来证明其他线段垂直。

例如，如果直线AB与直线CD相交于点E，且∠AED=∠BEC=π/2，则直线AB垂直于直线CD。

2.垂直线段法：如果两条线段的斜率之积为-1，则这两条线段垂直。

例如，如果直线AB和直线CD的斜率之积为-1，则AB⊥CD。

3.反证法：假设AB和CD不垂直，然后通过构造形式，证明得到矛盾。

例如，如果直线AB和CD不垂直，则可以证明存在一条直线EF与这两条直线相交于点G，且所形成的两个内角∠GAC和∠GDB之和小于π/2，这与直线EF垂直的性质矛盾，所以AB⊥CD。

综上所述，平行与垂直证明可以通过公共光线法、反证法、平行线性质法、垂直线性质法、垂直线段法等方法和技巧来解决。

在实际问题中，可以根据已知条件选择合适的方法和技巧，灵活运用来解决平行与垂直的证明问题。

专题20立体几何中的平行与垂直问题(解析版)

专题20 立体几何中的平行与垂直问题一、题型选讲题型一、线面平行与垂直知识点拨：证明直线与平面的平行与垂直问题，一定要熟练记忆直线与平面的平行与垂直判定定理和性质定理，切记不可缺条件。

直线与平面的平行有两种方法：一是在面内找线；二是通过面面平行转化。

直线与平面垂直关键是找两条相交直线例1、（2019南通、泰州、扬州一调）如图，在四棱锥PABCD中，M, N分别为棱PA, PD的中点.已知侧面PAD丄底面ABCD,底面ABCD是矩形，DA=DP.求证：（1）MN〃平面PBC；MD丄平面PAB.【证明】（1）在四棱锥P-ABCD中，M, N分别为棱PA, PD的中点，所以MN〃AD.（2分）又底面ABCD是矩形，所以BC〃AD.所以MN〃BC.（4分）又BC U平面PBC，MN Q平面PBC，所以MN〃平面PBC. （6分）（2）因为底面ABCD是矩形，所以AB丄AD.又侧面PAD丄底面ABCD，侧面PAD n底面ABCD=AD, AB U底面ABCD，所以AB丄侧面PAD.（8分）又MD U侧面PAD，所以AB丄MD.（10分）因为DA=DP,又M为AP的中点，从而MD丄PA. （12分）又PA，AB在平面PAB内，PA n AB=A，所以MD丄平面PAB.（14分）例2、（2019扬州期末）如图所示，在三棱柱ABCA1B1C1中，四边形AA1B1B为矩形，平面AA1B1B丄平面ABC,点E，F分别是侧面AA1B1B，BB1C1C对角线的交点.（1）求证：EF〃平面ABC；（2）求证：BB］丄AC.规范解答（1）在三棱柱ABCA1B1C1中，四边形AA1B1B,四边形BB1C1C均为平行四边形，E, F分别是侧面AA1B1B, BB1C1C对角线的交点，所以E, F分别是AB1，CB1的中点，所以EF〃AC.（4分）因为EF Q平面ABC, AC U平面ABC，所以EF〃平面ABC.（8分）（2）因为四边形AA1B1B为矩形，所以BB1丄AB.因为平面AA1B1B丄平面ABC,且平面AA1B1B n平面ABC=AB, BB1U平面AA1B1B, 所以BB1丄平面ABC.（12分）因为AC U平面ABC，所以BB1丄AC.（14分）例3、（2019南京、盐城二模）如图，在三棱柱ABCA1B1C1中，AB=AC, A1C丄BC］, AB］丄BC1，D, E 分别是AB1和BC的中点.求证：（1）DE〃平面ACC1A1；（2）AE丄平面BCC1B1.A _________ c,规范解答⑴连结A1B，在三棱柱ABCA1B1C1中，AA1#BB1且AA1=BB1，所以四边形AA1B1B是平行四边形．又因为D是AB1的中点，所以D也是BA1的中点.（2分）在厶BA1C中，D和E分别是BA1和BC的中点，所以DE〃A］C.又因为DE G平面ACC1A1，A1C U平面ACC1A1，所以DE〃平面ACC1A1.（6分）（2）由（1）知DE〃A］C，因为A1C丄BC” 所以BC］丄DE.（8 分）又因为BC］丄AB1，AB1H DE=D，AB1，DE U平面ADE，所以BC1丄平面ADE.又因为AE U平在ADE,所以AE丄BC1.（10分）在厶ABC中，AB=AC，E是BC的中点，所以AE丄BC.（12分）因为AE丄BC1，AE丄BC，BC1H BC=B，BC1，BC U平面BCC1B1，所以AE丄平面BCC1B1. （14 分）例4、（2019苏锡常镇调研）如图，三棱锥DABC中，已知AC丄BC，AC丄DC，BC=DC，E，F 分别为BD，CD 的中点．求证：（1）EF〃平面ABC；（2）BD丄平面ACE.所以EF 〃平面ABC.（6分）（2）因为AC丄BC，AC丄DC，BC H DC = C，BC，DC U平面BCD所以AC丄平面BCD，（8分）因为BD U平面BCD，所以AC丄BD，（10分）因为DC=BC，E为BD的中点，所以CE丄BD，（12分）因为AC n CE = C, AC，CE U平面ACE，所以BD丄平面ACE.（14分）例5、（2019苏州三市、苏北四市二调）如图，在直三棱柱ABCA1B1C1中，侧面BCC1B1为正方形，A1B1 丄B1C1•设A1C与AC1交于点D, B1C与BC1交于点E.求证：（1） DE〃平面ABB1A1；（2） BC］丄平面A1B1C.规范解答（1）因为三棱柱ABCA1B1C1为直三棱柱，所以侧面ACC1A1为平行四边形．又A1C 与AC1 交于点D,所以D为AC]的中点，同理，E为BC]的中点•所以DE〃AB.（3分）又AB U平面ABB]A], DE G平面ABB]A], 所以DE〃平面ABB]A].（6分）（2）因为三棱柱ABCA]B]C]为直三棱柱，所以BB]丄平面A]B]C]. 又因为A]B]U平面A]B]C],所以BB]丄A]B i.（8分）又A]B]丄B]C], BB], B]C] U 平面BCC]B], BB]n B]C1=B1，所以A]B]丄平面BCC]B].（10 分）又因为BC]U平面BCC]B1，所以A]B丄BC].（12分）又因为侧面BCC]B1为正方形，所以BC]丄BQ.又A1B1n B1C=B1，A1B1，B1C U平面A1B1C, 所以BC1丄平面A1B1C.（14分）例6、（2017苏北四市一模）如图，在正三棱柱ABCA1B1C1中，已知D, E分别为BC, B1C1的中点，点F 在棱CC1上，且EF丄CD.求证：（1）直线A1E〃平面ADC1；⑴证法1连结ED,因为D, E分别为BC, B1C1的中点，所以B&/BD且B1E=BD, 所以四边形BBDE是平行四边形，（2分）所以BB/DE且BB1=DE. 又BB]〃AA]且BB]=AA], 所以AA/DE且AA1=DE, 所以四边形AA]ED是平行四边形，所以A]E〃AD.（4分）又因为AE G平面ADC, AD U平面ADC，所以直线AE〃平面ADC.（7分）1 1 1畀 ------ 1B证法2连结ED,连结A1C, EC分别交AC” DC1于点M, N,连结MM,则因为D, E分别为BC,B1C1的中点，所以C1E^CD且C、E=CD,所以四边形C1EDC是平行四边形，所以N是CE的中点.（2分）因为A1ACC1为平行四边形，所以M是A1C的中点，（4分）所以MN//A\E.又因为A]E G平面ADC，MN U平面ADC，，所以直线Af〃平面ADC、.（7分）（2）在正三棱柱ABCA1B1C1中，BB]丄平面ABC.又AD U平面ABC，所以AD丄BB、.又A ABC是正三角形，且D为BC的中点，所以AD丄BC.（9分）又BB，，BC U 平面BBCC，，BB1A BC=B，所以AD丄平面B,BCC,，又EF U平面BBCC，所以AD丄EF.（11分）又EF丄CD，CD，AD U平面ADC,，C,D A AD=D，所以直线EF丄平面ADC,.（14分）题型二、线面与面面平行与垂直证明平面与平面的平行与垂直问题，一定要熟练记忆平面与平面的平行与垂直判定定理和性质定理，切记不可缺条件。

立体几何直线平面平行的判定和性质课件文

2023-11-06•直线与平面平行的判定•直线与平面平行的性质•直线与平面平行的重要结论•立体几何直线平面平行问题建模•立体几何直线平面平行问题的求解策略目录01直线与平面平行的判定直线与平面平行是指直线与平面内任意一条直线都无公共点，即直线与平面平行。

直线与平面平行的基本性质是：如果直线与平面平行，则直线与平面内的任意一条直线都平行。

直线与平面平行的定义直线与平面平行的判定定理如果一条直线与一个平面平行，那么这条直线与此平面内的任何一条直线都平行。

如果一条直线与一个平面平行，那么这条直线的方向向量与此平面的法向量垂直。

如果一条直线与一个平面平行，那么这条直线的斜率与此平面的法向量的斜率互为相反数的倒数。

在工程学中，直线与平面平行的判定定理也被广泛应用，例如在机械加工、建筑设计等领域中，都需要用到这个定理来计算和设计物体的位置和形状。

直线与平面平行判定的应用在立体几何中，我们常常需要判断一条直线是否与一个平面平行，或者判断一个平面是否与另一个平面平行。

通过直线与平面平行的判定定理，我们可以很容易地判断出直线与平面的位置关系，从而解决一些立体几何的问题。

02直线与平面平行的性质直线与平面平行的性质定理直线与平面平行，则该直线与平面内的任意一条直线均无交点，因此它们平行或异面。

若直线与平面平行，则该直线与平面的垂线互相垂直。

若两条直线都与同一平面平行，则它们的夹角为0度。

直线与平面平行性质的应用在建筑学中，可以利用直线与平面平行的性质来设计建筑物的结构，确保其稳定性和安全性。

在机械加工中，可以利用直线与平面平行的性质来加工和测量工件的尺寸和形状。

在实际生活中，可以利用直线与平面平行的性质来检测平直的物体或线段是否平行。

直线与平面平行性质的证明方法方法一01利用直线与平面平行的判定定理证明直线与平面平行，然后根据性质定理得出结论。

方法二02利用反证法证明直线与平面平行。

假设直线与平面不平行，根据性质定理可得出矛盾，从而证明直线与平面平行。

完整)高中立体几何证明平行的专题

完整)高中立体几何证明平行的专题在此文章中，存在一些格式错误和明显有问题的段落，需要进行修改和删除。

修改后的文章如下：立体几何——平行的证明例1】如图，四棱锥P-ABCD的底面是平行四边形，点E、F分别为棱AB、PD的中点。

求证：AF∥平面PCE。

分析：取PC的中点G，连EG，FG，则易证AEGF是平行四边形。

例2】如图，已知直角梯形ABCD中，AB∥CD，AB⊥BC，AB=1，BC=2，CD=1+3，过A作AE⊥CD，垂足为E，G、F分别为AD、CE的中点，现将△ADE沿AE折叠，使得DE⊥EC。

Ⅰ）求证：BC⊥面CDE；（Ⅱ）求证：FG∥面BCD。

分析：取DB的中点H，连GH、HC，则易证FGHC是平行四边形。

例3】已知直三棱柱ABC-A1B1C1中，D、E、F分别为A1A、C1C、AB的中点，M为BE的中点，AC⊥BE。

求证：（Ⅰ）C1D⊥BC；（Ⅱ）C1D∥平面B1FM。

分析：连EA，易证C1EAD是平行四边形，于是MF//EA。

例4】如图所示，四棱锥P-ABCD底面是直角梯形，BA⊥AD，CD⊥AD，CD=2AB，E为PC的中点。

证明：EB//平面PAD。

分析：取PD的中点F，连EF、AF，则易证ABEF是平行四边形。

例5】如图，已知E、F、G、M分别是四面体的棱AD、CD、BD、BC的中点，求证：AM∥平面EFG。

分析：连MD交GF于H，易证EH是△AMD的中位线。

例6】如图，ABCD是正方形，O是正方形的中心，E是PC的中点。

求证：PA∥平面BDE。

AEBGMFCD例7】如图，三棱柱ABC-A1B1C1中，D为AC的中点。

求证：AB1//面BDC1.分析：连B1C交BC1于点E，易证ED是△B1AC的中位线。

例8】如图，平面ABEF⊥平面ABCD，四边形ABEF与ABCD都是直角梯形，∠BAD=∠FAB=90，BC//AD，BE//AF，G、H分别为FA、FD的中点。

Ⅰ）证明：四边形BCHG是平行四边形；Ⅱ）C、D、F、E四点是否共面？为什么？例9】正方体ABCD-A1B1C1D1.例10：在四棱锥P-ABCD中，AB∥CD，AB=DC，E为PD中点。

立体几何中的向量方法——证明平行及垂直

立体几何中的向量方法(一)——证明平行与垂直1．直线的方向向量与平面的法向量的确定(1)直线的方向向量：在直线上任取一非零向量作为它的方向向量．(2)平面的法向量可利用方程组求出：设a ，b 是平面α两不共线向量，n 为平面α的法向量，则求法向量的方程组为⎩⎨⎧n ·a ＝0，n ·b ＝0.2．用向量证明空间中的平行关系(1)设直线l 1和l 2的方向向量分别为v 1和v 2，则l 1∥l 2(或l 1与l 2重合)⇔v 1∥v 2.(2)设直线l 的方向向量为v ，与平面α共面的两个不共线向量v 1和v 2，则l ∥α或l ⊂α⇔存在两个实数x ，y ，使v ＝x v 1＋y v 2.(3)设直线l 的方向向量为v ，平面α的法向量为u ，则l ∥α或l ⊂α⇔v ⊥u .(4)设平面α和β的法向量分别为u 1，u 2，则α∥β⇔u 1 ∥u 2.3．用向量证明空间中的垂直关系(1)设直线l 1和l 2的方向向量分别为v 1和v 2，则l 1⊥l 2⇔v 1⊥v 2⇔v 1·v 2＝0.(2)设直线l 的方向向量为v ，平面α的法向量为u ，则l ⊥α⇔v ∥u .(3)设平面α和β的法向量分别为u 1和u 2，则α⊥β⇔u 1⊥u 2⇔u 1·u 2＝0.【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”)(1)直线的方向向量是唯一确定的．( )(2)平面的单位法向量是唯一确定的．( )(3)若两平面的法向量平行，则两平面平行．( )(4)若两直线的方向向量不平行，则两直线不平行．( )(5)若a ∥b ，则a 所在直线与b 所在直线平行．( )(6)若空间向量a 平行于平面α，则a 所在直线与平面α平行．( )1．下列各组向量中不平行的是( )A ．a ＝(1,2，－2)，b ＝(－2，－4,4)B ．c ＝(1,0,0)，d ＝(－3,0,0)C ．e ＝(2,3,0)，f ＝(0,0,0)D ．g ＝(－2,3,5)，h ＝(16,24,40)2．已知平面α有一点M (1，－1,2)，平面α的一个法向量为n ＝(6，－3,6)，则下列点P 中，在平面α的是( )A ．P (2,3,3)B ．P (－2,0,1)C ．P (－4,4,0)D ．P (3，－3,4)3．已知AB →＝(1,5，－2)，BC →＝(3,1，z )，若AB →⊥BC →，BP →＝(x －1，y ，－3)，且BP ⊥平面ABC ，则实数x ，y ，z 分别为______________．4．若A (0,2，198)，B (1，－1，58)，C (－2,1，58)是平面α的三点，设平面α的法向量n ＝(x ，y ，z )，则x ∶y ∶z ＝________.题型一证明平行问题例1 (2013·改编)如图，在四面体A －BCD 中，AD ⊥平面BCD ，BC ⊥CD ，AD ＝2，BD ＝22，M 是AD 的中点，P 是BM 的中点，点Q 在线段AC 上，且AQ ＝3QC .证明：PQ ∥平面BCD .如图，在棱长为2的正方体ABCD－A1B1C1D1中，E，F，M，N分别是棱AB，AD，A1B1，A1D1的中点，点P，Q分别在棱DD1，BB1上移动，且DP＝BQ＝λ(0<λ<2)．(1)当λ＝1时，证明：直线BC1∥平面EFPQ；(2)是否存在λ，使平面EFPQ与平面PQMN所成的二面角为直二面角？若存在，求出λ的值；若不存在，说明理由．题型二证明垂直问题例2如图所示，正三棱柱(底面为正三角形的直三棱柱)ABC—A1B1C1的所有棱长都为2，D为CC1的中点．求证：AB1⊥平面A1BD.如图所示，在四棱锥P－ABCD中，PC⊥平面ABCD，PC ＝2，在四边形ABCD中，∠B＝∠C＝90°，AB＝4，CD＝1，点M在PB上，PB＝4PM，PB与平面ABCD成30°角．(1)求证：CM∥平面PAD；(2)求证：平面PAB⊥平面PAD.题型三解决探索性问题例3 如图，棱柱ABCD－A1B1C1D1的所有棱长都等于2，∠ABC和∠A1AC均为60°，平面AA1C1C⊥平面ABCD.(1)求证：BD⊥AA1；(2)求二面角D－A1A－C的余弦值；(3)在直线CC1上是否存在点P，使BP∥平面DA1C1，若存在，求出点P的位置，若不存在，请说明理由．如图所示，四棱锥S—ABCD的底面是正方形，每条侧棱的长都是底面边长的2倍，P为侧棱SD上的点．(1)求证：AC⊥SD.(2)若SD⊥平面PAC，则侧棱SC上是否存在一点E，使得BE∥平面PAC.若存在，求SE∶EC的值；若不存在，试说明理由．利用向量法解决立体几何问题典例：如图，四棱锥P－ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点．(1)证明：PB∥平面AEC；(2)设二面角D－AE－C为60°，AP＝1，AD＝3，求三棱锥E－ACD的体积．A 组专项基础训练1．若直线l 的方向向量为a ＝(1,0,2)，平面α的法向量为n ＝(－2,0，－4)，则( )A ．l ∥αB ．l ⊥αC ．l ⊂αD ．l 与α相交2．若AB →＝λCD →＋μCE →，则直线AB 与平面CDE 的位置关系是( )A ．相交B ．平行C ．在平面D ．平行或在平面3．已知A (4,1,3)，B (2，－5,1)，C (3,7，－5)，则平行四边形ABCD 的顶点D 的坐标是( )A ．(2,4，－1)B ．(2,3,1)C ．(－3,1,5)D ．(5,13，－3)4．已知a ＝(2，－1,3)，b ＝(－1,4，－2)，c ＝(7,5，λ)，若a ，b ，c 三向量共面，则实数λ等于( )A.627B.637C.607D.6575．如图，在长方体ABCD —A 1B 1C 1D 1中，AB ＝2，AA 1＝3，AD ＝22，P 为C 1D 1的中点，M 为BC 的中点．则AM 与PM 所成的角为( )A ．60°B ．45°C ．90°D ．以上都不正确6．已知平面α的三点A (0,0,1)，B (0,1,0)，C (1,0,0)，平面β的一个法向量n ＝(－1，－1，－1)，则不重合的两个平面α与β的位置关系是________．7．设点C (2a ＋1，a ＋1,2)在点P (2,0,0)、A (1，－3,2)、B (8，－1，4)确定的平面上，则a ＝________.8．如图，在正方体ABCD —A 1B 1C 1D 1中，棱长为a ，M 、N 分别为A 1B 和AC 上的点，A 1M ＝AN ＝2a 3，则MN 与平面BB 1C 1C 的位置关系是________． 9．如图，四边形ABCD 为正方形，PD ⊥平面ABCD ，PD ∥QA ，QA ＝AB ＝12PD .证明：平面PQC ⊥平面DCQ .10．如图，在底面是矩形的四棱锥P －ABCD 中，PA ⊥底面ABCD ，E ，F 分别是PC ，PD 的中点，PA ＝AB ＝1，BC ＝2.(1)求证：EF ∥平面PAB ；(2)求证：平面PAD ⊥平面PDC .B 组专项能力提升11．如图，正方形ABCD 与矩形ACEF 所在平面互相垂直，AB ＝2，AF ＝1，M 在EF 上，且AM ∥平面BDE ，则M 点的坐标为( )A ．(1,1,1)B ．(23，23，1)C ．(22，22，1) D ．(24，24，1) 12．设u ＝(－2,2，t )，v ＝(6，－4,4)分别是平面α，β的法向量，若α⊥β，则t 等于( )A ．3B ．4C ．5D ．613．在正方体ABCD —A 1B 1C 1D 1中，P 为正方形A 1B 1C 1D 1四边上的动点，O 为底面正方形ABCD 的中心，M ，N 分别为AB ，BC 的中点，点Q 为平面ABCD 一点，线段D 1Q 与OP 互相平分，则满足MQ →＝λMN →的实数λ有________个．14．如图所示，已知直三棱柱ABC —A 1B 1C 1中，△ABC 为等腰直角三角形，∠BAC ＝90°，且AB ＝AA 1，D 、E 、F 分别为B 1A 、C 1C 、BC的中点．求证：(1)DE ∥平面ABC ；(2)B 1F ⊥平面AEF .15．在四棱锥P—ABCD中，PD⊥底面ABCD，底面ABCD为正方形，PD＝DC，E、F分别是AB、PB的中点．(1)求证：EF⊥CD；(2)在平面PAD求一点G，使GF⊥平面PCB，并证明你的结论．。

立体几何平行证明方法[20210409]

线面平行的判定✓平行四边形法
9、如图，在四棱柱1111ABCD
A B C D 中，侧棱1A A ABCD ⊥底面,AB AC ⊥,1AB ,
12,
5
AC
AA AD CD ,且点M 和N 分别为11C D B D 和的中点.
(I)求证： MN ∥平面ABCD
10、如图,四棱锥
中,,
,
分别为
的中点
(Ⅰ)求证:;
11、如图，四棱锥P ABCD -中，PA ⊥底面ABCD ，AD BC ，=3AB AD AC ==，4PA BC ==，M 为
线段AD 上一点，2AM MD =，N 为PC 的中点．（Ⅰ）证明MN
平面PAB ；
P
A
B
D
C N M
✓ 中位线法的判定
3 如图，四棱锥P —ABCD 中，ABCD 为矩形，△PAD 为等腰直角三角形，∠APD=90°，面PAD ⊥面ABCD ，且AB=1，AD=2，E 、F 分别为PC 和BD 的中点．（1）证明：EF ∥面PAD ；
4、如图，四棱锥P ABCD -中，AP PCD ⊥平面，AD BC ∥，
1
,,2AB BC AD E F ==
分别为线段,AD PC
的中点. （Ⅰ）求证：AP BEF ∥平面；
5、如图，四棱锥P ABCD -中，底面ABCD 为矩形，PA ⊥平面ABCD ，E 为PD 的中点．
（Ⅰ）证明：PB ∥平面AEC ；
✓ 通过面面平行证线面平行
3、如图四棱锥P ABCD -的底面ABCD
是平行四边形，BA BD ==
2AD =
,PA PD ==,E ,F 分
别是棱AD ,PC 的中点．（Ⅰ）证明: EF ∥平面PAB ；。

高考数学专题讲解：立体几何平行证明

高考数学专题讲解：立体几何平行证明第一部分：三角形中位线平行于底边第一部分：三角形自现原则一（原创方法）例题一：已知：E 为PA 的中点，F 为PB 的中点。

分析方法：确定目标三角形（有中位线的三角形）E 为PA 的中点⇒点P 和点A 为目标三角形的两个端点；F 为PB 的中点⇒点P 和点B 为目标三角形的两个端点；中位线：EF点P 和点A ，点P 和点B ⇒目标三角形⇒PAB AB EF //⇒。

底边：AB分析：①两个中点的连线为中位线；②目标三角形的四个端点，去掉两个相同端点，两个不同端点组成的边为底边。

证明方法：E 为PA 的中点，F 为PB 的中点EF ⇒为PAB ∆的中位线AB EF //⇒。

例题二：已知：A 为DE 的中点，B 为DF 的中点。

分析方法：确定目标三角形（有中位线的三角形）A 为DE 的中点⇒点D 和点E 为目标三角形的两个端点；B 为DF 的中点⇒点D 和点F 为目标三角形的两个端点；中位线：AB点D 和点E ，点D 和点F ⇒目标三角形⇒DEF EF AB //⇒。

底边：EF证明方法：A 为DE 的中点，B 为DF 的中点AB ⇒为DEF ∆的中位线EF AB //⇒。

训练一：已知：M 为AB 的中点，N 为AC 的中点。

训练二：已知：P 为MA 的中点，Q 为MB 的中点。

训练一证明：M 为AB 的中点，N 为AC 的中点MN ⇒为ABC ∆的中位线BC MN //⇒。

训练二证明：P 为MA 的中点，Q 为MB 的中点PQ ⇒为MAB ∆的中位线AB PQ //⇒。

例题一：2012年高考数学浙江卷：如下图所示，在四棱锥ABCD P -中，底面是边长为32的菱形，且0120=∠BDA ，且⊥PA 平面ABCD ，62=PA ，M 、N 分别为PB 、PD 的中点。

（Ⅰ）证明：//MN 平面ABCD 。

证明：M 为PB 的中点，N 为PD 的中点MN ⇒为PBD ∆的中位线BD MN //⇒，⊂BD 平面ABCD //MN ⇒平面ABCD 。

立体几何中的向量方法——证明平行及垂直

立体几何中的向量方法(一)——证明平行与垂直1．直线的方向向量与平面的法向量确实定(1)直线的方向向量：在直线上任取一非零向量作为它的方向向量．(2)平面的法向量可利用方程组求出：设a ，b 是平面α两不共线向量，n 为平面α的法向量，则求法向量的方程组为⎩⎨⎧n ·a ＝0，n ·b ＝0.2．用向量证明空间中的平行关系(1)设直线l 1和l 2的方向向量分别为v 1和v 2，则l 1∥l 2(或l 1与l 2重合)⇔v 1∥v 2.(2)设直线l 的方向向量为v ，与平面α共面的两个不共线向量v 1和v 2，则l ∥α或l ⊂α⇔存在两个实数*，y ，使v ＝*v 1＋y v 2.(3)设直线l 的方向向量为v ，平面α的法向量为u ，则l ∥α或l ⊂α⇔v ⊥u .(4)设平面α和β的法向量分别为u 1，u 2，则α∥β⇔u 1∥u 2.3．用向量证明空间中的垂直关系(1)设直线l 1和l 2的方向向量分别为v 1和v 2，则l 1⊥l 2⇔v 1⊥v 2⇔v 1·v 2＝0.(2)设直线l 的方向向量为v ，平面α的法向量为u ，则l ⊥α⇔v ∥u .(3)设平面α和β的法向量分别为u 1和u 2，则α⊥β⇔u 1⊥u 2⇔u 1·u 2＝0.【思考辨析】判断下面结论是否正确(请在括号中打"√〞或"×〞)(1)直线的方向向量是唯一确定的．()(2)平面的单位法向量是唯一确定的．()(3)假设两平面的法向量平行，则两平面平行．()(4)假设两直线的方向向量不平行，则两直线不平行．()(5)假设a ∥b ，则a 所在直线与b 所在直线平行．()(6)假设空间向量a 平行于平面α，则a 所在直线与平面α平行．()1．以下各组向量中不平行的是()A ．a ＝(1,2，－2)，b ＝(－2，－4,4)B ．c ＝(1,0,0)，d ＝(－3,0,0)C ．e ＝(2,3,0)，f ＝(0,0,0)D ．g ＝(－2,3,5)，h ＝(16,24,40)2．平面α有一点M (1，－1,2)，平面α的一个法向量为n ＝(6，－3,6)，则以下点P 中，在平面α的是()A ．P (2,3,3)B ．P (－2,0,1)C ．P (－4,4,0)D ．P (3，－3,4)3．AB →＝(1,5，－2)，BC →＝(3,1，z )，假设AB →⊥BC →，BP →＝(*－1，y ，－3)，且BP ⊥平面ABC ，则实数*，y ，z 分别为______________．4．假设A (0,2，198)，B (1，－1，58)，C (－2,1，58)是平面α的三点，设平面α的法向量n ＝(*，y ，z )，则*∶y ∶z ＝________.题型一证明平行问题例1(2013·改编)如图，在四面体A －BCD 中，AD ⊥平面BCD ，BC ⊥CD ，AD ＝2，BD ＝22，M 是AD 的中点，P 是BM 的中点，点Q 在线段AC 上，且AQ ＝3QC .证明：PQ ∥平面BCD .如图，在棱长为2的正方体ABCD －A 1B 1C 1D 1中，E ，F ，M ，N 分别是棱AB ，AD ，A 1B 1，A 1D 1的中点，点P ，Q 分别在棱DD 1，BB 1上移动，且DP ＝BQ ＝λ(0<λ<2)．(1)当λ＝1时，证明：直线BC 1∥平面EFPQ ；(2)是否存在λ，使平面EFPQ 与平面PQMN 所成的二面角为直二面角？假设存在，求出λ的值；假设不存在，说明理由．题型二证明垂直问题例2 如下图，正三棱柱(底面为正三角形的直三棱柱)ABC —A 1B 1C 1的所有棱长都为2，D 为CC 1的中点．求证：AB 1⊥平面A 1BD .如下图，在四棱锥P －ABCD 中，PC ⊥平面ABCD ，PC ＝2，在四边形ABCD 中，∠B ＝∠C ＝90°，AB ＝4，CD ＝1，点M 在PB 上，PB ＝4PM ，PB 与平面ABCD 成30°角．(1)求证：CM ∥平面PAD ；(2)求证：平面PAB ⊥平面PAD .题型三解决探索性问题例3 如图，棱柱ABCD－A1B1C1D1的所有棱长都等于2，∠ABC和∠A1AC均为60°，平面AA1C1C⊥平面ABCD.(1)求证：BD⊥AA1；(2)求二面角D－A1A－C的余弦值；(3)在直线CC1上是否存在点P，使BP∥平面DA1C1，假设存在，求出点P的位置，假设不存在，请说明理由．如下图，四棱锥S—ABCD的底面是正方形，每条侧棱的长都是底面边长的2倍，P为侧棱SD上的点．(1)求证：AC⊥SD.(2)假设SD⊥平面PAC，则侧棱SC上是否存在一点E，使得BE∥平面PAC.假设存在，求SE∶EC的值；假设不存在，试说明理由．利用向量法解决立体几何问题典例：如图，四棱锥P－ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点．(1)证明：PB∥平面AEC；(2)设二面角D－AE－C为60°，AP＝1，AD＝3，求三棱锥E－ACD的体积．A组专项根底训练1．假设直线l的方向向量为a＝(1,0,2)，平面α的法向量为n＝(－2,0，－4)，则()A．l∥αB．l⊥αC．l⊂αD．l与α相交2．假设AB→＝λCD→＋μCE→，则直线AB与平面CDE的位置关系是()A．相交B．平行C．在平面D．平行或在平面3．A(4,1,3)，B(2，－5,1)，C(3,7，－5)，则平行四边形ABCD的顶点D的坐标是() A．(2,4，－1) B．(2,3,1)C．(－3,1,5) D．(5,13，－3)4．a＝(2，－1,3)，b＝(－1,4，－2)，c＝(7,5，λ)，假设a，b，c三向量共面，则实数λ等于()A.627B.637C.607D.6575．如图，在长方体ABCD —A 1B 1C 1D 1中，AB ＝2，AA 1＝3，AD ＝22，P 为C 1D 1的中点，M 为BC 的中点．则AM 与PM 所成的角为()A ．60°B ．45°C ．90°D ．以上都不正确6．平面α的三点A (0,0,1)，B (0,1,0)，C (1,0,0)，平面β的一个法向量n ＝(－1，－1，－1)，则不重合的两个平面α与β的位置关系是________．7．设点C (2a ＋1，a ＋1,2)在点P (2,0,0)、A (1，－3,2)、B (8，－1，4)确定的平面上，则a ＝________.8．如图，在正方体ABCD —A 1B 1C 1D 1中，棱长为a ，M 、N 分别为A 1B 和AC 上的点，A 1M ＝AN ＝2a 3，则MN 与平面BB 1C 1C 的位置关系是________． 9．如图，四边形ABCD 为正方形，PD ⊥平面ABCD ，PD ∥QA ，QA ＝AB＝12PD .证明：平面PQC ⊥平面DCQ . 10．如图，在底面是矩形的四棱锥P －ABCD 中，PA ⊥底面ABCD ，E ，F 分别是PC ，PD 的中点，PA ＝AB ＝1，BC ＝2.(1)求证：EF ∥平面PAB ；(2)求证：平面PAD ⊥平面PDC .B 组专项能力提升11．如图，正方形ABCD 与矩形ACEF 所在平面互相垂直，AB ＝2，AF ＝1，M 在EF 上，且AM ∥平面BDE ，则M 点的坐标为()A ．(1,1,1)B ．(23，23，1) C ．(22，22，1) D ．(24，24，1)12．设u ＝(－2,2，t )，v ＝(6，－4,4)分别是平面α，β的法向量，假设α⊥β，则t 等于()A ．3B ．4C ．5D ．613．在正方体ABCD —A 1B 1C 1D 1中，P 为正方形A 1B 1C 1D 1四边上的动点，O 为底面正方形ABCD 的中心，M ，N 分别为AB ，BC 的中点，点Q 为平面ABCD 一点，线段D 1Q 与OP 互相平分，则满足MQ →＝λMN→的实数λ有________个．14．如下图，直三棱柱ABC —A 1B 1C 1中，△ABC 为等腰直角三角形，∠BAC ＝90°，且AB ＝AA 1，D 、E 、F 分别为B 1A 、C 1C 、BC 的中点．求证：(1)DE ∥平面ABC ；(2)B 1F ⊥平面AEF .15．在四棱锥P —ABCD 中，PD ⊥底面ABCD ，底面ABCD 为正方形，PD ＝DC ，E 、F 分别是AB 、PB 的中点．(1)求证：EF ⊥CD ；(2)在平面PAD 求一点G ，使GF ⊥平面PCB ，并证明你的结论．。

立体几何平行证明题常见模型及方法2018.10

1FESA BCDEA BCFEA BCDDABC DEF 立体几何平行证明题常见模型及方法线面平行面面平行变式2、如图，在直三棱柱ABC—A1B1C1中，AA1=2，AC=BC=2，∠C=90°，点D是A1C1的中点. 求证：BC1//平面AB1D；变式 3正方形ABCD与正方形ABEF所在平面相交于AB，在AE，BD上各有一点P，Q，且AP＝DQ，求证：PQ∥平面BCE.○1EF∥平面SAD○2BF∥平面SDE变式1：若E、F分别为AD SB,的中点．证明EF∥平面SCD变式2 若E、F分别为SD B,A的中点．证明EF∥平面SCB变式3 如图，在直四棱柱ABCD-A1B1C1D1中，底面ABCD为等腰梯形，AB//CD，AB=4, BC=CD=2, AA1=2, E、E1分别是棱AD、AA1的中点.设F是棱AB的中点,证明：直线EE1//平面FCC1方法3：面面平行法（略）例 4 如图，已知AB⊥平面A C D，DE⊥平面ACD，△ACD为等边三角形，2AD DE AB==，F为CD的中点.求证：//AF平面BCE；变式1几何体E-ABCD是四棱锥，△ABD为正三角形，CB＝CD，EC⊥BD.2(1)求证：BE ＝DE ；(2)若∠BCD ＝120°，M 为线段AE 的中点，求证：DM ∥平面BEC .类型二：面面平行证明例5、如图，在三棱柱ABC －A 1B 1C 1中，E ，F ，G ，H 分别是AB ，AC ，A 1B 1，A 1C 1的中点，求证：(1)B ，C ，H ，G 四点共面； (2)平面EFA 1∥平面BCHG .变式1、如图所示，在正方体ABCD －A 1B 1C 1D 1中，O 为底面ABCD 的中心，P 是DD 1的中点，设Q 是CC 1上的点，问：当点Q 在什么位置时，平面D 1BQ ∥平面PAO?类型三：线线平行证明例6、四边形ABCD 是平行四边形，点P 是平面ABCD 外一点，M 是PC 的中点，在DM 上取一点G ，过G 和AP 作平面交平面BDM 于GH .求证：AP ∥GH .类型四：探索性问题例7、在三棱柱ABC -A 1B 1C 1中，点E 在线段B 1C 1上，B 1E ＝3EC 1，试探究：在AC 上是否存在点F ，满足EF ∥平面A 1ABB 1？若存在，请指出点F 的位置，并给出证明；若不存在，请说明理由．变式1、如图所示，在斜三棱柱ABC —A 1B 1C 1中，点D ，D 1分别为AC ，A 1C 1上的点．(1)当A 1D 1D 1C 1的值等于何值时，BC 1∥平面AB 1D 1； (2)若平面BC 1D ∥平面AB 1D 1，求ADDC 的值．备选、1、直三棱柱ABC -A 1B 1C 1中，D ，E 分别是AB ，BB 1的中点．证明：BC 1∥平面A 1CD ；2、在正方体ABCD -A 1B 1C 1D 1中，棱长为2，E 是棱CD 的中点，P 是棱AA 1的中点．求证：PD ∥平面AB 1E.3、在三棱柱ABC -A 1B 1C 1中，D 是棱CC 1的中点，问在棱AB 上是否存在一点E ，使DE∥平面AB 1C 1？若存在，请确定点E 的位置；若不存在，请说明理由．3。

专题11 立体几何 11.3平行与垂直证明题型归纳讲义-2022届高三数学一轮复习(解析版)

因为点 E 是 AC 中点，点 F 为 AB 的中点，
所以 EF∥BC．
又因为 EF⊄平面 PBC，BC⊂平面 PBC，
△PAD 是正三角形，平面 PAD⊥平面 PBD．
（Ⅰ）求证：PA⊥BD；
（Ⅱ）设二面角 P﹣BD﹣A 的大小为α，直线 PA 与平面 PBC 所成角的大小为β，求 cos
（α+β）的值．
【解答】（Ⅰ）证明：∵∠BAD＝45°，AD＝1，�� = 2，
∴由余弦定理，得：
BD=
1 + 2 − 2 × 1 × 2 × ��45° =1，…（2 分）
性质定理
行，则过这条直线的任一
∵l∥α，
平面与此平面的交线与
l⊂β，α∩β
该直线平行(简记为“线面
＝b，∴l∥b
平行⇒线线平行”)
2．平面与平面平行的判定定理和性质定理
文字语言
判定定理
图形语言
符号语言
一个平面内的两条相交
∵a∥β，b
直线与另一个平面平行，
∥β，a∩b
则这两个平面平行(简记
＝P，a⊂α，
⊥AC，
所以 PA⊥面 ABC，
因为 BC⊂平面 ABC，
所以 PA⊥BC．
又因为 AB⊥BC，且 PA∩AB＝A，
所以 BC⊥面 PAB．
…．（9 分）
（Ⅲ）解：当点 F 是线段 AB 中点时，过点 D，E，F 的平面内的任一条直线都与平面 PBC
平行．
取 AB 中点 F，连 EF，连 DF．
由（Ⅰ）可知 DE∥平面 PBC．
��
理由．
【解答】（Ⅰ）证明：取 AB 中点 O，连接 EO，DO．
因为 EA＝EB，所以 EO⊥AB． …（2 分）

立体几何证明题 ppt课件

法二：向量法，已知异面直线 a, b 的方向向量为
uuur
uuur
AB (x1, y1),CD (x2, y2) ，则
uuur uuur cos AB,CD
uuur uuur uAuBur CuuDur
AB CD
x1x2 y1 y2 x12 y12 x22 y22
注意：
uuur uuur
M F
O
范例 2：两个全等的正方形 ABCD 和 ABEF 所在平面交于 AB ，
P AE,Q DB,且 AP DQ ．
求证： PQ // 平面 BCE
A
D
Q F
P
B
C
E
二．垂直证明
线线垂直 ƒ 线面垂直 ƒ 面面垂直，其核心是线线垂直！
（一）证线线垂直的方法：法一：等腰三角形的底边上的中线法二：勾股定理法三：线面垂直的性质定理法四：三垂线定理及其逆定理法五：向量
结论汇总1：
P
三垂线定理：在平面内的一条
直线，如果和这个平面的一条斜线的射影垂直，那么，它就和这条斜线垂直。
证明过程分析：
A
PA⊥
a
PA ⊥a AO⊥a
Oa
板书证明过程
a⊥平面PAO
PO平面PAO
a⊥PO
结论应用：
例1 已知P 是平面ABC 外一点， PA⊥平面 ABC ，AC ⊥ BC，求证： PC ⊥ BC
求证：AC⊥BD'
D′
C′
A′
B′
D A
C B
范例 3：如图，在长方体 ABCD A1B1C1D1 中，
AA1 AD 1， E 、 F 、 G 分别为CD 、 CB 、

届数学一轮复习第七章立体几何第四节平行关系教师文档教案文

第四节平行关系授课提示:对应学生用书第131页［基础梳理]1．直线与平面平行的判定定理和性质定理文字语言图形语言符号语言判定定理平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行（线线平行⇒线面平行)因为l∥a，aα，lα，所以l∥α性质定理一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行（简记为“线面平行⇒线线平行”）因为l∥α，lβ，α∩β＝b，所以l∥b2.平面与平面平行的判定定理和性质定理文字语言图形语言符号语言判定定理一个平面内的两条相交直线与另一个平面平行，则这两个平面平行（简记为“线面平行⇒面面平行”)因为a∥β,b∥β，a∩b＝P，aα，bα，所以α∥β性质定理如果两个平行平面同时和第三个平面相交，那么它们的交线平行因为α∥β,α∩γ＝a，β∩γ＝b，所以a∥b1．判定定理序号文字语言图形语言符号语言判定定理2如果两个平面同垂直于一条直线,那么这两个平面平行错误!⇒α∥β判定定理3平行于同一个平面的两个平面平行错误!⇒α∥γ2.性质定理序号文字语言图形语言符号语言性质定理2如果两个平面平行，那么在一个平面内的所有直线都平行于另一个平面α∥β且aα⇒a∥β性质定理3如果两个平行平面中有一个垂直于一条直线，那么另一个平面也垂直于这条直线α∥β且l⊥α⇒l⊥β3。

线线平行、线面平行、面面平行的相互转化利用线线平行、线面平行、面面平行的相互转化，解决平行关系的判定时,一般遵循从“低维"到“高维”的转化,即从“线线平行”到“线面平行”,再到“面面平行"；而应用性质定理时，其顺序正好相反．在实际应用中,判定定理和性质定理一般要相互结合,灵活运用．[四基自测］1．(易错点：线面平行的性质)下列命题中正确的是() A．若a，b是两条直线,且a∥b,那么a平行于经过b的任何平面B．若直线a和平面α满足a∥α,那么a与α内的任何直线平行C．平行于同一条直线的两个平面平行D．若直线a，b和平面α满足a∥b，a∥α，bα,则b∥α答案：D2．(基础点:线面平行的判定）下列四个正方体图形中,A，B为正方体的两个顶点，M,N，P分别为其所在棱的中点，能得出AB∥平面MNP的图形的序号是(）A．①③B．②③C．①④ D．②④答案：C3．（基础点：空间平行关系的判定）在正方体ABCD。

高中数学《立体几何》证明平行的一般方法

例4：正方形ABCD与正方形ABEF所在的平面相交于 AB，P、Q分别是AE、BD的的点，且AP=DQ。求证：PQ∥平面BCE
A FP
MB E
D
Q
NC
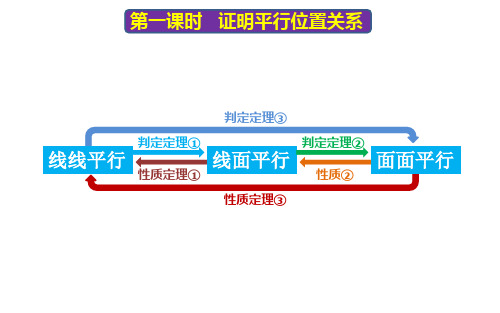
第一课时证明平行位置关系
判定定理①
判定定理②
线线平行
线面平行
面面平行
性质定理①
性质②
判定定理① 平面外一条直线与平面内的一条直线平行，那么该直线与此平面平行。
解：连接AB，设交BD于点Q，连接PQ
A
D
在△BEC中， ∵点P，Q分别是AE，AC的中点 ∴PQ∥EC
F P
Q
又∵ EC⊂平面BCE，PQ⊄平面BCE ∴ PQ∥平面BCE
B
C
E
第一课时证明平行位置关系
判定定理①
判定定理②
线线平行
线面平行
面面平行
性质定理①
性质②
判定定理① 平面外一条直线与平面内的一条直线平行，那么该直线与此平面平行。
例4：正方形ABCD与正方形ABEF所在的平面相交于 AB，P、Q分别是AE、BD的的点，且AP=DQ。求证：PQ∥平面BCE
A FP
MB E
D
Q
NC
第一课时证明平行位置关系
判定定理①
判定定理②
线线平行
线面平行
面面平行
性质定理①
性质②
判定定理① 平面外一条直线与平面内的一条直线平行，那么该直线与此平面平行。
F
Q
P
B
C
E
第一课时证明平行位置关系
判定定理①
判定定理②
线线平行
线面平行
面面平行
性质定理①

用空间向量证(解)立体几何题之——证明线面平行PPT优秀课件

用空间向量证(解)立体几何题之
(五 )
-----证明线面平行
用空间向量证(解)立体几何题是现阶段的热门话题。它可以把一些复杂的证明或计算题用“程序化”的计算来给出解答。
前段时间我们研究了用空间向量求角(包括线线角、线面角和面面角)、求距离(包括线线距离、点面距离、线面距离和面面距离)和证明垂直(包括线线垂直、线面垂直和面面垂直)。
通过本例的练习，同学们要进一步掌握平面法向量的求法：即用平面内的两个相交向量与假设的法向量求数量积等于0，利用解方程组的方法求出平面法向量(在解的过程中可令其中一个未知数为某个数)。
( 1 , 1 , 1 ) 同理可得平面 CB1D 1的法向量为m
例4.在正方体ABCDA1B1C1D1中，E、F、 G、H分别是A1B1、 B1C1、C1D1、D1A1的中点. 求证：平面AEH∥平面BDGF
例3.在正方体ABCDA1B1C1D1中，求证： A 1 平面A1BD∥平面CB1D1
平行四边形A1BCD1 A1B∥D1C 平行四边形DBB1D1 B1D1∥BD
D1
B1
C1
D A B
C
于是平面A1BD∥平面CB1D1
证明：建立如图所示的空间直角坐标系o-xyz 设正方形边长为1， A1 ( 1 ,0 , 1 ) 则向量 DA 1
MH∥AB,NG ∥AB AH=FG CH=BG MH=NG
MH∥NG CH:CA=BG:BF
PH∥CB,PG∥BE
平面HPG∥平面CBE
C
D
H B E G
HG∥平面CBE
P
F
A
C
oB G
2 2 ( 1 a , 0 , a ),而平面CBE的法向故 HG H 2 2 n 量为n (0,1,0), 故 HG ,而平面CBE

高考数学一轮复习-空间立体几何中的平行、垂直证明课件

F
构造平面法
(1) 证明如图所示，取线段 PB 的中点 H，连接 EH、ＡＨ.
在△PBC 中，E、Ｈ和分别为 PC、PB 的中点， ∴EH // BC. 在直角梯形 ABCD 中， ∵AD∥BC，且 AD＝1，BC＝２ ∴AD // 12BC. ∴AD // EH. ∴四边形 ABFD 是平行四边形， ∴ＥD∥AH.
➳性质：如果两个平面平行，那么其中一个平面内的任何一条直线都平行于另外一个平面。
a
//
a
//
☺ 简称：面面平行，线面平行.
复习定理
空间中的平行
5.平面与平面平行的判定与性质
➳性质：如果两个平行平面同时和第三个平面相交，那么它们的交线平行．
//
a
a
// b
b
☺ 简称：面面平行，线线平行.
分析： (1)证明线面平行只需在平面内找一条和该直线平行的直线即可，也可转化为经过这条直线的平面和已知平面平行；(2)证明面面垂直，只需在一个平面内找到另一个平面的垂线.
(1) 证明如图所示，取线段 BC 的中点 F，连接 EF、FD.
在△PBC 中，E、F 分别为 PC、CB 的中点， ∴EF∥PB. 在直角梯形 ABCD 中，F 为 CB 的中点， ∴BF＝12BC＝1. 又∵AD∥BC，且 AD＝1， ∴AD // BF. ∴四边形 ABFD 是平行四边形， ∴FD∥AB. 又∵EF∩FD＝F，PB∩BA＝B， ∴平面 EFD∥平面 PAB. 又∵DE⊂平面 EFD，∴DE∥平面 PAB.
b
b
b
☺ 简称：线面垂直，面面垂直.
复习定理
空间中的垂直
4．平面与平面垂直性质
性质：如果两个平面互相垂直，则其中一个平面内垂直于交线的直线必垂直于另一个平面.

立体几何平行证明题教程文件

用空间向量证(解)立体几何题之——证明线面平行ppt 人教课标版

方法技巧专题05 立体几何中平行与垂直证明(解析版)

方法技巧专题05立体几何中平行与垂直证明

专题20立体几何中的平行与垂直问题(解析版)

立体几何直线平面平行的判定和性质课件文

完整)高中立体几何证明平行的专题

立体几何中的向量方法——证明平行及垂直

立体几何平行证明方法[20210409]

高考数学专题讲解：立体几何平行证明

立体几何中的向量方法——证明平行及垂直

立体几何平行证明题常见模型及方法2018.10

专题11 立体几何 11.3平行与垂直证明 题型归纳讲义-2022届高三数学一轮复习(解析版)

立体几何证明题 ppt课件

届数学一轮复习第七章立体几何第四节平行关系教师文档教案文

高中数学《立体几何》证明平行的一般方法

用空间向量证(解)立体几何题之——证明线面平行PPT优秀课件

高考数学一轮复习-空间立体几何中的平行、垂直证明课件

专题11 立体几何 11.3平行与垂直证明题型归纳讲义-2022届高三数学一轮复习(解析版)