【华中科技大学结构力学习题练习及讲解】5平面桁架习题课

合集下载

李廉锟《结构力学》(上册)课后习题详解(5-7章)【圣才出品】

第5章静定平面桁架复习思考题1．桁架的计算简图作了哪些假设？它与实际的桁架有哪些差别？答：（1）桁架的计算简图假设①各结点都是无摩擦的理想铰；②各杆轴都是直线，并在同一平面内且通过铰的中心；③荷载只作用在结点上并在桁架的平面内。

（2）桁架的计算简图与实际桁架的差别①结点的刚性。

②各杆轴线不可能绝对平直，在结点处也不可能准确交于一点。

③非结点荷载（例如杆件自重、风荷载等）。

④结构的空间作用，等等。

2．如何根据桁架的几何构造特点来选择计算顺序？答：根据桁架的几何构造特点来选择计算顺序的方法（1）找出零杆根据节点的几何特征和外部受力特点判断出零杆。

（2）选择合适的方法求解桁架①用节点法解简单桁架时，在求出支座反力后，可按与几何组成相反的顺序，从最后的结点开始，依次倒算回去，便能顺利地用结点法求出所有杆件的内力。

②求解联合桁架时，用结点法将会遇到未知力超过两个的结点，可以先用截面法将联合杆件的内力求出，再用结点法求解其它杆件的内力。

③求解复杂桁架时，根据桁架的几何构造特点看，可先算出截面单杆的内力，再选择合适的计算方法求解剩余杆的内力。

3．在结点法和截面法中，怎样尽量避免解联立方程？答：在结点法和截面法中，尽量避免解联立方程的方法：（1）采用结点法时，为避免解联立方程，可改选投影轴方向或者改用力矩平衡方程（向力的汇交点取矩）。

（2）采用截面法时，使用力矩法的关键在于选取合理的力矩中心，因此应尽量选取多力汇交点作为力矩中心；使用投影法的过程中，应尽量选择多个力所在方向作为力分解的坐标轴。

4．零杆既然不受力，为何在实际结构中不把它去掉？答：在实际结构中不把零杆去掉的原因：（1）在实际结构中，工况更复杂，荷载不是一成不变的，荷载改变后，“零杆”可能变为非零杆。

因此，为了保证结构的几何形状在任何载荷作用下都不会改变，零杆不能从桁架中除去。

（2）在理想桁架（做了诸多假设）中“零杆”才是零杆，而实际结构中，零杆的内力也不是零，只是较小而已。

第二节平面桁架问题

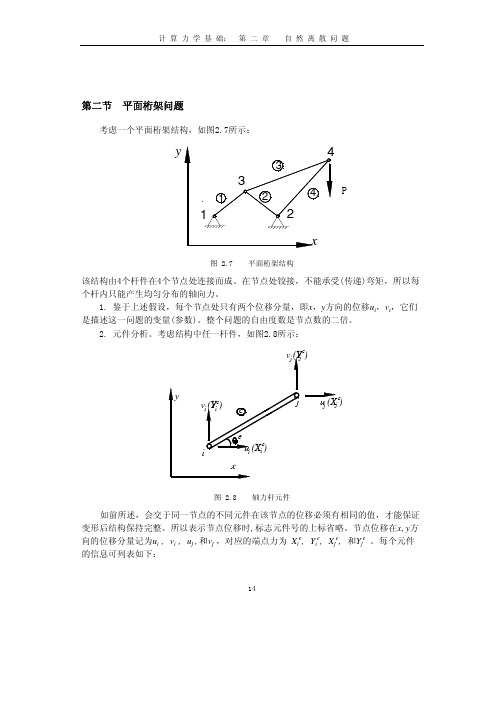
第二节平面桁架问题考虑一个平面桁架结构，如图2.7所示：图 2.7 平面桁架结构该结构由4个杆件在4个节点处连接而成。

在节点处铰接，不能承受(传递)弯矩，所以每个杆内只能产生均匀分布的轴向力。

1. 鉴于上述假设，每个节点处只有两个位移分量，即x，y方向的位移u i，v i，它们1415元件号节点号节点坐标弹性模量横截面积 e i , j ( x i , y i )；(x j , y j ) E e A e杆件的长度可由下式计算()()L x y x x y y e eej i j i =+=−+−∆∆2222()()ij i j e x x y y tg −−=θ其中e θ是杆件的轴向与x 轴正方向的夹角。

对于图2.8所示的结构，每个元件的节点号如下所示：424433322311j i e杆件产生节点位移u i ,v i ,u j ,v j 后,杆的长度变化为（以受拉为正，受压为负） ))sin cos (sin cos (e i e i e j e j e v u v u L θθθθ+−+=∆ 在节点 j 处的端点轴向力为ee ee e e e e eee jL L LA E L L A E F ∆=∆=∆=κ 其中e ee eLA E =κ 该力在x , y 方向的分量就是X j e 和Y j e ，其表达式为：ee e e e j e j L F X θκθcos cos ∆== j e e e j e e i e e e i e e v u v u θθκθκθθκθκsin cos cos cos sin cos 22++−−=e e e e e j e j L F Y θκθsin sin ∆== j e e j e e e i e e i e e e v u v u θκθθκθκθθκ22sin cos sin sin sin cos ++−−=由杆件本身的平衡得到 F i e = －F j e 即（2.11）（2.14a）（2.12）（2.14b）（2.13）16j eeej eei eeei eee je i v u v u X X θθκθκθθκθκsin cos cos cos sin cos 22−−+=−=j eej eeei eei eeeej e i v u v u Y Y θκθθκθκθθκ22sin cos sin sin sin cos −−+=−=把以上4式合并起来,写成矩阵形式如下⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡−−−−−−−−=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧j j i i e ee ee e e e e ee ee e e ee e e e e ee e e e j e j e i e i v u v u Y X Y X θθθθθθθθθθθθθθθθθθθθθθθθκ22222222sin cos sin sin cos sin cos sin cos cos sin cos sin cos sin sin cos sin cos sin cos cos sin cos 上式写成分块形式为F F k k k k d d i ej e ii eijejie jj e i j ⎧⎨⎪⎩⎪⎫⎬⎪⎭⎪=⎡⎣⎢⎢⎤⎦⎥⎥⎧⎨⎩⎫⎬⎭上式中各子矩阵，各子向量的意义是很明确的。

17 桁架平面力系习题课

A E
解: 1. 以DC为研究对象, 受力如图。
B
F D
M C (F ) 0 :
FDy l W l 0 2 (1)
C
FDy
C
FCy FCx
FDy W 2
FDx D
W
A
E
B
2. 再以整体为研究对象:
F D
Fy 0:
FAy FDy 3W 0 (2)
C
FAy
A E
y
A
联立求解，得 FAx= －2 kN FAy= 2 kN FB = 2 kN
FAy A FAx
F a a
E FE
a
FB B
C D FC
a
FAF A FAx FAC
取节点A，受力分析如图。由平衡方程
FAy
F A E FE
F 0， F 0,
x
FAx FAC FAF cos 45 0
a
C
a FC
FDE
D
a
D
a
B
取节点D，受力分析如图。由平衡方程
F 0, F 0,
x
FDB FDC 0
y
FDE 0
FDC
FDB
解得 FDB 2 kN , FDE 0
FBE
FB
取节点B，受力分析如图。由平衡方程
F
B
x
0,
0,
FBD FBE cos 45 0
F A a C FC a E FE a D a B
【解】先取整体为研究对象,受力如图所示。由平衡方程
F 0， FAx FE 0 F 0, FB FAy FC 0 M F 0,

结构力学第五章平面桁架详解

1‘ 2‘ 3‘ 4‘ e
a
cd
b
4d d3
A 1 2 3 4 5
B
P PP 6d
VA 1.5P
(1) Na Nb
1‘ 2‘
4
Na
d 3
1 2 Nb
1.5P
P
Y 0 M 2 0
VB 1.5P
Na P VA 0.5P
Nb
4 3
d
1.5P 2d
0
Nb 2.25 P
1‘ 2‘ 3‘ 4‘ e
a
cd
b
A 1 2 3 4 5
P PP 6d
4d d3
B
(2) N c
VA 1.5P
Yc 1.5P P 0.5P
Nc
5 4
Yc
0.625P
VB 1.5P
4‘ e
d
Nc
B
45
P 1.5P
A VA 1.5P
1‘
2‘
3‘
4‘
e
a
cd
b
12345 P P P 6d
4d d3
B
VB 1.5P
5-1 桁架的特点和组成分类
桁架是由链杆组成的格构体系，当荷载仅作用在结点上时，
杆件仅承受轴向力，截面上只有均匀分布的正应力，是最理想
的一种结构形式。
上弦杆
理想桁架：
腹杆
下弦杆
（1）桁架的结点都是光滑无摩擦的铰结点；（2）各杆的轴线都是直线，并通过铰的中心；（3）荷载和支座反力都作用在结点上
主应力、次应力
桁架的分类（按几何构造） 1、简单桁架
2、联合桁架
3、复杂桁架
§5-2 结点法
分析时的注意事项：

5 平面桁架结构力学

F
M G 0 F N 4 2 F P
2FP
FN3
F
E
2
Ⅱ—Ⅱ截面
C
D
M D 0 F N 3 2 F P
结点C
2FP F N 2
C
Y0 F N 222 F P
Ⅲ—Ⅲ截面 F N1
FP
A
B
C
D
综上所求，得：
X0 F N 12F P
F N 1 2 F P ， F N 2 2 2 F P ,F N 3 2 F P ， F N 4 2 F P
+
一、平面汇交力系
3 -90 5
7
结点2
40
H=0
60
60
1
2 40kN 4 60kN 6 80kN 8
4m
N23
N23 40
60 2
N24 N24 60
V1=80kN
结点1 5
3
Y13
1 80
X13 N12
4×3m=12m
40
V8=100kN
4
Y13 80
X138
036
4
0
VA 1.5P
Yc1.5PP0.5P Nc 54Yc 0.62P 5
VB 1.5P
4‘ e
d
Nc
B
45
P 1.5P
A
VA 1.5P
1‘
2‘
3‘
4‘
e
a
cd
b
12345 P P P 6d
4d d3
B
VB 1.5P
(3) Nd
Xe
Ne
4‘ Y e
Nd
45

华中科技大学——结构力学题库及详解

结构力学第一题绪论和基本概念1.从几何角度来看，结构可分为哪几类？（）A.杆系结构、板和壳结构和实体结构B.复杂的杆系和板壳C.飞机蒙皮D.轮船发动机2.何为结构？（）A. 建筑物中门、窗。

B.建筑物中承受载荷而起骨架作用的部分。

C. 建筑物中玻璃。

D. 建筑物中水泥。

3.结构力学中的杆是指（）A. 一个方向的尺寸远小于其它两方向的尺寸的构件。

B. 一个方向的尺寸远大于其它两方向的尺寸的构件。

C.三个方向的尺寸几乎相等。

D. 曲面构件。

4.计算简图是指（）A建筑结构平面设计图。

B. 建筑结构三维立体图。

C. 用一个简化的图形来代替实际结构。

D实际建筑结构效果图5.选择计算简图的原则是（）A把实际构件变为平面结构。

B.计算越简单越好C. 保留实际构件所有的材料。

D从实际出发，分清主次，略去细节。

6.结构力学中的外力类型有（）A集中力、分布力和外力矩。

B. 应力、分布力和力矩。

C. 集中力、剪力和力矩。

D集中力、分布力和轴力。

7.结构力学中杆件简化是用（）A. 其中性轴表示B. 其形心表示C.其轴线表示D. 其实际图形表示8.结构力学中按计算简图分类，可分为（）A. 砖石、钢混、钢结构和高层结构。

B. 砌体结构、多层结构。

C. 蒙皮结构、拱和组合结D.梁和钢架、桁架、拱和组合结构。

1. A2. B3. B4. C5. D6. A7. C8. D第二题单选题（几何组成分析内力计算）1.用几何组成规则分析图示体系是:( ):A.无多余约束的几何不变体系；B.有多余约束的几何不变体系；C.可变体系；D.瞬变体系。

2.叠加原理用于求解静定结构时，需满足的条件是（）。

A．位移微小且材料是线弹性的。

B．位移是微小的。

C．应变是微小的。

D. 材料是理想弹朔性的。

3. 图示结构是单跨静定梁的一种，称为（）A.简支梁B.外伸梁C.悬臂梁D.多跨静定梁4.拱结构和曲梁的区别（）A.截面形状不同B. 材料不同C.在竖向荷载作用下有无水平推力D.轴线形状不同5. 下列结论哪些是正确的____:A.几何不变且无多余约束的体系其自由度为零；B.三个刚片之间用三个铰两两相连，组成无多余约束几何不变体系；C.两个刚片之间用一个铰和一根链杆相连，组成无多余约束几何不变体系；D.两个刚片之间用三根链杆相连，组成无多余约束几何不变体系；6. . 区别拱和梁的主要标志是________：A 杆轴线的形状B 弯矩和剪力的大小C 在竖向荷载作用下是否产生水平推力D 是否具有合理轴线7.大门雨蓬可选择的计算简图是（）。

第五章静定平面桁架(李廉锟结构力学)全解PPT课件

X0， FN CE FN CH 0
Y0 ， 10 2 F k N Cs N Ei n F N C D 0
得
FN CD 1k 0N 215(22.3 61kk 0N N)
F N CH F N CE 2.3 2 6kN
退出
返回
*
§5-2 结点法
5 kN 2m
A 20 kN
10 kN
10 kN 10 kN
通常假定未知的轴力为拉力，计算结果得负值表示轴力为压力。
退出
返回
*
§5-2 结点法
结构力学
例5-1 试用结点法求三角形桁架各杆轴力。
5 kN 2m
A 20 kN
10 kN
10 kN 10 kN
C
E
F
G
DHBiblioteka 2 m 4=8 m5 kN
B 20 kN
解: (1) 求支座反力。
FxA 0
FyA 20kN(↑)
X0 Y 0
F N AE co sF N AG 0
2k 0 N 5 k N F N Ac E o 0 s
有所以
FN AE 1k 5N 533.k5N （4压）
F N AG F N AE co s33.2 5 53k 0（N 拉）
退出
返回
*
§5-2 结点法
10 kN
10 kN 10 kN
5 kN
退出
返回
*
§5-1 平面桁架的计算简图
二、按外型分类
1. 平行弦桁架
2. 三角形桁架
3. 抛物线桁架
退出
返回
结构力学
*
§5-1 平面桁架的计算简图
三、按几何组成分类

《平面桁架习题》课件

04 平面桁架的优化设计
平面桁架的尺寸优化
总结词
尺寸优化是平面桁架优化设计的重要环节，主要涉及对杆件长度、截面尺寸等参数的调整，以达到更好的力学性能和经济效益。
详细描述
在平面桁架的尺寸优化过程中，通常采用数学模型和计算机模拟技术，通过对杆件长度、截面面积等参数的调整，使整个结构在满足承载能力的前提下，具有更小的重量和成本。同时，尺寸优化还可以改善结构的稳定性和振动性能。
平面桁架习题
目录
• 平面桁架的基本概念 • 平面桁架的内力分析 • 平面桁架的位移分析 • 平面桁架的优化设计 • 平面桁架的应用实例
01 平面桁架的基本概念
平面桁架的定义
总结词
平面桁架是一种由杆件组成的结构，其所有杆件都在同一平面内相互连接。
详细描述
平面桁架是由若干直杆在端点以铰链连接组成的结构，所有杆件都在同一平面内，形成了一个几何不变体系。
总结词
高层建筑中，平面桁架用于连接高层建筑竖向结构和水平楼板，提高整体稳定性。
详细描述
在高层建筑中，平面桁架被广泛应用于连接高层建筑的竖向结构和水平楼板。通过合理设计平面桁架的结构形式和尺寸，可以有效地提高高层建筑的整体稳定性，增强结构的承载能力和抗风能力，确保高层建筑的安全性和稳定性。
05 平面桁架的应用实例
桥梁工程中的平面桁架
总结词
桥梁工程中，平面桁架常被用于主梁和桥墩的连接，以承受和传递荷载。
详细描述
在桥梁工程中，平面桁架结构因其高强度的承载能力和稳定性而被广泛应用。通过合理设计平面桁架的结构形式和尺寸，可以有效地将桥面荷载传递到桥墩上，确保桥梁的整体稳定性和安全性。
平面桁架的结构优化

工程力学第5节平面静定桁架的内力计算

F1 sin 30 G 0
n
Fiy 0
i1
F1 cos 30 F2 0
得 F1 40 kN（拉） F2 34.6 kN（压）
节点 B：
n
Fix 0
i1 n
Fiy 0
i1
F2 F6 0
得
F3 G 0
F6 34.6 kN（压） F3 20 kN（拉）
i1 n
Fiy 0
i1
FS1 sin 60 FS4 sin 60 0 FS1 cos 60 FS4 cos 60 FS3 0
解得
FS4 FS1 2F（压）校核计算结果
将各杆内力计算结果列表如下
杆号
1
2
3
内力 2F 1.73F 2F
半部分为研究对象进行受力分析，列平衡方程：
n
M E (Fi ) 0
FS1 1sin 60 FAy 1 0
i1
n
M D (Fi ) 0
i1 n
Fiy 0
i1
F1

1 2

FS3
1
sin
60

FAy

2 3

0
FAy FS2 sin 60 F1 0
• 因为只有三个独立平衡方程，因此作假想截面时，一般每次最多只能截断三根杆件。
注意
• 由于平面汇交力系只能列出两个独立平衡方程，所以应用节点法必须从只含两个未知力大小的节点开始计算。
例2-15 平面桁架的受力及尺寸如图所示，试求桁架各杆的内力。
解 1）先求支座反力：以整体桁架为研究对象进行

静力学-5平面桁架

Fix 0, FDB
4 4 FDB 0 ; FDB 2.5kN; 5 5
FAD
FDA
FDB
3 3 FDA FDE 0 ; FDE 3kN; 5 5
[D]
FDE
[B]
4 4 Fiy 0, FBD FBE 0 ; FBE 2.5kN; A 5 5
FR
左螺旋
当空间力系简化为一合力时，合力矩定理仍然成立。空间一般力系的平衡条件空间一般力系平衡的充分和必要条件：
FR Fi 0
M O M Oi 0
FR Fi 0
M O M Oi 0
——空间一般力系的平衡方程
刚体系的平衡
刚体系平衡系统中每个刚体平衡平面任意力系的平衡方程
F2 F1
F3
解: 1、选取截面
2、画出研究对象受力图 3、建立平衡方程研究整体:
FB
研究部分桁架
M
A
0 FB
F
y
0 F1
例: 求图示结构中, CB杆上C端的约束力和杆1的内力已知:M, P, AE=EC=CD=DB=DH=EG=L 解: 1、研究整体
FAy F Ax
A
E
C
F
P
一、节点法：将每个节点视为平面汇交力系平衡对像，逐个节点求解内力。二、截面法：截取桁架每一部份视为平面力系平衡对像，应用三个平衡方程求解内力。
二、平面桁架内力的计算方法
1、节点法：以节点为研究对象计算杆件内力的方法 A D 4 例: 在图示桁架中,已知水平杆 1 和铅垂杆等长, 节点E上作用有 7 3 5 铅垂力P, 求各杆内力. E 6 C 2 B 节点法的特点: P 研究节点E－>杆1、2的内力研究节点C－>杆3、6的内力研究节点D－>杆4、5的内力研究节点B－>杆7内力和B处的约束力

《结构力学习题》(含答案解析)

第三章静定结构的位移计算一、判断题：1、虚位移原理等价于变形谐调条件，可用于求体系的位移。

2、按虚力原理所建立的虚功方程等价于几何方程。

3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下，静定结构不产生内力，但会有位移且位移只与杆件相对刚度有关。

4、求图示梁铰C 左侧截面的转角时，其虚拟状态应取：A.;; B.D.C.=1=15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。

6、已知M p 、M k 图，用图乘法求位移的结果为：()/()ωω1122y y EI +。

M k M p 21y 1y 2**ωω( a )M =17、图a 、b 两种状态中，粱的转角ϕ与竖向位移δ间的关系为：δ=ϕ 。

8、图示桁架各杆E A 相同，结点A 和结点B 的竖向位移均为零。

a a9、图示桁架各杆EA =常数，由于荷载P 是反对称性质的，故结点B 的竖向位移等于零。

二、计算题：10、求图示结构铰A 两侧截面的相对转角ϕA ，EI = 常数。

q l l l /211、求图示静定梁D 端的竖向位移 ∆DV 。

EI = 常数，a = 2m 。

a a a 10kN/m12、求图示结构E 点的竖向位移。

EI = 常数。

l l l /3 2 /3/3q13、图示结构，EI=常数，M =⋅90kN m , P = 30kN 。

求D 点的竖向位移。

P 3m 3m 3m14、求图示刚架B 端的竖向位移。

ql15、求图示刚架结点C 的转角和水平位移，EI = 常数。

q16、求图示刚架中Ｄ点的竖向位移。

EI ＝常数。

l/217、求图示刚架横梁中Ｄ点的竖向位移。

EI＝常数。

18、求图示刚架中D点的竖向位移。

E I = 常数。

qll l/219、求图示结构Ａ、Ｂ两截面的相对转角，EI＝常数。

l/23l/320、求图示结构A、B两点的相对水平位移，E I = 常数。

ll21、求图示结构B点的竖向位移，EI = 常数。

第五章桁架及组合结构习题解答-推荐下载

N
N 45

X 34 N35
56

N54 3kN 1kN
X 32 X Y34 Y32
Y32 2/3
36

2
0 Y36
X36 1.5kN，Y，36 0.5kN N36 1.58kN ； X32 4.5kN，Y，32 1.5kN N32 4.74kN

3 1
，知：
4.5 1.5
/
3
X 32 1 Y32
Y36
N67 0 0.5 0

，知：

X 21 X Y21 Y27
Y21
1 3

X

36 0 Y36 0
X 36，Y32

N67
N 62
27

1 3
0 1.5
X

解。其中垂直于 AB 分量对 C 点有矩。
A
a/2
(a)
a
a/2
B
NEA
5-5d 解：（1）取 I-I 截面上边部分为研究对象，受力如图（b）所示。
A
a
a
B
E
P I
C
b
4m
（a）
a cI II D
4m
MC (F)
D

M B (F) MO (F)
FE
I O2
0 10 3
（4）6
（5）2
由比例：
结点：
结点：
X 21 2

X Y
X Y
Y21 2/3

结构力学第5章静定平面桁架(f)

§5-1 平面桁架的计算简图
实际结构与计算简图之间的差别
（1）结点的刚性。
（2）各杆轴不可能绝对平直，在结点处也不可能准确交于一点。（3）非结点荷载（自重，风荷载等）。
（4）结构的空间作用等。
主应力：按理想平面桁架算得的应力称之。次应力：将上述一些因素所产生的附加应力称之。次应力影响不大，可以忽略不计。
A
N1
C
2 D D B

P1
P2 N2 2 A C D
MC 0
B
N 2

例1、求图示平面桁架结构中指定杆件的内力。 1‘ 2‘ 3‘ 4‘ e c d a
A
1
b 2 3 4 5 P P P 6d
4 d d 3
B
VA 1.5P
VB 1.5P
(1)
N a Nb
1‘ 2‘
M M
F
0 FNDE 112.5kN
取截面II-II右侧部分为隔离体，由
G
0 FxHC 37.5kN
FNHC 40.4kN
§5-5 各式桁架比较
弦桁的内力计算公式
平行弦桁架
M0 FN r M0：相应简支梁与矩心对应的点的弯矩； r ：内力对矩心的力臂。
结论抛物线形桁架（1）平行弦桁架内力分布不均匀，弦杆内力向跨中递增；（2）抛物线形桁架内力分布均匀，材料使用上最为经济；（3）三角形桁架内力分布不均
§5-3 一、平面一般力系
截面法
X 0 Y 0 M 0
截取桁架的某一局部作为隔离体，由平面任意力系的平衡方程即可求得未知的轴力。
对于平面桁架，由于平面任意力系的独立平衡方程数为3，因此所截断的杆件数一般不宜超过3 截面法可分为力矩法和投影法。

结构力学章节习题及参考答案

第1章绪论（无习题）第2章平面体系的机动分析习题解答习题2.1是非判断题(1) 若平面体系的实际自由度为零，则该体系一定为几何不变体系。

( )(2) 若平面体系的计算自由度W=0，则该体系一定为无多余约束的几何不变体系。

( )(3) 若平面体系的计算自由度W＜0，则该体系为有多余约束的几何不变体系。

( )(4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。

( )(5) 习题2.1(5) 图所示体系去掉二元体CEF后，剩余部分为简支刚架，所以原体系为无多余约束的几何不变体系。

( )习题2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC后，成为习题2.1(6) (b)图，故原体系是几何可变体系。

( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF后，成为习题2.1(6) (c)图，故原体系是几何可变体系。

()(a)(b)(c)习题2.1(6)图习题2.2填空(1) 习题2.2(1)图所示体系为_________体系。

习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系。

习题2-2(2)图(3) 习题 2.2(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。

习题2.2(3)图(4) 习题2.2(4)图所示体系的多余约束个数为___________。

习题2.2(4)图(5) 习题2.2(5)图所示体系的多余约束个数为___________。

习题2.2(5)图(6) 习题2.2(6)图所示体系为_________体系，有_________个多余约束。

习题2.2(6)图(7) 习题2.2(7)图所示体系为_________体系，有_________个多余约束。

习题2.2(7)图习题2.3对习题2.3图所示各体系进行几何组成分析。

(a)(b)(c)(d)(e)(f)(h)(g)(i)(j)(k)(l)习题2.3图第3章静定梁与静定刚架习题解答习题3.1 是非判断题(1) 在使用内力图特征绘制某受弯杆段的弯矩图时，必须先求出该杆段两端的端弯矩。

第5章静定平面桁架

- 23/85页 -
FP
FP 1
D
FP
C
3FP
E
1.5FP -
2
1m B 1m
A
3FP F
G
H
2m 2m 2m 2m
1.5FP
1.5FP
FP C
3FP A
F
即
FNAC
1.5FP
可由比例关系求得
Fy1
FN1
D Fx1
G
Fx2
Fy2
FN2
24
《第5章静定平面桁架》
- 24/85页 -
【例】用结点法求AC、AB杆轴力。
F6=120kN
6
4
3
F7H=120kN 7
F7V=45kN
4m
5 15kN 4m
2 15kN 4m
3m
1 15kN
按结点1，2，…，6依次计算各结点相关杆件轴力。
结点7用于校核。
17
《第5章静定平面桁架》
- 17/85页 -
2. 零杆和等力杆
(1) 关于零杆的判断在给定荷载作用下，桁架中轴力为零的杆件，称为零杆。 1) L形结点：成L形汇交的两杆结点无荷载作用，则这两杆皆为零杆。
FyAC
FyAB
4m
2m
1 2
3 2
27
《第5章静定平面桁架》
- 27/85页 -
【例】用结点法求各杆轴力。解： 1）支座反力
FAy=FBy=30kN(↑)
FAx=0
2）判断零杆
3）求各杆轴力取结点隔离体顺序为：A、E、D、C。结构对称，荷载对称，只需计算半边结构。
28
《第5章静定平面桁架》