中考数学系统复习第六单元圆滚动小专题(八)三角形的内心与外心练习

三角形内心和外心练习题

CEB 内心和外心一、选择题：1、对于三角形的外心，下列说法错误的是（）A.它到三角形三个顶点的距离相等B.它到三角形任意一个顶点的距离等于其外接圆的半径C.它是三角形三条角平分线的交点D.它是三角形三条边垂直平分线的交点2、下列命题正确的个数有（）○1过两点可以作无数个圆；○2经过三点一定可以作圆；○3任意一个三角形有一个外接圆，而且只有一个外接圆；○4任意一个圆有且只有一个内接三角形.A.1个B.2个C.3个D.4个2、在Rt△ABC中，∠C=90°，AC=6cm，BC=8cm，则它的外心与顶点C的距离是（）A. 5cmB. 6cmC. 7cmD. 8cm3、下列说法错误的是（）A.三角形有且只有一个内切圆B.若I为△ABC的内心，则AI平分∠BACC.三角形的内心不一定都在三角形的内部D.等腰三角形的内心一定在它底边的高上4、在Rt△ABC中，∠C=90°，AC=3cm，BC=4cm，则△ABC的外接圆的面积为（）A.254cm2 B.5πcm2 C.254πcm2 D.25cm25、⊙O与△ABC分别相切于点D、E、F，△ABC的周长为20cm，AF=5cm，CF=3cm，则BE的长度为（）A.1cmB. 2cmC.3cmD.2.5cm第5题第7题第9题6、△ABC内接于⊙O，∠A=60°，⊙O的半径为5，则BC的长为（）527、已知，如图在Rt△ABC中，∠C=90°，AC=3cm，BC=4cm，⊙O为Rt△ABC的内切圆，切点为D、E、F，则⊙O的半径为（）A.12cm B.1cm C.32cm D.2cm8、等边三角形的内切圆半径为r，外接圆半径为R，高为h，则r：R：h的值为（）A.1：2：3 B.1 2 C.2：1：3 D.19、如图，⊙O为△ABC的内切圆，∠C=90°，AO的延长线交BC于点D，AC=4，CD=1，则⊙O的半径为( )A.45B.54C.34D.5610、△ABC内接于⊙O，∠A=60°，∠ABC、∠ACB的角平分线分别交AC、AB于点D、E，CE、BD相交于点F.以下四个结论：○1∠BFE=60°；○2BC=BD；○3EF=FD；○4BF=2DF.其中结论一定正确的是（）A. ○1○2○3B.○1○3C. ○1○2○4D. ○1○2○3○4第10题第15题第16题二、填空题11、已知I是△ABC的内心，且∠BIC=130°，则∠A= ；12、已知⊙O为△ABC的内切圆，D、E、F为切点，则△DEF一定是三角形；13、已知等腰Rt△的外接圆半径是5，则其内切圆半径是；14、三角形的周长为20，面积为35，则其内切圆半径是；15、如图，⊙O是边长为2的等边△ABC的内切圆，则图中阴影部分的面积为16、如图，网格中的小正方形的边长均为1，小正方形的顶点叫做格点，△ABC的三个顶点都在格点上，那么△ABC的外接圆半径是17、等边三角形的边长为6cm，则这个等边三角形的外接圆半径为 cm，外接圆的面积是 cm2；18、等腰△ABC的外接圆半径是5，其底BC=4 ，则S△ABC= .三、解答题19、在Rt△ABC中，∠C=90°，AC=8，BC=6，求其内心和外心之间的距离.。

中考数学复习----《三角形的内切圆与内心》知识点总结与专项练习题(含答案解析)

中考数学复习----《三角形的内切圆与内心》知识点总结与专项练习题（含答案解析）知识点总结1. 相交弦定理：圆内的两条相交弦，被交点分成的两条线段长的积相等。

几何语言：若弦CD AB ，交于点P ，则PD PC PB PA ⋅=⋅。

推论：如果弦与直径垂直相交，那么弦的一半是它分直径所成的两条线段的比例中项。

几何语言：若AB 是直径，CD 垂直AB 于点P ，则PB PA PD PC ⋅==22。

2. 弦切角定理：（1）弦切角的定义：如图像∠ACP 这样，顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角。

（2）弦切角定理：弦切角的度数等于它所夹的弧的圆心角的度数的一半。

等于这条弧所对的圆周角。

即∠PCA=∠PBC 。

3. 切线长定理：（1）切线长定义：经过圆外一点作圆的切线，这点和切点之间的线段的长，叫做这点到圆的切线长。

（2）切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线，平分两条切线的夹角。

4. 切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。

几何语言：∵PT切⊙O于点T，PBA是⊙O的割线∴PT2=PA•PB（切割线定理）。

推论：从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等。

几何语言：∵PBA，PDC是⊙O的割线∴PD•PC=PA•PB由上可知：PT2=PA•PB=PC•PD。

5. 三角形的内切圆与内心：内切圆与内心的概念：与三角形各边都相切的圆叫三角形的内切圆，三角形的内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形。

三角形的内心就是三角形三个内角角平分线的交点。

练习题1、（2022•恩施州）如图，在Rt△ABC中，∠C＝90°，AC＝4，BC＝3，⊙O为Rt△ABC的内切圆，则图中阴影部分的面积为（结果保留π）．【分析】根据题意，先作出相应的辅助线，然后求出内切圆的半径，再根据图形可知：阴影部分的面积＝△ABC的面积﹣正方形CEOD的面积﹣⊙O面积的，代入数据计算即可．【解答】解：作OD⊥AC于点D，作OE⊥CB于点E，作OF⊥AB于点F，连接OA、OC、OB，如图，∵∠C＝90°，OD＝OE＝OF，∴四边形CEOD是正方形，∵AC＝4，BC＝3，∠C＝90°，∴AB＝＝＝5，∵S△ABC＝S△AOC+S△COB+S△BOA，∴＝，解得OD＝OE＝OF＝1，∴图中阴影部分的面积为：﹣1×1﹣π×12×＝5﹣π，故答案为：5﹣π．2、（2022•泰州）如图，△ABC中，∠C＝90°，AC＝8，BC＝6，O为内心，过点O的直线分别与AC、AB边相交于点D、E．若DE＝CD+BE，则线段CD的长为．【分析】连接BO，CO，结合内心的概念及平行线的判定分析可得当DE＝CD+BE时，DE∥BC，从而利用相似三角形的判定和性质分析计算．【解答】解：如图，过点O的直线分别与AC、AB边相交于点D、E，连接BO，CO，∵O为△ABC的内心，∴CO平分∠ACB，BO平分∠ABC，∴∠BCO＝∠ACO，∠CBO＝∠ABO，当CD＝OD时，则∠OCD＝∠COD，∴∠BCO＝∠COD，∴BC∥DE，∴∠CBO＝∠BOE，∴BE＝OE，则DE＝CD+BE，设CD＝OD＝x，BE＝OE＝y，在Rt△ABC中，AB＝＝10，∴，即，解得，∴CD＝2，过点O作D′E′⊥AB，作DE∥BC，∵点O为△ABC的内心，∴OD＝OE′，在Rt△ODD′和Rt△OE′E中，，∴△ODD′≌△OE′E（ASA），∴OE＝OD′，∴D′E′＝DE＝CD+BE＝CD′+BE′＝2+＝，在△AD′E′和△ABC中，，∴△AD′E′∽△ABC，∴，∴，解得：AD′＝，∴CD′＝AC﹣AD′＝，故答案为：2或．3、（2022•黔东南州）如图，在△ABC中，∠A＝80°，半径为3cm的⊙O是△ABC的内切圆，连接OB、OC，则图中阴影部分的面积是cm2．（结果用含π的式子表示）【分析】根据角A的度数和内切圆的性质，得出圆心角DOE的度数即可得出阴影部分的面积．【解答】解：∵∠A＝80°，⊙O是△ABC的内切圆，∴∠DOE＝180°﹣（）＝180°﹣（180°﹣∠A）＝130°，∴S扇形DOE＝＝（cm2），故答案为：．4、（2022•宜宾）我国古代数学家赵爽的“弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形（如图所示）．若直角三角形的内切圆半径为3，小正方形的面积为49，则大正方形的面积为．【分析】如图，设内切圆的圆心为O，连接OE、OD，则四边形EODC为正方形，然后利用内切圆和直角三角形的性质得到AC+BC＝AB+6，（BC﹣AC）2＝49，接着利用完全平方公式进行代数变形，最后解关于AB的一元二次方程解决问题．【解答】解：如图，设内切圆的圆心为O，连接OE、OD，则四边形EODC为正方形，∴OE＝OD＝3＝，∴AC+BC﹣AB＝6，∴AC+BC＝AB+6，∴（AC+BC）2＝（AB+6）2，∴BC2+AC2+2BC×AC＝AB2+12AB+36，而BC2+AC2＝AB2，∴2BC×AC＝12AB+36①，∵小正方形的面积为49，∴（BC﹣AC）2＝49，∴BC2+AC2﹣2BC×AC＝49②，把①代入②中得AB2﹣12AB﹣85＝0，∴（AB﹣17）（AB+5）＝0，∴AB＝17（负值舍去），∴大正方形的面积为289．故答案为：289．。

初中数学《三角形的内切圆、外切圆》专题练习试卷及答案

6《三角形的内切圆、外接圆》专题练习试卷1. 如图，⊙O 为△ABC 的内切圆，AC ＝10，AB ＝8，BC ＝9，点D ，E 分别为BC ，AC 上的点，且DE 为⊙O 的切线，则△CDE 的周长为（）A ．9B ．7C ．11D ．81题图 2题图 3题图2. 如图，AB 、AC 、BD 是⊙O 的切线，切点分别是P 、C 、D ．若AB ＝5，AC ＝3，则BD 的长是（）A ．4B ．3C ．2D ．13. 如图，△ABC 内接于圆，D 是BC 上一点，将∠B 沿AD 翻折，B 点正好落在圆点E 处，若∠C ＝50°，则∠BAE 的度数是（）A ．40°B ．50°C ．80°D ．90°4．已知：如图，∠C ＝90°，内切圆O 分别与BC 、AC 相切于点D 、E ，判断四边形ODCE 的形状，并说明理由．4题图65．如图，在△ABC 中，∠A ＝60°，∠C ＝70°，点O 是△ABC 的内心，BO 的延长线交AC 于点D ，求∠BDC 的度数．5题图弧长和扇形面积题型：1. 已知正六边形的边长为8，则较短的对角线长为．2. 如图，正六边形ABCDEF 内接于⊙O 其边长为2，则⊙O 的内接正三角形ACE 的边长为．2题图 5题图 3．一圆锥的侧面积是底面积的2倍，这个圆锥的侧面展开图所对应的扇形的圆心角是( )．A ．120° B．180° C．240° D．300°4．底面圆半径为3cm ，高为4cm 的圆锥侧面积是( )．A ．7.5π cm 2B ．12π cm 2C ．15πcm 2D ．24π cm 25．如图是两个半圆，点O 为大半圆的圆心， AB 是大半圆的弦关与小半圆相切，且AB =24．问：能求出阴影部分的面积吗？若能，求出此面积；若不能，试说明理由．6．如图，若⊙O的周长为20πcm，⊙A、⊙B的周长都是4πcm，⊙A在⊙O内沿⊙O滚动，⊙B在⊙O外沿⊙O滚动，⊙B转动6周回到原来的位置，而⊙A只需转动4周即可，你能说出其中的道理吗？6题图参考答案1. C. 解析：设AB，AC，BC和圆的切点分别是P，N，M，CM＝x，根据切线长定理，得CN＝CM＝x，BM＝BP＝9﹣x，AN＝AP＝10﹣x．则有9﹣x+10﹣x＝8，解得：x＝5.5．所以△CDE的周长＝CD+CE+QF+DQ＝2x＝11．故选：C．1题图2. C. 解析：∵AC、AP为⊙O的切线，∴AC＝AP＝3，∵BP、BD为⊙O的切线，∴BP＝BD，∴BD＝PB＝AB﹣AP＝5﹣3＝2．故选：C．63. C. 解析：连接BE，如图所示：，由折叠的性质可得：AB＝AE，∴AB AE∴∠ABE＝∠AEB＝∠C＝50°，∴∠BAE＝180°﹣50°﹣50°＝80°．故选：C．Array3题图4. 解：四边形ODCE为正方形，理由如下：∵内切圆O分别与BC、AC相切于点D、E，∴OE⊥AC，OD⊥BC．∵∠C＝90°，∴四边形ODCE为矩形．又∵OD＝OE，∴四边形ODCE为正方形．5. 解：∵∠A＝60°，∠C＝70°，∴∠ABC＝50°，∵点O为△ABC的内心，∴∠DBC＝∠ABC＝25°，∵∠ACB＝78°，∠DBC+∠C+∠BDC＝180°，∴∠BDC＝180°﹣78°﹣25°＝77°．66弧长和扇形面积题型：1. 8. 解析：如图，六边形ABCDEF 是正六边形，连接BF ，作AH ⊥BF 于点H ，1题图根据题意可知：BF 为较短对角线，∵六边形ABCDEF 是正六边形，∴AB ＝AF ＝8，∠BAF ＝120°，∵AH ⊥BF ，∴∠BAH=12∠BAF ＝60°， ∴∠ABH ＝30°，∴AH=12AB ＝4，根据勾股定理，得4，∴BF ＝2BH ＝8．故答案为：8．2. 2. 解析：连接OB 交AC 于H ．2题图在正六边形ABCDEF 中，∵AB ＝BC ，∠ABC ＝120°，6∴AB BC =，∴OB ⊥AC ，∴∠ABH ＝∠CBH ＝60°，AH ＝CH ，∴AH，∴AC ＝，故答案为．3. B. 解析：由得，∴．∴n ＝180°． 4. C. 解析：可求圆锥母线长是5cm ．∴圆锥的侧面积为：π×3×5=15π.5. 解：将小圆向右平移，使两圆变成同心圆，如图，连OB ，过O 作OC ⊥AB 于C 点，则AC=BC =12，∵AB 是大半圆的弦且与小半圆相切，∴OC 为小圆的半径，∴S 阴影部分=S 大半圆-S 小半圆=12π•OB 2-12π•OC 2=12π（OB 2-OC 2）=12πAC 2=72π．故答案为72π．5题图6. 解：∵圆O 的周长为20πcm ，∴圆O 的半径=10cm ，∵圆A 圆B 周长都是4πcm ，∴圆A 圆B 周长半径都是2，∴圆A 在圆O 内沿圆O 滚动半径是10﹣2=8，圆B 在圆O 外沿圆O 滚动半径是10+2=12∴要回到原来的位置，圆B 转动的周数=12÷2=6，圆A 转动的周数=8÷2=4．22rl r ππ=2l r =22180n r r ππ=。

2023年人教版数学中考复习考点专练——三角形的内切圆与内心(含答案)

2023年人教版数学中考复习考点专练——三角形的内切圆与内心一、单选题1．如图，⊙O内切于⊙ABC，切点为D，E，F，若⊙B=50°，⊙C=60°，连接OE，OF，DE，DF，⊙EDF等于（）A．45°B．55°C．65°D．70°2．下列命题是真命题的是（）A．对顶角相等B．平行四边形的对角线互相垂直C．三角形的内心是它的三条边的垂直平分线的交点D．三角分别相等的两个三角形是全等三角形3．如图，已知⊙ABC与⊙ACD都是直角三角形，⊙B=⊙ACD=90°，AB=4，BC=3，CD=12。

则⊙ABC的内切圆与⊙ACD的内切圆的位置关系是（）A．内切B．相交C．外切D．外离4．如图，⊙ABC中，⊙C＝90°，AC＝12，BC＝5，⊙O与⊙ABC的三边相切于点D、E、F，则AD长为（）A．8B．10C．12D．14 5．下列四个命题中，正确的个数是（）①经过三点一定可以画圆；②任意一个三角形一定有一个外接圆；③三角形的内心是三角形三条角平分线的交点；④三角形的外心到三角形三个顶点的距离都相等；⑤三角形的外心一定在三角形的外部．A ．4个B ．3个C ．2个D ．1个 6．在⊙ABC 中，O 为内心，⊙A=80°，则⊙BOC=（）A ．140°B ．135°C ．130°D ．125° 7．若等腰直角三角形的外接圆半径的长为2，则其内切圆半径的长为（）A ．2 ﹣2B ．2﹣C ﹣1D 8．有如下四个命题：（1）三角形有且只有一个内切圆；（2）四边形的内角和与外角和相等；（3）顺次连接四边形各边中点所得的四边形一定是菱形；（4）一组对边平行且一组对角相等的四边形是平行四边形．其中真命题的个数有（）A ．1个B ．2个C ．3个D ．4个 9．已知一个三角形的三边长分别为5、7、8，则其内切圆的半径为（）A ．2B ．32CD ．10．如图，在 ABC ∆ 中， 60BAC ∠=︒ 其周长为20，⊙I 是 ABC ∆ 的内切圆，其半径为，则 BIC ∆ 的外接圆半径为（）A ．7B ．C ．2D 二、填空题11．在⊙ABC 中，⊙C=90°，AB=10，且AC=6，则这个三角形的内切圆半径为．12．已知一个三角形的三边长分别为5、7、8，则其内切的半径为．13．如图，在平面直角坐标系中，矩形 OACB 的顶点 ()68C ，，点 I 是 ABC 的内心，将 ABC 绕原点顺时针旋转 90︒ 后， I 的对应点 I ' 的坐标是．14．从一个边长为 cm 的正三角形钢板上裁下一个面积最大的圆，则这个圆的半径是 cm ．15．若直角三角形的两边a 、b 是方程 27120x x -+= 的两个根，则该直角三角形的内切圆的半径r = ．三、解答题16．如图，在⊙ABC 中，⊙C=90°，⊙O 是⊙ABC 的内切圆，切点分别为D ，E ，F ，若BD=6，AD=4，求⊙O 的半径r ．17．如图⊙ABC 内接于圆O ，I 是⊙ABC 的内心，AI 的延长线交圆O 于点D ．（1）求证：BD=DI ；（2）若OI⊙AD ，求AB AC BC+的值．18．如图，在⊙ABC中，内切圆I和边BC、CA、AB分别相切于点D、E、F，若⊙A=70°，求⊙FDE．19．如图，⊙ABC中，⊙C=90°，⊙O是⊙ABC的内切圆，D、E、F是切点．（1）求证：四边形ODCE是正方形；（2）如果AC=6，BC=8，求内切圆⊙O的半径．20．如图：在三角形ABC中，AB=5，AC=7，BC=8，求其内切圆的半径.21．如图，点E是⊙ABC的内心，AE的延长线交BC于点F，交⊙ABC的外接圆⊙O 于点D，连接BD，过点D作直线DM，使⊙BDM=⊙DAC．（⊙）求证：直线DM是⊙O的切线；（⊙）求证：DE2=DF•DA．答案解析部分1．【答案】B2．【答案】A3．【答案】C4．【答案】B5．【答案】B6．【答案】C7．【答案】A8．【答案】C9．【答案】C10．【答案】D11．【答案】212．13．【答案】(64)-，14．【答案】115．【答案】1或1 216．【答案】解：连接EO，FO，∵⊙O是⊙ABC的内切圆，切点分别为D，E，F，∴OE⊙BC，OF⊙AC，BD=BE，AD=AF，EC=CF，又∵⊙C=90°，∴四边形ECFO是矩形，又∵EO=FO，∴矩形OECF是正方形，设EO=x，则EC=CF=x，在Rt⊙ABC中BC2+AC2=AB2故（x+6）2+（x+4）2=102，解得：x=2，即⊙O的半径r=2．17．【答案】（1）证明：∵点I 是⊙ABC 的内心 ∴⊙BAD=⊙CAD ，⊙ABI=⊙CBI∵⊙CBD=⊙CAD∴⊙BAD=⊙CBD∴⊙BID=⊙ABI+⊙BAD ，⊙BAD=⊙CAD=⊙CBD ， ∵⊙IBD=⊙CBI+⊙CBD ，∴⊙BID=⊙IBD∴ID=BD ；（2）解：连接OA 、OD 、BD 和BI ，∵OA=OD ，OI⊙AD∴AI=ID ，∵I 为⊙ABC 内心，∴⊙BAD=⊙BCD ，∴弧BD=弧CD ，∵弧CD=弧CD ，∴⊙BCD=⊙BAD ，∴⊙DBI=⊙BCD+⊙CBI=⊙CAD+⊙CBI ， =12（⊙BAC+⊙ACB ）， ∵⊙DIB=⊙DAB+⊙ABI=12（⊙BAC+⊙ABC ）， ∴⊙DIB=⊙DBI ，∴BD=ID=AI ，BD DC ∧∧=，故OD⊙BC ，记垂足为E ，则有BE=12BC ，作IG⊙AB于G，又⊙DBE=⊙IAG，而BD=AI，∴Rt⊙BDE⊙Rt⊙AIG，于是，AG=BE=12BC，但AG=12（AB+AC﹣BC），故AB+AC=2BC，∴AB ACBC=2．18．【答案】解：连接IE，IF，∵内切圆I和边BC、CA、AB分别相切于点D、E、F，∴⊙AEI=⊙AFI=90°，∵⊙A=70°，∴⊙EIF=110°，∴⊙FDE=55°．答：⊙FDE的度数为55°．19．【答案】（1）解：∵⊙O是⊙ABC的内切圆，∴OD⊙BC，OE⊙AC，又⊙C=90°，∴四边形ODCE是矩形，∵OD=OE，∴四边形ODCE是正方形.（2）解：∵⊙C=90°，AC=6，BC=8，∴AB= =10，由切线长定理得，AF=AE ，BD=BF ，CD=CE ， ∴CD+CE=BC+AC ﹣BD ﹣AE=BC+AC ﹣AB=4，则CE=2，即⊙O 的半径为2．20．【答案】解：如图，作 AD BC ⊥ ，设 BD x = ，则 8CD x =- ，由勾股定理可知： 2222AB BD AC CD -=- ，则 ()2225498x x -=-- ，解得 52x = ，则 2AD = ，故 118222ABC S BC AD =⋅=⨯⨯= ，由三角形的内切圆性质，可得： ()12ABC S r AB BC AC =++2ABC S r AB BC AC ∴===++ . 21．【答案】解：（⊙）如图所示，连接OD ， ∵点E 是⊙ABC 的内心，∴⊙BAD=⊙CAD ，∴BD = CD ，∴OD⊙BC ，又∵⊙BDM=⊙DAC ，⊙DAC=⊙DBC ， ∴⊙BDM=⊙DBC ，∴BC⊙DM ，∴OD⊙DM ，∴直线DM 是⊙O 的切线；（⊙）如图所示，连接BE ，∵点E 是⊙ABC 的内心，∴⊙BAE=⊙CAE=⊙CBD ，⊙ABE=⊙CBE ， ∴⊙BAE+⊙ABE=⊙CBD+⊙CBE ，即⊙BED=⊙EBD，∴DB=DE，∵⊙DBF=⊙DAB，⊙BDF=⊙ADB，∴⊙DBF⊙⊙DAB，∴DFDB=DBDA，即DB2=DF•DA，∴DE2=DF•DA．。

2025年九年级中考数学复习专题六圆

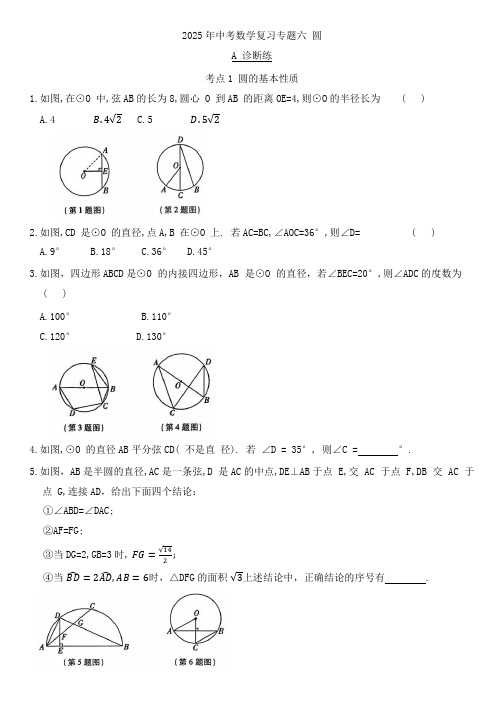
2025年中考数学复习专题六圆A 诊断练考点1 圆的基本性质1.如图,在⊙O 中,弦AB的长为8,圆心 O 到AB 的距离OE=4,则⊙O的半径长为 ( )A.4B.4√2C.5D.5√22.如图,CD 是⊙O 的直径,点A,B 在⊙O 上. 若AC=BC,∠AOC=36°,则∠D= ( )A.9°B.18°C.36°D.45°3.如图，四边形ABCD是⊙O 的内接四边形，AB 是⊙O 的直径，若∠BEC=20°,则∠ADC的度数为( )A.100°B.110°C.120°D.130°4.如图,⊙O 的直径AB平分弦CD( 不是直径). 若∠D = 35°, 则∠C =°.5.如图，AB是半圆的直径,AC是一条弦,D 是AC的中点,DE⊥AB于点 E,交 AC 于点 F,DB 交 AC 于点 G,连接AD，给出下面四个结论：①∠ABD=∠DAC;②AF=FG;;③当DG=2,GB=3时,FG=√142̂=2AD̂,AB=6时，△DFG的面积√3上述结论中，正确结论的序号有 .④当BD考点2 与圆有关的位置关系6.如图,⊙O 中,弦AB 的长为√3,点 C在⊙O 上,OC⊥AB,∠ABC30°.⊙O所在的平面内有一点 P,若OP=5,则点 P与⊙O 的位置关系是 ( )A.点 P在⊙O上B.点 P在⊙O内C.点P在⊙O外D.无法确定7.如图,以AB 为直径的⊙O与AC相切于点 A，以AC 为边作平行四边形ACDE,点 D,E 均在⊙O 上,DE 与AB交于点F,连接CE,与⊙O交于点 G,连接 DG. 若 AB = 10,DE = 8,则 AF = ,DG=.8.如图,⊙O 是△ABC的外接圆，D 是直径AB 上一点，∠ACD 的平分线交AB 于点E,交⊙O于另一点F,FA=FE.(1)求证:CD⊥AB;(2)设FM⊥AB,垂足为M.若OM=OE=1,求AC的长.9.如图,△ABC 内接于⊙O,AB=AC=10,过点A作AE∥BC,交⊙O 的直径 BD的延长线于点 E，连接CD.(1)求证:AE 是⊙O 的切线;,求 CD 和DE 的长.(2)若tan∠ABE=12考点3 与圆有关的计算10.两个半径相等的半圆按如图方式放置，半圆O'的一个直径端点与半圆O的圆心重合，若半圆的半径为2，则阴影部分的面积是 ( )A.43π−√3B.43πC.23π−√3D.43π−√3411.已知圆锥的底面圆半径为 4，母线长为 5，则圆锥的侧面积为 .12.铁艺花窗是园林设计中常见的装饰元素.如图是一个花瓣造型的花窗示意图，由六条等弧连接而成，六条弧所对应的弦构成一个正六边形，中心为点O，AB所在圆的圆心C恰好是△ABO 的内心，若.AB=2√3,则花窗的周长 ( 图中实线部分的长度 ) = .(结果保留π)B 考点突破练考点4 圆的基本性质基础考向1 弧、弦、圆心角的关系1.如图,AB是⊙O 的直径，BC=CD,∠COD=52°,,则∠AOD 的大小为 .2.如图,在⊙O中,AB̂=CD,有下列结论:①AB = CD;②AC = BD;③∠AOC=∠BOD;④AĈ=BD̂,其中正确的是 (填序号).考向2 垂径定理及其推论3.如图,OA,OB,OC都是⊙O的半径,AC,OB 交于点 D.若AD=CD=8,OD=6,则BD的长为 ( )A.5B.4C.3D.24.如图，⊙O 是一个盛有水的容器的横截面，⊙O的半径为10 cm，水的最深处到水面AB 的距离为4 cm，则水面AB的宽度为 cm.考向3 圆周角定理及其推论5.如图,在⊙O 中,弦AB,CD 相交于点 P,若∠A= 48°,∠APD=80°,则∠B的度数为( )A.32°B.42°C.48°D.52°6.如图,四边形 ABCD 内接于⊙O,AC,BD 为对角线,BD 经过圆心 O. 若∠BAC=40°,则∠DBC的度数为( )A.40°B.50°C.60°D.70°7.如图，将一个量角器与一把无刻度直尺水平摆放，直尺的长边与量角器的外弧分别交于点A，B，C，D，连接AB，则∠BAD的度数为 .8.如图,AB 为⊙O 的直径,CD 为⊙O 的一条弦，∠BCD 的平分线交⊙O 于点E,AD,BE 的延长线交于点 F.(1)若∠BAD=70°,求∠ABE 的度数. (2)求证:AB=AF.考向4 圆内接四边形9.如图，圆内接四边形ABCD 中,∠BCD = 105°,连接 OB,OC,OD,BD,∠BOC=2∠COD.则∠CBD 的度数是( )A.25°B.30°C.35°D.40°10.如图,四边形ABCD 内接于⊙O,BC∥AD,AC⊥BD. 若∠AOD =120°,AD √3 则∠CAO 的度数与 BC 的长分别为 ( )A.10°,1B.10°， √2C.15°,1D.15°， √211.如图,四边形ABCD 内接于 ⊙O,点 E 在 CD 的延长线上. 若∠ADE=70°,则∠AOC= °.12.如图，四边形AB-CD 内接于 ⊙O,连接 AC,BD, ∠ABD =∠ADC,过点D 作DP∥AB,交⊙O 于点M,交BC 的延长线于点 P. (1)求证:BP=BD;诊断区检测区突破区,AB=10,求 CP 的长.(2)若cos∠ABD=2513.下列说法中正确的个数是 ( )①同圆或等圆中，同弧所对的圆周角相等；②在同圆或等圆中，同一条弦所对的圆周角相等；③相等的圆心角所对的弧相等；④平分弦的直径垂直于弦，并且平分弦所对的弧.A.1B.2C.3D.4提升1.如图，已知点A,B,C,D都在⊙O上,OB⊥AC,BC=CD,下列说法错误的是 ( )̂=BĈ B.∠AOD=3∠BOCA.ABC. AC=2CDD. OC⊥BD2.如图,在⊙O中,OA⊥BC,∠ADB=30°,BC=√3,则OC( )A.1B.2C.√3D.43.在半径为2的⊙O中,弦AB的长度为2,点C 为⊙O上异于A,B两点的一个动点,则∠BCA=°.,E,F 分别为AC,BC的中点，弦EF 分别4.如图,AB 为半圆O的直径，C为半圆上一点且sin∠CAB=35交AC,CB 于点 M,N. 若MN=3√2,则 AB =5.如图,OA,OB,OC都是⊙O 的半径,∠ACB=2∠BAC.(1)求证:∠AOB=2∠BOC;(2)若AB=4,BC=√5，求⊙O的半径.6.如图,以△ABC的边AC为直径作⊙O,交 BC 边于点 D,过点 C 作CE ∥AB 交⊙O 于点 E, 连接AD, DE,∠B=∠ADE.(1)求证:AC=BC;(2)若 tan B=2,CD=3,求AB 和DE 的长.7.如图，在扇形 AOB 中,OA=8,点 C 在半径 OA 上,将△BOC沿BC翻折,点 O 的对应点 D 恰好落在弧 AB 上,再将弧 AD 沿着 CD 翻折至弧A₁D(点A₁是点A的对应点),那么 OA₁的长为 .考点5 与圆有关的位置关系基础考向1 点、直线和圆的位置关系1.在同一平面内，已知⊙O的半径为2，圆心O到直线l的距离为3，点P为圆上的一个动点，则点P 到直线l的最大距离是 ( )A.2B.5C.6D.82.已知平面内有⊙O 和点A,B,若⊙O 的半径为3 cm,线段OA=4cm,OB=3cm,则直线AB与⊙O的位置关系为 ( )A.相离B.相交C.相切D.相交或相切3.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD 是AB 边上的高,AB=4，若圆C是以点 C 为圆心，2为半径的圆，那么下列说法正确的是 ( )A.点 D 在圆 C 上,点 A,B 均在圆C外B.点 D 在圆 C 内,点 A,B 均在圆C外C.点A,B,D 均在圆C外D.点A在圆C外，点D在圆C内，点B在圆C上考向2 切线的性质及判定4.如图,AC 是⊙O 的切线,B 为切点,连接OA,OC.若∠A=30°,AB=√3,BC=3则OC的长度是( )A,3 B.√3C√13 D.65.如图,AB 切⊙O 于点B,连接OA交⊙O 于点C,BD∥OA交⊙O 于点D.连接CD,若∠OCD=25°,则∠A的度数为( )A.25°B.35°C.40°D.45°̂上. 已知∠A = 50°, 6.如图,点 A 是⊙O 外一点,AB,AC分别与⊙O 相切于点 B,C,点 D 在BDC则∠D 的度数是 .7.如图,已知△ABC 内接于⊙O,CO 的延长线交AB 于点 D,交⊙O 于点E,交⊙O 的切线AF于点F,且AF∥BC.(1)求证:AO∥BE;(2)求证:AO 平分∠BAC.∠A,点O在BC上，以点O为圆心的8.如图,在△ABC 中,∠ACB=90°,点 D 是 AB 上一点,且∠BCD=12圆经过C,D两点.(1)试判断直线 AB 与⊙O 的位置关系，并说明理由；,⊙O的半径为3，求AC的长.(2)若sinB=35考向3 三角形的外接圆与内切圆9.如图,点O 是△ABC外接圆的圆心，点I 是△ABC 的内心，连接OB,IA.若∠CAI=35°,则∠OBC的度数为( )A.15°B.17.5°C.20°D.25°10.如图的方格纸中，每个方格的边长为1，A，O两点皆在格线的交点上.今在此方格纸格线的交点上另外找两点 B，C,使得△ABC 的外心为 O,求 BC 的长度（）A.4B.5C.√10D.√2011.如图，⊙O是锐角三角形 ABC 的外接圆,OD⊥AB,OE⊥BC,OF⊥AC,垂足分别为 D,E,F,连接 DE,EF,FD.若DE+DF=6.5,△ABC 的周长为21,则EF 的长为 ( )A.8B.4C.3.5D.312.如图,△ABC的内切圆⊙I与BC,CA,AB 分别相切于点 D,E,F,若⊙I的半径为r,∠A=α,则(BF+CE-BC)的值和∠FDE 的大小分别为 ( )A.2r,90°-αB.0,90°-αC.2r,90∘−α2D.0,90∘−α213.如图所示的网格由边长为1个单位长度的小正方形组成，点A，B，C在直角坐标系中的坐标分别为(3，6),(-3,3),(7,-2),则△ABC 内心的坐标为 .14.在同一平面内，点P不在⊙O上，若点P到⊙O上的点的最大距离是11，最小距离是5，则⊙O的半径是 .提升1.已知点A在半径为3的圆O 上，如果点 A 到直线a 的距离是6，那么圆O与直线a的位置关系是( )A.相交B.相离C.相切D.以上答案都不对2.已知一个三角形的内心与外心重合，若它的内切圆的半径为2，则它的外接圆的面积为 ( )A.4πB.8πC.12πD.16π3.如图,在四边形AB-CD中,AB∥CD,AD⊥AB,以 D 为圆心,AD 为半径的弧恰好与 BC 相切，切点为E.若ABCD =13,则 sin C的值 ( )A 23 c 344.如图是一个圆形餐盘的正面及其固定支架的截面图，凹槽ABCD 是矩形.当餐盘正立且紧靠支架于点A ，D 时，恰好与 BC 边相切，则此餐盘的半径等于 cm.5.如图，在平面直角坐标系中,已知点A(1,0),P(-1,0),⊙P 过原点O ，且与x 轴交于另一点D ，AB 为⊙P 的切线,B 为切点,BC 是⊙P 的直径,则∠BCD 的度数为 °.6.如图,在△ABC 中,AB=BC,以BC 为直径作⊙O 与AC 交于点D,过点 D 作DE⊥AB,交CB 延长线于点 F,垂足为点 E.(1)求证:DF 为⊙O 的切线;(2)若 BE =3,cosC =45,求 BF 的长.B.√53D.√747.如图，分别过矩形ABCD的四个顶点作其内部的⊙O 的切线，切点分别为E，F，G，H，若AE = a,BF = b, DH = c, 则 CG 的长为 .(用含a,b,c的代数式表示)考点6 与圆有关的计算基础考向1 圆内接正多边形的计算1.如图,正五边形ABCDE内接于⊙O,连接OC,OD,则∠BAE-∠COD= ( )A.60°B.54°C.48°D.36°2.如图,点 P₁~P₈是⊙O 的八等分点.若△P₁P₃P₇,四边形 P₃P₄P₆P₇的周长分别为a，b，则下列正确的是( )A. a<bB. a=bC. a>bD. a，b大小无法比较考向2 弧长与扇形面积的计算3.圆心角为90°，半径为3的扇形弧长为 ( )A.2πB.3π C32D.12π4.“莱洛三角形”也称为圆弧三角形，它是工业生产中广泛使用的一种图形.如图，分别以等边△ABC 的三个顶点为圆心，以边长为半径画弧，三段圆弧围成的封闭图形是“莱洛三角形”.若等边△ABC的边长为3，则该“莱洛三角形”的周长等于 ( )A.πB.3πC.2πD.2π−√35.马面裙(图(1))，又名“马面褶裙”，是我国古代女子穿着的主要裙式之一.将图(1)中的马面裙抽象成数学图形，如图(2)中的阴影部分所示，AD 和BC所在圆的圆心均为点O，且点A在 OB 上,点 D 在 OC 上,若OA=AB=6 dm,OA⊥OD，则该马面裙裙面(图(2)中阴影部分)的面积为 ( )A.36πdm²B.27πdm²C.18πdm²D.12πdm²6.如图，在矩形ABCD中,AB=3,BC=6,E为BC的中点,连接AE，DE.以E为圆心，EB 长为半径画弧，分别与AE，DE交于点M，N，则图中阴影部分的面积和是 (结果保留π).考向3 圆锥的有关计算7.如图,用圆心角为120°半径为6的扇形围成一个圆锥的侧面(接缝忽略不计)，则这个圆锥的高是.8.如图，小珍同学用半径为8cm ，圆心角为 100°的扇形纸片，制作一个底面半径为2cm 的圆锥侧面，则圆锥上粘贴部分的面积是 cm².9.如图，圆锥形烟囱帽的底面半径为30cm ，母线长为50cm ，则烟囱帽的侧面积为 cm².(结果保留π)10.如图,在△ABC 中,AC=3,AB=4,BC 边上的高AD=2,将△ABC 绕着BC 所在的直线旋转一周得到的几何体的表面积为 .考向4 与圆有关的阴影部分面积11.如图,在△ABC 中,∠ABC=90°,∠ACB=30°,AB=4,点O 为BC 的中点，以O 为圆心，OB 长为半径作半圆，交AC 于点 D ，则图中阴影部分的面积是( )A.5√3−√33π B.5√3−4πC.5√3−2πD.10√3−2π12.如图,矩形ABCD 内接于⊙O,分别以AB,BC,CD,AD 为直径向外作半圆.若AB=4，BC=5，则阴影部分的面积是 ( )检测区突破区A.414π−20B.412π−20C.20πD.2013.如图,Rt△BCO中,∠BCO=90°,∠CBO=30°,BO=4cm,将△BCO绕点 O逆时针旋转至△B'C'O,点 C'恰好落在 BO 延长线上，则边 BC 扫过区域(图中阴影部分)的面积为 ( )A.πcm²B.(π+√3)cm2C.4πcm²D.(4π+√3)cm214.如图，点B在半圆O 上,直径AC=12,∠BAC=40°,则图中阴影部分的面积为(结果保留π).15.如图,△ABC的周长为20,⊙O 的半径为1,⊙O从与AB 相切的切点D的位置出发，在△ABC外部，按顺时针方向沿三角形的边无滑动滚动，当滚动一周又回到点 D 的位置时，⊙O的圆心O运动的长度 (填“>”“=”或“<”)三角形的周长，运动长度为 .提升1.如图，正六边形AB-CDEF内接于⊙O,点P在AB上,点Q是DÊ的中点，则∠CPQ的度数为 ( ) A.30° B.45° C.36° D.60°2.如图,正六边形AB-CDEF的外接圆⊙O 的半径为2，过圆心 O 的两条直线l₁，l₂的夹角为60°，则图中的阴影部分的面积为 ( )A.43π−√3B.43π−√32C.23π−√3D.23π−√323.如图，已知点 C 为圆锥母线 SB 的中点，AB 为底面圆的直径，SB=6，AB=4，一只蚂蚁沿着圆锥的侧面从A 点爬到C 点，则蚂蚁爬行的最短路程为 ( )A.5B.√3C.3√2D.2√34.如图,在▱ABCD中,AB=√3+1,BC=2,AH⊥CD,垂足为H,AH=√3.以点 A 为圆心，AH 长为半径画弧，AB,AC,AD 分别交于点E,F,G.若用扇形AEF围成一个圆锥的侧面，记这个圆锥底面圆的半径为r₁；用扇形AHG 围成另一个圆锥的侧面，记这个圆锥底面圆的半径为r₂，则r₁−r₂=.(结果保留根号) 5.如图,在△ABC 中,AB=4,∠C=64°,以AB 为直径的⊙O 与AC 相交于点 D,E 为ABD̂上一点,且∠ADE=40°.(1)求BÊ的长；(2)若∠EAD=76°, 求证:CB为⊙O 的切线.6.将三个相同的六角形螺母并排摆放在桌面上，其俯视图如图(1)，正六边形边长为2且各有一个顶点在直线l上.两侧螺母不动，把中间螺母抽出并重新摆放后，其俯视图如图(2)，其中，中间正六边形的一边与直线l平行，有两边分别经过两侧正六边形的一个顶点.则图(2)中(1)∠α= 度;(2)中间正六边形的中心到直线l的距离为 (结果保留根号).C 检测验收练一、选择题(每小题5分，共20分)1.如图,AB是⊙O 的直径,∠E=35°,则∠BOD= ( )A.80°B.100°C.120°D.110°2.数学活动课上，同学们要测一个如图所示的残缺圆形工件的半径，小明的解决方案是在工件圆弧上任取两点A,B,连接AB,作AB 的垂直平分线 CD 交AB于点D,交AB 于点 C,测出AB=40 cm, CD=10cm，则圆形工件的半径为 ( )A.50cmB.35 cmC.25 cmD.20cm3.刘徽(今山东滨州人)是魏晋时期我国伟大的数学家，中国古典数学理论的奠基者之一，被誉为“世界古代数学泰斗”.刘徽在注释《九章算术》时十分重视一题多解，其中最典型的是勾股容方和勾股容圆公式的推导，他给出了内切圆直径的多种表达形式. 如图,Rt△ABC 中,∠C =90°, AB,BC,CA 的长分别为c,a,b.则可以用含c，a，b的式子表示出△ABC 的内切圆直径d，下列表达式错误的是 ( )A. d=a+b-cB.d=2aba+b+cC.d=√2(c−a)(c−b)̅̅̅̅̅̅̅̅̅ D. d=|(a-b)(c-b)|4.如图，两个半径长均为 1 的直角扇形的圆心分别在对方的圆弧上,扇形 CFD 的圆心 C 是弧 AB的中点,且扇形 CFD 绕着点 C 旋转,半径 AE,CF交于点G，半径BE，CD交于点 H，则图中阴影部分的面积等于 ( )A.π2−1B.π2−12C.π-1D.π-2二、填空题(每小题5分，共30分)5.如图，AB 是圆的直径,∠1,∠2,∠3,∠4的顶点均在 AB上方的圆弧上，∠1，∠4的一边分别经过点A，B，则∠1+∠2+∠3+∠4=°.6.如图,四边形ABCD是⊙O 的内接四边形，点O 在四边形ABCD内部，过点C作⊙O 的切线交AB的延长线于点P,连接 OA,OB. 若∠AOB = 140°,∠BCP =35°,则∠ADC 的度数为 .7.[2024 浙江杭州校级二模]如图，正六边形AB-CDEF与正方形AGDH都内接于⊙O，则劣弧BG 所对圆周角的度数为 .8.如图,△ABC 内接于⊙O,点 O 在AB上,AD 平分∠BAC 交⊙O 于D,连接BD.若AB=10,BD=√5,则BC的长为 .9.如图，在边长为6的正六边形 ABCDEF中,以点 F为圆心,以 FB 的长为半径作BD，剪下图中阴影部分做一个圆锥的侧面，则这.个圆锥的底面半径为 .̂的圆心10.如图，四边形ABCD 是正方形，曲线DA₁B₁C₁D₁A₂B₂…叫做“正方形的渐开线”，其中DA1为点A,半径为AD;A₁B₁的圆心为点B，半径为BA₁;B₁C₁的圆心为点C，半径为(CB₁;C₁D₁的圆心为点 D，半径为DC₁;……,DA₁,A₁B₁,B₁C₁,C₁D₁,…I的圆心依次按A,B,C,D 的顺序循环,当AB=1时,的长是 .三、解答题(11 题 10 分,12 题 12 分, 13 题13分,14题15分,共50分)11.日晷仪也称日晷，是观测日影计时的仪器，主要根据日影的位置，以指定当时的时辰或刻数，是我国古代较为普遍使用的计时仪器，如图(1)所示. 小东为了探究日晷的奥秘，在不同时刻对日晷进行了观察探究.(1)探究1：如图(2)，日晷的平面是以点O为圆心的圆，直线l是日晷的底座，OA⊥l于点A,与⊙O交于点B,点P在⊙O 上,OP 为某一时刻晷针的影长，PB的延长线与直线l交于点 C.连接A P,当AP=AC时,求证:AP与⊙O相切.(2)探究2：当小东观察到影长OP 落在图(3)所示位置时，连接AP，交⊙O 于点D,若∠POD=90∘,OA=√10,AD=√2,求⊙O的半径.12.已知△AOB 中,∠ABO =30°,AB为⊙O 的弦,直线MN与⊙O 相切于点 C.(1)如图(1),若AB∥MN,直径 CE 与 AB 相交于点 D,求∠AOB 和∠BCE的大小;(2)如图(2),若OB∥MN,CG⊥AB,垂足为G,CG与OB 相交于点 F,OA=3,求线段 OF的长.13.如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点 D,交AC于点 E,过点 D 作DF⊥AC 于点 F,FD 的延长线交AB 的延长线于点 G.(1)若AB=10,BC=12,求△DFC的面积;(2)若 tan C=2,AE=6,求 BG的长.14.如图(1),O 是正方形ABCD对角线上一点，以O为圆心，OC长为半径的⊙O 与AD 相切于点E，与AC 相交于点 F.(1)求证:AB 与⊙O 相切;(2)若正方形ABCD 的边长为√2+1,求⊙O的半径；̂于点 N.(3)如图(2),在(2)的条件下,若点 M是半径OC 上的一个动点,过点 M 作MN⊥OC 交CE当CM:FM=1:4时,求CN的长.。

河北省2019届中考数学系统复习第六单元圆滚动小专题三角形的内心与外心练习

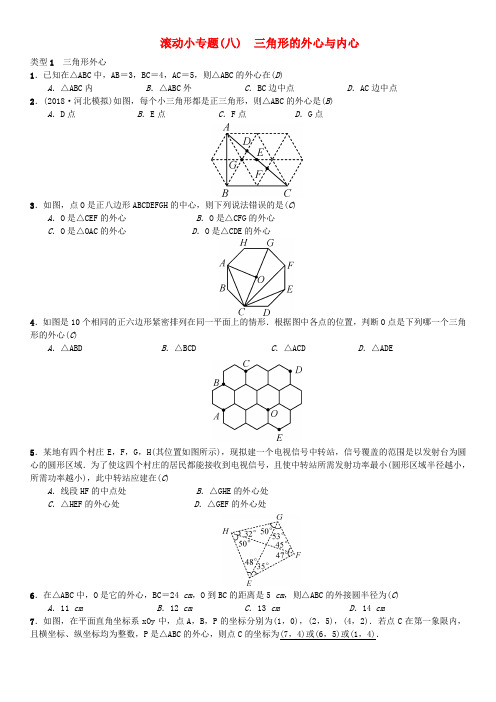
滚动小专题(八) 三角形的外心与内心类型1三角形外心1．已知在△ABC中，AB＝3，BC＝4，AC＝5，则△ABC的外心在(D)A．△ABC内B．△ABC外C．BC边中点D．AC边中点2．(2018·河北模拟)如图，每个小三角形都是正三角形，则△ABC的外心是(B)A．D点B．E点C．F点D．G点3．如图，点O是正八边形ABCDEFGH的中心，则下列说法错误的是(C)A．O是△CEF的外心B．O是△CFG的外心C．O是△OAC的外心D．O是△CDE的外心4．如图是10个相同的正六边形紧密排列在同一平面上的情形．根据图中各点的位置，判断O点是下列哪一个三角形的外心(C)A．△ABD B．△BCD C．△ACD D．△ADE5．某地有四个村庄E，F，G，H(其位置如图所示)，现拟建一个电视信号中转站，信号覆盖的范围是以发射台为圆心的圆形区域．为了使这四个村庄的居民都能接收到电视信号，且使中转站所需发射功率最小(圆形区域半径越小，所需功率越小)，此中转站应建在(C)A．线段HF的中点处B．△GHE的外心处C．△HEF的外心处D．△GEF的外心处6．在△ABC中，O是它的外心，BC＝24 cm，O到BC的距离是5 cm，则△ABC的外接圆半径为(C) A．11 cm B．12 cm C．13 cm D．14 cm7．如图，在平面直角坐标系xOy中，点A，B，P的坐标分别为(1，0)，(2，5)，(4，2)．若点C在第一象限内，且横坐标、纵坐标均为整数，P是△ABC的外心，则点C的坐标为(7，4)或(6，5)或(1，4)．8．如图，在△ABC 中，∠BAC＝70°，AB ＝AC ，O 为△ABC 的外心，△OCP 为等边三角形，OP 与AC 相交于点D ，连接OA.(1)求∠OAC 的度数； (2)求∠AOP 的度数．解：(1)∵O 为△ABC 的外心， ∴AO 垂直平分BC. ∵AB＝AC ，∴AO 平分∠BAC. ∴∠OAC＝12∠BAC＝35°.(2)∵O 为△ABC 的外心， ∴AO＝CO.∴∠OAC＝∠OCA＝35°.∴∠AOC＝110°. ∵△OCP 为正三角形，∴∠POC＝60°. ∴∠AOP＝50°.类型2 三角形内心9．如图为5×5的网格图，点A ，B ，C ，D ，O 均在格点上，则点O 是(B )A ．△ACD 的外心B ．△ABC 的外心 C ．△ACD 的内心 D ．△ABC 的内心10．如图，△ABC 是等腰直角三角形，点D ，E 在BC 上，△ADE 是等边三角形．若点O 是△ABC 的内心，则下列说法正确的是(C )A ．点O 是△ADE 的内心B ．点O 是△ADE 的外心C ．点O 不是△ABE 的内心D ．点O 是△ABC 的外心提示：易知OA平分∠BAC，由于OA不平分∠BAE，所以点O不是△ABE的内心．11．如图，I点为△ABC的内心，D点在BC上，且ID⊥BC.若∠B＝44°，∠C＝56°，则∠AID的度数为(A) A．174° B．176° C．178° D．180°提示：连接CI，∠AID＝∠AIC＋∠CID＝112°＋62°＝174°.12．如图，△ABC中，AB＝7 cm，AC＝8 cm，BC＝6 cm，点O是△ABC的内心，过点O作EF∥AB，与AC，BC分别交于点E，F，则△CEF的周长为(A)A．14 cm B．15 cm C．13 cm D．10.5 cm提示：连接OA，OB.C△CEF＝CE＋CF＋EF＝CE＋EA＋CF＋FB＝CA＋CB＝14 cm.13．如图，I是△ABC的内心，AI的延长线和△ABC的外接圆相交于点D，连接BI，BD，DC.下列说法中错误的一项是(D)A．线段DB绕点D顺时针旋转一定能与线段DC重合B．线段DB绕点D顺时针旋转一定能与线段DI重合C．∠CAD绕点A顺时针旋转一定能与∠DAB重合D．线段ID绕点I顺时针旋转一定能与线段IB重合提示：根据I是△ABC的内心，得到AI平分∠BAC，BI平分∠ABC，由角平分线的定义得到∠BAD＝∠CAD，∠AB I ＝∠CBI.根据三角形外角的性质得到∠DBI＝∠DIB，根据等腰三角形的性质得到BD＝DI.14．(2018·娄底)如图，P是△ABC的内心，连接PA，PB，PC，△PAB，△PBC，△PAC的面积分别为S1，S2，S3.则S1＜S2＋S3.(填“＜”“＝”或“＞”)15．如图所示，在Rt △ABC 中，∠ACB＝90°，在斜边AB 上分别截取AD ＝AC ，BE ＝BC ，DE ＝6，点O 是△CDE 的外心，则点O 到△ABC 的三边的距离之和是9．提示：由题意知：点O 是EC ，CD 垂直平分线的交点，∵AD＝AC ，BE ＝BC ，∴EC 的垂直平分线经过点B 且平分∠B，CD 的垂直平分线经过点A 且平分∠A.∴点O 是△ABC 的内心．∵∠ACB＝90°，∴r＝12(AC ＋BC －AB)＝12(AD ＋BE －AB)＝12DE ＝3.∴点O 到△ABC 的三边的距离之和是3r ＝9.16．三角形内角平分线的交点为三角形的内心．如图，D 是△ABC 的内心，E 是△ABD 的内心，F 是△BDE 的内心．若∠BFE 的度数为整数，则∠BFE 至少是113°．17．已知I 是△ABC 的内心，AI 的延长线交△ABC 的外接圆于点D ，连接BD.(1)在图1中，求证：DB ＝DI ；(2)如图2，若AB 为直径，且OI⊥AD 于点I ，DE 切圆于点D ，求sin ∠ADE 的值．解：(1)证明：连接BI. ∵I 是△ABC 的内心，∴AD 平分∠CAB，BI 平分∠ABC. ∴∠CAD＝∠BAD，∠ABI＝∠CBI. ∵∠CAD＝∠DBC，∴∠DAB＝∠DBC. ∵∠DBI＝∠DBC＋∠CBI， ∠DIB＝∠DAB＋∠ABI， ∴∠DIB＝∠DBI.∴DB＝DI. (2)连接BD ，DO.∵AB 为直径，∴∠ADB＝90°. ∵OI⊥AD，∴AD＝2DI. ∵BD＝DI ，∴AD＝2BD.∴AB＝AD 2＋BD 2＝5BD.∵DE 切圆于点D ，∴∠ADE＋∠ADO＝90°.又∵∠ADO＋∠ODB＝90°，∠ODB＝∠OBD， ∴∠ABD＝∠ADE.∴sin ∠ADE＝sin ∠ABD＝AD AB ＝2BD 5BD ＝255.。

中考数学模拟题汇总《三角形的内切圆与内心》专项练习及答案

中考数学模拟题汇总《三角形的内切圆与内心》专项练习及答案一、单选题1．下列四个命题：①直角三角形斜边上的中线等于斜边的一半；②对角线相等的平行四边形是菱形；⑨一组邻边相等的矩形是正方形；④三角形三条角平分线的交点是三角形的外心．其中真命题共有（） A ．1个B ．2个C ．3个D ．4个2．内心和外心重合的三角形是( )A ．直角三角形B ．钝角三角形C ．等腰三角形D ．等边三角形3．如图，在ABC 中， 906,8,ACB AC BC O ∠===，是 ABC 的内切圆，连结 AO ，BO ，则图中阴影部分的面积之和为（）A ．3102π-B ．5142π-C ．12D ．144．如图，ABC 的内切圆O 与AB BC CA ，，分别相切于点D ，E ，F ，若50DEF ∠=︒，则A ∠的度数是（）A ．50︒B ．100︒C ．90︒D ．80︒5．在△ABC 中，点I 是内心，△BIC=114°，则△A 的度数为（）A ．57°B ．66°C ．48°D ．78°6．如图，△O 内切于△ABC ，切点分别为D ，E ，F ，连接OE ，OF ，DE ，DF ，乙组△A=80°，则△EDF等于（）A ．40°B ．45°C ．50°D ．80°7．在△ABC 中，已知△C=90°，BC=3，AC=4，则它的内切圆半径是（）A ．32B ．1C ．2D ．238．设边长为a 的等边三角形的高、内切圆的半径、外接圆的半径分别为h 、r 、R ，则下列结论不正确．．．的是（）A ．h R r =+B ．2R r =C ．3r =D ．3R =9．将正方形ABCD 绕点A 按逆时针方向旋转30°，得正方形AB 1C 1D 1，B 1C 1交CD 于点E ，3则四边形AB 1ED 的内切圆半径为（） A 31+B 33- C 31+D 33- 10．已知一个三角形的三边长分别为5、7、8，则其内切圆的半径为（）A ．3B ．32C 3D ．23二、填空题11．如图，在ABC 中，点O 是 ABC 的内心， 48A ∠=︒ ， BOC ∠= ︒ ．12．如图，在扇形CAB 中，CD△AB ，垂足为D ，△E 是△ACD 的内切圆，连接AE ，BE ，则△AEB 的度数为 .13．设两直角边分别为3、4的直角三角形的外接圆和内切圆的半径长分别为R 和r ，则R—r = . 14．《九章算术》是我国古代的数学名著，书中有这样的一个问题：“今有勾八步，股十五步，问勾中容圆径几何？”．其意思是：“如图，现有直角三角形，勾（短直角边）长为 8 步，股（长直角边）长为 15 步，问该直角三角形所能容纳的最大圆的直径是多少？”答：该直角三角形所能容纳的最大圆的直径是步．15．如图，点I 为△ABC 的内心，连AI 交△ABC 的外接圆于点D ，若2AI CD ＝，点E 为弦AC 的中点，连接EI ，IC ，若6IC ＝，5ID ＝，则IE 的长为．三、解答题16．如图，在Rt△ABC 中，△ACB=90°，△O 是Rt△ABC 的内切圆，其半径为1，E ，D 是切点，△BOC=105°.求AE 的长.17．如图，圆O 是ABC 的内切圆，其中75AB BC ==，，8AC =，求其内切圆的半径．18．如图，在△ABC 中，I 是内心，O 是AB 边上一点，△O 经过B 点且与AI 相切于I 点．（1）求证：AB=AC ；（2）若BC=16，△O 的半径是5，求AI 的长．19．如图1，点I 是△ABC 的内心，AI 的延长线交△ABC 的外接圆△O 于点D ．（1）求证：DB=DC=DI ；（2）若AB 是△O 的直径，OI△AD ，求tan2CAD的值． 20．如图：在三角形ABC 中，AB=5，AC=7，BC=8，求其内切圆的半径.21．如图，点E是△ABC的内心，AE的延长线交BC于点F，交△ABC的外接圆△O于点D，连接BD，过点D作直线DM，使△BDM=△DAC．（△）求证：直线DM是△O的切线；（△）求证：DE2=DF•DA．参考答案1．【答案】B 2．【答案】D 3．【答案】B 4．【答案】D 5．【答案】C6．【答案】C 7．【答案】B 8．【答案】C 9．【答案】B 10．【答案】C11．【答案】114 12．【答案】135° 13．【答案】1.5 14．【答案】6 15．【答案】416．【答案】解：连结OD，OE，如图所示，则OD=OE=1.∵O是△ABC的内切圆圆心，∴BO，CO分别是△ABC，△ACB的平分线，即△OBD=△OBE= 12△ABC，且△OCD=12△ACB.又∵△ACB=90°，∴△OCD= 12△ACB=45°.∵OD，OE是过切点的半径，∴OD△BC且OE△AB，∴△OCD+△COD=90°，∴△COD=△OCD=45°，∴CD=OD=1.∵△COB=105°，∴△DOB=△COB-△COD=60°.∵△OBD+△BOD=90°，∴△OBD=30°.∵OD=1，∴OB=2，∴DB=3.∵△OBD=△OBE= 12△ABC=30°，∴△ABC=60°，∴△A=30°.∵BC=BD+CD=1+ 3，∴AB=2+23.在Rt△OBE中，∵OE=1，△OBE=30°，∴BE= 3.∴AE=AB-BE=2+ 317．【答案】解：过B 作BD△AC 于D ，切点分别为E 、F 、G ，连结OE ，OF ，OG ，设AD=x ，CD=8-x ，其内切圆的半径为r ，根据勾股定理2222AB AD BC CD -=-，即()2222758x x -=--，解方程得112x =， ∴BD=22221157322AB AD ⎛⎫-=-= ⎪⎝⎭， ∵圆O 是ABC 的内切圆，∴OE△AC ，OF△AB ，OG△BC ，OE=OF=OG=r ， ∴S △ABC=()1111122222AC BD AB OF BC OG AC OE AB BC AC r ⋅=⋅+⋅+⋅=++⋅， ∴()AC BD AB BC AC r ⋅=++⋅，∴5832320AC BDr AB BC AC⨯⋅===++． 18．【答案】解：（1）延长AI 交BC 于D ，连结OI ，作BH△AC 于H ，如图，∵I 是△ABC 的内心，∴BI 平分△ABC ，即△OBI=△DBI ， ∵OB=OI ， ∴△OBI=△OIB ，∴△DBI=△OIB，∴OI△BD，∵AI为△O的切线，∴OI△AI，∴BD△AD，∵AI平分△BAC，∴△ABC为等腰三角形，∴AB=AC；（2）∵OI△BC，∴△AOI△△ABD，∴AO OI AI AB BD AD==，∴558 ABAB-=，∴AB=403，∴2232 3AB BD-=，∴AI=OIBD•AD=53220833⨯=．19．【答案】（1）证明：∵点I是△ABC的内心，∴△BAD=△CAD，△ABI=△CBI，∵△CBD=△CAD，∴△BAD=△CBD，∴△BID=△ABI+△BAD，∴△ABI=△CBI，△BAD=△CAD=△CBD，∵△IBD=△CBI+△CBD，∴△BID=△IBD，∴ID=BD ， ∵△BAD=△CAD ， ∴BD CD ∧∧=， ∴CD=BD ， ∴DB=DC=DI ；（2）∵AB 是△O 的直径， ∴BD△AD ，OI△AD ， ∴OI△BD ， ∵OA=OB ， ∴AI=DI ，由（1）知ID=BD ， ∴AD=2BD ，BD=2OI ，设OI=x ，则BD=AI=2x ，AD=4x ， ∴22AD BD +5，如图2，过O 作OE△BD 交△O 于E ，连接AE 交OI 于F ，则OE△AI ， ∴AI IF OE OF=， 5IFX IF x=-， ∴52+， ∵OE△BD ， ∴BE DE ∧∧=， ∴△DAE=12△BAD=12△CAD ， ∴tan△DAE=tan2CAD∠=52xIF AI+=5﹣2．20．【答案】解：如图，作 AD BC ⊥ ，设 BD x = ，则 8CD x =- ，由勾股定理可知： 2222AB BD AC CD -=- ，则 ()2225498x x -=-- ，解得 52x =，则 53AD = ，故 11538103222ABCSBC AD =⋅=⨯⨯=，由三角形的内切圆性质，可得： ()12ABCS r AB BC AC =++ 22033578ABC S r AB BC AC ∴===++++ .21．【答案】解：（△）如图所示，连接OD ，∵点E 是△ABC 的内心， ∴△BAD=△CAD ， ∴BD = CD ， ∴OD△BC ，又∵△BDM=△DAC ，△DAC=△DBC ， ∴△BDM=△DBC ， ∴BC△DM ， ∴OD△DM ，∴直线DM 是△O 的切线；（△）如图所示，连接BE，∵点E是△ABC的内心，∴△BAE=△CAE=△CBD，△ABE=△CBE，∴△BAE+△ABE=△CBD+△CBE，即△BED=△EBD，∴DB=DE，∵△DBF=△DAB，△BDF=△ADB，∴△DBF△△DAB，∴DFDB=DBDA，即DB2=DF•DA，∴DE2=DF•DA．。

(名师整理)最新数学中考专题复习《三角形的内心与外心》考点精讲精练

数学中考专题考点精讲精练
第六单元圆第30讲三角形的内心与外心
考点解读
三角形与圆 1．确定圆的条件：过一点可以作①无数个圆；过两点的圆有②无数个，其圆心在③这两点连线的中垂线上；④ 不在同一直线上的三个点可以确定一个圆．
2．三角形的外接圆与内切圆外接圆
内切圆
图形
圆心是三角形的外心，三条边圆心是三角形的内心，三个
(3)证明：在图2中， ∵∠PCA＝2×7.5°＝15°，∠BCE＝∠ACB－∠PCA＝75°，∠ECA＝ ∠EBA＝15°，∠EBC＝∠EBA＋∠ABC＝75°， ∴∠BCE＝∠EBC. ∴BE＝EC.
学习了本课后，你有哪些收获和感想？告诉大家好吗？
在数学的天地里，重要的不是我们知道什么，而是我们如何知道什么
-------毕达哥拉斯
【自主解答】
解：(1)连接OC. ∵射线CP与△ABC的外接圆相切， ∴∠OCP＝90°. ∵OA＝OC，∴∠ACO＝∠A＝30°.
∴射线CP旋转度数是120°.
(2)∵∠BCA＝90°， ∴△ABC的外接圆就是量角器所在的圆．当CP过△ABC外心时(即过O点)，∠BCE＝60°. ∴∠BOE＝120°，即E处的读数为120. 当CP过△ABC的内心时(如图1)，∠BCE＝45°，∠EOB＝90°， ∴E处的读数为90.
圆心
中垂线的交点
内角的平分线的交点
三角形的外心到三角形的三个三角形的内心到三角形的三
性质
顶点的距离⑤相等
条边的距离⑥ 相等
外接圆
内切圆
Hale Waihona Puke ∠BOC＝2∠A，∠OBC＝角度关系
⑦ ∠OCB
∠BOC＝90°＋12∠A

三角形内心和外心练习题上课讲义

CEB 内心和外心一、选择题：1、对于三角形的外心，下列说法错误的是（）A.它到三角形三个顶点的距离相等B.它到三角形任意一个顶点的距离等于其外接圆的半径C.它是三角形三条角平分线的交点D.它是三角形三条边垂直平分线的交点2、下列命题正确的个数有（）○1过两点可以作无数个圆；○2经过三点一定可以作圆；○3任意一个三角形有一个外接圆，而且只有一个外接圆；○4任意一个圆有且只有一个内接三角形.A.1个B.2个C.3个D.4个2、在Rt △ABC 中，∠C=90°，AC=6cm ，BC=8cm ，则它的外心与顶点C 的距离是（）A. 5cmB. 6cmC. 7cmD. 8cm3、下列说法错误的是（）A.三角形有且只有一个内切圆B.若I 为△ABC 的内心，则AI 平分∠BACC.三角形的内心不一定都在三角形的内部D.等腰三角形的内心一定在它底边的高上4、在Rt △ABC 中，∠C=90°，AC=3cm ，BC=4cm ，则△ABC 的外接圆的面积为（）A.254cm 2B.5πcm 2C. 254πcm 2 D.25cm 2 5、⊙O 与△ABC 分别相切于点D 、E 、F ，△ABC 的周长为20cm ，AF=5cm ，CF=3cm ，则BE 的长度为（）A.1cmB. 2cmC.3cmD.2.5cm第5题第7题第9题6、△ABC 内接于⊙O ，∠A=60°，⊙O 的半径为5，则BC 的长为（）527、已知，如图在Rt △ABC 中，∠C=90°，AC=3cm ，BC=4cm ，⊙O 为Rt △ABC 的内切圆，切点为D 、E 、F ，则⊙O 的半径为（）A.12cm B.1cm C.32cm D.2cm8、等边三角形的内切圆半径为r，外接圆半径为R，高为h，则r：R：h的值为（）A.1：2：3 B.1 2 C.2：1：3 D.19、如图，⊙O为△ABC的内切圆，∠C=90°，AO的延长线交BC于点D，AC=4，CD=1，则⊙O的半径为( )A.45B.54C.34D.5610、△ABC内接于⊙O，∠A=60°，∠ABC、∠ACB的角平分线分别交AC、AB于点D、E，CE、BD相交于点F.以下四个结论：○1∠BFE=60°；○2BC=BD；○3EF=FD；○4BF=2DF.其中结论一定正确的是（）A. ○1○2○3B.○1○3C. ○1○2○4D. ○1○2○3○4第10题第15题第16题二、填空题11、已知I是△ABC的内心，且∠BIC=130°，则∠A= ；12、已知⊙O为△ABC的内切圆，D、E、F为切点，则△DEF一定是三角形；13、已知等腰Rt△的外接圆半径是5，则其内切圆半径是；14、三角形的周长为20，面积为35，则其内切圆半径是；15、如图，⊙O是边长为2的等边△ABC的内切圆，则图中阴影部分的面积为16、如图，网格中的小正方形的边长均为1，小正方形的顶点叫做格点，△ABC的三个顶点都在格点上，那么△ABC的外接圆半径是17、等边三角形的边长为6cm，则这个等边三角形的外接圆半径为 cm，外接圆的面积是 cm2；18、等腰△ABC的外接圆半径是5，其底BC=4 ，则S△ABC= .三、解答题19、在Rt△ABC中，∠C=90°，AC=8，BC=6，求其内心和外心之间的距离.。

中考数学系统复习第六单元圆滚动小专题三角形的内心与外心练习

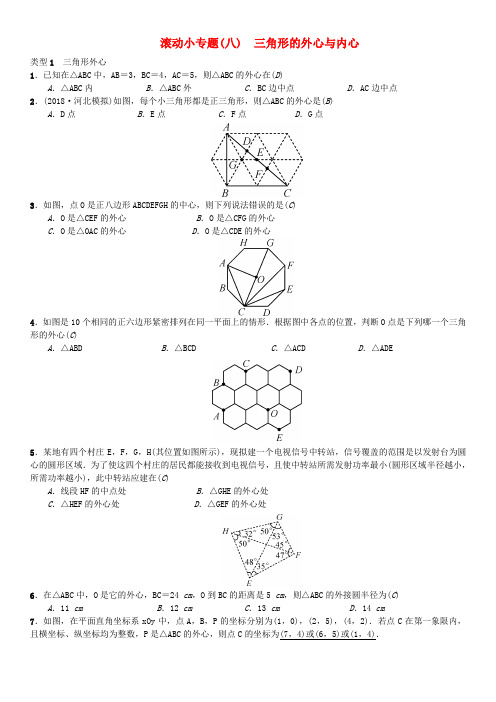
滚动小专题(八) 三角形的外心与内心类型1三角形外心1．已知在△ABC中，AB＝3，BC＝4，AC＝5，则△ABC的外心在(D)A．△ABC内B．△ABC外C．BC边中点D．AC边中点2．(2018·河北模拟)如图，每个小三角形都是正三角形，则△ABC的外心是(B)A．D点B．E点C．F点D．G点3．如图，点O是正八边形ABCDEFGH的中心，则下列说法错误的是(C)A．O是△CEF的外心B．O是△CFG的外心C．O是△OAC的外心D．O是△CDE的外心4．如图是10个相同的正六边形紧密排列在同一平面上的情形．根据图中各点的位置，判断O点是下列哪一个三角形的外心(C)A．△ABD B．△BCD C．△ACD D．△ADE5．某地有四个村庄E，F，G，H(其位置如图所示)，现拟建一个电视信号中转站，信号覆盖的范围是以发射台为圆心的圆形区域．为了使这四个村庄的居民都能接收到电视信号，且使中转站所需发射功率最小(圆形区域半径越小，所需功率越小)，此中转站应建在(C)A．线段HF的中点处B．△GHE的外心处C．△HEF的外心处D．△GEF的外心处6．在△ABC中，O是它的外心，BC＝24 cm，O到BC的距离是5 cm，则△ABC的外接圆半径为(C) A．11 cm B．12 cm C．13 cm D．14 cm7．如图，在平面直角坐标系xOy中，点A，B，P的坐标分别为(1，0)，(2，5)，(4，2)．若点C在第一象限内，且横坐标、纵坐标均为整数，P是△ABC的外心，则点C的坐标为(7，4)或(6，5)或(1，4)．8．如图，在△ABC 中，∠BAC＝70°，AB ＝AC ，O 为△ABC 的外心，△OCP 为等边三角形，OP 与AC 相交于点D ，连接OA.(1)求∠OAC 的度数； (2)求∠AOP 的度数．解：(1)∵O 为△ABC 的外心， ∴AO 垂直平分BC. ∵AB＝AC ，∴AO 平分∠BAC. ∴∠OAC＝12∠BAC＝35°.(2)∵O 为△ABC 的外心， ∴AO＝CO.∴∠OAC＝∠OCA＝35°.∴∠AOC＝110°. ∵△OCP 为正三角形，∴∠POC＝60°. ∴∠AOP＝50°.类型2 三角形内心9．如图为5×5的网格图，点A ，B ，C ，D ，O 均在格点上，则点O 是(B )A ．△ACD 的外心B ．△ABC 的外心 C ．△ACD 的内心 D ．△ABC 的内心10．如图，△ABC 是等腰直角三角形，点D ，E 在BC 上，△ADE 是等边三角形．若点O 是△ABC 的内心，则下列说法正确的是(C )A ．点O 是△ADE 的内心B ．点O 是△ADE 的外心C ．点O 不是△ABE 的内心D ．点O 是△ABC 的外心提示：易知OA平分∠BAC，由于OA不平分∠BAE，所以点O不是△ABE的内心．11．如图，I点为△ABC的内心，D点在BC上，且ID⊥BC.若∠B＝44°，∠C＝56°，则∠AID的度数为(A) A．174° B．176° C．178° D．180°提示：连接CI，∠AID＝∠AIC＋∠CID＝112°＋62°＝174°.12．如图，△ABC中，AB＝7 cm，AC＝8 cm，BC＝6 cm，点O是△ABC的内心，过点O作EF∥AB，与AC，BC分别交于点E，F，则△CEF的周长为(A)A．14 cm B．15 cm C．13 cm D．10.5 cm提示：连接OA，OB.C△CEF＝CE＋CF＋EF＝CE＋EA＋CF＋FB＝CA＋CB＝14 cm.13．如图，I是△ABC的内心，AI的延长线和△ABC的外接圆相交于点D，连接BI，BD，DC.下列说法中错误的一项是(D)A．线段DB绕点D顺时针旋转一定能与线段DC重合B．线段DB绕点D顺时针旋转一定能与线段DI重合C．∠CAD绕点A顺时针旋转一定能与∠DAB重合D．线段ID绕点I顺时针旋转一定能与线段IB重合提示：根据I是△ABC的内心，得到AI平分∠BAC，BI平分∠ABC，由角平分线的定义得到∠BAD＝∠CAD，∠AB I ＝∠CBI.根据三角形外角的性质得到∠DBI＝∠DIB，根据等腰三角形的性质得到BD＝DI.14．(2018·娄底)如图，P是△ABC的内心，连接PA，PB，PC，△PAB，△PBC，△PAC的面积分别为S1，S2，S3.则S1＜S2＋S3.(填“＜”“＝”或“＞”)15．如图所示，在Rt △ABC 中，∠ACB＝90°，在斜边AB 上分别截取AD ＝AC ，BE ＝BC ，DE ＝6，点O 是△CDE 的外心，则点O 到△ABC 的三边的距离之和是9．提示：由题意知：点O 是EC ，CD 垂直平分线的交点，∵AD＝AC ，BE ＝BC ，∴EC 的垂直平分线经过点B 且平分∠B，CD 的垂直平分线经过点A 且平分∠A.∴点O 是△ABC 的内心．∵∠ACB＝90°，∴r＝12(AC ＋BC －AB)＝12(AD ＋BE －AB)＝12DE ＝3.∴点O 到△ABC 的三边的距离之和是3r ＝9.16．三角形内角平分线的交点为三角形的内心．如图，D 是△ABC 的内心，E 是△ABD 的内心，F 是△BDE 的内心．若∠BFE 的度数为整数，则∠BFE 至少是113°．17．已知I 是△ABC 的内心，AI 的延长线交△ABC 的外接圆于点D ，连接BD.(1)在图1中，求证：DB ＝DI ；(2)如图2，若AB 为直径，且OI⊥AD 于点I ，DE 切圆于点D ，求sin ∠ADE 的值．解：(1)证明：连接BI. ∵I 是△ABC 的内心，∴AD 平分∠CAB，BI 平分∠ABC. ∴∠CAD＝∠BAD，∠ABI＝∠CBI. ∵∠CAD＝∠DBC，∴∠DAB＝∠DBC. ∵∠DBI＝∠DBC＋∠CBI， ∠DIB＝∠DAB＋∠ABI， ∴∠DIB＝∠DBI.∴DB＝DI. (2)连接BD ，DO.∵AB 为直径，∴∠ADB＝90°. ∵OI⊥AD，∴AD＝2DI. ∵BD＝DI ，∴AD＝2BD.∴AB＝AD 2＋BD 2＝5BD.∵DE 切圆于点D ，∴∠ADE＋∠ADO＝90°.又∵∠ADO＋∠ODB＝90°，∠ODB＝∠OBD， ∴∠ABD＝∠ADE.∴sin ∠ADE＝sin ∠ABD＝AD AB ＝2BD 5BD ＝255.。

中考数学系统复习第六单元圆滚动小专题(八)三角形的内心与外心练习

滚动小专题(八) 三角形的外心与内心类型1三角形外心1．已知在△ABC中，AB＝3，BC＝4，AC＝5，则△ABC的外心在(D)A．△ABC内B．△ABC外C．BC边中点D．AC边中点2．(2018·河北模拟)如图，每个小三角形都是正三角形，则△ABC的外心是(B)A．D点B．E点C．F点D．G点3．如图，点O是正八边形ABCDEFGH的中心，则下列说法错误的是(C)A．O是△CEF的外心B．O是△CFG的外心C．O是△OAC的外心D．O是△CDE的外心4．如图是10个相同的正六边形紧密排列在同一平面上的情形．根据图中各点的位置，判断O点是下列哪一个三角形的外心(C)A．△ABD B．△BCD C．△ACD D．△ADE5．某地有四个村庄E，F，G，H(其位置如图所示)，现拟建一个电视信号中转站，信号覆盖的范围是以发射台为圆心的圆形区域．为了使这四个村庄的居民都能接收到电视信号，且使中转站所需发射功率最小(圆形区域半径越小，所需功率越小)，此中转站应建在(C)A．线段HF的中点处B．△GHE的外心处C．△HEF的外心处D．△GEF的外心处6．在△ABC中，O是它的外心，BC＝24 cm，O到BC的距离是5 cm，则△ABC的外接圆半径为(C) A．11 cm B．12 cm C．13 cm D．14 cm7．如图，在平面直角坐标系xOy中，点A，B，P的坐标分别为(1，0)，(2，5)，(4，2)．若点C在第一象限内，且横坐标、纵坐标均为整数，P是△ABC的外心，则点C的坐标为(7，4)或(6，5)或(1，4)．8．如图，在△ABC 中，∠BAC＝70°，AB ＝AC ，O 为△ABC 的外心，△OCP 为等边三角形，OP 与AC 相交于点D ，连接OA.(1)求∠OAC 的度数； (2)求∠AOP 的度数．解：(1)∵O 为△ABC 的外心， ∴AO 垂直平分BC. ∵AB＝AC ，∴AO 平分∠BAC. ∴∠OAC＝12∠BAC＝35°.(2)∵O 为△ABC 的外心， ∴AO＝CO.∴∠OAC＝∠OCA＝35°.∴∠AOC＝110°. ∵△OCP 为正三角形，∴∠POC＝60°. ∴∠AOP＝50°.类型2 三角形内心9．如图为5×5的网格图，点A ，B ，C ，D ，O 均在格点上，则点O 是(B )A ．△ACD 的外心B ．△ABC 的外心 C ．△ACD 的内心 D ．△ABC 的内心10．如图，△ABC 是等腰直角三角形，点D ，E 在BC 上，△ADE 是等边三角形．若点O 是△ABC 的内心，则下列说法正确的是(C )A ．点O 是△ADE 的内心B ．点O 是△ADE 的外心C ．点O 不是△ABE 的内心D ．点O 是△ABC 的外心提示：易知OA平分∠BAC，由于OA不平分∠BAE，所以点O不是△ABE的内心．11．如图，I点为△ABC的内心，D点在BC上，且ID⊥BC.若∠B＝44°，∠C＝56°，则∠AID的度数为(A) A．174° B．176° C．178° D．180°提示：连接CI，∠AID＝∠AIC＋∠CID＝112°＋62°＝174°.12．如图，△ABC中，AB＝7 cm，AC＝8 cm，BC＝6 cm，点O是△ABC的内心，过点O作EF∥AB，与AC，BC分别交于点E，F，则△CEF的周长为(A)A．14 cm B．15 cm C．13 cm D．10.5 cm提示：连接OA，OB.C△CEF＝CE＋CF＋EF＝CE＋EA＋CF＋FB＝CA＋CB＝14 cm.13．如图，I是△ABC的内心，AI的延长线和△ABC的外接圆相交于点D，连接BI，BD，DC.下列说法中错误的一项是(D)A．线段DB绕点D顺时针旋转一定能与线段DC重合B．线段DB绕点D顺时针旋转一定能与线段DI重合C．∠CAD绕点A顺时针旋转一定能与∠DAB重合D．线段ID绕点I顺时针旋转一定能与线段IB重合提示：根据I是△ABC的内心，得到AI平分∠BAC，BI平分∠ABC，由角平分线的定义得到∠BAD＝∠CAD，∠AB I ＝∠CBI.根据三角形外角的性质得到∠DBI＝∠DIB，根据等腰三角形的性质得到BD＝DI.14．(2018·娄底)如图，P是△ABC的内心，连接PA，PB，PC，△PAB，△PBC，△PAC的面积分别为S1，S2，S3.则S1＜S2＋S3.(填“＜”“＝”或“＞”)15．如图所示，在Rt △ABC 中，∠ACB＝90°，在斜边AB 上分别截取AD ＝AC ，BE ＝BC ，DE ＝6，点O 是△CDE 的外心，则点O 到△ABC 的三边的距离之和是9．提示：由题意知：点O 是EC ，CD 垂直平分线的交点，∵AD＝AC ，BE ＝BC ，∴EC 的垂直平分线经过点B 且平分∠B，CD 的垂直平分线经过点A 且平分∠A.∴点O 是△ABC 的内心．∵∠ACB＝90°，∴r＝12(AC ＋BC －AB)＝12(AD ＋BE －AB)＝12DE ＝3.∴点O 到△ABC 的三边的距离之和是3r ＝9.16．三角形内角平分线的交点为三角形的内心．如图，D 是△ABC 的内心，E 是△ABD 的内心，F 是△BDE 的内心．若∠BFE 的度数为整数，则∠BFE 至少是113°．17．已知I 是△ABC 的内心，AI 的延长线交△ABC 的外接圆于点D ，连接BD.(1)在图1中，求证：DB ＝DI ；(2)如图2，若AB 为直径，且OI⊥AD 于点I ，DE 切圆于点D ，求sin ∠ADE 的值．解：(1)证明：连接BI. ∵I 是△ABC 的内心，∴AD 平分∠CAB，BI 平分∠ABC. ∴∠CAD＝∠BAD，∠ABI＝∠CBI. ∵∠CAD＝∠DBC，∴∠DAB＝∠DBC. ∵∠DBI＝∠DBC＋∠CBI， ∠DIB＝∠DAB＋∠ABI， ∴∠DIB＝∠DBI.∴DB＝DI. (2)连接BD ，DO.∵AB 为直径，∴∠ADB＝90°. ∵OI⊥AD，∴AD＝2DI. ∵BD＝DI ，∴AD＝2BD.∴AB＝AD 2＋BD 2＝5BD.∵DE 切圆于点D ，∴∠ADE＋∠ADO＝90°.又∵∠ADO＋∠ODB＝90°，∠ODB＝∠OBD， ∴∠ABD＝∠ADE.∴sin ∠ADE＝sin ∠ABD＝AD AB ＝2BD 5BD ＝255.。

中考考点(8-4)：三角形的内心与外心【★★】

中考考点（8-4）：三角形的内心与外心【★★】说明：（1）本节知识点：三角形的内心、外心的性质与作图；（2）最大难度：☆☆☆一、选择题（共3小题；共15分）1 .边长分别等于6cm，8cm，10cm的三角形的内切圆的半径为( )A. 3cmB. 2cmC. 32cmD. 6cm√√2 .如图，若等边△퐴퐵퐶的边长为6，内切圆푂分别切三边于퐷，퐸，퐹，则阴影部分的面积是( )√31C. π4A. πB. π D. 3π√23 .点푂是△퐴퐵퐶的外心，若∠퐵푂퐶=80∘，则∠퐵퐴퐶的度数为( )A. 40∘B. 100∘C. 40∘或140∘D. 40∘或100∘二、填空题（共4小题；共20分）4 .如图，⊙푂是△퐴퐵퐶的内切圆，其切点分别为퐷，퐸，퐹，且퐵퐷=3，퐴퐸=2，则퐴퐵=．第4题图第5题图第7题图56. 如图，点푂是△퐴퐵퐶的内切圆的圆心，∠퐵퐴퐶=70∘，则∠퐵푂퐶=．. 直角三角形的外接圆半径为5cm，内切圆半径为1cm，则此三角形的周长是．푘7 .如图，在平面直角坐标系中有一正方形퐴푂퐵퐶，反比例函数푦=的图象经过正方形퐴푂퐵퐶对角푥线的交点，半径为(6−3√2)的圆内切于△퐴퐵퐶，则푘的值为三、解答题（共4小题；共52分）．8 .制作铁皮桶，需在一块三角形余料上截取一个面积最大的圆，请画出该圆．9 1 1 . 如图，已知 △ 퐴퐵퐶，利用尺规完成下列作图（不写画法，保留作图痕迹）．（1）作 △ 퐴퐵퐶 的外接圆；（2）若 △ 퐴퐵퐶 所在平面内有一点 퐷，满足 ∠퐶퐴퐵 = ∠퐶퐷퐵，퐵퐶 = 퐵퐷，求作点 퐷．0. 如图，点 퐼 是 △ 퐴퐵퐶 的内心，퐴퐼 交边 퐵퐶 于点 퐷，交 △ 퐴퐵퐶 外接圆于点 퐸．求证：퐼퐸 是 퐴퐸和 퐷퐸 的比例中项．1. 如图，△ 퐴퐵퐶 中，퐴퐵 = 퐴퐶，⊙ 푂 是 △ 퐴퐵퐶 的外接圆，퐵퐷 ⊥ 퐴퐶 于点 퐷，交 ⊙ 푂 于点 퐹，퐴푂的延长线交 퐵퐷 于点 퐸，连接 퐴퐹．（（ 1）求证：퐴퐸 = 퐴퐹；42）若 sin∠퐵퐴퐶 = ，퐴퐸 = 5，求 퐸퐹 的长．5∘ ∘ ∘．∴ ∠퐵푂퐶 = 180 − 55 = 125 答案6 7 . 22 cm . 9 第一部分 . B 【解析】∵ 62 + 82 = 36 + 64 = 100 =1第三部分. 作出三角形的角平分线 퐵퐷，퐶퐸，交于点 푂， 02，1 8∴ 此三角形为直角三角形．푂 就是所画的圆的圆心．设此直角三角形的内切圆的半径为 푟．过 푂 做 푂퐹 ⊥ 퐵퐶 于点 퐹，以 푂 为圆心，푂퐹长为半径作 ⊙ 푂．由直角三角形的面积公式，1111得 푆 = × 6 × 8 = × 6푟 + × 8푟 + × 10푟，2222如图，⊙ 푂 即为所求的圆．解得 푟 = 2．2 . A 【解析】连接 푂퐴，푂퐷，푂퐸，푂퐹，퐴퐷，9 . （1）如图 1 所示：则 퐴퐷 过 푂，依题意可得：三角形内接圆的圆心为角平分线的交点，∴ ∠푂퐵퐷 = 30∘，퐵퐷 = 퐶퐷 = 3，则푂퐷 = √3，1 3 20 602∠ 퐵푂퐶 = 120∘，푆阴影 . C = × π × (√3) = π ．3【解析】如图所示：∵ 푂 是 △ 퐴퐵퐶 的外心，∠퐵푂퐶 = 80∘，⊙ 푂 即为所求； 2）如图 2 所示：∴∠퐴 = 40∘，∠퐴′ = 140∘，（故 ∠퐵퐴퐶 的度数为：40∘ 或 140∘．点 퐷 即为所求．第二部分 10. 如图，连接 퐼퐵，4 5. 5. 125∘ 【∴ 解析】∵ ∠퐵퐴퐶 = 70∘， ∘ ∘，∠퐴퐵퐶 + ∠퐴퐶퐵 = 180 − ∠퐵퐴퐶 = 110 ∴∠푂퐵퐶 + ∠푂퐶퐵 = 55∘，3∴ 퐷퐸 = 푎， 23√5 2∴ ∵ ∴퐴퐸 = √퐴퐷2+ 퐷퐸2 = 푎， 퐴퐸 = 5， 3 √52푎 = 5， 2 √53解得：푎 =， ∵ ∴ 퐼 是 △ 퐴퐵퐶 的内心，∴ 퐸퐹 = 2퐷퐸 = 3푎 = 2√5．∠퐴퐵퐼 = ∠퐶퐵퐼，∠퐵퐴퐼 = ∠퐶퐴퐼．又 ∵ ∠퐵퐼퐸 = ∠퐵퐴퐼 + ∠퐴퐵퐼，∠퐸퐵퐼 = ∠퐶퐵퐼 + 퐸퐵퐶，∠퐸퐵퐶 = ∠퐸퐴퐶， ∠∴ ∠퐸퐼퐵 = ∠퐸퐵퐼， 퐸퐼 = 퐸퐵．∴易证 △ 퐵퐷퐸∽ △ 퐴퐵퐸， 퐵퐸 퐸퐴，∴== 퐸퐷 퐼퐸 퐵퐸 퐸퐴，퐼퐸即 퐸퐷 퐼퐸= 퐴퐸 × 퐷퐸．2 ∴即 퐼퐸 是 퐴퐸 和 퐷퐸 的比例中项．11. （1） ∵ 퐴퐵 = 퐴퐶， ⏜ ⏜ ， ∴ 퐴퐵 = 퐴퐶 ∴ ∴ ∵ ∴ ∴ ∴ ∴ ∴ 퐴퐸 ⊥ 퐵퐶， ∠퐸퐴퐶 + ∠퐶 = 90∘，퐵퐷 ⊥ 퐴퐶，∠퐵퐷퐶 = ∠퐵퐷퐴 = 90∘，∠퐷퐵퐶 + ∠퐶 = 90∘，∠퐸퐴퐶 = ∠퐶퐵퐷， ∠퐶퐵퐷 = ∠퐶퐴퐹， ∠퐶퐴퐹 = ∠퐶퐴퐸，在 △ 퐸퐴퐷 和 △ 퐹퐴퐷 中， 퐸퐴퐷 = ∠퐹퐴퐷, 퐴퐷 = 퐴퐷, ∠ { ∠ 퐸퐷퐴 = ∠퐹퐷퐴, ∴△ 퐸퐴퐷≌ △ 퐹퐴퐷， ∴ 퐴퐸 = 퐴퐹．퐵퐷 퐴퐵4= ，5（ 2） ∵ sin∠퐵퐴퐶 = 设 퐵퐷 = 4푎，퐴퐵 = 5푎，则 퐴퐷 = 3푎，퐶퐷 = 2푎，∵ ∴ ∠퐸퐴퐶 = ∠퐶퐵퐷，∠퐴퐷퐸 = ∠퐵퐷퐶， Rt △ 퐷퐴퐸∽Rt △ 퐷퐵퐶， 퐴퐷 퐵퐷 퐷퐸 퐷퐶 3푎 4푎 퐷퐸2푎∴ = ，即 = ，。

备考2021年中考数学复习专题：图形的性质_圆_三角形的外接圆与外心,填空题专训及答案

C在第一象限内，且横坐标、纵坐标均为整数，EH= ，则坐标是（1，2），那么这条圆弧所在圆的圆心坐标是7、(2019天台.中考模拟) 如图，在平面直角坐标系中，△ABC的顶点在坐标轴上，A，B，C三点的坐标分别为 (0，2)，(1，0)，(0，-0．5)，D为线段AB上-个动点(不与点A，B重合)，过B，D，0三点的圆与直线BC交于点E，当△OED面积取得最小值时，ED的长为________．8、(2017宁波.中考模拟) 直角三角形两直角边为3，4，则其外接圆和内切圆半径之和为________．9、(2017金乡.中考模拟) 直角三角形的外接圆半径为5cm，内切圆半径为1cm，则此三角形的周长是________．10、(2018临沂.中考真卷) 如图．在△ABC中，∠A=60°，BC=5cm．能够将△ABC完全覆盖的最小圆形纸片的直径是____ ____cm．11、(2018烟台.中考真卷) 如图，方格纸上每个小正方形的边长均为1个单位长度，点O，A，B，C在格点（两条网格线的交点叫格点）上，以点O为原点建立直角坐标系，则过A，B，C三点的圆的圆心坐标为________．12、(2017襄阳.中考模拟) 若点O是等腰△ABC的外心，且∠BOC=60°，底边BC=2，则△ABC的面积为________．13、(2017港南.中考模拟) 如图等边三角形ABC内接于圆，点P是圆上任意一点（P不与A、B、C重合），则∠APB=_____ ___．14、(2018内江.中考真卷) 已知的三边、、满足，则的外接圆半径________.15、(2012资阳.中考真卷) 直角三角形的两边长分别为16和12，则此三角形的外接圆半径是________．16、(2012宜宾.中考真卷) 如图，在⊙O中，AB是直径，点D是⊙O上一点，点C是的中点，弦CE⊥AB于点F，过点D的切线交EC的延长线于点G，连接AD，分别交CF、BC于点P、Q，连接AC．给出下列结论：①∠BAD=∠ABC；②GP=GD；③点P是△ACQ的外心；④AP•AD=CQ•CB．其中正确的是________（写出所有正确结论的序号）．17、(2016成都.中考真卷) 如图，△ABC内接于⊙O，AH⊥BC于点H，若AC=24，AH=18，⊙O的半径OC=13，则AB=___ _____．18、(2016宁夏回族自治区.中考真卷) 已知正△ABC的边长为6，那么能够完全覆盖这个正△ABC的最小圆的半径是______ __．19、(2020徐州.中考真卷) 在中，若，，则的面积的最大值为________.20、(2020泰州.中考模拟) 如图，在平面直角坐标系xOy中，点A，B，C的坐标分别是（0，4），（4，0），（8，0），⊙M是△ABC的外接圆，则点M的坐标为________.备考2021中考数学复习专题：图形的性质_圆_三角形的外接圆与外心，填空题答案1.答案：2.答案：3.答案：4.答案：5.答案：6.答案：7.答案：8.答案：9.答案：10.答案：11.答案：12.答案：13.答案：14.答案：15.答案：16.答案：17.答案：18.答案：19.答案：20.答案：。

中考数学系统复习第六单元圆滚动小专题(八)三角形的内心与外心练习

三角形内心和外心练习题

中考数学复习----《三角形的内切圆与内心》知识点总结与专项练习题(含答案解析)

初中数学《三角形的内切圆、外切圆》专题练习试卷及答案

2023年人教版数学中考复习考点专练——三角形的内切圆与内心(含答案)

2025年九年级中考数学复习专题六 圆

河北省2019届中考数学系统复习第六单元圆滚动小专题三角形的内心与外心练习

中考数学模拟题汇总《三角形的内切圆与内心》专项练习及答案

(名师整理)最新数学中考专题复习《三角形的内心与外心》考点精讲精练

三角形内心和外心练习题上课讲义

中考数学系统复习第六单元圆滚动小专题三角形的内心与外心练习

中考数学系统复习第六单元圆滚动小专题(八)三角形的内心与外心练习

中考考点(8-4)：三角形的内心与外心【★★】

备考2021年中考数学复习专题：图形的性质_圆_三角形的外接圆与外心,填空题专训及答案

2025年九年级中考数学复习专题六圆