三角函数中考数学考试知识点分析
初中九年级数学中考锐角三角函数知识点总结

初中九年级数学中考锐角三角函数知识点总结1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
2、如下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B):3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。
4、任意锐角的正切值等于它的余角的余切值;任意锐角的余切值等于它的余角的正切值。
5、0°、30°、45°、60°、90°特殊角的三角函数值(重要)A 90B 90∠-︒=∠︒=∠+∠得由B A 对边邻边 CA 90B 90∠-︒=∠︒=∠+∠得由B A6、正弦、余弦的增减性:当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。
7、正切、余切的增减性:当0°<α<90°时,tan α随α的增大而增大,8、解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和角。
依据:①边的关系:222c b a =+;②角的关系:A+B=90°;③边角关系:三角函数的定义。
(注意:尽量避免使用中间数据和除法)9、应用举例:(1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。
(2)坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)。
用字母i 表示,即hi l=。
坡度一般写成1:m 的形式,如1:5i =等。
把坡面与水平面的夹角记作α(叫做坡角),那么tan hi lα==。
3、从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角。
如图3,OA 、OB 、OC 、OD 的方向角分别是:45°、135°、225°。
4、指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角。
如图4,OA 、OB 、OC 、OD 的方向角分别是:北偏东30°(东北方向) , 南偏东45°(东南方向), 南偏西60°(西南方向), 北偏西60°(西北方向)。
中考数学-锐角三角函数(解析版)

知识点一:锐角三角函数 1.三角函数定义 在 Rt△ABC 中,若∠C=90°
sin A A的对边 a
斜边
c
A的邻边
b
cos A
斜边
c
A的对边
a
tan A A的邻边 b
A的邻边
b
cot A A的对边 a
2.同角三角函数的关系
(1)平方关系: sin2 Acos2 A1
(1)三边之间的关系为 a2 b2 c2 (勾股定理)
(2)锐角之间的关系为∠A+∠B=90°
(3)30°角所对直角边等于斜边的一半。
(4)直角三角形斜边上的中线等于斜边的一半。
(5)边角之间的关系为:(三角函数定义)
2.其他有关公式
(1)
S
1 2
ab sin C
=
1 2
bc sin
A
=
1 2
ac sin
B
(2)Rt△面积公式:
S
1 2
ab
1 2
ch
(3)直角三角形外接圆的半径
R c 2
,内切圆半径
r abc 2
结论:直角三角形斜边上的高 h ab c
3.实际问题中术语的含义
(1)仰角与俯角
在视线与水平线所成的角中,视线在水平线上方的角叫做仰角,在水平线下方的角叫做俯角。
(2)坡度:如图,我们通常把坡面的铅直高度和水平宽度的比叫做坡度(或坡比),用字母 i 表示,即 i h . l
见问题,这也是以后中考命题的趋势。 5.解决实际问题的关键在于建立数学模型,要善于把实际问题的数量关系转化为解直角三角形的问题.在 解直角三角形的过程中,常会遇到近似计算,应根据题目要求的精确度定答案.
中考数学三角函数公式汇总与解析

中考数学三角函数公式汇总与解析1.锐角三角函数锐角三角函数定义:锐角角A的正弦(si n),余弦(c o s)和正切(t a n),余切(c o t)以及正割(se c),余割(c sc)都叫做角A的锐角三角函数。
正弦(si n):对边比斜边,即si n A=a/c余弦(c o s):邻边比斜边,即c o sA=b/c正切(t a n):对边比邻边,即t a n A=a/b余切(c o t):邻边比对边,即c o t A=b/a正割(se c):斜边比邻边,即se c A=c/b余割(c sc):斜边比对边,即c s c A=c/a2.3.互余角的关系s i n(π-α)=c o sα,c o s(π-α)=si nα,t a n(π-α)=c o tα,c o t(π-α)=t a nα.4.平方关系sin^2(α)+cos^2(α)=1tan^2(α)+1=sec^2(α)cot^2(α)+1=csc^2(α)5.积的关系s i nα=t a nα·c o sαc o sα=c o tα·si nαt a nα=si nα·se cαc o tα=c o sα·c s cαs e cα=t a nα·c scαc s cα=se cα·c o tα6.倒数关系t a nα·c o tα=1s i nα·c scα=1c o sα·se cα=17.诱导公式公式一:设α为任意角,终边相同的角的同一三角函数的值相等:s i n(2kπ+α)=si nαk∈zc o s(2kπ+α)=c o sαk∈zt a n(2kπ+α)=t a nαk∈zc o t(2kπ+α)=c o tαk∈z公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:s i n(π+α)=-si nαc o s(π+α)=-c o sαt a n(π+α)=t a nα8.两角和差公式(1)si n(A+B)=si n A c o sB+c o sA si n B(2)si n(A-B)=si n A c o s B-si n B c o sA(3)c o s(A+B)=c o sA c o sB-si n A si n B(4)c o s(A-B)=c o sA c o sB+si n A si n B(5)t a n(A+B)=(t a n A+t a n B)/(1-t a n A t a n B)(6)t a n(A-B)=(t a n A-t a n B)/(1+t a n A t a n B)(7)c o t(A+B)=(c o t A c o t B-1)/(c o t B+c o t A)(8)c o t(A-B)=(c o t A c o t B+1)/(c o t B-c o t A)除了以上常考的三角函数公式外,掌握下面半角公式,积化和差和万能公式有利于快速解决选择题,达到事半功倍的效果哦!1.半角公式注:正负由α/2所在的象限决定。
中考数学三角函数的基础应用

中考数学三角函数的基础应用数学是一门广泛应用于各个领域的学科,其中三角函数是数学中的重要内容之一。
在中考数学中,三角函数的基础应用也是考试内容的一部分。
本文将探讨三角函数的基础应用,包括角度的表示、正弦、余弦、正切函数的定义与性质,以及在几何图形中的应用等方面,旨在帮助读者更深入地理解和掌握三角函数的应用。
一、角度的表示角度是三角函数中的基本概念之一,它通常用度数来表示。
在三角函数中,常见的度数制表示方法包括度(°)、分(')和秒('')三个单位。
其中,1°可以分为60',1'可以再分为60''。
通过这种度数制的表示方法,我们可以更加准确地描述角度的大小。
二、正弦、余弦、正切函数的定义与性质1. 正弦函数在三角函数中,正弦函数是最常见的一种函数。
它是一个周期函数,周期为360°(或2π弧度)。
正弦函数的定义域是全体实数,值域是闭区间[-1, 1]。
我们可以通过观察其图像来了解正弦函数的性质,例如在第一象限和第二象限中,正弦函数的值大于0;而在第三象限和第四象限中,正弦函数的值小于0。
2. 余弦函数与正弦函数类似,余弦函数也是一个周期函数,周期也是360°(或2π弧度)。
余弦函数的定义域和值域与正弦函数相同,即定义域是全体实数,值域是闭区间[-1, 1]。
与正弦函数相比,余弦函数在第一象限中的值大于0,而在第二、三、四象限中的值小于0。
3. 正切函数正切函数是另一个常见的三角函数,它的定义域通常是除去所有与余弦函数为零的实数。
正切函数的值域是全体实数。
与正弦、余弦不同,正切函数的图像并没有周期性,我们可以通过观察其图像来了解正切函数的性质。
三、三角函数的应用三角函数的基本应用之一是在几何图形中的应用。
例如,在矩形、三角形等几何图形中,我们可以利用三角函数来求解边长、角度等问题。
在解题过程中,我们可以根据已知条件,利用正弦、余弦、正切等函数来建立方程,进而求解未知量。
2023 数学浙教版新中考 考点29锐角三角函数(解析版)

考点29锐角三角函数考点总结1.锐角三角函数的意义:如图,在Rt △ABC 中,设∠C =90°,∠α为Rt △ABC 的一个锐角,则: ∠α的正弦sin α=∠α的对边斜边;∠α的余弦cos α=∠α的邻边斜边;∠α的正切tan α=∠α的对边∠α的邻边2.同角三角函数之间的关系: sin 2A +cos 2A = 1 ,tan A =s inA cos A .3.互余两角三角函数之间的关系:(1)sin α=cos (90°-α),cos α=sin (90°-α). (2)tan α·tan (90°-α)=1.(3)锐角的正弦值或正切值随着角度的增大而增大,锐角的余弦值随着角度的增大而减小.(4)对于锐角A 有0<sin A <1,0<cos A <1,tan A >0. 4.特殊的三角函数值:5.如图,直角三角形的三条边与三个角这六个元素中,有如下的关系:(1)三边的关系(勾股定理):a 2+b 2=c 2. (2)两锐角间的关系:∠A +∠B =90°. (3)边与角的关系:sin A =cos B =a c, cos A =sin B =b c ,tan A =a b ,tan B =b a.6.直角三角形的边角关系在现实生活中有着广泛的应用,它经常涉及测量、工程、航海、航空等,其中包括了一些概念,一定要根据题意理解其中的含义才能正确解题. (1)仰角:向上看时,视线与水平线的夹角,如图.(2)俯角:向下看时,视线与水平线的夹角, (3)坡角:坡面与水平面的夹角.(4)坡度:坡面的铅直高度与水平宽度的比叫做坡度(或坡比),一般情况下,我们用h 表示坡的铅直高度,用l 表示坡的水平宽度,用i 表示坡度,即i =hl=tan α,显然,坡度越大,坡角就越大,坡面也就越陡,如图.(5)方向角:指北或指南的方向线与目标方向线所成的小于90°的锐角叫做方向角,如图324.真题演练一、单选题1.(2021·浙江台州·中考真题)如图,将长、宽分别为12cm ,3cm 的长方形纸片分别沿AB ,AC 折叠,点M ,N 恰好重合于点P .若∠α=60°,则折叠后的图案(阴影部分)面积为( )A .(36-cm 2B .(36-cm 2C .24 cm 2D .36 cm 2【答案】A 【分析】过点C 作CF MN ⊥,过点B 作BE MN ⊥,根据折叠的性质求出60PAC α∠=∠=︒,30EAB PAB ∠=∠=︒,分别解直角三角形求出AB 和AC 的长度,即可求解.【详解】解:如图,过点C 作CF MN ⊥,过点B 作BE MN ⊥,∵长方形纸片分别沿AB ,AC 折叠,点M ,N 恰好重合于点P , ∵60PAC α∠=∠=︒, ∵30EAB PAB ∠=∠=︒,∵90BAC ∠=︒,6cm sin BE AB EAB ==∠,sin CFAC α==,∵12ABCSAB AC =⋅=∵(212336cm ABCS S S=-=⨯-=-阴矩形,故选:A .2.(2021·浙江金华·中考真题)如图是一架人字梯,已知2AB AC ==米,AC 与地面BC 的夹角为α,则两梯脚之间的距离BC 为( )A .4cos α米B .4sin α米C .4tan α米D .4cos α米 【答案】A 【分析】根据等腰三角形的性质得到12BD DC BC ==,根据余弦的定义即可,得到答案. 【详解】过点A 作AD BC ⊥,如图所示:∵AB AC =,AD BC ⊥, ∵BD DC =, ∵DCco ACα=, ∵cos 2cos DC AC αα=⋅=, ∵24cos BC DC α==, 故选:A .3.(2021·浙江温州·中考真题)图1是第七届国际数学教育大会(ICME )的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形OABC .若1AB BC ==.AOB α∠=,则2OC 的值为( )A .211sin α+ B .2sin 1α+ C .211cos α+ D .2cos 1α+【答案】A 【分析】根据勾股定理和三角函数求解. 【详解】∵在Rt OAB 中,AOB α∠=,1AB = ∵1=sin sin AB OB αα= 在Rt OBC 中,1BC =,2222221111sin sin OC OB BC αα⎛⎫=+=+=+ ⎪⎝⎭故选:A .4.(2021·浙江·中考真题)如图,已知在矩形ABCD 中,1,AB BC ==P 是AD 边上的一个动点,连结BP ,点C 关于直线BP 的对称点为1C ,当点P 运动时,点1C 也随之运动.若点P 从点A 运动到点D ,则线段1CC 扫过的区域的面积是( )A .πB .π+C D .2π【答案】B 【分析】先判断出点Q 在以BC 为直径的圆弧上运动,再判断出点C 1在以B 为圆心,BC 为直径的圆弧上运动,找到当点P 与点A 重合时,点P 与点D 重合时,点C 1运动的位置,利用扇形的面积公式及三角形的面积公式求解即可. 【详解】解:设BP 与CC 1相交于Q ,则∵BQC =90°,∵当点P 在线段AD 运动时,点Q 在以BC 为直径的圆弧上运动, 延长CB 到E ,使BE =BC ,连接EC , ∵C 、C 1关于PB 对称, ∵∵EC 1C =∵BQC =90°,∵点C 1在以B 为圆心,BC 为直径的圆弧上运动, 当点P 与点A 重合时,点C 1与点E 重合, 当点P 与点D 重合时,点C 1与点F 重合,此时,tanPC AB PBC BC BC ∠=== ∵∵PBC =30°,∵∵FBP =∵PBC =30°,CQ =12BC =BQ 32=,∵∵FBE =180°-30°-30°=120°,11322BCFS CC BQ =⨯==线段1CC 扫过的区域的面积是2120360BCFSππ⨯+=故选:B .5.(2021·浙江丽水·中考真题)如图,AB 是O 的直径,弦CD OA ⊥于点E ,连结,OC OD .若O 的半径为,m AOD α∠=∠,则下列结论一定成立的是( )A .tan OE m α=⋅B .2sin CD m α=⋅C .cos AE m α=⋅D .2sin CODSm α=⋅【答案】B 【分析】根据垂径定理、锐角三角函数的定义进行判断即可解答. 【详解】解:∵AB 是O 的直径,弦CD OA ⊥于点E , ∵12DE CD =在Rt EDO ∆中,OD m =,AOD α∠=∠ ∵tan =DEOEα ∵=tan 2tan DE CDOE αα=,故选项A 错误,不符合题意; 又sin DEODα=∵sin DE OD α=∵22sin CD DE m α==,故选项B 正确,符合题意; 又cos OEODα=∵cos cos OE OD m αα== ∵AO DO m ==∵cos AE AO OE m m α=-=-,故选项C 错误,不符合题意; ∵2sin CD m α=,cos OE m α=∵2112sin cos sin cos 22COD S CD OE m m m αααα∆=⨯=⨯⨯=,故选项D 错误,不符合题意; 故选B .6.(2021·浙江宁波·中考真题)如图,在ABC 中,45,60,B C AD BC ∠=︒∠=︒⊥于点D ,BD =E ,F 分别为AB ,BC 的中点,则EF 的长为( )A B C .1 D 【答案】C 【分析】根据条件可知∵ABD 为等腰直角三角形,则BD =AD ,∵ADC 是30°、60°的直角三角形,可求出AC 长,再根据中位线定理可知EF =2AC。
上海数学中考知识点必看

上海数学中考知识点必看中考数学知识点:直角三角形一、三角函数1.定义:在Rt△ABC中,∠C=Rt∠,则sinA= ;cosA= ;tgA= ;ctgA= .2. 特殊角的三角函数值:0° 30° 45° 60° 90°sinαcosαtgα /ctgα /3. 互余两角的三角函数关系:sin(90°-α)=cosα;…4. 三角函数值随角度变化的关系5.查三角函数表二、解直角三角形1. 定义:已知边和角(两个,其中必有一边)→所有未知的边和角。
2. 依据:①边的关系:②角的关系:A+B=90°③边角关系:三角函数的定义。
注意:尽量避免使用中间数据和除法。
三、对实际问题的处理1. 俯、仰角:2.方位角、象限角:3.坡度:4.在两个直角三角形中,都缺解直角三角形的条件时,可用列方程的办法解决。
中考数学知识点复习:正负数1、正数:像小学学过的大于0的数叫做正数。
2、负数:在正数前面加上负号“-”的数叫做负数。
3、正数负数的判断方法:⑴具体的数:看是否有负号“-”,如果有“-”就是负数,否则是正数。
⑵含字母的数:如-a要看a本身的符号,如a是负的,则-a是正数,如a是正的则-a是负数,如a是0则-a是0。
4、 0的含义:①0表示起点。
②0表示没有。
③0表示一种温度。
④0表示编号的位数。
⑤0表示精确度。
⑥0表示正负数的分界。
⑦0表示海拔平均高度。
5、具有相反意义的量;6、正负数的作用:在同一问题中,用正负数表示的量具有相反的意义。
中考数学《整式》知识点总结单项式和多项式统称为整式。
1.单项式:1)数与字母的乘积这样的代数式叫做单项式。
单独的一个数或字母(可以是两个数字或字母相乘)也是单项式。
2)单项式的系数:单项式中的数字因数及性质符号叫做单项式的系数。
3)单项式的次数:一个单项式中,所有字母的指数的和叫做这个单项式的次数。
2.多项式:1)几个单项式的和叫做多项式。
考点20 锐角三角函数及其应用-备战2023届中考数学一轮复习考点梳理(解析版)
考点20 锐角三角函数及其应用锐角三角函数及其应用是数学中考中比较重要的考点,其考察内容主要包括①正弦、余弦、正切三函数、②特殊角的三角函数值、③解直角三角形与其应用等。
而且,因为锐角三角函数的性质的特点,出题时除了会单独出题以外,还常和四边形、圆、网格图形等结合考察。
特别是三角函数的应用,是近几年中考填空压轴题常考题型。
学生在复习这块考点时,需要付出更多的努力,已达到熟练掌握这块考点的要求。
一、锐角三角函数的定义及其性质二、特殊角的三角函数值三、解直角三角形四、解直角三角形的应用考向一:锐角三角函数的定义及其性质一.锐角三角函数的定义:在Rt △AABC 中,∠C=90°,AB=c ,BC=a ,AC=b则:∠A 正弦:;ACBabc∠A余弦:;∠A正切:;二.锐角三角函数的函数关系当∠A+∠B=90°时,有以下两种关系:(1).同角三角函数的关系:;(2)互余两角的三角函数的关系:;1.如图,在Rt△ABC中,∠C=90°,AB=5,AC=3,则cos B的值为( )A.B.C.D.【分析】先根据勾股定理计算出BC,再根据三角函数的定义,即可得解.【解答】解:根据勾股定理可得,则cos B==.故选:B.2.Rt△ABC中,∠C=90°,AC=1,BC=2,tan A的值为( )A.B.C.D.2【分析】根据勾股定理求出AB的值,代入正切公式即可得到答案;【解答】解:∵∠C=90°,AC=1,BC=2,∴.故选:D.3.在Rt△ABC中,∠C=90°,sin A=,BC=6,则AC=( )A.10B.8C.5D.4【分析】在Rt△ABC中,利用锐角三角函数的定义求出AB,再根据勾股定理进行计算即可解答.【解答】解:在Rt△ABC中,∠C=90°,sin A=,BC=6,∴sin A===,∴AB=10,∴AC===8.故选:B.4.已知0°<θ<45°,则下列各式中正确的是( )A.cosθ<B.tanθ>1C.sinθ>cosθD.sinθ<tanθ【分析】根据逐项进行判断即可.【解答】解:A.由于一个锐角的余弦值随着锐角的增大而减小,而0°<θ<45°,所以cosθ>cos60°,即cosθ>,因此选项A不符合题意;B.由于一个锐角的正切值随着锐角的增大而增大,而所以tanθ<tan45°,即tanθ<1,因此选项B不符合题意;C.由于cosθ=sin(90°﹣θ),而0°<θ<45°,即45°<90°﹣θ<90°,所以sinθ<sin(90°﹣θ),即sinθ<cosθ,因此选项C不符合题意;D.由于sinθ=,tanθ=,而锐角的邻边小于斜边,所以sinθ<tanθ,因此选项D符合题意.故选:D.5.如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,则下列结论中不正确的是( )A.a2+b2=c2B.sin B=cos A C.tan A=D.sin B=【分析】根据直角三角形的边角关系逐项进行判断即可.【解答】解:在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,由勾股定理可得a2+b2=c2,因此选项A不符合题意;由锐角三角函数的定义可得sin B==cos A,因此选项B不符合题意;由锐角三角函数的定义可知,tan A=,因此选项C符合题意;由于sin2A+cos2A=()2+()2===1,因此选项D不符合题意;故选:C.考向二:特殊角的三角函数值特殊角的三角函数值表αsinαcosαtanα30°45°60°1.下列三角函数中,值为的是( )A.cos45°B.tan30°C.sin5°D.cos60°【分析】根据特殊锐角三角函数值逐项进行判断即可.【解答】解:A.由于cos45°=,因此选项A不符合题意;B.由于tan30°=,因此选项B不符合题意;C.sin5°<sin30°,即sin5°<,因此选项C不符合题意;D.由于cos60°=sin30°=,因此选项D符合题意;故选:D.2.计算tan45°+tan30°cos30°的值为( )A.B.1C.D.2【分析】根据特殊角三角函数值,可得实数的运算,根据实数的运算,可得答案.【解答】解:原式=1+×=1+=,故选:C.3.4sin260°的值为( )A.3B.1C.D.【分析】根据特殊角的三角函数值计算即可得出答案.【解答】解:.故选:A.4.若sin(x+15°)=,则锐角x= 45 °.【分析】根据特殊角的三角函数值,即可解答.【解答】解:∵sin(x+15°)=,∴x+15°=60°,解得:x=45°,故答案为:45.5.计算:tan60°﹣sin245°+tan45°﹣2cos30°= .【分析】直接利用特殊角的三角函数值代入,进而得出答案.【解答】解:原式=﹣()2+1﹣2×=﹣+1﹣=.故答案为:.6.在△ABC中,,则△ABC的形状是 等边三角形 .【分析】非负数的和为0,则每个加数都等于0,求得相应的三角函数,进而求得∠A,∠B的度数.根据三角形的内角和定理求得∠C的度数.【解答】解:由题意得:2cos A﹣1=0,﹣tan B=0,解得cos A=,tan B=,∴∠A=60°,∠B=60°.∴∠C=180°﹣60°﹣60°=60°,∴△ABC是等边三角形.故答案为:等边三角形.7.计算:.【分析】根据特殊角三角函数值的混合计算法则求解即可.【解答】解:=====.考向三:解直角三角形解直角三角形相关:三边关系:在Rt△ABC中,∠C=90°两锐角关系:AB=c,BC=a,AC=b边与角关系:,,,锐角α是a、b的夹角面积:1.如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P.则tan∠APD的值是( )A.2B.1C.0.5D.2.5【分析】连接格点AE,BE.根据题图和勾股定理先判断△ABE的形状,再求出∠APD的正切,利用平行线的性质可得结论.【解答】解:如图,连接格点AE,BE.由网格和勾股定理可求得;,,,∴BE2+AE2=AB2,∴△ABE是直角三角形.在Rt△ABE中,.∵BE∥CD,∴∠APD=∠ABE,∴tan∠APD=2,故选:A.2.如图,在△ABC中,∠C=90°,AC=8cm,AB的垂直平分线MN交AC于D,连接BD,若tan∠BDC =,则BC的长是( )A.6cm B.5cm C.4cm D.2cm【分析】设CD为xcm,则有AD为(8﹣x)cm,根据垂直平分线得到AD=BD,根据得到BC,最后根据勾股定理即可得到答案.【解答】解:设CD为xcm,则有AD为(8﹣x)cm,∵AB的垂直平分线MN交AC于D,∴AD=BD=8﹣x,∵,∴,∴,∵∠C=90°,∴,解得:x1=3,x2=﹣12(不符合题意舍去),∴,故答案为:C.3.如图,在Rt△ABC中,∠CAB=90°,sin C=,AC=8,BD平分∠CBA交AC边于点D.求:(1)线段AB的长;(2)tan∠DBA的值.【分析】(1)先解Rt△ABC,得出sin C==,设出AB=3k,则BC=5k,由BC2﹣AB2=AC2,得出方程(5k)2﹣(3k)2=82,解方程求出k的值,进而得到AB;(2)过D点作DE⊥BC于E,设AD=x,则CD=8﹣x.根据角平分线的性质得出DE=AD=x,利用HL 证明Rt△BDE≌Rt△BDA,得到BE=BA=6,那么CE=BC﹣BE=4.然后在Rt△CDE中利用勾股定理得出DE2+CE2=CD2,即x2+42=(8﹣x)2,解方程求出x的值,即为AD的长,再根据正切函数的定义即可求解.【解答】解:(1)∵在Rt△ABC中,∠CAB=90°,∴sin C==,BC2﹣AB2=AC2,∴可设AB=3k,则BC=5k,∵AC=8,∴(5k)2﹣(3k)2=82,∴k=2(负值舍去),∴AB=3×2=6;(2)过D点作DE⊥BC于E,设AD=x,则CD=8﹣x.∵BD平分∠CBA交AC边于点D,∠CAB=90°,∴DE=AD=x.在Rt△BDE与Rt△BDA中,,∴Rt△BDE≌Rt△BDA(HL),∴BE=BA=6,∴CE=BC﹣BE=5×2﹣6=4.在Rt△CDE中,∵∠CED=90°,∴DE2+CE2=CD2,∴x2+42=(8﹣x)2,解得x=3,∴AD=3,∴tan∠DBA===.4.如图,⊙O是△ABC的外接圆,点D在BC延长线上,且满足∠CAD=∠B.(1)求证:AD是⊙O的切线;(2)若AC是∠BAD的平分线,sin B=,BC=4,求⊙O的半径.【分析】(1)连接OA,OC与AB相交于点E,如图,由OA=OC,可得∠OAC=∠OCA,根据圆周角定理可得,由已知∠CAD=∠B,可得∠AOC=2∠CAD,根据三角形内角和定理可得∠OCA+∠CAO+∠AOC=180°,等量代换可得∠CAO+∠CAD=90°,即可得出答案;(2)根据角平分线的定义可得∠BAC=∠DAC,由已知可得∠BAC=∠B,根据垂径定理可得,OC⊥AB,BE=AE,在Rt△BEC中,根据正弦定理可得sin B===,即可算出CE的长度,根据勾股定理可算出BE=的长度,设⊙O的半径为r,则CE=OC﹣CE=r﹣,在Rt△AOE中,OA2=OE2+AE2,代入计算即可得出答案.【解答】证明:(1)连接OA,OC与AB相交于点E,如图,∵OA=OC,∴∠OAC=∠OCA,∵,∴,∵∠CAD=∠B,∴∠AOC=2∠CAD,∵∠OCA+∠CAO+∠AOC=180°,∴2∠CAO+2∠CAD=180°,∴∠CAO+∠CAD=90°,∴∠OAD=90°,∵OA是⊙O的半径,∴AD是⊙O的切线;解:(2)∵AC是∠BAD的平分线,∴∠BAC=∠DAC,∵∠CAD=∠B,∴∠BAC=∠B,∴OC⊥AB,BE=AE,在Rt△BEC中,∵BC=4,∴sin B===,∴CE=,∴BE===,设⊙O的半径为r,则CE=OC﹣CE=r﹣,在Rt△AOE中,OA2=OE2+AE2,r2=(r﹣)2+,解得:r=.5.如图,△ABC中,AB=AC=6cm,BC=8cm,点P从点B出发,沿线段BC以2cm/s的速度向终点C运动,点Q从点C出发,沿着C→A→B的方向以3cm/s的速度向终点B运动,P,Q同时出发,设点P运动的时间为t(s),△CPQ的面积为S(cm2).(1)sin B= ;(2)求S关于t的函数关系式,并直接写出自变量t的取值范围.【分析】(1)过点A作AD⊥BC,垂足为D,利用等腰三角形的三线合一性质求出BD的长,再利用勾股定理求出AD的长即可解答;(2)分两种情况,当0<t≤1时,当1<t<2时.【解答】解:(1)过点A作AD⊥BC,垂足为D,∵AB=AC=6cm,AD⊥BC,∴BD=BC=4cm,在Rt△ABD中,AB=6cm,BD=4cm,∴AD==2,∴sin B==;故答案为:.(2)过点Q作QE⊥BC,垂足为E,∵AB=AC,∴∠B=∠C,∴sin B=sin C=,分两种情况:当0<t≤1时,由题意得:CQ=3t,BP=2t,∴CP=BC﹣BP=8﹣2t,在Rt△CQE中,QE=CQ sin C=3t•=t,∴S=CP•QE=•(8﹣2t)•t=4t﹣t2=﹣t2+4t,当1<t<2时,由题意得:CA+AQ=3t,BP=2t,∴CP=BC﹣BP=8﹣2t,BQ=AB+AC﹣(CA+AQ)=12﹣3t,在Rt△BQE中,QE=BQ sin B=(12﹣3t)•=4﹣t,∴S=CP•QE=•(8﹣2t)•(4﹣t)=,∴S=.考向四:解直角三角形的应用解直角三角形的应用:仰角和俯角仰角:在视线与水平线所成的角中,视线在水平线上方的叫仰角.俯角:视线在水平线下方的叫俯角坡度:坡面的铅直高度h和水平宽度l的比叫做坡面的坡度(或坡比),记作坡度和坡角坡度越大,坡角越大,坡面越陡1. 在实际测量高度、宽度、距离等问题中,常结合平面几何知识构造直角三角形,利用三角函数或相似三角形来解决问题,常见的构造的基本图形有如下几种:(1)不同地点看同一点,如图①(2)同一地点看不同点,如图②(3)利用反射构造相似,如图③2. 常用结论:1.在山坡上植树,要求两棵树间的坡面距离是3,测得斜坡的倾斜角为27°,则斜坡上相邻两棵树的水平距离是( )A.3sin27°B.3cos27°C.D.3tan27°【分析】根据坡角的定义、余弦的概念列式计算即可.【解答】解:如图,过点A作AB⊥BC于B,∴∠ABC=90°,cos∠BAC=,∵AC=3,∠BAC=27°,∴AB=AC cos∠BAC=3cos27°;故选:B.2.如图,在天定山滑雪场滑雪,需从山脚下A处乘缆车上山顶B处,缆车索道与水平线所成的∠BAC=α,若山的高度BC=800米,则缆车索道AB的长为( )A.800sinα米B.800cosα米C.米D.米【分析】利用直角三角形的边角关系定理列出关系式即可得出结论.【解答】解:在Rt△ACB中,∵∠ACB=90°,sin BAC=,∴AB=.∵∠BAC=α,BC=800米,∴AB=(米).故选:C.3.如图,为了估算某河流的宽度,在该河流的对岸选取一点A,在近岸取点D,C,使得A、D、C在一条直线上,且与河流的边沿垂直,测得CD=15m,然后又在垂直AC的直线上取点B,并量得BC=30m,若cos B=,则该河流的宽AD为 25 m.【分析】根据三角形函数的定义可得AB的长,利用勾股定理可得AC的长,由线段的和差关系可得答案.【解答】解:∵∠C=90°,BC=30m,cos B==,∴AB=50m,∴AC==40(m),∵CD=15m,∴AD=AC﹣CD=25(m),故答案为:25.4.某古村落为方便游客泊车,准备利用长方形晒谷场长60m一侧,规划一个停车场,已知每个停车位需确保有如长5.5m,宽2.5m的长方形AEDF供停车,如图平行四边形ABCD是其中一个停车位,所有停车位都平行排列,∠ABD为60°,则每个体车位的面积大约为 17 m2(结果保留整数),这个晒谷场按规划最多可容纳 20 个停车位.()【分析】由题意,在Rt△ABF中,由直角三角形的边角关系得出AB,BF的长,讲而可以解决问题.【解答】解:由题意,在Rt△ABF中,∠AFB=90°,∠ABF=60°,AF=2.5m,∴AB===≈2.94(m),∴BF=AB≈1.47(m),∴BD=DF+BF≈5.5+1.47=6.97(m),∵CD=AB≈2.94m,∴S平行四边形ABDC=BD•AF≈6.97×2.5≈17 (m2),∴每个停车位的面积大约为17m2;∵60÷2.94≈20.4,∴这个晒谷场按规划最多可容纳20个停车位.故答案为:17;20.5.夏秋季节,许多露营爱好者晚间会在湖边露营,为遮阳和防雨会搭建一种“天幕”,其截面示意图是轴对称图形,对称轴是垂直于地面的支杆AB,用绳子拉直AD后系在树干EF上的点E处(EF⊥BF),使得A,D,E在一条直线上,通过调节点E的高度可控制“天幕”的开合,幕布宽AC=AD=2m,CD⊥AB 于点O,支杆AB与树干EF的横向距离BF=2.2m.(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)(1)天晴时打开“天幕”,若∠CAE=140°,求遮阳宽度CD.(2)下雨时收拢“天幕”,∠CAE由140°减小到90°,求点E下降的高度.【分析】(1)根据在Rt△AOD中,,先算出OD的长,再根据AD=2OD即可得到答案;(2)过点E作EH⊥AB于H,在Rt△AHE中,,得,当∠CAE=140°时和当∠CAE=90°时,分别求出AH的值,作差即可得到答案.【解答】解:(1)∵∠CAE=140°,AC=AD,AO⊥CD,∴,CD=2DO,在Rt△AOD中,,即,解得:OD≈1.88m,∴CD=2OD≈3.76m,答:遮阳宽度CD约为3.76m;(2)如图,过点E作EH⊥AB于H,∴∠BHE=90°,∵AB⊥BF,EF⊥BF,∴∠ABF=∠EFB=90°,∴∠ABF=∠EFB=∠BHE=90°,∴EH=BF=2.2m,在Rt△AHE中,,∴,当∠CAE=140°时,∠EAO=70°,m,当∠CAE=90°时,∠EAO=45°,AH=2.2m,2.2﹣0.8=1.4m,答:点E下降的高度为1.4m.6.近几年中学生近视的现象越来越严重,为响应国家的号召,某公司推出了如图1所示的护眼灯,其侧面示意图(台灯底座高度忽略不计)如图2所示,其中灯柱BC=18cm,灯臂CD=31cm,灯罩DE=24cm,BC⊥AB,CD、DE分别可以绕点C、D上下调节一定的角度.经使用发现:当∠DCB=140°,且ED∥AB时,台灯光线最佳.求此时点D到桌面AB的距离.(精确到0.1cm,参考数值:cos50°≈0.77,cos50°≈0.64,tan50°≈1.19)【分析】根据题意,作出合适的辅助线,然后根据锐角三角函数,即可得到DF的长,再根据FG=CB,即可求得DG的长,从而可以解答本题.【解答】解:过点D作DG⊥AB,垂足为G,过点C作CF⊥DG,垂足为F,如右图所示,∵CB⊥AB,FG⊥AB,CF⊥FG,∴∠B=∠BGF=∠GFC=90°,∴四边形BCFG为矩形,∴∠BCF=90°,FG=BC=18cm,又∵∠DCB=140°,∴∠DCF=50°,∵CD=31cm,∠DFC=90°,∴DF=CD•sin50°≈31×0.77=23.87(cm),∴DG≈23.87+18≈41.9(cm),答:点D到桌面AB的距离约为41.9cm.1.(2022•扬州)在△ABC中,∠C=90°,a、b、c分别为∠A、∠B、∠C的对边,若b2=ac,则sin A的值为 . .【分析】根据勾股定理和锐角三角函数的定义解答即可.【解答】解:在△ABC中,∠C=90°,∴c2=a2+b2,∵b2=ac,∴c2=a2+ac,等式两边同时除以ac得:=+1,令=x,则有=x+1,∴x2+x﹣1=0,解得:x1=,x2=(舍去),当x=时,x≠0,∴x=是原分式方程的解,∴sin A==.故答案为:.2.(2022•荆州)如图,在平面直角坐标系中,点A,B分别在x轴负半轴和y轴正半轴上,点C在OB上,OC:BC=1:2,连接AC,过点O作OP∥AB交AC的延长线于P.若P(1,1),则tan∠OAP的值是( )A.B.C.D.3【分析】根据OP∥AB,证明出△OCP∽△BCA,得到CP:AC=OC:BC=1:2,过点P作PQ⊥x轴于点Q,根据∠AOC=∠AQP=90°,得到CO∥PQ,根据平行线分线段成比例定理得到OQ:AO=CP:AC=1:2,根据P(1,1),得到PQ=OQ=1,得到AO=2,根据正切的定义即可得到tan∠OAP的值.【解答】解:如图,过点P作PQ⊥x轴于点Q,∵OP∥AB,∴△OCP∽△BCA,∴CP:AC=OC:BC=1:2,∵∠AOC=∠AQP=90°,∴CO∥PQ,∴OQ:AO=CP:AC=1:2,∵P(1,1),∴PQ=OQ=1,∴AO=2,∴tan∠OAP===.故选:C.3.(2022•天津)tan45°的值等于( )A.2B.1C.D.【分析】根据特殊角的三角函数值,进行计算即可解答.【解答】解:tan45°的值等于1,故选:B.4.(2022•荆门)计算:+cos60°﹣(﹣2022)0= ﹣1 .【分析】先化简各式,然后再进行计算即可解答.【解答】解:+cos60°﹣(﹣2022)0=﹣+﹣1=0﹣1=﹣1,故答案为:﹣1.5.(2022•金华)计算:(﹣2022)0﹣2tan45°+|﹣2|+.【分析】直接利用零指数幂的性质以及特殊角的三角函数值、绝对值的性质、算术平方根分别化简,进而计算得出答案.【解答】解:原式=1﹣2×1+2+3=1﹣2+2+3=4.6.(2022•贵港)如图,在4×4网格正方形中,每个小正方形的边长为1,顶点为格点,若△ABC的顶点均是格点,则cos∠BAC的值是( )A.B.C.D.【分析】延长AC到D,连接BD,由网格可得AD2+BD2=AB2,即得∠ADB=90°,可求出答案.【解答】解:延长AC到D,连接BD,如图:∵AD2=20,BD2=5,AB2=25,∴AD2+BD2=AB2,∴∠ADB=90°,∴cos∠BAC===,故选:C.7.(2022•广西)如图,某博物馆大厅电梯的截面图中,AB的长为12米,AB与AC的夹角为α,则高BC 是( )A.12sinα米B.12cosα米C.米D.米【分析】直接根据∠A的正弦可得结论.【解答】解:Rt△ABC中,sinα=,∵AB=12米,∴BC=12sinα(米).故选:A.8.(2022•宜宾)如图,在矩形纸片ABCD中,AB=5,BC=3,将△BCD沿BD折叠到△BED位置,DE 交AB于点F,则cos∠ADF的值为( )A.B.C.D.【分析】利用矩形和折叠的性质可得BF=DF,设BF=x,则DF=x,AF=5﹣x,在Rt△ADF中利用勾股定理列方程,即可求出x的值,进而可得cos∠ADF.【解答】解:∵四边形ABCD是矩形,∴∠A=90°,AB∥CD,AD=BC=3,AB=CD=5,∴∠BDC=∠DBF,由折叠的性质可得∠BDC=∠BDF,∴∠BDF=∠DBF,∴BF=DF,设BF=x,则DF=x,AF=5﹣x,在Rt△ADF中,32+(5﹣x)2=x2,∴x=,∴cos∠ADF=,故选:C.9.(2022•广元)如图,在正方形方格纸中,每个小正方形的边长都相等,A、B、C、D都在格点处,AB 与CD相交于点P,则cos∠APC的值为( )A.B.C.D.【分析】把AB向上平移一个单位到DE,连接CE,则DE∥AB,由勾股定理逆定理可以证明△DCE为直角三角形,所以sin∠APC=sin∠EDC即可得答案.【解答】解:把AB向上平移一个单位到DE,连接CE,如图.则DE∥AB,∴∠APC=∠EDC.在△DCE中,有EC==,DC==2,DE==5,∵EC2+DC2=DE2,故△DCE为直角三角形,∠DCE=90°.∴cos∠APC=cos∠EDC==.故选:B.10.(2022•陕西)如图,AD是△ABC的高.若BD=2CD=6,tan C=2,则边AB的长为( )A.3B.3C.3D.6【分析】利用三角函数求出AD=6,在Rt△ABD中,利用勾股定理可得AB的长.【解答】解:∵2CD=6,∴CD=3,∵tan C=2,∴=2,∴AD=6,在Rt△ABD中,由勾股定理得,AB=,故选:D.11.(2022•常州)如图,在四边形ABCD中,∠A=∠ABC=90°,DB平分∠ADC.若AD=1,CD=3,则sin∠ABD= .【分析】过点D作DE⊥BC,垂足为E,如图,由已知∠A=∠ABC=90°,可得AD∥BC,由平行线的性质可得∠ADB=∠CBD,根据角平分线的定义可得∠ADB=∠CDB,则可得CD=CB=3,根据矩形的性质可得AD=BE,即可得CE=BC﹣BE,在Rt△CDE中,根据勾股定理DE=,在Rt△ADB中,根据勾股定理可得,根据正弦三角函数的定义进行求解即可得出答案.【解答】解:过点D作DE⊥BC,垂足为E,如图,∵∠A=∠ABC=90°,∴AD∥BC,∴∠ADB=∠CBD,∵DB平分∠ADC,∴∠ADB=∠CDB,∴CD=CB=3,∵AD=BE=1,∴CE=BC﹣BE=3﹣1=2,在Rt△CDE中,DE===,∵DE=AB,在Rt△ADB中,==,∴sin∠ABD==.故答案为:.12.(2022•齐齐哈尔)在△ABC中,AB=3,AC=6,∠B=45°,则BC= 3+3或3﹣3 .【分析】利用分类讨论的思想方法,画出图形,过点A作AD⊥BC于点D,利用勾股定理解答即可.【解答】解:①当△ABC为锐角三角形时,过点A作AD⊥BC于点D,如图,∵AB=3,∠B=45°,∴AD=BD=AB•sin45°=3,∴CD==3,∴BC=BD+CD=3+3;②当△ABC为钝角三角形时,过点A作AD⊥BC交BC延长线于点D,如图,∵AB=3,∠B=45°,∴AD=BD=AB•sin45°=3,∴CD==3,∴BC=BD﹣CD=3﹣3;综上,BC的长为3+3或3﹣3.13.(2022•连云港)如图,在6×6正方形网格中,△ABC的顶点A、B、C都在网格线上,且都是小正方形边的中点,则sin A= .【分析】先构造直角三角形,然后即可求出sin A的值.【解答】解:设每个小正方形的边长为a,作CD⊥AB于点D,由图可得:CD=4a,AD=3a,∴AC===5a,∴sin∠CAB===,故答案为:.14.(2022•长春)如图是长春市人民大街下穿隧道工程施工现场的一台起重机的示意图,该起重机的变幅索顶端记为点A,变幅索的底端记为点B,AD垂直地面,垂足为点D,BC⊥AD,垂足为点C.设∠ABC =α,下列关系式正确的是( )A.sinα=B.sinα=C.sinα=D.sinα=【分析】根据直角三角形的边角关系进行判断即可.【解答】解:在Rt△ABC中,∠ACB=90°,∠ABC=α,由锐角三角函数的定义可知,sinα=sin∠ABC=,故选:D.15.(2022•沈阳)如图,一条河的两岸互相平行,为了测量河的宽度PT(PT与河岸PQ垂直),测量得P,Q两点间距离为m米,∠PQT=α,则河宽PT的长为( )A.m sinαB.m cosαC.m tanαD.【分析】根据垂直定义可得PT⊥PQ,然后在Rt△PQT中,利用锐角三角函数的定义进行计算即可解答.【解答】解:由题意得:PT⊥PQ,∴∠APQ=90°,在Rt△APQ中,PQ=m米,∠PQT=α,∴PT=PQ•tanα=m tanα(米),∴河宽PT的长度是m tanα米,故选:C.16.(2022•福建)如图所示的衣架可以近似看成一个等腰三角形ABC,其中AB=AC,∠ABC=27°,BC=44cm,则高AD约为( )(参考数据:sin27°≈0.45,cos27°≈0.89,tan27°≈0.51)A.9.90cm B.11.22cm C.19.58cm D.22.44cm【分析】根据等腰三角形性质求出BD,根据角度的正切值可求出AD.【解答】解:∵AB=AC,BC=44cm,∴BD=CD=22cm,AD⊥BC,∵∠ABC=27°,∴tan∠ABC=≈0.51,∴AD≈0.51×22=11.22cm,故选:B.17.(2022•六盘水)“五一”节期间,许多露营爱好者在我市郊区露营,为遮阳和防雨会搭建一种“天幕”,其截面示意图是轴对称图形,对称轴是垂直于地面的支杆AB,用绳子拉直AD后系在树干EF上的点E 处,使得A,D,E在一条直线上,通过调节点E的高度可控制“天幕”的开合,AC=AD=2m,BF=3m.(1)天晴时打开“天幕”,若∠α=65°,求遮阳宽度CD(结果精确到0.1m);(2)下雨时收拢“天幕”,∠α从65°减少到45°,求点E下降的高度(结果精确到0.1m).(参考数据:sin65°≈0.90,cos65°≈0.42,tan65°≈2.14,≈1.41)【分析】(1)根据对称性得出AD=2m,再根据锐角三角函数求出OD,即可求出答案;(2)过点E作EH⊥AB于H,得出EH=BF=3m,再分别求出∠α=65°和45°时,AH的值,即可求出答案.【解答】解:(1)由对称知,CD=2OD,AD=AC=2m,∠AOD=90°,在Rt△AOD中,∠OAD=α=65°,∴sinα=,∴OD=AD•sinα=2×sin65°≈2×0.90=1.80m,∴CD=2OD=3.6m,答:遮阳宽度CD约为3.6米;(2)如图,过点E作EH⊥AB于H,∴∠BHE=90°,∵AB⊥BF,EF⊥BF,∴∠ABF=∠EFB=90°,∴∠ABF=∠EFB=∠BHE=90°,∴EH=BF=3m,在Rt△AHE中,tan a=,∴AH=,当∠α=65°时,AH=≈≈1.40m,当∠α=45°时,AH==3,∴当∠α从65°减少到45°时,点E下降的高度约为3﹣1.40=1.6m.18.(2022•盐城)2022年6月5日,“神舟十四号”载人航天飞船搭载“明星”机械臂成功发射.如图是处于工作状态的某型号手臂机器人示意图,OA是垂直于工作台的移动基座,AB、BC为机械臂,OA=1m,AB=5m,BC=2m,∠ABC =143°.机械臂端点C到工作台的距离CD=6m.(1)求A、C两点之间的距离;(2)求OD长.(结果精确到0.1m,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈2.24)【分析】(1)过点A作AE⊥CB,垂足为E,在Rt△ABE中,由AB=5m,∠ABE=37°,可求AE和BE,即可得出AC的长;(2)过点A作AF⊥CD,垂足为F,在Rt△ACF中,由勾股定理可求出AF,即OD的长.【解答】解:(1)如图,过点A作AE⊥CB,垂足为E,在Rt△ABE中,AB=5m,∠ABE=37°,∵sin∠ABE=,cos∠ABE=,∴=0.60,=0.80,∴AE=3m,BE=4m,∴CE=6m,在Rt△ACE中,由勾股定理AC==3≈6.7m.(2)过点A作AF⊥CD,垂足为F,∴FD=AO=1m,∴CF=5m,在Rt△ACF中,由勾股定理AF==2m.∴OD=2≈4.5m.1.(2022•滨州)在Rt△ABC中,若∠C=90°,AC=5,BC=12,则sin A的值为 .【分析】根据题意画出图形,进而利用勾股定理得出AB的长,再利用锐角三角函数关系,即可得出答案.【解答】解:如图所示:∵∠C=90°,AC=5,BC=12,∴AB==13,∴sin A=.故答案为:.2.(2022•湖州)如图,已知在Rt△ABC中,∠C=90°,AB=5,BC=3.求AC的长和sin A的值.【分析】根据勾股定理求AC的长,根据正弦的定义求sin A的值.【解答】解:∵∠C=90°,AB=5,BC=3,∴AC===4,sin A==.答:AC的长为4,sin A的值为.3.(2022•广东)sin30°= .【分析】熟记特殊角的三角函数值进行求解即可得出答案.【解答】解:sin30°=.故答案为:.4.(2022•绥化)定义一种运算:sin(α+β)=sinαcosβ+cosαsinβ,sin(α﹣β)=sinαcosβ﹣cosαsinβ.例如:当α=45°,β=30°时,sin(45°+30°)=×+×=,则sin15°的值为 .【分析】把15°看成是45°与30°的差,再代入公式计算得结论.【解答】解:sin15°=sin(45°﹣30°)=sin45°cos30°﹣cos45°sin30°=×﹣×=﹣=.故答案为:.5.(2022•张家界)计算:2cos45°+(π﹣3.14)0+|1﹣|+()﹣1.【分析】根据特殊锐角三角函数值,零指数幂,绝对值以及负整数指数幂的性质进行计算即可.【解答】解:原式==.6.(2022•岳阳)计算:|﹣3|﹣2tan45°+(﹣1)2022﹣(﹣π)0.【分析】先化简各式,然后再进行计算即可解答.【解答】解:|﹣3|﹣2tan45°+(﹣1)2022﹣(﹣π)0=3﹣2×1+1﹣1=3﹣2+1﹣1=1.7.(2022•通辽)如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C,D,则cos∠ADC的值为( )A.B.C.D.【分析】由格点构造直角三角形,由直角三角形的边角关系以及圆周角定理可得答案.【解答】解:∵AB为直径,∴∠ACB=90°,又∵点A,B,C都在格点上,∴∠ADC=∠ABC,在Rt△ABC中,cos∠ABC====cos∠ADC,故选:B.8.(2022•乐山)如图,在Rt△ABC中,∠C=90°,BC=,点D是AC上一点,连结BD.若tan∠A=,tan∠ABD=,则CD的长为( )A.2B.3C.D.2【分析】过D点作DE⊥AB于E,由锐角三角函数的定义可得5DE=AB,再解直角三角形可求得AC的长,利用勾股定理可求解AB的长,进而求解AD的长.【解答】解:过D点作DE⊥AB于E,∵tan∠A==,tan∠ABD==,∴AE=2DE,BE=3DE,∴2DE+3DE=5DE=AB,在Rt△ABC中,tan∠A=,BC=,∴,解得AC=,∴AB=,∴DE=1,∴AE=2,∴AD=,∴CD=AC﹣AD=,故选:C.9.(2022•泸州)如图,在平面直角坐标系xOy中,矩形OABC的顶点B的坐标为(10,4),四边形ABEF是菱形,且tan∠ABE=.若直线l把矩形OABC和菱形ABEF组成的图形的面积分成相等的两部分,则直线l的解析式为( )A.y=3x B.y=﹣x+C.y=﹣2x+11D.y=﹣2x+12【分析】分别求出矩形OABC和菱形ABEF的中心的坐标,利用待定系数法求经过两中心的直线即可得出结论.【解答】解:连接OB,AC,它们交于点M,连接AE,BF,它们交于点N,则直线MN为符合条件的直线l,如图,∵四边形OABC是矩形,∴OM=BM.∵B的坐标为(10,4),∴M(5,2),AB=10,BC=4.∵四边形ABEF为菱形,BE=AB=10.过点E作EG⊥AB于点G,在Rt△BEG中,∵tan∠ABE=,∴,设EG=4k,则BG=3k,∴BE==5k,∴5k=10,∴k=2,∴EG=8,BG=6,∴AG=4.∴E(4,12).∵B的坐标为(10,4),AB∥x轴,∴A(0,4).∵点N为AE的中点,∴N(2,8).设直线l的解析式为y=ax+b,∴,解得:,∴直线l的解析式为y=﹣2x+12,故选:D.10.(2022•益阳)如图,在Rt△ABC中,∠C=90°,若sin A=,则cos B= .【分析】根据三角函数的定义即可得到cos B=sin A=.【解答】解:在Rt△ABC中,∠C=90°,∵sin A==,∴cos B==.故答案为:.11.(2022•西宁)在Rt△ABC中,∠C=90°,AC=1,BC=,则cos A= .【分析】根据勾股定理求出AB,再根据锐角三角函数的定义求出cos A即可.【解答】解:由勾股定理得:AB===,所以cos A===,故答案为:.12.(2022•通辽)如图,在矩形ABCD中,E为AD上的点,AE=AB,BE=DE,则tan∠BDE= ﹣1 .【分析】用含有AB的代数式表示AD,再根据锐角三角函数的定义进行计算即可.【解答】解:∵四边形ABCD是矩形,∴∠A=90°,∵AB=AE,设AB=a,则AE=a,BE==a=ED,∴AD=AE+DE=(+1)a,在Rt△ABD中,tan∠BDE===﹣1,故答案为:﹣1.13.(2022•张家界)我国魏晋时期的数学家赵爽在为天文学著作《周髀算经》作注解时,用4个全等的直角三角形和中间的小正方形拼成一个大正方形,这个图被称为“弦图”,它体现了中国古代数学的成就.如图,已知大正方形ABCD的面积是100,小正方形EFGH的面积是4,那么tan∠ADF= .【分析】根据两个正方形的面积可得AD=10,DF﹣AF=2,设AF=x,则DF=x+2,由勾股定理得,x2+(x+2)2=102,解方程可得x的值,从而解决问题.【解答】解:∵大正方形ABCD的面积是100,∴AD=10,∵小正方形EFGH的面积是4,∴小正方形EFGH的边长为2,∴DF﹣AF=2,设AF=x,则DF=x+2,由勾股定理得,x2+(x+2)2=102,解得x=6或﹣8(负值舍去),∴AF=6,DF=8,∴tan∠ADF=,故答案为:.14.(2022•金华)一配电房示意图如图所示,它是一个轴对称图形.已知BC=6m,∠ABC=α,则房顶A 离地面EF的高度为( )A.(4+3sinα)m B.(4+3tanα)m C.(4+)m D.(4+)m【分析】过点A作AD⊥BC于点D,利用直角三角形的边角关系定理求得AD,.用AD+BE即可表示出房顶A离地面EF的高度.【解答】解:过点A作AD⊥BC于点D,如图,∵它是一个轴对称图形,∴AB=AC,∵AD⊥BC,∴BD=BC=3m,在Rt△ADB中,∵tan∠ABC=,∴AD=BD•tanα=3tanαm.∴房顶A离地面EF的高度=AD+BE=(4+3tanα)m,故选:B.15.(2022•枣庄)北京冬奥会开幕式的巨型雪花状主火炬塔的设计,体现了环保低碳理念.如图所示,它的主体形状呈正六边形.若点A,F,B,D,C,E是正六边形的六个顶点,则tan∠ABE= .【分析】由正六边形的性质得AB=BC=AC,BE垂直平分AC,再由等边三角形的性质得∠ABC=60°,则∠ABE=∠ABC=30°,即可得出结论.【解答】解:如图,连接AB、BC、AC、BE,∵点A,F,B,D,C,E是正六边形的六个顶点,∴AB=BC=AC,BE垂直平分AC,∴△ABC是等边三角形,∴∠ABC=60°,∵BE⊥AC,∴∠ABE=∠ABC=30°,∴tan∠ABE=tan30°=,故答案为:.16.(2022•绵阳)如图,测量船以20海里每小时的速度沿正东方向航行并对某海岛进行测量,测量船在A 处测得海岛上观测点D位于北偏东15°方向上,观测点C位于北偏东45°方向上.航行半个小时到达B 点,这时测得海岛上观测点C位于北偏西45°方向上,若CD与AB平行,则CD= (5﹣5) 海里(计算结果不取近似值).【分析】过点D作DE⊥AB,垂足为E,根据题意可得:AB=10海里,∠FAD=15°,∠FAC=45°,∠FAB=90°,∠CBA=45°,从而可得∠DAC=30°,∠CAB=45°,进而利用三角形内角和定理求出∠ACB=90°,然后在Rt△ACB中,利用锐角三角函数的定义求出AC的长,设DE=x海里,再在Rt△ADE 中,利用锐角三角函数的定义求出AE的长,在Rt△DEC中,利用锐角三角函数的定义求出EC,DC的长,最后根据AC=5海里,列出关于x的方程,进行计算即可解答.【解答】解:如图:过点D作DE⊥AB,垂足为E,由题意得:AB=20×=10(海里),∠FAD=15°,∠FAC=45°,∠FAB=90°,∠CBA=90°﹣45°=45°,∴∠DAC=∠FAC﹣∠FAD=30°,∠CAB=∠FAB﹣∠FAC=45°,∴∠ACB=180°﹣∠CAB﹣∠CBA=90°,在Rt△ACB中,AC=AB•sin45°=10×=5(海里),设DE=x海里,在Rt△ADE中,AE===x(海里),∵DC∥AB,∴∠DCA=∠CAB=45°,在Rt△DEC中,CE==x(海里),DC===x(海里),∵AE+EC=AC,∴x+x=5,∴x=,∴DC=x=(5﹣5)海里,故答案为:(5﹣5).17.(2022•荆门)如图,一艘海轮位于灯塔P的北偏东45°方向,距离灯塔100海里的A处,它沿正南方向以50海里/小时的速度航行t小时后,到达位于灯塔P的南偏东30°方向上的点B处,则t= (1+) 小时.【分析】根据题意可得:∠PAC=45°,∠PBA=30°,AP=100海里,然后在Rt△APC中,利用锐角三角函数的定义求出AC,PC的长,再在Rt△BCP中,利用锐角三角函数的定义求出BC的长,从而求出AB的长,最后根据时间=路程÷速度,进行计算即可解答.【解答】解:如图:由题意得:∠PAC=45°,∠PBA=30°,AP=100海里,在Rt△APC中,AC=AP•cos45°=100×=50(海里),PC=AP•sin45°=100×=50(海里),在Rt△BCP中,BC===50(海里),∴AB=AC+BC=(50+50)海里,∴t==(1+)小时,故答案为:(1+).18.(2022•桂林)如图,某雕塑MN位于河段OA上,游客P在步道上由点O出发沿OB方向行走.已知∠AOB=30°,MN=2OM=40m,当观景视角∠MPN最大时,游客P行走的距离OP是 20 米.【分析】先证OB是⊙F的切线,切点为E,当点P与点E重合时,观景视角∠MPN最大,由直角三角形的性质可求解.【解答】解:如图,取MN的中点F,过点F作FE⊥OB于E,以直径MN作⊙F,∵MN=2OM=40m,点F是MN的中点,∴MF=FN=20m,OF=40m,∵∠AOB=30°,EF⊥OB,∴EF=20m,OE=EF=20m,∴EF=MF,又∵EF⊥OB,∴OB是⊙F的切线,切点为E,∴当点P与点E重合时,观景视角∠MPN最大,此时OP=20m,故答案为:20.19.(2022•内江)如图所示,九(1)班数学兴趣小组为了测量河对岸的古树A、B之间的距离,他们在河边与AB平行的直线l上取相距60m的C、D两点,测得∠ACB=15°,∠BCD=120°,∠ADC=30°.(1)求河的宽度;(2)求古树A、B之间的距离.(结果保留根号)【分析】(1)过点A作AE⊥l,垂足为E,设CE=x米,则DE=(x+60)米,先利用平角定义求出∠ACE =45°,然后在Rt△AEC中,利用锐角三角函数的定义求出AE的长,再在Rt△ADE中,利用锐角三角函数的定义列出关于x的方程,进行计算即可解答;(2)过点B作BF⊥l,垂足为F,CE=AE=BF=(30+30)米,AB=EF,先利用平角定义求出∠BCF =60°,然后在Rt△BCF中,利用锐角三角函数的定义求出CF的长,进行计算即可解答.【解答】解:(1)过点A作AE⊥l,垂足为E,设CE=x米,∵CD=60米,∴DE=CE+CD=(x+60)米,∵∠ACB=15°,∠BCD=120°,∴∠ACE=180°﹣∠ACB﹣∠BCD=45°,在Rt△AEC中,AE=CE•tan45°=x(米),在Rt△ADE中,∠ADE=30°,。
三角函数的应用(1个知识点4种题型1个易错点1种中考考法)(解析版)-初中数学北师大版9年级上册

专题04三角函数的应用(1个知识点4种题型1个易错点1种中考考法)【目录】倍速学习四种方法【方法一】脉络梳理法知识点1.解直角三角形的应用(重点、难点)【方法二】实例探索法题型1.方向角问题题型2.坡度、坡角问题题型3.方案决策问题题型4.一题多解——求建筑物的高【方法三】差异对比法易错点:对俯角的意义理解错误【方法四】仿真实战法考法.解直角三角形的应用-坡角问题【方法四】成果评定法【学习目标】1.进一步体会三角函数在解决实际问题中的作用。
2.能够把实际问题转化数学问题,能够借助计算器进行有关s'j函数的计算,并能够进一步对结果的意义进行说明,提高解决实际问题的能力。
3.能利用解直角三角形的有关知识,解决测量、航海、工程技术等生活中的实际问题。
重难点:把实际问题转化为直角三角形问题,通过解直角三角形形达到求解的目的。
【倍速学习四种方法】【方法一】脉络梳理法知识点1.解直角三角形的应用(重点、难点)1.水平线:水平面上的直线以及和水平面平行的直线.2.铅垂线:垂直于水平面的直线,我们通常称为铅垂线.3.在测量时,如图,在视线与水平线所成的角中,视线在水平线上方的角叫做仰角,视线在水平线下方的角叫做俯角.4.如图,坡面的铅垂高度(h )和水平宽度(l )的比叫做坡面的坡度(或坡比),记作i ,即h i l=.坡度通常写成1:m 的形式,如i =1︰1.5.5.坡面与水平面的夹角叫做坡角,记作α.坡度i 与坡角α之间的关系:h i tan lα==.知识延伸※1.方向角:以观测者的位置为中心,将正北或正南方向作为起始方向,旋转到目标的方向线所成的小于90°的角,通常表达成北(南)偏东(西)*度.若正好为45°,则表示为西(东)南(北)方向.2.方位角:从标准方向的北端起,顺时针方向到直线的水平角称为该直线的方位角.方位角θ的取值范围为0360θ≤< .【例1】.(2023秋•成都期中)如图,一座古塔座落在小山上(塔顶记作点A ,其正下方水平面上的点记作点)B ,小李站在附近的水平地面上,他想知道自己到古塔的水平距离,便利用无人机进行测量,但由于某些原因,无人机无法直接飞到塔顶进行测量,因此他先控制无人机从脚底(记为点)C 出发向右上方(与地面成45︒,点A ,B ,C ,O 在同一平面)的方向匀速飞行4秒到达空中O 点处,再调整飞行方向,继续匀速飞行8秒到达塔顶,已知无人机的速度为5米/秒,75AOC ∠=︒,(求小李到古塔的水平距离即BC 的长.(结果精确到1m 1.41≈ 1.73)≈【分析】过点O作OD BC⊥,交BC的延长线于点D,过点O作OE AB⊥,垂足为E,根据题意可得:40AO=米,20OC=米,OE BD=,//OE BD,从而可得45EOC OCD∠=∠=︒,进而可得30AOE∠=︒,然后在Rt OCD∆中,利用锐角三角函数的定义求出CD的长,再在Rt AOE∆中,利用锐角三角函数的定义求出OE的长,从而求出BD的长,最后利用线段的和差关系进行计算,即可解答.【解答】解:过点O作OD BC⊥,交BC的延长线于点D,过点O作OE AB⊥,垂足为E,由题意得:8540AO=⨯=(米),4520OC=⨯=(米),OE BD=,//OE BD,45EOC OCD∴∠=∠=︒,75AOC∠=︒,30AOE AOC EOC∴∠=∠-∠=︒,在Rt OCD∆中,2cos452022CD OC=⋅︒=⨯=),在Rt AOE∆中,3cos304032OE AO=⋅︒=⨯=(米),3OE BD∴==),310221BC BD CD∴=-=-≈(米),∴小李到古塔的水平距离即BC的长约为21米.【点评】本题考查了解直角三角形的应用-仰角俯角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.【例2】.(2023秋•盘州市期中)某超市利用一个带斜坡的平台装卸货物,其纵断面ACFE如图所示.AE为台面,AC垂直于地面,AB表示平台前方的斜坡.斜坡的坡角ABC∠为43︒,坡长AB为2m.为保障安全,又便于装卸货物,决定减小斜坡AB的坡角,AD是改造后的斜坡(D在直线BC上),坡角ADC∠为31︒.求斜坡AD底端D与平台AC的距离CD.(结果精确到0.1)m【参考数据:sin430.68︒=,cos430.73︒=,tan430.93︒=;sin310.52︒=,cos310.86︒=,tan310.60︒=】【分析】首先在Rt ABC∆中,求出AC的长,再在Rt ADC∆,由tanACADCCD∠=,即可求出CD的长.【解答】解:在Rt ABC∆中,sinAC ABCAB∠=,sin4320.68 1.36() AC AB m∴=⋅︒=⨯=,在Rt ADC∆中,tanAC ADCCD ∠=,∴1.362.3()tan310.60ACCD m ==≈︒,∴斜坡AD底端D与平台AC的距离CD约为2.3m.【点评】本题考查了解直角三角形的应用,解答本题的关键是利用三角函数知识解直角三角形.【例3】.(2023秋•九龙坡区校级月考)如图,海岸边上有三个观测站A,B,C,观测站B在观测站A的东北方向,观测站C在观测站B的正东方向,观测站B,C之间的距离为30海里.某天,观测站A,B,C同时收到一艘轮船在D处发出的求救信号,经分析,D在观测站C的南偏东15︒方向,在观测站B的东南方向,在观测站A的正东方向.(1)求CD的长度.(结果精确到个位)(2)目前只有观测站A与B配备了搜救艇,搜救艇航速为30海里/时.收到求救信号后,因观测站B的搜救艇在检修,接到任务后不能马上出发,需30分钟后才能出发,而且必须先去C处,才能再去D处(在C 处停留时间可忽略不计);而观测站A的搜救艇接到任务后可马上出发,并直接到达D处.请问哪一个观测站的搜救艇可以更快到达D 1.414≈ 1.732)≈【分析】(1)过点C 作CE BD ⊥于点E ,利用方向角的意义,等腰直角三角形的性质和含30︒角的直角三角形的性质解答即可;(2)过点B 作BF AD ⊥于点F ,利用(1)的结论和等腰直角三角形的判定与性质求得AD 的长度,通过比较两个搜救艇到达D 处所需的时间解答即可.【解答】解:(1)由题意得://AD BC ,45CBD ∠=︒,9015105BCD ∠=︒+︒=︒,30BC =海里.过点C 作CE BD ⊥于点E ,如图,则CBE ∆为等腰直角三角形,45BCE ∴∠=︒,21522BE CE ===(海里),60DCE BCD BCE ∴∠=∠-∠=︒,30CDE ∴∠=︒,2242CD CE ∴==≈(海里);(2)观测站A 的搜救艇可以更快到达D 处.理由:由(1)知:152BE =海里,22156DE CD CE =-=(海里),(152156)BD BE DE ∴=+=海里.过点B 作BF AD ⊥于点F ,由题意得:45NAB BAD ∠=∠=︒,//BF AN ,45ABF ∴∠=︒,45DAF ∠=︒ ,90ABD ∴∠=︒,ABD ∴∆为等腰直角三角形,23030382AD BD ∴==+≈(海里).∴观测站A 的搜救艇到达D 处需要8230 2.73÷=(小时). 观测站B 的搜救艇到达D 处需要:1(3042)300.5 2.4 2.92++÷=+=(小时),∴观测站A 的搜救艇可以更快到达D 处.【点评】本题主要考查了解直角三角形的应用,方向角,直角三角形的边角关系定理,特殊角的三角函数值,利用已知条件恰当的添加辅助线,构造直角三角形是解题的关键.【方法二】实例探索法题型1.方向角问题1.(2023•高碑店市模拟)如图为东西流向且河岸平行的一段河道,点A ,B 分别为两岸上一点,且点B 在点A 正北方向,由点A 向正东方向走a 米到达点C ,此时测得点B 在点C 的北偏西55︒方向上,则河宽AB 的长为()A .tan 55a ︒米B .cos55a ︒米C .tan 35a ︒米D .tan 55a ︒米【分析】连接AB ,BC ,根据三角函数的定义即可得到结论.【解答】解:连接AB ,BC ,由题意得,90BAC ∠=︒,55ABC ∠=︒,AC a =米,tan tan 55AC ABC AB ∴∠=︒=,tan 55tan 55AC a AB ∴==︒︒,【点评】本题考查了解直角三角形的应用-方向角问题,熟练掌握三角函数的定义是解题的关键.2.(2023•金东区二模)如图,小明在C 处看到西北方向上有一凉亭A ,北偏东35︒的方向上有一棵大树B ,已知凉亭A 在大树B 的正西方向,若50BC =米,则AB 的长等于()米.A .5050sin 35cos35-︒︒B .5050sin 35cos35+︒︒C .50(cos35sin 35)︒-︒D .50(cos35sin 35)︒+︒【分析】过点C 作CD AB ⊥,垂足为D ,先在Rt BCD ∆中,利用锐角三角函数的定义求出BD ,CD 的长,然后在Rt ADC ∆中,利用锐角三角函数的定义求出AD 的长,从而利用线段的和差关系进行计算,即可解答.【解答】解:过点C 作CD AB ⊥,垂足为D ,在Rt BCD ∆中,35BCD ∠=︒,50BC =米,sin 3550sin 35BD BC ∴=⋅︒≈︒(米),cos 4550cos 35CD BC =⋅︒=︒(米),在Rt ADC ∆中,45ACD ∠=︒,tan 4550cos 35AD CD CD ∴=⋅︒==︒(米),50cos3550sin 3550(cos35sin 35)AB AD BD ∴=+=︒+︒=︒+︒米,【点评】本题考查了解直角三角形的应用-方向角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.3.(2023秋•徐汇区期末)如图,一段东西向的限速公路MN 长500米,在此公路的南面有一监测点P ,从监测点P 观察,限速公路MN 的端点M 在监测点P 的北偏西60︒方向,端点N 在监测点P 的东北方向,那么监测点P 到限速公路MN 的距离是米(结果保留根号).【分析】过点P 作PA MN ⊥于点A ,则90PAM PAN ∠=∠=︒,设PA x =米,证PAN ∆是等腰直角三角形,得NA PA x ==米,再由锐角三角函数定义得MA =米,然后由MA NA MN +=,求出250x =-,即可得出结论.【解答】解:如图,过点P 作PA MN ⊥于点A ,则90PAM PAN ∠=∠=︒,设PA x =米,由题意可知,60MPA ∠=︒,45NPA ∠=︒,PAN ∴∆是等腰直角三角形,NA PA x ∴==米,tan tan 60MAMPA PA∠==︒= ,MA ∴==(米),500MA NA MN +== ,∴500x +=,解得:250x =-,即监测点P 到限速公路MN 的距离是250)-米,故答案为:250)-.【点评】本题考查了解直角三角形的应用—方向角问题,正确作出辅助线构造直角三角形是解题的关键.4.(2023春•沙坪坝区校级期中)在公园里,同一平面内的五处景点的道路分布如图所示,经测量,点D 、E 均在点C 的正北方向且600CE =米,点B 在点C 的正西方向,且BC =点B 在点A 的南偏东60︒方向且400AB =米,点D 在点A 1.414≈, 1.732≈ 2.449)≈.(1)求道路AD 的长度(精确到个位);(2)若甲从A 点出发沿A —D —E 的路径去点E ,与此同时乙从点B 出发,沿B —A —E 的路径去点E ,其速度为40米/分钟.若两人同时到达点E ,请比较谁的速度更快?快多少?(精确到十分位)【分析】(1)过点A 作AF CB ⊥,交CB 的延长线于点F ,过点A 作AG DC ⊥,垂足为G ,根据题意可得:AF CG =,AG CF =,然后在Rt AFB ∆中,利用锐角三角函数的定义求出AF ,BF 的长,从而求出CF 的长,再在Rt ADG ∆中,利用锐角三角函数的定义求出AD 的长,即可解答;(2)利用(1)的结论可求出EG 的长,再在Rt AGE ∆中,利用勾股定理可求出AE 的长,然后在Rt ADG ∆中,利用锐角三角函数的定义求出DG 的长,从而求出甲和乙的路程,最后进行计算即可解答.【解答】解:(1)过点A 作AF CB ⊥,交CB 的延长线于点F ,过点A 作AG DC ⊥,垂足为G ,由题意得:AF CG =,AG CF =,在Rt AFB ∆中,60BAF ∠=︒,400AB =米,∴1cos604002002AF AB=⋅︒=⨯=(米),sin60400BF AB=⋅︒=⨯(米),200CG AF∴==米,BC=∴CF BF BC=+=+=(米),∴AG CF==米,在Rt ADG∆中,904545DAG∠=︒-︒=︒,∴980cos45AGAD==︒(米),∴道路AD的长度约为980米;(2)600CE=米,200CG=米,400EG CE CG∴=-=(米),在Rt AGE∆中,AG=米,∴800AE=(米),在Rt ADG∆中,45DAG∠=︒,∴tan45DG AG=⋅︒=),∴甲的路程400)AD DE AD DG EG=+=+-=米,乙的路程4008001200AB AE=+=+=(米),乙的速度为40米/分钟,∴乙所用的时间12003040==(分钟),∴甲所用的时间也是30分钟,∴甲的速度42.4=≈(米/分钟),42.440 2.4∴-=(米/分钟),∴若两人同时到达点E,甲的速度更快,快2.4米/分钟.【点评】本题考查了解直角三角形的应用-方向角问题,勾股定理的应用,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.5.(2023秋•沙坪坝区校级月考)如图,五边形ABCDE 是某公园的游览步道,把公园的五个景点连接起来,为方便游览,增设了步道AC .经勘测,90BAE ∠=︒,景点C 在景点A 的东北方向,且在景点B 的南偏东60︒方向的800米处,景点D 在景点C 的正南方向500米处,150AED ∠=︒ 1.414≈ 1.732)≈(1)求景点A 与景点E 的距离;(结果精确到1米)(2)甲、乙两人同时从景点A 出发,选择相反的路线依次游览其余四个景点,最后回到景点A ,两人在各景点处停留时间忽略不计.其中甲的游览路线是A B C D E A →→→→→,甲游览的平均速度是100米/分,乙游览的平均速度是80米/分.请通过计算说明在游览过程中,甲、乙谁先到达景点C ?【分析】(1)延长AE ,CD 交于点G ,连接AC ,过点C 作CF AB ⊥于点F ,利用含30︒角的直角三角形的性质,等腰直角三角形的性质解答即可;(2)利用(1)的结论分别计算出甲,乙两人的走的路程,再计算出到达点C 的时间即可.【解答】解:(1)延长AE ,CD 交于点G ,连接AC ,过点C 作CF AB ⊥于点F ,如图,由题意得:800BC =米,500CD =米,60ABC ∠=︒,景点C 在景点A 的东北方向,45BAC CAG ∴∠=∠=︒.在Rt BFC ∆中,60B ∠=︒ ,30BCF ∴∠=︒,400BF ∴=(米),CF ==(米).90AFC ∠=︒ ,45BAC ∠=︒,AF FC ∴==),AC ∴==),45CAG ∠=︒ ,90G ∠=︒,2AG GC AC ∴===(米),500)DG CG CD ∴=-=米,150AED ∠=︒ ,30DEG ∴∠=︒,21000)DE DG ∴==米,(1200EG ∴==-米,1200359AE AG EG ∴=-=-≈(米).答:景点A 与景点E 的距离359米.(2)乙先到达景点C ,理由:由(1)知:4008001893AB AF BF =+=++≈(米),35910005001245AE DE CD ++=++=(米),∴甲到达点C 所有的时间为189310018.93÷=(分),乙到达点C 所有的时间为12458015.56÷≈(分),18.9315.56> ,∴乙先到达景点C .【点评】本题主要考查了直角三角形的应用,含30︒角的直角三角形的性质,等腰直角三角形的性质,勾股定理,方向角,近似数和有效数字,恰当的构造直角三角形是解题的关键.6.(2023秋•九龙坡区校级期中)如图,五边形ABCDE 是一个公园沿湖的健身步道(步道可以骑行),BD 是仅能步行的跨湖小桥.经勘测,点B 在点A 的正北方935米处,点E 在点A 的正东方,点D 在点B 的北偏东74︒,且在点E 的正北方,90C ∠=︒,800BC =米,600CD =米.(参考数据:sin 740.96︒≈,cos 740.27︒≈,tan 74 3.55)︒≈(1)求AE 的长度(结果精确到1米);(2)小明和爸爸在健身步道锻炼,小明以200米/分的速度从点A 出发沿路线A B C D E A →→→→→的方向骑行,爸爸以150米/分的速度从点B 出发沿路线B D E A →→→的方向跑步前行.两人约定同时出发,那么小明和爸爸谁先到达A 点?请说明理由.【分析】(1)过点B 作BF DE ⊥,垂足为F ,根据垂直定义可得90BFE BFD ∠=∠=︒,再根据题意可得:74GBD ∠=︒,90A E ∠=∠=︒,从而可得四边形ABFE 是矩形,进而可得AB FE =,AE BF =,//AB EF ,然后利用平行线的性质可得74GBD BDF ∠=∠=︒,在Rt BCD ∆中,利用勾股定理求出BD 的长,再在Rt BFD ∆中,利用锐角三角函数的定义求出BF 的长,即可解答;(2)在Rt BFD ∆中,利用锐角三角函数的定义求出DF 的长,从而求出DE 的长,然后进行计算,比较即可解答,【解答】解:(1)如图:过点B 作BF DE ⊥,垂足为F ,90BFE BFD ∴∠=∠=︒,由题意得:74GBD ∠=︒,90A E ∠=∠=︒,∴四边形ABFE 是矩形,935AB FE ∴==米,AE BF =,//AB EF ,74GBD BDF ∴∠=∠=︒,90C ∠=︒ ,800BC =米,600CD =米1000BD ∴===(米),在Rt BFD ∆中,sin 7410000.96960BF BD =⋅︒≈⨯=(米),960BF AE ∴==米,AE ∴的长度约为960米;(2)爸爸先到达A 点,理由:在Rt BFD ∆中,74BDF ∠=︒,1000BD =米,cos 7410000.27270DF BD ∴=⋅︒≈⨯=(米),935EF = 米,9352701205DE DF EF ∴=+=+=(米),∴小明从点A 出发沿路线A B C D E A →→→→→的方向骑行需要的时间450022.5200200AB BC CD DE AE ++++===(分钟),爸爸从点B 出发沿路线B D E A →→→的方向跑步前行需要的时间316521.1150150BD DE EA ++===(分钟),21.1 分钟22.5<分钟,∴爸爸先到达A 点.【点评】本题考查了解直角三角形的应用-方向角问题,矩形的判定与性质,勾股定理的应用,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.7.(2023秋•沙坪坝区校级月考)如图,小明家A 和商店C 都在地铁站D 的正西方向,小亮家B 在地铁站的西北方,且在小明家北偏东15︒方向.一天,小明和小亮相约去地铁站坐地铁,小明到离家4千米的商店C 时,小亮家B 恰在商店C 的北偏西30︒方向. 1.41≈, 2.45)≈(1)求小明和小亮家的距离(保留根号);(2)小明从商店出发继续前往地铁站,此时小亮也从家出发乘坐公交车沿BD 方向前往地铁站,其中小明的步行速度为每小时8千米,公交车的行驶速度为每小时25千米,谁先到达地铁站呢?请说明理由.【分析】(1)过点A 作AE BC ⊥,垂足为E ,根据题意可得:75BAC ∠=︒,60BCA ∠=︒,从而利用三角形内角和定理可得45ABC ∠=︒,然后在Rt AEC ∆中,利用锐角三角函数的定义求出AE 和CE 的长,再在Rt ABE ∆中,利用锐角三角函数的定义求出AB 的长,即可解答;(2)过点B 作BF AC ⊥,垂足为F ,在Rt ABE ∆中,利用锐角三角函数的定义求出BE 的长,从而求出BC 的长,然后在Rt BCF ∆中,利用锐角三角函数的定义求出BF 和CF 的长,再在Rt BFD ∆中,利用锐角三角函数的定义求出DF 和BD 的长,从而求出CD 的长,最后进行计算即可解答.【解答】解:(1)过点A 作AE BC ⊥,垂足为E,由题意得:901575BAC ∠=︒-︒=︒,903060BCA ∠=︒-︒=︒,18045ABC BAC BCA ∴∠=︒-∠-∠=︒,在Rt AEC ∆中,4AC =千米,1cos 60422CE AC ∴=⋅︒=⨯=(千米),3sin 60432AE AC =⋅︒=⨯=(千米),在Rt ABE ∆中,2326sin 4522AE AB ===︒,∴小明和小亮家的距离为26千米;(2)小明先到达地铁站,理由:过点B 作BF AC ⊥,垂足为F,在Rt ABE ∆中,45ABE ∠=︒,AE =千米,tan 45AE BE ∴==︒,2CE =千米,(2BC BE CE ∴=+=+千米,在Rt BCF ∆中,60BCF ∠=︒,sin 60(2(32BF BC ∴=⋅︒=+⨯=+千米,1cos 60(2(12CF BC =⋅︒=+⨯=千米,在Rt BFD ∆中,904545BDF ∠=︒-︒=︒,(3tan 45BF DF ∴==︒千米,sin 45BF BD ==︒千米,3(12CD DF CF ∴=-=++=(千米), 小明的步行速度为每小时8千米,公交车的行驶速度为每小时25千米,∴小明到达地铁站需要的时间210.2584===(小时),小亮到达地铁站需要的时间0.27=(小时),0.25 小时0.27<小时,∴小明先到达地铁站.【点评】本题考查了解直角三角形的应用-方向角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.题型 2.坡度、坡角问题8.(2023•秦都区校级模拟)菏泽某超市计划更换安全性更高的手扶电梯,如图,把电梯坡面的坡角由原来的37︒减至30︒,已知原电梯坡面AB 的长为8米,更换后的电梯坡面为AD ,点B 延伸至点D ,求BD 的长.(结果精确到0.1米.参考数据:sin 370.60︒≈,cos 370.80︒≈,tan 370.75︒≈,3 1.73)≈【分析】根据正弦的定义求出AC ,根据余弦的定义求出BC ,根据正切的定义求出CD ,结合图形计算,得到答案.【解答】解:在Rt ABC ∆中,8AB =米,37ABC ∠=︒,则sin 80.60 4.8AC AB ABC =⋅∠≈⨯=(米),cos 80.80 6.40BC AB ABC =⋅∠≈⨯=(米),在Rt ADC ∆中,30ADC ∠=︒,则 4.88.30tan tan 3033AC CD ADC ===≈∠︒(米),8.30 6.40 1.9BD CD BC ∴=-=-≈(米),答:BD 的长约为1.9米.【点评】本题考查的是解直角三角形的应用—坡度坡角问题,掌握锐角三角函数的定义是解题的关键.题型3.方案决策问题9.(2023秋•大东区期末)如图1是某越野车的侧面示意图,折线段ABC 表示车后盖,已知1AB m =,0.6BC m =,123ABC ∠=︒,该车的高度 1.7AO m =.如图2,打开后备箱,车后盖ABC 落在AB C ''处,AB '与水平面的夹角27B AD '∠=︒.(1)求打开后备箱后,车后盖最高点B '到地面l 的距离;(2)若小明爸爸的身高为1.83m ,他从打开的车后盖C 处经过,有没有碰头的危险请说明理由.(结果精确到0.01m ,参考数据:sin 270.454︒≈,cos 270.891︒≈,tan 270.510︒≈3 1.732)≈【分析】(1)过点B E AD '⊥于E ,根据正弦的定义求出B E ',进而求出车后盖最高点B '到地面l 的距离;(2)过点C '作C F B E '⊥'于点F ,根据题意求出60C B F ∠''=︒,根据余弦的定义求出B F ',再求出点C '到地面l 的距离,比较大小证明结论.【解答】解:(1)如图2,过点B E AD '⊥于E ,在Rt △AB E '中,1AB AB m '==,27B AD ∠'=︒,sin B E B AE AB '∠'=',sin 1sin 270.454()B E AB B AE m ∴'='⋅∠'=⨯︒≈,∴点B '到地面l 的距离为:0.454 1.7 2.154 2.15()m +=≈,答:车后盖最高点B '到地面l 的距离约为2.15m ;(2)没有碰头的危险,理由如下:如图2,过点C '作C F B E '⊥'于点F ,在Rt △AB E '中,27B AD ∠'=︒,则902763AB E ∠'=︒-︒=︒,123AB C ABC ∠'=∠=︒ ,60C B F ∴∠''=︒,0.6B C BC m ''== ,1cos 0.60.3()2B F BC C B F m ∴'=''⋅∠''=⨯=,∴点C '到地面l 的距离为:2.150.3 1.85()m -=,1.85 1.8> ,∴没有碰头的危险.【点评】本题考查的是解直角三角形的应用-坡度坡角问题,正确作出辅助线、熟记锐角三角函数的定义是解题的关键.题型4.一题多解——求建筑物的高10.(2023秋•长春期末)在综合与实践活动中,要利用测角仪测量塔的高度.如图,塔AB 前有一座高为3m 的观景台DE ,已知30DCE ∠=︒,点E 、C 、A 在同一条水平直线上.某学习小组在观景台C 处测得塔顶部B 的仰角为45︒,在观景台D 处测得塔顶部B 的仰角为27︒.求塔AB 的高度.【参考数据:tan 270.5︒=,3 1.7=】.【分析】根据题意可得:DE EC ⊥,然后在Rt DEC ∆中,利用含30度角的直角三角形的性质得333CE DE m ==,过点D 作DF AB ⊥,垂足为F ,设AB h =m ,根据题意得:(33)DF EA h m ==,3DE FA m ==,则(3)BF h m =-,然后在Rt BDF ∆中,利用锐角三角函数的定义求出BF 的长,从而列出关于h 的方程,进行计算即可解答.【解答】解:由题意得:DE EC ⊥,在Rt DEC ∆中,30DCE ∠=︒,90DEC ∠=︒,3DE m =,∴333CE DE m ==,BA EA ⊥ ,在Rt ABC ∆中,45BCA ∠=︒,AB h =m ,tan 45AB AC h m ∴==︒,∴)AE EC AC h m =+=,过点D 作DF AB ⊥于点F ,由题意得:3DE FA m ==,)DF EA h m ==,AB h = m ,(3)BF AB AF h m ∴=-=-,在Rt BDF ∆中,27BDF ∠=︒,tan 270.5(33)BF DF h m ∴=⋅︒=+,∴3)h h -=,∴611.1h =+=,11.1AB m ∴=,∴塔AB 的高度约为11.1m .【点评】本题考查解直角三角形的应用-仰角俯角,熟练掌握直角三角形中的边角关系是解题的关键.11.(2023秋•闵行区月考)如图,AB ,CD 表示两栋建筑,小明想利用建筑CD 玻璃幕墙的反射作用来测建筑AB 的高度,首先他在建筑AB 的底部A 处用测角仪测得其顶部B 在建筑CD 玻璃幕墙上的反射点E 的仰角为α,然后他沿AC 前进了10米到达点F 处,再用测角仪测得建筑AB 的顶部B 在建筑CD 玻璃幕墙上的反射点G 的仰角为β,已知1tan 3α=,1sin 3β=,测角仪置于水平高度1.5米的M 、N 处.试求建筑AB 的高度.【分析】延长BE .BG 分别交MN 的延长线于M ',N ',MM '于CD 相交于H ,设NH xm =,则(10)MH x m =+,(210)N M x m '=+,(220)MM x m '=+,在Rt △MM B '中,1tan (210)3BM MM x α='=+ ,在Rt △MN B '中,tan BM MN β=' ,根据1sin 3β=求得2tan 4β=,于是得到210)4BM x =+,列方程解得30235x =+,于是得到1[2(30235)20] 1.5(20231.5)3AB m =⨯+++=+.【解答】解:延长BE .BG 分别交MN 的延长线于M ',N ',MM '于CD 相交于H ,设NH xm =,则(10)MH x m =+,(210)N M x m '=+,(220)MM x m '=+,在Rt △MM B '中,1tan (220)3BM MM x α='=+ ,在Rt △MN B '中,tan BM MN β=' ,1sin 3β=,22cos 3β∴=,2tan 4β∴=,210)BM x ∴=+,∴12(220)10)34x x +=+,解得:30235x =,1[2(30235)20] 1.5(20231.5)3AB m ∴=⨯+++=+.答:建筑AB 的高度为(20231.5)m .【点评】本题考查了解直角三角形的应用-仰角俯角,解答本题的关键是根据仰角构造直角三角形,利用三角函数的知识求解.【方法三】差异对比法易错点:对俯角的意义理解错误12.(2023秋•诸城市期中)如图,数学兴趣小组用无人机测量一幢楼AB 的高度.小亮站立在距离楼底部94米的D 点处,操控无人机从地面F 点,竖直起飞到正上方60米E 点处时,测得楼AB 的顶端A 的俯角为30︒,小亮的眼睛点C 看无人机的仰角为45︒(点B 、F 、D 三点在同一直线上).求楼AB 的高度.(参考数据:小亮的眼睛距离地面1.7米,3 1.7)≈【分析】过点C 作CG EF ⊥,垂足为G ,延长BA 交HE 于点I ,根据题意可得:BI EH ⊥, 1.7GF CD ==米,CG DF =,EI BF =,60EF IB ==米,94BD =米,从而可得58.3EG =米,然后在Rt EGC ∆中,利用锐角三角函数的定义求出CG 的长,从而求出IE 的长,再在Rt AIE ∆中,利用锐角三角函数的定义求出AI 的长,最后利用线段的和差关系进行计算,即可解答.【解答】解:如图:过点C 作CG EF ⊥,垂足为G ,延长BA 交HE 于点I ,由题意得:BI EH ⊥, 1.7GF CD ==米,CG DF =,EI BF =,60EF IB ==米,94BD =米,60 1.758.3EG EF FG ∴=-=-=(米),在Rt EGC ∆中,45ECG ∠=︒,58.3tan 45EG CG ∴==︒(米),58.3CG DF ∴==米,9458.335.7IE BF BD DF ∴==-=-=(米),在Rt AIE ∆中,30AEI ∠=︒,tan 3035.7AI IE ∴=⋅︒=⨯(米),6039.77AB IB IA ∴=-=-≈(米),∴楼AB 的高度约为39.77米.【点评】本题考查了解直角三角形的应用-仰角俯角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.【方法四】仿真实战法考法.解直角三角形的应用-坡角问题1.(2023•淄博)如图,与斜坡CE 垂直的太阳光线照射立柱AB (与水平地面BF 垂直)形成的影子,一部分落在地面上,另一部分落在斜坡上.若2BC =米,8.48CD =米,斜坡的坡角32ECF ∠=︒,则立柱AB 的高为米(结果精确到0.1米).科学计算器按键顺序计算结果(已取近似值)0.5300.8480.625【分析】延长AD 交BF 于点H ,根据余弦的定义求出CH ,进而求出BH ,再根据正切的定义计算,得到答案.【解答】解:如图,延长AD 交BF 于点H ,在Rt CDH ∆中,8.48CD =米,32DCH ∠=︒,cos CD DCH CH ∠=,8.4810cos 0.848CD CH DCH ∴=≈=∠(米),10212BH CH BC ∴=+=+=(米),90CDH ∠=︒ ,32DCH ∠=︒,903258DHC ∴∠=︒-︒=︒,AB BF ⊥ ,905832BAH ∴∠=︒-︒=︒,在Rt ABH ∆中,tan BH BAH AB ∠=,1219.2tan 0.625BH AB BAH ∴=≈=∠(米),故答案为:19.2.【点评】本题考查的是解直角三角形的应用-坡度坡角问题,熟记锐角三角函数的定义是解题的关键.2.(2023•十堰)如图所示,有一天桥高AB 为5米,BC 是通向天桥的斜坡,45ACB ∠=︒,市政部门启动“陡改缓”工程,决定将斜坡的底端C 延伸到D 处,使30D ∠=︒,则CD 的长度约为()(参考数据:1.414≈ 1.732)≈A .1.59米B .2.07米C .3.55米D .3.66米【分析】由90BAC ∠=︒,45ACB ∠=︒,得45ABC ACB ∠=∠=︒,则5AC AB ==米,由90BAD ∠=︒,30D ∠=︒,得60ABD ∠=︒,则tan 603AD AB =︒=,所以3AD AB =,则3 3.66CD AD AC AB AC =-=-≈米,于是得到问题的答案.【解答】解:在Rt ABC ∆中,90BAC ∠=︒,45ACB ∠=︒,45ABC ACB ∴∠=∠=︒,5AC AB ∴==米,在Rt ABD ∆中,90BAD ∠=︒,30D ∠=︒,60ABD ∴∠=︒,∴tan tan 603AD ABD AB=∠=︒=,3AD AB ∴=,3 1.73255 3.66CD AD AC AB AC ∴=-=-≈⨯-≈(米),CD ∴的长度约为3.66米,故选:D .【点评】此题重点考查直角三角形的两个锐角互余、等腰直角三角形的判定、锐角三角函数与解直角三角形等知识,推导出3AD AB =是解题的关键.3.(2023•深圳)爬坡时坡面与水平面夹角为α,则每爬1m 耗能(1.025cos )J α-,若某人爬了1000m ,该坡角为30︒,则他耗能()(参考数据:3 1.732≈,2 1.414)≈A .58J B .159J C .1025J D .1732J【分析】根据题意可得:他耗能1000(1.025cos30)=⨯-︒,进行计算即可解答.【解答】解:由题意得:某人爬了1000m ,该坡角为30︒,则他耗能1000(1.025cos30)1000(1.025159()J =⨯-︒=⨯-≈,故选:B .【点评】本题考查了解直角三角形的应用-坡度坡角问题,准确熟练地进行计算是解题的关键.4.(2023•辽宁)暑假期间,小明与小亮相约到某旅游风景区登山.需要登顶600m 高的山峰,由山底A 处先步行300m 到达B 处,再由B 处乘坐登山缆车到达山顶D 处.已知点A ,B ,D ,E ,F 在同一平面内,山坡AB 的坡角为30︒,缆车行驶路线BD 与水平面的夹角为53︒(换乘登山缆车的时间忽略不计).(1)求登山缆车上升的高度DE ;(2)若步行速度为30/m min ,登山缆车的速度为60/m min ,求从山底A 处到达山顶D 处大约需要多少分钟(结果精确到0.1)min .(参考数据:sin 530.80︒≈,cos 530.60︒≈,tan 53 1.33)︒≈【分析】(1)根据直角三角形的边角关系求出BM ,进而求出DE 即可;(2)利用直角三角形的边角关系,求出BD 的长,再根据速度、路程、时间的关系进行计算即可.【解答】解:(1)如图,过点B 作BM AF ⊥于点M ,由题意可知,30A ∠=︒,53DBE ∠=︒,600DF m =,300AB m =,在Rt ABM ∆中,30A ∠=︒,300AB m =,11502BM AB m EF ∴===,600150450()DE DF EF m ∴=-=-=,答:登山缆车上升的高度DE 为450m ;(2)在Rt BDE ∆中,53DBE ∠=︒,450DE m =,sin DE BD DBE∴=∠4500.80≈562.5()m =,∴需要的时间t t t =+步行缆车300562.53060=+19.4()min ≈,答:从山底A 处到达山顶D 处大约需要19.4分钟.【点评】本题考查解直角三角形的应用,掌握直角三角形的边角关系是正确解答的前提.5.(2023•大庆)某风景区观景缆车路线如图所示,缆车从点A 出发,途经点B 后到达山顶P ,其中400AB =米,200BP =米,且AB 段的运行路线与水平方向的夹角为15︒,BP 段的运行路线与水平方向的夹角为30︒,求垂直高度PC .(结果精确到1米,参考数据:sin150.259︒≈,cos150.966︒≈,tan150.268)︒≈【分析】过点B 作BD PC ⊥,垂足为D ,过点B 作BE AC ⊥,垂足为E ,根据题意可得:CD BE =,然后分别在Rt ABE ∆和Rt BDP ∆中,利用锐角三角函数的定义求出BE 和DP 的长,从而利用线段的和差关系进行计算,即可解答.【解答】解:过点B 作BD PC ⊥,垂足为D ,过点B 作BE AC ⊥,垂足为E ,由题意得:CD BE =,在Rt ABE ∆中,15A ∠=︒,400AB =米,sin154000.259103.6BE AB ∴=⋅︒≈⨯=(米),103.6CD BE ∴==米,在Rt BDP ∆中,30PBD ∠=︒,200BP =米,11002DP BP ∴==(米),204PC PD DC ∴=+≈(米),∴垂直高度PC 约为204米.【点评】本题考查了解直角三角形的应用-坡度坡角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.【方法五】成果评定法一、单选题A .10tan 40⋅︒米B 【答案】A 【分析】本题主要考查解直角三角形,熟练掌握三角函数的定义是解题的关键.【详解】解:∵ABC 为直角三角形,A .170m【答案】D 【分析】本题主要考查了解直角三角形的实际应用,矩形的性质与判定,过点四边形ABED 是矩形,得到可求出答案.【详解】解:如图所示,过点由题意得AB CD AD ∥,∴AB AD ⊥,又∵BE CD ⊥,∴四边形ABED 是矩形,∴10m DE AB AD ==,在Rt EBC 中,tan α=∴105m CE =,∴115m CD DE CE =+=故选D .4.(2023上·四川资阳则AC的长是()A.53米B【答案】A【分析】本题考查了坡比计算,熟练掌握定义是解题的关键.【详解】∵堤高5BC=米,迎水坡∴:5:1:==BC AC AC解得53AC=(米),故选A.5.(2023上·山西长治·九年级校联考期末)该支架三个脚长度相同且与地面夹角相同.如图∠脚AB的长为2米,BA.2tan70︒米B.2sin【答案】B【分析】本此题主要考查了解直角三角形的应用,直接利用锐角三角函数关系得出。
中考总复习锐角三角函数综合复习--知识讲解

中考总复习锐角三角函数综合复习--知识讲解锐角三角函数是初中数学中的一个重要内容,也是中考数学考试中常考的内容之一、掌握了锐角三角函数的定义、性质和相关的计算方法,可以帮助我们解决与角度有关的各种问题,如计算角度的大小、求角的三角函数值等。
下面是锐角三角函数的综合复习知识讲解。
1.弧度制和角度制在介绍锐角三角函数之前,我们首先要了解弧度制和角度制。
在角度制中,一个圆的周长被定义为360度,而在弧度制中,一个圆的周长被定义为2π弧度。
所以可以得到以下关系:360度=2π弧度180度=π弧度90度=π/2弧度2.定义对于任意一个锐角A,我们可以在一个单位圆上面取点P,使得∠POA 的顶点为O,点O为圆心,点P在单位圆上。
这样,我们可以定义以下几个锐角三角函数:正弦函数sinA、余弦函数cosA、正切函数tanA、余切函数cotA。
3.性质(1) 正弦函数sinA:在单位圆上,点P的纵坐标就是正弦值sinA。
(2) 余弦函数cosA:在单位圆上,点P的横坐标就是余弦值cosA。
(3) 正切函数tanA:tanA的值等于sinA/cosA。
(4) 余切函数cotA:cotA的值等于cosA/sinA。
(5) 错位现象:sinA等于cos(90度-A),cosA等于sin(90度-A)。
4.基本关系式(1) sin²A + cos²A = 1,即sin²A = 1 - cos²A,cos²A = 1 -sin²A。
(2) tanA = sinA/cosA,cotA = 1/tanA = cosA/sinA。
(3) sin(180度 - A) = sinA,cos(180度 - A) = -cosA。
(4) cos(360度 - A) = cosA,sin(360度 - A) = -sinA。
5.锐角三角函数的值(1)0度、30度、45度、60度、90度的正弦、余弦、正切值是特殊的,需要进行熟记。
数学中考一轮复习:三角函数-锐角三角函数要点集锦
初中数学锐角三角函数要点集锦考点考纲要求分值考向预测锐角三角函数要点1. 理解正弦、余弦、正切的定义及计算公式;2. 能够推导并掌握特殊角的三角函数值;3. 能够理解与锐角三角函数有关的公式。
3~5分主要考查为利用三角函数的定义求值,利用特殊角的三角函数值进行计算,难度不大,分值也不高,理解定义是解决问题的关健。
一、锐角三角函数基本定义:在Rt△ABC中,∠C=90°,我们把∠A的对边与斜边的比叫做∠A的正弦,记作sin A;把∠A的邻边与斜边的比叫做∠A的余弦,记作cos A;把∠A的对边与邻边的比叫做∠A 的正切,记作tan A。
即:sinA=;cosA=;tanA=。
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数。
ABCabc对边邻边斜边【随堂练习】(贵阳)在Rt△ABC中,∠C=90°,AC=12,BC=5,则sinA的值为()A. B. C. D.思路分析:首先画出图形,进而求出AB的长,再利用锐角三角函数求出即可。
答案:解:如图所示:∵∠C=90°,AC=12,BC=5,∴AB===13,则sinA==,故选:D。
三角函数角度αsinαcosαtanα30°45° 160°【重要提示】1. 各三角函数值可通过直角三角形性质及勾股定理求出边长从而求出比值;2. 锐角三角函数值的取值范围及增减情况:①∠A的正弦函数、余弦函数的取值范围是:0<sinA<1,0<cosA<1,即任意锐角的正弦、余弦值都大于0而小于1;而正切是两直角边的比,所以∠A的正切函数取值范围是:tanA>0,即任意锐角的正切值都大于0。
②当角度在0°~90°间变化时,正弦值随着角度的增大(或减小)而增大(或减小),余弦值随着角度的增大(或减小)而减小(或增大);正切值随着角度的增大(或减小)而增大(或减小)。
三、同角、互余两角的锐角三角函数值的关系:1. 任意锐角的正弦值等于它的余角的余弦值,任意锐角的余弦值等于它的余角的正弦值;即:。
2023福州中考数学考点分析

2023福州中考数学考点分析学习是每个一个学生的职责,而学习的动力是靠自己的梦想,也可以这样说没有自己的梦想就是对自己的一种不责任的表现,同时知识也不是也不是随意的摘取。
要通过自己的努力,要把我自己生命的钥匙。
今天小编在这给大家整理了一些福州中考数学考点分析,我们一起来看看吧!福州中考数学考点分析1一、锐角三角函数正弦等于对边比斜边余弦等于邻边比斜边正切等于对边比邻边余切等于邻边比对边正割等于斜边比邻边二、三角函数的计算幂级数c0+c1x+c2x2+...+cnxn+...=∑cnxn(n=0..∞)c0+c1(x-a)+c2(x-a)2+...+cn(x-a)n+...=∑cn(x-a)n(n=0..∞)它们的各项都是正整数幂的幂函数,其中c0,c1,c2,...及a都是常数,这种级数称为幂级数.泰勒展开式(幂级数展开法)f(x)=f(a)+f'(a)/1!_(x-a)+f''(a)/2!_(x-a)2+...f(n)(a)/n!_(x-a)n+...三、解直角三角形1.直角三角形两个锐角互余。
2.直角三角形的三条高交点在一个顶点上。
3.勾股定理:两直角边平方和等于斜边平方四、利用三角函数测高1、解直角三角形的应用(1)通过解直角三角形能解决实际问题中的很多有关测量问.如:测不易直接测量的物体的高度、测河宽等,关键在于构造出直角三角形,通过测量角的度数和测量边的长度,计算出所要求的物体的高度或长度.(2)解直角三角形的一般过程是:①将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题).②根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.福州中考数学考点分析21.代数式与有理式用运算符号把数或表示数的字母连结而成的式子,叫做代数式。
单独的一个数或字母也是代数式。
整式和分式统称为有理式。
2.整式和分式含有加、减、乘、除、乘方运算的代数式叫做有理式。
初中九年级数学中考锐角三角函数知识点总结

九年级数学中,锐角三角函数是一个重要的知识点。
锐角三角函数是指对于锐角的正弦、余弦和正切函数。
下面我将对锐角三角函数的基本概念、性质和应用进行总结。
一、基本概念1.弧度和角度:角度是常用的角度度量单位,弧度是角度的另一种度量单位。
1个弧度对应360°/2π≈57.3°。
角度和弧度之间的关系式:弧度=角度×π/180°。
2.锐角:指角度小于90°的角。
3. 三角函数:对于一个锐角A,定义其正弦(sin A)为对边与斜边的比值,余弦(cos A)为邻边与斜边的比值,正切(tan A)为对边与邻边的比值。
二、性质1.正弦函数的性质:(1)对于锐角A,0 < A < 90°,sin A > 0;(2)sin A = sin (180° - A) = sin (A + 360°);(3)sin (90° - A) = cos A;(4)sin A ≠ 0,当且仅当A是锐角。
2.余弦函数的性质:(1)对于锐角A,0 < A < 90°,cos A > 0;(2)cos A = cos (180° - A) = cos (360° + A);(3)cos (90° - A) = sin A;(4)cos A ≠ 0,当且仅当A是锐角。
3.正切函数的性质:(1)对于锐角A,0 < A < 90°,tan A > 0;(2)tan A = tan (180° + A);(3)tan (90° - A) = 1/tan A;(4)tan A ≠ 0,当且仅当A是锐角。
4.三角函数的关系:(1)sin^2 A + cos^2 A = 1;(2)tan A = sin A / cos A。
三、应用1.解三角形:利用已知角的正弦、余弦和正切的值,可以求解未知边长或角度的三角形问题。
中考数学考点:三角函数公式关系_考点解析

中考数学考点:三角函数公式关系_考点解析中考是初中升高中的一个重要阶段,查字典数学网精心为大家搜集整理了中考数学考点:三角函数公式关系,希望对大家的数学学习有所帮助!中考数学考点:三角函数公式关系倒数关系tan cot=1sin csc=1cos sec=1商的关系sin/cos=tan=sec/csccos/sin=cot=csc/sec平方关系sin^2()+cos^2()=11+tan^2()=sec^2()1+cot^2()=csc^2()同角三角函数关系六角形记忆法构造以上弦、中切、下割;左正、右余、中间1的正六边形为模型。
倒数关系对角线上两个函数互为倒数;商数关系六边形任意一顶点上的函数值等于与它相邻的两个顶点上函数值的乘积。
(主要是两条虚线两端的三角函数值的乘积,下面4个也存在这种关系。
)。
由此,可得商数关系式。
平方关系在带有阴影线的三角形中,上面两个顶点上的三角函数值的平方和等于下面顶点上的三角函数值的平方。
两角和差公式sin(+)=sincos+cossinsin(-)=sincos-cossincos(+)=coscos-sinsincos(-)=coscos+sinsintan(+)=(tan+tan )/(1-tan tan)tan(-)=(tan-tan)/(1+tan tan)二倍角的正弦、余弦和正切公式sin2=2sincoscos2=cos^2()-sin^2()=2cos^2()-1=1-2sin^2()tan2=2tan/(1-tan^2())tan(1/2*)=(sin )/(1+cos )=(1-cos )/sin半角的正弦、余弦和正切公式sin^2(/2)=(1-cos)/2cos^2(/2)=(1+cos)/2tan^2(/2)=(1-cos)/(1+cos)tan(/2)=(1cos)/sin=sin/1+cos万能公式sin=2tan(/2)/(1+tan^2(/2))cos=(1-tan^2(/2))/(1+tan^2(/2))tan=(2tan(/2))/(1-tan^2(/2))三倍角的正弦、余弦和正切公式sin3=3sin-4sin^3()cos3=4cos^3()-3costan3=(3tan-tan^3())/(1-3tan^2())三角函数的和差化积公式sin+sin=2sin((+)/2) cos((-)/2)sin-sin=2cos((+)/2) sin((-)/2)cos+cos=2cos((+)/2)cos((-)/2)cos-cos=-2sin((+)/2)sin((-)/2)三角函数的积化和差公式sincos=0.5[sin(+)+sin(-)]cossin=0.5[sin(+)-sin(-)]coscos=0.5[cos(+)+cos(-)]sinsin=-0.5[cos(+)-cos(-)]经过精心的整理,有关中考数学考点:三角函数公式关系的内容已经呈现给大家,祝大家学习愉快!。
中考数学重要知识点解析三角函数的计算与应用

中考数学重要知识点解析三角函数的计算与应用三角函数是中学数学中的重要知识点,它在几何学和三角学的相关领域中有着广泛的应用。
掌握三角函数的计算与应用,对于中考数学的学习至关重要。
本文将对三角函数的计算方法和应用进行解析。
一、弧度制和角度制的转换在计算三角函数时,有时会涉及到角度的转换。
在数学中,角度的计量方式有角度制和弧度制两种。
角度制是将一个圆周等分为360等份,以度(°)作为计量单位;而弧度制是以圆的弧长所对应的圆心角作为计量单位。
在数学中,我们常常使用45°和π/4两种表示方式,它们是等价的。
具体转换公式如下:弧度制角度 = 弧度× (180/π)角度制角度 = 角度× (π/180)二、常用三角函数的计算在三角函数中,最常用的三个函数是正弦函数(sin)、余弦函数(cos)和正切函数(tan)。
这些函数的值与角度的大小有着密切的关系。
可以通过查表或计算器进行具体数值的计算。
1. 正弦函数正弦函数的定义为:sinθ = 对边/斜边其中θ为角度,对边指的是与角度θ相对的边,斜边指的是三角形中斜边的长度。
正弦函数的取值范围是[-1, 1]。
2. 余弦函数余弦函数的定义为:cosθ = 邻边/斜边其中θ为角度,邻边指的是与角度θ相邻的边,斜边指的是三角形中斜边的长度。
余弦函数的取值范围也是[-1, 1]。
3. 正切函数正切函数的定义为:tanθ = 对边/邻边其中θ为角度,对边指的是与角度θ相对的边,邻边指的是与角度θ相邻的边。
正切函数的取值范围是(-∞, +∞)。
三、三角函数的应用三角函数在几何学、物理学、工程学等领域中有着广泛的应用。
在中考数学中,我们也常常需要运用三角函数来解决一些实际问题。
以下是几个常见的应用场景:1. 三角形的边长计算已知一个三角形的两个角度和一个边长,我们可以利用三角函数来计算其他边长的值。
例如,已知一个直角三角形的一个锐角为30°,另一个锐角为60°,我们可以利用sin30°和cos30°来计算三角形的边长。
中考复习初中数学三角函数复习重点整理

中考复习初中数学三角函数复习重点整理数学三角函数是中学数学中一个较为重要的内容,对于中考来说,复习三角函数是非常重要的。
下面是初中数学三角函数的复习重点整理。
一、基本概念1. 角度与弧度制:角度制是我们常用的度数表示方法,弧度制是更精确的表示方法,可以通过角度制与弧度制的换算进行转化。
2. 正弦、余弦和正切:正弦是一个角的对边与斜边的比值,余弦是一个角的邻边与斜边的比值,正切是一个角的对边与邻边的比值。
3. 特殊角的三角函数值:例如,30°的正弦值为1/2,余弦值为√3/2,正切值为1/√3。
二、基本关系1. 三角函数的正负:在不同象限中,正弦、余弦和正切的正负情况是不同的,要根据象限关系来确定正负值。
2. 三角函数的基本关系:在一个直角三角形中,正弦、余弦和正切之间存在一定的关系,可以通过正弦定理、余弦定理和正切定理进行推导和计算。
三、诱导公式1. 正弦和余弦的诱导公式:通过三角函数的基本关系,可以得到正弦和余弦的诱导公式,例如,sin(α±β)=sinαcosβ±cosαsinβ。
2. 正切的诱导公式:通过正切的定义和基本关系,可以得到正切的诱导公式,例如,tan(α±β)=(tanα±tanβ)/(1∓tanαtanβ)。
四、同角三角函数间的关系1. 同角三角函数的关系:在一个直角三角形中,正弦、余弦和正切之间存在一定的关系,例如,tanα=sinα/cosα。
2. 同角三角函数的平方和关系:例如,sin²α+cos²α=1,tan²α+1=sec²α,等等。
五、解三角形问题1. 利用正弦定理和余弦定理解三角形问题:通过正弦定理和余弦定理,可以求解各种类型的三角形问题,例如,已知两边和夹角,求第三边或第三角;已知两边和一个对角,求其他未知量等等。
六、图象与性质1. 正弦曲线、余弦曲线和正切曲线:三角函数的图象具有一定的特点,通过观察和探究,可以得到正弦曲线、余弦曲线和正切曲线的性质。
中考数学三角函数知识点归纳

2019中考数学三角函数知识点归纳三角函数(也叫做圆函数)是角的函数;它们在研究三角形和建模周期现象和许多其他应用中是很重要的。
相信对于大多数同学来说三角函是一大难点,为此下文为各位考生整理了2019中考数学三角函数知识点的内容供大家参考。
【三角函数解题思路】很多人都认为成绩是用大量的题堆出来的,其实不然,要想提高成绩,我们还需要对所学的知识点进行总结。
我们要对它格外重视。
解题思想方法有转化思想、数形结合思想、函数思想、方程思想法。
【全文】【锐角三角函数定义】锐角角A的正弦(sin),余弦(cos)和正切(tan),余切(cot)以及正割(sec),余割(csc)都叫做角A的锐角三角函数。
正弦(sin)等于对边比斜边;sinA=a/c余弦(cos)等于邻边比斜边;cosA=b/c正切(tan)等于对边比邻边;tanA=a/b余切(cot)等于邻边比对边;cotA=b/a正割(sec)等于斜边比邻边;secA=c/b余割(csc)等于斜边比对边。
cscA=c/a【互余角的三角函数间的关系】sin(90°-α)=cosα,cos(90°-α)=sinα,tan(90°-α)=cotα,cot(90°-α)=tanα.平方关系:sin^2(α)+cos^2(α)=1 tan^2(α)+1=sec^2(α) cot^2(α)+1=csc^2(α)积的关系:sinα=tanα·cosαcosα=cotα·sinαtanα=sinα·secαcotα=cosα·cscαsecα=tanα·cscαcscα=secα·cotα倒数关系:tanα·cotα=1sinα·cscα=1cosα·secα=1。
初中三角函数知识点+题型总结+课后练习
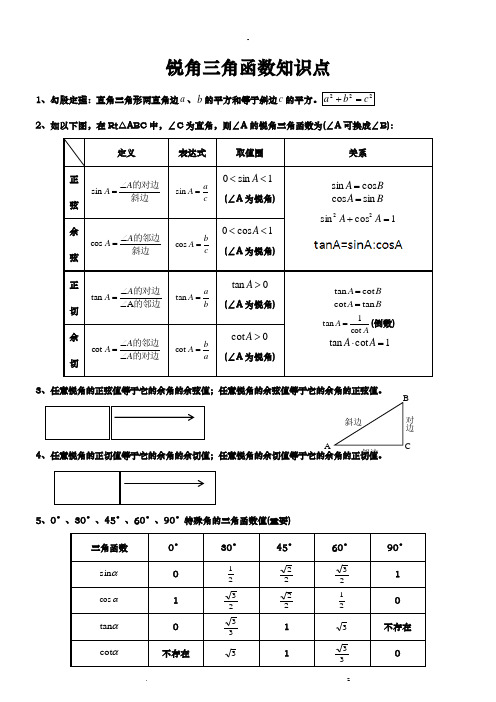
锐角三角函数知识点1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
222c b a =+2、如以下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B):定义表达式取值围关系正弦 斜边的对边A A ∠=sin caA =sin1sin 0<<A(∠A 为锐角)B A cos sin = B A sin cos =1cos sin 22=+A A余弦 斜边的邻边A A ∠=cos c bA =cos 1cos 0<<A(∠A 为锐角)正切 的邻边的对边A tan ∠∠=A A b aA =tan 0tan >A(∠A 为锐角)B A cot tan = B A tan cot =AA cot 1tan =(倒数) 1cot tan =⋅A A余切的对边的邻边A A A ∠∠=cot abA =cot0cot >A(∠A 为锐角)3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。
4、任意锐角的正切值等于它的余角的余切值;任意锐角的余切值等于它的余角的正切值。
5、0°、30°、45°、60°、90°特殊角的三角函数值(重要)三角函数 0° 30°45°60°90° αsin 0 21 22 23 1 αcos1 23 2221 0 αtan 0 33 1 3 不存在 αcot不存在3133 0对边邻边 斜边 B锐角三角函数题型训练类型一:直角三角形求值1.Rt △ABC 中,,12,43tan ,90==︒=∠BC A C 求AC 、AB 和cos B .2.:如图,⊙O 的半径OA =16cm ,OC ⊥AB 于C 点,⋅=∠43sin AOC 求:AB 及OC 的长.3.:⊙O 中,OC ⊥AB 于C 点,AB =16cm ,⋅=∠53sin AOC(1)求⊙O 的半径OA 的长及弦心距OC ; (2)求cos ∠AOC 及tan ∠AOC . 4.A ∠是锐角,178sin =A ,求A cos ,A tan 的值 类型二. 利用角度转化求值:1.:如图,Rt △ABC 中,∠C =90°.D 是AC 边上一点,DE ⊥AB 于E 点.DE ∶AE =1∶2.求:sin B 、cos B 、tan B .2. 如图4,沿AE 折叠矩形纸片ABCD ,使点D 落在BC 边的点F 处.8AB =,10BC =,则tan EFC ∠的值为 ( ) A.34 B.43C.35D.453. 如图6,在等腰直角三角形ABC ∆中,90C ∠=︒,6AC =,D 为AC 上一点,假设1tan 5DBA ∠=,则AD 的长为( )A .2 B .2 C .1 D .224. 如图6,在Rt △ABC 中,∠C =90°,AC =8,∠A 的平分线AD =3316求∠B 的度数及边BC 、AB 的长. 类型三. 化斜三角形为直角三角形例1〔2021•〕如图,在△ABC 中,∠A=30°,∠B=45°,AC=23,求AB 的长.例2.:如图,△ABC 中,AC =12cm ,AB =16cm ,⋅=31sin A(1)求AB 边上的高CD ; (2)求△ABC 的面积S ; (3)求tan B .例3.:如图,在△ABC 中,∠BAC =120°,AB =10,AC =5.求:sin ∠ABC 的值.对应训练 1.〔2021•〕如图,在Rt△ABC 中,∠BAC=90°,点D 在BC 边上,且△ABD 是等边三角形.假设AB=2,求△ABC 的周长.〔结果保存根号〕2.:如图,△ABC 中,AB =9,BC =6,△ABC 的面积等于9,求sin B . 类型四:利用网格构造直角三角形例1 〔2021•江〕如下图,△ABC 的顶点是正方形网格的格点,则sinA 的值为〔 〕 A .12 B .55 C .1010 D .255DABC对应练习:1.如图,△ABC 的顶点都在方格纸的格点上,则sin A =_______.特殊角的三角函数值例1.求以下各式的值︒-︒+︒30cos 245sin 60tan 2=. 计算:3-1+(2π-1)0-33tan30°-tan45°= 030tan 2345sin 60cos 221⎪⎪⎭⎫ ⎝⎛︒-︒+︒+= ︒-︒+︒60tan 45sin 230cos 2tan 45sin 301cos 60︒+︒-︒=在ABC ∆中,假设0)22(sin 21cos 2=-+-B A ,B A ∠∠,都是锐角,求C ∠的度数 例2.求适合以下条件的锐角.(1)21cos =α (2)33tan =α (3)222sin =α(4)33)16cos(6=- α〔5〕为锐角,且3)30tan(0=+α,求αtan 的值〔〕在ABC ∆中,假设0)22(sin 21cos 2=-+-B A ,B A ∠∠,都是锐角,求C ∠的度数 例3. 三角函数的增减性 1.∠A 为锐角,且sin A <21,则∠A 的取值围是 A. 0°< A < 30° B. 30°< A <60° C. 60°< A < 90° D. 30°< A < 90° 2. A 为锐角,且030sin cos <A ,则 〔 〕A. 0°< A < 60°B. 30°< A < 60°C. 60°< A < 90°D. 30°< A < 90° 例4. 三角函数在几何中的应用1.:如图,在菱形ABCD 中,DE ⊥AB 于E ,BE =16cm ,⋅=1312sin A 求此菱形的周长.2.:如图,Rt △ABC 中,∠C =90°,3==BC AC ,作∠DAC =30°,AD 交CB 于D 点,求:(1)∠BAD ;(2)sin ∠BAD 、cos ∠BAD 和tan ∠BAD .3. :如图△ABC 中,D 为BC 中点,且∠BAD =90°,31tan =∠B ,求:sin ∠CAD 、cos ∠CAD 、tan ∠CAD . 解直角三角形:1.在解直角三角形的过程中,一般要用的主要关系如下(如下图): 在Rt △ABC 中,∠C =90°,AC =b ,BC =a ,AB =c , ①三边之间的等量关系:________________________________.②两锐角之间的关系:__________________________________. ③边与角之间的关系:==B A cos sin ______;==B A sin cos _______;==BA tan 1tan _____;==B A tan tan 1______.④直角三角形中成比例的线段(如下图).在Rt △ABC 中,∠C =90°,CD ⊥AB 于D .CD 2=_________;AC 2=_________; BC 2=_________;AC ·BC =_________.类型一例1.在Rt △ABC 中,∠C =90°.(1):a =35,235=c ,求∠A 、∠B ,b ;(2):32=a ,2=b ,求∠A 、∠B ,c ; (3):32sin =A ,6=c ,求a 、b ;(4):,9,23tan ==b B 求a 、c ; (5):∠A =60°,△ABC 的面积,312=S 求a 、b 、c 及∠B .例2.:如图,△ABC 中,∠A =30°,∠B =60°,AC =10cm .求AB 及BC 的长.例3.:如图,Rt △ABC 中,∠D =90°,∠B =45°,∠ACD =60°.BC =10cm .求AD 的长. 例4.:如图,△ABC 中,∠A =30°,∠B =135°,AC =10cm .求AB 及BC 的长. 类型二:解直角三角形的实际应用 仰角与俯角:例1.〔2021•〕如图,从热气球C 处测得地面A 、B 两点的俯角分别是30°、45°,如果此时热气球C 处的高度CD 为100米,点A 、D 、B 在同一直线上,则AB 两点的距离是〔 〕 A . 200米 B . 200米 C . 220米 D . 100〔〕米例2.:如图,在两面墙之间有一个底端在A 点的梯子,当它靠在一侧墙上时,梯子的顶端在B 点;当它靠在另一侧墙上时,梯子的顶端在D 点.∠BAC =60°,∠DAE =45°.点D 到地面的垂直距离m 23=DE ,求点B 到地面的垂直距离BC .例3〔昌平〕19.如图,一风力发电装置竖立在小山顶上,小山的高BD =30m . 从水平面上一点C 测得风力发电装置的顶端A 的仰角∠DCA =60°, 测得山顶B 的仰角∠DCB =30°,求风力发电装置的高AB 的长.例4.如图,小聪用一块有一个锐角为30︒的直角三角板测量树高,小聪和树都与地面垂直,且相距33米,小聪身高AB 为1.7米,求这棵树的高度.例5.:如图,河旁有一座小山,从山顶A 处测得河对岸点C 的俯角为30°,测得岸边点D 的俯角为45°,又知河宽CD 为50m .现需从山顶A 到河对岸点C 拉一条笔直的缆绳AC ,求山的高度及缆绳AC 的长(答案可带根号). 例5.〔2021•〕如图,为测量*物体AB 的高度,在D 点测得A 点的仰角为30°,朝物体AB 方向前进20米,到达点C ,再次测得点A 的仰角为60°,则物体AB 的高度为〔 〕 A . 10米 B . 10米 C . 20米 D .米 例6.〔2021•〕超速行驶是引发交通事故的主要原因之一.上周末,小明和三位同学尝试用自己所学的知识检测车速.如图,观测点设在A 处,离大道的距离〔AC 〕为30米.这时,一辆小轿车由西向东匀速行驶,测得此车从B 处行驶到C 处所用的时间为8秒,∠BAC=75°. 〔1〕求B 、C 两点的距离;〔2〕请判断此车是否超过了大道60千米/小时的限制速度.〔计算时距离准确到1米,参考数据:sin75°≈0.9659,cos75°≈0.2588,tan75°≈3.732,3≈1.732,60千米/小时≈16.7米/秒〕 类型四. 坡度与坡角A B CD EA例.〔2021•〕如图,*水库堤坝横断面迎水坡AB 的坡比是1:3,堤坝高BC=50m ,则应水坡面AB 的长度是〔 〕A .100mB .1003mC .150mD .503m类型五. 方位角1.:如图,一艘货轮向正北方向航行,在点A 处测得灯塔M 在北偏西30°,货轮以每小时20海里的速度航行,1小时后到达B 处,测得灯塔M 在北偏西45°,问该货轮继续向北航行时,与灯塔M 之间的最短距离是多少"(准确到0.1海里,732.13≈) 综合题:三角函数与四边形:〔西城二模〕1.如图,四边形ABCD 中,∠BAD=135°,∠BCD=90°,AB=BC=2, tan∠BDC=63. (1)求BD 的长; (2)求AD 的长.〔2021东一〕2.如图,在平行四边形ABCD 中,过点A 分别作AE BC E AF ⊥CD 于点F . 〔1〕求证:∠BAE =∠DAF ; 〔2〕假设AE =4,AF =245,3sin 5BAE ∠=,求CF 的长.三角函数与圆:1. 如图,直径为10的⊙A 经过点(05)C ,和点(00)O ,,与*轴的正半轴交于点D ,B 是y 轴右侧圆弧上一点,则cos∠OBC 的值为〔 〕 A .12 B .32C .35D .45〔延庆〕19.:在⊙O 中,AB 是直径,CB 是⊙O 的切线,连接AC 与⊙O 交于点D,(1) 求证:∠AOD=2∠C(2) 假设AD=8,tanC=34,求⊙O 的半径。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角函数中考数学考试知识点分析
锐角三角函数定义
锐角角A的正弦,余弦和正切,余切以及正割,余割都叫做角A的锐角三角函数。
正弦等于对边比斜边;sinA=a/c
余弦等于邻边比斜边;cosA=b/c
正切等于对边比邻边;tanA=a/b
余切等于邻边比对边;cotA=b/a
正割等于斜边比邻边;secA=c/b
余割等于斜边比对边。
cscA=c/a
互余角的三角函数间的关系
sin=cos,cos=sin,
tan=cot,cot=tan。
平方关系:
sin^2+cos^2=1
tan^2+1=sec^2
cot^2+1=csc^2
积的关系:
sin=tancos
cos=cotsin
tan=sinsec
cot=coscsc
sec=tancsc
csc=seccot
倒数关系:
tancot=1
sincsc=1
cossec=1
锐角三角函数公式
两角和与差的三角函数:
sin=sinAcosB+cosAsinB
sin=sinAcosB-cosAsinB?
cos=cosAcosB-sinAsinB
cos=cosAcosB+sinAsinB
tan=/
tan=/
cot=/
cot=/
三角和的三角函数:
sin=sincoscos+cossincos+coscossin-sinsinsin cos=coscoscos-cossinsin-sincossin-sinsincos tan=/
辅助角公式:
Asin+Bcos=^sin,其中
cost=A/^
tant=B/A
Asin+Bcos=^cos,tant=A/B
倍角公式:
sin=2sincos=2/
cos=cos^2-sin^2=2cos^2-1=1-2sin^2 tan=2tan/
三倍角公式:
sin=3sin-4sin^3
cos=4cos^3-3cos
半角公式:
sin=/2)
cos=/2)
tan=/)=sin/=/sin
降幂公式
sin^2=)/2=versin/2
cos^2=)/2=covers/2
tan^2=)/)
万能公式:
sin=2tan/
cos=/
积化和差公式:
sincos=
cossin=
coscos=
sinsin=-
和差化积公式:
sin+sin=2sincos
sin-sin=2cossin
cos+cos=2coscos
cos-cos=-2sinsin
推导公式:
tan+cot=2/sin2
tan-cot=-2cot2
1+cos2=2cos^2
1-cos2=2sin^2
1+sin=^2
其他:
sin+sin+sin+sin++sin=0
cos+cos+cos+cos++cos=0以及sin^2+sin^2+sin^2=3/2 tanAtanBtan+tanA+tanB-tan=0
函数名正弦余弦正切余切正割余割
在平面直角坐标系xOy中,从点O引出一条射线OP,设旋转角为,设OP=r,P点的坐标为有
正弦函数sin=y/r
余弦函数cos=x/r
正切函数tan=y/x
余切函数cot=x/y
正割函数sec=r/x
余割函数csc=r/y
正弦:角的对边比上斜边
余弦:角的邻边比上斜边
正切:角的对边比上邻边
余切:角的邻边比上对边
正割:角的斜边比上邻边
余割:角的斜边比上对边
三角函数万能公式
万能公式
^2+^2=1
1+^2=^2
1+^2=^2
证明下面两式,只需将一式,左右同除^2,第二个除^2即可
对于任意非直角三角形,总有
tanA+tanB+tanC=tanAtanBtanC
证:
A+B=-C
tan=tan
/=/
整理可得
tanA+tanB+tanC=tanAtanBtanC
得证
同样可以得证,当x+y+z=n时,该关系式也成立
由tanA+tanB+tanC=tanAtanBtanC可得出以下结论
cotAcotB+cotAcotC+cotBcotC=1
cot+cot+cot=cotcotcot
^2+^2+^2=1-2cosAcosBcosC
^2+^2+^2=2+2cosAcosBcosC
万能公式为:
设tan=t
sinA=2t/
tanA=2t/
cosA=/kZ)
就是说都可以用tan来表示,当要求一串函数式最值的时候,就可以用万能公式,推导成只含有一个变量的函数,
最值就很好求了。
三角函数关系
倒数关系
tancot=1
sincsc=1
cossec=1
商的关系
sin/cos=tan=sec/csc
cos/sin=cot=csc/sec
平方关系
sin^2+cos^2=1
1+tan^2=sec^2
1+cot^2=csc^2
同角三角函数关系六角形记忆法
构造以上弦、中切、下割;左正、右余、中间1的正六边形为模型。
倒数关系
对角线上两个函数互为倒数;
商数关系
六边形任意一顶点上的函数值等于与它相邻的两个顶点上函数值的乘积。
由此,可得商数关系式。
平方关系
在带有阴影线的三角形中,上面两个顶点上的三角函数值的平方和等于下面顶点上的三角函数值的平方。
两角和差公式
sin=sincos+cossin
sin=sincos-cossin
cos=coscos-sinsin
cos=coscos+sinsin
tan=/
tan=/
二倍角的正弦、余弦和正切公式
sin2=2sincos
cos2=cos^2-sin^2=2cos^2-1=1-2sin^2
tan2=2tan/)
tan=/=/sin
半角的正弦、余弦和正切公式
sin^2=/2
cos^2=/2
tan^2=/
tan=/sin=sin/1+cos
万能公式
sin=2tan/)
cos=)/)
tan=)/)
三倍角的正弦、余弦和正切公式
sin3=3sin-4sin^3
cos3=4cos^3-3cos
tan3=)/)
诱导公式
诱导公式的本质
所谓三角函数诱导公式,就是将角n的三角函数转化为角的三角函数。
常用的诱导公式
公式一:设为任意角,终边相同的角的同一三角函数的值相等:
sin=sinkz
cos=coskz
tan=tankz
cot=cotkz
公式二:设为任意角,的三角函数值与的三角函数值之间的关系:
sin=-sin
cos=-cos
tan=tan
cot=cot。
