理论力学课件：第四章_转动参照系
合集下载
四章转动参考系-PPT精选文档
牵连加速度vt是动参考系（刚体）上与点P重合的点（牵连点
）的瞬时加速度。
牵连加速度vt也可以看成是在该瞬时将P点固结在动参考刚体
上，跟随动参考刚体一起运动时所具有的加速度，即受动参考
刚2体0s‘s的系系拖中中带的的或观观牵察察连者者而只只产能能生观观的测测加到到速v度v和 观和 。无a测a法不区到分 中v 的v 、 v e 、 va 和 、 a vt和 ea c
v
a ( x y y ) i ( y x x ) j ( x y ) d i ( y x ) d j
牵
3、 (y ix j)由 于 平r 板作变角速度转动所引起
连 加
的加速度，切向加速度
速
度
第四章
？ 4、2 ( y i x j ) 2 k 称v 为 科2 里 奥v 利加速度
方向垂直于与 v构成的平面，在平板平面内。
第四章
OP ＝R 时的速度
动点－P
定系－地面OXY
动系－直管oxy
绝对速度 va＝？
相对速度 vr ＝u＝ui 牵连速度 ve ＝(Rω) j
yY
va x
vr P
X
O
P
v a v e v r v e j v r i R j u i
第四章
二、加速度合成公式
牵连速度ve是动参考系（平面转动参考系）上与点P重
合的点(称为牵连点）的瞬时速度。
牵连速度ve也可以看成是在该瞬时将P点固结在
动参考刚体上，跟随动参考刚体一起运动时所具 有的速度，即受动参考刚体的拖带或牵连而产生 的速度。
）的瞬时加速度。
牵连加速度vt也可以看成是在该瞬时将P点固结在动参考刚体
上，跟随动参考刚体一起运动时所具有的加速度，即受动参考
刚2体0s‘s的系系拖中中带的的或观观牵察察连者者而只只产能能生观观的测测加到到速v度v和 观和 。无a测a法不区到分 中v 的v 、 v e 、 va 和 、 a vt和 ea c
v
a ( x y y ) i ( y x x ) j ( x y ) d i ( y x ) d j
牵
3、 (y ix j)由 于 平r 板作变角速度转动所引起
连 加
的加速度，切向加速度
速
度
第四章
？ 4、2 ( y i x j ) 2 k 称v 为 科2 里 奥v 利加速度
方向垂直于与 v构成的平面，在平板平面内。
第四章
OP ＝R 时的速度
动点－P
定系－地面OXY
动系－直管oxy
绝对速度 va＝？
相对速度 vr ＝u＝ui 牵连速度 ve ＝(Rω) j
yY
va x
vr P
X
O
P
v a v e v r v e j v r i R j u i
第四章
二、加速度合成公式
牵连速度ve是动参考系（平面转动参考系）上与点P重
合的点(称为牵连点）的瞬时速度。
牵连速度ve也可以看成是在该瞬时将P点固结在
动参考刚体上，跟随动参考刚体一起运动时所具 有的速度，即受动参考刚体的拖带或牵连而产生 的速度。
第四章 转动参照系
由动系角速度变化引起 m r mat 2 惯性离心力 m r mac 2m v 科里奥利力
d a a r r 2 v 2、定点转动参照系 dt d 2 ac 2 v at r r r dt m r 由动系角速度变化引起 2 mat m r m r 2 或 m r ＝m R “惯性离轴力” mac 2m v 科里奥利力 d note特例： 若 常矢， 0 dt
二、平面上任一点的速度 P点的绝对速度：
y
p
P点的位矢r ，在动系中表示为： r xi yj
* d r d d r v xi yj r dt dt dt
O
/z
r
x
k
i y j yi xj v r v x
dt
a v
三、平面上任一点的加速度：
dv d a v r dt dt d v d dr r dt dt dt a r 2 v r
解：如图建立固定在三角形上的坐标系。
y
A P
平面转动参照系问题，满足：
v v r 2 a a r r 2 v
b b v j k bi j 2i 1 2 j 2 2
设任意p点的位矢在动系中表示为： r xi yj zk dr d *r 1、速度 v r dt dt * d v d v 2、加速度 a v dt dt * * d* d r d r r r dt dt dt
转动参考系
x 0, y 2gt cos , z g
两次积分, 并考虑初始条件, 得
x 0, y 1 gt3 cos , z h 1 gt 2
3
2
消去时间, 得到轨道方程
y2 8 2 cos2 z h3
9g
到达地面
y 1 8h3 cos
力的水平分量指向运动的右侧, 这样长年累月的作用, 使得北半球河岸右侧冲刷比左侧厉害, 因为比较陡峭.
而在南半球 (sin＜0) 情况与此相反, 是左侧磨损或者
冲刷比较厉害. 双轨单行列车也是同样的问题.
c．落体偏东问题
假定质点由高度h自由下落,认为重力不变,且不受其他 外力, 显然有
t 0, x y z 0, x y 0, z h
2 科里奥利力
当物体 (质点) 相对地球运动时, 应同时考虑惯性 离心力和科里奥利力的作用. 由于质点离地轴的距离 的变化不太大, 惯性离心力可以用重力代替. 研究质点 运动只要考虑科里奥利力.
例一质 点在北半球的某点P上以 速度 v' 相对于地球运动, P点的纬
度的 角为 速. 度图中就S沿N是着地该轴轴,.
也可以简写a为
a'
相对加速度
at
牵连加速度
ac
科里奥利加速度
其中
aa'tddd2td**2rt
r
r
d *
dt
r
r
2
r
ac
2
d*r dt
2
v'
两次积分, 并考虑初始条件, 得
x 0, y 1 gt3 cos , z h 1 gt 2
3
2
消去时间, 得到轨道方程
y2 8 2 cos2 z h3
9g
到达地面
y 1 8h3 cos
力的水平分量指向运动的右侧, 这样长年累月的作用, 使得北半球河岸右侧冲刷比左侧厉害, 因为比较陡峭.
而在南半球 (sin＜0) 情况与此相反, 是左侧磨损或者
冲刷比较厉害. 双轨单行列车也是同样的问题.
c．落体偏东问题
假定质点由高度h自由下落,认为重力不变,且不受其他 外力, 显然有
t 0, x y z 0, x y 0, z h
2 科里奥利力
当物体 (质点) 相对地球运动时, 应同时考虑惯性 离心力和科里奥利力的作用. 由于质点离地轴的距离 的变化不太大, 惯性离心力可以用重力代替. 研究质点 运动只要考虑科里奥利力.
例一质 点在北半球的某点P上以 速度 v' 相对于地球运动, P点的纬
度的 角为 速. 度图中就S沿N是着地该轴轴,.
也可以简写a为
a'
相对加速度
at
牵连加速度
ac
科里奥利加速度
其中
aa'tddd2td**2rt
r
r
d *
dt
r
r
2
r
ac
2
d*r dt
2
v'
理论力学第四章 转动参照系
y
2 v
j
v
科里奥利加速度
科氏加速度2 v 是由牵连运动 和相对运动相互影响产 生的。
P
O
z
i k
x
2 a a' r r 2 v '
相对加速度 牵连加速度 科里奥利加速度
aa a at ac
真实性
质点的相对运动微分方程式
o1 是惯性坐标系(定系)，oxyz 是非惯性坐标系(动系)，
M 为所研究的质点(动点)。
牛顿第二运动定律相对惯性系适用
maa F
引入 Se mae
aa ae ar ac
（牵连惯性力） （科氏惯性力）
mar F mae mac
牵
o
Ny Nz
vz
v
x
z f 2mx c
f t mx vx
mg
由运动微分方程第1式得
dx dx dx 2x x x dx dt dx
xdx xdx
2
对xdx xdx 两边同时积分
2
x
0
dx xdx x
2 ma' F m R 2m v '
（3）相对平衡
z
O
x
2mx
P
Rz
m 2 x
x
a 0 A B t 0, x a, x 2 a t x e e t ach t 2
a t 2m Rz 2mx e e t 2ma 2 sht 2
2
Ry mg
2 v
j
v
科里奥利加速度
科氏加速度2 v 是由牵连运动 和相对运动相互影响产 生的。
P
O
z
i k
x
2 a a' r r 2 v '
相对加速度 牵连加速度 科里奥利加速度
aa a at ac
真实性
质点的相对运动微分方程式
o1 是惯性坐标系(定系)，oxyz 是非惯性坐标系(动系)，
M 为所研究的质点(动点)。
牛顿第二运动定律相对惯性系适用
maa F
引入 Se mae
aa ae ar ac
（牵连惯性力） （科氏惯性力）
mar F mae mac
牵
o
Ny Nz
vz
v
x
z f 2mx c
f t mx vx
mg
由运动微分方程第1式得
dx dx dx 2x x x dx dt dx
xdx xdx
2
对xdx xdx 两边同时积分
2
x
0
dx xdx x
2 ma' F m R 2m v '
（3）相对平衡
z
O
x
2mx
P
Rz
m 2 x
x
a 0 A B t 0, x a, x 2 a t x e e t ach t 2
a t 2m Rz 2mx e e t 2ma 2 sht 2
2
Ry mg
理论力学第4章转动参考系
v v r
相对速度 牵连速度
▪ 对于刚体来说，上一章的 公式显然没有第一项 v 。
▪ P 点对静止系的加速度
▪ 科里奥利加速度, 简称科氏加速度.
▪ 在静止系中的观察者看来, 牵连运动(即 ) 可使相对速度 v 发生改变, 而相对运动 ( 即 v ) 又同时使牵连速度 r 中的 r 发生 改变, 即科里奥利加速度 2 v 是由牵连 运动与相对运动相互影响所产生的. ▪ 其方向垂直于 及 v 所决定的平面并且依右
手螺旋法则定其指向. ▪ 如 与v 者中有一为零, 则此项加速度即为零.
§4.2 空间转动参考系
G Gx i G y j Gz k
di dj dk i , j, k dt dt dt
§4.1 平面转动参考系
▪ 在平板参考系上取坐标系 O xy, 它的原点 和静止坐标系原点 O 重合, O xy绕着通过
O点并垂直于平板的直线(即z轴)以角速度
转动.令单位矢量 i , j 固着在平板上的
x轴
和 y 轴上. P 为平板上运动着的一质点
▪ 因 P 和坐标轴都以 转动 所以有 di dj j , i dt dt
为 a0
2 ma F ma0 m r m( r ) m r 2m v
§4.4 地球自转所产生的影响
第24讲结束
r xi yj
▪ 则 P 点相对静止坐标系的速度（不是对平板， 因为对平板， i , j 都是常矢量）为
dr di dj dk i y j z k x v x y z dt dt dt dt y )i ( y x) j (x
第四章_转动参照系
a = a + at + ac
d 2*r a 2 dt
at
相对加速度
d r ( r ) 2 r 牵连加速度 dt d *r ac 2 2 v 科里奥利加速度 dt
上页 下页
地球自转： 是一个恒矢量(量值和方向都不变),可以 OB 表之，
d 0 ,则 故 dt
d 2 at r ( r ) r dt ( r cos ) r 2
OM 2 (OM MP) 2 2 R
在此情形下
2 a a R 2 v
上页 下页
更一般的情况
S ′系的原点不与S系重合，且相对速度为 v 0 相对 加速度为 a 0，则
得小球的运动微分方程为
mx = m 2 x my 0 Ry mg mz 0 2m x Rz (1) (2) (3)
（1）式的通解为 微分得
x Aet Bet x A et B et
(4) (5)
a （6） 2
利用起始条件 t 0, x a, x 0 ，可得 A B
a t 相等.当 a = 0,ac 0 时，
F mat = 0
即当质点在非惯性系中处于平衡时， 主动力、 约束反作用力和由牵 连运动而引起的惯性力的矢量和等于零. 这种平衡叫做相对平衡.
上页
下页
§4.4地球自转所产生的影响
（1）惯性离心力 地球自转的角速度约为 7.3× 10-5 弧度/秒 惯性离心力使重力常小于引力 重力随着纬度发生变化，纬度越低重力越小 只有两极重力和引力才相等 除两极外重力的方向也不与引力的方向一致 引力通过地心，而重力一般并不通过地心
第四章转动参照系
ma F Ft Fc A ( B C ) B( A C ) C ( A B) d F [m r m ( r )] 2m dt
r xi yj zk(空间关系) k
d dr d 0 ( xi yj zk ) dt dt dt d ( xi yj zk ) ( xi yj zk ) dt
第四章 转动参照系
一、空间转动参照系
S 固定参照系
r
P
z
强调： r 具有双重身份！！！
S 运动参照系（绕定点O转动）
o
y
dr dt
*
x
r
d r dt dr d = xi yj zk dt dt * dr = r dt
特例2：角速度为常矢量的空间转动参照系
y
r
x
o
y )i ( y x ) j zk ( x
*
z S系 S 系
P o
o xyz
R
d d 2 a r r r 2 dt dt * d 2 a 0 R 2 dt
* d d a a dt dt * d d r a dt dt * * * d d d d * r r r dt dt dt dt r d * d * d *r r 2 r r dt dt dt * d d r dt dt * d d 2 a r r r dt dt d 2 a a at ac a r r r t dt ac 2
r xi yj zk(空间关系) k
d dr d 0 ( xi yj zk ) dt dt dt d ( xi yj zk ) ( xi yj zk ) dt
第四章 转动参照系
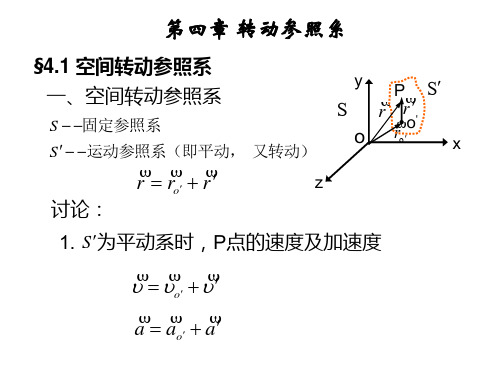
一、空间转动参照系
S 固定参照系
r
P
z
强调： r 具有双重身份！！！
S 运动参照系（绕定点O转动）
o
y
dr dt
*
x
r
d r dt dr d = xi yj zk dt dt * dr = r dt
特例2：角速度为常矢量的空间转动参照系
y
r
x
o
y )i ( y x ) j zk ( x
*
z S系 S 系
P o
o xyz
R
d d 2 a r r r 2 dt dt * d 2 a 0 R 2 dt
* d d a a dt dt * d d r a dt dt * * * d d d d * r r r dt dt dt dt r d * d * d *r r 2 r r dt dt dt * d d r dt dt * d d 2 a r r r dt dt d 2 a a at ac a r r r t dt ac 2
第4章 转动参照系
第四章 转动参照系 §4.1 平面转动参照系考虑一旋转的平面参照系oxy ，记为S ′（如平板），其角速度ω沿轴，其原点与静止坐标系(z S ξηo )的原点重合。
令单位矢量、固着在平板上的o i j x 轴和轴上，ω可表为y k ωω=。
再考虑平板上的运动质点P (想象为一小虫)，其位矢为j i r y x += 严格应为：)()()()()(t t y t t x t j i r +=d d d x y x y dt dt dt ==+++r i j v i j ) ()(xy y x ωω=++−+i j i j 其中v j i ′=+y x 应为相对速度（即对转动参照系而言）；0v r ωj i =×=+−x y ωω应为点所在处的牵连速度 P 于是，点的速度为：P r ωv v ×+′=与刚体力学中定轴转动公式r ωv ×=比较可见此处多出了相对速度这一项，原因是刚体上的质点相对刚体是没有相对运动的。
v ′ya j i ′=+yx 为相对加速度； r j i 222ωωω−=−−y x 为平板转动引起的向心加速度；(方向由点指向o 点)P r ωj i ×=+− x y ωω为平板作变角速转动引起的切向加速度（方向与r 垂直，在平板上。
匀速转动时为0）；向心加速度 + 切向加速度 = 牵连加速度；(用表示)t a v ωj i ′×=+−222x yωω为科里奥利加速度。
(用表示)c a 故上式又可写成v ωr r ωa a ′×+−×+′=22ω 或简写为t c ′=++a a a a与平动情况相比，不仅牵连加速度项不同，这里还多了一项，这是转动参照系所特有的。
c a 必须明确两点：1. 平面转动参照系是非惯性系。
这是因为对固结在平面上的点来说，0,0′′≡=v a 。
这时，质点的加速度就等于牵连加速度，所以是非惯性系。
第四章 转动参照系
η
P x v • r θ
(
)
o
ξ
v v & 2 i + r θ& + 2 r θ& v & & j a = && − r θ r
(
)
(
)
§4.2 平面转动参照系
y
η
v r
P • x
一、建立平面转动参照系
S系 S ′系 o − ξηζ o − xyz
ζ
ω
z
v
o
ξ
v ′系绕oζ轴以角速度ω转动。 使原点o重合，oζ轴与oz轴重合，S
平动牵连加速度 转动牵连加速度
v
v
3.当 S ′作任意运动（平动+转动）时，而P点相对 S ′ 系运动时，P点的速度及加速度
v v v *v v v dr dro′ dr ′ v d r ′ 速度： υ = +ω ×r′ = + =υo′ + dt dt dt dt *v v v d r′ = υ o′ + ω × r ′ + dt v v = υt + υ ′ 牵连速度 加速度： v v v dυ ′ v dυ dυo′ d v v a= = + (ω × r ′) + dt dt dt dt v v v dω v v dr ′ dυ ′ v = ao ′ + ×r′+ω × + dt dt dt v v *v dω v v d r ′ dυ ′ v v = ao ′ + ×r′+ω ×( + ω × r ′) + dt dt dt
v
v
v
2.当 S ′作任意运动（平动+转动）时，而P点相对 S ′ 系静止时，P点的速度及加速度(如刚体)
第4章 转动参考系
⎧ x = −4ω 2 y sin λ ⎡ x sin λ + ( z − h ) cos λ ⎤ ⎣ ⎦ ⎪ ⎪ y = 2 gtω cos λ − 4ω 2 y ⎨ ⎪ z = − g − 4ω 2 cos λ ⎡ x sin λ + ( z − h ) cos λ ⎤ ⎣ ⎦ ⎪ ⎩
青岛科技大学数理学院
青岛科技大学数理学院
14
§4.4 地球自转所产生的影响
一 惯性离心力
考虑地球自转时，可以认为其角速度是沿着地轴的一个恒 矢量，即 ω = 0. 因此，只需考虑惯性离心力和科里奥利力 即可；若质点相对于地球静止，则只需考虑惯性离心力 . 惯性离心力产生的影响： a) 重力与引力大小不相等（两极除外）. b) 重力与引力方向不一致（两极除外）. 注 惯性离心力所产生的影响一般都比较小，当研究 质点相对于地球的运动时，惯性离心力的效应只要用重 力来代替引力即可 .
a ωt x = ( e + e −ωt ) = achωt 2
管对小球的竖直反作用力和水平反作用力分别为
Ry = mg
a ωt −ωt Rz = 2mω x = 2mω ( e − e ) = 2maω 2shωt 2
2
惯性系
⎧m r − rθ 2 = Fr = 0 ⎪ ⎨ ⎪m rθ + 2rθ = Rθ ⎩
所以质点 P 的绝对加速度可简写为
dω ⎧ at = × r + ω (ω ⋅ r ) − ω 2 r ⎪ ⎪ dt ⎨ d *r ⎪a = 2ω × = 2ω × v′ c ⎪ dt ⎩
青岛科技大学数理学院
a = a′ + at + ac
8
若 S ′系以匀角速度转动，则
转动参照系
r
C
B A
S'
S ''
r 与 均发生变化
ae
牵连速度变化引起的加速度（ a ） v ' 0
16
理论力学
第四章 转动参照系
许杰制作
科里奥利加速度产生的原因：
由 ac 2 v ' 2v 'sin 可知:
① 0 ② v'0 ③ v ' ( 0, v ' 0)
z
r
x
z'
P
r'
O'
y'
即 v vt r ' v ' ve v '
rt
O
x'
y
为静系观察者看到质点P的总角速度
绝对速度=相对速度 + 牵连速度
8
理论力学
第四章 转动参照系
许杰制作
质点速度合成原理 v vt r ' v ' ve v ' 各项物理含义：
质点的速度合成原理 v vt r ' v ' ve v '
13
理论力学
第四章 转动参照系
许杰制作
d dr ' dv ' 于是 a at r ' dt dt dt
d at r ' (v ' r ') (a ' v ') dt
O
15
为静系观察者看到质点P的总角速度
C
B A
S'
S ''
r 与 均发生变化
ae
牵连速度变化引起的加速度（ a ） v ' 0
16
理论力学
第四章 转动参照系
许杰制作
科里奥利加速度产生的原因：
由 ac 2 v ' 2v 'sin 可知:
① 0 ② v'0 ③ v ' ( 0, v ' 0)
z
r
x
z'
P
r'
O'
y'
即 v vt r ' v ' ve v '
rt
O
x'
y
为静系观察者看到质点P的总角速度
绝对速度=相对速度 + 牵连速度
8
理论力学
第四章 转动参照系
许杰制作
质点速度合成原理 v vt r ' v ' ve v ' 各项物理含义：
质点的速度合成原理 v vt r ' v ' ve v '
13
理论力学
第四章 转动参照系
许杰制作
d dr ' dv ' 于是 a at r ' dt dt dt
d at r ' (v ' r ') (a ' v ') dt
O
15
为静系观察者看到质点P的总角速度
理论力学-转动参考系
′ i 、j 、k 随S 系以同一角速度ω 转动 ∴ 在静止参照系S上所看到的G的变化率为：
di dj dk dG dGx dGy dGz = + Gy + Gz k + Gx i+ j+ dt dt dt dt dt dt dt
i 以ω 绕O转动，即i 是距离O为单位长的动点对O的位矢
则
v = v′ + ω × r
即绝对速度等于相对速度与牵连速度的矢量和。
2. P点对静止坐标系S的加速度： dv d − ωy )i + ( y + ωx ) j (x a= = dt dt 2 2 yi + ω xj − 2ωy − ω x )i + ( − 2ωx − ω y) j − ω x y = ( 2 ( yi − xj ) i + j ) − ω ( xi + yj ) − 2ω (− x j + y i ) − ω x y = ( 2 = a ′ − ω r + ω × r + 2ω × v ′
、y 为P对转动参照系诸轴的分速度， 其中x 合成为v ′ − 相对速度
y
j
P
S′
r i
O
x
ξ
若P在平板上不动，则此项速度为零。
ω k
z
又-ωy及 ωx 为由于平板转动而带着P一同转动所引起， 故为牵连速度在坐标轴上的分量，即轴向分量。
∴ 两者的合成即牵连速度：
ω × r = ωk × ( xi + yj ) = ωxj − ωyi
理论力学chapt
y
2y sin 2x sin
g l g l
x y
0 0
令 则
02
g l
,
sin
x
2
y
2 0
x
0
y 2x 02 y 0
令
x iy
将两式合并，有
2i 02 0
上式的通解为
Ae n1t Be n2t
其中 n1 , n2 是特征根方程
n 2 2in 02 0
风，南半球上的西北贸易风。（２）轨道磨损和河岸冲
刷：北半球铁轨右轨，河流右岸磨损冲刷严重；南半球
铁轨左轨，河流做岸磨损冲刷严重。
以下讨论另外科氏力的两种效应：落体偏东和傅科摆 １、落体偏东
考虑仅在重力作用下的落体。初始条件为
t 0 x y z 0, x y 0, z h
对动力学方程积分一次，得
x 2y sin
y 2x sin (z h) cos
z gt 2y cos
将以上结果代回并略去 2 项，得
x 0
y 2gt cos
z g
对上式积分两次后，得
可见落体的轨迹在 yz平面内，
x y
0 1 3
gt 3
cos
并有偏东的趋势。 轨迹方程
z
h
1 2
gt
2
y 2 8 2 cos2 (z h)3
x s in
t
y c os t
x x1 (A B) cos0t
y
y1
(A
B)sin 0t
上式表明在旋转系中，又恢复了单摆的椭圆轨道运动
1851年傅科在巴黎( 49,sin 0.75)
采用67m摆长，28kg的摆锤进行实验，摆的振动周期 为16s，椭圆旋转周期为32小时， 与理论计算相吻合。
第四章 转动参照系
式中 r ′ 为质点相对 o′ 的位矢。
P197例 秒后p P197例4.3 求t秒后p点的速度和加速 度 建立坐标系o 解：建立坐标系o-xyz
ω α R P v’ y
v v v v = v′ + vt v v v v vt = ω × r = −ωv′t sinαi v v v v ∴v = v′sinα j − v′cosαk −ωv′t sinαi
解 建 动 o− xy ： 立 系
v v dv′ a′ = =0 dt
x ω v’ ac
r v & ω ×r = 0 v 2r 2 −ω r = −ω xi v v v v v 2ω × v′ = 2ωk × v′i = 2ωv′j
r r r 2 a = −ω xi + 2ωv′j
•
4.2 空间转动参考系
任一矢量： 2. 任一矢量： G = G x i + G y j + G z k
dG y dG z dG dG x di dj dk = i+ j+ k + Gx + G y + Gz dt dt dt dt dt dt dt
由泊松公式：
di =ω ×i dt
dj =ω × j dt
dk = ω × k 代入上式得： dt
a= dv di dj & & & & = ( && − yω − yω )i + ( && + xω + xω ) j + ( x − yω ) + ( y + xω ) x & y & dt dt dt
& & & & = ( && − yω − xω 2 − 2 yω )i + ( && + xω − yω 2 + 2 xω ) j x y
理论力学课件：第四章_转动参照系
为r 的圆柱上作纯滚动，圆管中心的速度 v0 u 。试求小球在图示
位置时的绝对速度和绝对加速度
解：运动分析： 小球相对圆管运动：圆周运动
C
o1h
u
j
牵连运动：平面平行运动（纯滚动）
v小tv球的uv绝j0 对u速i度：3vrorMj
v' vt
3r
ui 2uj
u
u 3r
ho
3
r
v0
a v sin 4 2t2 7
§4.2非惯性系动力学
一、相对运动微分方程
在惯性系下：
ma
F
m{a
'
a0
d0 dt
r
20
v
'
0
(0
r
)}
F
牵m连a惯' 性 力FF：tm{maa00dmdtd0dt0
r
0 (0
r
m0
(0
r )}
r)
2m0
v
'
平动惯性力 转动惯性力 惯性离心力
科里奥利力：
第四章 转动参考系
§4.1(2)转动参照系 §4.3 非惯性系动力学 §4.4 地球自转的影响
1
§4.1转动参照系
z
复习平动参考 系、相对运动：
r
ro'
r ',
v
vo'
v',
r'
o'
ro '
r
x'
a
ao'
a'
O x
y z
ma' F (mao' )
**********************************
理论力学课件
第四章转动参照系本章应掌握①转动参照系中的速度、加速度计算公式及有尖概念；②转动参照系中的动力学方程；③惯性力的有矢概念、计算公式；④地球自转产生的影响。
第一节平面转动参照系本节应掌握：①绝对运动、相对运动、牵连运动的有矢概念及相互矢系；特别是科里奥利加速度的产生原因；②平动转动参照系中的速度和加速度。
一、绝对运动、相对运动、牵连运动有定系oEnZ，另一平面以角速度3绕轴旋转，平板上固定坐标系oxyz , oz轴与oZ轴重合。
运动质点P相对板U运动。
由定系oEnZ看到的质点的运动叫绝对运动；动系oxyz看到的质点运动叫相对运动；定系上看到的因动系转动导致质点所在位置的运动叫牵连运动。
绝对速度、加速度记为’」；相对速度、加速度记为V',a'。
二、平动参照系中的速度、加速度1、v和a的计算公式速度：（为牵连速度）F T Z f fa = a + -- x r -G） r + Zt/jxv = a + 甸+□百加速度：」’其中，牵连加速度a为：/八切二——X厂+ J—（D T \（转动加速度+向心加速度）科里奥利加速度：2、科里奥利加速度ac① 它产生条件是：动系对定系有转动；质点相对动系的运动速度不为零，而且运动方向与转轴方向不平行。
② 它产生原因是：科氏加速度的产生在于牵连运动与相对运动的相互影响：从静止系看来，一方面牵连运动使相对速度’发生改变，另一方面，相对运动也使牵连速度刁：」中的L发生改变，两者各贡献2 - \结果科氏加速度为hi。
三、平面转动参照系问题解答例尖键是分清定系，动系和运动物体；然后适当选取坐标系，按公式计算。
[例1]P263 4.1 题等腰直角三角形OAB，以匀角速3绕点0转动，质点P以相对速度沿AB 边运动。
三角形转一周时，P点走过AB。
求P质点在A点之速度、加速度（已知AB=b ）解：（1 ）相对动系（直角三角形）的速度Vr=b/T=b/ （2 n3） =b 3/2 n （方向丄•）A点的牵连速度一,2>（方向垂直」）由V=Vr+Ve，利用矢量合成法则，得到________________ b ______v = + V? +2%协cosff = ---- F4JT + 192咒（2 ）加速度•人，因匀速，所以相对加速度a*=0 又匀角速转动，所以角加速'J牵连加速度. ，大小・，方向沿一’科氏加速度'< 2t,J■「注意到| ■-，所以其大小占血2①-------------W 「兀方向与AB边垂直（见图4.1.1 ）由-,利用矢量合成法则则得到:a - Ja/ + 2a s a c cos45° = -----+2 加+1召二绘冷2吐与斜边的夹角->■ 1第二节空间转动参照系本节要求：①掌握空间转动参照系中绝对、相对、牵连变化率等概念；②掌握空间转动参照系中的速度V、加速度a的计算公式。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
为r 的圆柱上作纯滚动，圆管中心的速度 v0 u 。试求小球在图示
位置时的绝对速度和绝对加速度
解：运动分析： 小球相对圆管运动：圆周运动
C
o1h
u
j
牵连运动：平面平行运动（纯滚动）
v小tv球的uv绝j0 对u速i度：3vrorMj
v' vt
3r
ui 2uj
u
u 3r
ho
3
r
v0
2
11
x a (e t e t ) ach( t)
2 管对小球的约束反作用力为：
R
y
mg
Rz
2m
x
2m 2
a (e t 2
e t )
2ma 2sh( t)
②选用惯性参照系，建立柱坐标系，小球受力分析如 图所示，运动微分方程为：
m(r
m(r
r2 ) 2r)
Fr R
0
mz Rz mg 0
Res Re
1 365
2
1 105 4
0.2
aces esv 1 0.003 ace ev 365
13
Ft mR02 cos
mg F Ft
F sin mg sin( )
Ft sin mg sin
mg(sin cos cos sin )
F mg cos Ft cos
Ft mx1A ma2 sin t
l g sin a2 cos sin t x l sin l , cos 1
OA
x
F
x1
M
y Ft mg
y1
x g x a2 sin t
l
若考虑空气阻力：
x 2 x e2x a2 sint
x Aet cos(t 0 ) B cos(t ) 10
ω
α P
R v’
v vsin j vcosk vt sini
y
a a ' d r 2R 2 v
dt
x
a dv 0, d 0, R vt sin j
dt
dt
at 2R 2vt sin j
ac 2 v 2k (vsin j vcosk ) 2v sini
a at ac 2v sini 2vt sin j
3
a
dv dt
d dt
(v
' 0
r)
d dt
(v ' 0
r ) 0
(v
' 0
r)
dv ' dt
d0
dt
r
0
dr dt
0
v
' 0
0
r
0 v '
d 0
dt
d 0
dt
0 0
d 0
dt
a
'
d0
dt
r
0
(0
r)
20
v
'
牵连加速度
at
科里奥利加速度 ，ac
如何产生？
4
讨论：
12)）若vac 02, ac 00v,a'， v0',则0a， at，0 如0同，刚v体' //上一0，点a的c 加速0 度
因为： =常数，故 0 ，则上式简化为：m2mrrmrR2
12
Rz mg
§4.4 地球自转的影响
一、对重力的影响
0
2
24 3600
7.29105 s1
R 6.37106 m
Nω k
Oj
λ
i
at 02R 0.0338m/ s2 3103 g
S
ac 20v
ates ate
2 es
e2
第四章 转动参考系
§4.1(2)转动参照系 §4.3 非惯性系动力学 §4.4 地球自转的影响
1
§4.1转动参照系
z
复习平动参考 系、相对运动：
r
ro'
r ',
v
vo'
v',
r'
o'
ro '
r
x'
a
ao'
a'
O x
y z
ma' F (mao' )
**********************************
di dt
0
i ,
dj dt
0
j,
dk dt
0 k
y
x
v
dr dt
dx i dt
dy dt
j
dz dt
k
0 (xi
yj
zk )
v ' 0 r
dA dt
dA dt
0
A
v'
dx
i
dy
j
dz
k,
动点相对于oxyz动系的速度；
0
drt:
dt dt 动系上与动点重合点相对于静系的速度，牵连速度
3） 一般参照系：既平动又转动
v v0 v ' 0 r '
a
a0
a
'
d0
dt
r
'
20
v
' 0
(0
r
')
若有：
0 (0 r )
B
R
P
d0
dt
0,
a0
0
0 (0 r ) 02r
(OB
OP)02
0
2
R
0
r
a a '02R 20 v ' 5
O
例2. 小球M在半径为3r 的圆管内以匀速u作圆周运动，而圆管又在半径
M
k
i
aaau''2aiat 0ua2dcdjt3rroM2i2(ui
3r 2r
roM
)
2
a0
u2 2r
v'
j, 圆管中心
o以
o1为
4u2
i
u2
j
圆心作圆周运动
6
3r 2r
P197习题4.3：求t秒后p点的速度和加速度 解：建立坐标系o-xyz
v v vt
vt r vt sini
y
动点在静系和转动参照系运动的关系 :
x
o- -固定系，oxyz - -转动系
oxyz 动系相对于固定系作定点转动， 转动角速度0
2
动r 点 x的i 运 y动j
zk
0
0
0
v dr dx i dy j dz k x di y dj z dk
z
dt dt dt dt
dt dt dt
sin R02 sin 2
2g
equator : 0
max
R02
2g
1.5103
6'
Ft
F
mg
F mg Ft m(g R02)
Fc
2m v'
ma ' F Ft FC
dv0 0, d0 0
dt
dt
Ft
8
mat
m02 R
B
R
Pm0 (0 r)
0
r
m02R
惯性离心力
O
注意：惯性离心力与离心力的区别
二、相对平衡方程
当v'
0,
a'
0,
0 F mat F Ft
9
例子：箱子左右作简谐振动。
Байду номын сангаас
ml mg sin Ft cos
P186例子
解：①选取非惯性参照系o xyz ，
小球受力分析
ma F m2r 2mω v
小球运动微分方程的分量形式为：
mx m 2 x
(1)
my Ry mg 0
(2)
mz 2m x Rz 0 (3)
（1）式的通解： x Ae t Be t
利用初始条件： t 0 x a x 0 A B a
a v sin 4 2t2 7
§4.2非惯性系动力学
一、相对运动微分方程
在惯性系下：
ma
F
m{a
'
a0
d0 dt
r
20
v
'
0
(0
r
)}
F
牵m连a惯' 性 力FF：tm{maa00dmdtd0dt0
r
0 (0
r
m0
(0
r )}
r)
2m0
v
'
平动惯性力 转动惯性力 惯性离心力
科里奥利力：