高等数学试卷2017-2018-1试卷 - 副本

合集下载

2017年-2018年普通高等学校招生全国统一考试数学试题文(天津卷,含答案)

高考衣食住用行衣：高考前这段时间，提醒同学们出门一定要看天气，否则淋雨感冒，就会影响考场发挥。

穿着自己习惯的衣服，可以让人在紧张时产生亲切感和安全感，并能有效防止不良情绪产生。

食：清淡的饮食最适合考试，切忌吃太油腻或者刺激性强的食物。

如果可能的话，每天吃一两个水果，补充维生素。

另外，进考场前一定要少喝水！住：考前休息很重要。

好好休息并不意味着很早就要上床睡觉，根据以往考生的经验，太早上床反而容易失眠。

考前按照你平时习惯的时间上床休息就可以了，但最迟不要超过十点半。

用：出门考试之前，一定要检查文具包。

看看答题的工具是否准备齐全，应该带的证件是否都在，不要到了考场才想起来有什么工具没带，或者什么工具用着不顺手。

行：看考场的时候同学们要多留心，要仔细了解自己住的地方到考场可以坐哪些路线的公交车？有几种方式可以到达？大概要花多长时间？去考场的路上有没有修路堵车的情况？考试当天，应该保证至少提前20分钟到达考场。

绝密★启用前2017年普通高等学校招生全国统一考试（天津卷）数学（文史类）本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试用时120分钟。

第Ⅰ卷1至2页，第Ⅱ卷3至5页。

答卷前，考生务必将自己的姓名、准考号填写在答题考上，并在规定位置粘贴考试用条形码。

答卷时，考生务必将答案涂写在答题卡上，答在试卷上的无效。

考试结束后，将本试卷和答题卡一并交回。

祝各位考生考试顺利！第Ⅰ卷注意事项：1.每小题选出答案后，用铅笔将答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

2.本卷共8小题，每小题5分，共40分。

参考公式：·如果事件A ，B 互斥，那么P (A ∪B )=P (A )+P (B )．·棱柱的体积公式V =Sh . 其中S 表示棱柱的底面面积，h 表示棱柱的高． ·球的体积公式34π3V R =.其中R 表示球的半径. 一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的. （1）设集合{1,2,6},{2,4},{1,2,3,4}A B C ===，则()A B C =U I （A ）{2}（B ）{1,2,4}（C ）{1,2,4,6}（D ）{1,2,3,4,6} （2）设x ∈R ，则“20x -≥”是“|1|1x -≤”的（A ）充分而不必要条件（B ）必要而不充分条件（C ）充要条件（D ）既不充分也不必要条件（3）有5支彩笔（除颜色外无差别），颜色分别为红、黄、蓝、绿、紫.从这5支彩笔中任取2支不同颜色的彩笔，则取出的2支彩笔中含有红色彩笔的概率为（A ）45（B ）35（C ）25（D ）15（4）阅读右面的程序框图，运行相应的程序，若输入N 的值为19，则输出N 的值为（A ）0 （B ）1（C ）2（D ）3（5）已知双曲线22221(0,0)x y a b a b-=>>的左焦点为F ，点A 在双曲线的渐近线上，OAF △是边长为2的等边三角形（O 为原点），则双曲线的方程为（A ）221412x y -=（B ）221124x y -=（C ）2213x y -=（D ）2213y x -= （6）已知奇函数()f x 在R 上是增函数.若0.8221(log ),(log 4.1),(2)5a fb fc f =-==，则,,a b c 的大小关系为（A ）a b c <<（B ）b a c <<（C ）c b a <<（D ）c a b << （7）设函数()2sin(),f x x x ωϕ=+∈R ，其中0,||πωϕ><.若5π11π()2,()0,88f f ==且()f x 的最小正周期大于2π，则（A ）2π,312ωϕ==（B ）211π,312ωϕ==-（C ）111π,324ωϕ==-（D ）17π,324ωϕ== （8）已知函数||2,1,()2, 1.x x f x x x x +<⎧⎪=⎨+≥⎪⎩设a ∈R ，若关于x 的不等式()||2x f x a ≥+在R 上恒成立，则a 的取值范围是（A ）[2,2]-（B）[2]-（C）[2,-（D）[-第Ⅱ卷注意事项：1．用黑色墨水的钢笔或签字笔将答案写在答题卡上。

【精品】吉林省近两年(2017,2018)高考理科数学试卷以及答案(word解析版)

绝密★启用前吉林省2017年高考理科数学试卷注意事项：1.答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在条形码区域内。

2.选择题必须使用2B 铅笔填涂；非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整，笔迹清楚3.请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效4.作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5.保持卡面清洁，不要折叠、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.31ii+=+（） A ．12i + B ．12i - C ．2i + D ．2i -2. 设集合{}1,2,4A =，{}240B x x x m =-+=．若{1}AB =，则B =（）A ．{}1,3-B ．{}1,0C ．{}1,3D ．{}1,53. 我国古代数学名著《算法统宗》中有如下问题：“远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？”意思是：一座7层塔共挂了381盏灯，且相邻两层中的下一层灯数是上一层灯数的2倍，则塔的顶层共有灯（）A ．1盏B ．3盏C ．5盏D ．9盏4. 如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为（）A ． 90πB ．63πC ．42πD ．36π5. 设x ，y 满足约束条件2330233030x y x y y +-≤⎧⎪-+≥⎨⎪+≥⎩，则2z x y =+的最小值是（）A ．15-B ．9-C ．1D ．96. 安排3名志愿者完成4项工作，每人至少完成1项，每项工作由1人完成，则不同的安排方式共有（）A ．12种B ．18种C ．24种D ．36种7. 甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩．老师说：你们四人中有2位优秀，2位良好，我现在给甲看乙、丙的成绩，给乙看丙的成绩，给丁看甲的成绩．看后甲对大家说：我还是不知道我的成绩．根据以上信息，则（）A ．乙可以知道四人的成绩B ．丁可以知道四人的成绩C ．乙、丁可以知道对方的成绩D ．乙、丁可以知道自己的成绩 8. 执行右面的程序框图，如果输入的1a =-，则输出的S =（）A ．2B ．3C ．4D ．59. 若双曲线C :22221x y a b-=（0a >，0b >）的一条渐近线被圆()2224x y -+=所截得的弦长为2，则C 的离心率为（）A ．2 BC10. 已知直三棱柱111ABC A B C -中，C 120∠AB =，2AB =，1C CC 1B ==，则异面直线1AB 与1CB所成角的余弦值为（） A．2 B．5 C．5D．3 11. 若2x =-是函数21`()(1)x f x x ax e -=+-的极值点，则()f x 的极小值为（）A.1-B.32e --C.35e -D.112. 已知ABC ∆是边长为2的等边三角形，P 为平面ABC 内一点，则()PA PB PC ⋅+的最小值是（）A.2-B.32-C. 43- D.1- 二、填空题：本题共4小题，每小题5分，共20分。

2017-2018-1《高等数学 ( I ) 》期末考试试卷A

北京化工大学2017——2018学年第一学期《高等数学（I ）》期终考试试卷A班级：姓名：学号：分数：一、填空题（3分×6=18分）1．若0x →时，1cos x -与kx 为同阶无穷小，则k = ；2. 1x =为函数 sin ()1xf x x π=-的间断点；3．设231()1x xf x dt t=+⎰，则(1)f '=； 4．曲线ln(y x =在点(0,0)处的曲率k = ； 5．120171(x dx-+=⎰；6．微分方程 20y y y '''-+= 的通解为。

二、解答题(6分×7=42分) 1. 求极限 0sin 22sin limtan x x xx x→--2. 设函数()y y x =由方程lncos sec x t y a t=⎧⎨=⎩确定，若()y y x =为微分方程x dyy e dx -=+的解，求常数a 的值。

3. 求不定积分ln(1dx +⎰4. 将函数()arctan f x x = 展开为带有拉格朗日型余项的3阶麦克劳林公式。

5.求曲线24(1)y x =--与22(2)y x =-- 围成的平面图形的面积。

6.求曲线22ln 1yx x =+-上拐点处的切线方程。

7. 计算曲线3sin ,(0)3a a θρ=>相应于03θπ≤≤的一段弧的长度。

三．解答题（7分×5=35分）1. 设101()10x xx xf x x e e -⎧≥⎪⎪+=⎨⎪<⎪+⎩，计算2(1)f x dx -∞-⎰。

2. 求微分方程cos y y x x ''+=+的通解。

3. 求由曲线sin ,cos ,(0)2y x y x x π==≤≤及直线0,2x x π==围成的平面图形绕x 轴旋转一周而成的旋转体的体积。

4. 设21sin ()x tf x dt t=⎰，求10()xf x dx ⎰。

湖北汽车工业学院制卷模板(A4)

1
2
3
4
5
6
7
8
9
10
三．判断题（共20分，每题2分）
1.
四．简答题（共20分，每题2分）
1.
2.
。。。。。。
答题区域：（答题不得超出答题区域）
五．综合题（共20分，每题2分）
1.
2.
1.答题区域由任课教师根据试卷进行设计。
2.试题部分和答题部分的每道题均应标注总分和分项得分。
3.试卷批改结束后，只装订答题卡。
湖北汽车工业学院2017-2018（1）学期考试试卷(题)
课程编号
课程名称
考试日期
考试形式
□闭卷□开卷
考试时长
□120分钟□100分钟分钟
试题内容：
一．填空题（共10分，每空1分）
1.
2.
二．单选题（共20分，每题2分）
1.
三．判断题（共10分，每题1分）
1.
四．简答题（共10分，每题1分）
1.
2.
五．综合题（共10分，每题1分）
。。。。。。
共2页，第1页
湖北汽车工业学院2017-2018（1）学期考试试卷(题)
高等数学（课程编号：150014）试卷答题纸
学号
姓名
班级
座位号
题号
一
二
三
四
五
六
七
八
九
十
得分
阅卷
答题区域：（答题不得超出答题区域）
一．填空题（共10分，每空1分）
1.，Leabharlann 2.，二．单选题（共20分，每题2分）

东北大学文科类高数期末试卷练习题 (3)

A ]；
…
(A) 5 / 2 ； (B) 2 ； (C) 2； (D) 3 .
x (et2 1)dt
解 lim 2 x0 x sin x ln(1 x)
…
… 线 …
5.向量组 1
1 1
,2
1
1
,3
1 2
,4
2
1
的最大无关组是[
D ];
… …
(A) 1,2,3 ； (B ) 1,3,4 ； (C) 1,2 ； (D) 1,3 .
0 不可能是
封 …
函数 f (x) 的 [ B ];
得分：
三.计算题（每题 3 分，共 15 分）
… …
(A) 可去间断点； (B ) 无穷间断点；
… …
(C ) 跳跃间断点； (D ) 连续点.
x (et2 1)dt
1. 求极限. lim 2 x0 x sin x ln(1 x)
○ …
2
4. |1 2x | dx [ 0
7 3
2 4
的代数余子式
A23
___ 4 ____ .
6 1 2 3
5，齐次线性方程组
x1 2 x1
2 x2 4 x2
x3 0 3x3 0
有非零解，则
______
2
________
.
3x1 2x2 x3 0
… …
3.设 lim x0
f
(
x)
k1,
lim
x0
f (x)
k2 ，其中 k1, k2 是确定的常数，则点 x
一.单项选择题（每题 2 分，共 10 分）
2. 函数 f (x) 2x3 9x2 12x 1 在区间____[1, 2]___单调减少.

大学高等数学习题答案17-18-1-高数1-1A答案

贵州大学2017-2018学年第一期学期考试试卷A《高等数学1-1》参考答案与评分标准一、选择题（每小题3分，共12分） 1. C 2. A 3. D 4.B二、填空题（每小题3分，共18分） 1.31e -+ 2.=a 1- 3. 1y ex =+ 4. π235. dx x x 21sin 2+6.21 三、求下列极限（每小题5分，共15分）1. 解：x xx x x xx x x x 22sin cos 2cos sin lim 2cos cos 1lim 020+=-→→ ……………….. 2分＝x x x x x 2)cos 4(cos sin lim 20+→ ……………….. 3分＝)2cos 4cos (sin lim20x x x x x +→=25……………….. 5分 2. 解：x x x 2tan)1(lim 1π-→=x xx x 2cos2sin)1(lim1ππ-→ ……………….. 1分xx x x x 2sin22cos2)1(2sin lim1πππππ-⨯-+-=→=2π……………….. 5分四、求下列导数（每题6分，共12分）1. 解：2sin 2cos21222222x x x x x y ⨯+---='=2cot 2)1(222x x x +-- …………….. 4分 2csc 2122)1(22422222x x x x x x x y ----⨯+--='' 2csc 212)2()3(22222xx x x x ----=…………….. 6分2. 解：dt dx dt dydx dy ==ttee --1=t t e e 2--- ……………….. 3分 dt dx dt dx dy d dxy d )(22= =t t t e e e ---22= t t e e 232--- ……………….. 6分五、求下列积分（每题6分，共24分）1. 解：⎰+dx x xcos 2sin 3=x d x x x d x x cos cos 234cos )cos (cos 2cos 122⎰⎰++-=-+- ………….. 3分 =x d x x cos cos 232cos ⎰⎥⎦⎤⎢⎣⎡++- ……………4分 =21cos 2cos 3ln(2cos )2x x x c -+++ ………….. 6分2. 解：dx xx x xx dx x ⎰⎰+-⨯-=221111arctan 1arctan …………….. 3分 =dx x xx x ⎰++211arctan …………….. 4分C x x x ++++=)1ln(211arctan 2 ………….. 6分3. 解：令x t 45-=，则dt tdx t x 2, 452-=-= 于是⎰--1145dx xx =⎰-⨯-1 3 2)2(45dt t t t ……………….. 3分 =⎰-31 285dt t ………………..4分 =3133124185t t -=16……………….. 6分4. 解：2sin ,2cos ,2,002x t dx tdt x t x t π======令时时原式222016sin cos t tdt π=⎰………………………………………………..……3分242013116sin sin 16().22422t tdt ππππ=-=⋅-⋅=⎰…………………………..6分4、解：六、（10分）解：所求面积 11ln ln 111 =⨯-==⎰⎰dx xx x x xdx A eee…………….. 5分旋转体体积dx x xx x x dx x V e ee x ⎰⎰⨯-==1122 1 ln 12)(ln )(ln πππ=(2)e π- ………….. 10分七、（8分）解: 如图建立坐标系，则在水深[0 , 5]上任取区间],[dz z z +，对应的体积元素2(25)dV z dzπ=-…………..2分将水吸到z 处所做的功元素2(25)dW g z z dzρπ=-………….. 5分故所求功为 24 5250 025625(25)[]().244z z W g z z dz g g J ρπρπρπ=-=-=⎰………….. 8分八、证明题（6分）证明：据罗尔定理，在(,)a b 内至少存在一点1ξ，使得0)(1='ξf …………….. 2分对导函数)(x f '分别在],[1ξa 与],[1b ξ上应用拉格朗日中值定理：0)()()()(1112<-'-=-'-'=''a a f a a f f f ξξξξ （12ξξ≤<a ） …………….. 3分0)()()()(1113>-'=-'-'=''ξξξξb b f b f b f f （b ≤<31ξξ） …………….. 4分由闭区间上连续函数的介质定理：在23(,)ξξ内至少存在一点ξ，有0)(=''ξf b a <≤≤<32ξξξ. …………….. 6分。

2017-2018学年度高一第一学期期末考试试卷以及答案

2018-2018学年度期末考试试卷高一数学第Ⅰ卷<选择题共50分）一、选择题<本大题共10小题，每小题5分，共50分，每题只有一个正确答案，请把你认为正确的答案填在答题卡上，答在试卷上的一律无效。

）Ke4U17Jcyx 1．若{}9,6,3,1=P {}8,6,4,2,1=Q ，那么=⋂Q P < C ） A.{1} B.{6} C. {1，6} D. 1，62．下列函数中哪个与函数y x =是同一个函数 < B ）A.2)(x y =B. 33x y = C . xx y 2=D.2x y =3．图<1）是由哪个平面图形旋转得到的< A ）图<1） A B CDKe4U17Jcyx 4．下列函数中有两个不同零点的是< D ）A ．lg y x =B ．2x y =C ．2y x =D ．1y x =-5．函数()12f x x=-的定义域是< A ） A ．[)()+∞⋃-,22,1B ．[)+∞-,1C ．()()+∞⋃∞-,22,D ． 1 22 -⋃+∞(，)(，)6．已知直线m ⊥平面α，直线n ⊂平面β，下面有三个命题：①//m n αβ⇒⊥；②//m n αβ⊥⇒；③//m n αβ⇒⊥；则真命题的个数为< B ）A ．0B ．1C ．2D ．37．若10x -<<，那么下列各不等式成立的是< D ）A ．220.2x x x -<<B ．20.22x x x -<<C ．0.222x x x -<<D ．220.2x x x -<< 8. 过2 3A -(，) ，2 1B (，) 两点的直线的斜率是< C ）A ．12B ．12-C ．2-D ．29. 已知函数)31(12)(≤≤+=x x x f ，则< B ） A ．)1(-x f =)20(22≤≤+x xB ． )1(-x f =)42(12≤≤-x xC ． )1(-x f =)20(22≤≤-x xD ． )1(-x f =)42(12≤≤+-x x10．．已知)(x f 是偶函数，当0<x 时，)1()(+=x x x f ，则当0>x 时，()f x 的值为< A ）A ．)1(-x xB ．)1(--x xC ．)1(+x xD ．)1(+-x x第Ⅱ卷<非选择题共100分）二、填空题<本大题共4小题，每小题5分，共20分. 请把你认为正确的答案填在答题卡上，答在试卷上的一律无效。

高数2017-2018年第1学期第1学期期末考试试卷

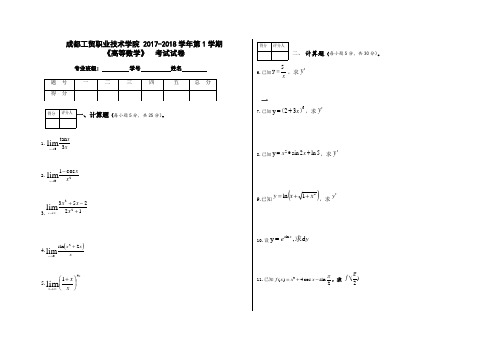
得分评分人得分评分人成都工贸职业技术学院 2017-2018学年第1学期《高等数学》考试试卷专业班级: 学号姓名一一、计算题（每小题5分，共25分）。

1.x xx 3tan lim 0→2.2cos 1lim x xx -→3.1225322lim +-+∞→x x x x4.()x xx x 2sin 20lim +→5.xx x x 41lim ⎪⎭⎫ ⎝⎛+∞→二、计算题（每小题5分，共30分）。

6.已知x5y =，求'y7.已知632y ）（x +=，求'y8.已知5ln 2sin y 2+∙=x x ，求'y9.已知()21ln x x y ++=，求'y10.设y e x d ,y sin 求=11.已知3()4cos sin2f x x x π=+-，求)2('πf得分评分人得分评分人得分评分人三、计算题（每小题5分，共20分）。

12. ()dx x x⎰+-32213.dx x x⎰+12214.dx xx ⎰+2ln15.dx x x⎰+1四、应用题（15分）。

16.已知函数()233+-=x x x f .定义区间[]3,2-。

（每小题5分，共15分）（1）求()x f 的极值；（2）求()x f 的单调性与最值；（3）求()x f 的凹凸性。

五、应用题（10分）。

17.在一条河的同旁有甲，乙两城，甲城位于河岸边，乙城离岸40km ，乙城到岸的垂足与甲城相距50km ，两城在河边合建一水厂取水，从水厂到甲城和乙城的水管费用分别为每公里3万元和5万元，问此水厂应该建在河边的何处才能使水管费用最少？。

2017—2018学年度第一学期高二理科数学试卷含答案

2017—2018学年度第一学期期末考试高二理科数学试卷（答题时间：120分钟满分：150分)一、选择题（本大题共12小题，每小题5分，满分60分）每小题只有一个．．．．正确选项,请将正确选项填到答题卡处1。

设集合{|(1)(2)0}A x x x =+-<， {|13}B x x =<<，则A B = A ．{|13}x x -<< B ．{|11}x x -<<C ．{|12}x x <<D ．{|23}x x <<2.已知抛物线y 2＝2px （p >0）的准线经过点(－1,1),则该抛物线的焦点坐标为A ．(－1，0)B ．（1,0）C ．（0，－1)D ．（0,1）3．设x ，y ∈R ，则“x ≥2且y ≥2”是“x 2＋y 2≥4”的A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件4．已知等差数列｛a n }的公差为d （d ≠0）,且a 3＋a 6＋a 10＋a 13＝32，若a m ＝8，则m 为A ．12B ．8C ．6D ．45．执行如图所示的程序框图,若输入的n ＝10，则输出的S 等于A .错误!B .错误!C 。

错误!D .错误!6．某学校组织学生参加数学测试，成绩的频率分布直方图如图，数据的分组依次为［20,40),[40,60)，［60,80），［80，100]．若低于60分的人数是15人，则该班的学生人数是A ．45B ．50C ．55D ．607。

若一个正三棱柱的三视图如图所示，则这个正三棱柱的表面积为A .318B 。

315C .3824+D 。

31624+8．已知a ＋b ＋c ＝0,｜a |＝2，|b |＝3，｜c ｜＝4，则向量a 与b 之间的夹角<a ,b 〉为A ．30°B ．45°C ．60°D ．以上都不对9．在长为10厘米的线段AB 上任取一点G ，用AG 为半径作圆,则圆的面积介于36π平方厘米到64π平方厘米的概率是A .错误!B 。

2017高等数学考试题及答案

2017高等数学考试题及答案一、选择题（每题4分，共40分）1. 极限的定义是：A. 数列的极限B. 函数的极限C. 无穷小的极限D. 无穷大的极限答案：B2. 以下哪个函数是偶函数？A. f(x) = x^2B. f(x) = x^3C. f(x) = x^2 + xD. f(x) = x^2 - x答案：A3. 以下哪个函数是周期函数？A. f(x) = e^xB. f(x) = sin(x)C. f(x) = ln(x)D. f(x) = x^2答案：B4. 以下哪个函数的导数为0？A. f(x) = x^2B. f(x) = x^3C. f(x) = x^0D. f(x) = x^(-1)答案：C5. 以下哪个函数的不定积分为ln|x|？A. f(x) = xB. f(x) = 1/xC. f(x) = x^2D. f(x) = 1/x^2答案：B6. 以下哪个选项是正确的洛必达法则的应用？A. 0/0 形式B. ∞/∞ 形式C. 0×∞ 形式D. ∞-∞ 形式答案：A7. 以下哪个选项是正确的二重积分的性质？A. 可交换积分顺序B. 可交换积分顺序，但需满足Fubini定理C. 不可交换积分顺序D. 可交换积分顺序，但需满足Lebesgue定理答案：B8. 以下哪个选项是正确的多元函数偏导数的定义？A. ∂f/∂x = lim(h->0) [(f(x+h, y) - f(x, y))/h]B. ∂f/∂x = lim(h->0) [(f(x, y+h) - f(x, y))/h]C. ∂f/∂y = lim(h->0) [(f(x+h, y) - f(x, y))/h]D. ∂f/∂y = lim(h->0) [(f(x, y+h) - f(x, y))/h]答案：D9. 以下哪个选项是正确的线性代数中矩阵的性质？A. 矩阵的行列式总是正数B. 矩阵的行列式可以是0C. 矩阵的行列式总是负数D. 矩阵的行列式总是1答案：B10. 以下哪个选项是正确的特征值和特征向量的定义？A. 特征值是矩阵的对角线元素B. 特征向量是矩阵的列向量C. 特征值是矩阵的非零行列式D. 特征值是满足Av=λv的λ，其中A是矩阵，v是特征向量答案：D二、填空题（每题4分，共20分）11. 函数f(x) = x^2 + 3x + 2的导数是______。

2017-2018学年高中毕业班第一次统测数学理科试题(终稿) 精品

试卷类型：A肇庆市中小学教学质量评估2018届高中毕业班第一次统一检测理科数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共23小题，满分150分. 考试用时120分钟. 注意事项：1. 答卷前，考生务必用黑色字迹的钢笔或签字笔，将自己所在县（市、区）、姓名、试室号、座位号填写在答题卷上对应位置．2. 选择题每小题选出答案后，用2B 铅笔把答题卷上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其它答案，答案不能写在试卷或草稿纸上．3. 非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卷各题目指定区域内相应的位置上；如需改动，先划掉原来的答案，然后再在答题区内写上新的答案；不准使用铅笔和涂改液．不按以上要求作答的答案无效．参考公式：22⨯列联表随机变量))()()(()(22d b c a d c b a bc ad n K ++++-=. )(2k K P ≥与k 对应值表：第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.（1）若集合(){}|40M x R x x =∈-<，集合{}0,4N =，则MN =A ．[]0,4B ．∅C ．{}0,4D ．()0,4 （2）设i 为虚数单位，复数3iz i+=，则z 的共轭复数z = A ．13i --B ．13i -C ．13i -+D ．13i +（3）已知向量()(),2,1,1m a n a ==+，若//m n ，则实数a 的值为A ．23-B ．2或1-C ．2-或1D ．2- （4）设复数z 满足()1(i z i i +=为虚数单位），则复数z 对应的点位于复平面内A ．第一象限B ．第二象限C ．第三象限D ．第四象限（5）原命题p ：“设,,a b c R ∈，若22ac bc >，则a b >”以及它的逆命题、否命题、逆否命题中，真命题的个数为 A ．0B ．1C ．2D ．4（6）执行右边的程序框图，为使输出S 的值小于91，则输入的正整数N 的最小值为 A ．5B ．4C ．3D ．2（7）变量,x y 满足约束条件2330233030x y x y y +-≤⎧⎪-+≥⎨⎪+≥⎩，则2z x y =+的最小值等于A ．15-B ．9-C ．1D ．9（8）如图所示的茎叶图记录了甲、乙两组各5名工人某日的产量数据（单位：件）.若这两组数据的中位数相等，且平均值也相等，则x 和y 的值分别为 A. 3，5B. 5，5C. 3，7D. 5，7 （9）为了研究某班学生的脚长x （单位：厘米）和身高y（单位：厘米）的关系，从该班随机抽取10名学生，根据测量数据的散点图可以看出y 与x 之间有线性相关关系，设其回归直线方程为ˆˆˆy bx a =+．已知101225i i x ==∑，1011600i i y ==∑，ˆ4b=．该班某学生的脚长为24，据此估计其身高为A. 160B. 163C. 166D.170（10）从区间[]0,1随机抽取2n 个数1x ,2x ，…，n x ，1y ，2y ，…，n y ，构成n 个数对()11,x y ，()22,x y ，…，(),n n x y ，其中两数的平方和小于1的数对共有m 个，则用随机模拟的方法得到的圆周率π的近似值为A.4n m B.2n mC.4m nD.2m n（11）四棱柱1111ABCD A BC D -的所有棱长均为1，且1160AAB A AD BAD ∠=∠=∠=︒，则1AC 的长为A ．3BC ．6D （12）下列命题中正确的是A ．有两个面平行，其余各面都是平行四边形的几何体是棱柱B ．将圆心角为23π，面积为3π的扇形作为圆锥的侧面，则圆锥的表面积为5π C ．若空间中n 个不同的点两两距离都相等，则正整数n 的值至多等于4D ．过两条异面直线外的一点，有且只有一个平面与这两条异面直线都平行第II 卷本卷包括必考题和选考题两部分. 第13题~第21题为必考题，每个试题考生都必须作答.第22题~第23题为选考题，考生根据要求作答.二、填空题：本大题共4小题，每小题5分.（13）若随机变量ξ～N (2，1)，且P (ξ>3)＝0.1587，则P (ξ≥1)＝ ▲ . （14）()522x x +-的展开式中3x 的系数是 ▲ .（用数字作答）.（15）由一个长方体和两个14圆柱体构成的几何体的三视图如右图，则该几何体的体积为 ▲ .（16）A ，B 两种规格的产品需要在甲、乙两台机器上各自加工一道工序才能成为成品．已知A 产品需要在甲机器上加工3小时，在乙机器上加工1小时；B 产品需要在甲机器上加工1小时，在乙机器上加工3小时．在一个工作日内，甲机器至多只能使用11小时，乙机器至多只能使用9小时．A 产品每件利润300元，B 产品每件利润400元，则这两台机器在一个工作日内创造的最大利润是 ▲ 元．三、解答题：解答应写出文字说明，证明过程或演算步骤. （17）（本小题满分12分）某公司为了解用户对其产品的满意度，从A ，B 两地区分别随机调查了40个用户，根据用户对产品的满意度评分，得到A 地区用户满意度评分的频率分布直方图和B 地区用户满意度评分的频数分布表.A 地区用户满意度评分的频率分布直方图B 地区用户满意度评分的频数分布表（Ⅰ）求A 地区用户满意度评分的众数和中位数；（Ⅱ）填写下列的列联表，并根据列联表判断是否有99%的把握认为用户满意度与地区有关？（18）（本小题满分12分）如图，在四棱锥V ABCD -，1//2AB CD ，,AB VA CD VD ⊥⊥，E 是VC 的中点. （Ⅰ）证明：//BE VAD 平面；（Ⅱ）证明：平面ABCD ⊥平VAD 面.405060708090满意度评分100 频率/C（19）（本小题满分12分）某公司进行抽奖活动，某抽奖箱里有2张印有“中奖”的卡片和3张印有“谢谢惠顾”的卡片.现场员工小王进行抽奖，每次随机抽取一张卡片，抽取后不放回，假如小王一定要将2张印有“中奖”的卡片全部抽完才停止.（Ⅰ）求小王恰好抽奖3次停止的概率；（Ⅱ）若抽奖一次需要费用100元，设X 表示小王停止抽奖前所需要的费用（单位：元），求X 的分布列和均值（数学期望）.（20）（本小题满分12分）如图，在四棱锥S ABCD -中，ABCD 是边长为1的菱形，且60DAB ∠=︒，SA SD == 2SB =.（Ⅰ）证明：AD SB ⊥；（Ⅱ）求二面角S AD B --的大小.（21）（本小题满分12分）如图，在三棱锥P ABC -中，PAB ABC ⊥平面平面，PAC ABC ⊥平面平面，BE AC ⊥于点E ，BC =30ACB ∠=︒，2,AC =1PA =，F 为线段PC 上的一点.（Ⅰ）证明：PA ABC ⊥平面；（Ⅱ）若直线EF 与平面PBC 所成角的，求三棱锥F CBE -的体积.请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分. 作答时，请用2B 铅笔在答题卡上将所选题号后的方框涂黑. （22）（本小题满分10分）选修4-4：坐标系与参数方程已知极坐标系的极点在直角坐标系的原点处，极轴与x 轴非负半轴重合，直线l 的参数方程为：1cos (sin x t t y t αα=-+⎧⎨=⎩为参数，[0,)απ∈)，曲线C 的极坐标方程为：4cos ρθ=.（Ⅰ）写出曲线C 的直角坐标方程;（Ⅱ）设直线l 与曲线C 相交于,P Q 两点, 若PQ =l 的斜率.（23）（本小题满分10分）选修4—5：不等式选讲设函数()12f x x x =++-. （Ⅰ）求不等式()5f x ≤的解集；（Ⅱ）当[]0,2x ∈时，()22f x x x m ≥-++恒成立，求m 的取值范围.。

2017年-2018年普通高等学校招生全国统一考试数学试题理(全国卷1,参考解析)

高考衣食住用行衣：高考前这段时间，提醒同学们出门一定要看天气，否则淋雨感冒，就会影响考场发挥。

穿着自己习惯的衣服，可以让人在紧张时产生亲切感和安全感，并能有效防止不良情绪产生。

食：清淡的饮食最适合考试，切忌吃太油腻或者刺激性强的食物。

如果可能的话，每天吃一两个水果，补充维生素。

另外，进考场前一定要少喝水！住：考前休息很重要。

好好休息并不意味着很早就要上床睡觉，根据以往考生的经验，太早上床反而容易失眠。

考前按照你平时习惯的时间上床休息就可以了，但最迟不要超过十点半。

用：出门考试之前，一定要检查文具包。

看看答题的工具是否准备齐全，应该带的证件是否都在，不要到了考场才想起来有什么工具没带，或者什么工具用着不顺手。

2017年普通高等学校招生全国统一考试（全国I卷）理科数学注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上，2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 已知集合{}{}131x A x x B x =<=<，，则（） A ．{}0=<I A B x x B ．A B =R U C ．{}1=>U A B x xD ．A B =∅I【答案】A【解析】{}1A x x =<，{}{}310xB x x x =<=<∴{}0A B x x =<I ，{}1A B x x =<U ，选A2. 如图，正方形ABCD 内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分位于正方形的中心成中心对称，在正方形内随机取一点，则此点取自黑色部分的概率是（）A ．14B ．π8C ．12D ．π4【答案】B【解析】设正方形边长为2，则圆半径为1则正方形的面积为224⨯=，圆的面积为2π1π⨯=，图中黑色部分的概率为π2则此点取自黑色部分的概率为ππ248=故选B3. 设有下面四个命题（）1p ：若复数z 满足1z∈R ，则z ∈R ；2p ：若复数z 满足2z ∈R ，则z ∈R ；3p ：若复数12z z ，满足12z z ∈R ，则12z z =； 4p ：若复数z ∈R ，则z ∈R ．A ．13p p ，B ．14p p ，C ．23p p ，D ．24p p ，【答案】B【解析】1:p 设z a bi =+，则2211a bi z a bi a b -==∈++R ，得到0b =，所以z ∈R .故1P 正确； 2:p 若z =-21，满足2z ∈R ，而z i =，不满足2z ∈R ，故2p 不正确；3:p 若1z 1=，2z 2=，则12z z 2=，满足12z z ∈R ，而它们实部不相等，不是共轭复数，故3p 不正确；4:p 实数没有虚部，所以它的共轭复数是它本身，也属于实数，故4p 正确；4. 记n S 为等差数列{}n a 的前n 项和，若4562448a a S +==，，则{}n a 的公差为（） A ．1 B ．2C ．4D ．8【答案】C【解析】45113424a a a d a d +=+++=61656482S a d ⨯=+= 联立求得11272461548a d a d +=⎧⎪⎨+=⎪⎩①②3⨯-①②得()211524-=d624d =4d =∴ 选C5. 函数()f x 在()-∞+∞，单调递减，且为奇函数．若()11f =-，则满足()121f x --≤≤的x 的取值范围是（） A ．[]22-， B ．[]11-， C ．[]04， D ．[]13，【答案】D【解析】因为()f x 为奇函数，所以()()111f f -=-=，于是()121f x --≤≤等价于()()()121f f x f --≤≤| 又()f x 在()-∞+∞，单调递减 121x ∴--≤≤3x ∴1≤≤ 故选D6. ()62111x x ⎛⎫++ ⎪⎝⎭展开式中2x 的系数为A ．15B ．20C ．30D ．35【答案】C.【解析】()()()66622111+1111x x x x x ⎛⎫+=⋅++⋅+ ⎪⎝⎭对()61x +的2x 项系数为2665C 152⨯== 对()6211x x⋅+的2x 项系数为46C =15， ∴2x 的系数为151530+= 故选C7. 某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形、该多面体的各个面中有若干是梯形，这些梯形的面积之和为A ．10B ．12C ．14D ．16【答案】B【解析】由三视图可画出立体图该立体图平面内只有两个相同的梯形的面 ()24226S =+⨯÷=梯6212S =⨯=全梯故选B8. 右面程序框图是为了求出满足321000n n ->的最小偶数n ，那么在和可以分别填入A ．1000A >和1n n =+B ．1000A >和2n n =+C ．1000A ≤和1n n =+D ．1000A ≤和2n n =+ 【答案】D【答案】因为要求A 大于1000时输出，且框图中在“否”时输出∴“”中不能输入A 1000> 排除A 、B又要求n 为偶数，且n 初始值为0， “”中n 依次加2可保证其为偶故选D9. 已知曲线1:cos C y x =，22π:sin 23C y x ⎛⎫=+ ⎪⎝⎭，则下面结论正确的是（）A ．把1C 上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线2CB ．把1C 上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线2CC ．把1C 上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线2CD ．把1C 上各点的横坐标缩短到原来的2倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线2C 【答案】D【解析】1:cos C y x =，22π:sin 23⎛⎫=+ ⎪⎝⎭C y x首先曲线1C 、2C 统一为一三角函数名，可将1:cos C y x =用诱导公式处理．πππcos cos sin 222⎛⎫⎛⎫==+-=+ ⎪ ⎪⎝⎭⎝⎭y x x x ．横坐标变换需将1=ω变成2=ω，即112πππsin sin 2sin 2224⎛⎫⎛⎫⎛⎫=+−−−−−−−−−→=+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭C 上各坐短它原y x y x x 点横标缩来 2ππsin 2sin 233⎛⎫⎛⎫−−→=+=+ ⎪ ⎪⎝⎭⎝⎭y x x ．注意ω的系数，在右平移需将2=ω提到括号外面，这时π4+x 平移至π3+x ，根据“左加右减”原则，“π4+x ”到“π3+x ”需加上π12，即再向左平移π12．10. 已知F 为抛物线C ：24y x =的交点，过F 作两条互相垂直1l ，2l ，直线1l 与C 交于A 、B 两点，直线2l 与C 交于D ，E 两点，AB DE +的最小值为（） A ．16B ．14C ．12D ．10【答案】A 【解析】设AB 倾斜角为θ．作1AK 垂直准线，2AK 垂直x 轴易知11cos 22⎧⎪⋅+=⎪⎪=⎨⎪⎛⎫⎪=--= ⎪⎪⎝⎭⎩AF GF AK AK AF P P GP Pθ（几何关系）（抛物线特性）cos AF P AF θ⋅+=∴同理1cos P AF θ=-，1cos PBF θ=+∴22221cos sin P PAB θθ==- 又DE 与AB 垂直，即DE 的倾斜角为π2θ+2222πcos sin 2P PDE θθ==⎛⎫+ ⎪⎝⎭而24y x =，即2P =．∴22112sin cos AB DE P θθ⎛⎫+=+ ⎪⎝⎭2222sin cos 4sin cos θθθθ+=224sin cos θθ=241sin 24=θ 21616sin 2θ=≥，当π4θ=取等号即AB DE +最小值为16，故选A11. 设x ，y ，z 为正数，且235x y z ==，则（）A ．235x y z <<B ．523z x y <<C ．352y z x <<D ．325y x z <<【答案】D【答案】取对数：ln 2ln3ln5x y ==.ln33ln 22x y => ∴23x y > ln2ln5x z = 则ln55ln 22x z =< ∴25x z <∴325y x z <<，故选D12. 几位大学生响应国家的创业号召，开发了一款应用软件，为激发大家学习数学的兴趣，他们推出了“解数学题获取软件激活码”的活动，这款软件的激活码为下面数学问题的答案：已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16，…，其中第一项是02，接下来的两项是02，12，在接下来的三项式62，12，22，依次类推，求满足如下条件的最小整数N ：100N >且该数列的前N 项和为2的整数幂．那么该款软件的激活码是（） A ．440 B ．330 C ．220 D ．110 【答案】A【解析】设首项为第1组，接下来两项为第2组，再接下来三项为第3组，以此类推．设第n 组的项数为n ，则n 组的项数和为()12n n +由题，100N >，令()11002n n +>→14n ≥且*n ∈N ，即N 出现在第13组之后第n 组的和为122112nn -=-- n 组总共的和为()2122212n nn n --=---若要使前N 项和为2的整数幂，则()12n n N +-项的和21k -应与2n --互为相反数即()*21214k n k n -=+∈N ，≥ ()2log 3k n =+→295n k ==，则()2912954402N ⨯+=+=故选A二、填空题：本题共4小题，每小题5分，共20分。

(完整word版)2017-2018高一数学上学期期末考试试题及答案,推荐文档

是符合题目要求的．
1．已知全集 U {0,1,2,3}, A {1,3} ，则集合 CU A （）
A． 0 B ． 1,2 C ． 0,2 D ． 0,1,2
2．空间中，垂直于同一直线的两条直线
（）
A．平行 B ．相交 C ．异面 D ．以上均有可能
2
3．已知幂函数 f x x 的图象经过点 2， 2 ，则 f 4 的值等于
18．（本小题满分 10 分）
已知函数 f (x) log a (1 x) log a( x 3) (0 a 1) . （Ⅰ）求函数 f ( x) 的零点；（Ⅱ）若函数 f ( x) 的最小值为 4 ，求 a 的值 .
3
19. （本小题满分 12 分）已知圆 C：x2＋ y2－ 8y＋ 12＝ 0，直线 l ： ax＋y＋ 2a＝0. ( Ⅰ ) 当 a 为何值时，直线 l 与圆 C相切； ( Ⅱ ) 当直线 l 与圆 C相交于 A，B两点，且 AB＝ 2 2时，求直线 l 的方程．
（）
A．若 m∥n，m∥α，则 n∥α
B．若 α⊥ β，m∥α ，则 m⊥ β
C．若 α⊥ β，m⊥β ，则 m∥ α
D．若 m⊥n，m⊥α， n ⊥β ，则 α⊥β
7．设 f x 是定义在 R 上的奇函数，当 x 0 时， f x 2x 2 x，则 f 1 等于（
）
A．－ 3
B
．－ 1
C
．1
D
．3
∵ 3 < x <1 ∴ 0 < -( x
2
1)
4
4
L L L L L L L 7分
∵0 < a <1∴ log a (x 1)2 4 log a 4
5

2017—2018学年度第一学期高三级数学试题及答案精装版

2017—2018学年度第一学期高三级数学试题一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1已知两个集合(){}2ln 2++-==x x y x A ，⎭⎬⎫⎩⎨⎧≤-+=212x e e xB 则=⋂B A （）A.⎪⎭⎫⎢⎣⎡-2,21 B ．⎥⎦⎤ ⎝⎛--21,1 C ．()e ,1- D ．()e ,22.要得到一个奇函数，只需将x x x f cos 3sin )(-=的图象（）A.向右平移6π个单位B.向右平移3π个单位C.向左平移6π个单位 D.向左平移3π个单位3．由下列条件解△ABC ，其中有两解的是( )A ．b ＝20，A ＝45°，C ＝80°B ．a ＝30，c ＝28，B ＝60°C ．a ＝14，c ＝16，A ＝45°D ．a ＝12，c ＝15，A ＝120° 4设函数()sin(2)3f x x π=+，则下列结论正确的是（）①()f x 的图象关于直线3x π=对称；②()f x 的图象关于点(,0)4π对称；③()f x 的图象向左平移12π个单位，得到一个偶函数的图象；④()f x 的最小正周期为π，且在[0,]6π上为增函数．A. ①③ B .②④ C. ①③④D .③5命题“存在R x ∈，使a ax x 42-+≤0为假命题”是命题“016≤≤-a ”的(A) 充要条件(B)必要不充分条件(C)充分不必要条件 (D)既不充分也不必要条件6已知函数f (x )＝A tan(ωx ＋φ)⎝⎛⎭⎫ω>0，|φ|<π2，y ＝f (x )的部分图象如图，则f ⎝⎛⎭⎫π24＝( )A ．2＋ 3B ．3C.33D ．2－ 37.已知sin α＋2cos α＝3，则tan α＝( )A.22B ．2C ．－22D ．－ 28已知ω＞0，函数f (x )＝sin(ωx ＋)在(，π)上单调递减，则ω的取值范围是( ) A ． B ． C ．(0，］ D ．(0,2］9设α、β都是锐角，且cos α＝55，sin(α＋β)＝35，则cos β等于( ) A.2525 B.255 C.2525或255D.55或52510.在ABC △中，若2sin sin sin A B C =⋅且()()3b c a b c a bc +++-=，则该三角形的形状是（）A ．直角三角形B ．钝角三角形C ．等腰三角形D ．等边三角形11.已知定义在实数集R 上的函数()f x 满足(1)3f =，且()f x 的导数()f x '在R 上恒有()2f x '<()x R ∈，则不等式()21f x x <+的解集为（）A ．(1,)+∞B ．(,1)-∞-C ．(1,1)-D ．(,1)-∞-⋃(1,)+∞12已知函数f (x )＝sin ωx ＋3cos ωx (ω>0)，f ⎝⎛⎭⎫π6＋f ⎝⎛⎭⎫π2＝0，且f (x )在区间⎝⎛⎭⎫π6，π2上递减，则ω＝( )A ．3B ．2C．6D ．5π4π21524⎡⎤⎢⎥⎣⎦，1324⎡⎤⎢⎥⎣⎦，12二、填空题：（本大题共4小题，每小题5分，共20分）13.已知53)30sin(0=+α，0015060<<α，则=αcos ___________.14如图，为测量山高MN ，选择A 和另一座山的山顶C 为测量观测点．从A 点测得M 点的仰角∠MAN ＝60°，C 点的仰角∠CAB ＝45°以及∠MAC ＝75°；从C 点测得∠MCA ＝60°.已知山高BC ＝100 m ，则山高MN ＝________m.15已知α，β都是锐角，tan α＝17，sin β＝1010，则α＋2β的大小为________。

2017-2018高等数学A(1) A卷答案

2017/2018学年第一学期高等数学A1课程考核试卷 A ■、B□参考答案一、填空题或选择填空题 (每小题 3分，满分15分) 1. 当0x →1−与是等价无穷小，则ax 12a=；(等价无穷小112x −∼) 2. 设，则(1)1f ′=0(1)(1)lim2x f x f x x→+−−=；(导数定义 00(1)(1)(1)(1)(1)(1)limlim 2(1)2x x f x f x f x f f x f f x x x →→+−−+−−−⎡⎤′=+=⎢⎥−⎣⎦=0) 3. 若函数由确定，则()y y x =e e xyx y +−=0d d x y x==；(微分形式：0d (0x y y =′=)d x xyy x y y )(隐函数求导：当时，，0x =0y =e e 0′′++−=，则e e x y y+′=，进而)(0)1y ′=y x−4. 设函数3()f x x =−x ，则在内(0,1)B()A 存在ξ，使得()2f ξ′=− ()B 存在ξ，使得()0f ξ′= ()C 存在ξ，使得()2f ξ′= (存在)D ξ，使得()3f ξ′=；(罗尔定理：()f x 在[0上连续，在(0内可导，,1],1)(0)(1)f f =，由罗尔定理知，(0,1)ξ∃∈，使得()0f ξ′=) 5. 若()f x 满足201()()d 11xf x f t t x =++∫，则C()A (0)0f ′= ()B (0)1f ′= ()C (0)2f ′= 无法确定()D (0)f ′的值.(导数定义结合洛必达法则和积分上限函数求导：(0)1f =，00022000()(0)(0)lim lim li 1()d ()d m lim 22(0)2(1)2121()x x x xx x f t t f t t f x f f f x f x x x x x x →→→→−′=====+++∫∫=)二、计算下列各题（每小题6分，共48分）1. 10(1)e limxx x x →+−； (0洛必达法则或者等价无穷小)解：(洛必达法则结合幂指函数求导)11ln(1)ln(1)20000(1)ln(1)(1)e 1lim lim lim e lim e 1x x x x x x x x x x x x x x x x x ++→→→→′⎡⎤+⎢⎥−+′⎡⎤+−⎣⎦+===⋅⎢⎥⎣⎦ln(1)22000(1)ln(1)ln(1)elim elime lim e lim (1)23232x xx x x x x x x x x x x x x x x +→→→→−++−+−−=⋅=⋅=⋅=+++2.(等价无穷小结合洛必达法则) 1ln(1)ln(1)1200000ln(1)1(1)e eee(e1)ln(1)limlimlimelim elim x x x xxx x x x x x x x x x xxxx++−→→→→→x +−+−−−+−==== 0011e 1elimelim 22(1)x x x x x x x →→−−+==+2=−. 2. 设33cos ,sin ,x t y t ⎧=⎪⎨=⎪⎩ 求22π4d d x y x =； (参数方程求导)解：2d 3cos sin d x t t =−t , 2d 3sin cos d y t t t =, 22d 3sin cos tan d 3cos sin y t t t x t t==−−， 22224d 3cos si sec 1d 3o n c n t t y ts si t t −==−, 22π4d d 3x y x==. x3.∫； (三角换元)解：令tan x t =，则2d sec d x t t =2csc d ln |csc cot |ln t t t t C C ==−+=∫+； 4.2(2+3)d 25x xx x ++∫；(分母二次的有理函数----凑微分)解：222222(2+3)d (25)+1d d(25)1d(1)252525(1)4x x x x x x x x x x x x x x x ′++++==+++++++++∫∫∫∫+ 211ln (25)arc tan 22x x x C +=++++； 5.e 1eln d x x ∫； (去绝对值，分部积分)解：[][]e 1e1e11111ee e2ln d (ln )d ln d ln ln 2e x x x x x x x x x x x x =−+=−−+−=−∫∫∫；6.1x +∞∫；(反常积分，倒代换)解：令1x t =，则21d d x t t =−，111211002(1)x t t t −+∞⎡⎤===−+=⎢⎥⎣⎦∫∫∫2；7. 求微分方程满足，2()0y y y ′′′−=(0)1y =(0)2y ′=的解； (可降阶微分方程) 解：令d d y p x =，则d d p y py ′′=，代入方程得2d 0d p y p p y −=，从而d 0d py p y−=，(舍) 0p = 分离变量得d d p yp y=，两边积分得 1ln ||ln ||ln ||p y C =+，则1p C y = 由，(0)1y =(0)2y ′=得，则12C =d 2d yy x=，分离变量的d 2d y x y =，两边积分得2ln ||2ln ||y x C =+，即22e xy C =，由(0)1y =得21C =，故2e xy =；8. 求函数的极值.2(1)y x x =−3)解：，(,D =−∞+∞32222(1)3(1)(1)(52)y x x x x x x x ′=−+−=−−当，0x =2x =，1x =时， 0y ′= 故极小值为()53125y =−(0)0y =.，极大值为三、(8分) 设0α>，讨论函数1sin ,0(),x x f x xx αβ⎧≠⎪=⎨⎪=⎩在0x =处的连续性与可导性.解：因0α>，则01lim sin0x x xα→=，(0)f β= 当0β=时，，0lim ()(0)0x f x f →==100()(0)1(0)limlim sin x x f x f f x x xα−→→−′== 当1α>时，；当(0)0f ′=01α<≤时，(0)f ′不存在. 故当0α>，0β≠时，()f x 在0x =处不连续且不可导. 当01α<≤，0β=时，()f x 在0x =处连续但不可导.当1α>，0β=时，()f x 在处连续且可导.0x = 四、(8分) 求由曲线y x =，及ln y x =0y =，1y =围成平面图形的面积，并求此图形绕x 轴旋转而成的旋转体的体积.为积分变量)：面积121003(e )d e e 22yy y A y y ⎡⎤=−=−=−⎢⎥⎣⎦∫ y 解：(选择体积131004π2π(e )d 2πe e 33y y yx y V y y y y ⎡⎤=−=−−=⎢⎥⎣⎦∫；为积分变量): 面积[]121ee10103d (1ln )d ln e 22x A x x x x x x x x ⎡⎤=+−=+−+=−⎢⎥⎣⎦∫∫x (选择体积131ee 22221014ππd π(1ln )d ππln 2ln 233x x V x x x x x x x x x x ⎡⎤⎡⎤=+−=+−+−=⎢⎥⎣⎦⎣⎦∫∫. 五、(7分) 求微分方程369e xy y y ′′′−+=的通解.解: 特征方程: 特征根 269r r −+=0123r r ==，对应齐次方程通解 312()e x Y C C x =+ 因3λ=是特征重根设非齐次方程特解为23*e xy ax =，代入方程得12a =故所求通解23312*()e e 2xxx y Y y C C x =+=++.六、(6分) 设()f x 是[0上单调递减连续函数，证明：对于任意,1](0,1)a ∈，成立不等式1()d ()d a f x x a f x x ≥∫∫.证明: 令0()d ()a f x x g a a=∫， (构造函数，利用单调性证明) (a 为自变量)0a <<1 则02()()d ()af a a f x xg a a⋅−′=∫，由积分中值定理知，()d ()a f x x f a ξ=⋅∫，0a ξ<<从而()()()f a f g a aξ−′=，因()f x 在[0上单调减少，则,1]()()f a f ξ≤，进而，故在(0上单调减少，，()0g a ′≤()g a ,1)10()(1)()d g a g f x x ≥=∫即1()d ()d a f x x a f x x ≥∫∫，(01)a <<.(另法) 令 (为了利用单调性，分割区间)100()()d ()d a g a f x x a f x x =−∫∫ 则11()()d (()d ()d )(1)()d ()d aa a aag a f x x a f x x f x x a f x x a f x x =−+=−−∫∫∫∫∫ 由积分中值定理知，10()d ()a f x x f a ξ=⋅∫，01a <，12()d ()(1)af x x f a ξ=⋅−∫，a 21<<<ξξ 从而12()(1)()(1)()g a a a f a a f ξξ=−⋅⋅−−⋅⋅因()f x 在[0上单调减少，,1]1201a ξξ<<<<，则12()()f f ξξ≥故，即()0g a ≥1()d ()d a f x x a f x x ≥∫∫，(01)a <<.七、(8分) 设()f x ，在[,上具有二阶导数，()g x ]a b ()()f a g a =，()()f b g b =，()()f x g x ≠，且在内(,)a b ()f x 与取得相等的最大值.()g x 证明：(1) 存在(,)a b ξ∈，使得()()f g ξξ=；(2) 存在(,)a b η∈，使得()()f g ηη′′′′=. 证明：(1) 若()f x 与均在()g x 0x 点取得相等的最大值，即00()()f x g x =，取0(,)x a b ξ=∈即可若()f x 与分别在点()g x 1x 与点2x 取得最大值，即12()()f x g x M ==，不妨设12x x <令，则在()()()F x f x g x =−()F x 12[,]x x 上连续，且1111()()()()0F x f x g x M g x =−=−>， 2222()()()()0F x f x g x f x M =−=−<由零点定理知，12(,)(,)x x a b ξ∃∈⊂，使得()0F ξ=，即()()f g ξξ=.(2) 因()()f a g a =，()()f g ξξ=，()()f b g b =，则()()()0F a F F b ξ===()F x 在[,]a ξ，[,]b ξ上连续，在(,)a ξ，(,)b ξ内可导， ()()()0F a F F b ξ===由罗尔定理知，1(,)a ξξ∃∈，2(,)b ξξ∈，使得1()0F ξ′=，2()0F ξ′=()F x ′在12[,]ξξ上连续，在12(,)ξξ内可导， 12()()F F ξξ′′=由罗尔定理知，12(,)(,)a b ηξξ∃∈⊂，使得()0F η′′=，即()()f g ηη′′′′=.。

武汉大学2017-2018学年第一学期末《高等数学C1》试卷(A卷)

x d x3 2 2 1+x s in x √ J √武汉大学2017-2018学年第一学期末《高等数学C1》试卷(A 卷)一. 计算 limn →∞√n [√n + 3 − √n ].(7分)二. 计算lim e tan x −e 3x. (7 分)x →0sin x三. 设f (x ) = ax + b,|x | ≤ 1x 2 + 2x − 2, |x | > 1, 求a, b 使得函数f (x )在x = ±1处连续.(7分)四. 若y = arctan 1+x , 求d y . (7分)1−x五. 设y = y (x )由方程ln ✓x 2 + y 2 = arctan y 确定, 求d y . 六. 设y = sin x − 1 sin 3 x , 验证y II − 3 sin 3x = −3 sin x . (7分)七. 求函数f (x ) = sin 2x − x 在区间[− π , π ]上的最大值与最小值. (8分)八. 已知f (x )的一个原函数为 sin x , 求J [1 + f (x )]f I (x )d x . (7分)九. 计算J 1 d x , 其中a 是正常数. (7分)(a 2−x 2)3十. 计算Jx sin x d x . (7分)十一. 计算 e 2 1√ x d x . (7分)1+ln x 十二. 计算J 22√ x √a rcsi n x d x . (7分)−1−x 2十三. 设函数f (x )在区间[a, b ]上有连续的导数, 在区间(a, b )内二阶可导,且f (a ) = f (b ) = f I (a ) = 0. 证明存在ξ ∈ (a, b ), 使得f II(ξ) = 0. (7分)十四. 求由直线y = x, y = 2 − x 与x 轴围成的图形分别绕x 轴与y 轴得到的旋转体体积. (8分)武汉大学2017-2018学年第一学期末《高等数学C1》试卷(A 卷)答案2 2x 2+y 2 x d x32 2 一. 计算 lim √n [√n +3 − √n ].(7分)n →∞√ √√ √ 解. lim n [ n + 3 − n ] = lim √n √ (4分) = 3 .(3分)n →∞ 二. 计算lim etan x −e 3x. (7分) n →∞n +3+ n2 x →0sin x解. I. limetan x −e 3x = lim etan x −1−(e 3x −1)= lim tan x −3x (5分) = −2.(2分)x →0sin x x →0 sin x x →0 sin x II. lim e tan x −e 3x = sec 2 xe tan x −3e 3x (5分) = −2.(2分) x →0sin x cos x 三. 设f (x ) =ax + b,|x | ≤ 1x 2 + 2x − 2, |x | >1, 求a, b 使得函数f (x )在x = ±1处连续.(7分)解. 由 lim − f (x ) = −3, lim + f (x ) = −a + b , limf (x ) = a + x →−1x →−1x →1−b, lim x →1+f (x ) = 1(4分), a = 2, b = −1.(3分) 四. 若y = arctan 1+x , 求d y . (7分)1−x解. 由y I =12 (5分), d y =12 d x .(2分)1+x1+x五. 设y = y (x )由方程ln ✓x 2 + y 2 = arctan y 确定, 求d y .解. 方程两边同时对x 求导得, x +yy lx 2+y 2= xy l−y (4分). 由此, x + yy I = xy I − y . 故d y = x +y (3分).d xx −y六. 设y = sin x − 1 sin 3x , 验证y II − 3 sin 3 x = −3 sin x . (7分) 证. 由y I = cos x − cos x sin 2 x = cos 3 x , y II = −3 sin x cos 2 x (5分). 故y II − 3 sin 3 x = −3 sin x (cos 2 x + sin 2 x ) = −3 sin x.(2分)七. 求函数f (x ) = sin 2x − x 在区间[− π , π ]上的最大值与最小值. (8分)3J I . f (x ) , [1 + f (x )]f (x )d x .(7 ) r J 1 6 6 2 222626626222 2 2 2 =(1 + x sin x )2 + 2 (a 2 − x 2)3 a 2 cos 2 t a 2 − x 2 J1 + lnx √21 + ln x 12 2解. 由f I (x ) = 2 cos x − 1, x 1 = − π , x 2 = π 为函数在区间[− π , π ]上的两个驻点(4分). 又f (− π) = π , f (− π ) = − √3 + π , f ( π ) = √3 − π , f ( π ) = − π .函数f (x )在区间[− π , π ]上的最大值与最小值分别为π, − π (4分). 八已知的一个原函数为 sin x 求分 1+x sin x解. 由f (x )的一个原函数为 sin x , f (x ) = cos x −sin2 x(3分). 故1+x sin x(1+x sin x )2r[1 + f (x )]f I (x )d x =f (x ) +1 f2 2(x ) + Ccos x − sin 2 x 1 ＿ cos x − sin 2 x ＿2九. 计算J1d x , 其中a 是正常数. (7分)解. 令x = a sin t , 则d x = a cos t d t (2分),1 1 1 ✓ d x = d t = tan t +C = x√ +C. (5分)十. 计算 x sin x d x . (7分)解.rx sin x d x = − r x d cos x (2分) = −x cos x + rcosx d x= − x cos x + sin x + C. (5分)十一. 计算 e 2d x. (7分) 解.e 2d x √ =e 2d(1 + ln x ) √ (4 分) = 2e 2 1 + ln x 1= 2(3 − 1). (3分) 十二. 计算J2√x √a rcsi n x d x . (7分)1−x 21 1 √ (1 + xsin x )2 + C. (4分) r a 2 a 2 √r x r √ 1 √ −− 2 r 211 2 − r解.√22 x a rcsin x √2 √1 − x 2 d x = −√2 2 √ arcsin x d − 21 − x2 √(3分) √2✓ 1 2 r 2= 4 −√ π. (4分) 2 2十三. 设函数f (x )在区间[a, b ]上有连续的导数, 在区间(a, b )内二阶可导,且f (a ) = f (b ) = f I (a ) = 0. 证明存在ξ ∈ (a, b ), 使得f II (ξ) = 0. (7分)证. 由罗尔中值定理, 存在η ∈ (a, b ), 使得f I (η) = 0(4分). 又导函数f I (x )在区间[a, η]上满足罗尔中值定理的条件, 故存在ξ ∈ (a, η) ⊂ (a, b ), 结论成立(3分).十四. 求由直线y = x , y = 2 − x 与x 轴围成的图形分别绕x 轴与y 轴得到的旋转体体积. (8分)解. 图形绕x 轴与y 轴得到的旋转体体积分别为V x = π 1 x 2d x + π 0 2 (2 x )2d x = 12π, (4分)3 V y = π√2d x − 2arcsin x √2 + − 22 1 − x = − r ✓r r r(2 −y)2d y −πy2d y = 2π.(4分) 0。

复旦大学2017～2018学年《高等数学C上》第一学期期末考试试卷及答案

复旦大学数学科学学院 2017～2018学年第一学期期末考试试卷 A 卷一、选择题()43⨯' 1. 已知()x f 的导数是x sin ，则()x f 的原函数是（）。

()A x sin 1+ ()B 1s i n x - ()C 1c o s x + ()D 1c o s x - 2. 设()x f 可导，()()()x x f x F sin 1+=，则()00=f 是()x F 在0=x 可导的（）。

()A 充要条件 ()B 充分非必要条件 ()C 必要非充分条件 ()D 即不充分又不必要条件 3.设()x f 在()+∞∞-,上有定义，且a x =∞→lim ，()⎪⎩⎪⎨⎧=≠⎪⎭⎫ ⎝⎛=0,00,1x x x f x g ，则（）。

()A 0=x 是()x g 的第一类间断点 ()B 0=x 是()x g 的第二类间断点 ()C ()x g 在0=x 的连续性与a 相关 ()D ()x g 在0=x 的连续 4. 设A 、B 为n 阶方阵，2=A ，3-=B ，则12-*B A =（）。

()A 12- ()B 34- ()C 3212--n ()D 321+-n 二、填充题()43⨯' 1. ⎰20sin ln πxdx = 。

：我已知悉学校对于考试纪律的严肃规定，将秉持诚实守信宗旨，严守考试纪律，不作弊，不剽窃；若有违反学校考试纪律的行为，自愿接受学校严肃处理。

签名: 年月日）2. ⎰∞+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛++-12111ln 1dx x x x = 。

3. 设⎪⎪⎪⎭⎫ ⎝⎛-----=1471481510A ，则1-A = 。

4. 已知()x f 在0=x 连续，()[]1sin 2ln lim 0=-+→x x x f x ，则()='0f 。

三、计算题()88⨯' 1. 22011lim x x x +-→2. ()[]x x dtt x x x 22030sin 1211ln lim 2-++⎰+→3. 设()x e x f x cos =，求()()x f n 。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2017-2018学年第1学期考试试题
课程名称高等数学A1、B1 任课教师签名王志宏等
出题教师签名题库抽题审题教师签名
考试方式（闭）卷适用专业全校17级工科本科各专业考试时间（120）分钟
一、判断题（共10分，每题2分） 1. 2
arctan lim π
=
∞
→x x . （）
2. 当0→x 时x x tan 1sin 1--+与x arcsin 是等价无穷小. （）
3. 函数在某点可导，则必在该点连续. （）
4. 若c x F dx x f +=⎰)()(，则c x F dx x f +=
⎰)2(2
1
)2(. （） 5.
()⎰b a
dx x f 表示以曲线()x f y =为曲边的曲边梯形的面积. （）
二、填空题（共15分，每小题3分）
1. 若22
lim 2
22=--++→x x b
ax x x , 则a = b = . 2. 设)(x f 可导，且满足()()
12311lim 0
-=--→x
x f f x ，则)1(f '= .
3. 设()x x
x f 2cos 2
sin
+=，则()()π27f = .
4. 若C x dx x
x f +=⎰
arctan )
(，则⎰
=dx x f )( . 5.
(2
1
1
x dx -+
⎰
= .
三、选择题（共15分，每小题3分，在每小题给出的四个选项内，只
有一项是符合题目要求的） 1．设当0→x 时,()()x x βα,都是无穷小()()0≠x β,则当0→x 时,下列表达式中不一定为无穷小的是（）
A 、()()()x x βα⋅+1ln
B 、()()x
x x 1sin 22
βα
+
C 、 ()()
x x βα2 D 、()()x x βα+
2．设()x ϕ在a x =连续，()()x a x x F ϕ-=，则（）
A 、)(x F 在a x =点间断
B 、)(x F 在a x =点连续但不可导
C 、)(x F 在a x =点可导
D 、)(x F 在a x =点的可导性与()a ϕ有关 3. 在区间]1,0[上，满足罗尔定理全部条件的函数为（）
A 、⎪⎪⎩⎪⎪⎨⎧
≥-<=21
12
1)(x x x x x f B 、 ⎩⎨⎧≥<=111)(x x x x f
C 、⎪⎪⎩⎪⎪⎨⎧≥<-=1411)2
1()(2x x
x x x f D 、⎩⎨⎧≥<=101)(2x x x x f
4. 设)(x F 为偶函数)(x f 的一个原函数，则（） A 、)()(x F x F -= B 、c x F x F +-=-)()( C 、c x F x F +-=)()( D 、)()(x F x F -=-
5. 下列命题中不正确的是（）
A 、若0x 为)(x f 的可导的极值点，则0)('0=x f ；
B 、若0)('0=x f ，0x 一定是)(x f 的极值点；
C 、连续函数从左到右,单调性改变的点是极值点，凹凸性改变的点
))(,(00x f x 是拐点；
D 、若0)(''0=x f ，则))(,(00x f x 不一定为曲线的拐点.
四、计算题（共48分，每小题6分）
1. ()()3
2
d cos ln lim
x
t
t t x
x ⎰+→.
2. ⎪⎭⎫
⎝
⎛--→x x x ln 111lim 1. 3. x x
e e
y cos cos +=, 求y '.
4. 求由参数方程2ln(1)
arctan x t y t t
ì=+ïí=-ïî所确定函数的二阶导数2
2dx y d . 5. 设1
2
+=
x x y ，求dy .
6. 计算不定积分
⎰
-+.922
dx x
x
7. 设21,0
()ln(1),0
x x f x x x ⎧+<=⎨+≥⎩，计算31
(2)d f x x -⎰.
8. 求⎰
∞+++0
2
8
4x x dx
.
五、综合题（共12分，每小题6分）
1.设函数()x f 在闭区间[]b a ,上连续，且()0>x f ，证明方程
()()
01
=+⎰
⎰
dt t f dt t f x
b
x a
在开区间()b a ,内有唯一的根。

2. 设有抛物线2
:(0,0)L y a bx a b =->>，试确定常数a ，b 的值，使得
（1）L 与直线1y x =-+相切；
（2）L 与x 轴所围图形绕y 轴旋转所得旋转体的体积最大。