弦振动的研究ppt课件
弦振动研究试验(教材)

弦振动研究试验传统的教学实验多采用音叉计来研究弦的振动与外界条件的关系。
采用柔性或半柔性的弦线,能用眼睛观察到弦线的振动情况,一般听不到与振动对应的声音。
本实验在传统的弦振动实验的基础上增加了实验内容,由于采用了钢质弦线,所以能够听到振动产生的声音,从而可研究振动与声音的关系;不仅能做标准的弦振动实验,还能配合示波器进行驻波波形的观察和研究,因为在很多情况下,驻波波形并不是理想的正弦波,直接用眼睛观察是无法分辨的。
结合示波器,更可深入研究弦线的非线性振动以及混沌现象。
【实验目的】1. 了解波在弦上的传播及弦波形成的条件。
2. 测量拉紧弦不同弦长的共振频率。
3. 测量弦线的线密度。
4. 测量弦振动时波的传播速度。
【实验原理】张紧的弦线4在驱动器3产生的交变磁场中受力。
移动劈尖6改变弦长或改变驱动频率,当弦长是驻波半波长的整倍数时,弦线上便会形成驻波。
仔细调整,可使弦线形成明显的驻波。
此时我们认为驱动器所在处对应的弦为振源,振动向两边传播,在劈尖6处反射后又沿各自相反的方向传播,最终形成稳定的驻波。
图 1为了研究问题的方便,当弦线上最终形成稳定的驻波时,我们可以认为波动是从左端劈尖发出的,沿弦线朝右端劈尖方向传播,称为入射波,再由右端劈尖端反射沿弦线朝左端劈尖传播,称为反射波。
入射波与反射波在同一条弦线上沿相反方向传播时将相互干涉,在适当的条件下,弦线上就会形成驻波。
这时,弦线上的波被分成几段形成波节和波腹。
如图1所示。
设图中的两列波是沿X轴相向方向传播的振幅相等、频率相同、振动方向一致的简谐波。
向右传播的用细实线表示,向左传播的用细虚线表示,当传至弦线上相应点时,相位差为恒定时,它们就合成驻波用粗实线表示。
由图1可见,两个波腹或波节间的距离都是等于半个波长,这可从波动方程推导出来。
下面用简谐波表达式对驻波进行定量描述。
设沿X轴正方向传播的波为入射波,沿X轴负方向传播的波为反射波,取它们振动相位始终相同的点作坐标原点“O”,且在X =0处,振动质点向上达最大位移时开始计时,则它们的波动方程分别为:Y1=Acos2 (ft-x/ )Y2=Acos2 (ft+x/ )式中A为简谐波的振幅,f为频率, 为波长,X为弦线上质点的坐标位置。
弦振动的研究

x实验2.5 弦振动的研究、实验目的1. 观察弦振动时形成的横驻波的特性.2. 通过不同途径,测量弦线上横波的传播速度,比较测得的结果.3. 研究弦振动时波长与张力的关系.、仪器设备WZB-4型驻波实验仪、弦线、天平.WZB-4型驻波实验仪如图2.5-1所示,该实验仪用金属导线作为弦线,由信号发生器提供低频信号(频率可以改变),在金属导线下面放一块磁铁,这样载流导 体在磁场中因受安培力的作用,按信号频率作横向振动而产生横波,再由入射波 和反射波相干而形成驻波.图中 AA 、BB 为连接弦线和信号发生器的两对接线 柱,A 和A ,B 和B'已经连接好.C 为定位杆,上有小孔,弦线穿过小孔,可以 定位弦线的位置.R 1、R 2为两块劈形滑块,用以调整弦线的振动区长度 I (简称弦长).D 为一测量标尺,用以测量金属滑块之间的距离. M 为磁铁,E 为滑轮,以图2.5-1 WZB-4型驻波实验仪的结构三、实验原理1. 驻波图2.5-2驻波形成示意图频率和传播速度都相同的两列相干波,在同一直线上沿相反挂钩连接砝码,每组有3个砝码:10克,20克,40克各1个.频率计]安培表IB'频率调节振幅调节接线柱 电源R ^ M "?DITR驻波是由振幅、为V 的简谐振动.当x =±(2K +1)t 时(其中K = 0,1,2……),这些点的振动幅度始终为零,4 称为波节.当x=±K 上时(K = 0,1,2……),这些点的振幅达到最大2A,称为2 波腹.相邻两波节(或波腹)之间的距离恰为 一。
因此在驻波实验中,只要测得2 相邻两波节(或波腹)间的距离,就可以确定其波长.2. 弦线上横波的传播速度11图2.5-3 实验装置图如图2.5-3所示,将弦线的一端穿过定位杆C 的小孔固定,另一端跨过滑轮E 系以方向传播时叠加而成的一种特殊形式的干涉现象.如图 2.5-2所示,设有两列频率相同、振幅相同、初相位为零的简谐波,分别沿 ox 轴正方向和ox 轴负方向传播,它们的波动方程分别为xy r = Acos2兀(vt -—)Ay 2 = Acos2 兀(vt + —)A(2.5-1 ) (2.5-2 )x x=Acos2 兀(vt —―) + Acos2 兀(vt +—)AAf2兀)(2.5-3 )这就是驻波的波函数,常称之为驻波方程,式中2AC0S 竺X 是各点的振幅,它只A与x 有关.上式表明,当形成驻波时,弦线上的各点作振幅为2兀2AC0S ——x,频率砝码W并接通正弦信号源.在磁铁M的作用下,通有电流的弦线就会受到与电流垂直的安培力的作用,当弦线上通有正弦交变电流时,安培力也随之呈正弦 变化.可认为磁铁 M 所在处对应的弦线为振源,振动向两边传播,在劈形滑块 R i和R 2两处反射后又沿着各自相反的方向传播而发生干涉.由于固定弦线的两端是 由劈形滑块R 和R 支撑的,故两端点为波节,只有当R i 和R 之间的距离(即弦长I ) 等于半波长的整数倍时,才能形成驻波,这就是均匀弦振动产生驻波的条件设正弦信号频率为V ,则波速为(2.5-4 )21若这个时候R 与Fb 之间有n 个半波长,则波长A =-,弦线上的波速为n2I V =v —n可以证明(见附录)在线密度(单位长度的质量)为 P ,张力F T 的弦线上, 横波的传播速度(2.5-6 )波长(2.5-7 )四、实验内容1. 测定弦线的线密度在天平上秤其质量 m 求出线密度P (或者由实验室预 先秤好给出).2. 观察弦线上的驻波(1)刮去漆包线两端的漆层,穿过定位杆 C 的小孔,接到接线柱 A .另一端跨 过滑轮E 系上砝码 W 然后再接到接线柱B',构成一个导电回路.系砝码时请注意,从砝码到接线柱 B'间的弦线要松些,不能紧绷.信号发生 器的输出端接接线柱A 和B.(2)将弦长I 设置为一定长度.在砝码钩上增减砝码,改变弦线的张力F T ,(2.5-5 )取约2米长的漆包线,仔细调节信号频率^^和信号强度,使弦线上产生若干个波形清晰、稳定的驻波.(3)选定一定的砝码质量和信号频率,仔细调节弦长I、使弦线上产生若干个波形清晰、稳定的驻波.3.测量弦线上横波的传播速度(1)弦线张力不变,弦长I也不变的条件下,调节振动频率V ,测量弦线上横波的传播速度.(2)弦线张力不变,振动频率^/也不变的条件下,调节弦长I,测量弦线上横波的传播速度.(3)改变张力,重复步骤(1)、(2)。
实验3%20弦振动实验ppt

大学物理实验
【实验原理及仪器】
引起弦线上质点的振动,于是振动就由A端沿弦 线向B端传播,形成的波称为入射波;传到支点 B后发生反射,弦线中产生由B端沿弦线向A端传 播的波,称为反射波。入射波与反射波在同一 条弦线上沿相反方向传播时将互相干涉,移动 劈尖B到适当位置,弦线上的波就形成驻波。这 时,弦线上的波就被分成几段且每段波两端的 点始终静止不动,而中间的点振幅最大。我们 把这些始终静止的点就称为波节,振幅最大的 点就称为波腹。
大学物理实验
Ln
2
(n 1, 2, 3L
)
)
2L (n 1, 2, 3L n
T V
f T
2 fL V n
)
n (n 1 , 2, 3L 2L
大学物理实验
【实验内容及步骤】 测定弦的线密度(可采用以下几种方法) (1)选取一个固定的弦长L,张力T由砝码的质量可 以求得,调节激振频率f,使弦上依次出现段驻波波 腹,并记录AB间距离L,并求的平均值。 (2)在频率一定的条件下,取一固定弦长,改变张 力的大小,测量弦线上横波的传播速度Vf。 (3)在张力T和频率f一定的条件下,改变L,使弦 上出现个驻波波腹。记录相应的 f、 n、 L,由(7)式 计算出弦上的横波速度的测量值VT,从 Y1 A cos 2 f t X Y2 A cos 2 f t
A
X(t=0)
X(t=T/4)
X(t=T/2) λ/2
图1 驻波的形成
X Y1 Y2 2 A cos 2 cos 2 f t
实验2.3 弦振动实验
Shenzhen lean-sigma consultant Co., LTD 版权所有 翻版必究
弦振动研究
弦振动研究【实验目的】1.了解波在弦上的传播及驻波形成的条件。
2.测量不同弦长和不同张力情况下的共振频率。
3.测量弦线的先行密度。
4.测量弦振动时波的传播速度。
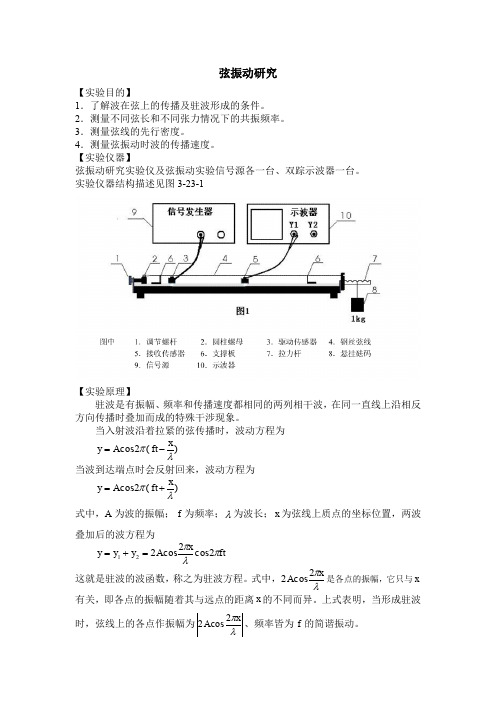
【实验仪器】弦振动研究实验仪及弦振动实验信号源各一台、双踪示波器一台。
实验仪器结构描述见图3-23-1【实验原理】驻波是有振幅、频率和传播速度都相同的两列相干波,在同一直线上沿相反方向传播时叠加而成的特殊干涉现象。
当入射波沿着拉紧的弦传播时,波动方程为)(2cos λπxft A y -=当波到达端点时会反射回来,波动方程为)(2cos λπxft A y +=式中,A 为波的振幅;f 为频率;λ为波长;x 为弦线上质点的坐标位置,两波叠加后的波方程为ft xA y y y πλπ2cos 2cos221=+=这就是驻波的波函数,称之为驻波方程。
式中,λπxA 2cos2是各点的振幅,它只与x有关,即各点的振幅随着其与远点的距离x 的不同而异。
上式表明,当形成驻波时,弦线上的各点作振幅为λπxA 2cos2、频率皆为f 的简谐振动。
由式(3-23-3)可知,另02cos2=λπxA ,可得波节的位置坐标为4)12(λ+±=k x ⋅⋅⋅=,,,210k另12cos2=λπxA ,可得波腹的位置坐标为2λkx ±= ⋅⋅⋅=,,,210k由式(3-23-4)、式(3-23-5)可得相邻两波腹(波节)的距离为半个波长,由此可见,只要从实验中的测得波节或波腹间的距离,就可以确定波长。
在本实验中,由于弦的两端是固定的,故两端点为波节,所以,只有当均匀弦线的连个固定端之间的距离(弦长)L 等于半波长的整数倍时,才能形成驻波。
即有 2λ=L 或 n L2=λ ⋅⋅⋅=,,,210n式中,L 为弦长;λ为驻波波长;n 为半波数(波腹数)。
另外,根据波动理论,假设弦柔韧性很好,波在弦上的传播速度v 取决于线密度μ和弦的张力T ,其关系为μTv =又根据波速、频率与波长的普遍关系式λf v =,可得μλTf v ==由式(3-23-6)、式(3-23-8)可得横波传播速度 nL f v 2= 如果已知张力和频率,由式(3-23-6)、式(3-23-8)可得线密度2)2(Lfn T =μ 如果已知线密度和频率,则由式(3-23-10)可得张力2)2(nLf T μ=如果已知线密度和张力,则由式(3-23-11)可得张力μTL n f 2=【实验内容】一、实验前准备1.选择一条弦,将弦的带有铜圆柱额一端固定在张力杆U型槽中,把带孔的一端套到调整螺杆上圆柱螺母上。
弦振动的实验研究

弦振动的实验研究弦振动的实验研究弦是指⼀段⼜细⼜柔软的弹性长线,⽐如⼆胡、吉它等乐器上所⽤的弦。
⽤薄⽚拨动或者⽤⼸在张紧的弦上拉动就可以使整个弦的振动,再通过⾳箱的共鸣,就会发出悦⽿的声⾳。
对弦乐器性能的研究与改进,离不开对弦振动的研究,对弦振动研究的意义远不只限于此,在⼯程技术上也有着极其重要的意义。
⽐如悬于两根⾼压电杆间的电⼒线、⼤跨度的桥梁等,在⼀定程度上也是⼀根“弦”,它们的振动所带来的后果可不象乐器上的弦的振动那样使我们们感到愉快。
对于弦振动的研究,有助于我们理解这些特殊“弦”的振动特点、机制,从⽽对其加以控制。
同时,弦的振动也提供了⼀个直观的振动与波的模型,对它的分析、研究是处理其它声与振动问题的基础。
欧拉最早提出了弦振动的⼆阶⽅程,⽽后达朗贝尔等⼈通过对弦振动的研究开创了偏微分⽅程论。
本实验意在通过对⼀段两端固定弦振动的研究,了解弦振动的特点和规律。
预备问题1.复习DF4320⽰波器的使⽤。
2.什么是驻波?它是如何形成的?3.什么是弦振动的模式?共振频率与哪些因素有关?4.张⼒对波速有何影响?试⽐较以基频和第⼀谐频共振时弦中的波速。
⼀、实验⽬的:1、了解驻波形成的条件,观察弦振动时形成的驻波;2、学会测量弦线上横波传播速度的⽅法:3、⽤作图法验证弦振动频率与弦长、频率与张⼒的关系。
⼆、实验原理⼀根两端固定并张紧的弦,静⽌时处于⽔平平衡位置,当在弦的垂直⽅向被拉离平衡位置后,弦会有回到平衡位置的趋势,在这种趋势和弦的惯性作⽤下,弦将在平衡位置附近振动。
令弦线长度⽅向为x 轴,弦被拉动的⽅向(与x 轴垂直的⽅向)为y 轴,如图1所⽰。
若设弦的长度为L ,线密度为ρ,弦上的张⼒为T ,对⼀⼩段弦线微元dl 进⾏受⼒分析,运⽤⽜顿第⼆定律定律,可得在y ⽅向的运动微分⽅程()2222tydx dx x y T ??=??ρ(1)若令ρ/2T v =,上式可写为222221tyv x y ??=?? (2)y 图1(2)式反映了弦的位移y 与位置x 、时间t 的关系,其中)/(ρT v =代表了在弦线上横波传播的波速。
基础物理实验--关于弦振动的探究附图

如何做好这个实验呢?这里有图有真相~一、首先了解一下实验目的:1、观察弦振动形成的驻波。
熟悉其性质2、测定弦振动张力与波速的关系3、测定音叉的频率二、实验原理一、驻波的性质柔软均匀的弦线被拉紧,一端固定,另一端以一个固定频率振动,于是激起一个由振动端传至固定端然后反射回来的波,前进波和反射波不断在弦线上传播,并发生干涉。
为了简便可见,我们视前进波与反射波的振幅相等,通过调整绳线的压力,当弦线的长度为半波长的整数倍时,形成振幅最大又稳定的驻波,即弦与音叉共振。
前进波为;y1=Asin2p(t/T-x/λ)y2=Asin〔2p(t/T-(X+2l)/λ)-p〕y=y1+y2 经三角函数变换,得y=〔2Asin2p(l/λ)〕cos2p〔t/T-(x+l)/λ〕此式即驻波方程,式中余弦符号前面的系数是驻播上各点振动的振幅,可见,驻波上不同的点(不同l)以不同的振幅振动,振动的振幅依点的位置而按正弦规律变化,振动的最大值等于2A,叫波腹;最小值等于0,叫波节。
可见驻波上某些点始终以最大的振幅振动,某些点则始终静止。
处sin2p(l/λ)=0,是波节的位置,即l=0,λ、2、2λ/2、3λ/2......波节的位置;处sin2p(l/λ)=1,是波腹的位置,即l=λ/4、3λ/4、5λ/4、7λ/4.......是波腹的位置可见,波节与波节,波腹与波腹的距离,叫做驻波的波长,它等于形成这个驻波的两个横波波长的一半,因此利用驻波可以方便的测出横波波长二、音叉以固有频率做等幅简谐振动的原理音叉两臂间装有一个电磁铁N,磁铁的线圈一端接直流电源,一端接螺钉尖端的固定架,螺钉尖端可与音叉一臂上的弹片接触,电源另一极在音叉座驾上,通电后,调整尖端与音叉的距离(这是重要操作,音叉与尖端不能接触,但要足够近,以至于产生尖端放电,形成回路),电磁铁线圈有电流通过,音叉臂在电磁铁的吸引下使得尖端断开,电流中断,电磁铁失去吸引力,音叉臂弹回,弹片与尖端重新接触电路接通,电磁铁又吸引如此反复,使音叉以固有频率不断振动,而且每次振动都能得到电磁铁补给的能量,因此,音叉按照它的固有频率做等幅振动。
弦振动的研究

3、计算波速 从以上测量中,选取合适的数据,用 两种方法求波速,说明其差异是否显著。 4、从测量纪录中,选一组数据 (T=40g),计算弦振动频率,求其与音 叉频率的百分差。
弦振动的研实验目的
1、观察弦振动时形成的驻波 2、验证弦振动的波长与张力 的关系 3、测量弦上横波的传播速度
实验仪器
• 电振音叉
• 弦线 • 滑轮 • 砝码 • 米尺
实验原理: 实验原理 由波动理论可以证明,横波沿着一条 拉紧的弦线传播时,波速v与弦线的张力T、 线密度ρ (单位长度的质量)间的关系为
T
实验内容: 实验内容: 1.观察驻波的形成和波形,波长的 变化。 (1)安装调试实验装置。如图所示, 接通电源后,调节螺钉 k ′ ,使音叉振 动; (2)改变弦线长(移动音叉)或砝码 质量,使之产生振幅最大且稳定的驻波 ,改变数次,观察波形、波长的变化情 况。
2、弦上横波的波长与张力的关系 增加砝码的质量,再细调弦长使其共 振,保持n=1或2个波段数,测出弦长l, 算出波长λ,重复测量取平均值。FT值 取20、40、60、80、100ɡ。 作 λ ~ FT 图,根据图求出斜率,求出 线密度ρ值,求其与测量值得百分差
v = FT
ρ
(1)
设f为弦线的波动频率;λ为弦线上传播 的横波波长,则根据v =fλ和(1)式得 1 F
λ=
T
f
ρ
当f、ρ一定时λ与 F 成正比。 形成驻波的条件:两列波,频率相同 ,振动方向相同,振幅基本相同,传播 方向相反。 λ l = n (n=1,2,3,……)时,得 当弦长 2 到稳定的最大幅度的驻波,波长 λ = 2l , n 则波速 v = f 2nl
大学物理实验讲义-弦振动与驻波研究

大学物理实验讲义-弦振动与驻波研究弦振动与驻波研究【实验目的】1.观察在弦上形成的驻波;2.确定弦线振动时驻波波长与张力的关系; 3.学习对数作图和最小二乘法进行数据处理。
【实验原理】在一根拉紧的弦线上,其中张力为T ,线密度为μ,则沿弦线传播的横波应满足下述运动方程:2222x yT t y ∂∂=∂∂μ(1)式中x 为波在传播方向(与弦线平行)的位置坐标,y 为振动位移。
将(1)式与典型的波动方程22222x y V t y ∂∂=∂∂相比较,即可得到波的传播速度: μTV =若波源的振动频率为f ,横波波长为λ,由于波速λf V =,故波长与张力及线密度之间的关系为:μλTf1=(2)为了用实验证明公式(2)成立,将该式两边取对数,得:11lg lg lg lg 22T f λμ=-- (3)固定频率f 及线密度μ,而改变张力T ,并测出各相应波长λ,作lg λ-lg T 图,若得一直线,计算其斜率值(如为21),则证明了λ∝21T的关系成立。
弦线上的波长可利用驻波原理测量。
当两个振幅和频率相同的相干波在同一直线上相向传播时,其所叠加而成的波称为驻波,一维驻波是波干涉中的一种特殊情形。
在弦线上出现许多静止点,称为驻波的波节。
相邻两波节间的距离为半个波长。
【实验仪器】1、可调频率数显机械振动源;2、振动簧片;3、弦线(铜丝);4、可动刀片支架;5、可动刀口支架;6、标尺;7、固定滑轮;8、砝码与砝码盘;9、变压器;10、实验平台;11、实验桌9123456781011图1 实验装置示意图图2 可调频率数显机械振动源面板图 (1、电源开关 2、频率调节 3、复位键 4、幅度调节 5、频率指示)实验装置如图1所示,金属弦线的一端系在能作水平方向振动的可调频率数显机械振动弦线上驻波实验仪电 源ON复位 幅度 调节上海复旦天欣科教仪器有限公司频率调节H Z1 2 3 45FD-SWE-II源的振簧片上,频率变化范围从0-200Hz 连续可调,频率最小变化量为0.01Hz ,弦线一端通过定滑轮⑦悬挂一砝码盘⑧;在振动装置(振动簧片)的附近有可动刀片支架④,在实验装置上还有一个可沿弦线方向左右移动并撑住弦线的可动刀口⑤。
实验8 固定均匀弦振动的研究

y2
2Acos
x
cos ft
因为在波节处振幅为零,即
cos2 x 0
2 x (2k 1)
2
(k 0, 1, 2, )
所以可得波节的位置为 x (2k 1)
4
相邻两波节之间的距离为:
xk 1
x1
2
又因为波腹处的质点振幅为最大,即
cos2 x 1
2 x k
(k 0,1, 2, )
对均匀弦线扰动引起弦线上质点的扰动引起弦线上质点的振动于是波动就由振动于是波动就由aa端端朝朝bb端方向传播称为入端方向传播称为入射波再由射波再由bb端反射沿弦端反射沿弦线朝aa端传播称为反射端传播称为反射波
大学物理实验
固定均匀弦振动的研究
杭州电子科技大学 物理实验中心
前 言 实验目的 实验仪器 实验原理 实验内容 注意事项
实验目的
1、了解固定均匀振动传播的规律; 2、观察固定弦振动传播时形成验波的波形; 3、测定均匀弦振动上横波传播的速度
实验仪器
固定均匀弦振动实验装置,砝码。
1、6香蕉插头座 2、频率显示 3、电源开关 4、频率调节旋钮 5、磁钢 7、砝码盘 8、米尺 9、弦线 10、滑轮及托架
实验原理
设一均匀弦线,一端 由劈尖A支住,另一端由 劈尖B支撑。对均匀弦线 扰动,引起弦线上质点的 振动,于是波动就由A端 朝B端方向传播,称为入 射波,再由B端反射沿弦 线朝A端传播,称为反射 波。入射波与反射波在同 一条弦线上沿相反方向传 播时将相互干涉,移动劈 尖B到适合位置。弦线上 的波就形成驻波。如图所 示:
用简谐表达式对驻波进行定量描述。设沿X轴正方向传 播的波为入射波,沿X轴负方向传播的波为反射波,取它 们振动位相始终相同的点作标原点,且在x=0处,振动质 点向上达最大位移时开始计时,则它们的波动方程为:
三年级下册音乐课件-3.1(活动)声音的奥秘—琴弦振动与弹拨乐器-接力版(共12张PPT)

人们在劳动和生活中发现弓
弦振动会发出声音,并受此启发 创造发明了弹拨类乐器。
古代的弹拨乐器
中国民族乐队中常见的弹拨乐器
试一试, 用文具探索琴弦弹拨的秘密。
音乐小知识
琴弦: 弦乐器上激发声音的线,在一定的张力下,通过摩擦、
弹击等手法激发弦振动,经过共鸣腔的放大,得到乐音, 是弦乐器最重要的组成部分。通常采用蚕丝、羊肠、金属、 或长丝塑料纤维制成。
音乐小知识
民谣吉他弦指的是钢弦,在1、2弦而讲,材质是种高
碳钢,它具有很好的伸展性和弹性,在锡中浸泡过后,涂
上了一层保护膜,减少了外界的腐蚀,延长了使用时间,
同时又具备了明亮的外表和光滑的手感。而3、4、5、6弦
则不同,除了内部的高碳钢外还裹了一层合成的金属线圈,
此时内部的高碳钢往往做成6角形而不是圆形起来,达到更好的共振效果。
音乐小知识
弹拨乐器是用手指或拨子拨弦,及用琴竹击弦而发音 的乐器总称。
音乐小知识
弹拨乐器分横式与竖式两类。横式,如:筝(古筝和转
调筝)、古琴、扬琴和独弦琴等;竖式,如:琵琶、阮、月
琴、三弦、柳琴、冬不拉和扎木聂等。
音乐小知识
弹拨乐器的历史悠久,种类形制繁多,是极富特色的 一类弦乐器。
弦振动驻波实验PPT课件

感谢您的观看。
第13页/共13页
数据表格
第11页/共13页
注意事项
• 驱动传感器与接收传感器不能靠得太近,否则会产生干 扰,两个传感器的距离应大于10cm。
• 改变砝码质量时要轻拿轻放,要使砝码静止后再进行测 量。
• 在移动劈尖调整驻波时,磁铁应在两劈尖之间,且不能 处于波节位置,要等波形稳定后,再记录数据。
第12页/共13页
mg
f 2 2
和E
Δ
计算 和
Δ
(2 f
)2
(2Δ
)2
Δ
(m
)2
f
m
第8页/共13页
实验内容
2. 测定弦线上横波的传播速度
(1)测得张力及所测线密度,测定弦线中的横波波速vf
T
vf
(2)在同一张力条件下,测出共振频率及波长,测量弦线中 的横波波速vf
vf f
第9页/共13页
数据表格
第10页/共13页
(3)
第2页/共13页
实验原理
令
2Acos 2x
0
可得波节的位置坐标为:
x (2m 1) , 4
m 0,1, 2
令
2Acos 2x
2A可得波腹的位置坐标为:
x m ,
2
m 0,1, 2
相邻两波节(或波腹)的距离为
xm xm1 2
因此,在驻波实验中,只要测得相邻两波节或相邻两波腹的距离, 就可以确定波长。
由于弦的两端分别由劈尖ab支撑故两端点劈尖必为波节又由于相邻两波节的距离为2所以当弦上出现稳定驻波时ab两点的距离l必为2的整数倍
实验原理
驻波可以由两列振动方向相同,频率相同,振幅相等, 传播方向相反的简谐波叠加和干涉产生。
质点振动学弦振动梁的纵振动-PPT文档资料

• •
Prof. Sheng Meiping Northwestern Polytechnical University
质点振动学
• •
Prof. Sheng Meiping Northwestern Polytechnical University
质点振动系统
振动系统分类及准则
• •
• 强迫振动方程:
• 解的一般形式: • 特解形式:
激励力
2 d d j t M 2 c K F e A dt dt
' j t 0
j t e Ae e F t
e 1 F
j t
F A F 2 M j cK
• 稳态振动、瞬态振动
课程简介
• •
Prof. Sheng Meiping Northwestern Polytechnical University
主要教学资源
教材:
盛美萍等编著《噪声与振动控制技术》
参考资料:
杜功焕等编著《声学基础》 R.G.White等编著《Noise and Vibration》 工程分析全部来自主讲教师工程实践 Journal of Sound and Vibration Applied Acoustics
质点振动系统的强迫振动
• 方程的解:
e Ae
t
包络曲线
' j t 0
' 2 2 0 0
振动衰减曲线
t
• •
Prof. Sheng Meiping Northwestern Polytechnical University
问题
拉力器的等效刚度分析
固定均匀弦振动的研究PPT优秀

固定均匀弦振动 的研究
大学物理实验教学中心
在自然界中,振动和波是一种普遍的运动形式, 它在力(包括声)、热、电、光各领域都广泛存在, 例如力学中的机械振动和机械波;电磁学中的电磁震 荡和电磁波;光学中的光波等等。振动与波具有自己 的特征:振动有振幅、频率与相位,在媒质中伴随着 能量以一定的速度传播。波具有反射、折射、干涉和 衍射等独特的现象。上述独特的运动形式帮助人们在 微观世界中发现了粒子的波动性,证实了物质的波粒 二象性,建立了量子力学(也常称波动力学),由此 可见振动与波的重要性。
注意事项
严禁两பைடு நூலகம்钢吸碰以免撞碎。 改变砝码时注意码槽的形状,从上往下轻轻放,严
禁用力挤压弄断弦线。 弦线两头与电极接线柱连接必须彻底去掉绝缘漆,
保证有良好的接触。 移动A、B两支撑劈尖调整波段时,磁钢应处于波腹
处,而且细心调节使形成的驻波达到最佳的稳定, 方可记录数据。
实验结束
若有不清楚的地方, 欢迎同学们自己重新播放 观看!
波仪具器有 介反绍射(、点8折击0射图H、片z干播,涉放和)1衍0射0等H独z特,的现1象2。0Hz, 140Hz, 160Hz, 调节支撑点A、B间 距离使弦上出现n=1、n=2个驻波段。记录相应值,计算此 仪器介绍(点击图片播放)
移动A、B两支撑劈尖调整波段时,磁钢应处于波腹处,而且细心调节使形成的驻波达到最佳的稳定,方可记录数据。 改变砝码时注意码槽的形状,从上往下轻轻放,严禁用力挤压弄断弦线。
1.测量均匀弦的线密度,测多次取平均值。
2.张力一定,改变频率测量弦线上横波传播的速度:
电本磁实学 验中研的究电波磁的震特将荡征和之弦电一磁:线波干;涉的现象一的特端例挂——上驻波。40.0g砝码、选取频率分别为60Hz,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
υ
T ρ
(2.8—2)
按波动公式 u f,结合式(2.8—2)
可得弦振动波长与张力的关系为
λ
1 f
T ρ
(2.8—3)
从式(2.8—1)容易得出前进波、反射波都是波动方程的
解,当满足一定条件时弦振动方式为驻波,为简明起见,
设x=0及x=L处 y≡0,即视弦的两端为固定,则驻波条件
可记为
L
(6)写出各测量结果不确定度表示方式。即
n
i
i i1 5
uc.i S2 i Nhomakorabea
2
λi λi ucλ.i (cm )
Si
n
( i i )2
i 1
n( n 1)
0.2 3
【注意事项】
(1) 调节滑轮C高度,使弦线成水平,并使 弦线和音叉腿成一直线,不能是折线
l2A
l2B
l2
/cm /cm /cm
n=3
l3A
l3B
l3
/cm /cm /cm
n=4
l4A
l4B
l4
/cm /cm /cm
/m/s-1
vf f /m/s-1 lg f
lg T
f = Hz
(4)取对数lgλ、lgT,并作lgλ—lgT图,以验证其 线性关系及振动频率。
(5)对本实验进行误差分析
m
才会使弦上出现一个半波区?
此课件下载可自行编辑修改,供参考! 感谢您的支持,我们努力做得更好!
弦振动的研究
➢实验目的 ➢实验原理 ➢实验内容 ➢注意事项 ➢思考题
【实验目的】
1.观察驻波的形成,归纳驻波性质. 2.弦振动的研究:弦振动的波长与
弦张力之间的关系.
【实验原理】
振幅相同、频率相同、振动方向相同、周相差恒定的两 列波在同一直线上相向传播叠加而形成的一种看起来停驻不 前的波形,称为驻波。波的叠加引起的驻波是一种重要的振 动现象,它广泛存在于自然现象之中,管、弦、板、膜的振 动都可形成驻波。驻波在声学、无线电学和光学等领域都有 重要的应用。利用驻波可以测定波长,也可确定振动系统的 固有频率。
(2) 测量时应使驻波波形稳定,且波节清晰, 砝码不要晃动,应保持静态。
(3) 电振音叉不起振或不使用时,应将触点 断开。
(4) 实验完毕,应立即将所有砝码取下放好。
【思考题】
(1)本实验是振动频率固定情况下的λ—T关系, 如果频率改变而波长不变则实验如何进行?
(2)弦在频率为f 的音叉策动下振动,当T为某 值时,若弦上出现m个半波区,则弦的基频应 为 f ,为什么?若频率不变,则应如何改变张力,
nλ 2
(n =1,2,…,为弦上半波个数)
可见形成驻波时可方便地测得波长λ。
本实验验证(2.8—3)式时测定λ,就是把弦振动调整 到驻波状态而进行的,弦线取适当长,在电动音叉带 动下,起振后适当调节张力(可先试以手按砝码盘) 即可看见驻波现象:某些点不振动为波节,波节中间 振幅最大处为波腹,应再细心调节注意观察,直至出 现波腹极大而且稳定,且仅限于y方向振动(没有z方 向的振动),这可在初选固定张力下慢慢移动支撑点 D的位置,细调弦长来获得。
验证(2.8—3)式还可采用直观的图解法,对式 (2.8—3)取对数:
lgλ1lgT 1lgρlgf 22
因ρ、f均为确定值,故以lgλ对lgT作图应为直线, 且其斜率为1/2
如果ρ事先测得,则由直线的截距还可求得弦振动频 率值,并与音叉的频率比较是否一致。
【实验内容】
1、观察弦振动驻波的形成
弦线的张力
,
TmgW
m为砝码及砝码托的质量和.
(2)通电,调节振子螺钉(注意不可过紧)使音叉振动起 来,固定弦长约70cm左右,手按弦线以改变张力,观察 弦上形成不同半波个数时的驻波。取n =1,2,3,4,5, 可从手感觉张力T 的不同,并估计其大概数值。
2、λ—T关系研究
(1)挂上适当的砝码,并使T一定,取n=1,微调弦长L (通过沿着弦线方向慢慢移动支撑点D),获得稳定、 最大的振幅,并且振动仅沿y方向(无z方向运动), 记下L、T求出λ。
(1)按图接好线路,弦线L的一端固定在音叉A的 一脚B,另一端跨过滑轮C悬一重物W. 音叉的 振动利用电磁铁来激发,电源E的一端接音叉, 另一端通过开关K、电磁铁B的线圈和可调螺丝 K’与音叉相接,调节K’使之与音叉相接触,则 电路接通,电磁铁吸引音叉. 音叉一被吸动后, 螺丝与音叉便不再接触,电流中断,电磁铁失 去吸引音叉的作用,音叉又回到原来的位置, 这样反复作用的结果,就使音叉按其固有频率 振动起来.
(2) T不改变,再分别取n—2,3,4,5,重复上述细
调过程,记下相应的L、T .求出λ,并与λ 的理论值比较。
(3)改变砝码值T,重复上述(1)(2)过程,求出相应的λ 值。
频率f不变,改变砝码(连托盘)质量m, 测定弦线中的横波波速vf
T =mg
n=1
l1A
l1B
l1
/cm /cm /cm
n=2
弦振动可视作一维的波动,绷紧的弦线上一点作横向受迫振 动,会导致横波沿弦线传播并在其端点发生反射,前进波与 反射波干涉便产生驻波。
分析可知弦振动满足波动方程:
2 y T 2 y
t2 x2
(2.8—1)
x为波动传播方向,y为振动位移方向,ρ为弦线的
线密度,T为弦线张力,弦上波速为
