平行四边形辅助线练习题

合集下载

人教版初二数学8年级下册第18章(平行四边形)含辅助线证明题训练(含答案)

人教版数学八年级下期第十八章平行四边形含辅助线证明题训练1.已知边长为2的正方形ABCD中，P是对角线AC上的一个动点（与点A，C不重合），过点P作PE⊥PB，PE交DC于点E，过点E作EF⊥AC，垂足为点F．（1）求证：PB＝PE；（2）在点P的运动过程中，PF的长度是否发生变化？若不变，求出这个不变的值；若变化，试说明理由．2.在▱ABCD中，BE平分∠ABC交AD于点E．（1）如图1，若∠D=30°，AB=6，求△ABE的面积；（2）如图2，过点A作AF⊥DC，交DC的延长线于点F，分别交BE，BC于点G，H，且AB=AF．求证：ED-AG=FC．3.如图，在平行四边形ABCD中，AC，BD交于点O，且AO＝BO，∠ADB的平分线DE交AB于点E．（1）求证：四边形ABCD是矩形．（2）若AB＝8，OC＝5，求AE的长．4.如图，在正方形ABCD中，E是边AB上一动点（不与点A，B重合），连接DE，点A关于直线DE的对称点为F，连接EF并延长交BC于点G，连接DG，过点E 作EH⊥DE交DG的延长线于点H，连接BH．（1）求证：GF＝GC；（2）用等式表示线段BH与AE的数量关系，并证明．5.如图，在平行四边形ABCD中，∠BAD的平分线交BC于点E，交DC的延长线于F，以EC，CF为邻边作平行四边形ECFG．（1）证明平行四边形ECFG是菱形；（2）若∠ABC=120°，连接BG，CG，DG，①求证：△DGC≌△BGE；②求∠BDG的度数；（3）若∠ABC=90°，AB=8，AD=14，M是EF的中点，求DM的长．6.已知正方形ABCD如图所示，连接其对角线AC，∠BCA的平分线CF交AB于点F，过点B作BM⊥CF于点N，交AC于点M，过点C作CP⊥CF，交AD延长线于点P．(1)求证：DP＝BF；(2)若正方形ABCD的边长为4，求DP的长；(3)求证：CP＝BM＋2FN．7.如图，四边形ABCD是菱形，E是AB的中点，AC的垂线EF交AD于点M，交CD的延长线于点F．（1）求证：AM=AE；（2）连接CM，DF=2．①求菱形ABCD的周长；②若∠ADC=2∠MCF，求ME的长．8.在菱形ABCD中，AB＝4，∠ABC＝60°，E是对角线AC上一点，F是线段BC延长线上一点．且CF＝AE，连接BE、EF．（1）如图1，若E是线段AC的中点，求EF的长；（2）如图2．若E是线段AC延长线上的任意一点，求证：BE＝EF．AC，将菱形ABCD绕着点B （3）如图3，若E是线段AC延长线上的一点，CE＝12顺时针旋转α°（0≤α≤360），请直接写出在旋转过程中DE的最大值．9.如图所示，在边长为1的菱形ABCD中，∠DAB=60°，M是AD上不同于A，D两点的一动点，N是CD上一动点，且AM+CN=1.（1）证明：无论M，N怎样移动，△BMN总是等边三角形；（2）求△BMN面积的最小值.10.如图，正方形ABCD中，F在CD上，AE平分∠BAF，E为BC的中点．求证：AF=BC+CF．11.已知：如图（1），点E、F分别为正方形ABCD的边BC、DC上的点，线段AE和AF分别交BD于点M和点N，连接MF，MF⊥AE于点M．（1）求证：∠EAF＝45°；（2）如图（2），连接EF，当AD＝5，DF＝1时，求线段EF的长度；BD．（3）如图（3），作FR⊥BD于R．求证：RM=12BC，CE⊥AB于点E，F是AD的中点，连接12.如图，在平行四边形ABCD中，AB=12EF，CF．求证：（1）EF=CF；（2）∠EFD=3∠AEF．13.如图1，点E为正方形ABCD的边AB上一点，EF⊥EC，且EF=EC，连接AF．（1）求∠EAF的度数；（2）如图2，连接FC交BD于M，交AD于N．求证：BD=AF+2DM．14.已知：如图，G为平行四边形ABCD中BC边的中点，点E在AD边上，且∠1＝∠2．（1）求证：E是AD的中点；（2）若F为CD延长线上一点，连接BF，得∠3＝∠2，求证：CD＝BF+DF．15.如图，四边形ABCD是平行四边形，AD=AC，AD⊥AC，E是AB的中点，F是AC延长线上一点．(1)若ED⊥EF，求证：ED=EF：(2)在(1)的条件下，若DC的延长线与FB交于点P，试判断四边形ACPE是否为平行四边形．并证明你的结论(请先补全图形，再解答)：(3)若ED=EF，则ED与EF垂直吗?若垂直给出证明，若不垂直说明理由．16.在▱ABCD中，∠BAD的平分线交直线BC于点E，交直线DC于点F。

八年级上册几何辅助线专题讲解和练习

八上数学辅助线的添加浅谈一、添辅助线有二种情况：1按定义添辅助线：如证明二直线垂直可延长使它们,相交后证交角为90°；证线段倍半关系可倍线段取中点或半线段加倍；证角的倍半关系也可类似添辅助线;2按基本图形添辅助线：每个几何定理都有与它相对应的几何图形,我们把它叫做基本图形,添辅助线往往是具有基本图形的性质而基本图形不完整时补完整基本图形,因此“添线”应该叫做“补图”这样可防止乱添线,添辅助线也有规律可循;举例如下：1平行线是个基本图形：当几何中出现平行线时添辅助线的关键,是添与二条平行线都相交的等第三条直线2等腰三角形是个简单的基本图形：出现一点发出的二条相等线段时,往往要连结已知点补完整等腰三角形;3等腰三角形中的重要线段是个重要的基本图形：出现等腰三角形底边上的中点,添底边上的中线；4直角三角形斜边上中线基本图形出现直角三角形斜边上的中点,往往添斜边上的中线;出现线段倍半关系且倍线段是直角三角形的斜边,要添直角三角形斜边上的中线;５全等三角形：全等三角形有轴对称形,中心对称形,旋转形与平移形等;如果出现两条相等线段或两个相等角关于某一直线成轴对称,就可以添加辅助线构造轴对称形全等三角形；或添对称轴,对应点连线的中垂线即为对称轴;当几何问题中出现一组或两组相等线段位于一组对顶角两边且成一直线时可添加辅助线构造中心对称形全等三角形加以证明,添加方法是将四个端点两两连结或过二端点添平行线６特殊角直角三角形当出现30,45,60,135,150度特殊角时可添加特殊角直角三角形,利用45角直角三角形三边比为1：1：√2；30度角直角三角形三边比为1：2：√3进行证明二、基本图形的辅助线的画法1.三角形问题添加辅助线方法方法1：倍长中线法;有关三角形中线的题目,常将中线倍长构造全等三角形;方法2：含有平分线的题目,常以角平分线为对称轴,利用角平分线的性质定理和题中的条件,构造出全等三角形,从而利用全等三角形的知识解决问题;方法3：结论是两线段相等的题目常画辅助线构成全等三角形,或利用角平分线、垂直平分线的性质定理进行转换;方法4：结论是一条线段与另一条线段之和等于第三条线段这类题目,常采用截长法或补短法进行转换,所谓截长法就是把第三条线段分成两部分,证其中的一部分等于第一条线段,而另一部分等于第二条线段;2.平行四边形中常用辅助线的添法平行四边形包括矩形、正方形、菱形的两组对边、对角和对角线都具有某些相同性质,所以在添辅助线方法上也有共同之处,目的都是造就线段的平行、垂直,构成三角形的全等、相似,把平行四边形问题转化成常见的三角形、正方形等问题处理,其常用方法有下列几种,举例简解如下：1连对角线或平移对角线：2过顶点作对边的垂线构造直角三角形3连接对角线交点与一边中点,或过对角线交点作一边的平行线,构造线段平行或中位线4连接顶点与对边上一点的线段或延长这条线段,构造三角形相似或等积三角形;5过顶点作对角线的垂线,构成线段平行或三角形全等.三、作辅助线的方法一：中点、中位线,延线,平行线;如遇条件中有中点,中线、中位线等,那么过中点,延长中线或中位线作辅助线,使延长的某一段等于中线或中位线；另一种辅助线是过中点作已知边或线段的平行线,以达到应用某个定理或造成全等的目的;二：垂线、角平分线,翻转全等连;如遇条件中,有垂线或角的平分线,可以把图形按轴对称的方法,并借助其他条件,而旋转180度,得到全等形,,这时辅助线的做法就会应运而生;其对称轴往往是垂线或角的平分线;三：边边若相等,旋转做实验;如遇条件中有多边形的两边相等或两角相等,有时边角互相配合,然后把图形旋转一定的角度,就可以得到全等形,这时辅助线的做法仍会应运而生;其对称中心,因题而异,有时没有中心;故可分“有心”和“无心”旋转两种;四：面积找底高,多边变三边;如遇求面积,在条件和结论中出现线段的平方、乘积,仍可视为求面积,往往作底或高为辅助线,而两三角形的等底或等高是思考的关键;如遇多边形,想法割补成三角形；反之,亦成立;另外,我国明清数学家用面积证明勾股定理,其辅助线的做法,即“割补”有二百多种,大多数为“面积找底高,多边变三边”;四、三角形中作辅助线的常用方法举例一、在证明三角形中多条线段的不等量关系时,若直接证不出来,可连接两点或延长某边构成三角形,使结论中出现的线段在一个或几个三角形中,再运用三角形三边的不等关系证明,如：例1：已知如图1-1：D 、E 为△ABC 内两点,求证:AB ＋AC ＞BD ＋DE ＋CE.证明：法一将DE 两边延长分别交AB 、AC 于M 、N,在△AMN 中,AM ＋AN ＞ MD ＋DE ＋NE;1 在△BDM 中,MB ＋MD ＞BD ； 2 在△CEN 中,CN ＋NE ＞CE ； 3 由1＋2＋3得：AM ＋AN ＋MB ＋MD ＋CN ＋NE ＞MD ＋DE ＋NE ＋BD ＋CE ∴AB ＋AC ＞BD ＋DE ＋EC法二：如图1-2, 延长BD 交 AC 于F,延长CE 交BF 于G,在△ABF 和△GFC 和△GDE 中有：AB ＋AF ＞ BD ＋DG ＋GF 三角形两边之和大于第三边1 GF ＋FC ＞GE ＋CE 同上………………………………2 DG ＋GE ＞DE 同上……………………………………3 由1＋2＋3得：AB ＋AF ＋GF ＋FC ＋DG ＋GE ＞BD ＋DG ＋GF ＋GE ＋CE ＋DE ∴AB ＋AC ＞BD ＋DE ＋EC;二、在证明三角形中某些角的不等量关系时,如直接证不出来时,可连接两点或延长某边,构造三角形,使求证的大角在某个三角形的外角的位置上,小角处于这个三角形的内角位置上,再利用外角定理：例如：如图2-1：已知D 为△ABC 内的任一点,求证：∠BDC ＞∠BAC;BDC 与∠BAC 不在同一个三角形中,没有直接的联系,可适当添加辅助线构造新的三角形,使∠BDC 处于在外角的位置,∠BAC 处于在内角的位置；证法一：延长BD 交AC 于点E,这时∠BDC 是△EDC 的外角,A BCDEN M 11-图ABCDEF G21-图AD E G∴∠BDC ＞∠DEC,同理∠DEC ＞∠BAC,∴∠BDC ＞∠BAC 证法二：连接AD,并延长交BC 于F ∵∠BDF 是△ABD 的外角∴∠BDF ＞∠BAD,同理,∠CDF ＞∠CAD ∴∠BDF ＋∠CDF ＞∠BAD ＋∠CAD 即：∠BDC ＞∠BAC;注意：利用三角形外角定理证明不等关系时,通常将大角放在某三角形的外角位置上,小角放在这个三角形的内角位置上,再利用不等式性质证明;三、有角平分线时,通常在角的两边截取相等的线段,构造全等三角形,如：例如：如图3-1：已知AD 为△ABC 的中线,且∠1＝∠2,∠3＝∠4,求证：BE ＋CF ＞EF;分析：要证BE ＋CF ＞EF ,可利用三角形三边关系定理证明,须把BE,CF,EF 移到同一个三角形中,而由已知∠1＝∠2,∠3＝∠4,可在角的两边截取相等的线段,利用三角形全等对应边相等,把EN,FN,EF 移到同一个三角形中;证明：在DA 上截取DN ＝DB,连接NE,NF,则DN ＝DC, 在△DBE 和△DNE 中：∵⎪⎩⎪⎨⎧=∠=∠=)()(21)(公共边已知辅助线的作法ED ED DB DN ∴△DBE ≌△DNE SAS∴BE ＝NE 全等三角形对应边相等同理可得：CF ＝NF在△EFN 中EN ＋FN ＞EF 三角形两边之和大于第三边 ∴BE ＋CF ＞EF;注意：当证题有角平分线时,常可考虑在角的两边截取相等的线段,构造全等三角形,然后用全等三角形的性质得到对应元素相等;四、有以线段中点为端点的线段时,常延长加倍此线段,构造全等三角形; 例如：如图4-1：AD 为△ABC 的中线,且∠1＝∠2,∠3＝∠4,求证：BE ＋CF ＞EF 证明：延长ED 至M,使DM=DE,连接 CM,MF;在△BDE 和△CDM 中,AB CD E FN13-图1234ACE F1234∵⎪⎩⎪⎨⎧=∠=∠=)()(1)(辅助线的作法对顶角相等中点的定义MD ED CDM CD BD ∴△BDE ≌△CDM SAS又∵∠1＝∠2,∠3＝∠4 已知 ∠1＋∠2＋∠3＋∠4＝180°平角的定义 ∴∠3＋∠2=90°,即：∠EDF ＝90° ∴∠FDM ＝∠EDF ＝90° 在△EDF 和△MDF 中∵⎪⎩⎪⎨⎧=∠=∠=)()()(公共边已证辅助线的作法DF DF FDM EDF MD ED∴△EDF ≌△MDF SAS∴EF ＝MF 全等三角形对应边相等∵在△CMF 中,CF ＋CM ＞MF 三角形两边之和大于第三边 ∴BE ＋CF ＞EF注：上题也可加倍FD,证法同上;注意：当涉及到有以线段中点为端点的线段时,可通过延长加倍此线段,构造全等三角形,使题中分散的条件集中;五、有三角形中线时,常延长加倍中线,构造全等三角形; 例如：如图5-1：AD 为 △ABC 的中线,求证：AB ＋AC ＞2AD;分析：要证AB ＋AC ＞2AD,由图想到： AB ＋BD ＞AD,AC ＋CD ＞AD,所以有AB ＋AC ＋ BD ＋CD ＞AD ＋AD ＝2AD,左边比要证结论多BD ＋CD,故不能直接证出此题,而由2AD 想到要构造2AD,即加倍中线,把所要证的线段转移到同一个三角形中去;证明：延长AD 至E,使DE=AD,连接BE,则AE ＝2AD ∵AD 为△ABC 的中线已知 ∴BD ＝CD 中线定义在△ACD 和△EBD 中⎪⎩⎪⎨⎧=∠=∠=)()()(辅助线的作法对顶角相等已证ED AD EDB ADC CD BD∴△ACD ≌△EBD SAS∴BE ＝CA 全等三角形对应边相等∵在△ABE 中有：AB ＋BE ＞AE 三角形两边之和大于第三边ABCDE15-图AEF∴AB ＋AC ＞2AD;练习：已知△ABC,AD 是BC 边上的中线,分别以AB 边、AC 边为直角边各向形外作等腰直角三角形,如图5-2, 求证EF ＝2AD;六、截长补短法作辅助线;例如：已知如图6-1：在△ABC 中,AB ＞AC,∠1＝∠2,P 为AD 上任一点;求证：AB －AC ＞PB －PC;分析：要证：AB －AC ＞PB －PC,想到利用三角形三边关系定理证之,因为欲证的是线段之差,故用两边之差小于第三边,从而想到构造第三边AB －AC,故可在AB 上截取AN 等于AC,得AB －AC ＝BN, 再连接PN,则PC ＝PN,又在△PNB 中,PB －PN ＜BN,即：AB －AC ＞PB －PC;证明：截长法在AB 上截取AN ＝AC 连接PN , 在△APN 和△APC 中∵⎪⎩⎪⎨⎧=∠=∠=)()(21)(公共边已知辅助线的作法AP AP AC AN ∴△APN ≌△APC SAS∴PC ＝PN 全等三角形对应边相等∵在△BPN 中,有 PB －PN ＜BN 三角形两边之差小于第三边 ∴BP －PC ＜AB －AC证明：补短法延长AC 至M,使AM ＝AB,连接PM, 在△ABP 和△AMP 中∵ ⎪⎩⎪⎨⎧=∠=∠=)()(21)(公共边已知辅助线的作法AP AP AM AB∴△ABP ≌△AMP SAS∴PB ＝PM 全等三角形对应边相等又∵在△PCM 中有：CM ＞PM －PC 三角形两边之差小于第三边 ∴AB －AC ＞PB －PC;七、延长已知边构造三角形：例如：如图7-1：已知AC ＝BD,AD ⊥AC 于A ,BC ⊥BD 于B, 求证：AD ＝BCA BCDNMP 16-图12分析：欲证 AD ＝BC,先证分别含有AD,BC 的三角形全等,有几种方案：△ADC 与△BCD,△AOD 与△BOC,△ABD 与△BAC,但根据现有条件,均无法证全等,差角的相等,因此可设法作出新的角,且让此角作为两个三角形的公共角;证明：分别延长DA,CB,它们的延长交于E 点, ∵AD ⊥AC BC ⊥BD 已知 ∴∠CAE ＝∠DBE ＝90° 垂直的定义在△DBE 与△CAE 中∵⎪⎩⎪⎨⎧=∠=∠∠=∠)()()(已知已证公共角AC BD CAE DBE E E∴△DBE ≌△CAE AAS∴ED ＝EC EB ＝EA 全等三角形对应边相等 ∴ED －EA ＝EC －EB 即：AD ＝BC;当条件不足时,可通过添加辅助线得出新的条件,为证题创造条件;八、连接四边形的对角线,把四边形的问题转化成为三角形来解决; 例如：如图8-1：AB ∥CD,AD ∥BC 求证：AB=CD;分析：图为四边形,我们只学了三角形的有关知识,必须把它转化为三角形来解决; 证明：连接AC 或BD∵AB ∥CD AD ∥BC 已知∴∠1＝∠2,∠3＝∠4 两直线平行,内错角相等在△ABC 与△CDA 中∵ ⎪⎩⎪⎨⎧∠=∠=∠=∠)(43)()(21已证公共边已证CA AC∴△ABC ≌△CDA ASA∴AB ＝CD 全等三角形对应边相等九、有和角平分线垂直的线段时,通常把这条线段延长;例如：如图9-1：在Rt △ABC 中,AB ＝AC,∠BAC ＝90°,∠1＝∠2,CE ⊥BD 的延长于E ;求证：BD ＝2CE分析：要证BD ＝2CE,想到要构造线段2CE,同时CE 与∠ABC 的平分线垂直,想到要将其延长;证明：分别延长BA,CE 交于点F; ∵BE ⊥CF 已知DAEFA BCD 18-图1234ABCDE17-图O∴∠BEF ＝∠BEC ＝90° 垂直的定义在△BEF 与△BEC 中,∵ ⎪⎩⎪⎨⎧∠=∠=∠=∠)()()(21已证公共边已知BEC BEF BE BE ∴△BEF ≌△BECASA ∴CE=FE=21CF 全等三角形对应边相等 ∵∠BAC=90° BE ⊥CF 已知∴∠BAC ＝∠CAF ＝90° ∠1＋∠BDA ＝90°∠1＋∠BFC ＝90° ∴∠BDA ＝∠BFC 在△ABD 与△ACF 中⎪⎩⎪⎨⎧∠=∠∠=∠)()()(已知＝已证已证AC AB BFC BDA CAF BAC∴△ABD ≌△ACF AAS ∴BD ＝CF 全等三角形对应边相等 ∴BD ＝2CE十、连接已知点,构造全等三角形;例如：已知：如图10-1；AC 、BD 相交于O 点,且AB ＝DC,AC ＝BD,求证：∠A ＝∠D; 分析：要证∠A ＝∠D,可证它们所在的三角形△ABO 和△DCO 全等,而只有AB ＝DC 和对顶角两个条件,差一个条件,,难以证其全等,只有另寻其它的三角形全等,由AB ＝DC,AC ＝BD,若连接BC,则△ABC 和△DCB 全等,所以,证得∠A ＝∠D;证明：连接BC,在△ABC 和△DCB 中 ∵ ⎪⎩⎪⎨⎧===)()()(公共边已知已知CB BC DB AC DC AB∴△ABC ≌△DCB SSS∴∠A ＝∠D 全等三角形对应边相等十一、取线段中点构造全等三有形;例如：如图11-1：AB ＝DC,∠A ＝∠D 求证：∠ABC ＝∠DCB;分析：由AB ＝DC,∠A ＝∠D,想到如取AD 的中点N,连接NB,NC,再由SAS 公理有△ABN ≌△DCN,故BN ＝CN,∠ABN ＝∠DCN;下面只需证∠NBC ＝∠NCB,再取BC 的中点M,连接MN,则由SSS 公理有△NBM ≌△NCM,所以∠NBC ＝∠NCB;问题得证;证明：取AD,BC 的中点N 、M,连接NB,NM,NC;则AN=DN,BM=CM,在△ABN 和△DCN 中DCBA110-图ODAN∵ ⎪⎩⎪⎨⎧=∠=∠=)()()(已知已知辅助线的作法DC AB D A DN AN ∴△ABN ≌△DCN SAS∴∠ABN ＝∠DCN NB ＝NC 全等三角形对应边、角相等在△NBM 与△NCM 中∵⎪⎩⎪⎨⎧)()()(公共边＝辅助线的作法＝已证＝NM NM CM BM NC NB∴△NMB ≌△NCM,SSS ∴∠NBC ＝∠NCB 全等三角形对应角相等∴∠NBC ＋∠ABN ＝∠NCB ＋∠DCN 即∠ABC ＝∠DCB;五、巧求三角形中线段的比值例1. 如图1,在△ABC中,BD：DC＝1：3,AE：ED＝2：3,求AF：FC;解：过点D作DG如图2,BC＝CD,AF＝FC,求EF：FD解：过点C作CG如图3,BD：DC＝1：3,AE：EB＝2：3,求AF：FD;解：过点B作BG如图4,BD：DC＝1：3,AF＝FD,求EF：FC;解：过点D作DG如图5,BD＝DC,AE：ED＝1：5,求AF：FB;2. 如图6,AD：DB＝1：3,AE：EC＝3：1,求BF：FC;答案：1、1：10； 2. 9：1六、辅助线总结一、由角平分线想到的辅助线口诀：图中有角平分线,可向两边作垂线;也可将图对折看,对称以后关系现;角平分线平行线,等腰三角形来添;角平分线加垂线,三线合一试试看;角平分线具有两条性质：a 、对称性；b 、角平分线上的点到角两边的距离相等;对于有角平分线的辅助线的作法,一般有两种;①从角平分线上一点向两边作垂线；②利用角平分线,构造对称图形如作法是在一侧的长边上截取短边; 通常情况下,出现了直角或是垂直等条件时,一般考虑作垂线；其它情况下考虑构造对称图形;至于选取哪种方法,要结合题目图形和已知条件;与角有关的辅助线一、截取构全等几何的证明在于猜想与尝试,但这种尝试与猜想是在一定的规律基本之上的,希望同学们能掌握相关的几何规律,在解决几何问题中大胆地去猜想,按一定的规律去尝试;下面就几何中常见的定理所涉及到的辅助线作以介绍;如图1-1,∠AOC=∠BOC,如取OE=OF,并连接DE 、DF,则有△OED ≌△OFD,从而为我们证明线段、角相等创造了条件;如图1-2,ABAC;3．已知：如图2-5, ∠BAC=∠CAD,AB>AD,CE ⊥AB,AE=21AB+AD.求证：∠D+∠B=180 ;4.已知：如图2-6,在正方形ABCD 中,E 为CD 的中点,F 为BC上的点,∠FAE=∠DAE;求证：AF=AD+CF;图1-1BDBC已知：如图2-7,在Rt △ABC 中,∠ACB=90 ,CD ⊥AB,垂足为D,AE 平分∠CAB 交CD 于F,过F 作FH 21证：BD=2CE;分析：给出了角平分线给出了边上的一点作角平分线的垂线,可延长此垂线与另外一边相交,近而构造出等腰三角形;例3．已知：如图3-3在△ABC 中,AD 、AE 分别∠BAC 的内、外角平分线,过顶点B 作BFAD,交AD 的延长线于F,于M;求证：AM=ME;分析：由AD 、AE 是∠BAC AF,从而BF2121图4-2图4-1ABBG已知,如图,∠C=2∠A,AC=2BC;求证：△ABC 是直角三角形;2．已知：如图,AB=2AC,∠1=∠2,DA=DB,求证：DC ⊥ACCABA 图2-6ECD图3-2CE3．已知CE 、AD 是△ABC 的角平分线,∠B=60°,求证：AC=AE+CD 4．已知：如图在△ABC 中,∠A=90°,AB=AC,BD 是∠ABC 的平分线,求证：BC=AB+AD二、由线段和差想到的辅助线口诀：线段和差及倍半,延长缩短可试验;线段和差不等式,移到同一三角去; 遇到求证一条线段等于另两条线段之和时,一般方法是截长补短法： 1、截长：在长线段中截取一段等于另两条中的一条,然后证明剩下部分等于另一条；2、补短：将一条短线段延长,延长部分等于另一条短线段,然后证明新线段等于长线段;对于证明有关线段和差的不等式,通常会联系到三角形中两线段之和大于第三边、之差小于第三边,故可想办法放在一个三角形中证明;在利用三角形三边关系证明线段不等关系时,如直接证不出来,可连接两点或廷长某边构成三角形,使结论中出现的线段在一个或几个三角形中,再运用三角形三边的不等关系证明,如：已知如图1-1：D 、E 为△ABC 内两点,求证:AB+AC>BD+DE+CE. 证明：法一将DE 两边延长分别交AB 、AC 于M 、N, 在△AMN 中,AM+AN>MD+DE+NE;1 在△BDM 中,MB+MD>BD ；2 在△CEN 中,CN+NE>CE ；3 由1+2+3得：AM+AN+MB+MD+CN+NE>MD+DE+NE+BD+CE ∴AB+AC>BD+DE+ECA BC D AEB D CABCD EN M 11-图AF法二：图1-2延长BD 交AC 于F,廷长CE 交BF 于G,在△ABF 和△GFC 和△GDE 中有： AB+AF>BD+DG+GF 三角形两边之和大于第三边…1 GF+FC>GE+CE 同上2 DG+GE>DE 同上3 由1+2+3得：AB+AF+GF+FC+DG+GE>BD+DG+GF+GE+CE+DE ∴AB+AC>BD+DE+EC;在利用三角形的外角大于任何和它不相邻的内角时如直接证不出来时,可连接两点或延长某边,构造三角形,使求证的大角在某个三角形的外角的位置上,小角处于这个三角形的内角位置上,再利用外角定理：例如：如图2-1：已知D 为△ABC 内的任一点,求证：∠BDC>∠BAC;BDC 与∠BAC 不在同个三角形中,没有直接的联系,可适当添加辅助线构造新的三角形,使∠BDC 处于在外角的位置,∠BAC 处于在内角的位置；证法一：延长BD 交AC 于点E,这时∠BDC 是△EDC 的外角, ∴∠BDC>∠DEC,同理∠DEC>∠BAC,∴∠BDC>∠BAC 证法二：连接AD,并廷长交BC 于F,这时∠BDF 是△ABD 的外角,∴∠BDF>∠BAD,同理,∠CDF>∠CAD,∴∠BDF+ ∠CDF>∠BAD+∠CAD,即：∠BDC>∠BAC;注意：利用三角形外角定理证明不等关系时,通常将大角放在某三角形的外角位置上,小角放在这个三角形的内角位置上,再利用不等式性质证明;有角平分线时,通常在角的两边截取相等的线段,构造全等三角形,如：例如：如图3-1：已知AD 为△ABC 的中线,且∠1=∠2,∠3=∠4,求证：BE+CF>EF;BE+CF>EF,可利用三角形三边关系定理证明,须把BE,CF,EF 移到同一个三角形中,而由已知∠1=∠2,∠3=∠4,可在角的两边截取相等的线段,利用三角形全等对应边相等,把EN,FN,EF 移到同个三角形中;证明：在DN 上截取DN=DB,连接NE,NF,则DN=DC, 在△DBE 和△NDE 中： DN=DB 辅助线作法 ∠1=∠2已知 ED=ED 公共边AB CD E F G12-图ABCD E FN13-图1234∴△DBE ≌△NDESAS∴BE=NE 全等三角形对应边相等同理可得：CF=NF在△EFN 中EN+FN>EF 三角形两边之和大于第三边 ∴BE+CF>EF;注意：当证题有角平分线时,常可考虑在角的两边截取相等的线段,构造全等三角形,然后用全等三角形的对应性质得到相等元素;截长补短法作辅助线;例如：已知如图6-1：在△ABC 中,AB>AC,∠1=∠2,P 为AD 上任一点求证：AB-AC>PB-PC;要证：AB-AC>PB-PC,想到利用三角形三边关系,定理证之,因为欲证的线段之差,故用两边之差小于第三边,从而想到构造第三边AB-AC,故可在AB 上截取AN 等于AC,得AB-AC=BN,再连接PN,则PC=PN,又在△PNB 中,PB-PN<BN,即：AB-AC>PB-PC;证明：截长法在AB 上截取AN=AC 连接PN,在△APN 和△APC 中 AN=AC 辅助线作法 ∠1=∠2已知 AP=AP 公共边∴△APN ≌△APCSAS,∴PC=PN 全等三角形对应边相等 ∵在△BPN 中,有PB-PN<BN 三角形两边之差小于第三边∴BP-PC<AB-AC 证明：补短法延长AC 至M,使AM=AB,连接PM,在△ABP 和△AMP 中ABCDNMP 16 图12AB=AM 辅助线作法 ∠1=∠2已知 AP=AP 公共边 ∴△ABP ≌△AMPSAS∴PB=PM 全等三角形对应边相等又∵在△PCM 中有：CM>PM-PC 三角形两边之差小于第三边 ∴AB-AC>PB-PC;例1．如图,AC 平分∠BAD,CE ⊥AB,且∠B+∠D=180°,求证：AE=AD+BE;例2如图,在四边形ABCD 中,AC 平分∠BAD,CE ⊥AB 于E,AD+AB=2AE,求证：∠ADC+∠B=180º例3已知：如图,等腰三角形ABC 中,AB=AC,∠A=108°,BD 平分∠ABC;求证：BC=AB+DC;例4如图,已知Rt △ABC 中,∠ACB=90°,AD 是∠CAB 的平分线,DM ⊥AB 于M,且AM=MB;求证：CD=21DB;1．如图,AB ∥CD,AE 、DE 分别平分∠BAD 各∠ADE,求证：AD=AB+CD;DECB AE BCDCM BDCA2.如图,△ABC 中,∠BAC=90°,AB=AC,AE 是过A 的一条直线,且B,C 在AE 的异侧,BD ⊥AE 于D,CE ⊥AE 于E;求证：BD=DE+CE三、由中点想到的辅助线口诀：三角形中两中点,连接则成中位线;三角形中有中线,延长中线等中线;在三角形中,如果已知一点是三角形某一边上的中点,那么首先应该联想到三角形的中线、中位线、加倍延长中线及其相关性质直角三角形斜边中线性质、等腰三角形底边中线性质,然后通过探索,找到解决问题的方法;一中线把原三角形分成两个面积相等的小三角形即如图1,AD 是ΔABC 的中线,则S ΔABD =S ΔACD =S ΔABC 因为ΔABD 与ΔACD 是等底同高的;例1．如图2,ΔABC 中,AD 是中线,延长AD 到E,使DE=AD,DF 是ΔDCE 的中线;已知ΔABC 的面积为2,求：ΔCDF 的面积;解：因为AD 是ΔABC 的中线,所以S ΔACD =S ΔABC =×2=1,又因CD 是ΔACE 的中线,故S ΔCDE =S ΔACD =1,因DF 是ΔCDE 的中线,所以S ΔCDF =S ΔCDE =×1=;∴ΔCDF 的面积为;二由中点应想到利用三角形的中位线ED CB A例2．如图3,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,BA、CD的延长线分别交EF的延长线G、H;求证：∠BGE=∠CHE;证明：连结BD,并取BD的中点为M,连结ME、MF,∵ME是ΔBCD的中位线,∴ME CD,∴∠MEF=∠CHE,∵MF是ΔABD的中位线,∴MF AB,∴∠MFE=∠BGE,∵AB=CD,∴ME=MF,∴∠MEF=∠MFE,从而∠BGE=∠CHE;三由中线应想到延长中线例3．图4,已知ΔABC中,AB=5,AC=3,连BC上的中线AD=2,求BC的长;解：延长AD到E,使DE=AD,则AE=2AD=2×2=4;在ΔACD和ΔEBD中,∵AD=ED,∠ADC=∠EDB,CD=BD,∴ΔACD≌ΔEBD,∴AC=BE,从而BE=AC=3;在ΔABE中,因AE2+BE2=42+32=25=AB2,故∠E=90°,∴BD===,故BC=2BD=2;例4．如图5,已知ΔABC中,AD是∠BAC的平分线,AD又是BC边上的中线;求证：ΔABC是等腰三角形;证明：延长AD到E,使DE=AD;仿例3可证：ΔBED≌ΔCAD,故EB=AC,∠E=∠2,又∠1=∠2,∴∠1=∠E,∴AB=EB,从而AB=AC,即ΔABC是等腰三角形;D CB A EDF CBA四直角三角形斜边中线的性质例5．如图6,已知梯形ABCD 中,AB2：如图,△ABC 中,E 、F 分别在AB 、AC 上,DE ⊥DF,D 是中点,试比较BE+CF 与EF 的大小.3：如图,△ABC 中,BD=DC=AC,E 是DC 的中点,求证：AD 平分∠BAE.EDCB A中考应用09崇文二模以ABC ∆的两边AB 、AC 为腰分别向外作等腰Rt ABD ∆和等腰Rt ACE ∆,90,BAD CAE ∠=∠=︒连接DE,M 、N 分别是BC 、DE 的中点．探究：AM 与DE 的位置关系及数量关系．1如图① 当ABC ∆为直角三角形时,AM 与DE 的位置关系是 ,线段AM 与DE 的数量关系是；2将图①中的等腰Rt ABD ∆绕点A 沿逆时针方向旋转︒θ0<θ<90后,如图②所示,1问中得到的两个结论是否发生改变并说明理由．14-图A B CD EFM1234A BCDE 15-图DMCE AB BA D C86B E CDA ABCD EF25-图 AB DC EFDAEDCBAP QCBA二、截长补短1.如图,ABC ∆中,AB=2AC,AD 平分BAC ∠,且AD=BD,求证：CD ⊥AC2：如图,AC ∥BD,EA,EB 分别平分∠CAB,∠DBA,CD 过点E,求证;AB ＝AC+BD3：如图,已知在ABC内,060BAC ∠=,040C ∠=,P,Q 分别在BC,CA 上,并且AP,BQ 分别是BAC ∠,ABC ∠的角平分线;求证：BQ+AQ=AB+BP4：如图,在四边形ABCD 中,BC ＞BA,AD ＝CD,BD 平分ABC ∠,求证：0180=∠+∠C ACDBAP 21DCBA5:如图在△ABC 中,AB ＞AC,∠1＝∠2,P 为AD 上任意一点,求证;AB-AC ＞PB-PC中考应用 08海淀一模三、平移变换为△ABC 的角平分线,直线MN ⊥AD 于为MN 上一点,△ABC 周长记为AP ,△EBC 周长记为BP .求证BP ＞AP .2：如图,在△ABC 的边上取两点D 、E,且BD=CE,求证：AB+AC>AD+AE.ED CB A四、借助角平分线造全等CBAFED CBA 1：如图,已知在△ABC 中,∠B=60°,△ABC 的角平分线AD,CE 相交于点O,求证：OE=OD2：06郑州市中考题如图,△ABC 中,AD ∠BAC,DG ⊥BC 且平分BC,DE ⊥AB 于E,DF ⊥AC 于明BE=CF 的理由；2如果AB=a ,AC=b ,求AE 、BE 的长.中考应用06北京中考如图①,OP 是∠MON 的平分线,请你利用该图形画一对以OP 所在直线为对称轴的全等三角形;请你参考这个作全等三角形的方法,解答下列问题：1如图②,在△ABC 中,∠ACB 是直角,∠B =60°,AD 、CE 分别是∠BAC 、∠BCA 的平分线,AD 、CE 相交于点F ;请你判断并写出FE 与FD 之间的数量关系；2如图③,在△ABC 中,如果∠ACB 不是直角,而1中的其它条件不变,请问,你在1中所得结论是否仍然成立若成立,请证明；若不成立,请说明理由;五、旋转1：正方形ABCD 中,E 为BC 上的一点,F 为CD 上的一点,BE+DF=EF,求∠EAF 的度数.2：D 为等腰Rt ABC ∆斜边AB 的中点,DM ⊥DN,DM,DN 分别交BC,CA 于点E,F;当MDN ∠绕点D 转动时,求证DE=DF; 若AB=2,求四边形DECF 的面积;EDGFCBA第23题OPAMN EB CD FACEFBD图图图3.如图,ABC ∆是边长为3的等边三角形,BDC ∆是等腰三角形,且0120BDC ∠=,以D 为顶点做一个060角,使其两边分别交AB 于点M,交AC 于点N,连接MN,则AMN ∆的周长为；BCNM中考应用 07佳木斯已知四边形ABCD中,AB AD ⊥,BC CD ⊥,AB BC =,120ABC =∠,60MBN =∠,MBN ∠绕B 点旋转,它的两边分别交AD DC ，或它们的延长线于E F ，．当MBN ∠绕B 点旋转到AE CF =时如图1,易证AE CF EF +=．当MBN ∠绕B 点旋转到AE CF ≠时,在图2和图3这两种情况下,上述结论是否成立若成立,请给予证明；若不成立,线段AE CF ，,EF 又有怎样的数量关系请写出你的猜想,不需证明．西城09年一模已知2,PB=4,以AB 为一边作正方形ABCD,使P 、D 两点落在直线AB 的两侧.1如图,当∠APB=45°时,求AB 及PD 的长;2当∠APB 变化,且其它条件不变时,求PD 的最大值,及相应∠APB 的大小.图1A BC D E FMN 图2 A BC D E FMN 图3ABC D EF M N。

初二数学辅助线题大全

10 道初二数学辅助线题题目一已知在三角形ABC 中，AB = AC，D 是BC 中点，求证：AD⊥BC。

解析：连接AD，因为AB = AC，D 是BC 中点，根据等腰三角形三线合一的性质，可知AD⊥BC。

题目二在平行四边形ABCD 中，E 是AB 中点，F 是CD 中点，连接EF，求证：EF 平行且等于AD 的一半。

解析：连接AF、EC，因为四边形ABCD 是平行四边形，所以AB⊥CD，AB = CD。

又因为E 是AB 中点，F 是CD 中点，所以AE = CF。

可得四边形AECF 是平行四边形，所以EF⊥AC，EF = AC 的一半。

又因为平行四边形ABCD 中，AD = BC，AC = 2AO（O 为对角线交点），所以EF 平行且等于AD 的一半。

题目三在三角形ABC 中，⊥A = 90°，AB = AC，D 是BC 中点，连接AD，E、F 分别是AB、AC 上的点，且BE = AF，求证：ED⊥DF。

解析：连接AD，因为AB = AC，⊥A = 90°，D 是BC 中点，所以AD = BD = CD，且AD⊥BC，⊥BAD = ⊥CAD = 45°。

可证⊥BDE⊥⊥ADF（SAS），所以⊥BDE = ⊥ADF，又因为⊥ADB = 90°，所以⊥EDF = 90°，即ED⊥DF。

题目四在梯形ABCD 中，AB⊥CD，⊥A + ⊥B = 90°，E、F 分别是AB、CD 的中点，求证：EF = (AB - CD) / 2。

解析：延长AD、BC 交于点G，因为AB⊥CD，所以⊥GDC = ⊥A，⊥GCD = ⊥B。

又因为⊥A + ⊥B = 90°，所以⊥G = 90°。

因为E、F 分别是AB、CD 的中点，所以EF 是梯形ABCD 的中位线，所以EF = (AB + CD) / 2。

在直角三角形GDC 和直角三角形GAB 中，F、E 分别是斜边CD、AB 的中点，所以GF = CD/2，GE = AB/2。

2020—2021学年人教版数学八年级下册第18章《平行四边形》常考题提高练习(一)

人教版数学八年级下册第18章《平行四边形》常考题提高练习（一）1．已知，△ABC、△ADE是等腰三角形，AB＝AC，AD＝AE，D是BC上一点，∠DAE＝∠BAC，过点E作BC的平行线交AB于点F，连接CF．（1）如图1，求证：四边形CDEF是平行四边形；（2）如图2，连接BE、DF，若AD⊥BC，在不添加任何辅助线的情况下，请直接写出图2中长度等于BC的长的的线段．2．如图，在▱ABCD中，点P在对角线AC上一动点，过点P作PM∥DC，且PM＝DC，连接BM，CM，AP，BD．（1）求证：△ADP≌△BCM；（2）若P A＝PC，设△ABP的面积为S，四边形BPCM的面积为T，求的值．3．如图，四边形ACFD是平行四边形，B，E，C，F在一条直线上，已知BE＝CF．（1）求证：四边形ABED是平行四边形．（2）若∠ABC＝60°，且AC⊥BF，AB＝6，BF＝5，求AD的长．4．如图，在▱ABCD中，AE⊥BC于点E，点F在线段DE上，且△ADF∽△DEC，若DC＝4cm，AD＝cm，AF＝cm．（1）求DE的长；（2）求▱ABCD的面积．5．如图，在菱形ABCD中，对角线AC，BD交于点O，过点A作AE⊥BC于点E，延长BC 到点F，使得CF＝BE，连接DF，（1）求证：四边形AEFD是矩形；（2）连接OE，若AB＝13，OE＝，求AE的长．6．如图，已知菱形ABCD的对角线AC、BD相交于点O，分别过A、D两点作AO、DO的垂线，两垂线交于点E．（1）求证：四边形AODE是矩形；（2）若四边形AODE的面积为12，AD＝5，求四边形AODE的周长．7．如图，在矩形ABCD中，E是BC上一点，DF⊥AE于点F，设＝λ（λ＞0）．（1）若λ＝1，求证：CE＝FE；（2）若AB＝3，AD＝4，且D、B、F在同一直线上时，求λ的值．8．如图，分别以Rt△ACB的直角边AC和斜边AB向外作等边△ACE，等边△ABD，取AB 的中点F，连接DF、EF，已知∠BAC＝30°．（1）求证：四边形ADFE是平行四边形；（2）若BD＝4，求四边形BCEF的面积．9．如图，在△ABC中，AB＝AC，D是BC中点、F是AC中点，AN是∠ABC的外角∠MAC 的平分线，延长DF交AN于点E，连接CE．（1）求证：四边形ADCE是矩形；（2）若AB＝BC＝4，则四边形ADCE的面积为多少？（3）直接回答：当△ABC满足时，四边形ADCE是正方形．10．如图，在矩形ABCD中，O为对角线AC的中点，过点O作直线分别与矩形的边AD，BC交于M，N两点，连接CM，AN．（1）求证：四边形ANCM为平行四边形；（2）若AD＝4，AB＝2，且MN⊥AC，求DM的长．11．已知：l∥m∥n∥k，平行线l与m、m与n、n与k之间的距离分别为d1，d2，d3，且d1＝d3＝2，d2＝3．我们把四个顶点分别在l，m，n，k这四条平行线上的四边形称为“线上四边形”．（1）如图1，正方形ABCD为“线上四边形”，BE⊥l于点E，EB的延长线交直线k于点F，求正方形ABCD的边长．（2）如图2，菱形ABCD为“线上四边形”且∠ADC＝60°，△AEF是等边三角形，点E在直线k上，连接DF，且直线DF分别交直线l、k于点G、M，求证：EC＝DF．12．如图，正方形ABCD，G是BC边上任意一点（不与B、C重合），DE⊥AG于点E，BF ∥DE，且交AG于点F．（1）求证：AF﹣BF＝EF；（2）四边形BFDE是否可能是平行四边形，如果可能，请指出此时点G的位置，如不可能，请说明理由．13．如图，在△ABC中，点D，E分别是BC，AC的中点，延长BA至点F，使得AF＝AB，连接DE，AD，EF，DF．（1）求证：四边形ADEF是平行四边形；（2）若AB＝6，AC＝8，BC＝10，求EF的长．14．矩形ABCD中，AB＝3，BC＝4．点E，F在对角线AC上，点M，N分别在边AD，BC 上．（1）如图1，若AE＝CF＝1，M，N分别是AD，BC的中点．求证：四边形EMFN为矩形．（2）如图2，若AE＝CF＝0.5，AM＝CN＝x（0＜x＜2），且四边形EMFN为矩形，求x 的值．15．如图，四边形ABCD的对角线AC⊥BD于点E，点F为四边形ABCD外一点，且∠FCA ＝90°，BC平分∠DBF，∠CBF＝∠DCB．（1）求证：四边形DBFC是菱形；（2）若AB＝BC，∠F＝45°，BD＝2，求AC的长．参考答案1．（1）如答图1，证明：连接BE，∵∠BAC＝∠DAE，∴∠DAC＝∠EAB，在△ACD和△ABE中，，∴△ACD≌△ABE（SAS），∴CD＝BE，∠ACD＝∠ABE，∵EF∥BC，∴∠ABC＝∠EFB，∴∠ABE＝∠EFB，∴EB＝EF，∴EF＝CD，∵EF∥BC，∴四边形EDCF是平行四边形；（2）∵AB＝AC，AD⊥BC，∴BD＝CD＝BC，由（1）知CD＝BE＝EF，∴BD＝EF，∵E作BC的平行线交AB于点F，即BD||EF，∴四边形BEFD是平行四边形，∴BD ＝CD ＝BE ＝EF ＝DF ＝BC ，故答案为：BD ，CD ，BE ，EF ，DF ．2．解：（1）∵PM ∥DC ，且PM ＝DC ，∴四边形CDPM 是平行四边形，∴PD ＝MC ，∵AB ∥DC ，且AB ＝DC ，PM ∥DC ，且PM ＝DC ，∴AB ∥PM ，且AB ＝PM ，∴四边形ABMP 是平行四边形，∴AP ＝BM ，∵四边形ABCD 是平行四边形，∴AD ＝BC ，∴△ADP ≌△BCM （SSS ）；（2）由（1）可得S △ADP ＝S △BCM ，∴S 四边形BMCP ＝S △BCM +S △BCP ＝S △ADP +S △BCP ＝S 平行四边形ABCD ，又∵P A ＝PC ，∴S △ABP ＝S △ABC ＝S 平行四边形ABCD ，∴的值为＝．3．证明：（1）∵四边形ACFD 是平行四边形，∴AD ∥CF ，AD ＝CF ，∵B ，E ，C ，F 在一条直线上，∴AD ∥BE ，∴AD＝BE，∴四边形ABED是平行四边形；（2）∵四边形ACFD是平行四边形，∴AD＝CF，∵∠ABC＝60°，且AC⊥BF，AB＝6，∴∠BAC＝30°，∴BC＝AB＝3，∵BF＝5，∴CF＝BF﹣BC＝2，∴AD＝2．4．解：（1）∵△ADF∽△DEC，∴，∴，∴DE＝6；（2）∵四边形ABCD为平行四边形，∠EAD＝∠AEB＝90°，∴在Rt△EAD中，，∴AE＝3（cm），∴S▱ABCD＝BC•AE＝．5．（1）证明：∵四边形ABCD是菱形，∴AD∥BC且AD＝BC，∵BE＝CF，∴BC＝EF，∴AD＝EF，∵AD∥EF，∴四边形AEFD是平行四边形，∵AE⊥BC，∴∠AEF＝90°，∴四边形AEFD是矩形；（2）解：∵四边形ABCD是菱形，AB＝13，∴BC＝AB＝13，AC⊥BD，OA＝OC＝AC，OB＝OD＝BD，∵AE⊥BC，∴∠AEC＝90°，∴OE＝AC＝OA＝2，AC＝2OE＝4，∴OB＝＝＝3，∴BD＝2OB＝6，∵菱形ABCD的面积＝BD×AC＝BC×AE，即×6×4＝13×AE，解得：AE＝12．6．（1）证明：∵四边形ABCD是菱形，∴AC⊥BD，∴∠AOD＝90°，∵EA⊥AO，DE⊥DO，∴∠EAO＝∠DOA＝90°，∴四边形AODE是矩形；（2）解：由（1）知，四边形AODE是矩形，∴∠AED＝90°，OA＝DE，OD＝AE，∵四边形AODE的面积为12，∴OA•OD＝12，在Rt△AOD中，根据勾股定理，得OA2+OD2＝AD2＝25，∴（OA+OD）2＝OA2+2OA•OD+OD2＝25+24＝49，∴OA+OD＝7，∴四边形AODE的周长为2（OA+OD）＝14．7．解：（1）证明：连接DE，如图：∵四边形ABCD为矩形，∴∠C＝90°，AD∥BC，∴∠ADE＝∠CED，∵DF⊥AE，∴∠DFE＝90°，∴∠DFE＝∠C，∵＝λ＝1，∴AD＝AE，∴∠ADE＝∠FED，∴∠FED＝∠CED，在△DFE和△DCE中，，∴△DFE≌△DCE（AAS），∴CE＝FE；（2）当D、B、F在同一直线上时，如图所示：∵四边形ABCD为矩形，∴∠BAD＝∠ABC＝90°，在Rt△ADB中，AB＝3，AD＝4，∴tan∠ABD＝＝，∵DF⊥AE，∴∠BFE＝90°，∵∠ABD+∠DBC＝90°，∠DBC+∠FEB＝90°，∴∠FEB＝∠ABD，∴＝tan∠FEB＝tan∠ABD＝，∵AB＝3，∴BE＝，在Rt△ABE中，由勾股定理得，AE＝＝，∴λ＝＝＝＝．8．（1）证明：∵Rt△ABC中，∠BAC＝30°，∴AB＝2BC，又∵△ABD是等边三角形，F是AB的中点，∴AD＝AB＝BD，AB＝2AF，DF⊥AB，∴AF＝BC，在Rt△AFD和Rt△BCA中，，∴Rt△AFD≌Rt△BCA（HL），∴DF＝AC，∵△ACE是等边三角形，∴∠EAC＝60°，AC＝AE，∴∠EAB＝∠EAC+∠BAC＝90°，∴DF＝AE，又∵DF⊥AB，∴DF∥AE，∴四边形ADFE是平行四边形；（2）解：由（1）得：△AEF的面积＝△ADF的面积＝△ABC的面积，AB＝BD＝4，BC ＝AB＝2，AC＝BC＝2，∴四边形BCEF的面积＝△ACE的面积+△ABC的面积﹣△AEF的面积＝△ACE的面积＝×（2）2＝3．9．（1）证明：∵AN是△ABC外角∠CAM的平分线，∴∠MAE＝∠MAC，∵∠MAC＝∠B+∠ACB，∵AB＝AC，∴∠B＝∠ACB，∴∠MAE＝∠B，∴AN∥BC，∵F为AC的中点，D为BC的中点，∴FD∥AB，∴四边形ABDE为平行四边形，∴AE＝BD，∵BD＝CD，∴AE＝CD，∴四边形ADCE为平行四边形，∵AB＝AC，点D为BC中点，∴AD⊥BC，∴AD⊥AE，∴∠DAE＝90°，∴四边形ADCE为矩形；（2）解：由（1）知四边形ADCE是矩形，∵BC＝AB＝4，AB＝AC，∴△ABC是等边三角形，∴AB＝AC＝BC＝4，∵D为BC的中点，∴∠ADC＝90°，BD＝CD＝2，∴AD＝2，∴四边形ADCE的面积为CD×AD＝2×2＝4；（3）解：答案不唯一，如当∠BAC＝90°时，四边形ADCE是正方形．∵∠BAC＝90°，AB＝AC，∴△ABC为等腰直角三角形，∵D为BC的中点，∴AD＝DC，∵四边形ADCE为矩形，∴四边形ADCE为正方形．故答案为：∠BAC＝90°．10．（1）证明：∵在矩形ABCD中，O为对角线AC的中点，∴AD∥BC，AO＝CO，∴∠OAM＝∠OCN，∠OMA＝∠ONC，在△AOM和△CON中，，∴△AOM≌△CON（AAS），∴AM＝CN，∵AM∥CN，∴四边形ANCM为平行四边形；（2）解：∵在矩形ABCD中，AD＝BC，由（1）知：AM＝CN，∴DM＝BN，∵四边形ANCM为平行四边形，MN⊥AC，∴平行四边形ANCM为菱形，∴AM＝AN＝NC＝AD﹣DM，∴在Rt△ABN中，根据勾股定理，得AN2＝AB2+BN2，∴（4﹣DM）2＝22+DM2，解得DM＝．11．解：（1）如图1，∵l∥m∥n∥k，BE⊥l，∴BE⊥k，BE⊥m，BE⊥n，∴∠AEB＝∠BFC＝90°，BE＝5，BF＝2，∴∠CBF+∠BCF＝90°，∵正方形ABCD为“线上四边形”，∴AB＝BC，∠ABC＝90°，∴∠ABE+∠CBF＝90°，∴∠ABE＝∠BCF，∴△ABE≌△BCF（AAS），∴FC＝BE＝5，∴BC＝＝＝；（2）如图2，连接AC，∵四边形ABCD是菱形，∴AD＝CD，∵∠ADC＝60°，∴△ADC是等边三角形，∴AD＝AC，∠CAD＝60°，∵△AEF是等边三角形，∴AE＝AF，∠EAF＝60°，∴∠EAF＝∠CAD，∴∠EAC＝∠DAF，∴△EAC≌△F AD（SAS），∴EC＝DF．12．解：（1）证明：∵四边形ABCD是正方形，∴AB＝AD，∠BAF+∠DAE＝90°，∵DE⊥AG，∴∠DAE+∠ADE＝90°，∴∠ADE＝∠BAF，又∵BF∥DE，∴∠BF A＝90°＝∠AED，∴△ABF≌△DAE（AAS），∴AE＝BF，∴AF﹣BF＝AF﹣AE＝EF；（2）不可能，理由是：如图，若要四边形BFDE是平行四边形，已知DE∥BF，则当DE＝BF时，四边形BFDE为平行四边形，∵DE＝AF，∴BF＝AF，即此时∠BAF＝45°，而点G不与B和C重合，∴∠BAF≠45°，矛盾，∴四边形BFDE不可能是平行四边形．13．（1）证明：∵点D，E分别是BC，AC的中点，∴DE是△ABC的中位线，∴DE∥AB，DE＝AB，∵AF＝AB，∴DE＝AF，DE∥AF，∴四边形ADEF是平行四边形；（2）解：由（1）得：四边形ADEF是平行四边形，∴EF＝AD，∵AB＝6，AC＝8，BC＝10，∴AB2+AC2＝BC2，∴△ABC是直角三角形，∠BAC＝90°，∵点D是BC的中点，∴AD＝BC＝5，∴EF＝AD＝5．14．（1）证明：连接MN，如图1所示：∵四边形ABCD是矩形，∴AD∥BC，AD＝BC，∠B＝90°，∴∠EAM＝∠FCN，AC＝＝＝5，∵M，N分别是AD，BC的中点，∴AM＝DM＝BN＝CN，AM∥BN，∴四边形ABNM是平行四边形，又∵∠B＝90°，∴四边形ABNM是矩形，∴MN＝AB＝3，在△AME和△CNF中，，∴△AME≌△CNF（SAS），∴EM＝FN，∠AEM＝∠CFN，∴∠MEF＝∠NFE，∴EM∥FN，∴四边形EMFN是平行四边形，又∵AE＝CF＝1，∴EF＝AC﹣AE﹣CF＝3，∴MN＝EF，∴四边形EMFN为矩形．（2）解：连接MN，作MH⊥BC于H，如图2所示：则四边形ABHM是矩形，∴MH＝AB＝3，BH＝AM＝x，∴HN＝BC﹣BH﹣CN＝4﹣2x，∵四边形EMFN为矩形，AE＝CF＝0.5，∴MN＝EF＝AC﹣AE﹣CF＝4，在Rt△MHN中，由勾股定理得：32+（4﹣2x）2＝42，解得：x＝2±，∵0＜x＜2，∴x＝2﹣．15．（1）证明：∵AC⊥BD，∠FCA＝90°，∠CBF＝∠DCB．∴BD∥CF，CD∥BF，∴四边形DBFC是平行四边形；∵BC平分∠DBF，∴∠CBF＝∠CBD，∵∠CBF＝∠DCB，∴∠CBD＝∠DCB，∴CD＝BD，∴四边形DBFC是菱形；（2）解：∵四边形DBFC是平行四边形，∴CF＝BD＝2，∵AB＝BC，AC⊥BD，∴AE＝CE，作CM⊥BF于M，如图：∵BC平分∠DBF，∴CE＝CM，∵∠F＝45°，∴△CFM是等腰直角三角形，∴CM＝CF＝，∴AE＝CE＝，∴AC＝2．。

第3课时：《平行四边形》(3)——梯形及梯形中常用的辅助线的作法

第3课时《四边形》（3）——梯形及梯形中常用的辅助线的作法【知识点拨】一、梯形的定义：一组对边平行，另一组对边不平行的四边形叫做梯形。

直角梯形的定义：有一个角是直角的梯形等腰梯形的定义：两腰相等的梯形。

等腰梯形的性质：等腰梯形同一底边上的两个角相等；等腰梯形的两条对角线相等。

等腰梯形判定定理：（1）同一底上两个角相等的梯形是等腰梯形。

（2）对角线相等的梯形是等腰梯形。

[例题1]1、下列命题中，正确的个数是（）①如果一个梯形是轴对称图形，则它一定是等腰梯形②有两个角相等的梯形，一定是等腰梯形③一组对边平行，另一组对边相等的四边形事实上是等腰梯形④对角线相等的梯形是等腰梯形 A ．1个B ．2个C ．3个D ．4个【答案】：B2、已知梯形的两个对角分别是78和120，则另两个角分别为（） A ．78和120 B ．102和60C ．120和78 D ．60和120【答案】：Ｂ3、如图所示，在四边形ABCD 中，AD BC E ∥，是AB 的中点，若DEC △的面积为S ，则四边形ABCD 的面积为（）A ．52S B ．2S C ．74SD ．94S 【答案】：B4、已知，如图所示，在等腰梯形ABCD 中，.AD BC PA PD =∥，求证：PB PC =．【答案】：证明：四边形ABCD 是等腰梯形．.B A D C D A ∴∠=∠ 又PA PD =，1 2..B A P C D P∴∠=∠∴∠=∠在PBA △和PCD △中，A B D C B A P C D P P A =∠=∠=，，．..P B A P C DP B P C ∴∴=△≌△12ADCPBA E BCD第3题图5、已知，如图，在梯形ABCD 中，AD ∥BC ，BC ＝DC ，CF 平分∠BCD ，DF ∥AB ，BF 的延长线交DC 于点E 。

求证（1）△BFC ≌△DFC ；（2）AD ＝DE 【答案】：二、梯形的中位线的性质：梯形的中位线平行于上下底边，且等于上下底边长度的和的一半。

平行四边形几何辅助线专题详解

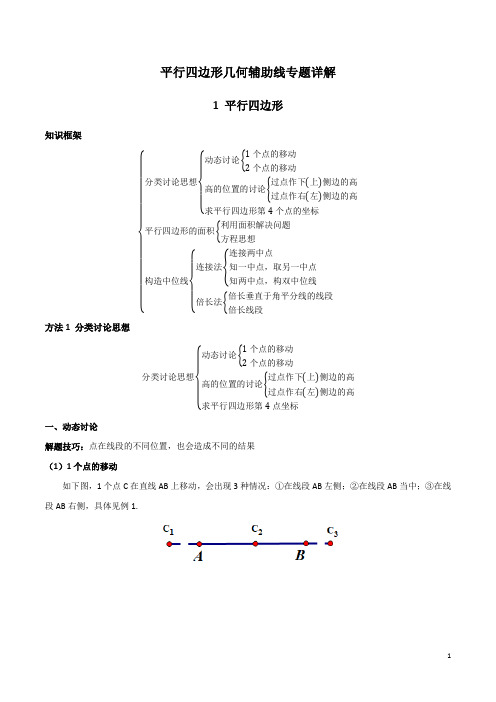
平行四边形几何辅助线专题详解1 平行四边形知识框架{分类讨论思想{动态讨论{1个点的移动2个点的移动高的位置的讨论{过点作下(上)侧边的高过点作右(左)侧边的高求平行四边形第4个点的坐标平行四边形的面积{利用面积解决问题方程思想构造中位线{连接法{连接两中点知一中点，取另一中点知两中点，构双中位线倍长法{倍长垂直于角平分线的线段倍长线段方法1 分类讨论思想分类讨论思想{动态讨论{1个点的移动2个点的移动高的位置的讨论{过点作下(上)侧边的高过点作右(左)侧边的高求平行四边形第4点坐标一、动态讨论解题技巧：点在线段的不同位置，也会造成不同的结果（1）1个点的移动如下图，1个点C 在直线AB 上移动，会出现3种情况：①在线段AB 左侧；②在线段AB 当中；③在线段AB 右侧，具体见例1.（2）2个点的移动如下图，2个点C、D在线段AB上移动（C、D两点在AB中），会出现2种情况：①点C在点D的左侧；②点C在点D的右侧，具体见例2.例1.▱ABCD的内角∠BCD的平分线CE交射线DA于点E，若AE=3，DE=4，求▱ABCD的周长。

例2.在▱ABCD中，AD=8，AE平分∠BAD交BC于点E，DF平分∠ADC交BC于点F，且EF=2，求AB的长。

二、高的位置的讨论解题技巧：在平行四边形中作高，会出现2种情况：①在图形内；②在图形外。

（1）过点作下（上）侧边的高如下图，过点A作▱ABCD下侧的边CD上的高AE。

因▱ABCD倾斜方向的变化，高会存在两种情况，具体见例1（2）过点右（左）侧边的高如下图，过点B作▱ABCD的右侧边AD上的高AE。

因▱ABCD倾斜大小的变化，高会存在两种情况，具体见例2上述两种情况实质是同一种情况经过翻折后得到的，为同一种情况。

例1.在面积为15的平行四边形ABCD中，过点A作AE垂直于直线BC于点E，若AB=5，BC=6，求CE的值。

例2.在▱ABCD中，AD=BD=4，BE是AD边上的高，∠EBD=30°，求△ABD的面积。

北师大版八年级下册数学第六章平行四边形含辅助线证明题—截长补短类训练

北师大版数学八年级下册第六章平行四边形含辅助线证明题——截长补短类1.在▱ABCD中，AE⊥BC于点E，F为AB边上一点，连接CF，交AE于点G，CF=CB=AE．（1）若AB=2√2，BC=√7，求CE的长；（2）求证：BE=CG-AG．2.在平行四边形ABCD中，以边AD为边在平行四边形内作等边△ADE，连接BE.（1）如图1，若点E在对角线BD上，且∠DAB=75°，AB=√6，求BE的长；（2）如图2，若点F是BE的中点，且CF⊥BE，过点E作MN∥CF，分别交AB，CD于点M，N，求证：DN=CN+EN.3.如图，在▱ABCD中，AE⊥BC，垂足为E，AE=CE.BF⊥AC，垂足为F，分别与AE，AD交于点G，H.（1）若AG=GE=BE=1，求▱ABCD的面积；（2）若CH平分∠BCD，求证：BC=AG+CH.4.已知在▱ABCD中，AE⊥CD，且AB=AE，F为AE上一点，且BF平分∠ABC，（1）若∠ABC=60°，AB=√3，求EF的长；（2）求证：AF+DE=BC.5.在平行四边形ABCD中，E为对角线AC上任意一点，连接BE（1）如图①所示，若AB=BE，AC=BC，∠BAC=75°，AB=2√2，求平行四边形ABCD的面积；（2）如图②所示，延长BE至F，使得EF=EB，连接CF，FD，求证：CE=AE+FD．6.在平行四边形ABCD中，连接BD，过点B作BE⊥BD于点B交DA的延长线于点E，过点B作BG⊥CD于点G．（1）如图1，若∠C=60°，∠BDC=75°，BD=6√2，求AE的长度；（2）如图2，点F为AB边上一点，连接EF，过点F作FH⊥FE于点F交GB的延长线于点H，在△ABE的异侧，以BE为斜边作Rt△BEQ，其中∠Q=90°，若∠QEB=∠BDC，EF=FH，求证：BF+BH=BQ．7.在平行四边形ABCD中，以AB为边作等边△ABE，点E在CD上，以BC为边作等边△BCF，点F在AE上，点G在BA延长线上且FG=FB．（1）若CD=6，AF=3，求△ABF的面积；（2）求证：BE=AG+CE．8.如图，在▱ABCD中，点F是对角线BD上一点，且满足AB=AF，过点F作EG交AD于E，交BC于G，作AH⊥BC于点H，交BD于M．（1）若F为MD中点，AF=2，AM=√3，求BC的长度；（2）若∠ABH=∠AFE，求证：BH+FG=HG．9.如图，平行四边形ABCD中，AB∥CD，AD∥BC，点G是线段BC的中点，点E是线段AD上的一点，点F是线段AB延长线上一点，连接DF，且∠ABE=∠CDG=∠FDG.（1）∠A=45°，∠ADF=75°，CD=3+√3，求线段BC的长；（2）求证：AB=BF+DF.10.如图，△ABC的高AD与中线BE相交于点F，过点C作BE的平行线，过点F作AB的平行线，两平行线相交于点G，连接BG，FG．（1）若AE＝2.5，CD＝3，BD＝2，求AB的长；（2）若∠CBE＝30°，求证：CG＝AD+EF．11.如图，在□ABCD中，E为BC边的中点，连接AE，F为CD边上一点，且满足∠DFA=2∠BAE.（1）若∠D=100°，∠DAF=30°，求∠FAE的大小；（2）求证：AF=CD+CF.12.已知在平行四边形ABCD中，过点D作DE⊥BC于点E，且AD=DE．连接AC交DE于点F，作DG⊥AC于点G．（1）如图1，若EFDF =12，AF=√13，求DG的长；（2）如图2，作EM⊥AC于点M，连接DM，求证：AM-EM=2DG．13.如图，在平行四边形ABCD中，AE⊥BC于点E，AE=AD，EG⊥AB于点G，延长GE、DC交于点F，连接AF.（1）若BE=2EC，AB=√13，求AD的长；（2）请猜想线段EG、BG、FC之间的等量关系并证明.14.如图，已知平行四边形ABCD中，DE⊥BC于点E，DH⊥AB于点H，AF平分∠BAD，分别交DC、DE、DH于点F、G、M，且DE=AD，CE=3，AB=5．(1)求线段CF的长度；(2)求证：AB=DG+CE．15.如图所示，在平行四边形ABCD中，∠DAC=60°，点E是BC边上一点，连接AE，AE=AB，点F是对角线AC边上一动点，连接EF.（1）如图1，若点F与对角线交点O重合，已知BE=4，OC：EC=5：3，求AC的长度；（2）如图2，若EC=FC，点G是AC边上一点，连接BG、EG，已知∠AEG=60°，∠AGB+∠BCD=180°，求证：BG+EG=DC.16.如图所示，平行四边形ABCD和平行四边形CDEF有公共边CD，边AB和EF在同一条直线上，AC⊥CD且AC=AF，过点A作AH⊥BC交CF于点G，交BC于点H，连接EG．（1）若AE=2，CD=5，求△BCF的周长；（2）求证：BC=AG+EG．。

八年级上册数学几何辅助线经典题

八年级上册数学几何辅助线经典题一、概述在数学几何学科中，辅助线是解决问题的重要方法之一。

在八年级上册数学教材中，有许多经典的数学几何辅助线题目，通过这些题目的练习，可以帮助学生更好地掌握辅助线的运用方法，提高解题能力。

本文将针对八年级上册数学几何辅助线经典题进行详细介绍和解析。

二、题目一：相似三角形的辅助线应用题目描述：如图所示，∠ABC=∠ACD=90°，AB=4cm，AC=6cm，CD=9cm，求AD的长度。

解析：根据题目给出的信息，我们可以通过绘制辅助线来解决这道题。

连接BD并延长至E点，使得BE=BC。

接下来，连接AE，可得到相似三角形ABE与ACD。

根据相似三角形的性质，我们可以得出以下等式：AB/AC=BE/AD，即4/6=4/(4+AD)。

通过解方程，可以求得AD=8cm。

三、题目二：三角形中的中位线问题题目描述：如图所示，△ABC中，D为AB的中点，E为AC的中点，连接DE，求证：DE//BC。

解析：这道题目考察了中位线的性质和应用。

根据△ABC的性质，可以得出AD=DC，AE=EB，通过连接DE可以得到四边形ADBE。

根据四边形的性质，可以得出ADBE是一个平行四边形，而平行四边形的对角线互相平分，因此DE//BC。

四、题目三：正方形中的选点问题题目描述：如图所示，ABCD为正方形，E为BC的中点，连接AE，求证：AE⊥CD。

解析：这道题目是典型的正方形中的选点问题。

首先根据正方形的性质可以得出AB⊥BC，BC⊥CD，AD⊥DC，因此AD//BC。

接下来连接AE，并可得到△ADE与△CDE，由△ADE≌△CDE，可得出AE⊥CD。

五、结语通过以上三道典型的数学几何辅助线经典题目的解析，我们可以看到辅助线在解决问题中的重要作用。

通过练习和掌握这些经典题目，不仅可以提高学生的数学运算能力，还可以加深对数学几何知识的理解。

希望学生能够在课堂上认真学习，多加练习，提高自己的解题能力，取得好成绩。

2024成都中考数学第一轮专题复习微专题遇到中点如何添加辅助线知识精练(含答案)

2024成都中考数学第一轮专题复习微专题遇到中点如何添加辅助线知识精练1. 如图，在Rt △ABC 中，∠BAC ＝90°，BC ＝4，E ，F 分别是BC ，AC 的中点，延长BA 到点D ，使AD ＝12AB ，则DF 的长为________．第1题图2. 如图，在△ABC 中，AB ＝AC ＝5，BC ＝6，点M 为BC 的中点，MN ⊥AC 于点N ，则MN 的长为________．第2题图3.如图，AD 是△ABC 的中线，点E 是AB 上一点，且BE ＝2AE ，连接CE 交AD 于点F ，若CF ＝3，则EF 的长为________．第3题图4. 如图，在Rt △ABC 中，∠ACB ＝90°，AD 为△ABC 的中线，点E 为AD 的中点，点F 为BE 的中点，连接DF .若DF ⊥BE ，则tan ∠DBE 的值为________．第4题图5. 如图，在▱ABCD 中，BC ＝2AB ，过点A 作AE ⊥CD 于点E ，F 为BC 的中点，连接EF ，若∠B ＝70°，则∠BFE 的度数为________．第5题图6. 如图，在四边形ABCD 中，∠BAD ＝90°，AD ＝2BA ＝6，M ，N 分别是BC ，CD 的中点，连接AM ，AN ，MN .若△CMN 的面积为32，则△AMN 的面积为________．第6题图7. 如图，在▱ABCD 中，E 为AD 的中点，F 是CD 边上一点，连接EF 交BD 于点G ，若DF ＝2，CF ＝4，DG ＝3，则BG 的长为________．第7题图8. 如图，已知△ABC 和△CEF 是等腰直角三角形，其中∠ABC ＝∠CEF ＝90°，且E 是中线AD 的中点，连接BF ，若AB ＝4，则线段BF 的长度为________．第8题图9. 如图，在矩形ABCD 中，点E 为AB 上一点，连接DE ，CE ，且EC 平分∠DEB ，点F 为CE 的中点，连接AF ，BF .求证：AF ⊥BF .第9题图参考答案与解析1. 2 【解析】如解图，连接EF ，AE .∵E ，F 分别为BC ，AC 的中点，∴BE ＝EC ，AF ＝CF ，∴EF ∥AB ，EF ＝12 AB .∵AD ＝12 AB ，∴AD ＝EF ，∴四边形ADFE 是平行四边形，∴DF ＝AE ，∵∠BAC ＝90°，∴AE ＝12BC ＝2，∴DF ＝AE ＝2.第1题解图2.125【解析】如解图，连接AM ，∵AB ＝AC ，点M 为BC 的中点，∴AM ⊥CM (三线合一)，BM ＝CM .∵AB ＝AC ＝5，BC ＝6，∴BM ＝CM ＝3，在Rt △ABM 中，AB ＝5，BM ＝3，∴根据勾股定理得AM ＝AB 2－BM 2 ＝52－32 ＝4.∵S △AMC ＝12 MN ·AC ＝12 AM ·CM ，∴MN ＝AM ·CM AC ＝4×35 ＝125.第2题解图一题多解3. 1 【解析】解法一：如解图①，过点D 作DG ∥AB 交CE 于点G ，则∠EAF ＝∠GDF .∵AD 是△ABC 的中线，∴点D 是BC 的中点，∴DG 是△BCE 的中位线，∴BE ＝2DG ，CG ＝EG .∵BE ＝2AE ，∴AE ＝DG .∵∠AFE ＝∠DFG ，∴△AEF ≌△DGF ，∴EF ＝GF ，∴EF ＝13 CF ＝13 ×3＝1.解法二：如解图②，过点D 作DH ∥CE 交AB 于点H ，∵AD 是△ABC 的中线，∴DH 是△BCE 的中位线，∴DH ＝12 CE ，BH ＝EH .∵BE ＝2AE ，∴AE ＝EH ，∴EF 是△ADH 的中位线，∴EF＝12 DH ，∴EF ＝14 CE ，∴EF ＝13 CF ＝13×3＝1.图①图② 第3题解图4.33【解析】如解图，连接CE ，设CD ＝a ，∵AD 是BC 边上的中线，∴CD ＝BD ＝a .∵点F 为BE 的中点，∴EF ＝BF .∵DF ⊥BE ，∴BD ＝ED ＝a .∵E 为AD 的中点，∠ACB ＝90°，∴CE ＝ED ＝CD ＝a ，∴△CED 为等边三角形，即∠CDE ＝60°.又∵BD ＝ED ，∴∠DEF ＝∠DBF ＝12 ∠CDE ＝30°，∴tan ∠DBE ＝33.第4题解图5. 165° 【解析】如解图，延长EF 交AB 的延长线于点M ，连接AF ，∵四边形ABCD 是平行四边形，∴AB ∥CD ，∴∠C ＝∠MBF .∵F 为BC 的中点，∴BF ＝CF .在△BFM 和△CFE 中，⎩⎪⎨⎪⎧∠MBF ＝∠C ，BF ＝CF ，∠BFM ＝∠CFE ， ∴△BFM ≌△CFE (ASA)，∴MF ＝EF ，∠CEF ＝∠M .∵AE ⊥CD ，∴∠AEC ＝90°，∴∠EAB ＝90°.∵MF ＝EF ，∴AF ＝EF ＝MF ，∴∠M ＝∠MAF .∵四边形ABCD 是平行四边形，∴∠D ＝∠ABC ＝70°，∠BCD ＝110°.∵BC ＝2AB ，∴AB ＝BF ，∴∠MAF ＝(180°－70°)÷2＝55°，∴∠M ＝55°，∴∠CEF ＝55°，∴∠CFE ＝180°－110°－55°＝15°，∴∠BFE ＝180°－15°＝165°.第5题解图6. 6 【解析】如解图，连接AC ，BD .∵M ，N 分别是BC ，CD 的中点，∴MN ＝12 BD ，MN ∥BD ，S △ACN ＝S △DAN ，S △ABM ＝S △AMC ，S △CMN ＝14 ·S △DBC .∵S △CMN ＝32 ，∴S △DBC ＝6.∵∠BAD ＝90°，AD ＝2BA ＝6，∴S △ABD ＝12AD ·AB ＝9，∴S四边形ABCD ＝S △BCD ＋S △ABD ＝15，∴S △ACN ＋S △ACM＝12 S 四边形ABCD ＝152，∴S △AMN ＝S △ACN ＋S △ACM －S △CMN ＝6.第6题解图7. 12 【解析】如解图，延长FE 交BA 的延长线于点H ，∵四边形ABCD 是平行四边形，∴AB ∥CD ，AB ＝CD ，∴∠H ＝∠DFE ，∠HAE ＝∠FDE .∵E 为AD 的中点，∴AE ＝DE ，∴△AEH ≌△DEF ，∴AH ＝DF ＝2，∴BH ＝AB ＋AH ＝CD ＋AH ＝4＋2＋2＝8.又∵AB ∥CD ，∴△BGH ∽△DGF ，∴BG DG ＝BH DF ，即BG 3 ＝82，解得BG ＝12.第7题解图8. 2 【解析】如解图，过点E 作EG ∥BC 交AC 于点G ，连接BG ，∵点E 是AD 的中点，∴点G 是AC 的中点．∵△ABC 和△CEF 是等腰直角三角形，∠ABC ＝∠CEF ＝90°，∴AB ＝BC ，CE ＝EF ，∴∠ACB ＝∠ECF ＝45°，CB ＝2 CG ，CF ＝2 CE ，∴∠GCE ＝∠BCF ，CG CB ＝CE CF ＝22 ，∴△GCE ∽△BCF ，∴GE BF ＝22 .∵BC ＝AB ＝4，AD 是中线，∴BD ＝CD ＝2.∵点E ，G 分别是AD ，AC 的中点，∴EG 是△ADC 的中位线，∴GE ＝12 CD ＝1，∴BF ＝2 .第8题解图9. 证明：∵四边形ABCD 是矩形， ∴AB ∥CD ，∴∠DCE ＝∠CEB . ∵EC 平分∠DEB ， ∴∠DEC ＝∠CEB ， ∴∠DCE ＝∠DEC ， ∴DE ＝DC . 如解图，连接DF ，∵DE ＝DC ，F 为CE 的中点， ∴DF ⊥EC ，∴∠DFC ＝90°.在矩形ABCD 中，AB ＝DC ，∠ABC ＝90°， ∴BF ＝CF ＝EF ＝12 EC ，∴∠ABF ＝∠CEB . ∵∠DCE ＝∠CEB ， ∴∠ABF ＝∠DCF . 在△ABF 和△DCF 中， ⎩⎪⎨⎪⎧BF ＝CF ，∠ABF ＝∠DCF ，AB ＝DC ，∴△ABF ≌△DCF (SAS)， ∴∠AFB ＝∠DFC ＝90°， ∴AF ⊥BF .第9题解图。

总结-平行四边形辅助线

平行四边形常用辅助线总结10组李子君一、构造平行四边形例1、如图，已知点O是平行四边形ABCD的对角线AC的中点，四边形OCDE是平行四边形.求证: OE与AD互相平分.思路：当已知条件中涉及到平行，且要求证的结论中和平行四边形的性质有关，可试通过添加辅助线构造平行四边形.（利用一组对边平行且相等构造平行四边形）例2、如图，在△ABC中，E、F为AB上两点，AE=BF，ED 求证: ED+FG=AC.思路：当图形中涉及到一组对边平行时，可通过作平行线构造另一组对边平行，得到平行四边形解决问题.（利用两组对边平行构造平行四边形）例3、如图，已知AD是△ABC的中线，BE交AC于E，交AD于F，且AE=EF.求证BF=AC.思路：本题通过利用对角线互相平分构造平行四边形，实际上是采用了平移法构造平行四边形.当已知中点或中线应思考这种方法.（利用对角线互相平分构造平行四边形）二、连结对角线例4.在正方形ABCD中，点P是对角线AC上一点，PE⊥AB，PF ⊥BC ，垂足分别是点E 、F.求证：DP=EF三、中心旋转例 5.如图，在正方形ABCD 中，分别是中点交于P,求证AP=AB四、平移对角线例6.在平行四边形ABCD 中，对角线AC 和BD 交于点O ，如果AC=12， BD=10，那么AB 的取值范围是（）五、做高线例7.已知：如图，四边形ABCD 为平行四边形 .求证：思路：当有一边是中点时，倍长中线转移三角形方法十分常见。

旋转三角形（中心对称）解决题目。

思路：当给的条件只见并无直接联系，可联想到转移条件在同一个三角形中，如题想到平移对角线构造一个三角形，转移条件。

222222DA CD BC AB BD AC +++=+思路：从题目入手，由形式可以联想到勾股定理，故试构造直角三角形解题。

A C DB P 思路：矩形对角线相等，欲证DP=EF ，已知EF 是对角线之一，于是想到连结另一条对角线解决题目。

辅助线(补形法)

辅助线（补形法）一些几何题的证明或求解，由原图形分析探究，有时显得十分繁难，若通过适当的“补形”来进行，即添置适当的辅助线，将原图形填补成一个完整的、特殊的、简单的新图形，则能使原问题的本质得到充分的显示，通过对新图形的分析，使原问题顺利获解。

这种方法，我们称之为补形法，它能培养思维能力和解题技巧。

我们学过的三角形、特殊四边形、圆等都可以作为“补形”的对象。

现就常见的添补的图形举例如下，以供参考。

一、补成三角形1.补成三角形例1.如图1，已知E为梯形ABCD的腰CD的中点；证明：△ABE的面积等于梯形ABCD面积的一半。

分析：过一顶点和一腰中点作直线，交底的延长线于一点，构造等面积的三角形。

这也是梯形中常用的辅助线添法之一。

证：2.补成等腰三角形例2 如图2.已知∠A＝90°，AB＝AC，∠1＝∠2，CE⊥BD，求证：BD＝2CE分析：因为角是轴对称图形，角平分线是对称轴，故根据对称性作出辅助线，不难发现CF＝2CE，再证BD＝CF即可。

证：3.补成直角三角形例3.如图3，在梯形ABCD中，AD∥BC，∠B＋∠C＝90°，F、G分别是AD、BC的中点，若BC＝18，AD＝8，求FG的长。

分析：从∠B、∠C互余，考虑将它们变为直角三角形的角，故延长BA、CD，要求FG，需求PF、PG。

解：图34.补成等边三角形例4.图4，△ABC是等边三角形，延长BC至D，延长BA至E，使AE＝BD，连结CE、ED。

证明：EC＝ED分析：要证明EC＝ED，通常要证∠ECD＝∠EDC，但难以实现。

这样可采用补形法即延长BD到F，使BF＝BE，连结EF。

证：二、补成特殊的四边形1.补成平行四边形例5.如图5，四边形ABCD中，E、F、G、H分别是AB、CD、AC、BD的中点，并且E、F、G、H 不在同一条直线上，求证：EF和GH互相平分。

分析：因为平行四边形的对角线互相平分，故要证结论，需考虑四边形GEHF是平行四边形。

第6章平行四边形题型解读7 直角坐标系中的平行四边形-2020-2021学年北师大版八年级数学下册

《平行四边形》题型解读7 直角坐标系中的平行四边形【知识梳理】： 1.总体解题分析思路线：2.常见添辅助线方法：①过平行四边形顶点作坐标轴的垂线段，把点的坐标转化成线段长； ②连接对角线，利用中点坐标公式求解点的坐标；【典型例题】例1.已知如图，平行四边形ABCD 的边AB 在轴上，顶点D 在轴上，AD=4，AB=5，点A 的坐标为（-2，0），则点B 的坐标为____________, 点C 的坐标为____________, 点D 的坐标为____________ 【解题过程】作CE ⊥x 轴，∵点A 的坐标为（-2，0），∴OA=2，∵四边形ABCD 是平行四边形，∴AD=BC=4,AB=CD=5,∴OB=3,∴BE=2,在Rt △OAD 中，由勾股定理可得OD=2√3,∵∠DAO=∠CBE,OA=BE=2,∠AOD=∠CEB=90º,∴△AOD ≌△BEC,∴CE=OB=2√3,∴B(3,0)、D(0,2√3)、C(5,2√3).例2.如图，在平面直角坐标系中，AB//OC ，A （0，12），B （a,12），C （b,0），且满足b =√a −21+√21−a +16. 动点P 从点A 出发，在线段AB 上以每秒2个单位长度的速度向点B 运动；动点Q 从点O 出发在线段OC 上以每秒1个单位长度的速度向点C 运动，点P 、Q 同时出发，当点P 运动到点B 时，点Q 随之停止运动.设运动时间为t （秒）. （1）求B ，C 两点的坐标；（2）当t 为何值时，四边形PQCB 是平行四边形？请求出此时P ，Q 两点的坐标；（3）当t 为何值时，△PQC 是以PQ 为腰的等腰三角形？并求出P 、Q 两点的坐标.【解题过程】（1）∵b =√a −21+√21−a +16，∴√a −21≥0，√21−a ≥0，∴a=21,∴b=16,∴B(21,12)、C(16,0)；（2）如图1，由题可知：AP=2t,PB=21-2t ，OQ=t,QC=16-t ，∵当四边形PQCB 是平行四边形时，∴PB=QC ，即21-2t=16-t ，解得t=5，此时AP=10,OQ=5，∵AB//OC ，∴点B 、P 的纵坐标相同，∴P(10,12)、Q(5,0)。

平行四边形中的辅助线

平行四边形中辅助线问题知识点一：平行四边形有关的辅助线作法第一类：连结对角线，把平行四边形转化成两个全等三角形。

例1如图，在平行四边形ABCD 中，点F E ,在对角线AC 上，且CF AE =,请你以F 为一个端点，和图中已标明字母的某一点连成一条新线段，猜想并证明它和图中已有的某一条线段相等第二类：平移对角线，把平行四边形转化为梯形。

例2如右图2，在平行四边形ABCD 中，对角线AC 和BD 相交于点O ，如果12=AC ，10=BD ，m AB =，那么m 的取值范围是（）A 111<<mB 222<<mC 1210<<mD 65<<m第三类：过一边两端点作对边的垂线，把平行四边形转化为矩形和直角三角形问题。

例3已知：如图，四边形ABCD 为平行四边形。

求证：222222DA CD BC AB BD AC +++=+第四类：延长一边中点与顶点连线，把平行四边形转化为三角形。

例4：已知：如图，在正方形ABCD 中，F E ,分别是CD 、DA 的中点，BE 与CF 交于P 点，求证：AB AP =证明：第五类：延长一边上一点与一顶点连线，把平行四边形转化为平行线型相似三角形。

第六类：把对角线交点与一边中点连结，构造三角形中位线例5已知：如图，在平行四边形ABCD 中，BN AN =,BC BE 31=,NE 交BD 于F ，求BD BF :综上所述，平行四边形中常添加辅助线是：连对角线，平移对角线，延长一边中点与顶点连线等，这样可将平行四边形转化为三角形（或特殊三角形）、矩形（梯形）等图形，为证明解决问题创造条件。

知识点二：和菱形有关的辅助线的作法和菱形有关的辅助线的作法主要是连接菱形的对角线，借助菱形的判定定理或性质定定理解决问题.例7 如图，在△ABC 中，∠ACB=90°，∠BAC 的平分线交BC 于点D ，E 是AB 上一点，且AE=AC ，EF//BC 交AD 于点F ，求证：四边形CDEF 是菱形.分析：要证明四边形CDEF 是菱形，根据已知条件，本题有量种判定方法，一是证明四边相等的四边形是菱形，二是证明对角线互相垂直平分的四边形是菱形.根据AD 是∠BAC 的平分线，AE=AC ，可通过连接CE ，构造等腰三角形，借助三线合一证明AD 垂直CE.求AD 平分CE.例8 如图，四边形ABCD 是菱形，E 为边AB 上一个定点，F 是AC 上一个动点，求证EF+BF 的最小值等于DE 长.分析：要证明EF+BF 的最小值是DE 的长，可以通过连结菱形的对角线BD ，借助菱形的对角线互相垂直平分得到DF=BF ，然后结合三角形两边之和大于第三边解决问题.说明：菱形是一种特殊的平行四边形，和菱形的有关证明题或计算题作辅助线的不是很多，常见的几种辅助线的方法有：（1）作菱形的高；（2）连结菱形的对角线.知识点三：与矩形有辅助线作法和矩形有关的题型一般有两种：（1）计算型题，一般通过作辅助线构造直角三角形借助勾股定理解决问题；（2）证明或探索题，一般连结矩形的对角线借助对角线相等这一性质解决问题.和矩形有关的试题的辅助线的作法较少.例9如图，已知矩形ABCD 内一点，PA=3，PB=4，PC=5.求 PD 的长.分析：要利用已知条件，因为矩形ABCD ，可过P 分别作两组对边的平行线，构造直角三角形借助勾股定理解决问题.说明：本题主要是借助矩形的四个角都是直角，通过作平行线构造四个小矩形，然后根据对角线得到直角三角形，利用勾股定理找到PD 与PA 、PB 、PC 之间的关系，进而求到PD 的长.知识点四：与正方形有关辅助线的作法正方形是一种完美的几何图形，它既是轴对称图形，又是中心对称图形，有关正方形的试题较多.解决正方形的问题有时需要作辅助线，作正方形对角线是解决正方形问题的常用辅助线.例10如图，过正方形ABCD 的顶点B 作BE//AC ，且AE=AC ，又CF//AE.求证：∠BCF=21∠AEB.分析：由BE//AC ，CF//AE ，AE=AC ，可知四边形AEFC 是菱形，作AH ⊥BE 于H ，根据正方形的性质可知四边形AHBO 是正方形，从AH=OB=21AC ，可算出∠E=∠ACF=30°，∠BCF=15°.说明：本题是一道综合题，既涉及正方形的性质，又涉及到菱形的性质.通过连接正方形的对角线构造正方形AHBO ，进一步得到菱形，借助菱形的性质解决问题.知识点五：与梯形有关的辅助线的作法和梯形有关的辅助线的作法是较多的.主要涉及以下几种类型：（1）作一腰的平行线构造平行四边形和特殊三角形；（2）作梯形的高，构造矩形和直角三角形；（3）作一对角线的平行线，构造直角三角形和平行四边形；（4）延长两腰构成三角形；（5）作两腰的平行线等.例11 已知，如图，在梯形ABCD 中，AD//BC ，AB=AC ，∠BAC=90°，BD=BC ，BD 交AC 于点0.求证：CO=CD.分析：要证明CO=CD ，可证明∠COD=∠CDO ，由于已知∠BAC=90°，所以可通过作梯形高构造矩形，借助直角三角形的性质解决问题.说明：在证明线段相等时，一般利用等角对等边来证明，本题作梯形的高将梯形转化为矩形和直角三角形，进而根据直角三角形知识解决.例12 如图，在等腰梯形ABCD 中，AD//BC ，AC ⊥BD ，AD+BC=10，DE ⊥BC 于E.求DE 的长.分析：根据本题的已知条件，可通过平移一条对角线，把梯形转化为平行四边形和直角三角形，借助勾股定理解决.说明:当有对角线或垂直成梯形时,常作梯形对角线的平行线,构造平行四边形,等腰三角形或直角三角形来解决.知识点六：和中位线有关辅助线的作法例13 如图，在四边形ABCD中，AC于BD交于点0，AC=BD，E、F分别是AB、CD 中点，EF分别交AC、BD于点H、G.求证：OG=OH.分析：欲证0G=OH，而OG、OH为同一个三角形的两边，又E、F分别是AB、CD 中点，所以可试想作辅助线，构造三角形中位线解决问题.说明：遇中点，常作中位线，借助中位线的性质解题.。

(完整版)平行四边形的判定练习及答案

诘你添加一个适当的条 A.1： 2 ：B.2 ： 2 ：C.2 ： 3 ：平行四边形的判定二、课中强化（10分钟训练）1•如图3,在匚ABCD 中，对角线F 满足F 列哪个条件时，四边形AC 、BD 相交于点0,E 、F 是对角线AC 上的两点，当E 、 DEBF 不一定是平行四边形（ A.AE=CFC.Z ADE=/CBFB.DE=BF D. / AED= / CFB 2•如图 4,AB\|DC, DC=EF=10 , DE=CF=8，则图中的平行四边形有由分别是 ___________________3.如图5,E 、F 是平行四边形ABCD 对角线BD 上的两点,'使四边形AECF 是平行四边形.4.如图6,AD=BC,要使四边形ABCD 是平行四边形，还需补充的一个条件是： __________三、课后巩固（30分钟训练）1 •以不在同一直线上的三个点为顶点作平行四边形最多能作（） A.4个 B.3个 C.2个 D.1个2. 下面给出了四边形ABCD 中/A 、/ B 、/ C 、/ D 的度数之比，其中能判定四边形ABCD 是平行四边形的是（）3. 九根火柴棒排成如右图形状，图中 __个平行四边形，你判断的根据是 __________________4. 已知四边形ABCD 的对角线AC 、BD 相交于点O,给出下列5个条件：①AB // CD ； OA=OC ; ③AB=CD :④/ BAD= / DCB ; ® AD // BC.（1）从以上5个条件中任意选取2个条件，能推出四边形ABCD 是平行四边形的有（用序图4图5 图6⑵对由以上5个条件中任意选取2个条件，不能推出四边形ABCD 是平行匹边形的，请选取一种情形举出反例说明 •5•若三条线段的长分别为平行四边形？20 cm,14 cm,16 cm,以其中两条为对角线，另一条为一边，是否可以画 6•如图，E 、F 是四边形ABCD 的对角线AC 上的两点，AF=CE , DF=BE , DF// BE.求证：(】)△AFD ©A CEB;(2)四边形ABCD 是平行四边形.17•如图，已知DC // AB ，且DC= —AB, E 为AB 的中点• 2⑴求证：△ AED EBC ;(2)观察图形，在不添加辅助线的情况下，除厶 EBC 夕卜，请再写出两个与厶AED 的面积相等的三角形(直接写出结果，不要求证明)： __________________________________8•如图，已知二1ABCD中DE丄AC,BF丄AC,证明四边形DEBF为平行四边形9•如图，已知■ ABCD中,E、F分别是AB、CD的中点•求证:(1) △ AFD ©A CEB;⑵四边形AECF是平行四边形•二、课中强化（10分钟训练）1懈析：当E、F满足AE=CF时，由平行四边形的对角线相等知OB=OD,OA=OC ,故OE=OF.可知四边形DEBF是平行四边形•当E、F满足/ ADE= / CBF 时，因为AD // BC,所以/ DAE= / BCF.又AD=BC，可证出厶ADE OA CBF，所以DE=BF，/ DEA= / BFC.故/ DEF= / BFE.因此DE// BF，可知四边形DEBF是平行四边形•类似地可说明D也可以•答案:B2•解析：因为ABWDC，根据一组对边平行且相等的四边形是平行四边形可判定四边形ABCD是平行四边形；DC=EF , DE=CF,根据两组对边分别相等的四边形是平行四边形可判定四边形CDEF是平行四边形•答案：四边形ABCD，四边形CDEF —组对边平行且相等的四边形是平行四边形两组对边分别相等的四边形是平行四边形3•解析：根据平行四边形的定义和判定方法可填BE=DF ; Z BAE= / CDF^-答案：BE=DF或ZBAE=ZCDF等任何一个均可4•解析：根据平行四边形的判定定理，知可填（DAD// BC,② AB=CD,③ ZA+ZB=180。

人教版初二数学8年级下册第18章(平行四边形)含辅助线证明专项训练(含答案)

人教版数学八年级下册第十八章平行四边形含辅助线证明训练一1.如图，□ABCD中，AC⊥AB，点E在线段AC上，AE=AB，BE的延长线交边AD于点F，AG⊥BC，且AG=AF，AG交BF于点O．（1）若AD=13，AC=12，求BE的长；（2）若点O恰好是线段AG的中点，连接GE，求证：AF=GE．2.已知正方形ABCD如图所示，连接其对角线AC，∠DAC的平分线AE交CD于点E，过点D作DM⊥AE于F，交AC于点M，共过点A作AN⊥AE交CB延长线于点N．(1)若AD=3，求△CAN的面积；(2)求证：AN=DM+2EF．3.如图1，已知正方形ABCD中，点E在BC上，连接AE，过点B作BF⊥AE于点G，交CD于点F.图1 图2（1）如图1，连接AF，若AB＝4，BE＝1，求AF的长；（2）如图2，连接BD，交AE于点N，连接AC，分别交BD、BF于点O、M，连接GO,求证：AG-BG=2GO4.如图，平行四边形ABCD中，BF⊥DC交DC于点F，且BF=AB，E点是BC边上一点，连接AE交BF于G；（1）若AE平分∠DAB，∠C=60∘，BE=3，求BG的长；（2）若AD=BG+FC，求证：AE平分∠DAB．5.如图，在□ABCD中，AD上有一点E，连接BE,AH⊥BC于H,AH、BE交于点G,连接CG并延长交AB于F,且GC=CD,∠GCD=90∘.(1) 若GC＝6，∠BAG＝30∘，求四边形AGCD的面积；(2) 求证：DE=2BG．6.如图，▱ABCD中，点E为BC边上一点，过点E作EF⊥AB于F，已知∠D=2∠AEF．（1）若∠BAE=70°，求∠BEA的度数；（2）连接AC，过点E作EG⊥AC于G，延长EG交AD于点H，若∠ACB=45°，求AC．证：AH=AF+227.如图，▱ABCD中，DF平分∠ADC交AC于点H，G为DH的中点．（1）如图①，若M为AD的中点，AB⊥AC，AC=9，CF=8，CG=25，求GM；（2）如图②，M为线段AB上一点，连接MF，满足∠MCD=∠BCG，∠MFB=∠BAC．求证：MC=2CG．8.如图，在▱ABCD中，连结BD，点E在BD上，且DE=DC，连结CE并延长它与AD交于点F，过点C作CG⊥BD垂足为G，交AD于点H．（1）若DG=3，CG=23，求△CDE的面积；（2）若∠DFC=45°，求证：EF+2FH=CF．9.如图所示，在正方形ABCD的边CB的延长线上取点F，连结AF，在AF上取点G，使得AG=AD，连结DG，过点A作AE⊥AF，交DG于点E．（1）若正方形ABCD的边长为4，且AB=2FB，求FG的长；（2）求证：AE+BF=AF．10.如图，▱ABCD中，E为平行四边形内部一点，连接AE，BE，CE．（1）如图1，AE⊥BC交BC于点F，已知∠EBC=45°，∠BAF=∠ECF，AB=5，EF=1，求AD的长；（2）如图2，AE⊥CD交CD于点F，AE=CF且∠BEC=90°，G为AB上一点，作GP⊥BE 且GP=CE，并以BG为斜边作等腰Rt△BGH，连接EP、EH．求证：EP=2EH．11.如图1，在等腰△ABO中，AB=AO，分别延长AO、BO至点C、点D，使得CO=AO、BO=BO，连接AD、BC．（1）如图1，求证：AD=BC；（2）如图2，分别取边AD、CO、BO的中点E、F、H，猜想△EFH的形状，并说明理由．12.已知，如图，▱ABCD的对角线AC、BD相交于点O，（1）如图1，若AC=AD过点A作AE⊥BC于点E，若AE=3,BC=5，求AB边的长；（2）如图2，过点A作BD的垂线，垂足为F，且AF=BF，过点B作BC的垂线，两条垂线相交于点G，若∠BAG=∠BFC，连接DG.求证：GF=4FO13.已知，在平行四边形ABCD中，AB⊥BD,E为射线BC上一点，连接AE交BD于点F，AB=BD.（1）如图1，若点E与点C重合，且AF=25，求AD的长；（2）如图2，若点E在BC边上时，过点D作DG⊥AE于G,延长DG交BC于H，连接FH.求证：AF=DH+FH;（3）如图3，当点E在射线BC上运动时，过点D作DG⊥AE于G,M为AG的中点，点N在BC边上且BN=1，已知AB=42，请直接写出MN的最小值。

第4章平行四边形-中位线常见的辅助线浙教版数学八年级下册课件

例2：四边形ABCD中，点E、F、G、H分别是BC、AD、BD、AC的中
点，求证:EF和GH互相平分
连结EG,GF,FH,EH
∵E,G分别为AD，BD的中点
∴

∵F,H分别为BC，AC的中点
∴

∴
∴四边形EGFH是平行四边形
∴EF和GH互相平分
例题演练掌握新知
练习1：已知：四边形ABCD中，AB=CD，M、N、E、F分
3、三角形中两边中点-------中位线定理
4、一般三角形中点-------倍长中线法
只有一边中点，取另一边中点构造中位线
例题演练掌握新知
例3：如图，△ABC中，AD是BC边上的中线，F是AD的中
点，BF的延长线交AC于点E
1
求证：AE AC
3
取BE中点M,连结DM
∵D,M分别为BC，BE的中点
中位线常见的辅助线
例题演练掌握新知
出现两边中点，添加第三边构造三角
形使其成为中位线
例1：任意四边形ABCD，四边中点E、F、G、H
组成的四边形是不是平行四边形？
顺次连接任意四边形各边中点的线段组成一个平行四边形
例题演练掌握新知
练习1：如图，已知△ABC是锐角三角形，分别以AB，AC
为边向外侧作两个等边△ABM和△CAN．D，E，F分别是MB，
CD的中点，EF交AC于M,交BD于N，
求证：OM=ON。
取BC中点G，连接EG、FG
∵E,G分别为AB，BC的中点

∴ ∥ , =

同理可得 ∥ , =

∴ =FG
∵AB=CD
∴∠GEF=∠GFE

2023年中考九年级数学高频考点专题训练--平行四边形的判定

2023年中考九年级数学高频考点专题训练--平行四边形的判定一、综合题1．如图，在□ ABCD中，点E、F在对角线BD上，且BE＝DF.（1）求证：AE＝CF；（2）求证：四边形AECF是平行四边形．2．如图，E、F是平行四边形ABCD对角线AC上两点，且AE=CF．（1）求证：四边形BFDE是平行四边形．（2）如果把条件AE=CF改为BE⊥AC，DF⊥AC，试问四边形BFDE是平行四边形吗？为什么？（3）如果把条件A E=CF改为BE=DF，试问四边形BFDE还是平行四边形吗？为什么？3．如图，平行四边形ABCD 中，AB=8 cm，BC=12 cm，⊥B=60°，G 是CD 的中点，E 是边AD 上的动点，EG 的延长线与BC 的延长线交于点F，连接CE，DF.（1）求证：四边形CEDF 是平行四边形；（2）①AE=cm 时，四边形CEDF 是矩形，请写出判定矩形的依据（一条即可）；②AE=cm 时，四边形CEDF 是菱形，请写出判定菱形的依据（一条即可）.4．如图，四边形ABCD中，AD⊥BC，AE⊥AD交BD于点E，CF⊥BC交BD于点F，且AE=CF.（1）求证：四边形ABCD是平行四边形.（2）若⊥BAE=⊥BDC,AE=3，BD=9，AB=4，求四边形ABCD的周长.5．如图，直线y=−2x+10与x轴交于点A，点B是该直线上一点，满足OB=OA.（1）求点B的坐标；（2）若点C是直线上另外一点，满足AB=BC，且四边形OBCD是平行四边形，试画出符合要求的大致图形，并求出点D的坐标.6．如图，在⊥ABCD中，点O是边BC的中点，连接DO并延长，交AB延长线于点E，连接BD，EC．（1）求证：四边形BECD是平行四边形；（2）若⊥A=50°，则当⊥BOD= °时，四边形BECD是矩形．7．如图，在⊥AFC中，⊥FAC=45°，FE⊥AC于点E，在EF上取一点B，连接AB、BC，使得AB=FC，过点A作AD⊥AF，且AD=BC，连接CD。

初中几何辅助线——四边形辅助线大全

初中几何辅助线——四边形辅助线大全题型1.平行四边形的两邻边之和等于平行四边形周长的一半.例1已知,□ABCD的周长为60cm，对角线AC、BD相交于点O，△AOB的周长比△BOC的周长多8cm，求这个四边形各边长.解：∵四边形ABCD为平行四边形∴AB = CD，AD = CB，AO = CO∵AB＋CD＋DA＋CB = 60AO＋AB＋OB－(OB＋BC＋OC) = 8∴AB＋BC = 30，AB－BC =8∴AB = CD = 19，BC = AD = 11答：这个四边形各边长分别为19cm、11cm、19cm、11cm.题型 2.平行四边形被对角线分成四个小三角形，相邻两个三角形周长之差等于邻边之差.（例题如上）题型3.有平行线时常作平行线构造平行四边形.例2已知，如图，Rt△ABC，∠ACB = 90o，CD⊥AB于D，AE平分∠CAB交CD于F，过F 作FH∥AB交BC于H求证：CE = BH证明：过F作FP∥BC交AB于P，则四边形FPBH 为平行四边形∴∠B =∠FP A，BH = FP∵∠ACB = 90o，CD⊥AB∴∠5＋∠CAB = 45o，∠B＋∠CAB = 90o∴∠5 =∠B∴∠5 =∠FP A又∵∠1 =∠2，AF = AF∴△CAF≌△P AF∴CF = FP∵∠4 =∠1＋∠5，∠3 =∠2＋∠B∴∠3 =∠4∴CF = CE∴CE = BH练习：已知，如图，AB∥EF∥GH，BE = GC求证：AB = EF＋GH54321PHFEDCB AGHFEB AC题型4.有以平行四边形一边中点为端点的线段时常延长此线段.例3已知，如图，在□ABCD中，AB = 2BC，M为AB中点求证：CM⊥DM证明：延长DM、CB交于N∵四边形ABCD为平行四边形∴AD = BC，AD∥BC∴∠A = ∠NBA∠ADN=∠N又∵AM = BM∴△AMD≌△BMN∴AD = BN∴BN = BC∵AB = 2BC，AM = BM∴BM = BC = BN∴∠1 =∠2，∠3 =∠N∵∠1＋∠2＋∠3＋∠N = 180o，∴∠1＋∠3 = 90o∴CM⊥DM题型5.平行四边形对角线的交点到一组对边距离相等.例4如图：OE=OF题型 6.平行四边形一边（或这边所在的直线）上的任意一点与对边的两个端点的连线所构成的三角形的面积等于平行四边形面积的一半.例5如图：S△BEC= 12S□ABCD题型7.平行四边形内任意一点与四个顶点的连线所构成的四个三角形中，不相邻的两个三角形的面积之和等于平行四边形面积的一半.例6如图：S△AOB＋S△DOC= S△BOC＋S△AOD = 12S□ABCDEDCBAODCBA321NM BAD CFEODCBA题型8.任意一点与同一平面内的矩形各点的连线中，不相邻的两条线段的平方和相等. 例7如图：AO 2＋OC 2 = BO 2 ＋DO 2题型9.平行四边形四个内角平分线所围成的四边形为矩形.例8如图：四边形GHMN 是矩形（题型5～题型9请自己证明）题型10.有垂直时可作垂线构造矩形或平行线.例9已知，如图，E 为矩形ABCD 的边AD 上一点，且BE = ED ，P 为对角线BD 上一点，PF ⊥BE 于F ，PG ⊥AD 于G 求证：PF ＋PG = AB证明：证法一：过P 作PH ⊥AB 于H ，则四边形AHPG 为矩形∴AH = GP PH ∥AD ∴∠ADB =∠HPB∵BE = DE ∴∠EBD = ∠ADB ∴∠HPB =∠EBD 又∵∠PFB =∠BHP = 90o∴△PFB ≌△BHP∴HB = FP∴AH ＋HB = PG ＋PF 即AB = PG ＋PF证法二：延长GP 交BC 于N ，则四边形ABNG 为矩形，（证明略）NP H G FE D C B AN M HG DCBAA DC B OO B CD A题型11.直角三角形常用辅助线方法⑴作斜边上的高例10已知，如图,若从矩形ABCD的顶点C作对角线BD的垂线与∠BAD的平分线交于点E 求证：AC = CE证明：过A作AF⊥BD，垂足为F，则AF∥EG∴∠F AE = ∠AEG∵四边形ABCD为矩形∴∠BAD = 90o OA = OD∴∠BDA =∠CAD∵AF⊥BD∴∠ABD＋∠ADB= ∠ABD＋∠BAF= 90o∴∠BAF =∠ADB =∠CAD∵AE为∠BAD的平分线∴∠BAE =∠DAE∴∠BAE－∠BAF =∠DAE－∠DAC即∠F AE =∠CAE∴∠CAE =∠AEG∴AC = EC⑵作斜边中线，当有下列情况时常作斜边中线①有斜边中点时例11已知，如图，AD、BE是△ABC的高，F是DE的中点，G是AB的中点求证：GF⊥DE证明：连结GE、GD∵AD、BE是△ABC的高，G是AB的中点∴GE = 12AB，GD =12AB∴GE = GD∵F是DE的中点∴GF⊥DE②有和斜边倍分关系的线段时例12已知，如图，在△ABC中，D是BC延长线上一点，且DA⊥BA于A，AC = 12 BD求证：∠ACB = 2∠B证明：取BD中点E，连结AE，则AE = BE = 12 BD∴∠1 =∠BGOFEDCBAFEDCBA∵AC =12BD ∴AC = AE∴∠ACB =∠2 ∵∠2 =∠1＋∠B ∴∠2 = 2∠B ∴∠ACB = 2∠B题型12.正方形一条对角线上一点到另一条对角线上的两端距离相等.例13已知，如图，过正方形ABCD 对角线BD 上一点P ，作PE ⊥BC 于E ，作PF ⊥CD 于F 求证：AP = EF证明:连结AC 、PC∵四边形ABCD 为正方形∴BD 垂直平分AC ，∠BCD = 90o∴AP = CP∵PE ⊥BC ，PF ⊥CD ，∠BCD = 90o ∴四边形PECF 为矩形 ∴PC = EF ∴AP = EF 题型13.有正方形一边中点时常取另一边中点.例14已知,如图，正方形ABCD 中，M 为AB 的中点，MN ⊥MD ，BN 平分∠CBE 并交MN 于N求证：MD = MN证明：取AD 的中点P ，连结PM ，则DP = P A =12AD ∵四边形ABCD 为正方形 ∴AD = AB , ∠A =∠ABC = 90o∴∠1＋∠AMD = 90o ，又DM ⊥MN ∴∠2＋∠AMD = 90o ∴∠1 =∠2 ∵M 为AB 中点∴AM = MB = 12AB∴DP = MB AP = AM ∴∠APM =∠AMP = 45o ∴∠DPM =135o ∵BN 平分∠CBE ∴∠CBN = 45o∴∠MBN =∠MBC ＋∠CBN = 90o ＋45o = 135o 即∠DPM =∠MBN ∴△DPM ≌△MBN21EDCBAP F ED CB A21P NEDCA∴DM = MN注意：把M 改为AB 上任一点，其它条件不变，结论仍然成立。

八年级初二数学平行四边形知识点及练习题含答案

一、选择题1．如图，正方形ABCD 和正方形CEFG 中，点D 在CG 上，1BC =，3CE =，H 是AF 的中点，那么CH 的长是( )A ．2B ．52C ．332D ．52．如图，正方形ABCD 的边长为4，点E 在边AB 上，AE ＝1，若点P 为对角线BD 上的一个动点，则△PAE 周长的最小值是（）A ．3B ．4C ．5D ．63．如图，正方形ABCD 中，点E F 、分别在边BC CD 、上，且AE EF FA ==，有下列结论：①ABE ADF ∆≅∆；②CE CF =；③75AEB ∠=︒；④BE DF EF +=；⑤A ABE DF CEF S S S ∆∆∆+=；其中正确的有（）个．A ．2B ．3C ．4D ．54．□ABCD 中，∠A=60°，点E 、F 分别在边AD 、DC 上，DE=DF ，且∠EBF=60°．若AE=2，FC=3，则EF 的长度为（）A 21B ．5C ．26D ．55．如图，菱形ABCD 中，∠A 是锐角，E 为边AD 上一点，△ABE 沿着BE 折叠，使点A 的对应点F 恰好落在边CD 上，连接EF ，BF ，给出下列结论：①若∠A =70°，则∠ABE =35°；②若点F 是CD 的中点，则S △ABE 13=S 菱形ABCD下列判断正确的是（）A ．①，②都对B ．①，②都错C ．①对，②错D ．①错，②对6．如图，在▭ABCD 中，AB ＝4，BC ＝6，∠ABC ＝60°，点P 为▭ABCD 内一点，点Q 在BC 边上，则PA +PD +PQ 的最小值为( )A ．3719++B ．6+23C ．53D ．107．如图，在平行四边形ABCD 中，对角线AC 、BD 相交于O ，2BD AD =，E 、F 、G 分别是OC 、OD 、AB 的中点，下列结论：①BE AC ⊥；②EG GF =；③EFG GBE ∆∆≌；④EA 平分GEF ∠；⑤四边形BEFG 是菱形．其中正确的是( )A ．①②③B ．①③④C ．①②⑤D ．②③⑤8．如图，正方形ABCD 中，点E 是AD 边的中点，BD 、CE 交于点H ，BE 、AH 交于点G ，则下列结论：①AG ⊥BE ；②BE:BC=5:2；③S △BHE =S △CHD ；④∠AHB=∠EHD ．其中正确的个数是A ．1B ．2C ．3D ．49．下列命题中，真命题的个数有（）①对角线相等的四边形是矩形；②三条边相等的四边形是菱形；③一组对边平行且相等的四边形是平行四边形．A ．3个B ．2个C ．1个D ．0个10．如图，在菱形ABCD 中，AB=AC=1，点E 、F 分别为边AB 、BC 上的点，且AE=BF ，连接CE 、AF 交于点H ，连接DH 交AC 于点O ，则下列结论：①△ABF ≌△CAE ；②∠FHC=∠B ；③△ADO ≌△ACH ；④=3ABCD S 菱形；其中正确的结论个数是（）A ．1个B ．2个C ．3个D ．4个二、填空题11．如图，某景区湖中有一段“九曲桥”连接湖岸A ，B 两点，“九曲桥”的每一段与AC 平行或BD 平行，若AB ＝100m ，∠A ＝∠B ＝60°，则此“九曲桥”的总长度为_____．12．如图，菱形ABCD 的BC 边在x 轴上，顶点C 坐标为(3,0)-，顶点D 坐标为(0,4)，点E 在y 轴上，线段//EF x 轴，且点F 坐标为(8,6)，若菱形ABCD 沿x 轴左右运动，连接AE 、DF ，则运动过程中，四边形ADFE 周长的最小值是_______．13．如图，ABC ∆是边长为1的等边三角形，取BC 边中点E ，作//ED AB ，//EF AC ，得到四边形EDAF ，它的周长记作1C ；取BE 中点1E ，作11//E D FB ，11//E F EF ，得到四边形111E D FF ，它的周长记作2C ．照此规律作下去，则2020C =______．14．如图，四边形ABCD 是菱形，∠DAB ＝48°，对角线AC ，BD 相交于点O ，DH ⊥AB 于H ，连接OH ，则∠DHO ＝_____度．15．如图，Rt ABE ∆中，90,B AB BE ︒∠==, 将ABE ∆绕点A 逆时针旋转45︒，得到,AHD ∆过D 作DC BE ⊥交BE 的延长线于点C ，连接BH 并延长交DC 于点F ，连接DE 交BF 于点O ．下列结论：①DE 平分HDC ∠；②DO OE =； ③CD HF =； ④2BC CF CE -=； ⑤H 是BF 的中点，其中正确的是___________16．在锐角三角形ABC 中，AH 是边BC 的高，分别以AB ，AC 为边向外作正方形ABDE 和正方形ACFG ，连接CE ，BG 和EG ，EG 与HA 的延长线交于点M ，下列结论：①BG=CE ；②BG ⊥CE ；③AM 是△AEG 的中线；④∠EAM=∠ABC ．其中正确的是_________．17．在ABCD 中，5AD =，BAD ∠的平分线交CD 于点E ，∠ABC 的平分线交CD 于点F ，若线段EF=2，则AB 的长为__________．18．如图，▱ABCD 中，∠DAB ＝30°，AB ＝6，BC ＝2，P 为边CD 上的一动点，则2PB+ PD 的最小值等于______.19．如图，有一张长方形纸片ABCD ，4AB =，3AD =．先将长方形纸片ABCD 折叠，使边AD 落在边AB 上，点D 落在点E 处，折痕为AF ；再将AEF ∆沿EF 翻折，AF 与BC 相交于点G ，则FG 的长为___________．20．如图，在四边形ABCD 中， //,5,18,AD BC AD BC E ==是BC 的中点．点P 以每秒1个单位长度的速度从点A 出发，沿AD 向点D 运动;点Q 同时以每秒3个单位长度的速度从点C 出发，沿CB 向点B 运动．点P 停止运动时，点Q 也随之停止运动，当运动时间为t 秒时，以点,,,P Q E D 为顶点的四边形是平行四边形，则t 的值等于_______．三、解答题21．在四边形ABCD 中，90A B C D ∠∠∠∠====，10AB CD ==，8BC AD ==．()1P 为边BC 上一点，将ABP 沿直线AP 翻折至AEP 的位置(点B 落在点E 处) ①如图1，当点E 落在CD 边上时，利用尺规作图，在图1中作出满足条件的图形(不写作法，保留作图痕迹，用2B 铅笔加粗加黑).并直接写出此时DE =______； ②如图2，若点P 为BC 边的中点，连接CE ，则CE 与AP 有何位置关系？请说明理由； ()2点Q 为射线DC 上的一个动点，将ADQ 沿AQ 翻折，点D 恰好落在直线BQ 上的点'D 处，则DQ =______； 22．如图1，ABC ∆是以ACB ∠为直角的直角三角形，分别以AB ，BC 为边向外作正方形ABFG ，BCED ，连结AD ，CF ，AD 与CF 交于点M ，AB 与CF 交于点N ．（1）求证：ABD FBC ∆≅∆；（2）如图2，在图1基础上连接AF 和FD ，若6AD =，求四边形ACDF 的面积．23．如图，在Rt ABC 中，∠B ＝90°，AC ＝60cm ，∠A ＝60°，点D 从点C 出发沿CA 方向以4cm/s 的速度向点A 匀速运动．同时点E 从点A 出发沿AB 方向以2cm/秒的速度向点B 匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D 、E 运动的时间是ts （0＜t≤15）．过点D 作DF ⊥BC 于点F ，连接DE ，EF ．（1）求证：AE ＝DF ；（2）四边形AEFD 能够成为菱形吗？如果能，求出相应的t 值，如果不能，说明理由；（3）当t 为何值时，DEF 为直角三角形？请说明理由．24．如图，在平行四边形ABCD 中，AB ⊥AC ，对角线AC ，BD 相交于点O ，将直线AC 绕点O 顺时针旋转一个角度α（0°＜α≤90°），分别交线段BC ，AD 于点E ，F ，连接BF ．（1）如图1，在旋转的过程中，求证：OE ＝OF ；（2）如图2，当旋转至90°时，判断四边形ABEF 的形状，并证明你的结论；（3）若AB ＝1，BC 5BF ＝DF ，求旋转角度α的大小．25．已知在ABC 和ADE 中， 180ACB AED ∠+∠=︒，CA CB =，EA ED =，3AB =．（1）如图1，若90ACB ∠=︒，B 、A 、D 三点共线，连接CE ：①若522CE =，求BD 长度； ②如图2，若点F 是BD 中点，连接CF ，EF ，求证：2CE EF =；（2）如图3，若点D 在线段BC 上，且2CAB EAD ∠=∠，试直接写出AED 面积的最小值．26．已知：如下图，ABC 和BCD 中，90BAC BDC ∠=∠=，E 为BC 的中点，连接DE AE 、.若DC AE ，在DC 上取一点F ，使得DF DE =，连接EF 交AD 于O . （1）求证：EF DA ⊥.（2）若4,23BC AD ==，求EF 的长.27．如图，四边形ABCD 为正方形.在边AD 上取一点E ，连接BE ，使60AEB ∠=︒.（1）利用尺规作图（保留作图痕迹）：分别以点B 、C 为圆心，BC 长为半径作弧交正方形内部于点T ，连接BT 并延长交边AD 于点E ，则60AEB ∠=︒；（2）在前面的条件下，取BE 中点M ，过点M 的直线分别交边AB 、CD 于点P 、Q . ①当PQ BE ⊥时，求证：2BP AP =；=时，延长BE，CD交于N点，猜想NQ与MQ的数量关系，并说明理由.②当PQ BE28．已知：在矩形ABCD中，点F为AD中点,点E为AB边上一点，连接CE、EF、CF，EF 平分∠AEC．(1)如图1，求证：CF⊥EF;(2)如图2，延长CE、DA交于点K, 过点F作FG∥AB交CE于点G若，点H为FG上一点，连接CH,若∠CHG=∠BCE, 求证：CH=FK;(3)如图3, 过点H作HN⊥CH交AB于点N,若EN=11,FH-GH=1,求GK长.29．已知E，F分别为正方形ABCD的边BC，CD上的点，AF，DE相交于点G，当E，F分别为边BC，CD的中点时，有：①AF=DE；②AF⊥DE成立．试探究下列问题：（1）如图1，若点E不是边BC的中点，F不是边CD的中点，且CE=DF，上述结论①，②是否仍然成立？（请直接回答“成立”或“不成立”），不需要证明）（2）如图2，若点E，F分别在CB的延长线和DC的延长线上，且CE=DF，此时，上述结论①，②是否仍然成立？若成立，请写出证明过程，若不成立，请说明理由；（3）如图3，在（2）的基础上，连接AE和BF，若点M，N，P，Q分别为AE，EF，FD，AD的中点，请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种，并证明你的结论．30．如图，已知正方形ABCD与正方形CEFG如图放置，连接AG，AE．=（1）求证：AG AE⊥于P，交AB、AD于M、N，交AE、AG于P、Q，交BC于（2）过点F作FP AEH，．求证：NH=FM【参考答案】***试卷处理标记，请不要删除一、选择题1．D解析：D【分析】连接AC、CF，根据正方形性质求出AC、CF，∠ACD=∠GCF=45°，再求出∠ACF=90°，然后利用勾股定理列式求出AF，再根据直角三角形斜边上的中线等于斜边的一半解答即可．【详解】如图，连接AC、CF，∵正方形ABCD和正方形CEFG中，BC=1，CE=3，∴AC=2，CF=32，∠ACD=∠GCF=45°，∴∠ACF=90°，由勾股定理得，22AF=AC CF=25，∵H是AF的中点，∴CH=12AF=12×25=5.故选D．【点睛】本题考查了直角三角形斜边上的中线等于斜边的一半的性质，正方形的性质，勾股定理，熟记各性质并作辅助线构造出直角三角形是解题的关键．2．D解析：D【分析】连接AC 、CE ，CE 交BD 于P ，此时AP +PE 的值最小，求出CE 长，即可求出答案．【详解】解：连接AC 、CE ，CE 交BD 于P ，连接AP 、PE ，∵四边形ABCD 是正方形，∴OA ＝OC ，AC ⊥BD ，即A 和C 关于BD 对称，∴AP ＝CP ，即AP +PE ＝CE ，此时AP +PE 的值最小，所以此时△PAE 周长的值最小，∵正方形ABCD 的边长为4，点E 在边AB 上，AE ＝1，∴∠ABC ＝90°，BE ＝4﹣1＝3，由勾股定理得：CE ＝5，∴△PAE 的周长的最小值是AP +PE +AE ＝CE +AE ＝5+1＝6，故选D ．【点睛】本题考查了正方形的性质与轴对称——最短路径问题，知识点比较综合，属于较难题型.3．C解析：C【分析】由已知得AB AD =，AE AF =，利用“HL ”可证ABE ADF ∆≅∆，利用全等的性质判断①②③正确，在AD 上取一点G ，连接FG ，使AG GF =，由正方形，等边三角形的性质可知15DAF ∠=︒，从而得30DGF ∠=︒，设1DF =，则2AG GF ==，3DG =AD ，CF ，EF 的长，判断④⑤的正确性．【详解】解：AB AD =，AE AF EF ==，()ABE ADF HL ∴∆≅∆，AEF ∆为等边三角形， BE DF ∴=，又BC CD =，CE CF ∴=，11()(9060)1522BAE BAD EAF ∴∠=∠-∠=︒-︒=︒， 9075AEB BAE ∴∠=︒-∠=︒，∴①②③正确，在AD 上取一点G ，连接FG ，使AG GF =，则15DAF GFA ∠=∠=︒，230DGF DAF ∴∠=∠=︒，设1DF =，则2AG GF ==，3DG =， 23AD CD ∴==+，13CF CE CD DF ==-=+，226EF CF ∴==+，而2BE DF +=，∴④错误，⑤12232ABE ADF S S AD DF ∆∆+=⨯⨯=+， 1232CEF S CE CF ∆=⨯=+ ∴⑤正确．∴正确的结论有：①②③⑤．故选C ．【点睛】本题考查了正方形的性质，全等三角形的判定与性质，勾股定理的运用．关键是利用全等三角形的性质，把条件集中到直角三角形中，运用勾股定理求解．4．A解析：A【解析】【分析】由DE=DF ，AE=2，FC=3可知AB-BC=1，过点E 作EM ⊥AB 于M ，根据30°角所对的直角等于斜边的一半可得AM=1，进而得出BM=BC ，将△BEM 顺时针旋转120°得△BEN ，连接FN ，可证△BEF ≌△BFN ，即可得出EF=FN ，过点N 作NG ⊥DC 交DC 的延长线于点G ，利用勾股定理即可求出答案.【详解】解：过点E 作EM ⊥AB 于M ，在Rt △AEM 中，∠A=60°，∴∠AEM=30°，∴AM=12AE=1，∴又∵DE=DF ，AE=2，FC=3，∴DC -AD=1，即AB-BC=1，∴BM=BC ，将△BEM 顺时针旋转120°得△BEN ，连接FN ，则BE=BN ，∵∠EBF=60°，∠EBN=120°，∴∠NBF=60°，∴∠EBF=∠NBF又∵BE=BN ，BF=BF ，∴△BEF≌△BFN ，∴EF=FN ，过点N 作NG⊥DC 交DC 的延长线于点G ，∵∠GCN=180°-60°-90°=30°，∴NG=1232= ∴FG=3+32=92=.【点睛】此题考查了平行四边形的性质、旋转的性质、勾股定理等知识，合理添加辅助线是解题关键.5．A解析：A【解析】【分析】只要证明BF BC =，可得ABF BFC C 70∠∠∠===，即可得出ABE 35∠=；延长EF 交BC 的延长线于M ，只要证明DEF ≌CMF ，推出EF FM =，可得EMB BCDE S S =四边形，BEF MBE 1S S 2=，推出ABE ABCD 1S S 3菱形=．【详解】①∵四边形ABCD是菱形，∴AB∥CD，∠C=∠A=70°．∵BA=BF=BC，∴∠BFC=∠C=70°，∴∠ABF=∠BFC=70°，∴∠ABE12=∠ABF=35°，故①正确；②如图，延长EF交BC的延长线于M，∵四边形ABCD是菱形，F是CD中点，∴DF=CF，∠D=∠FCM，∠EFD=∠MFC，∴△DEF≌△CMF，∴EF=FM，∴S四边形BCDE=S△EMB，S△BEF12=S△MBE，∴S△BEF12=S四边形BCDE，∴S△ABE13=S菱形ABCD．故②正确，故选A．【点睛】本题考查了菱形的性质、等腰三角形的判定和性质、全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．6．C解析：C【分析】如下图，将△APD绕点A逆时针旋转60°至△AFE处，通过边长转换，可将PA+PD+PQ转化为PF+EF+PQ的形式，再利根据两点之间线段最短，得出最小值．【详解】如下图，将△APD绕点A逆时针旋转60°至△AFE处，连接FP，过点E作BC的垂线，交BC于点G，AD于点H，过点A作BC的垂线，交BC于点K∵△AFE是△APD绕点A逆时针旋转60°得到∴∠FAP=60°，∠EAD=60°，AF=AP，EF=PD∴△APF是等边三角形，∴AP=PF∴PA+PD+PQ=PF+FE+PQ≥EG∵四边形ABCD是平行四边形，BC=6∴AE=AD=BC=6，AD∥BC∴在Rt△AHE中，AH=3，3∵HG⊥BC，AK⊥BC，AD∥BC∴AK⊥AD，GH⊥AD，∴AK=HG∵∠ABC=60°，AB=4∴在Rt△ABK中，BK=2，3∴3∴32353=故选：C【点睛】本题考查最值问题，解题关键是旋转△APD，将PA+PD+PQ转化为PF+EF+PQ的形式．7．B解析：B【分析】由平行四边形的性质可得OB＝BC，由等腰三角形的性质可判断①正确，由直角三角形的性质和三角形中位线定理可判断②错误，通过证四边形BGFE是平行四边形，可判断③正确，由平行线的性质和等腰三角形的性质可判断④正确，由∠BAC≠30°可判断⑤错误．【详解】解：∵四边形ABCD是平行四边形∴BO＝DO＝12BD，AD＝BC，AB＝CD，AB∥BC，又∵BD＝2AD，∴OB＝BC＝OD＝DA，且点E 是OC中点，∴BE⊥AC，故①正确，∵E、F分别是OC、OD的中点，∴EF∥CD，EF＝12 CD，∵点G是Rt△ABE斜边AB上的中点，∴GE＝12AB＝AG＝BG∴EG＝EF＝AG＝BG，无法证明GE＝GF，故②错误，∵BG＝EF，AB∥CD∥EF∴四边形BGFE是平行四边形，∴GF＝BE，且BG＝EF，GE＝GE，∴△BGE≌△FEG（SSS）故③正确∵EF∥CD∥AB，∴∠BAC＝∠ACD＝∠AEF，∵AG＝GE，∴∠GAE＝∠AEG，∴∠AEG＝∠AEF，∴AE平分∠GEF，故④正确，若四边形BEFG是菱形∴BE＝BG＝12 AB，∴∠BAC＝30°与题意不符合，故⑤错误故选：B．【点睛】本题考查了菱形的判定，平行四边形的性质，全等三角形的判定和性质，三角形中位线定理等知识，灵活运用相关的性质定理、综合运用知识是解题的关键．8．D解析：D【分析】首先根据正方形的性质证得△BAE≌△CDE，推出∠ABE＝∠DCE，再证△ADH≌△CDH，求得∠HAD＝∠HCD，推出∠ABE＝∠HAD:求出∠ABE+∠BAG＝90°;最后在△AGE中根据三角形的内角和是180°求得∠AGE＝90°即可得到①正确；因为点E是AD边的中点，求出AB= 2AE，即可求得，故②正确；根据 AD ∥BC，求出S△BDE=S△CDE，推出 S△BDE﹣S△DEH=S△CDE﹣S△DEH，即；S△BHE=S△CHD，故③正确；由∠AHD ＝∠CHD ，得到邻补角和对顶角相等得到∠AHB ＝∠EHD ，故④正确【详解】∵四边形ABCD 是正方形，E 是AD 边上的中点，∴AE=DE ，AB=CD ，∠BAD=∠CDA=90°，在△BAE 和△CDE 中∵AE DE BAE CDE AB CDA =⎧⎪∠=∠⎨⎪=⎩∴△BAE ≌△CDE （SAS ），∴∠ABE=∠DCE ，∵四边形ABCD 是正方形，∴AD=DC ，∠ADB=∠CDB=45°，∵在△ADH 和△CDH 中，AD CD ADH CDH DH DH =⎧⎪∠=∠⎨⎪=⎩∴△ADH ≌△CDH （SAS ），∴∠HAD=∠HCD ，∵∠ABE=∠DCE∴∠ABE=∠HAD ，∵∠BAD=∠BAH+∠DAH=90°，∴∠ABE+∠BAH=90°，∴∠AGB=180°-90°=90°，∴AG ⊥BE ，故①正确；∵点E 是AD 边的中点，∴AB= 2AE ，∴∴，故②正确；∵AD ∥BC ，∴S △BDE =S △CDE ，∴S △BDE ﹣S △DEH =S △CDE ﹣S △DEH ，即；S △BHE =S △CHD ，故③正确；∵△ADH ≌△CDH ，∴∠AHD=∠CHD ，∴∠AHB=∠CHB ，∵∠BHC=∠DHE ，∴∠AHB=∠EHD ，故④正确；故选：D．【点睛】本题考查了全等三角形的判定与性质和正方形的性质，解题的关键是熟练掌握其性质. 9．C解析：C【分析】正确的命题是真命题，根据矩形的判定定理，菱形的判定定理及平行四边形的判定定理依次判断.【详解】①对角线相等且互相平分的四边形是矩形，故该项错误；②四条边相等的四边形是菱形，故该项错误；③一组对边平行且相等的四边形是平行四边形，故该项正确；故选：C.【点睛】此题考查真命题的定义，正确掌握矩形、菱形、平行四边形的判定定理是解题的关键. 10．B解析：B【分析】根据菱形的性质，利用SAS证明即可判断①；根据△ABF≌△CAE得到∠BAF=∠ACE，再利用外角的性质以及菱形内角度数即可判断②；通过说明∠CAH≠∠DAO，判断△ADO≌△ACH不成立，可判断③；再利用菱形边长即可求出菱形面积，可判断④.【详解】解：∵在菱形ABCD中，AB=AC=1，∴△ABC为等边三角形，∴∠B=∠CAE=60°，又∵AE=BF，∴△ABF≌△CAE（SAS），故①正确；∴∠BAF=∠ACE，∴∠FHC=∠ACE+∠HAC=∠BAF+∠HAC=60°，故②正确；∵∠B=∠CAE=60°，则在△ADO和△ACH中，∠OAD=60°=∠CAB，∴∠CAH≠60°，即∠CAH≠∠DAO，∴△ADO≌△ACH不成立，故③错误；∵AB=AC=1，过点A作AG⊥BC，垂足为G，∴∠BAG=30°，BG=12，∴∴菱形ABCD 的面积为：BC AG ⨯=312⨯=32，故④错误；故正确的结论有2个，故选B.【点睛】本题考查了全等三角形判定和性质，菱形的性质和面积，等边三角形的判定和性质，外角的性质，解题的关键是利用菱形的性质证明全等.二、填空题11．200m【分析】如图，延长AC 、BD 交于点E ，延长HK 交AE 于F ，延长NJ 交FH 于M ，则四边形EDHF ，四边形MNCF ，四边形MKGJ 是平行四边形，△ABC 是等边三角形，由此即可解决问题．【详解】如图，延长AC 、BD 交于点E ，延长HK 交AE 于F ，延长NJ 交FH 于M由题意可知，四边形EDHF ，四边形MNCF ，四边形MKGJ 是平行四边形∵∠A ＝∠B ＝60°∴18060E A B ∠=-∠-∠=∴△ABC 是等边三角形∴ED ＝FM+MK+KH ＝CN+JG+HK ，EC ＝EF+FC ＝JN+KG+DH∴“九曲桥”的总长度是AE+EB ＝2AB ＝200m故答案为：200m ．【点睛】本题考查了平行四边形、等边三角形、三角形内角和的知识；解题的关键是熟练掌握平行四边形、等边三角形、三角形内角和的性质，从而完成求解．12．18【分析】由题意可知AD 、EF 是定值，要使四边形ADFE 周长的最小，AE ＋DF 的和应是最小的，运用“将军饮马”模型作点E 关于AD 的对称点E 1，同时作DF ∥AF 1，此时AE ＋DF 的和即为E 1F 1，再求四边形ADFE 周长的最小值．【详解】在Rt △COD 中，OC ＝3，OD ＝4，CD ＝22OC +OD =5，∵ABCD 是菱形，∴AD ＝CD ＝5，∵F 坐标为(8,6)，点E 在y 轴上，∴EF ＝8，作点E 关于AD 的对称点E 1，同时作DF ∥AF 1，则E 1（0，2），F 1（3，6），则E 1F 1即为所求线段和的最小值，在Rt △AE 1F 1中，E 1F 1＝22211EE +EF =-+(8-5)=52(62)， ∴四边形ADFE 周长的最小值＝AD ＋EF ＋AE ＋DF ＝ AD ＋EF ＋ E 1F 1＝5＋8＋5＝18．【点睛】本题考查菱形的性质、“将军饮马”作对称点求线段和的最小值，比较综合，难度较大．13．201812【分析】根据几何图形特征，先求出1C 、2C 、3C ，根据求出的结果，找出规律，从而得出2020C ．【详解】∵点E 是BC 的中点，ED ∥AB ，EF ∥AC∴DE 、EF 是△ABC 的中位线∵等边△ABC 的边长为1∴AD=DE=EF=AF =12 则1C =1422⨯= 同理可求得：2C =1，3C =12 发现规律：规律为依次缩小为原来的12 ∴2020C =201812 故答案为：201812．【点睛】本题考查找规律和中位线的性质，解题关键是求解出几组数据，根据求解的数据寻找规律．14．24【分析】由菱形的性质可得OD ＝OB ，∠COD ＝90°，由直角三角形的斜边中线等于斜边的一半，可得OH ＝12BD ＝OB ，可得∠OHB ＝∠OBH ，由余角的性质可得∠DHO ＝∠DCO ，即可求解．【详解】【解答】解：∵四边形ABCD 是菱形，∴OD ＝OB ，∠COD ＝90°，∠DAB ＝∠DCB ＝48°，∵DH ⊥AB ，∴OH ＝12BD ＝OB ， ∴∠OHB ＝∠OBH ，又∵AB ∥CD ，∴∠OBH ＝∠ODC ，在Rt △COD 中，∠ODC +∠DCO ＝90°，在Rt △DHB 中，∠DHO +∠OHB ＝90°，∴∠DHO ＝∠DCO ＝12∠DCB ＝24°，故答案为：24．【点睛】本题考查了菱形的性质，直角三角形斜边中线的性质，余角的性质，是几何综合题，判断出OH是BD的一半，和∠DHO＝∠DCO是解决本题的关键．15．①②④⑤【分析】根据∠B=90°，AB=BE，△ABE绕点A逆时针旋转45°，得到△AHD，可得△ABE≅△AHD，并且△ABE和△AHD都是等腰直角三角形，可证AD//BC，根据DC⊥BC，可得∠HDE=∠CDE，根据三角形的内角和可得∠HDE=∠CDE，即DE平分∠HDC，所以①正确；利用∠DAB=∠ABC=∠BCD=90°，得到四边形ABCD是矩形，有∠ADC=90°，∠HDC=45°，由①有DE平分∠HDC，得∠HDO=22.5°，可得∠AHB=67.5°，∠DHO=22.5°，可证OD=OH，利用 AE=AD易证∠OHE=∠HEO=67.5°，则有OE=OH，OD=OE，所以②正确；利用AAS证明ΔDHE≅ΔDCE，则有DH=DC，∠HDE=∠CDE=22.5°，易的∠DHF=22.5°，∠DFH=112.5°，则△DHF不是直角三角形，并DH≠HF，即有：CD≠HF，所以③错误；根据△ABE是等腰直角三角形，JH⊥JE，∵J是BC的中点，H是BF的中点，得到2JH=CF，2JC=BC，JC=JE+CE，易证BC−CF=2CE，所以④正确；过H作HJ⊥BC于J，并延长HJ交AD于点I，得IJ⊥AD，I是AD的中点，J是BC的中点，H是BF的中点，所以⑤正确；【详解】∵Rt△ABE中，∠B=90°，AB=BE，∴∠BAE=∠BEA=45°，又∵将△ABE绕点A逆时针旋转45°，得到△AHD，∴△ABE≅△AHD，并且△ABE和△AHD都是等腰直角三角形，∴∠EAD=45°，AE=AD ，∠AHD=90°，∴∠ADE=∠AED，∴∠BAD=∠BAE+∠EAD=45°+45°=90°，∴AD//BC，∴∠ADE=∠DEC，∴∠AED=∠DEC，又∵DC⊥BC，∴∠DCE=∠DHE=90°∴由三角形的内角和可得∠HDE=∠CDE，即：DE平分∠HDC，所以①正确；∵∠DAB=∠ABC=∠BCD=90°，∴四边形ABCD是矩形，∴∠ADC=90°，∴∠HDC=45°，由①有DE平分∠HDC，∴∠HDO=12∠HDC=12×45°=22.5°，∵∠BAE=45°，AB=AH，∴∠OHE=∠AHB= 12(180°−∠BAE)=12×(180°−45°)=67.5°，∴∠DHO=∠DHE−∠FHE=∠DHE−∠AHB=90°−67.5°=22.5°，∴OD=OH，在△AED中，AE=AD，∴∠AED=12(180°−∠EAD)=12×(180°−45°)=67.5°，∴∠OHE=∠HEO=67.5°，∴OE=OH，∴OD=OE，所以②正确；在△DHE和△DCE中，DHE DCEHDE CDEDE DE∠=∠⎧⎪∠=∠⎨⎪=⎩，∴ΔDHE≅ΔDCE(AAS)，∴DH=DC，∠HDE=∠CDE=12×45°=22.5°，∵OD=OH，∴∠DHF=22.5°，∴∠DFH=180°−∠HDF−∠DHF=180°−45°−22.5°=112.5°，∴△DHF不是直角三角形，并DH≠HF，即有：CD≠HF，所以③不正确；如图，过H作HJ⊥BC于J，并延长HJ交AD于点I，∵△ABE是等腰直角三角形，JH⊥JE，∴JH=JE，又∵J是BC的中点，H是BF的中点，∴2JH=CF，2JC=BC，JC=JE+CE，∴2JC=2JE+2CE=2JH+2CE=CF+2CE=BC，即有：BC−CF=2CE，所以④正确；∵AD//BC，∴IJ⊥AD，又∵△AHD是等腰直角三角形，∴I是AD的中点，∵四边形ABCD是矩形，HJ⊥BC，∴J是BC的中点，∴H是BF的中点，所以⑤正确；综上所述，正确的有①②④⑤，故答案为：①②④⑤．【点睛】本题考查了全等三角形的判定与性质、旋转的性质、矩形的性质、角平分线的性质以及等腰直角三角形的判定与性质；证明三角形全等和等腰直角三角形是解决问题的关键．16．①②③④【分析】根据正方形的性质和SAS可证明△ABG≌△AEC，然后根据全等三角形的性质即可判断①；设BG、CE相交于点N，AC、BG相交于点K，如图1，根据全等三角形对应角相等可得∠ACE＝∠AGB，然后根据三角形的内角和定理可得∠CNG＝∠CAG＝90°，于是可判断②；过点E作EP⊥HA的延长线于P，过点G作GQ⊥AM于Q，如图2，根据余角的性质即可判断④；利用AAS即可证明△ABH≌△EAP，可得EP＝AH，同理可证GQ＝AH，从而得到EP ＝GQ，再利用AAS可证明△EPM≌△GQM，可得EM＝GM，从而可判断③，于是可得答案．【详解】解：在正方形ABDE和ACFG中，AB＝AE，AC＝AG，∠BAE＝∠CAG＝90°，∴∠BAE+∠BAC＝∠CAG+∠BAC，即∠CAE＝∠BAG，∴△ABG≌△AEC（SAS），∴BG＝CE，故①正确；设BG、CE相交于点N，AC、BG相交于点K，如图1，∵△ABG≌△AEC，∴∠ACE＝∠AGB，∵∠AKG＝∠NKC，∴∠CNG＝∠CAG＝90°，∴BG⊥CE，故②正确；过点E 作EP ⊥HA 的延长线于P ，过点G 作GQ ⊥AM 于Q ，如图2，∵AH ⊥BC ，∴∠ABH +∠BAH ＝90°，∵∠BAE ＝90°，∴∠EAP +∠BAH ＝90°，∴∠ABH ＝∠EAP ，即∠EAM ＝∠ABC ，故④正确；∵∠AHB =∠P =90°，AB =AE ，∴△ABH ≌△EAP （AAS ），∴EP ＝AH ，同理可得GQ ＝AH ，∴EP ＝GQ ，∵在△EPM 和△GQM 中，90P MQG EMP GMQ EP GQ ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩，∴△EPM ≌△GQM （AAS ），∴EM ＝GM ，∴AM 是△AEG 的中线，故③正确．综上所述，①②③④结论都正确．故答案为：①②③④．【点睛】本题考查了正方形的性质、三角形的内角和定理以及全等三角形的判定和性质，作辅助线构造出全等三角形是难点，熟练掌握全等三角形的判定和性质是关键．17．8或12【分析】根据平行四边形的性质得到BC=AD=5，∠BAE=∠DEA ，∠ABF=∠BFC ，根据角平分线的性质得到DE=AD=5，CF=BC=5，即可求出答案.【详解】在ABCD 中，AB ∥CD ，BC=AD=5，∴∠BAE=∠DEA ，∠ABF=∠BFC ，∵BAD ∠的平分线交CD 于点E ，∴∠BAE=∠DAE，∴∠DAE=∠DEA，∴DE=AD=5，同理：CF=BC=5，∴AB=CD=DE+CF-EF=5+5-2=8或AB=DE+CF+EF=5+5+2=12，故答案为：8或12.【点睛】此题考查平行四边形的性质，角平分线的性质，等腰三角形的等角对等边的判定，解题中注意分类思想的运用，避免漏解.18．6【分析】过点P作PE⊥AD交AD的延长线于点E，根据四边形ABCD是平行四边形，得到 AB∥CD，推出PE=12PD，由此得到当PB+PE最小时2PB+ PD有最小值，此时P、B、E三点在同一条直线上，利用∠DAB＝30°，∠AEP=90°，AB=6求出PB+PE的最小值=12AB=3，得到2PB+PD的最小值等于6.【详解】过点P作PE⊥AD交AD的延长线于点E，∵四边形ABCD是平行四边形，∴AB∥CD，∴∠EDC=∠DAB＝30°，∴PE=12 PD，∵2PB+ PD=2（PB+12PD）=2(PB+PE)，∴当PB+PE最小时2PB+ PD有最小值，此时P、B、E三点在同一条直线上，∵∠DAB＝30°，∠AEP=90°，AB=6，∴PB+PE的最小值=12AB=3，∴2PB+ PD的最小值等于6，故答案为：6.【点睛】此题考查平行四边形的性质，直角三角形含30°角的问题，动点问题，将线段2PB+PD转化为三点共线的形式是解题的关键.19．2【解析】【分析】根据折叠的性质可得∠DAF=∠BAF=45°，再由矩形性质可得FC=ED=1，然后由勾股定理求出FG即可．【详解】由折叠的性质可知，∠DAF=∠BAF=45°，∴AE=AD=3，EB=AB-AD=1，∵四边形EFCB为矩形，∴FC=BE=1，∵AB∥FC，∴∠GFC=∠DAF=45°，∴GC=FC=1，∴22112=+=+=，FG GC FC故答案为：2．【点睛】本题考查了折叠变换，矩形的性质是一种对称变换，理解折叠前后图形的大小不变，位置变化，对应边和对应角相等是解决此题的关键．20．2或3.5【分析】分别从当Q运动到E和B之间、当Q运动到E和C之间去分析求解即可求得答案．【详解】如图，∵E 是BC 的中点，∴BE=CE= 12BC=9， ①当Q 运动到E 和B 之间，则得：3t ﹣9=5﹣t ，解得：t=3.5；②当Q 运动到E 和C 之间，则得：9﹣3t=5﹣t ，解得：t=2，∴当运动时间t 为2秒或3.5秒时，以点P ，Q ，E ，D 为顶点的四边形是平行四边形．【点睛】“点睛”此题考查了梯形的性质以及平行四边形的判定与性质．解题时注意掌握辅助线的作法，注意掌握数形结合思想、分类讨论思想与方程思想的应用．三、解答题21．（1）①6；②结论：//P EC A ；（2）为4和16．【分析】()1①如图1中，以A 为圆心AB 为半径画弧交CD 于E ，作EAB ∠的平分线交BC 于点P ，点P 即为所求.理由勾股定理可得DE ．②如图2中，结论：EC//PA.只要证明PA BE ⊥，EC BE ⊥即可解决问题． ()2分两种情形分别求解即可解决问题．【详解】解：()1①如图1中，以A 为圆心AB 为半径画弧交CD 于E ，作EAB ∠的平分线交BC 于点P ，点P 即为所求．在Rt ADE 中，90D ∠=，10AE AB ==，8AD =，22221086DE AE AD ∴-=-=，故答案为6．②如图2中，结论：//P EC A ．理由：由翻折不变性可知：AE AB =，PE PB =，PA ∴垂直平分线段BE ，即PA BE ⊥，PB PC PE ==，90BEC ∠∴=，EC BE ∴⊥，//EC PA ∴．()2①如图31-中，当点Q 在线段CD 上时，设DQ QD'x ==．在Rt AD'B 中，AD'AD 8==，AB 10=，AD'B 90∠=，22BD'AB AD'6∴=-=，在Rt BQC 中，222CQ BC BQ +=， 222(10x)8(x 6)∴-+=+，x 4∴=，DQ 4∴=．②如图32-中，当点Q 在线段DC 的延长线上时，DQ //AB ，DQA QAB ∠∠∴=，DQA AQB ∠∠=，QAB AQB ∠∠∴=，AB BQ 10∴==，在Rt BCQ 中，CQ BQ 6==，DQ DC CQ 16∴=+=，综上所述，满足条件的DQ 的值为4或16．故答案为4和16．【点睛】本题属于几何变换综合题，考查了矩形的性质，翻折变换，勾股定理等知识，解题的关键是学会利用参数构建方程解决问题，学会用分类讨论的思想思考问题，属于中考压轴题．22．（1）详见解析；（2）18【分析】（1）根据正方形的性质得出BC=BD ，AB=BF ，∠CBD=∠ABF=90°，求出∠ABD=∠CBF ，根据全等三角形的判定得出即可；（2）根据全等三角形的性质得出∠BAD=∠BFC ，AD=FC=6，求出AD ⊥CF ，根据三角形的面积求出即可．【详解】解：（1）四边形ABFG 、BCED 是正方形，AB FB ∴=，CB DB =，90ABF CBD ∠=∠=︒，ABF ABC CBD ABC ∴∠+∠=∠+∠，即ABD CBF ∠=∠在ABD ∆和FBC ∆中，AB FB ABD CBF DB CB =⎧⎪∠=∠⎨⎪=⎩()ABD FBC SAS ∴∆≅∆；图1 图2（2）ABD FBC ∆≅∆，BAD BFC ∴∠=∠，6AD FC ==，180AMF BAD CNA ∴∠=︒-∠-∠ 180()BFC BNF =︒-∠+∠1809090=︒-︒=︒AD CF ∴⊥-ACD ACF DFM ACM ACDF S S S S S ∆∆∆∆∴=++四边形11112222AD CM CF AM DM FM AM CM =⋅+⋅+⋅-⋅ 1133(6)(6)1822CM AM AM CM AM CM =++---⋅= 【点睛】本题考查了正方形的性质，全等三角形的性质和判定，三角形的面积等知识点，能求出△ABD ≌△FBC 是解此题的关键．23．（1）证明见解析；（2）能，10；（3）152，理由见解析；【分析】（1）利用题中所给的关系式，列出CD ，DF ，AE 的式子，即可证明．（2）由题意知，四边形AEFD 是平行四边形，令AD=DF ，求解即可得出t 值．（3）由题意可知，当DE ∥BC 时，△DEF 为直角三角形，利用AD+CD=AC 的等量关系，代入式子求值即可．【详解】（1）由题意知：三角形CFD 是直角三角形∵∠B ＝90°，∠A ＝60°∴∠C=30°，CD=2DF ，又∵由题意知CD=4t ，AE=2t ，∴CD=2AE∴AE=DF ．（2）能，理由如下；由（1）知AE=DF又∵DF⊥BC，∠B＝90°∴AE∥DF∴四边形AEFD是平行四边形．当AD=DF时，平行四边形AEFD是菱形∵AC＝60cm，DF=12CD，CD=4t，∴AD=60-4t，DF=2t，∴60-4t=2t∴t=10．（3）当t为152时，△DEF为直角三角形，理由如下；由题意知：四边形AEFD是平行四边形，DF⊥BC，AE∥DF，∴当DE∥BC时，DF⊥DE∴∠FDE=∠DEA=90°在△AED中，∵∠DEA=90°，∠A＝60°，AE=2t∴AD=4t，又∵AC＝60cm，CD=4t，∴AD+CD=AC，8t=60，∴t=152．即t=152时，∠FDE=∠DEA=90°，△DEF为直角三角形．【点睛】本题主要考查了三角形、平行四边形及菱形的性质，正确掌握三角形、平行四边形及菱形的性质是解题的关键．24．（1）证明见解析；（2）平行四边形，理由见解析；（3）45°【分析】（1）由平行四边形的性质得出∠OAF＝∠OCE，OA＝OC，进而判断出△AOF≌△COE，即可得出结论；（2）先判断出∠BAC＝∠AOF，得出AB∥EF，即可得出结论；（3）先求出AC＝2，进而得出A＝1＝AB，即可判断出△ABO是等腰直角三角形，进一步判断出△BFD是等腰三角形，利用等腰三角形的三线合一得出∠BOF＝90°，即可得出结论．【详解】（1）证明：在▱ABCD中，AD∥BC，∴∠OAF＝∠OCE，∵OA＝OC，∠AOF＝∠COE，∴△AOF≌△COE（ASA），∴OE＝OF；（2）当旋转角为90°时，四边形ABEF是平行四边形，理由：∵AB⊥AC，∴∠BAC＝90°，∵∠AOF＝90°，∴∠BAC＝∠AOF，∴AB∥EF，∵AF∥BE，∴四边形ABEF是平行四边形；（3）在Rt△ABC中，AB＝1，BC∴AC＝2，∴OA＝1＝AB，∴△ABO是等腰直角三角形，∴∠AOB＝45°，∵BF＝DF，∴△BFD是等腰三角形，∵四边形ABCD是平行四边形，∴OB＝OD，∴OF⊥BD（等腰三角形底边上的中线是底边上的高），∴∠BOF＝90°，∴∠α＝∠AOF＝∠BOF﹣∠AOB＝45°．【点睛】此题是四边形综合题，主要考查了平行四边形的性质和判定，全等三角形的判定和性质，等腰三角形的判定和性质，等腰直角三角形的性质，旋转的性质，判断出△ABO是等腰直角三角形是解本题的关键．25．（1）①7；②证明见解析；（2，理由见解析【分析】（1）①如图1中，延长BC交DE的延长线于T，过点T作TH⊥BD于H，设BD=2x．证明△BDT是等腰直角三角形，四边形ACTE是矩形，进而利用勾股定理构建方程求解即可；②如图2中，延长BC交DE的延长线于T，连接TF，进而利用全等三角形的性质证明△CEF是等腰直角三角形即可解决问题；（2）如图3中，根据题意设∠EAD=x，则∠BAC=2x．证明△ABC是等边三角形，再根据垂线段最短即可解决问题．【详解】解：（1）①如图1中，延长BC交DE的延长线于T，过点T作TH⊥BD于H，设BD=2x．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1、如图，□ABCD 中，对角线AC 和BD 相交于点O ，如果AC=12，BD=10，AB=m ，那么m 的取值范围是（）
A 、111<<m
B 、222<<m
C 、1210<<m
D 、65<<m
2、如图，平行四边形的两邻边长分别为b a ,，两对角线的长分别为n m ,。

求证：)(22222b a n m +=+。

3、如图，在□ABCD 中，点E 为边CD 上任一点，请你在该图的基础上，适当添加辅助线填写两对相似三角形：△_________∽△________,△_________∽△________。

4、如图，过□ABCD 的顶点A 作一条直线l ，且111,,BB CC DD 两两平行，分别交直线l 于111,,B C D 。

求证：111BB DD CC +=。

5、如图，在□ABCD 中，E 、F 分别为AB 、CD 的中点，连结DE 、BF 、BD 。

（1）求证：△ADE ≌△CBF 。

（2）若AD ⊥BD ，则四边形BFDE 是什么特殊四边形？请证明你的结论。

6、如图，已知△ABC 是等边三角形，D 、E 分别在BC 、AC 上，且CD=CE ，连结DE 并延长至点F ，使EF=AE ，连结AF 、BE 和CF 。

（1）请在图中找出一对全等三角形，用符号“≌”表示，并加以证明；
（2）判断四边形ABDF 是怎样的四边形，并说明理由；
（3）若AB=6，BD=2DC ，求四边形ABEF 的面积。