相似三角形解题方法学生版
相似三角形的性质及判定知识点总结+经典题型总结(学生版)学习资料

中考要求板块考试要求A级要求B级要求C级要求相似三角形了解相似三角形掌握相似三角形的概念,判定及性质,以及掌握相关的模型会运用相似三角形相关的知识解决有关问题知识点睛、相似的有关概念1 •相似形具有相同形状的图形叫做相似形•相似形仅是形状相同,大小不一定相同•相似图形之间的互相变换称为相似变换.2 •相似图形的特性两个相似图形的对应边成比例,对应角相等.3. 相似比两个相似图形的对应角相等,对应边成比例.、相似三角形的概念1. 相似三角形的定义对应角相等,对应边成比例的三角形叫做相似三角形.如图,△ ABC与厶ABC相似,记作△ ABCABC,符号s读作相似于”2•相似比相似三角形对应边的比叫做相似比.全等三角形的相似比是1.全等三角形”一定是相似形” 相似形”不一定是全等形”、相似三角形的性质1.相似三角形的对应角相等如图,△ ABC与厶ABC相似,则有A A , B B , C C .2 •相似三角形的对应边成比例△ ABC与厶ABC相似,则有-AB BC AC k(k为相似比)AB BC AC3•相似三角形的对应边上的中线,高线和对应角的平分线成比例,都等于相似比.如图1,△ ABC与厶ABC相似,AM是厶ABC中BC边上的中线,AM 是厶ABC中BC边上的中线, 则有上邑匹竺k上也(k 为相似比).AB BC AC AM如图则有2, △ ABC与厶ABC相似,AB BC AC kAB BC AC AHAH3, △ ABC 与厶ABC分线,则有2AB -BCAB BC AC如图相似,AC k1AH是△ ABC中BC边上的高线,AH是厶ABC中BC边上的高线,(k为相似比).AD是厶ABC中BAC的角平分线,AD是厶ABC 竺(k为相似比).AD图2中BAC的角平4. 相似三角形周长的比等于相似比.如图4, △ ABC与厶ABC相似, 则有AB BC ACkAB B C AC(k为相似比).应用比例的等比性质有AB BC AC AB BC ACAB BC AC AB BC A C5•相似三角形面积的比等于相似比的平方.四、相似三角形的判定1 •平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.2 •如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似•可简单说成:两 角对应相等,两个三角形相似.3 •如果一个三角形的两边和另一个三角形的两边对应成比例,并且夹角相等,那么这两个三角形相似.4. 如果一个三角形的三条边与另一个三角形的你对应成比例,那么这两个三角形相似.可简单地说成:三 边对应成比例,两个三角形相似.5. 如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这 两个直角三角形相似. 6 •直角三角形被斜边上的高分成的两个直角三角形相似(常用但要证明)7 •如果一个等腰三角形和另一个等腰三角形的顶角相等或一对底角相等,那么这两个等腰三角形相似;如 果它们的腰和底对应成比例,那么这两个等腰三角形也相似.五、相似证明中的比例式或等积式、比例中项式、倒数式、复合式证明比例式或等积式的主要方法有三点定形法”.1 .横向定型法AB BC欲证一一 —一,横向观察,比例式中的分子的两条线段是AB 和BC ,三个字母A , B , C 恰为△ ABC 的顶BE BF点;分母的两条线段是 BE 和BF ,三个字母B , E , F 恰为△ BEF 的三个顶点.因此只需证 △ ABCEBF •2. 纵向定型法欲证一一 匹,纵向观察,比例式左边的比 AB 和BC 中的三个字母 A , B , C 恰为△ ABC 的顶点;右边的 BC EF 比两条线段是 DE 和EF 中的三个字母 D , E , F 恰为A DEF 的三个顶点.因此只需证 △ ABC DEF .AH 是厶ABC 中BC 边上的高线,则有ABBC AC k AH ( k 为相似比) .进而可得比ABCABBCACAHABC-BC AH BC 2BC 空k 2•AH如图5, △ ABC 与厶ABC 相似,AH 是厶ABC 中BC 边上的高线,如图:S A ABCACD 1BC AH21CD AH2BCCD如图:SA ABC12BC AHAHSA BCD1BC DG DG2S A ABD S A ABD S A AED AB AD AB AD SA ACESA AEDSA ACEAE AC AE AC3. 中间比法由于运用三点定形法时常会碰到三点共线或四点中没有相同点的情况,此时可考虑运用等线,等比或等积进行变换后,再考虑运用三点定形法寻找相似三角形•这种方法就是等量代换法•在证明比例式时,常用到中间比.比例中项式的证明,通常涉及到与公共边有关的相似问题。
专题 相似三角形中的对角互补模型(学生版)
专题09相似三角形中的基本模型-对角互补模型相似三角形在中考数学几何模块中占据着重要地位。
相似三角形与其它知识点结合以综合题的形式呈现,其变化很多,难度大,是中考的常考题型。
如果大家平时注重解题方法,熟练掌握基本解题模型,再遇到该类问题就信心更足了。
本专题就对角互补模型进行梳理及对应试题分析,方便掌握。
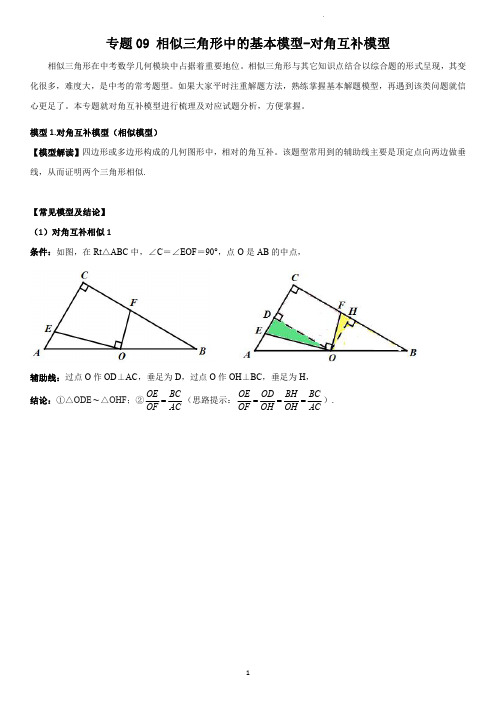
模型1.对角互补模型(相似模型)【模型解读】四边形或多边形构成的几何图形中,相对的角互补。
该题型常用到的辅助线主要是顶定点向两边做垂线,从而证明两个三角形相似.【常见模型及结论】(1)对角互补相似1条件:如图,在Rt△ABC中,∠C=∠EOF=90°,点O是AB的中点,辅助线:过点O作OD⊥AC D,过点O作OH⊥BC,垂足为H,结论:①△ODE∼△OHF;②OE BCOF AC=(思路提示:OE OD BH BCOF OH OH AC===).(2)对角互补相似2条件:如图,已知∠AOB =∠DCE =90°,∠BOC =α.辅助线:作法1:如图1,过点C 作CF ⊥OA ,垂足为F ,过点C 作CG ⊥OB ,垂足为G ;结论:①△ECG ∼△DCF ;②CE =CD·tan α.(思路提示:CE CG CD CF =,CF =OG ,在Rt △COG 中,CG tan OGα=)辅助线:作法2:如图2,过点C 作CF ⊥OC ,交OB 于F ;结论:①△CFE ∼△COD ;②CE =CD·tan α.(思路提示:CE CF tan CD CO α==,在Rt △OCF 中,CF tan OC α=)(3)对角互补相似3条件:已知如图,四边形ABCD 中,∠B+∠D=180°辅助线:过点D 作DE ⊥BA ,垂足为E ,过点D 作DF ⊥BC ,垂足为F ;结论:①△DAE ∼△DCF ;②ABCD 四点共圆。
例1.(2022·黑龙江·鸡西九年级期末)如图,在Rt ABC 中,90ABC ∠=︒,6AB =,8BC =,在Rt MPN △中,90MPN ∠=︒,点P 在AC 上,PM 交AB 于点E ,PN 交BC 于点F ,当2PE PF =时,AP 的长为()A .4B .6C .245D .256例3.(2022·江西·吉水县九年级期末)【问题情境】如图①,直角三角板ABC中,∠C=90°,AC=BC,将一个用足够长的细铁丝制作的直角的顶点D放在直角三角板ABC的斜边AB上,再将该直角绕点D旋转,并使其两边分别与三角板的AC边、BC边交于P、Q两点.【问题探究】(1)在旋转过程中,①如图2,当AD=BD时,线段DP、DQ的数量关系是()A、DP<DQB、DP=DQC、DP>DQD、无法确定②如图3,当AD=2BD时,线段DP、DQ有何数量关系?并说明理由.③根据你对①、②的探究结果,试写出当AD=nBD时,DP、DQ满足的数量关系为(直接写出结论,不必证明)。
相似三角形的判定--知识讲解(提高)学生版

相似三角形的判定--知识讲解(提高)【要点梳理】要点一、相似三角形在和中,如果我们就说与相似,记作∽.k就是它们的相似比,“∽”读作“相似于”.要点诠释:(1)书写两个三角形相似时,要注意对应点的位置要一致,即∽,则说明点A的对应点是A′,点B的对应点是B′,点C的对应点是C′;(2)对于相似比,要注意顺序和对应的问题,如果两个三角形相似,那么第一个三角形的一边和第二个三角形的对应边的比叫做第一个三角形和第二个三角形的相似比.当相似比为1时,两个三角形全等.要点二、相似三角形的判定定理1.判定方法(一):平行于三角形一边的直线和其他两边相交,所构成的三角形和原三角形相似;2.判定方法(二):如果两个三角形的三组对应边的比相等,那么这两个三角形相似;3.判定方法(三):如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.要点诠释:此方法要求用三角形的两边及其夹角来判定两个三角形相似,应用时必须注意这个角必需是两边的夹角,否则,判断的结果可能是错误的.4.判定方法(四):如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.要点诠释:要判定两个三角形是否相似,只需找到这两个三角形的两个对应角相等即可,对于直角三角形而言,若有一个锐角对应相等,那么这两个三角形相似.要点三、相似三角形的常见图形及其变换:【典型例题】类型一、相似三角形1. 判断对错:(1)两个直角三角形一定相似吗?为什么?(2)两个等腰三角形一定相似吗?为什么?(3) 两个等边三角形一定相似吗?为什么?举一反三:【变式】下列说法错误的是().A.有一对锐角对应相等的两个直角三角形相似B.全等的两个三角形一定相似C.对应角相等的两个多边形相似D.两条邻边对应成比例的两个矩形相似类型二、相似三角形的判定2.(2015•湖州模拟)如图,在正方形ABCD中,E、F分别是边AD、CD上的点,,连接EF并延长交BC的延长线于点G.(1)求证:△ABE∽△DEF;(2)若正方形的边长为4,求BG的长.举一反三:【变式】(2015•大庆模拟)如图,△ABC中,AB=5,BC=3,CA=4,D为AB的中点,过点D的直线与BC交于点E,若直线DE截△ABC所得的三角形与△ABC相似,则DE=.3.如图,小正方形边长均为1,则图中的三角形(阴影部分)与相似的是哪一个?图(1)图(2)图(3)图(4)4. 已知:如图,,,,当BD与a、b之间满足怎样的关系时,这两个三角形相似?举一反三:【变式】如图,正方形ABCD和等腰Rt,其中,G是CD与EF的交点.(1)求证:≌.(2)若,,,求的值.。
专题 相似三角形半角模型(学生版)

专题06相似三角形中的半角模型相似三角形在中考数学几何模块中占据着重要地位。
相似三角形与其它知识点结合以综合题的形式呈现,其变化很多,难度大,是中考的常考题型。
如果大家平时注重解题方法,熟练掌握基本解题模型,再遇到该类问题就信心更足了。
本专题就半角模型进行梳理及对应试题分析,方便掌握。
模型1.半角模型(相似模型)【常见模型及结论】1)半角模型(正方形中的半角相似模型)条件:已知,如图,在正方形ABCD 中,∠EAF 的两边分别交BC 、CD 边于M 、N 两点,且∠EAF =45°结论:如图1,△AMN ∽△AFE 且AF AE EF AM AN MN===.(思路提示:∠ANM=∠AEF ,∠AMN=∠AFE );图1图2结论:如图2,△MAN ∽△MDA ,△NAM ∽△NBA ;结论:如图3,连接AC ,则△AMB ∽△AFC ,△AND ∽△AEC .且AF AC AM AB==;图3图4结论:如图4,△BME ∽△AMN ∽△DFN.2)半角模型(特殊三角形中的半角相似模型)(1)含45°半角模型图1图2条件:如图1,已知∠BAC =90°,45ABC ACB DAE ∠=∠=∠=︒;结论:①△ABE ∽△DAE ∽△DCA ;②AB AD CD BE AE AC==;③AB AC BE CD ⋅=⋅(2AB BE CD =⋅)(2)含60°半角模型条件:如图1,已知∠BAC =120°,60ADE DAE ∠=∠=︒;结论:①△ABD ∽△CAE ∽△CBA ;②AD CE AC BD AE AB==;③AD AE BD CE ⋅=⋅(2DE BD CE =⋅)AC例4.(2023·广东·九年级专题练习)如图,段CD上一点,且1CE=,AB=AE例7.(2023·广东佛山·九年级校考阶段练习)EF与AC交于点G.AC课后专项训练1.(2022春·浙江绍兴·九年级校考阶段练习)如图,在正方形ABCD 中,点E 、F 分别在边BC ,DC 上,AE 、AF分别交BD 于点M 、N ,连接CN 、EN ,且CN =EN .下列结论:①AN =EN ,AN ⊥EN ;②BE+DF=EF ;③∠DFE =2∠AMN ;④22222EF BM DN =+;⑤图中有4对相似三角形.其中正确结论个数是()A .5B .4C .3D .22.如图,在矩形纸片ABCD 中,点E 、F 分别在矩形的边AB 、AD 上,将矩形纸片沿CE 、CF 折叠,点B 落在H 处,点D 落在G 处,点C 、H 、G 恰好在同一直线上,若AB =6,AD =4,BE =2,则DF 的长是()A .2B .74C .322D .33.如图,等腰直角三角形,90ABC BAC ∠=︒,D 、E 是BC 上的两点,且BD CE =,过D 、E 分别作DM AB ⊥、EN AC ⊥,垂足分别为M 、N ,DM 、EN 交于点F ,连接AD 、AE .以下四个结论:①四边形AMFN 是正方形;②ABE ACD △≌△;③222CE BD DE +=;④当45DAE ∠=︒时,2AD DE CD =⋅.其中正确的结论有()A .1个B .2个C .3个D .4个分别是正方形的两个外角的平分线,点A.1个B.2个5.(2022·河南安阳·统考一模)如图,在RtADC△绕点A顺时针旋转90︒后,得到△③AE ADBE CD=;④点C转至点B经过的弧长为A.1个B.2个6.(2023·山东·统考一模)如图,在同一平面内,将两个全等的等腰直角三角形顶点,∠BAC=∠AGF=90°,它们的斜边长为别为D、E(点D不与点B重合,点E不与点的三角形;(2)m•n=2;(3)BD2+CE2=DE分别在边A.222+=B.BN DM MN9.如图,已知△PMN是等边三角形,∠APB=120︒.求证:AM·PB=PN·AP10.已知:如图边长为2的正方形ABCD中,∠MAN的两边分别交BC、CD边于M、N两点,且∠MAN=45°①求证:MN=BM+DN;②若AM、AN交对角线BD于E、F两点.设BF=y,DE=x,求y与x的函数关系式.12.(2023江苏九年级期末)已知正方形ABCD的边长为4,一个以点A为顶点的45°角绕点A旋转,角的两边分别与边BC、DC的延长线交于点E、F,连接EF.设CE=a,CF=b.(1)如图1,当∠EAF被对角线AC平分时,求a、b的值;(2)当△AEF是直角三角形时,求a、b的值;(3)如图3,探索∠EAF绕点A旋转的过程中a、b满足的关系式,并说明理由.分别是14.(2022秋·广东广州·九年级广州市第三中学校考期中)在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°.(1)若点G在边CB的延长线上,且BG=DF,(如图①),求证:△AEG≌△AEF;(2)若直线EF与AB,AD的延长线分别交于点M,N(如图②),求证:222EF ME NF=+;(3)将正方形改为长与宽不相等的矩形(如图③),∠EAF=∠CEF=45°,BE=4,DF=1,请你直接写出△CEF的面积.。
专题 相似三角形手拉手模型(学生版)

专题03相似三角形中的重要模型-手拉手模型相似三角形是初中几何中的重要的内容,常常与其它知识点结合以综合题的形式呈现,其变化很多,是中考的常考题型。
手拉手模型相似是手拉手模型当中相对于手拉手全等模型较难的一种模型,在实际的应用和解题当中出现时,对于同学们来说,都比较困难。
而深入理解模型内涵,灵活运用相关结论可以显著提高解题效率,本专题重点讲解相似三角形的“手拉手”模型(旋转模型)。
手拉手相似证明题一般思路方法:①由线段乘积相等转化成线段比例式相等;②分子和分子组成一个三角形、分母和分母组成一个三角形;③第②步成立,直接从证这两个三角形相似,逆向证明到线段乘积相等;④第②步不成立,则选择替换掉线段比例式中的个别线段,之后再重复第③步。
模型1.“手拉手”模型(旋转模型)【模型解读与图示】“手拉手”旋转型定义:如果将一个三角形绕着它的项点旋转并放大或缩小(这个顶点不变),我们称这样的图形变换为旋转相似变换,这个顶点称为旋转相似中心,所得的三角形称为原三角形的旋转相似三角形。
1)手拉手相似模型(任意三角形)条件:如图,∠BAC=∠DAE=α,AD AE k AB AC ==;结论:△ADE ∽△ABC ,△ABD ∽△ACE ;EC k BD=.2)手拉手相似模型(直角三角形)条件:如图,90AOB COD ∠=∠=︒,OC OD k OA OB==(即△COD ∽△AOB );结论:△AOC ∽△BOD ;BD k AC =,AC ⊥BD ,12ABCD S AB CD =⨯.3)手拉手相似模型(等边三角形与等腰直角三角形)条件:M 为等边三角形ABC 和DEF 的中点;结论:△BME ∽△CMF ;BE CF 条件:△ABC 和ADE 是等腰直角三角形;结论:△ABD ∽△ACE.例1.(2022·山西长治·九年级期末)问题情境:如图1,在△ABC 中,AB =6,AC =5,点D ,E 分别在边AB ,AC 上,且∥DE BC .数学思考:(1)在图1中,BD CE 的值为;(2)图1中△ABC 保持不动,将△ADE 绕点A 按逆时针方向旋转到图2的位置,其它条件不变,连接BD ,CE ,则(1)中的结论是否仍然成立?并说明理由;(3)拓展探究:在图2中,延长BD ,分别交AC ,CE 于点F ,P ,连接AP ,得到图3,探究∠APE 与∠ABC 之间有何数量关系,并说明理由;(4)若将△ADE 绕点A 按逆时针方向旋转到图4的位置,连接BD ,CE ,延长BD 交CE 的延长线于点P ,BP 交AC 于点F ,则(3)中的结论是否仍然成立,若成立,请说明理由;若不成立,请直接写出∠APE 与∠ABC 之间的数量关系.例2.(2022·山东济南·八年级期末)某校数学活动小组探究了如下数学问题:(1)问题发现:如图1,ABC 中,90BAC ∠=︒,AB AC =.点P 是底边BC 上一点,连接AP ,以AP 为腰作等腰Rt APQ △,且90PAQ ∠=︒,连接CQ 、则BP 和CQ 的数量关系是______;(2)变式探究:如图2,ABC 中,90BAC ∠=︒,AB AC =.点P 是腰AB 上一点,连接CP ,以CP 为底边作等腰Rt CPQ △,连接AQ ,判断BP 和AQ 的数量关系,并说明理由;(3)问题解决:如图3,在正方形ABCD 中,点P 是边BC 上一点,以DP 为边作正方形DPEF ,点Q 是正方形DPEF两条对角线的交点,连接CQ .若正方形DPEF ,CQ =ABCD 的边长.例3.(2022·河南信阳·九年级期末)如图1,在Rt△ABC中,∠C=90°,∠A=30°,BC=1,点D,E分别为AC,BC的中点.△CDE绕点C顺时针旋转,设旋转角为α(0°≤α≤360°),记直线AD与直线BE的交点为点P.(1)如图1,当α=0°时,AD与BE的数量关系为______,AD与BE的位置关系为______;(2)当0°<α≤360°时,上述结论是否成立?若成立,请仅就图2的情形进行证明;若不成立,请说明理由;(3)△CDE绕点C顺时针旋转一周,请直接写出运动过程中P点运动轨迹的长度和P点到直线BC距离的最大值.例4.(2022·江苏·无锡市天一实验学校一模)如图,在等边ABC 边长为6,O 是中心;在Rt ADE △中,90ADE ∠=︒,60DAE ∠=︒,2AD =.将ADE 绕点A 按顺时针方向旋转一周.(1)当AD 、AE 分别在AC 、AB 边上,连结OD 、OE ,求ODE 的面积;(2)设DE 所在直线与ABC 的边AB 或AC 交于点F ,当O 、D 、E 三点在一条直线上,求AF 的长;(3)连结CE ,取CE 中点M ,连结DM ,DM 的取值范围为_________.例5.(2022·山东烟台·中考真题)(1)【问题呈现】如图1,△ABC 和△ADE 都是等边三角形,连接BD ,CE .求证:BD =CE .(2)【类比探究】如图2,△ABC 和△ADE 都是等腰直角三角形,∠ABC =∠ADE =90°.连接BD ,CE .请直接写出BD CE的值.(3)【拓展提升】如图3,△ABC 和△ADE 都是直角三角形,∠ABC =∠ADE =90°,且AB BC =AD DE =34.连接BD ,CE .①求BD CE的值;②延长CE 交BD 于点F ,交AB 于点G .求sin ∠BFC 的值.例6.(2023·四川·成都九年级期中)如图1,已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.(1)证明:四边形CEGF是正方形;(2)探究与证明:将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图2所示,试探究线段AG与BE 之间的数量关系,并说明理由;(3)拓展与运用:正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图3所示,当B,E,F三点在一条直线上时,延长CG交AD于点H,若AG=9,GH=,求BC的长.课后专项训练1、如图,AB=3,AC=2,BC=4,AE=3,AD=4.5,DE=6,∠BAD=20°,则∠CAE的度数为()A.10°B.20°C.40°D.无法确定2、如图,△ABC∽△ADE,∠BAC=∠DAE=90°,AB与DE交于点O,AB=4,AC=3,F是DE的中点,连接BD,BF,若点E是射线CB上的动点,下列结论:①△AOD∽△FOB,②△BOD∽△EOA,③∠FDB+∠FBE=90°,④BF=56AE,其中正确的是()A.①②B.③④C.②③D.②③④,D、E分别在边AC、BC上,CD=1,DE∥AB,将△CDE3、如图,△ABC中,∠C=90°,∠B=30°,AC绕点C旋转,旋转后点D、E对应的点分别为D′、E′,当点E′落在线段AD′上时,连接BE′,此时BE′的长为()A.B.C.D.4、已知正方形DEFG 的顶点F 在正方形ABCD 的一边AD 的延长线上,连结AG ,CE 交于点H ,若3AB =,2DE =,则CH 的长为________.5.(2022·浙江国·九年级课时练习)观察猜想(1)如图1,在等边ABC 中,点M 是边BC 上任意一点(不含端点B 、C ),连接AM ,以AM 为边作等边AMN ,连接CN ,则ABC ∠与ACN ∠的数量关系是______.(2)类比探究:如图2,在等边ABC 中,点M 是BC 延长线上任意一点(不含端点C ),(1)中其它条件不变,(1)中结论还成立吗?请说明理由.(3)拓展延伸:如图3,在等腰ABC 中,BA BC =,点M 是边BC 上任意一点(不含端点B 、C ),连接AM ,以AM 为边作等腰AMN ,使顶角AMN ABC ∠=∠.连按CN .试探究ABC ∠与ACN ∠的数量关系,并说明理由.6.(2022湖北·九年级专题练习)如图,ABC为等边三角形,D为AC边上一点,连接BD,M为BD的中点,连接AM.(1)如图1,若AB=,∠ABD=45°,求AMD的面积;(2)如图2,过点M作MN AM⊥与AC交于点E,与BC的延长线交于点N,求证:AD=CN;(3)如图3,在(2)的条件下,将ABM沿AM翻折得'AB M,连接B'N,当B'N取得最小值时,直接写出BN DE MN-的值.7.(2023·广西·九年级课时练习)某校数学活动小组在一次活动中,对一个数学问题作如下探究:(1)问题发现:如图1,在等边ABC 中,点P 是边BC 上任意一点,连接AP ,以AP 为边作等边APQ ,连接CQ ,BP 与CQ 的数量关系是________;(2)变式探究:如图2,在等腰ABC 中,AB BC =,点P 是边BC 上任意一点,以AP 为腰作等腰APQ ,使AP PQ =,APQ ABC ∠=∠,连接CQ ,判断ABC ∠和ACQ ∠的数量关系,并说明理由;(3)解决问题:如图3,在正方形ADBC 中,点P 是边BC 上一点,以AP 为边作正方形APEF ,Q 是正方形APEF的中心,连接CQ .若正方形APEF 的边长为5,2CQ =,求正方形ADBC 的边长.8.(2022·河南开封·九年级期末)某数学兴趣小组在学习了尺规作图、等腰三角形和相似三角形的有关知识后,在等腰△ABC 中,其中AB AC =,如图1,进行了如下操作:第一步,以点A 为圆心,任意长为半径画弧,分别交BA 的延长线和AC 于点E ,F ,如图2;第二步,分别以点E ,F 为圆心,大于12EF 的长为半径画弧,两弧相交于点D ,作射线AD ;第三步,以D 为圆心,DA 的长为半径画弧,交射线AE 于点G ;(1)填空;写出∠CAD 与∠GAD 的大小关系为___;(2)①请判断AD 与BC 的位置关系,并说明理由.②当6,2AB AC BC ===时,连接DG ,请直接写出AD AG =___;(3)如图3,根据以上条件,点P 为AB 的中点,点M 为射线AD 上的一个动点,连接PM ,PC ,当CPM B ∠=∠时,求AM 的长.9.(2022·山东济南·一模)在Rt ABC 中与Rt DCE 中,90,30ACB DCE BAC DEC ∠=∠=︒∠∠=∠=︒,AC DC =Rt DCE 绕点C 顺时针旋转,连接,BD AE ,点,F G 分别是,BD AE 的中点,连接,CF CG .(1)观察猜想:如图1,当点D 与点A 重合时,CF 与CG 的数量关系是__________,位置关系是__________;(2)类比探究:当点D 与点A 不重合时,(1)中的结论是否成立?如果成立,请仅就图2的情形给出证明;如果不成立,请说明理由.(3)问题解决在Rt DCE 旋转过程中,请直接写出CFG △的面积的最大值与最小值.10.(2022•莱芜区一模)在△ACB中,∠ACB=120°,AC=BC,点P在AB边上,AP=AB,将线段AP绕点P顺时针旋转至PD,记旋转角为a,连接BD,以BD为底边,在线段BD的上方找一点E,使∠BED=120°,ED =EB,连接AD、CE.(1)如图1,当旋转角a=180°时,请直接写出线段CE与线段AD的数量关系;(2)当0<a<180°时,①如图2,(1)中线段CE与线段AD的数量关系是否还成立?并说明理由.②如图3,当点A、D、E三点共线时,连接CD,判断四边形CDBE的形状,并说明理由.11.(2022·江苏·九年级课时练习)观察猜想(1)如图1,在等边ABC 中,点M 是边BC 上任意一点(不含端点B 、C ),连接AM ,以AM 为边作等边AMN ,连接CN ,则ABC ∠与ACN ∠的数量关系是______.(2)类比探究:如图2,在等边ABC 中,点M 是BC 延长线上任意一点(不含端点C ),(1)中其它条件不变,(1)中结论还成立吗?请说明理由.(3)拓展延伸:如图3,在等腰ABC 中,BA BC =,点M 是边BC 上任意一点(不含端点B 、C ),连接AM ,以AM 为边作等腰AMN ,使顶角AMN ABC ∠=∠.连按CN .试探究ABC ∠与ACN ∠的数量关系,并说明理由.12、如图1,在Rt ABC 中,90C ∠=︒,30A ∠=︒,1BC =,点D ,E 分别为AC ,BC 的中点.CDE △绕点C 顺时针旋转,设旋转角为α(0360α︒≤≤︒,记直线AD 与直线BE 的交点为点P .(1)如图1,当0α=︒时,AD 与BE 的数量关系为_________,AD 与BE 的位置关系为_______;(2)当0360α<≤︒︒时,上述结论是否成立?若成立,请仅就图2的情形进行证明;若不成立,请说明理由;(3)CDE △绕点C 顺时针旋转一周,请直接写出运动过程中P 点运动轨迹的长度和P 点到直线BC 距离的最大值.13、尝试:如图①,ABC 中,将ABC 绕点A 按逆时针方向旋转一定角度得到AB C '',点B 、C 的对应点分别为B ′、C ',连接BB '、CC ',直接写出图中的一对相似三角形_______;拓展:如图②,在ABC 中,90C ∠=︒,AC BC =,将ABC 绕点A 按逆时针方向旋转一定角度得到AB C '',点B 、C 的对应点分别为B ′、C ',连接BB '、CC ',若8BB '=,求CC '的长;应用:如图③,在Rt ABC △中,90ACB ∠=︒,2AB =,30ABC ∠=︒,将ABC 绕点A 按逆时针方向旋转一周,在旋转过程中,当点B 的对应点B ′恰好落在Rt ABC △的边所在的直线上时,直接写出此时点C 的运动路径长.14、问题背景:如图(1),已知A ABC DE ∽△△,求证:ABD ACE ∽;尝试应用:如图(2),在ABC 和ADE 中,90BAC DAE ︒∠=∠=,30ABC ADE ︒∠=∠=,AC 与DE 相交于点F .点D 在BC 边上,AD BD=DF CF 的值;拓展创新:如图(3),D 是ABC 内一点,30BAD CBD ︒∠=∠=,90BDC ︒∠=,4AB =,AC =AD 的长.15、如图,四边形ABCD 和四边形AEFG 都是正方形,C ,F ,G 三点在一直线上,连接AF 并延长交边CD 于点M .(1)求证:△MFC ∽△MCA ;(2)求证△ACF ∽△ABE ;(3)若DM=1,CM=2,求正方形AEFG 的边长.16.(2022•南山区校级一模)(1)【问题发现】如图①,正方形AEFG的两边分别在正方形ABCD的边AB和AD 上,连接CF.填空:①线段CF与DG的数量关系为;②直线CF与DG所夹锐角的度数为.(2)【拓展探究】如图②,将正方形AEFG绕点A逆时针旋转,在旋转的过程中,(1)中的结论是否仍然成立,请利用图②进行说明.(3)【解决问题】如图③,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=10,O为AC的中点.若点D在直线BC上运动,连接OE,则在点D的运动过程中,线段OE长的最小值为(直接写出结果).17、某校数学活动小组在一次活动中,对一个数学问题作如下探究:(1)问题发现:如图1,在等边ABC 中,点P 是边BC 上任意一点,连接AP ,以AP 为边作等边APQ ,连接CQ ,BP 与CQ 的数量关系是________;(2)变式探究:如图2,在等腰ABC 中,AB BC =,点P 是边BC 上任意一点,以AP 为腰作等腰APQ ,使AP PQ =,APQ ABC ∠=∠,连接CQ ,判断ABC ∠和ACQ ∠的数量关系,并说明理由;(3)解决问题:如图3,在正方形ADBC 中,点P 是边BC 上一点,以AP 为边作正方形APEF ,Q 是正方形APEF的中心,连接CQ .若正方形APEF 的边长为5,2CQ =,求正方形ADBC 的边长.。
相似三角形重要模型之(双)A字型与(双)8字型(学生版)-2024年中考数学常见几何模型

相似三角形重要模型之(双)A字型与(双)8字型相似三角形是初中几何中的重要的内容,常常与其它知识点结合以综合题的形式呈现,其变化很多,是中考的常考题型。
本专题重点讲解相似三角形的(双)A字模型和(双)8(X)字模型.A字型和8(X)字型的应用难点在于过分割点(将线段分割的点)作平行线构造模型,有的是直接作平行线,有的是间接作平行线(倍长中线就可以理解为一种间接作平行线),这一点在模考中无论小题还是大题都是屡见不鲜的。
模型1. “A”字模型【模型解读与图示】“A”字模型图形(通常只有一个公共顶点)的两个三角形有一个“公共角”(是对应角),再有一个角相等或夹这个公共角的两边对应成比例,就可以判定这两个三角形相似.图1 图2 图31)“A”字模型条件:如图1,DE∥BC;结论:△ADE∽△ABC⇔ADAB =AEAC=DEBC.2)反“A”字模型条件:如图2,∠AE D=∠B;结论:△ADE∽△ACB⇔ADAC =AEAB=DEBC.3)同向双“A”字模型条件:如图3,EF∥BC;结论:△AEF∽△ABC,△AEG∽△ABD,△AGF∽△ADC⇔EGBD=FGCD=AGAD1(2023·湖北十堰·统考中考真题)如图,在菱形ABCD中,点E,F,G,H分别是AB,BC,CD,AD上的点,且BE=BF=CG=AH,若菱形的面积等于24,BD=8,则EF+GH=.2(2023·安徽·九年级期末)如图,在三角形△ABC中,点D、E分别在边AB、AC上,AD=3,BD=1,AE =2,EC=4.(1)求证:∠ADE=∠C;(2)若∠BAC的平分线交DE于点F,交BC于点G,求AFFG.3(2022·山东东营·中考真题)如图,在△ABC 中,点F 、G 在BC 上,点E 、H 分别在AB 、AC 上,四边形EFGH 是矩形,EH =2EF ,AD 是△ABC 的高.BC =8,AD =6,那么EH 的长为.4(2022·浙江宁波·中考真题)(1)如图1,在△ABC 中,D ,E ,F 分别为AB ,AC ,BC 上的点,DE ∥BC ,BF =CF ,AF 交DE 于点G ,求证:DG =EG .(2)如图2,在(1)的条件下,连接CD ,CG .若CG ⊥DE ,CD =6,AE =3,求DEBC的值.(3)如图3,在▱ABCD 中,∠ADC =45°,AC 与BD 交于点O ,E 为AO 上一点,EG ∥BD 交AD 于点G ,EF ⊥EG 交BC 于点F .若∠EGF =40°,FG 平分∠EFC ,FG =10,求BF 的长.5(2023•安庆一模)如图,在△ABC 中,点D 、E 、F 分别在边BC 、AB 、CA 上,且DE ∥CA ,DF ∥AB .(1)若点D 是边BC 的中点,且BE =CF ,求证:DE =DF ;(2)若AD ⊥BC 于D ,且BD =CD ,求证:四边形AEDF 是菱形;(3)若AE =AF =1,求1AB +1AC的值.模型2.“X ”字模型(“8”模型)【模型解读与图示】“8”字模型图形的两个三角形有“对顶角”,再有一个角相等或夹对顶角的两边对应成比例就可以判定这两个三角形相似.图1图2图3图41)“8”字模型条件:如图1,AB ∥CD ;结论:△AOB ∽△COD ⇔AB CD =OA OC =OBOD .2)反“8”字模型条件:如图2,∠A =∠D ;结论:△AOB ∽△DOC ⇔AB CD =OA OD =OBOC.3)平行双“8”字模型条件:如图3,AB ∥CD ;结论:AE DF =BE CF =ABCD4)斜双“8”字模型条件:如图4,∠1=∠2;结论:△AOD ∽△BOC ,△AOB ∽△DOC ⇔∠3=∠4.1(2022·辽宁·中考真题)如图,在正方形ABCD 中,E 为AD 的中点,连接BE 交AC 于点F .若AB =6,则△AEF 的面积为.2(2023·黑龙江·哈尔滨九年级阶段练习)如图,AB ∥CD ,AE ∥FD ,AE ,FD 分别交BC 于点G ,H ,则下列结论中错误的是()A.DH FH =CHBHB.GE DF =CGCBC.AF CE =HGCGD.FH AG =BFFA3(2021·上海·中考真题)如图,在梯形ABCD 中,AD ⎳BC ,∠ABC =90°,AD =CD ,O 是对角线AC 的中点,联结BO 并延长交边CD 或边AD 于E .(1)当点E 在边CD 上时,①求证:△DAC ∽△OBC ;②若BE ⊥CD ,求ADBC的值;(2)若DE =2,OE =3,求CD 的长.4(2022·贵州铜仁·中考真题)如图,在四边形ABCD 中,对角线AC 与BD 相交于点O ,记△COD 的面积为S 1,△AOB 的面积为S 2.(1)问题解决:如图①,若AB ⎳CD ,求证:S 1S 2=OC ⋅ODOA ⋅OB(2)探索推广:如图②,若AB 与CD 不平行,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由.(3)拓展应用:如图③,在OA 上取一点E ,使OE =OC ,过点E 作EF ∥CD 交OD 于点F ,点H 为AB的中点,OH 交EF 于点G ,且OG =2GH ,若OE OA=56,求S 1S 2值.模型3. “AX ”字模型(“A 8”模型)【模型解读与图示】图1图2图3 1)一“A”一“8”模型条件:如图1,DE∥BC;结论:△ADE∽△ABC,△DEF∽△CBF⇔ADAB=AEAC=DEBC=DFFC=FEBF2)两“A”一“8”模型条件:如图2,DE∥AF∥BC;结论:1BC +1DE=1AF.3)四“A”一“8”模型条件:如图3,DE∥AF∥BC,1BC+1DE=1AF=1AG;结论:AF=AG1(2022·山东东营·中考真题)如图,点D为△ABC边AB上任一点,DE∥BC交AC于点E,连接BE、CD 相交于点F,则下列等式中不成立的是()A.ADDB =AEECB.DEBC=DFFCC.DEBC=AEECD.EFBF=AEAC2(2021·江苏南京·中考真题)如图,AC与BD交于点O,OA=OD,∠ABO=∠DCO,E为BC延长线上一点,过点E作EF⎳CD,交BD的延长线于点F.(1)求证△AOB≌△DOC;(2)若AB=2,BC=3,CE=1,求EF的长.3(2022·重庆九年级期中)如图,AD与BC相交于点E,点F在BD上,且AB∥EF∥CD,求证:1AB +1CD=1EF.证明:∵AB∥EF,∴△DEF∽△DAB,∴EFAB=DFDB.又∵EF∥CD,∴△BEF∽△BCD.∴EFCD=BFBD.∴EF AB +EFCD=DFDB+BFBD=BDBD=1.∴1AB+1CD=1EF.4(2022•安庆模拟)在四边形ABCD中,对角线AC、BD相交于点O.(1)如图①,若四边形ABCD为矩形,过点O作OE⊥BC,求证:OE=12CD.(2)如图②,若AB∥CD,过点O作EF∥AB分别交BC、AD于点E、F.求证:EFAB =EFCD=2.(3)如图③,若OC平分∠AOB,D、E分别为OA、OB上的点,DE交OC于点M,作MN∥OB交OA于一点N,若OD=8,OE=6,直接写出线段MN长度.课后专项训练1(2021·山东淄博·中考真题)如图,AB,CD相交于点E,且AC⎳EF⎳DB,点C,F,B在同一条直线上.已知AC=P,EF=r,DB=q,则p,q,r之间满足的数量关系式是()A.1r +1q=1pB.1p+1r=2qC.1p+1q=1rD.1q+1r=2p2(2023秋·山西阳泉·九年级统考期末)如图,在四边形ABCD中,AB=AC,对角线AC与BD相交于点E,DE=3BE,AC⊥AD,∠ACB=75°,AE=33,则对角线AC与BD的长分别是()A.AC=43,BD=123B.AC=9,BD=419C.AC=6,BD=83D.AC=8,BD=4193(2023·福建福州·校考二模)在数学综合实践课上,某学习小组计划制作一个款式如图所示的风筝.在骨架设计中,两条侧翼的长度设计AB=AC=50cm,风筝顶角∠BAC的度数为110°,在AB,AC上取D,E 两处,使得AD=AE,并作一条骨架AF⊥DE.在制作风筝面时,需覆盖整个骨架,根据以上数据,B,C两点间的距离大约是( )(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)A.41cmB.57cmC.82cmD.143cm4(2022·湖北十堰·中考真题)如图,某零件的外径为10cm,用一个交叉卡钳(两条尺长AC和BD相等)可测量零件的内孔直径AB.如果OA:OC=OB:OD=3,且量得CD=3cm,则零件的厚度x为()A.0.3cmB.0.5cmC.0.7cmD.1cm5(2022·湖南怀化·中考真题)如图,△ABC中,点D、E分别是AB、AC的中点,若S△ADE=2,则S△ABC=.6(2023·广东梅州·九年级统考期末)如图,在△ABC中,点F、G在BC上,点E、H分别在AB、AC上,四边形EFGH是矩形,EH=2EF,AD是△ABC的高,BC=15,AD=5,那么EH的长为.7(2023·广东深圳·校考三模)如图,在Rt△ABC中,∠ACB=90°,AC=BC=6,D是AB上一点,点E 在BC上,连接CD,AE交于点F,若∠CFE=45°,BD=2AD,则CE=.8(2022·四川宜宾·中考真题)如图,△ABC中,点E、F分别在边AB、AC上,∠1=∠2.若BC=4,AF =2,CF=3,则EF=.9(2022·辽宁阜新·中考真题)如图,在矩形ABCD中,E是AD边上一点,且AE=2DE,BD与CE相交于点F,若△DEF的面积是3,则△BCF的面积是.10(2022·湖北荆门·中考真题)如图,点G 为△ABC 的重心,D ,E ,F 分别为BC ,CA ,AB 的中点,具有性质:AG :GD =BG :GE =CG :GF =2:1.已知△AFG 的面积为3,则△ABC 的面积为.11(2023·福建·统考中考真题)阅读下列材料,回答问题任务:测量一个扁平状的小水池的最大宽度,该水池东西走向的最大宽度AB 远大于南北走向的最大宽度,如图1.工具:一把皮尺(测量长度略小于AB )和一台测角仪,如图2.皮尺的功能是直接测量任意可到达的两点间的距离(这两点间的距离不大于皮尺的测量长度);测角仪的功能是测量角的大小,即在任一点O 处,对其视线可及的P ,Q 两点,可测得∠POQ 的大小,如图3.小明利用皮尺测量,求出了小水池的最大宽度AB ,其测量及求解过程如下:测量过程:(ⅰ)在小水池外选点C ,如图4,测得AC =am ,BC =bm ;(ⅱ)分别在AC ,BC ,上测得CM =a 3m ,CN =b3m ;测得MN =cm .求解过程:由测量知,AC =a ,BC =b ,CM =a 3,CN =b3,∴CM CA=CN CB =13,又∵①,∴△CMN ∽△CAB ,∴MN AB=13.又∵MN =c ,∴AB =②m .故小水池的最大宽度为m .(1)补全小明求解过程中①②所缺的内容;(2)小明求得AB 用到的几何知识是;(3)小明仅利用皮尺,通过5次测量,求得AB .请你同时利用皮尺和测角仪,通过测量长度、角度等几何量,并利用解直角三角形的知识求小水池的最大宽度AB ,写出你的测量及求解过程.要求:测量得到的长度用字母a ,b ,c ⋯表示,角度用α,β,γ⋯表示;测量次数不超过4次(测量的几何量能求出AB ,且测量的次数最少,才能得满分).12(2023秋·山西运城·九年级统考期末)综合与实践问题情境:如图1,在Rt△ABC中,∠C=90°,AC=3,BC=4,点D是AC上一点,将△BCD沿直线BD折叠,点C落在AB上的点E,连接DE.独立思考(1)如图1,求tan∠DBC的值;问题拓展如图2,点F是图1中AB上一动点,连接CF,交BD于点G.(2)当点F是AB的中点时,求证:DGBG =49;(3)当点G是BD的中点时,请你直接写出AFBF的值.13(2023·湖南郴州·统考中考真题)已知△ABC是等边三角形,点D是射线AB上的一个动点,延长BC 至点E,使CE=AD,连接DE交射线AC于点F.(1)如图1,当点D在线段AB上时,猜测线段CF与BD的数量关系并说明理由;(2)如图2,当点D在线段AB的延长线上时,①线段CF与BD的数量关系是否仍然成立?请说明理由;②如图3,连接AE.设AB=4,若∠AEB=∠DEB,求四边形BDFC的面积.14(2023·浙江·九年级专题练习)已知:如图,四边形ABCD是平行四边形,在边AB的延长线上截取BE=AB,点F在AE的延长线上,CE和DF交于点M,BC和DF交于点N,联结BD.(1)求证:△BND∽△CNM;(2)如果AD2=AB•AF,求证:CM•AB=DM•CN.15(2023·湖北武汉·统考模拟预测)问题背景:如图1,在四边形ABDC中,点F,E,G分别在AB,AD,AC上,EF∥BD,EG∥CD,求证:EFBD =EG DC尝试应用:如图2,AM是△ABC的中线,点E在AM上,直线BE交AC于点G,直线CE交AB于点F,若BE EC =2,求EF EG的值.迁移拓展:如图3,在等边△ABC 中,点D 在BC 上,点E 在AD 上,若BD =mDC ,∠BEC =120°,直接写出BE CE的值.(用含m 的式子表示)16(2023·浙江杭州·统考中考真题)在边长为1的正方形ABCD 中,点E 在边AD 上(不与点A ,D 重合),射线BE 与射线CD 交于点F .(1)若ED =13,求DF 的长.(2)求证:AE ⋅CF =1.(3)以点B 为圆心,BC 长为半径画弧,交线段BE 于点G .若EG =ED ,求ED 的长.17(2022·四川内江·中考真题)如图,在矩形ABCD 中,AB =6,BC =4,点M 、N 分别在AB 、AD 上,且MN ⊥MC ,点E 为CD 的中点,连接BE 交MC 于点F .(1)当F 为BE 的中点时,求证:AM =CE ;(2)若EF BF =2,求AN ND 的值;(3)若MN ∥BE ,求AN ND的值.18(2023•重庆中考模拟)问题提出:如图1,D 、E 分别在△ABC 的边AB 、AC 上,连接DE ,已知线段AD =a ,DB =b ,AE =c ,EC =d ,则S △ADE ,S △ABC 和a ,b ,c ,d 之间会有怎样的数量关系呢?问题解决:探究一:(1)看到这个问题后,我们可以考虑先从特例入手,找出其中的规律.如图2,若DE ∥BC ,则∠ADE =∠B ,且∠A =∠A ,所以△ADE ∽△ABC ,可得比例式:a a +b =c c +d 而根据相似三角形面积之比等于相似比的平方.可得S △ADE S △ABC =a 2a +b 2.根据上述这两个式子,可以推出:S △ADE S △ABC =a 2a +b2=a a +b ⋅a a +b =a a +b ⋅c c +d =ac a +b c +d.(2)如图3,若∠ADE =∠C ,上述结论还成立吗?若成立,请写出证明过程;着不成立,请说明理由.探究二:回到最初的问题,若图1中没有相似的条件,是否仍存在结论:S △ADE S △ABC =ac a +b c +d?方法回顾:两个三角形面积之比,不仅可以在相似的条件下求得,当两个三角形的底成高具有一定的关系时,也可以解决.如图4,D 在△ABC 的边上,做AH ⊥BC 于H ,可得:S △ABD S △ADC =12BD ⋅AH 12DC ⋅AH =BD DC .借用这个结论,请你解决最初的问题.延伸探究:(1)如图5,D 、E 分别在△ABC 的边AB 、AC 反向延长线上,连接DE ,已知线段AD =a ,AB =b ,AE =c ,AC =d ,则S △ADE S △ABC=.(2)如图6,E 在△ABC 的边AC 上,D 在AB 反向延长线上,连接DE ,已知线段AD =a ,AB =b ,AE =c ,AC =d ,S △ADE S △ABC =.结论应用:如图7,在平行四边形ABCD 中,G 是BC 边上的中点,延长GA 到E ,连接DE 交BA 的延长线于F ,若AB =5,AG =4,AE =2,▱ABCD 的面积为30,则△AEF 的面积是.19(2023·河南郑州·校考三模)【问题发现】小明在一次利用三角板作图的过程中发现了一件有趣的事情:如图1,在Rt △ABC 中,∠A =30°,AB =6,点M 和点P 分别是斜边AB 上的动点,并且满足AM =BP ,分别过点M 和点P 作AC 边的垂线,垂足分别为点N 和点Q ,那么MN +PQ 的值是一个定值.问题:若AM =BP =2时,MN +PQ 值为;【操作探究】如图2,在Rt △ABC 中,∠C =90°,∠A =α,AB =m ;爱动脑筋的小明立即拿出另一个三角板进行了验证,发现果然和之前发现的结论一样,于是他猜想,对于任意一个直角三角形,当AM =BP 时,MN +PQ 的值都是固定的,小明的猜想对吗?如果对,请利用图2进行证明,并用含α和m 的式子表示MN +PQ 的值.【解决问题】如图3,在菱形ABCD 中,AB =8,BD =14.若M 、N 分别是边AD 、BC 上的动点,且AM =BN ,作ME ⊥BD ,NF ⊥BD ,垂足分别为E 、F ,则ME +NF 的值为.20(2022·湖北武汉·中考真题)问题提出:如图(1),△ABC 中,AB =AC ,D 是AC 的中点,延长BC 至点E ,使DE =DB ,延长ED 交AB 于点F ,探究AF AB的值.(1)先将问题特殊化.如图(2),当∠BAC =60°时,直接写出AF AB的值;(2)再探究一般情形.如图(1),证明(1)中的结论仍然成立.问题拓展:如图(3),在△ABC 中,AB =AC ,D 是AC 的中点,G 是边BC 上一点,CG BC =1n n <2 ,延长BC 至点E ,使DE =DG ,延长ED 交AB 于点F .直接写出AF AB的值(用含n 的式子表示).21(2023·浙江温州·统考中考真题)如图,已知矩形ABCD ,点E 在CB 延长线上,点F 在BC 延长线上,过点F 作FH ⊥EF 交ED 的延长线于点H ,连结AF 交EH 于点G ,GE =GH .(1)求证:BE=CF.(2)当ABFH =56,AD=4时,求EF的长.。
专题 相似三角形一线三等角模型(学生版)
专题04相似三角形重要模型-一线三等角模型相似三角形在中考数学几何模块中占据着重要地位。
相似三角形与其它知识点结合以综合题的形式呈现,其变化很多,难度大,是中考的常考题型。
如果大家平时注重解题方法,熟练掌握基本解题模型,再遇到该类问题就信心更足了.本专题就一线三等角模型进行梳理及对应试题分析,方便掌握。
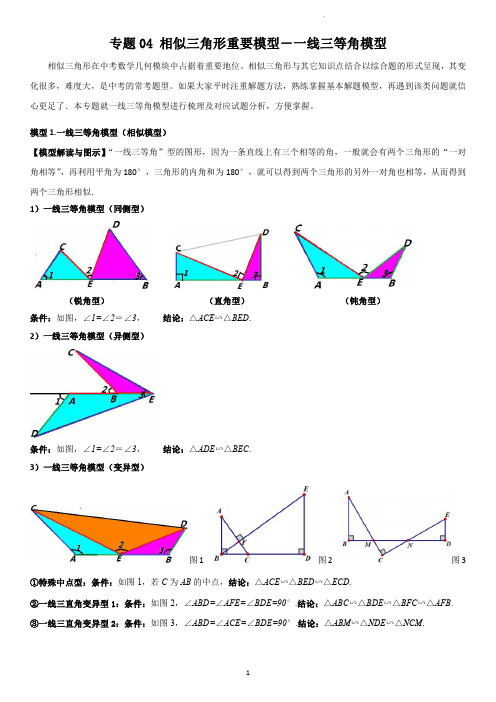
模型1.一线三等角模型(相似模型)【模型解读与图示】“一线三等角”型的图形,因为一条直线上有三个相等的角,一般就会有两个三角形的“一对角相等”,再利用平角为180°,三角形的内角和为180°,就可以得到两个三角形的另外一对角也相等,从而得到两个三角形相似.1)一线三等角模型(同侧型)(锐角型)(直角型)(钝角型)条件:如图,∠1=∠2=∠3,结论:△ACE∽△BED.2)一线三等角模型(异侧型)条件:如图,∠1=∠2=∠3,结论:△ADE∽△BEC.3)一线三等角模型(变异型)图1图2图3①特殊中点型:条件:如图1,若C为AB的中点,结论:△ACE∽△BED∽△ECD.②一线三直角变异型1:条件:如图2,∠ABD=∠AFE=∠BDE=90°.结论:△ABC∽△BDE∽△BFC∽△AFB.③一线三直角变异型2:条件:如图3,∠ABD=∠ACE=∠BDE=90°.结论:△ABM∽△NDE∽△NCM.是边A.3B.5C.2D.1B (1)如图2,在53⨯个方格的纸上,小正方形的顶点为格点、边长均为1,AB 为端点在格点的已知线段.请用三种不...同连接格点.....的方法,作出以线段AB 为等联线、某格点P 为等联点的等联角,并标出等联角,保留作图痕迹;(2)如图3,在Rt APC △中,90A ∠=,AC AP >,延长AP 至点B ,使AB AC =,作A ∠的等联角CPD ∠和PBD ∠.将APC △沿PC 折叠,使点A 落在点M 处,得到MPC ,再延长PM 交BD 的延长线于E ,连接CE 并延长交PD 的延例5.(2022·浙江·嘉兴一中一模)阅读材料:我们知道:一条直线经过等腰直角三角形的直角顶点,过另外两个顶点分别向该直线作垂线,即可得三垂直模型”如图①:在△ABC 中,∠ACB =90°,AC =BC ,分别过A 、B 向经过点C 直线作垂线,垂足分别为D 、E ,我们很容易发现结论:△ADC ≌△CEB .(1)探究问题:如果AC ≠BC ,其他条件不变,如图②,可得到结论;△ADC ∽△CEB .请你说明理由.(2)学以致用:如图③,在平面直角坐标系中,直线y =12x 与直线CD 交于点M (2,1),且两直线夹角为α,且tanα=32,请你求出直线CD 的解析式.(3)拓展应用:如图④,在矩形ABCD 中,AB =4,BC =5,点E 为BC 边上一个动点,连接AE ,将线段AE 绕点E 顺时针旋转90°,点A 落在点P 处,当点P 在矩形ABCD 外部时,连接PC ,PD .若△DPC 为直角三角形时,请你探究并直接写出BE 的长.例6.(2023·浙江·九年级专题练习)在Rt ABC 中,90BAC ∠=︒,2AB AC ==,点D 在BC 所在的直线上运动,作45ADE ∠=︒(A 、D 、E 按逆时针方向).(1)如图,若点D 在线段BC 上运动,DE 交AC 于E .①求证:ABD DCE △△∽;②当ADE V 是等腰三角形时,求AE 的长;(2)如图,若点D 在BC 的延长线上运动,DE 的反向延长线与AC 的延长线相交于点E ',是否存在点D ,使ADE '△是等腰三角形?若存在,求出线段CD 的长度;若不存在,请简要说明理由;(3)若点D 在BC 的反向延长线上运动,是否存在点D ,使ADE V 是等腰三角形?若存在,写出所有点D 的位置;若不存在,请简要说明理由.上一点,轴9,23A.()9,3B.()3.(2023·湖南长沙·九年级专题练习)如图,在矩形4.(2021·浙江台州·中考真题)如图,点E,F,G分别在正方形ABCD的边AB,BC,AD上,AF⊥EG.若AB=5,AE=DG=1,则BF=_____.分别在边6.(2022秋·安徽淮北·九年级校考阶段练习)如图,在四边形分别在线段AD、DC上(点E与点A、CD=,在BC边上取中点E,连接DE,过点E 8.(2023·山东烟台·九年级统考期末)如图,在正方形ABCD中,4做EF ED⊥与AB交于点G,与DA的延长线交于点F.(1)求证:BEG CDE△∽△;(2)求AFG的面积.⊥交AB于点M,9.(2023·上海·九年级假期作业)在矩形ABCD中,3AB=,4=AD,点E是边AD上一点,EM EC∠=∠.(1)求证:AE是AM和AN的比例中项;(2)当点N在线段AB的延点N在射线MB上(如图),且ANE DCE长线上时,联结AC,且AC与NE互相垂直,求MN的长.的两个等腰直角三角形,(3)【拓展探究】在整个运动过程中,请直接写出N点运动的路径长,及CN的最小值.312.(2023·广东深圳·九年级校考阶段练习)如图,在ABC 中6cm AB AC ==,8cm BC =,点E 是线段BC 边上的一动点(不含B 、C 两端点),连接AE ,作AED B ∠=∠,交线段AB 于点D .(1)求证:BDE CEA△∽△(2)设BE x =,AD y =,请求y 与x 之间的函数关系式.(3)E 点在运动的过程中,ADE V 能否构成等腰三角形?若能,求出BE 的长;若不能,请说明理由.13.(2023春·广东深圳·八年级校考期中)【操作发现】如图1,在边长为1个单位长度的小正方形组成的网格中,ABC 的三个顶点均在格点上.①请按要求画图:将ABC 绕点A 顺时针方向旋转90︒,点B 的对应点为点B ',点C 的对应点为点C ',连接BB ';②在①中所画图形中,AB B '∠=______︒.【问题解决】如图2,在Rt ABC △中,190BC C =∠=︒,,延长CA 到D ,使1CD =,将斜边AB 绕点A 顺时针旋转90︒到AE ,连接DE ,求ADE ∠的度数.【拓展延伸】如图3,在四边形ABCD 中,AE BC ⊥,垂足为E ,BAE ADC ∠=∠,1BE CE ==,3CD =,2=AD AB ,求BD 的长.14.(2023·浙江·九年级专题练习)在平面直角坐标系中,O 为坐标原点,直线AB 与y 轴交于点A ,与x 轴交于点B ,2OA =,AOB 的面积为2.(1)如图1,求直线AB 的解析式.(2)如图2,线段OA 上有一点C ,直线BC 为2(0)y kx k k =-<,AD y ⊥轴,将BC 绕点B 顺时针旋转90︒,交AD 于点D ,求点D 的坐标.(用含k 的式子表示)(3)如图3,在(2)的条件下,连接OD ,交直线BC 于点E ,若345ABC BDO ∠-∠=︒,求点E 的坐标.九年级专题练习)某数学兴趣小组在学习了尺规作图、等腰三角形和相似三角形的有关知识后,在BC=.点E是线段AD上的动点(点E不与18.(2022·湖南郴州·中考真题)如图1,在矩形ABCD中,4AB=,6⊥,交AB于点F.点A,D重合),连接CE,过点E作EF CE∽;(1)求证:AEF DCE⊥,垂足为G,连接AG.点M是线段BC的中点,连接GM.(2)如图2,连接CF,过点B作BG CF①求AG GM+的最小值;②当AG GM+取最小值时,求线段DE的长.。
专题7 类比探究—图形旋转中三角形相似题型(学生版)

专题7类比探究—图形旋转中三角形相似题型知识归纳图形的类比探究常以三角形、四边形为背景,与翻折、旋转相结合,考查三角形全等或相似的性质与判定,难度较大.此类题目第一问相对简单,后面的问题需要结合第一问的方法进行类比解答.根据其特征大致可分为:几何变换类比探究问题、旋转综合问题、翻折类问题等。
本专题主要对类比探究—图形旋转中三角形相似题型进行总结,对其解法进行归纳总结,所选题型为近几年期末考试中的常考题型。
知识点睛(1)类比探究属于几何综合题,类比(类比字母,类比辅助线,类比思路)是解决此问题的主要方法,做好类比需要把握变化过程中的不变特征.(2)类比探究问题中常见结构举例①旋转结构②中点结构(类)倍长中线平行夹中点中位线方法总结(1)类比探究是一类共性条件与特殊条件相结合,由特殊情形到一般情形(或由简单情形到复杂情形)逐步深入,解决思想方法一脉相承的综合性题目,常以几何综合题为主.(2)解决类比探究问题的一般方法:①根据题干条件,结合分支条件先解决第一问;②用解决第一问的方法类比解决下一问,整体框架照搬.整体框架照搬包括照搬字母,照搬辅助线,照搬思路。
(3)用铅笔做讲义第1,2题,并将计算、演草保留在讲义上,先看知识点睛,再做题,思路受阻时(某个点做了2~3分钟)重复上述动作,若仍无法解决,课堂重点听.常考题型专练一、解答题1.在△ABC中,AB=AC,∠BAC=α,点P为线段CA延长线上一动点,连接PB,将线段PB绕点P逆时针旋转,旋转角为α,得到线段PD,连接DB,DC.(1)如图1,当α=60°时,①求证:PA=DC;②求∠DCP的度数;(2)如图2,当α=120°时,请直接写出PA和DC的数量关系.(3)当α=120°时,若AB=6,BP=31,请直接写出点D到CP的距离为.2.如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=2,Rt△ABC绕点C按顺时针方向旋转得到Rt△A′B′C,A′C与AB交于点D.(1)如图1,当A′B′∥AC时,过点B作BE⊥A′C,垂足为E,连接AE.①求证:AD=BD;②求S△ACE S△ABE的值;(2)如图2,当A′C⊥AB时,过点D作DM∥A′B′,交B′C于点N,交AC的延长线于点M,求DN NM的值.3.(1)问题发现如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:①的值为;②∠AMB的度数为.(2)类比探究如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断的值及∠AMB的度数,并说明理由;(3)拓展延伸在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=,请直接写出当点C与点M重合时AC的长.4.在△ABC中,CA=CB,∠ACB=α.点P是平面内不与点A,C重合的任意一点.连接AP,将线段AP绕点P逆时针旋转α得到线段DP,连接AD,BD,CP.(1)观察猜想如图1,当α=60°时,的值是,直线BD与直线CP相交所成的较小角的度数是.(2)类比探究如图2,当α=90°时,请写出的值及直线BD与直线CP相交所成的小角的度数,并就图2的情形说明理由.(3)解决问题当α=90°时,若点E,F分别是CA,CB的中点,点P在直线EF上,请直接写出点C,P,D在同一直线上时的值.5.已知,ABC中,AB=AC,∠BAC=2α°,点D为BC边中点,连接AD,点E为线段AD上一动点,把线段CE 绕点E顺时针旋转2α°得到线段EF,连接FG,FD.(1)如图1,当∠BAC=60°时,请直接写出BFAE的值;(2)如图2,当∠BAC=90°时,(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请写出正确的结论,并说明理由;(3)如图3,当点E在AD上移动时,请直接写出点E运动到什么位置时DFDC的值最小.最小值是多少?(用含α的三角函数表示)6.在ABC ∆中,CA CB =,(0180)ACB αα∠=<<.点P 是平面内不与A ,C 重合的任意一点,连接AP ,将线段AP 绕点P 逆时针旋转α得到线段DP ,连接AD ,CP 点M 是AB 的中点,点N 是AD 的中点.(1)问题发现,如图1,当60α=时,MN PC 的值是,直线MN 与直线PC 相交所成的较小角的度数是;(2)类比探究,如图2,当120α=时,请写出MN PC的值及直线MN 与直线PC 相交所成的较小角的度数,并就图2的情形说明理由;(3)解决问题,如图3,当90α=时,若点E 是CB 的中点,点P 在直线ME 上,MN =请直接写出点B ,P ,D 在同一条直线上时PD 的长.7.如图(1),在矩形ABCD中,AD=nAB,点M,P分别在边AB,AD上(均不与端点重合),且AP=nAM,以AP和AM为邻边作矩形AMNP,连接AN,CN.【问题发现】(1)如图(2),当n=1时,BM与PD的数量关系为,CN与PD的数量关系为.【类比探究】(2)如图(3),当n=2时,矩形AMNP绕点A顺时针旋转,连接PD,则CN与PD之间的数量关系是否发生变化?若不变,请就图(3)给出证明;若变化,请写出数量关系,并就图(3)说明理由.【拓展延伸】(3)在(2)的条件下,已知AD=4,AP=2,当矩形AMVP旋转至C,N,M三点共线时,请直接写出线段CN的长8.(1)问题发现如图1,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=45°,点D是线段AB上一动点,连接BE.填空:①BEAD的值为;②∠DBE的度数为.(2)类比探究如图2,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,点D是线段AB上一动点,连接BE.请判断BEAD的值及∠DBE的度数,并说明理由.(3)拓展延伸如面3,在(2)的条件下,将点D改为直线AB上一动点,其余条件不变,取线段DE的中点M,连接BM、CM,若AC=2,则当△CBM是直角三角形时,线段BE的长是多少?请直接写出答案.。
小学数学知识归纳三角形的相似判定及性质

小学数学知识归纳三角形的相似判定及性质三角形是初中数学中重要的几何形状之一,它具有丰富的性质与判定方法。
相似性是三角形研究中一项重要的内容,通过相似判定及相似性质可以帮助我们更深入地理解三角形的特性。
本文将归纳总结小学阶段数学中关于三角形相似判定及性质的知识,帮助小学生更好地掌握和运用。
一、相似判定方法1. AAA相似判定法当两个三角形对应的三个角分别相等时,可以判定它们相似。
例如,当三角形ABC和三角形DEF满足∠A = ∠D,∠B = ∠E,∠C = ∠F 时,可以得出三角形ABC ∽三角形DEF。
2. AA相似判定法当两个三角形中一对对应角相等,并且另一对对应角相等时,可以判定它们相似。
例如,当三角形ABC和三角形DEF满足∠A = ∠D,∠B = ∠E或∠A = ∠E,∠B = ∠D时,可以得出三角形ABC ∽三角形DEF。
3. SAS相似判定法当两个三角形中一对对应边成比例,并且夹角也相等时,可以判定它们相似。
例如,当三角形ABC和三角形DEF满足AB/DE = AC/DF,并且∠B = ∠E时,可以得出三角形ABC ∽三角形DEF。
4. SSS相似判定法当两个三角形对应的三条边成比例时,可以判定它们相似。
例如,当三角形ABC和三角形DEF满足AB/DE = AC/DF = BC/EF时,可以得出三角形ABC ∽三角形DEF。
二、相似性质1. 对应角相等性质如果两个三角形相似,它们对应的角相等。
例如,在∆ABC ∽∆DEF中,∠A = ∠D,∠B = ∠E,∠C = ∠F。
2. 对应边成比例性质如果两个三角形相似,它们对应的边成比例。
例如,在∆ABC ∽∆DEF中,AB/DE = AC/DF = BC/EF。
3. 相似三角形的周长比性质如果两个三角形相似,它们的对应边长之比等于它们的周长之比。
例如,在∆ABC ∽ ∆DEF中,AB/DE = BC/EF = AC/DF = 周长(∆ABC)/周长(∆DEF)。
相似三角形的性质及判定知识点总结+经典题型总结(学生版)

一、相似的有关概念1.相似形具有相同形状的图形叫做相似形.相似形仅是形状相同,大小不一定相同.相似图形之间的互相变换称为相似变换. 2.相似图形的特性两个相似图形的对应边成比例,对应角相等. 3.相似比两个相似图形的对应角相等,对应边成比例.二、相似三角形的概念1.相似三角形的定义对应角相等,对应边成比例的三角形叫做相似三角形.如图,ABC △与A B C '''△相似,记作ABC A B C '''△∽△,符号∽读作“相似于”.2.相似比相似三角形对应边的比叫做相似比.全等三角形的相似比是1.“全等三角形”一定是“相似形”,“相似形”不一定是“全等形”.三、相似三角形的性质1.相似三角形的对应角相等A 'B 'C 'CB A中考要求知识点睛相似三角形的性质及判定2.相似三角形的对应边成比例ABC △与A B C '''△相似,则有AB BC ACk A B B C A C===''''''(k 为相似比).3.相似三角形的对应边上的中线,高线和对应角的平分线成比例,都等于相似比.如图1,ABC △与A B C '''△相似,AM 是ABC △中BC 边上的中线,A M ''是A B C '''△中B C ''边上的中线,则有AB BC AC AM k A B B C A C A M ====''''''''(k 为相似比).图1如图2,ABC △与A B C '''△相似,AH 是ABC △中BC 边上的高线,A H ''是A B C '''△中B C ''边上的高线,则有AB BC AC AH k A B B C A C A H ====''''''''(k 为相似比).图2如图3,ABC △与A B C '''△相似,AD 是ABC △中BAC ∠的角平分线,A D ''是A B C '''△中B A C '''∠的角平分线,则有AB BC AC ADk A B B C A C A D ====''''''''(k 为相似比).图34.相似三角形周长的比等于相似比. 如图4,ABC △与A B C '''△相似,则有AB BC ACk===(k 为相似比).应用比例的等比性质有A 'B 'C 'CB AM 'MA 'B 'C 'C BAH 'H AB C C 'B 'A 'D 'D A 'B 'C B AAB BC AC AB BC ACk A B B C A C A B B C A C ++====''''''''''''++. 图45.相似三角形面积的比等于相似比的平方.如图5,ABC △与A B C '''△相似,AH 是ABC △中BC 边上的高线,A H ''是A B C '''△中B C ''边上的高线,则有AB BC AC AH k A B B C A C A H ====''''''''(k 为相似比).进而可得21212ABC A B C BC AHS BC AH k S B C A H B C A H '''⋅⋅==⋅=''''''''⋅⋅△△.图5四、相似三角形的判定1.平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似. 2.如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.可简单说成:两角对应相等,两个三角形相似.3.如果一个三角形的两边和另一个三角形的两边对应成比例,并且夹角相等,那么这两个三角形相似. 4.如果一个三角形的三条边与另一个三角形的你对应成比例,那么这两个三角形相似.可简单地说成:三边对应成比例,两个三角形相似.5.如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.6.直角三角形被斜边上的高分成的两个直角三角形相似(常用但要证明)7.如果一个等腰三角形和另一个等腰三角形的顶角相等或一对底角相等,那么这两个等腰三角形相似;如果它们的腰和底对应成比例,那么这两个等腰三角形也相似.五、相似证明中的比例式或等积式、比例中项式、倒数式、复合式证明比例式或等积式的主要方法有“三点定形法”. 1.横向定型法欲证AB BCBE BF =,横向观察,比例式中的分子的两条线段是AB 和BC ,三个字母A B C ,,恰为ABC △的顶点;分母的两条线段是BE 和BF ,三个字母B E F ,,恰为BEF △的三个顶点.因此只需证ABC EBF △∽△.A 'B 'C 'CB AH 'H AB C C 'B 'A '欲证AB DEBC EF=,纵向观察,比例式左边的比AB 和BC 中的三个字母A B C ,,恰为ABC △的顶点;右边的比两条线段是DE 和EF 中的三个字母D E F ,,恰为DEF △的三个顶点.因此只需证ABC DEF △∽△. 3.中间比法由于运用三点定形法时常会碰到三点共线或四点中没有相同点的情况,此时可考虑运用等线,等比或等积进行变换后,再考虑运用三点定形法寻找相似三角形.这种方法就是等量代换法.在证明比例式时,常用到中间比.比例中项式的证明,通常涉及到与公共边有关的相似问题。
初中数学重难点易错专题 相似三角形中的“8”字模型(3种题型)(学生版)

相似三角形中的“8”字模型(3种题型)一、【知识梳理】8字_平行型条件:CD∥AB,结论:ΔPAB∼ΔPCD(上下相似);左右不一定相似,不一定全等,但面积相等;四边形ABCD为一般梯形.条件:CD∥AB,PD=PC.结论:ΔPAB∼ΔPCD∼ΔPDC(上下相似)ΔPAD≅ΔPBC左右全等;四边形ABCD为等腰梯形;8字_不平行型条件:∠CDP=∠BAP.结论:ΔAPB∼ΔDPC(上下相似);ΔAPD∼ΔBPC(左右相似);二、【考点剖析】8字-平行型1.直接利用“8”字型解题1如图,在平行四边形ABCD中,点E在边DC上,若DE:EC=1:2,则BF:BE=.2如图,P为▱ABCD对角线BD上任意一点.求证:PQ∙PI=PR∙PS.3如图,在平行四边形ABCD中,CD的延长线上有一点E,BE交AC于点F,交AD于点G.求证:BF2=FG∙EF.4如图,点C在线段AB上,ΔAMC和ΔCBN都是等边三角形.求证:(1)MDDC=AMCN;(2)MD∙EB=ME∙DC.5如图,已知AB⎳CD⎳EF.AB=m,CD=n,求EF的长.(用m、n的代数式表示).6如图,E 为平行四边形ABCD 的对角线AC 上一点,AE EC=13,BE 的延长线交CD 的延长线于点G ,交AD 于点F ,求BF :FG 的值.7如图,l 1⎳l 2,AF :FB =2:5,BC :CD =4:1,求AE :EC 的值.2.添加辅助线构造“8”字模型解题8过ΔABC 的顶点C 任作一直线,与边AB 及中线AD 分别交于点F 、E .求证:AE ED =2AF FB.9如图,AD 是ΔABC 的内角平分线.求证:AB AC=BD DC .8字-不平行型1如图,∠BEC=∠CDB,下列结论正确的是()A.EF•BF=DF•CFB.BE•CD=BF•CFC.AE•AB=AD•ACD.AE•BE=AD•DC1.【过关检测】一、选择题(共3小题)1(2023•静安区校级一模)如图,在△ABC中,中线AD与中线BE相交于点G,联结DE.下列结论成立的是()A. B. C. D.2(2023•徐汇区一模)如图,点D在△ABC边AB上,∠ACD=∠B,点F是△ABC的角平分线AE 与CD的交点,且AF=2EF,则下列选项中不正确的是()A. B. C. D.3(2022秋•闵行区期末)如图,某零件的外径为10cm,用一个交叉卡钳(两条尺长AC和BD相等)可测量零件的内孔直径AB.如果==3,且量得CD=4cm,则零件的厚度x为()A.2cmB.1.5cmC.0.5cmD.1cm二、填空题(共8小题)4(2022秋•奉贤区期中)如图,已知点D为△ABC中AC边的中点,AE∥BC,ED交AB于点G,交BC的延长线于点F,若,BC=8,则AE的长为.5(2022•浦东新区校级模拟)如图,已知点D、E分别在△ABC的边CA、BA的延长线上,DE∥BC.DE:BC=2:3,设=,试用向量表示向量,= .6(2022•静安区二模)如图,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,点E、F分别是边AB、CD的中点,AO:OC=1:4,设=,那么= .(用含向量的式子表示)7(2023•静安区校级一模)在矩形ABCD内作正方形AEFD(如图所示),矩形的对角线AC交正方形的边EF于点P.如果点F恰好是边CD的黄金分割点(DF>FC),且PE=2,那么PF= .8(2022春•浦东新区校级期中)如图,梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,如果△BCD的面积是△ABD面积的2倍,那么△BOC与△BDC的面积之比是.9(2022秋•虹口区校级月考)如图,梯形ABCD中,AD∥BC,,点E为边BC的中点,点F在边CD上且3CF=CD,EF交对角线AC于点G,则AG:GC=.10(2022秋•黄浦区期末)如图是一个零件的剖面图,已知零件的外径为10cm,为求出它的厚度x,现用一个交叉卡钳(AC和BD的长相等)去测量零件的内孔直径AB.如果==,且量得CD的长是3cm,那么零件的厚度x是cm.11(2022春•闵行区校级月考)如图,梯形ABCD中,∠D=90°,AB∥CD,将线段CB绕着点B按顺时针方向旋转,使点C落在CD延长线上的点E处.联结AE、BE,设BE与边AD交于点F,如果AB=4,且=,那么梯形ABCD的中位线等于.三、解答题(共12小题)1(2023•普陀区一模)如图,已知梯形ABCD中,AD∥BC,E是BC上一点,AE∥CD,AE、BD相交于点F,EF:CD=1:3.(1)求的值;(2)联结FC,设,,那么= ,= .(用向量、表示)2(2023•奉贤区一模)已知:如图,在梯形ABCD中,AD∥BC,点E在对角线BD上,∠EAD=∠BDC.(1)求证:AE•BD=AD•DC;(2)如果点F在边DC上,且,求证:EF∥BC.3(2023•青浦区一模)如图,在平行四边形ABCD中,点F在边AD上,射线BA、CF相交于点E,DF=2AF.(1)求EA:AB的值;(2)如果,,试用、表示向量.4(2022秋•金山区校级期末)已知:如图,在△ABC中,点D在边BC上,AE∥BC,BE与AD、AC 分别相交于点F、G,AF2=FG•FE.(1)求证:△CAD∽△CBG;(2)联结DG,求证:DG•AE=AB•AG.5(2022•松江区二模)已知:如图,两个△DAB和△EBC中,DA=DB,EB=EC,∠ADB=∠BEC,且点A、B、C在一条直线上,联结AE、ED,AE与BD交于点F.(1)求证:;(2)如果BE2=BF•BD,求证:DF=BE.6(2023•宝山区二模)如图,四边形ABCD中,AD∥BC,AC、BD交于点O,OB=OC.(1)求证:AB=CD;(2)E是边BC上一点,联结DE交AC于点F,如果AO2=OF•OC,求证:四边形ABED是平行四边形.7(2022秋•徐汇区期中)如图,在四边形ABCD中,对角线AC与BD交于点E,DB平分∠ADC,且AB2=BE•BD.(1)求证:△ABE∽△DCE;(2)AE•CD=BC•ED.8(2022春•杨浦区校级期中)如图1,在△ABC中,点E在AC的延长线上,且∠E=∠ABC.(1)求证:AB2=AC•AE;(2)如图2,D在BC上且BD=3CD,延长AD交BE于F,若=,求的值.9(2023•崇明区二模)已知:如图,在平行四边形ABCD中,对角线AC、BD交于E,M是边DC延长线上的一点,联结AM,与边BC交于F,与对角线BD交于点G.(1)求证:AG2=GF•GM;(2)联结CG,如果∠BAG=∠BCG,求证:平行四边形ABCD是菱形.10(2021秋•虹口区期末)如图,在梯形ABCD中,∠ABC=90°,AD∥BC,BC=2AD,对角线AC 与BD交于点E.点F是线段EC上一点,且∠BDF=∠BAC.(1)求证:EB2=EF•EC;(2)如果BC=6,sin∠BAC=,求FC的长.11(2021秋•嘉定区期末)如图,在梯形ABCD中,AD∥BC,点E在线段AD上,CE与BD相交于点H,CE与BA的延长线相交于点G,已知DE:AE=2:3,BC=4DE,CE=10.求EH、GE的长.12(2021秋•杨浦区期末)如图,已知在Rt△ABC中,∠ACB=90°,AC=BC=5,点D为射线AB 上一动点,且BD<AD,点B关于直线CD的对称点为点E,射线AE与射线CD交于点F.(1)当点D在边AB上时,①求证:∠AFC=45°;②延长AF与边CB的延长线相交于点G,如果△EBG与△BDC相似,求线段BD的长;(2)联结CE、BE,如果S△ACE=12,求S△ABE的值.。
相似三角形判定1-学生版

基本内容相似三角形的判定(一)知识精要1、相似三角形:若一个三角形的三个角与另一个三角形的三个角对应相等,且它们各有的对应边成比例,那么这两个三角形叫做相似三角形.即:两个对应角相等,对应边成比例的三角形叫做相似三角形.说明:证两个三角形相似时和证两个三角形全等一样,通常把表示对应顶点的字母写在对应的位置上,这样便于找出相似三角形的对应角和对应边.2、相似比:两个相似三角形对应边的比k,叫做这两个相似三角形的相似比(相似系数).如:若△DEF与△ABC相似,则AB BC AC DE EF DF==.3、相似三角形的预备定理:平行于三角形一边的直线截其他两边所在的直线,截得的三角形与原三角形相似.说明:这个定理反映了相似三角形的存在性,所以有的书把它叫做相似三角形的存在定理,它是证明三角形相似的判定定理的理论基础.4、三角形相似的判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.可简单说成:两角对应相等,两三角形相似.三角形相似的判定定理2:如果一个三角形的两边与另一个三角形的两边对应相等,并且夹角相等,那么这两个三角形相似.可简单说成:两边对应成比例且夹角相等,两三角形相似.热身练习1、在△ABC中,E、F分别在AC、AB上,且AF AB AE AC⋅=⋅,则下列各式中正确的是()A.EF AFAC BC=;B.AF BCAE AB=;C.EF AEBC AC=;D.BC ABEF AE=.2、BD、CE是△ABC的两条高,BD、CE相交于点O.下列结论中不正确的是()A.△ADE∽△ABC;B.△DOE∽△COB;C.△BOE∽△COD;D.△BOE∽△BDE.3、下列各组有可能不相似的是()A .各有一个角是45︒的两个等腰三角形;B .各有一个角是60︒的两个等腰三角形;C .各有一个角是105︒的两个等腰三角形;D .两个等腰直角三角形.4、在Rt △ABC 中,90C ∠=︒,CD ⊥AB ,垂足D 在斜边AB 上,则下列四个结论中正确的是( )①2AC AD AB =⋅; ②2BC BD AB =⋅; ③2CD AD BD =⋅; ④AC BC AB CD ⋅=⋅. A .①②④; B .②③④; C .①③④; D .①②③④.5、已知点P 是△ABC 的边BC 的中点,过点P 作直线截△ABC ,使截得的三角形与原三角形相似,那么这样的直线最多有( )条A .5;B .4;C .3;D .2.精解名题例1、已知在△ABC 中,点D 是边AB 的中点,DE ∥BC ,DE 交AC 于点E , △ADE 与△ABC 有什么关系?例2、根据下列条件,判断△ABC 与△'''A B C 是否相似,并说明理由:(1)120A ∠=︒,7AB =cm ,14AC =cm ; '120A ∠=︒,''3A B =cm ,''6A C =cm . (2)4AB =cm ,6BC =cm ,8AC =cm ; ''12A B =cm ,''18B C =cm ,''21A C =cm .例3、四边形ABCD 的对角线AC 与BD 相交于点O ,1OA =,1.5OB =,3OC =,2OD =,求证:△OAD 与△OBC 是相似三角形.备选例题GF E DCBA例1、点D 是△ABC 的边AB 上的一点,且2AC AD AB =⋅,求证:△ACD ∽△ABC .例2、如图,在同一平面内,将两个全等的等腰直角三角形ABC 和AFG 摆放在一起, A 为公共顶点,90BAC AGF ∠=∠=︒, 它们的斜边长为2, 若△ABC 固定不动,△AFG 绕点A 旋转,AF 、AG 与边BC 的交点分别为D 、E (点D 不与点B 重合,点E 不与点C 重合),设BE m =,CD n =.(1)请在图中找出两对相似而不全等的三角形,并选取其中一对进行证明. (2)求m 与n 的函数关系式,直接写出自变量n 的取值范围.(3)以△ABC 的斜边BC 所在的直线为x 轴,BC 边上的高所在的直线为y 轴,建立平面直角坐标系(如图2).在边BC 上找一点D ,使BD CE =,求出D 点的坐标,并通过计算验证222BD CE DE +=.(4)在旋转过程中,(3)中的等量关系222BD CE DE +=是否始终成立,若成立,请证明;若不成立,请说明理由.巩固练习1、下列命题中,不正确的是( )Gy xOFE DCBAA .如果两个三角形相似,且相似比为1,那么这两个三角形全等;B .等腰直角三角形都是相似三角形;C .有一个角为60︒的两个等腰三角形相似;D .有一个锐角相等的两个等腰三角形相似. 2、下列结论中,不正确的是( )A .有一个角相等,有两条边对应成比例的两个三角形相似;B .顺次连结三角形各边中点所得的三角形与原三角形相似;C .如果三角形两边和其中一边上的中线与另一个三角形的对应部分成比例,那么这两个三角形相似;D .两条边长分别是7、4和14、8的两个直角三角形相似. 3、△ABC ∽△'''A B C 且相似比为13错误!未找到引用源。
相似三角形的求法

相似三角形的求法相似三角形是指具有相同形状但尺寸不同的三角形。
在几何学中,相似三角形是一个重要的概念,它在解决实际问题中有着广泛的应用。
相似三角形的求法有几种常见的方法,下面我们将逐一介绍。
一、比较边长比例法:我们需要比较两个三角形的对应边的比例是否相等。
如果两个三角形的对应边的比例相等,则它们是相似的。
具体步骤如下:1. 对两个三角形的对应边进行比较,比较边长可以通过测量或已知条件得到。
2. 比较两个三角形的对应边的比例是否相等。
如果比例相等,则两个三角形相似。
3. 如果两个三角形相似,可以通过已知的边长比例来确定未知边的长度。
二、对应角相等法:相似三角形还可以通过比较两个三角形的对应角是否相等来确定。
具体步骤如下:1. 对两个三角形的对应角进行比较,可以通过测量或已知条件得到。
2. 比较两个三角形的对应角是否相等。
如果两个三角形的对应角相等,则它们是相似的。
3. 如果两个三角形相似,可以通过已知的角度关系来确定未知边的长度。
三、边角对应法:在某些情况下,我们可以通过比较两个三角形的边角对应关系来确定它们是否相似。
具体步骤如下:1. 对两个三角形的边角进行比较,可以通过测量或已知条件得到。
2. 比较两个三角形的边角对应关系是否相等。
如果边角对应关系相等,则两个三角形相似。
3. 如果两个三角形相似,可以通过已知的边角关系来确定未知边的长度。
相似三角形的求法还有其他一些特殊情况,比如利用圆的切线与半径的关系、利用勾股定理等。
但以上提到的三种方法是最常见和基础的方法。
相似三角形在实际问题中有着广泛的应用。
例如,在测量高塔的高度时,可以利用相似三角形的性质来计算。
又如,在计算不规则图形的面积时,可以利用相似三角形的面积比来简化计算过程。
相似三角形的求法是解决几何问题中的重要方法。
通过比较边长比例、对应角的相等关系以及边角的对应关系,我们可以确定两个三角形是否相似,并进一步计算未知边的长度或解决实际问题。
学生-相似三角形的存在性问题解题策略

相似三角形的存在性问题解题策略专题攻略相似三角形的判定定理有3个,其中判定定理1和判定定理2都有对应角相等的条件,因此探求两个三角形相似的动态问题,一般情况下首先寻找一组对应角相等.判定定理2是最常用的解题依据,一般分三步:寻找一组等角,分两种情况列比例方程,解方程并检验,如例题1、2、3、4.应用判定定理1解题,先寻找一组等角,再分两种情况讨论另外两组对应角相等,如例题6.应用判定定理3解题不多见,如例题5,根据三边对应成比例列连比式解方程(组). 例题解析例❶ 如图1-1,抛物线213482y x x =-+与x 轴交于A 、B 两点(A 点在B 点左侧),与y 轴交于点C .动直线EF (EF //x 轴)从点C 开始,以每秒1个单位的速度沿y 轴负方向平移,且分别交y 轴、线段BC 于E 、F 两点,动点P 同时从点B 出发,在线段OB 上以每秒2个单位的速度向原点O 运动.是否存在t ,使得△BPF 与△ABC 相似.若存在,试求出t 的值;若不存在,请说明理由.图1-1例❷如图2-1,在平面直角坐标系中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AO=BO=2,∠AOB=120°.(1)求这条抛物线的解析式;(2)连结OM,求∠AOM的大小;(3)如果点C在x轴上,且△ABC与△AOM相似,求点C的坐标.图2-1例❸如图3-1,抛物线y=ax2+bx-3与x轴交于A(1, 0)、B(3, 0)两点,与y轴交于点D,顶点为C.(1)求此抛物线的解析式;(2)在x轴下方的抛物线上是否存在点M,过M作MN⊥x轴于点N,使以A、M、N 为顶点的三角形与△BCD相似?若存在,求出点M的坐标;若不存在,请说明理由.图3-1例❹如图4-1,在平面直角坐标系中,A(8,0),B(0,6),点C在x轴上,BC平分∠OBA.点P在直线AB上,直线CP与y轴交于点F,如果△ACP与△BPF相似,求直线CP的解析式.图4-1例❺如图5-1,二次函数y=x2+3x的图象经过点A(1,a),线段AD平行于x轴,交抛物线于点D.在y轴上取一点C(0, 2),直线AC交抛物线于点B,连结OA、OB、OD、BD.求坐标平面内使△EOD∽△AOB的点E的坐标;图5-1例❻如图6-1,在△ABC中,AB=AC=BC=8.⊙A的半径为2,动点P从点B出发沿BC方向以每秒1个单位的速度向点C运动.延长BA交⊙A于点D,连结AP交⊙A于点E,连结DE并延长交BC于点F.设点P运动的时间为t秒,当△ABP与△FBD 相似时,求t的值.图6-1因动点产生的相似三角形问题课前导学相似三角形的判定定理有3个,其中判定定理1和判定定理2都有对应角相等的条件,因此探求两个三角形相似的动态问题,一般情况下首先寻找一组对应角相等.判定定理2是最常用的解题依据,一般分三步:寻找一组等角,分两种情况列比例方程,解方程并检验.如果已知∠A=∠D,探求△ABC与△DEF相似,只要把夹∠A和∠D的两边表示出来,按照对应边成比例,分AB DEAC DF=和AB DFAC DE=两种情况列方程.应用判定定理1解题,先寻找一组等角,再分两种情况讨论另外两组对应角相等.应用判定定理3解题不多见,根据三边对应成比例列连比式解方程(组).还有一种情况,讨论两个直角三角形相似,如果一组锐角相等,其中一个直角三角形的锐角三角比是确定的,那么就转化为讨论另一个三角形是直角三角形的问题.求线段的长,要用到两点间的距离公式,而这个公式容易记错.理解记忆比较好.如图1,如果已知A、B两点的坐标,怎样求A、B两点间的距离呢?我们以AB为斜边构造直角三角形,直角边与坐标轴平行,这样用勾股定理就可以求斜边AB的长了.水平距离BC的长就是A、B两点间的水平距离,等于A、B两点的横坐标相减;竖直距离AC就是A、B两点间的竖直距离,等于A、B两点的纵坐标相减.图1例 1 2014年湖南省衡阳市中考第28题二次函数y=a x2+b x+c(a≠0)的图象与x轴交于A(-3, 0)、B(1, 0)两点,与y轴交于点C(0,-3m)(m>0),顶点为D.(1)求该二次函数的解析式(系数用含m的代数式表示);(2)如图1,当m=2时,点P为第三象限内抛物线上的一个动点,设△APC的面积为S,试求出S与点P的横坐标x之间的函数关系式及S的最大值;(3)如图2,当m取何值时,以A、D、C三点为顶点的三角形与△OBC相似?图1 图22014年湖南省益阳市中考第21题如图1,在直角梯形ABCD中,AB//CD,AD⊥AB,∠B=60°,AB=10,BC=4,点P 沿线段AB从点A向点B运动,设AP=x.2·1·c·n·j·y(1)求AD的长;(2)点P在运动过程中,是否存在以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似?若存在,求出x的值;若不存在,请说明理由;(3)设△ADP与△PCB的外接圆的面积分别为S1、S2,若S=S1+S2,求S的最小值.例3 2015年湖南省湘西市中考第26题如图1,已知直线y=-x+3与x轴、y轴分别交于A、B两点,抛物线y=-x2+bx+c 经过A、B两点,点P在线段OA上,从点O出发,向点A以每秒1个单位的速度匀速运动;同时,点Q在线段AB上,从点A出发,向点B结PQ,设运动时间为t秒.(1)求抛物线的解析式;(2)问:当t为何值时,△APQ为直角三角形;(3)过点P作PE//y轴,交AB于点E,过点Q作QF//y轴,交抛物线于点F,连结EF,当EF//PQ时,求点F的坐标;(4)设抛物线顶点为M,连结BP、BM、MQ,问:是否存在t的值,使以B、Q、M为顶点的三角形与以O、B、P为顶点的三角形相似?若存在,请求出t的值;若不存在,请说明理由.图1。
专题 相似三角形母子型(共边共角模型)(学生版)

专题02相似三角形重要模型-母子型(共边共角模型)相似三角形是初中几何中的重要的内容,常常与其它知识点结合以综合题的形式呈现,其变化很多,是中考的常考题型。
在相似三角形中存在众多的相似模型,其中“母子型”相似模型应用较为广泛,深入理解模型内涵,灵活运用相关结论可以显著提高解题效率,本专题重点讲解相似三角形的“母子”模型。
母子相似证明题一般思路方法:①由线段乘积相等转化成线段比例式相等;②分子和分子组成一个三角形、分母和分母组成一个三角形;③第②步成立,直接从证这两个三角形相似,逆向证明到线段乘积相等;④第②步不成立,则选择替换掉线段比例式中的个别线段,之后再重复第③步。
模型1.“母子”模型(共边角模型)【模型解读与图示】“母子”模型的图形(通常有一个公共顶点和另外一个不是公共的顶点,由于小三角形寓于大三角形中,恰似子依母怀),也是有一个“公共角”,再有一个角相等或夹这个公共角的两边对应成比例就可以判定这两个三角形相似.图1图2图31)“母子”模型(斜射影模型)条件:如图1,∠C=∠ABD;结论:△ABD∽△ACB,AB2=AD·AC.2)双垂直模型(射影模型)条件:如图2,∠ACB=90o,CD⊥AB;结论:△ACD∽△ABC∽△CBD;CA2=AD·AB,BC2=BD·BA,CD2=DA·DB.3)“母子”模型(变形)条件:如图3,∠D=∠CAE,AB=AC;结论:△ABD∽△ECA;例1.(2022·贵州贵阳·中考真题)如图,在ABC 中,D 是AB 边上的点,B ACD ∠=∠,:1:2AC AB =,则ADC 与ACB △的周长比是()A .B .1:2C .1:3D .1:4例2.(2023·广东·九年级课时练习)如图,在Rt △ABC 中,∠ACB =90°,CD ⊥AB 于点D ,已知AD =94,55BD =,那么BC =_______.例3.(2022.山西九年级期中)如图,点C ,D 在线段AB 上,△PCD 是等边三角形,且∠APB =120°,求证:(1)△ACP ∽△PDB ,(2)CD 2=AC•BD .例4.(2022·浙江·九年级期中)如图,在Rt△ABC中,∠ACB=90°,点D在AB上,且ADAC=ACAB.(1)求证△ACD∽△ABC;(2)若AD=3,BD=2,求CD的长.例5.(2022.浙江中考模拟)如图,在ABC中,∠ACB=90°,CD⊥AB.(1)图1中共有对相似三角形,写出来分别为(不需证明):(2)已知AB=5,AC=4,请你求出CD的长:(3)在(2)的情况下,如果以AB为x轴,CD为y轴,点D为坐标原点O,建立直角坐标系(如图2),若点P从C点出发,以每秒1个单位的速度沿线段CB运动,点Q出B点出发,以每秒1个单位的速度沿线段BA运动,其中t秒是否存在点P,使以点B、P、Q为顶点的三角形与△ABC相似?若存在,请求出点P的坐标;若不存在,请说明理由.例6.(2022·浙江绍兴·九年级期末)如果两个相似三角形的对应边存在2倍关系,则称这两个相似三角形互为母子三角形.(1)如果DEF 与ABC 互为母子三角形,则DE AB 的值可能为()A .2B .12C .2或12(2)已知:如图1,ABC 中,AD 是BAC ∠的角平分线,2,AB AD ADE B =∠=∠.求证:ABD △与ADE 互为母子三角形.(3)如图2,ABC 中,AD 是中线,过射线CA 上点E 作//EG BC ,交射线DA 于点G ,连结BE ,射线BE 与射线DA 交于点F ,若AGE 与ADC 互为母子三角形.求AG GF 的值.A .ABP C ∠=∠B .APB ABC ∠=∠2.(2023成都市九年级期中)如图,矩形ABCD 中,F 是DC 上一点,BF ⊥AC ,垂足为E ,AD AB =12,△CEF 的面积为S 1,△AEB 的面积为S 2,则S 1S 2的值等于()A .116B .15C .14D .1253.(2023浙江九年级期中)如图,在△ABC 中,∠ACB =90°,CD 是AB 边上的高.如果BD =4,CD =6,那么BC :AC 是()A .3:2B .2:3C .3:13D .2:13.任意长为半径作弧,5.(2023•宜宾)如图,已知直角△ABC 中,CD 是斜边AB 上的高,AC =4,BC =3,则AD =.6.(2022·江苏盐城·中考真题)如图,在ABC 与A B C '''V 中,点D 、D ¢分别在边BC 、B C ''上,且ACD A C D '''∽△△,若___________,则ABD A B D '''△∽△.请从①BD B D CD C D ''='';②AB A B CD C D ''='';③BAD B A D '''∠=∠这三个选项中选择一个作为条件(写序号),并加以证明.7.(2022秋·陕西西安·九年级校联考期中)如图,在ABC 中,点D 是边AB 上的一点,ADC ACB ∠=∠,2AD =,8AB =.求边AC 的长.8.(2022•惠山区九年级专项)如图,在Rt △ABC 中,∠BAC=90o ,AD ⊥BC 于D .(1)图中有多少对相似三角形?(2)求证:AB 2=BD BC ,AC 2=CD CB ,AD 2=BD CD ;(3)求证:AB AC=BC AD的边2三角形来加以证明的(填“全等12.(2022·湖北武汉·一模)在Rt △ABC 中,∠ACB =90°,点D 为AB 上一点.(1)如图1,若CD ⊥AB ,求证:AC 2=AD ·AB ;(2)如图2,若AC =BC ,EF ⊥CD 交CD 于H ,交AC 于F ,且49FH HE =,求AD BD 的值;(3)如图3,若AC =BC ,点H 在CD 上,∠AHD =45°,CH =3DH ,则tan ∠ACH 的值为________.13.(2023·安徽合肥·九年级期中)中,90ABC ∠=︒,BD AC ⊥,点E 为BD 的中点,连接AE 并延长交BC 于点F ,且有AF CF =,过F 点作FH AC ⊥于点H .(1)求证:ADE CDB ∽;(2)求证:=2AE EF ;(3)若FH BC 的长.14.如图1,在ABC 中,在BC 边上取一点P ,在AC 边上取一点D ,连AP 、PD ,如果APD △是等腰三角形且ABP △与CDP 相似,我们称APD △是AC 边上的“等腰邻相似三角形”.(1)如图2,在ABC 中AB AC =,50B ∠=︒,APD △是AB 边上的“等腰邻相似三角形”,且AD DP =,PAC BPD ∠=∠,请直接写出PAC ∠的度数;(2)如图3,在ABC 中,2A C Ð=Ð,在AC 边上至少存在一个“等腰邻相似APD △”,请画出一个AC 边上的“等腰邻相似APD △”,并说明理由;(3)如图4,在Rt ABC △中4AB AC ==,APD △是AB 边上的“等腰邻相似三角形”,求出AD 长度的所有可能值.15.(2022•静安区期末)如图1,四边形ABCD 中,∠BAD 的平分线AE 交边BC 于点E ,已知AB =9,AE =6,AE 2=AB•AD ,且DC ∥AE .(1)求证:DE 2=AE•DC ;(2)如果BE =9,求四边形ABCD 的面积;(3)如图2,延长AD 、BC 交于点F ,设BE =x ,EF =y ,求y 关于x 的函数解析式,并写出定义域.16.(2022·安徽·校联考三模)在ABC 中,2ABC ACB ∠=∠,BD 平分ABC ∠.(1)如图1,若3AB =,5AC =,求AD 的长.(2)如图2,过A 分别作AE AC ⊥交BC 于E ,AF BD ⊥于F .①求证:ABC EAF ∠=∠;②求BF AC 的值.ACD(1)求证:ABE CAD≌;△△(2)求证:AC FB∥;(3)若点D,E,F在同一条直线上,如图2,求AB的值.(温馨提示:请用简洁的方式表示角)BC、。
初中相似三角形解题技巧集锦

运用角平分线
1. 角平分线的基本概念和性质:角平分线是指将一个角平分成两个相等的 角的线段,具有对称性和比例性质。 2. 利用角平分线求相似三角形的边长比例:在一些相似三角形的题目中, 可以通过利用角平分线的比例性质,以及已知三角形中某个角的度数或边 长比例,求解出其他角的度数或相应边的比例。 3. 利用角平分线证明两条线段平行:当两条平行线段中夹角被角平分线平 分时,这两条线段与角平分线所形成的两个小三角形必定相似,因此它们 之间的对应边也成比例关系,从而可以通过此法证明两条线段平行。
利用比例求两直线平行
1. 利用角的对应性质确定直线之间的关系:当两直线上的对应角相等时,这两直线平行。 2. 利用对应线段成比例的性质求解:在相似三角形中,两直线与三角形相对的边成比例,因此可以利用已知边长求解未知边长,从而判断两直线是否 平行。
04
知识点巩固题型
Knowledge point consolidation question type
VIEW MORE
05
实例分析解题
Example analysis and problem-solving
实例分析解题
图形比较 关键词 关键词 关键词 关键词 关键词 关键词
边长比较 比较边长的大小关系
内角相等 边长比例
比例计算 比例的性质 求解未知量
实际应用
06
解题技巧总结
Summary of problem-solving techniques
02
角度相等法解题
Solving problems using the method of equal angles
相等角作边比
1. 什么情况下可以使用相等角作边比法? 2.需要强调的是,只有在两个三角形中存在对应的相等角才能使用相等角作边比法进行解题。如果没有找到相等角,就不能使用这个解题方法。 3. 如何判断哪些边是对应边? 4.可以观察两个三角形的图形,找出它们的相等角,然后根据对应角对应边的关系,就可以判断出两个三角形的对应边。
相似图形(学生版)

相似图形【基础知识回顾】相似三角形:1、定义:如果两个三角形的各角对应各边对应那么这两个三角形相似2、性质:⑴相似三角形的对应角对应边⑵相似三角形对应点的比、对应角平分线的比、对应的比都等于⑶相似三角形周长的比等于面积的比等于1、判定:⑴基本定理:平行于三角形一边的直线和其它两边或两线相交,三角形与原三角形相似⑵两边对应且夹角的两三角形相似⑶两角的两三角形相似⑷三组对应边的比的两三角形相似【名师提醒:1、全等是相似比为的特殊相似2、根据相似三角形的性质的特质和判定,要证四条线段的比相等相等一般要先证判定方法中最常用的是三组对应边成比例的两三角形相似多用在点三角形中】相似多边形:1、定义:各角对应各边对应的两个多边形叫做相似多边形2、性质:⑴相似多边形对应角对应边⑵相似多边形周长的比等于面积的比等于【名师提醒:相似多边形没有专门的判定方法,判定两多边形相似多用在矩形中,一般用定义进行判定】相似三角形的性质及其应用例1 (2012•重庆)已知△ABC∽△DEF,△ABC的周长为3,△DEF的周长为1,则ABC 与△DEF的面积之比为.对应训练1.(2012•沈阳)已知△ABC∽△A′B′C′,相似比为3:4,△ABC的周长为6,则△A′B′C′的周长为.相似三角形的判定方法及其应用例2(2012•徐州)如图,在正方形ABCD中,E是CD的中点,点F在BC上,且FC= 14 BC.图中相似三角形共有()A.1对B.2对C.3对D.4对例3 16.(2012•资阳)(1)如图(1),正方形AEGH的顶点E、H在正方形ABCD的边上,直接写出HD:GC:EB的结果(不必写计算过程);(2)将图(1)中的正方形AEGH绕点A旋转一定角度,如图(2),求HD:GC:EB;(3)把图(2)中的正方形都换成矩形,如图(3),且已知DA:AB=HA:AE=m:n,此时HD:GC:EB的值与(2)小题的结果相比有变化吗?如果有变化,直接写出变化后的结果(不必写计算过程).(2012•义乌市)在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;(2)如图2,连接AA1,CC1.若△ABA1的面积为4,求△CBC1的面积;(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1,求线段EP1长度的最大值与最小值.1.(2012•潍坊)已知矩形ABCD中,AB=1,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,则AD=()A.512-B.512+C.3D.22(2012福州,15,4分,)如图,已知△ABC,AB=AC=1,∠A=36°,∠ABC的平分线BD交AC于点D,则AD的长是,cosA的值是 .(结果保留根号3(2012•日照)在菱形ABCD中,E是BC边上的点,连接AE交BD于点F,若EC=2BE,则BFFD的值是()A.12B.13C.14D.154 (2012江苏泰州市,18,3分)如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则tan∠APD的值是.5(2012•菏泽)如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,P1,P2,P3,P4,P5是△DEF边上的5个格点,请按要求完成下列各题:(1)试证明三角形△ABC为直角三角形;(2)判断△ABC和△DEF是否相似,并说明理由;(3)画一个三角形,使它的三个顶点为P1,P2,P3,P4,P5中的3个格点并且与△ABC相似(要求:用尺规作图,保留痕迹,不写作法与证明).6(2012•天门)如图,△ABC为等边三角形,点E在BA的延长线上,点D在BC边上,且ED=EC.若△ABC的边长为4,AE=2,则BD的长为()A.2 B.3 C.3D.317(2012•宁德)如图,在矩形ABCD中,AB=2,BC=3,点E、F、G、H分别在矩形ABCD 的各边上,EF∥AC∥HG,EH∥BD∥FG,则四边形EFGH的周长是()A.10B.13C.210D.2138.(2012•荆州)下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是()A.B.C.D.9(2012•海南)如图,点D在△ABC的边AC上,要判定△ADB与△ABC相似,添加一个条件,不正确的是()A.∠ABD=∠C B.∠ADB=∠ABC C.AB C BBD C D=D.AD ABAB AC=如图,在△ABC中,EF∥BC,12AEEB=,S四边形BCFE=8,则S△ABC=()A.9 B.10 C.12 D.1310(2012•宜宾)如图,在四边形ABCD中,DC∥AB,CB⊥AB,AB=AD,CD= 12 AB,点E、F分别为AB、AD的中点,则△AEF与多边形BCDFE的面积之比为()A.17B.16C.15D.1411(2012•自贡)正方形ABCD的边长为1cm,M、N分别是BC、CD上两个动点,且始终保持AM⊥MN,当BM= cm时,四边形ABCN的面积最大,最大面积为cm2.12(2012•资阳)如图,O为矩形ABCD的中心,M为BC边上一点,N为DC边上一点,ON⊥OM,若AB=6,AD=4,设OM=x,ON=y,则y与x的函数关系式为。
(完整版)相似三角形证明技巧(整理)

相似三角形解题方法、技巧、步骤、辅助线解析一、相似三角形(1)三角形相似的条件:①;② ;③ . 二、两个三角形相似的六种图形:只要能在复杂图形中辨认出上述基本图形,并能根据问题需要舔加适当的辅助线,构造出基本图形,从而使问题得以解决.三、三角形相似的证题思路:判定两个三角形相似思路:1)先找两对内角对应相等(对平行线型找平行线),因为这个条件最简单; 2)再而先找一对内角对应相等,且看夹角的两边是否对应成比例; 3)若无对应角相等,则只考虑三组对应边是否成比例;找另一角 两角对应相等,两三角形相似找夹边对应成比例 两边对应成比例且夹角相等,两三角形相似找夹角相等 两边对应成比例且夹角相等,两三角形相似找第三边也对应成比例 三边对应成比例,两三角形相似找一个直角 斜边、直角边对应成比例,两个直角三角形相似找另一角 两角对应相等,两三角形相似找两边对应成比例 判定定理2 找顶角对应相等 判定定理1找底角对应相等 判定定理1 找底和腰对应成比例 判定定理3e)相似形的传递性 若△1∽△2,△2∽△3,则△1∽△3四、“三点定形法”,即由有关线段的三个不同的端点来确定三角形的方法。
具体做法是:先看比例式前项和后项所代表的两条线段的三个不同的端点能否分别确定一个三角形,若能,则只要证明这两个三角形相似就可以了,这叫做“横定”;若不能,再看每个比的前后两项的两条线段的两条线段的三个不同的端点能否分别确定一个三角形,则只要证明这两个三角形相似就行了,这叫做“竖定”。
有些学生在寻找条件遇到困难时,往往放弃了基本规律而去乱碰乱撞,乱添辅助线,这样反而使问题复杂化,效果并不好,应当运用基本规律去解决问题。
例1、已知:如图,ΔABC 中,CE ⊥AB,BF ⊥AC. 求证: BAAC AF AE(判断“横定”还是“竖定”? )a)已知一对等b)己知两边对应成比c)己知一个直d)有等腰关例2、如图,CD是Rt△ABC的斜边AB上的高,∠BAC的平分线分别交BC、CD于点E、F,AC·AE=AF·AB吗?说明理由。
第3课 相似三角形的判定方法(学生版)

永昌三中九年级数学(下)第二十七章学案 主备人:苏建礼 审核人:九年级数学备课组 班级: 姓名: 时间:2016/3/2第3课 相似三角形的判定方法一、知识回顾: 1.相似多边形的定义:如果两个多边形的对应角____ __,并且 对应边___ ___,那么这两个多边形相似. 2.如图,在△ABC 中,DE∥BC,则AD DE, = .BD BC== 二、探究新知:相似三角形的判定方法 知识点一、相似三角形判定的预备定理平行于三角形一边的直线和其他两边相交,所成的三角形与原来三角形相似. 可记忆为:两直线平行,两三角形相似. 几何语言:∵∴△ADE ∽△ABC对应练习:如图,AB ∥EF ∥CD ,图中共有 对相似三角形.写出来并说明理由; 由AB ∥EF 可得△AOB ∽ , 由EF ∥CD 可得 , 由AB ∥CD 可得 .这三个三角形都相似吗? 【说明】相似三角形具有传递性. 知识点二、相似三角形的判定定理Ⅰ 相似三角形的判定定理1 三边对应成比例的两个三角形相似.可记忆为:边边边(SSS ) 几何语言:∵∴△ABC ∽△DEF例1.根据下列条件,判断△ABC 与△DEF 是否相似,并说明理由. AB=4cm ,BC=6cm ,AC=7cm ,DE=12cm ,EF=18cm ,DF=21cm.【对应练习】1.如图,在正方形网格上有△A 1B 1C 1和△A 2B 2C 2,它们相似吗?如果相似,求出相似比;如果不相似,请说明理由.2.如图,小正方形的边长均为1,则图中的阴影部分三角形与△ABC 相似的是( )Ⅱ 相似三角形的判定定理2两边对应成比例,并且夹角相等的两个三角形相似. 可记忆为:边角边(SAS )几何语言:∵∴△ABC ∽△DEF例2.根据下列条件,判断△ABC 与△DEF 是否相似,并说明理由. (1)AB=4cm ,AC=5cm , ∠A=340,DE=1.6cm ,DF=2cm ,∠D=340. (2)AB=4cm ,AC=5cm , ∠A=340,DE=1.6cm ,DF=2cm ,∠E=340. (3)AB=4cm ,AC=5cm , ∠A=340,DE=1.6cm ,EF=2cm ,∠D=340.Ⅲ 相似三角形的判定定理3 两角分别相等的两个三角形相似. 可记忆为:角角(AA ) 例3.如图,在△ABC 中,∠1=∠2=∠3.求证:△ABC ∽△DEF三、巩固练习:如图,D 为△ABC 内一点,E 为△ABC 外一点,且∠1=∠2,∠3=∠4. 求证:(1)△ABD ∽△CBE. (2)△ABC ∽△DBE.四、作业布置:如图,AD=4,AE=3, AB=4.8,AC=3.6,∠1=∠2. 求证:△ADE ∽△ABCEBACD。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相似三角形解题方法、技巧、步骤、辅助线解析一、 相似、全等的关系全等和相似是平面几何中研究直线形性质的两个重要方面, 全等形是相似比为1的特殊 相似形,相似形则是全等形的推广.因而学习相似形要随时与全等形作比较、 明确它们之间 的联系与二、 相似三角形(1)三角形相似的条件:① ___________________ :② ________________________ :③_______________________________ . 三、 两个三角形相似的六种图形:四、三角形相似的证题思路:判定两个三角形相似思路:1) 先找两对内角对应相等(对平行线型找平行线),因为这个条件最简单; 2) 再而先找一对内角对应相等,且看夹角的两边是否对应成比例; 3) 若无对应角相等,则只考虑三组对应边是否成比例;尺 f 找另一角 --------- ►两角对应相等,两三角形相似a )已知一对等[找夹边对应成比例 ——两边对应成比例且夹角相等,两三角形相似找夹角相等 ►两边对应成比例且夹角相等,两三角形相似 找第三边也对应成比例 三边对应成比例,两三角形相似、二m 人击冷 J 找另一角 ------------ 两角对应相等,两三角形相似 c ) 己知'—个直角 ■L 找两边对应成比例 判定定理1或判定定理4找顶角对应相等判定定理1d ) 有等腰关系-找底角对应相等 判定定理1 I 找底和腰对应成比例 ---- ►判定定理3e )相似形的传递性若2, △ 3,则3五、“三点定形法”,即由有关线段的三个不同的端点来确定三角形的方法。
具体做法是: 先看比例式前项和后项所代表的两条线段的三个不同的端点能否分别确定一个三角形, 若能,则只要证明这两个三角形相似就可以了,这叫做“横定” ;若不能,再看每个比的前后两项的两条线段的两条线段的三个不同的端点能否分别确定一个三角形,则只要证明这两个三角形相似就行了,这叫做“竖定” 。
例1、已知:如图,△ AB (中 ,CE 丄AB,BF 丄AC. 求证:AE AC気AF BAb )己知两边对应成比無件条件厶条件三上乙日築件务件4■厶D 条件AD 是RtABC 斛边上的高只要能在复杂图形中辨认出上述基本图形,并能根据问题需要舔加适当的辅助线,构造出 基本图形,从而使问题得以解决•(判断“横定”还是“竖定”?例2、如图,CD 是Rt △ ABC 的斜边 AB 上的高,/ BAC 的 平分线分别交 BC 、CD 于点E 、F , AC • AE=AF • AB 吗? 说明理由。
分析方法:1) ________________________ 先将积式 2) ______________ ( “横定”还是“竖定”?)例1、已知:如图,△ ABC 中,/ ACB=90, AB 的垂直平分线交AB 于D,交BC 延长线于F 。
分析方法: 1) 先将积式2) ( “横定”还是“竖定”? )L» C '求证:CD 2=DE- DF 。
六、过渡法(或叫代换法)有些习题无论如何也构造不出相似三角形, 这就要考虑灵活地运用 过渡”,其主要类型 有三种,下面分情况说明. 1、等量过渡法(等线段代换法) 遇到三点定形法无法解决欲证的问题时, 即如果线段比例式中的四条线段都在图形中的同 一条直线上,不能组成三角形,或四条线段虽然组成两个三角形, 但这两个三角形并不相 似,那就需要根据已知条件找到与比例式中某条线段相等的一条线段来代替这条线段, 如 果没有,可考虑添加简单的辅助线。
然后再应用三点定形法确定相似三角形。
只要代换得 当,问题往往可以得到解决。
当然,还要注意最后将代换的线段再代换回来。
例1:如图3, △ABC 中,AD 平分/ BAC , AD 的垂直平分线 FE 交BC 的延长线于 E .求证:DE 2 = BE- CE . 分析: 2、等比过渡法(等比代换法) 当用三点定形法不能确定三角形,同时也无等线段代换时,可以考虑用等比代换法, 即考虑利用第三组线段的比为比例式搭桥, 也就是通过对已知条件或图形的深入分析, 找到与求证的结论中某个比相等的比,并进行代换,然后再用三点定形法来确定三角 形。
例2:如图4,在△ABC 中,/ BAC=90 , AD 丄BC , E 是AC 的中点, 交AB 的延长线于点F . 求证: AB AC DFAF思考冋题的基本途径是:用三点定形法确定两个三角形,然后通过三角形相似推出线段代换,或用等比代换,然后再用三点定形法确定相似三角形,若以上三种方法行不通时,则考虑用等积代换法。
例3:如图5,在△ABC中,/ ACB=90 , CD是斜边AB上的高,G是DC延长线上一点,过B作BE丄AG,垂足为E,交CD于点F. J 求证:CD2= DF-DG ./£A圏§I)E“遇等积,化比例:横找竖找定相似; 不相似,不用急:等线等比来代替。
2. 如图,A ABC中,点DE在边BC上,且A ADE是等边三角形,/ BAC=120 求证:(1 )A ADB^A CEA; (2)DE2=BD- CE;(3)AB • AC=AD BC.3.如图,平行四边形ABCD中,E为BA延长线上一点,/ D=Z ECA.求证:AD- EC=AC EB .£小结:证明等积式思路口诀:同类练习:1. 如图,点D、E分别在边AB、AC上,且/ ADEN C求证:(1)A ADE^A ACB; (2)AD-AB=AE- AC.(1题图)(2题图)5. 如图,E 是平行四边形的边 DA 延长线上一点,EC 交AB 于点G,交BD 于点F, 求证:FC2=FG ・ EF.6. 如图,E 是正方形 ABCD 边BC 延长线上一点,连接 AE 交CD 于F,过F 作FMI BE 交DE 于 M.求证:FM=CF.7. 如图,△ ABC 中,AB=AC 点D 为BC 边中点, 点F 、G,连接FC.求证:(1) BF=CF. (2)BF 2=FG- FE.&如图,/ ABC=90 ,AD=DB,DE1 AB,9. 如图,ABCD 为直角梯形, AB// CD,AB 丄 BC,AC 丄 BC 。
AD= BD 过 E 作 EF / AB 交 AD 于 F. 是说明:(1) AF=BE;(2)AF2=AE ・EC.CE// AB,BE 分别交 AD AC 于10. A ABC 中,/ BAC=90 ,AD 丄 BC,E 为 AC 中点。
求证:AB:AC=DF:AF 。
11. 已知,CE 是RT A ABC 斜边AB 上的高,在 EC 延长线上任取一点 P,连接AP,作BGLAP, 垂足为G ,交CE 于点D.例2 如图6, CABCD 中,E 是BC 上的一点,AE 交BD 于点F ,已知BE : EC = 3: 1 ,S ^FBE = 18,求:(1)BF : FD(2)S 济DA七、证比例式和等积式的方法:对线段比例式或等积式的证明: 常用三点定形法”、等线段替换法、中间比过渡法、面积法 等•若比例式或等积式所涉及的线段在同一直线上时,应将线段比 转移”必要时需添辅助线),使其分别构成两个相似三角形来证明.图6 EC例3 如图7在△ABC 中,AD 是BC 边上的中线, 于N .求:AN : AB 的值;例4 如图8在矩形 ABCD 中,E 是CD 的中点,BE 丄AC 交AC 于F ,过F 作FG // AB 交 AE 于 G .求证:AG 2= AF XFCl例5 如图在 A ABC 中,D 是BC 边的中点,且 AD = AC , DE 丄BC ,交AB 于点E , EC例6如图10过MBC 的顶点C 任作一直线与边 AB 及中线AD 分别交于点F 和E .过 点D 作DM // FC 交AB 于点M .⑴若S ^AEF : ⑵求证:AE XFB = 2AF XEDM 是AD 的中点,CM 的延长线交AB交AD 于点F .⑴求证: △ABCFCD ;⑵若 S ZFCD = 5,D IVI CS 四边形 图例7 己知如图11在正方形ABCD 的边长为1 ,P 是CD 边的中点,Q 在线段BC 上, 当BQ 为何值时, A ADP 与A QCP 相似?ABCD 中,AD // BC ,/ A = 90°, AB = 7, AD = 2, BC = 3.试 使得以 P 、A 、D 为顶点的三角形与以 P 、B 、C 为顶点的三角形相似.例11.如图,已知△ ABC 中,AB=AC , AD 是BC 边上的中线, CF / BA , BF 交AD 于P 点,交AC 于E 点。
求证:BP 2=PE • PF 。
九、相似三角形中的辅助线在添加辅助线时,所添加的辅助线往往能够构造出一组或多组相似三角形,或得到 成比例的线段或得出等角,等边,从而为证明三角形相似或进行相关的计算找到等 量关系。
主要的辅助线有以下几种:例8己知如图 在边AB 上确定点 12在梯形 P 的位置, 中,/ BAC=900 , AD 丄 BC , E 是 AC求证:朋 DF、作平行线例1.如图, ABC 的AB 边和AC 边上各取一点 D 和E ,且使AD = AE , DE 延长线与BC例4、如图4-7,已知平行四边形 ABCD 中,对角线AC 、BD 交于0点,E 为AB 延长线上 一点,0E 交 BC 于 F ,若 AB=a , BC=b , BE=c ,求 BF 的长.例5、△ ABC 中,在AC 上截取 AD ,在CB 延长线上截取 BE ,使AD=BE ,求证:DF ?AC=BC ?FE延长线相交于F ,求证:BFCFBDCEAE= __________E 为BD 的中点,贝U AF : C例6:如图△ ABC 中,AD 为中线,CF 为任一直线,CF 交AD 于E ,交AB 于F ,求证:AE ED=2AF FBo于G .求AG : AC 的值.二、作延长线例7.如图,Rt ABC 中,CD 为斜边 AB 上的高,E 为CD 的中点,AE 的延长线交 BC 于F , FG AB 于G ,求证:2FG 2=CF ?BFAF例&如图4-1,已知平行四边ABCD 中,E 是AB 的中点,1 AD3 ,连 E 、F 交 ACB三、作中线例10: 已知:如图,△ ABC中,AB = AC , BD丄AC于D .求证:BC2= 2CD • AC .。
