“活结与死结”“活动杆与固定杆”
(新课标)高考物理大一轮复习物理模型2“动杆”、“定杆”和“死结”、“活结”模型

A.当m一定时,θ越大,轻杆受力越小 B.当m一定时,θ越小,滑块对地面的压力越大 C.当θ一定时,M越大,滑块与地面间的摩擦力越大 D.当θ一定时,M越小,可悬挂重物C的质量m越大
解析:选A.将与C相连的绳子的拉力按照作用效果分解,如 1 mg 2 mg 图所示.根据平行四边形定则有F1=F2= = , sin θ 2sin θ
故m一定时,θ越大,轻杆受力越小,选项A正确;对A、 2M+m B、C组成的整体分析可知,对地面压力为FN= g,与θ无 2 关,选项B错误;对A受力分析,受重力、杆的推力、支持力和 mg 向右的静摩擦力,根据平衡条件有f=F1cos θ= ,与M无 2tan θ 关,选项C错误;只要动摩擦因数足够大,即可满足F1cos θ≤μF1sin θ,不管m多大,滑块都不会滑动,选项D错误.
解析:选C.对C点受力分析,如图所示,C点受向下的拉力,沿 CA方向的拉力F1及沿BC方向的支持力F2;三力 的合力为零;A上移,使AC、CD的夹角变大, 由于ACD为同一根绳,所以绳的拉力大小相等 即F1=G,故细绳的拉力不变,两绳对C点的作 用力的合力减小,即BC杆所受压力变小,故选 项C正确.
[典例]
如图甲所示,轻绳AD跨过固定的水平横梁BC右端
的定滑轮挂住一个质量为M1的物体,∠ACB=30° ;图乙中轻杆 HG一端用铰链固定在竖直墙上,另一端G通过细绳EG拉住,EG 与水平方向也成30° ,轻轩的G点用细绳GF拉住一个质量为M2的 物体,求:
(1)轻绳AC段的张力FTAC与细绳EG的张力FTEG之比; (2)轻杆BC对C端的支持力; (3)轻杆HG对G端的支持力.
解析:选D.细线上的弹力处处相等,因此细线BO对天花板 的拉力大小是G,选项A错误.两段细线上弹力均为G,构成菱 形,合力为2Gsin 30° =G,大小等于a杆对滑轮的作用力,选项B 错误、D正确.a杆和细线对滑轮的合力大小是0,选项C错误.
2020高中物理同步重难讲练专题11“活结”和“死结”、“动杆”和“定杆”模型学案 新人教版必修1

专题11“活结”和“死结”、“动杆”和“定杆”模型重难讲练1.“活结”和“死结”问题(1)活结:当绳绕过光滑的滑轮或挂钩时,由于滑轮或挂钩对绳无约束,因此绳上的力是相等的,即滑轮只改变力的方向不改变力的大小,例如图乙中,两段绳中的拉力大小都等于重物的重力.(2)死结:若结点不是滑轮,是固定点时,称为“死结”结点,则两侧绳上的弹力不一定相等.“死结”一般是由绳子打结而形成的,“死结”两侧的绳子因打结而变成两根独立的绳子。
死结的特点:a.绳子的结点不可随绳移动b.“死结”两侧的绳子因打结而变成两根独立的绳子,因此由“死结”分开的两端绳子上的弹力不一定相等 2.“动杆”和“定杆”问题(1)动杆:若轻杆用光滑的转轴或铰链连接,当杆处于平衡时杆所受到的弹力方向一定沿着杆,否则会引起杆的转动.如图甲所示,若C 为转轴,则轻杆在缓慢转动中,弹力方向始终沿杆的方向.(2)定杆:若轻杆被固定不发生转动,则杆所受到的弹力方向不一定沿杆的方向.如图乙所示.【典例1】(2016·全国卷Ⅲ·17)如图所示,两个轻环a 和b 套在位于竖直面内的一段固定圆弧上;一细线穿过两轻环,其两端各系一质量为m 的小球.在a 和b 之间的细线上悬挂一小物块.平衡时,a 、b 间的距离恰好等于圆弧的半径.不计所有摩擦.小物块的质量为( )A.m2B.32m C.m D.2m【答案】 C【解析】如图所示,【典例2】如图所示,一轻绳的两端分别固定在不等高的A、B两点,现用另一轻绳将一物体系于O点,设轻绳AO、BO相互垂直,α>β,且两绳中的拉力分别为F A、F B,物体受到的重力为G,下列表述正确的是( )A.F A一定大于G B.F A一定大于F BC.F A一定小于F B D.F A与F B大小之和一定等于G【答案】 B【解析】分析O点受力如图所示,由平衡条件可知,F A与F B的合力与G等大反向,因F A⊥F B,故F A、F B均小于G;因α>β,故F A>F B,B正确,A、C错误;由三角形两边之和大于第三边可知,|F A|+|F B|>G,D错误.【典例3】如图甲所示,轻绳AD跨过固定的水平横梁BC右端的定滑轮挂住一个质量M1的物体,∠ACB=30°;图乙中轻杆HG一端用铰链固定在竖直墙上,另一端G通过细绳EG拉住,EG与水平方向也成30°,轻杆的G点用细绳GF拉住一个质量M2的物体,求:(1)轻绳AC段的张力F T AC与细绳EG的张力F T EG之比;(2)轻杆BC对C端的支持力;(3)轻杆HG对G端的支持力.【答案】(1)M12M2(2)M1g方向和水平方向成30°指向右上方(3)3M2g方向水平向右【解析】题图甲和乙中的两个物体M1、M2都处于平衡状态,根据平衡的条件,首先判断与物体相连的细绳,其拉力大小等于物体的重力;分别取C点和G点为研究对象,进行受力分析如图甲和乙所示,根据平衡规律一一求解.【跟踪训练】1. 如图所示,将一细绳的两端固定于两竖直墙的A、B两点,通过一个光滑的挂钩将某重物挂在绳上,下面给出的四幅图中有可能使物体处于平衡状态的是()【答案】C2.如图所示,当重物静止时,节点O受三段绳的拉力,其中AO沿水平方向,关于三段绳中承受拉力的情况,下列说法中正确的是A . AO 承受的拉力最大B . BO 承受的拉力最大C . CO 承受的拉力最大D . 三段绳承受的拉力一样大 【答案】B【解析】以结点O 为研究对象,分析受力情况,受力分析如图:由平衡条件得: 1tan T G θ=, 2cos GT θ=,故T1小于T2,G 小于T2;所以BO 承受的拉力最大;故B 正确。
人教版2020高中物理同步重难讲练专题11“活结”和“死结”、“动杆”和“定杆”模型学案 新人教版必修1

专题11“活结”和“死结”、“动杆”和“定杆”模型重难讲练1.“活结”和“死结”问题(1)活结:当绳绕过光滑的滑轮或挂钩时,由于滑轮或挂钩对绳无约束,因此绳上的力是相等的,即滑轮只改变力的方向不改变力的大小,例如图乙中,两段绳中的拉力大小都等于重物的重力.(2)死结:若结点不是滑轮,是固定点时,称为“死结”结点,则两侧绳上的弹力不一定相等.“死结”一般是由绳子打结而形成的,“死结”两侧的绳子因打结而变成两根独立的绳子。
死结的特点:a.绳子的结点不可随绳移动b.“死结”两侧的绳子因打结而变成两根独立的绳子,因此由“死结”分开的两端绳子上的弹力不一定相等2.“动杆”和“定杆”问题(1)动杆:若轻杆用光滑的转轴或铰链连接,当杆处于平衡时杆所受到的弹力方向一定沿着杆,否则会引起杆的转动.如图甲所示,若C为转轴,则轻杆在缓慢转动中,弹力方向始终沿杆的方向.(2)定杆:若轻杆被固定不发生转动,则杆所受到的弹力方向不一定沿杆的方向.如图乙所示.【典例1】(2016·全国卷Ⅲ·17)如图所示,两个轻环a和b套在位于竖直面内的一段固定圆弧上;一细线穿过两轻环,其两端各系一质量为m的小球.在a和b之间的细线上悬挂一小物块.平衡时,a、b间的距离恰好等于圆弧的半径.不计所有摩擦.小物块的质量为( )A.m2B.32mC.mD.2m【答案】 C【解析】如图所示,【典例2】如图所示,一轻绳的两端分别固定在不等高的A、B两点,现用另一轻绳将一物体系于O点,设轻绳AO、BO相互垂直,α>β,且两绳中的拉力分别为F A、F B,物体受到的重力为G,下列表述正确的是( )A.F A一定大于G B.F A一定大于F BC.F A一定小于F B D.F A与F B大小之和一定等于G【答案】 B【解析】分析O点受力如图所示,由平衡条件可知,F A与F B的合力与G等大反向,因F A⊥F B,故F A、F B 均小于G;因α>β,故F A>F B,B正确,A、C错误;由三角形两边之和大于第三边可知,|F A|+|F B|>G,D 错误.【典例3】如图甲所示,轻绳AD跨过固定的水平横梁BC右端的定滑轮挂住一个质量M1的物体,∠ACB =30°;图乙中轻杆HG一端用铰链固定在竖直墙上,另一端G通过细绳EG拉住,EG与水平方向也成30°,轻杆的G点用细绳GF拉住一个质量M2的物体,求:(1)轻绳AC段的张力F T AC与细绳EG的张力F T EG之比;(2)轻杆BC对C端的支持力;(3)轻杆HG对G端的支持力.【答案】(1)M12M2(2)M1g方向和水平方向成30°指向右上方(3)3M2g方向水平向右【解析】题图甲和乙中的两个物体M1、M2都处于平衡状态,根据平衡的条件,首先判断与物体相连的细绳,其拉力大小等于物体的重力;分别取C点和G点为研究对象,进行受力分析如图甲和乙所示,根据平衡规律一一求解.【跟踪训练】1. 如图所示,将一细绳的两端固定于两竖直墙的A、B两点,通过一个光滑的挂钩将某重物挂在绳上,下面给出的四幅图中有可能使物体处于平衡状态的是()【答案】C2.如图所示,当重物静止时,节点O 受三段绳的拉力,其中AO 沿水平方向,关于三段绳中承受拉力的情况,下列说法中正确的是A . AO 承受的拉力最大B . BO 承受的拉力最大C . CO 承受的拉力最大D . 三段绳承受的拉力一样大 【答案】B【解析】以结点O 为研究对象,分析受力情况,受力分析如图:由平衡条件得: 1tan T G θ=, 2cos GT θ=,故T1小于T2,G 小于T2;所以BO 承受的拉力最大;故B 正确。
绳的活结与死结模型、动杆和定杆模型-2024年高考物理一轮复习热点(解析版)

绳的活结与死结模型、动杆和定杆模型特训目标特训内容目标1绳子类的“死结”问题(1T -4T )目标2绳子类的“活结”问题(5T -8T )目标3有关滑轮组的“活结”问题(9T -12T )目标4定杆和动杆问题(13T -16T )【特训典例】一、绳子类的“死结”问题1如图所示,质量为m =2.4kg 的物体用细线悬挂处于静止状态。
细线AO 与天花板之间的夹角为53°,细线BO 水平,若三根细线能承受最大拉力均为100N ,重力加速度g 取10m/s 2,不计所有细线的重力,sin37°=0.6,cos37°=0.8。
下列说法正确的是()A.细线BO 上的拉力大小30NB.细线AO 上的拉力大小18NC.要使三根细线均不断裂,则细线下端所能悬挂重物的最大质量为8kgD.若保持O 点位置不动,沿顺时针方向缓慢转动B 端,则OB 绳上拉力的最小值为19.2N 【答案】C【详解】AB .以结点O 为研究对象,受到重力、OB 细线的拉力和OA 细线的拉力,如图所示根据平衡条件结合图中几何关系可得细线BO 上的拉力大小为F BO =mg tan37°=18N 同理,可解得细线AO 上的拉力大小F AO =mgcos37°=30N 故AB 错误;C .若三根细线能承受的最大拉力均为100N ,根据图中力的大小关系可得,只要OA 不拉断,其它两根细线都不会拉断,故有m max g =F max cos37°解得m max =F max cos37°g =100×0.810kg =8kg ,故C 正确;D .当OB 与OA 垂直时,OB 细线的拉力最小,根据几何关系结合平衡条件可得F min =mg sin37°=2.4×10×0.6N =14.4N 故D 错误。
故选C 。
2如图所示,两个质量均为m 的小球a 和b 套在竖直固定的光滑圆环上,圆环半径为R ,一不可伸长的细线两端各系在一个小球上,细线长为23R 。
高中物理:专题11 “活结”和“死结”、“动杆”和“定杆”模型-高一上学期同步重难讲练之相互作用

重难讲练1.“活结”和“死结”问题(1)活结:当绳绕过光滑的滑轮或挂钩时,由于滑轮或挂钩对绳无约束,因此绳上的力是相等的,即滑轮只改变力的方向不改变力的大小,例如图乙中,两段绳中的拉力大小都等于重物的重力.(2)死结:若结点不是滑轮,是固定点时,称为“死结”结点,则两侧绳上的弹力不一定相等.“死结”一般是由绳子打结而形成的,“死结”两侧的绳子因打结而变成两根独立的绳子。
死结的特点:a.绳子的结点不可随绳移动b.“死结”两侧的绳子因打结而变成两根独立的绳子,因此由“死结”分开的两端绳子上的弹力不一定相等2.“动杆”和“定杆”问题(1)动杆:若轻杆用光滑的转轴或铰链连接,当杆处于平衡时杆所受到的弹力方向一定沿着杆,否则会引起杆的转动.如图甲所示,若C为转轴,则轻杆在缓慢转动中,弹力方向始终沿杆的方向.(2)定杆:若轻杆被固定不发生转动,则杆所受到的弹力方向不一定沿杆的方向.如图乙所示.【典例1】(2016·全国卷Ⅲ·17)如图所示,两个轻环a和b套在位于竖直面内的一段固定圆弧上;一细线穿过两轻环,其两端各系一质量为m 的小球.在a 和b 之间的细线上悬挂一小物块.平衡时,a 、b 间的距离恰好等于圆弧的半径.不计所有摩擦.小物块的质量为( )A.m 2B.32m C.mD.2m【☆答案☆】 C 【解析】 如图所示,【典例2】 如图所示,一轻绳的两端分别固定在不等高的A 、B 两点,现用另一轻绳将一物体系于O 点,设轻绳AO 、BO 相互垂直,α>β,且两绳中的拉力分别为F A 、F B ,物体受到的重力为G ,下列表述正确的是( )A.F A一定大于G B.F A一定大于F BC.F A一定小于F B D.F A与F B大小之和一定等于G【☆答案☆】 B【解析】分析O点受力如图所示,由平衡条件可知,F A与F B的合力与G等大反向,因F A⊥F B,故F A、F B均小于G;因α>β,故F A>F B,B正确,A、C错误;由三角形两边之和大于第三边可知,|F A|+|F B|>G,D错误.【典例3】如图甲所示,轻绳AD跨过固定的水平横梁BC右端的定滑轮挂住一个质量M1的物体,∠ACB=30°;图乙中轻杆HG一端用铰链固定在竖直墙上,另一端G通过细绳EG拉住,EG与水平方向也成30°,轻杆的G点用细绳GF拉住一个质量M2的物体,求:(1)轻绳AC段的张力F T AC与细绳EG的张力F T EG之比;(2)轻杆BC对C端的支持力;(3)轻杆HG对G端的支持力.【☆答案☆】(1)M12M2(2)M1g方向和水平方向成30°指向右上方(3)3M2g方向水平向右【解析】题图甲和乙中的两个物体M1、M2都处于平衡状态,根据平衡的条件,首先判断与物体相连的细绳,其拉力大小等于物体的重力;分别取C点和G点为研究对象,进行受力分析如图甲和乙所示,根据平衡规律一一求解.【跟踪训练】1. 如图所示,将一细绳的两端固定于两竖直墙的A、B两点,通过一个光滑的挂钩将某重物挂在绳上,下面给出的四幅图中有可能使物体处于平衡状态的是( )【☆答案☆】C2.如图所示,当重物静止时,节点O 受三段绳的拉力,其中AO 沿水平方向,关于三段绳中承受拉力的情况,下列说法中正确的是A . AO 承受的拉力最大B . BO 承受的拉力最大C . CO 承受的拉力最大D . 三段绳承受的拉力一样大 【☆答案☆】B【解析】以结点O 为研究对象,分析受力情况,受力分析如图:由平衡条件得: 1tan T G θ=,2cos GT θ=,故T1小于T2,G 小于T2;所以BO 承受的拉力最大;故B 正确。
绳上的活结、死结问题与活动杆、固定杆问题-高考物理一轮复习热点专题突破
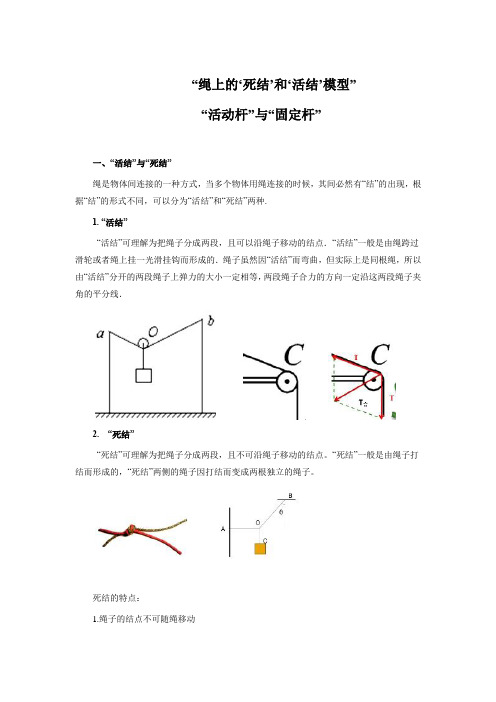
“绳上的‘死结’和‘活结’模型”“活动杆”与“固定杆”一、“活结”与“死结”绳是物体间连接的一种方式,当多个物体用绳连接的时候,其间必然有“结”的出现,根据“结”的形式不同,可以分为“活结”和“死结”两种.1. “活结”“活结”可理解为把绳子分成两段,且可以沿绳子移动的结点.“活结”一般是由绳跨过滑轮或者绳上挂一光滑挂钩而形成的.绳子虽然因“活结”而弯曲,但实际上是同根绳,所以由“活结”分开的两段绳子上弹力的大小一定相等,两段绳子合力的方向一定沿这两段绳子夹角的平分线.2. “死结”“死结”可理解为把绳子分成两段,且不可沿绳子移动的结点。
“死结”一般是由绳子打结而形成的,“死结”两侧的绳子因打结而变成两根独立的绳子。
死结的特点:1.绳子的结点不可随绳移动2.“死结”两侧的绳子因打结而变成两根独立的绳子,因此由“死结”分开的两端绳子上的弹力不一定相等【典例1】如图所示,将一细绳的两端固定于两竖直墙的A、B两点,通过一个光滑的挂钩将某重物挂在绳上,下面给出的四幅图中有可能使物体处于平衡状态的是()【答案】C【解析】由于重物是通过一个光滑的挂钩挂在绳上,绳子张力处处相等,而两边绳子的合力大小等于物体的重力,方向竖直向上,由对称性可知两边绳子与竖直方向的夹角相等,所以C正确。
【典例2】如图所示,一轻绳的两端分别固定在不等高的A、B两点,现用另一轻绳将一物体系于O点,设轻绳AO、BO相互垂直,α>β,且两绳中的拉力分别为F A、F B,物体受到的重力为G,下列表述正确的是( )A.F A一定大于GB.F A一定大于F BC.F A一定小于F BD.F A与F B大小之和一定等于G【答案】B【典例3】如图所示,在水平天花板的A点处固定一根轻杆a,杆与天花板保持垂直.杆的下端有一个轻滑轮O.另一根细线上端固定在该天花板的B点处,细线跨过滑轮O,下端系一个重为G的物体,BO段细线与天花板的夹角为θ=30°.系统保持静止,不计一切摩擦.下列说法中正确的是( )GA.细线BO对天花板的拉力大小是2GB.a杆对滑轮的作用力大小是2C.a杆和细线对滑轮的合力大小是GD.a杆对滑轮的作用力大小是G【答案】D二、“活动杆”与“固定杆”轻杆是物体间连接的另一种方式,根据轻杆与墙壁连接方式的不同,可以分为“活动杆”与“固定杆”.所谓“活动杆”,就是用铰链将轻杆与墙壁连接,其特点是杆上的弹力方向一定沿着杆的方向;而“固定杆”就是将轻杆固定在墙壁上(不能转动),此时轻杆上的弹力方向不一定沿着杆的方向。
高一物理上册专题—“活结”和“死结”及“动杆”和“定杆”模型

“活结”和“死结”、“动杆”和“定杆”模型重难讲练1.“活结”和“死结”问题(1)活结:当绳绕过光滑的滑轮或挂钩时,由于滑轮或挂钩对绳无约束,因此绳上的力是相等的,即滑轮只改变力的方向不改变力的大小,例如图乙中,两段绳中的拉力大小都等于重物的重力.(2)死结:若结点不是滑轮,是固定点时,称为“死结”结点,则两侧绳上的弹力不一定相等.“死结”一般是由绳子打结而形成的,“死结”两侧的绳子因打结而变成两根独立的绳子。
死结的特点:a.绳子的结点不可随绳移动b.“死结”两侧的绳子因打结而变成两根独立的绳子,因此由“死结”分开的两端绳子上的弹力不一定相等2.“动杆”和“定杆”问题(1)动杆:若轻杆用光滑的转轴或铰链连接,当杆处于平衡时杆所受到的弹力方向一定沿着杆,否则会引起杆的转动.如图甲所示,若C为转轴,则轻杆在缓慢转动中,弹力方向始终沿杆的方向.(2)定杆:若轻杆被固定不发生转动,则杆所受到的弹力方向不一定沿杆的方向.如图乙所示.【例1】(2016·全国卷Ⅲ·17)如图所示,两个轻环a和b套在位于竖直面内的一段固定圆弧上;一细线穿过两轻环,其两端各系一质量为m的小球.在a和b之间的细线上悬挂一小物块.平衡时,a、b间的距离恰好等于圆弧的半径.不计所有摩擦.小物块的质量为( )A.m2B.√32mC.mD.2m【答案】C【解析】如图所示,圆弧的圆心为0,悬挂小物块的点为c,由于ab=R,则△aOb为等边三角形,同一条细线上的拉力相等, F T=mg,,合力沿Oc方向,则Oc为角平分线,由几何关系知,∠acb=120°,故线的拉力的合力与物块的重力大小相等,即每条线上的拉力F T= G=mg,,所以小物块质量为m,故C对.【例2】如图甲所示,轻绳AD跨过固定的水平横梁BC右端的定滑轮挂住一个质量M₁的物体,∠ACB=30°;图乙中轻杆HG一端用铰链固定在竖直墙上,另一端G通过细绳EG 拉住,EG与水平方向也成30°,轻杆的G点用细绳GF拉住一个质量M₂的物体,求:(1)轻绳AC段的张力F TAC与细绳EG的张力F TEG;之比;(2)轻杆BC对C端的支持力;(3)轻杆HG对G端的支持力.【答案】(1)M12M2(2)M1g方向和水平方向成30°指向右上方(3)√3M2g方向水平向右【解析】题图甲和乙中的两个物体M₁、M₂都处于平衡状态,根据平衡的条件,首先判断与物体相连的细绳,其拉力大小等于物体的重力;分别取C点和G点为研究对象,进行受力分析如图甲和乙所示,根据平衡规律一一求解.(1)图甲中轻绳AD跨过定滑轮拉住质量为M₁的物体,物体处于平衡状态,轻绳AC段的拉力F24c=F TCD=M1g图乙中由.F TEG sin30∘=M2g,得F TEG=2M2g.所以F14CF126=M12M2(2)图甲中,三个力之间的夹角都为120°,根据平衡规律有F AC=F DAC=Mg,方向和水平方向成30°,指向右上方.(3)图乙中,根据平衡方程有F TEG sin30∘=Mg,F TBG cos30∘=F XG,所以F NG=M2gcot30∘=√3M2g,方向水平向右.专项训练1.如图所示,当重物静止时,节点O受三段绳的拉力,其中AO沿水平方向,关于三段绳中承受拉力的情况,下列说法中正确的是A.AO承受的拉力最大B.BO承受的拉力最大C.CO承受的拉力最大D.三段绳承受的拉力一样大【答案】B【解析】以结点O为研究对象,分析受力情况,受力分析如图:由平衡条件得:T₁=Gtanθ,T2=Gcosθ,故T1小于T2,G小于T2;所以BO承受的拉力最大;故B正确。
“活结与死结”“活动杆与固定杆”

mg 50 TB = = = 62.5N cosq 0.8
T A =T B sin q = 62.5? 0.6 37.5N
mg
1.用三根轻绳将质量为m的物块悬挂在空中,如图所 示.已知ac和bc与竖直方向的夹角分别为30°和 A 60°,则ac绳和bc绳中的拉力分别为( )
2.建筑工人要将建筑材料运送到高处,常在楼顶装置一个 定滑轮(图中未画出),用绳AC通过滑轮将建筑材料提到 某一高处,为了防止材料与墙壁相碰,站在地面上的工人还 另外用绳CD拉住材料,使它与竖直墙面保持一定的距离L。 若不计两根绳的重力,在提起材料的过程中,绳AC和CD的 拉力T1和T2的大小变化情况是( C ) A.T1增大、T2增大 B.T1增大、T2不变 C.T1增大、T2减小 D.T1减小、T2减小
解析:由于重物是通过一个光滑的挂钩挂在绳上,绳子张 力处处相等,而两边绳子的合力大小等于物体的重力,方 向竖直向上,由对称性可知两边绳子与竖直方向的夹角相 等,所以C正确。
1.如图所示,有两根立于水平地面上的竖直杆, 将一根不能伸长的、柔软的轻绳的两端,分别 系于竖直杆上不等高的两点a、b上,用一个光 滑的动滑轮O悬挂一个重物后再挂在绳子上, 达到平衡状态。现保持轻绳的a端不动,将b端 缓慢下移。在此过程中,轻绳的张力的变化情 况是( C ) A.保持不变 B.不断增大 C.不断减小 D.先增大,后减小
B
θ O A C
方法一:合成法
分析:
θ
TB
TC = mg = 50N
mg 50 TB = = = 62.5N cosq 0.8
T A = mg tanq = 50? 0.75 37.5N
TA
TC
方法二:正交分解法
专题10 活结与死结绳模型、动杆和定杆模型和受力分析-2025版高三物理一轮复习多维度导学与分层专练
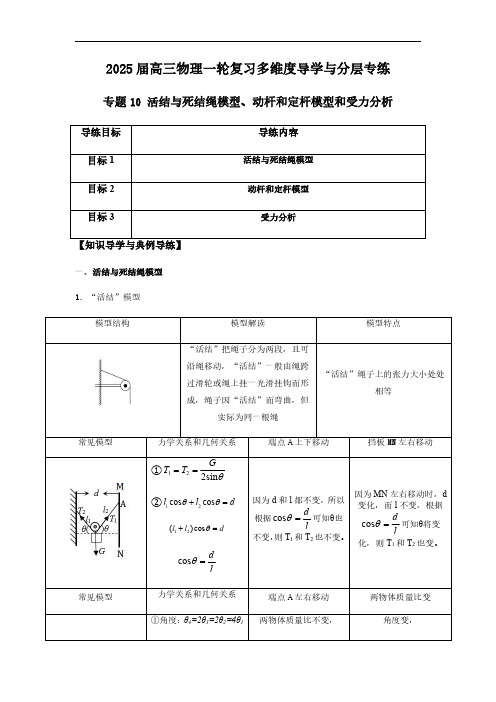
2025届高三物理一轮复习多维度导学与分层专练专题10活结与死结绳模型、动杆和定杆模型和受力分析导练目标导练内容目标1活结与死结绳模型目标2动杆和定杆模型目标3受力分析【知识导学与典例导练】一、活结与死结绳模型1.“活结”模型模型结构模型解读模型特点“活结”把绳子分为两段,且可沿绳移动,“活结”一般由绳跨过滑轮或绳上挂一光滑挂钩而形成,绳子因“活结”而弯曲,但实际为同一根绳“活结”绳子上的张力大小处处相等常见模型力学关系和几何关系端点A 上下移动挡板MN 左右移动①θsin 221G T T ==②dl l =+θθcos cos 21dl l =+θcos )(21ld =θcos 因为d 和l 都不变,所以根据ld=θcos 可知θ也不变,则T 1和T 2也不变。
因为MN 左右移动时,d 变化,而l 不变,根据ld=θcos 可知θ将变化,则T 1和T 2也变。
常见模型力学关系和几何关系端点A 左右移动两物体质量比变①角度:θ4=2θ3=2θ2=4θ1两物体质量比不变,角度变,②拉力:T=M Q g③2M Q cosθ2=M P 左右移动轻绳端点,角度都不变。
但让保持原有倍数关系。
【例1】如图所示,衣服悬挂在不可伸长的轻绳上,衣架的挂钩是光滑的,轻绳的两端固定在两根竖直杆上的A、B两点,衣服处于静止状态。
保持A端位置不变,将B端分别移动到1B、2B两点。
下列说法正确的是()A.B端移到1B,绳子张力变大B.B端移到1B,绳子张力变小C.B端移到2B,绳子张力变大D.B端移到2B,绳子张力不变【答案】D【详解】设绳子间的夹角为2θ,绳子总长为L,两杆间距离为d,如图所示根据几何关系有12sin sinL L dθθ+=得12sin d dL L Lθ==+当B端移到B1位置或B2位置时,d、L都不变,则θ也不变;由平衡条件可知2cosF mgθ=解得2cosmgFθ=可见,绳子张力F也不变,故D正确,ABC错误。
专题整理活结死结活杆死杆

共点力的平衡“活结,死结”、“活杆,死杆”问题1、“活结”与“死结”绳是物体间连接的一种方式,当多个物体用绳连接的时候,其间必然有“结”的出现,根据“结”的形式不同,可以分为“活结”和“死结”两种。
“活结”是绳子间的一种光滑连接,其特点是结的两端同一绳上的张力相等;而“死结”是绳子间的一种固定连接,结的两端绳子上的张力不一定相等。
2、“活杆”与“死杆”死杆是不可转动,所以杆所受弹力的方向不一定沿杆方向.活杆是可以转动的杆所以杆所受弹力的方向沿杆方向。
(一)“死结”和“活结”问题。
1. 如图所示,长为5 m的细绳的两端分别系于竖立在地面上的相距为4 m的两杆的顶端A、B,绳上挂一个光滑的轻质挂钩,其下连着一个重为12 N的物体,平衡时绳中的张力F T为多大?当A点向上移动少许,重新平衡后,绳与水平面夹角、绳中张力如何变化?2.如图所示,AO、BO和CO三根绳子能承受的最大拉力相等,O为结点,OB与竖直方向夹角为θ,悬挂物质量为m。
求:①OA、OB、OC三根绳子拉力的大小。
②A点向上移动少许,重新平衡后,绳中张力如何变化?3.如图所示,用绳AC和BC吊起一个物体,绳AC与竖直方向的夹角为60°,能承受的最大拉力为100N绳BC与竖直方向的夹角为30°,能承受的最大拉力为150N.欲使两绳都不断,物体的重力不应超过多少?4. 如图所示,轻绳绕过一光滑的小圆柱B,上端固定于A点,下端系一重为200 N的物体C,AB段绳子与竖直方向的夹角为60°,则绳中张力大小为____________ N,小圆柱B受到的压力大小为____________ N.(二)“死杆”和“活杆”问题。
5. 如图所示,质量为m的物体用细绳OC悬挂在支架上的O点,轻杆OB可绕B点转动,求细绳OA中张力T 大小和轻杆OB受力N大小。
6. 如图所示,水平横梁一端A 插在墙壁内,另一端装有小滑轮B ,一轻绳一端C 固定于墙壁上,另一端跨过滑轮后悬挂一质量为m =10 kg 的重物,∠CBA =30°,(g 取10 N /kg )则滑轮受到绳子作用力为【 】A .50 NB .50 3 N C .100 N D .100 3 N针对训练题1.三段不可伸长的细绳OA 、OB 、OC 能承受的最大拉力相同,它们共同悬挂一重物,如图所示,其中OB 是水平的,A 端、B 端固定。
2018-2019学年高中物理同步重难讲练之相互作用专题11“活结”和“死结”、“动杆”和“定杆”

专题11“活结”和“死结”、“动杆”和“定杆”模型重难讲练1•“活结”和“死结”问题(1)活结:当绳绕过光滑的滑轮或挂钩时,由于滑轮或挂钩对绳无约束,因此绳上的力是相等的,即滑轮只改变力的方向不改变力的大小,例如图乙中,两段绳中的拉力大小都等于重物的重力(2)死结:若结点不是滑轮,是固定点时,称为“死结”结点,则两侧绳上的弹力不一定相等•“死结” 一般是由绳子打结而形成的,“死结”两侧的绳子因打结而变成两根独立的绳子。
死结的特点:a.绳子的结点不可随绳移动b•“死结”两侧的绳子因打结而变成两根独立的绳子,因此由“死结”分开的两端绳子上的弹力不一定相等2•“动杆”和“定杆”问题(1)动杆:若轻杆用光滑的转轴或铰链连接,当杆处于平衡时杆所受到的弹力方向一定沿着杆,否则会引起杆的转动•如图甲所示,若C为转轴,则轻杆在缓慢转动中,弹力方向始终沿杆的方向•(2)定杆:若轻杆被固定不发生转动,则杆所受到的弹力方向不一定沿杆的方向•如图乙所示•【典例1】(2016 •全国卷川• 17)如图所示,两个轻环a和b套在位于竖直面内的一段固定圆弧上;一细线穿过两轻环,其两端各系一质量为m的小球•在a和b之间的细线上悬挂一小物块•平衡时,a、b间的B.~fmC.mD.2 m【答案】C【解析】如图所示,圆弧的圆心为6悬挂切砌块的点为G由于於二凡则&已为等边三角形,同一条细线上的拉力相等,Fr=mg f合力沿仇方向,则处为角平分线,由几何关系知,Zac5= 12<F,故线的拉力的合力与物块的重力大小相等,即每条线上的拉力所以小物块质量为叫故住对一【典例2】如图所示,一轻绳的两端分别固定在不等高的A、B两点,现用另一轻绳将一物体系于0点,设轻绳AO B0相互垂直, a >B ,且两绳中的拉力分别为F A、F B,物体受到的重力为G下列表述正确的是()CA. F A一定大于GB. F A一定大于F BC. F A定小于F BD. F A与F B大小之和一定等于G【答案】B【解析】分析0点受力如图所示,由平衡条件可知,F A与F B的合力与G等大反向,因F A丄F B,故F A、F B 均小于G;因a >B,故F A>F B, B正确,A C错误;由三角形两边之和大于第三边可知,|F A| + | F B| > G D 错误.【典例3】如图甲所示,轻绳AD跨过固定的水平横梁BC右端的定滑轮挂住一个质量M的物体,/ ACB=30°;图乙中轻杆HG —端用铰链固定在竖直墙上,另一端G通过细绳EG拉住,EG与水平方向也成30°,轻杆的G点用细绳GF拉住一个质量M的物体,求:⑴轻绳AC段的张力F TAC与细绳EG的张力F TEG之比;⑵轻杆BC对C端的支持力;⑶轻杆HG对G端的支持力.M L【答案】⑴2M⑵Mg方向和水平方向成30°指向右上方(3) .3Mg方向水平向右【解析】题图甲和乙中的两个物体M、M都处于平衡状态,根据平衡的条件,首先判断与物体相连的细绳,其拉力大小等于物体的重力;分别取C点和G 点为研究对象,进行受力分析如图甲和乙所示,根据平衡规律一一求解.甲乙⑴图甲中轻绳Q跨过定滑轮拉住质量为Vi的物体,物体处于平衡状态』轻绳AC段的拉力也二團乙中由KK—得F T備疽所以瓷二磊⑵團甲中,三个力之间的夹甬都为□俨』根据平衡规律有用方向和水平方向成30% 指向右上方.⑶图乙中,根据平衡方程有用宓血13旷=施』码盼遊3呼=再叭所以尬=隔血33=击陀,方向水平向右+【跟踪训练】1.如图所示,将一细绳的两端固定于两竖直墙的A、E两点,通过一个光滑的挂钩将某重物挂在绳上,下面给出的四幅图中有可能使物体处于平衡状态的是()【答案】C【解析】由于重韧是通过一个光滑的挂钩挂在绳上*绳子张力处处相等,而两边绳子的合力犬小等于 物体的重力,方向竖直向上,由对称性可知两边绳子与竖直方向的夹角相等,所以住正确。
高中物理“动杆”和“定杆”与“活结”和“死结”问题 —人教版高一暑假综合易错点、易混淆点突破专题讲义

七、“动杆”和“定杆”与“活结”和“死结”问题--易错点、易混淆点突破1.“动杆”和“定杆”问题(1)动杆:若轻杆用光滑的转轴或铰链连接,当杆处于平衡时杆所受到的弹力方向一定沿着杆,否则会引起杆的转动.如图甲所示,若C为转轴,则轻杆在缓慢转动中,两绳对BC杆弹力方向:始终沿BC杆的方向.(2)定杆:若轻杆被固定不发生转动,图乙中,轻杆是插入墙中的,则杆所受到的弹力方向不一定沿杆的方向,即C Bm对轻杆A B的作用力就不一定沿BA方向。
2.“活结”和“死结”问题(1)“死结”可理解为把绳子分成两段,且不可以沿绳子移动的结点。
“死结”两侧的绳因“结”而变成了两根独立的绳,因此由“死结”分开的两段绳子上的弹力不一定相等。
(2)“活结”可理解为把绳子分成两段,且可以沿绳子移动的结点。
“活结”一般由绳跨过滑轮或者绳上挂一光滑挂钩而形成。
绳子虽然因“活结”而弯曲,但实际上“活结”两侧的绳子是同一根绳,所以由“活结”分开的两段绳子上弹力的大小一定相等,两段绳子合力的方向一定沿这两段绳子夹角的角平分线。
1.(2020·天津市南开中学月考)如图为两种形式的吊车的示意图,OA为可绕O点转动的轻杆,重量不计,AB为缆绳,当它们吊起相同重物时,杆OA在图(a)、(b)中的受力分别为F a、F b,则下列关系正确的是()A.F a=F b B.F a>F bC.F a<F b D.大小不确定答案:A解析:对题图中的A点受力分析,则由图(a)可得F a=F a′=2mg cos 30°=3mg,由图(b)可得tan30°=mgF b′,则F b=F b′=3mg,故F a=F b,A正确.2.(多选)如图所示,质量均可忽略的轻绳与轻杆,A端用铰链固定,滑轮在A点正上方(滑轮大小及摩擦均可不计),B端吊一重物.现将绳的一端拴在杆的B端,用拉力F将B端缓慢上拉,在AB杆达到竖直前()图11A.绳子拉力不变B.绳子拉力减小C.AB杆受力增大D.AB杆受力不变答案:BD解析:以B点为研究对象,受力分析如图所示,B点受重物的拉力F T1(等于重物的重力G)、轻杆的支持力F N和绳子的拉力F T2由平衡条件得,F N和F T2的合力与F T1大小相等、方向相反,根据三角形相似可得:F N AB =F T2BO =F T1AO 又F =F T2,F T1=G 解得:F N =AB AO ·G ,F =BO AO·G∠BAO 缓慢变小时,AB 、AO 保持不变,BO 变小,则F N 保持不变,F 变小,故选项B 、D 正确.3.如图所示,两个轻环a 和b 套在位于竖直面内的一段固定圆弧上;一细线穿过两轻环,其两端各系一质量为m 的小球.在a 和b 之间的细线上悬挂一小物块.平衡时,a 、b 间的距离恰好等于圆弧的半径.不计所有摩擦.小物块的质量为( )A .m 2B .32m C .m D .2m答案:C解析:如图所示,圆弧的圆心为O ,悬挂小物块的点为c ,由于ab =R ,则△aOb 为等边三角形,同一条细线上的拉力相等,F T =mg ,合力沿Oc 方向,则Oc 为角平分线,由几何关系知,∠acb =120°,故细线的拉力的合力与物块的重力大小相等,则每条细线上的拉力F T =G =m ′g ,所以小物块质量为m ′=m ,故C 对.4.如图甲所示 , 细绳AD 跨过固定的水平轻杆BC 右端的光滑定滑轮挂住一个质量为M 1的物体, ∠ACB =30°; 图乙中轻杆HG 一端用铰链固定在竖直墙上,另一端G 通过细绳EG 拉住,EG 与水平方向也成30°角,轻杆的G 点用细绳GF 拉住一个质量为M 2的物体,重力加速度为g ,求:(1)细绳AC 段的张力F T AC 与细绳EG 的张力F T EG 之比; (2)轻杆BC 对C 端的支持力; (3)轻杆HG 对G 端的支持力.解析:(1)图甲中细绳AD 跨过定滑轮拉住质量为M 1的物体,物体处于平衡状态, 细绳AC 段的拉力F T AC =F T CD =M 1g ,图乙中由F T EG sin 30°=M 2g ,得F T EG =2M 2g , 所以F T AC F TEG =M 12M 2.(2)图甲中,三个力之间的夹角都为120°,根据平衡条件有F N C =F T AC =M 1g ,方向与水平方向成30°角指向右上方.(3)图乙中,根据平衡条件有 F T E G sin 30°=M 2g , F T E G cos 30°=F N G ,所以F N G =M 2g tan 30°=3M 2g ,方向水平向右.答案:(1)M 12M 2(2)M 1g ,与水平方向成30°角指向右上方 (3) 3M 2g ,方向水平向右【题后反思】 (1)轻绳中的“活结”两侧实际是同一根轻绳,“死结”两侧是两根不同的轻绳. (2)轻杆模型中,杆顶端所受的各力中,除杆的弹力外,如果其他力的合力沿着杆的方向,则杆的弹力也必然沿着杆,如果其他力的合力不沿着杆,则杆的弹力也不会沿着杆.。
第五讲死结与活结,死杆与活杆

第五讲:绳上的‘死结’和‘活结’杆中的“活杆”与“死杆”模型一、“活结”与“死结”绳是物体间连接的一种方式,当多个物体用绳连接的时候,其间必然有“结”的出现,根据“结”的形式不同,可以分为“活结”和“死结”两种.1. “活结”“活结”可理解为把绳子分成两段,且可以沿绳子移动的结点.“活结”一般是由绳跨过滑轮或者绳上挂一光滑挂钩而形成的.绳子虽然因“活结”而弯曲,但实际上是同根绳,所以由“活结”分开的两段绳子上弹力的大小一定相等,两段绳子合力的方向一定沿这两段绳子夹角的平分线.2. “死结”“死结”可理解为把绳子分成两段,且不可沿绳子移动的结点。
“死结”一般是由绳子打结而形成的,“死结”两侧的绳子因打结而变成两根独立的绳子。
死结的特点:1.绳子的结点不可随绳移动2.“死结”两侧的绳子因打结而变成两根独立的绳子,因此由“死结”分开的两端绳子上的弹力不一定相等【典例1】如图所示,将一细绳的两端固定于两竖直墙的A、B两点,通过一个光滑的挂钩将某重物挂在绳上,下面给出的四幅图中有可能使物体处于平衡状态的是()【典例2】如图所示,一轻绳的两端分别固定在不等高的A、B两点,现用另一轻绳将一物体系于O点,设轻绳AO、BO相互垂直,α>β,且两绳中的拉力分别为F A、F B,物体受到的重力为G,下列表述正确的是( )A.F A一定大于G B.F A一定大于F BC.F A一定小于F B D.F A与F B大小之和一定等于G第2题图第3题图【典例3】如图所示,在水平天花板的A点处固定一根轻杆a,杆与天花板保持垂直.杆的下端有一个轻滑轮O.另一根细线上端固定在该天花板的B点处,细线跨过滑轮O,下端系一个重为G的物体,BO段细线与天花板的夹角为θ=30°.系统保持静止,不计一切摩擦.下列说法中正确的是( )A.细线BO对天花板的拉力大小是2G B.a杆对滑轮的作用力大小是2G C.a杆和细线对滑轮的合力大小是G D.a杆对滑轮的作用力大小是G 【典例4】如图所示,长为5 m的细绳的两端分别系于竖立在地面上的相距为4 m的两杆的顶端A、B,绳上挂一个光滑的轻质挂钩,其下连着一个重为12 N的物体,平衡时绳中的张力F T为多大?当A点向上移动少许,重新平衡后,绳与水平面夹角、绳中张力如何变化?.【典例5】如图所示,AO、BO和CO三根绳子能承受的最大拉力相等,O为结点,OB与竖直方向夹角为θ,悬挂物质量为m。
高考物理模型讲练结合—04静力学部分(2)

模型04 静力学部分(2)-冲刺36模型模型+典例+方法+练习目录动态平衡 (2)五、动杆死结死杆活结模型 (2)六、挂件模型 (4)斜面模型 (6)轻绳轻杆轻弹簧 (10)一、轻绳 (10)二、弹簧(橡皮筋) (11)三、轻杆 (13)环杆模型 (15)动态平衡五、动杆死结死杆活结模型【模型+方法】1.动杆和定杆问题杆所受到的弹力方向可以沿着杆,也可以不沿杆,因此在分析问题时,要注意是动杆还是定杆。
若轻杆用转动轴或铰链连接,当处于平衡时杆所受到的弹力方向一定沿着杆,否则会引起杆的转动;若轻杆被固定不发生转动,则杆所受到的弹力方向不一定沿杆的方向。
2.“活结”和“死结”问题当绳绕过滑轮或挂钩时,由于滑轮或挂钩对绳无约束,因此绳上各处的力是相等的,即滑轮或挂钩只改变力的方向不改变力的大小;若结点不是滑轮,是称为“死结”的结点,则两侧绳上的弹力不一定相等。
3.物体的平衡问题中,常常遇到“动杆和定杆活结与死结”的问题,我们要明确几个问题:①动杆上的弹力必须沿着杆子的方向,定杆上的弹力可以按需供给;②活结两边的绳子上的张力一定相同,死结两边的绳子上的张力可以不同;③动杆配死结,定杆配活结。
【典例】城市中的路灯、无轨电车的供电线路等,经常用三角形的结构悬挂.如图是这类结构的一种简化模型,硬杆左端可绕通过B点且垂直于纸面的轴无摩擦的转动,右端O点通过钢索挂于A点,钢索和硬杆所受的重力均可忽略.有一质量不变的重物悬挂于O点,现将钢索缓慢变短,并使钢索的悬挂点A缓慢向下移动,以保证硬杆始终处于水平.则在上述变化过程中,下列说法中正确的是( )A.钢索对O点的拉力变大B.硬杆对O点的弹力变小C.钢索和硬杆对O点的作用力的合力变大D.钢索和硬杆对O点的作用力的合力变小【答案】A【解析】以O点为研究对象,分析受力,作出受力分析图,根据平衡条件得:钢索AO对O点的拉力F AO sin θ=G=mg,则F AO=mgsin θ,杆BO对O点的支持力F BO=Gtan θ=mgtan θ,将钢索缓慢变短,并使钢索的悬挂点A缓慢向下移动,θ减小,则F AO增大,F BO 增大,故A正确,B错误;BO始终水平,O点始终平衡,钢索和硬杆对O点的作用力的合力与重力平衡,保持不变,故C、D错误.【练习】如图所示,不计重力的轻杆OP能以O点为圆心在竖直平面内自由转动,P端用轻绳PB挂一重物,另用一根轻绳通过光滑定滑轮系住P端.在力F的作用下,当杆OP和竖直方向的夹角α(0<α<π)缓慢增大时,力F的大小应( )A.逐渐增大B.恒定不变C.逐渐减小D.先增大后减小六、挂件模型【模型+方法】利用对称性,做反向延长线求解【典例】如图所示,轻质不可伸长的晾衣绳两端分别固定在竖直杆M、N上的a、b两点,悬挂衣服的衣架钩是光滑的,挂于绳上处于静止状态。
2-2-3-核心素养培养:“活结”和“死结”、“动杆”和“定杆”模型
8
@《创新设计》
目录
题组剖析
【例2】 水平横梁的一端A插在墙壁内,另一端装有一个轻质 小滑轮B,一轻绳的一端C固定于墙壁上,另一端跨过滑轮后悬 挂一质量m=10 kg的重物,CB与水平方向夹角为30°,如图13 所示,则滑轮受到杆的作用力大小为(g取10 m/s2)( )
A.50 N
B.50 3 N
10
@《创新设计》
目录
本节内容结束
11
核心素养培养:“活结”和“死结”、“动杆”和“定杆”模型
01
1.“活结”和“死结”的比较
02
2.“动杆”和“定杆”的比较
目录
CONTENTS
03
@《创新设计》
04
1
目录
课堂互动
1.“活结”和“死结”的比较 “活结”可理解为把绳子分成两段,且可以沿绳子移动的结点。“活结” 一般是由绳跨过滑轮或者绳上挂一光滑挂钩而形成的。绳子虽然因“活结” 而弯曲,但实际上是同一根绳,所以由“活结”分开的两段绳子上弹力的 大小一定相等,两段绳子合力的方向一定沿这两段绳子夹角的平分线。 “死结”可理解为把绳子分成两段,且不可以沿绳子移动的结点。“死 结”两侧的绳因结而变成了两根独立的绳,因此由“死结”分开的两段绳 子上的弹力不一定相等。
转到解析
3
@《创新设计》
目录
题组剖析
【延伸拓展】 (多选)在【例1】中若将拉力F的方向变为水平方向,使物块a在细 绳拉力作用下匀速上升,则( ) A.桌面对物块b的支持力增大 B.桌面对物块b的摩擦力减小 C.细绳OO′的拉力减小 D.细绳OO′与竖直方向的夹角增大
转到解析
5
@《创新设计》
目录
题组剖析
2
专题09 绳的活结与死结模型、动杆和定杆模型(解析版)

2023届高三物理一轮复习重点热点难点专题特训专题09 绳的活结与死结模型、动杆和定杆模型特训目标特训内容目标1 绳子类的“死结”问题(1T—4T)目标2 绳子类的“活结”问题(5T—8T)目标3 有关滑轮组的“活结”问题(9T—12T)目标4定杆和动杆问题(13T—16T)一、绳子类的“死结”问题1.如图所示,将三段轻绳相结于O点,其中OA绳的一端拴在墙上,OB绳的下方悬挂甲物体,OC绳跨过光滑定滑轮悬挂乙物体。
OC绳与竖方向的夹角为α=70°。
OA绳与竖直方向的夹角为β(未知)。
若甲、乙两物体的质量均为m=2kg,重力加速度g取10m/s2,sin55°≈0.82。
根据所学的知识,不需计算,推理出OA绳的拉力约为()A.16N B.23N C.31N D.41N【答案】B【详解】甲、乙两物体的质量均为m=2kg,则OC绳的拉力与OB绳的拉力均为20N,这两个力的合力与OA绳的拉力大小相等,方向相反。
由几何关系可知OC绳的拉力与OB绳的拉力夹角为110°,而夹角为120°均为20N的两个力的合力大小为20N。
所以OC绳的拉力与OB绳的拉力的合力接近20N。
所以根据所学的知识,不需计算,推理出OA绳的拉力约为B选项的23N。
故选B。
2.如图所示,两个轻环P和Q套在位于竖直面你的一固定“∧”形光滑框架上,框架两边与竖直方向的夹角均为30°,两段伸长可忽略的细绳,一端分别系在P、Q环上,另一端与绳套系在一起,结点为O。
现在绳套上挂一小物块,平衡时细绳OP所受拉力大小为F,拉直时两段细绳长度相等,不计细绳与绳套的重力。
小物块的重力大小为()A .2FB .FC 3D 23【答案】B 【详解】如图所示对P 、Q 小环分析,小环受光滑杆的支持力和绳子的拉力,根据平衡条件,这两个力是一对平衡力,支持力是垂直于杆子向上的,故绳子的拉力也是垂直于杆子的,故两细绳之间的夹角为120︒,由几何关系可知,两根绳子与竖直方向之间的夹角都是903060︒-︒=︒所以绳子OQ 的拉力也是F ,两根绳子的长度相等,对结点O 受力分析如图所示,根据平衡条件可知,由几何关系可知,三个力之间的夹角都是120︒,所以G F =故B 正确,ACD 错误。
死结、活结与固定杆、活动杆学案、试题、答案

绳子死结、活结与固定杆、活动杆一、“活结”与“死结”1. “活结”“活结”一般是由绳跨过滑轮、光滑钉子或者绳上挂一光滑挂钩而形成的,结点可以沿绳子移动。
绳子虽然因“活结”而弯曲,但实际上是同根绳,两段绳子上弹力的大小一定相等,两段绳子合力的方向一定沿这两段绳子夹角的平分线。
2.“死结”“死结”一般是由绳子打结而形成的,结点不可沿绳子移动。
可理解为绳子因打结而变成两根独立的、拉力可不相同的绳子。
1、如图,一个重为G 的吊椅用三根轻绳AO 、BO 固定,绳AO 、BO 相互垂直,α>β,且两绳中的拉力分别为FA 、FB ,物体受到的重力为G ,则( )A .F A 一定大于GB .F A 一定大于F BC .F A 一定小于F BD .F A 与F B 大小之和一定等于G2、如图所示,A 、B 两物体的质量分别为、,且,整个系统处于静止状态,滑轮的质量和一切摩擦均不计,如果绳一端由Q 点缓慢地向左移到P 点,整个系统重新平衡后,绳的拉力F 和两滑轮间绳、水平方向的夹角θ与物体A 的高度变化情况是( )A .F 变大,θ角变大,A 升高B .F 变小,θ角变小,A 升高C .F 不变,θ角变小,A 降低D .F 不变,θ角不变,A 升高3、如图,将一根不可伸长、柔软的轻绳左、右两端分别系于A 、B 两点上,一物体用动滑轮悬挂在轻绳上,达到平衡时,两段绳子间的夹角为1θ,绳子张力为1F ;将绳子右端移到C 点,待系统达到平衡时,两段绳子间的夹角为2θ,绳子张力为2F ;将绳子右端再由C 点移到D 点,待系统达到平衡时,两段绳子间的夹角为3θ,绳子张力为3F ,不计摩擦,并且BC 为竖直线,则( )A.123θθθ==B.123θθθ=<C.123F F F >>D.123F F F =>二、“活动杆”与“固定杆”1.“活动杆”“活动杆”就是用铰链或者转动轴将轻杆与墙壁连接,其特点是杆上的弹力方向一定沿着杆的方向;2.“固定杆”“固定杆”就是将轻杆固定在墙壁上(不能转动),此时轻杆上的弹力方向不一定沿着杆的方向。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
轻绳也称细线,它的质量可忽略不计;轻绳是软的;同 时它的劲度系数非常大,可认为在受外力作用时它的形 变极微小,看作不可伸长.
其弹力的主要特征:
①不能承受压力,不能产生侧向力,只能产生沿绳收缩 方向的拉力.
②轻绳只有两端受力时,任何一个横截面上的张力大小 都等于绳的任意一端所受拉力的大小,即同一轻绳张力 处处相等.
而“固定杆”就是将轻杆固定在墙壁上(不能转 动),此时轻杆上的弹力方向不一定沿着杆的方向。
O
O活死来自GG例1.如图甲所示,轻绳AD跨过固定的水平横梁BC右端的定滑轮挂住
一个质量为M1的物体,∠ACB=30°;图乙中轻杆HG一端用铰链固 定在竖直墙上,另一端G通过细绳EG拉住,EG与水平方向也成30°,
可能使物体处于平衡状态的是( C )
解析:由于重物是通过一个光滑的挂钩挂在绳上,绳子张 力处处相等,而两边绳子的合力大小等于物体的重力,方 向竖直向上,由对称性可知两边绳子与竖直方向的夹角相 等,所以C正确。
1.如图所示,有两根立于水平地面上的竖直杆 ,将一根不能伸长的、柔软的轻绳的两端,分 别系于竖直杆上不等高的两点a、b上,用一个 光滑的动滑轮O悬挂一个重物后再挂在绳子上 ,达到平衡状态。现保持轻绳的a端不动,将b 端缓慢下移。在此过程中,轻绳的张力的变化
③轻绳的弹力大小可发生突变.
模型2:轻杆 轻杆的质量可忽略不计,轻杆是硬的,它的劲度系数 非常大,可认为在受外力作用时形变极微小,看作不可伸 长或压缩. 其弹力的主要特征是: ①轻杆既可产生压力、也可产生拉力,且能产生侧向 力(力的方向不一定沿着杆的方向); ②轻杆各处受力大小相等,且与运动状态无关; ③轻杆的弹力可发生突变.
模型3:轻弹簧 轻弹簧的质量可忽略不计,可以被压缩或拉伸。 其弹力的主要特征是: ①轻弹簧能产生沿弹簧轴线伸缩方向的压力或拉力; ②轻弹簧各处受力大小相等,且与弹簧形变的方向相反; ③在弹性限度内,弹力的大小与弹簧的形变量成正比,即 F=kΔx,其中k为弹簧的劲度系数,Δx为弹簧的伸长量或缩 短量。
例1.AO,BO,和CO三根绳子,O为节点,OB与数值 方向夹角为θ,悬挂物质量为m。已知θ角为37°, 物体质量为5kg. 求AO,BO,CO三根绳子拉力的大小。
B
θ O A
C
方法一:合成法
分析:
TB
TC mg 50N
θ
mg 50
TA
TB cos
62.5N 0.8
T A m gta n 5 00 .7 53 7 .5 N
A.T1增大、T2增大 B.T1增大、T2不变 C.T1增大、T2减小 D.T1减小、T2减小
二、“活动杆”与“固定杆”
轻杆是物体间连接的另一种方式,根据轻 杆与墙壁连接方式的不同,可以分为“活动杆” 与“固定杆”.
所谓“活动杆”,就是用铰链将轻杆与墙壁连接, 其特点是杆上的弹力方向一定沿着杆的方向;
轻杆的G点用细绳GF拉住一个质量为M2的物体,求: (1)轻绳AC段的张力TAC与 细绳EG的张力TEG之比; (2)轻杆BC对C端的支持力;
(3)轻杆HG对G端的支持力。
解:
总结: 1.什么是活结,什么是死结? 2.什么是活动杆,什么是固定杆? 2.它们各有什么特点?
TC
方法二:正交分解法
分析:
TC mg 50N
TB cos mg
TA A
mg 50
TB cos
62.5N 0.8
TA TB sin 62.5 0.6 37.5N
B TB θ θ O
mg
1.用三根轻绳将质量为m的物块悬挂在空中,如图所 示.已知ac和bc与竖直方向的夹角分别为30°和 60°,则ac绳和bc绳中的拉力分别A为( )
2.建筑工人要将建筑材料运送到高处,常在楼顶装置一个 定滑轮(图中未画出),用绳AC通过滑轮将建筑材料提到 某一高处,为了防止材料与墙壁相碰,站在地面上的工人还 另外用绳CD拉住材料,使它与竖直墙面保持一定的距离L。 若不计两根绳的重力,在提起材料的过程中,绳AC和CD的
拉力T1和T2的大小变化情况是(C )
情况是(C )
A.保持不变
B.不断增大
C.不断减小
D.先增大,后减小
(二)“死结”
“死结”可理解为把绳子分成两段,且不 可沿绳子移动的结点。“死结”一般是由绳子 打结而形成的,“死结”两侧的绳子因打结而 变成两根独立的绳子。
死结的特点: 1.绳子的结点不可随绳移动 2.“死结”两侧的绳子因打结而变成两根独立的 绳子,因此由“死结”分开的两端绳子上的弹 力不一定相等
一、“活结”与“死结”
绳是物体间连接的一种方式,当多个物体 用绳连接的时候,其间必然有“结”的出现,根 据“结”的形式不同,可以分为“活结”和“死 结”两种.
(一)“活结”
“活结”可理解为把绳子分成两段,此 时绳子为同一根绳子,张力大小处处相等.
T
T合
T
例1:如图3所示,将一细绳的两端固定于两 竖直墙的A、B两点,通过一个光滑的挂钩 将某重物挂在绳上,下面给出的四幅图中有
