山东省烟台市2020届高三上学期期末考试数学试题

合集下载

2020届山东省新高考高三优质数学试卷分项解析专题05 三角函数与解三角形(原卷版)

专题5 三角函数与解三角形1.近几年高考在对三角恒等变换考查的同时，对三角函数图象与性质的考查力度有所加强，往往将三角恒等变换与三角函数的图象和性质结合考查，先利用三角公式进行化简，然后进一步研究三角函数的性质.其中三角函数的定义域值域、单调性、奇偶性、周期性、对称性以及图象变换是主要考查对象，难度以中档以下为主.2.高考对正弦定理和余弦定理的考查较为灵活，题型多变，往往以小题的形式独立考查正弦定理或余弦定理，以解答题的形式综合考查定理的综合应用，多与三角形周长、面积有关；有时也会与平面向量、三角恒等变换等结合考查，试题难度控制在中等或以下，主要考查灵活运用公式求解计算能力、推理论证能力、数学应用意识、数形结合思想等．预测2020年将突出考查恒等变换与三角函数图象和性质的结合、恒等变换与正弦定理和余弦定理的结合.一、单选题1．（2020届山东省潍坊市高三上期中）sin 225︒= （）A ．12-B ．2-C ．D ．1-2．（2020届山东省泰安市高三上期末）“1a <-”是“0x ∃∈R ，0sin 10+<a x ”的（） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件3．（2020届山东省潍坊市高三上期末）已知345sin πα⎛⎫-= ⎪⎝⎭，0,2πα⎛⎫∈ ⎪⎝⎭，则cos α=（）A ．10B ．10C ．2 D ．104．（2020届山东省枣庄市高三上学期统考）设函数2sin cos ()(,0)x x xf x a R a ax +=∈≠，若(2019)2f -=，(2019)f =( )A ．2B ．-2C ．2019D ．-20195．（2020届山东省枣庄市高三上学期统考）已知函数()cos()(0)f x x ωϕω=+>的最小正周期为π，且对x ∈R ，()3f x f π⎛⎫⎪⎝⎭…恒成立，若函数()y f x =在[0,]a 上单调递减，则a 的最大值是（） A ．π6 B ．π3C ．2π3D ．5π66．（2020届山东省滨州市三校高三上学期联考）若π1sin 34α⎛⎫-= ⎪⎝⎭，则πcos 23α⎛⎫+= ⎪⎝⎭（）．A ．78-B ．14-C ．14 D ．787．（2020届山东省潍坊市高三上期中）已知函数()sin cos f x x x =+，则（） A ．()f x 的最小正周期为π B ．()y f x =图象的一条对称轴方程为4x π=C ．()f x 的最小值为2-D ．()f x 的0,2π⎡⎤⎢⎥⎣⎦上为增函数8．（2020届山东省九校高三上学期联考）如图是一个近似扇形的鱼塘，其中OA OB r ==，弧AB 长为l （l r <）.为方便投放饲料，欲在如图位置修建简易廊桥CD ，其中34OC OA =，34OD OB =.已知1(0,)2x ∈时，3sin 3!x x x ≈-，则廊桥CD 的长度大约为（）A ．323432r r l - B ．323432l l r - C ．32324l l r-D ．32324r r l-9．（2020·武邑县教育局教研室高三上期末（理））已知()cos 2cos 2παπα⎛⎫-=+ ⎪⎝⎭，且()1tan 3αβ+=，则tan β的值为（） A ．-7B ．7C ．1D ．-110．（2020届山东师范大学附中高三月考）为了得函数23y sin x π⎛⎫=+ ⎪⎝⎭的图象，只需把函数2y sin x =的图象（） A ．向左平移6π个单位 B ．向左平移3π单位 C ．向右平移6π个单位 D ．向右平移3π个单位11．（2020届山东省枣庄、滕州市高三上期末）将曲线()cos 2y f x x =上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移4π个单位长度，得到曲线cos 2y x =，则6f π⎛⎫= ⎪⎝⎭（）A ．1B ．-1C D ．12．（2020届山东省济宁市高三上期末）在ABC ∆中,1,3,1AB AC AB AC ==⋅=-u u u r u u u r,则ABC ∆的面积为( )A ．12B ．1CD ．213．（2020届山东省潍坊市高三上学期统考）将函数()πsin 23f x x ⎛⎫=+ ⎪⎝⎭的图像向右平移()0a a >个单位得到函数()πcos 24g x x ⎛⎫=+ ⎪⎝⎭的图像，则a 的值可以为（）A ．5π12B ．7π12C ．19π24D ．41π2414．（2020届山东省临沂市高三上期末）已知函数2()2cos 12f x x πω⎛⎫=- ⎪⎝⎭(0)>ω的图象关于直线4x π=对称，则ω的最小值为（） A ．13B ．16C ．43D ．5615．（2020届山东省潍坊市高三上学期统考）已知△ABC 的内角,,A B C 的对边分别为,,a b c ，若2cos cos cos b B a C c A =+，2b =，则△ABC 面积的最大值是A ．1B C ．2D ．416．（2020届山东省烟台市高三上期末）若x α=时，函数()3sin 4cos f x x x =+取得最小值，则sin α=（）A ．35B ．35-C ．45D ．45-17．（2020届山东实验中学高三上期中）在ABC △中，若 13,3,120AB BC C ==∠=o ，则AC =（） A ．1B ．2C ．3D ．418．（2020届山东实验中学高三上期中）已知()cos 2cos 2παπα⎛⎫-=+ ⎪⎝⎭，且()1tan 3αβ+=，则tan β的值为（） A ．-7B ．7C ．1D ．-119．（2020届山东省济宁市高三上期末）函数22cos cos 1y x x =-++，,22x ππ⎡⎤∈-⎢⎥⎣⎦的图象大致为( ) A ． B ．C ．D ．20．（2020届山东师范大学附中高三月考）泉城广场上矗立着的“泉标”，成为泉城济南的标志和象征．为了测量“泉标”高度，某同学在“泉标”的正西方向的点A 处测得“泉标”顶端的仰角为45︒，沿点A 向北偏东30︒前进100 m 到达点B ，在点B 处测得“泉标”顶端的仰角为30︒，则“泉标”的高度为（） A ．50 mB ．100 mC ．120 mD ．150 m21．（2020届山东实验中学高三上期中）已知函数()sin 23f x a x x =的图象关于直线12x π=-对称，若()()124f x f x ⋅=-，则12a x x -的最小值为（） A ．4πB ．2π C ．πD ．2π22．（2020届山东省滨州市高三上期末）已知函数()2sin(2)f x x ϕ=+的图象过点,26A π⎛⎫⎪⎝⎭，则( ) A ．把()y f x =的图象向右平移6π个单位得到函数2sin 2y x =的图象B ．函数()f x 在区间,02π⎛⎫- ⎪⎝⎭上单调递减C ．函数()f x 在区间[]0,2π内有五个零点D ．函数()f x 在区间0,3π⎡⎤⎢⎥⎣⎦上的最小值为1 二、多选题23．（2020届山东省滨州市三校高三上学期联考）设函数()sin 23f x x π⎛⎫=- ⎪⎝⎭，则下列结论正确的是（） A ．π-是()f x 的一个周期 B ．()f x 的图像可由sin 2y x =的图像向右平移3π得到 C ．()f x π+的一个零点为6x π=D ．()y f x =的图像关于直线1712x π=对称 24．（2020届山东师范大学附中高三月考）在平面直角坐标系xOy 中，角α顶点在原点O ，以x 正半轴为始边，终边经过点()()1,0P m m <，则下列各式的值恒大于0的是（） A ．sin tan ααB ．cos sin αα-C ．sin cos ααD ．sin cos αα+25．（2020·蒙阴县实验中学高三期末）关于函数()22cos cos(2)12f x x x π=-+-的描述正确的是（）A ．其图象可由2y x =的图象向左平移8π个单位得到 B ．()f x 在(0,)2π单调递增C ．()f x 在[]0,π有2个零点D ．()f x 在[,0]2π-的最小值为26．（2020·山东省淄博实验中学高三上期末）已知函数()sin cos f x x x =-，()g x 是()f x 的导函数，则下列结论中正确的是（）A ．函数()f x 的值域与()g x 的值域不相同B ．把函数()f x 的图象向右平移2π个单位长度，就可以得到函数()g x 的图象 C ．函数()f x 和()g x 在区间,44ππ⎛⎫-⎪⎝⎭上都是增函数 D ．若0x 是函数()f x 的极值点，则0x 是函数()g x 的零点27．（2020届山东省枣庄市高三上学期统考）将函数()sin 23f x x π⎛⎫=+ ⎪⎝⎭的图象向右平移2π个单位长度得到()g x 图象，则下列判断正确的是（） A ．函数()g x 在区间,122ππ⎡⎤⎢⎥⎣⎦上单调递增 B ．函数()g x 图象关于直线712x π=对称 C ．函数()g x 在区间,63ππ⎡⎤-⎢⎥⎣⎦上单调递减 D ．函数()g x 图象关于点,03π⎛⎫⎪⎝⎭对称28．（2020届山东省潍坊市高三上期末）已知()()22210f x cos x x ωωω=->的最小正周期为π，则下列说法正确的有（） A ．2ω= B ．函数()f x 在[0,]6π上为增函数C ．直线3x π=是函数()y f x =图象的一条对称轴D ．5π,012骣琪琪桫是函数()y f x =图象的一个对称中心29．（2020届山东省潍坊市高三上学期统考）在ABC V 中，内角A ，B ，C 所对的边分别为a ，b ，c ，若1tan A ，1tan B ，1tan C依次成等差数列，则下列结论中不一定成立．．．．．的是（） A ．a ，b ，c 依次成等差数列B C ．2a ，2b ，2c 依次成等差数列 D ．3a ，3b ，3c 依次成等差数列30．（2020届山东省济宁市高三上期末）将函数()sin 2f x x =的图象向右平移4π个单位后得到函数()g x 的图象,则函数()g x 具有性质( )A ．在0,4π⎛⎫⎪⎝⎭上单调递增,为偶函数 B ．最大值为1,图象关于直线32x π=-对称 C ．在3,88ππ⎛⎫-⎪⎝⎭上单调递增,为奇函数 D ．周期为π,图象关于点3,04π⎛⎫⎪⎝⎭对称 31．（2020届山东实验中学高三上期中）己知函数()()()sin 0,023f x x f x ππωϕωϕ⎛⎫=+><<- ⎪⎝⎭，为的一个零点，6x π=为()f x 图象的一条对称轴，且()()0f x π在，上有且仅有7个零点，下述结论正确．．的是（） A ．=6πϕB ．=5ωC ．()()0f x π在，上有且仅有4个极大值点D ．()042f x π⎛⎫⎪⎝⎭在，上单调递增32．（2019·山东师范大学附中高三月考）在平面直角坐标系xOy 中，角α顶点在原点O ，以x 正半轴为始边，终边经过点()()1,0P m m <，则下列各式的值恒大于0的是（） A ．sin tan ααB ．cos sin αα-C ．sin cos ααD ．sin cos αα+33．（2020届山东省烟台市高三上期末）已知函数()()sin 322f x x ππϕϕ⎛⎫=+-<< ⎪⎝⎭的图象关于直线4x π=对称，则（） A ．函数12f x π⎛⎫+⎪⎝⎭为奇函数 B ．函数()f x 在,123ππ⎡⎤⎢⎥⎣⎦上单调递增 C ．若()()122f x f x -=，则12x x -的最小值为3πD ．函数()f x 的图象向右平移4π个单位长度得到函数cos3y x =-的图象三、填空题34．（2020届山东省枣庄市高三上学期统考）已知1sin 4x =，x 为第二象限角，则sin 2x =______. 35．（2020届山东省日照市高三上期末联考）已知tan 3α=，则sin cos sin cos αααα-+的值为______.36．（2020届山东师范大学附中高三月考）已知1tan 3α=，则2sin 2sin 1cos 2ααα-+的值为________．37．（2020届山东省枣庄、滕州市高三上期末）在平面直角坐标系xOy 中，角α的顶点是O ，始边是x 轴的非负半轴，02απ<<，点1tan,1tan1212P ππ⎛⎫+- ⎪⎝⎭是α终边上一点，则α的值是________. 38．（2020·全国高三专题练习（文））已知sin cos 11cos 2ααα=-，1tan()3αβ-=，则tan β=________.39．（2020届山东实验中学高三上期中）在ABC ∆中，,,a b c 分别为内角,,A B C 的对边，若32sin sin sin ,cos 5B AC B =+=，且6ABC S ∆=，则b =__________． 40．（2020届山东省日照市高三上期末联考）已知函数()9sin 26f x x π⎛⎫=-⎪⎝⎭，当[]0,10x π∈时，把函数()()6F x f x =-的所有零点依次记为123,,,,n x x x x ⋅⋅⋅，且123n x x x x <<<⋅⋅⋅<，记数列{}n x 的前n 项和为n S ，则()12n n S x x -+=______.41．（2020届山东省德州市高三上期末）已知函数()()sin f x A x =+ωϕ0,0,||2A πωϕ⎛⎫>><⎪⎝⎭的最大值2π，且()f x 的图象关于直线3x π=-对称，则当,66x ππ⎡⎤∈-⎢⎥⎣⎦时，函数()f x 的最小值为______.42．（2020届山东省泰安市高三上期末）在△ABC 中，内角A ，B ，C 的对边分别为,,a b c ，若cos cos sin A B C a b c +=，22265b c a bc +-=，则tan B =______．四、解答题43．（2020届山东省临沂市高三上期末）在①3cos 5A =，cos C =，②sin sin sin c C A b B =+，60B =o，③2c =，1cos 8A =三个条件中任选一个补充在下面问题中，并加以解答. 已知ABC V 的内角A ，B ，C 的对边分别为a ，b ，c ，若3a =，______，求ABC V 的面积S . 44．（2020届山东省泰安市高三上期末）在①函数()()1sin 20,22f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭的图象向右平移12π个单位长度得到()g x 的图象，()g x图象关于原点对称；②向量),cos 2m x x ωω=u r，()11cos ,,0,24n x f x m n ωω⎛⎫=>=⋅ ⎪⎝⎭r u r r ；③函数()1cos sin 64f x x x πωω⎛⎫=+- ⎪⎝⎭()0ω>这三个条件中任选一个，补充在下面问题中，并解答．已知_________，函数()f x 的图象相邻两条对称轴之间的距离为2π．（1）若02πθ<<，且sin θ=()f θ的值；（2）求函数()f x 在[]0,2π上的单调递减区间．45．（2020届山东省枣庄市高三上学期统考）ABC ∆的内角A ，B ，C 的对边分别为,,a b c ，已知()2cos cos 0a c B b A ++=.（I ）求B ；（II ）若3,b ABC =∆的周长为3ABC +∆的面积.46．（2020届山东省滨州市三校高三上学期联考）已知函数()sin()f x A x ωϕ=+，其中0A >，0>ω，(0,)ϕπ∈，x ∈R ，且()f x 的最小值为-2，()f x 的图象的相邻两条对称轴之间的距离为2π，()f x 的图象过点,03π⎛-⎫ ⎪⎝⎭.（1）求函数()f x 的解析式和单调递增区间；（2）若[0,2]x πÎ函数()f x 的最大值和最小值.47．（2020届山东省潍坊市高三上期中）在ABC ∆中，内角A ，B ，C 所对的边分别为a ，b ，c ．已知10a b +=，5c =，sin 2sin 0B B +=．（1）求a ，b 的值：（2）求sin C 的值．48．（2020届山东省烟台市高三上期末）在条件①()(sin sin )()sin a b A B c b C +-=-，②sin cos()6a Bb A π=+，③sinsin 2B Cb a B +=中任选一个，补充到下面问题中，并给出问题解答. 在ABC ∆中，角,,A B C 的对边分别为,,a bc ，6b c +=，a =， . 求ABC ∆的面积.49．（2020届山东省泰安市高三上期末）如图所示，有一块等腰直角三角形地块ABC ，90A ∠=o ，BC 长2千米，现对这块地进行绿化改造，计划从BC 的中点D 引出两条成45°的线段DE 和DF ，与AB 和AC 围成四边形区域AEDF ，在该区域内种植花卉，其余区域种植草坪；设BDE α∠=，试求花卉种植面积()S α的取值范围．50．（2020届山东省日照市高三上期末联考）在①ABC ∆面积2ABC S ∆=，②6ADC π∠=这两个条件中任选一个，补充在下面问题中，求AC . 如图，在平面四边形ABCD 中，34ABC π∠=，BAC DAC ∠=∠，______，24CD AB ==，求AC .51．（2020届山东省滨州市三校高三上学期联考）在ABC ∆中，内角A ，B ，C 所对的边分别为a ，b ，c ，23sin 2cos02A CB +-=. （1）求角B 的大小；（2）若2sin 2sin sin B A C =，且ABC ∆的面积为3ABC ∆的周长.52．（2020届山东省德州市高三上期末）已知a ，b ，c 分别为ABC ∆内角A ，B ，C 的对边，若ABC ∆同时满足下列四个条件中的三个：①2633()b a ac c a b -+=+；②2cos 22cos 12A A +=；③6a =④2b =（1）满足有解三角形的序号组合有哪些？（2）在（1）所有组合中任选一组，并求对应ABC ∆的面积. （若所选条件出现多种可能，则按计算的第一种可能计分）53．（20203(cos )sin b C a c B -=；②22cos a c b C +=；③sin 3sin2A Cb A a += 这三个条件中任选一个，补充在下面问题中的横线上，并解答相应的问题.在ABC ∆中，内角A ，B ，C 的对边分别为a ，b ，c ，且满足________________，23,b =4a c +=，求ABC ∆的面积.54．（2020届山东师范大学附中高三月考）ABC V 的内角A ，B ，C 的对边分别为a ，b ，c ，且满足cos cos 2c A a C a +=．（1）求a b的值；（2）若1a =，7c =，求ABC V 的面积． 55．（2020·蒙阴县实验中学高三期末）在非直角ABC ∆中，a ，b ，c 分别是A ，B ，C 的对边.已知4a =，5AB AC ⋅=u u u r u u u r ，求：（1）tan tan tan tan A A B C+的值；（2）BC 边上的中线AD 的长.56．（2020届山东师范大学附中高三月考）设函数5()2cos()cos 2sin()cos 122f x x x x x ππ=++++. （1）设方程()10f x -=在(0,)π内有两个零点12,x x ，求12x x +的值；（2）若把函数()y f x =的图象向左平移6π个单位，再向下平移2个单位，得函数()g x 图象，求函数()g x 在[,]33ππ-上的最值. 57.（2020届山东省潍坊市高三上期末）在①34asinC ccosA =;②252B C bsinasinB +=这两个条件中任选-一个，补充在下面问题中，然后解答补充完整的题.在ABC V 中，角,,A B C 的对边分别为,,a b c ，已知，32a =.(1)求sinA ;(2)如图，M 为边AC 上一点，,2MC MB ABM π=∠=，求ABC V 的面积58．（2020·山东省淄博实验中学高三上期末）在ABC ∆中，角A ，B ，C 的对边分别为a ，b ，c ，已知4cos cos cos a A c B b C =+.（1）若4a =，ABC ∆的面积为15，求b ，c 的值；（2）若()sin sin 0B k C k =>，且角C 为钝角，求实数k 的取值范围.59．（2020届山东省潍坊市高三上学期统考）已知函数()()23sin cos sin 10f x x x x ωωωω=-+>图象的相邻两条对称轴之间的距离为2π.（1）求ω的值及函数()f x 的单调递减区间；（2）如图，在锐角三角形ABC 中有()1f B =，若在线段BC 上存在一点D 使得2AD =，且6AC =，31CD =-，求三角形ABC 的面积.60．（2020届山东省济宁市高三上期末）已知()()23sin sin cos 2f x x x x ππ⎛⎫=-+- ⎪⎝⎭. (1)若1210f α⎛⎫= ⎪⎝⎭,求2cos 23πα⎛⎫+ ⎪⎝⎭的值; (2)在△ABC 中,角A ,B ,C 所对应的边分别,,a b c ,若有()2cos cos a c B b C -=,求角B 的大小以及()f A 的取值范围.61．（2020届山东省济宁市高三上期末）如图,某市三地A ,B ,C 有直道互通.现甲交警沿路线AB ､乙交警沿路线ACB 同时从A 地出发,匀速前往B 地进行巡逻,并在B 地会合后再去执行其他任务.已知AB =10km ,AC =6km ,BC =8km ,甲的巡逻速度为5km /h ,乙的巡逻速度为10km /h .(1)求乙到达C 地这一时刻的甲､乙两交警之间的距离;(2)已知交警的对讲机的有效通话距离不大于3km ,从乙到达C 地这一时刻算起,求经过多长时间,甲､乙方可通过对讲机取得联系.62．（2020·全国高三专题练习（文））在ABC V 中，a ，b ，c 分别为内角A ，B ，C 的对边，且满()(sin sin )(3sin sin )b a B A c B C -+=-.（1）求A 的大小；（2）再在①2a =，②4B π=，③3=c b 这三个条件中，选出两个使ABC V 唯一确定的条件补充在下面的问题中，并解答问题.若________，________，求ABC V 的面积.63．（2020届山东实验中学高三上期中）己知函数()23sin cos sin 244f x x x x a ππ⎛⎫⎛⎫=++++ ⎪ ⎪⎝⎭⎝⎭的最大值为1.（1）求实数a 的值；（2）若将()f x 的图象向左平移6π个单位，得到函数()g x 的图象，求函数()g x 在区间0,2π⎡⎤⎢⎥⎣⎦上的最大值和最小值.64．（2020届山东实验中学高三上期中）“我将来要当一名麦田里的守望者，有那么一群孩子在一块麦田里玩，几千万的小孩子，附近没有一个大人，我是说……除了我”《麦田里的守望者》中的主人公霍尔顿将自己的精神生活寄托于那广阔无垠的麦田.假设霍尔顿在一块成凸四边形ABCD 的麦田里成为守望者，如图所示，为了分割麦田，他将BD 连接，设ABD ∆中边BD 所对的角为A ，BCD ∆中边BD 所对的角为C ，经测量已知2AB BC CD ===，23AD =.（1）霍尔顿发现无论BD 3cos A C -为一个定值，请你验证霍尔顿的结论，并求出这个定值；（2）霍尔顿发现麦田的生长于土地面积的平方呈正相关，记ABD ∆与BCD ∆的面积分别为1S 和2S ，为了更好地规划麦田，请你帮助霍尔顿求出2212S S +的最大值.。

【高考数学】立体几何中的截面

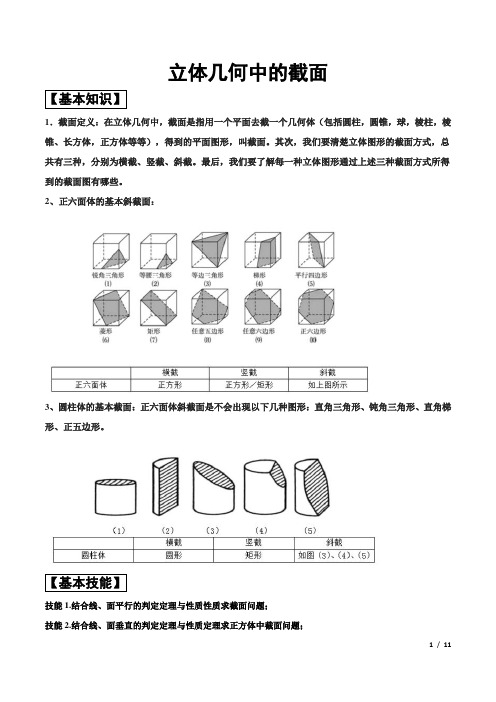
立体几何中的截面【基本知识】1．截面定义：在立体几何中，截面是指用一个平面去截一个几何体（包括圆柱，圆锥，球，棱柱，棱锥、长方体，正方体等等），得到的平面图形，叫截面。

其次，我们要清楚立体图形的截面方式，总共有三种，分别为横截、竖截、斜截。

最后，我们要了解每一种立体图形通过上述三种截面方式所得到的截面图有哪些。

2、正六面体的基本斜截面：3、圆柱体的基本截面：正六面体斜截面是不会出现以下几种图形：直角三角形、钝角三角形、直角梯形、正五边形。

【基本技能】技能1.结合线、面平行的判定定理与性质性质求截面问题；技能2.结合线、面垂直的判定定理与性质定理求正方体中截面问题；技能 3.猜想法求最值问题：要灵活运用一些特殊图形与几何体的特征，“动中找静”：如正三角形、正六边形、正三棱锥等；技能4.建立函数模型求最值问题：①设元②建立二次函数模型③求最值。

例1 一个正方体内接于一个球，过这个球的球心作一平面，则截面图形不可能．．．是（）例2 如图，在透明的塑料制成的长方体ABCD-A 1B 1C 1D 1容器内灌进一些水，固定容器底面一边BC 于地面上，再将容器倾斜，随着倾斜程度的不同，有下列四个命题：① 水的部分始终呈棱柱状； ② 水面EFGH 的面积不改变； ③ 棱A 1D 1始终与水面EFGH 平行；④ 当容器倾斜到如图5（2）时，BE·BF 是定值；其中正确的命题序号是______________例3 有一容积为1 立方单位的正方体容器ABCD-A 1B 1C 1D 1，在棱AB 、BB 1及对角线B 1C 的中点各有一小AB C H A 1 B 1 C 1 D 1E F GDA B C DA 1B 1C 1D 1EF G H图（2）图（1）ACBD孔E 、F 、G ，若此容器可以任意放置，则该容器可装水的最大容积是（）A ．21B ．87C ．1211 D ．4847例4 正四棱锥P ABCD -的底面正方形边长是3，O 是P 在底面上的射影，6, PO Q =是AC 上的一点，过Q 且与, PA BD 都平行的截面为五边形EFGHL ，求该截面面积的最大值.基本方法介绍①公理法：用平面基本性质中的公理来作平面； ②侧面展开法：将立体图形展开为平面图形进行研究；例5 能否用一个平面去截一个正方体，使得截面为五边形？进一步，截面能否为正五边形呢？C 1 A B CD A 1D 1 B 1EG F 图（1）例6 已知一个平面截一个棱长为1的正方体所得的截面是一个六边形（如图所示），证明：此六边形的周长≥一、单选题1．【江西省吉安市2019-2020学年高二上学期期末数学】在正方体1111ABCD A B C D -中，F 为AD 的中点，E 为棱1D D 上的动点(不包括端点)，过点,,B E F 的平面截正方体所得的截面的形状不可能是（） A ．四边形B ．等腰梯形C ．五边形D ．六边形2．【2020届辽宁省实验中学、大连八中、大连二十四中、鞍山一中、东北育才学校高三上学期期末】如图圆锥PO ，轴截面PAB 是边长为2的等边三角形，过底面圆心O 作平行于母线PA 的平面，与圆锥侧面的交线是以E 为顶点的抛物线的一部分，则该抛物线的焦点到其顶点E 的距离为( )A ．1B ．12C ．13D ．144．如图，在正方体1111ABCD A B C D -中，点E ，F ，G 分别是棱AB ，BC ，1BB 的中点，过E ，F ，G 三点作该正方体的截面，则下列说法错误的是（）A ．在平面11BDDB 内存在直线与平面EFG 平行 B ．在平面11BDD B 内存在直线与平面EFG 垂直C ．平面1//AB C 平面EFGD ．直线1AB 与EF 所成角为45︒5．【云南省昆明市2019-2020学年高三下学期1月月考数学】某同学在参加《通用技术》实践课时，制作了一个工艺品，如图所示，该工艺品可以看成是一个球被一个棱长为，若其中一个截面圆的周长为4π，则该球的半径是（）A ．2B ．4C ．D ．6．美学四大构件是：史诗、音乐、造型（绘画、建筑等）和数学.素描是学习绘画的必要一步，它包括了明暗素描和结构素描，而学习几何体结构素描是学习素描最重要的一步.某中学2018级某同学在画“切面圆柱体”（用与圆柱底面不平行的平面去截圆柱，底面与截面之间的部分叫做切面圆柱体）的过程中，发现“切面”是一个椭圆，若“切面”所在平面与底面成45︒角，则该椭圆的离心率为（）A ．12B ．2C D ．137．如图，已知三棱锥V ABC -，点P 是VA 的中点，且2AC =，4VB =，过点P 作一个截面，使截面平行于VB 和AC ，则截面的周长为（）A ．12B ．10C ．8D ．68．【2020届广东省东莞市高三期末调研测试理科数学试题】已知球O 是正四面体A BCD -的外接球，2BC =，点E 在线段BD 上，且3BD BE =，过点E 作球O 的截面，则所得截面圆面积的最小值是（） A ．89πB ．1118πC ．512π D ．49π 9．【2020届福建省福州市高三适应性练习卷数学理科试题】在三棱锥P ABC -中，PA ⊥底面ABC ，,6,8AB AC AB AC ⊥==，D 是线段AC 上一点，且3AD DC =.三棱锥P ABC -的各个顶点都在球O 表面上，过点D 作球O 的截面，若所得截面圆的面积的最大值与最小值之差为16π，则球O 的表面积为（） A ．72πB ．86πC ．112πD ．128π10．【2020届重庆南开中学高三第五次教学质量检测考试数学文科试题】正三棱锥P ABC -，Q 为BC 中点，PA =，2AB =，过Q 的平面截三棱锥P ABC -的外接球所得截面的面积范围为（）A ．13,45ππ⎡⎤⎢⎥⎣⎦B ．12,23ππ⎡⎤⎢⎥⎣⎦C ．[],2ππD ．3,2ππ⎡⎤⎢⎥⎣⎦11．一个三棱锥的各棱长均相等，其内部有一个内切球，即球与三梭锥的各面均相切（球在三棱锥的内部，且球与三棱锥的各面只有一个交点），过一条侧棱和对边的中点作三棱锥的截面，所得截面是下列图形中的（）A ．B ．C ．D ．12．【2020届湖北省部分重点中学高三第二次联考数学试卷理科试题】如图，已知四面体ABCD 的各条棱长均等于4，E ，F 分别是棱AD 、BC 的中点.若用一个与直线EF 垂直，且与四面体的每一个面都相交的平面α去截该四面体，由此得到一个多边形截面，则该多边形截面面积最大值为（）A ．B ．4C ．D ．613．【2020届辽宁省实验中学、大连八中、大连二十四中、鞍山一中、东北育才学校高三上学期期末】仿照“Dandelin 双球”模型，人们借助圆柱内的两个内切球完美的证明了平面截圆柱的截面为椭圆面．如图，底面半径为1的圆柱内两个内切球球心距离为4，现用与两球都相切的平面截圆柱所得到的截面边缘线是一椭圆，则该椭圆的离心率为( )A ．12B C ．2D 14．已知正方体1111ABCD A B C D -的边长为2，边AB 的中点为M ，过M 且垂直1BD 的平面被正方体所截的截面面积为（）A B C ．D ．15．在棱长为2的正方体1111ABCD A B C D -中，P ，Q ，R 分别是AB ，AD ，11B C 的中点，设过P ，Q ，R 的截面与面11ADD A ，以及面11ABB A 的交线分别为l ，m ，则l ，m 所成的角为（）A ．90︒B ．30C ．45︒D ．60︒16．在立体几何中，用一个平面去截一个几何体得到的平面图形叫截面，如图，在正方体ABCD ﹣A 1B 1C 1D 1中，点E 、F 分别是棱B 1B 、B 1C 中点，点G 是棱CC 1的中点，则过线段AG 且平行于平面A 1EF 的截面图形为（）A ．矩形B ．三角形C ．正方形D ．等腰梯形17．【2020届山西省吕梁市高三上学期第一次模拟考试数学（理)试题】如图四面体A BCD -中，2,AD BC AD BC ==⊥，截面四边形EFGH 满足//EF BC ；//FG AD ，则下列结论正确的个数为（） ①四边形EFGH 的周长为定值 ②四边形EFGH 的面积为定值 ③四边形EFGH 为矩形④四边形EFGH 的面积有最大值1A ．0B ．1C ．2D ．318．【2018年全国普通高等学校招生统一考试理科数学（新课标I 卷)】已知正方体的棱长为1，每条棱所在直线与平面α所成的角都相等，则α截此正方体所得截面面积的最大值为A B C ．4D 19．【四川省内江市2019-2020学年高二上学期期末数学（文)试题】已知正三棱锥A BCD -的外接球是球O ，正三棱锥底边3BC =，侧棱AB =E 在线段BD 上，且BE DE =，过点E 作球O 的截面，则所得截面圆面积的取值范围是（）A ．9,34ππ⎡⎤⎢⎥⎣⎦B ．[]2,3ππC ．11,44ππ⎡⎤⎢⎥⎣⎦D ．9,44ππ⎡⎤⎢⎥⎣⎦20．【云南省曲靖市2019-2020学年高三第一次教学质量检测数学文科试题】在四面体ABCD 中，3AB BD AD CD ====，4AC BC ==，用平行于AB ，CD 的平面截此四面体，得到截面四边形EFGH ，则四边形EFGH 面积的最大值为（）A ．43B ．94C ．92D ．3二、填空题21．【山东省烟台市2019-2020学年高三上学期期末考试数学试题】已知三棱锥P ABC -的四个顶点都在球O 的表面上，PA ⊥平面ABC ，6PA =，AB =2AC =，4BC =，则：（1）球O 的表面积为__________；（2）若D 是BC 的中点，过点D 作球O 的截面，则截面面积的最小值是__________．22．【新疆维吾尔自治区乌鲁木齐市2019-2020学年高三第一次诊断性测试数学文试题】如图，已知正方体1111ABCD A B C D -的棱长为2，E 、F 、G 分别为11,,AB AD B C 的中点，给出下列命题：①异面直线EF 与AG 所成的角的余弦值为6；②过点E 、F 、G 作正方体的截面，所得的截面的面积是 ③1A C ⊥平面EFG④三棱锥C EFG -的体积为1其中正确的命题是_____________（填写所有正确的序号）23．如图所示，在长方体1111ABCD A B C D -中，点E 是棱1CC 上的一个动点，若平面1BED 交棱1AA 于点F ，给出下列命题：①四棱锥11B BED F -的体积恒为定值；②对于棱1CC 上任意一点E ，在棱AD 上均有相应的点G ，使得//CG 平面1EBD ； ③O 为底面ABCD 对角线AC 和BD 的交点，在棱1DD 上存在点H ，使//OH 平面1EBD ；11 / 11④存在唯一的点E ，使得截面四边形1BED F 的周长取得最小值.其中为真命题的是____________________.（填写所有正确答案的序号）24．【2020届河南省驻马店市高三上学期期末数学(文科)试题】在棱长为2的正方体1111ABCD A B C D -中，E 是正方形11BB C C 的中心，M 为11C D 的中点，过1A M 的平面α与直线DE 垂直，则平面α截正方体1111ABCD A B C D -所得的截面面积为______.三、解答题25．【2015年全国普通高等学校招生统一考试文科数学（新课标Ⅱ带解析)】如图，长方体1111ABCD A B C D -中,116,10,8AB BC AA ===，点,E F 分别在1111,A B D C 上，114A E D F ==，过点,E F 的平面α与此长方体的面相交，交线围成一个正方形．（1）在图中画出这个正方形（不必说明画法与理由）；（2）求平面α把该长方体分成的两部分体积的比值．。

江苏省13市2020届高三上学期期中期末考试数学试题分类汇编：圆锥曲线

江苏省13市2020届高三上学期期中期末考试数学试题分类汇编圆锥曲线一、填空题1、（常州市2020届高三上学期期末考试）在平面直角坐标系xOy 中，双曲线2222:1(0,0)x y C a b a b-=>>的右顶点为A,过A 做x 轴的垂线与C 的一条渐近线交于点B,若2OB a =，则C 的离心率为2、（常州市2020届高三上学期期末考试）在平面直角坐标系xOy 中，圆222:22210C x ax y ay a -+-+-=上存在点P 到点（0,1）的距离为2，则实数a 的取值范围是3、（南京、盐城市2020届高三上学期期末考试）在平面直角坐标系 xOy 中，若抛物线 y 2 = 4x 上的点 P 到其焦点的距离为 3，则点 P 到点O 的距离为________.4、（南通、泰州市2020届高三上学期期末）在平面直角坐标系 xOy 中，已知点 A ，B 分别在双曲线C : x 2 - y 2 ＝1 的两条渐近线上，且双曲线C 经过线段 AB 的中点.若点 A 的横坐标为 2 ，则点 B 的横坐标为______.5、（苏北四市（徐州、宿迁、淮安、连云港）2020届高三上学期期末考试）在平面直角坐标系xOy中，双曲线2213x y -=的右准线与渐近线的交点在抛物线22y px =上，则实数p 的值为______.6、（苏州市2020届高三上学期期末考试）在平面直角坐标系xOy 中，己知点F 1，F 2是双曲线22221x y a b-=(a ＞0，b ＞0)的左、右焦点，点P 的坐标为(0，b )，若∠F 1PF 2＝120°，则该双曲线的离心率为．7、（无锡市2020届高三上学期期末考试）双曲线22:143x y C -=的左右顶点为,A B ，以AB 为直径作圆O ，P 为双曲线右支上不同于顶点B 的任一点，连接PA 角圆O 于点Q ，设直线,PB QB 的斜率分别为12,k k ，若12k k λ=，则λ=_____.8、（徐州市2020届高三上学期期中考试）在平面直角坐标系xOy 中，若双曲线C ：22221(0,0)x y a b a b-=>>的一条渐近线的倾斜角为30º，期C 的离心率为． 9、（扬州市2020届高三上学期期末考试）在平面直角坐标系xOy 中，顶点在原点且以双曲线2213y x -=的右准线为准线的抛物线方程是10、（扬州市2020届高三上学期期中考试）双曲线1422=-x y 的渐近线方程为． 11、（扬州市2020届高三上学期期中考试）抛物线x y 42=上横坐标为4的点到焦点的距离为．12、（镇江市2020届高三上学期期末考试）顶点在原点且以双曲线221124x y -=的右焦点为焦点的抛物线方程是．参考答案：1、22、117117,01,⎡⎤⎡⎤-+⎢⎥⎢⎥⎣⎦⎣⎦U 3、23 4、12 5、146、26 7、34- 8、23 9、22y x =- 10、2y x =±11、5 12、216y x =二、解答题1、（常州市2020届高三上学期期末考试）如图，在平面直角坐标系xOy 中，椭圆2222:1(0)x y C a b a b+=>>的左右焦点分别为12,F F ，椭圆右顶点为A ，点2F 在圆22(2)1x y -+=上。

山东省实验中学2020届高三第一次模拟考试数学（理）试卷含解析

山东省实验中学2020届高三第一次模拟考试数学（理）试卷一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.在直角坐标平面内，已知A（-2,0）,3（2,0）以及动点。

是AABC的三个顶点，且sin Asin B-2cosC=0,则动点C的轨迹曲线「的离心率是()\/2a/3A.2B.2 c.扬 D.右2.若函数f(x)=l+\x\+x\贝0/(lg2)+/flg|k/(lg5)+/flg^=()A.2b.4 C.6 D.83.在AA3C中，CA_CA AB.则sinA:sin3:sinC=（）543A.9:7:8b.c.6:8:7D何.3：由4.如图为我国数学家赵爽（约3世纪初）在为《周髀算经》作注时验证勾股定理的示意图，现在提供5种颜色给其中5个小区域涂色，规定每个区域只涂一种颜色，相邻区域颜色不相同，则不同的涂色方案共有（）种A.120B.260C.340D.4205.已知直线y=kx-1与抛物线J=8y相切，则双曲线x2-k2y2=l的离心率为（）73A.打B.右C.D.26.已知数列｛%｝的前〃项和S"满足S"+a"=2n(nwN*),则％=()1_127321385A.3b.64 c.32d.64x+y>l,7.设x，y满足约束条件\x-y>-l,若目标函数z=ax+3y仅在点（1,0）处取得最小值，则。

的取值范围2x-y<2,为()A.(—6,3)B.(-6,-3)C.(。

，3)D.(-6,0]8.已知集合M=(x|y=log2(-4x-x2)},2V=(x|(-)x>4},则肱N=()A.d-2]b.[-2,0) c.(-4,2]D(-co,-4)9.如图，已知等腰梯形A3CD中，AB=2DC=4,AD=BC=^5,E是OC的中点，P是线段BC±的动点，则的最小值是（）_9_4A.5B.0C.5D.110.已知^A={x\a-l<x<a+2},B=(x|3<x<5},则能使A^B成立的实数。

山东省烟台市2025届高三英语上学期期末考试试卷含解析

2024—2025学年度第一学期期末学业水平诊断高三英语试题说明：本试卷由四个部分组成，共12页，满分150分，考试用时120分钟。

请把答案全部涂写在答题卡上，考试结束后，只交答题卡。

第一部分听力(共两节，满分30分)做题时，先将答案标在试卷上。

录音内容结束后，你将有两分钟的时间将试卷上的答案转涂到答题卡上。

第一节(共5小题；每小题1.5分，满分7.5分)听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1．What will the man probably do next?A．Watch TV． B．Go out for dinner． C．Do his homework．2．How did the woman lose weight?A．By eating special Meals．B．By going on a diet．C．By doing exercise occasionally．3．Which foreign language does Mr．Smith do well in?A．French． B．Japanese． C．Spanish．4．What does the woman complain about?A．The desk． B．The messy room． C．The heavy box．5．What color is the woman’s dress?A．Red． B．Blue． C．Black．其次节(共15小题；每小题1.5分，满分22.5分)听下面5段对话或独白。

每段对话或独白后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听每段对话或独白前，你将有时间阅读各个小题，每小题5秒钟；听完后，各小题将给出5秒钟的作答时间。

考点17 分组求和法(1月)(期末复习热点题型)(人教A版2019)(解析版)

考点17 分组求和法一、单选题1．若数列{}n a 的通项公式是()()131nn a n =--，则1210···+a a a ++= A ．15 B ．12 C ．12-D ．15-【试题来源】吉林省蛟河市第一中学校2020-2021学年第一学期11月阶段性检测高二（理）【答案】A【解析】因为()()131nn a n =--，所以12253a a +=-+=，348113a a +=-+=，5614173a a +=-+=，7820233a a +=-+=，91026293a a +=-+=，因此1210···+3515a a a ++=⨯=．故选A ． 2．已知数列{}n a 满足11n n a a λ+=+，且11a =，23a =，则数列{}n a 前6项的和为 A ．115 B ．118 C ．120D ．128【试题来源】河南省豫北名校2020-2021学年高二上学期12月质量检测（文）【答案】C【分析】由题干条件求得2λ=，得到121n n a a +=+，构造等比数列可得数列{}n a 的通项公式，再结合等比数列求和公式即可求得数列{}n a 前6项的和．【解析】21113a a λλ=+=+=，则2λ=，可得121n n a a +=+，可化为()1121n n a a ++=+，有12nn a +=，得21n n a =-，则数列{}n a 前6项的和为()()6262122226612012⨯-+++-=-=-．故选C ．3．设数列{a n }的前n 项和为S n ，且a 1＝2，a n +a n +1＝2n （n ∈N *），则S 2020＝A ．2020223-B ．202022 3+C ．202122 3-D ．202122 3+【试题来源】河南省濮阳市2019-2020学年高二下学期升级考试（期末）（文）【答案】C【分析】根据递推公式a n +a n +1 ＝2n （n ∈N *）的特点在求S 2020时可采用分组求和法，然后根据等比数列的求和公式即可得到正确选项．【解析】由题意，可知2020122020123420192020()()()S a a a a a a a a a =+++=++++++132019222=+++2021223-=．故选C ． 4．定义：在数列{}n a 中，0n a >，且1n a ≠，若1n an a +为定值，则称数列{}n a 为“等幂数列”．已知数列{}n a 为“等幂数列”，且122,4,n a a S ==为数列{}n a 的前n 项和，则2009S 为 A ．6026 B ．6024 C ．2D ．4【试题来源】山西省长治市第二中学2019-2020学年高一下学期期末（文）【答案】A【分析】根据数列新定义求出数列的前几项，得出规律，然后求和．【解析】因为122,4a a ==，所以334242a a a ==，32a =，4216a =，44a =，所以212n a -=，24n a =，*n N ∈，2009(24)100426026S =+⨯+=．故选A ．【名师点睛】本题考查数列的新定义，解题关键是根据新定义计算出数列的项，然后寻找出规律，解决问题． 5．数列111111,2,3,4,,248162n n +++++的前n 项和等于 A ．21122n n n +-++B ．2122n n n++C ．2122n n n +-+D ．【试题来源】四川省三台中学实验学校2019-2020学年高一6月月考（期末适应性）【答案】A 【解析】因，故，故选A ．6．已知一组整数1a ，2a ，3a ，4a ，…满足130m m a a +++=，其中m 为正整数，若12a =，则这组数前50项的和为 A ．-50 B ．-73 C ．-75D ．-77【试题来源】四川省自贡市旭川中学2020-2021学年高一上学期开学考试【答案】C【分析】先利用已知条件写出整数列的前五项，得到其周期性，再计算这组数前50项的和即可．【解析】因为130m m a a +++=，12a =，所以2130a a ++=，得25a =-；3230a a ++=，得32a =-；4330a a ++=，得41a =-；5430a a ++=，得52a =-，由此可知，该组整数从第3项开始，以-2，-1，-2，-1，…的规律循环，故这组数的前50项和为()()25212475+-+--⨯=-．故选C ．7．已知n S 为数列{}n a 的前n 项和，且满足11a =，23a =，23n n a a +=，则2020S = A ．1010232⨯-B ．101023⨯C ．2020312-D ．1010312+【试题来源】山西省孝义市第二中学校2019-2020学年高一下学期期末【答案】A【分析】利用递推关系得出数列的奇数项与偶数项分别成等比数列，对2020S 进行分组求和．【解析】因为11a =，23a =，23n n a a +=，所以数列{}n a 的奇数项成等比数列，偶数项也成等比数列，且仅比均为3，所以101010102020132019242020133(13)()()1313S a a a a a a --=+++++++=+--1010232=⨯-．故选A ．【名师点睛】本题考查等比数列的判定，等比数列的前n 项和公式，考查分组求和法，解题时注意对递推式23n n a a +=的认识，它确定数列的奇数项与偶数项分别成等比数列，而不是数列{}n a 成等比数列．8．已知数列{(1)(21)}n n -+的前n 项和为n S ，*N n ∈，则11S = A ．13- B ．12- C ．11-D ．10-【试题来源】山东省青岛胶州市2019-2020学年高二下学期期末考试【答案】A【分析】本题根据数列通项公式的特点可先求出相邻奇偶项的和，然后运用分组求和法可计算出11S 的值，得到正确选项．【解析】由题意，令(1)(21)nn a n =-+，则当n 为奇数时，1n +为偶数， 1(21)[2(1)1]2n n a a n n ++=-++++=，111211S a a a ∴=++⋯+ 123491011()()()a a a a a a a =++++⋯+++222(2111)=++⋯+-⨯+2523=⨯-13=-．故选A ．【名师点睛】本题主要考查正负交错数列的求和问题，考查了转化与化归思想，整体思想，分组求和法，以及逻辑推理能力和数学运算能力．本题属中档题．9．已知数列{}n a 的前n 项和为n S ，且11a =，13nn n a a +=，那么100S 的值为A ．()50231-B ．5031-C ．5032-D ．50342-【试题来源】吉林省四平市公主岭范家屯镇第一中学2019-2020学年高一下学期期末考试【答案】A【分析】根据题中条件，得到23n na a +=，推出数列{}n a 的奇数项和偶数项都是成等比数列，由等比数列的求和公式，分别计算奇数项与偶数项的和，即可得出结果．【解析】因为11a =，13nn n a a +=，所以23a =，1123n n n a a +++=，所以1213n n n n a a a a +++=，即23n na a +=，所以135,,,a a a ⋅⋅⋅成以1为首项、3为公比的等比数列，246,,,a a a ⋅⋅⋅也成以3为首项、3为公比的等比数列，所以()()()5050100139924100313131313Sa a a a a a --=++⋅⋅⋅++++⋅⋅⋅+=+--505050313532322-+⋅-==⋅-．故选A ．【名师点睛】本题主要考查等比数列求和公式的基本量运算，考查分组求和，熟记公式即可，属于常考题型．10．已知数列{}n a 满足12321111222n n a a a a n -++++=，记数列{2}n a n -的前n 项和为n S ，则n S =A ．2222nn n--B ．22122nn n---C ．212222n n n +--- D ．2222nn n--【试题来源】河北省秦皇岛市第一中学2020-2021学年高二上学期第一次月考【答案】C【分析】利用递推关系求出数列{}n a 的通项公式，然后利用等差数列和等比数列的前n 项和公式进行求解即可．【解析】因为12321111(1)222n n a a a a n -++++=，所以有11a =，当2,n n N *≥∈时，有1231221111(2)222n n a a a a n --++++=-，(1)(2)-得，111122n n n n a a --=⇒=，显然当1n =时，也适合，所以12()n n a n N -*=∈，令 2n n a n b -=，所以2n n b n =-，因此有：2323(21)(22)(23)(2)(2222)(123)n n n n S n =-+-+-++-=++++-++++22112(12)(1)222 2.1222222n n n n n n n n n ++-+=-=---=----故选C.【名师点睛】本题考查了由递推关系求数列的通项公式，考查了等差数列和等比数列的前n 项和公式，考查了数学运算能力．11．已知数列{}n a 的前n 项和为n S ，且(),n P n a 为函数221x y x =+-图象上的一点，则n S =A ．2122n n ++-B ．212n n ++C ．22n -D ．22n n +【试题来源】四川省仁寿第二中学2020-2021学年高三9月月考（理）【答案】A【分析】根据已知条件求得n a ，利用分组求和法求得n S【解析】因为(),n P n a 为函数221x y x =+-图象上的一点，所以()212nn a n =-+，则()()121212322121321222nnn S n n =++++⋅⋅⋅+-+=++⋅⋅⋅+-+++⋅⋅⋅+()()212121212nn n -+-=+-1222n n +=+-．故选A ．12．数列112、134、158、1716、的前n 项和n S 为A ．21112n n -+-B ．2122n n +-C ．2112n n +-D ．21122n n -+-【试题来源】安徽省亳州市涡阳县第四中学2019-2020学年高一下学期线上学习质量检测【答案】C【分析】归纳出数列的通项公式为1212nn a n ⎛⎫=-+ ⎪⎝⎭，然后利用分组求和法可求得n S ．【解析】数列112、134、158、1716、的通项公式为1212nn a n ⎛⎫=-+ ⎪⎝⎭，所以，2341111113572122222n n S n ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=+++++++++-+ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭()()231111211111221352112222212n n n n n ⎛⎫- ⎪+-⎛⎫⎝⎭=++++-+++++=+⎡⎤ ⎪⎣⎦⎝⎭-2112n n =+-．故选C ．13．若数列{}n a 的通项公式是1(1)(32)n n a n +=-⋅-，则122020a a a ++⋯+=A ．-3027B ．3027C ．-3030D ．3030【试题来源】江苏省扬州市宝应中学2020-2021学年高二上学期阶段考试【答案】C【分析】分组求和，结合等差数列求和公式即可求出122020a a a ++⋯+．【解析】12202014710...60556058a a a ++⋯+=-+-++-()()101010091010100917...6055410...60551010610104622⨯⨯⎛⎫=+++-+++=+⨯-⨯+⨯ ⎪⎝⎭3030=-．故选C ．14．在数列{}n a 中，129a =-，()*13n n a a n +=+∈N ，则1220a a a +++=A ．10B ．145C ．300D ．320【试题来源】山西省太原市2021届高三上学期期中【答案】C【分析】由等差数列的性质可得332n a n =-，结合分组求和法即可得解．【解析】因为129a =-，()*13n n a a n N +=+∈，所以数列{}n a 是以29-为首项，公差为3的等差数列，所以()11332n a a n d n =+-=-，所以当10n ≤时，0n a <；当11n ≥时，0n a >；所以()()12201210111220a a a a a a a a a +++=-++⋅⋅⋅++++⋅⋅⋅+1101120292128101010103002222a a a a ++--+=-⨯+⨯=-⨯+⨯=．故选C ． 15．数列{}n a 的通项公式为2π1sin 2n n a n =+，前n 项和为n S ，则100S = A ．50 B ．-2400 C ．4900-D ．9900-【试题来源】河南省焦作市2020—2021学年高三年级第一次模拟考试（理）【答案】C【分析】由πsin2n y =的周期为4，可得22222210010013579799S =+-+-+⋅⋅⋅+-，利用并项求和可得解．【解析】2111a =+，21a =，2313a =-，41a =，…，考虑到πsin2n y =的周期为4，所以()222222100100135797991002135799S =+-+-+⋅⋅⋅+-=-⨯++++⋅⋅⋅+(199)50100249002+⨯=-⨯=-．故选C ．16．已知{}n a 的前n 项和为n S ，11a =，当2n ≥时，12n n a S n -+=，则2019S 的值为 A ．1008 B ．1009 C ．1010D ．1011【试题来源】广东省广州市增城区增城中学2020-2021学年高二上学期第一次段考【答案】C【分析】由2n ≥时，可得1n n n S S a -=-，结合题设条件，推得11n n a a -+=，进而求得2019S 的值，得到答案．【解析】由题意，当2n ≥时，可得1n n n S S a -=-，因为12n n a S n -+=，所以2()n n n S a a n +-=，即2n n S a n =+，当2n ≥时，1121n n S a n --=+-，两式相减，可得121n n n a a a -=-+，即11n n a a -+=，所以2345671,1,1,a a a a a a +=+=+=，所以()()()12345201820120991201911110102a a a a a a a S -=+++++++=+⨯=．故选C ． 17．冬春季节是流感多发期，某地医院近30天每天入院治疗流感的人数依次构成数列{}n a ，已知11a =，22a =，且满足()211+-=+-nn n a a （n *∈N ），则该医院30天入院治疗流感的共有（）人 A ．225 B ．255 C ．365D ．465【试题来源】山东省烟台市2020-2021学年高二上学期期末月考【答案】B【分析】直接利用分类讨论思想的应用求出数列的通项公式，进一步利用分组法求出数列的和【解析】当n 为奇数时，2n n a a +=，当n 为偶数时，22n n a a +-=，所以13291a a a ==⋅⋅⋅==， 2430,,,a a a ⋅⋅⋅是以2为首项，2为公差的等差数列，所以30132924301514()()1515222552S a a a a a a ⨯=++⋅⋅⋅++++⋅⋅⋅+=+⨯+⨯=，故选B 18．意大利数学家斐波那契以兔子繁殖为例，引入“兔子数列”：1，1，2，3，5，8，13，21，34，55，…即()()121F F ==，()()()12F n F n F n =-+- （3n ≥，n *∈N ），此数列在现代物理、化学等方面都有着广泛的应用，若此数列的每一项被2除后的余数构成一个新数列{}n a ，则数列{}n a 的前2020项的和为 A ．1348 B ．1358 C ．1347D ．1357【试题来源】江苏省镇江市八校2020-2021学年高三上学期期中联考【答案】C【分析】由题意可知，得数列{}n a 是周期为3的周期数列，前3项和为1102++=，又202067331=⨯+，由此可得答案.【解析】由数列1，1，2，3，5，8，13，21，34，55，…，各项除以2的余数，可得数列{}n a 为1,1,0,1,1,0,1,1,0,⋅⋅⋅，所以数列{}n a 是周期为3的周期数列，前3项和为1102++=，因为202067331=⨯+，所以数列{}n a 的前2020项的和为673211347⨯+=，故选C. 19．已知数列{}n a 的前n 项和为n S ，11a =，当2n ≥时，12n n a S n -+=，，则S 2019的值为 A ．1008 B ．1009 C ．1010D ．1011【试题来源】江苏省南通市2020-2021学年高三上学期期中考前热身【答案】C【分析】由2n ≥时，12n n a S n -+=，得到121n n a S n ++=+，两式相减，整理得()112n n a a n ++=≥，结合并项求和，即可求解．【解析】当2n ≥时，12n n a S n -+=，①，可得121n n a S n ++=+，②，由②－①得，112()1n n n n a a S S +--+-=，整理得()112n n a a n ++=≥，又由11a =，所以20191234520182019()()()1010S a a a a a a a =+++++++=．故选C ．20．已知数列{}n a 的前n 项和为n S ，且()11213n n n n S S a n +++=+-+，现有如下说法：①541a a =；②222121n n a a n ++=-；③401220S =．则正确的个数为 A ．0 B ．1 C ．2D ．3【试题来源】百校联盟2021届普通高中教育教学质量监测考试（全国卷11月）（文）试卷【答案】D【分析】由()11213n n n n S S a n +++=+-+得到()11132n n n a a n ++=-+-，再分n 为奇数和偶数得到21262k k a a k +=-+-，22165k k a a k -=+-，然后再联立递推逐项判断．【解析】因为()11213n n n n S S a n +++=+-+，所以()11132n n n a a n ++=-+-，所以()212621k k a a k +=-+-，()221652k k a a k -=+-，联立得()212133k k a a +-+=，所以()232134k k a a +++=，故2321k k a a +-=，从而15941a a a a ===⋅⋅⋅=，22162k k a a k ++=-，222161k k a a k ++=++，则222121k k a a k ++=-，故()()()4012345383940...S a a a a a a a a =++++++++()()()()234538394041...a a a a a a a a =++++++++()()201411820622k k =+⨯=-==∑1220，故①②③正确．故选D.21．已知正项数列{}n a 中，11a =，前n 项和为n S ，且当*2,n n N ≥∈时，2n a =，数列()1cos 12n n n a π⎧⎫-⋅+⎨⎬⎩⎭的前64项和为 A ．240 B ．256 C ．300D ．320【试题来源】重庆市第一中学2019-2020学年高一下学期期末【答案】D【分析】由题意结合数列n a 与n S 2-=，由等差数列的性质即可得21n =-，进而可得当2n ≥时，88n a n =-，结合余弦函数的性质、分组求和法可得()()()642664648264T a a a a a a --=+++⋅⋅⋅+-，即可得解．【解析】由题意，当*2,n n N ≥∈时，12n n n S a S -==-，即2=，由0n S >2=，所以数列1=，公差为2的等差数列，()12121n n =+-=-，所以当2n ≥时，()222121188n a n n n ==-+--=-⎡⎤⎣⎦，设数列()1cos12nn n a π⎧⎫-⋅+⎨⎬⎩⎭的前n 项和为数列n T ，所以该数列前64项的和为 164234234cos 1cos 1cos 1cos 12222T a a a a ππππ⎛⎫⎛⎫⎛⎫⎛⎫=-⋅++⋅++-⋅++⋅+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭6464cos 12a π⎛⎫+⋅⋅⋅+⋅+ ⎪⎝⎭ ()()()262642664624486464a a a a a a a a a a =-+-⋅⋅⋅-+=+++⋅⋅⋅--+-641616320=+⨯=．故选D ．【名师点睛】本题考查了数列n a 与n S 的关系、等差数列的判断及性质的应用，考查了分组求和法求数列前n 项和的应用，属于中档题． 22．数列{}n a 的前n 项和为n S ，项n a 由下列方式给出1121231234,,,,,,,,,,2334445555⋅⋅⋅⋅⋅⋅．若100k S ≥，则k 的最小值为 A ．200 B ．202 C ．204D ．205【试题来源】福建省莆田市第二中学2020-2021学年高二10月阶段性检测【答案】C【分析】首先观察数列中项的特征，先分组求和，之后应用等差数列求和公式，结合题中所给的条件，建立不等关系式，之后再找其满足的条件即可求得结果．【解析】11212312112312334442222n n S n nn --⎛⎫⎛⎫⎛⎫=+++++++++⋅⋅⋅+=+++⋅⋅⋅+⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ (1)1004n n -=≥．所以(1)400n n -≥，21n ≥．而当20n =时，95S =，只需要125212121m++⋅⋅⋅+≥，解得14m ≥．所以总需要的项数为1231914204+++⋅⋅⋅++=，故选C ．【名师点睛】该题考查的是有关数列的问题，涉及到的知识点有等差数列求和公式，分组求和法，属于中档题目．23．已知数列{} n a 中，10a =，21a =，且当n 为奇数时，22n n a a +-=；当n 为偶数时，23n n a a +=，则此数列的前20项的和为A ．10311102-+B ．1131902-+C ．1031902-+D ．11311102-+【试题来源】福建省莆田市第二中学2020-2021学年高二10月阶段性检测【答案】C【分析】根据n 为奇数时，22n n a a +-=；n 为偶数时，23n n a a +=，得到数列{}n a 中所有奇数项构成以0为首项，以2为公差的等差数列；所有偶数项构成以1为首项，以3为公比的等比数列；然后分别利用等差数列和等比数列前n 项和求解．【解析】因为10a =，21a =，且当n 为奇数时，22n n a a +-=；当n 为偶数时，23n n a a +=，则此数列的前20项的和：数列{}n a 中所有奇数项构成以0为首项，以2为公差的等差数列；数列{}n a 中所有偶数项构成以1为首项，以3为公比的等比数列；所有()()2013192420......S a a a a a a =+++++++()()10113101012100213⨯-+=⨯++-1031902-=+，故选C ． 24．已知数列{}n a 的通项公式为2(1)n n a n =-，设1n n n c a a +=+，则数列{}n c 的前200项和为 A ．200- B ．0 C ．200D ．10000【试题来源】安徽省六安市第一中学2019-2020学年高一下学期期中（理）【答案】A【分析】利用分组求和法及等差数列求和公式求解．【解析】记数列{}n c 的前200项和为n T ，122001223199200200201n T c c c a a a a a a a a =++=++++++++123419920012012[()()()]a a a a a a a a =++++++-+()()()2222[41169200199]1201=-+-++-+-22[3711399]1201=⨯+++++-()2100339921201402004040112002+=⨯+-=-+=-．故选A ．25．已知等差数列{}n a 的首项为1a ，公差0d ≠，记n S 为数列(){}1nn a -⋅的前n 项和，且存在*k N ∈，使得10k S +=成立，则 A ．10a d > B ．10a d < C ．1a d >D ．1a d <【试题来源】浙江省浙考交流联盟2020-2021学年高三上学期8月线上考试【答案】B【分析】由题意按照k 为奇数、k 为偶数讨论，利用并项求和法可得1k S +，转化条件得存在*k N ∈且k 为偶数时，102ka d --=，即可得解．【解析】因为等差数列{}n a 的首项为1a ，公差0d ≠，n S 为数列(){}1nn a -⋅的前n 项和，所以当*k N ∈且k 为奇数时，112341k k k S a a a a a a ++=-+-++⋅⋅⋅-+()()()12341102k k k a a a a a a d ++=-++-++⋅⋅⋅+-+=≠；当*k N ∈且k 为偶数时，1123411k k k k S a a a a a a a +-+=-+-++⋅⋅⋅-+-()()()()1234111122k k k k ka a a a a a a d a kd a d -+=-++-++⋅⋅⋅+-+-=-+=--；所以存在*k N ∈且k 为偶数时，102k a d --=即102ka d =-≠，当2k =时，1a d =-，此时1a d =，故排除C 、D ；所以1a 与d 异号即10a d <，故A 错误，B 正确．故选B ． 26．已知函数()2*()sin2n f n n n N π=∈，且()(1)n a f n f n =++，则1232020a a a a ++++的值为A ．4040B ．4040-C ．2020D ．2020-【试题来源】四川省宜宾市叙州区第一中学校2020-2021学年高二上学期开学考试（文）【答案】A【分析】由题意得2222(1)sin(1)sin sin (1)cos 2222n n n n n a n n n n ππππ+=++=++，从而可求出11a =，222232018201920203,,2019,2021a a a a a ==-⋅⋅⋅==-=，然后通过分组求和可得答案．【解析】因为()2*()sin2n f n n n N π=∈，且()(1)n a f n f n =++，所以2222(1)sin (1)sin sin (1)cos 2222n n n n n a n n n n ππππ+=++=++，所以11a =，222223452018201920203,5,,2019,2021a a a a a a a ==-==⋅⋅⋅==-=，所以1232020a a a a ++++13520192462020()()a a a a a a a a =+++++++++22222222222[(13)(57)(20172019)][(35)(79)(20192021)]=-+-+⋅⋅⋅+-+-++-++⋅⋅⋅+-+2(135720172019)2(35720192021)=-++++⋅⋅⋅++++++⋅⋅⋅++10102020101020242222⨯⨯=-⨯+⨯1010202010102024=-⨯+⨯4040=，故选A.27．已知数列{}n a 中，11a =，23a =，*122(3,)n n n a a a n n N --=+≥∈，设211(2)(2)n n n b a a n n --=-≥，则数列{}n b 的前40项的和为A ．860B ．820C ．820-D ．860-【试题来源】河南省开封市河南大学附属中学2020-2021学年高二9月质检【答案】A【分析】本题先对数列{}n a 的递推公式进行转化可发现数列{}12n n a a --是以1为首项，1-为公比的等比数列，通过计算出数列{}12n n a a --的通项公式可得1n b -的表达式，进一步可得数列{}n b 的通项公式，最后在求和时进行转化并应用平方差公式和等差数列的求和公式即可得到前40项的和．【解析】由题意，可知当3n ≥时，122n n n a a a --=+，两边同时减去12n a -，可得112112222(2)n n n n n n n a a a a a a a -------=+-=--，2123211a a -=-⨯=，∴数列{}12n n a a --是以1为首项，1-为公比的等比数列， 11121(1)(1)n n n n a a ---∴-=⋅-=-，*(2,)n n ≥∈N ，21211(2)(1)n n n n b a a n n ---∴==-⋅-，故2(1)(1)n n b n ⋅=-+，令数列{}n b 的前n 项和为n T ，则4012343940T b b b b b b =++++⋯++22222223454041=-+-+-⋯-+222222[(23)(45)(4041)]=--+-+⋯+-[(23)(45)(4041)]=--+-+-⋯-+23454041=++++⋯++40(241)2⨯+=860=．故选A ．【名师点睛】本题主要考查数列由递推公式推导出通项公式，以及数列求和问题．考查了转化与化归思想，整体思想，定义法，平方差公式，以及逻辑推理能力和数学运算能力．本题属中档题．28．在数列{}n a 中，122,2a a ==，且11(1)(*),nn n a a n N +-=+-∈则100S =A ．5100B ．2600C ．2800D ．3100【试题来源】河南省洛阳市第一中学2020-2021学年高二上学期10月月考【答案】A【分析】转化条件为22n n a a +-=，进而可得21k a -，2k a ，由分组求和法结合等差数列的前n 项和公式即可得解．【解析】因为11(1)(*)n n n a a n N +-=+-∈，所以1211(1)n n n a a +++-=+-，所以()()122121n n n n a a ++-=+--+=，因为122,2a a ==，所以()211212k a a k k -=+-=，()22212k k a k a =+-=，*k N ∈，所以()()100123499100139924100S a a a a a a a a a a a a =++++⋅⋅⋅++=++⋅⋅⋅++++⋅⋅⋅+()()2100241002410025051002+=++⋅⋅⋅++++⋅⋅⋅+=⨯⨯=．故选A ．【名师点睛】本题考查了等差数列通项公式及前n 项和公式的应用，考查了分组求和法的应用及转化化归思想，属于中档题．29．正项数列{}n a 的前n 项和为n S ，且()2*2n n n S a a n N =+∈，设()2112nn n na c s +=-，则数列{}n c 的前2020项的和为A ．20192020-B ．20202019-C ．20202021-D ．20212020-【试题来源】2020届广东省华南师范大学附属中学高三年级月考（三）（理）【答案】C【分析】先根据和项与通项关系得11n n a a --=，再根据等差数列定义与通项公式、求和公式得,n n a S ，代入化简n c ，最后利用分组求和法求结果．【解析】因为()2*2,0n n n nS a a n Na=+∈>，所以当1n =时，21112a a a =+，解得11a =，当2n ≥时，()()2211122n n n n n n n a S S a a a a ---=-=+-+，所以 ()()1110n n n n a a a a --+--=，因为0n a >，所以11n n a a --=，所以数列{}n a 是等差数列，公差为1，首项为1，所以()()111,2n n n n a n n S +=+-==，所以()()21111121n n n n na c s n n +⎛⎫=-=-+ ⎪+⎝⎭，则数列{}n c 的前2020项的和11111111202011223342020202120212021⎛⎫⎛⎫⎛⎫⎛⎫=-+++-++++=-+=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭．故选C ． 30．若数列{}n a 的通项公式为21nn a =-，在一个n 行n 列的数表中，第i 行第j 列的元素为()1,2,,,1,2,,ij i j i j c a a a a i n j n =⋅++=⋅⋅⋅=⋅⋅⋅，则满足11222021nn c c c ++⋅⋅⋅+<的n 的最大值是 A ．4B ．5C ．6D ．7【试题来源】山西省运城市2021届高三（上）期中（理）【答案】B【分析】求得1122nn c c c ++⋅⋅⋅+关于n 的表达式，利用数列的单调性可求得满足11222021nn c c c ++⋅⋅⋅+<的n 的最大值．【解析】数列{}n a 的通项公式为21nn a =-，在一个n 行n 列的数表中，第i 行第j 列的元素为()1,2,,,1,2,,ij i j i j c a a a a i n j n =⋅++=⋅⋅⋅=⋅⋅⋅，所以()()2121212121iji j i jij i j i j c a a a a +=⋅++=--+-+-=-．令1122n nn S c c c =+++，则()102,n n nn S S c n n N *--=>≥∈，所以，数列{}n S 为递增数列，当11222021nn c c c +++<时，所有的元素之和为246212121212021n n n S +=-+-+-++-<，当4n =时，24684222243362021S =+++-=<，当5n =时，246810522222513592021S =++++-=<，当6n =时，246810126222222654542021S =+++++-=>，故n 的最大值为5，故选B ．【点评】关键点【名师点睛】本题考查数列不等式的求解，解题的关键在于求出1122nn c c c ++⋅⋅⋅+关于n 的表达式，在求解数列不等式时，要充分结合数列的单调性求解．31．公元1202年列昂那多·斐波那契（意大利著名数学家）以兔子繁殖为例，引入“兔子数列”{}n a ：1，1，2，3，5，8，13，21，34，55，……，即11a =，21a =，()*12,2n n n a a a n n --=+∈>N ，此数列在现代物理、化学等学科都有着十分广泛的应用．若将此数列{}n a 的各项除以2后的余数构成一个新数列{}n b ，设数列{}n b 的前n 项的和为n T ；若数列{}n a 满足：212n n n n c a a a ++=-，设数列{}n c 的前n 项的和为n S ，则20202020T S +=A ．1348B ．1347C ．674D ．673【试题来源】浙江省宁波市慈溪市2020-2021学年高三上学期期中【答案】B【分析】根据题意写出数列{}n a 的前若干项，观察发现此数列是以3为周期的周期数列，可得2020T ，再计算1n nc c +，结合等比数列的通项公式和求和公式，可得2020S ，进而得到所求和．【解析】“兔子数列”的各项为1，1，2，3，5，8，13，21，34，55，⋯，∴此数列被2除后的余数依次为1，1，0，1，1，0，1，1，0，⋯⋯，即11b =，21b =，30b =，41b =，51b =，60b =，⋯⋯， ∴数列{}n b 是以3为周期的周期数列，20201231673()673211347T b b b b ∴=+++=⨯+=，由题意知22212112221121222121212()()1n n n n n n n n n n n n n n n n n n n n n n c a a a a a a a a a a a c a a a a a a a a a +++++++++++++++++-+---====----，由于212131c a a a =-=-，所以(1)n n c =-，所以2020(11)(11)(11)0S =-++-++⋯+-+=．则202020201347T S +=．故选B.【名师点睛】确定数列数列{}n b 是以3为周期的周期数列，利用周期性求出数列的和，摆动数列(1)n n c =-可以利用分组求和，是解决问题的关键，属于中档题． 32．已知函数()()()22,,n n f n n n ⎧⎪=⎨-⎪⎩当为奇数时当为偶数时且()(1)n a f n f n =++，则121100a a a a ++++等于A ．0B ．100C ．-100D ．10200【试题来源】广东省普宁市2020-2021学年高二上学期期中质量测试【答案】B【分析】先求出通项公式n a ，然后两项一组，即可求解数列的前100项的和【解析】()(1)n a f n f n =++，∴由已知条件知，2222(1),(1),n n n n a n n n ⎧-+=⎨-++⎩为奇数为偶数，即()21,21,n n n a n n ⎧-+=⎨+⎩为奇数为偶数，(1)(21)n n a n ∴=-+，12(n n a a n +∴+=是奇数），123100123499100()()()2222100a a a a a a a a a a ∴+++⋯+=++++⋯++=+++⋯+=故选B ．【名师点睛】解答本题的关键是求出数列{}n a 的通项(1)(21)n n a n =-+，即得到12(n n a a n ++=是奇数）．33．已知数列{}n a 为等差数列，首项为2，公差为3，数列{}n b 为等比数列，首项为2，公比为2，设n n b c a =，n T 为数列{}n c 的前n 项和，则当2020n T <时，n 的最大值是 A ．8 B ．9 C ．10D ．11【试题来源】山东省菏泽市2021届高三上学期期中考试（A ）【答案】A【分析】由已知分别写出等差数列与等比数列的通项公式，求得数列{}n c 的通项公式，利用数列的分组求和法可得数列{}n c 的前n 项和n T ，验证得答案．【解析】由题意得323(1)1n a n n ⨯-=+-=，2nn b =，2321n n n n b c a a ==⨯-=，123n T c c c ∴=+++…n c +123321321321=⨯-+⨯-+⨯-+…321n +⨯-(1233222=⨯+++…)2nn +-()212312n n ⨯-=⨯-- 1326n n +=⨯--，当8n =时，98326815222020T =⨯--=<；当9n =时，109326930572020T =⨯--=>，n ∴的最大值为8．故选A ．【名师点睛】本题解题的关键是求出数列{}n c 的通项公式，利用分组求和求出数列{}n c 的前n 项和n T ．34．已知数列{}n a 满足11a =，1(1)(1)n n na n a n n +=+++，*n N ∈，且23n n b π=，记n S 为数列{}n b 的前n 项和，则2020S =A ．1B ．12C ．12-D ．-1【试题来源】山西省孝义市第二中学校2019-2020学年高一下学期期末【答案】C【分析】由题设条件以及等差数列的性质得出2n a n =，进而得出2cos3n n b n π=，利用诱导公式求出32313,,k k k b b b --，即可求得2020S ．【解析】1(1)(1)n n na n a n n +=+++，111n na a n n+∴-=+， ∴数列n a n ⎧⎫⎨⎬⎩⎭是等差数列，公差与首项都为1，21(1)n n a n a n n ∴=+-⇒=，2cos3n n b n π∴=，3241(32)cos 2(32)32k b k k k ππ-⎛⎫=--=-- ⎪⎝⎭， 3121(31)cos 2(31)32k b k k k ππ-⎛⎫=--=-- ⎪⎝⎭，33cos 23k b k k k π==， 3231332k k k b b b --+∴=+，20203674212020(36742)101022b b ⨯-=-⨯-=-=-=， ()()()1234562017201820192020202031673101022b b b b b b b b b S b ++++++++++==⨯-=-故选C ．35．设()f n ()*n ∈N 的整数，如()()()()()11,21,324252f f f f f =====，，，若正整数m 满足()()()()11114034123f f f f m ++++=，则m = A ．20162017⨯ B ．20172018⨯ C ．20182019⨯D ．20192020⨯【试题来源】陕西省西安市高新一中2018-2019学年高二上学期期末（理）【答案】B【解析】设()f x j =，,*x j N ∈，n 是整数，则221124n n n ⎛⎫+=++ ⎪⎝⎭不是整数，因此任意正整数的正的平方根不可能是1()2n n Z +∈形式，所以1122j j -<<+，221144j j x j j -+<<++，因为,*x j N ∈，所以221j j x j j -+≤≤+，故()f x j =时，2221,2,,x j j j j j j =-+-++共2j 个，设222111(1)(2)()p a f j j f j j f j j =+++-+-++，则22p ja j==，*p N ∈，由题意()()()()11114034123f f f f m ++++=，403422017=⨯，所以()()()()1111111111123(1)(2)(3)(4)(5)(6)f f f f m f f f f f f ⎡⎤⎡⎤++++=+++++++⎢⎥⎢⎥⎣⎦⎣⎦1114034(220171)(220172)()f m f m f m ⎡⎤+++=⎢⎥-⨯+-⨯+⎣⎦，故()2017f m =，m 为方程2017f =的最大整数解，所以22017201720172018m =+=⨯．故选B ．【名师点睛】本题主要考查数列与函数的关系、数列的应用，解题关键是设()f x j =，,*x j N ∈，确定x 的范围，得出x 的个数，然后计算出满足()f x j =的所有1()f x 的和为2．二、多选题1．将2n 个数排成n 行n 列的一个数阵，如下图：111213212223231323331312n n n n n n nna a a a a a a a a a a a a a a a ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 该数阵第一列的n 个数从上到下构成以m 为公差的等差数列，每一行的n 个数从左到右构成以m 为公比的等比数列（其中0m >）．已知112a =，13611a a =+，记这2n 个数的和为S ．下列结论正确的有A ．3m =B ．767173a =⨯C ．1(31)3j ij a i -=-⨯D ．()1(31)314n S n n =+- 【试题来源】湖南省长沙市第一中学2020-2021学年高三上学期月考（三）【答案】ACD【解析】由题意，该数阵第一列的n 个数从上到下构成以m 为公差的等差数列，每一行的n 个数从左到右构成以m 为公比的等比数列，且112a =，13611a a =+，可得2213112a a m m ==，6111525a a d m =+=+，所以22251m m =++，解得3m =或12m =-（舍去），所以选项A 是正确的；又由6666761(253)3173a a m ==+⨯⨯=⨯，所以选项B 不正确；又由1111111(3[((1)][2(1)3]31)3j j j j ij i a ma i m m i i a ----==+-⨯⨯==-⨯+-⨯⨯，所以选项C 是正确的；又由这2n 个数的和为S ，则111212122212()()()n n n n nn S a a a a a a a a a =++++++++++++11121(13)(13)(13)131313n n n n a a a ---=+++---1(231)(31)22nn n +-=-⋅ 1(31)(31)4n n n =+-，所以选项D 是正确的，故选ACD ．【名师点睛】本题主要考查了数表、数阵数列的求解，以及等比数列及其前n 项和公式的应用，其中解答中合理利用等比数列的通项公式和前n 项和公式，准确计算是解答的关键，着重考查了分析问题和解答问题的能力，属于中档试题．2．将n 2个数排成n 行n 列的一个数阵，如图：该数阵第一列的n 个数从上到下构成以m 为公差的等差数列，每一行的n 个数从左到右构成以m 为公比的等比数列（其中m ＞0）．已知a 11＝2，a 13＝a 61+1，记这n 2个数的和为S ．下列结论正确的有A ．m ＝3B ．767173a =⨯C ．()1313j ij a i -=-⨯D ．()()131314n S n n =+- 【试题来源】江苏省扬州市仪征中学2020-2021学年高二上学期期中模拟（2）【答案】ACD【分析】根据第一列成等差，第一行成等比可求出1361,a a ，列式即可求出m ，从而求出通项ij a ，再按照分组求和法，每一行求和可得S ，由此可以判断各选项的真假．【解析】因为a 11＝2，a 13＝a 61+1，所以2m 2＝2+5m +1，解得m ＝3或m 12=-（舍去），所以a ij ＝a i 1•3j ﹣1＝[2+（i ﹣1）×m ]•3j ﹣1＝（3i ﹣1）•3j ﹣1，所以a 67＝17×36，所以S ＝(a 11+a 12+a 13+……+a 1n )+(a 21+a 22+a 23+……+a 2n )+……+(a n 1＋a n2＋a n 3＋……＋a nn )11121131313131313nn n n a a a ---=+++---（）（）（）12=（3n ﹣1）•2312n n +-（） 14=n （3n +1）（3n ﹣1），故选ACD ．【名师点睛】本题主要考查等差数列，等比数列的通项公式的求法，分组求和法，等差数列，等比数列前n 项和公式的应用，属于中档题．三、填空题1．已知数列{}n a 的前n 项和为n S ，满足112a =-，且()1222n n a a n N n n *++=∈+，则10S =__________．【试题来源】广西桂林市第十八中学2021届高三上学期第二次月考（理）【答案】1011【分析】根据题中条件，由裂项的方法得到1112n n a a n n ++=-+，根据裂项相消与并项求和的方法，即可得出结果．【解析】因为()122211222n n a a n n n n n n ++===-+++，则()()()()()1012345678910S a a a a a a a a a a =+++++++++11111111113355779911⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-+-+- ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭11011111=-=．2．设n S 为数列{}n a 的前n 项和，10a =，若11(1)(2)n n n na a +⎡⎤=+-+-⎣⎦（*n N ∈），则100S =__________．【试题来源】江苏省徐州市沛县2020-2021学年高三上学期第一次学情调研【答案】101223- 【分析】分n 为奇数、n 为偶数两种情况讨论，可得数列{}n a 的特点，然后可算出答案．【解析】当n 为奇数时，()12nn a +=-，则()122a =-，()342a =-，，()991002a =-，当n 为偶数时，()12222nn n n n a a a +=+-=+，则232220a a =+=，454220a a =+=，，989998220a a =+=，又10a =，所以10110024100223S a a a -=+++=． 3．已知数列{}n a 满足：11a =，12n n n a a a +=+，则数列1n a ⎧⎫⎨⎬⎩⎭的前n 项和n S =__________．【试题来源】安徽省亳州市涡阳县第四中学2019-2020学年高一下学期第二次质量检测（理）【答案】122n n +--【分析】根据题中条件，得到11211221n n n a a a +⎛⎫+=+=+ ⎪⎝⎭，判定数列11n a ⎧⎫+⎨⎬⎩⎭是以2为公比的等比数列，求出121n na =-，由分组求和的方法，即可求出结果．【解析】由12n n n a a a +=+得12121n n n n a a a a ++==+，所以11211221n n n a a a +⎛⎫+=+=+ ⎪⎝⎭，因此数列11n a ⎧⎫+⎨⎬⎩⎭是以2为公比的等比数列，又11a =，所以1112a +=，因此111222n n n a -+=⨯=，所以121n n a =-，因此()()2121222 (22212)n nn n n n S n +-=+++-=-=---．故答案为122n n +--．【名师点睛】求解本题的关键在于，根据12n n n a a a +=+，由构造法，得到111121n n a a +⎛⎫+=+ ⎪⎝⎭，再根据等比数列的求和公式，以及分组求和的方法求解即可． 4．数列{}n a 的通项公式22cos4n n a n n π=-，其前n 项和为n S ，则2021S =__________．【试题来源】甘肃省永昌县第一中学2020-2021学年高三上学期第一次月考数学理试题【答案】1010．【分析】由于22cos(1cos )cos 422n n n n a n n n n n πππ=-=+-=，可得数列{}n a 的所有奇数项为0，前2021项的所有偶数项共有202010102=项，从而可求得其结果【解析】因为22cos (1cos )cos 422n n n n a n n n n n πππ=-=+-=，所以数列{}n a 的所有奇数项为0，前2021项的所有偶数项共有202010102=项，所以2021246820182020S a a a a a a =++++⋅⋅⋅++246820182020=-+-+-⋅⋅⋅-+(24)(68)(20182020)=-++-++⋅⋅⋅+-+1010210102=⨯=．故答案为1010 5．2020年疫情期间，某医院30天每天因患新冠肺炎而入院就诊的人数依次构成数列{}n a ，已知11a =，22a =，且满足21(1)nn n a a +-=--，则该医院30天内因患新冠肺炎就诊的人数共有__________．【试题来源】山东省聊城市2020-2021学年高三上学期期中【答案】255【分析】根据题目所给递推关系式，求得数列{}n a 项的规律，由此进行分组求和，求得数列前30项的和．【解析】由于()211nn n a a +-=--，当n 为偶数时，20n na a +-=，因此前30项中的偶数项构成常数列，各项都等于22a =，共有15项，和为15230⨯=；当n 为奇数时，22n n a a +-=；又11a =，所以前30项中的奇数项构成首项为1，公差为2的等差数列，共有15项，和为151415122252⨯⨯+⨯=．故30天的总人数为30225255+=．故答案为255． 6．数列{}n a 的前n 项和为n S ，若()*1cos2n n a n n N π=+⋅∈，则2020S =__________．【试题来源】上海市复兴高级中学2021届高三上学期期中【答案】3030【分析】根据题意，先确定cos2n π的周期，再求出一个周期的和，即可得出结果．【解析】由()4coscos 2cos 222n n n ππππ+⎛⎫=+= ⎪⎝⎭，知cos 2n π的周期为4，又11cos12a π=+=，212cos 12a π=+=-， 3313cos12a π=+=， 414cos 214a π=+=+，则1234426a a a a +++=+=，所以20202020630304S =⨯=．故答案为3030．7．已知数列{}n a 的前n 项和为n S ，且21n n S a =-．则数列{}n S 的前n 项和n T =__________．【试题来源】重庆市巴蜀中学2021届高三上学期适应性月考（四）【答案】122n n +--【分析】通过前n 项和n S 与n a 的关系式以及等比数列的定义得出{}n a 及{}n S 的表达式，进而利用分组求和即可．【解析】由21n n S a =-，得111211a a a =-⇒=，由21n n S a =-，有1121(2)n n S a n --=-≥，两式相减，11222(2)n n n n n a a a a a n --=-⇒=，故数列{}n a 是首项为1，公比为2的等比数列，12n na ，122112nn n S -==--，()12122212n n n T n n +-∴=-=---．8．设函数()f x 的定义域为R ，满足()()12f x f x +=，且当[)0,1x ∈时，()sin f x x π=，当[)0,x ∈+∞时，函数()f x 的极大值点从小到大依次记为1a 、2a 、3a 、、n a 、，并记相应的极大值为1b 、2b 、3b 、、n b 、，则数列{}n n a b +前9项的和为__________．【试题来源】湖北省荆州中学2020-2021学年高三上学期8月月考【答案】11032【分析】求出函数()y f x =在区间[)()1,n n n N*-∈上的解析式，利用导数求出函数()y f x =在区间[)()1,n n n N *-∈上的极大值点与极大值，可得出数列{}n n a b +的通项公式，再利用分组求和法可求得数列{}n n a b +的前9项的和．【解析】函数()f x 的定义域为R ，满足()()12f x f x +=，则()()21=-f x f x ，且当[)0,1x ∈时，()sin f x x π=，则当[)()1,x n n n N *∈-∈，()[)10,1x n --∈，()()()()()2112122212sin 1n n f x f x f x f x n x n ππ--=-=-==--=--⎡⎤⎡⎤⎣⎦⎣⎦，()()12cos 1n f x x n πππ-'=--⎡⎤⎣⎦，当[)()1,x n n n N*∈-∈时，()[)10,1x n --∈，则()[)10,x n πππ--∈⎡⎤⎣⎦，令()0f x '=，可得()12x n πππ--=，解得12x n =-，当112n x n -<<-时，()0f x '>，当12n x n -<<时，()0f x '<．所以，函数()y f x =在12x n =-处取得极大值，即1122n n b f n -⎛⎫=-= ⎪⎝⎭，又12n a n =-，1122n n n a b n -∴+=-+，因此，数列{}n n a b +的前9项的和991199121103222122S ⎛⎫+-⨯ ⎪-⎝⎭=+=-．【名师点睛】本题考查了数列的分组求和，同时也考查了利用导数求函数的极值点和极值，考查计算能力，属于中等题．9．在数列{}n a 中，若121,(1)2nn n a a a +=+-=，记n S 是数列{}n a 的前n 项和，则100S =__________．【试题来源】江苏省盐城市响水中学2020-2021学年高二上学期期中【答案】2550【分析】当n 为奇数时，可得数列{}n a 的奇数项为公差为2的等差数列，当n 为偶数时，可得偶数项的特征，将所求问题转化为奇数项和偶数项求和即可．【解析】因为121,(1)2nn n a a a +=+-=，所以当n 为奇数时，22n n a a +-=，即数列{}n a 的奇数项为公差为2的等差数列，当n 为偶数时，22n n a a ++=，所以135995049501225002a a a a ⨯++++=⨯+⨯=， ()()()()24681012485022550a a a a a a a a ++++++++=⨯=，所以1002500502550S =+=，故答案为2550．【名师点睛】（1）得到数列{}n a 的奇数项为公差是2的等差数列；（2）得到数列{}n a 的偶数项满足22n n a a ++=．10．已知数列{}n a 的前n 项和为n S ，21122n n a a a =＋，=+，则5S 的值为__________．【试题来源】河南省豫南九校2020-2021学年高二第一学期第二次联考试题（理）【答案】732【解析】122n n a a +=+，()1222n n a a +∴+=+，故数列{}2n a +是以2为公比，以223a +=为第二项的等比数列，故2232n n a -+=⋅，故2322n n a -=⋅-，()5531273225122S -∴=-⨯=-，故答案为732. 【名师点睛】1n n a pa q +=+(1,0p q ≠≠的常数)递推关系求通项，构造等比数列是解题关键，属于基础题． 11．设数列{}n a 是以4为首项，12为公比的等比数列，其前n 项和为{}n S ，则{}n S 的前n 项和为__________．【试题来源】江苏省宿迁中学2020-2021学年高三上学期期中巩固测试【答案】3288n n -+-【分析】先根据题意得382nn S -=-，由于数列{}32n-是以4为首项，12为公比的等比数列，进而利用分组求和法求和即可得答案．【解析】由等比数列的前n 项和公式得()1314112821112n nn na q S q -⎡⎤⎛⎫-⎢⎥ ⎪-⎝⎭⎢⎥⎣⎦===---，由于数列{}32n-是以4为首项，12为公比的等比数列，。

山东省济南市2020-2021学年高三上学期期末考试数学试题(含解析)

山东省济南市2021届高三第一学期期末检测数学试卷一、单项选择题（本大题共8小题，每小题5分，共计40分．在每小题给出的四个选项中，只有一个是符合题目要求的，请把答案添涂在答题卡相应位置上） 1．设集合{}2A |60x x x =−−≤，{}B |10x x =−<，则AB =A ．{}|3x x ≤B ．{}|31x x −≤<C ．{}|21x x −≤<−D ．{}|21x x −≤< 2．已知复数i1i z =+（其中i 为虚数单位），则z 的共轭复数为 A ．11i 22−+ B ．11i 22−− C ．11i 22+ D ．11i 22−3．已知直线l 过点(2，2)，则“直线l 的方程为y ＝2”是“直线l 与圆224x y +=相切”的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4．十二生肖是中国特有的文化符号，有着丰富的内涵，它们是成对出现的，分别为鼠和牛、虎和兔、龙和蛇、马和羊、猴和鸡、狗和猪六对．每对生肖相辅相成，构成一种完美人格．现有十二生肖的吉祥物各一个，按照上面的配对分成六份．甲、乙、丙三位同学依次选一份作为礼物，甲同学喜欢牛和马，乙同学喜欢牛、狗和羊，丙同学所有的吉祥物都喜欢．如果甲、乙、丙三位同学选取的礼物中均包含自己喜欢的生肖，则不同的选法种数共有A ．12种B ．16种C ．20种D ．24种5．已知菱形ABCD 的边长为2，∠BAD ＝120°，点E ，F 分别在边BC ，CD 上，且满足BEEC =，CD 2CF =，则AE AF +=AB ．3C ．D ．46．把物体放在空气中冷却，如果物体原来的温度是1C θ︒，空气的温度是0C θ︒，那么min t后物体的温度θ（单位：C ︒）满足公式010()e kt θθθθ−=+−（其中k 为常数）．现有52C ︒的物体放在12C ︒的空气中冷却，2min 后物体的温度是32C ︒．则再经过4min 该物体的温度可冷却到A ．12C ︒B ．14.5C ︒ C ．17C ︒D ．22C ︒7．已知双曲线C ：22221(00)x y a b a b−=>>，的左、右顶点分别为A ，B ，其中一条渐近线与以线段AB 为直径的圆在第一象限内的交点为P ，另一条渐近线与直线PA 垂直，则C 的离心率为A ．3B ．2C D8．已知函数()(1)e x f x a x x =+−，若存在唯一的正整数0x ，使得0()0f x <，则实数a 的取值范围是 A ．[12e −，334e ) B ．[334e ，223e ) C ．[223e ，12e ) D ．[12e ，12) 二、多项选择题（本大题共4小题，每小题5分，共计20分．在每小题给出的四个选项中，至少有两个是符合题目要求的，请把答案添涂在答题卡相应位置上）9．为落实《山东省学生体质健康促进条例》的要求，促进学生增强体质，健全人格，锤炼意志，某学校随机抽取了甲、乙两个班级，对两个班级某一周内每天的人均体育锻炼时间（单位：分钟）进行了调研．根据统计数据制成折线图如下：下列说法正确的是A ．班级乙该周每天的人均体育锻炼时间的众数为30B ．班级甲该周每天的人均体育锻炼时间的中位数为72C ．班级甲该周每天的人均体育锻炼时间的极差比班级乙的小D ．班级甲该周每天的人均体育锻炼时间的平均值比班级乙的大10．已知函数12()sin(2)cos(2)f x a x b x ϕϕ=+++(()f x 不恒为0)，若()06f π=，则下列说法一定正确的是A ．()12f x π−为奇函数 B ．()f x 的最小正周期为πC ．()f x 在区间[12π−，125π]上单调递增 D ．()f x 在区间[0，2021π]上有4042个零点 11．如图，在正四棱柱ABCD—A 1B 1C 1D 1中，AA 1＝2AB ＝2，点P 为线段AD 1上一动点，则下列说法正确的是 A ．直线PB 1∥平面BC 1DB ．三棱锥P—BC 1D 的体积为13C ．三棱锥D 1—BC 1D 外接球的表面积为32π D ．直线PB 1与平面BCC 1B 112．已知红箱内有5个红球、3个白球，白箱内有3个红球、5个白第11题球，所有小球大小、形状完全相同．第一次从红箱内取出一球后再放回去，第二次从与第一次取出的球颜色相同的箱子内取出一球，然后再放回去，依次类推，第k ＋1次从与第k 次取出的球颜色相同的箱子内取出一球，然后再放回去．记第n 次取出的球是红球的概率为n P ，则下列说法正确的是A ．21732P =B ．117232n n P P +=+C ．211221()2n n n n n n P P P P P P ++++−=−+D ．对任意的i ，j N *∈且1i j n ≤<≤，11111()()(14)(14)22180n n i ji j nP P −−≤<≤−−=−−∑ 三、填空题（本大题共4小题，每小题5分，共计20分．请把答案填写在答题卡相应位置上）13．已知1sin()63απ+=，则5sin()6απ−的值为． 14．若实数x ，y 满足lg lg lg()x y x y +=+，则xy 的最小值为． 15．已知奇函数()f x 在(0，+∞ )上单调递减，且(4)0f =，则不等式(1)0xf x +>的解集为．16．已知直线l 与抛物线C ：28y x =相切于点P ，且与C 的准线相交于点T ，F 为C 的焦点，连接PF 交C 于另一点Q ，则△PTQ 面积的最小值为；若|TF |5=，则|PQ |的值为．（本小题第一空2分，第二空3分）四、解答题（本大题共6小题，共计70分．请在答题卡指定区域内作答．解答时应写出文字说明、证明过程或演算步骤）在平面四边形ABCD 中，AB ＝2，BC ＝5，∠ABC ＝120°，AD，∠ADC ＝2∠ACD ，求△ACD 的面积． 18．（本小题满分12分）已知数列{}n a 的前n 项和2n S n =．（1）求数列{}n a 的通项公式；（2）在①218()n n n nb a a +=⋅，②2n n n b a =⋅，③(1)n n n b S =−⋅这三个条件中任选一个，补充在下面的问题中，并求解该问题．若，求数列{}n b 的前n 项和n T ．注：如果选择多个条件分别解答，按第一个解答计分．19．（本小题满分12分）如图，在三棱柱ABC—A 1B 1C 1中，AB ＝AC ＝2，D 为BC 的中点，平面BB 1C 1C ⊥平面ABC ，设直线l 为平面AC 1D 与平面A 1B 1C 1的交线．（1）证明：l ⊥平面BB 1C 1C ；（2）已知四边形BB 1C 1C 为边长为2的菱形，且∠B 1BC ＝60°，求二面角D—AC 1—C 的余弦值．某县在实施脱贫工作中因地制宜，着力发展枣树种植项目．该县种植的枣树在2020年获得大丰收，依据扶贫政策，所有红枣由经销商统一收购．为了更好的实现效益，县扶贫办从今年收获的红枣中随机选取100千克，进行质量检测，根据检测结果制成如图所示的频率分布直方图．右表是红枣的分级标准，其中一级品、二级品统称为优质品．经销商与某农户签订了红枣收购协议，规定如下：从一箱红枣中任取4个进行检测，若4个均为优质品，则该箱红枣定为A 类；若4个中仅有3个优质品，则再从该箱中任意取出1个，若这一个为优质品，则该箱红枣也定为A 类；若4个中至多有一个优质品，则该箱红枣定为C 类；其它情况均定为B 类．已知每箱红枣重量为10千克，A 类、B 类、C 类的红枣价格分别为每千克20元、16元、12元．现有两种装箱方案：方案一：将红枣采用随机混装的方式装箱；方案二：将红枣按一、二、三、四等级分别装箱，每箱的分拣成本为1元．以频率代替概率解决下面的问题．（1）如果该农户采用方案一装箱，求一箱红枣被定为A 类的概率；（2）根据所学知识判断，该农户采用哪种方案装箱更合适，并说明理由．21．（本小题满分12分）已知椭圆C ：22221(0)x y a b a b+=>>（1）求椭圆C 的标准方程；（2）若折线0)y k x =≠与C 相交于A ，B 两点（点A 在直线x =的右侧），设直线OA ，OB 的斜率分别为1k ，2k ，且212k k −=，求k 的值．22．（本小题满分12分）已知函数()ln(1)f x a x x =−+．（1）讨论()f x 的单调性；（2）若1()e 1x f x x −≥−+对任意的x ∈(0，+∞)恒成立，求实数a 的取值范围．山东省济南市2021届高三第一学期期末检测数学试卷一、单项选择题（本大题共8小题，每小题5分，共计40分．在每小题给出的四个选项中，只有一个是符合题目要求的，请把答案添涂在答题卡相应位置上） 1．设集合{}2A |60x x x =−−≤，{}B |10x x =−<，则AB =A ．{}|3x x ≤B ．{}|31x x −≤<C ．{}|21x x −≤<−D ．{}|21x x −≤< 答案：D解析：{}2A |60x x x =−−≤＝[﹣2，3]，{}B |10x x =−<＝(−∞，1)，故AB =[﹣2，1)．选D ．2．已知复数i1i z =+（其中i 为虚数单位），则z 的共轭复数为 A ．11i 22−+ B ．11i 22−− C ．11i 22+ D ．11i 22−答案：D解析：i i(1i)1i1i (1i)(1i)22z −===+++−，则1i 22z =−．选D ． 3．已知直线l 过点(2，2)，则“直线l 的方程为y ＝2”是“直线l 与圆224x y +=相切”的 A ．充分不必要条件 B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件答案：A解析：“直线l 的方程为y ＝2”⇒“直线l 与圆224x y +=相切”, “直线l 与圆224x y += 相切”“直线l 的方程为y ＝2”，故选A ．4．十二生肖是中国特有的文化符号，有着丰富的内涵，它们是成对出现的，分别为鼠和牛、虎和兔、龙和蛇、马和羊、猴和鸡、狗和猪六对．每对生肖相辅相成，构成一种完美人格．现有十二生肖的吉祥物各一个，按照上面的配对分成六份．甲、乙、丙三位同学依次选一份作为礼物，甲同学喜欢牛和马，乙同学喜欢牛、狗和羊，丙同学所有的吉祥物都喜欢．如果甲、乙、丙三位同学选取的礼物中均包含自己喜欢的生肖，则不同的选法种数共有A ．12种B ．16种C ．20种D ．24种答案：B解析：甲若选牛，则有1124C C 种；甲若选马，则有1124C C 种．故共有16种，选B ．5．已知菱形ABCD 的边长为2，∠BAD ＝120°，点E ，F 分别在边BC ，CD 上，且满足BEEC =，CD 2CF =，则AE AF +=AB ．3 C．D ．4答案：B解析：由题意知△AEF 的等边三角形，故AE AF +=3，选B ．6．把物体放在空气中冷却，如果物体原来的温度是1C θ︒，空气的温度是0C θ︒，那么min t后物体的温度θ（单位：C ︒）满足公式010()e kt θθθθ−=+−（其中k 为常数）．现有52C ︒的物体放在12C ︒的空气中冷却，2min 后物体的温度是32C ︒．则再经过4min 该物体的温度可冷却到A ．12C ︒B ．14.5C ︒ C ．17C ︒D ．22C ︒ 答案：C解析：221321240e e 2k k −−=+⇒=，6311240e 1240()172k θ−=+=+⨯=，故选C ． 7．已知双曲线C ：22221(00)x y a b a b−=>>，的左、右顶点分别为A ，B ，其中一条渐近线与以线段AB 为直径的圆在第一象限内的交点为P ，另一条渐近线与直线PA 垂直，则C 的离心率为A ．3B ．2CD 答案：B解析：将直线AP 与斜率为正数的渐近线方程联立：()a y x a bb y x a ⎧=+⎪⎪⎨⎪=⎪⎩，解得P(322a b a −，222a b b a −)，因为OP ＝a ，则322222222()()a a b a b a b a+=−−，化简得2222222334a b a c a c a =⇒=−⇒=2e ⇒=，选B ．8．已知函数()(1)e x f x a x x =+−，若存在唯一的正整数0x ，使得0()0f x <，则实数a 的取值范围是 A ．[12e −，334e ) B ．[334e ，223e ) C ．[223e ，12e ) D ．[12e ，12) 答案：C解析：0()0f x <，参变分离得：000(1)e x x a x <+，令000()(1)(1)e x x g x x x =≥+，2000201()0(1)e x x x g x x +−'=−<+，所以0()g x 在[1，+∞)且0x Z ∈单调递增，求得1(1)2e g =，22(2)3eg =，故要使存在唯一的正整数0x ，使得0()0f x <，则223e ≤a ＜12e，选C ．二、多项选择题（本大题共4小题，每小题5分，共计20分．在每小题给出的四个选项中，至少有两个是符合题目要求的，请把答案添涂在答题卡相应位置上）9．为落实《山东省学生体质健康促进条例》的要求，促进学生增强体质，健全人格，锤炼意志，某学校随机抽取了甲、乙两个班级，对两个班级某一周内每天的人均体育锻炼时间（单位：分钟）进行了调研．根据统计数据制成折线图如下：下列说法正确的是A ．班级乙该周每天的人均体育锻炼时间的众数为30B ．班级甲该周每天的人均体育锻炼时间的中位数为72C ．班级甲该周每天的人均体育锻炼时间的极差比班级乙的小D ．班级甲该周每天的人均体育锻炼时间的平均值比班级乙的大答案：AC解析：班级甲该周每天的人均体育锻炼时间的中位数为65，故B 错误；班级甲该周每天的人均体育锻炼时间的平均值比班级乙的小，故D 错误．综上选AC ．10．已知函数12()sin(2)cos(2)f x a x b x ϕϕ=+++(()f x 不恒为0)，若()06f π=，则下列说法一定正确的是 A ．()12f x π−为奇函数 B ．()f x 的最小正周期为π C ．()f x 在区间[12π−，125π]上单调递增 D ．()f x 在区间[0，2021π]上有4042个零点答案：BD解析：()12f x π−为偶函数，故A 错误；()f x 在区间[12π−，125π]上单调，但不一定是单调递增，故C 错误．综上选BD ．11．如图，在正四棱柱ABCD—A 1B 1C 1D 1中，AA 1＝2AB ＝2，点P 为线段AD 1上一动点，则下列说法正确的是A ．直线PB 1∥平面BC 1DB ．三棱锥P—BC 1D 的体积为13C ．三棱锥D 1—BC 1D 外接球的表面积为32πD ．直线PB 1与平面BCC 1B 1答案：ABD解析：因为平面AB 1D 1∥平面BC 1D ，PB 1⊂平面AB 1D 1，所以直线PB 1∥平面BC 1D ，A 正确；V P—BC1D ＝V A—BC1D ＝V C1—ABD ＝111112=323⨯⨯⨯⨯，故B 正确；三棱锥D 1—BC 1D=S 球＝246ππ=，故C 错误；PB 1min 点P 到平面BCC 1B 1的距离为1，所以直线PB 1与平面BCC 1B 1所成角的正弦值的最，故D 正确．综上选ABD ．12．已知红箱内有5个红球、3个白球，白箱内有3个红球、5个白球，所有小球大小、形状完全相同．第一次从红箱内取出一球后再放回去，第二次从与第一次取出的球颜色相同的箱子内取出一球，然后再放回去，依次类推，第k ＋1次从与第k 次取出的球颜色相同的箱子内取出一球，然后再放回去．记第n 次取出的球是红球的概率为n P ，则下列说法正确的是A ．21732P =B ．117232n n P P +=+C ．211221()2n n n n n n P P P P P P ++++−=−+D ．对任意的i ，j N *∈且1i j n ≤<≤，11111()()(14)(14)22180n n i ji j nP P −−≤<≤−−=−−∑ 答案：ACD解析：第n 此取出球是红球的概率为n P ，则白球概率为(1)n P −，对于第1n +次，取出红球有两种情况． ①从红箱取出1(1)58n n P P +=⋅（条件概率）， ②从白箱取出2(1)3(1)8n nP P +=−⋅，对应121(1)(1)3184n n n n P P P P +++=+=+（转化为数列问题），所以1111()242n n P P +−=−，令12n n a P =−，则数列{n a 为等比数列，公比为14，因为158P =，所以118a =，故2(21)2n n a −+=即对应(21)122n n P −+=+，所以21732P =，故选项A 正确； [2(1)1](21)231111112[2]222224n n n n n P P −++−+−−+−=+−⨯+=−，故117232n n P P +=+不成立，故选项B 错误；经验证可得，211221()2n n n n n n P P P P P P ++++−=−+，故选项C 正确；1(21)(21)11111()()2222n ni j i j i j n i j i P P −−+−+<==+−−=⋅∑∑∑ 1(21)(23)(23)142[22]3n i i n i −−+−+−+==⋅−∑11(44)(23)(21)114[222]3n n i n i i i −−−+−+−+===−∑∑ 844(23)3214164[(22)2(22)]3153n n n −−−−+−−−=−−⋅− 424141122218045369n n n −−−=−⋅−⋅+⋅ 421(14252)180n n −−=+⋅−⋅ 221(142)(12)180n n −−=−⋅−11(14)(14)180n n −−=−−，故D 正确．三、填空题（本大题共4小题，每小题5分，共计20分．请把答案填写在答题卡相应位置上）13．已知1sin()63απ+=，则5sin()6απ−的值为．答案：13解析：51sin()sin[()]sin()6663ππαπααπ−=−+=+=． 14．若实数x ，y 满足lg lg lg()x y x y +=+，则xy 的最小值为．答案：4解析：11lg lg lg()1x y x y xy x y x y+=+⇒=+⇒+=， 11()()24y xxy x y x y x y x y=+=++=++≥，当且仅当x ＝y ＝2时取“＝”．15．已知奇函数()f x 在(0，+∞ )上单调递减，且(4)0f =，则不等式(1)0xf x +>的解集为．答案：(0，3)(﹣5，﹣1)解析：0(1)0(1)0x xf x f x >⎧+>⇒⎨+>⎩或003(1)0x x f x <⎧⇒<<⎨+<⎩或51x −<<−，故原不等式的解集为(0，3)(﹣5，﹣1)．16．已知直线l 与抛物线C ：28y x =相切于点P ，且与C 的准线相交于点T ，F 为C 的焦点，连接PF 交C 于另一点Q ，则△PTQ 面积的最小值为；若|TF |5=，则|PQ |的值为．（本小题第一空2分，第二空3分）答案：16，252解析：当PQ 为抛物线通径时△PTQ 的面积最小，为16；当TF ＝5时，可得线段PQ 中点的纵坐标为3或﹣3，故PQ 的斜率为43或43−，故PQ ＝2228254sin 2()5p α==．四、解答题（本大题共6小题，共计70分．请在答题卡指定区域内作答．解答时应写出文字说明、证明过程或演算步骤） 17．（本小题满分10分）在平面四边形ABCD 中，AB ＝2，BC ＝5，∠ABC ＝120°，AD，∠ADC ＝2∠ACD ，求△ACD 的面积．解：在△ABC 中，由余弦定理可得：所以在△ACD 中，由正弦定理可得：，即所以所以因为，所以所以所以18．（本小题满分12分）已知数列{}n a 的前n 项和2n S n =．（1）求数列{}n a 的通项公式；（2）在①218()n n n nb a a +=⋅，②2n n n b a =⋅，③(1)n n n b S =−⋅这三个条件中任选一个，补充在下面的问题中，并求解该问题．若，求数列{}n b 的前n 项和n T ．注：如果选择多个条件分别解答，按第一个解答计分．解：（1）因为所以所以当时，适合上式，所以（2）若选①：因为所以若选②：因为所以则两式相减可得：所以若选③：当n为偶数时，当n为奇数时，综上：19．（本小题满分12分）如图，在三棱柱ABC—A1B1C1中，AB＝AC＝2，D为BC的中点，平面BB1C1C⊥平面ABC，设直线l为平面AC1D与平面A1B1C1的交线．（1）证明：l⊥平面BB1C1C；（2）已知四边形BB1C1C为边长为2的菱形，且∠B1BC＝60°，求二面角D—AC1—C的余弦值．解：（1）证明：因为AB＝AC＝2，D为BC的中点，所以AD⊥BC，又因为平面BB1C1C⊥平面ABC，且平面BB1C1C平面ABC＝BC，AD 平面ABC，所以AD⊥平面BB1C1C，而AD∥平面A1B1C1，且AD⊂平面AC1D，平面AC1D平面A1B1C1＝l，所以AD∥l，所以l⊥平面BB1C1C；（2）因为AD⊥平面BB1C1C，AD⊂平面AC1D，所以平面AC1D⊥平面BB1C1C，在平面BB1C1C内，过C作CH⊥DC1于点H，则CH⊥平面AC1D，过C作CG⊥AC1于点G，则G为线段AC1的中点，连接HG，则∠CGH就是二面角D—AC1—C的平面角，在直角中，在中，，在中，，在直角中，，所以所以二面角D—AC1—C的余弦值为20．（本小题满分12分）某县在实施脱贫工作中因地制宜，着力发展枣树种植项目．该县种植的枣树在2020年获得大丰收，依据扶贫政策，所有红枣由经销商统一收购．为了更好的实现效益，县扶贫办从今年收获的红枣中随机选取100千克，进行质量检测，根据检测结果制成如图所示的频率分布直方图．右表是红枣的分级标准，其中一级品、二级品统称为优质品．经销商与某农户签订了红枣收购协议，规定如下：从一箱红枣中任取4个进行检测，若4个均为优质品，则该箱红枣定为A 类；若4个中仅有3个优质品，则再从该箱中任意取出1个，若这一个为优质品，则该箱红枣也定为A 类；若4个中至多有一个优质品，则该箱红枣定为C 类；其它情况均定为B 类．已知每箱红枣重量为10千克，A 类、B 类、C 类的红枣价格分别为每千克20元、16元、12元．现有两种装箱方案：方案一：将红枣采用随机混装的方式装箱；方案二：将红枣按一、二、三、四等级分别装箱，每箱的分拣成本为1元．以频率代替概率解决下面的问题．（1）如果该农户采用方案一装箱，求一箱红枣被定为A 类的概率；（2）根据所学知识判断，该农户采用哪种方案装箱更合适，并说明理由．解：（1）从红枣中任意取出一个，则该红枣为优质品的概率是，记“如果该农户采用方案一装箱，一箱红枣被定为A 类”为事件A ，则（2）记“如果该农户采用方案一装箱，一箱红枣被定为B 类”为事件B ，“如果该农户采用方案一装箱，一箱红枣被定为C 类”为事件C ，则所以如果该农户采用方案一装箱，每箱红枣收入的数学期望为：元；由题意可知，如果该农户采用方案二装箱，则一箱红枣被定为A 类的概率为，被定为C 类的概率也为，所以如果该农户采用方案二装箱，每箱红枣收入的数学期望为：元；所以该农户采用方案二装箱更合适．21．（本小题满分12分）已知椭圆C ：22221(0)x y a b a b+=>>（1）求椭圆C 的标准方程；（2）若折线0)y k x =≠与C 相交于A ，B 两点（点A 在直线x =的右侧），设直线OA ，OB 的斜率分别为1k ，2k ，且212k k −=，求k 的值．解：（1）由题可知22c a b a⎧=⎪⎪⎨⎪=⎪⎩，又因为，所以所以椭圆C 的标准方程为（2）因为折线与椭圆C 相交于A ，B 两点，设点B 关于x 轴的对称点为B′，则直线与椭圆C 相交于A ，B′两点，设则由得所以所以整理得解得22．（本小题满分12分）已知函数()ln(1)f x a x x =−+．（1）讨论()f x 的单调性；（2）若1()e 1x f x x −≥−+对任意的x ∈(0，+∞)恒成立，求实数a 的取值范围．解：（1）若，，此时在上单调递减；若，由得，此时在上单调递减，在上单调递增；综上所述，，在上单调递减；，在上单调递减，在上单调递增；（2）因为记所以在上单调递增，所以，所以恒成立；若不合题意；若，由（1）知，在上单调递减，所以不合题意；若，记记所以在上单调递增，所以所以符合题意；综上实数a的取值范围是．。

山东省烟台市莱州一中等高三数学上学期期末考试题理(

山东省烟台市莱州一中等2015届高三数学上学期期末考试题理（含解析）新人教A 版【试卷综析】本试卷是高三理科试卷，以基础知识为载体，以基本能力测试为主导，重视学生科学素养的考查.知识考查注重基础、兼顾覆盖面.试题重点考查：集合、复数、导数、函数模型、函数的性质、命题，数列，立体几何等；考查学生解决实际问题的综合能力，是份比较好的试卷一、选择题：本大题共10小题；每小题5分，共50分.在每小题给出的四个选项中，只有一个选项符合题目要求，把正确选项的代号涂在答题卡上.【题文】1.已知集合{}11M x x =-<，集合{}223N x x x =-<，则R M C N ⋂= A. {}02x x <<B. {}2x x -1<<C. {}1023x x x -<≤≤<或 D. ∅【知识点】集合及其运算A1 【答案】D【解析】M= {02}x x <<,N={13}x x -<<,则R M C N ⋂=∅. 【思路点拨】先求出M,N 再求结果。

【题文】2.若函数()()3,5,2,5x x f x f x x -≥⎧⎪=⎨+<⎪⎩则()2f 的值为 A.2 B.3 C.4 D.5【知识点】函数及其表示B1 【答案】B【解析】由题意得f(2)=f(2+2)=f(2+4)=6-3=3。

【思路点拨】由f(2)=f(2+2)=f(2+4)=6-3=3。

【题文】3.将函数sin 23y x π⎛⎫=-⎪⎝⎭的图象向右平移12π个单位，然后纵坐标不变横坐标伸长为原来的2倍，得到函数解析式为 A. 5sin 12y x π⎛⎫=-⎪⎝⎭B. cos y x =C. cos y x =-D. sin y x =- 【知识点】函数sin()y A x ωϕ=+的图象与性质C4【思路点拨】根据三角函数图象变换的公式，结合诱导公式进行化简，可得两次变换后所得到的图象对应函数解析式．【题文】4.如右图放置的六条棱长都相等的三棱锥，则这个几何体的侧视图是 A.等腰三角形 B.等边三角形 C.直角三角形D.无两边相等的三角形【知识点】空间几何体的三视图和直观图G2 【答案】A【解析】因为六条棱长都相等的三棱锥，分析易得这个几何体的侧视图是等腰三角形。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

……………………………………4 分
（2）平面 SCD 平面 ABCD，平面 SCD 平面 ABCD CD ， BC 平面
ABCD ，
BC CD ，所以 BC 平面 SCD . …………………………………5 分
以 C 为坐标原点，CD,CB 所在的方向分别为 y 轴、z 轴的正方向，与 CD,CB
B. x∈R, x2-x+1<0 D. x∈R, x2-x+l≤0
3. 若双曲线
(a>0,b>0)的离心率为，则其渐近线方程为
A. 2x±3y=0 B. 3x±2y=0 C. x±2y=0 D. 2x±y=0
4.设 a=,b=,c=
,则 a,b,c 的大小关系为
<b<c B. a<c<b
C. b<a<c
因为 AD // BC ，所以 AFD 与 BCF 相似.
所以 BF BC 2 . FD AD
………………………………………………1 分
又 BE BF =2 ，所以 EF // SD . ……………………………………2 分 ES FD
因为 EF 平面 ACE ， SD 平面 ACE ，所以直线 SD // 平面 ACE .
.
15. 设点 P 是曲线 y=ex+x2 上任一点，则点 P 到直线 x-y-1=O 的最小距离为
.
16.已知三棱锥 P-ABC 的四个顶点都在球 O 的表面上，PA 丄平面 ABC，PA=6,AB=2 ,AC=2,BC=4，
则：（1）球 O 的表面积为；（2）若 D 是 BC 的中点，过点 D 作球 O 的截面，则截面面
-
A. B.
C. D.
8.函数
,若方程 f(x)=-2x+m 有且只有两个不相等的实数根，则实数 m 的取值
范围是 A. (-∞,4)
B. (-∞,4]
C. (-2,4)
D. (-2,4]
二、多项选择题：本題共 4 小题，每小题 5 分，共 20 分。在每小题给出的选项中，有多项符合題目要求，全部选对得 5 分，部分选对得 3 分，有选错的得 0 分.
(2) 求二面角 S-AC-E 的余弦值。
22. (12 分)
已知椭圆的
的离心率为，F 是其右焦点，直线 y=kx 与椭圆交于 A,B 两点，
|AF|+|BF|=8. (1) 求椭圆的标准方程； (2) 设 Q(3,0),若∠AQB 为锐角,求实数 k 的取值范围.
23. ` 24. (12 分)
两式相减得：
3Tn 4+2 (42 +43 + +4n ) (2n 1) 4n1 ， …………………9 分
3Tn
4+2 42 4n+1 1 4
(2n 1) 4n1 ，
…………………11 分
6n
5)4n1 9
.
……………………………………12 分
19.解：（1）连接 BD交 AC 于点 F ,连接 EF .
积的最小值是。（本题第一空 2 分，第二空 3 分）
四、解答题：本题共 6 小题，共 70 分。解答应写出文字说明、证明过程或演算步驟。
17. （10 分）
在条件①(a+b)(sinA-sinB）=（c-b）sinC,②asinB=bcos(A+ ),③bsin =asinB 中任选一个，补充到下面问题中，并给出问题解答. 在ΔABC 中，角 A,B,C 的对边分别为 a,b,c, b+c=6,a= ,________________________ ,
D. 直线 C1P 与平面 A1C1D 所成角的正弦值的最大值为 12. 已知抛物线 C:y2=4x 的焦点为 F、准线为 l，过点 F 的直线与抛物线交于两点 P(x1,y1),G(x2,y2)，
点 P 在 l 上的射影为 P1，则 A. 若 X1+X2=6.则|PQ|=8 B. 以 PQ 为直径的圆与准线 l 相切
9.某大学为了解学生对学校食堂服务的满意度，随机调査了 50 名男生和
满意不满意
50 名女生，每位学生对食堂的服务给出满意或不满意的评价，得到如图
男 30
20
所示的列联表.经计算 K2 的观测值 k≈，则可以推断出 A. 该学校男生对食堂服务满意的概率的估计值为
女
:
10
P(k2≥k)
40
k
^
B. 调研结果显示，该学校男生比女生对食堂服务更满意
a 2 6 ， b c 6 ，所以 bc 4 ， ………………………………………8 分
所以
SABC
1 2
bc sin
A
1 4sin 2
3
3.
…………………………10 分
18.解：（1）因为 2Sn (n 1)an ， n N* ，
所以 2Sn 1 (n 2)an 1 ， n N* .
两式相减得 2an1 (n 2)an1 (n 1)an ，
】
整理得 nan 1 (n 1)an ，. ………………………………………………2 分
即 an 1 an ， n N* ，所以{ an } 为常数列.
n1 n
n
所以 an a1 2 ， n1
………………………………………4 分
所以 an 2n .
C. 设 M（O,1）,则|PM|+|PP1|≥
D. \ E. 过点 M（0,1）与抛物线 C 有且只有一个公共点的直线至多有 2 条
三、填空題：本題共 4 小題，每小题 5 分，共 20 分。
13. 己知向量 a,b 满足|a|=l,|b|= ,a⊥（a+b）,则 a 与 b 夹角为 .
14. 已知随机变量 X N（1, 2）,P（-1<X<1）=,则 P（X≥3）=
%
求ΔABC 的面积.
注：如选择多个条件分别解答，按第一个解答计分.
18. （12 分）已知数列{an}的前 n 项和 Sn 満足 2Sn=(n+1)an（n∈N）且 a1=2.
（1）求数列｛an｝的通项公式;
（2）设 bn=（an-1）2an.求数列{bn}的前 n 项和 Tn.
19. (12 分) 20. . 21. 如图，在四棱锥 S-ABCD 中，ABCD 为直角梯形，AD∥BC,BC⊥CD，平面 SCD 丄平面 ABCD. ΔSCD 是以 CD 为斜边的等腰直角三角形，BC=2AD=2CD=4,E 为 BS 上一点，且 BE=2ES. (1) 证明：直线 SD∥平面 ACE；
某企业拥有 3 条相同的生产线，每条生产线每月至多出现一次故障.各条生产线是否出现故
障相互独立，且出现故障的概率为 .
(1) 求该企业每月有且只有 1 条生产线出现故障的概率； (2) 为提高生产效益，该企业决定招聘 n 名维修工人及时对出现故障的生产线进行修.已知每名维修工人每月只有及时维修 1 条生产线的能力，且每月固定工资为 1 万元.此外，统计表明，每月在不岀现故障的情况下，每条生产线创造 12 万元的利润；如果出现故障能及时维修，每条生产线创造 8 万元的利润；如果出现故障不能及时维修，该生产线将不创造利润.以该企业每月实际获利的期望值为决策依据，在 n=1 与 n=2 之中选其一，应选用哪个(实际获利=生产线创造利润一维修工人工资)
…………………………………………………5 分
（2） bn (an 1)2an =(2n 1)4n . ……………………………………………6 分
所以 Tn 1 41+3 42 +5 43 + +(2n 1)4n
4Tn
1 42 +3 43 + +(2n 3) 4n (2n 1) 4n1 . ……7 分
2bc
2bc 2
因为 A(0, ) ，所以 A . …………………………………………6 分 3
又 a2 b2 c2 bc (b c)2 3bc ，
a 2 6 ， b c 6 ，所以 bc 4 ， …………………………………………8 分
所以
SABC
1 2
bc sin
A
1 4sin 2
25. (12 分)
已知函数 (1) 求函数 f(x)的单调区冋； (2) 讨论函数 f(x)零点的个数；
,其中 O<a<e.
(3) ~
(4) 若 f(x)存在两个不同的零点 x1,x2,求证：x1x2<e2.
2019-2020 学年度第一学期期末学业水平诊断
高三数学参考答案
一、单项选择题 6. D
二、多项选择题
三、填空题
13. 3 14. 0.1 4
$
四、解答题
15. 2 16. 52 ， 4
17.解：若选①：由正弦定理得 (a b)(a b) (c b)c ， ………………………………2 分
即 b2 c2 a2 bc ，
所以 cos A b2 c2 a2 bc 1 ， ……………………………………4 分
D. 】 E. 函数 f(x)的图象向右平移个单位长度得到函数 y=-cos3x 的图象
11. 如图,在正方体 ABCD-A1B1C1D1 中，点 P 在线段 B1C 上运动，则
A. 直线 BD1 丄平面 A1C1D B. 三棱锥 P-A1C1D 的体积为定值 C. 异面直线 AP 与 A1D 所成角的取值范用是[45°,90°]
烟台 2019-2020 学年度第一学期期末学业水平诊断
高三数学
注意事项： 1. 本试题满分 150 分,考试时间为 120 分钟。 2. 答卷前务必将姓名和准考证号填涂在答题纸上。 3. 使用答题纸时，必须使用毫米的黑色签字笔书写，要字迹工整，笔迹淸晰。超出答题区书写